Sharp EL-546W, EL-506W User Manual [sv]

/

EL-506W
EL-546W

TEKNISK RÄKNARE

BRUKSANVISNING

MODELL

MEM RESET

0 1

DRG FSE TA B

0 1

SVENSKA

P (x,y )

X

Y

0

y

x

P (r,θ )

X

Y

0

r

θ

y

x

b

xx

xx

a

0

13

2

y

a

b

x

x
x
x

x

1

0

2
3

PRINTED IN CHINA / TRYCKT I KINA / PAINETTU KIINASSA

INLEDNING

Vi tackar för köpet av denna tekniska räknare av modell EL-506W/546W.
Vi hänvisar till motsatt sida i den engelska bruksanvisningen för detaljer om

räkneexemplen (inklusive vissa formler och tabeller). Vi hänvisar till
numret till höger om varje rubrik i bruksanvisningen för närmare detaljer.

När du läst denna bruksanvisning bör du förvara den på lämplig plats, om
du behöver den igen.
Obs: Det kan hända att några av de modeller som beskrivs i denna

bruksanvisning inte finns tillgängliga i vissa länder.

Handhavande

• Bär aldrig räknaren i bakfickan då den kan förstöras om du råkar glömma
och sätter dig. Bildskärmen är tillverkad av glas och väldigt skör.

•Håll räknaren borta från ställen som utsätts för höga temperaturer, såsom
instrumentbrädan i en bil eller ett element, och undvik att utsätta den för
fukt och damm.

• Eftersom denna produkt inte är vattentät bör den inte användas eller
förvaras där den kan komma i kontakt med vätska (t ex vatten).
Regndroppar, vattenspray, juice, kaffe, ånga, svett etc. orsakar också
funktionsstörningar.

• Rengör den endast med en mjuk, torr trasa. Använd aldrig några
rengöringsmedel eller en fuktig trasa.

• Tappa inte räknaren och utsätt den inte för våld.

• Försök aldrig att bränna förbrukade batterier.

• Förvara batterier utom räckhåll för barn.

• Av uppgraderingsskäl kan utformningen av denna produkt, inklusive
dess tillbehör, ändras utan föregående meddelande.

OBSERVERA!

• SHARP rekommenderar verkligen att skriftliga säkerhetskopior görs
av alla viktiga data. Data kan i praktiskt taget vilken elektronisk
minnesprodukt som helst gå förlorade eller ändras under vissa
förhållanden. Därför tar SHARP inte på sig något ansvar för data som
gått förlorade eller på annat sätt blivit oanvändbara till följd av olämplig
användning, reparation, felaktighet, batteribyte, användning efter att
specificerad batterilivslängd har gått ut eller någon annan orsak.

• SHARP åtar sig inget ansvar för några som helst obetydliga eller
betydande skador eller förluster till följd av felaktigt bruk och/eller
felfunktioner hos denna produkt och dess kringutrustning, såvida inte
sådant ansvar är lagfäst.

♦ Tryck enbart i nedanstående fall in omkopplaren RESET (på baksidan)

med en kulspetspenna eller liknande föremål. Använd inte ett föremål
som är alltför vasst eller vars spets kan brytas. Tänk på att ett tryck på
omkopplaren RESET raderar alla data som lagrats i minnet.

• Då räknaren används för första gången

• Då du bytt batterier

• För att tömma innehållet i alla minnen

• Då räknaren låst sig och inga tangenter fungerar.
Om räknaren behöver teknisk service ska du endast anlita en SHARP­återförsäljare med service, en av SHARP godkänd serviceverkstad eller
SHARPs reparationsservice, där sådan finns.

Hårt fodral

SKÄRM

Ekvationsvisning

• Vid normal användning syns inte alla symboler på samma gång.

• Det kan hända att även vissa inaktiva symboler syns, när skärmen ses ur

en smal vinkel.

• Endast de symboler som är nödvändiga för det användningssätt som

beskrivs visas på skärmen och i räkneexemplen i denna bruksanvisning.

: Visas då en hel ekvation inte får plats. Tryck på </> så

xy/r

visas resten av ekvationen.

θ

: Indikerar att resultaten visas som komplexa tal.
: Indikerar att data ovanför/nedanför det som syns på skärmen

kan rullas fram. Tryck på [/] för att rulla uppåt/neråt
på skärmen.

2ndF : Visas när @ trycks in.
HYP : Indikerar att man har tryckt på h och de hyperboliska

ALPHA : Visas när K (STAT VAR), O eller R trycks in.
FIX/SCI/ENG: Indikerar den notation som används för att visa ett värde.

funktionerna går att nå. Om man trycker på @H visas
symbolerna “2ndF HYP” och man kan nå de inverterade
hyperboliska funktionerna.

→

04DGK (TINSZ0726EHZZ)

←Symbol

ExponentMantissa

DEG/RAD/GRAD: Indikerar vinkelenheter.

: Visas medan matrisläget är valt.
: Visas medan listläget är valt.
: Visas medan statistikläget är valt.

M:Indikerar att ett värde är lagrat i det oberoende minnet.

? : Anger att räknaren väntar på att ett numeriskt värde ska matas in,

i : Indikerar att räknaren visar ett imaginärt tal som resultat vid

exempelvis under simuleringsberäkning.

: Indikerar att räknaren visar en vinkel som resultat vid beräkning

med komplexa tal.

beräkning med komplexa tal.

INNAN DU ANVÄNDER RÄKNAREN

Så skrivs tangenterna i denna bruksanvisning

I denna bruksanvisning beskrivs tangenttryckningarna så här:

Så skrivs ex: @e
Så skrivs ln : I
Så skrivs F : Kü

För att använda en funktion som står skriven med orange text ovanför en
tangent måste @ tryckas in före aktuell tangent. Tryck först på K vid
val av minne. Siffror för inmatning visas inte som tangenter utan som vanliga
siffror.

Slå på och stänga av

Tryck på ª för att starta räknaren och på

Nollställning av inmatning och minne

Nollställnings- Inmatning M A-F, X,Y STAT*1matA-D*
metod (visat värde) F1-F4 ANS STAT VAR*2L1-4*

ª ×× × ×
@c ×

Val av arbetsläge ×

@∏00*
@∏10*

RESET-knapp

: Nollställs × : Värdet finns kvar

1

*

Statistiska data (inmatade data).

2

x¯, sx, σx, n, Σx, Σx2, ¯y, sy, σy, Σy, Σy2, Σxy, r, a, b, c.

*

3

*

Matrisminnen (matA, matB, matC och matD)

4

Listminnen (L1, L2, L3 och L4)

*

5

Samtliga variabler nollställs.

*

6

*

Denna tangentkombination har samma funktion som RESET-knappen.

[Tangent för nollställning av minne]

Tryck på @∏ för att ta fram menyn.

• För att nollställa alla variabler (M, A-F, X, Y, ANS,
F1-F4, STAT VAR, matA-D, L1-4): Tryck på
00 eller 0®.

• För att nollställa räknaren (RESET): Tryck på 10 eller 1®.
Vid nollställning av räknaren (RESET) raderas alla data som lagrats i minnet
samtidigt som räknaren återgår till grundinställningarna.

5

6

@F

för att stänga av den.

4

3

Inmatning och korrigering av ekvation

[Markörtangenter]

• Tryck på < eller > för att flytta markören. Det är också möjligt att
återgå till ekvationen efter att ett resultat har fåtts fram genom att trycka på
> (<). Vi hänvisar till nästa avsnitt angående användning av
tangenterna [ och ].

• Vi hänvisar till ‘SET UP-meny’ angående användning av markören på SET
UP-menyn.

[Infogningsläge och överskrivningsläge vid ekvationsvisning]

• Tryck på @‘ för att växla mellan de två redigeringslägena:
infogningsläge (grundinställning) och överskrivningsläge. En triangulär
markör anger att en inmatning kommer att infogas vid markören, medan en
rektangulär markör anger att redan existerande data skrivs över vid
inmatning.

• För att foga in en siffra i infogningsläget: Flytta markören till platsen direkt
efter önskat infogningsställe och mata därefter in önskad siffra. I
överskrivningsläget skrivs data som befinner sig under markören över av
den siffra som matas in.

• Valt läge kvarstår tills RESET-funktionen för nollställning av räknaren
används nästa gång.

[Raderingstangent]

• Radera en siffra/funktion genom att flytta markören till siffran/funktionen
du vill radera och tryck sedan på d. Om markören står vid den högra
ändan av en ekvation fungerar tangenten d som en backstegstangent.

Ta fram flera rader

Tidigare ekvationer kan återkallas i normalt läge. Ekvationerna innefattar även
instruktioner som avslutar beräkningen såsom “=” och högst 142 tecken får
plats i minnet. När minnet är fullt raderas de äldsta sparade ekvationerna ut
först. Tryck på [ för att visa den förra ekvationen. Tryck på [ igen så
visas föregående ekvation (då du ser den föregående kan du trycka på ]
för att se ekvationerna i tur och ordning). Dessutom kan du trycka på
@[ för att komma till den äldsta ekvationen.

• Minnet för flera rader nollställs av följande åtgärder: @c,
lägesändring, RESET och N-basomvandling och minnestömning
(@∏).

Prioritetsnivåer vid beräkning

Operationer utförs i följande prioritetsordning:
Q Bråkdelar (1
före funktionen (x
värde i ett minne (2Y etc.) Y Funktioner med argument efter funktionen (sin,
cos etc.) U Implicit multiplikation med en funktion (2sin30 etc.) I

O ×, ÷ P +, – { AND } OR, XOR, XNOR q =, M+, M–, ⇒M, |DEG,
|RAD, |GRAD, DATA, CD, →rθ, →xy och andra instruktioner som avslutar

beräkning.

4 etc.) W ∠, tekniska prefixer E Funktioner med argument

l

-1

, x2, n! etc.) R Yx, x¿ T Implicit multiplikation med ett

nCr, nPr

• Då parenteser används har beräkningar inom parentes förtur framför alla
andra beräkningar.

VIKTIGA INSTÄLLNINGAR

Val av arbetsläge

m0: Normalt läge (NORMAL)
m1: Statistikläge (STAT)
m2: Ekvationsläge (EQN)
m3: Läge för komplexa tal (CPLX)
m4: Matrisläge (MAT)
m5: Listläge (LIST)

SET UP-meny

Tryck på ” för att ta fram SET UP-menyn.

• Ett menyalternativ kan väljas genom att:

• flytta den blinkande markören med hjälp av

>< och trycka på ® (tangenten =), eller

• trycka på den siffertangent som motsvarar numret på menyalternativet

ifråga.

• Om

eller visas på skärmen, tryck på [ eller ] för att ta fram

föregående/nästa menysida.

• Tryck på ª för att lämna SET UP-menyn.

[Ställ in rätt vinkelenhet]

Följande tre vinkelenheter (grader, radianer och decimalgrader) kan anges.

• DEG (°) : Tryck på ”00.

• RAD (rad) : Tryck på ”01.

• GRAD (g) : Tryck på ”02.

[Val av hur tal visas och antal decimaler]

Fyra notationssystem används för visning av beräkningsresultat: flyttal, fast
decimalpunkt, vetenskaplig notation och teknisk notation.

• Medan symbolen FIX, SCI eller ENG visas kan antalet decimaler (TAB)
ställas in på mellan 0 och 9. Visade värden avkortas till motsvarande antal
siffror.

[Inställning av system för flyttalsvärden i vetenskaplig notation]

Två inställningslägen för visning av flyttalsvärden används: NORM1
(grundinställning) och NORM2. Ett tal visas automatiskt i vetenskaplig notation
utanför ett förinställt omfång:

• NORM1: 0.000000001 ≤ x ≤ 9999999999

• NORM2: 0.01 ≤ x ≤ 9999999999

TEKNISKA BERÄKNINGAR

• Tryck på m0 för att välja normalläge.

• Tryck innan varje ny beräkning på ª för att tömma skärmen. Om
indikeringen FIX, SCI eller ENG visas på skärmen, välj NORM1 på SET UP­menyn för att ta bort indikeringen.

Aritmetiska operationer

• Den avslutande parentesen ) precis före = eller ; kan
utelämnas.

Konstanträkning

•I konstantberäkningarna blir addenden en konstant. Subtraktion och division
utförs på samma sätt. Vid multiplikation blir multiplikanden en konstant.

• Vid konstantberäkning visas en konstant som K.

Funktioner

• Vi hänvisar till räkneexemplen för detaljer om varje funktion.

• Välj vinkelenhet innan beräkningar görs.

Differential-/integralkalkyl

Differential- och integralkalkyl kan endast utföras i normalt arbetsläge.
Beräkningsvillkor som x värdet vid differentialkalkyl eller startpunkt vid
integrering kan endast anges som numeriska värden och formler som 2
inte användas. Man kan använda samma formel flera gånger efter varann och
göra om beräkningen med ändrade villkor utan att skriva om formeln.

• När en beräkning utförs nollställs värdet i minnet X.

• Vid utförande av en differentialberäkning ska formeln anges först och
därefter värde x i differentialberäkning och minutintervall (dx). Om inget
numeriskt värde är specificerat för minutintervall, så kommer x≠0 att vara

x

×10–5 och x=0 att vara 10–5 från värdet på det numeriska derivatat.

• Vid utförande av en integralberäkning ska formeln anges först och därefter
gränsvärden (a, b) och delintervaller (n). Om inget numeriskt värde är
specificerat för delintervaller, så kommer beräkning att utföras med hjälp
av n=100.

Differential- och integralkalkyl utförs med nedanstående formler. Resultatet
kan i vissa sällsynta fall bli felaktigt, då funktionen är diskontinuerlig.

Integralkalkyl (Simpsons formel):

1

S=—h{ƒ(a)+4{ƒ(a+h)+ƒ(a+3h)+······+ƒ(a+(N–1)h)}

3

+2{ƒ(a+2h)+ƒ(a+4h)+······+ƒ(a+(N–2)h)}+f(b)}

Differentialkalkyl:

f’(x)=————————

[Beräkning av integraler]

Integralkalkyl kräver lång
beräkningstid beroende på
integrander och underintervall.
Under pågående beräkning
visas meddelandet “Calculat­ing!”. Tryck på ª för att
avbryta beräkningen. Notera att
det blir större integrala fel när
stora fluktuationer förekommer

dx2dx

f(x+––)–f(x –––)

dx

2



h=



N=2n




a ≤x ≤b

b – a

——

N

2

kan






i de integrala värdena vid ytterst liten förskjutning av det integrala omfånget

P (x,y )

X

Y

0

y

x

P (r,θ )

X

Y

0

r

θ

liksom för periodiska funktioner etc., där positiva och negativa integrala värden
förekommer beroende på intervallen.
I det första fallet bör integrationsintervallen göras så små som möjligt. I det
senare fallet ska de positiva och negativa värdena skiljas åt. Följ dessa råd så
blir beräkningens resultat noggrannare och beräkningstiden kortare.

Slumpvalsfunktion

Slumpvalsfunktionen har fyra inställningslägen för användning i normalt läge,
statistikläget, matrisläget och listläget. (Denna funktion kan inte utföras när
funktionen N-Base används.) Tryck på ® för att generera ytterligare
slumptal i följd. Tryck på ª för att avsluta.

• De genererade serierna med pseudoslumptal är lagrade i minnet Y. Varje
slumptal är baserat på en talserie.

[Slumptal]

Ett pseudoslumptal med tre signifikanta siffror, från 0 till 0.999, kan genereras
genom tryckning på @`0®.

[Slumptärning]

Ett tärningskast kan simuleras genom tryckning på @`1
® för slumpmässig generering av ett heltal mellan 1 och 6.

[Slumpmynt]

Slantsingling kan simuleras genom tryckning på @`2
® för slumpmässig generering av 0 (krona) eller 1 (klave).

[Slumpheltal]

Ett slumpmässigt heltal mellan 0 och 99 kan genereras genom tryckning på
@`3®.

Vinkelenhetsomvandling

Varje gång @g trycks in ändras vinkelenheten i följd.

Minnesberäkningar

Arbetsläge ANS M, F1-F4 A-F, X,Y
NORMAL

STAT ××
EQN × ××
CPLX ×
MAT ×
LIST ×

: Finns × : Saknas

[Tillfälliga minnen (A-F, X och Y)]

Tryck på O och en variabeltangent för att lagra ett värde i minnet.
Tryck på R och en variabeltangent för att återkalla ett värde från minnet.
Tryck på K följt av önskad variabeltangent för att placera en variabel i en
ekvation.

[Det oberoende minnet (M)]

Fungerar som de tillfälliga minnena och dessutom kan ett värde adderas till
eller subtraheras från det värde som finns i minnet.
Tryck på ªOM för att nollställa det oberoende minnet (M).

[Minnet för senaste resultat (ANS)]

Beräkningens resultat lagras automatiskt i minnet för senaste resultat då man
tryckt på = eller utfört en instruktion som avslutar beräkningen. Ett
resultat i matris- eller listformat lagras inte.

[Formelminnen (F1-F4)]

Formler innehållande upp till 256 tecken totalt kan lagras i minnena F1 - F4
(funktioner såsom sin etc. räknas som ett tecken). Vid lagring av en ny
ekvation i något av minnena ersätter denna automatiskt en redan existerande
ekvation.

Observera:

• Beräkningsresultat från de funktioner som anges nedan lagras automatiskt
i minnet X eller Y och ersätter där tidigare existerande värden.

• Slumpvalsfunktion ....... i minnet Y

• →rθ, →xy ....................

• Vid användning av R eller K återkallas värdet som lagrats i minnet
med användning av upp till 14 siffror.

i minnet X (r eller x), i minnet Y (θ eller y)

Bråkdelar kan inte skrivas in i de binära, pentala, oktala och hexadecimala
systemen. Om ett decimalt tal som innehåller en bråkdel omvandlas till ett
binärt, pentalt, oktalt eller hexadecimalt tal, så stympas bråkdelen. Bråkdelen
tas på samma sätt bort, om resultatet av en binär, pental, oktal eller
hexadecimal beräkning inkluderar en bråkdel. I de binära, pentala, oktala
och hexadecimala systemen visas negativa tal som komplement.

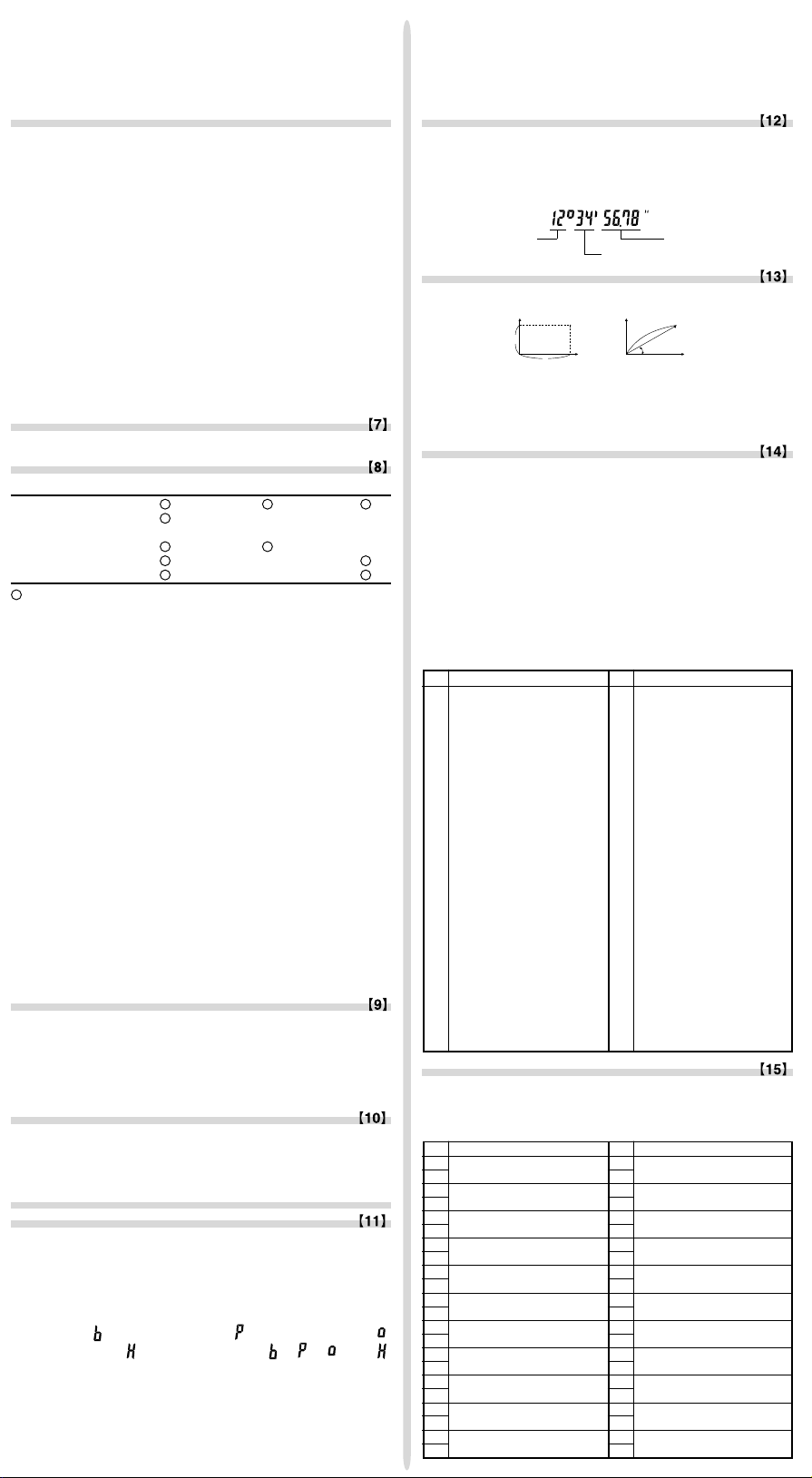
Beräkningar med tid, decimal och sexagesimal

Omvandling kan utföras mellan decimala och sexagesimala tal. Vid
användning av sexagesimala tal kan omvandling utföras till notation med
sekunder och minuter. De fyra grundläggande aritmetiska räknesätten och
minnesberäkningar kan utföras med det sexagesimala systemet. Sexagesimal
har följande notation:

Koordinatomvandling

• Innan en beräkning görs ska man välja vinkelenhet.

• Beräkningens resultat lagras automatiskt i minnena X och Y.

Beräkningar med hjälp av fysiskalika konstanter

Vi hänvisar till snabbreferenskortet och till baksidan på bruksanvisningen
på engelska. En konstant återkallas genom att trycka på ß följt av den
fysikaliska konstantens tal, vilket anges av ett 2-siffrigt nummer.
Den återkallade konstanten visas på skärmen enligt valt visningsläge med
angivet antal decimaler.
Fysikaliska konstanter kan återkallas i det normala läget (när inte det binära,
pentala, oktala eller hexadecimala systemet är inställt), statistikläget,
ekvationsläget, matrisläget eller listläget.

Observera: Fysikaliska konstanter och metriska omvandlingar är baserade

Kedjeberäkningar

• Det senaste beräkningsresultatet kan användas i efterföljande beräkning.
Det kan emellertid inte återkallas efter inmatning av flera instruktioner eller
när beräkningsresultatet är i matris- eller listformat.

• Vid användning av efterfixeringsfunktioner (¿ , sin etc.) kan en
kedjeberäkning utföras även om resultatet av föregående beräkning har
nollställts med hjälp av tangenten ª eller tangenterna @c.

Bråktal

Aritmetiska operationer och minnesberäkningar kan utföras med hjälp av
bråktal eller genom omvandling mellan ett decimalt tal och ett bråktal.

• Om det antal siffror som ska visas är större än 10, omvandlas talet till och
visas som ett decimaltal

.

Metriska omvandlingar

Vi hänvisar till snabbreferenskortet och till baksidan på bruksanvisningen
på engelska. Enhetsomvandlingar kan utföras i det normala läget (när inte
det binära, pentala, oktala eller hexadecimala systemet är inställt),
statistikläget, ekvationsläget, matrisläget eller listläget.

Binära, pentala, oktala, decimala
och hexadecimala operationer (N-bas)

Omvandlingar kan utföras mellan olika N-bastal. Beräkningar med de fyra
grundläggande aritmetiska räknesätten, beräkningar med parenteser och
minnesberäkningar kan också utföras, liksom de logiska operationerna AND,
OR, NOT, NEG, XOR och XNOR på binära, pentala, oktala och hexadecimala
tal.
Omvandling till önskad notation görs med hjälp av följande tangenter:

@ê ( “
visas), @ì (“
slocknar)

Observera: Med denna räknare skiver man de hexadecimala talen A – F med

” visas), @û (“ ” visas), @î (“ ”

” visas), @í (“ ”, “ ”, “ ” och “ ”

ß, ™, L, ÷, l och I. Talen visas på
följande sätt:

A → ï, B → ∫, C → ó, D → ò, E → ô, F → ö

grad sekund

Rätvinkliga
koordinater

•

Värdet på r eller x: i minnet X

på antingen rekommenderade värden i 2002 CODATA eller 1995
års upplaga av “Guide for the Use of the International System of
Units (SI)” (vägledning för användning av det internationella
enhetssystemet SI) utgiven av NIST (National Institute of
Standards and Technology) eller på ISO-standarder.

Nr Konstant

01 Ljusets hastighet i vakuum
02 Newtons gravitationskonstant
03 Standardacceleration för tyngdkraft
04 Elektronmassa
05 Protonmassa
06 Neutronmassa
07 Muonmassa
08 Sambandet mellan atomviktsenhet

och kilogram
09 Elementär laddning
10 Plancks konstant
11 Boltzmanns konstant
12 Magnetisk konstant
13 Elektrisk konstant
14 Klassisk elektronradie
15 Finstrukturkonstant
16 Bohrs radie
17 Rydbergs konstant
18 Magnetisk flödesmängd
19 Bohrmagneton
20 Elektronmagnetiskt moment
21 Kärnmagneton
22 Protonmagnetiskt moment
23 Neutronmagnetiskt moment
24 Muonmagnetiskt moment
25 Comptonvåglängd
26 Protons Comptonvåglängd
27 Stefan-Boltzmanns konstant

Nr Förklaring

1in : tum
2cm: centimeter
3ft : fot
4m : meter
5yd: yard
6m : meter
7 mile : mile
8km: kilometer

9n mile : nautiska mil
10 m : meter
11 acre : acre
12 m2: kvadratmeter
13 oz : uns
14 g : gram
15 lb : pund
16 kg : kilogram
17 °F : grader Fahrenheit
18 °C : grader Celsius
19 gal (US) : gallon (USA)
20 l : liter
21 gal (UK) : gallon (GB)
22 l : liter

minut

↔

Polära
koordinater

•

Värdet på θ eller y: i minnet Y

Nr Konstant

28 Avogadros konstant
29 Molvolym hos ideal gas

(273,15 K, 101,325 kPa)
30 Molar gaskonstant
31 Faradays konstant
32 Von Klitzings konstant
33 Kvot mellan elektrons laddning

och massa
34 Cirkulationskvantum
35 Protons gyromagnetiska kvot
36 Josephsons konstant
37 Elektronvolt
38 Celsius-temperatur
39 Astronomisk enhet
40 Parsek
41 Molmassa hos kol-12
42 Plancks konstant genom 2 pi
43 Hartree-energi
44 Konduktansmängd
45 Omvänd finstrukturkonstant
46 Massförhållande mellan proton

och elektron
47 Molar masskonstant
48 Neutrons Comptonvåglängd
49 Första strålningskonstanten
50 Andra strålningskonstanten
51 Vakuums karakteristiska impedans
52 Standardatmosfär

Nr Förklaring

23 fl oz(US) :
24 ml : milliliter
25 fl oz(UK) : ounce för vätska (GB)
26 ml : milliliter
27 J : joule
28 cal : kalorier
29 J : joule
30 cal15 : kalorier (15 n°C)
31 J : joule
32 calIT : I.T.-kalorier
33 hp : hästkrafter
34 W : watt
35 ps : franska hästkrafter
36 W : watt
37
38 Pa : pascal
39 atm : atmosfär
40 Pa : pascal
41 (1 mmHg = 1 Torr)
42 Pa : pascal
43
44 J : joule

ounce för vätska (USA)

Beräkningar med hjälp av tekniska prefixer

/

EL-506W
EL-546W

TEKNISK RÄKNARE

BRUKSANVISNING

MODELL

SHARP CORPORATION

MEM RESET

0 1

DRG FSE TA B

0 1

P (x,y )

X

Y

0

y

x

P (r,θ )

X

Y

0

r

θ

y

x

b

xx

xx

a

0

13

2

y

a

b

x

x
x
x

x

1

0

2
3

Beräkningar kan utföras i det normala läget (utom med N-basfunktionen)
med hjälp av följande 9 typer av prefixer.

Prefix Operation Enhet

k(kilo) ∑10 10
M(mega) ∑11 10
G (giga) ∑12 10
T (tera) ∑13 10
m (milli) ∑14 10
µ(mikro) ∑15 10
n (nano) ∑16 10
p (piko) ∑17 10
f (femto) ∑18 10

Modifieringsfunktion

Beräkningsresultat erhålls internt i vetenskaplig notation med upp till 14
siffror i mantissan. Beräkningens interna (verkliga) resultat kan skilja sig
något från det som visas på skärmen, eftersom resultatet visas i form du
ställt in och med inställt antal decimaler. Modifieringsfunktionen omvandlar
det interna värdet till det värde som visas, så att nästa beräkning utgår från
det visade värdet.

Ekvationslösare

Det är möjligt att finna det x-värde som minskar en inmatad ekvation till “0”.

• Denna funktion använder sig av Newtons metod för att erhålla en
approximation. Beroende på funktionen (t.ex. periodisk) eller startvärdet
kan ett fel inträffa (Error 2) på grund av att det inte finns någon konvergens
till lösningen för ekvationen.

• Det värde som erhålls med denna funktion kan inkludera en felmarginal.
Ändra värdena ‘Start’ (startvärde) och dx och beräkna därefter om
lösningen, om felmarginalen är oacceptabelt stor.

• Ändra ‘Start’-värdet (t.ex. till ett negativt värde) eller dx-värdet (t.ex. till
ett mindre värde), om:

• ingen lösning kan finnas (Error 2),

• fler än två lösningar tycks vara möjliga (t.ex. en kubisk ekvation),

• den aritmetiska precisionen behöver förbättras.

• Beräkningsresultatet lagras automatiskt i minnet X.

[Användning av ekvationslösare]

Q Tryck på m0.
W Mata in en formel med en x variabel.
E Tryck på ∑0.
R Mata in ett ‘Start’-värde och tryck på ®. Grundvärdet är “0”.
T Mata in ett dx-värde (minutintervall).
Y Tryck på ®.

SIMULERINGSBERÄKNING (ALGB)

Om du behöver finna ett värde genom att i följd använda samma formel, för
att exempelvis rita en kurva för 2x
=14, så är det enda du behöver göra efter att ha matat in ekvationen att ange
värdet på variabeln i formeln.
Användbara variabler: A-F, M, X och Y
Användbara funktioner: Slumpvalsfunktion

• Simuleringsberäkning kan endast genomföras i normalt läge.

• Inga beräkningsavslutande instruktioner förutom = kan användas.

2

+ 1 eller finna en variabel för 2x + 2y

Utförande av beräkningar

Q Tryck på m0.
W Mata in en formel med minst en variabel.
E Tryck på @≤.
R Läget för variabelinmatning visas på skärmen. Mata in värdet för den

blinkande variabeln och tryck sedan på ® för att bekräfta.
Beräkningsresultatet visas efter att värdena för alla använda variabler har
angetts.

• Endast numeriska värden godkänns som variabler. Inmatning av
formler är inte tillåtet.

• Tryck på @≤, efter att beräkningen är klar, för att utföra fler
beräkningar med hjälp av samma formel.

• Variabler och numeriska värden som finns lagrade i minnena visas på
skärmen i läget för variabelinmatning. Ändra ett numeriskt värde
genom att mata in det nya värdet och sedan trycka på ®.

• Vid utförande av simuleringsberäkning skrivs minnesplatser över med
nya värden.

STATISTISKA BERÄKNINGAR

Tryck på m1 för att välja statistikläget. Följande sju statistiska
beräkningar kan utföras. När du har valt statistikläget väljer du önskat
beräkningssätt genom att trycka på motsvarande siffertangent.
För att ändra till ett annat statistikberäkningssätt: välj statistikläget på nytt
(tryck på m1) och välj därefter önskat statistikberäkningssätt.

0 (SD) : Statistikberäkningar med en variabel
1 (LINE) : Linjär regression
2 (QUAD) : Kvadratisk regression
3 (EXP) : Exponentiell regression
4 (LOG) : Logaritmisk regression
5 (PWR) : Potensregression
6 (INV) : Invers regression

Följande statistik kan erhållas för varje statistisk beräkning (vi hänvisar till
tabellen nedan):

Statistiskberäkningar med en variabel

Statistik för Q och den normala sannolikhetsfunktionens värde.

Beräkning med linjär regression

Statistik för Q och W och dessutom uppskattning av y för ett givet x
(uppskatta y´) och uppskattning av x för ett givet y (uppskatta x´)

Beräkning med exponentiell regression, logaritmisk
regression, potensregression och invers regression

Statistik för Q och W. Dessutom uppskattning av y för ett givet x och

3

6

9

12

–3

–6

–9

–12

–15

uppskattning av x för ett givet y. (Eftersom räknaren omvandlar varje
formel till en formel med linjär regression innan en egentlig beräkning
påbörjas, erhåller den all statistik, förutom koefficienterna a och b, från
omvandlat data istället för från inmatat data.)

Kvadratisk regressionsanalys

Statistik för Q och W och koefficienterna a, b och c i den kvadratiska
regressionsformeln (y = a + bx + cx
ingen korrelationskoefficient (r).) Tryck på @≠, när två x´-värden
förekommer.

Vid beräkningar med a, b och c kan endast ett numeriskt värde sparas.

¯

x Medelvärde av stickprov (x data)

2

). (Kvadratisk regressionsanalys ger

sx Stickprovens standardavvikelse (x data)

σ

Q

x Populationens standardavvikelse (x data)

n Antal stickprov

Σ

x Summan av stickproven (x data)

Σ

x2Summan av kvadrater av stickprov (x data)

¯

y Medelvärde av stickprov (y data)

sy Stickprovens standardavvikelse (y data)

σ

y Populationens standardavvikelse (y data)

Σ

W

y Summan av stickproven (y data)

Σ

y2Summan av kvadrater av stickprov (y data)

Σ

xy Summa av stickprovsprodukter (x, y)
r Korrelationskoefficient
a Regressionsekvationens koefficient
b Regressionsekvationens koefficient
c Kvadratiska regressionsekvationens koefficient

• Använd K och R för beräkning med STAT-variabel.

Inmatning och korrigering av data

Inmatade data kvarhålls i minnet tills @c eller lägesval. Innan nya
data matas in ska minnets innehåll tas bort.

[Inmatning av data]

Data med en variabel

Data

k

Data & frekvens

Data med två variabler

Data

x &

Data

x &

samma x- och y-data)

• Upp till 100 dataposter kan inmatas. För data med en variabel räknas en
datauppgift utan frekvenstilldelning som en datauppgift, medan en
datauppgift som tilldelats frekvens lagras som en mängd av två data­uppgifter. För data med två variabler räknas en mängd datauppgifter utan
frekvenstilldelning som två datauppgifter, medan en mängd datauppgifter
som tilldelats frekvens lagras som en mängd av tre datauppgifter.

[Ändring av data]

Ändring före tryck på k direkt efter en datainmatning:

Ta bort felaktigt data med ª och mata därefter in korrekt data.

Ändring efter tryck på k:

Använd [] till att ta fram det tidigare inmatade datat.
Tryck på ] för att ta fram data i framåtgående ordning (äldsta först).
Tryck på [ för att ta fram data i bakåtgående ordning (senaste först).
Varje post visas med ‘Xn=’, ‘Yn=’ eller ‘Nn=’ (n är sekvensnumret för
datasatsen).
Uppvisa dataposten som ska modifieras, mata in det rätta värdet och
tryck sedan på k. Med hjälp av & går det att korrigera alla
värden i datasatsen samtidigt.

• Radera en datasats genom att uppvisa en post i datasatsen som ska
raderas och sedan trycka på @J. Datasatsen raderas.

• Lägg till en nya datasats genom att trycka på ª, mata in värdena och
sedan trycka på k.

k (då samma värde återkommer flera gånger)

Data

y k

Data

y &

frekvens

k (för inmatning av multipler av

Statistiska beräkningsformler

Typ Regressionsformel
Linjär y = a + bx
Exponentiell y = a • e
Logaritmisk y = a + b • ln x
Potens y = a • x

Invers

Kvadratisk y = a + bx + cx

Ett fel uppstår i de statistiska beräkningsformlerna:

• då absolutvärdet av ett delresultat eller beräkningsresultat är lika med eller

större än 1 × 10

• vid division med noll.

• vid försök att dra kvadratroten ur ett negativt tal.

• då ingen lösning existerar vid kvadratisk regressionsanalys.

Normala sannolikhetsberäkningar

•P(t), Q(t) och R(t) tar alltid positiva värden, också då t<0, eftersom dessa
funktioner följer samma princip som används vid problemlösning för en
yta.
Värden för P(t), Q(t) och R(t) ges med upp till sex decimaler.

SIMULTANA LINJÄRA EKVATIONER

En simultan linjär ekvation med två obekanta (2-VLE) eller med tre obekanta
(3-VLE) kan eventuellt lösas med hjälp av denna funktion.

Q 2-VLE: m20
W 3-VLE: m21

• Om determinanten D = 0, så uppstår ett fel.

y = a + b —

100

.

bx

b

1

x

2

• Om det absoluta värdet av ett delresultat eller ett beräkningsresultat är

100

eller mer, så uppstår ett fel.

1 × 10

• Koefficienter (a

• Tryck på @c för att ta tömma angivna koefficienter.

• Vid tryck på ® medan determinanten D visas på skärmen återkallas
koefficienterna. Med vart tryck på ® visas en koefficient enligt den
ordningsföljd de matats in, så att varje angiven koefficient kan verifieras.
(Vid tryck på @® visas koefficienterna i motsatt ordningsföljd.)
Mata in det korrekta värdet och tryck på ® för att vid behov korrigera
en viss koefficient medan den visas på skärmen.

1 etc.) kan anges med hjälp av vanliga aritmetiska operationer.

KVADRATISK OCH KUBISK EKVATIONSLÖSARE

En kvadratisk ekvation (ax2 + bx + c = 0) eller en kubisk ekvation (ax3 + bx
+ cx + d = 0) kan eventuellt lösas med hjälp av denna funktion.

Q Kvadratisk ekvationslösare: m22
W Kubisk ekvationslösare: m23

• Tryck på ® efter inmatning av varje koefficient.

• Tryck på ® efter inmatning av alla koefficienter för att få fram resultatet.
När fler än 2 resultat förekommer visas följande lösning.

• Om resultatet är ett imaginärt tal visas symbolen “xy”. Genom att trycka på
@≠ är det möjligt att växla mellan visning av imaginära och reella
delar.

BERÄKNINGAR MED KOMPLEXA TAL

Det går att utföra addition, subtraktion, multiplikation och division med komplexa
tal. Tryck på
Resultat av beräkningar med komplexa tal uttrycks på två olika sätt:

Q @}: Som rätvinkliga koordinater (xy visas).
W @{: Som polära koordinater (

m3

för att välja läget för komplexa tal.

r

θ

visas).

Inmatning av komplexa tal

Q Rätvinkliga koordinater

x-koordinat

eller

W Polära koordinater

r

r: absolut värde θ: argument

• Vid val av ett annat läge nollställs den imaginära delen av ett eventuellt
komplext tal lagrat i det oberoende minnet (M).

• Ett komplext tal som uttrycks som rätvinkliga koordinater med y-värdet noll
eller som polära koordinater med vinkeln noll behandlas som ett reellt tal.

• Tryck på ∑0 för att återhämta det komplexa konjugatet till det
angivna komplexa talet.

x-koordinat

Ö

θ

+

y-koordinat

+ Ü

Ü

y-koordinat

MATRISBERÄKNINGAR

Med hjälp av denna funktion är det möjligt att spara upp till 4 matriser (4
rader × 4 kolumner) för beräkningar. Tryck på m4 för att välja
matrisläget.

• Matrisdata måste matas in innan några beräkningar görs. Tryck på [/
], så att matrisredigeringsbufferten visas tillsammans med
Mata in värdet för varje post (‘ROW’ (rad), ‘COLUMN’ (kolumn) och därefter
varje element, t.ex. ‘MAT1,1’) och tryck på k efter varje. Tryck på
ª efter att alla poster har matats in. Tryck därefter på °2 och
ange matA-D för att spara datat.

• För att ändra data sparat i matA-D: tryck på °1 och ange matA-D
för att återkalla datat till matrisredigeringsbufferten. Tryck på ª efter
att önskade ändringar har gjorts. Tryck därefter på °2 och ange
matA-D för att spara datat.

• Tryck på ª för att stänga matrisredigeringsbufferten, innan beräkningar
påbörjas.

• När resultat av beräkningar är i matrisformat visas matrisredigerings­bufferten med de aktuella resultaten. (I detta läge är det inte möjligt att
återgå till ekvationen.) Resultaten kan sparas i matA-D genom att trycka
först på ª och därefter på °2 och sedan ange matA-D.

• Eftersom det bara finns en matrisredigeringsbuffert skrivs tidigare data
över av en ny beräkning.

• Förutom de 4 aritmetiska funktionerna (utom divisioner mellan matriser),

3

, x2 och x–1 är följande kommandon tillgängliga:

x

dim(

matrisnamn,

rad,kolumn

fill(

värde,rad,kolumn

cumul

matrisnamn

aug(

matrisnamn,

matrisnamn

identity

värde

rnd_mat(

rad,kolumn

det

matrisnamn

trans

matrisnamn

mat→list
(∑5)

matA→list
(∑6)

)

)

Beräknar en matris med dimensioner ändrade såsom
specificerats.

) Fyller varje element med ett angett värde.

Beräknar den kumulativa matrisen.
Lägger till den andra matrisen till den första matrisen som

nya kolumner. Den första matrisen måste ha lika många
rader som den andra.

Beräknar identitetsmatrisen med angivet värde för rader
och kolumner.

) Beräknar en slumpmatris med angivna värden för rader och

kolumner.
Beräknar determinanten i en kvadratisk matris.
Beräknar matrisen med kolumnerna omkastade till rader

och raderna omkastade till kolumner.
Skapar listor med element från den vänstra kolumnen i

varje matris. (matA→L1, matB→L2, matC→L3, matD→L4)
Läget ändras från matrisläge till listläge.

Skapar listor med element från varje kolumn i matrisen.
(matA→L1, L2, L3, L4)
Läget ändras från matrisläge till listläge.

LISTBERÄKNINGAR

Med hjälp av denna funktion är det möjligt att spara upp till 4 listor med 16
element för beräkningar. Tryck på m5 för att välja listläget.

• Listdata måste matas in innan några beräkningar görs. Tryck på [/
], så att listredigeringsbufferten visas tillsammans med
in värdet för varje post (‘SIZE’(storlek) och därefter varje element, t.ex.
‘LIST1’) och tryck på k efter varje. Tryck på ª efter att alla poster
har matats in. Tryck därefter på °2 och ange L1-4 för att spara
datat.

. Mata

2

.

• För att ändra data sparat i L1-4: tryck på °1 och ange L1-4 för att

SHARP CORPORATION

P (x,y )

X

Y

0

y

x

P (r,θ )

X

Y

0

r

θ

återkalla datat till listredigeringsbufferten. Tryck på ª efter att önskade
ändringar har gjorts. Tryck därefter på °2 och ange L1-4 för att
spara datat.

• Tryck på ª för att stänga listredigeringsbufferten, innan beräkningar
påbörjas.

• När resultat av beräkningar är i listformat visas listredigeringsbufferten
med de aktuella resultaten. (I detta läge är det inte möjligt att återgå till
ekvationen.) Resultaten kan sparas i L1-4 genom att trycka först på ª
och därefter på °2 och sedan ange L1-4.

• Eftersom det bara finns en listredigeringsbuffert skrivs tidigare data över av
en ny beräkning.

• Förutom de 4 aritmetiska funktionerna, x
tillgängliga:

sortA

listnamn

sortD

listnamn

dim(

listnamn,storlek

fill(

värde,storlek

cumul

listnamn

df_list

listnamn

aug(

listnamn,listnamn

min

listnamn

max

listnamn

mean

listnamn

med

listnamn

sum

listnamn

prod

listnamn

stdDv

listnamn

vari

listnamn

o_prod(

listnamn,listnamn

i_prod(

listnamn,listnamn

abs

listnamn

list→mat
(∑5)

list→matA
(∑6)

Sorterar lista i stigande ordning.
Sorterar lista i fallande ordning.

) Beräknar en lista med storlek ändrad såsom

specificerats.

)

Matar in det angivna värdet för alla poster.
Kumulerar varje post på listan i följd.
Beräknar en ny lista med hjälp av skillnaden mellan

angränsande poster på listan.

) Beräknar en lista fäst vid den angivna listan.

Beräknar det minimala värdet på listan.
Beräknar det maximala värdet på listan.
Beräknar medelvärdet för poster på listan.
Beräknar
Beräknar summan av poster på listan.
Beräknar produkten av poster på listan.
Beräknar standardavvikelsen för posterna på listan.
Beräknar variansen för posterna på listan.

) Beräknar den yttre produkten av två listor (vektorer).

) Beräknar den inre produkten av två listor (vektorer).

Beräknar det absoluta värdet för listan (vektor).
Skapar matriser med vänsterkolumnsdata från varje

lista. (L1→matA, L2→matB, L3→matC, L4→matD)
Läget ändras från listläge till matrisläge.

Skapar en matris med kolumndata från varje lista.
(L1, L2, L3, L4→matA)
Läget ändras från listläge till matrisläge.

3

, x2 och x–1 är följande kommandon

medianvärdet för poster på listan.

FEL OCH DEFINITIONSOMRÅDEN

Fel

Ett fel uppstår om en operation ligger utanför definitionsområdet eller om
man försöker utföra en otillåten matematisk operation. När ett fel uppstår
trycker man på < (eller >) så flyttas markören automatiskt tillbaka
till den plats i ekvationen där felet uppstod. Ändra ekvationen eller tryck på
ª för att ta bort ekvationen.

Felkoder och feltyper

Syntaxfel (Error 1):

• Du har försökt utföra en ogiltig operation.

Ex. 2 @{

Beräkningsfel (Error 2):

• Absolutvärdet av ett delresultat eller slutresultat är lika med eller större än

100

.

10

• Division med 0 (eller en delberäkning har gett ett nollresultat).

• Under pågående beräkning har definitionsområdets gränser överskridits.

Djupfel (Error 3):

• Tillgängligt antal buffertminnen har överskridits. (Det finns 10 buffertminnen*
för numeriska värden och 24 för beräkningskommandon i normalt läge).
*5 buffertminnen i andra lägen och 1 buffertminne för matris- och listdata.

• Antalet dataposter överstiger 100 i statistikläget.

Ekvationen är för lång (Error 4):

• Ekvationen får inte plats i buffertminnet för inmatning (142 tecken).
En ekvation måste vara kortare än 142 tecken.

Ekvationsåterkallningsfel (Error 5):

• Den lagrade ekvationen innehåller en funktion som inte är tillgänglig i det läge
som används för att återkalla ekvationen. Om exempelvis ett numeriskt värde
med andra tal än 0 och 1 finns lagrat som en decimal, så kan det inte återkallas
medan räknaren är inställd för binärt talsystem.

Minnet överskridet (Error 6):

• Ekvationen överskred minnesbufferten för formler (256 tecken totalt i minnena
F1 - F4).

Ogiltighetsfel (Error 7):

• Matrisdefinitionsfel eller inmatning av ett ogiltigt värde.

Dimensionsfel (Error 8):

• Dimensioner på en matris/lista är inkonsekventa under beräkning.

Ogiltig DIM (Error 9):

• Storlek på matris/lista överstiger beräkningsomfång.

Definition saknas (Error 10):

• En odefinierad matris/lista används i beräkning.

Definitionsområden

• Inom de omfång som anges är denna räknare exakt till ±1 hos den minst
signifikanta siffran i mantissan. Om det uppstår ett räknefel i en
kontinuerlig beräkning minskar dock exaktheten då varje ny beräkning
gör felet större. (Detta gäller även för y
listberäkningar o.dyl. då kontinuerlig beräkning utförs internt.)
Ett räknefel kan också ackumuleras och bli allt större i närheten av
inflexionspunkter och enskilda punkter i funktionerna.

• Definitionsområden

–99

~ ±9.999999999×1099 och 0.

±10
Om absolutvärdet av ett inmatat värde eller ett slutresultat eller delresultat i en
beräkning är mindre än 10
skärmen.

–99

, anses värdet vara 0 i beräkningar och på

x, x

¿

x

e

,

, ln, matris- och

BATTERIBYTE

Att tänka på vid batteribyte

Batterier som hanteras felaktigt kan orsaka explosion eller läcka ut elektrolyt.
Följ dessa regler:

• Byt båda batterierna på samma gång.

• Blanda inte gamla och nya batterier.

• Kontrollera att de nya batterierna är av rätt typ.

• Vänd varje batteri rätt enligt instruktionen i räknaren då det sätts i.

• Batterierna sätts i på fabriken innan leverans och kan ta slut på kortare tid
än vad specifikationen anger.

Observera angående radering av minnesinnehåll

Minnesinnehållet raderas vid batteribyte. Radering kan också inträffa vid
fel på räknaren eller i samband med reparation. Se till att anteckna alla
viktiga minnesuppgifter som säkerhet i händelse av oförutsedd radering.

När ska batterierna bytas?

Om visningen på skärmen har svag kontrast eller om ingenting visas på
skärmen ens då ª trycks in vid dålig belysning, så är det dags att byta
ut batterierna.

Varning

• Vätska från ett läckande batteri som råkar tränga in i ett öga kan leda till
allvarliga skador. Skölj med rent vatten och uppsök omedelbart läkare om
detta inträffar.

• Skulle vätska från ett läckande batteri komma i kontakt med huden eller
kläderna ska du omedelbart skölja av med rent vatten.

• För att undvika skador på enheten från läckande batterier bör du ta ur
batterierna och förvara dem på ett säkert ställe om enheten inte ska
användas under en längre tid.

• Lämna inte kvar urladdade batterier i enheten.

• Blanda inte gamla och nya batterier och ej heller batterier av olika typ.

• Förvara batterier utom räckhåll för barn.

• Om använda batterier får sitta kvar i räknaren kan de läcka och skada
räknaren.

• Olämplig hantering kan skapa risk för explosion.

• Kasta inte batterier i öppen eld eftersom de kan explodera.

Byt batterier så här

1. Stäng av räknaren med en tryckning på @F.

2. Skruva bort två skruvar. (Fig. 1)

3. Skjut batterifackets lock ett litet stycke och lyft bort det.

4. Bänd försiktigt bort de använda batterierna med en kulspetspenna eller
liknande. (Fig. 2)

5. Sätt i två nya batterier. Se till att “+” är uppåt.

6. Sätt tillbaka baksidans lock och skruvar.

7. Tryck på knappen RESET (på baksidan).

• Kontrollera att skärmen ser ut som på bilden nedan. Om det inte ser ut så,
tar du ur batterierna och sätter i dem och kontrollerar igen.

(Fig. 1) (Fig. 2)

Automatisk avstängning

Räknaren stänger av sig för att spara på batterierna om man inte trycker på
någon tangent under ca 10 minuter.

SPECIFIKATIONER

Beräkningar: Vetenskapliga beräkningar, beräkningar med

Interna beräkningar: Mantissa med upp till 14 siffror
Väntande operationer: 24 beräkningar, 10 numeriska värden i normalt

Strömkälla: Inbyggda solceller

Drifttemperatur: 0°C – 40°C
Yttermått:
Vikt: Ca 97 g (inklusive batterier)
Tillbehör: Batterier × 2 (installerade), bruksanvisning,

FÖR MER INFORMATION OM
TEKNISK RÄKNARE

Besök vår webbplats.
http://sharp-world.com/calculator/

komplexa tal, ekvationslösare, statistiska
beräkningar etc.

läge (5 numeriska värden i övriga lägen och
1 numeriskt värde för matris- och listdata)

3 V ¶ (DC):
Stödbatterier
(2 st alkaliska batterier (LR44))

79,6 mm (b) × 154,5 mm (d) × 13,2 mm (h)

snabbreferenskort och hårt fodral

EL-506W

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

4

3

x =

Σx

n

y =

Σy

n

sy =

Σy

2

– ny

2

n – 1

sx =

Σx

2

– nx

2

n – 1

σy =

Σy

2

– ny

2

n

σx =

Σx

2

– nx

2

n

EL-546W

CALCULATION EXAMPLES
ANWENDUNGSBEISPIELE
EXEMPLES DE CALCUL
EJEMPLOS DE CÁLCULO
EXEMPLOS DE CÁLCULO
ESEMPI DI CALCOLO
REKENVOORBEELDEN
PÉLDASZÁMÍTÁSOK

PŘÍKLADY VÝPOČTŮ

RÄKNEEXEMPEL
LASKENTAESIMERKKEJÄ

икаеЦкх ЗхуалгЦзав

UDREGNINGSEKSEMPLER

CONTOH-CONTOH PENGHITUNGAN
CONTOH-CONTOH PERHITUNGAN

[]

13(5+2)= ª 3 ( 5 + 2 )=
23×5+2= 3 * 5 + 2 =
33×5+3×2= 3 * 5 + 3 * 2 =

→1 @[
→2 ]
→3 ]
→2 [

”

100000÷3=
[NORM1] ª 100000 / 3 =
→[FIX] ”10
[TAB 2] ”2 2

→[SCI] ”11
→[ENG] ”12
→[NORM1] ”13

3÷1000=
[NORM1] ª 3 / 1000 =

→[NORM2] ”14 3.×
→[NORM1] ”13

+-*/()±E

45+285÷3= ª 45 + 285 / 3 =

18+6

=

15–8 ( 15 - 8 =

42×(–5)+120= 42 *± 5 + 120 =

(5×103)÷(4×10–3)= 5 E 3 / 4 E

34+57= 34 + 57 =
45+57= 45 + 57 =

68×25= 68 * 25 =
68×40= 68 * 40 =

sutSUTVhH
Ile¡•L÷⁄™
$#!qQ%

sin60[°]= ªs 60 =

π

cos — [rad]=

4

tan–11=[g] ”02@T 1 =

(cosh 1.5 + ª(hu 1.5 +h
sinh 1.5)2 = s 1.5 )L=

tanh–1— =

5
7

••••

( 18 + 6 )/

*1 (5 ±) *

± 3 =

”01u(
@V/ 4 )=

”00

@Ht( 5
/ 7 )=

1

33’333.33333
33’333.33333

33’333.33

33’333.33333

21.

17.

21.

21.

17.

21.

17.

3.33×10

33.33×10

0.003
10

0.003

140.

3.428571429

–90.

1’250’000.

91.

102.

1’700.
2’720.

0.866025403

0.707106781

50.

20.08553692

0.895879734

••••

ln 20 = I 20 =

log 50 = l 50 =

e3 = @e 3 =

1.7

10

= @¡ 1.7 =

1

1

— + — =

6

7

8–2 – 34 × 52 =8 ™± 2 - 3 ™

1
4

(123)—=

3

8

¿

49 –4¿

3

¿

27 @# 27 =

4! = 4 @!=

= 10 @q 3 =

10P3

=5 @Q 2 =

5C2

500×25%= 500 * 25 @%

120÷400=?% 120 / 400 @%

500+(500×25%)= 500 + 25 @%

400–(400×30%)= 400 - 30 @%

04–

03–

6 @•+ 7 @

•=

4 * 5 L=

12 ™ 3 ™ 4

@•=

8 ÷=

81 = @⁄ 49 - 4 @$

81 =

θ = sin–1 x, θ = tan–1 x θ = cos–1 x

DEG –90 ≤ θ ≤ 90 0 ≤ θ ≤ 180

–03

RAD – — ≤ θ ≤ — 0 ≤ θ ≤ π

GRAD –100 ≤ θ ≤ 100 0 ≤ θ ≤ 200

π2π

2

Åè

d/dx (x4 – 0.5x3 + 6x2) ªKˆ™ 4 - 0.5 K



x=2 ˆ÷+ 6 KˆL



dx=0.00002 @Å 2 ®®




x=3 ® 3 ® 0.001 ®



dx=0.001



8

(x2 – 5)dx ªKˆL- 5

∫

2

n=100 è 2 ® 8 ®®
n=10 ®®® 10 ®

g

90°→ [rad] ª 90 @g
→ [g] @g
→ [°] @g

sin–10.8 = [°] @S 0.8 =

→ [rad] @g
→ [g] @g
→ [°] @g

KRO;:?≥∆˚¬

24÷(8×2)= 24 /KM=
(8×2)×5= KM* 5 =

$150×3:M1 150 * 3 ;
+)$250:M2 =M1+250 250 ;
–)M2×5% RM* 5 @%
M @:RM

••••

ª 8 * 2 OM

ªOM

2.995732274

1.698970004

20.08553692

50.11872336

0.309523809

–2’024.984375

6.447419591

512.

24.

720.

10.

125.

30.

625.

280.

50.

130.5000029

138.

138.

1.570796327

100.

90.

53.13010235

0.927295218

59.03344706

53.13010235

16.

1.5

80.

450.

250.

35.

665.

••••

$1=¥110 110 OY
¥26,510=$? 26510 /RY=

$2,750=¥? 2750 *RY=

r=3cm (r→Y) 3 OY
πr2=? @VKYL=

24

—— = 2.4...(A) 24 /( 4 + 6 )=

4+6

3×(A)+60÷(A)=

πr2⇒F1 @VKYL

V = ? R≥* 4 / 3 =

3 *K?+ 60 /

K?=

O≥
3 OY

4.

3.

6+4=ANS ª 6 + 4 =
ANS+5 + 5 =

8×2=ANS 8 * 2 =

2

ANS

44+37=ANS 44 + 37 =

√

ANS= @⁄=

L=

\|

124

3— + — = [a—] ª 3 \ 1 \ 2 +

→[a.xxx] \
→[d/c] @|

10

7

(—)

5

1

(—)

8

—— = @⁄ 64 \ 225 =

225

3

2
— =

4

3

1.2
—– =

2.3
1°2’3”

——– =

2

1×10
——– =

2×10
A = 7 ª 7 OA

4

— =4 \KA=

A

1.25 + — = [a.xxx] 1.25 + 2 \ 5 =
→[a—] \

*

4 l5 l6

b

c

3

2

—

3

= @¡ 2 \ 3 =

5

=7 \ 5 ™ 5 =

1

—

3

=

64

3

3

2
5

b
c

= 4—

4 \ 3 =

1 \ 8 ™ 1 \ 3

=

( 2 ™ 3 ) \
( 3 ™ 4 ) =

1.2 \ 2.3 =

1 o 2 o 3 \ 2 =

1 E 3 \ 2 E 3 =

5
6

кыомнгв†д
аб

DEC(25)→BIN ª@í 25 @ê

HEX(1AC) @ì 1AC

→BIN @ê
→PEN @û
→OCT @î
→DEC @í

BIN(1010–100) @ê( 1010 - 100 )
×11 = * 11 =

BIN(111)→NEG ã 111 =

HEX(1FF)+ @ì 1FF @î+
OCT(512)= 512 =
HEX(?) @ì

2FEC– ªOM@ì 2FEC ­2C9E=(A) 2C9E ;

+)2000– 2000 -

1901=(B) 1901 ;

(C) RM

1011 AND ª@ê 1011 †
101 = (BIN) 101 =

5A OR C3 = (HEX) @ì 5A ä C3 =

NOT 10110 = @êâ 10110 =
(BIN)

0.

24 XOR 4 = (OCT) @î 24 à 4 =

B3 XNOR @ì B3 á
2D = (HEX) 2D =
→DEC @í

110.

241.

302’500.

28.27433388

32.2

37.69911184

256.

4 l5 l6

4.833333333
29 l6

4.641588834

16807 l3125

1 l2

8 l15

8 l81

12 l23

0°31’1.5”

1 l2

4 l7

1.65

1 l13 l20

11001.

110101100.

3203.

654.

428.

10010.

1111111001.

1511.

349.

34E.

6FF.
A4d.

db.

1111101001.

20.

FFFFFFFF61.

–159.

1.

3.

2.4

F1

3.

10.

15.

16.

81.

9.

*

7.

b

b

P

0

b

b

0

H

H

H

H

b

H

b

0

H

o_° (→sec, →min)

x =

Σx

n

y =

Σy

n

sy =

Σy

2

– ny

2

n – 1

sx =

Σx

2

– nx

2

n – 1

σy =

Σy

2

– ny

2

n

σx =

Σx

2

– nx

2

n

12°39’18.05” ª 12 o 39 o 18.05
→[10] @_

123.678→[60] 123.678 @_

3h30m45s + 3 o 30 o 45 + 6 o
6h45m36s = [60] 45 o 36 =

1234°56’12” + 1234 o 56 o 12 +
0°0’34.567” = [60] 0 o 0 o 34.567 =

3h45m – 3 o 45 - 1.69 =

1.69h = [60] @_

sin62°12’24” = [10] s 62 o 12 o 24=

24°→[ ” ] 24 o°2

1500”→[ ’ ]0 o 0 o 1500 °3

12.65501389

123°40’40.8”

10°16’21.”

1234°56’47.”

2°3’36.”

0.884635235

{},≠





x = 6 →r = @{[





y = 4 θ = [°] @≠[θ]







r = 14 →x = @}[x]



θ = 36[°] y = @≠[y]



ª 6 @, 4

@≠[r]

14 @, 36





@≠[x]

r

]

7.211102551

33.69006753

7.211102551

11.32623792

8.228993532

11.32623792

ß

V0 = 15.3m/s ª 15.3 * 10 + 2 @•*
t = 10s ß 03 * 10 L=

1

V0t+ — gt2 = ?m

2

643.3325

¥

125yd = ?m ª 125 @¥ 5 =

∑ (k, M, G, T, m,

100m×10k= 100 ∑14*

ÌÌ

Ì, n, p, f)

ÌÌ

10 ∑10=

j”

5÷9=ANS ª”10”2 1
ANS×9= 5 / 9 =
[FIX,TAB=1] * 9 =*

5 / 9 =@j
* 9 =*

1

5.5555555555555×10–1×9

*

2

*

0.6×9

”13

1

2

∑ (SOLV)

sin x–0.5 ªsKˆ- 0.5
Start= 0 ∑0 0 ®®
Start= 180 ® 180 ®®

≤

3

f(x) = x

–3x2+2 Kˆ™ 3 - 3 K

x = –11 ±®
x = –0.5 @≤ 0.5 ±®

2

A2+B

A = 2, B = 3 2 ® 3 ®
A = 2, B = 5 @≤® 5 ®

m0

ˆL+ 2 @≤

@⁄(KAL+
KBL)@≤

3.605551275

5.385164807

86’400.

25.

114.3

1’000.

0.6

5.0

0.6

5.4

30.

150.

–2.

1.125

k&~£pnzw^
¢PZWvrab©
xy≠° (→t, P(, Q(, R()

DATA

95 m10
80 95 k
80 80 k
75 k
75 75 & 3 k
75 50 k
50

–

x= R~

σx= Rp

n= Rn

Σx= Rz

Σx2= Rw

sx= R£

sx2= L=

(95––x)

×10+50=

sx

x = 60 → P(t) ? °1 60 °0)=

t = –0.5 → R(t) ? °3 0.5 ±)=

xy m11

2 5 2 & 5 k
2 5 k
12 24 12 & 24 k
21 40 21 & 40 & 3 k
21 40 15 & 25 k
21 40 Ra
15 25 Rb

x=3 → y′=? 3 @y
y=46 → x′=? 46 @x

xy m12

12 41 12 & 41 k
8 13 8 & 13 k
5 2 5 & 2 k
23 200 23 & 200 k
15 71 15 & 71 k

x=10 → y′=? 10 @y
y=22 → x′=? 22 @x

( 95 -K~)
/K£* 10
+ 50 =

Rr
R£
R¢

Ra
Rb
R©

@≠
@≠

–3.120289663

–3.432772026

k[]

DATA

30 m10
40 30 k
40 40 & 2 k
50 50 k

↓

DATA

30 ]]]

45 45 & 3 k X2=
45 ] N2=
45
60 ] 60 k X3=

Σx = x1 + x2 + ··· + x

2

Σx2 = x

2

+ x

+ ··· + x

1

2

75.71428571

12.37179148

530.

41’200.

13.3630621

178.5714286

64.43210706

0.102012

0.691463

1.050261097

1.826044386

0.995176343

8.541216597

15.67223812

6.528394256

24.61590706

5.357506761

0.503334057

24.4880159

9.63201409

9.63201409

45.

60.

n

2

n

0.

1.

2.

3.

4.

5.

7.

0.

1.

2.

3.

4.

5.

0.

1.

2.

3.

4.

5.

0.

1.

2.

3.

3.

Σxy = x1y1 + x2y2 + ··· + xny
Σy = y1 + y2 + ··· + y

2

Σy2 = y

2

+ y

+ ··· + y

1

2

n

n

2

n

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

t = ––––

x – x

σx

Standardization conversion formula
Standard Umrechnungsformel
Formule de conversion de standardisation
Fórmula de conversión de estandarización
Fórmula de conversão padronizada
Formula di conversione della standardizzazione
Standaardisering omzettingsformule

Standard átváltási képlet
Vzorec pro přepočet rozdělení

Omvandlingsformel för standardisering
Normituksen konversiokaava

îÓÏÛ· Òڇ̉‡ÚËÁÓ‚‡ÌÌÓ„Ó ÔÂÓ·‡ÁÓ‚‡ÌËfl

Omregningsformel for standardisering

Rumus penukaran pemiawaian
Rumus konversi standarisasi

y

x

A

B

r

r2

θ1

θ2

r1

θ

4

3

x =

Σx

n

y =

Σy

n

sy =

Σy

2

– ny

2

n – 1

sx =

Σx

2

– nx

2

n – 1

σy =

Σy

2

– ny

2

n

σx =

Σx

2

– nx

2

n

m (2-VLE)

a1x + b1y = c
a2x + b2y = c



2x + 3y = 4 2 ® 3 ® 4 ®



5x + 6y = 7 5 ® 6 ® 7



x = ? ® [x]

1

2

m20

y = ? ® [y]
det(D) = ? ® [det(D)]

D =

a1 b
a2 b

1

2

m (3-VLE)

a1x + b1y + c1z = d

a2x + b2y + c2z = d
a3x + b3y + c3z = d

1

2

3

m21

x + y – z = 9 1 ® 1 ® 1 ±® 9 ®



6x + 6y – z = 17 6 ® 6 ® 1 ±® 17 ®



14x – 7y + 2z = 42 14 ® 7 ±® 2 ® 42



x = ? ® [x]
y = ? ® [y]
z = ? ® [z]

det(D) = ? ® [det(D)]

D =

a1 b1 c

a2 b2 c
a3 b3 c

1

2

3

3.238095238

–1.638095238

m (QUAD, CUBIC)

m22

@®

m23

@≠

@≠

m3

@≠ [y]
@≠ [x]

@≠ [y]

@≠ [y]

–6.333333333

–1.233600307

0.216800153

+

1.043018296

0.216800153

–

1.043018296

13.85640646

2

+ 4x – 95 = 0 3 ® 4 ®± 95

3x

x1 = ? ®
x2 = ? ®

3

+4x2+3x +7=0 5 ® 4 ® 3 ® 7

5x

x1 = ? ®
x2 = ? ®

x3 = ? ®

m (CPLX)

(12–6i) + (7+15i) – 12 - 6 Ü+ 7 + 15 Ü-
(11+4i) = ( 11 + 4 Ü)= [x]

6×(7–9i) × 6 *( 7 - 9 Ü)*
(–5+8i) = ( 5 ±+ 8 Ü)= [x]

16×(sin30°+ 16 *(s 30 +

icos30°)÷(sin60°+ Üu 30 )/(s 60 +
icos60°)= Üu 60 )= [x]

••••

+

–7.4

105.

+

222.

606.

+

••••

@{ 8 Ö 70 + 12 Ö 25
= [r]
@≠ [θ]

r1 = 8, θ1 = 70°
r2 = 12, θ2 = 25°

↓
r = ?, θ = ?°

(1 + i) @} 1 +Ü=
↓ @{ [r]
r = ?, θ = ?° @≠ [θ]

2

= = [x]

(2 – 3i)

@}( 2 - 3 Ü)L

@≠ [y]

1 ( 1 +Ü)@•= [x]

—— =
1 + i @≠ [y]

CONJ(5+2i)

∑0( 5 + 2 Ü)= [x]
@≠ [y]

m (MAT)

1 2

→ matA

3 4 3 k 4 k

3 1

→ matB

2 6

=

7 13
17 27

–2

1

1.5 –0.5

matA × matB =

–1

matA

dim(matA,3,3) = 1 2 0

dim(matA,3,3) = 3 4 0

dim(matA,3,3) = 0 0 0

fill(5,3,3) = 5 5 5

fill(5,3,3) = 5 5 5

fill(5,3,3) = 5 5 5

–1.

2.

–3.

cumul matA =

1 2
4 6

aug(matA,matB) =

identity 3 = 1 0 0

identity 3 = 0 1 0 ª∑34 3 =

identity 3 = 0 0 1

rnd_mat(2,3)

det matA = –2

trans matB =

mat → list

3 2
1 6

L1: {1 3}
L2: {3 2}

m4
] 2 k 2 k 1 k 2 k

ª∑20
] 2 k 2 k
3 k 1 k 2 k 6 k
ª∑21

ª∑00*∑01=

ª∑00@•=

ª∑30∑00
@, 3 @, 3 )=

ª∑31 5 @,
3 @, 3 )=

ª∑32∑00=

1 2 3 1 ª∑33∑00
3 4 2 6 @,∑01)=

ª∑35 2 @, 3 )=

ª∑40∑00=

ª∑41∑01=

ª∑5

m (LIST)

2, 7, 4 → L1 ] 3 k 2 k 7 k 4 k

–3, –1, –4 → L2

5.

5.

L1+L2 = {–1 6 0}

sortA L1 = {2 4 7}

i

sortD L1 = {7 4 2}

i

i

dim(L1,5) = {2 7 4 0 0}

i

i

fill(5,5) = {5 5 5 5 5}

cumul L1 = {2 9 13}

df_list L1 = {5 –3}

aug(L1,L2) = {2 7 4 –3 –1 –4} ª∑36∑00

8.

i

5.

i

min L1 = 2

8.

i

max L1 = 7

mean L1 = 4.333333333

i

i

med L1 = 4

sum L1 = 13

prod L1 = 56

i

8.

i

••••

m5

ª∑20
] 3 k
± 3 k± 1 k± 4 k
ª∑21

ª∑00+∑01=

ª∑30∑00=

ª∑31∑00=

ª∑32∑00
@, 5 )=

ª∑33 5 @,
5 )=

ª∑34∑00=

ª∑35∑00=

@,∑01)=

ª∑40∑00=

ª∑41∑00=

ª∑42∑00=

ª∑43∑00=

ª∑44∑00=

ª∑45∑00=

18.5408873

∠

42.76427608

1.414213562

•••• ••••

stdDv L1 = 2.516611478

i

vari L1 = 6.333333333

i

o_prod(L1,L2) = {–24 –4 19}

ª∑46∑00=

ª∑47∑00=

ª

∑48∑00

@,∑01)=

ª

i_prod(L1,L2) = –29

∑49∑00

@,∑01)=

abs L2 = 5.099019514

1.

i

list → matA matA: 2 –3

i

∠

–

–

list → matA matA: 7 –1 ª∑6

45.

i

list → matA matA: 4 –4

–5.

i

12.

i

0.5

0.5

–

i

i

5.

i

2.

i

Function Dynamic range
Funktion zulässiger Bereich
Fonction Plage dynamique

Función Rango dinámico

Função Gama dinâmica

ª∑4A∑01=

Funzioni Campi dinamici

Functie Rekencapaciteit

Függvény Megengedett számítási tartomány

Funkce Dynamický rozsah

Funktion Definitionsområde

Funktio Dynaaminen ala

îÛÌ͈Ëfl СЛМ‡ПЛ˜ВТНЛИ ‰Л‡Ф‡БУМ

Funktion Dynamikområde

Fungsi Julat dinamik
Fungsi Kisaran dinamis

DEG: | x | < 10

sin x, cos x,

RAD: | x | < —– × 10

tan x (tan x : | x | ≠ — (2n–1))*

GRAD: | x | < —– × 10

sin–1x, cos–1x | x | ≤ 1

3

tan–1x,

x | x | < 10

¿

In x, log x 10

x

y

–99

≤ x < 10

• y > 0: –10

• y = 0: 0 < x < 10

• y < 0: x = n

• y > 0: –10

x

¿y • y < 0: x = 2n–1

x

e

x

10
sinh x, cosh x,

tanh x

• y = 0: 0 < x < 10

100

–10

< x ≤ 230.2585092

100

–10

< x < 100

| x | ≤ 230.2585092

sinh–1 x | x | < 10
cosh–1 x 1 ≤ x < 10
tanh–1 x | x | < 1

2

x

3

x

x 0 ≤ x < 10

¿

–1

x

| x | < 10
| x | < 2.15443469 × 10

| x | < 10

10

(tan x : | x | ≠ 90 (2n–1))*

π

10

180

10

9

(tan x : | x | ≠ 100 (2n–1))*

100

100

100

< x log y < 100

(0 < l x l < 1: — = 2n–1, x ≠ 0)*,

100

–10

< x log | y | < 100

100

< — log y < 100 (x ≠ 0)

(0 < | x | < 1 : — = n, x ≠ 0)*,

100

–10

< — log | y | < 100

50

50

50

100

100

(x ≠ 0)

π

2

10

100

1

x

1

x

100

1

x

1

x

33

n! 0 ≤ n ≤ 69*

nPr

0 ≤ r ≤ n ≤ 9999999999*

n!

100

—— < 10

(n-r)!

0 ≤ r ≤ n ≤ 9999999999*

nCr

↔

DEG, D°M’S

x, y → r, θ x2 + y2 < 10

r, θ → x, y RAD: | θ | < —– × 10

DRG |

(A+Bi)+(C+Di) | A + C | < 10
(A+Bi)–(C+Di)| A – C | < 10

(A+Bi)×(C+Di)

0 ≤ r ≤ 69

n!

100

—— < 10

(n-r)!

0°0’0.00001” ≤ | x | < 10000°

100

100

0 ≤ r < 10
DEG: | θ | < 10

GRAD : | θ | < — × 10

DEG→RAD, GRAD→DEG: | x | < 10
RAD→GRAD: | x | < — × 10

(AC – BD) < 10
(AD + BC) < 10

10

π

10

180
10

10

9

π

2

100

, | B + D | < 10

100

, | B – D | < 10

100

100

98

100

100

100

••••

x =

Σx

n

y =

Σy

n

sy =

Σy

2

– ny

2

n – 1

sx =

Σx

2

– nx

2

n – 1

σy =

Σy

2

– ny

2

n

σx =

Σx

2

– nx

2

n

AC + BD

(A+Bi)÷(C+Di)

→DEC DEC : | x | ≤ 9999999999
→BIN BIN : 1000000000 ≤ x ≤ 1111111111
→PEN 0 ≤ x ≤ 111111111
→OCT PEN : 2222222223 ≤ x ≤ 4444444444
→HEX 0 ≤ x ≤ 2222222222

AND OCT : 4000000000 ≤ x ≤ 7777777777
OR 0 ≤ x ≤ 3777777777
XOR HEX : FDABF41C01 ≤ x ≤ FFFFFFFFFF
XNOR 0 ≤ x ≤ 2540BE3FF

NOT

NEG

C2 + D

BC – AD

C2 + D

C2 + D2 ≠ 0

BIN : 1000000000 ≤ x ≤ 1111111111

PEN : 2222222223 ≤ x ≤ 4444444444

OCT : 4000000000 ≤ x ≤ 7777777777

HEX : FDABF41C01 ≤ x ≤ FFFFFFFFFF

BIN : 1000000001 ≤ x ≤ 1111111111

PEN : 2222222223 ≤ x ≤ 4444444444

OCT : 4000000001 ≤ x ≤ 7777777777

HEX : FDABF41C01 ≤ x ≤ FFFFFFFFFF

100

< 10

2

100

< 10

2

0 ≤ x ≤ 111111111

0 ≤ x ≤ 2222222221

0 ≤ x ≤ 3777777777

0 ≤ x ≤ 2540BE3FE

0 ≤ x ≤ 111111111

0 ≤ x ≤ 2222222222

0 ≤ x ≤ 3777777777

0 ≤ x ≤ 2540BE3FF

* n, r: integer / ganze Zahlen / entier / entero / inteiro / intero /

geheel getal / egész számok / celé číslo / heltal /
kokonaisluku / ˆÂÎ˚ / heltal /

/ /

integer / bilangan bulat

In Europe:

This equipment complies with the requirements of Directive 89/336/
EEC as amended by 93/68/EEC.

Dieses Gerät entspricht den Anforderungen der EG-Richtlinie 89/336/
EWG mit Änderung 93/68/EWG.

Ce matériel répond aux exigences contenues dans la directive 89/336/
CEE modifiée par la directive 93/68/CEE.

Dit apparaat voldoet aan de eisen van de richtlijn 89/336/EEG,
gewijzigd door 93/68/EEG.

Dette udstyr overholder kravene i direktiv nr. 89/336/EEC med tillæg
nr. 93/68/EEC.

Quest’ apparecchio è conforme ai requisiti della direttiva 89/336/EEC
come emendata dalla direttiva 93/68/EEC.

      
    89/336/, ! 
"! ! "#$ !   93/68/.

Este equipamento obedece às exigências da directiva 89/336/CEE na
sua versão corrigida pela directiva 93/68/CEE.

Este aparato satisface las exigencias de la Directiva 89/336/CEE
modificada por medio de la 93/68/CEE.

Denna utrustning uppfyller kraven enligt riktlinjen 89/336/EEC så som
kompletteras av 93/68/EEC.

Dette produktet oppfyller betingelsene i direktivet 89/336/EEC i
endringen 93/68/EEC.

Tämä laite täyttää direktiivin 89/336/EEC vaatimukset, jota on
muutettu direktiivillä 93/68/EEC.

чÌÌÓ ÛÒÚÓÈÒÚ‚Ó ÒÓÓÚ‚ÂÚÒÚ‚ÛÂÚ Ú·ӂ‡ÌËflÏ ‰ËÂÍÚË‚˚ 89/336/
EEC Ò Û˜ÂÚÓÏ ÔÓÔ‡‚ÓÍ 93/68/EEC.

Ez a készülék megfelel a 89/336/EGK sz. EK-irányelvben és annak 93/
68/EGK sz. módosításában foglalt követelményeknek.

Tento pfiístroj vyhovuje poÏadavkÛm smûrnice 89/336/EEC v platném
znûní 93/68/EEC.

Endast svensk version/For Sweden only:

Miljöskydd

Denna produkt drivs av batteri.
Vid batteribyte skall följande iakttagas:

• Det förbrukade batteriet skall inlämnas till er lokala handlare
eller till kommunal miljöstation för återinssamling.

• Kasta ej batteriet i vattnet eller i hushållssoporna. Batteriet
får ej heller utsättas för öppen eld.

OPMERKING: ALLEEN VOOR NEDERLAND/
NOTE: FOR NETHERLANDS ONLY

• Physical Constants and Metric Conversions are shown in the
tables.

• Physikalischen Konstanten und metriche Umrechnungen sind
in der Tabelle aufgelistet.

• Les constants physiques et les conversion des unités sont
indiquées sur les tableaux.

• Las constants fisicas y conversiones métricas son mostradas
en las tables.

• Constantes Fisicas e Conversões Métricas estão mostradas
nas tablelas.

• La constanti fisiche e le conversioni delle unità di misura
vengono mostrate nella tabella.

• De natuurconstanten en metrische omrekeningen staan in de
tabellen hiernaast.

• A fizikai konstansok és a metrikus átváltások a táblázatokban
találhatók.

• Fyzikální konstanty a převody do metrické soustavy jsou

/

uvedeny v tabulce.

• Fysikaliska konstanter och metriska omvandlingar visas i
tabellerna.

• Fysikaaliset vakiot ja metrimuunnokset näkyvät taulukoista.

• З Ъ‡·ОЛˆ‡ı ФУН‡Б‡М˚ ЩЛБЛ˜ВТНЛВ НУМТЪ‡МЪ˚ Л

ПВЪЛ˜ВТНЛВ ФВУ·‡БУ‚‡МЛfl.

• Fysiske konstanter og metriske omskrivninger vises i tabellen.

•

•

•

• Pemalar Fizik dan Pertukaran Metrik ditunjukkan di dalam

jadual.

• Konstanta Fisika dan Konversi Metrik diperlihatkan di dalam
tabel.

PHYSICAL CONSTANTS ß 01 — 52

No. SYMBOL UNIT No. SYMBOL UNIT No. SYMBOL UNIT
01 - c, c0m s
02 - G m3 kg–1 s–220 ­03 - gnm s
04 - mekg 22 ­05 - mpkg 23 ­06 - mnkg 24 ­07 - mµkg 25 ­08 - lu kg 26 ­09 - e C 27 -
10 - h J s 28 - N
11 - k J K
12 -

µ

13 -

ε

14 - rem 32 - RKOhm 50 - c2m K
15 -

α

16 - a0m 34 - h/2mem2 s
17 - R∞m
18 - Φ0Wb 36 - KJHz V

–1

19 -

–2

21 -

–1

29 - Vmm3 mol–147 - Mukg mol

–2

N A

0

F m

0

30 - R J mol–1 K–148 -

–1

31 - F C mol–149 - c1W m

33 - -e/meC kg–151 - Z0Ω

–1

35 -

–1

µ

J T

Β

–1

µ

J T

e

–1

µ

J T

Ν

–1

µ

J T

p

–1

µ

J T

n

–1

µ

J T

µ

λ

m43 - EhJ

c

λ

m44 - G0s

c, p

σ

W m–2 K–445 -

–1

,

L mol

Α

–1

s–1 T

–1

–1

γ

p

37 - eV J
38 - t K
39 - AU m
40 - pc m
41 - M(12C) kg mol
42 - h-J s

–1

α

46 - mp/m

e

λ

m

c, n

52 - Pa

–1

–1

2

Nur für Deutschland/For Germany only:

Umweltschutz

Das Gerät wird durch eine Batterie mit Strom versorgt.
Um die Batterie sicher und umweltschonend zu entsorgen,
beachten Sie bitte folgende Punkte:

• Bringen Sie die leere Batterie zu Ihrer örtlichen Mülldeponie,
zum Händler oder zum Kundenservice-Zentrum zur
Wiederverwertung.

• Werfen Sie die leere Batterie niemals ins Feuer, ins Wasser
oder in den Hausmüll.

Seulement pour la France/For France only:

Protection de l’environnement

L’appareil est alimenté par pile. Afin de protéger
l’environnement, nous vous recommandons:

• d’apporter la pile usagée ou à votre revendeur ou au service
après-vente, pour recyclage.

• de ne pas jeter la pile usagée dans une source de chaleur,
dans l’eau ou dans un vide-ordures.

METRIC CONVERSIONS

No. UNIT No. UNIT No. UNIT
1in→cm 16 kg→lb 31 J→calIT
2cm→in 17 °F→°C32calIT→J
3ft→m18°C→°F33hp→W
4m→ft 19 gal (US)→l 34 W→hp
5yd→m20l→gal (US) 35 ps→W
6m→yd 21 gal (UK)→l 36 W→ps
7 mile→km 22 l→gal (UK) 37 kgf/cm2→Pa
8km→mile 23 fl oz (US)→ml 38 Pa→kgf/cm
9 n mile→m24ml→fl oz (US) 39 atm→Pa
10 m→n mile 25 fl oz (UK)→ml 40 Pa→atm
11 acre→m
12 m2→acre 27 J→cal 42 Pa→mmHg
13 oz→g 28 cal→J 43 kgf·m→J
14 g→oz 29 J→cal15 44 J→kgf·m
15 lb→kg 30 cal15→J

2

26 ml→fl oz (UK) 41 mmHg→Pa

x @¥ 1 — 44

2