Page 1
http://www.ee.washington.edu/class/ConsElec/Chapter6.html
Chapter 6 - A Brief Introduction to Laser
Diodes
6.1 A very brief introduction to lasers
6.1.1 What is a laser?
The word LASER is an acronym for Light Amplification by Stimulated Emission of
Radiation. It is one of the few acronyms which is now accepted as a word. Thus, the verb
forms "to lase" and "lasing" are accepted as real words (check a dictionary!).
But, what does "Light Amplification by Stimulated Emission of Radiation" mean?
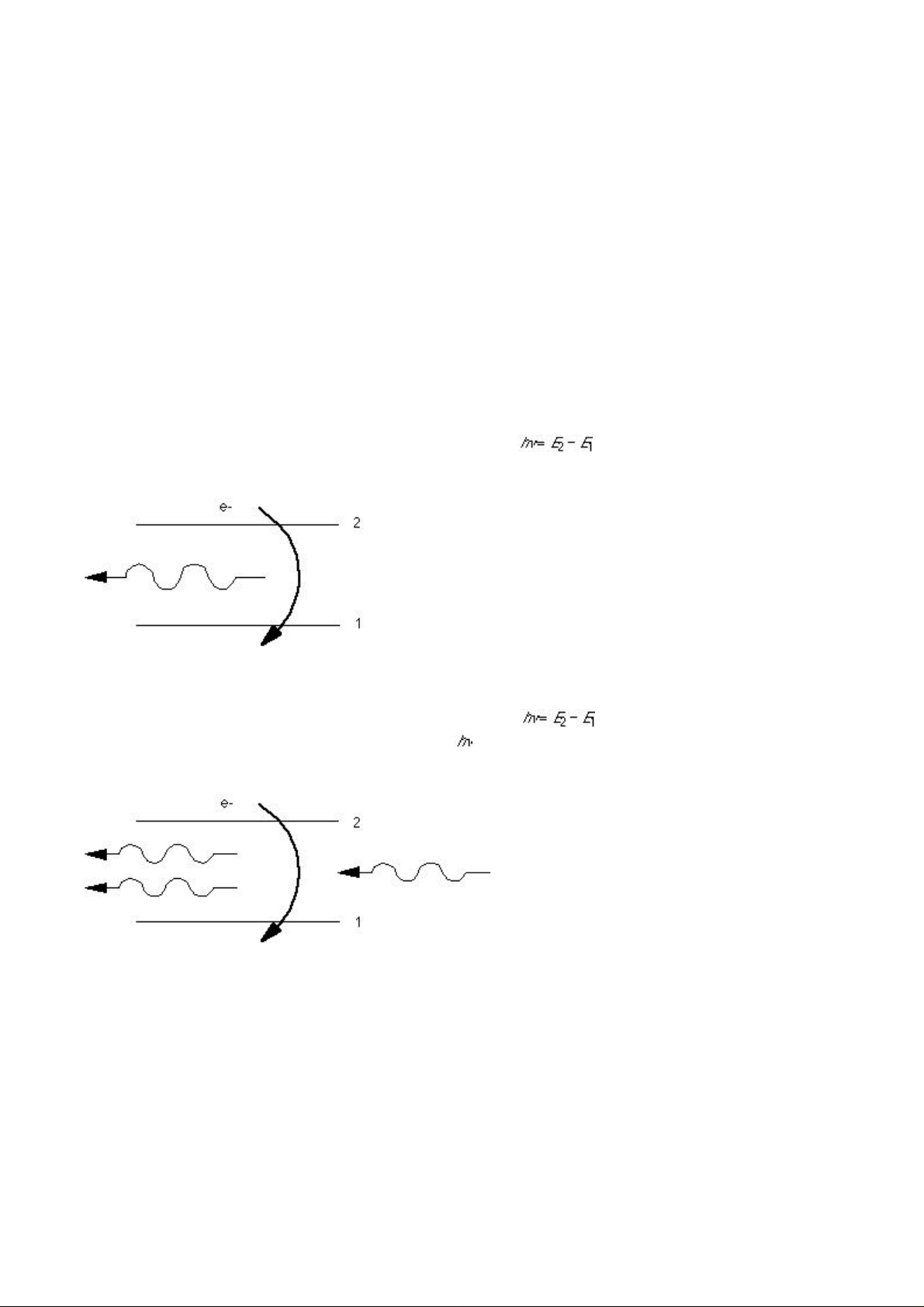
Consider how photons are created in an atom. If an electron spontaneously decays from
one state to another, it emits a photon of the energy . This process is called
"spontaneous emission".
However, it is also possible to force a transition from one state to another by means of a
photon. In other words, a photon of the energy h can force an electron to transfer between
states 2 and 1 yielding another photon of the energy . This "stimulated emission"
process results in two photons of the energy . Furthermore, these two photons will be in
phase.
Thus, ideal laser light is formed of groups of photons where all the photons are at exactly
the same frequency (wavelength) and all the photons are in phase.
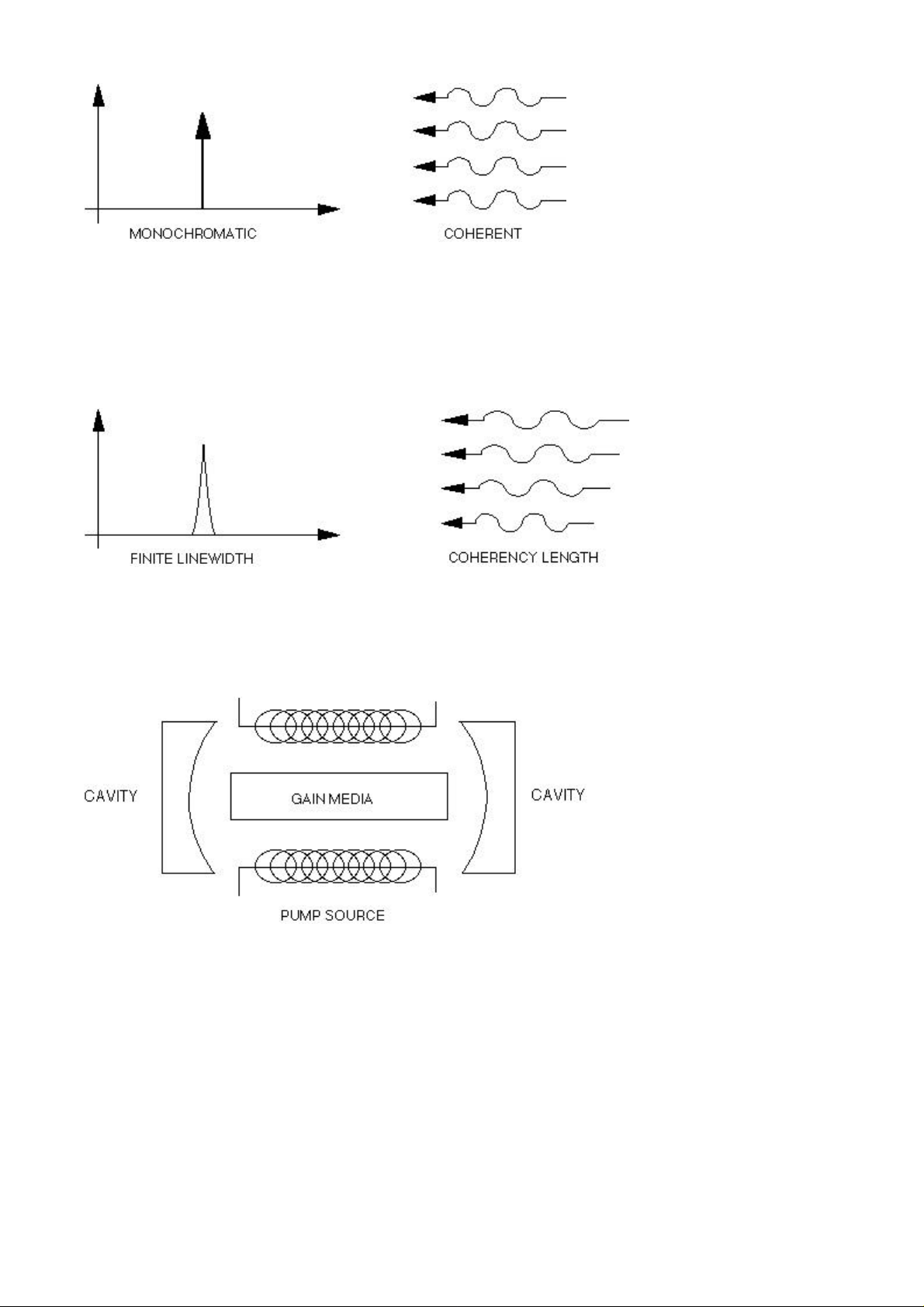
6.1.2 Monochromaticity and Coherency
The property of having the same frequency is referred to as monochromaticity and the
property of having the same phase is referred to as coherency. Thus, lasers are often
termed monochromatic and coherent sources of light. (Notice that this is a redundant
definition for an ideal laser, because a perfectly coherent source of light must be
monochromatic. However, notice that a perfectly monochromatic source of light, such as
spontaneous emission, need not be coherent.)
1 of 10 99/05/20 15:48
Page 2
http://www.ee.washington.edu/class/ConsElec/Chapter6.html
Now, real lasers are neither perfectly monochromatic nor perfectly coherent. However,
when characterizing a real laser system, it is generally assumed that the laser beam was
initially in phase and the incoherence of the laser arises only from the lack of
monochromaticity of the source. (This is a reasonable assumption for conventional lasers
with feedback -- but may not be accurate for unusual laser systems.) Thus, coherency and
monochromaticity are generally assumed to measure the same parameter.
6.1.3 Typical laser construction
Most lasers are constructed of three important elements, a gain media, a pumping source
and a resonant cavity.
The gain media is the location of the energy states which participate in stimulated
emission, the pumping source provides the energy to set the states up so stimulated
emission can occur, and the resonant cavity provides the path for the photons.
In many lasers, the resonant cavity is not even necessary. The functions of the resonant
cavity are simply to 1) physically shorten the laser and 2) tailor the profile of the
electromagnetic mode. In essence, the laser is simply "folded up" between the two cavity
mirrors.
2 of 10 99/05/20 15:48
Page 3
http://www.ee.washington.edu/class/ConsElec/Chapter6.html
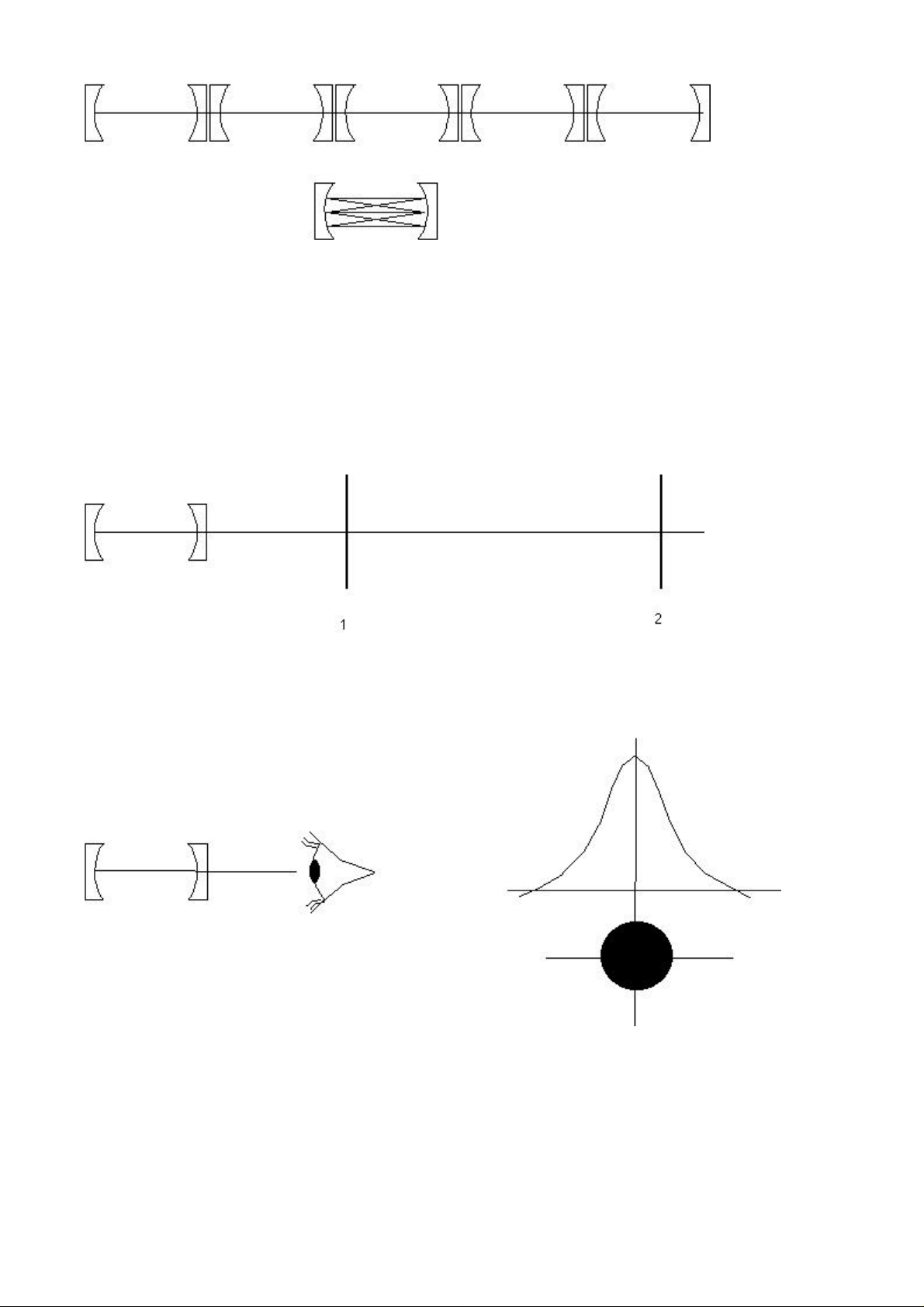
Now, it is certainly possible to make a laser long enough so that a reasonable intensity of
light beam emerges from the cavity (most x-ray lasers are made this way). However, such
lasers have poor output beam quality.
6.1.4 Basic Laser Concepts
When the laser beam exits the laser, it is consider collimated if the beam size remains
constant as the beam propagates. In other words, if the laser is collimated, the beam size
at location 2 will be the same as the beam size at location 1.
The output "spot" of the laser beam is termed the transverse electro-magnetic mode
(TEM). In most commercial lasers the transverse mode is TEMoo, which is a round mode
with a Gaussian profile in cross-section.
A laser can only lase at those wavelengths for which an integral multiple of wavelengths fit
into the cavity. The set of possible integral multiples of the cavity length is termed the set of
longitudinal modes of the cavity.
3 of 10 99/05/20 15:48
Page 4

http://www.ee.washington.edu/class/ConsElec/Chapter6.html
Now clearly, there are an infinite number of integral multiples of cavity length. However,
only a finite number (1-2000, depending on the laser) will fit into the gain profile of the laser
gain media. Thus, the actual output of the laser is the intersection of the set of possible
longitudinal modes with the gain curve.
The wavelength of the laser is the center of the operating wavelength. For example, a
He-Ne has a wavelength of 632.8 nm (or a wavenumber, 1/ = 15802.7 cm-1).
is the wavelength linewidth of the laser, generally expressed in angstroms.
4 of 10 99/05/20 15:48
Page 5

http://www.ee.washington.edu/class/ConsElec/Chapter6.html
is the frequency linewidth of the laser, generally expressed in Hz.
6.2 Semiconductors as photon sources
6.2.1 A brief introduction
Semiconductors (typically direct band-gap semiconductors) can be used as small, highly
efficient photon sources. Such semiconductor photon sources find application in displays,
optical storage, communications, printing, surveying, and as small efficient optical pumps
for other optical processes.
Semiconductor photon sources come in two major categories -- laser diodes and
light-emitting diodes. Although both photon sources are fundamentally the same (in other
words, a failed laser diode is an LED); application-based manufacturing differences mean
that laser diode and LED products are constructed in fundamentally different ways -- and
so possess fundamentally different optical properties.
Semiconductor photon sources can be "pumped" by a variety of techniques. These include
pumping with another optical source (photopumping), pumping with an electron beam, or
pumping via a pn-junction. However, the most common technique is via a pn-junction.
6.2.2 Pumping semiconductor photon sources with a pn-junction
5 of 10 99/05/20 15:48
Page 6

http://www.ee.washington.edu/class/ConsElec/Chapter6.html
Consider the energy band diagram for a simple pn-junction intended for use in a
semiconductor photon source. Initially, one side of the junction is heavily doped n and the
other side is heavily doped p. In general, both materials are doped degenerately (meaning
that the quasi-Fermi level is above the bandedge).
In equilibrium the quasi-Fermi levels align and the structure looks something like this:
When a positive voltage is applied to the p-region and a negative voltage is applied to the
n-region, then the diode is forward biased. The quasi-Fermi levels will misalign by the value
of the applied voltage. Under the influence of the forward bias, the holes will drift to the
n-region and the electrons will drift into the p-region. The holes and electrons are now
spatially coincident -- and hole-electron recombination can occur.
Notice that in the non-equilibrium situation, the quasi-Fermi levels for the electrons and
holes have separated. The spatial distance between the quasi-Fermi levels is essentially
the depth d of the active region.
In III-V semiconductors, the electrons are MUCH more mobile than the holes. Therefore,
the depth of the active region is principally determined by the mobility of the electrons. This
distance is approximately given by (Verdeyen, pg. 388),
where np is the electron concentration in the p-region. Typical numbers for d are on the
order of 1 m. Notice that this is on the order of the same size as the wavelength of the
electromagnetic mode being amplified.
6.3 Laser diodes
6.3.1 Basic construction
Semiconductor lasers are the most basic of the existing laser types. In their simplest form
they consist of a small rectangular slab of semiconductor material with two cleaved facets
6 of 10 99/05/20 15:48
Page 7

http://www.ee.washington.edu/class/ConsElec/Chapter6.html
to act as mirrors. The other facets are destroyed in some way (etched, ground, sawn, ion
implanted...) in order to avoid spurious laser modes.
Semiconductor lasers are quite different from conventional lasers. In particular:
1. The gain of the laser material is very high and is generated by a population inversion
between the conduction and valence bands of the semiconductors. In some sense, a
semiconductor laser is a two-state laser system.
2. Since the electromagnetic mode is on the order of the size of the laser device, then
the transverse mode of the semiconductor laser is quite different from that of a
conventional laser. In particular, the beam is not Gaussian, the beam profile tends to
be elliptical, and the beam divergence tend to be large.
3. The gain spectrum is quite large (many THz or hundreds of angstroms).
4. The short cavity (several hundred microns) means that the longitudinal mode spacing
is much larger than that of a conventional gas or solid state laser (on the order of
GHz or angstroms).
6.3.2 propagation in a laser diode
Light propagates in a laser diode somewhat differently than in an LED. In an LED, the
emitted photons can generally be modeled as independent entities propagating through the
structure in a ray-like fashion.
In a laser diode, the photons must be modeled as collective entities traveling in a confined
fashion down a waveguide. This gives a dramatically different character to the issue of
modeling light output from a laser diode.
In general, the far-field pattern from a laser diode is determined by the Fourier integral of
the electromagnetic field propagating in the waveguide. The electro-magnetic field within in
the waveguide can be calculated relatively straightforwardly using the eigenvalue equations
7 of 10 99/05/20 15:48
Page 8

http://www.ee.washington.edu/class/ConsElec/Chapter6.html
for wave propagation in a slab waveguide (essentially the same problem as electron
confinement in a quantum well -- but with slightly different constants).
For a symmetrical DH laser, the experimental far-field intensity pattern is given (Casey and
Panish, pg. 76) by the expression
where
This is not exactly straightforward ... so an approximate expression has been given (Casey
and Panish, pg. 78) as,
6.3.3 Various semiconductor laser types
Homostructure lasers:
This was the very first type of semiconductor laser structure demonstrated. It consists of a
highly doped p and n region with a small undoped region in the p material at the pn
junction. There is a slight refractive index change at the n-junction which permits some
index guiding.
Threshold current density at 300K is on the order of 30000-50000 A/cm2.
Single heterostructure: (Kressel and Nelson, Panish)
8 of 10 99/05/20 15:49
Page 9

http://www.ee.washington.edu/class/ConsElec/Chapter6.html
Threshold current density at 300K on the order of 6000-8000 A/cm2.
Double-heterostructure: (Alferov)
Threshold current density at 300K on the order of 500 A/cm2.
GRINSCH (Graded-index separate confinement heterostructure)
GRINSCH lasers separate optical and electrical confinement in an effort to achieve lower
thesholds and narrower beam patterns. The optical distribution in a GRINSCH laser is
principally a function of the graded index region, while the electrical confinement is
principally determined by the thin active region.
9 of 10 99/05/20 15:49
Page 10

References:
http://www.ee.washington.edu/class/ConsElec/Chapter6.html
W. Koechner, Solid State Laser Engineering, 3rd Edition, Springer-Verlag., ISBN
0-387-53756-2.
Joseph Verdeyen, Laser Electronics, Prentice Hall Series in Solid State Physical
Electronics, Prentice Hall, second edition, 1989; ISBN 0-13-523630-4
Amnon Yariv, Optical Electronics, Saunders College Publishing, fourth edition, 1991; ISBN
0-03-047444-2
Peter Milonni and Joseph Eberly, Lasers, John Wiley and Sons, first edition, 1988; ISBN
0-471-62731-3
P. Das, Lasers and Optical Engineering, Springer-Verlag, 1991, ISBN 0-387-97108-4
Anthony E. Siegman, Lasers, University Science Books, 1986, ISBN 0-935702-11-5
Eugene Hecht, Optics, Addison-Wesley, second edition, 1987; ISBN 0-201-11609-X
J. Wilson and J.F.B. Hawkes, Optoelectronics, Prentice Hall 1989, ISBN 0-13-638461-7
H.C. Casey and M.B Panish, Heterostructure Lasers, Academic Press, first edition, 1978;
ISBN 0-12-163101-X (Two volumes. Part A: Fundamental Principles and Part B: Materials
and Operating Characteristics.)
H. Kressel and J. Butler, Semiconductor lasers and LEDs, Academic Press, first edition,
1977; ISBN 0-12-426250-3
10 of 10 99/05/20 15:49
 Loading...
Loading...