Page 1
®
Instruction Manual with
Experiment Guide
012-09842B
*012-09842*
Ballistic Pendulum Accessory
ME-9892
Page 2

Ballistic Pendulum Accessory Table of Contents
Contents
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Equipment Set-up . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Assemble the Apparatus, 4
Load the Launcher, 5
Prepare the Sensor, 6
Test Fire, 6
Foam Insert Replacement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Experiment 1: Ballistic Pendulum . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Theory, 7
Experiment Set-up, 7
Procedure, 7
Analysis, 9
Question, 9
Further Study, 9
Experiment 2: Conservation of Momentum and Energy . . . . . . . . . . . . . . . . . . . . . . . . 10
Background, 10
Part 1: Measure Launch Velocity, 10
Part 2: Record Ballistic Pendulum Data, 10
Part 3: Determine Rotational Inertia of Pendulum-ball System, 11
Analysis, 13
Questions, 13
Further Study I: Different Launch Speeds, 14
Further Study II: Different Projectile Mass, 14
Further Study III: Different Center of Mass, 14
Further Study IV: Elastic Collision, 14
Further Study V: Alternative Determination of Rotational Inertia, 15
Further Study VI: Horizontal Collision, 16
Technical Support . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
Page 3
Ballistic Pendulum Accessory
®
1
2
3
4
5
6
7
ME-9892
Included Equipment Part Number
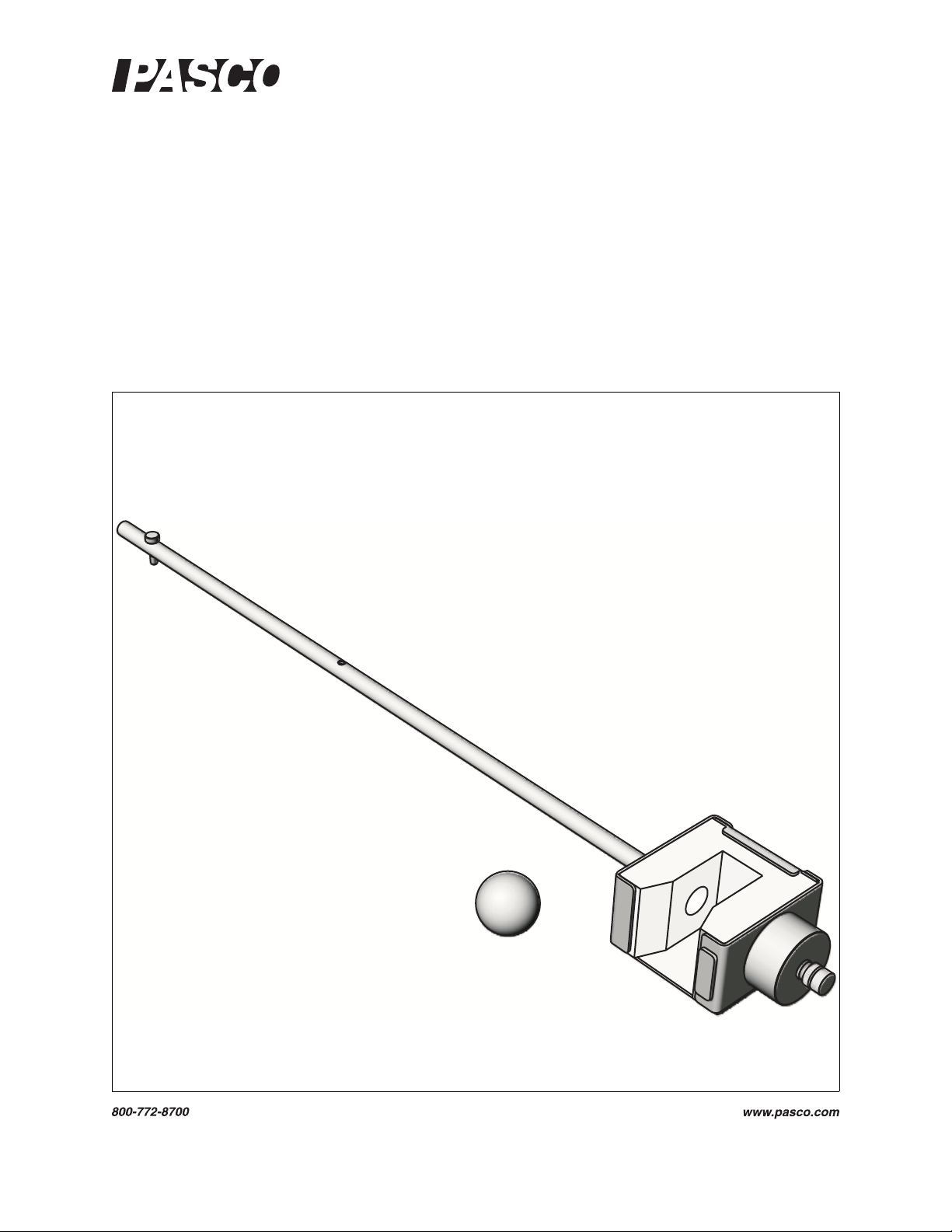
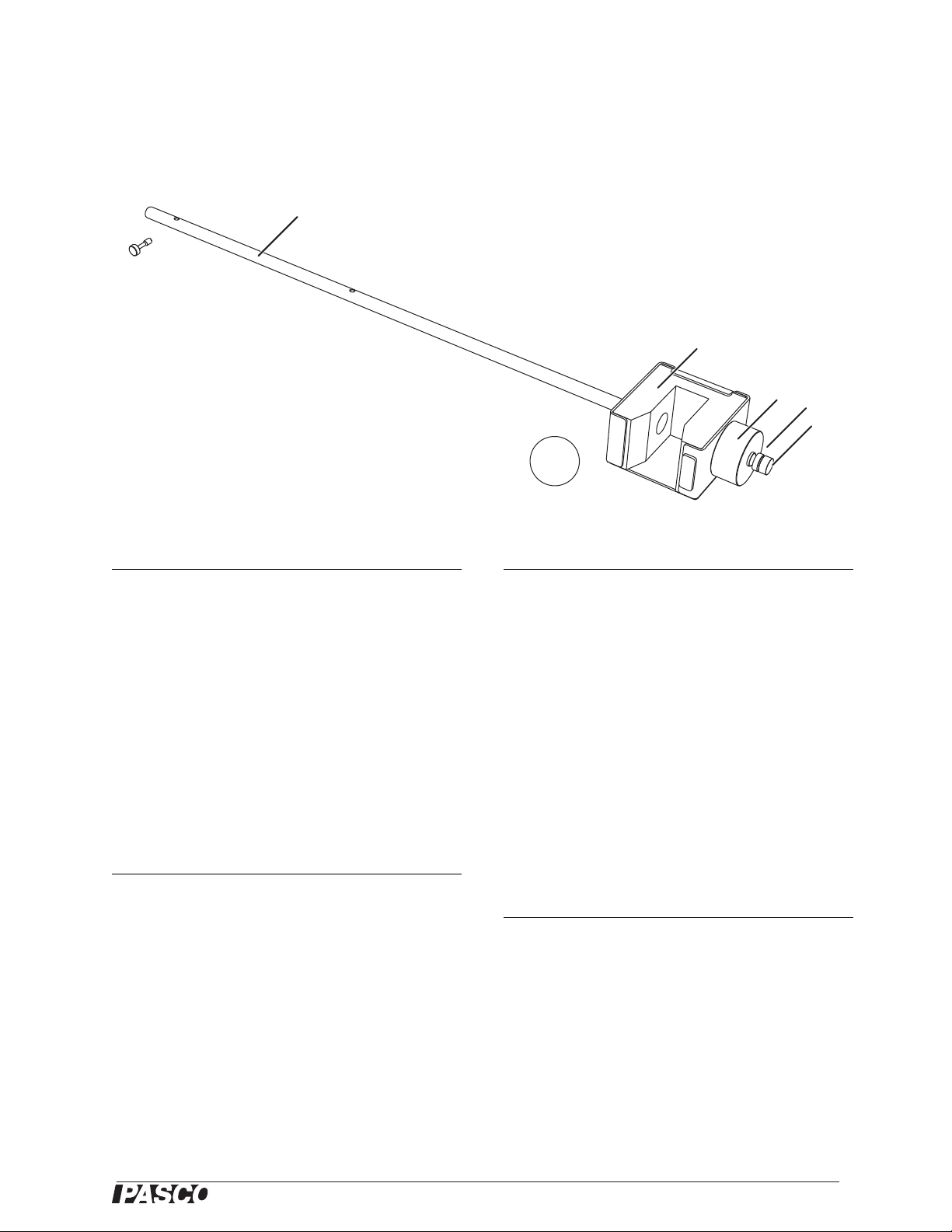
1. Catcher and pendulum
ME-9892
rod
2. Pendulum attachment
613-076
screw
3. Replaceable foam
ME-9894 (5-pack)
insert
4. Ballast mass 648-06511
5. Ballast lock nut 614-029
6. Ballast fastening screw 617-027
7. Steel ball ME-9864 (4-pack)
Required Equipment
Short Range Launcher ME-6800
PASPORT Rotary Motion
Sensor with three-step
1
pulley
Table Clamp ME-9472 or similar
PS-2120
90 cm mounting rod ME-8738 or similar
C-clamp SE-7286 or similar
Optional Equipment Part Number
Photogates (qty. 2)
Digital Adapter
2
1, 2
Photogate Mounting
Bracket
2
Super Pulley with Clamp
Hanging mass
2
Mini Rotational Accessory
Spherical Mass Set
Additional three-step
pulley
5
45 cm mounting rod
Multi clamp
1
Sensor requires a PASPORT interface.
2
For measuring launch velocity and rotational inertial. See
Experiment 2, page 10.
3
Required for experiment 2
4
For Experiment 2, Further Study II: Different Projectile Mass
(page 14)
5
For Experiment 2, Further Study VI: Horizontal Collision
(page 16)
5
4
5
ME-9498A or similar
PS-2159
ME-6821
2
ME-9448A
ME-9348 or similar
3
CI-6691
ME-8968
CI-6693
ME-8736 or similar
SE-9442 or similar
3
Page 4
®
Ballistic Pendulum Accessory Introduction
Three-step
pulley
Figure 2: Three-step
pulley on RMS
Introduction
Use the Ballistic Pendulum Accessory in combination with a Short Range Launcher
and Rotary Motion Sensor (RMS) to measure the velocity of a steel ball and study
rotational collisions. The launcher shoots the ball into the Ballistic Pendulum Accessory. The RMS measures the resulting angular displacement and velocity of the pendulum. The pendulum can be configured to catch the ball or allow the ball to bounce
off. With the addition of the Mini Rotational Accessory, the apparatus can be configured as a physical pendulum or rotational system with adjustable moment of inertia.
This manual includes set-up instructions and experiment instructions.
Equipment Set-up
Assemble the Apparatus
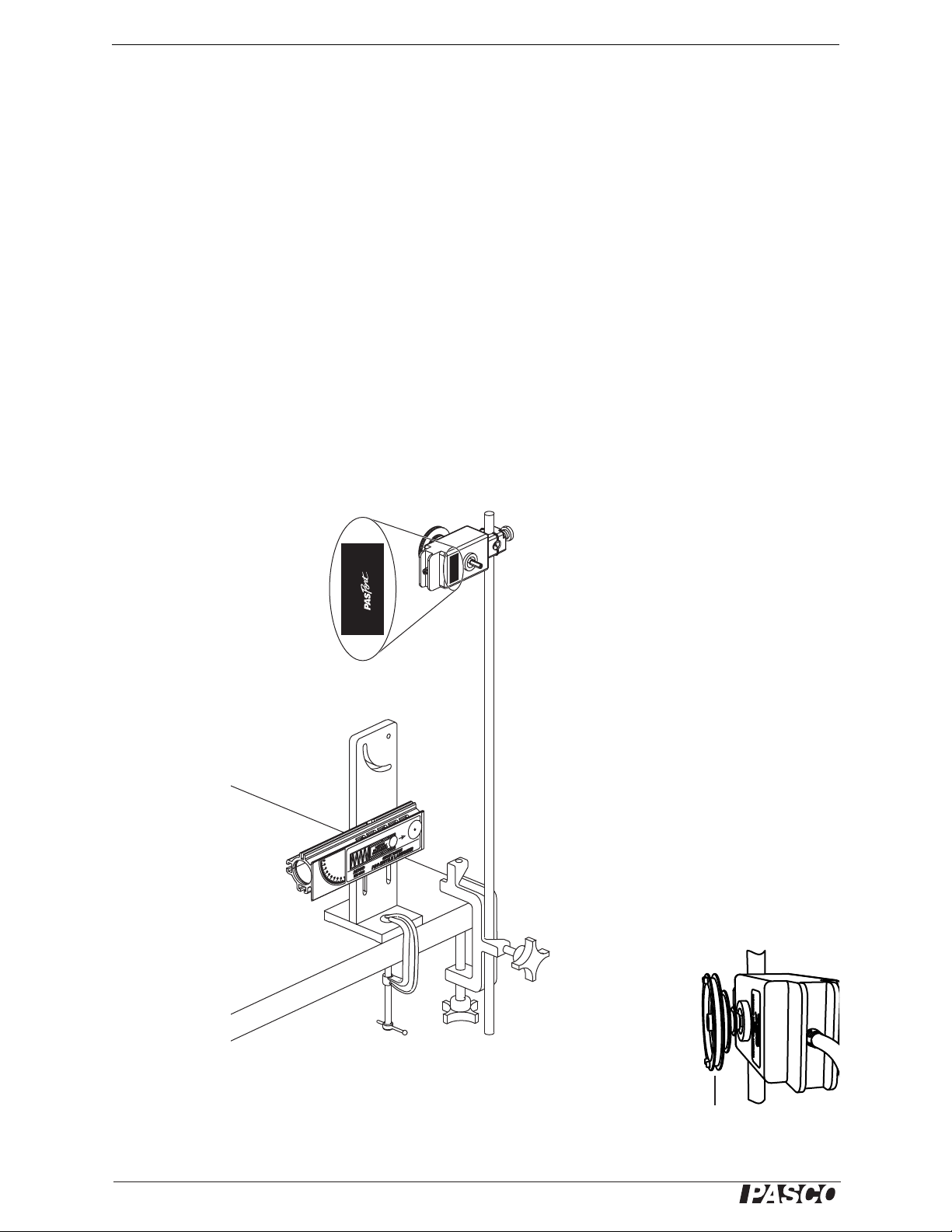
1. Set up the launcher, C-clamp, table clamp, mounting rod, and RMS as shown in
Figure 1. The exact position of the RMS is not important yet. Note that the side
of the RMS without the model number on the label is facing you. (If the RMS is
mounted the other way, it will measure negative displacement.)
ä
FOR
INTERFACES
ROTARY MOTION SENSOR
Figure 1: Launcher and RMS mounted on rod
2. Slide the three-step pulley onto the RMS shaft with the largest pulley out as
shown in Figure 2.
4
Page 5
®
Model No. ME-9892 Equipment Set-up
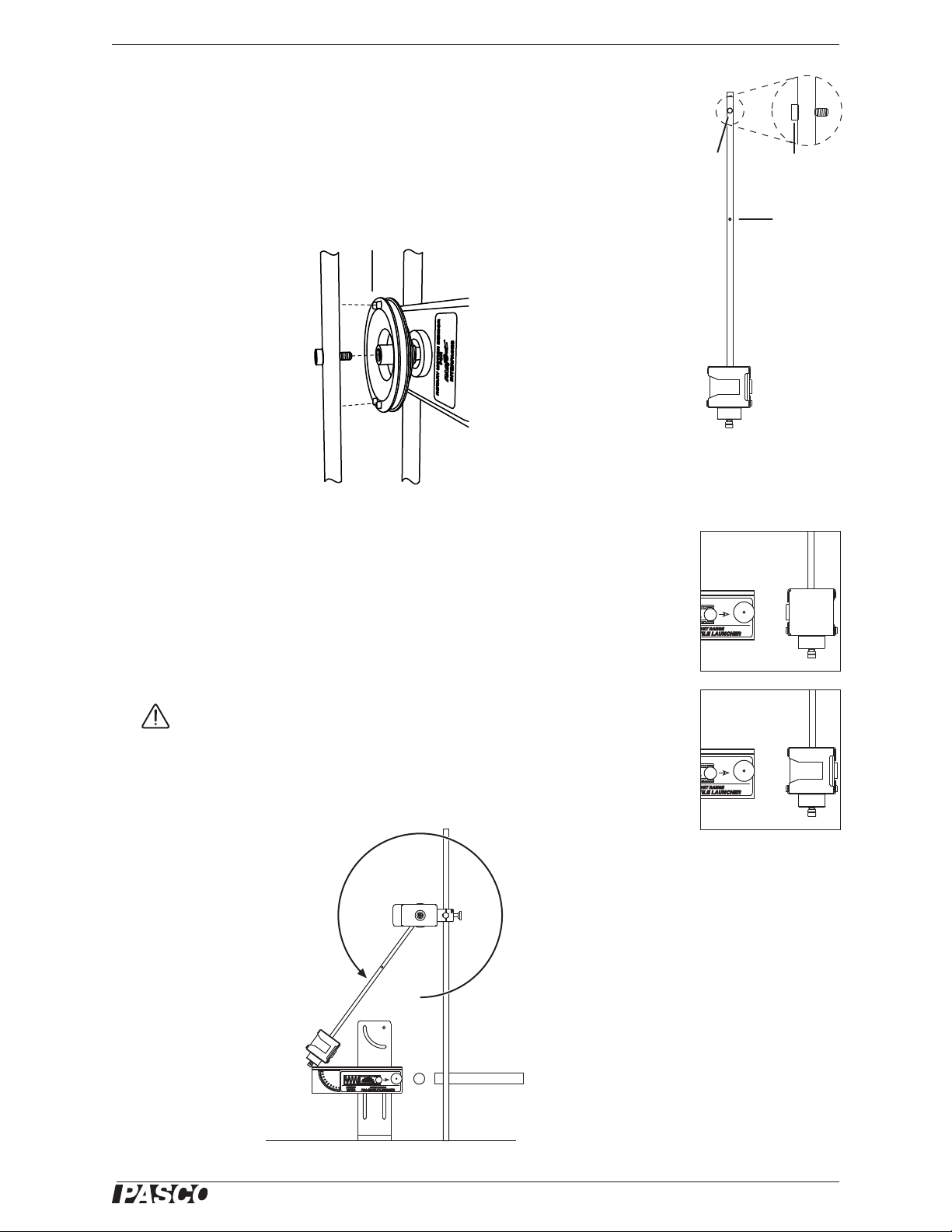
End
hole
Attachment
screw
Center hole
Figure 3: Attachment
screw loosely captured
in center hole
Align rod with tabs
Figure 5: Pendulum
aligned with launcher,
catcher side (top) and
bumper side (bottom)
PushrodBall
Swing pendulum
out of the way
3. Select one of the holes on the pendulum rod: either the center hole or the end
hole. Also select a side of the pendulum: either the catcher or the bumper. Thread
the attachment screw into the hole as shown in Figure 3. Screw it all the way in
so it is loosely captured.
4. Thread the screw into the end of the RMS shaft. Align the pendulum rod with the
tabs on the pulley as shown in Figure 4. Tighten the screw.
Figure 4: Attaching pendulum to RMS
5. Adjust the position of the RMS so the pendulum is aligned with the launcher as
shown in Figure 5. Leave a 2.5 cm gap between the launcher and the pendulum.
Load the Launcher
1. Swing the pendulum out of the way as shown in Figure 6.
2. Place the steel ball in the end of the barrel.
Caution: Use extra caution when using the launcher with a steel ball. Do not look down
the barrel. Do not leave the launcher loaded and unattended.
3. Use the pushrod included with the launcher to push the ball down the barrel until
the trigger catches in the first, second, or third position (for a slow, medium, or
fast launch).
Figure 6: Loading the launcher
5
Page 6
®
Ballistic Pendulum Accessory Foam Insert Replacement
Figure 7: Typical data
4. Return pendulum to its normal hanging position.
Prepare the Sensor
1. Connect the RMS to a PASPORT interface. If you will be using a computer, connect the interface to it and start your data collection software.
2. Set the sampling rate of the RMS to 40 Hz.
3. Prepare a graph to show angular position versus time.
For detailed instructions, refer to the documentation that came with your interface or
press F1 to launch the software’s on-line help.
Test Fire
1. Start data recording.
2. Pull the trigger of the launcher.
3. Stop data collection.
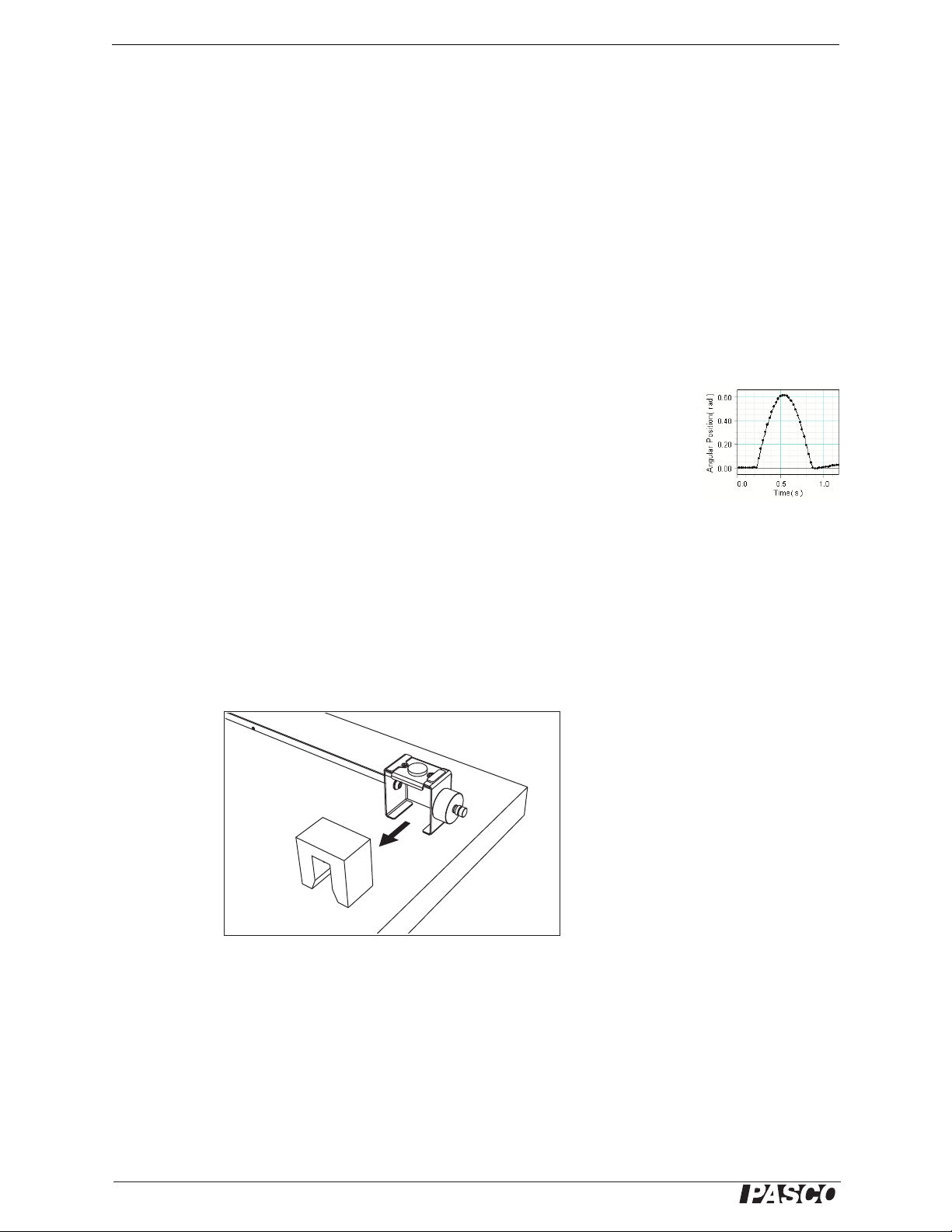
Figure 7 shows typical data for an inelastic collision. If your data shows negative
angular displacement, disassemble the RMS from the mounting rod and pendulum
and remount it with the pendulum attached to the other end of the RMS shaft.
Foam Insert Replacement
With age and repeated use, the foam catcher insert may lose elasticity. If the catcher
does not reliably hold the ball, remove the foam insert and replace it with a new one
(PASCO part ME-9894 is a five pack of foam inserts).
Figure 8: Removable foam insert
6
Page 7

®
Model No. ME-9892 Experiment 1: Ballistic Pendulum
m
ballV0
MV=
1
2
---
MV
2
Mgh=
V
0
1
m
pend
m
ball
-------------
+
2gh=
Figure 1.1: Set-up
Catcher
side
Ballast
mass
Experiment 1: Ballistic Pendulum
Theory
The ballistic pendulum has historically been used to measure the launch velocity of a
high speed projectile. In this experiment, a projectile launcher fires a steel ball (of
mass m
As the momentum of the ball is transferred to the catcher-ball system, the pendulum
swings freely upwards, raising the center of mass of the system by a distance h.
The pendulum rod is hollow to keep its mass low, and most of the mass is concentrated at the end so that the entire system approximates a simple pendulum. During
the collision of the ball with the catcher, the total momentum of the system is conserved. Thus the momentum of the ball just before the collision is equal to the
momentum of the ball-catcher system immediately after the collision:
(eq. 1.1)
where V is the speed of the catcher-ball system just after the collision, and
) at a launch velocity, V0. The ball is caught by a pendulum of mass m
ball
pend
.
(eq. 1.2) M = m
ball
+ m
pend
During the collision, some of the ball's initial kinetic energy is converted into thermal
energy. But after the collision, as the pendulum swings freely upwards, we can
assume that energy is conserved and that all of the kinetic energy of the catcher-ball
system is converted into the increase in gravitational potential energy.
(eq. 1.3)
where g =9.81 m/s
2
, and the distance h is the vertical rise of the center of mass of the
pendulum-ball system.
Combining equations 1.1 through 1.3 (eliminating V) yields
(eq. 1.4)
Experiment Set-up
1. Attach the ballast mass to the bottom of the catcher.
2. Set up the equipment and software as described on pages 4–6
with the pendulum rod attached to the RMS at the end hole and
the catcher side of the pendulum facing the launcher.
Procedure
Record Data
1. Load the launcher and push the ball in to the third (fastest) posi-
2. Start data collection.
tion.
7
Page 8

®
Ballistic Pendulum Accessory Experiment 1: Ballistic Pendulum
Table 1.1: Maximum
Angular Displacement
Trial Angle
Tr i a l 1
Tr i a l 2
Tr i a l 3
Tr i a l 4
Tr i a l 5
Tr i a l 6
Avg:
max
=
r
Balance point
Figure 1.2: Pendulum-ball system balanced on table edge
3. Launch the ball so that it is caught in pendulum.
4. After the pendulum has swung out and back, stop data collection.
5. Note the maximum angular displacement measured by the RMS. Record it in
Table 1.1.
6. Repeat steps 1 through 5 several times.
7. Calculate the average maximum displacement,
max
.
Find the Mass and Center of Mass
1. Fire the ball one more time (without recording data). Catch the pendulum near
the top of its swing so it does not swing back and hit the launcher (this will prevent the ball from falling out or shifting).
2. Remove the pendulum from the RMS.
3. Remove the screw from the pendulum shaft.
4. With the ball still in the catcher, place the pendulum at the edge of a table with
the pendulum shaft perpendicular to the edge and the counterweight hanging over
the edge. Push the pendulum out until it just barely balances on the edge of the
table. The balance point is the center of mass. (See Figure 1.2.)
5. Measure the distance, r, from the center of rotation (where the pendulum was
attached to the RMS) to the center of mass. r = _____________________.
6. Remove ball from the catcher.
7. Measure the mass of the pendulum (without the ball). m
8. Measure the mass of the ball. m
8
= _____________________
ball
= _______________
pend
Page 9

®
Model No. ME-9892 Experiment 1: Ballistic Pendulum
x
h
r
q
max
x = r cos (
max
)
r = x + h
Figure 1.3:
Calculating
h
Analysis
1. Use your value of
, the distance r, and Equation 1.5 to calculate the maxi-
max
mum height (h) that the center of mass rises as the pendulum swings up (see Figure 1.3).
(eq. 1.5) h = r (1 - cos (
max
))
h = _____________________
2. Use your value of h and Equation 1.4 to calculate the launch velocity of the ball.
V
= _____________________
0
Question
The theory for this experiment ignores the rotational inertia of the pendulum. Because
the pendulum is not really a simple pendulum (a point mass on a massless rod), a systematic error is introduced. Does this simplistic analysis tend to give a launch velocity
that is too high or too low? (See Experiment 3 for a more exact treatment.)
Further Study
Use two photogates to measure the launch velocity of the ball. Compare this value to
the value you found using the ballistic pendulum.
9
Page 10

®
Ballistic Pendulum Accessory Experiment 2: Conservation of Momentum and Energy
Figure 2.1: Launcher
with photogates
Counterweight
Experiment 2: Conservation of Momentum and Energy
Background
In this experiment you will analyze the angular collision between a ball and a physical
pendulum. You will compare the rotational momentum of the ball before the collision
to the rotational momentum of the pendulum-ball system after the collision. Both
rotational momenta are measured about the pendulum’s pivot point.
You will also compare the kinetic energy of the ball before the collision, the kinetic
energy of the pendulum-ball system just after the collision, and the maximum potential energy of the system after the collision.
The data-taking phase of this experiment has three parts. In Part 1 you will use photogates to measure the launch velocity of the ball. In Part 2 you will measure the maximum rotational velocity and angular displacement of the pendulum after the collision.
In Part 3 you will measure the rotational inertia of the pendulum-ball system.
Part 1: Measure Launch Velocity
Set up the launcher with two photogates and a photogate bracket (see Figure 2.1).
Measure the launch velocity (
als and use the average value.
If you will be doing the Advanced Study part of this experiment, also measure the
launch velocity for the medium and slow settings.
V
) of the ball on the fastest setting. Do several tri-
launch
Part 2: Record Ballistic Pendulum Data
Set-up
1. Set up the equipment and software as described on pages 4 through 6 with the
pendulum rod attached to the RMS at the center hole and the catcher side of the
pendulum facing the launcher. Do not attach the ballast mass to the bottom of the
catcher.
2. Install one of the sliding masses from the Mini Rotational Accessory as a counterweight. Slide it onto the pendulum rod above the RMS attachment point.
Adjust the position of the counterweight so the pendulum is perfectly balanced
without the ball. If you release the pendulum in the horizontal position, it should
not move. (See Figure 2.2.)
10
Figure 2.2: Pendulum balanced horizontally
3. Prepare a graph to display angular velocity versus time and position versus time.
Page 11

®
Model No. ME-9892 Experiment 2: Conservation of Momentum and Energy
Procedure
1. Load the launcher and push the ball in to the third (fastest) position.
2. Move the pendulum into the vertical position. If it does not stay that way by
itself, hold it very lightly with one finger.
3. Start data collection.
4. Launch the ball so that it is caught by pendulum.
5. After the pendulum has swung out and back, stop data collection.
6. Note the maximum angular displacement measured by the RMS. Record it in
Table 2.1
7. Record the initial angular velocity (just after the collision) in Table 2.1. Because
this velocity occurs close to the collision, the RMS cannot measure it accurately.
Instead, note the maximum negative velocity that occurs when the pendulum
swings back toward the launcher (record it as a positive value). Though this
might be slightly smaller than the actual initial velocity (due to friction), it is a
more reliable measurement.
8. Repeat steps 1 through 7 several times.
9. Calculate the average maximum displacement (
velocity (
10. Measure the mass of the ball. m
).
0
Table 2.1: Angular Displacement and Velocity
Trial Maximum
Angle
Tr i a l 1
Tr i a l 2
Tr i a l 3
Tr i a l 4
Tr i a l 5
Tr i a l 6
Average:
=
max
= _____________________
ball
) and the average initial
max
Initial Angular
Veloci ty
=
0
11. Fire the ball into the catcher one more time (without recording data). Catch the
pendulum near the top of its swing so it does not swing back and hit the launcher
(this will prevent the ball from falling out or shifting).
12. Measure the distance, , from the center of rotation (where the pendulum attaches
to the RMS) to the center of ball. = _____________________
Part 3: Determine Rotational Inertia of Pendulum-ball System
Set-up
1. Remove the RMS from the mounting rod. (Leave the pendulum attached to the
RMS and leave the ball in the catcher.)
11
Page 12

®
Ballistic Pendulum Accessory Experiment 2: Conservation of Momentum and Energy
Hanging
mass
Clamped-on
pulley
a
mg
F
T
Figure 2.4: Free-body
diagram of hanging
mass
2. Clamp the RMS on the mounting rod so that the pendulum can rotate in a horizontal plane (see Figure 2.3).
Figure 2.3: Setup for determining rotational inertia
3. Clamp a pulley to the RMS and set up a string and hanging mass (approximately
20 g to 30 g) as shown in Figure 2.3. Wind the string a few times around the middle step of the three-step pulley. Adjust the angle and height of the clamped-on
pulley so that the string will unwind and run over the pulley with as little friction
as possible.
Procedure
1. Start data collection.
2. Release the hanging mass.
3. After the string has unwound from the three-step pulley, stop data collection.
4. Determine the angular acceleration of the pendulum () from the slope of the
angular velocity versus time graph. = _____________________
5. Measure the radius of the middle step of the three-step pulley.
R
= _____________________
pulley
6. Measure the mass of the hanging mass. m = _____________________
7. Calculate the acceleration (a) of the hanging mass.
a = R
pulley
12
8. Calculate the tension in the string (FT). Since the hanging mass is accelerating,
the string tension is not the weight of the mass. Writing Newton’s 2nd Equation
for the free-body diagram in Figure 2.4 yields:
ma = mg F
T
where g = 9.8 m/s2.
F
= _____________________
T
Page 13

®
Model No. ME-9892 Experiment 2: Conservation of Momentum and Energy
Figure 2.5: Calculating h
q < 90°
h
q < 90°
h
Center of ball
K
launch
1
2
---
m
ballV0
2
=
K
0
1
2
---
I
0
2
=
9. Calculate the torque () applied to the pulley by the string.
= R
pulleyFT
10. Calculate the rotation inertia (I) of the pendulum-ball sys-
tem using the rotational form of Newton’s 2nd Law:
= I
I = _____________________
Analysis
1. Calculate the initial angular momentum of the ball
(L
is calculated about the pendulum pivot.
2. Calculate the angular momentum of the ball-pendulum
system (L
) just before the collision. The angular momentum
launch
V
launch
= m
ball
launch
L
) immediately after the collision.
0
L
= I
0
0
3. Calculate the kinetic energy of the ball (K
launch
collision.
4. Calculate the kinetic energy of the ball-pendulum system
(K
) immediately after the collision.
0
5. Use the maximum angular displacement of the pendulum
(
) to calculate the change in height (h
max
) of the ball.
max
Refer to Figure 2.5.
6. Calculate the gain in potential energy of the ball (U
U
= m
ball
g h
max
ball
Questions
) before the
).
ball
1. Why did you calculate the ball’s rotational momentum
rather than the linear momentum? Why did you calculate
the rotational momentum around the pendulum pivot rather
than the center of the ball?
2. Compare the rotational momentum of the ball before the
collision to the rotational momentum of the pendulum-ball
system just after the collision. Was momentum conserved?
13
Page 14

®
Ballistic Pendulum Accessory Experiment 2: Conservation of Momentum and Energy
3. Compare the kinetic energy of the ball before the collision to the kinetic energy
of the pendulum-ball system just after the collision. Was energy conserved in the
collision?
4. What was the gain in potential energy of the pendulum (not including the ball)?
What was the purpose of the counterweight?
5. Compare the kinetic energy of the pendulum-ball system just after the collision to
the gain in potential energy of the ball. Was energy conserved as the pendulum
swung after the collision?
Further Study I: Different Launch Speeds
Repeat the experiment for the slow and medium launch speeds. How does changing
the launch speed affect how well momentum is conserved?
Look at the ratio of initial kinetic energy (of just the ball) to the kinetic energy of the
pendulum-ball system (just after the collision). How does the launch speed of the ball
affect this ratio?
Further Study II: Different Projectile Mass
Repeat the experiment with the lower-mass nylon ball (included with the launcher), or
one of the balls from the Spherical Mass Set (ME-8968).
Further Study III: Different Center of Mass
Repeat the experiment without the counterweight. This time, you will need to find the
center of mass of the pendulum-ball system (see Experiment 1). Measure the distance
(r) from the axis of the RMS to the center of mass. When you calculate the potential
energy gain of the system, the height (h) is the change in height of the center of mass
of the system, not the ball.
Further Study IV: Elastic Collision
Examine the difference between catching the ball (completely inelastic collision) and
allowing the ball to hit the bumper on the back of the catcher:
1. Place the counter-weight on the lower half of the pendulum rod between the middle hole and the catcher. Fasten the pendulum to the RMS using the middle hole
with the bumper side towards the launcher. There should be a gap of a few centimeters between the end of the launcher and the bumper.
2. Launch the ball at its slowest speed. What happens to the ball when it hits the
rubber bumper on the catcher? Adjust the position of the counter weight so that
the ball drops straight down after the collision. If the counterweight is positioned
too low, the ball bounces backwards. If the counterweight is too high, the ball
still has some forward velocity. You want the horizontal velocity of the ball to be
zero after the collision.
3. Perform the experiment as before and measure the maximum displacement
(
) and initial angular velocity (0) of the pendulum.
max
4. Measure the rotational inertia of the pendulum without the ball.
Find the pendulum’s center of mass (without the ball). Measure the distance r
from the axis of the RMS to the center of mass.
14
Page 15

®
Model No. ME-9892 Experiment 2: Conservation of Momentum and Energy
T 2
I
Mgr
-----------=
5. Perform the analysis for energy and momentum as before. What is the kinetic
energy of the ball immediately after the collision? Why?
When you calculate the gain in potential energy, remember that h is the change in
height of the center of mass of the pendulum, not including the ball.
Is this a perfectly elastic collision? What is the percentage of the kinetic energy
lost (converted to thermal energy) during the collision?
6. Turn the pendulum around and repeat the experiment for catching the ball. (Do
not change the position of the counterweight.) Note that both the rotational inertia and the center of mass (and thus the distance r) will change due to the ball
being in the catcher.
7. For the two cases (ball hitting the bumper and ball being caught), compare the
angular velocity of the pendulum just after the collision. Compare the maximum
angular displacement for the two cases. Which type of collision causes the
greater angular displacement? Why?
Further Study V: Alternative Determination of Rotational Inertia
In the procedure above, you found the rotational inertia of the pendulum by applying
a known torque and measuring the resulting angular acceleration. An alternate
method is to measure the period of oscillation.
For a physical pendulum of rotational inertia I and mass M, the theoretical period (for
low-amplitude oscillations) is given by
where r is the distance from the axis of rotation to the center of mass of the pendulum.
Measure the period of the pendulum (with a low amplitude) and calculate its rotational inertia. Compare this to the answer you got by applying a known torque.
15
Page 16

®
Ballistic Pendulum Accessory Experiment 2: Conservation of Momentum and Energy
Sliding masses
Additional three-step
pulley
Disk
Sliding masses
Additional three-step
pulley
Disk
Ring
Further Study VI: Horizontal Collision
Repeat the experiment with the apparatus in one of the configurations shown in Figure 2.6 and 2.7 using parts from the Mini Rotational Accessory (ME-8968) and a second three-step pulley. Use two sliding masses to balance the system with the ball in
the catcher. Add the disk and (optionally) the ring to increase the moment of inertial.
After the collision, stop the catcher with your hand before it swings around and hits
the back of the launcher.
In this variation of the experiment, there is no maximum displacement because the
system would continue to rotate indefinitely if it were allowed to. What is the change
in potential energy of the system?
16
Figure 2.6: Setup for horizontal collision with disk only
Figure 2.7: Setup for horizontal collision with disk and ring
Page 17

®
Model No. ME-9892 Technical Support
Technical Support
For assistance with any PASCO product, contact PASCO at:
Address: PASCO scientific
10101 Foothills Blvd.
Roseville, CA 95747-7100
Phone: 916-786-3800 (worldwide)
800-772-8700 (U.S.)
Fax: (916) 786-7565
Web: www.pasco.com
Email: support@pasco.com
Limited Warranty
For a description of the product warranty, see the PASCO catalog.
Copyright
The PASCO scientific 012-09842B Ballistic Pendulum Accessory Instruction Manual is copyrighted with all rights reserved. Permission is granted to non-profit educational institutions for reproduction of any part of this manual, providing the reproductions are used
only in their laboratories and classrooms, and are not sold for profit. Reproduction under any other circumstances, without the written
consent of PASCO scientific, is prohibited.
Trademarks
PASCO, PASCO scientific, DataStudio, PASPORT, Xplorer, and Xplorer GLX are trademarks or registered trademarks of PASCO scientific, in the United States and/or in other countries. All other brands, products, or service names are or may be trademarks or service marks of, and are used to identify, products or services of, their respective owners. For more information visit
www.pasco.com/legal.
Authors: Jon Hanks
Alec Ogston
17
 Loading...
Loading...