PASCO ME-9833 User Manual

Download

Page 1

Instruction Manual

Manual No. 012-10461A

Physical Pendulum

Set

Model No. ME-9833

Page 2

Model No. ME-9833 Physical Pendulum Set

Equipment ................................................................................................... 3

Introduction................................................................................................. 4

Basic Setups ............................................................................................... 4

Background Information............................................................................ 5

Experiment 1: Parallel Axis Theorem ....................................................... 7

Experiment 2: Minimum Period for an Oscillating Bar ......................... 11

Experiment 3: Moment of Inertia Based on Period of Oscillation........ 15

Experiment 4: Use a Physical Pendulum to Measure ‘g’ ...................... 19

Appendix A: Specifications ......................................................................23

Appendix B: DataStudio Instructions......................................................23

Appendix C: Technical Support, Copyright, Warranty ..........................24

Appendix D: Teacher’s Notes...................................................................25

Page 3

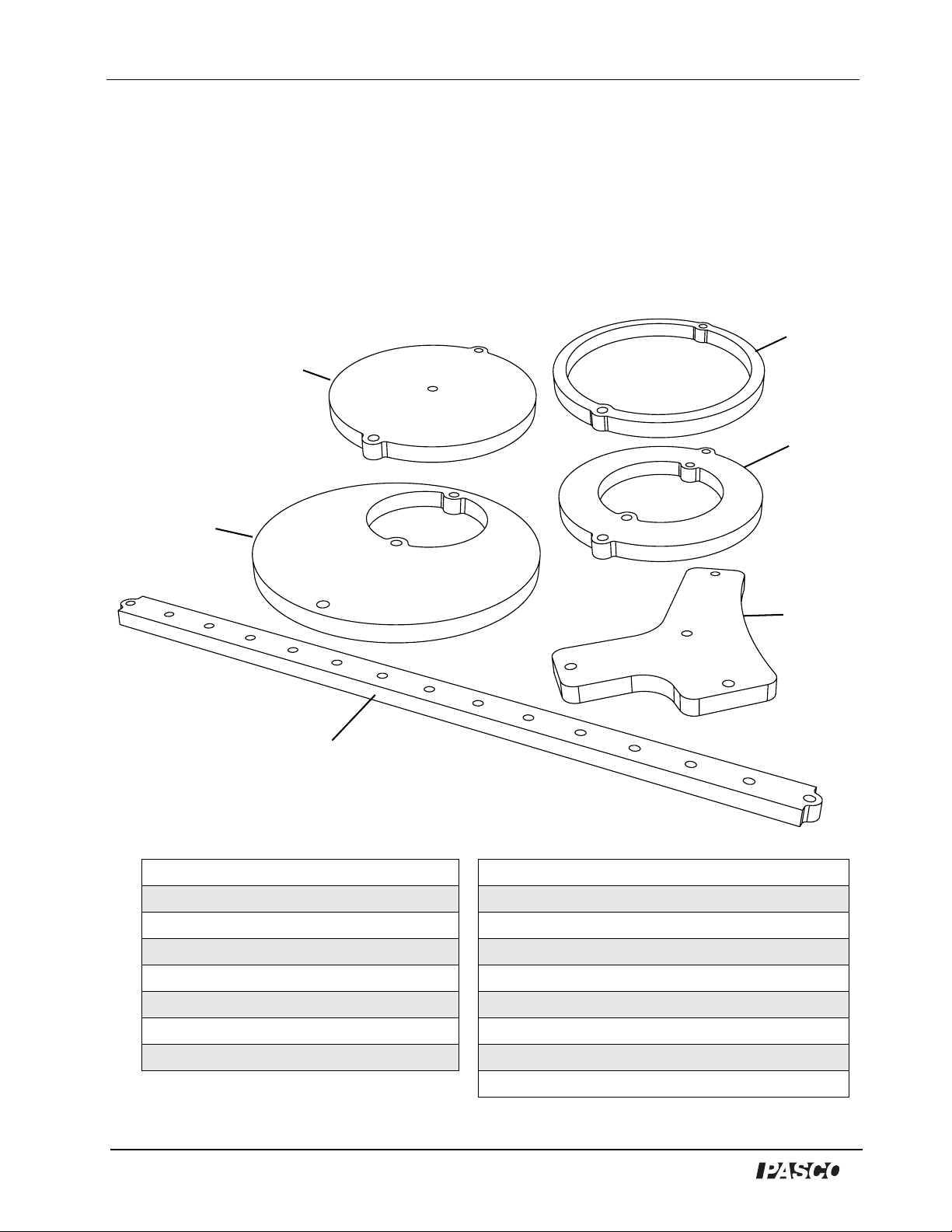
Physical Pendulum Set Model No. ME-9833

Physical Pendulum Set

Model No. ME-9833

Equipment

Included Equipment Recommended Equipment

1. Pendulum Bar, 28 cm Rotary Motion Sensor (PS-2120 or CI-6538)

2. Offset Hole Base and Support Rod (see PASCO catalog)

3. Solid Disk Super Pulley with Clamp (ME-9448A)

4. Thin Ring Mass and Hanger Set (ME-8979)

5. Thick Ring PASCO Computer Interface (see PASCO catalog)

6. Irregular Shape Vernier Caliper (SF-9711)

7. Mounting Screws (qty. 6) (not shown) String or Thread (see PASCO catalog)

Balance (see PASCO catalog

Page 4

Model No. ME-9833 Physical Pendulum Set

Introduction

The Physical Pendulum Set consists of six parts: pendulum bar (28 cm), offset hole, solid disk, thin ring, thick ring, and irregular shape. This set of objects allows the study of physical pendula, moments of inertia, and the parallel axis theorem. It includes six mounting screws for attaching the physical pendula to a Rotary Motion Sensor in order to measure the object’s acceleration due to an applied torque, or the object’s period of oscillation when the pendulum swings freely.

Basic Setups

Using the Rotary Motion Sensor to Measure Moment of Inertia

You can use the Rotary Motion Sensor (RMS) to measure the motion of a rotating object as it is accelerated by a net torque. The ratio of net torque to angular acceleration is the object’s moment of inertia.

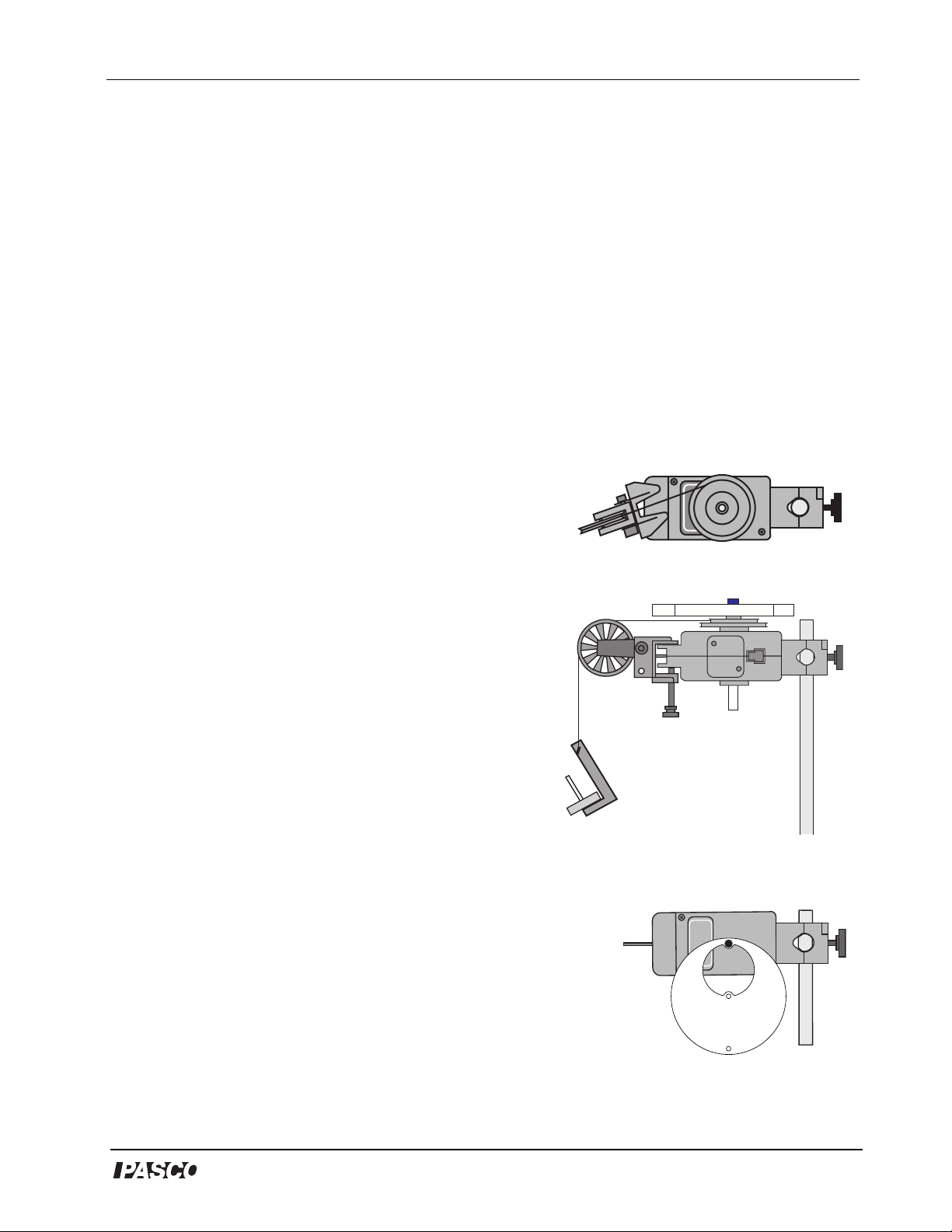
• Mount the Rotary Motion Sensor horizontally on a support rod with the three step pulley on top.

• Arrange the three step pulley on the shaft on top of the sensor so that the largest diameter step is nearest to the sensor.

• Mount a Super Pulley with Clamp to the platform area at the

Figure 1: Top view - Adjust the angle of the Super Pulley.

end of the sensor opposite to the support rod.

• Connect a string to one of the steps on the three step pulley and drape the string over the Super Pulley. Adjust the angle of the Super Pulley with Clamp so that the string is tangent to the step on the three step pulley (see Fig. 2).

• Put the object to be measured onto the shaft of the sensor above the three step pulley. Secure it in place with one of the mounting screws.

• Attach a mass hanger to the end of the string that is draped

Figure 2: Moment of Inertia setup

over the Super Pulley.

Using the Rotary Motion Sensor to Measure Period of Oscillation

You can use the Rotary Motion Sensor to measure the period of oscillation of the objects in the Physical Pendulum Set.

• Mount the Rotary Motion Sensor horizontally on a support rod so that the three step pulley is on one side (oriented vertically).

• Remove the mounting screw and the three step pulley.

• Use a mounting screw to attach the object to be measured to the shaft of the sensor.

Object

Figure 3: Period of oscillation setup

Page 5

Physical Pendulum Set Model No. ME-9833

Setting Up the Rotary Motion Sensor and Interface

Connect the Rotary Motion Sensor to the interface and connect the interface to a computer. For the PASPORT Rotary Motion Sensor, connect the sensor’s plug to a compatible PASPORT interface (e.g., USB Link, PowerLink, Xplorer, Xplorer GLX). For the ScienceWorkshop Rotary Motion Sensor, connect the yellow plug to digital channel 1 and the black plug to digital channel 2 of a compatible ScienceWorkshop interface (e.g., ScienceWorkshop 500 or ScienceWorkshop 750).

In general, the set up of the DataStudio program will be for measuring angular acceleration or for measuring period. To determine angular acceleration, find the slope of the plot of data on an angular velocity versus time graph display. To determine period, use the Smart Cursor to find the time for ten oscillations of the physical pendulum and then divide the total time for ten oscillations by ten.

Figure 4: Smart Cursor

For more information about setting up the DataStudio program, refer to the Appendix.

Background Information

Pendulum Period

If a body is suspended from a fixed point other than its center of mass and set in motion, it has a periodic motion that is very nearly simple harmonic motion. The period of the angular motion depends on the pull of gravity and the moment of inertia of the body.

For that reason, the physical pendulum is a useful device for determining the acceleration due to gravity and the moment of inertia. The analytical relationships for the period, T, are as follows:

for a simple pendulum:

T2π

and for a physical pendulum: where

----=

T2π

------------------=

MgL

T is the period L is the length of the simple pendulum g is the acceleration due to gravity I is the moment of inertia about an axis through the pivot point M is the mass of the pendulum, and

is the distance from the pivot point to the center of gravity, cg

The first equation is seen to be a special case of the second if ML

formulas give good results if the angular amplitude is small.

Torque and Moment of Inertia

mgsinθ

Figure 5: Physical pendulum

is substituted for I. These

For an object accelerating about an axis, the torque is the product of the force and the moment arm (the distance from the pivot point perpendicular to the line of action of the force):

Page 6

Model No. ME-9833 Physical Pendulum Set

τ Iα r ⊥F==

For the basic setup for measuring moment of inertia shown in Figure 2, where T is the

τ rT=

tension in the string and r is the radius of the step pulley to which the string is attached. The net

ΣFmgT– ma==

force is the difference between the tension, T, and the weight, mg, of the hanging mass. Therefore, the tension, is where “a” is related to the angular acceleration, α, by

Tmgma–=

a = rα. The torque becomes:

τ rT rmg rma– rmg rm rα()–== =

τ rm g rα–()=

where the angular acceleration is measured by the Rotary Motion Sensor.

Parallel Axis Theorem

For a physical pendulum, the moment of inertia about an axis through the point of suspension can

be found using the parallel axis theorem, where I

pivotIcg

2 cg

is the moment of inertia

pivot

about the point of suspension, Icg is the moment of inertia about the center of mass, m is the mass of the pendulum, and Lcg is the perpendicular distance from the pivot point to the center of mass. In other words, the moment of inertia about a parallel axis is the moment of inertia about the center of

mass plus the moment of inertia of the entire object treated as a point mass at the center of gravity.

Description of the Experiments

1.Parallel axis theorem: Measure the moment of inertia, Icg, around the center of gravity of an object, and the moment of inertia, I

center of mass. Confirm that I

pivot

, around a pivot point of the object that is not through the

pivot

= Icg + ML

where m is the mass of the object and Lcg is the

distance from the pivot point to the center of gravity.

2.Minimum period of a bar: Given a bar of length, L, calculate Lcg, the distance from the pivot point to the center of gravity that would give the minimum period of oscillation for the bar.

Measure the distance that gives the minimum period and compare it to the calculated result.

3.Determine moment of inertia: Use the period, T, of a physical pendulum to calculate the moment of inertia, I. Compare the calculated value to the theoretical value for I.

4.Acceleration due to gravity: Measure the acceleration due to gravity, g, using period, T, moment of inertia, I, mass, m, and the distance from the pivot point to the center of gravity, Lcg.

Page 7

Physical Pendulum Set Model No. ME-9833

Experiment 1: Parallel Axis Theorem

Equipment

Item

PASCO Interface and DataStudio software Base and Support Rod

Rotary Motion Sensor String or thread

Irregular Shape from Physical Pendulum Set Mass and Hanger Set

Super Pulley with Clamp Vernier calipers

Balance

Item

Theory

The moment of inertia about a parallel axis, I

, is the moment of inertia about the center of

pivot

gravity, Icm, plus the moment of inertia of the entire object treated as a point mass at the center of gravity:

pivotIcm

where L is the perpendicular distance from the center of gravity (cog) to the pivot

point.

Procedure

Use the Rotary Motion Sensor to measure the angular acceleration of a rotating irregular shaped object when it rotates about its center of gravity due to a net torque, and also when it rotates about a parallel axis a distance “L” away from the center of gravity. Use the angular acceleration and the known applied torque to determine the moment of inertia about the center of gravity and the moment of inertia about the parallel axis.

Equipment Setup: Center of Gravity

1. Set up the Rotary Motion Sensor horizontally on a support rod so that the three step pulley is

on top. Start the DataStudio program on the computer and connect the sensor to the computer interface.

2. Mount a Super Pulley with Clamp to the platform area at the end of the sensor opposite to the support rod.

3. Connect a string to one of the steps on the three step pulley and drape the string over the Super Pulley. Adjust the angle of the Super Pulley with Clamp so that the string is tangent to the step on the three step pulley.

4. Use calipers to carefully measure the diameter of the step to which you attached the string. Calculate the radius of the step and record it in the data table (Table 1).

5. Measure and record the mass, M, of the irregular shape object to be measured.

Page 8

Model No. ME-9833 Physical Pendulum Set

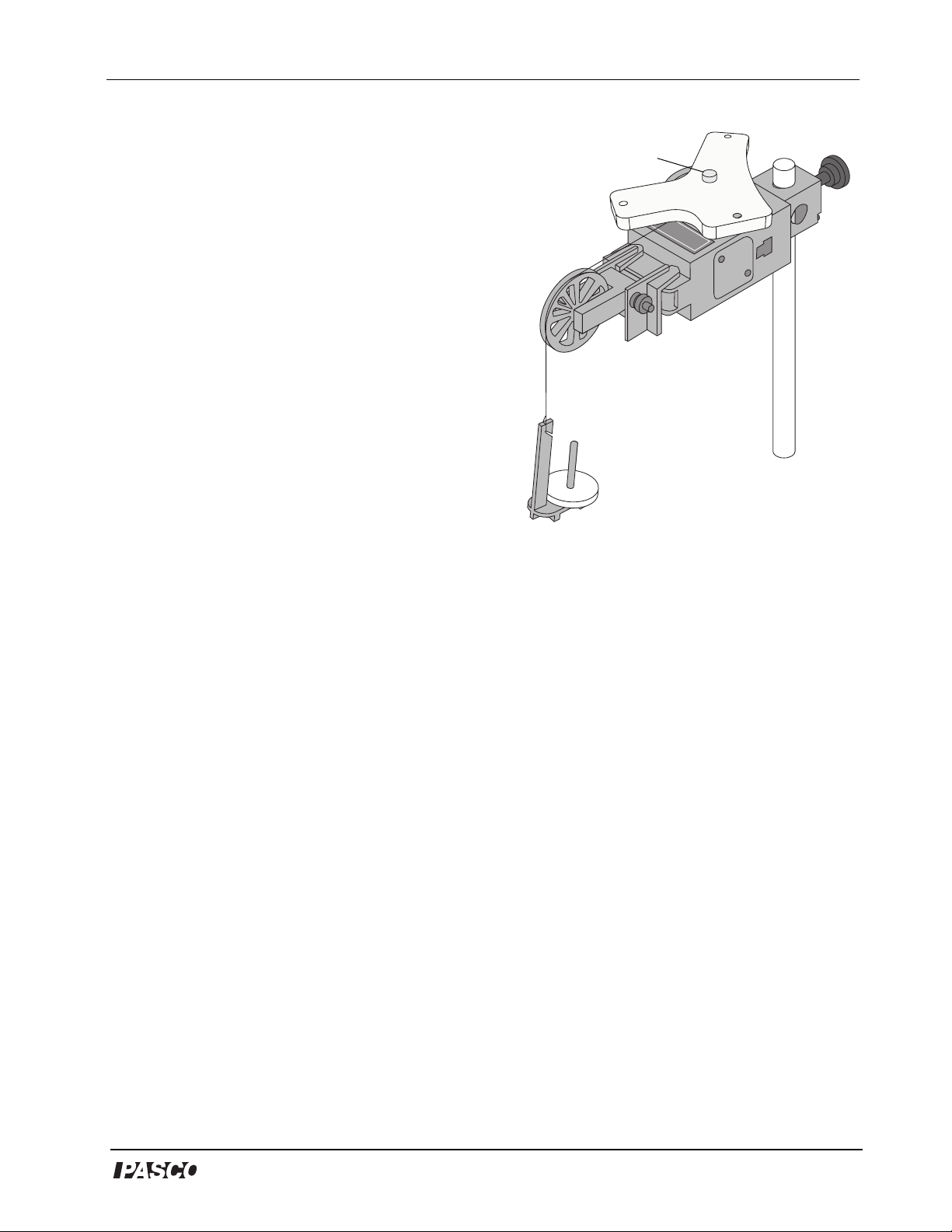
6. Put the object to be measured onto the shaft of the sensor above the three step pulley. Secure it in place with one of the mounting screws.

7. Measure and record the mass, m, of a mass hanger.

8. Attach the mass hanger to the end of the string that is draped over the Super Pulley.

Data Recording: Center of Gravity

1. Wind the string about the step pulley so that

the mass hanger is just below the Super Pulley. Hold the irregular shape in place.

2. Start recording data and then release the irregular shape so that it rotates freely.

3. Stop recording data when the mass hanger reaches its lowest point.

Mounting screw

Figure 1-1: Irregular shape mounted on the RMS at the center of gravity

4. Repeat the process a total of three times.

Analysis: Center of Gravity

Find the moment of inertia about the center of gravity.

1. Set up a graph display in the software of angular velocity versus time.

2. Select a region of the first run of angular velocity data and select ‘Linear Fit’ from the

‘Fit’ menu.

3. Record the value of the slope as the first value of angular acceleration around the center of gravity.

4. Repeat the process for the other two runs of data.

5. Find the average angular acceleration, α

, and record it in the data table.

6. Calculate the net torque, τ = rm(g - rα). Calculate the moment of inertia about the center of gravity by dividing the net torque by the average angular acceleration. Record the result

--------

as the moment of inertia about the center of gravity, Icg. ( )

Equipment Setup: Parallel Axis

1. Temporarily remove the irregular shape from the top of the Rotary Motion Sensor.

Page 9

Physical Pendulum Set Model No. ME-9833

2. Use calipers to carefully measure the distance, Lcg, from the center of gravity to

Measure L

one of the other pivot points on the irregular shape. Record the measurement as Lcg, the

distance from the center of gravity to the pivot point.

3. Replace the irregular shape on the Rotary Motion Sensor by attaching it with one of the mounting screws through the pivot point that you used for the measurement.

Data Recording: Parallel Axis

1. Wind the string about the step pulley so that the

mass hanger is just below the Super Pulley. Hold the irregular shape in place.

Figure 1-2: Irregular shape mounted through a parallel axis

2. Start recording data and then release the irregular shape so that it rotates freely.

3. Stop recording data when the mass hanger reaches its lowest point.

4. Repeat the process a total of three times.

Analysis: Parallel Axis

Find the moment of inertia about the parallel axis.

1. Use the same setup in the software to find the average angular acceleration.

2. Calculate the net torque (τ = rm(g - rα)). Calculate the moment of inertia about the

parallel axis by dividing the net torque by the average angular acceleration the results as the moment of inertia about the parallel axis, I

3. Calculate ML

, the moment of inertia about the parallel axis of the irregular shape as if

pivot

all its mass is concentrated at its center of gravity. Use the distance from the pivot point to the center of gravity as L

. Record

4. Calculate the sum of Icg and ML parallel axis, I

pivot

5. Find the percent difference between I percent difference. Set up a graph display in the software of angular velocity versus time.

Extensions

. Compare the sum to the moment of inertia about the

and the sum of Icg and ML

pivot

and record the

Page 10

Model No. ME-9833 Physical Pendulum Set

1.Repeat the procedure for the other two ‘legs’ of the irregular shape. Determine whether or not the moment of inertia about the parallel axis (the pivot point) is equal to the sum of the moment of

inertia about the center of mass plus ML

2.Repeat the procedure for another physical pendulum object, such as the solid disk.

Measurements and Calculations

Table 1: Parallel Axis Theorem for Irregular Shape

Item (units) 1 2 3

Object irregular shape

Mass of object, M (kg)

Step diameter (m)

Step radius, r (m)

Mass of hanger, m (kg)

, avg. angular accelerationcg (rad/s2)

, torque, rm(g - rαcg) (N m)

, moment of inertia (kg m2)

, distance - pivot to center of gravity (m)

, moment of inertia, parallel axis (kg m2)

pivot

Percent difference, I

+ ML

(kg m2)

, avg. angular acceleration

, torque, rm(g - rα

pivot

) (N m)

pivot

(rad/s2)

, moment of inertia, pivot point (kg m2)

and Icg + ML

pivot

Questions

1. How does the value of the moment of inertia about the pivot point compare to the sum of the

moment of inertia about the center of gravity Icg plus ML

2. Do your results confirm the parallel axis theorem? Why or why not?

3. How do you know that the center hole is the center of gravity?

Page 11

Physical Pendulum Set Model No. ME-9833

Experiment 2: Minimum Period for an Oscillating Bar

Equipment

Item

PASCO Interface and DataStudio software Base and Support Rod

Rotary Motion Sensor Metric ruler

28-cm Bar from Physical Pendulum Set

The first section outlines the calculation of the distance from the pivot point to the center of mass of a long bar that produces the minimum period of oscillation for the bar at small amplitudes. The next section describes the measurements needed to determine the minimum period.

Calculating Distance for Minimum Period

------

Recall that the moment of inertia of a “long rod” about its center of gravity is: where M

is the mass of the long rod and L is the overall length of the rod. A more precise physical model of the 28-cm Pendulum Bar as a rectangular-type rod has a moment of inertia about its center of

2b2

gravity that is: where M is the mass of the rectangular bar, “a” is the length, and

“b” is the thickness. However, if a>>b, can be used as a very good approximation.

------

+()=

------

The parallel axis theorem enables us to write the moment of inertia of the bar about a pivot point

not at the center of gravity as: where Lcg is the distance from the pivot point to the

pivotIcg

center of gravity.

The period of a physical pendulum depends on its moment of inertia, its mass, and the distance

from the pivot point to the center of gravity. The period is: . For the 28-cm Pendulum

T2π

pivot

-----------------=

mgL

Bar, the period becomes:

T2π

------

---------------------------------------- 2π

MgL

Use calculus to find the derivative of the period, T, with respect to L

------

----------------------------==

, the distance between the

pivot and the center of gravity.

Set the derivative equal to zero and solve for L

. Confirm that the minimum distance is:

----------

Page 12

Model No. ME-9833 Physical Pendulum Set

Measurement of Period for Different L

Equipment Setup

1. Measure and record the length, L, of the bar.

2. Mount the Rotary Motion Sensor on a support rod so

that the shaft of the sensor is horizontal (parallel to the table).

3. Use a mounting screw to attach the bar to the shaft of the sensor through the first hole above the center hole of the bar. In other words, attach the bar so the pivot point is 2 cm above the center of gravity.

Computer Setup

1. Connect the sensor to a PASCO interface and connect the

interface to a computer.

2. On the computer, start the DataStudio program. Set up the program so that it has a Graph display of Angular Position (rad) versus Time (s).

Figure 2-1: Setup

Data Recording

1. Gently start the pendulum bar swinging

with a small amplitude (about 20 degrees total).

2. Click ‘Start’ to begin recording data. After about 25 seconds, click ‘Stop’ to end recording data. Data will appear in the graph of angular position versus time and also in the graph of period versus

Figure 2-2: Graph display

time.

3. Move the mounting screw to the next hole (4 cm from the center hole).

4. Start the pendulum bar swinging and record data for about 25 seconds.

5. Repeat the process for the holes that are 6 cm, 8 cm, 10 cm, 12 cm, and 14 cm from the

center hole.

Analysis

1. Create a Table display to show period versus length. In the ‘Experiment’ menu, select ‘New Empty Data Table’.

Page 13

Physical Pendulum Set Model No. ME-9833

2. Double click the label of the new Table display in the Summary panel to open the Data Properties window. Give the table a Measurement Name of ‘Period versus Length’, an ‘X’ Variable Name of ‘Length’ with ‘cm’ for units, and a ‘Y’ Variable Name of ‘Period’ with ‘s’ for units.

3. Find the period of oscillation for the ‘2 cm’ setup. (a) Click the ‘Smart Cursor’ button in the toolbar. (b) Move the Smart Cursor to one of the first peaks of Angular Position. (c) Hover the cursor over the Smart Cursor until the ‘delta’ symbol appears. (d) Click and drag the ‘delta’ symbol to the tenth peak of Angular Position. (e) Divide the time for ten oscillations by ten and record the number as the period of oscillation.

Figure 2-3: Typical data

4. In the Table display, enter ‘2’ as the first length in the ‘x’ column and the period of oscillation for the 2 cm length as the first period in the ‘y’ column. Continue to enter data points in the Table display.

5. Click and drag a Graph display icon from the ‘Displays’ part of the Summary panel to the ‘Data’ under ‘Period versus Length’ in the top part of the Summary panel. The Graph display opens with ‘Period’ on the Y-axis and ‘Length’ on the X-axis.

6. Determine which length gives the minimum period of oscillation of the pendulum bar and record this length in the data section.

Data Section

Length of pendulum bar, L: _________________

----------

Calculated value for length that gives minimum period ( ): _________________

Measured value for length that gives minimum period: __________________

Percent difference: ___________________

Questions

1. What is the percent difference between the calculated value for the length that gives minimum period of oscillation and the measured value for the length?

2. Would a pendulum bar with different mass but with the same dimensions have a different value for the length that gives minimum period of oscillation? Why or why not?

Page 14

Model No. ME-9833 Physical Pendulum Set

Page 15

Physical Pendulum Set Model No. ME-9833

Experiment 3: Moment of Inertia Based on Period of

Oscillation

Equipment

Item

PASCO Interface and DataStudio software Balance

Rotary Motion Sensor Vernier caliper

Physical Pendulum Set Mass and Hanger Set

Base and Support Rod String or thread

Item

Use the period of oscillation of a physical pendulum to calculate the moment of inertia. Measure the moment of inertia and compare the measured value to the calculated value.

Background Information

The period of oscillation, T, of a physical pendulum depends on the moment of inertia about a pivot point, I

The Parallel Axis Theorem states that the moment of inertia about a pivot point, I

, the mass, M, and the distance from the pivot point to the center of gravity, Lcg.

pivot

T2π

pivot

------------------ 2π MgL

-------------------------------==

MgL

pivot

, is equal to

the sum of the moment of inertia about the center of gravity, Icg, and the moment of inertia of the

object as if all its mass were at the center of gravity, ML

Conversely, the moment of inertia about the center of gravity could be found as follows:

T2MgL

-------------------------

4π

Measurement: Period of Oscillation

Equipment Setup

1. Measure and record the mass M, of the disk.

2. Measure and record the distance, L

, from the

pivot point on the edge of the disk to the center of the disk.

3. Mount the Rotary Motion Sensor on a support rod so that the shaft of the sensor is horizontal (parallel to the table).

–=

Figure 3-1: Setup

Page 16

Model No. ME-9833 Physical Pendulum Set

4. Use a mounting screw to attach the disk to the shaft of the sensor through a hole on the edge of the disk.

Computer Setup: Period of Oscillation

1. Connect the sensor to a PASCO interface and connect the interface to a computer.

2. On the computer, start the DataStudio

program. Set up the program so that it has a Graph display of Angular Position (rad) versus Time (s).

3. Open the ‘Setup’ window and increase the sampling rate from 10 Hz to 100 Hz.

4. Open the Calculator and select ‘period(10,10,1,x)’ from the ‘Special’ menu in the Calculator. [This function

Figure 3-2: Calculator window

determines the period of oscillation from the angular position versus time data.]

5. To define the variable ‘x’ in the Calculator, click the menu down arrow under ‘Variables’ and select ‘Data Measurement’. Select ‘Angular Position’ from the window that opens.

6. Click ‘Properties’ in the Calculator window. Give the function ‘Period’ as the measurement name and the variable name. Enter ‘sec’ (seconds) as the unit.

7. Create a graph of ‘period versus time’. Click and drag the Graph icon from the Displays list in the Summary panel to the period function in the Data section of the Summary panel.

8. In the ‘Statistics’ menu of the ‘period versus time’ Graph display, select ‘Mean’. Click the ‘Statistics’ button in the toolbar so that the legend box will show both the data run and the mean.

Data Recording: Period of Oscillation

1. Gently start the disk swinging with a small amplitude (about 20 degrees total).

2. Click ‘Start’ to begin recording data. After about 25 seconds, click ‘Stop’ to end

recording data. Data will appear in the graph of angular position versus time and also in the graph of period versus time.

3. Repeat the process for several more trials. Determine the average of the values of the period of oscillation and record the average value in the Data Section.

Page 17

Physical Pendulum Set Model No. ME-9833

Analysis

1. Calculate the moment of inertia using the period, T, the mass, M, and the distance from the pivot point to the center of gravity, Lcg.

T2MgL

-------------------------

4π

–=

2. Record the calculated value for the moment of inertia in the Data Section.

Measurement: Moment of Inertia

Equipment Setup

1. Set up the Rotary Motion Sensor horizontally on a support rod with the three step pulley on

top. Start the DataStudio program on the computer and connect the sensor to the computer interface.

2. Mount a Super Pulley with Clamp to the platform area at the end of the sensor opposite to the support rod.

4. Use calipers to carefully measure the diameter of the step to which you attached the string. Calculate the radius of the step and record it in the Data Section.

5. Put the solid disk onto the shaft of the sensor above the three step pulley. Secure it in place with one of the mounting screws.

6. Measure and record the mass, m, of a mass hanger.

7. Attach the mass hanger to the end of the string that is draped over the Super Pulley.

Data Recording

1. Wind the string about the step pulley so that the mass hanger is just below the Super Pulley.

Hold the irregular shape in place.

2. Start recording data and then release the irregular shape so that it rotates freely.

3. Stop recording data when the mass hanger reaches its lowest point.

4. Repeat the process a total of three times.

Analysis

Find the moment of inertia about the center of gravity.

1. Set up a graph display in the software of angular velocity versus time.

Page 18

Model No. ME-9833 Physical Pendulum Set

2. Select a region of the first run of angular velocity data and select ‘Linear Fit’ from the ‘Fit’ menu.

3. Record the value of the slope as the first value of angular acceleration around the center of gravity.

4. Repeat the process for the other two runs of data.

5. Find the average angular acceleration, αcg, and record it in the Data Section.

6. Calculate the net torque, τ = rm(g - rα).

7. Calculate the moment of inertia about the center of gravity by dividing the net torque by

the average angular acceleration. Record the result as the moment of inertia about the

center of gravity, Icg. ( )

--------

8. Determine the percent difference between the calculated moment of inertia and the

measured moment of inertia and record the result in the Data Section.

Table 2: Data Section

Item Value Item Value

Mass of solid disk, M: Mass of hanger, m:

Distance from pivot to center of gravity, L

Average measured period of oscillation, T:

Calculated value for moment of inertia, I:

Radius of step pulley, r: Percent difference:

Average angular acceleration, α

Torq ue, τ:

Measured value for moment of inertia, I:

Questions

1. How does your value for the calculated moment of inertia compare to the measured moment of inertia?

2. Do your results support or disprove the idea that the moment of inertia of a physical pendulum can be determined from its period of oscillation. Why or why not?

Extensions

Repeat the procedure for the thin ring, thick ring, and offset hole. To measure the moment of inertia of the thin ring, for example, fasten it to the top of the solid disk, find the combined moment of inertia and then subtract the moment of inertia of the solid disk.

Page 19

Physical Pendulum Set Model No. ME-9833

Experiment 4: Use a Physical Pendulum to Measure the Acceleration Due to Gravity, g

The purpose of this experiment is to use a physical pendulum to measure the acceleration due to gravity.

Equipment

Item

PASCO Interface and DataStudio software Balance

Rotary Motion Sensor Vernier caliper

Physical Pendulum Set Base and Support Rod

Background Information

For small amplitudes of oscillation, the motion of a physical pendulum is approximately ‘simple harmonic motion’ and its theoretical period of oscillation, T, is given by

pivot

------------------=

MgL

where I

T2π

is the moment of inertia of the physical pendulum about its pivot point, M is the mass

pivot

of the pendulum, and Lcg is the distance from the pivot point to the center of gravity. The Parallel Axis Theorem states that the moment of inertia about the pivot point, I

, is the sum of the

pivot

moment of inertia about the center of gravity, Icg, and the moment of inertia of the pendulum as if all the mass is concentrated at the center of gravity. The period, T, is then given by

T2π

-------------------------------=

MgL

For a physical pendulum such as the 28-cm Pendulum Bar, the moment of inertia about the center

2b2

of gravity is very close to where “a” is the length of the physical pendulum and

------

+()Icg=

“b” is the width.

Solving for g gives

g4π

IcgML

⎛⎞

-------------------------------

⎜⎟ ⎝⎠

Page 20

Model No. ME-9833 Physical Pendulum Set

Procedure: Measurement of Period

Equipment Setup

1. Measure and record the length, a, and width, b, of the

bar.

2. Measure and record the mass, M, of the bar.

3. Mount the Rotary Motion Sensor on a support rod

so that the shaft of the sensor is horizontal

Figure 4-1: Equipment setup

(parallel to the table).

4. Use a mounting screw to attach the bar to the shaft of the sensor through the hole at the end of the bar. In other words, attach the bar so the pivot point is at the very end of the bar.

Computer Setup

1. Connect the sensor to a PASCO interface

and connect the interface to a computer.

2. On the computer, start the DataStudio program. Set up the program so that it has a Graph display of Angular Position (rad) versus Time (s).

3. Open the Calculator and select ‘period(10,10,1,x)’ from the ‘Special’ menu in the Calculator. [This function

Figure 4-2: Calculator window

determines the period of oscillation from the angular position versus time data.]

4. To define the variable ‘x’ in the Calculator, click the menu down arrow under ‘Variables’ and select ‘Data Measurement’. Select ‘Angular Position’ from the window that opens.

5. Click ‘Properties’ in the Calculator window. Give the function ‘Period’ as the measurement name and the variable name. Enter ‘sec’ (seconds) as the unit.

6. Create a graph of ‘period versus time’. Click and drag the Graph icon from the Displays list in the Summary panel to the period function in the Data section of the Summary panel.

7. In the ‘Statistics’ menu of the ‘period versus time’ Graph display, select ‘Mean’. Click the ‘Statistics’ button in the toolbar so that the legend box will show both the data run and the mean.

Data Recording

1. Gently start the pendulum bar swinging with a small amplitude (about 20 degrees total).

Page 21

Physical Pendulum Set Model No. ME-9833

2. Click ‘Start’ to begin recording data. After about 30 seconds, click ‘Stop’ to end recording data. Data will appear in the graph of angular position versus time and also in the graph of period versus time.

3. Repeat the process for two more trials.

Analysis

1. Determine the average period of oscillation, T, for the pendulum bar and record the value in the Data Section.

2. Assume that the center of gravity is at the midpoint of the pendulum bar. Measure and record the distance from the pivot point to the center of gravity, Lcg.

3. Calculate and record the theoretical moment of inertia about the center of gravity, Icg.

4. Calculate and record the acceleration due to gravity, g, based on the length from the pivot

point to the center of gravity, Lcg, mass, M, moment of inertia about the center of gravity, Icg, and period, T.

5. Calculate and record the percent different between the measured value for g, acceleration

due to gravity, and the accepted value (9.8 m/s2).

Data Section

Length of pendulum bar, a: _________________ Width of pendulum bar, b: __________________

Mass of pendulum bar, M: _________________

Average period of oscillation, T: ________________

Distance from pivot to center of gravity, Lcg: ________________

Calculated value for the moment of inertia about the center of gravity, Icg: _______________

Calculated value for acceleration due to gravity, g: __________________

Percent difference: ___________________

Questions

1. How does the calculated value for g based on the period compare to the accepted value for g,

9.8 m/s

2. Do your results confirm that the acceleration due to gravity, g, can be measured accurately using a physical pendulum? Why or why not?

Page 22

Model No. ME-9833 Physical Pendulum Set

Page 23

Physical Pendulum Set Model No. ME-9833

Appendix A: Specifications

Item Dimensions

Irregular shape L

1 = 0.051, Lcg 2 = 0.044, Lcg 3 = 0.035, thickness = 0.00635 m

Solid disk Diameter = 0.08 m, thickness = 0.00635 m

Thin ring Outside diameter = 0.085 m, inside diameter = 0.075 m, thickness = 0.00635 m

Thick ring Outside diameter = 0.08 m, inside diameter = 0.04964 , thickness = 0.00635 m

Offset hole Outside diameter = 0.096 m, diameter of hole = 0.043 m, thickness = 0.00635 m

Pendulum bar Length = 0.28 m, width = 0.015 m , thickness = 0.00635 m

Appendix B: DataStudio Setup Instructions

The instructions below are for using DataStudio to plot graphs of Angular Position versus Time and Angular Velocity versus Time. For information on the latest version of DataStudio, go to the PASCO web site (www.pasco.com).

Procedure

PART 1: Connect the interface to the computer and the sensor to the interface.

PART 2: Open a new DataStudio file.

Start DataStudio. If the Welcome to DataStudio screen opens, select ‘Create Experiment’. If a PASPORT Rotary Motion Sensor is connected to the computer through a PASPORT interface, an empty Graph display of Angular Position versus Time will open. OR If a ScienceWorkshop Rotary Motion Sensor is connected to the computer through a ScienceWorkshop interface, click ‘Setup’ in the toolbar to open the Experiment Setup window. Click digital channel 1 to open the sensor selection window and select ‘Rotary Motion Sensor’. Click ‘OK’ to close the sensor selection window. The sensor’s icon will appear in the Experiment Setup window under the image of the interface.

PART 3: Change ‘Sample Rate’ and select ‘Measurements’ to display.

If the Experiment Setup window is not open, click ‘Setup’ in the Toolbar to open the Experiment Setup window. The icon of the sensor will appear in the Experiment Setup window under the image of the interface. In the Setup window, change the ‘Sample Rate’ from the default to 100 Hz. Under the ‘Measurements’ tab, select the measurement that you want to use (for example, ‘Angular Position’ or ‘Angular Velocity’.) The ‘Measurement’ that you select will appear in the Summary panel under ‘Data’.

PART 4: Set up a data display

If you are using PASPORT, the Graph display automatically opens with Angular Position versus Time. OR

Page 24

Model No. ME-9833 Physical Pendulum Set

If you are using ScienceWorkshop, click and drag the Graph icon from the list under ‘Displays’ to the measurement name under ‘Data’ that you want to display. An empty Graph display will open with the measurement name on the vertical axis and ‘Time’ on the horizontal axis.

To change the measurement shown in the Graph display, click and drag the measurement name from the list under ‘Data’ to the vertical axis of the Graph display. OR To change the measurement shown in the Graph display, hover the cursor over the measurement name on the vertical axis of the Graph display until the cursor changes to a ‘List’ icon. Click the mouse once to open the List and select the measurement that you want to use.

Appendix C: Technical Support, Copyright, Warranty

For assistance with the Physical Pendulum Set (ME-9833) or any other PASCO products, contact PAS CO a s f ol low s:

Address: PASCO scientific

10101 Foothills Blvd.

Roseville, CA 95747-7100

Phone: (916) 786-3800

FAX: (916) 786-7565

Web: www.pasco.com

Email: support@pasco.com

The PASCO scientific 012-10461A Physical Pendulum Set manual is copyrighted and all rights reserved. However, permission is granted to non-profit educational institutions for reproduction of any part of the 012-10461A Physical Pendulum Set manual, providing the reproductions are used only for their laboratories and are not sold for profit. Reproduction under any other circumstances, without the written consent of PASCO scientific, is prohibited.

Warranty

For a description of the product warranty, see the PASCO catalog.

Page 25

Physical Pendulum Set Model No. ME-9833

Appendix D: Teacher’s Notes

Sample Data for Experiment 1: Parallel Axis Theorem

The table shows typical data for the parallel axis theorem using the irregular shape physical pendulum object. The three columns of data are for the three ‘legs’ of the irregular shape object.

Table 1: Parallel Axis Theorem for Irregular Shape

Item (units) 1 2 3

Object irregular shape A irregular shape B irregular shape C

Mass of object, M (kg) 0.06339 0.06339 0.06339

Step diameter (m) 0.0298 0.0298 0.0298

Step radius, r (m) 0.0149 0.0149 0.0149

Mass of hanger, m (kg) 0.00512 0.00512 0.00512

, avg. angular accelerationcg (rad/s2)

, torque, rm(g - rαcg) (N m) 0.0007347 0.0007347 0.0007347

, moment of inertia, center of mass (kg m2)

, distance - pivot to center of gravity (m) 0.0512 0.0439 0.0350

, moment of inertia, parallel axis (kg m2)

pivot

Percent difference, I

+ ML

(kg m2)

, avg. angular acceleration

, torque, rm(g - rα

) (N m) 0.00074417 0.00074332 0.00074199

pivot

(rad/s2)

, moment of inertia, pivot point (kg m2)

and Icg + mL

pivot

11.0 11.0 11.0

0.00006679 0.00006679 0.00006679

0.00016610 0.00012216 0.00007765

0.00023289 0.00018895 0.00014444

3.03 3.78 4.953

0.00024560 0.00019717 0.00015050

5.1% 4.1% 4.0%

Questions

1. How does the value of the moment of inertia about the pivot point compare to the sum of the

moment of inertia about the center of gravity plus mL

The values of the moment of inertia about the pivot point for all three ‘legs’ of the irregular shape

object compare well to the sum of the moment of inertia about the center of gravity plus mL

2. Do your results confirm the parallel axis theorem? Why or why not?

The results confirm the parallel axis theorem because of the close agreement between measurement and theory.

Page 26

Model No. ME-9833 Physical Pendulum Set

3. How do you know that the center hole is the center of gravity?

Answers will vary. One way to confirm that the center hole is the center of gravity is to balance the irregular shape on a fingertip.

Sample Data for Experiment 2: Minimum Period of an Oscillating Bar

The screenshot shows typical data for the length from the pivot point to the center of gravity of an oscillating pendulum bar and the corresponding period of oscillation for each length.

Calculations

----------

Derivation of the length for minimum period, . Find the derivative of the expression for

the period of oscillation, T.

T2π

------------

------

⎛⎞

⎜⎟

-------------------------------

⎜⎟

⎝⎠

------

------------

⎛⎞

⎜⎟

-------------------------------

⎜⎟

⎝⎠

Set the derivative equal to zero and solve for L

------

-------------------------------------------=

–

MgL

---

⎛⎞

------

⎝⎠

---------------------------------------------------------------------------

×=

---

–

⎛⎞

------

⎝⎠

--------------------------------------------------------------

×=

. For example,

L2L

gLcg()

(()

gLcg2Lcg()–

2Lcg()

–

Page 27

Physical Pendulum Set Model No. ME-9833

------

–+

------

----------

L2L

– 0==

Data Section

Length of pendulum bar: 28 cm

Calculated value for length that gives minimum period: 8.0829 cm

Measured value for length that gives minimum period: 8 cm

Percent difference: 1.02%

Questions

1. What is the percent difference between the calculated value for the length that gives minimum period of oscillation and the measured value for the length?

The percent difference between the calculated value for the length (8.0829 cm) and the measured value for the length (8 cm) that gives minimum period of oscillation is 1.02%

2. Would a heavier bar or a lighter bar with the same dimensions have a different value for the length that gives minimum period of oscillation? Why or why not?

No, a heavier or lighter bar with the same dimensions should have the same value for the length that gives minimum period of oscillation. Mass is not a factor in the calculation of the length for minimum period.

Page 28

Model No. ME-9833 Physical Pendulum Set

Sample Data for Experiment 3: Moment of Inertia Based on Period of Oscillation

Determine the calculated moment of inertia and the measured moment of inertia and record the results in the Data Section.

Table 3: Data Section

Item Value Item Value

Mass of solid disk, M: 0.08818 kg Mass of hanger, m: 0.00512 kg

Distance from pivot to center of gravity, L

Average measured period of oscillation, T:

Calculated value for moment of inertia, I:

Radius of step pulley, r: 0.0149 m Percent difference: 9.6%

0.40 m

0.497 s Torque, τ: 0.000737 N m

0.000075 kg m

Average angular acceleration, α

Measured value for moment of inertia, I:

8.87 rad/s

0.000083 kg m

Questions

1. How does your value for the calculated moment of inertia compare to the measured moment of inertia?

The value for the calculated moment of inertia compares relatively well with the measured moment of inertia.

2. Do your results support or disprove the idea that the moment of inertia of a physical pendulum can be determined from its period of oscillation. Why or why not?

The results support the idea that the moment of inertia of a physical pendulum can be determined from its period of oscillation. The calculated and measured values for the moment of inertia compare relatively well.

Page 29

Physical Pendulum Set Model No. ME-9833

Sample Data for Experiment 4: Use a Physical Pendulum to Measure the Acceleration Due to Gravity, g.

The following are typical data for the experiment.

Data Section

Length of pendulum bar, a: 0.28 m Width of pendulum bar, b: 0.015 m

Mass of pendulum bar, M: 0.70 kg

Average period of oscillation, T: 0.876 s

Distance from pivot to center of gravity, Lcg: 0.14 m

Calculated value for the moment of inertia about the center of gravity, Icg: 0.0004586 kg m

Calculated value for acceleration due to gravity, g: 9.608 m/s

Percent difference: 1.95%

Questions

1. How does the calculated value for g based on the period compare to the accepted value for g,

9.8 m/s2?

The calculated value for g compares relatively well to the accepted value for g.

2. Do your results confirm that the acceleration due to gravity, g, can be measured accurately using a physical pendulum? Why or why not?

The results confirm that the acceleration due to gravity, g, can be measured accurately using a physical pendulum. The calculated value based on the measured period is very close to the accepted value.

Page 30

Model No. ME-9833 Physical Pendulum Set

Notes

PASCO ME-9833 User Manual

Model No. ME-9833

Table of Contents