PASCO ME-9502 User Manual

Download

PASCO Mechanics

Statics System

ME-9502

Instruction Manual

012-12876B

*012-12876*

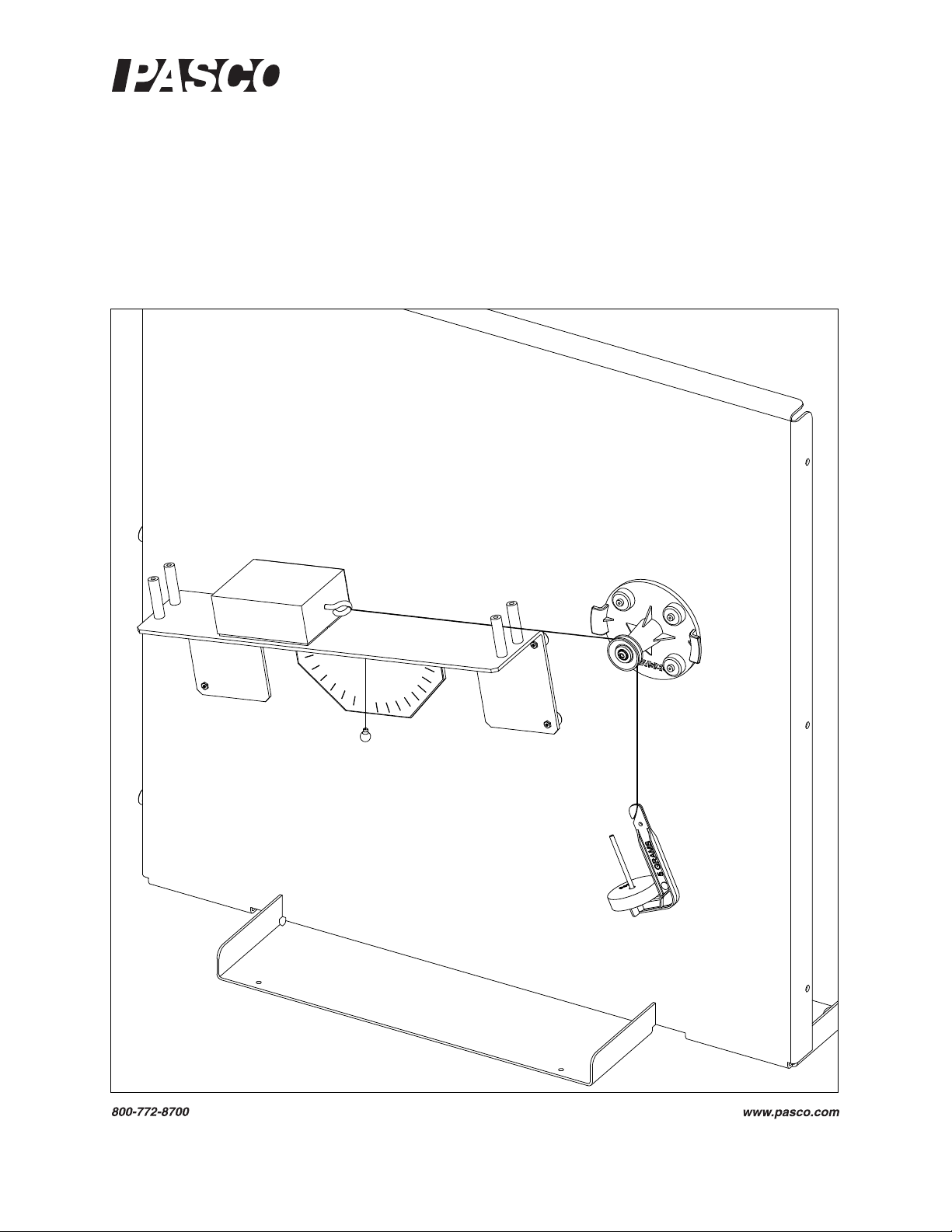
The cover page shows a a Friction Block on the Statics System Inclined Plane with a PASCO Mass Hanger from the ME-8979 Mass and Hanger Set suspended by a thread over a Small Pulley. Most of the components of the Statics System are held magnetically to the included workboard. This manual contains fifteen copy-ready experiments about the fundamentals of statics.

Table of Contents

Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1

Equipment . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1

Recommended Equipment . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

Spares Package. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

Components Package . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

About the Manual. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10

EXPERIMENTS

1. Hooke’s Law - Measuring Forces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11

2. Adding Forces - Resultants and Equilibriants . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

3. Resolving Forces - Components . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17

4. Torque - Parallel Forces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

5A. Center of Mass . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25

5B. Equilibrium of Physical Bodies . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

6. Torque - Non-Parallel Forces. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33

7. The Inclined Plane . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37

8. Sliding Friction and Static Friction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41

9. Simple Harmonic Motion - Mass on a Spring. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47

10. Simple Harmonic Motion - The Simple Pendulum . . . . . . . . . . . . . . . . . . . . . . . . . . 53

11A: Simple Harmonic Motion - Physical Pendulum . . . . . . . . . . . . . . . . . . . . . . . . . . . 57

11B: Minimum Period for a Physical Pendulum. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63

11C: Simple Harmonic Motion - Beam on a Spring . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67

12. Simple Machines - The Lever . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73

13. Simple Machines - The Inclined Plane. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77

14. Simple Machines - The Pulley . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81

15. Forces on a Boom . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83

Technical Support, Warranty, and Copyright. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85

iii

Statics System

iv 012-12876B

Statics System

If F 0 then a = 0=

net

----------

Statics Board

ME-9502

Introduction

The study of mechanics often begins with Newton’s Laws of Motion. The first law describes the conditions for an object to maintain its state of motion. If the net force on an object is zero, the acceleration of the object is zero.

The second law describes what happens if the net force on an object is not zero. The acceleration is directly proportional to net force, in the same direction as the net force, and inversely proportional to mass, or

Much of what is studied in an introductory course deals with the ways that forces interact with physical bodies. The PASCO Statics System is designed to help you investigate the nature of forces for the special case in which there is no acceleration. In other words, the vector sum of all the forces acting on the body is zero.

One reason to study the case of no acceleration is because it is easier to measure non-accelerating systems than it is to measure accelerating systems. A great deal can be learned about the vector nature of forces by studying the many ways in which forces can be applied to an object without causing acceleration.The second reason is that in our everyday experience, non-accelerated systems are the rule, not the exception.

Equipment

The ME-9502 Statics System consists of the Statics Board, Spares Package, Components Package, and Mass and Hanger Set.

ME-9503 Statics Board

The Statics Board is a ferrous metal plate approximately 45 by 45 centimeters (18 by 18 inches) with a writable white board finish on both sides.)

The board has rubber bumpers on its base. White board pens (or “dry erase” pens) can be used to write and draw directly on the board. The pens are available from stationery stores and the ink can be erased with a cloth or a white board eraser.

The Mounted Scale Assembly, Large and Small Pulley Assemblies, Balance Arm Assembly , Force Wheel Assembly, Torque Wheel Assembly, Inclined Plane Assembly, and Utility Mount Assembly all attach magnetically to t he board. Components can be stored on the rear side of the board when not in use. Except for the Inclined Plane Assembly, all the components that can mount on the board have a rubber ring on the base that protects the board and the component. The round magnetic base is 6.5 centimeters (cm) in diameter.

Statics System Equipment

Yes

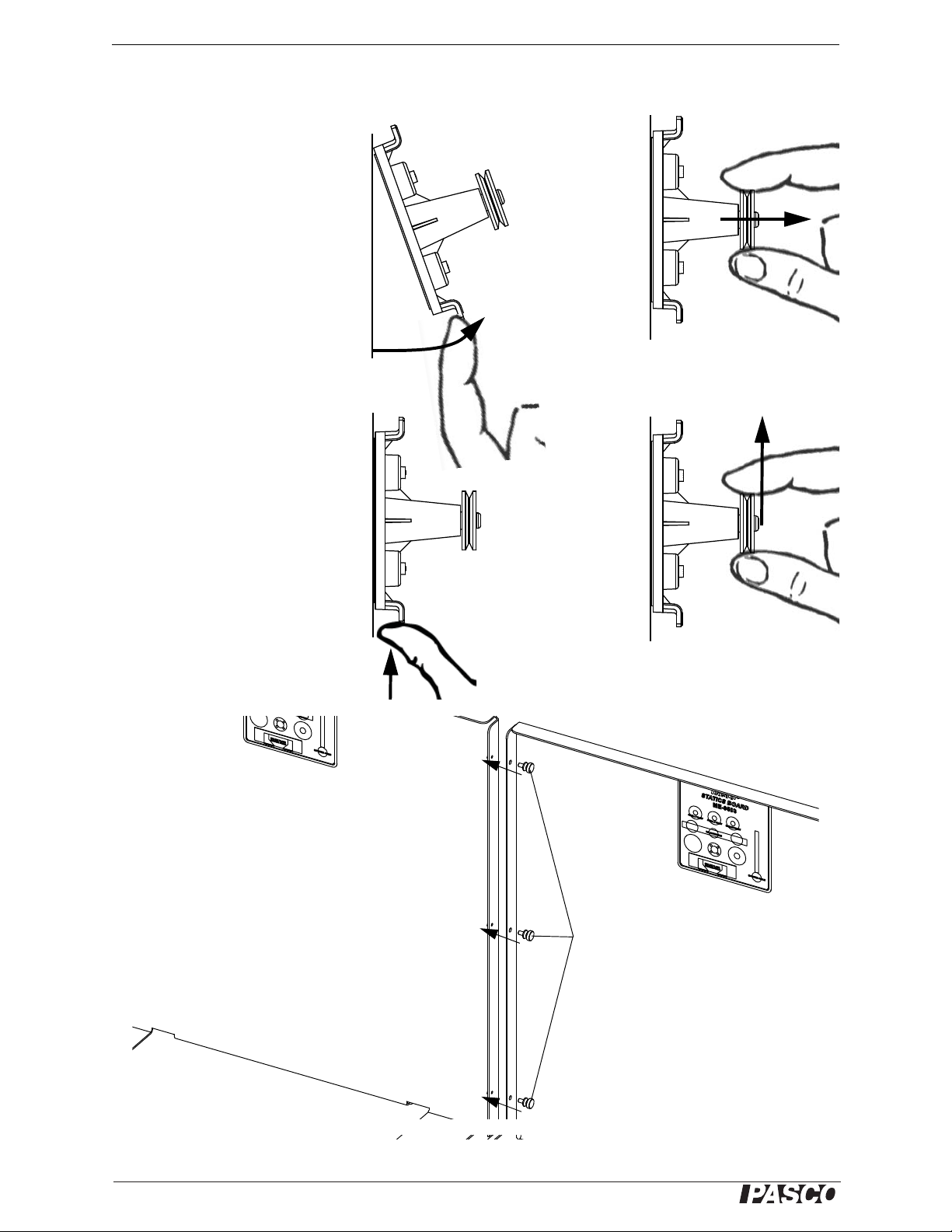
Moving Components on the Board

Rear view of Statics Boards

Connector

screws

Use the Connector screws to join two Statics Boards together.

Important

When moving or removing any of the magnetically mounted components from the board, handle the component by the magnetic base rather than by the component itself. This will reduce the strain on the component.

A second board (available separately) can be attached to the first board with the three included connector screws. To join the boards, remove the connector screws from the threaded holes on the side of the first board. Put the edge of the second board next to the first board. Align the holes and join the two boards with the connector screws

012-12876B

Model No. ME-9502 Recommended Equipment*

ME-8979 Mass and Hanger Set

PS-2201 5 N Load Cell

Amplifier Model

Load Cell Amplifier (PASPORT) PS-2198 Dual Load Cell Amplifier PS-2205 Load Cell Amplifier (ScienceWorkshop) CI-6464

ME-9504 Spares Package

Item Qty Item Qty

String Tie Assembly 3 Thumbscrew 6-32 by 5/8” (for Cord Clip) 2 Torque Indicator Assembly 6 Thumbscrew 4-40 by 1/2” (for balance arm protractor) 2 Nylon Thread, spool 1 Thumbscrew 6-32 by 1/4” (for balance arm pivot) 1 Cord Tensioning Clip 2 Washer 0.285” OD (for balance arm protractor) 2 Angle Indicator Arm 2 Plumb bob, brass (for inclined plane) 1

ME-9505 Components Package

Item Qty Item Qty

Large Pulley Assembly 1 Utility Mount Assembly 1 Small Pulley Assembly 2 Mass Cart Assembly 1 Mounted Scale Assembly 1 Torque Wheel Assembly 1 Balance Arm Assembly 1 Inclined Plane Assembly 1 Force Wheel Assembly 1 Friction Block Assembly 1 Double Pulley Assembly 1 Asymmetrical Plate 1

ME-8979 Mass and Hanger Set

Components from the ME-8979 P ASCO Mass and Hanger Set are used in most of the statics experiments. The set includes four mass hangers, a storage box, and twenty-seven masses ranging from 0.5 g to 100 g made from brass, aluminum, or polycarbonate plastic.

Recommended Equipment*

Load Cell and Load Cell Amplifier

A PS-2201 5 N Load Cell can be used to measure force. When it is connected through an amplifier to a PASCO interface or to a PASCO hand-held data logger, the force data from the Load Cell can be recorded, displayed, and analyzed.

*See the PASCO catalog or Web site at www.pasco.com for information about PASCO load cells, load cell amplifiers, interfaces, hand-held data loggers, and data acquisition software.

012-12876B 3

Statics System Spares Package (ME-9504)

Mass Balances

Stop Watch

Inner part

(force disk)

Outer part

Tab

Put threads through

this hole.

String Tie Assembly

T orque Indicator Assembly

Tie a thread to this hole.

Snap connects

to Torque Wheel

Stopwatch (ME-1234)

The PASCO Stopwatch has a liquid crystal display (LCD) with two display modes. Its precision is 0.01 seconds up to 3599.99 seconds, and 1 second up to 359999 seconds. Its memory holds up to nine event times.

Mass Balance

Use a mass balance such as the OHAUS Scout Pro Balance 2000 g (SE-8757A) or the OHAUS Cent-O-Gram Balance (SE-8725).

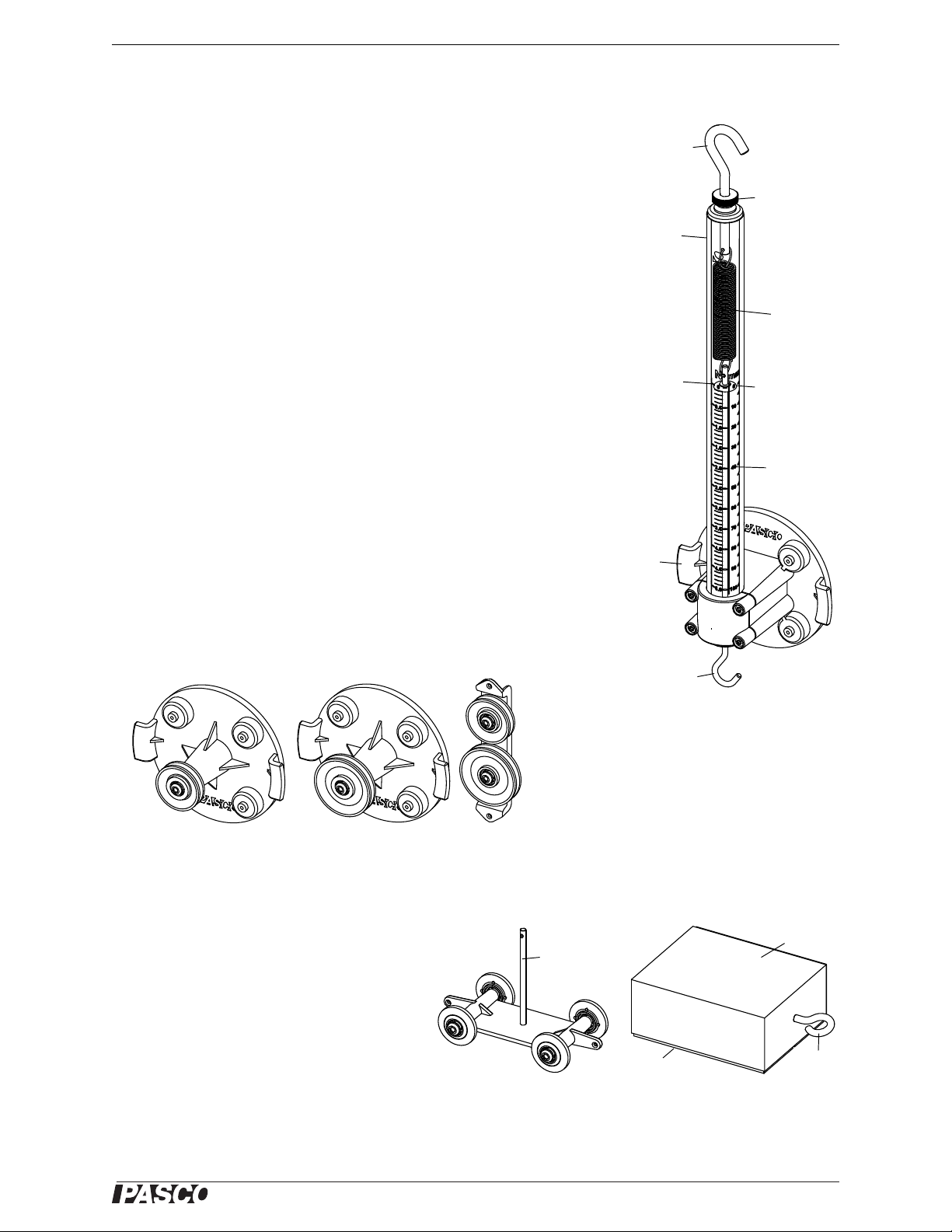
Mounted Scale Assembly (ME-9824A)

The Mounted Scale Assembly (included in the ME-9505 Components Package) is also available separately as a replacement or as an extra spring scale for experiments where measuring more than one force is required.

Spares Package (ME-9504)

The Spares Package contains some items which are used with assemblies from the Components Package. For example, the String Tie Assembly snaps into the center of the Force Wheel Assembly and the Torque Indicator Assembly snaps into the Torque Wheel Assembly. The Cord Tensioning Clip is used on the Utility Mount Assembly. Other items such as the Angle Indicator Arms, thumbscrews, washers, and brass weight are replacement parts.

String Tie Assembly.

When the String Tie Assembly is snapped into the center of the Force Wheel Assembly, you can use the apparatus to study force vectors. The String Tie Assembly has two parts: a clear plastic inner part (the “force disk”) that is free to move around in the center of the outer part, which has a center hole and two tabs that snap into the Force Wheel Assembly. (The two parts are not meant to be separated.)

Initial Setup

Get three threads that are 38 cm (15”) long. Put the threads through the hole in the inner part of the String Tie Assembly. Tie the ends of the threads together (for example, with an overhand knot) so that they cannot be pulled back through the inner part.

Torque Indicator Assembly

Note that the Torque Indicator Assembly has a snap that can be connected to the Torque Wheel Assembly . The other three assemblies are spares.

Initial Setup

Tie a 30 cm (12”) thread to each of three Torque Indicator Assemblies.

012-12876B

Model No. ME-9502 Components Package (ME-9505)

Spring

Indicator

disk

Scale

Base

Bottom

hook

Thumbnut

Top hook

Tab

Tube

Mounted Scale Assembly

Zero

mark

Small Pulley (2) Large Pulley Double Pulley Block

Mass Cart Friction Block

Felt

Hook

Rod for

stacking

masses

Wood

Components Package (ME-9505)

Mounted Scale Assembly

The mounted scale has four strong magnets in its base. The tube is marked in newtons (N), ounces (oz.) and millimeters (mm). The thumbnut allows the top hook to be raised or lowered in order to align the red indicator disk with the zero mark on the tube.

T o zero the scale, mount the scale on the statics board. Leave the bottom hook empty. Unscrew the thumbnut a few turns. Rotate the top hook clockwise (left-to-right) to lower the indicator disk and counter-clockwise (right-to-left) to raise the indicator disk. When the disk is aligned with the zero mark on the tube label, tighten the thumbnut to hold the top hook in place.

To move the scale on the statics board, hold the scale by the tabs on the base and push or pull the scale to the desired location. To remove the scale from the statics board, lift one or both of the tabs on either side of the base away from the board.

Large and Small Pulleys and Double Pulley Block

The Statics System comes with two Small Pulleys and one Large Pulley mounted on magnetic bases. It also includes a Double Pulley Block (that does not have a magnetic base). The Double Pulley Block is designed for block-and-tackle experiments. A support thread can be tied to either end of the Double Pulley Block.

All the pulleys have low friction ball bearings. The smaller pulleys are 2.41 cm (0.850”) outside diameter (OD) and 1.65 cm (0.650”) inside diameter (ID). The larger pulleys are 2.79 cm (1.10”) OD and 2.28 cm (0.90”) ID.

Please use the tabs on the base of the components when moving them around or removing them from the statics board.

Mass Cart and Friction Block

The Mass Cart and Friction Block are designed to be used with the Inclined Plane Assembly. The Mass Cart has low friction ball bearings in each wheel and a metal rod in the center for stacking extra masses. A thread can be attached at either end.

The Friction Block is made of beech wood. It has an “eye” hook at one end and is covered with felt on the bottom and one side. Its dimensions are 2.54 cm by 5.08 cm by 6.35 cm (1.0” by 2.0” by 2.5”).

012-12876B 5

Statics System Components Package (ME-9505)

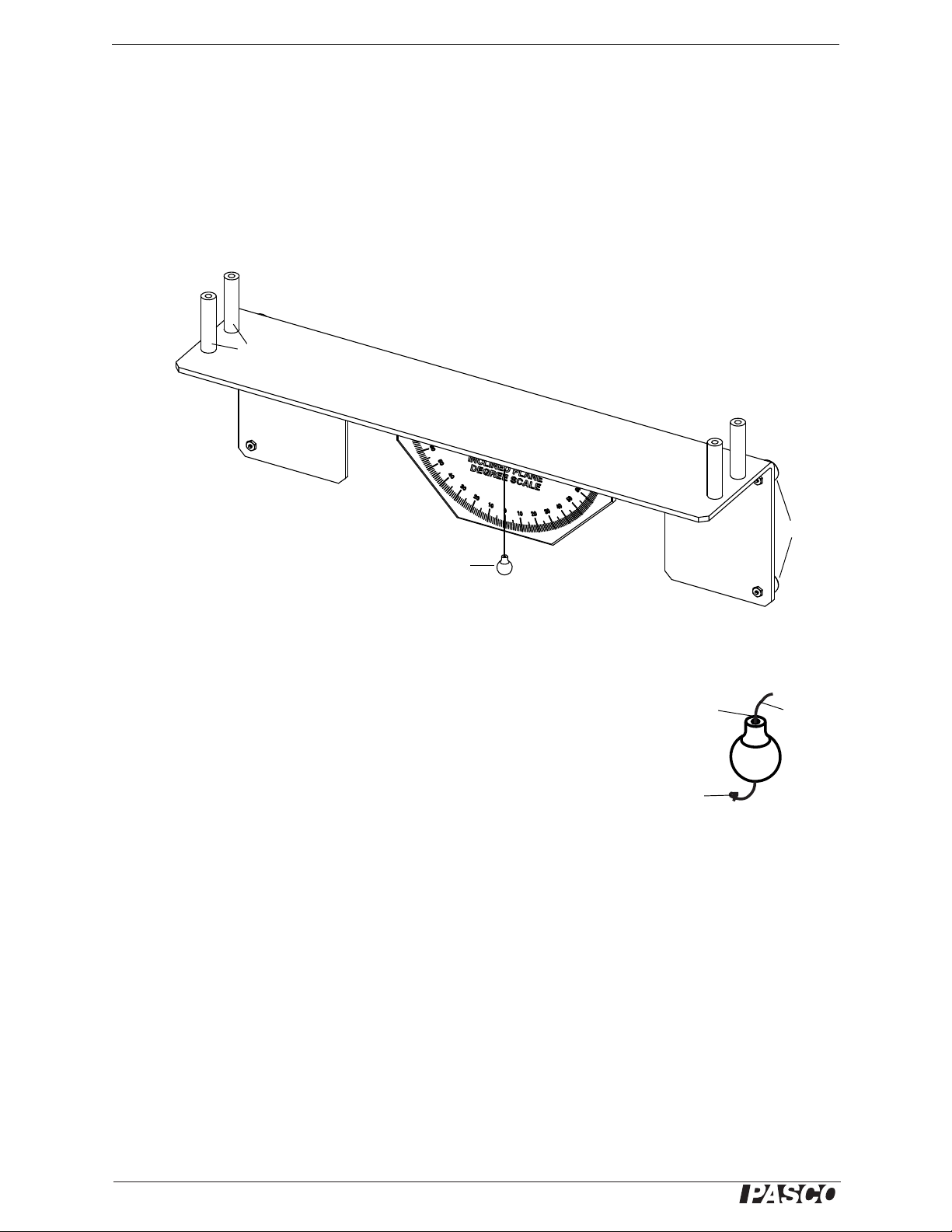
Inclined Plane Assembly

End stops

Plumb bob

Brass Weight

Put thread

through

the hole.

Tie a

knot.

Thread

Inclined Plane Assembly

The Inclined Plane Assembly has four strong magnets on its back side that hold it in position on the Statics Board.

CAUTION: The magnets on the Inclined Plane Assembly are not covered with protective material. Be careful to firmly hold the inclined plane when placing it on the board so that the magnets are not damaged by “snapping” against the board.

The inclined plane has end stops at each end of the plane and a degree scale with a brass plumb bob for determining the angle of the incline.

Replacing the Plumb Bob

The ME-9504 Spares package includes a spare plumb bob (brass weight). To replace the plumb bob, use a Phillips head (“crosshead”) screwdriver to loosen the screw on the back of the degree scale. Remove the piece of thread and get a new piece approximately 10 cm (4”) long. Put one end of the thread through the hole in the brass weight and tie a double knot in that end of the thread so it will not slip back through the hole. Put the other end of the thread through the small hole near the top of the degree scale. Adjust the length of the thread so the plumb bob can swing freely and then wind the end of the thread around the screw on the back. Tighten the screw to hold the thread in place.

Magnets

012-12876B

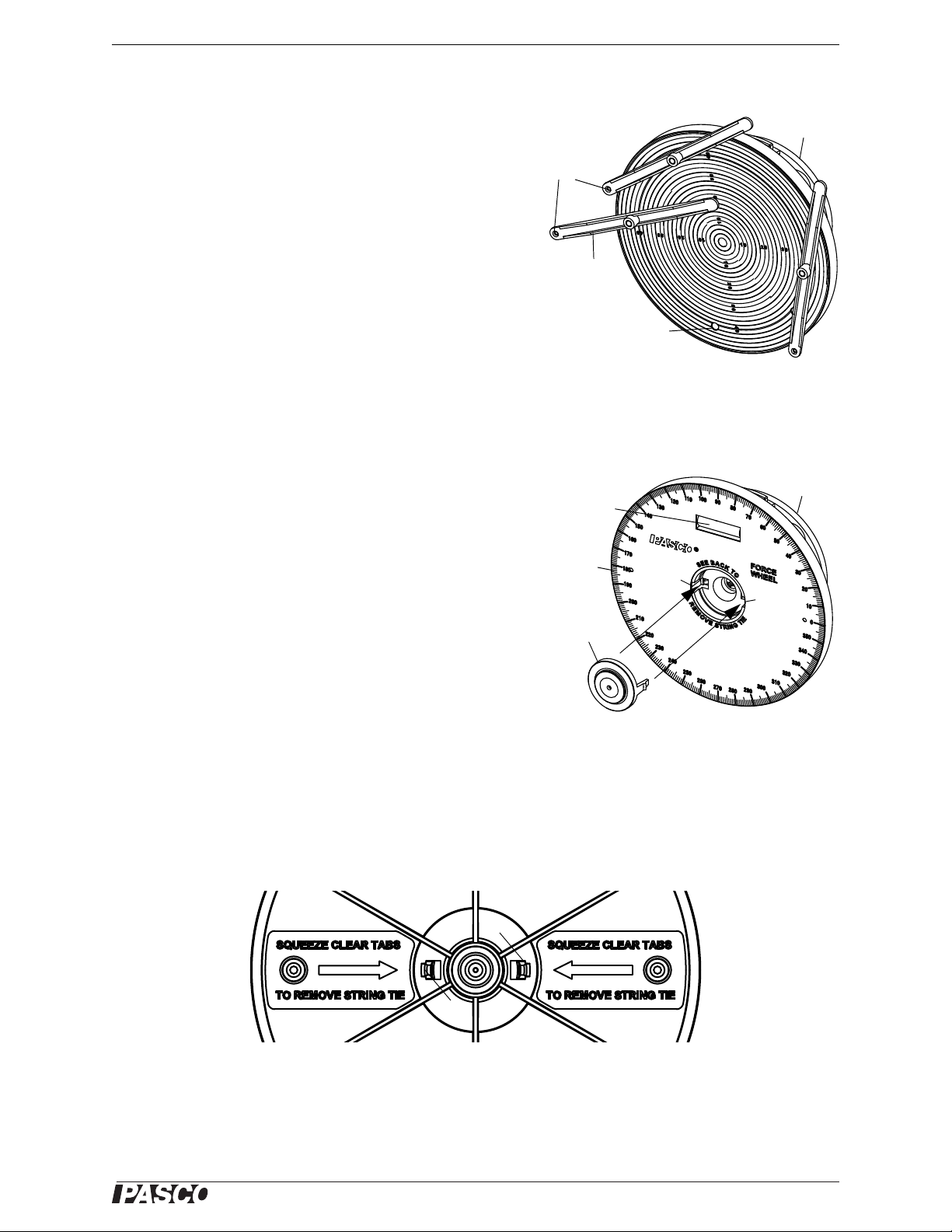
Model No. ME-9502 Components Package (ME-9505)

Torque Wheel Assembly Torque Indicator Assembly

Tie a thread

to the hole.

Hole

Base

Torque

Indicator

Force Wheel Assembly String Tie Assembly

Notch

String

Tie

Bubble

level

Base

Degree

scale

Notch

Tab

Torque Wheel Assembly and Torque Indicator Assembly

The Torque Wheel Assembly has a 5 cm radius disk with a label that has concentric circles 2 mm apart. The disk rotates freely on a ball bearing and has five holes for attaching a T orque Indicator Assembly. The Torque Indicator snaps into the hole and rotates freely. Tie a 30 cm (12”) thread to the hole in the end of each indicator.

To remove a Torque Indicator, firmly grasp the indicator at the pivot in the middle and pull outwards while pushing on the end of the snap from the other side of the disk.

Force Wheel Assembly and String Tie Assembly

The Force Wheel Assembly has a 5 cm radius disk with a 360° label and a bubble level for leveling the Force Wheel. Unlike the Torque Wheel, the Force Wheel does not rotate freely but the disk can be turned in order to level the wheel. Once leveled, the wheel will stay in position until moved again.

REMINDER: Be sure to put tie three threads through the hole in the center of the String Tie before putting the String Tie into the Force Wheel.

The String Tie Assembly snaps into the hole in the center of the Force Wheel Assembly. Align the tabs on the String Tie with the notches inside the hole at the center of the Force Wheel. Push the String Tie firmly into the Force Wheel until both tabs “snap” into place. Note that the surface of the outer part of the String Tie will be very slightly below the surface of the Force Wheel, but the inner part of the String Tie will be flush with the Force Wheel.

Removing the String Tie Assembly

If you need to remove the String Tie (in order to replace the threads, for example), remove the Force Wheel from the Statics Board. On the underside of the disk are instructions about removing the String Tie.

Remove String Tie

012-12876B 7

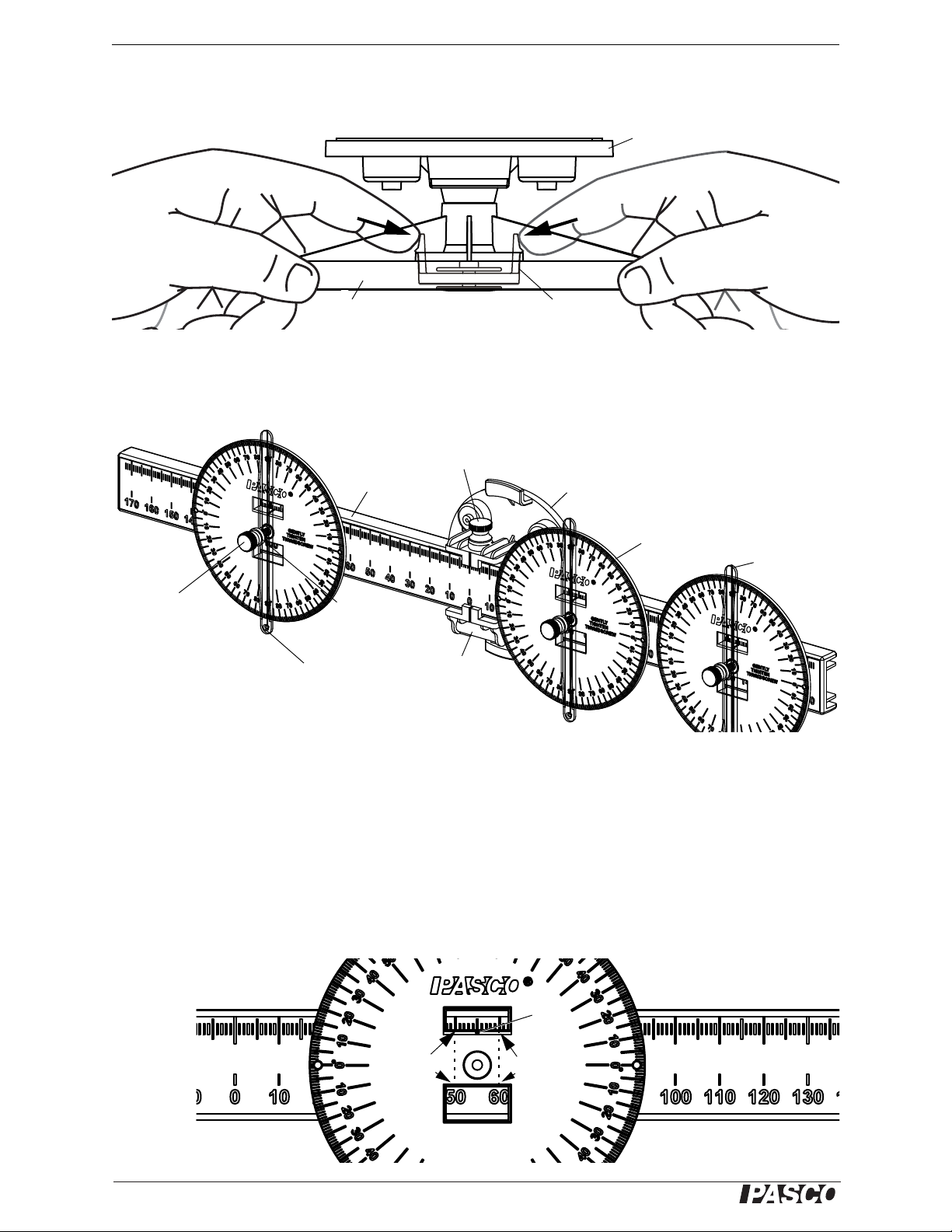
Statics System Components Package (ME-9505)

String Tie

Base

Force Wheel

Remove String Tie

Beam

Pivot base

Bubble

level

Protractor

Tie a thread to the hole.

Angle Indicator

Thumbscrew

Washer

Balance Arm Assembly

Indicator

line

This tick

mark is at

50 mm.

This tick

mark is at

60 mm.

Note: The Angle Indicator is not shown in this example.

Reading the Scale

(Imagine that the Force Wheel disk is transparent so that you can see the String Tie.) Hold the Force Wheel as shown and push the clear plastic tabs inward with your forefingers until the String Tie pops out of the Force Wheel.

Balance Arm Assembly

The Balance Arm Assembly consists of a Beam, a Pivot, and three Protractors that can be mounted on the beam. Each protractor has a transparent Angle Indicator. The pivot has a bubble level for leveling the beam.

Adjust the beam by loosening the thumbscrew on the top of the pivot and sliding the beam one way or the other. Move the protractors by loosening the thumbscrew at the center of the protractor and sliding the protractor along the beam. Note that not all experiments need three protractors.

Reading the Scale

Read the position of the protractor relative to the midpoint through the two rectangular windows on the protractor. The bottom window shows the position to the nearest centimeter, and the top window shows the position to the millimeter. The top window has a small indicator line on its bottom edge. The bottom window in the example shows the position as between 50 mm and 60 mm and the top window shows it at 55 mm.

012-12876B

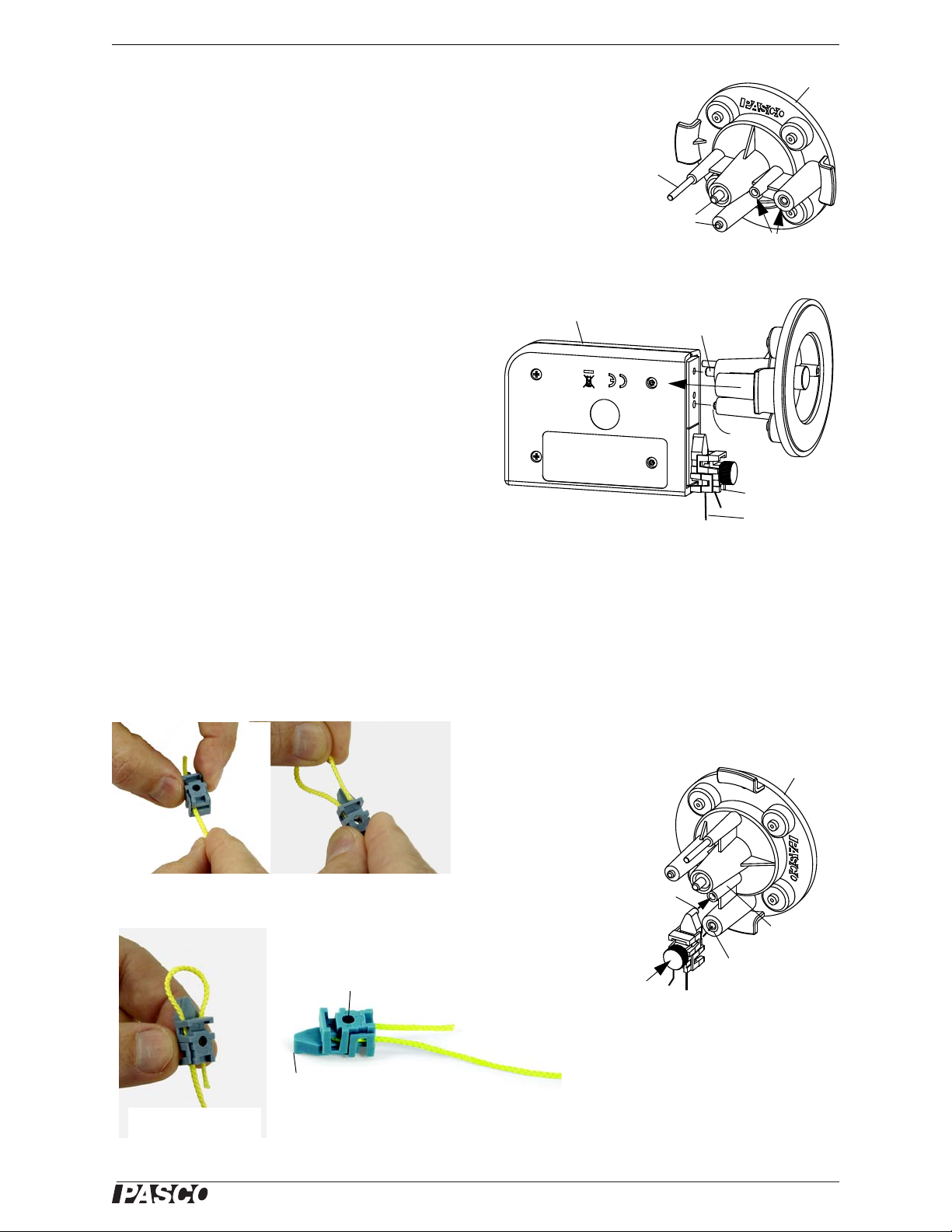
Model No. ME-9502 Components Package (ME-9505)

Utility Mount

Base

Rod for

Asymmetrical

Plate

Thumbscrew and

post for Load Cell

Attach a Cord

Clip here.

Attaching a Load Ce ll

Thumbscrew

Post

Cord Clip

Thread

Load Cell

Figure A: Hold the cord clip so the two parts separate

Figure B: Loop the thread back through the cord clip

Figure C: The thread goes around the screw hole

Figure D: The cord clip is ready to be attached to a Utility Mount or a Load Cell

Thumbscrew

hole

Peg

Threaded

post

Peg

Attaching a Cord Clip

Small

diameter

post

Base

Align the peg of the Cord Clip with the hole in the small diameter post. Use the 5/8” thumbscrew to attach the Cord Clip to the threaded post.

Utility Mount Assembly

The Utility Mount has several functions. It can support a PS-2201 5 N Load Cell, it has a rod from which you can hang the Asymmetrical Plate, and the included Cord Tensioning Clip allows you to connect a thread to the mount. The thumbscrew for the Load Cell is “captured” by a rubber O-ring so that it will not fall out of the mount.

Attaching a Load Cell

You can use a 5N Load Cell (available separately) with the Statics System to measure a force in much the same way that the Mounted Scale can be used to measure a force. (In fact, after the Load Cell is calibrated, it could be used to calibrate the Mounted Scale.) First, loop a thread through a Cord Clip (see below) and then attach the clip to the “LOAD” position that is imprinted on the side of the Load Cell. Next, attach the Load Cell’s “FIXED” end to the thumbscrew and post on the Utility Mount.

Using a Cord Clip

The Cord Clip connects to the Utility Mount so that to a thread and be attached to the Mount itself. Use the Clip to attach a thread to a Load Cell (see above) that is mounted on the Utility Mount.

It is best to attach the thread through the clip before the clip is installed on the mount or on a Load Cell. The Cord Clip has two parts but it does not come apart. Start by holding the top part of the clip so the two parts are separate as shown in Figure A, leaving an opening through which the thread can be threaded. Insert the thread into the flat end (not the pointed end) of the clip. Loop the thread back through the clip as shown in Figure B and Figure C. Attach the Cord Clip to the Load Cell or the Utility Mount using the thumbscrew to tighten the clip shut.

012-12876B 9

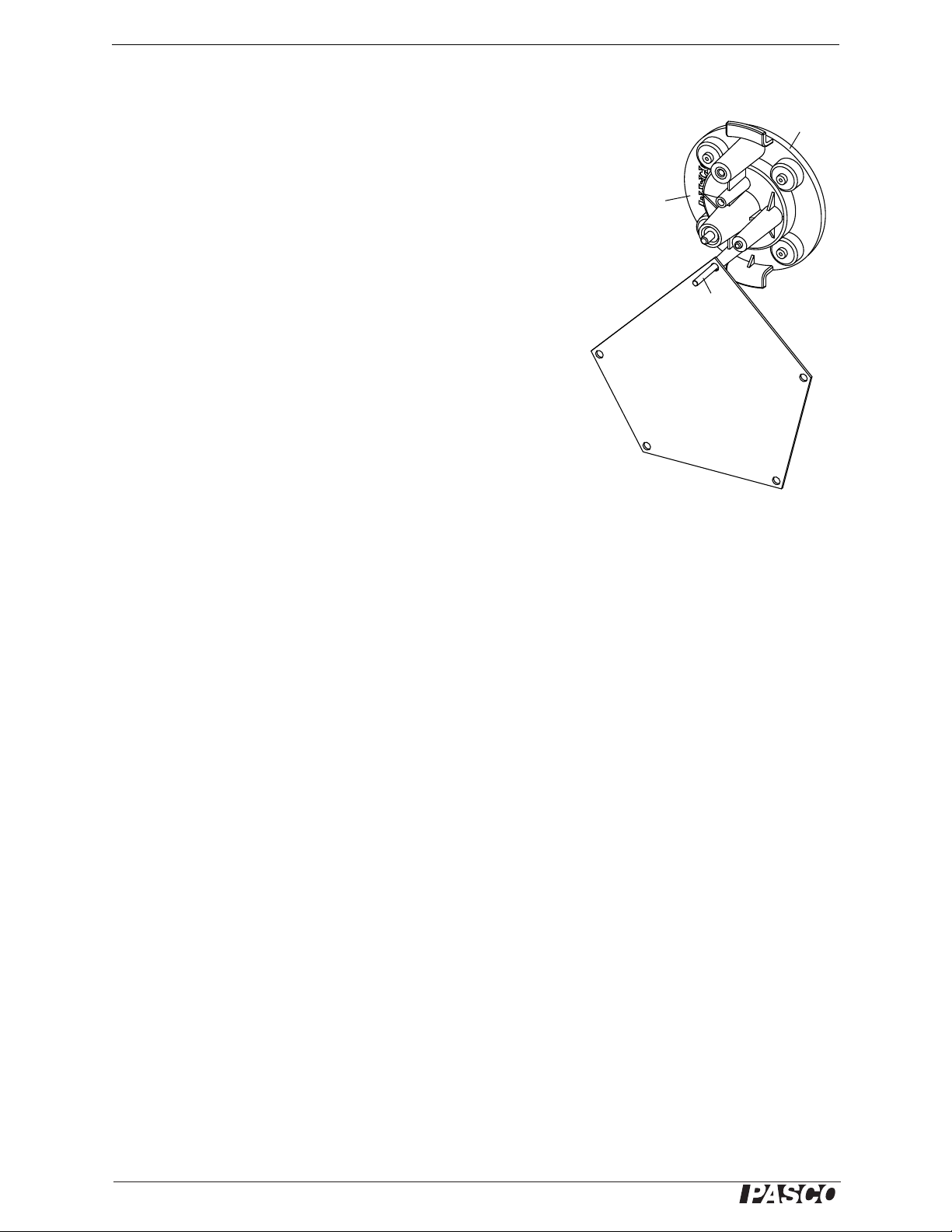
Statics System About the Manual

Rod

Asymmetrical Plate

Base

Suspend the Asymmetrical Plate

Utility

Mount

Asymmetrical Plate

The Asymmetrical Plate is a five-sided polygon with a small hole at each corner. The Utility Mount has a slender metal rod designed to support the Asymmetrical Plate so that the plate can swing on the rod until it reaches equilibrium.

About the Manual

The ME-9502 Statics System provides an introduction to static mechanics. The experiments first introduce force as a vector quantity and then build on this concept so that students will understand the equilibrium of a physical body under the application of a variety of forces and torques. Experiments to demonstrate simple harmonic motion with a pendulum and a spring/mass system are also included.

The experiments are presented in three groups: Basic Experiments, Advanced Experiments, and Simple Machines. Each experiment is copy-ready.

Basic Experiments provide the essentials for a solid introduction to static mechanics. The concepts of vector forces, torques, and center of mass are explored.

Advanced Experiments allow the student to combine the principles already studied to understand such phenomena as static equilibrium. Friction and simple harmonic motion are also investigated.

Simple Machines provide an opportunity for the student to investigate applications of the principles already studied and also to introduce important new concepts. Levers, inclined planes, and pulley systems are studied using the principles of static equilibrium, work, and conservation of energy.

In addition to the equipment in the Statics System, a few common items such as pencils, rulers, protractors, paper, a stop watch, and a mass balance will be needed for some experiments. Check the “Equipment Needed” section at the beginning of each experiment.

NOTE: Vector quantities are designated with boldface font, such as F, W, or F

. When the same letters are used in

normal style font, they refer to the magnitude (size) of the vector quantity. Since the vector nature of torques is not introduced in these experiments, boldface font is not used to designate torques.

012-12876B

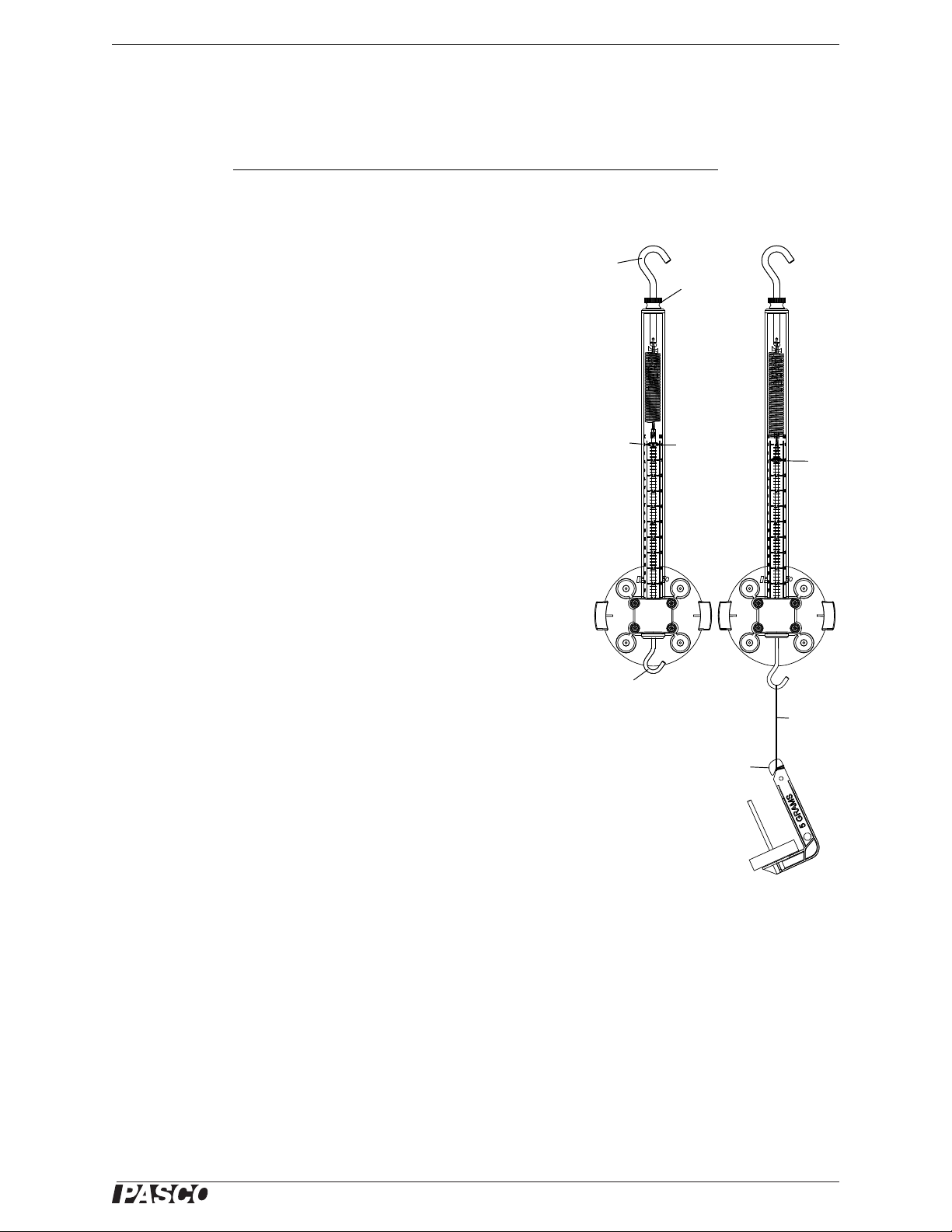
Model No. ME-9502 Exp. 1: Hooke’s Law—Measuring Force

Top

hook

Thumbnut

Indicator

Zero

mark

Bottom

hook

Figure 1.1: Setup and Procedure

Mass

hanger

Thread

Exp. 1: Hooke’s Law—Measuring Force

Equipment Needed

Item Item

Statics Board Mounted Spring Scale Mass and Hanger Set Thread

Introduction

At a practical level, a force is simply a push or a pull. A force is also a vector quantity that has magnitude (size) and direction. There are different ways to apply and measure a force. One way to apply a force is to hang a known mass, and determine the force based on the assumption that gravity pulls the mass downward toward the center of the earth with a magnitude F = mg, where m is the known mass and g is the acceleration due to gravity (9.8 m/s be expressed as 9.8 N/kg. Another way to apply a force is to pull with a spring. A spring stretches when it is pulled, and if he amount it stretches is directly proportional to the applied force, then the spring can be calibrated to measure unknown forces. In this experiment you will use the known force associated with gravity pulling on calibrated masses to investigate the properties of the Mounted Spring Scale.

). Note that the value of g can also

Hooke’s Law

Hooke’s Law describes the relationship between the amount of force and the amount of stretch for an “ideal” spring. The law states that the force and the stretch are directly proportional. In other words, the ratio of the force divided by the stretch is a constant, k. The constant is called the “spring constant”.

Setup

Place the Spring Scale on the Statics Board so that the spring hangs vertically in the tube. Do not hang anything on the bottom hook. The indicator must be aligned with the zero mark on the label. To zero the Spring Scale, loosen the thumbnut at the top of the scale. Turn the top hook clockwise to lower the indicator, and counter-clockwise to raise the indicator. Once the indicator is aligned with the zero mark on the label, tighten the thumbnut.

Procedure

1. Attach a thread to the bottom hook and hang a mass hanger from the thread.

2. Add mass to the mass hanger until the indicator is aligned with the 10 mm mark on the label. Adjust the mass

3. Record the total amount of mass (including the mass hanger) in the data table. Record the uncertainty.

so that the indicator is as close as possible to the mark. Estimate the uncertainty in your measurement. (If you add or remove 0.5 g, can you see a change? What happens if you add or remove 1 g or 2 g?)

4. Add more mass to the mass hanger until the indicator is aligned with the 20 mm mark on the label and record

the total amount of mass and the uncertainty.

5. Repeat the process to move the indicator down by 10 mm each time until the indicator is aligned with the 80

mm mark. Record the total mass and the uncertainty each time.

012-12876B 11

Statics System Exp. 1: Hooke’s Law—Measuring Force

Weight - Spring Scale

Weight

---------------------------------------------------- -

X100

Data Table

Spring Displacement (m) Mass (kg) Uncertainty Weight (N)

0.010 m (10 mm)

0.020 m (20 mm)

0.030 m (30 mm)

0.040 m (40 mm)

0.050 m (50 mm)

0.060 m (60 mm)

0.070 m (70 mm)

0.080 m (80 mm)

Calculations

1. Using the formula F = mg, where m is the mass and g is the a cceleration due to gravity, calculate the weight in

newtons for each trial. Record the weight in the data table. (To get the correct force in newtons, you must convert the mass value to kilograms.)

2. On a sheet of graph paper, construct a graph of Weight (N) versus Spring Displacement (m) with Spring Dis-

placement on the x-axis.

3. Draw the line that best fits your data points on the graph. The slope of this line on the graph is the ratio of the

force that stretched the spring divided by the amount of stretch. In other words, the slope is the spring constant, k, for the spring in the Spring Scale.

4. Determine the spring constant, k, from your graph and record the result. Remember to include the units (new-

tons per meter).

Spring constant = _____________________________

Using a Spring Scale to Measure Force

• Hang 160 g (0.160 kg) on the Spring Scale. Calculate the weight based on F = mg. Read the force in newtons

from the Spring Scale.

Weight = _______________ Spring Scale reading = ______________

• How does the measurement from the Spring Scale compare to the actual weight?

• Calculate the percent difference:

Percent Difference = _______________

Questions

1. Hooke’s Law states that the relationship between force and displacement in springs is a linear relationship. If

2. In what way is Hooke’s Law useful when calibrating a spring for measuring forces?

3. On your graph of Weight versus Spring Displacement, did the best fit line go through the origin (zero)? If it

Hooke’s Law was not valid, could a spring still be used successfully to measure forces? If so, how?

didn’t, what does that mean?

012-12876B

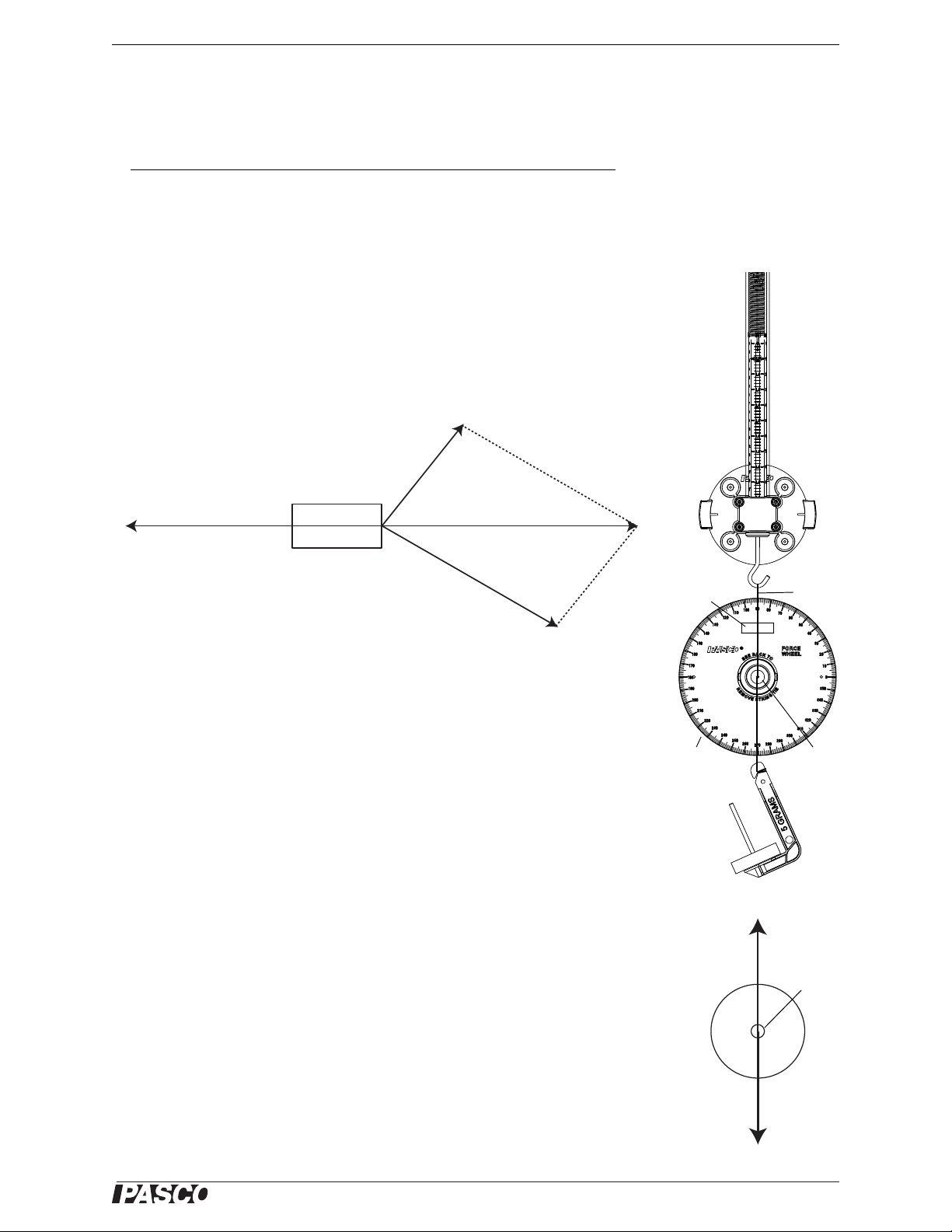
Model No. ME-9502 Exp. 2: Adding Forces—Re sultants and Equilibriants

Figure 2.2: Setup

Force

Wheel

Bubble

level

Force

disk

Spring

Scale

Thread

Force

disk

Fg = mg

= mg

Figure 2.1: Resultant and Equilibriant

Car

Exp. 2: Adding Forces—Resultants and Equilibriants

Equipment Needed

Item Item

Statics Board Mounted Spring Scale Force Wheel Large and Small Pulleys Mass and Hanger Set Thread

Theory

In figure 2.1, Person A and Person B are pulling with forces represented by FA and F

on a car stuck in the mud. Since these forces are acting on the same point of the

car, they are called concurrent forces. Each force is defined both by is direction (the direction of the vector arrow), and by its magnitude, which is proportional to the length of the vector arrow. (The magnitude of the force is independent of the length of the tow rope.)

The total force applied by the two people can be determined by adding vectors F and F

. The parallelogram method is used in the example. The diagonal of the par-

allelogram is called the resultant, F combination of F

and FB.

. It shows the magnitude and direction of the

Because the car is not moving, the net force on the car must be zero. The friction between the car and the mud is equivalent to the resultant force, F opposing force is called the equilibriant, F the resultant, F

Setup

, and it has the opposite direction of the resultant.

. This force has the same magnitude as

. This equivalent

Set up the Spring Scale and Force Wheel on the Statics Board as shown. Twist the Force Wheel until the bubble level shows that the Force Wheel is level. Attach one of the threads from the force disk (inner part of the String Tie) in the center of the Force Wheel to the bottom hook of the Spring Scale. Connect a second thread to a mass hanger (let the third thread dangle). Add 80 g (0.080 kg) to the mass hanger.

Adjust the Spring Scale up or down so that the force disk is centered in the Force Wheel. The mass hanger applies a force downward, F ity, where m is the total mass of the mass hanger). When the force disk is centered, the system is in equilibrium, so the downward force F equal and opposite force, the equilibriant, F

, is applied by the Spring Scale.

. In this case, the equilibriant force,

= mg (the force due to grav-

must be balanced by an

012-12876B 13

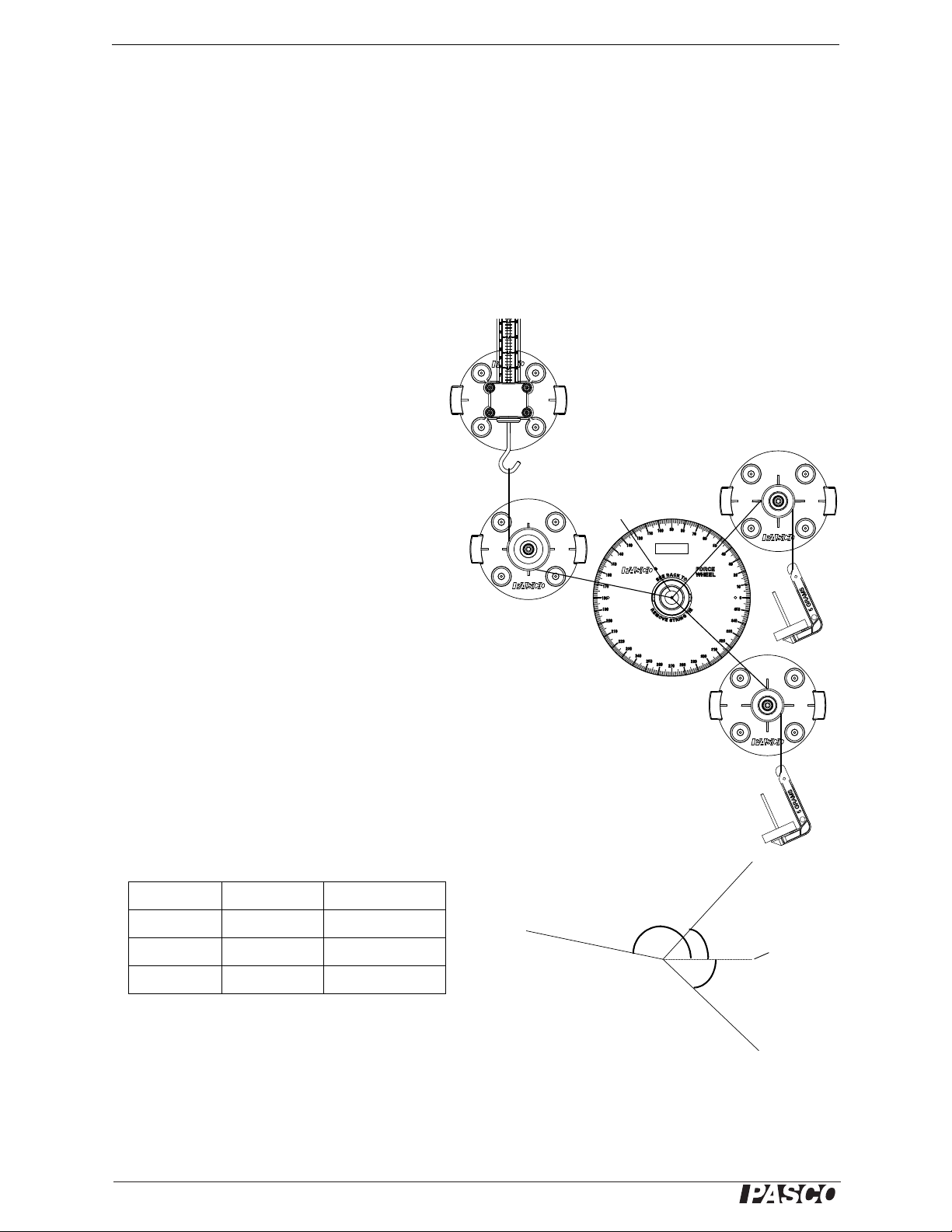
Statics System Exp. 2: Adding Forces—Resultants and Equilibriants

Figure 2.3: Find the Equilibriant

Small

Pulley

Small

Pulley

Large

Pulley

Force

Wheel

Force

disk

Spring

Scale

Vector diagram



Zero

line on

the

Force

Wheel

Procedure: Two Forces

1. Add or remove 0.5 g to the mass hanger. Did the force disk move away from the center position? How much

can you change the mass on the mass hanger without changing where the force disk is centered?

2. What are the magnitude and direction of F

• F

: Magnitude ________________ Direction ________________

, the gravitational force applied by the hanger, where Fg = mg?

3. Use the Spring Scale and Force Wheel to determine the magnitude and direction of F

• F

: Magnitude ________________ Direction ________________

Procedure: Three Forces

1. Attach the Large Pulley and the two Small

Pulleys to the Statics Board and move the Spring Scale as shown in the figure.

2. Attach threads to the bottom hook of the

Spring Scale and to mass hangers over the Small Pulleys.

3. Add 30 g (0.030 kg) to the upper mass

hanger and add 50 g (0.050 kg) to the lower mass hanger.

4. Adjust the Large Pulley and the Spring

Scale so that the force disk is centered in the Force Wheel.

, the equilibriant.

5. How much can you change the mass on the

hangers and still leave the force disk centered in the Force Wheel?

Data

Record the values of the hanging masses M1 and M

(including the mass of the mass hangers), the

magnitude in newtons of the forces F

, and the angles 1, 2, and E with respect to

the zero-degree line on the Force Wheel..

Mass (kg) Force (N) Angle (°)



, F2, and

012-12876B

Model No. ME-9502 Exp. 2: Adding Forces—Re sultants and Equilibriants

Analysis

1. On a separate piece of graph paper, use the values you recorded in the table to construct a vector diagram for F

, F2, and FE. Choose an appropriate scale, such as 2.0 centimeters per newton, and make t he l engt h of eac h

vector proportional to the magnitude of the force. Label each vector and indicate the magnitude of the force it represents.

2. On your vector diagram, use the parallelogram method to draw the resultant of F F

. Measure the length of FR to determine the magnitude of the resultant force and record this magnitude on

and F2. Label the resultant

your vector diagram.

3. On your diagram, measure the direction of F angle 

relative to the horizontal axis of your diagram and label the

Questions

1. Does the magnitude of the equilibriant force vector, FE, exactly balance the magnitude of the resultant force vector, F

2. Ho w does the dire ction of the equilibriant force vector, F tor, F

. If not, what are some possible reasons for the difference?

, compare to the direction of the resultant force vec-

Extension

Vary the magnitudes and directions of F1 and F2 and repeat the experiments.

012-12876B 15

Statics System Exp. 2: Adding Forces—Resultants and Equilibriants

012-12876B

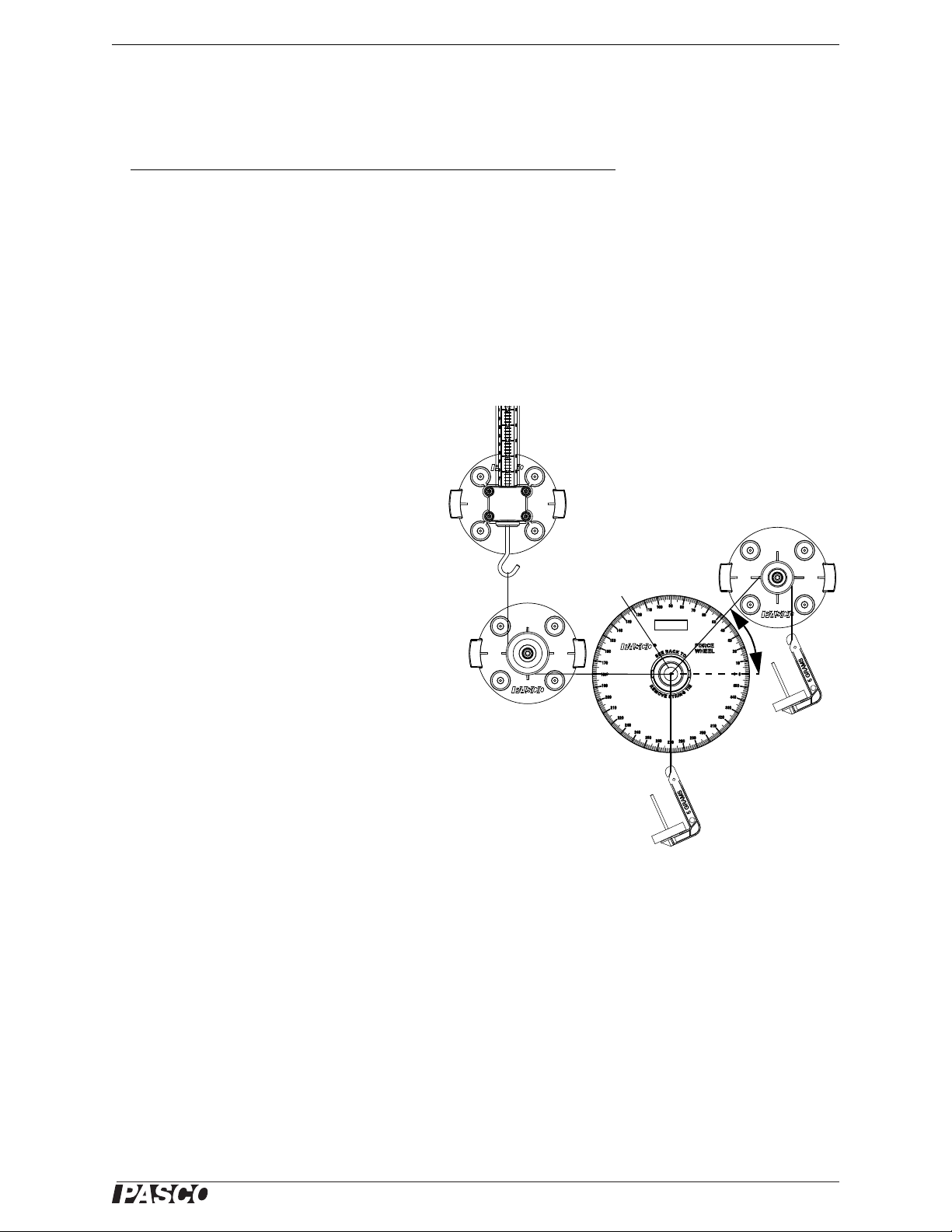
Model No. ME-9502 Exp. 3: Resolving Forces—Components

-F

Spring

Scale

Pulley

Force

Wheel

Force

disk

Figure 3.1: Setup

Exp. 3: Resolving Forces—Components

Equipment Needed

Item Item

Statics Board Mounted Spring Scale Force Wheel Pulleys (2) Mass and Hanger Set Thread

Theory

In experiment 2, you added concurrent forces vectorially to determine the magnitude and direction of the combined forces. In this experiment, you will do the reverse: you will find two forces which, when added together, have the same magnitude and direction as the original force. As you will see, any force vector in the X-Y plane can be expressed as a vector in the x-direction and a vector in the y-direction.

Setup

Set up the equipment as shown in the figure. As shown, create a force vector F by hanging a mass, M center of the Force Wheel over a pulley.

, on a thread from the force disk in the

Set up the Spring Scale and a pulley so that the thread from the Spring Scale is horizontal from the bottom of the pulley to the force disk. Hang a second mass hanger directly from the force disk in the center of the Force Wheel.

Now pull the Spring Scale toward or away from the pulley to adjust the horizontal or x-component of the force, F on the vertical mass hanger , M tical or y-component of the force, F

. Adjust the amount of mass

, to adjust the ver-

. Adjust the

x- and y-components in this way until the force disk is centered in the Force Wheel.

Note: These x- and y-components are actually the x- and y-components of the equilibriant, F

of the force F, rather than the components of F itself.

Procedure 1

1. Calculate and record the magnitude of F (based on F = mg). Use the Force Wheel to measure the angle of F and then record the angle.

• Magnitude, F = _________________ Angle,  = ____________________

2. Record the magnitude of the x-component of the equilibriant of F and calculate and record the y-component of the equilibriant of F.

• X-component = _________________ Y-component = ____________________

012-12876B 17

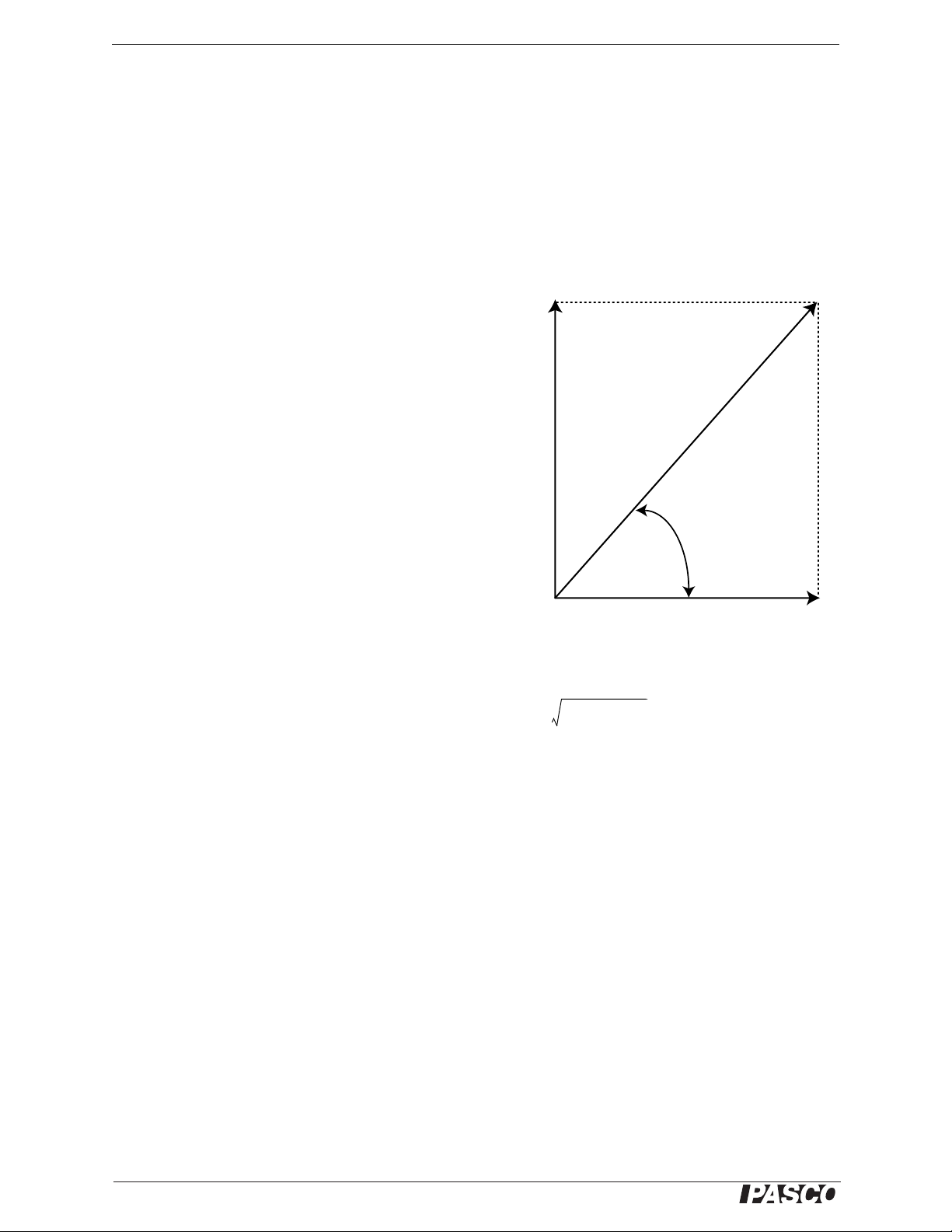
Statics System Exp. 3: Resolving Forces—Components

Fx = F cos 

= F sin 



Figure 3.2: Vector components

Rx2Ry



----- -





atan=

3. What are the magnitudes of F

• F

= _________________ Fy = ____________________

and Fy, the x- and y-components of F?

4. Change the magnitude and direction of the force vector F and repeat the experiment.

5. Record the magnitude and angle of the new force vector, F, and the magnitudes of F

• Magnitude, F = _________________ Angle,  = ____________________

• F

= _________________ Fy = ____________________

Background

Why use components to specify vectors? One reason is that using components makes it easier to add vectors mathematically. The figure shows the x- and y-components of a vector of length F, and an angle  with respect to the x-axis. Since the components are at right angles to each other, the parallelogram used to determine their resultant is a rectangle. Using right triangle AOX, the components of F can be calculated:

and Fy.

• F

, the x-component of F is F cos 

• F

, the y-component of F is F sin 

If you want to add several vectors, find the x- and y-components for each vector. Add all the x-components together and all the y-components together. The resulting values are the x- and y-components for the resultant. The magnitude of the resultant, F

the resultant’s x-component (R

) and the y-component (Ry).

, is the square root of the sum of the squares of

The angle of the resultant is the arctangent of the y-component divided by the x-component.

Procedure 2

Make sure that the Force Wheel is level. Set up a new force, F. Put one thread from the force disk over a pulley and tie a mass hanger to the end of the thread. Add mass to the mass hanger.

1. Calculate and record the magnitude of the force, F, that you set up with the pulley and mass hanger. Use the Force Wheel to determine the angle.

• Magnitude, F = _________________ Angle,  = ____________________

2. Calculate the magnitudes of F and F

• F

= _________________ Fy = ____________________

= F sin .)

3. Now, set up the Spring Scale with a pulley and a thread from the force disk so it can apply the x-component, F

, of the new force F. Adjust the Spring Scale so that it pulls the force disk horizontally by the amount, Fx.

4. Next, attach a mass hanger to the third thread from the force disk so the thread hangs vertically. Add mass to the hanger so it pulls the force disk vertically by the amount, F

and Fy, the x- and y-components of the new force, F. (Remember, Fx = F cos 

012-12876B

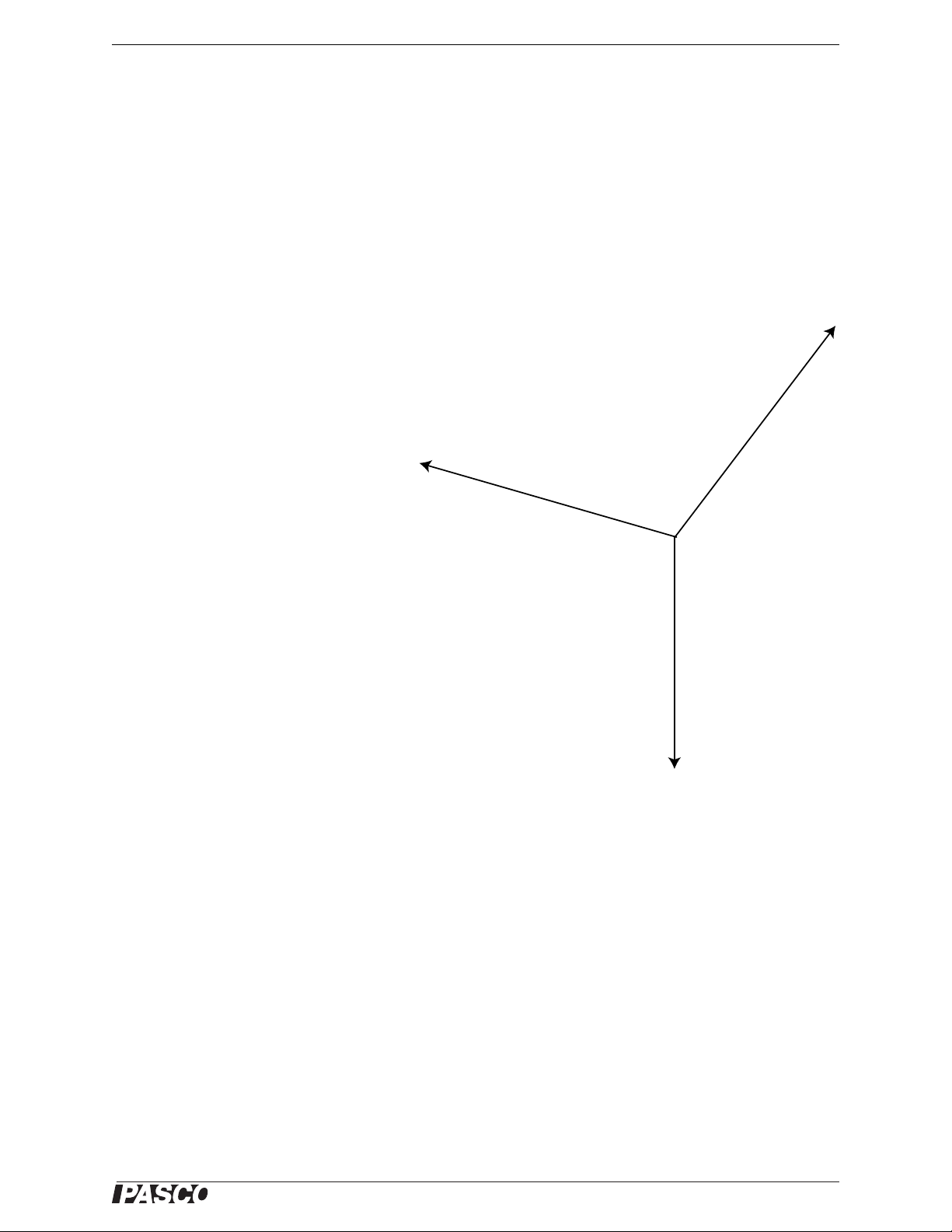
Model No. ME-9502 Exp. 3: Resolving Forces—Components

NOTE: The diagram is

not to scale.

Figure 3.3: Extension vectors

Question

1. Is the force disk at equilibrium in the center of the Force Wheel?

2. Why or why not?

Extensions

1. Generally it is most useful to find the components of a vector along perpendicular axes, as you did above. However, it is not necessary that the axes be perpendicular. If time permits, try setting up the equipment to find the components of a vector along non-perpendicular axes. Use pulley to redirect the component forces to non-perpendicular directions.

2. The figure shows a classic vector combination. For the force disk to be in equilibrium, the x-components of force

and force F2 must be equal and

opposite, and the y-components of F and F

must add to equal the magni-

tude of force F

, the vertical force. Set

up the equipment so that the Spring Scale applies force F

. Once the sys-

tem is in equilibrium, determine the xand y-components of the vectors and compare them.

3. For the setup in the figure, change the

angles of F are closer to the x-axis. Calculate the x-components and notice the change. What happens to the x-components as the two forces become closer and closer to parallel? What amount of force would be needed if F were both horizontal?

and F22 so that the vectors

and F2

012-12876B 19

Statics System Exp. 3: Resolving Forces—Components

012-12876B

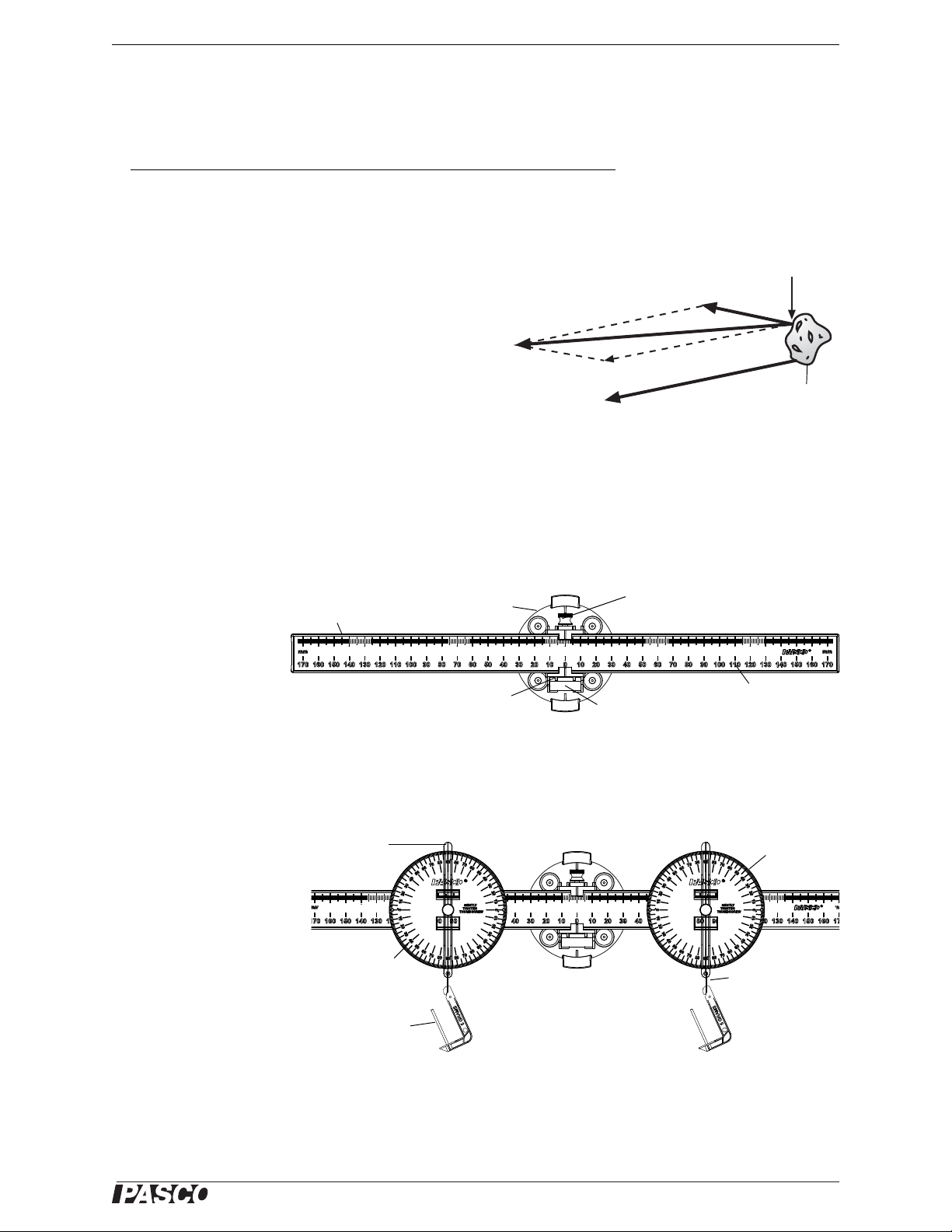
Model No. ME-9502 Exp. 4: Torque—Parallel Forces

Figure 4.1: Non-concurrent forces

Object

Figure 4.2: Balance Arm

Base

Thumbscrew

Bubble level

Beam

Pivot

Scale

Figure 4.3: Setup

Angle

Indicator

Protractor 2

Protractor 1

Thread

Mass

hanger

Exp. 4: Torque—Parallel Forces

Equipment Needed

Item Item

Statics Board Balance Arm and Protractors Mass and Hanger Set Thread

Theory

In experiment 2, you found resultants and equilibriants for concurrent forces—forces that act upon the same point. In the real world, forces are often not concurrent. They act upon different points on an object. In the figure, for example, two forces are pulling on different points of an object. Two questions can be asked:

1. In which direction will the object be accelerated?

2. Will the object rotate?

If the two forces were both applied at point A, the resultant would be the force vector shown, F

. In fact, FR points

in the direction in which the object will be accelerated. (This idea will be investigated further in later experiments,) What about question 2? Will the object rotate? In this experiment you will begin to investigate the types of forces that cause rotation in physical bodies. In doing so, you will encounter a new concept—torque.

Setup

Mount the Balance Arm near the center of the Statics Board.

Level the Beam

Loosen the thumbscrew and adjust the beam so that the zero mark on the beam is aligned with the indicator marks on the pivot. When the beam is level, the bubble in the bubble level will be midway between the two lines on the level.

Add the Protractors

First, find the mass of two of the protractors and record the masses. (Note that you can use the Spring Scale to measure the mass.)

• Protractor 1 = __________

• Protractor 2 = __________

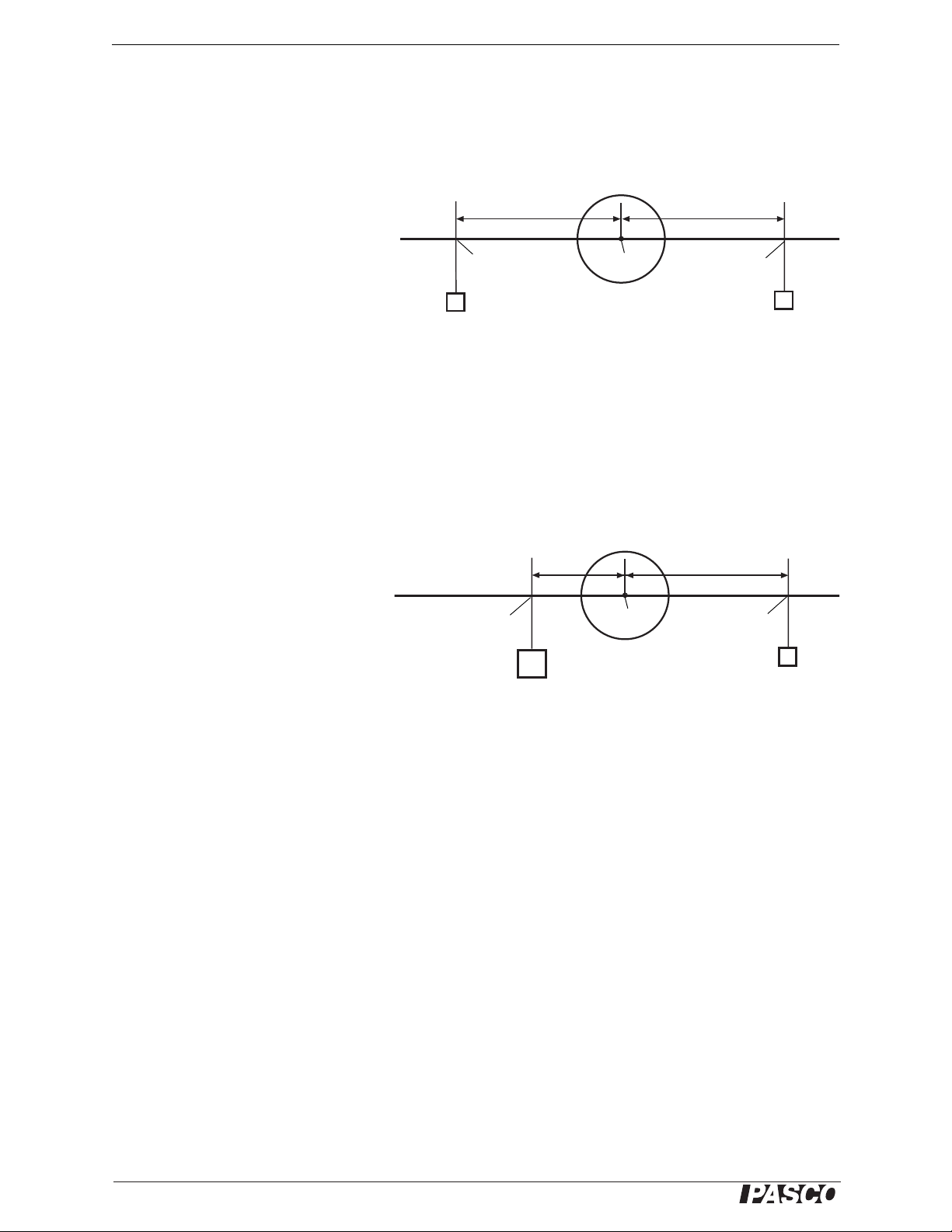
Loosen the thumbscrews on the two protractors and slide one onto each end of the beam. Tie a mass hanger to the thread on the angle indicator of each protractor.

012-12876B 21

Statics System Exp. 4: Torque—Parallel Forces

Figure 4.4: Measuring Torques

center of

protractor 1

center of

protractor 2

pivot

Figure 4.5: More Torques

center of

protractor 1

pivot

center of

protractor 2

Procedure: Equal Distance, Equal Mass

Position one of the protractors near one end the beam and tighten its thumbscrew to hold it in place. Adjust the position of the other protractor until the beam is perfectly balanced, and then tighten its thumbscrew to hold it in place.

1. Measure d

and d2, the distances

from the pivot to the center of each protractor.

•d

= _______________

•d

= _______________

2. Add a 50-gram mass to each mass hanger.

• Is the beam still balanced?

3. Add an ad ditional 20-gram to one of the mass hangers.

• Can you restore the balance of the beam by repositioning the other protractor and mass hanger?

Procedure: Unequal Distance, Unequal Mass

Position one of the protractors approximately halfway between the pivot point and the end of the beam and tighten its thumbscrew to hold it in place. Add 75 grams of mass to the mass hanger, M

Place various masses on the other mass hanger (M

) and slide it along the beam

as needed to rebalance the beam.

1. At the first balanced position, measure the total mass, M

and M2, on each side of the pivot (protractor, mass

hanger, added masses) and record the masses in the data table.

2. Measure the distances, d

and d2, between the centers of the protractors and the pivot and record the values in

the data table.

3. Take measurements for five more different valu es of M

and record your results in the data table. Be sure to

include the units of your measurements.

4. If there is time, vary M

and repeat the procedure.

• Reminder: For accurate results, include the mass of the protractor, mass hanger, and added masses when measuring M

and M2.

Calculations

Calculate the gravitational force (weight = mg) produced by the total mass on each side of the beam for each case. Calculate the torques,  of the net force and the lever arm. Since the distance and the direction of the force are at right angles in this experiment, the torque, , is F d (where F balanced position of the beam.

and 2, on each side of the beam for each case. Remember, torque, , is the cross product

= mg). Record your calculated values of weight, Fg, and torque, , for each

012-12876B

Model No. ME-9502 Exp. 4: Torque—Parallel Forces

Data Table

Case Total Mass

(kg)

1 2 3 4 5 6

Weight

F1 (N)

Distance

d1 (m)

Torque

1 = F1 d

Total Mass

(kg)

Weight

F2 (N)

Distance

d2 (m)

2 = F2 d

Questions

1. From your results, what mathematical relationship must there be between 1 and 2 in order for the beam to be balanced?

2. What torque is exerted on the balance beam by the upward pull of the pivot point?

Extension

If you have time, try adding a third Protractor and Mass Hanger to the beam on the same side of the beam as the second Protractor.

Torque

Question

What relationship must there be between  protractors and mass hangers?

, 2, and 3 in order for the beam to be balanced when there are three

012-12876B 23

Statics System Exp. 4: Torque—Parallel Forces

012-12876B

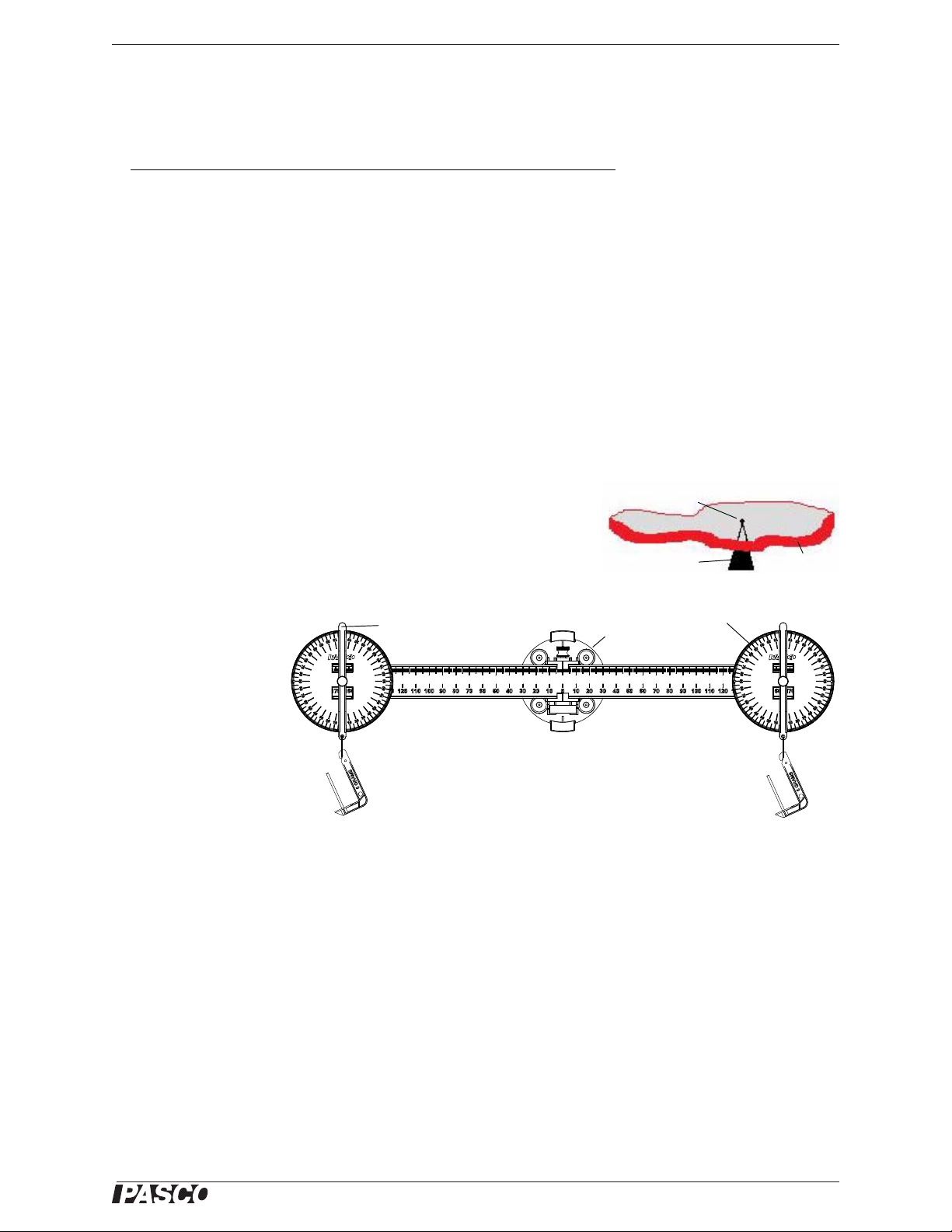
Model No. ME-9502 Exp. 5A: Center of Mass

Support

Center of mass

Object

Figure 5.1: Equipment Setup

Pivot base

Protractor

Angle

Indicator

Exp. 5A: Center of Mass

Equipment Needed

Item Item

Statics Board Balance Arm and Protractors Asymmetrical Plate Thread Mass and Hanger Set

Theory

Gravity is a universal force; every bit of matter in the universe is attracted to every other bit of matter. Therefore, when the Balance Arm is supported by the pivot, every bit of matter in the Balance Arm is attracted to every bit of matter in the Earth.

Fortunately , the sum of all these individual gravitational forces produces a single resultant. This resultant acts as if it were pulling between the center of the Earth and the center of mass of the Balance Arm. The magnitude of the force is the same as if all the matter of the Earth were located at the center of the Earth, and all the matter of the Balance Arm were located at the center of mass of the Balance Arm.

An object thrown so that it rotates tends to rotate about its center of mass, and the center of mass follows a parabolic path. An object whose center of mass is above a support tends to remain in rotational equilibrium (balanced on the support). In this experiment you will use your knowledge of torque to understand and locate the center of mass of an object.

Setup

Measure and record the mass of the beam.

Next, find the mass of two of the protractors and record the masses. (Note that you can use the Spring Scale to measure the mass.)

• Beam = ________

• Protractor 1 = __________

• Protractor 2 = __________

Loosen the thumbscrews on the two protractors and slide one onto each end of the beam so each protractor is at the 165 mm mark. Tie a mass hanger to the thread on the angle indicator of each protractor

Mount the Balance Arm near the center of the Statics Board.

Record the total mass of the beam plus protractors plus mass hangers (5 grams each).

• Mass of system = _____________

012-12876B 25

Statics System Exp. 5A: Center of Mass

Pivot

Center of mass

of the beam

Figure 5.2: Torques and the Center of Mass

Level the Beam and Mark the Center of Mass

Loosen the thumbscrew and adjust the beam so that the indicator marks on the pivot are aligned with the zero mark on the beam. If necessary, adjust the positions of the two protractors until the bubble in the bubble level is midway between the two lines on the level. Once the beam is balanced and level, tighten the thumbscrews to hold the protractors and beam in place.

Put a pencil mark on the beam to indicate the center of mass of the system. All of the mass of the system (beam, protractors, mass hangers) acts as if it is concentrated at the center of mass.

Once the beam is in balance, the force at the pivot point must be the equilibriant of the total gravitational force acting on the beam. Since the beam does not rotate, the gravitational force and its equilibriant must be concurrent forces.

Experiment

1. Why would the Balance Arm necessarily rotate if the resultant of the gravitational forces and the force provided by the pivot were not concurrent forces?

• Think of the Balance Arm as a collection of many small hanging masses. Each hanging mass is pulled down by gravity and therefore produces a torque about the pivot point of the Balance Arm.

2. What is the relationship between the sum of the clockwise torques about the center of the mass and the sum of the counterclockwise torques about the center of mass? Explain.

• Add 50 grams to one mass hanger and 100 grams to the other mass hanger. Loosen the thumbscrew on the beam and slide the beam through the pivot until the beam and masses are balanced. Tighten the thumbscrew.

• The pivot is still supporting everything (beam, protractors, mass hangers, and hanging masses), but at the new center of mass of the system–the pivot point.

3. Calculate the three torques,  and 

provided by the three forces

, F2, and F3 acting about the new

, 2,

pivot point position. Be sure to indicate whether each torque is clockwise (cw) or counterclockwise (ccw).

Position Mass (kg) Force (F = mg) Distance (m) Torque ( = F d)

1 0.050 2 0.100 3

4. Are the clockwise and counte rclockwise torques balanced?

• Remove the 50 gram mass from the left hand mass hanger, but leave the hanger and protractor in place. (Removing the mass effectively removes F balances the torque provided by F

and the beam is level again.

). Reposition the beam in the pivot until the torque provided by F3

012-12876B

Model No. ME-9502 Exp. 5A: Center of Mass

Mass

hanger

Asymmetrical

Plate

Force Sensor

Mount

Thread

Rod

Figure 5.3: Finding the Center of Mass

• Recalculate the torques about the pivot point.

Position Force (F = mg) Torque ( = F d)

2 3

5. Are the torques balanced?

Asymmetrical Plate

Replace the Balance Arm with the Force Sensor Mount. Hang the Asymmetrical Plate from the rod on the Force Sensor Mount.

Since the force of the rod acting on the plate is the equilibriant to the sum of the gravitational forces acting on the plate, the line of force exerted by the rod must pass through the center of the mass of the plate. Loop a piece of thread over the rod and attach a mass hanger to the end of the thread.

Use a pencil or a “dry erase” pen to draw a line on the Asymmetrical Plate that marks the position of the thread on the plate.

Remove the thread and mass hanger. Hang the plate from a different hole. Put the thread and mass hanger back on the rod. Draw a new line on the plate that marks the position of the thread.

Repeat the process for a third different hole. Draw a third line on the plate.

6. Does the line showing where the thread is hanging pass through the center of mass of the plate?

7. Would this method work for a three dimensional object? Why or why not?

Extension

Remove the thread and plate from the rod. Try to balance the Asymmetrical Plate on your finger by placing the tip of you finger under the point where the three drawn lines intersect. What happens?

012-12876B 27

Statics System Exp. 5A: Center of Mass

012-12876B

Model No. ME-9502 Exp. 5B: Equilibrium of Physical Bodies

Figure 5.4: Non-concurrent, non-parallel forces

Object

Spring

Scale

Force

diagram

Point of

suspension

Center of mass

of the beam

C.O.M.

Figure 5.5: Equipment Setup

Exp. 5B: Equilibrium of Physical Bodies

Equipment Needed

Item Item

Statics Board Balance Arm and Protractors Pulley (1) Mounted Spring Scale Mass and Hanger Set Thread

Theory

Any force acting on a body may produce both translational motion (movement of the center of mass of the body in the direction of the force) and rotational motion (rotation about a pivot point).

In this part of the experiment you will investigate the interplay between forces and torques by examining all the forces acting on a body in physical equilibrium.

Setup

Find the center of mass of the balance beam and mark it with a pencil. Use the Spring Scale, mass hangers, and three protractors on the Balance Arm to set up the equipment as shown.

By supporting the Balance Arm from the Spring Scale, you can now determine all the forces acting on the Balance Arm.

As shown in the diagram, these forces include F weight of the mass, M the weight of the mass M

, the weight

, F2,

, the

of the balance beam acting through its center of mass, and

, the upward pull of the Spring Scale.

Experiment

Fill in the data table listing M (in kilograms), F (in newtons), d (the distance in meters from the applied force to the suspension point), and  (the torque acting about the point of suspension in newton • meters. Indicate whether each torque is clockwise (cw) or counterclockwise (ccw)

012-12876B 29

Statics System Exp. 5B: Equilibrium of Physical Bodies

Figure 5.6: Change the Origin

Origin

Data Table.

Position mass (M) force (F) distance (d) torque ()

1 2 3 4—

Calculations

1. Calculate and record the sum of the clockwise and counterclockwise torques.



= _________________________ 

• Are the torques balanced?

2. Calculate and record the sum of the upward and downward forces.

F

= _________________________ F

= _______________________

ccw

= _______________________

down

• Are the translational forces balanced?

3. On the basis of your answers to the questions, what conditions must be met for a physical body to be in equilibrium (no acceleration)?

Change the Origin

In measuring the torques the first time, all the distances were measured from the point of suspension of the Balance Arm. This measures the tendency of the beam to rotate about this point of suspension. You can also measure the torques about any other point, on or off the beam. Using the same forces as you used before, re-measure the distances, measuring from the left end of the balance beam as shown in the diagram.

Recalculate the torques to determine the tendency of the beam to rotate about the left end of the beam.

Record your data in the second table. As before, indicate whether each torque is clockwise (cw) or counterclockwise (ccw).

012-12876B

Model No. ME-9502 Exp. 5B: Equilibrium of Physical Bodies

Data Table: Change the Origin.

Position force (F) distance (d) torque ()

1 2 3 4

Calculations

1. Calculate and record the sum of the clockwise and counterclockwise torques.



= _________________________ 

= _______________________

ccw

• Are the torques balanced?

Extension

Use a pulley, hanging mass, and a thread to produce an additional upward force at one end of the beam. You may need to use tape to secure the thread to the beam.) Adjust the positions of the remaining hanging masses and the Spring Scale to bring the beam back into balance so it is level horizontally.

• Are all the forces balanced, both for translational and rotations motion?

• Diagram your setup and show your calculations on a separate sheet of paper.

012-12876B 31

Statics System Exp. 5B: Equilibrium of Physical Bodies

012-12876B

Model No. ME-9502 Exp. 6: Torque—Non-Paralle l Forces

Figure 6.1: Torque





Pivot

point

Lever

arm





 Fd sin=

Exp. 6: Torque—Non-Parallel Forces

Equipment Needed

Item Item

Statics Board Balance Arm and Protractors Pulley Mounted Spring Scale Mass and Hanger Set Thread

Theory

In a previous experiment, you investigated torques appled to the Balance Arm and discovered that when the torques about the point of rotation are balanced, the beam remains balanced. All the forces in that experiment were perpendicular to the beam and parallel to each other. What happens when one or more of the forces is not perpendicular to the beam?

It turns out that the formula for torque can be generalized to account for this case. Torque is the cross product of the force vector and the lever arm where the lever arm is the distance from the pivot point to where the force is applied. The generalized formula is:

where F is the magnitude of the force vector, d is the distance from the pivot point to the point at which the force is applied (that is, the “lever arm”), and  is the angle between the force vector, F, and the lever arm, d. Note that F sin  is F is d



perpendicular distance, d

, the component of the force vector, F, that is perpendicular to the lever arm, d. Note also that d sin 



the component of the lever arm, d, that is perpendicular to the force vector, F. In other words, d sin  is the

, from the pivot point to the line of force.



Setup

Mount the Balance Arm on the left half of the Statics Board. Adjust the beam so that the zero marks on the beam align with the indicator marks on the pivot.

Put a protractor on each end of the beam (for example, between 130 and 140 mm from the pivot). Adjust the position of the protractors if necessary so that the beam is balanced and level.

012-12876B 33

Statics System Exp. 6: Torque—Non-Parallel Forces

Figure 6.2: Equipment Setup

Spring

Scale

Pulley

Protractor

Beam



Pivot point

Figure 6.3: Schematic

12–12+2

Suspend a mass, M

, from one protractor. Mount the Spring Scale on the Statics Board and connect it to the other

protractor using a thread and a Pulley as shown.

Procedure

1. Measure d1 and d2 and record the values.

2. Record the total mass, M

tude of the force, F

, and the magni-

(weight of the hanging

mass). Use your measured values to calculate the torque, 

, produced by the force, F2.

Be sure to include the units for each value.

d1 (m) d2 (m) M2 (kg) F2 (N)  (N•m)

• By moving the pulley, you can adjust the angle of the force, F

. Note that when you move the pulley, you also

need to move the Spring Scale in order to keep the thread perfectly vertical between the Spring Scale and the pulley.

3. Set the angle of F toward or away from the pulley as needed so that the magnitude of F

to each of the values shown in the table below. At each angle, move the Spring Scale

is sufficient to balance the beam.

Record the force reading on the Spring Scale in newtons.

Angle F

30° 40° 50° 60°

(N) 1 = F1d1 sin 

70° 80°

012-12876B

Model No. ME-9502 Exp. 6: Torque—Non-Paralle l Forces













Line of force

Line of

force

Pivot point

Figure 6.4: Non-Parallel Forces

Figure 6.5: Using the Torque Wheel

1



Line of

force

4. Perform the calculations to determine the torque, 1, provided by the Spring Scale, and the percent difference between 

and 2. [The percent difference is the difference of the two torques divided by the average of the

two torques.]

• T o provide a consistent mathematical definition of torque, 

and 2 must be determined according to the same

formula.

5. Apply the generalized definition of torque ( = F d sin ) to the calculation of  What is the angle between the force, F

, and the lever arm, d2?] Does the calculated value using the general-

ized definition change the results?

Analyzing Non-Parallel Forces

Imagine two non-parallel forces acting on an object at different distances from its pivot point. The figure shows a diagram for a calculation of torque provided by two non-parallel forces. The force F torque  produces a torque 

about the point O with a magnitude of F1 d1 sin 1. The force F2

about the point O with a magnitude of F2 d2 sin 2.

However, it would be misleading to simply add the two torques together to determine the total torque because 

and 2 cause rotation about point

O in opposite directions. When adding two or more torques, add together the magnitudes of all the torques that tend to cause clockwise rotation, then add together the magnitudes of all the torques that tend to cause counterclockwise rotation. For the system to be balanced, the sum of the clockwise torques must equal the sum of the counterclockwise torques.

Remember that the perpendicular distance, d

, from the pivot point to the



force is equal to d sin  and that the angle is measured between the lever arm, d, and the line of force.

produces a

in step 2 previously. [Hint:

Torque Wheel

A Torque Wheel provides an easy method for creating an equilibrium among several non parallel forces. Figure 6.5 shows a force F applied at an angle  to the line from the center of the Torque Wheel to the point of application of the force. The torque can be calculated as  = F d sin . However, as shown, d sin  is just the perpendicular distance, d between the center of the Torque Wheel and the line of force, when that line is extended far enough.

Imagine a To rque Wheel with tw o non-parallel forces. The angle between the force F tance d fore, the torque 

The radial scale on the Torque Wheel label allows you to measure the perpendicular distance from the pivot point to the line of force. Each concentric circle on the label is 2 mm larger in radius. Each Torque Indicator Arm is transparent and has a centerline that shows the line of force.

and the lever arm d1 is . The perpendicular dis-

from the pivot point O to the line of force is d1 sin . There-

1

produced by F1 is F1 d1





012-12876B 35

Statics System Exp. 6: Torque—Non-Parallel Forces

1

2

3

Pivot point

Torque

Indicator

Arm

Figure 6.6: Set up the Torque Wheel

Torque Wheel

Radial

scale

Set Up the Torque Wheel

Remove the Balance Arm and set up the Torque Wheel on the Statics Board as shown in the diagram. Use pulleys, thread, and hanging masses to apply three torques to the wheel.

Use the radial scale on the T orque Wheel label to measure the perpendicular distance from each line of force to the pivot point. Record the distances in the data table. Calculate and record the forces. Calculate and record the torque for each force using = F d

. Be sure



to indicate whether the torque is clockwise or counterclockwise.

Subtract the sum of the clockwise torques from the sum of the counterclockwise torques to determine the total net torque.

Data Table

Force, F (N) Perpendicular Distance, d

1 2 3

(m) Torque,



= F d

(N•m)



Total Torque = ________________

Question

Within the limits of your experimental error, is the total net torque equal to zero when the Torque Wheel is in equilibrium.

Extension

Repeat the procedure with different forces and angles.

012-12876B

Model No. ME-9502 Exp. 7: The Inclined Plane

Figure 7.1: The Inclined Plane





Object

Inclined

plane





Figure 7.2: Equipment Setup

Inclined

Plane

Pulley

Spring

Scale

Cart

100-g mass

Keep the thread

parallel to the plane.

Exp. 7: The Inclined Plane

Equipment Needed

Item Item

Statics Board Inclined Plane and Cart Pulley (2) Mounted Spring Scale Mass and Hanger Set Thread

Introduction

Suppose you must design a ramp with a cable to hold a heavy object on an inclined ramp. For a given angle of inclination of the ramp, how much force must the cable deliver to hold the object on the ramp? How much force must the ramp be able to support?

You could solve this problem by building ramps and cable and testing them, or by testing scale models. Alternatively, you could use your knowledge of forces and vectors to solve the problem mathematically. In the diagram, for example, the weight, F, of the object on the inclined plane can be resolved into two components: one perpendicular to the plane, F the plane, F

. The angle, , is the angle of inclination of the inclined plane. In this experiment, you will compare



the mathematical solution with data taken directly from a scale model.

, and one parallel to



Experiment

1. Add a 100-g mass to the cart and measure and record the total mass of the cart. Calculate and record the weight of the cart-plus-mass.

• total mass of cart = _______________ weight of cart = _________________

2. Set up the Inclined Plane on the Statics Board. Start with the plane at 15°. Put the cart on the Inclined Plane and use thread connected under a pulley to the Spring Scale to hold the cart in place on the ramp.

012-12876B 37

Statics System Exp. 7: The Inclined Plane

measured - calculatedmeasured + calculated2 x 100%

Figure 7.3: Normal Force Equipment Setup

The force provided by the Spring Scale, F the Inclined Plane, F

The calculated component of force that is parallel to the Inclined Plane, F





measured

, equals the component of the force of gravity that is parallel to



calculated

, is F sin

, where  is the angle of the plane.

3. Adjust the angle of inclination of the Inclined Plane to each of the values shown in the table. For accurate values, adjust the pulley and Spring Scale so that the thread remains parallel to the plane. At each value, record the measured value, F



measured

4. At each value, calculate the magnitude of the force parallel to the plane, F

, of the force parallel to the plane.



calculated

= F sin and record the

calculated value.

5. Calculate the percent difference between the measured and calculated values of the force parallel to the plane.

Angle F

15° 30° 45° 60° 75°

*The Percent Difference is the absolulte value of the ratio of the difference of the measured and calculated values, divided by the average of the measured plus calculated values, converted to a percentage.



measured



calculated

= F sin  Percent Difference*

Question

How well does the calculated force based on the vector model compare to your measured force?

Normal Force

The force that the Inclined Plane provides to support the cart is called the normal force (a force perpendicular – “normal” – to the surface.) In the vector model of the force, the component of force that is perpendicular to the plane, F surface.

To measure the force of the cart on the Inclined Plane, reset the Inclined Plane to 15°. Replace the Spring Scale with a mass hanger connected by a thread over the pulley to the cart. Add masses to the mass hanger until the cart and the hanging mass are in equilibrium. (In other words, the force provided by the tension in the thread equals the component of the cart’s weight that is parallel to the plane.)

, is F cos . The normal force is equal to the force of the cart on the Inclined Plane, perpendicular to its



012-12876B

Model No. ME-9502 Exp. 7: The Inclined Plane

Figure 7.4: Measure the Normal Force

Tie the thread to the

hole in the post.

Record the total mass of the mass hanger and calculate and record the weight.

• total mass of mass hanger = _______________ weight of mass hanger = _________________

• How does the weight of the mass hanger compare to value of F



calculated

, the component of the cart’s weight

that is parallel to the plane? (See the data table for the value at 15°.)

Add a second pulley to the Statics Board and set up the Spring Balance above the pulley. Tie a thread to the hole at the top of the post of the cart. Arrange the pulley so the thread from the post is in line with the post, and therefore is perpendicular to the plane. Arrange the Spring Scale so that the angle of the thread from the pulley up to the scale is vertical.

Pull the Spring Scale up until the force just barely lifts the mass cart off the Inclined Plane.

Record the value of the Spring Scale as the perpendicular force, F

Calculate the value of the perpendicular force as predicted by the vector model, F value

Question

How well does the calculated force based on the vector model compare to your measured force?

measured

calculated

= __________________





calculated

= F cos Record the

012-12876B 39

Statics System Exp. 7: The Inclined Plane

012-12876B

Model No. ME-9502 Exp. 8: Slidin g Fr iction

Plumb bob

Figure 8.1: Equipment Setup

Friction

Block

The thread must be parallel to the

Inclined Plane.

Level the

Inclined Plane

Mass

Pulley

Mass

Hanger

Exp. 8: Sliding Friction

Equipment Needed

Item Item

Statics Board Inclined Plane and Friction Block Pulley Mounted Spring Scale Mass and Hanger Set Thread

Theory

Friction is a force between two objects that resists motion between the two objects. Static friction (or sticking friction) is friction between objects that are not moving relative to each other. For example, static friction can prevent an object from sliding down an inclined plane. If a net external force on an object is greater than the force of static friction, the object begins to slide. Sliding friction (or kinetic friction) occurs when two objects are moving relative to each other. In most cases, the static friction between two objects is greater than the sliding friction between the two objects. Once sliding begins, if the sliding object’s motion is constant, then the external force equals the force of sliding friction.

An explanation of friction assumes that surfaces are atomically close to each other over a small fraction of their overall area. The surfaces that are atomically close to each other will exert retarding forces on each other. This contact area is proportional to the normal force, and therefore the friction force is proportional to the normal force, or f  F is called the coefficient of friction, . The friction force is f = F that is between zero and one for several common surface-to-surface combinations and is determined empirically.

where f is the friction force and FN is the normal force. The ratio of the friction force to the normal force

. The coefficient of friction is a unitless number

In this experiment you will investigate how the normal force, the contact materials, and the contact area affect the sliding friction.

Procedure

1. Use the Spring Scale to measure the weight of the Friction Block and then record the value.

•weight, W, of friction block = _________________

2. Mount the Inclined Plane on the Statics Board and use the plumb bob to level the plane. Set the Friction Block on the Inclined Plane and use thread to connect it over a pulley to a mass hanger as shown.

3. Adjust the pulley so that the thread is parallel to the Inclined Plane.

4. Add or subtract masses on the mass hanger until the Friction Block moves at a very slow, constant speed

when you give it a small push.

012-12876B 41

Statics System Exp. 8: Sliding Friction

• If the Friction Block stops, the mass is too light. If the Friction Block accelerates, the mass is too heavy.

• The weight of the hanging mass that is sufficient to pull the Friction Block at a constant speed is f

, the force

of the sliding (kinetic) friction between the Friction Block and the Inclined Plane.

Variables

Change the following factors and measure the sliding friction force.

• Normal Force: Add mass to the top of the Friction Block to increase the normal force between the block and the Inclined Plane.

• Contact Material: Two sides of the Friction Block are bare wood. Two other sides are covered with felt. Compare the sliding friction force for a wood surface to the sliding friction force for an equally sized felt surface.

• Contact Area: The top and bottom surfaces have a larger area than the side surfaces. Compare the sliding friction force for a larger area to the sliding friction force for a smaller area.

Reminders for each trial:

• Carefully adjust the mass on the mass hanger until the weight of the hanging mass is enough so that the Friction Block moves at a very slow, constant speed after you give it a small push.

• Record the total mass of the Friction Block, M, and the hanging mass, m, (total mass of the mass hanger and added masses).

• Calculate and record the normal force, F force, f

(weight of the hanging mass).

, of the Friction Block on the Inclined Plane and the sliding friction

• Calculate and record the coefficient of friction, , which is the ratio of the sliding friction force, f the normal force, F

Data Table

Trial Added Mass

(kg)

1 0.000 2 0.050 3 0.100 4 0.150 5 0.200 6 0.250

Trial Surface Total Mass,

7 Wood, Large 8 Felt, Large

Total Mass, M, of Block

M, of Block*

Normal Force,

= Mg

Normal Force,

= Mg

Hanging Mass, m

Friction

force, fk = mg

Friction

force, fk = mg

, divided by

Coefficient of

friction,  = fk/F

Coefficient of

friction, k = fk/F

9 Wood, Small

10 Felt, Small

*For trials 7 through 10, let the total mass of the Friction Block be constant.

012-12876B

Model No. ME-9502 Sliding Friction on an Incline d Plane

Figure 8.2: The Inclined Plane





Object





Inclined

plane







Friction

Block

Direction

of motion.

Inclined

plane

Figure 8.3: Force Diagram

Questions

1. In trials 1 through 6, what happens to the sliding friction as the normal force increases?

2. In trials 1 through 6, what happens to the coefficient of friction as the normal force increases?

3. How does the sliding friction for the large wood surface compare to the sliding friction for the large felt sur-

face? How does the sliding friction for the small wood surface compare to the sliding friction for the small felt surface?

4. Based on your measurements, does the sliding friction between two objects depend on the materials that are in contact?

5. How does the sliding friction for the large wood surface compare to the sliding friction for the small wood surface? How does the sliding friction for the large felt surface compare to the sliding friction for the small felt surface?

6. Based on your measurements, does the sliding friction between two objects depend on the area of contact between the objects?

Sliding Friction on an Inclined Plane

If the Friction Block is not on a horizontal surface, will the coefficient of sliding friction, 

, be different?

When an object is on the Inclined Plane at an angle, one component of the object’s weight (F = mg) is parallel to the surface of the plane (F the plane (F

), and another component of F is perpendicular to



. In theory , this perpendicular component is equal



to the normal force of the surface of the plane.

If there was no friction between the object and the plane, the parallel component of the object’s weight would accelerate the object down the plane. However, because there is friction between the object and the plane, the force of friction (f = F

)

opposes the parallel component of force. In other words, the vector for the force of friction would point up the plane as the object slides down the plane.

Imagine that the object is being pulled up the plane by the tension of a thread connected to a hanging mass. Would the sliding friction (f

= kFN) oppose the parallel component of

the object’s weight, or would the vector for the sliding friction be in the same direction as the parallel component? Both forces would point down the plane as the object is pulled up the plane. If the object is pulled at a constant speed, then the net force on the object is zero. Would the tension in the thread, T, equal the sum of the parallel component and the sliding friction?

Prediction

How will the sum of the parallel component of the block’s weight (F) plus the sliding friction (fk) compare to the weight of the hanging mass?

012-12876B 43

Statics System Sliding Friction on an Inclined Plane

Figure 8.4: Friction on an In clin ed Plan e Se tup

Friction

Block

The thread

must be parallel

to the plane.

Hanging

mass

Procedure

1. Measure and record the weight, W, of the Friction Block.

• weight, W =__________

2. Mount the Inclined Plane on the Statics Board and set the angle, , to 15°. Set up the pulley, mas s hanger , thread, and Friction Block as shown in the figure. Make sure that the thread is parallel to the Inclined Plane.

3. Carefully adjust the mass on the mass hanger until the weight of the hanging mass is enough so that the Friction Block moves at a very slow, constant speed up the inclined after you give it a small push.

4. Record the total mass of the hanging mass, m, (mass of the mass hanger and added masses).

Calculations

• Remember that the weight of the Friction Block, W = F = Mg.

5. Calculate and record the parallel component, F

6. Calculate the perpendicular component, F force, F

7. Use the normal force, F

, and the coefficient of sliding friction, k, for the surface material of the block

(either wood or felt) to calculate the sliding friction force, f

8. Calculate the weight of the hanging mass, F

9. Calculate and record the sum of the parallel component of the block’s weight, F

force, f

= Mg sin , of the block’s weight.



= Mg cos , of the block’s weight and record this as the normal



= kFN.

= mg and record this as the tension in the thread, T.

hanging

, and the sliding friction



Data Table

Angle,



Block

Mass, M

Hanging Mass, m

Parallel Component,

= Mg sin 



Normal Force,

= F

= Mg cos 





Friction Force,

= k F

Tension,

T = mg

• Sum of the parallel component of the block’s weight, F, and the sliding friction force, fk = ______________.

Question

How does the tension in the thread compare to the sum of the parallel component of the block’s weight and the sliding friction force?

012-12876B

Model No. ME-9502 Static Friction on an Inclined Plane





Object





Inclined

plane

Figure 8.5: Static Friction Diagram

Mg sin sMg cos=



Mg sin

Mg cos

--------------------

tan==

Figure 8.6: Increase the Angle

Static Friction on an Inclined Plane

Imagine that the Friction Block is placed on the Inclined Plane, and one end of the plane is tilted upward until the parallel component of the block’s weight begins to pull the block down the plane. Static friction holds the block in place on the plane until the parallel component of the block’s weight is larger than the static friction. If the block will almost — but not quite — start sliding, then the static friction is as large as possible and equals the parallel component of the block’s weight.

One way to measure the coefficient of static friction,  find the maximum angle at which the plane can be tilted before the block begins sliding down the plane. The component of the weight of the block that is parallel to the plane, F is Mg sin , where M is the mass of the block. The normal force, F weight, or F coefficient of static friction,  force. Therefore, f

, is the perpendicular component of the block’s

= Mg cos . The force of static friction, fs, is the



= s Mg cos .

, multiplied by the normal

When the block is at rest, the static friction force equal s th e component of the block’s weight that is parallel to the incline, or . Solving for the coefficient of static friction, 

, gives the following:

Procedure

1. Mount the Inclined Plane on the Statics Board and set the angle to zero. Place the Friction Block on the Inclined Plane.

2. Carefully raise one end of the Inclined Plane until the Friction Block just begins to slide. Record the angle, .

, is to



3. Switch the Friction Block to a different surface material and repeat the procedure.

Data Table

Surface Material Angle Coefficient of Static Friction

Wood

Felt

Calculations

• Calculate the coefficient of static friction for both wood and felt.

Question

• How does the coefficient of static friction for wood compare to the coefficient of static friction for felt?

012-12876B 45

Statics System Static Friction on an Inclined Plane

012-12876B

Model No. ME-9 502 Exp. 9: Simple Harmonic Motion–Mass on a Spring

Equilibrium

position

Figure 9.1: Spring Constant

T 2

---- -=

Figure 9.2: Setup

Spring

Scale

120 g

Mass

hanger

Exp. 9: Simple Harmonic Motion–Mass on a Spring

Equipment Needed

Item Item

Statics Board Mounted Spring Scale Mass and Hanger Set Thread Stopwatch (ME-1234)

Theory

Imagine a mass hanging from a spring. At rest, the mass hangs in a position such that the spring force just balances the gravitational force on the mass (its weight). When the mass is pulled below this original point (called the equilibrium position), the spring exerts a force to pull it back up. When the mass is above this original point, gravity pulls it down. The net force on the mass is therefore a restoring force because it always acts to accelerate the mass back toward its equilibrium position.

Previously you may have investigated Hooke’s Law , which states that the force exerted by a spring is proportional to the distance beyond its normal length to which it is stretched. (This also is true for the compression of a spring.) This relationship is stated as F = -kx, where F is the force exerted by the spring, x is the displacement of the end of the spring from the equilibrium position, and k is the constant of proportionality, called the spring constant.

Whenever an object is acted on by a restoring force that is proportional to the displacement of the object from its equilibrium position, the resulting motion is called Simple Harmonic Motion (SHM). When the si mple harmonic motion of a mass, M, on a spring is analyzed mathematically using Newton’s Second Law (and calculus), the period of the motion, T, is as follows:

The period, T, is the amount of time for one complete oscillation (down-up-down). In this experiment you will investigate this equation for the period of simple harmonic motion.

Procedure

1. Measure and record k, the spring constant for the spring in the Spring Scale (see Exp: Hooke’s Law).

• spring constant, k = _________________ (N/m)

2. Mount the Spring Scale on the Statics Board so that the scale is perfectly vertical. Use thread to hang a mass hanger from the scale, and add 120 g of mass to the hanger (for a total hanging mass of 125 g (0.125 kg).

• Practice the following: Pull the mass hanger down several centimeters and release it smoothly so that the mass hanger oscillates up and down without moving from side to side.

012-12876B 47

Statics System Exp. 9: Simple Harmonic Motion–Mass on a Spring

T 2

---- -=

3. Pull the mass hanger down and release it smoothly. Let it oscillate a few times before taking any measurements. When the oscillations are smooth and regular, measure the time for at least ten complete oscillations (down-up-down). If possible, measure the time for as many oscillations as you can before the amplitude of the oscillations becomes too small. Record the number of oscillations and the total time.

4. Calculate and record the Measured Period, T

measured

, by dividing the total time by the number of oscillations.

5. Repeat the measurement for the 125 g mass five times. Calculate and record the Average Measured Period.

6. Use M and k to calculate the Theoretical Period, T

theoretical

, and record the result.

7. Repeat the procedure using masses of 175 g and 225 g (total mass including the mass hanger).

Data Table

Mass (kg) Oscillations Total Time (s) Measured Period (s) Theoretical Period (s)

0.125 kg

Average Measured Period (s)

0.175 kg

Average Measured Period (s)

0.225 kg

Average Measured Period (s)

Questions

1. How well does the theoretical value for the period of oscillation compare to the measured period of oscillation?

2. Does the equation for the period of a mass on a spring provide a good mathematical model for the physical reality? Why or why not?

012-12876B

Model No. ME-9 502 Exp. 9: Simple Harmonic Motion–Mass on a Spring

total

T2k

4

-------- -

new

2

total

-------------- -=

Extension

In addition to the hanging mass, there is other mass that is oscillating up and down. The rod inside the Spring Scale moves up and down as well. A portion of the spring itself moves as the hanging mass oscillates. Would this unaccounted for mass make a difference in your calculation of the theoretical period, T

theoretical

To find out, used the equation for the period of oscillation to calculate what the total oscillating mass, M should be based on the spring constant and the Average Measured Period, T

measured

, for each mass. Use the for-

total

mula,

where T is the Average Measured Period and k is the spring constant.

Hanging Mass (kg) Average Measured Period (s) Calculated Total Mass (kg) New Theoretical Period (s)

0.125 kg

0.175 kg

0.225 kg

After calculating the total mass based on the average measured period and the spring constant, recalculate the theoretical period based on the calculated total mass and the spring constant:

Compare the calculated total mass, M

, to the hanging mass, M. Approximately how much “extra” mass is

total

oscillating in addition to the hanging mass?

•M

= _____________

extra

Question

1. For each trial, how well does the new theoretical value for the period of oscillation compare to the average measured period of oscillation?

2. Does the equation for the period of an oscillating mass on a spring provide a good mathematical model for the physical reality? Why or why not?

012-12876B 49

Statics System Simple Harmonic Motion–Beam on a Spring

Hinge

Beam

Spring

Figure 9.3: Beam on a String

---- -=





kxL–

mL

--------------

kxL–

----------------

kx–

----------

----- -

x–=

2x–

----- -

x–=



----- -



----- -=

T 2

----- -=

Simple Harmonic Motion–Beam on a Spring

Imagine a horizontal beam that is supported by a hinge at one end and a vertical spring at the other end. If the end of the beam is pulled down, the spring exerts a restoring force, F = -kx, to return the beam to its equilibrium position. The beam will oscillate up and down with a period, T mass on a spring, the period, T, is as follows:

where M is the total oscillating mass and k is the spring constant. What is the period for a beam on a spring?

The beam rotates about the hinge as the end attached to the spring oscillates. The force of the spring on the oscillating end of the beam, F = -kx, produces a torque on the beam. Let L be the length of the lever arm of the beam. The torque due to the spring is = FL. A net torque causes angular acceleration, , that is directly proportional to the torque, , and inversely proportional to the rotational inertia, I. That is,0,

beam

. For a

or  = I. Setting the two expressions for torque equal to each other gives FL = I. Assume that the beam is like a thin rod pivoted around one end. The rotational inertia of the thin rod is I = 1/3 m L

where m is the mass of the

beam. Since the force on the beam is F = -kx, the equation FL = I becomes:

The angular acceleration, , and the tangential (linear) acceleration, a related. The tangential acceleration, a the lever arm, L, so a

= L, or  = aT/L. The expression becomes:

= r where r is the radius of rotation. In this case, the radius of rotation is

, of the oscillating end of the beam are

which simplifies to

Solving for the tangential acceleration gives:

The tangential acceleration, a

= -2x, so the expression becomes:

Since the angular frequency,  = 2/T, the period, T = 2/or

012-12876B

Model No. ME-9502 Simple Harmonic Motion–Beam on a Spr ing

Spring

Scale

Pivot

Protractor

Figure 9.4: Equipment Setup

In this part of the experiment you will investigate this equation for the simple harmonic motion of a beam on a spring.

Procedure

1. Mount a Protractor on one end of the Balance Arm. Measure and record the total mass of the arm plus protractor.

• mass, m = ____________

2. Ad d the Pivot to the other end of the Balance Arm and mount the Balance Arm on the Statics Board.

3. Mount the Spring Scale on the Statics Board so that the scale is perfectly vertical. Use thread to connect the

Angle Indicator on the Protractor to the bottom hook of the Spring Scale.

4. Adjust the Balance Arm and the Spring Scale so that the ar m is horizontal and the scale is vertical and directly above the center of the protractor.

5. Push the balance arm down and release it smoothly. Measure the time for at least ten complete oscillations (down-up-down). Record the number of oscillations and the total time.

6. Calculate and record the Measured Period, T

measured

, by dividing the total time by the number of oscillations.

7. Repeat the measurement five times. Calculate and record the Average Measured Period.

8. Use m and k to calculate the Theoretical Period, T

theoretical

, and record the result.

012-12876B 51

Statics System Simple Harmonic Motion–Beam on a Spring

Data Table

Trial Oscillations Total Time (s) Measured Period (s) Theoretical Period (s)

1 2 3 4 5

Average Measured Period (s)

Questions

1. How well does the theoretical value for the period of oscillation compare to the average measured period of oscillation?

2. Does the equation for the period of a beam on a spring provide a good mathematical model for the physical reality? Why or why not?

Extension

The rod and part of the spring in the Spring Scale oscillate up and down as the beam oscillates. Use your results from the first part of this experiment to calculate the total mass that oscillates: the arm and protractor plus the mass of the parts of the Spring Scale that also oscillate. Recalculate the theoretical period, T

theoretical

• How does the re-calculated theoretical period compare to the average measured period?

012-12876B

Model No. ME-9502 Exp. 10: Simple Harmonic Motion –The Simple Pendulum

Figure 10.1: Pendulum



radial

tangential

mg sin 

mg cos 

Equilibrium

position

Pivot point

Mass

String

T 2

-------

------- 2 

-- -==

Exp. 10: Simple Harmonic Motion–The Simple Pendulum

Equipment Needed Item Item

Statics Board Utility Mount and Cord Clip Thread Mass and Hanger Set Stopwatch (ME-1234)

Theory

Simple harmonic motion is not limited to masses on springs. In fact, it is one of the most common and important types of motion found in nature. From the vibrations of atoms to the vibrations of airplane wings, simple harmonic motion plays an important role in many physical phenomena.

A swinging pendulum, for example, shows behavior that is very similar to that of a mass on a spring. By making comparisons between these two phenomena, some predictions can be made about the period of oscillation for a pendulum.

The figure shows a simple pendulum with a string and a mass at an angle  from the vertical position. Two forces act on the mass: the force of the string, T, and the force of gravity. The gravitational force, F = mg, can be resolved into two components. One component, F component, F

tangential

, is perpendicular to the string and tan-

, is along the string. The other

radial

gent to the arc of the mass as it swings. The radial component of the weight, mg cos , equals the force, T, through the string. The tangential component of the weight, mg sin , is in the direction of motion and accelerates or decelerates the mass.

Using the congruent triangles in the figure, it can be seen that the displacement of the mass from the equilibrium position is an arc whose length, x, is approximately L tan . If the angle, , is relatively small (less than 20°), then it is very nearly true that sin  = tan . Therefore, for small swings of the pendulum, it is approximately true that

tangential

= mg tan  = mg x/L. Since the tangential force is a restoring force, the equation should be = - mg x/L. Comparing this equation to the equation for the restoring force of a mass on a spring,

F = -kx, it can be seen that the quantity mg/L has the same mathematical role as k, the spring constant. On the basis of this similarity, you can say that the period of oscillation for a pendulum is as follows:

where m is the mass, g is the acceleration due to gravity, and L is the length of the pendulum from the pivot point to the center of mass of the hanging mass.

In this part of the experiment you will investigate this equation for the period of the simple harmonic motion of a pendulum.

012-12876B 53

Statics System Exp. 10: Simple Harmonic Motion–The Simple Pendulum

Fig. 10.2: Setup

Utility

Mount

Mass

Cord

Clip

Thread

Procedure

1. Place the Utility Mount near the top edge of the Statics Board. Loop a thread approximately 45 cm long through a Cord Clip and attach the Cord Clip to the mount.

2. Attach a 10 g mass to the thread and adjust the length of the thread so that the pendulum is as long as possible on the board.

3. Measure and record L, the length of the pendulum from the pivot point to the center of mass of the hanging mass. Record m, the hanging mass.

4. Set the mass swinging but keep the angle of the swing reasonably small (less than 20°). Measure the time for 30 oscillations. Record the total time.

5. Repeat the measurement five times.

6. Change the mass. Repeat the procedure for a 20 g hanging mass and then a 50 g hang-

ing mass.

7. Change the length. Repeat the procedure for the original mass and two different pendulum lengths; one-half of the original length and then one-quarter of the original length.

Data Table

Mass 1 (kg) Length 1 (m) Oscillations Total Time (s) Measured Period (s) Theoretical Period (s)

0.010

Average Measured Period (s)

Mass 2 (kg) Length 1 (m) Oscillations Total Time (s) Measured Period (s) Theoretical Period (s)

0.020

Average Measured Period (s)

Mass 3 (kg) Length 1 (m) Oscillations Total Time (s) Measured Period (s) Theoretical Period (s)

0.050

Average Measured Period (s)

012-12876B

Model No. ME-9502 Exp. 10: Simple Harmonic Motion –The Simple Pendulum

T 2

L g

-- -=

Data Table

Mass 1 (kg) Length 2 (m) Oscillations Total Time (s) Measured Period (s) Theoretical Period (s)

0.010

Average Measured Period (s)

Mass 1 (kg) Length 3 (m) Oscillations Total Time (s) Measured Period (s) Theoretical Period (s)

0.010

Average Measured Period (s)

Calculations

1. Calculate and record the Measured Period by dividing the total time by the number of oscillations.

2. Calculate and record the Average Measured Period.

3. Calculate the Theoretical Period.

Questions

1. How well does the theoretical value for the period of oscillation for a simple pendulum compare to the measured period of oscillation?

2. Does the equation for the period of a simple pendulum provide a good mathematical model for the physical reality? Why or why not?

3. How does increasing the mass of the simple pendulum affect the period of the pendulum?

4. How does changing the length of the simple pendulum affect the period of the pendulum?

012-12876B 55

Statics System Exp. 10: Simple Harmonic Motion–The Simple Pendulum

012-12876B

Model No. ME-9502 Exp. 11A: Simple Harmonic Motion–Physical Pendulum

Figure 11.1: Physical Pendulum



mg sin 

mg cos 

Equilibrium

position

Pivot point

Center of

mass

T 2

-----------------=

T 2

---- -=

Fig. 11.2: Moment of Inertia

----- -

parallelIcm

----- -

mL2mL

+==

T 2

----- -

--------------------------------------- - 2 

----- -

------------------------------ -==

Exp. 11A: Simple Harmonic Motion–Physical Pendulum

Equipment Needed Item Item

Statics Board Balance Arm Stopwatch (ME-1234)

Theory

A simple pendulum is a mass on the end of a “massless” length of string. A physical pendulum is any rigid body that pivots at some point of the body so that it can rotate freely in a vertical plane under the force of gravity. Let L the center of mass of the body.

The torque that causes the rotation is produced by the component of the force of gravity that is perpendicular to the line that joins the pivot point to the center of mass, mg sin . The torque is the product of the lever arm, L  = L

mg sin For small angles, sin  = , so the expression for

the torque becomes  = L

be the distance from the pivot point to

, and the perpendicular force, or

mg or= kwhere k = Lcm mg.

Since the expression for torque matches the expression for the restoring force, F = -kx, on an object in simple harmonic motion, the period of oscillation for the physical pendulum can be written as follows:

where I, the moment of inertia (rotational inertia) for the physical pendulum, replaces M and L

mg replaces k in the equation for the

period of oscillation of a mass on a spring,

Assume that the Balance Arm beam is a rectangular-type rod. For a rod pivoting around an axis through its center of mass, the moment of inertia around the center of mass is:

where m is the mass and L is the length of the rod.

What happens if the rod pivots around one end rather than its center of mass? If the rod pivots around any other axis that is parallel to the axis through the center of mass, you can use the Parallel Axis Theorem to calculate the moment of inertia around that parallel axis. The moment of inertia about the parallel axis, I of the rod and L

, is the sum of the moment of inertia around the center of mass, Icm, plus mL

parallel

is the perpendicular distance from the center of mass to the pivot point, or

, where m is the mass

The formula for the period of oscillation becomes

012-12876B 57

Statics System Exp. 11A: Simple Harmonic Motion–Physical Pendulum

Pivot point

Beam

Center of

mass

Fig. 11.3: Setup

T 2

----- -

------------------------------ -=

In this part of the experiment you will investigate this equation for the period of the simple harmonic motion of a physical pendulum with a fixed distance between the pivot point and the center of mass.

Procedure

1. Move the pivot of the Balance Arm to the 170 mm mark at one end of the beam, and mount the pivot near the top of the Statics Board.

2. Measure and record the total length, L, of the beam of the Balance Arm and the distance, L

3. Start the beam swinging but keep the angle of the swing reasonably small (less than 20°).

4. Measure and record the total time for 10 oscillations.

5. Repeat the measurement a total of five times.

, from the pivot point to the center of mass (presumably at “0”).

Data Table

• Length, L (m) = _________________ Distance, Lcm (m) = _______________

Trial Oscillations Total Time (s) Measured Period (s) Theoretical Period (s)

1 2 3 4 5

Average Measured Period (s)

Calculations

1. For each trial, calculate and record the Measured Period by dividing the total time by the number of oscillations. Calculate the Average Measured Period.

2. Calculate the Theoretical Period:

Questions

1. How well does the theoretical value for the period of oscillation compare to the measured period of oscillation?

012-12876B

Model No. ME-9502 Exp. 11A: Simple Harmonic Motion–Physical Pendulum

parallelIcm

----- -

mL2mL

----- -

mL2m

-- -





----- -

1 4

-- -

1 3

-- -

== = = =

T 2

parallel

Lcmmg

------------------- -2

1 3

-- -

Lcmmg

----------------- 2 

1 3

-- -

---

------------- -2

------====

2. Does the equation for the theoretical period of this physical pendulum provide a good mathematical model for the physical reality? Why or why not?

Try This

• If you assume that the distance L the rod, then the formula for I

from the pivot point to the center of mass is L/2, exactly half the length of

gives a simpler expression:

parallel

• Substituting this expression into the formula for the period of oscillation of a physical pendulum gives:

• Use this expression to re-calculate the theoretical period of the physical pendulum and compare the result to the measured period of oscillation.

• How much difference is there between the re-calculated theoretical period and the previous theoretical period?

012-12876B 59

Statics System Exp. 11A: Simple Harmonic Motion–Physical Pendulum

2. Draw an arc.

3. Replace the Balance Arm with the Force Wheel and use a thread from the Force Wheel to determine the angles.

4. Put a mark every 5°.

Balance Arm

Pivot

1. Draw the outline of the pivot base.

Figure 11.4: Large Angle Oscillation Setup

Extension: Period of Oscillation for Large Angles

The motion of a physical pendulum is simple harmonic motion for small angles. When the angle becomes larger, sin  . How does the period of oscillation for a physical pendulum vary as the initial angle of swing increases?

Equipment Needed Item Item

Statics Board Force Wheel Balance Arm Stopwatch (ME-1234) Pencil or Dry Erase Marker Pen Thread

Setup

1. Slide the Balance Arm pivot to one end of the beam, and mount the pivot in a top corner of the Statics Board.

2. Use a dry erase marker pen or a pencil to draw the outline of the pivot base onto the board.

3. Hold the dry erase pen or pencil at the end of the beam and perpendicular to the board, and move the beam

and pen so you draw an arc from the bottom corner of the board to the opposite top corner.

4. After you draw the arc, remove the Balance Arm and place the base of the Force Wheel into the outline of the

pivot base. Level the Force Wheel.

012-12876B

Model No. ME-9502 Exp. 11A: Simple Harmonic Motion–Physical Pendulum

5. S tretch one of the threads from the Force Disk to the arc on the board. Arrange the thread so it is straight down

from the Force Wheel, and put a mark on the arc and label it as 0°.

6. Keep the thread taut and move it so the angle relative to vertical is 5°. Put a mark on the arc and label it.

7. Continue to move the thread along the arc and put a mark at every 5° interval until the string is horizontal.

8. Remove the Force Wheel and replace the Balance Arm on the board in its original position.

Procedure

1. Hold the beam of the Balance Arm so its center line points at the 5° mark on the arc. Release the beam and

measure the time for at least ten oscillations. Record the time and the number of oscillations.

2. Hold the beam so its center line points at the 10° mark and repeat the measurement.

3. Continue to measure and record the total time for at least ten oscillations at each angle until you reach 90°.

Data Table

Angle Oscillations Total Time (s) Period (s) Angle Oscillations Total Time (s) Period (s)

550 10 55 15 60 20 65 25 70 30 75 35 80 40 85 45 90

Analysis

1. Calculate and record the period for each angle by dividing the total time by the number of oscillations.

2. Create a graph of period versus angle.

Question

1. At what angle does the period of the physical pendulum begin to change?

2. Does the period increase or decrease as the initial angle increases?

012-12876B 61

Statics System Exp. 11A: Simple Harmonic Motion–Physical Pendulum

012-12876B

Model No. ME-9 502 Exp. 11B: Minimum Period of a Physical Pendulum

Figure 11.5: Physical Pendulum



mg sin 

mg cos 

Equilibrium

position

Pivot point

Center of

mass

T 2

-----------------=

----- -

2b2

+=

----- -

parallelIcm

----- -

mL2mL

+==

T 2

----- -

------------------------------ -=

Exp. 11B: Minimum Period of a Physical Pendulum

Equipment Needed Item Item

Statics Board Balance Arm Stopwatch (ME-1234)

Theory

The period of oscillation for a physical pendulum can be written as follows:

where I is the moment of inertia (rotational inertia) for the physical pendulum, L point to the parallel axis at the center of mass, cm, and m is the mass of the pendulum.

is the perpendicular distance from the axis at the pivot

The moment of inertia, I

, for a rectangular-type rod about its center

of mass is:

where a is the length and b is the thickness of the rectangular-type rod. However, if the length, a, is much greater than the thickness, b, then the following can be used as a very good approximation of the moment of inertia around the center of mass:

where m is the mass and L is the length of the rod.

If the rod pivots around any other axis that is parallel to the axis through the center of mass, the Parallel Axis Theorem states that the moment of inertia about the parallel axis, I the center of mass, I center of mass to the pivot point, or

, plus mL

, where m is the mass of the rod and Lcm is the perpendicular distance from the

, is the sum of the moment of inertia around

parallel

The formula for the period of oscillation becomes

At what distance, L

In this experiment you will determine the distance, L minimum period of oscillation for the physical pendulum.

, does the period of oscillation, T, become a minimum?

, from the pivot point to the center of mass that gives the

012-12876B 63

Statics System Exp. 11B: Mi nimum Period of a Physical Pendulum

Pivot point

Beam

Center of

mass

Fig. 11.6: Setup

Procedure

1. Move the pivot of the Balance Arm to a position one centimeter (cm) above the

midpoint of the beam (presumably the center of mass of the beam). Mount the pivot on the Statics Board.

2. S tart the beam swinging but keep the angle of the swing reasonably small (less than

20°)..

3. Measure and record the total time for 10 oscillations.

4. Change the position of the beam so that the pivot point is one centimeter farther

from the center of mass. Repeat the measurement for the total time of oscillation.

5. Increase the distance, L

6. Increase the distance, L

, by one centimeter again and repeat the procedure.

, by one centimeter until you reach the 170 mm mark on

the beam.

7. Record the total length, L, of the beam.

• T otal length, L = ____________ m

Data Table

Trial Distance, Lcm (m) Oscillations Total Time (s) Measured Period (s)

1 2 3 4 5

6 7 8

9 10 11 12 13 14 15 16 17

012-12876B

Model No. ME-9 502 Exp. 11B: Minimum Period of a Physical Pendulum

T 2

----- -

------------------------------ -=

--------- -

Calculations

1. For each distance, Lcm, calculate and record the Measured Period by dividing the total time by the number of

oscillations.

2. Create a graph of Measured Period versus distance, L

, to determine which length gives the minimum

period.

• Minimum L

= _______________

3. Use calculus to find the derivative of the period:

• Set the derivative equal to zero and solve for L

• Calculate and record the value for L

• Theoretical L

= _______________

based on the total length, L.

to confirm that this distance is .

Questions

1. Based on the graph, for which distance from the pivot point to the center of mass (Lcm) is the period a mini-

mum?

2. How does the value from the graph for the distance that gives minimum period compare to the theoretical

(calculated) value for the distance?

3. What would happen if you move the pivot point to the beam’s center of mass and then pulled the beam aside

at a small angle less than 20°? Assume that the pivot is perfectly frictionless.

012-12876B 65

Statics System Exp. 11B: Mi nimum Period of a Physical Pendulum

012-12876B

Model No. ME-9 502 Exp. 11C: Simple Harmonic Motion–Beam on a Spring

Hinge

Beam

Spring

lever

Figure 11.3: Beam on a Spring

---- -=





kxL

lever

–

lever

--------------

lever

------------------- -



lever

------------------- - L

lever

--==

2

lever

--------------

I k

--=

Exp. 11C: Simple Harmonic Motion–Beam on a Spring

Equipment Needed

Item Item

Statics Board Mounted Spring Scale Mass and Hanger Set Balance Arm and Protractor Stopwatch (ME-1234) Thread

Theory

Imagine a horizontal beam that is supported by a hinge at one end and a vertical spring at the other end. If the beam is displace, the spring exerts a restoring force, F = -kx, to return the beam to its equilibrium position. The beam will oscillate up and down with a period, T

For a mass on a spring, the period, T, is as follows:

beam

where M is the oscillating mass and k is the spring constant. What is the period for a beam on a spring?

The beam rotates at the hinge as the spring oscillates up and down. The force of the spring on the beam, F = -kx, produces a torque on the beam. Let L is = FL

. A net torque causes angular acceleration, , that is directly proportional to the torque, , and

lever

be the length of the lever arm of the beam. The torque due to the spring

lever

inversely proportional to the moment of inertia, I. That is,

or  = I. Setting the two expressions for torque equal to each other gives FL

= I or -kxL

lever

= I where x is

lever

the displacement of the spring up and down as it oscillates.

The angular acceleration, , and the tangential (linear) acceleration, a acceleration, a

= L

lever

Solving for a

This expression has the form of a

= r where r is the radius of rotation. In this case, the radius of rotation is the lever arm, L

, or  = aT/L

gives:

.The expression becomes:

lever



x, where  is the angular frequency, so  is:

, of the beam are related. The tangential

lever

, so

Since the angular frequency,  = 2/T, the period, T = 2/or

012-12876B 67

Statics System Exp. 11C: Simple Harmonic Motion–Beam on a Spring

----- -

parallelIcm

----- -

ML2ML

+==

Spring

Scale

Pivot base

Protractor

Figure 11.7: Equipment Setup

Thread

Center of

mass

Balance Arm

beam

where I is the moment of inertia and k is the spring constant. If you assume that the beam is like a rectangular-type rod, then the moment of inertia about the center of mass of the rod is:

where M is the mass and L is the length of the rod. The Parallel Axis Theorem predicts that the moment of inertia about an axis at the end of the rod is

where L

Of course, any other mass added to the beam would alter the moment of inertia. For example, if a point mass, m, is at a distance, r, from the pivot point, its moment of inertia is I = mr

is the distance from the center of mass of the rod to the parallel axis (the pivot point).

. The moment of inertia would be the sum.

Procedure

1. Measure and record the mass of the of the Balance Arm beam. Measure and record the mass of a Protractor.

2. Place the Pivot at the 170 mm mark on the Balance Arm beam. Mount the Protractor on the beam at the 110

mm mark. Mount the Balance Arm beam on the Statics Board.

3. Mount the Spring Scale on the Statics Board so that the scale is perfectly vertical. Use thread to connect the

Angle Indicator on the Protractor to the bottom hook of the Spring Scale.

4. Adjust the Balance Arm and the Spring Scale so that the arm is horizontal and the scale is directly above the

center of the protractor.

5. Push the Balance Arm beam down to a small angle (less than 20°) and release it smoothly. Measure the time

for ten complete oscillations (or as many oscillations as possible). Record the number of oscillations and the total time.

6. Calculate and record the Measured Period, T

measured

, by dividing the total time by the number of oscillations.

7. Repeat the measurement for the first position of the Protractor five times.

8. Change the position of the Protractor by moving it 10 millimeters (mm) farther away from the pivot point and

repeat the measurements.

9. Repeat the procedure for 90 mm, 80 mm, and 70 mm for a total of five distances.

012-12876B

Model No. ME-9 502 Exp. 11C: Simple Harmonic Motion–Beam on a Spring

beam

----- -

ML2ML

++==

beam

----- -

ML2ML

lever

++==

2

lever

--------------

I k

2

lever

--------------

----- -

lever

--------------------------------------------------------------------- -==

10. Measure and record the length of the beam, L, and the distance from the pivot point to the center of mass

(c.o.m.) of the beam, L

11. See the experiment Hooke’s Law to find the spring constant, k, of the Spring Scale and record its value.

Calculations

1. Calculate and record the Measured Period for each trial.

2. Calculate and record the Average Measured Period for each lever arm length.

Assume that the Protractor is a point mass, m, at a distance r from the axis of rotation. Its moment of inertia added to the beam’s moment of inertia gives the following:

Since the distance r from the axis of rotation is also the length of the lever arm, L becomes:

and the period of oscillation, T, becomes:

3. Calculate the Theoretical Period, T

theoretical

, for each trial and record the result.

Data

• mass of beam, M = ____________ mass of protractor, m = ________________

• length, L = _____________ distance from pivot point to c.o.m., L

• spring constant, k = ________________

= ________________

, the moment of inertia

lever

012-12876B 69

Statics System Exp. 11C: Simple Harmonic Motion–Beam on a Spring

Data Table

(m) Oscillations Total Time (s) Measured Period (s) Theoretical Period (s)

lever

0.060

Average Measured Period (s)

0.070

Average Measured Period (s)

0.080

0.090

0.100

Average Measured Period (s)

Questions

1. How well does the theoretical value for the period of oscillation compare to the average measured period of

oscillation for each trial?

2. Does the equation for the period of a beam on a spring provide a good mathematical model for the actual

period of a beam on a spring? Why or why not?

012-12876B

Model No. ME-9 502 Exp. 11C: Simple Harmonic Motion–Beam on a Spring

2

----- -

lever

--------------------------------------------------------------------- -

Extension

• Plot a graph of period, T, versus the reciprocal of L slope’s value to the following:

. Determine the slope of the line and compare the

lever

012-12876B 71

Statics System Exp. 11C: Simple Harmonic Motion–Beam on a Spring

012-12876B

Model No. ME-9502 Exp. 12: Simple Machines–The Lever

Figure 12.1: Lever

Figure 12.2: Equipment Setup

Spring

Scale

Pivot

Balance

Arm

Protractor

Large Pulley

Hanging

Mass

Thread

Exp. 12: Simple Machines–The Lever

Equipment Needed

Item Item

Statics Board Mounted Spring Scale Mass and Hanger Set Balance Arm and Protractors Large Pulley Thread Pencil or Dry Erase Marker Pen

Theory

The workings of a lever can be understood using the concept of torque. When the torque produced by the applied force (called the “effort”) becomes greater than the torque of the object being lifted (called the “load”), the lever will rotate about its pivot point (sometimes called the “fulcrum”), raising the load. However, levers can also be explained in terms of work and the conservation of energy.

In physics, the precise mathematical definition of work is the force applied to an object multiplied by the distance over when that force acts, or W = Fd where W is the work, F is the applied force, and d is the displacement of the object in the direction of the force. (If a force is applied to an object, but the object does not move in the direction of the force, then, technically, no work is done.) Whenever work is done on an isolated system, the energy of the system will change by exactly the amount of work that was performed, or



E = W where E is the change of

energy.

In this experiment, you will apply a measurable amount of work to a lever and observe the change in the gravitational potential energy of the load.

Setup

1. Put a Protractor at each end of the Balance Arm beam and mount the Balance Arm on the Statics Board with the beam centered in the pivot.

012-12876B 73

Statics System Exp. 12: Simple Machines–The Lever

Figure 12.3: Raise the Spring Scale

Spring

Scale

Pivot

Protractor

Large Pulley

Hanging

Mass

Thread

Outline

2. Mount a Large Pulley and Spring Scale at one end of the Balance Arm and use thread to connect the Spring Scale to the Protractor on the Balance Arm.

3. Use thread to hang a mass hanger from the other Protractor and add 200 g of mass to the hanger.

4. Adjust the Large Pulley and the Spring Scale so that the Balance Arm beam is horizontal and level.

Procedure

1. Make and record the necessary measurements to show that the torques produced by the Spring Scale and the weight of the Hanging Mass are balanced.

2. Use a pencil or dry erase marker pen to outline the base of the Spring Scale and the position of the top of the Hanging Mass on the Statics Board.

3. Slowly push the Spring Scale upward. (If you perform this movement slowly enough, the reading on the Spring Scale will not vary appreciably.)

4. Mark the new positions of the Hanging Mass and the Spring Scale.

5. Measure and record the distances, d Also record F

, the reading on the Spring Scale, and M1 and W1, the mass and weight of the Hanging Mass.

6. Move the protractor with the hanging mass to a new location about halfway to the pivot point and repeat the experiment. Measure and record the new values for d

(distance Hanging Mass moved) and d2 (distance Spring Scale moved).

, d2, and F2.

012-12876B

Model No. ME-9502 Exp. 12: Simple Machines–The Lever

Figure 12.4: Class II Lever

Applied

force

Load

Data Table

Item Trial 1 Trial 2 Item Trial 1 Trial 2

Distance hanging mass moved, d

Distance Spring Scale moved, d

Force of Spring Scale, F

Mass of hanging mass, M

Weight of hanging mass, W

Calculations

1. Calculate and record the work done on the system as you raised the Spring Scale, where Work = F2 d2.

2. Calculate and record the change in potential energy of the Hanging Mass as it was raised in the Earth’s gravi-

tational field, where E

Trial Work Change of potential energy

1 2

= M1 g d1 and g = 9.8 N/kg.

potential

Questions

1. How did the work done on the system compare to the change in potential energy of the system?

2. How does a lever make it easier to perform work, such as raising a heavy load? Explain in terms of conserva-

tion of energy.

Extension

The type of lever that has the fulcrum between the load (hanging mass) and the applied force (Spring Scale) is called a Class I Lever. A Class II Lever has the load between the fulcrum and the applied force, and the Class III lever has the applied force between the fulcrum and the load.

Fulcrum

012-12876B 75

Statics System Exp. 12: Simple Machines–The Lever

Figure 12.6: Class III Lever

Load

Applied

force

A wheelbarrow is an example of a Class II Lever, and the human forearm is an example of a Class III Lever.

Fulcrum

When a lever is in equilibrium, the sum of the clockwise torques about the pivot point (fulcrum) is equal to the sum of the counterclockwise torques about the pivot point.

Make and record the measurements that are necessary to determine if the sum of the clockwise torques equals the sum of the counterclockwise torques for the Class II and Class III levers. Will you need to take the mass of the protractors and the mass of the Balance Arm beam into account?

Diagram your results and show your measurements and calculations on a separate sheet of paper.

Data Table

Table 16.1:

Lever  clockwise torque  counterclockwise torque Net torque

Class II

Class III

Questions

1. For the Class II Lever, is the net torque equal to zero when the lever is in equilibrium?

2. For the Class III Lever, is the net torque equal to zero when the lever is in equilibrium?

012-12876B

Model No. ME-9502 Exp. 13: Simple Machine s–The Inclined Plane

Figure 13.1: Inclined Plane

height

parallel

= W sin 

Fup = W



Figure 13.2: Equipment Setup

Inclined

Plane

Pulley

Spring

Scale

Mass

Cart

100-g mass

Keep the thread

parallel to the plane.

Exp. 13: Simple Machines–The Inclined Plane

Equipment Needed

Item Item

Statics Board and Pulley Mounted Spring Scale Mass and Hanger Set Inclined Plane and Mass Cart Pencil or Dry Erase Marker Pen Thread

Introduction

The inclined plane, like the lever, is often used to help raise heavy objects. In a previous experiment, you analyzed this use of the inclined plane in terms of the forces that are involved. In this experiment you will take a second look at the inclined plane, using the concepts of work and conservation of energy as you applied them in previous experiments.

The work to lift an object with a weight, W, is the product of the weight and the height. To push the same object up the inclined plane requires a smaller force, W

sin



, than the object’s weight, but the distance over which the force acts is longer. The angle  is the incline of the

plane.

Procedure

1. Put a 100 g mass on the peg of the Mass Cart and use the Spring Scale to measure the total weight, W, of the cart plus mass.

• Weight, W = ______________

2. Put the Inclined Plane on the Statics Board at a relatively small angle (such as 15°). Put a Pulley and the Spring Scale on the board near one end of the Inclined Plane. Put the Mass Cart on the Inclined Plane and use thread to connect the end of the Mass Cart to the Spring Scale.

Mark the outline of

the Spring Scale.

012-12876B 77

Statics System Exp. 13: Simple Machines–The Inclined Plane

Fig. 13.3: Measure d

Outline

Figure 13.4: Calculate height

d1 sin 



Original position

3. Measure and record the magnitude of the force, F angle



of the Inclined Plane.

• Force, F

= _____________ Angle, 

, exerted by the Spring Scale on the Mass Cart, and the

4. Use a pencil or dry erase marker pen to outline the base of the Spring Scale on the Statics Board.

5. Slowly raise the Spring Scale – slowly enough that there is no appreciable change

in the reading on the Spring Scale.

6. Measure and record the distance, d

• Distance, d

= _______________

, that the Spring Scale pulled the Mass Cart.

Calculations

1. Calculate and record the height that the Mass Cart was lifted as it was pulled up the Inclined Plane by the Spring Scale.

•Height, d

sin  = ________________

Question

Procedure

2. Calculate and record the amount of work done by the Spring Scale.

• Work = F

= _________________.

1 d1

3. Calculate and record the change in gravitational potential energy of the Mass Cart.

• E = Weight x height = W d

sin  = __________________.

• How does the change in gravitational potential energy of the Mass Cart compare to the work done by the Spring Scale?

1. Carefully hang the Mass Cart plus the 100 g mass from the Spring Scale. Record the force, F2, exerted by the Spring Scale.

• Force, F

= ______________

012-12876B

Model No. ME-9502 Exp. 13: Simple Machine s–The Inclined Plane

d1 sin 

Outline

Original position

Fig. 13.5: Raise the Mass Cart

2. Slowly push the Spring Scale straight up a distance, d1 sin the height to which the Mass Cart was raised when it was on the Inclined Plane. (Raise the Spring Scale slowly so that there is no appreciable change in the reading of the Spring Scale.)

Calculations

1. Calculate and record the amount of work that was done on the Mass Cart by lifting it straight up by a distance of d

sin 

• Work = F d = F

sin  = ___________________

2 d1

2. Calculate and record the change in gravitational potential energy of the Mass Cart.

• E = Weight x height = W d

sin  = __________________.

Questions

1. How does the work done on the Mass Cart when it was on the Inclined Plane compare to the work done when it was lifted directly by the Spring Scale?

2. How does an inclined plane make it easier to perform work, such as raising a heavy load? In other words, what is the advantage of using the inclined plane?

012-12876B 79

Statics System Exp. 13: Simple Machines–The Inclined Plane

012-12876B

Model No. ME-9502 Exp. 14: Simple Machines–The Pulley

Fig. 14.1: Simple Pulley

Mass

Force

Figure 14.2: Equipment Setup

Pulley

Spring

Scale

Hanging

Mass

Pulley

Exp. 14: Simple Machines–The Pulley

Equipment Needed

Item Item

Statics Board and Pulley Mounted Spring Scale Large Pulley and Small Pulleys (2) Double Pulley Block Mass and Hanger Set Thread

Theory

In previous experiments, you used pulleys to change the direction of applied forces. However, systems of pulleys can be arranged to translate relatively small applied forces into much larger forces, much the same way as a lever or inclined plane. In this experiment you will take a second look at pulleys and investigate how systems of pulleys can be used to amplify the applied force as work is done.

In an ideal pulley system there would be not friction in the pulleys. For example, the applied force would be transferred completely to the hanging mass.

As with the lever and the inclined plane, pulley systems can be understood by analyzing either the forces acting on the system or the work performed on and by the system. In this experiment you will investigate several pulley systems.

Procedure

The effects of friction are more noticeable in this experiment than with the lever or the inclined plane. Start by investigating the effects of friction in the pulleys.

1. Put 200 g of mass on a mass hanger and use the Spring Scale to measure the total weight, W, of the mass hanger plus mass. Record your measurement.

• Weight, W = ______________

2. Put the Spring Scale and two Pulleys on the Statics Board as shown and use thread to attach the Spring Scale to the hanging mass. Record the reading of the force, F, on the Spring Scale.

• Force, F = _______________

Question

• How does the force reading, F, on the Spring Scale for the pulley setup compare to the weight, W, of the hanging mass?

3. Set up each of the three pulley systems shown below. For each pulley system, perform work on the system by slowing raising the Spring Scale. Measure and record the following:

Symbol Description Symbol Description

F Force reading on the Spring Scale d

W/F Ratio of weight of hanging mass to force Work Work done by raising the Spring Scale (F x d

Distance that the Spring Scale is raised E Change in gravitational potential energy (W x d2)

Distance that the hanging mass is raised

012-12876B 81

)

Statics System Exp. 14: Simple Machines–The Pulley

Figure 14.3: Pulley Systems

Outline

ABC

Note that the drawings are not to scale. Allow more vertical distance between the components.

Small

Pulley

Large

Pulley

Double

Pulley

Hanging

Mass

Loop the thread around the pulley.

Original position

4. Use a pencil or dry erase marker pen to outline the base of the Spring Scale. Also mark the position of the top of the hanging mass.

5. Slowly raise the Spring Scale – slowly enough that there is no appreciable change in the reading on the Spring Scale.

6. Measure and record the distance, d d

, that the hanging mass was raised.

Data Table

System W F W/F d

A B C

Questions

1. How does the relationship of weight (W) and force (F) compare to the relationship of the distance the Spring Scale was raised (d

) and the distance the hanging mass was raised (d2)?

, that the Spring Scale was raised. Also measure and record the distance,

2. Compare the value of W/F to the number of threads that crosses the dotted line in the figure of the pulley sys-

tem.

012-12876B

Work E

Model No. ME-9502 Exp. 15: Forces on a Boom

Fig. 15.1: Suspended Mass

Cable

Mass

c.o.m.

Pivot

Boom

normal



clockwise

WL cosWcmL

cos+=



counterclockwise

cos=

WL cosW

cmLcm

cos+

cos

---------------------------------------------------------------------- -

Exp. 15: Forces on a Boom

Equipment Needed

Item Item

Statics Board Mounted Spring Scale and Pulley Balance Arm and Protractors) Thread Mass and Hanger Set

Theory

A boom supported by a cable has a mass suspended at its upper end. The lower end of the boom is supported by a pivot.

For example, if the mass is 100 kg and the boom has a mass of 50 kg, what is the tension, T, in the cable? Assume that the cable is attached at the boom’s center of mass and is at an angle relative to the boom. The boom is at an angle of 50° to the horizontal.

For the boom to be in equilibrium, all of the translational forces (F

and Fy)

and all of the torques must add up to zero. One torque is produced by the tension in the cable. Another torque is produced by the weight of the beam. A third torque is produced by the weight of the hanging mass.

where W is the weight of the hanging mass, L is the lever arm from the pivot point to the place where the hanging mass is attached, W

is the weight of the boom, Lcm is the lever arm from the pivot point to the center of mass,

boom

 is the angle of the boom, T is the tension in the cable, and  is the angle of the cable relative to the normal of the boom.

If the boom is in equilibrium, the net torque is zero. The expression for the tension, T, in the cable becomes:

012-12876B 83

Statics System Exp. 15: Forces on a Boom

Figure 15.2: Equipment Setup

Pulley

Spring

Scale

Hanging

Mass

Balance

Arm

Protractor

Pivot





Thread

beam

Pivot

Procedure

1. Set up the Balance Arm with the pivot at one end, a protractor at the midpoint, and a second protractor at the other end. Mount the Balance Arm in a lower corner of the Statics Board.

2. Mount the Spring Scale and a Pulley on the board and use thread to attach the Spring Scale to the protractor at the midpoint of the beam.

3. Use thread to attach a hanging mass to the protractor at the end of the beam.

4. Make and record the necessary measurements.

Data Table

Item Value

Angle, , of Balance Arm

Angle, , of thread

Weight, W, of hanging mass

Weight, W

Weight of protractor Lever arm, L Lever arm, L, to hanging mass

Tension, T, in the thread

, of beam

beam

, pivot to c.o.m.

Calculations

1. Calculate the sum of the clockwise torques about the pivot point.

•  torque

clockwise

= _____________________

2. Calculate the theoretical tension, T, in the thread.

•Tension

Question

theoretical

= ________________________

• How does the force reading on the Spring Scale compare to the theoretical value for the tension in the cable?

012-12876B

Model No. ME-9502 Exp. 16: Modifie d Atwood’s Machine

Mass

M2g

Pulley

Thread

Fig. 16.1: Atwood’s FBD

M1g

T1M1g– F

net

M1a==

2M2

g– F

net

M2a–==

2M1

–

2M1

---------------------

----- -

Exp. 16: Modified Atwood’s Machine

Equipment Needed

Item Item

Statics Board Small Pulley (2) Mass and Hanger Set Thread Stopwatch Dry-erase Marker Pen or Pencil

Theory

The acceleration of an object depends on the net applied force and the object’s mass. In an Atwood’s Machine, the difference between two hanging masses determines the net force acting on the system of the two masses. The net force accelerates both of the hanging masses; the heaver mass is accelerated downward and the lighter mass is accelerated upward.

The Atwood’s Machine was invented in 1784 by the Reverend George Atwood to demonstrate the principles of acceleration and net force. In an ideal Atwood’s Machine, two unequal masses are attached to a flexible, massless string which passes over a frictionless, massless pulley. A real Atwood’s Machine is not as simple as its ideal counterpart. Strings and pulleys are not massless and pulleys are not frictionless. The rotational inertia of the pulley complicates the demonstration.

In the free body diagram (FBD) of the Atwood’s Machine, T is the tension in the string, Mass Mass

, and g is the acceleration due to gravity. Using the convention that up is positive and down is negative, the

is greater than

net force equations for the two masses are:

Ideally (where the string is massless and doesn’t stretch and the pulley is massless and frictionless), the tension, T, is the same for both hanging masses. Let T

The theoretical acceleration is the difference in the two forces (M

= T2 and solve for the theoretical acceleration, a:

g - M1g) divided by the sum of the two masses.

In this experiment you will investigate the acceleration of the masses in an Atwood’s Machine. You can determine the acceleration, a, by measuring the time, t, it takes for one of the masses to fall a known distance, d.

Compare your measured acceleration to the theoretical acceleration.

012-12876B 85

Statics System Exp. 16: Modified Atwood ’s M achine

Figure 16.2: Equipment Setup

Pulley

Thread

Mass

hanger

Mass

hanger

Pulley

Bottom edge of

mass hanger

Setup

1. Place the two Small Pulleys on the Statics Board near

the top edge of the board and close to each other. Make sure that the two pulleys are level.

2. Connect a thread from one Mass Hanger to a second

Mass Hanger so the hangers are suspended over the two pulleys.

• NOTE: Make the thread long enough so that the heavy mass almost reaches the base of the Statics Board when the light mass is almost up to the pulley.

3. Pull the M M

mass hanger is just below the base of the pulley.

mass hanger down so that the top of the

Use a dry-erase marker or a pencil to put a horizontal mark on the Statics Board for the position of the bottom edge of the M

mass hanger.

4. Measure vertically down from the first mark a distance of 20 cm (0.020 m) and put a second horizontal mark on the board.

Procedure

Part 1: Keep Total Mass Constant

1. Put the following on the ‘light’ (M ing on the ‘heavy’ (M

) mass hanger: 1 x 50-g, 3 x 20-g, 1 x 10-g, 1 x 5-g.

2. Including each 5-g mass hanger, record the total mass for M

3. Move the 1-g mass from the light mass hanger to the heavy mass hanger (so the difference in mass is 1 g). Pull

the light mass hanger down so that the bottom edge of the heavy mass hanger is aligned with the starting mark on the Statics Board.

• NOTE: Stop the hangers from spinning or swinging.

4. Release the light mass hanger and start timing at the same instant. Stop timing when the bottom edge of the heavy mass hanger reaches the finish mark on the Statics Board. Record the time, t the trial two more times and record the results.

) mass hanger: 1 x 50-g, 3 x 20-g, 2 x 5-g, 2 x 2-g, 1 x 1-g. Put the follow-

and the total mass for M2 in the Data Table.

, in the Data T able. Repeat

5. For the second trial, return the 1-g mass to the light hanger and move one of the 2-g masses to the heavy hanger (M = 2 g). Repeat the data recording procedure three times.

6. For the third trial, move the 1-g mass from the light hanger to the heavy hanger (M = 3 g) and repeat the pro- cedure three times.

7. For the fourth trial, move the 1-g mass from the heavy hanger back to the light hanger and move the 2-g mass from the light hanger over to the heavy hanger (M = 4 g) and repeat the procedure three times.

8. F or the f ift h trial , move th e 1-g mas s fro m the light hanger to the heavy hanger (M = 5 g) and repeat the pro- cedure three times.

012-12876B

Model No. ME-9502 Exp. 16: Modifie d Atwood’s Machine

Data Table 1: Constant Total Mass

Trial M1 (kg) M2 (kg)

1 0.001 2 0.002 3 0.003 4 0.004 5 0.005

M

(kg)

avg

theoreticalameasured

% diff.

Part 2: Keep Net Force Constant

1. P ut a 50-g mass on the ‘light’ (M

) mass hanger and put a 50-g mass and a 5-g mass on the ‘heavy’ (M2) mass

hanger.

2. Including each 5-g mass hanger, record the total mass for M

and the total mass for M2 in the Data Table.

3. Pull the light mass hanger down so that the bottom edge of the heavy mass hanger is aligned with the starting mark on the Statics Board.

• NOTE: Stop the hangers from spinning or swinging.

4. Release the light mass hanger and start timing at the same instant. Stop timing when the bottom edge of the heavy mass hanger reaches the finish mark on the Statics Board. Record the time, t

, in the Data T able. Repeat

the trial two more times and record the results.

5. For the second trial, add 20 g of mass to each hanger (but M still is 5 g). Repeat the data recording procedure three times.

6. For the third trial, add another 20 g of mass to each hanger and repeat the procedure three times.

7. For the fourth trial, add another 20 g of mass to each hanger and repeat the procedure three times.

8. For the fifth trial, add another 20 g of mass to each hanger and repeat the procedure three times.

Data Table 2: Constant Net Force

Trial M

1 0.005 2 0.005 3 0.005 4 0.005 5 0.005

(kg) M2 (kg)

M

(kg)

avg

theoreticalameasured

% diff.

Calculations

1. Calculate and record the average time for each trial.

2. Calculate and record the theoretical acceleration and the measured acceleration for each trial.

012-12876B 87

Statics System Exp. 16: Modified Atwood ’s M achine

% diff=

theoreticalameasured

–

theoretical

--------------------------------------------------------- -

100

3. Calculate and record the percent difference of the theoretical acceleration and the measured acceleration for each trial.

4. For the Constant Total Mass data, calculate the net force (F

= M x g) for each trial. Plot a graph of net

net

force (vertical axis) versus measured acceleration (horizontal axis).

Questions

1. Describe the graph of net force versus measured acceleration. What does the slope of this graph represent?

2. How does the plot of net force versus measured acceleration relate to Newton’s Second Law?

3. Compare the percent difference for the theoretical and measured accelerations. What are some reasons that

might account for the percent difference?

012-12876B

Model No. ME-9502 Technical Support

Technical Support

For assistance with any PASCO product, contact PASCO at:

Address: PASCO scientific

10101 Foothills Blvd. Roseville, CA 95747-7100

Phone: 916-786-3800 (worldwide)

800-772-8700 (U.S.) Fax: (916) 786-7565 Web: www.pasco.com Email: support@pasco.com

For more information about the Statics System and the latest revision of this Instruction Manual, visit the PASCO web site and enter ME-9502 into the Search window.

Limited Warranty For a description of the product warranty, see the PASCO catalog. Copyright The PASCO scientific 012-12876B S tatics System Instruction Manual is copyrighted with all rights reserved. Permission is

granted to non-profit educational institutions for reproduction of any part of this manual, providing the reproductions are used only in their laboratories and classrooms, and are not sold for profit. Reproduction under any other circumstances, without the written consent of PASCO scientific, is prohibited.

Trademarks PASCO and PASCO scientific are trademarks or registered trademarks of PASCO scientific, in the United States and/or in other countries. All other brands, products, or service names are or may be trademarks or service marks of, and are used to identify, products or services of, their respective owners. For more information visit www.pasco.com/legal.

012-12876B 89

Statics System Technical Support

012-12876B

PASCO ME-9502 User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual

Introduction

Equipment

ME-9503 Statics Board

Important

ME-8979 Mass and Hanger Set

ME-9504 Spares Package

ME-9505 Components Package

Recommended Equipment*

T orque Indicator Assembly

Spares Package (ME-9504)

String Tie Assembly.

Mounted Scale Assembly

Components Package (ME-9505)

Large and Small Pulleys and Double Pulley Block

Mass Cart and Friction Block

Inclined Plane Assembly

Torque Wheel Assembly and Torque Indicator Assembly

Force Wheel Assembly and String Tie Assembly

Balance Arm Assembly

Utility Mount Assembly

Using a Cord Clip

Asymmetrical Plate

About the Manual

Introduction

Hooke’s Law

Setup

Procedure

Data Table

Calculations

Using a Spring Scale to Measure Force

Questions

Theory

Setup

Procedure: Two Forces

Procedure: Three Forces

Data

Analysis

Questions

Extension

Theory

Setup

Procedure 1

Background

Procedure 2

Question

Extensions

Theory

Setup

Procedure: Equal Distance, Equal Mass

Procedure: Unequal Distance, Unequal Mass

Calculations

Data Table

Questions

Exp. 5A: Center of Mass

Theory

Setup

Experiment

Asymmetrical Plate

Exp. 5B: Equilibrium of Physical Bodies

Theory

Setup

Experiment

Calculations

Calculations

Extension

Theory

Setup

Procedure

Analyzing Non-Parallel Forces

Torque Wheel

Data Table

Question

Extension

Exp. 7: The Inclined Plane

Introduction

Experiment