PASCO ME-6950 User Manual

Download

Instruction Manual and Experiment Guide for the PASCO scientific Model ME-6950

PAScar with Mass

012-07361B

250g

012-07361B

PAScar with Mass

Introduction

The PASCO Model ME-6950 PAScar with Mass performs high quality motion experiments through its low-friction design.

The PASCar with Mass has several excellent features:

• Extremely low friction ball-bearing design provides smooth motion.

• Built-in spring plunger, activated by a convenient trigger (button), with three positions of launching amplitude enables the car to be launched without using additional apparatus.

• Unique suspension system allows the wheels to collapse inside the body of the car to prevent damage to the internal components of the car caused by being dropped or other misuse (such as the car being used as a roller skate).

• Convenient holes located at the top of the end cap on each end of the PAScar facilitate the use of string, springs, etc.

• Hook and loop fasteners on the front of each PAScar enable the user to perform inelastic collision experiments without using additional apparatus.

• The mass of the PAScar is approximately 250g. The additional mass also has an approximate mass of 250g.

NOTE: For best results, measure the mass of the car and mass bar with an accurate balance or scale.

The spring plunger of the PAScar has three cocking positions. Determine the one that gives you a range that fits your situation best, taking into account the limitations of space. Most experiments require a range of at least 2 meters or more.

Practice launching the PAScar by placing the cart on the floor with its cocked plunger against a wall or a secured brick.

NOTES:

1. Before performing experiments with the PAScar and Mass, calibrate to insure accurate results from your experiments. We suggest performing Experiment #2 before Experiment #5 and #4 before #6.

2. To insure that you do not give the cart an initial velocity, other than that supplied by the spring plunger, release the trigger by tapping it with a rod or stick using a flat edge.

3. Rolling distance can be shortened by adding more mass to the car.

4. For even less friction, use 1/4-inch plate glass as surface for the car.

• Other features include a tray on top of the cart for application of additional mass and the ability of the cars to be stacked.

While performing experiments, you may find that you get better results by making the surface over which the car rolls more uniform and clean. One way to achieve this is by taping a long piece of butcher paper to the surface on which the cart rolls.

PAScar with Mass

012-07361B

Equipment

The ME-6950 PAScar with Mass includes the following:

• (2) PAScars, 1 red, 1 blue

• (2) 250 g mass

• Instruction Manual/Experiments Guide

Additional Equipment Required

• A spool of thread

• Masses, such as the Slotted Mass Set (SE-8704)

• A pulley and clamp, such as the Super Pulley with Clamp (ME-9448A) or the Super Pulley (ME-9450) used with the Model ME-9376B Universal Table Clamp and Model SA-9242 Pulley Mounting Rod

• Metric ruler, such as the Metric Measuring Tape (SE-8712A).

• Stopwatch, such as the Digital Stopwatch (SE-

8702)

• Mass balance, such as the Triple-Beam Balance (SE-8723)

• A friction block that can fit in the car's accessory tray (such as PASCO's Friction Block, part number 003-04708)

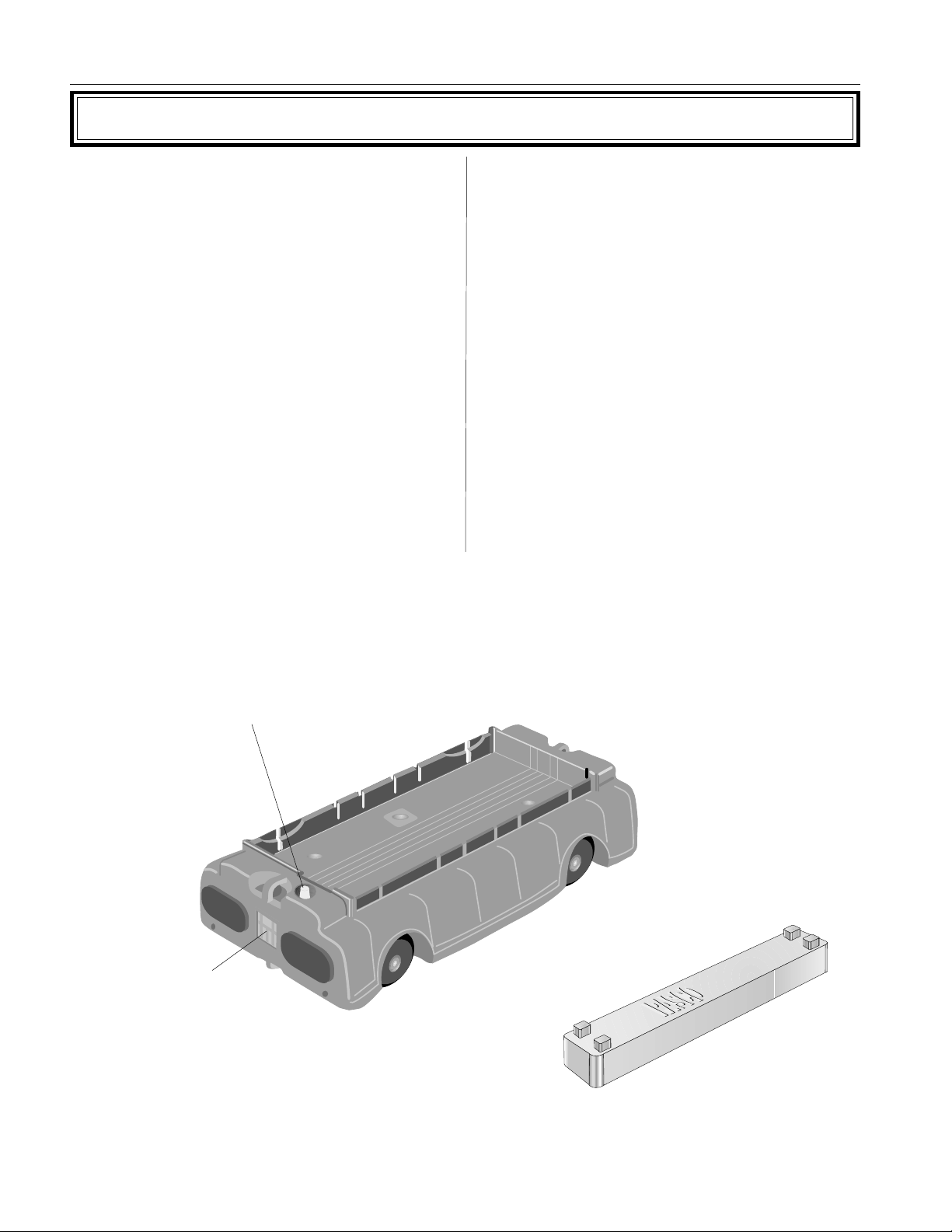
Plunger bar

release button

Accessory

tray

Additional mass

(250 g)

PAScar

(250 g)

250g

012-07361B

EQUIPMENT NEEDED:

– PAScar (ME-6950)

– Metric tape (SE-8712)

– Stopwatch (SE-8702)

Purpose

In this lab, the PAScar will be used to investigate one dimensional accelerated motion. The car will be launched over the floor using the built-in spring plunger. The car will “decelerate” over the floor under the combined action of rolling friction and floor slope. You will be able to establish whether or not the acceleration of the car is constant. This will be done by initially assuming a constant acceleration and then by examining the results to see if they are consistent with this assumption.

PAScar with Mass

Experiment 1: Kinematics

(Average vs. Instantaneous Velocities)

Figure1.1

Theory

The car will be allowed to roll to a stop. The distance D covered and the total elapsed time T from launch to stop will be measured and recorded. The average velocity over this interval is given by:

(EQN-1):

If the acceleration of the car is constant as it rolls to a stop over the floor, then the initial instantaneous velocity of the car at the final moment of launch is given by:

(EQN-2):

= 2vav =

And the value of the acceleration would be given by:

(EQN-3):

If the acceleration and v

a = = = –

are known, then the time t1 required to cover the distance d

0 – v

to some intermediate point (i.e. short of the final stopping point!) can be calculated by applying the quadratic formula to:

(EQN-4):

d = v

+ 1/2at

0t1

Calculated values of t1 will be compared with directly measured values. The extent to which the calculated values agree with the directly measured values is an indication of the constancy of the acceleration of the car.

Note your theoretical values in Table 1.1.

PAScar with Mass

Procedure

1. Once you have roughly determined the range of the cart, clearly mark a distance d that is about half way out from the start. Measure this distance and record it at the top of Table

1.1.

012-07361B

2. Using a stopwatch with a lap timer and metric tape, it is possible to determine t for each launch. Practice this step a few times before you start recording data.

NOTE: To eliminate reaction time errors, it is very important to have the person who launches the cart also be the timer!

3. Launch the car and record the data described in the previous step for six trials. To cock the spring plunger, push the plunger in, and then push the plunger slightly upward to allow one of the notches on the plunger bar to “catch” on the edge of the small metal bar at the top of the hole. (Don’t count the trials in which the timer feels that a distraction interfered with the measurement.) Record your best trials in Table 1.1.

4. Using the equations described in the theory section and the data recorded in the table, do the calculations needed to complete the table.

Data Analysis

d = _______cm

Table 1.1

TheoryExperiment

Trial

t1 (sec) T (sec)

D (cm)

vo (cm/s) a (cm/s2)t1 (sec)

, T and D

% Diff.

Questions

1. Is there a systematic difference between the experimental and calculated values of t1? If so, suggest possible factors that would account for this difference.

2. Can you think of a simple follow-up experiment that would allow you to determine how much the cart’s “deceleration” was affected by floor slope?

012-07361B

EQUIPMENT NEEDED:

– PAScar (ME-6950)

– Metric tape (SE-8712)

– Stopwatch (SE-8702)

Purpose

In this lab, the PAScar will be launched over the floor using the on-board spring launcher. The car will “decelerate” over the floor under the combined action of rolling friction and the average floor slope. To determine both the coefficient of rolling friction µ ments must be done. (Recall that to determine the value of two unknowns, you must have two equations.)

Experiment 2: Coefficient of Friction

and θ, the small angle at which the floor is inclined, two separate experi-

PAScar with Mass

Theory

UPSLOPE

Figure 2.1

DOWNSLOPE

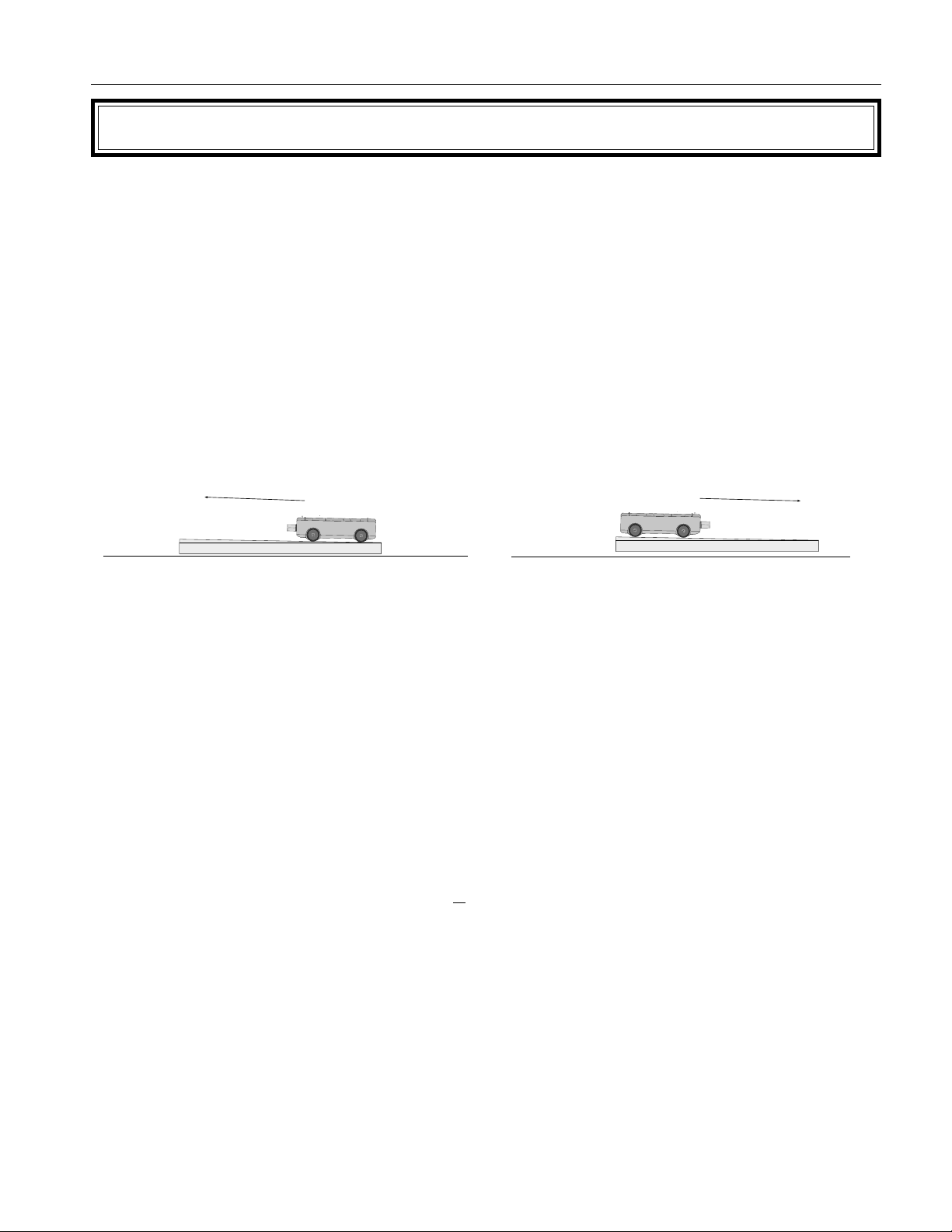
The car will be launched several times in one direction, and then it will be launched several times along the same course, but in the opposite direction. For example, if the first few runs are toward the east, then the next few runs will be toward the west. See Figure 2.1. In the direction which is slightly downslope, the acceleration of the car is given by:

(EQN-1):

a1 = + gsinθ – µrg (since cos2θ + sin2θ =1)

And the acceleration in the direction that is slightly upslope will be:

= – gsinθ – µrg

(EQN-2):

Numerical values for these accelerations can be determined by measuring both the distance d that the car rolls before stopping and the corresponding time t. Given these values, the acceleration can be determined from:

(EQN-3):

Having obtained numerical values for a

a =

and a2, EQN-1 and EQN-2 can be simultaneously solved

for µr and θ.

PAScar with Mass

Procedure

1. Place the car in its starting position and then launch it. To cock the spring plunger, push the plunger in, and then push the plunger slightly upward to allow one of the notches on the plunger bar to “catch” on the edge of the small metal bar at the top of the hole. Using a stopwatch and metric tape, determine the range d and the total time spent rolling t. Record these in Table 2.1.

2. Repeat step 1six times for each direction and enter your results in Table 2.1.

3. Using EQN-3, compute the accelerations corresponding to your data and an average acceleration for each of the two directions.

012-07361B

4. Using the results of step 3, determine µ unknowns.

Trial

First Direction

d (cm) t (sec)

a ( )

and θ by algebraically solving for the two

Table 2.1

Second Direction

Trial

d (cm) t (sec)

a ( )

Average Acceleration = __________

Data Analysis

Coefficient of rolling friction = ________________ Floor Angle = ________________

Questions

1. Can you think of another way to determine the acceleration of the car? If you have

time, try it!

2. How large is the effect of floor slope compared to that of rolling friction?

012-07361B

PAScar with Mass

Experiment 3: Newton's Second Law

(Predicting Accelerations)

EQUIPMENT NEEDED:

– PAScar (ME-6950)

– Pulley and pulley clamp (ME-9448)

– Mass set (SE-8704)

– Stopwatch (SE-8702)

– String

– Paper clips

– Block (to act as bumper)

– Balance (SE-8723 or equiv.)

Purpose

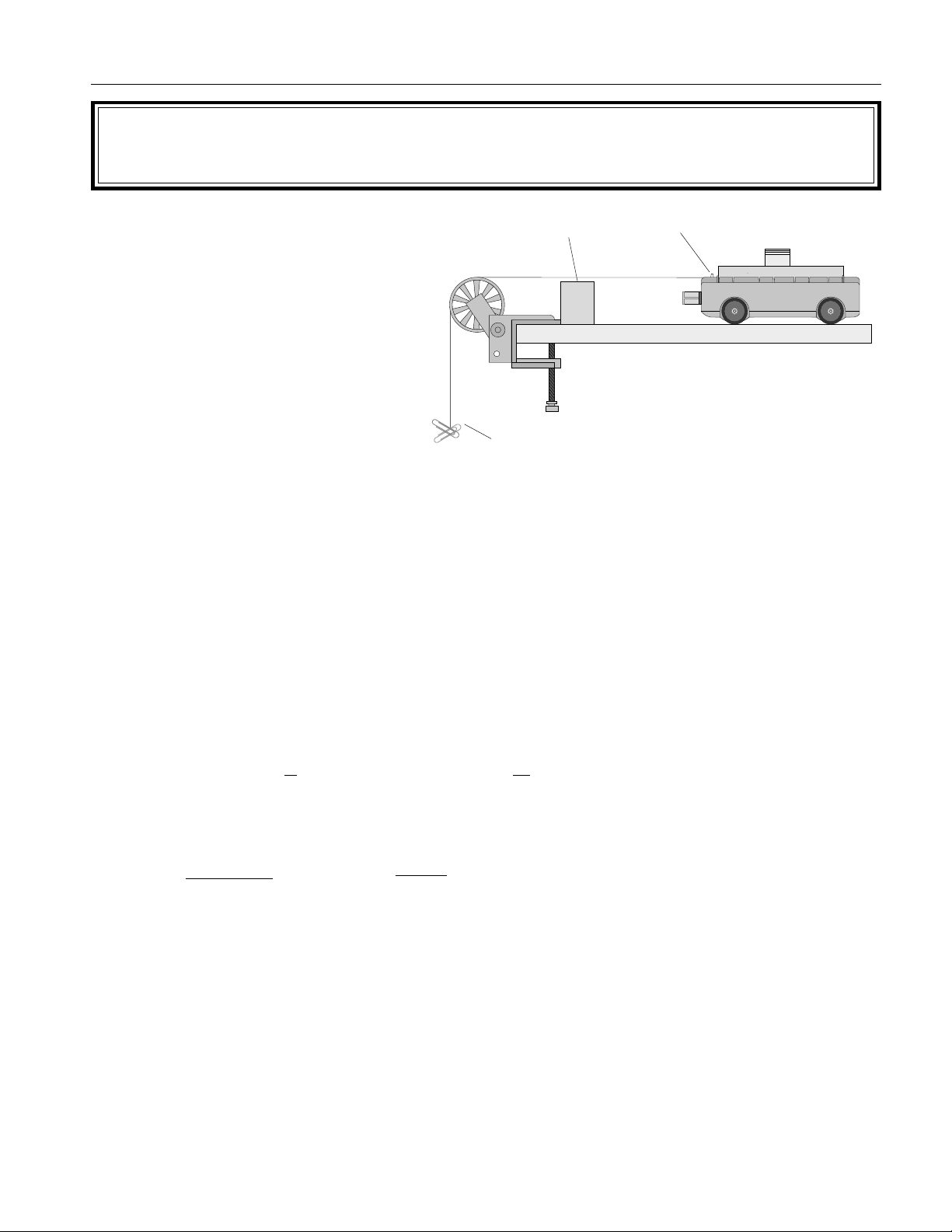
In this lab, a small mass m will be connected to the PAScar by a string as shown in Figure

3.1. The string will pass over a pulley at the table’s edge so that as the mass falls the car will be accelerated over the table’s surface. As long as the string is not too elastic and there is no slack in it, both the falling mass and the PAScar will have the same acceleration. The resulting acceleration of this system will be experimentally determined and this value will be compared to the acceleration predicted by Newton’s Second Law.

Theory

Bumper

block

Paper clips

Trigger

Figure 3.1

The car will be released from rest and allowed to accelerate over a distance d. Using a stopwatch, you will determine how long it takes, on average, for the car to move through the distance d. An experimental value for the car’s acceleration a can be determined from:

d = at

which leads to: a = (Experimental Value)

Assuming that the tabletop is truly horizontal (i.e. level), Newton’s Second Law ( F = ma) predicts that the acceleration of this system will be:

net

TOTAL

a = or

a = ( ) g (Theoretical Value)

TOTAL

Procedure

1. Set up the pulley, car, and a bumper of some sort to prevent the car from hitting the pulley at the end of its run. Add the following masses to the bed of the car: 10 g, 50 g, 500 g and two 20-gram masses.

2. Carefully level the table until the car has no particular tendency to drift or accelerate in either direction along its run.

3. Put a loop in one end of the string and place this loop over the spring-release trigger on the PAScar. Drape the string over the pulley. Adjust the pulley so the string is level.

4. Adjust the length of the string so that the longest arrangement of masses that you intend to use will not hit the floor before the car has reached the end of its run. Put a loop in this end of the string.

PAScar with Mass

NOTE: The car’s acceleration falls to zero when the falling mass hits the floor.

5. Hang enough paper clips onto the dangling loop in the string until the car will just continue to move without apparent acceleration when barely nudged. This small added mass will compensate for friction in the system and will be ignored in the following calculations. The paper clips will remain attached to the loop throughout the experiment!

6. Move a 10 gram mass from the bed of the car to the hanging loop and pull the car back to a clearly marked starting point. Determine the distance d that the car will move from the starting point to the bumper block and record this distance at the top of Table 3.1.

NOTE: The total mass of the system will remain constant throughout the experiment.

7. Practice releasing the car being careful not to give it any push or pull as you do so. The best way to do this is to press your finger into the table in front of the car thereby blocking its movement. Quickly pull your finger away in the direction that the car wants to move. At the instant you pull your finger away, start your stopwatch. Stop your stopwatch at the instant the car arrives at the bumper. To eliminate reaction time errors, it is best that the person who releases the car also does the timing!

012-07361B

8. Determine the average time for the car to move through the distance d, having been released from rest. Record the average of the four time trials in which you have the most confidence in Table 3.1. Repeat for all of the masses given in the data table.

9. Excluding the pulley, determine the total mass of your system, M

(car, added

Total

masses, string) and record at the top of Table 3.1. (It will be close to 1100 grams, but you might want to check it on a balance.)

10. Fill in the table using your data and the equations given in the Theory section.

012-07361B

Data Analysis

PAScar with Mass

Trial

d = __________ cm M

m (grams)

Average time

(sec.)

TOTAL

Table 3.1

= __________ grams

exp

% Diff.

Questions

1. Can you think of any systematic errors that would effect your results? Explain how each would skew your results.

PAScar with Mass

012-07361B

Notes:

012-07361B

Purpose

Theory

PAScar with Mass

Experiment 4: Cart Calibration

(Measuring the Spring Constant)

EQUIPMENT NEEDED:

– PAScar (ME-6950) – 250g mass

– Mass set (SE-8704) – Stopwatch (SE-8702)

– Pan for holding masses

– Balance (SE-8723 or equiv.)

The PAScar has a spring plunger, which can be used for producing relatively elastic collisions and providing a reproducible launch velocity.

For this and the following experiments, it will be necessary to find the spring constant k of the car’s spring plunger. As compressional forces F are applied to the spring, the spring will compress a distance x, which is measured with respect to its uncompressed equilibrium position. If F is plotted versus x on graph paper, the spring constant is given by the slope of the graph as:

k = ∆F/∆x

= kx

= x

by using conservation of



(EQN-1):

Once k is known, it is possible to predict the launch velocity v energy, since the elastic potential energy stored in the spring is converted into kinetic energy at the time of launch. The launch velocity can be found from:

(EQN-2):

which leads to:

(EQN-3):

This predicted launch velocity can be experimentally checked by measuring the total rolling distance d on a horizontal surface and the corresponding time t for given launch conditions. This leads to:

(EQN-4):

vo = 2

It is assumed that the acceleration of the car is constant, so that the initial velocity of the car at the moment of launch is twice the average velocity of the car over its whole run.

Total added mass

Note the initial position

of the plunger.

15 cm ruler attached

to car

1/2 total added mass

Spring plunger

Note the final

position of the end

Pan for holding

masses

Figure 4.1

of the plunger.

PAScar with Mass

Procedure

1. Stand the PAScar on its end so that the spring plunger is aimed up, as shown in Figure

4.1. Using masking tape or rubber bands, fix a ruler to the car and adjust it so that the

0 cm mark on the ruler lines up with the upper surface of the plunger. Take care to avoid parallax errors!

2. Carefully add enough mass to the top of the plunger so that it is nearly fully depressed. Record this mass and the corresponding compression x (initial position) of the spring in Table 4.1.

3. Remove approximately one quarter of the mass used in step 2. Record the new mass and x values in Table 4.1.

4. Repeat step 3 until no mass remains on the plunger.

5. Plot a graph of F versus x using your data and determine the slope of the best line through your data points. This slope is the spring constant for your car. Show your slope calculations on the graph and record k below.

6. Determine the mass of the car using a mass balance and record this value below.

012-07361B

7. Using EQN-3 and your values for m, x and k, predict the launch velocity of your car and record this below.

8. Cock the spring plunger to the value of x its starting position and launch it. Using a stopwatch and a meter stick, determine the average range d and the average total time spent rolling t. Record these below.

NOTE: To avoid reaction time errors, the person who launches the car should also time the car’s motion.

9. Using EQN-4, determine the observed value of v value.

Data and Analysis

Mass of car = _________ kg

k = ________ x

Predicted value of launch velocity v

Average d = _________ m Average t = __________ sec

(i.e. the compression of the cocked spring)

that you have chosen, then place the car in

and compare it with the predicted

= ________ m

= __________

Observed value of the launch velocity v

= __________

% Difference between observed and expected values of v

= __________

012-07361B

PAScar with Mass

Table 4.1

Trial

m (kg)

F (= mg)

(newtons)

x (meters)

PAScar with Mass

012-07361B

Notes:

012-07361B

Experiment 5: Rackets, Bats and "Sweet Spots"

EQUIPMENT NEEDED:

– PAScar (ME-6950) – Metric tape (SE-8712)

– Meter stick or a long rod

Purpose

When a batter or tennis player strikes a ball, a portion of the rotational kinetic energy of the bat or racket is transferred to the ball. In a somewhat oversimplified picture, the motion of the bat or racket can be thought of as a simple rotation about a pivot which is located near its end and close to the batter’s wrists. The portion of the bat’s original kinetic energy that is transferred to the ball depends on the distance y between the point of impact and the pivot point. The position on the bat corresponding to the maximum energy transfer is called a “sweet-spot." We will call this maximum energy sweet-spot

SS1.

NOTE: For simplicity, it is assumed

that the collisions are perfectly elastic.

Pivot point

PAScar with Mass

Theory

As any batter can tell you, if you hit the ball at a certain point on the bat, there will be no shock, or impulse, transferred to your hands! This “sweet-spot” is generally located at a different position than SS1 and is called the “percussion point." We will call this zero-impulse sweet-spot SS2. For a given “bat” and pivot, the position of SS2 can be found from:

(EQN-1):

SS2

NOTE: Release the stick from the same

position each trial.

Figure 5.1

where I is the rotational inertia of the bat for the corresponding pivot, m is the total mass of the bat, and y

is the distance from the pivot to the center of mass of the bat. (e.g. If a

uniform rod of length L is pivoted about an end-point, SS2 is located at 0.67L from the pivot.)

The positions of both SS1 and SS2 can be found theoretically, or by using the Sweet-Spot computer program (see page 18 for details). The position of SS2 can be found experimentally using the PASCO Force Sensor or, roughly, by actually hitting a ball at a variety of positions on the bat and noting where the least shock to your wrists occurs. In this experiment, a method for determining the location of SS1 is described.

Using a meter stick or rod as a bat (see Figure 5.1), the PAScar can play the role of a ball. By observing how far the car rolls after impact, the relative, or even absolute energy transfer can be determined for various values of y. In this manner, SS1 can be found.

PAScar with Mass

If you have already done the experiment to determine the coefficient of rolling friction for your cart for the same surface that you will be using in this experiment, you can determine the kinetic energy of the car at the moment after impact since:

012-07361B

(EQN-2):

mv2 = µmgx

Procedure

1. Set up the system as shown in Figure 5.1. Position the car so that its plunger hangs over the edge of the table several centimeters.

NOTE: You will need a long, horizontal table, or board for this experiment. A 3/4 inch by 1 foot by 8 foot plywood board is recommended.

2. Arrange to have a stop of some sort to insure that you always use the same pull-back angle for the hanging meter-stick.

3. Pull the meter-stick or rod back to the pull-back angle that you have chosen and release it, allowing it to strike the car plunger. Record the corresponding values of y and x in Table 5.1.

4. Repeat step 3 four times for each value of y, changing it from roughly 10 to 90 cm in 10 cm increments.

5. Compute the average value of x for each value of y.

6. By interpolation, determine the location of SS1 from your data and record it below Table

5.1.

7. Using EQN-1, compute the location of SS2 and record it below Table 5.1.

8. If time permits, repeat the above after either repositioning the pivot (i.e. “choking up”) or

adding 100 grams or so at some point on the stick.

NOTE: This would add a little realism to the experiment since neither a bat nor a tennis racket is uniform!

012-07361B

Data and Analysis

PAScar with Mass

Table 5.1

Trial

y (cm)

x (cm)

Average

x (cm)

Optional

µmgx (joules)

y-position of SS1 = _________ cm & y-position of SS2 = _________ cm

Questions

1. Is it possible to construct a “Super-bat” for which both SS1 and SS2 coincide? If so, what

changes would have to occur to the uniform rod to bring SS1 and SS2 closer together? (You might use the Sweet-Spot computer program to help you answer this!)

2. What assumptions have we made in analyzing this system? How do they affect our results?

PAScar with Mass

“Sweet Spot” Computer Program

The following is a listing of the “Sweet Spot” computer program written by

Scott K. Perry of American River College, Sacramento, CA., using Quickbasic 4.5.

REM Program: SWEET SPOTS and PERCUSSION POINTS (Fixed Pivot)

REM (Version: 15DEC91)

CLS

LOCATE 1, 1

INPUT “What pullback angle will you be using for this experiment (deg.)”; theta

INPUT “What is the mass of your meter-stick ’bat’ (kg); Ms

012-07361B

PRINT: PRINT

COLOR 14

PRINT “Y-Impact (m)”; TAB(16); “Cart-Speed (m/ s)”; TAB(35); “Omega (rad/sec)”; TAB(54); “Impulse at Pivot (N∗sec)”

COLOR 15

FOR k = 1 TO 9

r = k / 10

g = 9.8: Mc = .5: L = 1: theta = theta / 57.3

COLOR 15

Begin:

CLS

LOCATE 1, 1

INPUT “How far from the center-of-mass is the pivot located (m)”; S

INPUT “How large is the load mass (kg)”; m

IF m = 0 GOTO Skip

INPUT “ How far is the load mass from the pivot (m)”; y

Skip:

I = (1 / 12) ∗ Ms ∗ L ^ 2 + Ms ∗ S ^ 2 + m ∗ y ^ 2 PE = (Ms ∗ S + m ∗ y) ∗ (1 – COS(theta)) ∗ g

Wo = SQR(2 ∗ PE / I)

h = (1 + 2 ∗ (y / L) ∗ (m / Ms)) ∗ (1 – COS(theta)) ∗ L / 2

a = Mc / 2 + (Mc ∗ r) ^ 2 / (2 ∗ I) b = –Mc ∗ Wo ∗ r c = –PE + (1 / 2) ∗ I ∗ Wo ^ 2

v = (–b + SQR(b ^ 2 – 4 ∗ a ∗ c)) / (2 ∗ a) w = (I ∗ Wo – Mc ∗ r ∗ v) / I DeltaP = Mc ∗ v + Ms ∗ w ∗ L / 2 – Ms ∗ Wo ∗ L / 2 v = INT(1000 ∗ v + .5) / 1000 w = INT(1000 ∗ w + .5) / 1000

DeltaP = INT(100 ∗ DeltaP + .5) / 100

PRINT TAB(5); r; TAB(20); v; TAB(39); w; TAB(60); DeltaP

PRINT: PRINT

INPUT “Would you like to input different values ”; a$

IF a$ < > “N” and a$ < > “n” GOTO Begin

END

012-07361B

EQUIPMENT NEEDED:

– PAScar (ME-6950) – Stopwatch (SE-8702)

– Metric tape (SE-8712A) – Brick or block of wood

– Long board that can be used as a ramp – Friction block (003-04708)

– Protractor

Purpose

In this lab, the PASCar will be launched down a ramp, as shown in Figure 6.1, while riding on a friction block. The initial elastic potential energy and gravitational potential energy of the car are converted to thermal energy as the car slides to a stop. The thermal energy generated on the surfaces is the same as the work done against sliding friction.

PAScar with Mass

Experiment 6: Sliding Friction and

Conservation of Energy

Friction block

Theory

Figure 6.1

Using the principle of conservation of energy, we can equate the initial energy of the system with the final (i.e. thermal) energy of the system. This leads to:

+ mgDsinθ = µkmgDcosθ

1/2kx

(EQN-1):

(elastic P.E.) + (Gravitational P.E.) = (work done against friction)

where k is the spring constant of the plunger (from Experiment 4), x is the distance that the plunger is pushed in, m is the mass of the car plus the friction block, D is the distance that the block slides after the car’s plunger is released,

θθ

θ is the angle of the ramp to the horizontal, and

θθ

µk is the coefficient of kinetic or “sliding” friction.

In this experiment, you will use the principle of the conservation of energy to predict D, given certain measurements you will make and the value of k determined in Experiment 4. First you will need to determine the coefficient of kinetic or “sliding” friction for the friction block.

Determining µ

: If the angle of the ramp is high enough, the friction block will slide

down the ramp with uniform acceleration, due to a net force on the block. The net force on the block is the difference between the component of the gravitational force (mgsinø) that is parallel to the surface of the ramp and the friction force (-µkmgcosø) that retards the motion. The angle ø is the angle of the ramp when the block slides down the ramp with uniform acceleration. The acceleration down the ramp is given by:

(EQN-2):

a = mgsinø - µkmgcosø

The average acceleration down the ramp is given by:

(EQN-3):

a = 2d/t

where d is the total distance the block slides and t is the time required to slide through that distance. If the acceleration is uniform, EQN-2 equals EQN-3. You can use the measured values of the angle ø (the angle of uniform acceleration), the distance d, and the time t to calculate the kinetic coefficient of friction µk.

PAScar with Mass

Procedure

NOTE: To get consistent results in this experiment, you must insure that the ramp you will be

using is both straight and clean. Wipe the surface of the ramp and the friction block with a rag.

Determining coefficient of kinetic or “sliding” friction:

1. Place the car with the friction block on the ramp. Set up the ramp at a relatively low angle (one that does not cause the friction block to begin sliding down the ramp by itself).

012-07361B

2. Increase the angle of the ramp until the block begins to slide down the ramp on its own, but

only after you “release” it by slapping the table (or tapping the ramp very lightly). Now increase the angle of the ramp by a few more degrees, so that the block will slide down the ramp with a uniform acceleration when you release it with a “slap” or tap. The angle of the ramp must be low enough so that the block does not begin to slide on its own - only when you release it. Measure the angle of the ramp with the protractor and record it as the angle of uniform acceleration (ø) in the data table.

3. Release the block from the grasp of static friction as described in the previous step and measure the time

Block or

brick

of the car’s descent down the ramp. Record this time as t in data Table 6.1. Measure the distance d that the block slides down the ramp and record this data in Table 6.1. Repeat the measurements four times. Use EQN-3 to compute the accelerations of the block and enter the values in data Table 6.1. Determine the

(about 1/2 the

slip angle)

average value of acceleration and enter it below data Table 6.1.

Figure 6.2

4. Use EQN-2 to calculate the coefficient of kinetic or “sliding” friction. Enter it below the data table.

Prediction of D and Measurement of D:

5. Now slightly reduce the angle of the ramp until the block will just barely slide down the ramp with a uniform

speed when you release it with a slap or tap. Measure this “slip” angle. Reduce the angle of the

ramp to about one half of the “slip” angle. Measure this new angle and record its value in data Table

6.2 as θ. Secure a brick or block at the upper end of the ramp as shown in Figure 6.2.

6. It is time to make a prediction – Using EQN-1 and the information that you have recorded, predict D, the distance that the car will slide down the ramp after being launched. Assume that the plunger on the car is fully cocked at the position of maximum spring compression. Record your prediction at the top of Table 6.2.

7. After double checking your work in the previous step, launch the car down the ramp by placing it on the ramp with its cocked plunger against the secured brick. Then tap the spring-release trigger with a rod or stick using a flat edge.

NOTE: This will help to insure that you do not give the car an initial velocity other than that supplied by the spring plunger.

8. For six trials, measure the distance D that the car slides and record these in Table 6.2.

NOTE: Sometimes the car will twist a bit as it descends, so use the midpoint of the back edge of your car as a reference point for measuring D.

9. Compare your results with your prediction. Compute the percent difference between these two values and enter it below Table 6.2.

012-07361B

Data and Analysis

ø = _________ Spring constant, k = _________ (from Experiment 4)

PAScar with Mass

Table 6.1

Trial

t (sec)

d (cm) a ( )

average acceleration = _________ coefficient of sliding friction = _________

θ = _________ Predicted value of D = _________ cm

Trial

Table 6.2

D (cm)

Average of measured value of D = _________ cm Percent of difference = _________%

Questions

1. In analyzing this system, has the energy been fully accounted for? Discuss.

2. How do your results agree with your prediction? Discuss.

3. What if you launched the car up the same ramp? How far up would it go?

PAScar with Mass

012-07361B

Notes:

012-07361B

Appendix

Replacing the Wheel-Axle Assemblies

1. Using a Phillips screwdriver, loosen the screws and remove the bottom cover plate.

NOTE: The screws that connect the two halves of the PAScar are thread-forming screws and may require substantial force to remove and reinstall. A #1 Phillips point screw driver is required.

Thread forming

screws

PAScar with Mass

Plunger release spring

Trigger bar

Plunger bar

Velcro tabs

Magnetic bumpers

Suspension springs

Figure 6.3: Components of the PAScar (Model ME-6950)

Bottom cover plate

Plunger spring

Wheel/axle assembly(includes wheel bearings)

2. With the car on a stable support, gently lift the wheel assemblies from the plastic grooves.

NOTE: Be sure to keep the components, such as springs, plunger, nuts and magnets in

their proper orientation, as shown in Figure 6.3. Rearranging or moving these items could change the operational capability of the PAScar.

3. Place the new wheel/axle assemblies over the suspension springs.

4. Place the bottom plastic cover over the wheel/axle assemblies, such that the vertical grooves on the cover align over the axles. Align the bottom cover flush with the frame. Replace the screws and tighten them until the cover fits snugly against the outside frame.

NOTE: When replacing the cover, be careful not to knock the

plunger release spring or plunger spring from its holding place.

PAScar with Mass

012-07361B

Additional or Replacement Parts

Description Part No. Qty

Wheel-axle set ME-6957 4

Plunger release spring 632-048 1

Suspension spring 632-034 4

Plunger Spring 632-07369 1

Thread-forming screws 611-033 8

Velcro tab, Loop 616-07427 1

Velcro tab, Hook 616-07428 1

250 g mass 648-07413 2

PAScar Accessories ME-6952 1

-Friction Pad 003-07398 1

-Magnet Neodym 634-022 2

Discover Friction Accessory ME-8574 1

012-07361B

PAScar with Mass

Technical Support

Feedback

If you have any comments about this product or this manual, please let us know. If you have any suggestions on alternate experiments or find a problem in the manual, please tell us. PASCO appreciates any customer feedback. Your input helps us evaluate and improve our product.

To Reach PASCO

For Technical Support, call us at 1-800-772-8700 (toll-free within the U.S.) or (916) 786-3800.

Email: techsupp@PASCO.com

Fax: (916) 786-3292

Web: http://www.pasco.com

Contacting Technical Support

Before you call the PASCO Technical Support staff, it would be helpful to prepare the following information:

• If your problem is computer/software related, note:

-Title and Revision Date of software

-Type of Computer (Make, Model, Speed)

-Type of external Cables/Peripherals

• If your problem is with the PASCO apparatus, note:

-Title and Model number (usually listed on the label)

-Approximate age of apparatus

-A detailed description of the problem/sequence of events. (In case you can't call PASCO right away, you won't lose valuable data.)

-If possible, have the apparatus within reach when calling. This makes descriptions of individual parts much easier.

• If your problem relates to the instruction manual, note:

-Part number and Revision (listed by month and year on the front cover)

-Have the manual at hand to discuss your questions.

PAScar with Mass

012-07361B

012-07361B PAScar with Mass

Table of Contents

Section Page

Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1

Equipment . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

Experiment 1: Kinematics (Average vs. Instantaneous Velocities) . . . . . . . . . 3

Experiment 2: Coefficient of Friction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

Experiment 3: Newton's Second Law (Predicting Accelerations) . . . . . . . . . . 7

Experiment 4: Cart Calibration (Measuring the Spring Constant) . . . . . . . . . 11

Experiment 5: Rackets, Bats and "Sweet Spots" . . . . . . . . . . . . . . . . . . . . . . 15

Experiment 6: Sliding Friction and Conservation of Energy . . . . . . . . . . . . . 19

Appendix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23

PAScar with Mass

Please—Feel free to duplicate this manual subject to the copyright restrictions below.

However, permission is granted to non-profit educational institutions for reproduction of any part of this manual providing the reproductions are used only for their laboratories and are not sold for profit. Reproduction under any other circumstances, without the written consent of PASCO scientific, is prohibited.

Limited Warranty

PASCO scientific warrants this product to be free from defects in materials and workmanship for a period of one year from the date of shipment to the customer. PASCO will repair or replace, at its option, any part of the product which is deemed to be defective in material or workmanship. This warranty does not cover damage to the product caused by abuse or improper use. Determination of whether a product failure is the result of a manufacturing defect or improper use by the customer shall be made solely by PASCO scientific. Responsibility for the return of equipment for warranty repair belongs to the customer. Equipment must be properly packed to prevent damage and shipped postage or freight prepaid. (Damage caused by improper packing of the equipment for return shipment will not be covered by the warranty.) Shipping costs for returning the equipment, after repair, will be paid by PASCO scientific.

012-07361B

Equipment Return

Should this product have to be returned to PASCO scientific, for whatever reason, notify PASCO scientific by letter or phone BEFORE returning the product.

Upon notification, the return authorization and shipping instructions will be promptly issued.

NOTE: NO EQUIPMENT WILL BE ACCEPTED FOR RETURN WITHOUT AN AUTHORIZATION.

When returning equipment for repair, the units must be packed properly. Carriers will not accept responsibility for damage caused by improper packing. To be certain the unit will not be damaged in shipment,

observe the following rules:

• The carton must be strong enough for the item

shipped.

• Make certain there is at least two inches of pack-

ing material between any point on the apparatus and the inside walls of the carton.

• Make certain that the packing material cannot

shift in the box, or become compressed, thus letting the instrument come in contact with the edge of the box.

Address: PASCO scientific

10101 Foothills Blvd.

P.O. Box 619011

Roseville, CA 95678-9011

PASCO ME-6950 User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual