PASCO ME-6831 User Manual

Download

Instruction Manual

Projectile Launcher

Base

Ballistic Pendulum

Vertical upright

Trigger String

Included: Ramrod, 2-D Collision Accessory, Steel Balls (2), Plastic Balls (3) Not shown: Safety Glasses (2 pair)

Angle indicator

Ballistic Pendulum/

Projectile Launcher

ME-6830, ME-6831

012-05375C

*012-05375*

The cover page shows the PASCO Ballistic Pendulum with the Short Range Projectile Launcher mounted on the vertical part of the base. The Ballistic Pendulum is designed for traditional ballistic pendulum exp eriments and can also be used for projectile motion experiments and demonstrations. When the Projectile Launcher is used for projectile motion experiments, the launch angle at the upper launch position can vary from 0 to 90 degrees, and the firing height is fixed for any launch angle. The Launcher can also mounted in a horizontal position that is height-adjustable. The vertical base of the Ballistic Pendulum also has a dedicated position for the Launcher fo r Ballistic Pendulum experiments. This manual contains copy-ready experiments and demonstrations for the ballistic pendulum and projectile launcher.

Table of Contents

Equipment . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1

Assembly . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2

Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

General Operation of the Projectile Launcher . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

Ballistic Pendulum Theory . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

Installation of the Optional Photogate Bracket. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

Installation of the Two-Dimensional Collision Attachment. . . . . . . . . . . . . . . . . . . . . . . . 9

Expectations for the Projectile Launcher . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

Expectations for the Ballistic Pendulum. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

EXPERIMENTS

1. Projectile Motion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11

2. Projectile Motion Using Photogates. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

3. Projectile Range versus Angle. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

4. Projectile Path . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23

5. Conservation of Energy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27

6. Conservation of Momentum. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31

7. Vary Angle to Maximize Height . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35

8. Projectile Velocity—Approximate Method). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37

9. Projectile Velocity—Exact Method) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39

DEMONSTRATIONS

10. Do 30° and 60° Launch Angles give the Same Range? . . . . . . . . . . . . . . . . . . . . . 43

11. Simultaneously Fire Two Balls Horizontally at Different Speeds. . . . . . . . . . . . . . . 45

12. Shoot through Hoops. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47

13. Elastic and Inelastic Collisions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49

Teacher’s Guide. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51

Technical Support, Warranty, and Copyright. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57

iii

Projectile Launcher

iv 012-05375C

Ballistic Pendulum / Projectile Launcher

ME-6830, ME-6831

Equipment

The ME-6830 Ballistic Pendulum / Projectile Launcher includes the following:

Included Equipment Part Number

Ballistic Pendulum and Base (unassembled) 003-05374 Short Range Projectile Launcher Assembly 003-10550 Plastic Balls, 25 mm diameter (3) see ME-6802* 2-D (two-dimensional) Collision Accessory see ME-6802* Ramrod see ME-6802* Steel Balls, 25 mm diameter (2) 699-064 Safety Glasses (2 pair) 699-066 Trigger String (45 cm (18”)) 699-067 Hex Key 726-046

Required Equipment Part Number

C-Clamp, Large SE-7285

Recommended Equipment Part Number

Launcher Spares Kit* ME-6802 Time-of-Flight Accessory ME-6810 Projectile Catcher Accessory ME-6815 Photogate Mounting Bracket ME-6821A Shoot-the-Target ME-6853 Photogate Head ME-9498A Laser Sight Accessory OS-8527A

*The ME-6802 Launcher Spares Kit includes: Ramrod (2), Plastic Balls (10-pack), 2-D Collision Accessory (2), Sights (5-pack), Plumb Bob (24-pack), Nylon Thread (1 spool), and Thumbscrews (10).

The ME-6831 Ballistic Pendulum does not include the Short Range Launcher. The ME-6831 Ballistic Pendulum includes two steel balls and the hex key.

ME-6802 Launcher Spares Kit

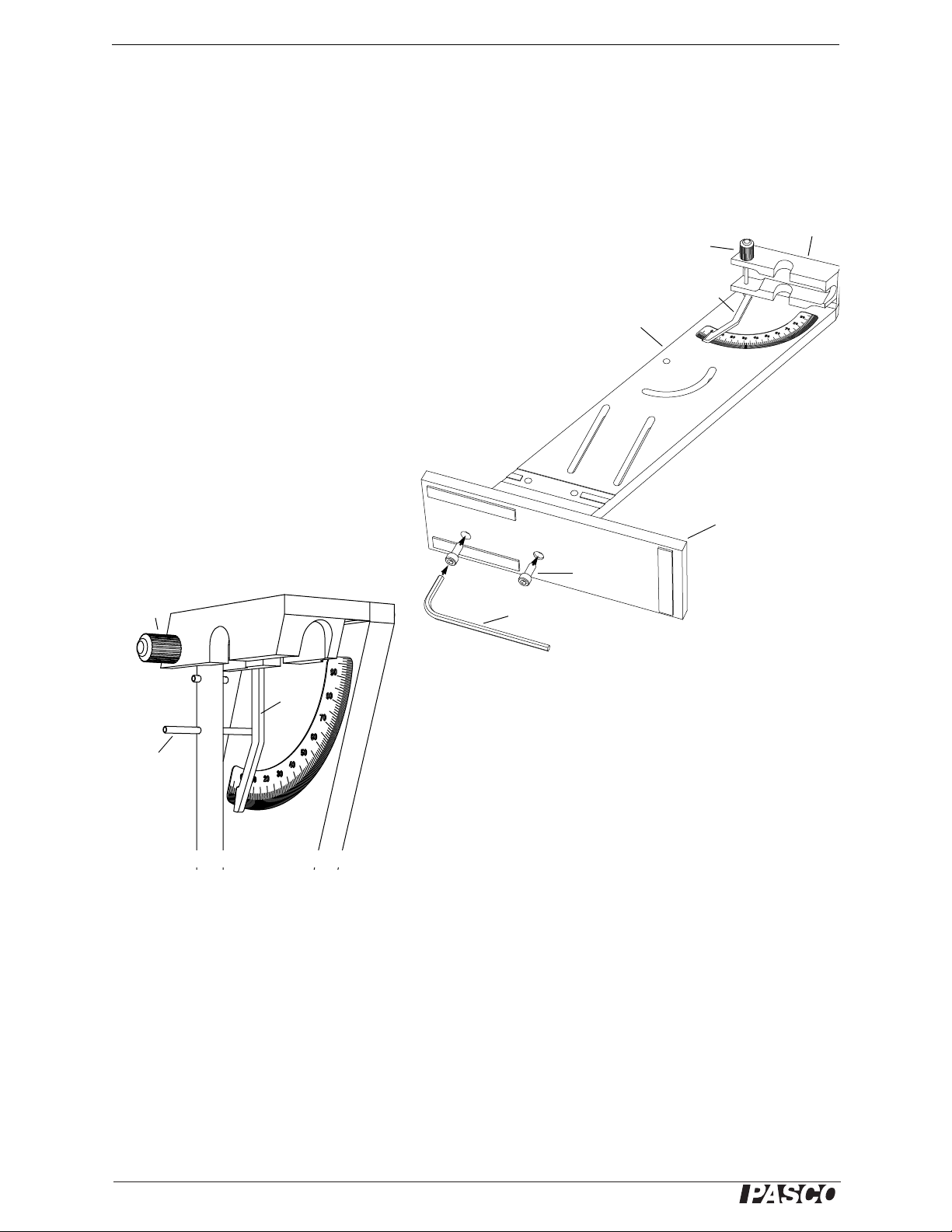
Ballistic Pendulum / Projectile Launcher Assembly

Upright

Base

Hex key

Socket head

screw

Axle

Angle Indicator

Assemble the Base

Angle

Indicator

Long pin

Axle

Mount the Ballistic Pendulum

Assembly

The Ballistic Pendulum / Projectile Launcher arrives in a custom-made package, and some assembly is required. The package has several cut-outs for the Ballistic Pendulum and ramrod, base, upright and Projectile Launcher, safety glasses, and miscellaneous small parts including a hex key (“Allen wrench”) used for assembly.

Assemble the Base

Unscrew the thumbscrew to temporarily remove the Projectile Launcher from the upright. Use the included hex key and the two socket head screws to attach the base to the upright. The screws are coated with a strong adhesive that activates when they are screwed into place.

Mount the Ballistic Pendulum

To attach the Ballistic Pendulum to the upright, unscrew the axle from the yoke. The Ballistic Pendulum has a hinge at the top of the rod with a hole through it. Line up the hole in the hinge with the axle hole in the yoke, and screw the axle back into place. Note that the long pin that extends from either side of the Ballistic Pendulum rod should be behind the angle indicator.

Yoke

Introduction

The PASCO Ballistic Pendulum / Projectile Launcher has been designed for ballistic pendulum and projectile motion experiments and demonstrations. The only addition equipment required is a C-clamp for mounting the base of the Ballistic Pendulum to a table or sturdy horizontal surface. The features of the Ballistic Pendulum include:

• Reliable Ball-Catcher Mechanism: The sensitive spring-loaded barb-type catch on the pendulum will catch

balls with a large range of speeds. In addition, the catcher holds the ball in line with the pendulum rod for best accuracy.

• Removable Pendulum: All moving parts of the pendulum may be removed so that the mass and center of

mass can be measured accurately. In addition, the pendulum can be reversed so that elastic collisions can be compared to inelastic collisions.

012-05375C

Model No. ME-6830, ME-6831 Introduction

Wear Safety Glasses

• Variable-Mass Pendulum: The pendulum includes masses that can be removed so that the pendulum can be

used with lightweight balls over a wide range of speeds. Leave the masses on the pendulum when you use heavyweight balls.

The features of the Projectile Launcher include:

• Launch at Any Angle: Balls can be launched from any angle from zero to ninety degrees measured from hor-

izontal (zero degrees). The angle is easily adjusted using thumbscrews and the built-in protractor and plumb-bob give an accurate way to measure the angle of inclination.

• Three Range Settings: Each version of Projectile Launchers has three range settings. The Short Range Pro-

jectile Launcher ranges are approximately 1.2 m, 3 m, and 5 m when the launch angle is 45°. (The Long Range Projectile Launcher ranges are approximately 2.5 m, 5 m, and 8 m. The Long Range Launcher has a stronger spring and is useful for large classroom demonstrations.)

• Fixed Elevation Independent of Launch Angle: The Projectile Launcher can pivot at the muzzle end so the

elevation of the ball as it leaves the barrel does not change as the angle is varied. The upright part of the Ballistic Pendulum base has three positions for mounting the Launcher. At the top is a hole and curved slot for use when you want to change the launch angle. The vertical slots let you mount the Launcher horizontall y at different heights so you can fire a ball into targets such as a ball catcher on a PASCO Cart on a track. At the bottom are two holes for use when you want to fire a ball horizontally into the Ballistic Pendulum.

• Repeatable Results: The piston keeps the ball from rubbing on the inside of the barrel as it travels so there is

no spin on the ball as it launches. When the base is secured to a table with a C-clamp, there is very little recoil. The trigger is pulled with a string to minimize jerking.

• Barrel Sights and Safety Precautions: There are sites built-in to the barrel for

aiming the Projectile Launcher. View the sites by looking through the back end of the barrel. WARNING: Never look down the front of the barrel because it may be loaded. Safety glasses are provided, so use them. Look for the yellow indicator through any of the five slots on the top of the barrel because the yellow indicator shows the position of the piston. If the indicator is between the first and second slots (relative to the muzzle end), the piston is not cocked.

• Computer Compatible: One or two photogates can be attached to the Projec-

tile Launcher using the ME-6821A Photogate Mounting Bracket. When used with a PASCO interface and data acquisition software, the photogates can measure the muzzle speed of the ball. Use a photogate and the ME-6810 Time of Flight Accessory to measure the time of flight of the ball

• Compact Storage: When the barrel of the Launcher is aligned vertically with the base, the Launcher takes up

minimal space. The included ramrod and the Ballistic Pendulum base have hook-and-pile material that allows the ramrod to be stored on the base.

012-05375C 3

Ballistic Pendulum / Projectile Launcher General Operation of the Projectile La uncher

Trigger

String

Trigger

Protractor

Plumb Bob

Muzzle

Thumbscrews

Range

setting slots

(1 of 5)

Launcher Parts

Label details

Yellow Band in Wi ndow Indicates Range

Launcher

on high

position

General Operation of the Projectile Launcher

Parts

Ready

• Attach the included Trigger String to the hole in the Trigger . (For example, loop the string through the hole and tie the ends together.)

• Always wear safety goggles when you are in a room where a Projectile Launcher is being used.

• Firmly clamp the base of the Ballistic Pendulum to a sturdy table or other surface.

• Mount the Projectile Launcher on the Ballistic Pendulum base. Mount the Launcher to the lower two holes in the base if you intend to shoot horizontally at the ball catcher of the Ballistic Pendulum.

• Use the hole and curved slot near the top of the base when you want to adjust the Launcher’s launch angle. Note: For this configuration, the Launcher should be mounted on the ‘back side’ of the Ballistic Pendulum base.

012-05375C

Model No. ME-6830, ME-6831 Genera l Operation of the Projectile Launcher

Bore Sights

Front

site

Rear

site

Launcher

Aim

• If you have the Launcher mounted on the top position, you can adjust the angle of inclination above the horizontal by loosening the two thumbscrews and rotating the Launcher barrel to the desired angle. Use the plumb bob and the protractor on the label to select the angle. Tighten both thumbscrews when the angle is set.

• You can ‘bore-sight’ through the barrel at a target, such as the ME-6853 Shoot-The Target. Look through the back end of the barrel when the Launcher is not loaded. There are two ‘tripod’ (three-spoke) sights inside the barrel, one at the end of the barrel and one at the end of the piston (about midway in the barrel). Each sight has a sighting hole at its center. Loosen the thumbscrews and C-clamp and adjust the angle and position of the Launcher to align the centers of both sights on your target. Tighten the thumbscrews and C-clamp when the Launcher is aimed.

Load

• T o load a ball in the Launcher when its mounted on the low position, either hold the Ballistic Pendulum out of the way or rotate the pendulum until the rod is horizontal and it catches in the component clip on the underside of the yoke.

• Place a ball in the muzzle of the Launcher. NOTE: Always cock the piston with a ball in the piston. You may damage the piston if you use the ramrod without a ball in the piston.

• Remove the ramrod from its storage place on the edge of the upright. While looking through the range-setting slots on the top side of the Launcher, push the ball down the barrel with the ramrod until the trigger catches the edge of the piston at the desired range setting. (The trigger will “click” into place.)

• When the yellow indicator tape on the piston is visible in the middle range-setting slot, the piston is in the SHORT RANGE position. When the indicator tape on the piston is visible in the next range-setting slot (fourth from the muzzle), the piston is in the MEDIUM RANGE position, and when the tape is visible in the last range-setting slot, the piston is in the LONG RANGE position.

• Remove the ramrod and return it to the storage place on the edge of the upright.

• When the Projectile Launcher is loaded, the yellow indicator tape is visible through one of the range-setting slots on the upper side of the barrel. Never look down the barrel! To check whether the Launcher is loaded, look through the range-setting slots on the barrel.

Shoot

• Before shooting the ball, make certain that no one is in the way.

• T o shoot the ball, pull straight up on the trigger string that is attached to the trigger. You only need to pull about one centimeter.

• The trigger will automatically return to its initial position after you release the string.

Maintenance and Storage

• The Ballistic Pendulum/Projectile Launcher does not need any special maintenance. Do not oil the Launcher!

• To store the Launcher in the least amount of space, align the barrel vertically. One way is to mount it in one of the two vertical slots. Tighten the thumbscrews to hold the Launcher in place.

012-05375C 5

Ballistic Pendulum / Projectile Launcher Ballistic Pendulum Theory

PE Mgh

hR1 cos–=

PE MgR

1 cos–=

1 2

-- -

------- -

2MKE=

Ballistic Pendulum Theory

Overview

The ballistic pendulum is a classic method of determining the velocity of a projectile. It is also a good demonstration of many of the basic principles of physics.

The ball is fired into the ballistic pendulum, which then swings up a measured amount. From the height reached by the pendulum, you can calculate its gravitational potential energy. The gravitational potential energy is equal to the kinetic energy of the pendulum at the bottom of the swing, just after the collision with the ball.

You cannot equate the kin etic energy of the pendulum after the collision with the kinetic energy of the ball before the swing since the collision between ball and pendulum is inelastic, and kinetic energy is not conversed in inelastic collisions. Momentum is conserved in all forms of collisions, so you know that the momentum of the ball before the collision is equal to the momentum of the pendulum after the collision. Once you know the momentum of the ball and the ball’s mass, you can determine the initial velocity.

There are two ways of calculating the velocity of the ball. The first method (called the “approximate method”) assumes that the pendulum and the ball together act as a point mass located at their combined center of mass. This method does not take rotational inertia into account. It is somewhat quicker and easier than the second method (called the “exact method”), but not as accurate.

The second method (exact method) uses the actual rotational inertia of the pendulum in the calculations. The equations are slightly more complicated, and it is necessary to take more data in order to find the moment of inertia of the pendulum, but the results are generally better.

Please note that the subscript “cm” used in the following equations stands for “center of mass”.

Approximate Method

Begin with the potential energy of the pendulum at the top of its swing after the collision with the ball:

where M is the combined mass of the pendulum and ball, g is the acceleration due to gravity, and h is the change in height. Substitute for the change in height:

where R energy is equal to the kinetic energy immediately after the collision:

where v the equation is:

is the distance from the pivot point to the center of mass of the pendulum/ball system. This potential

is the speed of the speed of the pendulum just after collision. The momentum of the pendulum just after

which you can substitute into the previous equation to give:

Solving this equation for the pendulum momentum gives:

012-05375C

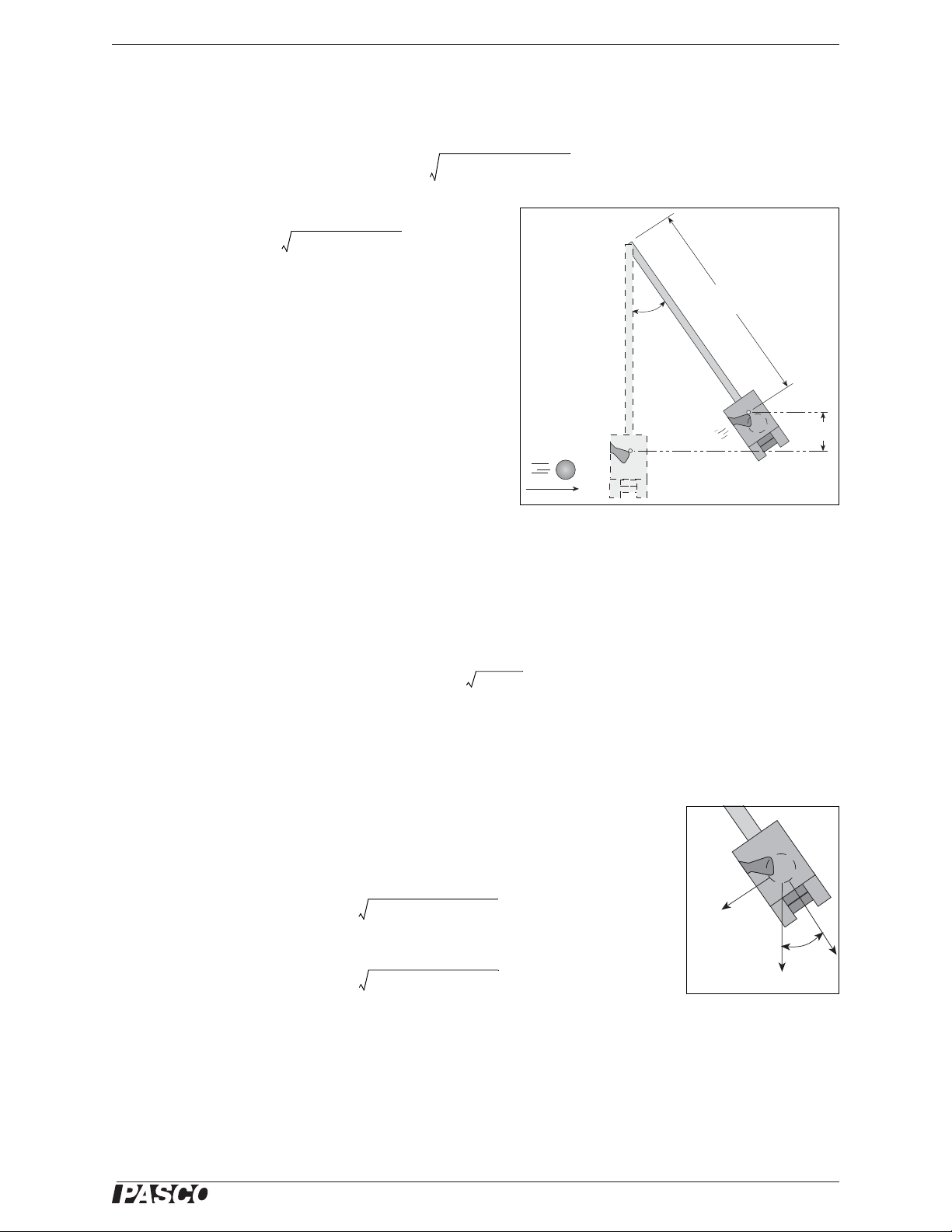
Model No. ME-6830, ME-6831 Ballistic Pendulum Theory

2M2gRcm1 cos–=

h



Figure 1

---- -

2gR

1 cos–=

PE MgRcm1 cos–=

1 2

-- -

I

I=

--------

2IKE=

LpmR

 mRbv==

-Mg sin



-Mg

Figure 2

mRbv 2IMgRcm1 cos–=

----------

2IM gR

1 cos–=

 I=

This momentum equal to the momentum of the ball just before the collision:

Setting these two equations equal to each other and replacing KE with our known potential energy gives:

Solve this for the ball’s velocity and simplify to get:

Exact Method

The potential energy is found in a way identical to the way shown previously:

For the kinetic energy, you can use the equation for angular kinetic energy instead of linear kinetic energy, and substitute into it the equation for angular momentum:

where I is the moment of inertia of the pendulum/ball combination, and  is the angular velocity immediately after the collision.

As you did previously, solve this last equation for angular momentum:

This angular momentum is equal to the angular momentum of the ball before the collision, as measured from the pendulum pivot point:

where R general equal to R

is the distance from the pendulum pivot to the ball. (NOTE: This radius is not in

, which is the distance from the pivot point to the center of mass for

the pendulum/ball system.)

These two angular momenta are equal to each other, so:

Solve for v:

Now you need to find I, the moment of inertia of the pendulum and ball. To do this, start with the rotational equivalent of Newton’s Second Law:

where  is torque, I is moment of inertia, and  is angular acceleration. The force on the center of mass of the pendulum is Mg, and the component of force directed towards the center of the pendulum swing is F = -Mg sin Figure 2.)

012-05375C 7



See

Ballistic Pendulum / Projectile Launcher Ballistic Pendulum Theory

I RcmMg sin–=



MgR

------------------

–=



--- -

x– 2x–==



MgR

------------------

MgR



------------------

MgR

4

------------------------

Projectile Launcher

barrel

Square

Nut

Thumb

screw

Photogate

Mounting

Bracket

T-slot

Thumb

screw

Install the Optional Photogate Bracket

The torque on the pendulum is thus:

For small angles, , sin so if you make this substitution and solve for  you get:

This angular equation is in the same form as the equation for linear simple harmonic motion:

So if you compare the two equations, linear and angular, you can see that the pendulum exhibits simple harmonic motion, and that the square of the angular frequency (

) for this motion is:

Solving for I gives the desired result:

where T is the period of the pendulum.

• NOTE: You used a small-angle approximation to find the equation for I, but I does not depend on . This means that you must measure the period T using small angle oscillations. Once you have calculated I with that period, you may use that value of I regardless of the amplitude reached during other parts of the experiment.

Installing the Optional Photogate Bracket (ME-6821A)

The Photogate Bracket is an optional accessory for mounting one or two photogates on the Projectile Launcher to measure the muzzle speed of the ball.

• Prepare the Photogate Bracket by loosening the thumbscrew near the end of the bracket. Leave the square nut in place on the end of the thumbscrew. Use the smaller (0.75 in) thumbscrews that are stored on the bottom side of the bracket to mount one or two photogates to the bracket

• Align the square nut of the bracket with the T-shaped slot on the bottom of the Launcher barrel and slide the nut into the slot until the photogate nearest to the barrel is as close to the muzzle as possible without blocking the photogate beam. Tighten the bracket thumbscrew to secure the bracket in place.

012-05375C

Model No. ME-6830, ME-6831 Ballistic Pendulum Theory

Plumb bob

Tie a triple knot

in the end.

Thread through

the hole.

Make the string

long enough.

Vertex

Repairing the Plumb Bob

50°

Projectile Launcher

barrel

Square

Nut

T-slot

Thumbscrew

2-D Collision Accessory

Repairing the Plumb Bob

If the string breaks that holds the plumb bob on the protractor of the Launcher, replace it with an equal length of nylon thread (such as the thread included in the ME-6802 Launcher Spares Kit). Make sure that the replacement string is long enough so that when the Launcher is inclined at an angle of 50°, the string extends well below the corner of the Launcher. Carefully thread the replacement string through the small hole at the vertex of the protractor and tie a triple knot at that end of the string. To put the plumb bob onto the string, thread the string through the hole in the center of the plumb bob and tie a triple knot in that end of the string.

Installing the 2-D (two dimensional) Collision Accessory

Introduction

The 2-D (two dimensional) Collision Accessory is a plastic bar with a thumbscrew and square nut. The bar has a post and you can balance a second ball on the post in front of the muzzle. When the launched ball collides with the second ball, they experience a two dimensional (2-D) collision.

Assembly

To assemble the Collision Accessory, insert the thumbscrew through the hole in the plastic bar and screw the square nut onto the thumbscrew. Leave the square nut loose on the thumbscrew until you install the Collision Accessory onto the Launcher.

To install the Collision Accessory onto the Launcher, slide the square nut into the T-shaped slot on the bottom side of the barrel. Adjust the position of the Collision Accessory and then tighten the thumbscrew. Place a ball on the top of the post, loosen the thumbscrew slightly, and rotate the Collision Accessory to one side or the other until the ball on the post is in a place where it will be hit by the launched ball at the angle that you want.

Expectations for the Projectile Launcher

• The muzzle speed will vary slightly with angle. The difference between muzzle speed when shot horizontally versus vertically can be between zero to eight percent, depending on the range setting.

• Although the muzzle end of the Projectile Launcher does not change height with angle, it is about 30 centimeters (12 inches) above table level. If you desire to show that projectiles fired with the same muzzle speed but at complementary angles will have the same range, you need to shoot to a horizontal target that is at the same height as the muzzle.

• The scatter pattern of projectiles with the Projectile Launcher is minimized when the Projectile Launcher is securely clamped to a sturdy table. Any wobble in the table will show up in the data.

• The angle of inclination can be determined to within one-half of a degree.

Expectations for the Ballistic Pendulum

• Angles reached by the swinging pendulum should be repeatable to within half a degree.

012-05375C 9

Ballistic Pendulum / Projectile Launcher Ballistic Pendulum Theory

• Overall error in measurement of ball velocity should not exceed 2.5% (exact method) or 10% (approximate method).

• NOTE: Adjustable leveling feet are not necessary for good results. Small deviations from the horizontal will not cause significant error.

012-05375C

Model No. ME-6830 Exp. 1: Projectile Motion

1 2

-- -

----- -=

yy0v0sint

1 2

-- -

–+=

Exp. 1: Projectile Motion

Equipment Needed

Item Item

Projectile Launcher and plastic ball Plumb bob and string Meter stick Carbon paper White paper Sticky tape

Purpose

The purpose of this experiment is to predict and verify the range of a ball launched at an angle. The initial speed of the ball is determined by shooting it horizontally and measuring the range of the ball and the height of the Launcher.

Theory

T o predict where a ball will land on the floor when it is shot from the Launcher at some angle above the horizontal, it is first necessary to determine the initial speed (muzzle velocity) of the ball. That can be determined by shooting the ball horizontally from the Launcher and measuring the vertical and horizontal distances that the ball travels. The initial speed can be used to calculate where the ball will land when the ball is shot at an angle above the horizontal.

• NOTE: For rest results, see the notes on “Repeatable Results” in the Introduction.

Initial Horizontal Speed

For a ball shot horizontally with an initial speed, v

, the horizontal distance travelled by the ball is given by x = v0t,

where t is the time the ball is in the air. (Neglect air friction.)

The vertical distance of the ball is the distance it drops in time t given by:

The initial speed can by determined by measuring x and y. The time of flight, t, of the ball can be found using

and the initial horizontal speed can be found using .

Initial Speed at an Angle

To predict the horizontal range, x, of a ball shot with an initial speed, v

, at an angle, , above the horizontal, first

predict the time of flight from the equation for the vertical motion:

where y the quadratic equation for t and then use x = v

is the initial height of the ball and y is the position of the ball when it hits the floor. In other words, solve

cost where v0 cos is the horizontal component of the initial

speed.

Setup

1. Put the Launcher in the top position on the Ballistic Pendulum upright. Clamp the Ballist ic Pendulum/Projectile Launcher to a sturdy table or other horizontal surface. Mount the Launcher near one end of the table and aimed away from the table.

012-05375C 11

Projectile Launcher Exp. 1: Projectile Motion

Bottom

of ball

AB– AB+

-------------

x100

2. Adjust the angle of the Projectile Launcher to zero degrees so the ball will by launched horizontally.

Part A: Determining the Initial Horizontal Speed of the Ball

1. Put a plastic ball in the Projectile Launcher and use the ramrod to cock it at the long range position. Fire one shot to locate where the ball hits the floor. At that point, tape a piece of white paper to the floor. Place a piece of carbon paper (carbon-side down) on top of the white paper and tape it in place.

• When the ball hits the carbon paper on the floor, it will leave a mark on the white paper.

2. Fire ten shots.

3. Measure the vertical distance from the bottom of the ball as it leaves the barrel to the

floor. Record this distance in the Data Table.

• The “Launch Position of Ball” in the barrel is marked on the label on the side of the Launcher.

4. Use a plumb bob to find the point on the floor that is directly beneath the release point on the barrel. Measure the horizontal distance along the floor from the release point to the leading edge of the piece of white paper. Record the distance in the Data Table.

5. Carefully remove the carbon paper and measure from the leading edge of the white paper to each of the ten dots. Record these distances in the Data Table and find the average. Calculate and record the total horizontal distance (distance to paper plus average distance from edge of paper to dots).

6. Using the vertical distance, y, and the total horizontal distance, x, calculate the time of flight, t, and the initial horizontal speed of the ball, v

. Record the time and speed in the Data Table.

Part B: Predicting the Range of a Ball Shot at an Angle

1. Adjust the angle of the Projectile Launcher to an angle between 30 and 60 degrees. Record this angle in the second Data Table.

2. Using the initial speed and vertical distance from the first part of this experiment, calculate the new time of flight and the new horizontal distance based on the assumption that the ball is shot at the new angle you have just selected. Record the predictions in the second Data Table.

3. Draw a line across the middle of a white piece of paper and tape the paper on the floor so that the line on the paper is at the predicted horizontal distance from the Projectile Launcher. Cover the white paper with carbon paper (carbon side down) and tape the carbon paper in place.

4. Shoot the ball ten times.

5. Carefully remove the carbon paper. Measure the distances to the ten dots and record the distances in the sec-

ond Data Table.

Analysis

1. Calculate the percent difference between the predicted theoretical distance (“A”) and the actual average distance (“B”) when shot at an angle.

2. Estimate the precision of the predicted range. How many of the final 10 shots landed within this range?

012-05375C

Model No. ME-6830 Exp. 1: Projectile Motion

Data Table A: Determine the Initial Speed

Vertical distance = __________ ___ Horizontal distance to edge of paper = _________________

Calculated time of flight = ________________ Initial speed = _____________

Trial Distance

1 2 3 4 5 6 7 8 9

Average

Total Distance

Data Table B: Predict the Range

Angle above horizontal = _____________ Horizontal distance to edge of paper = _________________

Calculated time of flight = ________________ Predicted range = _____________

Trial Distance

1 2 3 4 5 6 7 8 9

Average

Total Distance

012-05375C 13

Projectile Launcher Exp. 1: Projectile Motion

Notes

012-05375C

Model No. ME-6830 Exp. 2: Projectile Motion Usin g Photogates

yy0v0sint

1 2

-- -

–+=

Exp. 2: Projectile Motion Using Photogates

Equipment Needed

Item Item

Projectile Launcher and plastic ball Plumb bob and string Photogate Head ME-9498A (2) Photogate Mounting Bracket ME-6821A PASCO Interface or Timer* PASCO Data acquisition software* Meter stick Carbon paper White paper Sticky tape

*See the PASCO web site at www.pasco.com for information about PASCO interfaces, timers, and data acquisition software.

Purpose

The purpose of this experiment is to predict and verify the range of a ball launched at an angle. Photogates are used to determine the initial speed of the ball.

Theory

T o predict where a ball will land on the floor when it is shot from the Launcher at some angle above the horizontal, it is first necessary to determine the initial speed (muzzle velocity) of the ball. The speed can be determined by shooting the ball and measuring a time using photogates. To predict the range, x, of the ball when it is shot with an initial speed at an angle, , above the horizontal, first predict the time of flight using the equation for the vertical motion:

where y equation to find the time, t. Use x = (v

is the initial height of the ball and y is the position of the ball when it hits the floor. Solve the quadratic

cos  t to predict the range.

• NOTE: For best results, see the notes on “Repeatable Results” in the Introduction.

Setup

2. Adjust the angle of the Projectile Launcher to an angle between 30 and 60 degrees and record the angle.

3. Attach the photogate mounting bracket to the Launcher and attach two photogates to the bracket. Check that

the distance between the photogates is 0.10 m (10 cm).

4. Plug the photogates into an interface or a timer.

Procedure

Part A: Determining the Initial Speed of the Ball

1. Put a plastic ball in the Projectile Launcher and use the ramrod to cock it at the long range position.

2. Setup the data acquisition software or the timer to measure the time between the ball blocking the two photo-

gates.

3. Shoot the ball three times and calculate the average of these times. Record the data in Data Table 2.1.

012-05375C 15

Projectile Launcher Exp. 2: Projectile Motion Using Photogates

Bottom

of ball

yy0v0sint

1 2

-- -

–+=

4. Calculate the initial speed of the ball based on the 0.10 m distance between the photogates. Record the value.

Data Table: Part A

Table 2.1: Determine the Initial Speed

Trial Time

1 2 3

Average Time

Initial Speed

Part B: Predicting the Range of a Ball Shot at an Angle

1. Keep the angle of the Projectile Launcher at the original angle above horizontal.

2. Measure the vertical distance from the bottom of the ball as it leaves the barrel to the

floor. Record this distance in Data Table 2.2.

• The “Launch Position of Ball” in the barrel is marked on the label on the side of the Launcher.

3. Use the vertical distance, the angle, and the initial speed to calculate the time of flight. Record the value.

4. Use the time of flight, t, angle, , and initial speed, v (range, x = (v

cos  t). Record the predicted range.

, to predict the horizontal distance

5. Draw a line across the middle of a white piece of paper and tape the paper on the floor so the line is at the predicted horizontal distance. Cover the white paper with carbon paper and tape the carbon paper in place.

6. Use a plumb bob to find the point on the floor that is directly beneath the release point on the barrel. Measure the horizontal distance along the floor from the release point to the leading edge of the piece of white paper. Record the distance in the Data Table.

7. Shoot the ball ten times.

8. Carefully remove the carbon paper and measure from the leading edge of the white paper to each of the ten

dots. Record these distances in the Data Table and find the average. Calculate and record the total horizontal distance (distance to paper plus average distance from edge of paper to dots).

Angle above horizontal = ______________ Horizontal distance to edge of paper = _______________

Calculated time of flight = _________________ Predicted range = ________________

012-05375C

Model No. ME-6830 Exp. 2: Projectile Motion Usin g Photogates

AB– AB+

-------------

x100

Data Table: Part B

Table 2.2: Confirm the Predicted Range

Trial Distance

1 2 3 4 5 6 7 8 9

Average

Total Distance

Analysis

1. Calculate the percent difference between the predicted theoretical distance (“A”) and the actual average distance (“B”) when shot at an angle.

1. Estimate the precision of the predicted range. How many of the final 10 shots landed within this range?

012-05375C 17

Projectile Launcher Exp. 2: Projectile Motion Using Photogates

Notes

012-05375C

Model No. ME-6830 Exp. 3: Projectile Rang e versus Angle

Figure 3.1: Shooting on a level surface

0 v0singt

peak

–==

t 2t

peak

sin

----------------





Figure 3.2: Shooting from a table

yy0v0sint

1 2

-- -

–+=

Exp. 3: Projectile Range versus Angle

Equipment Needed

Item Item

Projectile Launcher and plastic ball Plumb bob and string Meter stick or measuring tape Box to make landing area same elevation as muzzle Graph paper Carbon paper White paper Sticky tape

Purpose

The purpose of this experiment is to determine how the range of the ball depends on the launch angle. The angle that gives the greatest range is determined for two cases: for shooting on level ground and for shooting off a table.

Theory

The range is the horizontal distance, x, between the muzzle of the Launcher and the place where the projectile hits, given by x = (v above horizontal, and t is the time of flight. See the figure.

cos  t, where v0 is the initial speed of the projectile as it leaves the muzzle,  is the launch angle

For the case in which the projectile hits on a surface that is the same level as the level of the muzzle of the Launcher, the time of flight of the projectile will be twice the time it takes for the projectile to reach the peak of its trajectory. At the peak, the vertical speed is zero, so:

where v

is the initial speed of the projectile. Solving for the time gives an expression for the total time of flight as:

For the case in which the projectile is launched at an angle above horizontal from a table onto the floor, the time of flight is found using the equation for vertical motion:

where y

is the initial height of the projectile in the

Launcher and y is the vertical position of the ball when it hits the floor.

Setup

012-05375C 19

Projectile Launcher Exp. 3: Projectile Range versus Angle

CAUTION! DO NOT LOOK DOW

N BARREL!

CAUTION! DO NOT LOOK DOW

N BARREL!

T LO

SHORT RANGE

PROJECTILE LAUNCHER

ME-6800

llow Ban

d i

n W

indow

Ind

ates R

ge.

7 0

6 0

5 0

3 0

WEAR

SAFETY GLASSES WHEN IN USE.

Figure 3.3: Shooting to a level surface

2. Adjust the angle of the Projectile Launcher to 10 degrees.

3. Put a plastic ball into the Projectile Launcher and cock it to the medium or long range setting.

• Note: In general, the experiment will not work as well on the short range setting because the muzzle speed is more variable with the change in angle.

4. Fire one shot to locate where the ball hits. Place a box or other horizontal surface at that location so the ball will hit the top of the box at the same level as the muzzle of the launcher.

Procedure

Part A: Shooting to a Level Surface

1. Fire one shot to locate where the ball hits the top of the box. Tape a piece of white paper on the box at this location. Tape a piece of carbon paper (carbon-side down) on top of the white paper.

• When the ball hits the carbon paper it will leave a mark on the white paper underneath.

2. Fire five shots.

3. Use a measuring tape to measure the horizontal distance from the muzzle to the leading edge of the paper. (If

a measuring tape is not available, use a plumb bob to find the point on the table that is directly beneath the release point on the barrel and mea sure the distance along the table from the muzzle to the leading edge of the paper.) Record the distance in the Data Table.

4. Carefully remove the carbon paper. Measure from the leading edge of the paper to each of the five dots and record these distances in the Data Table.

5. Increase the launch angle by 10 degrees and repeat all the steps.

6. Keep repeating for angles up to and including 80 degrees (the complementary angle of 10 degrees).

Table 3.1: Shooting to a Level Surface

Angle 1020304050607080

1 2 3 4 5

Horizontal Distance

Average

Paper distance

Total distance

Part B: Shooting Off the Table

1. Turn the Projectile Launcher so it will launch the ball to the floor.

012-05375C

Model No. ME-6830 Exp. 3: Projectile Rang e versus Angle

2. Repeat the procedure and record the data in the Data Table.

Table 3.2: Shooting off the Table

Angle 1020304050607080

1 2 3 4

Horizontal Distance

Average

Paper distance

Total distance

Analysis

1. Find the average of the five distances in each case and record the results in the Data Tables.

2. Add the average distance to the distance from the Launcher to the leading edge of the white paper to get the

total distance (range) in each case. Record the results in the Data Tables.

3. For each Data Table, plot the range versus the angle and draw a smooth curve through the points.

Questions

1. From the graph, what angle give the maximum range for each case?

2. Is the angle for the maximum range greater or less for shooting off the table?

3. Is the maximum range further when the ball is shot off the table or on the level?

Notes

012-05375C 21

Projectile Launcher Exp. 3: Projectile Range versus Angle

012-05375C

Model No. ME-6830 Exp. 4: Projectile Path

---- -

1 2

-- -

--------







--------

CAUTIO

N! D O NO

T LOO

N BA

RREL!

CAUTIO

N! D O NO

T LOO

N BA

RREL!

A U T I

D O

N O T L

D O

W N

T H E B

L .

L ON

RANGE

DIUM

AN GE

SHOR

RANG

o s i

t i

o n o f B a l

a u n c h

SHOR

T RANGE

PROJECTILE LAUNCHER

ME-6800

e l

w B

a n d in

d o

w In d i

a t

e s

R a n g

e .

9 0

8 0

7 0

6 0

4 0

3 0

2 0

1 0

E A

A F

E T

L A

S S

E S

H E

N I

N U

U s

e 2

b a ll

s O

Y !

Figure 4.1: Launcher setup

Target board

Exp. 4: Projectile Path

Equipment Needed

Item Item

Projectile Launcher and plastic ball Movable vertical target board* Meter stick or measuring tape Sticky tape Graph paper Carbon paper White paper

*The target board should be as tall as the distance from the muzzle to the floor.

Purpose

The purpose of this experiment is to determine how the vertical distance a projectile drops is related to the horizontal distance the projectile travels when the projectile is launched horizontally .

Theory

The range is the horizontal distance, x, between the muzzle of the Launcher and the place where the projectile hits, given by x = v

t, where v0 is the initial speed of the projectile as it leaves the muzzle and t is the time of flight.

If the projectile is launched horizontally, the time of flight of the projectile will be

The vertical distance, y, that the projectile falls during time, t, is given by

where g is the acceleration due to gravity. Substituting for t in the second equation gives

A plot of y versus x

will give a straight line with a slope equal to .

Setup

1. Clamp the Projectile Launcher

to a sturdy table or other horizontal surface. Mount the Launcher near one end of the table with the Launcher aimed away from the table.

2. Adjust the angle of the Projec-

tile Launcher to zero degrees so the ball will be launched horizontally.

3. Fire a test shot on medium

range to determine the initial position of the vertical target board. Place the target board on the floor so that the ball hits the board near the bottom. See Figure 4.1

012-05375C 23

Projectile Launcher Exp. 4: Projectile Path

4. Cover the target board with white paper. Tape carbon paper over the white paper.

Procedure

1. Measure the vertical height from the floor to the muzzle and record the height in the Table 4.1. Mark this

height on the target.

2. Measure the horizontal distance from the muzzle of the Launcher to the target board and record it in the Data

Table.

3. Shoot the ball.

4. Move the target board about 10 to 20 cm closer to the Launcher.

5. Repeat steps 2 through 4 until the height of the ball when it strikes the target board is about 10 to 20 cm below

the height of the muzzle.

Data Table 4.1

Height of Muzzle = ____________________

Table 4.1: x, y Data

Horizontal (x) Vertical (y) x

Analysis

1. On the target board, measure the vertical distances from the muzzle level mark down to the ball marks and

record them in Table 4.1.

2. Calculate x2 for all the data points and record them in the Data Table.

3. Plot a graph of y versus x2 and draw the best-fit light through th e data points.

4. Calculate the slope of the graph and record it in Table 4.2.

5. From the slope of the graph, calculate the initial speed of the ball as it leaves the muzzle. Record the initial

speed in Table 4.2.

6. Pick any x, y data point from Table 4.1. Use the vertical distance, y, to calculate the time, t. Calculate the ini-

tial speed using this time and the horizontal distance, x. Record the results in Table 4.2.

012-05375C

Model No. ME-6830 Exp. 4: Projectile Path

AB–

AB+

-------------





------------------ -

x100

7. Calculate the percent difference between the two initial speeds that were found using the different methods.

Record the percent difference in Table 4.2. (To calculate the percent difference, let A be one of the initial speed values and let B be the other initial speed value.)

Data Table 4.2

Table 4.2: Compare Methods for Initial Speed

Item Value

Slope of graph

Initial speed from slope

Time of flight

Initial speed from x,y

Percent difference

Question

1. From the graph, was the best-fit line straight?

2. What does the shape of the best-fit line on the y versus x

graph tell you about the relationship of y and x2?

3. If you plotted a graph of y versus x, how would the graph differ from the y versus x

4. What shape is the path of the projectile?

graph?

012-05375C 25

Projectile Launcher Exp. 4: Projectile Path

Notes

012-05375C

Model No. ME-6 830 Exp. 5: Conservation of Energy

CAUTION!

DO NOT LOOK DOWN BARREL!

CAUTION!

DO NOT LOOK DOWN BARREL!

CAUTION!

DO NOT LOOK

DOWN THE BARREL.

LONG RANGE

MEDIUM

RANGE

SHORT RANGE

Position

of Ball

Launch

SHORT RANGE

PROJECTILE LAUNCHER

ME-6800

Yellow Band in Window

Indicates Range.

WEAR

SAFETY

GLASSES

WHEN IN USE.

Use 25 mm

balls ONL Y!

Figure 5.1: Conservation of Energy

final

position

initial

position

1 2

-- -

GPE mgh=

Figure 5.2: Find the initial speed

1 2

-- -

----- -=

Exp. 5: Conservation of Energy

Equipment Needed

Item Item

Projectile Launcher and plastic ball Plumb bob and string Meter stick or measuring tape Sticky tape White paper Carbon paper Photogate Head ME-9498A (2) optional* Photogate Mounting Bracket ME-6821A optional*

*Use the Photogates and Photogate Mounting Bracket with a PASCO Interface or Timer to measure the initial speed of the ball directly (see Experiment 2).

Purpose

The purpose of this experiment is to confirm that the initial kinetic energy of a projectile shot straight up is transformed into an equal amount of gravitational potential energy.

Theory

The total mechanical energy of a projectile is the sum of its gravitational potential energy and its kinetic energy. In the absence of friction, total mechanical energy is conserved. When a projectile is shot straight up, the initial gravitational potential energy (GPE) can be defined as zero. The initial kinetic energy (KE) depends on the mass, m, of the projectile and the initial speed, v

When the projectile reaches its maximum height, h, the speed of the projectile is zero and therefore the kinetic energy is zero. The gravitational potential energy depends on the mass of the projectile and the height:

where g is the acceleration due to gravity. If friction in the form of air resistance is ignored, the initial kinetic energy should equal the final gravitational potential energy.

The initial speed of the projectile must be determined in order to calculate the initial kinetic energy. To calculate the initial speed, v

, of a projectile fired horizontally, the horizontal distance travelled by the projectile is x = v0t

where t is the time that the projectile is in the air.

The vertical distance that projectile drops in time, t, is given by

The initial speed of the projectile can be calculated by measuring x and y and using y to calculate the time, t. The time of flight of the projectile can be found using

and then the initial speed can be found using

012-05375C 27

Projectile Launcher Exp. 5: Conservation of Energy

Setup

1. Clamp the Projectile Launcher to a sturdy table or other horizontal surface. Mount the Launcher near one end

of the table with the Launcher aimed away from the table.

2. Point the Launcher straight up and fire a test shot on medium range to make sure that the ball doesn’t hit the

ceiling. (If it does, use the short range setting for this experiment or put the Launcher closer to the floor.)

3. Adjust the angle of the Projectile Launcher to zero degrees so the ball will be launched horizontally.

Procedure

Part A: Determine the Initial Speed (without photogates)

1. Put the plastic ball into the Launcher and cock it to the medium range setting. Fire one shot to locate where the

ball hits the floor. At that position, tape a piece of white paper to the floor. Place a piece of carbon paper (carbon-side down) on top of the white paper and tape it in place

• When the ball hits the carbon paper, it will leave a mark on the white paper.

2. Fire ten shots.

3. Measure the vertical distance from the bottom of the ball as it leaves the barrel to the floor. Record this dis-

tance in the Table 5.1. Use the distance to calculate the time of flight and record it.

• The “Launch Position of Ball” in the barrel is marked on the label on the side of the Launcher.

4. Use a plumb bob to find the point on the floor that is directly beneath the release point on the barrel. Measure

the horizontal distance along the floor from the release point to the leading edge of the piece of white paper. Record the distance in Table 5.1.

5. Carefully remove the carbon paper. Measure from the leading edge of the white paper to each of the ten dots

and record these distances in Table 5.1.

6. Find the average of the ten distances and record it.

7. Using the horizontal distance and the time of flight, calculate the initial speed of the ball. Record the speed.

Table 5.1:

Item Value Item Value

Vertical distance Calculated time of flight

Horizontal distance to edge of paper Initial speed

012-05375C

Model No. ME-6 830 Exp. 5: Conservation of Energy

Table 5.1

Trial Distance Trial Distance

16 27 38 49 510

Average

Total distance

Alternate Method for Determining the Initial Speed of the Ball (using photogates)

1. Attach the photogate mounting bracket to the Launcher and attach two photogates to the bracket. Check that

the distance between the photogates is 0.10 m (10 cm).

2. Plug the photogates into an interface or a timer.

3. Adjust the angle of the Launcher to 90 degrees (straight up).

4. Put a plastic ball in the Projectile Launcher and use the ramrod to cock it at the medium range setting.

5. Setup the data acquisition software or the timer to measure the time between the ball blocking the two photo-

gates.

6. Shoot the ball three times and calculate the average of these times. Record the data in the Table 5.2.

7. Calculate the initial speed of the ball based on the 0.10 m distance between the photogates. Record the value.

Table 5.2

Table 5.2: Initial Speed Using Photogates

Trial Time

1 2 3

Average Time

Initial Speed

012-05375C 29

Projectile Launcher Exp. 5: Conservation of Energy

KE GPE– KE GPE+

--------------------------

-------------------------- -

x100

Part B: Measure the Height of the Ball

1. Adjust the angle of the Launcher to 90 degrees (straight up).

2. Shoot the ball on the medium range setting several times and then measure the maximum heigh t attained by

the ball. Record the maximum height in Table 5.3.

3. Determine the mass of the ball and record it in Table 5.3.

Analysis

1. Calculate the initial kinetic energy and record it in Table 5.3.

2. Calculate the final gravitational potential energy and record it in Table 5.3.

3. Calculate the percent difference between the initial kinetic energy and the final gravitational potential energy

and record it in Table 5.3.

Table 5.3: Results

Item Value

Maximum height of ball

Mass of ball

Initial Kinetic Energy

Final Potential Energy

Percent difference

Questions

1. How does the initial kinetic energy compare to the final gravitational potential energy?

2. How does friction in the form of air resistance affect the result for the conservation of energy?

3. When the Launcher is cocked, it has elastic potential energy. If energy is conserved, how should the elastic

potential energy compare to the initial kinetic energy?

012-05375C

Model No. ME-6830 Exp. 6: Conservation of M omentum

(υ = 0)

(a)

(b)

Figure 6.1: Conservation of Momentum

(a) before collision (b) after collision

before

m1v0x

after

m1v1xm2v

+xˆm1v1ym2v

+y

m1v

m2v

–=

m1v

m1v1xm2v

1 2

-- -

1v0

1 2

-- -

1v1

1 2

-- -

2v2

Exp. 6: Conservation of Momentum

Equipment Needed

Item Item

Projectile Launcher and 2 plastic balls 2-D Collision Accessory Meter stick or measuring tape Sticky tape White paper, large sheet Carbon paper (2 or 3 sheets) Protractor Plumb bob and string

Purpose

The purpose of this experiment is to confir m that moment um is conserved for elastic and inelastic collisions in two dimensions.

Theory

A ball is shot toward another ball that is initially at rest, resulting in a collision after which the two balls move in different directions. In the system consisting of just the balls, both balls are falling under the influence of gravity so momentum is not conserved in the vertical direction. However, there is no net force in the horizontal plane (if air resistance is ignored), so momentum is conserved in the horizontal plane.

Before collision, since all the momentum is in the direction of Ball #1 (m

), it is convenient to define the x-axis in

this direction. Momentum before the collision is:

where v

is the initial speed of Ball #1 and is the unit vector in the x-direction. The momenta of the two balls

after the collision consists of both horizontal and vertical components, so the momentum after the collision is:

where v

= v1 cos 1, v1y = v1 sin 1. v2x = v2 cos 2, and v2y = v2 sin 2.

Since there is no momentum in the y-direction before the collision, there is zero net momentum in the y-direction after the collision. Therefore, t

Equating the momentum in the x-direction before the collision to the momentum in th e x-directi on after the collision gives:

In a perfectly elastic collision, kinetic energy is conserved as well as momentum.

Also, when energy is conserved, the paths of two balls of equal mass will be at right angles to each other after the collision.

012-05375C 31

Projectile Launcher Exp. 6: Conservation of Momentum

Target

ball

“tee”

Setup

1. Clamp the Projectile Launcher to a sturdy table. Mount the

Launcher near one end of the table with the Launcher aimed inward toward the table.

2. Adjust the angle of the Projectile Launcher to zero degrees

so the ball will be launched horizontally onto the table.

3. Cover the table with white paper (such as butcher paper).

NOTE: The paper must reach the base of the Launcher.

4. Fire a test shot on the short range setting to make sure that

the ball lands on the table. Tape a piece of carbon paper (carbon-side down) over the spot where the ball lands.

5. Mount the 2-D Collision Accessory to the front of the

Launcher.. Put a target ball on the post (“tee”) of the accessory.

6. Loosen the thumbscrew and rotate the 2-D Collision Accessory slightly to one side.

• The “tee” must be located so that the launched ball does not rebound into the Launcher but does hit the target ball so that both balls land on the table at the same time.

• Tighten the thumbscrew to hold the accessory in place.

7. Load the Launcher and fire a test shot to check that both balls hit the table at the same time. Tape a piece of carbon paper on the white paper at each spot where the two balls land on the table.

Procedure

A. No Collision

1. Put “ball 1” into the Launcher and cock it to the short range setting. Do not put a target ball on the “tee”.

2. Shoot the ball straight ahead and repeat the procedure five times.

B. Elastic Collision

1. Use two balls. Load Ball 1into the Launcher at the short range setting. Place Ball 2 on the “tee” of the 2-D Collision Accessory.

2. Shoot Ball 1 so it collides with the target ball (Ball 2). Repeat the procedure five times.

C. Inelastic Collision

1. Use two balls. Load Ball 1into the Launcher at the short range setting. Put a small loop of sticky tape (sticky-side out) on Ball 2 and place it on the “tee”.

2. Orient the tape side of Ball 2 so that it will be struck by the launched ball (Ball 1), causing an inelastic collision.

3. Fire a test shot to locate where the two balls hit the table. Tape a piece of carbon paper to the white paper.

4. Shoot Ball 1 and if the two balls stick together but miss the carbon paper, relocate the carbon paper and shoot

once more.

012-05375C

Model No. ME-6830 Exp. 6: Conservation of M omentum

• Since the tape does not produce the same inelastic collision each time, it is only useful to record this collision once.

5. Use a plumb bob to locate on the paper the spot directly below the point of contact of the two balls. Mark this spot on the paper as the “point-of-contact” spot. Carefully remove the carbon paper from the white paper.

Analysis

The time of flight for each shot is the same because the vertical distance for each shot is the same. Therefore, the horizontal length of each path is proportional to the speed of the ball. Since the masses are the same, the horizontal length of each path is also proportional to the momentum of the ball.

A. No Collision

1. Draw straight lines from the “point-of-contact” spot to each of the dots made by the ‘no collision’ shots.

2. Measure each straight line and record the length. Find the average of the five lengths and record the length as

the “initial x-momentum” in Table 6.1 and Table 6.2. (For example, if the length is 65 cm, record “65” as the value for the “initial x-momentum” but do not include any units.)

B. Elastic Collision

1. Draw a straight line from the “point-of-contact” through the center of the group of dots made by the ‘no colli- sion’ shots. (This is the center line from which all of the angles will be measured.)

2. Draw straight lines from the “point-of-contact” spot to each of the dots made by the ‘elastic collision’ shots. (There should be five lines on each side of the center line.)

3. Measure from the “point-of-contact” to each of the dots made by Ball 1. Find the average of the five lengths. Draw a straight line from the “point-of-contact” through the center of the group of dots made by Ball 1.

4. Measure the angle from the centerline to the straight line for Ball 1. Use this angle and the average length of the line for Ball 1 to calculate the x-component for Ball 1 and the y-component for Ball 1. Record the values.

5. Measure from the “point-of-contact” to each of the dots made by Ball 2. Find the average of the five lengths. Draw a straight line from the “point-of-contact” through the center of the group of dots made by Ball 2.

6. Measure the angle from the centerline to the straight line for Ball 2. Use this angle and the average length of the line for Ball 2 to calculate the x-component for Ball 2 and the y-component for Ball 2. Record the values.

7. Add the x-momentum for Ball 1 and the x-momentum for Ball 2 and record the result in Table 6.1 as “Final x-momentum”.

8. Calculate the initial kinetic energy of Ball 1 and the sum of the kinetic energy of Ball 1 and Ball 2 after the collision.

9. Calculate the percent differences.

Table 6.1: Data for the Elastic Collisions

Item Value Item Value Percent difference

Initial x-momentum.

Ball 1

Final y-momentum,

Ball 1

Initial kinetic energy,

Ball 1

Final x-momentum,

Ball 1 + Ball 2

Final y-momentum,

Ball 2

Final kinetic energy,

Ball 1 + Ball 2

012-05375C 33

Projectile Launcher Exp. 6: Conservation of Momentum

C. Inelastic Collision

1. Draw straight lines from the “point-of-contact” spot to the dots made by the ‘inelastic collision’ shot. (Th e re should be two lines.)

2. Measure from the “point-of-contact” to each of the dots made by the ‘inelastic collision’ shot.

3. Measure the angle from the centerline to the straight line for each dot of the ‘inelastic collision’ shot.

4. Use the angle and the length of the lines for the shot to calculate the x-component and the y-component for

each ball in the ‘inelastic collision’ shot. Record the values.

5. After the collision, add the x-momentum for Ball 1 and the x-momentum for Ball 2 and record the result in Table 6.2 as “Final x-momentum”.

6. Calculate the initial kinetic energy of Ball 1 and the sum of the kinetic energy of Ball 1 and Ball 2 after the collision.

7. Calculate the percent differences.

Table 6.2: Data for the Inelastic Collisions

Item Value Item Value Percent difference

Initial x-momentum.

Ball 1

Final y-momentum,

Ball 1

Initial kinetic energy,

Ball 1

Final x-momentum,

Ball 1 + Ball 2

Final y-momentum,

Ball 2

Final kinetic energy,

Ball 1 + Ball 2

Questions

1. Was momentum conserved in the x-direction for each type of collision?

2. Was momentum conserved in the y-direction for each type of collision?

3. W as kinetic energy conserved for the elastic collision?

4. W as kinetic energy conserved for the inelastic collision?

5. For the elastic collision, was the angle between the paths of the balls after the collision equal to 90 degrees as

expected?

6. For the inelastic collision, what was the angle between the paths of the balls after the collision? Why is it less than 90 degrees?

012-05375C

Model No. ME-6830 Exp. 7: Vary the Angle to Maxim ize the Height

TIO

T LO

N BAR

TIO

T LO

N BAR

CAUTION!

DO NOT LOOK

DOWN THE

SHOR

T RANGE

ME-6800

WEAR

SAFETY GLASSES

WHEN IN USE.

e 25 m

lls

Figure 7.1: Maximizing Height

Range

Initial

height

Angle

Initial

speed

yy0v0sint

1 2

-- -

–+=

xv0cost=

cos

-----------------

yy0x 



cos

---------------------- -

–tan+=

dy d

------

x 

gx2

sectan

----------------------------------

–sec 0==



max

tan

----- -

Exp. 7: Vary the Angle to Maximize the Height

Equipment Needed

Item Item

Projectile Launcher and plastic ball Board to protect wall Meter stick or measuring tape Sticky tape White paper, large sheet Carbon paper (several sheets) Plumb bob and string

Purpose

The purpose of this experiment is to find the launch angle that will maximize the height on a vertical wall for a projectile launched at a fixed horizontal distance from the wall.

Theory

When the ball is shot at an angle at a fixed distance, x, from a target such as a vertical wall, the ball hits the wall at a height y given by:

where y

is the initial height of the ball, v0 is the initial speed

of the ball as it leaves the muzzle,  is the angle of inclination above horizontal, g is the acceleration due to gravity, and t is the time of flight. The range is the horizontal distance, x, between the muzzle of the Launcher and the place where the ball hits, given by

Solving this equation for the time of flight, t, gives

Substituting for t in the equation for y gives

T o find the angle, , that gives the maximum height, y, find the first derivative of the equation for y and set it equal to zero. Solve for the angle, .

Solving for the angle, , gives:

Since the second derivative is negative for  the fixed distance, x, and the maximum height, y



max

, and x.

, the angle is a maximum. To find the initial speed of the ball, use

max

. Solve the y-equation for v0 and plug in the values for y

max

012-05375C 35

Projectile Launcher Exp. 7: Vary the Angle to Maximize the Height

Difference

AB–

AB+

-------------

x100=

Setup

1. Clamp the Projectile Launcher to a sturdy table. Mount the Launcher near one end of the table with the Launcher aimed toward a wall about 2 meters from the table.

2. Use a vertical board to the protect the wall and cover the board with white paper.

3. Fire a test shot to see where the ball hits the board and tape a piece of carbon paper (carbon-side down) at that

position.

Procedure

1. Shoot the ball at various angles and pinpoint whi c h angle gives the maximum height by checking the marks on the white paper. (Move the carbon paper as necessary.)

2. Measure the angle that produces the maximum height and record its value in Table 7.1.

3. Measure the maximum height and record the value in the Data Table.

4. Measure the horizontal distance from the muzzle to the vertical board and record the value.

5. Measure the initial height of the ball where it leaves the muzzle and record the value..

Table 7.1: Data and Results

Item Value

Measured Angle for Maximum Height Maximum Height Horizontal Distance Initial Height Calculated Initial Speed Calculated Angle for Maximum Height Percent Difference between Angles

Analysis

1. Calculate the initial speed by solving the y-equation for v0 and substituting the values for y from Table 7.1.

2. Calculate the angle for maximum height using the initial speed calculated in step 1 and the horizontal distance from the wall to the launcher.

3. Calculate the percent difference between the measured angle and the calculated angle. (Let A be one of the angles and B be the other angle).

max

, 

max

, and x

Questions

1. For the angle that gives the maximum height, when the ball hits the wall, has it already reached the peak of its trajectory?

2. For what distance from the wall would the height be maximized for a launch angle of 45°? What would the maximum height be in this case?

012-05375C

Model No. ME-6 830 Exp. 8: Projectile Velocity—Approximate Method

M m

---- -

2gR

1 cos–=

String loop

Figure 8.1: Setup

Exp. 8: Projectile Velocity—Approximate Method

Equipment Needed

Item Item

Ballistic Pendulum/Projectile Launcher Steel ball C-clamp Mass balance String

Purpose

The muzzle velocity of the projectile launcher is determined by launching the ball into the ballistic pendulum and observing the angle to which the pendulum swings.

As derived earlier in the manual, the equation for the velocity of the ball is approximately:

where M is the mass of the pendulum and ball combined, m is the mass of the ball, g is the acceleration due to gravity, R by the pendulum after the collision.

is the distance from the pivot point to the center of mass of the pendulum, and  is the angle reached

Setup

1. Put the Projectile Launcher on the Ballistic Pendulum upright at the level of the ball catcher (the low position). Make sure that the pendulum can hang vertically without touching the launcher.

2. Clamp the Ballistic Pendulum base to a sturdy table. Make sure that the clamp does not interfere with the pendulum swing.

Procedure

1. Latch the pendulum at 90° so it is out of the way temporarily, and then load the projectile launcher with the steel ball. Allow the pendulum to hang freely, and move the angle indicator to zero degrees.

2. Fire the launcher and record the angle reached. If you want to do the experiment with a lower or higher angle, add to or remove mass from the pendulum. Repeat these test measurements until you are satisfied with the mass of the pendulum.

3. Once you have chosen the mass to use for your experiments, remove the pendulum from the upright by unscrewing and removing the axle. Use a mass balance to find the mass of the pendulum and ball together. Record this value as M in Table 8.1.

4. Measure the mass of the ball alone and record this as m.

• Tie a loop in a piece of string, and hang the pendulum horizontally from the loop. (See Figure 8.1.) With the ball latched in position in the ball catcher, adjust the position of the pendulum in the loop until the pendulum balances. Measure the distance from the pivot point to this balance point, and record the distance as R

012-05375C 37

Projectile Launcher Exp. 8: Projectile Velocity—Approximate Method

• NOTE: It may be easier to balance the pendulum on the edge of a ruler or similar object.

5. Reattach the pendulum to the upright, making sure that it is facing the right way. Be sure that the angle indicator is in front of the long pin of the pendulum.

6. Load the launcher, and then set the angle indicator to an angle one or two degrees less than the angle reached in step 2. This will nearly eliminate the friction against the pendulum caused by the angle indicator, since the pendulum will only move the angle indicator for a short distance.

7. Fire the launcher, and record the angle reached by the pendulum in T able 8.1. Repeat several times, setting the angle indicator to an angle one or two degrees less than the previous angle reached by the pendulum each time.

Table 8.1

M = ____________________ m = ____________________ Rcm = ___________________

Table 8.1: Data

Item Value



Average 

Muzzle velocity

Calculations

1. Find the average angle reached by the pendulum and record the value in Table 8.1.

2. Calculate the muzzle velocity of the ball fired from the projectile launcher.

Questions

1. Is there another way to measure the muzzle velocity that you could use to check your results? You may want to use that second method and compare the two answers.

2. What sources of error are there in this experiment? How much do these errors affect your result?

3. It would simplify the calculations if kinetic energy were conserved in the collision between the ball and the

pendulum (see “Ballistic Pendulum Theory” in the Introduction). What percentage of the kinetic energy is lost in the collision between the ball and pendulum? Would it be valid to assume that energy was conserved in that collision?

4. How does the angle reached by the pendulum change if the ball is not caught by the ball catcher? Y ou may test this by turning the pendulum around so the ball strikes the back of the ball catcher. Is there more energy or less energy transferred to the pendulum?

012-05375C

Model No. ME-6830 Exp. 9: Projectile Velocity—Exact Method

----------

2IMgR

1 cos–=

MgR

4

------------------------

Exp. 9: Projectile Velocity—Exact Method

Equipment Needed

Item Item

Ballistic Pendulum/Projectile Launcher and steel ball Ruler C-clamp Mass balance String Stopwatch

Purpose

The muzzle velocity of the projectile launcher is determined by launching the ball into the ballistic pendulum and observing the angle to which the pendulum swings.

As derived earlier in the manual, the equation for the velocity of the ball is approximately:

where M is the mass of the pendulum and ball combined, m is the mass of the ball, g is the acceleration due to gravity, R pivot point to the ball,  is the angle reached by the pendulum, and I is the moment of inertia of the pendulum with the ball in the catcher.

is the distance from the pivot point to the center of mass of the pendulum, Rp is the distance from the

The value of I can be found by measuring the period of small oscillations of the pendulum/ball combination and by using the equation:

where T is the period.

Setup

1. Put the Projectile Launcher on the Ballistic Pendulum upright at the level of the ball catcher (the low position). Make sure that the pendulum can hang vertically without touching the launcher.

2. Clamp the Ballistic Pendulum base to a sturdy table. Make sure that the clamp does not interfere with the pendulum swing.

Procedure

4. Measure the mass of the ball alone and record this as m.

012-05375C 39

Projectile Launcher Exp. 9: Projectile Velocity—Exact Method

String loop

Figure 9.1: Setup

5. Tie a loop in a piece of string, and hang the pendulum horizontally from the loop. (See Figure 9.1.) With the ball latched in position in the ball catcher, adjust the position of the pendulum in the loop until the pendulum balances. Measure the distance from the pivot point to this balance point, and record the distance as R

• NOTE: It may be easier to balance the pendulum on the edge of a ruler or similar object.

6. Measure the distance between the pivot point and the center of the ball. Record this as R

7. Remove the launcher so that the pendulum can swing freely. With the ball in the ball catcher, give the pendulum an initial displacement of 5° or less. Using the stopwatch, time how long it takes to go through ten oscillations. Divide this time by the number of oscillations and record the result as T in Table 9.1.

8. Calculate the value of I, and record it in Table 9.1.

9. Reattach the launcher and load it. Set the angle indicator to an angle one or two degrees less than the angle

reached in step 2. This will nearly eliminate the friction against the pendulum caused by the angle indicator, since the pendulum will only move the angle indicator for a short distance.

10. Fire the launcher, and record the angle reached by the pendulum in Table 9.1. Repeat several times, setting the angle indicator to an angle one or two degrees less than the previous angle reached by the pendulum each time.

Table 9.1

M = ____________________ m = ____________________ Rcm = ___________________

= ____________________ T = ____________________ I = _____________________

Table 9.1: Data

Item Value



Average 

Muzzle velocity

Calculations

1. Find the average angle reached by the pendulum and record the value in Table 9.1.

2. Calculate the muzzle velocity of the ball fired from the projectile launcher.

012-05375C

Model No. ME-6830 Exp. 9: Projectile Velocity—Exact Method

M m

---- -

2gR

1 cos–=

Questions

1. Is there another way to measure the muzzle velocity that you could use to check your results? You may want to use that second method and compare the two answers.

2. What sources of error are there in this experiment? How much do these errors affect your result?

3. It would simplify the calculations if kinetic energy were conserved in the collision between the ball and the

4. Does increasing the mass of the pendulum increase or decrease the efficiency of the energy transfer in the collision? Try it.

5. The “Projectile Velocity—Approximate Method” experiment uses the approximate equation for velocity:

• What is the value of velocity when you use this equation? Is there a significant difference between these two calculated values? What factors would increase the difference between these two results? How would you build a ballistic pendulum so that the approximate equation gave better results?

012-05375C 41

Projectile Launcher Exp. 9: Projectile Velocity—Exact Method

012-05375C

Model No. ME-6830 Exp. 10 (Demo ): Do 30° and 60° Give the Same Range?

t 2t

peak

2v0sin

------------------- -

cossin

------------------------------- -

2sin

------------------- -

CAUTION!

T LOO

N BARREL!

CAUTION!

T LOO

N BARREL!

T L

osition of Ball

Laun

PROJECTILE LAUNCHER

-6

9 0

8 0

lls

Figure 10.1: Set up to shoot on level surface.

Box

Exp. 10 (Demo): Do 30° and 60° Give the Same Range?

Equipment Needed

Item Item

Projectile Launcher and steel ball Box to make landing area same height as muzzle

Purpose

The purpose of this demonstration is to confirm that the range of a ball launched at 30° is the same as one launched at 60° if the ball lands at the same height from which it was launched.

Theory

The range is the horizontal distance, x, between the muzzle of the Launcher and the place where the projectile lands, given by x = (v above horizontal, and t is the time of flight.

If the ball lands on a target that is at the same height as the level of the muzzle of the launcher, the time of flight of the ball will be twice the time it takes the ball to reach the peak of its trajectory, when its vertical component of speed reaches zero.

cos ) t where v0 is the initial speed of the ball as it leaves the muzzle,  is the launch angle

where g is the acceleration due to gravity. Substituting for t in the equation for x gives:, and t is the time of flight.

and using a trigonometry identity gives:

The ranges for the angles 30° and 60° are the same since sin 60° = sin 120°.

Setup

1. Clamp the Projectile Launcher to a sturdy table. Mount the Launcher near one end of the table with the Launcher aimed toward the middle of the table.

2. Adjust the angle of the Launcher to 30°.

3. Put the steel ball into the Launcher and cock

it to the medium range or long range setting.

• NOTE: In general, this demonstration will not work as well on the short range setting because the muzzle speed is more variable with the change in angle.

4. Fire a test shot to see where the ball hits. Place the box in front of that location so that the next ball will hit the top of the box.

Procedure

1. Shoot the ball at 30° to demonstrate that the ball lands on the box.

012-05375C 43

Projectile Launcher Exp. 10 (Demo): Do 30° and 60° Give the Same Range?

2. Change the angle of the Launcher to 60° and shoot the ball again . Call attent ion to the fact that the ball again lands on the box (confirming that the ranges are the same).

3. Change the angle to 45° and shoot the ball again to show that the ball now lands further away, missing the box.

4. Ask the question: What other pairs of angles will have a common range? Will 20° and 70° have the same range? Will 35° and 55° have the same range?

• This demonstration can be done for any two angles that add up to 90°.

012-05375C

Model No. ME-6 830 Exp. 11 (Demo): Sim ultaneous Shots at Different Speeds

----- -=

short

long

0(long)

0(short)

Figure 9.1: Shots fired simultaneously

Exp. 11 (Demo): Simultaneous Shots at Different Speeds

Equipment Needed

Item

Projectile Launcher (2) and plastic ball (2)

Purpose

The purpose of this demonstration is to confirm that regardless of the initial speed of projectiles fired horizontally, the projectiles will hit the floor at the same time.

Theory

Two projectiles are shot horizontally from the same height, y. The muzzle speeds of the two projectiles are different.

The vertical and horizontal motions of a projectile are independent of each other. The horizontal distance, x, travelled by the projectile depends on the initial speed, v

The time of flight depends on the vertical distance that the projectile falls.

, and the time of flight, t. The distance x = v0t.

where g is the acceleration due to gravity. Since the vertical distance is the same fore each projectile, the time of flight is the same for each projectile.

Setup

1. Clamp two Projectile Launchers adjacent to each other on a sturdy table. Mount the Launchers near one end of the table with the Launchers aimed away from the table so the balls will land on the floor.

2. Adjust the angle of the Launcher to 0° so the balls will fire horizontally.

Procedure

1. Put a plastic ball into each Launcher. Cock one Launcher to the short range setting and clock the other Launcher to the long range setting.

2. Ask the class to be quiet and listen for the balls striking the floor.

• NOTE: If there is only one click, that means that the balls hit the floor simultaneously.

3. Put both trigger release strings in the same hand and pull them at the same time so that the balls are launched simultaneously.

4. After the balls hit the floor, ask the class if they heard one click or two.

012-05375C 45

Projectile Laun cher Exp. 11 (Demo): Simultaneous Shots at Different Sp eeds

012-05375C

Model No. ME-6830 Exp. 12 (Demo): Shooting Through Hoops

xv0t=

1 2

-- -





– gt

1 2

-- -





– g

---- -





ax2b+==

Exp. 12 (Demo): Shooting Through Hoops

Equipment Needed

Item Item

Projectile Launcher and plastic ball Ring clamp on stand (5) Photogate Head ME-9498A (2) optional Photogate Mounting Bracket ME-6821A optional Meter stick Two-meter stick

Purpose

The purpose of this demonstration is to confirm that the part of a projectile is parabolic.

Theory

The range is the horizontal distance, x, between the muzzle of a Launcher and the place where the projectile hits, given by:

where v

is the initial speed of the projectile as it leaves the muzzle and t is the time of flight. The vertical position,

y, of the projectile at time t is given by:

where y0 is the initial height of the projectile and g is the acceleration due to gravity.

Solving the x-equation for t and substituting the expression in the y-equation gives:

where “a” and “b” are constants. The y-equation (y = ax

+b) describes a parabola.

Pre-Lab

Before the demonstration begins, find the initial speed of the bal. Use two photogates and a photogate mounting bracket with a P ASCO Interface or T imer or shoot the ball horizontally and measure x and y. (Use y to calculate the time of flight. See experiments 1 and 2.)

Setup

1. Clamp the Projectile Launcher to a sturdy table near one end of the table with the Launchers aimed away from the table so the balls will land on the floor.

2. Adjust the angle of the Launcher to 0° so the balls will fire horizontally.

Procedure

1. Measure and record the initial height, y0, of the ball at muzzle level.

012-05375C 47

Projectile Launcher Exp. 12 (Demo): Shooting Through Hoops

C A

U T

D O

O T

O K

D O

W N

A R

E L

C A

U T

D O

O T

O K

D O

W N

A R

E L

A U

T I O

N !

D O

N O

T L

O O

D O

N T

H E

L O N

N G

E D

IU M

R A N

G E

H O

R T

A NG

P o s

i t io

o f B

l l

L a u

n c

O R

T R

PROJECTILE LAUNCHER

E-6800

Y e l

l o w B

a n

d i n

W i n

d o w

I n d

i c a t e s

a n g

e .

EAR SAFETY GLASS

WHEN

IN US

e 2

5 m

ll s O

N L

ME-6831

BALLISTIC PENDULUM

Figure 12.1: Demonstration setup

2. Calculate and record the horizontal and vertical positions of the ball each 1/10 second until the vertical posi-

tion is zero.

Table 10.1: X- and y-positions

t (sec) x = v

t (cm) y = y0 - (1/2)gt2 (cm)

0.1

0.2

0.3

0.4

0.5

3. Lay the two-meter stick on the floor in a straight line away from the Launcher. Remove the back mounting

screw from the Launcher base so that the back of the Launcher can rotate upward. Look through the Launcher at the end of the two-meter stick. Adjust the end of the stick until the end is aligned with the sites in the Launcher and the stick is along the path of the ball when it is fired.

4. Starting at the muzzle of the Launcher, measure off each set of x and y distances and place a ring clamp on a

stand at each position corresponding to one-tenth of a second (see Figure 10.1).

5. Shoot the ball through the rings.

6. Ask the class: What shape of curve is formed by the rings? What is the path of the projectile?

012-05375C

Model No. ME-6830 Exp. 13 (Demo): Ela stic and Inelastic Collisions

Exp. 13 (Demo): Elastic and Inelastic Collisions

Equipment Needed

Item

Projectile Launcher and plastic or steel ball

Purpose

The purpose of this demonstration is to show the difference in kinetic energy transfer between an elastic collision and an inelastic collisions.

Theory

The amount of kinetic energy transferred between colliding objects depends on the elasticity of the collision. By reversing the pendulum of the Ballistic Pendulum so the ball bounces off instead of being caught, it is possible to demonstrate this effect.

Setup

1. Clamp the Ballistic Pendulum/Projectile Launcher to a sturdy table with the launcher mounted in the lower

position on the upright.

Procedure

1. Shoot the ball into the pendulum and record the angle reached.

2. Remove the pendulum and reinstall it in the reversed position so that the ball opening is away from the

launcher.

3. Shoot the same ball again at the same launcher setting and note the angle reached.

Analysis

• The collision between the ball and the pendulum is not perfectly elastic, so kinetic energy is still not conserved. However, the collision is more nearly elastic than the completely inelastic collision in step 1. There is a greater transfer of kinetic energy.

012-05375C 49

Projectile L auncher Exp. 13 (Demo): Elastic and Inelastic Collisions

012-05375C

Model No. ME-6830 Teacher’s Guide

 v0sin22gy0y–++sin

---------------------------------------------------------------------------------- -

Teacher ’s Guide

Exp. 1: Projectile Motion

NOTE: For best results, make sure that the Launcher is securely clamped to a sturdy table. Any movement of the Launcher will result in inconsistent data.

The muzzle speed of the Launcher tested was 6.5 m/s (on the long range setting).

To find the range at the chosen angle, it is necessary to solve the quadratic equation given in the Theory section. The solution is:

Analysis

1. The difference depended on the angle at which the Launcher was fired. The table gives typical results: range

Angle Predicted Range Actual Range Percent Error

30 5.22 5.19 0.57% 45 5.30 5.16 2.64% 60 4.35 4.23 2.87% 39 5.39 5.31 1.48%

NOTE: The maximum angle is not 45° in this case. The range at 60° is not equal to the range at 30°. This is because the initial height of the ball is not the same as the impact point. The maximum range for this setup (with the Launcher 1.15 m above ground level) was calculated to be at 39°. This was verified experimentally.

2. Answers will vary depending on the method for estimating the precision. The primary source of error is ignoring the effect of air resistance.

Exp. 2: Projectile Motion Using Photogates

Except for the method of determining initial speed, this experiment is identical to ex periment 1.

012-05375C 51

Ballistic Pendulum/Projectile Launcher Teacher’s Guide



0.5

1.5

2.5

3.5

4.5

0 102030405060708090

Range (m)

Angle (degrees)



0 102030405060708090

Range (m)

Angle (degrees)

Exp. 3: Projectile Range Versus Angle

Procedure

• Shooting off a level surface:

• Shooting off a table:

• NOTE: The curves show the calculated ranges in each case. The data points are the actual measured ranges.

Questions

1. On a level surface, the maximum range is at 45°. For a non-level surface, the angle of maximum range depends on the initial height of the projectile. For the experimental setup, with an initial height of 1.15 m, the maximum range is at 40° (versus the theoretical value of 39°).

2. The angle of maximum range decreases with table height.

3. The maximum distance increases with table height.

Exp. 4: Projectile Path

Analysis

1. Alternately, measure your distances from the ground up.

012-05375C

Model No. ME-6830 Teacher’s Guide



0.05

0.1

0.15

0.2

0.25

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

Vertical Distance (m)

Horizontal Distance Squared (m^2)

f(x) = -1.181345E-1*x + 2.609457E-1 R^2 = 9.997926E-1

--------

2. Vertical distances were measured from the ground up for this graph. The intercept is the height of the launcher above the ground when done this way.

3. The slope (measuring from the ground) is -0.118 for this example. Measuring down from the initial height will give the same value, except positive.) In either case, the slope is:

4. The slope calculated here gives us an initial speed of 6.44 m/s. This compares favorably with the speed calculated in experiments 1 and 2.

5. Results will vary with this method: the point of the activity is that individual measurements are not as accurate as a large number of measurements and a curve fit.

Questions

1. Yes. This tells us that y is a function of x

2. A plot of y versus x would be parabolic instead of linear.

3. The projectile moves in a parabolic curve (if air resistance is neglected).

Exp. 5: Conservation of Energy

Analysis

1. Using the photogate method, the initial speed of the ball was found to be 4.93 m/s (for the short range launcher at the medium range setting). The ball mass was 9.6 g, so the total kinetic energy was 0.117 J.

2. The ball reached an average height of 1.14 m (above the muzzle). The gravitational potential energy was

0.107 J.

3. The energy difference was 8.5% of the original kinetic energy.

4. NOTE: It seems unlikely that this much energy is lost due to air resistance, especially when you consider the

extraordinarily good results for labs 3 and 4. It is likely that the error here enters the calculation in the actual measurements of initial velocity and maximum height.

012-05375C 53

Ballistic Pendulum/Projectile Launcher Teacher’s Guide

yy0x 

max



max

cos

------------------------------- -

–tan+=

dy dx

----- -



max



max

cos

------------------------------ -

–tan=

Exp. 6: Conservation of Momentum in Two Dimensions

Setup

• If possible, use medium range setting instead of the short range setting. The medium range setting gives more predictable results than the short-range setting.

Analysis

• Results for the x component of momentum should be within 5% of initial values. The total y component should be very small compared to the x component.

Questions

1. Momentum is conserved on both axes.

2. Kinetic energy is nearly conserved in the elastic collision. There is some loss of energy which indicates that

the collision is not perfectly elastics.

3. Momentum is conserved for the inelastic collision, but kinetic energy is not conserved.

4. The angle should be nearly 90°. (Trials had angles of about 84°.)

5. In the inelastic case, the angle will be less than in the elastic case. The exact angle will depend on the degree

of inelasticity, which will depend on the type and amount of tape used.

Exp. 7: Vary the Angle to Maximize the Height

Procedure

1. Yo u should be able to measure the angle of maximum height to within ±2%.

2. Measure the distance to the front edge of the ball.

3. Measure the initial height to the center of the ball.

Analysis

1. The initial speed should be close to the initial speed determined by other methods. You may wish to determine the initial speed by the method in experiment 1, and use that value in your calculations for the rest of the experiment.

2. Measured value and calculated vale should agree to within 3%.

Questions

1. The ball will have passed its peak by the time it reaches the wall. To show this, take the derivative of y with respect to x:

012-05375C

Model No. ME-6830 Teacher’s Guide



max

--------------







1–

tan=

dy dx

----- -

max

--------------

max

--------------







1–

tan







cos

--------------------------------------------------------

–=

a b

-- -





1–

tan





cos

2b2

---------------------

dy dx

----- -

max

--------------

max

g2x

max

-------------------------------- -







-----------------------------------------------

–

max

--------------

g2x

max

+

max

---------------------------------------

–==

dy dx

----- -

max

--------------

max

-----------------

–

----- -

–=

dy dx

----- -

max

--------------

–=



max

tan

----- -

x

---- -







----------------

–+ y

---- -

–+==

• substitute

• Substitute

• and simplify:

•When x = x

, the value of this derivative is negative.

max

• Therefore, the ball has already reached the peak and is on its way down.

2. Solve the equation for maximum angle to determin e x:

• Substitute this value into the equation for y to determine the maximum height.

Exp. 8: Projectile Motion—Approximate Method

Procedure

1. The exact mass used is not critical. Pick a value that gives a fairly large swing for best results.

2. With the steel ball and extra masses on the pendulum, the balance point will be somewhere on the ball catcher

itself. This makes it difficult to use string, but it is relatively easy to find the center of mass by balancing the pendulum on a straightedge.

3. The angle reached by the pendulum should not vary by more than one degree between successive trials.

012-05375C 55

Ballistic Pendulum/Projectile Launcher Teacher’s Guide

Calculations

• Use the equations given in the theory section for the approximate method.

Questions

1. The best other method of measuring velocity is described in the first part of experiment 1.

2. The greatest source of error is the equation used. This is an approximate equation, based on the assumption

that the masses involved are point masses. The amount of effect this equation has on the results will depend on the exact geometry of the pendulum and ball, and should be between five and eight percent.

3. Typically, 70% of the kinetic energy of the ball is ‘lost’. It is not valid to assume that kinetic energy is conserved.

Exp. 9: Projectile Motion—Exact Method

Procedure

1. The exact mass is not critical. Pick a value that gives a fairly large swing for best results.

2. With the steel ball and extra masses on the pendulum, the balance point will be somewhere on the ball catcher

itself. This makes it difficult to use string, but it is relatively easy to find the center of mass by balancing the pendulum on a straightedge.

3. Measure this period as exactly as possible, using the smallest measurement angle that is practical.

4. The angle reached by the pendulum should not vary more than one degree between successive trials.

Calculations

• Use the equations given in the theory section for the approximate method.

Questions

1. The best other method of measuring velocity is described in the first part of experiment 1.

2. Sources of error include friction and measurement error.

3. Typically, 70% of the kinetic energy of the ball is ‘lost’. It is not value to assume that kinetic energy is con-

served.

4. The energy transfer is less efficient when there is a larger difference in the masses involved.

5. The exact method will give results that are typically within 2.5% of the actual value.

012-05375C

Model No. ME-6830 Technical Support

Technical Support

For assistance with any PASCO product, contact PASCO at:

Address: PASCO scientific

10101 Foothills Blvd. Roseville, CA 95747-7100

Phone: 916-786-3800 (worldwide)

800-772-8700 (U.S.) Fax: (916) 786-7565 Web: www.pasco.com Email: support@pasco.com

For more information about the Ballistic Pendulum/Projectile Launcher and the latest revision of this Instruction Manual, visit the PASCO web site and enter ME-6830 or ME-6831 into the Search window.

Limited Warranty For a description of the product warranty, see the PASCO catalog. Copyright The PASCO scientific 012-05375C Ballistic Pendulum/Projectile Launcher Instruction Manual is copyrighted with all rights

reserved. Permission is granted to non-profit educational institutions for reproduction of any part of this manual, providing the reproductions are used only in their laboratories and classrooms, and are not sold for profit. Reproduction under any other circumstances, without the written consent of PASCO scientific, is prohibited.

Trademarks PASCO and PASCO scientific are trademarks or registered trademarks of PASCO scientific, in the United States and/or in other countries. All other brands, products, or service names are or may be trademarks or service marks of, and are used to identify, products or services of, their respective owners. For more information visit www.pasco.com/legal.

012-05375C 57

Ballistic Pendulum/Projectile Launcher Technical Support

012-05375C

PASCO ME-6831 User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual

Equipment

Assembly

Introduction

General Operation of the Projectile Launcher

Parts

Ready

Load

Shoot

Maintenance and Storage

Ballistic Pendulum Theory

Overview

Approximate Method

Exact Method

Installing the Optional Photogate Bracket (ME-6821A)

Repairing the Plumb Bob

Installing the 2-D (two dimensional) Collision Accessory

Expectations for the Projectile Launcher

Expectations for the Ballistic Pendulum

Exp. 1: Projectile Motion

Purpose

Theory

Setup

Analysis

Data Table A: Determine the Initial Speed

Data Table B: Predict the Range

Notes

Exp. 2: Projectile Motion Using Photogates

Purpose

Theory

Setup

Procedure

Analysis

Notes

Exp. 3: Projectile Range versus Angle

Purpose

Theory

Setup

Procedure

Analysis

Questions

Notes

Exp. 4: Projectile Path

Purpose

Theory

Setup

Procedure

Question

Notes

Exp. 5: Conservation of Energy

Purpose

Theory

Setup

Procedure

Analysis

Questions

Exp. 6: Conservation of Momentum

Purpose

Theory

Setup

Procedure

Analysis

Questions

Exp. 7: Vary the Angle to Maximize the Height

Purpose

Theory

Setup

Procedure

Analysis

Questions

Purpose

Setup

Procedure

Table 8.1

Calculations

Questions

Purpose