Palisade RISK FOR SIX SIGMA User Manual

Guide to Using

@RISK for Six

Sigma

Version 5.5

May, 2009

Palisade Corporation
798 Cascadilla St.
Ithaca, NY USA 14850
[phone]
[phone] (fax)
http://www.palisade.com (website)
[e-mail] (e-mail)

Copyright Notice

Copyright © 2009, Palisade Corporation.

Trademark Acknowledgments

Microsoft, Excel and Windows are registered trademarks of Microsoft, Inc.
IBM is a registered trademark of International Business Machines, Inc.
Palisade, TopRank, BestFit and RISKview are registered trademarks of Palisade
Corporation.
RISK is a trademark of Parker Brothers, Division of Tonka Corporation and is used under
license.

Welcome

Welcome to @RISK, the world’s most powerful risk analysis tool!
@RISK has long been used to analyze risk and uncertainty in any
industry. With applications in finance, oil and gas, insurance,
manufacturing, healthcare, pharmaceuticals, science and other fields,
@RISK is as flexible as Excel itself. Every day tens of thousands of
professionals use @RISK to estimate costs, analyze NPV and IRR,
study real options, determine pricing, explore for oil and resources,
and much more.

A key application of @RISK is Six Sigma and quality analysis.
Whether it’s in DMAIC, Design for Six Sigma (DFSS), Lean projects,
Design of Experiments (DOE), or other areas, uncertainty and variable
lies at the core of any Six Sigma analysis. @RISK uses Monte Carlo
simulation to identify, measure, and root out the causes of variability
in your production and service processes. A full suite of capability
metrics gives you the calculations you need to step through any Six
Sigma method quickly and accurately. Charts and tables clearly show
Six Sigma statistics, making it easy and effective to illustrate this
powerful technique to management. The Industrial edition of @RISK
adds RISKOptimizer to your Six Sigma analyses for optimization of
project selection, resource allocation, and more.

Industries ranging from engine manufacturing to precious metals to
airlines and consumer goods are using @RISK every day to improve
their processes, enhance the quality of their products and services,
and save millions. This guide will walk you through the @RISK Six
Sigma functions, statistics, charts and reports to show you how
@RISK can be put to work at any stage of a Six Sigma project.
Example case studies round out the guide, giving you pre-built
models you can adapt to your own analyses.

The standard features of @RISK, such as entering distribution
functions, fitting distributions to data, running simulations and
performing sensitivity analyses, are also applicable to Six Sigma
models. When using @RISK for Six Sigma modeling you should also
familiarize yourself with these features by reviewing the @RISK for
Excel Users Guide and on-line training materials.

Table of Contents

Chapter 1: Overview of @RISK and Six Sigma Methodologies 1

Introduction.........................................................................................3

Six Sigma Methodologies..................................................................7

@RISK and Six Sigma........................................................................9

Chapter 2: Using @RISK for Six Sigma 13

Introduction.......................................................................................15

RiskSixSigma Property Function....................................................17

Six Sigma Statistics Functions .......................................................21

Six Sigma and the Results Summary Window ..............................35

Six Sigma Markers on Graphs.........................................................37

Case Studies 39

Example 1 – Design of Experiments: Catapult..............................41

Example 2 – Design of Experiments: Welding...............................47

Example 3 – Design of Experiments with Optimization................53

Example 4 – DFSS: Electrical Design.............................................61

Example 5 – Lean Six Sigma: Analysis of Current State – Quotation

Process...........................................................................................63

Example 6 – DMAIC: Roll Through Yield Analysis........................73

Example 7 – Vendor Selection ........................................................77

Table of Contents v

Example 8 – Six Sigma DMAIC Failure Rate..................................81

Example 9 – Six Sigma DMAIC Failure Rate using RiskTheo......85

vi Introduction

Chapter 1: Overview of @RISK and Six Sigma Methodologies

Introduction.........................................................................................3

What is Six Sigma?...................................................................................3

The Importance of Variation..................................................................5

Six Sigma Methodologies..................................................................7

Six Sigma / DMAIC .................................................................................7

Design for Six Sigma (DFSS).................................................................7

Lean or Lean Six Sigma...........................................................................8

@RISK and Six Sigma........................................................................9

@RISK and DMAIC.................................................................................9

@RISK and Design for Six Sigma (DFSS) .........................................10

@RISK and Lean Six Sigma..................................................................11

@RISK 5.0 Help System © Palisade Corporation, 1999

Chapter 1: Overview of @RISK and Six Sigma Methodologies 1

2 Introduction

Introduction

In today’s competitive business environment, quality is more
important than ever. Enter @RISK, the perfect companion for any Six
Sigma or quality professional. This powerful solution allows you to
quickly analyze the effect of variation within processes and designs.

In addition to Six Sigma and quality analysis, @RISK can be used to
analyze any situation in which there is uncertainty. Applications
include analysis of NPV, IRR, and real options, cost estimation,
portfolio analysis, oil and gas exploration, insurance reserves, pricing,
and much more. To learn more about @RISK in other applications,
and the use of @RISK in general, refer to the @RISK User’s Guide
included with your software.

What is Six Sigma?

Six Sigma is a set of practices to systematically improve processes by
reducing process variation and thereby eliminating defects. A defect
is defined as nonconformity of a product or service to its
specifications. While the particulars of the methodology were
originally formulated by Motorola in the mid-1980s, Six Sigma was
heavily inspired by six preceding decades of quality improvement
methodologies such as quality control, TQM, and Zero Defects. Like
its predecessors, Six Sigma asserts the following:

• Continuous efforts to reduce variation in process outputs is key

to business success

• Manufacturing and business processes can be measured,

analyzed, improved and controlled

• Succeeding at achieving sustained quality improvement

requires commitment from the entire organization, particularly
from top-level management

Six Sigma is driven by data, and frequently refers to “X” and “Y”
variables. X variables are simply independent input variables that
affect the dependent output variables, Y. Six Sigma focuses on
identifying and controlling variation in X variables to maximize
quality and minimize variation in Y variables.

Chapter 1: Overview of @RISK and Six Sigma Methodologies 3

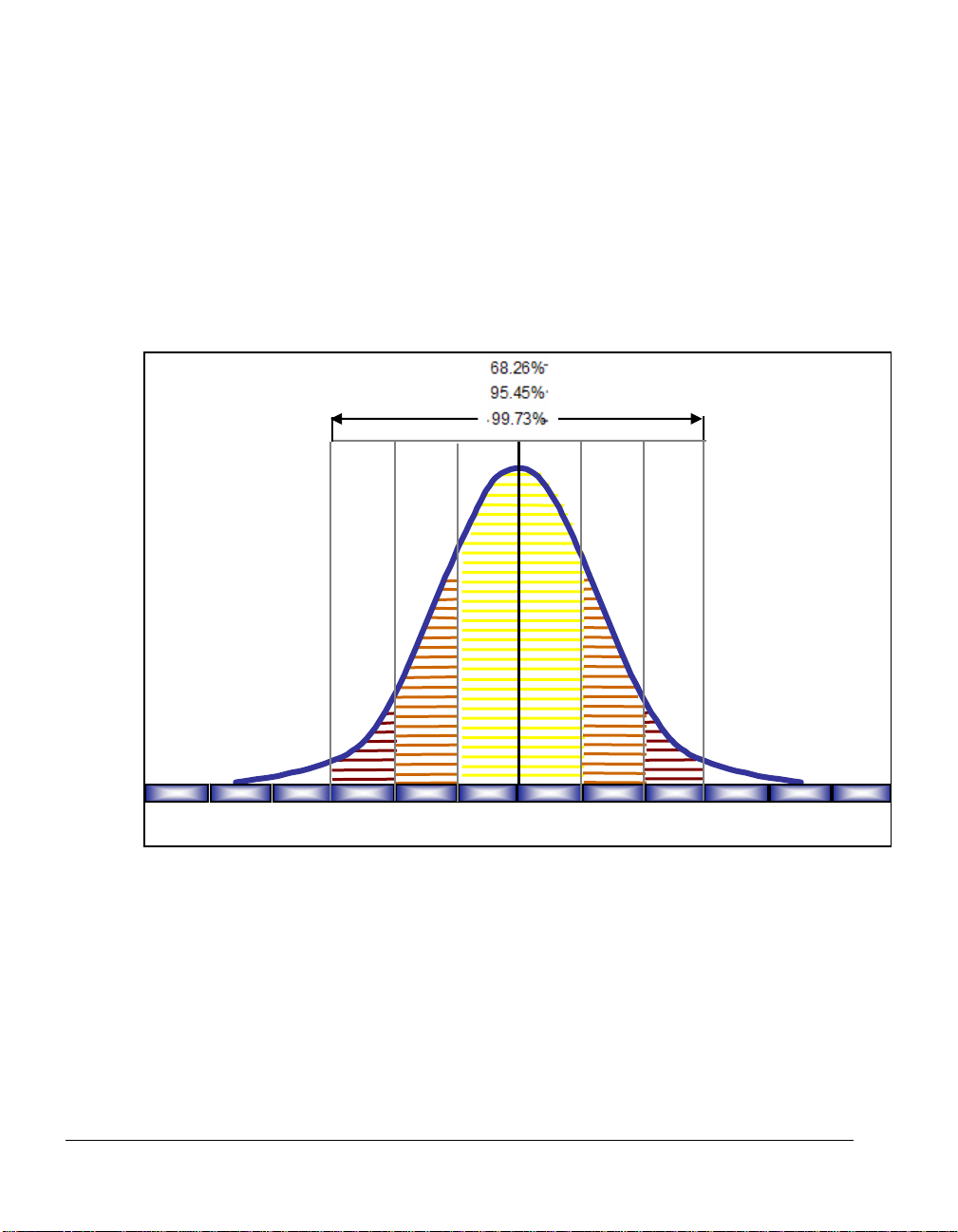
The term Six Sigma or 6σ is very descriptive. The Greek letter sigma
(σ) signifies standard deviation, an important measure of variation.
The variation of a process refers to how tightly all outcomes are
clustered around the mean. The probability of creating a defect can
be estimated and translated into a “Sigma level.” The higher the
Sigma level, the better the performance. Six Sigma refers to having

six standard deviations between the average of the process center
and the closest specification limit or service level. That translates to

fewer than 3.4 defects per one million opportunities (DPMO). The
chart below illustrates Six Sigma graphically.

-6

-3 -4 -5

-2

-1

+1

+4 +3 +2

+5

Six sigmas – or standard deviations – from the mean.

The cost savings and quality improvements that have resulted from
Six Sigma corporate implementations are significant. Motorola has
reported $17 billion in savings since implementation in the mid 1980s.
Lockheed Martin, GE, Honeywell, and many others have experienced
tremendous benefits from Six Sigma.

4 Introduction

+6

The Importance of Variation

Too many Six Sigma practitioners rely on static models that don’t
account for inherent uncertainty and variability in their processes or
designs. In the quest to maximize quality, it’s vital to consider as
many scenarios as possible.

That’s where @RISK comes in. @RISK uses Monte Carlo simulation to
analyze thousands of different possible outcomes, showing you the
likelihood of each occurring. Uncertain factors are defined using over
35 probability distribution functions, which accurately describe the
possible range of values your inputs could take. What’s more, @RISK
allows you to define Upper and Lower Specification Limits and
Target values for each output, and comes complete with a wide range
of Six Sigma statistics and capability metrics on those outputs.

@RISK Industrial edition also includes RISKOptimizer, which
combine the power of Monte Carlo simulation with genetic algorithm­based optimization. This gives you the ability to tackle optimization
problems like that have inherent uncertainty, such as:

• resource allocation to minimize cost

• project selection to maximize profit

• optimize process settings to maximize yield or minimize cost

• optimize tolerance allocation to maximize quality

• optimize staffing schedules to maximize service

The figure here illustrates how @RISK helps to identify, quantify, and
hone in on variation in your processes.

Chapter 1: Overview of @RISK and Six Sigma Methodologies 5

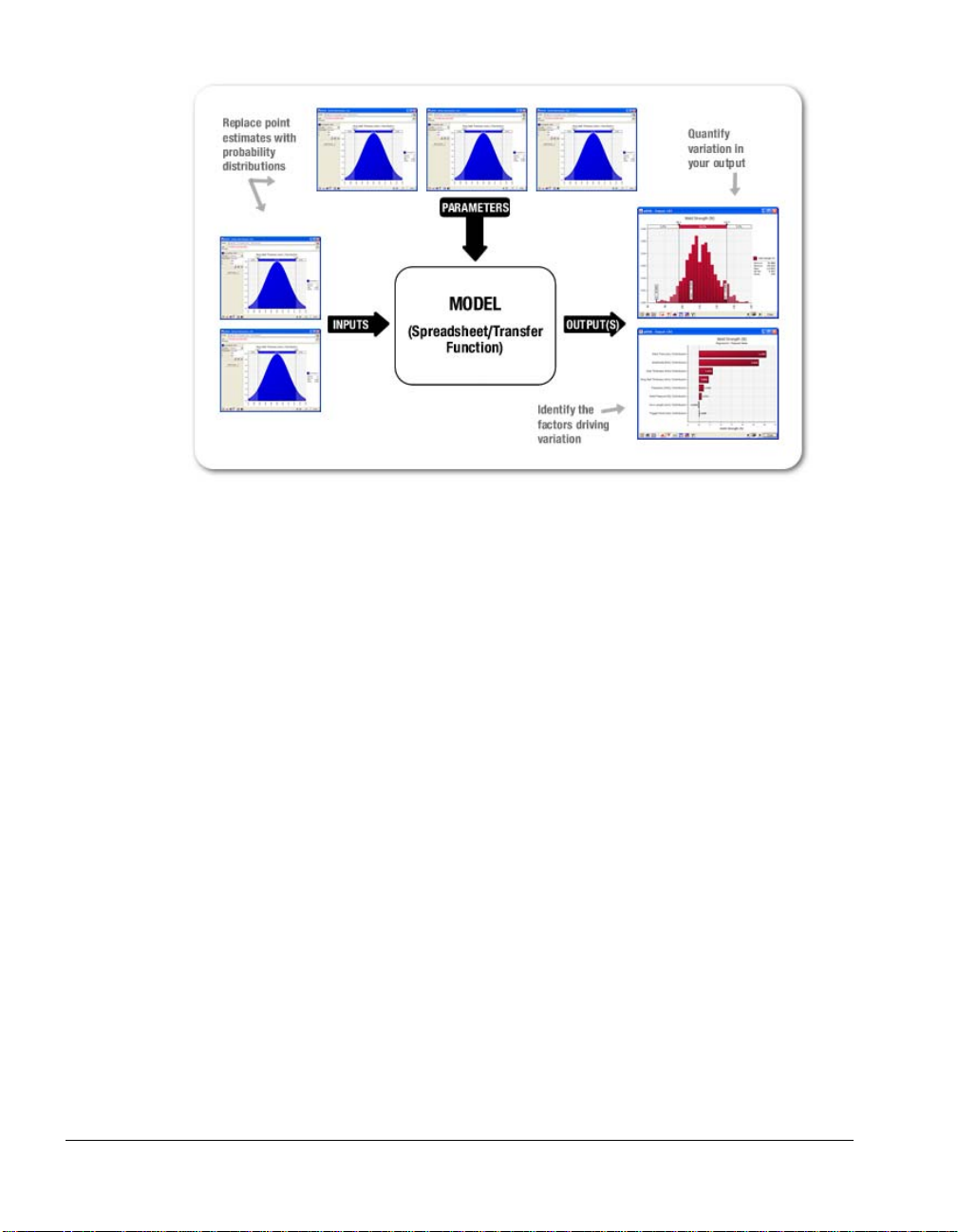
6 Introduction

Six Sigma Methodologies

@RISK can be used in a variety of Six Sigma and related analyses. The
three principal areas of analysis are:

• Six Sigma / DMAIC / DOE

• Design for Six Sigma (DFSS)

• Lean or Lean Six Sigma

Six Sigma / DMAIC

When most people refer to Six Sigma, they are in fact referring to the
DMAIC methodology. The DMAIC methodology should be used
when a product or process is in existence but is not meeting customer
specification or is not performing adequately.

DMAIC focuses on evolutionary and continuous improvement in
manufacturing and services processes, and is almost universally
defined as comprising of the following five phases: Define, Measure,

Analyze, Improve and Control:

1) Define the project goals and customer (internal and external

Voice of Customer or VOC) requirements

2) Measure the process to determine current performance

3) Analyze and determine the root cause(s) of the defects

4) Improve the process by eliminating defect root causes

5) Control future process performance

Design for Six Sigma (DFSS)

DFSS is used to design or re-design a product or service from the
ground up. The expected process Sigma level for a DFSS product or

service is at least 4.5 (no more than approximately 1 defect per
thousand opportunities), but can be 6 Sigma or higher depending on
the product. Producing such a low defect level from product or
service launch means that customer expectations and needs (Critical­To-Qualities or CTQs) must be completely understood before a design
can be completed and implemented. Successful DFSS programs can
reduce unnecessary waste at the planning stage and bring products to
market more quickly.

Chapter 1: Overview of @RISK and Six Sigma Methodologies 7

Unlike the DMAIC methodology, the phases or steps of DFSS are not
universally recognized or defined -- almost every company or
training organization will define DFSS differently. One popular
Design for Six Sigma methodology is called DMADV, and retains the
same number of letters, number of phases, and general feel as the
DMAIC acronym. The five phases of DMADV are defined as: Define,
Measure, Analyze, Design and Verify:

1) Define the project goals and customer (internal and external

VOC) requirements

2) Measure and determine customer needs and specifications;

benchmark competitors and industry

3) Analyze the process options to meet the customer needs

4) Design (detailed) the process to meet the customer needs

5) Verify the design performance and ability to meet customer

needs

Lean or Lean Six Sigma

“Lean Six Sigma” is the combination of Lean manufacturing
(originally developed by Toyota) and Six Sigma statistical
methodologies in a synergistic tool. Lean deals with improving the

speed of a process by reducing waste and eliminating non-value
added steps. Lean focuses on a customer “pull” strategy, producing

only those products demanded with “just in time” delivery. Six
Sigma improves performance by focusing on those aspects of a
process that are critical to quality from the customer perspective and
eliminating variation in that process. Many service organizations, for
example, have already begun to blend the higher quality of Six Sigma
with the efficiency of Lean into Lean Six Sigma.

Lean utilizes “Kaizen events” -- intensive, typically week-long
improvement sessions -- to quickly identify improvement
opportunities and goes one step further than a tradition process map
in its use of value stream mapping. Six Sigma uses the formal DMAIC
methodology to bring measurable and repeatable results.

Both Lean and Six Sigma are built around the view that businesses are
composed of processes that start with customer needs and should end
with satisfied customers using your product or service.

8 Six Sigma Methodologies

@RISK and Six Sigma

Whether it’s in DMIAC, Design of Experiments or Lean Six Sigma,
uncertainty and variability lie at the core of any Six Sigma analysis.
@RISK uses Monte Carlo simulation to identify, measure, and root out
the causes of variability in your production and service processes.
Each of the Six Sigma methodologies can benefit from @RISK
throughout the stages of analysis.

@RISK and DMAIC

@RISK is useful at each stage of the DMAIC process to account for
variation and hone in on problem areas in existing products.

1) Define. Define your process improvement goals,

incorporating customer demand and business strategy.
Value-stream mapping, cost estimation, and identification of
CTQs (Critical-To-Qualities) are all areas where @RISK can
help narrow the focus and set goals. Sensitivity analysis in
@RISK zooms in on CTQs that affect your bottom-line
profitability.

2) Measure. Measure current performance levels and their

variations. Distribution fitting and over 35 probability
distributions make defining performance variation accurate.
Statistics from @RISK simulations can provide data for
comparison against requirements in the Analyze phase.

3) Analyze. Analyze to verify relationship and cause of

defects, and attempt to ensure that all factors have been
considered. Through @RISK simulation, you can be sure all

input factors have been considered and all outcomes
presented. You can pinpoint the causes of variability and risk
with sensitivity and scenario analysis, and analyze tolerance.
Use @RISK’s Six Sigma statistics functions to calculate
capability metrics which identify gaps between
measurements and requirements. Here we see how often
products or processes fail and get a sense of reliability.

Chapter 1: Overview of @RISK and Six Sigma Methodologies 9

4) Improve. Improve or optimize the process based upon the

analysis using techniques like Design of Experiments.

Design of Experiments includes the design of all information­gathering exercises where variation is present, whether under
the full control of the experimenter or not. Using @RISK
simulation, you can test different alternative designs and
process changes. @RISK is also used for reliability analysis
and – using RISKOptimizer - resource optimization at this
stage.

5) Control. Control to ensure that any variances are corrected

before they result in defects. In the Control stage, you can
set up pilot runs to establish process capability, transition to
production and thereafter continuously measure the process
and institute control mechanisms. @RISK automatically
calculates process capability and validates models to make
sure that quality standards and customer demands are met.

@RISK and Design for Six Sigma (DFSS)

One of @RISK’s main uses in Six Sigma is with DFSS at the planning
stage of a new project. Testing different processes on physical
manufacturing or service models or prototypes can be cost
prohibitive. @RISK allows engineers to simulate thousands of
different outcomes on models without the cost and time associated
with physical simulation. @RISK is helpful at each stage of a DFSS
implementation in the same way as the DMAIC steps. Using @RISK
for DFSS gives engineers the following benefits:

• Experiment with different designs / Design of Experiments

• Identify CTQs

• Predict process capability

• Reveal product design constraints

• Cost estimation

• Project selection – using RISKOptimizer to find the optimal

portfolio

• Statistical tolerance analysis

• Resource allocation – using RISKOptimizer to maximize

efficiency

10 @RISK and Six Sigma

@RISK and Lean Six Sigma

@RISK is the perfect companion for the synergy of Lean
manufacturing and Six Sigma. “Quality only” Six Sigma models may
fail when applied to reducing variation in a single process step, or to
processes which do not add value to the customer. For example, an
extra inspection during the manufacturing process to catch defective
units may be recommended by a Six Sigma analysis. The waste of
processing defective units is eliminated, but at the expense of adding
inspection which is in itself waste. In a Lean Six Sigma analysis,
@RISK identifies the causes of these failures. Furthermore, @RISK can
account for uncertainty in both quality (ppm) and speed (cycle time)
metrics.

@RISK provides the following benefits in Lean Six Sigma analysis:

• Project selection – using RISKOptimizer to find the optimal

portfolio

• Value stream mapping

• Identification of CTQs that drive variation

• Process optimization

• Uncover and reduce wasteful process steps

• Inventory optimization – using RISKOptimizer to minimize

costs

• Resource allocation – using RISKOptimizer to maximize

efficiency

Chapter 1: Overview of @RISK and Six Sigma Methodologies 11

12 @RISK and Six Sigma

Chapter 2: Using @RISK for Six Sigma

Introduction.......................................................................................15

RiskSixSigma Property Function....................................................17

Entering a RiskSixSigma Property Function ....................................18

Six Sigma Statistics Functions .......................................................21

RiskCp......................................................................................................23

RiskCpm ..................................................................................................23

RiskCpk ...................................................................................................24

RiskCpkLower........................................................................................25

RiskCpkUpper........................................................................................25

RiskDPM .................................................................................................26

RiskK........................................................................................................26

RiskLowerXBound.................................................................................27

RiskPNC ..................................................................................................27

RiskPNCLower.......................................................................................28

RiskPNCUpper.......................................................................................28

RiskPPMLower.......................................................................................29

RiskPPMUpper.......................................................................................29

RiskSigmalLevel ....................................................................................30

RiskUpperXBound.................................................................................31

RiskYV .....................................................................................................31

RiskZlower..............................................................................................32

RiskZMin.................................................................................................33

RiskZUpper.............................................................................................33

Six Sigma and the Results Summary Window ..............................35

Six Sigma Markers on Graphs.........................................................37

Chapter 2: Using @RISK for Six Sigma 13

14

Introduction

@RISK’s standard simulation capabilities have been enhanced for use
in Six Sigma modeling through the addition of four key features.
These are:

The standard features of @RISK, such as entering distribution
functions, fitting distributions to data, running simulations and
performing sensitivity analyses, are also applicable to Six Sigma
models. When using @RISK for Six Sigma modeling you should also
familiarize yourself with these features by reviewing the @RISK for
Excel Users Guide and on-line training materials.

1) The RiskSixSigma property function for entering

specification limits and target values for simulation outputs

2) Six Sigma statistics functions, including process capability

indices such as RiskCpk, RiskCpm and others which return
Six Sigma statistics on simulation results directly in
spreadsheet cells

3) New columns in the Results Summary window which give

Six Sigma statistics on simulation results in table form

4) Markers on graphs of simulation results which display

specification limits and the target value

Chapter 2: Using @RISK for Six Sigma 15

16 Introduction

RiskSixSigma Property Function

In an @RISK simulation the RiskOutput function identifies a cell in a
spreadsheet as a simulation output. A distribution of possible
outcomes is generated for every output cell selected. These
probability distributions are created by collecting the values
calculated for a cell for each iteration of a simulation.

When Six Sigma statistics are to be calculated for an output, the
RiskSixSigma property function is entered as an argument to the
RiskOutput function. This property function specifies the lower
specification limit, upper specification limit, target value, long term
shift, and the number of standard deviations for the six sigma
calculations for an output. These values are used in calculating six
sigma statistics displayed in the Results window and on graphs for
the output. For example:

RiskOutput(“Part Height”,,RiskSixSigma(.88,.95,.915,1.5,6))

specifies an LSL of .88, a USL of .95, target value of .915, long term
shift of 1.5, and a number of standard deviations of 6 for the output
Part Height. You can also use cell referencing in the RiskSixSigma
property function.

These values are used in calculating Six Sigma statistics displayed in
the Results window and as markers on graphs for the output.

When @RISK detects a RiskSixSigma property function in an output,
it automatically displays the available Six Sigma statistics on the
simulation results for the output in the Results Summary window and
adds markers for the entered LSL, USL and Target values to graphs of
simulation results for the output.

Chapter 2: Using @RISK for Six Sigma 17

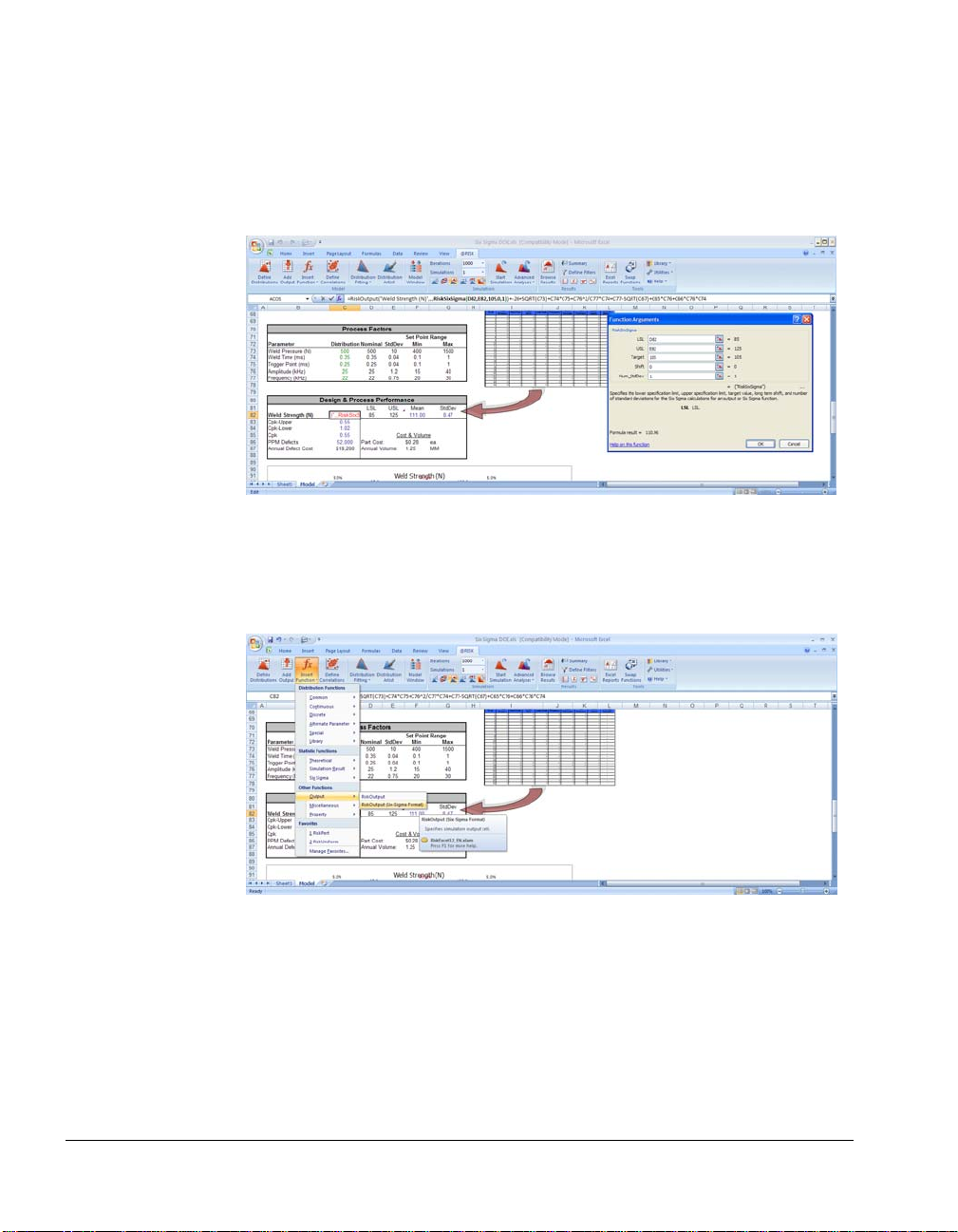
Entering a RiskSixSigma Property Function

The RiskSixSigma property function can be typed directly into a cell’s
formula as an argument to a RiskOutput function. Alternatively the
Excel Function Wizard can be used to assist in entering the function
directly in a cell formula.

@RISK’s Insert Function command allows you to quickly insert a
RiskOutput function with an added RiskSixSigma property function.
Simply select the Output menu RiskOutput (Six Sigma Format)
command from @RISK’s Insert Function menu and the appropriate
function will be added to the formula in the active cell.

18 RiskSixSigma Property Function

Output Properties – Six Sigma Tab

@RISK also provides a Function Properties window which can be
used to enter a RiskSixSigma property function into a RiskOutput
function. This window has a tab titled Six Sigma that has entries for
the arguments to the RiskSixSigma function. Access the RiskOutput
Function Properties window by clicking on the properties button in
the @RISK Add Output window.

Chapter 2: Using @RISK for Six Sigma 19

The default settings for an output to be used in Six Sigma calculations
are set on the Six Sigma tab. These properties include:

• Calculate Capability Metrics for This Output. Specifies that

capability metrics will be displayed in reports and graphs for
the output. These metrics will use the entered LSL, USL and
Target values.

• LSL, USL and Target. Sets the LSL (Lower Specification

Limit), USL (Upper Specification Limit) and Target values for
the output.

• Use Long Term Shift and Shift. Specifies an optional shift

for calculation of long-term capability metrics.

• Upper/Lower X Bound. The number of standard deviations

to the right or the left of the mean for calculating the upper or
lower X-axis values.

Entered Six Sigma settings result in a RiskSixSigma property
function being added to the RiskOutput function. Only outputs
which contain a RiskSixSigma property function will display Six
Sigma markers and statistics in graphs and reports. @RISK Six Sigma
statistics functions in Excel worksheets can reference any output cell
that contains a RiskSixSigma property function.

Note: All graphs and reports in @RISK use the LSL, USL, Target,
Long Term Shift and the Number of Standard Deviations values from
RiskSixSigma property functions that existed at the start of a
simulation. If you change the specification limits for an output (and
its associated RiskSixSigma property function), you need to re-run
the simulation to view changed graphs and reports.

20 RiskSixSigma Property Function

Six Sigma Statistics Functions

A set of @RISK statistics functions return a desired Six Sigma statistic
on a simulation output. For example, the function RiskCPK(A10)
returns the CPK value for the simulation output in Cell A10. These
functions are updated real-time as a simulation is running. These
functions are similar to the standard @RISK statistics functions (such
as RiskMean) in that they calculate statistics on simulation results;
however, these functions calculate statistics commonly required in Six
Sigma models. These functions can be used anywhere in spreadsheet
cells and formulas in your model.

Some important items to note about @RISK’s Six Sigma statistics
functions are as follows:

• If a cell reference is entered as the first argument to the statistics

function and that cell has a RiskOutput function with a
RiskSixSigma property function, @RISK will use the LSL, USL,
Target, Long Term Shift and Number of Standard Deviation
values from that output when calculating the desired statistic.

• If a cell reference is entered as the first argument, the cell does not

have to be a simulation output identified with a RiskOutput
function. However, if it is not an output, an optional

RiskSixSigma property function needs to be added to the
statistic function itself so @RISK will have the necessary settings

for calculating the desired statistic.

• Entering an optional RiskSixSigma property function directly in a

statistics function causes @RISK to override any Six Sigma

settings specified in the RiskSixSigma property function in a
referenced simulation output. This allows you to calculate Six

Sigma statistics at differing LSL, USL, Target, Long Term Shift
and Number of Standard Deviation values for the same output.

• If a name is entered instead of cellref, @RISK first checks for an

output with the entered name, and the reads its RiskSixSigma
property function settings. It is up to the user to ensure that
unique names are given to outputs referenced in statistics
functions.

• The Sim# argument entered selects the simulation for which a

statistic will be returned when multiple simulations are run. This
argument is optional and can be omitted for single simulation
runs.

Chapter 2: Using @RISK for Six Sigma 21

• When an optional RiskSixSigma property function is entered

directly in a Six Sigma statistics function, different arguments
from the property function are used depending on the calculation
being performed.

• Statistics functions located in template sheets used for creating

custom reports on simulation results are only updated when a
simulation is completed.

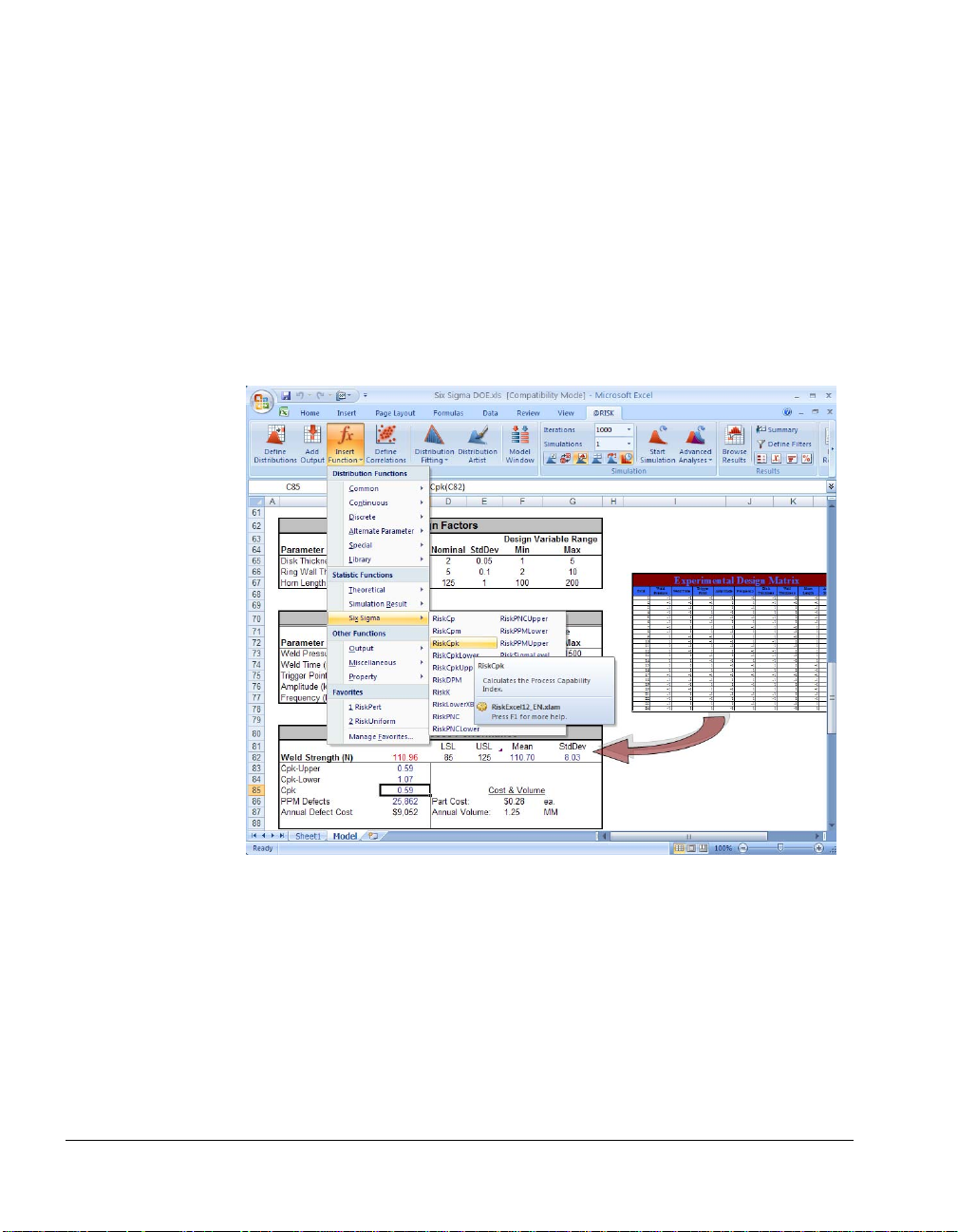
Entering Six Sigma Statistics Functions

@RISK’s Insert Function command allows you to quickly insert a Six
Sigma Statistics Function. Simply select the Six Sigma command in
the Statistics function category on the @RISK’s Insert Function menu,
then select the desired function. The selected function will be added
to the formula in the active cell.

22 Six Sigma Statistics Functions

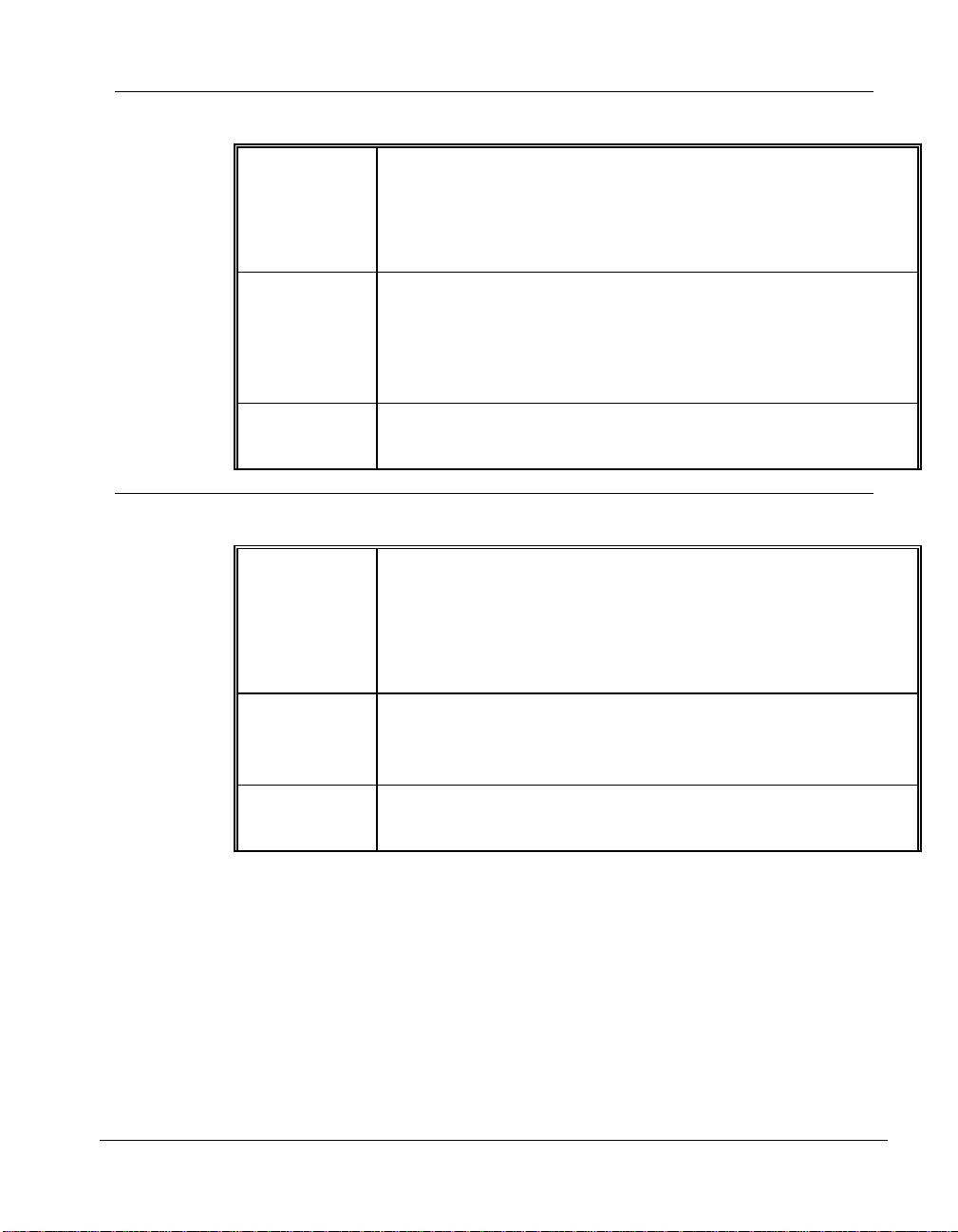
RiskCp

RiskCpm

Description

Examples

Guidelines

Description

Examples

Guidelines

RiskCp(cellref or output name, Sim#, RiskSixSigma(LSL,USL,

Target,LongTerm Shift,Number of Standard Deviations)) calculates
the Process Capability for cellref or output name in Sim#, optionally
using the LSL and USL in the included RiskSixSigma property
function. This function will calculate the quality level of the
specified output and what it is potentially capable of producing.

RiskCP(A10) returns the Process Capability for the output cell
A10. A RiskSixSigma property function needs to be entered in the
RiskOutput function in Cell A10.

RiskCP(A10, ,RiskSixSigma(100,120,110,1.5,6)) returns the
Process Capability for the output cell A10, using an LSL of 100 and
a USL of 120.

A RiskSixSigma property function needs to be entered for cellref
or output name, or a RiskSixSigma property function needs to be
included

RiskCpm(cellref or output name, Sim#, RiskSixSigma(LSL,USL,
Target,LongTerm Shift,Number of Standard Deviations)) returns

the Taguchi capability index for cellref or output name in Sim #,
optionally using the USL, LSL, and the Target in the RiskSixSigma
property function. This function is essentially the same as the Cpk
but incorporates the target value which in some cases may or may
not be within the specification limits.

RiskCpm(A10) returns the Taguchi capability index for cell A10 .
RiskCpm(A10,, RiskSixSigma(100, 120, 110, 0, 6)) returns the

Taguchi capability index for cell A10, using an USL of 120, LSL of
100, and a Target of 110.

A RiskSixSigma property function needs to be entered for cellref
or output name, or a RiskSixSigma property function needs to be
included

Chapter 2: Using @RISK for Six Sigma 23