Open office CALC User Manual

Az OpenOffice.org Calc használata

Táblázatkezelés az alapoktól

Pallay Ferenc

Szerző: Pallay Ferenc

CC – Néhány jog fenntartva

2010. július

A kiadvány létrejöttét az

támogatta.

Lektorálták:

Dr. Blahota István

Gibizer Tibor

Zahemszky Gábor

az FSF.hu Alapítvány aktivistái

LATEX-re átültette:

Papp István

Borító:

Baráth Gábor

Fotó:
ansik

A 2. kiadást szerkesztette:

Tímár András

ISBN 978-963-06-9218-2

Ez a Mű a Creative Commons Nevezd meg!-Így add tovább! 2.5 Magyarország Licenc feltételeinek megfelelően
szabadon felhasználható. További információk: http://creativecommons.org/licenses/by-sa/2.5/hu/

Előszó a 2. kiadáshoz

Ebből a könyvből az OpenOffice.org táblázatkezelőjének, a Calcnak a használatát lehet elsajátítani. Az anyag
teljes mértékben lefedi mind az érettségi, mind az ECDL táblázatkezelő moduljának a témaköreit. A tanulást
több, mint 150 szemléletes kép könnyíti meg, illetve 35 gyakorló feladat segít az ismeretek elmélyítésében. A

2. kiadásra azért került sor, mert a Calc munkalapfüggvényeinek nevei az OpenOffice.org újabb verzióiban
már magyarul vannak, ugyanúgy, ahogy az oktatásban és a munkahelyeken elterjedt magyar nyelvű Microsoft
Excelben, ezért a függvényneveket magyarra kellett fordítani a könyv szövegében és ábráiban is. Egyúttal
jónéhány sajtóhibát is sikerült javítani.

Az OpenOffice.org egy teljes körű irodai alkalmazáscsomag szövegszerkesztéshez, táblázatkezeléshez,
bemutatók és illusztrációk készítéséhez, adatbázisok használatához és egyéb feladatokhoz. Előnyei között
említhetjük, hogy több nyelven (kb. 70) és több platformon (Windows, Linux, Mac OS X stb.) elérhe­tő, nemzetközileg szabványosított formátumban tárolja az adatokat, valamint írja és olvassa a Microsoft
Office állományait. Letöltése és használata bármilyen célra – beleértve az üzleti alkalmazást is – teljesen
ingyenes. Ennek köszönhetően az egész világon és Magyarországon is számos állami szervezet, vállalkozás és
magánszemély tért át vagy tér át a használatára, illetve tervezi az áttérést a közeljövőben.

Az OpenOffice.org története 1986-ban kezdődött, ekkor kezdte el fejleszteni egy német cég, a Star Division
a StarWriter nevű szövegszerkesztőt az akkoriban elterjedt DOS platformra. 1993-ban megszületett a termék
windowsos verziója, melyet egy évvel később az OS/2-es és a macintoshos verzió követett. 1995-ben a
StarOffice nevet vette fel a termék, ekkor már több jelentős komponenst tartalmazott: szövegszerkesztőt
(StarWriter), egyszerű rajzprogramot (StarImage), táblázatkezelőt (StarCalc), grafikonkészítőt (StarChart)
és egy vektoros rajzolóprogramot (StarDraw). A későbbi változatok már böngészőt és HTML-szerkesztőt,
bemutatókészítőt (StarImpress) és adatbázis-kezelőt (StarBase) is tartalmaztak.

A StarDivision története 1999-ben ért véget, amikor a Sun felvásárolta a céget. Simon Phipps, volt
Sun-alkalmazott szerint „a StarDivision felvásárlásának legfontosabb oka az volt, hogy abban az időben a

Sun alkalmazottainak száma elérte a 42 ezret és minden munkatárs rendelkezett egy Unix-munkaállomással
és egy windowsos laptoppal. Olcsóbb volt megvenni egy céget, amely irodai alkalmazást fejlesztett Solaris és
Linux operációs rendszerre, mint 42 ezer Microsoft Office licencet venni a Microsofttól.” A StarOffice 5.2-es

verzióját a Sun ingyenesen letölthetővé tette, hogy így próbálja meg növelni a termék piaci részesedését. A
későbbi változatok már fizetős, kereskedelmi termékekként kerültek a felhasználókhoz.

A szabad szoftveres közösség számára a „nagy nap” 2000. október 13-án jött el, amikor a Sun Open­Office.org néven szabaddá tette az irodai csomag forráskódját. Több, harmadik fél által készített, licencelt
komponenst ki kellett venni, illetve szükség volt több átalakításra is, mielőtt megszülethetett volna az Open­Office.org kiindulási forrása. Az OpenOffice.org körülbelül másfél év alatt érte el az első nagy mérföldkövet:
az 1.0-s verzió 2002. május elsején jelent meg.

A közelmúltig a Sun volt az OpenOffice.org legnagyobb támogatója és a fejlesztés vezetője. 2010-ben
zárult le a Sun felvásárlása az Oracle által, de ez nem okoz változást. Az Oracle átvette a fejlesztőket,
továbbra is fejleszti és támogatja a nyílt forrású OpenOffice.org-ot, mint a közösség legjelentősebb tagja. A
StarOffice Oracle Open Office néven él tovább.

2002. február 1-től 4-ig, egy maratoni „fordítóbuli” keretén belül készült el az OpenOffice.org irodai
programcsomag magyarul beszélő változata. A hivatalos bemutatóra 2002. február 23-án került sor. A mun­kában mintegy 150 ember vett részt. Ez a munka teremtette meg a lehetőségét minden további fejlesztésnek,
és ez az esemény vezetett el az FSF.hu Alapítvány megalapításához is. A magyar OpenOffice.org elkészítését
azóta is az FSF.hu Alapítvány koordinálja. 2003 során tovább folyt a közösségi fordítói munka, februárban a
súgóból készültek el részek, novemberben pedig a részletes tippek lettek lefordítva. A súgó fordítása 2005-re
lett kész. Azóta csak az új verziókban megjelenő módosítások és újdonságok lefordítása, valamint a fordítás
folyamatos javítgatása ad feladatot.

A magyar OpenOffice.org-gal kapcsolatos aktuális hírek és információk a http://hu.openoffice.org/

honlapon olvashatók.

Tímár András

szoftverhonosító

OpenOffice.org

Tartalomjegyzék

1. Bevezetés 1

1.1. A Calc program ablaka . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1

1.2. A Súgó használata . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

2. Első lépések a Calckal 4

2.1. Adatok bevitele és módosítása . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

2.2. Kijelölés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

2.3. Cellák formázása . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

2.4. Karakterformázás . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

2.5. Szegélyek és háttér . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

2.6. Munkafüzet mentése . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10

2.7. 1. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11

3. Egyszerű számítások a munkalapon 12

3.1. Aritmetikai operátorok használata . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

3.2. Cellahivatkozások alkalmazása . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

3.3. 2. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

3.4. Képletek másolása . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

3.5. 3. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

3.6. Abszolút hivatkozás . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

3.7. 4. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

3.8. Vegyes cellahivatkozások . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

3.9. 5. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

3.10. 6. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18

4. Függvények használata 20

4.1. Függvények beszúrása . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20

4.2. Egyszerűbb statisztikai függvények használata . . . . . . . . . . . . . . . . . . . . . . 21

4.3. 7. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

4.4. 8. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25

5. Számformátumok 27

5.1. Százalék és pénznem formátum . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27

5.2. 9. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28

5.3. Dátum- és időformátum . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

5.4. Számformátumkódok . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32

6. Diagramok 34

6.1. Diagramtündér használata . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34

6.2. A diagram módosítása . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37

ii

TARTALOMJEGYZÉK iii

6.3. 10. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38

6.4. Pont (XY) diagram építése . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40

6.5. 11. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40

7. Logikai függvények. Beágyazott függvények használata 42

7.1. A HA függvény . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42

7.2. Egyéb logikai függvények . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42

7.3. 12. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43

7.4. A SZUMHA és a DARABTELI függvények . . . . . . . . . . . . . . . . . . . . . . . 47

7.5. 13. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47

8. Matematikai függvények 50

8.1. Egyszerűbb matematikai függvények . . . . . . . . . . . . . . . . . . . . . . . . . . . 50

8.2. 14. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51

8.3. 15. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52

8.4. Logaritmusfüggvények . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55

8.5. 16. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55

8.6. Trigonometrikus függvények . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55

8.7. 17. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57

9. Szövegfüggvények 59

9.1. 18. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60

9.2. 19. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62

10.Keresőfüggvények használata 64

10.1. Az FKERES, VKERES függvények . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64

10.2. 20. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64

10.3. 21. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66

10.4. A HOL.VAN és az INDEX függvények . . . . . . . . . . . . . . . . . . . . . . . . . . 68

10.5. 22. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69

11.Nevek és listák 71

11.1. Cellák elnevezése . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71

11.2. 23. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71

11.3. Rendezett listák . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72

11.4. Sorozatok létrehozása . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73

11.5. Cellatartomány érvényesítése . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74

11.6. 24. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74

12.Adattartományok a Calcban 75

12.1. Rendezés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75

12.2. Az automatikus szűrő használata . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76

12.3. Általános szűrő . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78

12.4. 25. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78

12.5. Irányított szűrés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79

13.Adatbázisfüggvények 81

13.1. 26. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82

14.Dátum- és időfüggvények 84

14.1. 27. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85

14.2. 28. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85

TARTALOMJEGYZÉK iv

15.Pénzügyi és statisztikai függvények 88

15.1. Pénzügyi függvények . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88

15.2. 29. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90

15.3. Statisztikai függvények . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90

16.Tömbképletek a Calcban 92

16.1. Tömbképletek létrehozása . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92

16.2. Mátrixok összeadása . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92

16.3. Mátrix szorzata skalárral . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92

16.4. Mátrixok szorzása . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94

16.5. Mátrix determinánsának meghatározása . . . . . . . . . . . . . . . . . . . . . . . . . 94

16.6. 30. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95

16.7. Mátrix inverze . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95

16.8. Transzponált mátrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96

16.9. 31. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96

17.Célértékkeresés 98

17.1. 32. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98

18.Űrlap-vezérlőelemek használata 102

18.1. 33. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103

19.Stílusok 107

19.1. Stílusok alkalmazása és módosítása . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107

19.2. Stílusok létrehozása . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108

19.3. Feltételes formázás . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109

19.4. Irányított beillesztés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109

19.5. Tartalom törlése . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110

19.6. 34. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111

20.Nyomtatási beállítások 112

20.1. Oldalbeállítás . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112

20.2. Élőfej és élőláb . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113

20.3. Munkalap . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113

20.4. Nyomtatási tartomány meghatározása . . . . . . . . . . . . . . . . . . . . . . . . . . 115

20.5. Ismétlődő sorok és oszlopok . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115

20.6. Nyomtatás . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115

21.A Megoldó használata 117

21.1. 35. feladat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117

1. fejezet

Bevezetés

A OpenOffice.org egy teljes körű irodai programcsomag. Ennek a programcsomagnak része az
OpenOffice.org Calc (továbbiakban Calc), ami egy kiváló táblázatkezelő program. Segítségével
számításokat, matematikai, pénzügyi elemzéseket végezhetünk, grafikusan ábrázolhatjuk számada­tainkat.

A jelenleg legelterjedtebb táblázatkezelő programmal – a Microsoft Excellel – szemben ez in-

gyenes, tetszőleges célra felhasználható szabad szoftver.

1.1. A Calc program ablaka

1.1. ábra. OpenOffice.org Calc ablak

A Calc programot elindítva figyeljük meg ablakának részeit (1.1 ábra). A Címsorban látjuk a

dokumentum és a program nevét. Nem mentett dokumentum esetén a „Névtelen” nevet látjuk. A

1. FEJEZET. BEVEZETÉS 2

címsor alatt a Menü található. Ezekre a menüpontokra kattintva kategóriákba rendezetten elér­hető a program összes funkciója. A leggyakrabban használt parancsokat kiadhatjuk az eszköztárak
ikonjai segítségével is. Alapértelmezés szerint három eszköztárat látunk: Standard, Formázás és
Képlet eszköztár. A Nézet menüpont Eszköztárak parancsával több eszköztár is bekapcsolha­tó. Az eszköztárak pozíciója megváltoztatható az egér „fogd és vidd” funkciójával, a bal szélükön
látható pontozott oszlopnál megfogva.

Az eszköztárak alatt a táblázatkezelő dokumentumablakát láthatjuk. Egy 1024 oszlopból és
1048576 sorból álló táblázatot, ahol az oszlopokat betűkkel (A, B, C, . . . , AA, . . . , AMJ), míg a
sorokat egész számokkal (1, 2, 3, . . . , 1048576) jelölik. Ezt a táblázatot Munkalapnak nevezzük.
A Calc induláskor három munkalapot hoz létre automatikusan. Ezek között a munkalapfülek
segítségével válthatunk. A munkalapfüleken a munkalapok neveit láthatjuk. A fülek bármelyikén
jobb egérgombbal kattintva, a megjelenő gyorsmenü segítségével átnevezhetjük a munkalapokat,
illetve további munkalapokat hozhatunk létre.

A munkalapfülektől balra a lapfüleket gördítő nyilakat találjuk. Több munkalap esetén elő­fordulhat, hogy nem látjuk mindegyik munkalapfület. Ilyenkor ezekkel a nyilakkal görgethetjük a
munkalapfülek sorát.

A munkalap legkisebb elemét cellának nevezzük. Minden cellának címe van, ami az oszlop és
a sorazonosítóból tevődik össze. Tehát a munkalap bal felső sarkában az A1-es cella található,
mellette közvetlenül a B1-es.

Az éppen használt munkalapnak mindig van aktív cellája. Ezt a cellát keret jelöli, és a sor- és
az oszlopazonosító, amelyek metszéspontján az aktív cella található, ki van emelve.

Az Állapotsor az ablak legalján található. Rajta az aktuális munkalapra vonatkozó különböző
információkat láthatunk.

Nagyobb táblázatoknál hasznos lehet, hogy a vízszintes és a függőleges osztósáv segítségével
feloszthatjuk a munkalapot több részre. Így megoldható, hogy egyszerre lássuk a képernyőn a
táblázat két, egymástól sok cellányi távolságra lévő sorát vagy oszlopát.

1.2. A Súgó használata

A Calc programban igen részletes, magyar nyelvű segítséget jeleníthetünk meg a Súgó menü Open­Office.org Súgó parancsával, vagy az F1 funkcióbillentyű lenyomásával. A megjelenő ablakban

(1.2 ábra) megtaláljuk a menük, eszköztárak elemeinek magyarázatát, a függvények kategória sze­rinti felsorolását és példákat a használatukhoz, de kereshetünk a Súgó teljes szövegében is. A
Súgó általunk hasznosnak ítélt oldalait ki is nyomtathatjuk a Nyomtatás. . . paranccsal, vagy
könyvjelzőt rendelhetünk az adott súgóoldalhoz.

A Calckal való ismerkedés során nagyon hasznos lehet, hogy a Súgó menü Mi ez? parancsával
a program ablakának több eleméről tippet kaphatunk. Ilyenkor az egér mutatója alakot vált, és
amire mutatunk vele, arról rövid magyarázatot olvashatunk a megjelenő szövegdobozban. Az 1.3
ábrán a Standard eszköztár Kivágás parancsáról megjelenő tippet láthatjuk.

1. FEJEZET. BEVEZETÉS 3

1.2. ábra. OpenOffice.org Súgó

1.3. ábra. OpenOffice.org Mi ez?

2. fejezet

Első lépések a Calckal

2.1. Adatok bevitele és módosítása

A Calc program elindítása után az A1 cella az aktív. A billentyűzeten begépelt karakterek ebbe
a cellába kerülnek. A beírt adatot az Enterrel vagy az iránybillentyűkkel nyugtázhatjuk. A cella
tartalmát módosíthatjuk az F2 funkcióbillentyűvel, vagy kettős kattintással az adott cellán.

2.1. ábra. Adatok bevitele

A 2.1 ábrán látjuk, hogy szám beírása esetén a Calc automatikusan jobbra igazítja a tartalmat,
szöveg esetén viszont balra. Amennyiben a beírt szöveg nem fér el a cellában, és a tőle jobbra lévő
cella üres, a cella tartalma átcsúszik ebbe a cellába.

Adatot írva a cellába, esetünkben a B3-ba, az A3-as tartalmának csak egy részét látjuk és a
Calc erre a cella jobb szélén megjelenő nyíllal figyelmeztet (2.2 ábra).

2.2. ábra. Adatcella határán túlérő tartalom

2. FEJEZET. ELSŐ LÉPÉSEK A CALCKAL 5

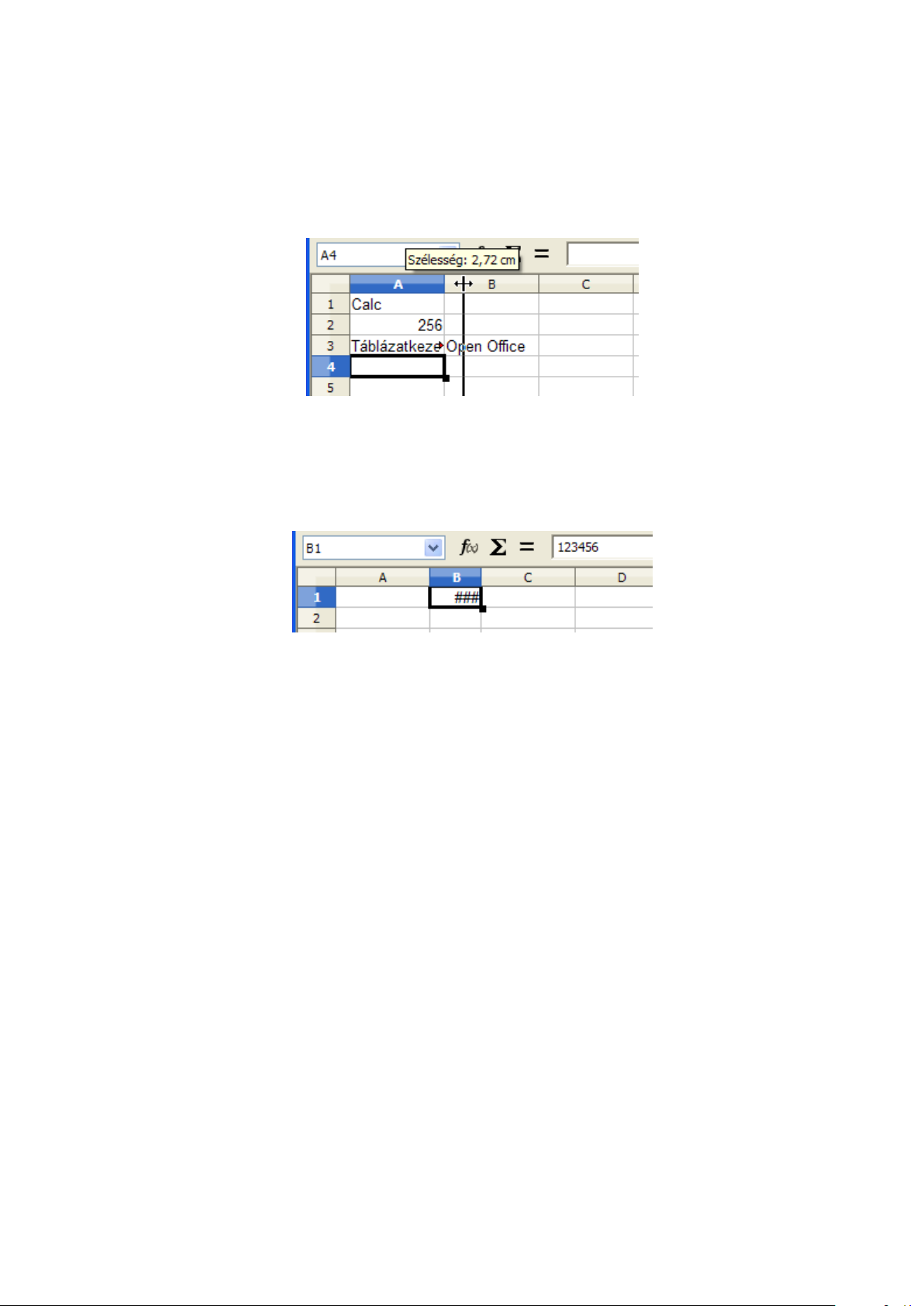
Az A oszlop szélességét módosíthatjuk, ha az egér mutatóját az A és a B oszlopazonosító elvá­lasztó vonalára vezetjük és bal gombját lenyomva tartva elmozdítjuk az egeret. Ilyenkor a leendő
oszlopszélességet a Calc megjeleníti cm-ben (2.3 ábra). Az oszlopazonosítók elválasztó vonalára
kettőt kattintva a Calc automatikusan a legtöbb karaktert tartalmazó cellához igazítja az oszlop­szélességet.

2.3. ábra. Oszlopszélesség

Számadattal nem fordulhat elő, hogy csak egy részét látjuk a cellában. Amennyiben a számje­gyek nem férnek el, a Calc mindig kettős keresztekkel figyelmeztet erre (2.4).

2.4. ábra. Kicsi oszlopszélesség ###

Többsoros szöveget is írhatunk a cellába, amennyiben a Ctrl+Enter billentyűkkel zárjuk a
sort. Hatására lehetőség nyílik az új sor kezdéséhez. Ilyenkor a Calc automatikusan megnöveli a
sormagasságot.

2.2. Kijelölés

Az aktív cellán különböző formázásokat, beállításokat végezhetünk. Több cella formátumának mó­dosításához kijelöléssel meghatározhatunk cellákat, téglalap alakú cellatartományokat. A Calcban
egyszerűen kijelölhetünk cellatartományokat: a tartomány egyik sarokcellájára kattintva, az egér
bal gombját lenyomva tartva átlósan húzva. Egy ilyen tartományt bal felső és a jobb alsó cellák
címeivel, és közöttük kettősponttal határozunk meg. Pl. A1:B5.

Billentyűzet segítségével, a Shift billentyűt lenyomva tartva az iránybillentyűkkel jelölhetünk
ki.

Több különálló cellát vagy cellatartományt is kijelölhetünk. Ehhez az első kijelölése után a
többit, a Ctrl billentyűt lenyomva tartva kell kijelölnünk.

Egy oszlop vagy sor minden celláját kijelölhetjük az oszlop-, illetve a sorazonosítóra kattintva.
A munkalap bal felső sarkában lévő üres téglalapra kattintva a munkalap minden celláját kijelöljük
(2.5 ábra)

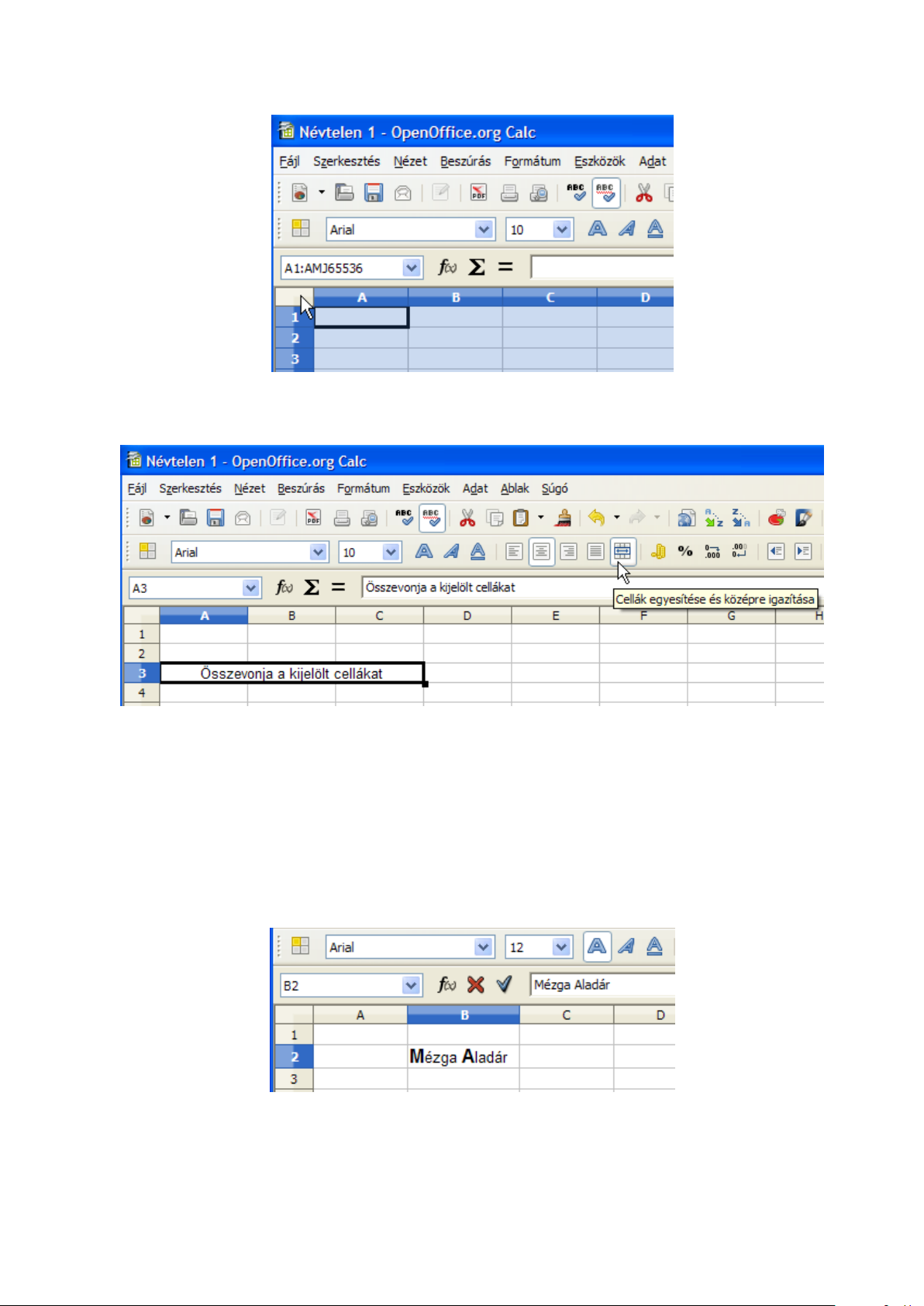
Két vagy több kijelölt cellát egyesíthetünk egy cellába a Formázás eszköztár Cellák egyesí-
tése parancsával. Az így kialakult terület elfoglalja a kijelölt cellákat, és erre a tartományra a bal
cella címével hivatkozhatunk. A 2.6 ábrán az A3:C3 tartományt egyesítettük egy cellává. Ennek a
cellacíme A3.

2. FEJEZET. ELSŐ LÉPÉSEK A CALCKAL 6

2.5. ábra. Munkalap kijelölése

2.6. ábra. Cellák összevonása

2.3. Cellák formázása

A gyakran használt cellákra vonatkozó formátumokat legegyszerűbben a Formátum eszköztáron
érhetjük el. A Calc képes a karakterek beírása közben módosítani a formátumot. A 2.7 ábrán
látható karakterformátumok a szöveg begépelése közben a Formátum eszköztár parancsaival lettek
kialakítva.

2.7. ábra. Cellák formázása

2. FEJEZET. ELSŐ LÉPÉSEK A CALCKAL 7

További, az eszköztáron nem elérhető formátumokat a Formátum menü Cellák..., vagy a
helyi menü Cellák formázása paranccsal állíthatunk be. A megjelenő párbeszédablakban a Be-
tűkészlet és a Betűhatások füleken a cellára vonatkozó karakterformátumokat módosíthatjuk.

Az Igazítás fülön (2.8 ábra) beállíthatjuk az aktuális vagy a kijelölt cellák tartalmának igazítá­sát. A vízszintes szövegigazítások közül az Alapértelmezett a számokat jobbra, a szöveget balra
igazítja. A következő négy (balra, jobbra, középre és sorkizárt) elérhető a Formázás eszköztáron is.
A Kitöltött szövegigazítás megismétli a cellatartalmakat (számokat és szövegeket), amíg a cella
látható területét ki nem tölti.

2.8. ábra. Cellák formázása – Igazítás

A Szöveg iránya részben megadhatjuk a kijelölt cellák elforgatásának szögét fokokban, de
megadhatjuk a szövegirányt az ABCD feliratú körlapra kattintva is.

Figyeljük meg a 2.9 ábrán látható cellaformátumokat. A C2 cellában a vízszintes és a függőleges
szövegigazítás beállítása: Középre. Az Automatikus szövegtördelés és az Elválasztás is be
van kapcsolva.

A D2 cella mind függőlegesen, mind vízszintesen középre igazított, és a Függőlegesen halmo-
zott formátum is be van kapcsolva.

A C1 cella balra igazított, a behúzás mértéke 10 pt.

Az A3 cella betűmérete és formátuma nem különbözik a C1 celláénál, de a Lekicsinyítve,
hogy beférjen kapcsoló be van kapcsolva.

A B4, D4 és az F4 szegéllyel ellátott cellákon az Alapél három beállítását figyelhetjük meg.
Mindhárom cellában a szöveg iránya 45 fokkal el van forgatva. A B4 cellában az elforgatott szöveg
a cella alsó szélétől kifelé jelenik meg. A D4 esetében a felső szélétől kifelé, az F4-ben pedig az
elforgatott szöveg csak a cellába kerül.

2. FEJEZET. ELSŐ LÉPÉSEK A CALCKAL 8

2.9. ábra. Cellaformátumok

2.4. Karakterformázás

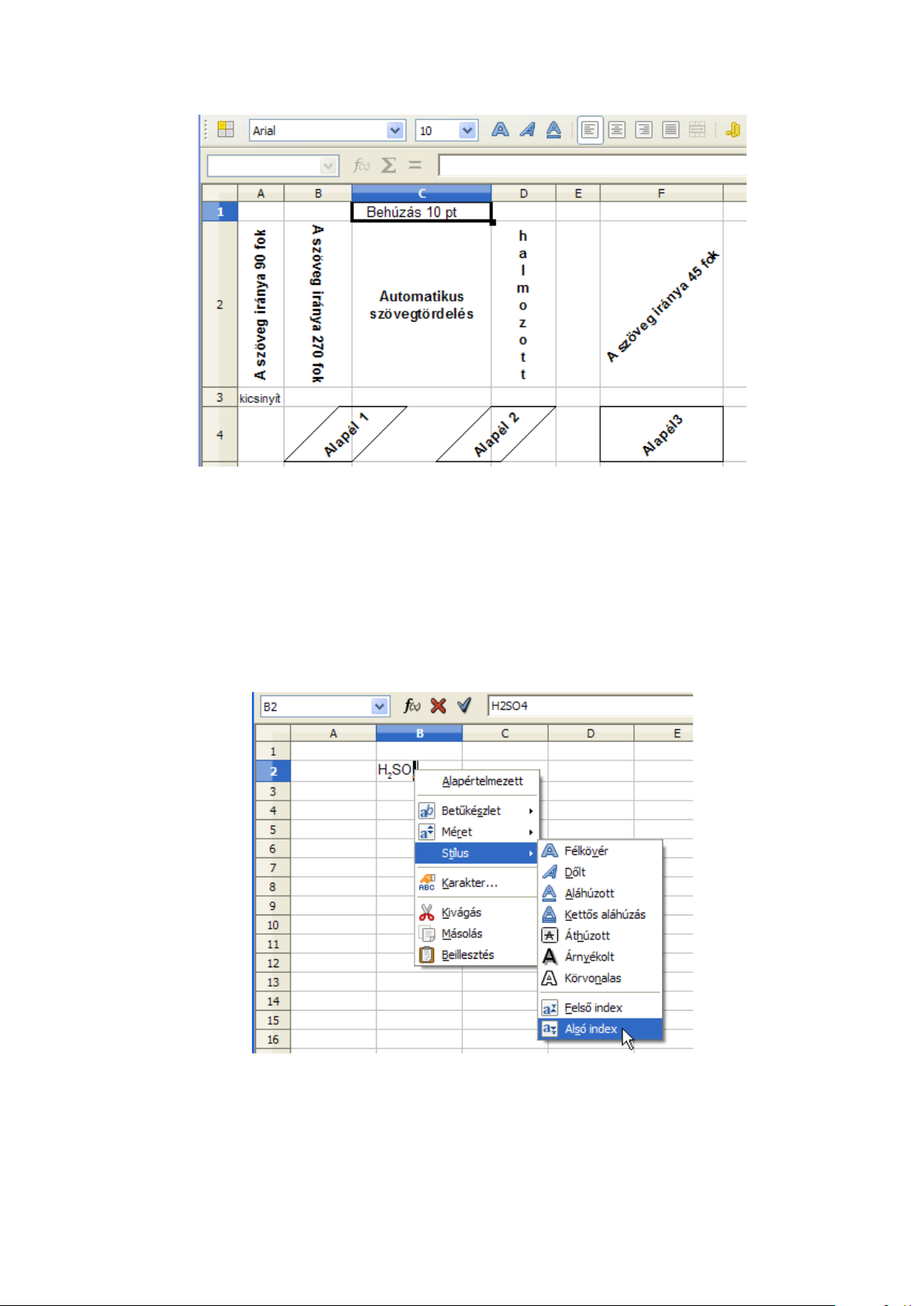
A cella tartalmának módosításakor a kijelölt karakteren különleges formázásokat is végrehajtha­tunk. Ezek elérhetőek a Formátum menü Karakter párbeszédablakban a Betűkészlet, Be-
tűhatások és Betűhelyzet fülekre kattintva. Gyorsmenü segítségével szintén elérhetők ezek a
beállítások, ha a kijelölt szövegrészen az egér jobb gombjával kattintunk (2.10 ábra).

2.10. ábra. Karakterformázás – Stílus

2. FEJEZET. ELSŐ LÉPÉSEK A CALCKAL 9

2.5. Szegélyek és háttér

A Calc alapbeállítása szerint a képernyőn látható szürke színű rácsvonalak nyomtatásban nem
jelennek meg. Nyomtatásban is látható rácsvonalakat legegyszerűbben a Formátum eszköztár
Szegélyek ikonjára kattintva hozhatunk létre (2.11 ábra). Ilyenkor az aktív cella, vagy a kijelölt
cellatartomány az általunk választott szegélytípust kapja.

2.11. ábra. Szegélyek ikon, menü

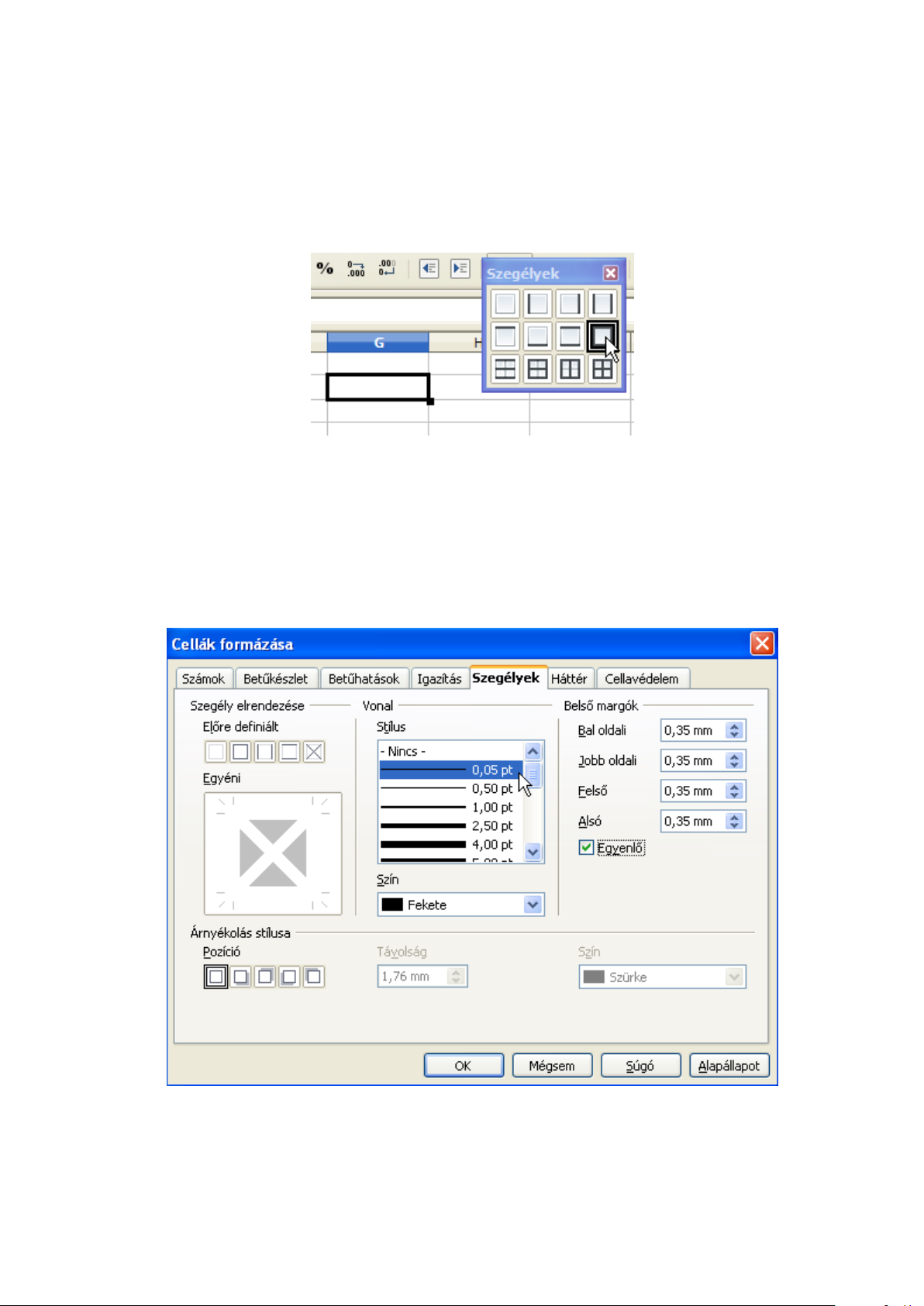
Egyéni szegélybeállításokat a Formátum menü Cellák parancsát választva, a párbeszédablak
Szegélyek lapján állíthatunk be (2.12 ábra). Választhatunk vonalvastagságot, stílust, színt és
akár árnyékolást is. A Szegély elrendezése terület másképp jelenik meg attól függően, hogy
cellát, cellákat egy oszlopban, cellákat egy sorban vagy nagyobb cellatartományt jelölünk ki. Ezek
a lehetőségek a cellatartományok belső, átlós és cellákon belüli átlós szegélyeire vonatkoznak.

2.12. ábra. Cellák formázása – Szegélyek

Az Egyéni területen kattintásokkal állíthatunk be vonalakat. Ezek jelentése a következő:

2. FEJEZET. ELSŐ LÉPÉSEK A CALCKAL 10

Fekete vonal – beállítja a kijelölt cellákra a kiválasztott stílusú vonalat. Szaggatott vonal akkor

jelenik meg, ha 0,05 pontos vonalstílus van kiválasztva.

Szürke vonal – a kijelölt cellák megfelelő vonala nem fog változni

Fehér vonal – a kijelölt cellák megfelelő vonalai törölve lesznek.

Az aktív cella, vagy a kijelölt cellatartomány háttérszínét a Formátum menü Cellák parancsát
választva, a párbeszédablak Szegélyek lapján állíthatjuk be.

2.6. Munkafüzet mentése

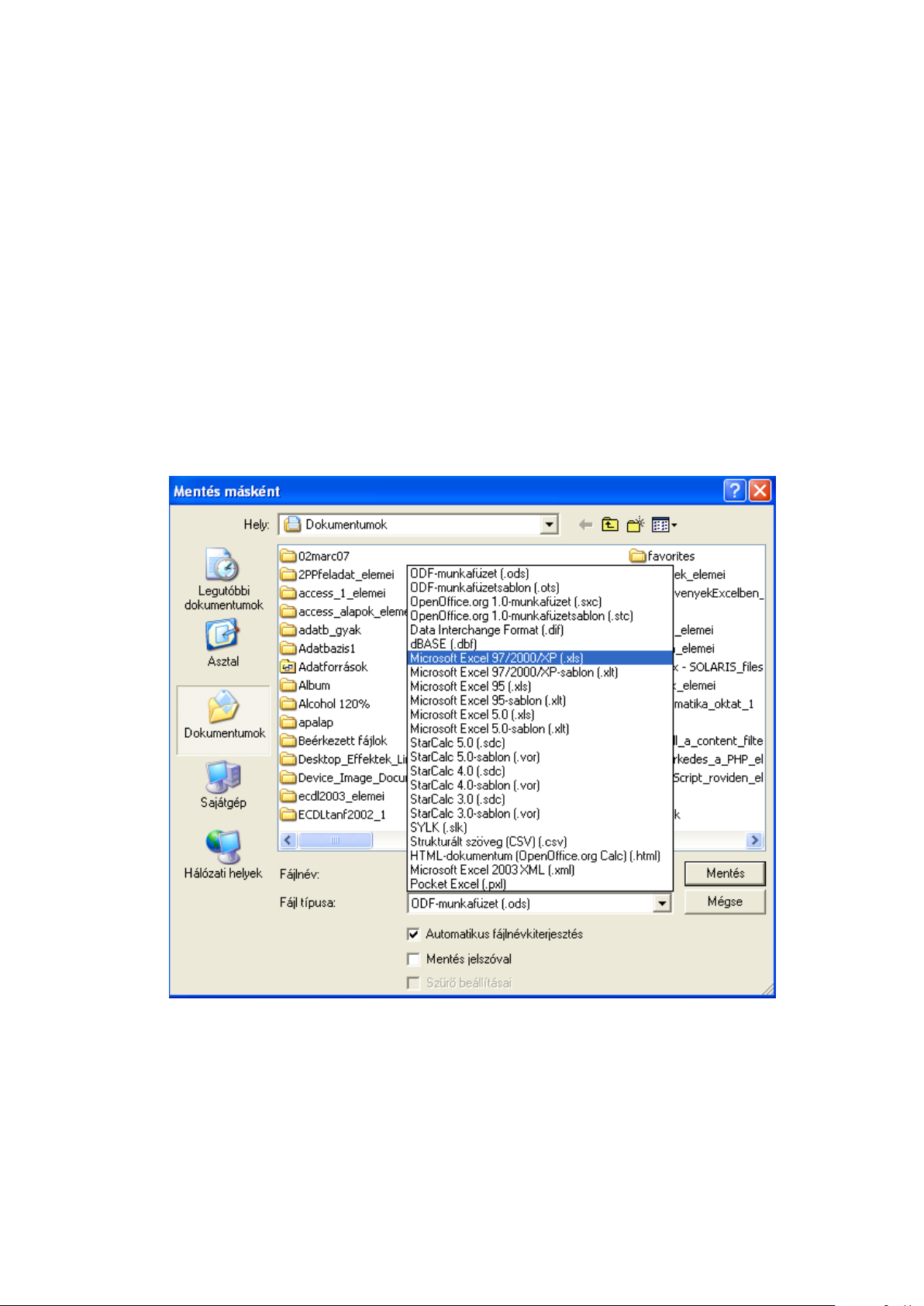
Munkafüzetünket a Fájl menü vagy a Standard eszköztár Mentés parancsával menthetjük el. A
Calc alapértelmezett formátuma az OpenDocument, amely az irodai dokumentumok új, nemzetközi
szabványa. Az OpenDocument munkafüzet állományának kiterjesztése .ods. A Calc képes Microsoft
Excel formátumba is menteni munkafüzetünket, amennyiben a Fájl típusánál ezt választjuk (2.13
ábra).

2.13. ábra. Fájl mentése – fájlformátumok

A Mentés ablak, attól függően, hogy milyen operációs rendszeren használjuk a Calcot, for­mailag különbözhet. A 2.13 ábrán a Microsoft Windows XP-re telepített Calc Mentés ablakát
látjuk.

Az alapértelmezett mentési formátum és mentési hely módosítható az Eszközök menüpont
Beállítások parancs kiadásakor megjelenő párbeszédablakban (2.14 ábra). A mentési helyet az

2. FEJEZET. ELSŐ LÉPÉSEK A CALCKAL 11

OpenOffice.org – Útvonalak – Dokumentumok lehetőséget választva módosíthatjuk. Az alap­értelmezett fájlformátum a Megnyitás és mentés – Általános ablakban állítható be, a doku­mentum típusánál a munkafüzetet választva.

2.14. ábra. Általános beállítások – Megnyitás és mentés

2.7. 1. feladat

Hozzuk létre a képen látható táblázatot (2.15 ábra) és mentsük el a munkafüzetet calc01 néven
OpenDocument formátumban!

A munkalap neve legyen ZH 01. Az egyesített B1:G1 tartományban Ctrl+Enter segítségével
hozzunk létre sortörést. A C4:G4 cellatartomány függőleges szegélyvonalai fehér színűek.

2.15. ábra. 1. feladat

3. fejezet

Egyszerű számítások a munkalapon

3.1. Aritmetikai operátorok használata

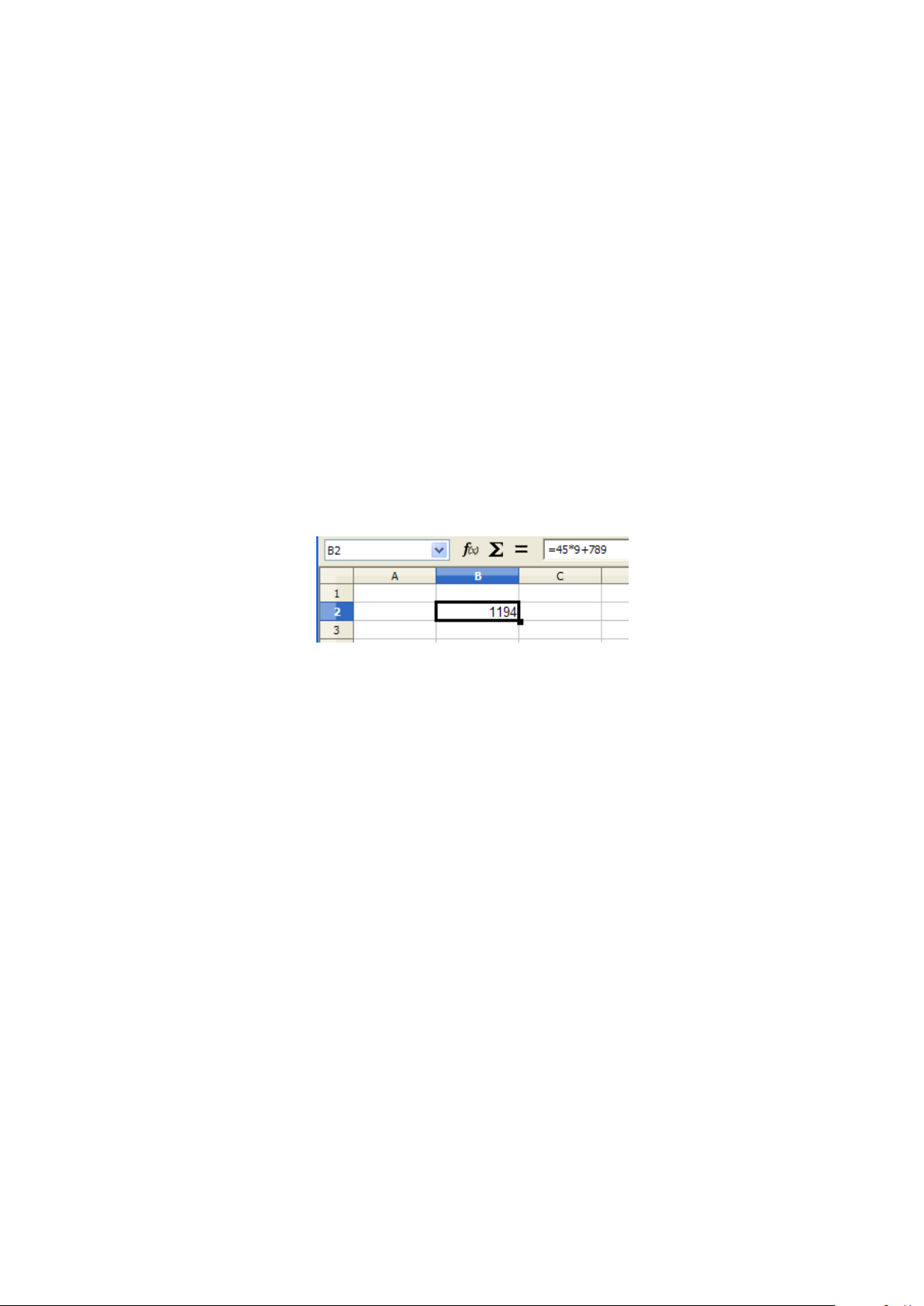
A Calc az egyenlő jellel (=) kezdődő matematikai kifejezést kiszámítja és a cellában az eredményt
megjeleníti.

Az „=45*9+789” beírásának 1194 lesz az eredménye. Aktívvá téve ismét a B2-es cellát a Képlet
eszköztár Névdobozában látjuk a cella címét, a Beviteli sorban pedig a kifejezést (3.1 ábra).

3.1. ábra. Aritmetikai operátorok

A számtani alapműveletek (például összeadás, kivonás, szorzás, osztás) végrehajtásához, számok
kombinálásához és számeredmények előállításához az alábbi számtani műveleti jeleket használhat­juk:

+ (pluszjel) Összeadás;

- (mínuszjel) Kivonás;

- (mínuszjel) Negálás;

* (csillag) Szorzás;

/ (törtjel) Osztás;

^ (kalap) Hatványozás (pl. 3ˆ2 – három a négyzeten).

Amennyiben egyetlen képletben több műveleti jelet vagy operátort adunk meg, a Calc a műve­leteket a következő sorrendben hajtja végre: hatványozás, szorzás és osztás, összeadás és kivonás. A
képlet azonos prioritású műveleteit (például szorzás és osztás) a Calc balról jobbra haladva értékeli
ki.

A végrehajtási sorrend módosításához az elsőnek kiértékelni kívánt képletrészt írjuk zárójelek
közé. Például az =5+2*3 eredménye 11 lesz, mivel a Calc a szorzást az összeadás előtt hajtja végre.
A képlet összeszorozza a 2-t a 3-mal, majd hozzáad 5-öt.

Amikor a képletet módosítva zárójeleket használunk =(5+2)*3, akkor a Calc összeadja az 5-öt
és a 2-t, majd az eredményt megszorozza 3-mal, melynek a végeredménye 21.

3. FEJEZET. EGYSZERŰ SZÁMÍTÁSOK A MUNKALAPON 13

3.2. Cellahivatkozások alkalmazása

Legtöbbször a cellákba nem konkrét számokat, hanem cellahivatkozásokat írunk. Módosítsuk a B2
cella tartalmát a számok helyett az A1, B1 és C1 cellacímeket írva. Ebbe a három cellába írjuk a
kifejezés számértékeit (3.2 ábra).

3.2. ábra. Cellahivatkozások

Módosítva az A1, B1 vagy a C1 cellák valamelyikét, a Calc újraszámítja a cellahivatkozást
tartalmazó cellát, esetünkben a B2-t.

3.3. 2. feladat

Készítsünk táblázatot, ami kiszámítja az A1 és a B1 cellákba írt két szám összegét, különbségét,
szorzatát és hányadosát (3.3 ábra)! Végezzük el az ábrán látható formázásokat is! Ellenőrizzük az
eredményeket a következő számpárokkal: 10, 2; 81, 9 és 8, 0. Figyeljük meg a hibaüzenetet az utolsó
számpár esetén a D4 cellában.

3.3. ábra. 2. feladat

3.4. Képletek másolása

Táblázatos adatok esetén gyakran előfordul, hogy valamelyik sort vagy oszlopot hasonló módon
kell kiszámítani. Ilyen esetben a képletet csak egyszer kell begépelnünk, és azt másolással sokszo­rosíthatjuk.

Nevezzük át a Munkalap3 munkalapot ZH 2-re és másoljuk ide az 1. feladat szegélyezett
cellatartományát. Ehhez jelöljük ki a B3:G9 tartományt, és válasszuk a Standard eszköztár Má-
solás parancsát. Ezután váltsunk a ZH 2 munkalap A1 cellájára és kattintsunk a Beillesztés
ikonra ugyanezen az eszköztáron. Egyesítsük a G1:G3 cellákat, ebbe kerüljön az Összesen szöveg.
Végezzük el a 3.4 ábrán látható formázásokat.

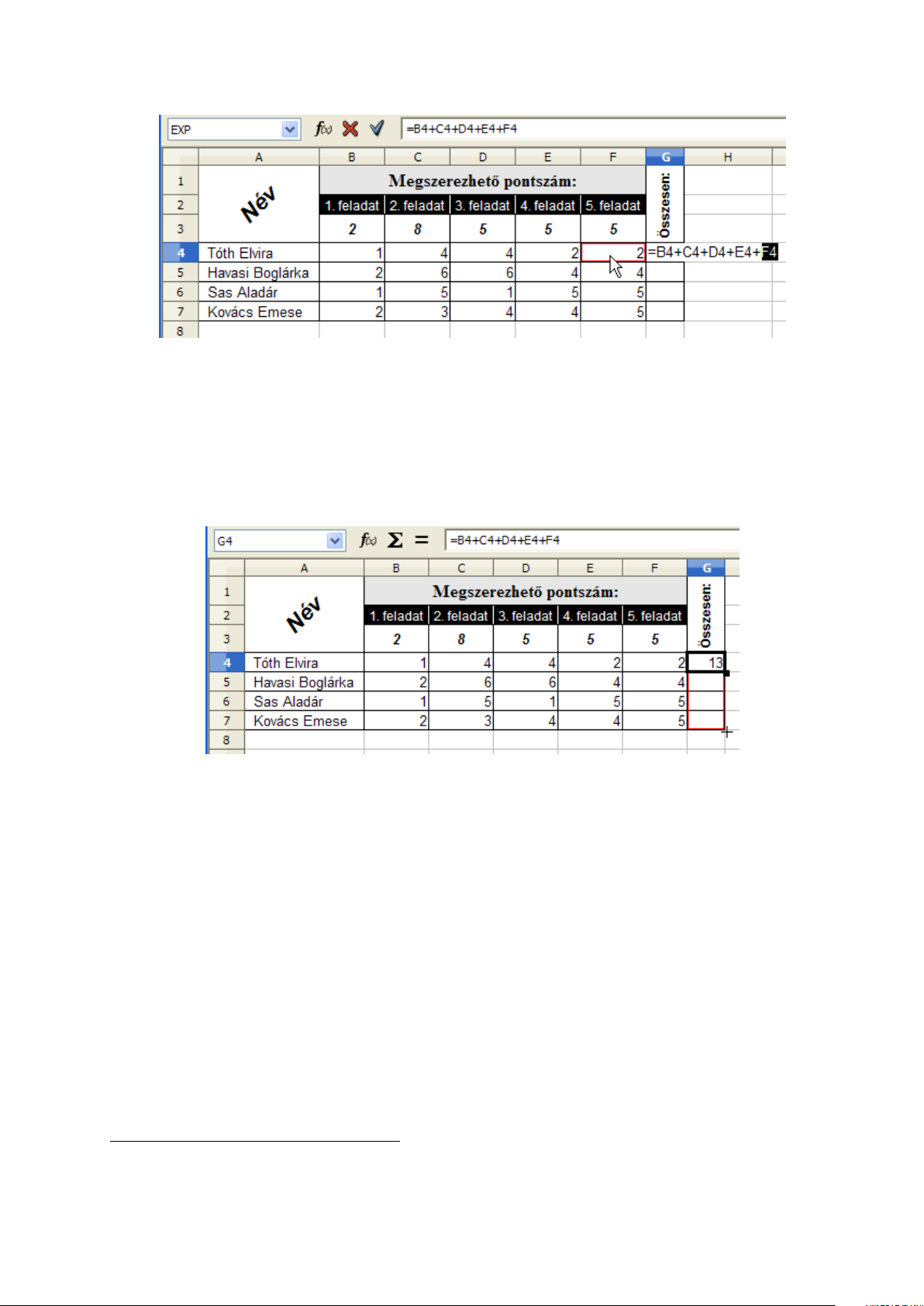
A G4 cellában számítsuk ki az első tanuló összpontszámát. A képletben szereplő cellahivatkozá­sokat egérrel is létrehozhatjuk egyszer kattintva az adott cellára. Ez általában gyorsabb módszer,
mintha a cellák címeit gépelnénk be.

3. FEJEZET. EGYSZERŰ SZÁMÍTÁSOK A MUNKALAPON 14

3.4. ábra. 2. feladat – Formázás

Az első tanuló összpontszámát a =B4+C4+D4+E4+F4 képlettel1számítjuk ki. A második
képletet már nem kell beírnunk, másolás segítségével létrehozhatjuk. Ehhez vezessük az egérmu­tatót az aktív G4 cella jobb alsó sarkába. Ott az keresztté változik és az egér gombját lenyomva
tartva töltsük ki (húzzuk lefelé) a G5:G7 tartományt. (3.5 ábra)

3.5. ábra. 2. feladat – Összegzés

A Calc minden cellában a megfelelő képletet hozza létre, mert a cellahivatkozásokat tartalmazó
képletet lefelé úgy másolja, hogy növeli eggyel a cellahivatkozásokban a sorszámot. Fölfelé máso­lásnál csökkenti. Az összpontszámokat úgy is kiszámolhattuk volna, hogy először a 7. sorban lévő
képletet írjuk be, és azt másoljuk fölfelé.

Jobbra másolásnál az oszlopazonosítót „növeli”, ha balra másolunk, csökkenti azt.

Amennyiben egy cella cellahivatkozásokat és számokat is tartalmaz, akkor a képlet másolásakor
az állandók nem változnak. Például, ha egy cella tartalma =5*C1*D2+12, akkor azt lefelé másolva
=5*C2*D3+12-t kapunk.

1

Természetesen létezik a Calcban ennél egyszerűbb megoldás is a cellatartomány összegének kiszámítására, amit
a függvények bemutatásánál tárgyalunk.

3. FEJEZET. EGYSZERŰ SZÁMÍTÁSOK A MUNKALAPON 15

3.5. 3. feladat

Válaszoljuk meg a következő kérdéseket, majd ellenőrizzük a Calc segítségével:

a) Az A1 cella tartalma =D3*2. Mi lesz az E5 tartalma, ha az A1 cellát lefelé három, majd
négy cellán át jobbra másoljuk?

b) Az A1 cella tartalma =A8+B8-412. Mi lesz a C2 tartalma, ha az A1-et lefelé eggyel, majd
két cellán át jobbra másoljuk?

3.6. Abszolút hivatkozás

Az eddig tárgyalt cellahivatkozásokat relatív hivatkozásoknak nevezzük. Ez azt jelenti, hogy az
ilyen hivatkozások a képletek másolásánál automatikusan módosulnak. Vannak esetek viszont,
amikor olyan képletre van szükségünk, amelyikben egy vagy több hivatkozás nem változik máso­láskor. Ilyenkor abszolút cellahivatkozást kell használnunk.

Abszolút hivatkozás az, ha egy az oszlop- és sorazonosító elé egy-egy $ jelet írunk. Például:
$B$3. Ez a hivatkozás ugyanúgy a B3-as cellára mutat, de ha így szerepel a képletekben, akkor
másoláskor nem változik.

A következő feladatban áttekintjük az abszolút cellahivatkozás használatát.

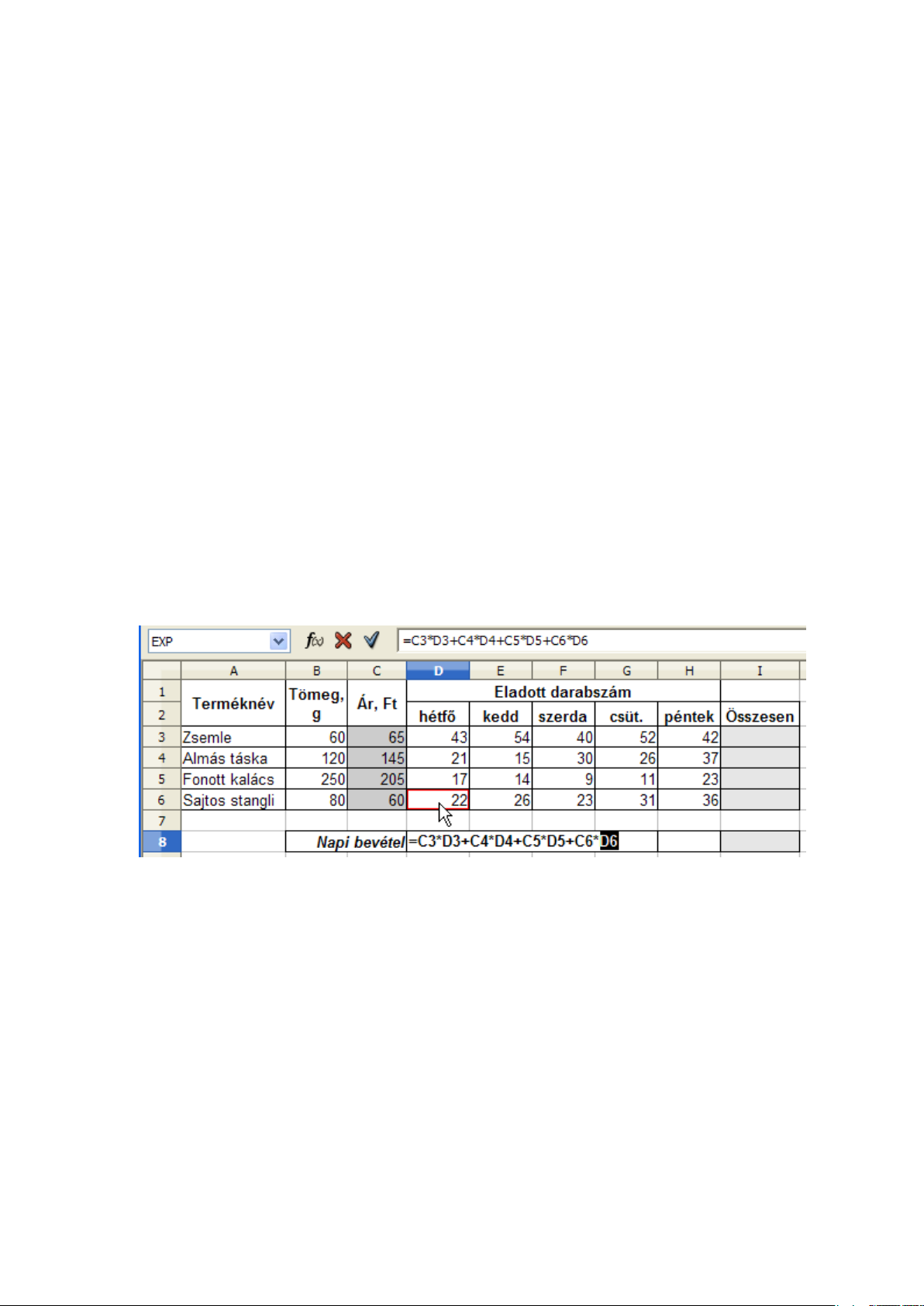
3.7. 4. feladat

A 3.6 ábrán egy üzletben eladott péksütemények napi adatait látjuk. Számítsuk ki a bevételt minden
napra és a heti összbevételt is. A 8. sorban a képleteket másolással hozzuk létre!

3.6. ábra. 4. feladat

Szúrjunk be egy új munkalapot és nevezzük át Bevétel-re. A hétfői bevétel kiszámítását
látjuk az ábrán: összeadjuk az egyes termékek eladásából befolyt összegeket, amelyeket a da­rabszám és az ár szorzataként kapunk meg. Ezt a képletet jobbra másolva hibás eredményt
kapnánk. Ahhoz, hogy a másolás helyes képletet hozzon létre, módosítanunk kell a D8 tar­talmát úgy, hogy az árakat megadó cellahivatkozások ne módosuljanak. A helyes képlet tehát:
=$C$3*D3+$C$4*D4+$C$5*D5+$C$6*D6. A $ jeleket be is írhatjuk (AltGr+É a billentyűze­ten), de sokkal gyorsabb megoldás, ha az adott cellahivatkozásra kattintva megnyomjuk a Shift+F4
billentyűkombinációt. A képletet jobbra másolva így már helyes eredményt kapunk (3.7 ábra).

3. FEJEZET. EGYSZERŰ SZÁMÍTÁSOK A MUNKALAPON 16

3.7. ábra. 4. feladat

3.8. Vegyes cellahivatkozások

Relatív és abszolút cellahivatkozásokon kívül léteznek még vegyes cellahivatkozások is. A vegyes
cellahivatkozás tartalma abszolút oszlop és relatív sor, vagy abszolút sor és relatív oszlop. Ilyen
hivatkozásokra akkor van szükség, ha azt akarjuk, hogy a hivatkozás egyik összetevője (az oszlop­vagy sorazonosító) állandó maradjon, a másik viszont változzon másoláskor. Példa a vegyes hivat­kozásra: =A$1 vagy =$A1. A Shift+F4 billentyűkombinációt többször lenyomva cellahivatkozás
beírásakor az abszolútra, vegyesre és ismét relatívra változik.

A vegyes hivatkozások begyakorlására készítsük el a következő feladatot.

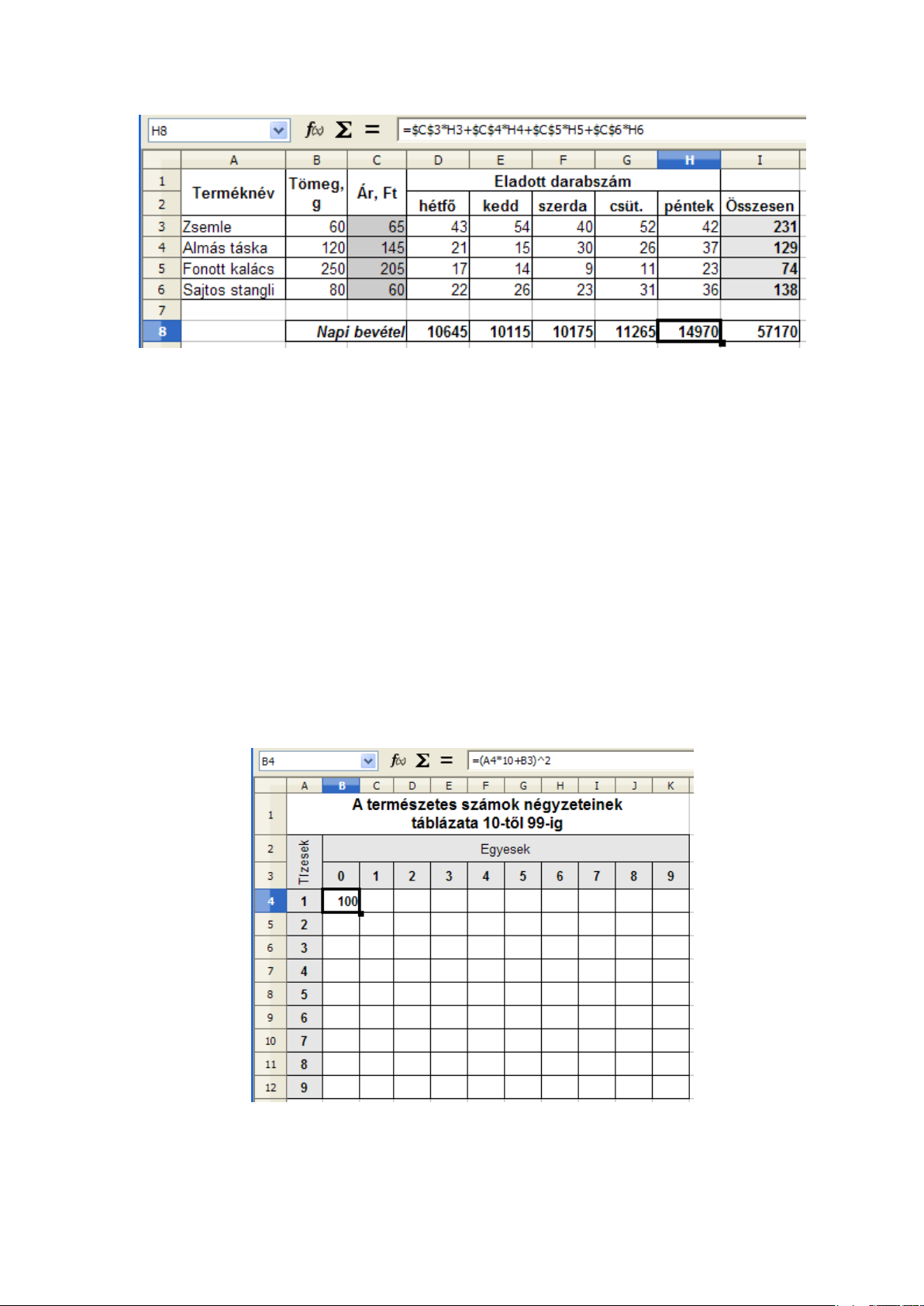
3.9. 5. feladat

Hozzuk létre a természetes számok négyzeteinek táblázatát 10-től 99-ig. A képletet csak egy cellába
írjuk be, a többit másolással töltsük fel.

3.8. ábra. 5. feladat

3. FEJEZET. EGYSZERŰ SZÁMÍTÁSOK A MUNKALAPON 17

Új munkalapon hozzuk létre a 3.8 ábrán látható táblázatot. Állítsuk be a cellaformátumokat.
Figyeljük meg a C4 cellába írt képletet. A képlet helyes, de jelenlegi formájában nem másolható.
Vízszintes másoláshoz úgy kell módosítani, hogy az A4 cellacím, ami 4-es sorban tízesek számát
tartalmazza, ne változzon. Viszont ha függőlegesen lefelé másoljuk az A4 cellacímnek A5-re kell
változnia. Tehát az A4 cellahivatkozásban az oszlopazonosítónak abszolútnak kell lennie, a sorazo­nosítónak pedig relatívnak: $A4.

Hasonlóképpen a B3 cellahivatkozás jobbra másoláskor változnia kell (relatív oszlopazonosító),
de lefelé történő másoláskor nem változhat (abszolút sorazonosító): B$3.

Megállapíthatjuk, hogy a helyes képlet esetünkben: =($A4*10+B$3)ˆ2.

Másoljuk a képletet jobbra (3.9 ábra).

3.9. ábra. 5. feladat

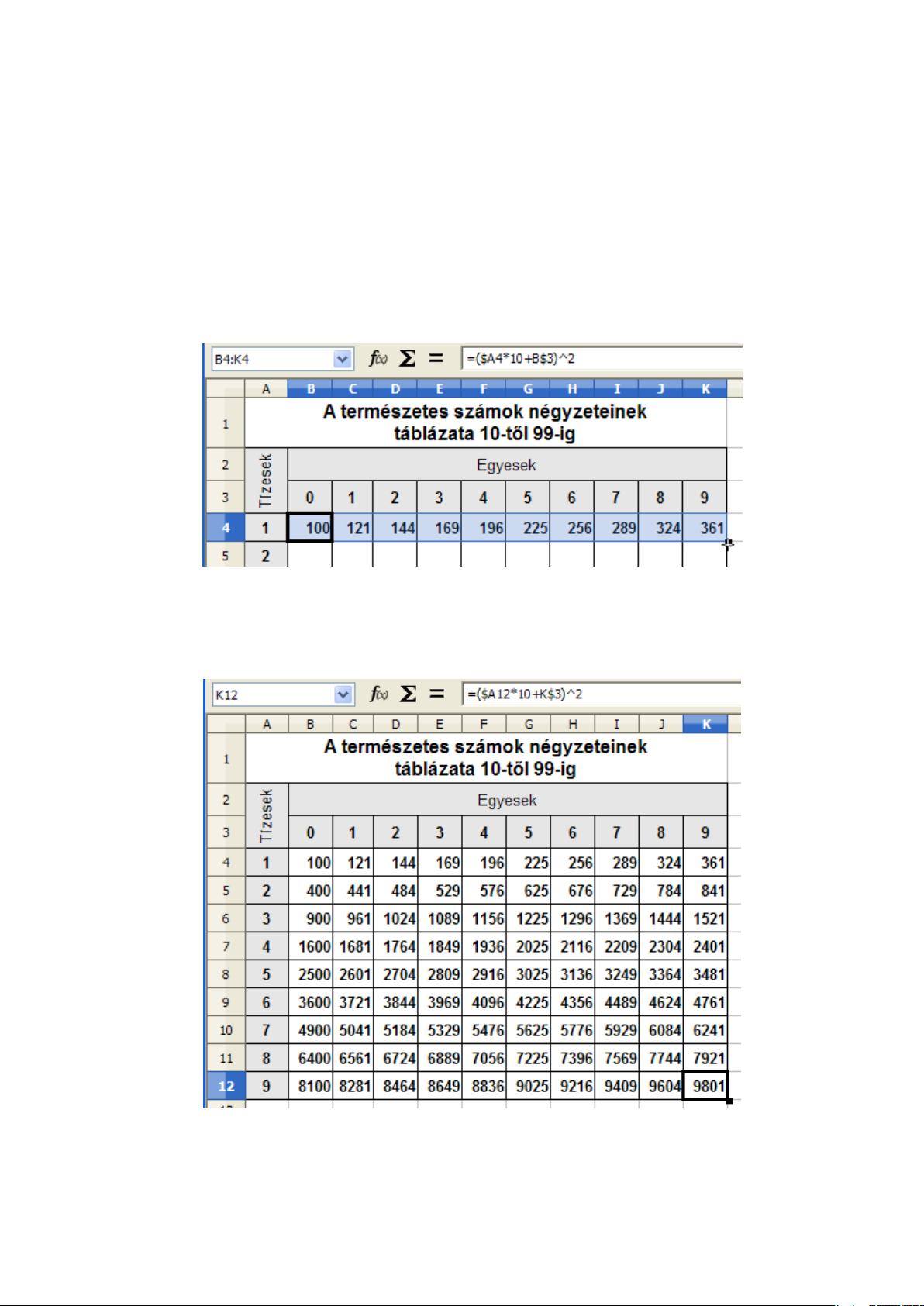
A kapott sort másoljuk lefelé, megkapva mind a 90 cellában az eredményt (3.10 ábra).

3.10. ábra. 5. feladat – megoldás

3. FEJEZET. EGYSZERŰ SZÁMÍTÁSOK A MUNKALAPON 18

Térjünk vissza az előző, 4. feladatra. A D8 cellában kiszámított hétfői bevételt jobbra másoltuk.
Ilyenkor csak a cellahivatkozás oszlopazonosító része változik. Tehát a képletben a sorazonosítók
előtti dollárjel fölösleges. A képlet helyes eredményt ad, de – szigorúan véve – itt is vegyes hivat­kozást kellett volna alkalmazni. A képlet helyesen: =$C3*D3+$C4*D4+$C5*D5+$C6*D6.

A vegyes és az abszolút cellacímzés begyakorlására oldjuk meg a következő feladatot.

3.10. 6. feladat

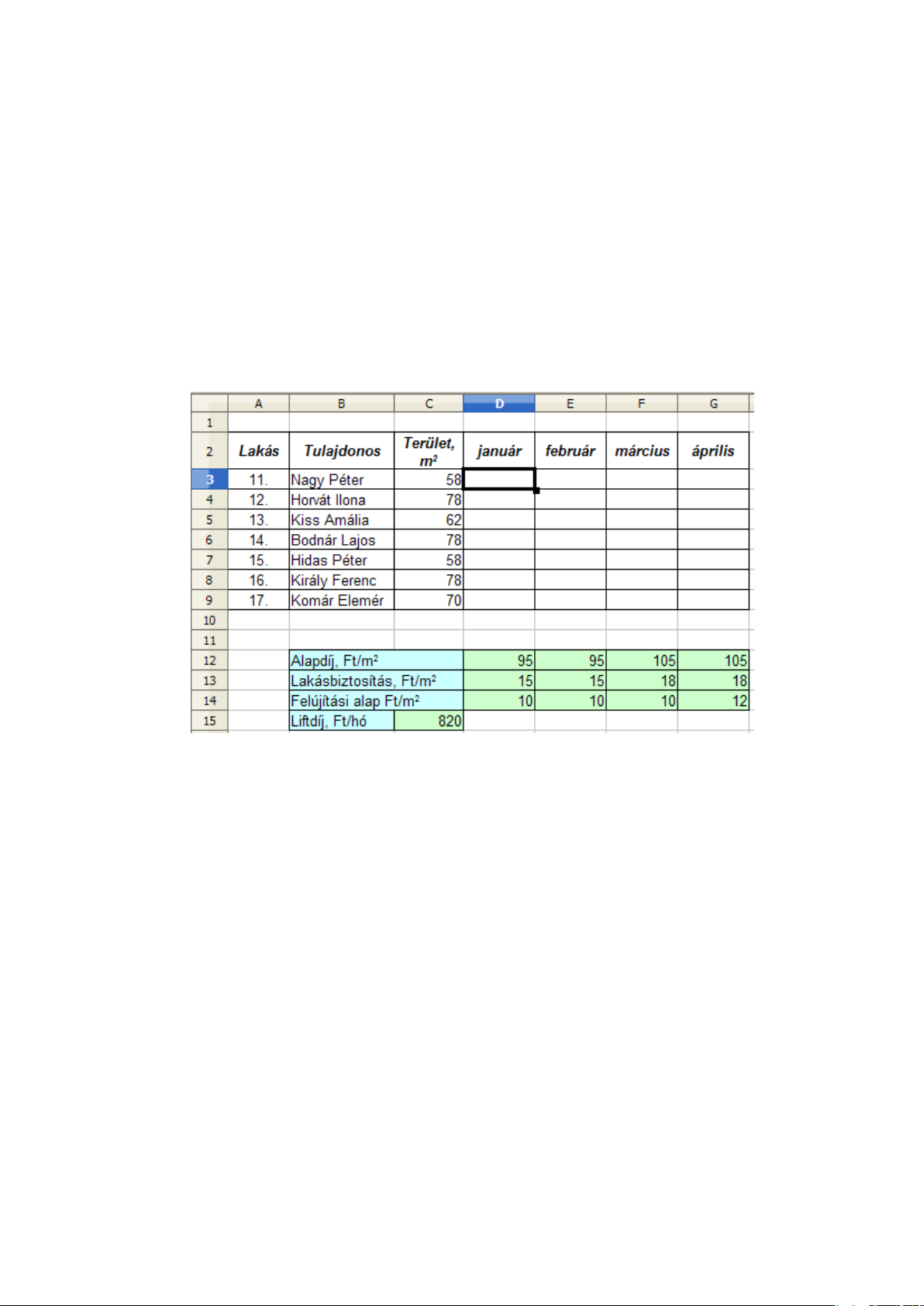
A 3.11 ábrán egy társasház lakásainak adatait látjuk. Számítsuk ki a lakások havi közös költségeit,
ha az a következő összetevőkből áll: négyzetméterenkénti alapdíj, lakásbiztosítási díj és felújítási
alap. A liftdíj állandó minden hónapban és nem függ a lakás területétől. A D3 cellába írt képlet
legyen másolható minden lakásra és hónapra!

3.11. ábra. 6. feladat

Az első lakás területét a C3 cella tartalmazza, a januári költségeket pedig a D12, D13 és D14
cellák. A liftdíjat a C15 cella. A közös költséget tehát a következő képlettel határozhatjuk meg:
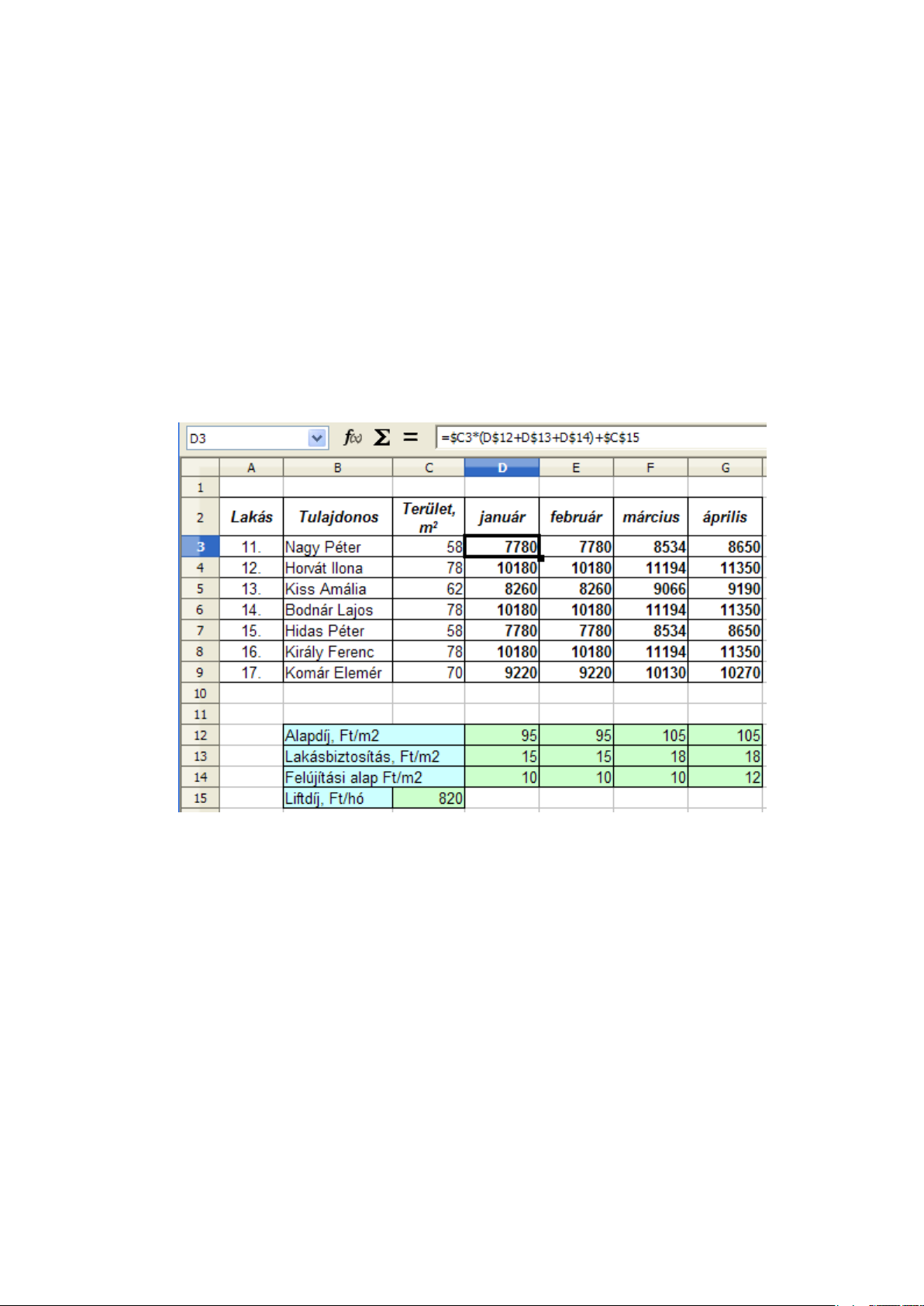
=C3*(D12+D13+D14)+C15. Ahhoz, hogy ez a képlet másolható legyen mind jobbra, mind
lefelé határozzuk meg a hivatkozások típusait. Mivel a liftdíj minden hónapban és minden la­kásra állandó, a C15-nek abszolútnak kell lenni. Jobbra másolásnál a születendő képleteknek
ugyanarra a lakásra kell hivatkoznia, lefelé másolásnál pedig a következőre. Tehát itt vegyes
hivatkozást alkalmazunk: $C3. A díjak esetén pedig fordítva kell eljárnunk, a vegyes hivatko­zásban az oszlopazonosítónak változni kell, a sorazonosító pedig állandó. A végleges képlet tehát:
=$C3*(D$12+D$13+D$14)+$C$15. Figyeljük meg, hogy ez a képlet csak ilyen hivatkozásokkal
másolható a D3:G9 tartományon, bármelyik hivatkozás módosítása hibás értékeket eredményezne.

A feladat megoldása a 3.12 ábrán látható.

3. FEJEZET. EGYSZERŰ SZÁMÍTÁSOK A MUNKALAPON 19

3.12. ábra. 6. feladat – megoldás

4. fejezet

Függvények használata

4.1. Függvények beszúrása

A függvények jelentősen megkönnyítik a számítási és egyéb feladatok elvégzését a táblázatkezelő
programokban.

A függvények két részből állnak: a függvény nevéből és argumentumból. Az argumentumot
zárójelek között kell megadnunk. Egy függvénynek több argumentuma is lehet, ilyenkor pontos­vesszővel választjuk el őket egymástól. A függvény általános alakja tehát:

=FÜGGVÉNYNÉV(argumentum1; argumentum2; ...)

Van olyan függvény is, amelynek nincs argumentuma, a zárójeleket ilyenkor sem hagyhatjuk el.
Például a matematikában használatos π számot meg tudjuk adni cellában függvénnyel: =PI().

A leggyakrabban használt függvény a SZUM, ami összeadja az argumentumlistájában lévő
számokat. A SZUM függvény a következő argumentummal =SZUM(A1:A4;C2) egyenértékű az
= A1 + A2 + A3 + A4 + C2 képlettel. Ezen az egyszerű példán is láthatjuk, hogy a függvények
használata megkönnyíti a számításokat.

Függvényeket a Beszúrás menüpont Függvény parancsával (Ctrl+F2) vagy a Képlet eszköz­tár ikonjaival hozhatunk létre. Ezek közül az első a Függvénytündér, a második az Összeg és a
harmadik a Függvény.

4.1. ábra. Függvénytündér

A Függvény ikon (a 4.1 ábrán az „=” feliratú) megkönnyíti a legutóbb használt függvények
ismételt kiválasztását (4.2 ábra). Nagyon hasznos funkció, hiszen a Calc több száz függvénye közül
egy munkalapon rendszerint csak néhányat használunk.

A 4.2 ábrán látható, hogy az eszköztár ikonjai is megváltoztak: megjelent a Mégse és az
Elfogadás parancs. Ezekkel, egér segítségével is nyugtázhatjuk a kiválasztott függvényeket és
argumentumokat.

4. FEJEZET. FÜGGVÉNYEK HASZNÁLATA 21

4.2. ábra. Függvény kiválasztása

4.2. Egyszerűbb statisztikai függvények használata

(SZUM, MIN, MAX, ÁTLAG, DARAB, DARAB2, KICSI, NAGY)

A Calc program magyar nyelvű változatában általában magyar függvénynevekkel találkozunk.
Ezek a magyar függvénynevek megegyeznek a magyar Excelben lévőkkel. Csak azok a függvényne­vek nincsenek lefordítva, amelyek nem léteznek a magyar Excelben, vagy abban nincsenek lefordít­va. Ezeknek az angolul maradt függvényeknek a használata az angol nyelvet nem ismerők számára
sem jelenthet gondot, hiszen a függvények magyarázata és a súgó példái magyar nyelvűek.

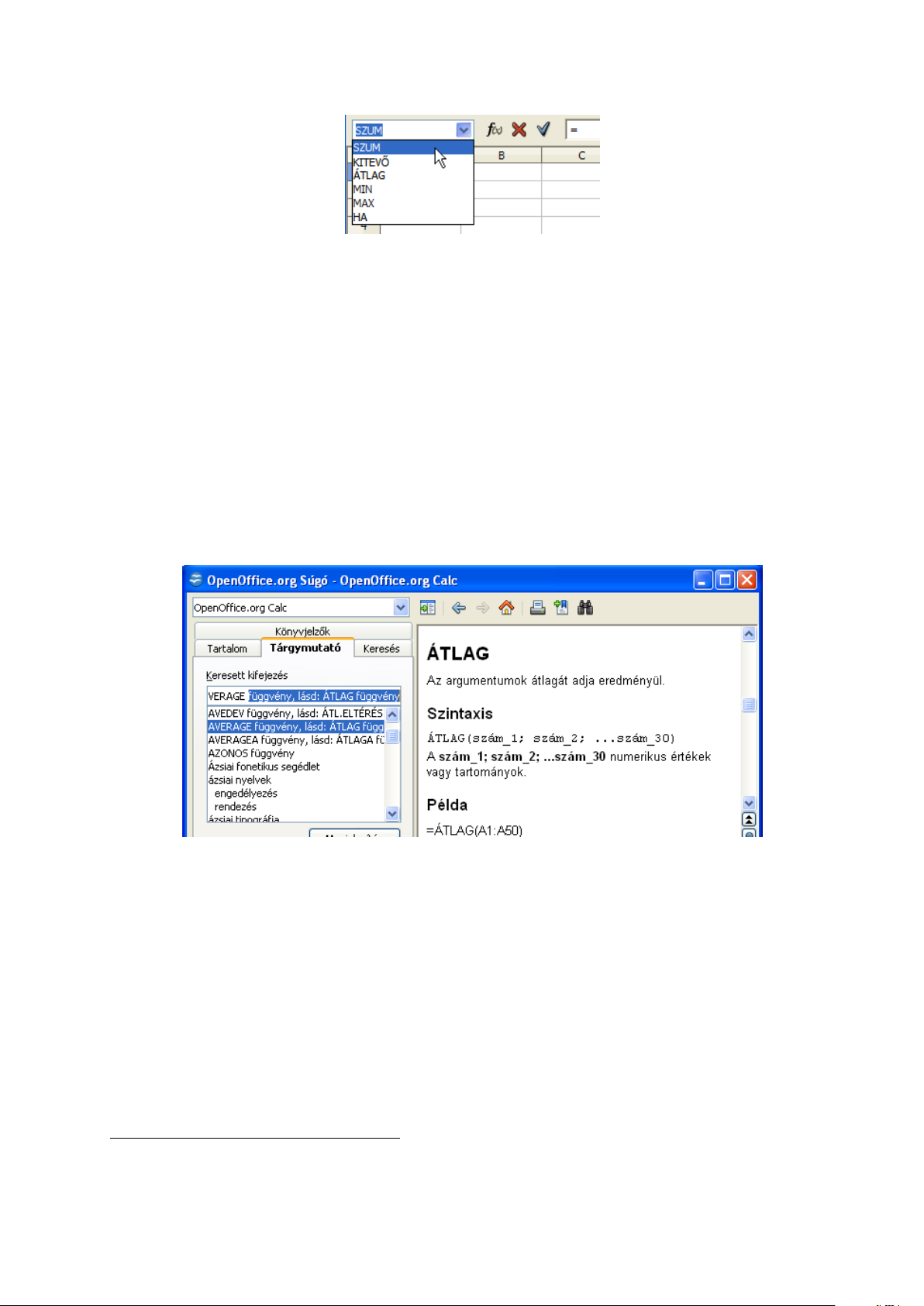
A Calc súgója megkönnyíti azok dolgát, aki csak az angol függvényneveket ismerik. A magyar
megfelelő kikereséséhez válasszuk a Súgó ablakában a Tárgymutatót, a Keresett kifejezéshez
pedig írjuk a függvény angol nevét (4.3 ábra).

1

4.3. ábra. OpenOffice.org Súgó – Átlag

A 4.1 táblázatban a négy leggyakrabban használt függvényt láthatjuk.

A Függvénytündér használatának begyakorlására készítsük el a következő feladatot.

4.3. 7. feladat

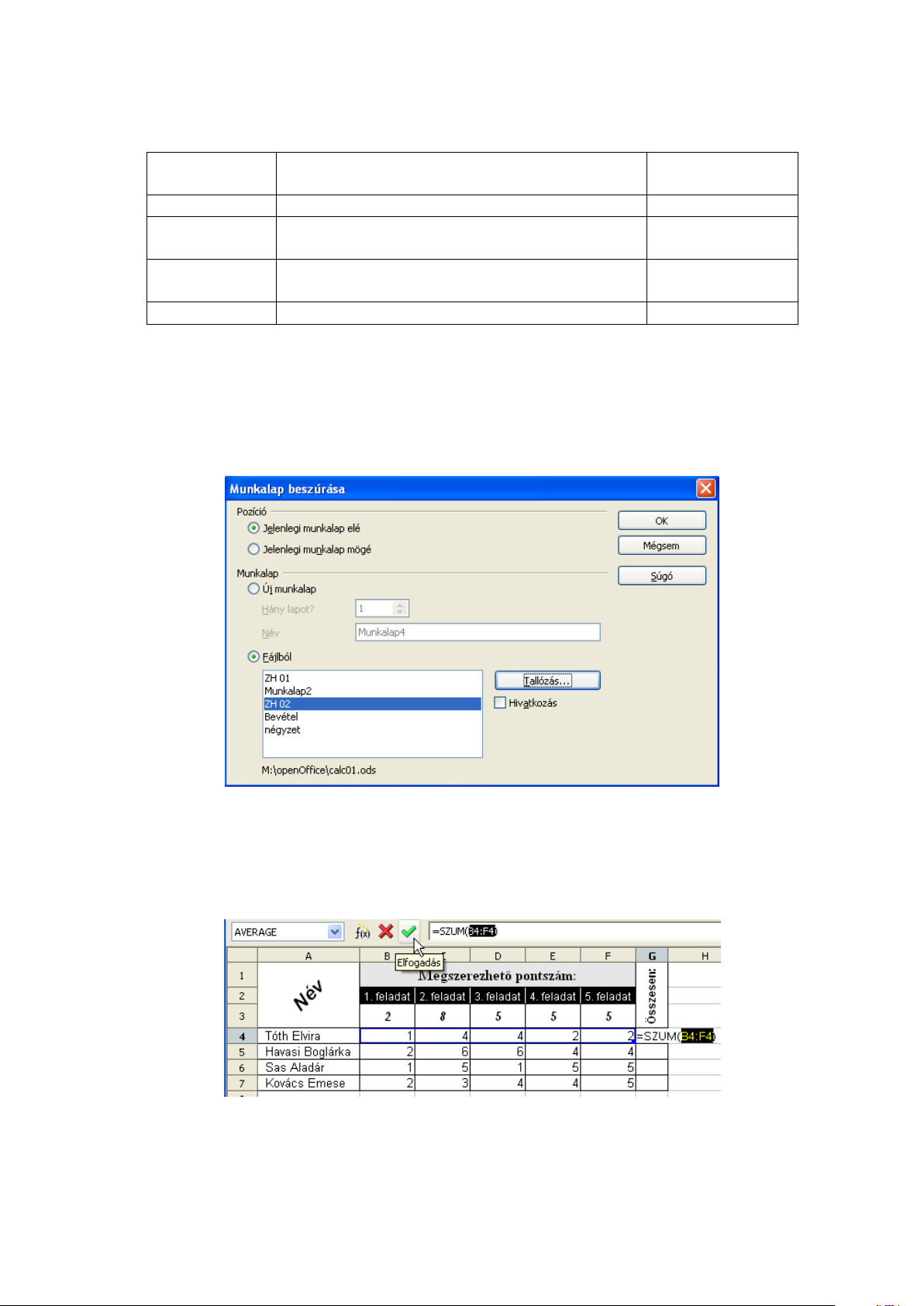
Másoljuk egy üres munkafüzetbe a ZH 02 munkalapot. A munkalapon töröljük a képlettel kiszá­mított cellák tartalmát. Számítsuk ki az összpontszámokat a G oszlopban a SZUM függvénnyel. A

8. sorban függvény segítségével jelenítsük meg a feladatok és az összpontszámok átlagát. Határoz­zuk meg a legnagyobb és a legkisebb összpontszámot, valamint azt, hogy a legtöbb pontszámot elért
tanulónak hány pont hiányzik a maximálisan elérhetőhöz. Mentsük a munkafüzetet calc02 néven.

1

A OpenOffice.org 3.2.1-es verziótól kezdve

4. FEJEZET. FÜGGVÉNYEK HASZNÁLATA 22

4.1. táblázat. Alapvető függvények

A függvény Funkciója A függvény

neve angol neve

SZUM Összeadja a cellatartományban lévő számokat. SUM

MIN

MAX

ÁTLAG

A munkalap tartalmát átmásolhatjuk kijelölve, másolva és a másik munkafüzetbe beillesztve
azt, de gyorsabb módszer a munkafüzet beszúrása (Beszúrás menüpont Munkalap parancs). Itt
válasszuk a Fájlból kapcsolót, majd a Tallózás parancs segítségével adjuk meg annak a munka­füzetnek a nevét, amelyik a szükséges munkalapot tartalmazza (4.4 ábra).

Az argumentumlista legkisebb értékét adja ered­ményül.
Az argumentumlista legnagyobb értékét adja
eredményül.
Az argumentumok átlagát adja eredményül. AVERAGE

MIN

MAX

4.4. ábra. 7. feladat – Munkafüzet beszúrása

Jelöljük ki a ZH 02 munkalap nevét és szúrjuk be az aktuális munkafüzetünkbe. A munkalapon
jelöljük ki a G4:G7 tartományt és a „Backspace” billentyűvel töröljük a tartalmát.

4.5. ábra. 7. feladat

4. FEJEZET. FÜGGVÉNYEK HASZNÁLATA 23

Tegyük aktívvá a G4 cellát és kattintsunk a Képlet eszköztár Összeg ikonjára. A cellában
megjelenik a SZUM függvény és a megfelelő argumentumok is. A Calc az aktív cellától balra egy
számsort talált és azt beírta a SZUM függvénybe argumentumként. Ez nagyon hasznos funkció,
hiszen gyakran fordul elő, hogy egy sor végén, vagy egy oszlop alján kell annak összegét kiszámolni.
A kék színű keret mutatja az automatikusan meghatározott tartományt (4.5 ábra).

A képletet három cellán át lefelé másolva megkapjuk mind a négy tanuló összpontszámát.

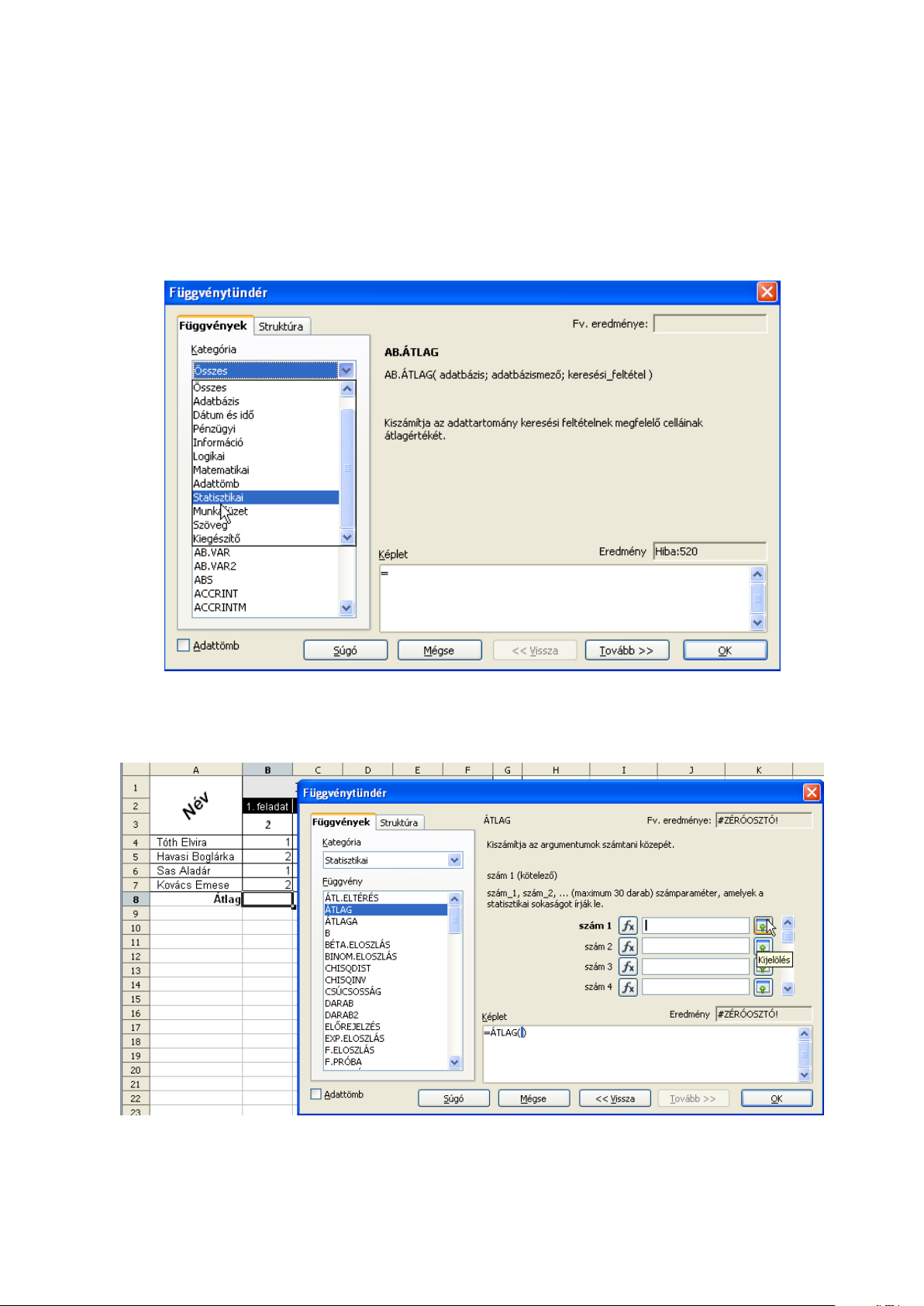
Az A8 cellába írjuk az „Átlag” szót és a B8 cellában válasszuk a függvénytündért (4.6 ábra).

4.6. ábra. 7. feladat – függvénytündér

4.7. ábra. 7. feladat

4. FEJEZET. FÜGGVÉNYEK HASZNÁLATA 24

Az ablakban kategóriákba rendezetten találjuk a Calc összes függvényét. Egy függvényt ki­választva az ablak jobb oldalán annak a magyarázatát olvashatjuk. A Statisztikai kategóriából
válasszuk az ÁTLAG függvényt. A Tovább gombra kattintva a párbeszédablak jobb oldalán megje-
lennek az argumentumbeviteli mezők (4.7 ábra). Jelöljük ki a B4:B7 tartományt és a cellahivatkozás
megjelenik az első beviteli mezőben. Természetesen megadhatunk szám- és egyéb értékeket, illetve
hivatkozásokat a párbeszédablak megfelelő részeiben.

A Zsugorítás ikon lecsökkenti a párbeszédablakot a beviteli mező méretére. Így könnyebb a
szükséges hivatkozást megjelölni a lapon. Az ikon ezután automatikusan átalakul a Maximalizálás
ikonra. Erre kattintva a párbeszédablakot visszaállíthatjuk eredeti méretére.

Bonyolultabb függvények esetén hasznos lehet a Súgó parancs. A megjelenő ablakban részletes
leírást és példákat olvashatunk a kiválasztott függvényről.

Másoljuk a függvénytündérrel létrehozott B8 cellát jobbra minden feladat és a csoport össz­pontszám átlagának kiszámításához.

A legtöbb és a legkevesebb összpontszámot jelenítsük meg a B11 és B10 cellákban a MAX és
MIN függvények segítségével. A B12 cella azt a pontszámot mutatja, amennyivel kevesebbet ért el a
legjobb tanuló az elérhető maximumnál. Ennek kiszámításához is használhatjuk a függvénytündért
az első függvény megadása után, a mínusz jelet beírva a Képlet párbeszédablakba és megadva a
második függvényt (4.8 ábra).

4.8. ábra. 7. feladat

Amennyiben pontosan ismerjük a használni kívánt függvény szintaxisát, nem kell feltétlenül
használnunk a függvénytündért, a cellába közvetlenül is beírhatjuk a kifejezést.

4. FEJEZET. FÜGGVÉNYEK HASZNÁLATA 25

Az elkészült feladat a 4.9 ábrán látható.

A következő feladatban a 4.2 táblázatban felsorolt statisztikai függvényeket fogjuk használni.

4.9. ábra. 7. feladat

4.2. táblázat. Statisztikai függvények

A függvény Funkciója A függvény

neve angol neve

DARAB

DARAB2

KICSI

NAGY

Megszámolja, hány szám van a paraméterlistá­ban. A szöveges bejegyzéseket kihagyja.
Megszámolja, hány érték van a paraméterlistá­ban. A szöveges elemek is számítanak.
Kiszámítja egy adathalmaz k-adik legkisebb ér­tékét.
Kiszámítja egy adathalmaz k-adik legnagyobb
értékét.

COUNT

COUNTA

SMALL

LARGE

4.4. 8. feladat

A 4.10 ábrán egy iskolai futóverseny eredményeit látjuk. Hozzuk létre a calc02 munkafüzet második
munkalapján az alábbi táblázatot. A D oszlopban jelenjen meg a tanulók jobbik eredménye. A G
oszlop számadatait függvény segítségével számítsuk ki.

A csoportlétszámot a DARAB2 függvénnyel, a résztvevők számát pedig a DARAB-bal szá­míthatjuk ki. Az argumentumlista lehet ugyanaz (D4:D12), hiszen a DARAB csak a számokat
tartalmazó cellák darabszámát adja meg.

A KICSI függvénnyel meghatározhatjuk egy cellatartomány k-adik legkisebb értékét. Két kö­telező paramétere van: az elsővel a tartományt adjuk meg, a másodikkal meghatározzuk, hogy

4. FEJEZET. FÜGGVÉNYEK HASZNÁLATA 26

4.10. ábra. 8. feladat

hányadik legkisebb elemre van szükségünk. Figyeljük meg a 4.10 ábrán, hogy ez a paraméter
relatív cellahivatkozás (F6). A képlet másolásakor ez az argumentum a megfelelő értéket fogja
felvenni. Az első paraméternél viszont vegyes cellahivatkozást használunk, hogy minden másolt
függvény ugyanarra a tartományra hivatkozzon.

A G13:G14 tartományt hasonlóan számítjuk ki, csak itt a NAGY függvényt alkalmazva.

5. fejezet

Számformátumok

5.1. Százalék és pénznem formátum

A számokat tartalmazó cellákon speciális formázásokat állíthatunk be. A leggyakrabban használt
számformátumok az eszköztáron is elérhetők: százalék és a pénznem formátum. E két alapvető
formátum megértéséhez írjuk be a következő adatokat (5.1 ábra).

5.1. ábra. Számformátumok

Az F3 cellán állítsunk be pénznem-, a G3 cellán pedig százalékformátumot. Látjuk az 5.2
ábrán, hogy a pénznem formátum ezres csoportosítást, két tizedesjegynyi pontosságot állított be
és hozzáadta az alapértelmezett pénznem megjelölést. A százalék formátum a számot százzal
megszorozva, két tizedesjegynyi pontossággal és a százalékjellel kiegészítve mutatja.

5.2. ábra. Százalék formátum

A tizedesjegyek számát növelhetjük és csökkenthetjük a Formátum eszköztár Számformá-
tum: tizedesjegy hozzáadása és a Számformátum: tizedesjegy törlése kapcsolókkal. A
Calc a matematika szabályai szerint kerekít a tizedesjegyek számának csökkentésekor, de vegyük

5. FEJEZET. SZÁMFORMÁTUMOK 28

figyelembe, hogy ilyenkor a cellában kerekítve látjuk a számértéket, de a cella tartalma közben nem
változik. Esetünkben, ha nullára csökkentjük a tizedesjegyek számát a G3 cellában, abban 13%-ot
fogunk látni, de a cella tartalma továbbra is 0,127 marad.

A százalékformátum ilyen megvalósítása megkönnyíti a százalékszámításokat: pl. az A1 cellába
írt szám B1 cellába felvett százalékát a két cella szorzatával számíthatjuk ki.

A Formátum eszköztár Számformátum: általános kapcsolóval törölhetjük a számformátu-
mokat a kijelölt cellákon, és a cella ismét alapértelmezett számformátumú lesz.

5.2. 9. feladat

Egy üzlet 20 db péksütemény vásárlásakor 5%, 50 db esetén 8% kedvezményt ad. Számítsuk ki a
kedvezményes árakat a D2:D6 és az E2:E6 tartományokban a D10, D11 cellákban felvett százalék­értékekkel számolva (5.3 ábra).

Az F oszlopban számítsuk ki egy kilogramm péksütemény árát az eredeti áron számolva. Ezekből
az árakból határozzuk meg, hogy hány százalékkal drágább a sajtos stangli, mint az almás táska.

A táblázatot a calc02 munkafüzet harmadik munkalapján hozzuk létre, amelyiket nevezzünk át
Kedvezményre.

5.3. ábra. 9. feladat

Az 5.3 ábrán figyeljük meg a D3 cella tartalmát: =(C3-C3*D$10)*20. Az eredeti árból (C3)
kivonjuk a kedvezményt, amit az eredeti ár és a kedvezmény szorzatával (C3*D$10) határozunk
meg. Ne feledjük, hogy a D10 cella számértéke 0,05.

A képletben zárójelből kiemelve a C3-at a következő kifejezést kapjuk: =20*C3*(1-D$10).

Az E3 cellát ezzel a módszerrel számítsuk ki (5.4 ábra).

Az F oszlopban egy kilogramm péksütemény árát a =C3/B3*1000 képlettel számíthatjuk ki,
hiszen a C3/B3 egy gramm árát adja meg.

Azt, hogy hány százalékkal több az F6 mint az F4, egy tört adja meg, aminek számlálója a két
cella különbsége, nevezője pedig az F4. A B14 cella tartalma tehát: =(F6-F4)/F4, számformátuma
százalék, tizedeshelyek száma nulla.

5. FEJEZET. SZÁMFORMÁTUMOK 29

5.4. ábra. 9. feladat

5.3. Dátum- és időformátum

A Calc a dátumot egész számként tárolja, mégpedig egy dátumértékhez viszonyított sorszámként.
Alapértelmezés szerint a kezdődátum 1899. december 30., ez a dátum a nullának felel meg. Az
ezt követő az egyes számnak, és így tovább. A kezdődátumnál korábbi dátumokat a program nem
értelmezi.

5.5. ábra. Dátumformátumok

Minden számformátumot, így a dátumformátumot is módosíthatjuk a Formátum menü Cel-
lák ablakában a Számok fület választva. Az 5.5 ábrán az A1 cella számformátumát látjuk, aminek
tartalma 35000. A Dátum kategóriát választva az előnézetmezőben láthatjuk, hogy ennek a szám­nak az 1995-10-28 dátum felel meg alapértelmezett dátumformátum esetén. A Formátumkód
ebben az esetben YYYY-MM-DD.

A Formátumkódot szerkeszthetjük is, a fenti példából is látjuk, hogy négy Y betű az évszámot
jeleníti meg. A dátumformátum gyakran használt formátumkódjait az 5.6 ábrán láthatjuk.

5. FEJEZET. SZÁMFORMÁTUMOK 30

5.6. ábra. Dátumformátumok formátumkódjai

A B4 cella tartalma =$A1, és ezt másoljuk a K4 celláig. Tehát a B4:K4 tartomány minden
cellája az A1 tartalmát mutatja. Ezeken a cellákon a fölöttük látható dátumformátum van beállítva.

Egyéni dátumformátumok használatára látunk három példát az 5.7 ábrán.

5.7. ábra. Egyedi dátumformátumok

A formátumkódot kiegészíthetjük tetszőleges szöveggel is, ilyenkor a szöveget idézőjelek ("...")
közé kell zárni.

Mind a dátumformátumot, mind a százalék- és pénznemformátumot a Calc beíráskor automa­tikusan alkalmazza. Ilyenkor a cella – mint számok beírásakor – jobbra igazított lesz. Írjuk három
cellába a következő tartalmakat: 2000Ft, 15%, 2008.08.01. Figyeljük meg, hogy a Calc automati­kusan alkalmazza a pénznem, százalék és a dátum formátumokat. A cellák tartalma pedig 2000,
0,15 és 39661 lesz, amit ellenőrizhetünk a Formátum eszköztár Számformátum: általános
parancsát alkalmazva.

A Calcban időértéket a szám tizedesjel utáni része határozza meg.

Írjuk a 39700,5 számot egy cellába és válasszuk az 5.8 ábrán látható dátumformátumot. Látjuk,
hogy esetünkben a 0,5 szám tizenkét óra nulla perc nulla másodpercnek felel meg.

Megadhatunk dátum nélküli időértéket is, értelemszerűen ilyenkor a szám egész része nulla lesz.

Az 5.8 ábrán látjuk, hogy az előnézetmezőben látható időformátumnak (12:00:00) a HH:MM:SS
formátumkód felel meg. További dátum- és időformátumokat az 5.9 ábrán találunk.

5. FEJEZET. SZÁMFORMÁTUMOK 31

5.8. ábra. Időformátumok

5.9. ábra. További időformátumok

5. FEJEZET. SZÁMFORMÁTUMOK 32

5.4. Számformátumkódok

Egyedi számformátumkódok használatával meghatározhatjuk, hogy milyen formában jelenjenek
meg a beírt számok a cellákban. Legfeljebb három, egymástól pontosvesszővel elválasztott formá­tumkódot határozhatunk meg egy cellára. Az első rész a pozitív értékekre, a második a negatívokra
és a harmadik a nullára fog vonatkozni. Akár feltételeket is megadhatunk a három részhez, a for­mátumkódok csak a feltételek teljesülésekor hatnak.

Számok jelölésére a nullát (0) vagy a kettős keresztet (#) használhatjuk helykitöltőként szám­formátumkódokban. A # csak a lényeges számjegyeket jeleníti meg, míg a 0, nullákat jelenít meg,
ha a kód több jegyből áll mint a beírt szám. Néhány számformátumkódot egyszerűen beállíthatunk
a Szám kategóriában (5.10 ábra).

5.10. ábra. Szám formátumkódok

Léptetőnyilak segítségével módosíthatjuk a tizedeshelyek és a vezető nullák számát. Az Ezres-
elválasztó bekapcsolása a ### kódrészletet hozza létre, ami ezres csoportokba rendezi a szám
egész részét. A Negatív számok pirossal kapcsoló a pontosvessző, színkód [RED] és a mínusz
jel után megismétli a számformátumot. Negatív számot írva a cellába az piros színű lesz, ezres cso­portosítású, két tizedes számjegyre kerekítve. Kettőnél kevesebb tizedes számjegy esetén, azokat
nullával helyettesíti.

Kérdőjel (?) felhasználásával létrehozhatunk formátumkódot, ami tört alakban jeleníti meg
a számot a cellában. A #?/? formátumkód és 2,5 cellatartalom esetén a cellában a következő
kifejezést fogjuk látni: 2 1/2.

5. FEJEZET. SZÁMFORMÁTUMOK 33

A tudományos számformátum segítségével nagyon nagy, vagy nagyon kicsi számok tömör meg­jelenítését valósíthatjuk meg. 200000000 (kétszázmillió) leírható 2*108módon is, amit a Calc a
következőképpen jelenít meg: 2,00E+8. A formátumkód ebben az esetben: 0,00E+#.

A következő formátumkód négy részből áll, a negyedik akkor fog végrehajtódni, ha a cellába
nem számot írunk. Ez hasznos lehet, hiszen figyelmezteti a felhasználót, ha az például a 0 számjegy
helyett O betűt ír:
[MAGENTA]###0" db";[RED]-###0" db";[GREEN]###0" db";"Ön nem számot írt!".

Tehát a formátumkód, pozitív számot beírva, azt ezres csoportosítással egészre kerekítve, bíbor
színnel jeleníti meg, a szám után szóköz és „db” karakterekkel. Negatív szám és nulla beírása
esetén a kódban megadott színnel jelennek meg a számok, a többi formátum ugyanaz mint pozitív
számnál. Szöveg beírásakor (pl. 5OO) a következő figyelmeztető üzenet jelenik meg: „Ön nem
számot írt!” Érdekes, hogy a kerekítés miatt az is előfordulhat, hogy három különböző színű „0
db”-t látunk a cellában. Ilyen számok pl. a -0,2; 0 és 0,2. Mindhárom szám egészre kerekítve a
cellában „0 db”-ként jelenik meg, de a színük bíbor, piros és zöld.

A Calcban a következő színkódokat használhatjuk: CYAN (cián), BLACK (fekete), MAGENTA
(bíbor), WHITE (fehér), GREEN (zöld), BLUE (kék), RED (piros) és YELLOW (sárga).

Meghatározhatunk olyan számformátumot, ami csak bizonyos feltétel esetén teljesül. A fel­tételekben számokat és matematikai operátorokat használhatunk. A Calc súgójában a következő
példát találjuk a feltételes számformátumra:

[BLUE][<0]#,0"◦C";[RED][>=30]#,0"◦C";[BLACK]#,0"◦C".

Ezt a formátumot alkalmazva egy cellára, a beírt negatív szám kék színű lesz, 0 és 30 fok között
fekete, 30 és annál nagyobb pedig piros. Mindhárom esetben a számok után megjelenik a „◦C”
kifejezés.

6. fejezet

Diagramok

Diagramok segítségével grafikusan ábrázolhatjuk a táblázatok számadatait. A diagramok automati­kusan követik a táblázat változásait. A Calc az adatok módosítását követően újraépíti a diagramot.
Többféle diagramtípus közül választhatunk és az elkészült diagramokat utólag is módosíthatjuk.

6.1. Diagramtündér használata

A Beszúrás menü vagy a Standard eszköztár Diagram parancsával kezdhetünk hozzá a diagram
elkészítéséhez. Mindkét esetben a Diagramtündér ablaka jelenik meg, ami végigvezet minket a
diagram elkészítésének négy lépésén. Megkönnyíti a diagram létrehozását, ha a Diagramtündér
indítása előtt kijelöljük azt a tartományt vagy tartományokat, amelyekből diagramunk felépül.

Nyissuk meg a calc01 munkafüzetet és a 4. feladat adatai alapján készítsünk diagramot, ami
a napi eladásokat mutatja. Jelöljük ki az A3:A6, majd a Ctrl billentyűt lenyomva tartva a D3:H6
tartományt (6.1 ábra).

6.1. ábra. Diagram készítése – tartomány kijelölése

Indítsuk el a Diagramtündért. Az első lépésben kiválaszthatjuk a diagram típusát és azon belül
az altípust. A számadatok típusa általában meghatározza a választható kategóriákat. Válasszuk
az Oszlop diagramtípust és a Halmozott altípust (6.2 ábra).

A diagramtündér használata közben a munkalapon kék színnel vannak kiemelve a kiindulási
cellák, és láthatjuk az e cellák adatai alapján létrejött, általunk választott típusú diagramot is.
Figyeljük meg, hogyan változik a diagram a normál és a halmozott altípust választva.

A Shift+F1 billentyűkombináció segítségével, a Diagramtündér ablakának elemeiről részletes
magyarázatot olvashatunk, ha az egér mutatóját az adott elemre vezetjük.

6. FEJEZET. DIAGRAMOK 35

6.2. ábra. Diagram készítése – diagramtípusok

A Tovább gombra kattintva a Diagramtündér második lépése, az Adattartomány következik
(6.3 ábra). Itt kijelölhetjük, vagy módosíthatjuk a diagram forrását.

6.3. ábra. Diagram készítése – adattartomány

Esetünkben az adattartomány két, pontosvesszővel elválasztott, abszolút címzésű cellatarto­mány, ahol a cellacímek előtt a munkalap nevét látjuk. Tehát a $Bevétel.$A$3:$A$6 hivatkozás
a Bevétel nevű munkalap A3:A6 tartományát jelöli abszolút címzéssel. Így hivatkozhatunk mun­kalapok között cellatartományokra a Calckal.

Amennyiben szükséges, hozzáadhatunk adattartományt pontosvesszőt írva a meglévők után és
az Adattartomány kijelölése gombra kattintva (a 6.3 ábrán az egér rá mutat). A Ctrl billentyűt
lenyomva tartva egérrel adhatunk meg további tartományokat.

Ebben a feladatban attól függően, hogy az Adatsorok sorokban vagy az Adatsorok osz-
lopokban választókapcsoló közül melyik aktív, a diagram vízszintes tengelyére a péksütemények

6. FEJEZET. DIAGRAMOK 36

nevei vagy a hét napjai kerülnek. Válasszuk az Adatsorok sorokban kapcsolót.

Az első sor legyen címke és Az első oszlop legyen címke kapcsolók automatikusan aktívak
mert a kijelölt területen az első sor és az első oszlop cellái szöveges információt tartalmaznak.

A következő lépés az Adatsorok (6.4 ábra). Ebben az ablakban az adatsorok sorrendjét mó­dosíthatjuk, és ha szükséges, újabb adatsorokat adhatunk a diagramhoz.

6.4. ábra. Diagram készítése – adatsorok

Az adatsorok valamelyikét választva látjuk, hogy melyik cellatartomány tartalmazza az adott
adatsor számértékeit és melyik cellában van az adatsor neve.

A Kategóriák részben látható cellatartomány a diagramon az X tengely felirata lesz. Esetünk­ben a hét napjai kerüljenek Ehhez válasszuk az Adattartomány kijelölése kapcsolót és jelöljük
ki a D2:H2 tartományt.

6.5. ábra. Diagram készítése – diagramelemek

A diagramtündér utolsó, negyedik ablakában címet és alcímet adhatunk a diagramnak és a
tengelyeknek (6.5 ábra). Cellahivatkozást nem adhatunk meg, a szöveget közvetlenül kell beírni.

6. FEJEZET. DIAGRAMOK 37

A jelmagyarázat tartalma a forrástartomány első sorból vagy oszlopból, illetve az Adatsorok
párbeszédpanelen megadott tartományból áll. Diagramon belüli pozícióját választókapcsolókkal
állíthatjuk be. Megjelenítését ki is kapcsolhatjuk, de olyan diagramoknál, amikor az adatsor értékek
tartománya több cellából áll, fontos információt hordoz. Esetünkben a halmozott oszlopdiagram
különböző színnel jelölt elemeinek magyarázatául szolgál.

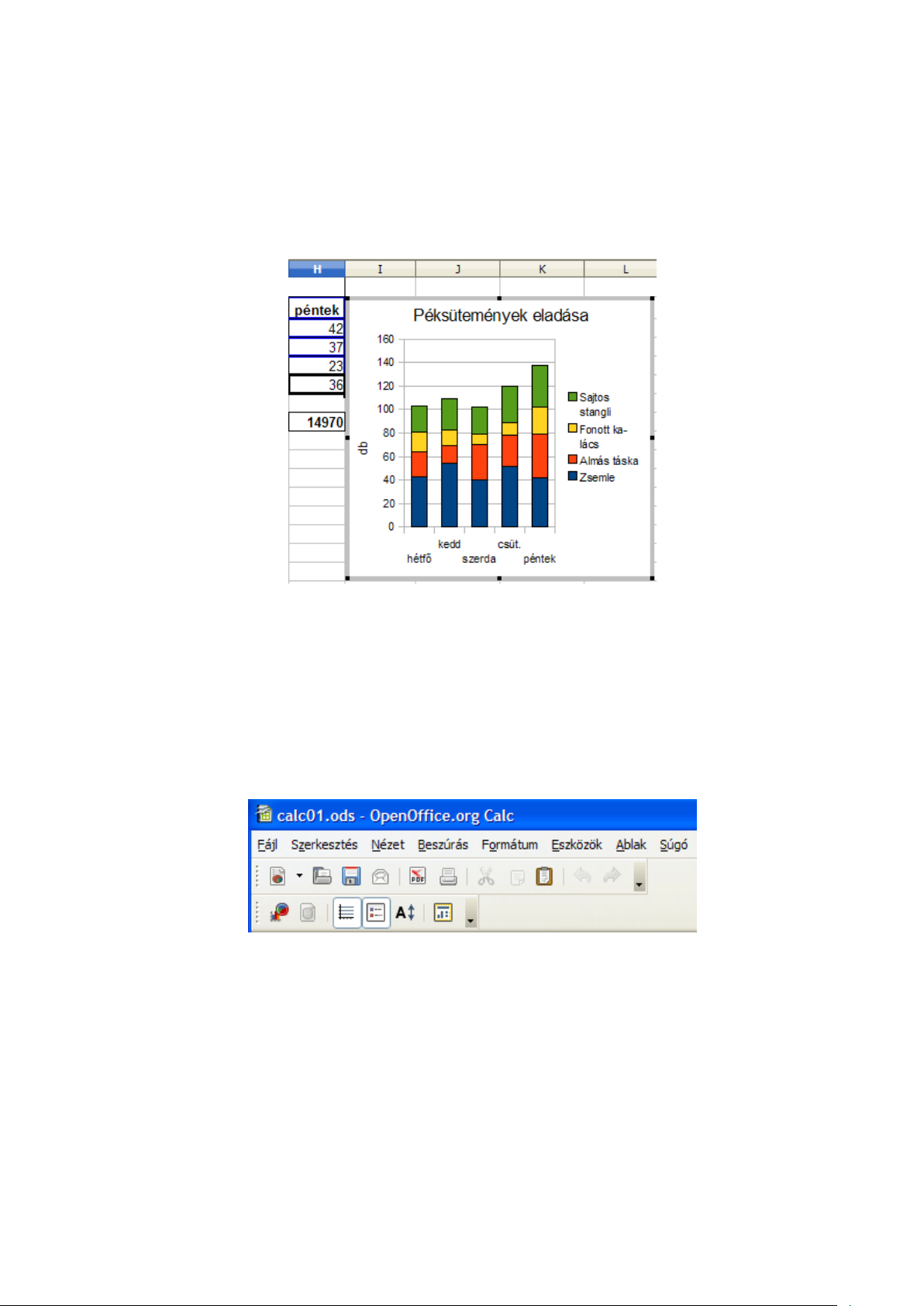
A Befejezés gombra kattintva megjelenik a munkalapon a diagram (6.6 ábra).

6.6. ábra. Diagram

Az elkészült diagramról a péksütemények napi eladásait olvashatjuk le. Az x tengelyen feltün­tetett napokhoz egy-egy oszlop tartozik, amelyek magassága az eladások összegének a darabszámát
mutatja az adott napon. Az oszlop különböző színű részekből áll, amelyek arányosak egyes termékek
napi eladásával. A színek magyarázatát a jelmagyarázatban találjuk.

A diagram diagramszerkesztési nézetben jelent meg. Ilyenkor a menüsor és az eszköztár is
átalakul (6.7 ábra).

6.7. ábra. Diagram szerkesztési menü

A munkalapra kattintva kilépünk a diagramszerkesztési nézetből, így módosíthatjuk a diagram
méretét és a munkalapon elfoglalt pozícióját.

6.2. A diagram módosítása

Az elkészült diagramot formailag, tartalmilag egyszerűen módosíthatjuk. A diagramra kettőt kat­tintva diagramszerkesztési nézetbe jutunk, ahol a gyorsmenüből (jobb egérgomb), vagy a 6.7 ábrán
látható menüsor és eszköztár parancsaival módosíthatjuk azt.

6. FEJEZET. DIAGRAMOK 38

A módosítandó diagramelemet kijelölve és azon kettőt kattintva, az adott elem tulajdonságait
mutató ablak jelenik meg, ahol elvégezhetjük a szükséges módosításokat.

6.3. 10. feladat

A 4. feladat adatai alapján készítsünk tortadiagramot, ami a keddi eladásokat mutatja. Módosítsuk
az elkészült diagramot a 6.8 ábrának megfelelően.

6.8. ábra. 10. feladat

A diagram építését kezdjük a diagramtündér indításával. Gyakorlásképpen az adattartományt
is itt adjuk meg. Az első lépésben válasszuk a Torta diagramtípust, Normál altípust és kapcsol-
juk be a Térhatású kapcsolót is. A második lépést az Adattartomány kijelölése paranccsal
kezdjük és jelöljük ki a péksütemények neveit. Ezután válasszuk ismét az Adattartomány kijelölé­sét, írjunk pontosvesszőt a hivatkozás után és a Ctrl billentyűt lenyomva tartva jelöljük ki a keddi
számadatokat (6.9 ábra).

6.9. ábra. 10. feladat – adattartomány

Kapcsoljuk ki Az első sor legyen címke kapcsolót. Monitorunk felbontásától függően a
diagramtündér ablaka takarhatja a készülő diagramot. Az ablakot a címsávnál fogva helyezhetjük
át ideiglenesen, hogy ellenőrizhessük a diagramot.

A harmadik ablakban semmit sem kell módosítani, kattintsunk a tovább gombra. A negyedikben
írjuk be a címet és az alcímet, a jelmagyarázat helye legyen Alul.

6. FEJEZET. DIAGRAMOK 39

A kész diagramot helyezzük át a munkalapon a táblázat alá és növeljük meg a méretét. Kettős
kattintással váltsunk diagramszerkesztési nézetre és a Formátum menü Térbeli nézet ablakának
Megjelenés fülén kapcsoljuk be az Árnyalást és az Objektumszegélyeket (6.10 ábra).

6.10. ábra. 10. feladat – térbeli nézet

A tortadiagram egyik adatpontjának módosításához ki kell jelöljük azt. Kettős kattintással,
a gyorsmenü segítségével (6.11 ábra), vagy a Formátum menüpont Objektum tulajdonságai
ablakban válasszuk a Terület fület.

6.11. ábra. 10. feladat – Objektum tulajdonságai

6. FEJEZET. DIAGRAMOK 40

Válasszuk a Szín kategóriából a Szürke 10%-ot. Fekete-fehér nyomtató estén hasznos lehet a
Vonalkázás kategória, de választhatunk díszes Színátmenetet és Bitképet is.

Hasonlóképpen módosítsuk a Jelmagyarázat tulajdonságait. A Karakterek fülön válasszunk
10 pt betűméretet és Arial betűtípust. A Szegélyek fülön Folyamatos stílust.

A diagram címének betűmérete legyen 14 pt és félkövér formátumú.

A Beszúrás menüpont Adatfeliratok ablakában kapcsoljuk be az adatsorok mellett a száza­lékérték megjelenítését is (6.12 ábra).

6.12. ábra. 10. feladat – adatfeliratok

A százalékértékek betűméretét módosítsuk 12-re, majd a legnagyobb százalékértéket (50%)
külön is kijelölve 14-re és félkövér betűstílusra.

A diagramterületet kijelölve állítsunk be folyamatos stílusú szegélyvonalat.

6.4. Pont (XY) diagram építése

Pont diagram segítségével értékpárokat (x, y) ábrázolhatunk. Ez az a diagramtípus, amelyik segít­ségével matematikai függvények grafikonjait is megrajzolhatjuk.

6.5. 11. feladat

Ábrázoljuk diagramon az y = a + (b + x)2függvény grafikonját az x -10, -9, . . . , 10 értékeinél. Az
a és a b értékeket a B1, B2 cella tartalmazza.

A diagram építéséhez először az x értékek oszlopát hozzuk létre. Írjuk az A5 cellába -10-et.
Automatikus kitöltéssel lefelé a Calc segít nekünk a számoszlop létrehozásában (6.13 ábra).

Az y értékek kiszámításánál a képlet =B$1+(A5+B$2)ˆ2 lesz, hiszen az x értéknek változnia
kell automatikus kitöltésnél, az a és b értékek pedig állandóak (64. ábra).

A diagramtípus kiválasztásánál az Pont (XY) típust és Csak vonalak altípust válasszuk. A
Sima vonalak kapcsoló legyen aktív. A Diagramelemek ablakban a jelmagyarázatot kikapcsol­hatjuk, hiszen csak egy adatsorunk van. A rácsot kapcsoljuk be az X tengelyre is (6.14 ábra).

6. FEJEZET. DIAGRAMOK 41

6.13. ábra. 11. feladat

6.14. ábra. 11. feladat – Megoldás

7. fejezet

Logikai függvények. Beágyazott függvények használata

7.1. A HA függvény

Az egyik leggyakrabban használt logikai függvény a HA. Egy logikai vizsgálat eredményétől füg­gően más-más értéket ad eredményül. Három argumentuma van, az első kötelező, a második és a
harmadik elhagyható. Szintaxisa:
=HA(teszt; akkor_érték; különben_érték).

Az első paraméter logikai kifejezés, tetszőleges érték, illetve kifejezés, amely IGAZ vagy HAMIS
értéket vehet fel. Ebben az argumentumban a Calc bármelyik összehasonlító operátorát használ­hatjuk. Ezeket a 7.1 táblázatban láthatjuk.

7.1. táblázat. Összehasonlító operátorok

Operátor Név

= Egyenlő
> Nagyobb mint

< Kisebb mint
>= Nagyobb vagy egyenlő
<= Kisebb vagy egyenlő
<> Nem egyenlő

A 7.1 ábrán látjuk, hogy a HA függvény az A1 cella tartalmától függően a B1 cellában a
„Felvételt nyert” vagy az „elutasítva” szöveget jeleníti meg. Megvizsgálja, hogy a teszt eredménye
igaz, vagy hamis. Igaz esetén a második paraméterben megadott szöveg jelenik meg, hamis esetén
a harmadikban.

Az első paraméter kötelező, a függvénytündér az ilyen paramétereket félkövér formázással jele­níti meg. A második és a harmadik nem ilyen, ezeket opcionális vagy elhagyható paramétereknek
nevezzük. Esetünkben ha elhagynánk a második és a harmadik paramétert, az IGAZ vagy a HAMIS
kifejezések valamelyike jelenne meg a B1 cellában.

7.2. Egyéb logikai függvények

Az ÉS logikai függvény akkor ad IGAZ eredményt, ha minden argumentuma igaz. Például az
=ÉS(A1>5; A2>5) eredménye akkor IGAZ, ha mind az A1, mind az A2 tartalma nagyobb mint
öt. Más esetben HAMIS.

7. FEJEZET. LOGIKAI FÜGGVÉNYEK. BEÁGYAZOTT FÜGGVÉNYEK HASZNÁLATA 43

7.1. ábra. HA függvény

A VAGY logikai függvény IGAZ értéket ad vissza, ha legalább egy argumentuma igaz. Például
a =VAGY(A1>5; A2>5) eredménye IGAZ, ha a két cella közül legalább az egyik nagyobb mint öt.

A NEM logikai függvény megfordítja a logikai értéket.

7.3. 12. feladat

7.2. ábra. 12. feladat

A 7.2 ábrán egy osztály tanulóinak osztályzatait és magaviseleti eredményeit látjuk. Készítsük
el a képen látható táblázatot a megfelelő formázásokkal. Számítsuk ki minden tanuló átlagát az
I oszlopban és a tantárgyak átlagát a 11. sorban. Az M oszlopban jelenjen meg a „Könyvjutalom”
szó azoknál a tanulóknál, akik átlaga jobb mint 4,5 és magviselete Jó vagy Példás.

7. FEJEZET. LOGIKAI FÜGGVÉNYEK. BEÁGYAZOTT FÜGGVÉNYEK HASZNÁLATA 44

Mentsük a munkafüzetet calc03 néven, a munkalap neve legyen Osztály.

Az átlagértékek kiszámítása után a K2 cellában válasszuk a függvénytündért.

Esetünkben a HA, az ÉS és a VAGY függvényt is használni kell, hogy a feladatot megoldjuk.
A HA függvény első argumentuma, le kell hogy ellenőrizze, hogy a tanuló megfelel-e a kritériu­moknak. Ezek a kritériumok logikai függvényekkel meghatározhatók. Tehát, a HA függvény első
argumentuma egy másik függvény lesz. A teszt szó utáni fxfeliratú gomb ezt teszi lehetővé, ezzel
a függvénybe további függvényeket is beágyazhatunk.

Amikor egy függvény argumentumaként függvényt használunk, azt beágyazott függvénynek ne­vezzük.

7.3. ábra. 12. feladat – HA függvény

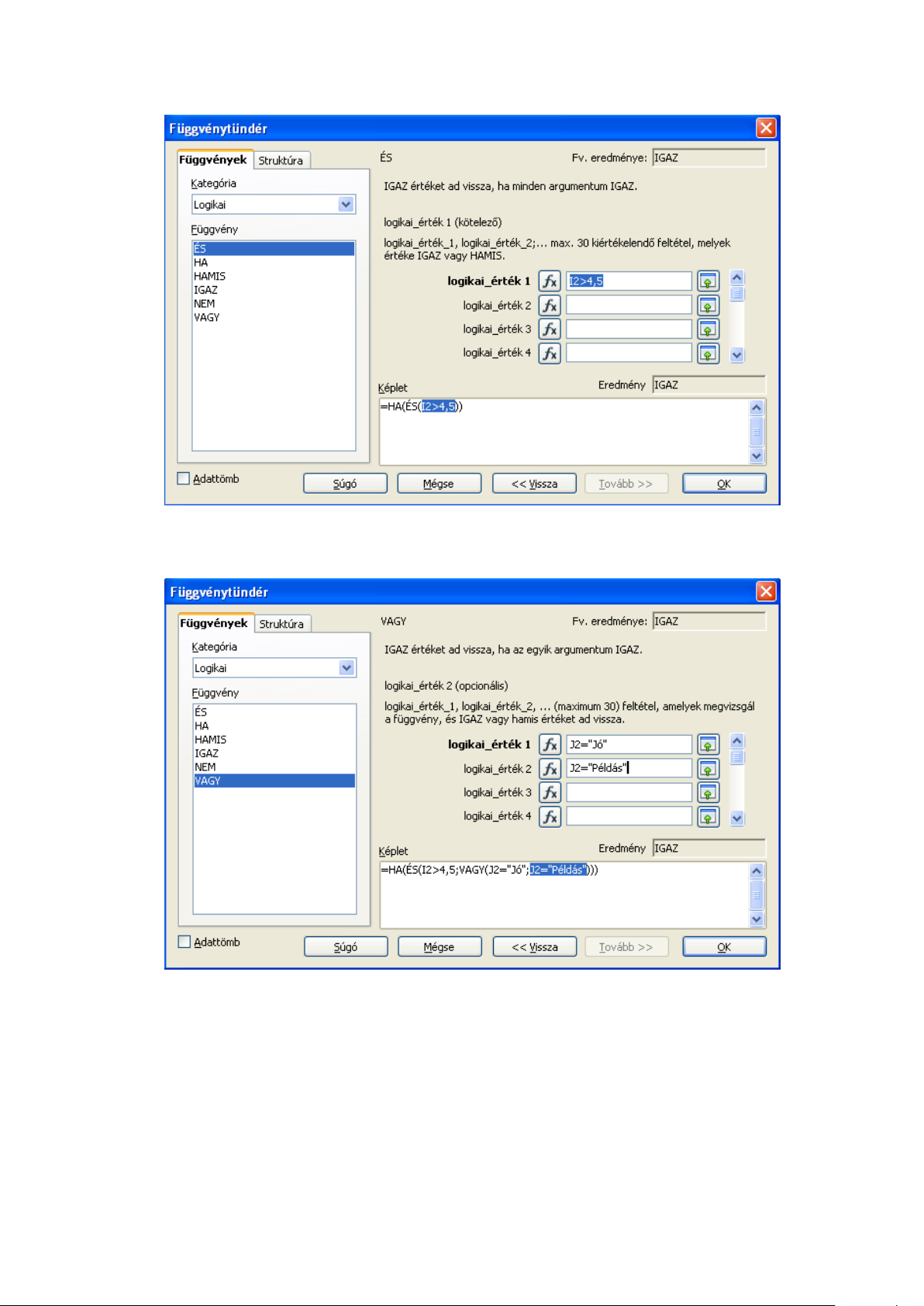
Kattintsunk az fxfeliratú gombra (7.3 ábra). A könyvjutalom elnyeréséhez egyszerre két fel­tételnek kell megfelelnie a tanulónak, vagyis az ÉS függvényt kell használnunk. Az egyik feltétel
az, hogy a tanuló átlaga jobb mint 4,5 (7.4 ábra). A másik feltétel viszont arról szól, hogy a két
lehetőség közül bármelyik esetén jár a könyvjutalom. Ismét beágyazott függvényt kell használnunk.

Az ÉS függvény második paraméterének sorában válasszuk az fxfeliratú kapcsolót és a VAGY
függvényt.

A függvények megkeresését megkönnyíti, hogy az első kezdőbetűket leütve a Calc kiválasztja
az adott függvényt. Leginkább akkor hasznos, amikor egy függvényről nem tudjuk, hogy melyik
függvénykategóriában található.

Írjuk be a VAGY függvény argumentumait (7.5 ábra).

A függvénytündér Képlet ablakában látjuk az eddigi lépések eredményeként létrehozott képletet.
Ezek között bármelyik függvényre kattintva újra módosíthatjuk azok argumentumait. Válasszuk a
HA függvényt és írjuk be a két argumentumot (7.6 ábra).

Az akkor_érték „Könyvjutalom” lesz, a különben_érték mezőbe pedig írjunk két idézőjelet.
Így a K oszlopban vagy a Könyvjutalom szó jelenik meg, vagy üres marad a cella. Amennyiben
nem írnánk semmit a harmadik paraméterhez, a HAMIS szó jelenne meg az üres cella helyett.

Másolással töltsük ki a K3:K10 tartományt.

A Calc igen áttekinthetően és látványosan jeleníti meg a beágyazott függvényeket. Válasszuk

7. FEJEZET. LOGIKAI FÜGGVÉNYEK. BEÁGYAZOTT FÜGGVÉNYEK HASZNÁLATA 45

7.4. ábra. 12. feladat – HA függvény argumentumok

7.5. ábra. 12. feladat – VAGY függvény

ismét a K2 cellát és kattintsunk a függvénytündér ikonjára. A Függvénytündér a képlet struktúráját
mutatja (7.7 ábra).

A Struktúra ablakban grafikusan látjuk a beágyazott függvényeket és azok argumentumait.
Bármelyiket választva a jobboldali ablakban látjuk az adott függvény részletes beállításait és ered­ményét is. A 7.7 ábrán látható, hogy az adott argumentumokkal a VAGY függvény eredménye

7. FEJEZET. LOGIKAI FÜGGVÉNYEK. BEÁGYAZOTT FÜGGVÉNYEK HASZNÁLATA 46

7.6. ábra. 12. feladat

7.7. ábra. 12. feladat – függvénytündér

IGAZ, a teljes képlet pedig a „Könyvjutalom” eredményt adja.

7. FEJEZET. LOGIKAI FÜGGVÉNYEK. BEÁGYAZOTT FÜGGVÉNYEK HASZNÁLATA 47

7.4. A SZUMHA és a DARABTELI függvények

Ezt a két függvényt nem a logikai, hanem a matematikai függvények kategóriájában találjuk, de
mivel mindkettő feltételt tartalmaz, tekintsük át használatukat ebben a fejezetben.

A SZUMHA függvény segítségével összeadhatjuk a megadott feltételnek megfelelő cellákat.
Szintaxisa: SZUMHA(tartomány; feltételek; összegtartomány).

A harmadik paraméter elhagyható, ha a feltétel az összegtartományra vonatkozik. Például a
=SZUMHA(A1:A10;">5") függvény az A1:A10 tartomány cellái közül azokat adja össze, melyek
nagyobbak ötnél.

A 7.8 ábrán látható példán azokat a cellákat adja össze a SZUMHA függvény az összegtarto­mányból, amelyek fölött esetünkben az „alma” szó szerepel.

7.8. ábra. SZUMHA függvény

A DARABTELI függvénnyel összeszámolhatjuk egy tartomány bizonyos feltételnek megfelelő
elemeit.

Szintaxisa: DARABTELI(tartomány; feltételek). Mindkét paraméter kötelező.

Például a =DARABTELI(A1:A10;">5") megadja, hogy hány olyan cella van az A1:A10 tarto­mányban, amelyek ötnél nagyobb számot tartalmaznak.

7.5. 13. feladat

A 12. feladatot bővítsük két sorral. A 12. sorban számítsuk ki a lányok átlagát, a 13-ban pedig a
fiúk átlagát minden tantárgyra.

Ahhoz, hogy a D12 cellában kiszámítsuk a lányok átlagát kémiából, össze kell adni a lányok
jegyeit és elosztani a lányok számával az osztályban.

A SZUMHA függvénnyel összeadjuk azokat a számokat a D oszlopból, amelyek mellett „L”
betű van (7.9 ábra).

A képlet után törtvonalat írva a DARABTELI függvénnyel meghatározzuk az „L” betűk da­rabszámát (7.10 ábra).

A képlet jobbra másolása előtt állítsuk be a megfelelő vegyes cellahivatkozásokat. A végleges
képlet a 7.11 ábrán látható.

A fiúk átlagát megadó képlet csak annyiban tér el a lányokétól, hogy a két „L” betűt „F”-re kell
cserélni. Ezért egyszerűbb a D12-ben lévő képletet a beviteli sorban kijelölni, másolni (Crtl+C),
majd a D13 cellába beilleszteni (Ctrl+V). Módosítva az említett argumentumot másoljuk jobbra a
képletet.

Az ebben a fejezetben tárgyalt függvényeket a 7.2 táblázatban találjuk meg.

7. FEJEZET. LOGIKAI FÜGGVÉNYEK. BEÁGYAZOTT FÜGGVÉNYEK HASZNÁLATA 48

7.9. ábra. 13. feladat – SZUMHA függvény

7.10. ábra. 13. feladat – DARABTELI függvény

7.11. ábra. 13. feladat – megoldás

7. FEJEZET. LOGIKAI FÜGGVÉNYEK. BEÁGYAZOTT FÜGGVÉNYEK HASZNÁLATA 49

7.2. táblázat. A fejezetben tárgyalt függvények

A függvény Funkciója A függvény

neve angol neve

HA Logikai feltételvizsgálat. IF

ÉS

VAGY

NEM Az argumentum értékét ellentettjére állítja. NOT

SZUMHA

DARABTELI

Igaz értéket ad vissza, ha minden argumentuma
igaz.
Igaz értéket ad vissza, ha egyik argumentuma
igaz.

Összeadja a megadott feltételnek megfelelő ar­gumentumokat.
Megszámolja a tartomány megadott feltételek­nek megfelelő elemeit.

AND

OR

SUMIF

COUNTIF

8. fejezet

Matematikai függvények

8.1. Egyszerűbb matematikai függvények

Az ABS függvény egy szám abszolút értékét számítja ki. Tehát negatív argumentum esetén a
függvény eredménye pozitív. Például: ABS(-7)=7.

A FAKT függvény kiszámítja egy szám faktoriálisát. Definíció szerint 4!=1*2*3*4.

Az INT függvény a legközelebbi egészre kerekít le egy számot. A negatív számok lefelé kerekí­tődnek a legközelebbi egészre. Például: INT(5,6)=5 és INT(-5,6)=-6.

A PÁROS függvény pozitív szám legközelebbi páros egészre felkerekített értékét, illetve egy ne-
gatív szám legközelebbi páros egészre lekerekített értékét adja eredményül. Például: PÁROS(4,6)=6
és PÁROS(-4,6) eredménye -6.

A PÁRATLAN függvény pozitív szám legközelebbi páratlan egészre felkerekített értékét, il-
letve egy negatív szám legközelebbi páratlan egészre lekerekített értékét adja eredményül. Például:
PÁRATLAN(4,6)=5 és PÁRATLAN(-4,6) eredménye -5.

A KITEVŐ függvény. Az e-t a megadott hatványra emeli. Az e állandó értéke megközelítőleg
2,71828. A KITEVŐ(1) eredménye maga az e szám.

A GCD függvény kiszámítja két vagy több egész szám legnagyobb közös osztóját. A legna­gyobb közös osztó az a legnagyobb pozitív egész szám, amellyel maradék nélkül osztható az összes
megadott egész szám. Például: a GCD(60;12;16) eredménye 4.

Az LCM függvény kiszámítja két vagy több szám legkisebb közös többszörösét. Például
LCM(18;30) eredménye 90, mert ez a legkisebb szám, ami mind a 18-al, mind a 30-al maradék
nélkül osztható.

Az ISEVEN függvény IGAZ értéket ad vissza, ha a szám páros egész, HAMIS értéket, ha
páratlan.

Az ISODD függvény IGAZ értéket ad vissza, ha a szám páratlan, HAMIS értéket, ha a szám
páros.

A HATVÁNY függvény hatványoz egy számot. Például a HATVÁNY(12;2) eredménye egyenlő
12ˆ2, tehát 144.

A SZORZAT függvény összeszorozza az argumentumban megadott számokat, eredményül a
szorzatot adja.

A MARADÉK függvény a maradékot adja eredményül egy egész szám másik egész számmal
való osztása után. Például MARADÉK(18;7) eredménye 4, mert a 18/7 osztás utáni maradék 4.

A KEREK függvény egy szám meghatározott számú tizedesjegyre kerekített értékét adja ered­ményül. Például KEREK(4,155;2) eredménye 4,16 lesz. Fontos tudni, hogy a cellaformátum mó­dosításával is elérhetjük ugyanezt az eredményt, de a cella valódi tartalma nem változik. Amikor
hivatkozunk rá, akkor az eredeti tartalmával fog számolni a Calc.

A GYÖK függvény egy szám négyzetgyökét számítja ki.

8. FEJEZET. MATEMATIKAI FÜGGVÉNYEK 51

A CSONK függvény levágja a szám tizedesjegyeit. Például CSONK(4,155;2) eredménye 4,15.
A második argumentum nem kötelező, elhagyva minden tizedesjegyet eldob: CSONK(4,155) = 4.

8.2. 14. feladat

Oldjuk meg, hogy az A1 cellába beírt, 1000-nél nem nagyobb pozitív egész számról a PRÍM szöveg
jelenjen meg az A2 cellában, ha a szám prímszám. Amennyiben a szám nem prím, ugyanebben a
cellában jelenjen meg az osztóinak a száma.

Az A1 cella csak az 1, 2, . . . , 1000 tartományból fogadjon értékeket.

A prímszámok csak eggyel és önmagukkal oszthatók maradék nélkül. A feladat tehát az, hogy
megállapítsuk egy számról, két osztója van. A definíció szerint az 1-et nem soroljuk a prímszámok
közé.

A calc03 munkafüzet második munkalapját nevezzük át „prím”-re. Írjunk egy tetszőleges, 1000­nél kisebb egész számot az A1 cellába. A B oszlopban hozzunk létre számoszlopot 1000-ig a 10.
feladatban tárgyalt módon. A C oszlopban pedig számítsuk ki az A1 cellába írt szám és a B oszlop
megfelelő elemének hányadosát (8.1 ábra).

8.1. ábra. 14. feladat

A C oszlopban mind az 1000 értéket kiszámíthatjuk, ha kettőt kattintunk a cella jobb alsó
részében megjelenő célkereszttel. Ilyenkor a Calc addig másolja a képletet, amíg a B oszlopban
kitöltött cellákat talál.

Kaptunk egy számoszlopot, amely egész számokból és tizedes törtekből áll. Az egész számok
darabszáma megadja az osztók számát. Ahhoz, hogy ezt meghatározzuk, a D oszlopban számítsuk
ki a C oszlop értékeinek egész részét a CSONK függvényt használva. Az E oszlopban pedig a
HA függvényt felhasználva jelenítsünk meg 1-et, ha a tőle balra lévő két cella tartalma egyenlő,
ellenkező esetben pedig 0-t. (8.2 ábra).

Az E oszlop összege megadja az A1-be írt szám osztóinak a számát. Az F1 cellában a SZUM
függvénnyel számítsuk ezt ki. A HA függvénnyel jelenítsük meg a PRÍM szöveget, ha az osztók
száma kettő (8.3 ábra).

Az A3 cellában megjeleníthetjük az „osztója van” szöveget is, abban az esetben, ha nem prím
számot írunk az A1 cellába. Prímszám esetén a cella üres marad (8.4 ábra).

A MARADÉK és a DARABTELI függvények segítségével egyszerűbben is megoldható a feladat.
Ezt végezzük el önállóan!

Ezernél nagyobb számot írva az A1 cellába hibás eredményt kaphatunk. A Calcban egyszerűen
megoldható, hogy cellába csak a megadott tartományból írhassunk be számot. Ehhez válasszuk az
Adatok menüpont Érvényesség parancsát. Állítsuk be a 8.5 ábrán látható értékeket.

Kapcsoljuk be a hibaüzenet megjelenítését és a Műveletek közül válasszuk a Leállítást (8.6
ábra).

8. FEJEZET. MATEMATIKAI FÜGGVÉNYEK 52

8.2. ábra. 14. feladat – HA

8.3. ábra. 14. feladat – PRÍM

8.4. ábra. 14. feladat – Van osztója

A Hibaüzenet szövegét megadva az fog megjelenni nem megfelelő tartalom beírása esetén (8.7
ábra).

8.3. 15. feladat

Az A2 és a A3 cellákba írt pozitív egész számokból kialakított törtet egyszerűsítsük a legnagyobb
közös osztóval. Amennyiben a kapott tört áltört, azt alakítsuk át vegyes törtté. Ebben az esetben a
D1 cellában jelenjen meg az „Áltört” szöveg. Amennyiben A2 és az A3 hányadosa egész szám, azt
is számítsuk ki, és a D1 cellában jelenjen meg az „Egész” szöveg.

A calc03 munkafüzet harmadik munkalapját nevezzük át tört-re. Az A2 cellába írjunk hatot,
az A3 cellába négyet. Amikor a két szám legnagyobb közös osztója eggyel egyenlő, „A tört nem
egyszerűsíthető” szöveg jelenik meg az A5 cellában. Ellenkező esetben az „A tört egyszerűsíthető”
szöveg (8.8 ábra), valamint D5 cellában megjelenik a GCD függvény eredménye is.

A D5 tartalma: =HA(GCD(A2;A3)<>1;GCD(A2;A3);"").

8. FEJEZET. MATEMATIKAI FÜGGVÉNYEK 53

8.5. ábra. 14. feladat – Érvényesség, feltételek

8.6. ábra. 14. feladat – Érvényesség, figyelmeztetés

Amikor az egyszerűsített tört számlálója nagyobb mint a nevezője, a D1 cella az „Áltört”
szöveget mutatja. Az „egész” szöveg jelenik meg, ha a nevező értéke 1, valódi tört esetén pedig
üres marad. A 8.9 ábrán látjuk, hogy ezt két egymásba ágyazott HA függvénnyel egyszerűen
megoldhatjuk.

Valódi tört beírásakor a D2 cellában az egyenlőség jele sem jelenik meg (8.10 ábra).

Az E2 cella tartalma csak akkor számítódik ki, ha a D2 egyenlőségjelet tartalmaz.

Az E2 tartalma: =HA(D2="=";CSONK(C2/C3);"").

8. FEJEZET. MATEMATIKAI FÜGGVÉNYEK 54

8.7. ábra. 14. feladat – Hibaüzenet

8.8. ábra. 15. feladat

8.9. ábra. 15. feladat – Egymásba ágyazott HA függvények

8.10. ábra. 15. feladat – Valódi tört

Az F2 és az F3 pedig csak áltört esetén:

Az F2 cella tartalma: =HA(D1="Áltört";C2-E2*F3;"").

Az F3 cella tartalma: =HA(D1="Áltört";C3;"").

8. FEJEZET. MATEMATIKAI FÜGGVÉNYEK 55

8.4. Logaritmusfüggvények

Az LN függvény kiszámítja egy szám „e” állandón alapuló természetes logaritmusát. Az e állandó
értéke megközelítőleg 2,71828182845904.
A LOG függvény szám megadott alapú logaritmusát adja eredményül. Szintaxisa: LOG(szám;alap)
A LOG10 függvény kiszámítja a szám tízes alapú logaritmusát.

8.5. 16. feladat

Számítsuk ki az A2:A76 tartományba létrehozott 0,1, 0,2, . . . , 7,5 értékeknél a következő függvények
eredményeit: log2(x), ln(x), log10(x), log

Az A2:A76 tartomány számadatainak létrehozásához írjuk be az első két értéket, ezeket kijelölve
és lefelé másolva (8.11 ábra) a Calc kitölti a tartományt.

(x) Építsük meg a függvények grafikonjait.

0,5

8.11. ábra. 16. feladat

A B1, C1, D1 és E1 cellákba írjuk a függvények neveit, és számítsuk ki az értékeket. A diagram­tündér segítségével könnyen elkészíthetjük a diagramot, előzőleg kijelölve az A2:E76 tartományt
(8.12 ábra).

8.6. Trigonometrikus függvények

A Calc beépített függvényei között megtaláljuk a trigonometrikus függvényeket és azok inverzeit is.
A fontosabb trigonometrikus, valamint azokkal kapcsolatos függvényeket a 8.1 táblázat mutatja.

8. FEJEZET. MATEMATIKAI FÜGGVÉNYEK 56

8.12. ábra. 16. feladat – grafikon

8.1. táblázat. A legfontosabb trigonometrikus függvények

SIN Kiszámítja egy radiánban adott szög szinuszát.

COS

SINH Kiszámítja egy szám szinusz hiperbolikuszát.
COSH Kiszámítja egy szám koszinusz hiperbolikuszát.
TAN Kiszámítja egy radiánban adott szög tangensét.
TANH Kiszámítja egy szám tangens hiperbolikuszát.

PI

RADIÁN Átszámítja a fok értéket radiánra.

Kiszámítja egy radiánban adott szög koszinu­szát.

A π matematikai állandó 14 tizedesjegy­re kerekített értékét adja vissza, ami
3,14159265358979.

8. FEJEZET. MATEMATIKAI FÜGGVÉNYEK 57

8.7. 17. feladat

Ábrázoljuk Pont(XY) diagramon az y = a ∗ sin(c ∗ (b + α)) függvény grafikonját a [-360; +360]
intervallumon. Az a, b és c értékeket az E1, H1 és K1 cellák tartalmazzák.

Az A2:A74 tartományban hozzuk létre az α értékeket. A függvény értékeinek kiszámításánál a
megfelelő cellahivatkozásoknál használjunk abszolút cellacímzést, és ne feledjük, hogy a fokértékeket
át kell alakítani radiánra (8.13 ábra).

8.13. ábra. 17. feladat – grafikon

Az ebben a fejezetben tárgyalt függvényeket a 8.2 táblázatban találjuk meg.

8. FEJEZET. MATEMATIKAI FÜGGVÉNYEK 58

8.2. táblázat. A fejezetben tárgyalt függvények

A függvény Funkciója A függvény

neve angol neve

ABS Egy szám abszolút értékét számítja ki. ABS
FAKT Egy szám faktoriálisát számítja ki. FACT
INT A legközelebbi egészre kerekít egy számot. INT
PÁROS
PÁRATLAN
KITEVŐ
GCD Legnagyobb közös osztó kiszámítása. GCD
LCM Legkisebb közös többszörös kiszámítása. LCM
ISEVEN Igaz értéket ad vissza, ha a szám páros. ISEVEN
ISODD Igaz értéket ad vissza, ha a szám páratlan. ISODD
HATVÁNY

SZORZAT

MARADÉK
KEREK Meghatározott számú tizedesjegyre kerekít. ROUND
GYÖK Egy szám négyzetgyökét számítja ki. SQRT
CSONK Levágja a szám tizedesjegyeit. TRUNC
LN Természetes logaritmust számol. LN
LOG Megadott alapú logaritmust számol. LOG
LOG10 Tízes alapú logaritmust számol. LOG10
SIN Egy adott szög szinuszát számítja ki. SIN
COS Egy adott szög koszinuszát számítja ki. COS
SINH Egy szám szinusz hiperbolikuszát számítja ki. SINH
COSH Egy szám koszinusz hiperbolikuszát számítja ki. COSH
TAN Egy szög tangensét számítja ki. TAN
TANH Egy szám tangens hiperbolikuszát számítja ki. TANH
PI A π matematikai állandót adja meg. PI
RADIÁN

A legközelebbi páros egészre kerekít. EVEN
A legközelebbi páratlan egészre kerekít. ODD
Az e-t a megadott hatványra emeli. EXP

Hatványoz egy számot. POWER
Összeszorozza az argumentumban megadott
számokat.
Osztási maradékot jeleníti meg. MOD

Fokot radiánná alakít. RADIANS

PRODUCT

9. fejezet

Szövegfüggvények

Ebben a kategóriában több tucat függvényt találunk, amelyek segítségével szövegtartalmú cellákkal
végezhetünk különböző műveleteket.

Az ÖSSZEFŰZ függvény segítségével egyetlen karakterlánccá egyesíthetjük az argumentum­ban megadott karakterláncokat. Az argumentumok lehetnek cellahivatkozások is.

Az AZONOS összehasonlít két szöveges karakterláncot. Amikor azok megegyeznek, IGAZ
értéket ad vissza. Ez a függvény különbséget tesz kis- és nagybetűk között.

A SZÖVEG.KERES függvény egy szövegrész karakterláncon belüli helyzetét adja eredmé­nyül. A keresés kezdőpontját paraméterként adhatjuk meg. A keresés nem különbözteti meg a
kis- és nagybetűket. A SZÖVEG.KERES("m";"Mamut") eredménye 1 lesz, mert a Mamut szó első
karaktere m.

A SZÖVEG.TALÁL függvény szöveget keres egy másikban, és megadja, hogy hányadik ka-
raktertől kezdődik. Opcionális paraméterként megadható, hogy a keresés melyik karaktertől kez­dődjön. A keresés megkülönbözteti a kis- és nagybetűket. A SZÖVEG.TALÁL("m";"Mamut")
eredménye 3 lesz, mert a kis m betű harmadik a Mamut szóban.

A BAL függvény egy szöveg első karaktereit adja eredményül. A BAL("rendszer";4) eredménye
a „rend” szó lesz. A második paramétert el is hagyhatjuk, ilyenkor csak az első karaktert adja
eredményül.

A JOBB függvénnyel egy szöveg utolsó karaktereit jeleníthetjük meg. A JOBB("alma";2)
eredménye a „ma” szó lesz.

A KÖZÉP függvény egy karakterlánc egy darabját adja vissza. A kezdőpozíciót, illetve a
karakterek számát a paraméterek határozzák meg. A KÖZÉP("karaktereit";4;3) eredménye az
„akt” szó lesz.

A HOSSZ függvény egy szövegnek a szóközökkel együtt vett hosszát adja eredményül.

A KISBETŰ függvény argumentumában megadott szöveg minden nagybetűjét kisbetűre cse­réli.

A TNÉV függvény nagybetűsre változtatja egy szöveg minden szavának első betűjét.

A NAGYBETŰS függvény argumentumában megadott szöveg minden kisbetűjét nagybetűre
cseréli.

A HELYETTE függvénnyel megadott karaktereket, másikra cserélhetünk. Szintaxisa: HE­LYETTE(szöveg; keresendő szöveg; új szöveg; előfordulás).

A HELYETTE("Varga Pál";"Pál";"Péter") eredménye Varga Péter lesz, mert a függvény az első
argumentumban megadott szövegben lecseréli a „Pál” minden előfordulását „Péter”-re.

A CSERE függvény kicseréli egy karakterlánc részét egy másik karakterláncra. Szintaxisa:
CSERE(szöveg; pozíció; hossz; új szöveg) A CSERE("Számológép";5;2;"ít") eredménye Számítógép.
Az 5. pozíciótól két karaktert lecseréli az „ít” karakterekre.

A SZÖVEG függvény egy számot szöveggé alakít, megadott formátum szerint. Szintaxisa:
SZÖVEG(szám; formátum). A SZÖVEG(39676;"yyyy.mmmm dd.") függvény a cellában a követ-

9. FEJEZET. SZÖVEGFÜGGVÉNYEK 60

kező szöveget eredményezi: 2008.augusztus 16.

A TRIM függvény eltávolítja a szóközöket egy karakterláncból, a szavak között csak egy szóköz
marad.

A RÓMAI függvény konvertálja a számot római számmá. Az értéktartománynak 0-3999 kö­zött kell lennie. Szintaxisa: RÓMAI(szám; mód). A mód 0-4 közötti egész szám, ami az egysze­rűsítés mértékét jelöli. Minél nagyobb az érték, annál nagyobb a római szám egyszerűsítése. A
RÓMAI(1998;2) eredménye MXMVIII lesz.

Az ARABIC1függvény egy római szám értékét adja meg arab számként. Az értéktartomány­nak 0-3999 között szükséges lennie. Az ARABIC(MCLXV) eredménye 1165.

Az ÉRTÉK függvény egy szöveget számmá alakít. Általában akkor van szükség a használatára,
amikor egy szövegformátumú cella, számot tartalmazó értékével kell műveletet végrehajtani.

A & operátorral összefűzhetünk szövegeket egy cellában. A BAL("kézikönyv";4)&"labda" ered­ménye a „kézilabda” szó lesz.

9.1. 18. feladat

A munkafüzet A oszlopában nevek vannak. Függvények segítségével oldjuk meg, hogy a B oszlopban
a nevek az esetleges „dr. ” vagy „Dr. ” előtag nélkül jelenjenek meg. A nevek közé beírt fölösleges
szóközöket is távolítsuk el.

Kézenfekvő megoldásnak a HELYETTE függvény használata tűnne, amivel üres karakterre
cserélnénk a megadottakat. Ez a függvény viszont különbséget tesz kis- és nagybetűk között.

Vizsgáljunk meg egy másik megoldást. Ellenőrizzük le az A1 cella tartalmának első három
karakterét. Amennyiben ez egyenlő a „dr.” karakterekkel, a cellában csak a jobbról vett karakterek
jelenjenek meg, melyek száma az eredeti karakterek számától hárommal kevesebb. Ezt kiszámíthat­juk a HOSSZ(A1)-3 kifejéssel. A „dr.” nélküli cellatartalmat a JOBB(A1;HOSSZ(A1)-3) kifejezés
adja meg. A B1 tartalma tehát: =HA(BAL(A1;3)=”dr. ”;JOBB(A1;HOSSZ(A1)-3);A1) (9.1
ábra).

9.1. ábra. 18. feladat

Figyeljük meg a kifejezés struktúráját a Függvénytündér ablakában (9.2 ábra). Több beágyazott
függvény használatakor a kifejezés működését segít megérteni, ha kiválasztjuk valamelyik beágya­zott függvényt, és megvizsgáljuk argumentumait és eredményét.

A nevekből távolítsuk el a fölösleges szóköz karaktereket. Az eddigi kifejezés legyen a TRIM
függvény argumentuma. A feladat megoldása a 9.3 ábrán látható.

Jól látható, hogy mind a vezeték-, mind a keresztnév elé beírt szóközökből csak egy maradt a
B oszlopban.

A & operátor, amivel szövegeket kapcsolhatunk össze, segítségünkre lehet számítási feladatok
esetén is. Vizsgáljuk meg ezt a következő feladatban.

1

Az Excelben nem létezik.

9. FEJEZET. SZÖVEGFÜGGVÉNYEK 61

9.2. ábra. 18. feladat – Függvénytündér – HA kifejezés struktúra

9.3. ábra. 18. feladat – Megoldás

9. FEJEZET. SZÖVEGFÜGGVÉNYEK 62

9.2. 19. feladat

Határozzuk meg, hogy a 12. feladatban vizsgált osztály tanulói közül hányan értek el az osztályátlag
fölötti átlagot.

A feladat megoldására a DARABTELI függvényt nem tudjuk alapesetben használni, hiszen a
függvény második feltétel argumentuma nem lehet sem függvény, sem hivatkozás. Még visszatérünk
ehhez a függvényhez, de először oldjuk meg a feladatot logikai függvények és segédoszlop felhasz­nálásával. Másoljuk a 12. feladat A1:I10 tartományát egy üres munkalapra. A J2 cellába pedig
írjuk a következő kifejezést: =HA(I2>ÁTLAG(D$2:H$10);1;0). Ez a cella 1-et fog felvenni, ha az
első tanuló átlaga az osztályátlagnál jobb, és 0-át, ha rosszabb. A képletet másolva számoszlopot
kapunk, aminek összege megadja a keresett eredményt (9.4 ábra).

9.4. ábra. 19. feladat

A DARABTELI függvény második argumentumában a & operátort felhasználva a következő
kifejezéssel adhatjuk meg a feltétel argumentumot: ">"&ÁTLAG(D2:H10)). A végleges kép-
let tehát: =DARABTELI(I2:I10;">"&ÁTLAG(D2:H10)). Írjuk be a képletet a J12 cellába és
ellenőrizzük, hogy ugyanazt az eredményt adja mint az előző esetben.

Az ebben a fejezetben áttekintett függvényeket a 9.1 táblázatban találjuk meg.

9. FEJEZET. SZÖVEGFÜGGVÉNYEK 63

9.1. táblázat. A fejezetben tárgyalt függvények

A függvény Funkciója A függvény

neve angol neve

ÖSSZEFŰZ
AZONOS Összehasonlít két szöveges karakterláncot. EXACT

SZÖVEG.KERES

SZÖVEG.TALÁL

BAL Megadja egy szöveg első karaktereit. LEFT
JOBB Megadja egy szöveg utolsó karaktereit. RIGHT
KÖZÉP
HOSSZ Szöveg karaktereinek számát adja. LEN
KISBETŰ

TNÉV

NAGYBETŰS
HELYETTE Megadott karaktereket cserél szövegben. SUBSTITUTE
CSERE Karaktereket cserél szövegben pozíció alapján. REPLACE

SZÖVEG

TRIM Eltávolítja a szükségtelen szóközöket. TRIM
RÓMAI
ARABIC Római számot arab számmá alakít. ARABIC
ÉRTÉK

Karakterláncokat egyesít. CONCATENATE

Egy szövegrész karakterláncon belüli helyzetét
adja eredményül. Kis és nagybetűk között nem
tesz különbséget.
Egy szövegrész karakterláncon belüli helyzetét
adja eredményül. Kis és nagybetűk között kü­lönbséget tesz.

Megadja egy karakterlánc egy darabját. MID

Kisbetűsre alakítja a szöveget. LOWER
Nagybetűsre változtatja minden szó első betű­jét.
Nagybetűsre alakítja a szöveget. UPPER

Megadott formátum alapján számot szöveggé
alakít.

Római számra alakít. ROMAN

Szöveget számmá alakít. VALUE

SEARCH

FIND

PROPER

TEXT

10. fejezet

Keresőfüggvények használata

A munkalapfüggvények kategóriában találjuk azokat a gyakran használt függvényeket, amelyek
segítségével adatokat kereshetünk a táblázatban.

10.1. Az FKERES, VKERES függvények

Az FKERES függvény egy tartomány bal szélső oszlopában megkeres egy értéket. Ennek az érték­nek a sora, és a harmadik paraméterben megadott tartományon belüli oszlop sorszámának met­széspontján található cella tartalmát adja eredményül.

Szintaxisa: =FKERES(keresési feltétel;tömb;index;rendezett)

Attól függően, hogy a negyedik, rendezett nevű, opcionális paraméternek milyen értéket adunk,
a függvény eltérően viselkedik. Amikor az oszlop, amiben keresünk egy értéket nem rendezett,
akkor ennek a paraméternek HAMIS értéket kell adjunk. Ilyenkor csak pontos egyezés esetén
ad eredményt a függvény. Rendezett oszlop esetén a negyedik paraméter lehet IGAZ, vagy el is
hagyhatjuk. A függvény ilyenkor közelítő eredményt is adhat.

Két feladaton keresztül vizsgáljuk meg az FKERES függvény működését.

10.2. 20. feladat

A 10.1 ábrán látható táblázat egy üzlet raktárkészletét mutatja. Minden árut egy kóddal azonosí­tanak. Oldjuk meg, hogy egy kódot az A19 cellába írva a B19:E19 tartományban megjelenjenek az
adott áru adatai.

A táblázatban létezik egy olyan tartomány, amelynek első oszlopában kell megkeresni a beírt
kód értékét, és tőle jobbra a második, harmadik, negyedik és ötödik oszlopból kell megjeleníteni a
hozzá tartozó értékeket. Ez a tartomány az A2:E17.

Írjunk be egy kódot az A19 cellába. A B19 cellában kell, hogy megjelenjen az e kódhoz tartozó
megnevezés. Ebben a cellában válasszuk a függvénytündért, és az FKERES függvényt (10.2 ábra).

Az első paraméter a keresési feltétel: mit keresünk a tömb első oszlopában. Esetünkben ez
az A19 cella. A második paraméter maga a tömb. A harmadik, hogy melyik oszlopból kell az
értéket venni. A feladat jellegéből következik, hogy most pontos egyezésre van szükség, a negyedik
paramétert is meg kell adni: HAMIS. A függvény tehát: =FKERES(A19;A2:E17;2;HAMIS) (10.2
ábra).

A függvény működését a következőképpen értelmezhetjük: keresd az A19 cella tartalmát az
A2:E17 tartomány első oszlopában. Pontos egyezés esetén jelenítsd meg a megtalált sor és a második
oszlop metszéspontján található cella tartalmát.

A további három cella csak abban különbözik a B19-től, hogy ott a harmadik, negyedik és
ötödik oszlop adatát kell megjeleníteni. A harmadik, index paramétert kell háromra, négyre és

10. FEJEZET. KERESŐFÜGGVÉNYEK HASZNÁLATA 65

10.1. ábra. 20. feladat

10.2. ábra. 20. feladat – FKERES függvény

ötre módosítani. Másolással ez nem oldható meg. Módosítsuk a hivatkozásokat és másoljuk a

10. FEJEZET. KERESŐFÜGGVÉNYEK HASZNÁLATA 66

cellákat jobbra. A C19, D19 és az E19 cellákban írjuk át az index paramétert. A D19 formátumát
változtassuk pénznemre, a tizedesjegyek száma nulla legyen.

A 10.3 ábrán a feladat megoldását látjuk.

10.3. ábra. 20. feladat – eredmény

Ellenőrizzük a függvény működését különböző kódokat írva az A19 cellába. Nem létező kódot
írva a #HIÁNYZIK hibaüzenetet kapjuk.

10.3. 21. feladat

10.4. ábra. 21. feladat

A 10.4 ábrán egy dolgozat eredményeit látjuk. Az elért pontszámok alapján függvény segítségével
határozzuk meg minden tanuló osztályzatát. A kritériumokat az M3:O7 cellatartomány tartalmazza:
12 pontig – Elégtelen (1), 12-től 16 pontig – Elégséges (2), 16-tól 19-ig – Közepes (3), 19-től 24-ig

10. FEJEZET. KERESŐFÜGGVÉNYEK HASZNÁLATA 67

– Jó (4) és 24 ponttól Jeles (5). A K oszlopban a legtöbb pontszámot elért tanulók sorában jelenjen
meg az „Igen” szó. Az L1 cella azt mutassa, hogy hány tanuló érte el a legtöbb pontszámot.

Ennek a feladatnak a megoldásához is az FKERES függvényt fogjuk használni. Az M3:O7
tartomány első oszlopában fogja megkeresni a függvény minden tanuló pontszámát. A második,
majd a harmadik oszlopból veszi az osztályzatot. Az M3:O7 tartomány első oszlopa növekvő
számsort tartalmaz. Az FKERES függvény ebben az esetben akkor is ad eredményt, ha nem talál
pontos egyezést, feltéve, hogy az érték a rendezett lista legalacsonyabb értékénél nagyobb.

Az első tanuló pontszáma 18 pont. Ez a 16 pontnál (Közepes) több, de a 19 pontnál (Jó)
kevesebb, tehát rá a harmadik sor vonatkozik (10.5 ábra).

10.5. ábra. 21. feladat – FKERES függvény

Ebben az esetben a negyedik paramétert nem kell megadni, az alapértelmezett értéke IGAZ.

A függvény másolása előtt abszolúttá kell tenni a mátrix paramétert. A végleges képlet tehát:
=FKERES(H2;$M$3:$O$7;2).

A J oszlopban a képlet csak a harmadik paraméterben különbözik. Itt a harmadik oszlopból
kell az eredményt venni (10.6 ábra).

Ahhoz, hogy a K oszlopban a legtöbb pontszámot elért tanulók sorában jelenjen meg az „Igen”
szó, használhatjuk a HA és a MAX függvényt. A függvénytündérrel hozzuk létre a következő
kifejezést: =HA(MAX(H$2:H$10)=H2;"Igen";"").

A legtöbb pontszámot szerzett tanulók számát kiszámíthatjuk az L1 cellában, összeszámolva az
„Igen”-ek darabszámát a K oszlopban: =DARABTELI(K2:K10;"Igen").

A megoldott feladatot a 10.7 ábrán látjuk.

A VKERES függvény pontosan úgy működik, mint az FKERES, csak a tartomány első oszlopa
helyett az első sorban keres. Erre utal a függvények nevében az első betű: F – függőleges, V –
vízszintes.

10. FEJEZET. KERESŐFÜGGVÉNYEK HASZNÁLATA 68

10.6. ábra. 21. feladat – FKERES függvény képlet

10.7. ábra. 21. feladat – HA képlet

10.4. A HOL.VAN és az INDEX függvények

A HOL.VAN függvény a keresett elem tömbben elfoglalt pozícióját adja vissza. A tömb egy sorból
vagy egy oszlopból állhat. Szintaxisa: HOL.VAN(keresési feltétel;keresési_tartomány;típus). A
harmadik típus paraméternek 0 értéket kell adni, ha pontos egyezést keresünk. Amikor több ilyen
is van, az első találatot adja eredményül. -1 esetén a függvény feltételezi, hogy a tömb csökkenő
rendbe rendezett. Ilyenkor az első nagyobb vagy egyenlő értéket adja vissza.

A harmadik paraméter elhagyása, vagy 1 értéke esetén a függvény az utolsóként előforduló, a
keresési feltételnél kisebb vagy azzal egyenlő értéket adja vissza.

Egy egyszerű példán könnyen megérthetjük a függvény működését. Az előző feladat táblázatá­ban találjuk meg, hogy a névsorban hányadik diák érte el a legkevesebb pontszámot.

A 10.8 ábrán látjuk, hogy az első paraméter a MIN(H2:H10) függvény, ami megadja a legkisebb
számot a H2:H10 tartományban. Ennek a számnak a sorszámát találja meg a HOL.VAN függvény,

10. FEJEZET. KERESŐFÜGGVÉNYEK HASZNÁLATA 69

mert keresési tartomány is a H2:H10. Látjuk, hogy az eredmény 5, tehát a névsorban az ötödik
tanuló érte el a legkevesebb pontszámot.

10.8. ábra. HOL.VAN függvény struktúrája

Az INDEX függvény adott sor és oszlop találkozásánál lévő cella tartalmát adja eredményül.
Szintaxisa: INDEX(hivatkozás;sor;oszlop;tartomány). Amennyiben a hivatkozás több tartomány­ból áll, zárójelek között kell megadni. A negyedik paraméter opcionális, csak akkor kell megadni,
ha több tartományból áll a hivatkozás.

A HOL.VAN függvényt gyakran használják az INDEX beágyazott függvényeként. Olyan kere­sési feladatokat is megoldhatunk ezekkel a függvényekkel, amelyeket az FKERES, VKERES függ­vényekkel nem. A következő feladatban vizsgáljunk meg egy ilyen esetet.

10.5. 22. feladat

A 10.9 ábrán az A oszlopban dátumértékek, a C oszlopban az adott napi bevétel van feltüntetve. A
C15 cellában jelenítsük meg legnagyobb bevételt, a C20-ban pedig hozzá tartozó dátumot.

A táblázatot megfigyelve láthatjuk, hogy itt a C oszlopban kell megkeresni egy értéket és a
tőle balra lévő oszlopból megjeleníteni a hozzá tartozó tartalmat. Az FKERES függvényt ezért itt
nem használhatjuk, illetve csak akkor, ha segédoszlopot alkalmazunk, másolatot készítve az A2:A13
tartományról a bevétel oszlopától jobbra, például a D oszlopba. Amikor nem alkalmazhatjuk ezt a
módszert, más függvényt kell használnunk.

A HOL.VAN függvénnyel keressük meg melyik sorban van a legnagyobb szám a B2:B12 tarto­mányban, és ez lesz az INDEX függvény sor paramétere. Az oszlop paraméter 1 lesz, a tartomány
pedig az A2:C13.

A függvénytündér segítségével hozzuk létre a kifejezést (10.10 ábra).

10. FEJEZET. KERESŐFÜGGVÉNYEK HASZNÁLATA 70

10.9. ábra. 22. feladat

10.10. ábra. 22. feladat INDEX függvény struktúrája

11. fejezet

Nevek és listák

11.1. Cellák elnevezése

Cellákhoz és cellatartományokhoz neveket rendelhetünk. Az elnevezett cellákra és cellatartomá­nyokra képletekben a nevükkel hivatkozhatunk. Ez megkönnyíti a képletek értelmezését és máso­lását. Neveket tartalmazó képleteket másolva, azok nem változnak. Érdemes olyan tartományhoz
vagy cellához nevet rendelni, amelyeket abszolút hivatkozásként használunk a képletekben.

Neveket legegyszerűbben úgy hozhatunk létre, hogy a szükséges cella vagy cellatartomány ki­jelölése után a névdobozba kattintunk egérrel, kitöröljük az ott lévő cellahivatkozást és beírjuk a
nevet (11.1 ábra).

11.1. ábra. Cellák elnevezése

A 11.1 ábrán a C3:C6 tartománynak az „árak” nevet adtuk.

A Calcban használt nevek betűket és számokat tartalmazhatnak, a speciális karakterek közül
csak az aláhúzásjelet ( _ ) és pontot ( . ). A név nem lehet lehetséges hivatkozásnév sem.

A neveket létrehozhatunk a Beszúrás menüpont Nevek – Meghatározás paranccsal, vagy
a Ctrl+F3 billentyűkombinációval (11.2 ábra). Az ablakban módosíthatjuk a nevekhez tartozó
cellahivatkozásokat és törölhetjük is őket.

11.2. 23. feladat

A negyedik feladatban kiszámított napi bevételt számítsuk ki függvény és cellák elnevezése segítségé­vel.

11. FEJEZET. NEVEK ÉS LISTÁK 72

11.2. ábra. Nevek megadása

A negyedik feladatban alkalmazott képlet (=$C$3*D3+$C$4*D4+$C$5*D5+$C$6*D6) szor­zatok összege, amire találunk függvényt is a Calcban. Ez a SZORZATÖSSZEG függvény.

A SZORZATÖSSZEG függvény összeszorozza az adott tömbök megfelelő elemeit, és ered-
ményül a szorzatok összegét adja. Szintaxisa: SZORZATÖSSZEG(tömb1; tömb2...tömb30).

Az előző képletet helyettesíthetjük a következő függvénnyel:

=SZORZATÖSSZEG($C$3:$C$6;D3:D6). Mivel a C3:C6 tartománynak az „árak” nevet adtuk:
=SZORZATÖSSZEG(árak;D3:D6) (11.3 ábra).

11.3. ábra. 23. feladat – SZORZATÖSSZEG függvény

11.3. Rendezett listák

Cella másolásakor annak tartalmától függően a Calc vagy másolást végez, vagy sorozattal tölti fel
a cellákat. Szöveges tartalom esetén általában megismétli a cella tartalmát. Ez alól két kivétel van.
Az egyik, ha a cellában a szöveg után szám található. Ilyenkor másoláskor folytatja a számozást.
A 11.4 ábrán látható három oszlop ezzel a módszerrel lett létrehozva.

Másolásnál a Ctrl billentyűt lenyomva tartva kikapcsolhatjuk a számsorozat létrehozását.

A második kivétel, ha olyan szöveget írunk be, ami eleme a Calc rendezett listáinak. Ezek a lis-

11. FEJEZET. NEVEK ÉS LISTÁK 73

11.4. ábra. Cellák tartalmának másolása

ták megtekinthetők az Eszközök menüpont Beállítások párbeszédablakban, az OpenOffice.org
Calc – Rendezett listák lehetőséget választva (11.5 ábra).

11.5. ábra. Rendezett listák

Lehetőség van saját listák létrehozására is. Ehhez csak be kell írni a listát egy tetszőleges
tartományba és a 11.5 ábrán látható Másolás majd az OK gombra kattintani.

11.4. Sorozatok létrehozása

A Calcban egyszerűen létrehozhatunk növekvő számtani és mértani sorozatokat. Írjuk be egy
cellába a sorozat első tagját, és jelöljük ki azt a tartományt, ahová a számsort létre akarjuk hozni.
Válasszuk a Szerkesztés – Kitöltés – Sorozat parancsot.

A 11.6 ábrán látható beállításokkal mértani sorozat jön létre, a sorozat hányadosa 2-vel egyenlő.
Számtani sorozatnál a sorozat különbségét kell a Növekmény mezőbe írni.

Dátumsorozatot is létrehozhatunk, a növekmény megadásán kívül ilyenkor időegységet is vá­laszthatunk.

11. FEJEZET. NEVEK ÉS LISTÁK 74

11.6. ábra. Kitöltés sorozattal

11.5. Cellatartomány érvényesítése

Az Adatok menüpont Érvényesség párbeszédablakában beállíthatjuk, hogy egy cellába ne be­írással, hanem listából való kiválasztással kerüljön adat. A lista egy sorból vagy oszlopból állhat,
és egyszerűbb, ha névvel azonosítjuk. Az Engedélyezés résznél válaszuk a Cellatartományt és
a Forráshoz írjuk be a meghatározott nevet.

11.6. 24. feladat

Módosítsuk a 20. feladatot, hogy az A19 cellában választható legyen bármelyik kód az A2:A17
cellatartományból.

Első lépésként jelöljük ki az A2:A17 cellatartományt és adjuk neki a kódok nevet. Az A19
cellát választva az Érvényesség párbeszédablakban válasszuk a Cellatartományt és a forráshoz
írjuk a kódok nevet. Ezután az A19 cellára kattintva a cella jobb oldalán egy nyilat ábrázoló gomb
jelenik meg, arra kattintva megjelenik a lista (11.7 ábra).

11.7. ábra. 24. feladat

Egérrel választhatunk a listából és a cella azt az értéket veszi fel. A B19:E19 tartományban az
FKERES függvény megkeresi az adott kódhoz tartozó adatokat.

12. fejezet

Adattartományok a Calcban

A Calc segítségével egyszerűbb adatbázis-funkciókat is megvalósíthatunk. Az adatokat kötött for­mátumú táblázatba kell beírnunk. Az ilyen táblázat oszlopai azonos típusú adatokat tartalmaznak,
az első sorba pedig az oszlopok neveit kell beírni. A táblában az oszlopokat mezőknek, a sorokat
rekordoknak, az első sor adatait pedig mezőneveknek nevezzük. A táblában lehetőleg ne legyenek
üres sorok vagy oszlopok. Ezeknek a kritériumoknak megfelelnek a 18. feladatban használt adatok.
Másoljuk az A1:E17 tartományt az újonnan létrehozott calc05 munkafüzet második munkalapjára
(12.1 ábra). A munkalap neve legyen Adatok.

12.1. ábra. Adattartományok

A táblában a következő mezőneveket látjuk: Kód, Megnevezés, Típus, Beszerzési ár, Készlet.
A tábla sorai pedig a rekordok lesznek.

12.1. Rendezés

Calcban különböző szempontok szerint rendezhetjük cellatartományok tartalmát. A Standard
eszköztár Rendezés növekvő sorrendbe és Csökkenő sorrend parancsait csak akkor használ-

12. FEJEZET. ADATTARTOMÁNYOK A CALCBAN 76

juk, ha egy tartományt a mellette lévő tartományoktól függetlenül akarunk rendezni. Olyan kötött
formátumú adattáblák rendezéséhez, mint amilyet a 12.1 ábrán is látunk, válasszuk a tábla egyik
kitöltött celláját és az Adatok menüpont Rendezés parancsát (12.2 ábra).

12.2. ábra. Rendezés – rendezési feltétel

Látjuk, hogy a Calc kijelölte az adattartományt. A megjelenő párbeszédablakban kiválaszthat­juk azt a mezőt, amelyik szerint rendezni szeretnénk adatainkat. Ismétlődő adatok esetén lehet
hasznos a másodlagos és a harmadlagos rendezés beállítása. Mindhárom rendezésnél a rendezés
irányát is megadhatjuk.

A Beállítások fület választva (12.3 ábra) megadhatjuk, hogy rendezésnél a kis- és nagybetűket
megkülönböztesse-e a program.

A tartomány oszlopcímeket tartalmaz kapcsoló meghatározza, hogy a mezőneveket, vagy
az oszlopazonosítókat használja az oszlopok azonosítására. Kikapcsolva az első sort is rendezi
a Calc. A rendezés eredményét egyszerűen átmásolhatjuk egy névvel megadott cellatartomány­ba, vagy megadhatunk egy cellacímet, ahova a másolat bal felső celláját helyezi. Ahhoz, hogy a
Munkalap3 nevű munkalapon jelenjen meg a táblázat másolata a beállított rendezésekkel, a Mun-
kalap3.A1 címet kell beírnunk.

12.2. Az automatikus szűrő használata

A Calcban különböző szűréseket végezhetünk adatainkon. Az adattartomány bármelyik cellájára
kattintva, az Adat menüpont Szűrő – Automatikus szűrő parancsával egy kombinált listát

12. FEJEZET. ADATTARTOMÁNYOK A CALCBAN 77

12.3. ábra. Rendezés – Beállítások

kapcsolhatunk be a mezőnevek cellái mellett. Ezek valamelyikére kattintva kiválaszthatunk egy
elemet. Ilyenkor csak azok a rekordok jelennek meg, amelyek eleget tesznek a szűrőfeltételben
megadottnak. A 12.4 ábrán azokat a rekordokat mutatja a szűrés eredménye, ahol a készlet értéke 8.

12.4. ábra. Automatikus szűrő használata

Az aktív szűrő oszlopában a nyílgomb kék színűre vált. További szűrőket választva, a legördülő
listában már csak a szűrt adatok közül választhatunk. Az aktív szűrőt a minden lehetőséget
választva kapcsolhatjuk ki.

12. FEJEZET. ADATTARTOMÁNYOK A CALCBAN 78

12.3. Általános szűrő

Az Adat menüpont Szűrő – Általános szűrő parancsával meghatározhatunk bonyolultabb szűrési feltételeket (12.5 ábra).

12.5. ábra. Általános szűrő

Módosíthatjuk az automatikus szűrővel kiválasztott feltételt, és meghatározhatunk még továb­bi kettőt. A három szűrőfeltétel között ÉS vagy VAGY kapcsolat lehet. A Részletek kapcsolóval
bekapcsolhatjuk a kis- és nagybetűk megkülönböztetését, a szűrt sorokat egy másik helyre másol­hatjuk, hasonlóképpen mint rendezésnél. A Reguláris kifejezés bekapcsolásával Egyenlő vagy
Nem egyenlő feltétel esetén az érték mezőbe reguláris kifejéseket is írhatunk. Ezek részletes
leírását az OpenOffice.org Calc Súgójában megtaláljuk.

12.4. 25. feladat

Szűrjük ki azokat a rekordokat az adattáblából amelyeknél a típusnév Z betűvel kezdődik, a beszerzési
ár pedig 10000 és 50000 közötti. Az E20 cellában függvénnyel határozzuk meg a készletértékek
összegét.

Azt hogy egy szöveg Z betűvel kezdődik a „Z.*” reguláris kifejezéssel adhatjuk meg, hiszen
a . (pont) bármilyen karaktert jelöl, a * (csillag) pedig az előtte lévő karakter nulla vagy több
előfordulását. Egyszerre kell érvényesülnie a másik két feltételnek is, tehát az ÉS kapcsolatot
válasszuk a sorok között (12.6 ábra).

A szűrt rekordok értékeinek összegzésére nem használhatjuk a SZUM függvényt, mert az tar­talmazni fogja a rejtett cellákban található értékeket is. A Képlet eszköztár Összeg ikonjára
kattintva a RÉSZÖSSZEG függvény jelenik meg (12.7 ábra).

Ez a függvény a szűrt eredményekkel végez különböző műveleteket, amit az első paraméterében
megadott számmal határozunk meg. 9 a SZUM függvénynek felel meg. A függvényindexek listáját
megtaláljuk a Calc súgójában.

12. FEJEZET. ADATTARTOMÁNYOK A CALCBAN 79

12.6. ábra. 25. feladat – Általános szűrő

12.7. ábra. 25. feladat – RÉSZÖSSZEG függvény

12.5. Irányított szűrés

Az Adat menüpont Szűrő – Irányított szűrő parancsával egy szűrőfeltételeket tartalmazó cel­latartomány alapján végezhetünk szűrést az adattartományon.

12.8. ábra. Irányított szűrő

Készítsünk másolatot az adattáblánk mezőneveit tartalmazó cellatartományról az A22:E22 tar­tományba. Az A22:E24 cellatartomány legyen szegélyezett. Az üres cellatartományba írjunk kü­lönböző feltételeket (12.8 ábra).

Ez a tartomány adja meg az irányított szűrő feltételeit. Egy sor cellái között ÉS logikai kapcsolat
lesz, a sorok között pedig VAGY. A 12.8 ábrán látható feltételek azokat a rekordokat határozzák
meg, amelyekből 8 db van és a beszerzési ár több mint 20000, és még minden olyan rekordot amelyik
megnevezése T betűvel kezdődik, függetlenül a beszerzési ártól és darabszámtól.

Válasszuk az eredeti adattartomány valamelyik celláját és az Adat menüpont Szűrő – Irányí-
tott szűrő parancsát. A megjelenő ablakban adjuk meg szűrőfeltételnek az A22:E24 tartományt,
és kapcsoljuk be a Reguláris kifejezések kapcsolót, hiszen a B24 cellába ilyet írtunk. A megjelenő,

12. FEJEZET. ADATTARTOMÁNYOK A CALCBAN 80

a feltételeknek megfelelő szűrt tartományt a 12.9 ábra mutatja.

12.9. ábra. Szűrés eredmények

A szűrőfeltételek módosítása után azok automatikusan nem jutnak érvényre. A szűrés aktuali­zálásához ismételten ki kell adni az Adat menüpont Szűrő – Irányított szűrő parancsát.

13. fejezet

Adatbázisfüggvények

Adatbázisfüggvények segítségével számításokat végezhetünk az adattábla értékeivel egy dinamiku­san változtatható keresési tartomány feltételei alapján. Az irányított szűrőhöz hasonlóan e tar­tomány egy sorának cellái között ÉS logikai kapcsolat lesz, a sorok között pedig VAGY. Minden
adatbázisfüggvénynek három argumentuma van: adatbázis, adatbázismező és keresési feltétel.

Az első magát az adattáblát adja meg. Az irányított szűrő tulajdonságait bemutató példánál
ez az A1:E17 tartomány (12.9 ábra).

A keresési feltétel a feltételeket tartalmazó cellatartomány. A 12.9 ábrán a A22:E24. Ebben
a tartományban csak akkor használhatunk reguláris kifejezéseket ha bekapcsoljuk az Eszközök –

Beállítások – OpenOffice.org Calc – Számítás panelen a Reguláris kifejezések engedé­lyezése képletekben kapcsolót.

Az adatbázismező annak az oszlopnak a sorszáma az adattáblán belül, amelyikben a függvény
működni fog. A 0 értékkel megadhatjuk a teljes adattartományt. Mezőnevet is megadhatunk
idézőjelek közé írva.

A 13.1 táblázat a gyakrabban használt adatbázisfüggvényeket mutatja.

13.1. táblázat. Gyakrabban használt adatbázisfüggvények

AB.SUM

AB.MAX

AB.MIN

AB.ÁTLAG

AB.DARAB

AB.DARAB2

A keresési feltételeknek megfelelő cellák összegét
számítja ki.
A keresési feltételeknek megfelelő cellák közül a
legnagyobb értékét adja vissza.
A keresési feltételeknek megfelelő cellák közül a
legkisebb értékét adja vissza.
A keresési feltételeknek megfelelő cellák átlagát
számítja ki.
Megszámolja a számokat tartalmazó rekordokat
az adattáblában, amelyek megfelelnek a keresési
feltételeknek.
Megszámolja a számokat vagy szöveget tartal­mazó (azaz nem üres) rekordokat az adattáblá­ban, amelyek megfelelnek a keresési feltételek­nek.

13. FEJEZET. ADATBÁZISFÜGGVÉNYEK 82

13.1. 26. feladat

Számítsuk ki adatbázisfüggvények felhasználásával a 12.8 ábrán látható feltételeknek megfelelő re­kordok:

a) darabszámát

b) készletszámok összegét

c) a legnagyobb beszerzési árat

d) a legkisebb beszerzési árat

e) a beszerzési árak átlagát

Módosítsuk a keresési feltételeket, hogy a K betűvel kezdődő, 10 000 Ft-nál kisebb beszerzési árú
rekordokat határozza meg.

A szűrő kikapcsolása után másoljuk az A1:E24 tartományt egy üres munkalapra. A Reguláris
kifejezések engedélyezése képletekben kapcsolót a Beállítások ablakban kapcsoljuk be. Az A26:A30
tartományba írjuk a 13.1 ábrán látható tartalmakat és adatbázisfüggvények segítségével számít­suk ki a C26:C30 tartomány celláit. A rekordok számának meghatározásánál használhatjuk az
AB.DARAB függvényt. Olyan mezőt válasszunk második argumentumnak, amelyiket az adattábla
módosításánál is mindenképp kitöltünk. Esetünkben ilyen lehet az első, a Kód mező.

A készlet összegének kiszámításának képletét látjuk a 13.1 ábrán. A további három függvény
argumentuma ugyanaz lesz: (A1:E17;4;A22:E24), a használt függvények pedig AB.MAX, AB.MIN
és AB.ÁTLAG. Az első két eredményt leellenőrizhetjük, összehasonlítva az Irányított szűrő példá­jában kapottakkal. A RÉSZÖSSZEG függvény ott ugyanúgy a készletszámok összegét határozta
meg, ugyanazokkal a keresési feltételekkel.

Módosítsuk a keresési feltételeket, és az adatbázisfüggvények az új feltételeknek megfelelő re­kordok alapján határozzák meg az értékeket (13.2 ábra).

Az ebben a fejezetben tárgyalt függvények a 13.2 táblázatban láthatóak.

13.2. táblázat. A fejezetben tárgyalt függvények

A függvény Funkciója A függvény

neve angol neve

AB.SZUM

AB.MAX

AB.MIN

AB.ÁTLAG

AB.DARAB

AB.DARAB2

A keresési feltételeknek megfelelő cellák összegét
számítja ki.
A keresési feltételeknek megfelelő cellák közül a
legnagyobb értékét adja vissza.
A keresési feltételeknek megfelelő cellák közül a
legkisebb értékét adja vissza.
A keresési feltételeknek megfelelő cellák átlagát
számítja ki.
Megszámolja a számokat tartalmazó rekordokat
az adattáblában, amelyek megfelelnek a keresési
feltételeknek.
Megszámolja a számokat vagy szöveget tartal­mazó (azaz nem üres) rekordokat az adattáblá­ban, amelyek megfelelnek a keresési feltételek­nek.

DSUM

DMAX

DMIN

DAVERAGE

DCOUNT

DCOUNTA

13. FEJEZET. ADATBÁZISFÜGGVÉNYEK 83

13.1. ábra. 26. feladat

13.2. ábra. 26. feladat – eredmény

14. fejezet

Dátum- és időfüggvények

A Függvénytündérben a dátum és idő kategóriát választva olyan függvényeket találunk, melyek
dátumok és időpontok beszúrására, valamint szerkesztésére szolgálnak.

A MA függvény a rendszer dátumát adja eredményül. A munkafüzetet megnyitva mindig
aktualizálja az értéket. Akkor is frissíti az értéket, amikor egy cellaértéket módosítunk, vagy
megnyomjuk az F9 funkcióbillentyűt. Szintaxisa: MA(), argumentuma nincs.

A MOST függvény a rendszer dátumát és idejét adja eredményül. Minden esetben frissíti az
értéket, amikor egy cellaértéket módosítunk, vagy megnyomjuk az F9 funkcióbillentyűt.

A DÁTUM függvény kiszámítja az argumentumaiban év, hónap, nap formában megadott
dátumot. Alapértelmezett formátuma a dátumformátum. Szintaxisa: DÁTUM(év;hónap;nap).
A hónapot és a napot megadhatjuk lehetséges dátumon kívül is. Ilyenkor átvitelre kerülnek a
következő számjegyre. A DÁTUM(2008;08;33) eredménye 2008-09-02 lesz.

A Calcban hat olyan függvény van, amelyek segítségével a dátum- és időértékből azok részeit
nyerhetjük ki. A 14.1 táblázat ezeket mutatja be.

14.1. táblázat. A dátum és az idő egyes részeinek kinyerése

ÉV
HÓNAP

NAP

ÓRA
PERC Időértékből a perceket adja vissza (0-59).
MPERC Időértékből a másodperceket adja vissza (0-59).

A függvényeknek egy argumentumuk van, az átalakítandó dátum- vagy időérték.

A HÉT.NAPJA függvény a dátumértéket a hét napjának a sorszámaként adja vissza. Szin­taxisa: HÉT.NAPJA(dátum;típus). A típus argumentum a számítás módját határozza meg. 1
esetén a hét napjai vasárnaptól számozódnak. 2 esetén a hét első napja a hétfő, 3 esetén pedig a
hétfő nullának (0) felel meg.

A WEEKNUM függvény egy dátumhoz tartozó hét számát adja vissza. Szintaxisa:
WEEKNUM(dátum;mód). A mód beállítja, hogy melyik legyen a hét első napja. Vasárnap esetén
értéke 1, hétfő esetén 2.

A NETWORKDAYS függvény két dátum közötti munkanapok számát adja vissza. Szinta-
xisa: NETWORKDAYS(kezdő dátum;befejező dátum;ünnepnapok). Az ünnepnapok a nem szom­batra vagy vasárnapra eső munkaszüneti napok listája.

A WORKDAY függvény megadja azt a dátumot, amelyik egy kezdő dátumhoz képest egy
adott számú munkanapra található. Szintaxisa: WORKDAY(kezdő dátum;napok;ünnepnapok).

Dátumértékből az évet adja vissza.
Dátumértékből a hónapot adja vissza.
Dátumértékből a hónap napját (1-31) adja
vissza.
Időértékből az órákat adja vissza (0-23).

14. FEJEZET. DÁTUM- ÉS IDŐFÜGGVÉNYEK 85

Az ünnepnapok a nem szombatra vagy vasárnapra eső munkaszüneti napok listája.

Az EASTERSUNDAY1függvénnyel az adott év Húsvét vasárnapjának dátumát számíthatjuk
ki. Szintaxisa: EASTERSUNDAY(év). Az év egy 1583 és 9956 közötti évszám. E függvény
segítségével más ünnepnapok is kiszámíthatók egyszerű összeadás segítségével:

Húsvéthétfő = EASTERSUNDAY(év) + 1

Nagypéntek = EASTERSUNDAY(év) - 2

Pünkösdvasárnap = EASTERSUNDAY(év) + 49

Pünkösdhétfő = EASTERSUNDAY(év) + 50

14.1. 27. feladat

Jelenítsük meg az ünnepek és emléknapok dátumait az A1 cellába beírt évben. Külön oszlopban
jelenjen meg, hogy az adott dátum milyen napra esik. A táblázat első sora az évszám legyen, vagy
szökőév esetén az „évszám – szökőév” felirat.

Azt, hogy az adott év szökőév-e, meghatározhatjuk a DÁTUM függvénnyel. Amennyiben a
HÓNAP(DÁTUM(A1;2;29)) függvény értéke 2, a DÁTUM függvény argumentuma létező dátum.
Tehát az A1 cellába írt évszám szökőév. Ahhoz, hogy egy cellában az évszám vagy az évszám és a
szökőév szöveg jelenjen meg logikai függvényt kell használnunk (14.1 ábra).

14.1. ábra. 27. feladat – szökőév

Azoknak az ünnepeknek a dátumát, amelyek egy bizonyos dátumra esnek egyszerűen meg­határozhatjuk a DÁTUM függvénnyel. Az államalapítás ünnepét például a =DÁTUM(A1;8;20)
függvény adja meg.

A hét napját legegyszerűbben úgy határozhatjuk meg, hogy az E5 cellába az =D5 képletet
írjuk, a cella dátumformátumának kódja pedig „nnnn” lesz (14.2 ábra).

14.2. 28. feladat

Magyarországon az Anyák napját május első vasárnapján ünneplik. Határozzuk meg ezt a dátumot
függvények segítségével az A1 cellába írt évben.

Az előző feladat táblázatában jelöljük ki az 10. sort és szúrjunk be egy újat. A B10 és a C10
cellákba írjuk a 14.3 ábrán látható tartalmakat.

Május első vasárnapjának dátumának meghatározásához tudnunk kell, hogy milyen napra esik
május elseje. Ezt a következő függvénnyel megtudhatjuk: HÉT.NAPJA(DÁTUM(A1;5;1);2). Ér-
téke 1 lesz ha hétfőre, 2 ha keddre, 3 ha szerdára és így tovább. Vasárnap esetén 7.

Az első vasárnap kiszámításához a május elsejei dátumhoz 6-ot kell adni ha az hétfőre esik,
5-öt ha keddre, 4-et ha szerdára stb., ha vasárnapra esik akkor nullát. A képlet tehát ez lesz (14.3
ábra): =DÁTUM(A1;5;1)+(7-HÉT.NAPJA(DÁTUM(A1;5;1);2)).

Az ebben a fejezetben tárgyalt függvények a 14.2 táblázatban láthatóak.

1

Az Excelben nem létezik.

14. FEJEZET. DÁTUM- ÉS IDŐFÜGGVÉNYEK 86

14.2. ábra. 27. feladat – DÁTUM függvény

14.3. ábra. 28. feladat – DÁTUM, HÉT.NAPJA függvények

14. FEJEZET. DÁTUM- ÉS IDŐFÜGGVÉNYEK 87

14.2. táblázat. A fejezetben tárgyalt függvények

A függvény Funkciója A függvény

neve angol neve

MA A rendszer dátumát adja eredményül. TODAY
MOST A rendszer dátumát és idejét adja eredményül. NOW
DÁTUM
ÉV
HÓNAP
NAP Dátumértékből a hónap napját adja vissza. DAY
ÓRA
PERC Időértékből a perceket adja vissza. MINUTE
MPERC Időértékből a másodperceket adja vissza. SECOND
HÉT.NAPJA
WEEKNUM A dátumhoz tartozó hét számát adja meg. WEEKNUM
NETWORKDAYS Két dátum közötti munkanapok száma. NETWORKDAYS
WORKDAY Adott számú munkanappal későbbi dátum. WORKDAY
EASTERSUNDAY Egy adott évben a Húsvétvasárnap dátuma. EASTERSUNDAY

Dátumértéket ad eredményül. DATE
Dátumértékből az évet adja vissza. YEAR
Dátumértékből a hónapot adja vissza. MONTH

Időértékből az órákat adja vissza. HOUR

A hét napjának sorszámát adja vissza. WEEKDAY

15. fejezet

Pénzügyi és statisztikai függvények

15.1. Pénzügyi függvények

Ebben a kategóriában több mint ötven függvényt találunk, ezek közül csak néhányat tekintünk át.
Az OpenOffice.org Calc súgójában részletes magyarázatot olvashatunk minden pénzügyi függvény­ről.

A JBÉ függvény egy befektetés jövőbeli értékét adja meg, állandó összegű befizetések és ka­matláb mellett.

Szintaxisa: JBÉ(kamatláb;időszakok_száma;részlet;jelenérték;típus). Az első három paraméter
kötelező, a két utolsó opcionális.

A 15.1 ábrán látjuk, hogy elhelyezve százezer forintot (jelenérték) egy 12% (kamatláb) évi kama­tozású számlán, és minden hó végén befizetve 20 000 forintot (részlet) 5 éven át (időszakok_száma),
a számlán az öt év elteltével a JBÉ függvénnyel meghatározható az összeg.

15.1. ábra. JBÉ függvény

Figyeljük meg, hogy azok a pénzösszegek, amelyek általunk befizetésre kerülnek, negatív érték­kel szerepelnek, a hozzánk befolyó összegek pozitív értéket kapnak. A havi kamatot az éves 12-ed
részével adjuk meg (B2/12) és az időszakok száma szintén hónapokban szerepel (B3*12). A típus
paramétert nem adtuk meg, mert a befizetések a hónapok végén történnek. Hó eleji törlesztés
esetén az értéke 1 lenne.

Az MÉ (mai érték) függvény segítségével kiszámítható az az összeg, amelyre – a mai napon, fix
kamatozással befektetve, egy meghatározott számú időszak múlva – egy adott összeget (annuitást)
kapunk kézhez. Megadható, hogy mennyi pénz maradjon az időszak letelte után. A függvényt a
jelenérték meghatározásának is nevezik.

Szintaxisa: MÉ(kamatláb; időszakok_száma; részlet; jövőérték; típus). A jövőérték opcionális
paraméterrel megadhatunk egy elérni kívánt értéket. Elhagyása esetén 0.

15. FEJEZET. PÉNZÜGYI ÉS STATISZTIKAI FÜGGVÉNYEK 89

A RÉSZLET függvénnyel egy kölcsönre vonatkozó törlesztési összeget számíthatunk ki, állandó
összegű törlesztőrészletek és kamatláb esetén.

Szintaxisa: RÉSZLET(kamatláb;időszakok_száma;jelenérték;jövőérték;típus). A jelenérték az
a jelenbeli egyösszegű kifizetés, amely egyenértékű a jövőbeli kifizetések összegével. A jövőérték
opcionális paraméter, az utolsó részlet kifizetése után elérni kívánt összeg. Amennyiben elhagyjuk,
a függvény 0-nak tekinti.

A 15.2 ábrán egy 5 millió forintos, 17%-os éves kamatrátájú, 10 év alatt havi részletekben
visszafizetendő kölcsön havi részleteit látjuk.

15.2. ábra. RÉSZLET függvény

A kiszámított összeg a tőketörlesztés összegét és a kamatokat adja meg, a kölcsönhöz kapcsolódó
egyéb költségeket, mint pl. adó vagy kezelési költség nem tartalmazza. Megszorozva a kiszámított
összeget a kifizetések számával megkapjuk a teljes kifizetendő összeget. Esetünkben: 10 427 869 Ft.

A PRÉSZLET függvény egy hiteltörlesztésen belül a tőketörlesztés nagyságát számítja ki egy
adott időszakra, adott nagyságú állandó törlesztőrészletek és állandó kamatláb mellett. Szintaxisa:
PRÉSZLET(kamat; időszak; időszakok_száma; jelenérték; jövőérték; típus). A két utolsó para­méter opcionális. A jelenérték az a jelenbéli egyösszegű kifizetés, amely egyenértékű a jövőbeli
kifizetések összegével. A jövőérték az utolsó részlet kifizetése után elérni kívánt összeg. Elhagyása
esetén a függvény 0-nak tekinti.

Az RRÉSZLET függvény egy hiteltörlesztésen belül a kamattörlesztés nagyságát számítja
ki egy adott időszakra, adott nagyságú állandó törlesztőrészletek és állandó kamatláb mellett.
Paraméterei megegyeznek a PRÉSZLET függvényével.

A 15.3 ábrán egy 6 hónap futamidejű, 200 000 Ft-os hitel tőke- és kamattörlesztés havi értékeit
és azok összegét látjuk.

15.3. ábra. PRÉSZLET függvény

15. FEJEZET. PÉNZÜGYI ÉS STATISZTIKAI FÜGGVÉNYEK 90

15.2. 29. feladat

Vizsgáljuk meg, hogy érdemes-e megvenni 400 000 Ft-ért egy értékpapírt, ami havi rendszeres
8000 Ft jövedelmet kínál 5 éven át. Az évi kamatláb 14%.

Akkor érdemes megvenni az értékpapírt, ha kiszámított jelenérték 400 000 Ft vagy több. Szá­mítsuk ki az MÉ függvénnyel (15.4 ábra).

15.4. ábra. 29. feladat – MÉ függvény

Az öt éven át történő kifizetés jelenértéke csak 343 816 Ft, tehát nem érdemes megvenni az
értékpapírt.

15.3. Statisztikai függvények

A statisztikai függvények közül az egyszerűbbeket áttekintettük a negyedik fejezetben. Most vizs­gáljunk meg néhány olyan függvényt ebből a kategóriából, amelyeket gyakran használnak mind
gazdasági elemzéseknél, mind mérnöki kutatómunka során.

A SZÓRÁS függvény minta alapján becslést ad a szórásra. A szórás azt méri, hogy az értékek a
várható értéktől (középértéktől) milyen mértékben térnek el. Szintaxisa: SZÓRÁS(szám1;szám2;...).
Az argumentumok numerikus értékek vagy tartományok. A SZÓRÁS függvény az argumentumo­kat statisztikai sokaság mintájának tekinti. Amikor az adatok a teljes sokaságot jelentik, akkor a
szórást a SZÓRÁSP függvénnyel számítjuk ki.

A SZÓRÁS függvény a szöveges és a logikai értékeket figyelmen kívül hagyja. A SZÓRÁSA
függvény a szórást úgy számítja ki, hogy a szöveget és a HAMIS logikai értéket nullának, az
IGAZ logikai értéket pedig 1-nek tekinti. A teljes sokaságra vett szórást, a logikai és szöveges
argumentumokat is figyelembe véve a SZÓRÁSPA függvénnyel számítjuk ki.

A MEDIÁN függvény kiszámítja a számhalmaz középső értékét. Páratlan számú értéket tar­talmazó halmazban a középső érték a halmaz közepén elhelyezkedő érték. Páros számú értéket
tartalmazó halmazban a középső érték a halmaz közepén elhelyezkedő két érték átlaga. Szintaxisa:
MEDIÁN(szám1;szám2;...). A szöveget, a logikai értékeket és üres cellákat figyelmen kívül hagyja.

A MÓDUSZ függvény kiszámítja az adathalmazban leggyakrabban előforduló értéket. Amikor
több, egyező gyakorisággal rendelkező érték létezik, akkor a függvény eredményül a legkisebbet adja.
Hibát ír ki, ha egy érték nem jelenik meg legalább kétszer. A szöveget, logikai értékeket és üres
cellákat figyelmen kívül hagyja.

A MÉRTANI.KÖZÉP függvény kiszámítja egy minta mértani közepét. Az argumentumai
számok, számokat tartalmazó tömbök, nevek, vagy hivatkozások lehetnek. Negatív számokat és
nullát nem tartalmazhat az argumentum. A szöveget, logikai értékeket és üres cellákat figyelmen
kívül hagyja. Két szám esetén a mértani közép a két szám szorzatának a négyzetgyökével egyenlő.

A 15.5 ábrán a tárgyalt statisztikai függvények eredményeit látjuk az A2:A11 tartományba írt
számhalmazra.

Az ebben a fejezetben tárgyalt függvények a 15.1 táblázatban láthatóak.

15. FEJEZET. PÉNZÜGYI ÉS STATISZTIKAI FÜGGVÉNYEK 91

15.5. ábra. Statisztikai függvények

15.1. táblázat. A fejezetben tárgyalt függvények

A függvény Funkciója A függvény

neve angol neve

JBÉ
MÉ

RÉSZLET

RRÉSZLET
PRÉSZLET
SZÓRÁS
SZÓRÁSP

SZÓRÁSA

SZÓRÁSPA

MEDIÁN

MÓDUSZ

MÉRTANI.KÖZÉP

Egy befektetés jövőbeli értékét számítja ki. FV
Egy befektetés mai értékét számítja ki. PV
A kölcsönre vonatkozó törlesztési összeget szá­mítja ki.
A kamattörlesztés nagyságát számítja ki. IPMT
A tőketörlesztés nagyságát számítja ki. PPMT
Minta alapján becslést ad a szórásra. STDEV
Sokaság egészéből kiszámítja annak szórását. STDEVP
Minta alapján becslést ad a szórásra. Szöveges
és logikai értékek is lehetnek argumentumok.
Sokaság egészéből kiszámítja annak szórását.
Szöveges és logikai értékek is lehetnek argumen­tumok.
Kiszámítja a számhalmaz középső értékét. MEDIAN
Kiszámítja az adathalmazban leggyakrabban
előforduló értéket.
Kiszámítja egy minta mértani közepét. GEOMEAN

PMT

STDEVA

STDEVPA

MODE

16. fejezet

Tömbképletek a Calcban

16.1. Tömbképletek létrehozása

A Calcban megoldhatjuk, hogy egy képletet beírva az eredményül több cellának is értéket adjon. Az
ilyen képletet tömbképletnek nevezzük. Tömbnek értékeket tartalmazó cellák kapcsolt tartományát
nevezzük. A tömb sorokból és oszlopokból áll. Egy 4 sorból és 3 oszlopból álló tömböt 4-szer 3­as tömbnek nevezünk. A 4 és a 3 a tömb dimenziói. A tömb dimenzióit mindig először a sorok
számával, majd az oszlopok számával adják meg.

A tömbökkel való munkát megkönnyíti, ha a tömbök cellatartományait nevekkel határozzuk
meg.

Tömbképletet úgy hozunk létre, hogy kijelöljük azt a tartományt, amelyik celláit tömbképlettel
akarunk feltölteni, beírjuk a képletet, majd a Shift+Ctrl+Enter billentyűkombinációt ütjük le.

A függvénytündér segítségével is létrehozhatunk tömbképletet, ha bekapcsoljuk az Adattömb
kapcsolót az ablak bal alsó sarkában.

A tömbök celláiba számokat írva a matematikából ismert mátrixokat kapunk. A mátrixokat
nagybetűvel jelölik és elemeit szögletes zárójelek közé írják. Mátrixokat használnak lineáris egyen­letek leírására és olyan adatok tárolására, amelyek két paramétertől függnek.

16.2. Mátrixok összeadása

Két mátrixot úgy adunk össze, hogy a megfelelő elemeit összeadjuk. Hozzunk létre a 16.1 ábrán
látható A és B mátrixokat. A B2:D4 tartomány neve legyen Atömb, az F2:H4 tartományé pedig
Btömb.

A szögletes zárójeleket megrajzolhatjuk a Rajz eszköztárt bekapcsolva, azon a Szimbolikus
alakzatok Nyitó zárójel és Záró zárójel objektumokat választva.

Jelöljük ki a J2:L4 tartományt és írjuk be a következő kifejezést: =Atömb+Btömb.

A kifejezés beírása után ne az Enter billentyűt, hanem a Shift+Ctrl+Enter billentyűkombinációt
üssük le. A cellatartományban megjelennek az értékek, tömbképletet hoztunk létre. Bármelyik
cellát is választva a J2:L4 tartományból a következő tartalmat látjuk: {=Atömb+Btömb} (16.2
ábra).

Ezek tömbhivatkozások, amit a Calc mindig kapcsos zárójelben mutat. A kapcsos zárójelek
kézi beírásával tömbképletet nem hozhatunk létre.

16.3. Mátrix szorzata skalárral

Egy mátrix skalárral való szorzatát úgy számítjuk ki, hogy a skalárral a mátrix minden elemét
megszorozzuk. A következő munkalapon számítsuk ki az A mátrix 3-al való szorzatát. A B2:D4

16. FEJEZET. TÖMBKÉPLETEK A CALCBAN 93

16.1. ábra. Mátrixok összeadása – Nevek megadása

16.2. ábra. Mátrixok összeadása

tartomány kijelölése után írjuk be a képletet majd a Shift+Ctrl+Enter billentyűkombinációval
érvényesítsük a tömbképletet (16.3 ábra)

16.3. ábra. Mátrix szorzata skalárral