nicomp 380 DLS User Guide

NNiiccoommpp 338800 DDLLSS
User Manual

Particle Sizing Systems, Inc.
Particle Sizing Systems makes every effort to ensure that this document is correct. However, due
to Particle Sizing Systems policy of continual product development we are unable to guarantee
the accuracy of this, or any other document after the date of publication. We therefore disclaim
all liability for any changes, errors or omissions after the date of publication. No reproduction or
transmission of any part of this publication is allowed without express written permission of
Particle Sizing Systems, Inc.
D
OOCCUUMMEENNTT
D
C
HHAANNGGEE
C
H
IISSTTOORRY
H
Y
Date Description of Document Revision of Review New Release Number
11/07/06 New Document - 01
Particle Sizing Systems
Nicomp 380 User Manual
PSS-380Nicomp-030806
11/06


TTaabbllee ooff CCoonntteennttss
GENERAL INFORMATION ............................................................................... SECTION 1
REGISTRATION ........................................................................................................................... 1
TECHNICAL SUPPORT..................................................................................................................1
SAFETY CONSIDERATIONS ..........................................................................................................2
CE MARK ...................................................................................................................................3
DLS THEORY ………………………………………………………………………………..SECTION 2
DYNAMIC LIGHT SCATTERING THEORY .................................................................................1
PRINCIPLES OF DLS – A QUALITATIVE REVIEW ............................................................................1
Dynamic scattering: the effects of diffusion...........................................................................3
Obtaining particle size from the diffusion coefficient............................................................. 7
Autocorrelation function: definition and motivation................................................................8
Ideal case: uniform particle size.......................................................................................... 11
Photon counting and digital autocorrelation functions.........................................................12
THE SIMPLEST APPROACH TO SIZE DISTRIBUTIONS: GAUSSIAN ANALYSIS ..................................16
Uniform particle size-trivial analysis ....................................................................................16
Broad unimodal distribution Gaussian Analysis ..................................................................21
Effects of weighting in the Gaussian Analysis.....................................................................30
Importance of acquiring data of sufficient accuracy ............................................................ 36
NICOMP DISTRIBUTION ANALYSIS ............................................................................................44
INITIAL HARDWARE SETUP …………………………………………………….............SECTION 3
SOFTWARE INSTALLATION ……………………………………………………………..SECTION 4
NICOMP SOFWARE ……………………………………………………………………….SECTION 5
FILE ...........................................................................................................................................1
Read......................................................................................................................................3
Read New .............................................................................................................................4
Save ......................................................................................................................................5
Save ASCII............................................................................................................................5
Add Data ...............................................................................................................................6
Subtract Data Point ...............................................................................................................6
Print .......................................................................................................................................7
Print Preview .........................................................................................................................9
Print Setup ...........................................................................................................................10
Nicomp 380 User Manual
PSS-380Nicomp-030806
11/06
Page i

TTaabbllee ooff CCoonntteennttss
VIEW MENU .............................................................................................................................. 12
Tool Bar ...............................................................................................................................12
Display Help for Current Task or Command .......................................................................16
Start Measurement..............................................................................................................16
Status Bar ............................................................................................................................ 18
Clock ...................................................................................................................................18
SETUP......................................................................................................................................19
Select Serial Port ................................................................................................................19
Multi-Angle Option...............................................................................................................19
Interrupter Angle .................................................................................................................20
Change Laser Wavelength..................................................................................................21
APD Overload Protection ....................................................................................................21
Intensity Overshoot Factor ..................................................................................................22
NICOMP Intens-Wt Threshold ............................................................................................22
Enable Intensity Monitor......................................................................................................22
Dual Particle Sizing DLS Detector ......................................................................................22
PARTICLE SIZING ......................................................................................................................23
Control Menu.......................................................................................................................24
Nicomp Input Menu .............................................................................................................36
Smoothing ...........................................................................................................................36
Read Menu File...................................................................................................................39
Save Menu File ................................................................................................................... 40
Change Graph Color ...........................................................................................................41
Control Buttons ...................................................................................................................42
Initialize ND Filter ................................................................................................................ 43
Corr. Function .....................................................................................................................45
Gaussian ............................................................................................................................. 46
Nicomp ................................................................................................................................50
Cumulative ..........................................................................................................................51
Corr. Data............................................................................................................................52
Channel Error......................................................................................................................53
Time History ........................................................................................................................54
Summary Result..................................................................................................................56
Gauss/Nicomp.....................................................................................................................57
Show Distributions ..............................................................................................................57
Time Plot Scale ...................................................................................................................58
WEIGHTING .............................................................................................................................. 59
Intensity...............................................................................................................................59
Volume ................................................................................................................................59
Number ...............................................................................................................................59
Intens/Vol ............................................................................................................................ 59
Nicomp 380 User Manual
PSS-380Nicomp-030806
11/06
Page ii

TTaabbllee ooff CCoonntteennttss
HELP MENU .............................................................................................................................. 60
Index ...................................................................................................................................60
Using Help...........................................................................................................................60
About CW388......................................................................................................................60
COMMAND KEYS .......................................................................................................................61
SAMPLE ANALYSIS RUN………………………………………………………………….SECTION 6
MATERIALS .................................................................................................................................1
Autodilution ...........................................................................................................................1
Drop-in Cell ........................................................................................................................... 1
Hardware...............................................................................................................................2
Procedure Autodilution..........................................................................................................2
Drop-in Cell ........................................................................................................................... 5
Review of Completed Sample Results
Print Sample Results
Post Measurement System Flush
SAMPLE MAINTENANCE …………………………………………………………………SECTION 7
MAINTENANCE ............................................................................................................................1
APPENDIX A
VOLUME WEIGHTED GAUSSIAN ...............................................................................................1
NUMBER WEIGHTED GAUSSIAN...............................................................................................3
INT/VOLUME WEIGHTED GAUSSIAN ........................................................................................4
VOLUME WEIGHTED NICOMP ................................................................................................... 5
INTENSITY WEIGHTED NICOMP................................................................................................6
NUMBER WEIGHTED NICOMP...................................................................................................7
INT/VOL WEIGHTED....................................................................................................................8
SUMMARY RESULT.....................................................................................................................9
GAUSSIAN/NICOMP ALL WEIGHTED ......................................................................................10
AUTOCORRELATION FUNCTION.............................................................................................11
AUTOCORRELATION DATA......................................................................................................12
TIME HISTORY PLOT ................................................................................................................13
Nicomp 380 User Manual
PSS-380Nicomp-030806
11/06
Page iii

TTaabbllee ooff CCoonntteennttss
CHANNEL ERROR PLOT...........................................................................................................14
APPENDIX B
NICOMP PARTS LIST.................................................................................................................. 1
APPENDIX C
NONAQUEOUS SOLVENTS FOR THE NICOMP .......................................................................1
APPENDIX D
SOLVENT, TEMPERATURE, VISCOSITY & INDEX REFRACTION TABLE..............................1
APPENDIX E
ESTIMATING MOLECULAR WEIGHT......................................................................................... 1
Nicomp 380 User Manual
PSS-380Nicomp-030806
11/06
Page iv

TTaabbllee ooff CCoonntteennttss
LIST OF FIGURES
Figure 1: Simplified block diagram -- NICOMP DLS Instrument ................................................... 1
Figure 2: Simplified scattering model: two diffusing particles .......................................................4
Figure 3: Typical intensity vs time for two diffusing particles ........................................................5
Figure 4 a,b,c: Representative intensity vs time for "small"(a), "medium"(b) and "large"(c) size
particles.........................................................................................................................................6
Figure 5: Computation of autocorrelation function C(t') ................................................................8
Figure 6:Autocorrelation function C(t') for diffusion of uniform particles: exponential ................ 11
decay
Figure 8a: Autocorrelation function for 91-nm latex standard. ....................................................16
Figure 8b: Block of raw data corresponding to Figure 8a ...........................................................18
Figure 8c: Log
Figure 9a: Autocorrelation function for an IV fat emulsion. .........................................................22
Figure 9b: Log
Figure l0a: Intensity-weighted Gaussian Analysis corresponding to the data of.........................27
Figure 9a and b...........................................................................................................................27
Figure l0b: Volume-weighted Gaussian Analysis corresponding to Figure l0a...........................31
and data of Figures 9a and b. .....................................................................................................31
Figure l0c: Number-weighted Gaussian Analysis corresponding to Figure l0a ..........................32
and data of Figure 9a and b........................................................................................................32
Figure 11a: Printout of volume-weighted Gaussian Analysis result for fat emulsion ..................33
(See Figure l0a.) .........................................................................................................................33
Figure 11b: Printout of volume-weighted Gaussian Analysis result for fat emulsion. .................34
(See Figure l0b.) .........................................................................................................................34
( C(t’)-B ) vs t’ for data of Figures 8a and 8b ......................................................19
e
( C(t’)-B) vs t’ for data of Figure 9a. ....................................................................24
e
Nicomp 380 User Manual
PSS-380Nicomp-030806
11/06
Page v

TTaabbllee ooff CCoonntteennttss
Figure 11c: Printout of number-weighted Gaussian Analysis result for .................35
fat emulsion. (See Figure l0c.) .................35
Figure 12a: Intensity-weighted Gaussian Analysis .....................................................................40
Figure 12b: Volume-weighted Gaussian Analysis ......................................................................41
Figure 12c: Intensity-weighted Gaussian Analysis .....................................................................41
Figure 13: Volume-weighted Distribution Analysis result for 91-nm latex standard.................... 50
Figure 14a: Volume-weighted Distribution Analysis result for 261-nm latex standard................ 52
Figure 14b: Volume-weighted Gaussian Analysis result for 261-nm latex standard................... 53
(See Figure 14a.) ........................................................................................................................53
Figure 15: Autocorrelation function for a test bimodal: 3:1 (vol.) ratio, ...52
91 and 261 nm latex particles ...53
Figure 16: Log
Figure 17: The volume-weighted Gaussian Analysis result corresponding to ............................57
to Figure 15 and Figure 16..........................................................................................................57
Figure 18a: The volume-weighted Distribution Analysis result for the 3:1 91/261 nm ................58
test bimodal after Data = 347K ...................................................................................................58
Figure 18b: The volume-weighted Distribution Analysis result for the test bimodal.................... 59
after Data = 840K (10 mm.) ........................................................................................................59
Figure 18c: The volume-weighted Distribution Analysis result for the ........................................60
test bimodal after Data = 1736K (23 mm.) ..................................................................................60
Figure 18d: The intensity-weighted Distribution Analysis result for the test bimodal, .................61
corresponding to Figure 18c .......................................................................................................61
Figure 18e: The number-weighted Distribution Analysis result for the test bimodal, ..................62
corresponding to Figures 18c,d ..................................................................................................62
Figure 19a Printout of the intensity-weighted Distribution Analysis result for the 3:1 .................64
91/261nm test bimodal................................................................................................................64
( C(t’)-B) vs t’ for data of Figure 15 .....................................................................54
e
Nicomp 380 User Manual
PSS-380Nicomp-030806
11/06
Page vi

TTaabbllee ooff CCoonntteennttss
Figure for the 19b: Printout of the volume-weighted Distribution Analysis result 63
91/261nm test bimodal................................................................................................................65
Figure 19c: Printout of the number-weighted Distribution Analysis result for the .......................66
91/261 nm test bimodal...............................................................................................................66
Figure 20: Log
ratio, 91 and 1091 nm .................................................................................................................68
Figure 21: The volume-weighted Distribution Analysis result for the 91/1091 sample (Figure
20) nm bimodal 69
Figure 22a: Printout of volume-weighted Distribution Analysis result for the 3:1........................70
91/261 bimodal sample after 7 min.............................................................................................70
Figure 22b: Printout of volume-weighted Distribution Analysis result for the 3:1........................71
91/261 bimodal sample -- after 10 min .......................................................................................71
Figure 22c: Printout of volume-weighted Distribution Analysis result for the 70 3:1
91/261 bimodal sample -- after 42 min 72
Figure 22d: Printout of volume-weighted Distribution Analysis result for the 3:1........................73
91/261 bimodal sample -- after 8 hrs, 10 min .............................................................................73
( C(t’)-B) vs. t’ for a widely-separated bimodal latex sample: 3:1 (vol.) ..............68
e
Nicomp 380 User Manual
PSS-380Nicomp-030806
11/06
Page vii


GGeenneerraall IInnffoorrmmaattiioonn
REGISTRATION
Please register your software by taking a moment to fill out the registration page provided. In
keeping with our promise, we can easily provide two years of free software upgrades.
Just call us if you need information about our other products, or information about upgrading
your existing system.
TECHNICAL SUPPORT
If technical support is needed please contact one of the following offices:
Particle Sizing Systems
8203 Kristel Circle
Port Richey, FL 34668
Tel: 727-846-0866
Fax: 727-846-0865
Or
Particle Sizing Systems
201 Woolston Drive, Ste. 1-C
Morrisville, PA 19067
Tel: 215-428-3424
Fax: 215-428-3429
Nicomp 380 Manual
PSS-380Nicomp-030806
06/06
Page 1 -1

GGeenneerraall IInnffoorrmmaattiioonn
SAFETY CONSIDERATIONS
The NICOMP
applicable requirements of 21 CFR Subchapter J, 1040.10 and 1040.11 (Radiation Control for
Health and Safety Act of 1968, 42 U.S.C 263f).
As presently constructed, this instrument is designated by the Bureau of Radiological Health
Class I product. Exposure to negligible levels of Laser Radiation during normal operation
results. The two labels below are affixed to the back panel of the Nicomp 380/Autodilute. They
attest to the above Safety Certification and also establish the place and date of manufacture of
the unit.
THIS EQUIPMENT CONFORMS
TM
(and Autodiluter) Submicron Particle Sizer, is certified to conform to the
TO PROVISIONS OF
US 21 CFR 1040.10
AND 1040.11
Important: Read carefully before attempting to operate the Nicomp
If the Nicomp is to be used with the Autodilution option, then all liquid samples will be introduced
into the system by means of a syringe or tube connected to the manual sampling valve that is
located on the front panel of the instrument. In this case, NO entry into the sample holder
space will be required.
Alternatively, if the Nicomp is to be used without the autodilution option, then all liquid samples
will be introduced into the light scattering cell using 6 mm disposable glass culture tubes or
standard 1-cm cuvettes. In this case, entry into the sample cell holder space will be required.
Nicomp 380 Manual
PSS-380Nicomp-030806
06/06
Page 1 - 2

GGeenneerraall IInnffoorrmmaattiioonn
Access to the sample cell holder, necessary for inserting or removing a sample cell, is provided
by a square opening at the front left corner of the top cover of the instrument. A rectangular
dust cover with handle and three thumb screws are provided to keep the scattering cell and
internal optical components free of excessive amounts of dust when the unit is not in use for
extended periods of time and to prevent the laser light from scattering outside the unit during
operation. During normal operation this cover can be secured with one screw and swung to one
side to provide easy access to the cell holder. It can be swung shut during operation to keep
out stray room light and keep in beam light being scattered by the particles.
During operation of the NICOMP
unit Must Remain Closed -- i.e. attached to the cabinet by means of the 3 screws provided. The
Warning label on the cover warns of the possible exposure to the laser beam (a minimum of 5
milliwatts, 632.8 nm wavelength) if the top cover is removed for any reason while power is
applied to the unit.
Important: Any attempt to remove the front panel while the instrument is in operation
may result in possible Direct Exposure to Dangerous Laser Radiation. Also, power
must be off to the unit if the Autodilution cell is being replaced by the drop-in cell.
TM
Autodilute Submicron Particle Sizer, the Top Cover of the
CE MARK
The CE mark (officially CE marking) is a mandatory marking on certain products, which is required if they are placed on the market in the CE marking, the manufacturer, or his representative, or the importer assures that that the item meets all the essential requirements of all applicable
The CE mark is a mandatory European marking for certain product groups to indicate
conformity with the essential health and safety requirements set out in European Directives. To
permit the use of a CE mark on a product, proof that the item meets the relevant requirements
must be documented. This has been achieved using an external test house which evaluates our
particle size analyzers and its documentation. CE originally stood for Communauté Européenne
or Conformité Européenne, French for European Conformity.
The following label is affixed to the back panel of the AccuSizer SIS to indicate that the
instrument has passed CE mark testing and conforms to the European Union Directives for
Electromagnetic Compatibility (EU EMC).
European Economic Area (EEA). By affixing the
EU directives.
Nicomp 380 Manual
PSS-380Nicomp-030806
06/06
Page 1 -3


DDLLSS TThheeoorryy
DYNAMIC LIGHT SCATTERING THEORY
In recent years, the technique of dynamic light scattering (DLS) -- also called quasi-elastic light
scattering (QELS) or photon correlation spectroscopy (PCS) -- has proven to be an invaluable analytical tool for characterizing the size distribution of particles suspended in a solvent (usually
water). The useful size range for the DLS technique is quite large -from below 5 am (0.005
micron) to several microns. The power of the technology is most apparent when applied to the
difficult Particularly for diameters below 300 nm submicron size range, where most competing
measurement techniques lose their effectiveness or fail altogether. Consequently, DLS-based
sizing instruments have been used extensively to characterize a wide range of particulate
systems, including synthetic polymers (e.g. latexes, PVCs, etc.), oil-in-water and water-in-oil
emulsions, vesicles, micelles, biological macromolecules, pigments, dyes, silicas, metallic sols,
ceramics and numerous other colloidal suspensions and dispersions.
PRINCIPLES OF DLS – A QUALITATIVE REVIEW
Classical light scattering: intensity vs. volume
A simplified schematic diagram of the DLS module is shown below. Light from a laser is focused
into a glass tube containing a dilute suspension of particles. The temperature of this scattering
cell is held constant, for reasons which will soon become apparent. Each of the particles
illuminated by the incident laser beam scatters light in all directions.
The intensity of light scattered by a single, isolated particle depends on its molecular weight and
overall size and shape, and also on the difference in refractive indices of the particle and the
surrounding solvent. The incident light wave can be thought of as consisting of a very rapidly
oscillating electric field, of amplitude E
(frequency approx. 1015 Hz).
o
Figure 1: Simplified block diagram -- NICOMP DLS Instrument
Nicomp 380 Manual
PSS-380Nicomp-030806
06/06
Page 2 -1

DDLLSS TThheeoorryy
The arrival of this alternating field in the vicinity of a particle causes all of the electrons which
are free to be influenced-the so-called "polarizable" electrons -- to oscillate at the same
frequency. These oscillating electrons, in turn, give rise to a new oscillating electric field which
radiates in all directions- the scattered light wave. The quantity of interest in a scattering
measurement is the intensity
intensity is given simply by the square
scattered light intensity I
particularly simple when the particle diameter is much smaller than the laser wavelength λ -- the
so-called Rayleigh region. In this case, all of the polarizable electrons within a particle oscillate
together in phase, because at any given time they all experience the same incident electric field.
Hence, the scattered wave amplitude E
electrons, times the incident wave amplitude, E
to the overall molecular weight of the particle, MW, or its volume, V (for a given particle density).
The constants of proportionality that connect these various physical quantities depend on the
indices of refraction of the particle (n
scatters light depends not only on MW, or V, but also on the polarizability of the particle (related
to n
) relative to that of the solvent (related to ns). For the very small particles in the Rayleigh
p
region, we arrive at simple expressions for the scattered intensity I
I
or
r, I
where I
is the incident laser intensity, and f(np,ns) and g(np,ns) are functions of the indices of
o
refraction of the particle and solvent, which are fixed for a given system composition (e.g. latex
particles in water). For these small particles in the Rayleigh region (i.e. diameters < approx. 0.1
micron, or 100 nm), there is negligible angular dependence in the scattered intensity.
The simple expressions above must be modified when the characteristic particle dimension (i.e.
the diameter, in the case of spheres) is no longer negligible compared to the wavelength of the
incident light beam. In this so-called Mie Scattering region, Equations la and 1b must be altered
to take account of intra-particle interference. With a larger particle, the oscillating electrons no
longer oscillate together in phase; the individual scattered waves originating from different
regions of the particle interfere
intensity I
is therefore diminished relative to the values given by Equations la and b, which
s
assume that all of the effective scattering mass is packed into a very small particle size. The
expressions in Equations la and 1b can be repaired to include the effects of interference by
multiplying them by a so-called Mie "form" factor; this quantity has a limiting value of 1.0 (i.e. no
effect) in the Rayleigh region, but falls below unity in a non-monotonic way as the particle size
grows.
of the scattered wave, Is, rather than its amplitude, Es. The
of the amplitude: Is = (Es)2. The dependence of the
on the molecular weight (MV) or volume (V) of the particle is
S
is simply proportional to the number of polarizable
s
. The former quantity is essentially proportional
o
) and solvent (nn). That is, how well a given particle
p
:
s
= f(np,ns) (MW)2 Io (1a)
s
= g(np,ns) V2 Io (1b)
s
at the distant point of detection. The resulting total scattered
Nicomp 380 Manual
PSS-380Nicomp-030806
06/06
Page 2 - 2

DDLLSS TThheeoorryy
Using Equation la or lb, one can, in principle, determine either the molecular weight or the
volume of the particles from a measurement of the scattered intensity I
standards, together with empirical determinations of f(n
) and g(np,ns). This forms the basis
p,ns
, using known calibration
s
for the technique of "classical" light scattering. The newer DLS method, however, departs
radically from this traditional approach to light scattering. The quantity of interest is no longer
the magnitude, per se, of the scattered light intensity. Rather, DLS concerns itself with the time
behavior of the fluctuations in the scattered intensity.
Dynamic scattering: the effects of diffusion
To understand why the scattered intensity fluctuates in time, we must appreciate that it is the
result of the coherent addition, or "superposition", of many individual scattered waves, each of
which originates from a different particle located in the illuminated/detected volume. This is the
physical phenomenon known as "interference". Each individual scattered wave arriving at the
detector bears a phase relationship with respect to the incident laser wave which depends on
the precise position of the suspended particle from which it originates. All of these waves mix
together, or interfere, at a distant slit on the face of a photomultiplier detector ("PMT" in Figure
1), which measures the resulting net scattering intensity at a particular scattering angle (90
degrees in the DLS Module).
The suspended particles are not stationary; rather, they move about, or diffuse, in random-walk
fashion by the process known as Brownian motion (caused by collisions of neighboring solvent
molecules). As a consequence, the phases of each of the scattered waves arriving at the PMT
detector fluctuate randomly in time, due to the random fluctuations in the positions of the
particles that scatter the waves. Because these waves interfere together at the detector, the net
intensity fluctuates randomly in time. It is important to appreciate that only relatively small
movements in particle position are needed to effect significant changes in phase and, therefore,
to create meaningful fluctuations in the final net intensity. This is because the laser wavelength
is relatively small -- only about 0.6 micron.
The connection between the diffusion of particles and the resulting fluctuations in scattered
intensity is perhaps more easily understood by considering a simplified situation in which there
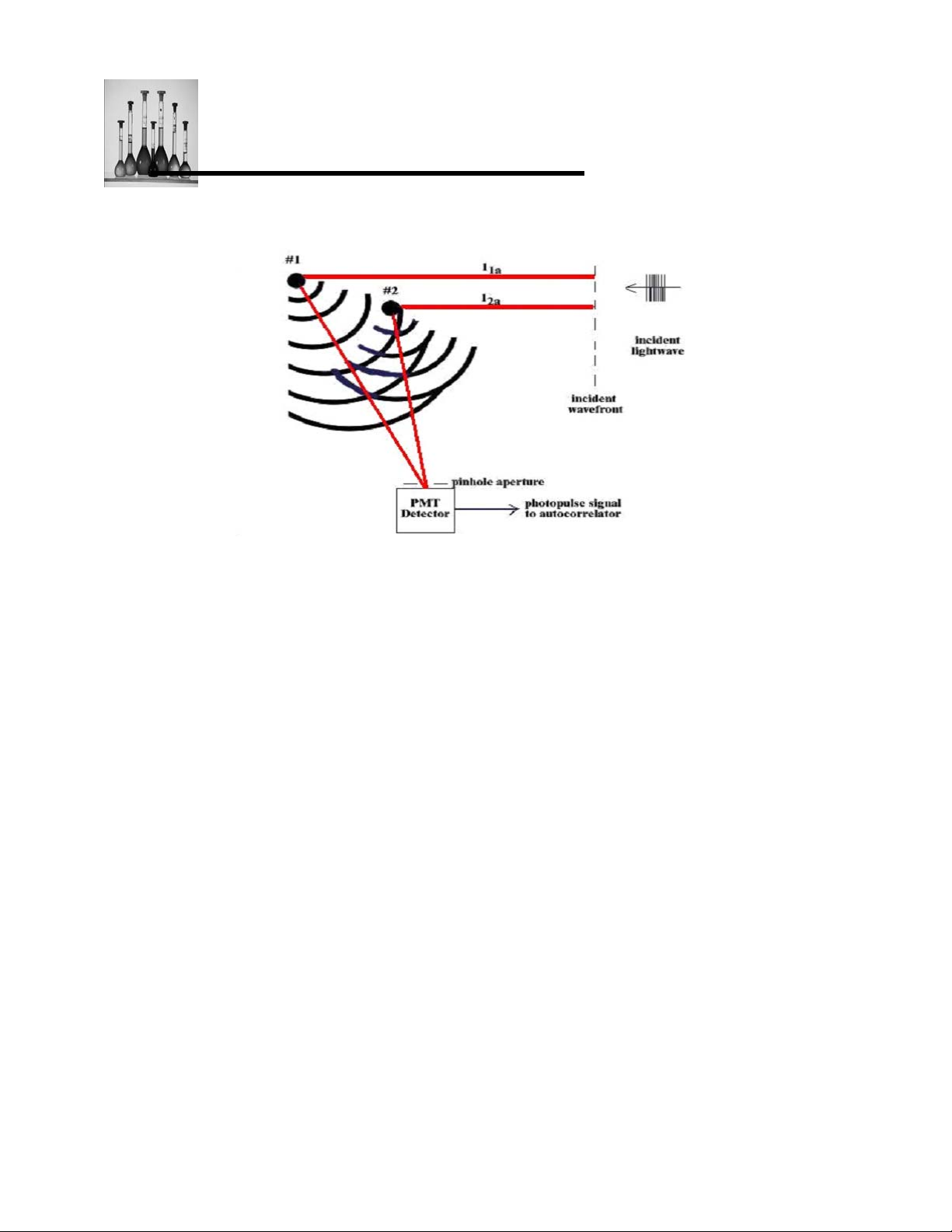
are only two particles in suspension, shown in Figure 2.
The net intensity at the detector (located far from the scattering cell, with a pinhole aperture) is a
result of the superposition of only two scattered waves. In Figure 2 we have defined the two
optical path lengths, L
distance corrected by the index of refraction, but for simplicity we assume an index of 1.0 and
show L
and L2 to be simple distances in Figure 2.) When the positions of the two particles are
1
such that the difference
multiple of the laser wavelength λ, then the two scattered waves will arrive in phase
detector. This is called total "constructive" interference and produces the largest possible
intensity at the detector.
= l1a + l1b and L2 = l2a + l2b. (More precisely, the optical path length is the
1
in optical path lengths, ΔL = L1 - L2 becomes equal to an integral
at the
Nicomp 380 Manual
PSS-380Nicomp-030806
06/06
Page 2 -3
DDLLSS TThheeoorryy
Figure 2: Simplified scattering model: two diffusing particles
At the other extreme, it is possible for the two particles to find themselves at positions such that
ΔL equals an odd number of half wavelengths, λ/2. In this case the two scattered waves arrive
at the detector totally out of phase with each other. This is total "destructive" interference,
resulting in zero net intensity. Over time, diffusion of the particles will cause the net intensity at
the detector to fluctuate in random fashion -- like a typical "noise" signal -- between these two
extreme values. A representative total intensity signal is shown in Figure 3. The intensity varies
between the maximum value and the minimum value (zero) when the optical path length
difference changes (i.e. increases or decreases) by λ/2.
Nicomp 380 Manual
PSS-380Nicomp-030806
06/06
Page 2 - 4

DDLLSS TThheeoorryy
Figure 3: Typical intensity vs time for two diffusing particles
The key physical concept that underlies the DLS particle sizing measurement is the fact that the
time scale of the fluctuations shown in Figure 3 depends on the size of the particles. For
simplicity at this point in the discussion, we assume the particles to be uniform in size, with a
single, well-defined diffusion coefficient. Small particles will "jitter" about in solution relatively
rapidly, resulting in a rapidly fluctuating intensity signal; by contrast, larger ones will diffuse
more slowly, resulting in a more slowly varying intensity.
At this point we make the simplifying assumption that the temperature of the particle suspension
is held constant. We shall see that the temperature plays as important a role as the particle
size in determining the diffusivity and, hence, the time scale of the resulting intensity
fluctuations. In any real situation of interest, of course, there are many more than two particles
in suspension which contribute to the scattered intensity signal. However, the principle of
interference remains the same. The resulting signal will be observed to fluctuate average level,
which is proportional to the number of particles illuminated/detected volume and their individual
scattering power -- Equations 1a and 1b. The time scale of the fluctuations depends on the
particle diffusivity, and hence on the particle size. This is illustrated in Figures 4a,b and c for
"small", "medium" and "large" size particles (using the same time scale on all three horizontal
axes). Again, it must be stressed that the fluctuations in the net scattered intensity are not
caused by the addition or subtraction of particles in the illuminated/detected volume. Rather,
they are the result of the variations in position of an essentially fixed number of particles within
the scattering volume.
Nicomp 380 Manual
PSS-380Nicomp-030806
06/06
Page 2 -5

DDLLSS TThheeoorryy
Figure 4 a,b,c: Representative intensity vs time for "small"(a), "medium"(b) and "large"(c) size
particles
Nicomp 380 Manual
PSS-380Nicomp-030806
06/06
Page 2 - 6

DDLLSS TThheeoorryy
Obtaining particle size from the diffusion coefficient
The goal of the DLS technique is to determine the diffusion coefficient D of the particles
(assumed uniform here) from the "raw" data -- i.e. the fluctuating light scattering signal, as
represented in Figure 4a,b,c. From D we can easily calculate the particle radius R. using the
well-known Stokes-Einstein relation,
D= kT/6πηR (2)
where k is Boltzmann's constant (1.38 X 10
the shear viscosity of the solvent (e.g. η = 1.002 X 10
that the rate at which the particles jitter about in the suspension, as measured by D, is inversely
related to the particle radius R.
From Equation 2 we see that, in general, the diffusion coefficient D of particles of a given size
increases with increasing temperature T. This is due primarily to the T-dependence of the
solvent viscosity η. (The fact that T is the numerator in Equation 2 is less small, in percentage,
when expressed in deg. Kelvin.) For example, η for pure water falls to 0.890 X 10
o
25
C -- i.e. more than a 10% change from the value at 20oC. Clearly, the less viscous the
solvent, the more rapid will be the random-walk diffusion of the particles and the faster the
resulting intensity fluctuations. Hence, changes in T are completely indistinguishable from
changes in particle radius R. as they affect D. For this reason, the sample temperature MUST
be constant (and accurately known) in order to obtain a meaningful measurement of D and,
hence, of R using Equation 2.
A cursory examination of the three fluctuating scattering signals in Figure 4a,b,c suggests that
extraction of the diffusion coefficient from the "noise" is not a straightforward matter. Signal (b)
clearly fluctuates faster than does (c), but is slower than (a); hence, its particle size must lie
between the values associated with (a) and (c). However, obtaining quantitative information
from these kinds of scattering signals is another matter altogether. What comes to our rescue is
the mathematical operation known as autocorrelation.
-16
erg K-1), T the temperature (oK, = oC + 273) and η
-2
poise for water at 20oC). Thus, we see
-2
poise at
Nicomp 380 Manual
PSS-380Nicomp-030806
06/06
Page 2 -7

DDLLSS TThheeoorryy
Autocorrelation function: definition and motivation
Let us consider the autocorrelation function of the net scattered light intensity I
fluctuates in time as shown in Figures 4a, b, and c. The autocorrelation function, which we
denote by C(t′) is used to study the correlation, or similarity, between the value of I
time, t, and the value of I
at a given time, t and the value of Is at an earlier time, t-t'. This
s
comparison is then made for many different values of t in order to obtain a good statistical
average for C(t') -- i.e. averaged over many "wiggles" of the fluctuating intensity I
evaluated according to,
C(t') = < I
(t) * Is(t-t')> (3)
s
The bracket symbols < > are shorthand for a summation over many values of t. That is, one
calculates a running sum of many products I
(t) * Is (t-t'), all having the same separation in time,
s
t', for many different values of t.
The ability of C(t') to extract useful information from the fluctuating scattering intensity I
best be understood by considering a portion of a typical signal I
arbitrarily choose a particular time t and record the value of I
consider a very small value of t', equal to t
I
(t-t1'). Because t1′ is presumed to be small, Is(t-t1') must be very similar to Is(t). The reason for
s
', and evaluate Is at this slightly earlier time, t-t1' --
1
(t), shown in Figure 5. We
s
at that time -- Is(t). We next
s
this, of course, is that the particles have not been able to change their positions significantly (i.e.
compared to λ) under diffusion in the (presumed) short time interval t
shown to be slightly larger than I
(t).
s
'. In Figure 5 Is(t-t1') is
1
(t), which
s
at a given
s
. C(t') is
s
(t) can
s
Figure 5: Computation of autocorrelation function C(t')
Nicomp 380 Manual
PSS-380Nicomp-030806
06/06
Page 2 - 8

DDLLSS TThheeoorryy
However, if t had been chosen differently in Figure 5, the order of the two values might have
been reversed. In any case, what matters is that the two intensity values that become multiplied
in Equation 3 are nearly the same. They are said to be highly correlated. Clearly, the choice of t
is irrelevant -- for any value of t, I
for a sufficiently small choice of t'.
Next, let us consider a larger value for t', equal to t
been chosen to be large enough relative to the time scale of the fluctuating signal that the two
sampled values of I
-- Is(t) and Is(t-t2') -- are now somewhat different. In this case, the two
s
sampled intensities are less well correlated. However, there still remains some relationship
between these two intensities. If t has been chosen so that I
intensity, then I
(t-t2') will still be a relatively low value. Similarly, if Is(t) lies near a maximum,
s
then it is apparent from Figure 5 that Is(t-t
not near a minimum), given the fact that t
characteristic time scale of the intensity signal shown in Figure 5.
Finally, we consider a very large time interval, t
large that I
has undergone two large fluctuations between the two sampling times, t and t-t3'. It
s
is clear, here, that the two sampled intensities will in general be almost completely uncorrelated
for such a large choice of t
'. The two values could easily be both high, both low, one high and
3
the other low, or any other intermediate possibility.
We have carried out these examples assuming a single choice for time t and three different
values of t'. In order to obtain a meaningful value for the autocorrelation function for a particular
choice of t' -- C(t') -- one must obtain many products I
for each value of t'. Only in this way will one average the value of C(t') over sufficiently many
"bumps" and "wiggles" in the fluctuating signal I
autocorrelation function. Then, one must repeat this process for sufficiently many values of t' so
as to obtain a well-defined, smooth representation of C(t') as a function of t'.
It is useful to have an idea at this point of the kinds of numbers that are involved when we use
the word "many". For a typical particle size measurement of duration 5 minutes on 0.2 micron
(200 nm) particles, the DLS Module performs approximately 15 million multiplications in order to
obtain C(t') for one value of t' (e.g. t' = 20 microseconds for "channel" #1). The instrument
makes 64 such sets of calculations simultaneously in order to obtain C(t') for 64 different values
of t'.
The essential point about the autocorrelation function is that it serves as a useful probe of the
characteristic lifetime, or duration, of the fluctuations in I
two sampled intensities exceeds the average width of a major "bump", or fluctuation, in I
two sampled intensity values will cease, on average, to be correlated. At this point, the value of
C(t') will have fallen substantially.
(t) and Is(t-t') must be highly correlated (i.e. nearly the same)
s
', as shown in Figure 5. In this case, t2' has
2
(t) is near a minimum in the
s
') must also be at a relatively high value (or certainly
2
' is not a very large time interval relative to the
2
', as seen in Figure 5. Here, we see that t3' is so
3
(t) * Is(t-t') using many different values of t,
s
to obtain a statistically meaningful value of the
s
(t). That is, once the interval t' between
s
(t), the
s
Nicomp 380 Manual
PSS-380Nicomp-030806
06/06
Page 2 -9

DDLLSS TThheeoorryy
What can we say about the shape of C(t') as a function of the sampling separation t'? Without
knowing anything about the physics of diffusion and its effect on I
something useful about C(t') in two limiting (extreme) cases: t' Æ0 and t'Æ:. In the limit in which
t' approaches zero, the two sampled intensities are essentially identical, because there is no
time for the particles to rearrange their positions. Hence,
C(O) = <I
2
(t)> (4)
s
That is, the value of C(t') for t'Æ0 is simply the sum over many values of t of the square
scattering intensity.
In the opposite limit, in which the sampling interval t' becomes very large (approaching infinity),
we have already seen (Figure 5) that there should be no correlation between the pair of
sampled intensities. Hence, Equation 3 reduces to the square of the average scattering
intensity, I
(t) -- i.e. the normalized sum of Is(t) values, taken over many values of t:
s
C(∞) = <I
(t)>2 (5)
s
It is known, and easily demonstrated, that for any fluctuating quantity, the average of the
squares of that quantity is always larger than the square of the average:
<I
2
(t)> > <Is(t)>2 (6)
s
The quantity on the right hand side of Equation 6 is the lowest value possible for the correlation
function; all other values of C(t') for finite values of t' must, in principle, be larger than the square
of the average of the I
values, because of the existence of correlations. This is referred to as
s
the baseline of the autocorrelation function. In practice, it can be effectively determined by
evaluating Equation 3 using a sufficiently large value for t'.
Hence, we can say with certainty that the function C(t') for our situation of diffusing particles
must fall from the value <I
2
(t)> at t'=0, to the baseline value, <Is(t)>2 at very large t'. The
s
problem remains -- what is the shape of C(t') between these two extreme values?
(t), we can nevertheless say
s
of the
Nicomp 380 Manual
PSS-380Nicomp-030806
06/06
Page 2 - 10

DDLLSS TThheeoorryy
Ideal case: uniform particle size
It turns out that for random diffusion of non-interacting particles, the autocorrelation function
C(t') of the fluctuating scattered light intensity I
t', as shown symbolically in Figure 6. This is described by the expression,
C(t') = A exp(-t'/τ) + B (7)
where A = <I
and B = <Is(t)>
2
(t)> - <Is(t)>
s
2
(t) is an exponentially decaying function of time
s
2
Figure 6:Autocorrelation function C(t') for diffusion of uniform particles: exponential
decay
Variable τ is the characteristic decay time constant of the exponential function; τ characterizes
quantitatively the speed with which the autocorrelation function C(t') decays toward the long-t'
limiting value (baseline B). In effect, the value of τ describes the characteristic lifetime, or
duration, of a major "bump", or fluctuation, in the scattered intensity I
particles, the slower the diffusivity and resulting fluctuations in I
s
. Hence, the larger the
s
' and the longer the decay time
constant τ.
As you might have predicted by now, we are able to obtain the diffusion coefficient D of the
particles from the decay constant τ; the precise relation is,
Nicomp 380 Manual
PSS-380Nicomp-030806
06/06
Page 2 -11

DDLLSS TThheeoorryy
1/τ = 2DK
2
(8a)
or
D = (1/2K
)(1/τ) (8b)
2
Here, the quantity K is called the "scattering wave vector". It is a constant that depends on the
laser wavelength λ in the solvent and the angle θ at which scattered light is intercepted by the
PMT detector. (θ = 90
o
for the DLS MODULE) In effect, K acts as an absolute calibration
constant, which relates the time scale of the diffusion process to the distance scale set by the
laser wavelength (making interference possible). Constant K is given by
K = (4πn/λ) sin θ/2 (9)
where n is the index of refraction of the solvent (e.g. 1.33 for water). In the case of the DLS
Module, with θ = 90
o
and λ = 632.8 nm, K equals 1.868 X 105 cm-l.
The rationale for particle sizing using the method of DLS should now be clear. We detect
scattered light (at a fixed angle) produced by an ensemble of particles suspended in a solvent.
The intensity fluctuates in time due to diffusion of the particles; there is a well defined
characteristic lifetime of the fluctuations, which is inversely proportional to the particle diffusivity.
We compute the autocorrelation function of the fluctuating intensity, obtaining a decaying
exponential curve in time. From the decay time constant τ, we obtain the particle diffusivity D.
Using the Stokes-Einstein relation (Equation 2), we finally compute the particle radius R
(assuming a sphere).
Photon counting and digital autocorrelation functions
We now consider the practical application of the theory discussed above in an actual DLS
particle sizing instrument. The first step is computation of the autocorrelation function C(t') from
the scattered light intensity I
fundamental operation of multiplication is most easily accomplished if both I
expressed as digital quantities. Fortunately, it turns out that this is already the case! In our
discussion thus far, we have represented I
magnitude as a function of time -- e.g. Figure 3 and 4a, b and c. However, in reality this is not
correct. The scattering signal I
produced by the PMT detector (Figure 1). That is, the particle suspension is sufficiently dilute
that the average scattering intensity at the PMT photocathode is extremely low, resulting in a
"photocurrent" which consists of discrete pulses (separated by zero baseline current),
corresponding to individual photons which comprise the weak scattering signal. Hence, the
DLS instrument is said to operate in the "photon counting" regime.
(t)' as prescribed in Equation 3. It should be apparent that the
s
(t) and Is(t-t') are
s
as an analog signal which varies continuously in
s
actually consists of a series of individual "photopulses"
s
Nicomp 380 Manual
PSS-380Nicomp-030806
06/06
Page 2 - 12

DDLLSS TThheeoorryy
If Is consists of a train of discrete pulses, rather than an analog signal, what is the quantitative
meaning of the "intensity" I
of photopulses per unit of time; the larger the number of pulses occurring in that time unit, the
larger the intensity. For example, in typical operation the DLS Module might show a photopulse
rate of, say, 300 kHz. This value is updated every one second and represents the number of
photopulses detected in the proceeding one-second interval. The sequence of values might
resemble the series 302, 297, 299, 304, 296, etc. We would therefore say that the average
"intensity" is approximately 300,000 -- meaning, pulses per one-second interval. However, it
would be equally valid to express the average intensity as 150,000 -- meaning per 0.5-second
interval; or as 30,000 -meaning per 0.1-second interval. That is, any
any other, for the purpose of defining the average value of the scattered intensity, depending on
the length of time which one wishes to use to define that average value.
Earlier we saw that it is typically necessary to sample the value of I
choose small values of t' between sampled pairs) in order to obtain an accurate autocorrelation
function, which is sensitive to rapid changes in I
this reason, it is therefore necessary to define I
small unit of time. In this way, the measurement of I
and approaches being an instantaneous value. For example, when 100 nm (0.1 micron)
particles are measured by the DLS Module, the sampling of I
every 10 microseconds. In this case, therefore, I
photopulses which occur during a given 10 microsecond interval. This short a time interval, or
smallest increment in t', is needed to compute the relatively rapid decay of C(t') versus t' which
occurs for these rapidly diffusing small particles. Of course, for smaller particles an even smaller
unit time interval would be needed to define I
Two observations should immediately be evident. First, given such small time intervals used to
define I
(t), the resulting number of pulses must be very small. Consider our example of a
s
typical average photopulse rate of 300,000 per second; this corresponds to an average
instantaneous intensity of 3 pulses per 10 microseconds. Second, we should expect this
number to change greatly from one time interval to the next, given such a small average value.
If the instantaneous photon rate were to follow Poisson statistics, we would expect the rms
standard deviation of the number of pulses per time interval to equal N
average number. For our example above, this gives a standard deviation of 1.7. Hence, from
purely a statistical point of view we expect the "intensity" I
vary from 0 to 5 photopulses with occasionally a 6, 7 or larger), independent of the effects of
diffusion. This is simply a consequence of our having chosen a very short time interval relative
to the average photopulse rate. When diffusion is added to the process, the resulting
fluctuations in I
(t) become even more pronounced.
s
The resulting integer numbers of photopulses per small time interval are, of course, the values
of I
(t) and Is(t-t') in Equation 3 which become multiplied together digitally to compute the values
s
of C(t'). A representative sequence of photopulses is shown in Figure 7. We have subdivided
the time base, t, into intervals of equal width Δt', equal to the "channel width" of the
at time t? Clearly, the intensity must be represented by the number
s
unit of time is as valid as
(t) very frequently (i.e. to
s
, caused by rapid diffusion of the particles. For
s
, in terms of the photopulse rate using a very
s
can be made as frequently as necessary
s
(t) is performed approximately
s
(t) is arbitrarily defined to be the number of
s
(t).
s
1/2
, where N is the
per 10 microsecond time interval to
s
Nicomp 380 Manual
PSS-380Nicomp-030806
06/06
Page 2 -13

DDLLSS TThheeoorryy
autocorrelator. Here, the instantaneous intensity Is(t) is defined as the number of pulses in the
interval Δt' which lies closest to time t. Over each interval we have recorded the instantaneous
"intensity" for that interval -- simply the number of photopulses produced by the PMT detector.
(Technically, the pulses which comprise the PMT photocurrent vary substantially in height, as
well as rate of Occurrence, owing to the statistical nature of the secondary-electron
multiplication mechanism in the PMT.
Figure 7: A typical photopulse sequence representing I
time width, t'
However, a discriminator with a low reference level is used to convert this signal to a
train of pulses of uniform height, suitable for manipulation by standard integrated logic circuits in
the autocorrelator.)
The procedure for computing the digital representation of C(t') should now be conceptually
clear. The train of photopulses from the PMT detector is divided into intervals of equal time, or
channel width, Δt'. Running sums of the products I
values of t' -- 64 in the case of the DLS Module. The separation times t' are "quantized" in
multiples of Δt': Δt', 2Δt', 3Δt',...64 Δt'. In addition, a long-delay baseline value is obtained:
t' = (64 + 1024) Δt'.
(t) * Is(t-t') are then produced for many
s
(t) divided into intervals of equal
s
Nicomp 380 Manual
PSS-380Nicomp-030806
06/06
Page 2 - 14
