MOTOROLA MPC180LMB User Guide

Download

查询MPC180LMB供应商

MPC180LMB Security Processor

User’s Manual

PRELIMINARY—SUBJECT TO CHANGE WITHOUT NOTICE

MPC180LMBUM/D

Rev. 0, 3/2002

DigitalDNA, PowerQUICC, and PowerQUICC II are trademarks of Motorola, Inc. The PowerPC name, the PowerPC logotype, and PowerPC 603e are trademarks of International Business Machines Corporation

used by Motorola under license from International Business Machines Corporation.

C is a registered trademark of Philips Semiconductors

This document contains information on a new product under development. Motorola reserves the right to change or discontinue this product without notice. Information in this document is provided solely to enable system and software implementers to use Motorola security processors. There are no express or implied copyright licenses granted hereunder to design or fabricate Motorola security processors integrated circuits or integrated circuits based on the information in this document.

Motorola reserves the right to make changes without further notice to any products herein. Motorola makes no warranty, representation or guarantee regarding the suitability of its products for any particular purpose, nor does Motorola assume any liability arising out of the application or use of any product or circuit, and specifically disclaims any and all liability, including without limitation consequential or incidental damages. “Typical” parameters can and do vary in different applications. All operating parameters, including “Typicals” must be validated for each customer application by customer’s technical experts. Motorola does not convey any license under its patent rights nor the rights of others. Motorola products are not designed, intended, or authorized for use as components in systems intended for surgical implant into the body, or other applications intended to support or sustain life, or for any other application in which the failure of the Motorola product could create a situation where personal injury or death may occur. Should Buyer purchase or use Motorola products for any such unintended or unauthorized application, Buyer shall indemnify and hold Motorola and its officers, employees, subsidiaries, affiliates, and distributors harmless against all claims, costs, damages, and expenses, and reasonable attorney fees arising out of, directly or indirectly, any claim of personal injury or death associated with such unintended or unauthorized use, even if such claim alleges that Motorola was negligent regarding the design or manufacture of the part. Motorola and are registered trademarks of Motorola, Inc. Motorola, Inc. is an Equal Opportunity/Affirmative Action Employer.

Motorola Literature Distribution Centers: USA/EUROPE: Motorola Literature Distribution; P.O. Box 5405; Denver, Colorado 80217; Tel.: 1-800-441-2447 or 1-303-675-2140/

JAPAN: Nippon Motorola Ltd SPD, Strategic Planning Office 4-32-1, Nishi-Gotanda Shinagawa-ku, Tokyo 141, Japan Tel.: 81-35487-8488

ASIA/PACIFC: Motorola Semiconductors H.K. Ltd.; 8B Tai Ping Industrial Park, 51 Ting Kok Road, Tai Po, N.T., Hong Kong;

Tel.: 852-26629298

Technical Information: Motorola Inc. SPS Customer Support Center 1-800-521-6274; electronic mail address:

crc@wmkmail.sps.mot.com.

Document Comments: FAX (512) 933-3873, Attn: Security Processor Applications Engineering. World Wide Web Addresses: http://www.motorola.com/smartnetworks/products/security

http://www.mot.com/netcomm http://www.mot.com/PowerPC http://www.mot.com/HPESD

Overview

Signal Descriptions

External Bus Interface and Memory Map

Data Encryption Standard Execution Unit

Arc Four Execution Unit

Message Digest Execution Unit

Public Key Execution Unit

Random Number Generator

Glossary of Terms and Abbreviations

PRELIMINARY—SUBJECT TO CHANGE WITHOUT NOTICE

GLO

Overview

6 7

Signal Descriptions External Bus Interface and Memory Map Data Encryption Standard Execution Unit Arc Four Execution Unit Message Digest Authentication Unit

Public Key Execution Unit Random Number Generator

GLO

Glossary of Terms and Abbreviations

PRELIMINARY—SUBJECT TO CHANGE WITHOUT NOTICE

CONTENTS

Paragraph Number

Title

Page

Number

Chapter 1

Overview

1.1 Features............................................................................................................... 1-1

1.2 System Architecture............................................................................................ 1-2

1.3 Architectural Overview....................................................................................... 1-3

1.3.1 Public Key Execution Unit (PKEU)............................................................... 1-4

1.3.2 Data Encryption Standard Execution Unit (DEU).......................................... 1-4

1.3.3 Arc Four Execution Unit (AFEU) .................................................................. 1-5

1.3.4 Message Authentication Unit (MAU)............................................................. 1-5

1.3.5 Random Number Generator (RNG)................................................................ 1-5

1.3.6 Software and Hardware Support..................................................................... 1-6

Chapter 2

Signal Descriptions

2.1 Signal Descriptions............................................................................................. 2-1

Chapter 3

External Bus Interface and Memory Map

3.1 Execution Unit Registers .................................................................................... 3–1

3.2 Address Map....................................................................................................... 3–2

3.3 External Bus Interface......................................................................................... 3–4

3.3.1 EBI Registers.................................................................................................. 3–5

3.3.1.1 Command/Status Register (CSTAT).......................................................... 3–5

3.3.1.2 ID Register.................................................................................................. 3–7

3.3.1.3 IMASK Register......................................................................................... 3–8

3.3.1.4 Input Buffer Control (IBCTL) and Output Buffer Control (OBCTL) Registers 3–9

3.3.1.5 Input Buffer Count (IBCNT) and Output Buffer Count (OBCNT) Registers... 3–11

3.4 EBI Controller Operation.................................................................................. 3–11

3.4.1 Buffer Accesses (FIFO Mode)...................................................................... 3–11

Contents

CONTENTS

Paragraph Number

Title

Page

Number

Chapter 4

Data Encryption Standard Execution Unit

4.1 Operational Registers.......................................................................................... 4–1

4.1.1 DEU Control Register (DCR)......................................................................... 4–2

4.1.2 DEU Configuration Register (DCFG)............................................................ 4–2

4.1.3 DEU Status Register (DSR)............................................................................ 4–3

4.1.4 Key Registers.................................................................................................. 4–4

4.1.5 Initialization Vector........................................................................................ 4–4

4.1.6 DATAIN......................................................................................................... 4–4

4.1.7 DATAOUT..................................................................................................... 4–4

Chapter 5

Arc Four Execution Unit

5.1 Arc Four Execution Unit Registers..................................................................... 5–1

5.1.1 Status Register ................................................................................................ 5–2

5.1.2 Control Register.............................................................................................. 5–3

5.1.3 Clear Interrupt Register .................................................................................. 5–3

5.1.4 Key Length Register....................................................................................... 5–3

5.1.5 Key (Low/Lower-middle/Upper-middle/Upper) Register.............................. 5–3

5.1.6 Message Byte Double-Word Register ............................................................ 5–4

5.1.7 Message Register............................................................................................ 5–4

5.1.8 Cipher Register............................................................................................... 5–4

5.1.9 S-box I/J Register............................................................................................ 5–5

5.1.10 S-box0 – S-box63 Memory............................................................................. 5–5

Chapter 6

Message Digest Execution Unit

6.1 Operational Registers.......................................................................................... 6–1

6.1.1 MDEU Version Identification Register (MID)............................................... 6–2

6.1.2 MDEU Control Register (MCR)..................................................................... 6–2

6.1.3 Status Register (MSR).................................................................................... 6–4

6.1.4 Message Buffer (MB0—MB15)..................................................................... 6–5

6.1.5 Message Digest Buffer (MA–ME) ................................................................. 6–5

Chapter 7

Public Key Execution Unit

7.1 Operational Registers.......................................................................................... 7–1

7.1.1 PKEU Version Identification Register (PKID) .............................................. 7–1

MPC180LMB Security Processor User’s Manual

CONTENTS

Paragraph Number

Title

Page

Number

7.1.2 Control Register (PKCR)................................................................................ 7–2

7.1.3 Status Register (PKSR)................................................................................... 7–3

7.1.4 Interrupt Mask Register (PKMR)................................................................... 7–4

7.1.5 EXP(k) Register.............................................................................................. 7–6

7.1.6 Program Counter Register (PC)...................................................................... 7–6

7.1.7 Modsize Register ............................................................................................ 7–7

7.1.8 EXP(k)_SIZE.................................................................................................. 7–7

7.2 Memories ............................................................................................................ 7–7

7.3 ECC Routines ..................................................................................................... 7–8

7.3.1 ECC Fp Point Multiply................................................................................... 7–8

7.3.2 ECC Fp Point Add........................................................................................ 7–11

7.3.3 ECC Fp Point Double................................................................................... 7–12

7.3.4 ECC Fp Modular Add................................................................................... 7–13

7.3.5 ECC Fp Modular Subtract ............................................................................ 7–14

7.3.6 ECC Fp Montgomery Modular Multiplication

B × R-1) mod N) 7–15

((A ×

7.3.7 ECC Fp Montgomery Modular Multiplication

B × R-2) mod N) 7–16

((A ×

7.3.8 ECC F2

7.3.9 ECC F2

7.3.10 ECC F2

7.3.11 ECC F2

7.3.12 ECC F2

((A ×

7.3.13 ECC F2

((A ×

Polynomial-Basis Point Multiply................................................. 7–17

Point Add...................................................................................... 7–19

Point Double................................................................................ 7–21

Add (Subtract)............................................................................. 7–22

Montgomery Modular Multiplication

B × R-1) mod N) 7–23

Montgomery Modular Multiplication

B × R-2) mod N) 7–24

7.4 RSA Routines ................................................................................................... 7–25

-1

EXP

)

7.4.1 (A ×

mod N .................................................................................... 7–25

7.4.2 RSA Montgomery Modular Multiplication

((A ×

B × R-1) mod N) 7–27

7.4.3 RSA Montgomery Modular Multiplication

((A ×

B × R-2) mod N) 7–28

7.4.4 RSA Modular Add........................................................................................ 7–29

7.4.5 RSA Fp Modular Subtract ............................................................................ 7–30

7.5 Miscellaneous Routines.................................................................................... 7–31

7.5.1 Clear Memory............................................................................................... 7–31

7.5.2 R

7.5.3 R

mod N Calculation................................................................................... 7–32

mod P Calculation .............................................................................. 7–33

7.6 Embedded Routine Performance ...................................................................... 7–35

Chapter 8

Random Number Generator

Contents

vii

CONTENTS

Paragraph Number

8.1 Overview............................................................................................................. 8–1

8.2 Functional Description........................................................................................ 8–1

8.3 Typical Operation ............................................................................................... 8–1

8.4 Random Number Generator Registers................................................................ 8–2

8.4.1 Status Register ................................................................................................ 8–2

Title

Page

Number

Glossary of Terms and Abbreviations

viii

MPC180LMB Security Processor User’s Manual

ILLUSTRATIONS

Figure Number

Title

Page

Number

1-1 Typical MPC8xx System Example............................................................................... 1-2

1-2 Typical MPC8260 System Example............................................................................. 1-3

1-3 MPC180 Block Diagram...............................................................................................1-3

2-1 MPC180 Pin Diagram................................................................................................... 2-4

3-1 MPC180 Execution Unit Registers...............................................................................3–1

3-2 Command/Status Register (CSTAT) ............................................................................3–6

3-3 ID Register....................................................................................................................3–8

3-4 IMASK Register ...........................................................................................................3–9

3-5 Input Buffer Control (IBCTL) and Output Buffer Control (OBCTL) Registers........3–10

3-6 Input Buffer Count (IBCNT) and Output Buffer Count (OBCNT) Registers...........3–11

4-1 DES Control Register (DCR)........................................................................................4–2

4-2 DEU Configuration Register (DCFG)..........................................................................4–2

4-3 DES Status Register (DSR) ..........................................................................................4–3

5-1 Arc Four Execution Unit Status Register......................................................................5–2

5-2 Arc Four Execution Unit Control Register...................................................................5–3

5-3 Arc Four Execution Unit Message Byte Double-Word Register..................................5–4

6-1 MDEU Control Register (MCR)...................................................................................6–2

6-2 MDEU Status Register (MSR)......................................................................................6–4

7-1 PKEU Control Register (PKCR) ..................................................................................7–2

7-2 PKEU Status Register (PKSR) .....................................................................................7–4

7-3 PKEU Interrupt Mask Register (PKMR)......................................................................7–5

7-4 ECC Fp Point Multiply Register Usage........................................................................7–9

7-5 ECC Fp Point Add Register Usage.............................................................................7–11

7-6 ECC Fp Point Double Register Usage........................................................................7–12

7-7 Modular Add Register Usage......................................................................................7–13

7-8 Modular Subtract Register Usage...............................................................................7–14

7-9 Modular Multiplication Register Usage......................................................................7–15

7-10 Modular Multiplication (with double reduction) Register Usage...............................7–16

7-11 ECC F2 7-12 ECC F2 7-13 ECC F2 7-14 F2 7-15 F2 7-16 F2

m m m

Point Multiply I/O......................................................................................7–18

Point Add Register Usage ..........................................................................7–20

Point Double Register Usage .....................................................................7–21

Modular Add (Subtract) Register Usage.............................................................7–22

Modular Multiplication Register Usage..............................................................7–23

Modular Multiplication (with double reduction) Register Usage.......................7–24

7-17 Integer Modular Exponentiation Register Usage........................................................7–26

7-18 Modular Multiplication Register Usage......................................................................7–27

Contents

ILLUSTRATIONS

Figure Number

Title

Page

Number

7-19 Modular Multiplication (with double reduction) Register Usage...............................7–28

7-20 Modular Add Register Usage......................................................................................7–29

7-21 Modular Subtract Register Usage...............................................................................7–30

7-22 Clear Memory Register Usage....................................................................................7–31

7-23 R 7-24 R

mod N Register Usage...........................................................................................7–33

mod P Register Usage ......................................................................................7–34

8-1 RNG Status Register.....................................................................................................8–2

MPC180LMB Security Processor User’s Manual

TABLES

Table Number

Title

Page

Number

2-1 Pin Descriptions............................................................................................................ 2-1

3-1 32-Bit System Address Map.........................................................................................3–2

3-2 EBI Registers................................................................................................................3–5

3-3 CSTAT Field Descriptions ...........................................................................................3–6

3-4 ID Field Descriptions....................................................................................................3–8

3-5 IMASK Field Descriptions...........................................................................................3–9

3-6 IBCTL Field Descriptions...........................................................................................3–10

3-7 OBCTL Register Field Descriptions...........................................................................3–10

4-1 Data Encryption Standard Execution Unit (DEU) Registers........................................4–1

4-2 DCR Field Descriptions................................................................................................4–2

4-3 DCFG Field Descriptions .............................................................................................4–3

4-4 DSR Field Descriptions ................................................................................................4–3

5-1 Arc Four Execution Unit (AFEU) Registers.................................................................5–1

5-2 AFEU Status Register Field Descriptions.....................................................................5–2

5-3 AFEU Control Register Field Descriptions..................................................................5–3

6-1 Message Digest Execution Unit (MDEU) Registers ....................................................6–1

6-2 MCR Field Descriptions...............................................................................................6–3

6-3 MSR Field Descriptions................................................................................................6–4

7-1 PKEU Registers............................................................................................................7–1

7-2 PKCR Field Descriptions..............................................................................................7–2

7-3 PKSR Field Descriptions..............................................................................................7–4

7-4 PKMR Field Descriptions.............................................................................................7–5

7-5 ECC Fp Point Multiply.................................................................................................7–8

7-6 ECC Fp Point Add......................................................................................................7–11

7-7 ECC Fp Point Double .................................................................................................7–12

7-8 Modular Add...............................................................................................................7–13

7-9 Modular Subtract ........................................................................................................7–14

7-10 Modular Multiplication...............................................................................................7–15

7-11 Modular Multiplication (with double reduction)........................................................7–16

7-12 ECC F2 7-13 ECC F2 7-14 ECC F2 7-15 F2 7-16 F2 7-17 F2

m m m

Point Multiply.............................................................................................7–17

Point Add....................................................................................................7–20

Point Double...............................................................................................7–21

Modular Add (Subtract)......................................................................................7–22

Modular Multiplication.......................................................................................7–23

Modular Multiplication (with double reduction) ................................................7–24

7-18 Integer Modular Exponentiation.................................................................................7–26

Contents

TABLES

Table Number

Title

Page

Number

7-19 Modular Multiplication...............................................................................................7–27

7-20 Modular Multiplication (with double reduction)........................................................7–28

7-21 Modular Add...............................................................................................................7–29

7-22 Modular Subtract ........................................................................................................7–30

7-23 Clear Memory.............................................................................................................7–31

7-24 R 7-25 R

mod N ....................................................................................................................7–32

mod P................................................................................................................7–34

7-26 Run Time Formulas ....................................................................................................7–35

8-1 Random Number Generator Registers..........................................................................8–2

8-2 RNG Status Register Field Descriptions.......................................................................8–2

xii

MPC180LMB Security Processor User’s Manual

Chapter 1 Overview

This chapter gives an overview of the MPC180 security processor, including the key features, typical system architecture, and the MPC180 internal architecture.

1.1 Features

The MPC180 is a ﬂexible and powerful addition to an y netw orking system currently using Motorola’s MPC8xx or MPC826x family of PowerQUICC™ communication processors. The MPC180 is designed to off-load computationally intensive security functions such as key generation and exchange, authentication, and bulk data encryption.

The MPC180 is optimized to process all of the algorithms associated with IPSec, IKE, WTLS/WAP and SSL/TLS. In addition, the MPC180 is the only security processor on the market capable of executing the elliptic curv e cryptography that is especially important for secure wireless communications.

MPC180 features include the following:

• Public key execution unit (PKEU), which supports the following: — RSA and Difﬁe-Hellman

– Programmable ﬁeld size 80- to 2048-bits – 1024-bit signature time of 32ms – 10 IKE handshakes/second

— Elliptic Curve operations in either F 2 m or F p

– Programmable ﬁeld size from 55- to 511-bits – 155-bit signature time of 11ms – 30 IKE handshakes/second

• Message authentication unit (MAU) — SHA-1 with 160-bit message digest — MD5 with 128-bit message digest — HMAC with either algorithm

• Data encryption standard execution units (DEUs) — DES and 3DES algorithm acceleration

– Two key (K1, K2, K1) or Three key (K1, K2, K3)

Chapter 1. Overview 1-1

System Architecture

— ECB and CBC modes for both DES and 3DES — 15 Mbps 3DES-HMAC-SHA-1 (memory to memory)

• ARC four execution unit (AFEU) — Implements a stream cipher compatible with the RC4 algorithm — 40- to 128-bit programmable key — 20 Mbps ARC Four performance (memory to memory)

• Random Number Generator (RNG) — Supplies up to 160 bit strings at up to 5 Mbps data rate

• Input Buffer (4kbits)

• Output Buffer (4kbits)

• Glueless interface to MPC8xx system or MPC826x local bus (50MHz and 66MHz operation)

• DMA hardware handshaking signals for use with the MPC826x

• 1.8v Vdd, 3.3v I/O

• 100pin LQFP package

• HIP4 0.25µm process

1.2 System Architecture

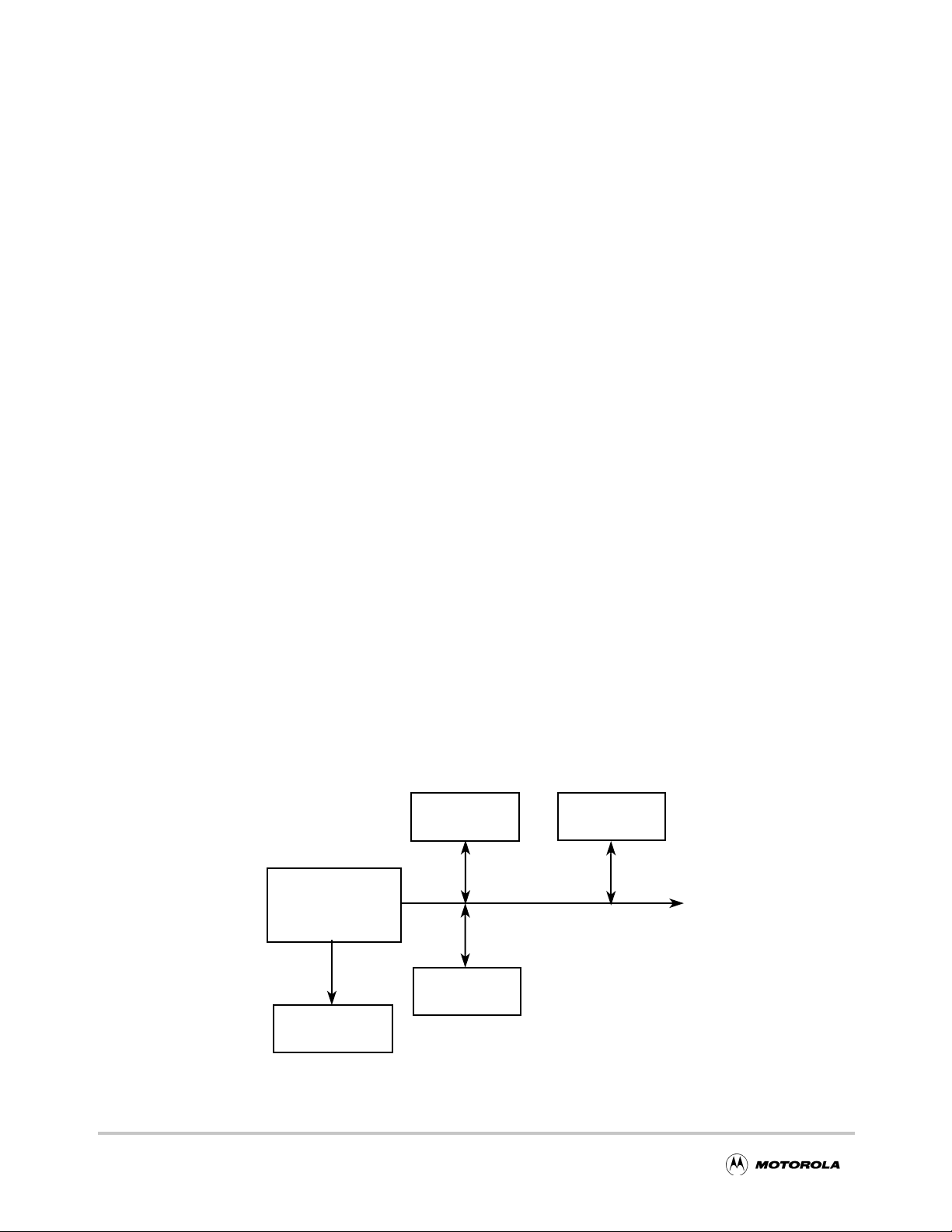
The MPC180 works well in most load/store, memory-mapped systems. An external processor may execute application code from its R OM and RAM, using RAM and optional non-volatile memory (such as EEPR OM) for data storage. Figure 1-1 shows an e xample of the MPC180 in an MPC8xx system, and Figure 1-2 shows the MPC180 connected to the local bus of the MPC826x. In these examples, the MPC180 resides in the memory map of the processor; therefore, when an application requires cryptographic functions, it reads and writes to the appropriate memory location in the security processor.

EEPROM

MPC860

MPC180

System Bus

1-2

SDRAM

I/O or Network

Interface

Figure 1-1. Typical MPC8xx System Example

MPC180LMB Security Processor User’s Manual

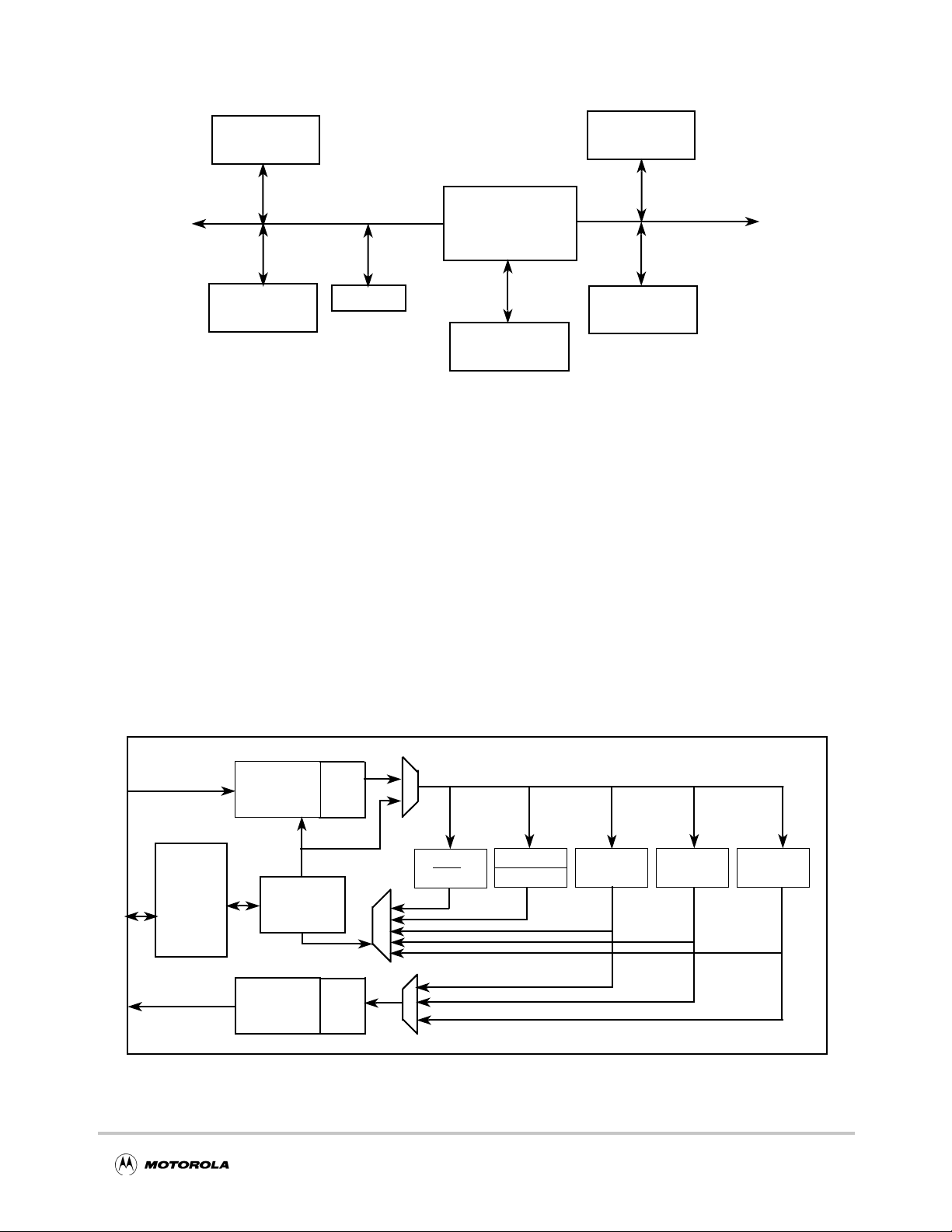
Architectural Overview

EEPROM

SDRAM

DIMMs

60x Bus

MPC8260

SDRAM

I/O or Network

Interface

MPC180

Local Bus

SDRAM

Figure 1-2. Typical MPC8260 System Example

1.3 Architectural Overview

The MPC180 has a slave interface to the MPC8xx system b us and MPC8260 local b us and maps into the host processor’s memory space. Each encryption algorithm is mapped to a unique address space. To perform encryption operations, the host reads and writes to the MPC180 to setup the execution unit and, then, transfers data to the execution unit directly or through the external bus interface.

In FIFO mode, the MPC180 accepts data into the 4-Kbit input buffer and returns b urst data through the output buffer. In this way, the host can automatically transfer bulk data through a given EU. This minimizes host management overhead and increases overall system throughput. Once the host conﬁgures the external bus interface (EBI), it receives an interrupt only after all data has been transferred or processed by the MPC180.

DMA Request

8xx/6xx

I/F

(Slave)

External Bus Interface

DMA Request

INPUT

4K bit FIFO

Controller

OUTPUT

4K bit FIFO

DMA Logic

RSA ECC

SHA-1

MD 5

DES/ 3DES

ARC4

RNG

Figure 1-3. MPC180 Block Diagram

Chapter 1. Overview 1-3

Architectural Overview

The interrupt controller organizes hardware interrupts coming from individual EUs into a single maskable interrupt, IRQ_B, for the host processor. Multiple internal interrupt sources are logically ORed to create a single, non-prioritized interrupt for the host processor. The controller lets the host read the unmasked interrupt source status as well as the request status of masked interrupt sources, thereby indicating whether a given unmasked interrupt source will generate an interrupt request to the host processor.

1.3.1 Public Key Execution Unit (PKEU)

The PKEU is capable of performing many advanced mathematical functions to support RSA and Difﬁe-Hellman as well as ECC in both F 2 m (polynomial-basis) and F p. The accelerator supports all levels of functions to assist the host microprocessor in performing its desired cryptographic function. For example, at the highest level, the accelerator performs modular exponentiations to support RSA and point multiplies to support ECC. At lower levels, the PKEU can perform simple operations such as modular multiplies.

1.3.2 Data Encryption Standard Execution Unit (DEU)

The DEU is used for bulk data encryption. It can also execute the Triple-DES algorithm, which is based on DES. The host processor supplies data to the DEU as input, and this data is encrypted and made available for reading. The session key is input to the DEU prior to encryption. The DEU computes the data encryption standard algorithm (ANSI X3.92) for bulk data encryption and decryption.

DES is a block cipher that uses a 56-bit key to encrypt 64-bit blocks of data, one block at a time. DES is a symmetric algorithm; therefore, each of the two communicating parties share the same 56-bit key. DES processing begins after this shared session key is agreed upon. The message to be encrypted (typically plain text) is partitioned into n sets of 64-bit blocks. Each block is processed, in turn, by the DES engine, producing n sets of encrypted (ciphertext) blocks. Decryption is handled in the rev erse manner. The ciphertext blocks are processed one at a time by a DES module in the recipient’s system. The same key is used, and the DEU manages the key processing internally so that the plaintext blocks are recovered.

The DES/3DES execution unit supports the following modes:

• ECB (electronic code book)

• CBC (cipher block chaining)

In addition to these modes, the DEU can compute T riple-DES. Triple-DES is an extension to the DES algorithm in which every 64-bit input block is processed three times. There are several ways that Triple-DES can be computed. The DES accelerator on the MPC180 supports two key (K1, K2, K1) or three key (K1, K2, K3) Triple-DES.

THe MPC180 supports two of the modes of operation deﬁned for Triple-DES (see draft ANSI Standard X9.52-1998):

• TECB (Triple DES analogue of ECB)

1-4 MPC180LMB Security Processor User’s Manual

Architectural Overview

• TCBC (Triple DES analogue of CBC)

1.3.3 Arc Four Execution Unit (AFEU)

The AFEU processes an algorithm that is compatible with the RC4 stream cipher from RSA Security, Inc. The RC4 algorithm is byte-oriented; therefore, a byte of plaintext is encrypted with a key to produce a byte of ciphertext. The key is variable length, and the AFEU supports 40-bit to 128-bit key lengths, providing a wide range of security levels. RC4 is a symmetric algorithm, so each of the two communicating parties share the same key .

AFEU processing begins after this shared session key is agreed upon. The plaintext message to be encrypted is logically partitioned into n sets of 8-bit blocks. In practice, the host processor groups 4 bytes at a time into 32-bit blocks and write that data to the AFEU. The AFEU internally processes each w ord one byte at a time. The AFEU engine processes each block in turn, byte by byte, producing n sets of encrypted (ciphertext) blocks. Decryption is handled in the reverse manner. The ciphertext blocks are processed one at a time by an AFEU in the recipient’s system. The same key is used, and the AFEU manages the key processing internally so that the plaintext blocks are recovered.

The AFEU accepts data in 32-bit words per write cycle and produces 4 bytes of ciphertext for every 4 bytes of plaintext. Before any processing occurs, the key data is written to the AFEU, after which an initial permutation on the key happens internally. After the initial permutation is ﬁnished, processing on 32-bit words can begin.

1.3.4 Message Authentication Unit (MAU)

The MAU can perform SHA-1, MD5 and MD4, three of the most popular public message digest algorithms. At its simplest, the MAU receives 16 32-bit registers containing a message, and produces a hashed message of 128 bits for MD4/MD5 and 160 bits for SHA-1. The MAU also includes circuitry to automate the process of generating an HMAC (hashed message authentication code) as speciﬁed by RFC 2104. The HMAC can be built upon any of the hash functions supported by MAU.

1.3.5 Random Number Generator (RNG)

Because many cryptographic algorithms use random numbers as a source for generating a secret value, it is desirable to have a private RNG for use by the MPC180. The anonymity of each random number must be maintained, as well as the unpredictability of the next random number. The private RNG allows the system to develop random challenges or random secret keys. The secret key can thus remain hidden from even the high-level application code, providing an added measure of physical security. The RNG is also useful for digital signature generation.

The RNG is a digital integrated circuit capable of generating 32-bit random numbers. It is designed to comply with FIPS-140 standards for randomness and non-determinism. The RNG creates an unpredictable sequence of bits and assembles a string of those bits into a register. The random number in that register is accessible to the host through the host

Chapter 1. Overview 1-5

Architectural Overview

interface of the RNG.

1.3.6 Software and Hardware Support

Customers will have access to device drivers integrated with the WindRiver VxWorks OS. Sample drivers will also be provided to customers wishing to integrate MPC180 support into other operating systems.

Third-party support for the MPC180 includes a development system for both the MPC860 and the MPC8260. The WindRiver/EST SBC8260C development system and Zephyr Engineering ZPC860C, both of which include a board support package, are available to accelerate customer design cycles.

1-6 MPC180LMB Security Processor User’s Manual

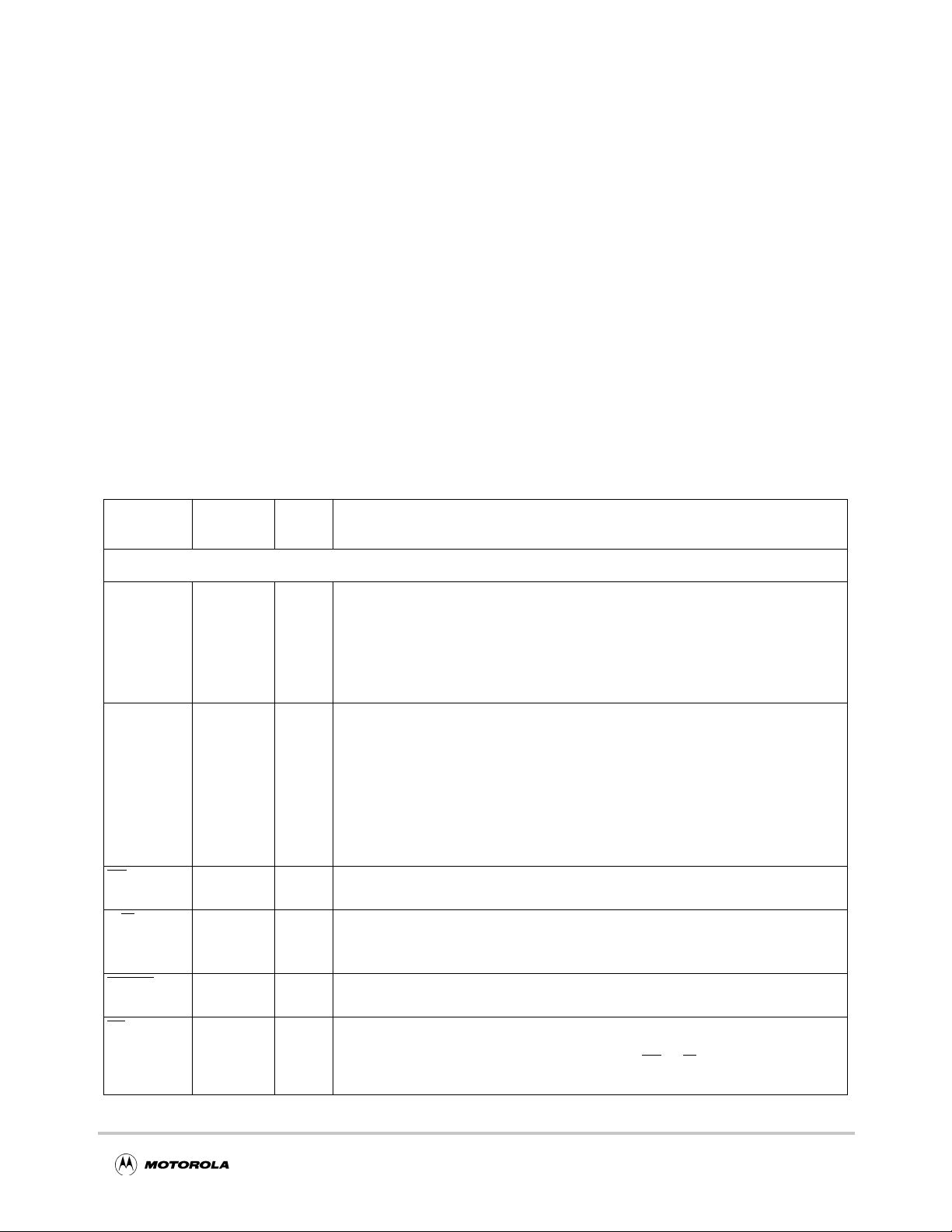
Chapter 2 Signal Descriptions

This chapter provides a pinout diagram and signal descriptions for the MPC180 security processor.

2.1 Signal Descriptions

Table 2-1 groups pins by functionality.

Table 2-1. Pin Descriptions

Signal name

A[18:29] 62, 64, 66,

D[0:31] 1, 2, 4, 6, 7,

R/W

URST 55 I Burst Transaction. Active low signal used in the 8260 interface that indicates when

locations

67, 68, 70, 72–75, 77,

9, 11, 12, 14, 16-18, 20, 22, 24, 28–32, 34, 36, 37, 38, 87, 89, 90, 92, 94, 96, 98, 99

56 I Chip Select. Active low signal that indicates when a data transfer is intended for

54 I Read/Write. Read/write line

Signal

type

Signal pins

I Address—address bus from the processor core. These bits are decoded in the

MPC180 to produce the individual module select lines to the execution units. Note that the processor address bus might be 32 bits wide, while the MPC180 address bus is only 12 bits wide.

msb = bit 0 lsb = bit 31

I/O Data—bidirectional data bus. This bus is connected directly to the processor core.

msb = bit 0 lsb = bit 31

the MPC180.

1 read cycle 0 write cycle

the current read/write is a burst transfer.

Description

53 I Transfer Start. Transfer start pin for control port. This signal is asserted by the

850/860 to indicate the start of a bus cycle that transfers data to or from the MPC180. This is used by the MPC180 along with CS transfer.

Chapter 2. Signal Descriptions 2-1

, R/W, and A to begin a

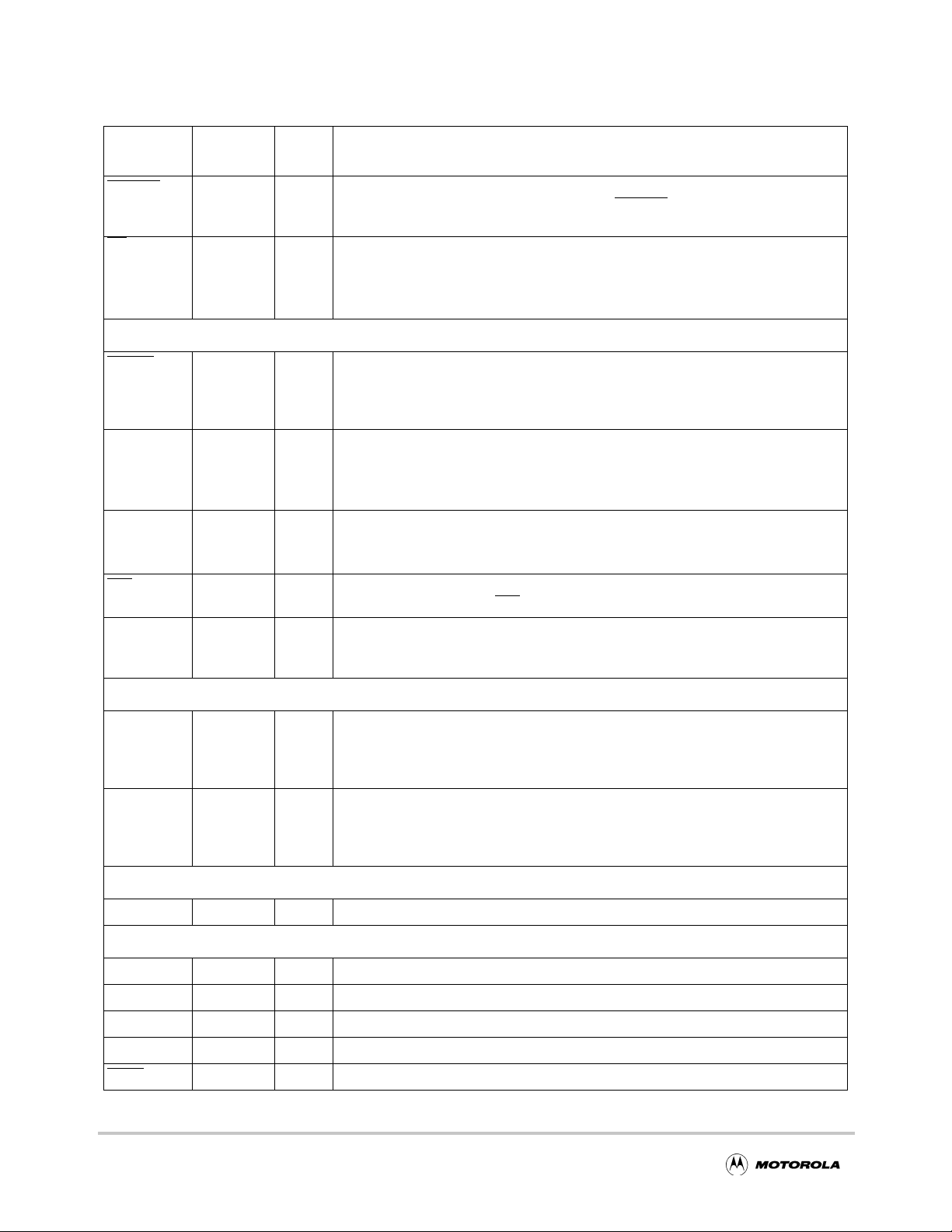
Signal Descriptions

Table 2-1. Pin Descriptions (Continued)

Signal name

PSDVAL 82 I Data valid. This active low signal is ignored when CONFIG=0 (MPC860 Mode), but

A /

LUPMWAIT

RESET

CONFIG 57 I Conﬁguration. Input that indicates whether the interface is to an MPC860 or

ENDIAN 40 I Endian. Active high for big endian mode. Low for little endian mode.

IRQ

locations

61 O Transfer Acknowledge. This active low signal is used in 860 mode and is asserted

52 I Reset. Asynchronous reset signal for initializing the chip to a known state. It is

85 O Interrupt Request. Interrupt line that signiﬁes that one or more execution units

Signal

type

Description

is active in MPC8260 Mode. The assertion of PSD valid on the data bus.

by the MPC180 when a successful read or write has occurred. Local UPM wait. This active high signal is used in 8260 mode and is asserted to

indicate the number of wait states for a transaction.

Miscellaneous pins

highly recommended that this signal be connected to a dual hardware/software reset function. Thus, the system designer can reset the MPC180 chip with optimal ﬂexibility.

MPC8260

1 8260 interface 0 860 interface

1 big endian 0 little endian

modules has asserted its IRQ

hardware interrupt.

VAL indicates that a data beat is

NC 26, 27, 49,

50, 51, 76, 100

DREQ1 83 O DMA Request 1. Active high signal which indicates that either the input or output

DREQ2 84 O DMA request 2. Active high signal which indicates that either the input or output

CLK 59 I Master clock input

TCK 47 I JTAG test clock TDI 48 I JTAG test data input TDO 44 I JTAG test data output TMS 46 I JTAG test mode select TRST

45 I JTAG test reset

— No connection to the pin

DMA Hardware Handshake pins

buffer is requesting data transfer by the host or DMA controller. DREQ1 and DREQ2 are each programmable to refer to the MPC180 chip input buffer or output buffer. This signal is designed to interoperate with a PowerQUICC IDMA channel.

buffer is requesting data transfer by the host or DMA controller. DREQ1 and DREQ2 are each programmable to refer to the MPC180 Chip input b uff er or output buffer. This signal is designed to interoperate with a PowerQUICC IDMA channel.

Clock

Test

2-2 MPC180LMB Security Processor User’s Manual

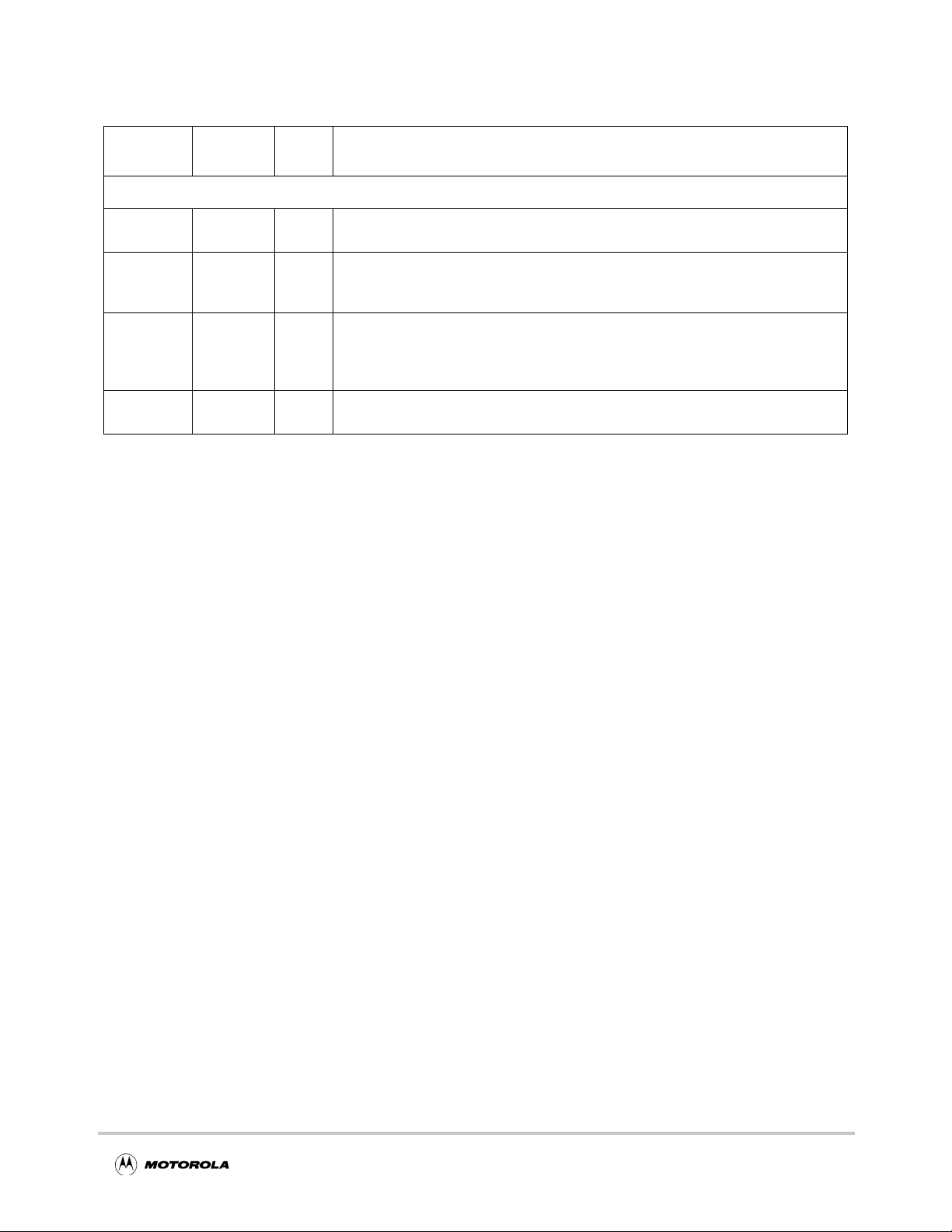
Table 2-1. Pin Descriptions (Continued)

Signal Descriptions

Signal name

IVDD 10, 21, 41,

OVDD 5, 15, 25,

OVSS 3, 13, 23,

IVSS 8, 19, 39,

locations

60, 71, 93

35, 43, 65, 81, 88, 97

33, 42, 63, 79, 80, 86, 95

58, 69, 91

Signal

type

Power and Ground

I +1.8 Volts (power pins for core logic)

I +3.3 Volts (Power pins for I/O pads)

I 0 V olts (Ground)

Description

Chapter 2. Signal Descriptions 2-3

Signal Descriptions

Figure 2-1 shows the MPC180 pinout.

D29 1 D21 2

OVSS 3

D13

OVDD 5

D28

IVSS 8

D20

IVDD 10

D12

OVSS 13

D27

OVDD 15

D19

D11 17

IVSS 19

D26

IVDD 21

D18

OVSS 23

D10 24

OVDD

6 7

11 12

100

D14

OVDD

D22

OVSS

D30

IVDD

IVSS

D1590D23

OVDD

MPC180 Pinout

30D931

D31

OVSS

DREQ2

IRQ

848382

VAL PSD

DREQ1

OVDD

OVSS

A29

A28

A27 A2674 A2573 A2472 IVDD71 A2370 IVSS69 A2268 A2167 A2066 OVDD65 A1964 OVSS63 A18

62 61

TA / LUPMWAIT

IVDD CLK

IVSS

CONFIG

CS56 BURST55

R/W

RESET

D25

D17

OVSS

D24

OVDD

D16

IVSS

IVDD

OVSS

ENDIAN

OVDD

TDO

TMS

TRST

Figure 2-1. MPC180 Pin Diagram

2-4 MPC180LMB Security Processor User’s Manual

TCK

TDI

Chapter 3 External Bus Interface and Memory Map

This chapter describes the MPC180 address map, the External Bus Interface (EBI), and EBI registers.

3.1 Execution Unit Registers

Each MPC180 execution unit has a dedicated set of registers. The MPC180 has a uniﬁed memory map that allows software addressibility to all internal registers. Figure 3-1 lists each MPC180 register and its 12-bit MPC180 chip address.

A00 A40 A80 B00 B01 B02 B03 B04 B05 B06 B07 B08 B09

000 010 015 016 017 018

PKEU

BRAM [64x32] ARAM [64x32]

NRAM[64x32]

EXP(k)

Control [CR]

Status [SR]

Mask [MR]

Instruction [IR]

Prog. counter [PC]

Clear interrupt

Modulus size

EXP(k) size

Device ID

MDEU

MDMB [0–15]

Digest [0–4]

Control [CR]

Status [SR]

Clear interrupt

Device ID

200 201 202 203 204 205 206 207 208 209 20A

20B 20C 20D 20E

600 602

DEU

Control

Status

Key1-right

Key1-left

Key2-right

Key2-left

Key3-right

Key3-left

IV-right

IV-left

DATAIN_R

DATAIN_L

DATAOUT_R

DATAOUT_L

Configuration

RNG

Command/status AutoRand output

A00 A80

B00 B01 B02 B03 B04 B05 B06

400 401 402 403 404 408 409 40A

40B 410

EBI

Input buffer

Output buffer

CSTAT

ID register

IMASK

IBCTL

IBCNT

OBCTL

OBCNT

AFEU

Control

Status

Clear interrupt

Key length Key data[0–3] Last sub msg

Plaintext-in

Ciphertext-out

Context I/J

Context SBox[0–63]

Figure 3-1. MPC180 Execution Unit Registers

Chapter 3. External Bus Interface and Memory Map 3-1

Address Map

Most of these registers are read and write, however some have special permissions. See Table 3-1 for more information. The 12-bit MPC180 address of each register is shown ne xt to the register name. All registers are assumed to be 32 bits wide; however, registers that contain fewer bits will return 0 (or a known value) on unused bits for that bus transaction only. Many registers contain multiple 32-bit words. If so, the number of words in the register set is shown in brackets after the name. Indi vidual e x ecution unit chapters describe how to use these registers, the bit assignments, and bit ordering.

3.2 Address Map

Table 3-1 lists the addresses for all registers in each execution unit. The 12-bit MPC180 address bus value is shown along with a 32-bit host processor address bus value.

Table 3-1. 32-Bit System Address Map

MPC180 12-Bit Address Processor 32-Bit Address Register Type

MDEU: 0x000–0x1FF

0x000 0x0000_0000 Message buffer(MB0) W 0x001 0x0000_0004 Message buffer(MB1) W 0x002 0x0000_0008 Message buffer(MB2) W 0x003 0x0000_000C Message buffer(MB3) W 0x004 0x0000_0010 Message buffer(MB4) W 0x005 0x0000_0014 Message buffer(MB5) W 0x006 0x0000_0018 Message buffer(MB6) W 0x007 0x0000_001C Message buffer(MB7) W 0x008 0x0000_0020 Message buffer(MB8) W

0x009 0x0000_0024 Message buffer(MB9) W 0x00A 0x0000_0028 Message buffer(MB10) W 0x00B 0x0000_002C Message buffer(MB11) W 0x00C 0x0000_0030 Message buffer(MB12) W 0x00D 0x0000_0034 Message buffer(MB13) W 0x00E 0x0000_0038 Message buffer(MB14) W

0x00F 0x0000_003C Message buffer(MB15) W

0x010 0x0000_0040 Message digest (MA) R/W

0x011 0x0000_0044 Message digest (MB) R/W

0x012 0x0000_0048 Message digest (MC) R/W

0x013 0x0000_004C Message digest (MD) R/W

0x014 0x0000_0050 Message digest (ME) R/W

0x015 0x0000_0054 Control (MCR) R/W

0x016 0x0000_0058 Status (MSR) R/W

0x017 0x0000_005C Clear interrupt (MCLRIRQ) W

3-2 MPC180LMB Security Processor User’s Manual

Address Map

Table 3-1. 32-Bit System Address Map (Continued)

MPC180 12-Bit Address Processor 32-Bit Address Register Type

0x018 0x0000_0060 Version Identiﬁcation (MID) R

DEU: 0x200–0x3FF

0x200 0x0000_0800 Control (DCR) R/W

0x201 0x0000_0804 Status (DSR) R

0x202 0x0000_0808 Key1_R R/W

0x203 0x0000_080C Key1_L R/W

0x204 0x0000_0810 Key2_R R/W

0x205 0x0000_0814 Key2_L R/W

0x206 0x0000_0818 Key3_R R/W

0x207 0x0000_081C Key3_L R/W

0x208 0x0000_0820 IV_R R/W

0x209 0x0000_0824 IV_L R/W 0x20A 0x0000_0828 DATAIN_R R/W 0x20B 0x0000_082C DATAIN_L R/W 0x20C 0x0000_0830 DATAOUT_R R 0x20D 0x0000_0834 DATAOUT_L R

0X20E 0x0000_0838 Conﬁguration (DCFG) R/W

AFEU: 0x400–0x5FF

0x400 0x0000_1000 Control W

0x401 0x0000_1004 Status R

0x402 0x0000_1008 Clear interrupt W

0x403 0x0000_100C Key Length W

0x404 0x0000_1010 Key Low W

0x405 0x0000_1014 Key Lower-Middle W

0x406 0x0000_1018 Key Upper-Middle W

0x407 0x0000_101C Key Upper W

0x408 0x0000_1020 Message Byte Double Word W

0x409 0x0000_1024 Plaintext-in W 0x40A 0x0000_1028 Ciphertext-out R 0x40B 0x0000_102C S-box I/J R/W

0x410 0x0000_1040 SBox [0] R/W

0x414 0x0000_1050 SBox [1] R/W

0x418 0x0000_1060 SBox [2] R/W

... ... ... ...

0x50C 0x0000_1430 SBox [63] R/W

Chapter 3. External Bus Interface and Memory Map 3-3

External Bus Interface

Table 3-1. 32-Bit System Address Map (Continued)

MPC180 12-Bit Address Processor 32-Bit Address Register Type

0x600 0x0000_1800 Status R

0x602 0x0000_1808 Random output R

0x800 0x0000_2000 Input buffer[128] R/W

0x880 0x0000_2200 Output buffer[128] R/W

0x900 0x0000_2400 CSTAT R/W

0x901 0x0000_2404 ID R

0x902 0x0000_2408 IMASK R/W

0x903 0x0000_240C IBCTL R/W

0x904 0x0000_2410 IBCNT R/W

0x905 0x0000_2414 OBCTL R/W

0x906 0x0000_2418 OBCNT R/W

RNG: 0x600–0x7FF

EBI: 0x800–0x9FF

PKEU: 0xA00–0xBFF

0xA00 0x0000_2800 BRAM R/W 0xA40 0x0000_2900 ARAM R/W 0xA80 0x0000_2A00 NRAM R/W 0xB00 0x0000_2C00 EXP(k) R/W 0xB01 0x0000_2C04 Control R/W 0xB02 0x0000_2C08 Status R 0xB03 0x0000_2C0C Interrupt mask R/W 0xB05 0x0000_2C14 Program counter R/W 0xB06 0x0000_2C18 Clear interrupt (CLRIRQ) W 0xB07 0x0000_2C1C Modulus size R/W 0xB08 0x0000_2C20 EXP(k) size R/W 0xB09 0x0000_2C24 Device ID R/W

3.3 External Bus Interface

The EBI handles the interface between the processor and MPC180’s internal execution units. It has the following features:

• Memory-mapped data transfers to/from the host to the MPC180 in single, burst, or DMA modes

• 4-Kbit input and output buffers that allows the host to set up an operation and pass control of interrupts and data ﬂow to the MPC180 until the operation completes

3-4 MPC180LMB Security Processor User’s Manual

External Bus Interface

• Automatic buffer ﬁlling and emptying. DREQ1 and DREQ2 stay asserted as long as memory space or data is in the buffers, letting the host load data for the next operation before the current operation ﬁnishes

• Interrupt routing and masking, which lets the host individually detect interrupts

• Interrupt auto-unmask, which lets the controller unmask an interrupt to the host when an operation ﬁnishes

3.3.1 EBI Registers

Table 3-2 describes the controller’s se v en 32-bit, host-addressable re gisters that are used to program MPC180.

Table 3-2. EBI Registers

Name R/W Description

CSTAT R/W Command/Status Register. Used to control global MPC180 functions and to monitor interrupts (see

Section 3.3.1.1, “Command/Status Register (CSTAT)”). ID R ID. Gives the ﬁxed ID number unique to the MPC180 (see Section 3.3.1.2, “ID Register”). IMASK R/W Interrupt Mask Register. Allows the masking of interrupts to the host (see Section 3.3.1.3, “IMASK

input buffer is to be written. Contains the counter mask ﬁeld (see Section 3.3.1.4, “Input Buffer

Control (IBCTL) and Output Buffer Control (OBCTL) Registers”). IBCNT R/W Input Buffer Count Register. Gives the total number of 32-bit words to be written to a speciﬁc

execution unit for a given operation. This number is not limited to 128 (4 Kbits), but is the total

number of words to be taken from the input buffer and written to the selected execution unit (see

Section 3.3.1.5, “Input Buffer Count (IBCNT) and Output Buffer Count (OBCNT) Registers”). OBCTL R/W Output Buffer Control Register. Contains the starting address in the MPC180’s address map from

where data should be transferred to the output buffer. Also contains the counter mask ﬁeld (see

Section 3.3.1.4, “Input Buffer Control (IBCTL) and Output Buffer Control (OBCTL) Registers”). OBCNT R/W Output Buffer Count Register. Contains the total number of 32-bit words a speciﬁc execution unit is

to write to the output buffer for a given operation. This number is not limited to 128 (4 Kbits), but is

the total number of words to be read from the selected (or enabled) execution unit (see

Section 3.3.1.5, “Input Buffer Count (IBCNT) and Output Buffer Count (OBCNT) Registers”).

3.3.1.1 Command/Status Register (CSTAT)

CSTAT, shown in Figure 3-2, is used to control the chip software reset and auto-unmask function and to report interrupt status. The controller synchronizes the software reset function to the rising edge of MCLK, guaranteeing sufﬁcient setup and hold times. Note that after the CSTAT register is read, bits 18-23 will be cleared, thus not allowing bitwise operations on these bits.

Chapter 3. External Bus Interface and Memory Map 3-5

External Bus Interface

05678101112131415

Field — DR2C DR1C — DEU AFEU MDEU RNG PKEU

Reset 0000_0000_0000_0000

R/W R/W

16 17 18 19 20 21 22 23 24 27 28 30 31

Field DR2A DR1A DEU AFEU MDEU RNG PKEU MPC180 Destination AUTO-UNMASK RST

Reset 0000_0000_0000_0000

R/W R/W

Addr 0x900

Figure 3-2. Command/Status Register (CSTAT)

Table 3-3 describes CSTAT ﬁelds.

Table 3-3. CSTAT Field Descriptions

Bits Name Description

0–5 — Reserved, should be cleared.

6 DR2C DREQ2 Control Bit

0 = DREQ2 displays the state of the output FIFO 1 = DREQ2 displays the state of the input FIFO

7 DR1C DREQ1 Control Bit

0 = DREQ1 displays the state of the input FIFO 1 = DREQ1 displays the state of the output FIFO

8–10 — Reserved, should be cleared.

11–15 Source interrupt indicators for the individual execution units. These are the masked interrupts from the

execution units. For bits 11–15: 0 interrupt not pending

1 interrupt pending 11 DEU Data Encryption Standard Execution Unit External Bus Interface interrupts 12 AFEU Arc Four Execution Unit External Bus Interface interrupts 13 MDEU Message Digest Execution Unit External Bus Interface interrupts 14 RNG Random Number Generator External Bus Interface interrupts 15 PKEU Public key Execution Unit External Bus Interface interrupts 16 DR2A DREQ2 Activation

0 = Inactive 1 = Active

17 DR1A DREQ1 Activation

0 = Inactive 1 = Active

18–22 Raw interrupt indicators for individual execution units. These are the unmasked interrupts from the

execution units.

For bits18–22:

0 interrupt not pending

1 interrupt pending

3-6 MPC180LMB Security Processor User’s Manual

External Bus Interface

Table 3-3. CSTAT Field Descriptions

Bits Name Description

18 DEU Data Encryption Standard Execution Unit interrupts 19 AFEU Arc Four Execution Unit interrupts 20 MDEU Message Digest Execution Unit interrupts 21 RNG Random Number Generator interrupts 22 PKEU Public key Execution Unit interrupts 23 MPC180 MPC180 IRQ. This bit, when set, indicates an interrupt is pending in the MPC180.

0 interrupt not pending 1 interrupt pending

24–27 Destination Destination bits. Only one execution unit on MPC180 can be active at a time through FIFO

accesses, so the host must program CSTAT to enable the appropriate execution unit. The host must guarantee that all data related to a speciﬁc operation has been processed before updating CSTAT, otherwise unpredictable results occur in MPC180 because the controller acts on one execution unit at a time. 1000 DEU

1001 AFEU 1010 MDEU 1011 RNG 1100 PKEU 0xxx no active module

28–30 AUTO-

UNMASK

31 RST Software reset. Performs the same function as asserting RESET

Auto-unmask bit. Enables or disables the auto-unmask function. This function is used to unmask an interrupt from the currently active execution unit. It is to be used when a execution unit sends a series of intermediate interrupts the host does not want to see. For example, if the DEU is enabled and active, many interrupts may be generated for intermediate results. The host, however, may only be interested in the ﬁnal interrupt that occurs when the DEU completes processing all of the data. To begin the operation, the host masks off the interrupts from the DEU and then writes to the auto-unmask bit. Then, when the DEU completes processing all the data, the controller unmasks the DEU interrupt and allows the ﬁnal DEU interrupt (signaling the completion of processing) to be sent to the host. The host can then read CSTAT to determine that the DEU generated an interrupt and take appropriate action. for bits 28–30: 000 disabled

001 enabled

on MPC180. Setting this bit resets the MPC180 within two MCLK cycles; the controller clears this bit. 0—

1 chip reset

The complete MPC180 register map, including all execution units, is available to the host. Although the host can access control registers and input and output buffers while an instruction is executing, it cannot access the execution unit itself.

3.3.1.2 ID Register

Figure 3-3 shows the ID register. Note that the ID register contains a 32-bit value that identiﬁes the version of MPC180. Its value at reset is 0x0065_1491and should be read with the ENDIAN mode set to big endian.

Chapter 3. External Bus Interface and Memory Map 3-7

External Bus Interface

0 7 8 1011 131415

Field — MPC180 MDEU DEU

Reset 0000_0000 011 0_01 01

R/W Read

16 17 19 20 22 23 25 26 28 29 31

Field DEU AFEU RNG — EBI PKEU

Reset 0 001 001 0_10 01_0 001

R/W Read

Addr 0x901

Figure 3-3. ID Register

Table 3-4 describes the ID ﬁelds.

Table 3-4. ID Field Descriptions

Bits Name Description

0–7 — Reserved, should be cleared.

8–10 MPC180 MPC180 version number. 11–13 MDEU Message Digest Execution Unit version number 14–16 DEU Data Encryption Standard Execution Unit version number 17–19 AFEU Arc Four Execution Unit version number 20–22 RNG Random Number Generator version number 23–25 — Reserved, should be cleared. 26–28 EBI Controller version number 29–31 PKEU Public key Execution Unit version number

3.3.1.3 IMASK Register

The built-in interrupt controller (IRQ module) gathers all execution unit interrupt signals and presents one output (IRQ interrupts from execution units by programming the IMASK register . In this w ay , interrupts can be controlled from a single source. Some execution-unit-speciﬁc conﬁguration is required to ensure proper response to any interrupt. The user can read the appropriate address in CSTAT to get the interrupt status of all execution units at once.

The interrupt port consists of the IRQ all pending interrupts from the execution units.

) to the host. It also lets the user selectively mask or disable

output, which is negated after the host responds to

All interrupts from the execution units have the same priority. Figure 3-4 shows the bit assignments in the IRQ register for all the MPC180 execution units. All enable (mask) registers operate on the corresponding bits. An interrupt is masked when its corresponding IMASK bit is a 1.

3-8 MPC180LMB Security Processor User’s Manual

External Bus Interface

0 15

Field —

Reset 0000_0000_0000_0000

R/W R/W

16 26 27 28 29 30 31

Field — DEU AFEU MDEU RNG PKEU

Reset 0000_0000_0000_0000

R/W R/W

Addr 0x902

Figure 3-4. IMASK Register

Table 3-5 describes the IMASK ﬁelds.

Table 3-5. IMASK Field Descriptions

Bits Name Description

0–26 — Reserved, should be cleared.

27 DEU Data Encryption Standard Execution Unit global interrupt control

0 interrupt unmasked 1 interrupt masked

28 AFEU Arc Four Execution Unit global interrupt control

0 interrupt unmasked 1 interrupt masked

29 MDEU Message Digest Execution Unit global interrupt control

0 interrupt unmasked 1 interrupt masked

30 RNG Random Number Generator global interrupt control

0 interrupt unmasked 1 interrupt masked

31 PKEU Public key Execution Unit global interrupt control

0 interrupt unmasked 1 interrupt masked

3.3.1.4 Input Buffer Control (IBCTL) and Output Buffer Control (OBCTL) Registers

The IBCTL register is used to control the input buffer starting address and address increment function.

The OBCTL register is used to control the output buffer starting address and address increment function.

Chapter 3. External Bus Interface and Memory Map 3-9

External Bus Interface

Figure 3-5 shows both the IBCTL and the OBCTL registers.

07815

Field — Count Mask

Reset 0000_0000_0000_0000

R/W R/W

16 19 20 31

Field — Starting Address

Reset 0000_0000_0000_0000

R/W R/W

Addr IBCTL: 0x903; OBCTL: 0x905

Figure 3-5. Input Buffer Control (IBCTL) and Output Buffer Control (OBCTL)

Registers

Table 3-6 describes IBCTL ﬁelds.

Table 3-6. IBCTL Field Descriptions

Bits Name Description

0–7 — Reserved, should be cleared. 8–15 Count mask Deﬁnes how the buffer controller presents addresses to execution units when data is

taken from the input buffer. The count mask bits deﬁne the number of 32-bit words to be transferred into each execution unit as deﬁned by the input block size upon which the

speciﬁc algorithms operate. 16–19 — Reserved, should be cleared. 20–31 Starting address Starting address of the input buffer data destination. The starting address is the internal

offset to which the ﬁrst word of data from the input buffer is written for a given operation.

All subsequent addresses are derived from this address.

Table 3-7 describes OBCTL ﬁelds.

Table 3-7. OBCTL Register Field Descriptions

Bits Name Description

0–7 — Reserved, should be cleared. 8–15 Count mask Deﬁnes how the buffer controller presents addresses to execution units when data is

read from the active execution unit and written to the output buffer. The count mask bits

deﬁne the number of 32-bit words to be transferred from each execution unit as deﬁned

by the output block size produced by the speciﬁc algorithms. 16–19 — Reserved, should be cleared. 20–31 Starting address Starting address of the output buffer data source. The starting address is the internal

offset from which the ﬁrst word of data to the output buffer is read for a given operation.

All subsequent addresses are derived from this address.

3-10 MPC180LMB Security Processor User’s Manual

EBI Controller Operation

3.3.1.5 Input Buffer Count (IBCNT) and Output Buffer Count (OBCNT) Registers

IBCNT indicates the number of 32-bit words to be used for an operation. For example, if the PKEU is to operate on 512 bits (16 words), IBCNT should be set to 0x0000_0010, corresponding to sixteen, 32-bit words to be taken from the input buffer and written to the PKEU.

When the input buffer counter reaches its terminus, IBCNT = 0, indicating that the number of words transferred to the active execution units matches the IBCNT value, data transfer stops automatically.

OBCNT contains the number of 32-bit words expected to be read for a particular operation. For example, if the DEU module is to operate on 512 bits, OBCNT should be set to 0x0000_0010, corresponding to sixteen 32-bit words to be read from the DEU module and written to the output buffer.

Figure 3-6 shows the IBCNT and OBCNT registers.

0 31

Field Count

Reset 0000_0000_0000_0000_0000_0000_0000_0000

R/W R/W

Addr IBCNT: 0x904; OBCNT: 0x906

Figure 3-6. Input Buffer Count (IBCNT) and Output Buffer Count (OBCNT)

Registers

3.4 EBI Controller Operation

The controller (EBI) is the interface between the host, the input and output FIFOs, and the individual execution units. It also contains control logic designed to help off load ﬂow control from the host. The controller facilitates single access or burst reads and writes from the host, and it also manages the interrupts that execution units send to the host. The controller also controls DREQ1 to and from the buffers.

The MPC180 EBI supports the MPC860 or MPC8260 processor interface, depending on the static state of the external pin CONFIG. When CONFIG is 0, the MPC180 interface is MPC860-compatible. When CONFIG is 1, the MPC180 interface is MPC8260-compatible. Burst access is only supported to/from the input and output FIFOs in MPC8260 mode. In MPC8260 mode, the MPC180 always assumes bursts to be eight 32-bit words.

and DREQ2, which can be used to signal DMA transfers

3.4.1 Buffer Accesses (FIFO Mode)

The controller contains an input buffer and an output b uffer of 4096 bits each. These buffers can be written to directly by the host or by using DMA. For direct access, the host simply

Chapter 3. External Bus Interface and Memory Map 3-11

EBI Controller Operation

writes or reads the address of the buffer. DREQ1

and DREQ2 (input/output buffer ready) are programmable handshak e signals used for buffer control. An external DMA controller can use this handshake to service the input or output buffer with data transfers as required. The EBI CSTAT register determines whether these signals reﬂect the state of the input buffer or output buffer. By default, DREQ1

refers to the state of the input buffer and DREQ2 refers to the state of the output buffer.

NOTE:

DREQx

refers to either DREQ1 or DREQ2. Either can be

programmed to refer to the state of the input or output buffer.

In FIFO mode, the input buffer automatically ﬁlls and the output buffer automatically empties. In the input buffer, this is accomplished by assertion of DREQx

whenev er at least eight 32-bit words (in MPC8260 mode) of space are available. Similarly, for the output buffer, DREQx

remains asserted as long as at least eight 32-bit words (MPC8260 mode)

are in the output buffer to be read.

3-12 MPC180LMB Security Processor User’s Manual

Chapter 4 Data Encryption Standard Execution Unit

This chapter explains how to program the DEU (Data Encryption Standard Ex ecution Unit) to encrypt or decrypt a message.

4.1 Operational Registers

All operational registers within the main control block are 32-bit addressable, howe ver they may contain less than 32 bits. The keys, initialization v ector , plaintext and ciphertext are all 64-bit, and each takes two registers. Each has a left (most signiﬁcant word) and a right (least signiﬁcant word) register. Table 4-1 lists DEU registers. These registers are described in more detail in the following sections.

Table 4-1. Data Encryption Standard Execution Unit (DEU) Registers

MPC180 12-Bit Address Processor 32-Bit Address Register Type

0x200 0x0000_0800 Control (DCR) R/W 0x201 0x0000_0804 Status (DSR) R 0x202 0x0000_0808 Key1_R R/W 0x203 0x0000_080C Key1_L R/W 0x204 0x0000_0810 Key2_R R/W 0x205 0x0000_0814 Key2_L R/W 0x206 0x0000_0818 Key3_R R/W 0x207 0x0000_081C Key3_L R/W 0x208 0x0000_0820 IV_R R/W

0x209 0x0000_0824 IV_L R/W 0x20A 0x0000_0828 DATAIN_R R/W 0x20B 0x0000_082C DATAIN_L R/W 0x20C 0x0000_0830 DATAOUT_R R 0x20D 0x0000_0834 DATAOUT_L R

0X20E 0x0000_0838 Conﬁguration (DCFG) R/W

Chapter 4. Data Encryption Standard Execution Unit 4-1

Operational Registers

4.1.1 DEU Control Register (DCR)

The control register, shown in Figure 4-1, contains static bits that deﬁne the encryption mode of operation for the DEU. This is typically written along with the keys and initialization vector at the start of each new encryption process. All unused bits of DCR are read as 0 values.

0 28 29 30 31

Field — MODE XDES E/D

Reset 0000_0000_0000_0000

R/W R

Addr

0x200

R/W

Figure 4-1. DES Control Register (DCR)

Table 4-2 describes control register ﬁelds.

Table 4-2. DCR Field Descriptions

Bits Name Description

0–28 — Reserved, should be cleared.

29 MODE Selects the DES mode of operation. Both Electronic Code Book (ECB) and Cipher Block

Chaining (CBC) are supported. 0 = ECB

1 = CBC

30 XDES Controls single DES or triple DES.

0 = Single DES 1 = Triple DES

31 E/D Controls whether the input data will be encrypted or decrypted.

0 = decrypt 1 = encrypt

4.1.2 DEU Conﬁguration Register (DCFG)

The conﬁguration register contains two bits that are set only during hardware initialization. All unused bits of DCFG are read as 0 values.

0 29 30 31

Field — RST IMSK

Reset 0000_0000_0000_0000

R/W R

Addr 0x20E

Figure 4-2. DEU Configuration Register (DCFG)

4-2 MPC180LMB Security Processor User’s Manual

W R/W

Table 4-3 describes DCFG ﬁelds.

Table 4-3. DCFG Field Descriptions

Bits Name Description

0–29 — Reserved, should be cleared.

Operational Registers

30 RST The DES can be reset by asserting the RESET signal or by setting the Software Reset bit in

31 IMSK Clearing the interrupt mask bit will allow interrupts on the IRQ

the Control Register. The software and hardware resets are functionally equivalent. The

software reset bit will clear itself one cycle after being set. 0 — 1 software reset

pin. It does not aff ect the IRQ bit in the status register. This bit is set (interrupts disabled) any time a hardware/software reset is performed. The user must clear this bit to enable hardware interrupts. 0 enable interrupts

1 disable interrupts

4.1.3 DEU Status Register (DSR)

The status register contains bits that giv e information about the state of the DEU. There are two bits which state when more input can be written to the input data register and read from the output data register. T o maximize throughput, data is b uffered, and reading and writing can be overlapped. When the IRDY bit is one, new data can be written to the input (DATA_IN) registers. It is possible to write three 64-bit blocks of data before any output data is read (and the IRDY signal goes low).

Figure 4-3 shows the DES status register.

0 29 30 31

Field — IDRY ORDY

Reset 0000_0000_0000_0000

R/W R

Addr 0x201

Figure 4-3. DES Status Register (DSR)

Table 4-4 describes DSR ﬁelds.

Table 4-4. DSR Field Descriptions

Bits Name Description

0–29 — Reserved, should be cleared.

30 IRDY Input Ready. Input Buffer ready to accept more data. 31 ORDY Output Ready. Output Buffer has data to send.

Upon completion of an encryption (or decryption), the ORDY signal will go high, indicating that the output is ready to be read from the DATA_OUT registers. If interrupts are enabled, then IRQ

will be asserted. After the ORDY signal goes high, new data in the

Chapter 4. Data Encryption Standard Execution Unit 4-3

Operational Registers

DATA_IN registers will start processing. When completed, the resulting output will be held in a working register until the output ciphertext is read from the DATA_OUT registers. Then the held data will be copied to the DATA_OUT registers and the ORDY signal asserted again. The interrupt IRQ

signal will be active as long as ODRY is asserted.

4.1.4 Key Registers

The DEU supports up to three independent 56-bit keys. Each key uses two 32-bit registers (56 bits of key plus 8 bits of parity). Note that key parity bits are ignored in processing.

For single DES, only one key is used (K ey1_L and K ey1_R); the other tw o are ignored. For Triple DES, all three ke ys are used. To simulate two-key T riple DES (in which the ﬁrst and third keys are identical), Key1_L and Key1_R are also written to Key3_L and Key3_R. When using three-key triple DES, the three keys must be written in order (K e y1, K ey2, and then Key3), otherwise the ﬁrst key may overwrite the third.

The key registers are read/write and must not be written while data is being encrypted/decrypted. Doing so will result in corrupted data.

4.1.5 Initialization Vector

The DEU supports CBC mode, which requires a 64-bit initialization vector (IV). The IV uses two 32-bit registers (IV_L and IV_R). The IV should be written before the ﬁrst block of data is encrypted. After each block of data is encrypted, the Initialization Vector register is updated to prepare for the next block of data. This register is readable so that the current encryption context (mode, keys, and IV) can be saved and restored.

The Initialization Vector registers must not be written while data is being encrypted or decrypted. Doing so will result in corrupted data.

4.1.6 DATAIN

Data to be encrypted or decrypted is written to the DATAIN registers. Data is ﬁrst written to DATAIN-R and then to DATAIN-L. DEU processing begins automatically with the completion of the write to the DATAIN-L register.

4.1.7 DATAOUT

Processed data is stored in the DATAOUT registers. Data must be read from DATAOUT-R ﬁrst. Reading data from DATA OUT-L indicates completion of the 64-bit block read, which allows the DEU to write the next 64 bits to DATAOUT-R and DATAOUT-L. If two 64-bit blocks have been written to the DATAIN registers while the DATAOUT registers haven’t been read, the DEU will stall to prevent an overwrite. IF three 64-bit blocks are written to DATAIN before any are read from DATAOUT, the IRDY bit in the Status register will go low, indicating that any additional blocks written to DATAIN will cause a loss of data due to overwrite.

4-4 MPC180LMB Security Processor User’s Manual

Chapter 5 Arc Four Execution Unit

This chapter explains how to program the AFEU (Arc Four Execution Unit) to encrypt or decrypt a message.

5.1 Arc Four Execution Unit Registers

All operational registers within the main control block are 32-bit addressable. However, they may contain less than 32 bits.

T able 5-1 lists AFEU registers. These re gisters are described in more detail in the following sections.

Table 5-1. Arc Four Execution Unit (AFEU) Registers

MPC180 12-Bit Address Processor 32-Bit Address Register Type

0x400 0x0000_1000 Control W 0x401 0x0000_1004 Status R 0x402 0x0000_1008 Clear interrupt W 0x403 0x0000_100C Key Length W 0x404 0x0000_1010 Key Low W 0x405 0x0000_1014 Key Lower-Middle W 0x406 0x0000_1018 Key Upper-Middle W 0x407 0x0000_101C Key Upper W 0x408 0x0000_1020 Message Byte Double Word W

0x409 0x0000_1024 Plaintext-in W 0x40A 0x0000_1028 Ciphertext-out R 0x40B 0x0000_102C S-box I/J R/W

0x410 0x0000_1040 SBox [0] R/W

0x414 0x0000_1050 SBox [1] R/W

0x418 0x0000_1060 SBox [2] R/W

... ... ... ...

0x50C 0x0000_1430 SBox [63] R/W

Chapter 5. Arc Four Ex ecution Unit 5-1

Arc Four Execution Unit Registers

5.1.1 Status Register

The AFEU Status Register, shown in Figure 5-1, contains seven bits of information. These bits describe the state of the AFEU circuit and are all active-high.

0 24 25 262728293031

Field — Input Buffer

empty

Reset 0000_0000_0000_0000

R/W Read

Addr 0x401

Figure 5-1. Arc Four Execution Unit Status Register

Table 5-2 describes the AFEU Status Register ﬁelds.

Table 5-2. AFEU Status Register Field Descriptions

Bit Name Description

Full msg

done

Sub-msg

done

Permute

done

Initialize

done

IRQ Busy

0–24 — Reserved, should be cleared. 25 Input Buffer empty Set when there is no data waiting in the AFEU Input Buffer. This can be used to monitor

when the AFEU is ready to receive the next sub-message while it is processing the current sub-message. Writing to the Message register will clear this bit.

26 Full message done Set when the last sub-message has been processed. This bit will remain set until a new

key is written. Reading from the Cipher register will clear this bit.

27 Sub-message done Set when the sub-message has been processed. Once the next sub-message is written,

the AFEU will begin processing it and this bit will clear.

28 Permute done Set once the memory is permuted with the key. Once the ﬁrst sub-message is written, the

AFEU will begin processing the message and this bit will clear.

29 Initialize done Set once memory initialization is complete. Once the key data and length is written, the

AFEU will begin permuting the memory and this bit will clear.

30 IRQ Asserted whenever an interrupt is pending (if interrupts are enabled). The following

conditions will generate an interrupt: Memory initialization done Memory permutation done Sub-Message processing done Full Message processing done The speciﬁc cause of the interrupt can be determined by reading the additional bits of the status register. Hardware interrupts are disabled following a reset. The IRQ bit in the status register is not affected by masking hardware interrupts in the control register.

31 Busy Asserted whenever the AFEU core is not in an idle state. Memory initialization or

permutation and message processing conditions will cause this bit to be set. The Busy bit will be set during context writes/reads.

5-2 MPC180LMB Security Processor User’s Manual

Arc Four Execution Unit Registers

5.1.2 Control Register

Figure 5-2 shows the AFEU Control Register.

0 29 30 31

Field — RST IMSK

Reset 0000_0000_0000_0001

R/W W

Addr

0x400

Figure 5-2. Arc Four Execution Unit Control Register

Table 5-3 describes the AFEU Control Register ﬁelds.

Table 5-3. AFEU Control Register Field Descriptions

Bit Name Description

0–29 — Reserved, should be cleared. 30 RST The AFEU can be reset by asserting the RESET signal or by setting the Software Reset bit in the

31 IMSK Clearing the interrupt mask bit will allow interrupts on the IRQ

Control Register. The software and hardware resets are functionally equivalent. The software

reset bit will clear itself one cycle after being set. 0 — 1 software reset

pin. It does not affect the IRQ bit in the status register. This bit is set (interrupts disabled) any time a hardware/software reset is performed. The user must clear this bit to enable hardware interrupts. 0 enable interrupts

1 disable interrupts

5.1.3 Clear Interrupt Register

The Clear Interrupt Register is a write-only register. Writing to this register will clear the IRQ

signal and the IRQ bit in the status register. The actual data written to this register is

ignored.

5.1.4 Key Length Register

The Key Length Register is a 4-bit write-only register that stores the number of bytes (minus one) in the key. Writing to this register will signal the AFEU to start permuting the memory with the key. Therefore, the key must be written before writing to this register.

5.1.5 Key (Lo w/Lower-mid dle/Upper-middle/Upper) Register

Each register is 32-bits wide (write-only). Because the key size may be 1 to 16 bytes in length, the key data is stored in four individually addressable re gisters. The ke y low re gister holds the lowest signiﬁcant four bytes of the key. The Ke y Lower -Middle Register holds the next lowest four bytes of the key. The Key Upper-Middle Register holds the next highest four bytes of the key. The Key Upper Register holds the most signiﬁcant four bytes of the key .

Chapter 5. Arc Four Ex ecution Unit 5-3

Arc Four Execution Unit Registers

NOTE:

If the key length is not divisible by four, the lower key data registers must be ﬁlled before writing to the upper key data registers.

5.1.6 Message Byte Double-Word Register

The Message Byte Double-Word Register is a 3-bit write-only register and is used to hold the number of bytes (minus one) in the last/partial sub-message. A 1 in the MSB of this register indicates to the AFEU that this is the last sub-message. Figure 5-3 shows the Message Byte Double-Word Register. The default number of sub-message bytes is four.

028293031

Field — Last1

sub-message

Reset 0000_0000_0000_0000

# sub-message

bytes - 1

R/W

Addr

Setting the Last Sub-message bit in this register will cause the AFEU to reset and start initializing once the full message is complete. The contents of the cipher register will hold the last processed sub-message.

0x408

Figure 5-3. Arc Four Execution Unit Message Byte Double-Word Register

5.1.7 Message Register

The Message Register is a 32-bit write-only register that stores the sub-message to be processed. This can either be the plaintext to be encrypted or ciphertext to be decrypted. Writing data to this register signals the AFEU to start processing the data.

5.1.8 Cipher Register

The Cipher Register is a 32-bit read-only register that stores the processed sub-message. This can either be the encrypted ciphertext or decrypted plaintext. Data in this register is valid when the sub- or full message done bit is set in the status register.

NOTE:

If the sub-message is less than 32-bits, the unused bits in the Cipher Register will be the same as the corresponding bits written to the Message Register.

5-4 MPC180LMB Security Processor User’s Manual

Arc Four Execution Unit Registers

5.1.9 S-box I/J Register

The Sbox I/J Register is a 24-bit read/write register where the Sbox I/J pointers are stored. The contents of this register must be read prior to context switching and must be written back to the AFEU before resuming message processing of an interrupted message. This register may be accessed whenever the AFEU is idle.

5.1.10 S-box0 – S-box63 Memor y

The S-box Memory consists of 64 read/write 32-bit blocks. The entire contents of the S-box memory must be read prior to context switching and must be written back to the AFEU before resuming message processing of an interrupted message. The S-box memory may be accessed whenever the AFEU is idle.

Chapter 5. Arc Four Ex ecution Unit 5-5

Arc Four Execution Unit Registers

5-6 MPC180LMB Security Processor User’s Manual

Chapter 6 Message Digest Execution Unit

This chapter explains how to program the MDEU (Message Digest Ex ecution Unit) within the MPC180 to hash a message for authentication.

6.1 Operational Registers

All operational registers within the MDEU are 32-bit addressable, however they may contain less than 32 bits.

Table 6-1 lists message registers. These registers are described in more detail in the following sections.

Table 6-1. Message Digest Execution Unit (MDEU) Registers

MPC180 12-Bit Address Processor 32-Bit Address Register Type

0x00F 0x0000_003C Message buffer(MB15) W

0x010 0x0000_0040 Message digest (MA) R/W

0x011 0x0000_0044 Message digest (MB) R/W

0x012 0x0000_0048 Message digest (MC) R/W

Chapter 6. Message Digest Execution Unit 6-1

Operational Registers

MPC180 12-Bit Address Processor 32-Bit Address Register Type

0x013 0x0000_004C Message digest (MD) R/W

0x014 0x0000_0050 Message digest (ME) R/W

0x015 0x0000_0054 Control (MCR) R/W

0x016 0x0000_0058 Status (MSR) R/W

0x017 0x0000_005C Clear interrupt (MCLRIRQ) W

0x018 0x0000_0060 Version Identiﬁcation (MID) R

6.1.1 MDEU Version Identiﬁcation Register (MID)

The Identiﬁcation Register contains a value reserved for a particular version and conﬁguration of the MDEU. As future hardware is developed to support dif ferent ﬁeld types or different microcode, each version will be assigned a different identiﬁer.

The value returned is ID = 0x0001.

6.1.2 MDEU Control Register (MCR)

The control register contains static bits that deﬁne the mode of operation for the MDEU. In addition to the static control bits, several bits are dynamic. These dynamic bits are set by a write to the MCR initiated by the host processor and are reset automatically by the MDEU after one cycle or operation. All unused bits of the MCR are read as 0 values.

Figure 6-1 shows the MDEU Control Register and Table 6-2 describes this register’s ﬁelds.

0 15

Field —

Reset 0000_0000

R/W R/W

16 19 20 21 22 23 24 23 26 27 28 29 30 31

Field — ENGO OPAD IPAD — MD5 MD4 RST IE GO BSWP STEP —

Reset 0000_0000

R/W R/W

Addr 0x015

Figure 6-1. MDEU Control Register (MCR)

6-2 MPC180LMB Security Processor User’s Manual

Operational Registers

Table 6-2. MCR Field Descriptions

Bits Name Description

0–19 — Reserved, should be cleared. 20 ENGO Enables automatic start of hashing as soon as the MDMB buffers ha v e all been written. It

is not necessary to set the GO bit manually.

21 OPAD The assertion of OPAD causes:

1. The value written to the 512 bit Message Buffer to be exclusive-ORed with the outer hash pad value

2. Unlik e IPAD, a procedur al change occurs: upon starting the hash of the value written to the Message Buffer , the contents of the Message Digest Buffer is copied to the Message Buffer, and is padded appropriately. By performing the copy from MDB to MB, the step of appending the inner hash result to the padded key is performed automatically. OPAD is autocleared upon completion of a hash of a single message block.

22 IPAD The assertion of IPAD causes the value written to the 512 bit Message Buffer to be

exclusive-ORed with the inner hash pad v alue. This value is autocleared upon completion of a hash of a single message block. Note that because this control bit affects the value stored in the 512 bit message buffer, if block chaining is to be used, it should be set only while the secret key is written to the 512 bit Message Buffer, and should be cleared

manually at the same time GO is asserted. 23 — Reserved, should be cleared. 24 MD5 The assertion of the MD5 bit signiﬁes that an MD5 hash will be computed. If both MD4

and MD5 are not asserted, a SHA-1 Hash will be computed. 25 MD4 The assertion of the MD4 bit signiﬁes that an MD4 hash will be computed. If both MD4

and MD5 are not asserted, a SHA-1 Hash will be computed. 26 RST The RST bit is a software reset signal. When activated, the MDEU will reset immediately,

halting any ongoing hash. All registers and buffers revert to their initial state. Normally,

asserting GO continues an existing hash function across multiple 512-bit message

blocks. Should a fresh-hash be desired for a new message block, the RST bit should be

asserted prior to loading the new message block into the Message Buffer. 27 IE The IE bit represents the Interrupt Enable ﬂag. When set to 1, the IRQ

thus when an interrupt occurs, the IRQ

all interrupts are disabled, and the IRQ

bit acts as the global interrupt enable. 28 GO The GO bit initiates the processing of the 512 bit message currently stored in the

Message Buffer. This hash will be a continuation of any existing hash of multiple

message blocks. In order to begin a new hash, the RST bit described below should be

asserted prior to loading the new 512 bit Message Block. The 512 bit Message Block is

double-buffered; a new block of message may be written while a hash is under process. If

a new block is so written, then hashing will continue with the new block without GO

needing to be reasserted. 29 BSWP The BSWP bit causes byte-swapping of the Message Digest Buffer Registers

(MDA-MDE) as they are read out of the MDEU.

signal will be activated. When the IE bit is set to 0,

output pin will be held inactive, that is, 0. The IE

signal is enabled,

30 STEP The STEP bit allows the MDEU to be stepped through on a single clock cycle basis.

When active, that is 1, the MDEU computes one “round” of the currently selected hash. 31 — Reserved, should be cleared.

Chapter 6. Message Digest Execution Unit 6-3

Operational Registers

6.1.3 Status Register (MSR)

The status register contains bits that give information about the state of the MDEU. Upon completion of a hash, DONE is asserted in bit 0 of MSR, followed by an interrupt on IRQ if interrupts are enabled. In addition, whenever the contents of the message buffer are copied for internal hash processing, BE is asserted. Assertion of BE will cause an interrupt only if interrupts are enabled and buffer -empty interrupt is enabled (MCR:BIE is asserted). Address Error (AE) is asserted by addressing MDEU but not specifying a valid address within MDEU.

The MSR is effectively a read-only register. Its contents cannot be modiﬁed by the host processor except to be reset, which occurs when the host processor performs a write to the MSR, regardless of the data value.

Figure 6-2 shows the MDEU status register and Table 6-3 describes this register’s ﬁelds.

0 15

Field —

Reset 0000_0000

R/W R/W

16 27 28 29 30 31

Field — IRQ AE BE DONE

Reset 0000_0000

R/W R/W

Addr 0x016

Figure 6-2. MDEU Status Register (MSR)

Table 6-3. MSR Field Descriptions

Bits Name Description

0–27 – Reserved, should be cleared. 28 IRQ 0 interrupt not indicated

29 AE 0 address error not detected

30 BE 0 message buffer not empty

31 DONE 0 hash not completed

1 interrupt indicated

1 address error detected

1 message buffer empty

1 hash completed

6-4 MPC180LMB Security Processor User’s Manual

Operational Registers

6.1.4 Message Buffer (MB0—MB15)

The MDEU hashes a message contained in the 16-word Message Buffer. The message should be processed such that a single-character message would be written to MB0. MB15 should only be programmed if the message block uses at least 481 bits.

The Message Buffer is not cleared upon completion of a computation process. Therefore, when programming the ﬁnal block of a multi-block message, all locations should be appropriately written using the padding required by the selected Message Digest algorithm.

The message is double-buffered; once hashing begins the MDEU does not depend on the value stored in the Message Buffer. Therefore, the next block of a multi-block message may be written as soon as MSR:BE is asserted.

If IPAD or OPAD are asserted while the Message Buffer is written, then the value stored will be the value applied to the data bus e xclusive-ORed with the appropriate pad value. In addition, assertion of OPAD causes the contents of the Message Digest Buffer to be copied into the ﬁrst four or ﬁve words of the Message Buffer , with all other words set appropriately for a two-block message.

6.1.5 Message Digest Buffer (MA–ME)

When DONE and IRQ are asserted, the current hash value for all message blocks processed since the last reset are available in Message Digest Buf fer locations MA–ME. For MD4 and MD5, which produce a 128 bit hash, ME is to be ignored.

Chapter 6. Message Digest Execution Unit 6-5

Operational Registers

6-6 MPC180LMB Security Processor User’s Manual

Chapter 7 Public Key Execution Unit

This chapter explains how to program the PKEU (Public Key Execution Unit) to perform mathematical functions.

7.1 Operational Registers

All operational registers within the main control block are 32-bit addressable, howe ver they may contain less than 32 bits.

Table 7-1 lists all PKEU registers. These registers are described in more detail in the following sections.

Table 7-1. PKEU Registers

MPC180 12-Bit Address Processor 32-Bit Address Register Type

7.1.1 PKEU Version Identiﬁcation Register (PKID)

The Identiﬁcation Register contains a value reserved for a particular version and conﬁguration of the PKEU. As future hardware is de veloped to support dif ferent ﬁeld types or different microcode, each version will be assigned a different identiﬁer.

The value returned is ID = 00021.

Chapter 7. Public Ke y Execution Unit 7-1

Operational Registers

7.1.2 Control Register (PKCR)

The Control Register contains static bits that deﬁne the mode of operation for the PKEU. In addition to the static control bits, several bits are dynamic. These dynamic bits are set by a write to the PKCR initiated by the host processor, and are reset automatically by the PKEU after one cycle of operation. All unused bits of the PKCR are read as 0 values. Figure 7-1 shows the PKEU control register.

012345678 9101112131415

Field regNsel regBsel regAsel — F2M XYZ RpRnRST IE GO ECC —

Auto clear N YNYNYY

Reset 0000_0000

R/W R/W

Addr 0xB01

Figure 7-1. PKEU Control Register (PKCR)

Table 7-2 describes the PKEU control register ﬁelds.

Table 7-2. PKCR Field Descriptions

Bits Name Description

0–1 regNsel 00 memory N block 0 select

2–3 regBsel 00 memory B block 0 select

4–5 regAsel 00 memory A block 0 select

6 — Reserved, should be cleared. 7F

8 XYZ The XYZ bit enables the PKEU point multiply operation to bypass certain processing used support

M The F2M bit causes the PKEU to perform arithmetic in the polynomial-basis. This must be set when

01 memory N block 1 select 10 memory N block 2 select 11 memory N block 3 select

01 memory B block 1 select 10 memory B block 2 select 11 memory B block 3 select

01 memory A block 1 select 10 memory A block 2 select 11 memory A block 3 select

executing operations f or ECC F This would be required for all RSA and ECC F 0 integer arithmetic (RSA or ECC F 1 polynomial-basis arithmetic (ECC F

systems that operate in afﬁne coordinates. Speciﬁcally, when set, the PKEU simply provides the ﬁnal results (i.e. the X, Y, and Z ﬁeld elements) which are no longer in the Montgomery format. When XYZ is zero, the PKEU assists the host in achie ving its desired afﬁne coordinate results . This is accomplished by including Z Montgomery residue system. It is the responsibility of the host to ﬁnd the inv erses of Z provide these back to the PKEU to compute the afﬁne coordinates. 0 afﬁne coordinates

1 projective coordinates

The regAsel, regBsel, and regNsel ﬁelds set pointers referencing memory blocks in the A, B, and N memories, respectively. Each memory, particularly where ECC is concerned, can be thought of as constituting four sub-memories (e.g. A(0), A(1), A(2), and A(3)). Each sub-memory contains 32 16-bit locations (or 512 bits). For ECC processing, these sub-memories are used to store the multitude of intermediate data and ﬁnal ﬁeld elements required during processing. These memory pointers are used to determine which memory block is to be referenced during arithmetic processing or moves from one location to another. All of this is transparent to the host and performed automatically by the PKEU for high-level functions. However, for low-level functions, such as ﬁeld add or multiplies, the host may set these pointers to ref erence a particular memory block. This ﬂexibility allows, for example, the following computation: A(3) * B(1) * R

m. When clear, all processing is performed using integer arithmetic.

)

and Z3 in addition to X, Y, and Z and leaving these results in the

processing.

-1

mod N(2).

and Z3 and

7-2 MPC180LMB Security Processor User’s Manual

Table 7-2. PKCR Field Descriptions (Continued)

Bits Name Description

Operational Registers

10 RST The RST bit is a software reset signal. When activated, the PKEU will reset immediately. All

11 IE The IE bit represents the Interrupt Enable ﬂag. When set to 1, the IRQ signal is enabled, thus when

12 GO The GO bit initiates the execution of the routine pointed to by the Program Counter (PC). This is

pRn

For a description of RpRn see Section 7.5.3, “RpRN mod P Calculation.”

0 R

mod N enabled

1 R

registers revert to their initial state, and the Program Counter (PC) will jump to 0. Instruction execution will halt, and any pending interrupt will be deactivated. All memories (A, B, and N) will indirectly be reset since this signal causes the “clear all” routine to be executed. 0 normal processing

1 reset the PKEU

an interrupt occurs, the IRQ signal will be activated. When the IE bit is set to 0, all interrupts are disabled, and the IRQ output pin will be held inactive, i.e. 0. The IE bit acts as the global interrupt enable. Note that this does not affect the SR[IRQ] bit. That bit is set regardless of IE. 0 interrupts disabled

1 interrupts enabled

accomplished by fetching the instruction addressed by the PC and to keep executing instructions until a jump to location 0 is encountered which tells the PKEU to stop executing. It is important to realize that once the PKEU is “going”, the host has limited access to the PKEU internal memory space. Speciﬁcally, reads and writes to the RAMs are ignored during this state and all other locations must be referenced with extreme caution. Under normal circumstances, only the Status Register and EXP(k) should be actively referenced during this mode. 0 rest condition

1 execute instructions without stopping

mod P enabled

pRn

13 ECC The ECC bit signiﬁes that one of the ECC-related routines will be executed. Conversely, by not

setting this bit, the PKEU will be conﬁgured to correctly execute RSA-related routines. 0 RSA processing enabled

1 ECC processing enabled

14–15 — Reserved, should be cleared.

7.1.3 Status Register (PKSR)

The Status Register contains bits that give information about the state of the PKEU. If an error occurs during normal operation, a bit in the PKSR will be set to 1. After a GO is issued to the PKCR, the next jump to location 0 will cause a bit in the Status Register to be set, followed by an interrupt on IRQ if interrupts are enabled.

The PKSR is effectiv ely a read-only register . Its contents cannot be directly modiﬁed by the host processor except to be reset, which occurs when the host processor performs a write to the PKSR, regardless of the data value. Note that the host may indirectly affect the contents of the PKSR, such as when GO is asserted.

Figure 7-2 shows the PKEU status register and Table 7-3 describes this register’s ﬁelds.

Chapter 7. Public Ke y Execution Unit 7-3

Operational Registers

0 10 11 12 13 14 15

Field — E_RDY IRQ OB Z DONE

Reset 0000_0000_0000_0001

R/W R

Addr 0xB02

Figure 7-2. PKEU Status Register (PKSR)

Table 7-3. PKSR Field Descriptions

Bits Name Description

0–10 — Reserved, should be cleared. 11 E_RDY The E_RDY (exponent or k ready) bit indicates that the execution unit is ready to accept the

next 32-bit word of exponent data or point multiplier (k) data in the EXP(k) register. The host processor may poll the status register to determine if this data needs to be provided or rely on IRQ (if enabled) to signal when to look at the register to determine what data needs to be provided. A write to the EXP(k) register will clear this bit as well as the associated IRQ (as long as no other condition has also cause IRQ’s assertion). Note that there is approximately a two cycle latency associated with the clearing of IRQ following a write to the EXP(k) register. Since the EXP(k) register is double-buffered, the host response time, while important, is not critical to meet maximum performance. At a minimum, the host will ha v e 8 integer multiplies for RSA or 8 point doubles for ECC to provide new data before adversely impacting the run time. Refer to the run-time formulae (see Table 7-26) to determine the exact time available for the target operating frequency. For those instances where the host does not need to know the status of E_RDY (i.e. lower-le v el routines), it is recommended that it mask this bit to prevent it from affecting the IRQ signal.

12 IRQ The IRQ bit of the Status Register reﬂects the value of the IRQ output pin of the PKEU.

However, it will be set regardless of CR[IE].

13 OB The OB bit of the Status Register is set to 1 if a read or write operation is to an unknown or

reserved address. The contents of the data bus on an out-of-bounds read is indeterminate.

14 Z The ERR bit of the Status Register is set to 1 if a general error occurs in the PKEU. Any error

not associated with one of the Status Register bits will cause the ERR bit to assert.

15 DONE The DONE bit of the Status Register is set to 1 when a branch to location 0 occurs. All of the

embedded routines cause the DONE bit to be asserted upon completion. Also, upon reset, the DONE bit is set. This signiﬁes to the host that the PKEU is ready for normal operation following the reset. Until that time, the PKEU is busy with its boot procedure. This primarily entails running the “clear all” routine, clearing all embedded RAM.

7.1.4 Interrupt Mask Register (PKMR)

The Interrupt Mask Register allows the host processor to individually disable certain interrupts. Normally, any change in the Status Register will cause a hardware interrupt on the IRQ pin, as long as the Interrupt Enable (IE) bit in the Control Register is set to 1. If a given bit of the PKMR is set to 1, the corresponding bit in the PKSR will no longer cause the interrupt.

The PKMR is a read-write register. Its contents may be read or written by the host processor.

7-4 MPC180LMB Security Processor User’s Manual

Operational Registers

All unused bits of the PKMR are read as 0 values. Since the PKMR is a 16-bit register, when the host processor reads the PKMR, its contents are copied onto D[15:0], and the upper half of D is driven with 0’s.

Figure 7-3 shows the PKEU Interrupt Mask Register and Table 7-4 describes this register’ s ﬁelds.

0 10 11 12 13 14 15

Field — E_RDY — OB — DONE

Reset 0000_0000

R/W R/W

Addr 0xB03

Figure 7-3. PKEU Interrupt Mask Register (PKMR)

Table 7-4. PKMR Field Descriptions

Bits Name Description

15–5 — Reserved, should be cleared. 4 E_RDY The E_RDY (exponent or k ready) bit indicates that the execution unit is ready to accept the

routines), it is recommended that it mask this bit to prevent it from affecting the IRQ signal. 3 — Reserved, should be cleared. 2 OB The OB bit of the Status Register is set to 1 if a read or write operation is to an unknown or

reserved address. The contents of the data bus on an out-of-bounds read is indeterminate. 1 — Reserved, should be cleared. 0 DONE The DONE bit of the status register is set to 1 when a branch to location 0 occurs. All of the

embedded routines cause the DONE bit to be asserted upon completion. Also, upon reset, the

DONE bit is set. This signiﬁes to the host that the PKEU is ready for normal operation following

the reset. Until that time, the PKEU is busy with its boot procedure. This primarily entails

running the “clear all” routine, clearing all embedded RAM.

Chapter 7. Public Ke y Execution Unit 7-5

Operational Registers

7.1.5 EXP(k) Register

The EXP(k) register contains the exponent (EXP) during exponentiation routines or the point multiplier (k) during ECC point multiply routines. EXP(k)_SIZE must be speciﬁed before writing to the EXP(k) register. Since EXP(k) is 32 bits in size, data must be written to it during exponentiations or point multiplies and never before. This data must be provided most signiﬁcant word (msw) to least signiﬁcant word (lsw). The host processor determines, via IRQ (if not masked) or IRD data is required. When IRQ is asserted, the host processor will look at the status word to see what was set. If the E(k) RDY bit is set, the host processor knows it must provide the next byte of EXP(k). If IRQ is masked, then it must poll the status register to determine when to provide the next word of EXP(k). When the host writes to the EXP(k) register, the E(k) RDY bit of the status register is cleared. As with all status register bits, the writing to the status register location will clear all of its bits, including the E(k) RDY bit.

There is an associated latency between the writing of the EXP(k) register and the deassertion of E(k) RDY (and IRQ). For this reason, it is recommended that the host waits a minimum of three cycles before polling the status register following a write to EXP(k).

Y (if selected to send via a DREQ pin), that new

The EXP(k) register is internally double-buf fered. As a result, the host response time, while important, is not critical to meet maximum performance. At a minimum, the host will ha v e 32 integer multiplies for RSA or 32 point doubles for ECC to provide new data before adversely impacting the run time. Refer to the run-time formulae (see Table 7-26) to determine the exact time available for the target operating frequency.

The host will be required to provide the ﬁrst byte of EXP(k) very shortly after initiating the routine (point multiply or exponentiation). Because of the double buf fering, the second byte will be allowed to be written very shortly after the ﬁrst written byte of EXP(k). For this reason, IRQ and E_RD Y is deasserted for only one cycle following the write of the ﬁrst byte of EXP(k). Once the second byte of EXP(k) is written, then there is a larger amount of time before the subsequent IRQ and E_RDY is asserted.

The maximum size for either the exponent or k is limited only by the EXP(k)_SIZE register that is, 64 words or 2048 bits). In practice, the values are typically less than or equal to the key size (for RSA) or ﬁeld size (ECC).

7.1.6 Program Counter Register (PC)

The Program Counter is an 11-bit register that contains the address of the next instruction to be executed. This register is a read-write register. During normal routine execution, this register is preloaded with the software routine’s entry address.

7-6 MPC180LMB Security Processor User’s Manual

Memories

7.1.7 Modsize Register

This register sets the maximum size of the modulus (or prime) for RSA and ECC Fp or the irreducible polynomial for ECC F digit = 16 bits) for RSA and ECC F

m. The maximum size of these vectors is 128 digits (1

and 32 digits for ECC F2m (Note that the value written

to modsize is not checked for validity). Thus, modsize represents the number of 16-bit blocks in the modulus or irreducible. If the number of bits in the modulus or irreducible is not evenly divisible by 16, then those remaining bits above the evenly divisible number of bits constitutes an entire 16-bit block in so far as setting modsize is concerned. Modsize is speciﬁed as a value between 0 and 127, which indicates a block size of 1 to 128 digits. On power-up or clear, modsize is set to 0. This register must be written to before initiating an arithmetic function.

All functions have a minimum modsize greater than zero for the function to operate properly.

7.1.8 EXP(k)_SIZE

EXP(k)_SIZE sets the maximum size of the exponent or multiplier vector in terms of 32-bit words. The minimum size is one 32-bit word, and the maximum size is 64 32-bit words. EXP(k)_SIZE will be speciﬁed as a value between 0 and 63, which indicates an exponent or multiplier size of 1 to 64 bytes. On power-up or clear, EXP(k)_SIZE is 0.

7.2 Memories

The PKEU uses four memory spaces (RAM) consisting of 128 16-bit words. Three of these memories, A, B, and N, are R/W accessible to the host during normal operation. The fourth memory, t (or tmp) is normally not accessible to the host accept when the PKEU is placed in test mode.

Each individual memory can be thought of as consisting of four, equally sized (32 16-bit words), separate sub-blocks (e.g. A(0), A(1), A(2), and A(3)). Depending on the function to be executed, it may be necessary to specify which sub-block is to be referenced for the operation. The host speciﬁes the sub-block for each memory via the PKCR. Note that it is not possible for the host to specify the tmp memory sub-blocks.

Prior to any operation, A, B, and N must be loaded with appropriate data. Once the operation is complete, the expected results may then be read from these memories. During processing, the PKEU uses all available memory to hold intermediate results. Memories can not be written to during processing or boot.

Note that despite being implemented as a series of 16 bit half -words, conversion from 32 bit words to 16 bit half-words is handled by the host interface. The RAM can only be written or read using 32 bit words.

Chapter 7. Public Ke y Execution Unit 7-7

ECC Routines

7.3 ECC Routines

7.3.1 ECC Fp Point Multiply

The PKEU performs the Elliptic Curve point multiply function which is the highest level of ECC abstraction supported by the device. It is the intention that the host processor use the PKEU in such a way as to support ECC schemes deﬁned in IEEE P1363 (and other ECC standards) where the point multiply is the critical and most computationally intensive, but not ﬁnal, step in many of these schemes. The point multiply is performed in a near fully-automated fashion; however , there is some interaction required by the host processor (described below).

Point multiplies in F

are carried out by the PKEU by performing repeated point add and

point double operations using projective coordinates. As a result, the host processor is responsible for providing the point P represented as the point (X, Y, Z). For systems that do not operate in the projective coordinate scheme (i.e. point P is represented as the point (x,y)), X is simply x, Y is y, and Z is 1. The complete set of I/O conditions is shown below.

NOTE:

The scalar ‘k’ is assumed to be positive. If k = 0, the results of the point multiply are (1, 1, 0). If k < 0, then k ← (-k) and Y ← -Y (modP).

NOTE:

The input ‘Z’ is assumed to be non-zero. If zero, then the results of the point multiply are (1, 1, 0).

Table 7-5. ECC Fp Point Multiply

Fp Point Multiply

Computation Q = k*P, where Q ≡ (X Entry name multkPtoQ

), P ≡ (X1,Y1, Z1)

3,Y3,Z3

Entry address 0x001(FpmultkPtoQ) Pre-conditions A0 = x

Run-time conditions

7-8 MPC180LMB Security Processor User’s Manual

(non-projective coordinate when XYZ=0) or X1 (projective coordinate when XYZ=1)

A1 = y

(non-projective coordinate when XYZ=0) or Y1 (projective coordinate when XYZ=1)

A2 = (z A3 = a elliptic curve parameter B0 = b elliptic curve parameter B1 = R N0 = prime p (modulus) of the ECC system

EXP(k) = ms 32-bits of k (provided in 32 bit words throughout the point multiply, msb to lsb); ﬁrst word provides following routine invocation per ERDY assertion.

≡1) (non-proj. coordinate when XYZ=0) or Z1 (projective coordinate when XYZ=1)

mod N value

Table 7-5. ECC Fp Point Multiply (Continued)

Fp Point Multiply

ECC Routines

Post-conditions B1 = X2 / X’

B2 = Y2 / Y’ B3 = Z2 / Z’ A2 = undeﬁned (when XYZ = 1) or Z A3 = undeﬁned (when XYZ = 1) or Z Unless explicitly noted, all other registers are not guaranteed to be any particular value.

Special

—

conditions

Initial Condition

mod N

b a

)

1 (or Z

y1 (or Y1)

(or X1)

prime p prime p

‘1’ - ECC enabled

k (run-time)

select ‘1’ or ‘0’

‘0’ - F

enabled same

set set

ECC

EXP(k)

XYZ

Modsize

EXP(k)_SIZE

B3 B2 B1 B0 A3 A2 A1 A0

N3 N2 N1 N0

F2M

(when XYZ = 0)

Final Condition

(or Z’2)

(or Y’2)

(or X’2)

? (or Z

)

? (or Z

)

? ?

? ? ?

same

? same

same same

Figure 7-4. ECC Fp Point Multiply Register Usage

It is important to note that unlike the RSA exponentiation routine, the point to be multiplied is not expected to be in the Montgomery residue system when loaded into the PKEU. All of the other ECC parameters are also expected to be loaded in standard format. This includes the a and b parameters of the ECC system. In addition, the “R

mod N” term is also required. This term is used by the PKEU to put the operands in the Montgomery residue system. See the full description of this function/value below.

It is the responsibility of the host processor to provide multiplier data to the PKEU during the operation. That is, the ‘k’ from the point multiplication ‘kP’ must be provided dynamically by the host micro-processor in 32-bit words. Note that the host must supply the k data starting with the most signiﬁcant 32-bit word and working down to the least signiﬁcant word. Each individual word, however, is formatted msb to lsb (i.e. “k_word[msb:lsb]”).

Chapter 7. Public Ke y Execution Unit 7-9

ECC Routines

PKEU asserts the IRQ signal when it is ready to accept more data. This tells the host processor to read PKSR to see what was set. If the E_RDY bit is set, the host processor knows it must provide the ne xt w ord of k - this data is written into the EXP(k) register one 8-bit word at a time. If this interrupt bit is masked, then it must poll the status register to determine when to provide the next word of k. The host should not look for the assertion of E_RDY until after the routine (i.e. PKCR[GO] bit). Any data written to EXP(K) prior to this will be ignored.

Pin IRD Y_B also is used to signify when PKEU is ready for the next 32 bit word of EXP(k). IRDY_B is active (low) whenever E_RDY bit in the status register is active (high).

The point multiplication is optimized to efﬁciently produce results for systems that work in the projective coordinate scheme but can accelerate afﬁne schemes as well. The host processor selects the scheme via the PKCR XYZ bit.

For afﬁne coordinate systems (CR [XYZ]= 0): The results of the calculation are returned to the A and B storage registers. Note that these

values correspond to the projectiv e coordinate v alues X, Y, Z, Z

, and Z3. X, Y, and Z are in the Montgomery residue system. In order to put the projective coordinates into their afﬁne form, the following equations which deﬁne their relationships must be calculated:

x = X/Z y = Y/Z

;

Because the PKEU does not support the inv erse function, it is the responsibility of the host processor to ﬁnd (Z

2)-1

and (Z3)-1 by using any number of available modulo-n inversion techniques. Once this is accomplished, the host may then provide these values back to the PKEU to perform the ﬁnal two ﬁeld (modular) multiplications to ﬁnd x and y. It is advisable that the user perform these multiplications in the PKEU to remove the values from the Montgomery residue system.

For projective coordinate systems (Control Register Bit XYZ = 1): The results of the calculation are returned to the B memory. Note that these values

correspond to the projective coordinate values X, Y, and Z and are no longer in the Montgomery residue system. The host may take these results as the complete point multiply (including the exit from the Montgomery residue system) (e.g. (XR)(Z

2)-1R-1

modN = X).

The following restrictions apply to the point multiply:

• The value of the k vector must be greater than one for this function to work properly.

• The point multiply operates with a minimum of ﬁve digits (Modsize = 4).

7-10 MPC180LMB Security Processor User’s Manual

ECC Routines

7.3.2 ECC Fp Point Add

This function is extensively utilized by the point multiply routine. However, its value as a stand-alone routine to the host processor is extremely limited. As a result, the information provided on the routine is primarily for testing and debug purposes.

Table 7-6. ECC F

Computation R = P + Q, where R ≡ (X Entry name FpaddPtoQ Entry address 0x002(FpaddPtoQ) Pre-conditions A0 = X’

A1 = Y’ A2 = Z’ A3 = a’ (elliptic curve parameter in Montgomery residue system) B0 = b’ (elliptic curve parameter in Montgomery residue system) B1 = X’ B2 = Y’ B3 = Z’ N0 = prime p (modulus) of the ECC system

Post-conditions A0 = X’

A1 = Y’ A2 = Z’1 A3 = a’ B0 = b’ B1 = X’ B2 = Y’ B3 = Z’3 Unless explicitly noted, all other registers are not guaranteed to be any particular value.

(projective coordinate in Montgomery residue system)

Point Add

Fp Point Add

), P ≡ (X1,Y1, Z1), and Q ≡ (X2,Y2, Z2)

3,Y3,Z3

Special conditions

All variables followed with the tick mark (‘) indicate it is in the Montgomery residue system.

Initial Condition

Z’ Y’ X’

Z’

Y’ X’

modulus N modulus N

‘1’ - ECC enabled

‘0’ - Fp enabled same

2 2 2

b’ a’

1 1

set

Modsize

EXP(k)_SIZE

B3 B2 B1 B0 A3 A2 A1 A0

N3 N2 N1 N0

ECC

EXP(k)

XYZ F2M

Final Condition

Z’

Y’

X’

b’ a’ Z’

Y’

X’

? ? ?

same

Figure 7-5. ECC Fp Point Add Register Usage

Chapter 7. Public Ke y Execution Unit 7-11

ECC Routines

7.3.3 ECC Fp Point Double

Table 7-7. ECC F

Computation R = Q + Q = 2 * Q, where R ≡ (X Entry name FpdoubleQ Entry address 0x003(FpdoubleQ) Pre-conditions B1 = X’

B2 = Y’ B3 = Z’ A3 = a’ (elliptic curve parameter in Montgomery residue system) B0 = b’ (elliptic curve parameter in Montgomery residue system) N0 = prime p (modulus) of the ECC system

Post-conditions B1 = X’

B2 = Y’ B3 = Z’3 A3 = a’ B0 = b’ Unless explicitly noted, all other registers are not guaranteed to be any particular value.

Special conditions

All variables followed with the tick mark (‘) indicate it is in the Montgomery residue system. While not explicitly mentioned or necessary, the contents registers A0, A1, and A2 a left undisturbed in anticipation that these will store the generator point (P) during a point multiply.

(projective coordinate in Montgomery residue system)

Point Double

Fp Point Double

), and Q ≡ (X3,Y3, Z3)

3,Y3,Z3

Initial Condition

Z’

Y’ X’

modulus N modulus N

‘1’ - ECC enabled

‘0’ - Fp enabled same

Modsize

EXP(k)_SIZE

B3 B2 B1 B0 A3 A2 A1 A0

N3 N2 N1 N0

ECC

EXP(k)

XYZ F2M

1 1

b’ a’

set

Final Condition

Z’

Y’

X’

b’ a’ same same same

? ? ?

same

Figure 7-6. ECC Fp Point Double Register Usage

7-12 MPC180LMB Security Processor User’s Manual

ECC Routines

7.3.4 ECC Fp Modular Add

Modular addition may be performed on any two vectors loaded into A (A0-A3) and B (B0-B3), where both of these vectors are less than the value stored in the modulus register N (N0-N3). The results are stored in the respective B register. For ECC functionality, this function is used by the point add and point double routines but is available to the host interface - typically for higher-level ECC-related functions. This function operates with a minimum of four digits (Modsize = 3).

Prior to initiating this function, the A, B and N register pointers must be set in the control register which indicate which sub-registers (e.g A0, B0, A1, B1, etc.) are the targeted operands. See Table 7-2 for a detailed description. Once this is performed, the host processor may successfully initiate this function.

Table 7-8. Modular Add

Modular Add

Computation C = D + E mod N, where D, E, and C are integers and are less than N Entry name modularadd Entry address 0x008(modularadd) Pre-conditions A0-3 = D (integer, exact A-location pre-selected in Control Register)

B0-3 = E (integer, exact B-location pre-selected in Control Register) N0-3 = prime p (modulus) of the ECC system

Post-conditions B0-3 = results of modular addition stored where the B operand was located

Unless explicitly noted, all other registers are not guaranteed to be any particular value.

Special conditions

The function operates the same regardless of whether or not the operands are in the Montgomery residue system.

Initial Condition

B3 B2 B1

regAsel regBsel regNsel

Modsize

EXP(k)_SIZE

B0 A3 A2 A1 A0

N3 N2 N1 N0

ECC

EXP(k)

XYZ F2M

E (if B0 selected)

D (if A0 selected)

modulus N (if N0 selected) modulus N (if N0 selected)

‘1’ - ECC enabled

‘0’ - Fp enabled same set (00, 01, 10, 11) set (00, 01, 10, 11) set (00, 01, 10, 11)

set

Final Condition

? ? ? C (if B0 selected)

? ?

same

same same same same

Figure 7-7. Modular Add Register Usage

Chapter 7. Public Ke y Execution Unit 7-13

ECC Routines

7.3.5 ECC Fp Modular Subtract

Modular subtraction may be performed on any two vectors loaded into A (A0–A3) and B (B0–B3), where both of these vectors are less than the value stored in the modulus re gister N (N0–N3). This is accomplished by computing A-B if A > B or A-B+N if A < B. The results are stored in the respective B register. For ECC functionality, this function is used by the point add and point double routines but is available to the host interface. This function operates with a minimum of four digits (Modsize = 3).

Before this function is initialized, the A, B and N register pointers must be set in the control register which indicate which sub-registers (A0, B0, A1, B1, etc.) are the targeted operands. See Table 7-2 for a detailed description. Once this is performed, the host processor may successfully initiate this function.

Table 7-9. Modular Subtract

Modular Subtract

Computation C = D - E mod N, where D, E, and C are integers and are less than N Entry name modularsubtract; Entry address 009h(modularsubtract) Pre-conditions A0-3 = D (integer, exact A-location pre-selected in Control Register)

B0-3 = E (integer, exact B-location pre-selected in Control Register) N0-3 = prime p (modulus) of the ECC system

Post-conditions B0-3 = results of modular subtraction stored where the B operand was located

Unless explicitly noted, all other registers are not guaranteed to be any particular value.

Special conditions

The function operates the same regardless of whether or not the operands are in the Montgomery residue system.

Initial Condition

B3 B2 B1

regAsel regBsel regNsel

Modsize

EXP(k)_SIZE

B0 A3 A2 A1 A0

N3 N2 N1 N0

ECC

EXP(k)

XYZ F2M

E (if B0 selected)

D (if A0 selected)

modulus N (if N0 selected) modulus N (if N0 selected)

‘1’ - ECC enabled

‘0’ - Fp enabled same set (00, 01, 10, 11) set (00, 01, 10, 11) set (00, 01, 10, 11)

set

Final Condition

? ? ? C (if B0 selected)

? ? ?

same

same same same same

Figure 7-8. Modular Subtract Register Usage

7-14 MPC180LMB Security Processor User’s Manual

ECC Routines

7.3.6 ECC Fp Montgomery Modular Multiplication

((A × B × R-1) mod N)

The (A × B × R-1) mod N calculation is the core function of the PKEU. It is used to assist the point add and double routines in completing their functions. For ECC purposes, this function will rarely be used directly by the host processor. This function operates with a minimum of ﬁve digits (Modsize = 4). The complete set of I/O conditions is sho wn below:

Table 7-10. Modular Multiplication

Modular Multiply

-1

Computation C = A * B * R

mod N, where A, B, and C are integers less than N and R = 2

number of digits of the modulus vector Entry name modularmultiply Entry address 0x00a(modularmultiply) Pre-conditions A0-3 = A (integer, exact A-location pre-selected in Control Register)

B0-3 = B (integer, exact B-location pre-selected in Control Register)

N0-3 = prime p (modulus) of the ECC system Post-conditions A0-3 = A operand is preserved

B0-3 = results of modular multiplication stored where the B operand was located

Unless explicitly noted, all other registers are not guaranteed to be any particular value.

16D

where D is the

Special conditions

Typically, though it is not mandatory, the operands will be in the Montgomery residue system. The

only time this would not be the case is when manually placing a value into the Montgomery residue

system.

Initial Condition

B3 B2 B1

regAsel regBsel regNsel

Modsize

EXP(k)_SIZE

B0 A3 A2 A1 A0

N3 N2 N1 N0

ECC

EXP(k)

XYZ F2M

B (if B0 selected)

A (if A0 selected)

modulus N (if N0 selected) modulus N (if N0 selected)

‘1’ - ECC enabled

‘0’ - Fp enabled same set (00, 01, 10, 11) set (00, 01, 10, 11) set (00, 01, 10, 11)

set

Final Condition

? ? ? C (if B0 selected)

A (if A0 selected)

? ? ?

same

same same same same

Figure 7-9. Modular Multiplication Register Usage

Chapter 7. Public Ke y Execution Unit 7-15

ECC Routines

7.3.7 ECC Fp Montgomery Modular Multiplication

((A × B × R-2) mod N)

The (A × B × R-2) mod N calculation is similar to the standard ‘R-1’ Montgomery multiplication except an additional R is divided out. This function is ideal for those ECC applications which work in afﬁne coordinates. In that case, the host may use this function to exit projectiv e coordinates. For example, the host could ﬁnd x, for x = X/Z

2)-1

are in the Montgomery residue system. Loading X and (Z2)-1 into the appropriate operand registers and initiating this function would yield x which is no longer in the Montgomery residue system. This function operates with a minimum of 5 digits (Modsize = 4). The complete set of I/O conditions is shown below:

Table 7-11. Modular Multiplication (with double reduction)

Modular Multiply (with double reduction)

-2

Computation C = A * B * R

number of digits of the modulus vector Entry name modularmultiply2 Entry address 0x00b (modularmultiply2)

mod N, where A, B, and C are integers less than N and R = 2

, where X and

16D

where D is the

Pre-conditions A0-3 = A (integer, exact A-location pre-selected in Control Register)

B0-3 = B (integer, exact B-location pre-selected in Control Register)

N0-3 = prime p (modulus) of the ECC system Post-conditions A0-3 = A operand is preserved

B0-3 = results of modular multiplication stored where the B operand was located

Unless explicitly noted, all other registers are not guaranteed to be any particular value. Special

— conditions

Initial Condition

B3 B2 B1

B (if B0 selected)

A (if A0 selected)

modulus N (if N0 selected) modulus N (if N0 selected)

‘1’ - ECC enabled

‘0’ - Fp enabled same set (00, 01, 10, 11) set (00, 01, 10, 11) set (00, 01, 10, 11)

set

B0 A3 A2 A1 A0

N3 N2 N1 N0

ECC

EXP(k)

XYZ

F2M regAsel regBsel regNsel

Modsize

EXP(k)_SIZE

Final Condition

? ? ? C (if B0 selected)

A (if A0 selected)

? ? ?

same

same same same same

Figure 7-10. Modular Multiplication (with double reduction) Register Usage

7-16 MPC180LMB Security Processor User’s Manual

ECC Routines

7.3.8 ECC F2m Polynomial-Basis Point Multiply

The PKEU performs the elliptic curve point multiply function which is the highest lev el of ECC abstraction supported by the device. It is the intention that the host processor use the PKEU in such a way as to support ECC schemes deﬁned in IEEE P1363 (and other ECC standards) where the point multiply is the critical and most computationally intensive, but not ﬁnal, step in many of these schemes. The point multiply is a nearly fully automated. However, some interaction is required by the host processor (described below).

Point multiplies in F

m are carried out by the PKEU by performing repeated point add and

point double operations using projective coordinates. As a result, the host processor is responsible for providing the point P represented as the point (X, Y, Z). For systems that do not operate in the projective coordinate scheme (that is, point P is represented as the point (x, y)), X is simply x, Y is y, and Z is 1. The complete set of I/O conditions is sho wn below:

Table 7-12. ECC F2m Point Multiply

F2m Point Multiply

Computation Q = k*P, where Q ≡ (X Entry name multkPtoQ(will probably be the same as F Entry address 0x001(multkPtoQ) Pre-conditions A0 = x

Run-time conditions

Post-conditions B1 = X

(when XYZ=0) or X1 (when XYZ=1)

A1 = y

(when XYZ=0) or Y1 (when XYZ=1)

A2 = (z A3 = a elliptic curve parameter B0 = c elliptic curve parameter B1 = R N0 = prime p (modulus) of the ECC system

EXP(k) = ms 8-bits of k (provided in 8 bit words throughout the point multiply, msb to lsb); ﬁrst word provides following routine invocation per ERDY assertion.

B2 = Y2 / Y’ B3 = Z2 / Z’ A2 = undeﬁned (when XYZ = 1) or Z A3 = undeﬁned (when XYZ = 1) or Z Unless explicitly noted, all other registers are not guaranteed to be any particular value.

≡1) (when XYZ=0) or Z1 (when XYZ=1)

mod N value

/ X’

2 2 2

), P ≡ (X1,Y1, Z1)

3,Y3,Z3

)

(when XYZ = 0)

Special conditions The ‘c’ elliptic curve parameter is a function of the ‘b’ parameter and ﬁeld size: .

m2–

Chapter 7. Public Ke y Execution Unit 7-17

ECC Routines

Initial Condition

mod N

1 (or Z

y1 (or Y1)

(or X1)

irred. poly. irred. poly.

‘1’ - ECC enabled

k (run-time)

select ‘1’ or ‘0’

‘1’ - F

B3 B2 B1

c a

)

m enabled same

set set

B0 A3 A2 A1 A0

N3 N2 N1 N0

ECC

EXP(k)

XYZ F2M

Modsize

EXP(k)_SIZE

Final Condition

(or Z’2)

(or Y’2)

(or X’2)

? (or Z

)

? (or Z

)

? ?

? ? ?

same ? same

same same

Figure 7-11. ECC F2m Point Multiply I/O

It is important to note that unlike the RSA exponentiation routine, the point to be multiplied is not expected to be in the Montgomery residue system when loaded into the PKEU. All of the other ECC parameters are also expected to be loaded in standard format. This includes the a, c, and modulus parameters of the ECC system. In addition, the “R

mod N” term is also required. This term is used by the PKEU to put the operands in the Montgomery residue system. See the full description of this function below.

It is the responsibility of the host processor to provide multiplier data to the accelerator during the operation. That is, the ‘k’ from the point multiplication ‘kP’ must be provided dynamically by the host micro-processor in 32-bit words. Note that the host must supply the k data starting with the most signiﬁcant 32-bit word and working down to the least signiﬁcant word. Each individual word, however, is formatted msb to lsb (i.e. “k_word[msb:lsb]”).

PKEU asserts the IRQ signal when it is ready to accept more data. This tells the host processor to read the status word to see what was set. If the E_RDY bit is set (or pin IRD Y_B active lo w), the host processor knows it must pro vide the next word of k - this data is written into the EXP(k) register one 32-bit word at a time. If this interrupt is masked, then it must poll the status register to determine when to provide the next word of k. The host should not look for the assertion of E_RD Y until after the routine (i.e. PKCR[GO] bit). Any data written to EXP(K) prior to this will be ignored.

7-18 MPC180LMB Security Processor User’s Manual

For afﬁne coordinate systems (XYZ = 0):

ECC Routines

The results of the calculation are returned to the A and B storage registers. Note that these values correspond to the projectiv e coordinate v alues X, Y, Z, Z

x = X/Z y = Y/Z

;

Since the PKEU does not support the inverse function, it is the responsibility of the host processor to ﬁnd (Z

2)-1

and (Z3)-1 by using any number of available modulo-irreducible-polynomial inversion techniques. Once this is accomplished, the host may then provide these values back to the PKEU to perform the ﬁnal two ﬁeld multiplications to ﬁnd x and y. It is advisable that the user perform these multiplications in the PKEU to remove the values from the Montgomery residue system.

For projective coordinate systems (XYZ = 1): The results of the calculation are returned to the B memory. Note that these values

2)-1R-1

modN = X).

The following restrictions apply to the point multiply:

• The value of the k vector must be greater than one for this function to work properly.

• The point multiply operates with a minimum of ﬁve digits (Modsize = 4).

7.3.9 ECC F2m Point Add

Chapter 7. Public Ke y Execution Unit 7-19

ECC Routines

Table 7-13. ECC F

Computation R = P + Q, where R ≡ (X Entry name F Entry address 0x005(F Pre-conditions A0 = X’

Post-conditions A0 = X’

maddPtoQ

maddPtoQ)

(projective coordinate in Montgomery residue system)

A1 = Y’ A2 = Z’

(projective coordinate in Montgomery residue system)

A3 = a’ (elliptic curve parameter in Montgomery residue system) B0 = c’ (elliptic curve parameter in Montgomery residue system) B1 = X’ B2 = Y’ B3 = Z’

(projective coordinate in Montgomery residue system)

N0 = irreducible polynomial of the ECC system

A1 = Y’

A2 = Z’1 A3 = a’ B0 = c’ B1 = X’

B2 = Y’

B3 = Z’3 Unless explicitly noted, all other registers are not guaranteed to be any particular value.

m Point Add

F2m Point Add

), P ≡ (X1,Y1, Z1), and Q ≡ (X2,Y2, Z2)

3,Y3,Z3

Special conditions The c elliptic curve parameter is a function of the ‘b’ parameter and ﬁeld size: .

m2–

All variables followed with the tick mark (‘) indicate it is in the Montgomery residue system.

Initial Condition

Z’ Y’ X’

Z’ Y’

X’

irred. poly. irred. poly.

‘1’ - ECC enabled

‘1’ - F2m enabled same

c’ a’

2 2 2

1 1

set

B3 B2 B1 B0 A3 A2 A1 A0

N3 N2 N1 N0

ECC

EXP(k)

XYZ F2M

Modsize

EXP(k)_SIZE

Final Condition

Z’

Y’

X’

c’ a’ Z’

Y’

X’

? ? ?

same

Figure 7-12. ECC F2m Point Add Register Usage

7-20 MPC180LMB Security Processor User’s Manual

ECC Routines

7.3.10 ECC F2m Point Double

Table 7-14. ECC F

m Point Double

F2m Point Double

Computation R = Q + Q = 2 * Q, where R ≡ (X Entry name F Entry address 0x006(F Pre-conditions B1 = X’

mdoubleQ

B2 = Y’ B3 = Z’

mdoubleQ)

(projective coordinate in Montgomery residue system)

), and Q ≡ (X3,Y3, Z3)

3,Y3,Z3

A3 = a’ (elliptic curve parameter in Montgomery residue system) B0 = c’ (elliptic curve parameter in Montgomery residue system) N0 = prime p (modulus) of the ECC system

Post-conditions B1 = X’

B2 = Y’

B3 = Z’3 A3 = a’ B0 = c’ Unless explicitly noted, all other registers are not guaranteed to be any particular value.

Special conditions The c elliptic curve parameter is a function of the ‘b’ parameter and ﬁeld size: .

m2–

Initial Condition

Z’

Y’ X’

irred. poly. irred. poly.

‘1’ - ECC enabled

‘1’ - F2m enabled same

Modsize

EXP(k)_SIZE

B3 B2 B1 B0 A3 A2 A1 A0

N3 N2 N1 N0

ECC

EXP(k)

XYZ F2M

1 1

c’ a’

set

Final Condition

Z’

Y’

X’

b’ a’ same same same

? ? ?

same

Figure 7-13. ECC F2m Point Double Register Usage

Chapter 7. Public Ke y Execution Unit 7-21

ECC Routines

7.3.11 ECC F2m Add (Subtract)

Field addition in F2m (polynomial-basis) may be performed on any two vectors loaded into A (A0-A3) and B (B0-B3), where both of these vectors are less than the value stored in the modulus (irreducible polynomial) register N (N0-N3). The results are stored in the respective B register. In F well as subtraction, therefore, it is sufﬁcient to support both of these functions with this single routine. This function operates with a minimum of 4 digits (Modsize = 3).

Prior to initiating this function, the A, B, and N register pointers must be set in the control register which indicate which sub-registers (e.g A0, B0, A1, B1, etc.) are the targeted operands. See Section 7.1.2, “Control Register (PKCR),” for a detailed description. Once this is performed, the host processor may successfully initiate this function.

m, this function provides identical results for both addition as

Table 7-15. F

m Modular Add (Subtract)

F2m Modular Add (Subtract)

Computation C = D + E mod N, where D, E, and C are integers and are less than N Entry name modularadd (same as with integer add) Entry address 0x008(modularadd) Pre-conditions A0-3 = D (binary polynomial, exact A-location pre-selected in control register)

B0-3 = E (binary polynomial, exact B-location pre-selected in control register) N0-3 = irreducible polynomial of the ECC system

Post-conditions B0-3 = results of modular addition (subtraction) stored where the B operand was located

Unless explicitly noted, all other registers are not guaranteed to be any particular value.

Special conditions

The function operates the same regardless of whether or not the operands are in the Montgomery residue system.

Initial Condition

E (if B0 selected)

D (if A0 selected)

B3 B2 B1 B0 A3 A2 A1 A0

Final Condition

? ? ? C (if B0 selected)

N3 N2 N1

EXP(k)_SIZE

ECC

EXP(k)

XYZ

F2M regAsel regBsel regNsel

Modsize

irred. poly. (if N0 selected) irred. poly. (if N0 selected)

‘1’ - ECC enabled

‘1’ - F2m enabled same set (00, 01, 10, 11) set (00, 01, 10, 11) set (00, 01, 10, 11)

set

? ? ?

same

same same same same

Figure 7-14. F2m Modular Add (Subtract) Register Usage

7-22 MPC180LMB Security Processor User’s Manual

ECC Routines

7.3.12 ECC F2m Montgomery Modular Multiplication

((A × B × R-1) mod N)

The (A × B × R-1) mod N calculation is the core function of the PKEU. This function is used to assist the point add and double routines in completing their functions. For ECC purposes, this function will rarely be used directly by the host processor. This function operates with a minimum of 5 digits (Modsize = 4). The complete set of I/O conditions is shown below:

Table 7-16. F

m Modular Multiplication

F2m Modular Multiply

-1

Computation C = A * B * R

mod N, where A, B, and C are integers less than N and R = 2

number of digits of the modulus vector

Entry name modularmultiply (same for F

or F2m)

Entry address 0x00a(modularmultiply) Pre-conditions A0-3 = A (binary polynomial, exact A-location pre-selected in Control Register)

B0-3 = B (binary polynomial, exact B-location pre-selected in Control Register) N0-3 = irreducible polynomial of the ECC system

Post-conditions A0-3 = A operand is preserved

B0-3 = results of modular multiplication stored where the B operand was located Unless explicitly noted, all other registers are not guaranteed to be any particular value.

Special conditions

Typically, though it is not mandatory, the operands will be in the Montgomery residue system. The only time this would not be the case is when manually placing a value into the Montgomery residue system.

Initial Condition

B (if B0 selected)

A (if A0 selected)

B3 B2 B1 B0 A3 A2 A1 A0

Final Condition

? ? ? C (if B0 selected)

A (if A0 selected)

16D

where D is the

N3 N2 N1

Modsize

EXP(k)_SIZE

ECC

EXP(k)

XYZ

F2M regAsel regBsel

regNsel

irred. poly. (if N0 selected) irred. poly. (if N0 selected)

‘1’ - ECC enabled

‘1’ - F2m enabled same set (00, 01, 10, 11) set (00, 01, 10, 11) set (00, 01, 10, 11)

set

? ? ?

same

same same same same

Figure 7-15. F2m Modular Multiplication Register Usage

Chapter 7. Public Ke y Execution Unit 7-23

ECC Routines

7.3.13 ECC F2m Montgomery Modular Multiplication

((A × B × R-2) mod N)

2)-1

, where X and

Table 7-17. F

m Modular Multiplication (with double reduction)

F2m Modular Multiply (with double reduction)

-2

Computation C = A * B * R

mod N, where A, B, and C are binary polynomials with order than N and R = 2

where D is the number of digits of the irreducible polynomial

Entry name modularmultiply2 (same as F

)

Entry address 0x00b (modularmultiply2) Pre-conditions A0-3 = A (binary polynomial, exact A-location pre-selected in Control Register)

B0-3 = B (binary polynomial, exact B-location pre-selected in Control Register) N0-3 = irreducible polynomial of the ECC system

Post-conditions A0-3 = A operand is preserved

B0-3 = results of modular multiplication stored where the B operand was located Unless explicitly noted, all other registers are not guaranteed to be any particular value.

Special

—

conditions

Initial Condition

B (if B0 selected)

A (if A0 selected)

B3 B2 B1 B0 A3 A2 A1 A0

Final Condition

? ? ? C (if B0 selected)

A (if A0 selected)

16D

N3 N2 N1

irred. poly. (if N0 selected) irred. poly. (if N0 selected)

‘1’ - ECC enabled

‘1’ - F2m enabled same set (00, 01, 10, 11) set (00, 01, 10, 11) set (00, 01, 10, 11)

set

ECC

EXP(k)

XYZ

F2M regAsel regBsel regNsel

Modsize

EXP(k)_SIZE

? ? ?

same

same same same same

Figure 7-16. F2m Modular Multiplication (with double reduction) Register Usage

7-24 MPC180LMB Security Processor User’s Manual

RSA Routines

7.4 RSA Routines

For the RSA-related descriptions which follow, it is generally recommended that all memory block pointers (regAsel, regBsel, etc.) are set to zero. For the modular exponentiation routine, the pointers are actually ignored. For the multiplies, add, subtract, and R settings.

While potentially dangerous due to the commonly large sizes of RSA operands, this ﬂexibility is allowed to support Chinese Remainder Theorem (CRT). CRT often generates intermediate values which must be stored for later use. By using pointers, these values may be stored in the PKEU and efﬁciently used again without the host having to store/retrieve these values to/from general memory . It is left to the application de veloper to use these tools to support CRT.

functions, it is possible to set these pointers and have the PKEU adhere to these

7.4.1 (A × R-1)

EXP

mod N

The PKEU carries out exponentiations by repeated multiply operations. The multiplies are controlled internally by the PKEU, howev er, it is the responsibility of the host processor to provide exponent data (32-bit words at a time) to the accelerator during the operation. Note that the host must supply the exponent data starting with the most signiﬁcant 32-bit word and working down to the least signiﬁcant word. Each individual word, however, is formatted msb to lsb (i.e. “exp_word[msb:lsb]”).

PKEU asserts the IRD Y_B and IRQ signals when it is ready to accept more exponent data (IRQ only if E_RD Y is not masked). This tells the host processor to read the SR to see what was set. If the E_RDY bit is set, the host processor knows it must provide the next word of the exponent - this data is written into the EXP(k) register one 32-bit word at a time. If this interrupt bit is masked, then it must poll the status register to determine when to provide the next word of the exponent. The host should not look for the assertion of E_RDY until after the routine (i.e. CR[GO] bit). Data previously written to EXP(K) is ignored.

The data to be exponentiated must be provided in the Montgomery format. Consider the vector A’, the data to be exponentiated where A’ = AR mod N. By providing A’, the results of (A’ × R

-1)EXP

mod N yields (A × R × R-1)

EXP

mod N, or equivalently, (A)

EXP

mod N.

The result of the calculation is returned to the B storage register . Note that this v alue has no remaining R terms and therefore is no longer in Montgomery format. The value of the exponent vector must be greater than one for this function to work properly. This function operates with a minimum of 5 digits (Modsize = 4). The exponent may be as small as one byte (EXP(k)_SIZE = 0).The complete set of I/O conditions is shown below:

Chapter 7. Public Ke y Execution Unit 7-25

RSA Routines

Table 7-18. Integer Modular Exponentiation

Integer Modular Exponentiation

-1)EXP

Computation S = (A’ * R Entry name expA Entry address 0x007(expA) Pre-conditions A0-3 = A’ (the value A in the Montgomery residue system)

N0-3 = modulus

mod N

Run-time conditions

EXP(k) = msb exponent word (provided in 8-bit words throughout the exponentiation); ﬁrst word provides following routine invocation per ERDY assertion.

Post-conditions B0-3 = S

Unless explicitly noted, all other registers are not guaranteed to be any particular value.

Special conditions

A, N, and B have the lsb digits in A0, N0, and B0, respectively. As required, data will occupy the more signiﬁcant memory blocks.

Initial Condition

B3 B2 B1

etc.

A’ (bits 1023:512)

A’ (bits 511:0)

N (bits 1023:512)

modulus N (bits 511:0) modulus N (bits 511:0)

exponent (run-time)

‘0’ - integer-mod-n enabled same

etc.

‘0’ - ECC disabled

set

B0 A3 A2 A1 A0

N3 N2 N1 N0

ECC

EXP(k)

XYZ

F2M

Modsize

EXP(k)_SIZE

Final Condition

etc. S (bits 1023:512) S (bits 511:0) etc. etc. A’ (bits 1023:512) A’ (bits 511:0)

etc. N (bits 1023:512)

same

same same

Figure 7-17. Integer Modular Exponentiation Register Usage

7-26 MPC180LMB Security Processor User’s Manual

RSA Routines

7.4.2 RSA Montgomery Modular Multiplication

((A × B × R-1) mod N)

The (A × B × R-1) mod N calculation is the core function of the PKEU. It is used to assist the exponentiation routine in completing its operation though it is also av ailable to the host processor - typically to put messages into the Montgomery format. This function operates with a minimum of ﬁve digits (Modsize = 4). The complete set of I/O conditions is shown below:

Table 7-19. Modular Multiplication

Modular Multiply

-1

Computation C = A * B * R

mod N, where A, B, and C are integers less than N and R = 2

number of digits of the modulus vector Entry name modularmultiply Entry address 0x00a(modularmultiply) Pre-conditions A0-3 = A

B0-3 = B

N0-3 = modulus

16D

where D is the

Post-conditions A0-3 = A operand is preserved

B0-3 = results of modular multiplication stored where the B operand was located

Unless explicitly noted, all other registers are not guaranteed to be any particular value. Special

conditions

Typically, though it is not mandatory, the operands will be in the Montgomery residue system. The only

time this would not be the case is when manually placing a value into the Montgomery residue system.

Initial Condition

B(⇑)

A(⇑)

modulus N(⇑) modulus N(⇑)

‘0’ - ECC disabled

‘0’ - integer-modulo-n enabled same

set (00) set (00) set (00)

set

regNsel

Modsize

EXP(k)_SIZE

B3 B2 B1 B0 A3 A2 A1 A0

N3 N2 N1 N0

ECC

EXP(k)

XYZ

F2M regAsel regBsel

Final Condition

C(⇑)

A(⇑)

same

same same same same

Figure 7-18. Modular Multiplication Register Usage

Prior to initiating this function, the A and B register pointers must be set in the control register which indicate which sub-registers (e.g A0, B0, A1, B1, etc.) are the targeted operands. See Table 7-2 for a detailed description. Once this is performed, the host processor may successfully initiate this function.

Chapter 7. Public Ke y Execution Unit 7-27

RSA Routines

7.4.3 RSA Montgomery Modular Multiplication

((A × B × R-2) mod N)

The (A × B × R-2) mod N calculation is similar to the standard ‘R-1’ Montgomery multiplication except an additional R is divided out. This function is particularly helpful when using the Chinese Remainder Theorem. This function operates with a minimum of ﬁve digits (Modsize = 4). The complete set of I/O conditions is shown below:

Table 7-20. Modular Multiplication (with double reduction)

Modular Multiply (with double reduction)

-2

Computation C = A * B * R

mod N, where A, B, and C are integers less than N and R = 2

number of digits of the modulus vector Entry name modularmultiply2 Entry address 0x00b(modularmultiply2) Pre-conditions A0-3 = A

B0-3 = B

N0-3 = modulus Post-conditions A0-3 = A operand is preserved

B0-3 = results of modular multiplication stored where the B operand was located

Unless explicitly noted, all other registers are not guaranteed to be any particular value.

16D

where D is the

Special

— conditions

Initial Condition

B3 B2 B1

B(⇑)

A(⇑)

modulus N(⇑) modulus N(⇑)

‘0’ - ECC disabled

‘0’ - integer-modulo-n enabled same

set (00) set (00) set (00)

set

B0 A3 A2 A1 A0

N3 N2 N1 N0

ECC

EXP(k)

XYZ

F2M regAsel regBsel regNsel

Modsize

EXP(k)_SIZE

Final Condition

C(⇑)

A(⇑)

same

same same same same

Figure 7-19. Modular Multiplication (with double reduction) Register Usage

7-28 MPC180LMB Security Processor User’s Manual

RSA Routines

7.4.4 RSA Modular Add

Modular addition may be performed on any two vectors loaded into A (A0-A3) and B (B0-B3), where both of these vectors are less than the value stored in the modulus register N (N0-N3). The results are stored in the respective B register. This function is particularly helpful when using the Chinese Remainder Theorem. This function operates with a minimum of 4 digits (Modsize = 3).

Table 7-21. Modular Add

Modular Add

Computation C = D + E mod N, where D, E, and C are integers and are less than N Entry name modularadd Entry address 0x008(modularadd) Pre-conditions A0-3 = D

B0-3 = E N0-3 = modulus

Post-conditions B0-3 = results of modular addition stored where the B operand was located

Unless explicitly noted, all other registers are not guaranteed to be any particular value.

Special conditions

The function operates the same regardless of whether or not the operands are in the Montgomery residue system.

Initial Condition

B3 B2 B1

EXP(k)_SIZE

B0 A3 A2 A1 A0

N3 N2 N1 N0

ECC

EXP(k)

XYZ

F2M regAsel regBsel regNsel

Modsize

E(⇑)

D(⇑)

modulus N(⇑) modulus N(⇑)

‘0’ - ECC disabled

‘0’ - integer-modulo-n enabled same

set (00) set (00) set (00)

set

Final Condition

C(⇑)

same

same same same same

Figure 7-20. Modular Add Register Usage

Chapter 7. Public Ke y Execution Unit 7-29

RSA Routines

7.4.5 RSA Fp Modular Subtract

Modular addition may be performed on any two vectors loaded into A (A0-A3) and B (B0-B3), where both of these vectors are less than the value stored in the modulus register N (N0-N3). This is accomplished by computing A-B if A > B or A-B+N if A < B. The results are stored in the respective B register. This function is particularly helpful when using the Chinese Remainder Theorem. This function operates with a minimum of 4 digits (Modsize = 3).

Table 7-22. Modular Subtract

Modular Subtract

Computation C = D - E mod N, where D, E, and C are integers and are less than N Entry name modularsubtract Entry address 0x009(modularsubtract) Pre-conditions A0-3 = D

B0-3 = E N0-3 = modulus

Post-conditions B0-3 = results of modular subtraction stored where the B operand was located

Unless explicitly noted, all other registers are not guaranteed to be any particular value.

Special conditions

The function operates the same regardless of whether or not the operands are in the Montgomery residue system.

Initial Condition

B3 B2 B1

E(⇑)

D(⇑)

modulus N(⇑) modulus N(⇑)

‘0’ - ECC disabled

‘0’ - integer-modulo-n enabled same

set (00) set (00) set (00)

set

B0 A3 A2 A1 A0

N3 N2 N1 N0

ECC

EXP(k)

XYZ

F2M regAsel regBsel regNsel

Modsize

EXP(k)_SIZE

Final Condition

C(⇑)

same

same same same same

Figure 7-21. Modular Subtract Register Usage

7-30 MPC180LMB Security Processor User’s Manual

Miscellaneous Routines

7.5 Miscellaneous Routines

The remaining routines are general in nature and are not speciﬁc to any particular cryptographic algorithm.

7.5.1 Clear Memory

This routine clears all of the RAM memory locations in the PKEU. This includes the A, B, and N RAMs. All locations are set to zero. All other registers are cleared either via a reset (software or hardware) or by explicitly writing zeros to each register. Following a reset (software or hardware), this routine is automatically in voked. This accounts for the majority of time between reset and the assertion of the DONE bit in the status register.

Table 7-23. Clear Memory

Clear Memory

Computation A, B, N, and t memories are overwritten with zeros Entry name clearmemory Entry address 0x00d(r2) Pre-conditions — Post-conditions A = B = N = 0 (all locations)

Unless explicitly noted, all other registers are not guaranteed to be any particular value.

Special

—

conditions

Initial Condition

regAsel regBsel regNsel

Modsize

EXP(k)_SIZE

B3 B2 B1 B0 A3 A2 A1 A0

N3 N2 N1 N0

EXP(k)

XYZ F2M

Final Condition

0 0 0 0 0 0 0 0

0 0 0 0

same same same same same same same same

Figure 7-22. Clear Memory Register Usage

Chapter 7. Public Ke y Execution Unit 7-31

Miscellaneous Routines

7.5.2 R2 mod N Calculation

The PKEU has the capability to calculate R2 mod N, where R = 2

16D

and D is the number of digits of the modulus vector (Modsize+1, where Modsize is speciﬁed independently). This function is used to assist in placing operands into the Montgomery residue system. When possible, this value should be pre-computed. If this value is not available, then the host processor may invoke this function to determine the value before the operation. This function takes a non-trivial amount of time (see Table 7-26) so if at all possible, this value should be stored for future use.

Note that this operation primarily exists to support RSA operations since R

mod N may not always be known prior to the execution of certain protocols. For ECC applications, the modulus is a system-wide parameter, which means that the R

mod N value may be pre-computed before any real-time operations by any other system entity and stored for future use. For this reason, R the control register bit F

mod N only supports integer-modulo-n computations (i.e.

M must be 0).

This function operates with a minimum of 4 digits (Modsize = 3) and with the most signiﬁcant digit (16-bits) of the modulus being non-zero. The complete set of I/O conditions is shown below:

Table 7-24. R2 mod N

R2 mod N

Computation R Entry name r2 Entry address 0x00c(r2) Pre-conditions Modsize = number of digits of the modulus vector - 1

Post-conditions B1 = R

Special conditions

mod N, where R = 2

N0-3 = modulus

mod N N0-3 = modulus Unless explicitly noted, all other registers are not guaranteed to be any particular value.

—

16D

and D is the number of digits of the modulus vector

7-32 MPC180LMB Security Processor User’s Manual

Miscellaneous Routines

Initial Condition

B3 B2 B1 B0 A3 A2 A1 A0

N3 N2 N1

Modsize

EXP(k)_SIZE

ECC

EXP(k)

XYZ

F2M regAsel regBsel regNsel

modulus N(⇑) modulus N(⇑)

‘0’ - ECC disabled

‘0’ - integer-modulo-n enabled same

set (00) set (00)

set

Final Condition

mod N(⇑)

same

Figure 7-23. R2 mod N Register Usage

7.5.3 RpRN mod P Calculation

The PKEU has the ability to calculate RpRN mod P, where Rp = 2

16D

, and RN = 2 the number of digits of the modulus P, and E is the number of digits of the modulus N, and D + 4 < E. This constant is used in performing Chinese Remainder Theorem calculations given modulus N = P × Q, where P and Q are prime numbers. Although labelled R P, this function can also compute R

mod Q. The requirement D + 4 < E is not a

QRN

requirement of the command, but a system requirement, as for all subfunctions of Chinese Remainder Theorem to be executable on the PKEU, the number of digits of P and Q must each be at least ﬁve.

16E

PRN

; D is

mod

As with the standard R and only works with the Control Register F

mod N operation, this operation exists primarily to support RSA

M bit set to zero.

To use this function, MOD_SIZE must be programmed with D-1, and EXP_SIZE must be programmed with E-1, and the prime modulus (either P or Q) is written into memory N. The complete set of I/O conditions is shown in Table 7-26.

Chapter 7. Public Ke y Execution Unit 7-33

Miscellaneous Routines

Table 7-25. R

pRN

mod P

RpRN mod P

Computation R

mod P, where Rp = 2

pRN

16D

, and RN = 2

16E

and E is the number of digits of the modulus N, and D + 4 < E Entry name r2 Entry address 0x00c(r2) Pre-conditions Modsize = number of digits of the vector D - 1

EXP(k) SIZE = number of digits of the vector E-1 Post-conditions B0-3 = RpRN mod P

N0-3 = modulus

Unless explicitly noted, all other registers are not guaranteed to be any particular value. Special

— conditions

Initial Condition

B3 B2 B1 B0 A3 A2 A1 A0

; D is the number of digits of the modulus P,

Final Condition

mod N(⇑)

N3 N2 N1

modulus P(⇑) modulus P(⇑)

‘0’ - ECC disabled

‘1’ - RpRn enabled

‘0’ - integer-modulo-n enabled same

set (00)

set (D-1)

set (E-1)

ECC

EXP(k)

RpRn

F2M regAsel regBsel regNsel

Modsize

EXP(k)_SIZE

same

same same

Figure 7-24. RPRN mod P Register Usage

7-34 MPC180LMB Security Processor User’s Manual

Embedded Routine Performance

7.6 Embedded Routine Performance

The formulas listed in Table 7-26 show the run times for the PKHA embedded routines. Many of these are data dependent, which result in variable length run times. F or these cases, the average run-time is noted.

Table 7-26. Run Time Formulas

Operation Symbol Run-Time Formula

multPtoQ t FpaddPtoQ t FpdoubleQ t multPtoQ t F2maddPtoQ t F2mdoubleQ t expA t modularmultiply t

modularmultiply2 t

modularadd t

modularsub t

r2 t clearmemory t

For these formulas, the following deﬁnitions apply: F = operating frequency MS = number of 16-bit blocks in the modulus (that is, the value assigned to the Modsize reg. plus one) Ne = number of bits in the exponent or multiplier (k) avg = average run time (applied to a nominal case which assumes 50% 1’s = in Ne wcs = worst-case run time bcs = best-case run time

(avg) Ne* t

mulfp addfp dblfp

(avg) Ne* t

mulf2m addf2m dblf2m

(avg) 1.5*Ne*[t

exp

(wcs)

mult1

(bcs)

mult1

(wcs)

mult2

(bcs)

mult2

(wcs)

add

(bcs)

add

(wcs)

sub

(bcs)

sub r2 clr_ram

+ 0.5*Ne* t

dblfp

16*(t 10*(t

20*(t 10*(t

(1/F) * [(MS) (1/F) * [(MS)

(1/F) *2* [(MS) (1/F) *2* [(MS)

(1/F) * [4*(MS)+ 11] (1/F) * [3*(MS)+ 6]

(1/F) * [3*(MS)+ 11] (1/F) * [2*(MS)+ 6]

<tbd> (1/F) * 4 * (MS+ 5)

mult1 mult1

dblf2m mult1 mult1

) + 4*(t

add

) + 11*(t

) + 7*(t ) + 4*(t

mult1

add

+ 0.5*Ne* t

add add

] + t

mult1

+ 10*(MS)+ 27]

+ 9*(MS)+ 22]

+ 10*(MS)+ 27]

+ 9*(MS)+ 22]

+ 8*(t

addfp

) + 5*(t

sub

)+2*(t

sub

+ 8*(t

addf2m

) + 15*(MS) ) + 9*(MS)

(wcs)

) + 6*(MS)

mult1

) + 19*(MS) ) + 10*(MS)

mult1

move

move move move

) + 6*(MS)

move

NOTE:

When t

without references to wcs or bcs is encountered,

mult1

assume that for 75% of the time, bcs will occur and for the other 25%, wcs (i.e. t

0.25*t The formulas given for t

mult1

(wcs)).

mulfp

↔ 0.75*t

mult1

and t

mulf2m

(bcs) +

mult1

are for XYZ bit of the Control Register set to one. If set to zero, the run-time would be nearly identical but additional support from the host processor would be required to fully complete the operation. See the point multiply descriptions in Embedded Routine Reference section for more details.

Chapter 7. Public Ke y Execution Unit 7-35

Embedded Routine Performance

7-36 MPC180LMB Security Processor User’s Manual

Chapter 8 Random Number Generator

This chapter explains how to program the RNG (Random Number Generator) to create a random number.

8.1 Overview

The RNG is a digital integrated circuit capable of generating 32-bit random numbers. It is designed to comply with the FIPS-140 standard for randomness and non-determinism. A linear feedback shift register (LSFR) and cellular automata shift register (CASR) are operated in parallel to generate pseudo-random data.

8.2 Functional Description

The RNG consists of six major functional blocks:

• Bus Interface Unit (BIU)

• Linear Feedback Shift Register (LFSR)

• Cellular Automata Shift Register (CASR)

• Clock Controller

• 2 Ring Oscillators

The states of the LFSR and CASR are advanced at unknown frequencies determined by the two ring oscillator clocks and the clock control. When a read is performed, the oscillator clocks are halted and a collection of bits from the LFSR and CASR are x’ored together to obtain the 32-bit random output. The BIU interfaces with the External Bus Interface (EBI) to allow communication between the EBI and the RNG.

8.3 Typical Operation

A typical procedure for reading random data is as follows. When a giv en operation calls for random data, the CPU writes the number of 32-bit random words required to the MPC180 EBI, speciﬁcally to the Output Buffer Count Register (see section 3.3.1.5). The EBI monitors the ORDY bit in the RNG Status Register (Fig 8-1). This bit signals whether the random data is ready . Once the ORDY bit goes low , the EBI reads the 32-bit word from the RNG Random Output Register (Table 8-1) and writes it to the MPC180 Output FIFO,

Chapter 8. Random Number Generator 8-1

Random Number Generator Registers

repeating this process until the required number of 32-bit random words have been generated. Reads by the EBI can be repeated as soon as the ORD Y bit is dri v en high again. The process is outlined as follows:

• CPU sets up MPC180 EBI to generate required number of random words.

• EBI waits for ORD

Y signal to be driven low.

• EBI reads autorand (Automatic Random Output Register), writes to Output FIFO.

• Repeat previous steps until Output Buffer Count Register reaches zero.

At this point, the EBI can generate an interrupt to inform the CPU that the required number of random words is waiting in the Output FIFO. These random words can be read by the CPU for immediate write back to the MPC180, or written into memory for later use.

8.4 Random Number Generator Registers

Table 8-1 shows RNG registers.

Table 8-1. Random Number Generator Registers

MPC180 12-Bit Address Processor 32-Bit Address Register Type

0x600 0x0000_1800 Status R 0x602 0x0000_1808 Autorand output R

8.4.1 Status Register

Figure 8-1 shows the RNG status register.

0171819 3031

Field — ORDY — ON/OFF

Reset 0000_0000_0000_0001

R/W R

Addr 0X600

Figure 8-1. RNG Status Register

Table 8-2 describes the RNG status register ﬁelds.

Table 8-2. RNG Status Register Field Descriptions

Bits Name Description

0–17 — Reserved. 18 ORDY The ORDY bit will be driven high when random data is ready. If the user performs a read

of the Random Output Register while the ORD Y bit is lo w, the RNG will assert wait states

until the ORDY bit goes high. 19–30 – Reserved. 31 ON/OFF A value of 1 indicates that the RNG is on and the shift registers are randomizing.

8-2 MPC180LMB Security Processor User’s Manual

Glossary of T erms and Abbre viations

The glossary contains an alphabetical list of terms, phrases, and abbreviations used in this book. Some of the terms and deﬁnitions included in the glossary are reprinted from IEEE Std 754-1985, IEEE Standard for Binary Floating-Point Arithmetic, copyright ©1985 by the Institute of Electrical and Electronics Engineers, Inc. with the permission of the IEEE.

AES. The Advanced Encryption Standard that will eventually replace DES

(Data Encryption Standard) around the turn of the century. The Rijndael algorithm has been chosen for the AES.

AFEU. Arc Four Execution Unit. Encryption engine which implements a

stream cipher compatible with the RC4 algorithm from RSA Security, Inc.

Authentication. The action of verifying information such as identity,

ownership, or authorization.

Architecture. A detailed speciﬁcation of requirements for a processor or

computer system. It does not specify details of how the processor or computer system must be implemented; instead it provides a template for a family of compatible implementations.

Big-endian. A byte-ordering method in memory where the address n of a

word corresponds to the most-signiﬁcant byte. In an addressed memory word, the bytes are ordered (left to right) 0, 1, 2, 3, with 0 being the most-signiﬁcant byte. See Little-endian.

Block cipher. A symmetric cipher which encrypts a message by breaking it

down into blocks and encrypting each block.

Block cipher based MAC. MAC that is performed by using a block cipher

as a keyed compression function.

Buffer count registers. Contain the number of 32-bit words to be transferred

to/from an execution unit for a given operation.

. Glossary-1

Bulk Data Encryption. The process of converting plaintext to ciphertext.

Refers to encryption operations other than key exchange and hashing.

Burst. A multiple-word data transfer whose total size is typically equal to a

cache block. In MPC8260 mode, eight words.

CBC. Cipher block chaining. Mode of DES encryption which uses IVs which

are altered by the context of the preceding block.

Chinese Remainder Theorem. Mathematical theorem based on the

congruence of greatest common denominator and least common multiple. CRT is used in support of asymmetric key exchange.

Ciphertext. Text (any information) which has been encrypted so as to render

it unreadable by parties without the proper decryption keys.

Clear. To cause a bit or bit ﬁeld to register a value of zero. See also Set. Context. Information associated with an encryption/decryption operation.

Typical context constituents are session keys, initialization vectors, and security associations.

Context memory. Local or system memory reserved for storage of security

context information.

Context switching. The act of changing session-speciﬁc parameters, such as

Keys and IVs, between the end of the current packet and the next.

Cryptography. The art and science of using mathematics to secure

information and create a high degree of trust in the electronic realm. See also public key, secret key, symmetric-key, and threshold cryptography.

Crypto-analysis. The art and science of code breaking. Dev elops methods of

attacking encryption algorithms to recover plaintext in signiﬁcantly less time that brute force attacks.

Decryption. The process of converting ciphertext to plaintext. Also referred

to as decoding.

DES. Data encryption standard. A block cipher that uses a 56-bit key to

encrypt 64-bit blocks of data, one block at a time.

3DES. Triple DES. Encryption operation which permutes 64 bit blocks of

plaintext with 64 bit keys three times. Triple DES is exponentially stronger than single DES encryption.

Glossary-2 MPC180LMB Security Processor User’s Manual

Difﬁe-Hellman key exchange. A key exchange protocol allowing the

participants to agree on a key over an insecure channel.

Digest. Commonly used to refer to the output of a hash function, e.g. message

digest refers to the hash of a message.

Digital signature. The encryption of a message digest with a private key. DMA. Direct Memory Access. DSA. Digital Signature Algorithm. DSA is a public-ke y method based on the

discrete logarithm problem. Proposed by NIST.

DSS. Digital signature standard proposed by NIST.

EBI. External Bus Interface. A functional block in the MPC180 that mediates

between internal and external signals.

ECB. Electronic code book. A mode of DES which uses initialization vectors

that are not modiﬁed by processing of the previous packet.

ECC. Elliptic curve cryptosystem. A public-key cryptosystem based on the

properties of elliptic curves.

Elliptic curve. The set of points (x, y) satisfying an equation of the form

y2 = x3 + ax + b, for variables x, y and constants a, b Î F, where F is a ﬁeld.

Encryption. The transformation of plaintext into an apparently less readable

form (called ciphertext) through a mathematical process. The ciphertext may be read by anyone who has the key that decrypts (undoes the encryption) the ciphertext.

Execution unit. Any device or silicon block which accelerates the

mathematical transformations associated with key exchange, data authentication, and bulk data encryption.

Exponent. In the binary representation of a ﬂoating-point number, the

exponent is the component that normally signiﬁes the integer power to which the value two is raised in determining the value of the represented number.

External Bus Interface. See EBI.

FIFO. First in, ﬁrst out. A buffer memory which supports in-order processing

of data.

FIPS. Federal Information Protection Standards.

. Glossary-3

Fraction. In the binary representation of a ﬂoating-point number, the ﬁeld of

the signiﬁcand that lies to the right of its implied binary point.

Hashing. A function that takes a variable sized input and has a ﬁxed size

output.

HMAC. Hashed message authentication code. MA C that uses a hash function

to reduce the size of the data it processes.

IKE. Internet Key Exchange. A process used by two more parties to e xchange

keys via the Internet, for future secure communication via the Internet.

Initialization V ector. Secret value that, along with the key, is shared by both

encryptor and decryptor . It is a string of bits used in lieu of plaintext at the start of DES. Used in CBC (Cipher Block Chaining) to complicate crypto-analysis.

Interrupt. An asynchronous exception. On PowerPC processors, interrupts

are a special case of exceptions.

Interrupt controller. Organizes the hardware interrupts coming from the

execution units into a maskable interrupt for the processor

Interrupt mask register. Allows masking of individual interrupts by the

host.

IPSec. A standard suite of protocols gov erning key e xchange, authentication,

and encryption of IP packets for transport or tunneling over the Internet.

IV. See Initialization vector.

Key. A string of bits used widely in cryptography, allowing people to encrypt

and decrypt data; a key can be used to perform other mathematical operations as well. Given a cipher, a key determines the mapping of the plaintext to the ciphertext.

Glossary-4 MPC180LMB Security Processor User’s Manual

Latency. The number of clock cycles necessary to execute an instruction and

make ready the results of that execution for a subsequent instruction.

Least-signiﬁcant bit (lsb). The bit of least value in an address, register, data

element, or instruction encoding.

Least-signiﬁcant byte (LSB). The byte of least value in an address, re gister,

data element, or instruction encoding.

Little-endian. A byte-ordering method in memory where the address n of a

word corresponds to the least-signiﬁcant byte. In an addressed memory word, the bytes are ordered (left to right) 3, 2, 1, 0, with 3 being the most-signiﬁcant byte. See Big-endian.

Masking. Hiding internal interrupts and signals from the external interface

via control registers.

MD4. Message Digest 4. Hashing algorithm developed by Rivest which

processes a series of 512-bit message blocks and produces a single 128-bit Hash representing the original message.

MD5. Message Digest 5. Hashing algorithm developed by Ri vest which pads

(if necessary) the message to be hashed to create a 512 bit block. This block is compressed by XOR-ing two inputs: the 512-bit message block, and a 128-bit key. Stronger than MD.

MDEU. Message Digest Execution Unit. A device or silicon block which

accelerates the hashing functions associated with message authentication.

Memory-mapped accesses. Accesses whose addresses use the page or block

address translation mechanisms provided by the MMU and that occur externally with the bus protocol deﬁned for memory.

Message Authentication Code (MAC). A MAC is a function that takes a

variable length input and a key to produce a ﬁx ed-length output. See also hash-based MAC, stream-cipher based MAC, and block-cipher based MAC.

Message Digest. The result of applying a hash function to a message. Modular arithmetic. A form of arithmetic where integers are considered

equal if they leave the same remainder when di vided by the modulus.

Modulus. The integer used to divide out by in modular arithmetic.

. Glossary-5

Most-signiﬁcant bit (msb). The highest-order bit in an address, registers,

data element, or instruction encoding.

Most-signiﬁcant byte (MSB). The highest-order byte in an address,

registers, data element, or instruction encoding.

NIST. National Institute of Standards. U.S. Government Agency responsible

for defining and certifying standards.

Padding. Extra bits concatenated with a key, password, or plaintext. Physical memory. The actual memory that can be accessed through the

system’s memory bus.

Pipelining. A technique that breaks operations, such as instruction

processing or bus transactions, into smaller distinct stages or tenures (respectively) so that a subsequent operation can begin before the previous one has completed.

PKEU. Public Key Execution Unit. A device or silicon block which

accelerates the mathematical algorithms associated with public key exchange. Typically uses the RSA or Difﬁe-Hellman algorithms.

PKI. Public Key Infrastructure. PKIs are designed to solve the key

management problem.

Plaintext. The data to be encrypted. Private key. In public-key cryptography, this key is the secret key. It is

primarily used for decryption but is also used for encryption with digital signatures.

PRNG. Pseudo Random Number Generator . A device or silicon block which

produces numbers or bits which are related to preceding and following numbers or bits, however this relationship is nearly imperceptible. Only predictable in a theoretical sense.

Public key. In public-key cryptography this key is made public to all, it is

primarily used for encryption but can be used for verifying signatures.

Public-key cryptography. Cryptography based on methods involving a

public key and a private key.

Glossary-6 MPC180LMB Security Processor User’s Manual

RC4 algorithm. Byte oriented, therefore a byte of plaintext is encrypted with

a permuted substitution box (S-box) key to produce a byte of ciphertext. The key is variable length and supports in byte increments key lengths from 40 bits to 128 bits, providing a wide range of strengths.

RNG. Random Number Generator . A de vice or silicon block which produces

numbers or bits which are non-deterministically related to preceding and following numbers or bits, thoroughly unpredictable.

RSA algorithm. A public-k e y cryptosystem based on the f actoring problem.

RSA stands for Rivest, Shamir and Adleman, the developers of the RSA public-key cryptosystem.

Secret key. In secret-key cryptography, this is the key used both for

encryption and decryption. Can be a symmetric (shared secret) key or an asymmetric private key.

Security Association (SA). In IPSec, the context which governs a one-way

session using encryption or authentication. A separate SA governs the one-way session by which the responder encrypts or authenticates messages.

Security Parameters Index (SPI). In IPSec, a speciﬁc ﬁeld in the packet

header which identiﬁes the Security Associations already established for the one-way session the packet belongs to.

Self-synchronous. Refers to a stream cipher, when the keystream is

dependent on the data and its encryption.

Session key. A key for symmetric-key cryptosystems that is used for the

duration of one message or communication session.

SHA-1. Secure-Hash Algorithm. Hashing algorithm which pads the message

to be hashed (if necessary) to create a 512 bit block. This block is compressed by XOR-ing two inputs: the 512-bit message block, and a 160-bit key. Stronger than MD-5.

Shared key. The secret key two (or more) users share in a symmetric-key

cryptosystem.

Slave. The de vice addressed by a master device. The slave is identiﬁed in the

address tenure and is responsible for supplying or latching the requested data for the master during the data tenure.

. Glossary-7

SSL Security socket layer protocol. Invented by Netscape Communications,

Inc. This protocol provides end-to-end encryption of application layer network trafﬁc.

Stall. An occurrence when an encryption operation cannot proceed to the next

stage.

Stream cipher. A secret-key encryption algorithm that operates on a bit at a

time.

Stream cipher based MAC. MAC that uses linear feedback shift registers

(LFSRs) to reduce the size of the data it processes.

Strong encryption. Conversion of plaintext to ciphertext which is highly

resistant to attack by crypto-analysis. Accomplished through inherently one-way mathematical functions.

Symmetric cipher. An encryption algorithm in which the same key is used

for encryption as decryption.

Symmetric key. A key that is used for both encryption and decryption. See

secret key.

Synchronization. A process to ensure that operations occur strictly in order. Synchronous. A property of a stream cipher, stating that the keystream is

generated independently of the plaintext and ciphertext.

System memory. The physical memory available to a processor.

Throughput. The bits-per-second measure of the amount of data that is

encrypted or hashed per clock cycle.

TLS. Transport Layer Security protocol. It is effectively SSL 3.1. Transaction. A complete exchange between two bus devices. A transaction

is typically comprised of an address tenure and one or more data tenures, which may overlap or occur separately from the address tenure. A transaction may be minimally comprised of an address tenure only.

Triple DES. See 3DES.

UPM. Universal Programmable Machine. Complex chip select device found

on the PowerQUICC and PowerQUICC II.

Glossary-8 MPC180LMB Security Processor User’s Manual

XOR. A binary bitwise operator yielding the result one if the two values are

different and zero otherwise. XOR is an abbreviation for exclusiveOR.

. Glossary-9

Glossary-10 MPC180LMB Security Processor User’s Manual

INDEX

Numerics

D, 2-1 signal description

D, 2-1 A, 2-1 signal description

A, 2-1

address map, 3–2 AFEU (Arc Four Execution Unit), 1-5, 5–1 AFEU Control Register, 5–3 AFEU Status Register, 5–2 Arc Four Execution Unit, 5–1 Arc Four Execution Unit (AFEU), 1-5 architecure

internal, 1-3

block diagram, 1-3 buffer accesses (FIFO mode), 3–11 BURST, 2-1

Cipher Register, 5–4 Clear Interrupt Register, 5–3 CLK, 2-2 CONFIG, 2-2 CS, 2-1 CSTAT, i>see Command/Status, 3–5

Data Encryption Standard (DEU), 4–1 Data Encryption Standard Execution Unit (DEU), 1-4 DATAIN, 4–4 DATAOUT, 4–4 DEU (Data Encryption Standard Execution Unit), 1-4 DEU (Data Encryption Standard), 4–1 DEU Configuration Register, 4–2 DEU Control Registers, 4–2 DEU Status Register, 4–3 DREQ1, 2-2 DREQ2, 2-2

EBI

operation summary, 3–11 EBI (External Bus Interface), 3–4 EBI seeExternal Bus Interface, 3–5 ECC routines

F2m Add (Subtract), 7–22

F2m Montgomery Modular

Multiplication, 7–23, 7–24 F2m Point Add, 7–19 F2m Point Double, 7–21 Fp Modular Add, 7–13 Fp Modular Subtract, 7–14 Fp Montgomery Modular

Multiplication, 7–15, 7–16 Fp Point Add, 7–11 Fp Point Double, 7–12 Fp Point Multipy, 7–8 Fp Polynomial-Basis Point Multiply, 7–17

embedded routine performance, 7–35 ENDIAN, 2-2 execution units

Arc Four (AFEU), 1-5 complete list, 3–1 Data Encryption Standard (DEU), 1-4 Message Digest (MDEU), 1-5 Public Key (PKEU), 1-4 Random Number Generator (RNG), 1-5

EXP(k) Register

PKEU, 7–6

EXP(k)_Size Register

PKEU, 7–7

External Bus Interface

operation summary, 3–11

External Bus Interface (EBI), 3–4

registers, 3–5

FIFO mode, 3–11

IBCNT,seeInput Buffer Count, 3–11 IBCTL,seeInput Buffer Control, 3–9 ID register, 3–7 IMASK, 3–8 Initialization Vector, 4–4

Index Index-1

INDEX

Input Buffer Control Register, 3–9 Input Buffer Count Register, 3–11 Interrupt Mask Register

PKEU, 7–4 IRQ, 2-2 IVDD, 2-3 IVSS, 2-3

Key Length Register, 5–3 Key Registers

low/lower-middle/upper-middle/upper, 5–3

MDEU (Message Digest Execution Unit), 1-5 MDEU Control Register, 6–2 MDEU Message Buffer Registers, 6–5 MDEU Message Digest Buffer Registers, 6–5 MDEU Status Register, 6–4 MDEU Version Identification Register, 6–2 memories

PKEU, 7–7 message buffer

MDEU register set, 6–5 Message Byte Double-Word Register, 5–4 message digest buffer

MDEU register set, 6–5 Message Digest Execution Unit (MDEU), 1-5 Message Digest Execution Unit (MDEU)

registers, 6–1 Message Register, 5–4 Miscellaneous routines

clear memory, 7–31 R2 mod N Calculation, 7–32 RpRn mod P Calculation, 7–33

Modsize Register

PKEU, 7–7

MPC180E

address map, 3–2 architecture

internal, 1-3

block diagram, 1-3 pinout, 2-4

NC, 2-2

OBCNT,seeOutput Buffer Count, 3–11 OBCTL,seeOutput Buffer Control, 3–9 Output Buffer Control Register, 3–9 Output Buffer Count Register, 3–11

OVDD, 2-3 OVSS, 2-3

pinout, 2-4 PKEU (Public Key Execution Unit), 1-4 Program Counter Register

PKEU, 7–6 PSDVAL, 2-2 Public Key Execution Unit, 7–1 Public Key Execution Unit (PKEU), 1-4 Public Key Execution Unit (PKEU) registers, 7–1 Public Key Execution Unit Control Register, 7–2 Public Key Execution Unit EXP(k) Register, 7–6 Public Key Execution Unit EXP(k)_Size Register, 7–7 Public Key Execution Unit Interrupt Mask

Register, 7–4 Public Key Execution Unit Memories, 7–7 Public Key Execution Unit Modsize Register, 7–7 Public Key Execution Unit Program Counter

R/W, 2-1 Random Number Generator, 8–1

functional description, 8–1

operation, 8–1 Random Number Generator (RNG), 1-5 Random Number Generator Status Register

registers

Random Number Generator

status, 8–2

DEU Control, 4–2 registers

AFEU

Cipher, 5–4 clear interrupt, 5–3 control, 5–3 key length, 5–3 key registers, 5–3 Message, 5–4 Message Byte Double-Word, 5–4 S-box I/J, 5–5 S-box0 – S-box63 Memory, 5–5

status, 5–2 Command/Status, 3–5 CSTAT, i>see Command/Status, 3–5 Data Encryption Standard (DEU), 4–1 DATAIN, 4–4

Index-2 MPC180LMB Security Processor User’s Manual

MOTOROLA MPC180LMB User Guide

Specifications and Main Features

Frequently Asked Questions

User Manual