Maplesoft MAPLE 10 User Manual

Maple User Manual

Maplesoft, Maple, Maple Application Center, Maple Student Center, Maplet, Maple T.A., and MapleNet are all trademarks of Waterloo Maple Inc.

© Maplesoft, a division of Waterloo Maple Inc. 2005. All rights reserved. No part of this book may be reproduced, stored in a retrieval system, or transcribed, in any form or by any means — electronic, mechanical, photocop ying, recording, or otherwise. Information in this document is subject to change without notice and does not represent a commitment on the part of the vendor. The software described in this document is furnished under a license agreement and may be used or copied only in accordance with the agreement. It is against the law to copy the software on any medium except as specifically allowed in the agreement.

Windows is a registered trademark of Microsoft Corporation. Java and all Java based marks are trademarks or registered trademarks of Sun Microsystems, Inc. in the United

States and other countries. Maplesoft is independent of Sun Microsystems, Inc. All other trademarks are the property of their respective owners. This document was produced using a special version of Maple and DocBook. Printed in Canada ISBN 1-894511-75-1

Preface .................................................................................................... xiii

1 Document Mode ...................................................................................... 1

1.1 Introduction ...................................................................................... 1

1.2 In This Chapter ................................................................................ 3

1.3 Simple Mathematical Expressions ................................................... 4

Rational Expressions (Fractions) ....................................................... 5

Powers ................................................................................................ 5

Products .............................................................................................. 5

Shortcuts for Entering Mathematical Expressions ............................. 6

Other Expressions .............................................................................. 7

1.4 Evaluating Expressions .................................................................... 8

1.5 Editing Expressions and Updating Output ...................................... 9

1.6 Entering Expressions ..................................................................... 10

Palettes ............................................................................................ 10

Symbol Names ................................................................................ 16

1.7 Performing Computations ............................................................. 19

Computing with Palettes ................................................................. 20

Context Menus ................................................................................ 20

Assistants and Tutors ....................................................................... 26

1.8 Document Mode Summary ............................................................ 30

1.9 Getting Help ................................................................................... 32

2 Worksheet Mode ................................................................................... 35

2.1 In This Chapter .............................................................................. 36

2.2 Input Prompt .................................................................................. 37

Suppressing Output .......................................................................... 38

1-D Math Input ................................................................................ 38

Input Separators ............................................................................... 39

2.3 Commands .................................................................................... 40

The Maple Library ........................................................................... 40

Top-Level Commands ...................................................................... 40

Package Commands ........................................................................ 42

2.4 Palettes .......................................................................................... 44

2.5 Context Menus .............................................................................. 46

2.6 Assistants and Tutors ..................................................................... 48

iii

iv • Contents

Launching an Assistant or Tutor ...................................................... 48

Example: Using the Interactive Plot Builder ................................... 49

2.7 Task Templates .............................................................................. 51

Viewing Task Templates .................................................................. 51

Inserting a Task Template ................................................................ 52

Performing the Task ......................................................................... 53

2.8 Text Regions ................................................................................... 54

2.9 Names ........................................................................................... 55

Assigning to Names ........................................................................ 55

Unassigning Names ........................................................................ 57

Valid Names .................................................................................... 58

2.10 Equation Labels .......................................................................... 59

Displaying Equation Labels ............................................................. 59

Referring to a Previous Result ......................................................... 59

Execution Groups with Multiple Outputs ........................................ 61

Label Numbering Schemes ............................................................. 61

Features of Equation Labels ............................................................ 62

3 Performing Computations .................................................................... 65

3.1 In This Chapter .............................................................................. 65

3.2 Symbolic and Numeric Computation ............................................ 66

Exact Computations ........................................................................ 67

Floating-Point Computations .......................................................... 68

Converting Exact Quantities to Floating-Point Values ................... 69

Sources of Error .............................................................................. 70

3.3 Integer Operations ......................................................................... 71

Non-Base 10 Numbers and Other Number Systems ........................ 74

3.4 Solving Equations .......................................................................... 78

Solving Equations and Inequations ................................................. 78

Other Specialized Solvers ................................................................ 88

3.5 Units, Scientific Constants, and Uncertainty ................................. 96

Units ................................................................................................ 97

Scientific Constants and Element Properties ................................ 105

Uncertainty Propagation ............................................................... 111

3.6 Restricting the Domain ................................................................ 115

Real Number Domain ................................................................... 115

Assumptions on Variables ............................................................. 117

Contents • v

4 Mathematical Computations .............................................................. 123

4.1 In This Chapter ............................................................................ 125

4.2 Algebra ........................................................................................ 126

Polynomial Algebra ...................................................................... 126

4.3 Linear Algebra ............................................................................ 135

Creating Matrices and Vectors ...................................................... 135

Accessing Entries in Matrices and Vectors ................................... 144

Linear Algebra Computations ....................................................... 145

Student LinearAlgebra Package .................................................... 152

4.4 Calculus ....................................................................................... 153

Limits ............................................................................................ 153

Differentiation ............................................................................... 155

Series ............................................................................................. 161

Integration ..................................................................................... 163

Differential Equations .................................................................... 166

Calculus Packages ......................................................................... 166

4.5 Optimization ............................................................................... 168

Point-and-Click Interface .............................................................. 169

Large Optimization Problems ....................................................... 171

MPS(X) File Support .................................................................... 173

Additional Information .................................................................. 173

4.6 Statistics ...................................................................................... 173

Probability Distributions and Random Variables .......................... 173

Statistical Computations ................................................................ 175

Plotting .......................................................................................... 177

Additional Information .................................................................. 179

4.7 Teaching and Learning with Maple ............................................ 180

Student Packages and Tutors ........................................................ 181

5 Plots and Animations .......................................................................... 189

5.1 In This Chapter ............................................................................ 189

5.2 Creating Plots .............................................................................. 190

Interactive Plot Builder ................................................................. 191

Context Menu ................................................................................ 204

Dragging to a Plot Region ............................................................. 207

The plot and plot3d Commands .................................................... 208

The plots Package ......................................................................... 211

vi • Contents

Multiple Plots in the Same Plot Region ......................................... 214

5.3 Customizing Plots ....................................................................... 216

Interactive Plot Builder Options ................................................... 216

Context Menu Options .................................................................. 217

The plot and plot3d Options ......................................................... 220

5.4 Analyzing Plots ........................................................................... 222

Point Probe, Rotate, Pan, and Scale Tools ..................................... 222

5.5 Creating Animations ................................................................... 223

Interactive Plot Builder ................................................................. 223

The plots[animate] Command ....................................................... 225

5.6 Playing Animations ..................................................................... 226

Animation Context Bar .................................................................. 226

5.7 Customizing Animations ............................................................. 228

Interactive Plot Builder Animation Options .................................. 228

Context Menu Options .................................................................. 228

The animate Command Options .................................................... 229

5.8 Exporting ..................................................................................... 230

5.9 Code for Color Plates .................................................................. 230

6 Creating Mathematical Documents ..................................................... 231

6.1 In This Chapter ............................................................................ 232

6.2 Document Formatting .................................................................. 233

Quick Character Formatting .......................................................... 233

Quick Paragraph Formatting .......................................................... 235

Copy and Paste ............................................................................... 236

Sections .......................................................................................... 237

Display Hidden Formatting Attributes ........................................... 238

Indentation and the Tab Key .......................................................... 238

Character and Paragraph Styles ..................................................... 239

Document Blocks ........................................................................... 247

Typesetting ..................................................................................... 252

Using Tables for Layout ................................................................. 252

Formatting Lists: Bullets, Numbers, and Indent ............................ 262

Bookmarks ..................................................................................... 264

Inserting Images ............................................................................. 265

Show or Hide Worksheet Content .................................................. 266

6.3 Embedded Components ............................................................... 268

Contents • vii

Adding Graphical Interface Components ...................................... 268

Editing Component Properties: General Process ........................... 269

Removing Graphical Interface Components .................................. 269

Example Component Properties .................................................... 270

Printing and Exporting a Document with Embedded Compon-

ents ................................................................................................. 271

6.4 Creating Graded Assignments ...................................................... 271

Creating a Question ........................................................................ 271

Viewing Questions in Maple .......................................................... 272

Saving Test Content ....................................................................... 272

6.5 Auto-Execute ................................................................................ 272

Setting the Auto-Execute Feature .................................................. 273

Removing the Auto-Execute Setting .............................................. 273

Repeating Auto-Execution ............................................................. 273

Security Levels ............................................................................... 273

6.6 Sketch Regions ............................................................................. 274

Insert a Sketch Pad ......................................................................... 274

Drawing .......................................................................................... 275

Canvas Style of Sketch Pad ............................................................ 275

Erase or Clear Content ................................................................... 276

Selection Tool ................................................................................ 277

6.7 Spell Checking ............................................................................. 277

How to Use the Spellcheck Utility ................................................. 278

Selecting a Suggestion ................................................................... 279

Spellcheck Usage and the Document ............................................. 279

User Dictionary .............................................................................. 279

6.8 Hyperlinks .................................................................................... 281

Inserting a Hyperlink in a Document ............................................. 281

6.9 Worksheet Compatibility ............................................................. 284

7 Maple Expressions .............................................................................. 285

7.1 In This Chapter ............................................................................ 285

7.2 Creating and Using Data Structures ............................................ 285

Expression Sequences ................................................................... 286

Sets ................................................................................................ 287

Lists ............................................................................................... 288

Arrays ............................................................................................ 289

viii • Contents

Tables ............................................................................................ 290

Matrices and Vectors ..................................................................... 291

Functional Operators ..................................................................... 292

Strings ........................................................................................... 297

7.3 Working with Maple Expressions ................................................ 298

Low-Level Operations ................................................................... 298

Manipulating Expressions ............................................................. 304

Evaluating Expressions ................................................................. 310

8 Basic Programming ............................................................................ 321

8.1 In This Chapter ............................................................................ 321

8.2 Flow Control ................................................................................ 322

Conditional Execution (if Statement) ........................................... 322

Repetition (for Statement) ............................................................. 325

8.3 Iterative Commands .................................................................... 333

Creating a Sequence ...................................................................... 333

Adding and Multiplying Expressions ........................................... 334

Selecting Expression Operands ..................................................... 335

Mapping a Command over a Set or List ....................................... 336

Mapping a Binary Command over Two Lists or Vectors ............... 336

Additional Information .................................................................. 337

8.4 Procedures ................................................................................... 338

Defining and Running Simple Procedures .................................... 338

Procedures with Inputs .................................................................. 339

Procedure Return Values ............................................................... 339

Displaying Procedure Definitions ................................................. 340

Displaying Maple Library Procedure Definitions ......................... 340

Modules ......................................................................................... 342

9 Maplets ................................................................................................ 343

9.1 In This Chapter ............................................................................ 343

9.2 Simple Maplet .............................................................................. 343

9.3 Using Maplets ............................................................................. 344

Maplet File .................................................................................... 344

Maple Document ............................................................................ 345

9.4 Authoring Maplets ...................................................................... 345

Maplet Builder .............................................................................. 346

Maplets Package ........................................................................... 355

Contents • ix

Saving ............................................................................................ 361

10 Input, Output, and Interacting with Other Products ......................... 363

10.1 In This Chapter .......................................................................... 363

10.2 Writing to Files ......................................................................... 363

Saving Data to a File ...................................................................... 363

Saving Expressions to a File .......................................................... 365

10.3 Reading from Files .................................................................... 366

Reading Data from a File ............................................................... 366

Reading Expressions from a File ................................................... 367

10.4 Exporting to Other Formats ...................................................... 369

Exporting Documents ................................................................... 369

MapleNet ........................................................................................ 372

Maple T.A. ..................................................................................... 373

10.5 Connectivity .............................................................................. 374

Translating Maple Code To Other Programming Languages ........ 374

Accessing External Products from Maple ...................................... 374

Accessing Maple from External Products ...................................... 375

Index ...................................................................................................... 379

x • Contents

List of Tables

Table 1.1: Shortcuts for Entering Mathematical Expressions .................... 6

Table 1.2: Entering a Definite Integral ..................................................... 13

Table 1.3: Symbol Completion Shortcut Keys ......................................... 17

Table 1.4: Summary of Document Mode Tools ....................................... 31

Table 1.5: Maple Help Resources ............................................................ 32

Table 3.1: Select Integer Commands ....................................................... 73

Table 3.2: Modular Arithmetic Operators ................................................ 76

Table 3.3: Overview of Solution Methods for Important Equation

Types ........................................................................................................ 78

Table 3.4: Sample Dimensions ................................................................ 98

Table 3.5: Scientific Constants ............................................................... 106

Table 4.1: Maple Resources for Mathematical Computation ................ 123

Table 4.2: Polynomial Arithmetic Operators ......................................... 127

Table 4.3: Polynomial Coefficient and Degree Commands ................... 132

Table 4.4: Select Other Polynomial Commands .................................... 134

Table 4.5: Additional Polynomial Help ................................................. 135

Table 4.6: Matrix and Vector Arithmetic Operators ............................... 146

Table 4.7: Select Matrix and Vector Operators ...................................... 148

Table 4.8: Select LinearAlgebra Package Commands ........................... 150

Table 4.9: Limits .................................................................................... 154

Table 4.10: Student and Instructor Resources ........................................ 180

Table 5.1: Windows of the Interactive Plot Builder ............................... 192

Table 5.2: Displaying a Plot of a Single Variable Expression ................ 193

Table 5.3: Displaying a Plot of Multiple Expressions of 1 Variable ..... 195

Table 5.4: Displaying a Plot of a Multi-variable Expression ................ 196

Table 5.5: Displaying a Conformal Plot ............................................... 198

Table 5.6: Displaying a Plot in Polar Coordinates ................................ 200

Table 5.7: Interactive Plotting ............................................................... 202

Table 5.8: The plot and plot3d Commands ............................................ 208

Table 5.9: Customizing Plots Using Interactive Plot Builder ................ 217

Table 5.10: Customizing 2-D Plots Using the Context Menu ................ 218

Table 5.11: Customizing 3-D Plots Using the Context Menu ................ 219

Table 5.12: Popular Plot Options ........................................................... 220

Table 5.13: Plot Analysis Options .......................................................... 222

xii • List of Tables

Table 5.14: Creating Animations Using the Interactive Plot Builder ..... 223

Table 5.15: The animate Command ....................................................... 225

Table 5.16: Animation Options .............................................................. 226

Table 5.17: Customizing Animations Using the Context Menu ............ 229

Table 8.1: Default Clause Values ........................................................... 327

Table 8.2: Iterative Commands .............................................................. 333

Table 8.3: The seq Command ................................................................ 333

Table 8.4: The add and mul Commands ................................................ 334

Table 8.5: The select, remove, and selectremove Commands ............... 335

Table 8.6: The map Command ............................................................... 336

Table 8.7: The zip Command ................................................................. 337

T able 10.1: Summary of Content T ranslation When Exporting to Dif ferent

Formats .................................................................................................. 371

Preface

The Maple Software

The MapleTM software is a powerful system that you can use to solve comple x mathematical problems. You can also create professional quality documents, presentations, and custom interactive computational tools in the Maple environment.

You can access the power of the Maple computational engine through a variety of interfaces.

DescriptionInterface

Standard Worksheet

Classic Worksheet

Command-line version

MaplesoftTMGraphing Calculator (Microsoft® Windows® only)

Full-featured graphical user interface offering features that help you create electronic documents that show all your assumptions, the calculations, and any margin of error in your results; or hide the computations to allow your reader to focus on the problem setup and final results. The advanced formatting features help you create the customized document you need. Because the documents are live, you can edit the parameters and, with the click of a button, compute the new results.

The User Manual was created using the Standard W orksheet interf ace to Maple. An interacti v e version of this manual is available in the Standard W orksheet interface. From the Help menu, select Manuals, Dictionary, and more>Manuals>User Manual.

Basic worksheet environment for older computers with limited memory.

Command-line interface, without graphical user interfaces features, for solving very large complex problems or batch processing with scripts.

Graphical calculator interface to the Maple computational engine. Using it, you can perform simple computations and create customizable, zoomable graphs.

xiii

xiv • Preface

DescriptionInterface

MapletTMApplications

Graphical user interface containing windows, textbox regions, and other visual interfaces, which gives you point-and-click access to the power of Maple. You can perform calculations and plot functions without using the worksheet or command-line interfaces.

This manual describes how to use the Standard Worksheet interface. Some features are not available in the Classic Worksheet interface and Commandline version. The Standard Worksheet interface has two modes: Document mode and Worksheet mode.

Document Mode - Using the Document mode, you can perform quick calculations. You can enter a mathematical expression, and then evaluate, manipulate, solve, or plot with a few keystrokes or mouse clicks.

Worksheet Mode - The Worksheet mode is designed for:

• Interactive use through Maple commands, which may offer advanced functionality or customized control not available using context menus or other syntax-free methods

• Programmatic use of the powerful Maple language

Using either mode, you can create high quality interactive mathematical presentations or documents.

In This Manual

This manual provides an overview of all Maple features including:

• Performing computations

• Creating plots and animations

• Creating interactive documents

• The Maple programming language

• Using and creating custom Maplet applications

Preface • xv

• File input and output, and using Maple with third party products

• Data structures For a complete list of manuals, study guides, toolboxes, and other resources,

visit the Maplesoft Web site at http://www.maplesoft.com.

Audience

The information in this manual is intended for Maple users who have read the Maple Getting Started Guide.

Conventions

This manual uses the following typographical conventions.

• bold font - Maple command, package name, option name, dialog, menu,

and text field

• italics - new or important concept

• Note - additional information relevant to the section

• Important - information that must be read and followed

Customer Feedback

Maplesoft welcomes your feedback. For suggestions and comments related to this and other manuals, contact doc@maplesoft.com

xvi • Preface

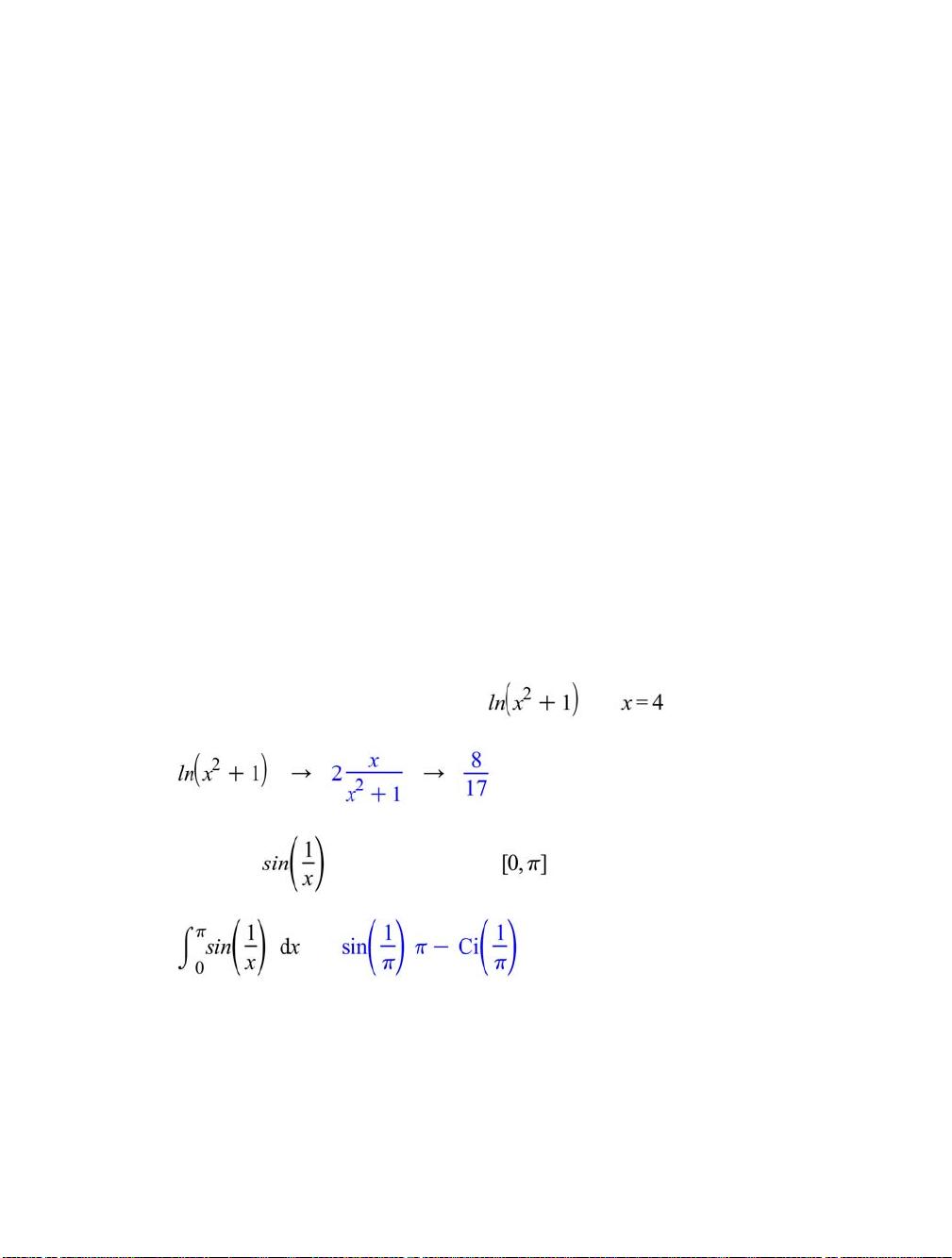
1 Document Mode

Using the Maple software, you can create powerful interactive documents. You can visualize and animate problems in two and three dimensions. You can solve complex problems with simple point-and-click interfaces or easyto-modify interactive documents. Y ou can also de vise custom solutions using the Maple programming language. While you work, you can document your process, providing text descriptions.

1.1 Introduction

Maple has two modes: Document mode and Worksheet mode. Using Document mode, you can quickly perform calculations. You can enter

a mathematical expression, and then evaluate, manipulate, solve, or plot it with a few keystrokes or mouse clicks. This chapter provides an overview of Document mode.

Document mode sample:

Find the value of the derivative of at .

Integrate over the interval .

Worksheet mode is designed for interactive use through commands and programming using the Maple language. The Worksheet mode supports the features available in Document mode described in this chapter . After revie w-

2 • 1 Document Mode

ing the information in this chapter, see Chapter 2, Worksheet Mode (page 35), for information on using Worksheet mode.

Worksheet mode sample:

Find the value of the derivative of at .

(1.1)

(1.2)

Integrate over the interval .

Important: In every Maple document, you can use Document mode and

Worksheet mode. Using either mode:

1.2 In This Chapter • 3

• You have access to the full mathematical engine.

• You can create high quality interactive documents: easy-to-use computational tools, presentations, or publications.

Interactive document features include:

• Embedded graphical interface components, like buttons, sliders, and check boxes

• Automatic execution of marked regions when a file is opened

• Tables

• Character and paragraph formatting styles

• Hyperlinks

These features are described in Chapter 6, Creating Mathematical Docu- ments (page 231).

Note: This chapter was created using Document mode. All other chapters were created using Worksheet mode.

1.2 In This Chapter

TopicsSection

Simple Mathematical Expressions - Introduction to Math and Text modes, and how to easily enter simple expressions

• Text and Math Modes

• Rational Expressions

• Powers

• Products

• Shortcuts for Entering Mathematical Ex-

• Other Expressions

pressions

4 • 1 Document Mode

TopicsSection

Evaluating Expressions - How to evaluate expressions

Editing Expressions and Regenerating Output

- How to update expressions and results

Entering Expressions - Overview of tools for creating complex mathematical expressions

Performing Computations - Overview of tools for computing and plotting

key Document mode features

in the Maple Help System

• Displaying the Value Inline

• Displaying the Value on the Following Line

• Updating a Single Computation

• Updating a Group of Computations

• Updating All Computations in a Document

• Palettes

• Symbol Names

• Computing with Palettes

• Context Menus

• Assistants and Tutors

• Table of Document Mode ToolsDocument Mode Summary - Summary of

• Table of Maple Help ResourcesGetting Help - A list of resources available

1.3 Simple Mathematical Expressions

In Document mode, you can enter two types of content: Text and Math. The Text mode and Math mode icons at the left end of the toolbar indicate the current mode. The toolbar is located near the top of the Maple window, immediately below the menu bar.

To switch between Text and Math modes, press the F5 key. (Alternatively, click the Text mode or Math mode toolbar icon.) Consequently, it is easy to enter sentences containing text and inline mathematical expressions.

1.3 Simple Mathematical Expressions • 5

Entering mathematical expressions, such as , , and , is natural in Math mode.

Rational Expressions (Fractions)

To enter a fraction:

1. Enter the numerator.

2. Press the forward slash (/) key.

3. Enter the denominator.

4. To exit the denominator, press the right arrow key.

Powers

To enter a power:

1. Enter the base.

2. Press the caret (^) key (Shift + 6).

3. Enter the exponent, which displays in math as a superscript.

4. To exit the exponent, press the right arrow key.

Products

To enter a product:

1. Enter the first factor.

2. Press the asterisk (*) key, which displays in math as .

3. Enter the second factor.

6 • 1 Document Mode

Implied Multiplication

In most cases, you do not need to include the multiplication operator, . Insert a space character between two quantities to multiply them.

Note: In some cases, you do not need to enter the multiplication operator or a space character. For example, Maple interprets a number followed by a variable as multiplication.

Shortcuts for Entering Mathematical Expressions

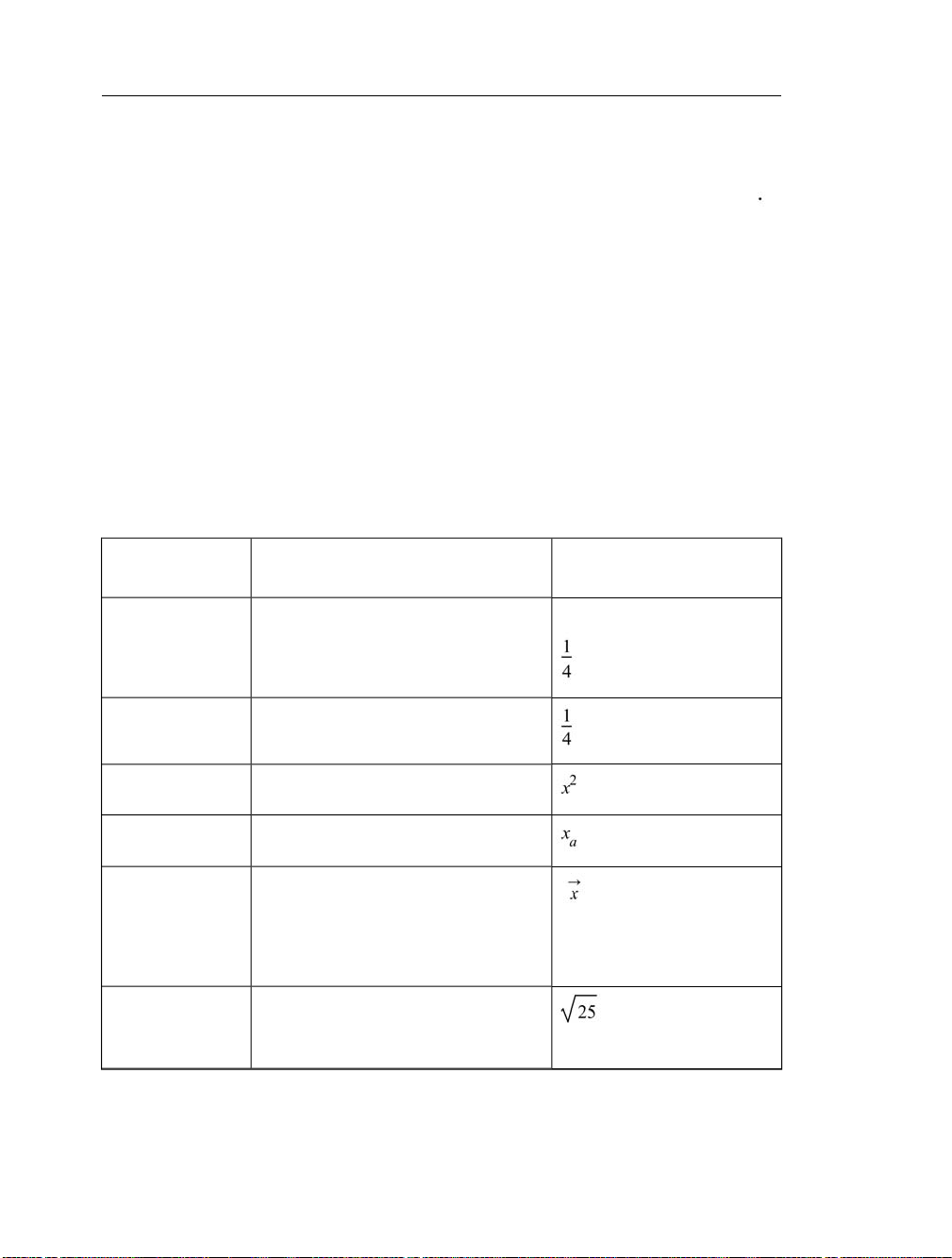
T able 1.1 lists shortcut keys for entering and na vigating mathematical expressions.

Table 1.1: Shortcuts for Entering Mathematical Expressions

Math and Text modes

Overscript

Square root

KeySymbol/Format

F5Switch between

/ (forward slash)Fraction

^ (caret)Exponent

_ (underscore)Subscript

• Ctrl + Shift + ", Windows and

UNIX®

• Command + Shift + ", Macin-

tosh®

Enter sqrt , and then press the command/symbol completion shortcut. (See the following row in this table.)

Automatically Generated in Document

Example using fraction:

(Math) versus 1/4 (Text)

1.3 Simple Mathematical Expressions • 7

Automatically Generated in Document

Command/symbol completion

pression

KeySymbol/Format

• Ctrl + Space, Windows

• Command + Shift + Space,

Macintosh

• Ctrl + Shift + Space, UNIX

Arrow keysNavigating an ex-

For a complete list of shortcut keys, refer to the Math Shortcut and Hints help page. To access this help page in the Maple software, in Math mode enter ?MathShortcuts and then press Enter. For information on the Maple Help System, see Getting Help (page 32).

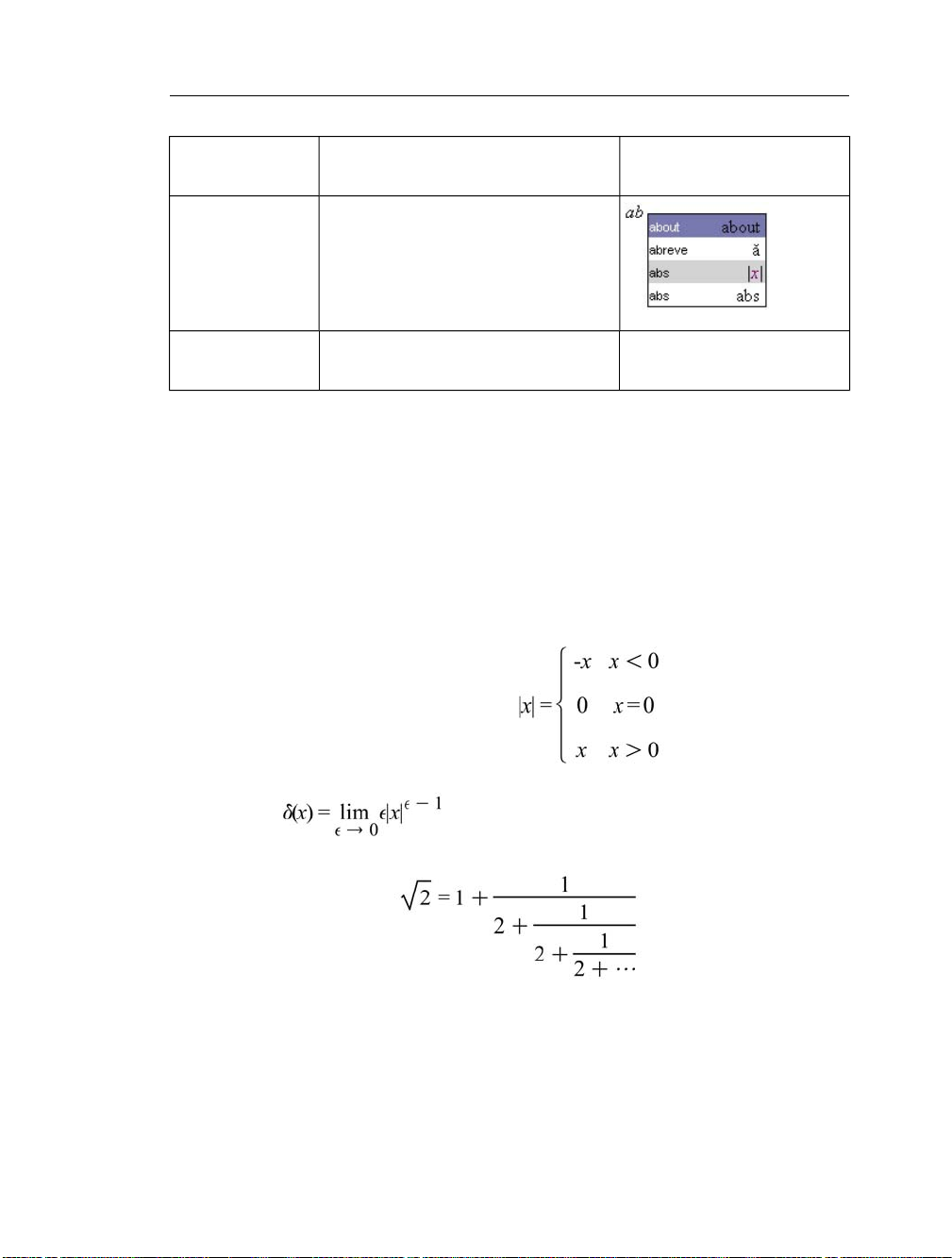
Other Expressions

It is also easy to enter mathematical expressions, such as:

• Piecewise-continuous functions:

• Limits:

• Continued fractions:

and more complex expressions. For information, see Entering Expres- sions (page 10).

8 • 1 Document Mode

1.4 Evaluating Expressions

To evaluate a mathematical expression, place the cursor in the expression and press Ctrl + = (Command + =, for Macintosh). That is, pr ess and hold the Ctrl (or Command) key, and then press the equal sign (=) key.

T o the right of the expression, Maple inserts an equal sign and then the v alue of the expression.

You can replace the inserted equal sign with text or mathematical content.

To replace the equal sign:

1. Select the equal sign. Press Delete.

2. Enter the replacement text or mathematical content. For example, you can replace the equal sign with the text "is equal to".

is equal to

In mathematical content, pressing Enterevaluates the e xpression and displays it centered on the following line. The cursor moves to a new line below the output.

By default, Maple labels output that is generated by pressing Enter. For information on equation labels, see Equation Labels (page 59). In this manual, labels are generally not displayed.

1.5 Editing Expressions and Updating Output • 9

In text, pressing Enter inserts a line break.

You can use the basic algebraic operators, such as and , with most expressions, including polynomials—see P olynomial Algebr a (page 126)—and

matrices and vectors—see Linear Algebra (page 135).

1.5 Editing Expressions and Updating Output

One important feature of Maple is that your documents are live. That is, you can edit expressions and quickly recalculate results.

To update one computation:

1. Edit the expression.

2. Press Ctrl + = (Command + =, for Macintosh) or Enter. The result is updated.

To update a group of computations:

1. Edit the expressions.

2. Select all edited expressions and the results to recalculate.

3. Click the Execute toolbar icon . All selected results are updated.

To update all output in a Maple document:

10 • 1 Document Mode

• Click the Execute All toolbar icon . All results in the document are updated.

1.6 Entering Expressions

Mathematical expressions can contain the following symbols.

• Numbers: integers, rational numbers, complex numbers, floating-point

values, finite field elements, , ∞, ...

• Operators: , , , /, , , , , ...

• Constants: π, e, ...

• Mathematical functions: sin(x), , Γ(2), ...

• Names (variables): x, y, z, α, β, ...

• Data structures: sets, lists, Arrays, Vectors, Matrices, ... Maple contains over a thousand symbols. For some numbers, operators, and

names, you can press the corresponding key , for e xample, 9, =, >, or x. Most symbols are not available on the keyboard, but you can insert them easily using two methods.

To insert a symbol, you can use:

• Palettes

• Symbol names

Palettes

Palettes are collections of related items that you can insert by clicking or dragging. Palettes contain:

• Numbers and constants, like i (the imaginary unit), π, and ∞. For example,

see the Common Symbols palette (Figure 1.1).

1.6 Entering Expressions • 11

• Layouts, like an item with a superscript and subscript. For example, see

the Layout palette (Figure 1.2).

• Mathematical operations, like a definite integral with placeholders for the integrand, variable of integration, and endpoints of the interval of integration. For example, see the Expression palette (Figure 1.3).

• Specialized tools. For example, see the Matrix palette (Figure 1.4). For information on the Matrix palette, see Creating Matrices (page 135).

Figure 1.2: Layout PaletteFigure 1.1: Common Symbols Palette

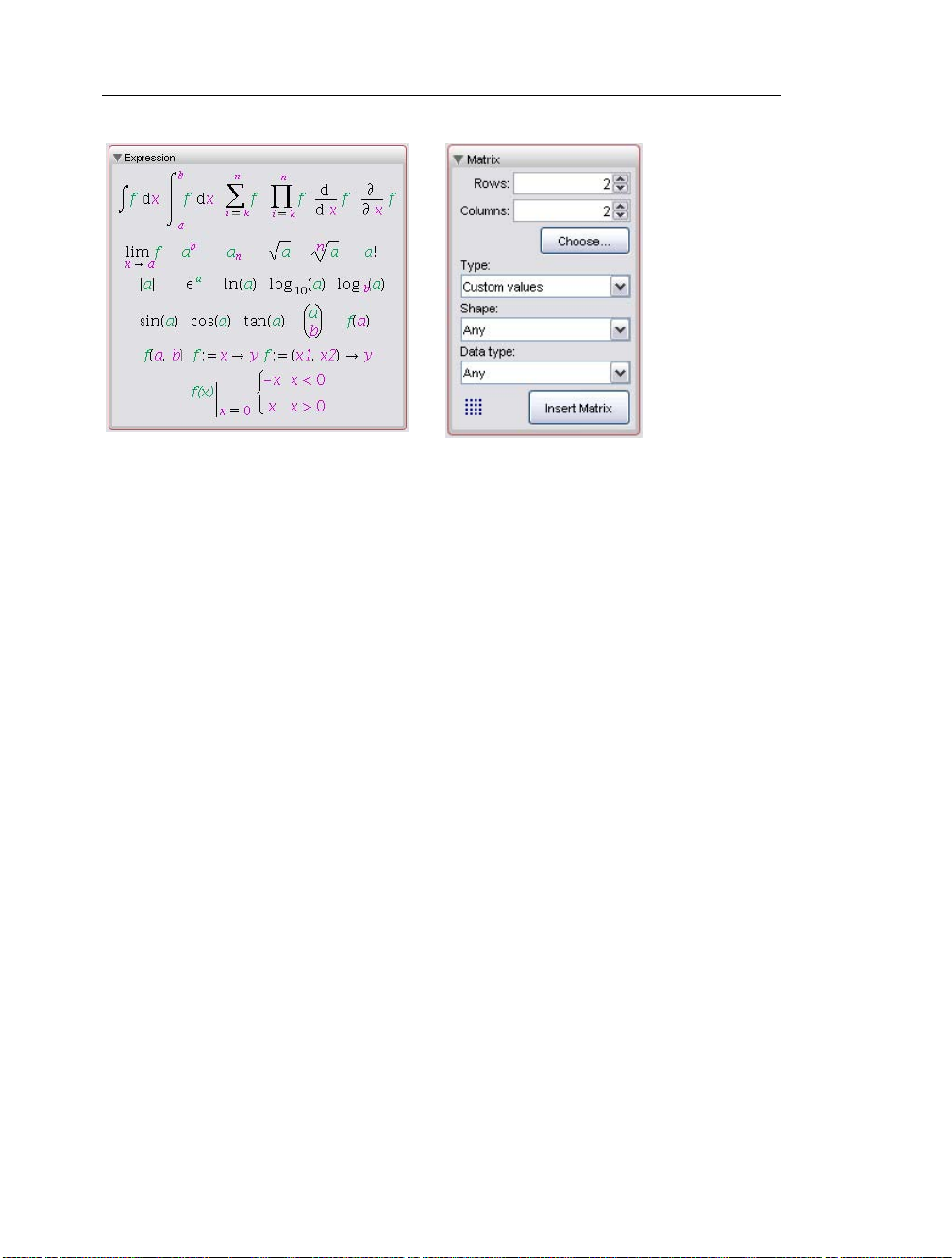
12 • 1 Document Mode

Figure 1.4: Matrix PaletteFigure 1.3: Expression Palette

Using Palettes

To insert a palette item:

1. In the palette, click the item to insert. The item is inserted at the cursor location.

2. If the item has colored placeholders, specify values for them.

• To move to the next placeholder, press the Tab key.

Note: You can drag palette items to any location in the document. For example, to insert the constant π:

• In the Common Symbols palette, click the π symbol. or

• From the Common Symbols palette, drag the π symbol to the appropriate

location in the document.

Table 1.2 shows how to enter a definite integral.

Table 1.2: Entering a Definite Integral

1. In the Expression palette, click the definite

integration item . Maple inserts the definite integral. The left endpoint placeholder is selected.

2. Enter 0, and then press Tab. The right end- point placeholder is selected.

3. Enter 1, and then press Tab. The integrand placeholder is selected.

1.6 Entering Expressions • 13

Result in DocumentAction

4. Enter , and then press Tab. The vari- able of integration placeholder is selected.

5. Enter x.

To evaluate the integral, press Ctrl+= (Command+=, for Macintosh) or Enter. For more information, see Computing with Palettes (page 20).

14 • 1 Document Mode

Defining a Mathematical Function

To define a function of one or two variables:

1. In the Expression palette, click one of the function definition items (Figure

1.5). Maple inserts the function definition.

2. Replace the placeholder f with the function name. Press Tab.

3. Replace the parameter placeholders, x or x1, x2, with the independent variable names. Press Tab.

4. Replace the final placeholder, y, with the expression that defines the function value. Press Enter.

Figure 1.5: Function Definition Palette Items

For example, define a function that doubles its input.

Note:T o insert the right arro w symbol , you can also enter the characters

->. Important: The expression is different from the function .

For more information on functions, see Functional Operators (page 292).

1.6 Entering Expressions • 15

Viewing and Arranging Palettes

By default, palettes are displayed in palette docks at the sides of the Maple window. If no palette dock is visible, use the following procedure.

To view palette docks:

• From the View menu, select Palettes, and then Expand Docks.

To expand a palette in a palette dock:

• Click the triangle at the left of the palette title.

To move a palette in a palette dock:

• Drag the palette (by clicking its title) to the new location.

Adding Palettes to the Palette Docks

Maple has over 20 palettes. By default, only a fe w palettes are in the palette docks. To add a palette to a palette dock, use the following procedure.

To add a palette:

1. Right-click (Control-click, for Macintosh) a palette dock. Maple displays

a context menu—a menu that lists actions you can perform on the object—near the palette.

2. From the context menu, select Show Palette, and then select the palette.

Symbol Recognition Palette

Finding the right symbol to insert can be time consuming. The Symbol Recognition palette provides an eff icient way to find and insert the right symbol.

You draw the symbol with your mouse and then Maple matches your input against items available in the system. See Figure 1.6.

16 • 1 Document Mode

Figure 1.6: Symbol Recognition Palette

To use the Symbol Recognition palette:

1. With your mouse, draw a symbol in the handwriting recognition region (sketch area).

2. Click the button. A list of potential matching symbols is displayed. To view more symbols (where indicated), click the drop-down arrows associated with the displayed symbols.

3. To insert a symbol, click the displayed symbol.

Symbol Names

Each symbol has a name, and some have aliases. By entering its name (or an alias) in Math mode, you can insert the symbol.

Note: If you hover the mouse pointer over a palette item, a tooltip displays the symbol's name.

1.6 Entering Expressions • 17

Using Symbol Names

To insert a symbol by entering its name:

1. In Math mode, enter the symbol name.

2. Press the symbol completion shortcut key. See Table 1.3.

Maple inserts the corresponding symbol.

Table 1.3: Symbol Completion Shortcut Keys

Shortcut KeyOperating System Ctrl + SpaceWindows Command + Shift + SpaceMacintosh Ctrl + Shift + SpaceUNIX

For example, to find the square root of :

1. Enter sqrt.

2. Press the completion shortcut key. Maple displays a pop-up list of exact

matches .

3. In the completion list, select . Maple inserts the symbol with the

placeholder selected.

4. Enter 603729.

5. Press Ctrl + = (Command + =, for Macintosh).

18 • 1 Document Mode

Using Partial Symbol Names

To enter a symbol quickly, you can enter the first few characters of its name and then press the completion shortcut key (see Table 1.3).

• If a unique symbol name matches the characters entered, Maple inserts the corresponding symbol.

• If multiple symbol names match the characters entered, Maple displays the completion list, which lists all matches. To select an item, click its name or symbol.

For example, if you enter iand then press the completion shortcut key, Maple displays:

For example, to multiply two complex numbers:

• Use the symbol name and completion list to enter the imaginary unit,

Example: Indefinite Integral

You can enter any expression using symbol names and the completion list.

For example, to enter the indefinite integral :

1.7 Performing Computations • 19

1. In Math mode, enter int. Press the completion shortcut key.

2. From the completion list, select the indefinite integral item .

3. Enter sin(x).

4. Enter d. Press the completion shortcut key.

5. From the completion list, select d (differential).

6. Enter x.

Note: From the int completion list, you can directly insert .

1.7 Performing Computations

Using the Document mode, you can access the power of the advanced Maple mathematical engine without learning Maple syntax. In addition to solving problems, you can also easily plot expressions.

The primary tools for syntax-free computation are:

• Palettes

• Context menus

• Assistants and tutors Note: The Document mode is designed for quick calculations, but it also

supports Maple commands. For information on commands, see Com- mands (page 40) in Chapter 2, Worksheet Mode (page 35).

Important: In Document mode, you can execute a statement only if you enter it in Math mode. To use a Maple command, you must enter it in Math mode.

20 • 1 Document Mode

Computing with Palettes

As discussed in Palettes (page 10), some palettes contain mathematical op- erations.

To perform a computation using a palette mathematical operation:

1. In a palette that contains operators, such as the Expression palette, click

an operator item.

2. In the inserted item, specify values in the placeholders.

3. To execute the operation and display the result, press Ctrl+= (Com-

mand+=, for Macintosh) or Enter.

For example, to evaluate inline:

1. Using the Expression palette, enter the definite integral. See Table

1.2 (page 12).

2. Press Ctrl+= (Command+=, for Macintosh).

Context Menus

A context menu is a pop-up menu that lists the operations and actions you can perform on a particular expression. See Figure 1.7.

1.7 Performing Computations • 21

Figure 1.7: Context Menu

To display the context menu for an expression:

• Right-click (Control-click, for Macintosh) the expression. The context menu is displayed beside the mouse pointer. You can evaluate expressions using context menus.

• The Evaluate and Display Inline operation (see Figure 1.7) is equiv alent to pressing Ctrl+= (Command+=, for Macintosh). That is, it inserts an equal sign (=) and then the value of the expression.

• The Evaluateoperation (see Figure 1.7) is equivalent to pressing Enter. That is, it evaluates the expression and displays the result centered on the following line.

For more information on evaluation, see Evaluating Expressions (page 8). From the context menu, you can also select operations different from e v alu-

ation. T o the right of the e xpression, Maple inserts a right arrow symbol (→) and then the result.

22 • 1 Document Mode

For example, use the Approximate operation to approximate a fraction:

Y ou can perform a sequence of operations by repeatedly using conte xt menus.

For example, to compute the second derivative of use the Differ- entiate operation on the expression, and then again on the output:

The following subsections provide detailed instructions on performing a fe w of the numerous operations available using context menus. Figures in the subsections show related context menus or palettes.

Approximating the Value of an Expression

To approximate a fraction numerically:

1. Enter a fraction.

2. Display the context menu. See Figure 1.8.

3. From the context menu, select Approximate, and then the number of significant digits to use: 5, 10, 20, 50, or 100.

1.7 Performing Computations • 23

Figure 1.8: Approximating the Value of a Fraction

You can replace the inserted right arrow with text or mathematical content.

To replace the right arrow ( ):

1. Select the arrow. Press Delete.

2. Enter the replacement text or mathematical content.

Note: To replace the the right arrow with text, you must first press F5 to switch to Text mode.

For example, you can replace the arrow with the te xt "is approximately equal to" or the symbol ≈.

is approximately equal to

24 • 1 Document Mode

Solving an Equation

You can find an exact (symbolic) solution or an approximate (numeric) solution of an equation. For more information on symbolic and numeric computations, see Symbolic and Numeric Computation (page 66).

To solve an equation:

1. Enter an equation.

2. Display the context menu.

3. From the context menu, select Solve or Solve Numerically.

For more information on solving equations, including solving inequations, differential equations, and other types of equations, see Solving Equa- tions (page 78).

Using Units

You can create expressions with units. To specify a unit for an expression, use the Units palettes. The Units (FPS) palette (Figure 1.9) contains important units from the foot-pound-second (FPS) system of units used in the United States. The Units (SI) palette (Figure 1.10) contains important units from the international system (SI) of units.

To insert an expression with a unit:

1. Enter the expression.

1.7 Performing Computations • 25

Figure 1.10: SI Units PaletteFigure 1.9: FPS Units Palette

2. In a unit palette, click a unit symbol.

Note: To include a reciprocal unit, divide by the unit. To evaluate an expression that contains units:

1. Enter the expression using the units palettes to insert units.

2. Right-click (Control-click, for Macintosh) the expression.

3. From the context menu, select Units and then Simplify.

For example, compute the electric current passing through a wire that conducts 590 coulombs in 2.9 seconds.

For more information on using units, see Units (page 97).

26 • 1 Document Mode

Assistants and Tutors

Assistants and tutors provide point-and-click interfaces, with buttons, text input regions, and sliders.

Assistants

Assistants help you accomplish many tasks, such as solving ordinary differ ential equations (ODEs) and ODE systems, creating plots and matrices, curve fitting, and performing unit conversions (Figure 1.11).

• From the Tools menu, select Assistants, and then one of the topic sub-

menus. For example: T o con v ert a quantity of 1 atomic mass unit to the equiv alent v alue in grams,

use the Unit Convert Assistant.

1. From the T ools menu, select Unit Con verter. The Unit Con verter dialog displays. See Figure 1.11.

2. In the Value text field, enter the value as measured in atomic mass units,

1.0.

3. In the Dimension drop-down list, select mass.

4. In the From drop-down list, select atomic mass units (u).

5. In the To drop-down list, select grams (g).

6. Click the Insert button. Maple inserts the value of the mass in grams,

, in the document. Note: The output has no units.

1.7 Performing Computations • 27

Figure 1.11: Unit Converter Assistant

Tutors

Over 40 interactive tutors help student users g ain insight and understanding of topics in courses such as precalculus, calculus, multivariate calculus, vector calculus, and linear algebra. Some tutors help you work through a problem step-by-step.

• From the T ools menu, select Tutors, and then one of the topic submenus. For example, you can create a plot of the compositions of two functions using

the Function Composition Tutor.

To use the Function Composition Tutor:

1. From the T ools menu, select Tutors, Precalculus, and then Compositions. The Function Composition Tutor is displayed. See Figure 1.12.

2. In the f(x) = and g(x) = text fields, enter the two functions.

3. Click the Display button. The tutor displays the compositions g(f(x)) and f(g(x)).

4. To insert the plot into your document, click the Close button.

28 • 1 Document Mode

Figure 1.12: Function Composition Tutor

Using a Context Menu to Launch the Plot Builder

You can plot a mathematical expression using the Interactive Plot Builder. The Plot Builder can be launched from the T ools menu or the conte xt menu

for an expression.

To create a plot using a context menu:

1. Enter or compute a mathematical expression with one or two independent variables.

2. Right-click (Control-click, for Macintosh) the expression to plot.

1.7 Performing Computations • 29

3. From the context menu, select Plots, and then PlotBuilder. The Interact- ive Plot Builder is displayed. See Figure 1.13.

4. In the Select Plot T ype dialog, select the plot type, for example, 3-D plot or 2-D contour plot.

5. To immediately create a plot, click the Plot button. To customize the plot before generating it, click the Options button.

Figure 1.13: Interactive Plot Builder: Select Plot Type Dialog

For example, Figure 1.14 shows a plot of .

30 • 1 Document Mode

Figure 1.14: 3-D Plot of an Expression

For more information on plots, see Plots and Animations (page 189).

1.8 Document Mode Summary

The key features of Document mode are summarized in Table 1.4.

1.8 Document Mode Summary • 31

Table 1.4: Summary of Document Mode Tools

MethodsAction

Entering Mathematical Expressions

For example:

Evaluating Mathematical Expressions (Result Inline)*

For example:

Evaluating Mathematical Expressions (Result Centered on Following Line)

For example:

• Math editing shortcut keys, including symbol name completion

• Palettes

• Ctrl + = (Command + =, for Macintosh)

• From the context menu, select Evaluate and Display Inline.

• Enter key

• From the context menu, select Evaluate.

Performing Computations and Other Operations on Expressions

For example, differentiate an expression:

Executing a Group of Evaluations, Computations, or Other Operations

• Context menus

• Assistants

• Tutors

• Execute toolbar icon

• Execute All toolbar icon

32 • 1 Document Mode

Inline evaluation is available in Document mode and document blocks. For information

on document blocks, see Document Blocks (page 247).

1.9 Getting Help

The Maple Help System contains resources to help you use Maple. See T able

1.5.

Table 1.5: Maple Help Resources

DescriptionResource

Maple Tour

Online Manuals

Quick Help

Quick Reference

An interactive overview of Maple.

• From the Help menu, select Take a Tour of Maple. Online manuals, including the Maple Getting Started Guide

and this manual. You can execute examples, copy content into other documents, and search the contents using the Maple Help System.

The Maple Getting Started Guide provides extensiv e information for new users on using Maple and the resources available on the Maplesoft W eb site (http://www .maplesoft.com). Each procedure and concept is accompanied by visual depictions of actions to help you identify Maple resources and tools.

• From the Help menu, select Manuals, Dictionary, and more>Manuals.

A list of key commands and concepts.

• From the Help menu, select Quick Help. Alternatively, press F1. For additional information, click an item in the Quick Help.

A table of commands and information for new users that opens in a new window . It contains h yperlinks to help pages for more information.

• From the Help menu, select Quick Reference. Alternatively, press Ctrl + F2 (Command + F2, for Macintosh).

1.9 Getting Help • 33

DescriptionResource

Help Pages

Task Templates

Applications and Example Worksheets

Mathematics and Engineering Dictionary

Help for Maple features, commands, packages, and more. Help pages include examples and screenshots to help you quickly learn.

• From the Help menu, select Maple Help. You can search for a help topic, perform a text search, or browse the Table

of Contents. You can also open a help page by entering ?<topic_name> at the input prompt (in Worksheet mode)

or in Math mode (in Document mode).

Set of commands with placeholders that you can use to quickly perform a task.

• From the Tools menu, select Tasks, and then Browse.

Executable documents that demonstrate the power and flexibility of the Maple interactive document or provide an o verview of computations in a particular field.

• From the Help menu, select Manuals, Dictionary, and more, and then Applications and Examples.

Over 5000 definitions, including 300 figures and plots.

• From the Help menu, select Manuals, Dictionary, and more, and then Dictionary.

For a complete list of resources, refer to the ?MapleResources help page. For more information on the Maple Help System, refer to the Maple Getting

Started Guide.

34 • 1 Document Mode

2 Worksheet Mode

The Worksheet mode of the Standard Worksheet interface is designed for:

• Interactive use through Maple commands, which may offer advanced functionality or customized control not available using context menus or other syntax-free methods

• Programming using the powerful Maple language

Using Worksheet mode, you have access to most of the Maple features described in Chapter 1 including:

• Math and Text modes

• Palettes

• Context menus

• Assistants and tutors

For information on these features, see Chapter 1, Document Mode (page 1). (For a summary, see Table 1.4 (page 30).)

Note: Using a document block, you can use all Document mode features in Worksheet mode. For information on document blocks, see Document Blocks (page 247).

Note: This chapter and the following chapters were created using Worksheet mode.

36 • 2 Worksheet Mode

2.1 In This Chapter

TopicsSection

Input Prompt - Where you enter input

Commands - Thousands of routines for performing computations and other operations

ing or dragging

operations Assistants and Tutors - Graphical interfaces

with buttons and sliders

Task Templates - Sets of commands with placeholders that you can insert and use to perform a task

• The Input Prompt (>)

• Suppressing Output

• 2-D and 1-D Math Input

• Input Separators

• The Maple Library

• Top-Level Commands

• Package Commands

• Using PalettesPalettes - Items that you can insert by click-

• Using Context MenusContext Menus - Pop-up menus of common

• Launching Assistants and Tutors

• Example: Using the Interactive Plot Builder

• Viewing Task Templates

• Inserting a Task Template

• Performing the Task

Text Regions - Areas in the document in which you can enter text

Names - References to the expressions you assign to them

• Inserting a Text Region

• Formatting Text

• Assigning to Names

• Unassigning Names

• Valid Names

2.2 Input Prompt • 37

TopicsSection

Equation Labels - Automatically generated labels that you can use to refer to expressions

• Displaying Equation Labels

• Referring to a Previous Result

• Execution Groups with Multiple Outputs

• Label Numbering Schemes

• Features of Equation Labels

2.2 Input Prompt

In Worksheet mode, you enter input at the Maple input prompt (>). The default mode for input is Math mode (2-D Math).

To evaluate input:

• Press Enter. Maple displays the result (output) below the input.

For example, to find the value of , enter the expression, and then press Enter.

For example, compute the sum of two fractions.

38 • 2 Worksheet Mode

Suppressing Output

To suppress the output, enter a colon (:) at the end of the input.

A set of Maple input and its output are referred to as an execution group.

1-D Math Input

You can also insert input using Text mode (1-D Math). The input is entered as a one-dimensional sequence of characters. 1-D Math input is red.

To enter input using 1-D Math:

• At the input prompt, press F5 to switch from 2-D Math to 1-D Math.

123^2 - 29857/120;>

Important: 1-D Math input must end with a semicolon or colon. If you use

a semicolon, Maple displays the output. If you use a colon, Maple suppresses the output.

123^2 - 29857/120:>

To set the default input mode to 1-D Math:

1. From the Tools menu, select Options. The Options dialog is displayed.

2.2 Input Prompt • 39

2. On the Display tab, in the Input display drop-down list, select Maple Notation.

3. Click Apply to Session (to set for only the current session) or Apply

Globally (to set for all Maple sessions). To convert 2-D Math input to 1-D Math input:

1. Select the 2-D Math input.

2. From the Format menu, select Convert To, and then 1-D Math Input. Important: In Document mode, you can execute a statement only if you

enter it in Math mode.

Input Separators

In 1-D and 2-D Math input, you can use a semicolon or colon to separate multiple inputs in the same input line.

If you do not specify a semicolon or colon, Maple interprets it as a single input.

40 • 2 Worksheet Mode

2.3 Commands

Maple contains a large set of commands and a powerful programming language. Most Maple commands are written using the Maple programming language.

You can enter commands using 1-D or 2-D Math. You must use 1-D Math input when programming in Maple. Basic Progr amming (page 321) provides an introduction to Maple programming.

To learn how to use Maple commands, use task templates. See Task Tem- plates (page 51).

The Maple Library

Commands are contained in the Maple library, which is divided into two groups: the top-level commands and packages.

• The top-level commands are the most frequently used Maple commands.

• Packages contain related specialized commands in areas such as student

calculus, linear algebra, vector calculus, and code generation.

For a complete list of packages and commands, refer to the index help pages. T o access the index o vervie w help page, enter ?index, and then press Enter. For information on the Maple Help System, see Getting Help (page 32).

Top-Level Commands

To use a top-level command, enter its name followed by parentheses (( )) containing any parameters. This is referred to as a calling sequence for the command.

command(arguments)

Note: In 1-D Math input, include a semicolon or colon at the end of the

calling sequence.

2.3 Commands • 41

For example, to differentiate an expression, use the diff command. The required parameters are the expression to differentiate, which must be specif ied first, and the independent variable.

For a complete list of functions (commands that implement mathematical functions), for example, BesselI and AiryAi, available in the library, refer to the ?initialfunctions help page. (T o display this help page, enter ?initial-

functions at the input prompt.)

For detailed information on the properties of a function, use the FunctionAdvisor command.

For detailed information on how to use a function in Maple, refer to its help page.

For example:

Note: In 1-D and 2-D Math input, when accessing a help page using ?, you

do not need to include a trailing semicolon or colon.

42 • 2 Worksheet Mode

Package Commands

To use a package command, the calling sequence must include the package name, and the command name enclosed in brackets ([ ]).

package[command](arguments)

If you are frequently using the commands in a package, load the package.

To load a package:

• Use the with command, specifying the package as an argument.

The with command returns a list of the package commands loaded (unless you suppress the output by entering a colon at the end of the calling sequence).

After loading a package, you can use its commands as top-level commands, that is, without specifying the package name.

For example, use the NLPSolve command from the Optimization package to find a local minimum of an expression and the value of the independent variable at which the minimum occurs.

For more information on optimization, see Optimization (page 168).

2.3 Commands • 43

To unload a package:

• Use the unwith command, specifying the package as an argument.

To use the examples in this manual, you may be required to use the unwith command between examples.

Some packages contain commands that have the same name as a top-level command. When you load one of these packages, Maple returns a warning.

For example, the plots package contains a changecoords command. Maple also contains a top-level changecoords command.

Warning, the name changecoords has been redefined

In general, this manual does not include the warning messages Maple returns. T o use the top-lev el command, unload the package. (For alternativ e methods

of accessing the top-level command, refer the ?with help page.)

44 • 2 Worksheet Mode

2.4 Palettes

Palettes are collections of related items that you can insert by clicking or dragging. See Figure 2.1.

Figure 2.1: Expression Palette

You can use palettes to enter input. For example, evaluate a definite integral using the definite integration item

in the Expression palette.

In 2-D Math, clicking the definite integration item inserts:

1. Enter values in the placeholders. To move to the next placeholder, press

Tab. Note: If pressing the Tab key inserts a tab, click the Tab icon in the toolbar.

2.4 Palettes • 45

2. To evaluate the integral, press Enter.

In 1-D Math, clicking the definite integration item inserts the corresponding command calling sequence.

int(f,x=a..b);>

Specify the problem values (using the Tab to move to the next placeholder), and then press Enter.

int(tanh(x), x = 0..1):>

Note: Some palette items cannot be inserted into 1-D Math because they are

not defined in the Maple language. When the cursor is in 1-D Math input, unavailable palette items are dimmed.

For more information on palettes, see Palettes (page 10) and Performing Computations (page 19) in Chapter 1.

46 • 2 Worksheet Mode

2.5 Context Menus

A context menu is a pop-up menu that lists the operations and actions you can perform on a particular expression. See Figure 2.2.

Figure 2.2: Integer Context Menu

In Worksheet mode, you can use context menus to perform operations on 2D Math and output.

To use a context menu:

1. Right-click (Control-click, for Macintosh) the expression. The context

menu is displayed.

2. From the context menu, select an operation.

Maple inserts a new execution group containing:

• The calling sequence that performs the operation

• The result of the operation

2.5 Context Menus • 47

For example:

To determine a rational expression (fraction) that approximates a floating-point number:

1. Right-click (Control-click, for Macintosh) the floating-point number.

2. From the context menu, select Conversions, and then Rational. The inserted calling sequence includes an equation label reference to the

number you are converting.

(2.1)

For information on equation labels and equation label references, see Equation Labels (page 59).

For more information on context menus, see Context Menus (page 20) in Chapter 1.

48 • 2 Worksheet Mode

2.6 Assistants and Tutors

Assistants and tutors provide point-and-click interfaces, with buttons, text input regions, and sliders. See Figure 2.3.

Figure 2.3: Interactive Plot Builder: Select Plot Type Dialog

Launching an Assistant or Tutor

To launch an assistant or tutor:

1. Open the Tools menu.

2. Select Assistants or Tutors.

3. Navigate to and select one of the assistants or tutors.

2.6 Assistants and Tutors • 49

Example: Using the Interactive Plot Builder

To plot an expression using the Interactive Plot Builder:

1. From the Tools menu, select Assistants, and then Plot Builder. Maple inserts the following command in the document and launches the Interactive

Plot Builder.

2. In the Interactive Plot Builder: Specify Expressions window (Figure

2.4), click Add. The Add/Edit Expression dialog is displayed.

Figure 2.4: Interactive Plot Builder: Specify Expressions Window

50 • 2 Worksheet Mode

3. In the Add/Edit Expression dialog, enter the expression to plot using 1-

D Math. See Figure 2.5.

Figure 2.5: Interactive Plot Builder: Add/Edit Expression Dialog

4. Repeat steps 2 and 3 for each expression to add to the plot.

5. After adding the expressions, in the Interactive Plot Builder: Specify

Expressions window (Figure 2.4), click Done.

6. In the Interactive Plot Builder: Select Plot Type dialog (Figure 2.3),

select the type of plot, for example, 3-D Plot or 3-D Contour Plot, and specify the variable ranges, for example, .

7. To immediately create a plot, click Plot. To customize the plot before

generating it, click Options. Set the plot options, and then click Plot. Maple inserts the plot in the document.

2.7 Task Templates • 51

For more information on assistants and tutors, see Assistants and Tu- tors (page 26) in Chapter 1.

2.7 Task Templates

Maple can solve a diverse set of problems. The task template facility helps you quickly find and use the commands required to perform common tasks.

After inserting a task template, specify the parameters of your problem in the placeholders, and then execute the commands, or click a button.

Viewing Task Templates

The Task Browser (Figure 2.6) organizes task templates by subject. To launch the Task Browser:

• From the Tools menu, select Tasks, and then Browse.

52 • 2 Worksheet Mode

Y ou can also bro wse the task templates in the Table of Contents of the Maple Help System.

Figure 2.6: Task Browser

Inserting a Task Template

To insert a task template from the Task Browser or Help Navigator:

1. Navigate to the task.

2. Click one of the insertion or copy buttons.

2.7 Task Templates • 53

• Click the Insert Default Content button. Maple inserts the default con- tent. The default content lev el is set using the Options dialog. For details, see the following steps.

• Click the Insert Minimal Content button. Maple inserts only the commands and embedded components, for example, a button to launch the related assistant or tutor.

• Click the Copy Task to Clipboard button. Place the cursor where you want to insert the task, and then paste the task. Maple inserts the default content. Use this method to quickly insert a task multiple times.

To change the default content level, use the Options dialog.

1. From the Tools menu, select Options. The Options dialog opens.

2. In the Options dialog, select the Display tab.

3. In the T ask content to insert drop-do wn list, select All Content, Standard

Content, or Minimal Content.

• Minimal Content - Only the commands and embedded components

• Standard Content - Commands, embedded components, and instructions for using the template

• All Content - All content in the task template, including hyperlinks to related help pages

Maple stores a list of the most recently inserted task templates.

To insert a recently inserted task:

• From the Tools menu, select Tasks, and then the task name.

Maple inserts the default content.

Performing the Task

After you insert a task template, enter the parameters for your task, and then compute the result.

54 • 2 Worksheet Mode

To use an inserted task template:

1. Specify values for the parameters in placeholders or using graphical interface components. You can move to the next placeholder by pressing Tab.

2. Execute all commands in the task by:

• Placing the cursor in the first task command, and then pressing Enter

repeatedly to execute each command.

• Selecting all the template commands, and then clicking the execute toolbar icon .

3. If the template contains a button that computes the result, click it.

For more information on task templates, refer to the Maple Getting Started Guide or the ?tasks help page.

2.8 Text Regions

To add descriptive text in Worksheet mode, use a text region.

To insert a text region:

• In the toolbar, click the Text region icon .

The default mode in a text region is Text mode. In a text region, you can:

• Enter text with inline mathematical content by switching between Text and Math modes. To toggle between Text mode and Math mode, press F5. Note: The mathematical content in a text region is not evaluated. To enter mathematical content that is evaluated, enter it at an Input Prompt (page 37).

• Insert any palette item. Palette items are inserted in Math mode (2-D Math).

2.9 Names • 55

You can format text in a text region. Features include:

• Character styles

• Paragraph styles

• Sections and subsections

• Tables For more information on formatting documents, see Creating Mathematical

Documents (page 231).

2.9 Names

Instead of re-entering an expression every time you need it, you can assign it to a name or add an equation label to it. Then you can quickly refer to the expression using the name or an equation label reference. For information on labels, see the following section Equation Labels (page 59).

Assigning to Names

You can assign any Maple expression to a name: numeric values, data structures, procedures (a type of Maple program), and other Maple objects.

Initially, the value of a name is itself.

The assignment operator (:=) associates an expression with a name.

56 • 2 Worksheet Mode

Recall that you can enter using the following two methods.

• Use the Common Symbols palette

• In 2-D Math enter pi, and then press the symbol completion short cut key. See Shortcuts for Entering Mathematical Expressions (page 6).

When Maple evaluates an expression that contains a name, it replaces the name with its value. For example:

For information on Maple evaluation rules, see Evaluating Expressions (page 310).

Mathematical Functions

To define a function, assign it to a name. For example, define a function that computes the cube of its argument.

For information on creating functions, see Defining a Mathematical Function (page 14).

Note: To insert the right arrow, enter the characters ->. In 2-D Math, Maple

replaces -> with the right arrow symbol . In 1-D Math, the characters are not replaced.

2.9 Names • 57

For example, define a function that squares its argument.

square := x -> x^2:>

square(32);>

For more information on functions, see Functional Operators (page 292).

Protected Names

Protected names are valid names that are predefined or reserved. If you attempt to assign to a protected name, Maple returns an error.

Error, attempting to assign to `sin` which is protected

For more information, refer to the ?type/protectedand ?pr otect help pages.

Unassigning Names

The unassign command resets the value of a name to itself. Note:You must enclose the name in right single quotes ('').

Right single quotes (unevaluation quotes) prevent Maple from evaluating the name. For more information on unevaluation quotes, see Delaying Evaluation (page 317) or refer to the ?uneval help page.

See also Unassigning a Name Using Unevaluation Quotes (page 319).

58 • 2 Worksheet Mode

Unassigning All Names

The restart command clears the Maple internal memory . The ef fects include unassigning all names and unloading all packages. For more information, refer to the ?restart help page.

Note: To use the examples in this manual, you may be required to use the unassign or restart command between examples.

Valid Names

A Maple name must be one of the following.

• A sequence of alphanumeric and underscore (_) characters that begins with an alphabetical character. Note: To enter an underscore character in 2-D Math, enter a backslash character followed by an underscore character, that is, \_.

• A sequence of characters enclosed in left single quotes (``).

Important: Do not begin a name with an underscore character. Maple reserves names that begin with an underscore for use by the Maple library.

Examples of valid names:

• a

• a1

• polynomial

• polynomial1_divided_by_polynomial2

• `2a`

• `x#y`

• `x y`

2.10 Equation Labels • 59

2.10 Equation Labels

Maple marks the output of each execution group with a unique equation label.

Note: The equation label is displayed to the right of the output.

(2.2)

Using equation labels, you can refer to the result in other computations.

(2.3)

Displaying Equation Labels

Important: By default, equation labels are displayed. If equation label display is turned off, complete both the following operations.

• From the Format menu, select Labels, and then ensure that Worksheet

is selected.

• In the Options dialog (Tools>Options), on the Display tab, ensure that Show equation labels is selected.

Referring to a Previous Result

Instead of re-entering previous results in computations, you can use equation label references. Each time you need to refer to a previous result, insert an equation label reference.

60 • 2 Worksheet Mode

To insert an equation label reference:

• From the Insert menu, select Label. (Alternatively, press Ctrl+L. For Macintosh, Command+L.)

• In the Insert Label dialog, enter the label value, and then click OK.

Maple inserts the reference. For example: To integrate the product of (2.2) and (2.3):

1. In the Expression palette, click the indefinite integration item .

The item is inserted and the cursor moves to the integrand placeholder.

2. Press Ctrl+L (Command+L, for Macintosh).

3. In the Insert Label dialog, enter 2.2. Click OK.

4. Press *.

5. Press Ctrl+L (Command+L, for Macintosh).

6. In the Insert Label dialog, enter 2.3. Click OK.

7. To move to the variable of integration placeholder, press Tab.

8. Enter x. Press Enter.

2.10 Equation Labels • 61

Execution Groups with Multiple Outputs

An equation label is associated with the last output within an execution group.

(2.4)

Label Numbering Schemes

You can number equation labels in two ways:

• Flat - Each label is a single number, for example, 1, 2, or 3.

• Sections - Each label is numbered according to the section in which it

occurs. For example, 2.1 is the first equation in the second section, and

1.3.2 is the second equation in the third subsection of the first section.

To change the equation label numbering scheme:

• From the Format menu, select Labels, and then Label Display. In the Format Labels dialog (Figure 2.7), select one of the formats.

• Optionally, enter a prefix.

62 • 2 Worksheet Mode

Figure 2.7: Format Labels Dialog: Adding a Prefix

Features of Equation Labels

Although equation labels are not descriptive names, labels of fer other important features.

• Each label is unique, whereas a name may be inadvertently assigned to more than once for different purposes.

• Maple labels the output values sequentially. If you remove or insert an output, Maple automatically renumbers all equation labels and updates the label references.

• If you change the equation label format (see Label Numbering Schemes (page 61)), Maple automatically updates all equation labels and label references.

For information on assigning to, using, and unassigning names, see Names (page 55).

For more information on equation labels, refer to the ?equationlabels help page.

The following chapters describe how to use Maple to perform tasks such as solving differential (and other types of) equations, producing plots and animations, and creating mathematical documents. The chapters were created

2.10 Equation Labels • 63

using Worksheet mode. Except where noted, all features are available in both Worksheet mode and Document mode.

64 • 2 Worksheet Mode

3 Performing Computations

This chapter discusses key concepts related to performing computations with Maple. It discusses important features that are relevant to all Maple users. After learning about these concepts, you will learn how to use Maple to solve problems in specific areas in the following chapter.

3.1 In This Chapter

TopicsSection

Symbolic and Numeric Computation - An overview of e xact and floating-point computation

Integer Operations - How to perform integer computations

Solving - How to solve standard mathematical equations

• Exact Computations

• Floating-Point Computations

• Converting Exact Quantities to FloatingPoint Values

• Sources of Error

• Important Integer Commands

• Non-Base 10 Numbers

• Finite Rings and Fields

• Gaussian Integers

• Equations and Inequations

• Ordinary Differential Equations

• Partial Differential Equations

• Integer Equations

• Integer Equations in a Finite Field

• Linear Systems

• Recurrence Relations

66 • 3 Performing Computations

TopicsSection

Units, Scientific Constants, and Uncertainty

- How to construct and compute with expressions that have units, scientific constants, or uncertainty

Units

• Conversions

• Applying Units to an Expression

• Performing Computations with Units

• Changing the Current System of Units

• Extensibility

Scientific Constants

• Scientific Constants

• Element and Isotope Properties

• Value, Units, and Uncertainty

• Performing Computations

• Modification and Extensibility

Uncertainty Propagation

• Quantities with Uncertainty

• Performing Computations with Quantities with Uncertainty

Restricting the Domain - How to restrict the domain for computations

• Real Number Domain

• Assumptions on Variables

3.2 Symbolic and Numeric Computation

Symbolic computation is the mathematical manipulation of expressions involving symbolic or abstract quantities, such as variables, functions, and

operators; and exact numbers, such as integers, rationals, π, and . The goal of such manipulations may be to transform an expression to a simpler

form or to relate the expression to other, better understood formulas.

3.2 Symbolic and Numeric Computation • 67

Numeric computation is the manipulation of expressions in the context of finite-precision arithmetic. Expressions in volving exact numbers, for example,

, are replaced by close approximations using floating-point numbers,

for example 1.41421. These computations generally involve some error. Understanding and controlling this error is often of as much importance as the computed result.

In Maple, numeric computation is normally performed if you use floatingpoint numbers (numbers containing a decimal point) or the evalf command. The plot command (see Plots and Animations (page 189)) uses numeric computation, while commands such as int, limit, and gcd (see Integer Oper - ations (page 71) and Mathematical Computations (page 123)) generally use only symbolic computation to achieve their results.

Exact Computations

In Maple, integers, rational numbers, mathematical constants such as π and ∞, and mathematical structures such as matrices with these as entries are

treated as exact quantities. Names, such as , , , and mathematical functions, such as sin(x) and LambertW(k, z), are symbolic

objects. Names can be assigned exact quantities as their values, and functions can be evaluated at symbolic or exact arguments.

Important: Unless requested to do otherwise (see the following section),

Maple evaluates expressions containing exact quantities to exact results, as you would do if you were performing the calculation by hand, and not to numeric approximations, as you normally obtain from a standard hand-held calculator.

68 • 3 Performing Computations

Floating-Point Computations

In some situations, a numeric approximation of an exact quantity is required. For example, the plot command requires the expression it is plotting to evaluate to numeric values that can be rendered on the screen: π cannot be

so rendered, but can be. Maple distinguishes approximate from exact quantities by the presence or absence of a decimal point: 9 is ap-

proximate, while is exact.

Note: An alternative representation of floating-point numbers, called e- notation, may not include an explicit decimal point: 1e5 , 3e-2

In the presence of a floating-point (approximate) quantity in an expression, Maple generally computes using numeric approximations. Arithmetic involving mixed exact and floating-point quantities results in a floating-point result.

3.2 Symbolic and Numeric Computation • 69

If a mathematical function is passed a floating-point argument, it normally attempts to produce a floating-point approximation to the result.

Converting Exact Quantities to Floating-Point Values

To convert an exact quantity to a numeric approximation of that quantity, use the evalf command or the Approximate context menu operation (see Approximating the Value of an Expression (page 22)).

By default, Maple computes such approximations using 10 digit arithmetic. You can modify this in one of two ways:

• Locally, you can pass the precision as an index to the evalf call.

• Globally, you can set the value of the Digits environment variable.

70 • 3 Performing Computations

For more information, see the ?evalf and ?Digits help pages. Note: When appropriate, Maple performs floating-point computations directly

using your computer's underlying hardware.

Sources of Error

By its nature, floating-point computation normally involves some error. Controlling the effect of this error is the subject of activ e research in Numer- ical Analysis. Some sources of error are:

• An exact quantity may not be exactly representable in decimal form:

and are examples.

• Small errors can accumulate after many arithmetic operations.

• Subtraction of nearly equal quantities can result in essentially no useful information. For example, consider the computation for

No correct digits remain. If, howev er , you use Maple to analyze this e xpression, and replace this form with a representation that is more accurate for

small values of , a fully accurate 10-digit result can be obtained.

3.3 Integer Operations • 71

For information on evaluating an expression at a point, see Substituting a Value for a Subexpression (page 310). For information on creating a series

approximation, see Series (page 161). For more information on floating-point numbers, refer to the ?float and

?type/float help pages.

3.3 Integer Operations

In addition to the basic arithmetic operators, Maple has many specialized commands for performing more complicated integer computations, such as factoring an integer, testing whether an integer is a prime number, and determining the greatest common divisor (GCD) of a pair of integers.

Note: Many integer operations are available as task templates (Tools>Tasks>Browse).

You can quickly perform many integer operations using context menus. Selecting an integer, and then right-clicking (for Macintosh, Contr ol-clicking) displays a context menu with integer commands, for example, Integer Factors, which applies the ifactor command. See Figure 3.1.

72 • 3 Performing Computations

Figure 3.1: Context Menu for an Integer

In Worksheet mode, Maple uses an equation label reference in the ifactor calling sequence.

(3.1)

For more information on equation labels, see Equation Labels (page 59). For more information on using context menus in Worksheet mode, see

Context Menus (page 46). For information on using conte xt menus in Document mode, see Context Menus (page 20).

3.3 Integer Operations • 73

You can also enter the ifactor command and specify the integer to factor as an argument.

Maple has many other integer commands, including those listed in Table

3.1.

Table 3.1: Select Integer Commands

DescriptionCommand

abs

factorial

mod

absolute value (displays in 2-D math as )

factorial (displays in 2-D math as ) factorizationifactor

greatest common divisorigcd quotient of integer divisioniquo remainder of integer divisionirem integer approximation of nth rootiroot test primalityisprime integer approximation of square rootisqrt maximum and minimum of a setmax, min modular arithmetic (See Finite Rings and

Fields (page 75)

set of positive divisorsnumtheory[divisors]

74 • 3 Performing Computations

For information on finding integer solutions to equations, see Integer Equations (page 94).

Non-Base 10 Numbers and Other Number Systems

Maple supports:

• Non-base 10 numbers

• Finite ring and field arithmetic

• Gaussian integers

Non-Base 10 Numbers

To represent an expression in another base, use the convert command.

3.3 Integer Operations • 75

For information on enclosing keywords in right single quotes ('), see Delaying Evaluation (page 317).

You can also use the convert/base command.

Note: The convert/base command returns a list of digit values in order of

increasing significance.

Finite Rings and Fields

Maple supports computations over the integers modulo m. The mod operator evaluates an expression over the integers modulo m.

By default, the mod operator uses positive representation (modp command). Symmetric representation is available using the mods command.

For information on setting symmetric representation as the default, refer to the ?mod help page.

The modular arithmetic operators are listed in Table 3.2.

76 • 3 Performing Computations

Table 3.2: Modular Arithmetic Operators

ExampleOperatorOperation

Multiplication (displays in 2-D Math as )

a superscript)

Division (displays in 2-D Math as )

+Addition

-Subtraction

^(-1)Multiplicative inv erse (displays in 2-D Math as

Exponentiation

To enter a caret (^) in 2-D Math, enter a backslash character followed by a caret, that is,

\^.

For information on solving an equation modulo an integer, see Integer Equations in a Finite Field (page 95).

The mod operator also supports polynomial and matrix arithmetic over finite rings and fields. For more information, refer to the ?mod help page.

3.3 Integer Operations • 77

Gaussian Integers

Gaussian integers are complex numbers in which the real and imaginary parts are integers.

The GaussInt package contains commands that perform Gaussian integer operations.

The GIfactor command returns the Gaussian integer factorization.

You can enter the imaginary unit using the following two methods.

• In the Common Symbols palette, click the i or j item. See

Palettes (page 10).

• Enter i or j, and then press the symbol completion key. See Symbol Names (page 16).

Note: In 1-D Math input, enter the imaginary unit as an uppercase i (I). The GIsqrt command approximates the square root in the Gaussian integers.

For more information on Gaussian integers including a list of GaussInt package commands, refer to the ?GaussInt help page.

78 • 3 Performing Computations

3.4 Solving Equations

You can solve a variety of equation types, including those described in Table

3.3.

Table 3.3: Overview of Solution Methods for Important Equation Types

Solution MethodEquation Type solve and fsolve commandsEquations and inequations ODE Analyzer Assistant (and dsolve command)Ordinary differential equations pdsolve commandPartial differential equations isolve commandIntegers equations msolve commandInteger equations in a finite field LinearAlgebra[LinearSolve] commandLinear systems rsolve commandRecurrence relations

Note: Many solve operations are available as task templates

(T ools>Tasks>Browse) and in context menus. This section focuses on other methods.

Solving Equations and Inequations

Using Maple, you can symbolically solve equations and inequations. You can also solve equations numerically.

To solve an equation or set of equations using context menus:

1. Right-click (for Macintosh, Control-click) the equations.

2. From the context menu, select Solve (or Solve Numerically). See Figure

3.2.

3.4 Solving Equations • 79

Figure 3.2: Context Menu for an Equation

In Worksheet mode, Maple inserts a calling sequence that solves the equation followed by the solutions.

If you select Solve, Maple computes exact solutions.

(3.2)

If you select Solve Numerically, Maple computes floating-point solutions.

80 • 3 Performing Computations

(3.3)

For information on solving equations and inequations symbolically using the solve command, see the following section. For information on solving equations numerically using the fsolve command, see Numerically Solving Equations (page 84).

Symbolically Solving Equations and Inequations

The solve command is a general solver that determines exact symbolic solutions to equations or inequations. The solutions to a single equation or inequation are returned as an expression sequence. If Maple does not find any solutions, the solve command returns the empty expression sequence.

It is recommended that you verify the solutions returned by the solve command. For details, see Working with Solutions (page 86).

To return the solutions as a list, enclose the calling sequence in brackets ([

]).

3.4 Solving Equations • 81

Expressions You can specify expressions instead of equations. The solve command automatically equates them to zero.

W represents the Lambert W function.

Multiple Equations To solve multiple equations or inequations, specify them as a set or list.

Solving for Specific Unknowns By default, the solve command returns

solutions for all unknowns. You can specify the unknowns for which to solve.

82 • 3 Performing Computations

To solve for multiple unknowns, specify them as a list.

Transcendental Equations In general, the solve command returns one

solution to transcendental equations.

To produce all solutions, set the _EnvAllSolutions environment v ariable to true.

Note: To enter an underscore character (_) in 2-D Math, enter \_.

Maple uses variables of the form _ZN~ , where N is a positive integer, to represent arbitrary integers. The tilde (~) indicates that it is a quantity with an assumption. For information about names with assumptions, see Assump- tions on Variables (page 117).

3.4 Solving Equations • 83

RootOf Structure The solve command may return solutions, for example, to higher order polynomial equations, in an implicit form using RootOf structures.

(3.4)

These RootOf structures are placeholders for the roots of the equation

. The index parameter numbers and orders the four

solutions. Like any symbolic expression, you can convert RootOf structures to a

floating-point value using the evalf command.

Some equations are difficult to solv e symbolically . For example, polynomial equations of order fiv e and greater do not in general hav e a solution in terms of radicals. If the solve command does not find any solutions, it is recommended that you use the Maple numerical solver, fsolve. For information, see the following section, Numerically Solving Equations.

For more information on the solve command, including how to solve equations defined as procedures and how to find parametric solutions, refer to the ?solve/details help page.

Maplesoft MAPLE 10 User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual

Maple User Manual

Contents

Preface

1 Document Mode

1.1 Introduction

1.2 In This Chapter

Rational Expressions (Fractions)

Powers

Products

Implied Multiplication

Shortcuts for Entering Mathematical Expressions

Other Expressions

1.4 Evaluating Expressions

1.6 Entering Expressions

Palettes

Using Palettes

Defining a Mathematical Function

Viewing and Arranging Palettes

Adding Palettes to the Palette Docks

Symbol Recognition Palette

Symbol Names

Using Symbol Names

Using Partial Symbol Names

Example: Indefinite Integral

1.7 Performing Computations

Computing with Palettes

Context Menus

Approximating the Value of an Expression

Solving an Equation

Using Units

Assistants and Tutors

Assistants

Tutors

Using a Context Menu to Launch the Plot Builder

1.8 Document Mode Summary

1.9 Getting Help

2 Worksheet Mode

2.1 In This Chapter

2.2 Input Prompt

Suppressing Output

1-D Math Input

Input Separators

2.3 Commands

The Maple Library

Top-Level Commands

Package Commands

2.4 Palettes

2.5 Context Menus

2.6 Assistants and Tutors

Launching an Assistant or Tutor

Example: Using the Interactive Plot Builder

2.7 Task Templates

Viewing Task Templates

Inserting a Task Template

Performing the Task

2.8 Text Regions

2.9 Names

Assigning to Names

Mathematical Functions

Protected Names

Unassigning Names

Unassigning All Names

Valid Names

2.10 Equation Labels

Displaying Equation Labels

Referring to a Previous Result

Execution Groups with Multiple Outputs

Label Numbering Schemes

Features of Equation Labels

3 Performing Computations

3.1 In This Chapter

Exact Computations

Floating-Point Computations

Converting Exact Quantities to Floating-Point Values

Sources of Error

3.3 Integer Operations