Irai Automgen 7 Manuel de référence [es]

Download

Page 1

Manual de referencia del lenguaje Ejemplos Las aventuras de Docteur R.

www.irai.com

Page 2

Page 3

Manual de referencia del lenguaje

1. Elementos comunes............................................................................................................... 7

1.1. Variables ..................................................................................................................................... 7

1.1.1. Variables booleanas............................................................................................................................. 7

1.1.2. Variables numéricas ............................................................................................................................ 8

1.1.3. Temporizaciones.................................................................................................................................. 8

1.2. Acciones .................................................................................................................................... 10

1.2.1. Asignación de una variable booleana................................................................................................ 10

Asignación complementada de una variable booleana................................................................................ 11

1.2.2. Puesta en uno de una variable booleana ............................................................................................ 12

1.2.3. Puesta en cero de una variable booleana ........................................................................................... 13

1.2.4. Inversión de una variable booleana ................................................................................................... 13

1.2.5. Puesta en cero de un contador, una palabra o un largo...................................................................... 14

1.2.6. Incremento de un contador, una palabra o un largo........................................................................... 15

1.2.7. Decremento de un contador, una palabra o un largo.......................................................................... 15

1.2.8. Temporizaciones................................................................................................................................ 16

1.2.9. Interferencias entre las acciones........................................................................................................ 17

1.2.10. Acciones de la norma CEI 1131-3................................................................................................... 17

1.2.11. Acciones múltiples .......................................................................................................................... 18

1.2.12. Código literal................................................................................................................................... 19

1.3. Tests........................................................................................................................................... 19

1.3.1. Forma general.................................................................................................................................... 20

1.3.2. Modificador de test............................................................................................................................ 20

1.3.3. Temporizaciones................................................................................................................................ 21

1.3.4. Prioridad de los operadores booleanos .............................................................................................. 21

1.3.5. Test siempre verdadero...................................................................................................................... 22

1.3.6. Test sobre variable numérica ....................................................................................................................... 22

1.3.7. Transiciones en varias líneas ............................................................................................................. 23

1.4. Utilización de símbolos..................................................................................................................... 23

1.4.1. Sintaxis de los símbolos .................................................................................................................... 23

1.4.2. Símbolos automáticos........................................................................................................................ 24

1.4.3. Sintaxis de los símbolos automáticos ................................................................................................ 24

1.4.4. ¿Cómo gestiona el compilador los símbolos automáticos? ............................................................... 24

1.4.5. Zona de atribución de las variables ................................................................................................... 25

1.5. A propósito de ejemplos .......................................................................................................... 26

1.6. Grafcet ...................................................................................................................................... 28

1.6.1. Grafcet simple ................................................................................................................................... 28

1.6.2. Divergencia y convergencia en « Y »................................................................................................ 31

1.6.3. Divergencia y convergencia en « O »................................................................................................ 33

1.6.4. Etapas pozos y fuentes, transiciones pozos y fuentes........................................................................ 36

AUTOMGEN7 3 (C)opyright 2002 IRAI

Page 4

Manual de referencia del lenguaje

1.6.5. Acciones múltiples, acciones condicionadas..................................................................................... 36

1.6.6. Sincronización................................................................................................................................... 38

1.6.7. Forzados de Grafcet........................................................................................................................... 39

1.6.8. Macro-etapas ..................................................................................................................................... 48

1.6.9. Contadores......................................................................................................................................... 51

1.7. Gemma ...................................................................................................................................... 52

1.7.1. Creación de un Gemma ..................................................................................................................... 54

1.7.2. Contenido de los rectángulos del Gemma ......................................................................................... 54

1.7.3. Obtener un Grafcet correspondiente.................................................................................................. 54

1.7.4. Anular los espacios vacíos en el Grafcet ........................................................................................... 55

1.7.5. Imprimir el Gemma........................................................................................................................... 55

1.7.6. Exportar el Gemma............................................................................................................................ 55

1.7.7. Ejemplo de Gemma........................................................................................................................... 55

1.8. Ladder....................................................................................................................................... 58

1.8.1. Ejemplo de Ladder............................................................................................................................. 59

1.9. Logigrama................................................................................................................................. 60

1.9.1. Diseño de los logigramas................................................................................................................... 61

1.9.2. Ejemplo de logigrama........................................................................................................................ 62

1.10. Lenguajes literales.................................................................................................................. 65

1.10.1. Cómo utilizar el lenguaje literal ...................................................................................................... 65

1.10.2. Definición de una caja de código..................................................................................................... 66

1.10.3. El lenguaje literal bajo nivel............................................................................................................ 67

1.10.4. Macro-instrucción.......................................................................................................................... 120

1.10.5. Biblioteca....................................................................................................................................... 121

1.10.6. Macro-instrucciones predefinidas.................................................................................................. 121

1.10.7. Descripción de las macro-instrucciones predefinidas.................................................................... 121

1.10.8. Ejemplo en lenguaje literal bajo nivel ........................................................................................... 123

1.11. Lenguaje literal extendido................................................................................................... 126

1.11.1. Escritura de ecuaciones booleanas................................................................................................. 127

1.11.2. Escritura de ecuaciones numéricas................................................................................................ 128

1.11.3. Estructura de tipo IF ... THEN ... ELSE ... .................................................................................... 130

1.11.4. Estructura de tipo WHILE ... ENDWHILE...................................................................................130

1.11.5. Ejemplo de programa en lenguaje literal extendido.......................................................................131

1.12. Lenguaje literal ST............................................................................................................... 132

1.12.1. Generalidades ................................................................................................................................ 132

1.12.2. Ecuaciones booleanas.................................................................................................................... 133

1.12.3. Ecuaciones numéricas.................................................................................................................... 134

1.12.4. Estructuras de programación ......................................................................................................... 135

1.12.5. Ejemplo de programa en lenguaje literal extendido.......................................................................137

AUTOMGEN7 4 (C)opyright 2002 IRAI

Page 5

Manual de referencia del lenguaje

1.13. Organigrama ........................................................................................................................ 137

1.13.1. Diseño de un organigrama............................................................................................................. 138

1.13.2. Contenido de los rectángulos......................................................................................................... 139

1.14. Ilustración............................................................................................................................. 139

1.15. Bloques funcionales.............................................................................................................. 142

1.15.1. Creación de un bloque funcional................................................................................................... 142

1.15.2. Diseño del bloque y creación del archivo « .ZON »...................................................................... 143

1.15.3. Creación del archivo « .LIB »........................................................................................................ 145

1.15.4. Ejemplo simple de bloque funcional ............................................................................................. 145

1.15.5. Ilustración...................................................................................................................................... 146

1.15.6. Complemento de sintaxis............................................................................................................... 149

1.16. Bloques funcionales evolucionados..................................................................................... 150

1.16.1. Sintaxis.......................................................................................................................................... 150

1.16.2. Diferenciar viejos y nuevos bloques funcionales........................................................................... 150

1.16.3. Ejemplo.......................................................................................................................................... 151

1.17. Bloques funcionales predefinidos ....................................................................................... 152

1.17.1. Bloques de conversión................................................................................................................... 152

1.17.2. Bloques de temporización.............................................................................................................. 153

1.17.3. Bloques de manipulación de cadena de caracteres ........................................................................ 153

1.17.4. Bloques de manipulación de tabla de palabras.............................................................................. 153

1.18. Técnicas avanzadas.............................................................................................................. 153

1.18.1. Código generado por el compilador............................................................................................... 153

1.18.2. Optimización del código generado................................................................................................ 154

2. Ejemplos............................................................................................................................. 157

2.1. A propósito de ejemplos ........................................................................................................ 157

2.1.1. Grafcet simple ................................................................................................................................. 157

2.1.2. Grafcet con diagrama en O.............................................................................................................. 158

2.1.3. Grafcet con divergencia en Y .......................................................................................................... 159

2.1.4. Grafcet y sincronización.................................................................................................................. 160

2.1.5. Forzado de etapas ............................................................................................................................ 161

2.1.6. Etapas pozos y fuentes..................................................................................................................... 162

2.1.7. Etapas pozos y fuentes..................................................................................................................... 163

2.1.8. Forzado de Grafcets......................................................................................................................... 164

2.1.9. Memorización de Grafcets............................................................................................................... 165

2.1.10. Grafcet y macro-etapas.................................................................................................................. 166

2.1.11. Folios en cadena ............................................................................................................................ 167

2.1.12. Logigrama...................................................................................................................................... 169

2.1.13. Grafcet y Logigrama...................................................................................................................... 170

2.1.14. Caja de lenguaje literal .................................................................................................................. 171

AUTOMGEN7 5 (C)opyright 2002 IRAI

Page 6

Manual de referencia del lenguaje

2.1.15. Organigrama.................................................................................................................................. 172

2.1.16. Organigrama.................................................................................................................................. 173

2.1.17. Bloque funcional............................................................................................................................ 174

2.1.18. Bloque funcional............................................................................................................................ 175

2.1.19. Ladder............................................................................................................................................ 176

2.1.20. Ejemplo desarrollado sobre una maqueta de tren ..........................................................................177

Manual pedagógico del usuario de AUTOMGEN............................................................... 183

Distribución ................................................................................................................................... 185

El Doctor R. en el reino de la domótica....................................................................................... 185

Primer ejemplo: « quién fue el primero, el interruptor o la bombilla … » ............................. 186

Solución 1: el lenguaje natural del electricista: ladder .............................................................................. 187

Solución 2: el lenguaje secuencial del automatista: Grafcet...................................................................... 187

A jugar … ...................................................................................................................................... 190

Segundo ejemplo: « temporizaciones, minuteros y otras diversiones temporales… »............ 190

Solución 1: la simplicidad ......................................................................................................................... 191

Solución 2: mejora..................................................................................................................................... 192

Tercer ejemplo: « variación sobre el tema del conmutador… »............................................... 193

He aquí una solución en logigrama: .......................................................................................................... 194

Una solución que utiliza el lenguaje literal de AUTOMGEN................................................................... 195

Otra más astuta:......................................................................................................................................... 196

Prueben esto: ............................................................................................................................................. 196

Cuarto ejemplo: « Y el botón pulsador se vuelve inteligente … » ............................................ 197

Las soluciones … ........................................................................................................................... 200

Las soluciones … ........................................................................................................................... 201

« quién fue el primero, el interruptor o la bombilla … »........................................................................... 201

« temporizaciones, minuteros y otras diversiones temporales… »............................................................ 201

« variación sobre el tema del conmutador …» ........................................................................... 203

AUTOMGEN7 6 (C)opyright 2002 IRAI

Page 7

Manual de referencia del lenguaje

1. Elementos comunes

Este capítulo detalla los elementos comunes a todos los lenguajes utilizables en AUTOMGEN.

El logo identifica las novedades utilizables en la versión 7 de AUTOMGEN.

1.1. Variables

Existen los siguientes tipos de variables:

Ö tipo booleano: la variable puede adoptar el valor verdadero (1) o falso (0). Ö tipo numérico: la variable puede adoptar un valor numérico; existen diferentes

subtipos: variables 16 bits, 32 bits y coma flotante.

Ö tipo temporización: tipo estructurado; es una combinación del booleano y el

numérico. A partir de la versión 6 la sintaxis de los nombres de variables puede ser la de AUTOMGEN o la de la norma CEI 1131-3.

1.1.1. Variables booleanas

La tabla siguiente ofrece la lista exhaustiva de variables booleanas utilizables.

Tipo Sintaxis

AUTOMGEN

Entradas I0

a I9999

Sintaxis CEI 1131-3

%I0 a %I9999

Comentario

Puede corresponder o no a entradas físicas (depende de la configuración de las E/S del destino).

Salidas O0

a O9999

Bits Sistema U0

a U99

Bits Usuario U100

a U9999

AUTOMGEN7 7 (C)opyright 2002 IRAI

%Q0 a %Q9999

%M0 a %M99 %M100 a %M9999

Puede corresponder o no a entradas físicas (depende de la configuración de las E/S del destino). Ver el manual sobre el entorno para el detalle de los bis Sistema. Bits internos de uso general.

Page 8

Manual de referencia del lenguaje

Etapas Grafcet

Bits de palabras

X0 a X9999

M0#0 a M9999#15

%X0 a %X9999

%MW0:X0 a %MW9999:X15

Bits de etapas Grafcet.

Bits de palabras: el número del bit se expresa en decimal y está comprendido entre 0 (bit de peso débil) y 15 (bit de peso fuerte).

1.1.2. Variables numéricas

La tabla siguiente ofrece la lista exhaustiva de variables numéricas.

Tipo Sintaxis

AUTOMGEN

Contadores C0

a C9999

Sintaxis

CEI 1131-3

%C0 a %C9999

Comentario

Contador de 16 bits; puede inicializarse, incrementarse, decrementarse y testearse con los lenguajes booleanos sin utilizar el lenguaje literal.

Palabras Sistema

Palabras Usuario

Largos L100

Flotantes F100

M0 a M199

M200 a M9999

a L4998

a F4998

%MW0 a %MW199

%MW200 a %MW9999

%MD100 a %MD4998

%MF100 a %MF4998

Ver el manual sobre el entorno para el detalle de las palabras Sistema.

Palabra de 16 bits de uso general.

Valor entero sobre 32 bits.

Valor real sobre 32 bits (formato IEEE).

1.1.3. Temporizaciones

La temporización es un tipo compuesto que agrupa dos variables booleanas (estado de lanzamiento, estado de fin) y dos variables numéricas sobre 32 bits (la consigna y el contador).

AUTOMGEN7 8 (C)opyright 2002 IRAI

Page 9

Manual de referencia del lenguaje

El esquema siguiente muestra el cronograma de funcionamiento de una temporización:

état de lancement

état de fin

consigne

valeur de comptage

El valor de consigna de una temporización está comprendido entre 0 ms y 4294967295 ms (vale decir, poco más de 49 días)

La consigna de la temporización puede modificarse por programa; ver el capítulo

(instrucción STA). 1.10.3. El lenguaje literal bajo nivel El contador de la temporización puede leerse por programa; ver el capítulo lenguaje literal bajo nivel

(instrucción LDA).

1.10.3. El

AUTOMGEN7 9 (C)opyright 2002 IRAI

Page 10

Manual de referencia del lenguaje

1.2. Acciones

Las acciones se utilizan en:

Ö los rectángulos de acción del lenguaje Grafcet,

Ö los rectángulos de acción del lenguaje logigrama,

Ö las bobinas del lenguaje ladder.

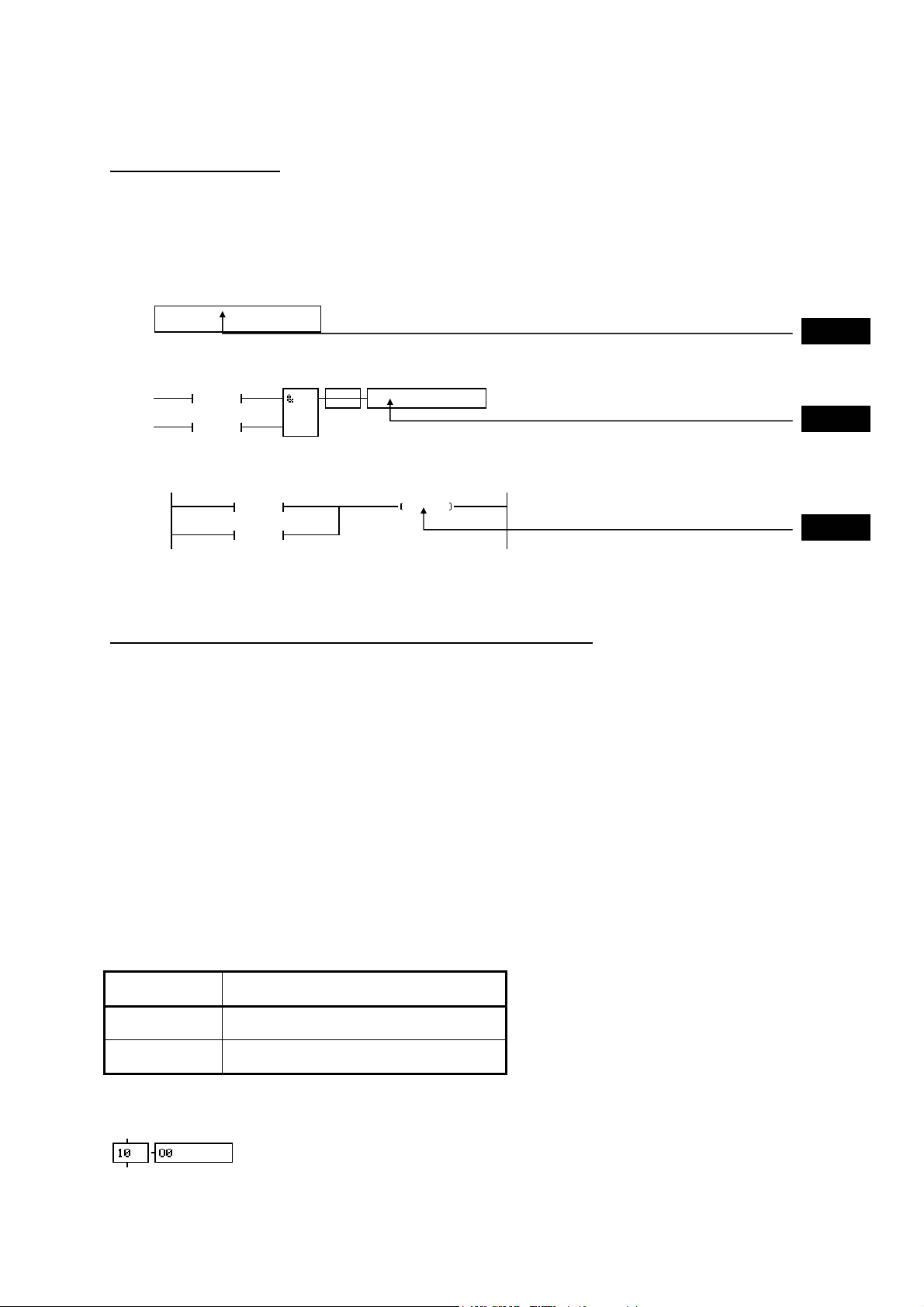
1.2.1. Asignación de una variable booleana

La sintaxis de la acción « Asignación » es: «variable booleana» Funcionamiento:

Action

Ö si el comando del rectángulo de acción o de la bobina está en estado verdadero,

la variable se pone en 1 (estado verdadero),

Ö si el comando del rectángulo de acción o de la bobina está en estado falso, la

variable se pone en 0 (estado falso).

Tabla de verdad:

Comando Estado de la variable (resultado)

0 0 1 1

Ejemplo:

Si la etapa 10 está activa, O0 adopta el valor 1; si no, O0 adopta el valor 0.

AUTOMGEN7 10 (C)opyright 2002 IRAI

Page 11

Manual de referencia del lenguaje

Es posible utilizar varias acciones « Asignación » para una misma variable dentro de un programa. En este caso, los diferentes comandos se combinan en « O » lógico.

Ejemplo:

Estado de X10 Estado de X50 Estado de O5

0 0 0 1 0 1 0 1 1 1 1 1

Asignación complementada de una variable booleana

La sintaxis de la acción « Asignación complementada » es: «N variable booleana» Funcionamiento:

Ö si el comando del rectángulo de acción o de la bobina está en estado verdadero,

la variable se pone en 0 (estado falso),

Ö si el comando del rectángulo de acción o de la bobina está en estado falso, la

variable se pone en 1 (estado verdadero).

Tabla de verdad:

Comando Estado de la variable (resultado)

0 1 1 0

Ejemplo:

Si la etapa 20 está activa, U100 adopta el valor 0; si no, U100 adopta el valor 1.

AUTOMGEN7 11 (C)opyright 2002 IRAI

Page 12

Manual de referencia del lenguaje

Es posible utilizar varias acciones « Asignación complementada» para una misma variable dentro de un programa. En este caso, los diferentes comandos se combinan en « O » lógico.

Ejemplo:

Estado de X100 Estado de X110 Estado de O20

0 0 1 1 0 0 0 1 0 1 1 0

1.2.2. Puesta en uno de una variable booleana

La sintaxis de la acción « Puesta en uno » es: «S variable booleana» Funcionamiento:

Ö si el comando del rectángulo de acción o de la bobina está en estado verdadero,

la variable se pone en 1 (estado verdadero),

Ö si el comando del rectángulo de acción o de la bobina está en estado falso, el

estado de la variable no se modifica.

Tabla de verdad:

Comando Estado de la variable (resultado)

0 no cambia 1 1

Ejemplo:

Si la etapa 5000 está activa, O2 adopta el valor 1; si no, O2 conserva su estado.

AUTOMGEN7 12 (C)opyright 2002 IRAI

Page 13

Manual de referencia del lenguaje

1.2.3. Puesta en cero de una variable booleana

La sintaxis de la acción « Puesta en cero » es: «R variable booleana» Funcionamiento:

Ö si el comando del rectángulo de acción o de la bobina está en estado verdadero,

la variable se pone en 0 (estado falso),

Ö si el comando del rectángulo de acción o de la bobina está en estado falso, el

estado de la variable no se modifica.

Tabla de verdad:

Comando Estado de la variable (resultado)

0 no cambia 1 0

Ejemplo:

Si la etapa 6000 está activa, O3 adopta el valor 0; si no, O3 conserva su estado.

1.2.4. Inversión de una variable booleana

La sintaxis de la acción « Inversión » es: «I variable booleana» Funcionamiento:

Ö si el comando del rectángulo de acción o de la bobina está en estado verdadero,

el estado de la variable se invierte a cada ciclo de ejecución,

Ö si el comando del rectángulo de acción o de la bobina está en estado falso, el

estado de la variable no se modifica.

AUTOMGEN7 13 (C)opyright 2002 IRAI

Page 14

Manual de referencia del lenguaje

Tabla de verdad:

Comando Estado de la variable (resultado)

0 no cambia 1 invertido

Ejemplo:

Si la etapa 7000 está activa, el estado de O4 se invierte; si no, O4 conserva su estado.

1.2.5. Puesta en cero de un contador, una palabra o un largo

La sintaxis de la acción « Puesta en cero de un contador, una palabra o un largo» es: «R contador o palabra» Funcionamiento:

Ö si el comando del rectángulo de acción o de la bobina está en estado verdadero,

el contador, la palabra o el largo se pone en cero,

Ö si el comando del rectángulo de acción o de la bobina está en estado falso, el

valor del contador, de la palabra o del largo no se modifica.

Tabla de verdad:

Comando Valor del contador, de la

palabra o del largo (resultado)

0 No cambia 1 0

Ejemplo:

Si la etapa 100 está activa, el contador 25 se pone en cero; si no, C25 conserva su valor.

AUTOMGEN7 14 (C)opyright 2002 IRAI

Page 15

Manual de referencia del lenguaje

1.2.6. Incremento de un contador, una palabra o un largo

La sintaxis de la acción « Incremento de un contador » es: «+ contador, palabra o largo» Funcionamiento:

Ö si el comando del rectángulo de acción o de la bobina está en estado verdadero,

el contador, la palabra o el largo se incrementa a cada ciclo de ejecución,

Ö si el comando del rectángulo de acción o de la bobina está en estado falso, el

valor del contador no se modifica.

Tabla de verdad:

Comando Valor del contador, de la

palabra o del largo (resultado)

0 No cambia 1 valor actual +1

Ejemplo:

Si la etapa 100 está activa, el contador 25 se incrementa; si no, C25 conserva su valor.

1.2.7. Decremento de un contador, una palabra o un largo

La sintaxis de la acción « Decremento de un contador » es: «- contador, palabra o largo» Funcionamiento:

Ö si el comando del rectángulo de acción o de la bobina está en estado verdadero, el

contador, la palabra o el largo se decrementa a cada ciclo de ejecución,

Ö si el comando del rectángulo de acción o de la bobina está en estado falso, el

valor del contador no se modifica.

AUTOMGEN7 15 (C)opyright 2002 IRAI

Page 16

Manual de referencia del lenguaje

Tabla de verdad:

Comando Valor del contador, de la

palabra o del largo (resultado)

0 no cambia 1 valor actual –1

Ejemplo:

Si la etapa 100 está activa, el contador 25 se decrementa; si no, C25 conserva su valor.

1.2.8. Temporizaciones

Las temporizaciones se consideran como variables booleanas y pueden utilizarse con las acciones « Asignación », « Asignación complementada », « Puesta en uno », « Puesta en cero » e « Inversión ». La consigna de la temporización puede escribirse a continuación de la acción. La sintaxis es: « temporización(duración) » La duración se expresa en forma predeterminada en décimas de segundo. El carácter « S » ubicado al final de la duración indica que se expresa en segundos.

Ejemplos:

La etapa 10 lanza una temporización de 2 segundos que permanecerá activa mientras la etapa permanezca activa. La etapa 20 arma una temporización de 6 segundos que permanecerá activa aunque la etapa 20 esté desactivada. Una misma temporización puede utilizarse en varios sitios con una misma consigna en momentos diferentes. En este caso, la consigna de la temporización debe indicarse una sola vez.

Observación: existen otras sintaxis para las temporizaciones. Ver el capítulo 1.3.3. Temporizaciones

AUTOMGEN7 16 (C)opyright 2002 IRAI

Page 17

Manual de referencia del lenguaje

1.2.9. Interferencias entre las acciones

Ciertos tipos de acción no pueden utilizarse simultáneamente con una variable. La siguiente tabla resume las combinaciones posibles.

Asignación

complementada

Puesta en uno

Puesta en cero

Inversión

Asignación

complementada

SÍ NO NO NO NO

NO SÍ NO NO NO

NO NO SÍ SÍ SÍ

Puesta en uno

Puesta

en cero

Inversión

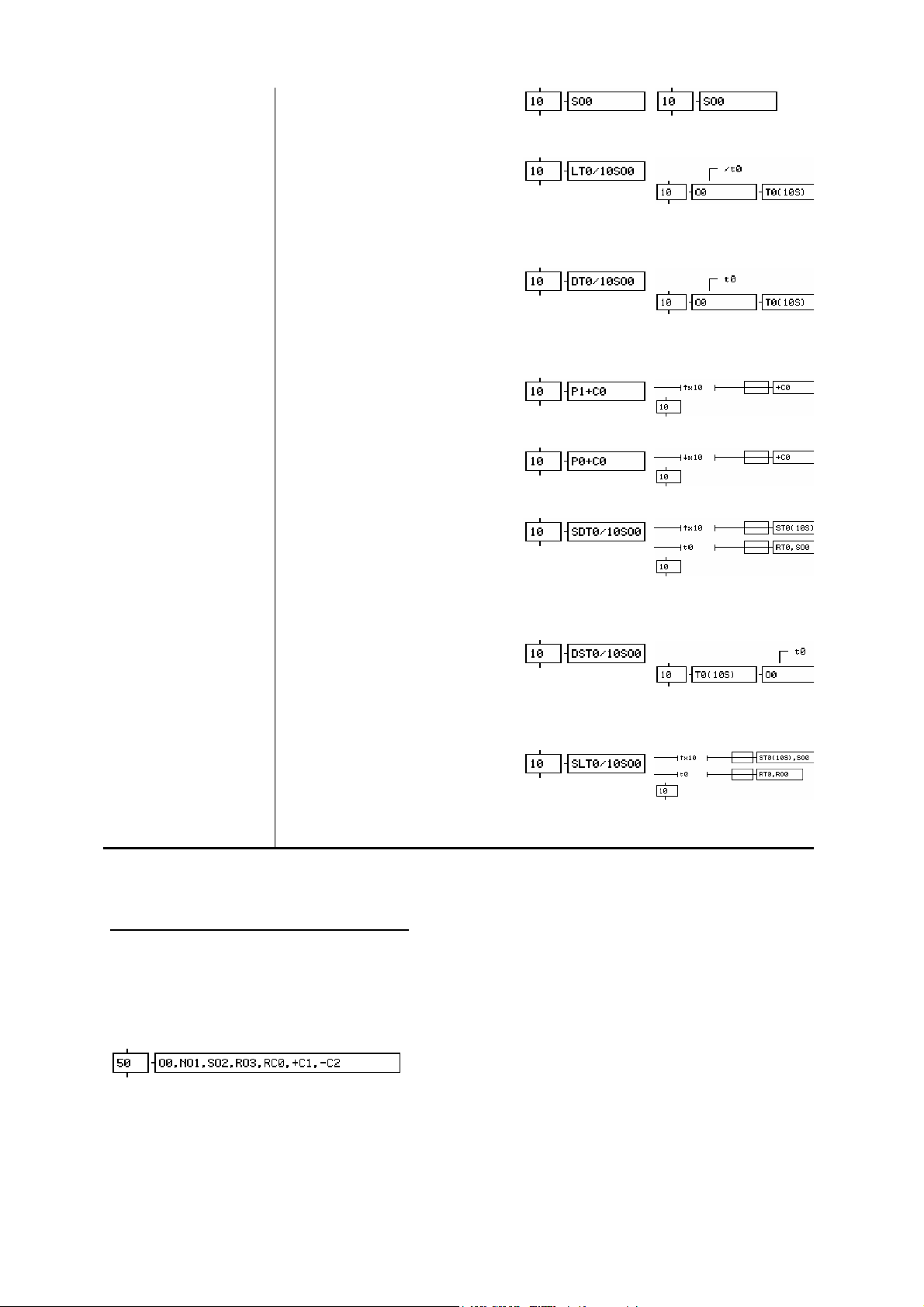
1.2.10. Acciones de la norma CEI 1131-3

La siguiente tabla ofrece la lista de acciones de la norma CEI 1131-3 utilizables en AUTOMGEN V>=6 con respecto a la sintaxis estándar de AUTOMGEN. V5.

Nombre Sintaxis

AUTOMGEN

V>=6

No memorizado Ninguno Ninguno

No memorizado N1 Ninguno

No memorizado complementado

Puesta en cero R R

N0 N

Sintaxis

AUTOMGEN

Ejemplo

AUTOMGEN

V>=6

Ejemplo

de equivalente

AUTOMGEN V5

AUTOMGEN7 17 (C)opyright 2002 IRAI

Page 18

Manual de referencia del lenguaje

Puesta en 1 S S

Limitado en el tiempo

Temporizado DTn/

Impulsión sobre frente ascendente

Impulsión sobre frente descendente

Memorizado

LTn/duración Inexistente

Inexistente

duración

P1 Inexistente

P0 Inexistente

SDTn/

Inexistente

y temporizado

Temporizado y memorizado

Memorizado y limitado en el tiempo

duración

DSTn/ duración

SLTn/ duración

Inexistente

1.2.11. Acciones múltiples

Dentro de un mismo rectángulo de acción o de una bobina, es posible escribir varias acciones separándolas con el carácter « , » (coma). Ejemplo:

Es posible yuxtaponer varios rectángulos de acción (Grafcet y logigrama) o bobinas (ladder). Consultar los capítulos correspondientes a estos lenguajes para más detalles.

AUTOMGEN7 18 (C)opyright 2002 IRAI

Page 19

Manual de referencia del lenguaje

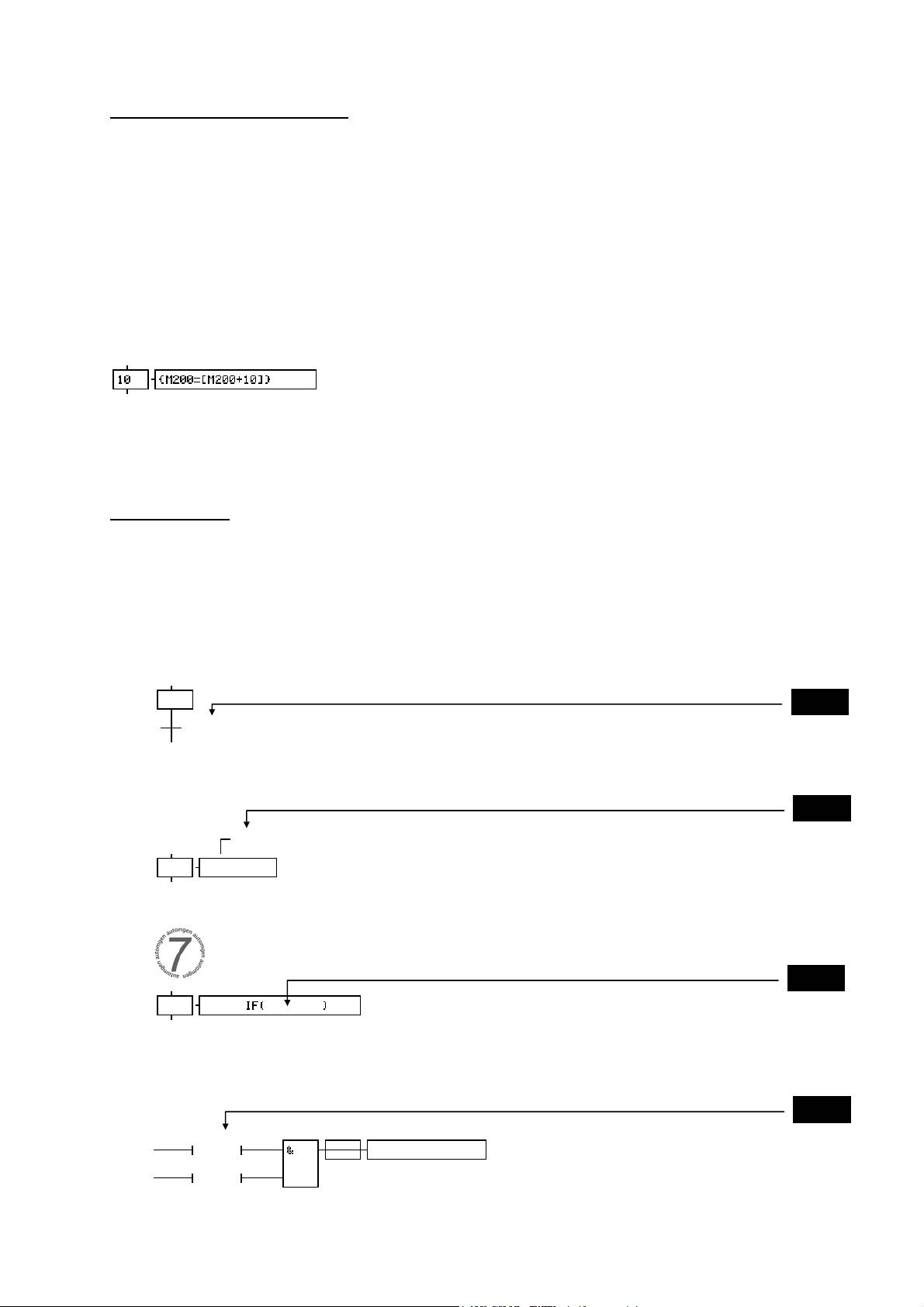
1.2.12. Código literal

En un rectángulo de acción o una bobina es posible insertar código literal. La sintaxis es: « { código literal } » Es posible escribir entre las llaves varias líneas de lenguaje literal. También aquí el separador es el carácter « , » (coma).

Ejemplo:

Consultar los capítulos « Lenguaje literal bajo nivel », « Lenguaje literal extendido » y « Lenguaje literal ST » para más detalles.

1.3. Tests

Los tests se utilizan en:

Ö transiciones del lenguaje Grafcet,

Ö condiciones sobre acción del lenguaje Grafcet,

Test

Ö tests del lenguaje logigrama,

AUTOMGEN7 19 (C)opyright 2002 IRAI

Test

Page 20

Manual de referencia del lenguaje

Ö tests del lenguaje ladder.

Test

1.3.1. Forma general

Un test es una ecuación booleana compuesta por una o por n variables separadas por los operadores « + » (o) o « . » (y).

Ejemplo de test:

i0 (test entrada 0)

i0+i2 (test entrada 0 « o » entrada 2)

i10.i11 (test entrada 10 « y » entrada 11)

1.3.2. Modificador de test

Si se especifica sólo el nombre de una variable, el test predeterminado es « si igual a uno» (si verdadero). Es posible utilizar modificadores para testear el estado complementado, el frente ascendente y el frente descendente:

Ö el carácter « / » ubicado delante de una variable testea el estado

complementado,

Ö el carácter « u » o el carácter « Ï

frente ascendente,

Ö el carácter « d » o el carácter « Ð

frente descendiente. Los modificadores de tests pueden aplicarse a una variable o a una expresión entre paréntesis.

» ubicado delante de una variable testea el

Ejemplos:

Ï i0

/i1

/(i2+i3) Ð(i2+(i4./i5))

Para obtener este carácter durante la edición de un test presione la tecla [Ï].

Para obtener este carácter durante la edición de un test presione la tecla [Ð].

AUTOMGEN7 20 (C)opyright 2002 IRAI

Page 21

Manual de referencia del lenguaje

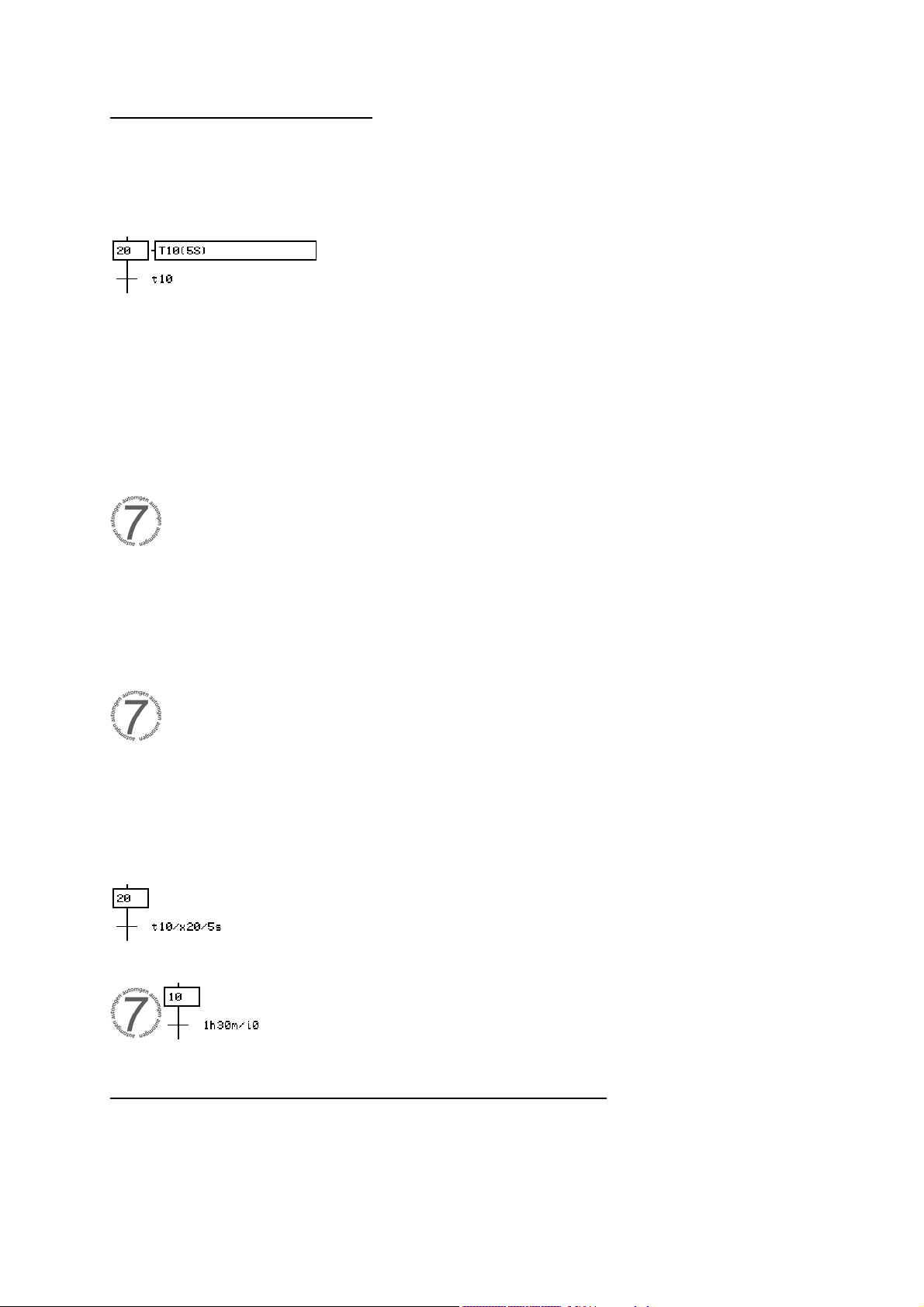
1.3.3. Temporizaciones

Hay cuatro sintaxis disponibles para las temporizaciones. En la primera, se activa la temporización en la acción y se menciona simplemente la variable temporización en un test para verificar el estado de fin:

En las otras, todo se escribe en el test. La forma general es: « temporización / variable de lanzamiento / duración » o « duración / variable de lanzamiento / temporización » o

« duración / variable de lanzamiento » En este caso, se atribuye una temporización automáticamente. La zona de atribución es la de los símbolos automáticos; ver el capítulo . 1.4.2. Símbolos automáticos

La duración se expresa en forma predeterminada en décimas de segundo.

La duración puede expresarse en días, horas, minutos, segundos y milisegundos con los operadores « d », « h », « m », « s » y « ms ». Por ejemplo: 1d30s = 1 día y 30 segundos.

Ejemplo con la segunda sintaxis:

Ejemplo con la sintaxis normalizada:

1.3.4. Prioridad de los operadores booleanos

El operador booleano « . » (Y) tiene una prioridad predeterminada mayor que el operador « + » (O). Es posible utilizar paréntesis para definir otra prioridad.

AUTOMGEN7 21 (C)opyright 2002 IRAI

Page 22

Manual de referencia del lenguaje

Ejemplos:

i0.(i1+i2)

((i0+i1).i2)+i5

1.3.5. Test siempre verdadero

La sintaxis del test siempre verdadero es: « » (ninguno) o « =1 »

1.3.6. Test sobre variable numérica

Los tests sobre variable numérica deben utilizar la siguiente sintaxis: « variable numérica » « tipo de test » « constante o variable numérica »

El tipo de test puede ser:

Ö « = » igual, Ö « ! » o « <> » diferente, Ö « < » menor (sin signo), Ö « > » mayor (sin signo), Ö « << » menor (con signo), Ö « >> » mayor (con signo), Ö « <= » menor o igual (sin signo), Ö « >= » mayor o igual (sin signo), Ö « <<= » menor o igual (con signo), Ö « >>= » mayor o igual (con signo).

Un flotante puede compararse sólo con otro flotante o con una constante real. Un largo puede compararse sólo con otro largo o con una constante larga. Una palabra o un contador puede compararse sólo con una palabra, un contador o una constante 16 bits. Las constantes reales deben estar seguidas del carácter « R ». Las constantes largas (32 bits) deben estar seguidas del carácter « L ». Les constantes enteras 16 o 32 bits están predeterminadas en decimal. Pueden escribirse en hexadecimal (sufijo « $ » o « 16# ») o en binario (sufijo « % » o « 2# »).

AUTOMGEN7 22 (C)opyright 2002 IRAI

Page 23

Manual de referencia del lenguaje

Los tests sobre variables numéricas se utilizan en las ecuaciones como los tests sobre variables booleanas. Pueden utilizarse con los modificadores de test siempre que estén encerrados por paréntesis.

Ejemplos:

m200=100

%mw1000=16#abcd

c10>20.c10<100

f200=f201

m200=m203

%md100=%md102

f200=3.14r

l200=$12345678L

m200<<-100

m200>>1000

%mw500<=12

/(m200=4) Ð(m200=100)

/(l200=100000+l200=-100000)

1.3.7. Transiciones en varias líneas

El texto de las transiciones puede ocupar varias líneas. El fin de una línea de transición debe ser indefectiblemente un operador « . » o « + ». Las combinaciones de teclas [CTRL] + [Ð] y [CTRL] + [Ï] permiten desplazar el cursor de una línea a otra.

1.4. Utilización de símbolos

Los símbolos permiten asociar un texto a una variable. Los símbolos pueden utilizarse con todos los lenguajes. Un símbolo debe asociarse a una y sólo una variable.

1.4.1. Sintaxis de los símbolos

Los símbolos están compuestos por:

Ö un carácter « _ » opcional (subrayado, generalmente asociado a la tecla [8] en

los teclados) que marca el principio del símbolo,

Ö el nombre del símbolo, Ö un carácter « _ » opcional (subrayado) que marca el fin del símbolo.

AUTOMGEN7 23 (C)opyright 2002 IRAI

Page 24

Manual de referencia del lenguaje

Los caracteres « _ » que encierran los nombres de los símbolos son opcionales. Deben utilizarse si el símbolo empieza con una cifra o un operador (+,-, etc…).

1.4.2. Símbolos automáticos

A veces es incómodo tener que definir la atribución entre cada símbolo y una variable, especialmente si la atribución precisa de un número de variable tiene poca importancia. Los símbolos automáticos son una solución a este problema, ya que confían al compilador la tarea de generar automáticamente la atribución de un símbolo a un número de variable. El tipo de variable a utilizar está dado por el nombre del símbolo.

1.4.3. Sintaxis de los símbolos automáticos

La sintaxis de los símbolos automáticos es la siguiente:

_« nombre del símbolo » %« tipo de variable »_

El « tipo de variable » puede ser: I , O o Q, U o M, T, C, M o MW, L o MD, F o MF.

Es posible reservar varias variables para un símbolo. Esto es útil para definir tablas. En este caso la sintaxis es:

_« nombre del símbolo » %« tipo de variable »« longitud »_

La « longitud » representa el número de variables a reservar.

1.4.4. ¿Cómo gestiona el compilador los símbolos automáticos?

Para compilar una aplicación, el compilador borra todos los símbolos automáticos que se encuentran en el archivo « .SYM » de la aplicación. Cada vez que encuentra un símbolo automático, crea una atribución única para ese símbolo en función del tipo de variable especificado en el nombre del símbolo. El símbolo generado se escribe en el archivo « .SYM ». Si un mismo símbolo automático aparece varias veces en una aplicación, hará referencia a la misma variable.

AUTOMGEN7 24 (C)opyright 2002 IRAI

Page 25

Manual de referencia del lenguaje

1.4.5. Zona de atribución de las variables

Cada tipo de variable tiene una zona de atribución predeterminada: Tipo Principio Fin I o %I 0 9999 O o %Q 0 9999 U o %M 100 9999 T o %T 0 9999 C o %C 0 9999 M o %MW 200 9999 L o %MD 100 4998 F o %MF 100 4998

La zona de atribución puede modificarse para cada tipo de variable utilizando la directiva de compilación #SR« tipo »=« principio », « fin » « tipo » designa el tipo de variable; « principio » y « fin », los nuevos límites a utilizar. Esta directiva modifica la atribución de las variables automáticas en cada sitio del folio donde está escrita hasta la siguiente directiva « #SR ».

AUTOMGEN7 25 (C)opyright 2002 IRAI

Page 26

Manual de referencia del lenguaje

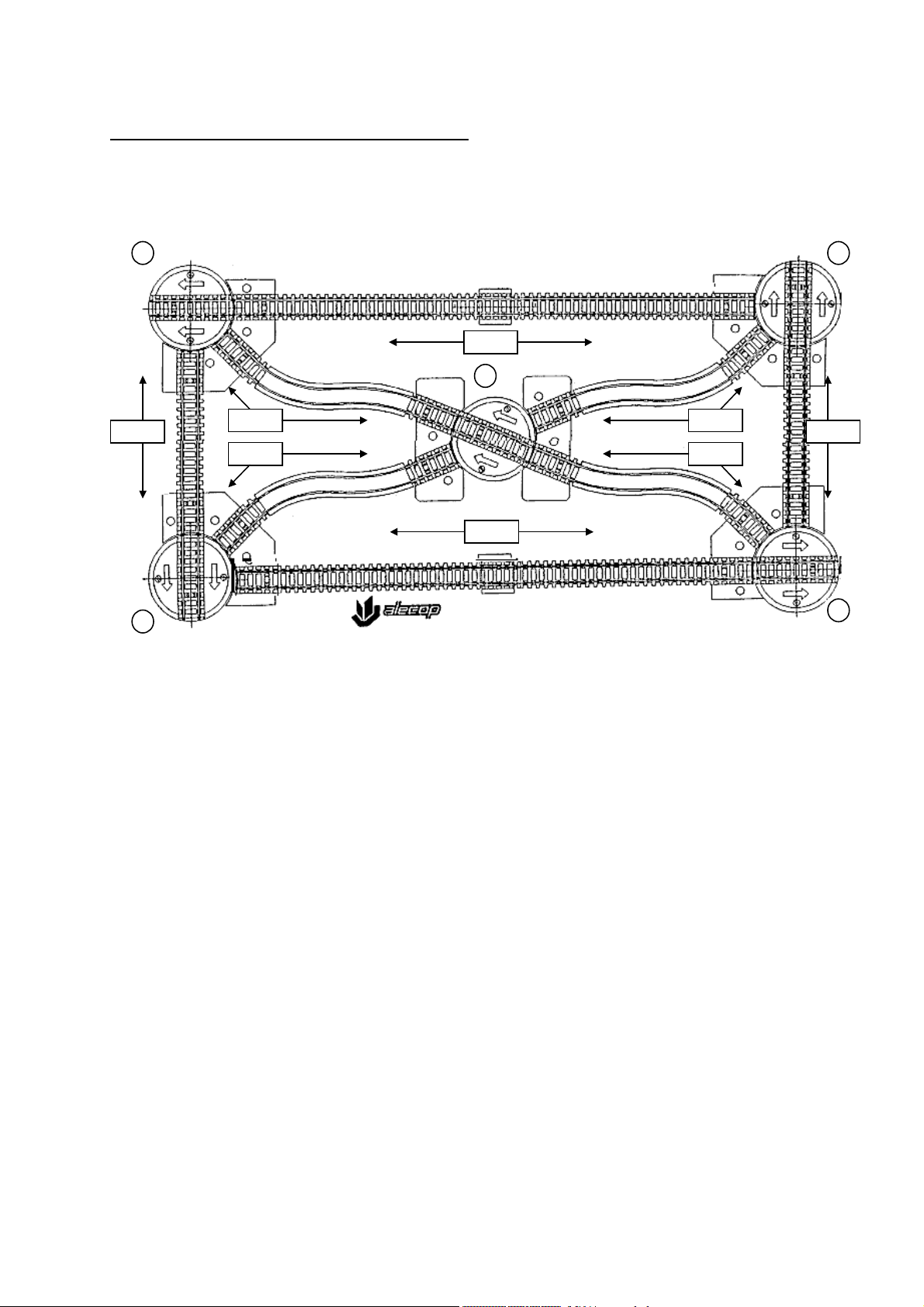
1.5. A propósito de ejemplos

Para ilustrar mejor este manual, hemos desarrollado ejemplos que funcionan con una maqueta de tren cuyo esquema es el siguiente:

1 4

S2A T2A

vía 2 vía 4

S2B T2B

vía 6

vía 7

S7I T7I

S1I T1I

S6I T6I

S3I T3I

MAQUETA AT-850

vía 1

S6D

T6D

S7D T7D

vía 3

S1D T1D

S5D

S5I

T5I

T5D

S4A T4A

vía 5

T8I

S8I

vía 8

S8D T8D

S3D T3D

S4B T4B

Para pilotear esta maqueta hemos utilizado mapas de E/S en PC. Los símbolos definidos por el constructor de la maqueta se han conservado.

AUTOMGEN7 26 (C)opyright 2002 IRAI

Page 27

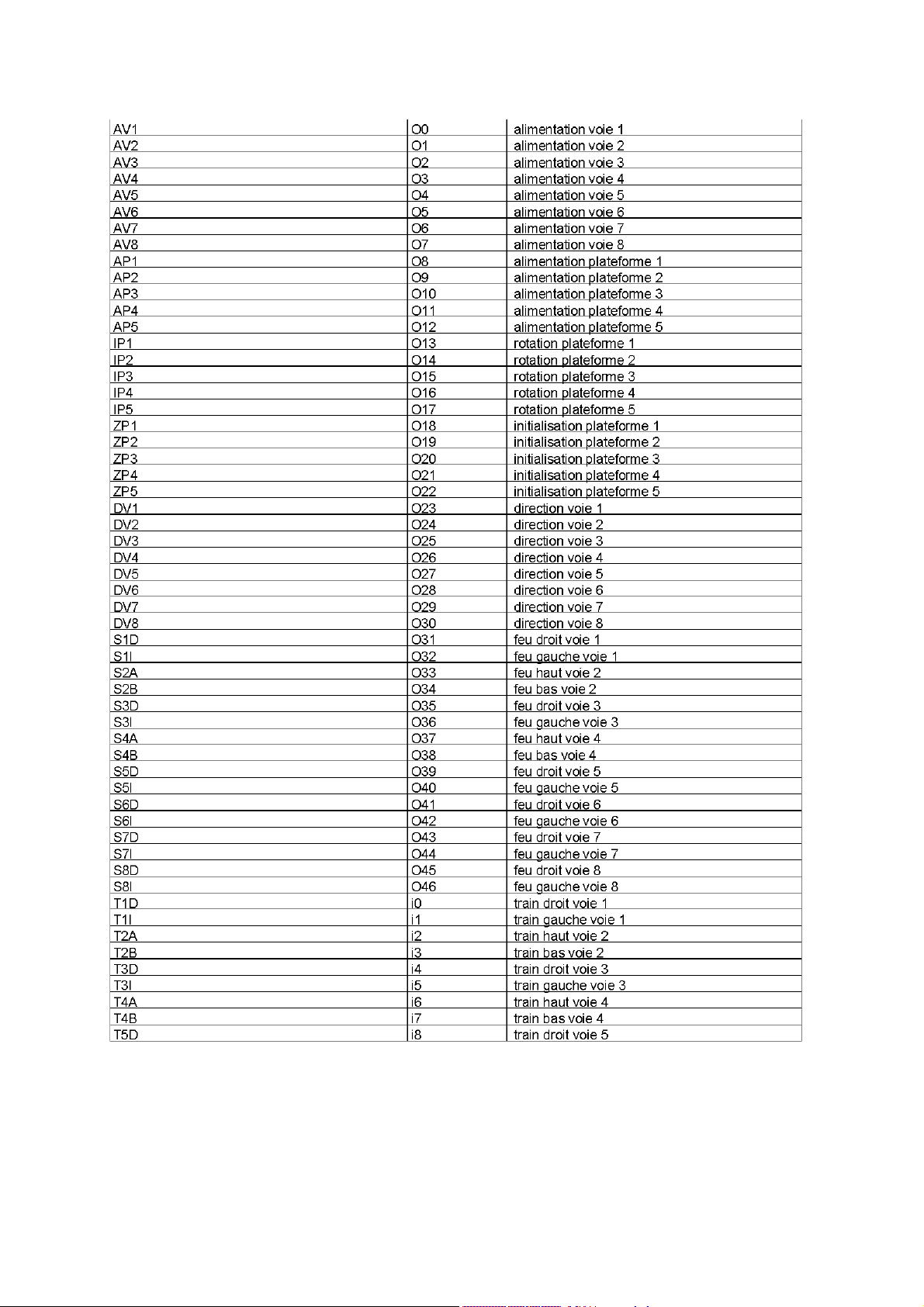
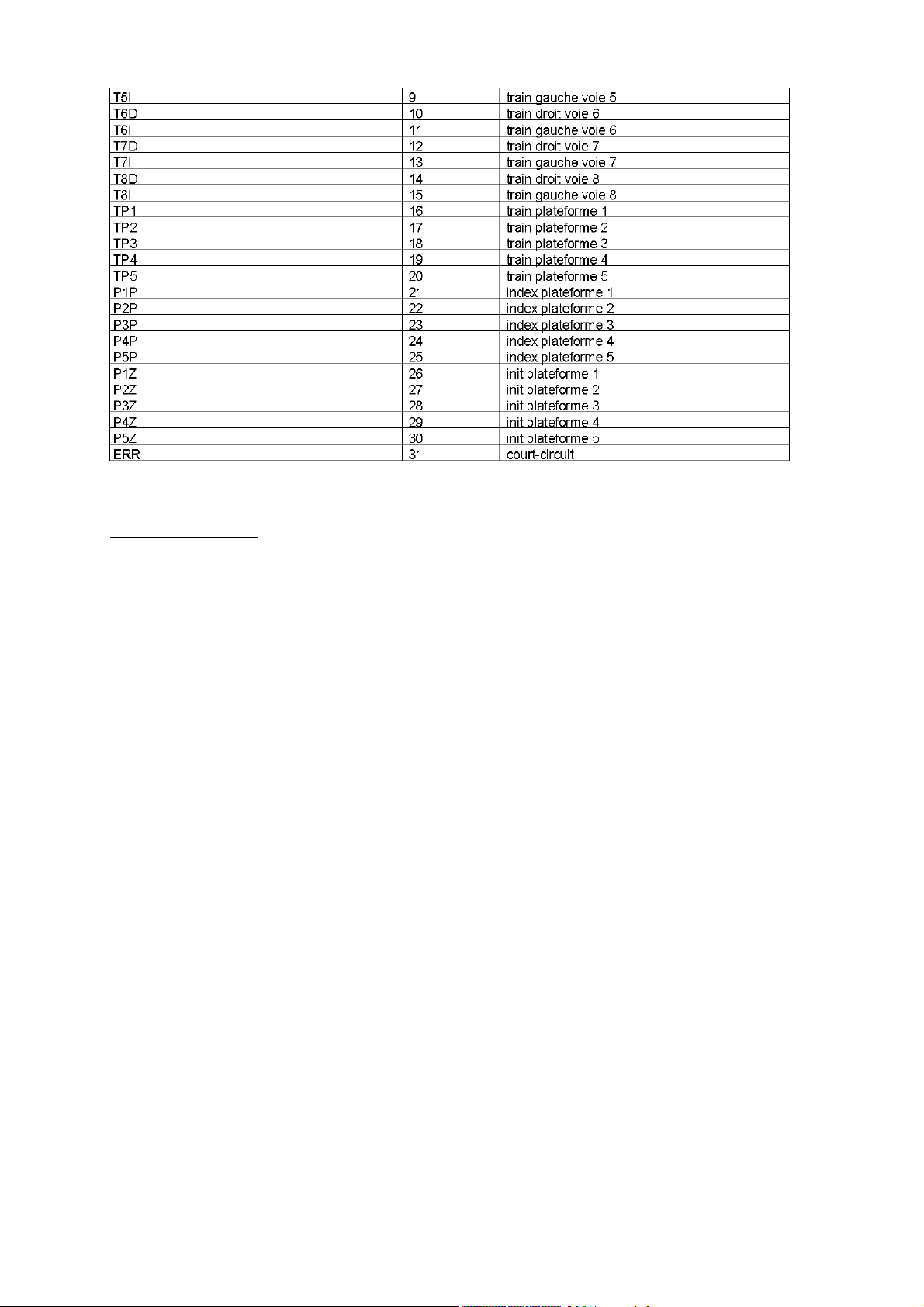
Manual de referencia del lenguaje

Se ha creado el siguiente fichero de símbolos:

AUTOMGEN7 27 (C)opyright 2002 IRAI

Page 28

Manual de referencia del lenguaje

1.6. Grafcet

AUTOMGEN soporta los elementos siguientes:

Ö divergencias y convergencias en « Y » y en « O », Ö etapas pozos y fuentes, Ö transiciones pozos y fuentes, Ö sincronización,

Ö forzados de Grafcets, Ö memorización de Grafcets, Ö fijación, Ö macro-etapas.

1.6.1. Grafcet simple

La escritura de Grafcet en línea se resume a la yuxtaposición de etapas y transiciones. Ilustremos un Grafcet en línea con el ejemplo siguiente: Condiciones: La locomotora debe partir por la vía 3 hacia la derecha, hasta el extremo de la vía. Luego regresa en sentido inverso hasta el otro extremo y vuelve a empezar.

AUTOMGEN7 28 (C)opyright 2002 IRAI

Page 29

Manual de referencia del lenguaje

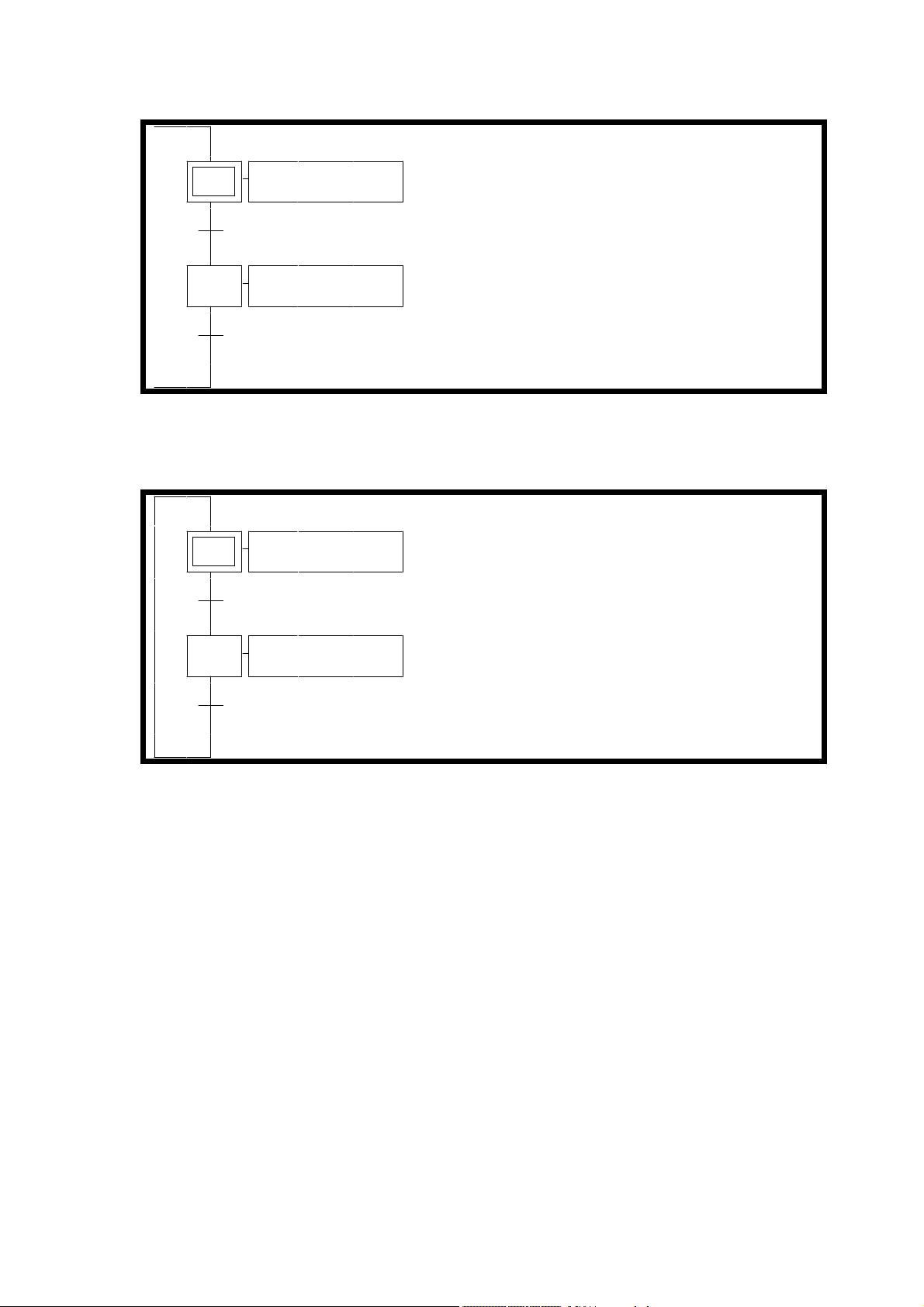
Solución 1:

0AV1

t1d

1 AV1 , DV1

t1i

 exemples\grafcet\simple1.agn

Solución 2:

0 S AV1 ,R DV1

Aller

t1d

1 S AV1 ,S DV1

Retou

t1i

 exemple\grafcet\simple2.agn

La diferencia entre estas dos soluciones reside en el uso de las acciones « Asignación » para el primer ejemplo y de las acciones « Puesta en uno » y « Puesta en cero » para el segundo. Modifiquemos las condiciones con una espera de 10 segundos cuando la locomotora llega a la derecha de la vía 1 y una espera de 4 segundos cuando la locomotora llega a la izquierda de la vía 1.

AUTOMGEN7 29 (C)opyright 2002 IRAI

Page 30

Manual de referencia del lenguaje

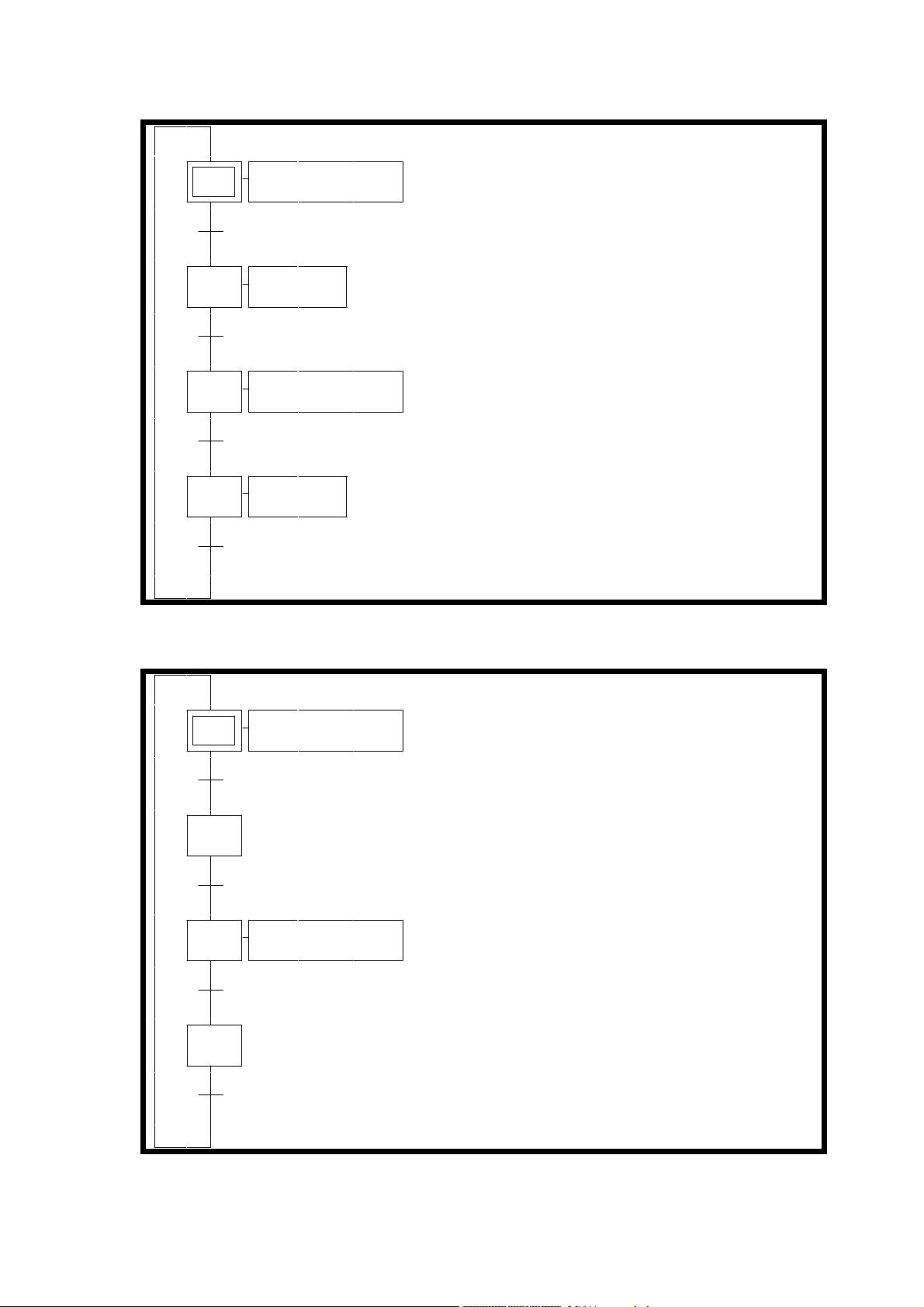
Solución 1:

0 AV1

Aller

t1d

10 T0(10S)

20 AV1 , DV1

Retou

t1i

30 T1(4S)

 exemple\grafcet\simple3.agn Solución 2:

0 AV1

t1d

10s/x10

20 AV1 , DV1

t1i

Aller

Retou

4s/x30

 exemple\grafcet\simple4.agn

AUTOMGEN7 30 (C)opyright 2002 IRAI

Page 31

Manual de referencia del lenguaje

La diferencia entre los ejemplos 3 y 4 reside en la elección de la sintaxis utilizada para definir las temporizaciones. El resultado desde el punto de vista funcional es idéntico.

1.6.2. Divergencia y convergencia en « Y »

Las divergencias en« Y » pueden tener n ramas. Lo importante es respetar la utilización de los bloques de función:

Obligatoirement un bloc [K] et pas un bloc [L]

Obligatoirement un bloc [M] et pas un bloc [L]

Obligatoirement un bloc [O] et pas un bloc [P]

Obligatoirement un bloc [Q] et pas un bloc [P]

Ilustremos la utilización de las divergencias y convergencias en « Y ». Condiciones: Vamos a utilizar dos locomotoras: la primera efectuará idas y vueltas por la vía 1, la segunda por la vía 3. Las dos locomotoras estarán sincronizadas (se esperarán en el extremo de la vía).

AUTOMGEN7 31 (C)opyright 2002 IRAI

Page 32

Manual de referencia del lenguaje

Solución 1:

0 AV1 50 AV3

t1d t3i

10 60

20 AV1 , DV1 70 AV3 , DV3

t1i t3d

30 80

 exemple\grafcet\divergence et 1.agn

AUTOMGEN7 32 (C)opyright 2002 IRAI

Page 33

Manual de referencia del lenguaje

Solución 2:

t1d t3i

0 AV1 10 AV3

t1d . t3i

t1i t3d

20 AV1 , DV1 30 AV3 , DV3

t1i . t3d

 exemple\grafcet\divergence et 2.agn Estas dos soluciones son equivalentes desde el punto de vista funcional. La segunda es una versión más compacta que utiliza acciones condicionadas.

1.6.3. Divergencia y convergencia en « O »

Las divergencias en « O » pueden tener n ramas. Lo importante es respetar la utilización de los bloques de función:

AUTOMGEN7 33 (C)opyright 2002 IRAI

Page 34

Manual de referencia del lenguaje

Las divergencias en « O » deben ramificarse obligatoriamente en vínculos descendentes. Por ejemplo:

incorrecto; el diseño correcto es:

AUTOMGEN7 34 (C)opyright 2002 IRAI

Page 35

Manual de referencia del lenguaje

Si el ancho de la página no permite escribir un gran número de divergencias, se puede adoptar una estructura del tipo:

Veamos un ejemplo para ilustrar la utilización de las divergencias y convergencias en « O »:

Condiciones: Retomemos las condiciones del primer ejemplo del capítulo: ida y vuelva de una locomotora por la vía 1.

Solución:

0 AV1

t1d t1i

ÇÇ

1 S

DV1 2 R DV1

 exemple\grafcet\divergence ou.agn

AUTOMGEN7 35 (C)opyright 2002 IRAI

Page 36

Manual de referencia del lenguaje

Este Grafcet podría resumirse en una etapa utilizando acciones condicionadas, como en este ejemplo:

t1d t1i

ÇÇ

0 AV1 S DV1 R DV1

 exemple\grafcet\action conditionnée.agn

1.6.4. Etapas pozos y fuentes, transiciones pozos y fuentes

Ilustremos estos principios con ejemplos: Condiciones: Tratemos de nuevo el segundo ejemplo de este capítulo: ida y vuelta de una locomotora por la vía 1 con espera al final de la vía. Solución:

0 S AV1

t1d t1i

ÇÇ

10 R AV1 30 R AV1

t0/x10/10s t1/x30/4s

20 S AV1 S DV1 40 S AV1 R DV1

=1 =1

 exemple\grafcet\étapes puits et sources.agn

1.6.5. Acciones múltiples, acciones condicionadas

Ya hemos utilizado en este capítulo acciones múltiples y acciones condicionadas. Detallemos estos dos principios.

AUTOMGEN7 36 (C)opyright 2002 IRAI

Page 37

Manual de referencia del lenguaje

Como se indica en el capítulo sobre el compilador, es posible escribir varias acciones en un mismo rectángulo; en este caso, el carácter « , » (coma) sirve como delimitador.

Cuando una condición se añade a un rectángulo de acción, se condiciona el conjunto de las acciones contenidas en el rectángulo.

Es posible asociar varios rectángulos de acción a una etapa:

Otra posibilidad:

Cada rectángulo puede recibir una condición diferente:

Para diseñar una acción condicionada, ubique el cursor en el rectángulo de acción, haga clic con el botón derecho del ratón y elija « Acción condicional » en el menú.

Para documentar la condición sobre acción, haga clic en el elemento

La sintaxis IF(condición) permite escribir una condición sobre acción en el rectángulo de acción.

AUTOMGEN7 37 (C)opyright 2002 IRAI

Page 38

Manual de referencia del lenguaje

1.6.6. Sincronización

Retomemos un ejemplo ya tratado para ilustrar la sincronización de Grafcets.

Condiciones:

Ida y vuelta de dos locomotoras por las vías 1 y 3 con espera entre las locomotoras en el extremo de la vía.

Este ejemplo se había tratado con una divergencia en « Y ».

Solución 1:

10 AV1 100 AV3

t1d t3i

20 110

x110 x20

30 AV1 , DV1 120 AV3 , DV3

t1i

40 130

x130

 exemple\grafcet\synchro1.agn

t3d

x40

AUTOMGEN7 38 (C)opyright 2002 IRAI

Page 39

Manual de referencia del lenguaje

Solución 2:

10 SX100,SX140

x110.x150

30 SX120,SX160

x130.x170

100 AV1 120 AV1 , DV1 140 AV3 160

t1d t1i t3i

110 130 150 170

x30 x10 x30

AV3 , DV3

t3d

x10

 exemple\grafcet\synchro2.agn

Esta segunda solución es un excelente ejemplo del arte de complicar las cosas más simples con fines pedagógicos.

1.6.7. Forzados de Grafcet

El compilador agrupa las etapas en función de los vínculos establecidos entre ellas. Para designar un Grafcet, es suficiente hacer referencia a una de las etapas que componen ese Grafcet.

Del mismo modo se puede designar el conjunto de Grafcets presentes en un folio mencionando el nombre del folio.

AUTOMGEN7 39 (C)opyright 2002 IRAI

Page 40

Manual de referencia del lenguaje

Por ejemplo:

Para designar este Grafcet hablaremos de Grafcet 200, Grafcet 201 o Grafcet 202. Al ser un conjunto de etapas, el Grafcet se convierte en una variable estructurada compuesta por n etapas; cada etapa puede estar activa o inactiva. Como hemos visto, AUTOMGEN divide las etapas en conjuntos independientes que pueden agruparse, lo cual permite considerarlos como un solo Grafcet. Para agrupar varios Grafcets se debe utilizar la directiva de compilación « #G:g1,g2 » (comando a incluir en un comentario). Este comando agrupa los Grafcets g1 y g2. Recordemos que la designación de un Grafcet se efectúa invocando el número de una de sus etapas. Veamos un ejemplo: #G:105,200 esta directiva de compilación agrupa estos dos Grafcets:

Observación: es posible utilizar varias directivas « #G » para agrupar más de dos Grafcets. Ahora vamos a detallar las órdenes de forzado utilizables. Se escribirán simplemente en rectángulos de acción como asignaciones clásicas. Soportarán tanto los operadores S(puesta en uno), R(puesta en cero), N(asignación complementada) e I(inversión) como las acciones condicionales.

AUTOMGEN7 40 (C)opyright 2002 IRAI

Page 41

Manual de referencia del lenguaje

1.6.7.1. Forzado de un Grafcet según una lista de etapas activas

Sintaxis: « F<Grafcet>:{<lista de etapas activas>} » o

« F/<nombre de folio>:{<lista de etapas activas>} » El o los Grafcets designados se forzarán al estado definido por la lista de etapas activas que se encuentra entre llaves. Si deben estar activas varias etapas, es necesario separarlas con el carácter « , » (coma). Si el o los Grafcets deben forzarse al estado vacío (ninguna etapa activa), no hay que precisar ninguna etapa entre las dos llaves.

El número de etapas puede estar precedido de « X ». Así se puede asociar un símbolo al nombre de una etapa. Ejemplos: « F10:{0} » fuerza todas las etapas del Grafcet 10 a 0 salvo la etapa 0, que se fuerza a 1. « F0:{4,8,9,15} » fuerza todas las etapas del Grafcet 0 a 0, salvo las etapas 4, 8, 9 y 15, que se fuerzan a 1. « F/marcha normal:{} » fuerza todos los Grafcets que se encuentran en el folio « marcha normal » al estado vacío.

1.6.7.2. Memorización del estado de un Grafcet

Estado actual de un Grafcet: Sintaxis: « G<Grafcet>:<N° de bit> » o

« G/<nombre de folio>:<N° de bit> » Este comando memoriza el estado de uno o varios Grafcets en una serie de bits. Es necesario reservar un espacio para almacenar el estado del o de los Grafcets

AUTOMGEN7 41 (C)opyright 2002 IRAI

Page 42

Manual de referencia del lenguaje

designados (un bit por etapa). Estos bits de almacenamiento deben ser consecutivos. Utilice un comando #B para reservar un espacio lineal de bit.

El número de la etapa que designa el Grafcet puede estar precedido de « X ». Así se puede asociar un símbolo al nombre de una etapa. El número del bit puede estar precedido de « U » o de « B ». Así se puede asociar un símbolo al primer bit de la zona de almacenamiento de estado.

Estado particular de un Grafcet: Sintaxis: « G<Grafcet>:<N° de bit> {lista de etapas activas} » o

« G/<nombre de folio>:<N° de bit> {lista de etapas activas} » Este comando memoriza el estado definido por la lista de etapas activas aplicadas a los Grafcets especificados a partir del bit indicado. También aquí es necesario reservar un número suficiente de bits. Si debe memorizarse una situación vacía, no debe aparecer ninguna etapa entre las dos llaves.

El número de las etapas puede estar precedido de « X ». Así se puede asociar un símbolo al nombre de una etapa. El número del bit puede estar precedido de « U » o de « B ». Así se puede asociar un símbolo al primer bit de la zona de almacenamiento de estado. Ejemplos: « G0:100 » memoriza el estado actual del Grafcet 0 a partir de U100. « G0:U200 » memoriza el estado vacío del Grafcet 0 a partir de U200. « G10:150{1,2} » memoriza el estado del Grafcet 10, en el que sólo las etapas 1 y 2 están activas, a partir de U150. « G/PRODUCCIÓN:_ GUARDAR ESTADO PRODUCCIÓN _ » memoriza el estado de los Grafcets que se encuentran en el folio « PRODUCCIÓN » en la variable _GUARDAR ESTADO PRODUCCIÓN_.

AUTOMGEN7 42 (C)opyright 2002 IRAI

Page 43

Manual de referencia del lenguaje

1.6.7.3. Forzado de un Grafcet a partir de un estado memorizado

Sintaxis: « F<Grafcet>:<N° de bit> » o

« F/<Nombre de folio>:<N° de bit> »

Fuerza el o los Grafcets con el estado memorizado a partir del bit precisado. El número de la etapa que designa el Grafcet puede estar precedido de ‘X’. Así se puede asociar un símbolo al nombre de una etapa. El número del bit puede estar precedido de « U » o de « B ». Así se puede asociar un símbolo al primer bit de la zona de almacenamiento de estado. Ejemplo: « G0:100 » memoriza el estado actual del Grafcet 0 « F0:100 » restaura ese estado

1.6.7.4. Fijación de un Grafcet

Sintaxis: « F<Grafcet> » o

« F/<Nombre de folio> » Fija uno o varios Grafcets: impide su evolución. Ejemplo: « F100 » fija el Grafcet 100 « F/producción » fija los Grafcets contenidos en el folio « producción » Ilustremos los forzados con un ejemplo.

AUTOMGEN7 43 (C)opyright 2002 IRAI

Page 44

Manual de referencia del lenguaje

Condiciones: Retomemos un ejemplo ya tratado: ida y vuelta de dos locomotoras por las vías 1 y 3 (esta vez sin espera entre las locomotoras). Añadamos una parada de urgencia. Cuando se detecta la parada de urgencia, todas las salidas se ponen en cero. Al desaparecer la parada de urgencia, el programa debe reanudar el recorrido desde donde se detuvo.

AUTOMGEN7 44 (C)opyright 2002 IRAI

Page 45

Manual de referencia del lenguaje

Solución 1:

#B104 réserve 4 bits pour la mémorisation de l'état des Grafcet

locomotive 1 locomotive 2

10 AV1 30 AV3

t1d t3i

20 AV1 , DV1 40 AV3 , DV3

t1i t3d

gestion de l'arrêt d'urgence

1000

arret urgence

1010 G10:100,G30:102

1020 F10:{},F30:{}

arret urgence

1030 F10:100,F30:102

 exemple\grafcet\forçage1.agn

La utilización de la directiva #B104 permite reservar cuatro bits consecutivos (U100 a U103) para memorizar el estado de los dos Grafcets.

AUTOMGEN7 45 (C)opyright 2002 IRAI

Page 46

Manual de referencia del lenguaje

« _parada urgencia_ » ha sido asociado a un bit (U1000). Por lo tanto su estado puede modificarse desde el entorno posicionándose encima y haciendo clic cuando la visualización dinámica está activada.

AUTOMGEN7 46 (C)opyright 2002 IRAI

Page 47

Manual de referencia del lenguaje

Solución 2:

#B104 réserve 4 bits pour la mémorisation de l'état des Grafcet

locomotive 1 locomotive 2

10 AV1 30 AV3

t1d t3i

20 AV1 , DV1 40 AV3 , DV3

t1i t3d

#G:10,30

gestion de l'arrêt d'urgence

1000

arret urgence

1010 G10:100

1020 F10:{}

arret urgence

1030 F10:100

 exemple\grafcet\forçage2.agn

AUTOMGEN7 47 (C)opyright 2002 IRAI

Page 48

Manual de referencia del lenguaje

Esta segunda solución muestra la utilización de la directiva de compilación « #G » que permite agrupar los Grafcets para los comandos de forzado.

1.6.8. Macro-etapas

AUTOMGEN implementa las macro-etapas. A propósito de este tema recordemos que: Una macro-etapa ME es la única representación de un conjunto único de etapas y transiciones llamado « expansión de ME ». Una macro-etapa obedece a las reglas siguientes:

Ö la expansión de ME implica una etapa particular llamada etapa de entrada y una

etapa particular llamada etapa de salida.

Ö la etapa de entrada tiene la propiedad siguiente: si superamos una transición

anterior a la macro-etapa, se activa la etapa de entrada de su expansión.

Ö la etapa de salida tiene la propiedad siguiente: participa de la validación de las

transiciones posteriores a la macro-etapa.

Ö fuera de las transiciones anteriores y posteriores a ME, no existe ningún vínculo

estructural entre, por una parte, una etapa o una transición de la expansión ME y, por otra, una etapa o una transición que no pertenece a ME.

La utilización de las macro-etapas en AUTOMGEN se define así:

Ö la expansión de una macro-etapa es un Grafcet en un folio distinto, Ö la etapa de entrada de la expansión de una macro-etapa deberá llevar el número

0 o la identificación Exxx (xxx = un número cualquiera),

Ö la etapa de salida de la expansión de una macro-etapa deberá llevar el número

9999 o la identificación Sxxx (xxx = un número cualquiera),

Ö fuera de estas dos últimas obligaciones, la expansión de una macro-etapa puede

ser un Grafcet cualquiera y como tal puede contener macro-etapas (la imbricación de macro-etapas es posible).

1.6.8.1. Cómo definir una macro-etapa

Debe utilizarse el símbolo . Para colocar este símbolo, haga clic en un sitio vacío del folio y elija « Más …/Macro-etapa » en el menú contextual. Para abrir el menú contextual, haga clic con el botón derecho del ratón sobre el fondo del folio.

AUTOMGEN7 48 (C)opyright 2002 IRAI

Page 49

Manual de referencia del lenguaje

Para definir la expansión de la macro-etapa, cree un folio, diseñe la expansión y modifique las propiedades del folio (haciendo clic con el botón derecho del ratón en el nombre del folio en el explorador). Ajuste el tipo de folio en « Expansión de macroetapas » y el número de la macro-etapa.

En modo ejecución, es posible visualizar una expansión de macro-etapa. Para ello, es necesario ubicar el cursor sobre la macro-etapa y hacer clic con el botón izquierdo del ratón.

Observaciones:

Ö las etapas y los bits Usuario utilizados en una expansión de macro-etapa son

locales, es decir que no tienen ninguna relación con las etapas y los bits de otros Grafcets. Los otros tipos de variables no presentan esta característica: son comunes a todos los niveles.

Ö si una zona de bits debe utilizarse de manera global, es necesario declararla con

la directiva de compilación « #B ».

Ö la asignación de variables no locales por diferentes niveles o diferentes

expansiones no es gestionada por el sistema. En otros términos, es necesario utilizar las asignaciones « S » « R » o « I » para garantizar un funcionamiento coherente del sistema.

Ilustremos la utilización de las macro-etapas con un ejemplo ya tratado: ida y vuelta de una locomotora por la vía 1 con espera en el extremo de la vía. Descompondremos la ida y la vuelta en dos macro-etapas distintas.

AUTOMGEN7 49 (C)opyright 2002 IRAI

Page 50

Manual de referencia del lenguaje

Solución:

macro-étape aller voie

10 S AV1 ,R DV1

t1d

20 R AV1

t0/x20/10s

macro-étape retour voie

10 S AV1 ,S DV1

t1i

20 R AV1

t1/x20/4s

AUTOMGEN7 50 (C)opyright 2002 IRAI

Page 51

Manual de referencia del lenguaje

 exemple\grafcet\macro-étape.agn

1.6.9. Contadores

Ilustremos la utilización de los contadores con un ejemplo. Condiciones: Una locomotora debe efectuar 10 idas y vueltas por la vía 1, inmovilizarse durante quince segundos y volver a arrancar.

AUTOMGEN7 51 (C)opyright 2002 IRAI

Page 52

Manual de referencia del lenguaje

Solución:

3 +C0

RC0

AV1

t1d

AV1 , DV1

t1i

c0<10 c0=10

15s/x4

 exemple\grafcet\compteur.agn

1.7. Gemma

AUTOMGEN implementa la descripción de Grafcet de gestión de los modos de marcha bajo forma de Gemma. El principio es un modo de edición transparente al modo Grafcet. Es posible pasar del modo de edición Grafcet al modo de edición Gemma. La traducción de un Gemma en Grafcet de gestión de modos de marcha es automático e inmediato. El comando « Editar bajo la forma de un Gemma » del menú « Caja de herramientas » permite pasar de un modo al otro.

AUTOMGEN7 52 (C)opyright 2002 IRAI

Page 53

Manual de referencia del lenguaje

ArrÛ

_ _

P.C. HORS

ENERGIE

remise en route

arrêt

mise en ou hors service

fonctionnement normal

is et vérifications

essa

P.C. HORS

ENERGIE

6 <Mise P.O. dans état initial>

AV1_,_D V1_

ramÞne la locomotive Ó

gauche

5 <Préparation pour remise en

route après défaillance>

rien pour l'instant

_arret urgence_

D1 <Marche ou arrêt en vue d'assurer la sécurit é>

F_GFN_:{}

RAZ du Grafcet de prod uction

r r ê t d a n s é t a t i n i t i a l

V O Y A N T I N I T

7 < Mise P.O. dans état

déterminé>

D2 <Diagnostic et/ou

traitement de

défaillance>

1 <Arrêt dans état initial>

fin de cycle obtenu_

PRODUCTION

2 <Arrêt

demandé en

fin de

cycle>

Grafcet de

production

D3 <Produc tion tout de mêm e>

PRODUCTION

VOYANT INIT_

t dans Útat initial

4 <Arrêt obtenu>

FIN_

t du

_depart cycle_

F2 <Marches de

préparation>

F3 < Marches de

clôture>

3 <Arrêt

demandé

dans état

déterminé>

F1 <Produc tion normale>

i n d e cy cl

DEPART_

Lancement du Grafcet de productio

ar re t

fonctionnement normal

ur g e

PRODUCTION

F4 <Marc

hes de vérification

dans l

e désordre>

F5 <Marc

hes de vérification

dans l'

ordre>

F6 <Marches de test>

is et vérifications

essa

# L " g e m m a 2 "

d e p a r t c y c l e

f i n d e c y c l e

A r r ê t d u G r a f c e t d e p r o d u c t i o n

2 F I N

f i n d e c y c l e o b t e n u

a n c e m e n t d u G r a f c e t d e p r o d u c t i o

D E P A R T

g e m m a 1 . g r 7

e x e m p l e d e l a n o t i c e d ' A U T O M G E N

( C ) o p y r i g h t 1 9 9 7 I R A I

0 5 / 0 3 / 1 9 9 4

R A Z d u G r a f c e t d e p r o d u c t i o n

5 F G F N : { }

a r r e t u r g e n c e

r i e n p o u r l ' i n s t a n t

= 1

r a m è n e l a l o c o m o t i v e à g a u c h e

7 A V 1 , D V 1

t 1 i

AUTOMGEN7 53 (C)opyright 2002 IRAI

Page 54

Manual de referencia del lenguaje

1.7.1. Creación de un Gemma

Para crear un Gemma:

Ö haga clic en el elemento « Folio » del explorador con el botón derecho del ratón y

seleccione el comando « Añadir un nuevo folio »,

Ö en la lista de tamaños elija « Gemma », Ö haga clic en el pulsador « OK », Ö haga clic con el botón derecho del ratón en el nombre del folio creado en el

explorador,

Ö elija « Propiedades » en el menú, Ö pinche la opción « Mostrar bajo la forma de un Gemma ».

La ventana contiene un Gemma en el que todos los rectángulos y vínculos están sombreados. Para validar un rectángulo o un vínculo hay que posicionarse encima y hacer clic con el botón derecho del ratón. Para modificar el contenido de un rectángulo o la naturaleza de un vínculo hay que posicionarse encima y hacer clic con el botón izquierdo del ratón. El contenido de los rectángulos del Gemma se ubicará en los rectángulos de acción del Grafcet. La naturaleza de los vínculos se ubicará en las transiciones del Grafcet. A cada rectángulo del Gemma puede asociarse un comentario, que aparecerá cerca del rectángulo de acción correspondiente en el Grafcet.

1.7.2. Contenido de los rectángulos del Gemma

Los rectángulos del Gemma pueden recibir cualquier acción utilizable en el Grafcet. Como se trata de definir una estructura de gestión de los modos de parada y de marcha, es conveniente utilizar órdenes de forzado hacia Grafcets de nivel más bajo; ver el capítulo 1.6.7. Forzados de Grafcet.

1.7.3. Obtener un Grafcet correspondiente

Una vez más, la opción « Mostrar bajo la forma de un Gemma » en las propiedades del folio permite volver a una representación Grafcet. Es posible volver en cualquier momento a una representación Gemma mientras la estructura del Grafcet no se modifique. Las transiciones, el contenido de los rectángulos de acción y los comentarios pueden modificarse con una actualización automática del Gemma.

AUTOMGEN7 54 (C)opyright 2002 IRAI

Page 55

Manual de referencia del lenguaje

1.7.4. Anular los espacios vacíos en el Grafcet

Es posible que el Grafcet obtenido ocupe más espacio del necesario en la página. El comando « Reorganizar la página » del menú « Herramientas » permite suprimir todos los espacios no utilizados.

1.7.5. Imprimir el Gemma

Cuando la edición está en modo Gemma, el comando « Imprimir » permite imprimir el Gemma.

1.7.6. Exportar el Gemma

El comando « Copiar en formato EMF » del menú « Edición » permite exportar un Gemma en formato vectorial.

1.7.7. Ejemplo de Gemma

Ilustremos la utilización del Gemma. Condiciones: Imaginemos un escritorio compuesto por los pulsadores « inicio ciclo », « fin de ciclo » y « parada de urgencia » y el testigo « INIT ». El propósito del programa principal será hacer efectuar idas y vueltas a una locomotora por la vía 1.

AUTOMGEN7 55 (C)opyright 2002 IRAI

Page 56

Manual de referencia del lenguaje

Solución:

P.C. HORS

ENERGIE

remise en rout e arrêt mise en ou hors servic e

fonc tionnement nor mal

essais et v érificat ions

P.C. HORS

ENERGIE

A6 <Mise P.O. dans état init ial>

_AV1_,_DV1_ ramÞne la locomotiv e Ó gauche

A7 <Mise P.O. dans état

déterminé>

A5 <Préparat ion pour remise en

route après défaillance >

rien pour l'ins tant

/_arret urgence_

D2 <Diagnost ic et/ou

traite ment de défai llance>

D1 <Marche ou arrêt en v ue d'ass urer la sécurit é>

F_GFN_:{} RAZ du Graf cet de produc tion

_t1i_

A1 <Arrêt dans état init ial>

_VOY ANT INIT_ ArrÛt dans Útat initial

_fin de cycle obtenu_

A4 <Arrêt obtenu>

PRODUC TION

A2 <Arrêt

demandé en fi n de cycle> _FIN_ ArrÛt du Grafc et de productio n

D3 <Product ion tout de même>

PRODUC TION PRODUC TION

A3 <Arrêt

demandé dans état déterminé>

_depart cy cle_

F2 <Marches de

préparation>

F1 <Produc tion normale>

_DEPART_ Lancement du Grafcet de productio

_fin de cycle_

_arret urgence_

fonc tionnement nor mal

F3 <Marches de

clôture>

F4 <Marches de vérif ication

dans le désordre>

F5 <Marches de vérif ication

dans l'ordr e>

F6 <Marches de test>

essais et v érificat ions

AUTOMGEN7 56 (C)opyright 2002 IRAI

Page 57

Manual de referencia del lenguaje

Arrêt dans état initial

0 VOYANT INIT

depart cycle

Lancement du Grafcet de produ ctio

1 DEPART

RAZ du Grafcet de production

fin de cycle 5FGFN:{}

Arrêt du Grafcet de productio n

2FIN

fin de cycle obtenu

arret urgence

22 F5:(5)

(editado bajo la forma de un Grafcet)

rien pour l'instant

ramène la locomotive à gauche

7 AV1,DV1

t1i

AUTOMGEN7 57 (C)opyright 2002 IRAI

Page 58

Manual de referencia del lenguaje

depart

100 AV1

t1d

110 AV1 , DV1

t1i . fin t1i . fin

120 FIN DE CYCLE OBTENU

fin de cycle obtenu

 exemple\gemma\gemma.agn

1.8. Ladder

El lenguaje Ladder, también llamado « esquema de contacto », permite describir gráficamente ecuaciones booleanas. Para realizar una función lógica « Y », es necesario escribir contactos en serie. Para realizar una función « O », es necesario escribir contactos en paralelo.

Función « Y »

Función « O » El contenido de los contactos debe respetar la sintaxis definida para los tests y detallada en el capítulo « Elementos comunes » de este manual.

AUTOMGEN7 58 (C)opyright 2002 IRAI

Page 59

Manual de referencia del lenguaje

El contenido de las bobinas debe respetar la sintaxis definida para las acciones y detallada en el capítulo « Elementos comunes » de este manual.

1.8.1. Ejemplo de Ladder

Empecemos con el ejemplo más simple. Condiciones: Ida y vuelta de una locomotora por la vía 1.

Solución 1:

AV1

t1i R DV1

t1d S DV1

 exemple\ladder\ladder1.agn

Solución 2:

AV1

t1i dv1 DV1

t1d

 exemple\ladder\ladder2.agn

La segunda solución es idéntica desde el punto de vista funcional. Su interés es mostrar la utilización de una variable en auto mantenimiento.

Enriquezcamos nuestro ejemplo. Condiciones: La locomotora deberá detenerse 10 segundos a la derecha de la vía 1 y 4 segundos a la izquierda.

AUTOMGEN7 59 (C)opyright 2002 IRAI

Page 60

Manual de referencia del lenguaje

Solución:

t1d T0(10S)

S DV1

t1i T1(4S)

R DV1

t1i t1d AV1

 exemple\ladder\ladder3.agn

Un último ejemplo un poco más complejo. Condiciones: Siempre una locomotora que va y viene por la vía 1. Cada 10 idas y vueltas deberá marcar un tiempo de parada de 15 segundos.

Solución:

b0 RC0

t1d

t1i RDV1

c0<10 AV1

c0=10 T0(15S)

dv1 +C0

SDV1

 exemple\ladder\ladder4.agn

1.9. Logigrama

AUTOMGEN implementa el lenguaje logigrama de la siguiente manera:

AUTOMGEN7 60 (C)opyright 2002 IRAI

Page 61

Manual de referencia del lenguaje

Ö utilización de un bloque especial llamado « bloque de asignación »; este bloque

separa la zona de acción de la zona test, tiene esta forma y está asociado a la tecla [0] (cero),

Ö utilización de las funciones « No », « Y » y « O », Ö utilización de rectángulos de acción a la derecha del bloque de acción.

El lenguaje logigrama permite escribir gráficamente ecuaciones booleanas. El contenido de los tests debe respetar la sintaxis definida en el capítulo « Elementos comunes » de este manual. El contenido de los rectángulos de acción debe respetar la sintaxis definida para las acciones y detallada en el capítulo « Elementos comunes » de este manual.

Zone « test »

Bloc

d’affectation

pour délimiter la

zone test de la

zone action

Zone « action »

1.9.1. Diseño de los logigramas

1.9.1.1. Número de entradas de las funciones « Y » y « O »

Las funciones « Y » y « O » se componen respectivamente de un bloque (tecla

[2]) o de un bloque

(tecla [3]), eventualmente de bloques (tecla [4]) para

añadir entradas a los bloques, y por último de un bloque (tecla [5]). Las funciones « Y » y « O » implican pues un mínimo de dos entradas.

AUTOMGEN7 61 (C)opyright 2002 IRAI

Page 62

Manual de referencia del lenguaje

1.9.1.2. Encadenamiento de las funciones

Las funciones pueden encadenarse.

1.9.1.3. Acciones múltiples

Es posible asociar varios rectángulos de acción a un logigrama después del bloque de asignación.

1.9.2. Ejemplo de logigrama

Empecemos con el ejemplo más simple. Condiciones: Ida y vuelta de una locomotora por la vía 1. Solución 1:

=1 AV1

t1d S DV1

t1i R DV1

 exemple\logigramme\logigramme1.agn

AUTOMGEN7 62 (C)opyright 2002 IRAI

Page 63

Manual de referencia del lenguaje

Solución 2:

=1 AV1

t1d DV1

dv1 &

t1i O

 exemple\logigramme\logigramme2.agn

La segunda solución es idéntica desde el punto de vista funcional. Su interés es consiste en mostrar la utilización de una variable en auto mantenimiento.

Enriquezcamos nuestro ejemplo. Condiciones: La locomotora deberá detenerse 10 segundos a la derecha de la vía 1 y 4 segundos a la izquierda.

Solución:

t1d T0(10S)

SDV1

t1i T1(4S)

RDV1

t0 AV1

 exemple\logigramme\logigramme3.agn Cabe notar la repetición del bloque « Y » de la parte inferior del ejemplo en las entradas « _t1d_ » y « _t1i_ ». Esto evita tener que escribir por segunda vez estos dos tests. Un último ejemplo un poco más complejo.

AUTOMGEN7 63 (C)opyright 2002 IRAI

Page 64

Manual de referencia del lenguaje

Condiciones: Siempre una locomotora que va y viene por la vía 1. Cada 10 idas y vueltas deberá marcar un tiempo de parada de 15 segundos.

Solución:

b0 RC0

t1d & +C0

dv1 O S DV1

t1i R DV1

c0<10 AV1

c0=10 T0(15S)

 exemple\logigramme\logigramme4.agn

AUTOMGEN7 64 (C)opyright 2002 IRAI

Page 65

Manual de referencia del lenguaje

1.10. Lenguajes literales

Este capítulo describe la utilización de las tres formas de lenguaje literal disponibles en AUTOMGEN:

Ö lenguaje literal bajo nivel, Ö lenguaje literal extendido, Ö lenguaje literal ST de la norma CEI 1131-3.

1.10.1. Cómo utilizar el lenguaje literal

El lenguaje literal puede utilizarse bajo la forma siguiente:

Ö archivo de código asociado a una acción (Grafcet, Ladder, logigrama), Ö caja de código asociada a una acción (Grafcet, logigrama), Ö código literal en un rectángulo de acción o una bobina (Grafcet, Ladder,

logigrama),

Ö caja de código utilizada bajo forma de organigrama (consultar el capítulo

« Organigrama »),

Ö archivo de código que rige el funcionamiento de un bloque funcional (consultar el

capítulo « Bloques funcionales »),

Ö archivo de código que rige el funcionamiento de una macro-instrucción; ver el

capítulo 1.10.4. Macro-instrucción.

1.10.1.1. Caja de código asociada a una etapa o un logigrama

Una caja de código asociada a una acción permite escribir algunas líneas de lenguaje literal en una página de la aplicación.

Ejemplos:

AUTOMGEN7 65 (C)opyright 2002 IRAI

Page 66

Manual de referencia del lenguaje

El código utilizado es escrutado mientras la acción es verdadera. Es posible utilizar conjuntamente rectángulos de acción y cajas de código.

Ejemplo:

1.10.1.2. Código literal en un rectángulo de acción o una bobina

Los caracteres « { » y « } » permiten insertar instrucciones en lenguaje literal directamente en un rectángulo de acción (lenguajes Grafcet y logigrama) o una bobina (lenguaje ladder). El carácter « , » (coma) se utiliza como separador si entre « { » y « } » hay varias instrucciones. Este tipo de inserción puede utilizarse con órdenes condicionadas.

Ejemplos:

1.10.2. Definición de una caja de código

Para diseñar una caja de código siga las etapas siguientes:

Ö haga clic con el botón derecho del ratón en un sitio vacío del folio, Ö elija en el menú « Más … / Caja de código »,

AUTOMGEN7 66 (C)opyright 2002 IRAI

Page 67

Manual de referencia del lenguaje

Ö haga clic sobre el borde de la caja de código para modificar su contenido.

Para salir de la caja después de modificarla utilice la tecla [Enter] o haga clic en el exterior.

1.10.3. El lenguaje literal bajo nivel

Este capítulo detalla la utilización del lenguaje literal bajo nivel. Este lenguaje es un código intermedio entre los lenguajes evolucionados Grafcet, logigrama, ladder, organigrama, bloques funcionales, literal extendido, literal ST y los lenguajes ejecutables. También se conoce con el nombre de código pivote. Los postprocesadores traducen el lenguaje literal bajo nivel en código ejecutable para PC, autómata o tarjeta con microprocesador. El lenguaje literal también puede utilizarse en una aplicación para efectuar diversos tratamientos booleanos, numéricos o algorítmicos. El lenguaje literal bajo nivel es un lenguaje de tipo ensamblador. Utiliza una noción de acumulador para los tratamientos numéricos. El lenguaje literal extendido y el lenguaje literal ST descritos en los capítulos siguientes ofrecen una alternativa simplificada y de más alto nivel para escribir programas en lenguaje literal. Sintaxis general de una línea de lenguaje literal bajo nivel: «acción » [[ [« Test »] « Test » ]...] Las acciones y los tests del lenguaje literal bajo nivel están representados por mnemónicos compuestos de tres caracteres alfabéticos. Cada instrucción va seguida de una expresión: variable, constante, etc... Una línea se compone de una sola acción y eventualmente de un test. Si una línea contiene únicamente una acción, la instrucción se ejecutará siempre, por convención.

1.10.3.1. Variables

Las variables utilizables son las mismas que las definidas en el capítulo « Elementos comunes ».

AUTOMGEN7 67 (C)opyright 2002 IRAI

Page 68

Manual de referencia del lenguaje

1.10.3.2. Acumuladores

Ciertas instrucciones utilizan la noción de acumulador. Los acumuladores son registros internos del sistema que ejecuta el programa final y permiten acumular valores temporalmente. Existen tres acumuladores: un acumulador entero 16 bits llamado AAA, un acumulador entero 32 bits llamado AAL y un acumulador flotante llamado AAF.

1.10.3.3. Banderas

Las banderas son variables booleanas posicionadas en función del resultado de las operaciones numéricas. Las cuatro banderas que permiten testear el resultado de un cálculo son:

Ö indicador de retención C: indica si una operación ha generado una retención (1) o

no (0),

Ö indicador de cero Z: indica si una operación ha generado un resultado nulo (1) o

no (0),

Ö indicador de signo S: indica si una operación ha generado un resultado negativo

(1) o positivo (0),

Ö indicador de exceso O: indica si una operación ha generado un exceso de

capacidad (1).

1.10.3.4. Modos de direccionamiento

El lenguaje literal bajo nivel posee 5 modos de direccionamiento. Un modo de direccionamiento es una característica asociada a cada una de las instrucciones del lenguaje literal. Los modos de direccionamiento utilizables son:

TIPO SINTAXIS EJEMPLO

Inmediato 16 bits {constante} 100 Inmediato 32 bits {constante}L 100000L Inmediato flotante {constante}R 3.14R Absoluto {variable} {identificación de variable} O540 Acumulador 16 bits AAA AAA Acumulador 32 bits AAL AAL

AUTOMGEN7 68 (C)opyright 2002 IRAI

Page 69

Manual de referencia del lenguaje

Acumulador flotante AAF AAF Indirecto {variable}{(identificación de palabra)} O(220) Label :{nombre de label}: :bucle:

Una instrucción posee dos características: el tipo de variable y el modo de direccionamiento. Una instrucción puede soportar o no ciertos modos de direccionamiento o ciertos tipos de variables. Por ejemplo, hay instrucciones que se aplican únicamente a palabras, y no a otros tipos de variables.

Observación: Las variables X y U no pueden asociarse a un direccionamiento indirecto debido a la no linealidad de sus asignaciones. Si es necesario acceder a una tabla de variables U, habrá que utilizar una directiva de compilación #B para declarar una tabla de bits lineales.

1.10.3.5. Tests

Los tests que pueden asociarse a las instrucciones se componen de un mnemónico, un tipo de test y una variable. Los mnemónicos de tests permiten definir tests combinatorios de varias variables (y, o). Si un test está compuesto por una sola variable, de todas maneras debe asociarse un operador AND. Existen solamente tres mnemónicos de test: AND y ORR o EOR fin de o He aquí algunos ejemplos de equivalencias entre ecuaciones booleanas y lenguaje literal bajo nivel:

o0=i1 : and i1

o0=i1.i2 : and i1 and i2

o0=i1+i2 : orr i1 eor i2

o0=i1+i2+i3+i4 : orr i1 orr i2 orr i3 eor i4

o0=(i1+i2).(i3+i4) : orr i1 eor i2 orr i3 eor i4

o0=i1.(i2+i3+i4) : and i1 orr i2 orr i3 eor i4

o0=(i1.i2)+(i3.i4) ; imposible traducir directamente,

; hay que utilizar

; variables intermedias:

AUTOMGEN7 69 (C)opyright 2002 IRAI

Page 70

Manual de referencia del lenguaje

equ u100 and i1 and i2

equ u101 and i3 and i4

equ o0 orr u100 eor u101

Los modificadores de tests permiten testear cosas que no son simplemente el estado verdadero de una variable:

Ö / no Ö # frente ascendente Ö * frente descendente Ö @ estado inmediato

Observaciones:

Ö las variables booleanas se actualizan después de cada ciclo de ejecución. En

otros términos, si durante un ciclo una variable binaria se posiciona en un estado, su nuevo estado será realmente reconocido en el ciclo siguiente. El modificador de test @ permite obtener el estado real de una variable booleana sin esperar el ciclo siguiente.

Ö los modificadores de tests no son utilizables con los tests numéricos.

Ejemplos:

set o100

equ o0 and @o100 ; test verdadero desde el primer ciclo

equ o1 and o100 ; test verdadero en el segundo ciclo

Para los tests, hay sólo dos modos de direccionamiento disponibles: el modo absoluto y el modo indirecto. Hay un test de contadores, palabras, largos y flotantes:

Sintaxis:

« {variable} {=, !, <, >, << , >>} {constante o variable} »

= significa igual, ! significa diferente, < significa menor sin signo, > significa mayor sin signo,

AUTOMGEN7 70 (C)opyright 2002 IRAI

Page 71

Manual de referencia del lenguaje

<< significa menor con signo, >> significa mayor con signo, Las constantes están predeterminadas en decimal. Los sufijos « $ » y « % » permiten escribirlas en hexadecimal o en binario. Las comillas permiten escribirlas en ASCII. Las constantes 32 bits deben estar seguidas del carácter « L ». Las constantes reales deben estar seguidas del carácter « R ». Una palabra o un contador puede compararse con una palabra, un contador o una constante 16 bits. Un largo puede compararse con un largo o una constante 32 bits. Un flotante puede compararse con un flotante o una constante real.

Ejemplos:

and c0>100 and m225=10

orr m200=m201 eor m202=m203 and f100=f101 and f200<f203

orr m200<<-100 eor m200>>200

and f200=3.14r

and l200=$12345678L

and m200=%1111111100000000

1.10.3.6. Comentarios

Los comentarios deben empezar con el carácter « ; » (punto y coma); todos los caracteres siguientes se ignoran.

1.10.3.7. Base de numeración

Los valores (identificaciones de variables o constantes) pueden escribirse en decimal, hexadecimal, binario o ASCII. La siguiente sintaxis debe aplicarse para las constantes 16 bits:

Ö decimal: eventualmente el carácter « - » y luego 1 a 5 dígitos « 0123456789 », Ö hexadecimal: prefijo « $ » o « 16# » seguido de 1 a 4 dígitos

« 0123456789ABCDEF »,

Ö binario: prefijo « % » o « 2# » seguido de 1 a 16 dígitos « 01 », Ö ASCII: carácter « " » seguido de 1 o 2 caracteres seguidos de « " ».

La siguiente sintaxis debe aplicarse para las constantes 32 bits:

AUTOMGEN7 71 (C)opyright 2002 IRAI

Page 72

Manual de referencia del lenguaje

Ö Decimal: eventualmente el carácter « - » y luego 1 a 10 dígitos « 0123456789 », Ö Hexadecimal: prefijo « $ » o « 16# » seguido de 1 a 8 dígitos

« 0123456789ABCDEF »,

Ö Binario: prefijo « % » o « 2# » seguido de 1 a 32 dígitos « 01 », Ö ASCII: carácter « " » seguido de 1 a 4 caracteres seguidos de « " ».

La siguiente sintaxis debe aplicarse para las constantes reales: [-] i [[.d] Esx] i es la parte entera d una eventual parte decimal s eventualmente el signo del exponente x eventualmente el exponente

1.10.3.8. Predisposiciones

Una predisposición permite fijar el valor de una variable al inicio de la aplicación. Las variables T o %T, M o %MW, L o %MD y F o %F pueden estar predispuestas.

La sintaxis es la siguiente:

« $(variable)=constante{,constante{,constante...}} »

Para las temporizaciones el valor debe estar escrito en decimal y comprendido entre 0 y 65535. Para las palabras debe utilizarse la siguiente sintaxis:

Ö Decimal: eventualmente el carácter « - » y luego 1 a 5 dígitos

« 0123456789 »,

Ö Hexadecimal: prefijo « $ » o « 16# » seguido de 1 a 4 dígitos

« 0123456789ABCDEF »,

Ö Binario: prefijo « % » o « 2# » seguido de 1 a 16 dígitos « 01 », Ö ASCII: (dos caracteres por palabra) el carácter « " » seguido de n

caracteres seguidos de « " »,

Ö ASCII: (un carácter por palabra) el carácter « ’ » seguido de n caracteres

seguidos de « ’ ».

AUTOMGEN7 72 (C)opyright 2002 IRAI

Page 73

Manual de referencia del lenguaje

Para los largos debe utilizarse la siguiente sintaxis:

Ö Decimal: eventualmente el carácter « - » y luego 1 a 10 dígitos « 0123456789 », Ö Hexadecimal: prefijo « $ » o « 16# » seguido de 1 a 8 dígitos

« 0123456789ABCDEF »,

Ö Binario: carácter « % » o « 2# » seguido de 1 a 32 dígitos « 01 », Ö ASCII: (cuatro caracteres por largo) carácter « " » seguido de n caracteres

seguidos de « " »,

Ö ASCII: (un carácter por largo) carácter « ’ » seguido de n caracteres seguidos de

« ’ »

Para los flotantes, el valor debe escribirse de la siguiente manera: [-] i [[.d] Esx] i es la parte entera d una eventual parte decimal s eventualmente el signo del exponente x eventualmente el exponente

Ejemplos:

$t25=100

fija la consigna de la temporización 25 en 10 s

$MW200=100,200,300,400

coloca los valores 100, 200, 300, 400 en las palabras 200, 201, 202, 203

$m200="ABCDEF"

coloca la cadena de caracteres « ABCDEF » a partir de m200 (« AB » en m200, « CD » en m201, « EF » en m202)

$m200=‘ABCDEF’

coloca la cadena de caracteres « ABCDEF » a partir de m200; cada palabra recibe un carácter.

$f1000=3.14

coloca el valor 3,14 en f1000

$%mf100=5.1E-15

coloca el valor 5,1 * 10 exponente -15 en %mf100

$l200=16#12345678

coloca el valor 12345678 (hexa) en el largo l200

AUTOMGEN7 73 (C)opyright 2002 IRAI

Page 74

Manual de referencia del lenguaje

Es más fácil escribir texto en las predisposiciones.

Ejemplo:

$m200=" Parada compuerta N°10 "

Coloca el mensaje a partir de la palabra 200 con dos caracteres en cada palabra.

$m400=‘ Defecto motor ‘

Coloca el mensaje a partir de la palabra 400 con un carácter en el byte de peso débil de cada palabra; el byte de peso fuerte contiene 0.

La sintaxis « $...= » permite proseguir una tabla de predisposiciones a continuación de la anterior.

Por ejemplo:

#$m200=1,2,3,4,5

#$...=6,7,8,9

Coloca los valores de 1 a 9 en las palabras m200 a m208.

Las predisposiciones pueden escribirse de la misma manera que el lenguaje literal bajo nivel o en una directiva de compilación en un folio. En este caso, la predisposición empieza con el carácter « # ». Ejemplo de predisposición escrita en una caja de código:

Ejemplo de predisposición escrita en una directiva de compilación:

AUTOMGEN7 74 (C)opyright 2002 IRAI

Page 75

Manual de referencia del lenguaje

1.10.3.9. Direccionamiento indirecto

El direccionamiento indirecto permite efectuar una operación con una variable señalada por un índice. Son las variables M (las palabras) las que sirven de índice. Sintaxis: « variable ( índice ) »

Ejemplo:

lda 10 ; carga 10 en el acumulador

sta m200 ; lo coloca en la palabra 200

set o(200) ; puesta en uno de la salida señalada por la palabra 200 (o10)

1.10.3.10. Direccionamiento de una variable

El carácter « ? » permite especificar el direccionamiento de una variable. Ejemplo:

lda ?o10 ; coloca el valor 10 en el acumulador

Esta sintaxis es interesante sobre todo si se utilizan símbolos.

Ejemplo:

lda ?_compuerta_ ; coloca en el acumulador el número de la variable

; asociada al símbolo « _compuerta_ »

Esta sintaxis también puede utilizarse en las predisposiciones para crear tablas de direccionamientos de variables.

Ejemplo:

$m200=?_compuerta1_,?_compuerta2_,?_compuerta3_

1.10.3.11. Saltos y labels

Los saltos deben hacer referencia a un label. La sintaxis de un label es: «:nombre del label: » Ejemplo:

jmp:continuación:

...

:continuación:

AUTOMGEN7 75 (C)opyright 2002 IRAI

Page 76

Manual de referencia del lenguaje

1.10.3.12. Lista de funciones por tipo

1.10.3.12.1. Funciones booleanas

SET puesta en uno RES puesta en cero INV inversión EQU equivalencia NEQ no-equivalencia

1.10.3.12.2. Funciones de carga y almacenamiento con enteros y flotantes

LDA carga STA almacenamiento

1.10.3.12.3. Funciones aritméticas con enteros y flotantes

ADA suma SBA resta MLA multiplicación DVA división CPA comparación

1.10.3.12.4. Funciones aritméticas con flotantes

ABS valor absoluto SQR raíz cuadrada

1.10.3.12.5. Funciones de acceso a los puertos de entrada/salida en PC

AIN lectura de un puerto AOU escritura de un puerto

1.10.3.12.6. Funciones de acceso a la memoria en PC

ATM lectura de una dirección de memoria MTA escritura de una dirección de memoria

1.10.3.12.7. Funciones binarias con enteros

ANA y bit a bit ORA o bit a bit XRA o exclusivo bit a bit TSA test bit a bit

AUTOMGEN7 76 (C)opyright 2002 IRAI

Page 77

Manual de referencia del lenguaje

SET puesta en uno de todos los bits RES puesta en cero de todos los bits RRA desfase a derecha RLA desfase a izquierda

1.10.3.12.8. Otras funciones con enteros

INC incremento DEC decremento

1.10.3.12.9. Funciones de conversión

ATB entero a booleanos BTA booleanos a entero FTI flotante a entero ITF entero a flotante LTI entero 32 bits a entero 16 bits ITL entero 16 bits a entero 32 bits

AUTOMGEN7 77 (C)opyright 2002 IRAI

Page 78

Manual de referencia del lenguaje

1.10.3.12.10. Funciones de ramificación

JMP salto JSR salto a un subprograma RET retorno de subprograma

1.10.3.12.11. Funciones de test

RFZ flag de resultado nulo RFS flag de signo RFO flag de exceso RFC flag de retención

1.10.3.12.12. Funciones de accesos asíncronos a entradas salidas

RIN lectura de entradas WOU escritura de salidas

1.10.3.12.13. Información contenida en la lista de funciones

Para cada instrucción se dan:

Ö Nombre: el mnemónico. Ö Función: una descripción de la función realizada por la instrucción. Ö Variables: tipos de variables utilizables con la instrucción. Ö Direccionamiento: tipos de direccionamientos utilizables. Ö Ver también: las otras instrucciones que tengan relación con este mnemónico. Ö Ejemplo: un ejemplo de utilización.

Los post-procesadores que generan lenguajes constructores están sujetos a ciertas restricciones. Consultar las notas sobre estos post-procesadores para conocer en detalle dichas restricciones.

AUTOMGEN7 78 (C)opyright 2002 IRAI

Page 79

Manual de referencia del lenguaje

BSS

Nombre : ABS - abs accumulator Función : calcula el valor absoluto del acumulador flotante Variables : ninguna Direccionamiento : acumulador Ver también : SQR Ejemplo : lda f200 abs aaf sta f201 ; deja en f201 el valor absoluto de f200

AUTOMGEN7 79 (C)opyright 2002 IRAI

Page 80

Manual de referencia del lenguaje

Nombre : ADA - adds accumulator Función : añade un valor al acumulador Variables : M o %MW, L o %MD, F o %MF Direccionamiento : absoluto, indirecto, inmediato Ver también : SBA Ejemplo : ada 200 ; añade 200 al acumulador 16 bits

ada f124

; añade el contenido de f124 al acumulador flotante

ada l200 ; añade el contenido de l200 al acumulador 32 bits

ada 200L ; añade 200 al acumulador 32 bits

ada 3.14R ; añade 3.14 al acumulador flotante

AUTOMGEN7 80 (C)opyright 2002 IRAI

Page 81

Manual de referencia del lenguaje

AII

Nombre : AIN - accumulator input Función : lectura de un puerto de entrada (8 bits) y almacenamiento en la parte baja del acumulador 16 bits;

Variables : M o %MW Direccionamiento: indirecto, inmediato Ver también : AOU Ejemplo : ain $3f8

lectura de un puerto de entrada 16 bits y almacenamiento en el acumulador 16 bits (en este caso la dirección del puerto debe escribirse como una constante de 32 bits) utilizable sólo con el ejecutor PC

; lectura del puerto $3f8 (8 bits)

ain $3f8l ; lectura del puerto $3f8 (16 bits)

AUTOMGEN7 81 (C)opyright 2002 IRAI

Page 82

Manual de referencia del lenguaje

Nombre : ANA - and accumulator Función : efectúa un Y lógico entre el acumulador 16 bits y una palabra o una constante o el acumulador 32 bits y un largo o una constante Variables : M o %MW, L o %MD Direccionamiento: absoluto, indirecto, inmediato

Ver también : ORA, XRA Ejemplo : ana %1111111100000000 ; oculta los 8 bits de peso débil del ; acumulador 16 bits

ana $ffff0000L ; oculta los 16 bits de peso débil del acumulador 32 bits

AUTOMGEN7 82 (C)opyright 2002 IRAI

Page 83

Manual de referencia del lenguaje

Nombre : AOU - accumulator output Función : transfiere la parte baja (8 bits) del contenido del acumulador 16 bits a un puerto de salida;

a un puerto de salida (en este caso la dirección del puerto

debe escribirse como una constante 32 bits)

utilizable sólo con el ejecutor PC Variables : M o %MW Direccionamiento: indirecto, inmediato Ver también : AIN Ejemplo : lda "A" aou $3f8 ; coloca el carácter « A » en el puerto de salida $3f8

lda $3f8 sta m200 lda "z"

transfiere los 16 bits del acumulador 16 bits

aou m(200) ; coloca el carácter « z » en el puerto de salida $3f8

lda $1234 aou $300l ; coloca el valor 16 bits 1234 en el puerto de salida $300

AUTOMGEN7 83 (C)opyright 2002 IRAI

Page 84

Manual de referencia del lenguaje

Nombre : ATB - accumulator to bit Función : transfiere los 16 bits del acumulador 16 bits a 16 variables booleanas sucesivas; el bit de peso débil corresponde a la primera variable booleana Variables : I o %I, O o %Q, B o %M, T o %T, U Direccionamiento: absoluto Ver también : BTA Ejemplo : lda m200 atb o0 ; recopia los 16 bits de m200 en las variables

; o0 a o15

Atención: para poder utilizar los bits U con esta función es necesario realizar una tabla lineal de bits

con la directiva de compilación #B.

AUTOMGEN7 84 (C)opyright 2002 IRAI

Page 85

Manual de referencia del lenguaje

Nombre : ATM - accumulator to memory Función : transfiere el acumulador 16 bits a una dirección memoria; la palabra o la constante especificada define el offset de la dirección de memoria a alcanzar; la palabra m0 debe estar cargada con el valor del segmento de la dirección de memoria a alcanzar; utilizable sólo con el ejecutor PC Variables : M o %MW Direccionamiento: indirecto, inmediato Ver también : MTA Ejemplo : lda $b800 sta m0 lda 64258 atm $10 ; coloca el valor 64258 en la dirección $b800:$0010

AUTOMGEN7 85 (C)opyright 2002 IRAI

Page 86

Manual de referencia del lenguaje

Nombre : BTA - bit to accumulator Función : transfiere 16 variables booleanas sucesivas a los 16 bits del acumulador 16 bits; el bit de peso débil corresponde a la primera variable booleana Variables : I o %I, O o %Q, B o %M, T o %T, U Direccionamiento: absoluto Ver también : ATB Ejemplo : bta i0 sta m200 ; recopia las 16 entradas i0 a i15 en la palabra m200

Atención: para poder utilizar los bits U con esta función es necesario realizar una tabla lineal de bits

con la directiva de compilación #B.

AUTOMGEN7 86 (C)opyright 2002 IRAI

Page 87

Manual de referencia del lenguaje

Nombre : CPA - compares accumulator Función : compara un valor al acumulador 16 bits o 32 bits o flotante; efectúa la misma operación que SBA pero sin modificar el contenido del acumulador Variables : M o %MW, L o %MD, F o %MF Direccionamiento: absoluto, indirecto, inmediato Ver también : SBA Ejemplo : lda m200 cpa 4 rfz o0 ; pone o0 en 1 si m200 es igual a 4, si no o0

; se pone en 0

lda f200 cpa f201 rfz o1 ; pone o1 en 1 si f200 es igual a f201, si no o1

; se pone en 0

AUTOMGEN7 87 (C)opyright 2002 IRAI

Page 88

Manual de referencia del lenguaje

16 bits o 32 bits

Nombre : DEC – decrement Función : decrementa una palabra, un contador, un largo, el acumulador

Variables : M o %MW, C o %C, L o %MD Direccionamiento: absoluto, indirecto, acumulador Ver también : INC Ejemplo : dec m200 ; decrementa m200

dec aal ; decrementa el acumulador 32 bits

dec m200 dec m201 and m200=-1 ; decrementa un valor 32 bits compuesto de

; m200 (peso débil) ; y m201 (peso fuerte)

AUTOMGEN7 88 (C)opyright 2002 IRAI

Page 89

Manual de referencia del lenguaje

bits el resto se coloca en la palabra m0; en caso de división por 0 el bit sistema 56 pasa a 1

Nombre : DVA - divides accumulator Función : división del acumulador 16 bits por una palabra o una constante; división del acumulador flotante por un flotante o una constante; división del acumulador 32 bits por un largo o una constante; para el acumulador 16

Variables : M o %MW, L o %MD, F o %MF Direccionamiento: absoluto, indirecto, inmediato Ver también : MLA Ejemplo : lda m200 dva 10 sta m201 ; m201 es igual a m200 dividido por 10, m0 contiene el ; resto de la división

lda l200 dva $10000L sta l201

AUTOMGEN7 89 (C)opyright 2002 IRAI

Page 90

Manual de referencia del lenguaje

Nombre : EQU - equal Función : fuerza una variable a 1 si el test es verdadero, en caso contrario, la variable se fuerza a 0 Variables : I o %I, O o %Q, B o %M, T o %T, X o %X, U Direccionamiento: absoluto, indirecto (salvo con las variables X) Ver también : NEQ Ejemplo : equ o0 and i10 ; fuerza la salida o0 al mismo estado que la entrada i10

lda 10 sta m200 equ o(200) and i0 ; fuerza o10 al mismo estado que la entrada i0

$t0=100 equ t0 and i0 equ o0 and t0 ; fuerza o0 al estado de i0 con un retraso en la activación ; de 10 segundos

, SET, RES, INV

AUTOMGEN7 90 (C)opyright 2002 IRAI

Page 91

Manual de referencia del lenguaje

TII

Nombre : FTI - float to integer Función : transfiere el acumulador flotante al acumulador 16 bits Variables : ninguna Direccionamiento: acumulador Ver también : ITF Ejemplo : lda f200 fti aaa sta m1000 ; deja la parte entera de f200 en m1000

AUTOMGEN7 91 (C)opyright 2002 IRAI

Page 92

Manual de referencia del lenguaje

IIN

Nombre : INC - increment Función : incrementa una palabra, un contador, un largo, el acumulador

Variables : M o %MW, C o %C, L o %MD Direccionamiento: absoluto, indirecto, acumulador

16 bits o 32 bits

Ver también : DEC Ejemplo : inc m200 ; añade 1 a m200

inc m200 inc m201 and m201=0 ; incrementa un valor sobre 32 bits, m200

; representa los ; pesos débiles, y m201 los pesos fuertes

inc l200 ; incrementa el largo l200

AUTOMGEN7 92 (C)opyright 2002 IRAI

Page 93

Manual de referencia del lenguaje

IIN

Nombre : INV - inverse Función : invierte el estado de una variable booleana, o invierte

Variables : I o %I, O o %Q, B o %M, T o %T, X o %X, U,

Direccionamiento: absoluto, indirecto, acumulador

todos los bits de una palabra, de un largo o del acumulador 16

bits o 32 bits

M o %MW, L o %MD

Ver también : EQU Ejemplo : inv o0 ; invierte el estado de la salida 0

inv aaa ; invierte todos los bits del acumulador 16 bits

inv m200 and i0 ; invierte todos los bits de m200 si i0 está en estado 1

, NEQ, SET, RES

AUTOMGEN7 93 (C)opyright 2002 IRAI

Page 94

Manual de referencia del lenguaje

IIT

Nombre : ITF - integer to float Función : transfiere el acumulador 16 bits al acumulador flotante Variables : ninguna Direccionamiento: acumulador

Ver también : FTI Ejemplo : lda 1000 itf aaa sta f200 ; deja la constante 1000 en f200

AUTOMGEN7 94 (C)opyright 2002 IRAI

Page 95

Manual de referencia del lenguaje

IIT

Nombre : ITL - integer to long Función : transfiere el acumulador 16 bits al acumulador 32 bits Variables : ninguna Direccionamiento: acumulador

Ver también : LTI Ejemplo : lda 1000 itl aaa sta f200 ; deja la constante 1000 en l200

AUTOMGEN7 95 (C)opyright 2002 IRAI

Page 96

Manual de referencia del lenguaje

JJM

Nombre : JMP - jump Función : salto a un label Variables : label Direccionamiento: label Ver también : JSR Ejemplo : jmp :fin de programa: ; ramificación incondicional en label :fin

; de programa:

jmp :continuación: and i0 set o0 set o1

:continuación:

; ramificación condicional en label :continuación: ; según el estado de i0

AUTOMGEN7 96 (C)opyright 2002 IRAI

Page 97

Manual de referencia del lenguaje

JJSSR

Nombre : JSR - jump sub routine Función : efectúa una ramificación a un subprograma Variables : label Direccionamiento: label Ver también : RET Ejemplo : lda m200 jsr :cuadrado: sta m201 jmp :fin:

:cuadrado: sta m53

mla m53 sta m53 ret m53

:fin:

; el subprograma « cuadrado » eleva al cuadrado ; el contenido del acumulador

AUTOMGEN7 97 (C)opyright 2002 IRAI

Page 98

Manual de referencia del lenguaje

flotante o una constante, carga un contador de temporización en el acumulador 16 bits

Nombre : LDA - load accumulator Función : carga en el acumulador 16 bits una constante, palabra o contador; carga en el acumulador 32 bits un largo o constante, carga en el acumulador flotante un

Variables : M o %MW, C o %C, L o %MD, F o %MF, T o %T Direccionamiento: absoluto, indirecto, inmediato Ver también : STA Ejemplo : lda 200 ; carga la constante 200 en el acumulador 16 bits

lda 0.01R ; carga la constante real 0.01 en el acumulador flotante

lda t10 ; carga el contador de la temporización 10 en

; el acumulador

AUTOMGEN7 98 (C)opyright 2002 IRAI

Page 99

Manual de referencia del lenguaje

TII

Nombre : LTI - long to integer Función : transfiere el acumulador 32 bits al acumulador

16 bits

Variables : ninguna Direccionamiento: acumulador Ver también : ITL Ejemplo : lda l200 lti aaa sta m1000 ; deja los 16 bits de peso débil de l200 en m1000

AUTOMGEN7 99 (C)opyright 2002 IRAI

Page 100

Manual de referencia del lenguaje

Nombre : MLA - multiples accumulator Función : multiplicación del acumulador 16 bits por una palabra o constante ; multiplicación del acumulador 32 bits por un largo o constante, multiplicación del acumulador flotante por un flotante o constante; para el acumulador

Variables : M o %MW, L o %MD, F o %MF Direccionamiento: absoluto, indirecto, inmediato Ver también : DVA Ejemplo : lda m200 mla 10

16 bits, los 16 bits de peso fuerte del resultado de la multiplicación se transfieren a m0

sta m201 ; multiplica m200 por 10, m201 está cargado con los

; 16 bits de peso débil, y m0 con los 16 bits de ; peso fuerte

AUTOMGEN7 100 (C)opyright 2002 IRAI