Hp 50g User Manual [es]

HP 50g calculadora gráfica

manual del usuario

H

Edición 1
Número de parte de HP F2229AA-90005

Nota

REGISTRO SU PRODUCTO EN : www.register.hp.com
ESTE MANUAL Y CUALQUIER EJEMPLO CONTENIDO AQUÍ SE

OFRECEN “TAL COMO ESTÁN” Y ESTÁN SUJETOS A CAMBIOS
SIN PREVIO AVISO. LA COMPAÑÍA HEWLETT-PACKARD NO
OFRECE GARANTÍAS DE NINGÚN TIPO CON RESPECTO A ESTE
MANUAL, INCLUYENDO, PERO NO LIMITÁNDOSE A LAS
GARANTÍAS IMPLÍCITAS DE COMERCIALIZACIÓN,

HEWLETT-PACKARD CO. NO SE HARÁ RESPONSABLE DE
NINGÚN ERROR O DE DAÑOS INCIDENTALES CONSECUENTES
ASOCIADOS A LA PROVISIÓN, FUNCIONAMIENTO O USO DE
ESTE MANUAL O A LOS EJEMPLOS AQUÍ CONTENIDOS.

© Copyright 2003, 2006 Hewlett-Packard Development Company, L.P.
La reproducción, adaptación o traducción de este manual está prohibida

sin previo permiso de la compañía Hewlett-Packard, excepto cuando lo
permitan las leyes de derecho de autor.

Hewlett-Packard Company
4995 Murphy Canyon Rd,
Suite 301
San Diego, CA 92123

Historial de impresión

Edición 1 Abril de 2006

Prefacio

Usted tiene en sus manos una calculadora que es efectivamente un
ordenador (computador, computadora) simbólico y numérico que facilita
el cálculo y análisis matemáticos de problemas en una gran variedad de
disciplinas, desde matemáticas elementales hasta temas avanzados de
ciencia e ingeniería.

Este manual contiene ejemplos que ilustran el uso de las funciones y
operaciones básicas de la calculadora. Los capítulos de este manual se
organizan en orden de dificultad: comenzando por la selección de los
modos de operación de la calculadoras, pasando a cálculos con números
reales y complejos, operaciones con listas, vectores y matrices, gráficas,
aplicaciones en el cálculo diferencial e integral, análisis vectorial,
ecuaciones diferenciales, probabilidad, y estadística.

Para ejecutar operaciones simbólicas la calculadora incluye un poderoso
Sistema Algebraico Computacional (Computer Algebraic System, o CAS),
que permite seleccionar diferentes modos de operación, por ejemplo,
números complejos vs. números reales, o modo exacto (simbólico) vs.
Modo aproximado (numérico). La pantalla puede ajustarse para
presentar los resultados en notación matemática, lo que puede ser útil
cuando se trabaja con matrices, vectores, fracciones, sumatorias,
derivadas, e integrales. Las gráficas de alta velocidad de la calculadora
son convenientes para producir figuras complejas en un tiempo mínimo.

A través de la conexión infrarroja, el cable USB, el puerto RS 232 y el
cable que se le entregará con la calculadora, puede conectar su
calculadora a otras calculadoras u ordenadores (computadores,
computadoras.) Esto permite un rápido y eficiente intercambio de datos
con otras calculadoras y ordenadores (computadores, computadoras). La
calculadora provee un puerto de tarjetas de memoria “flash” para facilitar
el almacenamiento e intercambio de datos con otros usuarios.

Esperamos que su calculadora sea una compañera inseparable para
Usted en sus actividades escolares y profesionales.

Nota: Los decimales que encontrará este manual están indicados por un
punto decimal en lugar de una coma. Éste es el ajuste por defecto de la
calculadora. Si prefiere trabajar con comas decimales, puede cambiar el
ajuste por defecto. Para más información, consulte el Capítulo 1.

Índice de materias

Chapter 1 - Preliminares

Operaciones Básicas, 1-1

Baterías, 1-1
Encendido y apagado de la calculadora, 1-2
Ajustando el contraste de la pantalla, 1-2
Contenidos de la pantalla, 1-3
Menús, 1-3
El menú de herramientas (TOOL), 1-4
Cambiando la hora del día y la fecha , 1-4

Introducción al teclado de la calculadora, 1-5
Cambiando los modos de operación, 1-6

Modo operativo, 1-7
Formato de los números y punto o coma decimal, 1-10

Formato Estándar , 1-10
Formato con número de decimales fijo, 1-11
Formato científico, 1-12
Formato de ingeniería, 1-13

Coma vs. Punto decimales , 1-13
Medidas angulares, 1-14
Sistema de coordenadas, 1-15

Seleccionando opciones del CAS, 1-15

Explicación de las opciones del CAS, 1-17

Selección de los modos de la pantalla, 1-18

Selección del tipo de caracteres (font), 1-19
Selección de las propiedades del editor de línea, 1-20
Selección de las propiedades de la pantalla (Stack) , 1-20
Selección de las propiedades del escritor de ecuaciones (EQW), 1-

21

Referencias, 1-22

Pagina -1 Índice de materias

Chapter 2 - Introducción a la calculadora

Objetos en la calculadora, 2-1
Edición de expresiones en la pantalla, 2-1

Creación de expresiones aritméticas, 2-1
Creación de expresiones algebraicas, 2-4

Uso del escritor de ecuaciones (EQW) para crear expresiones, 2-4

Creación de expresiones aritméticas, 2-5
Creación de expresiones algebraicas, 2-7

Organización de los datos en la calculadora, 2-8

El directorio HOME, 2-8
Sub-directorios, 2-9

Variables, 2-9

Escritura del nombre de variables , 2-10
Creación de variables, 2-11

Modo algebraico, 2-11
Modo RPN, 2-12

Examinando el contenido de una variable, 2-13

Modo algebraico, 2-13
Modo RPN,
Utilizando la tecla seguida de la tecla del menú, 2-14
Listado de las variables en la pantalla, 2-14

Eliminación de las variables, 2-15

Usando la función PURGE en la pantalla en Modo algebraico,
2-15

Utilizando la función PURGE en la pantalla en Modo RPN, 2-15

Las funciones UNDO y CMD , 2-16
Opciones CHOOSE boxes y Soft MENU, 2-16
Referencias, 2-19

2-13

Chapter 3 - Cálculos con números reales

Ejemplos de cálculos con números reales , 3-1

Utilizando potencias de 10 al escribir datos, 3-4

Las funciones de números reales en el menú MTH, 3-5

Usando los menús de la calculadora: , 3-6

Índice de materias Pagina -2

Las funciones hiperbólicas y sus inversas, 3-6

Operaciones con unidades, 3-7

El menú de UNIDADES , 3-8

Unidades disponibles, 3-10

Agregando unidades a los números reales, 3-10

Prefijos de unidades, 3-11
Operaciones con unidades , 3-12
Conversión de unidades, 3-13

Constantes físicas en la calculadora, 3-13
Definiendo y usando funciones, 3-16
Referencia, 3-17

Chapter 4 - Cálculos con números complejos

Definiciones, 4-1
Seleccionando el modo complejo (COMPLEX), 4-1

Escritura de números complejos, 4-2
Representación polar de un número complejo, 4-3

Operaciones elementales con números complejos, 4-4
Los menús CMPLX , 4-4

El menú CMPLX a través del menú MTH , 4-4
El menú CMPLX en el teclado, 4-6

Funciones aplicadas a números complejos, 4-6
Función DROITE: la ecuación de una línea recta, 4-7
Referencia, 4-7

Chapter 5 - Operaciones algebraicas y aritméticas

Escritura de los objetos algebraicos, 5-1
Operaciones elementales con objetos algebraicos, 5-2

Funciones en el menú ALG , 5-4

Operaciones con funciones trascendentes, 5-6

Expansión y factorización utilizando las funciones log-exp, 5-6
Expansión y factorización utilizando funciones trigonométricas, 5-7

Funciones en el menú ARITHMETIC , 5-8
Polinomios, 5-9

Pagina -3 Índice de materias

La función HORNER , 5-9
La variable VX, 5-9
La función PCOEF, 5-10
La función PROOT, 5-10
Las funciones QUOT y REMAINDER, 5-10
La función PEVAL, 5-11

Fracciones, 5-11

La función SIMP2, 5-11
La función PROPFRAC , 5-11
La función PARTFRAC , 5-12
La función FCOEF, 5-12
La función FROOTS , 5-12

Operaciones con polinomios y fracciones, paso a paso, 5-13
Referencia, 5-14

Chapter 6 - Solución de las ecuaciones

Solución simbólica de las ecuaciones algebraicas, 6-1

La función ISOL , 6-1
La función SOLVE, 6-3
La función SOLVEVX, 6-4
La función ZEROS, 6-5

Menú de soluciones numéricas, 6-6

Ecuaciones polinómicas, 6-6

Solución(es) de una ecuación polinómica, 6-7
Generación de coeficientes de un polinomio dadas las raíces, 6-

7

Generación de una expresión algebraica para el polinomio, 6-8
Cálculos financieros, 6-9
Solución de ecuaciones con una sola incógnita con el NUM.SLV, 6-

9

La función STEQ, 6-9

Solución de ecuaciones simultáneas con MSLV, 6-11
Referencia, 6-12

Índice de materias Pagina -4

Chapter 7 - Operaciones con listas

Creación y almacenamiento de listas, 7-1
Operaciones con listas de números, 7-1

Cambio de signo , 7-1
Adición, substracción, multiplicación, y división, 7-1
Funciones aplicadas a listas, 7-4

Listas de números complejos, 7-4
Listas de objetos algebraicos, 7-5
El menú MTH/LIST , 7-5
La función SEQ, 7-7
La función MAP, 7-7
Referencia, 7-8

Chapter 8 - Vectores

La escritura de vectores, 8-1

Escritura de vectores en la pantalla, 8-1
Almacenamiento de vectores en variables, 8-2
Utilizando el escritor de matrices (MTRW) para escribir vectores, 8-

3

Operaciones elementales con vectores, 8-5

Cambio de signo , 8-5
Adición, substracción, 8-5
Multiplicación o división por un escalar, 8-6
Función valor absoluto, 8-6

El menú MTH/VECTOR, 8-7

Magnitud, 8-7
Producto escalar (producto punto) , 8-7
Producto vectorial (producto cruz), 8-8

Referencia, 8-9

Chapter 9 - Matrices y álgebra lineal

Escritura de matrices en la pantalla, 9-1

Utilizando el editor de matrices, 9-1
Como se hizo con los vectores (véase el Capítulo 8), las matrices

Pagina -5 Índice de materias

pueden escribirse utilizando el editor o escritor de matrices. Por
ejemplo, para escribir la matriz:, 9-1

Escribiendo la matriz directamente en la pantalla, 9-2

Operaciones con matrices, 9-3

Adición y substracción, 9-3
Multiplicación, 9-4

Multiplicación por un escalar, 9-4

Multiplicación de una matriz con un vector, 9-4

Multiplicación de matrices, 9-5

Multiplicación término-a-término, 9-5

Elevar una matriz a una potencia real, 9-6

La matriz identidad, 9-6

La matriz inversa, 9-7

El menú NORM de matrices, 9-7

La función DET, 9-7
La función TRACE , 9-8

Solución de sistemas lineales, 9-8

Utilizando la solución numérica de sistemas lineales, 9-9
Solución utilizando la matriz inversa, 9-11
Solución a través de “división” de matrices, 9-11

Referencias, 9-11

Chapter 10 - Gráficas

Opciones gráficas en la calculadora, 10-1
Gráfica de una expresión de la forma y = f(x), 10-2
Tabla de valores de una función, 10-4
Gráficas tridimensionales de acción rápida (Fast 3D plots), 10-5
Referencia, 10-7

Chapter 11 - Aplicaciones en el Cálculo

El menú CALC (Cálculo), 11-1
Límites y derivadas, 11-1

La función lim, 11-1
Las funciones DERIV y DERVX, 11-3

Índice de materias Pagina -6

Anti-derivadas e integrales, 11-3

Las funciones INT, INTVX, RISCH, SIGMA y SIGMAVX, 11-3
Integrales definidas, 11-4

Series infinitas, 11-5

Las funciones TAYLR, TAYLR0, y SERIES, 11-5

Referencia, 11-6

Chapter 12 - Aplicaciones en el Cálculo Multivariado

Derivadas parciales, 12-1
Integrales múltiples, 12-2
Referencia, 12-2

Chapter 13 - Aplicaciones en Análisis Vectorial

El operador ‘del’, 13-1
Gradiente, 13-1
Divergencia, 13-2
Rotacional (Curl), 13-2
Referencia, 13-2

Chapter 14 - Las ecuaciones diferenciales

El menú CALC/DIFF, 14-1
Solución de las ecuaciones lineales y no lineales, 14-1

La función LDEC , 14-1
La función DESOLVE, 14-3
La variable ODETYPE, 14-3

Transformadas de Laplace, 14-4

Transformadas de Laplace y sus inversas en la calculadora, 14-5

Series de Fourier, 14-6

La función FOURIER, 14-6
Serie de Fourier para una función cuadrática, 14-6

Referencia, 14-7

Chapter 15 - Distribuciones de probabilidad

El sub-menú MTH/PROBABILITY.. - parte 1, 15-1

Factoriales, combinaciones, y permutaciones, 15-1

Pagina -7 Índice de materias

Números aleatorios, 15-2

El sub-menú MTH/PROBABILITY.. - parte 2, 15-3

La distribución normal, 15-3
La distribución de Student, 15-4
La distribución Chi cuadrada , 15-4
La distribución F, 15-4

Referencia, 15-4

Chapter 16 - Aplicaciones Estadísticas

Entrada de datos, 16-1
Cálculos estadísticos para una sola variable, 16-2
Muestra vs. población, 16-2
Cálculo de distribuciones de frecuencias, 16-3
Ajustando datos a la función y = f(x), 16-5
Medidas estadísticas adicionales, 16-6
Intervalos de confianza, 16-7
Prueba de hipótesis, 16-9
Referencia, 16-11

Chapter 17 - Números en bases diferentes

El menú BASE, 17-1
Escritura de números no decimales, 17-2
Referencia, 17-2

Chapter 18 - Utilizando tarjetas de memoria SD

Insertar y eliminar una tarjeta SD, 18-1
Formatear una tarjeta SD, 18-1
Acceder a objetos en una tarjeta SD, 18-2
Almacenando objetos en la Tarjeta SD, 18-3
Copiando un objeto de la tarjeta SD, 18-3
Eliminando objetos de la tarjeta SD, 18-4
Purgar todos los objetos en la tarjeta SD (reformateando), 18-4
Especificar un directorio en una tarjeta SD, 18-4

Índice de materias Pagina -8

Chapter 19 - La biblioteca de ecuaciones

Reference, 19-4
Garantía Limitada

Servicio
Regulatory information
Eliminación de residuos de equipos eléctricos y electrónicos por parte de

usuarios particulares en la Unión Europea

, G-3

, G-1

, G-5

, G-7

Pagina -9 Índice de materias

Capítulo 1
Preliminares

El presente capítulo está destinado a proveer la información básica sobre
la operación de la calculadora. Los ejercicios que se presentan a
continuación permiten al usuario familiarizarse con las operaciones
básicas y la selección de los modos de operación de la calculadora.

Operaciones Básicas

Los ejercicios siguientes tienen el propósito de describir la calculadora
misma.

Baterías

La calculadora utiliza 4 baterías AAA (LR03) como fuente de alimentación
principal y una batería de litio CR2032 para copia de seguridad de la
memoria.

Antes de utilizar la calculadora, instale las baterías siguiendo el
procedimiento que se describe a continuación.

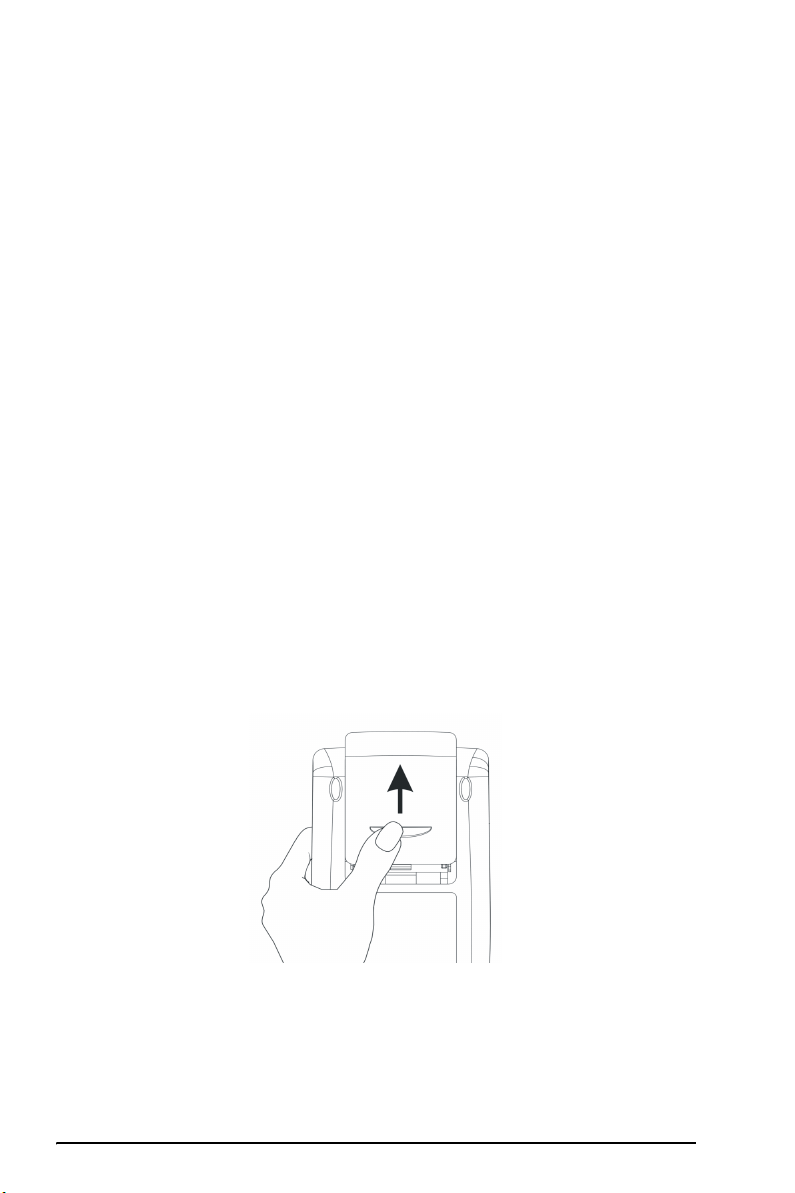
Para instalar las baterías principales

a. Compruebe que la calculadora esté apagada. Deslice la

tapa del compartimento de las baterías hacia arriba tal y como se
indica la figura.

b. Inserte 4 baterías AAA (LR03) nuevas en el compartimento principal.

Asegúrese de que cada batería se inserta en la dirección indicada.

Página 1-1

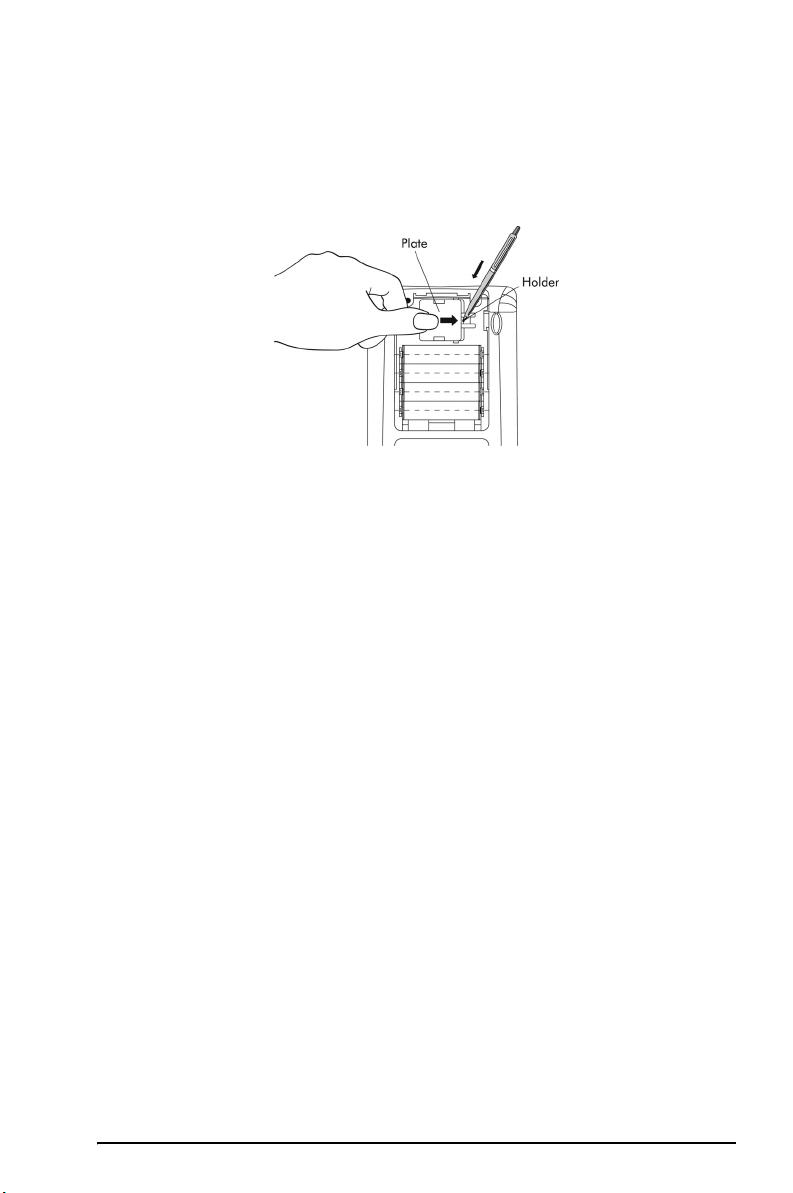
Para instalar las baterías de seguridad

a. Compruebe que la calculadora esté apagada. Presione el

elemento de sujeción hacia abajo. Empuje la placa en la dirección
mostrada y levántela.

b. Inserte una nueva batería de litio CR2032. Asegúrese de que el polo

positivo (+) mira hacia arriba.
c. Vuelva a colocar la placa y acóplela en su ubicación original.
Después de instalar las baterías, presione $ para activar la

alimentación.
Advertencia: cuando el icono de batería baja aparezca en la pantalla,

reemplace las baterías cuanto antes. No obstante, intente no retirar la
batería de seguridad y las baterías principales al mismo tiempo para
evitar la pérdida de datos.

Encendido y apagado de la calculadora

La tecla $ se localiza en la esquina inferior izquierda del teclado. Pulse
esta tecla para encender la calculadora. Para apagar la calculadora,
pulse la tecla @ (primera tecla en la segunda fila contada de la parte
inferior del teclado), seguida de la tecla $. La tecla $ tiene un rótulo
indicando OFF (apagar) en la esquina superior derecha para recalcar la
operación de apagar la calculadora.

Ajustando el contraste de la pantalla

Uno puede ajustar el contraste de la pantalla al mantener presionada la
tecla $ mientras pulsa la tecla + ó - simultáneamente.

La combinación $(mantener) + produce una pantalla más oscura.
La combinación $(mantener) - produce una pantalla más clara.

Página 1-2

Contenidos de la pantalla

Encienda la calculadora una vez más. En la parte superior de la pantalla
encontrará dos líneas de información que describen las características
operativas de la calculadora. La primera línea muestra los caracteres:

RAD XYZ HEX R= 'X'

Los detalles de estos símboloss se muestran en el Capítulo 2 de esta guía.
La segunda línea muestra los caracteres:

{ HOME }

que indican que el directorio HOME es el directorio activo para
almacenar archivos en la memoria de la calculadora

Al pié de la pantalla se encuentran varios rótulos, a saber,

@EDIT @VIEW @@RCL@@ @@STO@ !PURGE !CLEAR

que están asociados con las seis teclas de menú, F1 a F6:

ABCDEF.

Los seis rótulos en la parte inferior de la pantalla cambian dependiendo
del menú activo. Sin embargo, la tecla A siempre se asocia con el
primer rótulo, la tecla B se asocial con el segundo rótulo, y así
sucesivamente.

Menús

Los seis rótulos asociados con las teclas Aa F forman parte de un

de funciones de la calculadora. Dado que la calculadora solamente

menú
tiene seis teclas de menú, solo se muestran seis rótulos a la vez. Sin
embargo, el menú puede tener más de seis opciones. Cada grupo de 6
opciones se conoce como una Página de Menú. Para mostrar la siguiente
página de menú (si existe), presiónese la tecla L (NeXT, es decir, el
siguiente menú). Esta tecla se localiza en la tercera columna y la tercera
fila del teclado.

Página 1-3

El menú de herramientas (TOOL)

El menú activo a este momento, conocido como el menú de herramientas
(TOOL), está asociado con operaciones relacionadas a la manipulación
de variables (véase la sección sobre variables in este Capítulo). Las
diferentes funciones del menú de herramientas son las siguientes:

EDITar el contenido de una variable (para información

A

@EDIT

@VIEW
@@RCL@
@@STO@
!PURGE
@CLEAR

Estas seis funciones forman la primera página del menú de herramientas
(TOOL). Este menú tiene actualmente ocho opciones organizadas en dos
páginas. La segunda página se obtiene al presionar la tecla L.

En la segunda página del menú solamente las dos primeras teclas de
menú tienen funciones asociadas. Estas funciones son:

@CASCM

@HELP

adicional, véase el Capítulo 2 en esta guía y el Capítulo 2 y
el Apéndice L en la guía del usuario)

Observar (VIEW) el contenido de una variable

B

Recobrar (ReCaLl) el contenido de una variable

C

Almacenar (STOre) el contenido de una variable

D

Eliminar o borrar (PURGE) una variable

E

Limpiar (CLEAR) la pantalla

F

CASCMD: CAS CoMmanD, se utiliza para modificar el CAS

A

(Computer Algebraic System, o Sistema Algebraico
Computacional)

HELP, menú informativo que describe las funciones

B

disponibles en la calculadora

Al presionar la tecla L nuevamente, se obtiene el menú de herramientas
(TOOL) original. Otra forma de recuperar el menú de herramientas
(TOOL) es al presionar la tecla I (tercera columna y segunda fila en el
teclado).

Cambiando la hora del día y la fecha

Véase el Capítulo 1 en la guía del usuario para aprender como cambiar
la hora del día y la fecha en la calculadora.

Página 1-4

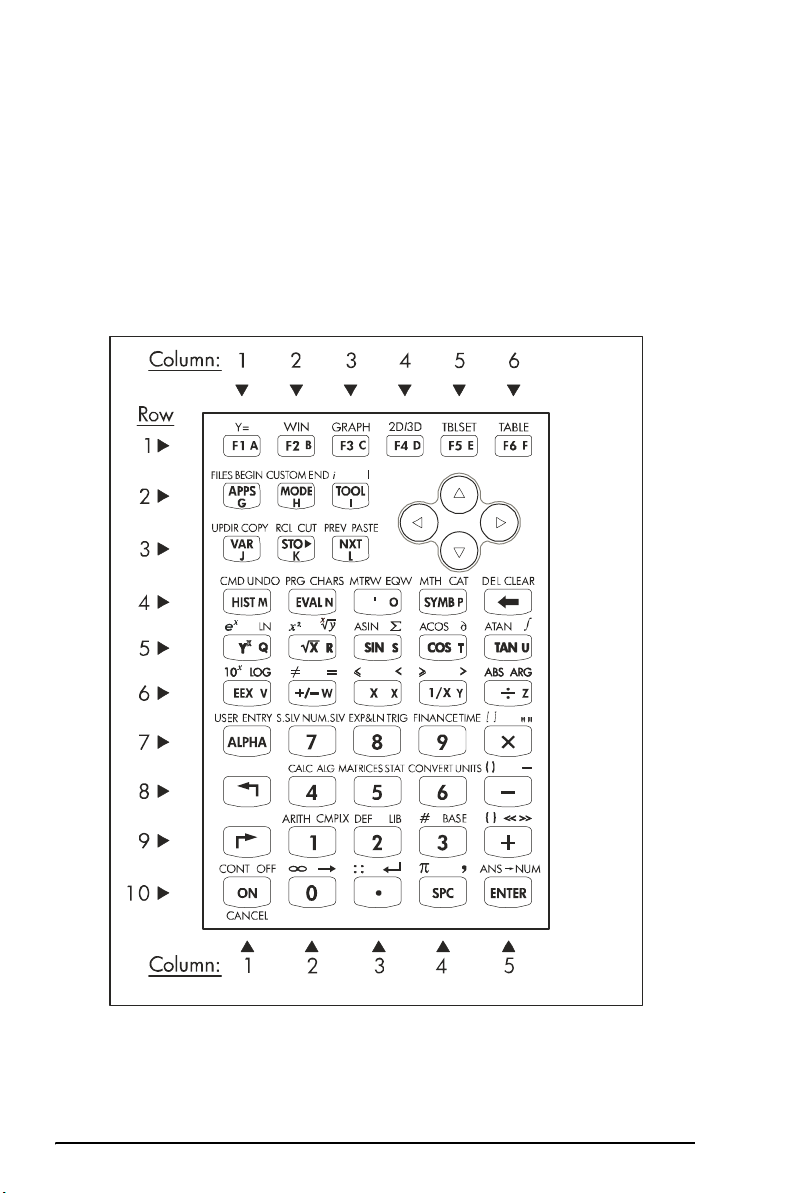
Introducción al teclado de la calculadora

La figura siguiente muestra un diagrama del teclado de la calculadora
enumerando sus filas y columnas. Cada tecla tiene tres, cuatro, o cinco
funciones asociadas. La función principal de una tecla corresponde al
rótulo más prominente en la tecla. La tecla de cambio izquierdo, tecla
(9,1), la tecla de cambio derecho, tecla (9,1), y la tecla alfa (ALPHA), tecla
(7,1), pueden combinarse con otras teclas para activar las funciones
alternas que se muestran en el teclado.

Página 1-5

Por ejemplo, la tecla P, tecla(4,4), tiene las siguientes seis funciones
asociadas:

P Función principal, para activar el menú de operaciones

simbólicas

„´ Función de cambio izquierdo, activa el menú de

…N Función de cambio derecho, activa el CATálogo de

~p Función ALPHA, para escribir la letra P mayúscula
~„p Función ALPHA-cambio izquierdo, escribe la letra p

~…p Función ALPHA-cambio derecho, escribe el símbolo

De las seis funciones asociadas con una tecla, solamente las cuatro
primeras se muestran en el teclado mismo. La figure siguiente muestra
estas cuatro funciones para la tecla P. Nótese que el color y la
posición de los rótulos de las funciones en la tecla, a saber, SYMB, MTH,
CAT y P, indican cual es la función principal (SYMB), y cual de las otras
tres funciones se asocian con la tecla de cambio izquierdo „(MTH), con
la tecla de cambio derecho …(CAT ), y con la tecla ~ (P).

matemáticas (MTH)

funciones

minúscula

Para información adicional sobre la operación del teclado de la
calculadora, refiérase al Apéndice B en la guía del usuario.

Cambiando los modos de operación

Esta sección asume que el usuario se ha familiarizado con el uso de los
menús y las formas interactivas de entradas de datos (si éste no es el caso,
refiérase al Apéndice A en la guía del usuario).

Presione la tecla H (segunda fila y segunda columna del teclado) para
activar la forma interactiva denominada CALCULATOR MODES:

Página 1-6

Presione la tecla !!@@OK#@ para recuperar la pantalla normal. Ejemplos de los
diferentes modos de operación se muestran a continuación.

Modo operativo

La calculadora presenta dos modos de operación: el modo Algebraico, y
el modo de Notación Polaca Reversa (Reverse Polish Notation, RPN). Si
bien el modo Algebraico es el modo predefinido de operación (como se
indica en la figure anterior), usuarios con experiencia en previos modelos
de las calculadoras HP podrían preferir el modo RPN.

Para seleccionar el modo operativo, actívese la forma interactiva titulada
CALCULATOR MODES presionando la tecla H. La opción Operating
Mode (Modo Operativo) es seleccionada automáticamente. Selecciónese
el modo operativo Algebraico o RPN usando, ya sea, la tecla \
(segunda columna y quinta fila en el teclado), o la tecla @CHOOS (escoger,
B). Si se usa el procedimiento ultimo, úsense las teclas direccionales
verticales, — ˜, para seleccionar el modo operativo, y presiónese la
tecla !!@@OK#@ para completar la operación.

Para ilustrar la diferencia entre los dos modos operativos, a continuación
procedemos a calcular la siguiente expresión en los dos modos
operativos:

1

⎛

0.50.3

−⋅

⎜
⎝

3

0.23

⎞
⎟

0.30.3

⋅

⎠

5.2

e+

Para escribir esta expresión, usaremos el escritor de ecuaciones (equation
writer), ‚O. Antes de continuar, le invitamos a identificar las

siguientes teclas, además de las teclas numéricas:

!@.#*+-/R

Q¸Ü‚Oš™˜—`

El escritor de ecuaciones representa un ambiente en el que uno puede
construir expresiones matemáticas usando notación matemática explícita

Página 1-7

incluyendo fracciones, derivadas, integrals, raíces, etc. Para escribir la
expresión antes mencionada en el escritor de ecuaciones, utilícense la
secuencia de teclas siguiente:

‚OR3.*!Ü5.-

1./3.*3.

—————

/23.Q3™™+!¸2.5`

Después de presionar la tecla ` la pantalla muestra la siguiente
expresión:

√ (3.*(5.-1/(3.*3.))/23.^3+EXP(2.5))

Al presionar la tecla ` una vez más produce el siguiente resultado
(acepte el cambio a modo Approx., de ser necesario, presionando la tecla
!!@@OK#@):

Uno puede escribir la expresión directamente en la pantalla sin usar el
escritor de ecuaciones, como se muestra a continuación:

R!Ü3.*!Ü5.-1/

3.*3.™

/23.Q3+!¸2.5`

Cámbiese el modo operativo a RPN comenzando al presionar la tecla
H. Selecciónese el modo operativo RPN utilizando ya sea la tecla \,
o la tecla @CHOOS del menú. Presiónese la tecla !!@@OK#@ ( F) del menú para
completar la operación. La pantalla en el modo operativo RPN se muestra
a continuación:

Nótese que la pantalla muestra varios niveles identificados por los
números 1, 2, 3, etc. Esta pantalla se denomina la pila (stack) de la
calculadora. Los diferentes niveles se denominan los niveles de la pila, es
decir, nivel 1, nivel 2, etc.

Página 1-8

Básicamente, en el modo operativo RPN en vez de escribir la operación 3
+ 2 de esta forma:

3+2`

se escriben primero los operandos, en el orden apropiado, seguidos del
operador, por ejemplo,

3`2+

A medida que se escriben los operandos, éstos pasan a ocupar diferentes
niveles en la pila. Al escribirse, por ejemplo, 3`, el número 3
aparece en el nivel 1. A continuación, escríbase 2 para promover el
número 3 al nivel 2. Finalmente, al presionar +, se indica a la
calculador que aplique el operador, o programa, + a los objetos que
ocupan los niveles 1 y 2. El resultado, es este caso 5, aparece en el nivel

1.
Calcúlense las siguientes operaciones antes de intentar las operaciones

presentadas anteriormente usando el sistema operativo algebraico:

123/32 123`32/

2

4

3

√(√27)

Obsérvese la posición de la y y la x en las dos operaciones últimas. La
base en la operación exponencial es y (nivel 2), mientras que el
exponente es x (nivel 1) antes de presionarse la tecla Q. De manera
similar, en la operación de la raíz cúbica, y (nivel 2) es la cantidad bajo el
signo radical, y x (nivel 1) es la raíz.

Ejecútese el siguiente ejercicio involucrando 3 factores: (5+3)

5`3+ Calcúlese (5 +3) primero.
2X Complétese la operación.

27R3@»

4`2Q

×2

Calcúlese la expresión propuesta anteriormente:

1

⎛

53

⎜
⎝

23

3` Escríbase 3 en el nivel1
5` Escríbase 5 en el nivel1, 3 pasa al nivel 2
3` Escríbase 3 en el nivel1, 5 pasa al nivel 2, 3 pasa

al nivel 3

3* Escríbase 3 y ejecútese la multiplicación, 9 se muestra en

el nivel1

Página 1-9

⎞

−⋅

⎟

33

⋅

⎠

5.2

3

e+

Y 1/(3

×3), último valor en nivel 1; 5 en el nivel2; 3 en

el nivel3

- 5 - 1/(3
* 3

×3), ocupa el nivel 1; 3 en el nivel2

× (5 - 1/(3×3)), ocupa el nivel 1

23`Escríbase 23 en el nivel1, 14.6666 pasa al nivel 2.
3Q

Escríbase 3, calcúlese 23

3

en nivel 1. 14.666 en

nivel 2.

/

× (5-1/(3×3)))/23

(3

3

en nivel 1

2.5Escríbase 2.5 en el nivel 1
!¸

+
R

2.5

e

, pasa al nivel 1, nivel 2 muestra el valor anterior

(3

× (5 - 1/(3×3)))/23

√((3× (5 - 1/(3×3)))/23

3

2.5

+ e

= 12.18369, en nivel 1

3

2.5

+ e

) = 3.49..., en nivel 1.

Para seleccionar modo operativo ALG vs. RPN, uno puede activar /
desactivar la señal de sistema número 95 utilizando las siguientes teclas:

H @FLAGS! 9˜˜˜˜ `

Formato de los números y punto o coma decimal

Al cambiar el formato de los números permite mostrar resultados en
diferentes formas. Esta opción es muy útil en operaciones que involucran
potencias de diez o si se quiere limitar el número de cifras decimales en
los resultados.

Para seleccionar el formato de los números, actívese primero la forma
interactiva denominada CALCULATOR MODES al presionar la tecla H.
Utilícese entonces la tecla direccional vertical, ˜, para seleccionar la
opción Number format. El valor preseleccionado es Std, o formato
estándar. En este formato, la calculadora mostrará números reales con
punto decimal flotante y con la máxima precisión disponible (12 cifras
significativas)Para mayor información sobre números reales en la
calculadora véase el Capítulo 2 en la guía del usuario. Ejemplos que
utilizan el formato estándar y otros formatos se muestran a continuación:

Formato Estándar

Este modo es el más utilizado dado que muestra los números en su
notación mas común. Presiónese la tecla de menú !!@@OK#@ , con la opción
Number format mostrando el valor Std, para recobrar la pantalla normal.
Escríbase el número 123.4567890123456 (con16 cifras significativas).
Presiónese la tecla `. El número se redondea al máximo de 12 cifras
significativas, y se muestra de la siguiente manera:

Página 1-10

Formato con número de decimales fijo

Presiónese la tecla H, y utilícese la tecla direccional vertical, ˜, para
seleccionar la opción Number format. Presiónese la tecla de menú @CHOOS (
B), y selecciónese la opción Fixed utilizando la tecla ˜.

Presiónese la tecla direccional horizontal, ™, y selecciónese el cero en
frente de la opción Fix. Presiónese la tecla de menú @CHOOS y selecciónese
el valor 3 (como ejemplo), utilizando las teclas direccionales verticales,
—˜.

Presiónese la tecla de menú !!@@OK#@ para completar la selección:

Presiónese la tecla de menú !!@@OK#@ para recobrar la pantalla normal. El
número que se utilizó anteriormente se muestra ahora como:

Página 1-11

Nótese que la parte decimal es redondeada, y no truncada. Por ejemplo,
con este formato, el número 123.4567890123456 se muestra como

123.457, y no como 123.456. Esto se debe a que el tercer decimal, 6 es
> 5.

Formato científico

Para seleccionar este formato, presiónese primero la tecla H. A
continuación, utilícese la tecla direccional vertical, ˜, para seleccionar
la opción Number format. Presiónese la tecla @CHOOS ( B), y
selecciónese la opción Scientific utilizando la tecla ˜. Manténgase el
número 3 en frente de Sci. (Este número puede cambiarse de la misma
manera en que se cambió la opción Fixed en el ejemplo anterior).

Presiónese la tecla !!@@OK#@ para recobrar la pantalla normal. El número
utilizado anteriormente se muestra ahora de la forma siguiente:

Este resultado, 1.23E2, es la versión de la notación de potencias de diez,

×

es decir 1.235

102, proveída por la calculadora. En este formato

científico, el número 3 en frente de la opción Sci representa el número de
cifras significativas que siguen al punto decimal. La notación científica
siempre incluye una cifra entera como se mostró anteriormente. En este
ejemplo, por lo tanto, el número de cifras significativas es cuatro.

Página 1-12

Formato de ingeniería

El formato de ingeniería (engineering format) es muy similar al científico,
excepto que el exponente en la potencia de diez es un múltiplo de 3.
Para seleccionar este formato, presiónese primero la tecla H, y utilícese
la tecla direccional, ˜, para seleccionar la opción Number format.
Presiónese la tecla @CHOOS (B), y selecciónese la opción Engineering con
la tecla ˜. Manténgase el número 3 delante de la opción Eng. (Este
número puede cambiarse de la misma manera en que se cambió para la
opción Fix del formato de número).

Presiónese la tecla !!@@OK#@ para recuperar la pantalla normal. El número
utilizado en los ejemplos anteriores se muestra ahora de la siguiente
manera:

Dado que este número posee tres cifras en la parte decimal, se muestra
con cuatro cifras significativas y un exponente de cero cuando se utiliza el
formato de ingeniería. Por ejemplo, el número 0.00256 se muestra como:

Coma vs. Punto decimales

Puntos decimales en números reales pueden re-emplazarse con comas, si
el usuario está acostumbrado a esa notación. Para re-emplazar los puntos
decimales con comas, cámbiese la opción FM en la forma interactiva
denominada CALCULATOR MODES como se muestra a continuación
(Nótese que hemos cambiado el formato de números a estándar, Std):

Presiónese primero la tecla H. Después, presiónese la tecla direccional
vertical, ˜, una vez, y la tecla direccional horizontal, ™, dos veces,

Página 1-13

seleccionando así la opción __FM,. Para seleccionar comas, presiónese
la tecla de menú (B). La forma interactiva lucirá como se muestra
a continuación:

Presiónese la tecla de menú !!@@OK#@ para recobrar la pantalla normal. Por
ejemplo, el número 123.4567890123456, utilizado anteriormente, se
mostrará de la forma siguiente utilizando comas:

Medidas angulares

Las funciones trigonométricas, por ejemplo, requieren argumentos que
representan ángulos en el plano. La calculadora provee tres modos
diferentes de medidas angulares, a saber:

• Grados (Degrees): Existen 360 grados (360

• Radianes: Existen 2

π radianes (2π

r

) en un círculo.

• Grados decimales (Grades): Existen 400 grades (400

Las medidas angulares afectan los resultados de funciones tales como
seno(SIN), COS, TAN y funciones asociadas.

Para seleccionar las medidas angulares utilícese el procedimiento
siguiente:

• Presiónese primero la tecla H. A continuación, utilícese la tecla

˜, dos veces. Selecciónese la opción Angle Measure utilizando ya

sea la tecla \ (segunda columna en la quinta fila contando de

abajo hacia arriba), o la tecla de menú @CHOOS (B). Si se utiliza la

última opción, utilícense las teclas direccionales verticales, — ˜,

para seleccionar la medida angular, y presiónese la tecla !!@@OK#@ para

completar la operación. Por ejemplo, en la siguiente pantalla, se

selecciona Radianes como la medida angular:

o

) en un círculo.

g

) en un círculo.

Página 1-14

Sistema de coordenadas

La selección del sistema de coordenadas afecta la forma en se escriben y
se muestran vectores y números complejos. Para mayor información sobre
números complejos y vectores, véanse los Capítulos 4 y 8,
respectivamente, en esta guía. Existen tres sistemas de coordenadas en la
calculadora: Rectangulares (RECT), Cilíndricas (CYLIN), y Esféricas
(SPHERE). Para seleccionar el sistema de coordenadas utilícese el
procedimiento siguiente:

• Presiónese primero la tecla H. A continuación, utilícese la tecla
direccional vertical, ˜, tres veces. Una vez seleccionada la opción
Coord System, selecciónese la medida angular utilizando la tecla \,
o la tecla @CHOOS (B). Si se sigue la última opción, utilícense las
teclas direccionales verticales, — ˜, para seleccionar el sistema de
coordenadas, y presiónese la tecla !!@@OK#@ (F) para completar la
operación. Por ejemplo, en la siguiente pantalla se seleccionan
coordenadas polares:

Seleccionando opciones del CAS

El término CAS significa Computer Algebraic System, o Sistema
Algebraico Computacional. El CAS es el centro matemático de la
calculadora donde residen las operaciones y funciones simbólicas de la
misma. El CAS presenta un número de opciones que pueden ajustarse de
acuerdo a la operación de interés. Para ver las opciones del CAS utilícese
el procedimiento siguiente:

Página 1-15

•Presiónese la tecla H para activar la forma interactiva denominada
CALCULATOR MODES.

• Para cambiar las opciones del CAS presiónese la tecla de menú @@CAS@@.
Los valores predefinidos de las opciones del CAS se muestran en la
figura siguiente:

• Para navegar a través de las diferentes opciones en la forma
interactiva denominada CAS MODES, utilícese las teclas direccionales:
š™˜—.

• Para seleccionar o remover cualquiera de las opciones indicadas
anteriormente, selecciónese la línea que precede a la opción de

interés, y presiónese la tecla de menú hasta que se obtenga la
opción apropiada. Una vez seleccionada cierta opción, aparecerá
una marca de aprobado () en la línea que precede a la opción
seleccionada (por ejemplo, véanse las opciones Rigorous y Simp Non-
Rational en la pantalla mostrada anteriormente). En las opciones que
no han sido seleccionadas no se mostrarán marcas de aprobado ()
en la línea precedente (por ejemplo, en las opciones _Numeric,
_Approx, _Complex, _Verbose, _Step/Step, y _Incr Pow mostradas
anteriormente).

• Después de haber seleccionado o removido todas las opciones
deseadas en la forma interactiva denominada CAS MODES,
presiónese la tecla de menú @@@OK@@@. Esta acción permite regresar a la
forma interactiva denominada CALCULATOR MODES. Para recobrar
la pantalla normal presiónese la tecla de menú @@@OK@@@ una vez más.

Página 1-16

Explicación de las opciones del CAS

•Indep var: La variable independiente para las aplicaciones del CAS.
Usualmente, VX = ‘X’.

•Modulo
almacena el módulo del anillo aritmético (véase el Capítulo 5 en la
guía del usuario de la calculadora).

•Numeric
resultados numéricos en las operaciones. Observe que las constantes
siempre se evaluarán numéricamente.

• Approx
modo denominado aproximado (Approx) y produce resultados
numéricos en las operaciones. Si esta opción no es seleccionada, el
CAS utiliza el modo exacto (Exact), el cual produce resultados
simbólicos en las operaciones algebraicas.

•Complex
números complejos son activadas. Si no se selecciona esta opción, la
calculadora opera en modo Real, lo que significa que se activan las
operaciones con números reales. Para mayor información sobre
operaciones con números reales véase el Capítulo 4 en esta guía.

•Verbose
información detallada al realizar ciertas operaciones del CAS.

•Step/Step
resultados intermedios detallados (paso-a-paso) en ciertas operaciones
que usan el CAS. Esta opción puede ser útil para obtener pasos
intermedios en sumatorias, derivadas, integrales, operaciones con
polinomios (por ejemplo, divisiones sintéticas), y operaciones
matriciales.

•Incr Pow
selecciona esta opción, los términos de los polinomios se mostrarán
con un orden reciente de las potencias de la variable independiente.

• Rigorous
función valor absoluto |X| a X.

• Simp Non-Rational
intentará simplificar expresiones no racionales tanto como sea posible.

: Para operaciones en la aritmética modular esta variable

: Cuando se selecciona esta opción la calculadora produce

: Cuando se selecciona esta opción, la calculadora usa el

: Cuando se selecciona esta opción, las operaciones con

: Si se selecciona esta opción la calculadora provee

: Si se selecciona esta opción, la calculadora provee

: Potencia creciente (Increasing Power), significa que, si se

: Si se selecciona esta opción la calculadora no simplifica la

: Si se selecciona esta opción la calculadora

Página 1-17

Selección de los modos de la pantalla

La pantalla de la calculadora posee un número de opciones que el usuario
puede ajustar a su gusto. Para ver las opciones disponibles, use el
procedimiento siguiente:

• Para empezar, presiónese la tecla H para activar la forma
denominada CALCULATOR MODE. Dentro de esta forma interactiva,
presiónese la tecla de menú @@DISP@ (D) para activar la forma
denominada DISPLAY MODES:

• Para navegar a través de las diferentes opciones en la forma interactiva
DISPLAY MODES utilícense las teclas direccionales: š™˜—.

• Para seleccionar o remover cualquiera de las opciones mostradas en la
figura anterior (las opciones selectas se indican con la marca de
aprobado, ), selecciónese la línea previa a la opción de interés, y

presiónese la tecla de menú hasta conseguir la opción deseada.
Cuando se selecciona una opción, se muestra una marca de
aprobado, , en la línea precedente (por ejemplo, en la opción
Textbook en la línea Stack: en la figura anterior). Opciones no
seleccionadas no mostrarán la marca de aprobado, , en la línea
precedente (por ejemplo, las opciones _Small, _Full page, e _Indent en
la línea Edit: en la figura anterior).

• Para seleccionar el tipo de caracteres (Font) para la pantalla,
selecciónese la opción Font: en la forma interactiva denominada
DISPLAY MODES, y utilícese la tecla de menú @CHOOS (B).

• Después de haber seleccionado y/o removido todas las opciones
deseadas en la forma interactiva DISPLAY MODES, presiónese la tecla
de menú @@@OK@@@. Esta acción permite al usuario recobrar la forma
interactiva denominada CALCULATOR MODES en la pantalla. Para
recobrar la pantalla normal, presiónese la tecla de menú @@@OK@@@ una vez

más.

Página 1-18

Selección del tipo de caracteres (font)

Para empezar, presiónese la tecla H para activar la forma interactiva
CALCULATOR MODES. Dentro de esta forma interactiva, presiónese la
tecla de menú @@DISP@ (D) para activar la forma interactiva denominada
DISPLAY MODES. La pantalla indicará que la opción Ft8_0:system 8 ha
sido seleccionada para la línea Font: en la forma interactiva DISPLAY
MODES. Este es el valor pre-selecto para la línea Font. Al presionar la
tecla de menú @CHOOS (B), la pantalla proveerá todas las opciones
posibles para el tipo de caracteres:

Existen tres opciones estándares disponibles System Fonts (de tamaños 8,
7, y 6) y una cuarta opción, Browse... Esta última opción permite al
usuario a buscar tipos adicionales que pueden ser creados por el usuario
o copiados en la memoria de la calculadora de otras fuentes.

Practique cambiar el tamaño de los caracteres a 7 y 6. Presiónese la tecla
@@OK@@ para aceptar la selección del tamaño de los caracteres. Una vez
seleccionado el tamaño de los caracteres, la tecla de menú @@@OK@@@ para
recobrar la forma interactiva denominada CALCULATOR MODES. Para
recobrar la pantalla normal, presiónese la tecla de menú @@@OK@@@ una vez
más. Obsérvese como la pantalla se ajusta al tamaño de caracteres
seleccionado por el usuario.

Página 1-19

Selección de las propiedades del editor de línea

Para empezar, presiónese la tecla H para activar la forma interactiva
CALCULATOR MODES. Dentro de esta forma interactiva, presiónese la
tecla de menú @@DISP@ (D) para activar la forma interactiva DISPLAY
MODES. Presiónese la tecla direccional vertical, ˜, una vez, para
alcanzar la línea Edit. Esta línea muestra tres propiedades del editor que
pueden ser modificadas. Cuando se seleccionan estas propiedades (se
muestra una marca de aprobado, ) se activan las siguientes opciones:

_Small Se cambia el tamaño de los caracteres a pequeño
_Full page Permite posicionar el cursor al final de una línea
_Indent Produce una auto-margen al presionar la tecla

alimentadora de líneas (Enter)

Instrucciones para el uso del editor de línea se presentan en el Capítulo 2
de la guía del usuario.

Selección de las propiedades de la pantalla (Stack)

Para empezar, presiónese la tecla H para activar la forma interactiva
CALCULATOR MODES. Dentro de esta forma interactiva, presiónese la
tecla de menú @@DISP@ (D) para activar la forma interactiva DISPLAY
MODES. Presiónese la tecla direccional vertical, ˜, dos veces, para
alcanzar la línea Stack. Esta línea muestra dos propiedades del editor
que pueden ser modificadas. Cuando se seleccionan estas propiedades
(se muestra una marca de aprobado, ) se activan las siguientes
opciones:

_Small Cambia el tamaño de los caracteres a pequeño. Esta

opción maximiza la cantidad de información presentada
en la pantalla. Esta selección precede a la selección del
tamaño de los caracteres de la pantalla.

_Textbook Muestra las expresiones matemáticas en notación

matemática propia

Para ilustrar estas opciones, ya sea en modo algebraico o RPN, utilícese el
escritor de ecuaciones para escribir la siguiente expresión:

‚O…Á0™„虄¸\x™x`

En modo algebraico, la siguiente pantalla muestra este resultado cuando
no se selecciona ni la opción _Small ni la opción _Textbook en la línea
Stack:

Página 1-20

Cuando se selecciona la opción _Small solamente, la pantalla muestra lo
siguiente:

Con la opción _Textbook seleccionada (este es el valor predefinido), ya
sea que se seleccione la opción _Small o no, la pantalla muestra el
siguiente resultado:

Selección de las propiedades del escritor de ecuaciones (EQW)

Para empezar, presiónese la tecla H para activar la forma interactiva
CALCULATOR MODES. Dentro de esta forma interactiva, presiónese la
tecla de menú @@DISP@ (D) para activar la forma interactiva DISPLAY
MODES. Presiónese la tecla direccional vertical, ˜, tres veces, para
activar la línea EQW (Equation Writer). Esta línea muestra dos
propiedades del editor que pueden ser modificadas. Cuando se
seleccionan estas propiedades (se muestra una marca de aprobado, ) se
activan las siguientes opciones:

_Small Cambia el tamaño de los caracteres a pequeño

_Small Stack Disp Muestra tamaño pequeño de caracteres después de

cuando se utiliza el escritor de ecuaciones

utilizar el escritor de ecuaciones

Instrucciones detalladas del uso del escritor de ecuaciones (EQW) se
presentan en otras secciones de esta guía.

Página 1-21

∞

−

En el ejemplo de la integral , que se presentó anteriormente, el

seleccionar la opción _Small Stack Disp en la línea EQW de la forma
DISPLAY MODES produce el siguiente resultado:

X

∫

dXe

0

Referencias

Referencias adicionales sobre las materias cubiertas en este Capítulo
pueden encontrarse en el Capítulo 1 y en el Apéndice C de la guía del
usuario.

Página 1-22

Capítulo 2
Introducción a la calculadora

En este Capítulo se presentan las operaciones básicas de la computadora
incluyendo el uso del escritor de ecuaciones (Equation Writer) y la
manipulación de los objetos (datos) en la calculadora. Analícense los
ejemplos en este Capítulo para conocer mejor la operación de la
calculadora en futuras aplicaciones.

Objetos en la calculadora

El término “objeto” se refiere un los números, listas, matrices, etc. que se
usan en la calculadora. Los objetos más comunes son: los reales (números
reales, escritos con un punto decimal, por ejemplo, -0.0023, 3.56), los
enteros (números enteros, escritos sin un punto decimal, por ejemplo,
1232, -123212123), los números complejos (escritos como pares
ordenados, por ejemplo, (3,-2)), las listas, etc. Los objetos en la
calculadora se describen en los Capítulos 2 y 24 de la guía del usuario.

Edición de expresiones en la pantalla

En esta sección se presentan ejemplos de la edición de expresiones
directamente en la pantalla de la calculadora.

Creación de expresiones aritméticas

Pare ejecutar este ejemplo, selecciónese el modo operativo Algebraic y el
formato Fix con 3 decimales para la pantalla. Escríbase la expresión:

0.1

0.1

+

0.5

⋅

Para escribir esta expresión, utilícense las siguientes teclas:

5.*„Ü1.+1/7.5™/

„ÜR3.-2.Q3

La expresión resultante es: 5*(1+1/7.5)/(
Presiónese la tecla ` para mostrar la expresión en la pantalla:

Página 2-1

5.7

0.20.3

−

√3-2^3).

3

Nótese que, es la opción EXACT se selecciona para el CAS (véase el
Apéndice C en la guía del usuario) y se escribe la expresión utilizando
números enteros para los valores enteros, el resultado es una expresión
simbólica, por ejemplo,

5*„Ü1+1/7.5™/

„ÜR3-2Q3

Antes de producirse el resultado, se solicita que el usuario cambie el modo
a Approximate (aproximado). Acéptese el cambio para obtener el
resultado mostrado a continuación (mostrado con formato Fix con tres
decimales – véase el Capítulo 1):

En este caso, cuando la expresión se escribe directamente en la pantalla,
en cuanto se presiona la tecla `, la calculadora intentará calcular el
valor de la expresión. Si la expresión va precedida por un tick, la
calculadora simplemente reproduce la expresión tal y como fue escrita.
Por ejemplo:

³5*„Ü1+1/7.5™/

„ÜR3-2Q3`

El resultado se muestra a continuación:

Para evaluar la expresión en este caso, utilícese la función EVAL:

µ„î`

Página 2-2

Si la opción Exact ha sido seleccionada para el CAS, se solicita que el
usuario cambie el modo a Approximate (aproximado). Acéptese el
cambio para obtener la evaluación de la expresión como se demostró en
un ejemplo anterior.

Una forma alternativa para evaluar la expresión escrita entre apóstrofes en
el ejemplo anterior, consiste en utilizar la función …ï.

A continuación, se escribe la expresión utilizada anteriormente con la
calculadora utilizando el modo operativo RPN. Selecciónese la opción
Exact para el CAS, la opción Textbook para la pantalla, y el formato
numérico a Standard. Utilícense las siguientes teclas para escribir la
expresión entre apóstrofes utilizada anteriormente, es decir,

³5*„Ü1+1/7.5™/

„ÜR3-2Q3`

El resultado se muestra en la siguiente pantalla:

Presiónese la tecla ` una vez más para producir dos copias de la
expresión en la pantalla. Evalúese la expresiónprimero pulsando:

µ!î` or @ï`

Esta expresión es semi-simbólica en el sentido de que existen componentes
reales (números reales) en el resultado, así como la expresión simbólica

√3. A continuación, intercámbiense las posiciones de los niveles 1 y 2 en

la pantalla y evalúese la expresión utilizando la función NUM, es decir,
™…ï.

Este último resultado es puramente numérico, de manera que, los dos
resultados en la pantalla, aunque representan la evaluación de la misma
expresión, aparecen en formas diferentes. Para verificar que el valor
resultante es el mismo, obténgase la diferencia de estos dos valores y
evalúese esta diferencia usando la función EVAL: -µ. El resultado
es cero(0.).

Para obtener información adicional en la edición de expresiones
aritméticas en la pantalla, véase el Capítulo 2 en la guía del usuario de la
calculadora.

Página 2-3

Creación de expresiones algebraicas

Las expresiones algebraicas incluyen no solamente números, sino también
variable. Por ejemplo, escríbase la siguiente expresión algebraica:

L212

Selecciónese el modo operativo Algebraico en la calculadora, la opción
Exact en el CAS, y la opción Textbook para la pantalla. Escríbase la
expresión propuesta utilizando las siguientes teclas:

³2*~l*R„Ü1+~„x/

~r™/„Ü

~r+~„y™+2*~l/~„b

Presiónese la tecla ` para obtener el siguiente resultado:

Esta expresión puede escribirse con la calculadora en modo operativo
RPN de la misma forma especificada anteriormente para el modo
operativo algebraico (ALG).

Para obtener información adicional en la edición de expresiones
algebraicas en la pantalla, véase el Capítulo 2 en la guía del usuario de
la calculadora.

x

+

R

yR

+

L

+

b

Uso del escritor de ecuaciones (EQW) para crear expresiones

El escritor de ecuaciones es una herramienta muy importante que permite
al usuario no solamente escribir o ver una ecuación, sino también
modificar y manipular expresiones, y aplicar funciones a las mismas.

El escritor de ecuaciones se activa al presionar ‚O (la tercera tecla
en la cuarta fila del teclado). La pantalla resultante es la siguiente.
Presiónese la tecla L para acceder la segunda página del menú:

Página 2-4

Las seis teclas de menú del escritor de ecuaciones activan las funciones
EDIT, CURS, BIG, EVAL, FACTOR, SIMPLIFY, CMDS, y HELP. Información
detallada sobre estas funciones se presenta en el Capítulo 3 de la guía del
usuario de la calculadora.

Creación de expresiones aritméticas

La escritura de expresiones en el Escritor de ecuaciones es muy similar a la
escritura de expresiones entre apóstrofes en la pantalla. La diferencia
principal es que en el Escritor de ecuaciones las expresiones producidas se
presentan en el estilo “textbook” (libro de texto, es decir, utilizando
notación matemática similar a la de un libro de texto) en vez de escribirse
como en el editor de línea en la pantalla. Por ejemplo, escríbase el
siguiente ejercicio en el escritor de ecuaciones: 5/5+2.

El resultado es la expresión

El cursor se muestra como una flecha apuntando hacia la izquierda. El
cursor indica la posición de edición actual en la pantalla del escritor de
ecuaciones. Por ejemplo, con el cursor en la posición mostrada
anteriormente, escríbase:

*„Ü5+1/3

La expresión así editada lucirá ahora de la siguiente manera:

Página 2-5

Supóngase que se desea reemplazar la expresión entre paréntesis en el

2

π

denominador (es decir, 5+1/3) con (5+
tecla de borrar (ƒ) para borrar la fracción 1/3, y reemplazarla con

2. Utilícense las siguientes teclas:

ƒƒƒ„ìQ2

A este punto, la pantalla lucirá de la siguiente manera:

/2). Para empezar, utilícese la

2

π

/

Para escribir el denominador 2 debajo de

2

π

expresión
horizontal ™, una sola vez. Después, escríbase:

La expresión resultante es:

Supóngase que se quiere sumar la cantidad 1/3 a esta expresión para
obtener:

completa. Esto se consigue al presionar la tecla direccional

/2

5

+⋅+

5(25

2

π

, es necesario seleccionar la

1

+

2

π

3

)

2

Para empezar, es necesario seleccionar todo el primer término utilizando,
ya sea, la tecla direccional horizontal (™) o la tecla direccional vertical
(—), repetidamente, hasta que la expresión completa haya sido
seleccionada, es decir, siete veces:

Página 2-6

NOTA: Como forma alternativa, comenzando en la posición original
del cursor (a la derecha del 2 en el denominador de

utilizar la combinación de teclas ‚—, que se interpreta como
(‚ ‘ ).

Una vez seleccionada la expresión como se mostró anteriormente,
escríbase +1/3 para agregar la fracción 1/3 a la expresión.
El resultado es:

2

π

/2), se puede

Creación de expresiones algebraicas

Una expresión algebraica es muy similar a una expresión aritmética,
excepto que en la última se pueden incluir letras castellanas y griegas. El
procedimiento de creación de una expresión algebraica sigue la misma
idea que el crear una expresión aritmética, excepto que se tiene que
utilizar el teclado alfanumérico.

Para ilustrar el uso del escritor de ecuaciones para escribir una expresión
algebraica se utilizará el siguiente ejemplo. Supóngase que se quiere
escribir la expresión:

∆⋅+

2

−

µ

⋅+

λ

LNe

3

Utilícense las siguientes teclas:

2/R3™™*~‚n+„¸\~‚m

™™*‚¹~„x+2*~‚m*~‚c

~„y———/~‚tQ1/3

Página 2-7

2

yx

⎛
⎜

⎝

µ

θ

⎞
⎟

3/1

⎠

El resultado es el siguiente:

En este ejemplo se utilizan varias letras minúsculas del Castellano, por
ejemplo, x (~„x), varias letras griegas, por ejemplo,
(~‚n), e inclusive una combinación de letras castellanas y griegas,

∆y (~‚c~„y). Obsérvese que para escribir una letra

castellana en minúscula es necesario utilizar la combinación de teclas
~„ seguida de la tecla de la letra a escribirse. Así mismo, se
pueden copiar caracteres especiales utilizando el menú CHARS (…±)
si no se desea memorizar la combinación de teclas que produce el
carácter deseado.

Para mayor información sobre la edición, evaluación, factorización, y
simplificación de expresiones algebraicas usando el escritor de
ecuaciones, véase el Capítulo 2 de la guía del usuario de la calculadora.

λ

Organización de los datos en la calculadora

Es posible organizar los datos en la calculadora al almacenar variables en
una colección de directorios. La base de esta colección es el directorio
HOME, que se describe a continuación.

El directorio HOME

Para acceder al directorio HOME, presiónese la función UPDIR („§)

-- repítase cuantas veces sea necesario -- hasta que la especificación

{HOME} se muestra en la segunda línea del encabezado de la pantalla.
Como una alternativa, utilícese „ (manténgase presionada la tecla)

§. En este ejemplo, el directorio HOME contiene solamente el sub-

directorio CASDIR. Presiónese la tecla J para mostrar las variables en
las teclas de menú:

Página 2-8

Sub-directorios

Para almacenar datos en una colección de directorios bien organizada, el
usuario podría crear una serie de sub-directorios dentro del directorio
HOME, y aún más sub-directorios dentro de estos sub-directorios, hasta
formar una jerarquía de directorios similar a los directorios en un
ordenador (computador, o computadora). Los sub-directorios pueden
identificarse con nombres que reflejen el contenido de los mismos, o con
cualquier nombre que el usuario quiera darles. Para mayor información
sobre la manipulación de directorios en la calculadora véase el Capítulo 2
en la guía del usuario.

Variables

Las variables en la calculadora son similares a los archivos en el disco
duro de un ordenador (computador, o computadora). Es posible
almacenar un objeto (valores numéricos, expresiones algebraicas, listas,
vectores, matrices, programas, etc.) en una variable. Las variables se
identifican por un nombre, el cual puede ser cualquier combinación de
caracteres alfabéticos o numéricos, comenzando siempre por una letra (ya
sea castellana o griega). Algunos caracteres no alfabéticos, tales como la
flecha (
combinan con un carácter alfabético. Por lo tanto, ‘
válido para una variable, pero ‘
pa ra u na var iab le son : ‘A’, ‘B’, ‘a ’, ‘b’, ‘
’Z0’, ’z1’, etc.

→), pueden utilizarse en el nombre de una variable, si se

→A’ es un nombre

→’ no lo es. Ejemplos de nombres válidos

α’, ‘β’, ‘A1 ’, ‘AB 12’, ‘A12’, ’Vel’,

No se puede asignar a una variable un nombre igual al de una función en
la calculadora. Algunos de los nombres reservados por la calculadora
son los siguientes: ALRMDAT, CST, EQ, EXPR, IERR, IOPAR, MAXR, MINR,
PICT, PPAR, PRTPAR, VPAR, ZPAR, der_, e, i, n1,n2, …, s1, s2, …,

ΣPAR, π, ∞

Las variables pueden organizarse en sub-directorio (véase el Capítulo 2 en
la guía del usuario de la calculadora para mayor información).

Página 2-9

ΣDAT,

Escritura del nombre de variables

Para identificar variables es necesario escribir una cadena de letras en un
solo tirón, las cuales pueden ser combinadas con números. Para escribir
cadenas de caracteres es posible asegurar el teclado de la calculadora en
el modo alfabético de la siguiente manera:

~~ asegura el teclado alfabético en mayúsculas. Cuando se
asegura el teclado alfabético de esta manera, es necesario presionar la
tecla „ antes de escribir la letra correspondiente en minúscula, mientras
que al presionarse la tecla ‚ antes de presionar una letra produce un
carácter especial. Si el teclado alfabético está ya asegurado en
mayúsculas, para asegurarlo en minúsculas utilícese „~

~~„~ asegura el teclado alfabético en minúsculas. Cuando
se asegura el teclado alfabético de esta manera, es necesario presionar la
tecla „ antes de escribir la letra correspondiente en mayúscula. Para
remover el teclado asegurado en minúsculas, presiónese „~

Para remover el teclado asegurado en mayúsculas, presiónese ~
Ejecútense los siguientes ejercicios:

~~math`

~~m„a„t„h`

~~m„~at„h`

La calculadora muestra los siguientes resultados (a la izquierda en modo
Algebraico, a la derecha en modo RPN):

Página 2-10

Creación de variables

La forma más simple de crear una variable es a través de la tecla K Los
ejemplos siguientes muestran como almacenar los objetos listados en la
tabla que se muestra a continuación (Presiónese J, de ser necesario,
para ver el menú de variables):

Nombre Contenido Tipo

α -0.25

A12
Q‘r/(m+r)'
R [3,2,1]
z1 3+5i
p1

Escójase el modo algebraico o RPN para ejecutar estos ejercicios.

5

×10

3

<<

→ r 'π*r^2'

Modo algebraico

Para almacenar el valor –0.25 en la variable α, utilícese:

0.25\K~‚a. Al terminar este ejercicio la
pantalla luce de esta manera:

real
real
algebraico
vector
complejo

>>

programa

Presiónese ` para crear la variable. La variable se muestra en las
teclas de menú J:

Los siguientes son los procedimientos requeridos para almacenar las
variables restantes:

A12: 3V5K~a12`
Q: ~„r/„Ü

~„m+~„r™™K~q`

R: „Ô3‚í2‚í1™K~r`
z1: 3+5*„¥K~„z1` (Aceptar cambio

a modo Complex, de ser necesario).

Página 2-11

p1: å‚é~„r³„ì*
~„rQ2™™™K~„p1`.

Al terminar estos ejercicios la pantalla lucirá de la forma siguiente:

Nótese que las teclas de menú muestran seis variables: p1, z1, R, Q,
A12, α.

Modo RPN

(Utilícese H\@@OK@@ para cambiar el modo operativo a RPN).
Utilícense las teclas siguientes para almacenar el valor –0.25 en la
variable α: .25\`³~‚a`. Al finalizar este
ejercicio, la pantalla muestra lo siguiente:

Con –0.25 en el nivel 2 de la pila y 'α' en el nivel 1 de la pila, puede usar
la tecla K para crear la variable. La variable se muestra en las teclas
del menú cuando presione J:

5

Para almacenar el valor 3×10

en la variable A12, se puede utilizar:

3V5³~a12`K

He aquí una forma de almacenar el contenido de la variable Q:
Q: ~„r/„Ü

~„m+~„r™™³~q`K

Para almacenar el contenido de R, utilícese, por ejemplo:
R: „Ô3#2#1™³~rK

Página 2-12

Nótese que para separar los elementos de un vector en modo RPN se
puede utilizar la tecla de espaciar (#), en vez de la coma (‚í)
como se requiere en modo algebraico.

z1: ³3+5*„¥³~„z1K
p1: ‚å‚é~„r³„ì*
~„rQ2™™™³ ~„p1™`K.
Al terminar estos ejercicios la pantalla RPN lucirá de esta manera:

Las teclas de menú mostrarán seis de las variables: p1, z1, R, Q, A12,

α.

Examinando el contenido de una variable

La forma más simple de examinar los contenidos de una variable consiste
en presionar la tecla de menú correspondiente al nombre de la variable.
Por ejemplo, para las variables utilizadas anteriormente, ejecútense las
siguientes instrucciones:

Modo algebraico

Presiónense las siguientes teclas: J@@z1@@ ` @@@R@@ `@@@Q@@@ `. Al
finalizar este ejercicio la pantalla lucirá de esta forma:

Modo RPN

En modos RPN, es necesario solamente presionar las teclas
correspondientes al nombre de las variables para examinar el contenido
de las mismas. Para el caso de interés, examínese el contenido de las
variables z1, R, Q, A12,
siguiente: J@@z1@@ @@@R@@ @@@Q@@ @@A12@@ @@»@@

Al finalizar este ejercicio, la pantalla lucirá de esta manera:

α, y α, creadas anteriormente, de la forma

Página 2-13

Utilizando la tecla seguida de la tecla del menú

Este procedimiento para examinar el contenido de las variables puede
utilizarse ya sea en modo algebraico como en modo RPN. Ejecútense los
siguientes ejemplos en cualquiera de los modos de operación:

J‚@@p1@@ ‚@@z1@@ ‚@@@R@@ ‚@@@Q@@ ‚ @@A12@@

Los resultados se muestran a continuación (Modo algebraico a la
izquierda, modo RPN a la derecha):

Nótese que en este caso el programa contenido en la variable p1 se lista
en la pantalla. Para ver el contenido de

@@@»@@L‚ @@@A@@

α, utilícese:

Listado de las variables en la pantalla

Utilícese la combinación ‚˜ para listar el contenido de todas las
variables en la pantalla. Por ejemplo:

Presiónese $ para recobrar la pantalla normal.

Página 2-14

Eliminación de las variables

La forma más simple de eliminar variables es utilizando la función PURGE
(eliminar). Esta función puede accederse directamente al utilizar el menú
TOOLS (I), o al utilizar el menú FILES (archivos) „¡@@OK@@ .

Usando la función PURGE en la pantalla en Modo algebraico

Nuestra lista de variables contiene las variables p1, z1, Q, R, y α. A
continuación se utiliza la función PURGE para eliminar las variable p1 y
A. Presiónese I@PURGE@ J @@p1@@ `, y a continuación I @PURGE@
J@@p1@@ `. La pantalla indica que las variables p1 y A han sido
eliminada:

La función PURGE puede utilizarse para eliminar más de una variable al
colocar sus nombres en una lista que pasa a ser el argumento de la
función. Por ejemplo, si quisiéramos eliminar las variables R y Q,
simultáneamente, se puede utilizar :

I @PURGE@ „ä³J@@@R!@@™‚í³J@@@Q!@@

La pantalla muestra la función PURGE a punto de activarse para eliminar
las variables R y Q:

Para completar el ejercicio, presiónese `. La pantalla muestra las
variables restantes:

Utilizando la función PURGE en la pantalla en Modo RPN

Asumiendo que nuestra lista de variables contiene p1, z1, Q, R, y α.
Utilizaremos la función PURGE para eliminar la variable p1. Presiónense

Página 2-15

las siguientes teclas ³ @@p1@@ `I @PURGE@. La pantalla indica que p1
ha sido eliminada de la memoria:

Para eliminar dos variables simultáneamente, por ejemplo, las variables R
y Q, créese primero una lista (en Modo RPN, los elementos de lista no
necesitan estar separados por comas como se requiere en Modo
algebraico):

J„ä³ @@@R!@@ ™³ @@@Q!@@ `

A continuación, presiónese I@PURGE@ para eliminar las dos variables.
Información adicional sobre la manipulación de variables se presenta en

el Capítulo 2 de la guía del usuario de la calculadora.

Las funciones UNDO y CMD

Las funciones UNDO y CMD son útiles para recobrar instrucciones previas
o para recobrar una operación en caso de que se haya cometido un error.
Estas funciones están asociadas con la tecla HIST: UNDO resulta al
escribir ‚¯, mientras que CMD resulta al escribir „®.

Opciones CHOOSE boxes y Soft MENU

En algunos de los ejercicios presentados en este Capítulo hemos
presentado listas de funciones en la pantalla. Estas listas de funciones se
denominan, en inglés, CHOOSE boxes (listas de menú). El ejercicio
siguiente indica como cambiar la opción (CHOOSE boxes) a Soft MENU
(teclas de menú), y viceversa.

Aunque el presente ejercicio no se aplica a un ejemplo específico, el
mismo muestra las dos opciones para los menús de funciones en la
calculadora (CHOOSE boxes y soft MENUs). En este ejercicio, se busca
la función ORDER, la cual se utiliza, en modo ALG, para reordenar las
variables en un directorio:

Página 2-16

„°˜ Mostrar el menú PROG. Seleccionar MEMORY.

@@OK@@ ˜˜˜˜ Mostrar el menú MEMORY. Seleccionar

DIRECTORY.

@@OK@@ —— Mostrar menú DIRECTORY. Seleccionar ORDER.

@@OK@@ Activar la función ORDER.

Una forma alternativa de mostrar las funciones de un menú es a través de
teclas de menú (soft MENU), al manipular la señal de sistema número 117
(system flag 117). (Para información adicional sobre señales de sistema
véanse los Capítulos 2 y 24 en la guía del usuario). Para seleccionar esta
señal utilícese:

H@FLAGS! ———————

La pantalla muestra la señal de sistema número 117 sin seleccionar (es
decir, con la opción CHOOSE boxes activa):

Página 2-17

Presiónese la tecla para seleccionar esta señal de sistema
activando la opción soft MENU. La pantalla reflejará esta selección:

Presiónese @@OK@@ dos veces para recobrar la pantalla normal.
A continuación, se busca la función ORDER utilizando teclas de menú.

Para comenzar, presiónese „°. Nótese que en vez de una lista de
menú se obtienen ahora teclas de menú para el menú PROG, es decir,

Presiónese B para seleccionar el menú MEMORY ()@@MEM@@). La pantalla
muestra las siguientes teclas de menú:

Presiónese E para seleccionar el menú DIRECTORY ()@@DIR@@)

La función ORDER no se muestra en esta página de menú. Para encontrar
esta función presiónese L:

Página 2-18

Para activar la función ORDER, presiónese la tecla de menú C(@ORDER).

Referencias

Para mayor información sobre la escritura y manipulación de expresiones
en la pantalla o en el escritor de ecuaciones véase el Capítulo 2 de la
guía del usuario. Para información sobre las opciones del CAS, véase el
Apéndice C en la guía del usuario. Para información sobre las señales de
sistema (system flags) en la calculadora, véase el Capítulo 24 en la guía
del usuario.

Página 2-19

Capítulo 3
Cálculos con números reales

Este Capítulo demuestra el uso de la calculadora para operaciones y las
funciones relacionadas un los números reales. Se asume que el usuario
está familiarizado con el teclado para identificar ciertas funciones
disponibles en el mismo (por ejemplo, SIN, COS, TAN, etc.). Así mismo,
se asume que el lector sabe como seleccionar el sistema operativo de la
calculadora (Capítulo 1), como usar menús y listas de selección (Capítulo

1), y como utilizar variables (Capítulo 2).

Ejemplos de cálculos con números reales

Para ejecutar cálculos con números reales es preferible que el CAS tenga
activa la opción Real (en contraste con la opción Complex). La opción
Exact es la opción pre-seleccionada por la calculadora para la mayoría
de las operaciones. A continuación se ilustran algunos cálculos con
números reales.

•Use la tecla \ para cambiar el signo de un número.
Por ejemplo, en modo ALG, \2.5`.
En modo RPN, 2.5\.

•Use la tecla Y para calcular el inverso de un número.
Por ejemplo, en modo ALG, Y2`.
En modo RPN, 4Y.

• Para adición, substracción, multiplicación, división, use la tecla
apropiada para esas operaciones, es decir, +-*/.
Ejemplos en modo ALG:

3.7+5.2`

6.3-8.5`

4.2*2.5`

2.3/4.5`

Ejemplos en modo RPN:

3.7` 5.2+

6.3` 8.5-

4.2` 2.5*

2.3` 4.5/

Página 3-1

Alternativamente, en modo RPN, uno puede separar los operandos con la
tecla espaciadora (#) antes de presionar la tecla de la operación.
Ejemplos:

3.7#5.2+

6.3#8.5-

4.2#2.5*

2.3#4.5/

• Los paréntesis („Ü) pueden utilizarse para agrupar operaciones,
así como para contener argumentos de funciones.
Ejemplo en modo ALG:

„Ü5+3.2™/„Ü7-

2.2`

En modo RPN uno no siempre necesita usar paréntesis, dado que los
cálculos se realizan directamente en la pantalla (stack):

5`3.2+7`2.2-/

En modo RPN, el escribir una expresión entre apóstrofes permite al
usuario a escribir expresiones como en el modo algebraico:

³„Ü5+3.2™/

„Ü7-2.2`µ

Para ambos modos, ALG y RPN, uno puede utilizar el escritor de
ecuaciones en el cálculo:

‚O5+3.2™/7-2.2

La ecuación puede ser evaluada dentro del escritor de ecuaciones al
utilizar las siguientes teclas:

————@EVAL@ ó, ‚—@EVAL@

• La función valor absoluto, ABS, se calcula usando „Ê.
Ejemplo en modo ALG:

„Ê\2.32`

Ejemplo en modo RPN:

2.32\„Ê

• La función cuadrado, SQ, se calcula usando „º.
Ejemplo en modo ALG:

„º\2.3`

Ejemplo en modo RPN:

2.3\„º

Página 3-2

La función raíz cuadrada, √, está disponible en la tecla R. Cuando se
calcula en la pantalla en modo ALG, escríbase la función antes del
argumento, por ejemplo,

R123.4`

En Modo RPN, escríbase el número primero, seguido por la función,
por ejemplo,

123.4R

• La función potencia, ^, se encuentra disponible en la tecla Q.
Cuando se calcula en la pantalla en modo ALG, escríbase la base (y)
seguida de la tecla Q, y del exponente (x), por ejemplo,

5.2Q1.25`

En Modo RPN, escríbase el número primero, seguido por la función,
por ejemplo,

5.2`1.25Q

• La función raíz, XROOT(y,x), está disponible a través de la
combinación de teclas ‚». Cuando se calcula en la pantalla en
modo ALG, escríbase la función XROOT seguida por los argumentos
(y,x), separados por comas, por ejemplo,

‚»3‚í27`

En Modo RPN, escríbase el argumento y, primero, después, x, y
finalmente la función, por ejemplo,

27`3‚»

• Los logaritmos de base 10 se calculan a través de la combinación de
teclas ‚Ã (función LOG) mientras que su inversa (ALOG, o
antilogaritmo) se calcula utilizando „Â. En modo ALG, la función
se escribe antes del argumento:

‚Ã2.45`

„Â\2.3`

En Modo RPN, el argumento se escribe antes de la función:

2.45‚Ã

2.3\„Â

Página 3-3

Utilizando potencias de 10 al escribir datos

Potencias de diez, es decir, números de la forma -4.5×10-2, etc., se
escriben utilizando la tecla V. Por ejemplo, en modo ALG:

\4.5V\2`

O, en modo RPN:

4.5\V2\`

• Los logaritmos naturales se calculan utilizando ‚¹ (función LN)
mientras que la función exponencial (EXP) se calcula utilizando

„¸. En modo ALG, la función se escribe antes del argumento:

‚¹2.45`

„¸\2.3`

En Modo RPN, el argumento se escribe antes de la función:

2.45`‚¹

2.3\`„¸

• Tres funciones trigonométricas se encuentran disponibles en el teclado:
seno (S), coseno (T), y tangente (U). Los argumentos de estas
funciones son ángulos ya sea en grados, radianes, o grados
decimales. Los siguientes ejemplos usan ángulos en grados (DEG):

En Modo ALG:

S30`

T45`

U135`

En Modo RPN:

30S

45T

135U

• Las funciones trigonométricas inversas disponibles en el teclado son el
arco seno („¼), el arco coseno („¾), y la arco tangente
(„À). Los resultados de estas funciones se darán en la medida
angular seleccionada por el usuario (DEG, RAD, GRD). Algunos
ejemplos se muestra a continuación:

En Modo ALG:

„¼0.25`

„¾0.85`

„À1.35`

Página 3-4

En Modo RPN:

0.25„¼

0.85„¾

1.35„À

Todas las funciones descritas anteriormente, es decir, ABS, SQ,
XROOT, LOG, ALOG, LN, EXP, SIN, COS, TAN, ASIN, ACOS, y ATAN,
pueden combinarse con las operaciones fundamentales (+-
*/) para formar expresiones más complejas. El escritor de
ecuaciones (Equation Writer), cuya operación se describe en el Capítulo
2, es el ambiente ideal para construir tales expresiones, sin importar el
modo operativo de la calculadora.

√, ^,

Las funciones de números reales en el menú MTH

El menú MTH („´) incluye un número de funciones matemáticas que
se aplican principalmente a los números reales. Utilizando la opción de
listas de funciones (CHOOSE boxes) para la señal de sistema número 117
(véase el Capítulo 2), el menú MTH muestra las siguientes funciones:

Las funciones se agrupan por el tipo de argumento (1. vectores, 2.
matrices, 3. listas, 7. probabilidad, 9. complejos) o por el tipo de función
(4. hiperbólicas, 5. reales, 6. de base, 8. fft (transformada rápida de
Fourier, o fast Fourier transform). El menú contiene así mismo una opción
para las constantes matemáticas disponibles en la calculadora, opción
número10.

En general, téngase cuidado del número y orden de los argumentos
requeridos para cada función, y téngase en cuenta que, en el modo ALG
uno debe seleccionar primero la función y después escribir el o los
argumentos, mientras que en Modo RPN, uno debe escribir el argumento
en la pantalla primero, y después seleccionar la función.

Página 3-5

Usando los menús de la calculadora:

1. Describiremos en detalle el uso del menú 4. HYPERBOLIC.. en esta
sección con la intención de describir la operación general de los
menús de la calculadora. Préstese atención particular al proceso de
selección de opciones.

2. Para seleccionar una de las opciones en una lista (CHOOSE box),
simplemente presiónese el número de esa opción en el teclado. Por
ejemplo, para seleccionar la opción 4. HYPERBOLIC.. en el menú
MTH, simplemente presiónese 4.

Las funciones hiperbólicas y sus inversas

Al seleccionar la opción 4. HYPERBOLIC.. , en el menú MTH, y al
presionar @@OK@@, se produce el menú de funciones hiperbólicas:

Por ejemplo, en Modo ALG, la secuencia de teclas para calcular tanh(2.5)
es la siguiente:

„´4 @@OK@@ 5 @@OK@@ 2.5`

En el modo RPN, las teclas para esta operación son las siguientes:

2.5`„´4 @@OK@@ 5 @@OK@@

Las operaciones mostradas anteriormente asumen que uno utiliza la
opción pre-definida para la señal de sistema número 117 (CHOOSE

boxes). Si uno ha cambiado esta señal de sistema (véase el Capítulo 2) a
SOFT menu, el menú MTH resulta ser como se muestra a continuación (a la

izquierda en modo ALG, a la derecha en Modo RPN):

Presiónese la tecla L para mostrar las demás opciones:

Página 3-6

Por lo tanto, para seleccionar, por ejemplo, el menú de las funciones
hiperbólicas, en este formato de menú presiónese la tecla )@@HYP@. Esta
acción produce el menú:

Finalmente, para seleccionar, por ejemplo, la función tangente hiperbólica
(tanh), simplemente presiónese la tecla @@TANH@.

Nota: Para ver opciones adicionales en este formato de menús,
presiónese la tecla L o las teclas „«.

Por ejemplo, para calcular tanh(2.5), en modo ALG, cuando se usan
menús de teclas (SOFT menus) en vez de menús de listas (CHOOSE
boxes), utilícese el procedimiento siguiente:

„´@@HYP@ @@TANH@ 2.5`

En Modo RPN, el mismo valor se calcula utilizando:

2.5`„´)@@HYP@ @@TANH@

Como ejercicio de aplicación de las funciones hiperbólicas, verifíquense
los siguientes valores:

SINH (2.5) = 6.05020.. ASINH(2.0) = 1.4436…
COSH (2.5) = 6.13228.. ACOSH (2.0) = 1.3169…
TANH(2.5) = 0.98661.. ATANH(0.2) = 0.2027…
EXPM(2.0) = 6.38905…. LNP1(1.0) = 0.69314….

Operaciones con unidades

Los números reales en la calculadora pueden escribirse con unidades de
medida. Por lo tanto, es posible calcular resultados que involucren un
sistema de unidades consistentes y producir un resultado con la
combinación de unidades apropiadas.

Página 3-7

El menú de UNIDADES

El menú de unidades (UNITS menu) se obtiene a través de la combinación
de teclas ‚Û(asociada con la tecla 6). Con la señal de sistema
número 117 indicando listas de menú (CHOOSE boxes), el resultado es el
siguiente menú:

Ls opción 1. Tools.. (herramientas) contiene las funciones usadas para
operar en unidades (se presentan más adelante). Las opciones 2.
Length.. a17.Viscosity.. contiene menús con varias unidades para cada
una de las cantidades descritas. Por ejemplo, al seleccionarse la opción

8. Force.. se muestra el siguiente menú de unidades:

El usuario reconocerá la mayoría de estas unidades de sus estudios de
física o química (algunas, por ejemplo, la dina (dyne), ya no se utilizan
muy comúnmente): N = newtons, dyn = dynes (dinas), gf = gramos –
fuerza (distinto de gramos-masa, ó simplemente gramos, una unidad de
masa), kip = kilo-poundal (1000 libras), lbf = libra-fuerza (distinto de
libra-masa), pdl = poundal.

Para adjuntar unidades a un número, el número debe seguirse de una
línea subrayada. Por lo tanto, una fuerza de 5 N se escribe como 5_N.

Página 3-8

El uso de teclas de menú (SOFT menus) provee una forma más conveniente
de agregar unidades cuando se utilizan números con unidades.
Cámbiese la señal de sistema número 117 a la opción SOFT menus
(véase el Capítulo 2), y utilícese la combinación de teclas ‚Û para
obtener los siguientes menús. Presiónese la tecla L para activar la
siguiente página del menú.

Al presionarse la tecla de menú apropiada se abrirá el sub-menú de
unidades para esa selección particular. Por ejemplo, para el menú @)SPEED
(rapidez, velocidad), se encuentran disponibles las siguientes unidades:

Al presionarse la tecla @)UNITS se reactiva el menú de UNIDADES.
Las opciones de un menú pueden listarse en la pantalla al usar las teclas

‚˜, por ejemplo, para las unidades @)ENRG (energía) se listan las
siguientes opciones:

Nota: Utilícense las teclas L ó „« para navegar a través de
los diferentes menús.

Página 3-9

Unidades disponibles

Véase el Capítulo 3 en la guía del usuario.

Agregando unidades a los números reales

Para adjuntar unidades a un número, el número debe seguirse de una
línea subrayada (‚Ý, tecla (8,5)). Por lo tanto, una fuerza de 5 N se
escribe como 5_N. La siguiente secuencia de teclas permite escribir este
número con unidades en modo ALG (la señal de sistema número 117
utiliza la opción CHOOSE boxes):

5‚Ý‚Û8@@OK@@ @@OK@@ `

Nota: Si se olvida uno de escribir la línea subrayada, el resultado es
la expresión algebraica 5*N, en la cual N representa una variable y
no las unidades de fuerza, Newtons.

Para escribir esta misma cantidad, con la calculadora en Modo RPN,
utilícense las teclas siguientes:

5‚Û8@@OK@@ @@OK@@

Nótese que la línea subrayada se escribe automáticamente al usarse el
modo RPN.

La secuencia de teclas para escribir unidades cuando la opción SOFT
menu ha sido seleccionada, en ambos modos, ALG y RPN, se ilustran a
continuación. Por ejemplo, en Modo ALG, para escribir la cantidad 5_N
use:

5‚Ý‚ÛL@)@FORCE @@@N@@ `

La misma cantidad escrita en Modo RPN utiliza las siguientes teclas:

5‚ÛL@)@FORCE @ @@N@@

Nota: Uno puede escribir una cantidad con unidades utilizando el
teclado alfanumérico ~, por ejemplo, 5‚Ý~n produce
la cantidad: 5_N.

Página 3-10

Prefijos de unidades

Uno puede escribir prefijos para las unidades de acuerdo con la siguiente
tabla de prefijos del Sistema Internacional (S.I.). La abreviatura del prefijo
se muestra primero, seguida del nombre, y del exponente x en el factor

x

correspondiente a cada prefijo:

10

Prefijo Nombre x Prefijo Nombre x
Yyotta+24 ddeci-1
Zzetta+21 ccenti-2
E exa +18 m milli -3
Ppeta+15
Ttera+12 nnano-9
Ggiga+9 p pico -12
Mmega+6 f femto-15
k,K kilo +3 a atto -18
h,H hecto +2 z zepto -21
D(*) deka +1 y yocto -24

(*) en el sistema SI, este prefijo se escribe da en vez de D. En la
calculadora, sin embargo, utilícese D en vez de deca.

Para escribir estos prefijos, simplemente utilícese el teclado alfanumérico

~. Por ejemplo, para escribir 123 pm (picómetro), use:

123‚Ý~„p~„m

La función UBASE (escriba el nombre de la función), que se usa para
convertir a la unidad base (1 m), produce lo siguiente:

µ micro -6

Página 3-11

Operaciones con unidades

A continuación se presentan algunos ejemplos de cálculos con unidades
en el modo ALG. Téngase en cuenta que, cuando se multiplican o dividen
cantidades con unidades, uno debe encerrar esas cantidades entre
paréntesis. Por lo tanto, para escribir, por ejemplo, el producto 12.5m

5.2 yd, úsese (12.5_m)*(5.2_yd) `:

×

que resulta en 65_(m
sistema SI, utilícese la función UBASE (use el catálogo de funciones para
ubicarla, ‚N):

Nota: Recuérdese que la variable ANS(1) se encuentra disponible a
través de la secuencia de teclas „î(asociada con la tecla `).

Para calcular una división, por ejemplo, 3250 mi / 50 h, escríbase como

la cual, transformada a unidades SI con la función UBASE, produce:

La adición y la substracción pueden ejecutarse, en modo ALG, sin usar
paréntesis, por ejemplo, 5 m + 3200 mm, se escribe simplemente como:

Expresiones más complicadas requieren el uso de paréntesis, por ejemplo,

⋅yd). Para convertir este resultado a unidades del

(3250_mi)/(50_h) `

5_m + 3200_mm `.

(12_mm)*(1_cm^2)/(2_s) `:

Página 3-12

Cálculos en la pantalla (stack) en modo RPN, no requieren que se
encierren los términos entre paréntesis, por ejemplo,

12 @@@m@@@ ` 1.5 @@yd@@ `*

3250 @@mi@@ ` 50 @@@h@@@ `/

Estas operaciones producen los siguientes resultados:

Conversión de unidades

El menú de unidades (UNITS menu) contiene un sub-menú de herramientas
(TOOLS), el cual provee las siguiente funciones:

CONVERT(x,y): convierte unidades x a unidades y
UBASE(x): convierte unidades x a unidades SI
UVAL(x): extrae el valor de la cantidad, x, con unidades
UFACT(x,y): factoriza las unidades y de la cantidad x
UNIT(x,y): combines valor de x con unidades de y

Ejemplos de aplicación de la función CONVERT se muestran a
continuación. Ejemplos de otras funciones del sub-menú UNIT/TOOLS se
presentan en el Capítulo 3 de la guía del usuario de la calculadora. Por
ejemplo, para convertir 33 watts a btu utilícese una de las siguientes
operaciones:

CONVERT(33_W,1_hp) `

CONVERT(33_W,11_hp) `

Constantes físicas en la calculadora

Las constantes físicas en la calculadora se localizan en una biblioteca de
constantes (constants library) que se activa con la función CONLIB. Para
activar esta función escríbase en la pantalla el nombre de la función:
~~conlib`, o, selecciónese la función CONLIB en el
catálogo de funciones siguiendo este procedimiento: Primero, ábrase el
catálogo de funciones utilizando: ‚N~c. A continuación,
utilícense las teclas direccionales verticales —˜ para seleccionar
CONLIB. Finalmente, presiónese @@OK@@. Presiónese `, de ser necesario.
utilícense las teclas direccionales verticales (—˜) para navegar a
través de la lista de constantes en la calculadora.

Página 3-13

Las teclas de menú correspondientes a la biblioteca de constantes
(CONSTANTS LIBRARY) incluyen las siguientes funciones:

SI cuando se selecciona esta opción, se usan unidades SI (*)
ENGL cuando se selecciona esta opción, se usan unidades

inglesas (*)

UNIT cuando se selecciona esta opción, se muestran unidades

(*)

VALUE cuando se selecciona esta opción, no se muestran

unidades
STK copia el valor (con ó sin unidades ) a la pantalla
QUIT abandona la biblioteca de unidades

(*) Activada solamente si la opción VALUE (valor) ha sido seleccionada.
La pantalla de la biblioteca de constantes (CONSTANTS LIBRARY)

aparece como se muestra a continuación si se ha seleccionado la opción
VALUE (unidades en el sistema SI):

Para ver los valores de las constantes en el sistema inglés (o sistema
imperial), presiónese la opción @ENGL :

Si se remueve la opción UNITS opción (presiónese @UNITS) se muestran
solamente los valores de las constantes (en este caso, en unidades
inglesas):

Página 3-14

Para copiar el valor de Vm a la pantalla, selecciónese el nombre de la
constante y presiónese @²STK, después, presiónese @QUIT@. Cuando se
utiliza el modo ALG, la pantalla mostrará el siguiente resultado:

La pantalla muestra lo que se denomina un valor rotulado (tagged value),
Vm:359.0394. En este resultado, Vm, es el rótulo (tag) del resultado.
Cualquier operación aritmética que utilice este número simplemente
ignora el rótulo en el resultado. Por ejemplo:

‚¹2*„î`

produce:

Esta misma operación en Modo RPN requiere las siguientes teclas
(después de extraer el valor de Vm de la biblioteca de constantes):

2`*‚¹

Página 3-15

Definiendo y usando funciones

Los usuarios pueden definir sus propias funciones a través de la partícula
DEFINE disponible a través de las teclas „à (asociada con la tecla

2). La función deberá escribirse en el siguiente formato:

Nombre_de_la_función(argumentos) =

expresión_contaniendo_argumentos

Por ejemplo, definamos una función relativamente simple,

H(x) = ln(x+1) + exp(-x)

Supóngase que uno tiene que evaluar esta función para un número de
valores discretos y que, por lo tanto, se requiere simplemente presionar
una tecla para esa evaluación. En el siguiente ejemplo, asumimos que la
calculadora opera en modo ALG. Escríbase la siguiente secuencia de
teclas:

„à³~h„Ü~„x™‚Å

‚¹~„x+1™+„¸~„x`

La pantalla lucirá como se muestra a continuación:

Presiónese la tecla J, nótese la existencia de una nueva variable en las
teces de menú (@@@H@@). Para examinar el contenido de esta variable
presiónese ‚@@@H@@. La pantalla mostrará lo siguiente:

La variable H, por lo tanto, incluye el siguiente programa:

<<  x ‘LN(x+1) + EXP(x)’ >>

Esto es un programa simple en el lenguaje de programacion del defecto
de lacalculadora. Este lenguaje de programación se denomina UserRPL
(Véanse los Capítulos 20 y 21 en la guía del usuario de la calculadora).

Página 3-16

El programa mostrado anteriormente es relativamente simple y consiste de
dos partes, contenidas entre los símbolos << >>:

•Entrada:  x  x

•Procesamiento: ‘LN(x+1) + EXP(x) ‘

Estas dos partes se interpretan de esta manera: escríbase un valor que se
asigna temporalmente al símbolo x (denominado una variable local),
evalúese la expresión entre apóstrofes que contiene a la variable local, y

muéstrese la expresión evaluada.
Para activar esta función en modo ALG, escríbase el nombre de la función

seguida por los argumentos entre paréntesis, por ejemplo, @@@H@@@
„Ü2`. He aquí algunos ejemplos:

Para activar la función en modo RPN, escríbase primero el argumento,
seguido de la tecla de menú con el nombre de la función, @@@H@@@ . Por
ejemplo, ejecútese esta operación: 2@@@H@@@. Los otros ejemplos
mostrados anteriormente pueden escribirse en modo RPN utilizando:

1.2@@@H@@@ , 2`3/@@@H@@@.

Referencia

Información adicional sobre operaciones con números reales con la
calculadora se presenta en el Capítulo 3 del guía del usuario.

Página 3-17

Capítulo 4
Cálculos con números complejos

Este Capítulo muestras ejemplos de cálculos y aplicación de funciones a
números complejos.

Definiciones

Un número complejo z es un número z = x + iy, donde x e y son números
reales, e i es la unida imaginaria definida por i² = –1. El número complejo
x + iy tiene una parte real, x = Re(z), y una parte imaginaria, y = Im(z). El
número complejo z = zx + iy se utiliza a menudo para representar un
punto P(x,y) en el plano x–y, conociéndose el eje x como eje real, y el eje
y como eje imaginario.

Se dice de un número complejo en la forma x + iy que está en
representación rectangular. Una representación alternativa es el par
ordenado z = (x,y). Un número complejo también puede representarse en

i

θ

coordenadas polares (representación polar) como z = re

θ, en donde r = |z| = es la magnitud del número

r·sin
complejo z, y

complejo z.
La relación entre la forma cartesiana y la representación polar de los

números complejos se da en la fórmula Euler: ei
conjugación compleja de un número complejo (z = x + iy = re

– iy = re
reflejo de z sobre el eje real (x). Igualmente, el negative de z, –z = –x –iy

i

θ

= –re

, puede considerarse como el reflejo de z sobre el origen.

θ = Arg(z) = arctan(y/x) es el argumento del número

i

θ

–

. La conjugación compleja de i puede considerarse como el

22

yx +

i

θ

= cos θ + i sin θ. La

= r·cosθ + i

i

θ

z

) es = x

Seleccionando el modo complejo (COMPLEX)

Para operaciones con números complejos selecciónese el modo complejo
(COMPLEX) del CAS:

H)@@CAS@ ˜˜™

El modo COMPLEX estará activo en la forma interactiva denominada CAS
MODES si se muestra un tick de aprobado () en la opción _Complex:

Página 4-1

Presione @@OK@@ , dos veces, para recobrar la pantalla normal de la
calculadora.

Escritura de números complejos

Los números complejos en la calculadora pueden escribirse en una de dos
representaciones Cartesianas: x+iy, o (x,y). Los resultados complejos en la
calculadora se muestran el formato de par ordenado, es decir, (x,y). Por
ejemplo, con la calculadora in modo ALG, el número complejo (3.5,-1.2),
se escribe con las siguientes teclas (accepte el cambio de modo a
Complex):

„Ü3.5‚í\1.2`

Un número complejo puede escribirse también en la forma x+iy. Por
ejemplo, en modo ALG, 3.5-1.2i se escribe con las siguientes teclas:

3.5-1.2*„¥`

Nota: para entrar el número unitario imaginario solamente, teclee

„¥, y la tecla I.

En modo RPN, estos números pueden escribirse de esta manera:

„Ü3.5‚í1.2\`

(Nótese que la tecla de cambio de signo se escribe después número 1.2,
en el orden contrario al del ejercicio anterior realizado en modo ALG).

Página 4-2

Representación polar de un número complejo

La representación polar del número complejo 3.5-1.2i, que se utilizó
anteriormente, se obtiene al cambiar el sistema de coordenadas de
Cartesianas (o rectangulares) a cilíndricas (o polares) usando la función
CYLIN. Esta función se puede obtener a través del catálogo de funciones
(‚N). Puede cambiarse a coordenadas polares (polar) usando H.
Cambiando las coordenadas a polares y las medidas angulares a
radianes, produce el siguiente resultado en modo RPN:

Este formato incluye una magnitud, 3.7, y un ángulo, 0.33029…. El
símbolo de ángulo (∠) se muestra delante de la medida angular.

Cámbiense las coordenadas de vuelta a Cartesianas o rectangulares
utilizando la función RECT (disponible en el catálogo de funciones,
‚N). Un número complejo en representación polar se escribe como

iθ

z = r⋅e
ordenado de la forma (r, ∠θ). El símbolo de ángulo (∠) puede escribirse
utilizando las teclas ~‚6. Por ejemplo, el número complejo z =

5.2e
muestran la pantalla RPN, es decir, el stack, antes y después de escribir el
número):

. Se puede escribir este número complejo utilizando un par

1.5i

, puede escribirse como se muestra a continuación (las figuras

Dado que el sistema de coordenadas activo es el sistema rectangular (o
Cartesiano), la calculadora automáticamente convierte el número a
Coordenadas Cartesianas, es decir, x = r cos θ, y = r sin θ, resultando,
para este caso, en el valor (0.3678…, 5.18…).

Ahora bien, si el sistema de coordenadas activo es el de coordenadas
cilíndricas (utilícese la función CYLIN para activarlo), al escribirse un
número complejo (x,y), en el cual x y y son números reales, se producirá
una representación polar. Por ejemplo, en coordenadas cilíndricas,
escríbase el número (3.,2.). Las figuras siguientes muestran la pantalla
RPN (stack), antes y después de escribir este número:

Página 4-3

Operaciones elementales con números complejos

Los números complejos pueden combinarse usando las cuatro operaciones
fundamentales (+-*/). Los resultados obtenidos siguen las
reglas del álgebra con la particularidad de que
con números complejos, por lo tanto, son similares a las operaciones con
números reales. Por ejemplo, con la calculadora en modo ALG y la
opción

Complex activa en el CAS, ejecútense las siguientes operaciones:

(3+5i) + (6-3i) = (9,2);

(5-2i) - (3+4i) = (2,-6)

(3-i)·(2-4i) = (2,-14);

(5-2i)/(3+4i) = (0.28,-1.04)

1/(3+4i) = (0.12, -0.16) ;

-(5-3i) = -5 + 3i

i2= -1. Las operaciones

Los menús CMPLX

Existen dos menús CMPLX (Números complejos) en la calculadora. Uno
de ellos se encuentra disponible a través del menú MTH (véase el Capítulo

3) y el otro se encuentra disponible directamente en el teclado (‚ß).
Los dos menús CMPLX se describen a continuación.

El menú CMPLX a través del menú MTH

Asumiendo que la opción lista de menú (CHOOSE boxes) esta activa
en la señal de sistema número 117 (véase el Capítulo 2), el sub-menú
CMPLX dentro del menú MTH se activa utilizando las teclas: „´9
@@OK@@ . Las funciones disponibles son las siguientes:

Página 4-4

El primer menú (opciones 1 a 6) muestra las siguientes funciones:
RE(z) Parte real de a número complejo

M(z) Parte imaginaria de a número complejo

→R(z) Separa las partes real e imaginaria de un número

C

complejo

→C(x,y) Forma el número complejo (x,y) dados los números reales

R

x y y
ABS(z) Calcula la magnitud de un número complejo.
ARG(z) Calcula el argumento de un número complejo.
SIGN(z) Calcula un número complejo de magnitud unitaria, es

decir, z/|z|.
NEG(z) Cambia el signo de z
CONJ(z) Produce el conjugado complejo de z

Ejemplos de aplicación de estas funciones se muestran a continuación en
coordenadas Cartesianas. Recuérdese que, en el modo ALG, la función
precede al argumento, mientras que en modo RPN, se debe escribir el
argumento primero, y después activar la función. Recuérdese también que
estas funciones están disponibles en las teclas de menú si la señal de
sistema número 117 tiene activa la opción SOFT menus (véase el Capítulo

2).

Página 4-5

El menú CMPLX en el teclado

El segundo menú CMPLX es accesible al utilizar las teclas ‚ß. si la
señal de sistema número 117 tiene activa la opción CHOOSE boxes, el
menú CMPLX en el teclado muestra las siguientes opciones:

El menú mostrado incluye algunas de las funciones presentadas
anteriormente, a saber, ARG, ABS, CONJ, IM, NEG, RE, y SIGN. Este
menú incluye así mismo la función
que las teclas „¥.

i que representa el mismo resultado

Funciones aplicadas a números complejos

Muchas de las funciones del teclado y del menú MTH definidas en el

x

Capítulo 3 para números reales (por ejemplo, SQ, LN, e
aplicarse a números complejos. El resultado es otro número complejo
como se ilustra en los siguientes ejemplos.

, etc.), pueden

Página 4-6

Nota: Cuando se utilizan las funciones trigonométricas y sus inversas
con números complejos los argumentos de estas no representan
ángulos como en el caso de los números reales. Por lo tanto, la
medida angular activa no tiene ningún efecto en los resultados de las
funciones antes mencionadas en el dominio de los números complejos.

Función DROITE: la ecuación de una línea recta

La función DROITE utiliza como argumentos dos números complejos, por
ejemplo, x

a+bx, que contiene los puntos (x
comprendida entre los puntos A(5,-3) y B(6,2) se puede obtener usando la

función DROITE como se muestra a continuación (el ejemplo se ejecuta en
el modo algebraico):

La función DROITE se puede activar utilizando el catálogo de funciones
(‚N). Si se activa el mode APPROX, el resultado sería Y = 5.*(X-5.)-

3.

+iy1 y x2+iy2, y la ecuación de una línea recta, es decir, y =

1

) y (x2,y2). Por ejemplo, la línea recta

1,y1

Referencia

Información adicional sobre las operaciones con números complejos se
presenta en el Capítulo 4 de la guía del usuario de la calculadora.

Página 4-7

Capítulo 5
Operaciones algebraicas y aritméticas

Un objeto algebraico es cualquier número, nombre de variable, o
expresión algebraica sobre el que se pueden efectuar operaciones, que
puede manipularse, o combinarse de acuerdo a las reglas del álgebra.
Algunos ejemplos de objetos algebraicos se presentan a continuación:

•Un número: 12.3, 15.2_m, ‘

•Un nombre de variable: ‘a’, ‘ux’, ‘width’, etc.

•Una expresión: ‘p*D^2/4’, ’f*(L/D)*(V^2/(2*g))’,

•Una ecuación: ‘

p*V = n*R*T’, ‘Q=(Cu/n)*A(y)*R(y)^(2/3)*√So’

π’, ‘e’, ‘i’

Escritura de los objetos algebraicos

Los objetos algebraicos pueden crearse al escribir el objeto entre
apóstrofes directamente en la pantalla, o utilizando el escritor de
ecuaciones (EQW). Por ejemplo, para escribir el objeto algebraico

π*D^2/4’ directamente en la pantalla utilícese:

‘

³„ì*~dQ2/4`

Un objeto algebraico puede construirse en el escritor de ecuaciones
(Equation Writer) y después enviado a la pantalla, o manipulado en el
Escritor de ecuaciones mismo. La operación del Escritor de ecuaciones se
describió en el Capítulo 2. Como ejercicio, constrúyase el siguiente objeto
algebraico en el Escritor de ecuaciones:

Después de construir el objeto algebraico, presiónese ` para mostrarlo
en la pantalla (las pantallas en modos ALG y RPN se muestran a
continuación):

Página 5-1

Operaciones elementales con objetos algebraicos

Los objetos algebraicos pueden sumarse, restarse, multiplicarse y dividirse
(excepto por cero), elevarse a una potencia, usarse como argumentos de
funciones (por ejemplo, exponenciales, logarítmicas, trigonométricas,
hiperbólicas, etc.), como se haría con cualquier número real o complejo.
Para demostrar las operaciones básicas con objetos algebraicos,
constrúyanse un par de objetos algebraicos, por ejemplo, ‘
‘g*t^2/4’, y almacénense en las variables A1 y A2 (véase el Capítulo 2
para aprender como crear variables y almacenar valores en ellas). He
aquí el procedimiento para almacenar la variable A1 en modo ALG:

³„ì*~rQ2™K~a1`

El resultado es:

Las instrucciones correspondientes en modo RPN son:

„ì~r`2Q*~a1K

Después de almacenar la variable A2, la pantalla mostrará las variables
como se muestra a continuación:

π*R^2’ y

En modo ALG, las siguientes instrucciones muestran varias operaciones
elementales con los objetos algebraicos contenidos en las variables @@A1@@ y

@@A2@@ (presiónese J para recobrar el menú de variables):

@@A1@@ + @@A2@@ ` @@A1@@ - @@A2@@ `

Página 5-2

@@A1@@ *@@A2@@ ` @@A1@@ / @@A2@@ `

‚¹@@A1@@ „¸@@A2@@

Los mismos resultados se obtienen en modo RPN si se utilizan las
instrucciones siguientes:

@@A1@@ @@A2@@ +µ @@A1@@ @@A2@@ -µ
@@A1@@ @@A2@@ *µ @@A1@@ @@A2@@ /µ
@@A1@@ ‚ ¹µ @@A2@@ „ ¸µ

Página 5-3

Funciones en el menú ALG

El menú ALG (Algebraico) se activa utilizando las teclas ‚×
(asociado con la tecla 4). Habiendo escogido la opción

boxes

siguientes funciones:

Utilícese la función informativa (HELP) de la calculadora para ver la
explicación de las diferentes funciones del menú ALG. Para activar la
función informativa (HELP) utilícense las siguientes teclas: IL @)HELP@
` . Para localizar una función particular en la función informativa,
escríbase la primera letra del nombre de la función. Por ejemplo, para
localizar la función COLLECT, utilícense las teclas ~c, y después
utilícense las teclas direccionales verticales —˜ para localizar la
palabra COLLECT dentro de la lista de la función informativa.

Para completar la operación presiónese la tecla @@OK@@. He aquí la
definición de la función COLLECT en la función informativa (HELP) de la
calculadora:

para la señal de sistema número 117, el menú ALG muestra las

CHOOSE

Nótese que la última línea contiene el texto “See: EXPAND FACTOR”
(traducción: Véase: EXPAND FACTOR). Esta línea sugiere enlaces a otras
definiciones dentro de la función informativa (HELP): las funciones EXPAND
y FACTOR. Para acceder esas funciones directamente, presiónese la tecla
de menú @SEE1! o @SEE2. Presiónese @SEE1! para la definición de la función
EXPAND. Presiónese @SEE2! para la definición de la función FACTOR.

Página 5-4

Para copiar a la pantalla los ejemplos mostrados en la definición
presiónese la tecla de menú @ECHO!. Por ejemplo, presiónese la tecla @ECHO
en la definición de la función EXPAND, mostrada anteriormente, para
obtener el ejemplo que se muestra a continuación (presiónese ` para
ejecutar el ejemplo):

Se invita al usuario a explorar las diferentes funciones en el menú ALG
utilizando la función informativa (HELP). Las siguientes listas muestra todas
las funciones en ese menú:

Por ejemplo, la función informativa (HELP) provee la siguiente definición y
ejemplo para la función SUBST:

Página 5-5

Nota: Recuérdese que para utilizar estas, y otras, funciones en el
modo RPN, debe escribirse primero el argumento de la función y
después activarse la misma. Por ejemplo, para el caso de la función
TEXPAND, mostrado anteriormente, utilícese:

³„¸+~x+~y`

A continuación, actívese la función TEXPAND en el menú ALG (o,
directamente, en el catálogo de funciones ‚N), para completar
la operación.

Operaciones con funciones trascendentes

La calculadora provee ciertas funciones que se utilizan para reemplazar
expresiones que contienen funciones logarítmicas y exponenciales
(„Ð), así como funciones trigonométricas (‚Ñ).

Expansión y factorización utilizando las funciones log-exp

El menú „Ð contiene las siguientes funciones:

Las definiciones de estas funciones, así como los ejemplos
correspondientes, se encuentran disponibles en la función informativa
(HELP) de la calculadora (IL @)HELP@ `). Por ejemplo, la
descripción de la función EXPLN se muestra en la figura siguiente a la
izquierda, mientras que el ejemplo correspondiente se muestra en la figura
siguiente a la derecha:

Página 5-6

Expansión y factorización utilizando funciones trigonométricas

El menú TRIG, que se obtiene utilizando ‚Ñ, muestra las siguientes
funciones:

Estas funciones permiten la simplificación de expresiones al reemplazar
ciertas categorías de funciones trigonométricas por otras categorías. Por
ejemplo, la función ACOS2S permite reemplazar la función
(acos(x)) por una expresión que involucra la función arco seno (asin(x)).

Las definiciones de estas funciones, así como los ejemplos
correspondientes, se encuentran disponibles en la función informativa
(HELP) de la calculadora (IL@)HELP@ `). Se invita al usuario a
investigar esa información por su propia cuenta.

arco coseno

Página 5-7

Funciones en el menú ARITHMETIC

El menú ARITHMETIC se activa utilizando „Þ (asociada con la tecla

1). Con la opción CHOOSE boxes seleccionada para la señal de

sistema número 117, la combinación „Þ muestra el siguiente menú:

De esta lista, las opciones 5 a 9 (DIVIS, FACTORS, LGCD, PROPFRAC,
SIMP2) corresponden a funciones que aplican a números enteros o a
polinomios. Las opciones restantes (1. INTEGER, 2. POLYNOMIAL, 3.
MODULO, y 4. PERMUTATION) son en realidad sub-menús de funciones
que aplican a objetos matemáticos específicos. Con la opción SOFT
menus seleccionada para la señal de sistema número 117, la
combinación „Þ muestra el siguiente menú:

A continuación se muestran las definiciones de las funciones FACTORS y
SIMP2 en el ARITHMETIC menu(IL@HELP ):

FACTORS: SIMP2:

Para ver las funciones disponibles en los sub-menús del menú
ARITHMETIC: INTEGER, POLYNOMIAL, MODULO, y PERMUTATION,
selecciónese el sub-menú apropiado. Definiciones y ejemplos se obtienen
en la función informativa (HELP) de la calculadora.

Página 5-8

Información adicional sobre las aplicaciones de las funciones del menú
ARITHMETIC se presenta en el Capítulo 5 en la guía del usuario de la
calculadora.

Polinomios

Los polinomios son expresiones algebraicas consistente de uno o más
términos que contienen potencias decrecientes de una variable o función.
Por ejemplo, ‘X^3+2*X^2-3*X+2’ es un polinomio del tercer orden
(cúbico) de la variable X, mientras que ‘SIN(X)^2-2’ es un polinomio de
segundo orden (cuadrático) de la función SIN(X). Las funciones COLLECT
y EXPAND, mostradas anteriormente, pueden utilizarse con polinomios.
Otras aplicaciones de polinomios en la calculadora se muestran a
continuación.

La función HORNER

La función HORNER („Þ, POLYNOMIAL, HORNER) produces la
división sintética de un polinomio P(X) por el factor (X­HORNER(P(X),a) = {Q(X), a, P(a)}, en la cual P(X) = Q(X)(X-a)+P(a). Por
ejemplo, HORNER(‘X^3+2*X^2-3*X+1’,2) = {‘X^2+4*X+5’ 2 11}, es

3

decir, X

es decir, X

es decir, X

+2X2-3X+1 = (X2+4X+5)(X-2)+11. Así mismo,

HORNER(‘X^3+2*X^2-3*X+1’,2) = {X^2+4*X+5 2 11}

3

+2X2-3X+1 = (X2+4X+5)(X-2)+11. Also,

HORNER(‘X^6-1’,-5)=

{X^5-5*X^4+25*X^3-125*X^2+625*X-3125 -5 15624}

6

-1 = (X5-5*X4+25X3-125X2+625X-3125)(X+5)+15624.

a), es decir,

La variable VX

La mayoría de los ejemplos con polynomios fueron escritos usando la
variable X. Esto es porque, en el directorio {HOME CASDIR} de la
calculadora, existe una variable denominada VX cuyo valor
preseleccionado es ‘X’. Este es el nombre de la variable independiente
preferida para aplicaciones en el álgebra y en el cálculo. Evítese utilizar la
variable VX en programas y ecuaciones, de manera que no se confunda
con la variable VX del CAS (Computer Algebraic System, o Sistema
Algebraico Computacional). Para obtener información adicional sobre las
variables del CAS véase el Apéndice C en la guía del usuario de la
calculadora.

Página 5-9

La función PCOEF

Dado un vector que contiene las raíces de un polinomio, la función PCOEF
genera un vector que contiene los coeficientes del polinomio
correspondiente. Los coeficientes corresponden al orden decreciente de
las potencias de la variable independiente. Por ejemplo:

PCOEF([-2, –1, 0, 1, 1, 2]) = [1. –1. –5. 5. 4. –4. 0.],

Este resultado representa el polinomio X6-X5-5X4+5X3+4X2-4X.

La función PROOT

Dado un vector que contiene lo coeficientes de un polinomio en orden
decreciente de las potencias, la función PROOT provee las raíces del

2

polinomio. Por ejemplo, para el polinomio X

+5X+6=0, PROOT([1, –5,

6]) = [2. 3.].

Las funciones QUOT y REMAINDER

Las funciones QUOT (cociente) y REMAINDER (residuo) proveen,
respectivamente, el cociente Q(X) y el residuo R(X), que resulta de la
división de dos polinomios, P

proveen los valores de Q(X) y R(X) en la expresión P
R(X)/P

(X). Por ejemplo,

2

QUOT (‘X^3-2*X+2’, ‘X-1’) = ‘X^2+X-1’

REMAINDER(‘X^3-2*X+2’, ‘X-1’) = 1.

Para este caso, por lo tanto: (X

(X) y P2(X). Es decir, estas funciones

1

(X)/P2(X) = Q(X) +

1

3

-2X+2)/(X-1) = X2+X-1 + 1/(X-1).

Nota: Este último resultado se puede obtener usando la función
PARTFRAC:

PARTFRAC(‘(X^3-2*X+2)/(X-1)’) = ‘X^2+X-1 + 1/(X-1)’.

Página 5-10

La función PEVAL

La función PEVAL (Polynomial EVALuation) se utiliza para evaluar un
polinomio

p(x) = a

dado un vector de coeficientes [
resultado es la evaluación
el menú ARITHMETIC, sino en el menú CALC/DERIV&INTEG. Ejemplo:

PEVAL([1,5,6,1],5) = 281.
Aplicaciones adicionales de las funciones relacionadas con polinomios se

presentan en el Capítulo 5 en la guía del usuario de la calculadora.

⋅

xn+a

n

p(x0). La función PEVAL no está disponible en

n-1

⋅

x

an, a

n-1

+ …+ a

, … a2, a1, a

n-1

⋅

2

x2+a

⋅

x+ a

1

,

0

] y un valor x0. El

0

Fracciones

Las fracciones pueden expandirse y factorizarse utilizando las funciones
EXPAND y FACTOR, localizadas en el menú ALG (‚×). Por ejemplo:

EXPAND(‘(1+X)^3/((X-1)*(X+3))’)= ‘(X^3+3*X^2+3*X+1)/(X^2+2*X-3)’
EXPAND(‘(X^2)*(X+Y)/(2*X-X^2)^2)’) = ‘(X+Y)/(X^2-4*X+4)’
FACTOR(‘(3*X^3-2*X^2)/(X^2-5*X+6)’) = ‘X^2*(3*X-2)/((X-2)*(X-3))’
FACTOR(‘(X^3-9*X)/(X^2-5*X+6)’ ) = ‘X*(X+3)/(X-2)’

La función SIMP2

La función SIMP2, en el menú ARITHMETIC, utiliza como argumentos dos
números o dos polinomios, los cuales representan el numerador y el
denominador de una fracción racional, y produce, como resultados, el
numerador y denominador simplificados. Por ejemplo:

SIMP2(‘X^3-1’,’X^2-4*X+3’) = { ‘X^2+X+1’,‘X-3’}

La función PROPFRAC

El función PROPFRAC convierte una función racional en una función
“propia”, es decir, una parte entera sumada a una parte fraccional, si tal
descomposición es posible. Por ejemplo:

PROPFRAC(‘5/4’) = ‘1+1/4’

PROPFRAC(‘(x^2+1)/x^2’) = ‘1+1/x^2’

Página 5-11

La función PARTFRAC

La función PARTFRAC descompone una fracción racional en fracciones
parciales que, al sumarse, producen la fracción original. Por ejemplo:

PARTFRAC(‘(2*X^6-14*X^5+29*X^4-37*X^3+41*X^2-16*X+5)/(X^5­7*X^4+11*X^3-7*X^2+10*X)’) =

‘2*X+(1/2/(X-2)+5/(X-5)+1/2/X+X/(X^2+1))’

La función FCOEF

La función FCOEF, disponible en el menú ARITHMETIC/POLYNOMIAL, se
utiliza par obtener una fracción racional dados las raíces y los polos de la
misma.

Nota: Si la expresión F(X) = N(X)/D(X) representa una función
racional, las raíces de la fracción se encuentran al resolver la ecuación
N(X) = 0, mientras que los polos de la fracción se encuentran al
resolver la ecuación D(X) = 0.

El argumento de esta función es un vector que incluye las raíces de la
fracción seguidas de su multiplicidad (es decir, cuantas veces la raíz se
repite), y los polos de la fracción, también seguidos de su multiplicidad,
esta última representada como un número negativo. Por ejemplo, si
queremos formar la fracción que tiene las raíces 2 con multiplicidad 1, 0
con multiplicidad 3, y -5 con multiplicidad 2, y los polos 1 con
multiplicidad 2 y –3 con multiplicidad 5, utilícese:

FCOEF([2,1,0,3,–5,2,1,–2,–3,–5])=‘(X--5)^2*X^3*(X-2)/(X+3)^5*(X-1)^2
Si se presiona µ„î`(or, simplemente µ, in RPN mode) se

obtiene:

‘(X^6+8*X^5+5*X^4-50*X^3)/(X^7+13*X^6+61*X^5+105*X^4-

45*X^3-297*X^2-81*X+243)’

’

La función FROOTS

La función FROOTS, en el menú ARITHMETIC/POLYNOMIAL, se utiliza
para obtener las raíces y los polos de una fracción. Por ejemplo, al
aplicar la función FROOTS a la fracción racional obtenida en el ejemplo
anterior, se obtiene el resultado: [1 –2. –3 –5. 0 3. 2 1. –5 2.]. Este
vector muestra primero los polos seguidos de su multiplicidad
(representada por un número negativo), y, a continuación, las raíces
seguidas por su multiplicidad (representada por un número positivo). En

Página 5-12

este caso, los polos son (1, -3) con multiplicidades (2,5), respectivamente,
y las raíces son (0, 2, -5) con multiplicidades (3, 1, 2), respectivamente.

Considérese también este segundo ejemplo:
FROOTS(‘(X^2-5*X+6)/(X^5-X^2)’) = [0 –2. 1 –1. 3 1. 2 1.].
En este caso, los polos son 0 (2), 1(1), y las raíces son 3(1), 2(1). Si se

hubiese seleccionado la opción Complex para el CAS, el resultado de este
ejemplo hubiese sido:

[0 –2. 1 –1. – ((1+i*

√3)/2) –1. – ((1–i*√3)/2) –1. 3 1. 2 1.].

Operaciones con polinomios y fracciones, paso a paso

Cuando se selecciona la opción Step/step en el CAS, la calculadora
mostrará las simplificaciones de fracciones o la operaciones con
polinomios detalladas paso a paso. Esta selección es útil, por ejemplo,
para ver los diferentes pasos de una división sintética. La división

23

2

−

X

se muestra en detalle en el Apéndice C la guía del usuario de la
calculadora. El siguiente ejemplo muestra otra división sintética, paso a
paso. Presiónese ` para ejecutar los pasos consecutivos. La función DIV2
se encuentra disponible en el menú ARITHMETIC/POLYNOMIAL.

9

1

X

−

2

1

−

X

235

XXX

−+−

Página 5-13

Referencia

Información adicional, definiciones, y ejemplos de operaciones
algebraicas y aritméticas se presentan en el Capítulo 5 de la guía del
usuario de la calculadora.

Página 5-14

Capítulo 6
Solución de las ecuaciones

Asociados con la tecla 7 existen dos menús de funciones para la
solución de ecuaciones, el Symbolic SOLVer („Î), o soluciones
simbólicas, y el NUMerical SoLVer (‚Ï), o soluciones numéricas. A
continuación se presentan algunas de las funciones disponibles en estos
menús.

Solución simbólica de las ecuaciones algebraicas

En esta sección se utiliza el menú de soluciones simbólicas (Symbolic
Solver). Actívese el menú utilizando las teclas „Î. Con la opción
CHOOSE boxes activa en la señal de sistema número 117, el menú de
soluciones simbólicas muestra las siguientes funciones:

Las funciones ISOL y SOLVE se utilizan para obtener la incógnita de una
ecuación polinómica. La función SOLVEVX se utiliza para resolver una
ecuación polinómica en la que la incógnita es la variable independiente
del CAS VX (usualmente la ‘X’). Finalmente, la función ZEROS provee los
ceros o raíces de una ecuación polinómica.

La función ISOL

La función ISOL(Ecuación, variable) produce la solución(es) de la Ecuación
al despejar la variable. Por ejemplo, con la calculadora en modo ALG,

para despejar

Página 6-1

t en la ecuación at

3

-bt = 0 utilícese:

Cuando la calculador usa el modo RPN, la solución se obtiene
escribiendo primero la ecuación en la pantalla (stack), seguida por la
variable, antes de activarse la función ISOL. La figura de la izquierda
muestra la pantalla RPN antes de aplicar la función ISOL, mientras que la
figura de la derecha muestra la pantalla después de aplicar la función
ISOL.

El primer argumento en la función ISOL puede ser una expresión (sin el
signo igual), como en el ejemplo anterior, o una ecuación. Por ejemplo,
en modo ALG, ejecútese el siguiente ejemplo:

Nota: Para escribir el signo igual (=) en una ecuación, utilícense las
teclas ‚Å (asociada con la tecla \).

El mismo problema puede resolverse en modo RPN como se ilustra a
continuación (las figuras siguientes muestran la pantalla RPN antes y
después de aplicar la función ISOL):

Página 6-2

La función SOLVE

La función SOLVE tiene la misma sintaxis que la función ISOL, excepto que
SOLVE puede utilizarse para resolver un sistema de ecuaciones
polinómicas. La función informativa de la calculadora (función HELP, que
se activa utilizando IL@HELP ) muestra la siguiente referencia para la
función SOLVE, incluyendo la solución de la ecuación X^4 – 1 = 3:

Los siguientes ejemplos muestran el uso de la función SOLVE en modo ALG
(use modo Complex en el CAS):

4

β

La figura anterior muestra dos soluciones. En la primera, SOLVE(
=125), no produce soluciones { }. En la segunda solución, SOLVE(β4 - 5β

= 6), produce cuatro soluciones, que se muestran en la línea inferior de la
pantalla. La última solución en la línea no es visible porque el resultado
ocupa más caracteres que el ancho de la pantalla. Sin embargo, uno
puede ver todas las soluciones al activar el editor de línea utilizando la
tecla direccional vertical ˜ (Esta operación puede utilizarse para
acceder a cualquier línea de la pantalla que sea más ancha que la
pantalla misma:

-5β

Las pantallas RPN correspondientes a los dos ejemplos anteriores, antes y
después de aplicar la función SOLVE, se muestran a continuación:

Página 6-3

La función SOLVEVX

La función SOLVEVX se utiliza para resolver una ecuación cuando la
incógnita es la variable CAS contenida en el registro VX. El valor pre­definido de VX es el símbolo ‘X’. Algunos ejemplos, en el modo ALG y
con la variable VX = ‘X’, se muestran a continuación:

En el primer caso, SOLVEVX no pudo encontrar una solución. En el
segundo caso, SOLVEVX encontró una solución única, X = 2.

Las siguientes figuras muestran la pantalla RPN en la solución de los
ejemplos anteriores (antes y después de aplicar la función SOLVEVX):

Página 6-4

La función ZEROS

La función ZEROS se utiliza para encontrar las raíces (o ceros) de una
ecuación polinómica, sin mostrar la multiplicidad de las mismas. La
función ZEROS requiere como argumentos una ecuación o expresión y la
variable a despejarse. Ejemplos en modo ALG se muestran a
continuación:

Para utilizar la función ZEROS en modo RPN, escríbase primero la
expresión o ecuación polinómica, seguida de la variable a ser despejada.
Después de esto, se deberá activar la función ZEROS. Las siguientes
figuras muestran la pantalla RPN en la solución de los ejemplos anteriores
(antes y después de aplicar la función ZEROS, con modo Complex
seleccionado para el CAS):

Las funciones de soluciones simbólicas (Symbolic Solver) presentadas
anteriormente producen soluciones para ecuaciones racionales
(principalmente, ecuaciones polinómicas). Si la ecuación a resolverse
tiene solamente coeficientes numéricos, es posible obtener una solución
numérica utilizando las funciones de soluciones numéricas (Numerical
Solver) en la calculadora.

Página 6-5