Hewlett-Packard 21S User Manual

Stat/Math

Calculator

Owner’s

Manual

(fifi

HEWLETT
PACKARD

[fi/’

P

B

INPUT

g

E

e\

STAT/MATH_/

\_

1.

Separates

2.

Executesaprogram.

3.

Activates

4.

Activates

5.

On;

clears

operation.

6.

Distribution

7.

df{and
freedom

two

numbers.

blue-labeled
yellow-labeled

display,

keys.

dfs

are

degrees

memory

8.

9.

keys.

10.

keys.

11.

cancels

12.

13.AthroughFkeys

of

aids. 14.

nthrough2xy
summation

Backspace.

Loads
Enters

Accumulates

builtinprograms.
Annunciator

memory

built-in
Program

statistical

Line.

programs.

are

statistical

aids.

mode.

for

labels

data.

and

df(ST0]1

(S)@0c(displays

[XEQ]B(displays

n-1
correct

ng/

x?)

degrees

U,)

5

of

\yes

freedom?

(QJ@xd)(displays

(XEQ)B(displays

x?)

U,)

\

¥

(XEQJF

0,

O,(NPUTIE,[R/S]

[INPUTIE,

(7S)

o

O,[INPUTJE

[XEQIA

unequil/

Expected

values

(\J([COADID

unequal

\Eual

or
equal?

OE]

and

Note:

start

For

at

another

"Which

test

test".

using

Test(CHI-2)

the
same

data,

press

[#][LOAD]C

[
Go

to
“Test

of
Hypothesis

or
Confidence

Interval?”

on
page

3
.

J

[«)(LOADIA

¥

y
givenx

x(XEQIE

given

x

slope

Which

mean

test?

of

particular

y

A
(displays

std.

err.
of

est.)

Linear

Regression

x,(INPUTy,

x,(INPUT]y,(2+]

[«)[COADIC

()L

Test

(£4)

Statistics

(Lr-StAt)

*i%
is

the
initial

guess

you

supply

for
the

interest

rate.

n

%

PV

PMT

Fv

(STO)4

~

TESXTVAMOSTE

Probability

N =

Upper-tail

Hypothesized

CHl-square

Student's

Standard

Degrees

of

normal

t

probability.

random

freedom.

random

value.

random

variable.

variable.

variable.

Observed

Expected

value.

value.

Variable

To
Store

To
Calculate

To
Review

Precision

('/,
width

of
confidence

interval).

value.

ATov

Population

Population

Sample

proportion.

mean.

proportion.

Note:

positive

For

value,

PV,

and

PMT,

money

and
FI/,

flowing

money

from

flowing

you

is

to

treated

you

is

as

treated

a
negative

as a

s

Sample

Sample

Population

standard

mean.

standard

deviation.

deviation.

Fv

Future

value

(the
final

cash

flow).

Sample

size.

PMT

i%

PV

Uniform,

Periodic

Present

value

interest

periodic

(the

rate

payment.

initial

as
a

cash

percent.

flow).

Symbols

Used

in
This

Guide

n

Total

number

of
compounding

[«2)(COADIF

periods.

Once

logic

HP-21S

and

you've

built-in

keystrokes

used

library,

your owner's

used

you

in

can

each

use

manual

of

this

the

guide

to

library

become

for

programs.

“quick

familiar

reference"

with

the

to
the

Time

Value

of
Money

(FinAnCE)

How

(for

To

the

Use

built-in

This

Guide

library)

x[XEQ)B(displays

x(XEQJA(displays

pr

pr

of

of

x

<x

successes)

successes)

HP-21S

Quick

Reference

Guide

Binomial

Distribution

(bin)

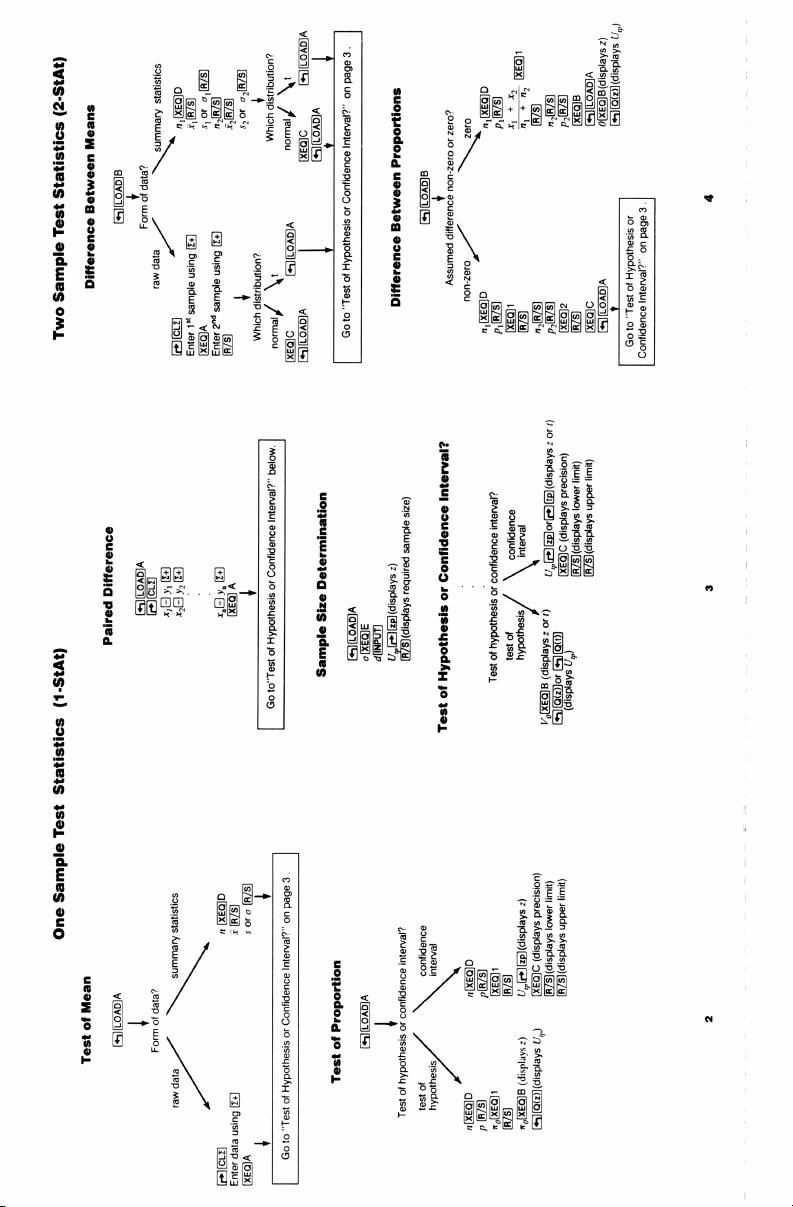
(2-StAt)

Means

Statistics

Between

Test

Difference

Sample

Two

statistics

n,(XEQ)D

summary

datj/
raw

(®JcT)

o,[R/S)

syor

x,[R/8)

(Z+]

using

sample
1%

Enter

(XEQJA

"zm

[T+

using

{

sample
2™

Enter

[R78)

x,[R/S)

o,[R/S]

¥

distribution?

s,0r

Which

\‘t

distribution?

/

Which

normal

(w)CoADIA

\'

¥

”0""3'/

(©)[COADIA l

(XEQIC

l

(©)COADIA

(XEQ)C

()CoADIA

J
.
3

on page

Interval?”

Confidence
or

Hypothesis
of

“Test
to

Go

I

Proportions

v

S)Coans

Between

Difference

zero?
or

\iero

non-zero

difference

/

Assumed

non-zero

(xeQ)
"22

x

+

+

[R7S)

n,(XEQID

"11

le

X

(XEQ]1

fi

n,(KEQID

n,[R7S)

plm

"zm

p,[R/S]

XEQ)2

sz

z)

(XEQ)B

(Q)CSADIA

0(XEQ)B(displays

Y

[R73)

(\J[LoAD)A

(XEQ)IC

U,,)

Bj@@)(displays

.
3

or

page
on

Hypothesis
of

Interval?”"

“Test
to

Go

Confidence

Difference

Paired

(1-StAt)

Statistics

Test

Sample

One

Mean
of

Test

B

[(©9)([LOADIA

(@)eLy

5By,

data?
of

(\)[LOADIA

Form

B

xEy,

statistics

summary

data
raw

(X3

A
XEQ)

I.B;".

(XEQJD
n

x[R/S)

(Z+]

using

data

Enter

¢

[R/S)

oro
s

below.

Interval?”’

Confidence
or

Hypothesis
of

to"Test
Go

.
3

'

page
on

Interval?’

Confidence
or

Hypothesis
of

"Test
to

¢

Go

L

Determination

Size

[«1)[COADIA

o[XEQJE

d[INPUT)

Sample

Proportion

(\)[LOADIA

of

Test

Interval?

size)

sample

z)

Confidence

required

or

[*)(zp)(displays

[R/S](displays

U,

Hypothesis
of

Test

interval?

interval

confidence

confidence
or

hypothesis

of

of

hypothesis

test

Test

n(XEQJD

pRS)

B/S)

n[XEQ)D

p

interval?

confidence
or

hypothesis
of

Test

n,(XEQ)1

limit)

precision)

lower

(displays

interval

confidence

u,[g]@or[a@(dispoayszorr)

[R7S)(displays

@C

P

hypothesis

testof

@(%ao;s[%fl@

VomB(displayszo”)

limit)

limit)

z)

precision)

upper

lower

(displays

[®)(zp)(displays

[R/S])(displays

[R7S])(displays

(XEQJC

U,

[R/S]

(xEQJ1

U,,)

z)

(displays

[R/S)

n,(XEQ)B

[w)@@)(displays

limit)

upper

[R7S)(displays

Help

By

takingamomenttofill

understand

Model:
Name
Address
City,

Age

1.

Whatisyour
001[Student
002[0Educator,
003[Professional

2.

Whatisyour
201[0Mechanical
202[JCivil
203[Electrical
204[JChemical

205[Other

206[Surveying
207[0Data
208[JQuality

3.Inwhat
301[JEducation
302[0Banking,
303OInsurance
304[JReal
305[0Business/Consulting
306[0Technical
307OSoftware,

308[JConstruction,
309[0Mining,

4.

Where
401[JRetail
402[JOffice
403[JBookstore
404[]Department
406[JCatalog

5.

How
501OPreviousHPOwner
502[JAdviceofFriends,
503[0MagazineorNewspaper
504[JPress

Us

your

HP-21S

State,

Zip

POSITIONOROCCUPATION?

AREAOFACTIVITYorFIELDOFWORK/STUDY?

Engineering

Engineering

Processing

Control

INDUSTRYdoyou

Estate

Oil

did

you

Computer

Equipment

Store

did

you

Articles

Help

needs.

Date

acquired:

Phone(__

Researcher

Staff

Engineering

Engineering

Engineering

Finance,

Investment

Consulting
Computer

Architectural

Drilling,
purchase

Store

Store

Store

first

hear

Colleagues,

Exploration

about

You!

out

this

Thank

you.

HELP

US

HELP

)

105[0Top
106[JOwner,
107

work?

Services

Services

yourHPcalculator?

Manager

(I Field

this

Advertising

Principal,VP110

Agent,

(SkipifStudentorRetired.

model?

Professor

card,

you

can

helpHPto

YOU!

Business

(Please

check

Rep

209[0Purchasing,
210[0Accounting,
211OFinance,
2120General

213[0Marketing

214

Sales
215[Customer
216[0Other

310[0Chemical,
311[0Agriculture,

3120

Food
313[0Manufacturing
314[0Manufacturing
3150

Transportation
3160Communication,
317OPublic
318(0Other

(Please

check
407[Mail
408[Specialty
4090PurchasedbyCompany/School
410[Directly
411[Other

505[JDirect
506(]Salesperson
507OBrochureorIn-Store
508[Other

or

Home

only

one)

109OIndependent,

Retired

1110Other

(Please

Scheduling,
Auditing

Investment

Administration/Management

Service,

Please
Refining

Forestry,

Processing/Distribution

Admin./Government

only

Order

Store

from

Mail

seif-employed

check

Analysis

Maintenance

check

Livestock

Industrial

Consumer

Utilities

one)

HP

Literature

better

only

one)

Inventory

only

one)

Goods

Goods

/Military

Cntrl.

39V.1SOd

AHVYSS3O3aN

ON

a3vin

3HL

NI

4i

S31V1S

a3lINN

I

I

I

L]

I

I

|

I

]

1IVIN

HO
'SITIVAHOO

A1d34

S€

335$3HAAV

"ON
1INY3d

SS3ANISNY

TIVIN

SSV10

1sHld

AQ
divd

39
11IM

39V1S0d

ANYdNOD

¢,66-0£€.6

IN3N1HV43d

aA1g

@HVMOVd-L13TM3IH

370410

HO

STIHINONI

SITIVAHOO

3N
00011

HP-21S

Stat/Math

Calculator

Owner’s

Manual

HEWLETT

(bfl]

Edition3June
Reorder

PACKARD

Number

1990

00021-90025

Notice

For

warranty

and

151.

This

manual

are

subjecttochange

no

warrantyofany

limited

particular
or

for

incidentalorconsequential

furnishing,

herein.

o

Hewlett-Packard
adaptation,ortranslationofthis
written
the

copyright

The

programs

are

reserved.
without
prohibited.

and

to,

the

purpose.

regulatory

and

any

implied

examples

kind

Hewlett-Packard

information

without

notice.

with

regardtothis

warrantiesofmerchantability

performance,oruseofthis

Co.

1989.

All

permissionofHewlett-Packard

laws.

that

Reproduction,

prior

written

control

your

adaptation,ortranslationofthose

permissionofHewlett-Packard

for

this

calculator,

contained

herein

are

Hewlett-Packard

manual,

Co.

shall

notbeliable

damagesinconnection

manualorthe

rights

reserved.

Reproduction,

manualisprohibited

Company,

calculator

are

exceptasallowed

copyrighted

see

provided

Company

including,

and

fitness

for

with

examples

without

and

Co.isalso

pages

“as

is”

and

makes

but

not

for

a

any

errors

the

contained

prior

under

all

rights

programs

148

Corvallis
1000
Corvallis,

Division

N.E.

Printing

Edition
Edition
Edition

1
2

3

Circle

OR

97330, U.S.A.

History

Blvd.

March
July
June

1989

1990

1989

Mfg.
Mfg.
Mfg.

No.

00021-90026

No.

00021-90042

No.

00021-90043

Welcome

Your

HP-21S
engineering
products
offer
service.

and

for50years.

expertisetosupport

to

reflects

the

manufacturing

Hewlett-Packard

Hewlett-Packard

Our

calculators

This
pollutants
variations

Both
caseofuse.Weadded
the

calculator.

Advanced

long
CMOS

toberetained
The

microprocessor

computations,
Extensive

adverse
and

data

are

madetoexcel

calculatorisdesignedtowithstand

(smog,

thatitmay

the

calculator

materials

keyboard

(low-power)

research

effectsofstatic

lossincalculators.

ozone),

life

indefinitely

using15digits

the

superior

its

that

use

HP-21S

quality

have

stands

(see

inside

Quality

andtobe

temperature

encounterineveryday

and

its

manual

many

and

permanent,

andapositive

electronics

and

has

been

has

createdadesign

electricity,apotential

have

examplestohighlight

feeltothe

andaliquid-crystal

the

batteriestolast

optimized

internally

and

attentiontodetail

distinguished

behind

back

easytouse.

the

extremes,

been

molded

for

for

that

this

cover)

drops,

and

work

life.

designed

key

lettering

keys.

fast

and

precise

has

minimized

causeofmalfunctions

in

Hewlett-Packard

calculator

and

worldwide

vibrations,

humidity

and

the

varied

display

a long

reliable

results.

tested

uses

provide

allow

time.

the

—we

for

of

a

data

Features

Probability

m

Normal

m

Student’stdistribution.

distribution

distribution.

mFdistribution.

m)?(Chi-square)

Six

built-in

m

Two

m

Linear
m
m

Binomial
m

Time

One
Factorial,
Essential
Polar
Keystroke
Large
Ten

Accurate

Detachable

programs.

One

sample
sample

regression

Chi-square

distribution.

valueofmoney.

and

two

variable

combinations,

scientific

/rectangular

programming,.

12-character

data

registers

math,

quick

statistics.
test

statistics.

test.

functions.

conversions.

display.

and99program

12-digits

reference

functions

and

distribution.

test

statistics.

statistics

with

permutations.

lines.

witha1

0:499

guide.

inverses.

linear

regression.

exponent

range.

Contents

1

10

10

10
12
12
12
13
14
14
15
15

15
16
17

17
18

19
20
20
21

Getting

On,

Simple
Understanding

Cursor
Clearing
Annunciators
Shift
INPUT
SWAP

Alpha
Introducing
Display

Specifying

Places
Displaying

Scientific

Interchanging
Full
RangeofNumbers
Messages

Started

Off,

and

Display

Arithmetic

the

the Calculator

Keys

Key

Key

Keys

the

FormatofNumbers

the

(FIX)

the

and

Precisionofa

Contrast

Calculations

Display

Math

NumberofDisplayed

Full

Engineering

the

Number

and

Keyboard

Functions

PrecisionofNumbers

Notation

Period

and

Comma

(SHOW)

Decimal

(ALL)

Contents

5

2

3

22

22
22
24
25
25
26

29

29
30
31

31

32
33
33
33
34
35
37
39

Arithmetic

Chain

Operator

Using
Reusing
Exchanging
Using

Numeric

General
Reciprocal
Percent

Percent

Percent
Pi

(7)

Trigonometric

Changing

Trigonometric

Angle

Coordinate
PartsofNumbers

and

Calculations

Priority
Parentheses
the

Previous

Two

Storage

Functions

and

Logarithmic

Functions

Change

the

and

Hour

Conversions

Storage

and

Pending

Result

Numbers

Registers

Modes

Trigonometric

Functions

Conversions

(SWAP)

Functions

and

Functions

Registers

Operations

(LAST)

Mode

4

6

Contents

40

40
40
40
41
42
43
44

44
45

Probability

Probability

Factorial
Combinations
Random

Distributions

Normal
InverseofUpper
Distribution
Student’stUpper
InverseofUpper
t

Distribution

Number

Upper

and

Distributions

and

Permutations

and

Seed

Tail

Probability

Tail

Probability—Normal

Tail

Probability

Tail

Probability—

Student’s

46
47
48

49

50

53
53
54
55
55
56
56
56
56
57
59

61

63
65
69

69
71

F

Distribution
InverseofUpper
Upper

Tail

Distribution

InverseofUpper
Distribution
HowtoConvert

Statistical
Clearing
SummaryofStatistical
Entering

Correcting

Mean,
Linear
Weighted

Built-in
One

Statistical

Statistical

One-Variable

Two-Variable

Correcting
Correcting

Standard

Regression

Sample
Population
Interval

Example:
Example:

Upper

Tail

Probability—Chi-Square

(x?)

Tail

(x?)

From

Calculations

Data

Calculations

Data
Statistics
Statistics

Statistical

One-Variable
Two-Variable

Mean

Library

Statistics

Mean—TestofHypothesis/Confidence

Estimate

Data

Deviations,

and

Estimation

(1-StAt)

Population
Population

Tail

Probability

Probability—F

Distribution

Probability—Chi-Square

Upper

Tail

and

Weighted

Mean

Data

Data

and

Summation

Standard

Standard

Deviation
Deviation

Statistics

Known

Unknown

74

74
75
77

79
80

Population

Example:

Example:
Example:
of

MeansofTwo

Example:

Two

Sample

Proportion

Confidence

Interval

TestofHypothesis

TestonPaired

Differences

Populations

Calculating

Test

Sample

Statistics

(2-StAt)

Estimate

Size

(Paired

t)

Contents

7

84

84

88

90

90

93
95

98

99

99
103
104

105
106

108

111
113
115
116
116
118
119

Difference
of

Hypothesis/Confidence
Example:
and

Example:

and

Difference

Example:

Example:

Linear

Data

Between

Population

Unknown

Population

Known

Between

Difference

Difference

Regression

Entry

Population

Population

Test

Statistics

Standard

Standard

Non-Zero

Zero

TestofHypothesis/Confidence

Example:
Example:

Example:

Given

Chi-Square

Example:
of

Fit)

Example:
of

Fit)

Binomial

Time

ValueofMoney
Example:
Example:
Example:
Example:
Example:
of

Non-Uniform

Slope
EstimatedyasaMean
EstimatedyasaParticular

x

Test

(CHI-2)

Single

Classification

With

Unequal

Single

With

Equal

Distribution

Expected

Classification

Expected

(bin)

(FinAnCE)
Student
Home
Savings
Compound
Net

Loan

Mortgage

Account

Present

Cash

Interest/Discount

Value

Flows

Means—Test

Interval

Deviations

Deviations

Proportions

(Lr-StAt)

Interval

(Including

Values

(Including

Values

(NPV)

Estimation

Equal

Unequal

Estimation

Value,

Given

Value,

Goodness

Goodness

Case

Tables

x

7

8

Contents

122

124
126
127
128
129

Programming

Creating

Positioning
Running

Programs
Program
Entering

Programs

Boundaries
Programs
the

Program

(LBL

Pointer

and

RTN)

129
130
130
131
131
132
133
134
138
138
139
141 Sample

143
143

144

144
144
145
145
146
147
148
149
151

Starting
Starting

Stopping

Clearing

Editing
Stepping
Sample

Programs
Programs

Programs

Programs

Programs

Through

Program:
Subroutines
Branching

Branching
Conditional

and

Conditionals

(GTO)

Instructions—Decisions

Program:

Data

Available

Program

Nonprogrammable

Support,

Calculator

Batteries,

Support
AnswerstoCommon
Environmental
Changing
Testing
The
Limited
If

Calculator

Self-Test

One-Year

the

Calculator

Regulatory

Limits

the

Batteries

Information

With

XEQ

With

GTO

Programs

Pythagorean

Standard

DeviationofGrouped

Memory

Functions

and

Questions

Operation

Warranty

Requires

Service

and

Theorem

Service

R/S

and

Control

152

154

Messages

Index

Contents

9

Getting

On,

Off,

Started

and

Display

Contrast

|

Since

the

information

itself

off

three

battery

possible

To

change

Simple

|

To

turnonyour

turn

the

()

(GFF)).

the

calculator

you’ve

approximately10minutes

alkaline

symbol

(page

the

batteries

(==1)inthe

145).

display

Arithmetic

||Ifyou

makeatyping

(¢]toerase

HP-21S,

calculator

has

continuous

stored.Toconserve

last

contrast,

off,

after

approximately

display,

hold

Calculations

mistake

the

incorrect

press

press

[®],

memory,

you

replace

down

digits.

(also

labeled

then

turningitoff

energy,

one

while

the

stop

using

year.Ifyou

the

batteriesassoon

and

press

enteringanumber,

“ON”).

(written

calculator

it.

as

does

not

The

calculator’s

see

the

or

[].

To

affect

turns

low-

as

press

10

1:

Getting

Started

Arithmetic

arithmetic
press

more

ignored

except

Operators.

operators

than

one

the

last

The

(4],

(=],

(x],

operator,

one.

following

(2],

and

for

example

examples

(¥*]

demonstrate

(exponentiation).Ifyou

(5]

(x]

(#],

all

using

are

the

Keys:

24.715

Afteracalculation

number

19

[x]

The

4.7

To

continueanoperation

1156.5

=

You

6.9

x5.35=+0.918:

6.9

918

62.471

key

startsanew

12.68

(=]

[y*]

keyisthe

3=

candochain

(x]

5.35

(3]

(=]

=)

exponentiation

calculations

Display:

87.1860

has

been

calculation:

240.9200

103.8230

1155

219.3230

36.9150

40.2124

completed

(chain

without

(by

pressing

operator:

calculation),

pressanoperator

using

(=]

Description:

Adds

24.715

and

62.471.

[=]),

pressing

Calculates19x

Calculates

Continues
Completes

a

12.68.

4.7°.

key.

calculation.

calculation

47+1155.

after

each

step.

Calculate

Pressing
intermediate

(resultof6.9x5.35).

Completes

(5]

displays

answer

calculation.

of

Chain

calculations

operatorsinthe

4[+]9(x

3

(=)

are

interpreted

expression.

9.0000

31.0000

accordingtothe

Calculate4+(9x

priority

3):

Delays
higher

of the

addition

priority

Calculates4+(9x

1:

Getting

Started

([x]

than

has

[+]).

3).

11

Negative

Calculate

Numbers.

-75

<+ 3.

Enter

the

number

and

press

[*/5].

Keys:

75
]3(5]

Calculate

411

(=)

0.4—e11,

Understanding

Cursor

The

cursor

(_)isvisible

Clearing

|

the

Calculator

Clearing
the

last

its

contents

Display:

-75_

-25.0000

-1.1_

0.3329

0.0671

the

digit

and

the

when

Display.

you

cancels

Display

you

are

entered.

the

Description:

Changes
Calculates

Calculatese11,
Completes

and

enteringanumber.

When

Otherwise,

calculation.

Keyboard

the

cursorison,

[¢]

clears

signof75.

result.

calculation.

[¢]

erases

the

display

of

While

you

are

enteringanumber,

zero.

Otherwise,

cancels

Clearing
HP-218Sisdisplayinganerror
restores

12

1:

the

Getting

Messages.

original

the

current

[¢]

contentsofthe

Started

clears

calculation.

and

also

message,

display.

pressing

the

displayofits

clear

messages.

[¢]

or

clears

clearsitto

contents

When

the

message

and

the

and

Clearing

Keys

()(CLPRGM]

Memory.

To

Clears

clear

portionsofmemory:

programs

wheninProgram

Description

mode.

(«1)(CLRG]

(]

To

clear

all

then

press

and

memoryiscleared.

Annunciators

Annunciators

calculator.

Annunciator

(¢

()

memory

hold

are

displayed

Clears

Clears
display.

The

Left

function

Right

function

been

registersR,throughR,.

statistical

and

reset

the

down

both

ALL

CLr

symbols

shiftisactive.

labeledinblueisexecuted

shiftisactive.

labeledinyellowisexecuted

has

been

enteredorreturned

registersR,throughR,and

calculator,

and

messageisdisplayed.

that

pressed,ortwo

[Z+].

indicate

Status

When

When

press

When

the

you

pressakey,

you

(page

and

hold

you

release

statusofthe

pressakey,

values

14).

down

(page

(page

them,

the

14).

have

[C],

all

the

14).

PEND

]

An

arithmetic

showsinthe
Battery

powerislow

operationispending

display.

(page

145).

1:

besides

Getting

what

Started

13

Annunciator

GRAD

The

calculatorisin

calculations

(page

Status

Grads

34).

mode

for

trigonometric

RAD

PRGM

Shift

Most
keys
labeled

Keys

keys

access

have

these

operation;

The

calculatorisin

trigonometric
The

calculatorisin

chapters6and

blueoryellow

labeled

the

yellow

operations:

functions

shift

operation.Toperformashifted

shift

annunciator.

For

example,

Radians
mode.

If
shift

To

If
annunciator.Ifyou
correct

mode.

thereisjust

keytoactivate

perform

you

accidentally

it.

Then,

press

the

pressing(]followed

Pressing

one

consecutive

[®](DEG]

shifted

it.

shifted

press

[€]or(],

press

function

the

wrong

operations,

Radians

calculations

Program

7.)

printed

the

blue

key

executesayellow

operation,

key

returns

label

press

that

has

by

the

aboveakey,

just

pressitagaintoturn

shift

key,

mode

for

(page

34).

mode.

above

shift

(Refer

the

key.

key

executesablue

labeled

(€]or[®]toturnonthe

the

desired

puts

the

calculatortoDegrees

hold

down

press

label.

calculator

you

can

the

shift

the

other

press

off

one

to

The

in

key.

the

to

shift

either

shift

INPUT

The

functionsortwo-variable

The:annunciatorisdisplayed
in

the
cursororan
the:annunciator.

14

Key

(INPUT]

keyisusedtoseparate

display,

1:

error

Getting

press

messageisvisibleinthe

Started

statistics.

to

erase

two

numbers

if

the:annunciator

has

been

display,

when

using

two-number

pressed.Ifa

and

the

press twicetoerase

number

display.Ifthe

is

SWAP

Key

m

The

divisionorsubtraction.

m

The

indicates

the

m

Thex-and

Alpha

TheA,B,C,D,E,andFlabelstothe

program

Pressing

last

two

resultsoffunctions

that

hidden

Keys

labels

Introducing the

(4q)(SWAP]

numbers

two

results

result.

y-values

andtoload

when

that

you

that

return

have

using

built-in

Math

exchanges

anyofthe

entered;

been

statistics.

programs.

for

two

values.

returned;

rightofthe

Functions

following:

instance,

top

the

The:annunciator

press

(€)[SWAP]tosee

row

keys

order

are

of

used

as

L

One-Number
number

use

Functions.

the

numberinthe

Math

functions

display.

1:

Getting

involving

Started

one

15

Keys:

Display:

Description:

89.25

3.57

(=)

2.36

Two-Number
numbers
evaluates

are

the

keystrokes

Keys:

Functions.

entered

current

calculate

9.4472

0.4237

3.9937

like
expression

the

Display:

17

29 29

(]

If

you

enter

pressing

number,
calculator

Display

numberl,

[INPUT],

press

uses

the

(INPUT],

the

Format

70.5882

then

calculator

and

same

Calculatesv89.25.

1/2.36iscalculated

Adds

Whenafunction

this:

numberl

and

percent

change

displays:.For

requires

number2.

between17and

Description:

17.0000

Enters

:

Enters

Calculates
change.

pressatwo-number

function

suppliesazeroasnumber2.Ifyou

then

pressatwo-number

number

of

for

both

Numbers

numberl

3.57

and

two

numbers,

Pressing

example,

29:

numberl,

annunciator.

number?2.

percent

key

without

function

and

number?2.

1/2.36.

the

following

displays

enter

key,

first.

the

a

the

When

you

turnonthe

with

four

decimal

format

controls

Regardlessofthe
signed,
pressing

the

calculationisa

12-digit

[€][x]inFIX4(four

numberisstoredas3.14159265359x10%%°.Ifthe

number
displayedinthe
to

fit,

but12digit

16

1:

Getting

HP-218S

for

the

places

andaperiodasthe

how

many

digits

appearinthe

current

mantissa

display

format,

withasigned,

decimal

current

containing

display

more

format,

precisionismaintained

Started

first

time,

each

three-digit

places)

significant

the displayed

internally.

numbers

decimal

are

point.

The

display.

numberisstoredasa

exponent.

displays

For

3.1416.

resultofa

digits

than

numberisrounded

displayed

display

example,

Internally,

can

be

Specifying
Places

(FIX)

To

enter

the

specify

the

appear

Number

the

of

Displayed

numberofdecimal

places,

numberofdigits(0through9)that

after

the

decimal

point.

Decimal

press(][FIX],

you

wish

then

to

Keys:

(«a](FIX]

45.6

[x]

(QJ[FIX]

(«)([FIX]

.1256

9

4

3

(=]

Whenanumberistoo
is

automatically

Displaying

L

oooocoo
oooooo
cCDOooOosOo
ooooo

ococoao

ooooo
oocoOoo

displayedinscientific

the

To

set

your

possible,

Display:

0.000

5.727

5.727360000

5.7274

largeortoo

Full

Precision

smalltobe

calculatortodisplay

press

[®][ALL].

displayedinFIX

notation.

of

Numbers

numbersasprecisely

Trailing

zeros

Description:

Displays

three

places.

Displays

places.

Restores

places.

nine

four

(ALL)

are

not

displayed.

decimal

decimal

decimal

format,

as

it

1:

Getting

Started

17

Scientific

and

Engineering

Notation

Sign

of

scientific
Press
Enter

point.

point,

Scientific
mantissa
the

exponent

Notation

leftofthe

mantissa

[*][SCI).

the

numberofdigits

Notation

mantissa

multipliedby10

thisisENG

Scientific
one

digittothe

To

specify

1.

2.

Engineering

numberasa

decimal

For

example,

and

engineering

multipliedbya

from

(SCI).

Digits
decimal

-1.234567

W

Mantissa

notation,

with

Scientific

decimal

after

point

E-S/

(ENG).

one,

4:

notation

powerof10.

the

mantissa.

notation

point.

For

Sign

of

_exponent__

that

you

wishtoappear

Engineering

two,orthree

raisedtoa

power

express

The

usesamantissa

example,

digitstothe

thisisSCI

Powerof10

notation

thatisa

the

numberasa

letterEseparates

with

6:

after

the

decimal

expresses

leftofthe

multipleof3.

a

Significant

digits after

first

digit

el

-12.345E-12

——
Sign
of

mantissa

18

1:

Getting

Mantissa

Started

Sign

of

exponent

Powerof10
(multiplesof3)

To

1.

2.

specify

Press
Enter

the

engineering

[¢q])(ENG].

the

first

digit.

notation,

numberofsignificant

digits

that

you

wishtoappear

after

Entering

display

an

exponent:

1.

2.

3.Ifthe

4.

Calculate

Keys:

4.78
8

[\])(E)25[5)

Calculate

2.36

+A-)(x]

Numbers

format,

Enter
the

Press

Enter

[¥)(E]13[

[*/=)[q](E]

you

the

mantissa.Ifthe

sign.

[¢q](E]tostart
exponentisnegative,

the

4.78x1013+8x10%.

—2.36x1075x12.

12(=)

Interchanging

With

can

always

exponent.

Display:

4.7800E13

5.9750E-13

15

-2.8320E-14

the

Exponents

enter a

the

exponent.

Period

numberasa

mantissaisnegative,

press

and

(E).

Regardlessofthe

mantissa

use

or

().

Description:

5975x10713,

-2.832x

Comma

followed

to

1074,

current

by

change

To

L

switch
International
separator,
displayed:

between

press

the

display)

(9][-/,).

1,000,000.0000

period

and

usedasthe

For

example,

or

comma

decimal

1.000.000,0000

one

1:

(United

point

million

Getting

States

and

digit

can

Started

and

be

19

Full

Precision

To

temporarily

numberinthe

(SHOW].

ofaNumber (SHOW)

view

all12stored

display,

The12digits

press

are

(€]

shown

mantissa

and

without

then

the

digitsofthe

hold

down

decimal

point.

Keys:

107
(«q)(SHOW
1

(2]80(/]

(«1)(SHOW

Range

The

rangeofnumbers

displays

the

largest

(=]

of

Numbers

zero.

Overflow

positiveornegative

Overflow

P,

-9.99999999999x10°%°

Display:

1.4286
142857142857

-0.0125

-125000000000

the

HP-21S

displays

Numbers

/Underflow\

-1x10499

the

number

the

~A—

can

storeisshown

OFLO

possible.

HP-21S

0

—r—

0

1x10-499

Description:

Displays12digits.

Displays12digits.

below.

Underflow

message

Can

foramoment,

Store

Overflow

—

9.99999999999x10°°°

then

20

1:

Getting

Started

Messages

The

HP-21S
informs
from
and

the

their

youifyou

display,

meanings.

displays

messages

attemptanincorrect

press

or

about

the

[¢].

Refertopage

statusofthe

calculator

or

operation.Toclearamessage

152

foralistofmessages

1:

Getting

Started

21

2

Arithmetic

Chain

Chain
each

operator

Keys:

750

360

Operator

Some
example,9+12=+3has

Calculations

calculationsdoa

operation.

priority

[x]12(2]

(=]

The

described

Priority

chain

calculations

HP-21S

and

sequenceofoperations

Display:

9,000.0000

25.0000

and

mightbeinterpreted

two

Storage

interprets

below.

Pending

interpretations:

9+

12

expressions

Calculate

or

9+—1:;2—

750x12+360.

Operations

Registers

without

Calculates
value.
is

Completes

calculation.

annunciatorisoff.

several

pressing

using

the

Description:

intermediate

PEND

on.

the

PEND

different

[=]

after

system

annunciator

ways.

of

For

22

2:

Arithmetic

and

Storage

Registers

The

HP-21S

(»*]

(exponentiation)

uses

the

following

systemofoperator

Highest

priority

priority:

Ble

(=]

The

HP-21S
enter

has
priority,
calculation912
Thus,

[+]isretainedasa

completed.

Keys:

9+

12

3

(=)

Calculate4x72+5%7%+

4(x]7

3

5

[x]

7

)

2

6

(=)

calculatesanintermediate

lowerorequal

the

HP-21S

retains

(5]3(=],

(5]

priority.

any

When

previous

division

pending

operation

Display:

12.0000

13.0000

6.

7.0000

1,372.0000

5.0000

7.0000

1,617.0000

1,623.0000

|

Lowest

result

hasahigher

when

the

next

numbers.

until

priority

Description:

Pressing

9+12.

The
calculation.

[»*]

than

Calculates4x

(x]

than

than

Adds

Completes

the

next

operator

For

example,inthe

priority

the

division

(=]

key

has

higher

[x].

has

higher

[+].

has

higher

[x].

5x7%to

operator

has

higher

than

addition.

is

(3]

does

not

completes

priority

7.

priority

priority

1,372.

calculation.

you

add

the

Ifacalculation

with

operator

parentheses.

*

There
four

pending

are

priority

You

fewer

left

requires

than
parentheses.

that

operationsbedoneinan

(for

example

can

useamaximumoffive

five

pending

Example:

addition

operations

you

can

2:

Arithmetic

before

pending

availableifthe

calculate1+

and

Storage

order

inconsistent

multlpllcatxon)

use

operations.

calculator
2+

has

(3+(4+(5+6.

more

Registers

than

23

Using

Use

they

be

25+

You

Parentheses

parenthesestogroup

are

performed.

omitted.

For

(3%(9+

can

calculate

operations

Closing

example,25+(3x(9+12=isequivalent

12))

=.

+

9

parenthesesatthe

12

by

placing

andtospecify

endofthe

parentheses

around

the

orderinwhich

expression

to

the

addition

can

so

thatitis

Keys:

Qo120

3G

Now

calculate

30

=@

85
&

12

D)

[

16.9

B8l

done

before

_30

85-12

the

division.

Display:

21.0000

7.0000

Vv

(169-8)

30.0000
85

85.0000

73.0000

0.4110
169

8.9000

2.9833

1.2260

Description:

Evaluates
inside

Completes

[0

prevents

by

85.

Evaluates
inside

Calculates30=

Evaluates
inside

CalculatesV'8.9.

Completes

expression

parentheses.

calculation.

divisionof30

expression

parentheses.

expression

parentheses.

calculation.

73.

24

2:

Arithmetic

and

Storage

Registers

Reusing

the

When

you

storedinthe

display,
following

Previous

startanew

LAST

press

[\q)

two

calculations:

Result

calculation,acopyofthe

register.Torecall

[LAST].

0.0821x(18+273.1)

2+

0.0821x(18+273.1)

For

13

(LAST)

example,

that

valuetothe

LAST

last

result

shortens

is

the

Keys:

.0821(x]

273.1

2

=

18

(5]

13(][«Q][LAST]

Exchanging

Pressing
entered
entered44(]
numbersto75

Display:

23.8993

23.8993

2.5439

Two

Numbers

(€)(SWAP]

duringacalculation.

exchanges

75,

[(1)[SWAP]

(3]

44.

Description:

Displays

whichisstoredinLAST

when
started.

(€]

previous
Displays

first

next

[LAST]

(SWAP)

the

last

two

For

example,ifyou

reverses

the

orderofthe

result,

calculation

recalls

result.
second

numbers

result.

have

that

is

you

2:

Arithmetic

and

Storage

Registers

25

Keys:

Display:

Description:

44(]75

[1][SWAP

B
8+

435

(1][SWAP

(=]

Whenafunction

Pressing

[¢q)[SWAP]

coordinates

returns

(10,-15)topolar

(][DEG]
10
15

(«Q)(>P]

(«][SWAP

You

can

also

use

[€q)(SWAP]

separatedby[INPUT].
statistical
(before

registers,

pressing

enter

[Z+])

75

44.0000

1.7045

5

4.0000

9.2500

two

results,

exchanges

the:annunciator

the

two

coordinates:

10.0000

-56.3099

18.0278

0.0000

with

functions

For

example,toaccumulate

x-value

exchanges

the

x-value

Oops!

Whatifyou

to

enter75<

Swaps75and

Completes
Whatifyou

toadd8+

SwapsS5and

Completes

comes

results.Toconvert

Sets

Degrees

Stores

x.

Displays
cates

another
Displays
Clears

display.

that

y-value

and

require

[Z+].

y-value.

(x,y)

Pressing

two

data

meant

44?

44.

calculation.

really

wanted

5+

4?

4.

calculation.

on.

the

rectangular

mode.

angle(:indi-

result).

radius.

numbers

pairsinthe

[q][SWAP]

Using

26

2:

Storage

Registers

RegistersRythroughRyare
accessed
statistics
summation

Arithmetic

using

functions,R4throughR,are

data.

and

Storage

and

(RCL].

Registers

usedtostore

When

you

usedtostore

numbers.

are

using

They

the

are

n

to

the

n

displayedinthe

The

following

n(nisaninteger0through9)copies

designated

n

copies

keystrokes

register,

the

contents ofR,to

current

with

display

useR;andR,to

(27.1+35.6)x1.0823

full12digit

the

display.

format.

calculate

(27.1+35.6)10823

the

numberinthe

precision.

The

number

display

is

Keys:

271

35.6

(=]

1

(x]

1.0823

2

=)

1
[»*]
(=]

To

Clearing
individual
storingavalue

value.

Storage
operations
resultisstoredinthe

cancel

2

or

Registers.

register,

since

Register

that

canbeperformedonnumbers

Display:

62.7000

62.7000

1.0823

67.8602

62.7000

1.0823

0.7699

[RCLJ,

press

Press

store0in

n

Arithmetic.

register.

Description:

Stores

Stores

Recalls
Recalls
Exponentiationisdone

before

or

[e].

[(][CLRG]toclear

it.Itis

unnecessarytocleararegister

replaces

the

This

previous

table

all

value

describes

storedinregisters.

62.7inR;.

1.0823inR,.

contents of

R;.

contentsofR,.

division.

registers.Toclear

before

with

the

new

the

arithmetic

The

an

2:

Arithmetic

and

Storage

Registers

27

The

following

Keys

[STO)[+]
(STO)E)

(STOJ(x]

(STO)(:]

keystrokes

n
n

n

n

New

Number

old

number+displayed

old

number-displayed

old

numberxdisplayed

old

number-displayed

use

two

registerstocalculate

1.097x25.6671=?

1.097x35.6671=?

in

Register

n

number
number

number

number

Keys:

1.097
(x]

25.6671

=]

0

(x)10(STO)

(RCL]

1

=

0

[+]

Display:

1.0970

1

25.6671

28.1568

1.0970

1

10.0000

35.6671

39.1268

Description:

Stores

1.097inR,,

Stores

25.6671inR;.
Displays
Recalls contents of

starts

Adds10to

Of

ContentsofR,
right-most
pending

Displays

new

Rl'

first

answer.

calculation.

contents

replace

number

expression.

second

answer.

Ry,

of

2:

28

Arithmetic

and

Storage

Registers

3

Numeric

HP-21S
number

functions
acted

m

Functions
example,

m

Functions
For

6

example,4(INPUT]5[*][%CHG]

between4and5.The

1+

3 2

between4and

m

Polar/rectangular
return

two

General

L

Seeco0o
oOOo0oo0oo
COoooo

ocooooa

ooooo
oocooo
ooooo

Functions

require

uponbya

with

one

calculates

with

two

S.

results.

and

Logarithmic

either

oneortwo

function):

argument

the

arguments

arguments

3

[»][%6CHG]

coordinate

arguments

actonthe
square

use

numberinthe

rootof6.

[INPUT]toseparate

calculates

canbeexpressions.

also

calculates

conversions

use

two

Functions

(an

the

the

percent

For

the

percent

arguments

argumentisa

display.

For

arguments.

change

example,

change

and

3:

Numeric

Functions

29

Key(s)

Description

Square

root.

Keys:

45

Calculate

45

(x]

=

105

()

3.7

[*/~)(«1)(10*]

Reciprocal

(¢)(x?)

(¢

(]

x1073”7,

Square.
Natural
Base10antilogarithm.

Natural

Base10logarithm.

Display:

6.7082

3.1623E-5

0.0002

6.3096E

antilogarithm.

logarithm.

-9

Description:

V

45.

Calculates
antilogarithmof-4.5.

Calculates

antilogarithmof-3.7.
Multiplies

antilogarithms.

base

base

two

10

10

3:

Press
display.

Numeric

Functions

(I

30

to

calculate

Calculate/5+

the

reciprocalofthe

1/,.

numberinthe

Keys:

Display:

Description:

3

=

The

exponentiation

positive

numbers.

3]
4

=

Percent

L

o000

0o
oOoooo00o
COoooo
ooooo
ocOoOsOOo
coooo
oocooo

Percent

4

0.2500

0.5833

operator,

For

example,

[y*],

can

alsobeusedtofind

findV3(whichisequivalentto3'/4):

3.0000

1.3161

Functions

The
subtractapercent,orcalculate
two

and

numbers.

keys

are

Calculates1+~3

4.

Defers

Adds

addition.

two

reciprocals.

roots

of

Exponentiation.
Reciprocalofpower

calculates

root.

usedtofindapercent,

the

percent

change

between

and1+

add

or

The

m

m

[¢q)(%]

When
was
by

function

thereisno

(x],

100.

When
displayed
number

performs

pending

(5],or(7],

or

[5]isthe

numberasa

preceding

pressing

pending

percent

the

or

two

different

operations:

operator,orthe

[4q)(%]

divides

operator,

and

returns

[q](%]

[5].

last

the

that

3:

Numeric

operator

displayed

interprets

percent

of the

Functions

you

number

the

entered

31

Example.

Find

27%of85.3.

Keys:

85.3

(x]27(\1](%]

(=)

Find

the

number

200

(=]25[v][%]

=

Percent

To

calculate

Change

the

(expressedasa

Example.

Calculate

Keys:

291.7

316.8

[*][%CHG]

Calculate

the

Display:

0.2700

23.0310

that1s25%

50.0000

150.0000

percent

change

percentageofn,)

the

percent

Display:

291.7000

8.6047

percent

change

Description:

Divides27by
Calculates

less

than

200.

Calculates
Completes

between

two

numbers,n;andn,,

enterny(INPUT]n,[*][%CHG].

change

between

291.7

Description:

Enters
Calculates

change.

between

(12xS)

and

(65+18).

100.

27%of85.3.

25%of200.

calculation.

and

316.8.

n;.

percent

12

65

32

[x]

5

18

[»][%CHG]

3:

Numeric

Functions

60.0000

38.3333

Calculates
Displays

between60and

and

percent

(65+18).

enters

change

n;.

Pi

()

Pressing
displayed

12-digit

Example.

Find

the

(A=4nr).

Keys:

4

(x]

[(«q])(m]

x]

4.5

(1)

(x3

(=)

Trigonometric

Changing

the

The

trigonometric
interpreted
conversion

[9q](x]

valueisactually

surface

displays

valueisroundedtothe

areaofa

Display:

3.1416

the

used.

sphere

20.2500

254.4690

Modes

and

Trigonometric

mode

determines

when

using

the

functions.Toexit

value of7.Although

current

witha4.5

display

inch

Description:

Displays

Displays

Calculates

square

inches.

Functions

Mode

how

numbers

trigonometric

one

mode,

and

press

the

format,

radius

.

4.5

surface

are
coordinate
another.

area

the

in

3:

Numeric

Functions

33

Keys

(]

()

(DEG]

(RAD]

Description

Sets

Degrees

degreesina

measuredindecimal

than

degrees-minutes-seconds).

Sets

Radians

radiansina

mode.

circle.

mode.

circle.

There

Angles

There

are

degrees

are

are

(rather

2«

360

Annunciator

None

()

(GRD]

Trigonometric

(SIN]

COS

Keys:

Sets

inacircle.

Angles

dependingonthe

Keys

Grads

mode.

There

Functions

are

interpretedindecimal

current

Function

sine
cosine
tangent

trigonometric

(«1][ASIN]
[«9)[ACOS]
(«1][ATAN]

Display:

are

400

grads

degrees,

Keys

Description:

GRAD

radians,orgrads

mode.

Function

arc

sine

arc

cosine

arc

tangent

[DEG]

(]

15

[SIN]

1

60

34

3:

Numeric

Functions

0.2588

1.7321

Degrees

Sets

Displays
Displays

mode.

sineof15°.

tangentof60°.

=
.35

[«](ACCS]

(=)

.62

[«1](ACOS)

=

Angle

Keys

(«1][=HR

and

2.7321

69.5127

51.6839

17.8288

Hour

Conversions

Function

To

hours;

hours(degrees)-minutes-seconds-decimal
seconds
decimal

converts

format

hours

the

(H.MMSSss

(or

degrees)

Calculates1+
Displays

0.35.
Displays

0.62.
Displays

0.35-arc

number

or

format.

arc

arc

arc

cosineof0.62.

from

D.MMSSss)

tan

cosine

cosine

cosine

to

60°.

of

of

of

(»][=HMS

(«q)[+DEG]

(»][=RAD]

To

hours-minutes-seconds;

from

decimal

hours(degrees)-minutes-seconds-decimal

seconds

To

degrees;

valuetoits

To

radians;

degree

hours

format

valuetoits

(H.MMSSss

converts

decimal

converts

(or

degree

the

radian

converts

degrees)

or

the

number

equivalent.

number

equivalent.

the

to

D.MMSSss).

fromaradian

fromadecimal

3:

Numeric

Functions

number

35

@lT@

Angleindecimal

Angle

radians

degrees

in

(D.d)

Decimal

(H.h)

hours

E@]lTEfl

Keys:

1.79

[x]

(«)(=DEG]

90.2015

25.2589

(«q)(SHOW

Angle

D.MMSSss

format

(«)(x]([=]

[«](>HR]

]

in

Display:

5.6235

322.2000

90.3375

25.1532

251532040000

I:-—:Jl

Hours

H.MMSSss

format

Description:

Calculates

Converts

degrees.
Converts90degrees,

minutes,15seconds

decimal

Converts

to25degrees,

minutes,32seconds.
Shows

(32.04

degrees.

decimal

seconds).

T

QG

in

1.79~.

1.79r

radians

25.2589
15

seconds

to

20

to

degrees

36

3:

Numeric

Functions

Coordinate

Conversions

L

oOo000oo
®S0O8e000

-

0000

ooooo

ooooo

cocooo
oococoo

To

convert

1.

2.

Coordinate

INPUT];6is

trigonometric

-—— = = =

from

rectangulartopolar
Enterx
Press

[q][SWAP]todisplay

conversions
interpreted

require

accordingtothe

mode.

==

-

- -

y

[«Q][>P]todisplay

r.

pairsofdata

x

-coordinate,y-coordinate

coordinates,

6.

separated

current

by

To

2.

convert

1.

Enterr
Press

from

polartorectangular

6

[*][>R]todisplay

(q]

to

display

coordinates,

y.

x.

3:

Numeric

Functions

37

Example.

Convert

coordinates.

the

rectangular

coordinates

(10,

—15)topolar

Keys:

(]

(DEG]

10

15

(«][SWAP

Convert

7
30

[*][+R]

[1][SWAP

(«q)(>P]

the

polar

Display:

10.0000

-56.3099

18.0278

coordinates

7.0000

3.5000

6.0622

(7,

30°)torectangular

Description:

Sets

Degrees

Enters

x.

mode.

Entersy,calculatesrand

6,

and

displays

Displays

6.

r.

coordinates:

Enters

r.

Enters6,calculatesxand

y,

and

displays

Displays

y.

x.

38

3:

Numeric

Functions

Parts

L

(«](IP)

Keys

of

Numbers

Integer

partofthe

Function

number.

()

(«1](ABS]
(r*](RND]

Keys:

12.3456789

(«1](SHOW

(][RND]

Fractional
integer

Absolute

Rounds
specifiedinthe
format.

(=]

[©q][SHOW]

partofthe

part).

valueofthe

the

number

(No

rounding

Display:

12.3457

123456789000

123457000000

internallytothe

current

number

number.

occursinALL

FIX,

SCI,orENG

(the

Description:

Entersanine-digit

number.

Displays

number.

Rounds
internally.

number

without

numberofdigits

display

mode.)

full

precision

number

its

of

3:

Numeric

Functions

39

Probability

Probability

and

Distributions

|

Factorial

Pressing
number

Combinations

The

numberofcombinationsofn

of

different

No

item

of

the

calculating

The

numberofpermutationsofn

of

different
ofnitems.Noitem
different
keystrokes

Your
permutations,
probabilities.

[*][nl]

mustbean

occurs

sameritems

orders of

calculates

sets

containingritems,

more

combinations:

arrangementsofr

for

calculating

HP-218S

integerinthe

and

than

are

can

the

provides

and

random

the

factorialofthe

Permutations

onceinthe

not

counted

n-value

objects

items

occur

more

sameritems

permutations:

factorials,

range0through

objects

taken

setof7

separately.

[INPUT]

that
than

are

combinations,

numberstohelp

numberinthe

takenratatimeisthe

fromalarger

items,

Use

r-value

takenratatimeisthe

canbetaken

onceinan

counted

n-value

separately.

you

253.

groupofn

and

different

these

keystrokes

[][Cn.r].

fromalarger

arrangement,

r-value

calculate

display.

number

items.

number

and

Use

these
[®][Pn,r].

The

orders

for

group

40

4:

Probability

and

Distributions

Keys:

Display:

Description:

5
3

[](Cn,]

5
3

[*][Pn,r]

Combination

Random

To

storeaseed
number
previous

To

and

contents.

generateasequenceofnumbers
(«(a)(RAN#].

and

Number

for

press

This

5.0000

10.0000

5.0000

60.0000

Permutation

and

the

random
[®](SEED].
The

first

producesapseudo-random

0<RAN#<1."

Cpp=——

BT

(mo-r)r!

Pnr‘_‘

’

(n

Seed

number

The

seedisstoredinR

random

numberinthe

from

Equations.

n!

n!

-r)

generator,

the

previously

numberinthe

Enters
Enters

calculates

the

n-value.

the

r-value;

combinations

of5objects,3atatime.
Enters
Enters

calculates

the

n-value.

the

r-value;

permutations

of5objects,3atatime.

enterapositive

and

writes

over

the

sequenceisdisplayed.

stored

seed,

press

range

*

The

numberispartofa

This

sequence

London:

Addison

passes

Wesley,

sequenceofuniformly

the

spectral

test

1981).

(D.

Knuth,

4:

Probability

distributed

Seminumerical

and

psuedo-random

Algorithms,

Distributions

numbers.

Vol.

41

2.

Distributions

under

that

tail

Using
HP-21S,
inverse.
under
You

valueofthe

the

are

other

chapter.

distribution

Distribution

Normal

L

ocooooo
ooOooo0o

CoOoo0o

oOoO0o0oo

ooooo

Oseses
0OooOooo

the

valueofthe

The

area
tables
endofthis

The

upper

the

The

the

can

random

curve

than

four

probability

you

can

calculateanupper

upper

tail

probability

curvetothe

calculate

random

variableifyou

thatiscalculatedisthe

upper

functions

rightofthe

the

area

variable.

tail,

Keys

=

know

use

are:

distribution

under

Conversely,

the

conversion

Inverse

(]

functionsonthe

tail

correspondstothe

random

the

curveifyou

the

area

upper

(zp]

probabilityorits

area

variable

you

under

tail.Ifyou

instructionsatthe

Keys

know

can

calculate

the

value.

the

curve.

are

using

These

distribution
textbooks.
determine

statistical

42

4:

Probability

Student’s

F

X

The

calculator

any

upper

tables.

t

functions

functions

tail

probability,

and

Distributions

()

(]

QEx)]

replace

the

statistical

expand

not

just

(>](tp]

(](Fp)

X%

tables

the

tablesbyallowing

the

selected

found

values

in

in

you

to

Normal

Upper

To

upper

Q(z)isthe

variableZis

calculate

tail

Tail

Probability

the

area

under

the

curvetothe

probability),

probability

greater

enter

the

thatastandard

than

z.

z value

and

normal

rightofz

press

[€][Q(z2)].

random

(the

Example.
the

probability

Keys:

1.7

[)[Q@)]

The

variableZisastandard

thatZis

greater

Display:

0.0446

than

1.7?

normal

random

Description:

Calculates

probability.

variable.

the

0

What

upper

tail

Q(z)=0.0446

z=1.7

is

4:

Probability

and

Distributions

43

InverseofUpper

Distribution

If

you

know

the

upper

to

calculatez,enter

the

Tail

Probability—

tail

probabilityp(area

probability

and

press

Normal

under

the

[*][zp].

curve)

and

want

Example.
of

0.025?

Keys:

.025

Whatisthezvalue

[*](zp]

Student’stUpper

To

calculate

first

store

value

and

The

label

df;isto

wheretostore

freedom,

numberofdegreesoffreedom

correspondingtoan

Display:

1.9600

Tail

Probability

the

area

under

the

Student’stdistribution

the

degreesoffreedominR,

press

(€]

[Q(1)].

the

lower

rightofthe

degreesoffreedom.Tostore

enter

the

value

and

press

the

upper

tail

Description:

Calculates

calculator

thezvalue.

then

enter

(1]

keytoremind

degrees

1.

The

can

probability

curve,

the

t

you

of

maximum

useis299.

44

4:

Probability

and

Distributions

7

Example.
distribution

Keys:

8

1.86

Inverse

Distribution

If

you

to

calculatet,store

(](te].

Whatisthe

with8degreesoffreedom

1

[Hq][Q(1)]

of

know

the

&

Upper

upper

the

upper

tail

probability

(df;)

Display:

8.0000

0.0500

df

-

6

.943

9

=

Tail

tail

probabilityp(area

degreesoffreedominRy,

.01

Probability—

associated

forat

valueof1.86?

Description:

Stores

freedom.
Calculates

probability.

.001

Student’s

under

the

then

withaStudent’s

the

degrees

the

curve)

enterp,and

upper

t

and

of

want

press

t

tail

4:

Probability

and

Distributions

45

Example.Ahypothesis

Student’stdistribution
foranupper

Keys:

26

.05

[>](tp)

F

Distribution

tail

1

with26degreesoffreedom

probabilityof0.05.

df
241

27

Upper

test

requires

Display:

26.0000

1.7056

1.711

the

criticaltvalue

.01

@

Tail

Probability

.

(df;).

Description:

Stores
freedom.

Calculates
value.

.001

from

the

Find

degrees

the

the
thetvalue

of

critical

t

and

(2]

keystoremind

store

the

numerator

1.Tostore

and

press

calculator

46

4:

Probability

To

calculate

store

the
denominator
value

and

The

df;

the

2.

The

can

useis299.

the

area

under

numerator

press

and

df,

you

degreesoffreedom,

denominator

maximum

and

Distributions

degreesoffreedominR;

degreesoffreedominR,.

[¥q]

[Q(F)].

appearaslabelstothe

wheretostore

degreesoffreedom,

numberofdegreesoffreedom

theFdistribution

Then

lower

the

degreesoffreedom.

enter

the

value

and

enter

curve,

first

and

the

enter

the

rightofthe

To

press

the

value

the

F

(1]

Example.
freedom

to

16,

foranF

Whatisthe

(df;)

equalto3

valueof5.29?

upper

and

denominator

tail

probability

with

numerator

degreesoffreedom

degrees

(df,)

equal

of

Keys:

3

16

5.29

Inverse

If
to
denominator

1

2

[¢][QF)] 0.0100

of

Upper

you

know

the

upper

calculateF,first

degreesoffreedominR,.

Display:

3.0000

16.0000

Description:

Stores

Stores

Calculates

probability.

DLevelofSignificance

|

14

17

tail

store

®

58388

PO

Tail

Probability

probabilityp(area

the

numerator

|

D

288D

PO0O0

—

under

degreesoffreedominR;

Then

enter

F

the curve)

p and

dfj.

df,.

the

upper

Distribution

and

and

press

[](Fp].

tail

want

the

4:

Probability

and

Distributions

47

%

7/

Z/y//////////////flmmfi_

F

.

Example.Ahypothesis
distribution
the

denominator

associated

Keys:

4

8

.05

[*][Fp]

Upper

L

1

2

Tail

with

the

numerator

degreesoffreedom

upper

tailFvalue

LeveI

aff

1

Probability—Chi-Square

To

calculate

the

degreesoffreedominR,

press

[\]

[Q(X?)].

test

requires

fora0.05

Display:

4.0000

8.0000

3.8379

of

Significance

2

the

area

the

criticalFvalue

degreesoffreedom

(df,)

equalto8.

levelofsignificance?

Description:

Stores

Stores
Calculates

Co|

under

the¥?distribution

then

enter

from

(df;)

equalto4

Whatisthe

df;.

df;.

F.

s

Distribution

curve,

the

x? value

the

F

and

(x?)

store

and

48

4:

Probability

To

store

degreesoffreedom

1.

The

calculator

and

maximum

can

useis299.

Distributions

(df,),

enter

the

value

and

numberofdegreesoffreedom

press

the

.

Example.
are17degreesoffreedom

Keys:

17

33.41

Inverse
Distribution

If

you

calculate

(]

B%e).

The)statistic

1

[q][Q(X?)]

of

Upper

know

the

upper

x?,

store

df|

15

&3

18

(x?)

tail

the

degreesoffreedominR,

calculated

(df;).

Display:

17.0000

0.0100

.10

Tail

Probability—

probability

fromasampleis33.41

Whatisthe

.05

upper

Description:

Stores

freedom.

Calculates
probability.

Chi-Square

(area

under

then

tail

probability?

the

the

curve),

enterpand

and

there

degrees

the

upper

and

press

of

tail

want

to

4:

Probability

and

Distributions

49

Example.Atest

value

correspondingtoan

Keys:

19

.001

How

The
probability.
curvetothe
with
some
equaltoone,
symmetric.
mirror

1

[](X3p)

to

Convert

distribution

areas

other

imageofthe

functions

The

upper

rightofthe

other

than

areaifyou

and

That

is,

sample

that

has19degreesoffreedom

upper

Display:

19.0000

43.8202

df

17|

27.59|

28.87|

30.14

31.41

From

return

tail

probability

given

upper

tail.Itis

remember

the

normal

the

portionofthe

portionofthe

.05

value.

\

X

tail

probabilityof0.001.

Description:

Stores
freedom.

Calculates

.01

33.41

34.80

Upper

values

Sometimes

easytoconvert
that
and

curvetothe

Tail

for

the

upper

correspondstothe

you

the

total

area

Student’stdistributions

curvetothe

rightofzero.

(df;).

Find

the

the

degrees

the»?value.

tail

camulative

area

under

will

needtowork

from

upper

tail

under

the

curve

are

leftofzeroisthe

x?

of

the

to

is

50

4:

Probability

and

Distributions

Example.

the

probability

The

probability

normal

1.7,

Q(1.7),

The

variableZisastandard

thatZis

thatZis

curvetothe

and

then

less

than

1.7?

less

than

1.7isthe

leftof1.7.

subtractitfrom1(the

You

can

calculate

normal

area

total

random

under

the

areatothe

area

variable.

area=Q(1.7)

the

standard

under

the

What

right

of

curve).

is

Keys:

1.7

[¢q](Q(2)]

1(3)

Example.
the

probability

The

variableZisastandard

thatZis

Display:

0.0446

0.9554

greater

-1.2

than

normal

1.2orless

0

Description:

Calculates
area.

Subtracts

from

1.

random

than

—1.2?

1.2

upper

tail

upper

tail

variable.

area=Q(1.2)

area

What

is

4:

Probability

and

Distributions

51

The
Since
you

desired

the

normal

can

calculate

areaisto

distributions

the

the

rightof1.2,

upper

tail

are

symmetric,

area,

plus

the

Q(1.2),

areatothe

the

areas

and

multiplyby2.

leftof—1.2.

are

the

same,

so

Keys:

1.2

[)[Qz)]

x]2(5]

Example.

so

that

0.95.

The

given

normal

(0.05=2=0.025).
of

0.025.

The

variableZisastandard

the

probability

areais0.95.

distributionissymmetric,

Display:

0.1151

0.2301

normal

thatZis

less

thanzand

N

O

The

area

not

includedis1—0.95=0.05.

halfofthis

The

desiredzcorrespondstoan

Description:

Calculates
area.

Calculates

random

greater

area=0.95

area=

N

areaisin

upper

upper

answer.

variable.

than-zis

1—’02—953

the

upper

tail

tail

probability

tail

Find

z

equal

to

=0.025=Q(1.96)

Since

the

Keys:

.025

You

52

(*](zp)

will

find

4:

Probability

other

examplesoftail

and

Display:

1.9600

Distributions

Description:

Desired

conversionsinchapter

valueofz.

6.

Statistical

Calculations

The
for
accumulatedinregistersR4through
at
storedineach
the

Mean

and

Linear
Linear
Weighted

regression
estimate

Summation

Clearing

Clear

the

statistical

you

don’t

clear
automatically
statistical

registers,

and

[€][Z-]

one-

and

two-variable

the

lower

rightofthe

register.

statistical

standard

mean.

functionstocalculate

deviation.

statistics.

and

forecasts.

statistics:n,2x,

Statistical

registers

the

registers,

includedinthe

press

(R4

data

summation

[®](CLZ].

keys

are

statistics.

keys

Once

£x%,

Xy,

Data

through

currently

(The

usedtoenter

Summation

indicate
you

enter

the

)2,

and

Lxy.

Ry)

before

storedinR4
calculations.Toclear
displayisalso

and

Rg.

The

what

statistical

the

data,

following:

entering

throughRyis

cleared.)

register

delete

data

you

new

the

data

is

labels

data

can

use

data.

is

If

5:

Statistical

Calculations

53

Summary

Some

functions

values

have

Keys

(=]

(]

Ew

()

of

Statistical

return

been

returned.

Arithmetic

(average)ofthe
Meanofthe

weightedbythe

Sample

deviationofthe

two

values.

Press

[4][SWAP]tosee

Description

mean

x-values.

x-values

y-values.

standard

x-values.*

Calculations

The:annunciator

(«1)[SWAP]toDisplay

Arithmetic

(average)ofthe

Sample

deviationofthe
you

entered

indicates

the

hidden

mean

standard

that

value.

y-values.

y-values

y-data.*

two

if

(](ox,0y]

y-value

()

x-value

(]3]

(«a)(m,b]

*

Sample

Population
t

The

correlation coefficientisa

how

closely
correlation,
indicates

Population

deviationofthe

Estimateofx

valueofy.

Estimateofy

valueofx.

Slope
calculated

standard

non-correlated

deviation

standard

and-1indicatesaperfect

the

data

deviation

fits

standard

foragiven

foragiven

(m)ofthe

line.

assumes

assumes

numberinthe

the

calculated

data.

x-values.*

dataisa

negative

samplingofa

the

data

constitutes

range—1through+1that

line.A+1

correlation.Avalue

Population
deviationofthe
you

entered

Correlation

Correlation

y-intercept

calculated

indicatesaperfect

standard

coefficient.t

coefficient.t

(b)ofthe

line.

larger,

the

entire

y-values

y-data.*

complete

population.

measures

positive

closetozero

if

set.

54

5:

Statistical

Calculations

Keys

4

(n)

Number

of

data

Description

points

entered.

5(x)

8

Entering

Thereisno

statistical

exceed

warning

(«1][CLRG].

One-Variable

To

enterxdata

1.

2.

3.

limittothe

registers.Ifstatistical

+9.99999999999x10*°,

(OFLO).

Clear
Enter

the

numberofitems

Continue

[Z+].

The

6

(Xy)

7

(&¢*)

(3y%)

9

(Xxy)

Sumofthe
Sumofthe

Sumofthe

Sumofthe
Sumofthe

x-values.
y-values.

squaresofthe

squaresofthe
productsofthex-and

Statistical

numberofvalues

Data

remains

Statistics

for

one-variable

the

contents ofR4throughRyby

first

value

accumulated.

accumulating

n-valueisincremented

Data

data causes

the

stored

statistics,

and

press

valuesbyentering

you

HP-21S

until

[Z+].

The

with

x-values.

y-values.

y-values.

can

accumulateinthe

the

valueofa

displaysatemporary

you

press

pressing

HP-21S

the

each

entry.

register

(]

[®](CLZ].

displaysn,the

numbers

and

to

overflow

or

pressing

5:

Statistical

Calculations

55

Two-Variable

To

enter

x,y

pairsofstatistical

1.

Clear

the

2.

Enter

the

3.

x-value

Enter

and

the

displaysn,the

4.

Continue

entry.

To

enter

data

for

x,

and

its

corresponding

Correcting

Statistics

and

data,

contentsofR,

first

x-value

throughRyby

and

press

the:annunciator

corresponding

y-value

numberofpairsofitems

entering

x,y

pairs.

calculating

the

The

weighted

weightasy.

Statistical

Weighted

pressing

(INPUT].

appearsinthe

and

The

press

Mean

[#][CLZ].

HP-21S

display.

[£+].

The

accumulated.

n-valueisincremented

mean,

enter

Data

each

displays

HP-21S

with

data

the

each

value

as

Incorrect
is

incorrect,

entries

Correcting

To

delete

and

1.

Keyinthe

2.

Press

3.

Enter

Correcting

To

delete

and

1.

Keyinthe

2.

Press

3.

Enter

canbedeleted

you

must

delete

One-Variable

reenter

[¢q)(Z-]todelete

the

reenter

[q)(Z-]todelete

the

statistical

x-valuetobe

correct

value

Two-Variable

x,y

pairsofstatistical

x-value,

correct

press

x,y

pair

using

and

reenter

data,

deleted.

the

value.

using

the

values.

using

(€](Z-].Ifeither

both

values.

Data

The

n-valueisdecreasedbyone.

[Z+].

Data

data,

and

then

keyinthe

The

n-valueisdecreasedbyone.

and

valueofanx,y

[Z+].

pair

y-value.

56

5:

Statistical

Calculations

Mean,

Standard

Statistics

L

OsseOs
O00000
CoOo0ooo
oooaoo
ooooo
OOoooo
OoOoO0OOos

You

can

calculate

deviation

summation

you

(S,),population

statistics,n,£x,

can

also

population

summation

Deviations,

the

sample

calculate

standard

statistics

the

deviationofthe

Ly,

mean

standard

and

mean,

£y?,

and

and

Summation

(x),

sample

deviation

£x?ofx-data.

sample

standard

y-data,

Zxy.

standard

(o,),and

For

and

the

x,y

data,

deviation,

Example

1.Ayacht

captain
averagetochangeasail.
observes

of

sample
square,

Keys:

()

4.5
4

2

3.25

3.6

3.6

3.5

3.75

[2)(z.7]
(>)(5x.8y]

minutes

standard

using

(]

themasthey

required:

deviationofthe

the

formulaV£x?/n

carry

4.5,4,2,

Display:

0.0000

1.0000

2.0000

3.0000

4.0000

5.0000

4.0000

5.0000

6.0000

3.5000

0.8515

wantstodetermine

She

randomly

out

the

sail

3.25,

3.5,

times.

.

chooses

change,

3.75.

Calculate

Also,

how

longittakes

six

membersofher

and

records

the

calculate

the

Description:

Clears

statistics

Enters

first
Enters
Enters
Enters

to

Oops!

enter

Deletes

second
third
fourth

Whatifyou

3.5?

3.6

n-valuebyone.

Enters

fifth

correctly.

Enters

sixth

Calculates

Calculates

standard

on
crew,

the

number

mean

and

root

mean

registers.

value.

value.

value.

value.

meant

and

decreases

time

time.

the

mean.

the

sample

dewviation.

5:

Statistical

Calculations

57

RCL])

7

8

4

=]

The

standard

[«1)[SWAP]

deviations

are

isasamplingofa

If

the

data

constitutes

deviations

canbecalculatedbypressing

[+2)(SWAP]todisplayo,.

the

sample

larger,

77.1250

6.0000

3.5853

calculatedby[®](Sx,Sy]

complete

the

entire

standard

deviations.

setofdata.

population,

[®][ox,0y]todisplayo,and

Displays

Displays
Calculates

square.

and

They

the

population

Tx?.

7.
the

[*][Sx,Sy]

assume

that

standard

root

the

mean

data

(]

Example

193,

182, 177,

kilograms.
heights

and

y-data).

Keys:

(]
193

182
177
185
()

(«](SWAP

[)lox,o

2.

The

and

Find

the

weights,

90

81
83
77

coach

185

centimeters

mean

then

has

four

and

population

find

the

Display:

0.0000

1.0000

2.0000

3.0000

4.0000

184.2500

82.7500

5.8041

new

playersonthe

and

weightsof90,

standard

total

weightofthe

team

with

81,

83,

and

deviationofboth

players

(sumofthe

Description:

Clears

statistics

Begins
and

Calculates
heights

Displays

entryofheights

weights.

mean

(x).

meanofweights

).

Calculates

standard

heights

population

deviation

(x).

heights

of

77

their

registers.

of

for

58

5:

Statistical

Calculations

(«)(SWAP

6

Linear

4.7104

331.0000

Regression

Least

squares

for

estimation

throughasetofx,y

x,y

pairs.Astraight

thex-and

slope

andbis

linear

and

y-variablesofthe

the

and

y-intercept.

Estimation

regressionisa

forecasting.Itis

data.

There

line

estimates

formy=mx+b,

Displays

standard

weights
Displays

(sumofy’s).

statistical

usedtofitastraight

mustbeat

the

population

deviation

(y).

total

method

least

two

relationship

wheremis

for

weight

used

line

different

between

the

Linear

Linear
canbeusedtoestimateay-value

linear

Regression.

1.

Enter

the

2.

Press

=

(Q)[E1]

correlation

m

[«¥)[m,b]todisplaym,the

displayb,the

Estimation.

estimation

1.

Enter

the

2.

Enter

the

mToestimatexfor

Todoa

x,y-data

using

[Q)([SWAP]

coefficient.

y-intercept.

The

calculations,

x,y-data

known

using

x-valueory-value.

linear

the

(or

straight

the

the

giveny,enter

[«)(zd.

mToestimateyfor

()

Bu).

the

givenx,enter

regression

instructionsonpage

(][]

slopeofthe

line

calculatedbylinear

foragiven

instructionsonpage

calculation,

[1](SWAP))todisplayr,the

line,

x-value,orvice

the

y-value,

the

x-value,

56.

then

56.

then

then

[¢](SWAP]

regression
versa.Todo

press

press

to

5:

Statistical

Calculations

59

Example.
concentrationofone

varying

are observed:

only

X

Y

The

rate

the

initial

|0.050

|[0.0062

of a

certain

chemical.

concentrationofthe

0.075

0.00941

chemical

When

0.10

0.0140

the

reaction

reactionisrun

chemical,

dependsonthe

0.125

0.0146

the following

initial

repeatedly,

rates

0.20

0.023

Calculate
line

fittedtothe

Keys:

(]
.05
.075

.00941

A

125

2

(«a)(m.b]
[«

[SWAP

[«Q](Zr]

Estimate
moles

.09

[«)([SWAP]

per

[](3.1]

the

slope

.0062

.014

.0146

.023

the

rateofthe

liter.

and

y-interceptofthe

data.

Also

Display:

0.0000

5.0000

0.1093

0.0014

0.9890

reaction

0.0113

calculate

when

least

the

correlation

the

concentration

squares

regression

coefficient.

Description:

Clears

statistics

Enters

x,y-data.

Displays
Displays

(:
result).

Displays
coefficient.

Calculates
forx=

slope.

y-intercept

indicates

correlation

equals

0.09.

straight

registers.

another

0.09

estimateofy

60

5:

Statistical

Calculations

Estimate

.02

the

(N][Z1]

Weighted

To

calculate

frequencies

1.

Use
frequenciesofthe

2.

Press

concentration

Mean

the

weighted

yy,

y2,...,

¥n,

and

[*][zw].

necessary

0.1700

0.0000

meanofdata

to

enter

x-values.

x,y

for

the

points

pairs.

rate

equalto0.0200.

Calculates

fory=0.02.

Clears

annunciator.

x;, x,,

...,X,occurring

The

y-values

estimateofx

display

are

the

and

:

with

Example.Asurveyof266

54ofthem

$216.

Keys:

(]

200

205
210

216

(]

rent

Whatisthe

54

32
88

92

[zw

for

$200

average

per

Display:

0.0000

1.0000

2.0000

3.0000

4.0000

209.4436

one-bedroom

month,32for

monthly

rent?

rental

apartments

$205,88for

$210,

Description:

Clears

statistics

Begins

entryofrents

numberofapartments.

Calculates
mean.

reveals

and92for

registers.

weighted

that

and

5:

Statistical

Calculations

61

Equations:

62

5:

Statistical

Calculations

Built-in

Program

Library

The

built-in

be

accessedbypressing

letter

keys,AthroughF,in

pressed,
abbreviated
released.

Name

A

B

C

D

program

the

top

row

program

One

Sample

Two

Sample
Linear
Chi-Square

library

consistsofsix

[€q])(LOAD]

the

keys

assume

nameisdisplayed

Title

Test

Statistics

Test

Statistics

Regression

Test

Test

Statistic

programs

followedbyoneofthe

top

row.

(When

their

letter

values.)

until

the

Statistics

that

[$]

An

letter

Message

1-StAt
2-StAt

Lr-StAt

CHI-2

key

can

is

is

E

you’ve

can

the

(However,

use
without

F

entered
and

Lr-StAt,

calculation,

Whenaprogramisloaded,itclears

memory.

Once
the

statistics
you
Lr-StAt
calculatingastatistic,
repeat

Binomial

Time

Probability

ValueofMoney

the storage

your

tests

describedinthis

load

affecting

youdonot

correcting

data

and

your

registers

(either

use

data.

needtoreenter

the

Distribution

any

other

programs

are

left

raworsummary),

chapterinany

1-StAt,

and

Also,ifyou

mistake.

that

intact.)

you

order.

then

reload

and

makeamistake

your

data.

6:

Built-in

bin

FinAnCE

maybein

can

calculate

For

instance,

use

You

simply

Library

63

This

table

lists

the
organizationofthe
quick

reference

guide.

symbols

programs.

usedinthe

The

diagramsinthis

flow

diagrams

chapter

that

show

the

makeupthe

The

restofthis

the

example

asaguidetofind

Symbols

Symbol

%3
»

3T

TESX,~NQAMOQT

that

in

Program

Sample
Sample
Sample
Population
Sample
Population

Population

Precision

Observed

Expected

Degreesoffreedom.
Standard
Student’strandom
Chi-square

Hypothesized

Upper

Probability.

size.
mean.
standard

proportion.

tail

chapter

describes

resembles

the

solution,

the

Flow

Description

deviation.

standard

proportion.

mean.

(1/,

widthofconfidence

value.

value.

normal

random

probability.

each

problem

mixing

random

value

program,

you

and

deviation.

variable.

variable.

(e.q.,

are

matching

Diagrams

interval).

variable.

mg,g,Dy,---)-

mainlybyexample.
tryingtosolve

the

parts.

and

Find

use

it

Quick
quick
perforated

64

Reference

reference

6:

Built-in

lines

Guide.

guide.

and

slipitinside

Library

You

The

diagramsinthis

can

detach

your

the

quick

calculator

chapter

reference

carrying

areinthe

guide

case.

along

the

One

1-StAt

Sample

calculates

test
varietyofone-sample
confidence

mean,

The

intervals,

degreesoffreedom,

1-StAt

programisorganizedasfollows.

Statistics

statistics

problems.

the

sample

and

and

confidence
You
size

standard

(1-StAt)

interval

can

calculate

required

for

error.

estimates

test

statistics,

estimation

test

for

a

of the

6:

Built-in

Library

65

Test

of

(«1)(COADJA

Formofdata?

Mean

ravV

(](CLz]

data

Enter

(XEQJA

Testofhypothesisorconfidence

V,(XEQ)B

(displays z or

[«\)[@@)]or

(displaysU,)

Testofhypothesisorconfidence

test

hypothesi

[Z+]

using

of

test
hypothesis

[«][Qt)

Test

of

\Tmary

¢)

U,

(e*)(ze)or(e])(te)(displays

(XEQ]C

[R7S](displays

[R/S](displays

of

Proportion

(«1)[COADJA

[XEQJD

n

[R/S]

x

soro

interval?

confidence

interval

(displays

lower

upper

interval?

confidence
interval

statistics

zor1)

precision)

limit)

limit)

n

D

p

m,(XEQ]1

n,(XEQ]B

[«)([@)(displays

6:

66

Built-in

Library

(displays z

)

U,,)

n

pR/S)

D

(XEQ]1

U,

[e*)(zp)(displays

[XEQ]C
(R/S](displays

[R/S](displays

(displays

lower

upper

2)

precision)

limit)

limit)

Paired

[«2)[LOADJA
[)[CLs)

x]E]

x=)y,4]

Difference

N

=

,.Elyn

V,(XEQ]B

(displays zorf)

[«)[Q&)or

(displays

Testofhypothesisorconfidence

test

of

hypothesis

[w][Q)

U,)

Sample

Size

Determination

confidence

interval

pE@]orE(displays

[XEQJC

(displays

[R/S)(displays

[R/S](displays

[«2)[LOAD]A

o[XEQJE

dm

U,

[*](zp](displays

fi(dlsplays

z)

required

sample

interval?

precision)

lower

upper

size)

zort)

limit)

limit)

6:

Built-in

Library

67

R4

through

LBLA

LBLB

LBLC

LBLD

LBL7

The

method

summary

If

you

are

1.

Clear

2.

Enter

3.

Press

(standard

4.

Optional:

m
m
m
m
m

statistics.

using

1-StAt

n,

the

The

degreesoffreedomn-1.

The

sample

The

standard

Ry

Statistics
Processes

storesinR,
Calculates

Calculates

or
Stores

testofone
Calculates

of

the

for

entering

raw

data,

the

statistics

sample

Press
Press
Press
Press
Press

deviationofthe

data

Atoprocess

deviationofthe

0todisplay
1todisplay
2todisplay
3todisplay

7tocalculate

Registers

sample

meanx

size.

and

or

proportion

deviation,Vp(1-p)

registers

summary

through

test

Aor

confidence

D.

summary

sample

standard

sampling

data

dependsonthe

registersbypressing
using

[Z+].

the

sampling

(page

statistics

Rj.

statistic

distribution.

data

sampling

the
the
the
the

the

distribution).

for

D.

interval.

statistics

meanorproportion.

error,

and

display

distribution).

sample
degreesoffreedom.
sample
sample

standard

Labels

p.

orvVx(1-

55).
for

1-StAt

and

hypothesis.

Used

intoR,throughR;for

the

standard

data

type:

[](CLZ].

the

size.

mean.
standard

error

Used

after

deviation

raw

data

standard

deviation.

(standard

error

).

after

A

or

68

6:

Built-in

Library

If

you

1.

2.

3.

4.

are

using

Enter

the

Enter

the

Enter

the

standard
Optional:

Press
Press
Press
Press

summary

sample
mean
standard

error

(standard

statistics,

size

and

press

and

press

[R/S].

deviation

deviationofthe

0todisplay

1todisplay
2todisplay
3todisplay

D.

and

press

[R/S].

sampling

the

sample

the

degreesoffreedom.

the

sample

the

sample

size.

mean.
standard

The

display

distribution).

deviation.

shows

the

Population

Interval

Example:
sampleof75

123.45

and

Part1.First,
statistics.

Keys:

(«1)[LOAD]
75

123.45

6.78

Now

you

interval

Part2.Calculate the
population
meanisnot

estimate

Mean

Estimate

Population

elementsistaken

the

population

enter

A

D

can

either

test

(part

meanis122.

equalto122atthe

—

Test

Standard

standard

the

data.Inthis

Display:

75.0000

123.4500

0.7829

the

hypothesis

3).

This

test

statistic

Testitagainst

of

Hypothesis/Confidence

Deviation

fromapopulation.

deviationis6.78.

example

example

for

the

0.05

significance

the

(part2)or

includes

null

hypothesis

the

alternative

dataissummary

Description:

Loads
Stores
Stores
Stores

and

error.

both.

level.

Known.

The

calculateaconfidence

A

sample

1-StAt.
sample
sample
standard

calculates

that

hypothesis

random

mean

size.
mean.

deviation

standard

the

that

is

the

6:

Built-in

Library

69

Because
distribution

The

statistics
the
translatedtoan

the

population

willbeusedtomake

problemisstatedsothat

fallinthe

normal

distribution key,

upper-tail

AN

Equation:

standard

areaofthe

the

0.025

deviationisknown,

the

test.

the

hypothesis

two

tailsofthe

two-tail

probability.

-

0.05

&)

o/Vn

the

normal

willberejectedifthe

normal

significance

distribution.Touse

level

is

test

Keys:

122

(]

Because

hypothesisisnot

Here’sanalternative

.025

122

Because
not

B

the

calculated

(*](zp]

B

the

rejected.

rejectedatthe

test

statisticisless

Display:

1.8521

0.0320

probabilityisgreater

0.05

levelinthis

proceduretotest

1.9600

1.8521

than

the

the

Description:

Enters
population
calculates

Calculates
probability.

than

0.025

two-tail

hypothesis:

Calculates
Calculates

criticalzvalue,

hypothesized

mean

and

test

statistic.

upper-tail

(0.05+2),

test.

criticalzvalue.
test

the

the

statistic.

hypothesis

is

70

6:

Built-in

Library

Part3.Calculate
mean.

Equations:

the

90%

confidence

interval

estimateofthe

population

The

inside

two-tail

90%

thatis(1—0.9)=2=

4%\_’/%»

Keys:

.05

[*](zp]

C

precision=——

.

confidence

confidence

0.05sothat

Display:

1.6449

1.2877

122.1623

124.7377

-

.

limits

level

you

zo

vn

—

=x

ZOo

+

T

n

willbetranslatedtoupper-tail,

can

use

the

[*](zp]

key.

Description:

Calculates

normal

Calculates

Calculates
confidence

Calculates

standard

variate.

precision.

lower

limit.

upper

limit.

Example:
followingisa

149.8,

129.6,

Population

random

109.3,

Part1.First,

Keys:

(«a)(LOAD]

A

()

enter

Standard

sampleof8

130.0,

133.4,

the

data.Inthis

Display:

0.0000

elements

116.4,

example

Deviation

Unknown.

fromapopulation:

and

134.8.

the

dataisraw.

Description:

Loads

Clears

1-StAt.

statistics

6:

Built-in

The

129.7,

registers.

Library

71

129.7

149.8

129.6

109.3
130

133.4

116.4

134.8
()

A

Now

you

interval

can

either

estimate

test

(part

1.0000

2.0000

3.0000

4.0000

5.0000

6.0000

7.0000

8.0000

129.1250

4.2975

the

hypothesis

3).

This

example

(part2)or

includes

Enters

Calculates

raw

data.

mean

(optional).

Processes

calculates

data

and

standard

calculateaconfidence

both.

error.

Part2.If

would

137,

Because

the

alternativeisthat

you

rejectornot

testingatthe

youdonot
distributionofthe
small,

the

normal

The

alternative

translatestoan

hypothesis

upper-tailsoyou

Equations:

degreesoffreedom

the

reject

the

hypothesis

0.1

levelofsignificance?

know

the

population

test

statisticist

distribution

cannotbeusedasan

impliesalower-tail

can

A=

G

t

=n

-1

population

that

standard

distributed.

Because

test.

use

the

[€]

N

s/\/;z—

meanislower

the

population

deviation,

the

sample

approximation.

This

procedure

key.

than

the

137,

mean

is

sampling

is

72

6:

Built-in

Library

Keys:

Display:

Description:

1

137

B

(«]

Because
the

Here’sanalternative

1

137

When
the

Part3.Calculate

the

calculated

hypothesisisrejected.

proceduretotest

[](tp)

B

the

two

values

are

critical

value.

Thus,

the

mean.

7.0000

-1.8325

1.8325

0.0548

tail

probabilityisless

the

hypothesis:

1.4149

-1.8325

1.8325

compared,

the

hypothesisisrejectedatthe

95%

confidence

the

calculated

interval

Checks

calculated
degreesoffreedom
(optional).

Enters
population
calculates

hypothesized

mean

test

statistic.

Convertstoupper

Calculates

upper-tail

probability.

than

0.1

(the

rejection

Calculatestdistribution
critical

Calculates

Convertstoupper

estimateofthe

value.

test

statistic.

statisticisgreater

0.1

level.

population

and

tail.

level),

tail.

than

The

inside

two-tail

probability,

thatis(1-0.95)+2=

Equations:

95%

confidence

/%\_’M

levelistranslatedtoan

0.025.

precision

upper-tail

ts

=

Vn

6:

Built-in

Library

73

confidence

limits

=X

,

s

vn

degreesoffreedom

Keys:

.025

(](tp)

C

=n

Display:

2.3646

10.1619

-1

118.9631

139.2869

Population

Example:

Proportion

Confidence

Interval

Estimate.Asampleof65
showed38favoringaproposaltoraise
servicetostudents.
population proportioninfavorofthe

Part1.First,

Keys:

enter

Whatisthe

the

summary

Display:

99%

confidence
proposal?

statistics.

the

Description:

Calculates

statistic.
Calculates

interval.

Calculates

confidence

Calculates

confidence

student

interval

Description:

required

precision

lower

limit.

upper

limit.

feetoprovide

estimateofthe

test

of

students

bus

[«a)[LOAD]

65
38

74

D

[:]65=]

1

6:

Built-in

A

65.0000

0.5846

0.4928

0.0611

Loads

1-StAt.

Enters

sample

Calculates
sample

proportion.

and

size.

stores

CalculatesVp (1-p).
Calculates

standard

error.

Library

Part2.The

key

for

impliedinthe

normal

the

calculations,

problem

(1-0.99)+2=

Equations:

approximation

translate

statementtoan

0.005.

4%_"/[%

methodisused.Touse

the

99%

inside-tail

upper-tail

probability:

the

confidence

[*](zp]

level

Keys:

.005

[*](zp]

C

Example:
their
new

logo

the

logo

at

least

Part1.First,

Keys:

TestofHypothesis.Afraternity

opinion

thatatleast

sweatshirt.Of75

sweatshirt,31madeapurchase.Tomeet

52%ofthe

confidence

members

enter

the

precision=zvp(-p)

vn

interval=p*zvp(

Display:

2.5758

0.1574

0.4272

0.7421

52%oftheir

randomly

would

summary

Display:

national

sampled

havetobuy.

statistics.

vn

Description:

Calculateszvalue.
Calculates

Calculates
Calculates

didamarket

members

members

their

Description:

precision.

lower
upper

studytotest

would

who

were

fund

raising

limit.

limit.

buy

their

offered

goal

[«<)[COAD]

75

A

D

75.0000

Loads

Enters

6:

Built-in

1-StAt.

sample

size.

Library

75

31

(5]75=)

52

0.4133

1

0.4996

0.0577

Calculates
sample

and

stores

proportion.

CalculatesVn(1-)
hypothesized

Calculates

proportion.

standard

for

Eerror.

Part2.Test

the

populationis0.52

0.52.

Use

the

normal

significance.

With

the

statementofthe
regionofthe
the

lower-tail to

This

test

wherepis

normal

statisticiscalculated:

the

sample

proportion.

Keys:

hypothesis

against

that

the

the

alternative

approximation

alternative

distributionisimplied.

the

upper-tail.

%{\

zZ

=

VvV

proportion

Display:

proportionofbuyersinthe

that

the

proportionisless

method

hypothesis,

and

Use

test at

the

lower-tail

the

the

M

(P-m)

m(1=mp)

vn

and7is

the

hypothesized

Description:

than

0.05

level

of

critical

keytotranslate

population

52

B

+/-

(«]

The

hypothesisisrejected

significance

76

6:

level.

Built-in

Library

-1.8490

1.8490

0.0322

because

the

Enters
population

and

statistic.
Convertstoupper
Calculates

probability.

tail

probabilityisless

hypothesized

proportion

calculates

upper-tail

than

test

tail.

the

Here’sanalternative

.05

[*](zp]

.52

B

proceduretotest

1.6449

-1.8490

1.8490

the

hypothesis:

Calculates
critical

Calculates

Convertstoupper

upper

value.

test

statistic.

tail

tail.

Because
fallsinthe

the

test

rejection

Example:

Means

Students
course
to

give

in

the

scores

hypothesis

is

greater

Part1.First,
using

of

have

has

exams

six

students

following

between

that

than

Student

Test

TestB

the

statisticisgreater

area

and

Test

on

Paired

Two

Populations

alleged

enter

key.

that

that

two

table.

the

two

TestAis

zero)?

Usea0.10

A

the

the

varyindifficulty.Inresponse,

different

Can

the

examsiszeroberejectedinfavorofthe

easier

1

90

83

difference

than

the

critical

the

hypothesisisrejected.

Differences

test

bank

foracertain

exams.

hypothesis

thanB(that

85

93 72

The

scoresofthe

that

the

the

mean

levelofsignificance.

2

3

78

between

4

75 80

68

each

value,

the

test

statistic

(Pairedt)of

large-enrollment

the

instructor

two

mean

difference

difference,A-

5

87

pairofobservations

agreed

exams

in

6

98

92

are

B,

Keys:

(«1)[COAD)
()] 0.0000

90

(-]

A

83

Display:

1.0000

Description:

Loads

1-StAt.

Clears

statistics

Enters

6:

raw

Built-in

data.

registers.

Library

77

85

(-]

93

78()72
75

(-]

68

80

(-]

87

98

(-]

92

(]

A

Now

you

estimate.

can

test

This

exampleisa

2.0000

3.0000

4.0000

5.0000

6.0000

1.8333

Processes

calculates

difference

2.9599

the

hypothesisorcalculateaconfidence

Calculates

€rror.

testofhypothesis.

data

and

mean

(optional).

standard

interval

Part2.Test the
and,

since

unknown,

hypothesis.

the

sampleissmall

thetdistributionisused.

The

and

Equation:

t

where

disthe
s41sthe
d,isthe

meanofthe

sample

standard

hypothesized

differencesofthe

deviationofthe

mean

difference.

degreesoffreedom=n—1(nis

problemisstatedasan

the

population

d.—-do

Sq

/\/n_

paired

standard

values.

differencesofthe

the

numberofdifferences).

upper-tail

deviation

paired

values.

test

is

78

6:

Built-in

Library

Keys:

Display:

Description:

1

0

B

(«]

Because
significance

the

tail

probabilityofthe

level,

the

Here’sanalternative

1

[](te]

0

B

5.0000

0.6194

0.2814

test

hypothesisisnot

A)%b_

proceduretotest

1.4759

0.6194

Reviews
degreesoffreedom
(optional).

Enters

mean

difference

calculates

Calculates
probability.

statisticisgreater

rejected.

the

hypothesis:

Calculatestdistribution

critical

Enters

mean

difference

calculates

calculated

hypothesized

and

test

statistic.

upper-tail

than

the

0.10

value.

hypothesized

and

test

statistic.

Because

the

calculated

hypothesisisnot

Example:

Suppose

random

Calculating

that

the

sample

size

within3unitsofthe

confidence?

The

problemisstatedasan

toanupper-tail

keytosolve

Use

probability,(1-

the

problem.

test

statisticisless

than

the

critical

rejected.

standard

Sample

deviation

Size

of a

populationis34.26.
mustbetakentoproduceanestimateofthe
true

the

population

normal

inside

mean(aprecisionof3)

probability

distribution.

two-tail

probability.Bytranslating

0.9)+2=0.05,

you

6:

can

Built-in

value,

What

with

use

the

Library

the

simple

mean

90%

this

[*](zp]

79

Equation:

A

N

Keys:

(«1][LOAD]

34.26

3
.05

[>](zp]

R/S

The

conventionisto

larger

integer,inthis

Two

2-StAt
statistics
between

standard

Sample

stores

and

population

dewviation.

A

E

the

statistics

confidence

h

Display:

34.2600

3.0000

1.6449

352.8472

round

the

case

353.

Test

meansorproportions.Italso

Statistics

neededtoprepare

interval

zo

=

|\———_

[

precision

calculated

estimates

2

]

Description:

Loads
Enters

deviation.

Enters
Calculates

normal

Calculates
sample

sample

(2-StAt)

for

involving

program

standard

precision.

variate.

size.

sizeupto

1-StAttocalculate

the

difference

calculates

A.

standard

required

the

next

the

pooled

test

2-StAtisorganizedasfollows:

80

6:

Built-in

Library

Difference

raw

dziy

Between

(«]([LOADIB

Formofdata?

Means

summary

statistics

e

Enter

15t

sample
(XEQJA
Enter2"sample

Which

normal

[XEQ)C

(«1][LOAD]A

distribution?

Test

V,(XEQ)B

[\)[@@)or

(displaysU,)

using

using

t

[«9)[COADJA

of

hypothesis

test

of

hypothesis

(displayszor

[w][Qt)

f)

normal

(XEQJC

[E]m/\

or

confldence

confidence

interval

U,

([e)(zplor(e*](tp]

(XEQ]C

(displays

[R/S)(displays

(R/S](displays

n,(XEQID

x,[R/S]

s,oro,[R/S]
n,[R/S)

%,[R/S)

s,0r

o,[R/S]

Which

distribution?

/

\t

interval?

(displayszor

precision)

lower

limit)

upper

limit)

[LOAD]A

1)

6:

Built-in

Library

81

Difference

Between

(«2)(LOAD]B

Proportions

Assumed

non-zero

difference

n,[(XEQJD

P1

(XEQ]1

n,[R/S)

p2

(XEQJ2

(XEQJC

[ElmA

Testofhypothesnsorconfidence

of

test

hypothesis

V,(XEQ)B

[\l

(displaysz)

[Q@)]or

[H][QM)]

(displaysU,)

non-zeroorzero?

zZero

n,[(XEQ]D

P1

X,+X,

n_+

nz

p,[R/S]

(XEQ]B
(<]

0(XEQ]B(displays

()@@

interval?

confidence

interval

U,(e)(zplor(e](tp]

[XEQ]C

(displays

(displays

(R/S](displays

(displaysz)

precision)

lower

limit)

upper

limit)

XEQJ!

[LOAD]A

(displays

z)

U,)

82

6:

Built-in

Library

1

(n—1+n_z)

Degreesoffreedomn;+n,-2.
Differenceinsample
Pooled

n,.

X5

S,.
n,.

X1

S

Calculates
entered.

Calculates

unknown

deviations.
Calculates

difference

deviations.
LBLD
LBL

1

LBL

2

Stores

Calculatesv/

Calculatesv/p,(1-p,).

2-StAt

1 1

standard

summary

Registers

or1ifBorCis

deviation.

and

moves

pooled

but

standard

when

standard

assumed

given

statistics

p(1-py)-

and

Labels

executed,

meansorproportions.

statistics

deviation

equal

population

errorofmean/proportion

unequal

from

respectively.

after

raw

estimate

standard

population

two

samples.

data

standard

is

of

The

method

summary

If

you

1.

2.

Enter

3.

Press

for

statistics.

are

using

Clear

the

sample

entering

raw

statistics

A.

data

data,

registersbypressing

data

for

dependsonthe

sample1using

data

type:

[®](CLZ].

[Z4].

6:

raw

Built-in

data

Library

or

83

If

you

1.

2.

3.

.

Enter

0

.

Press

.

Optional:
registers

are

using

Enter

Enter
Enter

display
sampling

Enter

.

Enter

.

Enter

.

Optional:
registers

sample

the

the
the

the
the

the

data

to

process

The

values

showninthe

summary

sample

mean

for

standard

shows

the

distribution).

sample
mean

for

standard

The

stored

showninthe

for

sample2using
the

data

stored

tableonpage

statistics,

size

for

sample1and

sample1and

deviation

standard

size

sample2and

deviation

error

for

sample2and

and

calculated

tableonpage

and

and

calculated

press

for

sample1and

(standard

press

for

sample2and

[Z+].

display

83.

press

[R/S].

press
[R/S].

values

83.

the

standard

canberecalled

error.

D.

press

[R/S].

deviationofthe

[R/S].

press

[R/S].

canberecalled

from

The

from

the

the

Difference

Between

Hypothesis/Confidence

Example:
Unknown.

variances

84

are

A|86|109

B|93|101

6:

Built-in

Population

Sample

given

Library

data

below.

Standard
from

11291

111|117

Population

Interval

Deviations

two

populations

|103

105

Means

Estimation

assumedtohave

121

107

|97 |99

—

Equal

100

Test

and

of

equal

97

Part1.First,

This

example

Equation:

enter

uses

the

data

and

raw

data.

oo

=g/ODT

calculate

nytn,

the

D

pooled

-2

standard

deviation.

Keys:

(«][LOAD]
(]

86

109
112

91

103
121
107
100

97

()

A

93

101
111
117

105
97
99

Display:

B

0.0000

1.0000

2.0000

3.0000

4.0000

5.0000

6.0000

7.0000

8.0000

9.0000

102.8889

Description:

Loads

2-StAt.

Clears

statistics

Enters

Calculates

sampleAdata.

mean

registers.

(optional).

0.0000

1.0000

2.0000

3.0000

4.0000

5.0000

6.0000

7.0000

Prepares
Enters

sampleBdata.

for

sample

B.

6:

Built-in

Library

85

(]

103.2857

9.8355

1

14.0000

Calculates
(optional).

Calculates
standard

Recalls
degreesoffreedom
(optional).

mean

pooled

dewviation.

calculated

Pressing

Now

you

can

either
interval
includes

Part2.Test
equal
distribution

The
translatedtothe

[«a)[Q®))

Equation:

whereDis

andSis

estimate

both.

the

against

the

anda0.10

alternative

key.

the

the

standard

B

displays

the

test

the

(part

3).

The

hypothesis

alternative

levelofsignificance.

hypothesis

upper

impliesatwo-tail

tail

0.10+2=0.05,sothat

A

hypothesized

errorofthe

pooled

hypothesis

that

hypothesis

_

standard

statisticist

the

meansofthe

(1

-x3)-Dy)

-

difference

difference.

(part2)or

distributed.

that

they

rejection

N

S

between

deviation

are

the

again.

calculateaconfidence

This

example

two

populations

not

equal.

Use

area.

This

you

can

use

the

population

means,

is

are

the

t

5pisdefinedinpart1on

degreesoffreedom

86

6:

Built-in

=n;+n,

Library

S=Sp

page

85.

-

2

"—1—+—"l—

nq

n»p

Keys:

Display:

Description:

[«<a][LOAD]

0

*/-

A

B

(«)

The

probabilityofgetting

approximately

hypothesis

that

0.47,

whichisgreater

the

two

Here’sanalternative

.05

[>][tp]

0

B

*/-

Because
is

not

rejected.

the

test

statisticisless

-0.0801

0.0801

0.4687

this

statisticifthe

than

means

are

equalisnot

proceduretotest

1.7613

-0.0801

0.0801

than

the

population

the

0.05
rejected.

the

hypothesis:

critical

Loads

1-StAt.

Enters

difference

population

calculatesttest
Convertstoupper

Calculates

hypothesized

between

means

upper

probability.

means

significance

Calculates

critical

Enters

difference

hypothesized

population

calculatesttest

are

level.

upper

value.

between

means

Convertstoupper

test

value,

the

hypothesis

and

statistic.

tail.

tail

equal

is

The

tail

and

statistic.

tail.

Part3.Calculate

between

The
probability,

the

inside

two

two

tail

thatis(1-

the

90%

confidence

population

90%

means.

confidence

0.9)+2=0.05,sothat

%’“’M

interval

estimateofthe

levelistranslatedtoan

you

can

use

6:

Built-in

difference

upper

the

[](tp]

Library

tail

87

Equations:

precision=(sp

: :

confidence

s,1sdefinedinpart1on

degreesoffreedom

interval=(x|-x,)*tsp

=n;

Keys:

(q](LOAD]

.05

[][tp]

A

1

C

R/S

R/S

..

page

85.

+n,-2

Display:

14.0000

1.7613

8.7302

-9.1270

8.3333

—

1 1

—

+

—

ny

np

Description:

Loads
Checks

freedom

calculated

(optional).

Calculatestvalue.

Calculates

Calculates

confidence

Calculates

1 1

—

+

ny

1-StAt.

that

have

—

)

degrees

been

and

stored

precision.

lower

limit.

upper

limit.

of

Example:

Known.
population

Population

Samples

standard

are

taken

deviations
of75hasameanof43.2
second

deviationof1.45.

Enter

is

statistics.

88

sampleof125

the

data

hasameanof38.1

and

calculate

calculatedbypressing

6:

Built-in

Library

Standard

from

arc

Deviations

two

populations

known

withapopulation

andapopulation

the

standard

C

after

you've

but

unequal.

standard

error.

The

entered

Unequal

for

which

The

and

the

first

sample

deviationof1.34.

standard

standard

the

error

summary

The

term

Equation:

m-m

-7

_

T

01

03

—

t—

hy

hp

Part1.First,

Keys:

[«1])(LOAD)

75

enter

B

D

43.2

1.34

125

38.1

1.45

C

Now

you

can

either

estimate.

confidence

Part2.Whatisthe

between

The

statisticisnormally

interval

the

population

the

data.

Display:

75.0000

43.2000

1.3400

125.0000

38.1000

1.4099

0.2019

test

the

hypothesisorcalculateaconfidence

estimate.

90%

confidence

means?

This

example

distributed.

uses

interval

summary

Description:

Loads

Enters
first

Enters

Enters
standard

Enters

second
Enters
Enters

of

second

statistics.

2-StAt.

sample

sample.

sample

population

deviation.

sample

sample.
sample
standard

Calculates
error.

This

example

estimateofthe

size

mean.

size

mean.

deviation

sample.

standard

interval

calculates

difference

from

of

the

For

these

Once

you've

upper-tail

conditions,

the

translated

probability,

4%\__)%

standard

the

inside

normal

two

distributionisused.

tail

90%

confidence

thatis(1—0.9)+2=0.05,

you

6:

can

Built-in

leveltoan

use

the

Library

[(*](zp]

89

Equations:

confidence

Keys:

(«](LOAD]

.05

[*](zp]

A

C

Difference

Example:
populations.
responding
proportion

Difference

“yes”

responding

Between

The

.

.

precision

interval=(x1-X3)*z

Display:

1.6449

0.3321

4.7679

5.4321

Population

Non-Zero.

first

was

sample

0.47.
“yes”

size

The

was

_

=z

was

second

0.35.

-7

0’1

—

hy

_

Samples

400

and

sample

0'2

4

=

nj

ol

1,22

o2

nq

n,

Description:

Loads

1-StAt.

Calculates
value.

Calculates
Calculates

estimateofdifference.

Calculates

upper-tail

precision.
lower

upper

Proportions

were

taken

from

the

proportionofpersons

size

was

500

and

limit

limit.

two

the

z

of

Part1.Enter

term.

Equation:

90

6:

Built-in

the

Tp.-ps

Library

summary

=\/

statistics

and

calculate

pi(1-py)+p2(1-p)

ny

the

h;

standard

error

Keys:

(«1)[LOAD]

400

D

47

1

500

.35

2

C

Now

you

can

interval

estimate

B

either

test

(part

Display:

400.0000

0.4700

0.4991

0.4991

500.0000

0.3500

0.4770

0.4869

0.0328

the

hypothesis

3).

This

example

(part2)or

includes

Description:

Loads

2-StAt.

Enters

sample.
Enters

first
Calculatesy/

Enters

Enters

sample.
Enters

second
Calculatesv/p,(1-p,).
Entersitand

data.

Calculates
for
assumedtobe

sizeoffirst

proportion

sample.

result.

sizeofsecond

proportion

sample.

standard

test

with

calculateaconfidence

both.

for

p(1-p»y).

for

processes

difference

non-zero.

error

Part2.Test
proportionsis0.04
Usea0.01

The

problem
two-tail
leveltoupper-tail,

the

hypothesis

levelofsignificance

statement

rejection

area.

that

AN

that

against

the

implies

Once

is,

0.01<+2=0.005,

the

differences

alternative that

and

the

normal

the

useofthe

you've

translated

N

between

the

differenceisnot

approximation

normal

the

you

distribution

two-tail

can

use

6:

Built-in

the

population

method.

significance

the

(4]

Library

0.04.

and

a

key.

91

Equation:

zZ

=

\/pl(l

(1

-p2)-Dy

-py)|,(1

hy

-po)

UPp)

D,isthe

Keys:

[«1][LOAD]

.04

hypothesized

A

B

difference.

Display:

2.4369

(«] 0.0074

Because
probabilityof0.005,

Here’sanalternative

.005

.04

Because
not

Part3.Calculatea95%
between

the

[*](zp]

B

the

rejected.

the

probabilityofthe

the

hypothesisisnot

proceduretotest

2.5758

2.4369

test

statisticisless

confidence

population

proportions.

test

statisticisgreater

rejected.

the

than

the

critical

interval

Description:

Loads

Enters

difference

test

statistic.

Calculates

normal

than

hypothesis:

Calculates

Calculates

value,

estimateofthe

1-StAt.

hypothesized

and

calculates

upper-tail

probability.

the

tail

criticalzvalue.

test

statistic.

the

hypothesis

difference

is

To

use

[](zp],

you

must

leveltoupper-tail:(1—

A

92

6:

Built-in

Library

also

translate

0.95)+2=

—

the

0.025.

inside

two-tail

95%

confidence

Equations:

confidence

precision

z\/pl(1

=

interval=(p;-p,)*z\/

py)

-

p2(1

s

p1)

-

h,

p1(1-py)sp2(1-py)

ny

h;

Keys:

(«1][LOAD]
.025

A

[](zp)

C

(R/S]

Example:
populations.
“yes”toa
replied
“yes”inthe

Part1.Enter
proportion.

Equation:

Difference

particular

“yes”tothat

two

Display:

1.9600

0.0643

0.0557

0.1843

Zero.

The

first

sample
question.
question.Itis

populationsisthe

the

data,

including

Samples

size

was

The

second
hypothesized

same.

the

—_

(x1

(ny+ny)

Description:

Loads
Calculateszvalue.

Calculates
interval.

Calculates

difference

population
Calculates

were

taken

from

250

and

117

respondents

sample

size

that

the

calculationofthe

+x3)

1-StAt.

precision

lower

between

proportions.

upper

two

was

283

proportion

pooled

limit

limit.

replied

and

124

of

sample

of

of

6:

Built-in

Library

93

Keys:

(x2)(LOAD]

250

117

(2]

117

B

D

250

=] 0.4680

124

(5]

(][@250

1

283

124

[z)

283

(5]

B

283

5]

Display:

250.0000

241.0000

0.4522

0.4977

0.4977

283.0000

0.4382

0.4977

Description:

Loads

2-StAt.

Enters

sizeoffirst

sample.

Calculates

first

Calculates
successes.

Calculates
proportion

sample

and

enters

proportion.

sum

of

pooled

p.

CalculatesVp(1-p).

Enters
Enters

result.
sizeofsecond

sample.
Calculates

sample
second

Processes
calculates

term.

and

enters

proportion

sample.

statistics
standard

of

and

error

Part2.Test
samples

0.10

In
the

tail:

94

are

significance

this

problem

(€]

0.10

=2=0.05.

6:

Built-in

the

hypothesis

equal

level

the

key,

AN

Library

against

and

normal

you

must

that

the

proportionsof“yes”inthe

the

alternative that

the

normal

approximation

they

approximationisused.

translate

the

two-tail

N

two

are not

equal.

Use

method.

And,inordertouse

rejection

areatoupper-

a