
10
10
18
Solid-State Soft Start Motor Controller and Starter
Application Note
February 2005
Supersedes January 2001
Contents
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
About This Guide . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
Basic Motor and Soft Start Theory
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
AC Motors . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
AC Motor Types . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
Induction Motors . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
Enclosures . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Ventilation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Control of AC Motors . . . . . . . . . . . . . . . . . . . . . . . . . 3
Soft Start Basics . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Soft Start Applications . . . . . . . . . . . . . . . . . . . . . . . . 5
Other Reduced Voltage Starting Methods . . . . . . . . 5
Basic Mechanics
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Torque . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Calculating Torque . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Calculating Horsepower . . . . . . . . . . . . . . . . . . . . . . . 7
Inertia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
Calculations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
Cylinders . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
Pulley/Gear . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
2
WK
Reflected to the Motor Shaft . . . . . . . . . . . . . . . 8
Speed Reducer Selection . . . . . . . . . . . . . . . . . . . . . . 9
Gear Reducer Selection . . . . . . . . . . . . . . . . . . . . . . . 9
Gear Reducer — Overhung Load . . . . . . . . . . . . . . . . 9
Other Gear Issues . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
Controllers and Starters, Theory and Application
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
Benefits of Using Soft Start Controllers and
Starters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Basic Principles of Soft Start Controllers and
Starters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Load Characteristics . . . . . . . . . . . . . . . . . . . . . . . . . . 11
Typical Soft Start Adjustments . . . . . . . . . . . . . . . . . 11
Motor Application Considerations . . . . . . . . . . . . . . 12
Installation Compatibility . . . . . . . . . . . . . . . . . . . . . . 12
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
. . . . . . . . . . . . . . . . 2
. . . . 10
Load Types and Characteristics
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
Load Types . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
Other Functional Considerations . . . . . . . . . . . . . . . 13
Typical Load Torque . . . . . . . . . . . . . . . . . . . . . . . . . . 13
Controller and Starter Selection
Selection Considerations . . . . . . . . . . . . . . . . . . . . . . 15
Selecting a Soft Start for a Machine . . . . . . . . . . . . . 15
Measuring Machine Torque . . . . . . . . . . . . . . . . . . . . 16
Soft Start Application Questions . . . . . . . . . . . . . . . . 16
Soft Starter Application Data Worksheet . . . . . . . . . 17
Formulae, Conversions and Tables
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
How to Calculate Torque . . . . . . . . . . . . . . . . . . . . . . 18
How to Calculate Horsepower . . . . . . . . . . . . . . . . . . 18
How to Calculate Surface Speed . . . . . . . . . . . . . . . . 18
How to Calculate Horsepower for Pumps . . . . . . . . 18
How to Calculate Horsepower for Fans and
Blowers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
How to Calculate Horsepower for Conveyors . . . . . 18
How to Calculate Accelerating Torque . . . . . . . . . . . 18
How to Calculate Maximum Motor Torque . . . . . . . 19
How to Calculate WK
How to Calculate Equivalent WK
Electrical Formulae . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Induction Motor Formulae . . . . . . . . . . . . . . . . . . . . . 20
Tables of Conversions and Abbreviations . . . . . . . . 20
Glossary
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
. . . . . . . . . . . . . . . . . . . 12
. . . . . . . . . . . . . . . . . . 15
. . . . . . . . . . . . . . . . 18
2
. . . . . . . . . . . . . . . . . . . . . . . . 19
2
at Motor Shaft . . 19
AP03902001E For more information visit: www.EatonElectrical.com
Application Note
Page 2
Introduction
About This Guide
The following material is intended to
acquaint the user with the theory and
operation of solid-state soft start
motor controllers and starters. This
material will enable the user to better
select the controller or starter and take
into consideration the parameters necessary for proper application to a
given load.
The reference material provided is for
the convenience of the user. It is taken
from current handbooks and standards such as NEC, NEMA, IEEE and
others. It is intended as reference
material for standard applications and
may not cover all actual and special
applications. Experienced factory
application engineers are available to
assist users in the application of motor
controllers and starters for most motor
loads. Specific ratings and external
signals used for control and logic are
the user’s responsibility.
The user must determine the final
suitability and acceptability for controllers and starters used on specific
equipment.
Basic Motor and Soft Start
Theory
Introduction
A solid-state soft start controller or
starter controls the starting torque and
current of an AC motor electronically.
They can be used in almost any
application such as:
■
commercial – HVAC fans and pumps
■
general industrial – fans, pumps,
conveyors, material handling and
processing equipment
■
others – forest products, mining,
metals and printing
The guide provides the basics required
to evaluate motor controller and
starter application needs.
Effective: February 2005
Solid-State Soft Start
Motor Controller and
Starter
AC Motor Types
AC motors can be divided into two
main types: Induction and Synchronous. In this guide we will only cover
the use of a three-phase induction
motor and soft starter device, although
in some cases a soft starter device
may be used with a single-phase
motor.
Induction Motors
The induction motor is the simplest
and most rugged of all electric motors.
The typical varieties are the standard
induction motor and the wound rotor
motor.
Three-Phase
The three-phase induction motor is
divided into four classifications
according to NEMA. (Note that there
are IEC design standards which differ
somewhat from the NEMA versions.)
The classification or design, is determined by the locked rotor torque and
current, breakdown torque, pull-up
torque and the percent slip. The
speed-torque curve and characteristics
of each design are given below. These
characteristics apply for operation
from fixed frequency and voltage as
normally supplied from commercial
utility power sources at 60 Hz.
■
Design A motors have a slightly
higher breakdown, and lower starting torque than Design B motors.
The slip is usually 3 to 5% or less.
The major difference between the
Design A and Design B motor is that
the starting current is limited on the
Design B, but not on the Design A.
Design A motors are applied to the
same applications as Design B
motors. Design A motors may be
used with solid-state soft start
devices.
%
Rated
Tor qu e
300
200
Breakdown
(Maximum)
To rq ue
■
Design B motors are general pur-
pose type motors and account for
the largest share of the induction
motors sold. The slip of a Design B
motor is approximately 3 to 5% or
less. Design B motors are used on
applications where starting torque
requirements are low such as general industry, fans, blowers and centrifugal pumps and compressors.
Design B motors are often used with
solid-state soft start devices.
%
Rated
Tor qu e
300
200
100
0
020406080100
% Rated Speed
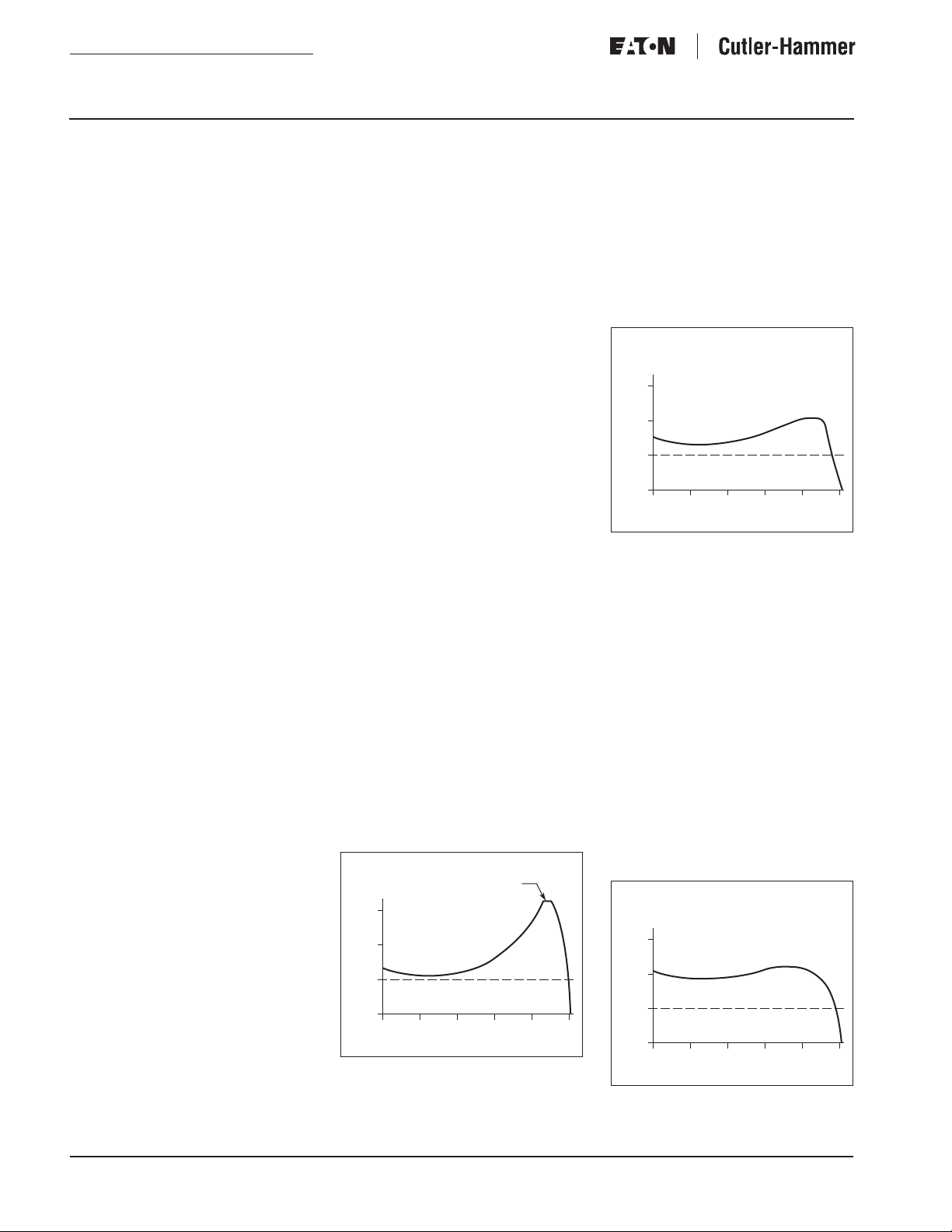
Figure 2. Design B Polyphase Motor
Design C motors have a high start-
■
ing torque with a normal starting
current and low slip. The Design C
motor is usually used where breakaway loads are high at starting, but
are normally run at rated full load,
and are not subject to high overload
demands after running speed has
been reached. The slip of the Design
C motor is 5% or less. Design C
motors are often used where high
starting torques under loaded conditions are required including crushers, agitators, reciprocating pumps
and high friction conveyors. Care
must be exercised when using a
Design C motor with a soft start controller or starter to assure that the
application starting torque and time
to start requirements can be met.
%
Rated
Tor qu e
300
AC Motors
Cutler-Hammer
and starters operate with standard
motors. In most cases, an existing
motor sized for another method of soft
start, can be directly applied. For new
installations the user must understand
the nature of the application in terms
of the load characteristic requirements
and the motor capability when used
with a soft start controller or starter.
®
soft start controllers
100
0
02040
% Rated Speed
Figure 1. Design A Polyphase Motor
For more information visit: www.EatonElectrical.com
60 80
100
200
100
0
020406080100
% Rated Speed
Figure 3. Design C Polyphase Motor
AP03902001E

■
Design D motors have high slip,
high starting torque, low starting
current and low full load speed.
Because of the high amount of slip,
the speed will vary if fluctuating
loads are encountered. The slip of
this type of motor is approximately
5 to 13%. Design D motors are used
on applications with high peak loads
with flywheels like punch presses,
shears, hoists, oil well pumps and
extractors. Care must be exercised
when using a Design D motor with a
soft start controller or starter, since
the limitation of the starting torque
or increase of the starting time may
cause thermal concerns for the
motor and soft start.
%
Rated
Tor que
300
200
100
0
020406080
% Rated Speed
Figure 4. Design D Polyphase Motor
100
Wound Rotor Motors
The wound rotor motor allows controllable speed and torque compared to
the conventional induction motor.
Wound rotor motors are generally
started with a secondary resistance in
the rotor. As the resistance is reduced,
the motor will come up to speed. Thus
the motor can develop substantial
torque while limiting the locked rotor
current. The secondary resistance can
be designed for continuous service to
dissipate the heat produced by continuous operation at reduced speed and
frequent start/stops or acceleration of
a large inertia load. This external resistance gives the motor a characteristic
that results in a large drop in rpm for a
small change in load. Reduced speed
typically can be provided down to
approximately 50% of rated speed,
although at a very low efficiency.
These motors are sometimes used (in
large horsepower ratings) in slip
recovery systems. In these systems
the external (secondary) resistance
element is replaced with a solid-state
circuit to convert the rotor slip energy
to useful AC power. These motors can
be used with a soft starter in some
applications. The use is dependent
Solid-State Soft Start
Motor Controller and
Starter
upon why the motor’s secondary resistance was selected and how the use of
the soft starter will impact the load
requirements. If the rotor resistance
was selected to be stepped through
various sizes to provide a gentle start,
a soft starter can likely be used. If the
resistor is just a single value and was
selected to give high starting torque,
the use of a soft starter might not
allow the same level of torque to be
generated. The application requirements must be determined.
Enclosures
The basic protective enclosures for AC
motors are: open dripproof (ODP),
totally enclosed fan cooled (TEFC),
totally enclosed non-ventilated (TENV)
and totally enclosed air over (TEAO).
Other special enclosures available
include: pipe-ventilated, weather protected, water cooled and explosion
proof.
Ventilation
The system for ventilating motors
depends on the type of motor enclosure as mentioned previously and
described below:
ODP (Open Dripproof) – The ODP
■
motor is ventilated (cooled) by
means of a shaft mounted internal
fan which drives air through the
open ends of the motor and discharges it out the sides. These
motors are often supplied as
protected, fully-guarded or
splash-proof.
TEFC (Totally Enclosed Fan Cooled)
■
– This type of motor is cooled by air
passing over the outer frame of the
motor. The air is supplied by a shaft
mounted fan opposite the shaft end
of motor.
TENV (Totally Enclosed Non-
■
Ventilated)
a shaft mounted internal fan used to
circulate air within the motor to prevent hot spots. No external fan or air
is supplied. These are suitable for
very dirty and contaminant laden
environments that would clog most
exposed cooling fans. These motors
dissipate their heat through their
frames and are thus oversized compared to other enclosure types.
They are generally available only in
smaller hp ratings (up to 7-1/2 hp).
– This type of motor has
Application Note
Effective: February 2005 Page 3
■
TEAO (Totally Enclosed Air Over) –
This type of motor is cooled by
externally provided air blowing over
the frame. The air may be supplied
by an integrally mounted blower
and motor or from a separate
source. This type of ventilation
provides constant cooling under
all operating conditions.
■
Special Enclosures – The Pipe-
Ventilated motor is available for
either an open or totally enclosed
type of enclosure and is used in very
dirty environments. Ventilating air
(supplied by the User) enters and
exits the motor through inlet and
outlet ducts or pipes. The air is circulated by means either integral or
external to the motor.
The Weather-Protected motor uses
an open type enclosure for ventilation. The motor is constructed to
minimize the entrance of rain, snow
and airborne particles to the electrical parts of the motor. External air
can be circulated through the motor
for cooling.
Totally Enclosed Air-to-Air and
Totally Enclosed Water-to-Air cooled
enclosures are normally used on
high horsepower motors that generate large amounts of heat. A heat
exchanger is used for both types to
remove the heat generated by the
motor. An AC motor driven blower
circulates air through the windings
and heat exchanger tubes. The heat
in the heat exchanger is removed by
either an external air system (air-toair) or water provided by the user
(water-to-air cooled).
Explosion Proof motors are
designed to operate in hazardous
environments such as explosive
vapors, coal or grain dust and other
classified areas. These are selected
on the basis of the appropriate
Class, Group, and Division of hazard, as defined by the National Electrical Code (NEC).
Control of AC Motors
The most common control of an AC
motor is by using a motor starter. This
device connects the motor to the commercial AC power line. It is rated to
operate with the typical high starting
(inrush) current that occurs when a
motor is directly connected to the utility line. A motor starter also contains a
protective device known as a motor
overload. This device is designed to
protect the motor from continued
overloads and stalling due to excessive machine loads on starting or jamming when operating.
AP03902001E For more information visit: www.EatonElectrical.com
Application Note
Page 4
With the above method of control, AC
motors will operate as described by
their NEMA (or IEC) characteristics for
their design type on industrial AC
power. This includes a prescribed
overload capability, regulation due to
slip, starting inrush current and starting (locked rotor) torque. The load on
the driven machine determines the
acceleration time and motor load (or
overload).
Special control hardware is available
to modify some of the above characteristics. Part winding, autotransformer and wye-delta motor starters
will reduce the inrush current when
starting an AC motor. But using these
devices does not provide for a soft
controlled stepless start.
Solid-state soft start motor controllers
and starters have the ability to control
the starting characteristics to match
the application requirements, such as
acceleration and deceleration time,
starting and overload current and
motor torque. In addition, motor
protection may be provided for a
number of potential damaging circumstances by the soft starter (a soft start
controller does not provide any motor
protection).
Soft Start Basics
Why do we want to use a reduced voltage soft starter?
The first reason is to limit the inrush
current that a motor draws from the
utility when it is first started. This is a
concern because the large starting current may cause the line voltage to dip,
impacting other loads which are sensitive to low voltages. There may also be
a concern if the utility limits the peak
current which can be drawn or charges
for exceeding the limit.
The second is reduced mechanical
system stress. When the large inrush
current occurs, there are significant
magnetic forces created in the motor
windings. These cause some parts of
the winding to be attracted to each
other and other parts repulsed. This
mechanical shock can damage the
winding insulation leading to early failure. The mechanical shock of the high
torques produced with the large starting current can cause failure of system
elements such as the motor shaft, belting, gear box, drive train and damage
to fragile product.
Effective: February 2005
Solid-State Soft Start
Motor Controller and
Starter
Current
600
Figure 5. Motor Current vs. Speed
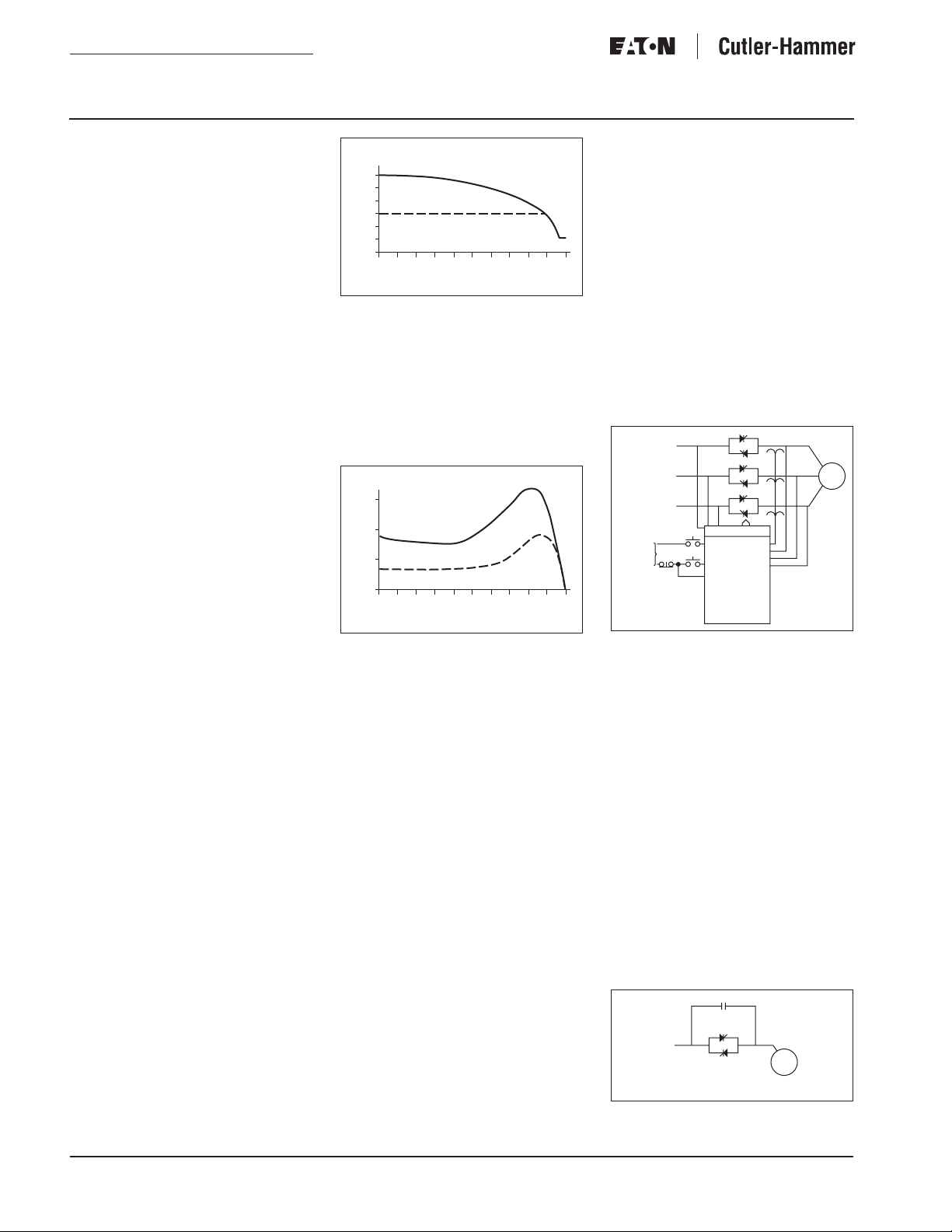
This graph shows the impact of using
a soft start. For this motor, the initial
current when it is started is 600 percent, or six times the motor’s full load
current rating. The soft starter can be
set to reduce this current, for example
in this case to 300 percent. This limits
the inrush current on the utility line.
Tor qu e
300
200
100
Figure 6. Motor Torque vs. Speed
As a result of the reduction in current,
the motor’s ability to generate torque
is also reduced. The upper curve
shows the same motor started across
the line. The initial torque is about 180
percent with a peak torque of over 300
percent. With the soft start limiting the
current, the torque speed curve is
reduced, reducing mechanical stress.
The torque available from the motor at
reduced current is equal to the locked
rotor or starting torque, times the
square of the reduced current divided
by the locked rotor current. Thus if we
reduce the current from 600 percent to
300 percent, the torque varies as the
square of this reduction. The torque is
thus reduced to 25 percent of the
across the line starting torque.
How Does Torque Vary?
Where:
T
T
I
1
I
2
V
V
Full Voltage Starter
%
Solid-State Starter
0
Speed RPM
%
Full Voltage
%
%
0
T2T
= Torque at recued current/voltage
2
= torque at locked rotor current
1
= Locked rotor current
Starter
Solid-State Starter
Speed RPM
2
I
2
T
≈=
----
1
I
1
V
2
------
1
V
1
2
= Reduced current
= Full voltage
1
= Reduced voltage
2
100
100
%
%
Some soft starters control voltage
instead of current. The torque available varies proportionately with the
square of the ratio of the reduced
voltage to the normal line voltage.
When the operator depresses the
START button, the soft starter logic
issues an ON command to the power
module, causing the SCRs to turn on
and gently increase the voltage across
the motor terminals, or the current
into the motor based on the adjustments made to the soft start logic.
When the SCRs are fully on, the motor
reaches full voltage.
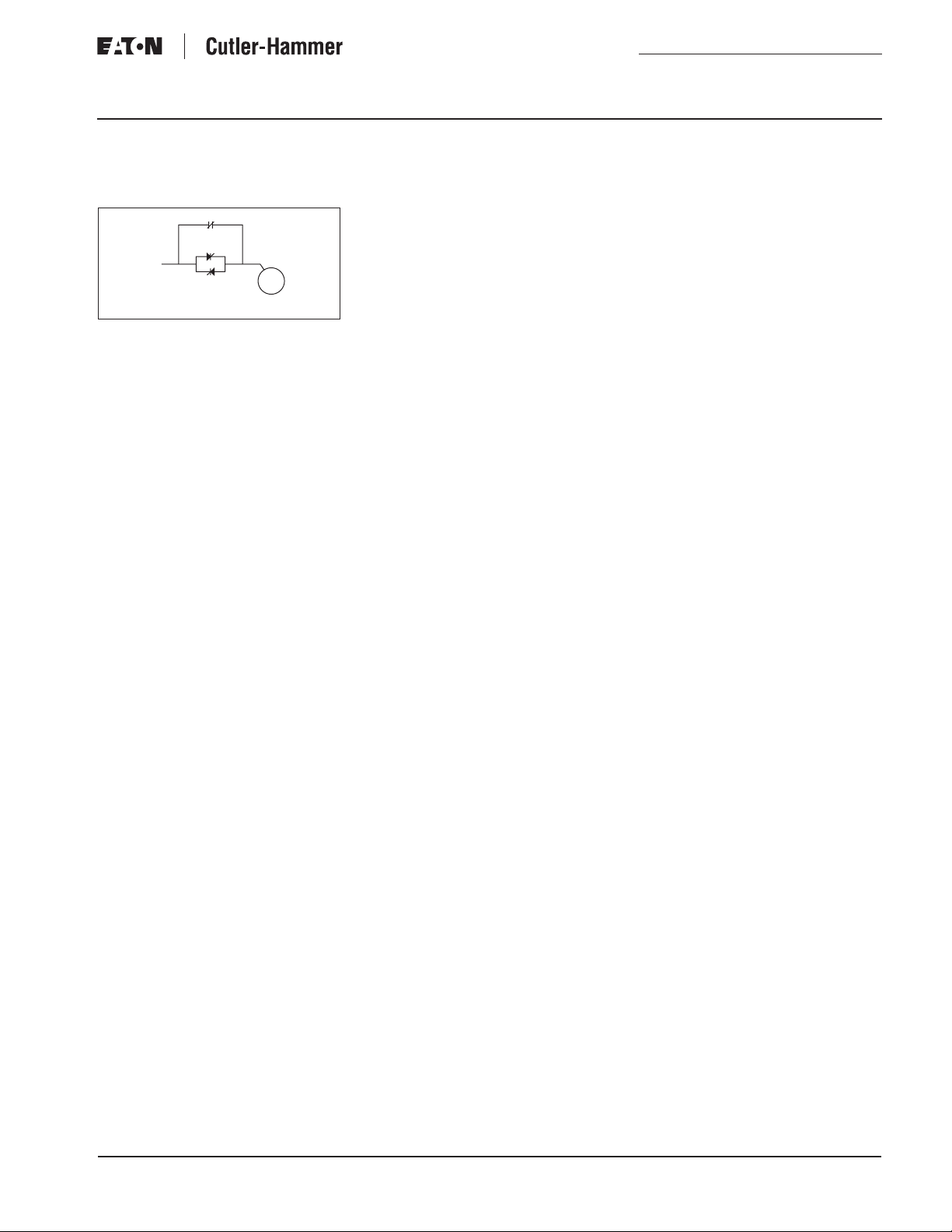
A block diagram of a typical soft start
starter would look like
L1
3-Phase
Power
Supply
Control
Power
Stop
L2
L3
Reset
Start
Figure 7 .
Control Logic
• Current limit
• Running
overload
protection
• Phase loss
protection
• Undervoltage
protection
• Energy saver
control
Motor
Figure 7. Typical Block Diagram
This solid-state starter utilizes six full
current rated SCRs as its power
devices. The logic circuit monitors
three-phase input voltage, three-phase
output voltage, and the three output
currents. From these inputs it can provide starting current limitation, running overcurrent protection, phase
loss and undervoltage protection.
This starter interfaces with standard
control circuits.
In some products a bypass contactor
may be closed to provide higher operating efficiency after the SCRs are fully
Figure 8 is a single-phase leg of the
on.
soft starter with the SCRs turning on
and becoming the current path for
power to flow from the utility to the
motor.
A
Motor
Figure 8. SCRs as Current Path
For more information visit: www.EatonElectrical.com
AP03902001E
Solid-State Soft Start
Motor Controller and
Starter
Application Note
Effective: February 2005 Page 5
After the motor has come up to speed,
the bypass contactor closes and it
becomes the current path for the
motor.
A
Motor
Figure 9. Bypass Contactor as Path
At this time the SCRs no longer conduct any current.
Bypass operation eliminates the SCR
losses once the motor is up to speed,
resulting in significantly lower heat
generation. Soft starters with internal
run bypass mode are typically much
smaller and lighter than devices without run bypass.
Soft Start Applications
We would like to identify problems
that can be solved by the use of a soft
starter. One challenge is that it can be
difficult for the user to recognize a
problem as a problem. Frequently the
problem is mistaken for a normal
operational or maintenance issue.
It is the intent of this section to help
to determine solutions, using soft
starters for both new and retrofit
installations.
Typical problems can be categorized
as mechanical, motor, starting equipment, inrush current, or fragile product
related.
Typical mechanical problems are:
stretching, squealing or breaking of
drive belts; breakage of gear boxes; couplings wearing out prematurely; shaft
breakage within the drive train; and,
water hammer in hydraulic systems.
To get an idea of the effect of starting
torque on the mechanical system, lets
consider an automobile. If you were to
put the transmission in neutral and
quickly press the accelerator to the
floor, you would feel the car reacting
to the sudden increase in motor torque
as it rotates slightly in response to the
torque being developed by the engine.
This same type of effect is what causes
these mechanical problems, except
that the torque levels may be considerably greater than those experienced
with an automobile.
Motor problems include: motor insulation deterioration or premature winding failure due to the mechanical
stresses put on the winding during
starting, or the high temperatures
imposed by high starting currents;
mechanical stresses on the system
such as foundation bolts or mounting
failures, bearing lock-up and failure,
and motor shaft cracking and breakage; coupling failures; and, excessive
energy losses due to duty cycle or frequent start/stop operation.
Benefits of Using Soft Start Starters:
■ Controlled starting – Limited start-
ing current, reduction of power line
disturbance on starting, lower
power demand on starting.
■ Controlled acceleration – Soft start,
adjustable acceleration based on
time or load, reduced motor size for
pure inertial load acceleration.
■ Adjustable torque limiting – Protects
machinery from damage, protects
process or product.
■ Controlled stopping – Soft slow
down, timed stopping, fast reversal
with much less stress on AC motor
than plug reverse.
Typical Fixed Speed Applications:
■ Conveyors, belts, chains, screws,
bulk material, packaged material
■ Fans, blowers, compressors, pumps
■ Machine tools, grinders, lathes,
stamping presses
■ Custom machinery, labelers, pack-
aging machines, bottle washers,
wire drawing, textiles, etc.
■ Extruders
■ Process machinery, kilns, grinders,
blenders, agitators. See the section
on load types for particular evaluation of specific loads.
Other Reduced Voltage Starting
Methods
There are several reduced voltage
starting methods that predate solidstate soft start motor controllers and
starters. Table 1 illustrates these meth-
ods and their typical applications.
AP03902001E For more information visit: www.EatonElectrical.com
Application Note
Page 6 Effective: February 2005
Solid-State Soft Start
Motor Controller and
Starter
Table 1. Comparison of Electromechanical Soft Starters
Type of
Starter
Autotransformer8065
Primary
Resistor
Part
Winding
Wye Delta 100 33 33 Open
Starting Characteristics in Percent of Full
Transition Extra
Voltage Values
% Line
Voltage at
Motor
50
% Motor
Locked Rotor
Amps
64
42
25
% of Motor
Locked
Rotor Torque
64
42
25
Closed No
65 65 42 Closed Yes
100 65 48 Closed Yes (but very
(Closed
available
for about
30% price
adder)
Acceleration
Steps
Available
uncommon)
No
Advantages Disadvantages Applications
■ Provides highest
torque per ampere of
line current
■ 3 different starting
torques available
through
■ In lower horsepower
ratings is most
expensive design
■ Low power factor
■ Large physical size
Blowers
Pumps
Compressors
Conveyors
autotransformer taps
■ Suitable for relatively
long starting periods
■ Motor current is
greater than line
current during starting
■ Smooth acceleration –
motor voltage
increases with speed
■ High power factor
during start
■ Less expensive than
autotransformer
starter in lower
horsepower ratings
■ Available with as
■ Low torque efficiency
■ Resistors give off heat
■ Starting time in excess
of 5 seconds requires
expensive resistors
■ Difficult to change
starting torques under
varying conditions
Belt and gear
drives
Conveyors
Textile
machines
many as 5 accelerating
points
■ Least expensive
reduced voltage
starter
■ Most dual voltage
motors can be started
part winding on lower
voltage
■ Small physical size
■ Unsuited for high
inertia, long starting
time loads
■ Requires special motor
design for voltage
higher than 230 volts
■ Motor will not start if
the torque demanded
Reciprocating
compressors
Pumps
Blowers
Fans
by the load exceeds
that developed by the
motor when the first
half of the motor is
energized
■ First step of
acceleration must not
exceed 5 seconds or
else motor will
overheat
■ Suitable for high
inertia, long
acceleration loads
■ High torque efficiency
■ Ideal for especially
stringent inrush
restrictions
■ Ideal for frequent
■ Requires special motor
■ Low starting torque
■ During open transition
there is a high
momentary inrush
when the delta
contactor is closed
Centrifugal
compressors
Centrifuges
starts
For more information visit: www.EatonElectrical.com AP03902001E

Solid-State Soft Start
Motor Controller and
Starter
Application Note
Effective: February 2005 Page 7
Basic Mechanics
Introduction
In order to apply a soft start properly,
certain mechanical parameters must
be taken into consideration. This section explains what these parameters
are and how to calculate or measure
them.
Torque
Torque is the action of a force producing or tending to produce rotation.
Unlike work (which only occurs during
movement) torque may exist even
though no movement or rotation
occurs.
Torque consists of a force (Lb.) acting
upon a length of a lever arm (Ft.). The
product of these two factors produces
the term lb-ft, which is the unit of measurement for torque (see Figure 10).
Mathematically, it is expressed as:
Torque (lb-ft) = Force (Lbs.) x
Distance (Ft.)
Example:
Torque = Force x Distance
Torque = 50 Lbs. x 1 Ft.
Torque = 50 lb-ft
Because most power transmission is
based upon rotating elements, torque
is important as a measurement of the
effort required to produce work.
Force
Lever Arm – 1 Ft.
Figure 10. Calculating Torque
Calculating Torque
Acceleration Torque Required for Rotating
Motion
Some machines must be accelerated
to a given speed in a certain period of
time. The torque rating of the motor
may have to be increased to accomplish this objective. The following
equation may be used to calculate the
average torque required to accelerate
a known inertia (WK
must be added to all the other torque
requirements of the machine when
determining the motor’s required peak
torque output.
2
). This torque
50 Lbs.
2
WK
xdN
-------------------------
T
=
308t
Where:
T = Acceleration Torque (lb-ft)
2
= Total system inertia (lb-ft2) that
WK
the motor must accelerate. This value
includes motor rotor, speed reducer
and load.
dN = Change in speed required (rpm)
t = Time to accelerate total system load
(seconds)
Note: The number substituted for (WK2) in
this equation must be in units of lb-ft
The same formula can also be rearranged to determine the minimum
acceleration time of a given system, or
if a motor can accomplish the desired
change in speed within the required
time period.
Rearranged Equation:
2
xdN
WK
-------------------------=
t
308T
2
.
Calculating Horsepower
Note: The following equations for calculating horsepower are to be used for estimating purposes only. These equations do not
include any allowance for machine friction,
windage or other factors. These factors
must be considered when selecting a motor
for an application. Once the machine torque
is determined, the required horsepower is
calculated using the formula:
TxN
hp
-------------=
5250
Where:
hp = Horsepower
T = Torque (lb-ft)
N = Speed of motor at rated load (rpm)
If the calculated horsepower falls
between standard available motor
ratings, select the higher available
horsepower rating. It is good practice
to allow some margin when selecting
the motor horsepower. Also note that
the motor’s torque output is reduced
during a soft start. The load requirements must be related to the soft
starter settings.
For many applications, it is possible
to calculate the horsepower required
without actually measuring the torque.
The following equations will be
helpful:
Conveyors
hp =
(Vertical)
hp =
(Horizontal
Where:
F/W = force/weight in Lbs.
V = Velocity in feet per minute
Coef. = Coefficient of friction
F / W (lbs) x V (fpm)
33,000 x Efficiency
F / W (lbs) x V (fpm) x Coef
)
33,000 x Efficiency
Fans and Blowers
hp =
cfm x Pressure (psi)
33,000 x Efficiency of Fan
hp =
cfm x Pressure (lb-ft
2
)
229 x Efficiency of Fan
cfm x (Inches of Water Gauge)
hp =
6356 x (Efficiency of Fan)
Pumps
gpm x Head (ft.) x (Specific Gravity)
hp =
Where:
psi = pounds per square inch
cfm = cubic feet per minute
gpm = gallons per minute
Specific gravity of water = 1.0
1 cubic foot per second = 448 gpm
1 psi = a head of 2.309 ft. for water
weighing 62.36 lbs. per cu. ft. at 62°F.
Efficiency of fan or pump = %/100
Displacement pump efficiency:
Displacement pumps vary between 85
and 90% efficiency depending on size
of pumps.
Centrifugal pump efficiency (at design
point):
500 to 1000 gal. per min. = 70 to 75%
1000 to 1500 gal. per min. = 75 to 80%
Larger than 1500 gal. per min. =
80 to 85%
3960 x (Efficiency of Pump)
AP03902001E For more information visit: www.EatonElectrical.com
Application Note
Page 8 Effective: February 2005
Solid-State Soft Start
Motor Controller and
Starter
Inertia
Inertia is a measure of a body’s resistance to changes in velocity, whether
the body is at rest or moving at a constant velocity. The velocity can be
either linear or rotational.
2
The moment of Inertia (WK
) is the
product of the weight (W) of an object
and the square of the radius of gyra-
2
tion (K
). The radius of gyration is a
measure of how the mass of the object
is distributed about the axis or rotation. Because of the distribution of
mass, a small diameter cylindrical part
has a much lower inertia than a large
diameter part.
The inertia calculations for typical
shapes follow.
WK2 or WR
2
WR2 refers to the inertia of a rotating
member that was calculated by
assuming the weight of the object
was concentrated around its rim at a
distance R (radius) from the center.
2
refers to the inertia of a rotating
WK
member that was calculated by
assuming the weight of the object was
concentrated at some smaller radius,
K (termed the radius of gyration). To
determine the WK
2
of a part, the
weight is normally required.
Calculations
When performing calculations, be consistent with the formulae and units
used. Common mistakes are substituting inches for feet, etc.
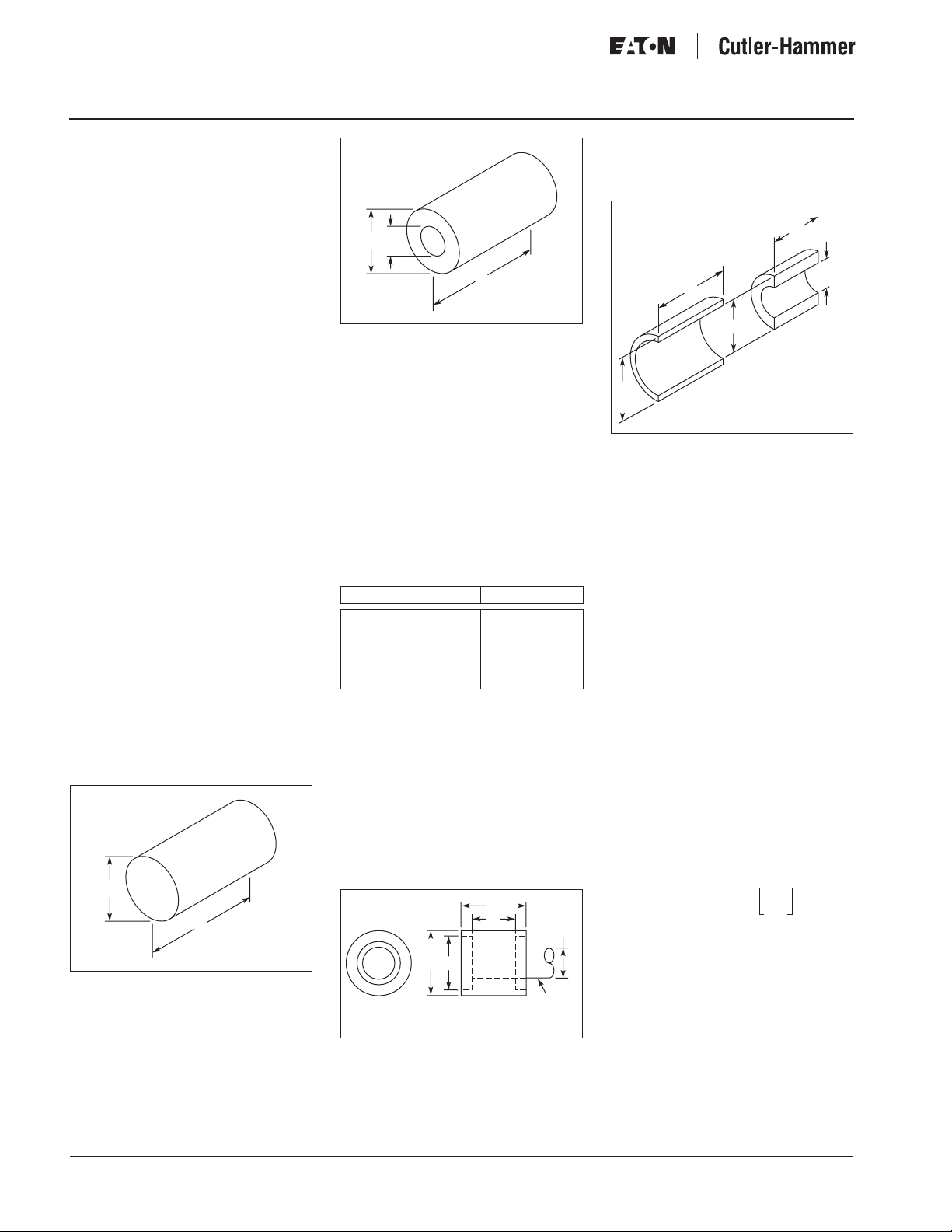
Cylinders
D
L
Figure 11. Solid Cylinder
Equations:
2
WK
= .000681 x p x L x (D)
4
D1D
2
L
Figure 12. Hollow Cylinder
Equations:
2
WK
= .000681 x p x L (D
4
- D1 4)
2
Where:
2
= inertia of a cylinder (lb-ft2)
WK
p = density of cylinder material in lb-in
(see density chart below)
= inside diameter of cylinder
D
1
(inches)
= outside diameter of cylinder
D
2
(inches)
L = Length of cylinder (inches)
Table 2. Common Material Densities (p)
Aluminum
Brass
Cast Iron
Steel
Rubber
Paper
0.0977
0.3110
0.2816
0.2816
0.0341
0.0250 to 0.0420
Pulley/Gear
To calculate the inertia of a pulley or
gear, divide up the piece (shown in
Figure 13) as shown in Figure 14.
Using the same equation for calculating hollow cylinders, perform the calculations of each separate part and
add them together for a total inertia.
End View
2
and WK
1
Note: WK
inertia calculations.
Figure 13. Complete Pulley/Gear
2
are the separate
2
3"
2.5"
Side View
3"
2"
1.375"
Motor
Shaft
In this example the pulley is made of
steel. We will divide it up to calculate
as shown.
3"
2.5"
3"
Figure 14. Pulley/Gear Components
3
WK
2
1
Equations:
2
= .000681 x p x L (D
WK
4
2
Calculations:
2
= .000681 x 0.2816 x 3 x
WK
1
4
– 2.54)
(3
= .0241 lb-ft
2
WK
= .000681 x 0.2816 x 2 x
2
(2.5
= .0136 lb-ft
Total Inertia = WK
2
4
– 1.3754)
2
2
+ WK
1
.0136
= .0377 lb-ft
2
WK2 Reflected to the Motor Shaft
In most mechanical systems not all the
moving parts operate at the same
speed. If speeds of the various parts
have a continuous fixed relationship
to the motor speed, the equation can
be used to convert all of the various
inertia values to an equivalent WK
applied to the motor shaft.
WK2 of Rotating Parts
2
WK
---------------DR()
2
N
--------N
Equivalent WK2 = WK2
Where:
2
= inertia of the moving part
WK
N = speed of the moving part (rpm)
= speed of the driving motor (rpm)
N
M
When using speed reducers, and the
machine inertia is reflected back to the
motor shaft, the equivalent inertia is
equal to the machine inertia divided by
the square of the drive reduction ratio.
2
Equivalent WK
=
2"
1.375"
2
WK
2
- D1 4)
2
= .0241 +
2
2
M
2
For more information visit: www.EatonElectrical.com AP03902001E
Solid-State Soft Start
Motor Controller and
Starter
Application Note
Effective: February 2005 Page 9
Where:
DR = drive reduction ratio =
Input
1 hp
3 lb-ft
1750 RPM
Reducer
N
---------
Output
(Less Efficiency)
76.5 lb-ft
57.5 Rpm
Gear
(30:1)
M
N
1 hp
Figure 15. Gear Reducer Characteristics
WK2 of Linear Motion
Not all driven systems involve rotating
motion. The equivalent WK
2
of linearly
moving parts can also be reduced to
the motor shaft speed as follows:
2
WV()
2
=
Equivalent WK
-----------------------------
39.5 NM()
2
Where:
W = weight of load (Lbs.)
V = linear velocity of rack and load or
conveyor and load (fpm)
= speed of the driving motor (rpm)
N
M
This equation can only be used where
the linear speed bears a continuous
fixed relationship to the motor speed,
such as a conveyor.
Speed Reducer Selection
The motor should always be coupled
to the driven machine by a power
transmission that will permit maximum motor rpm at maximum
machine speed. The power transmission may be a simple belt-sheave or
sprocket-chain arrangement or a
compact gear reducer. In most applications requiring speed reductions
greater than 5:1, the gear reducer
may be the most economical choice.
Gear Reducer Selection
A gear reducer transmits power by an
arrangement of various forms of
gears. It provides an efficient, positive
method to change speed, direction,
and torque. This may mean a change
of speed with a corresponding change
in torque, or a change in output direction or position. A common result is a
combination of the above.
The gear reducer serves as a torque
amplifier, increasing the torque by a
factor proportional to the reducer
ratio, less an efficiency factor. See
Figure 13.
A 1 hp, 1750 rpm motor has an output
torque of 3 lb-ft. If a 30:1 ratio reducer
with 85% efficiency is used, the
reducer output torque will be
3x30x0.85 = 76.5 lb-ft.
A typical application involves selecting
a gear reducer that permits the drive
motor to operate at nameplate speed
when the driven machine is at maximum speed. The gear reducer should
also provide adequate torque to drive
the machine.
Application Example
A 1750 rpm motor is selected for a
machine which is to operate at 57.5
rpm maximum speed and requires
70 lb-ft of torque.
To find the answer, the following two
steps must be accomplished.
1. Determine the required ratio:
Reducer =
Ratio
Maximum Motor rpm
Maximum Driven
Machine rpm
1750
Reducer Ratio = = 30.4 or a 30:1
Note: When the calculated reducer ratio is
not close to a standard speed reducer ratio,
a chain, belt or additional gears with further
reduction are necessary (located on the
input or output side).
-------------
57.5
ratio
2. Determine the motor torque &
horsepower
A 30:1 gear reducer is selected which
is capable of supplying 70 lb-ft of output torque. Since the machine torque
requirement is known, this value is
divided by the reduction ratio and an
efficiency factor, to arrive at the
required motor torque (TM).
TM =
Required torque (lb-ft)
Reducer Ratio x
Efficiency Factory
70
------------------------
TM = = 2.75 lb-ft
30 0.85×
Since a 1 hp, 1750 rpm motor delivers
3 lb-ft of torque, it is chosen for this
application along with a 30:1 gear
reducer with a minimum of 70 lb-ft
output torque.
Where the reduction ratio permits the
use of a chain or belt, the same formulae are used as with the reducers.
Gear Reducer — Overhung Load
An overhung load (OHL) is defined as
dead weight the gear reducer bearings
can support on an output shaft at a
distance equal to the shaft diameter.
This distance is measured from the
outside end of the bearing housing
along the shaft (see Figure 16). If the
acting load is at a point different from
the OHL point, it must be converted to
the reference point and compared to
the manufacturer’s catalog value.
Overhung Load
Reference Points
Side
Thrust
Side
Thrust
Output
Side
Gear
Reducer
Figure 16. Overhung Load
When a gear reducer is driven by a
belt, chain or gear drive, or when the
gear reducer drives a driven unit
through a belt, chain or gear drive,
an overhung load (side thrust) is
produced. The overhung load must
not exceed the rating of the gear
reducer as listed by the manufacturer.
The magnitude of the overhung load
should always be kept to a minimum.
Excessive loads could lead to fatigue
failure of either the bearing or shaft.
The sprocket or pulley should always
be located as close to the gear housing
as possible.
Increasing the sprocket or pulley diameter results in a reduced overhung
load. Use the following equation to
determine the overhung load:
=2 x Shaft Torque (lb-in) x K
OHL
(lb. )
Diameter (in)
Where:
Diameter is of the sprocket, sheave,
pulley or gear.
Note: K is a constant which is:
1.00 for chain drives
1.25 for gears or gear-belt drives
1.50 for V belt drives
2.50 for flat belt drives
Input
Side
AP03902001E For more information visit: www.EatonElectrical.com

Application Note
Page 10 Effective: February 2005
Solid-State Soft Start
Motor Controller and
Starter
No overhung loads are encountered
when the gear reducer is directly coupled to the motor and/or the driven
machine shaft. However, care must
be taken in aligning the shafts to
avoid pre-loading the bearings by
misalignment.
Other Gear Issues
1. Service Factor — The application
determines the amount of shock
load the gearbox will be subjected
to. Based on the operating hours
per day and the degree of shock
loading, the gearbox may need to
be oversized with a service factor
of up to 250%.
2. Thermal Rating — It is possible
that the gearbox will have a
mechanical rating larger than its
thermal rating. The gearbox manufacturer should advise under
what situations this might occur.
Controllers and Starters,
Theory and Application
Introduction
Soft Start Controller and Starter
Description — A soft start controller or
starter gently starts a motor limiting
both the initial torque levels and current levels to meet given application or
utility power system requirements.
Soft start controllers and starters are
used with three-phase motors. The
controller or starter interfaces with
normal operator or machine controls
as used in conjunction with a standard
across the line starter.
Benefits of Using Soft Start
Controllers and Starters
Soft starts are used for a number of
reasons, either to provide a required
starting characteristic or to prevent or
reduce a machine or system related
problem such as:
■ Mechanical
❑ Belts stretching, squealing, or
breaking
❑ Gears breaking
❑ Couplings wearing out
❑ Drive train shafts breaking
■ Motor
❑ Motor insulation deterioration or
premature winding failure
❑ Foundation bolts and mounting
failures
❑ Bearing lock-up and failure
❑ Motor shaft cracking and breaking
❑ Excessive energy consumption
■ Starting Equipment
❑ Contact pitting and wear
❑ Coil burnout
❑ Mechanical failure
■ Inrush Current
❑ Voltage dips causing electrome-
chanical starter coils to drop out
❑ Soft supply lines may mean the
starting current will not be acceptable to the utility
❑ Lighting brown outs or electronic
control hiccups
■ Fragile Product
❑ Materials chip, crack, spill or
break
❑ Positioned products are shifted
Basic Principles of Soft Start
Controllers and Starters
The following description applies to
the operation of a soft starter which is
used to control the motor torque or
current during the start sequence and
also provides, at minimum, motor
overload protection. A soft start
controller does not control torque or
current nor provide motor protection.
An adjustment is provided on the soft
start controller for initial starting
torque which is based on setting an
initial start voltage.
The soft starter controls motor current
or torque by controlling the voltage
applied to the motor. The voltage is
controlled by changing the phase
angle at which the silicon controlled
rectifiers, SCRs, are gated (or turned)
on. Once turned on, the SCRs stay on
until the magnitude of the current
through them passes through zero
each half cycle of the AC waveform.
Conduction phase angle may be considered as beginning at the zero
degree crossing of a phase through
zero VAC, and progressing back in
time towards 180 degrees, as seen in
Figure 17. At a 180 degree conduction
phase angle, full voltage is applied to
the motor phase, since the SCR conducts through the full 180 degrees. At
0 degrees no voltage is applied. As the
conduction phase angle is gradually
phased back from 0 degrees towards
180 degrees on subsequent gatings of
the SCRs, the effective voltage to the
motor increases, resulting in higher
current and motor torque. With the
proper feedback and control algorithms, current and torque can be controlled during start and stop.
800
600
180° 0°
400
200
0
-200
-400
180° 0°
-600
-800
30° 45° 60° 90° 155° Full On
Conduction Phase Angle
Figure 17. SSRV SCR Phase-Up
The effect of controlling the voltage or
current applied to the motor can be
seen in Figure 18 with the starting current being shown at the normal across
the line level, and at a current limit
level of 500% and 400%. As a result of
the current being limited to a lower
level, the torque developed by the
motor is also limited to a lower level.
As was noted in basic theory section of
this guide, the torque varies as the
square of the motor current. Figure 18
illustrates this.
For more information visit: www.EatonElectrical.com AP03902001E

Solid-State Soft Start
Motor Controller and
Starter
Application Note
Effective: February 2005 Page 11
% Torque
and
Current
700
600
500
400
300
200
100
0
0102030405060708090
Current Limit 1
Current Limit 2
Line StartingTorque
Available Torque 1
Available Torque 2
% Synchronous Speed
Note: When Current = Line Starting Current,
Available Torque = Line Starting Torque
Line Starting
Current
See
Note
Figure 18. Effects of Current Limiting on Motor Torque
Where:
= available torque at reduced
T
AV
current
= torque at full voltage and line
T
R
current
= reduced current
I
A
= current at full voltage
I
R
For example, a motor has an initial
across-the-line starting current of
670% and a torque capability of 150%
of its nameplate rating at start. If the
initial starting current is limited to
500%, the available torque will be limited to 83.5%.
= 150% = 83.5%
T
AV
2
500
----------
670
This same proportionality holds true
across the entire motor start time. The
available torque will be reduced until
the current being drawn drops below
the limited value and equals the normal across-the-line current. At this
point the available starting torque
equals the normal across-the-line
starting torque.
This means that to have a successful
motor start the available torque must
always be greater than the load’s
required torque. If the load torque is
greater than the available torque the
motor will not start.
The second element to be considered
is the acceleration time of the motor.
The available torque must exceed the
load torque by a great enough margin
to assure that the motor will have
enough acceleration torque available
to start in the desired start time.
Load Characteristics
There are three basic components
which contribute to the required
torque that must be considered. The
first is friction, the second inertia, and
the third the driven process. Each of
these can affect the motor and starter
choice. In this guide we are paying
specific attention to their effects on the
starter selection.
Friction
Friction can determine how difficult it
is to initially start the load. The higher
the friction at start, the larger the
amount of the motor’s torque that is
required to breakaway the mechanical
system and begin rotation. The friction
levels at start are often referred to
as stiction. After the load begins to
rotate, the friction levels tend to
decrease, reducing the motor torque
requirements.
Inertia
Inertia determines how quickly a load
can be accelerated or decelerated. The
larger the inertia, the longer the time it
will take to accelerate it up to full
speed with a given acceleration torque
level, or vice versa the larger the acceleration torque required to accelerate it
up to full speed in a given time.
Driven Process
Often times the driven process is
entirely a frictional load such as a
conveyor or an inertial load such as a
centrifuge. In some cases the driven
process may require torque in addition
to that to overcome friction or to accelerate it. For example a centrifugal load
will likely have a low friction require-
100
%FLA Current (Line Start)
500% FLA I Limit
400% FLA I Limit
% Rated Motor Torque
(Full Voltage)
% Rated Motor Torque
@ 500% I Limit
% Rated Motor Torque
@ 400% I Limit
ment, and may have a low inertia, but
has a process torque requirement
which varies with the square of speed.
When first started the load torque is
virtually zero, but as the speed
increases the load torque increases
quickly until it reaches full load at full
speed. A centrifugal pump has low
friction and typically low inertia and its
driven load requirement varies with
speed. The starter would be sized
purely on the basis of the driven load.
A centrifugal fan has low friction but
often high inertia, so the starter would
be sized on the basis of both the
driven load torque and the acceleration torque requirements.
Typical Soft Start Adjustments
Ramp Start
In order to properly start the motor
and minimize time at zero speed when
first starting, an initial current or
torque level is set for the soft start to
apply at start-up. For most applications, this initial value is set to just
break away the motor and its load. In
the case of a large friction load, a kick
start would be used instead, as noted
below, because of the large torque
required for breakaway.
Tor qu e
100%
Initial
To rq ue
(T2)
t
r
Start
Time (Seconds)
Figure 19. Ramp Start
After the initial step torque is applied,
the motor torque is increased linearly
by increasing the soft start output voltage over a user selected ramp time
(note that the torque generated during
this time period can approach the
motor’s locked rotor value dependent
upon the settings and the load requirements). At the completion of the ramp
time, the motor and load should be at
full speed and the motor current at its
normal level.
Full
Vol tage
Run
AP03902001E For more information visit: www.EatonElectrical.com

Application Note
Page 12 Effective: February 2005
Solid-State Soft Start
Motor Controller and
Starter
Current Limit Start
If a requirement exists for the motor
and load to start with a controlled
torque level, a current limit start can
be chosen. In this case the motor
torque level is set and it is held at this
value during start-up, until the load
requirements fall below this value or
the ramp time expires.
Tor que
Initial
To rq ue
(T2)
100%
t
r
Start Run
Time (Seconds)
Full
Vol tage
Figure 20. Current Limit Start
Kick Start
A kick start allows the motor to draw
greater current at start to develop
additional torque to breakaway a high
friction load. After a time delay the
current is reduced to the normal
preset starting level. The kick start
current level and time duration are
programmable.
Tor que
T
1
T
2
Kick Start
t
k
t
r
Start Run
Time (Seconds)
Full
Voltage
Figure 21. Kick Start
Ramp Stop
In some high friction load applications,
the user may desire that the load does
not stop suddenly. A ramp stop can be
applied to lengthen the stopping
period beyond the normal coast down
value. This stop works by gradually
decreasing the motor voltage thus
extending the stop time.
Percent
Voltage
100%
Run
Coast
to Stop
Soft
Stop
t
s
Soft Stop
Tim e (Seconds)
Figure 22. Ramp Stop
Note: This is not an electronic brake function, and cannot make the load stop faster
than its normal coast-to-stop time. This feature can only extend the stop time. In some
applications the motor will come to a stop
in less than the selected stop time, if the
load torque requirements are too high and
the stop time is set too long.
Motor Application Considerations
Motor Sizing
Motors are sized for use with a soft
starter or controller as they would be
for any other reduced voltage starting
device. If a large number of starts will
be made in a short period of time, the
motor must be able to thermally and
mechanically withstand this. In many
cases the soft start will be better for
the motor because of the reduction in
winding stress.
Multiple Motor Operation
The use of multiple motors connected
to one soft starter is not recommended
because of loss of motor protection. If
it is desired to do this, individual overload protection must be supplied for
each motor.
Motor Protection
Motor overload protection is provided
as required as a standard feature of
a soft starter. Soft start controllers
do not provide any motor overload
protection and require separate user
supplied overload devices as required
by the applicable codes.
Installation Compatibility
The successful application of a soft
starter or controller requires the assurance that it will be compatible with the
environment in which it will be
installed. The following are some of
the aspects of compatibility which
should be considered.
Cooling Air
Even though a soft starter or controller
is very efficient, the heat produced can
be substantial. The electronic circuitry
is subject to immediate failure if its
operating temperature limits are
exceeded. Junction temperatures of
SCRs typically can only increase 20 –
25°C from full load to failure level, so it
is important to remove heat through
the usual mechanisms of radiation,
conduction (heatsinks) or convection
(fans). Soft starters with run bypass
mode will significantly reduce the heat
generated once the motor is up to
speed, reducing enclosure sizes and/or
ventilating requirements. The enclosure must be located away from direct
sunlight and hot surfaces. The room
temperature must be kept within the
specified limits and adequate cooling
air must be allowed to flow around the
enclosure. Excessively moist, corrosive or dirty air must be prevented
from entering the enclosure.
Power Factor Correction Capacitors
Power factor correction capacitors
must not be connected on the soft
starter or controller output or at the
motor terminal box. To do so would
result in SCR failure. Power factor
correction should be done on a plantwide basis. If capacitors must be
located at the soft start input, they
should be connected as far upstream
from the soft start as possible.
Input Harmonics
During operation no harmonic currents
are caused by the use of a soft start.
During motor starting, harmonic currents may be drawn from the utility line,
but the duration of such is very short.
Load Types and
Characteristics
Introduction
The process of selecting a soft start is
dependent upon the characteristics of
the load to which it is being applied.
It is important to understand its torque
characteristics and how they vary
at start as well as during normal
operation.
When considering load characteristics,
the following should be evaluated:
■ What type of load is associated with
the application?
■ Does the load have a shock compo-
nent?
■ Are large inertial loads involved?
■ What are the motor considerations?
■ Are there frequent starts and stops?
For more information visit: www.EatonElectrical.com AP03902001E

Solid-State Soft Start
Motor Controller and
Starter
Application Note
Effective: February 2005 Page 13
Motor loads can be classified into
three basic components that contribute to load torque, friction, inertia and
the driven process, as was noted previously. The driven process can be
broken down into a few basic load
types.
Load Types
Constant Torque Load
This type of load is frequently encountered. In this group, the torque
demanded by the load during start and
run is constant. The load requires the
same amount of torque at start and
during normal operation. Loads of this
type are essentially friction loads. In
other words, the constant torque
characteristic is needed to overcome
friction. This load can be difficult to
start with a soft starter, and still limit
current, because it means that a high
level of current must be used to start
the load moving and maintain its
movement.
Examples of this type of load are conveyors, extruders and surface winders.
Variable Torque Load
With this type of load, the torque is
directly proportional to some mathematical power of speed, usually varying linearly with speed or speed
squared (Speed
2
).
An example of a load which varies linearly with speed is a mixer. Loads that
vary as the square of speed are centrifugal fans, pumps and blowers. These
types of loads require much lower
torque at low speed than at full speed.
Other Functional Considerations
Shock Loads
Soft starts for crushers, separators,
grinders, conveyors, winches, cranes
and vehicular systems often must
manage loads which range from a
small fraction of the rated load to
several hundred percent.
Under these conditions the soft starter
must function properly yet protect the
motor and driven equipment. Many
soft starters provide additional motor
protection beyond that of electromagnetic starters, such as jam, stall and
underload. The soft starter must be
appropriately sized for the load as well
as have its protective features adjusted
as required by the application.
Note: A soft start controller does not provide any motor or driven load protection. It
only provides a soft start capability.
Inertial Load
A high inertia load may require oversizing of the motor and soft start to
account for the heating caused by the
long acceleration times.
Duty Cycle
Certain applications may require cyclic
overloads or frequent start/stop cycles
which may result in severe motor
heating if not considered in the selection process.
Most motors and soft starts have a
specified duty cycle capability.
Typical Load Torque
Table 3. Typical Load Torque Requirements
Name of Application Load Torque as Percent of Full-Load Drive Torque
Breakaway Accelerating Peak Running
Actuators:
Screw-down (rolling mills)
Positioning
Agitators:
Liquid
Slurry
Blowers, centrifugal:
Valve closed
Valve open
Blowers, positive-displacement, rotary, bypassed
Calendars, textile or paper
Card machines, textile
Centrifuges (extractors)
Chippers, wood, starting empty
Compressors, axial-vane, loaded
Compressors, reciprocating, start unloaded
Conveyors, belt (loaded)
Conveyors, drag (or apron)
Conveyors, screw (loaded)
Conveyors, Shaker-type (vibrating)
Coolers, hot solids, rotary (loaded)
Cranes, traveling:
Bridge motion
Trolley motion
Hoist motion
Draw presses (flywheel)
Drill presses
Edgers (starting unloaded)
Elevators, bucket (starting loaded)
Elevators, freight (loaded)
Elevators, man lift
200
150
100
150
100
100
150
175
200
150
175
100
100
150
100
150
110
100
100
30
40
40
75
40
50
40
50
50
25
40
50
110
110
110
100
130
150
100
150
140
300
200
200
175
125
125
50
40
60
40
50
50
50
30
125
100
100
100
100
100
100
100
125
200
100
100
100
100
100
100
100
100
190
200
150
200
150
100
100
40
75
AP03902001E For more information visit: www.EatonElectrical.com

Application Note
Page 14 Effective: February 2005
Solid-State Soft Start
Motor Controller and
Starter
Table 3. Typical Load Torque Requirements — Continued
Name of Application Load Torque as Percent of Full-Load Drive Torque
Breakaway Accelerating Peak Running
Elevators, personnel (loaded)
Escalators, stairways (starting unloaded)
Extruders (rubber or plastic)
Fans, centrifugal, ambient:
Valve closed
Valve open
Fans, centrifugal, hot gases:
Valve closed
Valve open
Fans, propeller, axial-flow
Feeders, belt (loaded)
Feeders, distributing, oscillating drive
Feeders, screw compacting rolls
Feeders, screw, filter-cake
Feeders, screw, dry
Feeders, vibration motor-driven
Frames, spinning, textile
Grinders, metal
Hoists, skip
Indexers
Ironer, laundry (mangles)
Jointers, woodworking
Kilns, rotary (loaded)
Looms, textile, without clutch
Machines, boring (loaded)
Machines, bottling
Machines, buffing, automatic
Machines, cinder-block, vibrating
Machines, keyseating
Machines, polishing
Mills, flour, grinding
Mills, rolling metal:
Billet, skelp and sheet, bar
Brass and copper finishing
Brass and copper roughing
Merchant mill trains
Plate
Reels, wire or strip
Rod
Sheet and tin (cold rolling)
Strip, hot
Structural and rail finishing
Structural and rail roughing
Tub e
Tube piercing and expanding
Tube reeling
Mills, rubber
Mills, saw, band
Mixers, chemical
Mills, concrete
Mixers, dough
Mixers, liquid
Mixers, sand, centrifugal
Mixers, sand, screw
Mixers, slurry
Mixers, solids
Planers, metalworking
Planers, woodworking
Plows, conveyor, belt (ore)
Positioners, indexing (machine tool)
Presses, pellet (flywheel)
Presses, printing, production type
Presses, punch (flywheel)
Puller, car
Pumps, adjustable-blade, vertical
Pumps, centrifugal, discharge open
Pumps, oil-field, flywheel
Pumps, oil, lubricating
Pumps, oil fuel
Pumps, propeller
110
150
100
150
150
150
175
150
100
150
250
125
150
150
150
120
100
150
100
175
175
100
175
150
175
150
150
100
150
150
150
50
25
25
25
25
40
50
25
50
50
50
25
50
50
50
40
50
40
90
40
40
40
50
50
50
50
40
50
50
50
50
50
40
40
40
40
150
150
110
200
110
120
150
100
100
100
150
125
150
200
125
125
125
150
150
100
100
110
100
125
100
100
100
125
125
150
125
150
200
150
110
100
200
150
150
100
75
60
60
50
50
50
75
50
75
75
30
30
30
30
50
30
30
30
30
30
30
75
75
50
75
75
40
100
100
100
100
100
175
100
100
100
100
100
100
100
100
100
100
150
125
125
125
150
100
100
100
100
100
100
200
200
200
200
250
100
200
200
200
200
250
200
250
200
200
200
100
100
100
100
100
100
100
175
150
150
200
100
150
150
100
100
125
100
200
150
150
100
50
70
For more information visit: www.EatonElectrical.com AP03902001E

Solid-State Soft Start
Motor Controller and
Effective: February 2005 Page 15
Application Note
Starter
Table 3. Typical Load Torque Requirements — Continued
Name of Application Load Torque as Percent of Full-Load Drive Torque
Breakaway Accelerating Peak Running
Pumps, reciprocating, positive-displacement
Pumps, screw-type, started dry
Pumps, screw-type, primed, discharge open
Pumps, slurry-handling, discharge open
Pumps, turbine, centrifugal, deep-well
Pumps, vacuum (paper-mill service)
Pumps, vacuum (other applications)
Pumps, vacuum, reciprocating
Pumps, vane-type, positive-displacement
Rolls, bending
Rolls, crushing (sugarcane)
Rolls, flaking
Sanders, woodworking, disk or belt
Saws, band, metalworking
Saws, circular, metal, cutoff
Saws, circular, wood, production
Saws, edger (see Edgers)
Saws, gang
Screens, centrifugal (centrifuges)
Screens, vibrating
Separators, air (fan-type)
Shakers, foundry or car
Shears, flywheel-type
Shovels, dragline, hoisting motion
Shovels, dragline, platform motion
Shovels, large, digging motion
Shovels, large, platform motion
Te nsion-maintaining drives
Textile machinery
To ols, machine
To ols, machine, broaching, automatic
To ols, machine, lathe, metal production
To ols, machine, mill, boring production metal
To ols, machine, milling, production
To ols, machine, planer, production, metal (See Planers, metalworking)
To ols, machine, shaper, metal, automatic
Vehicles, freight
Vehicles, passenger
Walkways, mechanized
Washers, laundry
Winches
175
150
150
150
150
150
100
150
100
100
100
200
100
125
75
50
60
40
50
30
30
30
25
50
60
40
50
40
50
50
50
50
50
50
50
50
50
50
25
30
30
100
100
100
100
60
60
150
150
110
50
50
50
50
30
30
60
150
100
150
50
150
100
200
100
100
100
150
150
200
125
100
75
200
400
50
75
150
175
100
100
100
100
150
100
150
175
100
125
100
100
100
150
150
150
125
100
120
100
100
200
100
100
100
150
200
100
100
150
200
200
100
100
100
70
70
90
Controller and Starter
Selection
value several times full-load torque.
The peak torque varies because of a
change in load conditions or mechanical nature of the machine. The motor
Selection Considerations
When selecting a soft starter or controller for an application, the following
points should be considered:
Environment
The environment in which the motor
and soft start will be placed is of prime
concern. Conditions such as ambient
temperature, cooling air supply, the
presence of gas, moisture and dust
should all be considered when choosing the soft start, its enclosure and
protective features.
Torque Requirements
The starting, peak and acceleration
torques are to be considered. Starting
torque requirements can vary from a
torque available to the driven machine
must be more than that required by
the machine from start to full speed.
The greater the excess torque, the
more rapid the acceleration potential.
Duty Cycle
Selecting the proper soft start also
depends on whether the load is
steady, varies, follows a repetitive
cycle of variation or has pulsating
torques. The duty cycle, which is
defined as a fixed repetitive load
pattern over a given period of time,
is expressed as the ratio of on-time to
the cycle period. When the operating
cycle is such that the soft start starts
and stops frequently, the duty cycle
becomes a factor.
small percentage of the full load to a
AP03902001E For more information visit: www.EatonElectrical.com
Heating
The temperature of a motor or controller is a function of ventilation and
losses. Frequent starts or high ambient
temperatures need to be considered.
Selecting a Soft Start for a
Machine
The application of a soft start and
motor to power a machine can be both
a mechanical and electrical issue.
When applying the soft start, the
speed-torque characteristics available
at the motor’s shaft must be considered, and how well these characteristics suit the machine.
Three essential parameters are:
1. Breakaway Torque
2. Process Torque
3. Accelerating Torque

Application Note
Page 16 Effective: February 2005
Solid-State Soft Start
Motor Controller and
Starter
Breakaway Torque
This is the torque required to start the
machine in motion. It is usually greater
(except for centrifugal pumps and
fans) than the torque required to maintain motion (process torque). Breakaway torque combined with process
torque frequently determines the soft
start selection. Typical breakaway
torques for various machine types are
given in Table 3.
Note: Many soft starts have a selectable kick
start feature which allows a large pulse of
current for a very short period of time to
break away the machine, after which the
current level is reduced to the preset level.
Process (Running) Torque
This is the torque required to pull,
push, compress, stretch or otherwise
process or act upon the material being
transported by or through the
machine. On some machines, process
torque may be so significant as to
determine the motor power rating. On
other machines, this load may be
insignificant. This includes any peaks
required during normal operation such
as a work piece entering the machine
or material property change.
Most machines can be classified into
the following load types:
■ Constant torque — load varies
linearly with speed.
■ Variable torque — load varies as
the square of speed.
Care must be exercised if the properties of the machine or material change
periodically, for example icing on an
outdoor conveyor, or the settling of
sludge in a pump when shut down, to
select the motor and soft start to
account for these conditions.
Accelerating Torque
This is the torque required to bring the
machine to an operating speed within
a given time. With most machines, the
load is largely friction and this will
need to be all that is considered, since
the acceleration torque requirements
will be small. However, certain
machines classified as “high inertia”
with flywheel, bull gears or other large
rotating masses may require motor
and soft start selection based upon the
power required to accelerate the load
within a given time.
Acceleration time is directly proportional to the total inertia and inversely
proportional to the torque available.
Measuring Machine Torque
To measure the torque required to
drive a machine, fasten a pulley
securely to the shaft which the motor
is to drive. Fasten one end of a cord to
the outer surface of the pulley and
wrap a few turns of the cord around
the pulley. Tie the other end of the cord
to a spring scale. See Figure 23.
Scale (lb.)
F
To rq ue = F x R
Figure 23. Measuring Torque
Pull gently on the scale until the shaft
turns. Do not yank. The force in
pounds or ounces, indicated on the
scale, multiplied by the radius of the
pulley (measured from the centerline
of the machine shaft) in inches gives
the torque value in lb-in or oz-in. On
some machines, this torque may vary
as the shaft rotates. The highest value
of torque must be used when selecting
a motor.
The running torque required by a
machine will be approximately equal
to the starting torque if the load is
composed almost entirely of friction.
If the load is primarily inertia or windage, the characteristics of the inertia or
windage producing elements must be
determined.
Most machines require a higher torque
value to break away, but once running,
the torque requirement will decrease.
Refer to specific soft starter or
controller specifications in the
product sections of the Cutler-Hammer
catalog to match the driven machine
requirements.
R
Pulley
Soft Start Application Questions
1. Does the environment have an
explosive atmosphere — If the
atmosphere is classified by the
NEC to be hazardous or semihazardous (Division I or Division
II), the soft start must be located in
a separate room away from the
explosive environment.
2. Does the environment have any
magnetic dust present? The soft
start must be placed away from
the magnetic dust, as it is also
most likely to be conductive and
could cause short circuits on
printed circuit boards and power
components.
3. Will the soft start be subject to
harsh chemicals or washdown? If
the soft start will be subject to
washdown or harsh chemicals, the
appropriate enclosure must be
selected or the soft starter must be
located in a clean environment.
4. What is the start duty cycle of the
machine? If more frequent than
permitted in the soft start catalog,
an oversized starter will be
required.
5. What is the type of load? Variable
torque loads are typical of centrifugal pumps and fans where
torque varies as the square of
speed or a mixer where torque
varies linearly with speed. Constant torque loads are typical of
conveyors, stamping presses and
extruders. The torque required by
the load remains constant regardless of motor speed. The load inertia needs to be specified.
Additional Questions
After running through the above, you
will find that a high percentage of
applications can be satisfied by using
a standard soft starter or controller.
There are some additional questions
which need to be answered for proper
application.
1. What is the input power that will
be connected to the soft start?
The input voltage and frequency
must be identified.
2. What are the nameplate ratings of
the motor — The first cut choice of
the soft start is based on the
motor’s current and voltage ratings. The choice is then refined
based on the machine load
requirements and knowledge of
the prior starting method.
For more information visit: www.EatonElectrical.com AP03902001E

Solid-State Soft Start
Motor Controller and
Effective: February 2005 Page 17
Application Note
Starter
Soft Starter Application Data Worksheet
This worksheet is to assist you in determining the information required for selecting the proper soft starter.
Application:
Motor nameplate ratings:
Horsepower
___
RPM
___
Efficiency
___
Operating environment
Altitude in feet
___
Total inertia at the motor shaft
Duty cycle
Load torque requirement (Attach curve if available)
Starting
Motor torque-speed data (Attach curve if available)
Locked rotor torque
Breakdown torque
What is the required ramp time at start
What is the required ramp time at stop
Utility required inrush current limit
Existing starter data
ft-lbs Running
___
___
___
ft-lbs Pull up torque
ft-lbs
Voltage
___
Full load amps
___
NEMA design type
___
Ambient temperature
___
___
___
___
___
___
2
lb-ft
starts per hour
ft-lbs Peak
___
sec
sec
amps
___
ft-lbs
Service factor
___
Locked rotor code
___
___
ft-lbs
Auto transformer, taps used
❑
Wye Start — Delta Run
❑
Time to full speed
sec Peak current
___
Full Voltage Starter
❑
Part winding starter
❑
___
amps
AP03902001E For more information visit: www.EatonElectrical.com

Application Note
T
WK
2
()dN()
308t
-------------------------------
=
t
WK
2
()dN()
308T
-------------------------------
=
Page 18 Effective: February 2005
Solid-State Soft Start
Motor Controller and
Starter
Formulae, Conversions and
Tables
Introduction
This section of your Application Note
provides a rich resource of formulae,
conversions and tables:
■ How to Calculate Torque
■ How to Calculate Horsepower
■ How to Calculate Surface Speed
■ How to Calculate Horsepower for
Pumps
■ How to Calculate Horsepower for
Fans and Blowers
■ How to Calculate Horsepower for
Conveyors
■ How to Calculate Accelerating
Torque
■ How to Calculate Maximum Motor
Torque
■ How to Calculate WK
■ How to Calculate Equivalent WK
Motor Shaft
■ Electrical Formulae
■ Induction Motor Formulae
■ Tables of Conversions and
Abbreviations
How to Calculate Torque
Torque (lb-ft) =
------------------------------------
Speed rpm()
How to Calculate Horsepower
Definition:
1 horsepower = 550 ft-lb per second.
For Rotating Objects
Torque (lbs-ft) x Speed (rpm)
hp =
Torque (in-lbs) x Speed (rpm)
hp =
For Object or Material in Linear Motion
Force (Lbs.) x Velocity (In./min.)
hp =
Force (Lbs.) x Velocity (Ft./min)
hp =
Tension may be substituted for force in
the above formulae.
hp 5250×
5250
63,000
396,000
33,000
2
2
at
How to Calculate Surface Speed
Surface speed (Ft./min) = rpm x Radius
(Ft.) x 6.283.
How to Calculate Horsepower for
Pumps
Flow x Head x Specific Gravity
hp =
3960 x Efficiency of Pump
(Flow in gal./min.; Head in Ft.)
Head in feet is pressure (lbs/in
Specific
Gravity
Density of water = 62.43 lbs/ft
39.2°F (4°C)
Specific Gravity of Water = 1.0
Efficiency is expressed as a decimal.
(Efficiency of 0.85 is 85% efficient).
Table 4. Typical Values of Efficiency for
Centrifugal Pump
=
Gallons per Minute Efficiency
500 to 1000
1000 to 1500
over 1500
Density of Fluid
Density of Water
0.70 to 0.75
0.75 to 0.80
0.80 to 0.85
2
) x 2.307.
3
at
Typical values of efficiency for positive
displacement pumps:
Efficiency = 85 to 90.
Effects of Changing Pump Speed; for
Centrifugal Pumps:
2
(rpm)
3
3
(head)
hp = K1(rpm)
Horsepower is proportional to cube of
speed.
Torque = K
Torque is constant at all speeds with a
constant head.
Flow = K
Flow is directly proportional to speed.
How to Calculate Horsepower for
Fans and Blowers
hp =
(Flow in Ft3/min.; Pressure in Lbs/in2)
hp =
(Flow in Ft3/min.; Pressure in Lbs/ft2)
Flow x Pressure
33,000 x Efficiency of Fan
Flow x Pressure
229 x Efficiency of Fan
hp =
Flow x Pressure
6356 x Efficiency of Fan
(Flow in Ft3/min.; Pressure in inches of
water gauge)
Efficiency is expressed as a decimal
(efficiency of 0.85 is 85% efficient).
How to Calculate Horsepower for
Conveyors
hp =
(Vertical)
hp =
(Horizontal
Where:
F = Force (Lbs)
V = Velocity (Ft/min)
Eff. = Efficiency
Coef. of Friction:
Ball or Roller Slide = 0.02
Dovetail Slide = 0.20
Hydrostatic Ways = 0.01
Rectangle Ways with Gib = 0.1 – 0.25
F x V x Coef. of Friction
)
F x V
33,000 x Efficiency
33,000 x Efficiency
How to Calculate Accelerating
Torque
In addition to the torque required to
drive a load at a steady speed, torque is
required to accelerate the load inertia
from standstill to operating speed. The
torque required for acceleration is determined by the inertia and the required
rate of acceleration. The following formula is used to calculate acceleration
torque (torque required above load
torque) of a rotating member:
where:
T = acceleration torque (lb-ft)
2
= total system inertia (lb-ft2) that
WK
the motor must accelerate. This value
includes motor rotor, reducer, and
load. See “How to Calculate WK
follows.
dN = change in speed required (rpm)
t = time to accelerate total system load
(seconds)
The formula can also be arranged to
calculate acceleration time given
inertia, available torque and required
speed change.
2
” that
For more information visit: www.EatonElectrical.com AP03902001E

Solid-State Soft Start
Motor Controller and
Starter
Application Note
Effective: February 2005 Page 19
The accelerating force required for linear motion is given by:
WdV()
Accelerating Force (F) =
------------------1933t
where:
W = weight (Lbs.)
dV = change in velocity (fpm)
t = time (seconds) to accelerate weight
For motor selection, this force must be
converted to motor torque and added
to the torque required for accelerating
the rotating parts of the machine. See
also “How to Calculate WK
2
” that
follows. The weight of the linear
moving parts can be converted to an
equivalent WK
2
at the motor shaft,
eliminating the force calculations.
How to Calculate Maximum Motor
Torque
Maximum Motor Torque = Running
Torque + Accelerating Torque
How to Calculate WK
The factor WK2 (inertia) is the weight
of a rotating object multiplied by the
square of the radius of gyration K. For
weight in pounds and radius of gyration in feet, WK
For a solid cylinder:
WK2 =
where:
Density of material is in pounds per
cubic inch. Length and diameter are in
inches. Given weight in pounds and
diameter in feet:
WK2 =
For a hollow cylinder:
WK2 =
where:
Density of materials is in pounds per
cubic inch. Length and diameter are in
inches. Given weight in pounds and
diameter in feet:
WK2 =
2
Density x Length x Diameter
Weight x Diameter
Density x Length x (OD4 - ID4)
Weight x (OD2 + ID2)
2
is in lbs-ft2.
1467
2
8
1467
8
Table 5. Density Values for Common
Materials
Material Density lb/in
Aluminum
Bronze
Cast Iron
Nylon
Paper
Steel
Rubber
0.0924
0.3200
0.2600
0.0510
0.0250 to 0.0420
0.2820
0.0341
WK2 of Solid Steel Cylinders One Inch
Long
Table 6 lists values of WK2 in lb-ft2 for
one inch long solid steel cylinders of
various diameters. For cylinders
longer or shorter than one inch,
multiply the value given by the actual
length in inches. Values can be determined for diameters not listed by
moving the decimal point in the
diameter in either direction and moving the decimal point in the corresponding value of WK
2
four places in
the same direction for every one place
the decimal is moved in the diameter.
For hollow cylinders, subtract the WK
given for the inside diameter from the
2
given from the outside diameter.
WK
2
The WK
of 0.2820 Lbs. per In.
are for steel with a density
3
. For other
materials, multiply the WK
the table by:
4
Lbs per In3 of material
0.2820
How to Calculate Equivalent WK2
at Motor Shaft
In most mechanical systems not all of
the moving parts operate at the same
speed. If speeds of the various parts
have a continuous fixed relationship to
the motor speed, the following formulae can be used to convert all of the
various inertia values to an equivalent
2
applied to the motor shaft.
WK
For rotating parts:
2
Equivalent WK
where:
2
= inertia of the moving part (lbs-ft2)
WK
N = speed of the moving part (rpm)
= speed of the driving motor (rpm)
N
M
When using speed reducers, and the
machine inertia is reflected back to the
motor shaft, the equivalent inertia is
equal to the machine inertia divided by
the square of the drive reduction ratio.
= WK2
--------N
2
from
N
M
2
WK
2
=
3
where:
DR = drive reduction ration N
Equivalent WK
---------------DR()
2
/N
M
For linear motion:
Not all driven systems involve rotating
motion. The equivalent WK
2
of linearly
moving parts can also be reduced to
the motor shaft speed as follows:
2
WV()
2
=
Equivalent WK
-----------------------------
39.5 NM()
2
where:
W = weight of load (Lbs.)
V = linear velocity of moving parts
(feet per minute)
= speed of the driving motor (rpm)
N
M
Electrical Formulae
Ohms Law
Amperes = Volts/Ohms, or I = E/R
Ohms = Volts/Amperes, or R = E/I
2
Volts = Amperes x Ohms, or E = IR
Power in DC Circuits
Watts = Volts x Amperes, or W = EI
Horsepower =
(hp)
Kilowatts =
(kW)
Kilowatts Hrs =
(kWh)
Power in AC Circuits
Kilovolt-Amperes(kVA)
kVA =
(1 ph)
kVA =
(3 ph)
2
Kilowatts (kW)
kW =
(1 ph)
kW =
(3 ph)
Kilovolt-Amperes Reactive (kVAR)
kVAR = kVA SIN Θ
Volts x Amperes
746
Volts x Amperes
1000
Volts x Amperes x Hrs
1000
Volts x Amperes
1000
Volts x Amperes x 1.73
1000
Volts x Amperes x PF
1000
Volts x Amperes x PF x 1.73
1000
AP03902001E For more information visit: www.EatonElectrical.com

Application Note
Page 20 Effective: February 2005
Solid-State Soft Start
Motor Controller and
Starter
Power Factor
PF = ∆ COS Θ =
kW input()
--------------------------------kVA input()
kVA
kW
kVAR
Figure 24. Power Factor
Induction Motor Formulae
Synchronous Speed
Sync. rpm =
120f
-----------p
Tables of Conversions and Abbreviations
Table 6. WK2 of Steel Cylinders One Inch Long
Diameter in
Inches
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
2
WK
0.000192
0.00308
0.01559
0.049278
0.12030
0.2494
0.46217
0.78814
1.262
1.924
2.818
3.991
5.497
7.395
9.745
12.61
16.07
20.21
25.08
30.79
37.43
45.09
53.87
63.86
75.19
87.96
102.30
118.31
136.14
155.92
177.77
201.8
228.2
257.2
288.8
323.2
360.7
401.3
445.3
492.78
Diameter in
Inches
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
2
WK
543.9
598.8
658.1
721.4
789.3
861.8
939.3
1021.8
1109.6
1203.07
1302.2
1407.4
1518.8
1636.7
1761.4
1893.1
2031.9
2178.3
2332.5
2494.7
2665.2
2844.3
3032.3
3229.5
3436.1
3652.5
3879.0
4115.7
4363.2
4621.7
4891.5
5172
5466
5772
6090
6422
6767
7125
7498
7885
where:
p = number of poles
f = frequency (Hz)
Operating Speed
rpm = Sync rpm - Slip rpm
Slip rpm ≈
2 x percent load
p
For Three-Phase Motors
Current (Amps)
--------------------------------------------------------------------------------=
hp 746×
3 Volts Efficiency PF×××
------------------------------------------------------------------=
Volts Efficiency PF××
hp 431×
Locked Rotor Current (Amps)
hp x start kVA / hp x 1000
Volts x
Diameter in
Inches
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
2
WK
8286
8703
9135
9584
10048
10529
11028
11544
12077
12629
13200
13790
14399
15029
15679
16349
17041
17755
18490
19249
20031
20836
21665
22519
23397
24302
25232
26188
27173
28183
29222
30289
31385
32511
33667
34853
36071
37320
28601
39914
3
Diameter in
Inches
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
At frequencies other than 60 Hz, LRA
can be estimated by:
f
LRA = LRA at 60 Hz x
------
60
For Any Motor
hp 0.746×
kW (input) =
------------------------------
efficiency
kW (output) = hp x 0.746
2
WK
41262
42643
44059
45510
46995
48517
50076
51672
53305
54978
56689
58440
60231
62063
63936
65852
67811
69812
71858
73948
76083
78265
80493
82768
85091
87463
89884
92355
94876
97449
100075
102750
105482
108268
111107
114002
116954
119962
123028
126152
Diameter in
Inches
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
2
WK
129336
132579
135883
139249
142676
146166
149720
153339
157022
160772
164588
168472
172424
176446
180537
184699
188933
193239
197618
202071
206599
211203
215883
220640
225476
230391
235386
240461
245619
250858
256182
261589
267081
272660
278325
284078
289920
295852
301874
307988
For more information visit: www.EatonElectrical.com AP03902001E

Table 7. Standard Abbreviation Descriptions
Temperature deg. = degrees
Electrical Ω = Ohms
Power/Energy hp = horsepower
C = Celsius (Centigrade)
F = Fahrenheit
Btu = British Thermal Unit
Length Yd. = yard
m = meter
mm = millimeter (1/1000 of a meter)
cm = centimeter (1/100 of a meter)
In. = inch
Ft. = feet
km = kilometer
Weight Oz. = ounce
Lb. = pound
kg = kilogram
gm = gram
= Phase
V = Volts
A = Amperes
mA = milliamperes
µA = microamperes
kV = kilovolts
mV = millivolts
kVA = kilovolt-amps
kVAR = kilovolt-amps reactive
Hz = Hertz, cycle per second
W = watt
kW = kilowatt
kWH = kilowatt-hours
J = Joule
Solid-State Soft Start
Motor Controller and
Starter
Work/Inertia ft-lb = foot pound
Rotation/Rate FPM = feet per minute
Mathematic
2
= moment of inertia
WK
2
= Newton meters
N•m
r = radius
k = radius of gyration
2
Area Ft.
Pressure
Volume cu. = cubic
= square foot
sq. m = square meter
mil = unit of length of angular measurement
2
= square millimeter
mm
2
= square inch
In.
FPS = feet per second
m/s = meters per seconds
mph = miles per hour
cfm = cubic feet per minute
π =“pi”
rad. = radians
= Density
∑ = Summation
∆ = Change
kg per sq. cm = kilograms per square centimeter
Hg = Mercury Symbol
PSI = pounds per square inch
PSF = pounds per square foot
3
= cubic inch
In.
gal. = gallon
3
= cubic foot
Ft.
ml = milliliter
fl. oz = fluid ounce (U.S.)
Application Note
Effective: February 2005 Page 21
2
AP03902001E For more information visit: www.EatonElectrical.com

Application Note
Page 22 Effective: February 2005
Solid-State Soft Start
Motor Controller and
Starter
Table 8. Useful Conversion Constants
To Convert From To Multiply By
Area
2
In.
2
Ft.
2
Yd.
2
Ft.
Energy
Btu (thermochemical)
Btu (thermochemical)
calorie (thermochemical)
hp-hr
ft-lb
ft-lb
ft-lb
kWH
Flow — Mass
lb/hp-hr
lb-hr
lb/min
lb/sec
oz/min
Flow — Vol.
gpm
gpm
3
/sec
in
gal/hp-hr
ft3/sec
cfm
Force
kg
oz (avoirdupois)
lb (avoirdupois)
gm
kg
ton (2000 Lb.)
ton (2000 Lb.)
oz (avoirdupois)
lb (avoirdupois)
Length
Ft.
In.
mile (statute)
mil
Mass
Lb. (avoirdupois)
Lb. (avoirdupois)
Oz. (avoirdupois)
slug
ton (2000 lb)
ton (metric)
Power
hp (550 ft-lb/sec)
ton (refrigeration)
ton (refrigeration
hp (550 ft-lb/sec)
Btu/min (thermochemical)
Btu/sec (thermochemical)
calorie/sec (thermochemical)
To To Convert From Divide By
2
cm
2
m
2
m
2
Yd.
Joule (J)
kWH
Joule (J)
kWH
Joule (J)
Btu
kWH
Joule (J)
kg/Joule
kg/hr
kg/sec
kg/sec
g/min
liter/min
3
/sec
m
cm3/sec
3
/Joule
m
m3/sec
m3/hr
Newtons (N)
Newtons (N)
Newtons (N)
Newtons (N)
lb (avoirdupois)
Newton
kg
gm
gm
meter (m)
cm
km
mm
kg
gm
gm
kg
kg
kg
watt
watt
hp
hp (metric)
watt
hp (550 ft-lb/sec)
watt
6.4516
9.2903 x 10
0.83613
0.11111
1054.4
2.9288 x 10
4.184
1.341
1.3558
1.2859 x 10
3.7662 x 10
3.6 x 10
1.6897 x 10
45359
7.5599 x 10
0.45359
28.35
3.7854
6.309 x 10
16.387
1.4101 x 10
2.8317 x 10
1.699
9.8067
0.27801
4.4482
9.8067 x 10
2.2046
8896.4
907.18
28.35
453.59
0.3048
2.54
1.6093
2.54 x 10
0.45359
453.59
28.35
14.594
907.18
1000
745.7
3516.8
4.7161
1.0139
17.573
1.4139
4.184
To Convert From To Multiply By
Pressure
-2
PSI
ft of water (39.2°F)
2
gm/cm
in Hg (32°F)
atmosphere
atmosphere
-4
-3
-7
6
-7
-3
in Hg (32°F)
ft of water (39.2°F)
in of water (39.2°F)
in of water (39.2°F)
mm Hg @ 0°C (=Torr)
mm Hg @ 0°C (=Torr)
Temp.
°F
°C
°C
°F
Torque
lb-in
lb-ft
oz-ft
-5
-9
-2
oz-ft
kg-m
oz-in
kg-m
dyne-cm
dyne-cm
kPa
kPa
Pa
kPa
kPa
PSI
PSI
PSI
PSI
kPa
kPa
PSI
°C
°F
°K
°R
N-m
N-m
N-m
lb-in
N-m
gm-cm
lb-in
oz-in
N-m
6.8948
2.989
98.067
3.3864
101.33
14.696
0.49115
0.43351
3.6126 x 10
0.24908
0.13332
1.9337 x 10
t°
= (t°f - 32)/1.8
c
= (1.8)(t°c) + 32
t°
f
= t°c + 273.15
t°
k
= t°f + 459.67
t°
r
0.11298
1.3558
8.4739 x 10
0.75
9.8067
72.008
86.796
1.4161 x 10
-7
1 x 10
-2
-2
-2
-5
Velocity
ft/min
mph
-3
mph
ft/sec
rpm
revolutions/sec
mph
kWH
meter/sec
meter/sec
radians/sec
radians/sec
1.1364 x 10
1.6093
0.44704
0.3048
0.10472
6.2832
-2
Volume
barrel (oil, 42 gal)
barrel (oil, 42 gal)
barrel (42 gal)
barrel (42 gal)
gallon (U.S. liquid)
-2
gallon (U.S. liquid)
gallon (U.S. liquid)
quart (U.S. liquid)
quart (U.S. liquid)
fluid oz (U.S. liquid)
fluid oz (U.S. liquid)
liter
liter
liter
3
In.
3
Ft.
3
Ft.
3
meter
gallon (U.S. liquid)
liter
3
ft
liter
3
in
3
meter
3
in
liter
3
in
3
cm
3
meter
3
cm
3
in
3
cm
3
in
liter
15699
42
158.99
5.6146
3.7854
231
3.7854 x 10-3
57.75
0.94635
1.8047
29.571
1 x 10-3
1000
61.024
16.387
1728
28.317
To To Convert From Divide By
How to Use
Direct Conversion
Multiply known value by conversion factor to obtain equivalent value in
desired units. For example, 203 in
2
x 6.4516 = 1309.67cm
203 in
Inverse Conversion
2
is converted to cm2, as follows:
2
Divide known value by conversion factor to obtain equivalent value in
desired units. For example, 10.82 N-m converted to oz-ft, as follows:
10.82 N-m
8.4739 x 10-2
Indicates Standard International (S) Unit
Specific fuel consumption (SFC)
= 127.69 oz-ft
For more information visit: www.EatonElectrical.com AP03902001E

Solid-State Soft Start
Motor Controller and
Effective: February 2005 Page 23
Starter
Table 9. Fractional Inch to Equivalent Millimeters and Decimals
Inch Equivalent Inch Equivalent
mm Decimal mm Decimal
1/64
1/32
3/64
1/16
5/64
3/32
7/64
1/8
9/64
5/32
11/64
3/16
13/64
7/32
15/64
1/4
17/64
9/32
19/64
5/16
21/64
11/32
23/64
3/8
25/64
13/32
27/64
7/16
29/64
15/32
31/64
1/2
0.3969
0.7938
1.1906
1.5875
1.9844
2.3813
2.7781
3.1750
3.5719
3.9688
4.3656
4.7625
5.1594
5.5563
5.9531
6.3500
6.7469
7.1438
7.5406
7.9375
8.3344
8.7313
9.1281
9.5250
9.9219
10.3188
10.7156
11.1125
11.5094
11.9063
12.3031
12.700
0.0156
0.0313
0.0469
0.0625
0.0781
0.0938
0.1094
0.1250
0.1406
0.1563
0.1719
0.1875
0.2031
0.2188
0.2344
0.2500
0.2656
0.2813
0.2969
0.3125
0.3181
0.3438
0.3594
0.3750
0.3906
0.4063
0.4219
0.4375
0.4513
0.4688
0.4844
0.5000
33/64
17/32
35/64
9/16
37/64
19/32
39/64
5/8
41/64
21/32
43/64
11/64
45/64
23/32
47/64
3/4
49/64
25/32
51/64
13/16
53/64
27/32
55/64
7/8
57/64
29/32
59/64
15/16
61/64
31/32
63/64
—
13.0969
13.4938
13.8906
14.2875
14.6844
15.0813
15.4781
15.8750
16.2719
16.6688
17.0656
17.4625
17.8594
18.2563
18.6531
19.0500
19.4469
19.8438
20.2406
20.6375
21.0344
21.4313
21.8281
22.2250
22.6219
23.0188
23.4156
23.8125
24.2094
24.6063
25.0031
—
Application Note
0.5156
0.5313
0.5469
0.5625
0.5781
0.5938
0.6094
0.6250
0.6406
0.6563
0.6719
0.6875
0.7031
0.7188
0.7344
0.7500
0.7656
0.7813
0.7969
0.8125
0.8281
0.8438
0.8594
0.8750
0.8906
0.9063
0.9219
0.9375
0.9531
0.9688
0.9844
—
Glossary
AC Contactor
An alternating current (AC) contactor
is designed for the specific purpose of
establishing or interrupting an AC
power circuit.
Ambient Temperature
Ambient temperature is the temperature of the medium, such as air, water
or earth, into which the heat of the
equipment is dissipated.
For self-ventilated equipment, the
ambient temperature is the average
temperature of the air in the immediate neighborhood of the equipment.
For air or gas cooled equipment with
forced ventilation, or secondary water
cooling, the ambient temperature is
taken as that of the ingoing air or cooling gas.
For self-ventilated enclosed (including
oil immersed) equipment, considered
as a complete unit, the ambient temperature is the average temperature
of the air outside of the enclosure in
the immediate neighborhood of the
equipment.
Auxiliary Contacts
Auxiliary contacts of a switching
device are contacts in addition to the
main circuit contacts and operate with
the movement of the latter.
Back of a Motor
The back of a motor is the end which
carries the coupling or driving pulley
(NEMA). This is sometimes called the
drive end (D.E.) or pulley end (P.E.).
Base Speed
Base speed is the manufacturer’s
nameplate rating where the motor will
develop rated hp at rated load and
voltage.
Bearing (Ball)
A “ball” shaped component that is
used to reduce friction and wear while
supporting rotating elements. For a
motor, this type of bearing provides a
relatively rigid support for the output
shaft.
Bearing (Roller)
A special bearing system with cylindrical rollers capable of handling belted
load applications that are too large for
standard ball bearings.
Braking
Braking provides a means of stopping
an AC motor and can be accomplished
in several ways:
1. Motor Mounted or Separately
Mounted Spring Set Brake – This
is a positive action, mechanical,
friction device. Normal configuration is such that when the power is
removed, the brake is set. This can
be used as a holding brake. (Note:
a separately mounted brake is one
which is located on some part of
the mechanical drive train other
than the motor).
2. Eddy-Current Brake – Eddy
currents are generated in the
brake drum to produce braking
torque for retarding or stopping
shaft rotation. Braking torque is
transmitted by the eddy-current
principle when voltage is applied
to the brake coil, with the rate of
shaft deceleration being determined by the amount of excitation
applied to the coil. Braking torque,
which is a function of speed and
AP03902001E For more information visit: www.EatonElectrical.com

Application Note
Page 24 Effective: February 2005
Solid-State Soft Start
Motor Controller and
Starter
brake coil excitation, is provided
throughout most of the speed
range, but drops to zero as the
shaft approaches zero rpm. Therefore, this brake cannot serve as a
holding brake.
3. Friction Brake — An electromag-
netic field is established between
the brake coil and armature
assemblies only while the brake
coil is energized. Upon energizing
the brake coil, these two assemblies are drawn together and stop
shaft rotation by friction. The rate
of shaft deceleration is determined
by the amount of excitation
applied to the coil. As long as
excitation is applied to the brake
coil, the two assemblies will
remain locked together, thereby
servicing as a holding brake.
4. DC Dynamic Braking — A low DC
voltage is applied to the AC motor
stator at low speed. A braking
torque is developed which will
slow the motor down quickly. No
braking torque exists if the shaft is
at zero speed.
Breakaway Torque
The torque required to start a machine
and its load from standstill.
Breakdown Torque
The breakdown torque of an AC motor
is the maximum torque which it will
develop with rated voltage applied at
rated frequency.
C-Face (Motor/Drive Mounting)
This type of motor mounting is used to
closely couple pumps and similar
applications where the mounting
holes in the face are threaded to
receive bolts from the pump. Normally, the C-Face is used where a
pump or similar item is to be overhung
on the motor. This type of mounting is
a NEMA standard design and available
with or without feet.
Cogging
A condition in which a motor does not
rotate smoothly, but “steps” or “jerks”
from one position to another during
shaft revolution. Cogging is most pronounced at low motor speeds and can
cause objectionable vibrations in the
driven machine.
Constant Torque Range
A speed range in which the motor is
capable of delivering a constant
torque, subject to cooling limitations
of the motor.
Contactor
A contactor is a two-state (On-Off)
device for repeatedly establishing and
interrupting an electric power circuit.
Interruption is obtained by introducing
a gap or a very large impedance.
Contactor Reversing
A method of reversing motor rotation
by the use of two separate contactors,
one of which produces rotation in one
direction and the other produces
rotation in the opposite direction.
The contactors are electrically (and
mechanically) interlocked so that both
cannot be energized at the same time.
Continuous Duty
Operation of a motor within the insulation temperature limits after it has
reached normal operating (equilibrium) temperature.
Continuous Rating
The continuous rating is the maximum
constant load that can be carried continuously without exceeding established temperature rise limitations
under prescribed conditions of load
and within the limitations of established standards.
Control Circuit
The control circuit of a control apparatus or system is the circuit which carries the electric signals directing the
performance of the controller, but
does not carry the main circuit power.
Control Device
A control device is an individual device
used to control functions.
Control Transformer Winding
A control transformer winding is a
voltage transformer utilized to supply
voltage suitable for the operation of
control devices.
Controller
A device for controlling a motor.
Critical Frequency or Speed
Any frequency or speed at which
mechanical resonance occurs in the
mechanical drive train or the driven
equipment. To avoid damage due to
vibration, the machine must be
designed to shift the critical speed
away from the operating speed.
Current Limit
An electronic method of limiting the
maximum current available to the
motor. This is adjustable so that the
motor’s maximum current can be controlled. It can also be preset as a protective device to protect both the
motor and controller from extended
overloads.
Current Limit Acceleration
A system of control in which acceleration is governed so that the motor
current does not exceed an adjustable
maximum value.
Current Limiting Fuse
A fuse that, when it is melted by a
current within its specified current limiting range, abruptly introduces a high
impedance to end the current flow.
Current Relay
A current relay functions at a predetermined value of current. It may be an
overcurrent relay, an undercurrent
relay, or a combination of both.
Definite Purpose Motor
A definite purpose motor is any motor
design, listed and offered in standard
ratings with standard operating characteristics and mechanical construction, for use under service conditions
other than usual or for use on a particular type of application (NEMA).
D-Flange (Motor Mounting)
This type of motor mounting is used
when the motor is to be built as part of
the machine. The mounting holes of
the flange are not threaded. The bolts
protrude through the flange from the
motor side. Normally D-Flange motors
are supplied without feet since the
motor is mounted directly to the
driven machine.
di/dt
The rate of change in current versus
time.
Dimension Drawing
A dimensioned or outline drawing
(base plan, floor plan, etc.) is one
which shows the physical space and
mounting requirements of a piece of
equipment. It may also indicate ventilation requirements and space provided for connections or the location
to which connections are to be made.
For more information visit: www.EatonElectrical.com AP03902001E

Solid-State Soft Start
Motor Controller and
Starter
Application Note
Effective: February 2005 Page 25
dv/dt
The rate of change in voltage versus
time. Specially designed resistorcapacitor networks can help protect
the SCRs from excessive dv/dt which
can result form line voltage spikes, line
disturbances and circuit configurations
with extreme forward conducting or
reverse blocking requirements.
Duty Cycle
The relationship between the operating and resting times or repeatable
operation at different loads.
Dwell
The time spend in one state before
moving to the next. In motion control
applications for example, a dwell time
may be programmed to allow time
for a tool change or part clamping
operation.
Eddy-Current
The electrical current induced in metallic components from the change in
magnetic fields. Motor stators are
often laminated to reduce the eddycurrent effect.
Eddy-Current Brake
An eddy-current brake consists of a
rotating member keyed to a straight
through, double extension shaft and a
field coil assembly. The brake rotor
rotates at the speed of the prime
mover until the field coil is energized.
Rotation of the rotor is retarded, by
controlling the current in the field coil.
Efficiency
Ratio of power output to power input
indicated as a percent. In motors, it is
the effectiveness of which a motor
converts electrical power into mechanical power.
EMF
The acronym for electromotive force,
which is another term for voltage or
potential difference.
Enable
To allow an action or acceptance of
data by applying an appropriate signal
to the appropriate input.
Enclosure
Enclosure refers to the housing in
which the controller is mounted.
Enclosures are available in designs for
various environmental conditions:
1. NEMA Type 1 — A general pur-
pose enclosure of either a ventilated or a non ventilated variety. It
is used for most indoor applications and is intended to protect
limited amounts of falling dirt and
accidental human contact with the
electrical circuit.
2. NEMA Type 4 — A watertight
enclosure, required whenever the
unit is subjected to a great amount
of water from any angle. It is normally used in areas that are
repeatedly hosed down. These
enclosures are not designed to be
submerged.
3. NEMA Type 7 — An enclosure
designed for an indoor hazardous
location, Class I (air), Group A, B,
C, or D, per the National Electrical
Code. This hazardous environment is one in which flammable
gases or vapors are or may be
present in the air in quantities sufficient to produce explosive or
ignitable mixtures. This explosion
proof enclosure shall be of such
substantial construction that is will
withstand the internal pressures
resulting from explosions without
bursting, permanently distorting
or loosening its joints.
4. NEMA Type 9 — An enclosure
designed for hazardous locations,
Class II, Groups E, F, and G per the
National Electrical Code. The
atmosphere in which this controller must operate may contain
carbon black, coal or coke dust,
flour, starch or grain dust.
5. NEMA Type 12 — Designed for
industrial use. This enclosure is
intended for use in applications
where it is desirable to exclude
such materials as cooling oil,
seepage, dust, lint, fibers, and filings. This is a non-ventilated
enclosure with an oil resistant,
synthetic gasket between the case
and the cover. The cover is hinged
to swing horizontally and is held in
place with suitable fasteners
which require the use of a tool.
6. JIC — Joint Industry Conference
enclosures are similar in specifications to the NEMA Type 4 and
Type 12 enclosures. The most
obvious difference is the way the
seal is obtained. They are suitable for the use of the standard
NEMA Type 4 and NEMA Type 12
enclosures.
7. Explosion proof enclosures normally meet some, or all of the
following specifications: Class I,
Group D; Class II, Groups E, F
and G; NEMA Type 7 and NEMA
Type 9.
a. Class I, Group D is designed to
meet the application requirements of the NEC and is in
accordance with the latest
specifications of Underwriters
Laboratories, Inc., for locations
having atmospheres containing
gasoline, hexane, naphtha,
benzine, butane, propane, alcohol, acetone, benzol, lacquer
solvent vapors or natural gas.
b. Class II, Groups E, F and G is
designed to meet the application requirements of the NEC
and is in accordance with UL
requirements for atmospheres
containing metal dust, including aluminum, magnesium and
their commercial alloys: and
other metals or similar hazardous characteristics, such as carbon black, coal or coke dust,
flour, starch or grain dusts.
Fault Current
Fault current is a current which results
from the loss of insulation between
conductors or between a conductor
and ground.
Force
The tendency to change the motion or
position of an object with a push or
pull. Force is measured in ounces or
pounds.
Frame Size
The physical size of motor, usually
consisting of NEMA defined “D” and
“F” dimensions at a minimum. The
“D” dimension is the distance in quarter inches from the center of the motor
shaft to the bottom of the mounting
feet. The “F” dimension relates to the
distance between the centers of the
mounting feet holes.
Front of a Motor
The end opposite the coupling or driving pulley (NEMA). This is sometimes
called the opposite pulley end (O.P.E.).
Full Load Current
The input current to a motor operated
at its full load torque and nameplate
voltage and frequency.
Full Load Speed
The speed that the output shaft of the
motor attains with rated load connected at rated voltage.
Full Load Torque
The full load torque of a motor is the
torque necessary to produce rated
horsepower at full load speed.
AP03902001E For more information visit: www.EatonElectrical.com

Application Note
Page 26 Effective: February 2005
Solid-State Soft Start
Motor Controller and
Starter
Gate
The control element of an SCR (silicon
controlled rectifier) commonly referred
to as a thyristor. When a small positive
voltage is applied to the gate momentarily, the SCR will conduct current
(when the anode is positive with
respect to the cathode of the SCR).
Current conduction will continue, even
after the gate signal is removed, as
long as the anode/cathode voltage
relationship is maintained.
General Purpose Motor
This motor has a continuous Class B
insulation rating and NEMA B design,
listed and offered in standard ratings
with standard operating characteristics
and mechanical construction, for use
under usual service conditions without
restriction to a particular application or
type of application (NEMA).
Head
A measurement of pressure, usually
expressed in feet of water. A 30 foot
head is the pressure equivalent to the
pressure found at the base of a column
of water 30 feet high.
Heater Coil (Thermal Overload Relay)
A heater coil is a part of a thermal
overload relay that is intended to produce heat when conducting current.
Heater coils are sometimes referred to
as heaters, thermal units, current elements or heater elements.
Horsepower
A measure of the amount of work that
a motor can perform in a given period
of time.
Hysteresis Loss
The resistance offered by materials to
becoming magnetized results in
energy being expended and a corresponding loss. Hysteresis loss in a
magnetic circuit is the energy
expended to magnetize and demagnetize the core.
Induction Motor
An alternating current motor in which
the primary winding, on one member
(usually the stator), is connected to the
power source. A secondary on the
other member (usually the rotor) carries the induced current. There is no
physical electrical connection to the
secondary winding, its current is
induced.
Inertia
A measure of a body’s resistance to
changes in velocity, whether the body
is at rest or moving at a constant
velocity. The velocity can be either
linear or rotational. The moment of
inertia (WK
weight (W) of an object and the square
of the radius of gyration (K
radius of gyration is a measure of how
the mass of the object is distributed
about the axis of rotation. WK
ally expressed in units of lb-ft
2
) is the product of the
2
). The
2
2
is usu-
.
Integral Horsepower Motor
A motor built in a frame having a continuous rating of 1 hp or more.
Interconnection Diagram
An interconnection diagram is a diagram which shows only the external
connections between controllers and
associated machinery and equipment.
Intermittent Duty
A motor that never reaches equilibrium temperature, but is permitted to
cool down between operations. For
example, a crane, hoist or machine
tool motor is often rated for 15 or 30
minute duty.
Interrupting Capacity
The interrupting capacity is the maximum value of current that a contact
assembly is required to successfully
interrupt at a specified voltage for a
limited number of operations under
specified conditions.
Jogging
Jogging is a means of accomplishing
momentary motor movement by
repetitive application of power.
Kick Start
The momentary application of a high
initial starting torque to break away a
hard to start load. After a short duration, the starting torque or current
limit level returns to the preset value.
Kinetic Energy
The energy of motion possessed by a
body.
Linear Acceleration/Deceleration
A circuit that controls the rate at which
the motor is to accelerate or decelerate
upon a start or stop command.
Locked Rotor Current
Steady state current taken from the
line with the rotor at standstill (at rated
voltage and frequency). This is the current when starting the motor and load.
Locked Rotor Torque
The minimum torque that a motor will
develop at rest for all angular positions of the rotor application of rated
voltage and frequency.
Megohm Meter
A device used to measure an insulation system’s resistance. This is usually measured in megohms and tested
by passing a low current at high voltage through the motor windings and
measuring the resistance of the various insulation systems.
Modular Construction
The major circuit elements are
mounted in replaceable modules,
which can readily be removed and
replaced.
Module
A unit of circuit elements usually packaged so it can be readily replaced.
Multi Motor Operation
A system in which one controller operates two or more motors simultaneously.
Multi-Speed Motor
An induction motor that can operate at
two, three, or four discrete (fixed)
speeds by the selection of various stator winding configurations.
NEC
The National Electrical Code is the
recommendation of the National Fire
Protection Association for electrical
safety and property protection and is
revised every three years. City, county,
or state regulations may differ from
these code regulations and take precedence over NEC rules.
NEMA
The National Electrical Manufacturers
Association is a non-profit organization, organized and supported by
manufacturers of electrical equipment
and supplies. Some of the standards
NEMA promulgates cover: horsepower ratings, speeds, frame sizes and
dimensions, torques and enclosures.
No Load
The state of machine rotating at normal speed under rated conditions, but
when no output is required from it.
OFF Delay
Off delay signifies that the timing
period of a time delay relay is initiated
upon de-energization of its coil.
ON Delay
On delay signifies that the timing
period of a time delay relay is initiated
upon energization of its coil.
Operating Overload
Operating overload is the overcurrent
to which an electric apparatus is subjected in the course of the normal
For more information visit: www.EatonElectrical.com AP03902001E

Solid-State Soft Start
Motor Controller and
Starter
Application Note
Effective: February 2005 Page 27
operating conditions that it may
encounter. For example, those currents in excess of running current
which occur for a short time as a
motor is started or jogged, are considered normal operating overloads for a
control apparatus.
Open Machine (Motors)
A machine having ventilating openings which permit passage of external
cooling air over and around the windings of the machine.
1. Dripproof is an open machine in
which the ventilating openings are
so constructed that successful
operation is not interfered with
when drops of liquid or solid particles strike or enter the enclosure at
any angle from 0 to 15 degrees
downward from vertical.
2. Splash proof is an open machine
in which the ventilating openings
are so constructed that successful
operation is not interfered with
when drops of liquid or solid particles strike or enter the enclosure at
any angle not greater than 100
degrees downward from the
vertical.
3. Semiguarded is an open machine
in which part of the ventilating
openings in the machine, normally
in the top half, are guarded as in
the case of a “guarded machine”,
while the other parts are left open.
4. Guarded (NEMA) is an open
machine in which all openings
giving direct access to live metal
or rotating parts (except smooth
rotating surfaces) are limited in
size by the structural parts of by
the screens, baffles, grilles,
expanded metal or other means to
prevent accidental contact with
hazardous parts. Openings giving
direct access to such live or rotating parts shall not permit the passage of a cylindrical rod 0.75 inch
in diameter.
5. Dripproof Guarded is a dripproof
machine whose ventilating openings are guarded in accordance
with the definition of a guarded
machine.
6. Open Externally Ventilated is one
which is ventilated by means of a
separate motor driven blower
mounted machine enclosure. This
machine is sometimes known as a
blower-ventilated or a force-ventilated machine.
7. Open Pipe Ventilated is basically
an open machine except that
openings for admission of ventilating air are so arranged that inlet
ducts or pipes can be connected to
them. Air may be circulated by
means integral with the machine
or by means external to the
machine (separately or forced ventilated).
8. Weather Protected is an open
enclosure divided into two types:
a. Type 1 enclosures have venti-
lating passages constructed to
minimize the entrance of rain,
snow, airborne particles and
prevent passage of a 0.75 in.
diameter cylindrical rod.
b. Type 2 enclosures provide addi-
tional protection through the
design of their intake and
exhaust ventilating passages.
The passages are so arranged
that wind and airborne particles blown into the machine
can be discharged without
entering directly into the electrical parts of the machine.
Additional baffling is provided
to minimize the possibility of
moisture or dirt being carried
inside the machine.
Overcurrent Relay
An overcurrent relay operates when
the current through the relay, during
its operating period, is equal to or
greater than its setting.
Overload Capacity
The ability of the controller to withstand currents beyond the system’s
continuous rating. It is normally specified as a percentage of full load current
for a specified time period.
Overload Relay
An overload relay is an overcurrent
relay which operates at a predetermined value of current in order to prevent overheating of the motor.
Phase Control
The process of varying the point
within the electrical cycle at which thyristor gating occurs to begin forward
conduction.
Pickup Voltage or Current
The pickup voltage or current of a
magnetically operated device is the
minimum voltage or current at which
the device operates.
Plugging
Plugging refers to a type of motor
braking provided by reversing phase
sequence so that the motor develops a
counter-torque which exerts a retarding force to brake the motor.
Power
Work done per unit of time. Measured
in horsepower or watts:
1 hp = 33,000 ft-lb/min. = 746 watts
Power Factor
Power factor is the ratio of the total
input kW divided by the total input
kVA.
Printed Circuit Board
A board for mounting of separately
manufactured components which
has the connections made by printed
circuitry.
Pull-Up Torque
The minimum torque available after
initial motor start to accelerate the
load to full speed (where breakdown
torque occurs), expressed in percent of
running torque.
Pulse
A pulse is a signal of relatively short
duration.
Pump Control
A special feature on a soft starter
which provides a special shaped ramp
start and stop to reduce the potential
for water hammer in a pump system.
Pushbutton
A pushbutton is a switch having a
manually operable plunger, rocker or
button for actuating the switch.
Reactance
The opposition to the flow of current
made by an inductor or a capacitor.
Relay
An electrically controlled device that
causes electrical contacts to change
status. Open contacts will close and
closed contacts will open when rated
voltage is applied to the coil of relay.
Remote Control
Remote control is a control function
which provides for initiation or change
or a control function from a remote
point.
Reset
To reset is to restore a mechanism,
stored characteristics or device to a
prescribed state.
AP03902001E For more information visit: www.EatonElectrical.com

Application Note
Page 28 Effective: February 2005
Solid-State Soft Start
Motor Controller and
Starter
Reversing
Changing the direction of rotation of
the motor rotor. An AC motor is
reversed by reversing the connection
of two legs on the three-phase power
line.
Rotor
The rotating member of a machine
with a shaft.
Rotor Time Constant
The inductance divided by the resistance of the motor rotor.
Schematic Diagram (Elementary Diagram)
A schematic or elementary diagram is
one that shows all circuits and devices
of a controller. The diagram does not
show the physical arrangement of the
devices or the actual wiring to the
devices.
Service Factor
When used on a motor nameplate, a
number which indicates how much
above the nameplate rating a motor
can be loaded without causing serious
degradation (i.e., a motor with 1.15 S.F.
can produce 15% greater torque than
one with 1.0 S.F.).
Service of a Controller
The service of a controller is the specific application in which the controller
is to be used; for example:
1. General Purpose
2. Definite Purpose
a. Crane and hoist
b. Elevator
c. Machine tool, etc.
Shock Load
The load seen by a clutch, brake or
motor in a system which transmits
high peak loads. This type of load is
present in crushers, separators, grinders, conveyors, winches and cranes.
Silicon Controlled Rectifier (SCR)
A solid-state switch, sometimes
referred to as a thyristor. The SCR has
an anode, cathode and control element called the gate. The device provides controlled rectification since it
can be turned on at will. The SCR can
rapidly switch large currents at high
voltages. It is small in size and low in
weight.
Slip
The difference between rotating magnetic field speed (synchronous speed)
and rotor speed of AC induction
motors. Usually expressed as a percentage of synchronous speed.
Soft Start
A thyristor controlled device for reducing motor inrush current by gradually
increasing the line voltage at start
from zero to full voltage.
Soft Start Controller
A soft start device which provides no
motor protection. Usually used in conjunction with an electromagnetic
motor starter.
Soft Starter
A soft start device which provides
motor overload protection and may
also provide undervoltage, jam or stall
protection.
Solid-State Reduced Voltage
A technique for reduction of line voltage for motor starting by use of a
semiconductor device, normally a thyristor (SCR).
Special Purpose Motor
A motor with special operating characteristics, special mechanical construction or both, designed for a particular
application and not falling within the
definition of a general purpose of definite purpose motor (NEMA).
SSRV
Sold-state reduced voltage.
Starting Torque
The torque exerted by the motor during the starting period (a function of
speed or slip).
Stator
The stationary portion of the magnetic
circuit and the associated windings
and leads of a rotating machine.
Surge
A transient wave of current, voltage or
power in an electric circuit. Note: A
transient has a high rate of change of
current or voltage in the system.
Surge Protection
The process of absorbing and clipping
voltage transients on an incoming AC
line or control circuit. MOVs (Metal
Oxide Varistors) and specially
designed RC (resistor-capacitor)
networks are usually used to accomplish this.
Switch
A switch is a device for opening and
closing, or for changing the connections of a circuit. Note: A switch is
understood to be manually operated,
unless otherwise stated.
Synchronous Speed
The speed of an AC induction motor’s
rotating magnetic field. It is determined by the frequency applied to the
stator and the number of magnetic
poles present in each phase of the stator windings. Mathematically, it is
expressed as: Sync Speed (RPM) = 120
x Applied Frequency (Hz)/Number of
Poles per Phase.
System Efficiency
System efficiency is the ratio of the
mechanical power supplied to load to
the total input power under specified
operating conditions. The input power
includes requirements for auxiliary
functions, such as phase control,
switching equipment, overload protection and fans.
Thermal Overload Relay
A thermal overload relay functions
(trips) by means of a thermal response
to current.
Thermal Protector (Rotating Machinery)
A protective device assembled as an
integral part of a machine that protects
the machine against overheating due
to an overload condition.
Notes:
1. It may consist of one or more temperature sensing elements integral with the machine and a
control device external to the
machine;
2. When a thermal protector is
designed to perform its function
by opening the circuit to the
machine and then automatically
closing the circuit after the
machine cools to a satisfactory
operating temperature, it is an
automatic reset thermal protector;
3. When a thermal protector is
designed to perform its function
by opening the circuit to the
machine but must be reset manually to close the circuit, it is a manual reset thermal protector.
Thyristor
A three junction semiconductor device
that can be switched from the OFFstate to the ON-state by a logic signal.
Also known as a silicon controlled
rectifier.
Time Delay
Time delay means that a time interval
is purposely introduced in the performance of a function.
For more information visit: www.EatonElectrical.com AP03902001E

Solid-State Soft Start
Motor Controller and
Starter
Application Note
Effective: February 2005 Page 29
Torque
A turning force applied to a shaft,
tending to cause rotation. Torque is
normally measured in pound feet and
is equal to the force applied, times the
radius through which it acts.
Totally Enclosed Machine (Motor)
A totally enclosed machine is one so
enclosed as to prevent the free
exchange of air between the inside and
the outside of the case, but not sufficiently enclosed to be termed airtight.
1. Totally Enclosed Fan-Cooled is a
totally enclosed machine
equipped for exterior cooling by
means of a fan or fans integral
with the machine, but external to
the enclosing parts.
2. Explosion Proof is a totally
enclosed machine whose enclosure is designed and constructed
to withstand an explosion of a
specified gas or vapor which may
occur within it, and to prevent the
ignition of the specified gas or
vapor surrounding the machine
by sparks, flashes or explosions
of the specified gas or vapor,
which may occur within the
machine casing.
3. Dust-Ignition-Proof is a totally
enclosed machine whose enclosure is designed and constructed
in a manner which will exclude
ignitable amounts of dust or
amounts that might affect performance or rating, and will not permit arcs, sparks or heat, otherwise
generated or liberated inside of
the enclosure, to cause ignition of
exterior accumulations or atmospheric suspensions of a specific
dust on, or in, the vicinity of the
enclosure.
4. Waterproof is a totally enclosed
machine constructed so that it will
keep out water sprayed onto it.
Leakage may occurred around the
shaft, but will be prevented from
entering the oil reservoir. Provision is made for automatically
draining the machine. The means
for automatic draining may be a
check valve or a tapped hole at the
lowest part of the frame which will
serve for application of a drain
pipe.
5. Totally Enclosed Water Cooled is a
totally enclosed machine which is
cooled by circulating water, the
water or water conductors coming
in direct contact with the machine
parts.
6. Totally Enclosed Water-Air Cooled
is a totally enclosed machine
which is cooled by circulating air
which, in turn, is cooled by circulating water. It is provided with a
water cooled heat exchanger for
cooling the internal air and a fan,
or fans integral with the rotor shaft
or separate, for circulating the
internal air.
7. Totally Enclosed Air to Air Cooled
is a totally enclosed machine
which is cooled by circulating the
internal air through a heat
exchanger which, in turn, is
cooled by circulating external air.
It is provided with an air to air heat
exchanger for cooling the internal
air, a fan or fans integral with the
rotor shaft, or separate for circulating the internal air and a separate fan for circulating the external
air.
8. Totally Enclosed Fan Cooled
Guarded is a totally enclosed fan
cooled machine, in which all openings giving direct access to the fan
are limited in size by the design of
the structural parts of by screens,
grilles, expanded metal, etc., to
prevent accidental contact the
with the fan. Such openings shall
not permit the passage of a cylindrical rod, 0.75 inch in diameter,
and a probe shall not contact the
blades, spokes or other irregular
surfaces of the fan.
9. Totally Enclosed Air-Over is a
totally enclosed machine intended
for exterior cooling by a ventilating means external to the
machine.
Transient
A momentary deviation in an electrical
or mechanical system.
Trigger Circuit
The circuit used to gate a thyristor that
causes it to conduct current.
Undervoltage Protection
Undervoltage or low voltage protection is the effect of a device, operative
on the reduction or failure of voltage,
to cause and maintain the interruption
of power to the main circuit. The main
objective of the device is to prevent
restarting of the equipment on an undervoltage condition.
Ventilated Enclosure
A ventilated enclosure is provided with
means to permit circulation of sufficient air to remove an excess of heat,
fumes, or vapors.
Voltage Relay
A voltage relay operates at a predetermined value of voltage. It may be an
overvoltage relay, an undervoltage
relay, or a combination of both.
Wiring (or Connection) Diagram
A wiring, or connection diagram is one
which locates, and identifies electrical
devices, terminals and interconnecting
wiring in an assembly.
Work
A force moving an object over a
distance. Measured in foot pounds
(ft-lbs).
Work = Force x Distance.
AP03902001E For more information visit: www.EatonElectrical.com
 Loading...
Loading...