CBS 1000

Cherokee NightRider-150, CBS 1000 User Manual

Wolfgang Rolke

Theoretische Untersuchung von Breitbandantennen mit Realisierung einer logarithmisch-periodischen Dipolantenne

Inhaltsverzeichnis

Einleitung................................................................................................................................................................. 2

1. Theorie der Antenne............................................................................................................................................ 3

1.1. Grundbegriffe...................................................................................................................................... 3

1.1.1. Definition der Antenne....................................................................................................... 3

1.1.2. Die elektromagnetische Welle........................................................................................... 3

1.2. Elementarquellen................................................................................................................................ 4

1.2.1. Isotroper Kugelstrahler......................................................................................................4

1.2.2. Hertzscher Dipol................................................................................................................ 4

1.2.3. Fitzgeraldscher Dipol ......................................................................................................... 5

1.2.4. Huygenssche Elementarquelle.......................................................................................... 5

1.3. Kenngrößen........................................................................................................................................ 6

1.3.1. Polarisation........................................................................................................................ 6

1.3.2. Richtcharakteristik und Richtdiagramm............................................................................. 6

1.3.3. Der Richtfaktor................................................................................................................... 6

1.3.4. Der Antennengewinn......................................................................................................... 7

1.3.5. Antennenimpedanz............................................................................................................ 7

1.3.6. Mittlerer Wellenwiderstand................................................................................................8

1.3.7. Verkürzungsfaktor .............................................................................................................8

1.3.8. Welligkeit und Stehwellenverhältnis.................................................................................. 9

1.3.9. Bandbreite......................................................................................................................... 9

2. Breitbandige Antennen...................................................................................................................................... 11

2.1. Dicker Leiter ..................................................................................................................................... 11

2.1.1. Dicker zylindrischer Dipol................................................................................................ 11

2.1.2. Ebener Flächenstrahler...................................................................................................13

2.2. Babinet-Prinzip ................................................................................................................................. 13

2.3. Winkelprinzip .................................................................................................................................... 14

2.4. Logarithmisch-periodisches Prinzip.................................................................................................. 15

2.5. Zusammenfassung........................................................................................................................... 16

3. Ausführungsformen von Breitbandantennen..................................................................................................... 17

3.1. Stabantennen und Dipole................................................................................................................. 17

3.1.1. Kegelantenne ..................................................................................................................17

3.1.2. Gefalteter Dipol................................................................................................................ 17

3.2. Abgeschlossene Langdrahtantenne................................................................................................. 18

3.3. Wendelantenne ................................................................................................................................ 19

3.4. Trichterantenne................................................................................................................................. 21

3.5. Spiralantenne ................................................................................................................................... 21

3.5.1. Winkelkonstante Spiralantenne....................................................................................... 21

3.5.2. Archimedische Spiralantenne.......................................................................................... 22

3.6. Logarithmisch-periodische Antenne................................................................................................. 23

3.7. Speisung von Breitbandantennen..................................................................................................... 25

3.7.1. Frequenzgangkompensation........................................................................................... 26

3.7.2. Impedanzwandler............................................................................................................ 26

3.7.3. Symmetrierglieder ........................................................................................................... 27

3.8. Epilog zu den Breitbandantennen..................................................................................................... 27

4. Entwicklung einer log.-per. Dipolantenne.......................................................................................................... 29

4.1. Elektrische Dimensionierung............................................................................................................ 29

4.1.1. Geometrie der LPDA.......................................................................................................29

4.1.2. Aktive Zone der LPDA.....................................................................................................31

4.1.3. Physikalische Kenngrößen.............................................................................................. 33

4.1.4. Impedanz der LPDA........................................................................................................34

4.1.5. Hinweise zur Dimensionierung........................................................................................ 36

4.1.6. Berechnung der LPDA-Parameter................................................................................... 37

4.2. Mechanischer Aufbau....................................................................................................................... 40

4.3. Meßergebnisse................................................................................................................................. 41

Anhang A: Programm-Listing................................................................................................................................. 43

Anhang B: Literaturverzeichnis.............................................................................................................................. 45

Anhang C: Meßkurven........................................................................................................................................... 46

Seite: 1

Breitbandantennen Seite 2

Einleitung

Die hohe Anzahl verschiedener Funkdienste mit ihren vielfältigen Übertragungsf ormen erfordern Antennen mit sehr individuellen Eigenschaften.

In diesem Dokument werden speziell Antennenformen mit einer großen Bandbreite beschrieben.

Breitbandantennen können für den Kurzwel lenbereich bis hin zum Mikrowellenbereich konstruiert werden.

Im Kurzwellenbereich ist man oft auf Breitbandantennen angewiesen, weil die tages- und jahreszeitabhängigen Änderungen der Weitverkehrs-Übertragungsbedingungen einen häufigen Frequenzwechsel erfordern.

Im Ultrakurz- und Mikrowellenbereich sind die Einsatzgebiete von breitbandigen Antennen sehr vielfältig. Diese werden von Funkdiensten mit breitbandigen Übertragungstechniken oder mit oft wechselnden Betriebsfrequenzen benötigt. Dazu gehören Meß- und Überwachungsdienste, Posten für elektronische Gegenmaßnahmen (ECM), der Satellitenfunk sowie die Radioastronomie.

Oft ist es auch sinnvoll, mehrere schmalbandige Einzelantennen durch eine Breitbandantenne zu ersetzen, um einen kontinuierlichen Frequenzverlauf über mehrere Bänder zu erhalten (z.B. beim Fernsehund Tonrundfunk). Zudem werden dadurch Materialkosten eingespart und die statische Auslastung eines Antennenträgers reduziert.

Als letztes sei der Einsatz von extrem breitbandigen Antennen in Meßlaboren erwähnt, in denen die elektromagnetische Verträglichkeit (EMV) von Geräten untersucht werden.

Dieses Dokument ist in vier Abschnitte unterteilt:

Im 1. Kapitel wird kurz auf die Theorie der Antenne eingegangen. Dabei werden alle Grundbegriffe erläutert, die für diese Abhandlung wichtig sind.

Die theoretischen Prinzipien von Breitbandantennen werden dann detailliert im 2. Kapitel besprochen.

Die praktischen Realisierungen bzw. die Beschreibung der wichtigsten Ausführungsformen von Breitbandantennen sind dann im Kapitel 3 zu finden.

Im letzten Kapitel wird abschließend, Schritt für Schritt, die Entwicklung einer logarithmisch-periodischen Dipolantenne geschildert.

Breitbandantennen Seite 3

1. Theorie der Antenne

1.1. Grundbegriffe

1.1.1. Definition der Antenne

In der drahtlosen Nachrichtenübertragungstechnik hat die Antenne im Sendefall die Aufgabe, die vom Sender gelieferte Leitungswelle in die Freiraumwelle umzuwandeln bzw. im Empfangsfall die Freiraumwelle in eine Leitungswelle zu wandeln, welche dann den Empfänger speist. Die Antenne wird deshalb auch als Wellentypwandler bezeichnet.

Damit die Abstrahlung bzw. der Empfang der elektromagnetischen Wellen reflexionsfrei erfolgt, muß die Antenne den Leitungswellenwiderstand Z

ZF0= 120πΩ (1)

anpassen. Dieses erreicht man durch Formgebung und Größe der Antenne.

an den Feldwellenwiderstand des freien Raums

Für alle normalen Antennenanordnungen, die keine nichtlinearen und nichtreziproken Elemente wie Verstärker und Ferrite enthalten, gilt das Reziprozitätstheorem [3], [6]. Das bedeutet, daß die gleiche Antenne zum Empfang und Senden verwendet werden kann, ohne das sich dabei ihre charakteristischen Eigenschaften bzw. Kenngrößen ändern. In diesem Dokument gelten alle Angaben bezüglich des Empfangsfalles also entsprechend auch im Sendefall und umgekehrt.

1.1.2. Die elektromagnetische Well e

Im Vergleich zur Schwingung, die durch eine zeitliche Änderung von physikalischen Größen beschrieben wird, wird die Welle durch zeitliche und räumliche Änderungen physikalischer Größen bestimmt.

Die Kenngrößen der elektromagnetischen Welle sind

• die Periodendauer T,

• die Frequenz f,

• die Wellenlänge

Zwischen ihnen besteht folgender Zusammenhang:

==⋅

=⋅

c 310

(2)

Die elektromagnetische Welle tritt beim offenen Schwingkreis auf, welcher als Antenne wirkt. Diese führt zu einer Abstrahlung und erzeugt ein elektromagnetisches Feld.

Die Kenngrößen des elektromagnetischen Feldes sind

• die elektrische Feldstärke

• die magnetische Feldstärke

• der Feldwellenwiderstand Z

, .

Breitbandantennen Seite 4

Zwischen ihnen besteht folgender Zusammenhang [7]:

== = ≈

Die Antennenstrahlung kann durch den Vektor der elektromagnetischen Leistungsdichte (Poynting-Vektor) charakterisiert werden. Er gibt die Richtung und den Leistungsfluß der Welle je m an.

Im Normalfall ist der Abstand zwischen der Sende- und Empfangsantenne sehr groß, verglichen mit den Abmessungen der Sendeantenne und der Freiraumwellenlänge. Vom Empfangsort aus betrachtet scheint dann die Antennenstrahlung von einem einzigen Punkt, dem sogenannten Phasenzentrum, auszugehen. In diesem Fall befindet sich die Empfangsantenne in der Fernfeldregion. Im Fernfeld kann eine ebene Wellenfront angenommen werden; d.h. Flächen gleicher Phase sind parallele Ebenen. Der Fernfeldabstand [7] ist gegeben durch

376 68 120, ΩπΩ (3)

D≥>2

, wobei . (4)

SEH=×

Dabei ist r der Abstand Sendeantenne - Empfangsantenne und D

die größte Antennenabmessung. Den

Bereich zwischen Sendeantenne und Fernfeldregion bezeichnet man als Nahfeldregion bzw. Nahfeld.

1.2. Elementarquellen

1.2.1. Isotroper Kugelstrahler

Der isotrope Kugelstrahler [9] ist eine hypothetische, verlustfreie Antenne, die in alle Richtungen des Kugelraumes gleichmäßig abstrahlt. Sie erzeugt im Abstand r winkelunabhängig die Leistungsdichte

ist dabei die Strahlungsleistung der Antenne.

Obwohl der isotrope Kugelstrahler praktisch nicht realisiert werden kann, ist er als theoretische Vergleichsantenne durchaus sinnvoll. So wird der Gewinn einer Antenne meistens in Bezug auf den isotropen Kugelstrahler angegeben.

1.2.2. Hertzscher Dipol

(5)

Der Hertzsche Dipol (elektrischer Elementardipol) [7], [9] ist ein fiktiver Strahler, dessen Länge

∆

infinitesimal kurz ist und bei dem eine konstante Stromverteilung angenommen wird. In der Praxis kann er durch einen Dipol angenähert werden, dessen Länge L klein gegenüber der Wellenlänge

L <

ist.

(6)

Eine nahezu konstante Strombelegung kann durch entsprechend große Dachkapazitäten gebildet werden. Der Hertzsche Dipol beschreibt das Feld eines elementaren Stromelements. Durch Überlagerung äquivalenter Hertzscher Dipole können die Felder stromführender Leiter berechnet werden. Dabei gilt für das Gesamtfeld des Hertzschen Dipols in der Fernfeldregion:

Breitbandantennen Seite 5

∆

sin( )

∆

−

sin( )

−

(7)

(8)

(9)

1.2.3. Fitzgeraldscher Dipol

Ersetzt man beim Hertzschen Dipol den eingeprägten elektrischen Strom I prägten magnetischen Strom I

, so erhält man den Fitzgeraldschen Dipol (magnetischer

durch einen dualen einge-

Elementardipol) [9]. In der Praxis erreicht man dieses, in dem man durch eine elektrisch kleine Leiterschleife der Fläche A einen konstanten Strom I

IIA

∆=ωµ

führt. Es gilt dann:

(10)

In der Fernfeldregion erhält man für den Fitzgeraldschen Dipol:

∆

=−

sin( )

∆

sin( )

−

(11)

(12)

1.2.4. Huygenssche Elementarquelle

Nach dem Huygensschen Gesetz bildet jeder Punkt einer primären Wellenfront ein Erregungszentrum einer sekundären Kugelwelle. Innerhalb eines Ausschnitts der Wellenfront mit den Seitenlängen

∆

und

∆

kann eine solche Sekundärquelle durch eine Überlagerung aus Hertzschem- und Fitzgeraldschem Dipol beschrieben werden. Diese bezeichnet man dann als Huygenssche Elementarquelle [9]. Ihre Felder erhält man durch folgende Gleichungen:

∆∆

cos( ) sin( )

∆∆

cos( ) cos( )

ϑϕ

−

(13)

(14)

−

(15)

Breitbandantennen Seite 6

=−

und EI

∆∆ ∆

(16)

Dabei ist

∆∆ ∆

Mit diesen Formeln kann z.B. das Strahlungsfeld bzw. die Richtcharakteristik einer

Aperturantenne be-

rechnet werden.

1.3. Kenngrößen

1.3.1. Polarisation

Die Polarisation [7], [10] gibt die Richtung des Vektors der elektrischen Feldstärke in der ausgestrahlten elektromagnetischen Welle an. Man unterscheidet dabei zwischen linearer und kreisförmiger Polarisation. Bei der linearen Polarisation verlaufen die elektrischen Feldlinien geradlinig. Sind sie senkrecht zur Erdoberfläche gerichtet, spricht man speziell von vertikaler Polarisation; verlaufen sie horizontal zur Erdoberfläche, so liegt horizontale Polarisation vor. Ist die Richtung der elektrischen Feldkomponente nicht fixiert, sondern läuft kontinuierlich in Kreisform, dann spricht man von zirkularer Polarisation. Je nach Umlaufsinn unterscheidet man hier noch in rechtsdrehender und linksdrehender Polarisation.

1.3.2. Richtcharakteristik und Ri cht di agramm

Die Richtcharakteristik bzw. Strahlungscharakteristik beschreibt die Richtungsabhängigkeit der Amplitude, Phase und Polarisation der von der Antenne erzeugten Feldstärke. In der Praxis bezieht man sich jedoch nur auf die Amplitude der elektrischen oder magnetischen Feldstärke E

die von einer Antenne aufgenommenen Empfangsspannung U

. Es wird die Richtcharakteristik auf

(ϕ,ϑ)

den Maximalwert bezogen angegeben:

(ϕ,ϑ)

bzw. H

(ϕ,ϑ)

oder auf

(,)

ϕϑ

ϕϑ ϕϑ ϕϑ

== = (17)

max

(,)

max

(,)

max

Betrachtet man lediglich eine oder mehrere Schnittebenen der Richtcharakteristik und stellt diese grafisch dar, erhält man das Richtdiagramm bzw. Strahlungsdiagramm. Schnitte durch die E-Ebene bzw. durch die H-Ebene werden speziell Vertikal- und Horizontaldiagramm genannt.

1.3.3. Der Richtfaktor

Gegenüber Rundstrahlantennen, welche in alle Raumrichtungen annähernd gleich stark strahlen, haben Richtantennen eine mehr oder minder stark ausgeprägte Vorzugsrichtung. Der Richtfaktor D ist das Verhältnis der Strahlungsleistungsdichte S

der Antenne in Hauptstrahlungsrichtung verglichen mit der

max

Strahlungsleistungsdichte des isotropen Kugelstrahlers als Referenzantenne bei gleicher Strahlungsleistung P

Flächenstrahler mit ebener Strahlungsöffnung

[9].

max

(18)

konst.

P==

Breitbandantennen Seite 7

⋅

ππ

Cdd

ges

ϑϕ

ges,max

(,)sin()

ϕϑ ϑ ϑ ϕ

(19)

1.3.4. Der Antennengewinn

Der Gewinn G ist das Verhältnis der Strahlungsleistungsdichte S

der Antenne in Hauptstrahlungsrich-

max

tung verglichen mit der Strahlungsleistungsdichte des isotropen Kugelstrahlers als Referenzantenne bei gleicher zugeführter Eingangsleistung P

max

konst.

Der Gewinn ist über den Antennenwirkungsgrad

=⋅

[7], [9].

(20)

mit dem Richtfaktor verknüpft.

(21)

Wird statt des isotropen Kugelstrahlers der Hertzsche Dipol als Referenzantenne benutzt, gilt:

(22)

15,

Bezieht man sich auf den Halbwellendipol:

(23)

164,

In der Praxis wird statt des Gewinnfaktors oft der Gewinnpegel g = 10 log G in dB angegeben.

1.3.5. Antennenimpedanz

Ri Ra=Rr+Rl

≈

Bild 1 Ersatzschaltbild der Antenne im Sendefall

jXa

Ra=Rr+Rl jXa

≈

Bild 2 Ersatzschaltbild der Antenne im Empfangsfall

Breitbandantennen Seite 8

Der Realteil des Antennenwiderstandes einer verlustbehafteten Antenne besteht aus dem Strahlungswiderstand R

Der Strahlungswiderstand des verlustlosen Hertzschen Dipols beträgt [7]:

Für die Antennenimpedanz eines infinitesimal dünnen Halbwellendipols mit sinusförmiger Stromverteilung gilt [6]:

und dem Verlustwiderstand Rl.

−2

t0 t

G H

∆

Ω

(24)

(25)

(26)

ZRX

AA A

=+ − +

=Ω

Dabei ist C die Eulersche Konstante (C = 0,577215664901532...)

Um nun den Halbwellendipol bei Resonanz betreiben zu können, muß jX Kürzen der Dipollänge h um den Faktor 0,96 erreicht.

=⋅048

Res

1.3.6. Mittlerer Wellenwiderstand

Antennen weisen eine bestimmte Induktivität und Kapazität auf, welche im Gegensatz zu gestreckten elektrischen Leitungen nicht entlang des Leiters konstant sind. So fällt bei Antennen die Kapazität zu den Strahlerenden hin ab. Dieses wird deutlich, wenn man durch Aufklappen einer Zweidrahtleitung einen Dipol entstehen läßt.

Analog zur Leitungstheorie wird der Wellenwiderstand einer verlustlosen Antenne wie folgt definiert [9]:

30 2 2 2

73 13 42 54

ln() () ()

Ci jSi

ππ πΩ

(27)

= 0 werden. Dieses wird durch

(28)

Dabei ist C' der Kapazitätsbelag. Er gibt die Kapazität pro Längeneinheit an der betrachteten Stelle des Antennenleiters an. Entsprechend ist L' der Induktivitätsbelag und gibt die Selbstinduktion pro Längeneinheit an. Werden C' und L' als konstant angenommen, so erhält man den mittleren Wellenwiderstand

1.3.7. Verkürzungsfaktor

Die in Gleichung 28 beschriebene elektrische Länge eines Strahlers gilt nur für einen unendlich dünnen Leiter der in völlig freier Umgebung betrieben wird. Reale Dipole müssen schon wegen der mechani-

′

(29)

Breitbandantennen Seite 9

schen Festigkeit eine Mindestdicke besitzen und befinden sich immer in der Nähe von Bäumen, Häusern und vor allem nahe des Erdbodens. Dadurch haben die Dipolenden mehr Kapazität als im Idealzustand, und die Resonanzfrequenz sinkt. Um die mechanische Länge einer Antenne zu bestimmen, muß der Verkürzungsfaktor V, welcher abhängig vom Schlankheitsgrad s der Antenne ist, berücksichtigt werden.

(30)

s=+1

= (31)

Es sind h die Leiterlänge und d der Leiterdurchmesser der Antenne. Die physikalische Antennenlänge eines Halbwellendipols erhält man also aus

Phy

λλ

.=⋅⋅=⋅+⋅048 048

(32)

1.3.8. Welligkeit und Stehwellenverhältnis

Ist der Antenneneingangswiderstand Z

gleich dem Wellenwiderstand ZL der Versorgungsleitung, nimmt

die Antenne genau den Strom auf, den die Leitung bei der angelegten Spannung führt. Es besteht Anpassung. Jede Abweichung bedeutet eine Fehlanpassung. Dabei kann die Antenne den Strom bzw. die Spannung nicht vollständig aufzehren, und ein Teil davon läuft in die Leitung zurück. Ist die Leitung offen oder kurzgeschlossen, wird die elektromagnetische Welle am Ende völlig reflektiert, und man spricht von Totalreflektion.

Ein Maß für die Anpassung ist der Welligkeitsfaktor s oder das Stehwellenverhältnis VSWR, das aus den Amplituden von hin- und rücklaufender Welle bestimmt wird.

VSWR

(33)

−

1.3.9. Bandbreite

Die Bandbreite einer Antenne beschreibt das Frequenzintervall, in dem die elektrischen Eigenschaften dieser Antenne konstant bleiben bzw. sich nur um zulässige Werte ändern. Dazu gehören in erster Linie

• die Kontinuität der Eingangsimpedanz,

• die Form des Richtdiagramms,

• das Polarisationsverhalten.

Man spricht allgemein von einer Breitbandantenne, wenn innerhalb einer Oktave das Stehwellenverhältnis den Faktor 2 nicht überschreitet [14].

VSWR

≤≥20 20,, im Bereich

(34)

Breitbandantennen Seite 10

Als Maß der Bandbreite wird bei Schmalbandantennen das Verhältnis von Arbeitsfrequenzintervall zur Mittenfrequenz in Prozent angegeben:

−

⋅100%

(35)

Bei Antennen mit größerer Bandbreite als das Verhältnis von oberer Grenzfrequenz zur unteren Grenzfrequenz:

(36)

Die Werte für f

und fu sind abhängig vom Typ und dem Einsatz der Antenne. Meistens werden die bei-

den Eckfrequenzen aufgeführt, in deren Bereich das Stehwellenverhältnis einen bestimmten Wert nicht überschreitet.

Bei Richtantennen ändert sich während entsprechender Frequenzvariation das Richtdiagramm und die Hauptstrahlungsrichtung oft mehr als die Eingangsimpedanz. Hier wird zur Bestimmung der Bandgrenzen die Formänderung des Richtdiagamms und vereinzelt der Abfall des Antennengewinns herangezogen.

Oberhalb einer bestimmten Frequenzgrenze wird die Polarisation von zirkular polarisierten Antennen zunehmend elliptisch. Zur Definition der Bandbreite wird hier ein Achsenverhältnis der Polarisationsellipse von 2:1 als Grenzwert benutzt.

Breitbandantennen Seite 11

2. Breitbandige Antennen

Es gibt mehrere Konzepte, eine Antenne breitbandig zu gestalten.

1. Prinzip des dicken Leiters: Die einfachste, aber auch uneffektivste Methode ist es, die Elemente ei-

ner Antenne aus dicken Leitern zu konstruieren.

2. Das erweiterte Babinet-Prinzip: Eine Antenne deren Form zu sich selber komplementär ist, hat ei-

nen frequenzunabhängigen Eingangswiderstand und ist somit breitbandig.

3. Das Winkelprinzip: Eine frequenzunabhängige Antenne erhält man, wenn die Geometrie der An-

tennenstruktur nur durch Winkel beschrieben wird.

4. Das logarithmisch-periodische Prinzip: Besteht die Struktur einer Antenne aus mehreren Reso-

nanzelementen, deren Abmessungen sich gemäß den Gliedern einer geometrischen Reihe abstufen, so erhält man eine pseudofrequenzunabhängige Antenne.

Fast alle praktischen Breitbandantennen können aus mindestens einem dieser vier Prinzipien ableitet werden. Sie werden in den folgenden Abschnitten im einzelnen beschrieben.

2.1. Dicker Leiter

2.1.1. Dicker zylindrischer Dipol

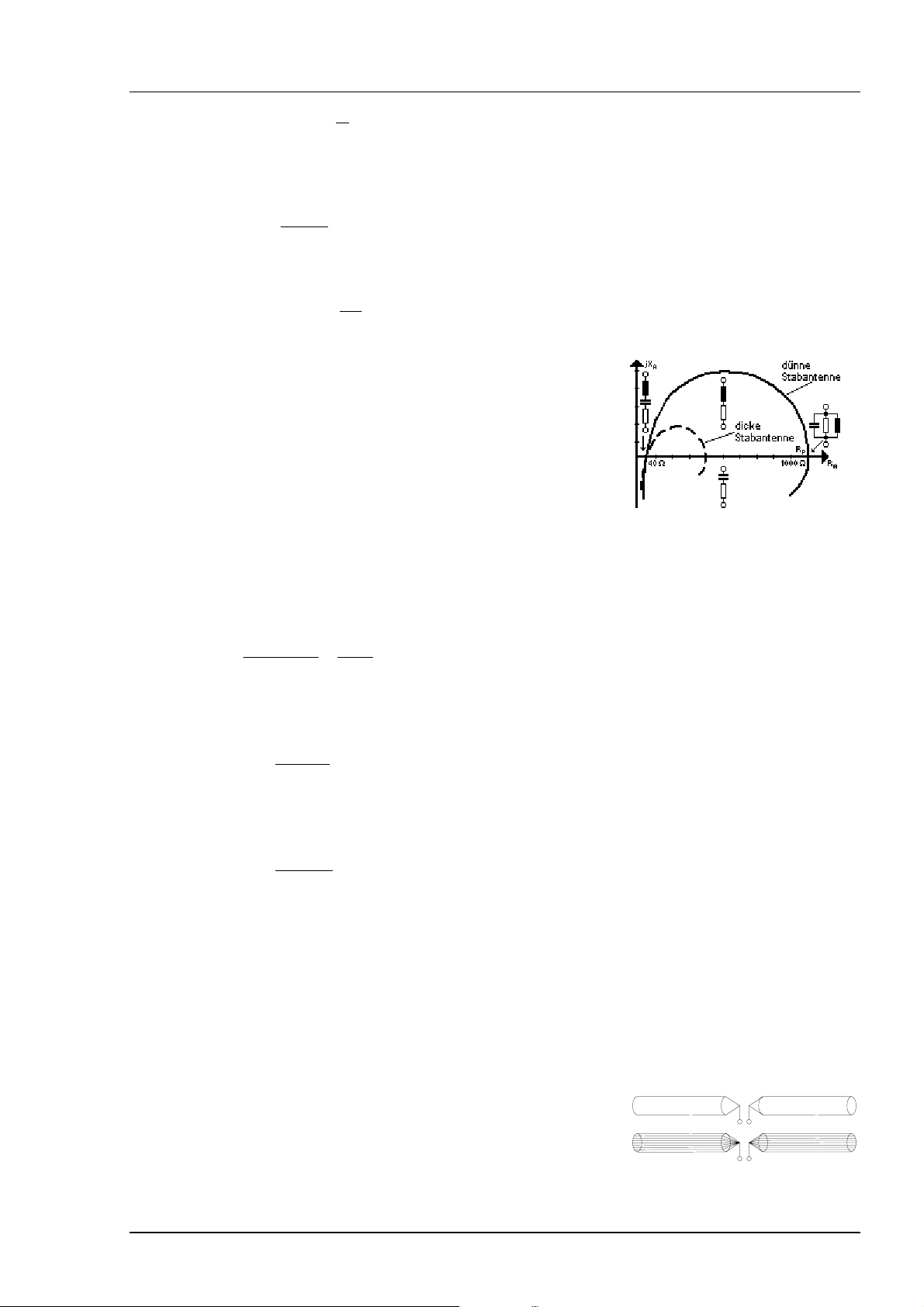
Innerhalb eines bestimmten Frequenzbereiches darf sich bei einer Breitbandantenne deren Antenneneingangsimpedanz nur geringfügig ändern. Diese ist vom Schlankheitsgrad der Antenne abhängig.

Bild 3 Impedanzverlauf eines Dipols

Bild 4 Eingangsimpedanz eines Dipols

Bild 5 Eingangsimpedanz bei der 2. Resonanz

Bild 6 VSWR bei unterschi edl i chem Schlankheits grad

Bild 3 zeigt den Eingangsimpedanzverlauf einer Dipolantenne als Funktion der Länge, jeweils für den Schlankheitsgrad 60 und 2000. Es ist zu sehen, daß die Änderung des Blindwiderstandes jX tennenimpedanz als Funktion der Länge bei dicken Strahlern kleiner ist als bei Strahlern mit großem Schlankheitsgrad. Bild 5 zeigt noch deutlicher, daß die Frequenzabhängigkeit der Antennenimpedanz bei kleinerem Schlankheitsgrad geringer ist. Entsprechend verbessert sich auch die Anpassung der Antenne (Bild 6).

Die Dicke eines Strahlers wirkt sich sehr stark auf den Antenneneingangswiderstand bei der zweiten Antennenresonanz R gleich bleibt. R

aus, während die Eingangsimpedanz bei der ersten Antennenresonanz R1 nahezu

beträgt bei der

/4-Stabantenne ca. 40 Ω und beim

/2-Dipol ca. 80 Ω. R2 ist mit R

über den natürlichen Antennenwiderstand Zn verknüpft [13]:

der An-

(37)

Breitbandantennen Seite 12

==150 150log log (38)

ist zudem vom mittleren Wellenwiderstand ZM abhängig. Bei relativ dünnen Stabantennen gilt:

≈

160

=−

120

Einen dicken Halbwellendipol erhält man, in dem man sich mehrere dünne Halbwellendipole parallelgeschaltet denkt. Dabei addieren sich die Kapazitätsbeläge, während sich die Induktivitätsbeläge vermindern. Der mittlere Wellenwiderstand Z und infolgedessen auch R hängigkeit der Eingangsimpedanz zur Folge.

Die Antennenimpedanz kann in Resonanznähe durch einen gleichwertigen Resonanzkreis dargestellt werden (Bild 7). An der ersten Antennenresonanz (h/ resonanz (h/ eine Kreisgüte Q definiert werden. Eine Anpassung der Antenne ist lediglich in einem begrenzten Frequenzbereich möglich:

≈ 1) durch einen Parallelkreis (Spannungsresonanz). Entsprechend kann für die Antenne

Ω

F H

. Dies hat eine geringere Frequenzab-

≈ 0,5) durch einen Reihenkreis (Stromresonanz) und an der zweiten Antennen-

(39)

1ln Ω (40)

wird dadurch kleiner

Bild 7 Impedanzverlauf einer Stabantenne

−

max min

ff Q

max min

Für eine

/4-Stabantenne berechnet sich die Antennengüte [3], [13] zu

und für eine

Bild 8 Äquivalente Kreisgüte Q einer Antenne

Bild 9 Größte mögliche Bandbreite

Man erhält für die erste Antennenresonanz etwas höhere Güten als an der zweiten Antennenresonanz (Bild 8). Da die Bandbreite der Antenne mit steigender Güte abnimmt, ist es für eine große Bandbreite vorteilhaft, die zweite Resonanzstelle zu wählen (Bild 9).

/2-Stabantenne gilt

⋅1π

⋅

≈

Res1

Res2

≈

310...

26...

⋅

(41)

(42)

(43)

Breitbanddipole bzw. breitbandige Stabantennen werden aus dicken Metallzylindern oder aus reusenförmigen Drahtkäfigen erstellt (Bild 10). Dabei weisen jedoch die Querschnittsflächen der Dipolhälften am Speisepunkt eine große Kapazität gegeneinander auf. Um nun die dünne Speiseleitung besser anpassen zu können, werden die dicken Elemente am Speisepunkt konisch verjüngt.

Bild 10 Dicke Dipole

Breitbandantennen Seite 13

2.1.2. Ebener Flächenstrahler

Um die Abhängigkeit der Eingangsimpedanz einer Antenne von der Frequenz zu verringern, ist es ausreichend, den Querschnitt eines Strahlers nur in einer Richtung zu vergrößern [3].

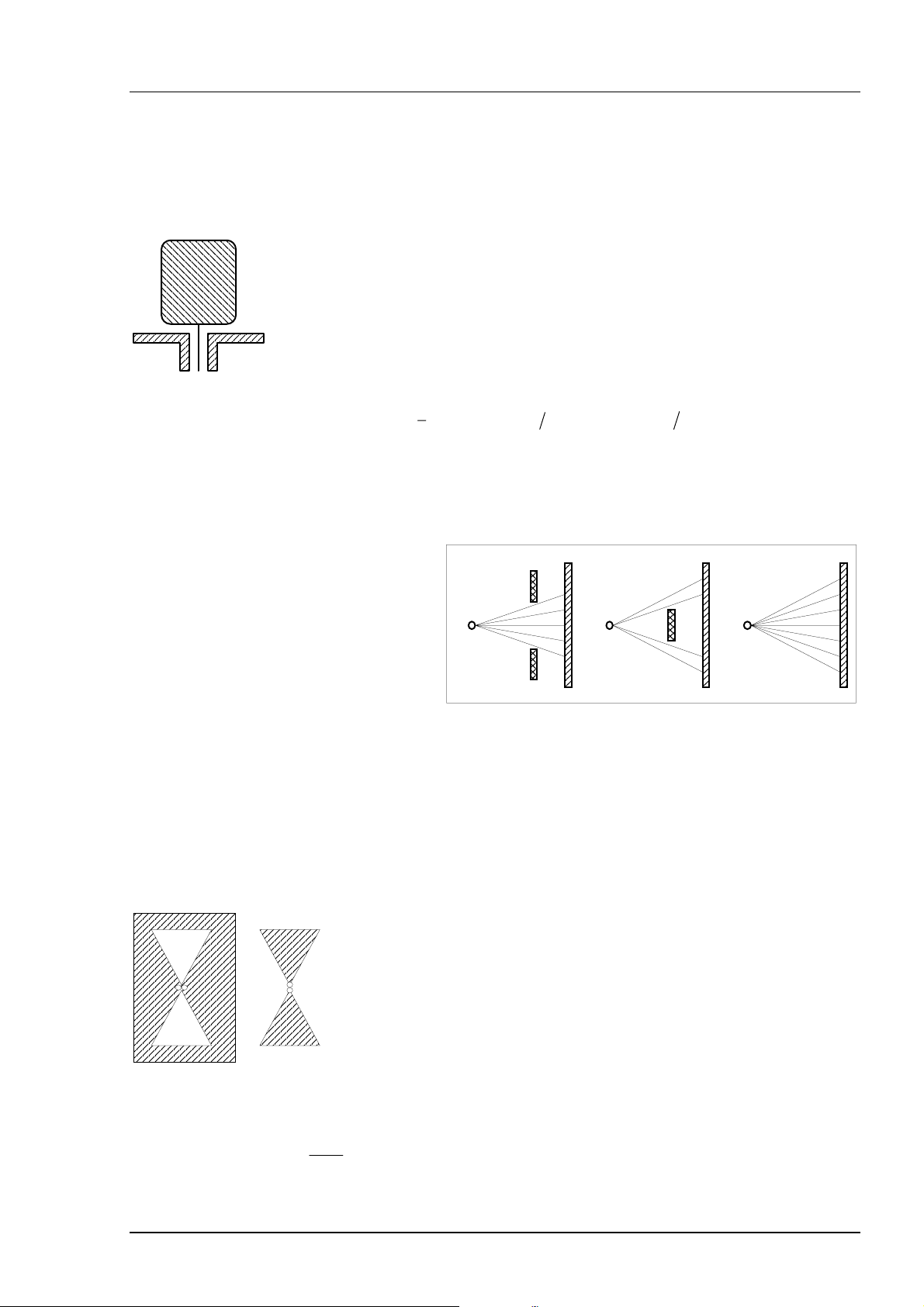
Wird eine rechteckige ebene Platte, dessen Speisepunkt in der Mitte einer Seite liegt, senkrecht zu einer leitenden Ebene montiert (Bild 11), so kann eine Bandbreite von 3:1 erreicht werden. Die Welligkeit ist stark von der Höhe des Strahlers über der leitenden Ebene abhängig und um so kleiner, je schmaler dieser Abstand ist.

Ein ebener Flächenstrahler der Länge L, der Breite b und der Dicke C hat den gleichen Eingangswiderstand (2. Antennenresonanz) wie ein Zylinder der Länge L und

Bild 11 Flächenstrahler

dem Durchmesser d, wenn

dbC b=+ >> <<

12 1( ) für L b und .π

2.2. Babinet-Prinzip

Das Babinetsche Prinzip [3], [4], [6] ist ein Gesetz aus der Optik und lautet:

Schirm

Schirm Schirm

"Wird der Lichtfluß einer Lichtquelle einmal durch eine Blende, ein anderes Mal durch eine dazu komplementäre Blende

Lichtquelle

Licht-

quelle

Licht-

quelle

abgeschirmt, so ist die Summe deren Felder auf einem Schirm mit konstanter Entfernung zur Quelle gleich dem ungestörten

Blende

Komplementär-Blende keine Blende

Bild 12 Babinetsches Theorem

Feld ohne Blende."

Wird das Babinetsche Prinzip erweitert und auf die vektorielle elektromagnetische Strahlung angewandt, gelten folgende Beziehungen:

EE E

HH H

, He bezeichnen die Felder hinter einer elektrischen Blende und Em, H

(45)

die hinter einer dazu komplementären magnetischen Blende. E0, H0 kennzeichnen das Feld ohne Blende. Wird die nicht realisierbare magnetische Blende durch einen elektrischen Leiter gleicher Größe ersetzt, müssen auch die Größen U, I, Z, E und H durch I, U, Y, H und E ausgetauscht werden. Dann hat zum Beispiel ein ebener Flächenstrahler, der aus zwei dreieckigen Scheiben besteht, das gleiche Strahlungsverhalten wie zwei an den Spitzen

Bild 13 Schlitzantenne und dazu komplementärer Flächenstrahler

gespeisten dreieckförmigen Öffnungen. Die Eingangsimpedanzen des Flächendipols und der komplementären Schlitzantenne haben zueinander die Beziehung [4], [6]

.⋅=

(46)

Breitbandantennen Seite 14

Aus dieser Gleichung ist zu ersehen, daß eine Antenne breitbandig ist, wenn deren komplementäre Antenne ebenfalls breitbandig ist. Ist eine Antenne selbstkomplementär, d.h. wenn deren Fläche in Form und ebenso in ihrer Größe gleich ihrer komplementären Fläche ist, so gilt folgender frequenzunabhängiger Ausdruck [4], [6]:

== ≈

60πΩ (47)

Es ist zu beachten, daß eine Struktur nur dann selbstkomplementär sein kann, wenn sie unendlich ausgedehnt ist. Bild 16 zeigt einige selbstkomplementäre Antennenformen.

2.3. Winkelprinzip

Die Strahlungscharakteristik und Eingangsimpedanz einer Antenne ist abhängig von der geometrischen Form und der Strahlerlänge bezogen auf die Wellenlänge. Bleiben jedoch die Abmessungen einer Antenne normiert auf die Wellenlänge gleich, so bleiben auch deren elektrischen Eigenschaften konstant. Eine Antenne deren Form bei einer Maßstabsänderung unverändert bleibt ist also frequenzunabhängig. Solch eine Struktur muß jedoch unendlich ausgedehnt sein und auch die Einspeisepunkte müssen unendlich nahe benachbart sein (Bild 14). Diese Forderungen sind dann erfüllt, wenn das Objekt nur durch die Angabe von Winkeln definiert werden kann. Beispiele für solche Gleichwinkelantennen sind Kegel- bzw. Konusdipole sowie ebene Ausführungen wie die Schmetterlingsantenne.

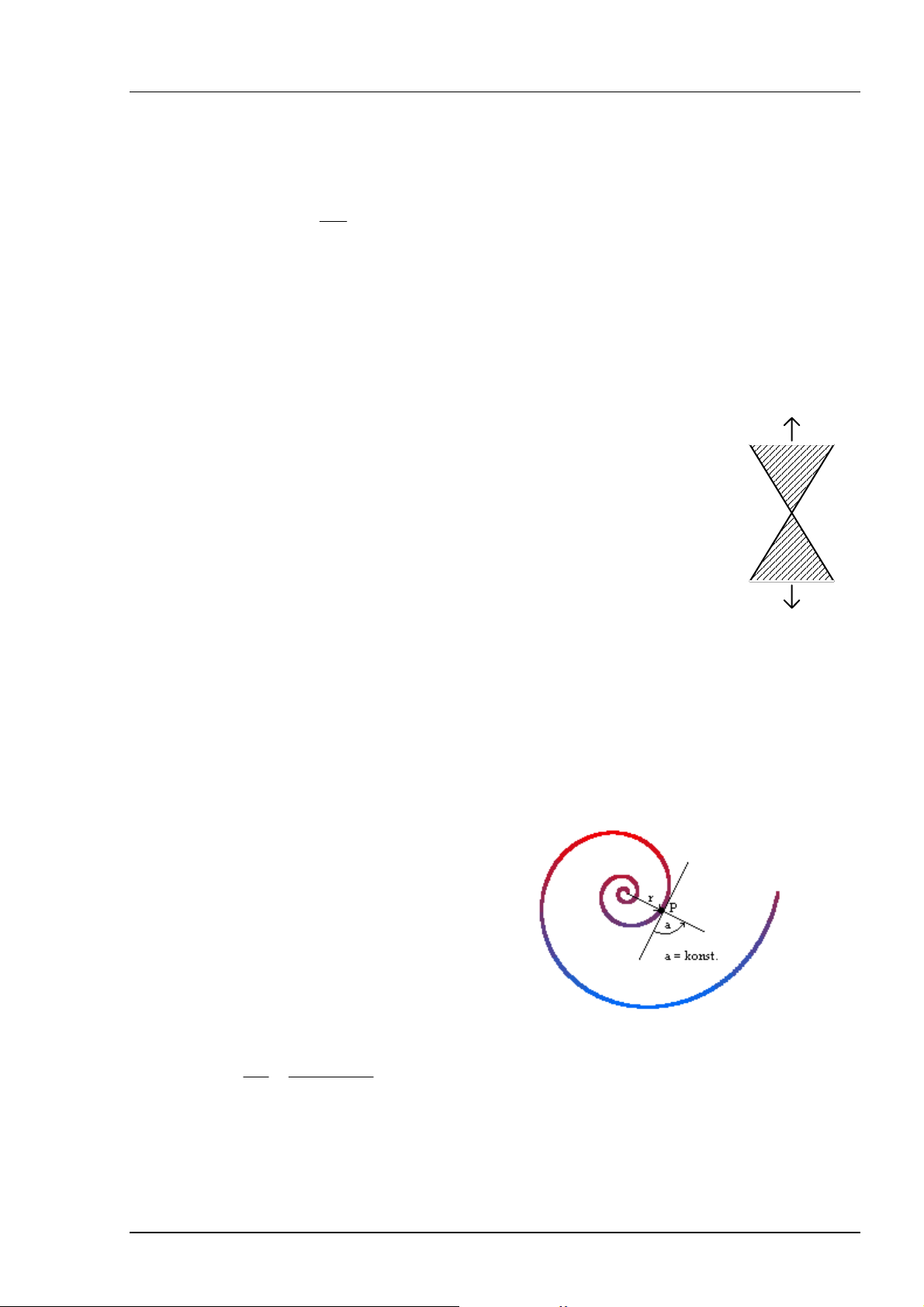
Dem Winkelprinzip gehorcht auch die logarithmische Spiralantenne. Die Kanten eines Spiralarms werden in Polarkoordinaten (r,

) durch folgende Gleichungen be-

schrieben:

ϕδ

−

rk Kr

−

= konst.; = konst.

∞

Bild 14

(48)

Der Winkel ϕ zwischen der Radiuskoordinate r und der Spiraltangente ist konstant (Bild 15). Es wird daher von einer winkelkonstanten Spiralantenne gesprochen. Bei einer ebenen Spirale ergibt das Verhältnis des Radius eines Spiralarmrandes, bezogen auf den Radius nach einer vollen Umdrehung, ebenfalls eine Konstante.

Bild 15 Logarithmische Spirale

Dabei bezeichnet man

===

als den Ausdehnungskoeffizient [14] einer Spiralantenne.

Wird bei einer zweiarmigen Spirale

in Formel 48 zu 90° gewählt, erhält man eine selbstkomplementäre

(49)

Struktur mit einer Eingangsimpedanz von 60π Ω.

Breitbandantennen Seite 15

Die Gleichwinkelantennen sind wie die selbstkomplementären Antennen frequenzunabhängig, solange sie eine unendliche Ausdehnung besitzen. In der Praxis führen die jeweiligen Minimal- und Maximalabmessungen jedoch zu einer oberen und unteren Grenzfrequenz.

Die obere Frequenzgrenze wird durch die Form der Speisestelle bestimmt. Wird die Frequenz weiter erhöht, treten höhere Schwingungsformen auf, welche

Bild 16 Selbstkomplementäre S trukturen

die Anpassung und Strahlungscharakteristik beeinflussen.

Die endliche Länge der Antenne verursacht bei tiefen Frequenzen an der Strukturbegrenzung Feldstörungen. Dieser Endeffekt wirkt sich auf Anpassung, Strahlung und bei Spiralantennen auch auf die Polarisation aus. Er legt damit die untere Frequenzgrenze fest.

Um die Rückwirkungen des Endeffektes zu verringern, muß entlang der Antennenstruktur eine starke Abstrahlung erfolgen. Dadurch ist der Strombelag der eingespeisten Leitungswelle bis zum Strukturende soweit abgesunken, daß keine oder nur geringe Reflexion auftritt. Antennen mit dieser Eigenschaft besitzen eine hohe Strahlungsdämpfung. Der Bereich der Antennenstruktur, der für die Abstrahlung sorgt, wird als aktive Zone bezeichnet (s. Kap. 4.1.2.). Da für große Strahlungsdämpfung kleine Wellenwiderstände erforderlich sind, müssen Antennen mit geringem Schlankheitsgrad verwendet werden.

2.4. Logarithmisch-periodisches Prinzip

Das logarithmisch-periodische Prinzip baut auf das Winkelprinzip des vorherigen Kapitels auf.

Um die Endeffekte bei den Gleichwinkelantennen abzuschwächen, und damit eine größere Bandbreite zu erreichen, muß die Strahlungsdämpfung dieser Antennen weiter erhöht werden. Dieses kann durch den Einbau von resonanzfähigen Elementen in die Winkelstruktur erfolgen. Solche Resonanzstellen erhält man z.B. durch periodisch über die Antennenstruktur eingefügten Schlitzen oder gezahnten Strukturrändern (Bild 17). Da diese Resonanzelemente jedoch frequenzabhängig sind, müssen sie ausreichend eng benachbart angelegt werden.

Analog zum Ausdehnungskoeffizienten der Spiralantenne (Gleichung 49) wird hier das Verhältnis dieser Abstände (bezogen auf den Scheitelpunkt) durch den Stufungsfaktor

festgelegt.

Bild 17 Ebene logarithmisch-periodisc he Strukturen

==<

−

(50)

Breitbandantennen Seite 16

τ ⋅

Besitzt ein Resonanzelement die Länge L0, so ist das nächst kleinere τ L0 lang, das dritte

L0, usw. Es

gilt

=⋅

. (51)

Werden beide Seiten logarithmiert, erhält man:

ln ln lnLLn

Da ln L

und ln τ konstant sind, erhöht sich bei verschiedenen Werten von n der Logarithmus von Ln in

(52)

gleichen periodischen Schritten. Eine solche Struktur nennt man daher logarithmisch-periodisch.

Die Bandbreite einer Periode beträgt dabei

mit .

(53)

Entsprechend gilt:

ln ln lnff

=−

nn+

(54)

Die elektrischen Eigenschaften einer logarithmisch-periodischen Antenne wiederholen sich also periodisch mit dem Logarithmus der Frequenz, da sich in demselben Maße auch die Struktur wiederholt.

Wählt man die Kontur der Antenne und die Periode ln

so, daß die Änderungen von Richtdiagramm und Scheinwiderstand innerhalb einer Periode klein bleiben, dann sind auch für alle übrigen Perioden diese Schwankungen klein. Trägt man den Betrag der Eingangsimpedanz gegen ln f auf, so schwankt dieser um einen Mittelwert der Periode 0,5 ln 1/ der Änderung der Frequenz. Die Formen wiederholen sich bei f und bei bestimmten Frequenzen genau

. Auch das Richtdiagramm verändert seine Form periodisch mit

f, da die Resonanzelemente nur

/4 lang sind. Der Stufungsfaktor τ sollte deshalb nur wenig vom

Wert 1 abweichen.

Wegen den Schwankungen kann man selbst bei unendlicher Ausdehnung nicht von einer frequenzunabhängigen Antenne sprechen. Antennen, die nach dem logarithmisch-periodischen Prinzip arbeiten, werden daher als pseudofrequenzunabhängige Antennen bezeichnet.

2.5. Zusammenfassung

Die ideale Breitbandantenne besitzt eine Struktur, die jeden der oben genannten Prinzipien gehorcht.

Eine solche Antenne muß einen Querschnitt besitzen, der vom Speisepunkt aus proportional mit der Entfernung zunimmt. Ein solcher dicker Strahler kann dabei ein flaches oder ein kreisförmiges Profil besitzen. Ferner muß die Strahlerlänge bezogen auf die Betriebsfrequenz lang sein, um Reflexionen am Antennenende zu vermeiden. Entlang dieser Strecke muß die Antenne eine fortschreitende Welle führen oder eine hohe Strahlungsdämpfung besitzen welche durch Eingliedern von Stoßstellen positiv beeinflußt werden kann.

Breitbandantennen Seite 17

3. Ausführungsformen von Breitbandantennen

3.1. Stabantennen und Dipole

3.1.1. Kegelantenne

Der Wellenwiderstand eines zylinderförmigen Dipols ist entlang seiner Achse nicht konstant und nimmt nach außen hin stetig zu (s. Kapitel 1.3.6.). Die dadurch entstehenden Teilreflektionen können verhindert werden, wenn die Antennenform an den Energieniveauflächen des Dipols angepaßt wird [3]. Günstig sind dabei kegelförmige oder tropfenförmige Antennenstrukturen.

So ist bei der Doppelkegelantenne der Wellenwiderstand konstant und nur vom Öffnungswinkel 2 Kegels abhängig [3], [6]:

Wird die Kegelantenne als Unipol über einer leitenden Ebene betrieben, so halbiert sich der Wert des Wellenwiderstandes.

Die bei tiefen Frequenzen entstehenden Feldstörungen am Kegelende kann man durch Aufsetzen eines kugelförmigen Daches reduzieren. Der Übergang vom Kegel zur Kuppel sollte möglichst fließend sein, um Stoßstellen zu vermeiden. Bild 18 zeigt die Welligkeit eines Kegels mit ebenem Dach im Vergleich zu Kegelantennen mit Ellipsoid- und Kegeldach.

Bild 18 Welligkeit von Kegelantennen

Die Welligkeit kann noch weiter verringert werden, in dem der obere Kegel einer Doppelkegelantenne durch eine runde Scheibe ersetzt wird. Dieser Antennentyp wird entsprechend Discone-Antenne [14] genannt und kann ein Eckfrequenzverhältnis von 1:8 aufweisen. Innerhalb dieses großen Frequenzbereiches sind die elektrischen Eigenschaften recht konstant. Lediglich der Erhebungswinkel nimmt mit steigender Frequenz zu.

Die Discone-Antenne kann sehr einfach und ohne Symmetrierglied mit einem Koaxial-Kabel gespeist werden, wenn es durch den feldfreien Kegelinnenraum geführt wird.

1202ln cotαΩ (55)

I K

des

3.1.2. Gefalteter Dipol

Wird parallel zu einem Dipol ein weiterer Leiter angebracht und deren Enden miteinander verbunden, so erhält man einen Faltdipol [3], [13]. Der Abstand D der beiden Leiter darf jedoch nicht größer als ein Zehntel der Wellenlänge betragen.

Die elektrischen Eigenschaften entsprechen denen des gestreckten Dipols. Lediglich der Antenneneingangswiderstand ist um ein vielfaches höher. Bei gleichen Stabradien gilt:

=⋅4 (56)

Sind die Radien unterschiedlich groß, so gilt folgende Gleichung [10], [13]:

Breitbandantennen Seite 18

log

⋅

D r

I J

J J

J K

F G

G G

G H

log

mit und

oder und

Beim Faltdipol existieren zwei verschiedene Ausbreitungsarten. Es überlagert sich eine zum zylindrischen Dipol äquivalente symmetrische Welle mit einer unsymmetrischen Welle die von der Doppelleitung des Faltdipols ausgeht. Aus dieser Gegebenheit resultiert eine höhere Bandbreite im Vergleich zum gestreckten Dipol.

Wird der gespeiste Stab dicker ausgelegt (Radius r Bandbreite weiter erhöht werden (Bild 19). Für optimales Breitbandverhalten wurden folgende Beziehungen ermittelt [3]:

D r

>> ≥

125

<≥

125

12 5

D r

) als der parasitäre Stab (Radius r2), so kann die

(57)

(58)

Die Dipollänge muß dabei 3/10 der größten Betriebswellenlänge betragen. Ein gefalteter Dipol mit diesen Abmessungen kann ein Eckfrequenzverhältnis von 1:2 erreichen.

Im Vergleich zum gewöhnlichen Dipol tritt beim Faltdipol eine geringere Kopplung zu einem eventuell vorhandenen Reflektor auf. Selbst bei Verwendung einer ebenen Reflektorwand mit nicht allzu großer Abmessung können die elektrischen Eigenschaften innerhalb

Bild 19 Flacher symmetrischer Faltdi pol

3.2. Abgeschlossene Langdrahtantenne

Im Kurzwellenbereich werden oft Langdrahtantennen [10], [13] verwendet. Dabei ist die Drahtlänge des Strahlers größer als eine Betriebswellenlänge und die Antenne wird mittels ihrer harmonischen Resonanzen erregt.

Bild 20 Bemessungskurven für Rhombusantennen

Um im Strahlungsdiagramm eine Vorzugsrichtung zu erhalten, kann der Strahler mit einem Lastwiderstand abgeschlossen werden (Bild 21). Solche Antennen nennt man abgeschlossene oder aperiodische Antennen. Der Wert des Abschlußwiderstandes muß reell und gleich dem Wellenwiderstand der Antenne sein. Es bilden sich dann, wie bei einer angepaßt abgeschlossenen Leitung, vom Speisepunkt in Richtung Abschlußwiderstand fortschreitende Wellen aus.

einer Oktave konstant gehalten werden.

≈

Bild 21 Abgeschlossene Langdrahtantenne

h/2

R=Z

Breitbandantennen Seite 19

Um Abstrahlung zu erhalten, müssen die beiden Leiter (Antennendraht und Erde) so weit von einander entfernt werden, daß sich die entgegengesetzten magnetischen Felder nicht aufheben. Da die nicht abgestrahlte Energie im Abschlußwiderstand geschluckt wird und sich keine stehenden Wellen ausbilden können, ist der Eingangswiderstand weitgehend frequenzunabhängig. Er beträgt je nach Aufbauhöhe und Leiterdurchmesser 500 bis 600 Ω - bei Rhombusantennen sogar bis zu 800 Ω. Ist die Antennenlänge ge- nügend groß (l/

> 4), ändert sich auch die Richtung der Hauptkeule über einen breiten Frequenzbereich

nur wenig. Es können Bandbreiten mit einem Frequenzverhältnis von 1:4 erreicht werden.

Zu den Antennentypen, die in erster Näherung eine einzelne fortschreitende Welle führen, gehören auch eine lange, in axialer Richtung strahlende Wendelantenne und ein langer, dicker linearer Leiter. Obwohl sie keine Abschlußwiderstände besitzen, verhalten sie sich in gleicher Weise wie abgeschlossene Antennen [6].

So hat ein dicker linearer Strahler eine ähnliche Stromverteilung wie ein dünner abgeschlossener linearer Leiter. Ist der Strahlerdurchmesser nicht allzu groß, dann ist auch die Strahlungscharakteristik gleichartig.

Die Resultate der fortschreitenden Welle bei linearen Leitern können auf die Wendelantenne übertragen werden, wenn man sich diese aus mehreren kurzen linearen Segmenten zusammengesetzt denkt.

3.3. Wendelantenne

Die Wendelantenne [6] kann als Querstrahler oder als Längsstrahler angeregt werden.

Ist die Windungslänge L sehr viel kleiner gegenüber der Wellenlänge richtung in der Ebene senkrecht zur Spulenachse. Wendelantennen in diesem Strahlungszustand werden jedoch selten verwendet und sind zudem sehr schmalbandig, da sich auf der Wendel stehende Wellen ausbilden.

Wird die Windungslänge L so gewählt, daß sie in die Größenordnung einer Wellenlänge fällt, strahlt die Antenne zirkular polarisierte Wellen in Richtung der Wendelachse aus. Dazu müssen sich die abgestrahlten Felder von zwei in Achsrichtung hintereinander liegender Spulenelemente gleichphasig überlagern. Die Phasenverzögerung der Welle entlang einer Windung vermindert um die Phasennacheilung der sich mit Lichtgeschwindigkeit zwischen den Wendelelementen ausbreitenden Raumwelle muß daher 2π bzw. 360° ergeben.

ππ

⋅− ⋅=

Dabei ist S die Ganghöhe bzw. der Windungsabstand der Wendel.

Für das Breitbandverhalten der Wendelantenne ist der Verlauf der relativen Phasengeschwindigkeit von Bedeutung. Nach umstellen der Gleichung 59 erhält man:

, so liegt die Hauptstrahlungs-

(59)

cLS

Verwendet man den Steigungswinkel

⋅π

(60)

der Wendel und den relativen Umfang

(61)

Breitbandantennen Seite 20

so folgt:

+cos sin

αα

Der Funktionsverlauf ist in Bild 22 für drei Steigungswinkel abgebildet.

1.4

1.3

1.2

1.1 Licht im freien Raum

1.0

0.9

0.8

0.7

0.6

0.5

0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5

Bild 22 Abhängigkeit der Phasengeschwindigkeit vom relativen Umfang

α = 0°

α = 10°

α = 30°

(62)

Da Cλ bei konstantem Durchmesser D der Frequenz proportional ist, gibt die Kurve gleichzeitig die Abhängigkeit der Phasengeschwindigkeit von der Frequenz an.

Wird z.B. die Frequenz erhöht, so wird auch die Phasengeschwindigkeit auf der Wendel größer. Die Phasengeschwindigkeit stellt sich also in einem größeren Frequenzbereich von selbst so ein, daß die einzelnen Windungen phasengleiche Strahlungsbeiträge liefern.

Die obere Frequenzgrenze liegt bei einer Antenne mit 3 Windungen bei C mender Windungszahl auf C

= 1,0 bei 50 Windungen ab. Die untere Frequenzgrenze liegt bei C

= 1,35 und nimmt mit zuneh-

= 0,77

und ist unabhängig von der Windungszahl. Werden diese Grenzen überschritten, entstehen neue Wellentypen mit verschieden Phasengeschwindigkeiten.

Die Antenneneingangsimpedanz ist nur wenig frequenzabhängig und beträgt im genannten Frequenzbereich [6]

= 140λΩ . (63)

Dabei muß die Windungszahl größer 3 betragen, um genügend Strahlungsdämpfung zu erhalten.

Die Polarisation bleibt im Frequenzbereich von 1:1,8 nahezu konstant und wird mit steigender Windungszahl günstiger.

Bild 23 Funktionsbereiche einer Wendelantenne

Bild 23 zeigt die Funktionsbereiche einer Wendelantenne mit einer Windungslänge von 1,6·λ bei der Mittenfrequenz. Für optimale Bandbreite sollte demnach

= 14°, S

= 0,24 und D

= 0,31 betragen.

Breitbandantennen Seite 21

3.4. Trichterantenne

Einen Trichterstrahler erhält man durch trichterförmiges Aufweiten eines Hohlleitungsrohres an dessen Ende. Durch das allmählich weiter werdende Rohr wird die Hohlleitungswelle stoßstellenfrei an den Wellenwiderstand Z tennenstruktur keine Resonanzstellen besitzt, haben Trichterantennen eine Bandbreite mit einem Eckfrequenzverhältnis von 1:3 und größer.

des freien Raumes angepaßt. Da nur sehr geringe Reflexion auftritt und die An-

Die untere Frequenzgrenze ist allein durch die kritische Frequenz f

des Hohlleiters [7] festgelegt. Diese

ist abhängig vom Wellentyp und von den Innenabmessungen des Hohlleiters.

Die obere Frequenzgrenze ist durch das Auftreten von Wellen höherer Ordnung bedingt. Es entstehen dann Nebenzipfel im Richtdiagramm.

Nebenzipfel entstehen ebenfalls durch den Phasenunterschied zwischen den Wellen, die an die Trichteröffnung in Achsrichtung ankommen und denen, die am Trichterrand entlang ankommen. Bei einer Tricherantenne mit großem Öffnungswinkel entsteht so durch die unterschiedliche Wegstrecke eine Kugelwelle. Die Wegdifferenz sollte deshalb in der E-Ebene 0,25⋅

und in der H-Ebene 0,4⋅

nicht über-

schreiten [6].

Durch Anbringen von Stegen längs des Trichters kann die Bandbreite noch weiter vergrößert werden. So kann ein Eckfrequenzverhältnis von 1:6 erreicht werden. Wird ein Doppelsteg verwendet und dieser über eine Koaxial-Leitung gespeist, können Frequenzverhältnisse von 1:12 und größer erzielt werden. Die kleinste nutzbare Wellenlänge ist durch den Abstand d der beiden Stege am Speisepunkt und die größte Wellenlänge durch den Abstand D der Stege am offenen Ende des Trichters bestimmt:

=⋅10 d (64)

min

=⋅2 D (65)

max

Die Stege sollten einen exponentiellen Verlauf besitzen und außerhalb der Trichteröffnung nach hinten kreisförmig gebogen werden, um Reflexionen zu vermeiden.

Die durch Reflexion entstandenen Welligkeiten können durch Abgleichschrauben am Trichterhals oder durch dielektrische Platten breitbandig kompensiert werden.

Die hier beschriebenen Trichterantennen besitzen alle einen relativ konstanten Eingangswiderstand. Ihr Gewinn wird jedoch mit steigender Frequenz größer und entsprechend die Halbwertsbreite des Richtdiagramms kleiner.

3.5. Spiralantenne

3.5.1. Winkelkonstante Spiral ant enne

Die winkelkonstante logarithmische Spiralantenne [3], [4], [6], [8], [14], deren Geometrie die Gleichung 48 in Kapitel 2.3. beschreibt, gehört zu den frequenzunabhängigen Antennenstrukturen (Bild 24).

Entlang der Spiralarme bildet sich eine aktive Strahlungszone aus, deren Länge proportional zur Betriebswellenlänge ist. Je länger die Arme sind, um so tiefer ist die untere Grenzfrequenz. Diese ist auch abhängig von der Armbreite und der Wickeldichte. Das Strahlungsdiagramm ist

Bild 24 Zweiarmige Spiralantenne

Breitbandantennen Seite 22

um so konstanter, je dicker die Spiralarme sind und um so dichter die Spiralanordnung ist. Da diese Parameter jeweils voneinander abhängig sind, gibt es keine Optimalwerte. Lediglich für die Winkelbreite des Spiralantennenarms mit 90° gibt es ein Optimum; denn dann erhält man eine selbstkomplementäre Struktur. In der Praxis liegen die Werte für

zwischen 0,1 und 0,5 sowie für k zwischen 0,4 und 0,9. Die

Windungszahl n liegt im Bereich zwischen 1,25 und 1,5 (Bild 25).

-5

MuPAD-Arbeitsblatt:

k:=0.6: a:=0.35: d:=PI/2: n:=3*PI: r1:=k*E^(a*phi): r2:=k*E^(a*(phi-d)): s1:=plot::polar([ r1, phi], phi = [0, n]): s2:=plot::polar([ r2, phi], phi = [0, n]): s3:=plot::polar([-r1, phi], phi = [0, n]): s4:=plot::polar([-r2, phi], phi = [0, n]): plot(s1, s2, s3, s4)

151050-5-10-15

xyx

Bild 25 Gleichwinklige Spiralantenne mit k = 0, 6;

= 0,35; δ = 90° und n = 1,5

Die obere Grenzfrequenz ist von der Ausbildung der Speisestelle abhängig. Der Abstand zwischen dem Spiralzentrum und dem Spiralarmanfang muß klein gegenüber der Wellenlänge sein:

(66)

Die Spiralantenne strahlt in beiden Richtungen senkrecht zur Antennenfläche und ist zirkular polarisiert. Soll eine einseitige Richtwirkung erzielt werden, kann die Spirale auf der Oberfläche eines Kegels angebracht werden (Bild 26 und 27). Diese Antennenart wird konische logarithmische Spirale genannt.

Bild 26 Konische Spiralantenne

Bild 27 Richtdiagramm einer konis chen Spiralantenne

Die Bandbreite von winkelkonstanten Spiralantennen ist sehr groß und kann ein Eckfrequenzverhältnis von 1:20 erreichen.

Die Eingangsimpedanz liegt zwischen 60 und 120 Ω bei der ebenen Spiralantenne und zwischen 100 und 160 Ω bei der konischen Spiralantenne. Sogar bei der selbstkomplementären Ausführung ist die Antenneneingangsimpedanz kleiner als der theoretische Wert von 60π Ω.

In der Praxis werden Spiralen mit zwei oder vier Armen verwendet, die entweder als Leiter oder als Schlitze in einer leitenden Ebene ausgebildet werden.

3.5.2. Archimedische Spiralantenne

Die archimedische Spiralantenne [3] gehört nicht zu den frequenzunabhängigen Antennenstrukturen, da sie nicht ausschließlich durch Winkel definiert ist. Die zwei Spiralarme liegen zueinander parallel und sind wie nachstehend definiert:

rrc

=+ −

konst.

(67)

Breitbandantennen Seite 23

Nahe des Speisepunktes sind die Ströme der beiden Spiralarme zueinander gegenphasig, und es wird nur wenig Energie abgestrahlt. Der Phasenunterschied wird um so geringer, je weiter man auf den Windungen nach außen hin fortschreitet. In dem Bereich, wo der Windungsumfang etwa eine Wellenlänge entspricht, sind die benachbarten Ströme praktisch phasengleich und die Antenne kann dort Leistung abstrahlen. Das Verhalten entspricht dem der Wendelantenne; Es kann jedoch mit der archimedischen Spiralantenne ein Eckfrequenzverhältnis von 1:10 erreicht werden. Die Eingangsimpedanz liegt bei diesem Antennentyp um 120 Ω.

3.6. Logarithmisch-periodische Antenne

Die logarithmisch-periodische Antenne [1], [2], [4], [5], [11], [12], [15], [16] ist aus der logarithmischen Spiralantenne entstanden. Man wollte eine linear polarisierte Struktur entwickeln, welche die gleichen guten Breitbandeigenschaften der Spiralantenne besitzt. Dazu wurden die geradlinigen Schenkel einer selbstkomplementären Dreieckflächenantenne durch eine Zahnstruktur ersetzt. Der Abstand der Zähne zueinander wurde dabei so gewählt, daß das Radienverhältnis enten der logarithmischen Spiralantenne entspricht (s. Kapitel 2.4.).

dieser Zähne dem Ausdehnungskoeffizi-

Die Länge und Breite von aufeinanderfolgenden Zähnen sind also jeweils um den Stufungsfaktor kürzer. Da sich im logarithmischen Maßstab die Zahnstruktur mit der konstanten Periode ln

wiederholt,

< 1

wird diese Antennenform logarithmisch-periodische Antenne genannt.

Die oben beschriebene logarithmisch-periodische Antenne wird speziell logarithmisch-periodische Kreisringsektor-Zahnantenne genannt. Das Grenzfrequenzverhältnis dieser Antenne beträgt 1:10 und die Eingangsimpedanz beläuft sich auf etwa 150 Ω. Sie strahlt doppelseitig senkrecht zur Antennenfläche.

Bild 28 Zweistöckige Kreisringsektor-Zahnantenne

Faltet man die beiden Strahlerhälften am Speisepunkt zweistöckig übereinander, so daß sie einen Winkel

einschließen, dann erhält man eine einseitige Strahlung in Richtung der Spitze (Bild 28). Diese Antenne strahlt also wie die konische logarithmische Spirale in die entgegengesetzte Richtung des Speisestromes. Die Antennenimpedanz wird um so kleiner, je geringer der Spreizwinkel tiefer die Zähne ausgespart werden (Winkel

Bild 29 Logarithmisch-periodische Trapez-Zahn-Antennen

). Er kann zwischen 100 und 170 Ω betragen.

wird und wird größer, je

Um lineare Polarisation zu erhalten, müssen die kreisförmigen Zähne durch zueinander parallel angeordneten Zähne ersetzt werden. Man erhält eine logarithmisch-periodische Trapez-Zahn-Antenne (Bild 29) deren elektrischen Eigenschaften annähernd gleich geblieben sind, aber dessen E

Zähnen polarisiert ist. Bei der dazu komplementären Schlitzantenne ist das E recht zu den Zähnen polarisiert. Günstige Werte für den Strukturöffnungshalbwinkel

-Feld parallel zu den

-Feld entsprechend senk liegen bei dieser

Antenne zwischen 20° und 30°.

Bild 30 Logarithmisch-periodische Dreiecks-Zahn-Antennen

Bild 31 Logarithmisch-periodische Antennentypen

Bild 32 Trapez-Zahn-Antenne für Kurzwelle

Bild 33 Speisung der Trapez-Zahn-Antenne

Die Metallflächen der logarithmisch-periodischen Antenne können durch Drahtgebilde ersetzt werden. Bei diesen Drahttypen wird dann meistens noch

= β gewählt, so daß beide Strukturhälften über je eine Speiseleitung versorgt werden (Bilder 31, 32, 33). Die logarithmisch-periodische Drahtantenne weist gegenüber der Vollmetallausführung eine geringere Eingangsimpedanz und eine etwas größere Halbwertsbreite auf.

Breitbandantennen Seite 24

Eine einfachere Bauweise mit geringerem Materialbedarf erhält man, wenn die trapezförmigen Zähne durch dreieckförmige Zähne ersetzt werden (Bild 30). Eine Antenne dieser Art wird logarithmisch-periodische Dreiecks-Zahn-Antenne oder logarithmisch-periodische Sägezahn-Antenne genannt. Sie besitzt eine günstigere Richtcharakteristik und einen etwa doppelt so großen Eingangswiderstand gegenüber der logarithmisch-periodischen Trapez-Zahn-Antenne.

Bei dieser Ausführung kann zudem die mittige Speiseleitung weggelassen werden, ohne daß sich die Dimensionierungs-Parameter ändern. Man erhält sodann die logarithmisch-periodische Zick-Zack-Antenne (Bild 31 Mitte).

Bild 34 Logarithmisch-periodische Dipol -Antenne

Bild 35 Log.-per. Dipol-Antenne über leitender Ebene

Bild 36 Log.-per. Dipol-Antenne für Kurzwelle

Den Antennentyp mit der größten Bedeutung stellt jedoch die logarithmisch-periodische Dipolantenne dar. Sie besteht aus einer Dipolzeile mit logarithmisch-periodischen Längen und Abständen, die über eine Zweidrahtleitung gespeist wird (Bild 34 und 36).

Die Doppelleitung wird dabei von Dipol zu Dipol gekreuzt (Kommutierung). Dadurch führen aufeinanderfolgende Dipole jeweils um 180° phasenverschobene Ströme die in Richtung kleinerer Dipole nacheilen. Durch diese Phasennacheilung ist die Strahlung zum Speisepunkt hin gerichtet, läuft also der Leitungswelle entgegen (Rückwärtswellenanregung). Um die Kreuzungen der Speiseleitung zu vermeiden, muß die Doppelleitung so angebracht werden, daß die einzelnen Dipolhälften alternierend an den einen und an den anderen Leitungszweig angeschlossen werden können (Bild 34 und 35).

Breitbandantennen Seite 25

Die Impedanz der logarithmisch-periodischen Dipolantenne ist im ganzen Betriebsfrequenzbereich konstant und kann unabhängig von der Strahlungscharakteristik zwischen 50 und 300 Ω eingestellt werden. Ein weiterer wichtiger Vorteil der logarithmisch-periodischen Dipolantenne ist, daß sie vollständig mathematisch berechenbar ist.

Bild 37 Logarithmisch-periodische V-Antenne

Bild 38 Verhalten der V-Antenne bei höheren Well enmoden

Eine Weiterentwicklung der logarithmisch-periodischen Dipolantenne ist die logarithmisch-periodische V-Antenne. Bei ihr werden die Dipole an den Einspeisestellen V-förmig in Strahlungsrichtung eingeknickt (Bild 37). Dadurch werden höhere Wellenmoden angeregt, die zu größerer Bandbreite und höherem Gewinn bei gleicher Baulänge führen. Die Werte für Gewinn und Impedanz sind jedoch nicht konstant, da sie mit den jeweiligen Wellenmoden springen (Bild 38).

Bild 39 Vertikale log.-per. Dipol-Antenne

Bild 40 Bifilare log.-per. Unipol-Antenne

Bild 41 Monofilare log.-per. Unipol-Antenne

Bild 42 Log.-per. Trapez-Unipol-Antenne

Bild 43 Log.-per. Trapez-Unipol-Antenne

Bild 44 Trapez-Zahn-Antenne für zirkulare Polarisation

Von geringerer Bedeutung ist die logarithmisch-periodische Unipolantenne über einer leitenden Ebene. Es gibt von diesem Typ recht viele Ausführungsformen, die jedoch in Entwicklung und Leistung sehr kritisch sind (Bilder 39 bis 43).

Bild 45 Log.-periodische Drehkreuz-Antenne

Abschließend sei noch die logarithmisch-periodische Drehkreuzantenne erwähnt, die ein zirkular-polarisierter Rundstrahler darstellt (Bild 45). Sie entsteht aus zwei zueinander senkrecht zusammengesetzten ebenen logarithmisch-periodischen Strukturen. Damit sich eine 90° Phasenvariation ergibt, muß hier zwi-

schen den senkrecht zueinander stehenden Strahlern ein Abstand von

bestehen.

Der Gewinn und die Richtschärfe von logarithmisch-periodischen Antennen können durch Gruppieren mehrerer identischer Strukturen erhöht werden. Die einzelnen Antennen müssen dabei so angeordnet werden, daß deren Strukturspitzen kongruieren. Sie müssen also entweder kreisringförmig nebeneinander oder aber in einem bestimmten Winkel übereinander montiert werden.

Eine breitbandige Antenne mit guten elektrischen Eigenschaften erhält man zudem, wenn eine logarithmisch-periodische Struktur als Erreger einer konventionellen Yagi-Uda-Antenne verwendet wird.

3.7. Speisung von Breitbandantennen

Ist die Antennenimpedanz ZA nicht identisch mit dem Wellenwiderstand ZL der Speiseleitung, so treten stehende Wellen auf. Dadurch sinkt der Wirkungsgrad, und im Sendebetrieb können Überspannungen auftreten. Um dieses zu vermeiden, muß die Antenne über den gesamten verwendeten Frequenzbereich an die Speiseleitung angepaßt sein. Bei abweichenden Wellenwiderständen muß ein Impedanzwandler zwischen Antenne und Speiseleitung geschaltet werden. Ist das eine der beiden Übertragungsglieder symmetrisch, während das andere von unsymmetrischer Form ist, so wird zusätzlich ein Symmetriewandler benötigt.

Breitbandantennen Seite 26

Diese Transformationsglieder sind jedoch sehr schmalbandig oder in breitbandiger Ausführung sehr aufwendig und teuer. Damit auf solche Anpassungsschaltungen verzichtet werden kann, sollte möglichst eine Antennenkonstruktion verwendet werden, deren Fußpunktwiderstand bereits dem Wellenwiderstand der Speiseleitung entspricht oder leicht auf diesen justiert werden kann.

So kann die Impedanz des Dipols weitläufig variiert werden, durch

• Änderung des Leiterdurchmessers (Gleichung 40),

• Ausführung als Halbwellen- oder Ganzwellendipol (Gleichung 37),

• Ausführung als gestreckter oder gefalteter Dipol (Gleichung 57),

• Ausführung als Leiter oder Schlitzantenne (Gleichung 46).

Bei der Kegelantenne ist die Antennenimpedanz direkt vom Öffnungswinkel abhängig (Gleichung 55), bei der Wendelantenne vom Durchmesser einer Windung (Gleichung 63).

Die Spiralantenne und die logarithmisch-periodische Dipolantenne kann über ein Koaxial-Kabel gespeist werden, ohne daß ein Symmetrierglied verwendet werden muß.

Dazu wird bei der Spiralantenne das Koaxial-Kabel, dessen Mantel abisoliert wurde, entlang eines Spiralarms aufgelötet. Um die Symmetrie der Antenne zu wahren, wird auch auf dem zweiten Spiralarm ein Koaxial-Kabel als Dummy angebracht.

Bei der logarithmisch-periodischen Dipolantenne wird das Koaxial-Kabel durch eines der Trägerrohre zum Speisepunkt geführt. Aufgrund der Rückwärtsstrahlung der Antenne ist das Speisekabel so gegen Mantelwellen abgeschirmt.

3.7.1. Frequenzgangkompensation

Antennen mit selbstkomplementärer Struktur, und viele andere der hier beschriebenen Antennentypen, weisen eine recht konstante Antennenimpedanz innerhalb eines größeren Frequenzbandes auf. Bei schmalbandigen Dipolantennen und Stabantennen mit hohem Schlankheitsgrad ändert sich jedoch der Blindwiderstand der Antennenimpedanz recht stark (s. Kapitel 2.1.1.).

Diese frequenzabhängige Blindwiderstandsänderung kann in gewissen Grenzen durch eine Kompensationsschaltung verringert werden [13]. Dazu muß diese Schaltung einen der Antenne entgegengesetzten Blindwiderstandsverlauf aufweisen. Zu den Antennenklemmen eines Halbwellendipols, der ja einen Impedanzverlauf eines Serienresonanzkreises besitzt, muß also eine Kompensationsschaltung mit dem Verhalten eines Parallelkreises zugeschaltet werden. Entsprechend kann ein Ganzwellendipol mittels eines Serienresonanzkreises im Frequenzgang kompensiert werden.

Die Kompensationsglieder können mit konzentrierten Schaltelementen oder durch

/2- bzw.

/4-Stich-

leitungen realisiert werden.

3.7.2. Impedanzwandl er

Um einen vom Wellenwiderstand der Speiseleitung abweichenden Antenneneingangswiderstand frequenzunabhängig anzupassen, muß auf konzentrierte Schaltelemente oder

/4-Stichleitungen verzichten

werden. Demgegenüber muß eine Transformationsleitung zwischengeschaltet werden, deren Wellenwiderstand ortsabhängig vom Eingang zum Ausgang langsam ansteigt bzw. abfällt (Bild 46). Dieses Verfahren (Taperung) funktioniert nur, wenn die Transformationsleitung lang genug und die Impedanzdifferenz nicht allzu groß ist. Für eine 2:1 Impedanzwandlung sollte die Länge

/2 nicht unterschrei-

max

ten [12].

Breitbandantennen Seite 27

So wie die Trichterantenne die Leitungswelle langsam an den Freiraum-Wellenwiderstand anpaßt, wird hier die Leitungswelle allmählich an den Eingangswiderstand der jeweiligen Antenne transformiert. Analog zur Trichterantenne ist auch hier ein exponentieller Verlauf der Transformationsleitung am günstigsten.

Die Taperung kann dabei kontinuierlich oder in mehreren Stufen ausgebildet werden (Bild 47). Das Stufenintervall sollte dabei kleiner

Bild 46 Exponentialleitung

Bild 47 Exponentialleitungen

/18 sein [12].

max

3.7.3. Symmetrierglieder

Den einfachsten breitbandigen Symmetriewandler erhält man durch Aufwickeln einer symmetrischen Bandleitung auf einen Spulenkörper [10]. Die aufgewickelte Zweidrahtleitung wirkt für unsymmetrische Ströme wie eine Drossel, schwächt aber die symmetrischen Ströme nur wenig. Die Länge der Doppelleitung sollte etwa

/4 betragen und kann zwischen 1/10 λ und 3/8 λ schwanken.

+180°

0°

+90°

0°

-90°

Symmetrierglieder mit gekoppelten Spulen können so gefertigt werden, daß sie zusätzlich zur Impedanzwandlung verwendet werden können. Leichte und kleine Symmetriewandler entstehen bei Verwendung von Ringkern-

Bild 49

Übertagern aus Ferrit [10], [13]. Sie können mit

Bild 48

Übersetzungsverhältnissen von 1:1 bis 10:1 hergestellt werden und weisen ein Grenzfrequenzverhältnis von 1:10 auf.

Symmetrierglieder aus Spulen sind im Sendebetrieb nicht unbeschränkt belastbar. Als Behelf kann eine mittels Taperung modifizierte Koaxial-Leitung verwendet werden [12]. Dazu wird das Kabel auf einer Länge von

/2 diagonal aufgeschlitzt, so daß an einem Ende der Außenleiter den gleichen Durch-

max

messer besitzt wie der Innenleiter (Bild 50).

Bild 50 Koaxial-Symmetriewandler

Bild 51 Erhebungswinkel in Abhängigkeit von der Masthöhe

3.8. Epilog zu den Breitbandantennen

In Analogie zum Schwingkreis gilt: Je breitbandiger eine Antenne ist, um so geringer ist ihre Güte und entsprechend kleiner ihr Gewinn.

Soll mangelnder Gewinn und zu geringe Richtwirkung mit Hilfe eines Reflektors verbessert werden, so wirkt sich das immer negativ auf die Bandbreite aus, da Größe und Abstand zum Strahler nur für eine Frequenz optimal sein können.

Die Breitbandeigenschaften einer Antenne können mittels Einfügen von aktiven Elementen in die Antennenstruktur erheblich verbessert werden [3]. Zu den aktiven Elementen gehören Transistoren, Tunneldioden, Varaktoren und auch gyromagnetische Stoffe wie Ferrite. Mit ihnen kann die empfangene bzw. abgestrahlte Welle verstärkt werden, eine Frequenzänderung hervorgerufen werden oder der Eingangswiderstand und die Stromverteilung verändert werden.

Breitbandantennen Seite 28

Wird bei Wendelantennen und logarithmisch-periodischen Antennen die Frequenz variiert, so wandert auch das Phasenzentrum entlang der Antennenstruktur. Dieses muß im Mikrowellenbereich beachtet werden, wenn eine solche Struktur als Erreger einer Spiegelantenne verwendet werden soll. Entsprechend muß eine logarithmisch-periodische Antenne im Kurzwellenbereich schräg zum reflektierenden Erdboden gerichtet werden, um einen konstanten Strahlungswinkel zu erreichen.

Breitbandantennen Seite 29

4. Entwicklung einer log.-per. Dipolantenne

In diesem Kapitel wird die Entwicklung einer logarithmisch-periodischen Dipolantenne (LPDA) für das VHF-Band beschrieben.

Für diese Antenne wurden nachstehende Spezifikationen vorgegeben:

• Frequenzbereich: 30 bis 300 MHz

• Eingangsimpedanz: 50 Ω

• Strukturlänge: ≤ 3,50 m

Die logarithmisch-periodische Dipolantenne soll drei vorhandene Rundfunkantennen der Bereiche VHF-I, UKW und VHF-III ersetzen.

4.1. Elektrische Dimensionierung

4.1.1. Geometrie der LPDA

dd d

LLL

12 3

123

Bild 52 Bemaßung der Strukturelemente ei ner LP DA

Virtuelle Sp itze

Speisepunkt

Die Strahlungseigenschaften der logarithmisch-periodischen Dipolantenne sind abhängig von dem Strukturöffnungswinkel den Elementabständen d

und dem Stufungsfaktor τ (s. Kapitel 2.4.). Zwischen α, τ, der Dipollänge Ln,

, und den Entfernungen Rn zur Spitze bestehen einfache geometrische Bezie-

hungen (s. Bild 52):

RLR

Das Verhältnis der Strecken R

RRRRRR

=⋅ =⋅ =⋅

τττ

tan

von der Spitze zu den einzelnen Elementen ist der Stufungsfaktor τ < 1:

;; (69)

nn2132 1

−

(68)

Breitbandantennen Seite 30

Daraus folgt weiter, daß

−

R R RR RR R

=⋅= = =

ττ τ τ τ

3121431

;; . (70)

Die gleichen Beziehungen gelten auch für die Dipollängen L

LLLLLL

=⋅ =⋅ =⋅

ττ τ

;; (71)

L L LL LL L

=⋅= = =

ττ τ τ τ

3121431

In gleicher Weise sind die Abstände d

dRRR RR

1121 11

dRRR RR

2232 22

dRR R RR

=− =−⋅= −

Das Verhältnis d

nnn n nn

dRRR RR

=−=−⋅= −

nnn n nn++++ ++

1121 11

zu dn ergibt wiederum τ, da

n+1

;; . (72)

ττ

nn2132 1

zwischen den Elementen festgelegt:

ττ

−

1=−=−⋅= −

−

(73)

(74)

(75)

(76)

++ +

11 1

So erhält man ebenfalls für d

dddddd d

=⋅ =⋅ = =

ττττ

213221

Für die weitere Betrachtung ist es bequemer, d lenlänge

der Resonanzfrequenz des ersten Dipols annäherungsweise das Vierfache von l1 (Element-

−

die Beziehungen

;;. (78)

−

auf die Wellenlänge zu beziehen. So ist die Freiraumwel-

(77)

länge = Dipol-Halblänge):

4≅⋅l (79)

würde gleich 4·l1 sein, wenn die Phasengeschwindigkeit der Welle auf der Speiseleitung gleich der der

Freiraumwelle wäre.

Gleiches gilt für alle anderen Elemente:

λλλ

444≅⋅ ≅⋅ ≅⋅lll

;; (80)

Die Abstände d

2233

, ausgedrückt in Wellenlängen der Resonanzfrequenzen der jeweils benachbarten Ele-

mente, sind

ddlddldd

≅

⋅

444

λλ λ

;;.

≅

⋅

≅

⋅

(81)

Es gilt ferner für jeden Wert von n:

Breitbandantennen Seite 31

σ, τ

dld

111

(82)

Man erhält schließlich folgenden Ausdruck:

444

⋅

≅

⋅

(83)

Diese Gleichung besagt, daß die Abstände zwischen den Elementen überall auf der Antenne gleich sind, wenn sie auf die Wellenlänge der Frequenz bezogen werden, die diesen Teil der Antenne erregt [1].

wird elektrische Periodizität oder relativer Abstand genannt. Sie nimmt wie die Parameter τ und

starken Einfluß auf die elektrischen Eigenschaften der Antenne.

Zwischen

Bild 53 Nomogramm zu Gleichung 84

Bild 54 Gewinn in Abhängigkeit von σ und τ

und α besteht nachfolgender Zusammenhang:

af af

−

⋅

ττατ

⋅

−

tan tan

−d

(84)

Bilder 55 und 56 Halbwertsbreite für E- und H-Ebene

Bild 53 stellt ein Nomogramm für Gleichung 84 dar. Die Abhängigkeit von Antennengewinn und Halbwertsbreite von der elektrischen Periodizität kennen, daß für jedes steigendem

verbessern.

ein optimaler Wert für σ existiert und daß sich die elektrischen Eigenschaften mit

ist in den Bildern 54, 55 und 56 zu ersehen. Es ist zu er-

4.1.2. Aktive Zone der LPDA

Bild 57 Spannungsverlauf entlang der Speiseleitung

Bild 58 Fußpunktströme der Elemente

In Bild 57 ist die Amplitude und Phase der Spannung auf der Speiseleitung als Funktion der Entfernung zur Strukturspitze aufgezeichnet. Dabei wurde die Frequenz so gewählt, daß der Dipol Nr. 4 eine halbe Wellenlänge lang ist.

Breitbandantennen Seite 32

Relative Amplitude in dB

Bis zum Dipol Nr. 6 hat die Amplitude und die Phase einen recht konstanten Verlauf. Die Antenne

Fußpunktstöme der Elemente

wirkt in diesem Bereich wie eine abgeschlossene Leitung. Innerhalb einer Strecke, die ein Viertel der Freiraum-Wellenlänge entspricht, ändert sich die Phase um etwa 150°. Die Phasengeschwindigkeit auf der Speiseleitung ist also langsamer als im freien Raum. Dieses resultiert von den kleineren parasitären Elementen, welche die Speiseleitung kapazitiv belasten.

Der Spannungswert fällt nach dem Dipol mit der Nr. 6 sehr stark ab. Damit sind hohe Ströme in den einzelnen Elementen verbunden. In Bild 58 ist zu sehen, daß die Ströme in den Elementen Nr. 4 bis Nr. 7 mehrfach größer sind als in den anderen Elementen. In dieser aktiven Zone strahlt die Antenne Energie ab. Die aktive Zone umfaßt also mehrere Elemente und wird durch den Dipol mit der Ausdehnung einer halben Wellenlänge begrenzt. Die Breite der aktiven Zone wird im allgemeinen durch ein Abfall der

-5

-10

-15

-20

-25

-30

-35 0,3 0,4 0,5 0,6 0,7

Relative Elementlänge

Strom Phase

Bild 59

180 150 120 90 60 30 0

-30

-60

-90

-120

-150

-180

-210

Relative Phase in Grad

Stromamplitude um 10 dB festgelegt.

In der Zeichnung ist auch zu sehen, daß die Phasen der Ströme in Richtung der kleineren Elemente hin nacheilen. Diese, für die Rückwärtsstrahlung erforderliche Bedingung, wurde durch die Kommutierung der Elemente erzwungen.

Bild 60 Aktive Zone und LPDA-Schema

Bild 61 Stomverteilung bei verschiedenen Frequenzen

Bild 62 Element-Fußpunktströme gegen rel at i ver Elementlänge

Für die Dimensionierung der logarithmisch-periodischen Dipolantenne ist die Breite der aktiven Zone und die Anzahl der Elemente innerhalb dieser Zone von großer Bedeutung.

Je höher der Antennengewinn sein soll, um so mehr Elemente müssen sich in der aktiven Zone befinden. Dieses kann durch Erhöhen des Stufungsfaktors aktiven Zone mit steigendem

kleiner wird; denn durch die höhere Anzahl der wirkenden Elemente tritt

erreicht werden. Es ist zu beachten, daß die Breite der

eine höhere Strahlungsdämpfung auf, und die Spannungsamplitude auf der Speiseleitung fällt schneller ab.

Damit die elektrischen Eigenschaften an den Bereichsgrenzen der logarithmisch-periodischen Dipolantenne die gleichen sind, wie denen bei jeder anderen Frequenz innerhalb dieses Bereiches, muß die Antennenstruktur dort die komplette aktive Zone unterstützen.

In den Bildern 58 und 62 ist zu sehen, daß sich das Zentrum der aktiven Zone vor dem Dipol mit der Resonanzlänge ( steigendem

/2) befindet. Ferner verschiebt sich die aktive Zone, aus oben aufgeführten Grund, mit

weiter zur Strukturspitze hin.

Die Breite der aktiven Zone und deren Verlauf bestimmt also die Ausdehnung des längsten und des kürzesten Dipols der Antenne.

=⋅≈

111

max

(85)

Breitbandantennen Seite 33

=⋅≈

ist die Struktur-Kürzungskonstante für die unterste Grenzfrequenz und K2 entsprechend für die obere

Grenzfrequenz. Ihre Werte, die von

min

(86)

und σ abhängen, können dem Bild 63 entnommen werden. Sie be-

ziehen sich auf einen Abfall der Fußpunktströme um 10 dB vom Spitzenwert.

Bild 63 Struktur-Kürzungsfaktoren

Für die Dimensionierung unter Verwendung eines Rechners ergeben folgende Funktionen Näherungswerte:

K10 9725 0 477=−⋅,,

71 213 2198 73

=− + −+

,,,,

ττ τ

21 82 66 62 12 18 29

+−+−

,,,

στττ

(87)

(88)

Die Bandbreite der aktiven Zone ergibt sich aus dem Verhältnis der beiden Struktur-Kürzungskonstanten:

In der Literatur wird jedoch meistens eine andere Funktion zur Bestimmung von B

Ba=+ −11 30 81,,

τσ

angegeben:

(89)

(90)

Allerdings ist nicht klar, auf welchem Amplitudenabfall der Fußpunktströme sie sich bezieht und in welchem Wertebereich von

und σ sie genau ist. Gleichung 90 ergibt kleinere Bandbreiten für die aktive Zone als Gleichung 89 und bezieht sich für die untere Bandgrenze immer auf den Dipol mit der Resonanzlänge

/2 (also K1 = 0,5).

4.1.3. Physikalische Kenngrößen

Die Länge der einzelnen Dipole berechnet sich nach Gleichung 72 zu

−

Dabei wird n soweit erhöht, bis L

. (91)

≤ Lx wird, um die volle Breite der aktiven Zone auch bei der größten

Frequenz zu unterstützen. Das Verhältnis des längsten zum kürzesten Dipol stellt die Strukturbandbreite dar:

−

(92)

Diese kann aber wegen der endlichen Breite der aktiven Zone nicht voll ausgenutzt werden. Die effektive Bandbreite ist daher nur

eff

= .

(93)

Um die Elementabstände berechnen zu können, muß Gleichung 75 aufgelöst werden zu

Breitbandantennen Seite 34

111

Aus Gleichung 92 kann die Anzahl der benötigten Dipole berechnet werden:

af af

=−= −=1

σλ

−

τσ

tan

(94)

(95)

(96)

log

=+ =+

log

⋅

log

G H

log

ττ τ

Bild 64 zeigt ein Nomogramm für diesen mathematischen Satz.

Bild 64 Nomogramm für die Anzahl der El emente

Die notwendige Baulänge der Antenne ergibt sich aus der Geometrie der LPDA zu

SRR

=−=

oder

=−

4.1.4. Impedanz der LPDA

−

cot .

J K

=−

1tan

−

(97)

(98)

(99)

Wie in Kapitel 4.1.2. beschrieben, wirkt die logarithmisch-periodische Dipolantenne wie eine abgeschlossene symmetrische Zweidrahtleitung die zusätzlich durch die kleineren Elemente vor der aktiven Zone kapazitiv belastet wird.

′

′+′

der einzelnen Dipole [12].

(100)

(101)

ist der mittlere Wellenwiderstand der Paralleldrahtleitung ohne kapazitive Belastung und R0 die An-

tenneneingangsimpedanz mit dem zusätzlichen Kapazitätsbelag C

Dieser Kapazitätsbelag ist vom Speisepunkt entlang der Doppelleitung bis zur abschließenden aktiven Zone konstant, da mit länger werdenden Elementen auch deren Abstände größer werden. Der Wert von

ist nicht nur von der Elementlänge und dem Elementabstand abhängig, sondern auch noch vom mitt-

leren Wellenwiderstand Z

Breitbandantennen Seite 35

ττ

==C

′

cd Z cZ

=−= −

120 2 25 120 2 25ΩΩln , ln ,

F H

I K

(102)

(103)

Der Funktionsverlauf von Z

kann aus Bild 65 entnommen werden.

Bild 65 Mittlerer Wellenwiderstand der LPDA-Elemente

Bild 66 Impedanz einer symmetris c hen Zweidrahtl ei tung

Wird für jedes Element der gleiche Schlankheitsgrad s verwendet (längere Elemente mit größerem Durchmesser), so bleibt C

Wird Gleichung 102 in Gleichung 101 eingesetzt, erhält man

Um die charakteristische Impedanz der Speiseleitung als Funktion des Eingangswiderstandes zu erhalten, muß die Gleichung umgestellt werden zu:

konstant und damit auch die Antenneneingangsimpedanz R

. (104)

Breitbandantennen Seite 36

=++

Der benötigte Wert für Z Leiter der symmetrischen Speiseleitung eingestellt werden.

Für eine Paralleldrahtleitung mit rundem Leiterprofil gilt (Bild 66):

Dabei ist s der Abstand zwischen den Leitern und d der Durchmesser der Leiter. Wird nach s umgestellt, ergibt sich:

=⋅cosh

Die Antenneneingangsimpedanz der logarithmisch-periodischen Dipolantenne kann durch einfaches Ändern dieses Abstandes zwischen 50 und 300 Ω eingestellt werden.

G G

kann nun durch entsprechende Wahl von Abstand und Durchmesser der beiden

120=⋅Ω arcosh (106)

120 Ω

(105)

(107)

4.1.5. Hinweise zur Dimensionierung

Die Dimensionierung der LPDA ist nicht einfach, da die einzelnen Antennenparameter voneinander abhängig sind und nicht einzeln bestimmt werden können (s. Gleichung 84 und 98).

Im Allgemeinen beginnt man die Dimensionierung, indem zwei Werte für den Stufungsfaktor τ und der elektrischen Periodizität nungswinkel, Dipolanzahl und Baulänge ermittelt werden. Wurde aufgrund einer Dimensionierungsvorschrift (z.B. min. Gewinn oder Richtschärfe) ein Wert für Wert für den anderen Parameter (Bilder 54, 55 und 56). Dieser kann jedoch meistens nicht verwendet werden, weil dadurch die Antenne viel zu lang oder die Anzahl der Dipole zu groß wird. Es muß also ein Kompromiß gefunden werden, wodurch mehrere Rechengänge erforderlich sind.

Um die beste Lösung zu erhalten und zu sehen, wie stark sich die einzelnen Dimensionierungs-Parameter beeinflussen, wurde ein Computerprogramm entwickelt. Das Listing dazu, ist im Anhang A zu finden.

Mit der nachstehenden Schrittfolge erhält man am schnellsten brauchbare Dimensionierungswerte:

1. Festlegen von Gewinn, Halbwertsbreite, Baulänge und Ausdehnung des längsten Elementes.

2. Auswählen von

(Bild 54).

3. Prüfen, ob die gewählten Werte von

und 56).

4. Schritte 2 und 3 mit kleinerem Wert von

Halbwertsbreiten nicht erfüllt sind.

5. Mit Hilfe von Gleichung 98 prüfen, ob die Baulänge den Höchstwert nicht überschreitet.

6. Falls erforderlich, Schritte 4 und 5 wiederholen.

7. Die Längen der Elemente mit Hilfe der Gleichungen 85 und 91 bestimmen.

8. Die Abstände der Elemente mit den Gleichungen 95 und 96 berechnen.

9. Konzipieren der Speiseleitung für die gewünschte Eingangsimpedanz (Gleichungen 105 und 107).

gewählt werden. Daraufhin können alle anderen Parameter, wie Strukturöff-

bzw. σ gefunden, so gibt es einen optimalen

und σ für den gewünschten Gewinn unter Verwendung des optimalen Wertes von

und σ den gewünschten Halbwertsbreiten genügen (Bilder 55

wiederholen, falls die Anforderungen bezüglich der

Breitbandantennen Seite 37

Bei der Wahl der Dimensionierungs-Parameter müssen diverse Punkte berücksichtigt werden:

Der Stufungsfaktor aktiven Zone befindet. Strukturen mit

sollte nicht kleiner als 0,80 gewählt werden, da sich sonst nur noch ein Dipol in der

> 0,975 sind im Mikrowellenbereich schwierig zu konstruieren

und bei kleinen Frequenzen sehr lang, schwer und teuer.

Die elektrische Periodizität ist darauf zurückzuführen, daß mit kleiner werdendem d

darf nicht kleiner als 0,05 werden, da sonst der Gewinn steil abfällt. Dies

= 2σ ln infolge der von Element zu Element

sich wiederholenden Phasenumkehr die Phase zwischen benachbarten Dipole sich dem Wert π nähert. Wird

größer 0,25 gewählt, entstehen große Nebenkeulen im Strahlungsdiagramm.

Für eine brauchbare Dimensionierung sollten sich die LPDA-Parameter innerhalb der folgenden Grenzen befinden:

081 095

≤≤

01 02

≤≤

(108)

420

°≤ ≤ °

50 300

≤≤

ΩΩR

Es ist zu beachten, daß diese Bereiche nur für die LPDA gelten. Bei anderen logarithmisch-periodischen Antennentypen, wie z.B. bei der logarithmisch-periodischen Trapez-Zahn-Antenne, können diese Wertebereiche anders liegen. Selbst bei völlig gleichen Dimensionierungs-Parameter unterscheiden sich oft die elektrischen Eigenschaften der jeweiligen Antennentypen.

Die Speiseleitung wird am niederfrequenten Ende im Abstand l

kurzgeschlossen. Dieser Stub liegt in der

Größenordnung

λλ

max

≤≤l .

10 8

max

(109)

Bei einer Speiseleitung aus Rohren vergrößert sich also die Baulänge um die Ausdehnung dieses Abschlusses. Im Kurzwellenbereich genügt eine Leiterschleife der gestreckten Länge l

≈ 200 mm.

Der Mittenabstand s der beiden Leiter der symmetrischen Speiseleitung muß kleiner sein als

min

s <

(110)

Die Ausdehnung g der beiden Pole am Speisepunkt der LPDA (Bild 67) ist ebenso begrenzt auf

min

g <

(111)

Alle in diesem Kapitel aufgeführten Formeln beziehen sich auf elektrische Längen. Endeffekt-Korrekturen und Verkürzungsfaktoren dürfen erst dann auf die Elementlängen angewandt werden, wenn die komplette Dimensionierung abgeschlossen ist.

4.1.6. Berechnung der LPDA-Parameter

Da für den extrem großen Frequenzbereich von 30 bis 300 MHz eine sehr große Baulänge zu erwarten war und keine Anforderungen bezüglich Gewinn und Richtschärfe vorlagen, wurden für den ersten Rechengang die Mindestwerte für

und σ gewählt.

Breitbandantennen Seite 38

Das Computerprogramm ergab mit τ = 0,81 und σ = 0,1 dennoch eine zu große Baulänge von 6 Metern. Der Frequenzbereich mußte also eingeschränkt werden. Es wurde der Bereich zwischen 54 MHz (Kanal 3 im VHF-I Band) und 230 MHz (Kanal 12 im VHF-III Band) gewählt.

Ein erneuter Rechengang ergab dann eine Baulänge von 3,12 m und blieb somit unter dem Maximalwert von 3,50 m. Daraufhin konnten die Antennen-Parameter mit höheren Werten von

und σ optimiert wer-

den.

Die günstigsten Werte und Abmessungen zeigen sich mit

= 0,84 und σ = 0,1:

Stufungsfaktor τ = 0,840 elektrische Periodizität σ = 0,100

untere Frequenzgrenze fu = 54,0MHz obere Frequenzgrenze fo = 230,8MHz effektive Bandbreite B = 4,27 Strukturbandbreite Bs = 6,81 Bandbreite der aktiven Zone Ba = 1,59

Öffnungshalbwinkel der Struktur α = 21,8° Erforderliche Dipolanzahl N = 12 Antennenbaulänge (ohne Stub) S = 2,96m Antennenbaulänge (mit Stub) A = 3,52m Länge der kleinsten Dipolhälfte L12 = 195mm Länge der größten Dipolhälfte L1 = 1325mm kleinster Dipolabstand d11 = 97mm größter Dipolabstand d1 = 556mm kleinster Dipoldurchmesser a12 = 2,6mm größter Dipoldurchmesser a1 = 17,9mm Mittenabstand der Doppelleitung s = 24,0mm

Wellenwiderstand der Dipole Za = 335,2Ω Wellenwiderstand der Doppelleitung Zo = 59,3Ω

Dipol Länge Abstand Durchmesser

1 1325 mm 0 mm 17,9 mm 2 1113 mm 556 mm 15,1 mm 3 935 mm 467 mm 12,6 mm 4 785 mm 392 mm 10,6 mm 5 660 mm 329 mm 8,9 mm 6 554 mm 277 mm 7,5 mm 7 465 mm 232 mm 6,3 mm 8 391 mm 195 mm 5,3 mm

9 328 mm 164 mm 4,4 mm 10 276 mm 138 mm 3, 7 m m 11 232 mm 116 mm 3, 1 m m 12 195 mm 97 mm 2,6 mm

Um genügend Stabilität zu erreichen, wurden für die beiden Leiter der symmetrischen Speiseleitung zwei Vierkantrohre mit einer Kantenlänge von 20 mm angegeben. Damit der Durchmesser des kürzesten Elementes nicht zu klein und der des längsten nicht größer als die Kantenlänge der Trägerrohre wird, wurde ein Schlankheitsgrad von 155 gewählt.

Der Gewinn der Antenne kann aus Bild 54 ermittelt werden und beträgt 8 dB. Die Halbwertsbreite in der E-Ebene beträgt etwa 65° und in der H-Ebene zirka 100°.

Der Rechengang mit den endgültigen Ergebnissen soll hier noch einmal detailliert aufgeführt werden.

Breitbandantennen Seite 39

Aus τ und σ kann mit Hilfe von Gleichung 84 der Strukturöffnungswinkel bestimmt werden:

rad

−

1084

⋅

401

=arctan arctan

038 (112)

αα

Da am höherfrequenten Ende der Antenne immer ein Dipol mehr angesetzt wird, um die komplette aktive Zone zu unterstützen, ist die resultierende Bandbreite immer etwas größer. In diesem Fall reichte für die gewünschte obere Frequenzgrenze ein Wert von 216 MHz aus.

Die Bandbreite der aktiven Zone beträgt nach Gleichung 90:

Ba=+ − =+ − =11 30 8 1 1 1 30 8 1 0 84 0 1 1 59,, ,, ,,,

Die Strukturbandbreite ist nach Gleichung 92:

Daraus ergibt sich eine effektive Bandbreite B

eff

180

rad

== =

038

ππ

MHz

216

MHz

af a f

−−

1112

== =

084 681,, (116)

681

159

180

τσ

428

=°

21 8

> B von:

eff

(113)

(114)

(115)

(117)

Die obere Grenzfrequenz beträgt also genau:

ffB

oueff

Mit Gleichung 97 wird die Anzahl der Dipole berechnet:

log

NB=+ =+ =1

log

Die Ausdehnung des längsten Dipols (elektrische Länge) ergibt sich aus Gleichung 85:

Der größte Elementabstand und Elementdurchmesser kann aus L

cf300 10

max

2 2 0 1 2 78 556==⋅⋅ =

MHz MHz=⋅ = ⋅ =54 4 28 231, (118)

54 10

556

⋅

log ,

log

1 s

278== =

681

084

, (120)

556

m==

bestimmt werden:

,,m mm (122)

(119)

(121)

Breitbandantennen Seite 40

278

155

17 9== =,,mmm

(123)

Ω

(124)

(125)

(127)

Die Größen der anderen Elemente erhält man jeweils durch die Multiplikation mit

Mit Gleichung 98 und 109 kann die Baulänge bestimmt werden:

=−

AS=+ = + =

Mit einem Schlankheitsgrad von s = 155 erhält man den mittleren Wellenwiderstand der Dipole:

=−= −=120 2 25 120 155 2 25 335ln , ln ,

Die charakteristische Impedanz der Speiseleitung beträgt:

=++

1278

max

afa f

G G

50 0 84

Ω

G G

⋅⋅

8 0 1 335

=−

297

ΩΩΩ(126)

Ω

556

Ω

G H

J K

G H

I J

681

353,

I J

J K

Ω

50 0 84

⋅⋅

8 0 1 335

038 297cot

cot , ,

Ω

59 3

Bei der Berechnung des Mittenabstandes der Trägerrohre (Kantenlänge = 20 mm) muß in der Gleichung 107 ein Korrekturfaktor k berücksichtigt werden, da die Leiter hier statt eines runden Querschnitts ein Vierkantprofil aufweisen:

cosh

=⋅

Damit ist die logarithmisch-periodische Dipolantenne dimensioniert.

4.2. Mechanischer Aufbau

Die Antenne ist mit einer Länge von 3,53 m und der größten Breite von 2,65 m ein recht gewaltiges Gebilde. Als Baumaterial kam daher nur Aluminium (AlMgSi05) in Frage.

Für die beiden Trägerrohre wurde ein Vierkantprofil mit einer Kantenlänge von 20 mm und einer Wandstärke von 2 mm gewählt.

Das Material für die Elemente konnte nicht jeweils mit dem errechneten Durchmesser erworben werden. Es wurden für die einzelnen Positionen folgende Abmessungen verwendet:

120

Ω

59 3 15

ΩΩ

mm mm

cosh

120

Ω

(128)

Breitbandantennen Seite 41

Dipol berechneter

Durchmesser

verwendeter

Durchmesser

1 17,9 mm 15,0 mm 2 15,1 mm 15,0 mm 3 12,6 mm 12,0 mm 4 10,6 mm 10,0 mm 5 8,9 mm 8,0 mm 6 7,5 mm 8,0 mm 7 6,3 mm 6,0 mm 8 5,3 mm 6,0 mm

9 4,4 mm 6,0 mm 10 3,7 mm 6, 0 m m 11 3,1 mm 6, 0 m m 12 2,6 mm 6, 0 m m

Die Dipole 1 bis 6 sind Aluminiumrohre, während die dünneren Dipole 7 bis 12 aus Vollmaterial bestehen. Die Elementrohre mußten an die beiden Trägerrohre angeschweißt werden, da es aufgrund der Kommutierung keine einfache Möglichkeit gibt, die langen Elemente stabil zu befestigen. Schließlich muß zur Selbstsymmetrierung ein Koaxial-Kabel durch eines der Trägerrohre geführt werden.

Da die beiden Trägerrohre als symmetrische Speiseleitung wirken, müssen sie zueinander isoliert fixiert werden. Dazu wurden vier 25 mm breite Kunststoffärmel gefertigt, die entlang der Antenne verteilt angebracht wurden. In der Mitte dieser Kunststoffärmel wurde waagerecht eine Kunststoffschraube der Größe M5 durchgeführt, um den Abstand der beiden Trägerrohre gegeneinander zu justieren. Der Abstand ist damit 1 mm größer als berechnet (Gleichung 128).

Die Antenne muß zusätzlich zum Antennenmast isoliert werden. Auch dafür wurde eine Halterung aus Kunststoff gefertigt.

Die Ausführung des Speisepunktes stellt die letzte

Koaxial-Speisekabel

Problematik bei der Konstruktion der logarithmisch-periodischen Dipolantenne dar. Eine elektrisch ideale Realisierung ist in Bild 67 zu sehen. Bei der praktischen Verwirklichung muß neben der elektrischen Funktion auch die Korrosionsfestigkeit gewährleistet sein:

Für beide Vierkant-Trägerrohre sind Aluminiumwürfel ge-

Elemente

Trägerrohre (Doppelleitung)

Elemente

Gap

I1 I2

fertigt worden, die in die Rohre eingepaßt wurden. In einem dieser Klötze wurde zusätzlich zentriert ein Loch gebohrt. Darin wurde dann eine BNC-Buchse so eingesetzt, daß der Buchsenverschluß in das Rohr hineinragt, während

Bild 67 Speisepunkt der LPDA

der Mittelkontakt nach außen frei absteht. Mittels eines Steges wurde dann von diesem Kontakt eine Verbindung zum anderen Trägerrohr geschaffen. Das Koaxial-Kabel kann so über ein BNC-Stecker wettergeschützt innerhalb des Rohres mit der BNC-Buchse verbunden werden. Die beiden Klötze und der Verbindungssteg wurden mit kleinen Edelstahlschrauben gesichert.

4.3. Meßergebnisse

Zur Messung der Antenneneingangsimpedanz und des Stehwellenverhältnisses wurde die logarithmischperiodische Dipolantenne senkrecht an einen Mast montiert, so daß diese ins Firmament strahlte. Dadurch konnten etwaige Beeinflussungen durch die Umgebung und den Erdboden weitgehend vermieden werden. Die Messungen wurden mit einem Network-Analyser durchgeführt und ausgeplottet. Ein Teil der Meßkurven ist im Anhang C zu finden.

Breitbandantennen Seite 42

Die erste Messung wurde im Bereich von 30 bis 300 MHz durchgeführt. In der Meßkurve war deutlich eine Fehlanpassung im unteren Frequenzbereich zu sehen. Um einen besseren Überblick zu erhalten, wurden weitere Meßdurchgänge mit kleineren Frequenzintervallen vorgenommen. Es zeigte sich, daß die Meßwerte unter 55 MHz und über 370 MHz gegen Unendlich liefen. Dieser Bereich entspricht in etwa der berechneten Strukturbandbreite von 6,81. Auffallend im Smith-Diagramm waren zwei große Schleifen im Bereich 50 bis 100 MHz und 100 bis 150 MHz. Es war ebenfalls deutlich zu sehen, daß die Meßwerte nicht um den Diagramm-Mittelpunkt (50 Ω) verliefen. Sie hatten einen leichten Versatz nach links; Die Antenne war also zu niederohmig (etwa 43 Ω).

Die Eingangsimpedanz der logarithmisch-periodischen Dipolantenne kann durch Vergrößern des Abstandes zwischen den beiden Trägerrohren erhöht werden. Dieser Abstand (5 mm) war bereits größer als berechnet. Er wurde dann auf 6 mm verbreitert.

Eine neue Meßreihe ergab dann den korrekten Wert von 50 Ω. Die Schleifen im Smith-Diagramm wur- den kleiner und verliefen um den Mittelpunkt. Es waren jedoch noch zwei Stellen bei 90 MHz und 125 MHz geblieben, an denen Fehlanpassung herrschte. Durch Verkürzen des Stubs konnten die Orte dieser Fehlanpassungen verändert werden, jedoch nicht deren Werte. Lediglich bei offener Speiseleitung (ohne Stub) verbesserte sich das Stehwellenverhältnis an diesen Stellen etwas. Nachteilig war jedoch, daß ohne Stub die untere Grenzfrequenz anstieg.

Im Idealfall müßten alle Strukturgrößen einer Breitbandantenne dem Winkelprinzip gehorchen. Bei der logarithmisch-periodischen Dipolantenne ist dieses aber nur bei der Elementlänge und deren Durchmesser gegeben. Die Ausdehnungen der Speiseleitung (Leiterdurchmesser und Abstand der Leiter) sind bei der LPDA jedoch konstant.

Da der Durchmesser der Trägerrohre nicht geändert werden konnte, wurde versucht, die elektrischen Eigenschaften der logarithmisch-periodischen Dipolantenne durch stetiges Vergrößern des Zwischenraumes der Trägerrohre zu verbessern.

Am Speisepunkt wurde der Abstand bei 6 mm belassen, um die Anpassung an 50 Ω zu gewährleisten. Der Trägerrohr-Abstand am niederfrequenten Ende wurde jedoch auf 9 mm aufgestockt. Durch diese Anordnung ergaben sich sodann deutlich bessere Meßergebnisse (siehe Anlage C). Weitere Ausdehnungen ergaben keine günstigeren Werte. Das Stehwellenverhältnis blieb in dieser Ausführung bis auf zwei schmale Stellen unter 1:1,5.

Um zu testen, ob sich die Meßwerte noch weiter verbessern ließen, wurde der Abstand der Trägerrohre weiter auf konstante 12 mm erhöht. Wie zu erwarten war, ergab sich dadurch eine Antenneneingangsimpedanz größer 50 Ω.

Die beste Lösung wäre jedoch gewesen, den Kapazitätsbelag am niederfrequenten Ende dadurch zu reduzieren, indem man den Durchmesser der langen Elemente verkleinern würde. So haben auch jeweils sämtliche Elemente der auf dem Markt erhältlichen logarithmisch-periodischen Dipolantennen eine gleiche Stärke (siehe z.B. Bild 34).

Breitbandantennen Seite 43

Anhang A: Programm-Listing

' LPDA.BAS von W.Rolke Version 1.01

DEFDBL a-z ' Alle Variablenbezeichner in doppelter Genauigkeit (64 Bit) ' # : doppeltgenaue Typen ' % : Integer-Typen

DO CLS PRINT PRINT " +-------------------------------------------------------------------------+ " PRINT " ¦ Dimensionierung einer logarithmisch-periodischen Dipol-Antenne (LPDA) ¦-+" PRINT " ¦ von W.Rolke V1.01 ¦ ¦" PRINT " +-------------------------------------------------------------------------+ ¦" PRINT " +-------------------------------------------------------------------------+" PRINT

DO INPUT " untere Frequenzgrenze fu / MHz "; fu INPUT " obere Frequenzgrenze fo / MHz "; fo LOOP UNTIL fu<fo AND fu>=10 AND fo/fu<50

DO INPUT " Stufungsfaktor (0.8 ≤ τ ≤ 0.975) "; Tau

LOOP UNTIL Tau>=0.8# AND Tau<=0.975#

OptSigma = 0.25#*Tau - 0.058# PRINT USING " Maximaler Gewinn mit σ=#.###"; OptSigma

DO INPUT " elektrische Periodizität (0.1 ≤ σ ≤ 0.2) "; Sigma

LOOP UNTIL Sigma>=0.1# AND Sigma<=0.2#

DO INPUT " Schlankheitsgrad der Dipole l/d "; s LOOP UNTIL s>=10 AND s<=1E4

DO INPUT " Resistanz der Speiseleitung Ro / Ω "; Ro

LOOP UNTIL Ro>=30 AND Ro<600

DO INPUT " Querschnitt der Doppelleitung rund oder quadratisch (r/q) "; Quer$ Quer$ = UCase$(Quer$) LOOP UNTIL Quer$="R" OR Quer$="Q"

IF Quer$="R" THEN Korrektur = 0 DO

INPUT " Durchmesser der Doppelleitung φ / mm "; dDoppel LOOP UNTIL dDoppel>0 AND dDoppel<=50 ELSE Korrektur = 15 DO INPUT " Kantenlänge der Doppelleitung a / mm "; dDoppel LOOP UNTIL dDoppel>0 AND dDoppel<=50 END IF

DO INPUT " Aktive Zone schmal oder breit (s/b) "; Breite$ Breite$ = UCase$(Breite$) LOOP UNTIL Breite$="S" OR Breite$="B"

AKBreit = 0 IF Breite$="B" THEN AKBreit = 1

Pi = 4*ATN(1) LambdaMax = 300/fu AlphaInRad = ATN( (1-Tau)/4/Sigma ) 'Öffnungshalbwinkel Alpha = AlphaInRad * 180/Pi 'Winkel in Grad B = fo/fu 'Mindestbandbreite K1 = -0.477#*Tau + 0.9725# 'Grenzfrequenzkonstanten K2 = 7.1#*Tau^3 - 21.3#*Tau^2 + 21.98#*Tau - 7.3# +_ Sigma * (21.82# - 66*Tau + 62.12#*Tau^2 - 18.29#*Tau^3)

Breitbandantennen Seite 44

IF AKBreit THEN 'Aktive Zone BAktiv = K1/K2 ELSE BAktiv = 1.1# + 30.8# * (1-Tau) * Sigma END IF Elemente = 1 + LOG10(B*BAktiv) / LOG10(1/Tau) 'Anzahl der Elemente N% = INT(Elemente) + 1 'Elemente aufrunden BStruktur = (1/Tau)^(N%-1) 'Strukturbandbreite Beff = BStruktur / BAktiv 'Effektive Bandbreite DIM L(N%), d(N%), a(N%) IF AKBreit THEN 'Längstes Element L1 = LambdaMax/2 * K1 ELSE L1 = LambdaMax/4 END IF Lang = L1 * (1-1/BStruktur) / TAN(AlphaInRad) 'Antennenbaulänge L(1) = L1 * 1000 'Längstes Element (mm) d(1) = 4 * L(1) * Sigma 'größter Dipolabstand a(1) = 2 * L(1) / s 'größter Durchmesser FOR i%=2 TO N% L(i%) = L(i%-1) * Tau 'Länge der Elemente d(i%) = d(i%-1) * Tau 'Dipolabstände a(i%) = 2 * L(i%) / s 'Elementdurchmesser NEXT i% ZDipol = 120 * (LOG(s) - 2.25#) 'Impedanz der Elemente Hilf = Ro * SQR(Tau)/Sigma / 8 / ZDipol Zo = Ro * (Hilf + SQR(Hilf^2 + 1)) 'Impedanz der Leitung h = dDoppel * (EXP( (Zo+Korrektur)/120 ) + EXP( -(Zo+Korrektur)/120 )) / 2

CLS PRINT PRINT " Die wichtigsten Werte der LPDA:" PRINT

PRINT USING " Stufungsfaktor τ=###.###"; Tau PRINT USING " elektische Periodizität σ=###.###"; Sigma

PRINT USING " untere Frequenzgrenze fu=#####.#MHz"; fu PRINT USING " obere Frequenzgrenze fo=#####.#MHz"; fu * Beff PRINT USING " effektive Bandbreite B=####.##"; Beff PRINT USING " Strukturbandbreite Bs=####.##"; BStruktur PRINT USING " Bandbreite der aktiven Zone Ba=####.##"; BAktiv

PRINT USING " Öffnungshalbwinkel der Struktur α=####.#°"; Alpha PRINT USING " Erforderliche Dipolanzahl N=#######"; N% PRINT USING " Antennenbaulänge (ohne Stub) A=###.##m"; Lang PRINT USING " Antennenbaulänge (mit Stub) A=###.##m"; Lang + LambdaMax/10 PRINT USING " Länge der kleinsten Dipolhälfte L##=#####mm"; N%, L(N%) * 0.48# * s/(1+s) PRINT USING " Länge der größten Dipolhälfte L1=#####mm"; L(1) * 0.48# * s/(1+s) PRINT USING " kleinster Dipolabstand d##=#####mm"; N%-1, d(N%-1) PRINT USING " größter Dipolabstand d1=#####mm"; d(1) PRINT USING " kleinster Dipoldurchmesser a##=###.#mm"; N%, a(N%) PRINT USING " größter Dipoldurchmesser a1=###.#mm"; a(1) PRINT USING " Mittenabstand der Doppelleitung s=###.#mm"; h

PRINT USING " Wellenwiderstand der Dipole Za=####.#Ω"; ZDipol PRINT USING " Wellenwiderstand der Doppelleitung Zo=####.#Ω"; Zo

PRINT INPUT " Antennenparameter ändern (j/n)"; NeueParam$ NeueParam$ = UCase$(NeueParam$) IF NeueParam$="N" THEN EXIT LOOP ERASE L, d, a LOOP

CLS PRINT PRINT " +-------------------------------------------------+" PRINT " ¦ Dipol ¦ Länge ¦ Abstand ¦ Durchmesser ¦" PRINT " ¦---------+-----------+-----------+---------------¦" PRINT USING " ¦ 1 ¦ ##### mm ¦ 0 mm ¦ ####.# mm ¦"; L(1) * 0.48# * s/(1+s), a(1) FOR i% = 2 TO N% PRINT USING " ¦ ## ¦ ##### mm ¦ ##### mm ¦ ####.# mm ¦"; i%, L(i%) * 0.48# * s/(1+s), d(i%-1), a(i%) IF i%=18 OR i%=40 THEN PRINT " ¦ Mit beliebiger Taste weiter... ¦" WHILE INKEY$="" : WEND END IF NEXT i% PRINT " +-------------------------------------------------+" ERASE L, d, a

Breitbandantennen Seite 45

Anhang B: Literaturverzeichnis

[1] CARREL, R.: THE DESIGN OF LOG.-PERIODIC DIPOLE ANTENNAS. IRE INT. CONV. REC.

OL. 9, PT. I, 1961, S. 61–75

[2] D

[3] D

U HAMEL, R. H., ORE, F.R.: LOGARITHMICALLY PERIODIC ANTENNA DESIGNS. IRE NAT.

ONV. REC. VOL. 6, PT. I, 1958, S. 139–151

UBOST, G., ZISLER, S.: BREITBAND-ANTENNEN. R. OLDENBOURG VERLAG, MÜNCHEN,

1977, 355 S. [4] H [5] J

EILMANN, A.: ANTENNEN III. BIBLIOGRAPHISCHES INSTITUT AG, MANNHEIM, 1970, 184 S.

ASIK, H.: ANTENNA ENGENEERING HANDBOOK. MCGRAW-HILL, NEW YORK, 1961,

S. 18.1–18.31 [6] K [7] K [8] K [9] M

[10] R

RAUS, J. D.: ANTENNAS. MCGRAW-HILL, NEW YORK, 1988, 892 S. RUG, J.: VORLESUNG IMPULSTECHNIK, FH NIEDERRHEIN KREFELD, 1989/90 ÜHN, R.: MIKROWELLEN ANTENNEN. VEB VERLAG TECHNIK, BERLIN, 1964, S. 650–664

EINKE, H., GUNDLACH, F. W.: TASCHENBUCH DER HOCHFREQUENZTECHNIK. SPRINGER-

ERLAG, BERLIN, 1986

OTHAMMEL, K.: ANTENNENBUCH. FRANCKH-KOSMOS VERLAG, STUTTGART, 10. AUFLAGE

[11] RUMSEY, V. H.: FREQUENCY-INDEPENDENT ANTENNAS. ACADEMIC PRESS, NEW YORK, 1966 [12] S

[13] S

MITH, C. E.: LOG-PERIODIC ANTENNA DESIGN HANDBOOK. SMITH-ELECTRONICS PRESS,

LEVELAND, OHIO, 1966, 375 S.

TIRNER, E.: ANTENNEN BAND 2: PRAXIS. ALFRED HÜTHIG VERLAG, HEIDELBERG, 1980,

215 S. [14] S

N [15] W [16] W

ANTENNEN. NTZ, 1969, HEFT 9, S. 531–542

TUTZMAN, W. L., THIELE, G. A.: ANTENNA THEORY AND DESIGN. JOHN WILEY & SONS,

EW YORK, 1981, 598 S.

EEKS, W. L.: ANTENNA ENGENEERING. MCGRAW-HILL, NEW YORK, 1968, 370 S. OHLLEBEN, R.: DIE TYPEN LINEAR-POLARISIERTER LOGARITHMISCH-PERIODISCHER

Breitbandantennen Seite 46

Anhang C: Meßkurven

Smith-Diagramm 30-300 MHz

Smith-Diagramm 50-100 MHz

Breitbandantennen Seite 47

Smith-Diagramm 100-150 MHz

Smith-Diagramm 150-200 MHz

Breitbandantennen Seite 48

Smith-Diagramm 200-250 MHz

Smith-Diagramm 250-300 MHz

Breitbandantennen Seite 49

Stehwellenverhältnis 30-300 MHz

Horizontaldiagramm 89 MHz

Breitbandantennen Seite 50

Horizontaldiagramm 99 MHz

Horizontaldiagramm 107 MHz

Breitbandantennen Seite 51

Horizontaldiagramm 203 MHz

Stand: 16. Mai 2003

Cherokee NightRider-150, CBS 1000 User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual