Page 1

Calculatrices CASIO Graph 80 à 100 1
(
)
3
Eléments de base
1°) Calculs usuels
•
Conseil : laissez votre calculatrice en radians et lorsque vous voulez un résultat en degrés,
multipliez-le par la constante 180/π. (Ex : 0,23 rad ≈ 13,178029288°)
•
Règles de priorité : les formules doivent être tapées comme si on les écrivait sur une feuille
de papier. Par exemple,
√ 3 → X EXE puis 2X LN(X) EXE permet de calculer 23.ln
•
On peut omettre les parenthèses fermantes situées immédiatement devant la touche EXE .
Il en est de même pour un signe x devant une parenthèse ouvrante ou un nom de mémoire.
•
La dernière formule frappée peut être modifiée en utilisant les touches de déplacement
horizontal. On peut revenir sur les formules précédentes en tapant AC ON puis en
utilisant les flèches de déplacement vertical.
•
Utilisation des 28 mémoires (de A à Z puis ρ et θ) :
9 x 8 → Alpha A EXE affiche 72 et le stocke dans la mémoire A.
*
2 Alpha A → Alpha B EXE affiche 144 et le stocke dans la mémoire B.
*
•
SCI 3 permet d'afficher tous les résultats avec une incertitude relative de l'ordre de 10-2 (3
chiffres significatifs).
•
Démarche à suivre pour écrire 11 h 34' 51" en heure décimale sur certaines calculatrices :
Option ANGL puis 11 F4 34 F4 51 F4 EXE .
On obtient alors 11,5808333 h.
•
Ecrivez la démarche à suivre pour écrire 3,74194445 h en notation traditionnelle :
.
(On obtient 3 h 44' 31")
Page 2
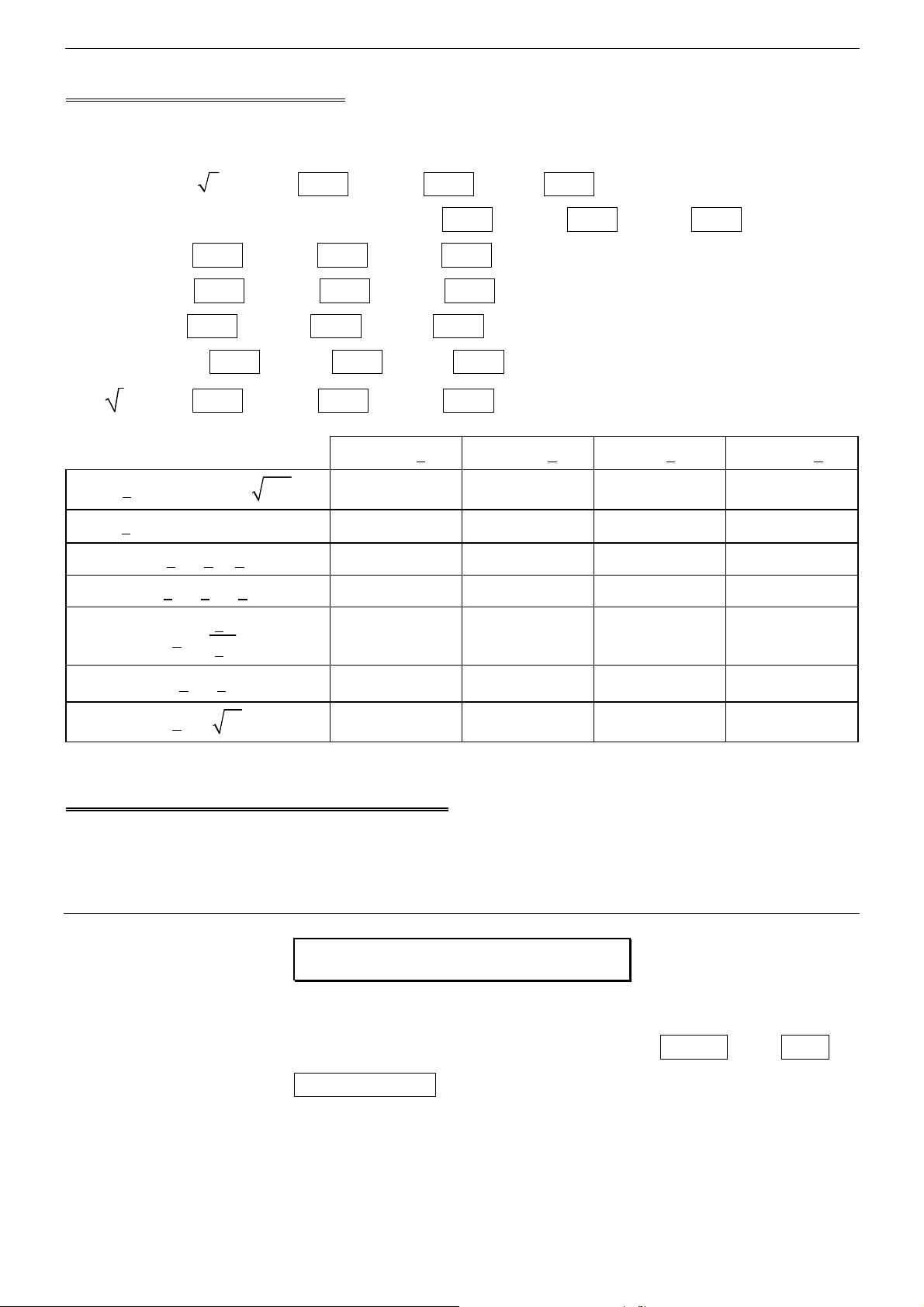
2 IUT VESOUL
1,9
3
5
5
z
x.ln(x).dx
(x.ln(x),1,2)
∫
2°) Opérations sur les complexes
Passez en mode complexe, les instructions suivantes permettent de compléter le tableau cidessous avec une incertitude relative de l'ordre de 10-3 (4 chiffres significatifs) :
sin(1,1) + i 1,9 → A EXE Abs(A) EXE Arg(A) EXE
ln(148).cos(0,6) + i.ln(148).sin(0,6) → B EXE Abs(B) EXE Arg(B) EXE
A*B → C EXE Abs(C) EXE Arg(C) EXE
B+C → D EXE Abs(D) EXE Arg(D) EXE
C/D → E EXE Abs(E) EXE Arg(E) EXE
E*E*E → F EXE Abs(F) EXE Arg(F) EXE
E → G EXE Abs(G) EXE Arg(G) EXE
Re (z) Im (z) |z| arg (z)
z1 = sin(1,1) + j
z2 = ln(148).exp(0,6j)
z3 = z1 . z2
z4 = z2 + z3
0,8912 1,378 1,641 0,9969
4,124 2,822 4,997 0,6000
- 0,2137 8,200 8,203 1,597
3,911 11,02 11,69 1,230
z3
z5 =
z6 = z
z7 =
z
4
0,6547 0,2517 0,7014 0,3670
0,1562 0,3077 0,3451 1,101
0,8234 0,1528 0,8375 0,1835
3°) Représentation graphique d'une fonction
Ecrivez la démarche à suivre pour superposer les représentations graphiques des fonctions
x → x2 – 3 et x → tan(x).
Calcul d'une intégrale
Pour calculer I =
2
∫
1
il suffit d'écrire
La calculatrice donne I ≈ 0,636 294 361 1 .
(Utilisez Option puis Calc ).
Page 3
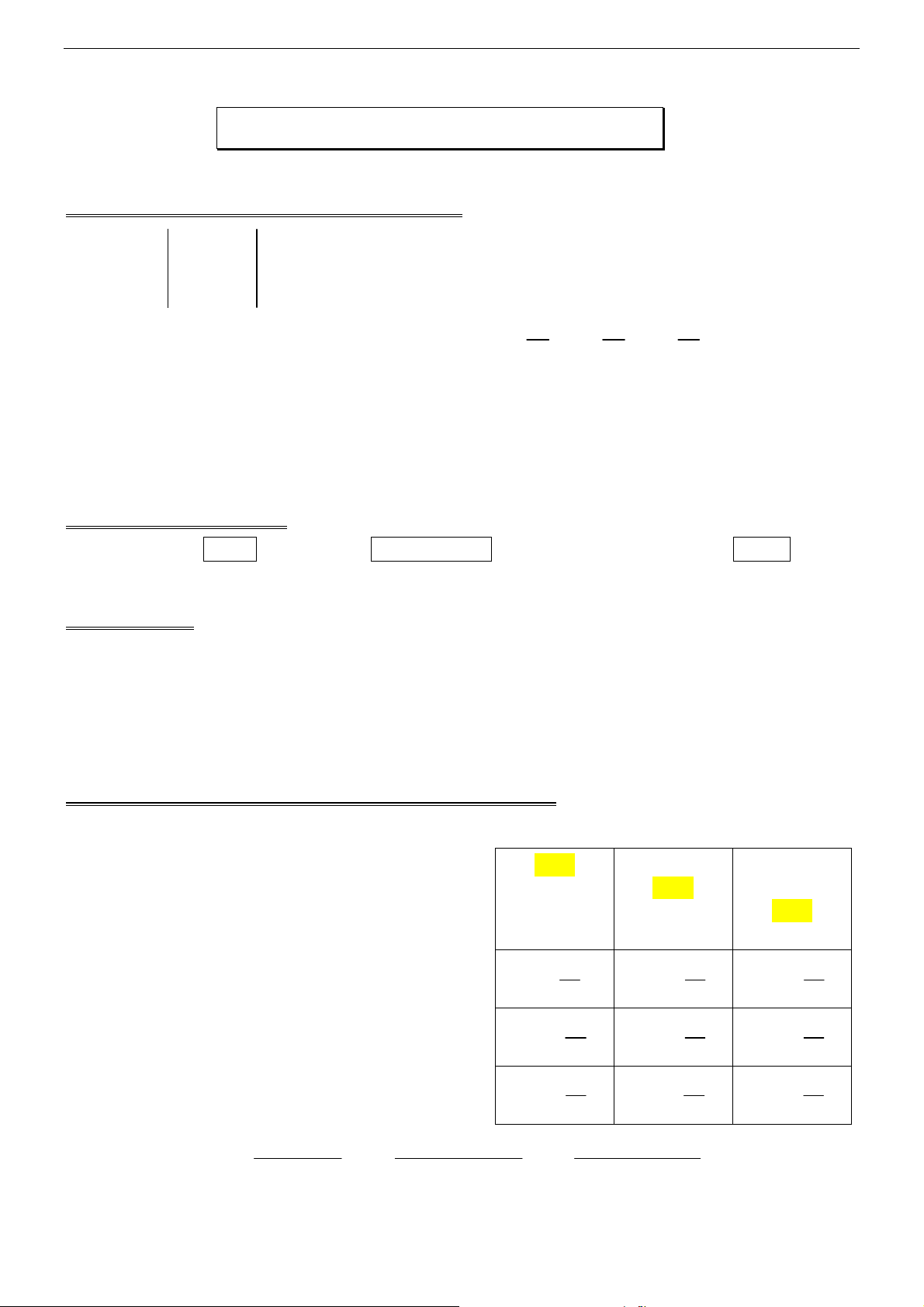
Calculatrices CASIO Graph 80 à 100 3
1 1 1 1
2 2 2 2
3 3 3 3
a x b y c z d
a x b y c z d
a x b y c z d
+ + =
1 1 1
2 2 2
3 3 3
a b c
a b c
a b c
x
∆
∆
y
∆
∆
z
∆
∆
7x 3y 3z a
8x 5y 4z b
5x 7y 5z c
− + − =
ère
3
54
6
54
−
3
54
−
20
54
50
54
−
52
54
−
31
54
−
64
54
59
54
−
3a 6b 3c
54
− −
20a 50b 52c
54
− − −
31a 64b 59c
54
− − −
+ + =
Résolution d'un système 3x3
+ + =
1°) Rappels du cours sur les systèmes linéaires
Soit ∆ =
•
Si ∆ ≠ 0, le système admet une solution unique x =
, le déterminant du système.
; y =
; z =
.
•
Si ∆ = 0 et ( ∆x ≠ 0 ou ∆y ≠ 0 ou ∆z ≠ 0), le système est impossible.
•
Si ∆ = 0 et ∆x = 0 et ∆y = 0 et ∆z = 0, suivez la démarche du cours.
2°) Résolution du système
Dans le menu Equa sélectionnez Simultaneous , suivez les instructions puis Solve .
3°) Remarques
•
La méthode ci-dessus permet de résoudre un système nxn quelconque.
•
Restez vigilant : Math Error signifie qu'il y a, soit aucune solution, soit une infinité de
solutions.
+ − =
4°) Exemple où les seconds membres sont des paramètres : (S)
− + =
•
Une 1
donne les coefficients de a dans x ; y et z.
•
Une 2
donne les coefficients de b dans x ; y et z.
•
Une 3
donne les coefficients de c dans x ; y et z.
•
On en déduit, x =
résolution pour a = 1 ; b = 0 ; c = 0
ème
résolution pour a = 0 ; b =1 ; c = 0
ème
résolution pour a = 0 ; b = 0 ; c = 1
; y =
a = 1
b = 0
c = 0
donne
x =
y =
z =
; z =
x =
−
y =
z =
a = 0
b = 1
c = 0
donne
−
x =
y =
z =
.
a = 0
b = 0
c = 1
donne
Page 4
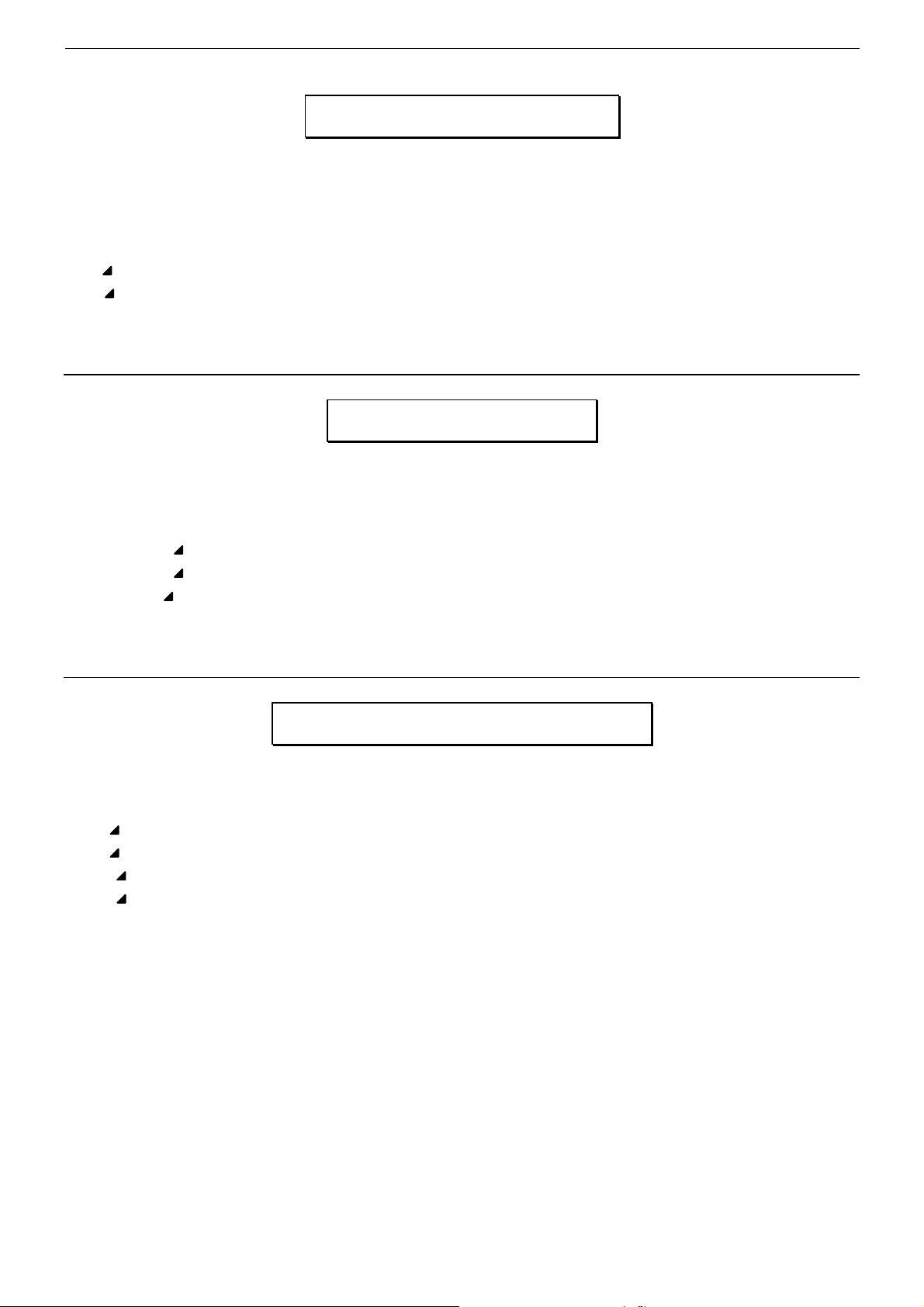
4 IUT VESOUL
Programme fraction
"Valeur numérique" ? → X : 1 → P : 0 → Q : Int(X) → R : 1 → S : 1/(X-R) → Y :
Lbl 1 : Int(Y) → A : AR + P → T : AS + Q → U : Abs(X-T/U) ≤ 10-9 ⇒ Goto 2 :
1/(Y-A) → Y : R → P : S → Q : T → R : U → S : Goto 1 : Lbl 2 : "X=" :
T
U
Produit vectoriel
"X1"? → A : "Y1"? → B : "Z1"? → C : "X2"? → D : "Y2"? → E : "Z2"? → F :
BF - CE → G : CD - AF → H : AE - BD → I :
"X3=" : G
"Y3=" : H
"Z3=" : I
Fonction de 2 variables
Programme "Aff"
X
Y
Y1
" "
Programme "Vérif"
"X"? → A : "Y"? → B :
A - 0.1 → X : B - 0.1 → Y : Prog "Aff" : B → Y : Prog "Aff" : B + 0.1 → Y : Prog "Aff" :
A → X : B - 0.1 → Y : Prog "Aff" : B → Y : Prog "Aff" : B + 0.1 → Y : Prog "Aff" :
A + 0.1 → X : B - 0.1 → Y : Prog "Aff" : B → Y : Prog "Aff" : B + 0.1 → Y : Prog "Aff"
Exécution du programme principal "Vérif"
Saisissez la fonction de 2 variables dans la ligne Y1 pour le tracé des fonctions.
Lancez le programme "Vérif" puis suivez les instructions.
Page 5

Calculatrices CASIO Graph 80 à 100 5
Statistiques à 1 variable
Exemple n°1
On considère la série statistique "Taille" décrite ci-dessous.
Taille (en cm) 180 173 167 165 189 195 156 178 182
•
Passez en mode STAT.
•
Remplissez la liste L1 avec les tailles (xi).
•
Calc puis SET (F6)
La calculatrice donne
E[Taille] ≈ 176,111 111 111
σn(Taille) ≈ 11,532 027 329
•
1 Var XList : L1
1 Var Freq : 1
•
EXIT
•
1 Var
σ
(Taille) ≈ 12,231 562 088
n-1
Exemple n°2
On considère la série statistique X qui étudie le nombre d'enfants.
Nombre d'enfants
0 1 2 3 4 5 6
Effectif 18 32 66 41 32 9 2
•
Passez en mode STAT.
•
Remplissez la liste L1 avec les nombres d'enfants (xi).
La calculatrice donne
E[X] = 2,36
Remplissez la liste L2 avec les effectifs (ni).
•
Calc puis SET (F6)
•
1 Var XList : L1
σn(X) ≈ 1,341 789 849
σ
n-1
1 Var Freq : L2
•
EXIT
•
1 Var
(X) ≈ 1,345 156 956
Page 6

6 IUT VESOUL
Exemple n°3
On considère la série statistique "Note".
Note ]0;3] ]3;6] ]6;9] ]9;12] ]12;15] ]15;18] ]18;20]
Effectif 2 6 7 9 9 6 1
Pour pouvoir effectuer le calcul, on remplace chaque classe par son centre. D'où le tableau
suivant. Ensuite on utilise le même mode opératoire qu'à l'exemple n°2.
Note 1,5 4,5 7,5 10,5 13,5 16,5 19
Effectif 2 6 7 9 9 6 1
La calculatrice donne E[Note] = 10,4125
σn(Note) ≈ 4,499 843 747
σ
(Note) ≈ 4,557168 909
n-1
Statistiques à 2 variables
Exemple n°1
Le tableau ci-dessous résume l'observation d'une série statistique à 2 variables X et Y.
X 67 63 67 62 68 62 70 68 70 72
Y 68 66 68 65 71 65 68 71 68 71
Solution
•
Passez en mode STAT.
•
Remplissez la liste L1 avec les xi.
Remplissez la liste L2 avec les yi.
•
Calc puis SET (F6)
La calculatrice donne
•
2 Var XList : L1
2 Var YList : L2
2 Var Freq : 1
•
EXIT
Pour obtenir moyennes et écarts-type :
•
2 Var puis Calc
Pour obtenir le coefficient de corrélation linéaire :
•
2 Var puis REG puis Linear
E[X] = 66,9
σn(X) ≈ 3,330 165 161
σ
(X) ≈ 3,510 302 298
n-1
E[Y] = 68,1
σn(Y) ≈ 2,211 334 439
σ
(Y) ≈ 2,330 951 165
n-1
r(X ; Y) ≈ 0,802 541 091
Page 7
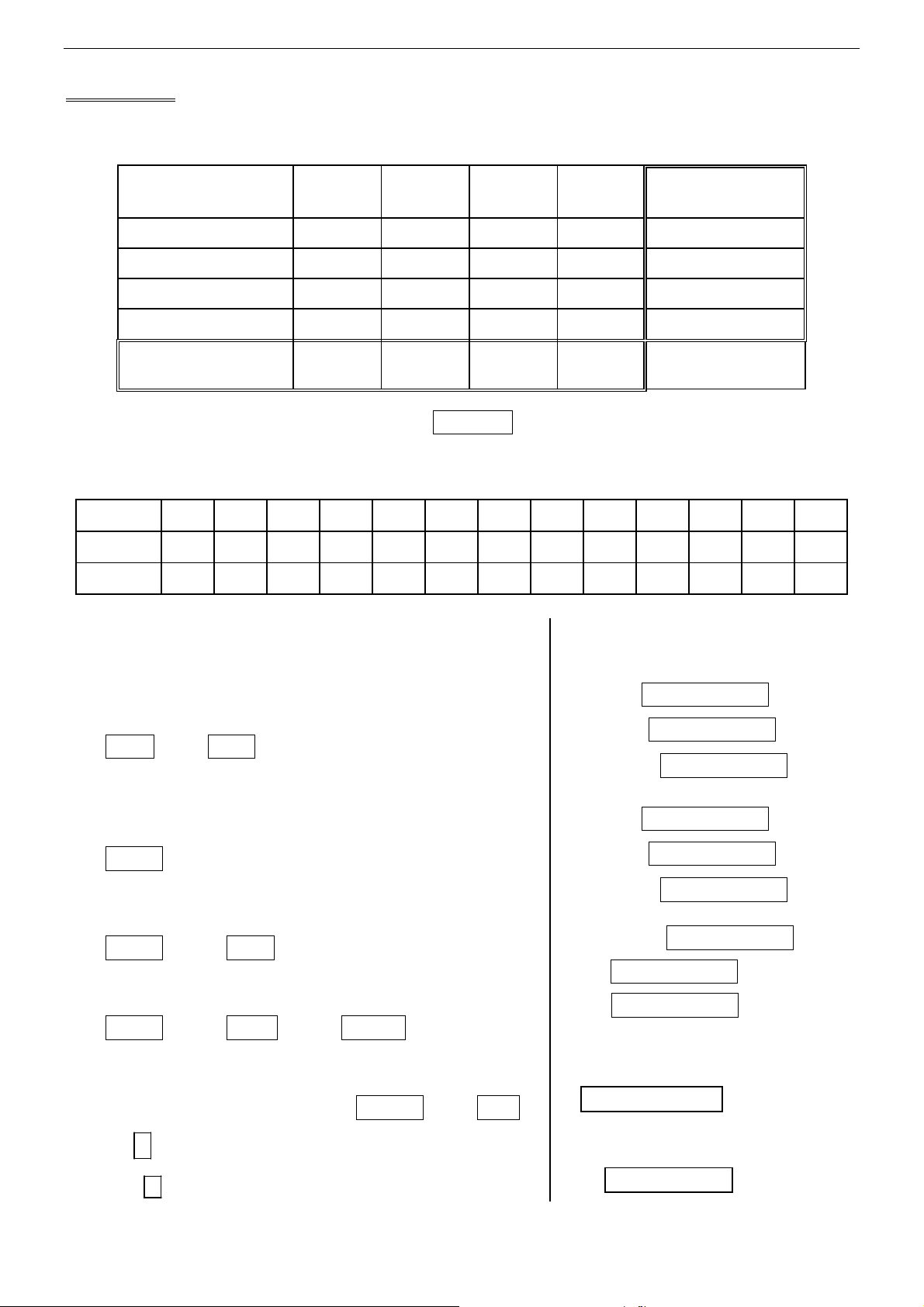
Calculatrices CASIO Graph 80 à 100 7
ˆ
y
ˆ
x
Exemple n°2
Sur une population de 70 personnes, on mesure la masse et la taille. Les observations sont
consignées dans le tableau ci-dessous.
Taille (en cm)
Masse (en kg)
]160;165] ]165;170] ]170;175] ]175;180]
série marginale
"Masse"
]48;56] 16 1 0 0 17
]56;64] 8 10 4 1 23
]64;72] 1 4 8 5 18
]72;80] 0 1 2 9 12
série marginale
"Taille"
25 16 14 15 70
Solution
Pour pouvoir effectuer le calcul, on remplace chaque classe par son centre. Ensuite, on
transforme le tableau de contingences en un tableau exhaustif. C'est le tableau ci-dessous.
Masse (xi) 52 52 60 60 60 60 68 68 68 68 76 76 76
Taille (yi) 162,5 167,5 162,5 167,5 172,5 177,5 162,5 167,5 172,5 177,5 167,5 172,5 177,5
Effectif (ni) 16 1 8 10 4 1 1 4 8 5 1 2 9
•
Passez en mode STAT.
•
Remplissez la liste L1 avec les xi.
Remplissez la liste L2 avec les yi.
La calculatrice donne
E[X] ≈ 62,857 142 86
Remplissez la liste L3 avec les ni.
σn(X) ≈ 8,229 365 041
•
Calc puis SET (F6)
σ
(X) ≈ 8,288 783 611
•
2 Var XList : L1
n-1
2 Var YList : L2
2 Var Freq : L3
E[Y] ≈ 168,857 142 9
•
EXIT
Pour obtenir moyennes et écarts-type :
•
2 Var puis Calc
Pour obtenir le coefficient de corrélation linéaire :
•
2 Var puis REG puis Linear
Pour obtenir les estimations du cours :
•
Passez en mode RUN. Ensuite Option puis Stat .
•
66
•
176
donne 170, 613 067 cm
donne 75, 641 855 kg
σn(Y) ≈ 5,789 240 548
σ
(Y) ≈ 5,831 040 662
n-1
r(X ; Y) ≈ 0,794 192 401
a ≈ 0,558 702 989
b ≈ 133,738 669 2
Une personne dont la masse est
66 kg aura une taille estimée de
170,613 067 cm .
Une personne dont la taille est
176 cm aura une masse estimée
de 75,641 855 kg .
Page 8

8 IUT VESOUL
Loi binomiale
0°) Menu "Distr" du mode "Stat " pour certains modèles
Si X suit une loi binomiale de paramètres n = 5 et p = 0,6,
•
Pour obtenir P(X=3) ≈ 34,56 % : Binmal puis P.D puis Data Var puis x=3 puis
Numtrial=5 puis p=0,6 puis Execute .
•
Pour obtenir P(0 ≤ X ≤ 4) ≈ 92,22 % : Binmal puis C.D puis Data : Var puis x=4 puis
Numtrial=5 puis p=0,6 puis Execute . Vous lisez : 0,92224.
•
Pour obtenir P(2 ≤ X ≤ 4) ≈ 83,52 % : stockez 4 et 1 dans la liste n°1 ensuite Binmal puis
C.D puis Data : List puis List : List1 puis Numtrial=12 puis p=0,6 puis
SaveRes : List2 puis Execute . Passez en mode "Run" puis List2[1] – List2[2]
( Option permet d'accéder aux listes).
1°) Programme
"N"? → N : "P"? → P : "A"? → A : "B"? → B : 0 → M :
Lbl 0 : NCA → C : C*(P ^ A*(1-P) ^ (N-A)) + M → M : If A=B : Then Goto 2 : IfEnd : Isz
A :
Goto 0 :
Lbl 2 : "P(A≤ X≤ B)=" : M
Remarque : Option Prob pour obtenir C (fonction nCr)
2°) Exécution
Si X suit une loi binomiale de paramètres n = 5 et p = 0,6,
•
Pour obtenir P(X=3) ≈ 34,56 % : N=5 ; P=0,6 ; A=3 ; B=3.
•
Pour obtenir P(2 ≤ X ≤ 4) ≈ 83,52 % : N=5 ; P=0,6 ; A=2 ; B=4.
Loi de POISSON
0°) Menu "Distr" du mode "Stat " pour certains modèles
Si X suit une loi de Poisson de paramètre λ = 1,7,
•
Pour obtenir P(X=3) ≈ 14,96 % : Poisson puis P.D puis Data Var puis x=3 puis
Lambda=1,7 puis Execute .
•
Pour obtenir P(0 ≤ X ≤ 4) ≈ 97,04 % : Poisson puis C.D puis Data : Var puis x=4 puis
Lambda=1,7 puis Execute . Vous lisez : 0,97039.
•
Pour obtenir P(2 ≤ X ≤ 4) ≈ 47,71 % : stockez 4 et 1 dans la liste n°1 ensuite Poisson puis
C.D puis Data : List puis List : List1 puis Lambda=1,7 puis
SaveRes : List2 puis Execute . Passez en mode "Run" puis List2[1] – List2[2]
( Option permet d'accéder aux listes).
Page 9

Calculatrices CASIO Graph 80 à 100 9
1°) Programme
"LAMBDA"? → L : "A"? → A : "B"? → B : 0 → M :
Lbl 0 : A! → C : (L ^ A/C)*e(-L) + M → M : If A=B : Then Goto 2 : IfEnd : Isz A :
Goto 0 :
Lbl 2 : "P(A≤ X≤ B)=" : M
2°) Exécution
Si X suit une loi de Poisson de paramètre λ = 1,7,
•
Pour obtenir P(X=3) ≈ 14,96 % : Lambda=1,7 ; A=3 ; B=3.
•
Pour obtenir P(2 ≤ X ≤ 4) ≈ 47,71 % : Lambda=1,7 ; A=2 ; B=4.
Loi normale : fonction π
0°) Menu "Distr" du menu "Stat " pour certains modèles
Si D suit une loi normale N(74;3),
•
Pour obtenir P(D<77) ≈ 84,13 % : Norm puis C.D puis Lower = -1E99 ; Upper = 77 ;
σ=3 ; µ=74. Remarque : -1E99 signifie -∞.
•
Pour obtenir P(70<D<76) ≈ 65,62 % : Norm puis C.D puis Lower = 70 ; Upper = 76 ;
σ=3 ; µ=74.
1°) Programme
•
Pour obtenir la fonction P (qui correspond à la fonction π) : Option Prob F6 F1 .
•
"M"? → M : "E"? → E :
Lbl 0 : "P(A<X<B) : TAPE 1" : "P(A<X) : TAPE 2" : "P(X<B) : TAPE 3" ? → R :
"A"? → A : "B"? → B :
If R=1 Then Goto 1 : IfEnd :
If R=2 Then Goto 2 : IfEnd :
If R=3 Then Goto 3 : IfEnd :
Lbl 1 : "P(A<X<B)=" : P((B-M)/E) - P((A-M)/E) Goto 0 :
Lbl 2 : "P(A<X)=" : 1 - P((A-M)/E) Goto 0 :
Lbl 3 : "P(X<B)=" : P((B-M)/E) Goto 0 :
2°) Exécution
Si D suit une loi normale N(74;3),
•
Pour obtenir P(D<77) ≈ 84,13 % : M=74 ; E = 3 ; Tape = 3 ; A=77 ; B=77.
•
Pour obtenir P(70<D<76) ≈ 65,62 % : M=74 ; E = 3 ; Tape = 1 ; A=70 ; B=76.
Page 10

10 IUT VESOUL
Loi normale réciproque
0°) Menu "Distr" du menu "Stat " pour certains modèles
•
Pour obtenir π
-1
(0,879) ≈ 1,17 : Norm puis Inverse puis Tail=Left ; Area=0,879.
•
Si D suit une loi normale N(74;3), pour obtenir le réel t ≈ 76,025 tel que P(D<t) = 0,75
Norm puis Inverse puis Tail=Left ; Area=0,75 ; σ=3 ; µ=74.
:
1°) Programme
•
Pour obtenir la fonction P (qui correspond à la fonction π) : Option Prob F6 F1 .
•
Lbl 3 : "B="? → B : 0 → X :
Lbl 1 : X → Y : X - (P(X) - B)* (2π) / e(-X2/2) → X :
If ABS(X-Y) < 0.0001 Then Goto 2 : IfEnd : Goto 1 :
Lbl 2 : "T = " : X Goto 3
2°) Exécution
Pour obtenir π
-1
(0,879) ≈ 1,17 : B = 0,879 et le programme donne T=1,17...
 Loading...
Loading...