CASIO Graph 60, Graph 30, CFX-9940GT User Manual [fr]

Download

MANUEL DE L’UTILISATEUR

GRAPH35 GRAPH65

CONNECTABLE

DEXXON DATAMEDIA

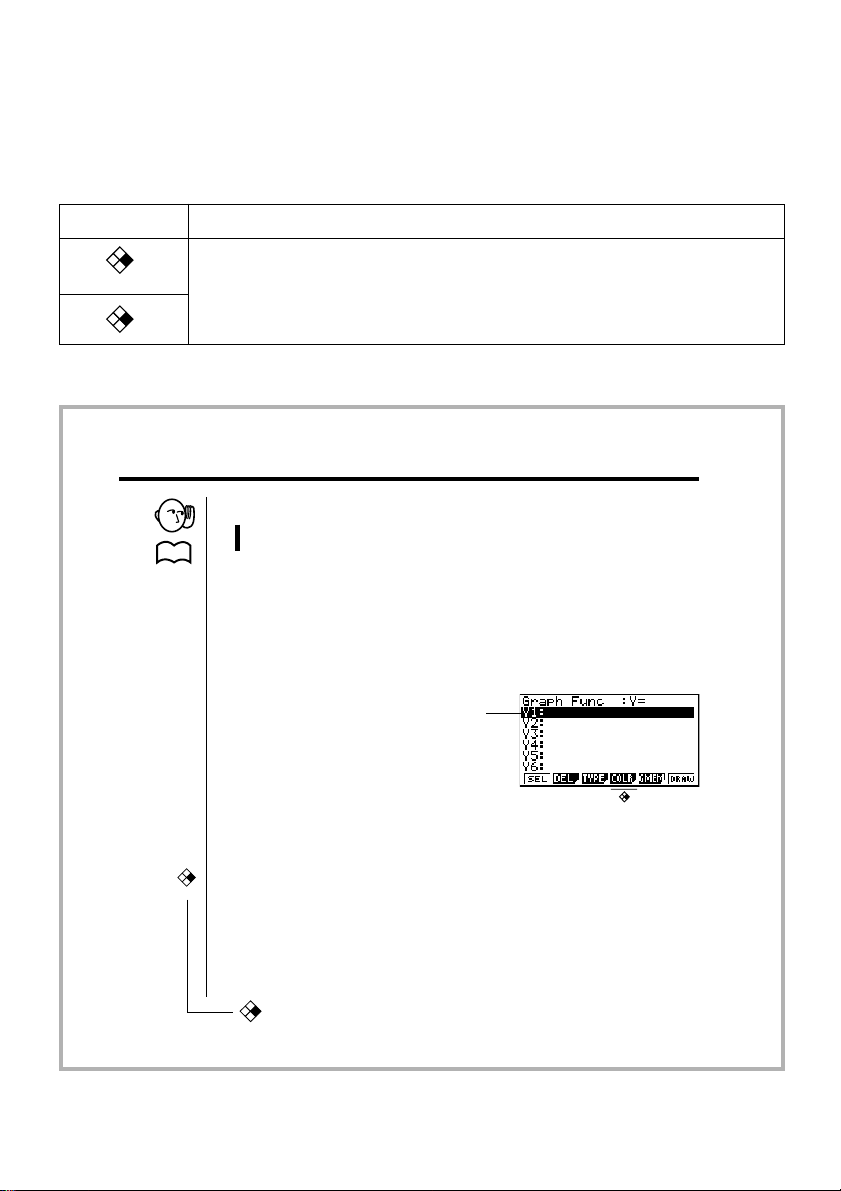
Utilisateurs de la GRAPH 35+ …

Ce manuel couvre différents modèles de calculatrices. Veuillez noter les symboles suivants lorsque vous utilisez ce manuel.

Symbole

couleur

Indique des informations qui ne concernent pas la GRAPH 35+. Vous pouvez ignorer les informations marquées de ce symbole.

8-1 Avant de tracer un graphe

k Réglage de la configuration

Avant de commencer un tracé de graphe, vérifiez le réglage de l’écran de configuration du menu GRAPH: Set Up.

P. 5 à 7

k Entrée dans le mode graphique

Sur le menu principal, sélectionnez le symbole GRAPH et appuyez sur w. Le menu de fonctions graphiques apparaît à ce moment à l’écran. Vous pouvez utiliser ce menu pour stocker, éditer, rappeler des fonctions et produire les graphes correspondants.

Zone de mémoire

Utilisez f et c pour changer de

Signification

sélection

couleur

• {SEL} ... {statut avec tracé/sans tracé}

• {DEL} ... {effacement de fonction}

• {TYPE} ... {menu de types de graphes}

• {COLR} ... {couleur de graphe}

• {GMEM} ... {sauvegarde/rappel de graphe}

• {DRAW} ... {tracé de graphe}

indique que {COLR} n’est pas supporté par la GRAPH 35+.

couleur

CARTE DE GARANTIE

GARANTIE 3 ANS

Ce modèle est garanti pendant TROIS ans, à compter de la date d’achat. Sont exclus de cette garantie:

• les piles livrées avec l’appareil

• tous dommages de l’ECRAN

•TOUS DEFAUTS OU DETERIORATIONS provoqués par un mauvais usage ou un accident.

• frais d’expédition au service après-vente CASIO.

De plus, pour que la prise en charge sous garantie soit acceptée, la calculatrice devra être accompagnée du présent certificat rempli(joindre éventuellement la facture ou le ticket d’achat). Afin de nous aider dans la recherche de la panne, veuillez indiquer l’organe ou la fonction incriminé.

Cachet du revendeur ou bon de caisse

GRAPH35+/GRAPH65

Date d’achat: (obligatoire)

Pour toute réparation dans le cadre de la garantie, le service après-vente CASIO peut exiger cette carte dûment complétée.

Agent DEXXON DATAMEDIA GENNEVILLIERS

Pour toute informations ou en cas de panne, contactez:

CONSOMMATEUR ASSISTANCE SERVICE

Tél: 08 92 68 33 44

INTERNET http://www.cas-calcul.com

Adresse: CASIO/Assistance Consommateur

DEXXON DATAMEDIA 8 rue Ferdinand de Lesseps 95190 Goussainville

* ( 0,34 C/min )

AVANT D’UTILISER LA CALCULATRICE

BACK UP

POUR LA PREMIÈRE FOIS...

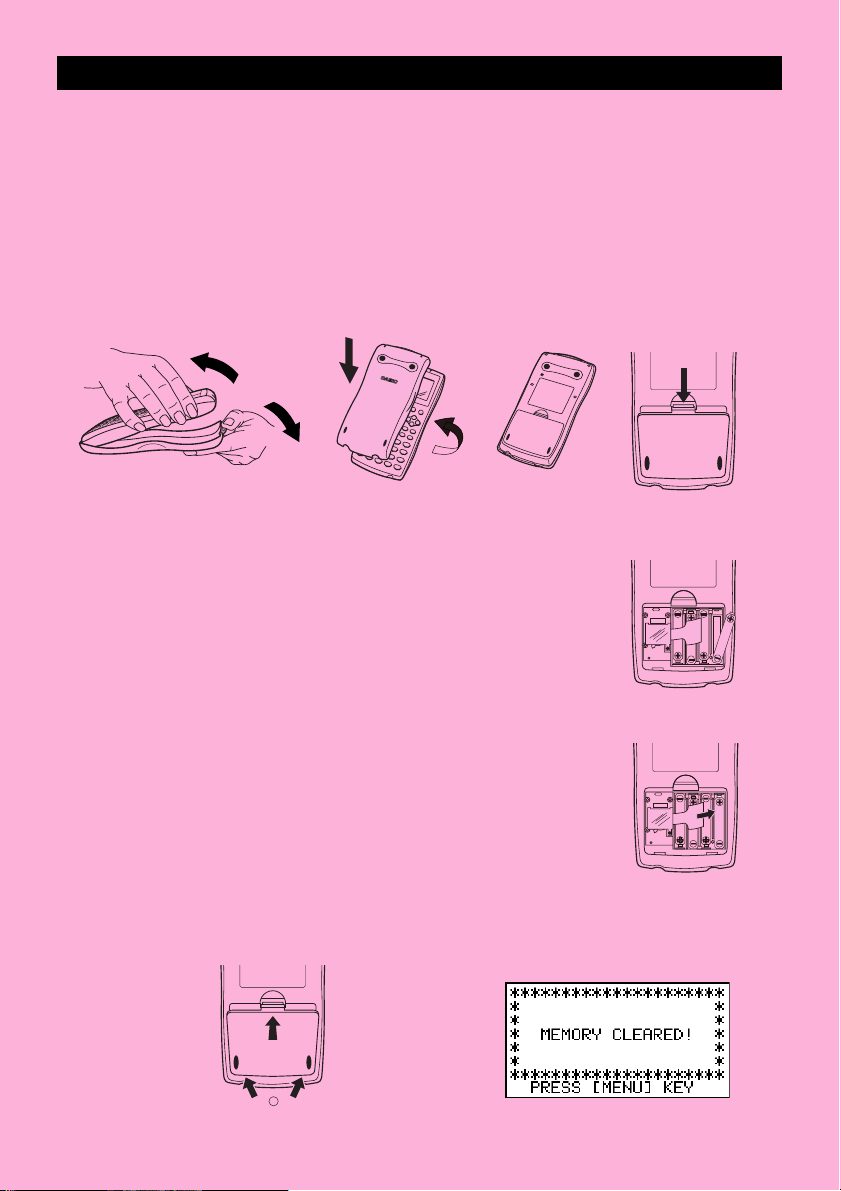
N’oubliez pas d’effectuer les opérations suivantes pour mettre les piles en place, reinitialiser la calculatrice et régler le contraste avant d’essayer d’utiliser la calculatrice.

1. A veillant à ne pas appuyer accidentellement sur la touche o, fixez l’étui à

la calculatrice et retournez la calculatrice. Enlevez le couvercle arrière de la calculatrice en tirant avec le doigt au point indiqué par

2. Insérez les quatre piles fournies avec la calculatrice.

• Assurez-vous que les extrémités positives (+) et négatives (–) des piles sont dirigées dans le bon sens.

3. Enlevez la pellicule isolante à l’endroit marqué “BACK UP” en tirant dans le sens de la flèche.

BACK UP

4. Remettez-le couvercle arrière en faisant bien entrer les griffes dans les orifices indiqués par

2 et retournez la calculatrice, face vers le haut. La calculatrice doit

s’allumer automatiquement et réinitialiser la mémoire.

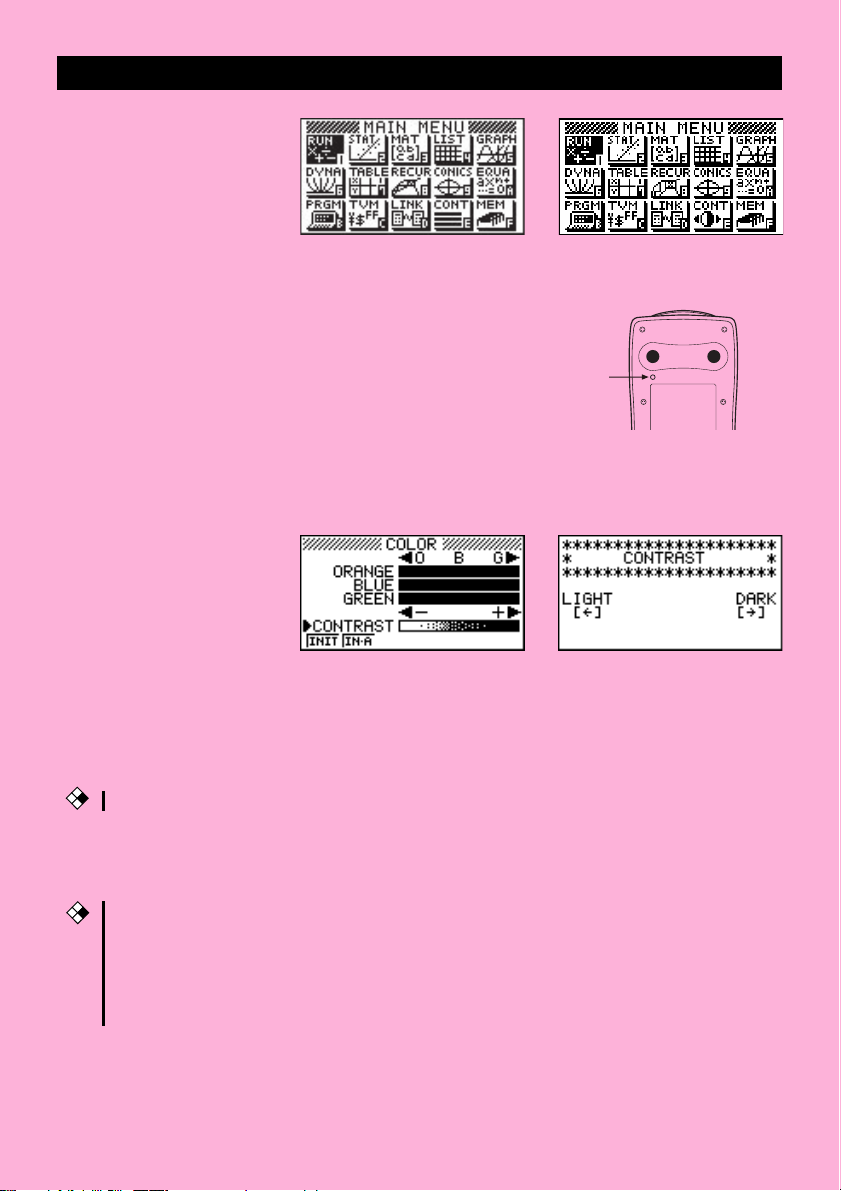
5. Appuyez sur m.

* L’écran ci-dessus est celui de la

GRAPH 65.

* L’écran ci-dessus est celui de la

GRAPH 35+ .

•Si le menu principal indiqué ci-dessus n’apparaît pas,

appuyez sur le bouton P au dos de la calculatrice pour réinitialiser la mémoire.

Bouton P

6. Utilisez les touches de curseur f, c, d et e pour sélectionner le symbole

CONT et appuyez sur w ou simplement sur

pour afficher l’écran de réglage du

contraste.

GRAPH 65

GRAPH 35

7. Ajustez le contraste.

uPour ajuster le contraste

•Utilisez f et c pour amener le pointeur devant CONTRAST.

couleur

• Appuyez sur e pour assombrir les caractères sur l’écran et sur d pour les

éclaircir.

uPour ajuster la teinte

couleur

1. Utilisez f et c pour amener le pointeur devant la couleur que vous voulez

ajuster (ORANGE, BLUE ou GREEN).

2. Appuyez sur e pour obtenir une couleur plus verte et sur d pour obtenir

une couleur plus orange.

8. Pour quitter l’écran de réglage du contraste, appuyez sur m.

couleur

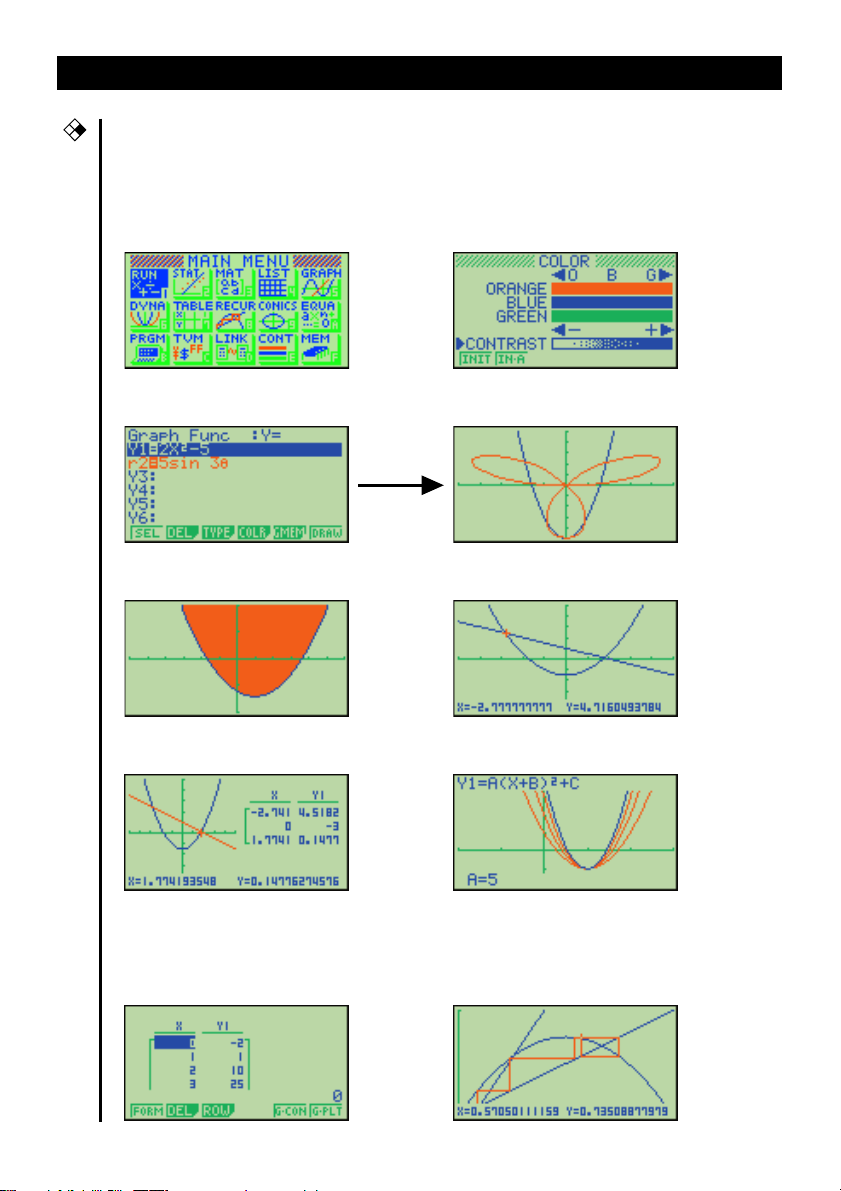
A PROPOS DE L’AFFICHAGE COULEUR

L’affichage utilise trois couleurs, l’orange, le bleu et le vert, pour faciliter la lecture des données.

•Menu principal • Réglage de la couleur

•Menu de fonctions graphiques

•

Affichage graphique (Exemple 1)•Affichage graphique (Exemple 2)

•Affichage de graphe à table • Affichage de graphe dynamique

•Table numérique de Table et • Exemple de graphe de Graphe divergence/convergence de

formule de récurrence

iii

couleur

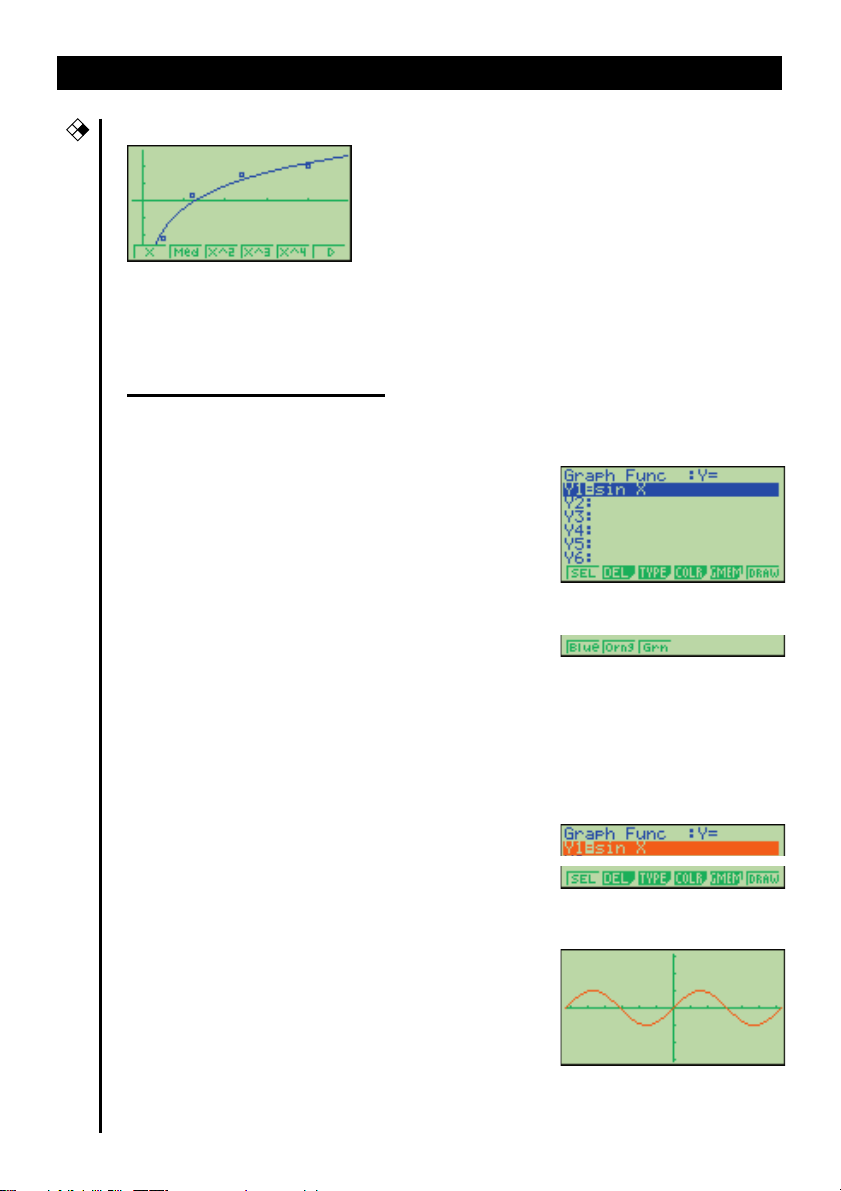
•Exemple de graphe de régression statistique

• Lorsque vous tracez un graphe ou mettez un programme en route, les textes de commentaires apparaissent normalement en bleu, mais vous pouvez changer la couleur du texte et choisir l’orange ou le vert.

Exemple:

1. Entrez dans le mode GRAPH et effectuez les opérations suivantes.

Tracer une sinusoïde

3(TYPE)1(Y=)

(Définit des coordonnées rectangulaires.)

svwf

(Stocke l’expression.)

4(COLR)

• Appuyez sur la touche de fonction qui correspond à la couleur que vous

voulez utiliser pour le graphe:

pour le vert.

3. 2(Orng)

(Définit la couleur du graphe.)

1 pour le bleu, 2 pour l’orange et 3

4. 6(DRAW)

(Trace le graphe.)

1234 56

1 2 3456

123456

Vous pouvez aussi tracer plusieurs graphes de différentes couleurs sur le même écran, de manière à bien les distinguer les uns des autres.

Touches

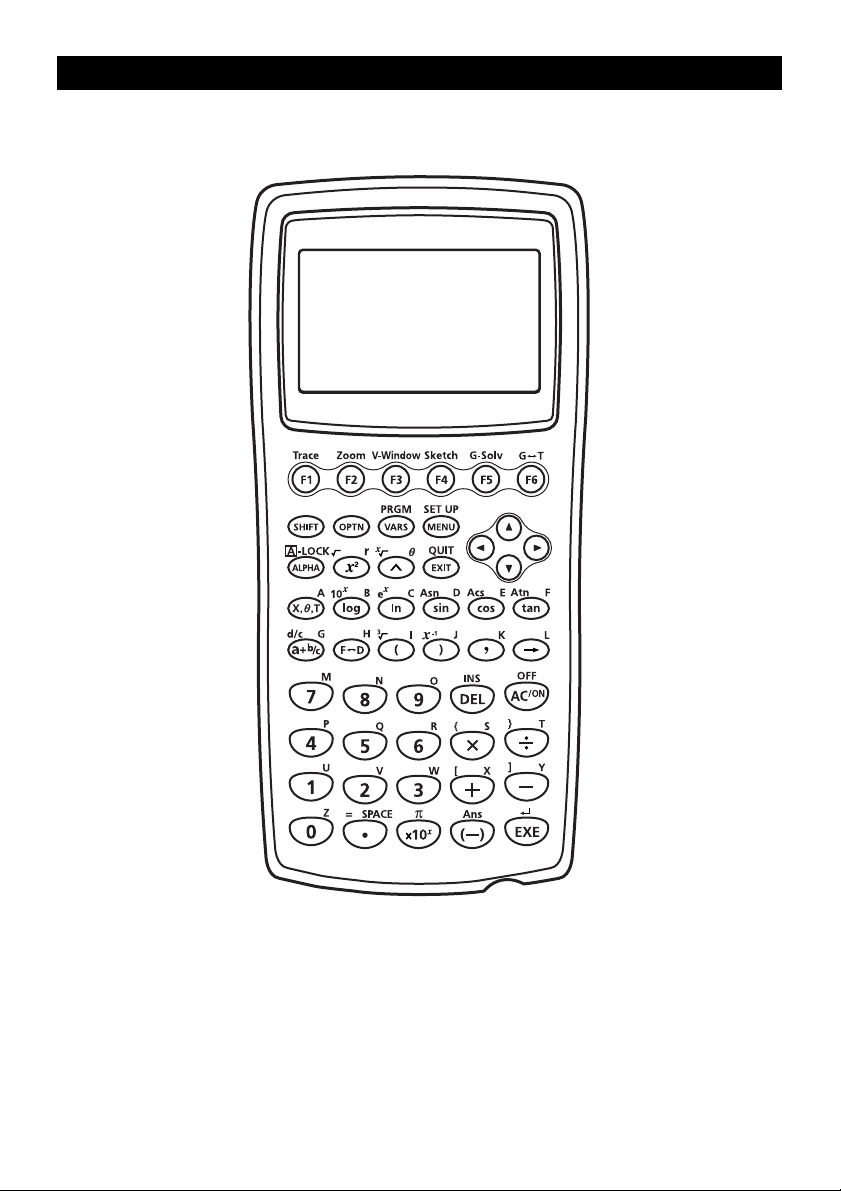
Verrouillage alpha

Normalement, après avoir appuyé sur a puis sur une touche pour entrer un caractère alphabétique, le clavier revient immédiatement à ses fonctions primaires. Si vous appuyez sur ! puis sur a, le clavier se verrouille en entrée alphabétique jusqu’à ce que vous appuyiez de nouveau sur a.

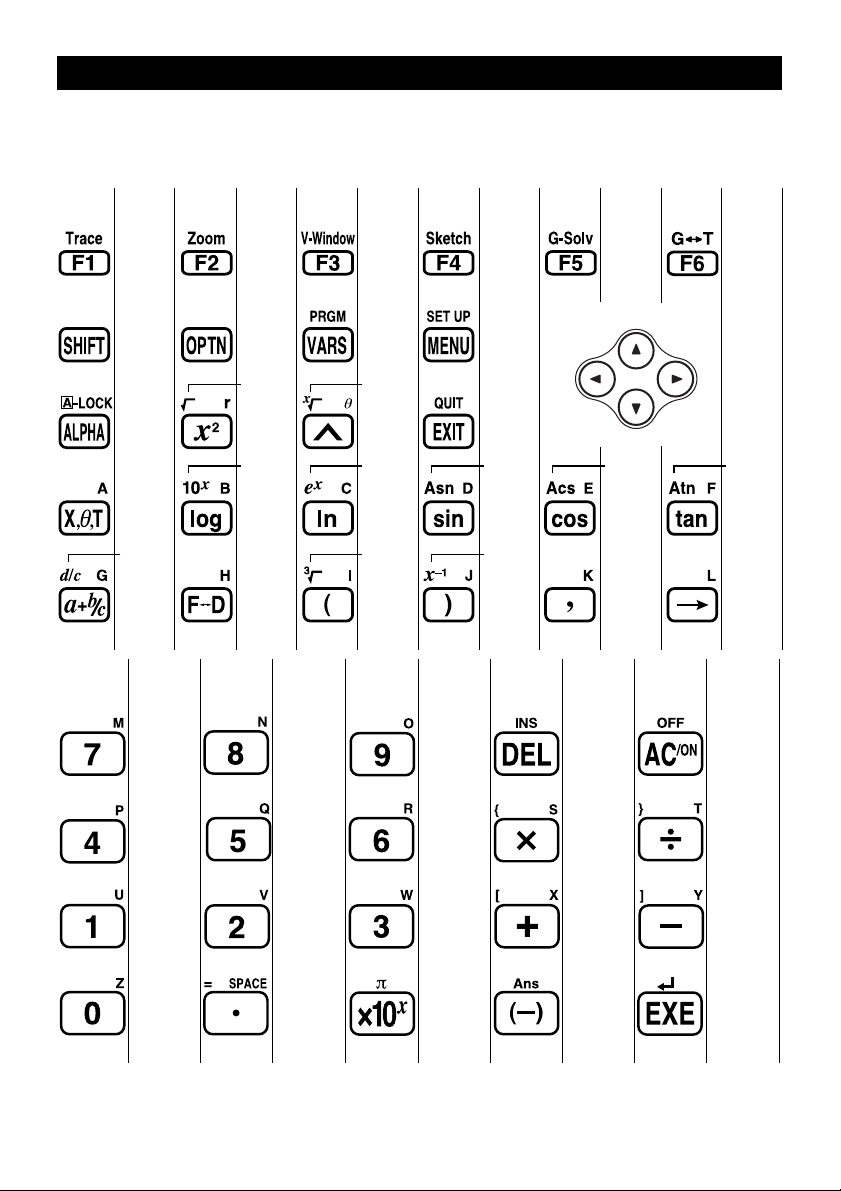
Tableau des touches

Page Page Page Page Page Page

128

227283

24746

Page Page Page Page Page

132 113

369 4

47 46

46 46

154 144 120

45 45

Démarrage rapide

Mise sous / hors tension Utilisation des modes Calculs de base Fonction de répétition Calculs de fractions Exposants Fonctions graphiques Graphe double Zoom sur cadre Graphe dynamique Fonction de table

Démarrage rapide

Bienvenue dans le monde des calculatrices graphiques.

Ce sommaire n’est pas un guide éducatif complet, mais il vous initie aux fonctions les

plus communes, de la mise sous tension à la spécification des couleurs et aux équations graphiques complexes. Quand vous l’aurez lu, vous maîtriserez les opérations de base

de cette calculatrice et serez prêt à aborder la suite de ce mode d’emploi pour faire connaissance avec toutes les fonctions disponibles.

Toutes les phases des exemples du sommaire sont illustrées graphiquement pour vous aider à comprendre rapidement et facilement l’opération. Si vous devez entrer le nombre 57 par exemple, nous l’indiquons comme suit:

Appuyez sur

Chaque fois que c’était nécessaire, nous avons inséré des exemples d’écran. Si votre écran ne correspond pas à l’exemple, vous pouvez recommencer depuis le début en appuyant sur le bouton

“All Clear” (vidage complet).

MISE SOUS/HORS TENSION

Pour mettre sous tension, appuyez sur o. Pour mettre hors tension, appuyez sur !o.

La calculatrice s’éteint automatiquement si vous ne réalisez pas d’opération pendant six minutes environ (60 minutes si un calcul est arrêté par la commande de sortie (^)).

OFF

UTILISATION DES MODES

Cette calculatrice facilite la réalisation d’un grande nombre de calculs par simple sélection du mode approprié. Avant d’aborder les calculs et les opérations d’exemples réels, voyons comment passer d’un mode à l’autre.

Pour sélectionner le mode RUN

1. Appuyez sur m pour afficher le menu principal.

* L’écran ci-dessus est celui de la

GRAPH 65.

viii

Démarrage rapide

2. Utilisez defc pour mettre RUN en

surbrillance et appuyez sur

C’est l’écran initial du mode RUN, dans lequel vous

pouvez effectuer les calculs manuels et exécuter des

programmes.

CALCULS DE BASE

Avec les calculs manuels, vous entrez vos formules de gauche à droite, simplement comme elles s’écrivent sur une feuille de papier. Avec les formules qui comprennent des opérateurs arithmétiques et des parenthèses, la calculatrice applique automatiquement la logique algébrique vraie pour calculer le résultat.

Exemple:

1. Appuyez sur o pour vider la calculatrice.

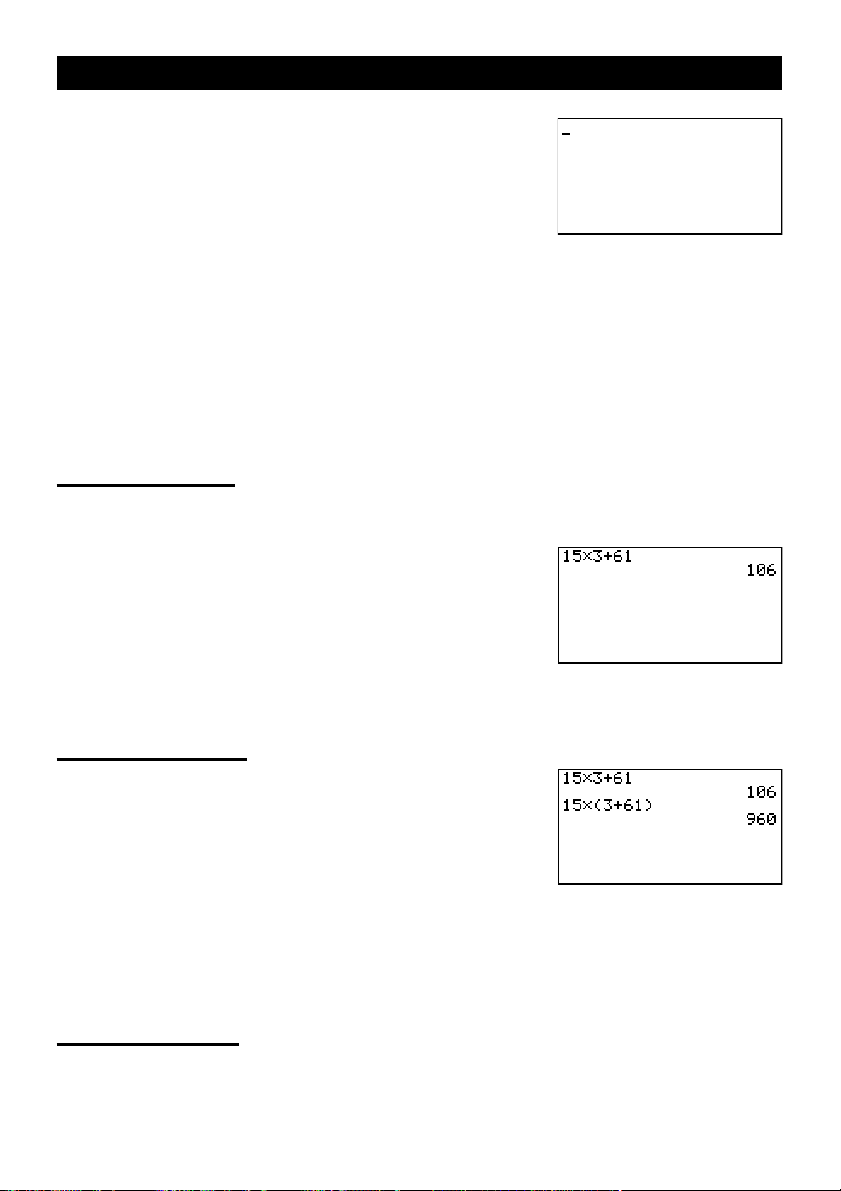
2. Appuyez sur

15 × 3 + 61

bf*d+gb

Calculs avec parenthèses

Exemple:

1. Appuyez sur

15 × (3 + 61)

bf*(d +gb)w.

Fonctions incorporées

Cette calculatrice comprend un certain nombre de fonctions scientifiques, dont les fonctions trigonométriques et logarithmiques.

Exemple:

25 × sin 45˚

Important!

Spécifiez bien Deg (degré) comme unité d’angle avant de tenter de réaliser cet exemple.

Démarrage rapide

1. Appuyez sur o.

SET UP

2. Appuyez sur !m pour afficher le menu de

configuration.

3. Appuyez sur

spécifier les degrés comme unité de mesure angu-

laire.

4. Appuyez sur J pour quitter le menu.

5. Appuyez sur o pour vider la calculatrice.

6. Appuyez surcf*sefw.

cccc1 (Deg) pour

FONCTION DE RÉPÉTITION

Avec la fonction de répétition, appuyez simplement sur d ou e pour rappeler

le dernier calcul exécuté. Une fois le calcul rappelé, vous pouvez faire des changements ou le recommencer tel qu’il est.

Exemple:

Changer le calcul de l'exemple précédent (25 × sin 45˚) en (25 × sin 55˚)

1. Appuyez sur

2. Appuyez deux fois sur d pour amener le curseur

sur 4.

3. Appuyez sur

4. Appuyez sur w pour exécuter le calcul à nouveau.

d pour afficher le dernier calcul.

Démarrage rapide

CALCULS DE FRACTIONS

Vous pouvez utiliser la touche N pour entrer des fractions dans un calcul. Le

symbole “ { ” est utilisé pour séparer les diverses parties d’une fraction.

Exemple:

151637

1+ + 1

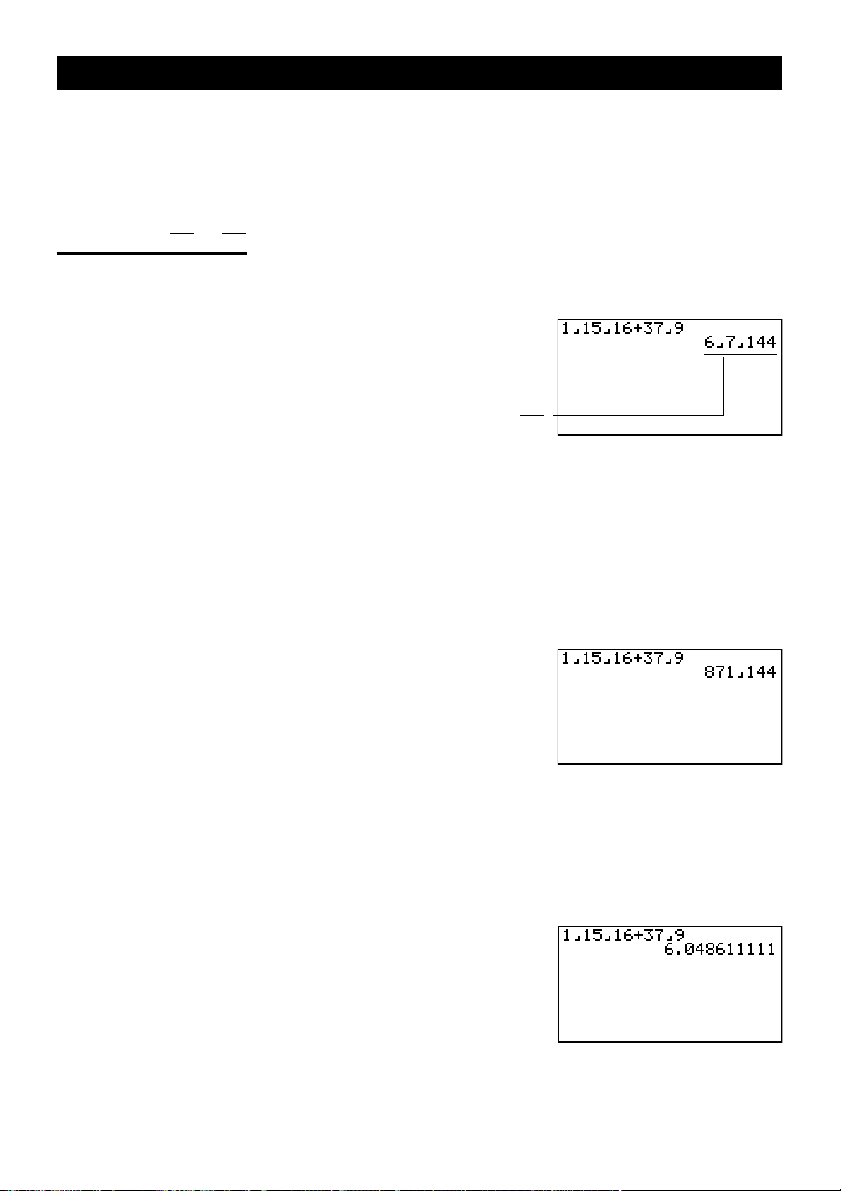
1. Appuyez sur

2. Appuyez sur bNbfN

bg+dhN jw.

Indique 6 +

Conversion d’une fraction mixte en un nombre fractionnaire

Quand une fraction mixte est affichée à l’écran, appuyez sur convertir en un nombre fractionnaire.

Appuyez à nouveau sur

! N

d/c

pour le reconvertir en une fraction mixte.

Conversion d’une fraction en son équivalent décimal

Lorsqu’une fraction est affichée à l’écran, appuyez sur M pour la convertir en son

équivalent décimal.

Appuyez à nouveau sur M pour revenir à la fraction.

144

d/c

! N

pour le

Démarrage rapide

EXPOSANTS

Exemple:

1. Appuyez sur o.

2. Appuyez sur bcfa*c.ag.

3. Appuyez sur

4. Appuyez sur f. Le ^5 à l’écran indique que 5 est

5. Appuyez sur

1250 × 2,06

l’exposant.

M. L’indicateur ^ apparaît à l’écran.

xii

Démarrage rapide

FONCTIONS GRAPHIQUES

Les capacités graphiques de la calculatrice permettent de tracer des graphes complexes à partir de coordonnées rectangulaires (axe horizontal: x ; axe vertical: y) ou de coordonnées polaires (angle: θ ; distance de l’origine: r).

Exemple

1. Appuyez sur

2. Utilisez d, e, f et c pour mettre

3. Entrez la formule.

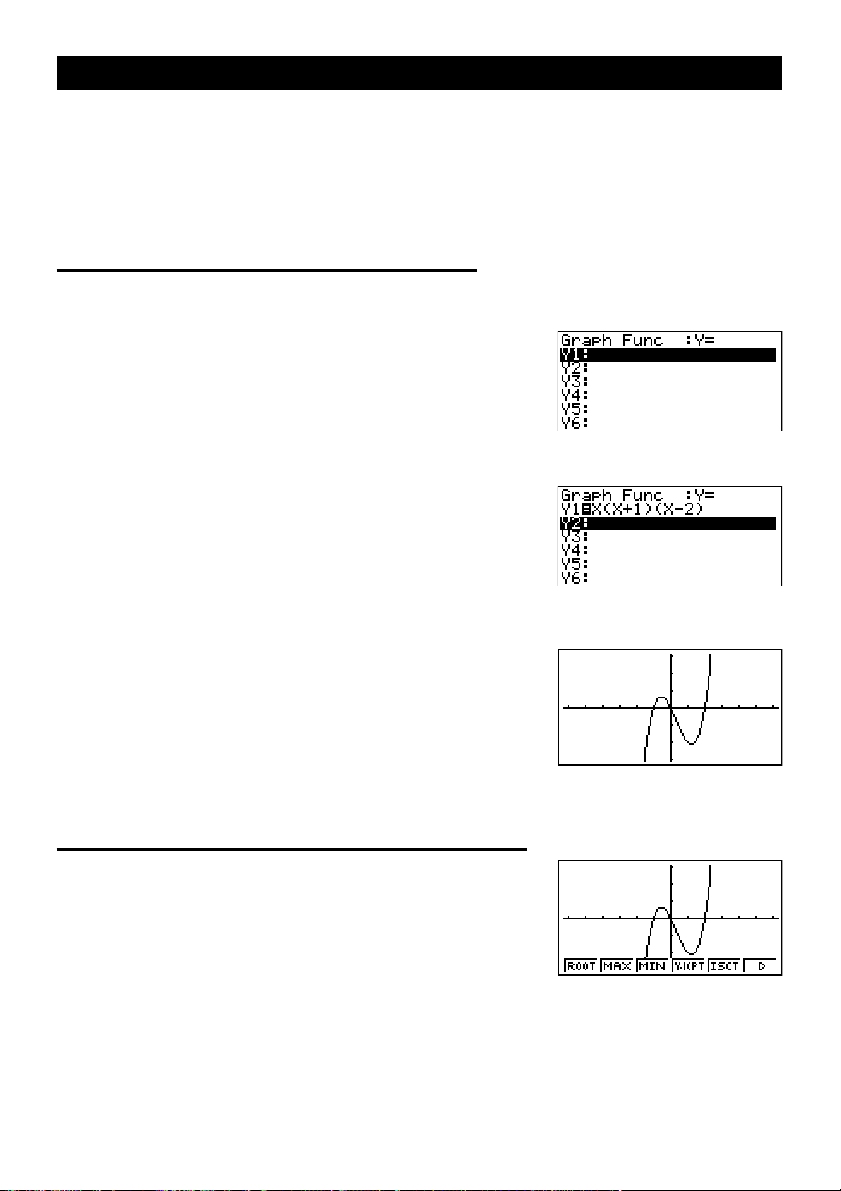
1: Tracer le graphe de Y = X(X + 1)(X – 2)

GRAPH en surbrillance, puis appuyez sur

v(v+b)

(v-c)w

4. Appuyez sur 6 (DRAW) ou w pour tracer le graphe.

Exemple

2: Déterminer les racines de Y = X(X + 1)(X – 2)

1. Appuyez sur

! 5 (G-Solv).

1 23456

xiii

Démarrage rapide

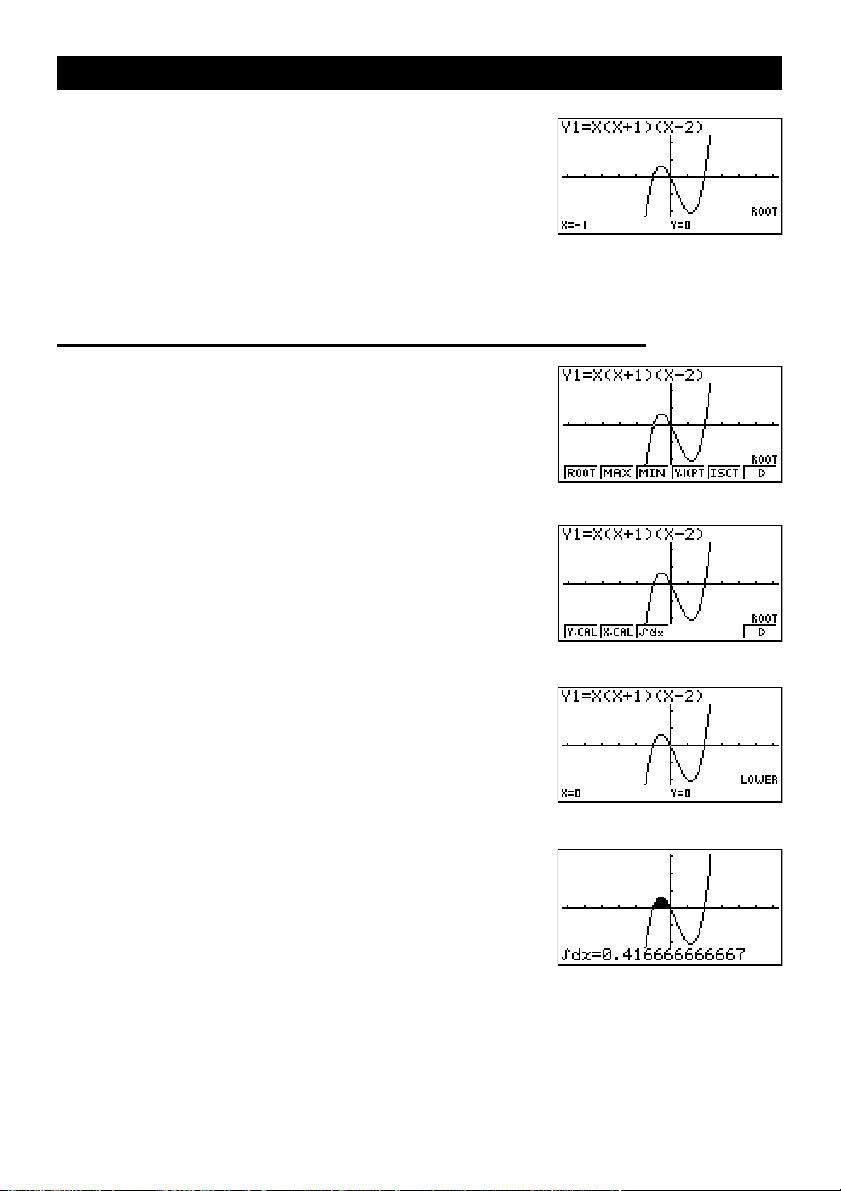
2. Appuyez sur 1 (ROOT).

Appuyez sur

Exemple

1. Appuyez sur

2. Appuyez sur

3. Appuyez sur

3: Déterminer la zone délimitée par l’origine et la racine X = –1

obtenue pour Y = X(X + 1)(X – 2)

e pour d’autres racines.

!5 (G-Solv).

6 (g).

3 (

dx).

∫

123456

123 456

4. Utilisez

X = –1 puis appuyez sur

amener le pointeur à l’endroit où X = 0, puis appuyez

sur

apparaît en sombre à l’écran.

xiv

d pour amener le pointeur à l’endroit où

w. Utilisez e pour

wpour entrer la plage d’intégration, qui

Démarrage rapide

GRAPHE DOUBLE

Cette fonction vous permet de diviser l’écran en deux zones et d’afficher deux graphes sur le même écran.

Exemple:

1. Appuyez sur !Zcc1(Grph)

2. Appuyez sur

Tracer les deux graphes suivants et déterminer les points d’intersection

Y1 = X(X + 1)(X – 2) Y2 = X + 1,2

pour spécifier “Graph” pour le réglage du double

écran.

J, puis entrez les deux fonctions.

v(v+b)

(v-c)w

v+b.cw

3. Appuyez sur 6(DRAW) ou wpour tracer les

graphes.

1 23456

ZOOM SUR CADRE

Utilisez la fonction “BOX” de zoom pour délimiter la zone d’un graphe que vous voulez agrandir.

1. Appuyez sur

2. Utilisez

pointeur sur un angle de la zone que vous voulez

spécifier, puis appuyez sur

!2 (Zoom) 1 (BOX).

d, e, f et c pour amener le

Démarrage rapide

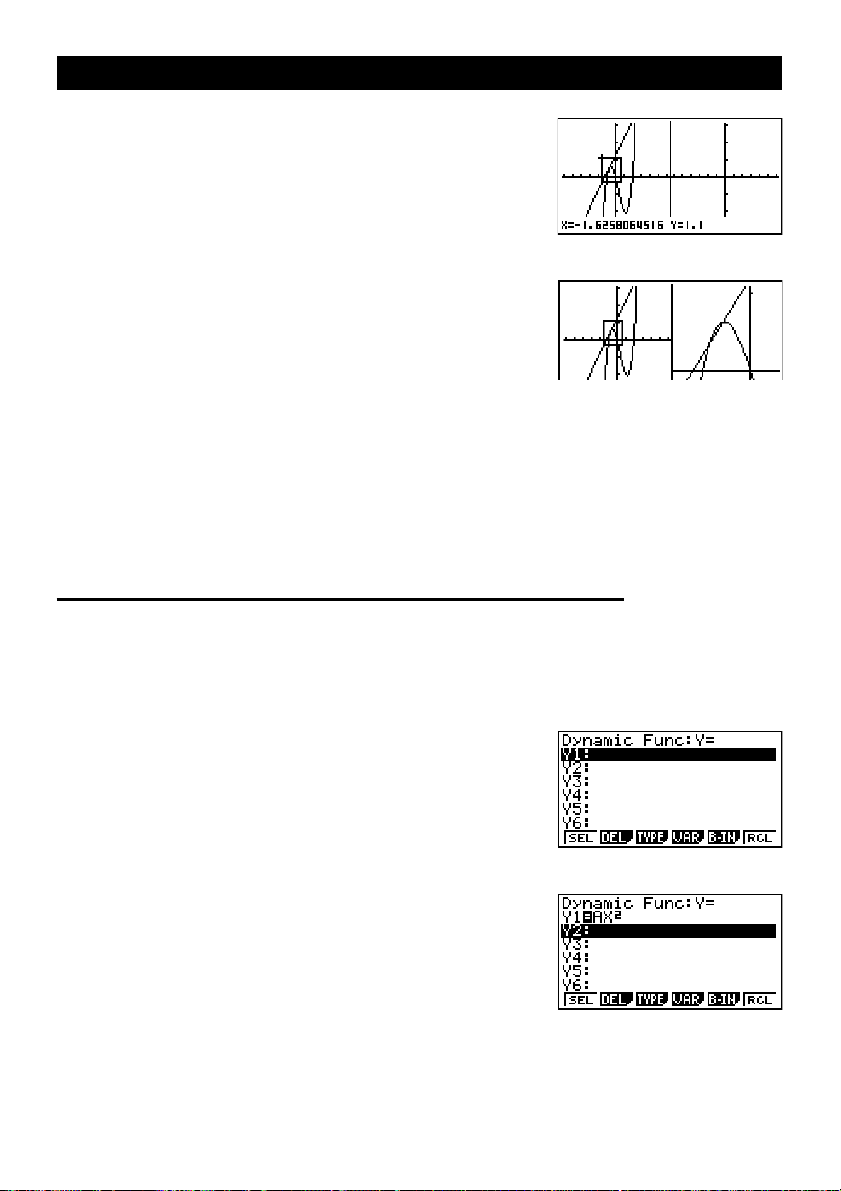
3. Utilisez d, e, f et c pour déplacer

une nouvelle fois le pointeur. Un cadre apparaît sur

l’écran. Déplacez le pointeur de façon à encadrer la

zone que vous voulez agrandir.

4. Appuyez sur

l’écran inactif (côté droit).

w. La zone agrandie apparaît sur

GRAPHE DYNAMIQUE

Le graphe dynamique vous permet de voir de quelle façon un graphe est affecté par le changement de valeur d’un des coefficients de sa fonction.

Exemple:

1. Appuyez sur m.

2. Utilisez d, e, f et c pour mettre

DYNA en surbrillance, puis appuyez sur

Tracer les graphes correspondant au changement de valeur du coefficient A de 1 à 3 dans la fonction suivante

Y = AX

3. Entrez la formule.

aAvxw

xvi

1234 56

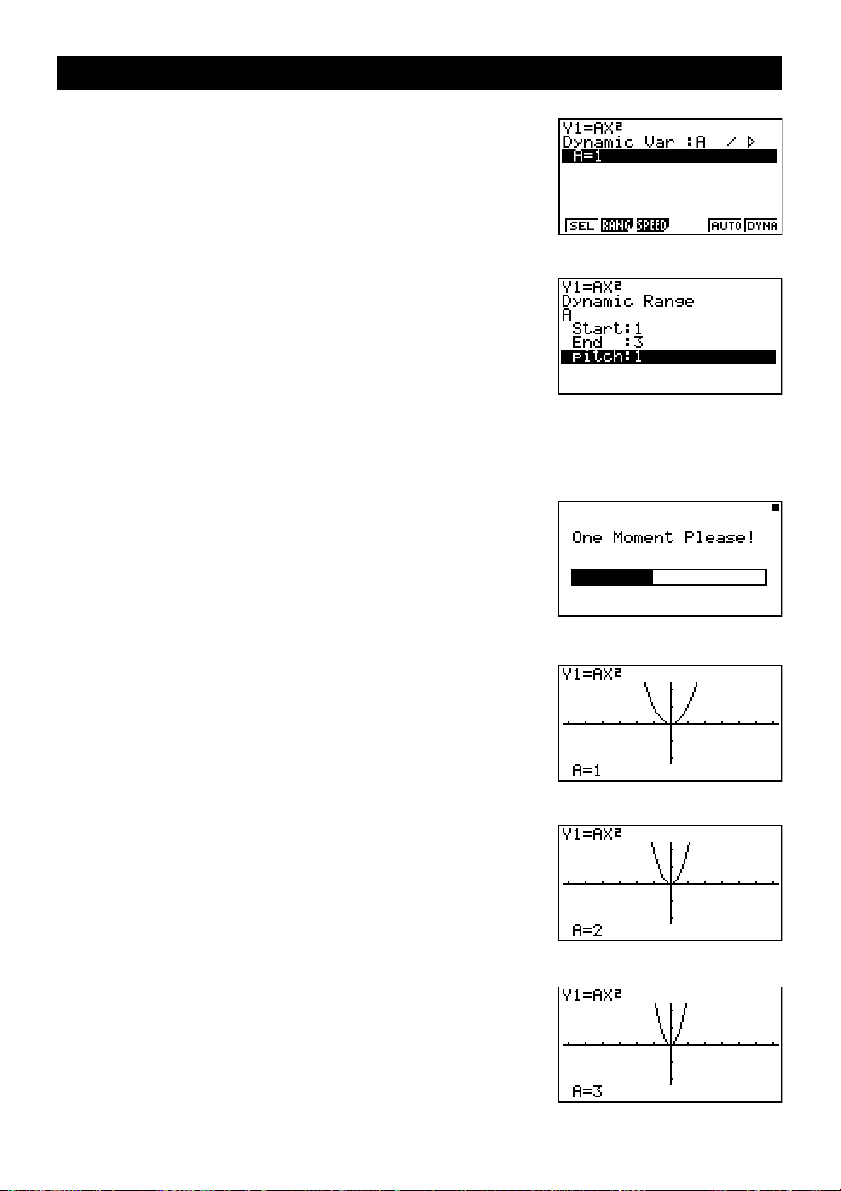
4. Appuyez sur 4 (VAR) bw pour affecter la

valeur initiale 1 au coefficient A.

5. Appuyez sur 2 (RANG)bwdw

bw pour spécifier la plage et l’incrément pour

le changement de valeur du coefficient A.

Démarrage rapide

1 2 3456

6. Appuyez sur

7. Appuyez sur 6(DYNA) pour commencer le tracé

de graphe dynamique. Les graphes sont tracés 10

fois.

↓

↓↑

xvii

Démarrage rapide

FONCTION DE TABLE

Cette fonction permet de produire une table de solutions quand différentes valeurs sont affectées aux variables d’une fonction.

Exemple:

1. Appuyez sur m.

2. Utilisezd, e, f et c pour mettre

3. Entrez la formule.

Créer une table numérique pour la fonction suivante

Y = X (X + 1) (X – 2)

TABLE en surbrillance, puis appuyez sur

v(v+b)

(v-c)w

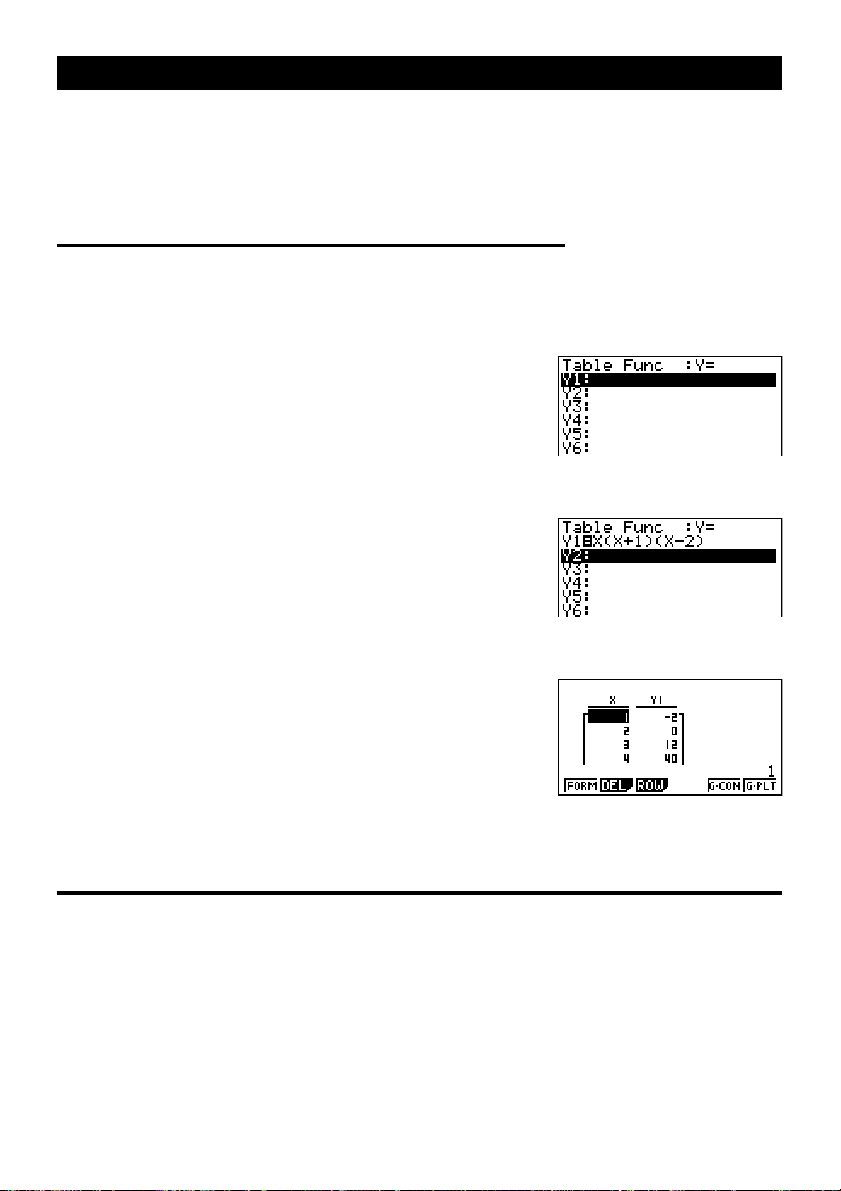
4. Appuyez sur 6 (TABL) ou w pour créer une

table numérique.

Pour tout connaître sur les nombreuses caractéristiques de cette calculatrice, lisez et explorez!

xviii

Précautions de manipulation

•Votre calculatrice est constituée de composants de précision et ne doit jamais être démontée.

•Eviter de la laisser tomber et de lui faire subir des chocs violents.

•Ne pas ranger la calculatrice ou la laisser dans des endroits exposés à une température et

humidité élevées ou à de grandes quantités de poussière. Lorsqu’elle est exposée à de faibles températures, la calculatrice peut nécessiter plus de temps pour afficher les réponses et même ne pas fonctionner du tout. L’affichage redevient normal lorsque la température atteint un niveau normal.

•L’affichage est vide et les touches ne fonctionnent pas pendant les calculs. Lorsque vous utilisez

le clavier, contrôlez l’affichage pour vérifier que toutes vos opérations de touches sont correctement effectuées.

•Remplacer les piles principales au moins une fois tous les 2 ans, même si la machine n’est pas

utilisée pendant cette période. Ne jamais laisser de piles mortes dans le logement des piles. Elles pourraient fuir et endommager la machine.

•Rangez les piles hors de portée des enfants en bas âge. En cas d’ingestion, consultez

immédiatement un médecin.

•Eviter d’utiliser des liquides volatils tels que diluant ou benzine pour nettoyer la machine.

L’essuyer avec un chiffon doux et sec ou un chiffon qui a été trempé dans une solution d’eau et de détergent neutre et essoré.

•Enlevez la poussière de l’écran avec précaution pour ne pas le rayer.

•En aucun cas le fabricant et ses fournisseurs ne seront tenus pour responsables de dégât,

dépense, perte de profits, perte d’économies ou autre dommage résultant d’une perte de données et/ou de formules survenue à la suite d’un fonctionnement défectueux, de réparations ou du remplacement des piles. L’utilisateur doit préparer des enregistrements physiques des données pour se protéger contre de telles pertes de données.

•Ne jamais incinérer les piles, le panneau à cristaux liquides ou d’autres composants .

• Lorsque le message ‘‘Low battery!’’ apparaît sur l’écran, remplacer aussitôt que possible les piles

de l’alimentation principale.

•Vérifier que la machine est hors tension lors du remplacement des piles.

•Si la calculatrice est exposée à de fortes charges d’électricité statique, le contenu de sa mémoire

peut être endommagé ou les touches cesser de fonctionner. Dans ce cas, effectuer une initialisation (Reset) pour effacer la mémoire et rétablir le fonctionnement normal des touches.

•Si la calculatrice cesse de fonctionner correctement pour une raison quelconque, appuyez sur la

touche P au dos de la calculatrice avec un objet fin et pointu. Notez qu’à ce moment toutes les données mémorisées sont effacées.

• Noter que de fortes vibrations ou de violents chocs pendant l’exécution des programmes peuvent

provoquer l’arrêt de l’exécution ou endommager le contenu de la mémoire de la calculatrice.

•L’utilisation de la calculatrice à proximité d’un téléviseur ou d’une radio peut provoquer des

interférences sur la réception de la télévision ou de la radio.

•Avant de supposer un mauvais fonctionnement de la calculatrice, veuillez relire avec soin ce

manuel et vous assurer que la panne n’est pas due à une alimentation insuffisante, des erreurs opérationnelles ou de programmation.

Table des matières

xix

Table des matières

Précautions de manipulation

Toujours garder des enregistrements physiques de toutes les données importantes!

La large capacité de mémoire de la calculatrice permet de sauvegarder de grandes quantités de données. Vous devriez cependant remarquer qu’une faible puissance des piles ou le remplacement incorrect des piles alimentant l’appareil peut entraîner une modification des données sauvegardées en mémoire ou même leur disparition complète. Les données sauvegardées peuvent également être affectées par une forte charge électrostatique ou un coup violent.

Comme la calculatrice emploie la mémoire libre comme zone de travail lorsqu’elle exécute des calculs internes, si la mémoire n’est pas suffisante, une erreur se produit. Pour éviter ce type de problème, il vaut mieux toujours laisser 1 ou 2 koctets de mémoire libre (inutilisée).

En aucun cas CASIO Computer Co., Ltd. ne sera tenu pour responsable de dommages spéciaux, collatéraux, indirects ou consécutifs liés à ou résultant de l’achat ou de l’utilisation de ce matériel. De plus, CASIO Computer Co., Ltd. ne sera pas tenu pour responsable de réclamation quelle qu’elle soit, faite contre l’utilisation de ce matériel par un parti tiers.

• Le contenu de ce manuel est susceptible d’être modifié sans préavis.

•Aucune partie de ce manuel ne peut être reproduite sous quelque forme que ce soit sans la permission écrite du fabricant.

• Les options décrites dans le chapitre 21 de ce manuel ne sont pas disponibles dans certaines zones géographiques. Demandez à votre distributeur ou au revendeur CASIO le plus proche quelles sont les options qui sont disponibles dans votre pays.

•••••••••••••••••••

• ••••••••••••••••••

•••••••••••••••••••

GRAPH 35

GRAPH 65

•••••••••••••••••••

• ••••••••••••••••••

•••••••••••••••••••

• ••••••••••••••••••

•••••••••••••••••••

• ••••••••••••••••••

•••••••••••••••••••

• ••••••••••••••••••

Table des matières

Familiarisation — A lire en premier! ................................................................... 1

1. Inscriptions sur le clavier ...................................................................................... 2

2. Sélection d’un symbole et du mode d’entrée ........................................................ 3

3. Affichage ............................................................................................................... 8

4. Réglage du contraste.......................................................................................... 11

5. En cas de problème... ......................................................................................... 12

Chapitre 1 Opérations de base ....................................................................... 13

1-1 Avant de commencer un calcul ................................................................... 14

1-2 Mémoire ...................................................................................................... 22

1-3 Menu d’options (OPTN)............................................................................... 27

1-4 Menu de données de variables (VARS) ...................................................... 28

1-5 Menu de programmation (PRGM) ............................................................... 34

Chapitre 2 Calculs manuels ............................................................................ 35

2-1 Calculs de base ........................................................................................... 36

2-2 Fonctions spéciales ..................................................................................... 39

2-3 Calculs de fonctions .................................................................................... 43

Chapitre 3 Calculs numériques....................................................................... 53

3-1 Avant d’effectuer un calcul .......................................................................... 54

3-2 Calculs de différentielles ............................................................................. 55

3-3 Calculs de différentielles quadratiques........................................................ 58

3-4 Calculs d’intégrations .................................................................................. 60

3-5 Calculs de valeurs maximale/minimale ....................................................... 63

3-6 Calculs de sommes (Σ) ............................................................................... 65

Chapitre 4 Nombres complexes...................................................................... 67

4-1 Avant de commencer le calcul d’un nombre complexe ............................... 68

4-2 Réalisation de calculs avec nombres complexes ........................................ 69

Chapitre 5 Calculs binaires, octaux, décimaux ou hexadécimaux .............. 73

5-1 Avant de commencer un calcul binaire, octal, décimal ou hexadécimal

avec entiers ........................................................................................... 74

5-2 Sélection du système numérique ................................................................ 76

5-3 Opérations arithmétiques ............................................................................ 77

5-4 Valeurs négatives et opérations à un bit ..................................................... 78

Chapitre 6 Calculs matriciels .......................................................................... 79

6-1 Avant d’effectuer des calculs matriciels....................................................... 80

6-2 Opérations sur les éléments d’une matrice ................................................. 83

6-3 Modification de matrices à l’aide des commandes de matrice .................... 88

6-4 Calculs matriciels ........................................................................................ 92

xxii

Table des matières

Chapitre 7 Calcul d’équations ......................................................................... 99

7-1 Avant de commencer le calcul d’une équation .......................................... 100

7-2 Équations linéaires de 2 à 6 inconnues..................................................... 101

7-3 Équations quadratiques et cubiques ......................................................... 104

7-4 Calculs avec résolution ............................................................................. 107

7-5 Que faire quand une erreur se produit ? ................................................... 110

Chapitre 8 Graphisme .................................................................................... 111

8-1 Avant de tracer un graphe ......................................................................... 112

8-2 Réglages de la fenêtre d’affichage (V-Window) ........................................ 113

8-3 Opérations avec fonctions graphiques ...................................................... 117

8-4 Mémoire de “Menus” de fonctions graphiques .......................................... 122

8-5 Tracé de graphes manuel.......................................................................... 123

8-6 Autres fonctions graphiques ...................................................................... 128

8-7 Mémoire de graphes ................................................................................. 139

8-8 Arrière-plan de graphe .............................................................................. 140

Chapitre 9 Résolution graphique ..................................................................143

9-1 Avant de résoudre un graphe .................................................................... 144

9-2 Analyse d’un graphe de fonction ............................................................... 145

Chapitre 10 Fonction de dessin ...................................................................... 153

10-1 Avant d’utiliser la fonction de dessin ......................................................... 154

10-2 Représentation graphique avec la fonction de dessin............................... 155

Chapitre 11 Graphe double ............................................................................. 167

11-1 Avant d’utiliser le graphe double ............................................................... 168

11-2 Définition des paramètres gauche et droite de la fenêtre d’affichage ....... 169

11-3 Tracé d’un graphe sur l’écran actif ............................................................ 170

11-4 Affichage d’un graphe sur l’écran inactif ................................................... 171

Chapitre 12 Graphe à table.............................................................................. 175

12-1 Avant d’utiliser la fonction graphe à table.................................................. 176

12-2 Utilisation de la fonction graphe à table .................................................... 177

Chapitre 13 Graphe dynamique ......................................................................181

13-1 Avant d’utiliser un graphe dynamique ....................................................... 182

13-2 Stockage, édition et sélection d’une fonction de graphe dynamique ........ 183

13-3 Tracé d’un graphe dynamique................................................................... 184

13-4 Utilisation de la mémoire de graphe dynamique ....................................... 190

13-5 Exemples de graphes dynamiques ........................................................... 191

xxiii

Table des matières

Chapitre 14 Graphes de sections coniques................................................... 193

14-1 Avant de représenter graphiquement une section conique ....................... 194

14-2 Pour représenter graphiquement une section conique ............................. 195

14-3 Analyse du graphe d’une section conique................................................. 199

Chapitre 15 Table et graphe ............................................................................ 205

15-1 Avant d’utiliser la fonction de table et graphe............................................ 206

15-2 Stockage d’une fonction et génération d’une table numérique ................. 207

15-3 Édition et suppression de fonctions........................................................... 210

15-4 Édition de tables et tracé de graphes ........................................................ 211

15-5 Copie d’une colonne d’une table dans une liste........................................ 216

Chapitre 16 Table de récurrence et graphe .................................................... 217

16-1 Avant d’utiliser une table de récurrence et une fonction graphique .......... 218

16-2 Entrée d’une formule de récurrence et génération d’une table ................. 219

16-3 Édition d’une table et tracé de graphes ..................................................... 223

Chapitre 17 Listes .......................................................................................................229

Mise en relation des données de différentes listes ............................................... 230

17-1 Constitution de listes (Menu LIST) ............................................................ 231

17-2 Édition et remise en ordre d’une liste (Menu LIST) ................................... 233

17-3 Traitement des données d’une liste (Menu RUN) ..................................... 237

17-4 Calculs arithmétiques à partir de listes (Menu RUN) ................................ 244

17-5 Changement de fichiers de listes .............................................................. 248

Chapitre 18 Graphes et calculs statistiques.................................................. 249

18-1 Avant d’effectuer des calculs statistiques.................................................. 250

18-2 Exemples de calculs statistiques à variable double .................................. 251

18-3 Calcul et représentation graphique de données statistiques

à variable unique ................................................................................. 257

18-4 Calcul et représentation graphique de données statistiques

à variable double ................................................................................. 261

18-5 Exécution de calculs statistiques............................................................... 270

18-6 Tests .......................................................................................................... 276

18-7 Intervalle de confiance .............................................................................. 294

18-8 Répartition ................................................................................................. 304

Chapitre 19 Calculs financiers ........................................................................ 321

19-1 Avant d’effectuer des calculs financiers .................................................... 322

19-2 Calculs d’intérêts simples .......................................................................... 324

19-3 Calculs d’intérêts composés...................................................................... 326

19-4 Evaluation d’un investissement ................................................................. 337

19-5 Amortissement d’un emprunt .................................................................... 341

19-6 Conversion entre taux effectif global et taux d’intérêt réel ........................ 345

xxiv

Table des matières

19-7 Calculs de coût, prix de vente, marge bénéficiaire.................................... 347

19-8 Calculs de jours et dates ........................................................................... 349

Chapitre 20 Programmation ............................................................................351

20-1 Avant la programmation ............................................................................ 352

20-2 Exemples de programmation .................................................................... 353

20-3 Mise au point d’un programme .................................................................. 358

20-4 Calcul du nombre d’octets utilisés par un programme .............................. 359

20-5 Accès secret .............................................................................................. 360

20-6 Recherche d’un fichier............................................................................... 362

20-7 Recherche de données à l’intérieur d’un programme ............................... 364

20-8 Édition d’un nom de fichier et d’un programme ......................................... 365

20-9 Effacement d’un programme ..................................................................... 368

20-10 Commandes de programmation pratiques ................................................ 369

20-11 Guide des commandes .............................................................................. 371

20-12 Affichage de texte ...................................................................................... 388

20-13 Utilisation des fonctions de la calculatrice dans un programme ................ 389

Chapitre 21 Communication de données ...................................................... 399

21-1 Connexion de deux calculatrices............................................................... 400

21-2 Connexion de la calculatrice à un ordinateur ............................................ 401

21-3 Connexion de la calculatrice à une imprimante d’étiquettes CASIO ......... 402

21-4 Avant de communiquer des données ........................................................ 403

21-5 Exécution d’un transfert de données ......................................................... 404

21-6 Transmission d’écran ................................................................................ 408

21-7 Précautions lors la communication de données ........................................ 409

Chapitre 22 Répertoire de programmes......................................................... 411

1. Analyse du facteur premier ............................................................................... 412

2. Plus grand dénominateur commun ................................................................... 414

3. Valeur test

4. Cercle et tangentes........................................................................................... 418

5. Rotation d’une figure......................................................................................... 425

t ....................................................................................................... 416

Appendice .......................................................................................................429

Appendice A Initialisation de la calculatrice ......................................................... 430

Appendice B Alimentation.................................................................................... 432

Appendice C Tableau de messages d’erreur ....................................................... 436

Appendice D Plages d’introduction ...................................................................... 438

Appendice E Spécifications ................................................................................. 441

Index .................................................................................................................. 443

Index des commandes.......................................................................................... 449

Index des touches................................................................................................. 450

Liste des commandes de programmation............................................................. 453

xxv

Table des matières

xxvi

Familiarisation

— A lire en premier!

A propos du manuel de l’utilisateur

uTouches de fonction et menus

•Un certain nombre d'opérations effectuées par la calculatrice peuvent être exécutées en

utilisant les touches de fonction 1 à 6. L'opération affectée à chaque touche de fonction dépend du mode dans lequel se trouve la calculatrice, et les opérations disponibles sont indiquées sur les menus de fonctions qui apparaissent au bas de l'écran.

•Dans ce manuel, l'opération actuellement affectée à une touche de fonction est indiquée

entre parenthèses après le nom de la touche. 1 (Comp), par exemple, indique que par une pression sur 1 vous sélectionnez {Comp}, qui apparaît aussi sur le menu de fonctions.

•Quand {g} est indiqué sur le menu de fonctions pour la touche 6, ce symbole signifie qu'en appuyant sur 6 vous afficherez la page suivante ou précédente des options de ce menu.

uTitres des menus

• Les titres des menus dans le manuel de l’utilisateur indiquent l'opération de touches nécessaire pour afficher le menu expliqué. Par exemple, [OPTN]-[MAT] indique qu'il faut appuyer sur K puis sur {MAT} pour afficher le menu.

• L'utilisation de la touche 6 (g) pour le changement de page d'un menu n'est pas indiquée dans les titres des menus.

Getting Acquainted — Read This First!

uListe de commandes

• La liste des commandes de programmation (page 453) fournit un organigramme des différents menus correspondant aux touches de fonction. Il vous indique comment accéder au menu de commandes souhaité.

Exemple: L'opération suivante affiche Xfct: [VARS]-[FACT]-[Xfct]

uSymboles utilisés dans le manuel de l’utilisateur

• La signification des symboles utilisés dans le manuel de l’utilisateur est la suivante.

: Fonction non supportée par la GRAPH 35+.

couleur

: Important : Remarque : Page de référence

P.000

1. Inscriptions sur le clavier

De nombreuses touches de la calculatrice sont utilisées pour exécuter plus d’une fonction. Les fonctions indiquées sur le clavier sont codées par couleur pour vous aider à trouver rapidement et aisément celle dont vous avez besoin.

Fonction Opération de touche

1 log l

2 10

3 B al

Le codage couleur utilisé pour les inscriptions du clavier est le suivant.

Couleur Opération de touche

Orange Appuyez sur ! puis sur la touche pour

exécuter la fonction indiquée.

Rouge Appuyez sur a puis sur la touche pour

exécuter la fonction indiquée.

2. Sélection d’un symbole et du mode d’entrée

Ce paragraphe décrit comment sélectionner un symbole sur le menu principal pour entrer dans le mode souhaité.

uPour sélectionner un symbole

1. Appuyez sur m pour afficher le menu principal.

Symbole actuellement

2. Utilisez les touches de curseur (d, e, f, c) pour mettre le symbole

souhaité en surbrillance.

3. Appuyez sur w pour afficher l’écran initial du mode correspondant au

symbole sélectionné.

•Vous pouvez aussi entrer dans un mode sans mettre le symbole en surbrillance dans le menu principal en entrant le nombre ou la lettre indiqué dans le coin inférieur droit du symbole.

•Utilisez seulement les méthodes indiquées ici pour entrer dans un mode. Toute autre méthode peut vous faire entrer dans un mode différent du mode sélectionné.

La signification de chaque symbole est la suivante.

sélectionné

* L’écran ci-dessus est celui de la

GRAPH 65.

Symbole Nom de mode Description

RUN Utilisez ce mode pour les calculs arithmétiques

et les calculs de fonction, ainsi que pour les calculs impliquant des valeurs binaires, octales, décimales et hexadécimales.

STATistics Utilisez ce mode pour effectuer des calculs (statistiques) statistiques à variable unique (écart-type) ou à

variable double (régression), pour effectuer des tests, analyser des données et pour tracer des graphes statistiques.

MATrix Utilisez ce mode pour stocker et éditer des (matrice) matrices.

LIST Utilisez ce mode pour stocker et éditer des (liste) données numériques.

GRAPH Utilisez ce mode pour stocker des fonctions (graphe) graphiques et pour tracer des graphes à partir

ces fonctions.

DYNAmic graph Utilisez ce mode pour stocker des fonctions (graphe graphiques et pour tracer plusieurs dynamique) versions d’un graphe en changeant les

valeurs affectées aux variables d’une fonction.

2 Sélection d’un symbole et du mode d’entrée

Symbole Nom de mode Description

couleur

GRAPH

35+

TABLE Utilisez ce mode pour stocker des fonctions, créer une

RECURsion Utilisez ce mode pour stocker les formules de (récurrence) récurrence, créer une table numérique présentant les

CONICS Utilisez ce mode pour tracer des graphes de (coniques) sections coniques.

EQUAtion Utilisez ce mode pour résoudre des équations linéaires (équation) de deux à six inconnues, des équations quadratiques et

PRoGraM Utilisez ce mode pour stocker des programmes dans la (programme) zone de programme et lancer des programmes.

Time Value of Utilisez ce mode pour effectuer des calculs financiers Money (valeur et tracer des graphes de cash-flow et d'autres types temporelle de de graphes. devises)

LINK Utilisez ce mode pour transférer le contenu de la (liaison) mémoire ou des données de sauvegarde sur une autre

CONTrast Utilisez ce mode pour ajuster le contraste de l’écran. (contraste)

table numérique présentant différentes solutions quand les valeurs affectées aux variables d’une fonction changent et pour en tracer les graphes.

différentes solutions quand les valeurs affectées aux variables d’une fonction changent et pour en tracer les graphes.

des équations cubiques.

machine.

MEMory Utilisez ce mode pour contrôler le volume de mémoire (mémoire) utilisé et libre, effacer des données en mémoire et

initialiser (Reset) la calculatrice.

k Utilisation de l’écran de configuration

L'écran de configuration de mode indique l'état actuel des réglages de mode et permet d'effectuer les changements souhaités. Vous pouvez changer les réglages d'un mode de la façon suivante.

uPour changer la configuration d’un mode

1. Sélectionnez le symbole souhaité et appuyez sur w pour entrer dans un

mode et en afficher l’écran initial. Ici nous choisissons le mode RUN.

2. Appuyez sur !Z pour afficher l’écran

de configuration de ce mode.

•Cet écran de configuration est utilisé à titre

d’exemple. Le contenu de l’écran peut être différent en fonction du mode dans lequel vous êtes et des réglages actuels de ce mode.

1 23456

P. 7 5

Sélection d’un symbole et du mode d’entrée 2

12345

3. Utilisez les touches de curseur f et c pour mettre le paramètre dont vous

voulez changer le réglage en surbrillance.

4. Appuyez sur la touche de fonction 1 à 6 qui indique le réglage que vous

voulez faire.

5. Quand vous avez fait les changements nécessaires, appuyez sur J pour

revenir à l’écran initial de ce mode.

k Menus de touches de fonction sur l’écran de

configuration

Ce paragraphe explique en détail les réglages que vous pouvez faire avec les touches de fonction sur l’écran de configuration.

uMode (mode de calcul/binaire, octal, décimal, hexadécimal)

•{Comp} ... {mode de calcul arithmétique}

•{Dec}/{Hex}/{Bin}/{Oct} ... {décimal}/{hexadécimal}/{binaire}/{octal}

P. 123 P. 125 P. 126

P. 128

P. 129 P. 177 P. 209

P. 1 4

uFunc Type (type de fonction graphique)

•{Y=}/{r=}/{Parm}/{X=c} ... graphe à {coordonnées rectangulaires}/

{coordonnées polaires}/{coordonnées paramétriques}/{X= constante}

•{Y>}/{Y<}/{Y }/{Y } ... graphe d'inégalité {y>f(x)}/{y<f(x)}/{y≥f(x)}/{y≤f(x)}

• La touche v sert à entrer un des trois noms de variables. Le nom de variable entré dépend du type de fonction sélectionnée.

uDraw Type (type de tracé de graphe)

•{Con}/{Plot} ... {points connectés}/{points séparés}

uDerivative (affichage de la valeur dérivée)

•{On}/{Off} ... {affichée}/{non affichée} quand le mode Graphe à table, Table et

Graphe et Lecture des coordonnées d'un point sont utilisés.

uAngle (unité de mesure d'angle par défaut)

•{Deg}/{Rad}/{Gra} ... {degré}/{radian}/{grade}

2 Sélection d’un symbole et du mode d’entrée

uCoord (affichage des coordonnées du pointeur sur le graphe)

P. 130

P. 121

P. 1 4 P. 1 5

P. 6 0

P. 251

•{On}/{Off} ... {affichées}/{non affichées}

uGrid (affichage de la trame du graphe)

•{On}/{Off} ... {affichée}/{non affichée}

uAxes (affichage des axes graphiques)

•{On}/{Off} ... {affichés}/{non affichés}

uLabel (affichage des noms d'axes)

•{On}/{Off} ... {affichés}/{non affichés}

uDisplay (format d'affichage)

•{Fix}/{Sci}/{Norm}/{Eng} ...{désignation d'un nombre fixe de décimales}/

{désignation du nombre de chiffres significatifs}/{changement à la plage d'affichage exponentiel}/{mode Ingénieur}

uIntegration (calcul d'intégration)

•{Gaus}/{Simp} ... calcul d'intégration en utilisant la {règle de Gauss-Kronrod}/

{règle de Simpson}

uStat Wind (méthode de réglage de la fenêtre d'affichage de

graphes statistiques)

•{Auto}/{Man} ... {automatique}/{manuel}

uGraph Func (affichage de la fonction pendant le tracé d'un graphe

et la lecture de coordonnées)

P. 187

•{On}/{Off} ... {affichée}/{non affichée}

uBackground (arrière-plan de graphe)

P. 140

•{None}/{PICT} ... {sans arrière-plan}/{désignation de l'image en arrière-plan

du graphe}

uPlot/Line (réglage de la couleur du graphe pointillé ou linéaire)

couleur

• {Blue}/{Orng}/{Grn} ... {bleu}/{orange}/{vert}

uResid List (calcul résiduel)

P. 267

•{None}/{LIST} ... {sans calcul}/{désignation d'une liste pour les données

résiduelles calculées}

P. 248

P. 168 P. 176

P. 215

P.132

P. 186 P. 187

couleur

P. 188

P. 208

Sélection d’un symbole et du mode d’entrée 2

uList File (désignation de fichier de listes)

•{File 1} à {File 6} ... {désignation du fichier de listes à afficher lorsque la

fonction Liste est utilisée}

uDual Screen (réglages en mode d'écran double)

Les réglages en mode d'écran double que vous pouvez effectuer dépendent du mode utilisé, GRAPH, TABLE ou RECUR lorsque vous appuyez sur !Z.

Mode GRAPH

•{Grph}/{GtoT}/{Off} ... {graphes sur les deux côtés de l'écran double}/

{graphe sur un côté et table numérique sur l'autre côté de l'écran double}/{écran double désactivé}

Mode TABLE/RECUR

•{T+G}/{Off} ... {graphe d'un côté et table numérique de l'autre côté de l'écran

double}/{écran double désactivé}

uSimul Graph (mode de tracé de graphes simultané)

•{On}/{Off} ... {activé (tous les graphes sont tracés simultanément)}/{désactivé

(tous les graphes sont tracés dans l'ordre numérique des zones)}

uDynamic Type (type de graphe dynamique)

•{Cnt}/{Stop} ... {sans arrêt (continu)}/{arrêt après 10 tracés}

uLocus (mode de lieu de graphe dynamique)

•{On}/{Off} ... {lieu identifié par une couleur}/{lieu non identifié}

uVariable (réglages pour la génération de table et le tracé de

graphes)

•{Rang}/{LIST} ... {utilisation de la plage d'une table}/{utilisation des données

d'une liste}

P. 224

P. 331

P. 324

uΣ Display (affichage de la valeur Σ dans la table de récurrence)

•{On}/{Off} ... {affichée}/{non affichée}

uSlope (affichage de la dérivée à la position actuelle du curseur

dans un graphe de section conique)

•{On}/{Off} ... {affichée}/{non affichée}

uPayment (désignation d'une période de paiement)

•{BGN}/{END} ... désignation {du début}/{de la fin} de la période de paiement

uDate Mode (désignation du nombre de jours par année)

•{365}/{360} ... calcul des intérêts pour {365}/{360} jours par année

* Il faut utiliser l'année de 365 jours pour les calculs de dates en mode

financier, sinon une erreur se produit.

2 Selecting Icons and Entering Modes

3. Affichage

k A propos de l’écran d’affichage

La calculatrice emploie deux types d’affichages: un affichage de texte et un affichage de graphe. L’affichage de texte peut contenir 21 caractères sur une ligne et huit lignes, y compris la ligne inférieure utilisée pour le menu de touches de fonction. L’affichage graphique utilise une zone de 127 points ( L ) × 63 points ( H ).

Affichage de texte Affichage de graphe

couleur

k A propos des couleurs d’affichage [OPTN]-[COLR]

La calculatrice peut afficher des données en trois couleurs: orange, bleu et vert. La couleur réglée par défaut pour les graphes et le texte de commentaire est le bleu, mais vous pouvez aussi spécifier l’orange et le vert, si vous le souhaitez.

•{Orng}/{Grn} ... {orange}/{vert}

• Les réglages précédents affectent la couleur des graphes et du commentaire. Désignez la couleur souhaitée avant d'entrer la fonction du graphe ou le commentaire dans un programme.

k A propos des types de paramètres des menus

La calculatrice emploie certaines conventions pour indiquer le type de résultat que vous devriez obtenir quand vous appuyez sur une touche de fonction.

• Menu suivant

Exemple:

La sélection de affiche un menu de fonctions hyperboliques.

• Entrée de commandes

Exemple:

La sélection de entre la commande sinh.

• Exécution directe de commandes

Exemple:

La sélection de exécute la commande DRAW.

k Affichage exponentiel

La calculatrice est capable normalement d’afficher des valeurs contenant 10 chiffres. Les valeurs qui dépassent cette limite sont automatiquement converties et affichées sous forme exponentielle. Vous pouvez choisir une des deux plages pour l’affichage automatique exponentiel.

Norm 1 ........... 10–2 (0,01) > |x|, |x| > 10

Norm 2 ........... 10–9 (0,000000001) > |x|, |x| > 10

uPour changer la plage d’affichage exponentiel

1. Appuyez sur !Z pour afficher l’écran de configuration.

2. Utilisez f et c pour mettre “Display” en surbrillance.

3. Appuyez sur 3 (Norm).

La plage d’affichage exponentiel alterne entre le format Norm 1 et le format Norm 2 chaque fois que vous effectuez les opérations précédentes. Il n’y a pas d’indicateur pour vous signaler la plage actuellement utilisée, mais vous pouvez toujours la vérifier en regardant le résultat d’un calcul.

Ab/caaw (Norm 1)

(Norm 2)

Tous les exemples de calculs dans ce manuel affichent des résultats avec Norm

uComment interpréter le format exponentiel

1.2E+12 indique que le résultat est égal à 1,2 × 1012. Cela signifie que vous devez déplacer la virgule des décimales dans 1,2 de douze rangs vers la droite, puisque l’exposant est positif. Le résultat est 1 200 000 000 000.

1.2E–03 indique que le résultat est équivalent à 1,2 × 10–3, ce qui signifie que vous devez déplacer la virgule des décimales dans 1,2 de trois rangs vers la gauche puisque l’exposant est négatif. Le résultat est 0,0012.

3 Affichage

k Formats d’affichage spéciaux

La calculatrice utilise des formats d’affichage spéciaux pour indiquer des fractions, des valeurs hexadécimales et des valeurs sexagésimales.

uFractions

..... Indique: 456+

––––

uValeurs hexadécimales

..... Indique: ABCDEF12(16), qui est égal

à –1412567278(10)

uValeurs sexagésimales

..... Indique: 12° 34’ 56,78"

•Outre ces formats spéciaux, la calculatrice utilise aussi d’autres indicateurs et symboles qui sont décrits dans chaque paragraphe concerné de ce mode d’emploi.

k Indicateur d’exécution de calcul

Quand la calculatrice est en train de dessiner un graphe ou d’exécuter un calcul ou un programme long et complexe, un carré noir (k) clignote dans le coin supérieur droit de l’écran. Ce carré vous signale que la calculatrice effectue une opération interne.

4. Réglage du contraste

Ajustez le contraste quand l’affichage n’est pas très visible ou sombre.

uPour afficher l’écran de réglage du contraste

Mettez le symbole CONT sur le menu principal en surbrillance, puis appuyez sur w.

uPour ajuster le contraste

Appuyez sur la touche de curseur e pour rendre l’écran plus foncé et sur la touche de curseur d pour le rendre plus clair. Si vous tenez ces touches enfoncées, le réglage change plus rapidement.

GRAPH 35+GRAPH 65

couleur

uPour ajuster la teinte de la couleur

Il est conseillé de régler d’abord le contraste.

1. Utilisez les touches de curseur f et cpour amener le pointeur devant la

couleur dont vous voulez régler la teinte (ORANGE, BLUE, GREEN).

2. Appuyez sur la touche de curseur e pour obtenir une couleur plus verte et sur la touche de curseur d pour obtenir une couleur plus orange. Si vous tenez ces touches enfoncées, le réglage change plus rapidement.

uPour initialiser les réglages de teinte de la couleur

•{INIT}/{IN·A} ... {initialisation de la couleur en surbrillance}/{initialisation de

toutes les couleurs}

uPour quitter l’écran de réglage du contraste

Appuyez sur m pour revenir au menu principal.

•Vous pouvez changer le contraste quand vous le souhaitez sans afficher

l’écran de réglage du contraste. Appuyez simplement sur ! puis sur d ou e pour changer de réglage. Appuyez une nouvelle fois sur ! quand l’écran est tel que vous le souhaitez.

5. En cas de problème...

Si vous rencontrez un problème pendant que vous effectuez une opération, faites les opérations suivantes avant de supposer que la calculatrice ne fonctionne pas.

k Retour aux réglages de mode par défaut

1. Sur le menu principal, sélectionnez le symbole RUN et appuyez sur w.

2. Appuyez sur ! Z pour afficher l’écran de configuration.

3. Mettez “Angle” en surbrillance et appuyez sur 2 (Rad).

4. Mettez “Display” en surbrillance et appuyez sur 3 (Norm) pour sélectionner la plage d’affichage exponentiel (Norm 1 ou Norm 2) que vous voulez utiliser.

P. 3

P. 431

5. Sélectionnez maintenant le mode correct et effectuez une nouvelle fois le calcul, en contrôlant les résultats sur l’écran.

k En cas de blocage

•Si la calculatrice se bloque et ne répond plus à l’entrée au clavier, appuyez sur la touche P au dos de la calculatrice pour réinitialiser la mémoire. Notez qu’à ce moment toutes les données mémorisées sont effacées.

k Message de faible tension des piles

Le message de faible tension des piles apparaît quand vous appuyez sur o pour mettre la calculatrice sous tension ou sur m pour afficher le menu principal quand la tension des piles principales est en dessous d’un certain niveau.

o ou m

P. 433

Au bout de 3 secondes environ

↓

* L’écran ci-dessus est celui de la

GRAPH 65.

Si vous continuez d’utiliser la calculatrice sans remplacer les piles, l’alimentation sera automatiquement coupée afin de protéger le contenu de la mémoire. Le cas échéant, il est impossible de remettre la calculatrice sous tension et le contenu de la mémoire peut être altéré ou entièrement perdu.

•Vous ne pouvez effectuer aucun transfert de données quand le message de faible tension des piles apparaît.

Chapitre

Opérations de base

1-1 Avant de commencer un calcul 1-2 Mémoire 1-3 Menu d’options (OPTN) 1-4 Menu de données de variables (VARS) 1-5 Menu de programmation (PRGM)

1-1 Avant de commencer un calcul

Avant d’effectuer un calcul pour la première fois, vous devez définir l’unité d’angle et le format d’affichage sur l’écran de configuration.

Effectuez les opérations de touche suivantes pour afficher l’écran de configuration: mRUN w!Z.

k Pour définir l’unité d’angle (Angle)

1. Affichez l’écran de configuration et utilisez les touches f et c pour mettre

“Angle” en surbrillance.

2. Appuyez sur la touche de fonction correspondant à l'unité d'angle que vous voulez définir.

•{Deg}/{Rad}/{Gra} ... {degré}/{radian}/{grade}

3. Appuyez sur J pour revenir à l'écran qui était affiché avant ce réglage.

• La relation entre les degrés, grades et radians est la suivante.

360° = 2π radians = 400 grades

90° = π/2 radians = 100 grades

k Pour définir le format d’affichage (Display)

1. Affichez l’écran de configuration et utilisez les touches f et c pour mettre “Display” en surbrillance.

2. Appuyez sur la touche de fonction correspondant au paramètre que vous voulez définir.

•{Fix}/{Sci}/{Norm}/{Eng} ...{désignation du nombre de décimales}/

{désignation du nombre de chiffres significatifs}/{changement à la plage d'affichage exponentiel}/{mode Ingénieur}

3. Appuyez sur J pour revenir à l'écran qui était affiché avant ce réglage.

u Pour définir le nombre de chiffres après la virgule (Fix)

Exemple Définir deux chiffres après la virgule

1 (Fix) 3 (2)

Appuyez sur la touche de fonction qui correspond au nombre de chiffres après la

virgule que vous souhaitez (

• Les valeurs affichées sont arrondies au nombre de chiffres après la virgule que vous avez spécifié.

= 0 à 9).

Avant de commencer un calcul 1 - 1

uPour définir le nombre de chiffres significatifs (Sci)

Exemple Définir trois chiffres significatifs

2 (Sci) 4 (3)

Appuyez sur la touche de fonction qui correspond au nombre de chiffres significatifs que vous souhaitez (

= 0 à 9).

• Les valeurs affichées sont arrondies au nombre de chiffres significatifs que vous avez spécifié.

•Si vous spécifiez 0, le nombre de chiffres significatifs est 10.

u Pour définir la plage d’affichage exponentiel (Norm 1/Norm 2)

Appuyez sur 3 (Norm) pour alterner entre les deux plages, Norm 1 et Norm

Norm 1: 10 Norm 2: 10

u Pour définir l’affichage en notation ingénieur (Eng)

–2

(0,01)>|x|, |x| >10

–9

(0,000000001)>|x|, |x| >10

Appuyez sur 4 (Eng) pour alterner entre la notation ingénieur et la notation normale.

L’indicateur “/E” apparaît sur l’écran quand la notation ingénieur est en service.

Voici une liste des 11 symboles utilisés par la calculatrice en notation ingénieur.

Symbole

GGiga10

MMéga 10

Signification

Unité

E Exa 10

P Péta 10

TTéra 10

k kilo 10

Symbole

mmilli 10

Signification

Unité

µ micro 10

n nano 10

ppico 10

ffemto 10

• La calculatrice sélectionne automatiquement le symbole ingénieur qui fait rentrer la valeur de la mantisse dans la plage de 1 à 1000 quand la notation ingénieur est en service.

–3

–6

–9

–12

–15

1 - 1 Avant de commencer un calcul

k Entrée de calculs

Lorsque vous êtes prêt à entrer un calcul, appuyez d’abord sur la touche A pour effacer l’affichage. Entrez ensuite vos formules de calcul, exactement comme elles sont écrites, de gauche à droite et appuyez sur w pour obtenir le résultat.

Exemple 1 2 + 3 – 4 + 10 =

Ac+d-e+baw

Exemple 2 2(5 + 4) ÷ (23 × 5) =

Ac(f+e)/

(cd*f)w

k Séquence de priorité de calcul

Cette calculatrice emploie la vraie logique algébrique pour calculer les parties d’une formule dans l’ordre suivant:

1 Transformation de coordonnées Pol (x, y), Rec (r, θ)

Calculs de différentielles, différentielles quadratiques, intégrations, Σ

d/dx, d

/dx2, ∫dx, Σ, Mat, Solve, FMin, FMax, List→Mat, Fill, Seq, SortA,

SortD, Min, Max, Median, Mean, Augment, Mat→List, List

2 Fonctions de type A

Avec ces fonctions, la valeur est entrée, puis la touche de fonction enfoncée.

, x–1, x !, ° ’ ”, symboles ENG

3 Puissance/Racine ^(xy),

4 Fractions a+

5 Format de multiplication abrégé devant π, le nom de mémoire ou de variable.

2π, 5A, X min, F Start, etc.

6 Fonctions de type B

Avec ces fonctions, la touche de fonction est enfoncée, puis la valeur entrée.

, 3, log, In, ex, 10x, sin, cos, tan, Asn, Acs, Atn, sinh, cosh, tanh, sinh–1,

cosh–1, tanh–1, (–), d, h, b, o, Neg, Not, Det, Trn, Dim, Identity, Sum, Prod, Cuml, Percent, AList

7 Format de multiplication abrégé devant les fonction de type B

2 , A log2, etc.3

8 Permutation, combinaison nPr, nCr

9 × , ÷

0 +, –

Avant de commencer un calcul 1 - 1

! Opérateur relationnel

=, G, >, <, ≥, ≤

@ And (opérateur logique), and (opérateur à un bit)

# Or (opérateur logique), or (opérateur à un bit), xor, xnor

• Lorsque des fonctions ayant la même priorité sont utilisées en série, l’exécution est effectuée de droite à gauche.

exIn → ex{In( )}120 120

Sinon, l’exécution se fait de gauche à droite.

• Les fonctions composées sont exécutées de droite à gauche.

•Tout ce qui se trouve entre parenthèses a la plus grande priorité.

Exemple 2 + 3 × (log sin2π2 + 6,8) = 22,07101691 (unité d’angle = Rad)

k Opérations de multiplication sans signe de multiplication

Vous pouvez omettre le signe de multiplication (×) dans toutes les opérations suivantes.

Exemple 2sin30, 10log1,2, 2 , 2Pol(5, 12), etc.

•Devant les constantes, noms de variables et de mémoires

Exemple 2π, 2AB, 3Ans, 3Y1, etc.

•Devant une ouverture de parenthèses

Exemple 3(5 + 6), (A + 1)(B – 1), etc.

1 - 1 Avant de commencer un calcul

2 3 4 5 4

( (

(

...

Pile de valeurs numériques Pile de commandes

k Piles

L’appareil utilise des blocs de mémoire appelés “ valeurs et des commandes de faible priorité. La niveaux, la niveaux. Une erreur se produit si vous effectuez un calcul trop complexe pour la capacité restante de la pile de valeurs numériques ou de la pile de commandes disponible, ou si l'exécution d'un sous-programme dépasse la capacité de la pile de sous-programmes.

Exemple

pile de commandes

26 niveaux et la

piles

” pour la sauvegarde des

pile de valeurs numériques

pile de sous-programmes

a 10

P. 1 6

P. 1 9

• Les calculs sont effectués en fonction de l’ordre de priorité. Une fois un calcul exécuté, il est effacé de la pile.

• La sauvegarde d’un nombre complexe occupe deux niveaux de la pile de valeurs numériques.

• La sauvegarde d’une fonction à 2 octets occupe deux niveaux de la pile de commandes.

k Limites d’entrée et de sortie de valeurs

La plage de valeurs d’entrée et de sortie admissible est de 10 chiffres pour la mantisse et de 2 chiffres pour l’exposant. Les calculs internes sont cependant effectués avec 15 chiffres pour la mantisse et 2 chiffres pour l’exposant.

Exemple 3 × 105 ÷ 7 – 42857 =

AdZf/hw

dZf/h-

ecifhw

P. 438

Avant de commencer un calcul 1 - 1

k Dépassement de capacité et erreurs

Le dépassement d’une plage de calcul ou d’une entrée spécifiée, ou une tentative d’entrée invalide entraîne l’apparition d’un message d’erreur sur l’affichage. Toute autre opération est impossible quand un message d’erreur est affiché. Les opérations suivantes entraînent l’apparition d’un message d’erreur sur l’affichage.

• Lorsqu’un résultat, intermédiaire ou final, ou une valeur en mémoire, dépasse ±9,999999999 × 1099 (“Ma ERROR”).

• Lorsque vous essayez d’effectuer un calcul de fonction qui dépasse la plage d’entrée (“Ma ERROR”).

• Lorsque vous faites une opération invalide pendant des calculs statistiques (“Ma ERROR”). Par exemple, tentative d’obtenir 1VAR sans introduction de données.

• Lorsque la capacité de la pile de valeurs numériques ou de la pile de commandes est dépassée (“Stk ERROR”). Par exemple, introduction de 25 ( successives, suivie de 2 + 3 * 4 w.

• Lorsque vous essayez d’effectuer un calcul en utilisant une formule invalide (“Syn ERROR”). Par exemple, 5 ** 3 w.

• Lorsque vous essayez d’effectuer un calcul qui provoque un dépassement de la mémoire (“Mem ERROR”).

• Lorsque vous utilisez une commande qui exige un argument mais qu’aucun argument valide n’est spécifié (“Arg ERROR”).

• Lorsque vous essayez d’utiliser une dimension invalide pendant des calculs matriciels (“Dim ERROR”).

P. 436

P. 4 1

•D’autres erreurs peuvent se produire pendant l’exécution d’un programme. Lorsqu’un message d’erreur est affiché, la plupart des touches de la calculatrice sont inopérantes. Vous pouvez reprendre l’opération en utilisant une des deux procédures suivantes.

•Appuyez sur la touche A pour effacer l’erreur et revenir au fonctionnement normal.

•Appuyez sur d ou e pour afficher l’erreur.

k Capacité de la mémoire

Chaque fois que vous appuyez sur une touche, un octet ou deux octets de mémoire sont utilisés. Les fonctions qui n’utilisent qu’un octet sont les suivantes: b, c, d, sin, cos, tan, log, In, et π. Les fonctions qui utilisent deux octets sont les suivantes: d/dx(, Mat, Xmin, If, For, Return, DrawGraph, SortA(, PxlOn, Sum et an+1.

Lorsque le nombre d’octets restants est égal ou inférieur à 5, le curseur “ _ ” prend automatiquement la forme “ v ”. Si vous voulez entrer d’autres données, vous devez diviser votre calcul en au moins deux parties.

• Lorsque vous entrez des valeurs numériques ou des commandes, elles apparaissent sur l’affichage à partir de la gauche. Cependant, les résultats des calculs sont affichés à partir de la droite.

1 - 1 Avant de commencer un calcul

k Affichages de graphe et de texte

L’appareil utilise un affichage de graphe et un affichage de texte. L’affichage de graphe est utilisé pour les graphiques alors que l’affichage de texte l’est pour les calculs et les instructions. Le contenu de chaque type d’affichage est sauvegardé dans des zones de mémoire indépendantes.

uPour alterner entre l’affichage de graphe et l’affichage de texte

Appuyez sur la touche !6(G↔T). Vous devez également noter que les opérations de touches utilisées pour effacer chaque type d’affichage sont différentes.

uPour effacer l’affichage de graphe

Appuyez sur !4(Sketch) 1(Cls) w.

uPour effacer l’affichage de texte

Appuyez sur A.

k Édition de calculs

Utilisez les touches d et e pour amener le curseur sur la position à changer, puis effectuez une des opérations décrites ci-dessous. Après avoir édité le calcul, vous pouvez l’exécuter en appuyant sur w, ou utiliser e pour passer à la fin du calcul et continuer à entrer des données.

uPour changer un pas

Exemple Changer cos60 en sin60

cga

ddd

uPour effacer un pas

Exemple Remplacer 369 × × 2 par 369 × 2

dgj**c

ddD

uPour insérer un pas

Avant de commencer un calcul 1 - 1

Exemple Remplacer 2,362 par sin2,36

c.dgx

ddddd

• Lorsque vous appuyez sur ![, le point d’insertion est indiqué par le

symbole ‘‘t’’. La fonction ou valeur suivante entrée est insérée à l’emplacement de ‘‘t’’. Pour abandonner l’opération sans rien entrer, déplacez le curseur et appuyez de nouveau sur ![, ou appuyez sur d, e ou w.

1-2 Mémoire

k Variables

Cette calculatrice est dotée de 28 variables en standard. Vous pouvez utiliser les variables pour sauvegarder les valeurs à utiliser à l’intérieur des calculs. Les variables sont identifiées par des noms d’une lettre, correspondant aux 26 lettres de l’alphabet plus r et θ. La taille maximale des valeurs que vous pouvez affecter aux variables est de 15 chiffres pour la mantisse et 2 chiffres pour l’exposant. Le contenu des variables est retenu même lorsque la calculatrice est mise hors tension.

uPour affecter une valeur à une variable

Exemple Affecter 123 à la variable A

[valeur] a [nom de la variable] w

AbcdaaAw

Exemple Ajouter 456 à la variable A et sauvegarder le résultat dans la

uPour afficher le contenu d’une variable

Exemple Afficher le contenu de la variable A

uPour effacer une variable

Exemple Effacer la variable A

•Pour vider toutes les variables, sélectionnez “Memory Usage” dans le mode

MEM.

uPour affecter la même valeur à plus d’une variable

•Vous ne pouvez pas utiliser “r” ou “θ” comme nom de variable dans

l’opération précédente.

Exemple Affecter la valeur 10 aux variables A à F

variable B

AaA+efgaaBw

AaAw

AaaaAw

[valeur]a[nom de la première variable]a3(~) [nom de la dernière variable]w

Abaa!aA

3(~)Fw

Mémoire 1 - 2

k Variables indicées

• Il était possible sur les calculatrices CASIO ne comportant pas de fonctions LISTES de créer des variables indicées du type A [ I ] ou Z [ J ] après avoir étendu la mémoire pour Defm.

• Les nouvelles calculatrices possèdent la fonction LISTE qui permet d’indicer le contenu d’une liste et de désigner ainsi chaque élément.

P. 229

P. 7 9

P. 2 7

Exemple List 1 [ J ] désigne le 4ème élément de cette liste si J = 4

(voir “17. Listes”).

•L’équivalent de Defm D est l’instruction: Seq (0, X, 1, D, 1) → List 1...ou : D→Dim List 1 La variable Z [ I ] sera remplacée par List 1 [ I ].

k Tableau à 2 dimensions

Voir “6. Calculs matriciels”.

k Mémoire de fonctions [OPTN]-[FMEM]

La mémoire de fonctions est pratique pour le stockage provisoire d’expressions souvent utilisées. Pour le stockage d’expressions à long terme, il est conseillé d’utiliser le mode GRAPH pour les expressions et le mode PRGM pour les programmes.

•{STO}/{RCL}/{fn}/{SEE} ... {sauvegarde de la fonction}/{rappel de la fonction}/

{désignation de la zone de la fonction comme nom de variable dans une expression}/{liste de fonctions}

uPour sauvegarder une fonction

Exemple Sauvegarder la fonction (A+B) (A–B) dans la mémoire de

fonctions n° 1

K6(g)6(g )3(FMEM)A

(aA+aB)

(aA-aB)

1(STO) 1(f1)

•Si le numéro de mémoire de fonctions auquel vous affectez une fonction contient déjà une fonction, la fonction précédente sera remplacée par la nouvelle.

uPour rappeler une fonction

Exemple Rappeler le contenu de la mémoire de fonctions n° 1

K6(g)6(g )3(FMEM)A

2(RCL)1(f1)

• La fonction rappelée apparaît à l’emplacement actuel du curseur sur l’écran.

1 - 2 Mémoire

uPour afficher une liste des fonctions disponibles

K6(g)6(g )3(FMEM)

4(SEE)

uPour effacer une fonction

Exemple Effacer le contenu de la mémoire de fonctions n° 1

K6(g)6(g )3(FMEM)A

1(STO) 1(f1)

•L’exécution de la sauvegarde quand l’affichage est vierge permet d’effacer la fonction de la mémoire de fonctions spécifiée.

uPour utiliser les fonctions mémorisées

Lorsqu’une fonction a été stockée en mémoire, elle peut être rappelée et utilisée pour un calcul. Cette fonction est pratique pour entrer rapidement des fonctions lors de la programmation ou du tracé de graphes.

P. 11 1

Exemple Stocker x3 + 1, x2 + x dans le mémoire de fonctions, puis

•Pour tous les détails au sujet de la représentation graphique, voir “8. Graphisme”.

k Statut de la mémoire (MEM)

Vous pouvez vérifier le volume de mémoire utilisé pour le stockage de chaque type de données et vous pouvez aussi voir combien d’octets de mémoire sont encore disponibles.

représenter graphiquement y = x3 + x2 + x + 1

Utilisez les paramètres de fenêtre d’affichage suivants:

Xmin = –4 Ymin =–10 Xmax = 4 Ymax = 10 Xscale = 1 Yscale = 1

!Zc1(Y=)JK6(g)6(g)3(FMEM)

AvMd+b1(STO)1(f1)(stocke (x3 + 1))

Avx+v1(STO)2(f2)(stocke (x2 + x))

A!4(Sketch)1(Cls)w

!4(Sketch)5(GRPH)1(Y=)

K6(g)6(g )3(FMEM)

3(fn)1(f1)+2(f2)w

Mémoire 1 - 2

uPour vérifier le statut de la mémoire

1. Sur le menu principal, sélectionnez le

symbole MEM et appuyez sur w.

2. Appuyez une nouvelle fois sur w pour

afficher l’écran de statut de la mémoire.

Nombre d’octets encore disponibles

3. Utilisez f et c pour déplacer la mise en surbrillance et voir la quantité de

mémoire (en octets) utilisée pour le stockage de chaque type de données.

Le tableau suivant indique tous les types de données qui apparaissent sur l’écran de statut de la mémoire.

Type de données Signification

Program Programmation

Statistics Calculs et graphes statistiques

Matrix Données de mémoire matricielle

List File Données de listes

Y= Fonctions graphiques

Draw Memory Conditions du tracé de graphe (fenêtre

d’affichage, facteur d’agrandissement/ réduction, écran graphique)

Graph Memory Données de graphes mémorisées

View Window Données de fenêtre d’affichage mémorisées

Picture Données d’écran graphique

Dynamic Graph Données de graphe dynamique

Table Données de Table et Graphe de fonction

Recursion Données de Table et Graphe de récurrence

Equation Données de calcul d’équation

Alpha Memory Données de la mémoire alpha

Function Mem Données de la mémoire de fonctions

Financial Données financières

1 - 2 Mémoire

k Suppression du contenu de la mémoire

Procédez de la façon suivante pour supprimer les données sauvegardées dans la mémoire.

1. Sur l'écran indiquant le statut de la mémoire, utilisez f et c pour mettre le

type de données que vous voulez supprimer en surbrillance.

Si le type de données sélectionné à l'étape 1 permet l'effacement de données particulières

2. Appuyez sur 1 (DEL).

123456

* Ce menu apparaît quand vous

sélectionnez le menu List File.

3. Appuyez sur la touche de fonction correspondant aux données que vous voulez effacer.

1 23456

• L'exemple précédent montre le menu de fonctions qui apparaît quand vous mettez {List File} en surbrillance à l'étape 1.

4. Appuyez sur 1 (YES).

Si le type de données que vous sélectionnez à l'étape 1 ne permet que l'effacement des données en bloc

2. Appuyez sur 1 (DEL).

1 23456

3. Appuyez sur 1 (YES) pour effacer toutes les données.

1-3 Menu d’options (OPTN)

Le menu d’options vous permet d’accéder aux fonctions et caractéristiques scientifiques qui ne sont pas indiquées sur le clavier de la calculatrice. Le contenu du menu d’options varie en fonction du mode dans lequel est la calculatrice quand vous appuyez sur la touche K.

Consultez la liste des commandes au dos du mode d'emploi pour les détails sur le menu d'options (OPTN).

uMenu d’options en modes RUN et PRGM

P.237

P.88 P.68 P.54

P.272

couleur

P.43 P.43 P.43 P.44

P.44

P.139

P.23 P.51

couleur

•{LIST} ... {menu de fonctions de liste}

•{MAT} ... {menu d’opérations matricielles}

•{CPLX} ... {menu de calculs avec nombres complexes}

•{CALC} ... {menu d’analyse de fonctions}

•{STAT} ... {menu de valeurs statistiques estimées à variable double}

•{COLR} ... {menu de couleurs de graphe}

•{HYP} ... {menu de calculs hyperboliques}

•{PROB} ... {menu de calculs de répartition/probabilité}

•{NUM} ... {menu de calculs numériques}

•{ANGL} ... {menu pour la conversion coordonnées/angles, conversion/entrée

•{ESYM} ... {menu de symboles ingénieur}

•{PICT} ... {menu de sauvegarde/rappel de graphes}

•{FMEM} ... {menu de mémoire de fonctions}

•{LOGIC} ... {menu d’opérateurs logiques}

Si vous appuyez sur K, le menu de touches de fonction suivant apparaît quand le système numérique par défaut est binaire, octal, décimal ou hexadécimal.

•{COLR} ... {menu de couleurs de graphe}

uMenu d’options pendant l’entrée de données numériques dans

sexagésimale}

les modes STAT, MAT, LIST, TABLE, RECUR et EQUA

•{LIST}/{HYP}/{PROB}/{NUM}/{ANGL}/{ESYM}/{FMEM}/{LOGIC}

uMenu d’options pendant l’entrée de formules dans les modes

GRAPH, DYNA, TABLE, RECUR et EQUA

•{List}/{CALC}/{HYP}/{PROB}/{NUM}/{FMEM}/{LOGIC}

La signification des paramètres du menu d’options est indiquée dans les paragraphes couvrant chaque mode.

1-4 Menu de données de variables (VARS)

Pour rappeler des données de variable, appuyez sur J pour afficher le menu de données de variables.

P. 11 3

{V-W IN}/{FACT}/{STAT}/{GRPH}/{DYNA}

Consultez la liste des commandes au dos du mode d'emploi pour les détails sur le menu de données de variables (VARS).

•Notez que les paramètres EQUA et TVM apparaissent pour les touches de fonction (3 et 4) seulement quand vous accédez au menu de données de variables à partir du mode RUN ou PRGM.

• Le menu de données de variables n’apparaît pas si vous appuyez sur J quand le système numérique par défaut est binaire, octal, décimal ou hexadécimal.

k V-WIN — Rappel des valeurs de la fenêtre d'affichage

En sélectionnant {V-WIN} sur le menu VARS, vous affichez le menu de rappel des valeurs de la fenêtre d'affichage.

u {X}/{Y}/{T,θ } ... {menu de l'axe x}/{menu de l'axe y}/{menu de T,

u {R-X}/{R-Y}/{R-T,θ } ... {menu de l'axe x}/{menu de l'axe y}/{menu de T,

pour le côté droit de l'écran double

Les paramètres suivants apparaissent dans ces menus.

• {min}/{max}/{scal}/{ptch} ...{valeur minimale}/{valeur maximale}/{gradua-

tion}/{incrément}

{TABL}/{RECR}/{EQUA}/{TVM}

}

P. 134

P. 259 P. 268

k FACT — Rappel des facteurs d'agrandissement/réduction

En sélectionnant {FACT} sur le menu VARS, vous affichez le menu de rappel des facteurs d'agrandissement/réduction.

• {Xfct}/{Yfct} ...{facteur de l'axe x}/{facteur de l'axe y}

k STAT — Rappel des données statistiques à variable

unique ou double

En sélectionnant {STAT} sur le menu VARS, vous affichez le menu de rappel des données statistiques à variable unique ou double

u {X}/{Y} ... {menu de données x}/{menu de données y}

Les paramètres qui apparaissent dans ce menu sont les suivants.

•{n} ... {nombre de données}

•{

o}/{

p} ... moyenne des {données x}/{données y}

•{Σx}/{Σy} ... somme des {données x}/{données y}

•{Σx2}/{Σy2} ... somme des carrés des {données x}/{données y}

•{Σxy} ... {somme des produits des données x et données y}

{X}/{Y}/{GRPH}/{PTS}/{TEST}/{RESLT}

Menu de données de variables (VARS) 1 - 4

xσn}/{yσn} ... écart-type d’une population de {données x}/{données y}

•{

xσn-1}/{yσn -1} ... écart-type d’un échantillon de {données x}/{données y}

•{minX}/{minY} ... valeur minimale de {données x}/{données y}

•{maxX}/{maxY} ... valeur maximale de {données x}/{données y}

u {GRPH} ...{menu de données graphiques}

Les paramètres qui apparaissent sur ce menu sont les suivants.

•{a}/{b}/{c}/{d}/{e} ... {coefficient de régression et coefficients polynomiaux}

•{r} ... {coefficient de corrélation}

•{Q1}/{Q3} ... {premier quartile}/{troisième quartile}

•{Med}/{Mod} ... {médiane}/{mode} des données entrées

•{Strt}/{Pitch} ... {division de départ}/{pas} de l'histogramme

u {PTS} ... {menu des points récapitulatifs}

Les paramètres qui apparaissent sur ce menu sont les suivants.

• {x1}/{y1}/{x2}/{y2}/{x3}/{y3} ... {menu des points récapitulatifs}

u {TEST} ... {rappel des données de test}

Voici les paramètres qui apparaissent sur ce menu.

• {n}/{

o}/{xσn-1} ... {nombre de données}/{moyenne des données}/{écart-type

• {n1}/{n2} ... nombre de {données 1}/{données 2}

• {

o1}/{

o2} ... moyenne des {données 1}/{données 2}

• {x1σ}/{x2σ} ... écart-type de l'échantillon de {données 1}/{données 2}

• {xpσ} ... {écart-type d'écart-type concentré}

• {F} ... {valeur F} (ANOVA)

• {Fdf}/{SS}/{MS} ... {degrés de liberté}/{somme des carrés}/{moyenne des

• {Edf}/{SSe}/{MSe} ... {degrés de liberté}/{somme des carrés}/{moyenne des

de l’échantillon}

carrés} du facteur

carrés} de l’erreur

u {RESLT} ... {rappel du résultat du test}

Voici les paramètres qui apparaissent sur ce menu.

• {p} ... {valeur p}

• {z}/{t}/{Chi}/{F} ... {valeur z}/{valeur t}/{valeur χ2}/{valeur F}

• {Left}/{Right} ... {limite inférieure (borne gauche) de l’intervalle de

confiance}/{limite supérieure (borne droite) de l’intervalle de confiance}

• {ˆp }/{ˆp 1}/{ˆp 2} ... {proportion estimée de l’échantillon}/{proportion estimée de

l’échantillon 1}/{proportion estimée de l’échantillon 2}

• {df}/{s}/{r}/{r2} ... {degrés de liberté}/{erreur standard}/{coefficient de

corrélation}/{coefficient de détermination}

1 - 4 Menu de données de variables (VARS)

k GRPH — Rappel de fonctions graphiques

En sélectionnant {GRPH} sur le menu VARS, vous affichez le menu de rappel des fonctions graphiques suivant.

P. 156

•{Y}/{r} ... {fonction à coordonnées rectangulaires ou d'inégalité}/{fonction à

coordonnées polaires}

•{Xt}/{Yt} ... fonction de graphe paramétrique {Xt}/{Yt}

•{X} ... {fonction de graphe avec constante = X}

(Appuyez sur ces touches avant d'entrer une valeur pour désigner la zone de stockage.)

Exemple Rappeler et tracer le graphe de la fonction à coordonnées

rectangulaires y = 2 x2 – 3, se trouvant dans la zone de stockage Y2

Utiliser les paramètres de fenêtre d’affichage suivants pour tracer le graphe.

Xmin = –5 Ymin = –5 Xmax = 5 Ymax = 5 Xscale = 1 Yscale = 1

!4(Sketch)5(GRPH)1(Y=)

J4(GRPH)1(Y)cw

P. 185

P. 208

k DYNA — Rappel des données de configuration de graphe

dynamique

En sélectionnant {DYNA} sur le menu VARS, vous affichez le menu de rappel des données de configuration de graphe dynamique

•{Strt}/{End}/{Pitch} ... {valeur initiale de la plage de coefficients}/{valeur

finale de la plage de coefficients}/{incrément de la valeur de coefficients}

k TABL — Rappel de la configuration d'une Table et Graphe

et de son contenu

En sélectionnant {TABL} sur le menu VARS, vous affichez le menu de rappel de la configuration d'une Table et Graphe et de son contenu.

•{Strt}/{End}/{Pitch} ... {valeur initiale de la plage de la table}/{valeur finale de

la plage de la table}/{incrément de la valeur de la table}

•{Reslt} ... {matrice du contenu de la table}

• Le paramètre Reslt apparaît pour la touche de fonction 4 seulement quand le menu précédent est affiché dans le mode RUN ou PRGM.

Menu de données de variables (VARS) 1 - 4

P. 218

P. 219

Exemple Rappeler le contenu de la table numérique pour la fonction

4(Reslt)w

k RECR — Rappel d'une formule de récurrence, de la plage

y = 3x

– 2, quand la plage de la table commence (Start) avec 0

et se termine (End) avec 6 et que l’incrément (pitch) est égal à 1

et du contenu de la table

En sélectionnant {RECR} sur le menu VARS, vous affichez le menu de rappel des données de récurrence suivant.

u {FORM} ... {menu de données de formules de récurrence}

Les paramètres qui apparaissent dans ce menu sont les suivants.

• {an}/{an+1}/{an+2}/{bn}/{bn+1}/{bn+2} ... expressions {an}/{an+1}/{an+2}/{bn}/{bn+1}/{bn+2}

u {RANG} ...{menu de données de plage de table}

Les paramètres qui apparaissent dans ce menu sont les suivants.

• {Strt}/{End} ... {valeur initiale de la plage d'une table}/{valeur finale de la

plage d'une table}

• {a0}/{a1}/{a2} ... {valeur ao du terme zéro}/{valeur a1 du premier terme}/

{valeur a2 du second terme}

• {b0}/{b1}/{b2} ... {valeur bo du terme zéro}/{valeur b1 du premier terme}/

{valeur b2 du second terme}

• {anSt}/{bnSt} ... origine du graphe de convergence/divergence de la

formule de récurrence {an }/{bn} (graphe WEB)

u {Reslt} ... {matrice du contenu de la table}

La sélection de {Reslt} permet d'afficher une matrice qui indique le contenu de la table de récurrence.

•Cette opération n'est possible que dans les modes RUN et PRGM.

Exemple Rappeler le contenu de la table numérique pour la formule de

récurrence an = 2n + 1, quand la plage de la table se situe entre Start = 1 et End = 6

3(Reslt)w

1 - 4 Menu de données de variables (VARS)

• Le contenu de la table rappelé au moyen de l’opération précédente est automatiquement stocké dans la mémoire matricielle de dernier résultat

(MatAns).

•Une erreur se produit si vous effectuez l’opération précédente quand aucune table numérique de fonctions ou formules de récurrence se trouve en mémoire.

k EQUA — Rappel des coefficients et solutions d'équations

En sélectionnant {EQUA} sur le menu VARS, vous affichez le menu de rappel des coefficients et solutions d'équations.

P. 101

P. 104

•{S-Rlt}/{S-Cof} ... matrice de {solutions}/{coefficients} pour les équations

linéaires de deux à six inconnues.

•{P-Rlt}/{P-Cof} ... matrice de {solutions}/{coefficients} pour les équations

quadratriques ou cubiques.

Exemple 1 Rappeler les solutions pour les équations linéaires suivantes à

Exemple 2 Rappeler les coefficients pour les équations linéaires suivantes

deux inconnues

2x + 3y =8 3x + 5y =14

1(S-Rlt)w

à trois inconnues

4x + y –2z =–1

x +6y +3z =1

–5x +4y + z =–7

2(S-Cof)w

Exemple 3 Rappeler les solutions pour l’équation quadratique suivante

2x2 + x – 10 = 0

3(P-Rlt)w

Exemple 4 Rappeler les coefficients pour l’équation quadratique suivante

2x2 + x – 10 = 0

4(P-Cof)w

Menu de données de variables (VARS) 1 - 4

• Les coefficients et solutions rappelés au moyen des opérations précédentes sont automatiquement stockés dans la mémoire matricielle de dernier résultat (MatAns).

•Dans les cas suivants une erreur se produit:

—Aucun coefficient n’a été entré pour l’équation

—Aucune solution n’a été obtenue pour l’équation

k TVM — Rappel des données de calculs financiers

En sélectionnant {TVM} sur le menu VARS, vous affichez le menu de rappel des données de calculs financiers.

•{n}/{I%}/{PV}/{PMT}/{FV} ... {périodes de paiement (versements)}/{%

d'intérêts}/{capital}/{montant du paiement}/{position du compte ou valeur capitalisée après le dernier versement}

•{P/Y}/{C/Y} ... {nombre de périodes de versement par année}/{nombre de

périodes de composition par année}

1-5 Menu de programmation (PRGM)

Pour afficher le menu de programmation (PRGM), entrez d'abord dans le mode RUN ou PRGM à partir du menu principal, puis appuyez sur ! W. Les sélections disponibles dans le menu de programmation (PRGM) sont les suivantes.

• {COM} … {menu de commandes de programmation}

• {CTL} … {menu de commandes de contrôle de programmation}

• {JUMP} … {menu de commandes de saut}

• {?} … {commande d’entrée}

• {

^} … {commande de sortie}

• {CLR} … {menu de commandes d’effacement}

• {DISP} … {menu de commandes d’affichage}

• {REL} … {menu d’opérateurs relationnels avec saut conditionnel}

• {I/O} … {menu de commandes d’entrée/sortie}

• { : } … {séparateur d’instructions multiples}

Le menu de touches de fonction apparaît si vous appuyez sur ! W dans le mode RUN ou PRGM, quand le système numérique par défaut est binaire, octal, décimal ou hexadécimal.

P. 351

• {Prog}/{JUMP}/{?}/{

Les fonctions attribuées aux touches de fonction sont identiques à celles du mode Comp.

Pour les détails au sujet des commandes disponibles dans les différents menus auxquels vous avez accès à partir du menu de programmation, voir “20. Programmation”.

^}/{REL}/{ : }

Chapitre

Calculs manuels

2-1 Calculs de base 2-2 Fonctions spéciales 2-3 Calculs de fonction

Choisir le menu RUN Régler l’écran de configuration !Z

2-1 Calculs de base

k Calculs arithmétiques

•Entrez les calculs arithmétiques comme ils sont écrits, de gauche à droite.

•Utilisez la touche - pour entrer une valeur négative.

•Utilisez la touche - pour les soustractions.

• Les calculs sont effectués internement avec une mantisse de 15 chiffres. Le résultat est arrondi à une mantisse de 10 chiffres avant d’être affiché.

•Pour les opérations arithmétiques mixtes, la multiplication et la division ont priorité sur l’addition et la soustraction.

Exemple Opération Affichage

23 + 4,5 – 53 = –25,5 23+4.5-53w –25.5

56 × (–12) ÷ (–2,5) = 268,8 56*-12/- 2.5w 268.8

P. 6

P. 4 3

(2 + 3) × 102 = 500 (2+3)*1Z2w*

500

1 + 2 – 3 × 4 ÷ 5 + 6 = 6,6 1+2-3*4/5+6w 6.6

100 – (2 + 3) × 4 = 80 100-(2+3)*4w 80

2 + 3 × (4 + 5) = 29 2+3*(4+5w*

(7 – 2) × (8 + 5) = 65 (7-2)(8+5)w*

= 0,3 6 /(4*5)w*

4 × 5

*1“(2+3)Z2” ne donne pas le bon résultat. Toujours entrer ce calcul de la

manière indiquée.

Les fermetures de parenthèses (immédiatement avant une opération de la touche w) peuvent être omises, quel qu’en soit le nombre nécessaire.

Un signe de multiplication se trouvant immédiatement avant une ouverture de

parenthèses peut être omis.

Identique à 6 / 4 / 5 w.

k Nombre de décimales, nombre de chiffres significatifs,

plage de notation exponentielle

•Ces réglages peuvent être effectués lors de la sélection du format d’affichage (Display) sur l’écran de configuration.

•Même après que le nombre de décimales ou le nombre de chiffres significatifs a été défini, les calculs internes sont effectués avec une mantisse de 15 chiffres et les valeurs affichées sont enregistrées avec une mantisse de 10 chiffres. Utilisez Rnd (4) du menu de calculs numériques (NUM) pour arrondir la valeur affichée et la stocker avec le nombre de décimales et de chiffres significatifs spécifié.

0.3

P. 323

Calculs de base 2 - 1

• Le réglage du nombre de décimales (Fix) et de chiffres significatifs (Sci) reste valide tant que vous ne les changez pas ou tant que vous ne changez pas le réglage d’affichage exponentiel (Norm). Notez cependant que le réglage Sci revient automatiquement à Norm 1 quand vous entrez dans le mode Financier.

•Pour changer le réglage d’affichage exponentiel (Norm), appuyez sur 3(Norm) quand le menu de format d’affichage (Display) est à l’écran. Chaque fois que vous effectuez cette opération, les deux réglages suivants alternent.

Norm 1 ........... affichage exponentiel des valeurs en dehors de la plage

Norm 2 ........... affichage exponentiel des valeurs en dehors de la plage

–2

à 10

10–9 à 10

Exemple 100 ÷ 6 = 16,66666666...

Condition Opération Affichage

100/6w 16.66666667

4 décimales !Z

ccccccccc

1(Fix)5(4)Jw 16.6667

5 chiffres significatifs !Z

Annule la spécification !Z

ccccccccc

2(Sci)6(g)1(5)Jw 1.6667E+01

ccccccccc

3(Norm)Jw 16.66666667

*1Les valeurs affichées sont arrondies à la décimale spécifiée.

Exemple 200 ÷ 7 × 14 = 400

Condition Opération Affichage

200/7*14w 400

3 décimales !Z

ccccccccc

1(Fix)4(3)Jw 400.000

Le calcul continue en utilisant l’affichage 200/7w 28.571 de 10 chiffres. * Ans × _

14w 400.000

•Si le même calcul est effectué avec le nombre de chiffres spécifié :

200/7w 28.571

La valeur interne sauvegardée est K6(g) arrondie au nombre 4(NUM)4(Rnd)w 28.571 de décimales spécifié. * Ans × _

14w 399.994

2 - 1 Calculs de base

k Calculs avec variables

193,2 ÷ 23 = 8,4 aA/23w 8.4

193,2 ÷ 28 = 6,9 aA/28w 6.9

Exemple Opération Affichage

193.2aaAw 193.2

2-2 Fonctions spéciales

k Fonction de réponse

Cette fonction sauvegarde le dernier résultat obtenu par une pression sur w(à moins que l’opération de la touche w n’entraîne une erreur). Le résultat est sauvegardé dans la mémoire de dernier résultat.

uPour utiliser le contenu de la mémoire de dernier résultat dans un

calcul

Exemple 123 + 456 = 579

789 – 579 = 210

Abcd+efgw

hij-!Kw

• La valeur la plus élevée que peut contenir la mémoire de dernier résultat a 15 chiffres pour la mantisse et 2 chiffres pour l’exposant.

• Le contenu de la mémoire de dernier résultat n’est pas effacé lorsque la touche A est enfoncée ou l’appareil mis hors tension.

•Notez que le contenu de la mémoire de dernier résultat n’est pas changé par une opération qui affecte des valeurs à la mémoire de valeurs (tel que: faaAw).

P. 1 6

k Exécution de calculs continus

La calculatrice vous permet d’utiliser le résultat d’un calcul comme un argument dans le calcul suivant. Pour ce faire, utilisez le résultat du calcul précédent qui est actuellement stocké dans la mémoire de dernier résultat.

Exemple 1 ÷ 3 =

1 ÷ 3 × 3 =

Ab/dw

(En continuant)*dw

Les calculs continus peuvent également être utilisés avec les fonctions de type A (x2, x-1, x!), +, –, ^(xy), x, ° ’ ”.

2 - 2 Fonctions spéciales

k Utilisation de la fonction de répétition

La fonction de répétition sauvegarde le dernier calcul effectué dans la mémoire de répétition. Vous pouvez rappeler le contenu de la mémoire de répétition par une pression sur d ou e. Si vous appuyez sur e, le calcul apparaît avec le curseur au début. Une pression sur d permet de faire apparaître le curseur à la fin du calcul. Vous pouvez procéder à volonté à des changements dans le calcul, puis le réexécuter.

Exemple Effectuer les deux calculs suivants

Ae.bc*g.ew

dddd

h.b

•Un calcul reste sauvegardé dans la mémoire de répétition jusqu’à ce que vous réalisiez un nouveau calcul ou changiez de mode.

• Le contenu de la mémoire de répétition n’est pas effacé lorsque vous appuyez sur la touche A, vous pouvez donc rappeler un calcul et l’exécuter même après avoir effectué un effacement général. Cependant, le contenu de la mémoire de répétition est vidé chaque fois que vous passez à un autre mode ou à un autre menu.

•Une fois que vous avez appuyé sur A, vous pouvez appuyer sur f ou sur c pour rappeler des calculs précédents, dans l’ordre, en commençant par le plus récent pour finir par le plus ancien (Fonction de multi-répétitions). Vous pouvez utiliser e ou d pour déplacer le curseur dans un calcul et faire des changements pour créer un nouveau calcul. Cependant, le contenu de la mémoire à multi-répétitions est vidé chaque fois que vous changez de menu.

4,12 × 6,4 = 26,368

4,12 × 7,1 = 29,252

Exemple

Abcd+efgw

cde-fghw

f(Un calcul précédent)

f(Deux calculs précédents)

Fonctions spéciales 2 - 2

k Pour faire des corrections dans le calcul d’origine

Exemple 14 ÷ 0 × 2,3 entré par erreur à la place de 14 ÷ 10 × 2,3

Abe/a*c.dw

Appuyez sur d ou e.

Le curseur se met automatiquement à l’emplacement de la cause de l’erreur.

Faites les changements nécessaires.

d![b

Réexécutez le calcul.

k Utilisation d’instructions multiples

Les instructions multiples sont formées en connectant un certain nombre d’instructions individuelles pour une exécution séquentielle. Vous pouvez utiliser les instructions multiples dans les calculs manuels et dans les calculs programmés. Deux moyens sont disponibles pour connecter des instructions afin de former des instructions multiples.

•Deux-points (:)

Les instructions qui sont connectées par deux-points sont exécutées de gauche à droite, sans arrêt.

• Commande d’affichage de résultat (

Lorsque l’exécution atteint la fin d’une instruction suivie d’une commande d’affichage de résultat, l’exécution s’arrête et le résultat jusqu’à ce point apparaît à l’écran. Vous pouvez reprendre l’exécution en appuyant sur la touche w.

2 - 2 Fonctions spéciales

Exemple 6,9 × 123 = 848,7

AbcdaaA!W6(g)

5(:)g.j*aA!W

5(^)aA/d.cw

•Notez que le résultat final d’une instruction multiple est toujours affiché, qu’il se termine ou non par une commande d’affichage de résultat.

•Vous ne pouvez pas construire une instruction multiple dans laquelle une instruction utilise directement le résultat de l’instruction précédente.

Exemple 123 × 456: × 5

123 ÷ 3,2 = 38,4375

Résultat intermédiaire au point

où “^” a été utilisé.

Invalide

2-3 Calculs de fonctions

k Menus de fonctions

La calculatrice comprend cinq menus de fonctions pour l’accès aux fonctions scientifiques qui ne sont pas indiquées sur le clavier.

• Le contenu de chaque menu de fonctions varie selon le mode que vous avez choisi sur le menu principal avant d’avoir appuyé sur la touche K. Les exemples suivants indiquent les menus de fonctions qui apparaissent dans le mode RUN ou PRGM.

uCalculs hyperboliques (HYP) [OPTN]-[HYP]

•{sinh}/{cosh}/{tanh} ... hyperbolique {sinus}/{cosinus}/{tangente}

•{sinh-1}/{cosh-1}/{tanh-1} ... hyperbolique inverse {sinus}/{cosinus}/{tangente}

uCalculs de probabilité/répartition (PROB) [OPTN]-[PROB]

•{x!} ... {appuyez après avoir saisie une valeur pour obtenir la factorielle de

cette valeur}

•{nPr}/{nCr} ... {permutation}/{combinaison}

•{Ran#}... {génération de nombre pseudo-aléatoire (0 à 1)}

P. 273

•{P(}/{Q(}/{R(} ... probabilité normale{P(t)}/{Q(t)}/{R(t)}

•{t(} ... {valeur de la variante normalisée t(x)}

uCalculs numériques (NUM) [OPTN]-[NUM]

•{Abs} ... {sélectionnez ce paramètre et entrez une valeur pour obtenir la

valeur absolue de cette valeur.}

•{Int}/{Frac} ... Sélectionnez le paramètre et entrez une valeur pour extraire la

partie {entière}/{fractionnaire}.

•{Rnd} ... {arrondit la valeur utilisée pour les calculs internes à 10 chiffres

significatifs (en fonction de la valeur enregistrée dans la mémoire de dernier résultat), ou au nombre de décimales (Fix) et au nombre de chiffres significatifs (Sci) que vous avez définis.}

•{Intg} ... {sélectionnez ce paramètre et entrez une valeur pour obtenir le plus

grand entier qui n’est pas supérieur à cette valeur.}

2 - 3 Calculs de fonctions

uUnités d’angle, conversion de coordonnées, opérations en

notation sexagésimale (ANGL)

°}/{r}/{g} ... {degré}/{radian}/{grade} pour une valeur saisie particulière

•{

° ’ ”} ... {définit les degrés (heures), minutes, secondes lors de l’entrée d’une

valeur sexagésimale}

←

•{° ’ ”} ... {convertit une valeur décimale en valeur sexagésimale}

•L’option {

•{Pol(}/{Rec(} ... conversion de coordonnées {rectangulaires en polaires}/

{polaires en rectangulaires}

uCalculs en notation Ingénieur (ESYM) [OPTN]-[ESYM]

•{m}/{µ}/{n}/{p}/{f} ... {milli (10-3)}/{micro (10-6)}/{nano (10-9)}/{pico (10

{femto}(10

•{k}/{M}/{G}/{T}/{P}/{E} ... {kilo (103)}/{méga (106)}/{giga 109)}/{téra (1012)}/{péta

(1015)}/{exa (1018)}

•{ENG}/{ENG} ... Déplace la virgule des décimales de la valeur affichée de

• Les options des menus {ENG} et {ENG} apparaissent seulement quand un

←

trois chiffres vers la {gauche}/{droite} et {réduit}/{augmente} l'exposant de trois.

Quand vous utilisez la notation Ingénieur, le symbole Ingénieur change aussi.

résultat de calcul est à l’écran.

[OPTN]-[ANGL]

←

° ’ ”

} apparaît seulement quand un résultat de calcul est à l’écran.

-15

)}

←

-12

)}/

P. 5

k Unités d’angle

•Après avoir spécifié une unité d’angle, celle-ci reste valide jusqu’à ce qu’une autre unité soit spécifiée. La spécification est retenue même si l’appareil est mis hors tension.

•Veillez à choisir le mode “Comp” pour le mode de calcul/binaire, octal, décimal, hexadécimal.

Exemple Opération Affichage

Convertir degrés. 1(Deg)J4.25K6(g)

47,3° + 82,5 rad = 4774,20181°

4,25

radians en !Zcccc

5(ANGL)2(r)w 243.5070629

47.3+82.52(r)w 4774.20181

P. 5

Calculs de fonctions 2 - 3

k Fonctions trigonométriques et trigonométriques inverses

•Toujours régler l’unité d’angle avant d’effectuer des calculs de fonction trigonométrique et de fonction trigonométrique inverse.

(90° = ––– radians = 100 grades)

•Veillez à choisir le mode “Comp” pour le mode de calcul/binaire, octal, décimal, hexadécimal.

Exemple Opération Affichage

sin 63° = 0,8910065242 !Zcccc

cos (

rad) = 0,5 !Zcccc

c(!7/d)w 0.5

tan (– 35gra) = – 0,6128007881 !Zcccc

2 • sin 45° × cos 65° = 0,5976724775 !Zcccc

2*s45*c65w*

1(Deg)J

s63w 0.8910065242

2(Rad)J

3(Gra)J

t-35w –0.6128007881

1(Deg)J

0.5976724775

cosec 30° =

sin-10,5 = 30° (x quand sin x = 0,5) !W0.5*2w

*1* peut être omis.

*2L’entrée du zéro initial n’est pas nécessaire.

= 2 1/s30w 2

sin30°

2 - 3 Calculs de fonctions

k Fonctions logarithmiques et exponentielles

P. 5

•Veillez à choisir le mode “Comp” pour le mode de calcul/binaire, octal, décimal, hexadécimal.

Exemple Opération Affichage

log 1,23 (log101,23) = 8,990511144 × 10

In 90 (loge90) = 4,49980967 I90w 4.49980967

1,23

= 16,98243652

(Pour obtenir l’antilogarithme du logarithme décimal 1,23) !01.23w 16.98243652

4,5

= 90,0171313

(Pour obtenir l’antilogarithme du logarithme népérien 4,5) !e4.5w 90.0171313

(–3)4 = (–3) × (–3) × (–3) × (–3) = 81 (-3)M4w 81

–34 = –(3 × 3 × 3 × 3) = – 81 -3M4w – 81

(= 1237)

123

= 1,988647795 7!q123w 1.988647795

2 + 3 × 3 – 4 = 10 2+3*3!q64-4w*

*1^ (xy) et x ont priorité sur la multiplication et la division.

–2

l1.23w 0.08990511144

P. 5

k Fonctions hyperboliques et hyperboliques inverses

•Veillez à choisir le mode “Comp” pour le mode de calcul/binaire, octal, décimal, hexadécimal.

Exemple Opération Affichage

sinh 3,6 = 18,28545536 K6(g)2(HYP)

1(sinh)3.6w 18.28545536

cosh 1,5 – sinh 1,5 K6(g)2(HYP) = 0,2231301601 2(cosh)1.5-1(sinh)1.5w 0.2231301601

–1,5

= e

(Preuve de cosh x ± sinh x =

cosh–1

= 0,7953654612

±x

)

5(cosh–1)(20/15)w 0.7953654612

I!Kw – 1.5

K6(g)2(HYP)

Déterminer la valeur de x lorsque tanh 4 x = 0,88

-1

tanh

0,88

x =

K6(g)2(HYP)

= 0,3439419141 6(tanh–1)0.88/4w 0.3439419141

P. 5

Calculs de fonctions 2 - 3

k Autres fonctions

•Veillez à choisir le mode “Comp” pour le mode de calcul/binaire, octal, décimal, hexadécimal.

Exemple Opération Affichage

+ =

3,65028154 !92+!95w 3.6502815425

(–3)2 = (–3) × (–3) = 9 (-3)xw 9

–32 = –(3 × 3) = –9 -3xw – 9

––––––––––– = 12

––– – –––

8! (= 1 × 2 × 3 × .... × 8) 8K6(g)3(PROB)

= 40320 1(x!)w 40320

Génération d’un nombre K6(g)3(PROB) aléatoire (nombre pseudo- 4(Ran#)w (Ex.) 0.4810497011 aléatoire entre 0 et 1)

Quelle est la valeur absolue du logarithme décimal de 3

log

Quelle est la partie entière K6(g)4(NUM) de – 3,5? 2(Int)-3.5w – 3

Quelle est la partie décimale K6(g)4(NUM) de – 3,5? 3(Frac)-3.5w – 0.5

Quel est le chiffre entier le K6(g)4(NUM) plus proche, ne dépassant 5(Intg)-3.5w – 4 pas – 3,5?

= 42

= 0,1249387366

(3!X-4!X)

!Xw 12

!#(36*42*49)w

K6(g)4(NUM)

1(Abs)l(3/4)w 0.1249387366

4236 × 42 × 49

2 - 3 Calculs de fonctions

k Conversion de coordonnées

u Coordonnées rectangulaires

•Avec des coordonnées polaires, θ peut être calculé et affiché dans une plage de –180°< θ < 180° (les radians et les grades ont la même plage).

u Coordonnées polaires

P. 5

•Veillez à choisir le mode “Comp” pour le mode de calcul/binaire, octal, décimal, hexadécimal.

Exemple Calculer r et θ° lorsque x = 14 et y = 20,7

Opération Affichage

!Zcccc1(Deg)J K6(g)5(ANGL)6(g) 1(Pol()14,20.7)w Ans

1–24.989–→ 24.98979792 (r) 2–55.928–→ 55.92839019 (θ)

•Pour rappeler r: ListAns [ 1 ]w, θ: ListAns [ 2 ]w

Exemple Calculer x et y lorsque r = 25 et θ = 56°

Opération Affichage

!Zcccc1(Deg)J K6(g)5(ANGL)6(g) 2(Rec()25,56)w Ans

•Pour rappeler les valeurs et les utiliser dans des calculs.

r : ListAns [ 1 ]wθ: ListAns [ 2 ]w x : ListAns [ 1 ]w y : ListAns [ 2 ]w

List est obtenu par K11.

k Permutation et combinaison

u Permutation

n! n!

nPr = ––––– nCr = –––––––

(n – r)! r! (n – r)!

1–13.979–→ 13.97982259 (x) 2–20.725–→ 20.72593931 (y)

u Combinaison

P. 5

•Veillez à choisir le mode “Comp” pour le mode de calcul/binaire, octal, décimal, hexadécimal.

Calculs de fonctions 2 - 3

Exemple Calculer le nombre possible d’arrangements différents quand

4 éléments sont sélectionnés parmi 10 éléments

Formule Opération Affichage

10P4 = 5040 10K6(g)3(PROB)

2(nPr)4w 5040

P. 5

Exemple Calculer le nombre possible de combinaisons différentes de 4

éléments sélectionnés parmi 10 éléments.

Formule Opération Affichage

10C4 = 210 10K6(g)3(PROB)

3(nCr)4w 210

k Fractions

•Attention: La touche M peut servir également au transfert de données.

Vérifiez son affectation et mettez-la dans l’état permettant le calcul de fractions.

Pour ce faire: m LINK w6 (IMGE) 1 (OFF)

• Les valeurs fractionnaires sont affichées avec le nombre entier en premier, puis le numérateur et enfin le dénominateur.

•Veillez à choisir le mode “Comp” pour le mode de calcul/binaire, octal, décimal, hexadécimal.

Exemple Opération Affichage

2 1 13

–– + 3 + –– = 3 + ––

5 4 20

= 3,65

––––– + –––––

2578 4572

= 6,066202547 × 10

–4

2N5+3N1N 4w 3{13{20

(Conversion en décimale*1)M 3.65

1N2578+1N4572w 6.066202547E–04*

(Format d’affichage Norm 1)

–– × 0,5 = 0,25

–––––– = 1 + ––

11 7

–– + ––

*1Les fractions peuvent être converties en valeurs décimales, et inversement.

Lorsque le nombre total de caractères, y compris le nombre entier, le numérateur, le

dénominateur et le séparateur, dépasse 10, la fraction introduite est automatiquement convertie en décimale.

Les calculs contenant à la fois des fractions et des décimales sont effectués sous forme

décimale.

Vous pouvez inclure des fractions dans le numérateur ou le dénominateur d’une fraction

en mettant le numérateur ou le dénominateur entre parenthèses.

1N(1N3+1N4)w*

1N2*

.5w 0.25*

1{5{7

2 - 3 Calculs de fonctions

k Calculs en notation Ingénieur

P. 4 4

P. 5

Entrez les symboles Ingénieur à partir du menu de notation Ingénieur.

•Veillez à choisir le mode “Comp” pour le mode de calcul/binaire, octal, décimal, hexadécimal.

Exemple Opération Affichage

999 k (kilo) + 25 k (kilo) 999K = 1,024 M (méga) 6(g)6(g)1(ESYM)

!Zccccc

cccc4(Eng)J

6(g)1(k)+251(k)w 1.024M

9 ÷ 10 = 0,9 = 900 m (milli) 9/10w 900.m

K6(g)6(g)1(ESYM)

6(g)6(g)

←

0.9

0.0009k

0.9

900.m

3(ENG)*

2(ENG)* 2(ENG)*

*1Convertit la valeur affichée à l’unité ingénieur supérieure suivante, en déplaçant la

virgule décimale de trois unités à droite.

Convertit la valeur affichée à l’unité ingénieur inférieure suivante, en déplaçant la

virgule décimale de trois unités à gauche.

P.52

P. 5

Calculs de fonctions 2 - 3

k Opérateurs logiques (AND, OR, NOT) [OPTN]-[LOGIC]

Le menu d’opérateurs logiques vous propose une variété d’opérateurs logiques.

•{And}/{Or}/{Not} ... {AND logique}/{OR logique}/{NOT logique}

•Veillez à choisir le mode “Comp” pour le mode de calcul/binaire, octal, décimal, hexadécimal.

Exemple Quel est le AND logique de A et B quand A = 3 et B = 2?

A AND B = 1

Opération Affichage

3aaAw

aAK6(g)6(g)

4(LOGIC)1(And)aBw 1

Exemple Quel est le OR logique de A et B quand A = 5 et B = 1?

A OR B = 1

Opération Affichage

aAK6(g)6(g)

4(LOGIC)2(Or)aBw 1

2aaBw

5aaAw

1aaBw

Exemple Mettre en négation A quand A = 10

NOT A = 0

Opération Affichage

10aaAw

K6(g)6(g )

4(LOGIC)3(Not)aAw 0

2 - 3 Calculs de fonctions

A propos des opérations logiques

•Une opération logique produit toujours 0 ou 1 comme résultat.

• Le tableau suivant indique tous les résultats qui peuvent être produits par les opérations AND et OR.

Valeur ou Expression A Valeur ou Expression B

A G 0B G 011

A G 0B = 001

A = 0 B G 001

A = 0 B = 0 0 0

• Le tableau suivant indique les résultats produits par l’opération NOT.

Valeur ou Expression

A G 00

A = 0 1

A NOT A

A AND B A OR B

Chapitre

Calculs numériques

3-1 Avant d’effectuer un calcul 3-2 Calculs de différentielles 3-3 Calculs de différentielles quadratiques 3-4 Calculs d’intégrations 3-5 Calculs de valeurs maximale/minimale 3-6 Calculs de sommes (Σ)

3-1 Avant d’effectuer un calcul

Ce paragraphe décrit les paramètres qui sont disponibles sur les menus que vous utilisez pour effectuer des calculs avec résolution, différentielles/ différentielles quadratiques, intégrations, valeurs maximale/minimale et Σ.

P.27

P.394

P.107

Quand le menu d'options est affiché, appuyez sur 4 (CALC) pour faire apparaître le menu d'analyse de fonction. Les paramètres de ce menu servent à effectuer des calculs de type particulier.

•{Solve}/{d/dx}/{d2/dx2}/{∫dx} ... Calculs de {résolution}/{différentielle}/

{différentielle quadratique}/{intégration}

•{FMin}/{FMax}/{Σ(} ... Calculs de {valeur minimale}/{valeur maximale}/{Σ

(sigma)}

Calcul de résolution

La syntaxe requise pour l'utilisation de la fonction de résolution dans un programme est la suivante.

Solve ( f(x), n, a, b)

Limite supérieure Limite inférieure Valeur initiale estimée

•Deux méthodes différentes peuvent être utilisées pour le calcul de résolution: l’affectation directe et l’entrée d'une table de variables.

Avec l’affectation directe (méthode décrite ici), vous attribuez directement des valeurs aux variables. Ce type d’entrée est identique à celle qui est utilisée avec la commande de résolution dans le mode de programmation.

L’entrée d’une table de variables est utilisée avec la fonction de résolution du mode d’équation. Cette méthode est recommandée pour la plupart des entrées de la fonction de résolution.

3-2 Calculs de différentielles [OPTN]-[CALC]-[d/dx]

Pour effectuer des calculs de différentielles, affichez d’abord le menu d’analyse de fonctions, puis entrez les valeurs indiquées dans la formule suivante.

2(d/dx) f(x),a,A x)

Accroissement/décroissement de

Point pour lequel la dérivée doit être déterminée

d/dx ( f (x), a, Ax) ⇒ ––– f (a)

La différentiation pour ce type de calcul est définie en tant que :

f '(a) = lim –––––––––––––

Dans cette définition, la valeur aux environs de f ' (a) calculée en tant que :

f '(a) –––––––––––––

Afin d’apporter la meilleure précision possible, la machine emploie la différence moyenne pour réaliser les calculs différentiels. L’exemple suivant illustre la différence moyenne.

f (a + Ax) – f (a)

Ax→0

f (a + Ax) – f (a)

infinitésimal

est remplacé par

suffisamment petit

Ax, avec

Les pentes des points a et a + Ax, et des points a et a – Ax dans la fonction

y = f(x) sont les suivantes :

f (a + Ax) – f (a) Ay f (a) – f (a – Ax) ∇y

––––––––––––– = ––– , ––––––––––––– = –––

Ax Ax Ax ∇x

Dans l’exemple ci-dessus, Ay/Ax est appelé la différence avant, tandis que ∇y/∇

x est la différence arrière. Pour calculer les dérivées, la machine prend la

moyenne entre les valeurs de Ay/Ax et ∇y/∇x, apportant ainsi une plus grande précision pour les dérivées.

3 - 2 Calculs de différentielles

Cette moyenne, qui est appelée la que :

uPour réaliser un calcul différentiel

Exemple Déterminer la dérivée au point x = 3 pour la fonction

Entrez la fonction f(x).

Entrez le point x = a pour lequel vous voulez déterminer la dérivée.

Entrez Ax, qui est l’accroissement/décroissement de x.

1 f (a + Ax) – f (a) f (a) – f (a – Ax)

f '(a) = –– ––––––––––––– + –––––––––––––

2 Ax Ax

f (a + Ax) – f (a – Ax)

= –––––––––––––––––

y = x

décroissement de x est défini par

AK4(CALC)2(d/dx)vMd+evx+v-g,

bZ-f)

2Ax

+ 4x2 + x – 6, lorsque l’accroissement ou le

différence moyenne

, est exprimée en tant

Ax = 1E – 5.

•Dans la fonction f(x), seule X peut être utilisée comme variable dans les

expressions. Les autres variables (A à Z, r, θ) sont traitées comme constantes, et la valeur affectée à cette variable est utilisée au cours du calcul.

•L’entrée de Ax et la fermeture de parenthèses peuvent être omises. Si vous omettez Ax, la calculatrice utilise automatiquement une valeur pour Ax qui est appropriée à la dérivée que vous essayez de déterminer.

• Les points ou sections discontinus soumis à un changement important peuvent affecter la précision du calcul ou même provoquer une erreur.

Calculs de différentielles 3 - 2

k Applications des calculs différentiels

• Les différentielles peuvent être additionnées, soustraites, multipliées ou divisées par chacune d’elles.

––– f (a) = f '(a), ––– g (a) = g '(a)

dx dx

Par conséquent:

f '(a) + g'(a), f '(a) × g'(a), etc.

• Les résultats de différentielles peuvent être utilisés dans les additions, soustractions, multiplications et divisions et dans les fonctions.

2 × f '(a), log ( f '(a)), etc.

• Les fonctions peuvent être utilisées pour tous les termes ( f (x), a, Ax) d’une différentielle.

––– (sinx + cosx, sin0,5), etc.

•Vous ne pouvez pas utiliser d’expression de calcul de résolution, différentielle, différentielle quadratique, intégration, valeur maximale/minimale ou de Σ à l’intérieur d’un terme de calcul différentiel.

• Le fait d’appuyer sur A pendant le calcul d’une différentielle (lorsque le

curseur n’est pas affiché à l’écran) interrompt le calcul.

•Utilisez toujours le radian (mode Rad) comme unité d’angle pour effectuer des différentielles trigonométriques.

3-3 Calculs de différentielles quadratiques

[OPTN]-[CALC]-[d2/dx2]

Après avoir affiché le menu d’analyse de fonctions, vous pouvez entrer des différentielles quadratiques en utilisant un des deux formats suivants.

3(d2/dx2) f(x),a,n)

Limite finale (n = 1 à 15)

Point de coefficient différentiel

––– ( f (x), a, n) ⇒ ––– f (a)

Les calculs de différentielles quadratiques produisent une valeur différentielle approximative à partir de la formule de différentielle de second ordre suivante qui est basée sur l’interprétation polynomiale de Newton.

– f (x – 2h) + 16 f(x – h) – 30 f(x) + 16 f(x + h) – f(x + 2h)

=–––––––––––––––––––––––––––––––––––––––––––––––

f''(x)

Dans cette expression, les valeurs pour les “incréments suffisamment petits de

x” sont calculées en séquence à partir de la formule suivante, avec la valeur de

m substituée par m = 1, 2, 3, et ainsi de suite.

h = ––––

Le calcul est terminé quand la valeur de f"(x) basée sur la valeur de h calculée en utilisant la dernière valeur de m, et la valeur de f"(x) basée sur la valeur de

h calculée en utilisant la valeur actuelle de m sont identiques avant que la limite

supérieure n soit atteinte.

12h

•Normalement, vous n’avez pas à entrer de valeur pour n. Il est conseillé d’entrer une valeur pour n si la précision des calculs l’exige.

•L’entrée d’une grande valeur pour n ne produit pas nécessairement une plus grande précision.

uPour effectuer un calcul de différentielle quadratique

Exemple Déterminer le coefficient différentiel quadratique au point où x

= 3 pour la fonction y = x3 + 4x2 + x – 6 Dans ce cas, entrez 6 pour n, qui est une limite finale.

Entrez la fonction f(x).

AK4(CALC)3(d2/dx2) vMd+

evx+v-g,

Calculs de différentielles quadratiques 3 - 3

Entrez 3 comme point

a qui est un point de coefficient différentiel.

Entrez 6 pour

n, qui est la limite finale.

•Dans la fonction f(x), seule X peut être utilisée comme variable dans des expressions. Toutes les autres variables (A à Z, r, θ) sont traitées comme constantes et la valeur actuelle attribuée à cette variable est utilisée pendant le calcul.

•L’entrée de la limite finale n et la fermeture de parenthèses peuvent être omises.

•Des points ou des sections discontinus avec d’importantes fluctuations peuvent affecter la précision, voire causer une erreur.

k Applications des calculs de différentielles quadratiques

• Les opérations arithmétiques peuvent être effectuées en utilisant deux différentielles quadratiques.

––– f (a) = f ''(a), ––– g (a) = g''(a)

Par conséquent:

f ''(a) + g''(a), f ''(a) × g''(a), etc.

• Le résultat d’un calcul de différentielle quadratique peut être utilisé dans un calcul ultérieur arithmétique ou de fonction.

2 × f ''(a), log ( f ''(a) ), etc.

• Les fonctions peuvent être utilisées à l’intérieur des termes ( f(x), a, n ) d’une expression différentielle quadratique.

––– (sin x + cos x, sin 0,5), etc.

•Utilisez uniquement des entiers de 1 à 15 comme valeur de limite finale n.

L'utilisation d'une valeur hors de cette plage produit une erreur.

•Vous pouvez interrompre un calcul de différentielle quadratique en cours en

appuyant sur la touche A.

•Utilisez toujours les radians (mode Rad) comme unité d’angle quand vous effectuez des différentielles quadratiques trigonométriques.

3-4 Calculs d’intégrations [OPTN]-[CALC]-[

Pour effectuer des calculs d’intégrations, affichez d’abord le menu d’analyse de fonctions, puis entrez les valeurs indiquées dans la formule suivante.

Règle de Gauss-Kronrod

4(∫dx) f(x) , a , b , tol )

Tolérance Point final Point initial

( f(x), a, b, tol) ⇒

∫

f(x)dx

∫

dx]

P. 6

Zone calculée par

Règle de Simpson

4(∫dx) f(x) , a , b , n )

Nombre de divisions (valeur de n dans N = 2n, n étant un entier de 1 à 9)

Point final

Point initial

( f(x), a, b, n) ⇒

∫

Comme indiqué sur l’illustration ci-dessus, les calculs d’intégration sont exécutés en calculant les valeurs intégrales de a à b pour la fonction y = f (x) quand a < x < b et f (x) > 0*. La surface de la zone ombrée sur l’illustration est ainsi calculée.

*Quand f (x) < 0 dans a < x < b, le calcul de l’aire produit des valeurs

négatives (aire sous l’axe x).

f(x)dx, N = 2

∫

f(x)dx

∫

k Changement des méthodes de calcul d'intégration

Cette calculatrice peut utiliser la règle de Gauss-Kronrod ou la règle de Simpson pour effectuer des calculs d'intégration. Pour sélectionner une méthode, affichez l’écran de configuration et sélectionnez “Gaus” (pour la règle de Gauss-Kronrod) ou "Simp" (pour la règle de Simpson) pour le paramètre Intégration.

Toutes les explications de ce mode d’emploi utilisent la règle de Gauss-Kronrod.

Calculs d’intégrations 3 - 4

uPour effectuer un calcul d’intégration

Exemple Effectuer un calcul d’intégration pour la fonction indiquée

Entrez la fonction f (x).

Entrez le point initial et le point final.

Entrez la valeur de tolérance.

•Dans la fonction f(x), seule X peut être utilisée comme variable dans les

expressions. Les autres variables (A à Z, r, θ) sont traitées comme constantes, et la valeur affectée à cette variable est utilisée au cours du calcul.

•L’entrée de “tol” dans la règle de Gauss-Kronrod, “n” dans la règle de

Simpson et la fermeture de parenthèses peuvent être omises avec les deux règles. Si vous omettez “tol”, la calculatrice utilisera automatiquement la valeur de 1E - 5. Dans le cas de “n”, la calculatrice sélectionne automatiquement la valeur mieux appropriée.

• Les calculs d'intégration peuvent prendre un certain temps.

ci-dessous avec une tolérance de “tol” = 1E - 4

(2x2 + 3x + 4) dx

∫

AK4(CALC)4(∫dx)cvx+dv +e,

b,f,

bZ-e)w

k Application des calculs d’intégration

• Les intégrales peuvent être utilisées dans les additions, soustractions, multiplications ou divisions.

f (x) dx +

∫

• Les résultats d’intégration peuvent être utilisés dans les additions, soustractions, multiplications, divisions et dans les fonctions.

2 ×

∫

• Les fonctions peuvent être utilisées dans chacun des termes ( f (x), a, b, n) d’une intégrale.

cos 0,5

∫

sin 0,5

g (x) dx, etc.

∫

f (x) dx, etc. log (

(sin x + cos x) dx = ∫(sin x + cos x, sin 0,5, cos 0,5, 5)

f (x) dx), etc.

∫

3 - 4 Calculs d’intégrations

• Le fait d’appuyer sur A pendant le calcul d’une intégrale (lorsque le

curseur n’est pas affiché à l’écran) interrompt le calcul.

•Utilisez toujours le radian (mode Rad) comme unité d’angle pour effectuer des intégrations trigonométriques.

• Les facteurs comme le type de fonction utilisés, les valeurs positives et négatives dans les divisions et la division où l’intégration est effectuée peuvent causer une erreur importante dans les valeurs d’intégration et des résultats de calculs erronés.

Notez les points suivants pour garantir de bonnes valeurs d’intégration.

(1) Lorsque les valeurs d’intégration de fonctions cycliques deviennent positives

ou négatives pour différentes divisions, effectuez le calcul pour des cycles uniques ou divisez entre négatif et positif, puis ajoutez les résultats.

Partie positive (S)

Partie négative (S)

f (x)dx =

∫

Partie positive (S) Partie négative (S)

(2) Lorsque des changements minimes dans les divisions d’intégration donnent

des changements importants dans les valeurs d’intégration, calculez séparément les divisions d’intégration (divisez les larges zones de changement en zones plus petites), puis ajoutez les résultats.

f (x)dx =

∫

f (x)dx +

f (x)dx + (–

∫

f (x)dx +.....+

∫

f (x)dx)

∫

f (x)dx

3-5 Calculs de valeurs maximale/minimale

[OPTN]-[CALC]-[FMin]/[FMax]

Après avoir affiché le menu d’analyse de fonctions, vous pouvez effectuer des calculs de valeurs maximale/minimale en utilisant les formats suivants et trouver le maximum et le minimum d’une fonction dans un intervalle tel que a < x < b.

uValeur minimale

6(g)1(FMin) f(x) , a , b , n )

Précision (n=1 à 9)

Point final de l’intervalle

Point initial de l’intervalle

uValeur maximale

6(g)2(FMax) f (x), a , b , n )

Précision (n=1 à 9)

Point final de l’intervalle

Point initial de l’intervalle

uPour effectuer des calculs de valeurs maximale et minimale

Exemple 1 Déterminer la valeur minimale pour l’intervalle défini

Entrez f(x).

Entrez l’intervalle a = 0, b = 3.

Entrez la précision n = 6.

par le point initial a = 0 et le point final b = 3, avec une précision de n = 6 pour la fonction y = x

AK4(CALC)6(g)1 (FMin) vx-ev+j,

a,d,

– 4x + 9

3 - 5 Calculs de valeurs maximale/minimale

Exemple 2 Déterminer la valeur maximale pour l’intervalle défini par le point

initial a = 0 et le point final b = 3, avec une précision de n = 6 pour la fonction y = –x

Entrez f(x).

AK4(CALC)6(g)2 (FMax) -vx +cv+c,

Entrez l’intervalle a = 0, b = 3.

a,d,

Entrez la précision n = 6.

•Dans la fonction f(x), seule X peut être utilisée comme variable dans les

expressions. Les autres variables (A à Z, r, θ) sont traitées comme constantes, et la valeur affectée à cette variable est appliquée au cours du calcul.

•L’entrée de n et la fermeture de parenthèses suivant la valeur de précision

peuvent être omises.

• Les points ou sections discontinus soumis à un changement important peuvent affecter la précision du calcul ou même provoquer une erreur.

•L’entrée d’une valeur supérieure pour n augmente la précision du calcul, mais aussi le temps de calcul requis.

+ 2x + 2

• La valeur entrée pour le point final de l'intervalle (b) doit être supérieure à la valeur entrée pour le point initial (a), sinon une erreur se produira.

•Vous pouvez interrompre un calcul de valeurs maximale/minimale en cours en appuyant sur la touche A.

•Vous pouvez entrer un entier de 1 à 9 comme valeur de n. L’utilisation d’une valeur hors de cette plage cause une erreur.

3-6 Calculs de sommes (Σ) [OPTN]-[CALC]-[Σ(]

Pour effectuer des calculs de Σ , affichez d’abord le menu d’analyse de fonctions, puis entrez les valeurs indiquées dans la formule suivante.

6(g)3(Σ() a k , k , α , β , n )

Distance entre les partitions

Terme final de la séquence

Terme initial de la séquence

Variable utilisée par la séquence

(ak, k, α, β, n) ⇒ Σ ak

Le calcul de Σ est le calcul de la somme partielle d’une séquence ak avec la formule suivante.

k = α

S = aα + a

k Exemple de calcul de Σ

Exemple Effectuer le calcul suivant

Entrez la séquence ak.

AK4(CALC)6(g)3(Σ()aKx-daK+f,

Entrez la variable utilisée par la séquence ak.

aK,

Entrez le terme initial de la séquence ak et le terme final de la séquence a k.

c,g,

Entrez n.

+........+ aβ = Σ ak

(k2 – 3k + 5)

k = 2

Utilisez n = 1 comme distance entre les partitions.

k = α

3 - 6 Calculs de sommes (Σ)

•Vous pouvez utiliser seulement une variable dans cette fonction comme

séquence d’entrée ak.

•Entrez les nombres entiers seulement pour le terme initial de la séquence ak et pour le terme final de la séquence ak.

•L’entrée de n et la fermeture de parenthèses peuvent être omises. Sous vous omettez n, la calculatrice utilise automatiquement n = 1.

k Applications des calculs de Σ

•Opérations arithmétiques utilisant des expressions avec calculs de Σ

Expressions:

Opérations possibles: Sn + Tn, Sn – Tn, etc.

•Opérations arithmétiques et de fonctions utilisant les résultats de calculs de Σ

2 × Sn, log (Sn), etc.

•Opérations de fonctions utilisant des termes de calculs de Σ (ak, k)

Σ (sink, k, 1, 5), etc.

Sn = Σ ak, Tn = Σ bk

k = 1 k = 1

• La valeur utilisée comme terme final β doit être supérieure à la valeur utilisée comme terme initial α, sinon une erreur se produira.

•Pour interrompre un calcul de Σ en cours (indiqué par l’absence de curseur sur l’écran), appuyez sur la touche A.

Chapitre

Nombres complexes

Avec les nombres complexes, cette calculatrice réalise les opérations suivantes.

•Opérations arithmétiques (additions, soustractions, multiplications, divisions)

• Calcul de réciproques, de racines carrées et du carré d’un nombre complexe

• Calcul de la valeur absolue et de l’argument d’un nombre complexe

•Calcul des nombres complexes conjugués

•Extraction de la partie réelle

•Extraction de la partie imaginaire

4-1 Avant de commencer le calcul d’un nombre complexe 4-2 Réalisation de calculs avec nombres complexes

Choisir le menu RUN

4-1 Avant de commencer le calcul d’un nombre

complexe

mRUNw

Avant de commencer un calcul de nombres complexes, appuyez sur K3 (CPLX) pour afficher le menu de calcul de nombres complexes.

•{i} ... {entrée de l’unité imaginaire i}

•{Abs}/{Arg} ... obtention de {la valeur absolue}/{l'argument}

•{Conj} ... {calcul du conjugué}

•{ReP}/{ImP} ... extraction de la partie {réelle}/{imaginaire}

4-2 Réalisation de calculs avec nombres

complexes

Les exemples suivants indiquent comment réaliser les calculs de nombres complexes, disponibles sur cette calculatrice.

k Opérations arithmétiques [OPTN]-[CPLX]-[i]

Les opérations arithmétiques sont les mêmes que celles que vous utilisez dans les calculs manuels. Vous pouvez même utiliser les parenthèses et la mémoire.

Exemple 1 (1 + 2i) + (2 + 3i)

AK3(CPLX)

(b+c1(i))

+(c+d1(i))w

Exemple 2 (2 + i) × (2 – i)

AK3(CPLX)

(c+1(i))

*(c-1(i))w

k Réciproques, racines carrées et carrés

Exemple

k Valeur absolue et argument [OPTN]-[CPLX]-[Abs]/[Arg]

La machine considère un nombre complexe dans la forme a + bi comme coordonnée sur un plan de Gauss et calcule la valeur absolue Z et l’argument (arg).

Exemple Calculer la valeur absolue (r) et l’argument (θ) du nombre

(3 + i)

AK3(CPLX)

!9(d+1(i))w

complexe 3 + 4i, avec le degré comme unité d’angle

Axe imaginaire

Axe réel

4 - 2 Réalisation de calculs avec nombres complexes

AK3(CPLX)2(Abs)

(d+e1(i))w

(Calcul de la valeur absolue)

AK3(CPLX)3(Arg)

(d+e1(i))w

(Calcul de l’argument)

• Le résultat du calcul de l’argument change selon l’unité d’angle (degré, radian, grade) sélectionnée.

k Nombres complexes conjugués [OPTN]-[CPLX]-[Conj]

Un nombre complexe de forme a + bi devient un nombre complexe conjugué de forme a – bi.

Exemple Calculer le nombre complexe conjugué pour le nombre

k Extraction des parties réelle et imaginaire

Utilisez la méthode suivante pour extraire la partie réelle a et la partie imaginaire b d’un nombre complexe dont la forme est a+bi.

Exemple Extraire les parties réelle et imaginaire d’un nombre complexe

complexe 2 + 4i

AK3(CPLX)4(Conj)

(c+e1(i))w

[OPTN]-[CPLX]-[ReP]/[lmP]

2 + 5i

AK3(CPLX)5(ReP)

(c+f1(i))w

(Extraction de la partie réelle)

AK3(CPLX)6(ImP)

(c+f1(i))w

(Extraction de la partie imaginaire)

CASIO Graph 60, Graph 30, CFX-9940GT User Manual [fr]

Specifications and Main Features

Frequently Asked Questions

User Manual