Page 1

F
GRAPH 100
Mode d’emploi
(
Fonctions supplémentaires
2
+
)
Site Internet pédagogique international de CASIO
http://edu.casio.com
FORUM PÉDAGOGIQUE CASIO
http://edu.casio.com/forum/
Page 2

Conservez la documentation à portée de main pour
toute référence future.
Page 3

•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
GRAPH 100
+
(Fonctions supplémentaires)
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
20001201
Page 4

1
Table des matières
Table des matières
Chapitre 1 Application statistiques avancées
1-1 Statistiques avancées (STAT) .......................................................... 1-1-1
1-2 Tests (TEST) .................................................................................... 1-2-1
1-3 Intervalle de confiance (INTR).......................................................... 1-3-1
1-4 Lois de probabilité (DIST)................................................................. 1-4-1
Chapitre 2 Calculs financiers (TVM)
2-1 Avant d’effectuer des calculs financiers ........................................... 2-1-1
2-2 Intérêt simple .................................................................................... 2-2-1
2-3 Intérêt composé................................................................................ 2-3-1
2-4 Cash-flow (Evaluation d’investissement).......................................... 2-4-1
2-5 Amortissement ................................................................................. 2-5-1
2-6 Conversion de taux d’intérêt............................................................. 2-6-1
2-7 Coût, prix de vente, marge ............................................................... 2-7-1
2-8 Calculs de jours/date ........................................................................ 2-8-1
2-9 Dépréciation ..................................................................................... 2-9-1
2-10 Obligations ..................................................................................... 2-10-1
2-11 Graphe TVM ................................................................................... 2-11-1
2-12 Exemples........................................................................................ 2-12-1
Chapitre 3 Equations différentielles
3-1 Utilisation du mode DIFF EQ............................................................ 3-1-1
3-2 Equations différentielles du premier ordre........................................ 3-2-1
3-3 Equations différentielles linéaires du deuxième ordre ...................... 3-3-1
3-4 Equations différentielles du N
3-5 Système d’équations différentielles du premier ordre ...................... 3-5-1
Chapitre 4 E-CON
4-1 Aperçu de la fonction E-CON ........................................................... 4-1-1
4-2 Configuration de l’EA-100 ................................................................ 4-2-1
4-3 Mémoire de configurations ............................................................... 4-3-1
4-4 Convertisseur de programme ........................................................... 4-4-1
4-5 Activation d’un échantillonnage ........................................................ 4-5-1
Index
e
ordre ................................................ 3-4-1
20001201
Page 5

Chapitre
1
Application statistiques avancées
1-1 Statistiques avancées (STAT)
1-2 Tests (TEST)
1-3 Intervalle de confiance (INTR)
1-4 Lois de probabilité (DIST)
20001201
Page 6
1-1-1
Statistiques avancées (STAT)
1-1 Statistiques avancées (STAT)
uu
uMenu de fonctions
uu
Les menus de fonctions pour l’écran de saisie de listes dans le mode STAT sont les
suivants.
Une pression d’une touche de fonction correspondant à l’élément ajouté affiche un menu
contenant les options suivantes.
• 3(TEST) ... Test (page 1-2-1)
• 4(INTR) ... Intervalle de confiance (page 1-3-1)
• 5(DIST) ... Probabilités (page 1-4-1)
Les fonctions SORT et JUMP se trouvent dans le menu TOOL (6(g)1(TOOL)).
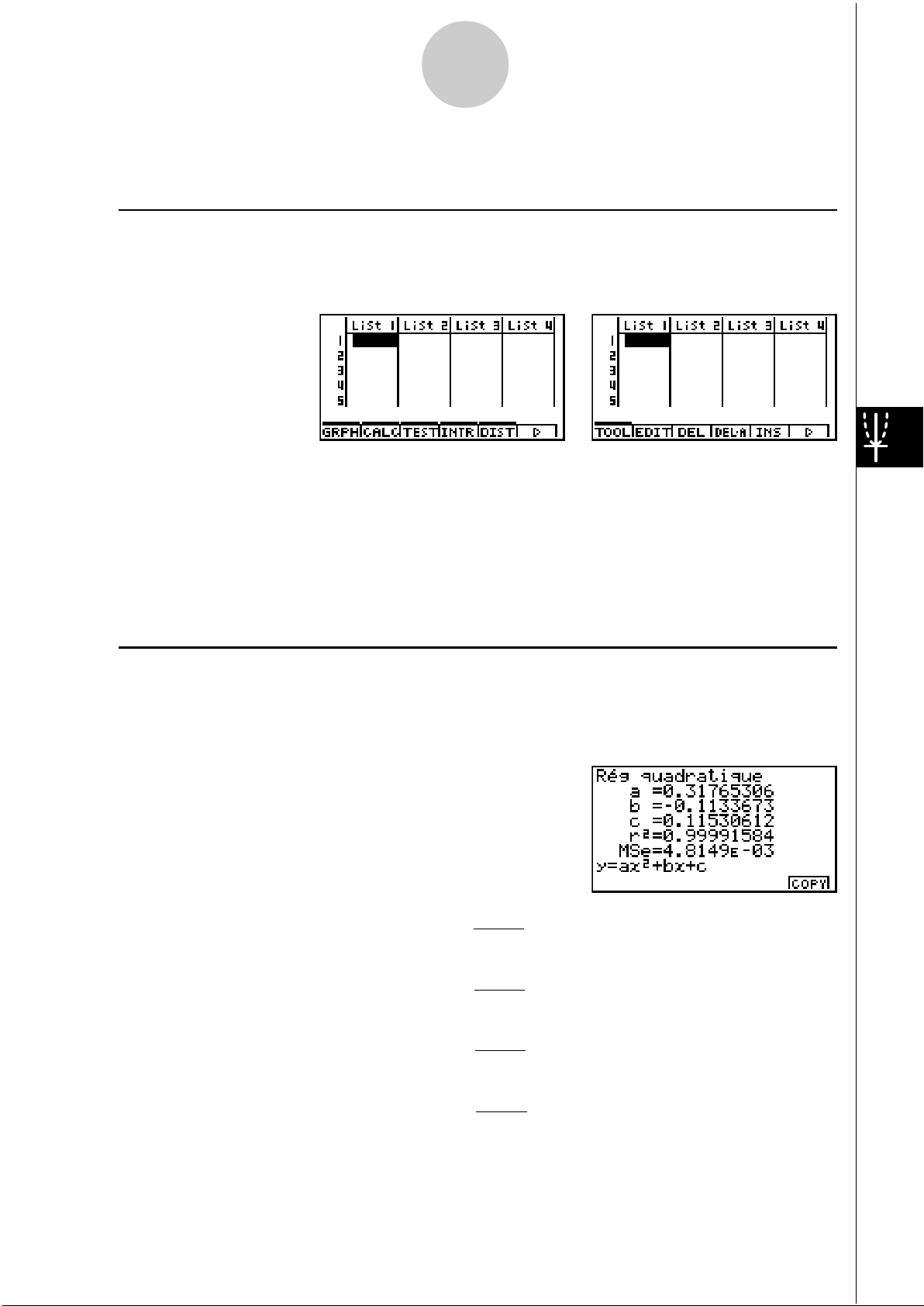
uu
uCalcul du coefficient de détermination (r
uu
2
) et de MSE
Vous pouvez utiliser le mode STAT pour calculer le coefficient de détermination (r2) pour une
régression quadratique, une régression cubique et une régression quartique. Les types de
calculs MSE suivants sont aussi disponibles pour chaque type de régression.
n
• Régression linéaire ...
• Régression quadratique ...
• Régression cubique ...
• Régression quartique ...
MSE =
MSE =
MSE =
MSE =
1
n – 2
1
n – 3
1
n – 4
1
n – 5
(yi – (axi+ b))
i=1
n
(yi – (axi + bxi+ c))
i=1
n
(yi – (axi3+ bxi + cxi +d ))
i=1
n
(yi – (ax
i=1
2
4
i
+ bx
2
2
i3
+ cx
2
2
i
+ dx
2
i
+ e))
2
20001201
Page 7
1-1-2
Statistiques avancées (STAT)
n
• Régression logarithmique ...
• Régression exponentielle ...
• Régression de puissance ...
• Régression sinusoïdale ...
• Régression logistique ...
uu
uCalcul de la valeur estimée pour les graphes de régression
uu
MSE =
MSE =
MSE =
MSE =
MSE =
1
(yi – (a + b ln xi ))
n – 2
n – 2
n – 2
n – 2
n – 2 1 + ae
i=1
n
1
1
1
1
(ln yi – (ln a + bxi ))
i=1
n
(ln yi – (ln a + b ln xi ))
i=1
n
(yi – (a sin (bxi + c) + d ))
i=1
i=1
n
y
i
–
C
-bx
2
2
2
2
2
i
Le mode STAT comprend aussi une fonction Y-CAL qui utilise la régression pour calculer la
valeur estimée de y pour une valeur x particulière après la représentation graphique d’une
régression statistique à variable double.
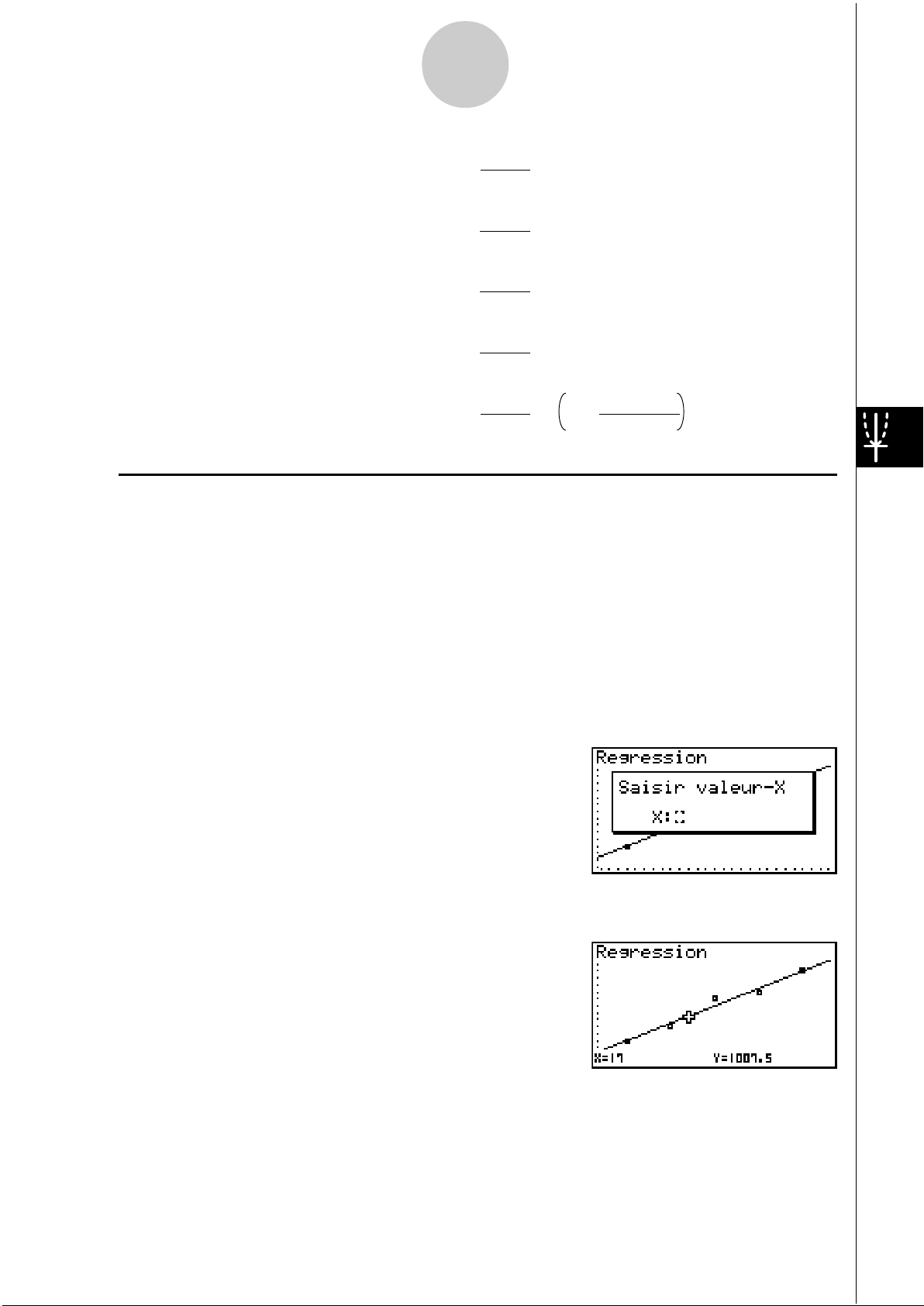
Pour utiliser la fonction Y-CAL procédez de la façon suivante.
1. Après avoir tracé un graphe de régression, appuyez sur 6(g)2(Y-CAL) pour accéder au
mode de sélection de graphe, puis appuyez sur w.
Si plusieurs graphes sont affichés, utilisez f et c pour sélectionner le graphe souhaité,
puis appuyez sur w.
• La boîte de dialogue de saisie de la valeur x apparaît.
2. Saisissez la valeur x souhaitée puis appuyez sur w.
• Les coordonnées x et y apparaissent au bas de l’écran, et le pointeur se positionne au
point correspondant sur le graphe.
3. Pour calculer une autre valeur, appuyez sur v ou sur une touche numérique à ce
moment pour faire réapparaître la boîte de dialogue de saisie de la valeur x.
20001201
Page 8

1-1-3
Statistiques avancées (STAT)
4. Lorsque vous avez terminé, appuyez sur i pour dégager les valeurs des coordonnées
et le pointeur de l’écran.
· Le pointeur n’apparaît pas si les coordonnées calculées ne sont pas dans la plage
d’affichage.
· Les coordonnées n’apparaissent pas si [Off] est spécifié pour l’option [Coord] de l’écran
[SETUP].
· La fonction Y-CAL peut aussi être utilisée avec un graphe tracé à l’aide de DefG.
uu
uCopie de la formule de régression depuis l’écran de résultat d’un calcul de
uu
régression
Outre la fonction de copie de formules de régression qui permet de copier le résultat d’un
calcul de régression après le tracé d’un graphe statistique (par ex. à points dispersés), le
mode STAT dispose aussi d’une fonction qui permet de copier la formule de régression
résultant de ce calcul. Pour copier cette formule, appuyez sur 6(COPY).
kk
k Calcul de tests, intervalle de confiance et de probabilité
kk
Le mode STAT comprend des fonctions permettant de réaliser des tests et des calculs
d’intervalle de confiance et de probabilité. Vous trouverez des explications sur chacune de
ces fonctions dans les paragraphes : 1-2 Tests, 1-3 Intervalle de confiance et 1-4 Probabilité.
uu
uRéglages des paramètres
uu
Vous pouvez utiliser les deux méthodes suivantes pour effectuer des calculs de test,
d’intervalle de confiance et de probabilité.
• Sélection
Il faut appuyer sur la touche de fonction correspondant au réglage souhaité sur le menu de
fonctions.
• Saisie de la valeur
Il faut saisir directement la valeur du paramètre. Dans ce cas, rien n’apparaît dans le menu
de fonctions.
· Une pression de i permet de revenir à l’écran de saisie de liste. Le curseur revient à sa
position originale avant le réglage des paramètres.
· Une pression de ! i(QUIT) ramène au début de l’écran de saisie de liste.
· Une pression de w sans pression de 1(CAL) pour l’option “Execute” exécute le calcul.
Pour revenir à l’écran de réglage des paramètres, appuyez sur i, A ou w.
20001201
Page 9

1-1-4
Statistiques avancées (STAT)
uu
uFonctions ordinaires
uu
• Le symbole “■” apparaît dans le coin supérieur droit de l’écran pendant l’exécution d’un
calcul et pendant le tracé d’un graphe. Si l’on appuie sur A à ce moment, le calcul ou le
tracé du graphique sera interrompu (Arrêt AC).
• Une pression de i ou w pendant l’affichage du résultat d’un calcul ou l’affichage d’un
graphe rétablit l’écran de réglage des paramètres. Il faut appuyer sur ! i(QUIT) pour
revenir au début de l’écran de saisie de liste.
· Une pression de A pendant l’affichage du résultat d’un calcul rétablit l’écran de réglage
des paramètres.
• Il faut appuyer sur u 5(GT) après le tracé d’un graphe pour passer à l’écran de
réglage des paramètres (fonction GT). Pour revenir à l’écran de graphe, appuyez à
nouveau sur u 5(GT).
· La fonction GT est désactivée lorsque vous changez de réglage sur l’écran de réglage
des paramètres, ou lorsque vous effectuez une opération u 3(SET UP) ou !
K(V-Window).
• Après le tracé d’un graphe, vous pouvez utiliser les fonctions de sauvegarde ou de rappel
d’écran du menu PICT.
· La fonction ZOOM et la fonction SKETCH sont désactivées.
La fonction TRACE est désactivée, sauf pour l’affichage de graphe ANOVA bidirectionnel.
Il n’est pas possible de faire défiler l’écran de graphe.
• Après le tracé d’un graphe, vous pouvez utiliser la fonction Save Result pour sauvegarder
les résultats des calculs dans une liste particulière. En principe, tous les éléments affichés
sont sauvegardés, à l’exception de la première ligne (titre).
· Chaque fois que vous exécutez Save Result, toutes les données de la liste sont
remplacées par les nouveaux résultats.
20001201
Page 10

1-2-1
Tests (TEST)
1-2 Tests (TEST)
Le Test Z permet d’effectuer divers tests standardisés. Par exemple, cette fonction permet
de vérifier si un échantillon représente de manière précise la population lorsque l’écart-type
de cette population (par ex. la population totale d’un pays) est connu de tests antérieurs.
Cette fonction est utilisée, entre autres, pour les études de marché et les enquêtes qui
doivent être effectuées rapidement.
Le Test
de cette population est connu.
Le Test Z à 2 échantillons teste l’égalité des moyennes de deux populations en se référant
à des échantillons indépendants lorsque les écarts-types des deux populations sont connus.
Le Test Z à 1 proportion teste une proportion inconnue de succès.
Le Test Z à 2 proportions teste la proportion de succès de deux populations pour les
comparer.
Le Test t teste l’hypothèse lorsque l’écart-type d’une population est inconnu. L’hypothèse qui
est l’opposé de l’hypothèse prouvée est appelée
prouvée est appelée
l’hypothèse nulle. Ensuite on détermine si l’hypothèse nulle ou l’hypothèse alternative doit
être adoptée.
Le Test t à 1 échantillon teste l’hypothèse pour une moyenne inconnue d’une population
lorsque l’écart-type de cette population est inconnu.
Le Test t à 2 échantillons compare les moyennes de populations lorsque les écart-types
sont inconnus.
Le Test t à régression linéaire calcule la force de l’association linéaire de paires de données.
Z à 1 échantillon teste la moyenne inconnue d’une population lorsque l’écart-type
hypothèse alternative
hypothèse nulle
. Le test t est normalement utilisé pour tester
, tandis que l’hypothèse
Le Test
d’un certain nombre de groupes indépendants. En général, ce test génère une tabulation
croisée de deux variables catégoriques (comme oui, non) et évalue l’indépendance de ces
variables. Il peut être utilisé, par exemple, pour évaluer la relation entre l’implication ou non
d’une personne dans un accident de la route et la connaissance du code de la route de cette
personne.
Le Test F à 2 échantillons teste l’hypothèse pour le taux des variances d’un échantillon. Il
peut être utilisé, par exemple, pour vérifier les effets cancérogènes de plusieurs facteurs, tels
que la consommation de tabac, l’alcool, la déficience en vitamines, une consommation
abusive de café, l’inactivité, une mauvaise hygiène de vie, etc.
ANOVA teste l’hypothèse selon laquelle les moyennes de populations des échantillons sont
égales en présence d’échantillons multiples. Ce test peut être utilisé, par exemple, pour
vérifier si différentes combinaisons de matériaux ont un effet sur la qualité et la durée du
produit fini.
One-Way ANOVA est utilisé en présence d’une variable indépendante et d’une variable
dépendante.
Two-Way ANOVA est utilisé en présence de deux variables indépendantes et d’une variable
dépendante.
2
teste l’hypothèse concernant la proportion d’échantillons compris dans chacun
20001201
Page 11

1-2-2
Tests (TEST)
Les diverses méthodes de calculs statistiques mentionnées ci-dessus sont expliquées aux
pages suivantes. Vous trouverez de plus amples informations sur les principes et sur la
terminologie statistiques dans les manuels de statistiques.
Sur l’écran du mode initial STAT, appuyez sur 3(TEST) pour afficher le menu de tests qui
contient les options suivants.
• 3(TEST)b(Z) ... tests
c(T) ... tests t (p. 1-2-10)
d(2) ...test 2 (p. 1-2-18)
e(F) ... test F à 2 échantillons (p. 1-2-20)
f(ANOVA) ... ANOVA (p. 1-2-22)
kk
k Tests Z
kk
uu
uFonctions ordinaires de Test
uu
Vous pouvez utiliser les fonctions d’analyse de graphe suivantes après le tracé d’un graphe.
• 1(Z) ... affiche le point z.
Une pression de 1(Z) affiche le point z au bas de l’écran et le pointeur à l’endroit
correspondant sur le graphe (à moins qu’il ne sorte de l’écran).
Deux points sont affichés dans le cas d’un test à deux extrémités. Utilisez d et e pour
déplacer le pointeur.
Appuyez sur i pour dégager le point z.
• 2(P) ... affiche la valeur p.
Z (p. 1-2-2)
Z
Une pression de 2(P) affiche la valeur p au bas de l’écran sans pointeur.
Appuyez sur i pour dégager la valeur p.
uu
u Test
uu
Ce test est utilisé lorsque l’écart-type d’un échantillon d’une population est connu pour
vérifier l’hypothèse. Le Test Z à 1 échantillon s’applique à la répartition normale.
Z à 1 échantillon
μ
o –
Z =
0
n
o : moyenne de l’échantillon
μ
o : moyenne supposée d’une population
: Ecart-type d’une population
n : taille de l’échantillon
# Les réglages de fenêtre d’affichage suivants
sont utilisés pour le tracé du graphe.
Xmin = –3,2, Xmax = 3,2, Xscale = 1,
Ymin = –0,1, Ymax = 0,45, Yscale = 0,1.
20001201
# L’exécution d’une fonction d’analyse
sauvegarde les valeurs
dans les variables Z et P.
z et p respectivement
Page 12

1-2-3
Tests (TEST)
Utilisez les touches suivantes à partir de la liste de données statistiques.
3(TEST)
b(Z)
b(1-Smpl)
La signification de chaque option en cas de spécification de données de listes est la
suivante.
Data ............................ type de données
μ
.................................. conditions du test de la valeur moyenne d’une population
(“G
μ
0” spécifie un test à deux extrémités, “< μ0” spécifie un
test à une extrémité inférieure, “>
μ
0” spécifie un test à une
extrémité supérieure.)
μ
0 ................................. moyenne supposée d’une population
.................................. écart-type d’une population ( > 0)
List .............................. liste dont le contenu doit être utilisé comme données
(Liste 1 à 20)
Freq ............................. fréquence (1 ou Liste 1 à 20)
Save Res..................... liste pour la sauvegarde des résultats des calculs
(Aucune ou List 1 à 20)
Execute ....................... exécution d’un calcul et tracé d’un graphe
Les options de spécification des données des paramètres qui sont différentes de la
spécification des données des listes ont la signification suivante.
o .................................. moyenne de l’échantillon
n .................................. taille de l’échantillon (entier positif)
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute], puis
appuyez sur une des touches de fonction suivantes pour effectuer le calcul ou tracer le
graphe.
• 1(CALC) ... exécution du calcul
• 6(DRAW) ... tracé du graphe
20001201
Page 13
1-2-4
Tests (TEST)
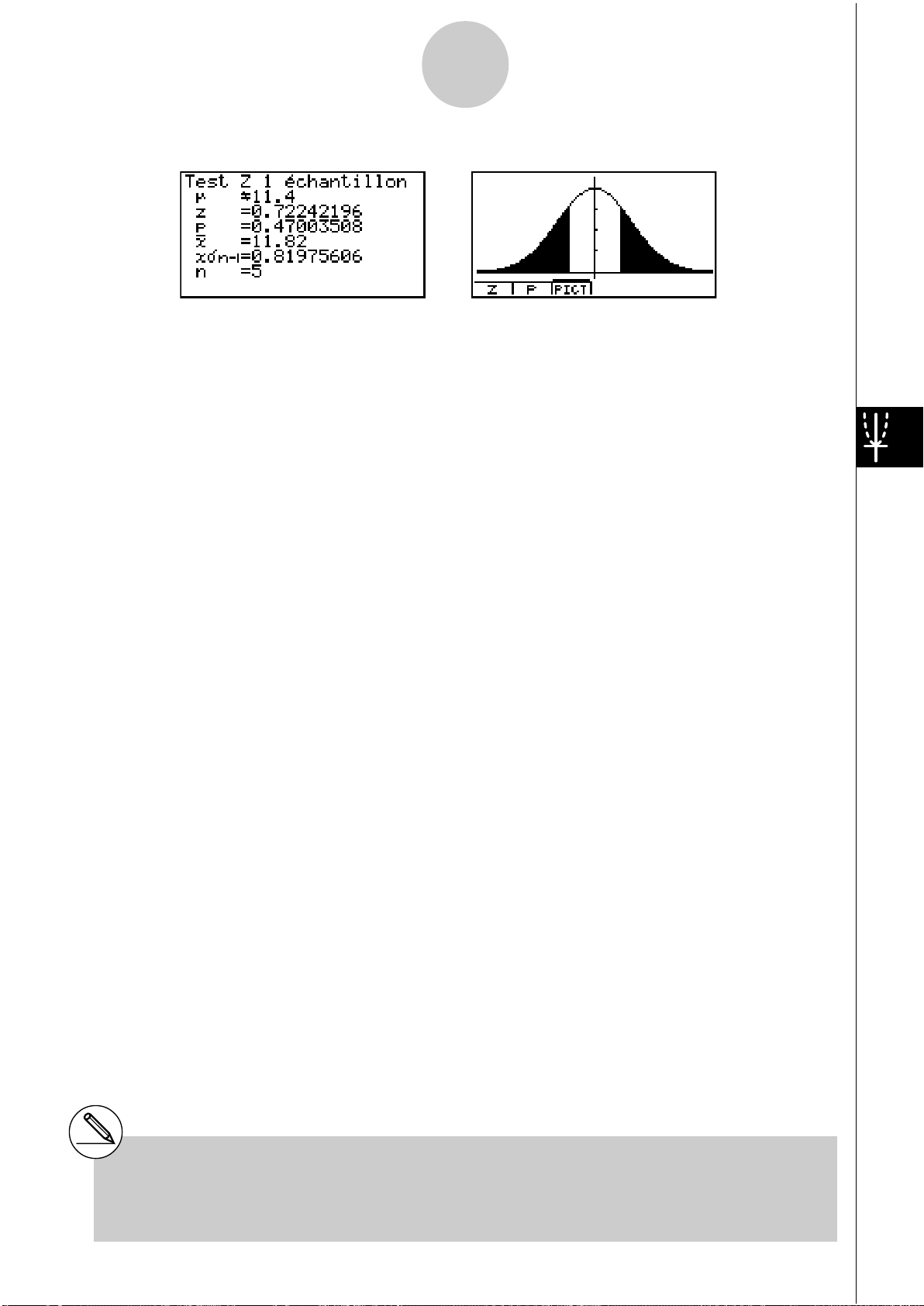
Exemple d’affichage des résultats d’un calcul
μ
G11.4
........................
sens du test
z .................................. point z
.................................. valeur p
p
o .................................. moyenne de l’échantillon
x
n-1 ............................. écart-type de l’échantillon (affiché seulement pour le réglage
Data: List)
n .................................. taille de l’échantillon
# [Save Res] ne sauvegarde pas la condition
de la deuxième ligne.
μ
20001201
Page 14

1-2-5
Tests (TEST)
uu
uTest
uu
Z à 2 échantillons
Ce test est utilisé pour vérifier l’hypothèse lorsque les écarts-types des échantillons de deux
populations sont connus. Le Test
o1 – o
Z =
2
1
+
n
n
1
Z à 2 échantillons s’applique à la répartition normale.
2
2
2
2
o1 : moyenne de l’échantillon 1
o2 : moyenne de l’échantillon 2
1 : écart-type de la population de l’échantillon 1
2 : écart-type de la population de l’échantillon 2
n1 : taille de l’échantillon 1
n2 : taille de l’échantillon 2
Utilisez les touches suivantes à partir de la liste de données statistiques.
3(TEST)
b(Z)
c(2-Smpl)
La signification de chaque option en cas de spécification de données de listes est la suivante.
Data ............................ type de données
μ
1 ................................. conditions du test de la valeur moyenne d’une population
(“G
μ
2” spécifie un test à deux extrémités, “< μ2” spécifie un
test à une extrémité où l’échantillon 1 est inférieur à
l’échantillon 2, “>
μ
2” spécifie un test à une extrémité où
l’échantillon 1 est supérieur à l’échantillon 2.)
1 ................................. écart-type de la population de l’échantillon 1 (1 > 0)
2 ................................. écart-type de la population de l’échantillon 2 (2 > 0)
List(1) .......................... liste dont le contenu doit être utilisé comme données
d’échantillon 1
List(2) .......................... liste dont le contenu doit être utilisé comme données
d’échantillon 2
Freq(1) ........................ fréquence de l’échantillon 1 (entier positif)
Freq(2) ........................ fréquence de l’échantillon 2 (entier positif)
Save Res..................... liste pour la sauvegarde des résultats des calculs
(Aucune ou List 1 à 20)
Execute ....................... exécution d’un calcul et tracé d’un graphe
Les options de spécification des données des paramètres qui sont différentes de la
spécification des données des listes ont la signification suivante.
20001201
Page 15
1-2-6
Tests (TEST)
o1 ................................. moyenne de l’échantillon 1
n1 ................................. taille (entier positif) de l’échantillon 1
o2 ................................. moyenne de l’échantillon 2
n2 ................................. taille (entier positif) de l’échantillon 2
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute] puis appuyez
sur une des touches de fonction suivantes pour effectuer le calcul ou tracer le graphe.
• 1(CALC) ... exécution du calcul
• 6(DRAW) ... tracé du graphe
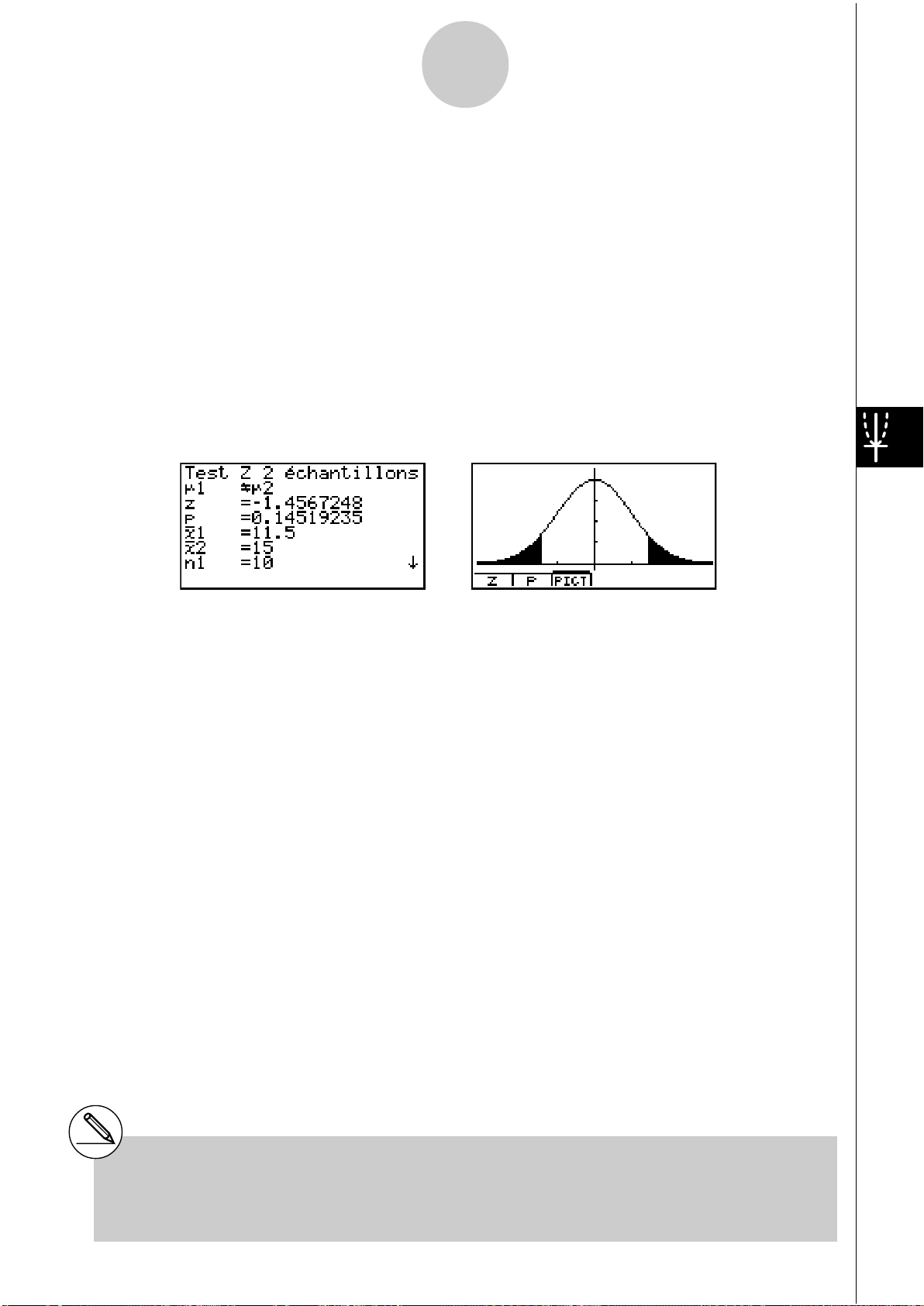
Exemple d’affichage des résultats d’un calcul
μGμ
2 ............................ sens du test
z ................................... point z
.................................. valeur p
p
o1 ................................. moyenne de l’échantillon 1
o2 ................................. moyenne de l’échantillon 2
x1
n-1 ............................ écart-type de l’échantillon 1
(affiché seulement pour le réglage Data: List)
x2
n-1 ............................ écart-type de l’échantillon 2
(affiché seulement pour le réglage Data: List)
n1 ................................. taille de l’échantillon 1
n2 ................................. taille de l’échantillon 2
# [Save Res] ne sauvegarde pas la condition
de la deuxième ligne.
μ
1
20001201
Page 16
1-2-7
Tests (TEST)
uu
uTest
uu
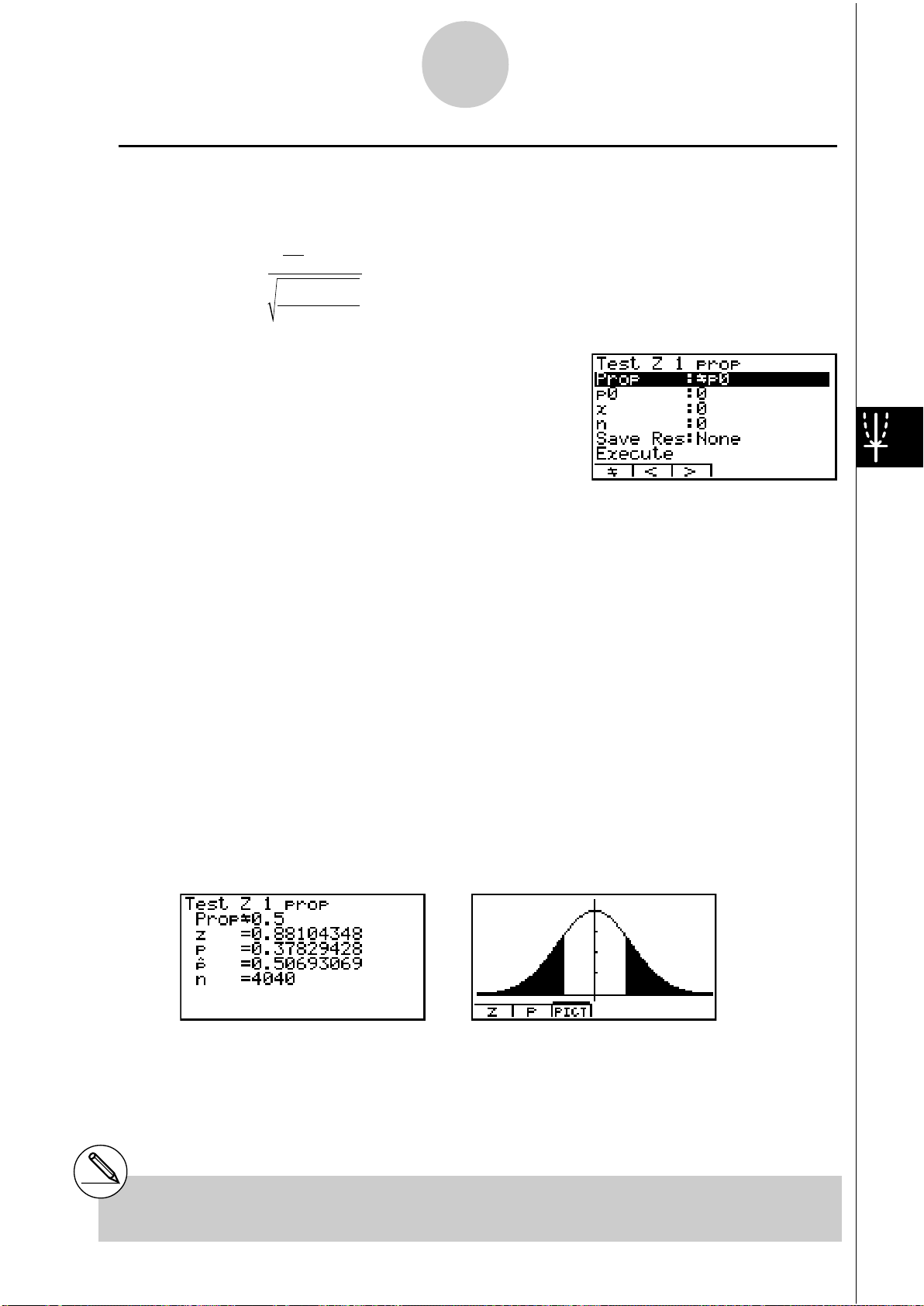
Ce test sert à vérifier une proportion inconnue de succès. Il s’applique à la probabilité
normale.
Z à 1 proportion
x
– p
Z =
n
p
(1– p0)
0
0
p0 : proportion attendue de l’échantillon
n : taille de l’échantillon
n
Utilisez les touches suivantes à partir de la liste de données statistiques.
3(TEST)
b(Z)
d(1-Prop)
Prop ............................ conditions du test de la proportion d’un échantillon (“G p0”
spécifie un test à deux extrémités, “< p0” spécifie un test à
une extrémité inférieure, “> p0” spécifie un test à une
extrémité supérieure)
p0 ................................. proportion attendue de l’échantillon (0 < p0 < 1)
x .................................. valeur de l’échantillon (x > 0 entier)
n .................................. taille de l’échantillon (entier positif)
Save Res..................... liste pour la sauvegarde des résultats des calculs
(Aucune ou List 1 à 20)
Execute ....................... exécution d’un calcul ou tracé d’un graphe
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute] puis appuyez
sur une des touches de fonction suivantes pour effectuer le calcul ou tracer le graphe.
• 1(CALC) ... exécution du calcul
• 6(DRAW) ... tracé du graphe
Exemple d’affichage des résultats d’un calcul
PropG0.5 .................... sens du test
z ................................... point z
p .................................. valeur p
ˆp .................................. proportion estimée de l’échantillon
n .................................. taille de l’échantillon
# [Save Res] ne sauvegarde pas la condition
Prop de la deuxième ligne.
20001201
Page 17
1-2-8
Tests (TEST)
uu
uTest
uu
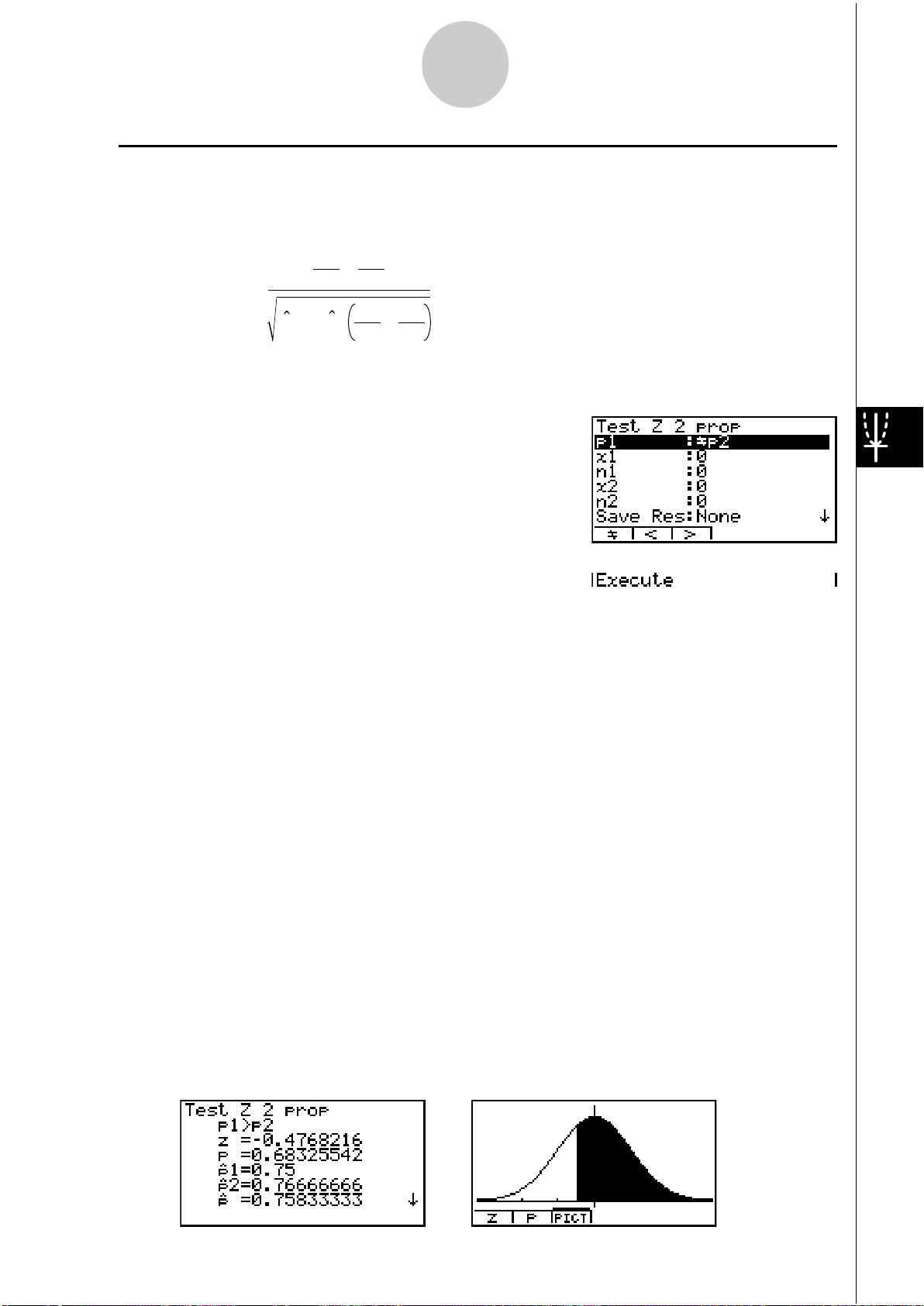
Ce test sert à comparer la proportion de succès. Il s’applique à la probabilité normale.
Z à 2 proportions
x
Z =
n
p(1 – p )
x
2
1
–
n
2
1
1
1
+
n
n
2
1
x1 : valeur des données de l’échantillon 1
x2 : valeur des données de l’échantillon 2
n1 : taille de l’échantillon 1
n2 : taille de l’échantillon 2
ˆp : proportion estimée de l’échantillon
Utilisez les touches suivantes à partir de la liste de données statistiques.
3(TEST)
b(Z)
e(2-Prop)
p1 ................................. conditions du test de la proportion d’un échantillon (“G p2”
spécifie un test à deux extrémités, “< p2” spécifie un test à
une extrémité où l’échantillon 1 est inférieur à l’échantillon 2,
“> p2” spécifie un test à une extrémité où l’échantillon 1 est
supérieur à l’échantillon 2.)
x1 ................................. valeur des données (x1 > 0 entier) de l’échantillon 1
n1 ................................. taille (entier positif) de l’échantillon 1
x2 ................................. valeur des données (x2 > 0 entier) de l’échantillon 2
n2 ................................. taille (entier positif) de l’échantillon 2
Save Res..................... liste pour la sauvegarde des résultats des calculs
(Aucune ou List 1 à 20)
Execute ....................... exécution d’un calcul ou tracé d’un graphe
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute] puis appuyez
sur une des touches de fonction suivantes pour effectuer le calcul ou tracer le graphe.
• 1(CALC) ... exécution du calcul
• 6(DRAW) ... tracé du graphe
Exemple d’affichage des résultats d’un calcul
20001201
Page 18

1-2-9
Tests (TEST)
p1>p2 ............................ sens du test
z .................................. point z
p .................................. valeur p
ˆp 1 ................................. proportion estimée de l’échantillon 1
ˆp 2 ................................. proportion estimée de l’échantillon 2
ˆp .................................. proportion estimée de l’échantillon
n1 ................................. taille de l’échantillon 1
n2 ................................. taille de l’échantillon 2
# [Save Res] ne sauvegarde pas la condition p
de la deuxième ligne.
20001201
Page 19

1-2-10
Tests (TEST)
kk
k Tests t
kk
uu
u Fonctions ordinaires Test t
uu
Vous pouvez utiliser les fonctions d’analyse de graphe suivantes après le tracé d’un graphe.
• 1(T) ... affichage du point t.
Une pression de 1(T) affiche le point t au bas de l’écran et le pointeur à l’endroit correspondant
sur le graphe (à moins qu’il sorte de l’écran).
Deux points sont affichés dans le cas d’un test à deux extrémités. Utilisez d et e pour
déplacer le pointeur.
Appuyez sur i pour dégager le point t.
•2(P) ... affichage de la valeur p.
Une pression de 2(P) affiche la valeur p au bas de l’écran sans pointeur.
Appuyez sur i pour dégager la valeur p.
# Les réglages de fenêtre d’affichage suivants
sont utilisés pour le tracé du graphe.
Xmin = –3,2, Xmax = 3,2, Xscale = 1,
Ymin = –0,1, Ymax = 0,45, Yscale = 0,1.
20001201
# L’exécution d’une fonction d’analyse
sauvegarde respectivement les valeurs
dans les variables T et P.
t et p
Page 20

1-2-11
Tests (TEST)
uu
uTest
uu
t à 1 échantillon
Ce test vérifie l’hypothèse pour la moyenne inconnue d’une population lorsque l’écart-type
de cette population est inconnu. Le Test
μ
o –
x
0
n–1
t =
n
t à 1 échantillon s’applique à la probabilité t.
o : moyenne de l’échantillon
μ
0 : moyenne supposée d’une
population
x
n-1 : écart-type d’un échantillon
n : taille de l’échantillon
Utilisez les touches suivantes à partir de la liste de données statistiques.
3(TEST)
c(T)
b(1-Smpl)
La signification de chaque option en cas de spécification de données de listes est la suivante.
Data ............................ type de données
μ
.................................. conditions du test de la valeur moyenne d’une population
(“G
μ
0” spécifie un test à deux extrémités, “< μ0” spécifie un
test à une extrémité inférieure, “>
μ
0” spécifie un test à une
extrémité supérieure.)
μ
0 ................................. moyenne supposée d’une population
List .............................. liste dont le contenu doit être utilisé comme données
Freq ............................. fréquence
Save Res..................... liste pour la sauvegarde des résultats des calculs
(Aucune ou List 1 à 20)
Execute ....................... exécution d’un calcul et tracé d’un graphe
Les options de spécification des données des paramètres qui sont différentes de la
spécification des données des listes ont la signification suivante.
o .................................. moyenne de l’échantillon
x
n-1 ............................. écart-type de l’échantillon (xn-1 > 0)
n .................................. taille de l’échantillon (entier positif)
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute] puis appuyez
sur une des touches de fonction suivantes pour effectuer le calcul ou tracer le graphe.
• 1(CALC) ... exécution du calcul
• 6(DRAW) ... tracé du graphe
20001201
Page 21
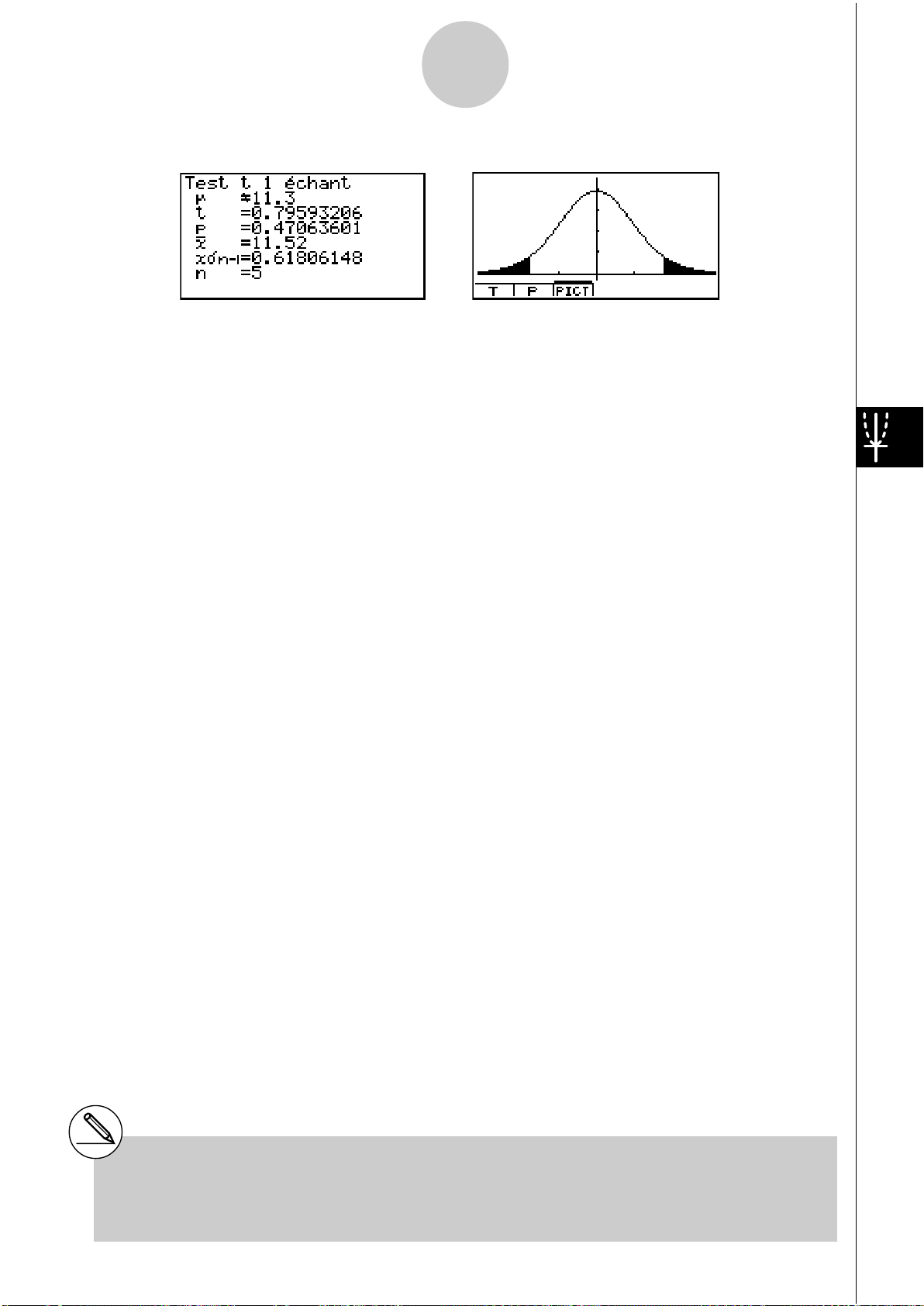
1-2-12
Tests (TEST)
Exemple d’affichage des résultats d’un calcul
μ
G 11.3 ...................... sens du test
t
...................................
.................................. valeur p
p
point t
o .................................. moyenne de l’échantillon
x
n-1 ............................. écart-type de l’échantillon
n .................................. taille de l’échantillon
# [Save Res] ne sauvegarde pas la condition μ
de la deuxième ligne.
20001201
Page 22

1-2-13
Tests (TEST)
uu
uTest
uu
t à 2 échantillons
Le Test t à 2 échantillons sert à comparer les moyennes de populations lorsque les écarts-
types sont inconnus. Le Test
t =
x
1 n–1
n
1
t à 2 échantillons s’applique à la répartition t.
o1 – o
2
+
2
x
2 n–1
n
2
2
o1 : moyenne de l’échantillon 1
o2 : moyenne de l’échantillon 2
x1
n-1 : écart-type de l’échantillon 1
x2
n-1 : écart-type de l’échantillon 2
n1 : taille de l’échantillon 1
n2 : taille de l’échantillon 2
Cette formule s’applique lorsque la mise en commun est activée. Le dénominateur est
différent lorsque la mise en commun est désactivée.
Les degrés de liberté df et xp
Lorsque l’option est validée la formule suivante s’applique.
df
= n1 + n2 – 2
n-1 dépendent de la validation ou non de l’option Pooled.
x
p n–1
=
(n
–1)x
1
2
+(n2–1)x
1
n–1
n
+ n
– 2
1
2
2
2
n–1
Lorsque l’option est invalidée la formule suivante s’applique.
df =
n
C =
x
2
C
–1
1
x
1 n–1
n
1
1
(1–C )
+
n
1 n–1
n
1
2
x
+
–1
2
2
2 n–1
n
2
2
2
Utilisez les touches suivantes à partir de la liste de données statistiques.
3(TEST)
c(T)
c(2-Smpl)
20001201
Page 23

1-2-14
Tests (TEST)
La signification de chaque option en cas de spécification de données de listes est la
suivante.
Data ............................ type de données
μ
1 ................................. conditions du test de la valeur moyenne d’un échantillon
(“G
μ
2” spécifie un test à deux extrémités, “< μ2” spécifie un
test à une extrémité où l’échantillon 1 est inférieur à
μ
l’échantillon 2, “>
2” spécifie un test à une extrémité où
l’échantillon 1 est supérieur à l’échantillon 2.)
List(1) .......................... liste dont le contenu doit être utilisé comme données
d’échantillon 1
List(2) .......................... liste dont le contenu doit être utilisé comme données
d’échantillon 2
Freq(1) ........................ fréquence de l’échantillon 1 (entier positif)
Freq(2) ........................ fréquence de l’échantillon 2 (entier positif)
Pooled ......................... On (activé) ou Off (désactivé)
Save Res..................... liste pour la sauvegarde des résultats des calculs
(Aucune ou List 1 à 20)
Execute ....................... exécution d’un calcul et tracé d’un graphe
Les options de spécification des données des paramètres qui sont différentes de la
spécification des données des listes ont la signification suivante.
o1 ................................. moyenne de l’échantillon 1
x1
n-1 ............................ écart-type de l’échantillon 1 (x1n-1 > 0)
n1 ................................. taille (entier positif) de l’échantillon 1
o2 ................................. moyenne de l’échantillon 2
x2
n-1 ............................ écart-type (x2n-1 > 0) de l’échantillon 2
n2 ................................. taille (entier positif) de l’échantillon 2
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute] puis appuyez
sur une des touches de fonction suivantes pour effectuer le calcul ou tracer le graphe.
• 1(CALC) ... exécution du calcul
• 6(DRAW) ... tracé du graphe
20001201
Page 24
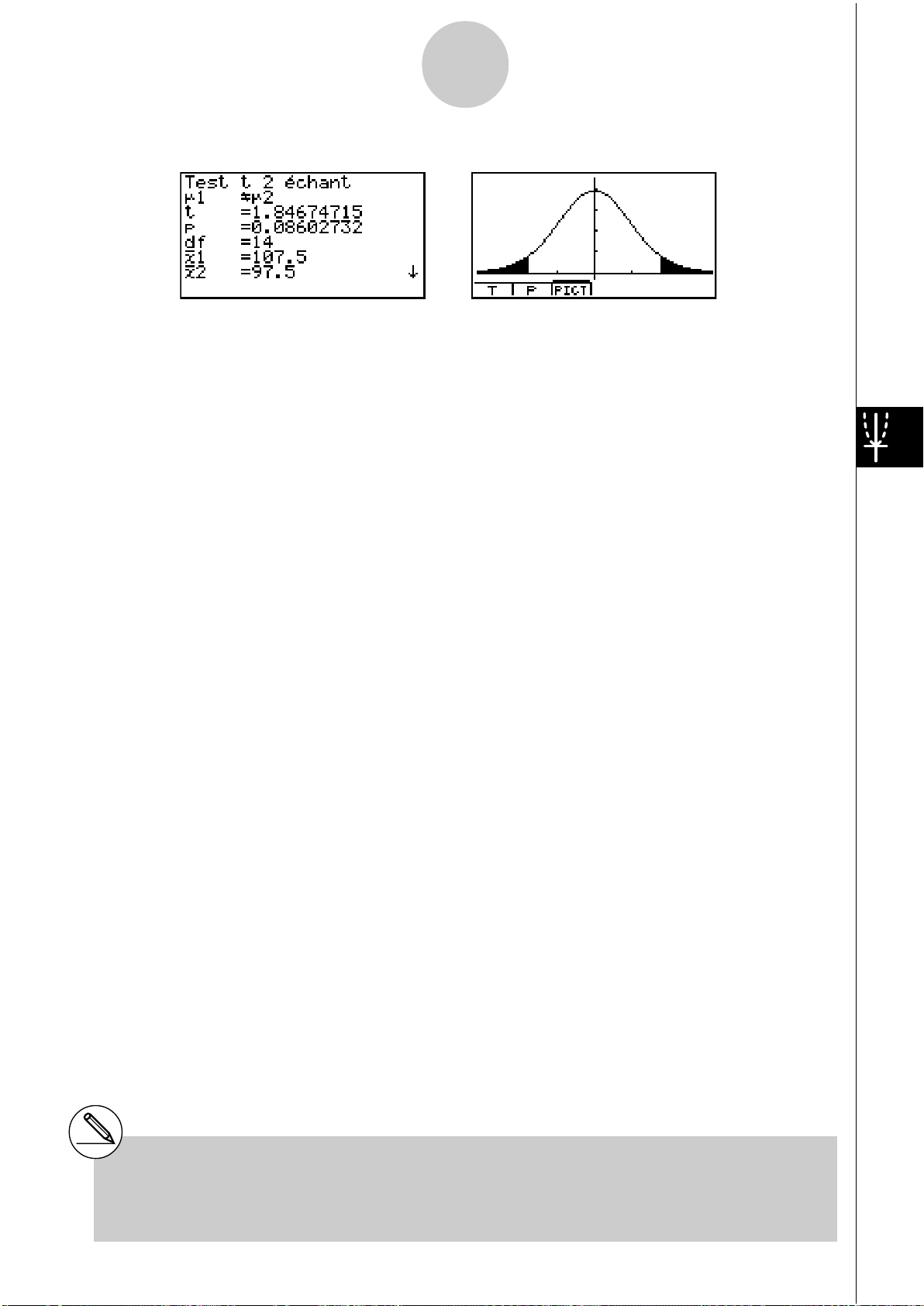
1-2-15
Tests (TEST)
Exemple d’affichage des résultats d’un calcul
μ1Gμ
2 ........................... sens du test
t
...................................
.................................. valeur p
p
point t
df ................................. degrés de liberté
o1 ................................. moyenne de l’échantillon 1
o2 ................................. moyenne de l’échantillon 2
x1
n-1 ............................ écart-type de l’échantillon 1
x2
n-1 ............................ écart-type de l’échantillon 2
xp
n-1 ............................ écart-type de l’échantillon mis en commun (apparaît seulement
pour le réglage Pooled : On.)
n1 ................................. taille de l’échantillon 1
n2 ................................. taille de l’échantillon 2
# [Save Res] ne sauvegarde pas la condition
de la deuxième ligne.
μ
1
20001201
Page 25

1-2-16
Tests (TEST)
uTest t à régression linéaire
Le Test t à régression linéaire traite des ensembles de données à variable double par
paires (
x, y) et marque toutes les données sur un graphe. Ensuite, une ligne droite (y = a +
bx) est tracée dans la zone où se trouve le plus grand nombre de points, et le degré où une
relation existe est calculé.
n
( x – o)( y – p)
i=1
b =
Utilisez les touches suivantes à partir de la liste de données statistiques.
La signification de chaque option en cas de spécification de données de listes est la
suivante.
n
(x – o)
i=1
3(TEST)
c(T)
d(LinReg)
2
a = p – bo t = r
n – 2
1 – r
a : intersection
b : pente de la ligne
n : taille de l’échantillon
2
(n > 3)
r : coefficient de
corrélation
2
r
: coefficient de
détermination
& ............................ conditions du test de la valeur p (“G 0” spécifie un test à
deux extrémités, “< 0” spécifie un test à une extrémité
inférieure, “> 0” spécifie un test à une extrémité supérieure.)
XList ............................ liste pour les données de l’axe
YList ............................ liste pour les données de l’axe y
Freq ............................. fréquence
Save Res..................... liste pour la sauvegarde des résultats des calculs
(Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute] puis appuyez
sur une des touches de fonction suivantes pour effectuer le calcul.
• 1(CALC) ... exécution du calcul
# Vous ne pouvez pas tracer un graphe pour le
Test t à régression linéaire.
x
20001201
Page 26

1-2-17
Tests (TEST)
Exemple d’affichage des résultats d’un calcul
G 0 &
G 0 .............. sens du test
t ................................... point t
.................................. valeur p
p
df ................................. degrés de liberté
a .................................. terme constant
b .................................. coefficient
s .................................. erreur standard
r .................................. coefficient de corrélation
2
r
................................. coefficient de détermination
Une pression de 6(COPY) pendant l’affichage du résultat d’un calcul copie la formule de
régression dans l’éditeur de formules graphiques.
Si une liste est spécifiée pour l’option [Resid List] de l’écran de réglage, les données résiduelles
de la formule de régression seront automatiquement sauvegardées dans la liste spécifiée après
le calcul.
# [Save Res] ne sauvegarde pas les conditions
et de la deuxième ligne.
# Lorsque la liste spécifiée par [Save Res] est
identique à la liste spécifiée par l’option
[Resid List] sur l'écran de réglage, seules
les données [Resid List] sont sauvegardées
dans la liste.
20001201
Page 27

j
1-2-18
Tests (TEST)
kk
k Test
kk
Le Test
2
2
crée un certain nombre de groupes indépendants et vérifie l’hypothèse en
fonction de la proportion de l’échantillon inclus dans chaque groupe. Le Test
aux variables dichotomiques (variables offrant deux possibilités, comme oui ou non).
Chiffres attendus
Fij =
2 =
k
i=1
k
=1
i=1
×
x
ij
j=1
n
(xij – Fij)
F
x
ij
ij
n : toutes les valeurs des
données
2
Utilisez les touches suivantes à partir de la liste de données statistiques.
3(TEST)
d(2)
2
s’applique
Spécifiez ensuite la matrice qui contient les données. La signification des options
précédentes est la suivante.
Observed .................... nom de la matrice (A à Z) contenant les chiffres observés
(entiers positifs de toutes les cellules)
Expected ..................... nom de la matrice (A à Z) réservée à la sauvegarde de la
fréquence attendue
Save Res..................... liste pour la sauvegarde des résultats des calculs
(Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul ou tracé d’un graphe
# La matrice doit avoir au moins deux lignes et
deux colonnes. Un erreur se produit si elle
n’a qu’une seule ligne et une seule colonne.
# Une pression de 2('MAT) pendant le
réglage des paramètres fait passer à l’éditeur
MATRIX où le contenu des matrices peut être
changé et vérifié.
20001201
Page 28
1-2-19
Tests (TEST)
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute] puis appuyez
sur une des touches de fonction suivantes pour effectuer le calcul ou tracer le graphe.
• 1(CALC) ... exécution du calcul
• 6(DRAW) ... tracé du graphe
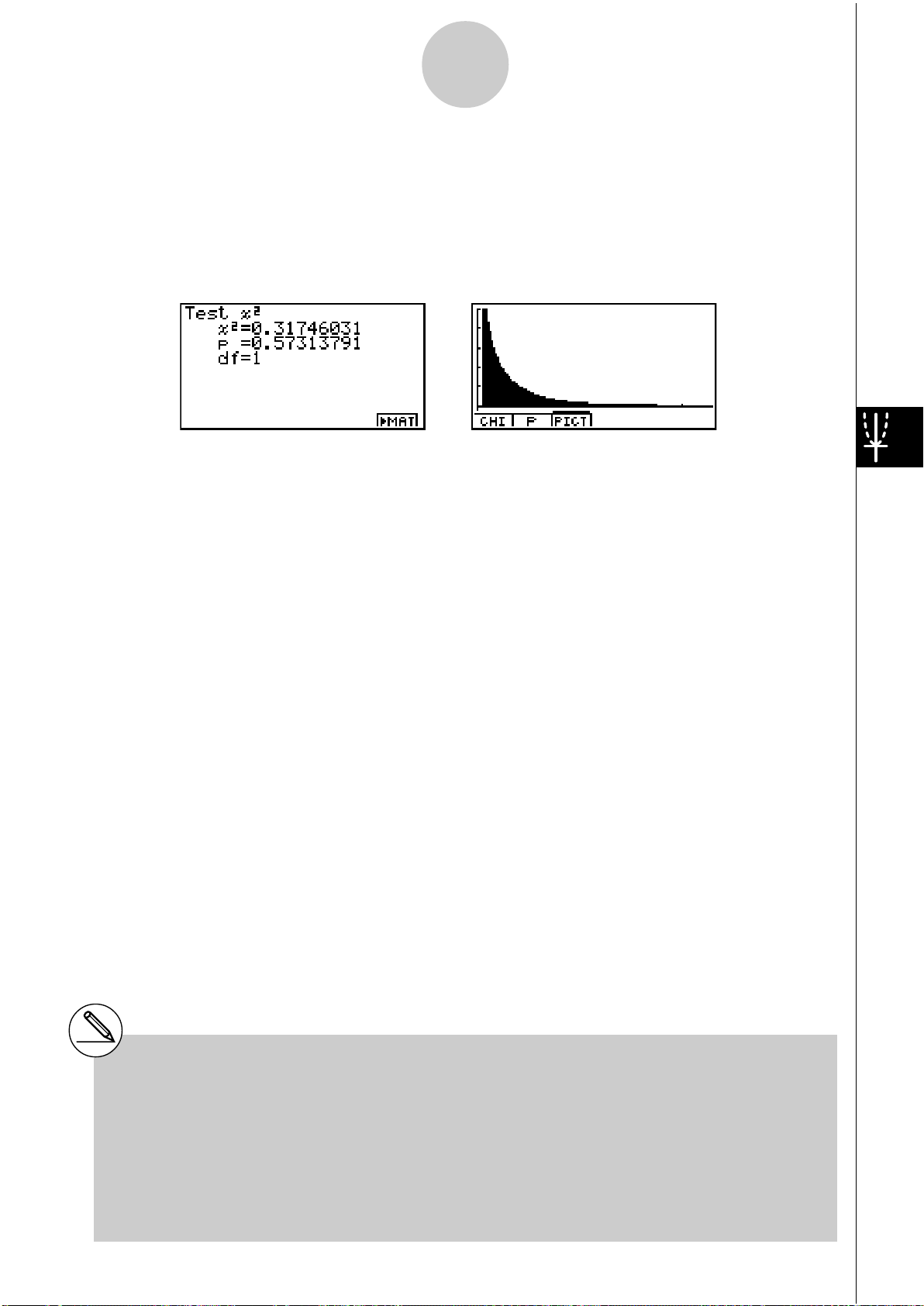
Exemple d’affichage des résultats d’un calcul
2
................................. valeur
2
p .................................. valeur p
df ................................. degrés de liberté
Vous pouvez utiliser les fonctions d’analyse de graphe suivantes après le tracé d’un graphe.
• 1(CHI) ... affichage de la valeur
Une pression de 1(CH1) affiche la valeur
correspondant sur le graphe (à moins qu’il ne sorte de l’écran).
Appuyez sur i pour dégager la valeur
• 2(P) ... affichage de la valeur p.
Une pression de 2(P) affiche la valeur p au bas de l’écran sans pointeur.
Appuyez sur i pour dégager la valeur p.
2
.
2
au bas de l’écran et le pointeur à l’endroit
2
.
# Une pression de 6('MAT) pendant
l'affichage du résultat d’un calcul fait passer à
l’éditeur MATRIX où le contenu des matrices
peut être changé et vérifié.
# Les réglages de fenêtre d’affichage suivants
sont utilisés pour le tracé du graphe.
Xmin = 0, Xmax = 11,5, Xscale = 2,
Ymin = –0,1, Ymax = 0,5, Yscale = 0,1
20001201
# L’exécution d’une fonction d’analyse
sauvegarde les valeurs
respectivement dans les variables C et P.
2
et p
Page 29

1-2-20
Tests (TEST)
kk
k Test
kk
F à 2 échantillons
Le Test F à 2 échantillons vérifie l’hypothèse pour le taux de variances d’un échantillon. Le
Test
F s’applique à la probabilité F.
2
x
1 n–1
F =
x
2 n–1
2
Utilisez les touches suivantes à partir de la liste de données statistiques.
3(TEST)
e(F)
La signification de chaque option en cas de spécification de données de listes est la suivante.
Data ............................ type de données
1 ................................. conditions du test de l’écart-type d’une population (“G 2”
spécifie un test à deux extrémités, “<
2” spécifie un test à
une extrémité où l’échantillon 1 est inférieur à l’échantillon 2,
“>
2” spécifie un test à une extrémité où l’échantillon 1 est
supérieur à l’échantillon 2.)
List(1) .......................... liste dont le contenu doit être utilisé comme données
d’échantillon 1
List(2) .......................... liste dont le contenu doit être utilisé comme données
d’échantillon 2
Freq(1) ........................ fréquence de l’échantillon 1
Freq(2) ........................ fréquence de l’échantillon 2
Save Res..................... liste pour la sauvegarde des résultats des calculs
(Aucune ou List 1 à 20)
Execute ....................... exécution d’un calcul et tracé d’un graphe
Les options de spécification des données des paramètres qui sont différentes de la
spécification des données des listes ont la signification suivante.
x1
n-1 ............................ écart-type (x1
n-1
>
0) de l’échantillon 1
n1 ................................. taille (entier positif) de l’échantillon 1
x2
n-1 ............................ écart-type (x2
n-1
>
0) de l’échantillon 2
n2 ................................. taille (entier positif) de l’échantillon 2
20001201
Page 30

1-2-21
Tests (TEST)
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute] puis appuyez
sur une des touches de fonction suivantes pour effectuer le calcul ou tracer le graphe.
• 1(CALC) ... exécution du calcul
• 6(DRAW) ... tracé du graphe
Exemple d’affichage des résultats d’un calcul
1G
2 .......................... sens du test
F .................................. valeur F
.................................. valeur p
p
o1 ................................. moyenne de l’échantillon 1 (apparaît seulement pour le réglage
Data: List)
o2 ................................. moyenne de l’échantillon 2 (apparaît seulement pour le réglage
Data: List)
x1
n-1 ............................ écart-type de l’échantillon 1
x2
n-1 ............................ écart-type de l’échantillon 2
n1 ................................. taille de l’échantillon 1
n2 ................................. taille de l’échantillon 2
Vous pouvez utiliser les fonctions d’analyse de graphe suivantes après le tracé d’un graphe.
• 1(F) ... affichage de la valeur F.
Une pression de 1(F) affiche la valeur F au bas de l’écran et le pointeur à l’endroit
correspondant sur le graphe (à moins qu’il sorte de l’écran).
Deux points apparaissent dans le cas d’un test à deux extrémités. Utilisez d et e pour
déplacer le curseur.
Appuyez sur i pour dégager la valeur F.
• 2(P) ... affichage de la valeur p.
Une pression de 2(P) affiche la valeur p au bas de l’écran sans pointeur.
Appuyez sur i pour dégager la valeur p.
# [Save Res] ne sauvegarde pas la condition
de la ligne 2.
# Les réglages de fenêtre d’affichage sont
automatiquement optimisés pour le tracé du
graphe.
1
20001201
# L’exécution d’une fonction d’analyse
sauvegarde les valeurs
respectivement dans les variables F et P.
F et p
Page 31

1-2-22
Tests (TEST)
kk
k ANOVA
kk
ANOVA vérifie l’hypothèse selon laquelle les moyennes de populations des échantillons sont
égales en présence d’échantillons multiples.
One-Way ANOVA est utilisé s’il y a une variable indépendante et une variable dépendante.
Two-Way ANOVA est utilisé s’il y a deux variables indépendantes et une variable
dépendante.
Utilisez les touches suivantes à partir de la liste de données statistiques.
3(TEST)
f(ANOVA)
La signification de chaque option en cas de spécification de données de listes est la
suivante.
How Many ................... sélection de One-Way ANOVA ou de Two-Way ANOVA (nombre
de niveaux)
Factor A ....................... liste de catégories
Dependnt .................... liste à utiliser pour les données d’échantillons
Save Res..................... liste pour la sauvegarde des résultats des calculs
Execute ....................... exécution d’un calcul et tracé d’un graphe (Two-Way ANOVA
seulement)
L’option suivante apparaît seulement dans le cas de Two-Way ANOVA.
Factor B....................... liste de catégories
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute] puis appuyez
sur une des touches de fonction suivantes pour effectuer le calcul ou tracer le graphe.
• 1(CALC) ... exécution du calcul
• 6(DRAW) ... tracé du graphe (Two-Way ANOVA seulement)
Les résultats des calculs sont affichés sous forme de tableau, comme dans les manuels de
sciences.
# [Save Res] sauvegarde chaque colonne
verticale du tableau dans sa propre liste. La
colonne extrême gauche est sauvegardée
dans la liste spécifiée, et chacune des autres
colonnes de droite est sauvegardée dans
l’ordre dans les autres listes. En tout cinq
listes peuvent être utilisées pour la
sauvegarde de colonnes. Vous pouvez
désigner un numéro de 1 à 16 pour la
première liste.
20001201
Page 32

1-2-23
Tests (TEST)
Exemple d’affichage des résultats d’un calcul
One-Way ANOVA
Line 1 (A) .................... valeur df, valeur SS, valeur MS, valeur F, valeur p de Facteur A
Line 2 (ERR) ............... valeur df, valeur SS, valeur MS de Erreur
Two-Way ANOVA
Line 1 (A) .................... valeur df, valeur SS, valeur MS, valeur F, valeur p de Facteur A
Line 2 (B) .................... valeur df, valeur SS, valeur MS, valeur F, valeur p de Facteur B
Line 3 (AB) .................. valeur df, valeur SS, valeur MS, valeur F, valeur p de Facteur A
× Facteur B
* La ligne 3 n’apparaît pas s’il y a un seul résultat dans
chaque cellule.
Line 4 (ERR) ............... valeur df, valeur SS, valeur MS de Erreur
F .................................. valeur F
.................................. valeur p
p
df ................................. degrés de liberté
SS ................................ somme des carrés
MS ............................... moyenne des carrés
Avec Two-Way ANOVA, des graphes interactifs peuvent être tracés. Le nombre de graphes
dépend du Facteur B, tandis que le nombre de données sur l’axe X dépend du Facteur A. L’axe
Y est la valeur moyenne de chaque catégorie.
Vous pouvez utiliser les fonctions d’analyse de graphe suivantes après le tracé d’un graphe.
• 1(TRACE) ... fonction d’affichage des coordonnées
Une pression de d ou e déplace le pointeur sur le graphe dans le sens correspondant. Si
plusieurs graphes sont tracés, vous pouvez passer d’un graphe à l’autre en appuyant sur f
et c.
Appuyez sur i pour dégager le pointeur de l’affichage.
# La représentation graphique n’est possible
qu’avec Two-Way ANOVA. Les réglages de la
fenêtre d’affichage sont automatiques, quels
que soient les réglages de l'écran de réglage.
# A l’emploi de la fonction TRACE, le nombre
de conditions est sauvegardé dans la variable
A et la valeur moyenne dans la variable M.
20001201
Page 33

1-2-24
Tests (TEST)
kk
k ANOVA (Two-Way)
kk
uu
uDescription
uu
Le tableau suivant montre les résultats des mesures effectuées sur un produit métallique
dont le processus de fabrication par soumission à la chaleur dépend de deux facteurs : la
durée (A) et la température (B). Les expériences ont été répétées deux fois, chacune dans
des conditions identiques.
B (Température de soumission à la chaleur)
A (Durée de soumission à la chaleur)
A1 113 , 116
A2
Effectuez une analyse de variance à partir de l’hypothèse zéro suivante, en utilisant 5%
comme niveau de signification.
Ho : Aucun changement de la résistance dû à la durée
Ho : Aucun changement de la résistance dû à la température
Ho : Aucun changement de la résistance dû à l’interaction de la durée et de la
température
uu
uSolution
uu
Utilisez Two-Way ANOVA pour vérifier l’hypothèse ci-dessus.
Saisissez les données précédentes, comme indiqué ci-dessous.
List1={1,1,1,1,2,2,2,2}
List2={1,1,2,2,1,1,2,2}
List3={113,116,139,132,133,131,126,122}
B1 B2
133 , 131
139 , 132
126 , 122
Définissez la liste 3 (les données de chaque groupe) comme Dependent. Définissez la liste
1 et la liste 2 (le nombre de facteurs pour chaque donnée de la liste 3) respectivement
comme Factor A et Factor B.
L’exécution du test produit les résultats suivants.
• Niveau de différence de durée (A) de signification P = 0,2458019517
Le niveau de signification (p = 0,2458019517) est supérieur au niveau de signification
(0,05) si l’hypothèse ne dément pas.
• Niveau de différentielle de température (B) de signification P = 0,04222398836
Le niveau de signification (p = 0,04222398836) est inférieur au niveau de signification
(0,05), si bien que l’hypothèse dément.
• Niveau d’interaction (A × B) de signification P = 2,78169946e-3
Le niveau de signification (p = 2,78169946e-3) est inférieur au niveau de signification
(0,05), si bien que l’hypothèse dément.
Le test ci-dessus indique que la différence de durée n’est pas significative, la différence de
température est significative et que l’interaction des deux est hautement significative.
20001201
Page 34

uu
uExemple de saisie
uu
uu
uRésultats
uu
1-2-25
Tests (TEST)
20001201
Page 35

1-3-1
Intervalle de confiance (INTR)
1-3 Intervalle de confiance (INTR)
Un intervalle de confiance est une plage (intervalle) comprenant la valeur moyenne d’une
population.
Un intervalle de confiance trop large ne permet pas de se faire une idée de l’endroit où se
trouve la valeur de la population (valeur vraie). Par contre, un intervalle de confiance étroit
limite la valeur de la population et ne permet pas d’obtenir des résultats fiables. Les niveaux
de confiance les plus courants se situent à 95% et 99%. Une augmentation du niveau de
confiance élargit l’intervalle de confiance, tandis qu’une diminution du niveau de confiance
restreint le niveau de confiance, mais augmente aussi le risque de ne pas voir la valeur de la
population. Avec un intervalle de confiance de 95%, par exemple, la valeur de la population
n’est pas incluse dans les intervalles obtenus dans 5% des cas.
Lorsque l’on prévoit de faire une enquête et de vérifier les données à l’aide du Test
Test Z, il faut aussi tenir compte de la taille de l’échantillon, de la largeur de l’intervalle de
confiance et du niveau de confiance. Le niveau de confiance change en fonction de
l’application.
L’ Intervalle Z à 1 échantillon calcule l’intervalle de confiance pour une moyenne inconnue
d’une population lorsque l’écart-type est connu.
L’ Intervalle Z à 2 échantillons calcule l’intervalle de confiance pour la différence entre
deux moyennes d’une population lorsque les écarts-types des deux échantillons sont
connus.
L’ Intervalle Z à 1 proportion utilise le nombre de données pour calculer l’intervalle de
confiance pour une proportion inconnue de succès.
L’ Intervalle Z à 2 proportions utilise le nombre de données pour calculer l’intervalle de
confiance pour la différence entre la proportion de succès de deux populations.
L’ Intervalle t à 1 échantillon calcule l’intervalle de confiance pour une moyenne inconnue
d’une population lorsque l’écart-type de cette population est inconnu.
L’ Intervalle t à 2 échantillons calcule l’intervalle de confiance pour la différence entre les
moyennes de deux populations lorsque les deux écarts-types de ces populations sont
inconnus.
t et du
Sur l’écran du mode STAT, appuyez sur 4(INTR) pour afficher le menu d’intervalle de
confiance, qui contient les paramètres suivants.
• 4(INTR)b(Z) ... Intervalles Z (p. 1-3-3)
c(T) ... Intervalles t (p. 1-3-8)
# Les fonctions d’intervalle de confiance ne
peuvent pas être représentées
graphiquement.
20001201
Page 36

1-3-2
Intervalle de confiance (INTR)
uu
uPrécautions générales concernant l’intervalle de confiance
uu
La saisie d’une valeur comprise entre 0 < C-Level < 1 pour le réglage C-Level définit la
valeur telle quelle. La saisie d’une valeur comprise entre 1 < C-Level < 100 définit une valeur
équivalente au 100e du nombre saisi.
# La saisie d’une valeur égale ou supérieure à
100 ou d’une valeur négative entraîne une
erreur (Erreur math).
20001201
Page 37

1-3-3
Intervalle de confiance (INTR)
kk
k Intervalle Z
kk
uu
u Intervalle
uu
L’ Intervalle Z à 1 échantillon calcule l’intervalle de confiance pour une moyenne inconnue
d’une population lorsque l’écart-type est connu.
L’intervalle de confiance est représenté de la façon suivante.
Toutefois, ne représente pas l’intervalle de confiance proprement dit. Le niveau de
confiance est représenté par 100 (1–)%.
Z à 1 échantillon
Left = o – Z
Right = o + Z
2
2
n
n
Lorsque le niveau de confiance est 95%, par exemple, la saisie de 0,95 produit 1 – 0,95 =
0,05 = .
Utilisez les touches suivantes à partir de la liste de données statistiques.
4(INTR)
b(Z)
b(1-Smpl)
La signification de chaque option en cas de spécification de données de listes est la
suivante.
Data ............................ type de données
C-Level ........................ niveau de confiance (0 < C-Level < 1)
.................................. écart-type d’une population ( > 0)
List .............................. liste dont le contenu doit être utilisé comme données
d’échantillon
Freq ............................. fréquence de l’échantillon
Save Res..................... liste pour la sauvegarde des résultats des calculs
(Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul
Les options de spécification des données des paramètres qui sont différentes de la
spécification des données des listes ont la signification suivante.
o .................................. moyenne de l’échantillon
n .................................. taille de l’échantillon (entier positif)
20001201
Page 38

1-3-4
Intervalle de confiance (INTR)
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute] puis
appuyez sur la touche de fonction indiquée ci-dessous pour effectuer le calcul.
• 1(CALC) ... exécution du calcul
Exemple d’affichage des résultats d’un calcul
Left .............................. limite inférieure de l’intervalle (bord gauche)
Right ............................ limite supérieure de l’intervalle (bord droit)
o .................................. moyenne de l’échantillon
x
n-1 ............................. écart-type de l’échantillon (apparaît seulement pour le réglage
Data: List)
n .................................. taille de l’échantillon
uu
u Intervalle
uu
L’ Intervalle Z à 2 échantillons calcule l’intervalle de confiance pour la différence entre les
moyennes de deux populations lorsque les écarts-types de deux échantillons sont connus.
L’intervalle de confiance est représenté de la façon suivante. La valeur 100 (1–)% est le
niveau de confiance.
Z à 2 échantillons
Left = (o1 – o2) – Z
Right = (o
– o2) + Z
1
2
1
n
2
1
2
2
2
+
n
2
2
2
1
2
+
n
n
1
2
o1 : moyenne de l’échantillon 1
o2 : moyenne de l’échantillon 2
1 : écart-type d’une population
pour l’échantillon 1
2 : écart-type d’une population
pour l’échantillon 2
n1 : taille de l’échantillon 1
n2 : taille de l’échantillon 2
Utilisez les touches suivantes à partir de la liste de données statistiques.
4(INTR)
b(Z)
c(2-Smpl)
20001201
Page 39

1-3-5
Intervalle de confiance (INTR)
La signification de chaque option en cas de spécification de données de listes est la
suivante.
Data ............................ type de données
C-Level ........................ niveau de confiance (0 < C-Level < 1)
1 ................................. écart-type de la population de l’échantillon 1 (1 > 0)
2 ................................. écart-type de la population de l’échantillon 2 (2 > 0)
List(1) .......................... liste dont le contenu doit être utilisé comme données
d’échantillon 1
List(2) .......................... liste dont le contenu doit être utilisé comme données
d’échantillon 2
Freq(1) ........................ fréquence de l’échantillon 1
Freq(2) ........................ fréquence de l’échantillon 2
Save Res .................... liste pour la sauvegarde des résultats des calculs
(Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul
Les options de spécification des données des paramètres qui sont différentes de la
spécification des données des listes ont la signification suivante.
o1 ................................. moyenne de l’échantillon 1
n1 ................................. taille (entier positif) de l’échantillon 1
o2 ................................. moyenne de l’échantillon 2
n2 ................................. taille (entier positif) de l’échantillon 2
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute] puis
appuyez sur une des touches de fonction indiquées ci-dessous pour effectuer le calcul.
• 1(CALC) ... exécution du calcul
Exemple d’affichage des résultats d’un calcul
Left .............................. limite inférieure de l’intervalle (bord gauche)
Right ............................ limite supérieure de l’intervalle (bord droit)
o1 ................................. moyenne de l’échantillon 1
o2 ................................. moyenne de l’échantillon 2
x1
n-1 ............................ écart-type de l’échantillon 1 (apparaît seulement pour le réglage
Data: List)
x2
n-1 ............................ écart-type de l’échantillon 2 (apparaît seulement pour le réglage
Data: List)
n1 ................................. taille de l’échantillon 1
n2 ................................. taille de l’échantillon 2
20001201
Page 40

1-3-6
Intervalle de confiance (INTR)
uu
uIntervalle
uu
L’ Intervalle Z à 1 proportion utilise le nombre de données pour calculer l’intervalle de
confiance pour une proportion inconnue de succès.
L’intervalle de confiance est représenté de la façon suivante. La valeur 100 (1–)% est le
niveau de confiance.
Utilisez les touches suivantes à partir de la liste de données statistiques.
La signification de chaque option en cas de spécification de paramètres est la suivante.
Z à 1 proportion
Left = – Z
Right = + Z
4(INTR)
b(Z)
d(1-Prop)
x
n
x
n
x
1
n
2
n1n
2
x
1–
n
n
x
x
1–
n
n : taille de l’échantillon
x : données
C-Level ........................ niveau de confiance (0 < C-Level < 1)
x .................................. données (0 ou entier positif)
n .................................. taille de l’échantillon (entier positif)
Save Res .................... liste pour la sauvegarde des résultats des calculs
(Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute] puis
appuyez sur une des touches de fonction indiquées ci-dessous pour effectuer le calcul.
• 1(CALC) ... exécution du calcul
Exemple d’affichage des résultats d’un calcul
Left .............................. limite inférieure de l’intervalle (bord gauche)
Right ............................ limite supérieure de l’intervalle (bord droit)
ˆp .................................. proportion estimée de l’échantillon
n .................................. taille de l’échantillon
20001201
Page 41

1-3-7
Intervalle de confiance (INTR)
uu
u Intervalle
uu
Z à 2 proportions
L’ Intervalle Z à 2 proportions utilise le nombre de données pour calculer l’intervalle de
confiance pour la différence entre la proportion de succès de deux populations.
L’intervalle de confiance est représenté de la façon suivante. La valeur 100 (1–) % est le
niveau de confiance.
n1, n2: taille de l’échantillon
x
2
n
2
x
2
n
2
2
x
x
1
Left = – – Z
n
Right = – + Z
2
n
1
2
x
x
1
2
n
n
1
2
x
n
2
2
x
x
x
n
1
1–
n
1
1
1
1–
n
n
1
2
1–
x1, x2: données
n
1
2
+
n
2
x
x
1
2
n
1
1–
n
2
+
n
1
1
Utilisez les touches suivantes à partir de la liste de données statistiques.
4(INTR)
b(Z)
e(2-Prop)
La spécification de paramètres est utilisée. La signification de chaque option est la suivante.
C-Level ........................ niveau de confiance (0 < C-Level < 1)
x1 ................................. valeur des données (x1 > 0) de l’échantillon 1
n1 ................................. taille (entier positif) de l’échantillon 1
x2 ................................. valeur des données (x2 > 0) de l’échantillon 2
n2 ................................. taille (entier positif) de l’échantillon 2
Save Res .................... liste pour la sauvegarde des résultats des calculs
(Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute] puis
appuyez sur une des touches de fonction indiquées ci-dessous pour effectuer le calcul.
• 1(CALC) ... exécution du calcul
Exemple d’affichage des résultats d’un calcul
20001201
Page 42

Left .............................. limite inférieure de l’intervalle (bord gauche)
Right ............................ limite supérieure de l’intervalle (bord droit)
ˆp 1 ................................. proportion estimée de l’échantillon 1
ˆp 2 ................................. proportion estimée de l’échantillon 2
n1 ................................. taille de l’échantillon 1
n2 ................................. taille de l’échantillon 2
kk
k Intervalle t
kk
1-3-8
Intervalle de confiance (INTR)
uu
u Intervalle
uu
L’ Intervalle t à 1 échantillon calcule l’intervalle de confiance pour une moyenne inconnue
d’une population lorsque l’écart-type de cette population est inconnu.
L’intervalle de confiance est représenté de la façon suivante. La valeur 100 (1–
niveau de confiance.
Utilisez les touches suivantes à partir de la liste de données statistiques.
La signification de chaque option en cas de spécification de données de listes est la suivante.
t à 1 échantillon
Left = o– t
Right = o+ t
4(INTR)
c(T)
b(1-Smpl)
n – 1
n – 1
) % est le
x
n–1
n
2
x
n–1
n
2
Data ............................ type de données
C-Level ........................ niveau de confiance (0 < C-Level < 1)
List .............................. liste dont le contenu doit être utilisé comme données
d’échantillon
Freq ............................. fréquence de l’échantillon
Save Res .................... liste pour la sauvegarde des résultats des calculs
(Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul
Les options de spécification des données des paramètres qui sont différentes de la
spécification des données des listes ont la signification suivante.
20001201
Page 43

1-3-9
Intervalle de confiance (INTR)
o .................................. moyenne de l’échantillon
x
n-1 ............................. écart-type de l’échantillon (xn-1 > 0)
n .................................. taille de l’échantillon (entier positif)
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute] puis
appuyez sur une des touches de fonction indiquées ci-dessous pour effectuer le calcul.
• 1(CALC) ... exécution du calcul
Exemple d’affichage des résultats d’un calcul
Left .............................. limite inférieure de l’intervalle (bord gauche)
Right ............................ limite supérieure de l’intervalle (bord droit)
o .................................. moyenne de l’échantillon
x
n-1 ............................. écart-type de l’échantillon
n .................................. taille de l’échantillon
uu
u Intervalle t à 2 échantillons
uu
L’ Intervalle t à 2 échantillons calcule l’intervalle de confiance pour la différence entre les
moyennes de deux populations lorsque les deux écarts-types de ces populations sont
inconnus. L’intervalle t s’applique à la répartition t.
L’intervalle de confiance suivant s’applique lorsque la mise en commun est activée. La
valeur 100 (1–) % est le niveau de confiance.
Left = (o1 – o2)– t
Right = (o
– o2)+ t
1
n1+n
2
n1+n
–2
xp
2
–2
2
2
n–1
xp
2
n–1
1
1
+
n
n
2
1
1
1
2
+
n
n
2
1
20001201
Page 44

1-3-10
Intervalle de confiance (INTR)
L’intervalle de confiance suivant s’applique lorsque la mise en commun est désactivée.
La valeur 100 (1–
) % est le niveau de confiance.
Left = (o1 – o2)– t
Right = (o
df =
C =
x
C
n
–1
1
1 n–1
n
1
– o2)+ t
1
1
2
+
x
1 n–1
n
2
+
(1–C )
n
2
2
1
x
2 n–1
n
df
–1
2
2
2
df
2
2
2
1 n–1
n
1
x
1 n–1
x
x
+
2
+
n
1
2 n–1
n
2
x
2 n–1
n
2
2
2
Utilisez les touches suivantes à partir de la liste de données statistiques.
4(INTR)
c(T)
c(2-Smpl)
La signification de chaque option en cas de spécification de données de listes est la suivante.
Data ............................ type de données
C-Level ........................ niveau de confiance (0 < C-Level < 1)
List(1) .......................... liste dont le contenu doit être utilisé comme données
d’échantillon 1
List(2) .......................... liste dont le contenu doit être utilisé comme données
d’échantillon 2
Freq(1) ........................ fréquence de l’échantillon 1
Freq(2) ........................ fréquence de l’échantillon 2
Pooled ......................... mise en commun On (activée) ou Off (désactivée)
Save Res..................... liste pour la sauvegarde des résultats des calculs
(Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul
Les options de spécification des données des paramètres qui sont différentes de la
spécification des données des listes ont la signification suivante.
20001201
Page 45

1-3-11
Intervalle de confiance (INTR)
o1 ................................. moyenne de l’échantillon 1
x1
n-1 ............................ écart-type (x1n-1 > 0) de l’échantillon 1
n1 ................................. taille (entier positif) de l’échantillon 1
o2 ................................. moyenne de l’échantillon 2
x2
n-1 ............................ écart-type (x2n-1 > 0) de l’échantillon 2
n2 ................................. taille (entier positif) de l’échantillon 2
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute] puis
appuyez sur une des touches de fonction indiquées ci-dessous pour effectuer le calcul.
• 1(CALC) ... exécution du calcul
Exemple d’affichage des résultats d’un calcul
Left .............................. limite inférieure de l’intervalle (bord gauche)
Right ............................ limite supérieure de l’intervalle (bord droit)
df ................................. degrés de liberté
o1 ................................. moyenne de l’échantillon 1
o2 ................................. moyenne de l’échantillon 2
x1
n-1 ............................ écart-type de l’échantillon 1
x2
n-1 ............................ écart-type de l’échantillon 2
xp
n-1 ............................ écart-type d’échantillons mis en commun (apparaît seulement
avec le réglage Pooled: On)
n1 ................................. taille de l’échantillon 1
n2 ................................. taille de l’échantillon 2
20001201
Page 46

1-4-1
Lois de probabilité (DIST)
1-4 Lois de probabilité (DIST)
Il existe toute une variété de lois de probabilité, mais la plus connue est la “répartition
normale” qui est essentielle aux calculs statistiques. La répartition normale est une
répartition symétrique centrée sur les plus fortes occurrences de données moyennes (la plus
grande fréquence), avec une fréquence décroissante lorsque l’on s’éloigne du centre. La loi
de Poisson, la répartition dans l’espace et d’autres formes de répartition sont également
utilisées en fonction du type de données disponibles.
Lorsque le type de probabilité a été déterminée, certaines tendances peuvent être
observées. Vous pouvez calculer la probabilité des données extraites d’une répartition
inférieure à une valeur donnée.
Par exemple, la répartition peut être utilisée pour calculer le taux de rendement pour la
fabrication d’un produit. Après avoir défini une valeur comme critère, vous pouvez calculer la
probabilité normale en estimant le pourcentage de produits répondant à ce critère.
Inversement, un taux de succès (par exemple 80%) peut être pris comme hypothèse pour
estimer la proportion de produits atteignant cette valeur par la répartition normale.
La densité de probabilité normale calcule la densité de la probabilité d’une répartition
normale depuis une valeur
La probabilité de répartition normale calcule la probabilité des données d’une répartition
normale tombant entre deux valeurs précises.
La répartition normale cumulée inverse calcule une valeur représentant le lieu à l’intérieur
d’une répartition normale pour une probabilité cumulée précise.
La densité de probabilité t de Student calcule la densité de probabilité t d’une valeur x
spécifiée.
La probabilité d’une répartition t de Student calcule la probabilité des données de
répartition t tombant entre deux valeurs précises.
Tout comme la loi de probabilité t, la probabilité peut être calculée pour les lois de probabilité
2, F, binomiale, Poisson et géométrique.
Sur l’écran du mode initial STAT, appuyez sur 5(DIST) pour afficher le menu de lois, qui
contient les options suivantes.
• 5(DIST)b(Norm) ... répartition normale (p. 1-4-3)
x spécifiée.
c(T) ... loi t de Student (p. 1-4-7)
d(2) ...loi 2 (p. 1-4-9)
e(F) ... loi F (p. 1-4-12)
f(Binmal) ... loi binomiale (p. 1-4-16)
g(Poissn) ... loi de Poisson (p. 1-4-19)
h(Geo) ... répartition dans l’espace (p. 1-4-21)
20001201
Page 47

1-4-2
Lois de probabilité (DIST)
uu
uFonctions de répartition ordinaires
uu
Après avoir tracé une graphe, vous pouvez utiliser la fonction P-CAL pour calculer une
valeur p estimée pour une valeur x particulière.
Procédez de la façon suivante pour utiliser la fonction P-CAL.
1.Après avoir tracé une graphe, appuyez sur 1(P-CAL) pour afficher la boîte de dialogue
de saisie de la valeur x.
2.Saisissez la valeur souhaitée pour x puis appuyez sur w.
• Les valeurs x et p apparaissent au bas de l’écran et le pointeur se positionne sur le point
correspondant du graphe.
3.Une pression de v ou d’une touche numérique à ce moment fait réapparaître la boîte
de dialogue de saisie de la valeur x pour effectuer un autre calcul de la valeur estimée.
4.Lorsque vous avez terminé, appuyez sur i pour dégager les valeurs des coordonnées et
le pointeur de l’écran.
# L’exécution d’une fonction d’analyse
sauvegarde les valeurs
dans les variables X et P.
x et p respectivement
20001201
Page 48

1-4-3
Lois de probabilité (DIST)
kk
k Répartition normale
kk
uu
uDensité d’une probabilité normale
uu
La densité d’une probabilité normale calcule la densité de la probabilité d’une répartition
normale depuis une valeur x particulière. La densité de probabilité normale s’applique à la
répartition normale.
2
μ
(x – μ)
–
f(x) =
2
1
2
2
e
( > 0)
Utilisez les touches suivantes à partir de la liste de données statistiques.
5(DIST)
b(Norm)
b(P.D)
La spécification de paramètres est utilisée. La signification de chaque option est la suivante.
x .................................. données
.................................. écart-type d’une population (
μ
.................................. moyenne d’une population
Save Res..................... liste pour la sauvegarde des résultats des calculs
(Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul ou tracé d’un graphe
• La répartition normale se spécifie par = 1 et μ = 0.
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute] puis
appuyez sur une des touches de fonction suivantes pour effectuer le calcul ou tracer le
graphe.
• 1(CALC) ... exécution du calcul
• 6(DRAW) ... tracé du graphe
Exemple d’affichage des résultats d’un calcul
> 0)
p .................................. densité d’une probabilité normale
# Les réglages de fenêtre d’affichage pour le
tracé du graphe sont automatiques lorsque le
réglage [Stat Wind] de l’écran de réglage est
[Auto]. Les réglages de fenêtre d’affichage
actuels sont utilisés pour le tracé du graphe
quand le réglage [Stat Wind] est [Manual].
20001201
Page 49

1-4-4
Lois de probabilité (DIST)
uu
uProbabilité d’une répartition normale
uu
La probabilité d’une répartition normale calcule la probabilité des données tombant entre
deux valeurs particulières.
p =
2
μ
(x – μ)
b
1
2
–
2
2
e
a
dx
: limite inférieure
a
b
: limite supérieure
Utilisez les touches suivantes à partir de la liste de données statistiques.
5(DIST)
b(Norm)
c(C.D)
La signification de chaque option en cas de spécification de paramètres est la suivante.
Lower .......................... limite inférieure
Upper .......................... limite supérieure
.................................. écart-type d’une population (
μ
.................................. moyenne d’une population
> 0)
Save Res..................... liste pour la sauvegarde des résultats des calculs
(Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute] puis
appuyez sur une des touches de fonction suivantes pour effectuer le calcul.
• 1(CALC) ... exécution du calcul
# La probabilité normale ne peut pas être
représentée graphiquement.
20001201
Page 50

1-4-5
Lois de probabilité (DIST)
Exemple d’affichage des résultats d’un calcul
p .................................. probabilité normale
z:Low ........................... valeur z:Low (convertie pour standardiser le point
valeur inférieure)
z:Up ............................. valeur z:Up (convertie pour standardiser le point
valeur supérieure)
uu
uRépartition normale cumulée inverse
uu
La répartition normale cumulée inverse calcule une valeur représentant le lieu d’une
probabilité cumulée particulière dans une répartition normale.
+
Extrémité :
Gauche
limite
supérieure
de l’intervalle
d’intégration
= ?
Spécifiez la probabilité et utilisez cette formule pour obtenir l’intervalle d’intégration.
Utilisez les touches suivantes en partant de la liste de données statistiques.
f (x)dx = p
Extrémité :
Droite
limite
inférieure de
l’intervalle
d’intégration
= ?
f (x)dx = p
Extrémité :
Centre
limites
supérieure et
inférieure de
l’intervalle
d’intégration
= ? = ?
z
z
de la
de la
f (x)dx = p
5(DIST)
b(Norm)
d(Invrse)
La signification de chaque option en cas de spécification de paramètres est la suivante.
Tail ............................... spécification de l’extrémité des valeurs de la probabilité
(gauche, droit, centre)
Area ............................ valeur de la probabilité (0 < Area < 1)
.................................. écart-type de la population (
μ
.................................. moyenne de la population
Save Res..................... liste de sauvegarde des résultats (Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul
20001201
> 0)
Page 51

1-4-6
Lois de probabilité (DIST)
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute], puis
appuyez sur une des touches de fonction suivantes pour effectuer le calcul.
• 1(CALC) ... exécution du calcul
Exemple d’affichage des résultats d’un calcul
x ....................................... répartition normale cumulée inverse
(Extrémité : Limite supérieure gauche de l’intervalle
d’intégration)
(Extrémité : Limite inférieure droite de l’intervalle
d’intégration)
(Extrémité : Limites supérieure et inférieure centrales de
l’intervalle d’intégration)
# La répartition normale cumulée inverse ne
peut pas être représentée graphiquement.
20001201
Page 52

f
1-4-7
Lois de probabilité (DIST)
kk
k Loi
kk
t de Student
uu
uDensité d’une probabilité t de Student
uu
La densité de la probabilité t de Student calcule la densité de probabilité t à une valeur x
particulière.
df+1
–
2
2
df + 1
(x) =
2
df
2
Utilisez les touches suivantes en partant de la liste de données statistiques.
5(DIST)
c(T)
b(P.D)
La signification de chaque option en cas de spécification de paramètres est la suivante.
1+
df
x
df
x .................................. donnée
df ................................. degrés de liberté (df > 0)
Save Res..................... liste de sauvegarde des résultats (Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul ou tracé d’un graphe
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute], puis
appuyez sur une des touches de fonction suivantes pour effectuer le calcul ou tracer le
graphe.
• 1(CALC) ... exécution du calcul
• 6(DRAW) ... tracé du graphe
Exemple d’affichage des résultats d’un calcul
p .................................. densité de la probabilité t de Student
# Les réglages de fenêtre d’affichage actuels
sont utilisés pour la représentation graphique
lorsque [Stat Wind] de l'écran de réglage est
réglé sur [Manual]. Les réglages de fenêtre
20001201
d’affichage suivants sont automatiques
lorsque [Stat Wind] est réglé sur [Auto].
Xmin = –3,2, Xmax = 3,2, Xscale = 1,
Ymin = –0,1, Ymax = 0,45, Yscale = 0,1
Page 53

1-4-8
Lois de probabilité (DIST)
uu
uProbabilité d’une répartition t de Student
uu
La probabilité d’une répartition t de Student calcule la probabilité de données de la
t
répartition
tombant entre deux valeurs particulières.
df + 1
p =
2
df
df
Utilisez les touches suivantes en partant de la liste de données statistiques.
5(DIST)
c(T)
c(C.D)
La signification de chaque option en cas de spécification de paramètres est la suivante.
Lower .......................... limite inférieure
Upper .......................... limite supérieure
df
................................. degrés de liberté (df > 0)
Save Res..................... liste de sauvegarde des résultats (Aucune ou Liste 1 à 20)
2
a
b
1+
df
df+1
–
2
2
x
dx
a
: limite inférieure
b
: limite supérieure
Execute ....................... exécution d’un calcul
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute], puis
appuyez sur une des touches de fonction suivantes pour effectuer le calcul.
• 1(CALC) ... exécution du calcul
# La probabilité d’une répartition t de Student
ne peut pas être représentée graphiquement.
20001201
Page 54

f
1-4-9
Lois de probabilité (DIST)
Exemple d’affichage des résultats d’un calcul
p .................................. probabilité d’une répartition t de Student
t:Low ........................... t:valeur inférieure (la valeur saisie la plus faible)
t:Up ............................. t:valeur supérieure (la valeur saisie la plus grande)
kk
k Loi de probabilité
kk
uu
uDensité d’une probabilité
uu
2
2
La densité d’une probabilité 2 calcule la densité de la probabilité pour la loi de probabilité
à une valeur x particulière.
df
(x) =
df
1
2
2
x e
1
df
2
x
–1
–
2
2
Utilisez les touches suivantes en partant de la liste de données statistiques.
5(DIST)
d(2)
b(P.D)
La signification de chaque option en cas de spécification de paramètres est la suivante.
2
x .................................. donnée
df ................................. degrés de liberté (entier positif)
Save Res..................... liste de sauvegarde des résultats des calculs
(Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul ou tracé d’un graphe
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute], puis
appuyez sur une des touches de fonction suivantes pour effectuer le calcul ou tracer le
graphe.
• 1(CALC) ... exécution du calcul
• 6(DRAW) ... tracé du graphe
20001201
Page 55

1-4-10
Lois de probabilité (DIST)
Exemple d’affichage des résultats d’un calcul
p .................................. densité de la probabilité
2
# Les réglages de fenêtre d’affichage actuels
sont utilisés pour la représentation graphique
lorsque [Stat Wind] de l'écran de réglage est
réglé sur [Manual]. Les réglages de fenêtre
d’affichage suivants sont automatiques
lorsque [Stat Wind] est réglé sur [Auto].
Xmin = 0, Xmax = 11,5, Xscale = 2,
Ymin = -0,1, Ymax = 0,5, Yscale = 0,1.
20001201
Page 56

1-4-11
Lois de probabilité (DIST)
uu
uProbabilité d’une répartition
uu
2
La probabilité d’une répartition 2 calcule la probabilité des données de répartition 2 tombant
entre deux valeurs particulières.
df
p =
b
df
1
df
2
2
1
2
x e dx
a
x
–1
–
2
2
a
: limite inférieure
b
: limite supérieure
Utilisez les touches suivantes en partant de la liste de données statistiques.
5(DIST)
d(2)
c(C.D)
La signification de chaque option en cas de spécification de paramètres est la suivante.
Lower .......................... limite inférieure
Upper .......................... limite supérieure
df
................................. degrés de liberté (entier positif)
Save Res..................... liste de sauvegarde des résultats des calculs
(Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute], puis
appuyez sur une des touches de fonction suivantes pour effectuer le calcul.
• 1(CALC) ... exécution du calcul
# La probabilité d’une répartition
pas être représentée graphiquement.
2
ne peut
20001201
Page 57

f
1-4-12
Lois de probabilité (DIST)
Exemple d’affichage des résultats d’un calcul
p .................................. probabilité d’une répartition
kk
k Loi de probabilité F
kk
uu
u Densité d’une probabilité F
uu
La densité d’une probabilité F calcule la fonction de la densité d’une probabilité F à une
valeur x particulière.
n + d
2
(x) =
n
2
Utilisez les touches suivantes en partant de la liste de données statistiques.
5(DIST)
e(F)
b(P.D)
d
2
n
n
–1
2
n
2
x
1 +
d
nx
d
–
n + d
2
2
La signification de chaque option en cas de spécification de paramètres est la suivante.
x .................................. donnée
n:df .............................. degrés de liberté du numérateur (entier positif)
d:df .............................. degrés de liberté du dénominateur (entier positif)
Save Res..................... liste de sauvegarde des résultats (Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul ou tracé d’un graphe
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute], puis
appuyez sur une des touches de fonction suivantes pour effectuer le calcul ou tracer le
graphe.
• 1(CALC) ... exécution du calcul
• 6(DRAW) ... tracé du graphe
20001201
Page 58

1-4-13
Lois de probabilité (DIST)
Exemple d’affichage des résultats d’un calcul
p .................................. densité d’une probabilité F
# Les réglages de fenêtre d’affichage actuels
sont utilisés pour la représentation graphique
lorsque [Stat Wind] de l'écran de réglage est
réglé sur [Manual]. Les réglages de fenêtre
d’affichage sont utilisés pour la
représentation graphique lorsque [Stat Wind]
est sur [Manual].
20001201
Page 59

1-4-14
Lois de probabilité (DIST)
uu
u Probabilité d’une répartition F
uu
La probabilité d’une répartition F calcule la probabilité des données de répartition F tombant
entre deux valeurs particulières.
a
n + d
p =
Utilisez les touches suivantes en partant de la liste de données statistiques.
5(DIST)
e(F)
c(C.D)
2
n
2
d
2
n
b
n
2
n
d
–1
2
1 +
x
a
nx
d
–
n + d
2
dx
: limite inférieure
b
: imite supérieure
La signification de chaque option en cas de spécification de paramètres est la suivante.
Lower .......................... limite inférieure
Upper .......................... limite supérieure
n:df
.............................. degrés de liberté du numérateur (entier positif)
d:df
.............................. degrés de liberté du dénominateur (entier positif)
Save Res..................... liste de sauvegarde des résultats (Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute], puis
appuyez sur une des touches de fonction suivantes pour effectuer le calcul.
• 1(CALC) ... exécution du calcul
# La probabilité d’une répartition F ne peut pas
être représentée graphiquement.
20001201
Page 60

1-4-15
Lois de probabilité (DIST)
Exemple d’affichage des résultats d’un calcul
p .................................. probabilité d’une répartition F
20001201
Page 61

f
1-4-16
Lois de probabilité (DIST)
kk
k Loi binomiale
kk
uu
u Probabilité binomiale
uu
La loi de probabilité binomiale calcule la probabilité d’une valeur particulière pour la loi
binomiale discrète avec le nombre d’essais et la probabilité de succès spécifiés à chaque
essai.
(x) = nCx px(1–p)
n – x
(x = 0, 1, ·······, n) p : probabilité de succès
(0 < p < 1)
n : nombre d’essais
Utilisez les touches suivantes en partant de la liste de données statistiques.
5(DIST)
f(Binmal)
b(P.D)
Les paramètres qui doivent être spécifiés lors de la spécification de listes ont la signification
suivante.
Data ............................ type de données
List .............................. liste dont le contenu doit être utilisé comme données
Numtrial....................... nombre d’essais
p .................................. probabilité de succès (0 < p < 1)
Save Res..................... liste de sauvegarde des résultats des calculs
(Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul
Les options de spécification des données des paramètres qui sont différentes de la
spécification des données des listes ont la signification suivante.
x .................................. entier de 0 à n
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute], puis
appuyez sur une des touches de fonction suivantes pour effectuer le calcul.
• 1(CALC) ... exécution du calcul
# La loi binomiale ne peut pas être représentée
graphiquement.
20001201
Page 62

1-4-17
Lois de probabilité (DIST)
Exemple d’affichage des résultats d’un calcul
p .................................. probabilité binomiale
uu
uDensité cumulée binomiale
uu
La densité cumulée binomiale calcule une probabilité cumulée à une valeur particulière pour
la loi binomiale discrète avec le nombre d’essais et la probabilité de succès spécifiés à
chaque essai.
Utilisez les touches suivantes en partant de la liste de données statistiques.
5(DIST)
f(Binmal)
c(C.D)
Les paramètres qui doivent être spécifiés lors de la spécification de listes ont la signification
suivante.
Data ............................ type de données
List .............................. liste dont le contenu doit être utilisé comme données
Numtrial....................... nombre d’essais
p .................................. probabilité de succès (0 < p < 1)
Save Res..................... liste de sauvegarde des résultats des calculs
(Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul
Les options de spécification des données des paramètres qui sont différentes de la
spécification des données des listes ont la signification suivante.
x .................................. entier de 0 à n
20001201
Page 63

1-4-18
Lois de probabilité (DIST)
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute], puis
appuyez sur une des touches de fonction suivantes pour effectuer le calcul.
• 1(CALC) ... exécution du calcul
Exemple d’affichage des résultats d’un calcul
p ......................................... densité cumulée binomiale
20001201
Page 64

1-4-19
Lois de probabilité (DIST)
kk
k Loi de Poisson
kk
uu
uProbabilité de Poisson
uu
La loi de probabilité de Poisson calcule la probabilité d’une valeur définie pour la répartition
discrète de Poisson à partir d’une moyenne particulière.
μ
–
x
μ
e
f(x) =
x!
(x = 0, 1, 2, ···)
μ
: moyenne d’une population (
Utilisez les touches suivantes en partant de la liste de données statistiques.
5(DIST)
g(Poissn)
b(P.D)
μ
> 0)
Les paramètres qui doivent être spécifiés lors de la spécification de listes ont la signification
suivante.
Data ............................ type de données
List .............................. liste dont le contenu doit être utilisé comme données
μ
.................................. moyenne d’une population (μ > 0)
Save Res..................... liste de sauvegarde des résultats (Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul
Les options de spécification des données des paramètres qui sont différentes de la
spécification des données des listes ont la signification suivante.
x .................................. ( x
> 0)
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute], puis
appuyez sur une des touches de fonction suivantes pour effectuer le calcul.
• 1(CALC) ... exécution du calcul
Exemple d’affichage des résultats d’un calcul
p .................................. probabilité de Poisson
# La loi de Poisson ne peut pas être
représentée graphiquement.
20001201
Page 65

1-4-20
Lois de probabilité (DIST)
uu
u Densité cumulée de Poisson
uu
La densité cumulée de Poisson calcule la probabilité cumulée d’une valeur définie pour la
répartition discrète de Poisson à partir d’une moyenne particulière.
Utilisez les touches suivantes en partant de la liste de données statistiques.
5(DIST)
g(Poissn)
c(C.D)
Les paramètres qui doivent être spécifiés lors de la spécification de listes ont la signification
suivante.
Data ............................ type de données
List .............................. liste dont le contenu doit être utilisé comme données
μ
.................................. moyenne d’une population (μ > 0)
Save Res..................... liste de sauvegarde des résultats des calculs
(Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul
Les options de spécification des données des paramètres qui sont différentes de la
spécification des données des listes ont la signification suivante.
x .................................. ( x
> 0)
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute], puis
appuyez sur une des touches de fonction suivantes pour effectuer le calcul.
• 1(CALC) ... exécution du calcul
Exemple d’affichage des résultats d’un calcul
p .................................. densité cumulée de Poisson
20001201
Page 66

f
1-4-21
Lois de probabilité (DIST)
kk
k Loi de répartition dans l’espace
kk
uu
uProbabilité géométrique
uu
La probabilité géométrique calcule la probabilité d’une valeur définie et le numéro de l’essai
où le premier succès se présente, pour la répartition discrète dans l’espace avec la
probabilité de succès spécifiée.
(x) = p(1– p)
x – 1
(x = 1, 2, 3, ···)
Utilisez les touches suivantes en partant de la liste de données statistiques.
5(DIST)
h(Geo)
b(P.D)
Les paramètres qui doivent être spécifiés lors de la spécification de listes ont la signification
suivante.
Data ............................ type de données
List .............................. liste dont le contenu doit être utilisé comme données
p .................................. probabilité de succès (0 < p < 1)
Save Res..................... liste de sauvegarde des résultats des calculs
(Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul
Les options de spécification des données des paramètres qui sont différentes de la
spécification des données des listes ont la signification suivante.
x .................................. entier positif (x > 1)
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute], puis
appuyez sur une des touches de fonction suivantes pour effectuer le calcul.
• 1(CALC) ... exécution du calcul
Exemple d’affichage des résultats d’un calcul
p .................................. probabilité géométrique
# La loi de répartition dans l’espace ne peut
pas être représentée graphiquement.
20001201
# Le nombre entier positif est calculé que les
données de liste (Data:List) ou la valeur x
(Data:variable) soient spécifiées.
Page 67

1-4-22
Lois de probabilité (DIST)
uu
uDensité cumulée géométrique
uu
La densité cumulée géométrique calcule la probabilité cumulée d’une valeur définie et le
numéro de l’essai où le premier succès se présente, pour la répartition discrète dans
l’espace avec la probabilité de succès spécifiée.
Utilisez les touches suivantes en partant de la liste de données statistiques.
5(DIST)
h(Geo)
c(C.D)
Les paramètres qui doivent être spécifiés lors de la spécification de listes ont la signification
suivante.
Data ............................ type de données
List .............................. liste dont le contenu doit être utilisé comme données
p .................................. probabilité de succès (0 < p < 1)
Save Res..................... liste de sauvegarde des résultats des calculs
(Aucune ou Liste 1 à 20)
Execute ....................... exécution d’un calcul
Les options de spécification des données des paramètres qui sont différentes de la
spécification des données des listes ont la signification suivante.
x .................................. entier positif (x > 1)
Lorsque tous les paramètres ont été réglés, positionnez le curseur sur [Execute], puis
appuyez sur une des touches de fonction suivantes pour effectuer le calcul.
• 1(CALC) ... exécution du calcul
Exemple d’affichage des résultats d’un calcul
p .................................. densité cumulée géométrique
# Le nombre entier positif est calculé que les
données de liste (Data:List) ou la valeur
(Data:variable) soient spécifiées .
x
20001201
Page 68

Chapitre
Calculs financiers (TVM)
2
2-1 Avant d’effectuer des calculs financiers
2-2 Intérêt simple
2-3 Intérêt composé
2-4 Cash-flow (Evaluation d’investissement)
2-5 Amortissement
2-6 Conversion de taux d’intérêt
2-7 Coût, prix de vente, marge
2-8 Calculs de jours/date
2-9 Dépréciation
2-10 Obligations
2-11 Graphe TVM
2-12 Exemples
20001201
Page 69

2-1-1
Avant d’effectuer des calculs financiers
2-1 Avant d’effectuer des calculs financiers
kk
k Mode TVM
kk
Sur le menu principal, sélectionnez l’icône TVM.
Un des écrans Finance suivants apparaît lorsque vous accédez au mode TVM.
Ecran Finance 1 Ecran Finance 2
• 1(SMPL) ....Intérêt simple
• 2(CMPD) ...Intérêt composé
• 3(CASH) .... Marge brut d’autofinancement (Evaluation d’investissement)
• 4(AMT) ......Amortissement
• 5(CNVT) ....Conversion de taux d’intérêt
• 6(g)1(COST) ... Coût, prix de vente, marge
2(DAYS) ... Calculs de jours/date
3(DEPR) ... Dépréciation
4(BOND) ... Obligations
5(TVMG) ... Graphe TVM (simulation d’intérêts composés)
20001201
Page 70

2-1-2
Avant d’effectuer des calculs financiers
kk
k Options SET UP
kk
uu
u Paiement
uu
•{BGN}/{END} ........ Spécification du {début de la période} / {fin de la période} de
paiement
uu
u Mode de Date
uu
•{365}/{360} ......... Spécification d’un calcul sur {365 jours} / {360 jours}
uu
u Périodes/YR. (Bond)
uu
•{Annual}/{SEMI} ... Indique une période {annuelle} / {semestrielle}
Notez les points suivants relatifs aux réglages de l’écran de configuration lorsque vous utilisez
le mode Finance.
• Lorsque l’option Label est activée et un graphe tracé, l’axe vertical (dépôts, retraits) est
nommé CASH et l’axe horizontal (fréquence) TIME. Les noms des axes n’apparaissent pas
sur le graphe TVM.
• Le nombre de chiffres affichés en mode Finance est différent du nombre de chiffres
affichés dans les autres modes. La calculatrice revient automatiquement à Norm1 quand
vous sélectionnez le mode Finance, et le nombre de chiffres significatifs (Sci) ou la notation
Ingénieur (Eng) désignés dans un autre mode sont annulés.
kk
k Représentation graphique dans le mode TVM
kk
Après avoir effectué un calcul financier, vous pouvez utiliser la touche 6(GRPH) pour le
représenter graphiquement, comme indiqué ci-dessous.
• Une pression sur 1(TRACE) quand un graphique est affiché permet d’obtenir d’autres
valeurs financières (Fonction Trace). Dans le cas d’un intérêt simple, par exemple, en
appuyant sur e les valeurs PV, SI et SFV sont affichées. En appuyant sur la touche d
les mêmes valeurs apparaissent dans l’ordre inverse.
• Le zoom, le défilement d’écran et les fonctions de dessin ne peuvent pas être utilisés en
mode Finance.
• La valeur actuelle (PV) ou le prix d’achat (PRC) devra être une valeur positive ou négative
selon le type de calcul que vous voulez effectuer.
• Les graphes ne doivent servir qu’à titre de référence lorsque vous consultez les résultats
d’un calcul en mode TVM.
• Notez que les résultats obtenus dans ce mode ne doivent servir qu’à titre de référence.
• Quand vous effectuez une transaction financière, veillez à toujours vérifier les résultats
obtenus sur cette calculatrice avec les sommes indiquées par votre service financier.
20001201
Page 71

2-2-1
Intérêt simple
2-2 Intérêt simple
Cette calculatrice utilise les formules suivantes pour calculer un intérêt simple.
uu
uFormule
uu
Mode 365 jours
Mode 360 jours
SI' =
SI' =
n
365
n
360
× PV × i
× PV × i
i =
i =
I%
100
I%
100
SI : intérêt
n : nombre de périodes
d’intérêt
PV : capital
I% : taux d’intérêt annuel
SFV : valeur capitalisée
SI = –SI'
SFV = –(PV + SI')
Appuyez sur 1(SMPL) sur l’écran Finance 1 pour afficher l’écran de saisie suivant destiné
au calcul d’intérêt simple.
1(SMPL)
n .................................. nombre de périodes d’intérêt (jours)
I% ............................... taux d’intérêt annuel
PV ............................... capital
Après avoir réglé les paramètres, appuyez sur une des touches de fonction mentionnées
ci-dessous pour effectuer le calcul correspondant.
• 1(SI) ....... Intérêt simple
• 2(SFV) ... Valeur capitalisée simple
20001201
Page 72

2-2-2
Intérêt simple
• Une erreur (Erreur math) se produit si les paramètres ne sont pas configurés correctement.
Utilisez les touches de fonction suivantes pour passer d’un écran de résultat à l’autre.
• 1(REPT) ... Ecran de saisie des paramètres
• 6(GRPH) ... Tracé de graphe
Après le tracé du graphe, vous pouvez appuyer sur 1(TRACE) pour activer la fonction
Trace et relever les résultats du calcul sur le graphe.
Lorsque la fonction Trace est activée, la valeur affichée change à chaque pression de e de
la façon suivante : valeur actuelle (PV) intérêt simple (SI) valeur capitalisée simple
(SFV). La valeur change en sens inverse si vous appuyez sur d.
Appuyez sur i pour désactiver la fonction Trace.
Appuyez une nouvelle fois sur i pour revenir à l’écran de saisie des paramètres.
20001201
Page 73

β
β
(
)
2-3-1
Intérêt composé
2-3 Intérêt composé
Cette calculatrice utilise les formules types suivantes pour calculer les intérêts composés.
uu
uFormule I
uu
(1+ i u S)[(1+ i)n–1] 1
PV+PMT
Ici:
u
i(1+ i)
n
+ FV
(1+ i)
= 0
n
I %
i =
100
PV= –(PMT
FV= –
PMT= –
log
{ }
n =
u
PMT
u
PV + FV u
(1+ i S ) PMT–FVi
(1+ i S ) PMT+PVi
log(1+ i)
(1+ i u S)[(1+ i)n–1]
α
=
i
1+ i
1
=
β
(1+ i)
n
α
+ FV
+ PV
α
α
n
β
u )
PV : valeur actualisée
FV : valeur capitalisée
PMT : paiement
n : nombre de périodes de
composition
I
%
: taux d’intérêt annuel
i est calculé à l’aide de la méthode de
Newton.
S = 0 supposé comme fin de période
S = 1 supposé comme début de période
F(i) = Formule I
F'(i)= –
uu
uFormule II (I% = 0)
uu
PV + PMT × n + FV = 0
Ici:
PV = – (PMT u n + FV )
PMT
(1+ i S)[1– (1+ i)
[
+S [1–(1+ i)–n]
ii
– FVun(1+ i)
]
20001201
20091001
–n
]
+ (1+ i S)[n(1+ i)
–n–1
–n–1
]
Page 74

Intérêt composé
FV = – (PMT u n + PV )
2-3-2
PMT = –
PV + FV
n
PV + FV
n = –
PMT
• Un dépôt est indiqué par un signe (+), tandis qu’un retrait est indiqué par un signe (–).
uu
u Conversion entre le taux d’intérêt nominal et le taux d’intérêt réel
uu
Le taux d’intérêt nominal (valeur I% entrée par l’utilisateur) est convertie en taux d’intérêt
réel (I%’) quand le nombre de versements à l’année (P/Y) est différent du nombre de
périodes de calcul des l’intérêts composés (C/Y). Cette conversion est nécessaire pour les
plans d’épargne échelonnée, les remboursements d’emprunts, etc.
I%' =
Pour calculer n, PV, PMT, FV
(1+ ) –1
{ }
100 × [C / Y ]
I%
[C / Y ]
[P / Y ]
×100
P/Y : périodes de
versement par
année
C/Y: périodes de
composition
par année
Le calcul suivant est effectué après la conversion du taux d’intérêt nominal en taux d’intérêt
réel et le résultat est utilisé pour tous les calculs ultérieurs.
i = I%'÷100
Pour calculer I%
Une fois que l’intérêt nominal (I%) a été obtenu, le calcul suivant est effectué pour obtenir le
taux d’intérêt réel (I%’).
La valeur de
[P / Y ]
[C / Y ]
I%' =
I%’ est obtenue à partir du résultat du calcul de I%.
(1+ ) –1
{ }
I%
100
×[C / Y ]×100
P/Y : périodes de
versement par
année
C/Y: périodes de
composition
par année
20001201
Page 75

2-3-3
Intérêt composé
Appuyez sur 2(CMPD) à partir de l’écran Finance 1 pour afficher l’écran de saisie suivant
pour le calcul d’intérêt composé.
2(CMPD)
n .................................. nombre de périodes de composition
I% ............................... taux d’intérêt annuel
PV ............................... valeur actualisée (montant du prêt dans le cas d’un emprunt,
capital dans le cas d’un plan d’épargne)
PMT ............................ paiement à chaque versement (paiement dans le cas d’un
emprunt, dépôt dans le cas d’un plan d’épargne)
FV ............................... valeur capitalisée (solde dû dans le cas d’un prêt, capital
plus intérêt dans le cas d’un plan d’épargne)
P/Y .............................. périodes de versement par année
C/Y .............................. périodes de composition par année
Important!
Saisie de valeurs
Une période (n) est exprimée par une valeur positive. La valeur actualisée (PV ) ou la valeur
capitalisée (FV) est positive, tandis que l’autre (PV ou FV ) est négative.
Précision
Cette calculatrice effectue des calculs d’intérêt au moyen de la méthode de Newton, qui
produit des valeurs approximatives dont la précision peut dépendre des différentes
conditions de calcul. Pour cette raison, tenez compte de sa limite lorsque vous utilisez les
résultats de calculs d’intérêt, ou bien vérifiez les résultats.
20001201
Page 76

2-3-4
Intérêt composé
Après avoir réglé les paramètres, appuyez sur une des touches de fonction mentionnées
ci-dessous pour effectuer le calcul correspondant.
• 1(n) ............ Nombre de périodes de composition
• 2(I
%) ......... Taux d’intérêt annuel
• 3(PV) ......... Valeur actuelle
(Prêt : montant du prêt, Epargne : solde)
• 4(PMT) ...... Paiement
(Prêt : versement ; Epargne : dépôt)
• 5(FV) ......... Valeur capitalisée
(Prêt : solde non payé ; Epargne : capital plus intérêts)
• 6(AMT) ...... Ecran d’amortissement
• Une erreur (Erreur math) se produit si les paramètres ne sont pas configurés correctement.
Utilisez les touches de fonction suivantes pour passer d’un écran de résultat à l’autre.
• 1(REPT) .... Ecran de saisie des paramètres
• 4(AMT) ...... Ecran d’amortissement
• 6(GRPH) .... Tracé de graphe
Après le tracé du graphe, vous pouvez appuyer sur 1(TRACE) pour activer la fonction
Trace et relever les résultats du calcul sur le graphe.
Appuyez sur i pour désactiver la fonction Trace.
Appuyez une nouvelle fois sur i pour revenir à l’écran de saisie des paramètres.
20001201
Page 77

2-4-1
Cash-flow (Evaluation d’investissement)
2-4 Cash-flow (Evaluation d’investissement)
Cette calculatrice utilise la méthode du “Cash-Flow en Escompte” (DCF) pour effectuer une
évaluation d’investissement par la sommation de cash-flow pour une période donnée. Elle
effectue les quatre types d’évaluations d’investissement suivants.
• Valeur actualisée nette (
• Valeur capitalisée nette (NFV)
• Taux de rendement interne (IRR )
• Période d’amortissement (PBP)
Le graphique de cash-flow suivant facilite la visualisation du mouvement des fonds.
NPV)
CF2
CF3
CF4
CF5
CF7
CF6
CF1
CF0
Dans ce diagramme, le montant de l’investissement initial est représenté par CF0. Le cashflow un an plus tard est représenté par CF1, deux ans plus tard par CF2, etc.
L’évaluation de l’investissement est utilisé pour montrer clairement si un investissement
apporte les bénéfices prévus à l’origine.
uNPV
1
CF
NPV = CF0 + + + + … +
(1+ i )
CF
2
(1+ i )
2
CF
3
(1+ i )
CF
n
3
(1+ i )
n
I%
i =
100
n: entier naturel jusqu’à 254
uNFV
NFV = NPV × (1 + i )
n
uIRR
1
CF
0 = CF0 + + + + … +
(1+ i )
Dans cette formule, NPV = 0 et la valeur IRR est équivalente à i × 100. Pendant les calculs
consécutifs effectués automatiquement par la calculatrice, de minuscules valeurs
fractionnaires s’accumulent néammoins et le NPV n’atteint jamais exactement la valeur zéro.
Plus NPV s’approche de zéro, plus IRR est précis.
CF2
(1+ i )
2
CF3
(1+ i )
CFn
3
(1+ i )
n
20001201
Page 78

2-4-2
Cash-flow (Evaluation d’investissement)
uu
uPBP
uu
Valeur initiale de N quand NPV > 0.
• Appuyez sur 3(CASH) sur l’écran Finance 1 pour afficher l’écran de saisie suivant lors du
calcul de la marge brut d’autofinancement.
3(CASH)
I% ............................... taux d’intérêt
Csh .............................. liste pour le cash-flow
Si vous n’avez pas encore introduit de données dans une liste, appuyez sur 5('LIST) et
introduisez des données dans une liste.
Après avoir réglé les paramètres, appuyez sur une des touches de fonction mentionnées cidessous pour effectuer le calcul correspondant.
• 1(NPV) ........ Valeur actuelle nette
• 2(IRR) ......... Taux de rendement interne
• 3(PBP) ........ Période d’amortissement
• 4(NFV) ........ Valeur capitalisée nette
• 5('LIST) .... Saisie des données d’une liste
• 6(LIST) ....... Spécification d’une liste pour la saisie de données
• Une erreur (Erreur math) se produit si les paramètres ne sont pas configurés correctement.
Utilisez les touches de fonction suivantes pour passer d’un écran de résultat à l’autre.
• 1(REPT) .... Ecran de saisie des paramètres
• 6(GRPH) .... Tracé de graphe
20001201
Page 79

2-4-3
Cash-flow (Evaluation d’investissement)
Après le tracé du graphe, vous pouvez appuyer sur 1(TRACE) pour activer la fonction
Trace et relever les résultats du calcul sur le graphe.
Appuyez sur i pour désactiver la fonction Trace.
Appuyez une nouvelle fois sur i pour revenir à l’écran de saisie des paramètres.
20001201
Page 80

2-5-1
Amortissement
2-5 Amortissement
Cette calculatrice permet de calculer le montant du capital et le montant des intérêts d’un
versement mensuel, le solde du capital et le montant total du capital et des intérêts
remboursés à un point donné.
uu
uFormule
uu
Montant d’un paiement unique
e
d
a
b
12 mn
(Nombre de paiements)
a: partie intérêts du versement PM1 (INT)
b: partie capital du versement PM1 (PRN)
c: solde du capital après le versement PM2 (BAL)
d: total du capital du versement PM1 au paiement du versement PM2 (PRN)
e: intérêt total du versement PM1 au paiement du versement PM2 (INT)
*a + b = un versement (PMT)
a : INTPM1 = I BALPM1–1 × i I × (signe PMT)
c
b : PRN
c : BAL
PM2
d : PRN = PRNPM1 + PRNPM1+1 + … + PRNPM2
PM1
PM2
e : INT = INTPM1 + INTPM1+1 + … + INTPM2
PM1
BAL0 = PV (INT1 = 0 et PRN1 = PMT au début de la période de versement)
PM1 = PMT + BALPM1–1 × i
PM2 = BALPM2–1 + PRNPM2
20001201
Page 81

2-5-2
Amortissement
uu
uConversion entre le taux d’intérêt nominal et le taux d’intérêt réel
uu
Le taux d’intérêt nominal (valeur I% entrée par l’utilisateur) est convertie en taux d’intérêt
réel (
I%’) pour les emprunts où le nombre de versements par année est différent du nombre
de périodes de calcul des intérêts composés.
[C / Y ]
I%' =
Le calcul suivant est effectué après la conversion du taux d’intérêt nominal en taux d’intérêt
réel, et le résultat est utilisé pour les calculs suivants.
(1+ ) –1
{ }
I%
100 × [C / Y ]
[P / Y ]
×100
i = I%'÷100
Appuyez sur 4(AMT) sur l’écran Finance 1 pour afficher l’écran de saisie suivant lors de la
conversion de taux d’intérêt.
4(AMT)
PM1 ............................. premier des versements 1 à n
PM2 ............................. second des versements 1 à n
.................................. versements
n
I% ............................... taux d’intérêt
PV ............................... capital
PMT ............................ paiement à chaque versement
FV ............................... solde après le dernier versement
P/Y .............................. versements par année
C/Y .............................. compositions par année
20001201
Page 82

2-5-3
Amortissement
Après avoir réglé les paramètres, appuyez sur une des touches de fonction mentionnées
ci-dessous pour effectuer le calcul correspondant.
• 1(BAL) ........ Solde du capital après le versement PM2
• 2(INT) ......... Partie intérêts du versement PM1
• 3(PRN) ....... Partie capital du versement PM1
• 4( INT) ...... Total des intérêts payés du versement PM1 au versement PM2
• 5( PRN) .... Capital total payé du versement PM1 au versement PM2
• 6(CMPD) .... Ecran d’intérêts composés
• Une erreur (Erreur math) se produit si les paramètres ne sont pas configurés correctement.
Utilisez les touches de fonction suivantes pour passer d’un écran de résultat à l’autre.
• 1(REPT) ..... Ecran de saisie des paramètres
• 4(CMPD) .... Ecran d’intérêts composés
• 6(GRPH) ..... Tracé de graphe
Après le tracé du graphe, vous pouvez appuyer sur 1(TRACE) pour activer la fonction
Trace et relever les résultats du calcul sur le graphe.
A la première pression de 1 (TRACE), INT et PRN sont indiqués pour n = 1. A chaque
pression suivante de e, INT et PRN sont indiqués pour n = 2, n = 3, etc.
Appuyez sur i pour désactiver la fonction Trace.
Appuyez une nouvelle fois sur i pour revenir à l’écran de saisie des paramètres.
20001201
Page 83

2-6-1
Conversion de taux d’intérêt
2-6 Conversion de taux d’intérêt
Les procédures décrites ici indiquent comment convertir le taux de pourcentage annuel en
taux d’intérêt réel, et inversement.
uu
uFormule
uu
EFF =
APR/100
1+
n
n
–1 × 100
APR : taux de pourcentage
annuel (%)
EFF : taux d’intérêt réel (%)
1
n
–1 × n ×100
APR =
Appuyez sur 5(CNVT) sur l’écran Finance 1 pour afficher l’écran de saisie suivant pour la
conversion du taux d’intérêt.
5(CNVT)
1+
EFF
100
n : nombre de compositions
n ....................................... nombre de compositions
I% ............................... taux d’intérêt
Après avoir réglé les paramètres, appuyez sur une des touches de fonction mentionnées cidessous pour effectuer le calcul correspondant.
• 1('EFF) ... Conversion du taux de pourcentage annuel en taux d’intérêt effectif
• 2('APR) ... Conversion du taux d’intérêt réel en taux de pourcentage annuel
• Une erreur (Erreur math) se produit si les paramètres ne sont pas configurés correctement.
Utilisez les touches de fonction suivantes pour passer d’un écran de résultat à l’autre.
• 1(REPT) ... Ecran de saisie des paramètres
20001201
Page 84

M
2-7-1
Coût, prix de vente, marge
2-7 Coût, prix de vente, marge
Le coût, le prix de vente ou la marge bénéficiaire peuvent être calculés lorsque les deux
autres valeurs sont définies.
uu
uFormule
uu
CST : coût
SEL : prix de vente
MRG : marge bénéficiaire
CST = SEL
SEL =
CST
1–
RG(%) =
Appuyez sur 1(COST) sur l’écran Finance 2 pour afficher l’écran de saisie suivant.
6(g)1(COST)
Cst ............................... coût
1–
MRG
100
1–
MRG
100
CST
SEL
× 100
Sel ............................... prix de vente
Mrg .............................. marge bénéficiaire
Après avoir réglé les paramètres, appuyez sur une des touches de fonction mentionnées
ci-dessous pour effectuer le calcul correspondant.
• 1(COST) ... Coût
• 2(SEL) ......Prix de vente
• 3(MRG) ..... Marge bénéficiaire
• Une erreur (Erreur math) se produit si les paramètres ne sont pas configurés correctement.
Utilisez les touches de fonction suivantes pour passer d’un écran de résultat à l’autre.
• 1(REPT) ... Ecran de saisie des paramètres
20001201
Page 85

2-8-1
Calculs de jours/date
2-8 Calculs de jours/date
Vous pouvez calculer le nombre de jours entre deux dates ou déterminer quelle est la date
un certain nombre de jours après ou avant une autre date.
Appuyez sur 2(DAYS) sur l’écran Finance 2 pour afficher l’écran de saisie suivant pour le
calcul de jours/date.
6(g)2(DAYS)
d1 ................................ date 1
d2 ................................ date 2
D ................................. nombre de jours
Important!
• Le format d’entrée des dates est le suivant: <mois>. <jour> <année>.
Pour saisir une date, mettez d’abord d1 ou d2 en surbrillance. Au moment où vous appuyez
sur une touche numérique pour indiquer le mois, un écran de saisie similaire à l’écran
suivant apparaît.
# L’écran de configuration peut être utilisé pour
désigner une année de 365 ou 360 jours pour
les calculs financiers. Les calculs de jours et
de dates sont aussi effectués en fonction du
nombre de jours préréglés pour une année,
mais les calculs suivants ne peuvent pas être
effectués quand une année de 360 jours est
20001201
préréglée. Toute tentative de calcul dans ce
cas provoquera une erreur.
(Date) + (Nombre de jours)
(Date) – (Nombre de jours)
# La plage de calcul va du 1
décembre 2099.
er
janvier 1901 au 31
Page 86

2-8-2
Calculs de jours/date
Indiquez le mois, le jour et l’année en appuyant sur w après chaque fois saisie.
Après avoir réglé les paramètres, appuyez sur une des touches de fonction mentionnées
ci-dessous pour effectuer le calcul correspondant.
• 1(PRD) ...... Nombre de jours de d1 à d2 (d2 – d1)
• 2(d1+D) ..... d1 plus le nombre de jours (d1 + D)
• 3(d1–D) ..... d1 moins le nombre de jours (d1 – D)
• Une erreur (Erreur math) se produit si les paramètres ne sont pas configurés correctement.
Utilisez les touches de fonction suivantes pour passer d’un écran de résultat à l’autre.
• 1(REPT) .... Ecran de saisie des paramètres
Calculs en mode 360 jours
Procédez de la façon suivante pour effectuer des calculs lorsque 360 jours est spécifié pour
le mode Date sur l’écran de configuration.
• Si d1 est le 31e jour du mois, d1 est considéré comme le 30e jour de ce mois.
• Si d2 et le 31e jour d’un mois, d2 est considéré comme le 1er jour du mois suivant, à moins que
d1 soit le 30.
20001201
Page 87

2-9-1
Dépréciation
2-9 Dépréciation
Chacune des méthodes suivantes peut être utilisée pour le calcul de dépréciation
(amortissement).
uu
uMéthode linéaire
uu
La méthode de calcul linéaire calcule la dépréciation sur une période donnée.
SL
SL
SL
1
=
(PV–FV )
j
=
n+1
=
n 12
u
n
(PV–FV )
n 12
{Y–1}(PV–FV )
12–{Y–1}
u
SL j : dotation aux amortissements
pour la je année
n : durée de service en années
PV : coût d’acquisition (base)
FV : valeur à la casse (valeur
résiduelle de récupération)
j : année
Y–1 : nombre de mois
({Y–1}G12)
La dépréciation d’un objet acquis en cours d’année peut être calculée par mois.
uu
uMéthode à pourcentage fixe
uu
La méthode à pourcentage fixe peut être utilisée pour calculer la dépréciation sur une
période donnée, ou pour calculer le taux de dépréciation.
amortissables sur la première
année
{Y–1}I%
FP
FP
1
j
= PV ×
= (RDV
×
100
j–1
+ FV ) ×
12
I%
100
FPj : dotation aux amortissements pour la
e
j
année
RDVj : valeur amortissable restante en fin
n+1
= RDVn ({Y–1}G12)
FP
RDV
1
= PV – FV – FP
I
%
1
de je année
: taux de dépréciation
RDV
j
= RDV
RDV
n+1
= 0 ({Y–1}G12)
La dépréciation d’un objet acquis en cours d’année peut être calculée par mois.
j–1
– FP
j
20001201
Page 88

2-9-2
Dépréciation
uu
uMéthode de la somme des chiffres d’une année
uu
La méthode utilisant la somme des chiffres d’une année calcule la dépréciation sur une
période donnée.
n (n +1)
Z =
12
{Y–1}
n' = n –
12
(partie entière de n' +1)(partie entière de n' + partie fractionnaire de 2*n' )
Z' =
SYD
1 =
n
{Y–1}
× (PV
Z
12
2
– FV )
n'– j+2
– FV – SYD1)( jG1)SYDj = (
)(PV
Z'
n+1 = (
n'– (n +1)+2
Z'
– FV – SYD1)({Y–1}G12)
)(PV
12–{Y–1}
×SYD
12
RDV
1 = PV – FV – SYD1
RDVj = RDVj –1 – SYDj
La dépréciation d’un objet acquis en cours d’année peut être calculée par mois.
uu
uMéthode d’amortissement progressif
uu
La méthode d’amortissement progressif calcule la dépréciation sur une période donnée.
Y–1I%
DB
1
= PV ×
RDV
1
= PV – FV – DB
j
= (RDV
DB
RDV
j
= RDV
100n
j–1
j–1
×
+ FV )
– DB
12
1
×
100n
j
SYDj : dotation aux amortissements pour la
e
j
année
RDVj : valeur amortissable restante en fin
de je année
DBj : dotation aux
amortissement pour la j
année
RDVj : valeur amortissable
I%
I
%
restante en fin de
: facteur (%)
e
j
année
e
DB
n +1
RDV
= RDVn
n+1
= 0
({Y–1}G12)
({Y–1}G12)
20001201
Page 89

2-9-3
Dépréciation
Appuyez sur 3(DEPR) sur l’écran Finance 2 pour afficher l’écran de saisie suivant.
La dépréciation d’un objet acquis en cours d’année peut être calculée par mois.
6(g)3(DEPR)
n .................................. durée de service en années
I% ............................... taux/facteur de dépréciation
PV ............................... coût d’acquisition (base)
FV ............................... valeur à la casse (valeur résiduelle de récupération)
j ................................... année
Y–1 .............................. nombre de mois amortissables sur la première année
• Les paramètres peuvent être affichés sous forme d’entiers ou de valeurs décimales. Une
fraction sera convertie en valeur décimale.
Après avoir réglé les paramètres, appuyez sur une des touches de fonction mentionnées
ci-dessous pour effectuer le calcul correspondant.
• 1(SL) .......... Méthode linéaire
• 2(FP) ......... 1. Méthode du pourcentage fixe
......... 2. Taux de dépréciation
• 3(SYD) ....... Méthode de la somme des chiffres d’une année
• 4(DB) ......... Méthode d’amortissement dégressif
20001201
Page 90

2-9-4
Dépréciation
• Une erreur (Erreur math) se produit si les paramètres ne sont pas configurés correctement.
Utilisez les touches de fonction suivantes pour passer d’un écran de résultat à l’autre.
• 1(REPT) .... Ecran de saisie des paramètres
• 6(TABL) ..... Tableau de résultats des calculs
Les touches de fonction suivantes apparaissent sur l’écran contenant le tableau de résultats
des calculs.
• 1(REPT) .... Ecran de saisie des paramètres
• 6(GRPH) .... Tracé de graphe
Après le tracé du graphe, vous pouvez appuyer sur 1(TRACE) pour activer la fonction
Trace et relever les résultats du calcul sur le graphe.
Appuyez sur i pour désactiver la fonction Trace.
Appuyez une nouvelle fois sur i pour revenir à l’écran de saisie des paramètres.
20001201
Page 91

2-10-1
Obligations
2-10 Obligations
Le calcul d’obligations permet d’obtenir le prix et le rendement d’une obligation.
uu
uFormule
uu
D
A B
PRC
: prix pour une valeur nominale de 100 $
CPN : taux d’intérêt contractuel annuel (%)
YLD : taux actuariel (%)
A : jours cumulés
M : nombre de paiements des coupons par an (1 = annuel, 2 = semestriel)
N : nombre de paiements des coupons entre la date de liquidation et la date
d’échéance
RDV : prix de rachat ou prix d’exercice pour une valeur nominale de 100 $
D : nombre de jours dans la période de coupons où la liquidation a lieu
B : nombre de jours de la date de liquidation jusqu’à la date de paiement du prochain
coupon = D – A
INT : intérêts courus
CST : prix, intérêts compris
• Moins de six mois jusqu’au rachat
CPN
RDV +
M
PRC = – ( )
B
YLD/100
A
D
CPN
×
M
1+ ( × )
D
• Six mois ou plus jusqu’au rachat
M
CPN
RDV
M
YLD/100
M
(K–1+B/D )
A MCPN
×
–
D
PRC = +
YLD/100
(N–1+B/D )
(1+ )
M
N
k=1
(1+ )
INT =
×
–
D
CST = PRC + INT
A MCPN
20001201
Page 92

2-10-2
Obligations
Appuyez sur 4(BOND) sur l’écran Finance 2 pour afficher l’écran de saisie suivant lors du
calcul de bond.
• 6(g)4(BOND)
d1 ................................ date d’acquisition
d2 ................................ date de rachat
RDV ............................ prix de rachat ou prix d’exercice pour une valeur
nominale de 100 $
CPN ............................ taux d’intérêt contractuel annuel (%)
PRC ............................ prix pour une valeur nominale de 100 $
YLD ............................. taux actuariel (%)
Pour introduire une date, mettez d’abord d1 ou d2 en surbrillance. Au moment où vous
appuyez sur une touche numérique pour saisir le mois, un écran de saisie similaire à l’écran
suivant apparaît.
Indiquez le mois, le jour et l’année en appuyant sur w après chaque saisie.
Après avoir réglé les paramètres, appuyez sur une des touches de fonction mentionnées
ci-dessous pour effectuer le calcul correspondant.
• 1(PRC) .... Prix pour une valeur nominale de 100 $
• 2(YLD) ..... Taux actuariel
20001201
Page 93

2-10-3
Obligations
• Une erreur (Erreur math) se produit si les paramètres ne sont pas configurés correctement.
Utilisez les touches de fonction suivantes pour passer d’un écran de résultat à l’autre.
• 1(REPT) ..... Ecran de saisie des paramètres
• 5(MEMO) ....Ecran des valeurs nécessaires au calcul d’obligation*
• 6(GRPH) ..... Tracé du graphe
Lorsque vous appuyez sur 5(MEMO) diverses valeurs nécessaires au calcul d’obligation
apparaissent, comme ci-dessous.
* La date de paiement des intérêts est calculée à partir de d2 lorsque 365 est spécifié pour
le mode Date sur l’écran de configuration.
• w~w
• 6(GRPH)
Après le tracé du graphe, vous pouvez appuyer sur 1(TRACE) pour activer la fonction
Trace et relever les résultats du calcul sur le graphe.
Appuyez sur i pour désactiver la fonction Trace.
Appuyez une nouvelle fois sur i pour revenir à l’écran de saisie des paramètres.
20001201
Page 94

2-11-1
Graphe TVM
2-11 Graphe TVM
Le graphe TVM permet d’attribuer deux des cinq paramètres (n, I%, PV, PMT, FV) aux axes
x et y d’un graphe, et la valeur y change lorsque la valeur x change.
Appuyez sur 5(TVMG) sur l’écran Finance 2 pour afficher l’écran de saisie suivant lors du
tracé de graphe TVM.
6(g)5(TVMG)
Après avoir configuré les paramètres, appuyez sur les touches de fonction mentionnées
ci-dessous pour affecter les paramètres aux axes x et y.
• 1(X) ... Affectation du paramètre sélectionné à l’axe x
• 2(Y) ... Affectation du paramètre sélectionné à l’axe y
Après les réglages, tracez le graphe.
• 6(GRPH) ... Tracé du graphe
Après le tracé du graphe, vous pouvez appuyer sur 1(TRACE) pour activer la fonction
Trace et relever les résultats du calcul sur le graphe.
Appuyez sur i pour désactiver la fonction Trace.
L’écran suivant s’affiche par une pression de 6(Y-CAL) après le tracé du graphe.
Lorsque vous indiquez une valeur x sur cet écran et appuyez sur w, la valeur
correspondante sur l’axe y est indiquée.
Appuyez une nouvelle fois sur i pour revenir à l’écran de saisie des paramètres.
• Le calcul peut durer un certain temps lorsque vous désignez I% pour l’axe y.
20001201
Page 95

2-12 Exemples
Intérêt simple
Réglage
1. Sur le menu principal, sélectionnez l’icône TVM.
Exécution
2. 1(SMPL) ........ Calcul d’intérêt simple
3. Réglez la calculatrice pour cet exemple.
4. Spécifiez les paramètres nécessaires au calcul.
5. 1(SI) .............. intérêt simple
2(SFV) ........... valeur capitalisée simple
2-12-1
Exemples
20001201
Page 96

2-12-2
Exemples
○○○○○
Exemple Quel sera le montant des intérêts et du capital plus les intérêts pour
un prêt de 1 500 $ s’étalant sur 90 jours si le taux annuel est de
7,25%?
Utilisez le mode 360 jours et deux décimales.
Procédure
1 m TVM
2 1(SMPL)
3 u3(SET UP)*1c2(360)
cccc1(Fix)cwi
4jaw( n = 90)
h.cfw(I % = 7,25)
-bfaaw(FV = –1 500)
5 1(SI)
1(REPT)
2(SFV)
Ecran de résultat
Résultat du calcul (SI) Résultat du calcul (SFV)
Le montant des intérêts s’élèvera à 27,19 $ et le montant du capital plus les intérêts à
1 527,19 $.
*1Sur l’écran de réglage, spécifiez “360” pour le
mode de date et “Fix2” pour l’affichage.
20001201
Page 97

2-12-3
Exemples
Intérêt composé
Réglage
1. Sur le menu principal, sélectionnez l’icône TVM.
Exécution
2. 2(CMPD) ........calcul d’intérêts composés
3. Réglez la calculatrice pour cet exemple.
4. Spécifiez les paramètres nécessaires au calcul.
5. 1(n)................. nombre de périodes de composition
2(I%) .............. taux d’intérêt annuel
3(PV) ..............valeur actuelle (montant du prêt en cas de prêt ; capital en cas
d’épargne)
4(PMT) ........... paiement à chaque versement (paiement en cas de prêt ; dépôt en
cas d’épargne)
5(FV) .............. valeur capitalisée (solde impayé en cas de prêt ; capital plus intérêts
en cas d’épargne)
6(AMT) ........... amortissement
20001201
Page 98

2-12-4
Exemples
kk
k Epargne (intérêts composés standard)
kk
Condition de la saisie : La valeur capitalisée doit être supérieure à la valeur actuelle.
Formule de la condition de saisie : PMT = 0
|PV| < |FV|
○○○○○
Exemple Calculer le taux d’intérêt nécessaire pour accroître un capital de
10 000 $ à 12 000 $ en trois ans, lorsque la composition est
semestrielle.
Procédure
1 m TVM
2 2(CMPD)
3 u3(SET UP)*12(End)c1(365)
cccc2(Norm)i
4dw(Saisir n = 3.)
c
-baaaaw(PV = –10 000)
aw(PMT = 0)
bcaaaw(FV = 12 000)
bw
cw(Composition semestrielle)
5 2(I%)
Ecran de résultat
Un taux d’intérêt d’au moins 6,17% sera nécessaire.
*1Sur l’écran de réglage, spécifiez “End” pour le
paiement, “365” pour le mode de date et “Norm1”
pour l’affichage.
20001201
Page 99

2-12-5
Exemples
kk
k Plan d’épargne échelonné
kk
Condition de la saisie : La valeur capitalisée doit être supérieure au total des paiements.
Formule de la condition de saisie :
PMT et FV ont des signes différents (positif, négatif) lorsque PV = 0.
–FV < n × PMT lorsque FV > 0
–FV > n × PMT lorsque FV < 0
○○○○○
Exemple Calculer le taux d’intérêt nécessaire pour obtenir un solde de 2 500 $
sur un plan d’épargne échelonné sur deux ans si 100 $ sont déposés
chaque mois et la composition des intérêts est semestrielle.
Procédure
1 m TVM
2 2(CMPD)
3 u3(SET UP)*12(End)i
4 c*bcw(Saisir n = 2 × 12.)
c
aw(PV = 0)
-baaw(PMT = –100)
cfaaw(FV = 2 500)
bcw(Mensualité)
cw(Composition semestrielle)
5 2(I%)
Ecran de résultat
Un taux d’intérêt d’au moins 4,28% sera nécessaire.
*1Sur l’écran de réglage, spécifiez “End” pour le
paiement.
20001201
Page 100

2-12-6
Exemples
kk
k Prêts
kk
Condition de la saisie : Le total des paiements doit être supérieur au montant du prêt.
Formule de la condition de saisie :
PMT et PV ont des signes différents (positif, négatif) lorsque FV = 0.
–PV > n × PMT lorsque PV > 0
–PV < n × PMT lorsque PV < 0
○○○○○
Exemple Calculer le taux d’intérêt nécessaire pour rembourser un solde de
2 300 $ sur un prêt échelonné sur deux ans à raison de 100 $ par mois,
lorsque la composition des intérêts est mensuelle.
Procédure
1 m TVM
2 2(CMPD)
3 u3(SET UP)*12(End)i
4 c*bcw(Saisir n = 2 × 12.)
c
cdaaw(PV = 2 300)
-baaw(PMT = –100)
aw(FV = 0)
bcw(Mensualité)
(Composition mensuelle)*
2
5 2(I%)
Ecran de résultat
Un taux d’intérêt maximal de 4,11% sera acceptable.
20001201
2
*
La valeur P/Y est automatiquement saisie pour
C/Y. La saisie de C/Y peut donc être ignorée.
*1Sur l’écran de réglage, spécifiez “End” pour le
paiement.
 Loading...
Loading...