Page 1

Page 2

This activities book introduces practical examples of problems and
exercises that are covered in middle school, high school, and college
classes using the CASIO Programmable Scientific Calculator.
As you will see as you go through the problems and exercises,
using a programmable scientific calculator does much more than
take the work out of calculations. It is also a highly effective
educational tool that can help students grasp important concepts
and stimulate their imagination.
This manual is a collection of actual problems and exercises,
including actual operations. It is intended as the first step for
educators who want to start using the programmable scientific
calculator in their own classrooms. The material presented here is
designed to make problem solving more enjoyable and to cultivate
a deeper understanding of mathematics by showing how the
programmable scientific calculator can be used to solve a blend of
textbook problems and problems faced in everyday life.
関数電卓事例集表
23.eps
Page 3

Table of Contents
Programming a Calculation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
01 Greatest Common Divisors . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
02 Fractions from recurring decimals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
03 Simultaneous Equations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
04 Solutions to quadratic equations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
05 Values of Functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
06 Summing Arithmetic Progressions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
07 Summing Geometric Progressions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
08 Approximate solutions to higher order equations(bisection method) . . . . . . . . . . . . 14
09 Approximate solutions to Equations of higher degree (Newton’s method) . . . . . . . 16
10 Limits . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
11 Limits . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
12 Definite Integrals(Trapezoidal rule) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
13 Definite integrals(Simpsons formula) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
14 Finding the area of a triangle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
15 The angle between two vectors . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
16 Finding the angles in a triangle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
17 The radius of the Inscribed circle. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
18 The radius of the Circumscribed circle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
19 Center of mass of a triangle(barycentre) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
20 The distance between a line and a point . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
21 The sum, difference and inner product of two vectors . . . . . . . . . . . . . . . . . . . . . . . 30
22 Rotation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
23 Complex numbers and polar coordinates . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
24 The inverse of a 2
25 Combinations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
26 The binomial distribution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
×2 matrix. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
27 Confidence Intervals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
28 Test on a mean with known (z-tests) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
29 Guess the number . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
30 Various areas and volumes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
µσ
2
1
Page 4

Basic Operation for fx-3650P/3950P
Programming a Calculation
• The program storage area has about 360 bytes, which can be
divided among up to four different programs named P1, P2, P3,
and P4.
• To perform program calculation operations, press ,
MODE MODE MODE
which displays the screen shown below. Next, press the number
key that corresponds to the mode you want to select.
P
RGM RUN PCL
1
2
1
(PRGM) . . Edit Prog Mode for inputting and editing programs.
2
(RUN) . . . Mode for running programs.
3
(PCL) . . . . Clear Prog Mode for deleting programs.
Storing a Program
3
PRGM
Use the following procedure to specify the Edit Prog Mode and
store a program in memory.
Edit Prog. . . . . . . . . . . . . . . . . . . . . . . . . . . .
MODE MODE MODE
1
• Example: To create a program that uses Heron’s formula to cal-
culate the area of a triangle based on the lengths of its three
sides
Formula: Note that: s = (A + B + C) /2.
SssA–()sB–()sC–()=
1. Enter the Edit Prog Mode, which displays the screen shown
below.
If there is already a
program in memory, its
PRGM
Ed i t P r o
g
number appears on the
display.
P-1234 308
Remaining capacity (bytes)
2. Select the program number (P1 to P4) to which you want to
assign the program.
2
Ex.: (Program P2)
PRGM
000
Number of bytes used by program P2.
3. Input the program.
Program
▲
? → A: ? → B: ? → C: (A + B + C) ÷ 2 → D
D × (D – A) × (D
– B) × (D – C):
√ Ans
• To input a colon (:), press .
• To input → A”, press .
• You can also input a variable name using the key. To input
“X” for example, press .
SHIFT
ALPHA
EXE
STO
A
ALPHA
X
• To input a question mark (?), right arrow ( → ), colon (:), or out-
▲
put command (
1
keys through to select the mark or command you
want. See “Useful Program Commands” on page 40 for more
), press , and then use number
SHIFT SHIFT
4
P-CMD
information.
4. Press to exit program input.
AC
MODE MODE MODE
2
■ Editing a Program
• While a program’s contents are on the display in the Edit Prog
Mode, you can use and to move the cursor to the location you want to edit.
• Press to delete the function at the current cursor location.
DEL
• Use the insert cursor (page 9) when you want to insert a new
statement into a program.
Executing a Program
RUN
The procedure in this section shows how to execute a program in
the COMP Mode.
Perform the following key operation to enter the COMP Mode.
21
COMP. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
MODE
• Example: To create a program that uses Heron’s formula to cal-
culate the area of a triangle whose three sides measure A = 30,
B = 40, C = 50
1. Execute the program.
(In the COMP Mode)
Prog
2
Specify the number of the program you want to execute.
2
PRGM PCL RUN
2. Input the values required for the calculation.
EXE
A? 30
EXE
B? 40
EXE
C? 50
3. Press to resume program execution.
EXE
(A+B+C) 2 D
60.
The program number disappears after
program execution is complete.
(Assigns the result of
D = (A + B + C) 2 to
Disp
variable D.)
Ans
600.
Deleting a Program
(Area)
PCL
Use the following procedure to specify the Clear Prog Mode and
delete a program from memory.
Clear Prog . . . . . . . . . . . . . . . . . . . . . . . . . . .
MODE MODE MODE
• You can also enter the Clear Prog Mode by pressing while
3
DEL
the Edit Prog screen is on the display.
• You can select programs individually by specifying a program
number from P1 through P4.
1. Enter the Clear Prog Mode, which displays the screen shown
below.
PRGM
C
l ea r Pr
P-1234 247
g
o
2. Select the program number (P1 to P4) of the program you want
to delete.
• Example: (Program P1)
1
• The number of the program you selected disappears from the
upper part of the display, and remaining memory capacity
increases by the size of the deleted program.
• Note that the only way to delete all the programs in memory (P1
through P4) is to perform the reset operation (page 11).
Useful Program Commands
In addition to mathematical calculations, there are also a number of
useful program commands you can use to perform loops and
define conditions.
■ Program Command Menus
Press to display a menu of available program com-
SHIFT
P-CMD
mands.
• The program command menu has three screens. Use the
and keys to display the menu screen you want.
• To input one of the commands currently on the screen, press a
number key from through
1
5
• Basic Commands
? :
1 2 3 4
1
(?) . . . . . Operator input command
2
( → ) . . . Assign to variable command
3
(:) . . . . . Multi-statement separator code
4
▲
) . . .Output command
(
• Conditional Jump Commands
1 2 3 4 5
1
( ⇒ ) . . .Jump code (when condition is met)
2
( = ) . . .Relational operator
3
( ≠ ) . . .Relational operator
4
( > ) . . .Relational operator
5
( ≧ ) . . .Relational operator
• Unconditional Jump Commands
G
o t o Lb l
1 2
(Goto) . . Jump command
1
(Lbl). . . .Label
2
Page 5

01 Greatest Common Divisors
Given two natural numbers, and , the greatest common divisor may be found using
AB
Euclid’s algorithm. A simplified explanation is given below:
1.Let and be two natural numbers.
2.Let be the remainder after dividing by .
3.If , set and and return to 2.
4.If =
AB AB>()
CAB
C 0≠ BA→ CB→
0 , then is the greatest common divisor.
CB
Greatest common divisor
Program
ON
MODE MODE MODE
PRGM
1
MODE
COMP1P1
1
Lbl 1:?→ A:?→ B:B > A ⇒ Goto 1:Lbl 2:A - B → A:A ≧ B
⇒ Goto 2:A =0⇒ Goto 3:A → C:B → A:C → B:Goto 2:Lbl
3:B < 60 STEP >
Execution Example:
Find the greatest common divisor of 210 and 60.
Prog
210
60
1
EXE
EXE
S A
S A
S A
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
G
G
G
3
Page 6

02
Fractions from recurring decimals
Recurring decimals may be converted to fraction by proceeding in the following way:
1
= 0.111111111111 = 0.01010101010
---
……
9
1
---------
= 0.001001001001001 = 0.000100010001
……
999
1
------
99
1
-----------9999
……
……
For example, 0.345345345…… is
0.345345345
……
=
345
--------999
=
115
--------333
Program
PRGM
ON
MODE MODE MODE
1
MODE
?→ A:?→ B:10^ A -1→ A:A → X:B → Y:Lbl 1:A - B → A:A ≧
B ⇒ Goto 1:A =0⇒ Goto 2:A → C:B → A:C → B:Goto 1:Lbl
2:Y ÷ B X÷B <73 STEP >
Execution Example:
COMP1P1
1
Write 0.345345••• as a fraction.
A? : The number of digits in the repeated pattern (e.g. 3 in the example)
B? : The recurring sequence of digits (e.g. 345 in the example)
Prog
3
1
EXE
3 4 5
EXE
EXE
S A
S A
S A
S A
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
D R
G
G
G
Disp
G
*This program deals only with the case in which the 1st to Ath digits immediately following
the decimal point are repeated.
4
i.e. 0.033333...= 1/30 and 0.166666...= 1/6 cannot be converted.
Page 7

03 Simultaneous Equations
When , the solution to the simultaneous equation:
AE BD– G 0
Ax By+C=
=
≠
Dx Ey+F=
is given by the formula:
x
EC FB–
---------------------=y,
G
AF CD–
----------------------=
G
Program
PRGM
ON
MODE MODE MODE
1
MODE
Lbl 1:?→ A:?→ B:?→ C:A → Y:B → X:C → M:?→ A:?→ B:?→
C:AX - BY → D:D =0⇒ Goto 1:(XC - BM)÷ D → X:(AM - CY)÷
D→Y:X Y < 81 STEP >
INPUT A,B,C (first time): A,B,C (second time):
Ax By+C=DxEy+F=
COMP1P1
1
OUTPUT X,Y: solutions to the simultaneous equation
Execution Example:
3xy+ 9=
The solution to is
Prog
3
1
1
EXE
EXE
8x 5y–1=
x 2 y, 3==
S A
S A
S A
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
G
G
G
5
Page 8

S A
EXE
9
M
P1P1P2 P3 P4
D R
G
8
1
EXE
S A
S A
S A
S A
M
M
M
M
EXE
EXE
5
EXE
When , we cannot guarantee that there is a unique solution. In this case
AE BD–0=
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
D R
G
G
G
G
please enter a different problem.
Disp
6
Page 9

04
<>
Solutions to quadratic equations
The solutions to the quadratic equation are given by the formula:
x
b– b
--------------------------------------=
2
4ac–±
ax
2
bx c++ 0=
2a
In particular, when two real solutions exist,
when
when there are two complex solutions
b24ac–0>
b24ac–0
= there is just one real solution and
b24ac–0<
Program
PRGM
ON
MODE MODE MODE
1
MODE
?→ A:?→ B:?→ C:B2-4 AC =0⇒ Goto 1:(- B -√(B2-4 AC))
÷2 A → M:M Lbl 1:(-B+√(B
2
-4 AC))÷2 A → M:M < 70 STEP >
Execution Example:
CMPLX
2
P1
1
i) Find solutions to the equation .
EXE
4
1 6
1
EXE
EXE
Prog
2
EXE
2x
2
4x–16–0=x24,–=()
S A
S A
S A
S A
M CMPLX
S A
M CMPLX
CMPLX
CMPLX
CMPLX
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
D R
D R
G
G
G
G
Disp
G
7
Page 10

ii) Find solutions to the equation .
2
x
6x–12+ 0=x33i±=()
Prog
1
1 2
1
EXE
EXE
SHIHT EXE
EXE
SHIHT EXE
S A
S A
EXE
6
M CMPLX
S A
M CMPLX
S A
M CMPLX
S A
M CMPLX
CMPLX
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
D R
D R
G
G
G
G
G
RI<>
Disp
RI<>
Disp
i
RI<>
RI<>
ii
When R ⇔ I appears in the display, the solution is complex.
Press to display the imaginary parts.
SHIHT EXE
8
Page 11

05 Values of Functions
FIX
FIX
For two variables and where the values of is
determined for given values of , we say that is a
function of . For example, for the function
yx32x
y 3–=x1–=
– x 1++=y13=x3=
when .
xy y
xy
x
2
, when , and
y
1
x
1
Program
PRGM
ON
MODE MODE MODE
1
MODE
?→ A:?→ B:?→ C:?→ D:Lbl 1:?→ X:AX3+BX2+CX+D→Y:
Y Goto 1 < 42 STEP >
INPUT A,B,C,D: X: value of
OUTPUT Y : value of
Ax3Bx
yAx3Bx2Cx D+++=
2
Cx D+++ x
Execution Example:
COMP1P1
1
Calculate values of , given , for the function .
Prog
1
1
3
1
EXE
EXE
EXE
EXE
yx yx
EXE
2
EXE
1
EXE
1
3
S A
S A
S A
S A
2
2x
– x 1++=
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
D R
G
G
G
Disp
G
Disp
To continue the calculation, press , enter some value of X and .
To end the calculation, presss .
EXE EXE
AC
9
Page 12

06
Summing Arithmetic Progressions
1. The sum up to the th term of an arithmetic progression with first term and
difference term , may be calculated by:
C
Ak1–()B+()
∑
k 1=
CA
B
AAB+()A 2B+()…AC1–()B+()++ ++=
C
---- 2AC1–()B+()=
2
Program
PRGM
ON
MODE MODE MODE
1
MODE
?→ A:?→ B:?→ C:C(2 A +(C -1)B)÷2→ D:D < 30 STEP >
OUTPUT D: sum of arithmetical progression
Execution Example:
COMP1P1
1
Calculate the sum up to the 10th term of the arithmetic progression with first term 1 and
difference term 3.
1+4+7+・・・+28=145
Prog
1
3
1 0
EXE
EXE
1
EXE
S A
S A
S A
S A
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
D R
G
G
G
G
10
Page 13

2. The sum of an arithmetic progression with first term
terms is given by
BA–
AA
-------------+
C 1–
…
B+++
C terms
Program
A
and final term B, consisting of
C
ON
MODE MODE MODE
PRGM
1
MODE
COMP1P1
1
?→ A:?→ B:?→ C:(A + B)C ÷2→ D:D < 24 STEP >
OUTPUT D: sum of arithmetical progression
Execution Example:
The of an arithmetic progression of 10th terms, with first term 1 and last term 28, is:
1+4+7+・・・+28=145
Prog
1
EXE
1
S A
S A
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
G
G
2 8
1 0
EXE
EXE
S A
S A
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
G
G
11
Page 14

07
Summing Geometric Progressions
1. The sum up to the th term of the geometric progression with first term and ratio
term may be calculated:
B
C
∑
k 1=
AB
k 1–
CA
AABAB
++ ++=
A 1 B
------------------------=
2
–()
…
n
AB
C 1–
1 B–
Program
PRGM
ON
MODE MODE MODE
1
MODE
?→ A:?→ B:?→ C:A(1- B ^ C)÷(1- B)→ D:D < 30 STEP >
OUTPUT D: sum of geometric progression
Execution Example:
COMP1P1
1
Calculate the sum up to the 5th term of the geometric progression with first term 1 and ratio
term 3.
1+3+9+27+81=121
Prog
1
3
5
EXE
EXE
EXE
1
S A
S A
S A
S A
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
D R
G
G
G
G
12
Page 15

2. The sum of a geometric progression with first term , last term and common ratio
AB C
is:
AACAC
2
…
BC⁄ B++ ++ +
ABC–
-----------------=
1 C–
Program
PRGM
ON
MODE MODE MODE
1
MODE
?→ A:?→ B:?→ C:(A - BC)÷(1- C)→ D:D < 28 STEP >
OUTPUT D: sum of geometric progression
Execution Example:
The sum of the geometric progression with first term 1, last term 81 and common ratio 3 is
1+3+9+27+81=121
Prog
1
COMP1P1
S A
1
D R
P1P1P2 P3 P4
G
1
8 1
3
EXE
EXE
EXE
S A
S A
S A
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
G
G
G
13
Page 16

08
f
f
f
f
f
Approximate solutions to higher
order equations
Let be a function continuous on the interval
that there must be at least one in with
fc() 0= c
must belong to one of the intervals. Thus by
comparing the signs of , and
we can half the interval in which we search.
Repeating this procedure will yield an approximate
solution of arbitrary accuracy.
x()
, with and having opposite signs, so
ab[,]
a()
b()
cab[,]
. If we divide the interval into two,
ab+
a()f
-------------
,
2
(bisection method)
b()
a
a+b
2
b
Program
PRGM
ON
Lbl 1:?→ A:?→ B:( )( )≧0
⇒ Goto 1:(
MODE MODE MODE
A3-2 A2-2A+4
3
A
-2 A2-2A+4
1
MODE
)>0⇒ Goto 2:B → C:A → B:C →
COMP1P1
1
3
-2 B2-2B+4
B
A:Lbl 2:(A + B )÷2 → X:X
3:X → B:Goto 2:Lbl 3:X → A:Goto 2 < 126 STEP >
Execution Example:
Find solutions to the equation . (Solutions are and )
EXE
1
1 5
Prog
1
EXE
x32x
–2x–4+0=2± 2
EXE
X3-2 X2-2X+4
2
S A
S A
S A
→ Y:Y >0⇒ Goto
D R
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
G
G
G
Disp
Disp
14
Page 17

EXE EXE
S A
P1P1P2 P3 P4
D R
G
Disp
To stop program, press the key.
AC
To calculate for other functions, alter the program where underlined.
15
Page 18

09
f
Approximate solutions to Equations
(
of higher degree
Newton’s method
)
Newton’s method is used to calculate approximate solutions to the equation . For a
initial value , the following recurrence relation gives successive approximate solutions:
x
i 1+
x
1
fx
()
i
------------–=
x
i
′
x
()
f
i
x() 0=
It should be noted that the series calculated above may not always converge, depending on
the initial value .
x
1
Program
PRGM
ON
?→ X:Lbl 1:X -( )÷( )→ X:
MODE MODE MODE
X3-2 X2-2X+4
1
MODE
X Goto 1 < 40 STEP >
Execution Example:
Find solutions to the equation . (Solutions are and )
x32x
2
–2x–4+0=2± 2
COMP1P1
1
2
3X
-4X-2
Prog
1
1
EXE
EXE
EXE EXE
To stop program, press the key.
To calculate for other functions, enter the apropriate function in the part indicated by a single
underline, and the derivative in the part with double underline.
AC
S A
S A
S A
S A
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
D R
G
G
Disp
G
Disp
G
Disp
16
Page 19

10 Limits
n
1
The value of the limit is the base of
1
lim
n
∞
→
---+
n
e
the natural logarithm, namely .
e
Program
PRGM
ON
MODE MODE MODE
1
MODE
1→ X:Lbl 1:(1+1÷ X)^X→Y:Y 2 X → X:Goto 1 < 28 STEP >
Execution Example:
x
1
Check the value of as X becomes large.
1
---+
x
COMP1P1
1
The limit is the base of the natural logarithm,
Prog
1
EXE
EXE EXE
For X too large, it may not be possible to calculate the exponent, and Y may become 1.
To stop program, press the key.
To calculate for other functions, alter the program where underlined.
AC
e
= 2.718281828.
S A
S A
S A
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
G
Disp
G
Disp
G
Disp
17
Page 20

11 Limits
It is known that the limit takes value 1.
lim
x 0→
----------
x
xsin
1
0
Program
PRGM
ON
MODE MODE MODE
1
MODE
1→ X:Lbl 1:sin X ÷ X →Y:Y X ÷2→ X:Goto 1 < 24 STEP >
Execution Example:
COMP1P1
1
Check the convergence of for values of close to 0.
xsin
---------- x
x
Rad
ON
Prog
MODE MODE MODE MODE
1
EXE
EXE EXE
When the value of X becomes too small, a “Math Error” may occur.
2
S A
S A
S A
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
R R
R R
R R
G
Disp
G
Disp
G
Disp
To stop program, press the key.
To calculate for other functions, alter the program where underlined.
18
AC
Page 21

12
Approximations of the value of definite integrals may be obtained as follows:
Definite Integrals
(Trapezoidal rule)
B
x()xd
∫
A
h
---
fA() 2fA h+()2fA 2h+()…2fB h–()fB()++ +++()≈
2
h
BA–
-------------= n
:number of trapezoids
n
For larger the approximation improves, and as
tends to infinity it agrees with the precise value of
the definite integral.
nn
a
b
Program
PRGM
ON
?→ A:?→ B:?→ C:1→ D:(√ A)÷2→ Y:Lbl 1:(A(C - D)+ DB)
÷C→X:Y+(√X
MODE MODE MODE
)→Y:D+1→D:D≠C⇒Goto 1:Y+(√B)÷2→
1
MODE
COMP1P1
1
Y:(B-A)Y÷C→Y:Y <89 STEP >
INPUT A,B : interval of integration [
OUTPUT Y : value of the definite integral
Execution Example:
Calculate the value of the definite integral .
Prog
0
1
EXE
A,B
] C: number of trapezoids
10
xxd
∫
0
20
10
-------------- 21.08185107==
3
S A
S A
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
G
G
19
Page 22

1 0
EXE
S A
P1P1P2 P3 P4
D R
G
2 0
EXE
S A
For large n, the calculation may take a considerable amount of time.
To calculate for other functions, alter the program where underlined.
P1P1P2 P3 P4
D R
G
20
Page 23

13
The value of a definite integral can be approximated by Simpsons formula,
Definite integrals
(Simpsons formula)
∫
B
fx()xd
A
h
---
fA() fB() 4 fA 2i 1–()h+()
≈
3
++ +
BA–
h
-------------= n
:number of stripes
∑
i 1=
n
n 1–
2 fA 2ih+()
∑
i 1=
2n
As becomes larger the approximation becomes better, and the limit as approaches
nn
infinity is consistent with the true answer.
In general, this method gives good approximations.
Program
PRGM
ON
?→ A:?→ B:?→ C:1→ D:(B-A)÷2C→M:√A→ Y:Lbl 1:A +
2DM-M→X:Y+4√X
D⇒Goto 1:B-M→X:Y+4√X
MODE MODE MODE
→Y:X+M→X:Y+2√X→ Y:D +1→ D:C >
1
MODE
+√ B → Y:YM ÷3→ Y:Y < 105 STEP >
COMP1P1
1
INPUT A,B : interval of integration [
OUTPUT Y : value of the definite integral
Execution Example:
10
Calculate .
Prog
0
1
EXE
∫
xxd
0
1 0
20
10
-------------- 21.08185107==
3
EXE
A,B
] C: number of stripes
S A
S A
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
G
G
21
Page 24

2 0
S A
EXE
M
For large n, the calculation may take a considerable amount of time.
To calculate for other functions, alter the program where underlined.
P1P1P2 P3 P4
D R
G
22
Page 25

14
A
Finding the area of a triangle
In general, when the length of the base and the height of a triangle are known, its area can be
calculated by (Length of base)×(Height)÷2 . However, it is also possible to determine
the area given the lengths of the three sides, using the following formula.
Let the lengths of the three sides be , and ,
and set . The area
DABC++()2÷=
calculated:
SDDA–()DB–()DC–()=
BC
S
is
A
B
S
C
Program
PRGM
ON
MODE MODE MODE
1
MODE
?→ A:?→ B:?→ C:(A + B + C)÷2→ D:√(D(D - A)(D - B)(D-C))
→ M:M < 47 STEP >
OUTPUT M : the area of a triangle
Execution Example:
COMP1P1
1
Find the area of the right-angled triangle with sides of length 3 , 4 and 5 .
(The answer may also be calculated as: 3×4÷2=6 )
Prog
3
4
5
EXE
EXE
EXE
1
S A
S A
S A
S A
M
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
D R
G
G
G
G
23
Page 26

15
The angle between two vectors
The angle between two vectors and , not equal to 0 for 0 being the origin, can be
θ
→
a
→
b
obtained in the following way:
→
→
ab⋅
cos
1–
------------=
→
→
a
b
,,()=
,,()=
3
3
a
b
θ
→
aa1a2a
→
bb1b2b
Program
PRGM
ON
MODE MODE MODE
1
MODE
?→ A:?→ B:?→ C:A → X:B → Y:C → M:?→ A:?→ B:?→ C:(AX+BY
2
+CM)÷√((A
INPUT < 1st >A,B,C:(
OUTPUT D : the angle between two vectors:
+B2+C2)(X2+Y2+M2))→D:cos-1 D→D:D < 79 STEP>
a
,
a
,
a
1
) < 2nd >A,B,C:(
2
3
θ
COMP1P1
1
b
,
1
b
,
b
)
2
3
Execution Example:
Find the angle between the vectors (0,0,1) and (2,3,4).
MODE MODE
DEG
MODE MODE
EXE
EXE
EXE
1
1
3
Prog
0
0
2
EXE
EXE
1
EXE
4
S A
S A
S A
S A
D R
P1P1P2 P3 P4
M
M
M
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D
D R
D R
G
GD
G
G
To obtain the answer in radians, press before
executing the program.
24
MODE MODE MODE MODE
2
Page 27

16
Finding the angles in a triangle
Law of cosines:The relationship between the length
of the sides of a triangle and the angle between is
given by:
2
a
2
b
c22bcθcos–+=
b
a
Solving this for we obtain the angle in terms of the
θ
lengths:
2
b
cos
1–
θ
c2a2–+
-----------------------------=
2bc
Program
PRGM
ON
? → A:? → B:? → C:C O S
MODE MODE MODE
-1
((B2+C2-A2)÷2 BC)→ D:D < 33 STEP >
Execution Example:
Find the angle in a triangle with sides of length 3, 4 and 5.
MODE MODE
DEG
MODE MODE
1
1
MODE
S A
COMP1P1
1
c
P1P1P2 P3 P4
D R
G
Prog
5
4
3
1
EXE
EXE
EXE
To obtain the answer in radians press before
executing the program.
S A
S A
S A
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
MODE MODE MODE MODE
D R
D R
D R
G
G
G
8
2
25
Page 28
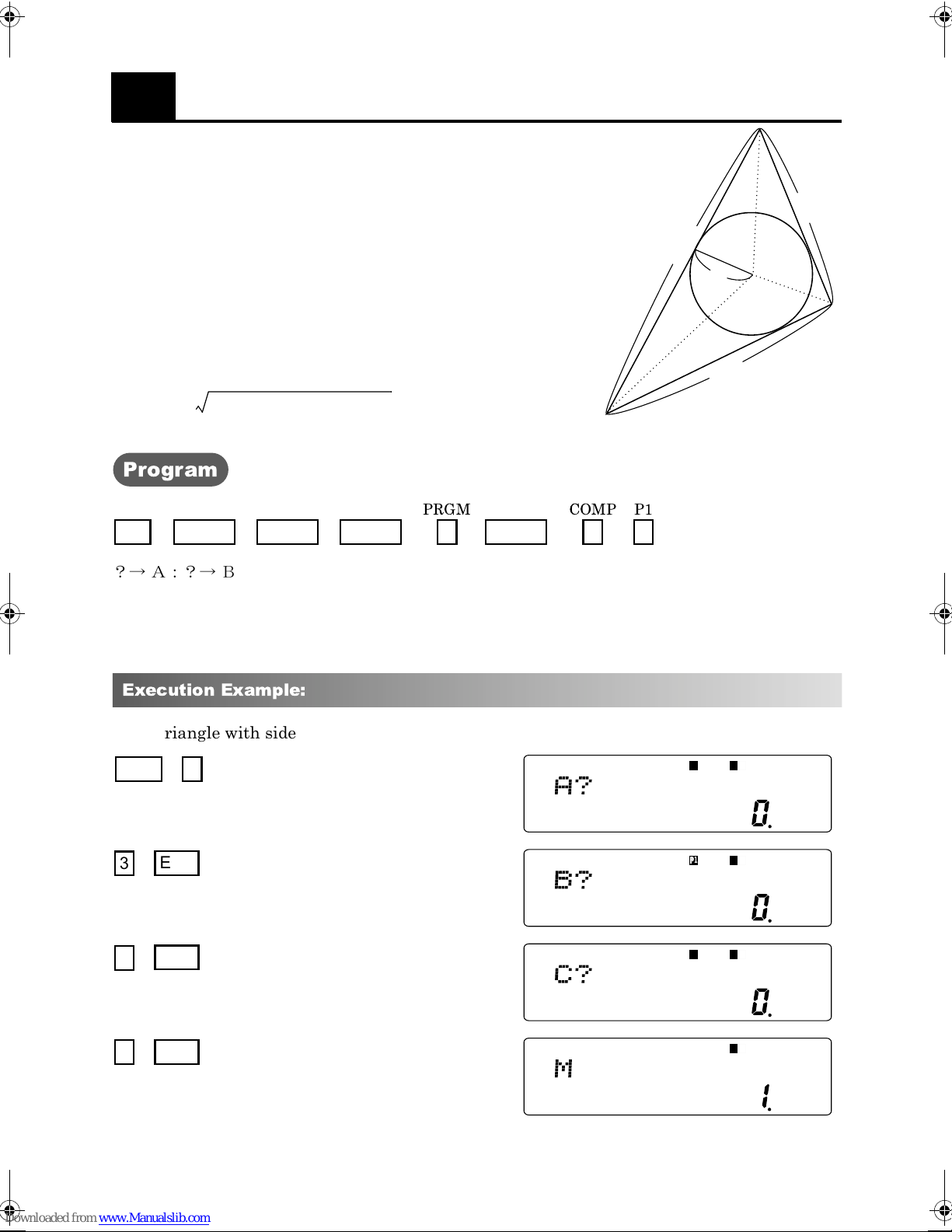
17
R
The inscribed circle is shown in the diagram on the
right.When the inscribed circle has radius , the area of
the appropriate triangle is:
The radius of the Inscribed circle.
B
AR
BR
S
------
2
Now, using herons formula it is possible to determine
the area of the triangle in terms of the length of the
three sides, whereby the radius of the circle is:
R
DD A
----------------------------------------------------------=
CR
------
------++
2
2
–()
DB
D
ABC
++()
-----------------------------==
2
–()
DC
–()
,
R
ABC
D
++
---------------------=
2
A
R
C
Program
PRGM
ON
?→ A:?→ B:?→ C:(A + B + C)÷2→ D:√(D(D - A)(D - B)(D-C))
÷ D → M:M < 49 STEP >
Execution Example:
MODE MODE MODE
OUTPUT M : the radius of the inscribed circle
1
MODE
COMP1P1
1
For a triangle with sides of length 3, 4 and 5, the radius of the inscribed circle is 1:
Prog
3
4
5
EXE
EXE
EXE
1
S A
S A
S A
S A
M
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
D R
G
G
G
G
26
Page 29

18
The radius of the Circumscribed circle
The law of sines:For △
diagram on the right, the following formula holds:
a
----------Asin
b
----------Bsin
----------- 2R===
ABC
, as shown in the
c
Csin
a
C
R
It is thereby possible, by the law of cosines and law of
b
sines, to calculate the radius of the circumscribed
circle given the lengths of the three sides of the
triangle.
=
R
-------------------------------------------------------------
sin
2
cos
A
2
C2A2–+
B
1–
------------------------------2BC
B
A
c
Program
PRGM
ON
?→ A:?→ B:?→ C:sin cos-1 ((B2+C2-A2)÷2 BC)→ D:
MODE MODE MODE
1
MODE
COMP1P1
1
A÷2D→M:M <41 STEP >
OUTPUT M : the radius of the circumscribed circle
Execution Example:
For a triangle with sides if length 3, 4 and 5, the radius of the circumscribed circle is 2.5:
Prog
3
4
EXE
EXE
1
S A
S A
S A
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
G
G
G
8 8 8 8 8 8 8 8 8 8
888888888
88
S A
EXE
5
M
P1P1P2 P3 P4
D R
G
27
Page 30

19
Center of mass of a triangle
(barycentre)
The three medians of a triangle all meet at a single
A
point. This point is called the “center of mass” (or
barycentre).
The center of mass divides each line in half.
For a triangle with corner points , and ,
AB C
B
P
the center of mass is given:
OP
OA OB OC++
---------------------------------------=
3
O
Program
PRGM
ON
MODE MODE MODE
1
MODE
?→ X:?→ Y:X → A:Y → B:?→ X:?→ Y:X → C:Y → D:?→ X:?→ Y:
(A + C + X)÷3→ X:(B + D + Y)÷3→ Y:X Y < 67 STEP >
COMP1P1
1
C
INPUT X, Y (first time):
OUTPUT X, Y: center of mass
A (X, Y
P(X, Y)
) X, Y(second time) : B (
X, Y
) X, Y(third time) : C(
Execution Example:
The center of mass for a triangle with corners A(1,0),B(0,3) and C(-1,0) is P(0,1).
Prog
1
0
EXE
EXE
EXE
1
1
EXE
0
EXE
3
EXE
EXE
0
S A
S A
S A
S A
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
D R
X, Y
)
G
G
G
Disp
G
28
Page 31

20
The distance between a line and a point
The distance between a point and a straight line
yaxb+=
, as in the diagram on the right, is given by the
formula:
ax y– b+
=
------------------------
AH
1 a2+
Axy(,)
A
(x, y)
y=ax+b
H
Program
PRGM
ON
MODE MODE MODE
1
MODE
? → X:? → Y:? → A:? → B:√((AX-Y+B)÷(1+ A2))→D:D <38 STEP >
INPUT X,Y: co-ordinates of the point
A(X, Y
) A : gradient B : y-intercept
COMP1P1
1
OUTPUT D: the distance between the line
y = Ax +B
and the point A(
X, Y
)
Execution Example:
Calculate the distance between the point (3, 4) and the straight line .
Prog
3
7
EXE
EXE
1
EXE
4
EXE
9
S A
S A
S A
M
y 7x 9+=
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
G
G
G
29
Page 32

21
→
The sum, difference and inner
product of two vectors
The sum and difference of two vectors in 3-dimensional space is obtained by adding and
subtracting their respective components.
For example, for , ,
→
→
αβ
+ abc,,()a′ b′ c′,,()+ aa′+ bb′+ cc′+,,()==
→
→
αβ
– abc,,()a′ b′ c′,,()– aa′– bb′– cc′–,,()==
The inner product is defined:
→
→
αβ⋅α
→
→
α ab
→
β
θ
cos aa′ bb′ cc′++==
→
c,,()=
β a′b
′ c′,,()=
α
β
α
β
α
β
Program
?→ A:?→ B:?→ C:A → X:B → Y:C → M:?→ A:?→ B:?→ C:A + X
→ A:B + Y → B:C + M → C:A B C 2X-A→A:2Y-B→B:2M
-C→C:A B C (X - A)X+(Y-B)Y+(M - C)M → D:D < 111 STEP >
INPUT A,B,C(first time) : A,B,C(second time):
α
→
abc,,()=
β
→
a′b′c
,,()=
′
OUTPUT A,B,C(first time) : sum of two vectors
A,B,C(second time): difference of two vectors
D : inner product
Execution Example:
→
For and ,
α
, ,
Prog
1 23,,()=
→
→
αβ
+ 3 100,,()=
1
→
β
→
αβ
– 1– 6– 6,,()=
28 3–,,()=
→
→
αβ
⋅
→
→
αβ
⋅ 9=
S A
P1P1P2 P3 P4
D R
G
30
Page 33

S A
EXE
1
EXE
2
EXE
3
M
P1P1P2 P3 P4
D R
G
2
EXE
EXE
EXE
EXE
EXE
3
8
EXE
EXE
S A
S A
S A
S A
S A
D R
M
M
M
M
M
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
D R
G
Disp
G
Disp
G
Disp
G
Disp
G
Disp
EXE
EXE
S A
S A
D R
M
M
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
G
Disp
G
88
31
Page 34

22 Rotation
(
(
(
The following matrix rotates a point , in the plane,
through an angle of in the anti-clockwise direction.
x′
y′
=
cos
sin
θ
θ
θ
sin–
cos
θ
θ
x y,
x
y
)
(x’, y’)
(x, y)
θ
Program
PRGM
x y,
1
MODE
)
x y,
)
ON
?→ X:?→ Y:?→ A:X → C:Y → D:Ccos A - Dsin A → X:Csin
A + Dcos A → Y:X Y < 43 STEP >
MODE MODE MODE
INPUT X, Y : point befor rotation A : rotation angle
OUTPUT X,Y : point after rotation
COMP1P1
1
θ
Execution Example:
Find the location of the point (1,0) after rotation through an angle of .
π
--3
MODE MODE
MODE MODE
EXE
1
0
π
EXP
Prog
1
SHIHT
EXE
Rad
EXE
2
EXE
3
S A
S A
S A
S A
D R
P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
G
G
G
G
8 8 8 8 8 8
Disp
To obtain the answer in radians, press before
executing the program.
32
MODE MODE MODE MODE
2
Page 35

23
Complex numbers and polar coordinates
As an example, for the complex number ,
we may write in polar coordinates, by letting
ω r θ
=
where .
ra2b2+
ω
cos i
θ
sin+()
a
θ
cos
---=θsin
r
ω
abi+=
a + bi
b
---=,,=
r
r
θ
The product of two complex numbers in polar form is
rθcos i
θ
sin+()r′
θ
cos i
θ
′sin+()× rr′
θθ′
+()cos i
θθ′
+()sin+()=
.
Program
?→ A:?→ B:√(A2+B2)→ X:cos-1 (A ÷ X)→ Y:X Y < 31 STEP >
a
INPUT A : real part
B : imaginary part b
OUTPUT X : the distance from the origin Y : the angle
Execution Example:
22i+=
ω
MODE MODE MODE
MODE
EXE
2
EXE
, when written in polar coordinates is .
Rad
2
Prog
EXE
2
1
ω
=
S A
S A
S A
from the real line
θ
22
---cos i
4
π
π
---sin+
4
P1P1P2 P3 P4
P1P1P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
G
G
8
Disp
G
To obtain the answer in degrees, press before
executing the program.
MODE MODE MODE MODE
1
33
Page 36

24
The inverse of a
2×2
matrix.
The inverse of the 2×2 matrix is . In other words,
1
-----------------ad bc–
As is clear from the formula above, when the denominator , no inverse exists.
db–
c– a
ab
cd
cd
1 0
=
0 1
ab
-----------------ad bc–
1
db–
c– a
a
d
bc– 0=
Program
Lbl 1:?→ A:?→ B:?→ C:?→ D:AD - BC → M:M =0⇒ Goto 1:
A→X:D÷M→A:X÷M→D:-B÷M→B:-C÷M→C:A B C D <71 STEP>
INPUT A, B, C, D : matrix
OUTPUT A, B, C, D : inverse of matrix
Execution Example:
ab
cd
ab
cd
The inverse matrix of is
EXE
EXE
1
4
4
Prog
1
2
EXE
EXE
EXE
1 4
24
EXE
EXE
1– 1
0.5 0.25–
S A
M
S A
M
S A
M
S A
M
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
D R
G
Disp
G
Disp
G
Disp
G
For , the inverse does not exist and the values and must be re-entered.
ad bc 0=– abc,, d
34
Page 37

25 Combinations
AAB
C
A
Let there be cards with the letter “”, cards with the
letter “” and cards with the letter “” written on them.
B
C
A
A
CB
Then number of possible different ways to arrange all
AB× C×()
abc++
cards in a row, is given by:
C
×
a
bc+
C
b
abc++()!
-----------------------------
a! bc+()!
bc+()!
------------------b!c!
a! 1 2×…× a×=
A
B
abc++()!
-----------------------------==
a!b!c!
B
C
A
AA
:
:
C
0! 1=
Program
PRGM
ON
MODE MODE MODE
1
MODE
?→ A:?→ B:?→ C:(A + B + C)!÷ A!÷ B!÷ C!→ Y:Y < 33 STEP >
INPUT A, B, C, : number of cards showing “A”, “B” and “C” respectively
OUTPUT Y : the number of combinations
COMP1P1
1
Execution Example:
How many combinations are possible for 3 “”s, 2 “”s and 2 “”s?
Prog
3
2
2
1
EXE
EXE
EXE
S A
S A
S A
S A
B
C
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
D R
G
G
G
G
35
Page 38

26 The binomial distribution
p
f
Assume that the probability that a tossed coin will land showing “heads” is , and that the
probability for “tails” is ( ). Then over tosses, the probability that the coin will land
1 p– x
times with “heads”-up, is:
x() C
=
mpx
x
1p–()
mx–
Program
?→ A:?→ B:?→ X:BCX × A ^ X(1- A)^(B - X)→ Y:Y < 34 STEP >
C:
nCr
INPUT A: throws B: probability of “heads” X: number of “heads”
Execution Example:
1
For a coin with probability of landing “heads”,
---
3
find the probability of getting 3 “heads” out of 7 throws.
Prog
1
S A
P1P1P2 P3 P4
D R
G
1 3
EXE
7
EXE
3
EXE
S A
S A
S A
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
G
G
G
36
Page 39

27 Confidence Intervals
For a random sample of size from normal distribution with known variance , the
confidence intervals for the population mean may be calculated as given by:
σ
x 1.64
-------
×–
µ
n
σ
x 1.96
-------
×–
µ
n
σ
-------
x 2.57
×–
µ
n
n
x 1.64
x 1.96
x 2.57
µ
σ
-------
(90% confidence interval)
×+<<
n
σ
-------
(95% confidence interval)
×+<<
n
σ
-------
(99% confidence interval)
×+<<
n
x
: sample mean
σ
2
Program
PRGM
x
1
SHIFT
:
MODE MODE
S-VAR1x
2
ON
?→ A: -1.96×√(A ÷ )→ B: +1.96×√(A ÷ )→ C:B C
< 39 STEP >
MODE MODE MODE
x nx n
n
SD1P1
1
SHIFT
:
S-SUM3n
1
INPUT A: Population variance
OUTPUT B,C: 95% confidence interval
Execution Example:
Calculate 95% confidence intervals.
Data: 1.4, 1.5, 1.3, 1.4, 1.7, 1.5, 1.3 Population variance
The interval of 95% certainty for is:
1.338< <1.548
MODE MODE
1 4
µ
SD
1
M+
DT
σ
µ
2
B
µ
C<<
2
S A
S A
σ
SD
SD
0.02=
D R
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
G
G
37
Page 40

1 5
M+
DT
S A
D R
SD
P1P1P2 P3 P4
G
1 3
1 4
1 7
1 5
1 3
M+
DT
M+
DT
M+
DT
M+
DT
M+
DT
S A
S A
S A
S A
S A
D R
SD
SD
SD
SD
SD
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
D R
D R
D R
G
G
G
G
G
Prog
1
0 0 2
EXE
EXE
S A
S A
S A
D R
SD
SD
SD
P1P1P1P1P2 P3 P4
P1P1P1P1P2 P3 P4
P1P1P1P1P2 P3 P4
D R
D R
G
G
Disp
G
Disp
38
Page 41

28
µ
2
T
est on a mean with known
σ
(z-tests)
The hypothesis of interest is that the mean is equal to a given value , versus the
alternative that it is not equal to . We calculate the test statistics
xµ–
Z
------------=
σ
-------
µ
0
µ
0
n
where is the sample mean and is the sample size. If , we reject the hypothesis
for the significance level .
For different significance levels, the confidence limits
are given below:
x nZ1.96≥
α
0.05=
α Confidence limits
0.10 1.64
0.05 1.96
0.01 2.57
-1.96
0
1.96
Program
PRGM
SHIFT
:
1
MODE MODE
σ
σ
2
2
S-VAR1x
2
ON
?→ A:?→ B:( - A)÷√(B ÷ )→ C:C < 24 STEP >
MODE MODE MODE
x n
x
INPUT A: given value B:population variance
OUTPUT C: value of Z
Execution Example:
Test : =1.2 :
H0µ
Data: 1.4, 1.5, 1.3, 1.4, 1.7, 1.5, 1.3 Population variance =0.02
0
H1µ
µ
0
1.2≠
0
SD1P1
n
:
1
SHIFT
S-SUM3n
1
`
39
Page 42

Answer
= 1.442857143
x
xµ–
Z
------------
σ
------n
As , we reject the hypothesis for the significance level
Z 1.96≥
MODE MODE
1 4
1.4428571 1.2111–
1.442857143- 1.2
-------------------------------------------------==
0.02
-------------7
1
M+
= 4.543441113
S A
S A
DT
α
0.05=
.
D R
SD
SD
P1P1P2 P3 P4
P1P1P2 P3 P4
D R
G
G
f
1 3
Prog
1
1 2
0 0 2
M+
DT
EXE
EXE
S A
S A
S A
S A
D R
SD
SD
SD
SD
P1P1P2 P3 P4
P1P1P1P1P2 P3 P4
P1P1P1P1P2 P3 P4
P1P1P1P1P2 P3 P4
D R
D R
D R
G
G
G
G
Disp
40
Page 43

29 Guess the number
Assume you wish to guess a randomly chosen number between 1 and 1000.
Simple guessing will require, on average, 500 tries to find the answer.
This program will tell you if your guess is larger or smaller than a number (which it chooses),
so that, proceeding logically, it should be possible to find the answer within 11 attempts.
Program
1000Ran#+l→X:?→A:0→D:Lbl 1:D+1→D:A=X⇒Goto
3:X > A ⇒ G o t o 2:? → A:G o t o 1:L b l 2:? → B:B → A:G o t o 1:
Lbl 3:X D < 68 STEP >
Running the Program
Prog
Enter a random number and press .
1
EXE
If the answer is smaller than the number you entered,
“A?” will be displayed.
If the answer is larger than the number you entered,
“B?” will be displayed.
When the number you enter is the correct answer,
“X” will be displayed, along with the answer
ff
S A
S A
S A
P1P1P2 P3 P4
P1P1P2 P3 P4
P1P1P2 P3 P4
R
G
R
G
R
G
Disp
and the number of attempts made.
S A
P1P1P2 P3 P4
R
G
Disp
41
Page 44

30 Various areas and volumes
A
Area: OUTPUT M: areas.
Triangle:(Base
?→ A:?→ B:AB ÷2→ M:M
Square:(Length of sides
?→ A:A2→ M:M
Rectangle:(Height
?→ A:?→ B:AB → M:M
A
)×(Height B)÷2
2
A
)
A
)×(Width B)
B
A
A
A
B
Trapezium:((Top length
?→ A:?→ B:?→ C:(A + B)C ÷2→ M:M
Circle:(Radius
?→ A:A
2
A
π → M:M
A
)+(Bottom length B))× (Height C) ÷2
)2×π
A
C
B
A
0
42
Page 45

Volume: OUTPUT M: volumes
A
Cube:(Length of sides
?→ A:A3→ M:M
Rectangular prism:(Depth
?→ A:?→ B:?→ C:ABC → M:M
A
3
)
A
)×(Width B)×(Height C)
A
A
A
C
B
Triangular, Quadrangular pyramid:(Base Area
?→ A:?→ C:AC ÷3→ M:M
Cone:(Radius
?→ A:?→ C:A
Sphere:4(Radius
?→ A:4 A
A
)2×π×(Height C)÷3
2
Cπ ÷3→ M:M
A
)3×π÷3
3
π ÷3→ M:M
A
) × (Height C) ÷3
C
A
C
A
A
43
Page 46

●
MEMO
MEMO
MEMOMEMO
●
Page 47

Authors
Dr. Yuichi Takeda Research and Development Initiative Chuo University
Page 48

 Loading...
Loading...