B&W 800 D User Manual

Development of the B&W 800D

Development of the B&W 800D

Contents

Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

Project brief . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

Overview . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

Drive units . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

Enclosures . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

Crossover. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

Performance. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

Industrial Design . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

Appendices

I Diamond Dome Tweeter. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14

II The FST Midrange Driver . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

III The use of Rohacell® in loudspeaker cones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24

IV Tapered tube theory . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

V Sphere/tube midrange enclosure . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28

VI Matrix™ cabinet . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30

VII Decoupling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32

VIII Finite Element Analysis. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34

IX Laser Interferometry. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36

3

Bowers and Wilkins’ 800 Series first saw the
light of day in 1979 with the introduction of
the original Model 801. Its radical shape,
composed of separate enclosures for each
drive unit, was to remain relatively constant for
almost 20 years, proving, like so many concepts
to come from the R&D division at Steyning, that
good ideas, based on sound principles stand
the test of time.

The development of the flagship Nautilus
speaker, launched in 1993, introduced a raft of
new ideas that clearly warranted adaptation to
a broader range of products, the result of which
was the Nautilus 800 Series. That Series was to
redefine the high-end audio speaker market and
the development of the then top model in the
range – the Nautilus 801 – was covered in a
previous paper. The subsequent development of
the Signature 800, which refined and extended
some of the principles used in the Nautilus 801,
was also the subject of a paper.

This paper describes the development of a new
generation 800 Series, using the top model
800D to describe the principles and techniques
to be found in the range. There are significant
new developments, but there is much in the
new models that carries over from the old.
These existing techniques are discussed here
once more, so that this paper may be read in
isolation, without reference to the previous
publications.

Project Brief

High-end audio products are about performance.
The investigation of new ideas, materials and
processes is a continual process, sometimes
coming as small steps and sometimes as
significant leaps. In this case, our engineers
had been pursuing several projects that
promised a significant improvement in
performance and the brief was simply to
incorporate the results into products.

Overview

A loudspeaker system can be divided into three
basic constituent parts:

• The drive units

• The crossover

• The enclosures and supporting structure

In an ideal situation, the drive units, seamlessly
blended by the crossover, should transmit
a perfect audio replica of the electrical input
signal. The rest of the structure should remain
perfectly stationary and serve only to support
the drive units, absorb the unwanted radiation
radiated from the rear side of each drive unit
diaphragm and be shaped to aid even
distribution of the sound away from the
loudspeaker. How good a speaker sounds
can be measured by how close the designer
can get to this ideal. In the real world, of
course, we fall somewhat short. Drivers suffer
from distortions of all kinds and enclosures
vibrate and add their own coloration to the
sound. Crossover components add unwanted
artifacts to the electrical signal before it even
reaches the drivers.

We shall examine our design philosophy to all
these categories separately, but in fact, in the
design process, they must be treated as a
whole, because they all interact. The choices
the designer makes in one area are affected
by what he has to work with in another.
Inevitably, choices have to be made and it is
down to the skill of the design engineer to
make a balanced judgement and optimise the
whole. It is a skill that combines science with
art. The science provides understanding and
points the way forward. For as long as the
scientific understanding is incomplete, however,
an understanding of the art of music is essential.
In high-end audio, it is not sufficient simply to
achieve a pleasant sound, the designer must
strive to recreate as closely as possible the
impression of being at an event, of being able
to imagine performers in front of the listener,
of raising the goose bumps on the skin and
hair on the back of the neck. That is the target,
and virtually impossible to describe by a set
of numbers.

The listener must be the final arbiter of how
well the target has been met. All we can do
within the scope of this paper is to examine
the science. In the sections immediately
following there is a general overview of each
of the techniques used and they are covered
in greater detail in the Appendices at the end
of the paper.

Introduction

4

Perhaps the most radical of the new
technologies used in the speaker is the
diamond dome of the tweeter. The acoustic
development is covered in detail in Appendix I.

One of the surprising outcomes of the new
design when compared with the existing
aluminium dome design is that the –6dB
frequency is lower (The blue horizontal line in
figure 4 represents the -6dB level after the
tweeters are equalised flat to 90dB by the
crossover). This may at first glance seem
strange, considering that diamond is much
stiffer and has a significantly higher break-up
frequency than aluminium. The answer is
simply to be found in the ‘ideal’ response of
an infinitely stiff dome of the same shape,
which suffers a deep dip in the response
around 70kHz because of the difference in
arrival times of sound generated at different
parts of the dome (Represented by the green
shaded area in figure 1). At 70kHz, the
wavelength of sound in air is 4.9mm (0.19 in)
at 20C, which is comparable with the height
of the dome. That the aluminium dome has
the higher –6dB frequency is simply because
the response is on the way down from a high
amplitude resonance at 30kHz.

We took the view that the diamond dome
should follow this ideal as closely as possible
and we should not attempt to achieve a flatter
acoustic response through various devices that
would either cause the total radiating area to
deliberately deviate from piston-like behaviour
at a lower frequency or by engineering cavity
effects in front of the diaphragm.

Our listening experience had repeatedly and
consistently shown that the most important
criterion affecting the sound quality was how
closely the radiating surface remained piston­like in the accepted range of human hearing
below 20kHz. We were therefore not tempted
by any perceived marketing need to follow
popular (mis)conceptions of what is required
to properly convey the improvements offered
by high sampling rate digital recording formats.
We kept the acoustic response of the infinitely
stiff dome as our target. If one removes the
acoustic time delay effects by examining the
structural acceleration response of the dome,

one sees that it is flatter and more extended,
as expected (see Appendix I).

It should be remembered that deviation from
piston-like behaviour does not suddenly happen
when the break-up resonance frequency is
reached. It builds up from a much lower
frequency. It is similar to the effect of anti­aliassing filters used in digital recording. Those
used in the standard 44.1kHz CD format may
have cut-off frequencies above the accepted
limit of human hearing, but deviations in the
phase and associated group delay begin well
below 20kHz. It is the shifting of these build
up effects well above the limit of hearing that
is most important, not necessarily maintaining
a flat acoustic amplitude response to 100kHz
or whatever, although, of course, the two
are related.

That it is possible to produce a diamond dome
at all is due to relatively recent developments in
the production of industrial diamonds.

The standard technique for synthesising
diamond is to simulate the conditions that
occur in nature, ie the high pressures and
temperatures that are found inside a volcano.
The technical difficulty in achieving temperatures
as high as 2,100C (3,800ºF) and pressures
exceeding 50 kbar limits the size and shape
of the diamond components that can be
manufactured by this process.

In the 1980s, the invention of a chemical
vapour deposition (CVD) technique for
growing diamond overcame this limitation:
the deposition temperature was halved and,
more critically, growth could now be achieved
at sub-atmospheric pressures. The technique
succeeds in producing diamond under
conditions for which graphite is the thermo­dynamically stable form of carbon by creating
a carefully balanced chemical environment
that stabilises the diamond surface as it
grows; in effect, the kinetics win over the
thermodynamics. This very specific environment
is generated by exciting a gas mixture of
hydrogen with a small percentage of an alkane
(carbon source gas) and other gases (such
as argon and oxygen). The resultant plasma
contains alkyl radicals, hydrogen atoms and

5

Drive Units Tweeter

30

20

10

0

-10

-20

-30
10000 20000 100000Frequency (Hz)

Simulated acoustic Frequency response

30

20

10

0

-10

-20

-30
10000 20000 100000Frequency (Hz)

Simulated acoustic Frequency response

1 FEA simulated acoustic responses of aluminium (top) and

diamond (bottom) domes. The response of an ‘ideal’ dome
is shown shaded in each case.

6 7

high-energy electrons. A range of power
sources can be used to excite the plasma,
the most common being microwaves, heated
filaments and arc discharges. The diamond is
deposited directly onto a suitable substrate
material, for instance tungsten, molybdenum
or silicon. This substrate can be removed after
deposition to leave a freestanding diamond
layer. The layers produced can be millimetres or
microns thick with areas greater than 100 cm2.
It is also possible to replicate complex shapes
machined into the substrate. The diamond itself
is polycrystalline and of high purity and,
because the properties are selected and
controlled, diamond materials grown by the
CVD process can actually outperform natural
diamond in many applications.

In developing the tweeter dome, B&W worked
closely with one of the world’s foremost
producers of industrial diamonds, Element 6,
based in Ascot, UK. As in so many industrial
applications, although the basic process was
well established, there were practical difficulties
peculiar to this application that had to be
overcome. Depositing diamond to the profile
of the spherical section of the dome itself
was fairly straightforward, but the vertical ring
location for the voice coil (see figure 3) proved
particularly tricky. Forming and ejecting with
parallel sides and maintaining material thickness
at the sharp corner were difficult. This part of
the profile is crucial both in ensuring repeatable
accurate location of the voice coil and also in
increasing the dome's stiffness to raise the first
break-up frequency. This is the first time such
a profile has been manufactured and the design
is patented.

The dome itself does not constitute the whole
of the radiating surface. The supporting surround
plays an important role in determining the
tweeter’s response.

During the development of the Nautilus 800
Series, deficiencies in the plastic film half roll
surround used on the then standard tweeter
design were ameliorated by using a flat foam
polymer surround. Its motion remained better
phase matched to that of the aluminium
dome and gave a smoother overall response.
However, in the new systems, we wanted to
use crossover filters with more gradual roll-off

2a

Tweeter continued

3 Diamond dome profile

5 Tweeter impedance with (red) and without (blue) a silver

layer on the magnet centre pole.

rates (see the subsequent section on the
crossover) and this necessitated lowering the
tweeter’s fundamental resonance frequency.
This could only be achieved by reverting to a
half roll profile to increase compliance, but we
were able to take advantage of a new synthetic
rubber material that avoided the shortcomings
of the original plastic film. We were thus able
to achieve good phase coherence with the
dome and usefully lower the fundamental
resonance frequency.

Frequency response deviations from the ideal
are not dependent solely on the dome and
surround. Any moving coil drive unit is a current
driven device, with the force on the voice coil
represented by the formula:

F = Bli

where F = force, B = magnetic flux density,
l = length of coil in the magnetic gap and
i = current.

Yet for various reasons, mainly to do with
controlling bass response, amplifiers are
voltage sources. The high frequency response
of a drive unit is therefore affected by the
inductance of the voice coil and, in order
to maintain high frequency response, the
inductance should be minimised. To that
end, not only does the tweeter employ a single
layer ribbon wire voice coil to minimise the
number of turns, it also uses a silver plated
centre pole in the magnet structure.

Copper is more usually used for this purpose.
The electrically conducting layer acts as a
shorted turn in the secondary windings of
what is in effect a transformer and reduces
the inductance of the primary windings (the
voice coil). Accommodating a layer of non­magnetic material widens the magnetic gap,
with a resultant decrease in flux density and
hence drive unit sensitivity. Silver, having a
higher conductivity than copper, is effective
with a thinner layer and is used here to
maximise sensitivity.

Both the tweeter and bass drive unit diaphragms
of the 800D are designed following the ‘stiff is
good’ principle. However, good reproduction in
the midrange has a particular requirement that
precludes this approach if a single drive unit
is to be used to cover the whole range. With
stiff diaphragms, the dispersion progressively
narrows as the frequency increases and the
wavelength becomes similar to or smaller than
the diameter of the diaphragm. With bass units,
this factor is never a problem, because the
wavelength is always significantly greater
than the size of the drive unit. At 400Hz,
the wavelength is just under 860mm (34 in),
compared to, say, 380mm (15 in) or 250mm
(10 in) or less for the bass drive unit. At 4kHz,
the wavelength is 86mm (3.4 in) and so with
any drive unit of a size large enough to give
high output levels with low distortion at the
bass-to-midrange crossover frequency,
beaming is likely to be a problem. Off centre
listeners are going to hear a sound with a
significantly different balance from that on axis,
and image precision will suffer.

Having established that we do want to achieve
high sound levels and do not want to use more
than one drive unit, the best option is to use a
drive unit with a more flexible cone material.
That does mean that the cone is virtually certain
to be operating in its break-up region for much
of its usable range, but the usual deleterious
effect of this (delayed resonances colouring
the sound) is ameliorated greatly if the correct
material is chosen.

Woven Kevlar®has been used by B&W since

1974. For the Nautilus 800 Series, the way we
used Kevlar in midrange-only (as opposed to
bass/midrange) drive units was improved by the
use of a new design of outer cone support or
surround. Such drive units go under the name
FST, standing for Fixed Suspension Transducer.

Midrange

For the Signature 800 and Nautilus 800, the
magnet structure was improved by using a
Neodymium-Iron-Boron (NeFeB) magnet driving
a thicker top plate. The use of a short coil in a
long magnetic gap lowered harmonic distortion
and improved detail retrieval. The reduced bulk
of the magnet had a minor secondary benefit
in reducing the bulk of obstructions behind the
cone and hence the amount of sound energy
from the rear of the cone being reflected back
through the cone to add delayed coloration.
This approach is carried over to all models in
the new 800 Series. Completely new to this
Series is the chassis (basket), which provides
greater strength than before without compro­mising the open area of the original. The use
of Kevlar®in the FST drive unit is discussed
in detail in Appendix II.

2b

2c

2 Diamond dome manufacture.

a Domes awaiting removal from the forming substrate.
b Laser cutting the outside diameter.
c Checking material thickness.

4 Responses of new diamond dome tweeter (black) and

Nautilus 800 Series tweeter (red)

14

12

10

8

6

4

Impedance magnitude (Ohms)

2

0

3

10

Frequency (Hz)

4

10

8 9

The midrange enclosure is carried over from the
Nautilus 800 Series with a small change to the
exterior design where the tweeter is mounted.
The tweeter is more enveloped, but this is an
aesthetic development with no acoustic
significance, except that the tweeter is mounted
further forward (see the section Crossover).

The unique sphere/tube design overcomes the
bandwidth limitations of simple tube loading and
is described in Appendix VI.

Because tube loading results in an overdamped
high-pass alignment, it is not applicable to
passive system bass cabinets because of the
inability to add boost equalisation. Therefore,
like the Nautilus™800 Series products, the 800D
employs a Matrix™-braced vented-box enclosure
(see appendix II).

The inertness of the cabinet is further enhanced
by using 38mm thick panels, also contributing
significant mass. In addition, smoothly curving
the rear surface greatly adds to the stiffness of
the cabinet and gives an interior shape that
modifies the internal acoustic resonance modes,
since there are fewer parallel surfaces. The
combination of an internal Matrix™construction,
together with both a massive and stiff external
‘skin’, makes the combination uniquely
resistant, not only to sound transmission from
inside to outside, but also to intrinsic cabinet
structural modes.

Bending thin wood laminations under heat and
pressure is widely used in the furniture industry
for the manufacture of chairs. However the
ability to accurately match and join two such
curved panels together without a witness
groove and to maintain the accuracy required
to fit the Matrix™panels inside is beyond the
capability of many suppliers. Special storage
conditions for the raw laminations, with
controlled temperatures and humidity are
essential and sophisticated CNC 5-axis routing
machines are required to shape the edges and
cut-outs of the curved panels.

The Tweeter incorporates Nautilus™technology
through the use of a tapered tube, filled with
wadding attached to the rear of the unit and
matching the hole through the pole (See
appendix V). The exponential profile has been
designed to ensure that the cut-off frequency
of the tube is low enough to absorb all the
energy in the operational bandwidth of the
tweeter, but allowing a shorter tube than in the
Nautilus™. It also allows the absorptive wadding
to be packed loosely at the mouth of the tube
and to become gradually compressed towards
the end. This allows the sound energy radiating
from the rear of the dome to pass through the
pole piece and into the tube without being
reflected back up towards the dome. This
variation in packing density ensures that the
acoustic impedance is varied smoothly, and
that there are no sudden changes that would
cause such a reflection of energy. As the
passband of the tweeter is similar to that in
Nautilus™, the onset of cross modes in the
tube is not a problem, occurring well above
audibility in the human ear.

A secondary use for the tube is as a heat sink.
The small dimensions of the magnet assembly
result in a low thermal mass. Making the tube
of zinc alloy and ensuring a good thermal bond
to the magnet back plate significantly reduced
the operating temperature of the unit. When
fed music from a 600W amplifier run just below
clipping, the operating temperature is reduced
by around 20C. In fact the tweeter was found
to be capable of withstanding unclipped high
frequency peaks from an amplifier rated up to
1kW, without the coil burning out. The tweeter/
tube combination is housed in an outer die-cast
shell which defines the outer housing of the
unit. The tweeter diaphragm only moves a
maximum of 0.5mm. Therefore, it is crucial

Bass Unit Enclosures Tweeter Bass

restricted and one cannot make up for lost
sensitivity by adding amplifier power, as is the
case with a powered subwoofer. So, work
began on finding a material that would add
further stiffness, increase inherent damping and
act as a better sound barrier than the materials
we had used in the past.

The material chosen has a composite sandwich
construction. Sandwich construction cones are
not new. The famous Leak Sandwich speaker
of the 1960s used a bass cone having an
expanded polystyrene core bounded by thin
aluminium skins, as did the flat fronted, oval
B139 from KEF that followed shortly after. Both
these diaphragms were thick and were a better
sound barrier than the paper cones common at
the time. However, they were fairly heavy and
expanded polystyrene as a core material can
now be improved on in terms of stiffness and
internal damping to achieve higher break-up
frequencies and better-controlled resonances.

The core material chosen was Rohacell®, again
an expanded foam material and one that is
commonly used in aircraft construction, due
to its light weight and relatively high strength.
This is bounded on both sides by carbon fibre
skins in woven mat form with a high level of
resin to add stiffness. Neither Rohacell®on its
own nor a Rohacell®/carbon fibre sandwich is
a new cone material, although the introduction
of both is relatively recent. What is novel in
the 800 Series is the cone thickness that has
been achieved through improvements in the
manufacturing process. Most Rohacell®cones
are in the 1-2mm thickness range. In the 800
Series, the core thickness is 8mm, which aids
the suppression of sound transmission
considerably.

The audible result of the new cone material,
with its enhanced stiffness and reduced sound
transmission is to improve what is referred to
as bass attack or dynamic bass. Most bass
lines in music do not consist of steady tones.
The waveforms have an extended frequency
range and the reduction in coloration in the
upper bass/lower midrange cleans up the
presentation significantly.

A detailed discussion of Rohacell®/carbon fibre
sandwich cones is to be found in Appendix III.

Midrange

to isolate it from mechanical energy arising
elsewhere in the system. To this end, the
tweeter and tube are held in the housing
with rings moulded with a Shore 1A hardness
elastomer. The housing in turn is decoupled
from the midrange enclosure below by the
use of two isolator pads of high compliance
gel material.

The top isolator has been shaped to sit in the
scallop of the midrange head enclosure and
cradle the underside of the tweeter housing.
Raised ribs have been designed into this
isolator to create maximum compliance at
this interface, in order to absorb any energy
transmission between the midrange head
enclosure and tweeter body. The bottom
isolator sits between the connector and the
underside of the midrange head enclosure
to ensure that both the sections of the Molex
cable connector are isolated from the midrange
head enclosure. The tweeter is allowed to float
free and reproduce the input signal without any
external interference.

The 800D uses two 250mm (10-in) diameter
bass drive units. At B&W, we have long
promoted the use of stiff, rigid cones for bass
drivers. Bass/midrange drivers are a different
matter, because of the same bandwidth
conditions that apply to the FST midrange
driver, but for bass-only drivers in 3-way
systems, the ability to withstand deformation
when subjected to the high pressure differences
inside and outside the cabinet is the best way
of achieving that dynamic performance often
described as ‘slam’. The stiffness also pushes
the onset of break-up to higher frequencies,
extending this piston-like behaviour.

At B&W, we have commonly used two materials
for this application – aluminium and a fibre pulp
mix of kraft paper and Kevlar, further stiffened
by resins. Both materials are stiff, but metals
in particular suffer high Q resonances outside
their working range, due to their low inherent
damping. They must be well attenuated by the
time the break-up region is reached to avoid
intrusive coloration. In the Nautilus 800 Series,
the paper/Kevlar®mix was chosen over
aluminium for two reasons:

• It was difficult in practice to form aluminium
cones of large diameter that fulfilled the bass
alignment criteria. Either they split during
forming or the thickness had to be increased
such that they became too heavy.

• Paper/Kevlar®has higher internal
damping and break-up resonances were
better controlled.

However, even paper/Kevlar®is fairly dense
and results in relatively thin section cones if a
reasonable sensitivity is to be achieved. This
can allow a certain amount of sound energy
from inside the cabinet to pass through and
cause low levels of coloration. As general
driver, cabinet and crossover quality has
improved in recent times, even this very low
level of coloration deserves corrective attention
and the sandwich construction of our PV1
subwoofer driver has shown that a thick cone
construction can have benefits in this area.

Simply adding thickness, however, is not a
universal panacea. In a passive speaker, we
cannot afford to add mass at the same time.
The choice of alignments becomes too

6 Forming curved cabinet sides at B&W Denmark

10

make it turbulent, which may be heard as wind
noise, particularly because it can excite the
organ-pipe resonances of the tube.

Far more serious problems occur when laminar
airflow tries to leave the tube at high velocities.
If the curvature of the diffuser (flare) is too
sharp, the minimal momentum of the air at the
base of the laminar boundary layer is insufficient
to pass the resulting sharp, adverse pressure
gradient without stopping or stagnation. Slightly
downstream, the pressure gradient (higher
velocity with lower pressure to lower velocity
with higher pressure) causes the flow at the
base of the boundary to reverse and a turbulent
eddy is created in the form of a rotating torus
(this is how smoke rings can be blown). The
boundary layer now becomes the region that is
between the eddy and the main flow, but it has
now separated from the surface of the diffuser.
It tries to follow the pressure gradient formed by
the turbulence, but may form more eddies trying
to do so, and so on.

The turbulent wake thus created is responsible
for the ‘chuffing’ noises that even gently flared
ports can produce under some conditions.
The separation can sometimes be so extreme
that a turbulent jet can hit a listener at some
distance from a speaker. The aerodynamics
of reflex ports is actually rather complex and
somewhat unusual in that it involves alternating
flow in two different pressure regimes (at and
below port resonance), three octaves of the
frequency spectrum (different systems have
different tunings), completely indeterminate
starting conditions and well over 100dB of
level difference.

Aerodynamics research into reflex ports at B&W
is still in its infancy. Classical wind tunnel work
is very difficult because the alternating flow
makes a mockery of smoke trails. Recent work
with Computational Fluid Dynamics has shown
that ports are very difficult to model accurately.
This is partly because of the large number of
variables, and also because the flow regime is
influenced so heavily by small-scale turbulence
creation, which is less well understood than
large-scale fully-developed turbulence (more
is known about how aircraft stay in the air than
how midge flies do). Therefore, work has been
largely empirical, using comparative rather than

11

The movement of air in and out of tuning ports,
which may represent quite a considerable
physical displacement, often causes ‘chuffing’
noises as the air interacts with the discontinuities
found at the internal and external ends of the
port tube. These noises occur as turbulence is
formed at the discontinuities. Even when the
inside and outside ends of the tube are given
smoothly rounded profiles, the problem is not
totally cured, though it is mollified.

The reflex port is a well-established device to
improve the bass response of a transducer in
an otherwise sealed box of finite dimensions.
As the power handling, excursion and linearity
of bass drivers have steadily improved over the
years, the limitations of a simple tuned port
have become apparent. At low levels the
behaviour of the air in the tube can be correctly
approximated to a solid piston bouncing on
a known air volume and at a specific tuning
frequency; a readily predictable and essentially
acoustic problem. At higher levels, aerodynamic
effects become increasingly important and the
associated loss means that a given rise in bass
driver input level will yield a smaller rise in clean
port output level. This also means that the port
is not reducing the excursion of the bass driver
as effectively and the system will thus behave
increasingly like a lossy sealed box design; the
combined effect is known as ‘port compression’
and can often create an ultimate ceiling to
achievable bass levels.

Well before any ceiling is reached, the energy
losses associated with port compression cause
problems and it is the way energy is lost rather
than the amount lost that causes serious
acoustic problems. At very low velocities, and
with a perfect entry, air travelling through a real
port tube will pass smoothly along streamlines,
which do not interfere with one another. Close
to the walls of the tube is a thin boundary layer
caused by skin friction, with a relatively high
velocity gradient. It provides the transition
between the stationary walls and the moving air.
Laminae of air rub against each other causing
pressure drag through noiseless viscous losses.
These are minimal at low levels but increase at
a geometric rate in proportion to velocity. At
high enough velocities, if the tube is excessively
long and rough (or just very rough), the high
shearing energies in the boundary layer can

Flowport

7 Representation of streamlines exiting port flare.

a Laminar airflow following curvature of flare
b Higher velocity turbulent airflow separates from surface

of flare causing large scale eddy formation

c Small scale turbulence due to dimples encourages

laminar streamlines to remain attached to boundary

a

b

c

absolute benchmarks, because it is difficult to
make reliable measurements of turbulent noise.

Theoretical predictions of air velocities down
the port were checked with a new Doppler
measurement system, to establish the kind of
flow regime operating around chuffing levels in
terms of the Reynolds number (a dimensionless
indicator of turbulence levels). This showed that,
with care, it was possible to maintain laminar

flow down the port tube, but that air could
detach from the flares at fairly modest levels.
Simply making the flares more gentle would
not guarantee silence.

Anyone studying aerodynamics will soon learn
that turbulence is not always a problem. In fact,
many aerodynamicists engineer turbulence to
their advantage (indeed, some aircraft would
not stay in the air without it). If a boundary layer
is turbulent prior to the stagnation point it will
be less inclined to separate because the base
layer has increased kinetic energy. This means
that the surface flow can be swept further
downstream before pressure conditions
stagnate it and the lower pressure in the layer
that results from the higher velocities within the
eddies adheres the main flow to the surface
profile better. Thus, small-scale turbulence can
be used to delay the large-scale turbulence
caused by separation.

Artificially creating turbulence in the air moving
down the tube can delay the onset of chuffing
to higher bass unit input levels, but problem
wind noise happens far earlier, especially when
turbulent air is sucked back in to the port as the
flow alternates. In addition, the thickened bound­ary layer effectively constricts the flow, causing
pressure drag and thus airflow compression.
This constriction also alters the effective area
of the port, which in turn affects the Helmholtz
tuning. Thus it is otherwise desirable to delay
the onset of turbulent flow down the tube to as
high a level as possible. A more optimal solution
would thus be to use a smooth tube and limit
artificial turbulence creation to the problematic
stagnation area. (figure 7)

It is quite easy to produce turbulence where
it is needed; aircraft use vortex generators,
(vertical strakes) ahead of separation points.
These strakes project into the main flow and
are very effective, but when the same technique
is applied to port flares it creates too much
wind noise at lower levels.

Enter the golf ball. It can travel twice as far
as an equivalent smooth ball because of its
distinctive dimpled surface. The dimples are
very carefully shaped to produce tiny separation
points and favourable conditions for the creation
of vortices within them. The ball is thus covered

by a thin turbulent boundary layer that moves
the separation point further round the ball. This
decreases the ball’s wake and hence its drag,
and it was this technology that was used to
improve the performance of the port flares.
Because a round port flare is axisymmetric,
it was first thought that a series of rings with
the cross section of a dimple might work (and
be easier to prototype). However, the regular
vortices formed simply became the new separa­tion points and at lower levels there was audible
wind noise because they were so abrupt. So
real, pseudo random dimples were tried on
the surface of the flare. These immediately
improved the chuffing phenomenon as
predicted, but there was still wind noise caused
by deep dimples at the edge of the tube where
flow velocities were highest. These were filled
but at the expense of earlier separation levels.

A process of experimentation refined the size,
shape and distribution of the dimples to
maximise headroom and minimise wind noise.
Small, smooth dimples are thus used where
velocities are highest and larger, more abrupt
dimples are used where velocities are lower.
This greatly refines the exit flow regime and also
ensures that a minimum of turbulence is carried
back down the tube when the flow is reversed.
It was found unnecessary to make the dimples
totally random over the whole flare, but as long
as they are locally irregular, perceptible wind
noise is incoherent and unobtrusive.

In the case of the 800D, the port is down firing,
so more wind noise is acceptable and the
dimples are optimised for maximum high level
flow. In use, the dimpled ports delay the
nuisance chuffing noise to significantly higher
levels. However, and perhaps of even greater
importance, when large-scale separation does
occur the resulting turbulence is far more
incoherent and thus less apparent. A reduction
of 6dB in certain regions of the noise spectrum
was measured, particularly around the problem
organ pipe frequencies. Port compression is
also decreased and the tuning frequency is
more stable at higher levels.

Having achieved excellent cabinets for each of
the drive units independently, it is important that
vibrations and radiation from each driver do not
leak into the enclosures of others. Decoupling
has been used extensively in the 800D to isolate
drive units, apart from bass units, from their
enclosures and the individual enclosures from
one another. A discussion of the technique can
be found in Appendix VIII.

Decoupling was not used for bass or bass/
midrange units in the Series. While it has the
potential for reducing vibration in cabinet walls,
listening tests have always confirmed that
this is more than offset by a reduction in the
speaker’s ability to portray ‘slam’. A similar
effect is noticed if the bass cabinet is not firmly
anchored to the floor, for example using spikes.
It should be noted that it is only bass drive units
that are required to operate in the stiffness
region, below their fundamental resonance
frequency. All others operate entirely in the
mass controlled region.

Decoupling

8 Gel gasket used for vibration isolation between tweeter and

midrange enclosures

12

that theoretical shape and with the units
nominally time aligned, it required the tweeter
to be connected in reverse polarity for the units
to be acoustically in phase with one another.

Reverse polarity connection of drive units has
always been avoided at B&W in recent years,
it being felt that the sound lacked coherence
and focus. There is inevitably phase distortion
and its associated group delay through any
practical crossover, but it has been deemed
preferable to restrict waveform distortion to the
limited frequency range immediately each side
of the crossover frequency rather than impose
a broadband change through polarity reversal
of any drive unit. In this case, positive polarity
connection would have led to a sharp null at
crossover, so this was avoided by realigning
the relative time delay of the drive units. Rather
than them being truly time aligned, the tweeter
is advanced by half a wavelength at the upper
crossover point of 4kHz to bring it in phase
with the midrange unit when fed with the simple
filter configuration. The addition of the drive
units is illustrated in figure 12. The tweeter sits
noticeably further forward than on the previous
series models. (figure 13)

It was strongly felt that this approach –
sacrificing true time alignment for a less
complex crossover – gave superior results
in terms of definition and imaging.

However, the bass drive unit’s high voice coil
inductance and the fact that the midrange drive
unit’s fundamental resonance frequency was
fairly close to the desired crossover frequency
meant that a higher component count was
the best solution for the bass to midrange
crossover. Nevertheless, the same in-phase
drive unit relationship and positive polarity
connection was followed.

13

Crossover Performance Industrial design

and, even though the drive units’ natural cut-off
frequencies may be well removed from the
crossover frequency, the phase response
associated with the drive unit magnitude
response usually intrudes through the frequency
range of the crossover to disrupt the way the
outputs of the two units add together.

In any case, a true 1st-order filter (assuming
one had drive units with perfectly flat responses)
is not particularly desirable. The two parts add
together in quadrature (constant 90º phase
difference) and, while this is of no consequence
in the one-dimensional world of current flowing
in a wire, when you have two drive units
separated in space, things are rather different.

On the reference axis, the responses add
together to give perfectly flat amplitude and
phase response. (figure 9)

As you change the measuring axis to move
downwards towards the lower drive unit, the
upper unit becomes delayed in time. The two
units become more in phase at crossover and
there is a peak in the response of up to 3dB.
(figure 10)

As the measuring position is moved up, the
lower unit becomes delayed and the units
become more out of phase, with a corresponding
dip in the response at crossover that reaches a
complete null when a 180º phase difference is
realised. (figure 11)

In both off-axis cases, the response oscillates
as the units go in and out of phase due to linear
time delay.

This situation of a lobe asymmetrically placed
around the reference axis is not ideal, leading
as it does to rapid changes in response with
relatively little height change. A preferable
situation is created when the units are in
phase at crossover. The lobe is aligned with
the reference axis and the same changes in
listening height result in much smaller changes
in response shape.

In the case of the midrange to tweeter crossover,
we were able to use a single capacitor in series
with the tweeter and achieve a response shape
very close to a 2nd-order Linkwitz-Riley. Like

Every effort was made to specify crossover
components of the highest calibre. The science
behind why certain crossover components
sound better than others is not fully understood.
That polypropylene capacitors sound better
than electrolytics is well accepted and can
be explained by the behaviour of the dielectric
properties as the signal changes. What is not
so clear-cut is why different capacitors, with
ostensibly the same specification, can sound
so different from one another. The difficulty in
mapping physical properties to the perceived
performance characteristics further compounds
this problem. Whilst we understand some of the
criteria, extensive listening tests are virtually
the only tool at our disposal to ensure that the
final choice of components is correct.

For the new 800 Series, we worked closely
with one of the foremost European capacitor
manufacturers to further optimise one of their
existing designs. All inductors are air core for
minimal distortion and thin film non-inductive
resistors were used in critical applications.
Where necessary for increased power handling,
the resistors are thermally bonded to the cast
aluminium plinth, which houses the crossover.

One of the notable things that comes from
critical listening tests is that, no matter how
good the crossover components are, all other
things being equal, the fewer of them there are
the better. That statement should be tempered
by the qualification that the response of the
speaker should be relatively flat with a good
phase relationship between the drive units,
but basic signal quality is never enhanced by
putting in an extra component. To that end,
one should try to minimise the component
count whenever possible.

The simplest filter configuration is 1st-order,
with a single series inductor for the low-pass
and a single series capacitor for the high-pass.
The fact of the matter is, however, that it is nigh
impossible to have a truly 1st-order crossover
in a passive loudspeaker system. One cannot
simply look at the component count. Drive units
themselves are inherently bandpass devices.
They have a 2nd-order high-pass characteristic
and usually a very high-order low-pass
characteristic. These shapes must be added
to the transfer function of the electrical network

10

dB

0

-10

-20

20 Hz 50 100 200 500 1000 2000 5000 10000 20000 50000

-30

-30

180°

Phase

0°

-180°

10

dB

0

-10

-20

20 Hz 50 100 200 500 1000 2000 5000 10000 20000 50000

-30

-30

180°

Phase

0°

-180°

10

dB

0

-10

-20

20 Hz 50 100 200 500 1000 2000 5000 10000 20000 50000

-30

-30

180°

Phase

0°

-180°

9 1st-order filter on axis

10 1st-order filter below axis

Several aspects of the speaker’s performance
are shown in figures 14 and 15, but many aspects
of performance cannot be represented simply
by a series of numbers or graphs; they can be
assessed only through careful listening tests.

The Nautilus 800 Series products always had
exceptional imaging, especially the ‘headed’
Nautilus 800, Nautilus 801 and Nautilus 802,
which was in no small measure a function of
the geometry of the enclosures. It is, for
example, quite easy to locate a central image
from a stereo pair, even when listening from
outside the area between the speakers. The
new 800 Series improves on this by adding still
better stability with a better impression of height
information. This last first became noticeable
when the simple electrical filter between
midrange and tweeter was incorporated.

The new Rohacell®sandwich cone material
delivers cleaner bass from a combination of
its higher transmission loss blocking sound
escaping from inside the cabinet more effectively
and having a more extended piston range.

However, no matter what other features the
new products employ, it is the diamond dome
tweeter that captures the imagination. What
it does not do is capture one’s attention when
listening. Rather it is an awareness that things
simply sound more natural. Bright sounds do
not become harsh, just bright. Everything is
there in correct proportion and the nuances in
the finest of detail in the input signal can be
discerned and appreciated.

Certainly the simple crossover design coupled
with the improvement in component quality
has helped bring out the full potential of the
diamond dome tweeter. It has also helped
combine the component parts of the speaker
into a coherent whole.

The styling of the 800D follows closely that of
its predecessor, the Nautilus 800. That latter
system’s bass cabinet was in fact styled
somewhat differently to the other two ‘headed’
products, the Nautilus 801 and Nautilus 802
in that the front baffle was curved round to
the base and the cabinet was supported on
the cast aluminium plinth by short pillars. That
general style has now been carried through
to the 801D and 802D. The bass grille has a
more sculpted outline compared to the original
Nautilus 800.

The Marlan ‘head’ design has altered slightly
in the way the tweeter is more enclosed by
the midrange cavity and, as mentioned above,
the tweeter is mounted further forward for
acoustic reasons.

12 graph of midrange (blue), tweeter (red) and sum (green)

responses

13 side view of tweeter on head.

14 800D – Horizontal responses and total harmonic distortion

15 800D – Modulus of impedance

11 1st-order filter above axis

10

2

10

3

10

4

30

40

50

60

70

80

90

10

0

11

0

Frequency (Hz)

Magnitude SPL (dB)

Frequency Response

Appendix I

Diamond Dome Tweeter

Introduction

B&W’s standard 26mm diameter aluminium
dome tweeter has gradually evolved over the
years to give a higher and higher break-up
frequency. The original tweeters had the first
break-up at a frequency of approximately 26kHz
whereas the latest tweeters, as used on the
Signature 800 Series, have a 30kHz break-up.
This improvement in break-up frequency has
resulted from minor modifications in the design
of the voice coil former (bobbin) such as
swaging the top edge inwards to follow the
dome profile (often referred to as crowning)
or changing its length.

There are, of course, various different flavours of
the standard tweeter in production, for example
those using neodymium-iron-boron (NeFeB) and
those using barium ferrite magnets, those with
silver coating to the pole and those without,
those with short and those with long rear
tapered tubes. Also over the years we have
used different surrounds (half roll plastic film
and flat section foam polymer), different lead­outs (beryllium copper strip and tinsels) and
a host of other variations in the quest to make
the most revealing tweeter possible.

Thus the increase in subjective performance
resulting from any increase in break-up
frequency had to be judged against a
background of many changing factors.
However, it is generally accepted within
B&W that a tweeter having its first resonance
at 30kHz sounds better than one having its
first resonance at 26kHz. This is perhaps
a little surprising when the normal audible limit
is generally considered to be 20kHz. However,
as discussed throughout this paper, there are
good reasons for pushing the break-up to very
high frequencies.

So, within B&W, there has always been a
motivation to increase the break-up frequency
of tweeters. However, over recent years,
provoked by high resolution audio formats
such as SACD and DVD-A with effective
sampling rates of 192kHz, the market has
started to demand so called Super Tweeters,
tweeters that are capable of reproducing
frequencies up to 96kHz.

The area of ultra high frequency audio in general
is somewhat controversial and debates rage
over which format is more accurate, whether
and why either format is better than standard

44.1kHz sampling rate CD, whether humans
can hear above 20kHz and so on. The resulting
lack of clarity has led the market to believe that
humans can hear above 20kHz and that a
supertweeter is therefore required to do this.
There is no credible scientific evidence at
present, that the author knows of, that proves
that frequencies above much 20kHz are audible,
and experiments to clarify this area are very
difficult to carry out.

Materials

In recent times, all B&W tweeters have used
aluminium domes. Aluminium is a comparatively
light and stiff material. This is beneficial
because, for simple structures such as domes
without formers, the break-up frequency is
directly proportional to √(E/), where E =
Young’s Modulus and  = density. Clearly
the stiffer or lighter a material is the better.
Although aluminium and titanium are good,
better materials are available. A comparison
of some relevant materials is shown below.

Material E (GPa) (kgm-3) √(E/) Relative
Aluminium 71 2700 5128 1.0
Titanium 120 4500 5164 1.0
Beryllium 318 1850 13111 2.6
Diamond 1000 3500 16903 3.3

Aluminium and titanium will give similar
performance, but beryllium is approximately

2.6 times better than aluminium and diamond

3.3 times better than aluminium in terms of
break-up frequency. To qualify this claim the
simulated (using Finite Element Analysis, FEA)
first break-up mode shape and frequency
for a 50µm aluminium and diamond dome
is compared in figure AI.1.

It is clear from the table above that diamond is
a better material to use than beryllium from a
break-up point of view. In fact diamond is the
best material to use from this point of view.
Beryllium does have the advantage, though,
of being almost half the density of diamond.
It is also claimed that beryllium has quite high
damping for a metal, though at present data
are not available to verify this claim.

Basic Tweeter Simulations

In Section 1, the superiority of diamond over
any other material from a break-up point of
view was discussed and simple simulations of
domes were used to illustrate the performance
improvements. However, what happens when
diamond is used in tweeters?

The Model

In figure AI.2 the Finite Element Model of a
tweeter is shown. In this case the surround
is not included in the model to simplify the
analysis and interpretation. Addition of a
surround generally causes a small and
consistent decrease in break-up frequency
and therefore for comparative purposes this
simplified model is justified. In addition the
surround may introduce features in the SPL
response caused by pure surround resonances
(that are largely decoupled from the rest of the
tweeter). These surround resonances will be
common, regardless of the material used
in the dome.

Modal Analysis

In figure AI.3, the first break-up frequency and
mode shape for an aluminium tweeter and a
diamond tweeter are compared. Taking each in
turn, the aluminium tweeter is shown to have
a break-up of approximately 28.5kHz. This is
a little lower than for the best current tweeters
used on the 700 Series mainly because a crown
has not been modelled. However, the result is
broadly representative of what is to be expected
of aluminium tweeters.

The diamond tweeter has a first break-up
frequency of approximately 80.8kHz. Here
the diamond tweeter is modelled with a 40µm
dome and ‘Skirt’. A 40µm thickness design
(cf 50µm aluminium dome) was chosen so
as to compensate for the increase in density
of diamond compared to aluminium ( 3500kgm

-3

cf 2700kgm-3).

In Section 1 it was discussed that the break-up
frequency of a diamond dome should be 3.3
times higher than an aluminium dome. Clearly
for the complete diamond tweeter, less of an
improvement has been achieved (approx 2.8
times). This compromised improvement results
partly because the dome thickness is less in the
diamond than the aluminium. However, a more

important factor is that the vibrational behaviour
of a complete tweeter is more complex than
for a simple dome and is partly dictated by
the former, which in this case is common to
both designs.

However, diamond domes clearly offer a means
of considerably increasing the break-up frequency
of a tweeter (at least in a virtual world).

Sound Pressure Level Response

Before comparing the aluminium and diamond
tweeters, some justification for the simulation
method will be made. Two approaches are
available: the Simple Source Method (SSM)
and the Boundary Element Method (BEM).
The SSM is the simpler, computationally cheap
technique that relies upon the assumption that
the vibrating surface is composed of a number
of simple sources, each set in an infinite baffle.
The BEM gives an approximate solution to
Helmholtz’ equation and is therefore a more
complete solution than the SSM, but at
increased computational expense. When using
the BEM there is no infinite baffle assumption,
so some kind of enclosure is required and in
this work a sphere of radius 100mm was used.

In figure AI.4, a comparison is made between
the SPL response from 1-100kHz of a standard
aluminium tweeter calculated using the SSM
and the BEM. The first thing to note is that,
with both methods, the low frequency response
is clearly wrong, as the surround and interior
acoustics have not been modelled. Secondly,
below 10kHz the BEM and SSM differ because
only the BEM incorporates the effects of the
enclosure. However, at higher frequencies,
although there are small differences between
the responses, use of the SSM is justified at
least for comparative purposes.

In figure AI.5, three tweeter responses are shown.
These are the responses of the aluminium and
diamond tweeters (with first break-up modes
corresponding to those shown in figure AI.3)
together with the response of an infinitely rigid
tweeter. The rigid response shows a character­istic roll off and deep null at approximately
70kHz caused by the interference effects owing
to path length differences, commonly referred
to as phase loss. The response of the diamond
tweeter is much closer to that of the perfect

1514

Mode 2 , 38785.9 Hz

Mode 2 , 128084.0 Hz

AI.1 First break-up mode shape and frequency for a 50µm Al

(top) and diamond (bottom) dome.
Note: In all simulations, the red profile represents the
dome’s static shape.

Mode 2 , 28556.0 Hz

Mode 2 , 80819.1 Hz

AI.2 Finite Element Model of a simplified tweeter

AI.3 Break-up frequency and mode shape for a standard Al

tweeter and a diamond tweeter

10

2

10

3

10

4

10

5

20

40

60

80

100

120

10

2

10

3

10

4

10

5

-200

-100

0

100

200

10

4

60

70

80

90

100

10

4

-60

-4

0

-2

0

0

2 2.2 2.4 2.6 2.8 3 3.2 3.4 3.6

x 10

3

-1

-0.5

0

0.5

1

1.5

2

2.5

3

3.5

4

Time (s)

Velocity re. m/s

Structural impulse response

AI.6 Diamond (red) versus aluminium (blue) magnitude (upper)

and phase (lower) responses

AI.7 Zoomed version of figure 6. Diamond (red) versus

aluminium (blue) magnitude (upper) and phase
(lower) responses

AI.8 Diamond (red) versus aluminium (blue) Structural

Impulse Response

Appendix I continued

Diamond Dome Tweeter

rigid tweeter below 20kHz than the aluminium
tweeter. More specifically, at 10kHz, the response
of the aluminium tweeter is approximately

0.8dB higher than the rigid tweeter whereas
the diamond tweeter's response differs by only

0.1dB. At 20kHz, the difference is increased to
approximately 4.6dB for the aluminium tweeter
but is less than 0.5dB for the diamond tweeter.
As discussed latter in the report, this absence
of coloration in the diamond tweeter when
compared to the perfect tweeter with a rigid
response is thought to be the reason for the
improved subjective performance.

Structural Acoustic Measurements

In the Section 2, the FEA was used to compare
the performance of aluminium and a diamond
tweeter. In this section structural measurements
are presented.

Structural Acceleration

In figure AI.6 the magnitude and phase response
for the diamond and aluminium tweeter measured
at the centre of the dome is shown and in figure
AI.7 a zoomed version is shown. The aluminium
tweeter, as expected, breaks up at 30kHz and
above this frequency a number of resonances
are apparent. The diamond tweeter’s magnitude
response is flat to approximately 40kHz before
rising to a break-up frequency of approximately
74kHz.

Note: this flatness of acceleration response is
really what should be quoted in specifications;
it indicates a purity in real performance which is
not obscured by acoustic effects such as phase
roll-off. A flat acoustic frequency response can
only be achieved by utilizing break-up.

Before 74kHz a number of small features are
evident, the most pronounced being a small
peak at approximately 65kHz. The cause
of these secondary features is not clear
though they could be as a result of surround
resonances, tube resonances, rocking of the
dome, etc.

The phase responses of the two tweeters start
to deviate from approximately 15kHz (figure AI.7)
with approximately 4 degrees difference at
20kHz. Though the phase responses are similar
to 15kHz, the magnitude responses for the two
tweeters show a far greater difference (approx

0.5dB at 10kHz and 3dB at 20kHz) and differ­ences are evident from approximately 10kHz. As
the simulations show in figure AI.5, we expect
the output of the diamond tweeter to be lower
than the aluminium tweeter – though care must
be taken as here we are comparing an acoustic
simulation with a structural measurement.

Structural Impulse Response

Figure AI.8 shows the structural impulse
response of a point at the centre of the two
types of tweeter (sampling rate 204.8kHz).
Both responses show approximately the same
rise time and overall low frequency response (to
be expected) but the response of the aluminium
tweeter is characterised by a high frequency
ripple which results from the 30kHz resonance
of the structure. When both responses are low
pass filtered to exclude information above
20kHz no significant difference is evident
(not shown). This makes sense because,
as has been shown in Section 3.1, below 20kHz
the phase responses show only very small
differences at relatively high frequencies
(though there is some magnitude difference).

Structural Time-Frequency Plots

In figure AI.9 the time-frequency responses
(created using a Wavelet transform) for diamond
and aluminium and tweeters are shown. There
are obvious differences in the transforms above
20kHz owing of course to the change in
frequency of the break-up frequency. However
below 20kHz the responses are largely the same.

Note: the apparent small resonant tails below
20kHz are thought to artefacts of the analysis
method. It is uncertain whether the resonant
tails between 20kHz and 60kHz in the diamond
tweeter are artefacts or not. The increased
amplitude of these tails compared to those
below 20kHz suggests they are genuine. It is
possible that like the small features apparent
in the structural frequency response they are
caused by surround or tube resonances.

Acoustic Measurements

In section 3, structural measurements were
presented that highlight the differences between
diamond and aluminium tweeters. In this section
acoustic measurements are presented.

On-Axis SPL response

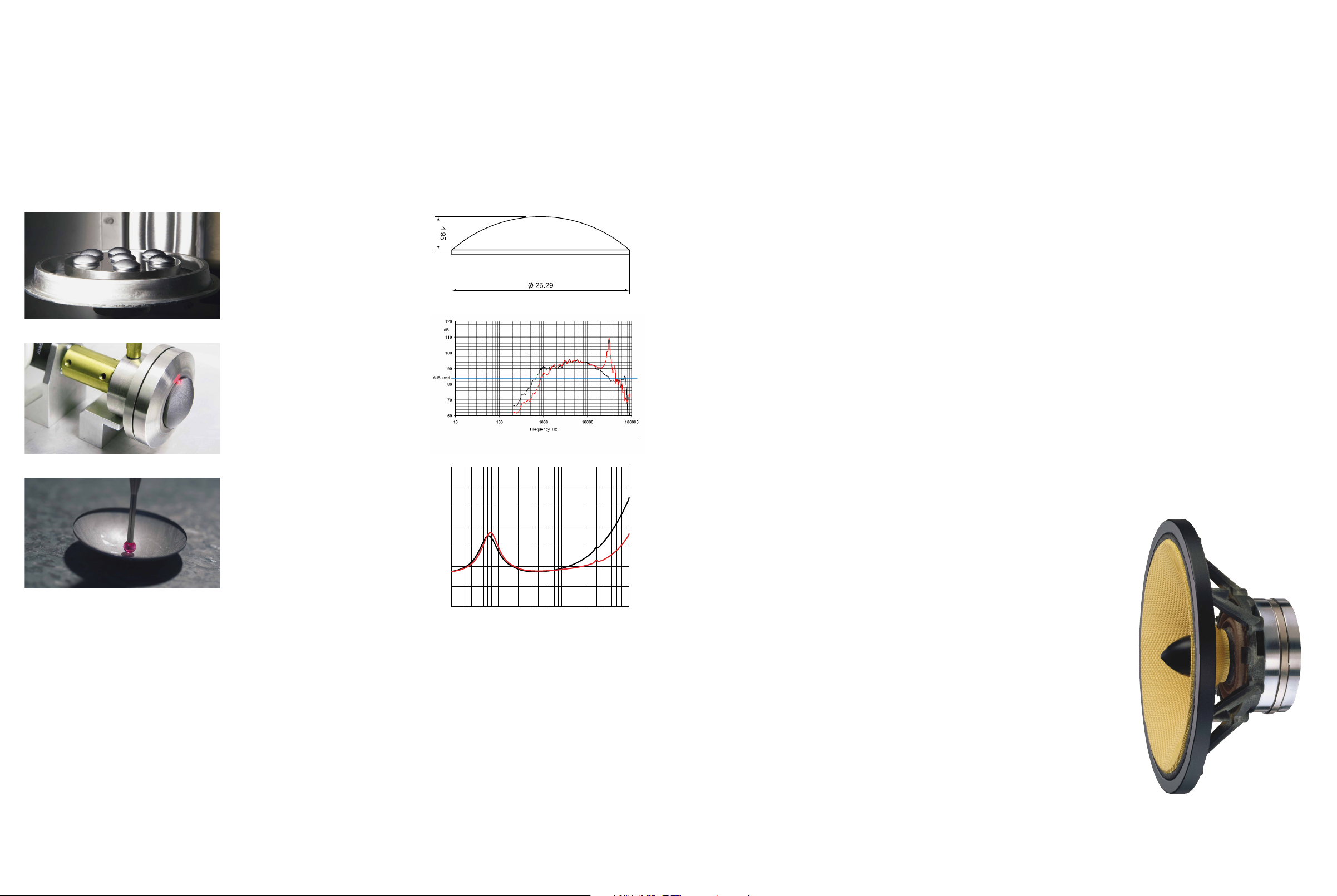
In figure AI.10, the on-axis SPL response for an
aluminium and diamond tweeter are compared.
The aluminium tweeter breaks-up at approximately
30kHz as expected. However, it is not so clear
from this plot at what frequency the diamond
breaks-up. The response of the diamond rolls
off smoothly to approximately 45kHz owing
to ‘phase loss’ (this effect is apparent in the
simulations). Above this frequency the response
rises before exhibiting two small peaks at
approximately 63kHz and 74kHz. Above
74kHz the response of the diamond tweeter
rolls off sharply.

As was shown in section 3 the actual break-up
frequency of the diamond tweeter is at 74kHz,
which compares to approximately 80kHz in
the simulation (see figure AI.3). The lower
frequency in the real tweeter is due to the effect
of the surround and uncertainty of the material
properties of the former/dome glue joint.

The peak in practice is much lower than in
the simulation. This is thought to be in part
because damping properties of the surround
at any frequency but especially high frequencies
are not known. Another explanation may be
that the peak is superimposed on a sharply
falling response so it appears to be lower than
it is. Another factor is likely to be the effect of
air absorption.

The degree of absorption is highly dependent
on factors such has humidity, temperature
and, of course, frequency. However, to illustrate
the effect, at 80kHz, 70% humidity and at
20 degrees, attenuation is approximately
3dB/metre. See (1) for a detailed discussion
of the effect of air absorption.

In figure AI.11 the acoustic phase response
of the aluminium and diamond tweeters are
compared. Below 20kHz the two responses
are similar but the aluminium shows anomalies
above this frequency. The phase differences
apparent in the structural measurements
(figures AI.6 and 7) are not so obvious in the
acoustic response.

The acoustic impulse response

Finally in figure AI.12, the acoustic impulse
response for aluminium and diamond tweeters
is shown. Whilst at first glance this looks like
convincing evidence that the diamond is better
than the aluminium; the leading edge of the
main pulse seems to be steeper than that of the
aluminium that could be equated with a ‘faster’
sound. The faster rise time would also equate
with more HF information. However when
considering figure AI.10, it might be concluded
then that the aluminium tweeter would have the
fastest rise time.

When the responses shown in figure AI.12
are low pass filtered to 20kHz (not shown) the
resulting impulses look largely the same. The
conclusion then is that the differences in rise
times are the result of ultrasonic frequencies –
though it is possible to argue that this result
is curious looking at figure AI.11. Thus the
responses in figure AI.12 are misleading and
are shown here just for completeness.

Distortion Measurements (an aside)

Other than the removal of the distortion features
that result from the 30kHz aluminium tweeter
break-up, there is no real reason that diamond
should be more linear than aluminium. THD+N
measurements for diamond and aluminium are
shown in figure AI.13, for reference. Below
3kHz, which is better depends on the frequency
considered and this variability is thought to be
more to do with manufacturing differences than
anything else (and this manufacturing variability
confounds all detailed comparisons of distortion).

1716

10

3

10

4

10

5

-25

-20

-15

-10

-5

0

5

10

15

20

25

Frequency (Hz)

Sound pressure level (dB)

Acoustic frequency response

AI.4 The SPL response of an Al tweeter calculated using

the SSM and the BEM

AI.9 Time-Frequency plots of aluminium and diamond

AI.5 The SPL response of aluminium, diamond and perfect,

rigid tweeters

110

100

90

80

70

Sound pressure level (dB)

60

50

3

10

Acoustic frequency response

Frequency (Hz)

4

10

BEM
SSM

5

10

there is no known credible evidence that
airborne sound can be perceived above 25kHz.

Against this background, there are a number of
controversial works that challenge the established
conclusions. In particular in (7), it is concluded
that ultrasonic information modifies measurable
brain response. This is not the same as normal
auditory perception. Instead it is postulated that
ultrasound could have a direct impact on the
brain. This work is the subject of debate.

Undoubtedly further experiments will be carried
out in this area, although convincing conclusions
will be difficult to make. Such experiments are
very difficult to carry out owing to the problem
of keeping a like-for-like comparison before and
after addition of ultrasonic information. One big
problem is that of intermodulation resulting from
speaker nonlinearity. Remember, another issue
that confounds this debate is the fact that the
ear is not linear (see figure AI.16) and therefore
does not perform a perfect Fourier transform.

So far, the bandwidth of the ear has been
discussed. Although related in a linear system
at least, there is some debate over whether
our hearing system can resolve very small time
differences. Two cases are to be considered.
Firstly, events that are closely separated in
time, implying fine monaural resolution and
consequently high bandwidth. Secondly,
binaural time difference errors, such as
differential dispersion or delay between
channels that help build up the auditory scene.
A number of investigations conclude that the
lowest limit of temporal resolution for both
monaural and binaural events is approximately
10µs (8-10).

So, on the one hand the audibility of ultrasonic
frequencies is not accepted by the audio
community, but on the other, 10µs time
discrimination is, which in a linear system
(which the ear is not) would imply a 50kHz
audible bandwidth.

As an aside, could the 10µs time discrimination
limit be an explanation as to why the diamond
tweeter sounds better than the aluminium
tweeter? In section 3.1 it was discussed that,

19

Appendix I continued

Diamond Dome Tweeter

However both the aluminium and diamond
tweeters have greatly improved distortion
compared to the Nautilus 800 tweeters or even
the Signature 800 tweeters. This is thought to
be firstly because the coil position has been
adjusted slightly to be correctly centred in the
gap and secondly because of the use of the
new roll surround. Over the important range,
from 3kHz –10kHz the distortion maximum is

0.4%, with dips as low as approximately 0.26%.

On standard CD programme, there is little infor­mation above 20kHz and almost none at 22kHz.
However, with high definition audio, information
up to 96kHz can be present. Thus considerable
effort was made to differentiate between diamond
and aluminium when applying a multitone
excitation from 20-40kHz and measuring the
resulting intermodulation distortion. Unfortunately,
without applying excessive power, little
difference could be found.

However, in figure AI.14, the distortion resulting
from a 20-40kHz multitone excitation applied
to a Nautilus 800 Series tweeter with a foam
surround and a new aluminium tweeter with roll

surround. The new tweeter gives up to 12dB
lower distortion at some frequencies.

On High Frequency Audibility

An excellent paper that touches on the issues
of high frequency audibility and high sampling
rates and which is also a good source of
references is (2, especially117-132). Much of
the following is paraphrased from this paper:

The advent of higher sampling rate formats
such as DVD-A and SACD have provoked
a debate over high frequency audibility. It is
generally accepted that higher sampling rate
formats sound better. Is this really because
high frequency components (above 20kHz)
are directly audible or because the increased
sampling rate gives a bigger gap than 44.1kHz
sampling, between 20kHz and the sampling
frequency, thus allowing for less severe filters
and/or less aliassing?

It is undoubtedly true that musical instruments
contain ultrasonic components. For example a
cymbal, which is said to have more content
above 20kHz than any other instrument, has
40% of its power in this range (3). However is
this audible?

It is worth first recalling briefly the function of
the ear. See figure AI.15 for a cross section of
an ear showing the three main sections; the
outer, middle and inner ear. The frequency
response of the outer and middle ear has a fast
cut-off rate owing to the combined action of
the acoustics of the ear canal and mechanical
transmission loss (4), typified by the well-known
Fletcher-Munson Curves (note the non-linearity).

The cochlear, the main structure of the inner
ear, behaves as a bank of mechanical filters
with the highest frequency filter closest to the
eardrum (the membrane separating the middle
from the outer ear). The centre frequency of the
highest filter is approximately 15kHz and data
suggests it has a bandwidth of 2kHz (5,6).
There is some evidence that supersonic
information that does manage to get to the
cochlear (by bone-conducted sound rather than
through the filters of the outer and middle ear),
ends up in the high frequency bin. However,

18

AI.11 Aluminium (blue) and diamond (red) phase response

AI.12 Impulse response of aluminium (blue) and diamond (red)

AI.15 The ear

AI.16 The Fletcher-Munson Curves

10

0

10

1

10

2

10

3

10

4

10

5

-140

-120

-100

-8

0

-6

0

-4

0

-2

0

Frequency (Hz)

SPL, dB (ref. 20uPa @1m, 2.84v)

10

3

10

4

10

1

10

0

10

1

Frequency (Hz)

THD+N, % ref fundamental

AI.14 Intermodulation distortion resulting from a multi-tone

stimulus 2-40kHz. aluminium tweeter with a roll surround
(Blue) and a foam surround (Red).

10

2

10

3

10

4

10

5

-200

-150

-100

-5

0

0

50

100

150

200

Frequency (Hz)

Phase, deg

AI.10 Blue – aluminium, Green – diamond acoustic frequency

response

AI.13 THD+N for aluminium (blue) and diamond (red)

105

100

95

90

85

80

75

70

SPL, dB (ref. 20uPa @1m, 2.84v)

65

60

2

10

1

0.

8

0.

6

0.

4

2

0.

0

0.2

Pressure amplitude

0.4

0.6

0.8

4.5 4.6 4.74.84.9 55.1

10

3

Frequency (Hz)

Time (ms)

4

10

5

10

2120

Appendix II

The FST Midrange Driver

At first sight 'perfect piston' drive units, (ie
those that move rigidly without bending and
with a total freedom from resonances), would
appear to satisfy the ultimate requirement for
perfect sound reproduction. However, there
are two limitations to this approach. Eventually,
even very stiff materials exhibit break-up and,
when they do, the resonances tend to be very
severe due to the low inherent damping of stiff
materials. Thus, one must ensure that the low­pass filter of the crossover to the next higher
drive unit can be set at least 1.5 and preferably
2 octaves below the first resonance frequency.
One must also have regard to the fact that the
loudspeaker has to convert a one-dimensional
electrical signal into a three dimensional sound
field. Beaming or directivity effects limit the
useful bandwidth of the drive unit. Much
research has shown that a wide and uniform
directivity pattern is important in creating a more
realistic sound image and enabling off-centre
listeners perceive a correct balance. In order to
maintain a more uniform off-axis response, one
must normally restrict the unit’s bandwidth to
below that frequency where the wavelength is
equal to the circumference of the diaphragm.

In the 800D, a single midrange drive unit is
required to cover the range 350Hz to 4kHz,
with useful output outside this bandwidth. At
the lower limit, the cone must be large enough
to radiate high sound pressure levels without
an excessive amount of excursion that would
compromise non-linear distortion. A very
stiff cone of that size would then exhibit the
resonance and beaming limitations outlined
above at the top end of the range. One must
therefore opt for the controlled break-up
approach and use a more flexible cone material.

The break-up pattern of woven Kevlar®has
proved beneficial for use in midrange and
bass/midrange units, being superior to
many other materials, not only because of
the inherent properties of Kevlar, but also
because the woven cone is not axi-symmetric.
We have used laser interferometry to examine
the motion of the surface of cones. In the
illustrations, the basic shape of the cone is
not evident, because velocity and not absolute
position is being measured.

In figure AII.1, there are two impulse progression
plots relating to a homogeneous plastic cone (a)
and a woven Kevlar®cone (b). In each case, the
drive unit voice coil is fed an electrical impulse.
In flexible materials, a bending wave is initiated
at the centre and moves out towards the rim of
the cone. Here we are looking at this bending
wave shortly after the impulse has been applied
and motion is still restricted to the area immedi­ately around the centre, but already the wave
front in the Kevlar®cone has begun to take up
a square shape imposed by the weave, as the
speed of the bending waves in the direction of
the fibres is significantly different from that at
45º to them.

As the bending wave progresses, the circular
form is maintained in the plastic cone. When the
wave hits the roll surround, most of the energy
passes into the surround, but because of the
surround's different mechanical impedance,
some of the energy is reflected back down the
cone. Further reflection takes place where the
surround is glued to the chassis and at the
centre of the cone where it joins the voice
coil, both again due to changes in mechanical
impedance. This wave motion up and down the
cone continues until internal damping dissipates
the energy as heat and, because the concentric
waves are efficient in radiating sound, the
motion is heard as delayed coloration.

In the woven Kevlar®case, these reflections
still occur, but at different times in different
radial directions. The non-symmetrical motional
pattern is less efficient at radiating sound,
because there is an almost equal area moving
forwards as there is moving backwards. So,
although there is cone break-up going on, there
is much less audible delayed coloration as a
result and the Kevlar®cone drive unit sounds
cleaner. (figure AII.2)

Up to now, we have examined cone behaviour
when excited by an impulse. If steady state sine
wave signals are applied, individual resonance
frequencies may be identified as the wave
reflections set up standing waves in the
cone/surround combination whenever a whole
number of half wavelengths exactly fits the out
and back path. In a single continuous material,
the standing wave patterns are the familiar
shapes shown in figures AII.3a & b.

AII.1a

AII.1b Bending wave progression in plastic (a) and woven

Kevlar

®

(b) cones shortly after an impulse signal has

been applied.

AII.2b Bending wave progression in plastic (a) and woven

Kevlar

®

(b) cones after reflections at boundaries.

AII.2a

References

1 Bazley, E.N. (1976) Absorption in Air at

Frequencies up to 100kHz. NPL Acoustics
Report Ac 74

2 Stuart, J.R. (2004) Coding for High-

Resolution Audio Systems, Journal of
the Audio Engineering Society, 52 (3)

3 Boyk, J. (2003) There is life above 20kHz!

A Survey of Musical Instrument Spectra to

102.4kHz, www.cco.caltech.edu/~boyk/
spectra/spectra.htm

4 Moore, B. J. C. Frequency Selectivity in

Hearing, Academic Press, New York

5 Moore, B.J.C and Patterson, R.D. (eds)

(1986) Auditory Frequency Selectivity, Buus,
S. et al. Tuning Curves at High Frequencies
and Their Relation to the Absolute
Threshold Curve, Plenum Press, New York).

6 Shailer M.J. et al. (1990) Auditory Filter

Shapes at 8 and 10 kHz, J. Acoustic Soc.
Am., vol 88 141-148.

7 Oohashi et al. (1993), On the mechanism

of Hypersonic Effect, Proc. Int. Computer
Music. Conf., Tokyo, Japan.

8 Nordmark, N.O. (1976) Binaural Time

Discrimination, J.Acoust Soc. Am.,
Vol 35 870-880.

9 Henning, B. G. (1974) Detectibility of

Interaural Delay in High-Frequency
Complex Waveforms, J. Acoust Soc.
Am. Vol 55 84-89

10 Klump, J.O and Eady, H.R. (1956)

Some Measurements of Interaural Time
Difference Threshholds, J. Acoust. Soc.
Am., Vol 28 859-860

11 Krumbholz, K. and Patterson, R.D (2003)

Microsecond Temporal Resolution in
Monaural Hearing without Spectral Cues?
J. Acoust. Soc. Am., Vol 113 2790-2800

at 20kHz, the structural phase response of the
two tweeters differs by 4 degrees (although this
difference is not apparent in the acoustic phase
response). A 4 degree phase difference at
20kHz relates to a timing error of approximately

0.5µs – well below the established threshold.

Discussion

Undoubtedly the diamond tweeter is a
significant improvement over the aluminium
tweeter in terms of audibility. Words and
phrases that are used to describe the
performance of the diamond tweeter are
effortless, detailed, producing a realistic sound
stage, the tweeter disappears and the tweeter
being well integrated with the system.

From an objective point of view the diamond can
be demonstrated to give a response more like
a perfect dome tweeter than the aluminium.
This is particularly evident when considering the
acoustic or structural magnitude response of
the system. There are smaller differences with
the structural phase response. Despite consider­able effort to demonstrate a difference in time mea­surements (below 20kHz), little could be found.

At this stage the detail as to why the diamond
sounds better than the aluminium tweeter is
not clear. Whilst we can say the diamond’s
response is more perfect in the sense it is
closer to an infinitely rigid tweeter (and this is
quite compelling), the actual reason in terms
of factors we normally consider, such as
phase, timing etc is not clear. Are the relatively
small differences more significant than
established wisdom would suggest or are
we looking in the wrong direction? Could,
for example, the perceived improvement in
performance be something to do with radial
modes? Experiments will continue.

Appendix I continued

Diamond Dome Tweeter

2322

Appendix II continued

The FST Midrange Driver

AII.6b

AII.6c Cone motion of plastic cone (upper) and FST (lower)

drive units at 210Hz (a), 690Hz (b) and 1890Hz (c)

AII.5 Cone motion of plastic cone (upper) and FST (lower)

drive units at 210Hz (a), 690Hz (b) and 1890Hz (c)

AII.6a

The proportions change somewhat in the case
of a cone attached to a (mechanically different)
surround. The cone is stiffer and will not bend
as much as the surround and the bending wave
velocity is much higher. The modified modal
patterns are illustrated in figure AII.4. The node
cusp shifts towards the cone to surround
junction. The fundamental resonance results
in a peak in the steady-state amplitude
response, when the outer edge of the cone
and the surround both move more than in the
simple pistonic motion case. The first harmonic
involves the cone moving more than it should in
one direction, while the surround moves in the
opposite direction. Whether this results in a dip,
peak or no change in the amplitude response
depends on the relative area velocity of the
cone and surround, but more often than not it
is a dip, often referred to as the surround dip.

These standing wave patterns can be modified
if attention is paid to the mechanical impedance
of both the surround and the voice coil. If these
can be matched to the mean mechanical
impedance of the outer rim and neck of the
cone respectively, bending wave reflections can
be reduced in magnitude, with a consequent
reduction in the level of delayed energy
coloration. The situation is a mechanical
analogy of the electrical practice of terminating
a coaxial cable with a resistor of a value equal
to the characteristic impedance of the cable.

It was found difficult fully to address both of
these criteria in a bass/midrange drive unit,
where the need to have a large excursion at low
frequencies imposes specific demands on the
design of both the surround and the voice coil.
If, however, one restricts the bandwidth to
midrange frequencies, there is much more
freedom to address the mechanical impedance
requirements.

In the case of the voice coil, this involves setting
the correct mass, which needs to be less than
that of a typical long-throw coil. In the case
of the surround, the solution was found by
replacing the normal half roll surround by a
foam polymer edge support that sits under the
rim of the cone and is compressed or stretched
as the cone moves back and forth (see figure
AII.5). The woven nature of the Kevlar®cone
does mean that the cone's mechanical

impedance is not the same at all points on the
circumference, but the particular support
material specification was chosen to have an
impedance as close as possible to the mean
value of the cone and
to be highly resistive. Thus not only does more
bending wave energy pass into the support,
but much of it is dissipated as heat before
reflection can take place at the boundary with
the chassis.

This is the basis of the FST (Fixed Suspension
Transducer) midrange drive unit. Laser measure­ments of the motion of the diaphragm and
support of the FST Kevlar®unit compared
to the motion of a plastic cone with rubber
roll surround are shown at three significant
frequencies in figure AII.4. In each case, the
FST drive unit is the lower of the two plots.

At 210Hz (figure AII.6a) we have the fundamental
standing wave shown clearly in the case of the
plastic cone, where the surround is moving in
the same direction as the cone, but with
excessive amplitude. At 690Hz (figure AII.6b),
the plastic cone is showing the first harmonic
and the surround is moving in the opposite
direction to the cone. At both these frequencies,
the FST cone is moving as a coherent whole.
The hole in the middle is simply a consequence
of the unit having a fixed central phase plug
and so there is no motion.

At 1890Hz (figure AII.6c), the plastic cone is
exhibiting a higher mode resonance. The
Kevlar®cone is beginning to break up and
one can detect the four-fold peak pattern
at the outer edge that is a consequence of the
material's woven nature. Like in the case of the
bending wave progression plot, this pattern
builds in the outer part of the cone to be largely
self-cancelling, leaving a smaller inner region as
the major sound radiating area. The effective
radiating area has roughly halved by 4kHz
and halved again by 6kHz, with a consequent
improvement in off-axis response compared
to a rigid piston.

a

b

AII.3 Standing wave patterns in a single continuous material

Fundamental (a) and first harmonic (b) node

a

b

AII.4 Standing wave patterns in a combination surround and

cone Fundamental (a) and first harmonic (b)

Rohacell case the mode at 1000 Hz is clearly
visible, though curiously the higher 2kHz mode
seems to have increased in frequency to
approximately 2.2kHz.

Transmission Loss

To assess the transmission loss for the paper
and Rohacell cones the following experiment
was carried out. An 8-inch driver was placed in
an enclosure, a whole cut in the outside of the
box and samples of 15-inch cones in the two
materials were rigidly mounted in the hole
(both at the edge and the neck of the cone).
The hole in the centre of the cone was blocked.
A measurement of the SPL was taken for the
two cones in the same position, approximately
1cm from the surface of the diaphragm.

In figure AIII.6, the measured responses clearly
show that the Rohacell has higher transmission
loss than the paper. For example, the
transmitted response through the Rohacell
cone is approximately 7dB lower at 300Hz
than for the paper cone.

Conclusions

A Rohacell/Carbon Fibre diaphragm is stiffer,
better damped and has higher transmission loss
than a Paper/Kevlar Diaphragm.

25

Appendix III

The use of Rohacell

®

in loudspeaker cones

Introduction

For the Nautilus 800 bass unit a combination
of paper and Kevlar fibres with a high resin
content was used for the diaphragm material.
This combination of materials resulted in a very
stiff cone. For the 800D, the bass performance
has been improved further by using of a
sandwich of 8mm Rohacell between two layers
of carbon fibre. In this report, measurements are
presented that show the differences between
Rohacell/Carbon Fibre and Paper/Kevlar cone
bass units.

Material Considerations

Rohacell®is a polymethacrylimide- (PMI-)
hard foam, that is used as a core material for
sandwich constructions. It shows outstanding
mechanical and thermal properties. In
comparison to all other foams it offers the
best ratio of weight and mechanical properties
as well as highest heat resistance. It comes in
different forms, but the material we are using
(Rohacell 31) has low density (31kgm-3) though
with low Young’s modulus (36MPa compared
to paper in the region of 2000MPa). It has
favourable (ie high) damping.

At first glance it might be thought that Rohacell
would be a worse material to use than paper.
The standard measure of dynamic stiffness
that we use is the ratio of stiffness to density.
Rohacell is very approximately six times worse
than paper according to this measure.

However, because the material is of such low
density, it is possible to use carbon fibre skins
while not adding excessive mass. These skins,
together with the Rohacell, result in a composite
that has high stiffness and damping, as will be
demonstrated in the following measurements.

Another important point to note is that the
transmission loss through the resulting
composite is higher than for paper. This is
because a relatively thick cone can be used,
owing to the low density of Rohacell.

Structural Measurements

The Structural Impulse Response

In figure AIII.1 the structural velocity response of
paper and Rohacell to an impulsive excitation is
compared. These plots highlight several advan­tages of Rohacell over paper. The most obvious
difference is the higher damping level, indicated
by a response with fewer wiggles. More generally
the Rohacell response indicates fewer resonant
features and a faster impulse (apparent when
looking at the response, both consistent with
improved stiffness of the composite.

Frequency responses and scans

In figure AIII.2, the average acceleration frequency
response of all the points comprising a surface
scan is shown for a paper and a Rohacell cone.
This clearly shows that the first main break-up
frequency for the Rohacell cone is higher than
that for the paper cone. Both graphs have
a common feature at approximately 320Hz,
which requires further investigation. Above this
frequency the paper has resonance frequencies
at approximately 700Hz and 1300Hz and the
Rohacell at approximately 1000Hz and 2000Hz.

The graph in figure AIII.2 clearly demonstrates
that the Rohacell is stiffer. In figure AIII.3,
scans at a number of frequencies are shown
for the two cases. At low frequency the
Rohacell bass unit is clearly more pistonic than
the paper. Another obvious feature at higher
frequencies is that the Rohacell bass unit rocks
less than the paper.

Time-Frequency Representations

In figure AIII.4, the wavelet transform has been
used to produce a time-frequency plot of
velocity at the edge of the cone in the two
cases. Once again the greater stiffness and
damping of the Rohacell is clear.

Acoustic Measurements

SPL Measurements

In figure AIII.5, the acoustic impulse and
frequency responses are shown, together with
the time-frequency plot for the paper and
Rohacell cones. These plots do not really tell
us any more than the structural plots shown
in Section 3. Once again the Rohacell is clearly
stiffer and better damped than the paper.
In the paper case (figure AIII.5, top) the 700Hz
and 1300Hz modes are clearly visible. In the

24

0.005 0.01 0.015 0.02 0.025 0.03 0.035

-5

0

5

10

15

20

25

x 10

3

Time, s

Magnitude, m/s/s

Paper
Rohacell

0.005 0.01 0.015 0.02 0.025 0.03 0.035

-0.01

-0.005

0

0.005

0.01

0.015

0.02

0.025

0.03

Time, s

Magnitude, m/s/s

Paper
Rohacell

10

1

10

2

10

3

10

4

-25

-2

0

-1

5

-1

0

-5

0

5

Frequency (Hz)

Magnitude, re. 0dB=1m/s/s

Average structural acceleration

Paper
Rohacell, 8mm

AIII.1 The velocity responses of paper (blue) and Rohacell (red)

cone bass units to an impulse measured at (top) the
neck of the cone and (bottom) the edge of the cone.

AIII.4 Cycle-Frequency plots created using the Wavelet

Transform for (top) paper and (bottom) Rohacell cones.

AIII.6 Frequency response exterior to a clamped cone, excited

via an internal speaker

AIII.5 Impulse (upper), frequency (middle) and time-frequency

(lower) plots of a paper cone (top) and Rohacell cone
(bottom) obtained using the Wavelet transform

AIII.2 Average structural acceleration response

AIII.3 Scans of Paper (left) and Rohacell (right) at 350Hz,

1375Hz and 2000Hz

120

Paper cone
Rohacell cone

110

Background noise

100

90

80

70

Absolute SPL, dB

60

50

40

2

10

Frequency (Hz)

3

10

Finite Element Analysis Abstract

The Finite Element Method was used to analyse
the interior acoustic field of an inverted horn
system. The finite element model was verified
by comparing simulated and measured sound
pressure level responses at an interior point.
Contours of equal pressure phase were used
to visualise the interior acoustic field. It is
concluded that the frequency range over which
the system can be used, is restricted by an
upper frequency which is dependent on the
diameter of the horn.

Introduction

A common source of distortion in loudspeaker
systems is internal acoustic resonances of the
cabinet. High pressures can build up behind
drivers at internal resonance frequencies of the
cabinet, which affect the movement of the driver
and thus colour the far-field sound. A solution
to this problem is to use an inverted horn. A
carefully designed inverted horn offers a smooth
change in acoustic impedance which, when
used in conjunction with an absorbent material,
can result in a cabinet structure free of internal
acoustic resonances.

In this paper, the results of Finite Element
Analysis (FEA) of a prototype inverted horn
designed for use in conjunction with an upper
midrange dome are reported. Initial listening
tests of the prototype revealed distortion
occurring at approximately 10kHz. The Finite
Element Method (FEM) was used to isolate
the cause of this distortion.

The finite element model is described in ‘The
Finite Element Model’. In ‘Verification of the
Finite Element Model’ the model is verified
against the sound pressure level (spl) frequency
response measured at an interior point. Finally,
in ‘Analysis of the Internal Pressure Field’ the
interior sound field is analysed in more detail.

The Finite Element Model

The FEM is a mathematical technique that can
be used to produce approximate solutions to
partial differential equations. By utilising the FEM
it is possible to carry out computer simulations
of structural and acoustic systems. This paper
is not intended to explain the FEM in detail. For
detailed descriptions of the FEM applied to
loudspeaker design see (Refs1+5), for example.

The main point is that by applying the FEM,
a virtual prototype can be constructed on
a computer that can reflect the real world
with sufficient accuracy to be useful in the
design and analysis of loudspeaker systems.
In this case a commercial FE package called
PAFEC FE (Refs 6-7) was used to carry out
the analysis.

The real prototype was composed of a 43mm
diameter aluminium dome driver and an
exponentially decreasing horn of length 680mm.
The interior of the horn was filled with polyester
fibre wadding, a material commonly used to
absorb unwanted sound. Figure AIV.1a shows
the FE model of the inverted horn prototype.
Note that the model was axisymmetric.

The model was composed of both structural
and acoustic finite elements. Structural finite
elements were used for the horn sides and the
dome driver. The structural break-up of the
dome driver was not modelled in detail and rigid
motion (constant acceleration) was imposed.
Detailed modelling of this component was
considered unnecessary as initial measurements
discounted structural break-up to be the cause
of distortion occurring at 10kHz. Acoustic finite
elements were used to model the wadding.
(figure AIV.1)

Verification of the Finite Element Model

To gain confidence in the accuracy of the FE
model a measurement of the spl response
at an on-axis point approximately 50mm from
the back of the driver was made using a
microphone inserted through the side of the
horn. This is compared to the simulated spl
response at the same point in figure AIV.1b.
Clearly the general trend is the same in both
cases – after an initial rise the responses
decrease with frequency to approximately
10kHz where a spike occurs.

27

Appendix IV

Tapered tube theory

26

The differences between the measurement and
the simulation probably arise because of:

• Small differences in measurement
position.

• The simulated response being taken
at a point whereas the microphone
essentially averages over an area.

• Simplification of the geometry in
the FE model.

• Uncertainty as to the acoustic
impedance of the wadding.

However, the correspondence between the
simulated and measured spl response is
generally good and it is therefore assumed
that the whole of the interior acoustic field
is modelled with sufficient accuracy.

Analysis of the Internal Pressure Field

To gain insight into the nature of the interior
acoustic field, animations of equal pressure
magnitude and equal pressure phase were
made. Such animations are a powerful means of
visualising the interior acoustic field. Contours of
equal pressure phase especially are significant
because wave fronts move in directions normal
to these. Snap shots of equal-pressure phase
animations are shown in figure AIV.2.

At 5kHz it is clear that the inverted horn is
behaving as expected – the direction of
propagation is down the tube. However, at
10kHz there is clear evidence of a resonance
across the diameter of the tube. This ties in well
with the spl responses shown in figure AIV.2 a-b,
where a spike is visible at approximately 10kHz.
At 11kHz, it is apparent that the main direction
of propagation is down the horn but with a
component across the diameter (this is very
clear in animations).

Concluding Discussion

The problem cross-diameter resonance could
be removed or the effects reduced by using:

• a more effective wadding

• a tube placed inside the horn

• a flatter radiator which would not

excite diameter modes so strongly.

Each of these cases were analysed using the
FEM and all resulted in either removing or
reducing the 10kHz spike. However, none offer
a realistic solution to the problem.

It is clear from the results presented in this
paper that inverted horns are only effective
up to a certain frequency dependent upon
its diameter at the throat. This is perhaps an
obvious result but by using the FEM the effects
can be quantified and clearly visualised.

Sound Propagation down Nautilus™Tubes
(Phases & Frequencies)

a Top plot shows a plane wave

moving smoothly down a Nautilus

™

tube at low frequencies.

b Middle Plot shows the wave at the

cut-on frequency of the first-order
mode of propagation. This occurs as
a resonance across the tube width.

c Bottom plot shows the propagation

above the cut-on frequency. Energy
then moves down the tube as a
combination of plane waves and first
order modes.

Note: all pipes and ducts will allow plane-only
waves to pass down them below a certain
frequency that depends on their cross sectional
dimensions. Above a first critical cut-on
frequency waves can also propagate in a zig
zag fashion along the tube. The angle of the zig
and zag changes with frequency and is at right
angles to the length of the tube at the cut-on
frequency – which therefore shows up as a
cross mode. Higher-order modes of propagation
also have their own cut-on frequencies, which
will also show up as cross resonances at higher
and higher frequencies. For best effect
therefore, Nautilus™tubes can only be used

AIV.1 The Finite Element Model

Upper – the entire mode,
Lower – close-up of the driver end

AIV.1b Interior SPL responses simulation

AIV.1a Interior SPL responses measurement

b

up to the cut-on frequency of their first higher­order mode. Ref: Book ‘Mechanical
Waveguides’ by Martin Redwood.

References

1 Jones, C.J.C

(1986) Finite Element Analysis of
Loudspeaker Diaphragm Vibration
and Prediction of the Resulting Sound
Radiation, PhD Thesis, Brighton
Polytechnic.

2 Jones, M.A, Henwood, D.J.

and Fryer P.A.
(1992) A Computer Model of the
Vibration and the Sound Radiated by
Loudspeaker Models and its
Validation, Acoustics Letters, 15(8)

3 Henwood, D.J.

(1993) The Boundary Element Method
and Horn Design, The Journal of the
Audio Engineering Society, 41(6).

4 Geaves, G.P.

(1995) Modelling and Optimal
Design of Loudspeaker Diaphragms
Using Numerical Methods,
PhD Thesis. University of Brighton.

5 Geaves, G.P.

(1996) Design and Validation of a
System for Selecting Optimised
midrange Loudspeaker Diaphragm
Profiles, The Journal of the Audio

Engineering Society, 44(3).
6 PAFEC Limited. (1984) PAFEC Theory
7 PAFEC Limited (1995) PAFEC-FE

Acoustics User Manual Level 8.1

a

b

c

AIV.2 Simulated results showing contours of equal pressure

phase a 5kHz, b 10kHz and c 11kHz

to be matched to the impedance of the driver
opposite to them in the sphere for maximum
power transfer from sphere to tube. Also, if
the taper rate is increased further, the horn
cut-off frequency will be correspondingly
increased, and with it the changes in acoustic
impedance that this represents. So these
changes will intrude into the pass band such
that the beneficial effects may be expected
to decrease. Furthermore, a closed-end horn
appears to be better than an open ended horn,
partly because the fundamental is at a higher
frequency and is therefore shorted out more
by the sphere. (figures AV.6)

The combination of GRP and Fibrecrete used
to construct the experimental enclosures did
not lend itself to mass production and so an
alternative material was required. It had to be
stiff and heavy to minimise vibration levels in the
walls and be mouldable into the complicated
shape required. The material chosen – Marlan®,
a synthetic resin – proved ideal for the applica­tion when used with the decoupling techniques
described below.

It appears, then, that the combination of a
sphere plus a tapering tube is greatly superior
to a simple sphere or a tube on its own.
Furthermore, when an easily achievable value
of absorption is placed in both the sphere and
the tube, closed at the far end, the remaining
small resonance effects present with the empty
sphere and tube combination are removed. The
ability to reduce the amount of internal wadding
maintains transparency on listening.

with the end of the first tube having the same
diameter as the beginning of the second tube.
However, when this routine was used to simulate
a sphere (modelled as a real box) with a pipe
attached, the theoretical results did not tally
with the experimental results at all. The
resonances in the real example corresponded
only to those found in the pipe part of the
combination, rather than to those of the box
and the pipe taken separately, and to those
of the combination of the two – which the
theoretical modelling showed. (figures AV.1, 2, 3)

Changing the modelling of the sphere to a
simple lumped parameter volume, but keeping
a ‘proper’ tube plugged into this, gave much
more realistic results, which agreed closely
with experiment. It seems that an empty sphere,
on its own, at the rear of the speaker acts
as a high Q resonance with Bessel function
harmonics. However, as soon as a hole is cut
into the sphere, particularly if it has the same
diameter as the driver, and a Nautilus™-style
tube is plugged into it, the sphere resonance
is greatly defused. The sphere then behaves
almost completely like a lumped parameter
spring, even with no absorption present in either
sphere or pipe. We are then only left with traces
of the resonances due to the length of the pipe
alone. Merely cutting a hole in the sphere,
with no tube present, gives rise to a classic
Helmholtz resonator, which has the usual low
frequency resonance, but which does not
stop the sphere’s internal resonances at high
frequencies to anything like the same extent.

The next step, having proved that the analytic
modelling tallies remarkably well with the
measurements (figures AV.4, 5), was to see
how much the various dimensions of the tube
could be pared down. Reducing the length to
around 300mm and increasing the taper rate
from -3 to -11 gives similar results to the long
tube with minimal absorption present, though
now the fundamental tube resonance frequency
is shifted into the region where the ‘shorting
effect’ of the lumped parameter volume reduces
its amplitude. If the diameter of the large end
of the tube is reduced to be smaller than that
of the driver, the effect of this appears to be
deleterious. This is because the acoustic
impedances of the near end of the tube and
of the matching section of the sphere both have

29

Appendix V

Sphere/Tube Midrange Enclosure

It was known that a simple Nautilus™tapered
tube would not work well over the bandwidth
required of the drive unit (see appendix II),
so other enclosure configurations were
investigated. In particular, a sphere is well
known to give a smooth diffraction-free exterior
shape. Initial experimentation was directed at
investigating how the performance was affected
by the size of the sphere and how the drive unit
was mounted in it. In all cases, the spheres
were constructed from a GRP outer shell, lined
on the inside with Fibrecrete. A sphere of
around 300mm proved to be the best size. Any
larger and imaging seemed to be impaired. Any
smaller and the unit sounded ‘closed in’. This is
a difficult phrase to explain succinctly, but is
akin to having traces of the effect obtained by
cupping the hands round one’s mouth when
speaking. The same effect is heard if tubes are
used above the frequency of the onset of cross
modes and this gave a clue as to what was
happening in the sphere.

In fact the way the drive unit chassis fitted into
the sphere was found to have a similar effect,
which was only removed if both the inside and
outside surfaces of the sphere blended
smoothly with the rim of the chassis. This
involved the sphere having a thin wall close to
the unit and so to maintain overall stiffness of
the enclosure, internal and external spherical
profiles were offset, with the internal sphere
centre being brought forward.

The sphere supports strong internal cross
modes, evident in delayed response waterfall
plots. These could only be damped by using
copious amounts of wadding inside the sphere.
Listening tests, however, revealed a loss of
transparency with this approach, even when
the waterfall plots apparently indicated a good
result. The combination of a sphere and an
inverse horn was then investigated both
experimentally and theoretically. Measurements
were made of spheres closed and open, with
and without absorption being present and
then with an added Nautilus™-style rear tube,
which had an open end and was either empty
or filled with absorption. Meanwhile some
theoretical predictions of these systems were
made to see which tallied with the reality.

To a reasonable degree of approximation a
sphere can be modelled internally by a pipe of
length and diameter equal to the diameter of
the sphere and having the same volume. When
this is done, the simulated cone output agrees
remarkably well with the measured output for
a cone in a closed sphere or cubical box.
The only difference between the box and the
sphere appears to be in the frequencies of the
harmonics. In a sphere these follow Bessel
function zero crossings, which are spaced
differently from those in a pipe, whose
resonances essentially follow a sine wave’s zero
crossings. However, the form and amplitude of
the response shape is remarkably similar. Exact
analytic modelling of a sphere adds only a little
extra accuracy to these features.

When a tube is added to the back of the
sphere, the combination might be expected to
behave like two tubes in series. To model this
involved the modification of existing modelling
routines to allow for a change in diameter at the
intersection of the two tubes. Previously there
had only been the possibility of a smooth join,

28

AV.3 Long Rear Inv Horn + short Tube

AV.1 Box and Sphere Internal & External Effects

AV.2 Prediction of simple sphere and piston responce

including external acoustic effects

AV.4 New Midrange Unit (measured)

In a Sphere – no absorption present – 1/24 Octave

AV.5 New Midrange Unit (measured)

In a Sphere with a Tube with absorption in Sphere and Tube

AV.6 Some simplified vector representations of the radiation

from a diaphragm visualised as a number of
omnidirectional high frequency virtual point sources.
This shows how the sphere/tube combination minimises
reflections back to the diaphragm.

Note: lossy wadding is placed in sphere and tube
and diaphragm’s rear suspension disperses/absorbs
coil area reflections

cheapest answer.

Conclusion

B&W’s patented Matrix™enclosure reinforce­ment system was used in the Matrix™801 to
greatly reduce cabinet vibration effects. Even
when using very strong and massive laminated
wood enclosures such as those found for
instance in the Signature™800, there will always
be cabinet panel resonances in evidence
without Matrix™stiffening. These, though they
may have been reduced in magnitude by the
cabinet’s own mass and stiffness and by the
judicious use of strategically placed bracing
members, will still radiate to some extent. This
radiation is compounded by the much larger
area that the whole cabinet represents when
compared with the area of the drive unit
diaphragm itself. This means that unwanted
movement of the cabinet’s surface must be
reduced to the smallest levels achievable. This
is where the Matrix™system comes into play
as shown in the next few pictures.

Effect of Matrix™Technology.

Cabinets damaging sound
(Impulse Plots, figure AVI.2a, b etc)
Lower image shows cabinet side
without Matrix™.
Upper image shows effect of Matrix

™

on cabinet side vibrations.

The lower picture shows the effect of an
impulse being fed into a speaker on the right
hand side, (not seen), at right angles to the side
we are looking at. Initially we see the impulse
spreading over the visible cabinet side and
ringing on for a very long time after that.

The upper picture shows the same speaker and
cabinet side, but now there is a Matrix™present.
The effect of the Matrix™is to virtually remove
all traces of the cabinet vibration except
immediately behind the speaker unit. The
vibrations have been reduced by at least 45dB.
In this illustration, the cabinet was made of thick
MDF material, (glued compressed sawdust),
often used in speaker cabinets.

31

Appendix VI

Matrix

™

cabinet

The phenomenon of cabinet radiation has been
recognised for as long as loudspeakers have
been used in boxes. In theory, the function of
the box is to act as a perfect obstruction to
the acoustic field generated within it by the
rear radiation from the drive units. Even vented
enclosures rely on the panels containing,
without deflection, the pressure element of
the resonant action of the port.

Of course, real materials have finite loss and
stiffness and hence will deflect in an acoustic
field, and the problem has been to minimise
this movement by judicious use of the available
materials within the constraints of economics
and ergonomics.

In general, at low frequencies the stiffness of
the walls dominates their behaviour, while at
high frequencies it is their mass which rules.
Between these two extremes they interact in
a resonant manner which can grossly magnify
and time smear the transmission at certain
frequencies. This situation is rendered tolerable
by resistive losses or damping.

In general one is trying to maximise all these
variables, although at times it can make more
sense to ensure that a resonance is outside the
frequency band to be used than it is to keep it
subdued with the use of mass or damping.

The stiffness of a panel for a given mass can
be increased dramatically by curving it. Hence
axially loaded tubes and spheres have long been
recognised as the most efficient users of mate­rials, though in our rectilinear society they have
usually been relegated to more exotic designs.

The mass of panels can be increased simply
through the use of dense material. Bricks, lead
and sand layers all offer increasing attenuation
with frequency, but these are all definitely for
the DIY enthusiast.

In the real world, cabinets were made of wood
with various degrees of panel bracing and
damping, like bituminous mats and suchlike,
which also helped increase the mass. By
increasing both the mass and the stiffness,
the lowest point in the curve corresponding to
the minimum transmission loss may be brought
up to reasonable levels. (figure AVI.1) In 1983

Celestion revealed their SL600, which for
the first time used Aerolam™panels in which
two sheets of material are separated by a
honeycomb structure. This structure makes the
best of a given mass and thickness of material
by ensuring that all forces act in the plane of
its sheet components. This greatly increases
the transmission loss at low frequencies by
extending the stiffness region of the curve
upwards in frequency. The result was a stiff
rather than light enclosure, with high frequency
resonances near the coincidence critical
frequency, which required damping with thin
pads. Aerolam™is, however, rather costly and
difficult to work with, and the lightness of the
panels makes the mass law part of the curve
lower than usual, which allows high frequencies
to be transmitted through the cabinet panels.

The Matrix™approach to the problem is to
extend the honeycomb principle of Aerolam

™

to the full width of the enclosure. The walls are
then being supported across their full area and,
in the limit, require no bending stiffness at all,
the displacement being entirely dependent on
the longitudinal stiffness and acoustic velocity
in the honeycomb.

To provide the support of the three pairs of walls,
an orthodox structure is preferable to the honey­comb. A wine box inspired the final structure of
the Matrix™which has now become a standard
feature in all the high-end B&W models.

The result when using wood is a cabinet that
exceeds the stiffness of Aerolam™for low
frequencies, has a higher mass for better high
frequency transmission loss, and the high
inherent damping of wood composites over
aluminium significantly damps the inevitable
resonances, which now occur at much higher
frequencies. The overall mass of the cabinet
is higher than that of Aerolam

™

, which is an
essential element in a decoupled driver
configuration, where it acts as a seismic mass
arrangement.

The B&W CM1 for instance traded mass for
stiffness by using a rigid phenolic resin cabinet,
which shifts the resonances well out of band.
Other ideas like moulded trays or 3-dimensional
weaving have all been examined but the original
‘low-tech’ solution still offers the simplest and

30

AVI.2a Whole Cabinet side Impulse Progression Plot,

at 480 u-sec

AVI.2b Whole Cabinet side Impulse Progression Plot,

at 1740 u-sec

AVI.2c Whole Cabinet side Impulse Progression Plot,

at 2010 u-sec

AVI.2d Whole Cabinet side Impulse Progression Plot,

at 3330 u-sec

AVI.1 Mass Law + Stiffness + Coincidence

The effect of the decoupling spring losses was
then investigated. As expected when the losses
are total (ie Q(decouple) very small) the system
defaults to a normal speaker plus chassis plus
enclosure. As Q(decouple) is increased, the dip
and peak in the response become more and
more pronounced. The effective Q of the lump
of test rubber was approximately 20, which
gave the correct ratio between peak and dip in
the response. Next, a more normal speaker
system was investigated and families of curves
were produced varying such parameters as
Q(decouple), the frequency of the magnet
resonating on the decoupling spring, and
so on. From these curves it becomes apparent
that either the decoupling resonance should
be very low, or it should be the same as that
of the cone mass resonating on the combined
stiffness of its suspension and the air in the
enclosure. In the interests of mainting
consistency of performance with variations in
the driver fundamental resonance frequency,
the former option was adopted.

Finally, the volume velocity being fed into the
cabinet was plotted – this of course is the
reason for decoupling the magnet in the first
place and it should be reduced as much as
possible within the pass band. Curves are
shown with the decouple frequency being
1Hz and Q(decouple) being 20. It is seen
that very little volume velocity is being fed into
the cabinet. Comparing this when Q(decouple)
is small and F(decouple) is 20 shows the size
of the relative problem that proper decoupling
will solve.

So decoupling is effective if it is correctly applied,
the big danger being that the resonance of the
magnet on the decoupling spring may fall within
the pass band. If that is the case, there will
be a peak and a dip in the response the size
of which depends on the decoupling spring
losses. Of course, the larger the losses the
less effective the decoupling will be.

Use of decoupling in the 800D

The 800D uses extensive vibration isolation
to minimise cabinet resonances and driver
interactions in a similar way to the previous
Nautilus 801 and Signature 800. The techniques
used have drawn from B&W research work,
which has shown, both theoretically and

practically, the benefits of decoupling. This work
has also shown how and where decoupling is
best applied, as well as the problems that can
arise if performed incorrectly.

Good isolation between components is relatively
easy to achieve on the laboratory bench, but
engineering it into a rugged product would have
been far more difficult without the application of
a new material. It is vital to ensure that the
fundamental spring /mass resonance of any
reliable decoupling scheme is below the
operating frequency range of the speaker
drive unit. If this is achieved then any damping
control is unnecessary and even undesirable. To
achieve the lowest resonance the spring must
be soft and the mass must be high. The trouble
has always been getting a soft spring to support
a high mass within tolerances. The midrange
driver isolation of the Nautilus™801, duplicated
in the 800D, was a particular challenge and one
that drove the search for new materials.

Despite the huge mass and stiffness of the
midrange enclosure, decoupling the midrange
driver from it produces huge reductions in
cabinet vibration. However, there must be
a complete seal that fits within the required
acoustic shape and point contacts (fixing
screws are undesirable because they
unnecessarily excite higher order modes).
A tensioned rod system was devised to hold
the driver against the cabinet with complete
axisymmetry. It was then necessary to find a
very compliant material to mate them.

Foams were easily soft enough but unable to
support a load long-term. Heavily plasticised
materials could be found with the low Shore
hardness required, but leached or crept in
the long-term and were often too lossy to be
effective across the band. Unfortunately, a fairly
large gulf separated the hardness of these
materials from the usable, homogenous, stable
rubbers – even the softest silicones. Armed
with an idealised specification, the purchasing
team succeeded in a more extensive search for
super-soft rubber suppliers.

The material finally chosen was an ultra-soft,
thermoplastic rubber, injection moulded using
cross-linked gel techniques. This material is
effectively a liquid suspended with complete

33

Appendix VII

Decoupling

Appendix VI continued

Matrix

™

cabinet

Points to note are

• A Matrix™completely prevents the box sides
vibrating where it connects to them

• A Matrix™damps out any remaining vibrations
in the much smaller unsupported regions

• Cabinet radiation is reduced by at least 45dB
relative to no Matrix™present

Effect of Insufficient Transmission loss inside to
outside (Impulse Plot) figure AVI.3

The plot shows the transmitted vibration of the
side of a long tubular cabinet in response to an
input impulse fed to a drive unit at the left hand
side. So we have distance from left to right, and
time moves away from us up the page.

Points to note are:

• The initial impulse moves from the speaker
at the left, along the tube from left to right

• It is reflected at the right hand side and moves
back again along the tube from right to left

• The wave speed can be determined from
the acute angle of the initial movement to
the x axis

• This is the speed of sound in air, not in the
material of the box

This clearly shows that the box is not massive
enough to stop the sound from leaking out
through the material of the box itself.

Note: that a vibration in the chassis of the driving
speaker can be seen at the left hand side.

The Effects of the Decoupling Spring on
Speaker Performance

The effects of the decoupling spring between
the magnet chassis and the speaker box have
been investigated theoretically and experimen­tally verified. The main results of this are hardly
surprising – the resonance frequency of the
magnet plus chassis on the decoupling spring
stiffness should be as low as possible to avoid
any undesirable effects on the speaker’s
response in its pass band. Also, if the resonance
frequency of the magnet plus chassis on the
decoupling spring, is the same as that of the
speaker cone on the combined stiffness of its
suspension and the air in the box, then there is
no effect on the speaker’s response. This latter
effect would drift in production and is probably
not a desirable solution to the decoupling
problem. The effects of the spring losses on
the response have also been investigated.

Method

As in time honoured style, an equivalent circuit
was derived by inspection for the three masses
and three springs and one force generator,
all fully floating, which this complete system
comprises. The fact that all three masses were
fully floating contributed to the difficulty of
finding the correct equivalent circuit, because
a reference to ground is always required for
equivalent circuit analysis. Once a mechanical
circuit had been derived, the ‘voltage’ electrical
model was derived from that mechanical circuit
with capacitors being equivalent to masses and
inductors to springs. Then the dual of that
circuit was produced to form the ‘impedance’
model, (inductors = masses, capacitors =
springs), which was analysed to produce the
volume velocities (ie currents) flowing into all
the parts of the system. These are used to give
the output response taking everything into
consideration.

Verification

A simple speaker system was built comprising
of a magnet and a cone of the same mass as
the chassis plus the magnet. This was
suspended on rubber bands to comprise a
fully floating system. The nearfield sound
pressure output of the cone was measured

• with the magnet equal to the cone mass and

• with the magnet being much heavier than
the cone (which is the normal situation)

Next, the whole system was supported on a
large lump of rubber and this constituted the
‘decoupling spring’ of a more normal speaker
system (this test system had no box of course).
The acceleration at various places in the system
was also measured with a small accelerometer.
The frequency responses of the accelerations
of these parts of the system are related to the
frequency response shapes of the volume
velocities of the same parts and thus to any
radiation which may take place.

Of course, parts like the decoupling spring
will not actually do any radiating, but other
parts like the speaker cone itself will. Thus
accelerations of the parts of the system may be
compared with each other, just like the acoustic
outputs of some parts may be. (figure AVII.1)

Points to note are:

• The shift of 1.414 in the basic resonance of
the system when the magnet mass changes
from ‘large’ to the same as the speaker cone.

• The dip followed by a peak in the cone
output with decoupling spring present.
The dip occurs at the frequency at which
the magnet plus chassis resonates on the
stiffness of the spring.

• The output of the cone at high frequencies
remains unchanged over a wide range of
magnet masses. This occurs because the
voice coil produces a force, which it exerts
equally in both directions, ie into the cone
and into the magnet system. They then
exhibit an appropriate acceleration according
to F = ma with F being the same in both
directions and the magnet and cone masses
determining the accelerations and hence the
radiation from both directions.

32

AVI.3 Single Slice Impulse Progression Plot – Box Side

AVII.1 The results show a high degree of correspondence

between the measured system and an equivalent
theoretical system

Introduction

Much work at B&W over the years has resulted
in proprietary Finite Element and Boundary
Element code capable of accurately predicting
the vibration and acoustic behaviour of
axisymmetrical shapes using Finite and
Boundary Element Analysis. Papers listed (refs)
include several on this topic. B&W proprietary
code runs at more than 10 times the speed of
any commercially available package and allows
in-house optimisation packages based on
‘simulated annealing’ to find the global minimum
of any target function we may like to specify.
The result of this is that a computer may be left
to search through the whole relevant design
space to find the best model that will fit our
requirements – and it will not be trapped in any
local minima along the way.

When non-axisymmetric modelling is needed,
commercial Finite Element packages have to
be used and one of these, PAFEC, allowed
the modelling of the total acoustics of normal
Nautilus™rearward inverted horns, though not
the coupling of a lumped parameter speaker
model at the near end. The tube was therefore
excited with an ‘ideal’ forced diaphragm for
this exercise. As expected, this shows up the
onset of the first higher order cross mode of
propagation as a resonance across the mouth
of the horn (ie where the speaker is situated).
This graphically illustrates that rearward
Nautilus™horns may not be used on their
own above this cut-on frequency, as this
transverse mode is clearly audible through
the speaker diaphragm.

The following report from Gary Geaves covers
the analysis of this phenomenon:

B&W Loudspeakers Ltd and Computer
Simulation

Computer simulation based on the Finite
Element and Boundary Element methods has
been widely exploited in many diverse scientific
and engineering applications. The Finite Element
Method was developed in the 1950s to aid in
the design of aircraft structures. Since then it
has been applied to structural, thermal,
electromagnetic, fluid flow and acoustic
problems. In many industries, such as the
automotive, it has been long regarded as an
essential design tool. However, it is only

relatively recently that sufficient computer power
has become readily available and the underlying
mathematical techniques sophisticated enough
to be of use in the design of loudspeakers.

Engineers at B&W were quick to spot the
potential of computer simulation in the design
of loudspeakers, first becoming involved
through collaborations with academic institutes
in the mid 1980s. At that time, if one wanted
to carry out simulation of an acoustic system,
it was necessary to develop and code the
algorithms from scratch. For this reason, B&W
has proprietary code, written in the Fortran
programming language, to solve a specific class
of problem. This code is used routinely and is
being constantly enhanced. It has also been
used as the basis for an optimisation system
that will automatically select designs fulfilling
specified design criteria.

Recently, especially in the last five years,
commercial, off the shelf systems have become
available that allow simulation of acoustic
systems to be performed. With the introduction
of such systems, computer simulation in the
loudspeaker industry is becoming increasingly
important, with many other companies investing
in the area. More recently, the task of porting
the Fortran code to Matlab, a popular high
level scientific programming language, has
commenced at B&W. Though Matlab code is
slow to execute in comparison to Fortran code,
it has numerous high level features and in-built
graphics routines that make it an ideal test bed
for quickly trying out new ideas.

A detailed description of B&W Loudspeakers’
research into and application of computer
simulation to the design of loudspeakers may
be found in the references section.

References

1 Jones, C.J.C (1985) Finite Element Analysis

of the Effect of Damping in the Piston and
the Outer Suspension of a Loudspeaker
Diaphragm, Proc spring Conf of the Institute
of Acoustics, York Univ.

2 Jones, C.J.C (1986) Finite Element Analysis

of Loudspeaker Diaphragm Vibration and
Prediction of the Resulting Sound Radiation,
PhD Thesis, Brighton Polytechnic

3 Jones, M.A. and Henwood, D.J. (1991)

Finite Element Modelling of Loudspeaker
Dive Units, In IMACS ‘91, Vol. 4, ed. R.
Vichnevetsky & J. J. Miller. Criterion Press,
Dublin

4 Jones, M.A, Binks, L.A. and Henwood, D.J.

(1992) Finite Element Methods Applied to
the Analysis of High Fidelity Loudspeaker
Transducers, Computers and Structures. 44

5 Jones, M.A, Henwood, D.J. and Fryer P.A.

(1992) A Computer Model of the Vibration
and the Sound Radiated by Loudspeaker
Models and its Validation, Acoustics Letters,
15(8)

6 Henwood, D.J. (1993) The Boundary

Element Method and Horn Design, The
Journal of the Audio Engineering Society,
41(6)

7 Geaves, G.P. (1994) An Investigation using

the Boundary-Element Method into the
Acoustic Field Resulting from Concave
Loudspeaker-Type Structures, Acoustics
Letters, 18(6)

8 Geaves, G.P. and Chakrabarti, R. (1995)

Modelling and Optimal Design of Tweeter
Loudspeakers, In Proceedings of Vibration
and Noise 95, 25th-27th April, Venice

9 Geaves, G.P. (1995) The Simulation of

midrange Loudspeakers using Numerical
Methods, In Proceedings of the IEE Audio
Engineering Colloquium, 1st May, London,
Digest No: 1995/089

10 Geaves, G.P. (1995) Modelling and Optimal

Design of Loudspeaker Diaphragms Using
Numerical Methods, PhD Thesis. University
of Brighton

11 Kirkup, S.M. and Jones, M.A. (1996)

Computational Methods for the Acoustic
Modal Analysis of an Enclosed Fluid With
Application to a Loudspeaker Cabinet,
Applied Acoustics, 48(4)

35

stability in a polymer molecular matrix. Its
mechanical properties are a reflection of this
structure. It is very compliant in shear and
stretch but has poor compressibility when
confined, much like a liquid but unlike
conventional elastomers. And while it is freely
elastic at low frequencies, it exhibits more
viscoelastic behaviour at much higher
frequencies (it has a high tan delta product)
giving it a useful transmission loss. The gel is
thus employed in an L-section gasket on the
rim of the midrange chassis. The mass is
supported by the thin edging, which provides
shear freedom, and the tension is held against
a thicker compressive region, the unconstrained
edge of which follows the critical internal profile
of the midrange cabinet. The gel is also
employed at the other end of the tensioned
rod to provide a fully floating assembly with
the required single degree of freedom at a
frequency well below the pass band.

Additional mass is coupled to the midrange
magnet to further lower the resonance
frequency and reduce chassis displacement,
this being of additional importance because the
cone impedance matching relies on the chassis
as a virtual ground. The high loss of the gel at
these elevated frequencies is thus invaluable,
because it provides damping control of any
structural modes in the chassis itself. To ensure
that low-frequency vibration from the bass
driver does not excite the midrange decoupling
resonance, and to shift cabinet on cabinet
resonances below the bandwidth of the bass
driver, the weighty midrange head is supported
on a bed of the gel at its base and at the rear
of the tailpipe.

A similar scheme is employed for the tweeter/
head interface. The tweeter motor is satisfactorily
isolated from the heavy cast housing by conven­tional rubber O rings, but the entire housing
is decoupled by a sculpted the gel interface.
Isolation is provided by shear freedom, but a
ribbed surface profile is employed to improve
compressibility and thus ensure that even
the rocking modes are well below band, yet
kept marginally above the midrange cabinet’s
fundamental resonance frequency.

It will of course be noted that the bass drivers
are not decoupled from the cabinet. This design
decision follows from the Nautilus™801 and was
made fairly early in that speaker’s development
stage, because the complications necessary to
do the job correctly would have been impractical
and perhaps unwarranted. Unlike the midrange
and treble drivers, a bass driver reacts against
a large air stiffness, so any orthodox compliance
scheme would involve losses or in-band
resonances unless the mass of the magnet was
unreasonably high. In passing, note that limited
magnet excursion has no effect on the acoustic
output of a mass-controlled diaphragm, as in
the mid and treble schemes.

However, decoupling cannot be ignored
because it will occur in a mechanical system at
some frequency whether it is desired or not. If
that frequency cannot be brought below band
then it is best to raise it above. To this end, the
hugely stiff bass chassis are bolted firmly into
the rigid Matrix™cabinet, which ensures that the
first chassis/cabinet resonance is just above
band and that there is minimal lost motion
between the two. The Matrix™construction
of the cabinet has long been proven to be
acoustically inert, so any vibration energy
imparted on the cabinet has no serious panel
modes to excite and is quickly dissipated. Lost
motion to the acoustic environment is also
minimised because the cabinet and plinth
assembly is massive enough to become
a virtual earth for the driver to react against.

12 Geaves, G.P. (1996) Design and Validation

of a System for Selecting Optimised
midrange Loudspeaker Diaphragm Profiles.
The Journal of the Audio Engineering
Society, 44(3)

13 Geaves, G.P. (1996) Horn Optimisation

using Numerical Methods, Presented at the
100th Convention of the AES, Copenhagen,
pre-print 4208 (J-5).

14 Geaves, G.P (1998) Finite Element Analysis

of an Inverted Horn. B&W Loudspeakers Ltd
White Paper

34

Appendix VIII

Finite Element Analysis

Appendix VII continued

Decoupling

and opposite region going downwards. The net
result of this is that air is merely shunted around
in the near field and very little sound energy
finds its way into the far field. What we are then
left with is any underlying perfect piston motion
and the radiation from the central regions,
which are still moving pistonically. When the hills
and dales are equal in number and height, we
have what is in effect a multipole source which,
when the wavelength of sound in air is greater
than that in the material, is very inefficient at
radiating. Just as with single frequency single
slice plots, the scans may be done with phase­sensitive detection or with a rectified output.
The surround resonance shows up as a
characteristic ‘flan dish’ shape with phase­sensitive detection, whereas with rectified plots
only a slight difference will be seen from perfect
piston motion.

Phase animated – single frequency –
full-surface scan

The full-surface phase-sensitive detection
method is used for this type of plot except that,
instead of just one whole surface scan, a set
of up to 20 surface scans are carried out,
each one being at a different phase though
the vibration cycle. When these 20 pictures
are placed in the computer’s memory, a second
programme allows all twenty pictures to be
repeatedly mapped onto the screen. This gives
the impression of animation and can often show
up features in a speaker’s response not clearly
visible from a single frozen-phase whole-cone
scan. For IBM PCs these can be produced as
‘AVI’ files which may be played with the
standard Windows™media viewer programme.

Phase Animated Single Frequency Plot
(20 Phases) figure AIX.3

• Complete single-frequency phase-sensitive
plot over whole cone

• A bell mode is evident, giving peaks and
dips around cone’s circumference

• A resonance in the surround can clearly
be seen – it is the first harmonic

• The surround pulls tight at top dead centre
(see single slice at the top left)

• The picture shown here is from top
dead centre

Note: The bell mode has an equal number of
sectors going upwards and downwards. These
are also of equal amplitude and therefore their
radiation cancels out in the near field (it’s an
‘acoustically fast’ multipole source). The
surround resonance is not cancelled out by
anything and is responsible for a major peak
and dip in the speaker’s response. The surround
pulling tight will cause distortion in the resulting
output sound.

Frequency animated full-surface scan

Either the phase-sensitive full-surface or the
rectified full-surface type of plot is used for
this technique, except that instead of just one
whole surface plot being carried out at a single
frequency, a set of 256 separate frequencies
are used from 200Hz to 20kHz, spaced at
approximately 80Hz intervals.

In this case, the scanning mechanism leaves
the laser spot at each of 126 x 126 positions
on the cone surface, while 256 measurements
are taken smoothly from 20kHz down to 200Hz
at each of the 256 separate frequencies. The
results are stored on a computer disc and the
spot is then moved on to the next position.
Complete surface plots for each frequency
are disentangled from the set of results at
a later date, using specially written software.

Just as with phase animated plots, the set of
256 separate frames can be projected onto
the computer screen as a movie, graphically
showing the development of surround and one
resonances which sweep in and out of view
as the frequency is changed. The differences
between the behaviour of say a Kevlar®cone
with a bending wave impedance matched
surround and a plastic cone with a conventional
surround is very striking when both animated
full-surface scans are visible on the screen at
the same time.

Frequency Slice Plots

In this case instead of the whole surface of the
cone being raster scanned at a single frequency
like a TV picture, a single strip of the cone from
edge to edge through the middle is repeatedly
scanned. Starting at the rear of the plot and at
a low frequency, the frequency is increased for
each succeeding sweep plotting in front of the
previous one, and the resulting 3-D plot shows

a frequency history of the behaviour of that
slice of cone as can be seen in figure AIX.4.
Once again this may be done using either
phase-sensitive detection or the rectified
method. Resonances and other problems
may be seen at a glance, particularly if the
cone is axisymmetric. This may be the only
kind of laser plot that is necessary to show
everything that is wrong (or right) with the
speaker cone/surround/coil combination.

The results of Finite Element Analysis are often
plotted in this way as well, so it forms a very
convenient test for the accuracy of finite
element predictions of cone vibration behaviour.

37

Introduction

Various laser test methods have been
extensively used in the development of
speakers at B&W. There now follows an
introduction to the armoury of laser test
methods available.

B&W was the first speaker company to use
a Harwell interferometer to make the vibrations
in cones visible. Over the years there have
been several significant improvements to the
system, and one entirely new technique has
been invented, which has great potential for
helping to improve the design of cones and
surrounds. Lasers are being used routinely
during the development of new cones and
surrounds at B&W.

The four main ways that a laser may be used
to show cone and cabinet vibrations are:

• Single Slice single frequency plots
(phase-sensitive or rectified)

• Single Slice multiple frequency plots
(phase-sensitive or rectified)

• Impulse Progression Plots
(single slice animated or as a 3-D plot)

• Whole cone plots of frequencies or impulses
(as individual plots or computer animated)

In addition, each of these techniques may be
applied to the air itself in front of the cone and
the speaker enclosure by utilising a very light
diaphragm to represent the movement of the
air in response to the sound radiated from the
driver and the cabinet.

Computer animation techniques may be used
to produce movies showing either the phase
response at any single frequency over the
whole cone or the progression of an impulse
as it spreads out from the cone neck.

Single Slice – single frequency – phase­sensitive or rectified

The laser is used to plot single slices across the
middle of the cone

A diameter across the cone is scanned with the
laser beam to produce two distinct types of plot
as shown in figures AIX.1a and b. This is done
at a single frequency of interest. On reflection
from a moving object, the frequency of the laser
light is changed by the cone movement due
to the Doppler effect. The motion of the object
is derived from that frequency shift by using
what is in effect an FM radio. The output of this
FM radio is then compared with the input signal
to the speaker. If they are in phase with one
another the result is plotted upwards on the
screen. If they out of phase it is plotted
downwards. The resulting phase-sensitive plot
shows which parts of the cone are moving in
the same direction as the voice coil and which
parts are moving in the opposite direction – that
is, it shows which parts are totally out of phase
with the voice coil. The disadvantage of this
type of plot is that those regions which are 90º
out of phase with the voice coil do not show
up at all. To overcome this disadvantage we
have the ‘rectified’ plot, which disregards phase
and always plots upwards if there is any cone
movement at all. Clearly there is a need for both
types of single slice plot for a compete picture
of cone movement to be obtained.

Full speaker surface scan – single
frequency – phase-sensitive or rectified

The second type of plot is produced by
scanning the whole surface of the speaker, still
at a single frequency of interest. On reflection,
the frequency of the laser light is still changed
by the cone motion because of the Doppler
effect. The motion is derived as before from the
frequency shift by using the FM radio principle
and the resulting information is now displayed
in 3-D, producing mountain like plots as shown
in figures AIX.2 and 3. A perfect piston-like
cone gives ‘top hat’ pictures, with every point
on the cone moving exactly the same amount
with so-called ‘piston’ motion. The hills and
dales produced by less than piston-like motion
are easy to see, but are possibly less easy to
interpret, and greatly aid the design and
development process. Figure AIX.2 shows
a classic cone surround mode where the
whole surround is moving out of phase with
the cone causing a dip in the resulting
frequency response. Figure AIX.3 shows a
totally symmetrical break-up pattern where for
every region going upwards there is an equal

36

Appendix IX

Laser Interferometry

AIX.1b Rectified Slice Plot – No Phase Information

AIX.1a Phase Sensitive Slice Plot – Surround out of Phase

AIX.2 Whole Cone Single Frequency Plots. Top Picture at

Low Frequency, Bottom at high Frequency.
Note: 4-way symmetry and smoothly reducing central area

AIX.3 Phase sensitive whole cone plot. Peaks and dips cancel

out, surround sound resonance does not.

Generalisations

As with all the above single slice types of
plot, this single slice impulse progression
plot is especially applicable to axisymmetrical
cone structures.

For materials such as woven Kevlar®, the whole
cone impulse progression plot has to be used.
In this case, a complete picture of the whole
cone is built up from each of the sampled
individual time elements making up the impulse
responses at each point on the cone. These
pictures are cycled from either the hard disc
or the memory of the computer onto the
screen, showing graphically an animation of
the progression of the impulse across the
whole of the cone surface.

Plots of the motion of the air motion
itself

As described in the paper ‘Laser Techniques
in Loudspeaker Design including the Impulse
Progression Plot’, B&W has a Laser Doppler
Velocimetric technique for observing the
passage of waves across the surface of a

speaker cone. As further shown in the Paper
‘New Pipe and Horn Modelling’, this technique
may be extended to measure air motion in order
to discover which parts of the speaker cone do
the radiating and which parts of the speaker
box allow waves to be diffracted, so spoiling the
resulting sound. The technique involves placing
a very light, highly stretched clingfilm diaphragm,
lightly dusted with talcum powder, in front of the
driver. Although this diaphragm is like gossamer
and is totally acoustically transparent, it does
move with the passage of any sound wave,
behaving almost like part of the air up to
supersonic frequencies. Since it moves with
the sound it may be observed with the Laser
Doppler velocimeter, which therefore detects
the movement of the air itself. (figure AIX.6)

This technique may be used in a number of
ways. The most obvious is to scan a whole
diaphragm placed in front of a cone or speaker
box. This allows us to observe the progression
of the impulse across the air in front of the cone
and across the surface of the box. The second
way is to place the diaphragm in a succession
of positions further and further away from the
speaker or box and measure either a slice
across the diaphragm, or indeed the whole
diaphragm at each position. Computer
processing then allows the passage of the
impulse in the air to be viewed as it passes
through each successive diaphragm, either
as a succession of ‘stills’ or as a computer
animated movie. This is very useful for
observing the transitions from near field
behaviour close to the driver or speaker box
to far field behaviour, which is what is usually
perceived by the listener, and to pin point
sources of diffraction and radiation within the
total speaker system.

The passage of an impulse though a single
diaphragm may be displayed as a 3-D plot,
rather like the slice plot for displaying the
behaviour of a single slice across a speaker
diaphragm at different frequencies. In this
case, the first arrival is plotted at the right hand
side and subsequent arrivals are displayed from
right to left. We thus see graphically with this
‘wavefront progression plot’ how energy comes
along well after the original impulse has passed
that point in space.

When observing the differences between
the impulse behaviour of axisymmetric cones
such as those made from plastic, with non
axisymmetric cones made from woven Kevlar

®

fibres, the difference is striking. The sound
energy radiated by the axisymmetric cone
consists of an initial wavefront, which largely
represents the music, followed by a series of
other waves, which are not the same in all
directions, representing the coloration of the
cone and caused by the waves bounding
backwards and forwards across the cone.
Measuring the behaviour of the air can also
be used to illustrate how cabinet edges really
do produce copies of the original sound, but
often out of phase with the original and delayed
by the time it took for the sound to get from
the driver to the diffracting sharp edge.
(figures AIX.7 and 8)

39

Appendix I

X

continued

Laser Interferometry

Phase Animated Frequency Slice Plots

(figure AIX.4)
Just as with the slice plot above, a complete set
of scans is done from a low frequency to a high
frequency at each of 20 different phases. The
resulting 20 plots are then animated, revealing
each slice’s behaviour as it moves though a
complete vibration cycle. This rather curious
‘frequency normalised’ phase animated
frequency slice plot shows the same 20 phases
for each frequency, so the animation proceeds
at the same rate for 20kHz as it would for
200Hz. Another form of plot, as yet to be
produced, would cycle though the phases at
20kHz at 100 times the rate that they are cycled
at 200Hz. It is doubtful though whether such
a plot would be of any use. The frequency­normalised phase-animated slice plot gives the
impression that energy passes down the plot
from low frequencies to high frequencies, but
this is merely an artefact of the normalisation.

Plots such as these show in graphic detail
phenomena such as the progression of energy
from the voice coil to the surround at high
frequencies, just like waves moving down
a length of rope being shaken up and down
at one end. Also often seen is the surround
lagging behind the movement of the otherwise
piston-like cone by 90º.

Phase Animated Frequency ‘Slices’ (20 Phases)

(figure AIX.4)

• Rear Slice is a scan across the middle
of the cone at 0.5kHz

• Front Slice is a scan across the middle
of the cone at 5.5kHz

• Each frame is at a different phase through
a complete cycle at each slice’s frequency

• This is a very bad cone, showing major
resonances and poor surround behaviour

• The single frame from the sequence
shown here illustrates the surround phase
lag at the rear

Note: The slice at the front, at 5.5kHz, is just
like a rope being waved at one end. No sound
will be radiated at this frequency. Even the slice
at the back, at 0.5kHz, shows that the surround
lags behind the cone (otherwise behaving like a
piston) by 90º. Thus the surround radiation will
cancel and reinforce the cone sound differently
depending on the direction. On axis there will
be little effect, but the directional pattern will
suffer peaks and dips as a result. The major
resonances produce peaks and dips in the
speaker’s response in all directions.

Impulse Progression Plots – in cones and
in the air – slices or full cone

The latest technique in the formidable armoury
of laser-based measurement techniques
available to B&W engineers is called the Impulse
Progression Plot.

In this case, the laser beam is pointed at a
position on the cone and the speaker is fed with
an impulse, rather than either a single frequency
or a sequence of frequencies as in the previous
methods. The resulting impulse response of the
point is stored in the computer and the beam is
moved on to the next point, where its impulse
response is translated into digits.

For the single slice impulse progression plot,
just a single line of impulse responses is used.
For the whole cone case obviously, impulse
responses from the whole cone surface have
to be translated for processing later.

With a single line of impulses, a plot is
produced across the whole diameter for each
time interval of the sampling of the individual
impulse responses. Each succeeding time

interval may be produced as a 3-D plot, with
time equals zero placed at any edge of the
page (usually at the left hand side). The resulting
cone behaviour is then displayed in 3-D as a
time history from left to right (or whatever).

Alternatively, the single line may be displayed
on the computer as a movie, and the line then
appears to waggle up and down as the impulse
progresses back and forth along it. However,
perhaps the most useful presentation technique
for the single slice impulse progression plot is
as a coloured contour plot, with time equals zero
at the left hand side – time therefore progresses
from left to right, with the voice coil in the
middle and the surround at top and bottom.
An example of this is shown in figure AIX.5.

This sort of presentation immediately reveals
that there are several different types of wave
motion conveying energy from the voice coil
to the surround and back again. The most
significant of these are bending waves and
compression waves, the latter travelling much
more quickly than the former. Figure AIX.6
shows the impulse coming in at the voice coil
in the centre. The cone begins to follow it and
the wave progresses outwards in both directions
to strike the surround near the edges of the pic­ture. This looks very much like ripples produced
when a stone is dropped into a round pond.

A computer animated version of this picture
shows in graphic detail how much of the
incoming bending wave is taken into the
surround and how much is reflected back down
into the cone again to form standing waves or
resonances. The impulse may also be seen
moving about in the surround itself, all the while
being absorbed and reflected during its travels.
The cone can clearly be seen to behave like a
transmission line for bending waves (and for
other types of waves as well) and for best effect
should be terminated in the characteristic
impedance of that line at both ends. This will
ultimately produce minimum reflections and
maximum absorption and consequently fewer
resonances and a cleaner sound output.

38

AIX.6 Impulse Progression Plot – Cone Diameter

AIX.5 Wavefront Arrival Plot – Sound in the Air

AIX.7 Phase Sensitive Frequency

AIX.8 Phase Sensitive Frequency

AIX.4 Phase Sensitive Frequency

Kevlar is a registered trademark of DuPont. Rohacell is a registered
trademark of Röhm GmbH & Co. KG. Marlan is a registered trademark
of Polylac Holland bv. Nautilus and Matrix are trademarks of B&W
Loudspeakers Ltd. Copyright © B&W Loudspeakers Ltd. E&OE.
Design by Thomas Manss & Company. Printed in the UK.
B&W Loudspeakers Ltd reserves the right to amend details of
specifications without notice in line with technical developments.

B&W Group UK
T [phone]
E [e-mail]

B&W Group North America
T [phone]
E [e-mail]

B&W Group Asia
T [phone]
E [e-mail]

B&W Loudspeakers Ltd
Dale Road
Worthing West Sussex
BN112BH England

T [phone]
F [phone]
[e-mail]
www.bwspeakers.com