Analog Devices EE261v01 Application Notes

Engineer-to-Engineer Note EE-261

=

{

a

Technical notes on using Analog Devices DSPs, processors and development tools

Contact our technical support at [e-mail] and at [e-mail]
Or vi sit our o n-li ne r esou rces htt p:/ /www.analog.com/ee-notes and http://www.analog.com/processors

Understanding Jitter Requirements of PLL-Based Processors

Contributed by Boris Lerner and Aaron Lowenberger Rev 1 – January 20, 2005

Introduction

With the advance of faster processors that
require faster lines of communication,
understanding and characterizing clock jitter has
become more important.

Jitter occurs in many different parts of digital
applications. Jitter of data with respect to clock
in synchronous protocols is one example; jitter of
the signal itself in CDR (clock data recovery)
applications is another.

This EE-Note describes jitter issues of the clock
from which PLL-based processors derive timing.
This document analyzes the given clock's jitter
with respect to an ideal clock, only as far as a
processor’s tolerance requires. This document is
intended for hardware design engineers
responsible for choosing the components to
satisfy a processor’s jitter requirements.

The specific processor being analyzed in this EE­Note is the ADSP-TS201S TigerSHARC®
processor. Some portions of this EE-Note apply
to jitter in general; other portions apply
specifically to our case in question.

Unfortunately, unlike more traditional data sheet
parameters like setup and hold, analyzing
acceptable system jitter is not as simple as
merely ensuring that specification numbers are
met. There are many ways to measure jitter; on
top of that, there are infinitely many different
kinds of jitter and the system may behave
differently depending on the jitter type. Thus,
before doing any analysis whatsoever, it is

Copyright 2005, Analog Devices, Inc. All rights reserved. Analog Devices assumes no responsibility for customer product design or the use or application of
customers’ products or for any infringements of patents or rights of others which may result from Analog Devices assistance. All trademarks and logos are property
of their respective holders. Information furnished by Analog Devices Applications and Development Tools Engineers is believed to be accurate and reliable, however
no responsibility is assumed by Analog Devices regarding technical accuracy and topicality of the content provided in Analog Devices’ Engineer-to-Engineer Notes.

important to supply all of the jitter terms and
definitions, first intuitively what they mean and
then the correct mathematical definition.

Terminology

We consider an ideal clock that is being jittered
(i.e., the clock’s edges experience movement
with respect to ideal locations).

The jitter of a particular waveform can be
measured/characterized as period, cycle-to-cycle,
or time interval error (TIE).

Period jitter. This measures the maximum
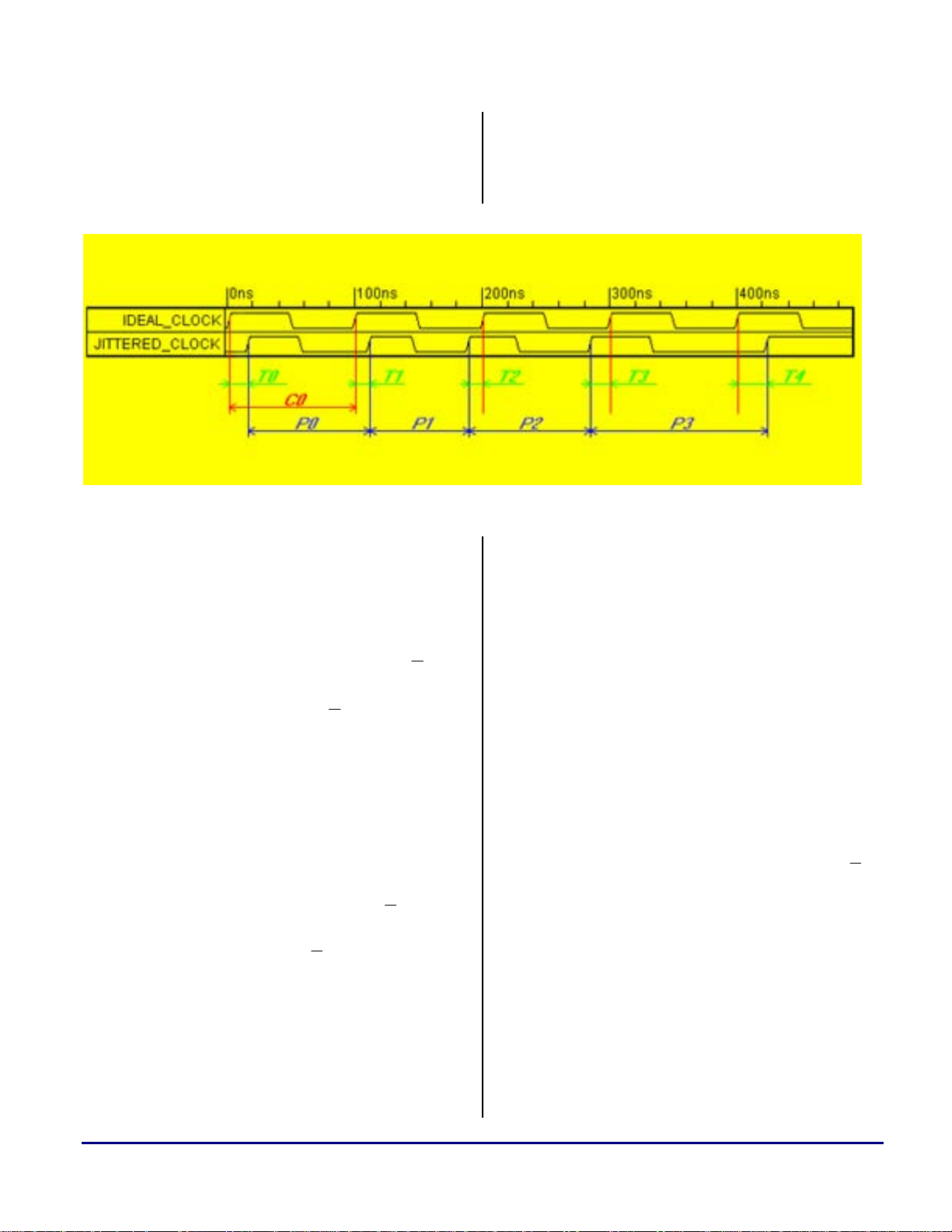
deviation of each single period of the jittered
clock from that of the ideal clock. In Figure 1, if

k

=

maxJitter TIE (3)

=

thenclock, Ideal of Period

{}

−=

k

,...3,2,1,0

=

{}

T

k

,..3,2,1,0

. maxJitter Period (1)

CP

0

1

+

,...3,2,1,0kkk

PP −=

C

0

Cycle-to-cycle jitter. This measures the
maximum deviation of each single period of the
jittered clock from the previous period of the
same clock. In Figure 1,

Time interval jitter. This mea sures t he maxi mum
deviation of the edge (Figure 1 shows this
relating to the rising edge; it can also relate to the
falling edge) of the jittered clock from the
corresponding edge of the ideal clock. In

Figure 1,

=

k

}

. maxJitter Cycle-to-Cycle (2)

(

(

−

=

()(

()(

=−=

a

Here we presume that at time t=0 of the
measurement, the edge of the jittered clock
aligns with the edge of the ideal clock. Note that
this is not just a simple aberration of the edge of

Figure 1. Jitter Definitions

It is time to put clock and jitter under a more
precise mathematical definition. We define the
ideal clock of period T and constant amplitude A
as the following function of time t:

⎧
⎪

⎪

(4)

Here, T is measured in units of time (usually
seconds) and A is measured in volts. Amplitude
of the ideal clock is irrelevant to the discussion
about jitter, so in all that follows we presume that
the clocks have unit amplitude and we consider
them as parameterized by T, (i.e., their period):

(5)

We also define

with jitter J

function of time J(t) (delay can be positive or
negative), mathematically:

Understanding Jitter Requirements of PLL-Based Processors (EE-261) Page 2 of 9

()

tC

=

,

T

⎨

TA

⎪
⎪

⎩

⎧
⎪

⎪

()

=

tC

⎨
⎪

⎪

⎩

()

tC

TJ ,

(t), as the ideal clock delayed by a

if

1

⎛

if 0

⎜
⎝

if 1

⎛

if 0

⎜
⎝

, the clock of period T

⎞

+

⎟

2

⎠

⎛
⎜

⎝

1

⎞

+

⎟

2

⎠

1

⎛
⎜

⎝

+<≤

⎞

TntnTA

+<≤

⎟

2

⎠

()

1

+<≤

1

⎞

TntnT

⎟

2

⎠

()

TntTn

1

+<≤

TntTn

the jittered clock from the nearest edge of the
ideal clock, because the edge of the jittered clock
may have “wandered” away from the edge of the
ideal clock by more than a full cycle period.

)()

(6)

,

There are several intuitive reasons for defining
jitter this way. The most compelling reason is
that jitter is usually generated in a laboratory by
applying a function generator signal to a delay
input of a pulse generator. This is the way
processor manufacturers test susceptibility to
jitter.

For simplicity we define
(7)

Note that G(t) matters only at points

These points are precisely where the clock
changes from low to high or high to low (thus
“r” for rising and “f” for falling edges). Since
what G does outside of these discrete points is
completely immaterial, we can presume that G
(and, thus J) are infinitely differentiable at all
points.

Since these definitions are mathematical in
nature and we must maintain real-life
plausibility, it is safe to assume that G must be a

TTJ

)()

)

tJtCtC

,

() ( )

and whereor TkfGkTrGfrt

TTJ

kkkk

)

. that so , :

tGCtCtJttG

1

⎛
⎜

⎝

⎞

+===

⎟

2

⎠

.

(

ε

ε

ε

(

π

=

()(

=

a

uniformly increasing function (that is,

() ()

the order of the edges, only their locations.
Going back to Figure 1, we see that

Thus, these definitions naturally lend themselves
to specifying jitter as TIE (simply because the
maximum amplitude of J(t) is the TIE jitter, as
defined in equation (3)). Unfortunately, clock
driver manufacturers do not typically specify
jitter as TIE. Thus, it becomes important to relate
different types of jitter with mathematical
formulas. This is the main reason for this
application note.

tGtGtt <⇒< , since G cannot change

2121

)

kTJTk= .

Jitter Examples

Let’s hesitate from this mild mathematical
onslaught and examine different examples of
jitter as consequences of our definitions.

T

In fact, its period is

Jitter Period

Intuitively, function J(t) is slowly increasing (or
decreasing, depending on the sign of epsilon),
and the edges shift uniformly. Note that infinite
TIE jitter implies that this jitter cannot be
generated by laboratory setup described above; it
would require the function generator to output a
signal of infinite amplitude. For the same reason,
this type of jitter does not occur in real-life
systems, so we will restrict our attention to jitter
of finite amplitude.

Example 3

P

k

T

=

ε

−

. Jitter TIE

∞=

, the same for all k.

ε

−=1

T

ε

T

=−

0, Jitter Cycle-to-Cycle

=

,

ε

11

−

Example 1

()

=

tJ

,

ε

() ( )

,

Period Jitter = 0
Cycle-to-Cycle Jitter = 0
TIE Jitter =

Example 2

()

ttJ

=

TTJ

,

ε

−=

tCtC

ε

() ( )()

,

ε

tCtC

−=

TTJ

)

This type of jitter is appropriately called the

sinusoidal jitter of frequency

Then number. real small a is where

phase a is which ,

clock. ideal original theofshift

Then number. real small a is where

jitter (which, as noted before, is the maximum
amplitude of J) is A. Deriving period and cycle­to-cycle jitter is not as trivial as in Example 1,
and derivation of period jitter will be done in a
following section.

Example 4

tCtJ

TA0,

and amplitude
the original clock by
Thus, provided that

T,

Period Jitter =
Cycle-to-Cycle Jitter =
TIE Jitter =

ofclock idealanother is which , 1

)2sin(

tfAtJ

0

f . In this case, TIE

0

)

, another ideal clock of period T0

A. It is easy to see that J(t) delays

A or does not delay it at all.

T

is reasonably smaller than

0

A

A

A

frequency. )0 (ifhigher or )0 (iflower

<>

εε

Understanding Jitter Requirements of PLL-Based Processors (EE-261) Page 3 of 9

Example 5

J(t) = White Gaussian noise. The implications of

this jitter type on period, cycle-to-cycle, and TIE
jitter are postponed to a latter section of this
applications note, when we discuss general case
jitter.

Statement of the Problem

All of the above is not intended to hopelessly
confuse this topic. It is, however, intended to
show the reader how confusing the subject can
be - there are infinitely many types of jitter and
several ways of measuring it. Let us state the
problem for a designer of a clock to a processor
specifically.

1.

Processor manufacturers care about how

short a clock pulse may become due to jitter
before it violates the processor’s guard­banded frequency spec. (Note that the
processor’s PLL usually has a jitter
frequency transfer function which needs to be
taken into account. It is the clock that comes
out of the PLL that must abide by the
frequency spec). Looking at the definitions of
the jitter measurements, it is clear that the
processor is concerned about the period jitter.

2.

When characterizing the jitter frequency

transfer function of the processor’s PLL,
processor manufacturers often use the lab
setup described above (i.e., they really
measure TIE jitter).

3.

Clock driver and oscillator manufacturers do

not artificially generate, but rather measure
jitter and usually specify it as cycle-to-cycle.

The hardware design engineer, who is faced with
three seemingly incompatible definitions, throws
in a towel, goes back to school, gets an MBA and
joins the marketing department instead. Or (and
this happens at least as often), the engineer

simply designs the board without checking the
jitter specs and hopes that it works.

a

Jitter Frequency Domain Transfer Function Through a PLL

Without a detailed discussion of PLLs (which, in
itself, has little to do with the subject at hand),
we can just state that a PLL, being a phase
locked loop, is linear in phase and, thus, is linear
in jitter. Although this statement is not as simple
as it looks, it is correct and we’ll leave it at that.
This is good news, because linear systems can be
analyzed in terms of their frequency domain
transfer function (i.e., frequency response). Note
that this transfer function is linear in jitter only; a
PLL itself is certainly not linear as output with
respect to input. Thus, the linear system
discussion that follows looks at the transfer of
jitter through the PLL only.

Generally, a PLL will have a fairly flat unity gain
response up to a certain frequency (because a
low-frequency jitter appears as a slowly varying
phase that the PLL has enough time to adjust
for). Also, as is the case with all real-life
systems, frequency response rolls off at the high
end. The locations of these cut-off points and the
response between these cut-off points varies
among PLLs. The jitter transfer function for
ADSP-TS201S processors with a base clock of
125 MHz and PLL multiplier set to 4 is shown in

Figure 2.

Another important factor to this analysis is:
given a clock at the processor maximum allowed
frequency, by how much can a clock period
shrink before failure. In case of ADSP-TS201S
TigerSHARC processors, this value is 40 ps (i.e.,
2% of the 2 ns period of a 500 MHz clock).

Armed with this data, it is time to analyze jitter
tolerance. We begin with sinusoidal jitter.

Understanding Jitter Requirements of PLL-Based Processors (EE-261) Page 4 of 9

π

π

(

(

(

()(

(

)

(

)

10

5

0

-5

transfer function (dB)

-10

ADSP-TS201S PLL Jitter Transfer Function

CLOCK MULTIPLIER = 4

SCLK = 125 MHz

-15

-20

0.1 1 10 100

jitter frequency (MHz)

Figure 2. Jitter Transfer Function

Sinusoidal Jitter

The sinusoidal jitter of amplitude A (measured in
time units, say seconds) and frequency

() ( )

= From

the previous discussion, we know that
TIE jitter.

This jitter inputs into the PLL of ADSP-TS201S
and outputs

() ( )

= , where

f

is taken from the graph in Figure 2. According to
formula (1), period jitter (which, stated above,
must be less than 40 ps), is given by:

{}

max CP

=

k

−

. Since G of equation (7) is

0

k

,...3,2,1,0

monotonically increasing, it is also invertible.
The edges of

()

tC

are at points kT , so the

T

. 2sinby given is Hz)(in ftAtJf

A is the

)

)2sin( ftfAtJ

fA

edges of

1

−

)

.

kTG

Thus,

k

)()()

−−

)()

1

−+= .

tGCtC

TTJ=,

11

kTGTkGP

are at points

We now invoke the Intermediate Value Theorem
from beginner calculus, which states that, given a
continuously differentiable function, the
difference of this function’s values at the end
points of an interval equals the length of that
interval times the derivative of the function at
some point inside the interval. We thus obtain:

−−

1

Gd

P

k

()( )()

0

dt

()

[]

0

+∈

=−+=

kTTkt

. 1, somefor

TkkTt

Gd
dt

1

()

1

Tt

0

Understanding Jitter Requirements of PLL-Based Processors (EE-261) Page 5 of 9

Again, using beginner calculus, if

=

π

()(

∗

=

()()(

()(

∗

=

()()()(

=

dy

dt

1

dt
dy

i.e. ,

===

.

tt

)

0

1

−

() ( )

1

−

Gd

()

()

t

dt

dG

dt

() ()

y

yGttGy

and then ,

==

11

dG

1

−

()

tG

dt

Substituting this into the above (with
gives:

P

k

(8)

=

T

dG

1

−

()

dt

P

=

k

−

.

()

tG

0

() ( )

−=

T

() ()

()

, 2sin)( Since ftfAttG

−

1

tfGffA

0

+

T

()

πππ

212cos21

ffA

≥

We now use Figure 2 to find the worst (i.e.,
maximal) value of

()

ffA . Note that the curve in

Figure 2 rolls off at the high end at the rate of
12 dB/oct. This means that every time we double
the frequency, amplitude is divided by 4. Thus,

()

ffA is maximized at the beginning of the roll-

off curve (i.e., at approximately 7 MHz) where
the PLL actually boosts the jitter amplitude by
about 5 dB. Thus,

(){}

f

5
6

66

.1046.121072max

AAffA

⋅⋅=⋅⋅≤

k

⋅=≤

a

396

−−

⋅≤⋅⋅⋅⋅≤− AAPT

12

−

, 101581021079

. sec 1040ps40 bemust which

Solving this inequality for A yields

9

ps 253 sec 10253.0

=⋅≤−A .

Thus, in the case of sinusoidal jitter, to satisfy
the 40 ps of period jitter required by ADSP­TS201S processors, we must ensure that the TIE
of that jitter is no more than 253 ps.
Unfortunately, one usually cannot assume that
the jitter will be sinusoidal in nature, in which
case the above analysis does not apply
completely. But it does show how estimating the
absolute value of the derivative of the jitter
relates TIE to period jitter. Note that the above
analysis can be performed more simply, without
referring to the derivative. The reason that we
did it in the more complicated way is because
most of this argument will apply when we
analyze general case jitter. We now turn our
attention to this more difficult case.

General Case Jitter

As shown in the analysis above, it is very
important to try to estimate the absolute value of
the derivative of the jitter function on the output
of the PLL.

Given jitter J(t) input to the PLL, its output is

Substituting this back into equation (8) gives:

≥

P

k

k

1079

=

T

π

−≤−

TPT

6

6

10791

1046.1221

T

10791

TA

⋅⋅⋅

A

⋅⋅+

≥

⋅⋅⋅+

6

⋅⋅+

A

6

1079

T

66

10791

TA

⋅⋅⋅≤

so ,

⋅⋅+

AA

h

transform of h evaluated on the unit circle

is given by the graph of Figure 2 (as a function of
f, of course).

)

thJtJ

, where the magnitude Laplace

)

22 ifhLifH

=

ππ

It follows that

The ideal clock input in this case is 500 MHz

)

thJtJ

''

(125 MHz input multiplied by PLL by a factor
of 4; see Figure 2), so

9−

sec 102ns2

⋅==T , so

h

i.e., J

' is the output of a filter whose impulse

h

response is h’ and input J. Since,

)

' ,

Understanding Jitter Requirements of PLL-Based Processors (EE-261) Page 6 of 9

shsLshL

(

)

(

)

(

)

a

the magnitude response of the filter h’, using the
notation of the previous section is given by

(9)

()( ) () ()

ffAifHfifhL

ππππ

2222' ==

which is maximum at f = 7 MHz, because the
high-frequency roll-off is at 12 dB/octave (this is
exactly as in the previous section).

Using standard mathematical notation

()

tg

()

∞

gtg

of boundupper smallest thedenote to

have now we), of amplitude pointwise (i.e.

66

⋅⋅⋅⋅⋅≤

JAJ

h

π

1071072'

∞∞

5

6

π

6

6

⋅⋅≤⋅⋅⋅⋅≤

JJ

107921072

∞∞

Now, just like in the previous section,

−−

()()()

k

1

Gd
dt

1

()( )()

0

11

=−+=

kTGTkGP

−−

1

Gd

()

==−+

1

kTTkt

dt

Tt

0

T

dG

−

1

()

()

tG

dt

Substituting

P

=

k

0

() ()

T

1

−

()

()

'1 tGJ

−

h

0

0

tJttG

−= gives

h

.

()

[]

+∈

. 1, somefor

TkkTt

Since T = 2 ns,

T

−≤−

TPT

k

−

= J

+

J

h

69

⋅⋅⋅⋅

J

1079102

6

⋅⋅+

J

10791

∞

To ensure that ≤−

−≤

T

∞

PT 40 ps, we must ensure

k

T

6

10791'1

−

3

⋅⋅≤

10158

⋅⋅+

J

∞∞

∞

that

123

−
∞

−

104010158

⋅≤⋅⋅ J

.

ps25310253

J gives

∞

Solving this inequality for

12

−

J

∞

=⋅≤

Thus, we end up deriving the same conclusion as
was the case with sinusoidal jitter (i.e., less than
253 ps of TIE jitter ensures that the pulse jitter
requirement of the processor is met).

Guidelines for Measuring TIE Jitter

Now that we know that the TIE jitter
measurement is ultimately what we want, some
guidelines are necessary to convert the definition
of TIE jitter as given by the equation (3) into a
measurement that makes sense in the real world
that we live in. The problem, of course, is that
the definition in (3) is theoretical in nature; the
maximum is taken over an infinite number of
indexes, in other words, over an infinitely long
period of time. This would be rather difficult to
reproduce in laboratory conditions. A greater
length of time is needed to analyze a lower
frequency content of jitter and, as shown by the
equation (9), our TIE jitter tolerance is inversely
proportional to the jitter’s frequency. So, let us
analyze the example at hand. Our clock
frequency is 125 MHz (i.e., each cycle is 8 ns
long). It is highly unlikely that this clock has
more than 100 ns of TIE jitter (it would have to
jitter by more than 12 periods of the clock!), if it
does, there is something fundamentally wrong
with the board’s design. We know from the
previous section that a 7 MHz jitter frequency
allows about 250 ps of TIE jitter. By the inverse
proportionality mentioned above, a 17.5 KHz
jitter frequency should allow about 100 ns of TIE
jitter (it is actually even better than that due to
the jitter boost at 7 MHz). Thus, if we presume
that the total TIE jitter is limited by 100 ns, all
jitter content below 17.5 KHz can be ignored.
Frequency of 17.5 KHz corresponds to a period
of less than 60 µs (i.e., measuring TIE over a
period of 60 µs should do the trick).

Understanding Jitter Requirements of PLL-Based Processors (EE-261) Page 7 of 9

a

Cycle-to-Cycle Jitter

The previous sections relate TIE and pulse jitter.
A few words need to be said in the relevance to
cycle-to-cycle jitter.

The problem with cycle-to-cycle jitter is that
given cycle-to-cycle jitter, no matter how small,
TIE and pulse jitter can be as large as desired. A
simple sinusoidal jitter of very low frequency
and large amplitude will change very little from
cycle to cycle (since its frequency is low), but the
accumulated total change from ideal period can
be very large. Thus, a board designer could not
use a clock driver whose jitter is specified as
cycle-to-cycle without some additional
information about the nature of that jitter. In
these cases, if such a driver must be used, it may
be necessary to obtain a driver evaluation board
and measure the TIE jitter. Then one must be
careful not to assume that the jitter will measure
the same on another board with a physically
different driver chip. It may be necessary to
contact the driver manufacturer to understand
board issues that contribute to jitter (such as the
power supply noise on the driver), deviation of
jitter numbers across the chips, and then guard­band the measured number appropriately to
ensure that the final result has no more than
250 ps of TIE jitter.

Thus, having reached this point in the application
note and having survived bombardment of

theoretical and practical calculations, the reader
still has not been given a way to select a clock
driver for our example processor! Fully realizing
that, simply leaving the issue “as is”, would,
most likely, also leave the unfortunate reader
more than just a little peeved at the authors, we
decided to contact a clock buffer manufacturer to
see if they can help us resolve this dilemma. We
sent the above portion of this EE-Note to the
applications folks at IDT, who were more than
helpful. They agreed that the cycle-to-cycle jitter
specification cannot be used in processor clock
designs and were happy to characterize their
recommended parts jitter as TIE. For our
processor example, they recommended their
IDT5T9070 driver. It turns out that the jitter that
this part produces depends almost entirely on the
quality of its power supply. The TIE jitter on
their clean evaluation board’s output measured
52 ps. At this point they were actually limited by
the quality of the input clock that measured TIE
jitter of 50 ps. Following this, they modulated the
power supply with a 400 mV peak-to-peak wave
and bypass capacitors removed (to ensure that
the supply is truly modulated this much). The
TIE jitter depended on the modulation frequency
as shown in Table 1. Keep in mind that the
frequency in Table 1. corresponds to the power
supply modulation frequency. The resulting jitter
frequency may be quite different.

1MHz 2MHz 3MHz 4MHz 5MHz 6MHz 7MHz 8MHz 9MHz 10MHz

314.5ps 200.2ps 163.2ps 143.6ps 140ps 127.8ps 136.1ps 148.1ps 122.6ps 125.1ps

Table 1. TIE Jitter of IDT5T9070 with Power Supply Modulated by 400mV Wave.

Note that 315 ps of jitter at 1 MHz will violate
the processor’s minimum spec derived above if
the jitter frequency is around 7 MHz — this is
unlikely to be caused by a 1 MHz modulation of
the power supply. Thus, even in the worst case of
the supply modulated by 400 mV and all of the
decoupling removed, the jitter spec is still met,

Understanding Jitter Requirements of PLL-Based Processors (EE-261) Page 8 of 9

except possibly, if the supply modulation is at
1 MHz (and even then, it is, most likely, met!).

The designer is encouraged to use the
IDT5T9070 that has already been specified to
meet the requirements, or, if another driver is
desired, to contact the driver manufacturer
directly for their TIE jitter specs.

References

[1] ADSP-TS201 TigerSHARC Processor Data Sheet. Rev 0, November 2004. Analog Devices, Inc.

Document History

Revision Description

Rev 1 – January 20, 2005

by Boris Lerner and
Aaron Lowenberger

Initial Release

Understanding Jitter Requirements of PLL-Based Processors (EE-261) Page 9 of 9