Page 1
Engineer-to-Engineer Note EE-211
a
Technical notes on using Analog Devices DSPs, processors and development tools
Contact our technical support at dsp.support@analog.com and at dsptools.support@analog.com
Or vi sit our o n-li ne r esou rces htt p:/ /www.analog.com/ee-notes and http://www.analog.com/processors
16-bit FIR Filters on ADSP-TS20x TigerSHARC® Processors
Contributed by Klas Brink and Rickard Fahlquist Rev 1 – January 13, 2004
Introduction
This document presents two assembly code
implementations with memory of direct-form
FIRs, capable of handling complex input and
output and complex or real coefficients with 16bit integer precision. These implementations
present methods of achieving high performance
while conserving memory.
General
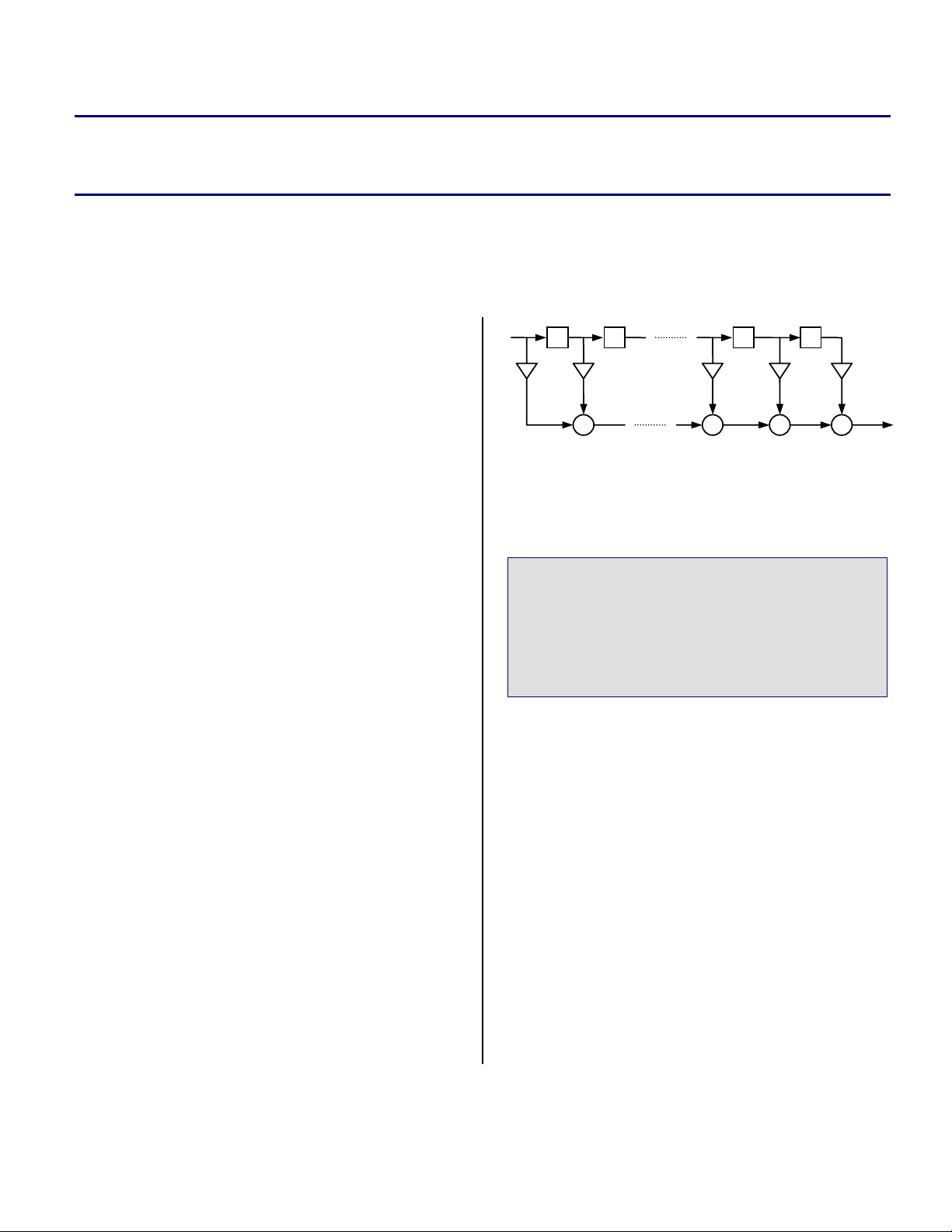
x[i]
Figure 1. Direct-form FIR.
x[i-1]
Z-1
h[0] h[1] h[M-3] h[M-2] h[M-1]
Z-1
+ + + +
x[i-M+3]
A C pseudo-code description of the same FIR is
given below, where ** represents complex
multiplication.
Z-1
x[i-M+2]
Z-1
x[i-M+1]
y[i]
A mathematical representation in direct form of a
FIR filter is given below.
−
10M
[] [ ] [ ]
∑
=
k
⋅−=
khkixiy
i 0, 1, …, N-1
N Number of samples
M Number of filter coefficients
y[i] Output sample number i
x[i-k] Input sample number i-k
h[k] Filter coefficient number k
Equation 1. Direct-form FIR
This equation is the result from the vector inner
product between the filter coefficient vector h
and the (time) order-reversed input data vector x.
This is also known as the convolution between h
and x.
Figure 1 presents the same equation graphically.
for(i=0; i< N; i++){
y[i] = 0;
Ncoeffs = i < (M-1) ? i : (M-1);
for(k=0; k<=Ncoeffs; k++){
y[i] = y[i] + x[i-k] ** h[k];
}
}
Listing 1. C pseudo-code algorithm of direct form FIR.
Parallelism in TigerSHARC Processors
ADSP-TS20x TigerSHARC® processors are
highly parallel computing devices that have three
distinct types of parallelism:
• Latency-2 computational pipeline
• Multiple compute units
• Wide memory structure
These three forms of parallelism complement
each other, and all three must be exploited to
achieve a high level of efficiency. The
computation rate and memory bandwidth in this
machine are balanced in such a way that failing
Copyright 2004, Analog Devices, Inc. All rights reserved. Analog Devices assumes no responsibility for customer product design or the use or application of
customers’ products or for any infringements of patents or rights of others which may result from Analog Devices assistance. All trademarks and logos are property
of their respective holders. Information furnished by Analog Devices Applications and Development Tools Engineers is believed to be accurate and reliable, however
no responsibility is assumed by Analog Devices regarding technical accuracy and topicality of the content provided in Analog Devices’ Engineer-to-Engineer Notes.
Page 2

a
to pay attention to one of the three components
of parallelism may result in sub-optimal
performance.
16-Bit Integer FIR with Complex Taps, Input and Output Data
Introduction
ADSP-TS20x TigerSHARC processors support
two complex multiplications (one in each
compute block) per core clock cycle along with
simultaneous data transfers. Filter calculations
like Equation 1 can, of course, be implemented
in a straightforward sequential fashion using one
(inner) loop for the summation, each iteration
performing a multiplication between an (old)
input sample and a coefficient, and adding that to
the output of the last iteration, and another
(outer) loop going through the same procedure
over and over again to produce the output
samples. However, using the parallel features
and high internal bandwidth of ADSP-TS20x
TigerSHARC processors, achieves higher
performance.
Pipelining and Parallel Resources Utilization
The FIR representations show that most data
used to compute output y[i] are the same as the
ones used to compute y[i+1]. The same applies
for y[i+1] when it comes to y[i+2] and so on. The
‘outer’ loop in the C pseudo-code performs all
the necessary steps to calculate all the output
samples. Unrolling this outer loop gains three
things:
1. Data can be reused between calculations of
different output samples.
2. MAC operations can be parallelized.
3. The effects of loop overhead are reduced.
Reducing loop overhead is not to be neglected as
this decreases the time required to perform the
conditional branching necessary for looping,
thereby increasing the percentage of time
available to perform the actual calculations.
Unrolling the outer loop four times yields an
algorithm described by the following C pseudocode:
for(i=0; i< N; i+=4){
y[i] = 0;
y[i+1] = 0;
y[i+2] = 0;
y[i+3] = 0;
Ncoeffs = i < (M-1) ? i : (M-1);
for(k=0; k<=Ncoeffs; k++){
y[i] = y[i] + x[i-k] **h[k];
y[i+1] = y[i+1]+ x[i+1-k]**h[k];
y[i+2] = y[i+2]+ x[i+2-k]**h[k];
y[i+3] = y[i+3]+ x[i+3-k]**h[k];
}
}
Listing 2. Outer loop unrolled 4 times.
What we have done so far is reuse the
coefficients. By also unrolling the ‘inner’ loop,
we achieve reuse of input data as well. Unrolling
of the inner loop by four gives the C pseudo-code
in Listing 3.
for(i=0; i< N; i+=4){
y[i] = 0;
y[i+1] = 0;
y[i+2] = 0;
y[i+3] = 0;
Ncoeffs = i < (M-1) ? i : (M-1);
for(k=0; k<=Ncoeffs; k+=4){
y[i] = y[i] + x[i-k] **h[k];
y[i] = y[i] + x[i-1-k]**h[k+1];
y[i] = y[i] + x[i-2-k]**h[k+2];
y[i] = y[i] + x[i-3-k]**h[k+3];
y[i+1] = y[i+1]+ x[i+1-k]**h[k];
y[i+1] = y[i+1]+ x[i-k] **h[k+1];
y[i+1] = y[i+1]+ x[i-1-k]**h[k+2];
y[i+1] = y[i+1]+ x[i-2-k]**h[k+3];
y[i+2] = y[i+2]+ x[i+2-k]**h[k];
y[i+2] = y[i+2]+ x[i+1-k]**h[k+1];
y[i+2] = y[i+2]+ x[i-k] **h[k+2];
y[i+2] = y[i+2]+ x[i-1-k]**h[k+3];
y[i+3] = y[i+3]+ x[i+3-k]**h[k];
y[i+3] = y[i+3]+ x[i+2-k]**h[k+1];
y[i+3] = y[i+3]+ x[i+1-k]**h[k+2];
y[i+3] = y[i+3]+ x[i-k] **h[k+3];
}
}
Listing 3. Outer and inner loops unrolled 4 times.
16-bit FIR Filters on ADSP-TS20x TigerSHARC® Processors (EE-211) Page 2 of 10
Page 3
b
r
b
r
–
a
We now have a high level of data reuse and a
possibility to parallelize calculations. What is not
so obvious in the C pseudo-code is that we also
have the possibility to do pipelining (i.e., fetch
data concurrent with performing the
calculations).
Data Partitioning
Complex 16-bit data is represented in ADSPTS20x TigerSHARC processors by a 32-bit word
as shown in Figure 2.
31 16 15 0
Imaginary Real
Figure 2. Complex 16-bit data representation.
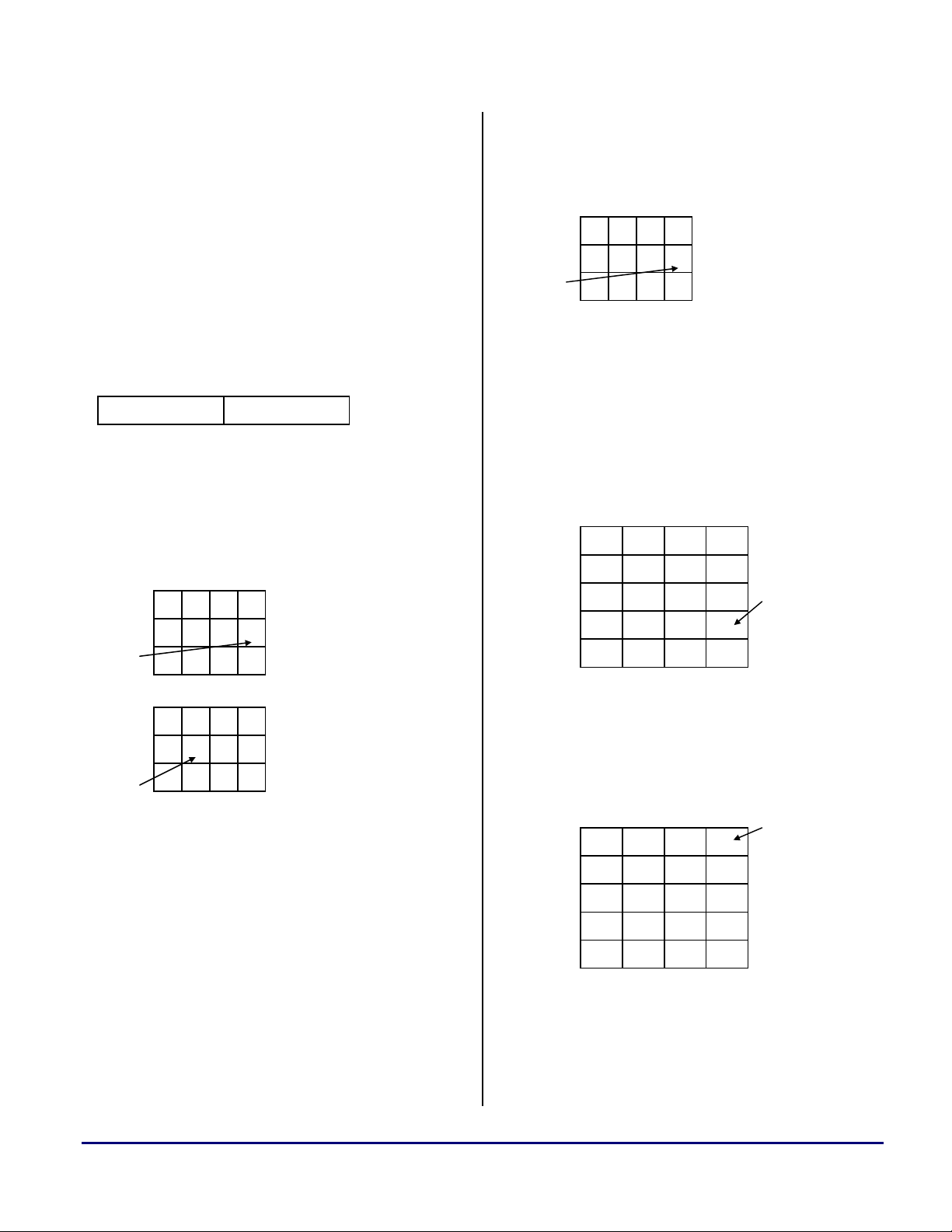
Input and Coefficient Buffer Structure
The input samples and coefficients are stored in
memory as described in Figure 3.
Input
x[3] x[2] x[1] x[0]
x[7] x[6] x[5] x[4]
31
0
Address
0xHHHH
0xHHHH + 4
word aligned storage is used when writing the
output samples to memory, and j4 keeps track of
the current position to be written.
Output
y[3] y[2] y[1] y[0]
y[7] y[6] y[5] y[4]
…
j4
Address
0 31
0xKKKK
0xKKKK + 4
Figure 4. Output storage in memory.
Delay Line Structure
The filter has memory in which it stores a history
of the last M input samples used by the filter.
This history is called the delay line. The samples
from the delay line are quad-word loaded, and
Figure 5 shows how they are stored.
Delay line Address
Circular
uffe
{
x[i-3] x[i-2]x[i-1]
0 31
x[i-M] x[i-M+1] x[i-M+2]x[i-M+3]
x[i-M+4] x[i-M+5] x[i-M+6]x[i-M+7]
…
x[i-4]
0xLLLL – M + 4
0xLLLL – M + 8
j0
0xLLLL
…
j5
Coefficients
h[3] h[2] h[1] h[0]
h[7] h[6] h[5] h[4]
…
k1
Figure 3. Input and coefficient storage in memory.
31
0
0xGGGG
0xGGGG + 4
The addresses are quad-word aligned. This type
of data storage enables quad-word loading,
which is used for the input samples. Quad-word
loading is used also for the coefficients. J5 points
to the position from where we are currently
loading input samples, and k1 points to the
current coefficient loading position.
Output Buffer Structure
The two compute blocks (CBX and CBY) each
calculate two output samples every outer loop
iteration. CBX produces samples y[i+3] and
y[i+1], and CBY produces y[i+2] and y[i]. Quad-
Figure 5. Delay line in memory.
The delay line is implemented as a circular
buffer with j0 as a pointer to the current
position/index in the buffer.
Delay line Address
Circular
uffe
{
x[i-3] x[i-2]x[i-1]
0 31
x[i] x[i+1] x[i+2]x[i+3]
x[i-M+4] x[i-M+5] x[i-M+6]x[i-M+7]
…
x[i-4]
j0
0xLLLL
0xLLLL – M + 8
0xLLLL
M + 4
Figure 6. Delay line after update.
Old samples are read from the delay line starting
at the position indicated by j0 and counting
backwards, wrapping at the circular buffer
boundaries. Assuming that Figure 5 shows the
16-bit FIR Filters on ADSP-TS20x TigerSHARC® Processors (EE-211) Page 3 of 10
Page 4

a
delay line just before samples y[i], y[i+1], y[i+2]
and y[i+3] have been generated, Figure 6 shows
the contents of the delay line after the output
generation and update of the delay line.
Interface
The interface to the filter function consists of the
following parts:
• A pointer to the output buffer
• A pointer to the input buffer
• The number of samples to be filtered
• A pointer to the filter state (including the
delay line and coefficient buffer)
The filter state consists of a pointer to the
coefficient buffer, the number of coefficients, a
pointer to the delay line buffer and an
index/pointer to where we are currently in the
delay line buffer.
16-Bit Integer FIR with Real Taps
and Complex Input/Output Data
Sometimes there is a need to filter the real and
imaginary parts of a complex sample separately.
One example is when the I and Q parts of
antenna data are treated as separate data streams,
both independently affected by the same filter
kernel.
Format
Both the taps and the real and imaginary parts of
the input data are 16 bits. Figures 7 and 8 show
how the input to the filter algorithm is formatted.
0 31 15
h[n] h[n+1]
h[n+3]
h[n+5]
h[n+2]
h[n+4]
typedef struct
{
int2x16 *h; // Filter coefficients
int2x16 *d; // Delay line
int2x16 *p; // Delay line Index
int k; // Number of coeff.
} fir_state_t;
Listing 4. Filter state structure
The filter state is given by the C-code in Listing
4. This structure must be initialized before the
filter is used for the first time (see Appendix for
an example of a C-code initialization ‘function’).
void fir_16_comp(
int2x16 *outdata,
int2x16 *indata,
int N,
fir_state_t *fir_state
);
Listing 5. Filter function prototype
Listing 5 shows a C-code prototype of the
interface.
.
.
.
.
.
.
Figure 7. Filter coefficients format
0
.
.
.
Im{x[i]}
Im{x[i+1]}
Im{x[i+2]}
.
.
.
15 31
Re{x[i]}
Re{x[i+1]}
Re{x[i+2]}
Figure 8. Input sample format
Since the data to be filtered is 32 bits wide with
each 16-bit short word treated independently,
one approach that facilitates the parallel structure
of the ADSP-TS20x TigerSHARC processor is
16-bit FIR Filters on ADSP-TS20x TigerSHARC® Processors (EE-211) Page 4 of 10
Page 5

a
to duplicate each filter coefficient and create
pairs of coefficients that occupy 32 bits each.
31 15 0
h[n] h[n]
Figure 9. Duplicated coefficients
This way four 16-bit MACs are performed per
cycle in each compute block, the real results are
accumulated in two of the MR registers, and the
imaginary results are stored in two other.
Implementation
One filtered output sample (y[i]) is calculated in
compute block X and the next (y[i+1]) is
simultaneously computed in compute block Y.
Using this approach, only half the number of
iterations are needed for a certain number of
input samples. To accomplish this, the
coefficients are skewed one position for one of
the compute blocks when loaded from memory.
In the filter implementation listed in appendix A
(
fir16_real.asm) the filter kernel was short
enough to be completely stored in the X and Y
register files.
Delay Line
The delay line is as long as the filter kernel.
Using the same delay line approach as the one
described for the complex filter, problems arise
because the filter taps are 16 bits, whereas the
input samples are 32 (16+16) bits. One way to
easily get around this is to place the last
processed samples (the delay line) directly before
the next buffer to filter in memory. The downside
is that between every call to the filter, the delay
line needs to be transferred to the beginning of
the next buffer. For a moderately long kernel,
however, the overhead is not significant.
Old
input
buffer
Delay line
buffer
Next
in
put
bu
ffer
Figure 10. Delay line handling
16-bit FIR Filters on ADSP-TS20x TigerSHARC® Processors (EE-211) Page 5 of 10
Page 6

a
Appendix
The assembly code for the filter functions are given, as well as a header file (*.h) specifying the filter state
structure, a filter state initialization ‘function’, and the filter function prototype, so that it can easily be
used in a C-code.
fir_16_comp.h
/* ********************************************************************************
*
* Copyright (c) 2003 Analog Devices Inc. All rights reserved.
*
* *******************************************************************************/
#include <i16.h>
typedef struct
{
int2x16 *h; // Filter coefficients
int2x16 *d; // Start of (circular) delay line
int2x16 *p; // Current index into delay line
int k; // Number of coefficients
} fir_state_t;
void fir_16_comp(int2x16 *outdata, int2x16 *indata, int N, fir_state_t *fir_state);
#define fir_init(state, coeffs, delay, ncoeffs) \
(state).h = (int2x16 *) (coeffs); \
(state).d = (int2x16 *) (delay); \
(state).p = (int2x16 *) (delay); \
(state).k = (int) (ncoeffs)
Listing 6. fir_16_comp.h
fir_16_comp.asm
/* ********************************************************************************
*
* Copyright (c) 2003 Analog Devices Inc. All rights reserved.
*
* *******************************************************************************/
.global _fir_16_comp;
.section program;
.align_code 4;
_fir_16_comp:
#define Yout j4 // Pointer to output sample buffer
#define Xin j5 // Pointer to input sample buffer
#define N j6 // Number of samples to be filtered
#define FState j7 // Pointer to filter state structure
#define h_offs 0 // Filter state structure offset to Coefficients
// buffer pointer
#define d_offs 1 // Filter state structure offset to Delay line pointer
16-bit FIR Filters on ADSP-TS20x TigerSHARC® Processors (EE-211) Page 6 of 10
Page 7

#define p_offs 2 // Filter state structure offset to Delay line index
#define k_offs 3 // Filter state structure offset to Number of
// coefficients
// Save stack so we can use the internal registers
// Stack PROLOGUE
J26 = J27 - 64; K26 = K27 - 64;;
[J27 += -28] = CJMP; K27 = K27 - 20;;
Q[J27 + 24] = XR27:24; Q[K27 + 16] = YR27:24;;
Q[J27 + 20] = XR31:28; Q[K27 + 12] = YR31:28;;
Q[J27 + 16] = J19:16; Q[K27 + 8 ] = K19:16;;
Q[J27 + 12] = J23:20; Q[K27 + 4 ] = K23:20;;
// Stack PROLOGUE ENDS
// Set number of samples to be generated/filtered
// (outerloop, 4 samples each iteration).
// Set number of times to go through filter kernel to use whole filter
// (innerloop, 4 coeffs/taps each iteration).
yR24 = N ; // Number of samples
xR24 = [FState + k_offs] ;; // Number of coeffs
j0 = [FState + p_offs] ;; // Set j0 to point to latest sample in delay
// line, i.e x[i+k-1]
jl0 = xR24 ; // Circular buffer length = Number of coeffs
R24 = ASHIFT R24 BY -2 ;; // Divide number of samples and coeffs by 4
LC1 = yR24 ; // Number of iterations for outerloop (LC1) =
// Number of samples/4
jb0 = [FState + d_offs] ;; // Circular buffer base address = delay line
// buffer base address
.align_code 4;
outerloop:
k1 = [FState + h_offs] ; // Set k1 to point to coefficient buffer
LC0 = xR24 ;; // Number of iterations for innerloop (LC0) =
// Number of coeffs/4
// Load input samples and coeffs.
R7:4 = q[Xin+=4] ;; // Get x[i+k+3]:x[i+k] from input sample buffer
R11:8 = q[k1+=4] ;; // Get c[k+3]:c[k] from coefficient buffer
R19:16 = R7:4 ; // Save x[i+k+3]:x[i+k] for later store in
// delay line
// Perform initial complex mult between data and coeffs and store in cleared
// MACs.
xMR3:2 += R7 ** R8 (CI) ; // y[i+3] = 0 + x[i+k+3] ** c[k]
yMR3:2 += R5 ** R8 (CI) ;; // y[i+1] = 0 + x[i+k+1] ** c[k]
xMR1:0 += R6 ** R8 (CI) ; // y[i+2] = 0 + x[i+k+2] ** c[k]
yMR1:0 += R4 ** R8 (CI) ; // y[i+0] = 0 + x[i+k+0] ** c[k]
R3:0 = CB Q[j0+=-4] ;; // Get x[i+k-1]:x[i+k-4]
.align_code 4;
innerloop:
// Iterate through filter length
xMR3:2 += R6 ** R9 (I) ; // y[i+3] = y[i+3] + x[i+k+2] ** c[k+1]
yMR3:2 += R4 ** R9 (I) ;; // y[i+1] = y[i+1] + x[i+k+0] ** c[k+1]
a
16-bit FIR Filters on ADSP-TS20x TigerSHARC® Processors (EE-211) Page 7 of 10
Page 8

xMR1:0 += R5 ** R9 (I) ; // y[i+2] = y[i+2] + x[i+k+1] ** c[k+1]
yMR1:0 += R3 ** R9 (I) ; // y[i+0] = y[i+0] + x[i+k-1] ** c[k+1]
R23:20 = q[k1+=4] ;; // Get c[k+7]:c[k+4]
xMR3:2 += R5 ** R10 (I) ; // y[i+3] = y[i+3] + x[i+k+1] ** c[k+2]
yMR3:2 += R3 ** R10 (I) ;; // y[i+1] = y[i+1] + x[i+k-1] ** c[k+2]
xMR1:0 += R4 ** R10 (I) ; // y[i+2] = y[i+2] + x[i+k+0] ** c[k+2]
yMR1:0 += R2 ** R10 (I) ; // y[i+0] = y[i+0] + x[i+k-2] ** c[k+2]
R9:8 = R21:20 ;; // Use c[k+5]:c[k+4]
xMR3:2 += R4 ** R11 (I) ; // y[i+3] = y[i+3] + x[i+k+0] ** c[k+3]
yMR3:2 += R2 ** R11 (I) ; // y[i+1] = y[i+1] + x[i+k-2] ** c[k+3]
R7:4 = R3:0 ;; // Shift x[i+k-1]:x[i+k-4] into x[i+k+3]:x[i+k]
xMR1:0 += R3 ** R11 (I) ; // y[i+2] = y[i+2] + x[i+k-1] ** c[k+3]
yMR1:0 += R1 ** R11 (I) ; // y[i+0] = y[i+0] + x[i+k-3] ** c[k+3]
R11:10 = R23:22 ;; // Use c[k+7]:c[k+6]
xR15:14 = MR3:2, MR3:2 += R7 ** R8 (I); // y[i+3] = y[i+3] + x[i+k-1] ** c[k+4]
yR15:14 = MR3:2, MR3:2 += R5 ** R8 (I);; // y[i+1] = y[i+2] + x[i+k-3] ** c[k+4]
if NLC0E, JUMP innerloop ; // All filter taps computed?
xR13:12 = MR1:0, MR1:0 += R6 ** R8 (I); // y[i+2] = y[i+2] + x[i+k-2] ** c[k+4]
yR13:12 = MR1:0, MR1:0 += R4 ** R8 (I); // y[i+0] = y[i+0] + x[i+k-4] ** c[k+4]
R3:0 = CB Q[j0+=-4] ;; // Get x[i+k-5]:x[i+k-8]
j0=j0+8 (CB) ;
sR12 = COMPACT R13:12 (IS);; // Transfer result from MACs and compact
// from 32-bit to 16-bit (with saturation).
CB q[j0+=j31] = xR19:16 ; // Store x[i+k+3]:x[i+k] in delay line buffer
sR13 = COMPACT R15:14 (IS);; // Transfer result from MACs and compact from
// 32-bit to 16-bit (with saturation).
.align_code 4;
if NLC1E, JUMP outerloop ; // All samples computed?
q[Yout+=4] = R13:12 ;; // Store 4 output samples in output buffer.
[FState + p_offs] = j0 ;; // Save j0 to point to latest sample in delay
// line, i.e x[i+k-1]
// Restore stack and return to calling function.
// EPILOGUE STARTS
CJMP = [J26 + 64];;
YR27:24 = q[K27 + 16]; XR27:24 = q[J27 + 24];;
YR31:28 = q[K27 + 12]; XR31:28 = q[J27 + 20];;
K19:16 = q[K27 + 8 ]; J19:16 = q[J27 + 16];;
K23:20 = q[K27 + 4 ]; J23:20 = q[J27 + 12];;
CJMP (ABS); J27:24=q[J26+68]; K27:24=q[K26+68]; nop;;
// EPILOGUE ENDS
_fir_16_comp.end:
a
Listing 7. fir_16_comp.asm
fir16_real.asm
.section program;
.global _fir16_real;
_fir16_real:
16-bit FIR Filters on ADSP-TS20x TigerSHARC® Processors (EE-211) Page 8 of 10
Page 9

// Local defines
#define Yout j4
#define Xin j5
#define INPUT_LEN j6
#define FIR_STATE j7
// Offsets to state struct elements
#define coeff_offs 0
#define delay_offs 1
#define idx_offs 2
#define nof_coeff_offs 3
//PROLOGUE
J26 = J27 - 64; K26 = K27 - 64;;
[J27 += -28] = CJMP; K27 = K27 - 20;;
Q[J27 + 24] = XR27:24; Q[K27 + 16] = YR27:24;;
Q[J27 + 20] = XR31:28; Q[K27 + 12] = YR31:28;;
Q[J27 + 16] = J19:16; Q[K27 + 8 ] = K19:16;;
Q[J27 + 12] = J23:20; Q[K27 + 4 ] = K23:20;;
//PROLOGUE ENDS
k0 = [FIR_STATE + coeff_offs];;
k0 = k0 + k0;; // Times 2 for short data access
j0 = k0;;
j0 = j0 + 0x1;;
xR3:0 = sDAB q[k0 += 0x8]; // Preload filter coeffs to CBX
yR3:0 = sDAB q[j0 += 0x8];; // Preload skewed coeffs copy into CBY
xR3:0 = sDAB q[k0 += 0x8];
yR3:0 = sDAB q[j0 += 0x8];;
xR20 = INPUT_LEN;;
// Expand the coeffs into 2 identical short words(16 bits) each
SR11:8 = MERGE R1:0, R1:0;;
SR15:12 = MERGE R3:2, R3:2;;
// Divide by two since two outputs are calculated simultaneously
xR20 = ASHIFT R20 by -1;;
j11 = -10;; // increment for i/p pointer
j0 = Xin + 0x2; // The first data will be picked from delay line
LC0 = xR20 ;;
R27:24 = DAB q[j0 += 4];; // Prefetch
R27:24 = DAB q[j0 += 4];;
j8 = [FIR_STATE + delay_offs];; // Get pointer to delay line
///////// Loop over number of input samples ////////
.align_code 4;
loop_:
R3:0 = R27:24;;
MR3:0 += R9:8 * R25:24 (CI);
R31:28 = DAB q[j0 += 4];;
MR3:0 += R11:10 * R27:26 (I);
R27:24 = DAB q[j0 += j11];;
MR3:0 += R13:12 * R29:28 (I);
R27:24 = DAB q[j0 += 4];;
MR3:0 += R15:14 * R31:30 (I);
R27:24 = DAB q[j0 += 4];;
sR23:22 = COMPACT MR3:0 (IS);;
a
16-bit FIR Filters on ADSP-TS20x TigerSHARC® Processors (EE-211) Page 9 of 10
Page 10
R7:4 = R31:28;;
sR21 = R23 + R22;;
if NLC0E, jump loop_; l[Yout += 0x2] = xyR21;;
/////////// End of loop_ ////////////////
q[j8 += 0x4] = xR3:0;; // Store delay line
q[j8 += j31] = xR7:4;;
// EPILOGUE STARTS
CJMP = [J26 + 64];;
YR27:24 = q[K27 + 16]; XR27:24 = q[J27 + 24];;
YR31:28 = q[K27 + 12]; XR31:28 = q[J27 + 20];;
K19:16 = q[K27 + 8 ]; J19:16 = q[J27 + 16];;
K23:20 = q[K27 + 4 ]; J23:20 = q[J27 + 12];;
CJMP (ABS); J27:24=q[J26+68]; K27:24=q[K26+68]; nop;;
// EPILOGUE ENDS
_fir16_real.end:
Listing 8. fir16_real.asm
Document History
a
Version Description
Rev 1 –January 13, 2004
by Klas Brink
Initial Release
16-bit FIR Filters on ADSP-TS20x TigerSHARC® Processors (EE-211) Page 10 of 10
 Loading...
Loading...