Page 1

Engineer To Engineer Note EE-186
a
Technical Notes on using Analog Devices' DSP components and development tools
Contact our technical support by phone: (800) ANALOG-D or e-mail: dsp.support@analog.com
Or v isi t ou r on -li ne r esou rc es h ttp :// www.analog.com/dsp and http://www.analog.com/dsp/EZAnswers
Extended-Precision Fixed-Point Arithmetic on the Blackfin® Processor
Platform
Contributed by DSP Apps May 13, 2003
Introduction
The Blackfin® Processor platform was designed
to efficiently perform 16-bit fixed-point
arithmetic operations. There are times, however,
when it may become necessary to increase
accuracy by extending precision up to 32 bits.
The first part of this document describes an
extended-precision, fixed-point arithmetic
technique that can be emulated on Blackfin
Processors using the native 16-bit ALU
instructions. The second part illustrates Blackfin
Processor assembly implementations of the 31and 32-bit- accurate FIR filters. An
accompanying source code package contains full
FIR and IIR assembly programs.
Addition
The Blackfin Processor instruction set contains a
single-cycle 32-bit addition of the form
R2
. Therefore, no emulation is necessary for
R0 = R1 +
adding two 32-bit numbers. Subtraction of 32bit numbers is also natively supported in the
same form as addition:
R0 = R1 - R2. Note that,
in these addition and subtraction instructions,
any combination of data registers can be used.
More detailed information on the native
L
Blackfin Processor operations can be
found in the Blackfin Processor
Instruction Set Reference.
Multiplication
In order to introduce the concept of extended-
Background
Extended-precision arithmetic is a natural
software extension for 16-bit fixed-point
processors. In machines with 16-bit register
files, two registers can be used to represent one
31-bit or 32-bit fixed-point number. Blackfin
precision multiplication, it is useful to review the
already familiar decimal multiplication.
Two-Digit Decimal Multiplication
Let’s start by recalling how any decimal
multiplication can be performed by knowing how
to multiply single-digit numbers.
Processors are ideally suited for extendedprecision arithmetic, because the register file is
based on 32-bit registers, which can either be
treated as 32-bit entities or two 16-bit halves.
Before getting into specific DSP algorithms, it is
important to see how basic arithmetic operations
can be implemented with extended precision.
Copyright 2003, Analog Devices, Inc. All rights reserved. Analog Devices assumes no responsibility for customer product design or the use or application of
customers’ products or for any infringements of patents or rights of others which may result from Analog Devices assistance. All trademarks and logos are property
of their respective holders. Information furnished by Analog Devices Applications and Development Tools Engineers is believed to be accurate and reliable, however
no responsibility is assumed by Analog Devices regarding technical accuracy and topicality of the content provided in Analog Devices’ Engineer-to-Engineer Notes.
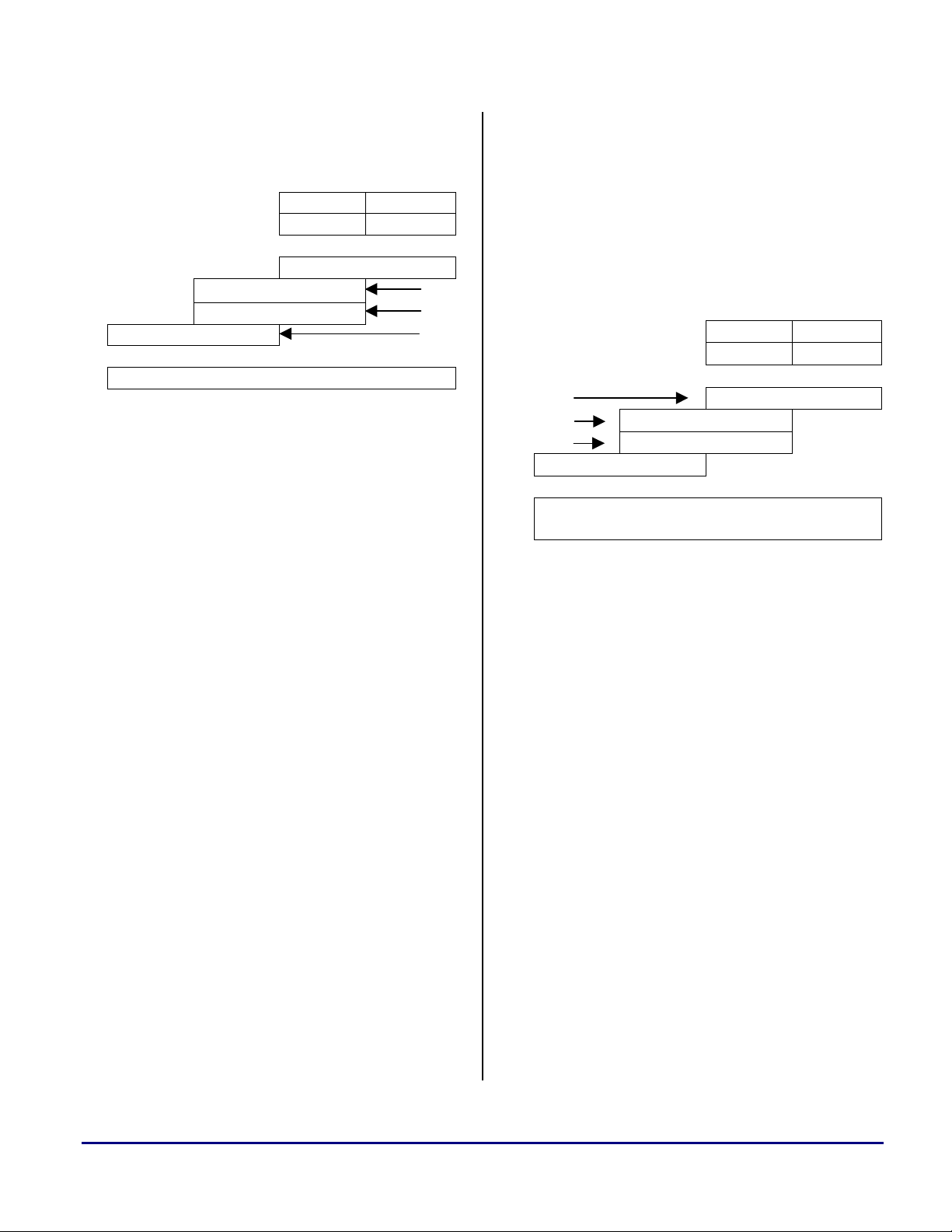
As an example, consider this two-digit by twodigit decimal multiplication:
23 x 98 = 2254
Figure 1 illustrates how this particular operation
can be broken down into smaller operations.
This is basically multiplication “by hand.”
Page 2
a
Figure 1 Decimal multiplication in detail
1000’s place 100’s place 10’s place 1’s place
2 3
x 9 8
{a} + 8 x 3 = 24
{b} + 8 x 2 = 16 x 10
{c} + 9 x 3 = 27 x 10
{d}+ 9 x 2 = 18 x 10
------------------------------------------------------------------------------------
{e}
2
+ 27 x 101 + 16 x 101 + 24 x 100 = 2254
18 x 10
------------------------------------------
1
1
2
To compute the final result, the following
operations are necessary:
• Four single-digit multiplications (lines {a},
{b}, {c}, {d} in Figure 1)
8 x 3 = 24, 8 x 2 = 16, 9 x 3 = 27, 9 x 2 = 18
• Three operations to shift the sub-products
into the correct digit-significant slot (lines
{b}, {c}, {d} in Figure 1)
18 x 10
2
, 27 x 101, 16 x 101
• Three additions (line {e} in Figure 1)
18 x 10
2
+ 27 x 101, 16 x 101 + 24, (18 x 10
2
+ 27 x 101) + (16 x101 + 24)
Two-Digit Hexadecimal Multiplication
Hexadecimal multiplication is not much different
from its decimal counterpart. Let’s consider a
multiplication of two 32-bit fractional numbers,
where the operands are stored in the 32-bit
general-purpose data registers
R0 and R1.
Blackfin Processors actually have a built-in 32bit multiply operation of the form:
R1 *= R0. It is
a multi-cycle instruction that takes 5 cycles to
execute from L1 memory. It is possible to
improve this performance with the 16-bit
multiplication technique that follows.
32-Bit Accuracy with 16-Bit Multiplication
Instead of relying on this instruction, one can use
elementary arithmetic to achieve a 32-bit
multiplication result with single-cycle 16-bit
multiplications.
Each of the two 32-bit operands (
be broken up into two 16-bit halves (
R1.H, and R1.L), as shown in Figure 2.
Figure 2 Hexadecimal multiplication in detail
bits 63:48 47:32 31:16 15:0
R0.H R0.L
xR1.H R1.L
{a} >> 32 + R1.L x R0.L
{b} >> 16 + R1.L x R0.H
{c} >> 16 + R1.H x R0.L
{d}+ R1.H x R0.H
------------------------------------------------------------------------------------
{e}
(R1.H x R0.H) + (R1.L x R0.H) >> 16 +
(R1.H x R0.L) >> 16 + (R1.L x R0.L) >> 32 = R1 x R0
------------------------------------------
R0 and R1) can
R0.H, R0.L,
From this figure, it is easy to see the operations
required to emulate the 32-bit multiplication
R1
with a combination of instructions using 16-
R0 x
bit multipliers:
• Four 16-bit multiplications to yield four 32bit results (lines {a}, {b}, {c}, {d} in Figure
2)
R1.L x R0.L, R1.L x R0.H,
R1.H x R0.L, R1.H x R0.H
• Three operations to shift the sub-products
into the correct digit-significant slot (lines
{a}, {b}, {c} in Figure 2). Since we are
performing fractional arithmetic, the result is
1.63 (1.31 x 1.31 = 2.62 with a redundant
sign bit). Most of the time, the result can be
truncated to 1.31 in order to fit in a native
32-bit data register. Therefore, the result of
the multiplication should be in reference to
the sign bit, or the most significant bit. In
this way, the rightmost least significant bits
can be safely discarded in a truncation.
Extended-Precision Fixed-Point Arithmetic on the Blackfin® Processor Platform (EE-186) Page 2 of 5
Page 3

a
(R1.L x R0.L) >> 32, (R1.L x R0.H) >> 16, (R1.H
x R0.L) >> 16
• Three operations to preserve bit place in the
final answer (line {e} in Figure 2):
(R1.L x R0.L) >> 32 + (R1.L x R0.H) >> 16,
(R1.H x R0.L) >> 16 + R1.H x R0.H
((R1.L x R0.L) >> 32 + (R1.L x R0.H) >> 16) +
((R1.H x R0.L) >> 16 + R1.H x R0.H)
,
The final expression for a 32-bit multiplication
is:
R1 x R0 = ((R1.L x R0.L) >> 32 + (R1.L x R0.H) >>
16) + ((R1.H x R0.L) >> 16 + R1.H x R0.H)
31-Bit Accuracy with 16-Bit Multiplication
From Figure 2, it is easy to see that the
multiplication of the least significant half-word
R1.L x R0.L does not contribute much to the final
result. In fact, if the final result is ultimately
truncated to 1.31 anyway, then this
multiplication can only have an effect on the
least significant bit of the 1.31 result. For many
applications, the loss of accuracy due losing to
this bit is balanced by the performance increase
over the 32-bit multiplication. Three operations
(one 16-bit multiplication, one shift, and one
addition) can be eliminated if 31-bit accuracy is
acceptable in the final design:
R1 x R0 = ((R1.L x R0.L) >> 32 + (R1.L x R0.H) >>
16) + ((R1.H x R0.L) >> 16 + R1.H x R0.H)
The remaining instructions necessary to get a 31bit-accurate 1.31 answer are three 16-bit
multiplications, two additions, and a shift:
R1 x R0 = ((R1.L x R0.H) >> 16) + ((R1.H x R0.L) >>
16 + R1.H x R0.H)
Further rearrangement of terms yields the final
form of 31-bit-accurate multiplication:
R1 x R0 = ((R1.L x R0.H) + R1.H x R0.L) >> 16 +
(R1.H x R0.H)
Double-Precision FIR Filter Implementation
32-Bit-Accurate FIR Filter
If we consider R0 to be the data value and R1 to
be a coefficient value, then each multiplication in
the FIR will be of the form described earlier:
R1 x R0 = ((R1.L x R0.L) >> 32 + (R1.L x R0.H) >>
16) + ((R1.H x R0.L) >> 16 + R1.H x R0.H)
The kernel for a 32-bit-accurate FIR
implementation is shown in Listing 1. The
number of cycles needed to execute the full
implementation is
where
N is the size of the input buffer and T is the
28 + N*(3*T+5) cycles,
number of filter taps.
Complete source code for 31- and 32-bit-
L
accurate FIR and IIR filters is contained
in the compressed package
accompanying this document.
Listing 1 Kernel of a 32-bit-accurate FIR
// I0 = address of the delay line buffer
// I1 = address of the input array
// I2 = address of the coefficient array
// I3 = address of the output array
// P0 = number of input samples
// P2 = number of coefficients
// The outer loop iterates over all the data
samples
LSETUP(FIR_START, FIR_END) LC0=P0;
FIR_START:
// The first section performs a multiplyaccumulate on the least significant halves
of the data and coefficients (R0.L*R1.L),
and implicitly shifts the result >> 32 by
placing it in accumulator A1
LSETUP(M_ST, M_ST) LC1=P2;
A0=R0.L*R1.L (FU) || R0=[I1--] ||
R1=[I2++];
M_ST: R3.L=(A0+=R0.L*R1.L) (FU) ||
R0=[I1--] || R1=[I2++];
A1=R3;
// In this section, the product of the
most significant words (R0.H*R1.H) gets
accumulated to A1, and the products
R0.L*R1.H and R1.L*R0.H get accumulated
into A0 onto the running sum from the
first section. The bit placement shift
is explicit in the R3=R3>>>15
instruction
A0=R0.H*R1.H, A1+=R0.H*R1.L (M) ||
[I3++]=R2;
LSETUP(MAC_ST,MAC_END) LC1=P2;
MAC_ST: A1+=R1.H*R0.L (M) || R0=[I1--]
|| R1=[I2++];
Extended-Precision Fixed-Point Arithmetic on the Blackfin® Processor Platform (EE-186) Page 3 of 5
Page 4

MAC_END: R2=(A0+=R0.H*R1.H),
A1+=R0.H*R1.L (M);
R3=(A1+=R1.H*R0.L) (M) || I4+=4 ||
R0=[I0++];
R3=R3>>>15 || [I1--]=R0 || R1=[I2++];
// The final sum gives the answer
FIR_END: R2=R2+R3 (S);
a
MAC_END: R3=(A1+=R1.H*R0.L) (M) ||
R0=[I1--] || R1=[I2++];
R3=R3>>>15 || I1+=M0 || R0=[I0++];
// R3 holds the final answer
R3=R2+R3 (S) || [I1--]=R0;
FIR_END: A1=A0=0 || [I3++]=R3;
31-Bit-Accurate FIR Filter
A 31-bit-accurate FIR filter can be useful for
extended precision in audio algorithms. The 31bit-accurate multiplication (illustrated above) can
be used for the FIR kernel computation:
R1 x R0 = ((R1.L x R0.H) + R1.H x R0.L) >> 16 +
(R1.H x R0.H)
The Blackfin Processor source code for the 31bit-accurate FIR filter is shown in Listing 2. The
number of cycles needed to execute the full
implementation is
23 + N*(2*T+4) cycles,
where N is the size of the input buffer and T is the
number of filter taps.
Listing 2 Kernel of a 31-bit-accurate FIR
// I0 = address of the delay line buffer
// I1 = address of the input array
// I2 = address of the coefficient array
// I3 = address of the output array
// P0 = number of input samples
// P2 = number of coefficients
// M0 = 8
// The outer loop iterates over all the data
samples
A1=A0=0 || R0=[I1--] || R1=[I2++];
LSETUP(FIR_START, FIR_END) LC0=P0;
FIR_START:
// Compared to the first section in the
32-bit-accurate FIR, this implementation
omits the least significant halves (R0.L
and R1.L) of the operands. The product of
the most significant words (R0.H*R1.H)
gets accumulated to A0, and the products
R0.L*R1.H and R1.L*R0.H get accumulated
into A1. The bit placement shift is
explicit in the R3=R3>>>15 instruction
LSETUP(MAC_ST,MAC_END) LC1=P2;
MAC_ST: R2=(A0+=R0.H*R1.H),
A1+=R0.H*R1.L (M);
Summary
This application note described an effective
method for implementing extended-precision
arithmetic on Blackfin Processors. The
discussion about the tradeoffs between 31-bit
accuracy and 32-bit accuracy was supported by
code segments for an FIR filter. Table 1
summarizes the performance of the FIR and IIR
filters found in the compressed package supplied
with this document.
Table 1 Computation time for 31-bit and 32-bit filter
implementations on a Blackfin Processor
FIR
IIR
32-bit accuracy 31-bit FIR accuracy
28+N*(3*T+5)
cycles
23+18*N cycles 23+12*N cycles
23+N*(2*T+4)
cycles
Extended-Precision Fixed-Point Arithmetic on the Blackfin® Processor Platform (EE-186) Page 4 of 5
Page 5

a
Document History
Version Description
May 13, 2003 by T. Lukasiak. Updated according to new naming conventions
April 1, 2003 by T. Lukasiak. Revision to source code snippets and accompanying source code
February 26, 2003 by T. Lukasiak. Initial release
Extended-Precision Fixed-Point Arithmetic on the Blackfin® Processor Platform (EE-186) Page 5 of 5
 Loading...
Loading...