Page 1
AN-604
a
APPLICATION NOTE
One Technology Way • P.O. Box 9106 • Norwood, MA 02062-9106 • Tel: 781/329-4700 • Fax: 781/326-8703 • www.analog.com
Using the ADXL202 Duty Cycle Output
by Harvey Weinberg
Calculation of the Acceleration Output
Acceleration experienced by the ADXL202 may be calculated using the following formula:
Acceleration in
As outlined in the data sheet, the nominal duty cycle
output of the ADXL202 is 50% at 0
cycle change per
from the duty cycle:
If the 0 g duty cycle output of the ADXL202 is other than
50%, and/or the duty cycle changes more or less than
12.5% per
rate. In practice, the 0
ADXL202 vary somewhat from device to device (see the
data sheet for details). So this formula can only be
used for low accuracy measurements. For higher
accuracy measurements, the actual offset and scale values must be substituted.
()
Acceleration in
g
, the acceleration calculation will be inaccu-
Duty Cycle Duty Cycle at
g
=
g
. Therefore to calculate acceleration
()
g =
g
output and the sensitivity of the
–
Duty Cycle per
g
and 12.5% duty
TT
()–%
12 50
.%
12 5
g
0
g
In addition, the result of this equation would be a number in the range of ±2 for an ADXL202. In general, it is
inconvenient to use real numbers in calculations with a
small microcontroller since floating point mathematics
would be required to get meaningful results. A preferred
method for calculation of acceleration with a small
microcontroller using fixed point math is included in
this application note, along with two simple methods of
calibration to find the actual offset and scale values.
This application note outlines methods to decode the duty
cycle output, conversion from duty cycle to acceleration
(or tilt angle), and calibration of the ADXL202. These methods are geared toward use with 8-bit microcontrollers
having limited computational capability.
Decoding the Output
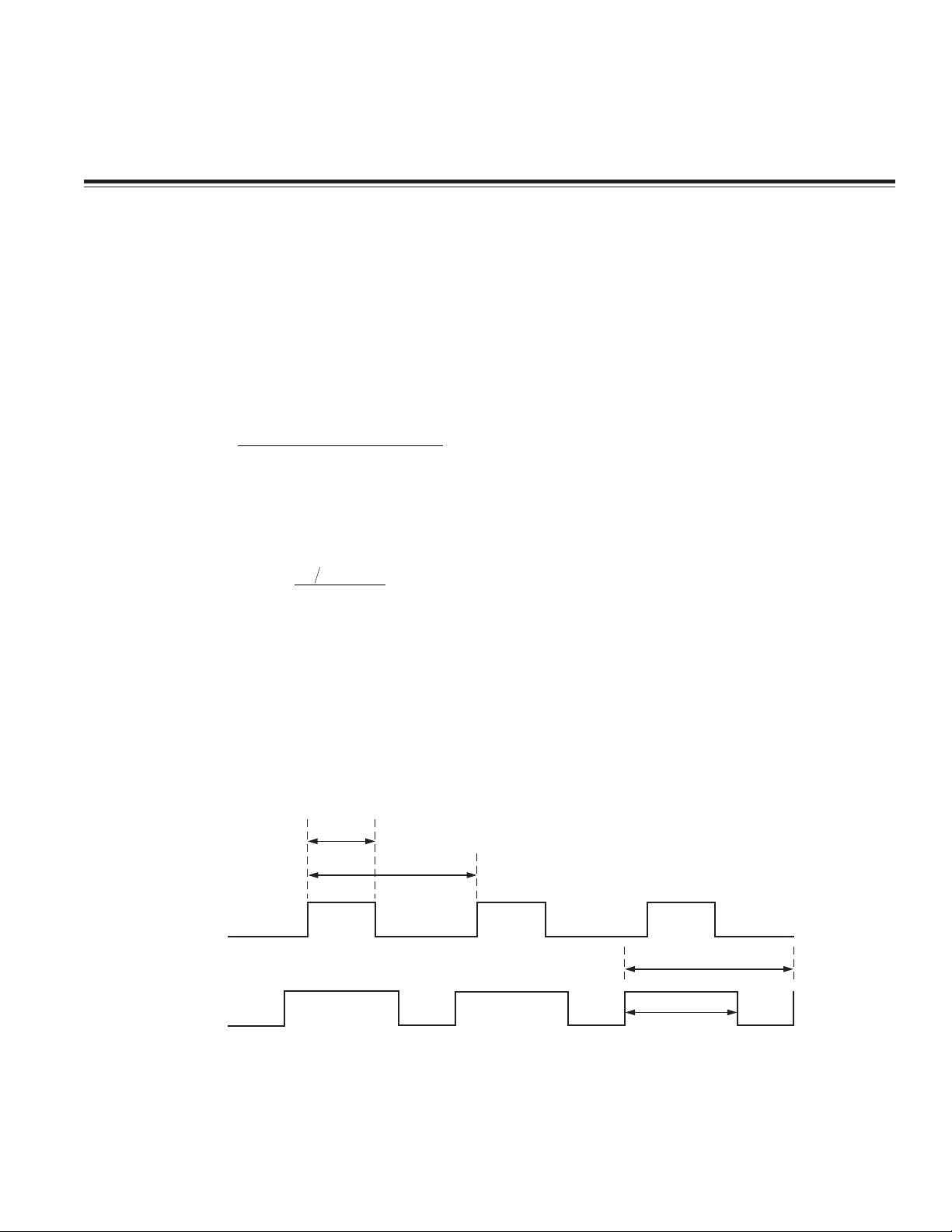
The most direct way to decode the duty cycle output is
shown in Figure 1. A counter is started at the rising edge
of the X output (Ta = 0). The count at the falling edge
(Tb) is recorded, and the timer is stopped at the next rising edge of the X output (Tc). This process is then
repeated for the Y output (Td, Te, and Tf).
REV. 0
T1
T2
X
OUT
Ta
Y
OUT
Figure 1. Basic Decode Technique for the ADXL202
Tb
Tc
Td
T2
T1
Te
© Analog Devices, Inc., 2002
Tf
Page 2
AN-604
While this technique is very easy to understand, you can
only acquire one sample of acceleration from both axes
every three cycles (i.e., 3 ⫻ T2) since you must wait for
the next rising edge of X
after Tf.
OUT
Note that while T2 is nominally constant, it does change
over temperature and contains some jitter. For systems
that do not require resolutions of better than 100 m
T2 may be measured only once. For more accurate
measurements, several T2 measurements should
be made and averaged. The average should be
updated periodically to account for T2 drift over
temperature.
T1
T2
X
OUT
Ta
Tb Te
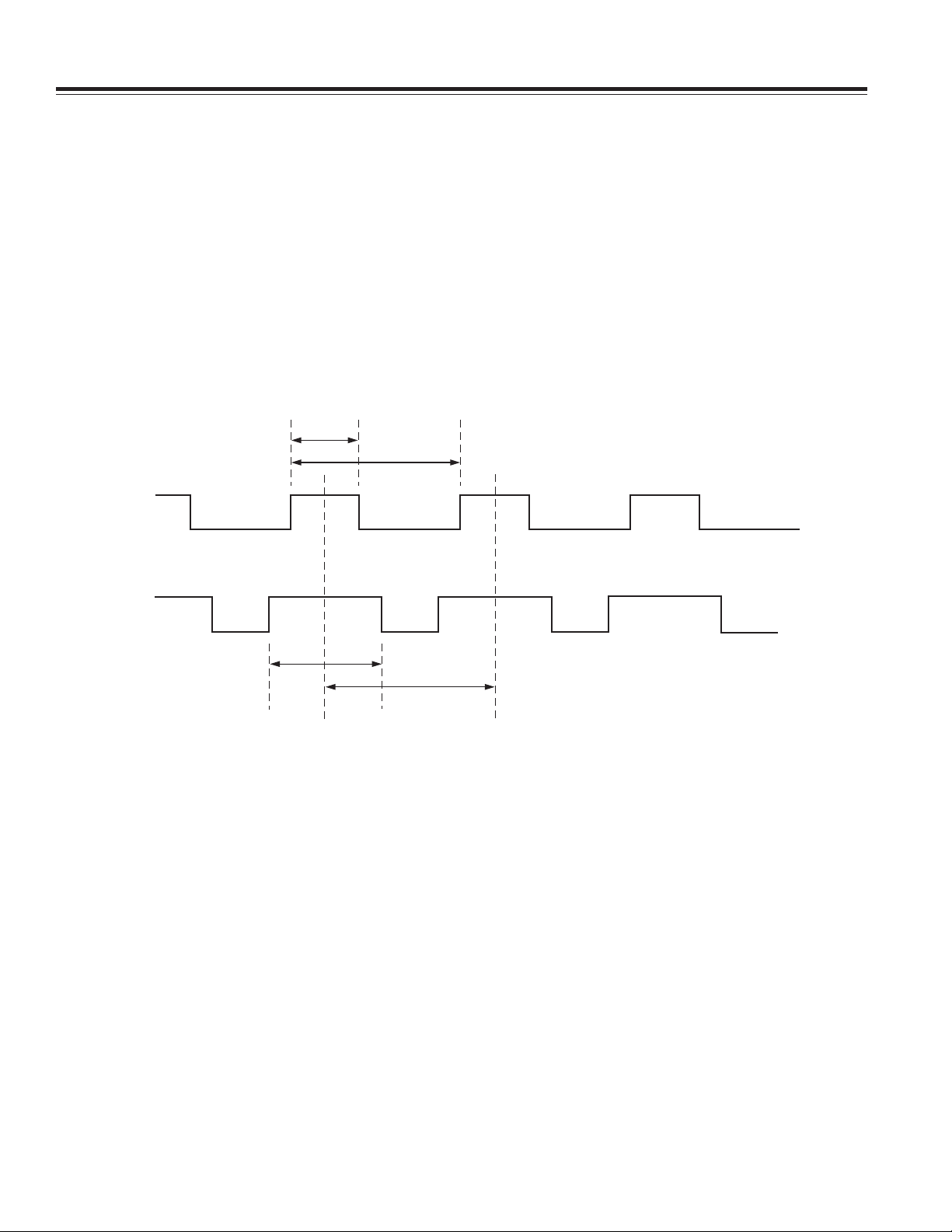
An Improved PWM Decode Scheme
Since the duty cycle modulator (DCM) uses the same triangle wave reference for the X and Y channels, the
midpoints of the T1 of each period must be coincident. This
is illustrated in Figure 2. Here it is shown that even
though the X and Y duty cycle outputs are different,
g
,
the midpoints of T1 are synchronized. Therefore, an
improved PWM decode technique can be used to speed up
the data acquisition time. Figure 2 shows the sequence of
events. A counter is started at the rising edge of the X output (Ta = 0). The count at the falling edge of the X output
(Tb) is recorded. Then the counts at the rising and falling
edges of the Y output (Tc and Td) are recorded. A flow chart
outlining this method of calibration is shown in Figure 3.
Y
OUT
T1
Tg
Tc
T2
Tf
Td
Figure 2. High Speed Decoding Technique for the ADXL202
By definition:T1x = Tb – Ta = Tb (if the counter is zero at Ta)
T1y
= Td –
T2x
= T2y = Te – Ta = Tg –
Tc
Tf
Since the midpoints of the high states of the X and Y duty cycle signals are coincident:
T
2 = [Td – ((Td – Tc)/2)] – [(Tb – Ta)/2]
T
2 = [Td – ((Td – Tc)/2)] – [Tb/2] (if the counter is zero at Ta)
The advantages of this system of decoding are:
1. One sample of acceleration from both axes can be acquired every two
2.
T
2 is only calculated once for both the X and Y signals.
T
2 cycles.
–2–
REV. 0
Page 3
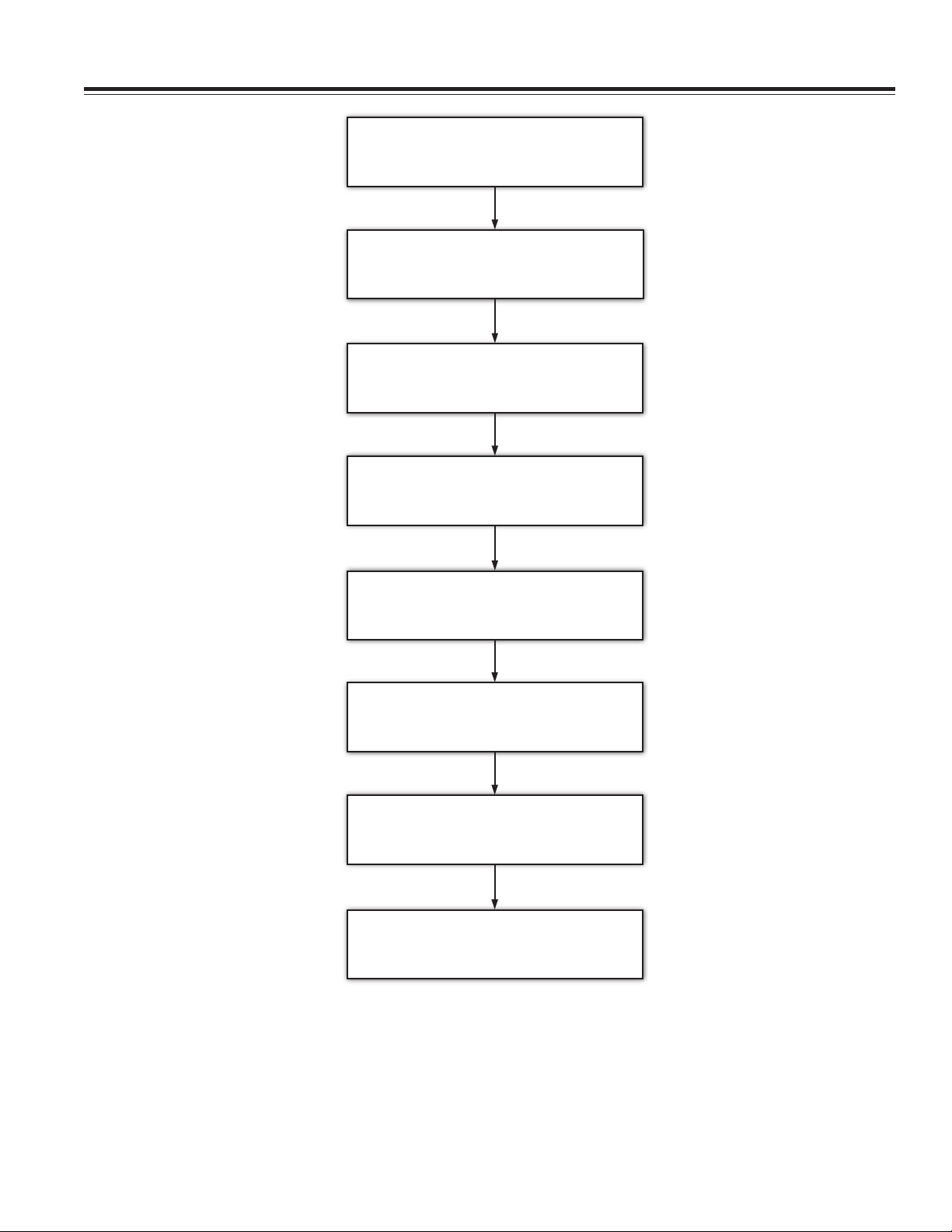
START TIMER AT Ta
RECORD TIME AT Tb
RECORD TIME AT Tc
RECORD TIME AT Td
AN-604
T1x = Tb
T1y = Td – Tc
T2 = [Td –
((Td – Tc)/2)] – [(Tb – Ta )/ 2 ) ]
DONE
Figure 3. Flow Chart for High Speed Decoding Technique for the ADXL202
REV. 0
–3–
Page 4

AN-604
Calibration of the ADXL202
The easiest way to calibrate the ADXL202 is by using the
earth’s gravity as a reference input. If your application
does not require high accuracy, you may use a “quick calibration” technique. Here we assume that the sensitivity of
the accelerometer is 12.5% duty cycle per
fication). One digital input may be used to tell the
microcontroller that it is in calibrate mode. When in calibrate
mode, the accelerometer must be level, with the X and Y axes
horizontal to the earth so both axes experience 0
When the microcontroller is told to calibrate, the
microcontroller reads the duty cycle output (T1) and
period (T2) of the accelerometer from each axis. Several
readings of T1 and T2 may be averaged to improve
accuracy. These values are stored as calibration constants and retained for use in calculating the acceleration
after calibration. A scale factor (K) used to scale the
acceleration output into an n-bit word should also be calculated. The calibration constants for each axis are:
1. T2cal = the value (from the microcontroller’s counter)
of T2 during calibration. T2cal must be stored, as the
value of T2 does drift over temperature and has jitter.
2. Zcal = the value (from the microcontroller’s counter)
of T1 during calibration.
3. Bit scale factor. You choose the bit scale factor to
determine the resolution (in bits) of the acceleration
calculation.
4.
K = [4 ⫻ (T2cal ⫻ bit scale factor)/T2cal]
Note that K need only be calculated once for the two
axes if you choose the same bit scale factor for both axes.
g
(the typical speci-
g
.
The bit scale factor will be determined by the size (in
bits) of the result desired. For example, if a result of ±1
= ± 128 counts (to result in an 8-bit number) is needed,
the scale factor would be 256. For a result of
±1
g
= ±90 counts (to approximate 1∞ per count), the
scale factor would be 180.
Calculation of Acceleration from Duty Cycle
Once the calibration constants are known, only two formulas are required for the calculation of acceleration.
They are:
Zcal T actual
Zactual
Where T2
formula corrects the 0
drift or jitter.
actual
is the current measurement of T2. This
g
Acceleration
Note that all of the operations are fixed point, and
therefore fairly easy and fast for any microcontroller
to perform.
Care should be taken in the correct ordering of operations to preserve resolution. When designing software,
keep an eye out for ways to order mathematical operations that will not drop significant bits. In general,
perform addition, multiplication, subtraction, and division in that order. Double and triple precision fixed point
arithmetic (16- and 24-bit) will be required in most applications. Algorithms for multibyte fixed point arithmetic
are widely available in application notes published by
microcontroller manufacturers.
¥ 2
=
T cal
2
value for changes in T2 due to
KT Zactual
¥ (– )1
=
T actual
2
g
–4–
REV. 0
Page 5

AN-604
High Accuracy Calibration Method for the ADXL202
Variance in sensitivity (i.e., duty cycle % per g ) from part
to part is normal and will result in a small error if not
accounted for. If your application requires high accuracy
measurements, the rotational calibration method presented below is preferred.
Simply place the ADXL202 such that the Z axis is horizontal and rotate the ADXL202 over at least 360∞. The
ADXL202 will then be exposed to ±1
Y axes. The rotation must be done slowly in order to
minimize the effects of centrifugal acceleration.
The following pieces of calibration data must be
retained for use in calculating the acceleration after
calibration:
1. T2cal. That is, the value of T2 during the calibration
procedure.
2.
Zcal
. That is, the 0 g value of T1 at the time of calibration.
It is calculated as follows:
TT
11
=
max min–
Zcal
3. Bit scale factor. You choose the bit scale factor to
determine the resolution (in bits) of the acceleration
calculation.
4.
K
. Where K is the scale factor. K may be calculated
as follows:
g
in both the X and
2
The bit scale factor used here is the same as outlined in
the quick calibration technique.
Variance in part-to-part sensitivity is corrected in the
denominator by calculating the actual duty cycle output obtained from exposure to 2
from gravity).
A flow chart outlining a calibration algorithm is shown
in Figure 4. One digital input is used to tell the
microcontroller that it is in calibrate mode.
Calculation of the acceleration is done as presented
above. That is:
Acceleration
Where:
Zactual
For maximum accuracy, several readings of T2 should
be averaged to reduce error induced by
flow chart (Figure 4) does not include this operation. It is
up to the user to determine how many averaged
samples of
four to eight averaged samples of
cient for systems with resolutions of 1 m
T
2 are suitable in the application. Generally
=
Zcal T actual
=
g
of acceleration (±1
KT Zactual
¥ (– )1
T actual
2
¥ 2
T cal
2
T
2 should be suffi-
g
T
2 jitter. The
or greater.
g
T cal bit scale factor
K
=
¥2
TT
11max min–
REV. 0
–5–
Page 6

AN-604
Calibration Algorithm
IS
CAL PIN
HIGH?
YES
CHANGE CAL
FLAG STATE
READ T1xmax
READ T1xmin
IS
CAL FLAG
HIGH?
NO
MAIN PROGRAM
YESNO
T2cal = T2
Zcal = (T1xmax + T1xmin)/2
SCALE = [T2/(T1xmax – Zcal)]
Figure 4. Flow Chart for the ADXL202 Calibration Algorithm
–6–
REV. 0
Page 7

–7–
Page 8

E03049-0-10/02(0)
–8–
PRINTED IN U.S.A.
 Loading...
Loading...