Page 1

AN-602
a
One Technology Way • P.O. Box 9106 • Norwood, MA 02062-9106 • Tel: 781/329-4700 • Fax: 781/326-8703 • www.analog.com
APPLICATION NOTE
Using the ADXL202 in Pedometer and Personal Navigation Applications
by Harvey Weinberg
INTRODUCTION
iMEMS® accelerometers have sparked the interest of
many designers looking for ways to build accurate
pedometers. The personal navigation system is an
extension of the pedometer with an electronic compass
integrated to the pedometer to allow a user to determine
their position relative to some starting point. This application note will discuss the issues that designers will
face in these applications and describe some strategies
for the implementation of personal navigation systems.
THE CLASSICAL IMPLEMENTATION
Accelerometers have been used as position sensors in
inertial navigation systems for many years. Inertial navigation systems use a combination of accelerometers
and gyroscopes to determine position by means of
“dead reckoning,” where the deviation of position from
a known reference (or starting point) is determined by
integration of acceleration in each axis over time. The
math is fairly straightforward:
However for low speed movement, the accuracy of such
a system over any reasonable length of time is poor
because small dc errors accumulate and eventually
amount to very large errors. This is most easily illustrated with an example of a person walking at 5 km/h
(1.39 m/s) over a five minute period. The average acceleration for the 416 m traveled would be:
Since the temperature coefficient of the ADXL202 is
approximately 2 m
0.5°C over the five minutes would add 1 m
more than the desired signal itself! In fact, a change in
inclination of the accelerometer of just 0.06°C would be
greater than 1 m
To minimize the error, we must know the orientation of
the accelerometer and have some method of “resetting”
Position Starting Position
A
=+
Displacement
×
2 833
=
avg
.. g
0 00926 0 944
g
/°C, a temperature deviation of even
g.
22
t
2
ms m
=
2
At
×
2
==
300
g
of error—
the integrator to known reference positions fairly often.
Many systems use GPS receivers or position switches to
provide this periodic reference position information. If
this absolute positional information was available fairly
often (say every 10 seconds), we could greatly reduce
the error.
In 10 seconds, the average acceleration would be
28.4 m
g.
Assuming we could hold all dc errors to 1 m
over 10 seconds and fix the orientation of the accelerometer, we would have a positional error of
approximately 0.5 m—much better than a GPS system
alone could do. So, using dead reckoning as an adjunct
to an existing positioning system may be very useful,
but it is not very accurate when used alone.
As an example of where dead reckoning works well,
consider an elevator. Magnetic position switches are
placed on its track every meter. However, we wish to
control the positioning of the elevator to 10 mm. The
classic solution is to use an optical encoder on a wheel
coupled to the track as a “fine position” sensor. Since
mechanical sensors are prone to wear, we wish to
replace the encoder wheel with an accelerometer to
improve long term reliability.
Assuming we can hold the dc errors stable to 1 m
a few seconds and the elevator travels at 1 m/s, we can
find the positional error as:
2
198 1
ms
=
g.
××
2
=
49
At m
E
pos
well within our target.
PEDOMETERS
When trying to determine how far a person has walked,
there is other information available to us. When people
walk, there is Z-axis (vertical) movement of the body with
each step. A simple but inaccurate way to measure distance walked is to use this Z-axis movement to determine
how many steps have been taken and then multiply the
number of steps taken by the average stride length.
A common algorithm for step counting uses some manner of peak detection. Generally, sampling is performed
×
=
2
.
mm
g
over
g
REV. 0
© Analog Devices, Inc., 2002
Page 2
AN-602
BOUNCE
LEFT
LEG
RIGHT
LEG
RIGHT
LEG
LEFT
LEG
␣
HIP
at 10 Hz to 20 Hz and then averaged down to 2 Hz to 3 Hz
to remove noise. The step detection routine then looks
for a change in slope of the Z-axis acceleration. These
changes in slope indicate a step.
Only looking for the change in slope at appropriate
times can improve step counting accuracy. Stride frequency tends to change no more than ±15% per step
during steady state walking. Looking for the peak only
during a time window as predicted by the last few steps
±15% will result in more accurate step counting.
IMPROVING THE ACCURACY
Unfortunately, using a fixed value for stride length will
always result in a low accuracy system. Stride length (at
a given walking speed) can vary as much as ±40% from
person to person and depends largely on leg length.
Some pedometers ask the user to program their stride
length to eliminate most of this error. However, each
individual’s stride length will vary by up to ±50%
depending on how fast one is walking (at low speeds,
people tend to take short steps while at high speeds,
their stride is much longer). Knowledge of leg length
cannot eliminate this error. But by looking closely at the
application, we can find ways to improve the situation.
While walking, the knee is bent only when the foot is off
the ground. Therefore we can look at the leg as being a
lever of fixed length while the foot is on the ground.
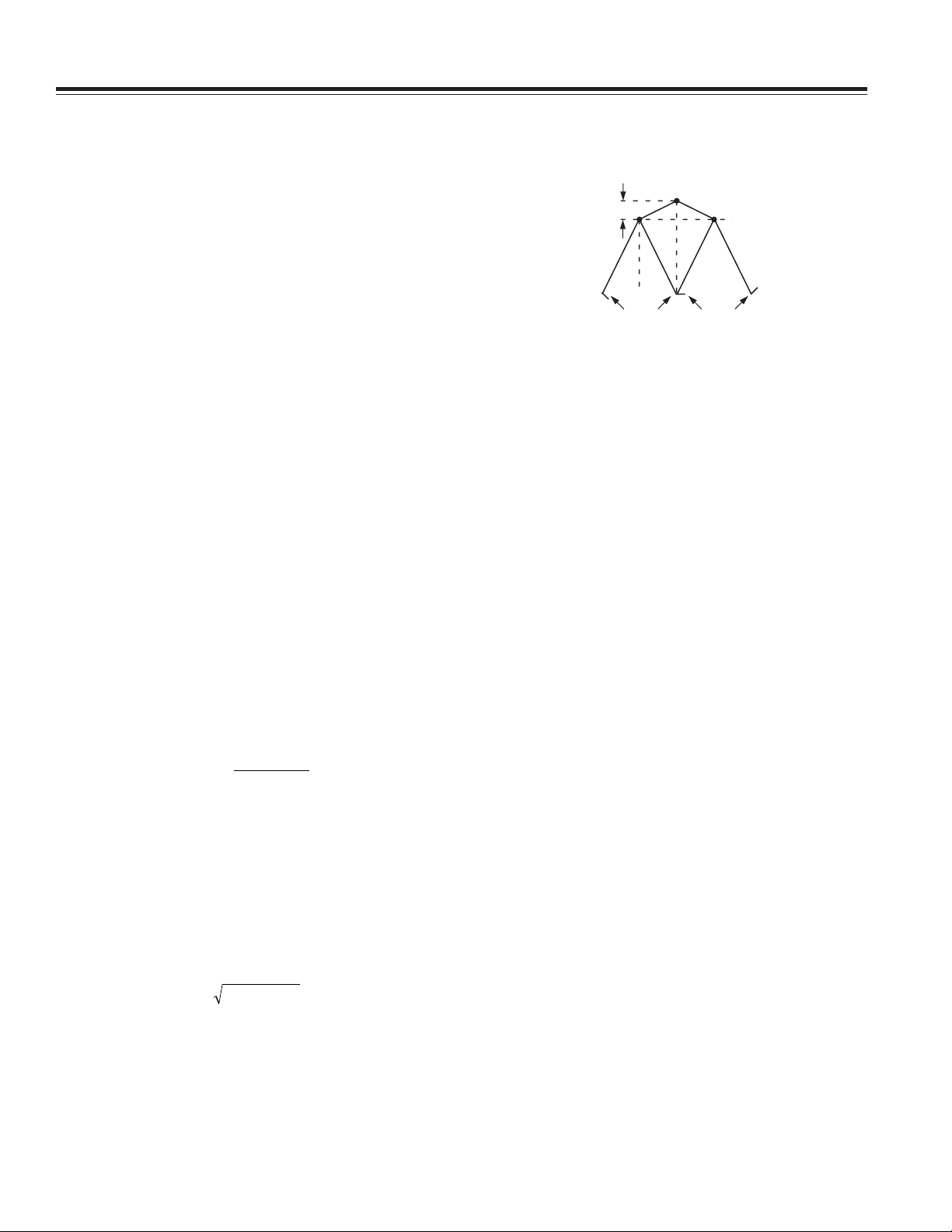
Figure 1 illustrates how the hip and, by extension, the
upper body move vertically when walking. By geometry
of similar angles we know that:
αθ=
So we can show that:
Bounce
×2
≈
α
Where
Bounce
Stride
is the vertical displacement (Z axis) of the
hip (or upper body).
Bounce
(Z-axis displacement) can be calculated as the
second integral of the Z-axis acceleration. ␣ is a small
angle and is difficult to measure since there is a lot of
shock present in all axes while walking. We have demonstrated empirically that we can simply use a constant
for ␣ without a large accuracy penalty. In fact, we can
approximate distance traveled by:
Distance ≈−××AAnK
4
max min
where:
•
A
is the minimum acceleration measured in the Z
min
axis in a single stride.
•
A
is the maximum acceleration measured in the Z
max
axis in a single stride.
•n is the number of steps walked.
•
K
is a constant for unit conversion (i.e., feet or meters
traveled).
Figure 1. Vertical Movement of Hip while Walking
This technique has been shown to measure distance
walked to within ±8% across a variety of subjects of different leg lengths. Close coupling of the accelerometer
to the body is important to maintain accuracy. An adaptive algorithm that “learns” the user's stride
characteristics could improve the accuracy significantly.
A BASIC program listing for the Parallax BASIC Stamp
(BS2) processor that performs step counting and distance calculation and displays distance and steps
walked on a standard 16 ⫻ 2 LCD display is included in
the Appendix of this application note.
ADDING DIRECTION SENSING
To fully implement a personal navigation system, some
method of direction sensing is required. An electronic
compass normally handles this task. Honeywell and
Phillips (among others) manufacture low cost electronic
compass sensor components and modules that are suitable for personal navigation applications. A
microcontroller is used to keep track of where you are
(relative to the starting position) by vector addition using the distance information derived from the
accelerometer along with directional information from
the electronic compass.
The accelerometer and microcontroller may also be
used to improve the accuracy of the electronic compass
by implementing a compass tilt correction algorithm
(consult electronic compass manufacturer’s application
notes regarding tilt correction techniques).
CONCLUSION
While dead reckoning can be used to improve the positional resolution of a system where the dead reckoning
time is short, it is not very useful for long-term position
measurement. Careful examination of the application
can often reveal surprisingly simple solutions. In this
case, a single simple mathematical equation along with
a simple step counting routine outperforms traditional
dead reckoning techniques.
®
BASIC Stamp is a registered trademark of Parallax, Inc.
–2–
REV. 0
Page 3

Appendix
STEP COUNTING AND DISTANCE CALCULATION
SOURCE CODE
For use with the Parallax BASIC Stamp (BS2). See the
“Using the ADXL202/210 with the PARALLAX BASIC
STAMP Module to Speed Algorithm Development” application note at www.analog.com/library/applicationNotes/
mems/StampXL202.pdf for more information.
DATAO VAR OUTH
RS VAR OUT1
RW VAR OUT2
E CON 3
STEPS VAR WORD
DIST VAR WORD
T1 VAR WORD
T2 VAR WORD
TEMP2 VAR WORD
ACCEL VAR WORD
Tn VAR WORD
Tn1 VAR WORD
XLMIN VAR WORD
XLMAX VAR WORD
STRIDE VAR WORD
AN-602
DELTA CON 190 ‘ACCELERATION DELTA BETWEEN SAMPLES. ADJUST
‘THIS CONSTANT TO CHANGE NOISE IMMUNITY
FUDGEMULT CON 7 ‘FUDGE FACTORS. STRIDE IS MULTIPLIED BY
FUDGEDIV CON 48 ‘(FUDGEMULT/FUDGEDIV)THESE FUDGE FACTORS
‘DETERMINE DISTANCE UNITS (FEET, m, etc.)
DIRH=%11111111 ‘INITIALIZE I/O FOR LCD
DIR2=1
DIR1=1
STEPS=0 ‘ZERO THE STEPS AND DISTANCE COUNTERS
DIST=0
HIGH 5 ‘TURN ON ACCELEROMETER
COUNT 7,500,TEMP2 ‘READ T2 PERIOD ONCE
T2=25000/(TEMP2/20) ‘T2 IS THE PERIOD IN µs
MAIN
GOSUB LCDSTART ‘DISPLAY THE TOP LINE
‘ONLY THE BOTTOM LINE GETS REFRESHED
XLMIN=10000 ‘INITIAL DUMMY VALUES
XLMAX=10000
LOOP
GOSUB SAMPLE ‘TAKE AN ACCELERATION SAMPLE
GOSUB FINDPEAK ‘LOOK FOR A PEAK
STRIDE=XLMAX-XLMIN ‘NORMALIZE STRIDE ACCELERATION
STRIDE=SQR STRIDE
STRIDE=STRIDE⫻16
STRIDE=SQR STRIDE
STRIDE=STRIDE/3
STRIDE=(STRIDE⫻FUDGEMULT)/FUDGEDIV
IF STRIDE>0 THEN MAIN1 ‘IF MATH UNDERFLOWS, THEN
STRIDE=1 ‘ANY STRIDE IS > 0
REV. 0
–3–
Page 4

AN-602
MAIN1
FREQOUT 4,35,2800 ‘BEEP WHEN A STEP IS DETECTED
GOSUB INCSTEPS ‘INCREMENT STEP AND DISTANCE COUNTERS
GOSUB SHOWSTEPS ‘UPDATE STEP AND DISTANCE DISPLAYS
GOTO LOOP
‘********* SUBROUTINES ************
SEND ‘USED TO PULSE THE ENABLE PIN ON LCD DISPLAY
‘NO REGISTERS USED OR MODIFIED
PULSOUT E,30
PAUSE 1
RETURN
SAMPLE ‘TAKES 2 SAMPLES OF T1X AND CONVERTS TO mg ⫻ 2
‘REGISTERS MODIFIED: T1, TEMP2, ACCEL
‘INPUTS: T2
‘OUTPUTS: ACCEL
T1=0
PULSIN 7,1,TEMP2 ‘ACCUMULATE 4 PULSES
T1=T1+TEMP2
PULSIN 7,1,TEMP2
T1=T1+TEMP2
PULSIN 7,1,TEMP2
T1=T1+TEMP2
PULSIN 7,1,TEMP2
T1=T1+TEMP2
T1=T1⫻80
TEMP2=T2/50
ACCEL=T1/TEMP2 ‘ACCEL=ACCELERATION IN mg
RETURN
FINDPEAK ‘FINDS THE ACCELERATION PEAK
‘INPUTS: ACCEL
‘REGISTERS MODIFIED: Tn, Tn1
‘OUTPUTS: XLMAX, XLMIN
Tn=(XLMIN/2)+(XLMAX/2) ‘THIS FORCES THIS ROUTINE TO FIND A NEW
Tn1=Tn ‘MIN AND MAX EVERY TIME
GOSUB SAMPLE ‘READ ACCELERATION (Nth SAMPLE)
Tn=ACCEL
PAUSE 50
P1
GOSUB SAMPLE
PAUSE 50
Tn1=ACCEL ‘(Nth + 1 SAMPLE)
IF Tn1>Tn THEN P2 ‘IF ACCELERATION IS INCREASING THEN JUMP
Tn=Tn1
XLMIN=Tn
GOTO P1
P2
Tn=Tn1
GOSUB SAMPLE
PAUSE 50
Tn1=ACCEL
IF Tn1+DELTA>Tn THEN P2
XLMAX=Tn1 ‘PEAK FOUND
PAUSE 50
RETURN
–4–
REV. 0
Page 5

LCDSTART ‘INITIALIZES THE LCD AND DISPLAYS TOP LINE
‘NO INPUT OR OUTPUT REGISTERS
‘REGISTERS MODIFIED: DATAO
PAUSE 200 ‘WAIT FOR POWER TO STABILIZE
RS=0 ‘LCD RESET ROUTINE
RW=0
DATAO=%00110000
GOSUB SEND
GOSUB SEND
GOSUB SEND
DATAO=%00111000
GOSUB SEND
DATAO=%00001000
GOSUB SEND
DATAO=%00000001
GOSUB SEND
DATAO=%00000111
GOSUB SEND
DATAO=%00001111
GOSUB SEND
DATAO=%00000110
GOSUB SEND
RS=1
DATAO=%01010011 ‘SEND S
GOSUB SEND
DATAO=%01010100 ‘T
GOSUB SEND
DATAO=%01000101 ‘E
GOSUB SEND
DATAO=%01010000 ‘P
GOSUB SEND
DATAO=%01010011 ‘S
GOSUB SEND
DATAO=%10100000 ‘SPACE
GOSUB SEND
DATAO=%10100000 ‘SPACE
GOSUB SEND
DATAO=%10100000 ‘SPACE
GOSUB SEND
DATAO=%01000100 ‘D
GOSUB SEND
DATAO=%01001001 ‘I
GOSUB SEND
DATAO=%01010011 ‘S
GOSUB SEND
DATAO=%01010100 ‘T
GOSUB SEND
DATAO=%01000001 ‘A
GOSUB SEND
DATAO=%01001110 ‘N
GOSUB SEND
DATAO=%01000011 ‘C
GOSUB SEND
DATAO=%01000101 ‘E
GOSUB SEND
RETURN
AN-602
SHOWSTEPS ‘DISPLAYS NUMBER OF STEPS
‘INPUT: STEPS, DIST
‘REGISTERS MODIFIED: DATAO
REV. 0
–5–
Page 6

AN-602
RS=0
RW=0 ‘CURSOR LOCATION START OF 2nd LINE
DATAO=%11000000
GOSUB SEND
RS=1 ‘SEND STEPS
DATAO=%00110000
DATAO.LOWNIB=STEPS.HIGHBYTE.HIGHNIB
GOSUB SEND
DATAO.LOWNIB=STEPS.HIGHBYTE.LOWNIB
GOSUB SEND
DATAO.LOWNIB=STEPS.LOWBYTE.HIGHNIB
GOSUB SEND
DATAO.LOWNIB=STEPS.LOWBYTE.LOWNIB
GOSUB SEND
RS=0 ‘CURSOR LOCATION 9th SPACE OF 2nd
DATAO=%11001000
GOSUB SEND
RS=1 ‘SEND DISTANCE
DATAO=%00110000
DATAO.LOWNIB=DIST.HIGHBYTE.HIGHNIB
GOSUB SEND
DATAO.LOWNIB=DIST.HIGHBYTE.LOWNIB
GOSUB SEND
DATAO.LOWNIB=DIST.LOWBYTE.HIGHNIB
GOSUB SEND
DATAO.LOWNIB=DIST.LOWBYTE.LOWNIB
GOSUB SEND
RETURN
INCSTEPS ‘INCREMENTS STEPS AND DISTANCE. ALSO CONVERTS HEX
‘INPUT TO DECIMAL
‘INPUTS: STEPS, DIST, STRIDE
‘REGISTERS MODIFIED: STEPS, DIST
STEPS=STEPS+1
IF STEPS.LOWBYTE.LOWNIB <= 9 THEN M1
STEPS=STEPS+6
M1
IF STEPS.LOWBYTE.HIGHNIB <= 9 THEN M2
STEPS=STEPS+96
M2
IF STEPS.HIGHBYTE.LOWNIB <= 9 THEN M3
STEPS=STEPS+1536
M3
DIST=DIST+STRIDE
IF DIST.LOWBYTE.LOWNIB <= 9 THEN M4
DIST=DIST+6
M4
IF DIST.LOWBYTE.HIGHNIB <= 9 THEN M5
DIST=DIST+96
M5
IF DIST.HIGHBYTE.LOWNIB <= 9 THEN M6
DIST=DIST+1536
M6
RETURN
–6–
REV. 0
Page 7

–7–
Page 8

E03047–0–7/02(0)
–8–
PRINTED IN U.S.A.
 Loading...
Loading...