Analog Devices AN600 Application Notes

TMP36

V

S

GND

OUT

ADXL202

V

S

V

S

R

SET

Y

FILT

X

FILT

GND

GND

X

OUT

Y

OUT

C

X

MICRO-

CONTROLLER

T = –20 C PERIOD = 1355␮s

T = +10

C PERIOD = 1855␮s

T = +40

C PERIOD = 2915␮s

R

SET

= 127k⍀

PWM OUTPUT = 60% IN ALL CASES SHOWN

R

SET

V

S

0.1␮F

C

Y

AN-600

a

One Technology Way • P.O. Box 9106 • Norwood, MA 02062-9106 • Tel: [phone] • Fax: [phone] • www.analog.com

INTRODUCTION

Many cases exist where it’s important to know the tem­perature of the ADXL202. Sometimes temperature
information is necessary for control or data logging
requirements (as in data loggers used to monitor how
articles are handled in shipping) or for high precision tilt
sensor applications (for temperature compensation of
the zero
verter is required when using the ADXL202’s duty cycle
outputs, it is preferable to have some means of acquir-

ing temperature information digitally.

This application note outlines a simple method of
embedding the temperature information from a TMP36
voltage output temperature sensor in the duty cycle
acceleration output of the ADXL202. No A/D converter is
required, and no additional I/O is necessary.

BASIC PRINCIPLE OF OPERATION

The duty cycle output period is proportional to the cur­rent flowing through R
typically 1.25 V. So for the recommended range of the
R

SET

10 µA. Normally R
and ground, but any noise free voltage source between
0V and 1.25 V is acceptable.

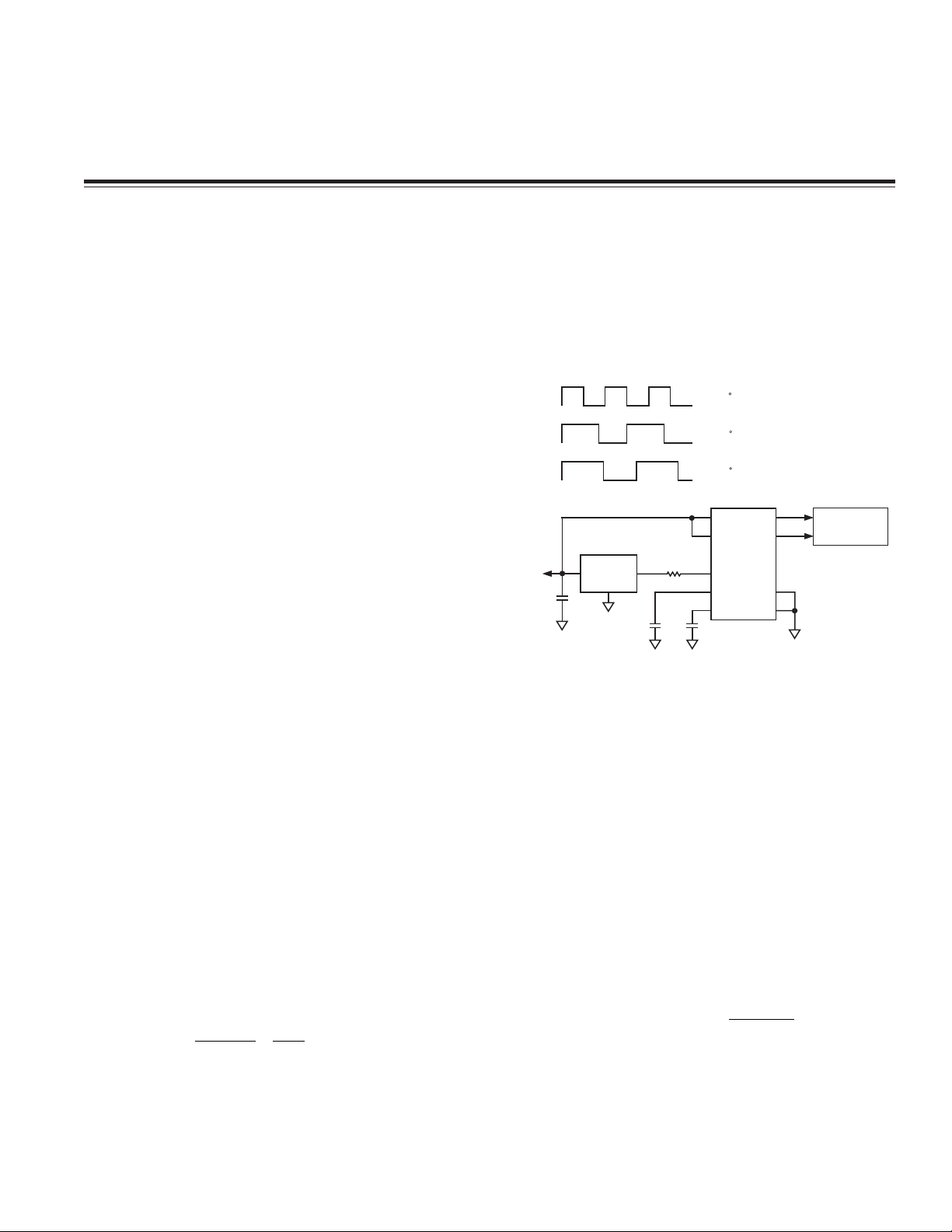
In Figure 1, a TMP36 voltage output temperature sensor
is connected to R
of:

where T = temperature in °C.

Over a range of –40°C to +70°C, the output is 0.1 V to

1.2 V. The resulting current is:

Using a 125 kΩ resistor for

0.4 µA over the –40°C to +70°C temperature range.

REV. 0

g

drift of the accelerometer). Since no A/D con-

resistor (125 kΩ to 1.25 MΩ) the current is 1 µA to

APPLICATION NOTE

Embedding Temperature Information in the ADXL202’s PWM Outputs

by Harvey Weinberg

Figure 1. Using a Temperature Sensor to
Embed Temperature Information into the
Acceleration Duty Cycle Output of the ADXL202

. The voltage at the T2 Pin is

SET

is connected between the T2 Pin

SET

. The TMP36 has an output voltage

SET

075 001..+×

()

125 125..

V

−

I

R

SET

=

R

RR

=−−

SET SET

T Volts

VR

()

R SET

R

, the current is 9.2 µA to

SET

In most applications, the period need not be measured
every cycle (this is discussed thoroughly in the “Using
the ADXL202 Duty Cycle Output” application note).
Since temperature change is normally a low speed phe­nomenon, this will not affect the accuracy of the
temperature measurements. Measuring the period a
few times per second should be more than sufficient.

A subroutine used to determine the temperature from
the T2 period must be added to the user’s firmware.
Since the change in T2 is not completely linear over tem­perature, the subroutine’s complexity will vary in
proportion to the temperature accuracy required. Table I
shows the typical T2 period versus temperature. Using a
simple calculation of:

−1735 2

26

where

TemperatureT=

Temperature

is in °C and T2 is in µs. This technique
will result in temperature readings that are accurate
±5.5°C over a range of –20°C to +40°C. If more accurate

© Analog Devices, Inc., 2002

to

AN-600

temperature readings are required, a simple look-up
table can be used. Alternatively, both the initial constant
(1735) and the divisor (26) may be modified for higher
accuracy over a narrower temperature range.

Table I. T2 vs. Temperature for the Circuit in Figure 1

Temp. (°C) T2 (␮s) Calculated Temp.

–30 1250 –18.7
–25 1300 –16.7
–20 1355 –14.5
–15 1420 –12.1
–10 1490 –9.4
–5 1565 –6.5
0 1650 –3.3
+5 1740 +0.2
+10 1855 +4.5
+15 1980 +9.5
+20 2110 +14.4
+25 2280 +21
+30 2450 +27.5
+35 2660 +35.6
+40 2915 +45.5
+45 3230 +57.5
+50 3620 +72.5

For example, consider a shipping conditions recorder
for an item that must be kept at 10°C ± 1°C. From Table I
we see that 10°C produces a T2 period of 1855 µs.
Assuming that we are interested in high accuracy over
the 5°C to 15°C range, we see that the T2 period changes
from 1980 µs at 15°C to 1740 µs at 5°C. Therefore we can
assume that the T2 change per °C is:

1980 1740

−

15 5

°−°

CC

We can then modify our temperature equation to:

TemperatureT=

in °C, which will be accurate to ±0.2°C over the 5°C to
15°C range.

24

=°

sCµ

−+2 1855

24

10

E03045–0–7/02(0)

–2–

PRINTED IN U.S.A.

REV. 0