Page 1
AN-584
a
APPLICATION NOTE
One Technology Way • P.O. Box 9106 • Norwood, MA 02062-9106 • Tel: 781/329-4700 • Fax: 781/326-8703 • www.analog.com
Using the AD813x
THEORY OF OPERATION
The AD813x differs from conventional op amps by the
external presence of an additional input and output. The
additional input, V
, controls the output common-
OGM
mode voltage. The additional output is the analog
complement of the single output of a conventional op
amp. For its operation, the AD813x makes use of two
feedback loops as compared to the single loop of conventional op amps. While this provides significant
freedom to create various novel circuits, basic op amp
theory can still be used to analyze the operation.
One of the feedback loops controls the output commonmode voltage, V
. Its input is V
OUT,cm
(Pin 2) and the
OCM
output is the common-mode, or average voltage, of the
two differential outputs (+OUT and –OUT). The gain of
this circuit is internally set to unity. When the AD813x is
operating in its linear region, this establishes one of the
operational constraints: V
OUT,cm
= V
OCM
.
The second feedback loop controls the differential operation.
Similar to an op amp, the gain and gain-shaping of
the transfer function is controllable by adding passive
feedback networks. However, only one feedback network is
constrain the
desired, two
possible as a
required to “close the loop” and fully
operation. But depending on the function
feedback networks can be used. This is
result of having two outputs that are each
inverted with respect to the differential inputs.
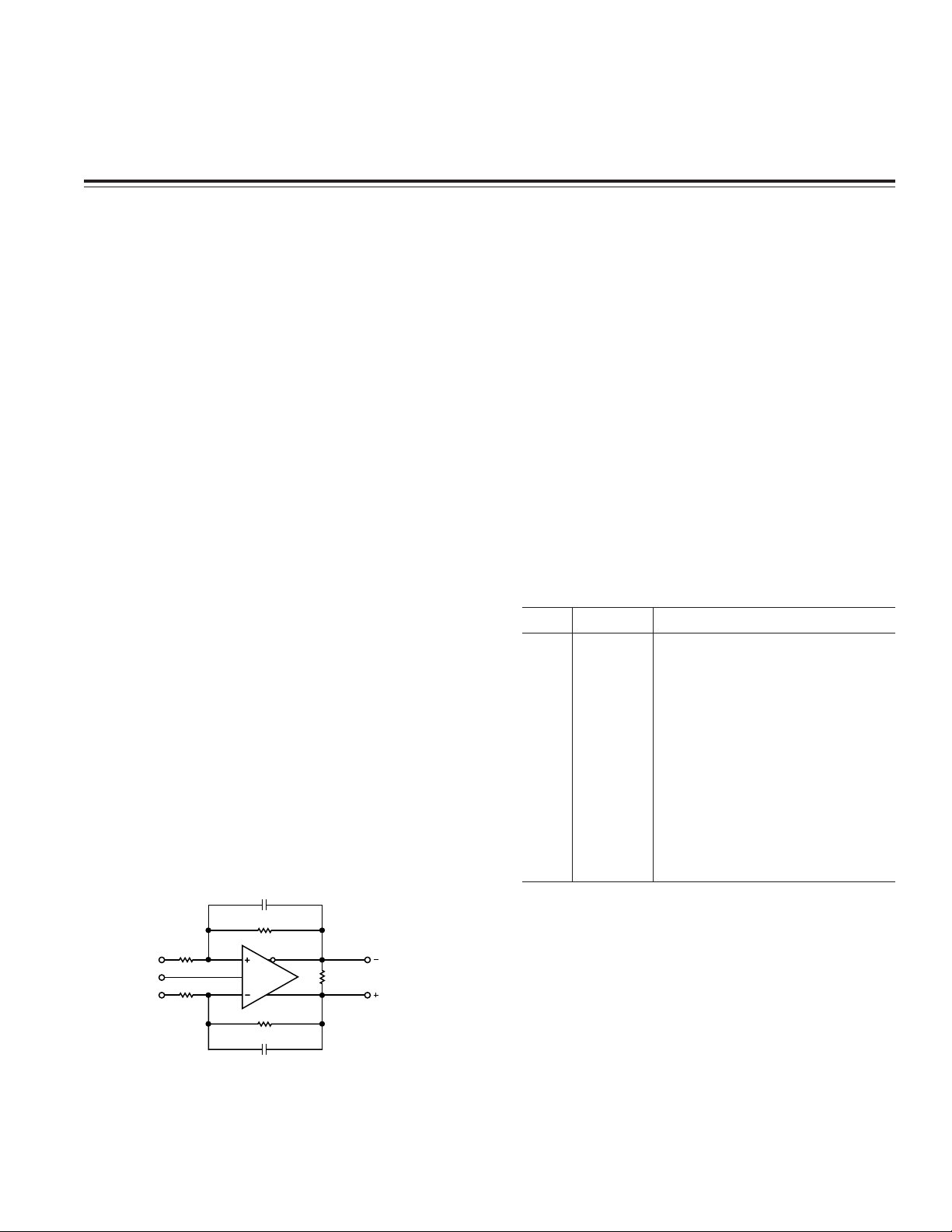
DEFINITION OF TERMS
C
F
R
F
R
G
+D
IN
V
OCM
–D
IN
+IN
–IN
R
G
AD813x
R
F
C
F
–OUT
+OUT
R
V
,dm
L
OUT
,dm
Figure 1. Circuit Definitions
Differential voltage refers to the difference between two
node voltages. For example, the output differential voltage (or equivalently output differential-mode voltage) is
defined as:
VVV
V
+OUT
=+(–)
OUT,dm OUT OUT
and
V
refer to the voltages at the +OUT and –OUT
–OUT
–
(1)
terminals with respect to a common reference.
Common-mode voltage refers to the average of two
node voltages. The output common-mode voltage is
defined as:
VVV
=+(+)/2
OUT,cm OUT OUT
–
(2)
PIN FUNCTION DESCRIPTIONS
Pin No. Mnemonic Function
1 –IN Negative Input
2V
OCM
Voltage applied to this pin sets the
common-mode output voltage with
a ratio of 1:1. For example, 1 V
dc
on VOCM will set the dc bias level
on +OUT and –OUT to 1 V.
3 V+ Positive Supply Voltage
4 +OUT Positive Output. Note: The voltage
is inverted at +OUT.
at –D
5 –OUT
IN
Negative Output. Note: The voltage
at +DIN is inverted at –OUT.
6 V– Negative Supply Voltage
7 NC No Connect
8 +IN Positive Input
GENERAL USAGE OF THE AD813x
Several assumptions are made here for a first-order
analysis, which are the typical assumptions used for the
analysis of op amps:
• The input impedances are arbitrarily large and their
loading effect can be ignored.
• The input bias currents are sufficiently small so they
can be neglected.
• The output impedances are arbitrarily low.
• The open-loop gain is arbitrarily large, which drives
the amplifier to a state where the input differential
voltage is effectively zero.
• Offset voltages are assumed to be zero.
REV. 0
© Analog Devices, Inc., 2002
Page 2
AN-584
While it is possible to operate the AD813x with a purely
differential input, many of its applications call for a circuit
that has a single-ended input with a differential output.
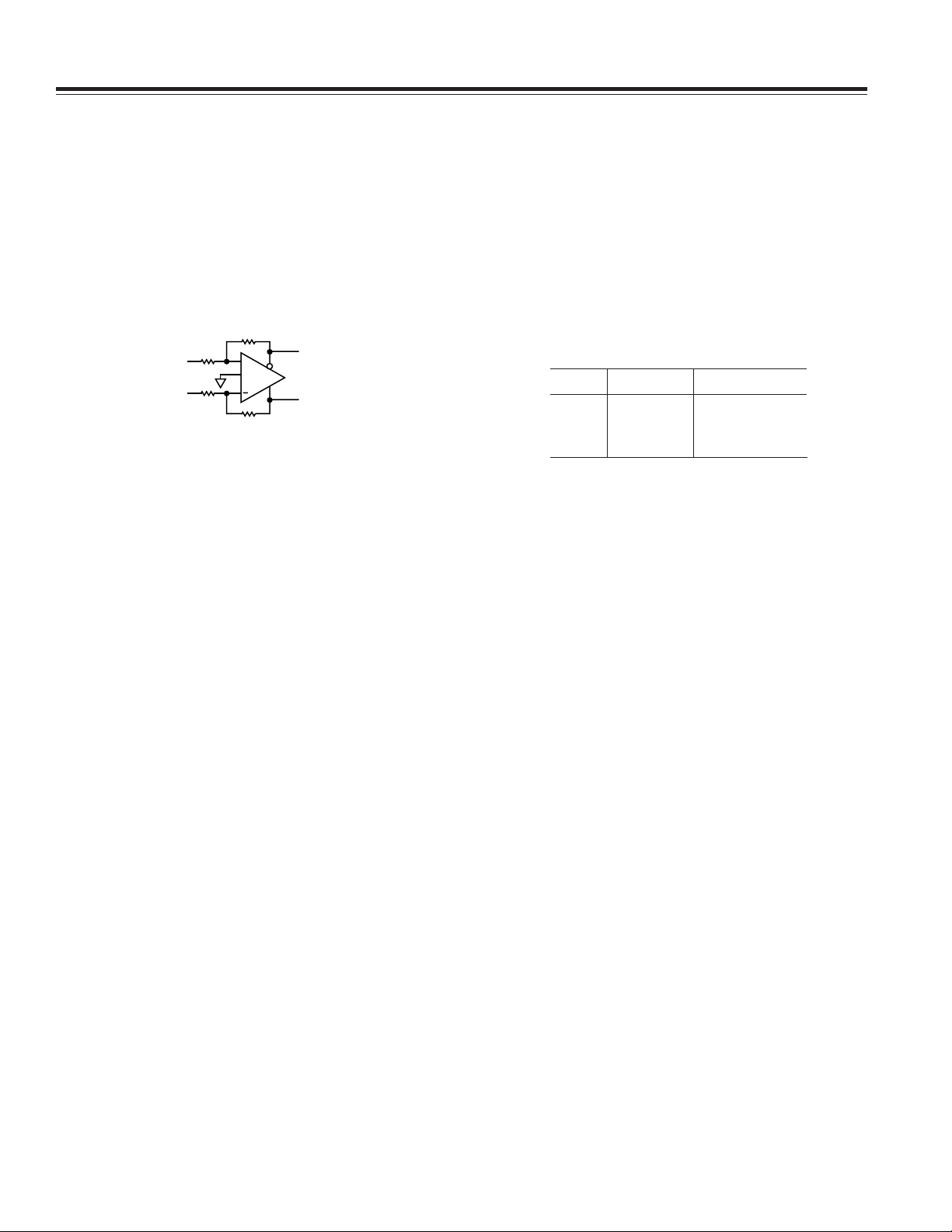
For a single-ended-to-differential circuit, the RG of the
undriven input will be tied to a reference voltage. For
now this is ground. Other conditions will be discussed
later. Also, the voltage at V
, and hence V
OCM
OUT,cm
will be
assumed to be ground for now. Figure 2 shows a generalized schematic of such a circuit using an AD813x with
two feedback paths.
R
F1
R
G1
+
R
G2
R
F2
Figure 2. Typical Four-Resistor Feedback Circuit
For each feedback network, a feedback factor can be
defined, which is the fraction of the output signal that is
fed back to the opposite-sign input. These terms are:
β1/( )
=+RRR
111
GGF
β2/( )
=+RRR
222
GGF
(3)
(4)
The feedback factor 1 is for the side that is driven, while
the feedback factor 2 is for the side that is tied to a reference voltage (ground for now). Note also that each
feedback factor can vary anywhere between 0 and 1.
A single-ended-to-differential gain equation can be
derived that is true for all values of 1 and 2:
G 2 (1 1) / ( 1 2)=× +–
βββ
(5)
This expression is not very intuitive. One observation
that can be made right away is that a tolerance error in
1 does not have the same effect on gain as the same
tolerance error in 2.
For RF1/RG1 = RF2/RG2 the gain equation simplifies to G = RF/RG.
BASIC CIRCUIT OPERATION
One of the more useful and easy to understand ways to
use the AD813x is to provide two equal-ratio feedback
networks. To match the effect of parasitics, these networks should actually be comprised of two equal-value
feedback resistors, R
tors, R
. This circuit is diagrammed in Figure 1.
G
and two equal-value gain resis-
F
Like a conventional op amp, the AD813x has two
dif
ferential inputs that can be driven with both a differential-mode input voltage, V
voltage, V
. Another input, V
IN,cm
conventional op amps, but provides another
consider on the AD813x. It is totally separate
above inputs. There are also two complementary
, and a common-mode input
IN,dm
OCM
, is not
present on
input to
from the
outputs
whose response can be defined by a differential-mode
output, V
and a common-mode output, V
OUT,dm
OUT,cm
.
Table I indicates the gain from any type of input to either
type of output.
Table I. Differential and Common-Mode Gains
Input V
V
IN,dm
V
IN,cm
V
OCM
OUT,dm
RF/R
0 0 (By Design)
0 1 (By Design)
The differential output (V
tial input voltage (V
) times RF/RG. In this case, it does
IN,dm
G
OUT,dm
V
OUT,cm
0 (By Design)
) is equal to the differen-
not matter if both differential inputs are driven, or only
one output is driven and the other is tied to a reference
voltage, like ground. As can be seen from the two zero
entries in the first column, neither of the common-mode
inputs has any effect on this gain.
The gain from V
IN,dm
to V
is 0 and to first-order does
OUT,cm
not depend on the ratio matching of the feedback networks. The common-mode feedback loop within the
AD813x provides a corrective action to keep this gain
term minimized. The term “balance error” describes the
degree to which this gain term differs from zero.
The gain from V
IN,cm
to V
does directly depend on
OUT,dm
the matching of the feedback networks. The analogous
term for this transfer function, which is used in conventional op amps, is “common-mode rejection ratio” or
CMRR. Thus, if it is desirable to have a high CMRR, the
feedback ratios must be well matched.
The gain from V
IN,cm
to V
is also ideally 0, and is
OUT,cm
first-order independent of the feedback ratio matching.
As in the case of V
IN,dm
to V
, the common-mode
OUT,cm
feedback loop keeps this term minimized.
The gain from V
OCM
to V
is ideally 0 only when the
OUT,dm
feedback ratios are matched. The amount of differential
output signal that will be created by varying V
OCM
is
related to the degree of mismatch in the feedback networks.
–2–
REV. 0
Page 3

V
controls the output common-mode voltage V
OCM
OUT,cm
with a unity-gain transfer function. With equal-ratio
feedback networks (as assumed above), its effect on
each output will be the same, which is another way to
say that the gain from V
OCM
to V
is zero. If not
OUT,dm
driven, the output common-mode will be at mid-supplies.
It is recommended that a 0.1 µF bypass resistor be connected to V
OCM
.
When unequal feedback ratios are used, the two gains
associated with V
become nonzero. This signifi-
OUT,dm
cantly complicates the mathematical analysis along
with any intuitive understanding of how the part operates. Some of these configurations will be in another
section.
AN-584
In the case of a single-ended input signal (for example if
–D
is grounded and the input signal is applied to +DIN),
IN
the input impedance becomes:
R
IN,dm
=
R
G
1
R
–
2
RR
×+
()
GF
The circuit’s input impedance is effectively higher than it
would be for a conventional op amp connected as an
inverter because a fraction of the differential output voltage
appears at the inputs as a common-mode signal, partially
bootstrapping the voltage across the input resistor R
F
(8)
G
.
ESTIMATING THE OUTPUT NOISE VOLTAGE
Similar to the case of a conventional op amp, the differential output errors (noise and offset voltages) can be
estimated by multiplying the input referred terms, at +IN
and –IN, by the circuit noise gain. The noise gain is
defined as:
R
F
1
R
G
(6)
G
=+
N
To compute the total output referred noise for the circuit
of Figure 1, consideration must also be given to the
contribution of the resistors
R
and
F
R
. Refer to Table II
G
for estimated output noise voltage densities at various
closed-loop gains.
Table II. Recommended Resistor Values and Noise Performance
for Specific Gains
Output Output
R
GRF
Gain (⍀)(⍀) –3 dB AD813x
Bandwidth Noise Noise
AD813x + RG, R
F
1 499 499 360 MHz 16 nV/Hz 17 nV/Hz
2 499 1.0 k 160 MHz 24.1 nV/Hz 26.1 nV/Hz
5 499 2.49 k 65 MHz 48.4 nV/Hz 53.3 nV/Hz
10 499 4.99 k 20 MHz 88.9 nV/Hz 98.6 nV/Hz
CALCULATING AN APPLICATION CIRCUIT’S INPUT
IMPEDANCE
The effective input impedance of a circuit such as that in
Figure 1, at +D
and –DIN, will depend on whether the
IN
amplifier is being driven by a single-ended or differential signal source. For balanced differential input signals,
the input impedance (R
) between the inputs (+D
IN,dm
IN
and –DIN) is simply:
=×
R2R
IN,dm G
(7)
INPUT COMMON-MODE VOLTAGE RANGE IN SINGLESUPPLY APPLICATIONS
The AD813x is optimized for level-shifting “ground”
referenced input signals. For a single-ended input this
would imply, for example, that the voltage at –DIN in Figure 1
would be zero volts when the amplifier’s negative power
supply voltage (at V–) was also set to zero volts.
SETTING THE OUTPUT COMMON-MODE VOLTAGE
The AD813x’s V
pin is internally biased at a voltage
OCM
approximately equal to the mid-supply point (average
value of the voltages on V+ and V–). Relying on this
internal bias will result in an output common-mode voltage
that is within about 100 mV of the expected value. In
cases where more accurate control of the output common
mode level is required, it is recommended that an external
source, or resistor divider (with R
< 10 kΩ), be used.
SOURCE
APPLICATION NOTES FOR THE AD813x DIFFERENTIAL AMPS
ADC DRIVING
High-Performance ADC Driving
The circuit in Figure 3 shows a simplified front-end
con
nection for an AD813x driving an AD9224, a 12-bit,
40 MSPS A/D converter. The A/D works best when
driven differentially, which minimizes its distortion as
described in its data sheet. The AD813x eliminates the
need for a transformer to drive the ADC and performs
single-ended-to-differential conversion, common-mode
level-shifting, and buffering of the driving signal.
The positive and negative outputs of the AD813x are
connected to the respective differential inputs of the
AD9224 via a pair of 49.9 Ω resistors to minimize the effects
of the switched-capacitor front-end of the AD9224. For
best distortion performance it is run from supplies of ±5 V.
-
REV. 0
–3–
Page 4

AN-584
The AD813x can also be configured with unity gain for a
single-ended input-to-differential output. The additional
23 Ω, 522 Ω total, at the input to –IN is to balance the
parallel impedance of the 50 Ω source and its 50 Ω termi-
nation that drives the noninverting input.
The signal generator has a ground-referenced, bipolar
output, i.e., it drives symmetrically above and below
ground. Connecting V
to the CML pin of the AD9224
OCM
sets the output common-mode of the AD813x at 2.5 V,
which is the mid-supply level for the AD9224. This voltage is bypassed by a 0.1 µF capacitor.
The full-scale analog input range of the AD9224 is set to
4 V p-p, by shorting the SENSE terminal to AVSS. This
has been determined to be the scaling to provide minimum harmonic distortion.
For the AD813x to swing a 4 V p-p, each output swings
2 V p-p, while providing signals that are 180 degrees out
of phase. With a common-mode voltage at the output of
2.5 V, this means that each AD813x output will swing
between 1.5 V and 3.5 V.
A ground-referenced 4 V p-p, 5 MHz signal at D
+ was
IN
used to test the circuit in Figure 3. When the combineddevice circuit was run with a sampling rate of 20 MHz
MSPS, the SFDR (spurious free dynamic range) was
measured at –85 dBc.
SINGLE 3 V SUPPLY DIFFERENTIAL A-TO-D DRIVER
Many newer A-to-D converters can run from a single 3 V
supply, which can save significant system power. In order
to increase the dynamic range at the analog input,
have differential inputs, which doubles the
they
dynamic
range with respect to a single-ended input. An added
benefit of using a differential input is that the distortion
can be improved.
The low distortion and ability to run from a single 3 V
supply make the AD813x suitable as an A-to-D driver for
some 10-bit, single-supply applications. Figure 4 shows
a schematic of a circuit for an AD813x driving an
AD9203, 10-bit, 40 MSPS A-to-D converter.
1V p-p
348⍀
49.9⍀
348⍀
24.9⍀
3V
10k⍀
10k⍀
0.1F
348⍀
348⍀
3V
AD813x
+
0.1F 10F
60.4⍀
60.4⍀
20pF
20pF
+5V
499⍀
50⍀
SOURCE
499⍀ 49.9⍀
49.9⍀
0.1pF
VINB
VINA
523⍀
+5V
0.1pF 0.1pF
AVSS DRVSS
+
AD813x
–5V
DRVDDAVDD
AD9224
SENSE CML
V
OCM
49.9⍀
499⍀
Figure 3. AD813x Driving an AD9224, a 12-Bit, 40 MSPS
A/D Converter
3V
0.1F
AVDD DRVDD
AINN
AD9203
AINP
AVSS DRVSS
0.1F
DIGITAL
OUTPUTS
Figure 4. AD813x Driving AD9203, a 10-Bit 40 MSPS A/D
Converter
The common-mode of the AD813x output is set at midsupply by the voltage divider connected to V
OCM
, and ac
bypassed with a 0.1 µF capacitor. This provides for
maximum dynamic range between the supplies at the
output of the AD813x. The 110 Ω resistors at the AD813x
output, along with the shunt capacitors form a one-pole,
low-pass filter for lowering noise and antialiasing.
Figure 5 shows an FFT plot that was taken from the combined devices at an analog input frequency of 2.5 MHz
–4–
REV. 0
Page 5

AN-584
and a 40 MSPS sampling rate. The performance of the
AD813x compares very favorably with a center-tapped
transformer drive, which has typically been the best way
to drive this A-to-D converter. The AD813x has the
advantage of maintaining dc performance, which a
transformer solution cannot provide.
10
–10
–20
–30
–40
–50
–60
–70
OUTPUT – dBc
–80
–90
–100
–110
–120
FUND
0
2ND
3RD
0
2.5 5.0 7.5 10.0 12.5 15.0 17.5 20.0
INPUT FREQUENCY – MHz
5TH
4TH
fS = 40MHz
= 2.5MHz
f
IN
6TH
9TH
7TH
8TH
Figure 5. FFT Response for AD813x Driving AD9203
BALANCED LINE DRIVING
TWISTED-PAIR LINE DRIVER
When driving a twisted-pair cable, it is desirable to drive
only a pure differential signal onto the line. If the signal
is purely differential (i.e., fully balanced), and the transmission line is twisted and balanced, there will be a
minimum radiation of any signal.
The complementary electrical fields will mostly be confined to the space between the two twisted conductors
and will not significantly radiate out from the cable. The
current in the cable will create magnetic fields that will
radiate to some degree. However, with each twist, the
two adjacent twists will have an opposite polarity magnetic field. If the twist pitch is tight enough, these small
magnetic field loops will contain most of the magnetic
flux, and the magnetic far-field strength will be negligible.
Any imbalance in the differential drive signal will appear
as a common-mode signal on the cable. This is the
equivalent of a single wire that is driven with the common-mode signal. In this case, the wire will act as an
antenna and radiate. Thus, in order to minimize radiation when driving differential twisted-pair cables, the
differential drive signal should be very well balanced.
The common-mode feedback loop in the AD813x helps
to minimize the amount of common-mode voltage at the
output, and therefore can be used to create a well-balanced
differential line driver.
Figure 6 shows a circuit of an AD813x driving a twistedpair line, like a Category 3 or Category 5 (Cat3 or Cat5),
already installed in many buildings for telephony and
data communications. The characteristic impedance of
such transmission lines is usually about 100 Ω. The out-
standing balance of the AD813x output will minimize the
common-mode signal and therefore the amount of EMI
generated by driving the twisted pair.
+5V
+
10F
0.1F
49.9⍀
3
8
5
24.9⍀
2
AD813x
1
6
–5V
4
49.9⍀
0.1F
+
10F
100⍀
AD8129/
AD8130
RECEIVER
49.9⍀
Figure 6. Single-Ended-to-Differential 100 Ω Line Driver
The two resistors in series with each output terminate
the line at the transmit end. Since the impedances of the
outputs of the AD813x are very low, they can be thought
of as a short circuit, and the two terminating resistors
form a 100 Ω termination at the transmit end of the
transmission line. The receive end is directly terminated
by a 100 Ω resistor across the line.
This back-termination of the transmission line divides
the output signal by two. The fixed gain-of-two of the
AD813x will create a net unity gain for the system from
end to end.
In this case, the input signal is provided by a signal
generator with an output impedance of 50 Ω. This is terminated with a 49.9 Ω resistor near +D
of the AD813x.
IN
The effective parallel resistance of the source and termination is 25 Ω. The 24.9 Ω resistor from –D
matches the +D
source impedance and minimizes any
IN
to ground
IN
dc and gain errors.
If +D
is driven by a low-impedance source over a short
IN
distance, such as the output of an op amp, no termination resistor is required at +D
. In this case, the –DIN can
IN
be directly tied to ground.
TRANSMIT EQUALIZER
Any length of transmission line will attenuate the signals
it carries. This effect is worse at higher frequencies than
at low frequencies. One way to compensate for this is to
provide an equalizer circuit that boosts the higher
quencies in the transmitter circuit, so that at the
fre-
receive
end of the cable the attenuation effects are diminished.
REV. 0
–5–
Page 6

AN-584
By lowering the impedance of the RG component of the
feedback network at higher frequency, the gain can be
increased at high frequency. Figure 7 shows a gain of a
two line driver that has its RGs shunted by 10 pF resistors. The effect of this is shown in the frequency
response plot of Figure 8.
499⍀
10pF
V
IN
24.9⍀
49.9⍀
249⍀
249⍀
10pF
499⍀
49.9⍀
49.9⍀
100⍀
V
OUT
Figure 7. Frequency Boost Circuit
20
10
0
–10
–20
– dB
IN
–30
/V
OUT
–40
V
–50
–60
–70
–80
1
10 100
FREQUENCY – MHz
1000
Figure 8. Frequency Response for Transmit Boost Circuit
MISCELLANEOUS APPLICATIONS
Balanced Transformer Driver
Transformers are among the oldest devices that have
been used to perform a single-ended-to-differential conversion (and vice versa). Transformers also can perform
the additional functions of galvanic isolation, step-up or
step-down of voltages, and impedance transformation.
For these reasons, transformers will always find uses in
certain applications.
However, when driving a transformer single-endedly
and then looking at its output, there is a fundamental
imbalance due to the parasitics inherent in the transformer. The primary (or driven) side of the transformer
has one side at dc potential (usually ground), while the
other side is driven. This can cause problems in systems
that require good balance of the transformer’s differential output signals.
If the interwinding capacitance (C
) is assumed to be
STRAY
uniformly distributed, a signal from the driving source
will couple to the secondary output terminal that is closest
to the primary’s driven side. On the other hand, no signal will be coupled to the opposite terminal of the
secondary, because its nearest primary terminal is not
driven (see Figure 9). The exact amount of this imbalance
will depend on the particular parasitics of the transformer, but will mostly be a problem at higher
frequencies.
SIGNAL WILL BE COUPLED
ON THIS SIDE VIA C
PRIMARY
52.3⍀
NO SIGNAL IS COUPLED
ON THIS SIDE
C
STRAY
C
STRAY
V
UNBAL
STRAY
500⍀
0.005%
500⍀
0.005%
SECONDARY V
DIFF
Figure 9. Transformer Single-Ended-to-Differential
Converter Is Inherently Imbalanced
The balance of a differential circuit can be measured by
connecting an equal-valued resistive voltage divider
across the differential outputs and then measuring the
center point of the circuit with respect ground. Since the
two differential outputs are supposed to be of equal
amplitude, but 180 degrees opposite phase, there
should be no signal present for perfectly balanced outputs.
The circuit in Figure 9 shows a Minicircuits T1-6T transformer connected with its primary driven single-endedly
and the secondary connected with a precision voltage
divider across its terminals. The voltage divider is made
up of two 500 Ω, 0.005% precision resistors. The voltage
V
, which is also equal to the ac common-mode volt-
UNBAL
age, is a measure of how closely the outputs are
balanced.
The plots in Figure 10 show a comparison between the
where the transformer is driven single-endedly by
generator and driven differentially using
The top signal trace of Figure 10 shows
the single-ended configuration, while the
the differentially driven balance response.
an AD813x.
the balance of
bottom shows
The 100 MHz
case
a signal
balance is 35 dB better when using the AD813x.
–6–
REV. 0
Page 7

AN-584
0
–20
V
, FOR TRANSFORMER
–40
–60
–80
OUTPUT BALANCE ERROR – dB
–100
0.3 500
UNBAL
WITH SINGLE-ENDED DRIVE
V
, DIFFERENTIAL DRIVE
UNBAL
1 10 100
FREQUENCY – MHz
Figure 10. Output Balance Error for Circuits of Figure 9
and Figure 11
The well-balanced outputs of the AD813x will provide a
drive signal to each of the transformer’s primary inputs
that are of equal amplitude and 180 degrees out of
phase. Thus, depending on how the polarity of the secondary is connected, the signals that conduct across the
interwinding capacitance will either both assist the
transformer’s secondary signal equally, or both buck the
secondary signals. In either case, the parasitic effect will
be symmetrical and provide a well-balanced transformer output. (See Figure 11.)
499⍀
C
STRAY
C
STRAY
V
UNBAL
500⍀
0.005%
500⍀
0.005%
V
DIFF
499⍀
499⍀
+IN
–IN
499⍀
49.9⍀
OUT–
AD813x
OUT+
49.9⍀
Figure 11. AD813x Forms a Balanced Transformer Driver
Full-Wave Rectifier
The balanced outputs of the AD813x, along with a
couple of Schottky diodes, can create a very high-speed
full-wave rectifier. Such circuits are useful for measuring
ac voltages and other computational tasks.
Figure 12 shows the configuration of such a circuit. Each
of the AD813x outputs drives the anode of an HP2835
Schottky diode. These Schottky diodes were chosen for
their high-speed operation. At lower frequencies (approximately
lower than 10 MHz), a silicon signal diode such as
a 1N4148 can be used. The cathodes of the two diodes
are connected together and this output node is connected to ground by a 100 Ω resistor.
+5V
R
F1
–5V
348⍀
R
348⍀
HP2835
F2
R
L
100⍀
V
OUT
R
G1
R
24.9⍀
T2
10k⍀
348⍀
R
G2
348⍀
5V
CR1
V
IN
R
T1
49.9⍀
Figure 12. Full-Wave Rectifier
The diodes should be operated such that they are
slightly forward-biased when the differential output voltage
is zero. For the Schottky diodes, this is about 400 mV.
The
forward biasing can be conveniently adjusted by CR1,
which, in this circuit, raises and lowers V
OUT,cm
without
creating a differential output voltage.
One advantage of this circuit is that the feedback loop is
never momentarily opened while the diodes reverse
their polarity within the loop. This is the scheme that is
sometimes used for full-wave rectifiers that use conventional op amps. These conventional circuits do not work
well at frequencies above about 1 MHz.
If there is not enough forward bias (V
too low), the
OUT,cm
lower sharp cusps of the full-wave rectified output
waveform will be rounded off. Also, as the frequency
increases, there tends to be some rounding of the lower
cusps. The forward bias can be increased to yield
sharper cusps at higher frequencies.
There is not a reliable, entirely quantifiable, means to
measure the performance of a full-wave rectifier. Since
the ideal waveform has periodic sharp discontinuities, it
should have (primarily even) harmonics that have no
upper bound on the frequency. However, for a practical
circuit, as the frequency increases, the higher harmonics
become attenuated and the sharp cusps that are present
at low frequencies become significantly rounded.
The circuit was run at a frequency up to 300 MHz and,
while it was still functional, the major harmonic that
remained in the output was the second. This made it
look like a sine wave at 600 MHz. Figure 13 is an oscilloscope plot of the output when driven by a 100 MHz,
2.5 V p-p input.
REV. 0
–7–
Page 8

AN-584
Sometimes a second harmonic generator is actually
useful, such as creating a clock to oversample a DAC by
a
factor of two. If the output of this circuit is run
through
a low-pass filter, it can be used as a second har-
monic generator.
1V
100mV 2ns
Figure 13. Full-Wave Rectifier Response with
100 MHz Input
Differential Filtering Applications
Similar to an op amp, various types of active filters can
be created with the AD813x. These can have singleended inputs and differential outputs, which can
provide an antialias function when driving a differential
A/D converter.
Figure 14 is a schematic of a low-pass, multiple feedback
filter. The active section contains two poles, and an
additional pole is added at the output. The filter was
designed to have a –3 dB frequency of 1 MHz. The actual
–3 dB frequency was measured to be 1.12 MHz as shown
in Figure 15.
2.15k⍀
549⍀
2k⍀
V
IN
24.9⍀
49.9⍀
100pF
100pF
2k⍀
953⍀
953⍀
2.15k⍀
33pF
33pF
549⍀
200pF
200pF
V
OUT
Figure 14. 1 MHz, 3-Pole Differential Output Low-Pass
Multiple Feedback Filter
10
0
–10
–20
–30
– dB
IN
–40
/V
OUT
–50
V
–60
–70
–80
–90
10k
100k 1M 10M 100M
FREQUENCY – Hz
Figure 15. Frequency Response of 1 MHz Low-Pass Filter
E02656–0–2/02(0)
–8–
PRINTED IN U.S.A.
REV. 0
 Loading...
Loading...