Page 1

AN-574
a
APPLICATION NOTE
One Technology Way • P.O. Box 9106 • Norwood, MA 02062-9106 • Tel: 781/329-4700 • Fax: 781/326-8703 • www.analog.com
A Tamper-Resistant Watt-Hour Energy Meter Based on the AD7751
with a Current Transformer and a Low Resistant Shunt
by William Koon
INTRODUCTION
This application note describes a low cost, high accuracy IEC1036 Class 1 watt-hour meter based on the
AD7751. The meter described is intended for use in
single phase, two-wire distribution systems.
The AD7751 is a low-cost, single chip solution for electrical energy measurement. The most distinctive feature of
the AD7751 is that it continuously monitors the phase
and neutral (return) currents. A FAULT condition occurs
if the two currents differ by more than 12.5%. Power calculation will be based on the larger of the two currents.
The meter calculates power correctly even if one of the
two wires does not carry any current. AD7751 provides
an effective way to combat any attempt to return the
current through earth, a very simple yet effective way of
meter tampering. The AD7751 comprises of two ADCs,
reference circuit and all the signal processing necessary for the calculation of real (active) power. The
AD7751 also includes direct drive capability for electromechanical counters (i.e., the energy register) and has
a high-frequency pulse output for calibration and
communications purposes.
This application note should be used in conjunction with
the AD7751 data sheet. The data sheet provides detailed
information on the functionality of the AD7751 and will
be referenced several times in this application note.
DESIGN GOALS
The international Standard IEC1036 (1996-09)—
Alternating current watt-hour meters for active energy (Classes
1 and 2)
, was used as the primary specification for this
design. For readers more familiar with the ANSI C12.16
specification, see the section at the end of this application which compares the IEC1036 and ANSI C12.16
standards. This section explains the key IEC1036 specifications in terms of their ANSI equivalents.
The design greatly exceeds this basic specification for
many of the accuracy requirements, e.g., accuracy at
unity power factor and at low (PF = ±0.5) power factor. In
addition, the dynamic range performance of the meter
has been extended to 500. The IEC1036 standard specifies accuracy over a range of 5% I
to I
B
—see Table I.
MAX
Typical values for I
are 400% to 600% of IB. Table I
MAX
outlines the accuracy requirements for a static watthour meter. The current range (dynamic range) for
accuracy is specified in terms of I
(basic current).
B
Table I. Accuracy Requirements
Current Value
1
0.05 IB ≤ I < 0.1 I
≤ I ≤ I
0.1 I
B
MAX
≤ I ≤ 0.2 I
0.1 I
B
2
PF
1 ±1.5% ±2.5%
B
1 ±1.0% ±2.0%
0.5 Lag ±1.5% ±2.5%
B
Percentage Error Limits
Class 1 Class 2
0.8 Lead ±1.5% —
0.2 IB ≤ I ≤ I
MAX
0.5 Lag ±1.0% ±2.0%
0.8 Lead ±1.0% —
NOTES
1
The current ranges for specified accuracy shown in Table I are expressed
in terms of the basic current (IB). The basic current is defined in IEC1036
(1996-09) section 3.5.1.2 as the value of current in accordance with which
the relevant performance of a transformer operated meter is fixed. I
is the maximum current at which accuracy is maintained.
2
Power Factor (PF) in Table I relates the phase relationship between the
fundamental (45 Hz to 65 Hz) voltage and current waveforms. PF in this
case can be simply defined as
between pure sinusoidal current and voltage.
3
Class index is defined in IEC1036 (1996-09) section 3.5.5 as the limits of
the permissible percentage error. The percentage error is defined as:
Percen
tage Error =
energy registered by meter true energy
PF = cos(θ)
true energy
, where θ is the phase angle
−
MAX
×100%
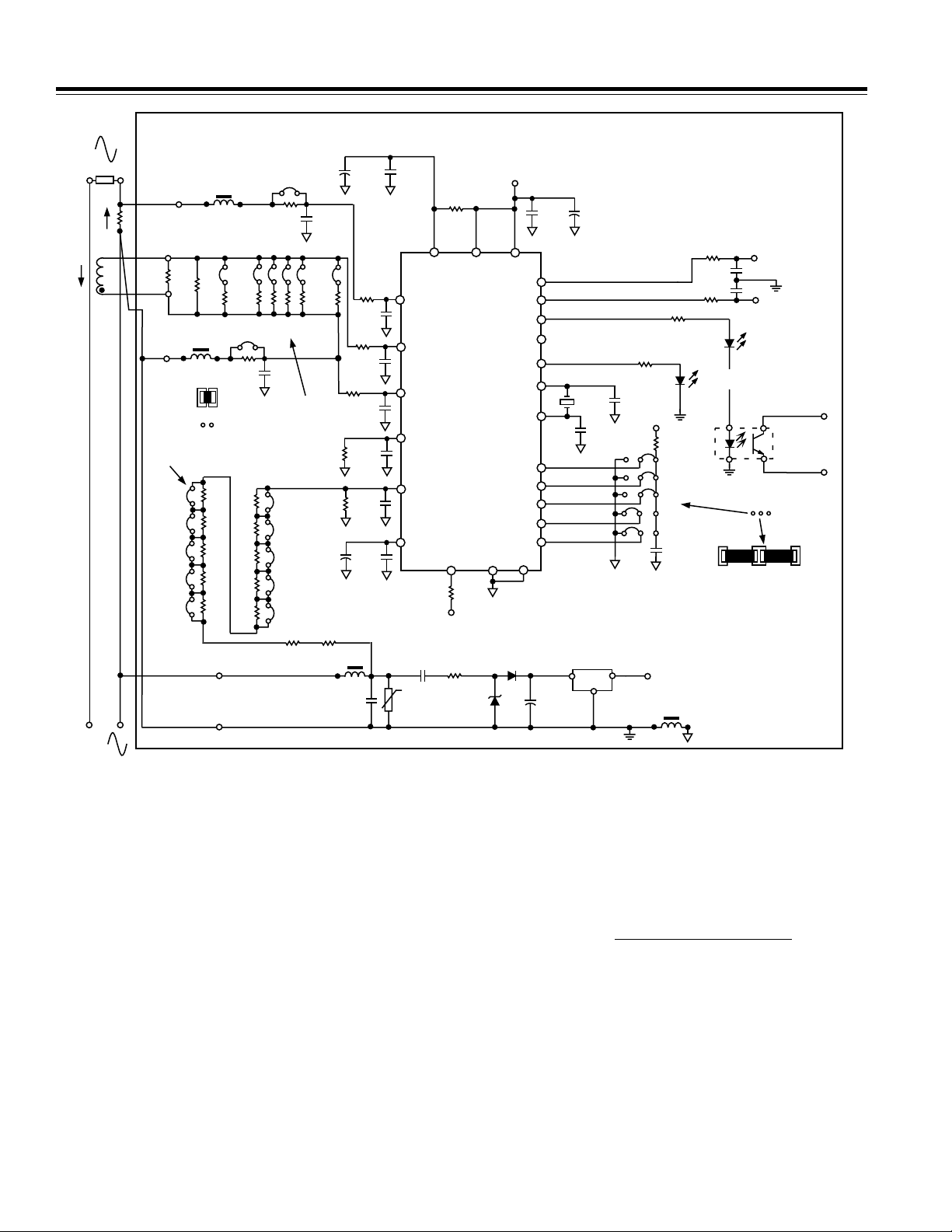
The schematic in Figure 1 shows the implementation of
a tamper-resistant, low-cost watt-hour meter using the
AD7751. A current transformer (CT) is used to detect the
current in the neutral wire, and the current flowing in the
phase is monitored by a current shunt. These two current sensors provide the current to voltage conversion
needed by the AD7751 and a simple divider network
attenuates the line voltage. The energy register (kWh) is
a simple electromechanical counter that uses a twophase stepper motor. The AD7751 provides direct drive
capability for this type of counter. The AD7751 also provides a high-frequency output at the CF pin for the meter
constant (3200 imp/kWh). Thus a high-frequency output
is available at the LED and optoisolator output. This
high-frequency output is used to speed up the calibration process and provides a means of quickly verifying
3
REV. 0
© Analog Devices, Inc., 2001
Page 2
AN-574
LOAD
–
+
–
+
PHASE
NEUTRAL
K1
K3
R6
R7
2.7
56
K4
K2
SOLDER JUMPERS
CALIBRATION
NETWORK
30%
J5
18k
J4
39k
J3
75k
J2
150k
J1
300k
FAULT TOLERANT ENERGY METER
= 40A, Ib = 5A, CLASS 1 (5% Ib – I
I
MAX
+
C12
C20
33nF
J21
R13
2.7k
R4A
1k
R4B
1k
10F
R25
330k
220F
6.3V
1.05k
R2
1k
+
C6
100nF
Z1
C17
10nF
X2
R5A
100
J18
J19
R10
R11
680
C21
33nF
CALIBRATION
NETWORK
J10
560
J9
1.2k
J8
2.2k
J7
5.1k
J6
9.1k
R24
330k
J22
J20
3%
R12
1.3k
Z3
J17
J16
R8
R9
82
160
330
J23
Z4
R5B
100
R18
R23
R17
R22
R16
R21
R15
R20
R14
R19
K5
K6
R1
1k
33nF
R3
33nF
33nF
33nF
33nF
C11
100nF
R33
10
P3 P1P2
AVDD AC/DC DVDD
P4
V1A
C1
P5
V1B
C3
P6
V1N
C2
P7
V2N
C4
P8
V2P
C5
P10
REF
C7
C18
470nF
MOV1
S20K275
U1
AD7751
IN/OUT
RESET AGND DGND
R27
10k
V
DD
R26
470
1N4744A
P11P9
D2
V
DD
DEVP
FAULT
CLKOUT
CLKIN
SCF
D2
1N4004
C13
100nF
P23
F1
P23
F2
P22
CF
P20
P19
P18
P17
P16
G0
P15
G1
P14
S0
P13
S1
P12
P21
POWER SUPPLY
81
C19
+
470F
35V
MAX
C14
+
10F
6.3V
3.579545MHz
Y1
C9
22pF
G0 = 1
G1 = 1
S0 = 1
S1 = 0
SCF = 0
U2
7805
2,3,6,7
)
TO IMPULSE COUNTER/
STEPPER MOTOR
D1
U3
1
2
PS2501-1
0R
K7
C16
100IMP/kWhr
C15
K8
CALIBRATION LED
HP HLMP-D150
4
3200IMP/kWhr
3
JUMPERS
USE 0
RESISTORS
0R
K9
K10
C10
22pF
R29
820
V
V
+5V
820
D4
DD
R28
10k
J15
J14
J13
J12
J11
C8
100nF
DD
Z2
R30
R32
20
R31
20
FAULT LED
HP HLMP-D150
240V
Figure 1. Tamper-Resistant Single Phase Watt-Hour Meter Based on the AD7751
meter functionality and accuracy in a production environment. The meter is calibrated in a two-step process:
Step 1. With current passing through only Channel
V1A’s shunt, the meter is first calibrated by varying
the line voltage attenuation using the resistor network
R14 to R23.
Step 2. With current passing through only Channel
V1B’s CT, the small gain mismatch between the CT’ in
Channel V1B and the shunt in Channel V1A is calibrated by shorting out the appropriate resistor in the
resistor network R8 to R13.
DESIGN EQUATIONS
The AD7751 produces an output frequency which is proportional to the time average value of the product of two
voltage signals. The input voltage signals are applied at
V1 and V2. The detailed functionality of the AD7751 is
explained in the AD7751 data sheet—see
Operation
section. The AD7751 data sheet also provides
Theory Of
an equation which relates the output frequency on F1
and F2 (counter drive) to the product of the rms signal
levels at V1 and V2. This equation is shown here again
for convenience and will be used to determine the correct signal scaling at V2 in order to calibrate the meter to
a fixed constant.
Frequency
.
=
2
V
REF
−
14
(1)
V V Gain F
×× × ×
574 1 2
The meter shown in Figure 1 is designed to operate at a
line voltage of 240 V and a maximum current (I
MAX
) of
40 A. However by correctly scaling the signals on Channel 1 and Channel 2, a meter operating of any line
voltage and maximum current could be designed.
The basic current (I
and the current range for accuracy will be 5% I
) for this meter is selected as 5 A,
B
to I
B
MAX
or
a dynamic range of 160 (maintains 1% accuracy from
250 mA to 40 A). The electromechanical register (kWh)
will have a constant of 100 imp/kWh, i.e., 100 impulses
–2–
REV. 0
Page 3

AN-574
from the AD7751 will be required in order to register
1 kWh. IEC1036 section 4.2.11 specifies that electromagnetic registers have their lowest values numbered in ten
division, each division being subdivided into ten parts.
Hence a display with a five plus one digits is used, i.e.,
10,000s, 1,000s, 100s, 10s, 1s, 1/10s. The meter constant
(for calibration and test) is selected as 3200 imp/kWh.
The on-chip reference circuit of the AD7751 has a temperature coefficient of typically 30 ppm/°C. However, on
A grade parts this specification is not guaranteed and
may be as high as 80 ppm/°C. At 80 ppm/°C the AD7751
error at –20°C/+60°C would be approximately +0.65%,
assuming a calibration at 25°C.
Shunt Selection
The shunt size (500 µΩ) is selected to maximize the use
of the dynamic range on Channel V1A (current Channel
A). However, there are some important considerations
when selecting a shunt for an energy metering application. First, minimize the power dissipation in the shunt.
The maximum rated current for this design is 40 A,
therefore the maximum power dissipated in the shunt is
2
(40 A)
× 500 µΩ = 800 mW. IEC1036 calls for a maximum
power disposition of 2 W (including power supply). Secondly, the higher power dissipation may make it difficult
to manage the thermal issues. Although the shunt is
manufactured from Manganin material which is an alloy
with a low temperature coefficient of resistance, high
temperatures may cause significant error at heavy
loads. A third consideration is the ability of the meter to
resist attempts to tamper by shorting the circuit externally. With a very low value of shunt resistance, the
effects of externally shorting the shunt are very much
minimized. Therefore, the shunt should always be
made as small as possible, but this must be offset
against the signal range on V1A (30 mV rms with a gain
of 16). If the shunt is made too small, it will not be possible to meet the IEC1036 accuracy requirements at light
loads. A shunt value of 500 µΩ was considered a good
compromise for this design.
Current Transformer (CT) Selection
The CTs and their burden resistors should be selected to
match the shunt selected for V1B input. However there
are some important considerations when selecting the
CTs and the burden resistors for energy metering application. First, one need to select CTs that have good
linearity in both their gain and phase characteristics
over the range of current specified in the accuracy
requirement. For IEC1036, the range is between 5% I
I
. CT manufacturers often recommend the burden
MAX
to
B
resistance to be as small as possible to preserve linearity over large current range. A burden resistance of less
than 15 Ω is recommended. Second, CT introduces a
phase shift between primary and secondary current. The
phase shift can contribute to a significant error at low
power factor. Note that at power factor of 0.5, a phase
shift as small as 0.1° translates to 0.3% error in the
power reading. In this design, the phase of the CT channel (V1B) is shifted to match the phase shift introduced
by the CT to eliminate any phase mismatch between the
current and voltage channel. This is achieved by moving the corner frequency of the antialiasing filter in the
current channel input—see Corrected Phase Matching
between Channels and Antialias Filters in this application note. In this design, a 5000 turn CT was chosen. The
nominal value of the burden resistor can be found by the
following calculation:
Burden Resistor = CT Turn Ratio × Shunt Resistance
Design Calculations
Design parameters:
Line Voltage = 240 V (Nominal)
I
= 40 A (IB = 5 A)
MAX
Counter = 100 imp/kWh
Meter Constant = 3200 imp/kWh
Shunt Resistance = 500 µΩ
CT Turn Ratio = 1:5000
Nominal Burden Resistor = 500 µΩ × 5000 = 2.5 Ω
100 imp/hour = 100 ÷ 3600 sec = 0.027777 Hz
Meter will be calibrated at I
Power dissipation at I
Frequency on F1 (and F2) at I
(5 A).
B
= 240 V × 5 A = 1.2 kW
B
= 1.2 × 0.027777 Hz
B
= 0.03333333 Hz
Voltage across the shunt at I
(V1A) = 5A × 500 µΩ =
B
2.5 mV.
To select the F
AD7751 data sheet—
Meter Application
frequency for Equation 1, see the
1-4
Selecting a Frequency for an Energy
. From Tables V and VI in the AD7751
data sheet it can be seen that the best choice of frequency for a meter with I
= 40 A is 3.4 Hz (F2). This
MAX
frequency selection is made by the logic inputs S0 and
S1—see Table II in the AD7751 data sheet. The CF
frequency selection (meter constant) is selected by
using the logic input SCF. The two available options are
64 × F1(6400 imp/kWh) or 32 × F1(3200 imp/kWh). For
this design, 3200 imp/kWh is selected by setting SCF
logic low. With a meter constant of 3200 imp/kWh and a
maximum current of 40 A, the maximum frequency from
CF is 8.53 Hz. Many calibration benches used to verify
meter accuracy still use optical techniques. This limits
the maximum frequency which can be reliably read to
about 10 Hz. The only remaining unknown from Equation 1 is V2 or the signal level on Channel 2 (the
voltage channel).
From Equation 1 on the previous page:
0 03333333
.
=
2
2
5
.
mV V Hz
××××
574 25 2 16 34
.. .
Hz
where:
V
2 = 266.8 mV rms
REV. 0
–3–
Page 4
AN-574
Therefore, in order to calibrate the meter, the line voltage
needs to be attenuated down to 266.8 mV.
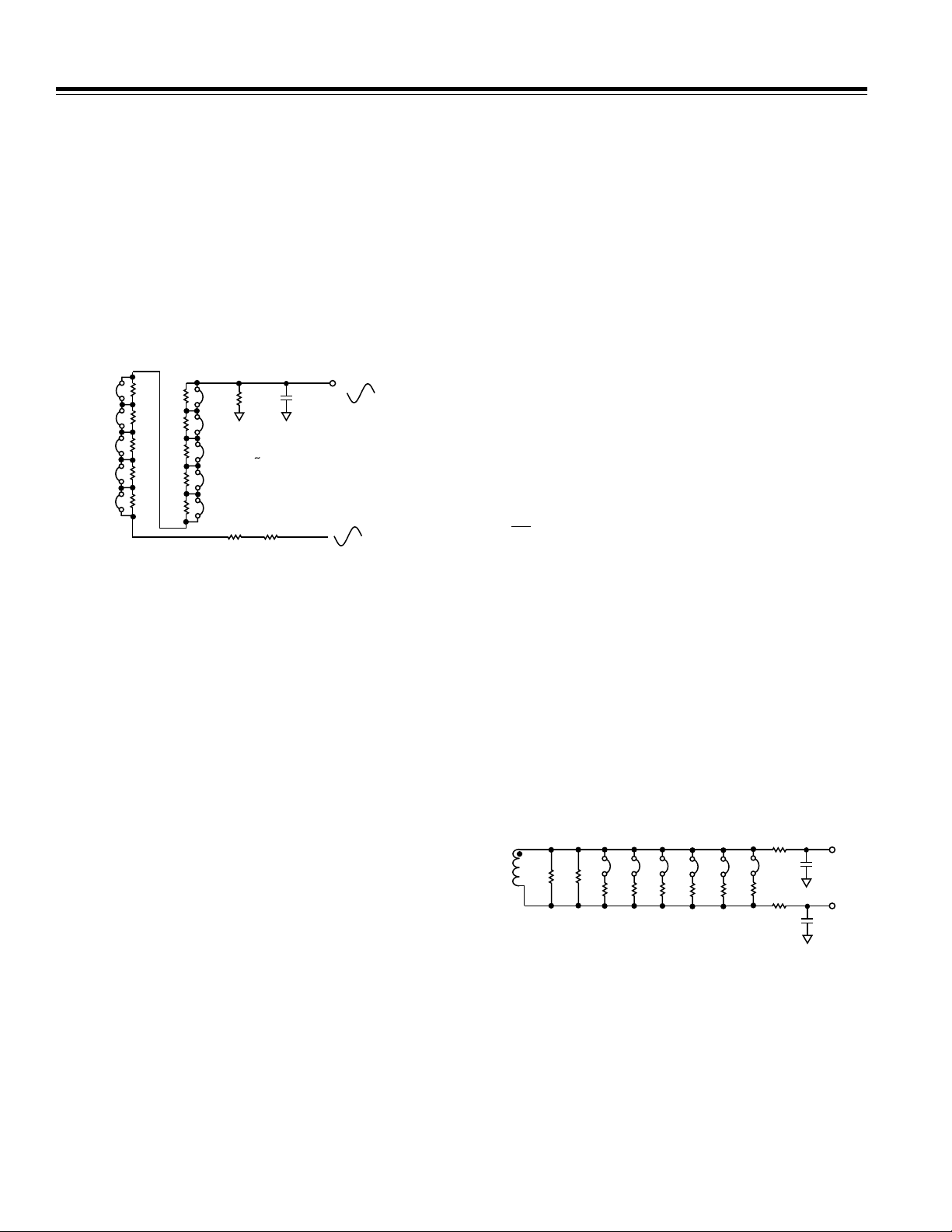
CALIBRATING THE METER: VOLTAGE CHANNEL
CALIBRATION
From the previous section it can be seen that the meter
is simply calibrated by attenuating the line voltage down
to 266.8 mV. The line voltage attenuation is carried out
by a simple resistor divider as shown in Figure 2. The
attenuation network should allow a calibration range of
at least ±30% to allow for CT/burden and the current
shunt resistance tolerances and the on-chip reference
tolerance of ±8%—see AD7751 data sheet.
J5
R18
R17
J4
J3
R16
R15
J2
R14
J1
R23
R22
R21
R20
R19
J10
R4B
J9
R14 + R15 +....+ R24 + R25 >> R4B
J8
f
= 1/(2..R4B.C5)
–3dB
J7
J6
R24
R25
266.8mV
C5
240V
Figure 2. Attenuation Network for Calibrating the
Voltage Channel (V2)
In addition, the topology of the network is such that the
phase matching between Channel 1 and Channel 2 is
preserved, even when the attenuation is being adjusted—
see Correct Phase Matching between Channels in this
application note.
As can be seen from Figure 2, the –3 dB frequency of this
network is determined by R4B and C5. Even with all the
jumpers closed, the total resistance of R24 and R25
(660 kΩ) is still much greater than R4B (1 kΩ). Hence
varying the resistance of the resistor chain R14 to R23
will have little effect on the –3 dB frequency of the network. The network shown in Figure 2 allows the line
voltage to be attenuated and adjusted in the range
190 mV to 363 mV with a resolution of 10 bits or 169 µV.
This is achieved by using the binary weighted resister
chain R14 to R23. This will allow the meter to be accurately calibrated using a successive approximation
technique.
During calibration, with current passing only the V1B
channel (current shunt side), starting with J1 each
jumper is closed in order of ascendance, e.g., J1, J2, J3
etc. If the calibration frequency on CF, i.e., 32 × 100 imp/
kWh (at I
= 5 A, CF frequency is expected to be 1.0667 Hz)
B
is exceeded when any jumper is closed, it should be
opened again. All jumpers are tested, J10 being the last
jumper. Note jumper connections are made with soldering together the jumper pins across the resistors in the
network. This approach is preferred over the use of trim
pots, as the stability of the latter over time and environmental conditions is questionable.
Since the AD7751 transfer function is extremely linear,
a one-point calibration (usually at I
) at unity power fac-
B
tor is all that is needed to calibrate the meter. If the
correct precautions have been taken at the design
stage, no calibration will be necessary at low power
factor (e.g., PF = 0.5).
CALIBRATING THE METER: MATCHING THE SHUNT AND
THE CT INPUTS
A calibration network, consisting of eight resistors and six
jumpers, is used to compensate gain variation between
the CT that is monitoring the phase current and the
shunt which detects the neutral currents. Because such
mismatch is often small, a more accurate calibration
network is used. In this design, a six-resistor parallel
resistor network is used for this purpose.
Because the signal at V1A and V1B must be the same to
provide accurate billing at both normal and fault mode,
Equation (2) shows the necessary condition for the V1A
and V1B signals to be the same.
R
B
=
R
S
N
where:
N
is the turn ratio of the CT.
R
is the CT’s burden resistance.
B
R
is the shunt resistance.
S
In this design, N = 5000, and RS = 500 µΩ, the nominal
value of R
is calculated to be at 2.5 Ω.
B
To generate the ±3% calibration range, the maximum
resistance (with J16 to J21 open) should be 2.5 Ω × 1.03
= 2.575 Ω and the minimum resistance (with J16 to J21
closed) should be 2.5 Ω × 0.97 = 2.425 Ω. The calibration
range is 2.575 – 2.425 = 0.15 Ω. Figure 3 shows the imple-
mentation of the calibration network in this design.
CURRENT TRANSFORMER
1:5000
J20
J19
R6 R7
J16 J17 J21
R8 R9 R13
J18
R10
R11
R12
Figure 3. Calibration Network for V1A and V1B Mismatch
R6 and R7 will produce the upper limit of the resistance
(2.575 Ω), and closing R8 to R13 will produce the lower
limit (2.425 Ω). R8 to R13 are binary weighted resistors,
i.e., closing jumper J16 will have twice as much effect to
the output than closing jumper J17. Again, successive
approximation technique is used to calibrate channel
matching.
During calibration, with current passing only the V1A
channel (CT side), the resistance is reduced by closing
appropriate jumpers J16 to J21. Starting from J16, each
–4–
(2)
R3
V1B
C3
R2
V1N
C2
REV. 0
Page 5
AN-574
jumper is closed. By putting extra resistor in parallel, the
total burden resistance is reduced and thus the output
signal is attenuated. If the calibration frequency falls
below the expected value after a jumper is closed, the
jumper should be opened again.
Note that similar to the voltage calibration network, the
phase angle is preserved to be the same as that of Channel V1A by selecting the appropriate resistance values
used in the network.
CORRECT PHASE MATCHING BETWEEN CHANNELS
The AD7751 is internally phase-matched over the frequency range 40 Hz to 1 kHz. Correct phase matching is
important in an energy metering application because
any phase mismatch between channels will translate
into significant errors at low power factor. This is easily
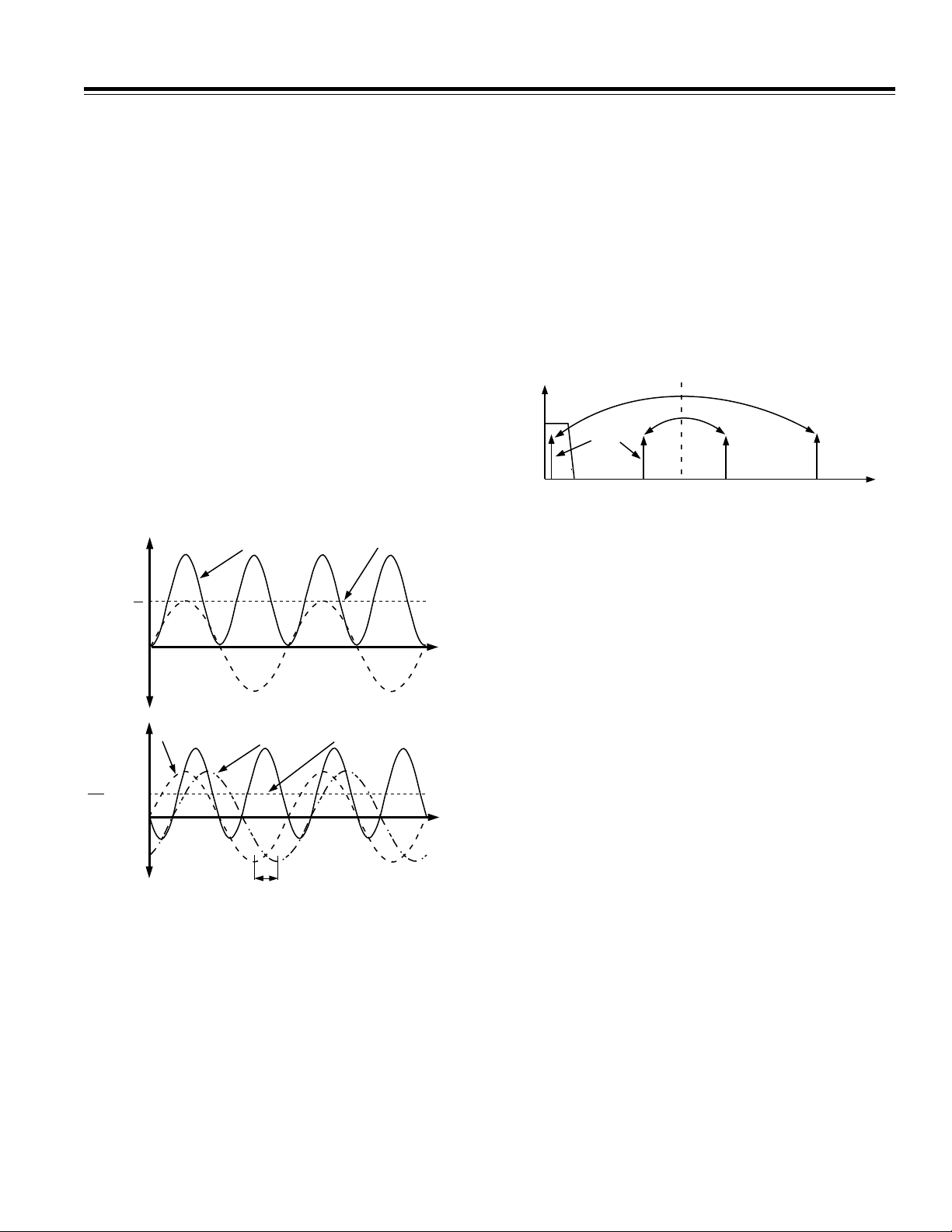
illustrated with the following example. Figure 4 shows
the voltage and current waveforms for an inductive
load. In the example shown, the current lags the voltage
by 60° (PF = 0.5). Assuming pure sinusoidal conditions,
the power is easily calculated as V rms × I rms × cos (60°).
INSTANTANEOUS REAL
POWER SIGNAL
INSTANTANEOUS REAL
POWER SIGNAL
V.I.
2
PF = 1
PF = 0.5
COS(60)
V.
2
I
CURRENT
VOLTAGE
CURRENT
INSTANTANEOUS
POWER SIGNAL
VOLTAGE
INSTANTANEOUS
POWER SIGNAL
60
Figure 4 . Voltage and Current Waveform
(Inductive Load)
If, however, a phase error (e) is introduced externally
to the AD7751, e.g., in the antialias filters, the error is
calculated as:
[
cos
(δ°) –
cos
(δ° + φe)]/
cos
(δ°) × 100% (3)
See Note 3 in Table I. Where δ is the phase angle between
voltage and current and φ
is the external phase error.
e
With a phase error of 0.2°, for example, the error at PF = 0.5
(60°) is calculated as 0.6%. As this example demonstrates, even a very small phase error will produce a
large measurement error at low power factor.
ANTIALIAS FILTERS
As mentioned in the previous section, one possible
source of external phase errors are the antialias filters
on Channel 1 and Channel 2. The antialias filters are lowpass filters that are placed before the analog inputs of
any ADC. They are required to prevent a possible distortion due to sampling called aliasing. Figure 5 illustrates
the effects of aliasing.
ALIASING EFFECTS
IMAGE
FREQUENCIES
0
450 900 2
FREQUENCY – kHz
Figure 5. Aliasing Effects
Figure 5 shows how aliasing effects could introduce
inaccuracies in an AD7751-based meter design. The
AD7751 uses two ⌺-⌬ ADCs to digitize the voltage and
current signals. These ADCs have a very high sampling
rate, i.e., 900 kHz. Figure 5 shows how frequency components (arrows shown in black) above half the
sampling frequency (also know as the Nyquist frequency), i.e., 450 kHz get imaged or folded back down
below 450 kHz (arrows shown in grey). This will happen
with all ADCs no matter what the architecture. In the
example shown it can be seen that only frequencies near
the sampling frequency, i.e., 900 kHz, will move into the
band of interest for metering, i.e., 0 kHz–2 kHz. This fact
will allow us to use a very simple LPF (Low-Pass Filter)
to attenuate these high frequencies (near 900 kHz) and
so prevent distortion in the band of interest.
The simplest form of LPF is the simple RC filter. This is a
single-pole filter with a roll-off or attenuation of
–20 dBs/dec.
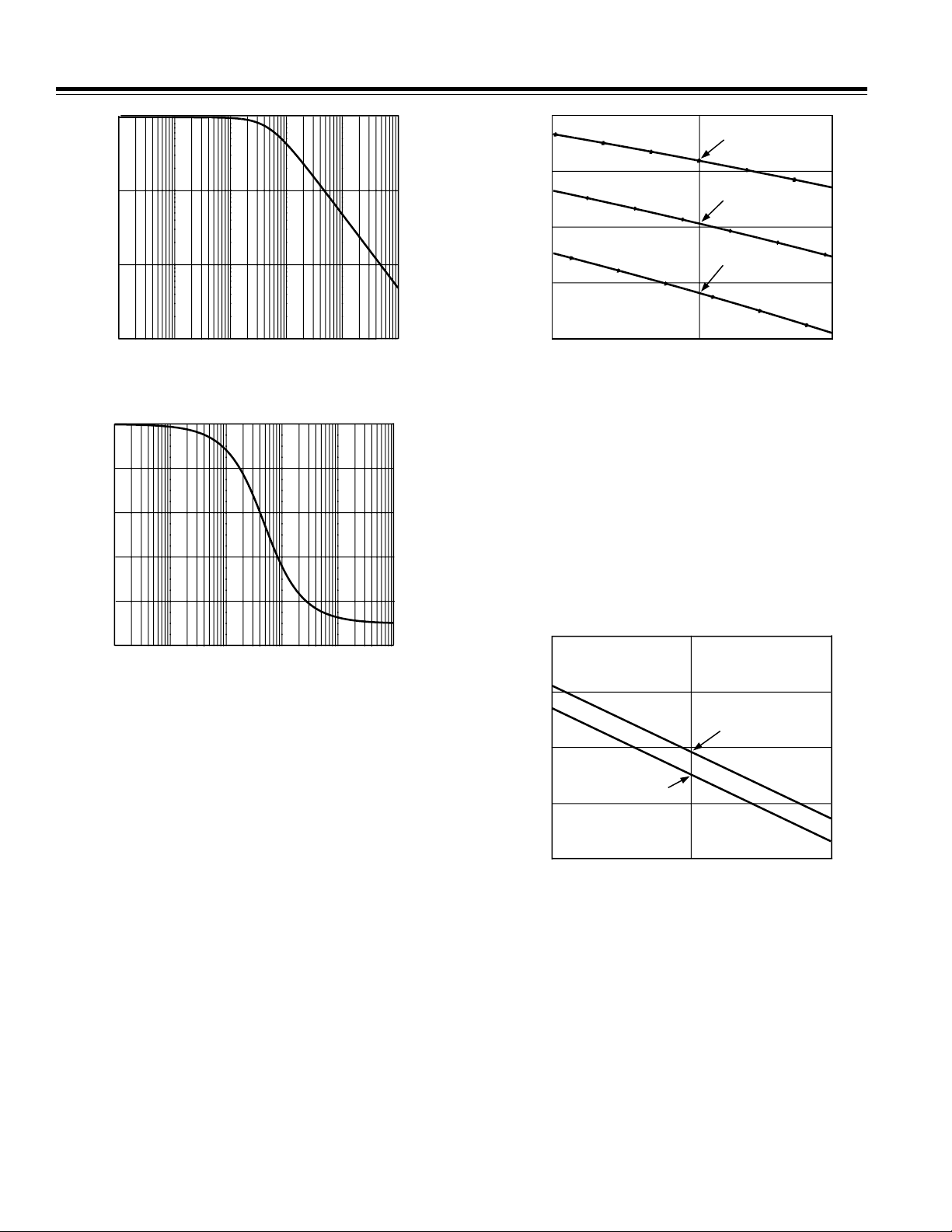
CHOOSING THE FILTER –3 dB FREQUENCY
As well as having a magnitude response, all filters also
have a phase response. The magnitude and phase
response of a simple RC filter (R = 1 kΩ, C = 33 nF) are
shown in Figures 6 and 7. From Figure 6 it is seen that
the attenuation at 900 kHz for this simple LPF is greater
than 40 dB. This is enough attenuation to ensure no ill
effects due to aliasing.
REV. 0
–5–
Page 6
AN-574
0dB
–20dB
–40dB
–60dB
10 100 1.0k 10k 100k 1.0M
FREQUENCY – Hz
Figure 6. RC Filter Magnitude Response
0
–20
–40
–60
–80
–0.4
(50Hz, –0.481)
(R = 900, C = 29.7nF)
–0.5
(50Hz, –0.594)
(R = 1k, C = 33nF)
–0.6
(50Hz, –0.718)
–0.7
(R = 1.1k, C = 36.3nF)
–0.8
45 50 55
FREQUENCY – Hz
Figure 8. Phase Shift at 50 Hz Due to Component
Tolerances
Note this is also why precautions were taken with the
design of the calibration network on Channel 2 (voltage
channel). Calibrating the meter by varying the resistance of the attenuation network will not vary the –3 dB
frequency and hence the phase response of the network on Channel 2—see Calibrating the Meter:
Voltage Channel Calibration. Shown in Figure 9 is a
plot of phase lag at 50 Hz when the resistance of the
calibration network is varied from 660 kΩ (J1–J10
closed) to 1.2 MΩ (J1–J10 open).
–100
10 100 1.0k 10k 100k 1.0M
FREQUENCY – Hz
Figure 7. RC Filter Phase Response
As explained in the last section, the phase response can
introduce significant errors if the phase response of the
LPFs on both Channel 1 and Channel 2 are not matched.
Phase mismatch can easily occur due to poor component tolerances in the LPF. The lower the –3 dB
frequency in the LPF (antialias filter), the more pronounced these errors will be at the fundamental
frequency component or the line frequency. Even with
the corner frequency set at 4.8 kHz (R = 1 kΩ, C = 33 nF),
the phase errors due to poor component tolerances can
be significant. Figure 8 illustrates the point. In Figure 8,
the phase response for the simple LPF is shown at 50 Hz
for R = 1 kΩ ± 10%, C = 33 nF ± 10%. Remember a phase
shift of 0.1°–0.2° can cause measurement errors of 0.6%
at low power factor. This design uses resistors of 1% tolerance and capacitors of 10% tolerance for the antialias
filters to reduce the possible problems due to phase
mismatch. Alternatively the corner frequency of the
antialias filter could be pushed out to 10 kHz–15 Hz.
However, the corner frequency should not be made too
high. This could allow enough high-frequency components to be aliased and cause accuracy problems in a
noisy environment.
–0.591
–0.592
J1–J10 CLOSED
(50Hz, –0.59308)
–0.593
J1–J10 OPEN
–0.594
–0.595
49.9 50.0 50.1
(50Hz, –0.59348)
FREQUENCY – Hz
Figure 9. Phase Shift Due to Calibration
For the resistor network used for matching the shunt and
the CT in V1A and V1B, the calibration network has no
phase shift property. The antialiasing filter for the CT has a
larger phase lag to offset the slight phase lead introduced by the CT. This is achieved by using a larger
resistor in the RC network.
–6–
REV. 0
Page 7
COMPENSATING FOR PARASITIC SHUNT INDUCTANCE
WITHOUT PARASITIC SHUNT INDUCTANCE
WITH PARASITIC SHUNT INDUCTANCE
10 100 1k 10k 100k 1M
–100
–80
–60
–40
–20
–0
–50dB
–40dB
–30dB
–20dB
–10dB
0dB
FREQUENCY – Hz
MAGNITUDE
PHASE
When used at low frequencies a shunt can be considered as a purely resistive element with no significant
reactive elements. However, under certain situations
even a small amount of stray inductance can cause
undesirable effects when a shunt is used in a practical
data acquisition system. The problem is very noticeable
when the resistance of the shunt is very low, in the order
of 200 µΩ. Shown below is an equivalent circuit for the
shunt used in this design. There are three connections to
the shunt. One pair of connections provide the current
sense inputs (V1A and V1N) and the third connection is
the ground reference for the system.
AN-574
The shunt resistance is shown as R
(500 µΩ). R
SH1
resistance between the V1N input terminal and the system
ground reference point. The main parasitic elements
(inductance) are shown as L
SH1
and L
. Figure 10 also
SH2
shows how the shunt is connected to the AD7751 inputs
(V1A and V1N) through the antialiasing filters. The function of the antialiasing filters is explained in the previous
section and their ideal magnitude and phase responses
are shown in Figures 6 and 7.
L
R
W1
1
V1A
C
R
SH1
L
SH1
L
W2
R
SH2
L
SH2
L
GND
1
OUT
SHUNT
R
2
C
R
GND
V1N
2
GND
PHASE
IN
Figure 10. Equivalent Circuit for the Shunt
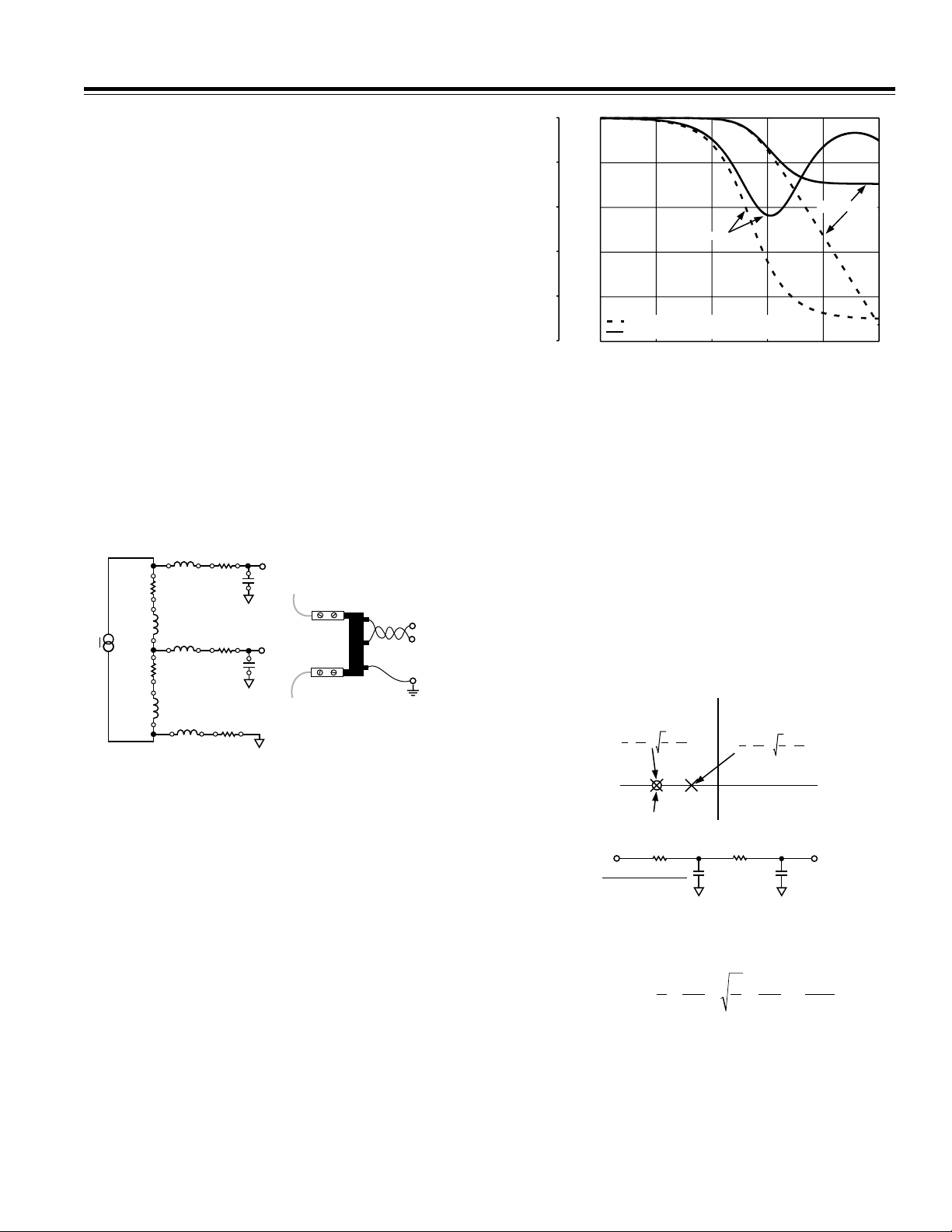
Canceling the Effects of the Parasitic Shunt Inductance
The effect of the parasitic shunt inductance is shown in
Figure 11. The plot shows the phase and magnitude
response of the antialias filter network with and without
(dashed) a parasitic inductance of 3 nH. As can be seen
from the plot, both the gain and phase response of the
network are effected. The attenuation at 1 MHz is now
only about –15 dB which could cause some repeatability
and accuracy problems in a noisy environment. More
importantly, a phase mismatch may now exist between
the current and voltage channels. Assuming the network
on Channel 2 has been designed to match the ideal
phase response of Channel 1, there now exists a phase
mismatch of 0.1° at 50 Hz. Note that 0.1 will cause a
0.3% measurement error at PF = ±0.5. See Equation (3)
in Correct Phase Matching Between Channels section.
500
SH2
is the
V1A
V1N
GND
Figure 11. Effect of Parasitic Shunt Inductance on the
Antialiasing Network
The problem is caused by the addition of a zero into the
antialias network. Using the simple model for the shunt
shown in Figure 10, the location of the zero is given as
R
SH1/LSH1
(in radians/sec).
One way of canceling the effects of this additional zero
in the network is to add an additional pole at the (or
close to) same location. The addition of an extra RC on
each analog input of V1A and V1N will achieve the additional pole required. The new antialias network for
Channel V1A is shown in Figure 12. To simplify the
calculation and demonstrate the principle, the Rs and Cs
of the network are assumed to be the same.
j
POLE #1
3 1 5 1
–
()
2 RC 4 RC
POLE #2
3 1 5 1
– –
()
2 RC 4 RC
ZERO #1
–(RSH/LSH)
2 R2 C2
S
R
1
S3RC 1
R
C
C
Figure 12. Shunt Inductance Compensation Network
The location of the pole #1 is given as:
For
R
= 500 µΩ,
SH
1
Pole
321541
#1
=× + ×
RC RCRL
L
= 3 nH, C = 33 nF.
SH
1
SH
1
=
SH
1
REV. 0
–7–
Page 8
AN-574
R is calculated as approximately 476 Ω (Use 470 Ω).
The location of Pole #1 is 166,667 rads or 26.53 kHz.
This places the location of Pole # 2 at:
Pole
321541
RC RC
kHz#.2
3 920=× + ×
=
To ensure phase matching between Channel 1 and
Channel 2, the pole at Channel 2 must also be positioned
at this location. With C = 33 nF, the new value of resistance
for the antialias filters on Channel 2 is approximately
1.23 kΩ (use 1.2 kΩ).
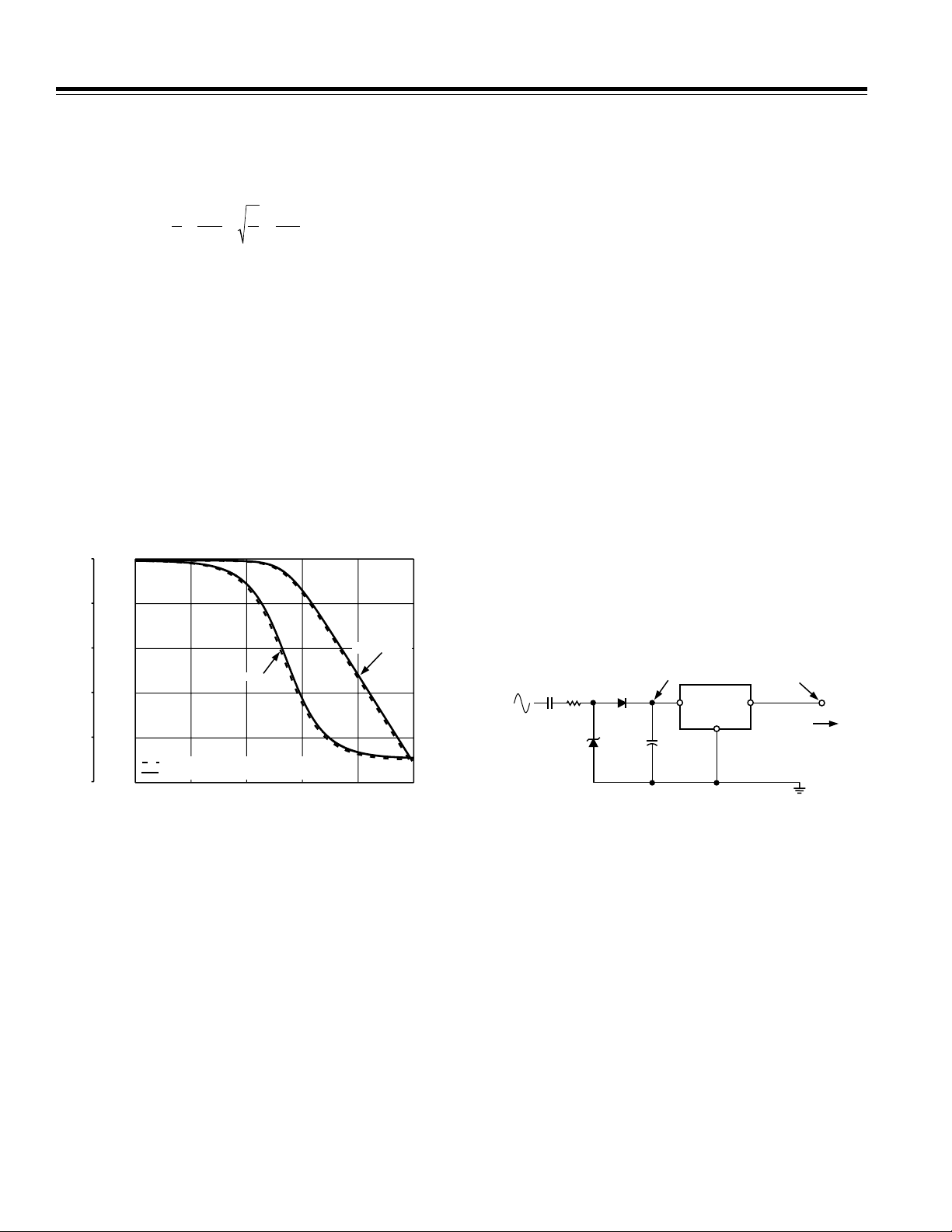
Figure 13 shows the effect of the compensation network
on the phase and magnitude response of the antialias
network in Channel 1. The dashed line shown the response
of Channel 2 using practical values for the newly calculated component values, i.e., 1.2 kΩ and 33 nF. The solid
line shows the response of Channel 1 with the parasitic
shunt inductance included. Notice phase and magnitude
responses match very closely. This is the objective of
the compensation network.
–0
0dB
–20
–10dB
–40
–60
–80
–100
–20dB
PHASE
–30dB
–40dB
WITHOUT PARASITIC SHUNT INDUCTANCE
–50dB
WITH PARASITIC SHUNT INDUCTANCE
10 100 1k 10k 100k 1M
FREQUENCY – Hz
MAGNITUDE
Figure 13. Antialiasing Network Phase and Frequency
Response after Compensation
The method of compensation works well when the poles
due to shunt inductance are greater than 25 kHz or so. If
zero is at a much higher frequency, its effects may simply
be eliminated by placing an extra RC on Channel 1 with
a pole that is a decade greater than that of the original
antialiasing filter. In this design, extra RC filters (R5A,
C20, and R5B, C21) are used for the purpose of eliminating the parasitic inductance.
NO LOAD THRESHOLD
The AD7751 has on-chip anticreep functionality. The
AD7751 will not produce a pulse on CF, F1, or F2 if the
output frequency falls below a certain level. This feature
ensures that the energy meter will not register energy
when no load is connected. IEC 1036 (1996-09), Section
4.6.4 specifies the start-up current as being not more
than 0.4% I
at PF = 1. With IB = 5 A, the meter has to start
B
registering energy at 20 mA. For this design, the start
current is calculated at 7.8 mA or 0.15% I
—see No Load
B
Threshold on the AD7751 data sheet.
POWER SUPPLY DESIGN
This design uses a simple low-cost power supply based
on a capacitor divider network, i.e., C18 and C19. Most of
the line voltage is dropped across C18, a 470 nF, 250 V
metalized polyester film capacitor. The impedance of
C18 dictates the effective VA rating of the supply. However, the size of C18 is constrained by the power
consumption specification in IEC1039. The total power
consumption in the voltage circuit including power supply is specified in Section 4.4.1.1 of IEC1039 (1996-9).
The total power consumption in each phase is 2 W and
10 VA under nominal conditions. The nominal VA rating
of the supply in this design is 8.5 VA. The total power
dissipation is approximately 0.59 W. Together with the
power dissipated in the shunt at 40 A load, the total
power consumption of the meter is 1.39 W. Figure 14
shows the basic power supply design.
240V
R26
V1
D2C18
D3
C19
+
U2
8
7805
2, 3, 6, 7
V2
1
5V
V
DD
I
Figure 14. Power Supply
The plots shown in Figures 15, 16, 17, and 18 show the
PSU performance under heavy load (50 A) with the line
voltage varied from 180 V to 250 V. By far the biggest
load on the power supply is the current required to drive
the stepper motor which has a coil impedance of about
400 Ω. This is clearly seen by looking at V1 (voltage on
C19) in the plots below. Figure 16 shows the current
drawn from the supply. Refer to Figure 14 when reviewing the following simulation plots.
Care should be taken when selecting a shunt to ensure
its parasitic inductance is small. This is especially true
of shunts with small values of resistance, e.g.,
<200 µΩ. Note the smaller the shunt resistance, the
lower the zero frequency for a given parasitic inductance (Zero = R
SH1/LSH1
).
–8–
REV. 0
Page 9

15
0246810
TIME – s
15
10
5
0
V2
V
DD
V1
(C19)
VOLTS
10
V1
(C19)
VOLTS
5
0
0 2 4 6 8 10
C19 VOLTAGE DROP DUE TO
STEPPER MOTOR DRIVE
V2
(V
)
DD
TIME – s
Figure 15. Power Supply Voltage Output at 220 V and
50 A Load
24
12.5mA
MOTOR DRIVE
20
16
4mA LED/OPTO DRIVE
12
mA
8
AN-574
Figure 18. Power Supply Voltage Output at 250 V and
50 A Load
DESIGN FOR IMMUNITY TO ELECTROMAGNETIC
DISTURBANCE
In Section 4.5 of IEC1036 it is stated that “the meter shall
be designed in such a way that conducted or radiated
electromagnetic disturbances as well as electrostatic
discharge do not damage nor substantially influence the
meter.” The considered disturbances are:-
1. Electrostatic Discharge
4
2. Electromagnetic HF Fields
3. Fast Transience Burst
0
0 1.0 2.0 3.0 4.0 5.0
TIME – s
Figure 16. Power Supply Current Output at 220 V and
50 A Load
15
All of the precautions and design techniques (e.g., ferrite
beads, capacitor line filters, physically large SMD resistors,
PCB layout including grounding) contribute to a certain
extent in protecting the sensitive meter electronics from
each form of electromagnetic disturbance. Some precautions (e.g., ferrite beads) however, play a more important
role in the presence of certain kinds of disturbances (e.g.,
RF and fast transience burst). The following discusses each
10
V2
V1
V
(C19)
VOLTS
5
DD
of the disturbances listed previously and details what protection has been put in place.
Electrostatic Discharge (ESD)
Although many sensitive electronic components contain a certain amount of ESD protection on-chip, it is not
possible to protect against the kind of severe discharge
described below. Another problem is that the effects of
an ESD discharge is cumulative, i.e., a device may sur-
0
0246810
TIME – s
Figure 17. Power Supply Voltage Output at 180 V and
50 A Load
vive an ESD discharge; however, this is no guarantee
that it will survive multiple discharges at some stage in
the future. The best approach is to eliminate or attenuate the effects of the ESD event before it comes in
contact with sensitive electronic devices. This holds true
for all conducted electromagnetic disturbances. This
test is carried out according to IEC1000-4-2, under the
following conditions:
REV. 0
–9–
Page 10

AN-574
• contact discharge;
• test severity level 4;
• test voltage 8 kV;
• 10 discharges.
Very often no additional components are necessary to
protect devices. With a little care those components
which are already required in the circuit can perform a
dual role. For example, the meter must be protected
from ESD events at those points where it comes in contact with the “outside world,” e.g., the connection to the
phase wire. For the current input, AD7751 is connected
to the neutral wire through a CT and antialias filter. The
CT insulates the AD7751 from outside contact. Therefore, for the current inputs (V1), the only path for ESD
comes from the shunt to V1A and V1N through a pair of
RC filters.
As for the voltage channel, the phase wire is connected
to the AD7751 voltage channel through an attenuation
resistor network. The neutral wire is connected to the
AD7751 through the ground plane.
Ferrite beads are placed in series with all connections to
the line (both phase and neutral wires). A ferrite choke is
particularly effective at slowing the fast rise time of an
ESD current pulse. The high frequency transient energy
is absorbed in the ferrite material rather than being
diverted or reflected to another part of the system—the
properties of ferrite are discussed later. The PSU circuit
is also connected directly to the terminals of the meter.
Here the discharge will be dissipated by the ferrite, the
line filter capacitor (C17) and the rectification diodes D2
and D3. The analog input V2P is also protected by the
large impedance of the attenuation network used for
calibration. This antialiasing (RC) filter can also be
enough to protect against ESD damage to CMOS
devices. However some care must be taken with the
type of components used. For example, the resistors
should not be wire-wound as the discharge will simply
travel across them. The resistors should also be physically large to stop the discharge arcing across the
resistor. In this design, 1/8 W SMD 1206 resistors were
used in the antialias filters.
Another very common low-cost technique used to arrest
ESD events is a spark gap on the component side of the
PCB—see Figure 19. However, since the meter will likely
operate in an open air environment and be subject to
many discharges, this is not recommended at sensitive
nodes like the shunt connection. Multiple discharges
could cause carbon buildup across the spark gap which
could cause a short or introduce an impedance. In time,
it will affect accuracy. A spark gap was introduced in the
PSU after the MOV to take care of any very high amplitude/fast rise time discharges.
8kV ESD
EVENT
TO EXTERIOR (I/O)
CONNECTION
6–9 MILS
NO SOLDER
MASK
TRACE (TRACK)
ESD DISCHARGED
ACROSS SPARK GAP
SIGNAL
GROUND
TO CIRCUIT
103
Figure 19. Spark Gap to Arrest ESD Events
ELECTROMAGNETIC HF FIELDS
Susceptibility of integrated circuits to RF tends to be
more pronounced in the 20 MHz–200 MHz region. Frequencies higher than this tend to be shunted away from
sensitive devices by parasitic capacitances. In general,
at the IC level, the effects of RF in the region 20 MHz–
200 MHz will tend to be broadband in nature, i.e., no
individual frequency is more troublesome than another.
However, there may be higher sensitivity to certain frequencies due to resonances on the PCB. These
resonances could cause insertion gain at certain frequencies which in turn could cause problems for
sensitive devices. By far the greatest RF signal levels are
those coupled into the system via cabling. These connection points should be protected. Some techniques
for protecting the system are:
1. Minimize circuit bandwidth
2. Isolate sensitive parts of the system
Minimize Bandwidth
In this application, the required analog bandwidth is
only 2 kHz. This is a significant advantage when trying to
reduce the effects of RF. The cable entry points can be
low-pass filtered to reduce the amount of RF radiation
entering the system. The shunt output is already filtered
before being connected to the AD7751. This is to prevent
aliasing effects described earlier. By choosing the correct
components and adding some additional components
(e.g., ferrite beads), these antialiasing filters can double
as very effective RF filters. Figures 6 and 7 show a somewhat idealized frequency response for the antialias
filters on the analog inputs. When considering higher
frequencies (e.g., > 1 MHz) the parasitic reactive elements
of each lumped component must be considered. Figure
20 shows the antialias filters with the parasitic elements
included. These small values of parasitic capacitance
and inductance become significant at higher frequencies
and therefore must be considered.
–10–
REV. 0
Page 11

LOW Z
Z3
K1
K2
R1
Z4
R2
V1A
C1
HIGH Z
V1N
C2
Figure 20. Antialiasing Filters Showing Parasitics
Parasitics can be kept at a minimum by using physically small components with short lead lengths (i.e.,
surface mount). Because the exact source impedance
conditions are not known (this will depend on the
source impedance of the electricity supply), some general precautions should be taken to minimize the
effects of potential resonances. Resonances which
result from the interaction of the source impedance
and filter networks could cause insertion gain effects
and so increase the exposure of the system to RF radiation at certain (resonant) frequencies. Lossy (i.e., having
large resistive elements) components like capacitors
with lossy dielectric (e.g., type X7R) and ferrite are
ideal components for reducing the “Q” of the input network. The RF radiation is dissipated as heat rather than
being reflected or diverted to another part of the system. The ferrite beads Z1 and Z2 perform very well in
this respect. Figure 21 shows how the impedance of the
ferrite beads varies with frequency.
250
LI 1806 B 151R
Z, R, X
VS. FREQUENCY
200
150
100
50
0
1 10 100
L
Z
R
X
L
FREQUENCY – MHz
Figure 21. Frequency Response of the Ferrite Chips
(Z3 and Z4) in the Antialias Filter
From Figure 21 it can be seen that the ferrite material
becomes predominately resistive at high frequencies.
Also note that the impedance of the ferrite material
increases with frequency, causing only high (RF) frequencies to be attenuated.
Isolation
On the current channels, the shunt connection is the
only location where the AD7751 is connected directly
(via antialiasing filter) to the phase wire. The system is
AN-574
connected to the phase and neutral lines for the purpose
of generating a power supply and voltage channel signal (V2). The ferrite bead (Z1) and line filter capacitor
(C17) should significantly reduce any RF radiation on the
power supply.
Another possible path for RF is the signal ground for the
system. A moating technique has been used to help isolate the signal ground surrounding the AD7751 from the
external ground reference point (K6). Figure 22 illustrates the principle of this technique called partitioning
or “moating.”
"MOAT" – NO
POWER OR
GROUND PLANE
I/O CONNECTION
POWER CONNECTION MADE USING
FERRITE "BEAD ON LEAD"
Figure 22. High-Frequency Isolation Using a “Moat”
Sensitive regions of the system are protected from RF
radiation entering the system at I/O connection. An area
surrounding the I/O connection does not have any
ground or power planes. This limits the conduction
paths for RF radiation and is called a “moat.” Obviously power, ground and signal connections must
cross this moat and Figure 21 shows how this can be
safely achieved by using a ferrite bead. Remember that
ferrite offers a large impedance to high frequencies—
see Figure 21.
ELECTRICAL FAST TRANSIENCE BURST TESTING (EFT)
This testing determines the immunity of a system to
conducted transients. Testing is carried out in accordance with IEC1000-4-4 under well-defined conditions.
The EFT (Electrical Fast Transience) pulse can be
particularly difficult to guard against because the disturbance is conducted into the system via external
connections, e.g., power lines. Figure 19 shows the
physical properties of the EFT pulse used in IEC1000-4-4.
Perhaps the most debilitating attribute of the pulse is
not its amplitude (which can be as high as 4 kV), but the
high-frequency content due to the fast rise times
involved. Fast rise times mean high-frequency content
that allows the pulse to couple to other parts of the system through stray capacitance, etc. Large differential
signals can be generated by the inductance of PCB
traces and signal ground. These large differential signals could interrupt the operation of sensitive electronic
REV. 0
–11–
Page 12

AN-574
components. Digital systems are generally most at
risk because of data corruption. Analog electronic
systems tend only to be affected for the duration of
the disturbance.
4kV
90%
50%
10%
5ns
50ns
TIME
Figure 23. Single EFT Pulse Characteristics
Another possible issue with conducted EFT is that the
effects of the radiation will, like ESD, generally be cumulative for electronic components. The energy in an EFT
pulse can be as high as 4 mJ and deliver 40 A into a 50 Ω
load—see Figure 26. Therefore continuous exposure to
EFT due to inductive load switching, etc., may have
implications for the long-term reliability of components.
The best approach is to protect those parts of the system
that could be sensitive to EFT.
The protection techniques described in the last section
(Electromagnetic HF Fields) also apply equally well in
the case of EFT. The electronics should be isolated as
much as possible from the source of the disturbance
through PCB layout (i.e., moating) and filtering signal
and power connections. In addition, a 10 nF capacitor
(C17) placed across the mains provides a low-impedance
shunt for differential EFT pulses. Stray inductance due
to leads and PCB traces will mean that the MOV will not
be very effective in attenuating the differential EFT
pulse. The MOV is very effective in attenuating high
energy, relatively long duration disturbances, e.g.,
due to lighting strikes, etc. The MOV is discussed in
the next section.
MOV Type S20K275
The MOV used in this design was of type S20K275 from
Siemens. An MOV is basically an voltage-dependant
resistor whose resistance decreases with increasing
voltage. MOVs are typically connected in parallel with
the device or circuit that is being protected. During an
overvoltage event they form a low-resistance shunt and
thus prevent any further rise in the voltage across the
circuit being protected. The overvoltage is essentially
dropped across the source impedance of the overvoltage source, e.g., the mains network source impedance.
Figure 24 illustrates the principle of operation.
V
S
OVERVOLTAGE SOURCE
V
B
V
V
S
VB, V
MOV
*
TAKEN FROM SIEMENS MATSUSHITA COMPONENTS
SIOV METAL OXIDE VARISTOR CATALOG
Z
S
1
MOV
V
"LOAD LINE"
OF THE OVERVOLTAGE
2
i*
LEAKAGE
CURRENT » 0
ELECTRONIC
CIRCUIT TO BE
PROTECTED
V/I CHARACTERISTIC
CURVE OF MOV
i*
SURGE CURRENT
it
Figure 24. Principle of MOV Overvoltage Protection
The plot in Figure 24 shows how the MOV voltage and
current can be estimated for a given overvoltage and
source impedance. A load line (open circuit voltage,
short circuit current) is plotted on the same graph as the
MOV characteristic curve. Where the curves intersect,
the MOV clamping voltage and current can be read.
Note, care must be taken when determining the shortcircuit current. The frequency content of the overvoltage
must be taken into account as the source impedance
(e.g., mains) may vary considerably with frequency. A
typical impedance of 50 Ω is used for mains source
impedance during fast transience (high-frequency)
pulse testing. The next section discusses IEC1000-4-4
and IEC1000-4-5 which are transience and overvoltage
EMC compliance tests.
IEC1000-4-4 and the S20K275
While the graphical technique just described is useful,
an even better approach is to use simulation to obtain a
better understanding of MOV operation. Siemens
Matsushita Components provides SPICE models for all
their MOVs and these are very useful in determining
device operation under the various IEC EMC compliance
tests. For more information on S&M SPICE models and
their applications see:
http://www.siemens.de/pr/index.htm
The purpose of IEC1000-4-4 is to determine the effect
of repetitive, low-energy, high-voltage, fast-rise-time
pulses on an electronic system. This test is intended to
simulate transient disturbances such as those originating from switching transience (e.g., interruption of
inductive loads, relay contact bounce, etc.).
Figure 21 shows an equivalent circuit which is intended
to replicate the EFT test pulse as specified in IEC1000-4-4.
The generator circuit is based on Figure 1 IEC1000-4-4
(1995-01). The characteristics of operation are:
–12–
REV. 0
Page 13

• Maximum Energy of 4mJ/pulse at 2 kV into 50 Ω
800V
600V
400V
200V
0V
20A
15A
10A
5A
0A
8kW
6kW
4kW
2kW
0W
3.00 3.04 3.08 3.12 3.16 3.20
TIME – s
CURRENT (INTO 50)
VOLTAGE
POWER (INTO 50)
• Source Impedance of 50 Ω ± 20%
• DC Blocking Capacitor of 10 nF
• Pulse Rise Time of 5 ns ± 30%
• Pulse Duration (50% Value) of 50 ns ± 30%
• Pulse Shape as Shown in Figure 23
AN-574
+
0.5kV
TO 5kV
SW1
C1
6F
SW2
R2
50
R1
0.01
C2
10nF
5nH
C17
10nF
50
L1
MOV
Figure 25. EFT Generator
The simulated output of this generator delivered to a
purely resistive 50 Ω load is shown in Figure 26. The
open circuit output pulse amplitude from the generator
is 4 kV. Therefore, the source impedance of the generator is 50 Ω as specified by the IEC1000-4-4, i.e., ratio of
peak pulse output unloaded and loaded (50 Ω) is 2:1.
4.0kV
50A
100kW
ENERGY = 80kW x 50ns = 4mJ
40A
3.0kV
2.0kV
1.0kV
30A
20A
10A
80kW
60kW
40kW
20kW
CURRENT
POWER
VOLTAGE
Figure 27. EFT Generator Output into 50 Ω with MOV
in Place
It should be noted that stray inductance and capacitance
could render the MOV unless. For example, Figure 28
shows the same simulation with the stay inductance
increased to 1 µH, which could easily happen if proper
care is not taken with the layout. The pulse amplitude
reaches 2 kV once again.
2.0k
1.6k
1.2k
0.8k
VOLTS
0.4k
0
VOLTAGE
–0.4k
3.00 3.05 3.10 3.15 3.20
TIME – s
Figure 28. EFT Generator Output into 50 Ω with MOV
µ
in Place and Stray Inductance of 1
H
When the 10 nF capacitor (C17) is connected, a lowimpedance path is provided for differential EFT pulses.
Figure 29 shows the effect of connecting C17. Here the
stray inductance (L1) is left at 1 µH and the MOV is in
place. The plot shows the current through C16 and the
voltage across the 50 Ω load. The capacitor C16 provides
a low-impedance path for the EFT pulse. Note the peak
current through C17 of 80 A. The result is the amplitude
of the EFT pulse is greatly attenuated.
0A
0V
0W
3.00 3.04 3.08 3.12 3.16 3.20
TIME – s
Figure 26. EFT Generator Output into 50
Ω
(No Protection)
The plot in Figure 26 also shows the current and instantaneous power (V × I) delivered to the load. The total
energy is the integral of the power and can be approximated by the rectangle method as shown. It is
approximately 4 mJ at 2 kV as per specification.
Figure 27 shows the generator output into 50 Ω load
with the MOV and some inductance (5 nH). This is
included to take into account stray inductance due to
PCB traces and leads. The simulation result shows that
the EFT pulse has been attenuated (600 V), and most of
the energy is being absorbed by the MOV (only 0.8 mJ is
delivered to the 50 Ω load).
REV. 0
–13–
Page 14

AN-574
300V
20A
0A
200V
–20A
100V
–100V
–40A
0V
CURRENT (INTO C17)
–60A
–80A
3.0 3.2 3.4 3.6 3.8 4.0
VOLTAGE (ACROSS 50 LOAD)
TIME – s
Figure 29. EFT Generator Output into 50 Ω with MOV
and C17 (10 nF) in Place and Stray Inductance of 1
µ
H
IEC1000-4-5
The purpose of IEC1000-4-5 is to establish a common
reference for evaluating the performance of equipment
when subjected to high-energy disturbances on the
power and interconnect lines. Figure 30 shows a circuit
which was used to generate the combinational wave
(hybrid) pulse described in IEC1000-4-5. It is based on
the circuit shown in Figure 1 of IEC1000-4-5 (1995-02).
Such a generator produces a 1.2/50 µs open-circuit volt-
age, which is why it is referred to as a hybrid generator.
The surge generator has an effective output impedance
of 2 Ω. This is defined as the ratio of peak open-circuit
voltage to peak short-circuit current.
+
0.5kV
TO 4kV
SW1
C1
20F
SW2
1.9
R1
3.9
L2
R1
10H
R1
50
5nH
C16
10nF
L1
MOV
S20K275
Figure 30. Surge Generator (IEC1000-4-5)
Figure 31 shows the generator voltage and current output wave forms. The characteristics of the combination
wave generator are:
Open-Circuit Voltage:
0.5 kV to at least 4.0 kV
Waveform as shown in Figure 31
Tolerance on open-circuit voltage is ±10%.
Short-Circuit Current:
0.25 kA to 2.0 kA
Waveform as shown in Figure 31
Tolerance on short-circuit current is ±10%.
Repetition Rate of at Least 60 Seconds.
2.0kA
4kV
1.5kA
3kV
1.0kA
2kV
0.5kA
1kV
0A
0V
0 20 40 60 80 100
TIME – s
Figure 31. Open-Circuit Voltage / Short-Circuit Current
The MOV is very effective in suppressing these kinds of
high energy/long duration surges. Figure 32 shows the
voltage across the MOV when it is connected to the generator as shown in Figure 30. Also shown are the current
and instantaneous power waveform. The energy absorbed
by the MOV is readily estimated using the rectangle
method as shown.
2.0kA
1.0kV
0.8kV
0.6kV
0.4kV
0.2kV
0V
1.5kA
1.0kA
0.5kA
0A
1.5mW
1.0mW
0.5mW
0W
0 50 100 150 200 250 300
TIME – s
Figure 32. Energy Absorbed by MOV During 4 kV Surge
Derating the MOV surge current
The maximum surge current (and therefore energy
absorbed) that an MOV can handle is dependant on the
number of times the MOV will be exposed to surges
over its lifetime. The life of an MOV is shortened every
time it is exposed to a surge event. The data sheet for an
MOV device will list the maximum nonrepetitive surge
current for an 8 µs/20 µs current pulse. If the current
pulse is of longer duration and if it occurs more than
once during the life of the device, this maximum current
must be derated. Figure 33 shows the derating curve for
the S20K275. Assuming exposures of duration 30 µs and
a peak current as shown in Figure 32, the maximum
number of surges the MOV can handle before it goes out
of specification is about 10. After repeated loading (10
times in the case just described) the MOV voltage will
change. After initially increasing, it will decay rapidly.
–14–
REV. 0
Page 15

AN-574
R
C
AD7751
5V
EMI
FILTER
35mA FROM PSU
ANALOG
GROUND
(QUIET)
DIGITAL
GROUND
(NOISY)
AREAS ISOLATED WITH
NO GROUND PRESENT
ON ANY LAYER
GROUNDS CONNECTED
VIA FERRITE BEAD
240V
80V
K5
K6
IN
OUT
CF
FAULT
K1
K2
SIOV-S20K275
4
10
3
10
MAX
I
2
10
1
10
0
10
–1
10
10 100 1k 10k
SIEMENS MATSUSHITA COMPONENTS
1x
2
10
2
10
3
10
4
10
5
10
6
10
8
s
VAR0169-F
I
T
r
T
MAX
r
Figure 33. Derating Curve for S20K275
PCB DESIGN
Both susceptibility to conducted or radiated electromagnetic disturbances and analog performance were
considered at the PCB design stage. Fortunately many of
the design techniques used to enhance analog and
mixed-signal performance also lend themselves well to
improving the EMI robustness to the design. The key
idea is to isolate that part of the circuit which is sensitive
to noise and electromagnetic disturbances. Since the
AD7751 carries out all the data conversion and signal
processing, the robustness of the meter will be determined to a large extent by how protected the AD7751 is.
In order to ensure accuracy over a wide dynamic range,
the data acquisition portion of the PCB should be kept as
quiet as possible, i.e., minimal electrical noise. Noise
will cause inaccuracy in the analog-to-digital conversion
process which takes place in the AD7751. One common
source of noise in any mixed-signal system is the
ground return for the power supply. Here highfrequency noise (from fast edge rise times) can be
coupled into the analog portion of the PCB by the common impedance of the ground return path. Figure 34
illustrates the mechanism.
One common technique used to overcome these kinds
of problems is to use separate analog and digital return
paths for the supply. Also, every effort should be made
to keep the impedance of these return paths as low as
possible. In the PCB design for the AD7751, separate
ground planes were used to isolate the noisy ground
returns. The use of ground plane also ensures the impedance of the ground return path is kept very low. The
AD7751 and sensitive signal paths are located in a “quiet”
part of the board which is isolated from the noisy elements of the design like the power supply, flashing LED,
etc. Since the PSU is capacitor-based, a substantial
current (approximately 35 mA at 240 V) will flow in the
ground return back to the phase wire (system ground).
This is shown in Figure 30. By locating the PSU in the
digital portion of the PCB, this return current is kept
away from the AD7751 and analog input signals. This
current is at the same frequency as the signals being
measured and could cause accuracy issues (e.g., crosstalk
between the PSU as analog inputs) if care is not taken
with the routing of the return current. In addition, part of
the attenuation network for the Channel 2 (voltage channel) is in the digital portion of the PCB. This helps to
eliminate possible crosstalk to Channel 1 by ensuring
analog signal amplitudes are kept as low as possible in
the analog (“quiet”) portion of the PCB. Figure 35 shows
the PCB design which was eventually adopted for the
watt-hour meter.
I
U
C
IT
G
O
L
A
N
A
+
Figure 34. Noise Coupling via Ground Return Impedance
REV. 0
R
Y
COMMON
IMPEDANCE
AL
T
GI
I
D
V
NOISE
Z
GROUND
= I
C
IR
I
NOISE
NOISE
UI
C
TR
x Z
Y
Figure 35. AD7751 Watt-Hour Meter PCB Design
The partitioning of the power planes in the PCB design
as shown in Figure 35 also allows us to implement the
idea of a “moat” for the purposes of immunity to electromagnetic disturbances. The digital portion of the PCB
is the only place where both phase and neutral wires are
connected. This portion of the PCB contains the transience suppression circuitry (MOV, ferrite, etc.) and
+
power supply circuitry. The ground planes are connected via a ferrite bead that helps to isolate the analog
ground from high frequency disturbances—see Design
for Immunity to Electromagnetic Disturbances section.
–15–
Page 16

AN-574
MEASUREMENT ACCURACY/TEST RESULTS
0.5
0.4
0.3
0.2
0.1
0
–0.1
ERROR – %
–0.2
–0.3
–0.4
–0.5
0.1 1.0 10 100
PF = 0.5
PF = 1.0
CURRENT – Amps
Figure 36. Measurement Error (% Reading, 240 V, 50 Hz)
ANSI C12.16 and IEC1039
The ANSI standard governing Solid-State Electricity
Meters is ANSI C12.16-1991. Since this application note
refers to the IEC 1036 specifications when explaining the
design, this section will explain some of those key
IEC1036 specifications in terms of their ANSI equivalents. This should help eliminate any confusion caused
by the different application of some terminology contained in both standards.
Class—IEC1036
The class designation of an electricity meter under
IEC1036 refers to its accuracy. For example, a Class 1
meter will have a deviation from reference performance
of no more than 1%. A Class 0.5 meter will have a maximum deviation of 0.5% and so on. Under ANSI C12.16
Class refers to the maximum current the meter can
handle for rated accuracy. The given classes are: 10, 20,
100, 200, and 320. These correspond to a maximum meter
current of 10 A, 20 A, 200 A, and 320 A, respectively.
I
(IB)—IEC1036
BASIC
The basic current (IB) is a value of current with which the
operating range of the meter is defined. IEC1036 defines
the accuracy class of a meter over a specific dynamic
range, e.g., 0.05 I
< I < I
B
. It is also used as the test
MAX
load when specifying the maximum permissible effect
of influencing factors, e.g., voltage variation and frequency variation. The closest equivalent in ANSI C12.16
is the Test Current. The Test Current for each meter class
(maximum current) is given below:
Class 10: 2.5 A
Class 20: 2.5 A
Class 100: 15 A
Class 200: 30 A
Class 320: 50 A
I
—IEC1036
MAX
I
is the maximum current for which the meter meets
MAX
rated accuracy. This would correspond to the meter
class under ANSI C12.16. For example, a meter with an
I
of 20 A under IEC 1026 would be designated Class
MAX
20 under ANSI C12.16.
–16–
REV. 0
Page 17

BILL OF MATERIALS
Part(s) Details Comments
R1, R2, R4A, R4B 1 kΩ, 1%, 1/8 W SMD 1206 Resistor Surface Mount,
Panasonic ERJ-8ENF1001
Digi-Key No. P1.00K FCT-ND
R3 1.05 kΩ, 1%, 1/8 W SMD 1206 Resistor Surface Mount,
Panasonic ERJ-8ENF1051
Digi-Key No. P1.05K FCT-ND
R5A, R5B 100 Ω, 1%, 1/8 W SMD 1206 Resistor Surface Mount,
Panasonic ERJ-8ENF1000
Digi-Key No. P 100 FCT-ND
R6 2.7 Ω, 1%, 1/8 W SMD 1206 Resistor Surface Mount,
Panasonic ERJ-8RQF2R7
Digi-Key No. P 2.7 RCT-ND
R7 56 Ω, 5%, 1.8 W, 200 V SMD 1206 Resistor Surface Mount,
Panasonic ERJ-8GEYJ560
Digi-Key No. P 56 ECT-ND
R8 82 Ω, 5%, 1.8 W, 200 V SMD 1206 Resistor Surface Mount,
Panasonic, ERJ-8GEYJ820
Digi-Key No. P 82 ECT-ND
R9 160 Ω, 5%, 1/8 W, 200 V SMD 1206 Resistor Surface Mount,
Panasonic, ERJ-8GEYJ161
Digi-Key No. P 160 ECT-ND
R10 330 Ω, 5%, 1/16 W, 50 V SMD 0402 Resistor Surface Mount,
Panasonic, ERJ-2GEJ331
Digi-Key No. P 330 JCT-ND
R11 680 Ω, 5%, 1/16 W, 50 V SMD 0402 Resistor Surface Mount,
Panasonic, ERJ-2GEJ681
Digi-Key No. P 680 JCT-ND
R12 1.3 kΩ, 5%, 1/16 W, 50 V SMD 0402 Resistor Surface Mount,
Panasonic, ERJ-2GEJ132
Digi-Key No. P 1.3K JCT-ND
R13 2.7 kΩ, 5%, 1/16 W, 50 V SMD 0402 Resistor Surface Mount,
Panasonic, ERJ-2GEJ272
Digi-Key No. P 2.7K JCT-ND
R14 300 kΩ, 5%, 1/8 W, 200 V SMD 1206 Resistor Surface Mount,
Panasonic, ERJ-8GEYJ304
Digi-Key No. P 300K ECT-ND
R15 150 kΩ, 5%, 1/8 W, 200 V SMD 1206 Resistor Surface Mount,
Panasonic, ERJ-8GEYJ154
Digi-Key No. P 150K ECT-ND
R16 75 kΩ, 5%, 1/8 W, 200 V SMD 1206 Resistor Surface Mount,
Panasonic, ERJ-8GEYJ753
Digi-Key No. P 75K ECT-ND
R17 39 kΩ, 5%, 1/16 W, 50 V SMD 0402 Resistor Surface Mount,
Panasonic, ERJ-2GEJ393
Digi-Key No. P 39K JCT-ND
R18 18 kΩ, 5%, 1/16 W, 50 V SMD 0402 Resistor Surface Mount,
Panasonic, ERJ-2GEJ183
Digi-Key No. P 18K JCT-ND
R19 9.1 kΩ, 5%, 1/16 W, 50 V SMD 0402 Resistor Surface Mount,
Panasonic, ERJ-2GEJ912
Digi-Key No. P 9.1K JCT-ND
R20 5.1 kΩ, 5%, 1/16 W, 50 V SMD 0402 Resistor Surface Mount,
Panasonic, ERJ-2GEJ512
Digi-Key No. P 5.1K JCT-ND
AN-574
REV. 0
–17–
Page 18

AN-574
Part(s) Details Comments
R21 2.2 kΩ, 5%, 1/16 W, 50 V SMD 0402 Resistor Surface Mount,
Panasonic, ERJ-2GEJ222
Digi-Key No. P 2.2K JCT-ND
R22 1.2 kΩ, 5%, 1/16 W, 50 V SMD 0402 Resistor Surface Mount,
Panasonic, ERJ-2GEJ122
Digi-Key No. P 1.2K JCT-ND
R23 560 Ω, 5%, 1/16 W, 50 V SMD 0402 Resistor Surface Mount,
Panasonic, ERJ-2GEJ561
Digi-Key No. P 560 JCT-ND
R24, R25 330 kΩ, 5%, 1/2 W, 200 V SMD 2010 Resistor Surface Mount,
Panasonic, ERJ-12ZY334
Digi-Key No. P 330K WCT-ND
R26 470 Ω, 5%, 1 W Through-Hole, Panasonic,
Digi-Key No. P470W-1BK-ND
R27, R28 10 kΩ, 5%, 1/8 W, 200 V SMD 1206 Resistor Surface Mount,
Panasonic, ERJ-8GEYJ103
Digi-Key No. P10K ECT-ND
R29, R30 820 Ω, 5%, 1/8 W, 200 V SMD 1206 Resistor Surface Mount,
Panasonic, ERJ-8GEYJ821
Digi-Key No. P 820 ECT-ND
R31, R32 20 Ω, 5%, 1/8 W, 200 V SMD 1206 Resistor Surface Mount,
Panasonic, ERJ-8GEYJ200
Digi-Key No. P 20 ECT-ND
R33 10 Ω, 5%, 1/8 W, 200 V SMD 1206 Resistor Surface Mount,
Panasonic, ERJ-8GEYJ100
Digi-Key No. P 10 ECT-ND
C1, C2, C3, C4, C5, C20, C21 33 nF, Multilayer Ceramic, 10% SMD 0805 Capacitor Surface Mount,
50 V, X7R Panasonic, ECJ-2VB1H333K
Digi-Key No. PCC 1834 CT-ND
C6, C14 10 µF, 6.3 V EIA Size A Capacitor Surface Chip-Cap,
Panasonic, ECS-TOJY106R
Digi-Key No. PCS 1106CT-ND – 3.2 mm × 1.6 mm
C7, C8, C11, C13, C15, C16 100 nF, Multilayer Ceramic, SMD 0805 Capacitor Surface Mount,
10%, 16 V, X7R Panasonic, ECJ-2VB1E104K
Digi-Key No. PCC 1812 CT-ND
C9, C10 22 pF, Multilayer Ceramic, 5%, SMD 0402 Capacitor Surface Mount,
50 V, NPO Panasonic, ECU-E1H220JCQ
Digi-Key No. PCC 220CQCT-ND
C12 6.3 V, 220 µF, Electrolytic Through-Hole Panasonic, ECA-OJFQ221
Digi-Key P5604 – ND
D = 6.3 mm, H = 11.2 mm,
Pitch = 2.5 mm, Dia. = 0.5 mm
C17 10 nF, 250 V, Class X2 Metallized Polyester Film
Through-Hole Panasonic, ECQ-U2A103MN
Digi-Key No. P4601-ND
C18 470 nF, 250 V AC Metallized Polyester Film
Through-Hole Panasonic, ECQ-E6474KF
Digi-Key No. EF6474-NP
C19 35 V, 470 µF, Electrolytic Through-Hole Panasonic, ECA-1VHG471
Digi-Key P5554 – ND
U1 AD7755AN Supplied by ADI – 24-Pin DIP, Use Pin Receptacles
(P1–P24)
U2 LM78L05 National Semiconductor, LM78L05ACM, S0-8
Digi-Key LM78L05ACM-ND
U3 PS2501-1 Opto, NEC, Digi-key No. PS2501-1NEC-ND
D1, D4 Low-Current LED HP HLMP-D150
Newark 06F6429 (Farnell 323-123)
–18–
REV. 0
Page 19

AN-574
Part(s) Details Comments
D2 Rectifying Diode 1 W, 400 V, DO-41, 1N4004,
Digi-Key 1N4004DICT-ND
D3 Zener Diode 15 V, 1 W, DO-41, 1N4744A
Digi-Key 1N4744ADICT-ND
Z1, Z2 Ferrite Bead Cores Axial-leaded (3.5 mm x 9 mm ) 0.6 mm Lead Diameter
Panasonic, EXC-ELSA39
Digi-Key P9818BK-ND
Z3, Z4 Ferrite SMD Beads SMD 1806 Steward, LI 1806 E 151 R
Digi-Key 240-1030-1-ND
Y1 3.579545 MHz XTAL Quartz Crystal, HC-49(US), ECS No. ECS-35-17-4
Digi-Key no. X079-ND
MOV1 Metal Oxide Varistors AC 275 V, 140 Joules
FARNELL No. 580-284, Siemens, S20K275
J1–J23 Solder Jumpers Jumpers Set Using Solder
P1–P24 Single Low Profile Sockets for U1
0.022’’ to 0.025’’ Pin Diameter ADI Stock 12-18-33.
ADVANCE KSS100-85TG
K1–K10 Pin Receptacles 0.037’’ to 0.043’’ Pin Diameter, Hex Press Fit
Mil-Max no. 0328-0-15-XX-34-XX-10-0
Digi-Key ED5017-ND
Current Shunt 500 µΩ, 1% ISOTEK Corporation, PVG-R0005-1
435 Wilbur Ave, Swansea, MA 02777, USA
Tel: 1-508-673-2900
Fax: 1-508-676-0885
Email: tekinfo@isotekcorp.com
Counter 2-Phase Stepper, 100 imp China National Electronics Import &
Export Shaanxi Co.
No.11 A, Jinhua northern Road, Xi’an, China.
Email: chenyf@public.xa.sn.cn
Tel: 86- 29 3218247,3221399
Fax: 86- 29 3217977, 3215870
REV. 0
–19–
Page 20

AN-574
PCB Design
Figure 37. PCB Assembly (Top Layer)
Figure 38. PCB Assembly (Bottom Layer)
Figure 39. PCB Top Layer
Figure 40. PCB Bottom Layer
–20–
REV. 0
Page 21

AN-574
R5A
R1
Z3 VAL
1
K1
K3
R6
2.7
K4
Z4 VAL
1
K2
Z1 VAL
2
1
K5
C17
0.01F
K6
2
2
MOV1
140J
100
J22
R7
56
R5B
100
J23
R24
330k
R25
330k
470
IN4744
CALV1BHI
CALV1BLO
R26
D3
C20
0.033F
SCHEMATIC 2
C21
0.033F
CALLOW
CALHI
SEE
SCHEMATIC 2
C1B
0.47F
D2
IN4004
C19
+
470F
35V
1k
SEE
R4A
1k
U2 7805
V
IN
G1 G2 G3 G4
2367
C1
0.033F
R4B
1k
V
R3
1.05k
0.033F
R4
1k
0.033F
C4
0.033F
OUT
1
Z2 VAL
C2
C5
0.033F
18
2
C3
10k
V
DD
5V
V
DD
R27
V
DD
C7
0.1F
R33
10
C14
+
10F
6.3V
AD7751
1
DVD D
2
AC/ DC
3
AV DD
4
V1A
5
V1B
6
V1N
7
V2N
8
V2P
9
RESET
10
REF
11
AGND
12
SCF
C6
+
10F
6.3V
C13
0.1F
U1
CLKOUT
+
F1
F2
CF
DGND
REVP
FAULT
CLKIN
G0
G1
S0
S1
C12
220F
6.3V
24
23
22
21
20
19
18
17
16
15
14
13
C11
0.1F
Y1
3.579545MHz
J15
J14
J13
J12
J11
R30
820
R32
20
R31
20
D1
HLMPD150
C10
22pF
C9
22pF
J15L
0
J14L
0
J13L
0
J12L
0
J11L
0
1
2
820
J15H
0
J14H
0
J13H
0
J12H
0
J11H
0
U3
PS2501
R29
HLMPD150
C15
0.1F
C16
0.1F
R28
10k
C8
0.1F
K7
K8
4
K9
3
K10
D2
V
DD
a. Schematic 1
J1
R14
300k
150k
J2
R15
J16
82
CALHIGH
J3
R16
75k
J17
R8
160
R9
J4
R17
39k
330
J18
R10
J5
R18
18k
680
J19
R11
J6
R19
9.1k
1.3k
J20
R12
J7
R20
5.1k
J21
R13
2.7k
J8
R21
2.2k
CALV1BHI
SEE SCHEMATIC 1
CALV1BLO
1.2k
J9
R22
J10
R23
560
SEE SCHEMATIC 1
CALLOW
b. Schematic 2
Figure 41. Circuit Schematic
REV. 0
–21–
Page 22

–22–
Page 23

–23–
Page 24

E01955–2.5–6/01(0)
–24–
PRINTED IN U.S.A.
 Loading...
Loading...