How it Works
X-Treme Audio
Loading...
MISI
User Manual
21 pgs5.01 Mb0

X-Treme Audio MISI User Manual

Download
Page 1
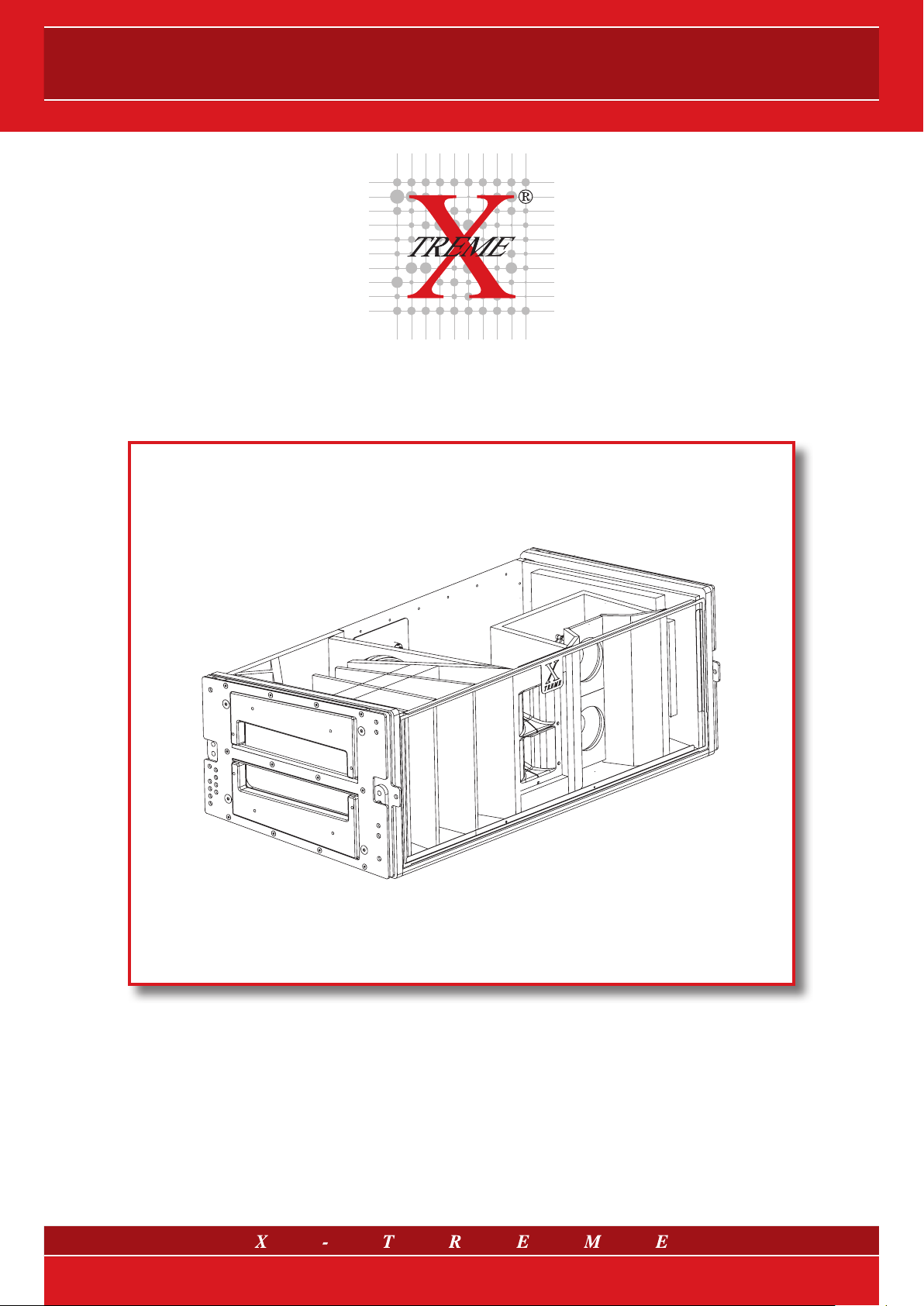
LINE ARRAYS
LINE ARRAYS
User’s manual
1/21
Page 2
User’s manual
LINE ARRAYS
User’s manual
CONTENTS
1. Free-field acoustics
2. Sound power and pressure levels
3. Physical-mathematical model: brief description
4. Linear sources: introduction
4.1 Infinite length linear source
4.2 Finite length linear source
5. Description of the sound field of a linear source
5.1 Directivity analysis
5.2 In-axis response analysis
6. Arc, J and progressive sources
7. Line arrays: “the state-of-the-art”
8.
X-Treme Vertical Line Array: product range
9.
X-Treme Vertical Line Array
10. MISITM system: from “AS IS” to “TO BE”
11. Types of installations
12. Stacking instructions
13. Suspension guidelines
13.1 X-Treme Installer (XTI)
13.2 Suspension instructions
: system design
13.3 “Straight to the… angle”
13.4 LSA: flying and lifting
1. Free-field acoustics
r >>λ/2π , r >> L , r >> πL2/2λ,
13.5 MISITM and MLA: enclosure suspension rigging
14. Subwoofers
15. Tri-amplification system configuration
16. System configurations: standard examples
16.1 Linear Source Array
16.2 MISI
16.3 Mini Line Array
TM
where L is the largest linear dimension of the source, λ is the long­est wavelength (therefore the lowest frequency) of the sound emit-
ted by the source (therefore λ is always ≤ 17.2 m - f ≥ 20 Hz) and the “much higher” symbol means at least 3 times higher (Bies, Hansen
1988). Note: a free-field variant is the so-called “free field on a reflect- ing surface”, such as a large open space on a rigid and highly reflecting surface (e.g. asphalt, ground) or a made-to-measure special environment known as “semi-anechoic” chamber. An omnidirectional source located near a reflecting surface acts as if it was associated to an image source having the same sound power: as a result, the intensity at every point of the acoustic field is worth double the sound intensity generated by the same source in a free field, therefore the intensity level will be 3 dB higher.
2/21
Page 3
LINE ARRAYS
2. Sound power and pressure levels
At present, one of the most common and interesting problems to face is the following: let the sound power (or the sound power level) of a certain source be given, a magnitude that characterizes it intrin­sically, determine the sound pressure (or the sound pressure level) at any point of the space where the source works. In a free field or in a free field on a reflecting surface, this problem can be easily solved by calculating all the necessary elements with the following simple formula:
Lp = Lw + ID
- 20 log(r) - 11 [dB].
θ,ϕ
Therefore this relationship, which is valid in far-field conditions (in fact, in this case all the real acoustic sources smaller than the wavelength of the sounds they produce can be approximated as pulsating point spheres known as “monopoles”), enables the calculation of the sound pressure level Lp produced by a source having a sound power level Lw (=10 log W/Wo with Wo= 1 pW; e.g. if the acoustic power of a speak­er system is 100 W its sound power level will be 140 dB), at a certain distance r in a direction such that the di rectivity index of the source is ID
(=10 log Q
θ,ϕ
with Q
θ,ϕ
being the direc tivity factor of the source in the
θ,ϕ
direction identified by angles θ and ϕ). For example, a source with a sound power level of 120 dB (there­fore with power W equal to 1 Watt) and a directivity index of 3 dB in the direction where the listener is positioned, produces a sound pressure level of 84 dB in a 25 m far free-field, because: Lp = 120 + 3 - 28 - 11 = 84 dB. Furthermore, if we know the sound pressure level Lp1 at a certain distance r1 from the source (for example, by measuring it through a sound-level meter) and in a certain direction, the sound pressure level Lp2 can be determined at another distance r2 in the same di­rection, without necessarily knowing the sound pressure level. In fact, by using the equation above, we obtain:
Lp2 = Lp1 - 20 log(r2/ r1) [dB].
If, for example, a source produces a sound pressure level Lp1 = 92 dB at a distance r1 = 8 m, the sound pressure level at r2 =16 m, in the same direction, will be 86 dB (as mentioned at the begin­ning, the sound pressure level decreases by 6 dB when distance doubles). Note: in a free-field on a reflecting surface, in the semi-space where the source is forced to radiate, as previously mentioned, the sound intensity is twice the intensity existing in a free field. Therefore, 3 dB should be added to the sound pressure level calculated with the formula above.
3. Physical-mathematical model: brief description
Most acoustic models are simplified solutions of a general equation (wave equation) which are subject to certain “constraints”, such as the environment’s volume or its known value at certain points in the listening space. Therefore, in an acoustic study the used formulas are a small set of specific solutions which is almost suitable for de­scribing with sufficient approximation the acoustic field in a listening environment. In general, these solutions are expressed in terms of pressure in relation to space and time variables. In indoor acoustics, the space characteristics are modelled as boundary conditions and they exert a remarkable influence on the acoustic field. It is the physical dimension of the space that makes the presence of waves with a certain length possible (or impos­sible). In mathematical terms this falls within the category of the eigenvalue problems. The solutions will be strictly dependent on frequency and will have periodical behaviours (in acoustical terms this is the so-called modal theory).
On the contrary, in outdoor acoustics, the boundary conditions imposed on the wave equation will commonly be radiation condi­tions, which are necessary to make the mathematical model coher­ent with the physical reality. The dependency on frequency is no longer regular as it occurs in closed spaces and the modal theory cannot be applied. Of course, the differences between open and closed spaces affect sound reproduction and the ability of a speak­er system to adjust to different reproduction contexts, especially if we consider the wide range of problems arising in open spaces. Line arrays can solve the various problems associated with sound reproduction. In this short introduction we will analytically describe a line array mathematical model and we will com ment on a few important results deriving from this model. Finally we will demonstrate that a simple theoretical model can suitably meet the coherence requirements with real measurement. This short introduction, having an analytical and general character, will not deal with the problems concerning the technological features of the models (waveguides, etc…) or with the electro-acoustics so­lutions that are nevertheless essential for designing and produc­ing line arrays.
4. Linear sources: introduction
Generally speaking, real sound sources are very complex and it is quite difficult to describe them in detail. Luckily, in most practi­cal cases, we can resort to substantial simplifications. The most drastic one, as previously mentioned, consists of considering a real source as an infinitely small point source whose dimensions are actually much smaller than the wavelength λ of the reproduced sound and/or if the listener is at a great distance from the source position. However, other more complex ideal sources can better represent the properties of the real sources: it is the case of the linear sources, namely point sources that are conveniently ar­ranged along a straight line, which are used in the literature to exemplify a stacked or flying vertical line array system. A row of cars along a straight road is another more common example of a real source which can be approximately represented as an infinite length linear source.
Line source
b=step
n
...
W
0
3
W
0
2
W
0
1
90°
r
0
β
η
P
fig. 1
3/21
Page 4
User’s manual
4.1 Infinite length linear source
With reference to fig. 1, let’s imagine an infinite sequence of unrelated sources, spaced out by a distance b and all having the same sound power Wo. As a result, the intensity of each source adds up to that of the other sources in determining the total intensity at the distance ro in a normal direction towards the linear source. Working from this hypoth­esis, we can demonstrate (Beranek, 1988) that with a distance value
ro >= b/π
and therefore at a distance such that the individual sources cannot be distinguished one from the other, the average sound intensity can be simply approximated by the relationship:
〈I〉=Wo/4bro [W/m2].
In other words, at distances exceeding the distance between one source and the next (these are exactly the listening conditions of the vertical line array sound reinforcement systems, since the dis­tance between the elements is generally one linear metre) the inten­sity no longer varies with the square of the distance as in the case of the monopole sources, but is inversely proportional to the distance. This means that these sound waves (often known as cylindrical) decrease by just 3 dB for each doubling of the distance rather than by 6 dB as it occurs in traditional systems (the previously mentioned “inverse-square” law).
4.2 Finite length linear source
If the sources arranged on a line are in a finite number n (>=3) and βn is the angle, in radians, below which the source line is seen from the observation point (as indicated in fig. 1), always at sufficiently large distances (ro >= b/π), the sound intensity can be determined according to the following relationship:
〈I〉 = Wo·βn /4πbro [W/m2].
In this case too it is inversely proportional to the distance and, obviously, it is directly proportional to the angle opening below which the linear source is seen from the listening point. In conclu­sion, in this case, one can state that a reasonably accurate de­scription of the ver tical line array behaviour has been reached, which is approximated as a finite linear source in its near field. In fact, owing to the di mensions of the magnitudes at issue, the b/π limit beyond which the array can be approximated as a linear source (and therefore it can be seen as a source of cylindrical waves) is much smaller than the above-mentioned limit between a far field and a near field (it should be recalled that this limit is represented by the larger distance between the following ones: r >>λ
/2π, r >> L , r >> πL2/2λ
max
max
).
5. Description of the sound field of a linear source
In order to analyse the sound field generated by a line array let’s start from a simple and ideal model: the finite linear source (or line source).
Far field
Line source
L/2
dl
x
dl sin(α)
fig. 2
The sound pressure generated by a linear source can be ob­tained analytically as a special solution of the wave equation, in relation to space and time coordinates. Moreover, it is also assumed that the source can only emit a sinusoidal signal. From a mathematical viewpoint, this simplification allows us to use a notation (known as phasorial) which simplifies calculations and ensures completeness without losing its general character. The Fourier theory shows that, within some hypotheses (which have been widely verified in the case of musical signals), any periodical signal can be modelled as the sum of individual sinusoids. Having said this, we can therefore express the sound pressure gen­erated from a linear source as:
where L is the line length, k is the wave number, A(l) and ϕ (l) are the signal amplitude and phase respectively on a point of the line (or rather on an infinitesimal segment dl) at a distance r(l) from a generic observation point or, rather, from a listening point P. In order to analytically verify the line array properties, a few ad­ditional hypotheses are required. For example, it can be easily no­ticed that, beyond a certain observation (or ‘listening’) distance, one will have:
Note: some empirical formulas can be found (Smith, Heil and others) in which the border distance from the near to the far
field depends on variables such as the array length or the reproduced frequency. However, it is better not to use them as they lack any general validity!
In the far field, on the contrary, it is right to apply the considerations mentioned just few lines earlier about the “inverse-square” law. In particular, in the case of linear sources, since the sound power of a single source Wo is known, the formula used to calculate the sound pressure level in the free-field conditions on a reflecting surface will be:
Lp = Lwo + 10 log(βn /r) – 8 [dB],
where βn is the angle below which the sources are seen from the listening point.
This further condition is precisely that of the far field, as previously mentioned. Thanks to the far field hypothesis we can rewrite the final expression of pressure in a form that we will use to evaluate the source directiv­ity (see paragraph 5.1):
4/21
Page 5
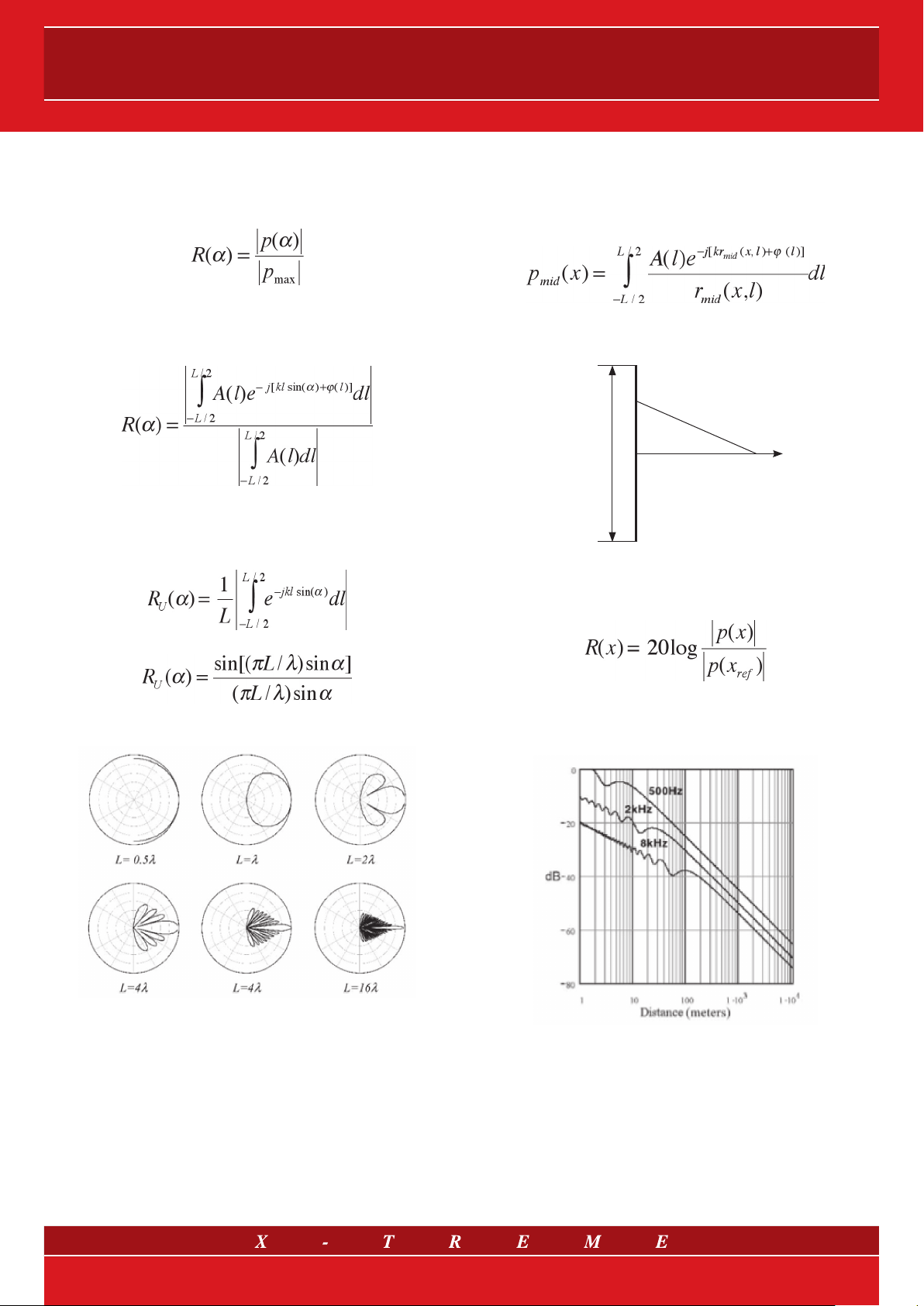
LINE ARRAYS
5.1 Directivity analysis
The directivity function enables us to evaluate the pressure distri­bution in relation to a definite emission direction. By using again the formulas of fig. 2, the directivity function R(α) can be defined as:
where
p
is the pressure in the maximum emission direction, in which from a mathematical viewpoint the exponential function be­low the integral sign assumes the maximum value (= 1). Following what has been stated above, one can obtain:
max
5.2 In-axis response analysis
Similarly to the directivity analysis, and referring to fig. 2, we force the (observation or “listening”) point P to lie on the axis x. Now let’s go back to the general case, thereby excluding the far-field hypothesis. The pressure form will therefore be of the following kind:
where r
The corresponding directivity function on the x axis is often expres­sed in a logarithmical form:
(x,l) is the distance traced in fig. 4
mid
Line source
r
dl
L
mid
fig. 4
(x,l)
P
mid
(x)
x
p
whose solution is:
rendering the wavelength λ explicit from the expression of the wave number k.
fig. 3
Figure 3 shows the polar diagrams of function RU(α). Let’s consider the L/λ ratio (0.5, 1, 2, 8, 16), i.e. the ratio between the line length and the wavelength. It can be easily noticed that a very high directivity is obtained in wavelengths that are much short­er (1/8, 1/16) than the line length (in the specific case of a few metre long line arrays, this leads to mid-high frequencies). In other words, in the case of a linear source, the narrower the main emission lobe is, the better the sound energy transmission can be forced into a narrow and orientable corner of the sound front.
Where x Note that R(x case of a 4 m long uniform linear source (as already seen in A(l)=A and ϕ= 0), will have a qualitative trend of the type shown in fig. 5
Each curve refers to a certain sinusoid frequency. A double slope is observed for each curve: as the distance from the source grows, at the beginning there is a decrease of 3 dB for each doubling of the distance, then there is a decrease of 6 dB for each doubling of the distance. The (theoretical) point in which the curve changes its slope is called transition distance and it is a function of both the fre quency and the dimension of the line source (L). The branch with a -3 dB slope is the near field, that with a -6dB slope is the far field.
is a reference distance, generally 1 m.
ref
)=0. The double logarithmic graph of r(x), in the specific
ref
fig. 5
5/21
Page 6
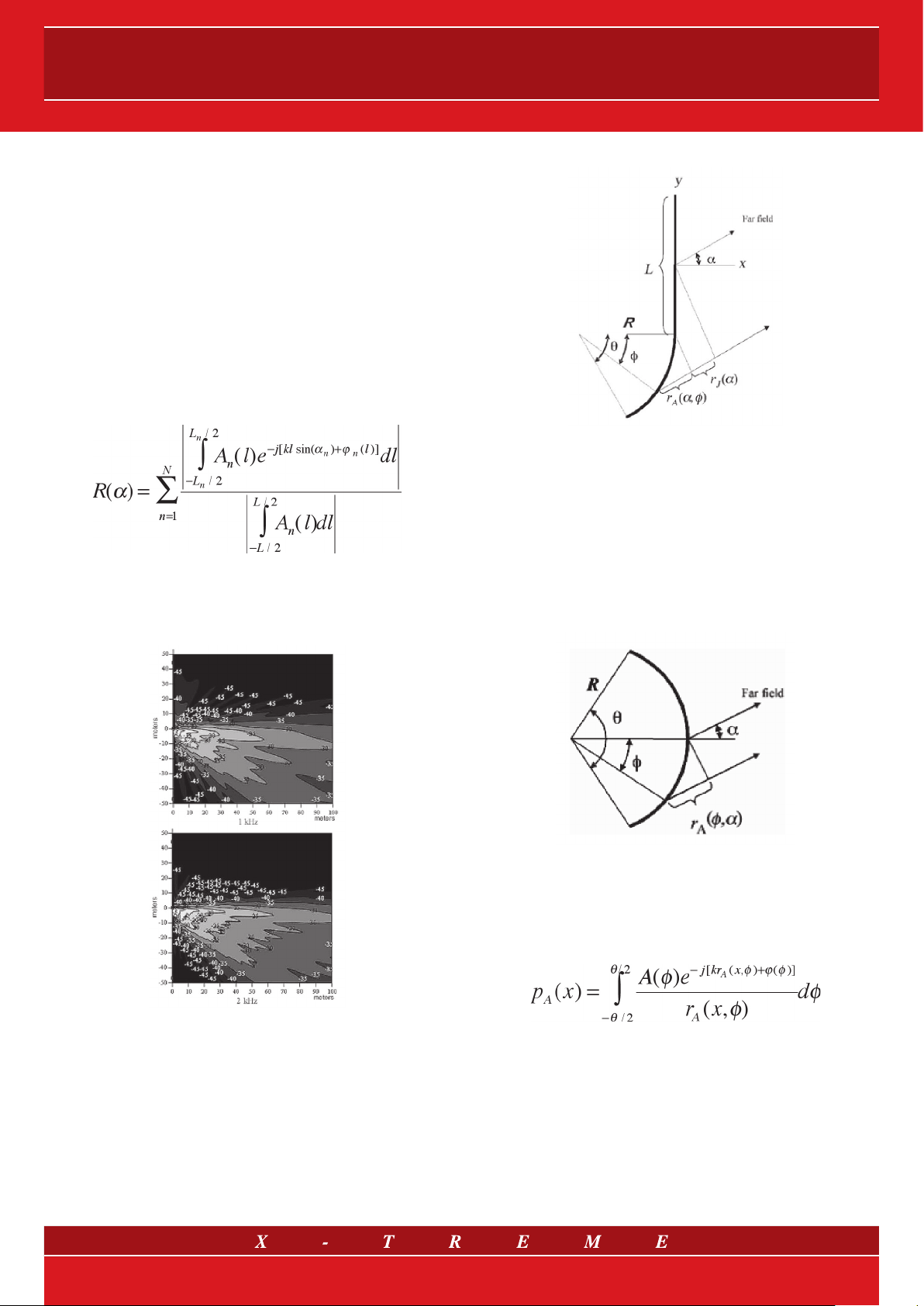
User’s manual
Therefore, in a linear source the in-axis response decreases by 3 dB for each doubling of the length instead of 6 dB as it occurs in a con ventional speaker system (point source) until the transition dis­tance is reached, which at medium-high frequencies can be dozens of metres for sources just a few metres long.
6. Arc, J and progressive sources
In a real configuration the wavefronts generated by the line array should be adjustable to the variables of the listening space (number and position of the listeners, listening space morphology, stage dimensions) to reach, in theory, the maximum listening uniformity from different positions. The general formulation of the directivity function, in case of N dif- ferent sources, sums up the effects of these N (linear or not) sources — the resulting function is as follows:
Given the freedom levels, this type of model can de scribe some real situations in a simplified way, such as those in fig. 6, relating to the measurement of a typical musical event with a line array sound reinforcement system.
fig. 7
The formal calculation of the expressions relating to the J source, despite having been substantially simplified, requires superfluous complex steps. On the contrary, the qualitative analysis of the con­tribution to directivity given by the lower semi-arc is quite interesting. Similarly to the considerations made for the linear source, an ideal arc source model can be created and the pressure expression can be analysed.
fig. 6
The directivity diagram as shown in fig. 6 can be used to approxi­mately represent a specific case of the suggested general for mula, where the sum has been reduced to two terms. The mathemati­cal sum of these two terms represents the overlapping of half an
arc source (which will be analytically described later) and a linear source. The resulting model is an important one, called J source.
Fig. 7 provides a further explanation of the link between the model we are trying to improve with the analytical description and the line arrays.
fig. 8
Skipping the mathematical steps required to replace the variables below the integral sign, we can write down directly the expression of the acoustic pressure as:
from which the directivity function is obtained.
A qualitative analysis of the polar diagrams of the arc source, indicated in fig. 9, reveals the same dependency between the lobe distribution and the frequency/arc length ratio noticed in the case of the linear sources. As far as linear sources are concerned, however, a greater width of the main lobe is observed as one can clearly see from the polar pattern chart in the following figure.
6/21
Page 7
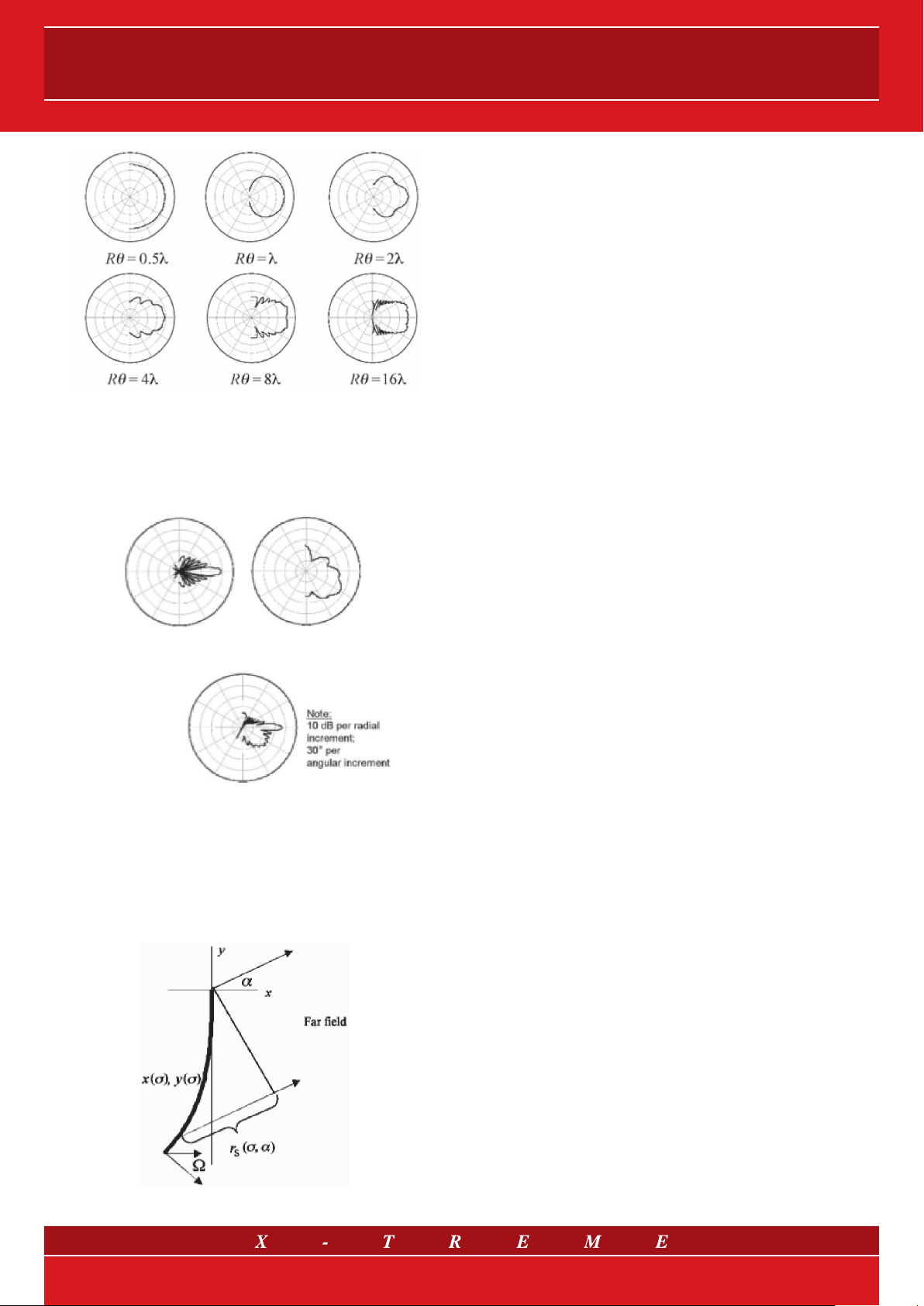
LINE ARRAYS
fig. 9
As a result of this property of arc sources, taking into account the lower semi-arc only and adding a linear source, one can see (fig.
Line source Arc source
J source
7. Line arrays: “the state-of-the-art”
The term “line array” (also called “sound columns”) applies to a sound reproduction system made up of a variable number of verti­cally arranged units (also called modules), which can achieve the effect of a single acoustic source having the dimen sions of all the component units and whose performance provides a coherent re­production, that is the result of the sum of its various compo nents. The vertical alignment allows narrowing of the reception zone to be achived as well as greater directivity and sound pressure compared to traditional systems. The idea is to create columns made up of low, middle and high fre­quency speakers; the systems consist of small, light modules joined into a wide acoustic source - the “line array”. The main advantage of this type of system is the energy saving deriving from narrowing the vertical directivity and a higher directivity of the sources which can also produce sound waves decreasing by 3 dB only for each dou­bling of distance instead of 6 dB as happens in traditional systems. These types of waves are defined as cylindrical and are generated while respecting certain parameters relating to the elements making up the array within a certain distance from the source (near field ), which depends on the frequency of the reproduced wave and on the lenght of the source itself. Having only two dispersion dimen­sions instead of three as in traditional spherical waves, the sound transmitted by the cylindrical waves decreases much more gradu­ally in relation to the distance from the source. As a result, the listen­ing experience does not change significantly in terms of sound level from a position far from the line array source to a position very near to it. Moreover, the vertical radiation for this type of system decays rapidly above and below the line array. As a result, less reverbera­tion is generated in case of indoor use because no wave is radi­ated towards any reflecting surfaces existing in the upper part of the room. Consequently, clarity and sound intelligibility are remarkably improved.
fig. 10
The J source model can be generalized in the progressive source (fig. 11), where the curvature is no longer null (or, better, infinite) and then constant such as in the J source, but it is parametrized in rela­tion to a coefficient σ. The analytical formulation is even more com­plex than the arc source but it is clear that a progres sive source can achieve complete control of the emission lobes.
8. X-Treme Vertical Line Array: product range
Created in 2001, the X-Treme brand identifies all the products man- ufactured by the Sound Corporation group business unit which produces “concert, touring and portable sound systems”, that is professional audio systems for concer ts, open air “live” events or any other indoor installation where music is played live. The X-Treme SBU (Strategic Business Unit) catalogue presents 3 different lines of vertical line array (VLA), all consisting of a 3-way module (the bi or tri-amplification mode can be selected by switch­ing the high current handling terminals in the crossover) and its cor­responding stacked or flying subwoofer, available in both active and passive versions. The Linear Source Array (LSA) system is the top solution of the range: in particular, the XTLSA module features high performances in terms of acoustic pressure as well as an innovative horn-loaded midrange configuration; the system has been designed to achieve an acoustic pressure similar to that of the above-mentioned “big” system, but with a higher re­sponse speed. Finally, the Mini Line Array (MLA) system stands out for its exceptional sonic accuracy with extremely reduced bulk and weight.
MISITM (Middle-Sized Line Array)
fig. 11
7/21
Page 8
User’s manual
Self-powered systems
The Linear Source Array XTLSA/A, MISITM XTMISI/A and Mini Line Array XTMLA/A active modules have been designed with the pur­pose of offering highly professional products combining the X-Treme audio system quality with new digital electronics technologies for the audio sector: in fact, both the power stage and the power sup­ply unit have been entirely designed with switching technology to achieve high performance with very reduced weight. The signal quality, in terms of distortion, is the same of that of the traditional professional amplification systems, while the pre-ampli­fication stage uses a powerful DSP (Digital Signal Processor) which allows extremely accurate processing of the signa l as well as the implementation of complex algorithms in infinitesimal times. In particular, the system management is innovative and accurate thanks to the remote connection thus enabling the creation of speaker system networks which can be controlled by a single sta­tion. The X-Treme designers’ efforts have led to the development of very interesting products for those working in the professional audio sector and appreciating continuous technological improvements.
9. X-Treme Vertical Line Array: system design
The X-Treme vertical line array (VLA) acoustic speaker systems have been designed to achieve broad horizontal and vertical cov­erage. This has been obtained thanks to a new waveguide for high range selection capable of producing a 120° coverage on a horizontal plane. Star ting from an array made up of side-by-side X-Treme speakers, the cabinets can be progressively opened by using the rear bars and by selecting the hole that ensures correct positioning, to obtain an array with different curvatures. A linear array can be created by using the hole corresponding to the low­est position in the rear of the cabinet handles. All X-Treme VLA loudspeaker systems have been designed as systems composed of identical elements in a vertical array configuration. When different loudspeaker systems (often called ‘line array mod- ules’) are configured in a line array, the electro-acoustic transducers are placed inside the cabinets in order to meet the Wavefront Sculp-
ture Technology© criteria for each frequency band (1. the wave fronts
generated by the electro-acoustic transducers for high frequencies are planar, 2. the “step”, that is the distance between acoustic cen­tres of the individual mid-low frequencies sources is smaller than half the wavelength correspon ding to the highest reproduced frequency = cut-off freq.). Therefore, each element generates a linear wave-front with a constant phase which enables several eleme nts to be as­sembled together creating a single broad sound source. Since the separation angle between the elements is adjustable, the wave-front can be modelled by changing the shape of the array. Thanks to a successful coupling right across the audible spec­trum, the X-Treme VL As generate a coherent wave-front on a large area with tiny variations in frequency response and sound pressure level. Therefore, these products are broadband sound reinforcement systems which ensure coherence up to the high­est frequencies. In terferences may occur as in all loudspeakers systems, but what makes X-Treme different is that interferences are constructive in the declared coverage area, and destructive outside this area. In a line array configuration, the bulk of the en­closures is smaller because all the array elements are coherently coupled, and fewer cabinets are required compared with conven­tional systems.
This means that the VLAs are highly competitive in case of touring applications in which transport, space availability and assembling can be very expensive. These properties make these systems very con­venient even for fixed installations where compact dimensions and coverage predictability are essential factors. In fact, one of the key benefits of the line arrays is predictability of the wave-front shape. Besides coverage accuracy, another important advantage resulting from using X-Treme array systems is their ability to extend the near field at high frequencies. In linear arrays, this leads to SPL reduction by 3 dB for each doubling of the distance versus 6 dB in the traditional systems. This property results from the physical features of cylindrical waves and spherical waves. This also means that these systems should not be evaluated on the basis of the classic “cost/kilowatt” ratio — since they gener- ate flat wave-fronts, they follow different attenuation laws compared with traditional systems. Determining the SPL value according to standard calculations is not meaningful because VLAs generate a combination of cylindrical and spherical wave-fronts which must be evaluated according to specific models (as shown in paragraph 4).
X-Treme curved arrays
When curved arrays are used, a combination of cylindrical and spherical propagations is obtained. Although the propagation of pure cylindrical waves does not always occur, reduction by 3 dB in relation to distance can be achieved through the extension of the near field and correct orientation of the system on the listening area. From a psycho-acoustic perspective, the near field extension allows the listener to be at a great distance from the systems and to perceive just a small difference in SPL terms due to the non con­ventional attenuation. In practice, the result is a high fidelity listening expe rience, a better stereophonic image and exceptional clarity. At a subjective level, listeners feel that the speaker systems are closer to them and that the sound is “right on your face”. The sound image localization is towards the stage, rather than towards the speaker systems. The near-field extension implies that not very high sound pressure levels are required near the system in order to obtain suit­able SPLs at the back of the listening area. Moreover, this property reduces the potential hearing loss for the audience and technicians alike. The near-field extension, combined with the coverage ac­curacy and predictability, can also effectively increase the critical distance in highly reverberating spaces (critical distance can be defined as the distance to which the direct sound energy equals that of the reflected sound). In many situations it is very important to prevent signals from reaching the ceiling, which means preventing energy from reaching any reflecting surfaces which have no relation with the sound event, such as in sports halls, arenas or amphithea­tres. Having less reverberation resulting from the sound acting on empty rooms or reflecting surfaces and by directing more energy to the listening area, critical distance can be increased in a specific room. Finally, another benefit of X-Treme VLA systems is the high decaying SPL level outside a well-defined wave field. This allows installation of the arrays behind or on top of the microphones with an exceptional resistance to feedback. Basically, if the bottom of the last module is visible, it means that one is outside the system cov­erage field. The FOH technicians too will prefer working with these loudspeaker systems for their low back-propagation, even at low frequencies, as the woofers will be positioned in a vertical array. The high SPL attenuation levels outside the coverage area make X-Treme VLAs an excellent solution for situations in which environ­mental noise should be avoided, such as, for example, in open air amphitheatres located near residential areas.
8/21
Page 9
LINE ARRAYS
10. MISI
The MISI
TM
system: from “AS IS” to “TO BE”
TM
(Middle-Sized line array) vertical line array can be de-
fined as a suitable compromise between power, weight and size. The designers of the MISITM system aimed to create a series of line array speakers capable of achieving considerable sound coverage with reduced bulk and weight. As a result, the system is particularly suitable for both middle-large tours as well as indoor and outdoor fixed installations. The MISI
TM
system provides the right solution to the needs of those
working in the live sector and/or dealing with sound reinforcement of large spaces. Each loudspeaker system offers 120° coverage horizon tally and 15° coverage vertically. The trapezoidal enclosure corners of the XTMISI unit have been designed so that a 2 x 7.5° an­gle is achieved when two loudspeaker systems are set side by side. Thanks to the suspension mechanics, starting from an array made of side-by-side XTMISI modules (7.5° x 2 = 15° between the different cabinets), the various cabinets can be progressively “opened” by us- ing the rear bars and selecting the hole ensuring correct positioning, in order to obtain arrays with different curvatures (fig. 12). The mechanical suspension system designed for the vertical line array module XTMISI allows the angle between two speakers to be adjusted, with a 1° reso­lution, from 0° to 15°, corresponding to two side-by-side loudspeaker systems and a line array respectively.
Array curvature adjustment system
On a horizontal plane, the whole line array, made of different XTMI- SI modules, shows the same directivity as a single element (120°). On a vertical plane, coverage is determined by the number of array elements and by a specific separation angle between them. Given this predictability, vertical coverage can be optimized in order to be adjusted to the specific geometry of the area to be covered. The high SPL attenuation levels outside the coverage area make the
TM
MISI
system an excellent solution for all situations in which envi-
ronmental noise should be avoided, such as, for example, in open air amphitheatres located near residentia l areas. The accuracy, flexibility and predictability of the X-Treme approach to sound reinforcement open up new horizons for sound design.
11. Types of installations
In practice, not all the line arrays permit a straight-line configura­tion. In fact, depending on the application and any specific needs, the array can be curved in order to obtain sufficient coverage for the entire listening area. For this reason, every loudspeaker system making up the line array can include a flying system by which it can be hooked and then oriented on a vertical plane. It should be noted that the flying system, being an integral part of the speakers, has been conceived so that the front hooking can ensure correct spac­ing out between the different units (while the rear hooking modifies the vertical orien tation consistently with theories on line arrays). Thus J-shaped systems are quite common although, of course, there are some constraints for their theoretical application such as a limit for the maximum opening angle that can be achieved. One of these conditions is specified below: in curved arrays, the opening angle is inversely proportional to the distance of the listening point ­to be more precise, in the farthest positions the angles must be very small and they should become progres sively larger as the listening point gets nearer to the line array. The vertical coverage of a curved array is given by the dimension and height of each loudspeaker sys­tem, by the opening angle between the various cabinets and by the number of flying modules.
Side-by-side speaker systems (15°)
fig. 12
Therefore, each element generates a linear wave-front with a con­stant phase and allows overall assembling of several elements pro­ducing a single and broad sound source. Since the separation angle between the elements is adjustable, the wave front can be modelled by varying the shape of the array. As regards the interferences occurring in all audio systems, the XTMISI line array module has been designed to obtain a construc­tive interference in the declared coverage area and destructive out­side this area. Moreover, thanks to successful coupling right across the audible spectrum, the XTMISI element generates a coherent wave-front on a large area with tiny variations in frequency response and sound pressure level. Therefore, MISI
TM
is a broadband audio
system, which remains coherent up to very high frequencies.
Ground stacked or flying?
Although flying systems are generally preferred by most sound technicians, there are a lot of arguments supporting both solutions. In many cases, however, the best solution depends on the logistical characteristics of the space to be sound reinforced or, simply, the system cannot be suspended at all. The perception of the sound image from the stage provided by the stacked systems is a positive element when small areas have to be sound reinforced. The stacking systems offer a higher SPL at low frequencies thanks to the coupling with the floor. In addition to these geometrical reasons, a stacked array can achieve a larger vertical coverage as compared with a flying one. For all these reasons, the stacking systems are more useful in small configurations where just a few elements are sufficient to achieve an excellent coverage of the audience. On the other hand, flying systems are the best solution to achieve a uniform sound pressure level if the total ratio between the number of flying elements and the area to be covered is sufficient to guaran­tee a suitable coverage from the front to the back. Flying systems also provide an excellent solution for the quite common sightline problems and allow high frequencies to better penetrate into listen­ing area with a reduced shadow effect. As for flying configurations, some additional loudspeaker systems are required to cover the central area of the first rows (“front-fill”) which enable the localiza­tion of the sound image on the stage for the first 10-20 rows of the audience.
9/21
Page 10
User’s manual
XTLSAS
XTLSAS
XTLSA
XTLSA
12. Stacking instructions
The stacked system has been designed for a maximum of 12 elements.
In this type of installations, the exact limits of vertical dispersion of X-Treme array systems don’t leave any small error margin. Of course, the FOH engineer should know if the audience will be standing or sitting, but in any case, the lowest part of the array will always be higher than the head of the first rows of the listening area. If the array bottom is placed far down, the received SPL level in first rows could be too high and the public standing in front of the system could act as an acoustic barrier for the next rows. Ideally, the array bottom should be located slightly above the audience (at least 2 metre high) and the volume of the lowest speaker should be set at a suitable level. Note: in the broad pass-band applications, a vertical stack of 4 sub- woofers provides a solid base if it is 2 metre high from the floor surface.
13. Suspension guidelines
As far as the anchoring points are concerned, the flying system has been designed for not more than 12 elements.
Pay special attention to the height at which the system is installed. In several cases, in fact, it is easier to optimize the area coverage at a specific height rather than another. In order to manage and carry out a complex operation such as the installation of curved arrays in a short time and safely, the X-Treme engineers have developed a dedicated software (XTI – see later), which allows calculation of the α angle of the vertical orientation. Note that the orientation should not be performed by considering only the coverage area on the axis, but also the geometry of the listening area outside the axis, in particular from 45° to 60°. It is also possible to sound reinforce places in which the two sections of the listening area have a differ­ent shape. In this case, coverage of the areas close to the borderline should be carefully determined and the array must be oriented dif­ferently in the two sections.
13.1 X-Treme Installer (XTI)
It is a “custom-made” software system designed and developed to favour a correct installation of the vertical line arrays (VLA) and of X-Treme conventional loudspeaker systems. Starting from geo­metric orientation, the software system calculates the sound field through an algorithm based on the acoustic wave amplitude and phase, according to the information available to the system. The operator can set a few installation parameters, such as, for ex­ample, the VLA position and the geometric variables associated with the audience. Through simulation he can also control the start-up and switching off of the VLA and the elemen ts making up the clusters, thus guaranteeing broad and effective control of the simulated sound field. Besides the VL As, the softwa re system enables the addition of other electro-acoustic speakers, such as subwoofers or double subwoofers, with the configuration chosen by the operator. Therefore, the sound field simulation allows inclu­sion of both VLAs and sub clusters, which can be conceived as horizontal arrays or, more commonly, as planar arrays working at low frequencies. It should be stressed that the essential purpose of this acoustic software tool is to allow the operator to check directly the effect of any change in the VLA vertical orientation angle (the α angle, that is the angle associated with the highest speaker), in the orientation angles between the various modules (splay angles) and in the other VLA installation parameters on the acoustic coverage of the audience area.
13.2 Suspension instructions
The STD-LSA, STD-MISI, STD-MLA bars (see fig. 13) construct­ed from martensitic steel tubular elements are designed to support big loads. Equipped with two flying points, they are made of a rein­forced central bar which is also used for lifting. The bars have a set of holes with a 2.6 cm diameter working as a collection point for the steel or lifting chains. The chosen collection point will determine the inclination angle of the whole array. The line passing through the two anchoring points crosses the barycenter of the flying system to guarantee an aligned and balanced suspension. The two anchor­ing points can be hooked separately to different suspension mo­tors in order to share the load between the two points and to allow the whole array to be inclined within certain limits. Alternatively, a single motor and a single suspension point can be used while mak­ing sure that a correct array inclination is achieved.
fig. 13
The new flying system without external hardware simplifies the in­stallation procedure so much that it can be carried out by just one person. No extra hardware must be hooked to the speaker system and the system dimensions are such that transport becomes easy.
13.3 “Straight to the… Angle!”
The XT-ANGLE is an electrical-mechanical device equipped with a motorized linear actuator for remote adjustment of the vertical tilt­ing of X-Treme arrays. The flying bar contains a worm screw which, when set to rotate by the motor, allows the lengthways movement of the coupling block and therefore the tilting of the flying bar (de­pending on the weight distribution of the array). This system, which is patent pending, offers unprecedented possibilities to professional riggers (that have never been seen before). In actual fact, it allows: a) the array to be lifted without having to decide the anchoring point
beforehand;
b) more precise angles to be set, compared with those offered by
the anchoring hole of a traditional rod;
c) the system to be adjusted after mounting, without ever having to
bring it back down to the ground.
13.4 LSA: flying and lifting
fig. 14
10/21
Page 11
LINE ARRAYS
fig. 17
Depending on the hole in which the (XT-PIN) pin is inserted in the upper part of the speaker system, the acoustic speaker systems will be arranged according to a specific angle. Lifting the structure with the hung loudspeaker systems and sliding the pins into the upper groove, on the holes delimiting the selected angles, the operation can be easily carried out as shown in figure 16. Once the array lifting has been completed, the STD-LSA, STD-MISI or STD-MLA bars must be fixed to avoid any rotation.
13.5 MISI™ and MLA: enclosure suspension rigging
The MISI™ and Mini Line Array systems are equipped with a fly- ing hardware placed on the front and the rear of the acoustic loud- speaker system. Two pull-out metallic bars are fitted on both sides of the loudspeaker system front (in the lower part). By unhooking and sliding out these two bars, the acoustic enclosure can be fixed to the lower element (that is the flying bar if the speaker is the first on the floor or any other line array module). Safe fixing is ensured by sliding the pins into the corresponding holes of the lower unit. On both sides of the rear part of the speaker two hinged joints are fitted; they are used to determine the angle between two succeed- ing cabinets. By releasing and rotating them, the joints can be fixed to the upper element (any speaker or the flying bar as for the module on top of the array), matching the fixing holes with the required angle and sliding the pins (XT-PIN), as shown in figure 18.
fig. 18
When a certain number of speaker systems are lifted (fig. 14 shows a line array system configuration in which the first two modules are made up of flying subwoofers and the others of line ar ray elements with a standard type of installation), they should be inter-connected (between them) on the floor, placing them on special wheelboards. Then follow the procedure shown in the following figure.
Slide the metallic joints of each loudspeaker system in the insert of the handle of the next system, fixing them with the pins in the final part only, which corresponds to the front part of the speakers (fig. 15). In the curved arrays, the vertical dispersion angles must be inversely proportional to the distance from the listening point. For example, regarding the farthest positions, the dispersion angle will be small, and will increase progressively as the listening point gets closer to the linear array. The coverage angle of the curved array is given by the di­mension or height of each speaker, the incli nation angle between the speakers and the number of units to be suspended. The maximum inclination angle between two Linear Source Array modules is 7.5°.
fig. 15
fig. 16
11/21
Page 12
User’s manual
fig. 19
The wheelable metallic joints are equipped with two holes - one above the other - corresponding to even or odd angles for a secure fixing, as indicated in figure 19. Also in this case, the coverage angle of the curved array depends on the dimensions of each loudspeaker system, the incli nation an­gle between the speakers and the number of units that must be suspended. The enclosures will be arranged with a specific angle (fig. 20) according to the hole in which the pin (XT-PIN) will slide into on the upper part of the loudspeaker system. The maximum inclina­tion angle between two subsequent MISITM or MLA modules is 15°.
fig. 20
14. Subwoofers
The subwoofers are used to extend the system frequency response up to 25-30 Hz and to increase the SPL level at low frequencies without increasing potential hearing damage to users.
General guidelines for using subwoofers
The number of subwoofers to be used depends on 3 parameters:
1) Number of flying elements
The recommended standard number of subwoofers corresponds to a 1:1 ratio (1 upper module - 1 subwoofer).
2) Type of programme to be reproduced
The standard subwoofer ratios are recommended for reprodu cing classical music or for conventions. In these applications subwoof­ers provide low frequencies extension of the line array modules and generate contribution of roughly 6 dB in the bands used. In this case, the resulting audio system will work as a 4-way broad pass band in tri-amplification mode. In live applications with rock music reproduction, 1:1.5 ratio (e.g. 2 modules and 3 subwoofers, 4:6, 8:12) or even 1:2 mended for strong reinforcement at low frequencies.
3) Type of location or installation
When the subwoofers are stacked outdoors, the ratios are those mentioned above. In the case of flying units, a higher number of subwoofers is required. They are usually installed on the floor, in a side-by-side configuration, in order to exploit the emphasis resulting from the floor coupling. When the flying modules and the subwoofers are physically separated, it is well-known that the phase alignment is valid in one position only, therefore a suitable compromise should be reached. When the systems are aligned, a position that is most representative of the listening area should be chosen. It is also well-known that when different subwoofer arrays are placed on the sides of the stage (left-right), sums and cancellations will oc­cur that vary according to the different listening positions. This phenomenon can be avoided by using the following tech­niques: a) using vertical subwoofer arrays placed on the sides of the stage (e.g. 4-4 left-right configuration). See drw. 21 a); b) placing n elements on the sides of the stage and 2n elements in the middle of the stage (e.g.: left-centre-right 2- 4-2 configu­ration), as shown in drw. 21 b). This ensures better coverage on the stage axis (where most of the audience is usually found) and a coherent sound image; c) physically curving the subwoofer arrays to create an L-shaped array rotating around the stage angle, see drw. 21 c). This orientates the main lobes of the left and right arrays out of the stage axis, thus reducing the central sum. It should be stressed that using a central horizontal line array with an electronic delay limiting its directionality will still generate excessive sound concentration in the middle of the audience. However, the advantage of a vertical omnidirectional directivity is achieved, which makes it a good solution for indoor use.
(1 upper module - 2 subwoofers)
STAGE
are recom-
STAGE
12/21
fig. 21 a) fig. 21 b)
STAGE
fig. 21 c)
Page 13
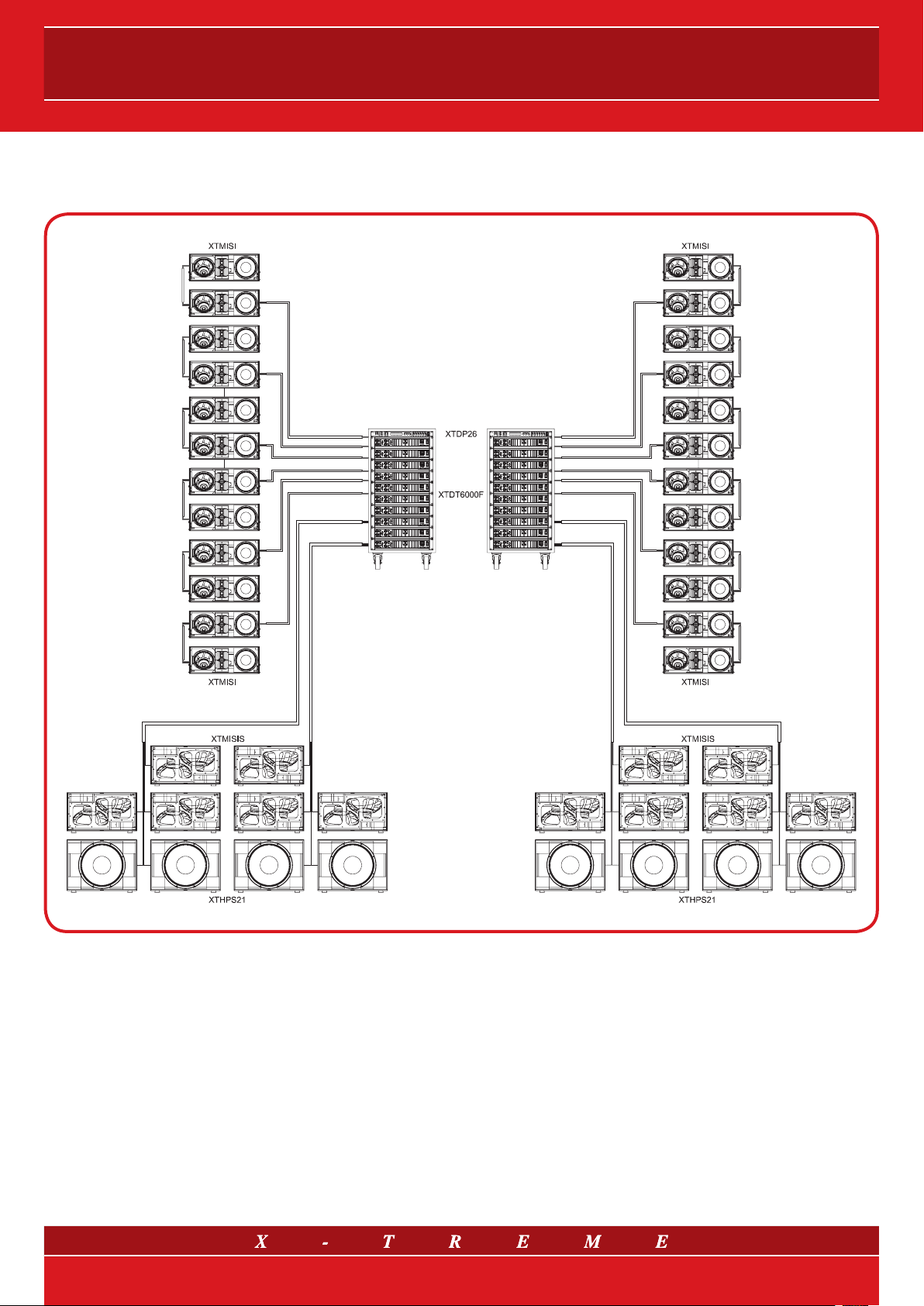
LINE ARRAYS
15. Tri-amplification system configuration
APPLICATIONS
• Large scale touring;
• Large open spaces, squares, etc…
• Stadiums, sports venues, large arenas;
• Huge fixed installations.
13/21
BRIEF DESCRIPTION
• Total Power Handling: 51600 W RMS
• Total Power Amplifiers:
• Horizontal coverage angle: 2 x 120°
• Reachable distance: 80-100 m
• Max potential audience: 20÷25000 people
120000
W RMS (@4 Ohm)
Page 14
UNITS
User’s manual
24 XTMISI
12 XTMISIS
8 XTHPS21
20 XTDT6000F
2 XTDP26
Middle-Sized Line Array module - Power handling RMS: 900 W - Impedance (bi-amp) 8+8 Ohm - Max SPL: 136 dB
Arrayable double subwoofer - Power handling RMS: 2400 W - Impedance: 4+4 Ohm - Max SPL: 140 dB
“Big Punch” Infra-bass subwoofer - Power handling RMS: 1500 W - Impedance: 8 Ohm - Max SPL: 139 dB
Stereo Switching Class D Amplifier with PFC (95-265 VAC) - Output Power RMS: 4x1500 W (@4 Ohm)
Digital Speaker Management System - Ways: 2 Input, 6 Output - Frequency response: 12÷20k Hz ±0.5 dB
CONNECTORS
The XTMISI and XTMISIS cabinets are fitted with a pair of Neu-
trik Speakon NL8 connectors, while XTHPS21 sub uses Neutrik
Speakon NL4. The double Speakon connector permits to connect
in parallel a fur ther loudspeaker system of the same type. All eight
Type
NL8
NL8
Pins
1+ 1- 2+ 2- 3+ 3- 4+ 4-
LF+
(XTMISI)
SW+
(XTMISIS)
SW-
(XTMISIS)
pins of both connectors are wired in parallel. The XTMISI uses the
pin assignments 2+/2- for woofer, 3+/3- for mid-high section in
bi-amp (this configuration) and 4+/4- for high section in tri-amp.
Pins 1+/1- are designed to XTMISIS and XTHPS21 subwoofers.
LF-
(XTMISI)
Mid/Hi+ (XTMISI
bi-amp)
Mid/Hi­(XTMISI bi-amp)
High+ (XTMISI tri-amp)
High­(XTMISI tri-amp)
NL4
SW+
(XTHPS21)
SW-
(XTHPS21)
= Utilize d louds peaker s ystems- power amplifier s conne ctions .
PROCESSOR PROGRAMS
DSP UNIT SOUND FILE
XTDP26
12_XTMISI+XTMISIS+XTHPS21_Mono.dfa ---
(*) The “Far” output has a boost in the ultra- high freque ncy zone; to be us ed for a set of upper modules whi ch are position ed in the top part of th e array (suspended or stacked), depe nding on installation
geome try and e nviron menta l condit ions (arc hitecture, humidity), to thr ow the ver y high fr equen cies far enough, despite air abso rption.
12_XTMISI_Mono.dfa Near/Far*
OUTPUT
OPTIONS
FUNCTION
Array made of 12 bi-amplified elements
without subwoofer
Array made of 12 bi-amplified elements
with subwoofer
ACCESSORIES
STD-MISI
XT-ANGLE
XT-ANGLERC Remote controller for XT-ANGLE with bright display (cable included, 10 m in length)
XT-D8P Connection panel specially designed for line arrays
XT-PSB32/8 Patch board 32A - 2 XLR IN, 2 XLR OUT - 4 Speakon OUT NL8MPR - 3 rack units
XT-NETINT Network Interface for XT-NET connection (PC adapter: from USB or RS232 to standard RJ45)
XT-NETPS Power unit for supplying up to 2 XT-NETINT (if a RS232 is used)
XTMISIS-SK Wheelboard for XTMISIS and XTMISIS/A double subwoofer
XTHPS21-SK Wheelboard for XTHPS21 infra-bass subwoofer
Flying bar for Middle-Sized Line Array
Electro-mechanical device for setting the pitch of the line array systems (flying bar not included)
14/21
Page 15
LINE ARRAYS
16. System configurations: standard examples
16.1 Linear Source Array: DSP active solution
APPLICATIONS BRIEF DESCRIPTION
• Large scale concert & touring;
• Large open-air events, public squares, etc...
• Stadium, sports halls, arenas;
• Large fixed installations.
15/21
• Total Power Amplifiers: 22800 W RMS (@4 Ohm)
• Horizontal coverage angle: 2 x 120°
• Reachable distance: 70-80 m
• Max potential audience: 8000 people
Page 16
UNITS
User’s manual
8 XTLSA/A
4 XTLSAS/A
Active bi-amplified line array module - Amp. Power: 800+800 W RMS - Digital DSP on board (2 preset)
Active arrayable double subwoofer - Amp. Power: 2500 W RMS (@ 4 Ohm) - Digital DSP on board (2 preset)
CONNECTORS
The input signal for XTLSA/A and XTLSAS/A uses a female XLR Bal connector. To wire the connector, use pin 2 for Hot (+), pin 3 for Cold (-) and pin 1 for ground (GND). Two internal presets are selectable through a switch positioned in the rear side of the speakers. Moreover, thanks to the power­ful DSP on board, it is possible to generate a cascade network of
Type
XLR
Pins
1 2 3
Ground
GND
Positive
(+)
Negative
(-)
N loudspeaker systems (XT-NET) via UTP CAT5 cable with RJ45 connectors – this allows the user to edit the audio parameters of the speakers and hence to read the history of the amplifier status from a single external PC. A second XLR male connector permits the signal to be linked to other additional loudspeaker systems.
PRESETS
DSP UNIT SOUND FILE
4_XTLSA_A_NoSub.dfa A (Near) / B (Far)*
XTLSA/A
4_XTLSA_A_Sub.dfa A (Near) / B (Far)*
XTLSAS/A XTLSAS_A.dfa
(*) Sele ctabl e via hard ware on the l oudsp eaker system’s rear pan el. The “Fa r” optio n (switch po sition: B) h as a boost i n the ultra -high fr equen cy zone; to be us ed for a set of upper mod ules wh ich are
positi oned in the top par t of the array (susp ended or stacked), dep ending on installa tion geom etry and en vironm ental con ditions (architecture, humi dity), to throw the ver y high frequencies far enou gh,
despi te air absorption. The sam e purpose can be ac compl ished w ith a manu al boos t in the 10 kHz zone.
(**) To use onl y with othe r upper module s - apar t from X TLSA - in ca se they hav e inver ted polarity re sponse .
HARDWARE
SWITCH OPTIONS
A (Polarity: normal) /
B (Polarity: inverted)**
FUNCTION
Array made of 4 active elements
without subwoofer
Array made of 4 active elements
with subwoofer
Subwoofer mode
ACCESSORIES
STD-LSA
XT-ANGLE
XT-ANGLERC Remote controller for XT-ANGLE with bright display (cable included, 10 m in length)
XT-NETINT Network Interface for XT-NET connection (PC adapter: from USB or RS232 to standard RJ45)
XT-NETPS Power unit for supplying up to 2 XT-NETINT (if a RS232 is used)
XTLSA-SK Wheelboard for XTLSA and XTLSA/A loudspeaker system
XTLSAS-SK Wheelboard for XTLSAS and XTLSAS/A double subwoofer
Flying bar for Linear Source Array
Electro-mechanical device for setting the pitch of the line array systems (flying bar not included)
16/21
Page 17
LINE ARRAYS
16.2 MISITM: passive solution powered by switching technology
APPLICATIONS BRIEF DESCRIPTION
• Medium/large scale touring;
• Central clusters, front fill, side fill, delay towers, etc...
• Medium/large open-air events, squares, etc…
• Stadiums, sports halls, arenas;
• Theme parks, circus shows;
• Theatres, auditoriums, music halls;
• Medium/large fixed installations;
• Large live clubs, music pubs and other live performance venues.
17/21
• Total Power Handling: 16800 W RMS
• Total Power Amplifiers: 15600 W RMS (@4 Ohm)
• Horizontal coverage angle: 2 x 120°
• Reachable distance: 60-70 m
• Max potential audience: 6000 people
Page 18
UNITS
User’s manual
8 XTMISI
4 XTMISIS
2 XTDT4800F
1 XTDT6000F
1 XTDP26
Middle-Sized Line Array module - Power handling RMS: 900 W - Impedance (bi-amp) 8+8 Ohm - Max SPL: 136 dB
Arrayable double subwoofer - Power handling RMS: 2400 W - Impedance: 4 Ohm - Max SPL: 140 dB
Stereo Switching Class D Amplifier with PFC (95-265 VAC) - Output Power RMS: 4x1200 W (@4 Ohm)
Stereo Switching Class D Amplifier with PFC (95-265 VAC) - Output Power RMS: 4x1500 W (@4 Ohm)
Digital Speaker Management System - Ways: 2 Input, 6 Output - Frequency response: 12÷20k Hz ±0.5 dB
CONNECTORS
The XTMISI and XTMISIS cabinets are fitted with a pair of Neutrik
Speakon NL8 connectors. The double Speakon connector per-
mits the parallel connecton of a further loudspeaker system of the
same type. All eight pins of both connectors are wired in parallel.
Type
NL8
NL8
Pins
1+ 1- 2+ 2- 3+ 3- 4+ 4-
LF+
(XTMISI)
SW+
(XTMISIS)
SW-
(XTMISIS)
The XTMISI uses pin assignments 2+/2- for woofer, 3+/3- for
mid-high section in bi-amp (this configuration) and 4+/4- for
high section in tri-amp. Pins 1+/1- are designed for XTMISIS
subwoofers.
LF-
(XTMISI)
Mid/Hi+ (XTMISI
bi-amp)
Mid/Hi­(XTMISI bi-amp)
High+ (XTMISI tri-amp)
High­(XTMISI tri-amp)
= Utilize d louds peaker s ystems- power amplifier s conne ctions .
PROCESSOR PROGRAMS
DSP UNIT SOUND FILE
XTDP26
(*) The “Far” output has a boost in the ultra- high freque ncy zone; to be us ed for a set of upper modules whi ch are position ed in the top part of th e array (suspended or stacked), depe nding on installation
geome try and e nviron menta l condit ions (arc hitecture, humidity), to thr ow the ver y high fr equen cies far enough, despite air abso rption.
4_XTMISI_BiAmp_Stereo.dfa Near/Far*
4_XTMISI_BiAmp+XTMISIS_Stereo.dfa ---
OUTPUT
OPTIONS
FUNCTION
Array made of 4 bi-amplified elements
without subwoofer
Array made of 4 bi-amplified elements
with subwoofer
ACCESSORIES
STD-MISI
XT-ANGLE
XT-ANGLERC Remote controller for XT-ANGLE with bright display (cable included, 10 m in length)
XT-D8P Connection panel specially designed for line arrays
XT-PSB32/8 Patch board 32A - 2 XLR IN, 2 XLR OUT - 4 Speakon OUT NL8MPR - 3 rack units
XT-NETINT Network Interface for XT-NET connection (PC adapter: from USB or RS232 to standard RJ45)
XT-NETPS Power unit for supplying up to 2 XT-NETINT (if a RS232 is used)
XTMISIS-SK Wheelboard for XTMISIS and XTMISIS/A double subwoofer
Flying bar for Middle-Sized Line Array
Electro-mechanical device for setting the pitch of the line array systems (flying bar not included)
18/21
Page 19
LINE ARRAYS
16.3 Mini Line Array: passive solution with “Big punch” powered by switching technology
APPLICATIONS BRIEF DESCRIPTION
• Medium/small scale concert & touring;
• Central clusters, front fill, side fill, delay towers, etc...
• Medium/small open-air events, public squares, etc…
• Theme parks, circus shows;
• Theatre sound reinforcement;
• Houses of worship;
• Medium fixed installations;
• Medium/large live clubs, music pubs and others;
• Multi-purpose venues and congress/fairs centres;
• Corporate A/V events;
• Small to medium sized portable PA systems.
19/21
• Total Power Handling: 13600 W RMS
• Total Power Amplifiers: 18400 W RMS (@4 Ohm)
• Horizontal coverage angle: 2 x 120°
• Reachable distance: 50-60 m
• Max potential audience: 4000 people
Page 20
UNITS
User’s manual
8 XTMLA
4 XTHPS36
2 XTDT3200
2 XTDT6000F
1 XTDP26
Mini Line Array module - Power handling RMS: 500 W - Impedance (bi-amp) 16+16 Ohm - Max SPL: 133 dB
“Big Punch” Double Subwoofer - Power handling RMS: 2400 W - Impedance: 4+4 Ohm - Max SPL: 143 dB
Stereo Switching Class D Amplifier with PFC (95-265 VAC) - Output Power RMS: 2x1600 W (@4 Ohm)
Stereo Switching Class D Amplifier with PFC (95-265 VAC) - Output Power RMS: 4x1500 W (@4 Ohm)
Digital Speaker Management System - Ways: 2 Input, 6 Output - Frequency response: 12÷20k Hz ±0.5 dB
CONNECTORS
The XTMLA cabinets are fitted with a pair of Neutrik Speakon NL8
connectors. All eight pins of both connectors are wired in parallel.
The XTMLA uses the pin assignments 2+/2- for woofer, 3+/3- for
mid-hi section in bi-amp (this configuration) and 4+/4- for high
Type
NL8
NL4
Pins
1+ 1- 2+ 2- 3+ 3- 4+ 4-
LF+
(XTMLA)
Woofer 1+
(XTHPS36)
Woofer 1-
(XTHPS36)
Woofer 2+
(XTHPS36)
section in tri-amp. The XTHPS36 uses a pair of NL4 Neutrik Spe-
akon. Pins 1+/1- are assigned to XTHPS36 woofer 1 and 2+/2- to
woofer 2. The double Speakon connector permits parallel con-
nection of a further loudspeaker system of the same type.
LF-
(XTMLA)
Woofer 2-
(XTHPS36)
Mid/Hi+ (XTMLA
bi-amp)
Mid/Hi-
(XTMLA
bi-amp)
High+
(XTMLA
tri-amp)
High­(XTMLA tri-amp)
= Utilize d louds peaker s ystems- power amplifier s conne ctions .
PROCESSOR PROGRAMS
DSP UNIT SOUND FILE
XTDP26
(*) The “Far” output has a boost in the ultra- high freque ncy zone; to be us ed for a set of upper modules whi ch are position ed in the top part of th e array (suspended or stacked), depe nding on installation
geome try and e nviron menta l condit ions (arc hitecture, humidity), to thr ow the ver y high fr equen cies far enough, despite air abso rption.
4_XTMLA_BiAmp_Stereo.dfa Near/Far*
4_XTMLA_BiAmp+XTHPS36_Stereo.dfa ---
OUTPUT
OPTIONS
FUNCTION
Array made of 4 bi-amplified elements
without subwoofer
Array made of 4 bi-amplified elements
with “Big punch” subwoofer
References
H. F. Olson, “Elements of acoustical engineering”, Van Nostrand, New York (1940)
D. L. Klepper, D. W. Steele, “Constant directional characteristics from a line source array”, AES (Audio Engineering Society), vol.11, no.3 (1963)
L. L. Beranek, “Acoustics”, AIP (American Institute of Physics), 3rd printing (1990)
C. Heil, “Sound fields radiated by multiple sound source arrays”, J. Audio Eng. Soc., vol.40 (1992)
M. S. Ureda, “Analysis of loudspeaker line arrays”, J. Audio Eng. Soc., vol.52, no.5 (2004)
20/21
Page 21
Contacts
www.x-tremeaudio.com
X-Treme Headquarters:
via Monti Urali, 33 - 42100 Reggio Emilia - Italy tel. +39 0522 557735 fax +39 0522 391268
X-Treme Audio reserves the rights to change or modify products and specifications at any time without prior notice.
X-Treme and the corresponding symbols, images and registered trademarks are of exclusive property of Sound Corporation group. © 2010 Sound Corporation group. All rights reserved.
21/21
For technical support/information: support@x-tremeaudio.com
For general information: info@x-tremeaudio.com
For commercial information: sales@x-tremeaudio.com
Loading...
Buy Points How it Works FAQ Contact Us Questions and Suggestions Privacy Policy Cookie Policy Terms of Use