XOR electronics Nerdseq User Manual
NerdSEQ Hybrid Tracker Sequencer
User Manual
(unfinished)
Please be aware that this is an ever growing manual and so it makes no
sense to print it out!
Nerdseq – a tracker based Eurorack sequencer Page 1
User Manual Revision V0.9.9 for Firmware V1.13 27 February 2018
Content
Introduction..........................................................................................................................................3
Technical Specification.........................................................................................................................5
Firmware Features................................................................................................................................6
Getting Started......................................................................................................................................7
Numbers, Values and Tracker basics....................................................................................................8
Buttons and Navigation......................................................................................................................10
General Screen information................................................................................................................12
Sequencer Screen................................................................................................................................13
Pattern Screen.....................................................................................................................................17
Patch Screen.......................................................................................................................................26
Recent Values Screen..........................................................................................................................27
Automation screen..............................................................................................................................32
Project screen......................................................................................................................................32
Setup Screen.......................................................................................................................................33
Load Sample window.........................................................................................................................35
Recording...........................................................................................................................................36
The Nerd Button.................................................................................................................................37
Expander Modules..............................................................................................................................38
Tips & Tricks......................................................................................................................................39
Firmware update.................................................................................................................................40
Document/Versions History................................................................................................................40
Disclaimer...........................................................................................................................................42
Nerdseq – a tracker based Eurorack sequencer Page 2
User Manual Revision V0.9.9 for Firmware V1.13 27 February 2018
Introduction
The NerdSEQ is a Tracker1 based sequencer for Eurorack systems.
It consist 6 Tracks for the CV/Trigger/Gate generation of 18 outputs (12 CV + 6 Trigger/Gate). They
are further 4 sample Tracks with 2 dedicated audio outputs for sample sequencing. Dedicated
clock/reset inputs and outputs are available for different clock types. 4 free assignable CV inputs
can be used for live manipulation or CV/Gate recording. So in complete they are 10 Tracks
available for sequencing.
The sequencer itself is inspired on old module trackers like Fasttracker2(PC)2, OctaMED(Amiga)3,
LittleSoundDJ(Gameboy)4 and Little Piggy Tracker(Multiple Platforms)5….. These to name only a
few, they are many more inspirations.
It contains many and very powerful functions for sequencing like an advanced live ability,
patternlength up to 64 steps, chaining, poly-rhythmic tracks, groove, glide, ratcheting/retrigger,
flexible trigger/gate/step lengths, patches, special effects, probability, tables and more. The
sampler tracks contain special functionality for sample playing, pitching, sample effects, retrigger
and many more. Samples can be loaded from a dedicated SD card available on the front panel.
The sequencer is able to make loops (as in many loops) and full songs (even multiple songs on
one project, depending on complexity, usage of patterns etc.) Projects can be saved and loaded
on/from the microSD card.
All editing is implemented in a very easy way (at least I tried so). So every screen or edit option
can be accessed through one key or Shift + Key. No complex submenus from submenus or menu
diving is needed. I also try to prevent that as much as possible for future updates.
1 https://nl.wikipedia.org/wiki/Moduletracker
2 https://en.wikipedia.org/wiki/FastTracker_2
3 https://en.wikipedia.org/wiki/OctaMED
4 http://www.littlesounddj.com/lsd/
5 http://littlegptracker.com/
Nerdseq – a tracker based Eurorack sequencer Page 3
User Manual Revision V0.9.9 for Firmware V1.13 27 February 2018
In the following picture you can see a front overview:
Nerdseq – a tracker based Eurorack sequencer Page 4
User Manual Revision V0.9.9 for Firmware V1.13 27 February 2018
Technical Specification
Power consumption:
- ~190mA on the +12Volt Rail
- ~32mA on the -12 Volt Rail
- +5 Volt Rail is not connected
Hardware:
- Colour Graphics IPS display with a resolution of 480 x 320 pixels
- 10 full size and 6 half size buttons
- 28 mini-Jack (mono), 4 CV Inputs (range 0..10 Volt) , Clock+Reset Inputs(5 Volt), 12 CV
outputs (Range -5 Volt /+5 Volt or 0 Volt / +10 Volt), 6 Trigger/Gate Outputs (5 Volt),
2 Sample outputs (-5 Volt/+5 Volt), Clock + Reset Output (5 Volt)
- 2 toggle switches to change the offset of the CV voltages
- 2 LED to indicate clocks
- microSD connector accessible on frontpanel
- 10 pin boxed bus connector (power)
- Expander connector (12 pin boxed) for IO-Expander (Midi In/Out + Sega Gamepad
connector) (Expander must be ordered seperately)
- Expander connector (14 pin boxed) for special Nerdseq extensions like a NSA (Nerd
Sound Adapter) which are dedicated Cartridges including full synthesizers. Those are totally
integrated in the Nerdseq sequencer. (Under development)
Tracker:
- 6 CV/Trigger/Gate tracks for 12 CV and 6 Trigger/Gate outputs
- 2x2 sample tracks for 2 sample outputs (mono)
- 239 Sequencer rows
- 175 Patterns with each 64 (and less) Steps
- 176 Patches
- 32 Tables with 16 (and less) steps
- 16 Automation slots (2do)
- 12 Sample slots
Nerdseq – a tracker based Eurorack sequencer Page 5
User Manual Revision V0.9.9 for Firmware V1.13 27 February 2018
- 200kB Sample memory (4 seconds with 44.1 kHz/8 Bit/Mono or more with lower
samplerate)
- Sample support for RAW 8 bit mono and WAV 8/16 bit, Mono/Stereo
- Projects as many as the SD card can hold
Firmware Features
- 8 Tracker tracks can be controlled independently, synchronised and not synchronised
- Pattern chaining
- Probability (0..100% with 1% resolution) for CV, Mod, Gate, Tables and FX (which can
contain every feature)
- Patterns with Note Scaled input, Patch selection, Trigger/Gate w retrigger/ratcheting, CV
Modulation manipulation, Groove, Fine pitch, Glide, Glide quantisation, Table selection
- 4 FX possibilities per pattern per step (Internal CV/Gate tracks)
- Groove per step per pattern to create different step lenghs, shuffle and weird rhythmics with
the possibility to create poly-rhythmic tracks
- Patches with all wanted functions directly accessible
- Tables (sequencer in the sequencer) for Transpose and all possible functions, different
speed scales and sources, synchronised and not synchronised to the main sequencer clock
- Automation slots to assign different automations (like LFO, Envelopes, Noise,
Randomness..etc) (2DO)
- Project management
- Sample management
- Clock Source can be Internal, 1/16 via Clock input, 24ppqn, Sync24, Midi Clock
- Clock Outputs can be 1/16, 24ppqn(2do), sync24 (2do), Midi Clock
- All Modular tracks can be manipulated from other Modular tracks
- Trigger functions with different timings for ON/OFF, OFF/ON, Retriggering
- Gate length can be as short or long as needed (much shorter than steplength possible)
- advanced Mark + Copy + Paste functions to copy marked parts within or between patterns
- Sample pitch in note scale
- Sample effects like Volume, Fine Pitch, Retrigger, Backwards, Bitcrush, Distortion … more
to come
- Enable/Disable edit mode so nothing can be changed accidentally on live situation
- Live editing while playing including pattern creation, manipulation, recording, nearly all
functions accessible while playing
Nerdseq – a tracker based Eurorack sequencer Page 6
User Manual Revision V0.9.9 for Firmware V1.13 27 February 2018
- pattern cloning
- patch cloning
- Free record routing
- free routing of CV inputs to different functions
Getting Started
To get started, insert the SD Card, connect the power cable properly. Take care that the red line is
connected to the -12Volt Rail on the Bus. Power on the System.
First there will be a splash screen followed by the current Firmware version number.
After that the system is checking if any NSA (Nerd Sound Adapter) are connected (those will be
available with the Cartridge expander in the future).
Without any cartridge expander, it should find the internal CV/TRIG/MOD for 4 tracks.
Then the SD card is being checked if it is correctly initialised, reading the calibration settings. And
at last, it will show if a Gamepad is detected (through the IO-Expander).
The startup is now ready and an empty sequencer screen will show up, waiting for you to get
started!
Attention, if the Splash screen the text or the background light appears to be weird somehow, then
it is a good indication that there is something wrong with the power. (For example, not enough
power -> Voltages are too low / not enough current). Check your supply, disconnect some other
modules to be sure your supply got enough power. (And be sure the NerdSEQ is working properly)
Next there will be a guide through some basics, related to values which you find back in most
trackers. Then there will be some basic information about Trackers and after that information about
the navigation with the NerdSEQ.
Nerdseq – a tracker based Eurorack sequencer Page 7
User Manual Revision V0.9.9 for Firmware V1.13 27 February 2018
Numbers, Values and Tracker basics
The history of trackers6 goes back to the late 80’s when some people developed a new way of
creating music by inserting music scores in a different way. It is mostly recognized by people as a
way to program music instead of composing, because of the input of the music data. This is actually
not really the case, once you know some of the basics it is composing all the way!
Trackers are often used to play samples (in a note scale) on different tracks as well as to control the
soundchips of old homecomputers directly. The workflow is different from other score based or
maybe piano roll based sequencing.
With most of the trackers the workflow goes from up to down, the sequencing running from the top
to the bottom. There you will find different columns and rows. Each row shows a step in the
sequence and the main columns are dedicated to the tracks and subcolumns to different commands.
Each track consists mostly the same kind of sub columns. (Modern trackers allow different kind of
tracks and sub-columns). Getting to the subcolumns there is often a subcolumn for the music note,
one for the volume and sometimes one for a special command. Sometimes they are additional
columns, depending on what tracker it is. Music notes are mostly filled in with their real note,
followed by the octave. For example:
“C-3” means Note C on octave 3.
“F-5” means Note F on octave 5.
“D#2” is the note D sharp on octave 2 (half tone higher than D-2)
The exact look of the notes can differ between the trackers. With the NerdSEQ the notes are filled in
like in the example.
Other values of the subcolumns like the volume are often shown as a hexadecimal numeral value7.
I will explain only the very basics of it. Refer to the footnotes for detailed information.
We count and calculate usually in a base 10 system. We count like this
0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18…….On every 10th number (10 overflow) the left
digit increases. On every 100th number the left and the second left digit increases..etc.
In a hexadecimal system the base is 16 and so with every 16th number the left digit will increase.
The numbers itself are also represented differently. A hexadecimal count goes like this:
0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F,10,11,12,13,14,15,16,17,18,19,1A,1B…….
6 https://en.wikipedia.org/wiki/Music_tracker
7 https://en.wikipedia.org/wiki/Hexadecimal
Nerdseq – a tracker based Eurorack sequencer Page 8
User Manual Revision V0.9.9 for Firmware V1.13 27 February 2018
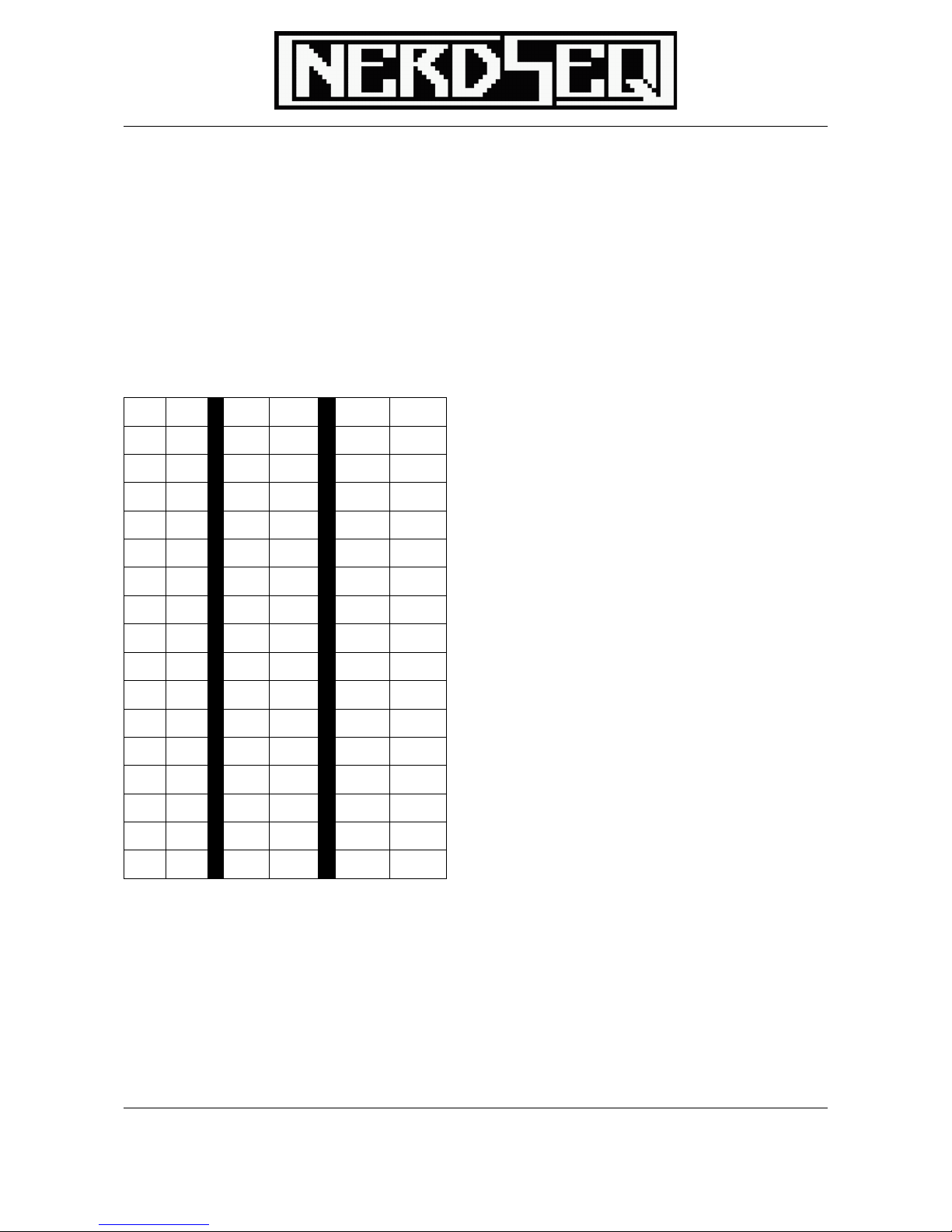
So instead of getting to the 10, letters are used to show the hexadecimal values until the 16th number
which will create the overflow for the digit on the left.
The decimal compared to the hexadecimal will show you the corresponding numbers:
Dec Hex Dec Hex Dec Hex
0 0 16 10 32 20
1 1 17 11 33 21
2 2 18 12 34 22
3 3 19 13 35 23
4 4 20 14 36 24
5 5 21 15 37 25
6 6 22 16 38 26
7 7 23 17 39 27
8 8 24 18 40 28
9 9 25 19 41 29
10 A 26 1A 42 2A
11 B 27 1B 43 2B
12 C 28 1C 44 2C
13 D 29 1D 45 2D
14 E 30 1E 46 2E
15 F 31 1F 47 2F
So in a hexadecimal system the number goes after 9F to A0 and after a FF to 100.
The Nerdseq uses also the hexadecimal system to show most of the values.
Furthermore, some trackers can show all content on one screen while some have to scroll to get to
other content and some have to switch to a different screen to get to the other content.
As the NerdSEQ got only a small display, the information is splitted logically into different screens.
Nerdseq – a tracker based Eurorack sequencer Page 9
User Manual Revision V0.9.9 for Firmware V1.13 27 February 2018
I will explain those later.
There is much more about trackers, check the links for more informations. I would also suggest to
check some tutorials about ‘LittleSoundDJ’ as it is the most similar to the tracker of the NerdSEQ.
Though they are some major differences, it gives a clue about how to work with dedicated screens.
I will also make a set of video tutorials at some point.
Buttons and Navigation
To navigate, change to other screens, edit values and more you use the Buttons.
On the top line the half buttons they are the buttons to go to another screen. These screens are:
Sequencer, Pattern, Patch, Table, Automate, Project. You can reach those screens by pressing the
corresponding buttons. (One footnote here, you can’t enter the pattern screen if there was no
pattern created first. Same for the patch screen. I will explain that later on. So no worries, your
buttons are not broken).
Those button have also a 2nd function which can be reached by pressing the Shift key together
(followed) by the other keys. Those are:
Mark - To start the marking of content on the screens
Copy – Copy earlier marked content
Delete – Delete current value or marked content
Record – to start/stop recording
Nerd – use for different functions (2do)
Setup – Enter the Setup screen
Further there are the buttons on the bottom left:
Start – Start sequencer or trigger a pattern
Stop – Stop a pattern (stop the sequencer in combination with SHIFT)
Shift - Get to the 2nd function of buttons or edit functionality
OK – Create a new pattern / patch. Enter/Accept
UP – Page up for 16 steps → move the cursor 16 rows up
DOWN – Page down for 16 steps → move the cursor 16 rows down
And the cursor keys on the right.
Note that they are also some other combinatons of the keys in different screens which will be
explained later on.
Nerdseq – a tracker based Eurorack sequencer Page 10
User Manual Revision V0.9.9 for Firmware V1.13 27 February 2018
For simple navigation you use the cursor keys:
Cursor up/down/left/right for simple navigation and scrolling
In most screens you can move your cursor and navigate like this. For example, in the sequencer
screen you change the Row by using cursor up/down and change the Track/Column by using
cursor left/right.
Using the cursor keys combined with the Shift key allows mostly some editing, as here explained
for the pattern screen:
SHIFT + CURSOR LEFT -> Decrease (-) value by 1 (value or semitone for notes)
SHIFT + CURSOR RIGHT -> Increase (+) value by 1 (value or semitone for notes)
SHIFT + DOWN/UP -> Decrease/Increase value by:
• 1 octave for notes
• 16 ($10) for regular values which can be < FF (255)
64 ($40) for values which can be > FF (255)
• 10 for FX types
So changing values is always in the smallest step by using cursor left/right and in bigger steps by
using cursor up/down
With SHIFT + DELETE you can delete/empty values
The button OK is mostly used to create new Patterns or Patches and to enter or agree/start a
menu option
Mute/Unmute track: Using the shortcut SHIFT+DOWN+START mutes or unmutes the current track
if in the Sequencer or Pattern screen. Mute does release the gate and keeps the CV voltage, but
won’t play anything else on the muted track until it is unmuted. It will sequence through though
while muted and the Break command is still working. So for example 16 step patterns will stay 16
step even if muted.
Solo/Unsolo track: Using SHIFT + UP + START solos the current track. That means all tracks will
be muted and the current track unmuted if needed. Unsoloing will unmute all tracks. Also, unmuting
other tracks or muting the solo track will release the solo function.
For fast unmuting all tracks you can press SHIFT + UP + START for the solo function twice and all
tracks are unmuted directly.
Nerdseq – a tracker based Eurorack sequencer Page 11
User Manual Revision V0.9.9 for Firmware V1.13 27 February 2018
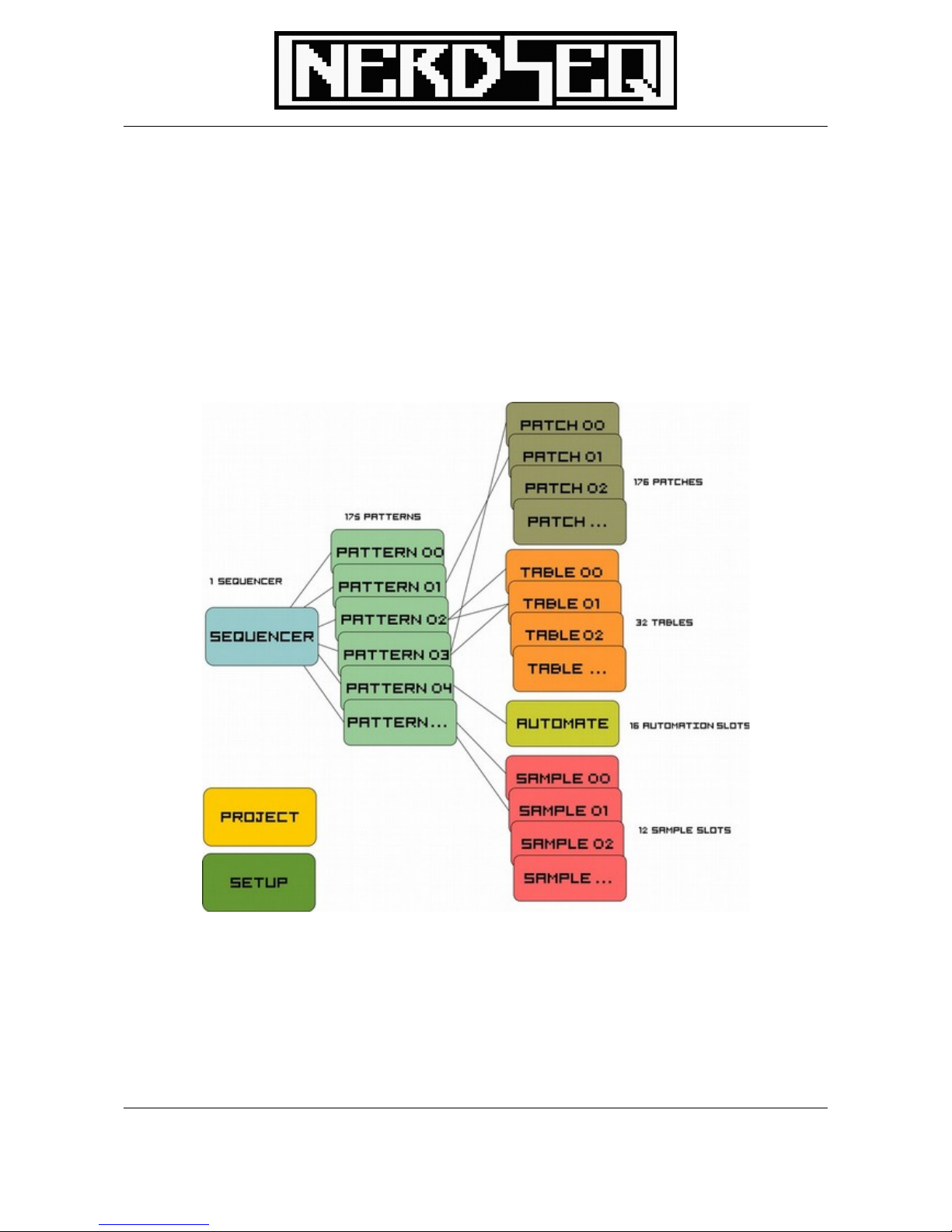
General Screen information
As mentioned before the main workflow is splitted into different screens.
The main screen is the Sequencer screen. From there you sequence the Patterns. You can
sequence each of the 176 patterns from each track if they are from the same type.
From the pattern you can access the different patches, tables, automations and/or samples.
Not directly dedicated to the sequencing are the Project and the Setup screen. Below a hopefully
simple view of the Sequencer → Patterns → Patch/Table/Automate/Sample relations.
Note that you can mostly freely use all patches, tables, automations or samples from the same or
different patterns. Also here, some are limited to the type which I will describe now. Depending on
which track the pattern is created, it is locked to the type of the track (not to the track itself). For
Nerdseq – a tracker based Eurorack sequencer Page 12
User Manual Revision V0.9.9 for Firmware V1.13 27 February 2018
example, if you create a pattern on a CV/Trigger/Gate track, then you can use it on any of the 6
CV/Trigger/Gate Tracks, but not on the sample tracks.
The same for the case if a pattern is created on a sample tracks, it can be used on the 2 sample
tracks, but not on the 6 CV/Trigger/Gate Tracks. The editor prevents this. The reason for this is that
the different types have some common but mostly different parameters which won’t fit to each
other. And to complete the explanation, when the Cartridge expanders with the Cartridges will be
released, many more types will appear for each kind of a cartridge.
The same goes for the patches which are then locked to the type of the pattern.
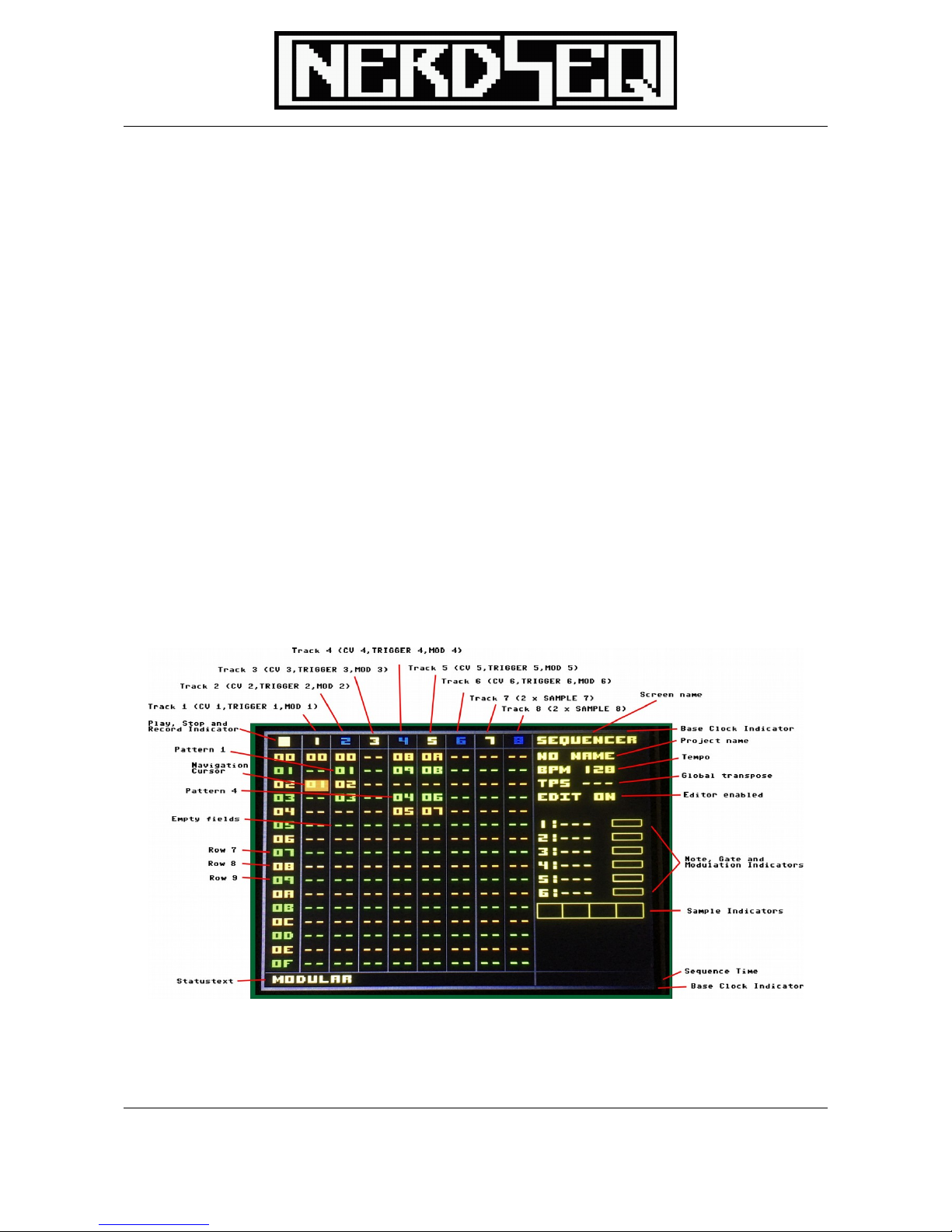
Sequencer Screen
In the sequencer screen you have different Rows and Columns. For the Columns they are 2 types.
One for the indication of the row, and the others are the actual Tracks of the sequencer.
Each track is dedicated to one output channel -> Track 1 for CV1, Trigger1 and MOD1
With the NerdSEQ, by default, there are 6 CV/TRIGGER/MOD tracks and 2 Sample tracks (with
each sample track being able to play 2 samples simultaneously, so 4 samples in total at any one
time).
Nerdseq – a tracker based Eurorack sequencer Page 13
User Manual Revision V0.9.9 for Firmware V1.13 27 February 2018
Loading...