WILEY ANTENNAS User Manual

Download

ANTENNAS

FROM THEORY TO PRACTICE

Yi Huang

University of Liverpool, UK

Kevin Boyle

NXP Semiconductors, UK

A John Wiley and Sons, Ltd, Publication

ANTENNAS

FROM THEORY TO PRACTICE

Yi Huang

University of Liverpool, UK

Kevin Boyle

NXP Semiconductors, UK

A John Wiley and Sons, Ltd, Publication

This edition ﬁrst published 2008



2008 John Wiley & Sons Ltd

Registered ofﬁce

John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex, PO19 8SQ, United Kingdom

For details of our global editorial ofﬁces, for customer services and for information about how to apply for permission to reuse the copyright material in this book please see our website at www.wiley.com.

The right of the author to be identiﬁed as the author of this work has been asserted in accordance with the Copyright, Designs and Patents Act 1988.

All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, except as permitted by the UK Copyright, Designs and Patents Act 1988, without the prior permission of the publisher.

Wiley also publishes its books in a variety of electronic formats. Some content that appears in print may not be available in electronic books.

Designations used by companies to distinguish their products are often claimed as trademarks. All brand names and product names used in this book are trade names, service marks, trademarks or registered trademarks of their respective owners. The publisher is not associated with any product or vendor mentioned in this book. This publication is designed to provide accurate and authoritative information in regard to the subject matter covered. It is sold on the understanding that the publisher is not engaged in rendering professional services. If professional advice or other expert assistance is required, the services of a competent professional should be sought.

Library of Congress Cataloging-in-Publication Data

Huang, Yi.

Antennas : from theory to practice / Yi Huang, Kevin Boyle.

p. cm. Includes bibliographical references and index. ISBN 978-0-470-51028-5 (cloth)

1. Antennas (Electronics) I. Boyle, Kevin. II. Title. TK7871.6.H79 2008



621.382

4—dc22 2008013164

A catalogue record for this book is available from the British Library.

ISBN 978-0-470-51028-5 (HB)

Typeset in 10/12pt Times by Aptara Inc., New Delhi, India. Printed in Singapore by Markono Print Media Pte Ltd, Singapore.

Preface xi

Acronyms and Constants xiii

1 Introduction 1

1.1 A Short History of Antennas 1

1.2 Radio Systems and Antennas 4

1.3 Necessary Mathematics 6

1.3.1 Complex Numbers 6

1.3.2 Vectors and Vector Operation 7

1.3.3 Coordinates 10

1.4 Basics of Electromagnetics 11

1.4.1 The Electric Field 12

1.4.2 The Magnetic Field 15

1.4.3 Maxwell’s Equations 16

1.4.4 Boundary Conditions 19

1.5 Summary 21 References 21 Problems 21

2 Circuit Concepts and Transmission Lines 23

2.1 Circuit Concepts 23

2.1.1 Lumped and Distributed Element Systems 25

2.2 Transmission Line Theory 25

2.2.1 Transmission Line Model 25

2.2.2 Solutions and Analysis 28

2.2.3 Terminated Transmission Line 32

2.3 The Smith Chart and Impedance Matching 41

2.3.1 The Smith Chart 41

2.3.2 Impedance Matching 44

2.3.3 The Quality Factor and Bandwidth 51

2.4 Various Transmission Lines 55

2.4.1 Two-wire Transmission Line 56

2.4.2 Coaxial Cable 57

2.4.3 Microstrip Line 60

vi Contents

2.4.4 Stripline 63

2.4.5 Coplanar Waveguide (CPW) 66

2.4.6 Waveguide 68

2.5 Connectors 70

2.6 Summary 74 References 74 Problems 74

3 Field Concepts and Radio Waves 77

3.1 Wave Equation and Solutions 77

3.1.1 Discussion on Wave Solutions 79

3.2 The Plane Wave, Intrinsic Impedance and Polarization 80

3.2.1 The Plane Wave and Intrinsic Impedance 80

3.2.2 Polarization 82

3.3 Radio Wave Propagation Mechanisms 83

3.3.1 Reﬂection and Transmission 83

3.3.2 Diffraction and Huygens’s Principle 91

3.3.3 Scattering 92

3.4 Radio Wave Propagation Characteristics in Media 93

3.4.1 Media Classiﬁcation and Attenuation 93

3.5 Radio Wave Propagation Models 97

3.5.1 Free Space Model 97

3.5.2 Two-ray Model/Plane Earth Model 98

3.5.3 Multipath Models 99

3.6 Comparison of Circuit Concepts and Field Concepts 101

3.6.1 Skin Depth 101

3.7 Summary 104 References 104 Problems 104

4 Antenna Basics 107

4.1 Antennas to Radio Waves 107

4.1.1 Near Field and Far Field 108

4.1.2 Antenna Parameters from the Field Point of View 112

4.2 Antennas to Transmission Lines 122

4.2.1 Antenna Parameters from the Circuit Point of View 122

4.3 Summary 125 References 126 Problems 126

5 Popular Antennas 129

5.1 Wire-Type Antennas 129

5.1.1 Dipoles 129

5.1.2 Monopoles and Image Theory 137

5.1.3 Loops and the Duality Principle 141

5.1.4 Helical Antennas 147

Contents vii

5.1.5 Yagi–Uda Antennas 152

5.1.6 Log-Periodic Antennas and Frequency-Independent Antennas 157

5.2 Aperture-Type Antennas 163

5.2.1 Fourier Transforms and the Radiated Field 163

5.2.2 Horn Antennas 169

5.2.3 Reﬂector and Lens Antennas 175

5.2.4 Slot Antennas and Babinet’s Principle 180

5.2.5 Microstrip Antennas 184

5.3 Antenna Arrays 191

5.3.1 Basic Concept 192

5.3.2 Isotropic Linear Arrays 193

5.3.3 Pattern Multiplication Principle 199

5.3.4 Element Mutual Coupling 200

5.4 Some Practical Considerations 203

5.4.1 Transmitting and Receiving Antennas: Reciprocity 203

5.4.2 Baluns and Impedance Matching 205

5.4.3 Antenna Polarization 206

5.4.4 Radomes, Housings and Supporting Structures 208

5.5 Summary 211 References 211 Problems 212

6 Computer-Aided Antenna Design and Analysis 215

6.1 Introduction 215

6.2 Computational Electromagnetics for Antennas 217

6.2.1 Method of Moments (MoM) 218

6.2.2 Finite Element Method (FEM) 228

6.2.3 Finite-Difference Time Domain (FDTD) Method 229

6.2.4 Transmission Line Modeling (TLM) Method 230

6.2.5 Comparison of Numerical Methods 230

6.2.6 High-Frequency Methods 232

6.3 Examples of Computer-Aided Design and Analysis 233

6.3.1 Wire-type Antenna Design and Analysis 233

6.3.2 General Antenna Design and Analysis 243

6.4 Summary 251 References 251 Problems 252

7 Antenna Manufacturing and Measurements 253

7.1 Antenna Manufacturing 253

7.1.1 Conducting Materials 253

7.1.2 Dielectric Materials 255

7.1.3 New Materials for Antennas 255

7.2 Antenna Measurement Basics 256

7.2.1 Scattering Parameters 256

7.2.2 Network Analyzers 258

viii Contents

7.3 Impedance, S11, VSWR and Return Loss Measurement 261

7.3.1 Can I Measure These Parameters in My Ofﬁce? 261

7.3.2 Effects of a Small Section of a Transmission Line or a Connector 262

7.3.3 Effects of Packages on Antennas 262

7.4 Radiation Pattern Measurements 263

7.4.1 Far-Field Condition 264

7.4.2 Open-Area Test Sites (OATS) 265

7.4.3 Anechoic Chambers 267

7.4.4 Compact Antenna Test Ranges (CATR) 268

7.4.5 Planar and Cylindrical Near-Field Chambers 270

7.4.6 Spherical Near-Field Chambers 270

7.5 Gain Measurements 272

7.5.1 Comparison with a Standard-Gain Horn 272

7.5.2 Two-Antenna Measurement 272

7.5.3 Three-Antenna Measurement 273

7.6 Miscellaneous Topics 273

7.6.1 Efﬁciency Measurements 273

7.6.2 Reverberation Chambers 274

7.6.3 Impedance De-embedding Techniques 275

7.6.4 Probe Array in Near-Field Systems 276

7.7 Summary 281 References 281 Problems 282

8 Special Topics 283

8.1 Electrically Small Antennas 283

8.1.1 The Basics and Impedance Bandwidth 283

8.1.2 Antenna Size-Reduction Techniques 299

8.2 Mobile Antennas, Antenna Diversity and Human Body Effects 304

8.2.1 Introduction 304

8.2.2 Mobile Antennas 305

8.2.3 Antenna Diversity 318

8.2.4 User Interaction 325

8.3 Multiband and Ultra-Wideband Antennas 334

8.3.1 Introduction 334

8.3.2 Multiband Antennas 334

8.3.3 Wideband Antennas 337

8.4 RFID Antennas 340

8.4.1 Introduction 340

8.4.2 Near-Field Systems 343

8.4.3 Far-Field Systems 349

8.5 Reconﬁgurable Antennas 352

8.5.1 Introduction 352

8.5.2 Switching and Variable-Component Technologies 352

8.5.3 Resonant Mode Switching/Tuning 354

Contents ix

8.5.4 Feed Network Switching/Tuning 355

8.5.5 Mechanical Reconﬁguration 355

8.6 Summary 356 References 356

Index 357

Preface

As an essential element of a radio system, the antenna has always been an interesting but difﬁcult subject for radio frequency (RF) engineering students and engineers. Many good books on antennas have been published over the years and some of them were used as our major references.

This book is different from other antenna books. It is especially designed for people who know little about antennas but would like to learn this subject from the very basics to practical antenna analysis, design and measurement within a relatively short period of time. In order to gain a comprehensive understanding of antennas, one must know about transmission lines and radio propagation. At the moment, people often have to read a number of different books, which may not be well correlated. Thus, it is not the most efﬁcient way to study the subject. In this book we put all the necessary information about antennas into a single volume and try to examine antennas from both the circuit point of view and the ﬁeld point of view. The book covers the basic transmission line and radio propagation theories, which are then used to gain a good understanding of antenna basics and theory. Various antennas are examined and design examples are presented. Particular attention is given to modern computer-aided antenna design. Both basic and advanced computer software packages are used in examples to illustrate how they can be used for antenna analysis and design. Antenna measurement theory and techniques are also addressed. Some special topics on the latest antenna development are covered in the ﬁnal chapter.

The material covered in the book is mainly based on a successful short course on antennas for practising professionals at the University of Oxford and the Antennas module for students at the University of Liverpool. The book covers important and timely issues involving modern practical antenna design and theory. Many examples and questions are given in each chapter. It is an ideal textbook for universityantenna courses, professionaltraining courses and self-study. It isalso a valuable reference forengineers anddesigners who work with RF engineering, radar and radio communications.

The book is organized as follows:

Chapter 1:Introduction.The objective of this chapter is tointroduce theconcept of antennas and review essential mathematics and electromagnetics, especially Maxwell’s equations. Material properties (permittivity,permeability and conductivity) are discussed and some common ones are tabulated.

Chapter 2: Circuit Concepts and Transmission Lines. The concepts of lumped and distributed systems are established. The focus is placed on the fundamentals and characteristics of transmission lines. A comparison of various transmission lines and connectors is presented. The Smith Chart, impedance matching and bandwidth are also addressed in this chapter.

xii Preface

Chapter 3: Field Concepts and Radio Waves. Field concepts, including the plane wave, intrinsic impedance and polarization, are introduced and followed by a discussion on radio propagation mechanisms and radio wave propagation characteristics in various media. Some basic radio propagation models are introduced, and circuit concepts and ﬁeld concepts are compared at the end of this chapter.

Chapter 4: Antenna Basics. The essential and important parameters of an antenna (such as the radiation pattern, gain and input impedance) are addressed from both the circuit point of view and ﬁeld point of view. Through this chapter, you will become familiar with antenna language, understand how antennas work and know what design considerations are.

Chapter 5:Popular Antennas. In this long chapter, some of the most popular antennas (wiretype, aperture-type and array antennas) are examined and analyzed using relevant antenna theories. The aim is to see why they have become popular, what their major features and properties are (including advantages and disadvantages) and how they should be designed.

Chapter 6: Computer-Aided Antenna Design and Analysis.Theaimofthis special and unique chapter is to give a brief review of antenna-modeling methods and software development, introduce the basic theory behind computer simulation tools and demonstrate how to use industry standard software to analyze and design antennas. Two software packages (one is simple and free) are presented with step-by-step illustrations.

Chapter 7: Antenna Manufacturing and Measurements. This is another practical chapter to address two important issues: how to make an antenna and how to conduct antenna measurement, with a focus placed on the measurement. It introduces S-parameters and equipment. A good overview of the possible measurement systems is provided with an in-depth example. Some measurement techniques and problems are also presented.

Chapter 8: Special Topics. This ﬁnal chapter presents some of the latest important developments in antennas. It covers mobile antennas and antenna diversity, RFID antennas, multiband and broadband antennas, reconﬁgurable antennas and electrically small antennas. Both the theory and practical examples are given.

The authors are indebted to the many individuals whoprovidedusefulcomments,suggestions and assistance to make this book a reality. In particular, we would like to thank Shahzad Maqbool, Barry Cheeseman and Yang Lu at the University of Liverpool for constructive feedback and producing ﬁgures, Staff at Wiley for their help and critical review of the book, Lars Foged at SATIMO and Mike Hillbun at Diamond Engineering for their contribution to Chapter 7 and the individuals and organizations who have provided us with their ﬁgures or allowed us to reproduce their ﬁgures.

Yi Huang and Kevin Boyle

Acronyms and Constants

AC Alternating current AF Antenna factor AM Amplitude modulation AR Axial ratio AUT Antenna under test BER Bit error rate CAD Computer-aided design CATR Compact antenna test range CDF Cumulative distribution function CEM Computational electromagnetics CP Circular polarization CPW Coplanar waveguide DC Direct current DCS Digital cellular system DRA Dielectric resonant antenna DUT Device under test EGC Equal gain combining EIRP Effective isotropic radiated power EM Electromagnetic EMC Electromagnetic compatibility ERP Effective radiated power FDTD Finite-difference time domain FEM Finite element method FNBW First null beamwidth GPS Global positioning system GSM Global System for Mobile communications GTD Geometrical theory of diffraction HPBW Half-power beamwidth HW Hansen–Woodyard (condition) ISI Inter-symbol interference

8.85419 ×10 4π ×10−7H/m

≈ 377 

−12

F/m

xiv Acronyms and Constants

LCP Left-hand circular polarization

Liquid crystal polymer LPDA Log-periodic dipole antenna MEMS Micro electromechanical systems MIMO Multiple-in, multiple-out MMIC Monolithic microwave integrated circuits MoM Method of moments MRC Maximal ratio combining NEC Numerical electromagnetic code OATS Open area test site PCB Printed circuit board PDF Power density function

Probability density function PIFA Planar inverted F antenna PO Physical optics PTFE Polytetraﬂuoroethylene RAM Radio-absorbing material RCP Right-hand circular polarization RCS Radar cross-section RF Radio frequency RFID Radio frequency identiﬁcation RMS Root mean square SAR Speciﬁc absorption rate SC Selection combining SI units International system of units (metric system) SLL Side-lobe level SNR Signal-to-noise ratio SWC Switch combining TE Transverse electric (mode/ﬁeld) TEM Transverse electromagnetic (mode/ﬁeld) TM Transverse magnetic (mode/ﬁeld) TV Television UHF Ultra-high frequency UTD Uniform theory of diffraction UWB Ultra-wide band VHF Very high frequency VNA Vector network analyzer VSWR Voltage standing wave ratio WLAN Wireless local area network WiMax Worldwide interoperability of microwave access

Introduction

1.1 A Short History of Antennas

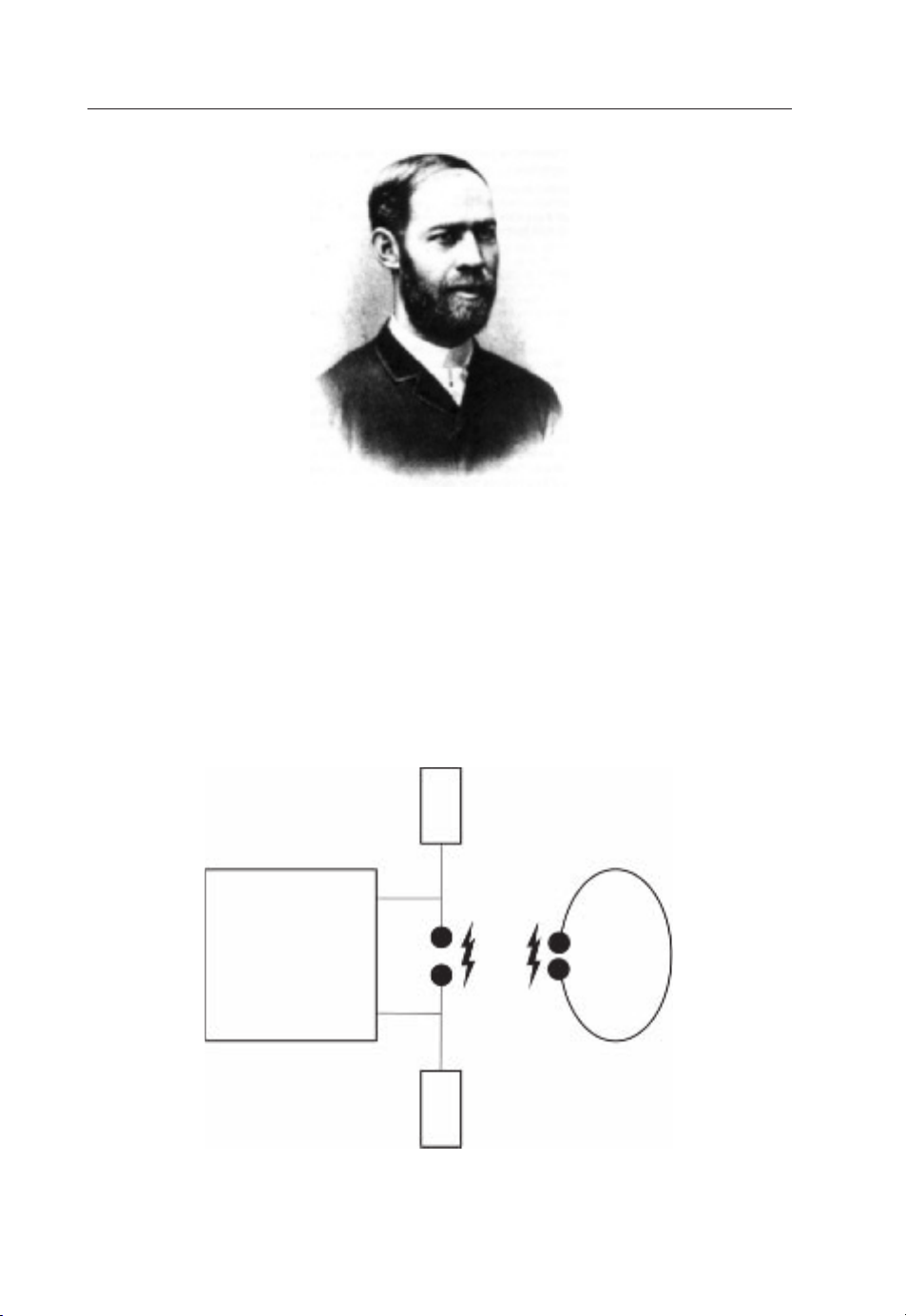
Work onantennasstartedmanyyears ago. The ﬁrstwell-knownsatisfactoryantennaexperiment was conducted by the German physicist Heinrich Rudolf Hertz (1857–1894), pictured in Figure 1.1. The SI (International Standard) frequency unit, the Hertz, is named after him. In 1887 he built a system, as shown in Figure 1.2, to produce and detect radio waves. The original intention of his experiment was to demonstrate the existence of electromagnetic radiation.

In the transmitter, a variable voltage source was connected to a dipole (a pair of one-meter wires) with two conducting balls (capacity spheres) at the ends. The gap between the balls could be adjusted for circuitresonance as well as forthe generation ofsparks. When the voltage was increased to a certain value, a spark or break-down discharge was produced. The receiver was asimple loop with two identical conducting balls. The gap between theballs wascarefully tuned to receive the spark effectively. He placed the apparatus in a darkened box in order to see the spark clearly. In his experiment, when a spark was generated at the transmitter, he also observed a spark at the receiver gap at almost the same time. This proved that the information from location A (the transmitter) was transmitted to location B (the receiver) in a wireless manner – by electromagnetic waves.

The information in Hertz’s experiment was actually in binary digital form, by tuning the spark on andoff.Thiscould be considered theveryﬁrst digital wireless system,which consisted of two of the best-known antennas: the dipole and the loop. For this reason, the dipole antenna is also called the Hertz (dipole) antenna.

Whilst Heinrich Hertz conducted his experiments in a laboratory and did not quite know what radio waves might be used for in practice, Guglielmo Marconi (1874–1937, pictured in Figure 1.3), an Italian inventor, developed and commercialized wireless technology by introducing a radiotelegraph system, which served as the foundation for the establishment of numerous afﬁliated companies worldwide. His most famous experiment was the transatlantic transmission from Poldhu, UK to St Johns, Newfoundland in Canada in 1901, employing untuned systems. He shared the 1909 Nobel Prize for Physics with Karl Ferdinand Braun ‘in recognition of their contributions to the development of wireless telegraphy’. Monopole antennas (near quarter-wavelength) were widely used in Marconi’s experiments; thus vertical monopole antennas are also called Marconi antennas.

Antennas: From Theory to Practice Yi Huang and Kevin Boyle



2008 John Wiley & Sons, Ltd

2 Antennas: From Theory to Practice

Figure 1.1 Heinrich Rudolf Hertz

During World War II, battles were won by the side that was ﬁrst to spot enemy aeroplanes, ships or submarines. To give the Allies an edge, British and American scientists developed radar technology to ‘see’ targets from hundreds of miles away, even at night. The research resulted in the rapid development of high-frequency radar antennas, which were no longer just wire-type antennas. Some aperture-type antennas, such as reﬂector and horn antennas, were developed, an example is shown in Figure 1.4.

Variable

Voltage Source

Figure 1.2 1887 experimental set-up of Hertz’s apparatus

Loop

Introduction 3

Figure 1.3 Guglielmo Marconi

Broadband, circularly polarized antennas, as well as many other types, were subsequently developed for various applications. Since an antenna is an essential device for any radio broadcasting, communication or radar system, there has always been a requirement for new and better antennas to suit existing and emerging applications.

More recently, one of the main challenges for antennas has been how to make them broadband and small enough in size for wireless mobile communications systems. For example, WiMAX (worldwide interoperability for microwave access) is one of the latest systems aimed at providing high-speed wireless data communications (>10 Mb/s) over long distances from point-to-point links tofull mobile cellular-typeaccess over a widefrequencyband. The original WiMAX standard in IEEE 802.16 speciﬁed 10 to 66 GHz as the WiMAX band; IEEE 802.16a

Figure 1.4 World War II radar (Reproduced by permission of CSIRO Australia Telescope National Facility)

4 Antennas: From Theory to Practice

was updated in 2004 to 802.16-2004 and added 2 to 11 GHz as an additional frequency range. The frequency bandwidth is extremely wide although the most likely frequency bands to be used initially will be around 3.5 GHz, 2.3/2.5 GHz and 5 GHz.

The UWB (ultra-wide band) wireless system is another example of recent broadband radio communication systems. The allocated frequency band is from 3.1 to 10.6 GHz. The beauty of the UWB system is that the spectrum, which is normally very expensive, can be used free of charge but the power spectrum density is limited to −41.3 dBm/MHz. Thus, it is only suitable for short-distance applications. The antenna design for these systems faces many challenging issues.

The role of antennas is becoming increasingly important. In some systems, the antenna is now no longer just a simple transmitting/receiving device, but a device which isintegrated with other parts of the system to achieve better performance. For example, the MIMO (multiple-in, multiple-out) antenna system has recently been introduced as an effective means to combat multipath effects in the radio propagation channel and increase the channel capacity, where several coordinated antennas are required.

Things have been changing quickly in the wireless world. But one thing has never changed since the very ﬁrst antenna was made: the antenna is a practical engineering subject. It will remain an engineering subject. Once an antenna is designed and made, it must be tested. How well it works is not just determined by the antenna itself, it also depends on the other parts of the system and the environment. The standalone antenna performance can be very different from that of an installed antenna. For example, when a mobile phone antenna is designed, we must take the case, other parts of the phone and even our hands into account to ensure that it will work well in the real world. The antenna is an essential device of a radio system, but not an isolated device! This makes it an interesting and challenging subject.

1.2 Radio Systems and Antennas

A radio system is generally considered to be an electronic system which employs radio waves, a type of electromagnetic wave up to GHz frequencies. An antenna, as an essential part of a radio system, is deﬁned as a device which can radiate and receive electromagnetic energy in an efﬁcient and desired manner. It is normally made of metal, but other materials may also be used. For example, ceramic materials have been employed to makedielectricresonatorantennas (DRAs). There are many things in our lives, such as power leads, that can radiate and receive electromagnetic energy but they cannot be viewed as antennas because the electromagnetic energy is not transmitted or received in an efﬁcient and desired manner, and because they are not a part of a radio system.

Since radio systems possess some unique and attractive advantages over wired systems, numerous radio systems have been developed. TV, radar and mobile radio communication systems are just some examples. The advantages include:

mobility: this is essential for mobile communications;

good coverage: the radiation from an antenna can cover a very large area, which is good for TV and radio broadcasting and mobile communications;

low pathloss: this is frequency dependent. Since the loss of a transmission line is an exponential function of the distance (the loss in dB =distance ×per unit loss in dB) and the loss

Introduction 5

of a radio wave is proportional to the distance squared (the loss in dB = 20 log10(distance)), the pathloss of radio waves can be much smaller than that of a cable link. For example, assume that the loss is 10 dB for both a transmission line and a radio wave over 100 m; if the distance is now increased to 1000 m, the loss for the transmission line becomes 10 × 10 = 100 dB but the loss for the radio link is just 10 + 20 = 30 dB! This makes the radio link extremely attractive for long-distance communication. It should be pointed out that optical ﬁbers are also employed for long-distance communications since they are of very low loss and ultra-wide bandwidth.

Figure 1.5 illustrates a typical radio communication system. The source information is normally modulatedand ampliﬁed in the transmitter and then passed on to thetransmit antenna via a transmission line, which has a typical characteristic impedance (explained in the next chapter) of 50 ohms. The antenna radiates the information in the form of an electromagnetic wave in an efﬁcient and desired manner to the destination, where the information is picked up by the receive antenna and passed on to the receiver via another transmission line. The signal is demodulated and the original message is then recovered at the receiver.

Thus, the antenna is actually a transformer that transforms electrical signals (voltages and currents from a transmission line) into electromagnetic waves (electric and magnetic ﬁelds), or vice versa. For example, a satellite dish antenna receives the radio wave from a satellite and transforms it into electrical signalswhich areoutput to a cable tobe further processed. Our eyes may be viewed as another example of antennas. In this case, the wave is not a radio wave but an optical wave, another form of electromagnetic wave which has much higher frequencies.

Now it is clear that the antenna is actually a transformer of voltage/current to electric/ magnetic ﬁelds, it can also be considered a bridge to link the radio wave and transmission line. An antennasystem isdeﬁned asthe combinationof theantenna andits feedline. Asan antenna is usually connected to a transmission line, how to best make this connection is a subject of interest, since the signal from the feed line should be radiated into the space in an efﬁcient and desired way. Transmission lines and radio waves are, in fact, two different subjects in engineering. To understand antenna theory, one has to understand transmission lines and radio waves, which will be discussed in detail in Chapters 2 and 3 respectively.

In some applications where space is very limited (such as hand-portables and aircraft), it is desirable to integrate the antenna and its feed line. In other applications (such as the reception of TV broadcasting), the antenna is far away from the receiver and a long transmission line has to be used.

Unlike other devices in a radio system (such as ﬁlters and ampliﬁers), the antenna is a very special device; itdeals with electrical signals (voltages and currents) as well aselectromagnetic waves (electric ﬁelds and magnetic ﬁelds), making antenna design an interesting and difﬁcult

Transmission

Transmitter

Line

Antenna

Electromagnetic

wave

Figure 1.5 A typical radio system

Antenna

Receiver

6 Antennas: From Theory to Practice

subject. For different applications, the requirements on theantenna may be verydifferent, even for the same frequency band.

In conclusion, the subject of antennas is about how to design a suitable device which will be well matched with its feed line and radiate/receive the radio waves in an efﬁcient and desired manner.

1.3 Necessary Mathematics

To understand antenna theory thoroughly requires a considerable amount of mathematics. However, the intention of this book is to provide the reader with a solid foundation in antenna theory andapply the theory to practical antenna design. Here weare justgoing tointroduce and review the essential and important mathematics required for this book. More in-depth study materials can be obtained from other references [1, 2].

1.3.1 Complex Numbers

In mathematics, a complex number, Z, consists of real and imaginary parts, that is

Z = R + jX (1.1)

where R is called the real part of the complex number Z , i.e. Re(Z), and X is deﬁned as the imaginary part of Z , i.e. Im(Z). Both R and X are real numbers and j (not the traditional notation i in mathematics to avoid confusion with a changing current in electrical engineering) is the imaginary unit and is deﬁned by

√

j =

−1 (1.2)

Thus

=−1 (1.3)

Geometrically, a complex number can be presented in a two-dimensional plane where the imaginary part is found on the vertical axis whilst the real part is presented by the horizontal axis, as shown in Figure 1.6.

In this model, multiplication by −1 corresponds to a rotation of 180 degrees about the origin. Multiplication by j corresponds toa 90-degree rotation anti-clockwise,and the equation

=−1 is interpreted as saying that if we apply two 90-degree rotations about the origin, the net resultis asingle 180-degree rotation. Notethat a 90-degree rotation clockwise also satisﬁes this interpretation.

Another representation of a complex number Z uses the amplitude and phase form:

Z = Ae

jϕ

(1.4)

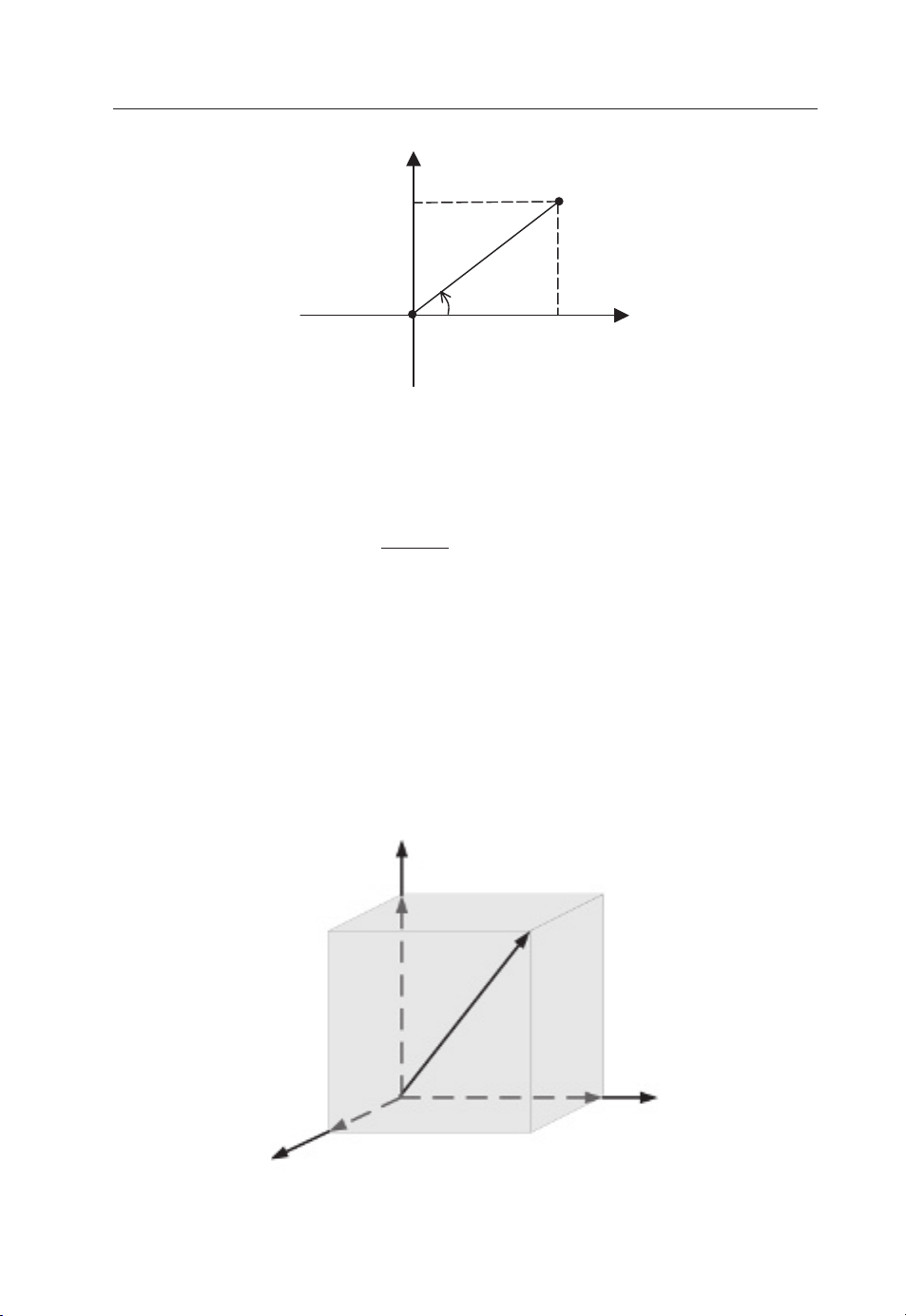
Introduction 7

Z (R, X)

Figure 1.6 The complex plane

where A is the amplitude and ϕ is the phase of the complex number Z; these are also shown in Figure 1.6. The two different representations are linked by the following equations:

Z = R + jX = Ae

√

A =

R2+ X2,ϕ= tan−1(X/R)

jϕ

;

(1.5)

R = A cos ϕ, X = A sin ϕ

1.3.2 Vectors and Vector Operation

A scalar is a one-dimensional quantity which has magnitude only, whereas a complex number is a two-dimensional quantity. A vector can be viewed as a three-dimensional (3D) quantity, and a special one – it has both a magnitude and a direction. For example, force and velocity are vectors (whereas speed is a scalar). A position in space is a 3D quantity, but it does not have a direction, thus it is not a vector. Figure 1.7 is an illustration of vector A in Cartesian

Figure 1.7 Vector A in Cartesian coordinates

8 Antennas: From Theory to Practice

coordinates. It has three orthogonal components (Ax, Ay, Az) along the x, y and z directions, respectively. To distinguish vectors from scalars, the letter representing the vector is printed in bold, for example A or a, and a unit vector is printed in bold with a hat over the letter, for exampleˆx orˆn.

The magnitude of vector A is given by



|A|

= A =

+ A

(1.6)

Now let us consider two vectors A and B:

A = A

B = B

x + A

x + B

y + A

y + B

The addition and subtraction of vectors can be expressed as

A + B = (A A − B = (A

+ Bx)ˆx + (Ay+ By)ˆy + (Az+ Bz)ˆz

− Bx)ˆx + (Ay− By)ˆy + (Az− Bz)ˆz

(1.7)

Obviously, the addition obeys the commutative law, that is A + B = B + A.

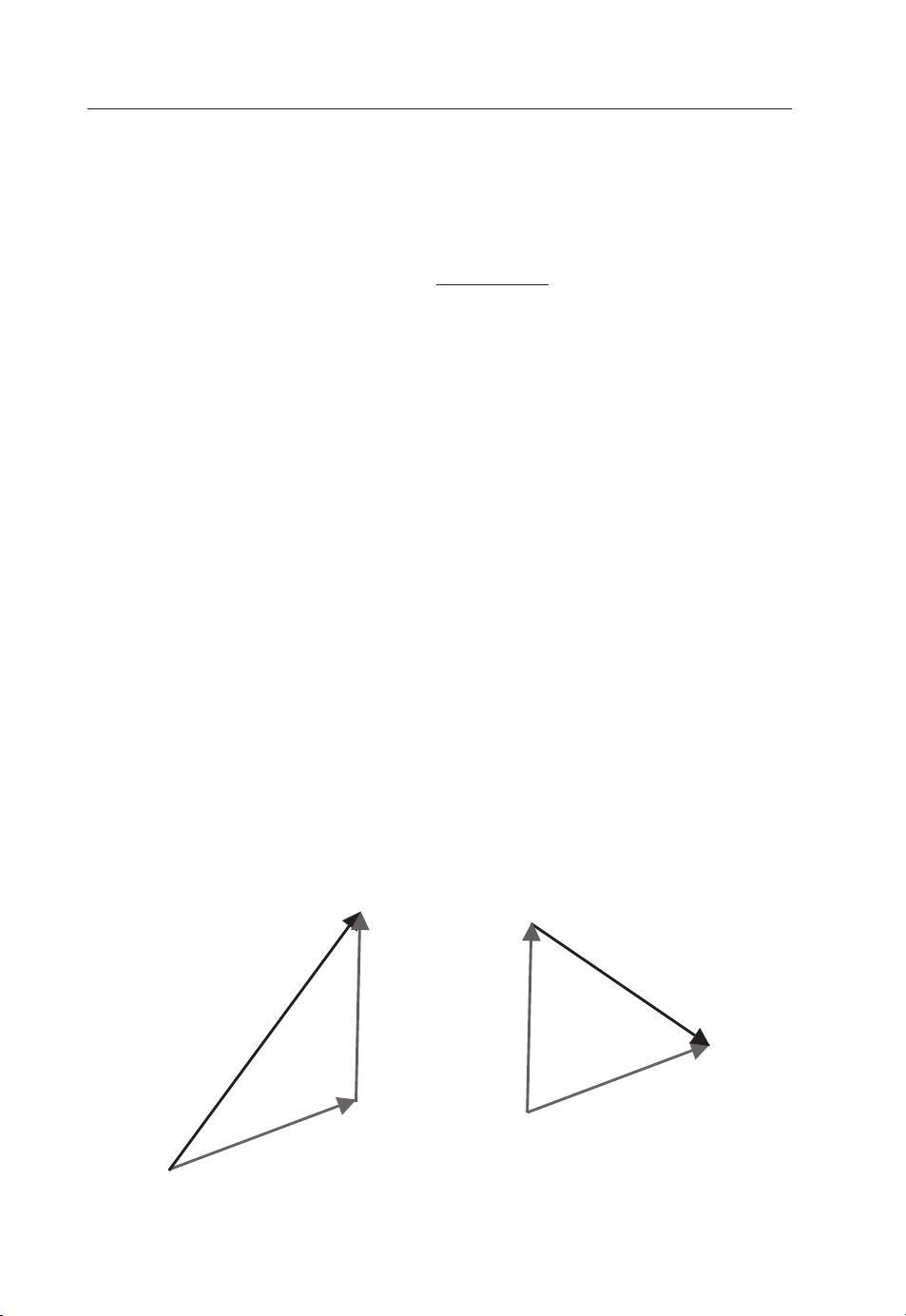
Figure 1.8 shows what the addition and subtraction mean geometrically. A vector may be multiplied or divided by a scalar. The magnitude changes but its direction remains the same. However, the multiplication of two vectors is complicated. There are two types of multiplication: the dot product and the cross product.

The dot product of two vectors is deﬁned as

ArB =|A||B|cos θ = A

+ AyBy+ AzB

xBx

(1.8)

where θ is the angle between vector A and vector B and cos θ is also called the direction cosine. The dotrbetween A and B indicates the dot product, which results in a scalar; thus, it is also called a scalar product. If the angle θ is zero, A and B are in parallel – thedot product is

A–B

A+B

Figure 1.8 Vector addition and subtraction

Introduction 9

Right-Hand

Rule

Figure 1.9 The cross product of vectors A and B

maximized – whereas for an angle of 90 degrees, i.e. when A and B are orthogonal, the dot product is zero.

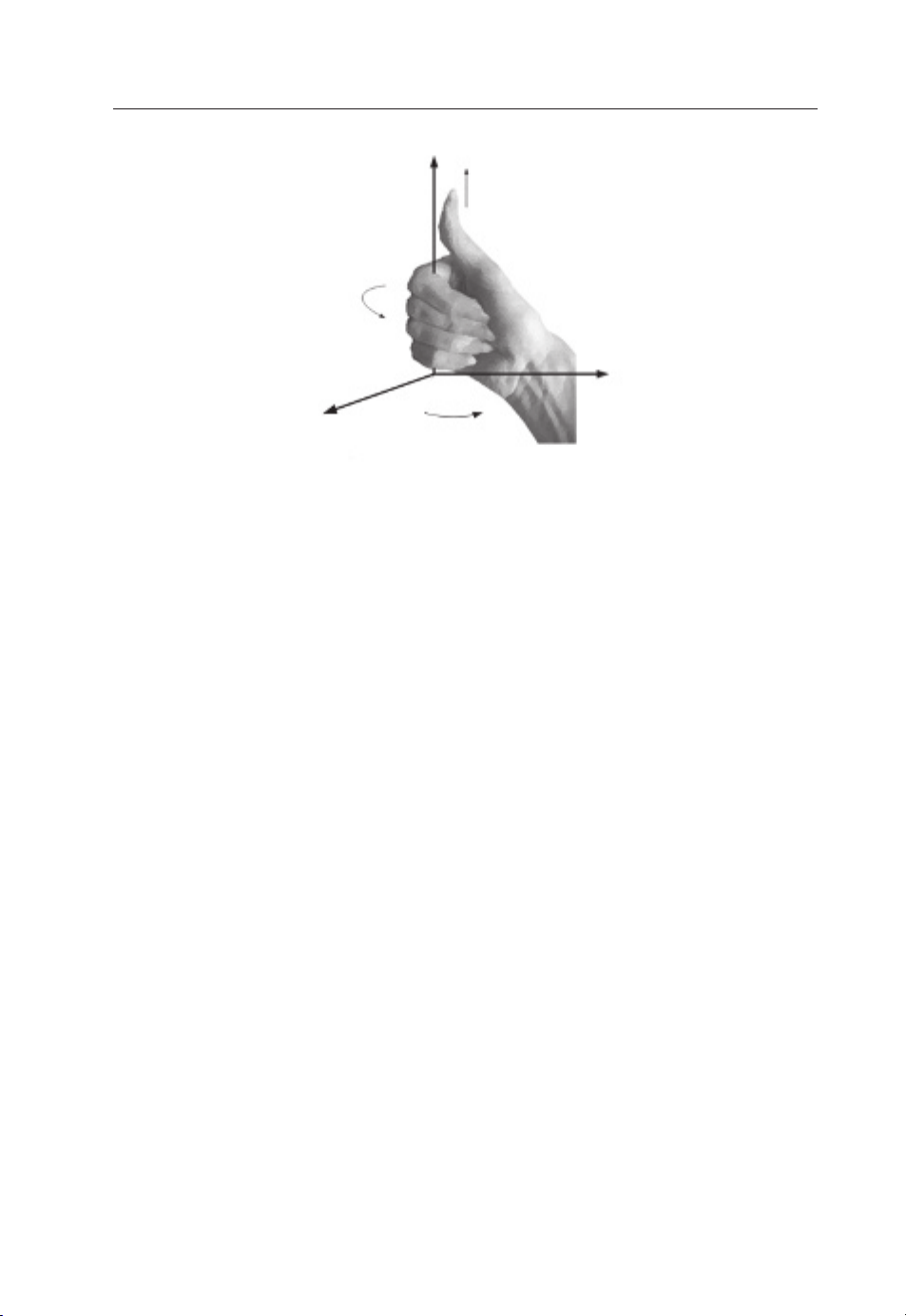
It is worth noting that the dot product obeys the commutative law, that is, ArB = BrA. The cross product of two vectors is deﬁned as

A × B =ˆn|A||B|sin θ = C

=ˆx(A

− AzBy) +ˆy( AzBx− AxBz) +ˆz( AxBy− AyBx)

yBz

(1.9)

whereˆn is a unit vector normal to the plane containing A and B. The cross × between A and B indicates the cross product, which results in a vector C; thus, it is also called a vector product. The vector C is orthogonal to both A and B, and the direction of C follows a so-called right-hand rule, as shown in Figure 1.9. If the angle θ is zero or 180 degrees, that is, A and B are in parallel, the cross product is zero; whereas for an angle of 90 degrees, i.e. A and B are orthogonal, the cross product of these two vectors reaches a maximum.Unlike the dot product, the cross product does not obey the commutative law.

The cross product may be expressed in determinant form as follows, which is the same as

Equation (1.9) but may be easier for some people to memorize:

A × B =

 

xˆy

 

  

AyA

BxByB

 

  

 

(1.10)

Another important thing about vectors is that any vector can be decomposed into three orthogonal components (such as x, y and z components) in 3D or two orthogonal components in a 2D plane.

Example 1.1: Vector operation. Given vectors A = 10

x + 5ˆy + 1ˆz and B = 2ˆy, ﬁnd:

A + B; A − B; A • B; and A × B

10 Antennas: From Theory to Practice

Solution:

A + B = 10ˆx + (5 +2)ˆy + 1ˆz = 10ˆx + 7ˆy + 1ˆz; A − B = 10ˆx + (5 −2)ˆy + 1ˆz = 10ˆx + 3ˆy + 1ˆz; A • B = 0 +(5 ×2) + 0 = 10; A × B = 10 ×2ˆz + 1 × 2ˆx = 20ˆz + 2ˆx

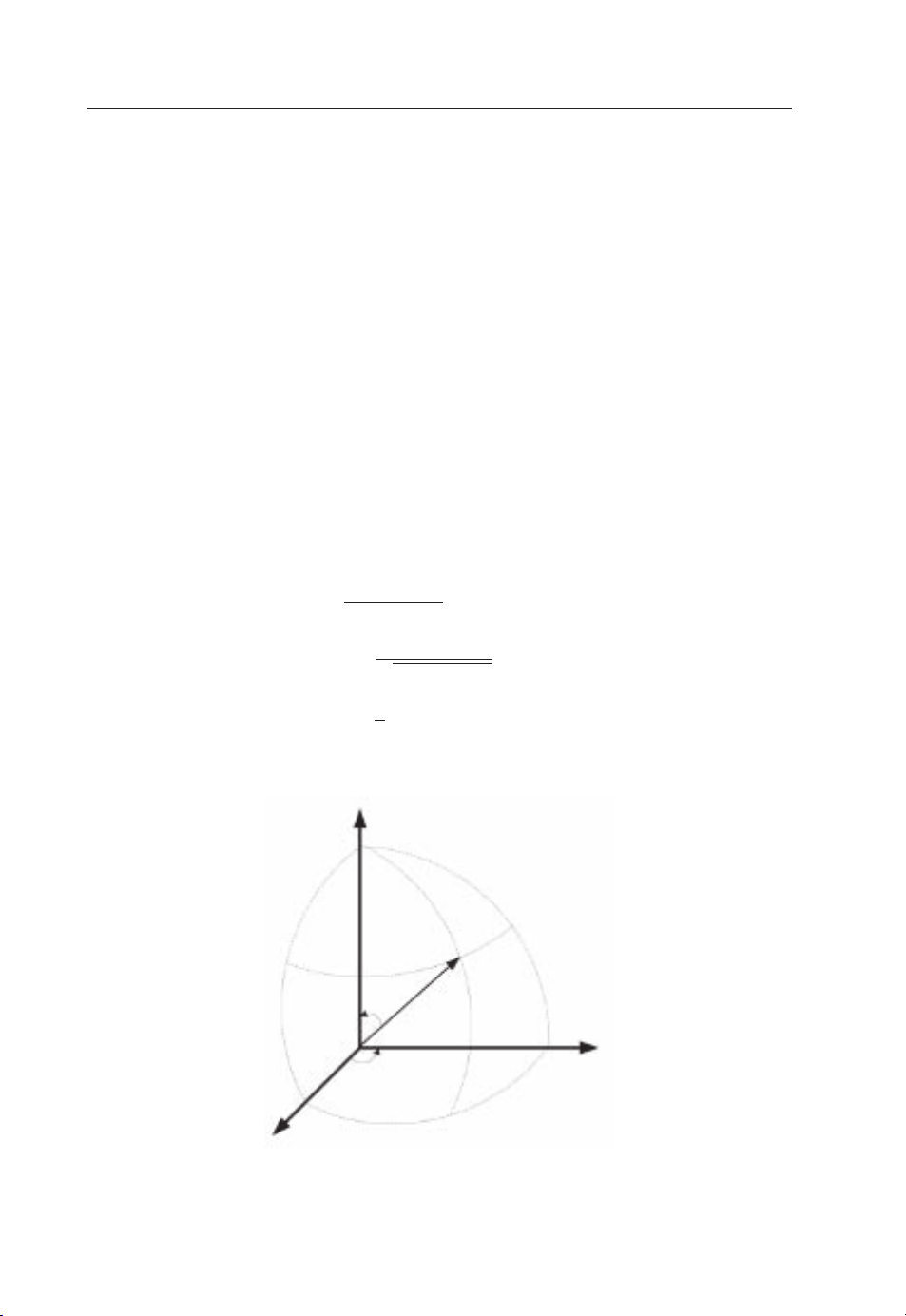
1.3.3 Coordinates

In addition to the well-known Cartesian coordinates, spherical coordinates (r, θ,φ), as shown in Figure 1.10,will also be used frequentlythroughout this book.These two coordinatesystems have the following relations:

x = r sin θ cosφ y = r sin θ sinφ z = r cos θ

and

(1.11)



r =

θ = cos

φ = tan

x2+ y2+ z

−1



x2+ y2+ z

−1

;0≤ φ ≤ 2π

;0≤ θ ≤ π (1.12)

Figure 1.10 Cartesian and spherical coordinates

Introduction 11

The dot products of unit vectors in these two coordinate systems are:

r = sin θ cosφ;ˆy

θ = cos θ cos φ;ˆy

φ =−sin φ;ˆy

r = sin θ sinφ;ˆz

θ = cos θ sin φ;ˆz

φ = cosφ;ˆz

φ = 0

r = cos θ

θ =−sin θ

(1.13)

Thus, we can express a quantity in one coordinate system using the known parameters in the other coordinate system. For example, if A

= A

x = Arsin θ cosφ + Aθcos θ cosφ − Aφsin φ

, Aθ, Aφare known, we can ﬁnd

1.4 Basics of Electromagnetics

Now let us use basic mathematics to deal with antennas or, more precisely, electromagnetic (EM) problems in this section.

EM waves cover the whole spectrum; radio waves and optical waves are just two examples of EM waves. We can see light but we cannot see radio waves. The whole spectrum is divided into many frequency bands. Some radio frequency bands are listed in Table 1.1.

Although the whole spectrum is inﬁnite, the useful spectrum is limited and some frequency bands, such as the UHF, are already very congested. Normally, signiﬁcant license fees have to be paid to use the spectrum, although there are some license-free bands: the most well-known ones are the industrial, science and medical (ISM) bands. The 433 MHz and 2.45 GHz are just two examples. Cable operators do not need to pay the spectrum license fees, but they have to pay other fees for things such as digging out the roads to bury the cables.

The wave velocity, v, is linked to the frequency, f , and wavelength, λ, by this simple equation:

v =

It is well known that the speed of light (an EM wave) is about 3 ×10

m/s in free space. The

(1.14)

higher the frequency,the shorter the wavelength. An illustration of how the frequency is linked

Table 1.1 EM spectrum and applications

Frequency Band Wavelength Applications

3–30 kHz VLF 100–10 km Navigation, sonar, fax 30–300 kHz LF 10–1 km Navigation

0.3–3 MHz MF 1–0.1 km AM broadcasting 3–30 MHz HF 100–10 m Tel, fax, CB, ship communications 30–300 MHz VHF 10–1 m TV, FM broadcasting

0.3–3 GHz UHF 1–0.1 m TV, mobile, radar 3–30 GHz SHF 100–10 mm Radar, satellite, mobile, microwave links 30–300 GHz EHF 10–1 mm Radar, wireless communications

0.3–3 THz THz 1–0.1 mm THz imaging

12 Antennas: From Theory to Practice

-2

Wavelength (m)

-4

-6

-8

-10

0 102 104 106 108 1010 1012 1014 1016

Optical

Communications

(1.7μm−0.8μm)

Conventional RF

1Hz−300MHz/1GHz

Microwave

300MHz−30GHz

(1m−1cm)

Millimeter Wave

30GHz−300GHz

Light

(0.76μm−0.4μm)

Frequency (Hz)

Figure 1.11 Frequency vs wavelength

to the wavelength is given in Figure 1.11, where both the frequency and wavelength are plotted on a logarithmic scale. The advantage of doing this is that we can see clearly how the function is changed, even over a very large scale.

Logarithmic scales are widely used in RF (radio frequency) engineering and the antennas community since the signals we are dealing with change signiﬁcantly (over 1000 times in many cases) in terms of the magnitude. The signal power is normally expressed in dB and is deﬁned as

P(dBW) = 10log

P(W)

; P(dBm) = 10 log

P(W)

1mW

(1.15)

Thus, 100 watts is 20 dBW, just expressed as 20 dB in most cases. 1 W is 0 dB or 30 dBm and 0.5 W is −3 dB or 27 dBm. Based on this deﬁnition, we can also express other parameters in dB. For example, since the power is linked to voltage V by P = V



R (so P ∝ V

), the

voltage can be converted to dBV by

V (dBV) = 20log



V (V )



(1.16)

Thus, 3 kVolts is 70 dBV and 0.5 Volts is –6 dBV (not −3 dBV) or 54 dBmV.

1.4.1 The Electric Field

The electric ﬁeld (in V/m) is deﬁned as the force (in Newtons) per unit charge (in Coulombs). From this deﬁnition and Coulomb’s law, the electric ﬁeld, E, created by a single point

Introduction 13

charge Q at a distance r is

E =

where

F is the electric force given by Coulomb’s law (F = ˆ

ris a unit vector along the r direction, which is also the direction of the electric ﬁeld E;

r (V /m) (1.17)

4πεr

Q1Q

r);

4πεr

ε is the electricpermittivity (it is also calledthe dielectric constant,but is normallya function

of frequency and not really a constant, thus permittivity is preferred in this book) of the material. Its SI unit is Farads/m. In free space, it is a constant:

= 8.85419 × 10

−12

F/m (1.18)

The product of the permittivity and the electric ﬁeld is called the electric ﬂux density, D,

which is a measure of how much electric ﬂux passes through a unit area, i.e.

where ε

D = εE = ε

= ε/ε0is called the relative permittivity or relative dielectric constant. The relative

E(C/m2) (1.19)

rε0

permittivities of some common materials are listed in Table 1.2. Note that they are functions of frequency and temperature. Normally, the higher the frequency, the smaller the permittivity in the radio frequency band. It should also be pointed out that almost all conductors have a relative permittivity of one.

The electric ﬂux density is also called the electric displacement, hence the symbol D.Itis also a vector. In an isotropic material (properties independent of direction), D and E are in the same direction and ε is a scalar quantity. In an anisotropic material, D and E may be in different directions if ε is a tensor.

If the permittivity isa complex number, it meansthatthe material hassome loss. The complex permittivity can be written as



− j ε



(1.20)

ε = ε

The ratio of the imaginary part to the real part is called the loss tangent, that is



tan δ =



(1.21)

It has no unit and is also a function of frequency and temperature.

The electric ﬁeld E is related to thecurrent density J (in A/m

), another importantparameter,

by Ohm’s law. The relationship between them at a point can be expressed as

J = σ E (1.22)

where σ is the conductivity, which is the reciprocal of resistivity. It is a measure of a material’s ability to conduct an electrical current and is expressed in Siemens per meter (S/m). Table 1.3

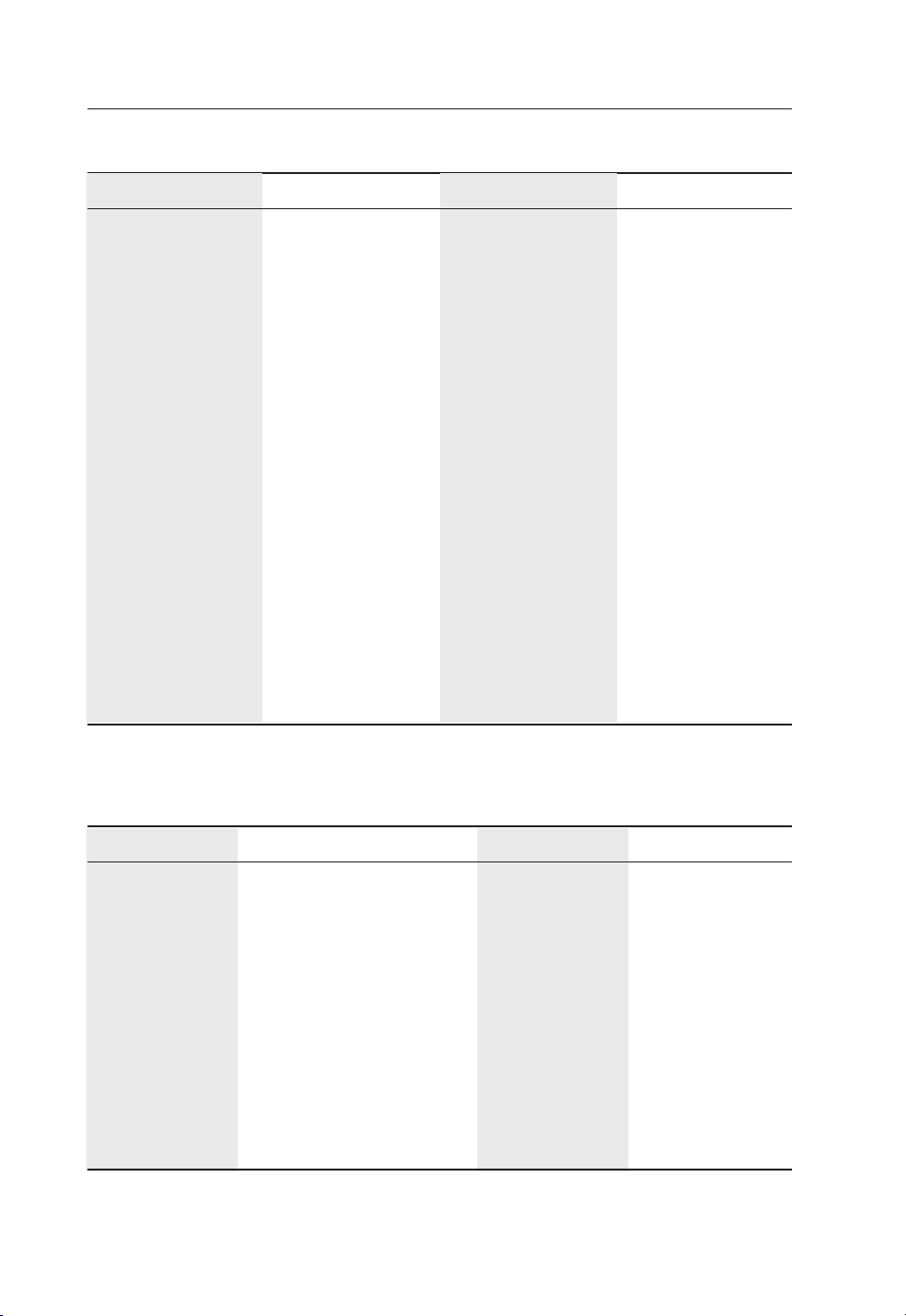
14 Antennas: From Theory to Practice

Table 1.2 Relative permittivity of some common materials at 100 MHz

Material Relative permittivity Material Relative permittivity

ABS (plastic) 2.4–3.8 Polypropylene 2.2 Air 1 Polyvinylchloride (PVC) 3 Alumina 9.8 Porcelain 5.1–5.9 Aluminum silicate 5.3–5.5 PTFE-teﬂon 2.1 Balsa wood 1.37 @ 1 MHz PTFE-ceramic 10.2

1.22 @ 3 GHz Concrete ∼8 PTFE-glass 2.1–2.55 Copper 1 RT/Duroid 5870 2.33 Diamond 5.5–10 RT/Duroid 6006 6.15@3GHz Epoxy (FR4) 4.4 Rubber 3.0–4.0 Epoxy glass PCB 5.2 Sapphire 9.4 Ethyl alcohol (absolute) 24.5 @ 1 MHz Sea water 80

6.5 @ 3 GHz FR-4(G-10) –low resin 4.9 Silicon 11.7–12.9 –high resin 4.2 GaAs 13.0 Soil ∼10 Glass ∼4 Soil (dry sandy) 2.59@1MHz

2.55 @ 3 GHz

Gold 1 Water (32

(68 (212

◦

F) 88.0

◦

F) 80.4

◦

F) 55.3

Ice (pure distilled water) 4.15 @ 1 MHz Wood ∼2

3.2 @ 3 GHz

Table 1.3 Conductivities of some common materials at room temperature

Material Conductivity (S/m) Material Conductivity (S/m)

Silver 6.3 ×10 Copper 5.8 × 10 Gold 4.1 ×10 Aluminum 3.5 ×10 Tungsten 1.8 ×10 Zinc 1.7 × 10 Brass 1 ×10 Phosphor bronze 1 ×10 Tin 9 × 10 Lead 5 ×10 Silicon steel 2 ×10 Stainless steel 1 × 10 Mercury 1 ×10 Cast iron ≈ 10

Graphite ≈ 10 Carbon ≈ 10 Silicon ≈ 10 Ferrite ≈ 10 Sea water ≈ 5 Germanium ≈ 2 Wet soil ≈ 1 Animal blood 0.7 Animal body 0.3 Fresh water ≈ 10 Dry soil ≈ 10 Distilled water ≈ 10 Glass ≈ 10 Air 0

−2

−3

−4

−12

Introduction 15

lists conductivities of some commonmaterials linked to antenna engineering. The conductivity is also a function of temperature and frequency.

1.4.2 The Magnetic Field

Whilst charges can generate an electric ﬁeld, currents can generate a magnetic ﬁeld. The magnetic ﬁeld, H (in A/m),is the vector ﬁeld which formsclosed loops aroundelectric currents or magnets. The magnetic ﬁeld from a current vector I is given by the Biot–Savart law as

I ×ˆr

H =

where

r is the unit displacement vector from the current element to the ﬁeld point and r is the distance from the current element to the ﬁeld point.

I,ˆr and H follow the right-hand rule; that is, H is orthogonal to both I andˆr, as illustrated

by Figure 1.12.

Like the electric ﬁeld, the magnetic ﬁeld exerts a force on electric charge. But unlike an electric ﬁeld, it employs force only on a moving charge, and the direction of the force is orthogonal to both the magnetic ﬁeld and the charge’s velocity:

(A/m) (1.23)

4πr

F = Qv × μH (1.24)

where

F is the force vector produced, measured in Newtons; Q is the electric charge that the magnetic ﬁeld is acting on, measured in Coulombs (C);

v is the velocity vector of the electric charge Q, measured in meters per second (m/s);

μ is the magnetic permeability of the material. Its unit is Henries per meter (H/m). In free

space, the permeability is

= 4π ×10−7H/m (1.25)

In Equation (1.24), Qv can actually be viewed as the current vector I and the product of μH is called the magnetic ﬂux density B (in Tesla), the counterpart of the electric ﬂux density.

Figure 1.12 Magnetic ﬁeld generated by current I

16 Antennas: From Theory to Practice

Table 1.4 Relative permeabilities of some common materials

Material Relative permeability Material Relative permeability

Superalloy ≈ 1 × 10 Puriﬁed iron ≈ 2 × 10 Silicon iron ≈ 7 × 10 Iron ≈ 5 ×10 Mild steel ≈ 2 × 10 Nickel 600 Silver ≈1

Aluminum ≈1 Air 1 Water ≈1 Copper ≈1 Lead ≈1

Thus

B = μH (1.26)

Again, in an isotropic material (properties independent of direction), B and H are in the same direction and μ is a scalar quantity. In an anisotropic material, B and E may be in different directions and μ is a tensor.

Like the relative permittivity, the relative permeability is given as

= μ/μ

(1.27)

The relative permeabilities of some materials are given in Table 1.4. Permeability is not sensitive to frequency or temperature. Most materials, including conductors, have a relative permeability very close to one.

Combining Equations (1.17) and (1.24) yields

F = Q(E + v × μH) (1.28)

This is called the Lorentz force. The particle will experience a force due to the electric ﬁeld

QE, and the magnetic ﬁeld Qv × B.

1.4.3 Maxwell’s Equations

Maxwell’s equations are a set of equations ﬁrst presented as a distinct group in the latter

half of the nineteenth century by James Clerk Maxwell (1831–1879), pictured in Figure 1.13. Mathematically they can be expressed in the following differential form:

d B

d D

(1.29)

where

ρ is the charge density;

∂

∇=

∂x

x +

y +

∂y

∇×E =−

∇×H = J + ∇rD = ρ

∇rB = 0

∂

z is a vector operator;

∂z

Introduction 17

Figure 1.13 James Clerk Maxwell

∇×is the curl operator, called rot in some countries instead of curl; ∇ris the divergence operator.

Here we have both the vector cross product and dot product.

Maxwell’s equations describe the interrelationship between electric ﬁelds, magnetic ﬁelds,

electric charge and electric current. Although Maxwell himself was not the originator of the

individual equations, he derived them again independently in conjunction with his molecular vortex model of Faraday’s lines of force, and he was the person who ﬁrst grouped these equations together into a coherent set. Most importantly, he introduced an extra term to Ampere’s Circuital Law, the second equation of (1.19). This extra term is the time derivative of the electric ﬁeld and is known as Maxwell’s displacement current. Maxwell’s modiﬁed version of Ampere’s Circuital Law enables the set of equations to be combined together to derive the electromagnetic wave equation, which will be further discussed in Chapter 3.

Now let us have a closer look at these mathematical equations to see what they really mean

in terms of the physical explanations.

1.4.3.1 Faraday’s Law of Induction

∇×E =

(1.30)

This equation simply means that the induced electromotive force is proportional to the rate of change of the magnetic ﬂux through a coil. In layman’s terms, moving a conductor (such as a metal wire) through a magnetic ﬁeld produces a voltage. The resulting voltage is directly proportional to the speed of movement. It is apparent from this equation that a time-varying magnetic ﬁeld (μ

d H

= 0) will generate an electric ﬁeld, i.e. E = 0. But if the magnetic ﬁeld

is not time-varying, it will NOT generate an electric ﬁeld.

18 Antennas: From Theory to Practice

1.4.3.2 Ampere’s Circuital Law

∇×H = J +

This equation was modiﬁed by Maxwell by introducing the displacement current

d D

. It means

(1.31)

that a magnetic ﬁeld appears during the charge or discharge of a capacitor. With this concept, and Faraday’s law, Maxwell was able to derive the wave equations, and by showing that the predicted wave velocity was the same as the measured velocity of light, Maxwell asserted that light waves are electromagnetic waves.

This equation shows that both the current (J) and time-varying electric ﬁeld (ε

d E

) can

generate a magnetic ﬁeld, i.e. H = 0.

1.4.3.3 Gauss’s Law for Electric Fields

∇rD = ρ (1.32)

This is the electrostatic application of Gauss’s generalized theorem, giving the equivalence relation between any ﬂux, e.g. of liquids, electric or gravitational, ﬂowing out of any closed surface and the result of inner sources and sinks, such as electric charges or masses enclosed within the closed surface. As a result, it is not possible for electric ﬁelds to form a closed loop. Since D = εE, it is also clear that charges (ρ) can generate electric ﬁelds, i.e. E = 0.

1.4.3.4 Gauss’s Law for Magnetic Fields

∇rB = 0 (1.33)

This shows that the divergence of the magnetic ﬁeld (∇rB) is always zero, which means that the magnetic ﬁeld lines are closed loops; thus, the integral of B over a closed surface is zero.

For atime-harmonic electromagnetic ﬁeld (which means a ﬁeldlinked to time by factor e

jωt

where ω is the angular frequency and t is the time), we can use the constitutive relations

D = εE, B = μH, J = σ E (1.34)

to write Maxwell’s equations in the following form

∇×E =−jωμH ∇×H = J + j ωεE = jωε1 − j

ωε



(1.35)

∇rE = ρ/ε ∇rH = 0

where B and D are replaced by the electric ﬁeld E and magnetic ﬁeld H to simplify the equations and they will not appear again unless necessary.

Introduction 19

It should be pointed out that, in Equation (1.35), ε(1 − j

) can be viewed as a complex

ωε

permittivity deﬁned by Equation (1.20). In this case, the loss tangent is



tan δ =



ωε

(1.36)

It is hard to predict how the loss tangent changes with the frequency, since both the permittivity and conductivity are functions of frequency as well. More discussion will be given in Chapter 3.

1.4.4 Boundary Conditions

Maxwell’s equations can also be written in the integral form as



Erdl =−



Hrdl =





Drds =





Brds = 0









(J +

d B

d D

)rds

ρdv = Q

(1.37)

Consider the boundary between two materials shown in Figure 1.14. Using these equations, we can obtain a number of useful results. For example, if we apply the ﬁrst equation of Maxwell’s equations in integral form to the boundary between Medium 1 and Medium 2, it is not difﬁcult to obtain [2]:

n × E

=ˆn × E

(1.38)

whereˆn is the surface unit vector from Medium 2 to Medium 1, as shown in Figure 1.14. This condition means that the tangential components of an electric ﬁeld (ˆn × E) are continuous across the boundary between any two media.

Medium 1

Medium 2

Figure 1.14 Boundary between Medium 1 and Medium 2

, σ1, μ

ε2, σ2, μ

20 Antennas: From Theory to Practice

Figure 1.15 Electromagnetic ﬁeld distribution around a two-wire transmission line

−

Similarly, we can apply the other three Maxwell equations to this boundary to obtain:

where J

n ×(H

nr(ε

nr(μ

is the surface current density and ρsis the surface charge density. These results can

− H2) = J

− ε2E2) = ρ

1E1

− μ2H2) = 0

1H1

be interpreted as

the change in tangential component of the magnetic ﬁeld across a boundary is equal to the surface current density on the boundary;

the change in the normal component of the electric ﬂux density across a boundary is equal to the surface charge density on the boundary;

the normal component of the magneticﬂuxdensityiscontinuousacrossthe boundary between two media, whilst the normal component of the magnetic ﬁeld is not continuous unless

= μ2.

(1.39)

Applying these boundary conditions on a perfect conductor (which means no electric and

magnetic ﬁeld inside and the conductivity σ =∞)intheair,wehave

n × E = 0;ˆn × H = J

;ˆnrE = ρs/ε;ˆnrH = 0 (1.40)

We can also use these results to illustrate, for example, the ﬁeld distribution around a twowire transmission line, as shown in Figure 1.15, where the electric ﬁelds are plotted as the solid lines and the magnetic ﬁelds are shown as broken lines. As expected, the electric ﬁeld is from positive charges to negative charges, whilst the magnetic ﬁeld forms loops around the current.

Introduction 21

1.5 Summary

In this chapter we have introduced the concept of antennas, brieﬂy reviewed antenna history and laiddown the mathematical foundations for further study. The focushas been on the basics of electromagnetics, which include electric and magnetic ﬁelds, electromagnetic properties of materials, Maxwell’s equations and boundary conditions. Maxwell’s equations have revealed how electric ﬁelds, magnetic ﬁelds and sources (currents and charges) are interlinked. They are the foundation of electromagnetics and antennas.

References

[1] R. E. Collin, Antennas and Radiowave Propagation, McGraw-Hill, Inc., 1985. [2] J. D. Kraus and D. A. Fleisch, Electromagnetics with Applications, 5th edition, McGraw-Hill, Inc., 1999.

Problems

Q1.1 What wireless communication experiment did H. Hertz conduct in 1887? Use a

diagram to illustrate your answer. Q1.2 Use an example to explain what a complex number means in our daily life. Q1.3 Given vectors A = 10ˆx +5ˆy + 1ˆz and B = 5ˆz, find

a. the amplitude of vector A;

b. the angle between vectors A and B;

c. the dot product of these two vectors;

d. a vector which is orthogonal to A and B. Q1.4 Given vector A = 10sin(10t + 10z)ˆx + 5ˆy, find

Q1.5 Vector E = 10e

Q1.6 Explain why mobile phone service providers have to pay license fees to use the Q1.7 Cellular mobile communications have become part of our daily life. Explain the

Q1.8 Which frequency bands have been used for radar applications? Give an example. Q1.9 Express 1 kW in dB, 10 kV in dBV, 0.5 dB in W and 40 dBμV/m in V/m and

Q1.10 Explain the concepts of the electric field and magnetic field. How are they linked

a. ∇

b. ∇×A;

c. (∇

∇) A;

d. ∇∇

a. find the amplitude of E;

b. plot the real part of E as a function of t ;

c. plot the real part of E as a function of z;

d. explain what this vector means.

spectrum. Who is responsible for the spectrum allocation in your country?

major differences between the 1st, 2nd and 3rd generations of cellular mobile

systems in terms of the frequency, data rate and bandwidth. Further explain why

their operational frequencies have increased.

μV/m.

to the electric and magnetic flux density functions?

j (10t−10z)

ˆx.

22 Antennas: From Theory to Practice

Q1.11 What are the material properties of interest to our electromagnetic and antenna

engineers?

Q1.12 What is the Lorentz force? Name an application of the Lorentz force in our daily

life.

Q1.13 If a magnetic field on a perfect conducting surface z = 0isH = 10cos(10t − 5z)ˆx,

find the surface current density J

Q1.14 Use Maxwell’s equations to explain the major differences betweenstatic EM fields

and time-varying EM fields.

Q1.15 Express the boundary conditions for the electric and magnetic fields on the surface

of a perfect conductor.

Circuit Concepts and Transmission Lines

In this chapter we are going to review the very basics of circuit concepts and distinguish the lumped element system from the distributed element system. The focus will be on the fundamentals of transmission lines, including the basic model, the characteristic impedance, input impedance, reﬂection coefﬁcient,return loss and voltagestanding wave ratio (VSWR) of a transmission line. The SmithChart, impedance-matching techniques,Q factor andbandwidth will also be addressed. A comparison of various transmission lines and associated connectors will be made at the end of this chapter.

2.1 Circuit Concepts

Figure 2.1 shows a very basic electrical circuit where a voltage source V is connected to a load Z via conducting wires. This simple circuit can represent numerous systems in our daily life, from a simple torch – a DC (direct current) circuit – to a more complicated power supply system – an AC (alternating current) circuit. To analyze such a circuit, one has to use the following four quantities:

Electric current I is a measure of the charge ﬂow/movement. The SI unit of current is the Ampere (A), which is equal to a ﬂow of one Coulomb of charge per second.

Voltage V is the difference in electrical potential between two points of an electrical or electronic circuit. The SI unit of voltage is the Volt (V). Voltage measures the potential energy of an electric ﬁeld to cause an electric current in a circuit.

Impedance Z = R + jX is a measure of opposition to an electric current. In general, the impedance is a complex number, its real part R is the electrical resistance (or just resistance) and reﬂects the ability to consume energy, whilst the imaginary part X is the reactance and indicates the ability to store energy. If the reactance is positive, it is called inductance since the reactance of an inductor is positive (ωL); if the reactance is negative, it is then

Antennas: From Theory to Practice Yi Huang and Kevin Boyle



2008 John Wiley & Sons, Ltd

24 Antennas: From Theory to Practice

Figure 2.1 A simple electrical circuit with a source and load

called capacitance since the reactance of a capacitor is negative (−1/ωC). The same unit, the Ohm (),is used forimpedance, resistance and reactance. The inverses of the impedance, resistance and reactance are called the admittance (Y ), conductance (G) and susceptance (B), respectively. Their unit is the Siemens (S) and it is 1 Ohm.

Power P is deﬁned as the amount of work done by an electrical current, or the rate at which electrical energy is transmitted/consumed. The SI unit of power is the Watt (W). When an electric current ﬂows through a device with resistance, the device converts the power into various forms, such as light (light bulbs), heat (electric cooker), motion (electric razor), sound (loudspeaker) or radiation for an antenna.

Ohm’s law is the fundamental theory for electrical circuits. It reveals how the current, voltage and resistance are linked in a DC circuit. It states that the current passing through a conductor/device from one terminal point on the conductor/device to another terminal point on the conductor/device is directly proportional to the potential difference (i.e. voltage) across the two terminal points and inversely proportional to the resistance of the conductor/device between the two terminal points. That is

I =

(2.1)

In an AC circuit, Ohm’s law can be generalized as

I =

(2.2)

i.e. the resistance R is replaced by the impedance Z. Since the impedance is acomplex number, both the current and voltage can be complex numbers as well, which means that they have magnitude and phase.

The average power can be obtained using

/R = RI2for DC (2.3)

0V0

for AC

where V

P = IV = V

and I0are the amplitudes of voltage and current, respectively.

Circuit Concepts and Transmission Lines 25

2.1.1 Lumped and Distributed Element Systems

In traditional circuit theory,we basically divide circuits into thosethat are DCand those that are AC. The voltage, current and impedance are real numbers in DC circuits but complex numbers in AC circuits. The effects of conducting wires can normally be neglected. For example, the current across the load Z in Figure 2.1 can be obtained usingOhm’slaw. It is given by Equation (2.2) and considered to be the same voltage across the load.

In most countries, the electrical power supply system operates at 50 or 60 Hz, which means a wavelength of 6000 or 5000 km (close to the radius of the Earth: 6378 km), much longer than any transmission line in use. The current and voltage along the transmission line may be considered unchanged. The system is called a lumped element system. However, in some applications the frequency of the source is signiﬁcantly increased, as a result the wavelength becomes comparable with the length of the transmission line linking the source and the load. The current and voltage along the transmission line are functions of the distance from the source, thus the system is called a distributed element system. If Figure 2.1 is a distributed element system, Equation (2.2) is no longer valid since the voltage across the load may now be very different from the source voltage. V the load.

Conventional circuit theory was developed for lumped element systems whose frequency is relatively low and where the wavelength is relatively large. However, the frequency of a distributed system is relatively high and the wavelength is relatively short. It is therefore important to introduce the transmissionlinetheory, which has beendeveloped forthedistributed element system and hastakenthedistributednatureof the parameters in thesystemintoaccount.

should therefore be replaced by the voltage across

2.2 Transmission Line Theory

A transmission line is the structure that forms all or part of a path from one place to another for directing the transmission of energy, such as electrical power transmission and optical waves.Examples of transmissionlinesinclude conducting wires,electrical power lines, coaxial cables, dielectricslabs, opticalﬁbers andwaveguides.In thisbook weare onlyinterested inthe transmission lines for RF engineering and antenna applications. Thus, dielectric transmission lines such as optical ﬁbers are not considered.

2.2.1 Transmission Line Model

The simplest transmission line is a two-wire conducting transmission line, as shown in Figure

2.2. It has been widely used for electrical power supply and also for radio and television systems. In the old days, the broadcasting TV signal was received by an antenna and then passed down to a TV via such a two-wire conducting wire, which has now been replaced by the coaxial cable. This is partially due to the fact that the antenna used now (the Yagi–Uda antenna, a popular TV antenna to be discussed in Chapter 5, which has an input impedance around 75 ohms) is different from the antenna used then (the folded dipole, which was a popular TV antenna many years ago and had an input impedance around 300 ohms). Also, the coaxial cable performs much better than the two-wire transmission line at the UHF (ultra-high frequency) TV bands.

26 Antennas: From Theory to Practice

z + Δz

I(z

I(z)

+ Δz)

V(z)

V(z + Δz)

z + Δ z

Figure 2.2 A two-wire transmission line model

As shown in Figure 2.2, if we divide the transmission line into many (almost inﬁnite) short segmentsof length z, which is muchsmallerthan the wavelength of interest,eachsegmentcan then be represented using a set oflumped elements.By doing so, a distributedtransmission line is modeled as an inﬁnite series of two-port lumped elementary components, each representing an inﬁnitesimally short segment of the transmission line. To make the analysis easier, the equivalent circuit of the segment of the transmission line is simpliﬁed to Figure 2.3, where

R = R

+ R2and L = L1+ L2.

The resistance R represents the conductive loss of the transmission line over a unit length, thus the unit is ohms/unit length (/m).

The inductance L is the self-inductance of the transmission line and is expressed in Henries per unit length (H/m).

The capacitance C between the two conductors is represented by a shunt capacitor with a unit of Farads per unit length (F/m).

The conductance G of the dielectric material separating the two conductors is represented by a conductance G shunted between the two conductors. Its unit is Siemens per unit length (S/m).

I(z)

V(z)

Figure 2.3 Schematic representation of the elementary component of a transmission line

I(z 

V(z 

Δz)

Circuit Concepts and Transmission Lines 27

It should be repeated for clarity that the model consists of an inﬁnite series of elements shown in Figure 2.3, and that the values of the components are speciﬁed per unit length. R, L, C and G may be functions of frequency.

Using this model we are going to investigate how the current and voltage along the line are changed and how they are linked to R, L, C and G.

It is reasonable to assume that the source is time-harmonic and has an angular frequency

ω(= 2π f, where f is the frequency), thus its time factor is e

jωt

Using Ohm’s law, we know that the voltage drop and current change over a segment of z can be expressed in the frequency domain as:

V (z + z) − V (z) =−(R + j ωL)z · I(z)

(2.4)

I(z + z) − I (z) =−(G + j ωC)z · V(z + z)

When z approaches zero, these two equations can be written in differential form as:

dV(z)

=−(R + j ωL) · I(z)

dI(z)

=−(G + jωC) ·V (z)

(2.5)

Differentiating with respect to z on both sides of the equations and combining them gives:

V (z)

= (R + j ωL)(G + jωC) · V(z)

I(z)

= (R + j ωL)(G + jωC) · I(z)

(2.6)

That is,

V (z)

− γ2V (z) = 0

I(z)

− γ2I(z) = 0

(2.7)

where



γ =

(R + jωL)(G + j ωC) (2.8)

and is called the propagation constant, which may have real and imaginary parts. Equation (2.7) is a pair of linear differential equations which describe the line voltage and current on a transmission line as a function of distance and time (the time factor e

jωt

is omitted here). They

are called telegraph equations or transmission line equations.

28 Antennas: From Theory to Practice

2.2.2 Solutions and Analysis

The general solution of V (z) in the telegraph equations can be expressed as the sum of the forward and reverse voltages [1, 2]

where A

V (z) = V

and A2are complex coefﬁcients to be determinedby the boundary conditions, which

(z) + V−(z) = A1e

−γ z

+ A2e

γ z

(2.9)

means the voltage, current and impedance at the input and the load of the transmission line – we need to know at least two of these in order to determine the two coefﬁcients.

Replacing V (z) in Equation (2.5) by Equation (2.9), we can ﬁnd the solution of the line

current as

I(z) =

R + jωL

−γ z

− A2e

γ z

) (2.10)

This can be written as

I(z) =

−γ z

(A1e

− A2e

γ z

) (2.11)

where



R + jωL

(z)

I+(z)

R + jωL

G + jωC

(2.12)

and is the ratio of the forward voltage to the current thus it is called the characteristic impedance of the transmission line. Its unit is theohm (). It is a function ofthe frequencyand parameters of the line. The industrial standard transmission line normally has a characteristic impedance of 50 or 75  when the loss can be neglected (R ≈ 0 and G ≈ 0).

Since the propagation constant is complex, it can be written as:

γ = α + jβ (2.13)

where α is called the attenuation constant(in Nepers/meter, or Np/m) and β is called the phase

constant. Because γ =

α =

β =

√

(R + jωL)(G + j ωC), we can ﬁnd that mathematically:







(R2+ ω2L2)(G2+ ω2C2) +( RG − ω2LC)







(R2+ ω2L2)(G2+ ω2C2) −( RG − ω2LC)



1/2





1/2



(2.14)

They are functions of frequency as well as the parameters of the transmission line.

Circuit Concepts and Transmission Lines 29

cos(ωt βz)

−

cos(ωt βz)

Figure 2.4 Forward- and reverse-traveling waves

If we take the time factor into account, the complete solution of the voltage and current along a transmission line can be expressed as

V (z, t) = A

I(z,t) =

jωt−γ z

(A1e

jωt−γ z

+ A2e

− A2e

jωt+γ z

= A1e

) =

−αz+j (ωt−β z)

(A1e

+ A2e

αz+j (ωt+β z)

− A2e

(2.15)

)

Physically, the line voltage solution can be considered the combination of two traveling voltage waves: the wave traveling towards the z direction (called the forward wave) has an amplitude of|V

(z)|=

 

towards the –z direction (called the reverse wave) has an amplitude of|A Figure 2.4.The amplitudesof A

A1e



−αz



, which attenuates as z increases, whereas the wave traveling

and A2are actuallythe voltage amplitudes of the forward and

αz

, as shown in

reverse waves at z = 0, respectively. If there is no reﬂection at the end of the transmission line, it means that the boundary conditions have forced A

to be zero, thus the reverse wave will be

zero and only the forward-traveling voltage will exist on the transmission line in this case.

Similarly, the line current can also be viewed as the combination of two traveling current waves. It is worth noting that the reverse-traveling current has aminus sign with the amplitude, this means a phase change of 180 degrees and reﬂects the direction change in the returned current.

The velocity of the wave is another parameter of interest and it can be determined from the phase term: ωt − β z. At a ﬁxed reference point, the wave moves z over a period of t, i.e. we have ωt − βz = 0, thus the velocity

dz dt

(2.16)

v =

Since the phase constant β is a function of the angular frequency, as shown in Equation (2.14), the velocity is a function of frequency, which is a well-known dispersion problem (change with frequency).

Using Equation (2.16), the phase constant can be expressed as

β =

2π f

2π

(2.17)

where λ is the wavelength. The phase constant is also called the wave number. For every one wavelength, the phase is changed by 2π.

30 Antennas: From Theory to Practice

These solutions are general and can be applied to any transmission line in principle. We can see that the characteristic impedance may be complex and the attenuation constant and phase constant are complicated functions of frequency. But, in practice, we always prefer something simpler and easier to use.

2.2.2.1 Lossless Transmission Lines

Since the function of the transmission line is to transmit information from one place to another with little change, the loss of the transmission line should be minimized – this is one of the requirements for transmission line manufacture. There are indeed many low-loss transmission lines available on the market.

For a lossless transmission line, elements R and G can be considered to be zero (R ≈ 0 and G ≈ 0). In this hypothetical case, the model depends only on elements L and C, which greatly simpliﬁes the analysis.

The characteristic impedance ofthetransmission line, Equation (2.12),cannowbesimpliﬁed to



(2.18)

This is just a real number (resistance) and is determined only by L and C; it is not a function of the frequency.

Similarly, Equation (2.14) becomes

α = 0 β = ω

√

(2.19)

This means that there isno attenuationand the propagation constant isnow just animaginary number:

√

γ = jβ = j ω

The voltage and current along the line are

V (z, t) = A

I(z,t) =

(A1e

j(ωt−βz)

+ A2e

− A2e

j(ωt+βz)

)

(2.20)

Neither the forwardnor thereversewaveis attenuated andtheir amplitudesare not afunction of the distance.

The velocity of the waves is now

v =

√

(2.21)

which is not a function of the frequency and is only determined by the transmission line itself–no dispersion. This is an important feature required for all transmission lines.

Circuit Concepts and Transmission Lines 31

2.2.2.2 Low-Loss Transmission Lines

In practice, most transmission lines cannot be considered lossless structures but, instead, are low-loss transmission lines.

The deﬁnition of ‘low loss’ is

R  ωL,

G  ωC

This seems to imply extremely high frequency. The reality is that both R and G are functions of frequency. Normally, the higher the frequency, the larger R and G. Thus, this conditiondoes not mean high frequency. It applies for any frequency when this condition is met.

For a low-loss transmission line, the characteristic impedance is



R + jωL

G + jωC



jωL(1 + R/j ωL)

jωC(1 + G/j ωC)



≈

jωL(1 +0) jωC(1 + 0)



(2.22)

Thus, it is the same as the lossless case. The characteristic impedance is a pure resistance and is determined by L and C; it is not a function of the frequency. This is why the characteristic impedance of industrial standard transmissions has a constant value, normally 50 or 75 ohms, over a large frequency band, even when the line loss is not zero.

Similarly, the attenuation and phase constants can be approximated as

α ≈

β ≈ ω



C/L +

√



L/C =

(2.23)

The loss (attenuation) is caused by the resistive loss R and the material loss G between the

conductors. The phase constant is again the same as for lossless lines.

However, the voltage and current are attenuated as they travel along the line (due to the loss)

and can be expressed as

V (z, t) = A

I(z,t) =

−αz+j (ωt−β z)

(A1e

−αz+j (ωt−β z)

+ A2e

− A2e

αz+j (ωt+β z)

)

where the attenuation constant is given by Equation (2.23).

Just like the lossless line, the velocity of the waves in a low-loss transmission line is only

determined by L and C , i.e.

v =

√

There is no dispersion (it is not changed with frequency).

(2.24)

(2.25)

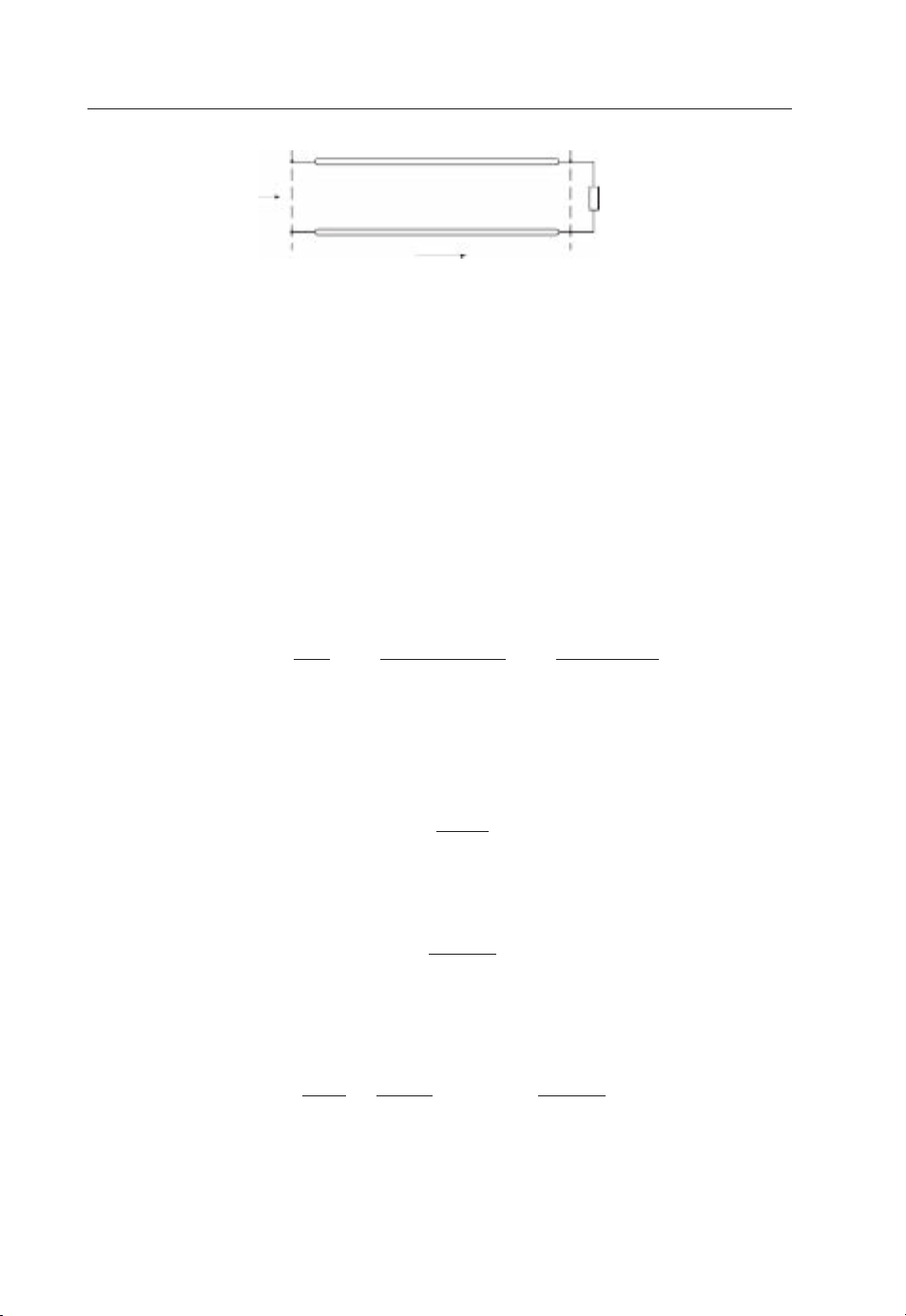
32 Antennas: From Theory to Practice

z  –l

z-axis

z  0

Figure 2.5 A transmission line terminated with a load

2.2.3 Terminated Transmission Line

It is now clearthat the voltage and current of a transmission lineare distributedquantities; they are functions of the position z. However, the characteristic impedance of a transmission line is not a distributed parameter but a constant. When the line is terminated with a load impedance

, as shown in Figure 2.5, what is the input impedance?

2.2.3.1 Input Impedance

The input impedance of a transmission line is deﬁned as the ratio of voltage to current at the input port and is the impedance looking towards the load, i.e.

−γ z

(z) =

V (z)

I(z)

= Z

A1e

−γ z

A1e



where 

= A

is called the reﬂection coefﬁcient at the load and is equal to the ratio of A

to A1,which are the complex coefﬁcients of the forward and reverse voltage waves at z = 0. The input impedance at the load should be the load impedance, that is

+ A2e

− A2e

γ z

= Z

−γ z

+ 0e

− 0e

γ z

(2.26)

1 +

(0) = Z

1 −

= Z

Thus, the reﬂection coefﬁcient at the load can be expressed as

− Z



ZL+ Z

A general expression of the reﬂection coefﬁcient on a transmission line at reference point z is

(z) =

(z)

−

V+(z)

A1e

γ z

= 0e

−γ z

2γ z

− Z

ZL+ Z

2γ z

This means that the reﬂection coefﬁcient is a distributed parameter and is a function of the load impedance as well as the transmission line characteristic impedance.

(2.27)

(2.28)

(2.29)

Circuit Concepts and Transmission Lines 33

Replacing 0in Equation (2.26) by Equation (2.28), we have

(z) = Z

= Z

(ZL+ Z0)e

γ z

ZL(e

γ z

Z0(e

+ e

−γ z

+ (ZL− Z0)e

−γ z

− (ZL− Z0)e

−γ z

) − Z0(e

−γ z

) − ZL(e

γ z

−γ z

− e

)

γ z

−γ z

− e

)

Thus

(z) = Z

ZL− Z0tanh(γ z)

Z0− ZLtanh(γ z)

(2.30)

where

γ z

−γ z

tanh(γ z) =

− e

γ z

−γ z

+ e

(2.31)

is the hyperbolic tangent function.

In practice, the input impedance is measured at a given distance l rather than at its z-axis

value, as shown in Figure 2.5. Thus, the input impedance at l meters away from the load is

(l) = Z

ZL+ Z0tanh(γ l)

Z0+ ZLtanh(γ l)

(2.32)

Note that there is a sign change from Equation (2.30) since the distance should not be

negative and we have used l =−z and tanh(−γ l) =−tanh(γ l).

If the loss of the transmission line can be neglected, that is γ ≈ jβ, Equation (2.32) can be

simpliﬁed to

(l) = Z

ZL+ jZ0tan(βl)

Z0+ jZLtan(βl)

(2.33)

This is a very useful equation. Special attention should be paid to the following cases:

Matched case: Z

= Z

Zin(l) = Z0, the input impedance is the same as the characteristic impedance and is not a function of the length of the line.

Open circuit: Z

=∞

(l) = Z

j tan(βl)

(2.34)

The input impedance has no resistance, just reactance (capacitive for small l).

Short circuit: Z

= 0

(l) = jZ0tan(βl) (2.35)

Again, the input impedance has no resistance, just reactance (inductive for small l).

34 Antennas: From Theory to Practice

Quarter-wavelength case: l = λ/4

(l) =

(2.36)

This special case is called the quarter-wavelength transform since the load impedance is transformed (after a quarter wavelength) to the input impedence given by this simple equation. It is often used for impedance-matching purposes.

It should be pointed out that, in calculating the wavelength λ and wave number β = 2π/λ, the wavelength inside the transmission line is generally different from that in free space. The dielectric properties of the material of the transmission line have to be takeninto account when doing such a calculation. The simplest case is that the wavelength is linked to the relative permittivity ε

(also called the relative dielectric constant) of the material by

λ =

√

(2.37)

where λ

is the free space wavelength. More details will be given later in this chapter.

Example 2.1: Input impedance. A lossless transmission line with a characteristic impedance

of 50  is loaded by a 75  resistor. Plot the input impedance as a function of the line length (up to two wavelengths).

Solution:

Since it is a lossless transmission line, Equation (2.33) is employed to calculate the input impedance. The result is shown in Figure 2.6 where both the resistance and reactance are plotted as a function of the normalized (to wavelength) line length. It is apparent that

Impedance (ohms)

–20

–40

0.5 1

Line length in wavelength

Resistance.

Reactance

1.5

Figure 2.6 Input impedance asa functionof thetransmission linelength forZL= 75  and Z0= 50 

Circuit Concepts and Transmission Lines 35

The input impedance is a periodic function of the line length. The period is half of a wavelength.

The input impedanceis a complex numberevenwhen the loadimpedance is a pureresistance. The resistance changes between 75  and 33 , whilst the reactance changes between

−20  and +20 .

There are two resonant points (where the reactance is zero) over one period. These are at l/λ = 0 and 0.25 in this case.

When 0 < l/λ<0.25, the reactance is negative, i.e. capacitive. When 0.25 < l/λ<0.5, the reactance is positive, i.e. inductive.

Example 2.2: Input impedance of a low-loss transmission line.A75 resistor is now

connected to a good transmission line with characteristic impedance of 50 . The attenuation constant is not zero but 0.2 Np/m at 1 GHz. Plot the input impedance as a function of the line length (up to 2λ). Assume that the effective relative permittivity is 1.5.

Solution:

For a low-loss transmission line, the characteristic impedance is still a constant (= 50  in this case). The line length changes from 0 to 2λ. Since the effective relative permittivity is 1.5 and the frequency is 1 GHz, the wavelength in the medium is

λ =

f√ε

3 ×10

√

≈ 0.245 (m)

1.5

Thus, the length l is from 0 to 0.49 m.

The propagation constant is γ = α + jβ = 0.2 + j2π/λ. Using Equation (2.32), we can plot the input impedance, as shown in Figure 2.7. It can be seen that the only change is that the input impedance is no longer a periodic function of the line length. However, it still exhibits a period feature if we neglect the amplitude changes. All other features remain the same as in the lossless case.

Impedance (ohms)

–20

–40

0.5

Line length in wavelength

Resistance.

Reactance

1.5

Figure 2.7 The input impedance along a low-loss transmission line for ZL= 75  and Z0= 50 

36 Antennas: From Theory to Practice

Example 2.3: Quarter-wavelength transform.A75 resistor is to be matched with a trans-

mission line of characteristic impedance50.Ifa quarter-wavelengthtransformerisemployed, what should its characteristic impedance be?

Solution:

Using Equation (2.36), we have

=ZinZL=√75 ·50 ≈ 61.2()

Since this is not a standard characteristic impedance of a transmission line, special dimen-

sions and/or materials will be needed to construct this line.

2.2.3.2 The Reﬂection Coefﬁcient and the Return Loss

The reﬂection coefﬁcient was deﬁned by Equation (2.29). If we replace the z-axis value by the length of the line l, it can be rewritten as

(l) =

ZL+ Z

−2γ l

= 0e

−2γ l

(2.38)

− Z

This is the voltage reﬂection coefﬁcient. Since the power is proportional to the voltage

squared, as shown in Equation (2.3), the power reﬂection coefﬁcient is



(l) =|(l)

=|

2e−2αl

(2.39)

Both reﬂection coefﬁcients are a good measure of how much signal/power is reﬂected back from the terminal. Obviously, when the load impedance is the same as the characteristic impedance, they are both zero and that is the matched case.

When the voltage reﬂection coefﬁcient and power reﬂection coefﬁcient are expressed in logarithmic forms, they give the same result, which is called the return loss:

(l) =−20 log10(|(l)|) =−10 log10(P(l)) (2.40)

Since thereturn lossshould not be smaller than zero, there is a minus sign in Equation (2.40) (but in practice some people ignore the minus sign, which is not correct). A 3 dB return loss corresponds to thereﬂectioncoefﬁcientbeing 1/

√

2 ≈ 0.707or the power reﬂectioncoefﬁcient

being 0.5.

It is worth noting the following special cases for a lossless transmission line:

Matched case: Z

= Z

(l) = 0= 0 – the reﬂection is zero at any point of the line (even for a non-perfect transmission line).

=∞dB – in practice, this means that the return loss is huge, say 50 dB.

Circuit Concepts and Transmission Lines 37

Open circuit: Z

= 1 and (l) = e



=∞

−j2β l

– the amplitude of the reﬂection coefﬁcient is 1 at any point of the

line.

= 0 dB – this means that all power is reﬂected back from the load.

Short circuit: Z



=−1 and (l) =−e

= 0

−j2β l

– the amplitudeofthe reﬂection coefﬁcient is1 at any reference point ofthe line; there is a phase shift of 180degrees between the input and reﬂected voltages at the end of the line.

= 0 dB – again, this means that all power is reﬂected back from the load.

Example 2.4: Reﬂection coefﬁcient and return loss of a lossless transmission line. A75

resistor is connected to a lossless transmission line with characteristic impedance of 50 .

a. What is the voltage reﬂection coefﬁcient for l = 0 and λ/4, respectively? b. What is the return loss for l = 0 and λ/4, respectively?

Solution:

For a lossless transmission line, the attenuation constant α is zero.

a. Using Equation (2.38), we have

(0) =

− Z

ZL+ Z

75 −50

75 +50

= 0.2

and







− Z

ZL+ Z

−2γ l

= 0.2e

−j2∗2π/4

= 0.2e

−jπ

=−0.2

This means that the phase of the reﬂection coefﬁcient is changed by 180 degrees when the length of the transmission line is increased by a quarter-wavelength.

b. The return loss can be obtained by using Equation (2.40), i.e.

=−20 log10(|(l)|) =−10 log10(P(l)) = 13.98

for l = 0 and λ/4, and actually any length of such a transmission line.

Example 2.5: Reﬂection coefﬁcient and return loss of a low-loss transmission line. A75

resistor is connected to a low-loss transmission line with characteristic impedance of 50 . The attenuation constant is 0.2 Np/m at 1 GHz.

a. What is the voltage reﬂection coefﬁcient for l = 0 and λ/4, respectively? b. Plot the return loss as a function of the line length. Assume that the effective relative

permittivity is 1.5.

38 Antennas: From Theory to Practice

Solution:

For this low-loss transmission line, the attenuation constant is α = 0.2 Np/m. At 1 GHz, the

wavelength in the line is

λ =

f√ε

3 ×10

√

≈ 0.245 (m)

1.5

a. Using Equation (2.38), we have

(0) =

− Z

ZL+ Z

75 −50 75 +50

= 0.2

and







− Z

ZL+ Z

−2γ l

−2∗0.2∗0.245/4−j2∗2π/4

= 0.2e

= 0.1952ejπ=−0.1952

This means that not only the phase of the reﬂection coefﬁcient but also the amplitude is changed when the length of the transmission line is increased by a quarter-wavelength.

b. The return loss can be obtained by using Equation (2.40), i.e.

(0) =−20 log10(|(l)|) = 13.98 dB

and





=−20 log

(|(l)|) = 14.19 dB

The return loss is slightly increased, as expected. Over two wavelengths, the change is shown in Figure 2.8. It follows 0.2e

(l) = 13.98 + 3.47l dB.

−2αl

and is a straight line on a logarithmic scale, i.e.

2.2.3.3 The Voltage Standing Wave Ratio (VSWR)

The VSWR (also known as the standing wave ratio, SWR) is deﬁned as the ratio of the magnitude of the maximum voltage on the line to the magnitude of the minimum voltage on the line, as shown in Figure 2.9. Mathematically, it can be expressed as

VSWR(l) =

|V|

max

min

|+| |−|

1 +|(l)

−

1 −|(l)

−

| |

(2.41)

Obviously, the VSWR is just another measure of how well a transmission line is matched with its load. Unlike the reﬂection coefﬁcient, the VSWR is a scalar and has no phase information. For a nonperfect transmission line, the VSWR is a function of the length of the line (l) as well as the load impedance and the characteristic impedance of the line. But for a lossless transmission line, the VSWR is the same at any reference point of the line.

Circuit Concepts and Transmission Lines 39

15.5

B d

14.5

urn loss in et R

13.5 0

0.5

Line length in wavelength

1.5 2

Figure 2.8 Return loss as a function of the line length

From Equation (2.41), we can prove that

VSWR −1

||

VSWR +1

This can be used to calculate the reﬂection coefﬁcient once the VSWR is known.

Note the following special cases:

Matched termination Z

= Zo:

VSWR = 1

Open circuit Z

=∞:

VSWR =∞

Short circuit Z

= 0:

VSWR =∞

(2.42)

min

max

min

Figure 2.9 Standing waves of the voltage and current on a transmission line

40 Antennas: From Theory to Practice

Thus, the VSWR of a line is bounded by unity and inﬁnity:

1 ≤ VSWR ≤∞

For most applications, the VSWR is required to be smaller than 2, which is considered a good match. But for the mobile phone industry, the desired VSWR is normally less than 3, which is due to the considerable effects of the human body on the performance of mobile phones.

Example 2.6: VSWR.A75 resistor is connected to a transmission line of characteristic

impedance of 50 . What is the VSWR at the termination?

Solution:

The reﬂection coefﬁcient at the termination is

(0) =

− Z

ZL+ Z

75 −50

75 +50

= 0.2

Using Equation (2.41) gives

VSWR(0) =

1 +|(0) 1 −|(0)

= 1.5

This is smaller than 2, thus this can be considered a very well-matched case.

In this section we have discussed the reﬂection coefﬁcient, the return loss and VSWR. All these quantities are measures of impedance matching. Table 2.1 is a list of some typical values to show how they are interrelated. It is interesting to note that, if Z

Table 2.1 Links between normalized impedance, reﬂection coefﬁcient, return loss and VSWR

ZL/Z

∞+10∞ Open circuit

5.8470 0.7079 3 5.8470 Half power returned

3.0096 0.5012 6 3.0096

1.9248 0.3162 10 1.9248 Close to VSWR = 2

1.2222 0.1000 20 1.2222

1.0653 0.0316 30 1.0653

1.0202 0.0100 40 1.0202

10 ∞ 1 Matched

0.9802 −0.0100 40 1.0202

0.9387 −0.0316 30 1.0653

0.8182 −0.1000 20 1.2222

0.5195 −0.3162 10 1.9248 Close to VSWR = 2

0.3323 −0.5012 6 3.0096

0.1710 −0.7079 3 5.8470 Half power returned 0 −10∞ Short circuit

 LRT(dB) VSWR Note

is a real number,

Circuit Concepts and Transmission Lines 41

when Z

> 1, ZL/Z0= VSWR;

L/Z0

< 1, ZL/Z0= 1/VSWR.

L/Z0

However, if Z

linking Z

L/Z0

we have  = j , L

is a complex number andits imaginary part is notzero, thesesimple relations

and VSWR do not hold. For example, for ZL= j 50 ohms and Z0= 50 ohms,

= 0dBandVSWR =∞= ZL/Z0.

2.3 The Smith Chart and Impedance Matching

2.3.1 The Smith Chart

The Smith Chart, as shown in Figure 2.10, was invented by Phillip H. Smith (1905–1987) and is a graphical aid designed for use by radio frequency (RF) engineers to solve transmission line and matching circuit problems. Although computer-aided tools have grown steadily over the years, the Smith Chart is still widely used today, not only as a problem-solving aid, but as a graphical demonstrator of how RF parameters behave and an alternative to using tabular information. The Smith Chart can be utilized to represent many parameters including impedances, admittances, reﬂection coefﬁcients, scattering parameters, noise ﬁgure circles, constant gain contours and regions for unconditional stability. It is most frequently used at, or within, the unity radius region. However, the remainder is still mathematically relevant, being used, for example, in oscillator design and stability analysis.

The Smith Chart is plotted on the complex reﬂection coefﬁcient plane in two dimensions, as shown in Figure 2.11. The horizontal axis is the real part of the reﬂection coefﬁcient while the vertical axis shows the imaginary part of the reﬂection coefﬁcient. The origin or center is

Toward generator

Short

180

170

160

150

140

0.0

0.2

130

120

0.2

100

110

0.5

2.0

5.0

Open

1.0

−170

Toward load

−160

−150

-0.2

−140

−130

−120

-0.5

−110

−100

-1.0

−90

−80

Figure 2.10 The standard Smith Chart

−70

-2.0

−60

−50

-5.0

−30

−40

Matched

-10

−20

42 Antennas: From Theory to Practice

Im (

)



|=1



|<1

0 <|



–1

Figure 2.11 The Smith Chart showing the complex reﬂection coefﬁcient

–j

1 Re (

)



||=0(VSWR = 1). In the standard Smith Chart, only the circle for ||=1 (VSWR =∞) is shown and other circles are not displayed to make the chart simple and neat.

Most information shown on the standard Smith Chart is actually the normalized complex impedance as shown in Figure 2.12: the resistance is displayed in circles and the reactance is shownas arched lines. Theupperhalfspace is inductive whilst the lower halfspaceiscapacitive. The middle line is pure resistance from 0 to inﬁnity. If a reference point on a transmission line is moved away from the load (i.e. towards the source), this can be shown on the Smith Chart as the impedance point is moved on the || (or VSWR) circle clockwise. When the reference point is moved towards the load, it means that the impedance point is moved on the || circle anti-clockwise. The distance is normalized to the wavelength.

The Smith Chart can also be shown in other forms, such as normalized admittance, which is often known as the Y Smith Chart. In thisbook weare mainly interested in using the impedance Smith Chart. Other forms which can be found in references such as [1] are not discussed in this book.

As impedances change with frequency, problems using the Smith Chart can only be solved manually using one frequency at a time, the result being represented by a point. This is often adequate for narrowband applications (typically up to about 10% bandwidth) but for wide bandwidths it is usually necessary to apply Smith Chart techniques at more than one frequency across the operating frequency band. Provided that the frequencies are sufﬁciently close, the resulting Smith Chart points may be joined by straight lines to create a locus. A locus of points on a Smith Chart covering a range of frequencies can be employed to visually represent:

how capacitive or inductive a load is across the frequency range;

how difﬁcult matching is likely to be at various frequencies;

how well matched a particular component is.

The accuracy of the Smith Chart is reduced for problems involving a large spread of impedances, although the scaling can be magniﬁed for individual areas to accommodate these.

Circuit Concepts and Transmission Lines 43

Constant inductive

0.5

Constant resistance

R =0

−0.5

0.5

Constant capacitive

−1



Figure 2.12 The Smith Chart showing the complex impedance

Example 2.7: Input impedance andreﬂectioncoefﬁcient. Use aSmith Chart toredo Example

2.1, and also display the reﬂection coefﬁcient on the chart.

Solution:

The characteristic impedance of the line is 50 , thus the normalized load impedance is 75/50 = 1.5, which can be uniquely identiﬁed as point A in the Smith Chart in Figure 2.13. The distance from the origin (center) to A is 0.2, thus the reﬂection coefﬁcient ||=0.2. Moving the reference plane away from this load means moving point A along the ||=0.2 circle clockwise into the capacitive half space, and then past the resonant point at R = 0.67 (i.e. 0.67 × 50  = 33.5 ) into the inductive half space. After 360 degrees (half wavelength), it is back to A. Over this period, the normalized reactance changes between – 0.4 and +0.4, i.e. −20  and +20 . The results are the same as in Example 2.1.

0.4

= 0

−0.4

0.67

Away from the load



R =1.5

Figure 2.13 The Smith Chart showing the complex reﬂection coefﬁcient

44 Antennas: From Theory to Practice

2.3.2 Impedance Matching

Impedance matching is the practice of making the output impedance of a source equal to the

input impedance of the load in order to maximize the power transfer and minimize reﬂections from the load. Mathematically, it means the load impedance being the complex conjugate of the source impedance. That is,

∗

= Z

= (RL+ jXL)∗= RL− jX

(2.43)

When the imaginary part is zero, the two impedances are the same:

= Z

∗

= ZL= R

(2.44)

Normally, we can use either lumped networks or distributed networks to match impedance.

2.3.2.1 Lumped Matching Networks

Lumped matching networks can be divided into three basic types: the Lnetwork, the T network and the pi(π) network.The aim of matchingisto make the equivalent impedanceofthe network the same as the desired resistance R

– usually the characteristic impedance of a transmission

line. Generally speaking, resistors are not employed for impedance matching since the power could be consumed by the resistor without making a useful contribution to the operation of the system.

In Figure 2.14(a) an L network is employed to match the impedance R

. It can be shown

that this impedance is linked to the network elements by the following equations:

√

B =±

X =±

n − 1

√

n − 1

− X

(2.45)

where n = R

and should be greater than 1. If this condition cannot be met, the second

in/RL

lumped L network, shown in Figure 2.14(b), may be used. The components are interrelated by

= 1/ZL= GL+ jB

B =±

√

m − 1

− B

(2.46)

√

where m = 1/(R

X =±R

) and should be greater than 1.

inGL

m − 1

It should be pointed out that lumped L networks have no degree of freedom to optimize the bandwidth, whilst the bandwidth is actually a very important consideration of many applications. To resolve this problem, one should consider adding further reactive elements to create Torπ networks to optimize the overall bandwidth.

Circuit Concepts and Transmission Lines 45

(a)

(b)

ZL=RL+ jX

YL=GL+jB

Figure 2.14 Lumped L networks (a) for Rin> RL; (b) for RinGL< 1

Figure 2.15 is a T network, which may be viewed as another reactance (jX2) added to the L network in Figure 2.14(a). The design process can be summarized by the following three steps:

Step 1: according to the load impedance and the desired bandwidth, choose X

 f

+ X

(2.47)

Step 2: since Z

= ZL+ jX1.

Step 3: use Z

and jX1are in series, the composite load impedance can be obtained as

and the L network design in Equation (2.45) to ﬁnd B and X2.

Another option for impedance matching is to use a π network, as shown in Figure 2.16, which can be seen as an admittance (jB

) added to the L network in Figure 2.14(b). The design

process is very similar to that of the T network. That is:

Figure 2.15 Lumped T network

46 Antennas: From Theory to Practice

Figure 2.16 Lumped π network

Step 1: according to the load impedance and the desired bandwidth, choose B1,

 f

Step 2: since Y

= YL+ jB1.

Step 3: use Y

Example 2.8: Impedance matching. A load with an impedance of 10 − j100  is to be

and jB1are in parallel, the composite load admittance can be obtained as

and the L network design in Equation (2.46) to ﬁnd X and B2.

+ B

(2.48)

matched with a 50  transmission line. Design a matching network and discuss if there are other solutions available.

Solution:

Since Z

= RL+ jXL= 10 − j100 and n = Rin/RL= 50/10 = 5 > 1, the L network in

Figure 2.14(a) is a suitable matching network. Using Equation (2.45) we obtain

√

B =±

X =±

n − 1

√

n − 1

=±

− X

=±0.04

=±

50 ×2

+ 100 =±20 + 100

Thus, there are two sets of solutions: (B,X) = (0.04, 120) and (B,X ) = (−0.04, 80).

Nowlet us seeifthere are otherpossible solutions. Because Y

j0.001and m =1/( R

) =1/0.05 = 20 > 1,we can alsouse the Lnetworkin Figure 2.14(b)

inGL

= 1/(RL+ jXL) ≈ 0.001 +

to match the impedance:

√

20 ×50

− 0.001 ≈±0.0043 − 0.001

B =±

√

m − 1

− BL=±

√

X =±R

m − 1 =±50√19 ≈±217.9

Therefore, we have obtained another two sets of solutions: (B, X) = (0.0033, 217.9) and (B,X) = (−0.0053, −217.9).

In addition, we can also use T and π networks to match the load with the transmission line

and the bandwidth can be controlled.

Circuit Concepts and Transmission Lines 47

It is apparent that, for a given load impedance, there is more than one matching network available. In practice, the decision as to which network to adopt normally depends on some other parameters such as the bandwidth (to be discussed in Example 2.9) and values of the elements.

2.3.2.2 Distributed Matching Networks

Distributed matching networks can be formed by a quarter-wavelength transmission line, an open-circuit transmission line, a short-circuit transmission line or their combinations. They can be represented mathematically by Equations (2.34)to (2.36). The process is best visualized on the Smith Chart.

The quarter-wavelength transformer mentioned earlier is a unique and popular narrowband impedance-matching technique and the process is quite straightforward. The short- and opencircuit stub tuning is very similar to the lumped matching circuit tuning: reactance and/or admittance is added to the matching network. The example below is a good illustration of how to realize matching using a distributed network.

Example 2.9: Impedance matching and bandwidth. A load with an impedance of 10 −

j100  is to be matched with a 50  transmission line. Design two distributed matching

networks and compare them in terms of the bandwidth performance.

Solution:

The normalized load impedance is:

= ZL/50 = 0.2 − j2

As shown in Figure 2.17, this corresponds to a unique point A on the Smith Chart. The reﬂection coefﬁcient is

− 50

 =

||

ZL+ 50

= 0.9235

= 0.5588 − j0.7353

The||= 0.9235 circle is shown in Figure 2.17 as a broken line. To match the impedance, we can move this point (A) clockwise (towards the source) along this circle to points B1, B2, B3 or B4, which are the crossover points with the circle of z = 1or1/z = 1. It can then be further moved either along circle z = 1or1/z = 1 to the center O–the matching point. The normalized admittances at B1 and B2 are −0.04 and +0.04, and the normalized reactances at B3 and B4 are +217.9 and −217.9, respectively. These four routes correspond to the four solutions from the L networks, as demonstrated in Example 2.8.

The matching network using B1 or B2 can be illustrated by Figure 2.18(a), where the openor short-circuit stub is in parallel with the load impedance, while the matching network using B3 or B4 can be shown by Figure 2.18(b), where the open- or short-circuit stub is in series with the load impedance. The rotational angles (from A to B1, B2, B3 or B4) on the Smith Chart determine the stub lengths l

and l2. There are at least four possible designs.

48 Antennas: From Theory to Practice

Inductive

= 0

0.2



Capacitive

2

Figure 2.17 Impedance matching using a Smith Chart

Figure 2.18 Stub-matching networks (a) parallel stub matching; (b) series stub matching

Circuit Concepts and Transmission Lines 49

To design a matching network using B1 we can follow the steps below:

◦

Step 1: Move from point A to B1, the rotational angle is about 0.582π (i.e. 104.8 Smith Chart, which corresponds to l

= 0.1455λ. Note that the rotational angle is twice βl

)onthe

(= 0.291π , not 0.582π, since the impedance period is π , not 2π). The impedance at point B1 is 0.0413 − j0.1984 while its admittance is 1.0 + j 4.8318.

Step 2: Move from point B1 to the center O. This can be achieved easily using a stub connected in parallel with the line, thus it is advantageous to work in admittances. The stub in parallel with the line should produce a susceptance of −4.8318. This can be achieved by the following two designs:

A. a short circuit with a stub length l B. an open circuit with a stub length l

= 0.0325λ;

= 0.2825λ.

The stub length can also be obtained from the Smith Chart.

Now let us examine the bandwidth of these two designs. Assuming the center frequency is 1 GHz, we have l

= 0.2825λ =8.475 cm for Design B. We can use the input impedance formula:

= 0.1455λ = 4.365 cm, and l2= 0.0325λ = 0.975 cm for Design A, and

(l) = Z

ZL+ jZ0tan(βl)

Z0+ jZLtan(βl)

and the following two equations:

− Z

 =

VSWR =

ZL+ Z

1 +| 1 −|

| |

to obtain the VSWR as a function of the frequency. The results are shown in Figure 2.19. It is apparent that

both designs have an excellent impedance match at the center frequency 1 GHz;

the stub length of Design A is shorter than that of Design B whilst the bandwidth of Design A is much wider than that of Design B. This is a very interesting and useful result.

Similar conclusions can be drawn from the matching networks built at the other points (B2, B3 and B4). To build a distributed matching network, the length should be as short as possible to maximize the bandwidth.

The frequency bandwidth limitation on matching networks has been investigated by many people. There exists a generallimit on the bandwidth over which an arbitrarilygood impedance match can be obtained in the case of a complex load impedance. It is related to the ratio of reactance to resistance, and to the bandwidth over which we wish to match the load.

Figure 2.20 shows four load impedances (series RL, series RC, parallel RC and parallel RL) with matching networks, which are speciﬁc examples of the L matching network discussed earlier.Take theparallel RC loadimpedance as an example; Bode andFano derived, for lumped

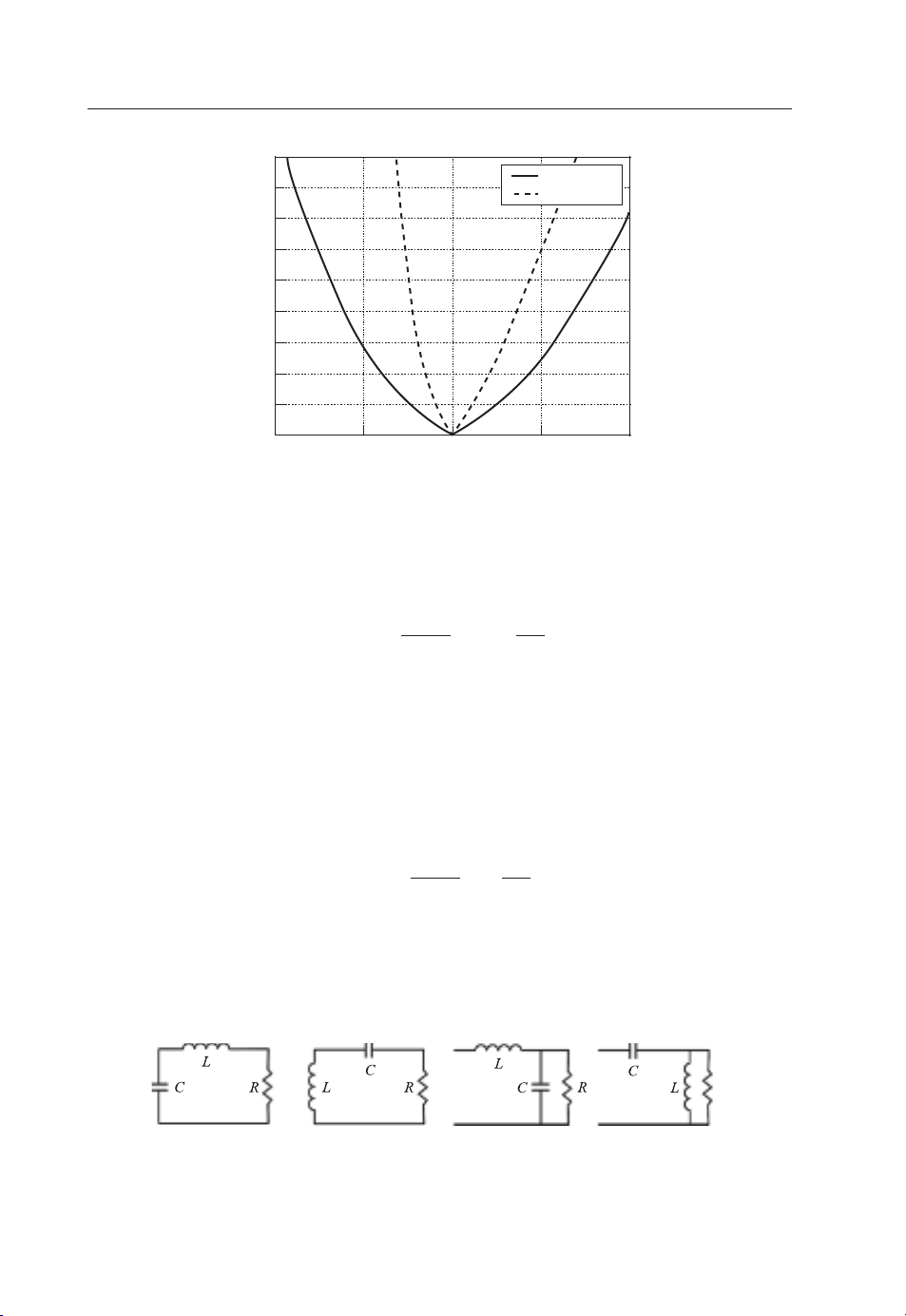
50 Antennas: From Theory to Practice

VSWR

900

Figure 2.19 VSWR of different designs as a function of frequency

950

Frequency in MHz

1000 1050

Design A

Design B

1100

circuits, a fundamental limitation for this, which can be expressed as [2]





∞

(ω)



dω ≤

(2.49)

This is known as the Bode–Fano limit for parallel RC. Since ln(1) = 0, there is no contribution to this integral over frequencies for||= 1, so it can be seen that it is desirable to have the maximum mismatch outside the band of interest if a broad bandwidth is required. If this condition is assumed, the integral is limited to the bandwidth of interest (ω), and we can get an idea of how well we can match an arbitrary complex impedance over that bandwidth. For an idealized case, this equation can be simpliﬁed to



ω ln

(ω)



≤

(2.50)

This clearly shows how the bandwidth (ω) is linked to the matching () and load impedance (RC). For a given reﬂection coefﬁcient (or VSWR) and the RC product, one can estimate the maximum bandwidth attainable.

RR R

Figure 2.20 Four load impedances with LC matching networks

Circuit Concepts and Transmission Lines 51

Similarly, the limits for the other three matching LC networks were obtained as:

Series RL: ω ln( Series RC: ω ln(

Parallel RL: ω ln(

(ω)

) ≤

) ≤ πω

) ≤

R/L

πω L/ R

2 0

There are similar limitations on other forms of complex impedance. A general implication of the Bode–Fano limit is that one should not waste any match out-of-band, and that the best in-band match is obtained with Tchebyscheff rather than maximally ﬂat networks. The best broadband impedance-matching practice incorporates the complex load impedance into, for example, a multisection ﬁlter structure with a design that includes the characteristics of the load.

2.3.3 The Quality Factor and Bandwidth

The bandwidth is indeed a very important parameter for any electric/electronic component and system. It is closely linked to the quality factor, Q, which is a measure of how much lossless reactive energy is stored in a circuit compared to the average power dissipated.

Antenna bandwidth is maximized when the power dissipation is comparatively high. In other words, a low Q is required for wide bandwidths. In turn, the extent to which this energy is associated with radiation (rather than conductor or dielectric losses) determines the antenna efﬁciency. For a circuit component such as an inductor or capacitor, we require the resistive losses to be low; hence Q is required to be high. It is often the case that antennas and circuit components have seemingly contradictory requirements: antennas are designed to have a low Q, whereas circuit components are designed for a high Q.

The quality factor is quoted as being either unloaded or loaded. For the latter, the losses of the external circuit – for example, the source – are included, whereas for the former they are not. The unloaded quality factor, Q, is deﬁned as

(

total energy stored

(

average power loss in the load

where W ﬁeld and P

Q ≡ ω

is the energy stored in the electric ﬁeld, WMis the energy stored in the magnetic

is the average power delivered to the load. The loaded quality factor, QL, can also

be given by Equation (2.51) but with P

replaced by the total power PT, which is dissipated

)

= ω

+ W P

in both the external circuit and the load.

At resonance, the electric and magnetic ﬁeld energies have the same magnitudes and the formulas simplify such that the unloaded quality factor at resonance Q

where ω

2ω

is the angular resonant frequency (= 2π f0, where f0is the resonant frequency).

0WE

≡

2ω

0WM

is given by

(2.51)

(2.52)

52 Antennas: From Theory to Practice

Figure 2.21 Series resonant circuit. (Reproduced by permission of Delft University Press)

There are many simpliﬁcations of these deﬁnitions that are widely used, but which only truly apply when they are derived directly from the above. For example, a relation that is often used is

where f

and f2are the frequencies at which the power reduces to half of its maximum value

at the resonant frequency, f

f2− f

, and where BFis the fractional bandwidth. This relation only

(2.53)

truly applies to simple circuits, but is considered to be a good approximation to a wide range of unloaded conﬁgurations. It has the advantage of providing a simple relationship between Q and fractional bandwidth, but we will see later that it only accurately applies to simple, single resonant circuits and should therefore be used with some care. The derivation of this relation is illustrated below.

Consider the series resonant circuit shown in Figure 2.21. The power dissipated in the resistance R is proportional to the square of the magnitude of the current I . This is plotted in Figure 2.22 with R = 50 , L = 79.5775 nH and C = 0.3183 pF. The half-power frequencies,

冟I冟

(mA)

0.7 0.8 0.9 1 1.1 1.2 1.3

Frequency (GHz)

f2f

Figure 2.22 Relative power dissipated in a series resonant circuit around resonance

Circuit Concepts and Transmission Lines 53

f1and f2, are found to be 0.9513 GHz and 1.0513 GHz respectively. As shown in Figure

2.22, the resonant frequency (when the current is maximized) is 1 GHz. Using Equation (2.53) yields a Q

of 10.

It is possibleto ﬁnd theunloaded quality factorof the circuitdirectly from thestored energies

of the inductor and capacitor. The magnetic and electric energies are given by

where V

is the voltage across the capacitor. Writing these and the power delivered to the load

, WE=

(2.54)

(i.e. the resistor, R) in terms of the current I gives

1 2

, WE=

(

ω C

)

I2, PL= RI

(2.55)

Further substitution in Equation (2.51) yields

Q =



ω L +





ω C

(2.56)

At resonance, the magnitudes of the electric and magnetic energies are equal and this relation simpliﬁes to

ω0CR

, and ω

√

(2.57)

This formula is often used, but it should beunderstood that it only applies at resonance. Taking

R = 50 , L = 79.5775 nH and C = 0.3183 pF gives Q

= 10, as previously.

It is interesting to evaluate the ratio of Q at any frequency to that at resonance. From

Equations (2.56) and (2.57), this is given by

q =





(2.58)

It can be seen thatthe unloaded qualityfactor is aminimum at resonance,although the variation with frequency is slow. For bandwidths of less than 20%, Q is approximately equal to Q

with an error of less than 0.5% – i.e. the term in the parentheses of Equation (2.58) is approximately equal to two over moderate bandwidths.

We wouldlike to derive a relationshipbetween the unloadedquality factor and thebandwidth of the circuit. The bandwidth is normally taken to be the range of frequencies over which the power dissipated; P

is greater than half of the maximum, PL0(at resonance). However, in the

sections that follow more general relations are derived based on a speciﬁed power transfer to the load.

54 Antennas: From Theory to Practice

The current in the circuit is given by

I =

R + jω L −





ω C

(2.59)

From Equation (2.59),the ratio ofthe power dissipatedat any frequency to the power dissipated at resonance is given by



p =



1 +



ω L

−

ω CR



(2.60)

This can be written

p =

1 +χ

(2.61)

where, from (2.57),

χ = Q





−

(2.62)

The relation given in Equation (2.61) can be solved to give







−

=±

1 − p

(2.63)

This is a quadratic equation in ω with two positive and two negative solutions. The difference between the two positive solutions is



1 − p

− ω1=

(2.64)

This gives the fractional bandwidth as



− f

1 − p

(2.65)

When p = 0.5, this simpliﬁes to the familiar expression

(2.66)

Circuit Concepts and Transmission Lines 55

Figure 2.23 Parallel anti-resonant circuit. (Reproduced by permission of Delft University Press)

as previously seen in Equation (2.53). This derivation does not make any assumptions about the numerical value of the quality factor or the bandwidth and is, therefore, applicable to both high- and low-Q systems.

The response of a parallel resonant circuit – shown in Figure 2.23 – can be found in much the same way as for series resonance.

The energies stored in the electric and magnetic ﬁelds of the capacitor and inductor respectively and the power dissipated in the resistance are given by

, WM=

V2, P = GV

(

)

ω L

(2.67)

where G is the conductance. Substitution in Equation (2.51) gives

Q =



ω C +





ω L

. (2.68)

At anti-resonance, the magnitudes of the electric and magnetic energies are equal and this relation simpliﬁes to

The ratio between Q and Q

is the same as for the series resonance, given by Equation (2.58).

ω0LG

(2.69)

It can also be shown (using the same method) that the fractional bandwidth is the same as for the series resonant circuit.

The formulas for Q that have been derived so far have been for series and parallel resonant circuits respectively. However, they are often applied – strictly incorrectly – to other circuit combinations. We will see later that this can give large errors, so some care is required in applying these formulas.

2.4 Various Transmission Lines

There are many transmission lines developed for various applications. The most popular ones are shown in Figure 2.24. They are the two-wire transmission line, the coaxial cable, the microstrip, the stripline, the coplanar waveguide (CPW) and the waveguide. We are going to examine these transmission lines in terms of their characteristic impedance, basic mode, frequency bandwidth, loss characteristic and costs.

56 Antennas: From Theory to Practice

StriplineTwo-Wire

Coaxial Cable

Microstrip

Figure 2.24 Various transmission lines

Coplanar Waveguide (CPW)

Wave

uide

2.4.1 Two-wire Transmission Line

This is the simplest transmission line and its cross-sectional view is given in Figure 2.25. The separation of the wires is D and the diameter of the wires is d. The medium between the wires has a permittivity of ε.

It can be shown that the per unit length inductance and capacitance of the transmission line

are [2]:

L =

If the medium between the wires has a conductivity of σ σ

, we can obtain the resistance and conductance of a unit length line as

R =

respectively.

D +

πd

√

D2− d



ωμ

2σ

, G =

, C =

D +

πε

√

, and the conductivity of the wire is

πσ

√

D2− d

D +

D2− d

(2.70)

(2.71)

Figure 2.25 Two-wire transmission line

Circuit Concepts and Transmission Lines 57

2.4.1.1 Characteristic Impedance

If the loss of the line can be considered very small, the characteristic impedance is given by Equation (2.22), i.e.



L C

π2ε

√

120

D +

≈

√

D2− d d

D +

√

D2− d

(2.72)

The typical value of industrial standard lines is 300 . This type of transmission line was commonly used to connect a television receiving antenna (usually a folded dipole with an impedance around 280 ) to a home television set many years ago. The uniform spacing is assured by embedding the two wires in a low-loss dielectric, usually polyethylene. Since the wires are embedded in the thin ribbon of polyethylene, the dielectric space is partly air and partly polyethylene.

2.4.1.2 Fundamental Mode

The electromagnetic ﬁeld distribution around the two-wire transmission line is illustrated by Figure 1.15. Both the electric ﬁeld and magnetic ﬁeld are within the transverse (to the propagation direction) plane, thus this mode is called the TEM (transverse electro magnetic) mode. This means that it is nondispersive and the velocity is not changed with the frequency. The plane wave can also be considered a TEM wave.

2.4.1.3 Loss

Since the lumped parameters of a transmission line are given by Equations (2.70) and (2.71), the attenuation constant α can be calculated using Equation (2.14). However, the principal loss of the two-wire transmission line is actually due to radiation, especially at higher frequencies. Thus, this typeof transmission line isnot suitable forhigherfrequency applications. Thetypical usable frequency is less than 300 MHz.

Some people may be familiar with the twisted-pair transmission line. As the name implies, the line consists of two insulated wires twisted together to form a ﬂexible line without the use of spacers. It has relatively good EMC (electromagnetic compatibility) performance – the twisted conﬁguration cancels out the radiation from both wires and results in a small and symmetrical total ﬁeld around the line; but it is not suitable for high frequencies because of the high dielectric losses that occur in the rubber insulation (low costs) as well as the radiation. When the line is wet, the losses increase signiﬁcantly.

2.4.2 Coaxial Cable

The coaxial cable consists of a central, insulated wire (inner conductor) mounted inside a tubular outer conductor, as shown in Figure 2.26. In some applications, the inner conductor is also tubular. The inner conductor is insulated from the outer conductor by insulating materials

58 Antennas: From Theory to Practice

Figure 2.26 The conﬁguration of a coaxial line

Copper

core

Outer jacket

Insulating

material

Braided outer conductor

Protective plastic covering

which are made of Pyrex, polystyrene, polyethylene plastic or some other material that has good insulating characteristics and low dielectric losses at high frequencies over a wide range of temperatures. In order to ensure good EMC performance, shielded and double-shielded coaxial cables have been developed and are available on the market. This type of transmission line is widely used for RF engineering and antenna measurements and for the connection between the antenna and transceiver.

Coaxial cablescome inthree basictypes: ﬂexible, semi-rigid and rigid. The rigid cable gives the best performance and is normally for high-performance and phase-sensitive applications, whilst the ﬂexible cables are cheap and, obviously, ﬂexible. The semi-rigid cable is a compromise. As shown in Figure 2.26, the diameters of the inner and outer conductors of a cable are denoted a and b respectively, and the relative permittivity of the insulating material is ε dielectric material reduces the velocity of the wave inside the cable to c/

√

εr. Some common

. The

loading materials and corresponding velocities are shown in Table 2.2 [3].

If the conductivities of the insulating material are zero and it can be shown that the per unit length parameters of the coaxial line are



2π

R =

G = 2πσ

L =

C = 2πεln

Table 2.2 Coaxial cable material and velocity

Dielectric type (ns/m) (% of c)

Solid polyethylene (PE) 5.05 65.9 Foam polyethylene (FE) 4.17 80.0 Foam polystyrene (FS) 3.67 91.0 Air space polyethylene (ASP) 3.77–3.97 84–88 Solid Teﬂon (ST) 4.79 69.4 Air space Teﬂon (AST) 3.71–3.94 85–90

f μ

πσ

Time delay velocity



(

)

Propagation

(2.73)

Circuit Concepts and Transmission Lines 59

Figure 2.27 Field distribution within a coaxial line

The velocity, as shown in Equation (2.25), is

v =

√

εμ

√

2.4.2.1 Characteristic Impedance

Normally, if the loss of the line can be considered very small, the characteristic impedance is given by Equation (2.22), i.e.





με

2π

√

(2.74)

The typical value for industrial standard lines is 50  or 75 .

2.4.2.2 Fundamental Mode

The electromagnetic ﬁeld distribution around the coaxial cable is illustrated by Figure 2.27. Again, both the electric ﬁeld and magnetic ﬁeld are within the transverse (to the propagation direction) plane, thus this ﬁeld is TEM mode.

However, this is only true for the frequencies below the cut-off frequency, which is [2]

π(a +b)

(2.75)

where v is the velocity of the wave in the cable and the cut-off wavelength is

= π(a + b) (2.76)

If theoperational frequency is above this cut-off frequency (or, say, the operational wavelength is below the cut-off wavelength), the ﬁeld within the coaxial cable may no longer be TEM mode; some higher modes such as TE

(a transverse electric ﬁeld, the magnetic ﬁeld has

nontransverse component) mode may exist, which is not a desirable situation since the loss could be signiﬁcantly increased.

60 Antennas: From Theory to Practice

2.4.2.3 Loss

Since the transmission line lumped parameters are given by Equation (2.73), the attenuation constant α canbe calculated using Equation (2.14)or Equation(2.23) for a low-loss line;that is

√

f μεr(1/a + 1/b)

120√πσ2ln(b/a)

60πσ

√

(2.77)

α ≈

which is a function of the coaxial dimensions a and b as well as the conductivity and permittivity of the materials. When b/a ≈ 3.592 (which means that the typical characteristic impedance should be around 77 ohms), the attenuation reaches the minimum. This is one of the most important considerations when making the cable.

In addition to the characteristic impedance, mode and loss of a cable, there are some other considerations when choosing a transmission line. Power-handling capacity is one of them, since it is very important for radar and high-power applications. The breakdown electric ﬁeld strength in air is about 30 kV/cm (this means thebest characteristic impedance should be close to 30 ohms). A list of some commercial cables with some important speciﬁcations is given in Table 2.3, where OD stands for the outer diameter and Vmax is the maximum voltage which may be applied to the cable in Volts. A more complete list can be found in [3]. It is clear that there are over 100 industry standard cables on the market with various speciﬁcations. The one with the smallest loss at 400 MHz is RG-211A, about 2.3 dB/100 ft. It is also one of the most expensive cables – normally the cost is inversely proportional to the loss of the cable.

2.4.3 Microstrip Line

As shown in Figure 2.28, a microstrip line may be viewed as a derivative of a two-wire transmission line and is perhaps the most widely used form of planar transmission line. One side of the structure is freely accessiblefor themounting of packaged devices andthe geometry lends itself extremely well to PCB patterning techniques to deﬁne the circuit. It has been used extensively in microwave and millimeter circuits and systems.

Due to the complexity of the structure, the analytical expressions of per unit length parameters are difﬁcult to obtain. The effective relative permittivity is approximated as

≈

+ 1

− 1

2√1 +12d /W

(2.78)

This is an empiricalexpressionand is a functionofthe material property andtheratio W/d.W is the widthof thestrip andd is the thickness of the substrate, which has a relative permittivity ε

2.4.3.1 Characteristic Impedance

The calculation of the characteristic impedance is not an easy task. From the transmission line theory, the relation between the velocity and per unit length inductance and capacitance is

v =

√

Circuit Concepts and Transmission Lines 61

Table 2.3 Some commercial coaxial cables and their speciﬁcations (Reproduced by permission of

RFCafe.com)

dB/100 ft

Dielectric Capacitance OD @400 Vmax

Type (/U) MIL-W-17 Z

RG-6A /2-RG6 75.0 PE 20.6 0.332 6.5 2700 Braid RG-8 52.0 PE 29.6 0.405 6.0 4000 Braid RG-8A 52.0 PE 29.6 0.405 6.0 5000 Braid RG-9 51.0 PE 30.2 0.420 5.9 4000 Braid RG-11A /6-RG11 75.0 PE 20.6 0.405 5.2 5000 Braid RG-55B 53.5 PE 28.8 0.200 11.7 1900 Braid RG-58A /28-RG58 52.0 PE 29.6 0.195 13.2 1900 Braid RG-58C /28-RG58 50.0 PE 30.8 0.195 14.0 1900 Braid RG-59/A /29-RG59 73.0 PE 21.1 0.242 10.5 2300 Braid RG-59B /29-RG59 75.0 PE 20.6 0.242 9.0 2300 Braid RG-141/A 50.0 ST 29.4 0.190 9.0 1900 Braid RG-142/A/B /60-RG142 50.0 ST 29.4 0.195 9.0 1900 Braid RG-164 /64-RG164 75.0 PE 20.6 0.870 2.8 10,000 Braid RG-174 50.0 ST 0.100 17.3 1200 Braid RG-177 /67-RG177 50.0 PE 30.8 0.895 2.8 11,000 Braid RG-178/A/B /93-RG178 50.0 ST 29.4 0.072 29.0 1000 Braid RG-180A/B /95-RG180 95.0 ST 15.4 0.140 17.0 1500 Braid RG-188 50.0 ST 0.050 17.5 700 Braid RG-211/A /72-RG211 50.0 ST 29.4 0.730 2.3 7000 Braid RG-223 /84-RG223 50.0 PE 19.8 0.211 8.8 1900 Dbl Braid RG-316 /113-RG316 50.0 ST 29.4 0.102 20.0 1200 Braid RG-393 /127-RG393 50.0 ST 29.4 0.390 5.0 5000 Braid RG-400 /128-RG400 50.0 ST 29.4 0.195 9.6 1900 Braid RG-401 /129-RG401 50.0 ST 29.4 0.250 4.6 3000 Cu. S-R RG-402 /130-RG402 50.0 ST 29.4 0.141 7.2 2500 Cu. S-R RG-403 /131-RG403 50.0 ST 29.4 0.116 29.0 2500 Braid RG-405 /133-RG405 50.0 ST 29.4 0.086 13.0 1500 Cu. S-R

() type (pF/ft) (in.) MHz (rms) Shield

Note: PE: Polyethylene; ST: Solid Teﬂon

Using Equation (2.18), the characteristic impedance can be expressed as



√

(2.79)

Thus, to compute the characteristic impedance, we just need to obtain the per unit length capacitance C once the effective permittivity is known. This approach makes a difﬁcult task

Figure 2.28 Microstrip line



62 Antennas: From Theory to Practice

slightly easier. When the thickness of the metal strip can be neglected, it has been found that [2]:

when W/d <1, the characteristic impedance of the line is



√

It decreases monotonically to 126/

when W/d >1, the characteristic impedance of the line is

√

εras W/d increases to 1.



126

√

(2.80)

√

εr(W/d + 1.393 + 0.667 ln(W/d + 1.44))

120π

It also decreases monotonically from 126/

√

εras W/d increases. That is, the larger the ratio

126

√

(2.81)

W/d, the smaller the characteristic impedance; also, the larger the permittivity, the smaller the characteristic impedance. Practical limitations exist on the range of impedances that can be manufactured. These limits depend on factors such as the dielectric constant, substrate height and manufacturing capability. In general, the thinnest line that can be etched routinely with a good photolithographicprocess is of the order of 0.1 mm. This then putsthe upperbound of the impedance at90–120 .The lower bound isdetermined bythe linewidth, whichshould not be comparable to a wavelength. The typical value of the characteristic impedance for industrial standard lines is 50  or 75 .

2.4.3.2 Fundamental Mode

The electromagneticﬁeld distributionaround themicrostrip line is illustrated by Figure (2.29). Both the electric ﬁeld and magnetic ﬁeld are seen to be within the transverse plane. But half of the wave is traveling in free space, which is faster than the other half wave traveling in the substrate, thus this ﬁeld is in what is called quasi-TEM mode, a sort of TEM mode.

A result of a microstrip line being an open structure is that circuits are subject to radiation. This does not mean that they are dangerous to get close to, but the performance of a device or circuit maybe affected. This is adirect consequenceof the ‘unterminated’ ﬁeld lines illustrated in Figure (2.29). Inreality, theﬁeldlines do notjusthang in free spacebutterminate on whatever is close to the line. The exact relations concerning radiation from a microstrip are complicated but, in general, narrow lines radiate less.

E H

Figure 2.29 The ﬁeld distribution of a microstrip

Circuit Concepts and Transmission Lines 63

The ﬁrst higher mode in a microstrip line is the transverse electric TE10mode, its cut-off wavelength is twice the strip width. After taking the material and fringing effects into account, the cut-off frequency can be expressed approximately as

≈√εr(2W + 0.8d) (2.82)

However, the mode analysis of a microstrip is actually more complicated than this. In addition to the conventional higher order modes, surface modes may exist. The surface mode does not need the metal strip; it only needs the ground plane and the substrate. The lowest transverse electric mode is TE

and its cut-off frequency is

√

( f

c)TE

8d√εr− 1

(2.83)

The lowest transverse magnetic mode is TM

and its cut-off frequency is

√

4d√εr− 1

, thus, in order to keep the quasi-TEM mode

(2.84)

Obviously ( f

c)TE

= 1.5 · ( fc)

( f

> ( fc)

c)TM

propagation, the operational frequency of a microstrip line should be smaller than the cut-off frequency of the TE

mode in Equation (2.82) and the cut-off frequency of the TM0mode in

Equation (2.84). Higher order modes will cause signiﬁcant power loss via conductive loss and radiation loss. The surface mode may transmit the power to any direction, which is, of course, not desirable.

2.4.3.3 Loss

The loss of a microstrip line comes from the conductor loss and dielectric substrate loss. The radiation loss is negligible at low frequencies. For most microstrip lines, conductor loss is much more signiﬁcant than dielectric loss. The attenuation constant can be calculated approximately by

Z0W

(2.85)

where R

=ωμ2σ is the surface resistivity of the conductor.

A summary of some of the common substrates is given in Table 2.4. The ﬁrst ﬁve are hard substrates and the rest are considered soft substrates.

2.4.4 Stripline

A stripline is a conductor sandwiched by a dielectric between a pair of ground planes. It may be viewed as an evolved structure from a coaxial cable, as shown in Figure 2.30. In practice, a stripline is usually made by etching circuitry on a substrate that has a ground plane on

64 Antennas: From Theory to Practice

Table 2.4 Some common substrates for a microstrip at 10 GHz

Substrate ε

Loss tangent Comments

Alumina (Al2O3) 9.8 0.0004 Low loss and cost, stable, difﬁcult to machine

but very hard-wearing

LaAlO

24 0.0001 Low loss, but very expensive MgO 9.8 0.00001 Very low loss but expensive and fragile Quartz (SiO

) 3.8 0.0004 Low loss and low permittivity, good for mm

range, fragile

Sapphire (Al

) 9.4 and 10.8 0.00002 Very low loss, single crystal and anisotropic

2O3

material, expensive

Epoxy (FR4) 4.43@ 1 GHz 0.01 Relatively high lossand low cost, popular PCB,

up to ∼ 2 GHz

FR2 (ﬂame resistant 2) 4.5@ 1 MHz 0.025 Similar to FR4, cheap, but recommend above

∼ 1 GHz GaAs 13.0 0.0006 Low loss, not cheap, widely used for MMICs LCP 3.1 0.002 Medium loss, low permittivity, up to 40 GHz,

cheap PTFE (Teﬂon) 2.1 0.0004 Low loss, medium cost, low permittivity PTFE-glass 2.1–2.55 ∼ 0.001 Medium loss and cost, low permittivity PTFE-ceramic 10.2 0.002 Medium loss, high permittivity soft substrate,

not cheap RT/Duroid 5870 2.33 0.0012 Medium loss, low cost and low permittivity, up

to 40 GHz RT/Duroid 5880 2.22 0.0009 Low loss, low cost and low permittivity, up to

77 GHz RT/Duroid 6002, 6202 2.94 0.0012 Medium loss, low cost and low permittivity RT/Duroid 6006, 6.15 0.0019 Mediumloss, lowcost and medium permittivity RT/Duroid 6010 10.2 0.0023 Medium loss, low cost andmediumpermittivity

the opposite face, then adding a second substrate (which is metalized on only one surface) on top to achieve the second ground plane. The stripline is often considered a ‘soft-board’ technology, but using low-temperature co-ﬁred ceramics (LTCC), ceramic stripline circuits are also possible.

Unlikea microstrip line, the stripline isbasicallyanenclosedstructure;theﬁeld is not affected

by nearby components. The effective permittivity is the same as the substrate permittivity.

Figure 2.30 From a coaxial cable to a stripline

Circuit Concepts and Transmission Lines 65

There are many advantages of using striplines. Whatever circuits are on a microstrip (which is a quasi-TEM mode structure), you can do better by using a stripline, unless you run into fabrication or size constraints. Stripline ﬁlters and couplers always offer better bandwidth than their counterparts in a microstrip. Another advantage of the stripline is that fantastic isolation between adjacenttraces can be achieved (unlike a microstrip). Thebest isolationresults when a picket-fence of vias surrounds eachtransmission line,spaced at less than aquarter-wavelength. The stripline can be used to route RF signals across each other quite easily when an offset stripline (i.e. the central conductor is not right at the middle between the two ground planes) is used.

There are two major disadvantages of a stripline:

1. It is much harder and more expensive to fabricate than the microstrip. Lumped-element and

active components either have to be buried between the ground planes (not as convenient as a microstrip), or transitions to the microstrip must be employed as necessary to get the components onto the top of the board.

2. Because of the second ground plane, the strip width is much narrower for given impedance

(such as 50 ohms) and the board is thicker than that for a microstrip. A common reaction to problems with microstrip circuits is to convert them to a stripline; this may result in a much larger thickness for the same loss of the transmission line.

2.4.4.1 Characteristic Impedance

The characteristic impedance can be calculated approximately by

30π

√



d − t

+ A



(2.86)

where

A =2B ln(B + 1) − (B − 1) ln(B



√

B = 1

1 −t /d

− 1)/π

The impedance is sensitive to the thickness of the central conductor. The typical value for industrial standard lines is 50  or 75 .

2.4.4.2 Fundamental Mode

Just as for the ﬁeld within a coaxial cable, the ﬁeld in a stripline is TEM mode. This means that it is nondispersive and the velocity is not changed with frequency.

It is also possible to generate higher order modes if the operational frequency is above the lowest cut-off frequency. The smallestwavelengthshould meet thefollowingcondition to avoid higher order modes:

> 2d√ε

min

> 2W√ε

(2.87)

66 Antennas: From Theory to Practice

t d

Figure 2.31 Evolution from a coaxial cable to CPW (G: gap: W: width; d: substrate height)



2.4.4.3 Loss

The loss characteristics of the stripline are similar to the microstrip but have little loss due to radiation, as the structure is almost screened.

2.4.5 Coplanar Waveguide (CPW)

The CPWis anotherpopular planar transmission line. Just like a stripline, it may be considered a structure evolved from a coaxial cable, as shown in Figure 2.31. This structure can also be viewed as a coplanarstripline. The central conductor is separated from a pair of ground planes. They all sit on a substrate with a dielectric permittivity of ε. In the ideal case, the thickness of the dielectric is inﬁnite; in practice, it is just thick enough so that EM ﬁelds die out before they get out of the substrate. A variant of the coplanar waveguide is formed when a ground plane is provided on the opposite side of the dielectric; this is called a grounded coplanar waveguide (GCPW) and was originally developed to counter the power dissipation problems of CPW.

The CPW offers many advantages, which include the following:

It iseasy tofabricate and to integrate into circuits. Circuit components can be easily mounted on top of the line (even easier than on a microstrip) due to the fact that both the conductor and ground plane are on the same side of the substrate. Unlike the microstrip and stripline, no vias are required.

It can work to extremely high frequencies (100 GHz or more). Connecting to a CPW does not entail any parasitic discontinuities in the ground plane.

Good circuit isolation can be achieved using a CPW, because there are always RF grounds between traces. Many examples of high-isolation RF switches have used a grounded CPW to get 60 dB isolation or more.

The characteristic impedance can be kept as a constant as the signal conductor’s width is tapered down/up tomeet apin. This is perfect formatching to a component pin width without changing the substrate thickness.

One disadvantage is potentially lousy heat dissipation - this depends on the thickness of the line and whether it makes contact with a heat sink. In addition, in terms of the circuit size, the CPW isat a disadvantage versus a stripline or microstrip circuit; becauseits effective dielectric constant is lower (half of the ﬁelds are in air). CPW circuits can be lossier than comparable microstrip circuits if a compact layout is required.

Circuit Concepts and Transmission Lines 67

2.4.5.1 Characteristic Impedance

The design formulas for aCPW are verycomplicated. There are four geometricparameters: the gap G, the conductor width W and thicknesst and thesubstrate thicknessd.It is not possible to obtain an accurate analytical expressionof the characteristic impedance. Some approximations have to be made. If the conductor thickness is neglected, the effective permittivity is given approximately by [2]



+ 1

tanh[0.775 ln(d/G) +1.75]

[0.04 −0.7k + 0.01(1 − 0.1ε

)(0.25 +k)]



(2.88)

where

k =

W + 2G

(2.89)

The effective dielectric constant of a CPW is very close to the average dielectric constant of the substrate and free space. One way to think about this is that half of the electric ﬁeld lines are in free space and half are in the dielectric.

The characteristic impedance is

√

K(k)

(2.90)

K(k)

30π

where K (k) is a complete elliptical function of the ﬁrst kind. We have



=√1 −k2; K(k) = K (k)

(2.91)

and



(k)

K(k)



1 +

ln(2

1 −√k



1 +

ln(2

1 −√k

√





)



)

if 0 < k < 0.707



−1

if 0.707 < k < 1 (2.92)

Again, the typical impedance value for industrial standard lines is 50  or 75 .

68 Antennas: From Theory to Practice

2.4.5.2 Fundamental Mode

The EMﬁeld distribution around the CPW is illustrated in Figure2.31 andis similarto that of a microstrip. The wave velocity in the air isfaster than that in the substrate, thus the fundamental ﬁeld of CPW is quasi-TEM mode.

Higher order modes and surface modes may be generated in a CPW just as in a microstrip line. Thus, ground straps (bounding wires) are normally needed to tie the two grounds together in a CPW. These are especially important around any discontinuity, such as a tee junction. Care has to be taken since the bounding wires themselves could be the cause of discontinuity!

2.4.5.3 Loss

The current on the CPWis concentrated aroundthe signal conductor. The current onthe ground planes is also very focused in a small area, which results in a relatively high conductor loss as well as a heat dissipation problem. Generally speaking, the CPW exhibits a higher loss than its microstrip counterpart.

2.4.6 Waveguide

This is a very special and unique electromagnetic transmission line. Unlike any other transmission lines, a waveguide consists of just one piece of metal, which is tubular, usually with a circular or rectangular cross-section. A rectangular waveguide is shown in Figure 2.32. Due to the boundary conditions that the electric and magnetic ﬁelds have to satisfy, there are many possible wave patterns, which are called transverse electric (m, n) modes (TE transverse magnetic (m, n) modes (TM the x and y axes respectively. For example, TE

modes). m and n represent thenumber of peaksalong

mode means that the electric ﬁeld is within

the transverse plane and there is no electric ﬁeld component along the propagation direction, whilst the magnetic ﬁeld is not conﬁned to the transverse plane, and the electric ﬁeld changes along the x -axis, having one peak, but it has no changes along the y-axis. Which modes will actually be generated inside a waveguide depend on the frequency and excitation.

If the frequency is below the cut-off frequency of the fundamental mode (which is TE mode for standard waveguides), no propagation mode can be generated. Thus, the operational frequency should be greaterthan thecut-off frequency, which means that the waveguide can be

modes) and

Figure 2.32 Rectangular waveguide

mode

Circuit Concepts and Transmission Lines 69

considered ahigh-pass ﬁlter. Anysignals below the cut-off frequency will be ﬁltered out by the waveguide. The larger the waveguide, the lower the cut-off frequency. Since large waveguides are heavy and expensive, they are not attractive for applications. Thus, waveguides are only used for microwave and millimeter wave frequency bands.

The main advantages of the waveguide are low loss and high power-handling capacities,

which are very important for high-power applications such as radar.

2.4.6.1 Fundamental Mode

The fundamental mode of a standard rectangular waveguide is TE

mode. The ﬁeld pattern

(along with some higher modes) is illustrated in Figure 2.32 (the ﬁeld patterns for some higher modes can be found in [2] and [4]). The width and height of the waveguide are a and b respectively. The electric ﬁeld can be expressed as

= E0sin(

Ex= Ez= 0

j(ωt−βz)

x)e

(2.93)

and the magnetic ﬁeld is given by

= H1sin(

Hy= 0 H

= H2cos(

j(ωt−βz)

x)e

j(ωt−βz)

x)e

(2.94)

The electric ﬁeld is indeed within the transverse plane and the maximum ﬁeld is at x = a/2, while the magnetic ﬁeld has two components, one along the propagation direction z. Neither the electric nor the magnetic ﬁeld is a function of y, i.e. the mode index n = 0.

2.4.6.2 Cut-off Frequency, Waveguide Wavelength and Characteristic Impedance

The cut-off wavelength for TE

and TMmnmodes is given by



(

)

+ (

(2.95)

)

and its corresponding cut-off frequency is



Thus, for TE

2√εμ

mode, the cut-off wavelength is λc= 2a. This means that the waveguide works

(

)

+ (

)

(2.96)

for the operational wavelength λ<2a.

Since the next highest mode to TE a higher mode than TE

) and its cut-off wavelength is λc= a, this waveguide is only suitable

is TE20(for a standard waveguide, 2b < a, i.e. TE01is

for the operational wavelength between these two cut-off wavelengths,i.e. a <λ<2a. Outside

70 Antennas: From Theory to Practice

Table 2.5 Standard waveguides

Waveguide Freq. (GHz) ID of a (mm) ID of b (mm) Freq. band

WR-137 5.85–8.2 34.85 15.80 C band WR-112 7.05–10.00 28.50 12.60 H band WR-90 8.2–12.4 22.86 10.16 X band WR-62 12.4–18.0 15.80 7.90 Ku band WR-51 15.0–22.0 12.96 6.48 K band WR-42 18.0–26.5 10.67 4.32 K band

the bounds, the frequency is either too low for transmission or too high to keep single-mode transmission. Higher modes are not desirable since they have higher loss and the ﬁeld pattern may be changed over the transmission. Thus, eachindustrialstandardwaveguide isonlysuitable for a certain frequency range. A list of some selected standard waveguides with their suitable frequency ranges and inside dimensions is given in Table 2.5.

The ﬁeld inside a waveguide exhibits a periodic feature and the period is one waveguide wavelength, which is actually different from (longer than) the free space wavelength. The waveguide wavelength can be calculated using





= λ

1 −(

)

(2.97)

It is determined by the free space wavelength λ and the cut-off frequency λ

The characteristic impedance is also mode-dependent. For TE



TE10



= 120π

1 −(

mode, it is

) (2.98)

which is not a constant but a function of frequency. This is one of the reasons why the single mode is preferred for waveguide applications.

In this sectionsix of themost popular transmissionlines have been introducedand discussed. The characteristic impedance, fundamental mode and loss characteristics have been presented. A brief summary is provided in Table 2.6.

2.5 Connectors

In practice, almost all transmission lines have to be terminated to suitable connectors, which make the device interconnection much easier. There are many types of industrial standard connectors. Sometimes, more than one connector is available. For example, RG58 cable can be assembled to SMA, SMB, BNC and Type N connectors. Making the right choice can be a problem and there is a lack of information on this practical subject in other books, hence we will address this issue in this section.

Connectors are developed as a pair: a male and a female (an example is shown in Figure 2.33), although some RF connectors are sexless (such as the APC-7 and the

Circuit Concepts and Transmission Lines 71

Table 2.6 Summary of various transmission lines

Two-wire Coax Microstrip Stripline CPW Wave-guide

Basic mode TEM TEM quasi-TEM TEM quasi-TEM TE Bandwidth narrow – low

freq Loss high med. med. med. med. low Cost low low/ med. med. med. med. high Ease of

integration

Application low freq.,

med. hard easy med. easy hard

short

distance

wide wide wide very wide narrow

general

purpose

PCB circuit

and MMIC

RF circuit

and MMIC

RF circuit

and MMIC

high power

and high freq.

General Radio GR874). It is very important to choose the right connector for the application, since the effects of the connector (which is an additional element and may not have been taken into account in the design) on the system performance and measurements may be quite signiﬁcant. This is especially true in antenna measurements.

A good summary of all RF/microwave connectors was given by Amphenol RF [5]. Table

2.7 is a selection of some popular connectors for antenna systems and measurements. These connectors are mainly for coaxial cables, but some of them can be used for other transmission lines. For example, theSMA straight PCBmount jack, tabterminal panel jack andstub terminal panel jack are available and widely used in the antenna community.

Since all RF test equipment comes with coaxial connectors (type N and SMA are popular connectors), direct connection with other forms of transmission lines (such as microstrip and CPW) would be tricky. Some adapters have been developed. For example, industrial standard coax-to-waveguide adaptors are now widely available on the market. Figure 2.34 shows how to connect an SMA connector directly to a microstrip and CPW (feed line to an antenna) in practice – no standard adaptor is available.

Figure 2.33 Male (left) and female (right) N-type connectors

72 Antennas: From Theory to Practice

Table 2.7 Some industry standard connectors (Reproduced by permission of Amphenol RF)

BNC Baby N connector (BNC). Bayonet-style coupling for quick connection and

disconnection. Available in 50 ,75 and 50  reverse polarity. DC–4GHz

K The K ConnectorTMis a precision coaxial connector system that operates up to 40 GHz. It is compatible with SMA, WSMA and 3.5 mm connectors. It is well suited to applications in components, systems or instrumentation.

MCX A snap-on miniature coaxial (MCX) connector that conforms to the European CECC 22220.Since the MCX has identicalinner contactand insulator dimensionsto the SMB while being 30% smaller, it provides designers with options where weight and physical space are limited. DC – 6 GHz.

MMCX A micro-miniature coaxial (MMCX) connector with a lock-snap mechanism allowing for 360 degrees rotation on a printed circuit board. Conforms to the European CECC 22000 speciﬁcation and comes in surface mount, edge card and cable connectors. DC – 6 GHz.

Precision:APC-2.4, APC-3.5, APC-7 and APC-N TheacronymAPCdescribeshighperformance precision connectors, and stands for Amphenol Precision Connectors. Developed by Amphenol and Hewlett-Packard engineers. DC – 50 GHz.

Mini BNC A new generation of miniature BNC connectors that maintain the positive characteristics of our full-size BNCs for 75  systems while allowing 40% more interconnects in the same area. DC – 11 GHz.

SMA Subminiature version A (SMA) connectors with a threaded coupling mechanism that perform through 18 GHz. Available in standard, phase adjustable and reverse polarity. Built in accordance with MIL-C-39012 and CECC 22110/111, SMA connectors can bemated with allconnectors that meetthese specs, regardless ofmanufacturer. Widely used with RG-55, 58, 141, 142, 223, 303, 122, 174, 188 and 316.

SMB Subminiature version B(SMB) connectors. Developedin the 1960s asasmaller alternative to the SMA, the SMB line features a snap-on coupling mechanism. Available in 50 ,75 and miniature 75 . DC – 4 GHz (usable to 10 GHz). Often used with RG-188 and 196.

(continued)

Circuit Concepts and Transmission Lines 73

Table 2.7 Some industry standard connectors (Reproduced by permission of Amphenol RF)

(Continued)

SMC Subminiature version C(SMC) connectors. Medium-sized 50  threaded con- nectors designed to meet MIL-C-39012 category D, as generated by the US Air Force. DC – 4 GHz (usable to 10 GHz). Often used with RG-188 and 196.

SMP Subminiature connectors with a frequency range up to 40 GHz. Used in miniaturized applications they feature both push-on and snap-on mating styles.

SSMB Scaled SMA (SSMA). Microminiature connectors with snap-on mating interface allowing quick installation in small spaces with excellent performance in devices up to 4 GHz.

TNC Features screw threads for mating and serves as a threaded version of the BNC connector. The TNC is a 50  connector available in both standard and reverse polarity. DC – 11 GHz.

Type NAvailable in standardN (coaxial cable) andcorrugated N (helical andannular cable), the Type N is a durable, weatherproof, medium-sized connector consistent through 11 GHz. Used with RG-8, 58, 141 and 225.

UHF Invented for use in the radio industry, UHF stands for ultra-high frequency. While at the time 300 MHz was considered high frequency, these are now general purpose connectors for low-frequency systems.

Figure 2.34 Wideband antennas fed by CPW and microstrip, which are directly connected/soldered to SMA connectors

74 Antennas: From Theory to Practice

2.6 Summary

This chapterhas provided comprehensive coverage of circuit concepts and transmission lines– this is essential knowledge for antenna feeding, matching and characterization. In summary:

An introduction to lumped element systems and distributed element systems has been given right at the beginning. The main idea is that the current, voltage and impedance are all functions of the frequency and the reference position at the transmission line.

A transmission line model has been developed to obtain the important parameters of a transmission line, which include the characteristic impedance, input impedance, attenuation constant, phase constant and velocity. An extensive study on terminated transmission lines has been carried out. The reﬂection coefﬁcient, return loss and VSWR have been introduced to evaluate the line impedance matching.

The Smith Chart has been introduced as a very useful tool to analyze impedance matching. Lumped and distributed matching networks and impedance-matching techniques have also been addressed.

The bandwidth and quality factor (Q factor) have been discussed in depth.

Six popular transmission lines have been examined and compared in terms of their characteristic impedance, fundamental mode, loss characteristics and frequency bandwidth.

Various RF/microwave cables and connectors have been presented at the end of this chapter along with their typical speciﬁcations and frequency bandwidths.

References

[1] J. D. Kraus and D. A. Fleisch, Electromagnetics with Applications, 5th edition, McGraw-Hill, Inc., 1999. [2] D. M. Pozar, Microwave Engineering, 2nd edition, John Wiley & Sons, Inc., 1997. [3] http://www.rfcafe.com/references/electrical/coax [4] C. S. Lee, S. W. Lee and L. L. Chuang, ‘Plot of modal ﬁeld distribution in rectangular and circular waveguides’,

IEEE Trans. on MTT, March, pp. 271–274, 1985.

[5] www.amphenolrf.com

chart.htm

Problems

Q2.1 Explain the concept of the characteristic impedance of a transmission line. Q2.2 For a low-loss transmission line, find its characteristic impedance, attenuation con-

stant and phase constant (or wave number using lumped elements). How does the frequency affect these parameters?

Q2.3 A uniform transmission line has constants R =500μ/m, G = 1.5mS/m, L =

0.5μH/m and C = 10nF/m. Find the characteristic impedance and the attenuation constant of the line at the following frequencies a) 50 Hz; b) 30 MHz; c) 1 GHz; d) 10 GHz. and comment on the results.

Circuit Concepts and Transmission Lines 75

Q2.4 A coaxial transmission line has a = 4 mm and b = 12 mm. Find the characteristic

impedance of the line if the dielectric is a) air space polyethylene (ASP); b) foam polyethylene (FE); c) solid Teflon (ST). Hint: Use Table 2.2 for permittivity.

Q2.5 A 100  resistor is connected to a good cable with characteristic impedance of

50 . The attenuation constant is not zero but 0.2 Np/m at 1 GHz, and the relative permittivity of the cable dielectric is 1.5. If the cable length is 10 m, find a) the reflection coefficient and return loss at the termination; b) the reflection coefficient and return loss at the input of the cable; c) the VSWR at both the terminal and the input of the cable; d) the input impedance at the input of the cable. Suggest a method to improve the matching of the system.

Q2.6 Obtain the theoretical characteristic impedance and the best impedance for maxi-

mum power-handling capacity of a coaxial cable. Use the results to justify why the most common coaxial cable impedances are 50  and 75 .

Q2.7 RG-59U, a popular cable for microwave applications, has an open-circuit

impedance of 130 + j 75 ohmsand short-circuitimpedance of30.3 − j 21.2ohms. Find the characteristic impedance of the line.

Q2.8 A quality transmission line is terminated in 100 + j 50 ohms. Find

a) the voltage reflection coefficient; b) the VSWR; c) the shortest length of line required to transform the impedance to purely resis-

tive.

If 220 V is applied to the line, find the maximum and minimum line voltages.

Q2.9 Explain the concept of impedance matchingand then comparea lumped matching

network and a distributed matching network. Q2.10 Explain what the Smith Chart is. Explain its application. Q2.11 A load with an impedance of 100 − j 100  is to be matched with a 50  trans-

mission line. Design a matching network and discuss if there are other solutions

available. Q2.12 A load with animpedance of 100 − j 100  is to be matchedwith a 50  transmis-

sion line. Design two stub-matching networks and then compare their bandwidth

performance. Q2.13 Explain what Bode–Fano limits are and how they may be applied to matching

networks. Q2.14 Discuss the relationship between bandwidth and quality factor. What is the major

difference between the loaded Q factor and the unloaded Q factor? Q2.15 Design a 50-ohm microstrip line using a PCB board with PTFE (Teflon) substrate

of 1 mm thickness. Find the cut-off frequency for the first higher mode in the line. Q2.16 Design a 50-ohm CPW using a PCB board with PTFE (Teflon) substrate of 1 mm

thickness. Q2.17 Rectangular waveguides are widely used for radar applications. WR-90 standard

waveguide (see Table 2.5) is mainly used for the X band. Find

a) the cut-off frequency for TE

b) the cut-off frequency for TE

c) the cut-off frequency for TE

10 01 20

mode; mode; mode.

Hence identify the most suitable frequency range for this waveguide.

Field Concepts and Radio Waves

In this chapter we will ﬁrst see how Maxwell’s equations can be used to obtain wave solutions. The concepts of the plane wave, intrinsic impedance and polarization will then be introduced, followed by a discussion on radio propagation mechanisms and radio wave propagation characteristics in various media. A few basic radio propagation models will be introduced, and circuit concepts and ﬁeld concepts will be compared at the end of this chapter. The concept of skin depth will be lookedinto from both the ﬁeldand circuitpoints of view. Althoughthe issues addressed in this chapter may not be used directly for antenna design, the knowledge will be extremely useful for gaining a better understanding of the antenna radiation characteristics as well asradio waves – generated/received by antennas. Because antennas and radio propagation are so closely linked, some countries and universities treat them as a single subject.

3.1 Wave Equation and Solutions

As mentioned in Chapter 1, Maxwell’s modiﬁed version of Ampere’s Circuital Law enables a set of equations to be combined together to derive the electromagnetic wave equation. The derivation is relatively straightforward.

Now let us discuss a time-harmonic case with the time factor e frequency and is the most common form of a wave in real life (according to Fourier’s theory, more complicated cases may be decomposed to a linear combination of harmonic waves). From Maxwell’s equations (1.29), we have

jωt

, which means a single

∇×E =−jωμH

∇×H = (σ + jωε)E

∇•E = ρ/ε

∇•H = 0

Take a curl operation on the ﬁrst equation to yield

∇×∇×E =∇(∇•E) −∇

Antennas: From Theory to Practice Yi Huang and Kevin Boyle



2008 John Wiley & Sons, Ltd

E =−jωμ∇×H

(3.1)

78 Antennas: From Theory to Practice

∂

∂z

where ∇2=∇•∇=

∂x

∂

∂y

Combine this with the second and third equations in Equation (3.1) to obtain

∇

E − jωμ(σ + j ωε)E =∇(ρ/ε) (3.2)

Now let



γ =

jωμ(σ + jωε) = α + jβ (3.3)

where α and β are theattenuation constant andphaseconstant, respectively. Similardeﬁnitions were introduced for a transmission line in Chapter 2. From Equation (3.3) we can represent these constants by the material properties and frequency as:



√

α = ω

με

β = ω√με





1 2







1 2

1 +

ε2ω



− 1

+ 1



1/2

(3.4)

Equation (3.2) can now be rewritten as

∇

E − γ2E =∇(ρ/ε) (3.5)

In the source-free region (ρ = 0), we have

∇

E − γ2E = 0 (3.6)

This is called the wave equation. There are many possible solutions to this equation. Boundary conditions and sources are required to obtain the speciﬁc solutions. In free space, one of the solutions is

E = ˆxE

jωt−γ z

= ˆxE0e

−αz+j (ωt−β z)

(3.7)

This can be validated easily by using this representation in the wave equation. Other possible solutions include, for example

E = ˆxE

jωt+γ z

; E = ˆyE0e

jωt+γ z

; E = ˆz E0e

jωt±γ x

; ...

Using the electric ﬁeld E in Equation (3.7) and Equation (3.1), the magnetic ﬁeld H is

H =

∇×E =−ˆy

ωμ

jγ

ωμ

−αz+j (ωt−β z)

(3.8)

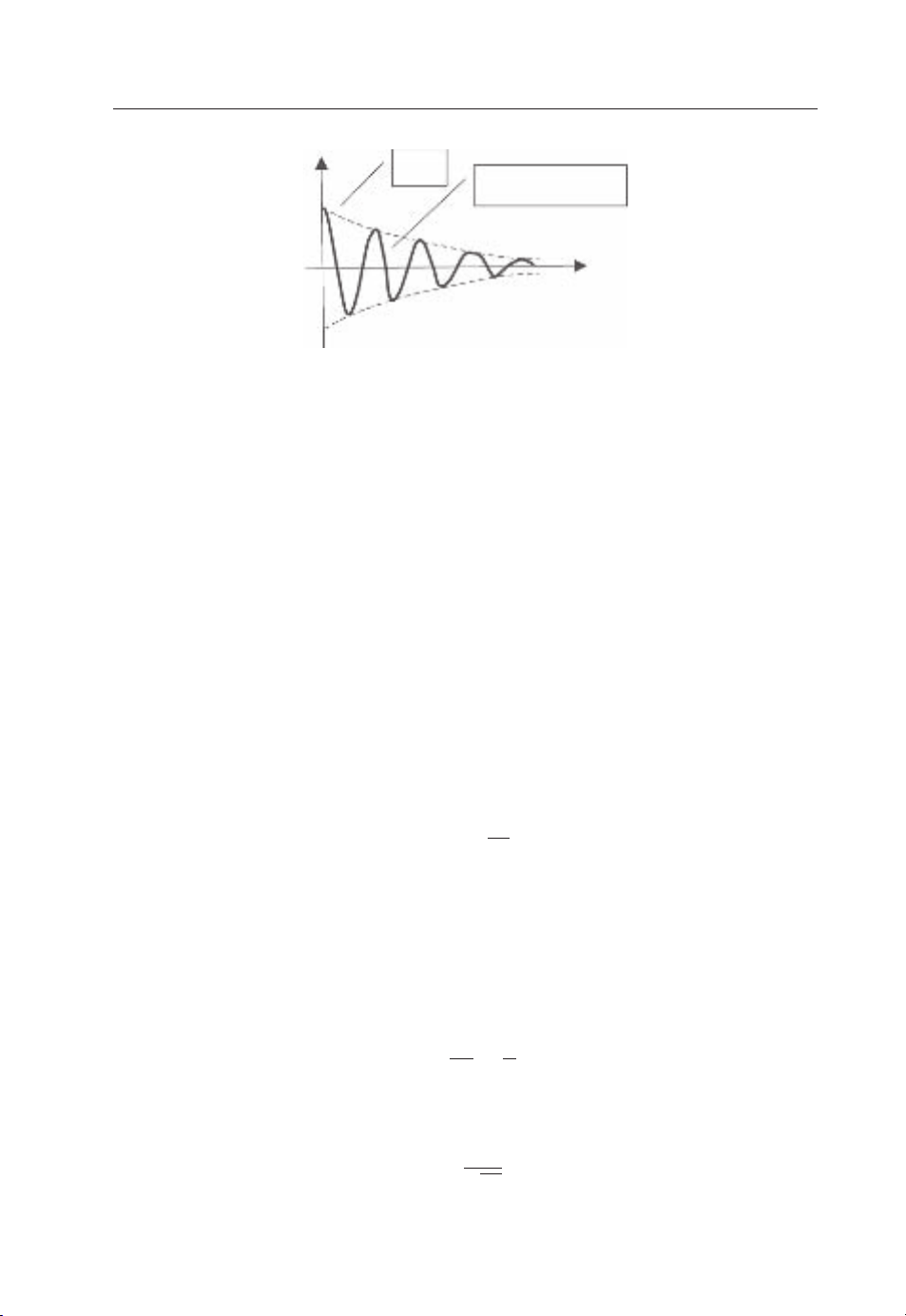
Field Concepts and Radio Waves 79

−αz

Figure 3.1 A traveling wave in a medium with loss

E0e

−αz

cos(ωt – βz)

Thus, themagnetic ﬁeld has only a y component in thiscase, whichis orthogonal to the electric ﬁeld. There is a phase difference between the electric and magnetic ﬁelds if the attenuation constant is not zero.

3.1.1 Discussion on Wave Solutions

Equation (3.7) can be illustrated by Figure 3.1; it is evident that

The wave solution is a vector. In this case, it has only an x component.

Its amplitude is decreased exponentially as a function of the propagation distance (z, in this case). The attenuation constant α, given by Equation (3.4), is determined by the material properties and frequency. When the conductivity σ is zero, the wave amplitude is a constant.

Its phase ϕ is of the form (ωt − βz), which is a function of time, frequency and propagation distance.

For the loss-free case, σ = 0, Equation (3.4) can be simpliﬁed to

α = 0 β = ω

√

με

(3.9)

If we ﬁx the phase and let the wave travel a distance of z over a period of time t, mathematically this is

ϕ = ω · t + β ·z = 0 (3.10)

Thus, the velocity of the wave can be obtained as

z t

(3.11)

v =

Replace β by Equation (3.9) to give

v =

√

με

(3.12)

80 Antennas: From Theory to Practice

This means that the wave velocity is determined by the permittivity and permeability of the medium in which the wave is traveling. In free space this velocity is

√

≈ 3 × 108m/s

μ0ε

v =

We can therefore conclude that the velocity of an electromagnetic wave (including light) in free space is about 3 × 10

m/s – this was what Maxwell obtained more than 120 years ago when he formulated the four equations (more precisely 20 equations in his original work), but at that time nobody could validate this important result. This is a good example of how mathematics can be used to solve real world engineering problems.

In addition, from Equation (3.11), we can see that

β =

2π f

2π

(3.13)

Thus, the phase constant is also called the wave number (for every one wavelength, the phase is changed by 2π ), which is the same as what we obtained for a transmission line in Chapter

2. In fact, the transmission line equation (2.7) is just a special case of the wave equation (3.6) when x and y are ﬁxed. The free space could be viewed as an open transmission line where the information is carried by electromagnetic (EM) waves.

Light, X-rays and radio waves are EM waves at different frequencies although they seem to be very different. One thing that all the forms of EM waves have in common is that they can travel through empty space. This is not true for other kinds of waves; sound waves, for example, need some kind of material, like air or water, in which to move. EM energy is carried by photons, the energy of a photon is hf, where h is Planck’s constant = 6.63 × 10

−34

Js, and

f is the frequency in Hz.

3.2 The Plane Wave, Intrinsic Impedance and Polarization

3.2.1 The Plane Wave and Intrinsic Impedance

When the conductivity of the medium is zero, the electric ﬁeld in Equation (3.7) can be simpliﬁed to

E = ˆxE

and the corresponding magnetic ﬁeld is

H = ˆy

ωμ

j(ωt−βz)

Thus, the electric and magnetic ﬁelds are in phase, of constant amplitude and orthogonal to each other, as well as being orthogonal to the propagation direction z. This EM wave is called the plane wave, and is illustrated by Figure 3.2. It is a special but common form of EM wave whose amplitude is a constant (in theory). The spherical wave is another common wave form.

j(ωt−βz)

= ˆy



(3.14)

j(ωt−βz)

(3.15)

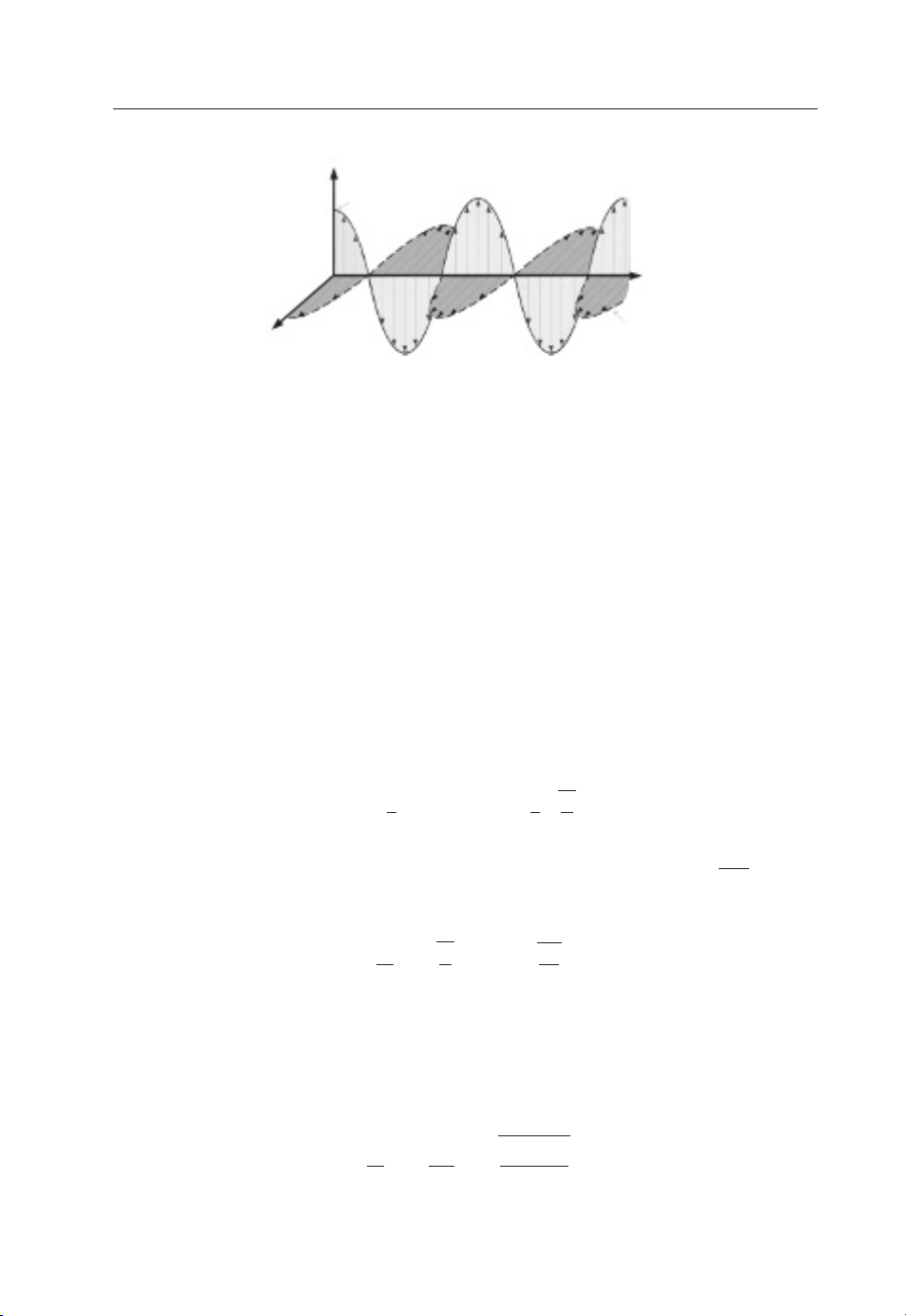
Field Concepts and Radio Waves 81

E = Ex x

Figure 3.2 A plane wave traveling in the z-direction

H = H

The plane wave can only existfar away from the source, whilstthe spherical wave is considered closer to the source.

The power ﬂow density of the EM wave, also known as the Poynting vector, is deﬁned as

the cross product of the electric and magnetic ﬁelds, i.e.

S = E × H

where * denotes the complex conjugate, i.e. (R + jX)

∗

(W/m2) (3.16)

∗

= R − jX. The Poynting vector de-

scribes the amplitude and direction of the ﬂow of power density in EM waves. It is named after the English physicist John Henry Poynting, who introduced it in 1884. The power ﬂow direction is orthogonal to E and H. Equation (3.16) gives the instantaneous Poynting vector. The averaged Poynting vector is obtained by integrating the instantaneous Poynting vector over one period and dividing by one period. Thus, the time-averaged power density of an EM wave is



Re(E × H

∗

) = ˆz

and it can be obtained by its electric ﬁeld amplitude and material properties

1 2

√

(3.17)

ε/μ – this is

actually the ratio of the electric ﬁeld to the magnetic ﬁeld:

η =



= 120π



() (3.18)

It is called the intrinsic impedance of the material and is determined by the ratio of the permittivity to the permeability of the medium for a loss-free medium. If the medium is lossy (conductivity is not negligible and/or the permittivity is complex), the intrinsic impedance is complex:

η =

=−

ωμ

jγ



σ + jωε

jωμ

() (3.19)

82 Antennas: From Theory to Practice

In free space it is



= 120π ≈ 377() (3.20)

and the time-averaged power density is

= ˆz

= ˆz60π E

(3.21)

3.2.2 Polarization

A very important feature of the EM wave is the polarization, which is described by the locus of the tip of the E vector as time progresses. If we use a trigonometric form (we can also use the exponential form), a wave propagating towards the z direction can be expressed as

E = ˆxA cos(ωt − βz) + ˆyB sin(ωt − β z) (3.22)

where A and B, also shown in Figure 3.3, are the amplitudes of the ﬁeld components in the x and y directions, respectively. It is not difﬁcult to verify that this E ﬁeld is also a solution of the wave equation (3.6).

If A or B = 0, this expression represents a linearly polarized wave; ifA = B = 0, it is an elliptically polarized wave; if A = B, it then represents a circularly polarized wave, which is widely employed insatellite communications. Becausethe ionosphere causesFaraday rotation to anEM wave, which means that alinearly polarizedEM wave may be rotated by an unknown amount (depending onthethickness and temperatureof the ionosphere, aswell as the frequency – the rotation is high at lower frequencies but small at higher frequencies), making the linearly polarized wave hard to match after passing through the ionosphere. However, there is no problem for circularly polarized waves; this is why satellite systems like GPS (global positioning system) have employed circular polarization, not linear polarization, for transmission.

The circularly polarized wave may be considered a combination of two linearly polarized waves. There are two types of circular polarization: right-hand circular polarization (RCP)

Linear

or B = 0

Elliptical

Figure 3.3 Wave polarizations

Circular

A = B

Field Concepts and Radio Waves 83

and left-hand circular polarization (LCP) – one linearly polarized wave is ahead of or behind the other one by 90 degrees. When the thumb points to the propagation direction, if the tip of the E vector follows the right-hand ﬁngers as time progresses, it is RCP. Otherwise, it is LCP. Equation (3.22) represents a right-hand circularly polarized wave if A = B > 0. Its corresponding left-hand polarized wave can be expressed as

E = ˆxA cos(ωt − βz) − ˆyB sin(ωt − β z) (3.23)

There is just a sign change: ‘+’ is changed to ‘−’ for the y component. The ratio of amplitudes

A to B is called the axial ratio:

AR =

(3.24)

For a circularly polarized wave, AR is one. For a linearly polarized wave, it is inﬁnite or zero, thus 0 ≤ AR ≤+∞.

It should be pointed out that a plane wave can be linearly polarized, circularly polarized or elliptically polarized. Equation (3.14) represents a linearly polarized plane wave, whilst Equations (3.22) and (3.23) are circularly polarized plane waves.

3.3 Radio Wave Propagation Mechanisms

Radio wave propagation is a special subject. A radio wave is considered a general term in this book for EM waves up to about 100 GHz. In this section we are going to brieﬂy review wave propagation mechanisms, which include wave reﬂection, transmission, diffraction and scattering.

3.3.1 Reﬂection and Transmission

As we understand now, an EM wave far away from its source may be considered a local plane wave. Let a linearly polarized plane wave be incident on the surface between Medium 1 and Medium 2, as shown in Figure 3.4. What is going to happen at the boundary? The wave will be partially reﬂected back to Medium 1 and partially transmitted (more precisely refracted; the refraction is the change in direction of a wave due to a change in velocity from one medium to another) into Medium 2. If the loss can be neglected, there are a few important points to note:

the incident angle θ

The reﬂection coefﬁcient is deﬁned as the ratio of the reﬂected wave to the incident wave, i.e.

is the same as the reﬂected angle θr, that is θi= θr;

is linked to the transmitted angle θtby Snell’s law:

√

sin θ sin θ

 =

ε1μ

E E

√

ε2μ

(3.25)

(3.26)

84 Antennas: From Theory to Practice

ε1, μ1,

Medium 1 Medium 2

ε2, μ2,

Et = T

Figure 3.4 Plane wave reﬂection and transmission, and its analogous transmission line

and the transmission coefﬁcient is deﬁned as the ratio of the transmitted wave to the incident wave, i.e.

T =

(3.27)

Both coefﬁcients are linked to the wave polarization. There are basically two orthogonal polarizations – parallel polarization (E is parallel to the incident plane formed by the incident and reﬂected waves) and perpendicular polarization (E is perpendicular to the incident plane), as shown in Figure 3.5. Any other polarizations can be considered to be combinations of these two principal polarizations.

We can employ either the ﬁeld approach or the circuit approach to obtain the reﬂection and transmission coefﬁcients. Using ﬁeld concepts, we need to employ the boundary conditions, which is relatively complicated. Thus, we are going to use the circuit approach to obtain these coefﬁcients.

From Figure 3.4, we can see that the two media can be replaced by two analogous transmission lines with characteristic impedances of Z

and Z2, respectively. They are determined by

Parallel Polarization Perpendicular Polarization

Figure 3.5 Two principal polarizations

WILEY ANTENNAS User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual

Contents

Preface

Acronyms and Constants

Introduction

1.1 A Short History of Antennas

1.2 Radio Systems and Antennas

1.3 Necessary Mathematics

1.3.1 Complex Numbers

1.3.2 Vectors and Vector Operation

1.3.3 Coordinates

1.4 Basics of Electromagnetics

1.4.1 The Electric Field

1.4.2 The Magnetic Field

1.4.3 Maxwell’s Equations

1.4.4 Boundary Conditions

1.5 Summary

References

Problems

Circuit Concepts and Transmission Lines

2.1 Circuit Concepts

2.1.1 Lumped and Distributed Element Systems

2.2 Transmission Line Theory

2.2.1 Transmission Line Model

2.2.2 Solutions and Analysis

2.2.3 Terminated Transmission Line

2.3 The Smith Chart and Impedance Matching

2.3.1 The Smith Chart

2.3.2 Impedance Matching

2.3.3 The Quality Factor and Bandwidth

2.4 Various Transmission Lines

2.4.1 Two-wire Transmission Line

2.4.2 Coaxial Cable

2.4.3 Microstrip Line

2.4.4 Stripline

2.4.5 Coplanar Waveguide (CPW)

2.4.6 Waveguide

2.5 Connectors

2.6 Summary

References

Problems

Field Concepts and Radio Waves

3.1 Wave Equation and Solutions

3.1.1 Discussion on Wave Solutions

3.2 The Plane Wave, Intrinsic Impedance and Polarization

3.2.1 The Plane Wave and Intrinsic Impedance

3.2.2 Polarization

3.3 Radio Wave Propagation Mechanisms