Victor V12 Owner's Manual

V12 Manual
1
Owners Guide
V12 Financial Calculator
Preface
Congratulations on your purchase of the V12
financial calculator from Victor Technology.
Victor has been serving customers since 1918.
Today, Victor offers a complete line of printing,
handheld, desktop, scientific, and financial
calculators. For more information please see
our website at www.victortech.com
or call us at
1-800-628-2420.
Victor: The Choice of Professionals
Copyright © 2007 by Victor Technology LLC
All rights reserved.

V12 Manual
32
Table of Contents
Chapter 1: Where to Start...................................5
Powering On and Off..............................................5
Controlling screen contrast.....................................5
Keyboard Dynamics ...............................................5
Entering Digits........................................................5
Decimal Placement ................................................5
Entering Large Amounts.........................................6
Entering Small Amounts.........................................6
Changing the Sign of a Number .............................7
Using the Clear Function........................................7
ALG and RPN Setting Functions............................7
RPN method...........................................................8
Sequential Calculations in RPN method.................8
Storage Capacity and Recalling Entered Data .......9
Chapter 2: The First Steps to Financial Functions
.....................................................................10
Using the Financial Storage Registers .................10
Saving to a Register.............................................10
Resetting Saved Data ..........................................10
Basic Interest Calculations ...................................10
Basic Financial Calculations.................................13
Positive and Negative Cash Flows.......................13
Payment Function ................................................14
The special relationship between i. and n..........14
Determining Interest Rate: Solving for i. ............14
Determining Present Value: Solving for PV ........16
Determining Payment Amount: Solving for PMT .17
Determining Future Value: Solving for FV..........17
Determining Number of Periods: Solving for n. .18
Loan With a Balloon Payment ..............................19
Amortization Function...........................................20
Chapter 3: Other Financial Calculations .........22
NPV (Net Present Value) .....................................22
Grouped Cash Flows............................................24
Replacing Current Cash Flow Value Data............26
Determining Values with Depreciation..................27
Determining Bond Values………………………….29
Percentages…………………………………………31
Calendar Operations……………………………….34
Determining Number of Days between Dates…...35
Chapter 4: Other Operational Features ............37
Full Figure Display ...............................................39
Other Display Settings..........................................39
LST X ...................................................................40
x ↔ y....................................................................41
Statistical Features and Functions .......................42
Recovering Incorrectly Entered Statistical Data ...43
Standard Deviation Entries...................................44
Mean Values ........................................................44
Linear Estimates for x and y.................................45

V12 Manual
54
Weighted Mean Values ........................................46
Mathematical Features and Functions .................48
Power Features in ALG method ...........................52
Power Features in RPN method...........................52
Chapter 5: The Basics of Programming............53
Creating Your Own Program ................................53
Executing Your Own Program..............................57
Program Memory Basics ......................................57
Determining Program Line Instructions ................58
Program line 000 and the GTO 000 instruction: ...60
Performing a Program One Line at a Time...........61
Setting the Calculator to a Specific Program Line 63
Interrupting a Program During Execution .............63
Stopping a Program During Execution .................65
Chapter 6: Branch & Loop Programs................67
Branching with Conditions....................................67
Storing More Than One Program .........................71
Chapter 7: Editing Your Programs....................72
Inserting Instructions Into a Program....................73
Inserting Instructions at the End of a Program .....76
Chapter 8: Error Messages...............................77
Chapter 1: Where to Start
Powering On and Off
Turn the unit on by touching the ON button. To turn the unit off,
touch the ON button again. The calculator will automatically
power off after 7 minutes if left not used.
When the calculator is experiencing a low battery charge, a
battery icon will appear in the top left corner of the display screen.
Controlling screen contrast
To change the contrast of the display screen for optimal viewing,
hold down the b button and touch X or ÷ keys until desired
contrast is reached.
Keyboard Dynamics
Most buttons perform multiple functions. The primary function is
displayed on the center of the button, while alternative functions
of the same button are imprinted on the bottom side of the button,
below the button, or above the button. Alternate functions are
obtainable by using one of two colored prefix buttons prior to
entering the function desired. The colors of the prefix buttons
match the alternative functions. The prefix buttons are b (blue)
and r (red).
Entering Digits
To enter a digit, touch the number buttons and decimal place ..
button in the same order as they would appear on paper.
Decimal Placement
On the display, digits are separated with commas left of the
decimal place. To change the decimal point period icon to a
comma and the comma icon to a decimal point, turn the V12 off,
touch and hold the decimal point button . , and touch the ON
V12 Manual
76
button. Repeat this process again to reset these placements to
the standard display.
Entering Large Amounts
The V12 displays numbers up to 10 digits. Scientific notation
allows numbers longer than 10 digits to be entered. To perform
this function, enter the number with the decimal point moved to
the left. Keep track of how many positions the decimal point
moved. Next touch the EEX button and enter the number of
positions the decimal point was moved. Touch the ENTER key
to complete the entry.
Example
To enter a value of 7,894,300,000,000 the decimal place should
move 12 spaces to the left leaving a mantissa of 7.8943 with an
exponent of 12.
YALPSID SEIRTNE
7.8943 EEX 12
7.894300 12
Displays the figure in scientific
notation.
These scientific notation numbers can be used in calculations
the same as any number.
Entering Small Amounts
Scientific notation allows numbers more than 10 decimal places
below zero to be entered. To perform this function, enter the
number with the decimal point moved to the right. Keep track of
how many positions the decimal point moved. Next touch the
EEX button and enter the number of positions the decimal point
was moved. Touch the CHS key to make the number negative.
Touch the ENTER key to complete the entry. For example, to
enter the number .00000000047823456 we move the decimal
point 10 positions. We enter 4.7823456, touch EEX, enter 10,
touch CHS, and touch ENTER The display will show 4.782345
-10.
Changing the Sign of a Number
The CHS button allows a changing of the sign of a number. If a
negative value is entered, or comes as a solution, touching the
CHS button will make it a positive. Likewise, touching the CHS
button after a positive value is displayed on the screen will
change its sign to a negative.
Using the Clear Function
Clearing replaces the displayed value with zero and replaces the
previous instruction with the r GTO 000 instruction when
programming. There are many ways of clearing data, outlined
here:
BUTTONS WILL CLEAR
.b CLEAR REG
Storage registers, block and last x register,
and display screen
.b CLEAR FIN
Financial registers
.b CLEAR ∑
Statistical registers (121- R)
1
block registers and display screen
.b CLEAR PRGM
Program memory (when touched in program
mode)
CLX
Display screen and x register
ALG and RPN Setting Functions
ALG MODE RPN MODE
4 ENTER 2 X. 4 X 2 =

V12 Manual
98
The ALG method enables calculations for addition, subtraction,
multiplication, and division (with or without parentheses) in the
standard method.
To select the ALG method. Touch b ALG , and the ALG icon
will appear.
Sequential Calculations in ALG method
To complete a sequential calculation, touch = at the end of your
entries and not after every entry.
Example: 5 X 2 + 3 – 4 ÷ 3 = 3.00
RPN method
To select the RPN method, touch b RPN , and the RPN icon
appears.
With RPN method enabled, you can perform basic calculations
with two numbers and with multiplication, addition, division, or
subtraction. It is necessary to enter both numbers in the
equation, and then select the mathematical operation to be used.
Touching ENTER between number entries allows a separation
of the different values within the calculator, and after entering the
second value, selecting the mathematical operation completes
the calculation.
Sequential Calculations in RPN method
Once a solution from a previous entry has been found and is on
the display screen, enter the next value and select the
mathematical operation to be performed.
Example: 5 ENTER 2 X 3 + 4 - 3 ÷ .
Note: The display will show the answer: 3.00
Storage Capacity and Recalling Entered Data
Information entered into the calculator is stored to memory in
different registers within the calculator. There are registers for
data storage during calculations called blocks (covered later in
this manual) and also a LST X register that stores the value last
on the display screen before an operation when using the RPN
method.
In addition to these storage registers, up to 20 more information
registers are available for storing values manually. The registers
are called R0 through R9, and R . 0 through R . 9 (with the
decimal point in front of the number). Note: In this manual, ..
represents the decimal point key.
To store numbers into a register, touch STO , and then touch
the register number desired [either (0, 1, 2, 3, 4, 5, 6, 7, 8, or 9),
or ( .. 0, . 1, . 2, . 3, . 4, . 5, . 6, . 7, . 8, . 9) ].
To recall a previously stored value, touch RCL , and similarly
select the desired stored value number, R0 through R9, and R ..
0 through R . 9.
To delete stored values, enter zero, touch STO , and select the
register to be deleted, R0 through R9, and R . 0 through R . 9.
(Note: Designating a new value instead of 0 also replaces the
old value set to the register)
V12 Manual
1110
Chapter 2: The First Steps to
Financial Functions
Using the Financial Storage Registers
Five specialty registers are used for financial calculations only.
These are n , i , PV , PMT , and FV and are located along
the top row of buttons. Saving data to these storage registers
makes it possible to calculate financial problems such as loan
payments.
Saving to a Register
To set the numbers into the registers, enter the number to be
stored, and touch the button to which the number is to be stored.
To recall the number, touch RCL followed by the register you
would like to recall ( n , i , PV , PMT , or FV )
Resetting Saved Data
To replace current financial register values simply enter the new
value and press the register key. To clear all financial registers
at once, touch b clear FIN. Financial storage registers are also
reset when b REG is entered, or when the continuous memory
is reset.
Basic Interest Calculations
Simple interest can be calculated with either 365-day or 360-day
cycles. Either can be displayed and the total amounts of
principal plus the accrued interest may be found by touching +
in RPN method, or + x ↔ y = in ALG method.
To perform this operation on a 365-day cycle, touch R↓ x↔ y
to find and show interest accrued after determining the 360 day
interest.
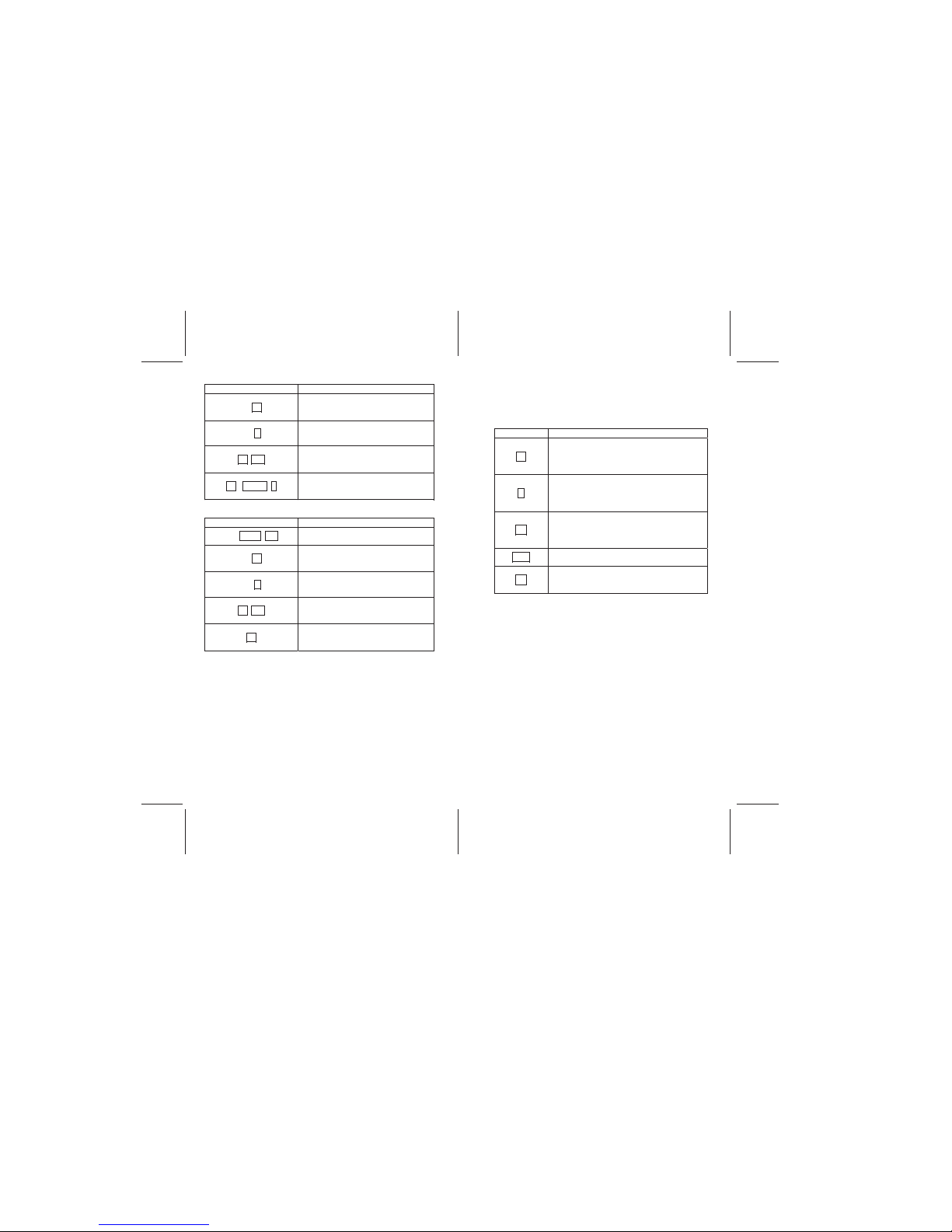
Example
Calculate the simple interest on a 100,000 amount with 12%
annual interest for 180 days using the 360 day cycle and the 365
day cycle.
YALPSID SEIRTNE
100000 CHS PV
-100,000.00
Displays the amount.
180 n.
180.00
Displays the number of days for
which interest will be calculated
12 i.
12.00
Displays the annual interest rate
.b INT
6,000.00
Displays the simple interest on a 360
day basis
R↓ x↔y
5,917.81
Displays the simple interest on a 360
day basis
In RPN method, touching + after the calculation places the
total principal and interest accrued into the display.
To display total principal and interest accrued in ALG method,
touch + x ↔ y = .
Example
You take out a loan of $900, which you have 90 days to repay.
You are lent the money at 4.3% simple interest, which is
calculated on a 360-day cycle. You want to find the total amount
of accrued interest you will owe in 90 days, the total amount you
will owe including principal.
ENTRIES (ALG) DISPLAY
900 CHS PV
-900.00
V12 Manual
1312
Displays the amount.
90 n.
90.00
Displays the number of days for
which interest will be calculated
4.3 i.
4.30
Displays the annual interest rate
b INT
9.68
Displays the simple interest on a 360
day basis
.+ x ↔ y =
909.68
Displays the simple interest plus
principal due on a 360 day basis
ENTRIES (RPN) DISPLAY
900 CHS PV
-900.00
Displays the amount.
90 n.
90.00
Displays the number of days for
which interest will be calculated
4.3 i.
4.30
Displays the annual interest rate
b INT
9.68
Displays the simple interest on a 360
day basis
+.
909.68
Displays the simple interest plus
principal due on a 360 day basis
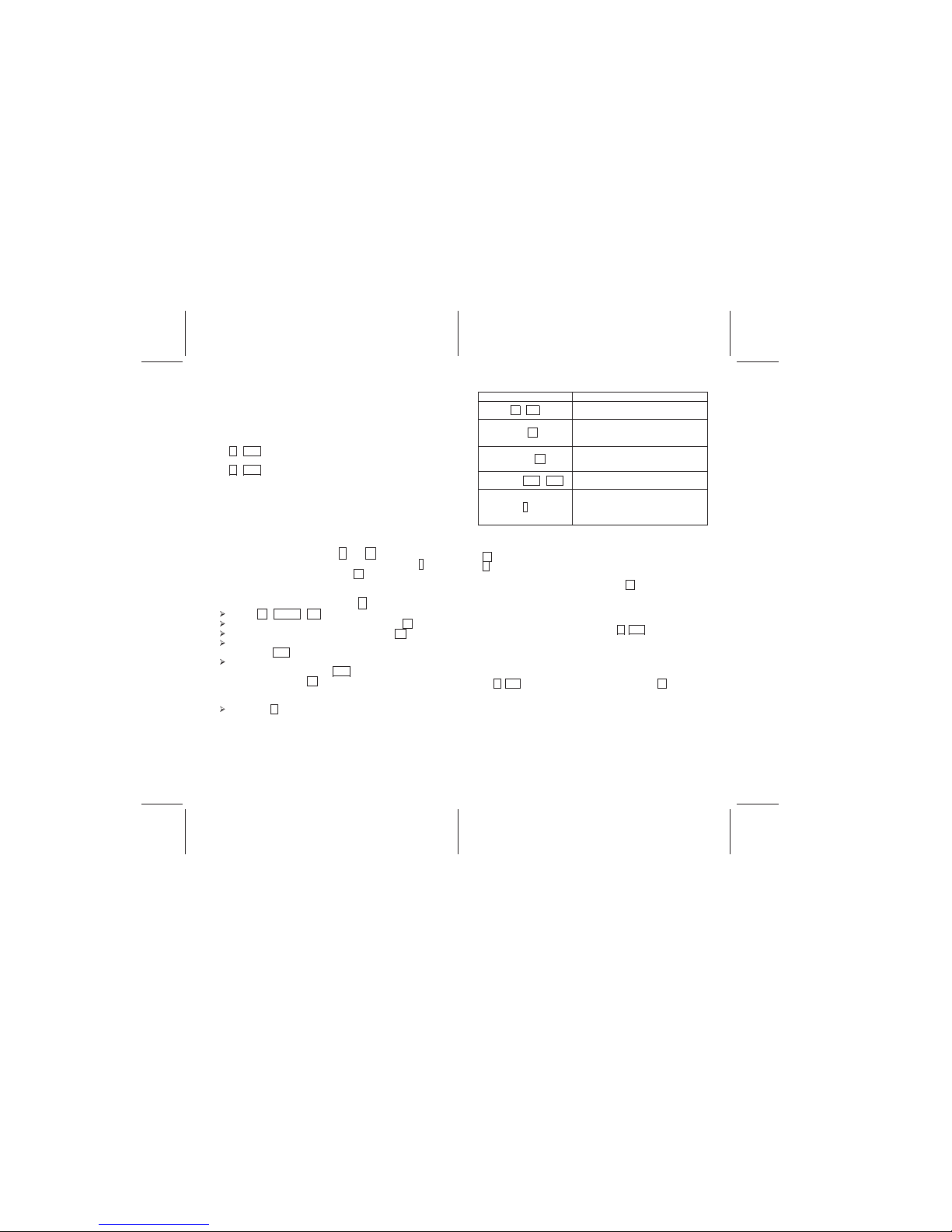
Basic Financial Calculations
Before describing Basic Financial Calculations, it is important to
review and understand five basic terms and keys used with the
V12.
TERM / KEY DEFINITION
n.
The number of periods in the financial
loan, often expressed in days, months, or
years. The interest rate must be defined
per period.
i.
The interest rate per period. Often an
annual rate is converted to monthly by
dividing by 12, weekly by dividing by 52, or
daily by dividing by 365.
PV
The initial cash value received or paid or
the present value of a series of future
payments when discounted at an interest
rate.
PMT
The payment made each period.
FV
The final cash value received or paid or
the future value of a series of payments
assuming an interest rate.
When using the V12, four of these five variables must be known
to perform a calculation. The unknown variable can then be
solved.
Positive and Negative Cash Flows
When performing financial calculations special care must be
taken to enter values with the proper sign. A payment or outflow
of cash must have a negative sign. A receipt of cash must have
a positive sign. For example, the initial cash received in a loan is
a positive amount. The payments are negative amounts.
V12 Manual
1514
Payment Function
Payments in compounding periods may be made either at the
beginning of a period (such as payments in advance, and
annuities due), or at the end of a period (such as regular
annuities or payments in arrears).
To select payment type:
Touch r END if the payment will be made at the end of the
period.
Touch r BEG if the payment will be made at the beginning of
the period.
Most transactions utilize an End of the period payment. Note:
This manual will only show examples using End of the period
payments.
If the BEGIN icon is not showing on the display, the payment
function is set to END.
The special relationship between i. and n.
In compound interest problems, the interest rate entered into i
must correlate to the compounding period n in time (as in years,
days, months, etc.)
Determining Interest Rate: Solving for i.
Touch b CLEAR FIN to reset financial registers
Enter the number of payment periods and touch n.
Enter the present value of the loan and touch PV.
Enter the payment value per period (a negative number)
and touch PMT.
Enter the future value of the amount owed at the end of
the payment periods, touch CHS to make the number
negative, and touch FV. Note: If the amount owed at
the end of the loan period will be zero, this step can be
skipped.
Touch the i key to calculate the interest rate per period.
Example
ENTRIES (RPN) DISPLAY
b FIN
0.00
Clears the financial registers.
360 n.
360.00
Enters 360 months for a 30 year
loan.
400000 PV
400,000.00
Enters the loan amount of $400,000.
2398.202 CHS PMT
-2,398.20
Displays the monthly payment
i.
-----------The V12 is calculating the value.
0.50
Displays the monthly interest rate.
Example
8 % annual interest, which is compounded quarterly for 3 years:
n is number of quarters (3 * 4=12)
i is interest rate per quarter (8% ÷ 4 = 0.02%)
If interest rate was compounded monthly, n would be 8% ÷ 12
=0.006
Since many financial calculations utilize an annual interest rate
compounded monthly, the V12 has two functions to simplify the
entry of interest rate and periods. The r 12÷ function will
divide an annual interest rate by 12 and enter the result as the
monthly interest rate.
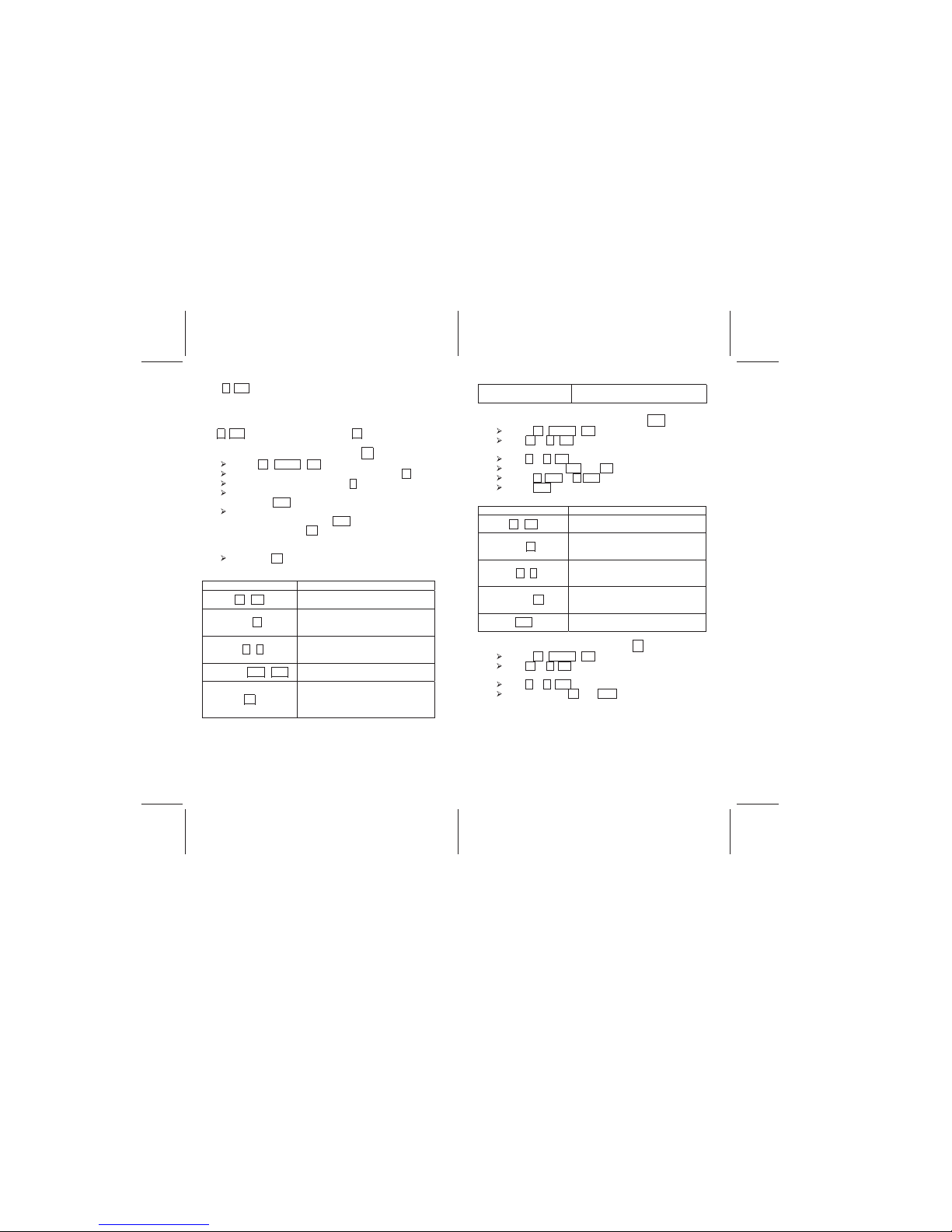
Example
24% annual interest which is compounded monthly
24 r 12÷ will enter an interest rate of 2% into the i. register.
V12 Manual
1716
The r 12x function will multiply a number of years by 12 and
enter the result as the number of monthly periods.
Example
30 year loan which is compounded monthly
30 r 12x will enter 360 periods into the n. register.
Determining Present Value: Solving for PV
Touch b CLEAR FIN to reset financial registers
Enter the number of payment periods and touch n.
Enter the interest rate and touch i..
Enter the payment value per period (a negative number)
and touch PMT.
Enter the future value of the amount owed at the end of
the payment periods, touch CHS to make the number
negative, and touch FV. Note: If the amount owed at
the end of the loan period will be zero, this step can be
skipped.
Touch the PV key to calculate the present value.
Example
YALPSID SEIRTNE
.b FIN
0.00
Clears the financial registers.
360 n.
360.00
Displays 360 months for a 30 year
loan.
6 r i.
0.50
Displays the interest rate of 6% per
year or 0.5% per month.
2398.202 CHS PMT
-2,398.20
Displays the monthly payment
PV
-----------The V12 is calculating the value.
400,000.00
Dis
play
s the loan amount or present
value. Actual amount may vary
slightly due to rounding
Determining Payment Amount: Solving for PMT
Touch b CLEAR FIN to reset financial registers
Use n or r 12x to enter number of periods or
payments
Use i or r 12÷ to enter periodic interest rate
Enter values for PV and FV
Touch r BEG or r END to select payment function
Touch PMT to calculate the amount of the payment
Example
ENTRIES DISPLAY
b FIN
0.00
Clears the financial registers.
360 n.
360.00
Displays 360 months for a 30 year
loan.
6 r i.
0.50
Displays the interest rate of 6% per
year or 0.5% per month.
400000 PV
400.000.00
Displays the loan amount or present
value.
PMT
-2,398.20
Displays the monthly payment
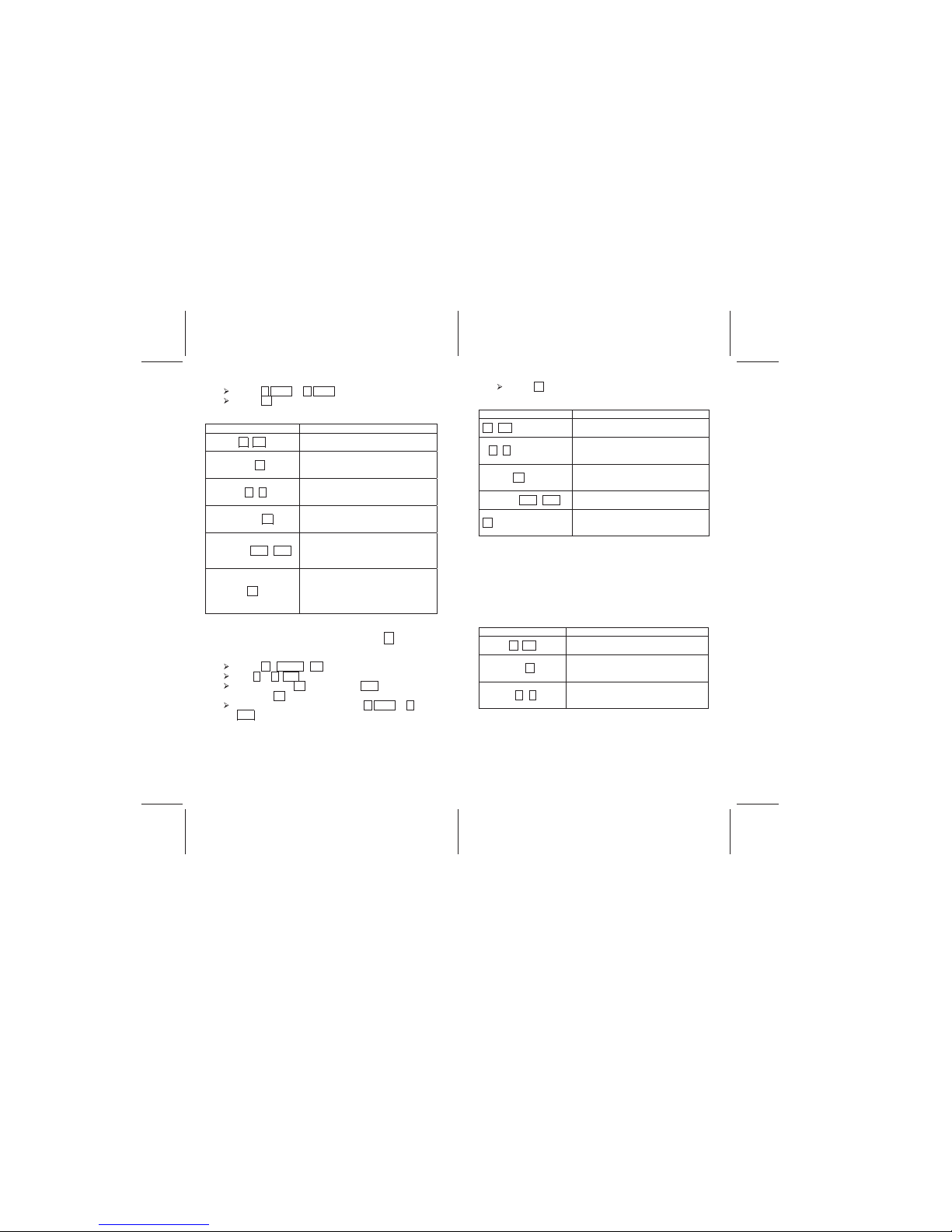
Determining Future Value: Solving for FV
Touch b CLEAR FIN to reset financial registers
Use n or r 12x to enter number of periods or
payments
Use i or r 12÷ to enter annual interest rate
Enter values for PV and PMT
V12 Manual
1918
Touch r BEG or r END to select payment function
Touch FV to calculate the future value
Example
ENTRIES (RPN) DISPLAY
b FIN
0.00
Clears the financial registers.
360 n.
360.00
Displays 360 months for a 30 year
loan.
6 r i.
0.50
Displays the interest rate of 6% per
year or 0.5% per month.
400000 PV
400.000.00
Displays the loan amount or present
value.
2397.202 CHS PMT
-2,397.20
Displays the monthly payment.
Notice the amount is reduced by $1
from previous examples.
FV
-1,004.62
Displays the amount still owed at the
end of the loan period. In this
example, the payments over 30
years did not pay off the entire loan.
Determining Number of Periods: Solving for n.
To determine the number of compounding periods and the
number of payments:
Touch b CLEAR FIN to reset financial registers
Use i or r 12÷ to enter periodic interest rate.
Enter values for PV(present value), PMT (amount of
payment), FV (future value)
Select payment function by touching r BEG or r.
END
Touch n to calculate number of periods or payments
Example
ENTRIES (RPN) DISPLAY
b FIN
0.00
Clears the financial registers.
6 r i.
0.50
Displays the interest rate of 6% per
year or 0.5% per month.
400000 PV
400.000.00
Displays the loan amount or present
value.
2398.202 CHS PMT
-2,398.20
Displays the monthly payment.
n.
360.00
Displays the number of periods
(months) required to pay off the loan.
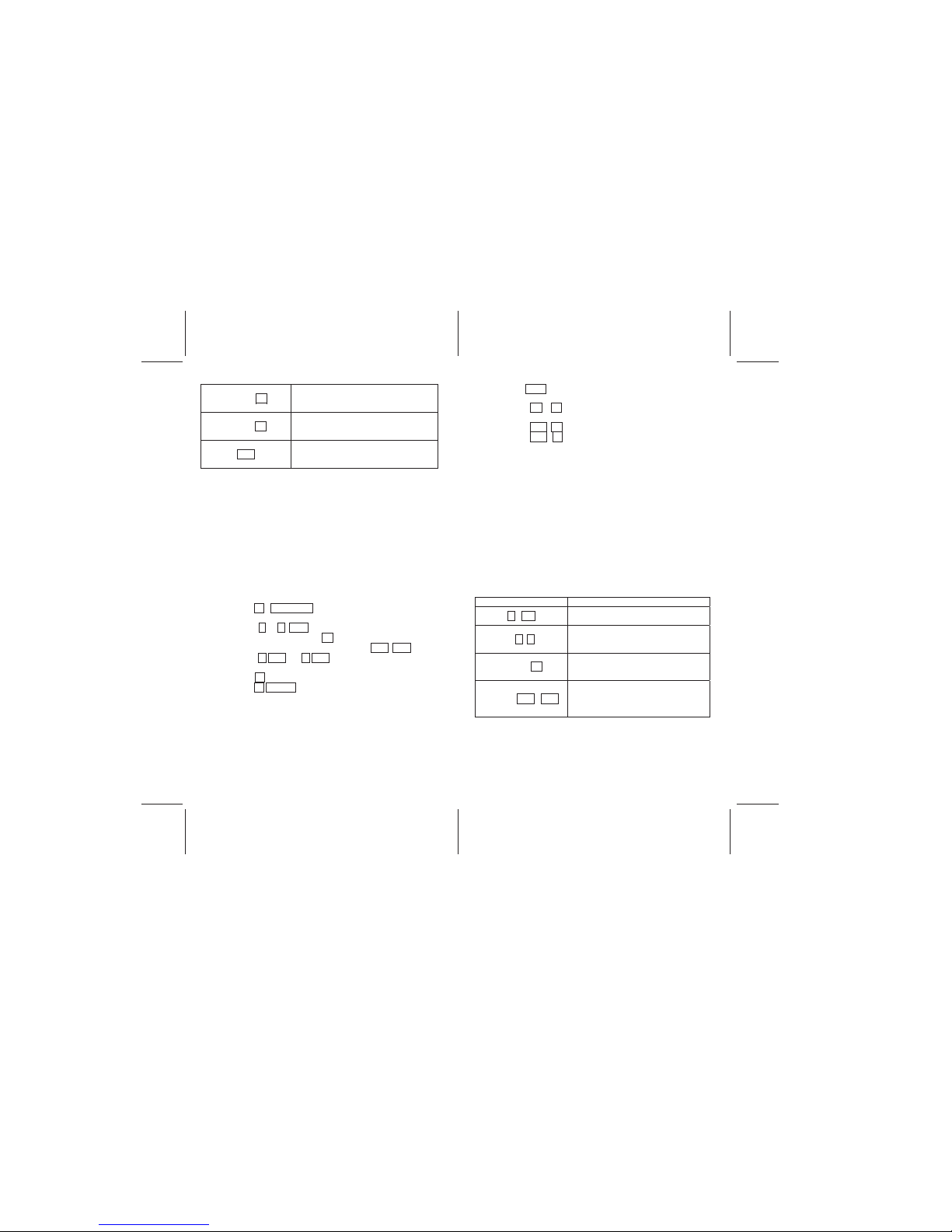
Loan With a Balloon Payment
A common transaction is a loan with a balloon payment. In this
case, the borrower makes a fixed payment each period until the
end of the loan term. At the end of the term, the borrower makes
one large final payment. The example below illustrates a
$400,000 loan, at 6% annual interest paid monthly for 30 years
with a balloon payment of $70,000.
Example
ENTRIES (RPN) DISPLAY
b FIN
0.00
Clears the financial registers.
360 n.
360.00
Displays 360 months for a 30 year
loan.
6 r i.
0.50
Displays the interest rate of 6% per
year or 0.5% per month.
V12 Manual
2120
400000 PV
400.000.00
Displays the loan amount or present
value.
-70000 FV
-70,000.00
Displays the future value required to
pay off the loan (the balloon payment)
PMT
-2,328.52
Displays the monthly payment required
to reach a $70.000 balloon payment.
Amortization Function
To Amortize is to liquidate a debt, such as a mortgage by
installment payments. Amortization is the gradual elimination of
a liability, such as a mortgage, in regular payments over a
specified period of time. Such payments must be sufficient to
cover both principal and interest. With the Amortization Function
the V12 can calculate the total amount of principle (liability) and
interest paid after a specified number of installments.
The following steps are required to determine the Amortization
status of a loan:
• Push b CLEAR FIN first to reset financial registers of
previous data
• Using i or r 12÷ , enter periodic interest rate
• Enter the principal using PV
• Enter the periodic payment, then push CHS PMT
• Select r BEG or r END to set the payment function
• Enter the number of payments that will be amortized
using n.
• Push b AMORT (will display amount from payments
that will be applied to interest)
• Push x↔y (will display amount from payments that will
be applied to principal)
• Push R↓ R↓ (will display number of payments to be
amortized)
• Push RCL PV (will display remaining balance)
• Push RCL n (will display total number of payments
amortized
If you repeat the Amortization function after an initial calculation,
the V12 picks up where you left off. In other words, after you
calculate the interest and principle paid after one year, the V12
resets the present value of the loan to the principle after one
year. Calculation of Amortization will start from this point.
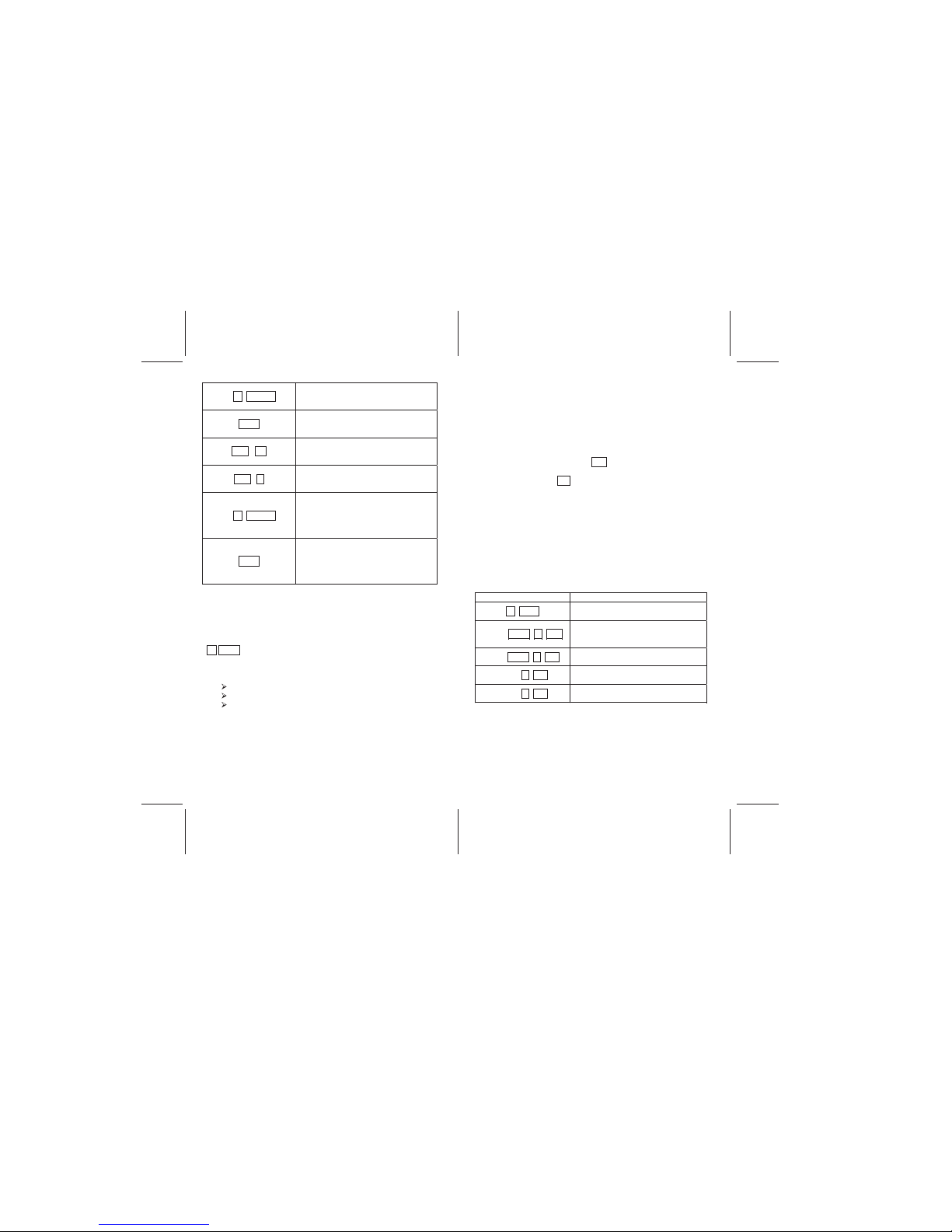
A common application of the Amortization function is to
determine the amount of interest and principle paid on a
mortgage for a given time period. The example below illustrates
a 30 year loan with a principle of $400,000, a 6% annual interest
rate, and monthly payment of $2,398.20. The task is to
determine the interest and principle paid after 5 years or 60
months.
Example
ENTRIES (RPN) DISPLAY
b FIN
0.00
Clears the financial registers.
6 r i.
0.50
Displays the interest rate of 6% per
year or 0.5% per month.
400000 PV
400.000.00
Displays the loan amount or present
value.
2398.20 CHS PMT
-2,398.20
Displays the payment required to pay
off the loan in 30 years (calculated in
an earlier example)
V12 Manual
2322
60 b AMORT
-116,109.58
Displays the total interest paid after
60 months.
x↔ y
-27,782.42
Displays the total principle paid after
60 months
RCL PV
372,217.58
Displays the remaining principle after
60 months of payments
RCL n
60.00
Displays the number of payments
amortized (60 months)
12 b AMORT
-22,152.81
Displays the amount of interest paid
in the next 12 months of payments
(after the initial 60 months already
amortized)
x↔ y
-6,625.59
Displays the amount of principle paid
in the next 12 months of payments
(after the initial 60 months already
amortized)
Chapter 3: Other Financial
Calculations
NPV (Net Present Value)
b NPV (net present value) represents the value of a series of
future cash flows discounted at a specified rate of return to
reflect the present value.
When NPV is positive, financial value increases.
When NPV is 0, financial value stays the same.
When NPV is negative, financial value decreases.
Therefore, the greater the value of NPV, the greater the increase
in financial value.
To find NPV, add the initial deposit (a negative cash flow) to
present value of future cash flow. (Here, i will describe the rate
of return, and NPV describes the result of the investment.)
Two keys not yet discussed in this manual are required to
perform NPV calculations. The CFo key is used to store the
initial cash flow. When touched, the contents of the x-register
are stored in R
0
. The CFj key is used to store additional cash
flows. When touched, the contents of the x-register are stored in
R
1
. If used again in the same cash flow problem, the contents of
the x-register are stored in first R
2
, then R3, R4, and so on.
Example
You want to buy a yacht for $23,000 and rent it to a skipper for a
share of tour revenue. You expect cash flows of the initial cost
($23,000), ($5000) in the first year for repairs, +$10,000 in the
second year from tours, +$15,000 in the third year, $17,000 in
the fourth year, and then you expect to sell the yacht in the fifth
year for $19,000. Your expected rate of return is 15%.
YALPSID SEIRTNE
b REG
0.00
Clears the x register
23000 CHS r CF
0
-23,000.00
Stores the initial cash out flow to buy
the yacht
5000 CHS r CF
j
-5,000.00
Stores the first year cash flow
10000 r CF
j
10,000.00
Stores the second year cash flow
15000 r CF
j
15,000.00
Stores the third year cash flow
 Loading...
Loading...