Texas instruments CBR User Manual [da]

Download

85-86

TRIGGER

CBR

)

Calculator-Based Ranger

™

(CBR

™

)

OM GODT I GANG MED OM GODT I GANG MED

MEDMED

ELEVOPGAVERELEVOPGAVER

5 5

CBR™CBR™

CBR

)

TRIGGER

85-86

CBR

)

TRIGGER

85-86

CBRé (Calculator-Based Rangeré) kabel mellem regner og CBR

klemme 4 AA-batterier

kabel mellem CBL og CBR

Vigtigt

Texas Instruments giver ingen garanti, hverken udtrykt eller underforstået, herunder, men ikke begrænset til, underforståede garantier for salgbarhed og egnethed til et bestemt formål, for programmateriale eller trykt materiale. Denne type materiale stilles alene til rådighed, som det måtte forefindes.

Texas Instruments kan under ingen omstændigheder gøres ansvarlig for specielle, affødte, tilfældige eller følgeskader i forbindelse med eller som måtte opstå på grund af købet af eller anvendelsen af disse materialer, og Texas Instruments eneste ansvar uanset handlingsform, kan ikke overstige udstyrets købspris. Desuden kan Texas Instruments ikke forpligtes ved krav af nogen art i forbindelse med anvendelsen af disse materialer.



1997 Texas Instruments Incorporated.

Alle rettigheder forbeholdes.

Hermed gives tilladelse til instruktører og lærere til at udskrive eller fotokopiere de sider i denne dokumentation, der er forsynet med Texas Instruments Copyright, i passende mængder til brug i klasseundervisning, øvelser eller seminarer. Disse sider er udvalgt til at blive reproduceret af instruktører og lærere til brug i klasseundervisning, øvelser eller seminarer under forudsætning af, at hver eneste kopi er forsynet med oplysningerne om copyright. Disse kopier må ikke gøres til genstand for salg, og videredistribution er udtrykkeligt forbudt. Undtagen som tilladt i henhold til ovenstående skal der indhentes forudgående skriftlig tilladelse fra Texas Instruments Incorporated til at reproducere eller overføre dette materiale eller dele heraf i nogen anden form eller på nogen anden elektronisk eller mekanisk måde, herunder alle systemer til lagring og søgning af informationer, medmindre det udtrykkeligt er tilladt i henhold til gældende lov. Forespørgsler bedes rettet til Texas Instruments Incorporated, PO Box 149149, Austin, TX, 78714-9149, M/S 2151, Attention: Contracts Manager.

Indholdsfortegnelse

CBR

)

Introduktion

Hvad er CBR? 2 Kom godt i gang med CBR — I tre lette trin 4 Tip om effektiv dataindsamling 6

Opgaver med instruktørnoter og arbejdsblade

TRIGGER

85-86

Opgave 1 — Efterlign grafen lineær 13

Opgave 2 — Legetøjsbil lineær 17

Opgave 3 — Pendul sinusformet 21

Opgave 4 — Hoppende bold parabolsk 25

Opgave 5 — Rullende bold parabolsk 29

Oplysninger til instruktøren 33

Tekniske oplysninger

CBR-data gemmes i lister 37 RANGER-indstillinger 38 Brug af CBR med CBL eller CBL-programmer 39 Programmeringskommandoer 40

Oplysninger om service

Batterier 42 Hvis der opstår problemer 43 Service og garanti 44

Oversigt over RANGER-menuerne indvendigt på det bageste omslag

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

Hvad er CBR?

CBRCBRé (Calculator-Based RangerCalculator-Based Rangeré

kan bruges sammen med TI-82, TI-83, TI-85/ aktuel dataindsamling og dataanalyse i klasseundervisningen

let at bruge, kræver ikke yderligere udstyr

det alsidige RANGER-program startes med et tryk på en knap

programmerne MATCH og BOUNCING BALL er en del af RANGER-programmet

de primære parametre er lette at definere

Hvad kan man gøre med CBR?

Med en bevægelsesdata uden besværlige målinger og manuel afbildning.

Med

CBR

afstand, hastighed, acceleration og tid ud fra de indsamlede data. Eleverne kan f.eks. udforske følgende matematiske og fysiske begreber:

-enhed og en grafisk TI-regner kan eleverne indsamle, få vist og analysere

CBR

kan eleverne udforske den matematiske og fysiske sammenhæng mellem

bevægelsesdetektor

CBL

ingen programmering nødvendig

RANGER-programmetRANGER-programmet

)

, TI-86 og TI-92

bevægelse: afstand, hastighed og acceleration

grafisk afbildning: akser i koordinatsystemer, hældning og skæringspunkter

funktioner: lineære funktioner, andengradspolynomier, eksponentielle funktioner og

sinusformede funktioner differentialregning: afledede funktioner og integraler

statistik og dataanalyse: dataindsamlingsmetoder og statistisk analyse

Hvad indeholder denne vejledning?

Kom godt i gang med CBR

uden særlig erfaring med regnere eller programmering. Den indeholder instruktioner til at komme hurtigt i gang med at bruge klasseopgaver til udforskning af de grundlæggende funktioner og egenskaber ved bevægelse. Disse opgaver (se side 13–32) består af:

instruktørnoter for hver opgave samt generelle oplysninger til instruktøren

trinvise instruktioner

en grundlæggende opgave om dataindsamling beregnet på elever på alle niveauer

øvelser, der undersøger disse data mere detaljeret, herunder forskellige scenarier af

typen hvad-nu-hvis forslag til avancerede emner beregnet på elever både med og uden kendskab til

differentialregning arbejdsblade, der kan kopieres, med åbne spørgsmål på mange forskellige niveauer

er udformet som en vejledning for lærere og instruktører

, tip om effektiv dataindsamling og fem

CBR

OM GODT I GANG MED

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

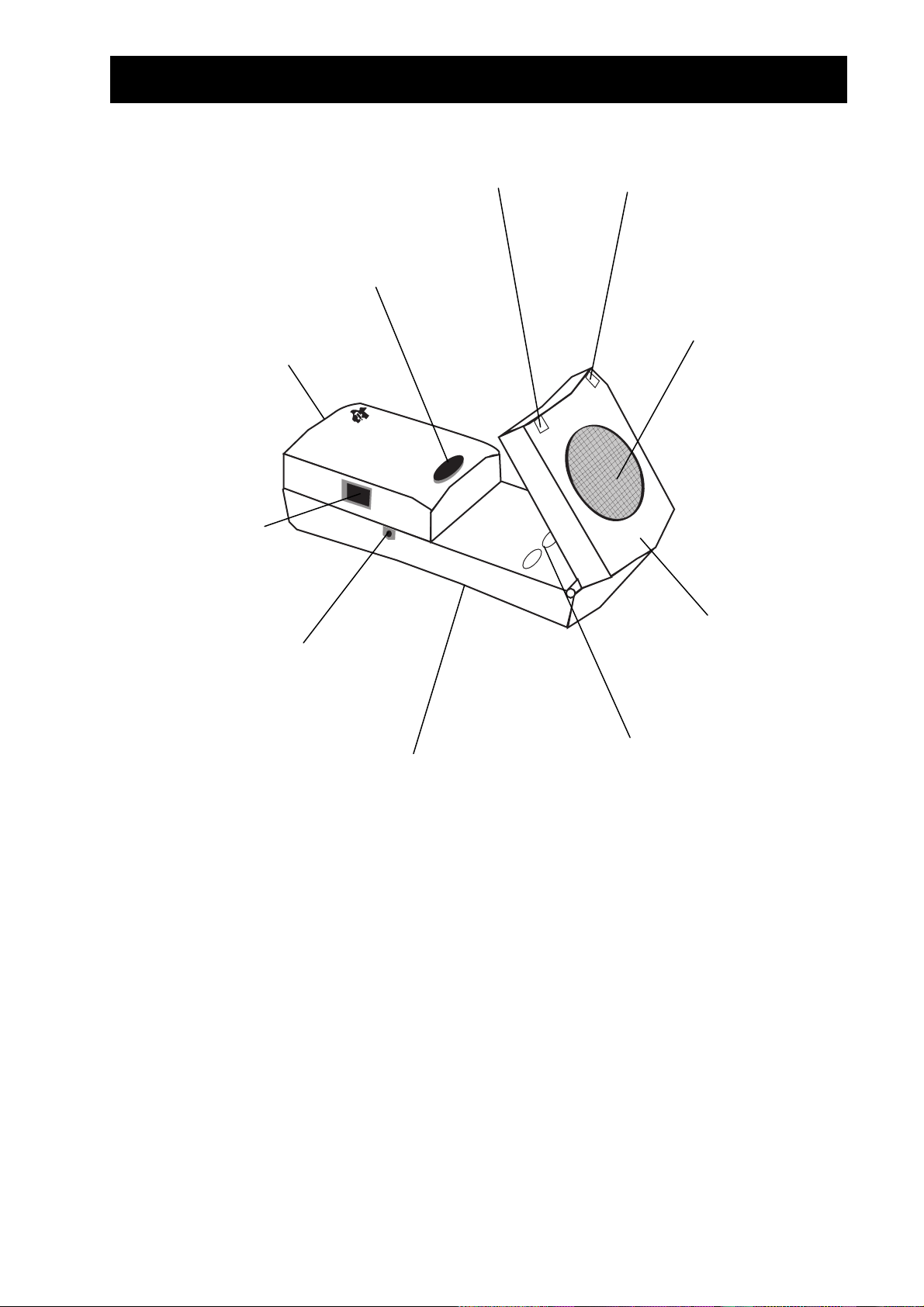
Hvad er CBR?

s g

(forts.)

at starte målingen

batteridæksel (i bunden)

port til tilslutning til CBL (valgfrit)

port til tilslutning til grafiske TIregnere via det medfølgende 2,25 meter lange kabel

rønt lys viser, at der foregår dataindsamling (lyd er også mulig)

knap til

CBR

)

rødt lys viser særlige forhold

lyddetektor, der kan foretage op til 200 målinger pr. sekund over en afstand på mellem 0,5 meter og 6 meter

TRIGGER

85-86

drejeligt hoved til at rette føleren nøjagtigt mod målet

tandardsokkel til et stativ eller den medfølgende monteringsklemme

indeholder alt, hvad du behøver for at komme i gang med klasseopgaverne let og hurtigt —

CBR

knapper til at overføre RANGER-programmet til regnere

det eneste andet, der skal bruges, er grafiske regnere fra TI (og noget ganske almindeligt udstyr til visse af opgaverne).

bevægelsesdetektor

RANGER

-programmet i

CBR

kabel mellem regner og CBR

4 AA-batterier

monteringsklemme

5 klasseopgaver

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

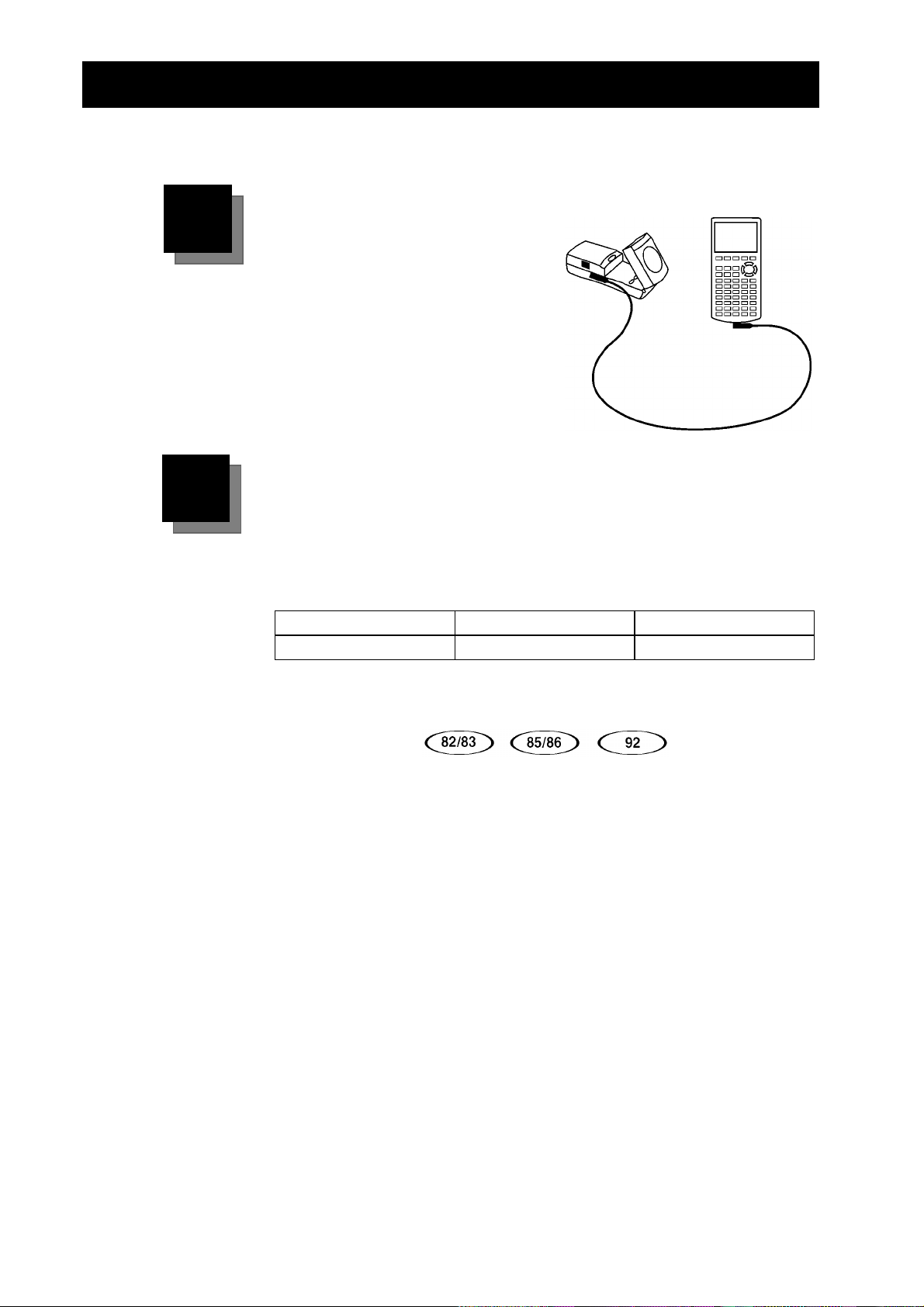
Kom godt i gang med CBR—I tre lette trin

ygg

Med

er du kun tre trin fra at have indsamlet de første data!

CBR

Tilslutning

Tilslut regner fra TI ved hjælp af kablet mellem regner og CBR-enhed.

Sæt det ender for at forbinde de to enheder.

Bemærk:

forbinde to regnere med hinanden, som følger med regneren, kan også bruges.

-enheden til en grafisk

CBR

omh

Det korte kabel til at

eligt fast

i begge

Overførsel

RANGER

er let at overføre det relevante program fra Først skal du gøre regneren klar til at modtage programmet (se

tastesekvenserne nedenfor).

, et specielt program for de forskellige regnere, findes i

-enheden til en regner.

CBR

. Det

TI-82 eller TI-83 TI-85/CBL eller TI-86 TI-92

LINK

[

Derefter skal du åbne det drejelige hoved på den relevante knap til overførsel af programmet.

Under overførslen viser displayet på regneren Når overførslen er slut, blinker den grønne lampe på gang, Hvis der opstår et problem, blinker den røde lampe på gange, og

Når du har overført skal du kun overføre det til den pågældende regner igen, hvis du sletter det fra regnerens hukommelse.

Bemærk:

byte. Du kan eventuelt slette andre programmer og data fra regneren. Du kan eventuelt først gemme disse programmer og data ved at overføre dem til en computer med TI-Graph Linké eller til en anden regner ved hjælp af et kabel til at forbinde to regnere med hinanden eller et kabel mellem regner og

CBR

›

]

-enheden bipper én gang, og displayet på regneren viser

-enheden bipper to gange.

CBR

RANGER

Program og data kræver typisk en hukommelse på ca. 17.500

CBR

-programmet fra

-enhed (se vejledningen til regneren).

[

LINK

]

-enheden og trykke på

CBR

RECEIVING

-enheden til en regner,

CBR

Gå til Home.

(undtagen TI-92).

-enheden én

CBR

-enheden to

CBR

DONE

OM GODT I GANG MED

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

Kom godt i gang med CBR—I tre lette trin

Kørsel

Kør

RANGER

Tryk på Væl Tryk på

Startskærmbilledet vises.

-programmet (se tastesekvenserne nedenfor).

TI-82 og TI-83 TI-85/CBL og TI-86 TI-92

RANGER

›

Tr Væl Tryk på

k på

RANGER

^ A

›

(forts.)

k på L [

Tr Væl Tryk på ¨

RANGER

VAR-LINK

›

Prøv en af de beskrevne klasseopgaver for at opnå hurtige resultater!

Tryk på

MAIN MENU

SETUPàSAMPLE SET DEFAULTS APPLICATIONS PLOT MENU TOOLS QUIT

Vælg på

› for at starte dataindsamlingen. Så let er det!

Vigtige oplysninger

›. Menuen

SET DEFAULTS

› for at vælge

i menuen

MAIN MENU

vis/skift indstillingerne før målingerne

Skift til standardindstillingerne

DISTANCE MATCH, VELOCITY MATCH, BALL BOUNCE

forskellige valg for grafer

GET CBR DATA, GET CALC DATA, STATUS, STOPàCLEAR

START NOW

vises.

MAIN MENU

. Skærmbilledet

SETUP

vises. Tryk

. Lav opstillingen til opgaven, og tryk på

Denne vejledning gælder for alle grafiske regnere fra TI, der kan bruges sammen med

. Derfor kan det forekomme, at nogle af

CBR

menunavnene ikke svarer nøjagtigt til dem på den aktuelle regner.

Når du laver opstillingen til opgaverne, skal du sørge for, at enheden er sikkert anbragt, og at man ikke kan komme til at falde over ledningen.

Afslut altid

RANGER

fuldstændig lukning af

-programmet med , når du vælger

CBR

. Programmet udfører en

QUIT

, og det sikrer, at

QUIT

bliver korrekt initialiseret næste gang.

Afbryd altid forbindelsen mellem

-enheden og regneren, før du

CBR

lægger dem til side.

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

Tip om effektiv dataindsamling

Bedre målinger

Hvordan fungerer CBR?

Hvis du forstår, hvordan en bevægelsesdetektor fungerer, kan du bedre opnå gode afbildninger af dine data. Bevægelsesdetektoren udsender et ultralydssignal og måler, hvor lang tid det tager, før dette signal kommer tilbage efter refleksion fra det nærmeste objekt.

Ligesom andre bevægelsesdetektorer måler ultralydssignalet, til det første ekko kommer tilbage, men microprocessor, som gør meget mere. Når målingen er foretaget, beregner

tiden fra udsendelsen af

CBR

har en indbygget

CBR

afstanden til objektet ved hjælp af lydens hastighed. Derefter beregnes den første og anden afledede af afstandsdataene med hensyn til tiden for at finde hastighed og acceleration. Disse målinger gemmes i listerne

Gennemførelse af de samme beregninger som

L1, L2, L3

CBR

og L4.

kan være en interessant øvelse

sammen med hele klassen.

Mål de ønskede data i tilstanden

➊

Brug måletiderne i

➋

sammen med afstandsdataene i L2 til at beregne objektets

REALTIME=NO

. Afslut

RANGER

-programmet.

hastighed i hvert måletidspunkt. Sammenlign derefter resultaterne med hastighedsdataene i

Brug hastighedsdataene i L3 (eller de værdier, eleverne selv har beregnet) sammen

➌

med måletiderne i Sammenlign derefter resultaterne med accelerationsdataene i

Objektets størrelse

Et lille objekt langt fra

(

n+1

til at beregne objektets acceleration i hvert måletidspunkt.

-enheden formindsker chancerne for en nøjagtig måling. På 5

CBR

)à2 N (

n+1

n-1

)à2

meters afstand er det meget lettere at måle en fodbold end en bordtennisbold.

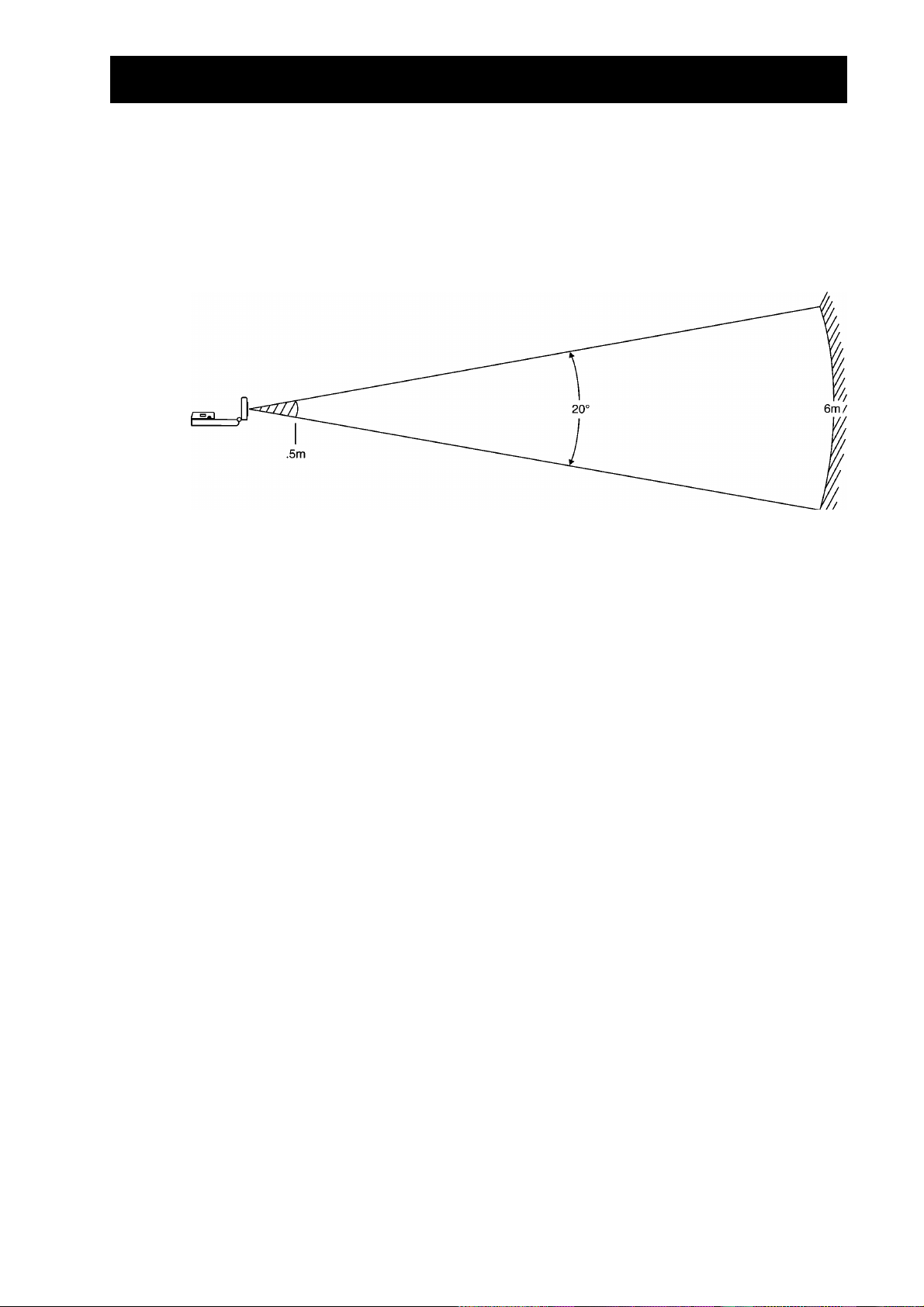
Mindste afstand til objektet

Når og modtages af flere signaler overlappe hinanden og føre til forkerte resultater. Derfor skal placeres mindst 0,5 meter fra objektet.

Største afstand til objektet

Når signalet går gennem luften, bliver det svagere og svagere. Efter en total distance på 12 meter (6 meter frem til objektet og 6 meter tilbage til for svagt til at blive korrekt registreret. Dette sætter en grænse på 6 meter (19 fod) for, hvor langt der kan være mellem

OM GODT I GANG MED

-enheden udsender et signal, rammer det objektet, hvorefter det sendes tilbage

CBR

-enheden. Hvis et objekt er nærmere end 0,5 meter (1,5 fod), kan

CBR

-enheden) er ekkoet blevet

CBR

-enheden og objektet.

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

-enheden

Tip om effektiv dataindsamling

Frit område mellem CBR-enheden og objektet

(forts.)

Ultralyden fra

-enheden er ikke en tynd stråle, men den breder sig ud i alle retninger

CBR

inden for en vinkel af 10°. For at undgå påvirkninger fra andre objekter i nærheden bør du sørge for et frit område

til ultralyden mellem ønskede bliver registreret.

Reflekterende overflader

-enheden og objektet for at undgå, at andre objekter end det

CBR

måler det nærmeste objekt i det frie område.

CBR

Nogle overflader reflekterer ultralydssignaler bedre end andre. Du kan f.eks. opnå bedre resultater med en bold med en forholdsvis hård, jævn overflade end med en tennisbold. Af samme grund er målinger i et lokale med hårde, reflekterende overflader mere udsatte for at blive forkerte. Målinger af uregelmæssige overflader (f.eks. en legetøjsbil eller en elev, der går rundt med regneren i hånden) kan give uensartede resultater.

En graf over afstanden som funktion af tiden af et stillestående objekt har små udsving i de beregnede afstandsværdier. Hvis en af disse værdier afviger lidt, kan der være små uregelmæssigheder i den forventede vandrette linie. Grafen over hastigheden som funktion af tiden kan være endnu mere ujævn, fordi ændringen i afstand mellem to tidspunkter pr. definition er hastigheden. Brug eventuelt en passende grad af udglatning på de målte data.

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

Tip om effektiv dataindsamling

RANGER-indstillinger

Måletider

er den totale tid i sekunder til udførelse af alle målinger. Angiv et helt tal mellem 1

TIME

sekund (for objekter, der bevæger sig hurtigt) og 99 sekunder (for objekter, der bevæger sig langsomt). I tilstanden

REALTIME=YES

(forts.)

altid 15 sekunder.

TIME

Jo mindre værdien for f.eks.

TIME=1 SECOND

er, jo nærmere skal objektet være ved

TIME

, kan objektet ikke være længere borte fra

CBR

-enheden end

CBR

1,75 meter (5,5 fod).

Start og stop

Skærmbilledet

SETUP

RANGER

-programmet indeholder flere muligheder for at starte og

stoppe målingerne.

BEGIN ON: [ENTER]

. Målingen startes med tasten

på regneren. Bruges, når den

›

person, der starter målingerne, er nærmest ved regneren.

BEGIN ON: [TRIGGER]

enheden

Bruges, når den person, der starter målingerne, er nærmest ved

. Målingen startes og stoppes med knappen

enheden. Du kan også vælge helt at fjerne forbindelsen mellem

-enheden og regneren. På

CBR

denne måde kan du lave opstillingen til målingen, tage ledningen ud af flytte målingerne, sætte ledningen tilbage i data. Brug

-enheden til det sted, hvor tingene sker, trykke på

CBR

-enheden og trykke på

CBR

BEGIN ON: [TRIGGER],

hvis ledningen ikke er tilstrækkelig lang eller ville

›

komme i vejen for dataindsamlingen. Dette kan ikke benyttes i tilstanden

REALTIME=YES

BEGIN ON: DELAY

(f.eks. funktionen

. Målingen starter automatisk med 10 sekunders forsinkelse fra det

tidspunkt, hvor du trykker på

MATCH

›

. Dette kan især være nyttigt, hvis der kun er én

person til at løse en opgave.

-enheden. Når

på

CBR CBR

-enheden,

CBR

, foretage

for at overføre

Knappen Trigger

Virkningen af knappen

DELAY

starter målingerne, også selvom der er valgt

. Den stopper også målingerne, men normalt vil du lade målingerne løbe til

afhænger af indstillingerne.

BEGIN ON: [ENTER]

eller

ende. I tilstanden

REALTIME=NO

gentages de seneste målinger med knappen

data overføres ikke til regneren. Hvis du vil overføre disse data, skal du vælge menuen

MAIN MENU

og derefter vælge målinger ved at vælge skærmbilledet

SETUP

REPEAT SAMPLE

GET CBR DATA

i menuen

. Du kan også gentage en række

PLOT MENU

eller

START NOW

BEGIN ON:

men

TOOLS

på

OM GODT I GANG MED

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

Tip om effektiv dataindsamling

Udglatning

(forts.)

De indbyggede muligheder for udglatning i

RANGER

-programmet kan reducere virkningen af fejlmålinger eller variationer i afstandsmålingerne. Undgå overdreven brug af udglatning. Start uden udglatning eller med

udglatning. Forøg graden af

LIGHT

udglatning, indtil du opnår tilfredsstillende resultater.

Hvis der er særlig stor chance for fejlmålinger, kan du eventuelt forøge udglatningen

på skærmbilledet Du kan anvende udglatning på allerede indsamlede data i tilstanden

Regneren skal være forbundet til vælg

SMOOTH DATA

Støj—hvad er det, og hvordan undgås det?

Når

-enheden modtager signaler, der er reflekteret fra andre objekter end det

CBR

før målingerne (se side 38).

SETUP

-enheden. Vælg

CBR

PLOT TOOLS

i menuen

, og vælg derefter den ønskede grad af udglatning.

REALTIME=NO

PLOT MENU

ønskede, vises der forkerte datapunkter (støj), som ikke passer med det generelle mønster for grafen. Du kan gøre følgende for at minimere støj:

Sørg for, at

på detektoren, mens du studerer en måling i tilstanden gode resultater, før du går i gang med at måle i tilstanden

Prøv at foretage målingerne i et område uden forstyrrende elementer (se tegningen af

-enheden peger direkte på det ønskede objekt. Prøv at justere hovedet

CBR

REALTIME=YES,

REALTIME=NO

indtil du opnår

det frie område på side 7). Vælg et større, mere reflekterende objekt, eller flyt objektet nærmere til

-enheden

CBR

(men stadig længere borte end 0,5 meter). Hvis der anvendes flere

-enheder i et lokale, bør den ene gruppe elever gøre deres

CBR

målinger færdige, før de andre begynder deres. Hvis du har en måling med meget støj i tilstanden

REALTIME=YES

, kan du gentage målingen med en højere grad af udglatning, indtil du opnår tilfredsstillende resultater. Du kan ikke ændre udglatningen i funktionerne eller

BALL BOUNCE

Hvis du har en måling med meget støj i tilstanden

DISTANCE MATCH, VELOCITY MATCH

REALTIME=NO

, kan du anvende en

højere grad af udglatning på de originale data.

Lydens hastighed

Afstanden til objektet beregnes under antagelse af en bestemt lydhastighed, men den aktuelle lydhastighed afhænger af flere faktorer, først og fremmest temperaturen. I forbindelse med relative bevægelser betyder dette ikke noget. Hvis der kræves meget nøjagtige målinger, kan du bruge en programmeringskommando til at angive temperaturen (se side 40–41).

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

Tip om effektiv dataindsamling

REALTIME=YES

(forts.)

Brug tilstanden

til langsomme objekter

for at se resultaterne samtidig med, at de bliver indsamlet

når du kun har behov for at indsamle eller afbilde én type data (afstand, hastighed

REALTIME=YES

eller acceleration)

I tilstanden

REALTIME=YES

beregner

de ønskede data (afstand, hastighed eller

CBR

acceleration) og overfører dem til regneren efter hver enkelt afstandsmåling. Derefter afsætter

RANGER

-programmet en enkelt pixel for den pågældende måling.

Da alle disse operationer skal være afsluttet, før den næste måling kan sættes i gang, er der en grænse for den hyppighed, hvormed data kan indsamles i tilstanden

REALTIME=YES

Det tager ca. 0,080 sekunder at måle, behandle og overføre data for et enkelt datapunkt. Dertil kommer tiden til andre operationer, f.eks. afbildning af punktet, så grænsen for, hvor hyppigt der kan måles i

RANGER

-programmet, går ved ca. 0,125

sekunder.

REALTIME=NO

Brug tilstanden

til hurtige objekter

når der kræves udglatning (se side 9)

hvis du bruger

når du samtidigt skal indsamle alle typer data (afstand, hastighed og acceleration)

REALTIME=NO

-enheden, uden at den er forbundet til regneren (se side 11)

CBR

I tilstanden

REALTIME=NO

lagres data i

og de overføres først til regneren, når alle

CBR,

målingerne er foretaget. Målingerne kan foretages så hyppigt som én måling for hver 0,005 sekunder for objekter, der er tæt på

-enheden. Data for tid, afstand, hastighed

CBR

og acceleration overføres til regneren. Da data lagres i

Hver gang du ændrer på udglatningen, anvender

, kan du overføre dem fra

CBR

til en regner igen og igen.

CBR

den nye udglatningsfaktor,

CBR

overfører de justerede data til regneren og gemmer de udglattede værdier i listerne. Når du vælger et område, ændres de lister, der er gemt i regneren. Hvis du får brug

for det, kan du hente de originale data fra i

RANGER

Du kan dele data med flere elever, også selvom de bruger forskellige typer grafiske

-programmet. Vælg

GET CBR DATA

igen. Vælg

CBR

i menuen

TOOLS

i menuen

MAIN MENU

regnere fra TI. På denne måde kan alle elever deltage i opgaver med dataanalyse på grundlag af de samme data (se side 11).

OM GODT I GANG MED

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

Tip om effektiv dataindsamling

(forts.)

Anvendelse af CBR uden at CBR-enheden er tilsluttet til regneren

Da forbundet, kræves der bestemte indstillinger. Gør følgende på skærmbilledet

Sæt

Programmet fortæller dig, hvornår du kan afbryde forbindelsen til hvornår du kan etablere den igen. Der kræves ingen specielle procedurer.

Deling af data

Hvordan kan du få en hel klasse til at analysere de samme data samtidigt? Med du hurtigt overføre data, der er indsamlet i tilstanden klassen.

➊

➋ ➌

➍

➎

-enheden ikke kan sende data til regneren med det samme, når de ikke er

CBR

REALTIME=NO BEGIN ON=[TRIGGER]

Overfør

RANGER

-enheden, og

CBR

REALTIME=NO,

til alle elever i

-programmet til alle elevernes regnere, før dataindsamlingen finder

sted. Foretag indsamling af data med Lad den første elev tilslutte sin regner til

regner med Vælg

TOOLS

menuen

TOOLS

-enheden eller et kabel til at forbinde to regnere med hinanden.

CBR

i menuen

. Teksten

MAIN MENU

TRANSFERRING...

Tryk på › for at vende tilbage til menuen

i tilstanden

CBR

RANGER

vises, og derefter vises grafen.

REALTIME=NO

-enheden med et kabel til at forbinde en

CBR

-programmet. Vælg

PLOT MENU

GET CBR DATA

, og vælg

QUIT

ud.

SETUP

kan

CBR

. Tag kablet

Tilslut en anden regner (af samme type) til regneren med dataene. Vælg

➏

menuen

i menuen

DATA

MAIN MENU

TOOLS

RANGER

. Listerne L1, L2, L3, L4 og L5 overføres automatisk til den anden

-programmet på den anden regner. Vælg

regner. Overfør data til en anden elevs regner fra

➐

mens andre elever fortsætter med at

CBR,

overføre data fra regner til regner.

Når alle elever har de samme data, kan de analysere disse data i hjælp af

PLOT MENU

eller uden for

RANGER

-programmet ved hjælp af regnerens

RANGER

funktioner til behandling af lister og tegning af grafer. Hvis du vil dele data på TI-85, skal du bruge funktionen

for

RANGER

-programmet.

til at overføre listerne uden

LINK

TOOLS

GET CALC

-programmet ved

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

Tip om effektiv dataindsamling

Meget mere end ren og skær dataindsamling

(forts.)

Når du har indsamlet og afbildet data i

RANGER

-programmet, kan du undersøge disse data i forhold til en funktion. Da data gemmes som lister og vises som statistiske grafer, kan du bruge

I RANGER-programmet

Udforsk graferne med

,  og œ til at undersøge den pågældende sammenhæng.

(standardindstillingen). På TI-85 skal du bruge den

TRACE

bevægelige markør. Bearbejd de pågældende data, f.eks. udglatning af data eller valg af område.

Uden for RANGER-programmet

Udforsk data ved hjælp af regnerens listeeditor.

Tilpas en funktion manuelt til dataene ved hjælp af regnerens redigeringsprogram Y=.

Fastlæg den ligning, der passer bedst til de pågældende data, ved hjælp af regnerens

funktioner til regressionsanalyse.

Andre sammenhæng end dem, der er repræsenteret af de forskellige valg for afbildning i

RANGER

hastigheden som funktion af tiden vises som statistiske grafer. Vælg

-programmet, kan undersøges. F.eks. kan samtidige målinger over afstanden og i menuen

QUIT

RANGER

-programmet, og definer

som L2 som funktion af L1 og

Plot1

Plot2

som

MAIN

som funktion af L1. Det kan eventuelt være nødvendigt at justere vinduet. Data og grafer kan sendes til en computer ved hjælp af TI-Graph Link. Dette er især

nyttigt, når eleverne laver mere omfattende rapporter over deres opgaver.

Anvendelse af CBR uden RANGER-programmet

Du kan bruge end

RANGER

Oplysninger om at bruge

Oplysninger om, hvordan du får fat i programmer og opgaver, findes på side 36.

Oplysninger om programmeringskommandoer til at skrive egne programmer findes på

som bevægelsesdetektor sammen med

CBR

sammen med

CBR

side 40–41.

CBL

findes på side 39.

CBL

eller andre programmer

OM GODT I GANG MED

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

Opgave 1—Efterlign grafen noter til instruktøren

Begreber

Den undersøgte funktion: lineær. Programmet

MATCH

indfører begreberne afstand og tid — eller mere præcist: begrebet afstand som funktion af tid. Når eleverne prøver at genskabe graferne ved at gå omkring, mens de ser deres bevægelse afbildet, kan begrebet position undersøges.

Under Undersøgelser bliver eleverne bedt om at konvertere deres hastighed fra meter i sekundet til kilometer i timen.

Når eleverne er blevet fortrolige med begrebet afstand som funktion af tid, kan de gå videre med at undersøge begrebet hastighed som funktion af tid.

Materialer

 regner

CBR



 kabel til at forbinde to regnere med hinanden

TI ViewScreené giver andre elever mulighed for at følge med og gør denne opgave meget sjovere.

Tip

Eleverne elsker denne opgave. Sørg for, at der er rigelig med tid, for alle vil selv prøve!

Denne opgave fungerer bedst, når den elev, der bevæger sig, (og resten af klassen) kan se bevægelsen afbildet på et lærred eller en skærm ved hjælp af TI ViewScreen.

Giv eleverne besked om at gå i en ret linie hen mod eller bort fra CBR-enheden. De prøver sommetider at gå vinkelret på retningen til CBR-enheden eller måske endda at hoppe op og ned!

Det foreslås, at opgaven løses i metersystemet, hvilket svarer til spørgsmålene på arbejdsbladet.

Der er tip om effektiv dataindsamling på side 6–12.

Typiske grafer

Typiske svar

1. tid (fra målingens start); sekunder; 1 sekund; afstand (fra CBR-enheden til objektet); meter; 1 meter

2. skæringen med y-aksen svarer til startafstanden

3. varierer fra elev til elev

4. tilbage (øg afstanden mellem CBR-enheden og objektet)

5. fremad (formindsk afstanden mellem CBRenheden og objektet)

6. stå stille; en hældning på nul kræver, at der ikke er nogen ændring i y (afstanden)

7. varierer fra graf til graf; @yà3,3

8. varierer fra graf til graf; @yà1

9. det liniestykke, der har den største hældning (positiv eller negativ)

10.dette er et drilsk spørgsmål - den flade del, fordi der slet ikke er nogen bevægelse!

11.ganghastighed; hvornår man skal ændre retning og/eller hastighed

12.fart (eller hastighed)

13.varierer fra graf til graf (eksempel: 1,5 meter på 3 sekunder)

14.varierer fra graf til graf; eksempel: 0,5 meter på 1 sekund

eksempel: (0,5 meter/sekund) Q (60 sekunderàminut) = 30 meteràminut

eksempel: (30 meteràminut) Q (60 minutteràtime) = 1800 meteràtime

eksempel: (1800 meteràtime) Q (1 kilometerà1000 meter) = 0.18 kilometeràtime.

Få eleverne til at sammenligne dette sidste tal med hastigheden af et motorkøretøj, f.eks. 96 kilometeràtime (60 mil i timen).

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

15.varierer fra graf til graf; summen af @y for hvert liniestykke.

OM GODT I GANG MED

CBR

Opgave 1—Efterlign grafen lineær

Dataindsamling

➊

Hold

-enheden i den ene hånd og regneren i den anden. Ret føleren direkte mod

CBR

en væg.

Den maksimale afstand for en graf er 4 meter (12 fod) fra

Tip:

CBR

mindste afstand er 0,5 meter (1,5 fod). Sørg for, at der ikke er noget i det frie område (se side 7).

-enheden. Den

Kør

➋ ➌ ➍

RANGER

Vælg Vælg

Programmet Tryk på › for at få vist den tilsvarende graf. Studer grafen et øjeblik, og besvar

➎

-programmet (se tastesekvenserne for de forskellige regnere på side 5).

APPLICATIONS DISTANCE MATCH

i menuen

DISTANCE MATCH

MAIN MENU

i menuen

sørger automatisk for de rigtige indstillinger.

APPLICATIONS

. Vælg

METERS

. Der vises nogle generelle anvisninger.

spørgsmål 1 og 2 på arbejdsbladet.

Placer dig selv, hvor du tror, grafen begynder, og tryk på › for at starte

➏

dataindsamlingen. Du kan høre en klikkende lyd og se den grønne lampe, mens data indsamles.

Gå frem og tilbage, og prøv at efterligne grafen. Din position vises på skærmen.

➐

Når målingen er færdig, kan du undersøge, hvor godt din “vandring” svarede til

➑

grafen. Besvar spørgsmål 3. Tryk på › for at få vist menuen

➒

OPTIONS,

og vælg

SAME MATCH

. Prøv at forbedre

resultatet af din gang, og besvar spørgsmål 4, 5 og 6.

OM GODT I GANG MED

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

Opgave 1—Efterlign grafen

Undersøgelser

(forts.)

lineær

DISTANCE MATCH

Tryk på › for at få vist menuen

➊

liniestykke, og besvar spørgsmål 7 og 8. Studer hele grafen, og besvar spørgsmål 9 og 10.

➋

Placer dig selv, hvor du tror, grafen begynder, tryk på › for at starte

➌

dataindsamlingen, og prøv at efterligne grafen.

➍

Besvar spørgsmål 11 og 12, når målingen stopper. Tryk på › for at få vist menuen

➎

Studer grafen, og besvar spørgsmål 13, 14 og 15.

➏

Tryk på › for at få vist menuen

➐

tilbage til menuen

Avancerede undersøgelser

De grafer, der blev dannet af programmet

VELOCITY MATCH

Det er noget sværere!

MATCH

er et meget populært program. Der findes andre udgaver, som undersøger mere

komplicerede relationer (se side 36).

består alle grafer af tre rette liniestykker.

MAIN MENU

OPTIONS,

OPTIONS

, og vælg

og vælg

NEW MATCH

. Gentag eventuelt opgaven, eller vend

for at afslutte

QUIT

DISTANCE MATCH,

var alle rette linier. Prøv nu

. Studer det første

RANGER

-programmet.

, hvor du skal efterligne en graf over hastighed som funktion af tiden.

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

Opgave 1—Efterlign grafen

Navn ____________________________________

Dataindsamling

1. Hvilken fysisk størrelse repræsenterer x-aksen? _____________________________________________ Hvilke enheder? Hvor langt er der mellem aksemærkerne? ________ Hvilken fysisk størrelse repræsenterer y-aksen? _____________________________________________ Hvilke enheder? Hvor langt er der mellem aksemærkerne? ________

2. Hvor langt fra

-enheden tror du, at du skal stå til at begynde med? _________________________

CBR

3. Begyndte du for tæt på, for langt væk eller i den rette afstand? _______________________________

4. Skal du gå frem eller tilbage for at efterligne et liniestykke, der går opad? ______________________

Hvorfor? _____________________________________________________________________________

5. Skal du gå frem eller tilbage for at efterligne et liniestykke, der går nedad? _____________________ Hvorfor? _____________________________________________________________________________

6. Hvad skal du gøre for at efterligne et liniestykke, der er fladt? ________________________________ Hvorfor? _____________________________________________________________________________

Undersøgelser

7. Hvis du tager ét skridt hvert sekund, hvor langt skal dette skridt så være? ______________________

8. Hvis du i stedet tager skridt, der er 1 meter lange (eller 1 fod), hvor mange skridt skal du så tage?

_____________________________________________________________________________________

9. For hvilket liniestykke skal du bevæge dig hurtigst? _________________________________________ Hvorfor? _____________________________________________________________________________

10. For hvilket liniestykke skal du bevæge dig langsomst? _______________________________________ Hvorfor? _____________________________________________________________________________

11. ,Hvilke andre faktorer indgår for at efterligne grafen nøjagtigt, ud over at finde ud af, om du skal bevæge dig frem eller tilbage? __________________________________________________________

_____________________________________________________________________________________

12. Hvilken fysisk størrelse repræsenterer hældningen, eller stejlheden, af liniestykket? _______________

13. Hvor mange meter skal du gå på hvor mange sekunder for at efterligne det første liniestykke? _____

sekund: ____________________________

14. Konverter værdien i spørgsmål 13 (hastigheden) til meter Konverter til meter Konverter til meter Konverter til kilometer

minut: ______________________________________________________________

àtime: _______________________________________________________________

àtime: ____________________________________________________________

15. Hvor langt gik du i virkeligheden? ________________________________________________________

OM GODT I GANG MED

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

Opgave 2—Legetøjsbil noter til instruktøren

Begreber

Den undersøgte funktion: lineær. Bevægelsen af en batteridrevet legetøjsbil kan

bruges til at illustrere begrebet konstant hastighed.

Materialer

 regner

CBR



 kabel mellem regner og CBR-enheden  batteridrevet legetøjsbil  TI ViewScreen (valgfri)

Tip

Legetøjsbiler varierer meget i størrelse, form og den vinkel, ultralyden reflekteres under. Derfor kan kvaliteten af de resulterende grafer også variere. Nogle biler kan kræve yderligere flader til refleksion for at give gode grafer. Prøv eventuelt at sætte et postkort eller lignende på bilen for at give føleren et godt mål.

Du kan eventuelt prøve flere forskellige legetøjsbiler, så eleverne kan udforske disse effekter.

Langsomme legetøjsbiler (f.eks. dem, der er beregnet på mindre børn) er de bedste til denne opgave. Find en bil, der kan køre med konstant hastighed.

Der er tip om effektiv dataindsamling på side 6–12.

Undersøgelser

Hældningen af grafen over afstanden som funktion af tiden for et objekt på et givet tidspunkt er et udtryk for objektets hastighed på det pågældende tidspunkt. For et objekt, der bevæger sig med konstant hastighed, er hældningen af grafen over afstanden som funktion af tiden derfor konstant. Det er derfor, grafen over afstanden som funktion af tiden viser en lineær sammenhæng.

Hvis du starter indsamling af data, før bilen begynder at bevæge sig, vil du bemærke, at grafen over afstanden som funktion af tiden ikke er lineær i starten af grafen. Hvorfor? Bilen begynder i hvile (v = 0). Den kan ikke pludselig opnå en konstant hastighed. Accelerationen er bestemt af:

∆

Hvis objektet pludselig skulle gå fra hvile til den konstante hastighed, skulle ∆t = 0, men dette kræver uendelig stor acceleration, hvilket ikke er fysisk muligt (Newtons anden lov, F = ma, siger, at en uendelig stor acceleration kun kan være resultatet af en uendelig stor kraft, hvilket er lige så umuligt). Vi må altså se objektet accelerere (øge hastigheden) til den konstante hastighed i løbet af en bestemt tid.

Typiske grafer

Svar på spørgsmål

1. den første eller sidste graf; afstanden øges med konstant hastighed

2. eleverne angiver værdier fra

TRACE

3. afstandsværdier øges med en konstant værdi

4. hastighed er et udtryk for, hvor hurtigt afstanden ændres; værdierne er de samme for lige store tidsrum

5. eleverne bør få en værdi svarende til de værdier, der er beregnet for m

svarende til m m svarer til bilens fart eller hastighed

6. b er skæringen med y-aksen; eksempel: y = 2x + 0

7. varierer; hvis f.eks. m = 2, er afstand (y) = 20 meter efter 10 sekunder (y = 2 Q 10 + 0); efter 1 minut er y = 120 meter

Avancerede undersøgelser

Hældningen af en graf over hastigheden som funktion af tiden for konstant hastighed er nul. Derfor viser grafen over accelerationen som funktion af tiden a = 0 (i det ideelle tilfælde) i den periode, hvor hastigheden er konstant.

Arealet under (t,v)-grafen er objektets forskydning (den afstand, det netto har flyttet sig) i tidsrummet fra t

til t2.

For elever, der har lært integralregning, kan forskydningen findes ud fra:

svdt

∫

hvor s er objektets forskydning i tidsrummet fra t1 til

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

Opgave 2—Legetøjsbil lineær

Dataindsamling

Placer bilen mindst 0,5 meter (1,5 fod) fra

➊

-enheden, så den vender bort fra

CBR

enheden i en ret linie.

Ret føleren direkte mod bilen, og sørg for, at der ikke er noget i det frie område

Tip:

(se side 7).

➋

Besvar spørgsmål 1 på arbejdsbladet, før du starter dataindsamlingen.

➌ ➍

Kør

RANGER

Vælg

-programmet (se tastesekvenserne for de forskellige regnere på side 5).

SETUPàSAMPLE

i menuen

MAIN MENU

. Til denne opgave skal indstillingerne

være:

CBR

REALTIME: NO

TIME (S): 5 SECONDS

DISPLAY: DISTANCE

BEGIN ON: [ENTER]

SMOOTHING: LIGHT

UNITS: METERS

Vejledning i at ændre indstillingerne findes på side 38. Vælg

➎ ➏

START NOW

Tryk på ›, når du er klar til at begynde. Start bilen, og gå selv hurtigt ud af det

frie område. Du kan høre en klikkende lyd, mens data indsamles, og meddelelsen

TRANSFERRING...

Når dataindsamlingen er færdig, viser regneren automatisk en graf over afstanden

➐

vises på regneren.

som funktion af tiden for de indsamlede data. Sammenlign grafen over resultaterne med din forudsigelse i svar 1 for at finde

➑

ligheder og forskelle.

OM GODT I GANG MED

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

Opgave 2—Legetøjsbil

Undersøgelser

Værdierne for x (tid) med intervaller på et halvt sekund findes i den første kolonne i

➊

spørgsmål 2. Udforsk grafen med (afstand) i den anden kolonne.

del af grafen. Det kan eventuelt være nødvendigt at se bort fra atypiske data i starten af dataindsamlingen. Det kan også være nødvendigt at tilnærme afstanden (regneren giver måske afstande for intervaller på 0,957 og 1,01 sekund i stedet for nøjagtig 1 sekund). Vælg det nærmeste, eller foretag et kvalificeret gæt.

➋

Besvar spørgsmål 3 og 4. Beregn ændringerne i afstand og tid mellem hvert datapunkt, og udfyld den tredje

➌

og fjerde kolonne. Hvis du f.eks. vil beregne @Afstand (i meter) for tidspunktet 1,5 sekunder, skal du trække værdien for Afstand ved 1 sekund fra værdien for Afstand ved 1,5 sekunder.

Den funktion, der illustreres i denne opgave, er y = mx + b. m er hældningen af en

➍

ret linie. Den beregnes efter:

(forts.) lineær

TRACE

, og angiv de tilhørende y-værdier

Bemærk:

Brug kun resultaterne fra den lineære

Skæringen med y-aksen svarer til b. Beregn m for hvert punkt. Skriv værdierne i tabellen i spørgsmål 2.

➎

Besvar spørgsmål 5, 6 og 7.

Avancerede undersøgelser

Hældningen af en graf over afstanden som funktion af tiden på et givet tidspunkt er et udtryk for objektets hastighed på det pågældende tidspunkt. Hældningen af en graf over hastigheden som funktion af tiden er et udtryk for objektets acceleration på det pågældende tidspunkt. Hvis hastigheden er konstant, hvad er accelerationen så?

Forudsig, hvordan grafen over accelerationen som funktion af tiden for denne graf over afstanden som funktion af tiden vil se ud.

Find arealet mellem grafen over hastigheden som funktion af tiden og x-aksen mellem to valgte tidspunkter, t flere rektangler, der hver især har et areal, der kan beregnes som:

Hvad repræsenterer det resulterende areal i virkeligheden?

@afstand

@tid

og t2. Det kan gøres ved at tage summen af arealerne af et eller

eller

afstand

areal = v∆t = v(t

N afstand

N tid

tid

2Nt1

eller

)

N y

x2 N x

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

Opgave 2—Legetøjsbil

Navn ____________________________________

Dataindsamling

1. Hvilken af disse grafer tror du svarer til grafen over afstanden som funktion af tiden for legetøjsbilen?

Hvorfor? _____________________________________________________________________________

Tid Afstand

Afstand

Tid

1 xxx xxx xxx

1,5

2,5

3,5

4,5

3. Hvad lægger man mærke til i forbindelse med afstandsværdierne?_____________________________

4. Hvordan viser disse resultater, at legetøjsbilen havde konstant hastighed?_______________________

5. Beregn

afstandà@tid

mellem Tid = 2 og Tid = 4. __________________________________________ Hvad bemærkede du i forbindelse med dette resultat? ______________________________________ Hvad tror du,

6. Hvad er værdien for

svarer til? ______________________________________________________________

i den lineære ligning y = mx + b,? ____________________________________

Skriv ligningen for linien på formen

= mx + b med angivelse af værdierne for m og b.___________

7. Hvor langt kunne legetøjsbilen bevæge sig på 10 sekunder? _________________________________ På 1 minut? __________________________________________________________________________

OM GODT I GANG MED

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

Opgave 3—Pendul noter til instruktøren

Begreber

Den undersøgte funktion: sinusformet. Undersøg en simpel harmonisk bevægelse i form af

et pendul, der svinger frit.

Materialer

 regner

CBR



 kabel mellem regner og CBR-enheden  monteringsklemme  stopur  pendul  målestok  TI ViewScreen (valgfri)

Forslag til lodder:

bolde med forskellige størrelser (≥ 50 mm i

diameter) sodavandsdåser (tomme og fyldte)

poser med forskelligt fyld

Tip

Der er tip om effektiv dataindsamling på side 6–12.

Fysiske forhold

Objekter, som foretager en periodisk bevægelse, der skyldes en genoprettende kraft, der er proportional med forskydningen fra ligevægtspositionen (hviletilstanden), siges at udføre simple harmoniske bevægelser. Simple harmoniske bevægelser kan beskrives ved to parametre:

Perioden T er den tid, det tager at gennemføre

én fuld svingning (svingningstiden). Amplituden A er den maksimale forskydning af

objektet fra ligevægtspositionen (hvilepositionen).

For et simpelt pendul er perioden T bestemt af:

T = 2p

hvor L er længden af snoren, og g er størrelsen af tyngdeaccelerationen. T afhænger ikke af objektets masse eller bevægelsens amplitude.

Frekvensen f (antallet af perioder i sekundet) kan beregnes som:

hvor f måles i hertz (Hz), når T måles i

f =

sekunder.

De afledede funktioner af en sinusformet graf er også sinusformede. Bemærk faseforskydningen mellem loddets position og hastighed.

Typiske grafer

Typiske svar

1. varierer (i meter)

2. varierer (i meter)

3. varierer (i sekunder); T (én periode) = den totale tid for 10 perioderà10; hvis der tages et gennemsnit over et større antal målinger, mindskes de naturlige målefejl

4. den totale kurvelængde, som bør være ca. 4 gange svaret på spørgsmål 2; fordi en kurve er længere end en ret linie

5. sinusformet, repetitiv, periodisk; afstand fra xaksen til ligevægtspositionen

6. hver periode er bredt ud i vandret retning; en graf over 10 sekunder skal have plads til flere perioder på samme plads på skærmen, og derfor vises perioderne tættere sammen

7. (det totale antal perioder)à(5 sekunder) = perioderàsekund; lettere at få vist hele perioder og færre målefejl

8. f = 1àT, hvor T er tiden for 1 periode

9. mindre periode; større periode Pendulets længde hænger direkte sammen med

perioden; jo længere snoren er, jo længere er perioden. Eleverne kan udforske denne sammenhæng ved hjælp af regnerens listeeditor, hvor de kan beregne perioden for forskellige værdier af L.

10.A (amplitude, udsving) = ¼ af den totale afstand, pendulet bevæger sig i 1 periode

11.begge sinusformede; forskellene ligger i amplitude og fase

12.ligevægtspositionen

13.når position = maksimum eller minimum (når loddet er i den største afstand fra ligevægtstilstanden).

14.Det gør den ikke. T afhænger kun af L og g, ikke af massen.

Avancerede undersøgelser

Dataindsamling: grafen over L2 som funktion af L3 er en ellipse.

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

Opgave 3—Pendul sinusformet

Dataindsamling

Hæng pendulet op. Juster det, så det svinger i en ret linie frem og tilbage mod

➊

enheden.

Tip:

Placer

-enheden mindst 0,5 meter (1,5 fod) fra den nærmeste position af

CBR

loddet. Sørg for, at der ikke er noget i det frie område (se side 7).

litude

equilibrium position

Mål afstanden fra

➋

-enheden til ligevægtspositionen med en målestok. Besvar

CBR

spørgsmål 1 på arbejdsbladet.

CBR

Mål, hvor langt du vil trække loddet bort fra ligevægtspositionen. Besvar

spørgsmål 2.

En pendulcyklus (en periode) består af et helt sving frem og tilbage. Tag tiden for ti

➌

hele perioder med et stopur. Besvar spørgsmål 3 og 4.

➍

Kør

RANGER

-programmet (se tastesekvenserne for de forskellige regnere på side 5). En effektiv metode er, at én person starter pendulet, mens en anden betjener regneren og

Tryk på › for at få vist indstillingerne. I denne opgave skal de være:

➎

REALTIME: NO

TIME (S): 10 SECONDS

DISPLAY: DISTANCE

BEGIN ON: [ENTER]

SMOOTHING: LIGHT

UNITS: METERS

Vejledning i at ændre indstillingerne findes på side 38. Vælg

➏

-enheden. Vælg

CBR

SETUPàSAMPLE

i menuen

MAIN MENU

START NOW,

når de er

korrekte. Tryk på ›, når du er klar til at begynde. Du kan høre en klikkende lyd, mens data

➐

indsamles, og meddelelsen Når dataindsamlingen er færdig, viser regneren automatisk en graf over afstanden

➑

TRANSFERRING...

vises på regneren.

som funktion af tiden på grundlag af de indsamlede data. Besvar spørgsmål 5.

OM GODT I GANG MED

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

Opgave 3—Pendul

Undersøgelser

Dataindsamling 2

(forts.)

sinusformet

Vælg

SETUPàSAMPLE

Gentag dataindsamlingen, og studer grafen. Besvar spørgsmål 6 og 7. Den størrelse, du har bestemt (antal perioder i sekundet), kaldes frekvensen. Du har

bestemt frekvensen i spørgsmål 7 ved hjælp grafen, men du kan også finde den matematisk ud fra:

hvor T er perioden i sekunder, og f er frekvensen i hertz (Hz).

f =

Besvar spørgsmål 8.

Dataindsamling 3 og 4

Gentag de 5 sekunders dataindsamling to gange til. Første gang skal du forkorte snoren, og anden gang skal du forlænge snoren. Besvar spørgsmål 9, når du har studeret disse grafer.

En anden vigtig størrelse, der har betydning for pendulets bevægelse, er amplituden. Svaret på spørgsmål 2 var amplituden af pendulets udsving. Besvar spørgsmål 10.

Avancerede undersøgelser

Dataindsamling 5

Vælg

VELOCITY-TIME

i menuen

MAIN MENU

PLOT MENU

. Ret tiden fra 10 til 5 sekunder under

. Besvar spørgsmål 11, 12 og 13.

SETUP

Dataindsamling 6

Gentag dataindsamlingen med et væsentlig lettere eller tungere lod, og besvar spørgsmål 14.

Lav en model over pendulets afstand som funktion af tiden ved hjælp af en sinusformet funktion, S = A sin (wt + d), hvor S er den øjeblikkelige position, A er amplituden, w er vinkelfrekvensen, d er fasevinklen, og t er tiden. Vinkelfrekvensen, w, forholder sig til perioden, T, efter formlen w = 2 pàT.

Skriv denne ligning i redigeringsprogrammet Y= med de beregnede værdier for A og w. Afbild samtidigt denne funktion og den statistiske graf over

(tid). Juster værdierne for A, w og d, indtil du opnår en god tilpasning. På TI-83 og

(afstand) som funktion af

TI-86 kan du bruge sinusregression til at bestemme værdierne. Undersøg forholdet mellem position og hastighed ved at afbilde

funktion af

(hastigheden). Hvordan tror du, den resulterende graf vil se ud?

(afstanden) som

Sammenlign det faktiske resultat med din forudsigelse.

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

Opgave 3—Pendul

Dataindsamling

Navn ____________________________________

1. Hvad er afstanden fra

-enheden til ligevægtspositionen? _________________________________

CBR

2. Hvor langt vil du trække pendulet bort fra ligevægtspositionen? ______________________________

3. Hvad var tiden for ti perioder? ___________________________________________________________

Beregn, hvor lang tid (i sekunder) det tog at fuldføre én periode. ______________________________ Hvad er fordelen ved at tage tiden for ti perioder i stedet for én? _____________________________

4. Brug svaret på spørgsmål 2 til at fastlægge den totale afstand, der er tilbagelagt i løbet af en periode. _____________________________________________________________________________

Hvorfor er denne værdi mindre end den afstand, der faktisk er tilbagelagt i løbet af en periode?

_____________________________________________________________________________________

5. Hvad lægger man mærke til i forbindelse med udseendet af grafen? ___________________________ På hvilken måde er værdien fra spørgsmål 1 repræsenteret på grafen? _________________________

Undersøgelser

6. Hvordan ændres grafens udseende? Hvorfor ? _____________________________________________

_____________________________________________________________________________________

7. Beregn antallet af perioder i sekundet ved hjælp af data fra grafen. ___________________________ Hvorfor er det lettere at bestemme dette ud fra den anden graf (der spænder over 5 sekunder) end

ud fra den første (der spænder over 10 sekunder)?__________________________________________

8. Beregn frekvensen ud fra perioden vha. ligningen. __________________________________________

9. Hvordan påvirker en forkortelse af snorens længde pendulets periode?_________________________ Hvordan påvirker en forlængelse af snorens længde pendulets periode? ________________________

10. Hvad er forholdet mellem amplituden af pendulets udsving og den totale afstand, som pendulet

bevæger sig i én periode? ______________________________________________________________

_____________________________________________________________________________________

Avancerede undersøgelser

11. Sammenlign grafen over afstanden som funktion af tiden med grafen over hastigheden som funktion af tiden. Angiv ligheder og forskelle. ______________________________________________

_____________________________________________________________________________________

12. I hvilken position er loddets hastighed størst?_______________________________________________

13. I hvilken position er loddets hastighed mindst? _____________________________________________

14. Hvordan påvirker en ændring af vægten af loddet grafen? Hvorfor? ___________________________

_____________________________________________________________________________________

OM GODT I GANG MED

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

Opgave 4—Hoppende bold noter til instruktøren

Begreber

Den undersøgte funktion: parabolsk. Begreber som objekter i frit fald og hoppende

objekter, tyngdekraft og konstant acceleration er eksempler på parabolske funktioner. Denne opgave undersøger størrelserne højde, tid og koefficienten A i andengradspolynomiet Y = A(X  H)

+ K,, som

beskriver den måde, en hoppende bold opfører sig på.

Materialer

 regner

CBR



 kabel mellem regner og CBR-enheden  stor bold (9 tommer)  TI ViewScreen (valgfri)

Tip

Denne opgave udføres bedst med to elever, en til at holde bolden og en til at trykke på ¤.

Der er tip om effektiv dataindsamling på side 6–12. Grafen skal se ud som en hoppende bold. Hvis den

ikke gør det, skal du gentage målingen og sikre dig,

CBR

-enheden er rettet lige mod bolden. Det

at anbefales at bruge en stor bold.

Typiske grafer

CBR

-enheden til bolden. Programmet

BOUNCE

vender afstandsdataene, så grafen bedre

BALL

svarer til elevernes opfattelse af, hvordan bolden opfører sig. y = 0 på grafen er det punkt, hvor bolden er længst væk fra

CBR

-enheden, når

bolden rammer gulvet.

4. Eleverne skal forstå, at x-aksen svarer til tiden, ikke den vandrette afstand.

7. Kurven for A = 1 er både vendt om og bredere end grafen.

8. A < L1

9. parabel med den konkave side opad; den konkave side nedad; lineær

12.samme; matematisk svarer koefficienten A til omfanget af parablens krumning; fysisk afhænger A af tyngdeaccelerationen, som er konstant i alle hoppene.

Avancerede undersøgelser

Boldens hoppehøjde (boldens største højde i et bestemt hop) kan tilnærmelsesvis beregnes som:

, hvor

y er boldens hoppehøjde

h er den højde, hvorfra bolden slippes

p er en konstant, der afhænger af boldens fysiske

egenskaber og gulvets overflade x er nummeret på det pågældende hop

Undersøgelser

Når et objekt slippes, påvirkes det kun af tyngdekraften (vi ser bort fra luftmodstanden). Så A afhænger af tyngdeaccelerationen, N9,8 meteràsekund

(N32 fodàsekund2). Minustegnet

skyldes, at accelerationen er rettet nedad. Værdien for A er ca. halvdelen af

tyngdeaccelerationen, eller N4,9 meteràsekund

(N16 fodàsekund2).

Typiske svar

1. tid (fra målingens start); sekunder; højdeàafstand af bolden over gulvet; meter eller fod

2. boldens starthøjde over gulvet (toppene repræsenterer den maksimale højde af hvert hop); gulvet er repræsenteret ved y = 0.

3. grafen over afstanden som funktion af tiden for denne opgave repræsenterer ikke afstanden fra

For en given bold og starthøjde aftager boldens hoppehøjde eksponentielt for hvert hop. Når x = 0 er y = h, så skæringen med y-aksen svarer til den højde, bolden oprindelig blev sluppet i.

Særlig ivrige elever kan finde koefficienterne i denne ligning ud fra de indsamlede data. Gentag opgaven med forskellige starthøjder eller med en anden bold eller en anden gulvoverflade.

Efter manuel tilpasning af kurven kan eleverne bruge regressionsanalyse til at finde den funktion, der giver den bedste afbildning af dataene. Vælg et enkelt hop ved hjælp af vælg derefter

QUIT

PLOT TOOLS

i menuen

SELECT DOMAIN

MAIN MENU

, og

. Følg regnerens procedurer for at udføre en andengradsregression på listerne

og L2.

Ekstraopgaver

Integrer grafen over hastigheden som funktion af tiden, hvilket giver forskydningen (den afstand, objektet netto har flyttet sig) for et givet tidsinterval. Bemærk, at forskydningen er nul for et fuldt hop (bolden starter og slutter på gulvet).

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

Opgave 4—Hoppende bold parabolsk

Dataindsamling

Start med et prøvehop. Slip bolden (kast den ikke).

➊

-enheden mindst 0,5 meter (1,5 fod) over højden af det højeste hop.

Placer

Tip:

Hold føleren direkte over bolden, og sørg for, at der ikke er noget i det frie område (se side 7).

CBR

Kør

➋ ➌ ➍

RANGER

Vælg Vælg

Programmet Hold bolden i udstrakte arme. Tryk på ›.

➎

-programmet (se tastesekvenserne for de forskellige regnere på side 5).

APPLICATIONS BALL BOUNCE

BALL BOUNCE

i menuen i menuen

sørger automatisk for de rigtige indstillinger.

MAIN MENU

APPLICATIONS

. Vælg

METERS

eller

FEET

. Der vises nogle generelle anvisninger.

RANGER

-programmet er nu i Triggertilstand. På dette tidspunkt kan du eventuelt afbryde forbindelsen mellem enheden og regneren.

Tryk på ¤. Slip bolden, når den grønne lampe begynder at blinke, og gå et

➏

skridt tilbage. Hvis bolden hopper til siden, kan du flytte over bolden, men sørg for ikke at ændre højden på

CBR

-enheden direkte hen

CBR

-enheden.

Du kan høre en klikkende lyd, mens data indsamles. Der indsamles data for tid og afstand, og hastighed og acceleration beregnes. Hvis du har afbrudt forbindelsen til

, skal du etablere den igen, når dataindsamlingen er færdig.

CBR

Tryk på ›. Hvis grafen ikke er pæn, skal du gentage målingen. Studer grafen, og

➐

besvar spørgsmål 1 og 2 på arbejdsbladet.

Bemærk, at programmet

➑

BALL BOUNCE

automatisk vender om på afstandsdataene.

Besvar spørgsmål 3 og 4.

CBR

OM GODT I GANG MED

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

Opgave 4—Hoppende bold

Undersøgelser

Grafen over afstanden som funktion af tiden for hoppet er en parabel.

(forts.)

parabolsk

Tryk på ›. Vælg

➊

PLOT TOOLS

i menuen

PLOT MENU

, og derefter

SELECT DOMAIN

ønsker at vælge det første fulde hop. Flyt markøren til grundlinien ved starten af hoppet, og tryk på pågældende hop, og tryk på

Grafen er i

➋

TRACE

›. Flyt markøren til grundlinien ved slutningen af det

›. Grafen tegnes igen med fokus på et enkelt hop.

-tilstand. Bestem toppen af hoppet. Besvar spørgsmål 5 på

arbejdsbladet. Tryk på › for at vende tilbage til menuen

➌

derefter Formen Y = A(X  H)

➍

Tryk på

QUIT

+ K på andengradspolynomiet er velegnet til denne analyse.

œ. Fravælg de funktioner i redigeringsprogrammet Y=, der måtte være

PLOT MENU

. Vælg

MAIN MENU

valgt. Angiv andengradspolynomiet på denne form: Yn=A(XH)^2+K. På skærmbilledet Home skal du gemme den værdi, du skrev ned i spørgsmål 5 for

➎

højden, i variablen K. Gem den tilhørende tid i variablen H, og gem 1 i variablen A. Tryk på  for at få vist grafen. Besvar spørgsmål 6 og 7.

➏

Prøv A = 2, 0, –1. Udfyld den første del af skemaet i spørgsmål 8, og besvar

➐

spørgsmål 9. Vælg egne værdier for A, indtil du har en god tilnærmelse til grafen. Skriv dine

➑

valg for A i skemaet i spørgsmål 8.

. Vi

Gentag opgaven, men denne gang skal du vælge det sidste fulde hop (længst til

➒

højre). Besvar spørgsmål 10, 11 og 12.

Avancerede undersøgelser

Gentag dataindsamlingen, men vælg ikke en enkelt parabel.

➊

Registrer tiden og højden for hvert hop.

➋

Bestem forholdet mellem højden for hvert hop og det foregående.

➌

Forklar betydningen af dette forhold.

➍

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

Opgave 4—Hoppende bold

Navn ____________________________________

Dataindsamling

1. Hvilken fysisk størrelse repræsenterer x-aksen? _____________________________________________ Hvilke enheder? _______________________________________________________________________ Hvilken fysisk størrelse repræsenterer y-aksen? _____________________________________________ Hvilke enheder? _______________________________________________________________________

2. Hvad repræsenterer det højeste punkt på grafen? __________________________________________ Det laveste punkt? ____________________________________________________________________

3. Hvorfor vendte programmet

BALL BOUNCE

om på grafen? ____________________________________

4. Hvorfor ser grafen ud, som om bolden hoppede hen over gulvet? _____________________________

Undersøgelser

5. Registrer den maksimale højde og den tilsvarende tid for det første fulde hop. __________________

6. Svarer kurven for

= 1 til din graf? ______________________________________________________

7. Hvorfor eller hvorfor ikke? ______________________________________________________________

8. Udfyld skemaet nedenfor.

A Hvordan svarer kurven til din graf?

1 2 0

9. Hvad betyder en positiv værdi for Hvad betyder en negativ værdi for Hvad betyder værdien nul for

? _____________________________________________________

? ____________________________________________________

? _________________________________________________________

10. Registrer den maksimale højde og den tilsvarende tid for det sidste fulde hop. __________________

11. Tror du,

12. Hvordan forholdt det sig i virkeligheden med

Hvad tror du,

OM GODT I GANG MED

er større eller mindre i det sidste hop? ___________________________________________

? ___________________________________________

kunne svare til? _________________________________________________________

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

Opgave 5—Rullende bold noter til instruktøren

Begreber

Den undersøgte funktion: parabolsk. Afbildning af bevægelsen af en bold, der ruller

ned ad en rampe med varierende stejlhed, giver en samling kurver, der kan repræsenteres af en række andengradspolynomier. Denne opgave undersøger værdierne af koefficienterne i andengradspolynomiet y = ax

+ bx + c.

Materialer

 regner

CBR



 kabel mellem regner og CBR-enheden  monteringsklemme  stor bold (9 tommer)  lang rampe (mindst 2 meter eller 6 fod lang—

et let bræt er udmærket)

 vinkelmåler  bøger til at understøtte rampen  TI ViewScreen (valgfri)

Tip

Diskuter, hvordan man kan måle vinklen på rampen. Lad eleverne udfolde deres kreativitet. De kan f.eks. bruge trigonometriske beregninger, foldet papir eller en vinkelmåler.

Der er tip om effektiv dataindsamling på side 6–12.

Typiske grafer

Typiske svar

1. den tredje graf

2. tid; sekunder; objektets afstand fra CBR-

enheden; fod eller meter

3. varierer (skal være halvdelen af en parabel med den konkave side opad)

4. en parabel (andengradspolynomium)

5. varierer

6. varierer (skal være parabolsk med voksende krumning)

7. 0¡ er en vandret rampe (bolden kan ikke rulle); 90¡ er det samme som en bold i frit fald

Undersøgelser

Bevægelsen af et objekt, der kun påvirkes af tyngdekraften, er et populært emne i fysikken. Sådanne bevægelser udtrykkes normalt med en bestemt form af andengradspolynomiet:

s = ½at

0 0 0 0

I andengradspolynomiet y = ax til afstanden fra

+ v

t + s

, hvor

s er objektets position til tiden t a er dets acceleration

er dets starthastighed

er dets startposition

+ bx + c svarer y

CBR

-enheden til bolden til tiden x, hvis boldens startposition var c, dens starthastighed b og dens acceleration 2a.

Avancerede undersøgelser:

Da bolden er i ro, når den bliver sluppet, bør b være tæt på nul i alle forsøg, og c bør være tæt på startafstanden, 0,5 meter (1,5 fod). a øges, når hældningen af rampen øges.

Hvis eleverne opbygger ligningen y = ax manuelt, kan det være nødvendigt at give dem nogle tip om værdierne for b og c. Du kan også opfordre dem til at udføre en kvadratisk regression på listerne

og L2 på deres regnere. Boldens acceleration skyldes Jordens tyngdekraft. Jo mere rampen peger nedad (jo stejlere den er), jo større er værdien af a. Den maksimale værdi af

a forekommer for q = 90¡, den mindste for q = 0¡. a er i virkeligheden proportional med

sinus til vinklen q.

+ bx + c

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

Opgave 5—Rullende bold parabolsk

Dataindsamling

➊

Besvar spørgsmål 1 på arbejdsbladet. Indstil rampen med en vinkel på 15° i forhold til vandret. Fastgør klemmen til rampens øverste kant, og fastgør enheden til klemmen. Åbn følerens hoved, og placer den vinkelret på rampen. Tilslut regneren til

-enheden.

CBR

Sæt et mærke på rampen 0,5 meter (1,5 fod) fra

-enheden. Få en af eleverne til

CBR

at holde bolden ved dette mærke, mens en anden holder regneren.

Ret føleren direkte mod bolden, og sørg for, at der ikke er noget i det frie

Tip:

område (se side 7).

Kør

➋

RANGER

Vælg Tryk på › for at få vist indstillingerne. I denne opgave skal de være:

➌

REALTIME: NO

TIME (S): 3 SECONDS

DISPLAY: DISTANCE

BEGIN ON: [ENTER]

SMOOTHING: LIGHT

-programmet (se tastesekvenserne for de forskellige regnere på side 5).

SETUPàSAMPLE

UNITS: METERS

i menuen

MAIN MENU

➍

➎

➏

➐

OM GODT I GANG MED

Vejledning i at ændre indstillingerne findes på side 38. Vælg

START NOW,

når indstillingerne er korrekte. Tryk på › for at begynde

målingerne. Slip straks bolden (uden at skubbe til den), og træd et skridt tilbage, når klikkene

begynder. Når målingen er færdig, vises grafen over afstanden som funktion af tiden

automatisk. Besvar spørgsmål 2 og 3. Tryk på › for at få vist menuen

DOMAIN

. Flyt markøren til det sted, hvor bolden blev sluppet, og tryk på ›. Flyt

PLOT MENU

markøren til det sted, hvor bolden nåede enden af rampen, og tryk på

. Vælg

PLOT TOOLS

og derefter

›. Grafen

SELECT

tegnes op igen med fokus på den del af målingen, der svarer til, at bolden ruller ned ad rampen. Besvar spørgsmål 4 og 5.

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

Opgave 5—Rullende bold

Undersøgelser

Undersøg, hvad der sker ved forskellige hældninger af rampen.

Forudsig, hvad der vil ske, hvis hældningen øges. Besvar spørgsmål 6.

➊

Juster hældningen til 30¡. Gentag trin 2 til 6. Tilføj denne graf på tegningen i

➋

spørgsmål 6, der er mærket 30¡. Gentag trin 2 til 6 for hældninger på 45¡ og 60¡, og tilføj dem på tegningen.

➌ ➍

Besvar spørgsmål 7.

Avancerede undersøgelser

Juster tidsværdierne, så x = 0 for starthøjden (på det tidspunkt, hvor bolden blev sluppet). Du kan gøre dette manuelt ved at trække x-værdien for det første punkt fra alle punkterne på grafen, eller du kan skrive

(forts.)

L1(1)"A:L1NA"L1

parabolsk

Beregn værdierne for a, b og c for de forskellige kurver på formen y = ax

➊

for vinklerne 0¡, 15¡, 30¡, 45¡, 60¡ og 90¡. Hvad er den mindste og største værdi for a? Hvorfor?

➋

Skriv et udtryk, der beskriver den matematiske relation mellem a og

➌

hældningsvinklen.

+ bx + c

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

Opgave 5—Rullende bold

Navn ____________________________________

Dataindsamling

1. Hvilken af disse grafer tror du bedst svarer til grafen over afstanden som funktion af tiden for en bold, der ruller ned ad en rampe?

2. Hvilken fysisk størrelse repræsenterer x-aksen? _____________________________________________ Hvilke enheder? _______________________________________________________________________ Hvilken fysisk størrelse repræsenterer y-aksen? _____________________________________________ Hvilke enheder? _______________________________________________________________________

3. Skitser, hvordan grafen virkelig ser ud. Navngiv akserne. Mærk grafen med de punkter, hvor bolden blev sluppet, og hvor den nåede enden af rampen.

4. Hvilken type funktion repræsenterer denne graf? ___________________________________________

5. Diskuter, hvordan din forståelse har ændret sig mellem den graf, du valgte i spørgsmål 1, og den

kurve, du skitserede i spørgsmål 3. _______________________________________________________

_____________________________________________________________________________________

Undersøgelser

6. Skitser, hvordan du tror, grafen vil se ud med en større hældning. Kald den forudsigelse.

og 90¡:

7. Skitser graferne for 0

OM GODT I GANG MED

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

Oplysninger til instruktøren

Hvordan ændres undervisningen med CBR?

er et enkelt system at bruge, og det indeholder funktioner, som gør det let hurtigt at

CBR

integrere det i undervisningsplanerne.

indeholder væsentlige forbedringer i forhold til andre dataindsamlingsmetoder, du

CBR

kan have brugt tidligere. Det kan føre til en omstrukturering af, hvordan du bruger tiden i klassen, når eleverne bliver mere entusiastiske i forbindelse med anvendelsen af data fra det virkelige liv.

Du vil opleve, at eleverne føler en større grad af tilknytning til data, fordi de selv

deltager i dataindsamlingsprocessen i stedet for at bruge data fra lærebøger, tidsskrifter eller statistiske oversigter. Dette forstærker deres oplevelse af, at de begreber, der undersøges i klassen, har rod i virkeligheden og ikke blot er abstrakte ideer. Men det betyder også, at alle eleverne på skift vil være med til at indsamle disse data.

Dataindsamling med

er væsentlig mere effektiv end oprettelse af scenarier og

CBR

manuel måltagning med lineal og stopur. Da flere målepunkter giver flere detaljer, og en bevægelsesdetektor er meget nøjagtig, bliver formen på kurverne mere letgenkendelige. Der skal bruges mindre tid til dataindsamling, så der bliver mere tid til analyse og undersøgelser.

Med

kan eleverne udforske pålideligheden i observationerne og variationer i

CBR

scenarier af typen hvad-nu-hvis? Spørgsmål som “Er det den samme parabel, hvis vi slipper bolden fra en større højde?” og “Er det den samme parabel for det første og det sidste hop?” bliver naturlige og værdifulde ekstraopgaver.

Med visualiseringen kan eleverne hurtigt forbinde de afbildede data med de fysiske

størrelser og matematiske funktioner, som disse data beskriver.

Der sker også andre ændringer, når der indsamles data fra virkelige hændelser. Med

CBR

kan eleverne udforske de tilgrundliggende forhold både numerisk og grafisk.

Grafisk undersøgelse af data

Brug de automatisk tegnede grafer over afstand, hastighed og acceleration som funktion af tiden til at undersøge f.eks.:

Hvad er den fysiske betydning af skæringen med y-aksen? skæringen med x-aksen?

hældningen? maksimum? minimum? de afledede funktioner? integralerne? Hvordan kan man genkende den funktion (lineær, parabolsk, etc.), der vises af

grafen? Hvordan kan man lave en datamodel med en repræsentativ funktion? Hvad er

betydningen af de forskellige koefficienter i funktionen (f.eks. AX

Numerisk undersøgelse af data

Eleverne kan anvende statistiske metoder (gennemsnit, median, standardafvigelse, etc.) på et passende niveau til at udforske de numeriske data. Når du afslutter programmet, bliver du mindet om listerne, hvor data fra tilstanden afstand, hastighed og acceleration er lagret.

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

+ BX + C)?

RANGER

REALTIME=NO

OM GODT I GANG MED

for tid,

CBR

Oplysninger til instruktøren

(forts.)

CBR-grafer—sammenhæng med fysik og matematik

De grafer, der oprettes ud fra data, der er indsamlet af

RANGER

-programmet, er en visuel repræsentation af forholdet mellem de fysiske og matematiske beskrivelser af bevægelsen. Eleverne skal opmuntres til at genkende, analysere og diskutere udseendet af grafen både i fysiske og matematiske vendinger. Det er muligt at komme frem til yderligere diskussioner og opdagelser, når der indtastes funktioner i redigeringsprogrammet Y=, og de vises som grafer.

En graf over afstanden som funktion af tiden svarer til et objekts omtrentlige position

(afstand fra

-enheden) på det tidspunkt, hvor målingen fandt sted. Y-aksens enhed

CBR

er meter eller fod; x-aksens enhed er sekunder. En graf over hastigheden som funktion af tiden svarer til et objekts omtrentlige

hastighed (i forhold til og i retning mod

-enheden) på det tidspunkt, hvor målingen

CBR

fandt sted. Y-aksens enhed er meteràsekund eller fodàsekund; x-aksens enhed er sekunder.

En graf over accelerationen som funktion af tiden svarer til et objekts omtrentlige

ændring af hastigheden (i forhold til og i retning mod hvor målingen fandt sted. Y-aksens enhed er meteràsekund

-enheden) på det tidspunkt,

CBR

eller fodàsekund2; x-

aksens enhed er sekunder. Den første afledede (hældningen) i et givet punkt på grafen over afstanden som

funktion af tiden er hastigheden i det pågældende øjeblik. Den første afledede (hældningen) i et givet punkt på grafen over hastigheden som

funktion af tiden er accelerationen i det pågældende øjeblik. Dette er også den anden afledede i et givet punkt på grafen over afstanden som funktion af tiden.

Et bestemt integral (arealet mellem grafen og x-aksen mellem to vilkårlige punkter) af

grafen over hastigheden som funktion af tiden svarer til forskydningen af objektet (den afstand, objektet netto har flyttet sig) i løbet af det pågældende tidsinterval.

Fart og hastighed bruges ofte synonymt, selvom der er tale om forskellige, men beslægtede, størrelser. Fart er en skalar, der har en størrelse, men ingen retning, f.eks. “6 meter i sekundet”. Hastighed er en vektor, der både har en bestemt retning og en størrelse, f.eks. “6 meter i sekundet mod nord”.

-graf over hastigheden som funktion af tiden svarer egentlig til farten,

En typisk

CBR

ikke hastigheden. Det er kun størrelsen (der kan være positiv, negativ eller nul), der er givet. Retningen er blot underforstået. En positiv hastighed viser bevægelse bort fra

-enheden, og en negativ værdi viser bevægelse hen mod

CBR

måler kun afstand langs en linie fra detektoren, så hvis et objekt bevæger sig i en

CBR

-enheden.

CBR

retning, der danner en vinkel med denne linie, er det kun den komponent af hastigheden, der er parallel med denne linie, der måles. Et objekt, der bevæger sig vinkelret på linien fra

-enheden, viser f.eks. hastigheden nul.

CBR

OM GODT I GANG MED

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

Oplysninger til instruktøren

(forts.)

Matematikken bag afstand, hastighed og acceleration

gennemsnitlig

N s

= hældningen af grafen over afstanden som funktion af tiden

N t

graf over afstanden som funktion af tiden

øjeblikkelig

lim

@t"

(

)

hvor s = afstand

graf over hastigheden som funktion af tiden

N v

gennemsnitlig

@v @t

= hældningen af grafen over hastigheden som funktion af

N t

tiden

øjeblikkelig

lim

@t"

(

)

Arealet under grafen over hastigheden som funktion af tiden fra t1 til t2 = @s = (s forskydningen fra t

t=t

Dvs. @s =

(

t=t

til t2 (den afstand, objektet netto har flyttet sig).

t=t

⌠

⌡

v(dt)

v(@t)

∑

eller @s =

)

2Ns1

) =

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

graf over accelerationen som funktion af tiden

OM GODT I GANG MED

CBR

Oplysninger til instruktøren

Web-adresse

(forts.)

På vores web-adresse

en liste over supplerende materialer til brug sammen med

fra TI et bibliotek med programmer til brug sammen med

en side med opgaver og programmer, der er udviklet af og til instruktører som dig selv

CBR

mere detaljerede oplysninger om indstillinger og programmeringskommandoer til

Andre ressourcer

Texas Instruments Explorations-bøger indeholder supplerende materiale til grafiske regnere fra TI, bl.a. bøger med klasseopgaver til fysikundervisningen på de mellemste klassetrin og i gymnasiet.

http:ààwww.ti.comàcalc

-programmer med endnu flere

-funktioner

CBR

kan du finde:

CBR, CBL

der er beregnet på matematik- og

CBR,

og grafiske regnere

og grafiske regnere fra TI

CBR

OM GODT I GANG MED

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

CBR-data gemmes i lister

De indsamlede data lagres i listerne L1, L2, L3 og L4

Når gang

indsamler data, bliver de automatisk overført til regneren og gemt i lister. Hver

CBR

RANGER

indeholder tidsdata.

indeholder afstandsdata.

indeholder hastighedsdata.

indeholder accelerationsdata.

-programmet afsluttes, får du en meddelelse om, hvor data er lagret.

For eksempel er det 5. element i listen L1 det tidspunkt, da det 5. datapunkt blev indsamlet, og det 5. element i listen

I tilstanden

REALTIME=YES

eller acceleration), der beregnes og overføres. I tilstanden overføres alle data.

Indstillingerne lagres i listen L5

Fra skærmbilledet

RANGER SETUP

(se side 38). Når du overfører

RANGER

med standardværdierne. På side 40–41 er der oplysninger om de programmeringskommandoer, der ændrer andre

indstillinger.

er afstanden for det 5. datapunkt.

er det kun data til den ønskede graf (over afstand, hastighed

beregnes og

-parametre

CBR

er det let at ændre de hyppigst brugte

-programmet fra

REALTIME=NO

, erstattes L5 automatisk med en ny liste

CBR

Brug af datalisterne

Listerne bliver ikke slettet, når yderligere grafiske, statistiske og numeriske undersøgelser og analyser.

Du kan afbilde én liste som funktion af en anden liste, få dem vist i listeeditoren, bruge regressionsanalyse på dem og udføre andre analytiske opgaver. Du kan f.eks. indsamle data fra en pendulbevægelse ved hjælp af hastigheden som en funktion af accelerationen for at udforske ellipseformede funktioner (det kan eventuelt være nødvendigt at justere vinduet).

RANGER

-programmet afsluttes. De kan derfor bruges til

RANGER

, afslutte

RANGER

og derefter afbilde

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

RANGER-indstillinger

Ændring af RANGER-indstillingerne

RANGER

-programmet viser de hyppigst brugte indstillinger, før dataindsamlingen

begynder.

➊

Vælg

SETUPàSAMPLE

i menuen

MAIN MENU

RANGER

-programmet. De aktuelle

indstillinger vises. 4 viser placeringen af markøren.

MAIN MENU

REALTIME:

TIME (S):

DISPLAY:

BEGIN ON:

SMOOTHING:

Tryk på c eller b for at gå til den indstilling, du vil ændre.

➋

Tryk på

➌

START NOW

eller

= 1–99

FEET

SECONDS

eller

(

ACCELERATION

10-SECOND DELAY

HEAVY

eller

kun for

REALTIME=NO

YES

TOTAL TIME

DISTANCE, VELOCITY

[ENTER], [TRIGGER]

NONE, LIGHT, MEDIUM

METERS

UNITS:

›

for at gå igennem de forskellige værdier for indstillingerne. Når

)

indstillingen er korrekt, skal du trykke på c for at gå til den næste indstilling. Hvis du vil ændre værdien af

Når alle indstillingerne er korrekte, skal du trykke på c eller b, indtil markøren står

➍

på

START NOW

Tryk på

Hvis du vil vende tilbage til menuen

›

på

for at fortsætte.

›

, skal du skrive 1 eller 2 cifre og trykke på c eller b.

TIME

MAIN MENU

, skal du trykke på e og derefter

De nye indstillinger forbliver i kraft, medmindre du vælger andet program, der ændrer indstillingerne. Hvis du ændrer programmet eller sletter listen næste gang du kører

RANGER

, kan indstillingerne blive ændret til standardværdierne,

-programmet.

Genetablering af standardindstillingerne for RANGER-programmet

Standardindstillingerne er velegnede til mange målesituationer. Hvis du er i tvivl om de bedste indstillinger, bør du starte med standardindstillingerne og derefter foretage de nødvendige justeringer.

➊

Vælg

SET DEFAULTS

i menuen

MAIN MENU

RANGER

-programmet. Indstillingerne ændres til standardværdierne, og skærmbilledet Hvis du vil ændre en indstilling til noget andet end standardværdien, skal du følge

➋

trinene ovenfor. Hvis du vil fortsætte, skal du trykke på

➌

, når markøren står på

›

Andre RANGER-indstillinger

RANGER

-programmet giver adgang til de indstillinger, der hyppigst ændres, men flere indstillinger. På side 40–41 er der oplysninger om de programmeringskommandoer, der ændrer disse indstillinger.

SET DEFAULTS

uden for

SETUP

eller kører et

RANGER

vises.

START NOW

CBR

har

OM GODT I GANG MED

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

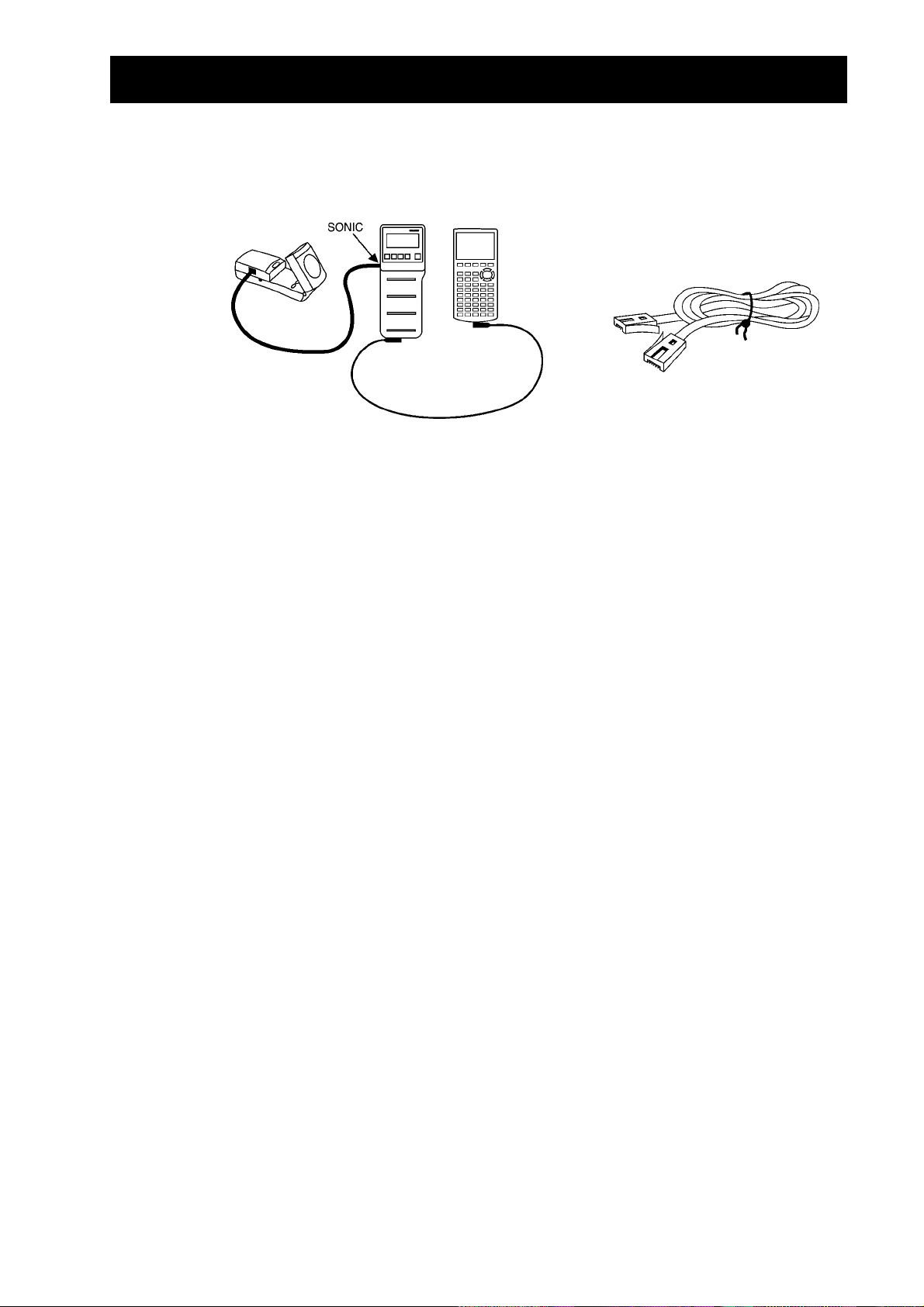
Brug af CBR med CBL eller CBL-programmer

Anvendelse af CBR som en normal bevægelsesdetektor sammen med CBL

kan bruges som en normal bevægelsesdetektor sammen med

CBR

(Calculator-Based Laboratoryé) fra Texas Instruments.

Det specielle kabel til at forbinde

-enheden til

CBR

Tilslut ikke Regneren skal være forbundet til

Det kan være nødvendigt at ændre programmet fungerer ikke sammen med

-enheden til

CBR

samtidig med, at

CBL

-programmet som vist nedenfor.

CBL

-enheden er tilsluttet til en regner.

CBR

Anvendelse af CBR sammen med programmer, der er skrevet til CBL

Du kan bruge

sammen med de fleste

CBR

-programmer, der kun er skrevet til en

CBL

bevægelsesdetektor, med få eller ingen ændringer af programmet. Stop målingerne: Med nogle

REALTIME=YES

, fortsætter

CBR

-programmer, der bruger dataindsamling i tilstanden

CBL

med at foretage målinger i det uendelige. Når du vil stoppe

dataindsamlingen efter fuldførelsen af målingerne, kan du gøre et af følgende:

CBL

-systemet

følger med.

CBL

RANGER

Tryk på ¤ på

Tilføj nogle linier i

-enheden.

CBR

-programmet, som sender kommandoen {6,0} til

CBL

skal indsættes et sted i programmet, efter at data er overført og vist, f.eks.:

{6,0}"L6:SEND L6

Slå lyden til eller fra: Hvis du vil slå lyden fra, skal du tilføje nogle linier i programmet, som sender kommandoen {6,3} til

Disse linier skal indsættes et sted i

CBR.

programmet, før dataindsamlingen begynder, f.eks.:

{6,3}"L6:SEND L6

Hvis du vil slå lyden til, behøver du blot køre

RANGER

Hvis der opstår problemer: Hvis du kører et låst, kan du køre

RANGER

der måske er en opdateret udgave af

-programmet. Prøv at se på TI’s web-adresse (se side 36), hvor

-programmet.

CBL

-programmet.

-program, og

CBL

ikke reagerer eller er

CBR

. Disse linier

CBR

CBL

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

Programmeringskommandoer

Kommando 0 Nulstiller systemet {0}

Nulstiller alt. Indsætter standardværdierne for startindstillingerne. Vælger automatisk Kanal 11.

Kommando 1 Nulstiller kanal {1,0}

Nulstiller kanal.

Kommando 1 Kanal {1,11,

operation

REALTIME=NO

operation

REALTIME=YES

efter_behandling

0 (standard) Intet 1( 2(

temperatur_konvertering

0 (standard) Deaktiverer temperaturkompensation. 1 Aktiverer temperaturkompensation.

REALTIME=NO REALTIME=NO

) Nulstiller alt. Indsætter standardværdierne for startindstillingerne. ) Meter ) Meter ) Fod

) Nulstiller alt. Indsætter standardværdierne for startindstillingerne. ) Meter ) Meter ) Fod ) Meter ) Fod ) Meter ) Fod

)dàdt (første afledede) )d

Kommando 2 Dataopsætning {2,

data_type

1 (standard) Liste

Kommando 3 Sample/Trigger {3,

sample_tid

0,005–1500 (0,1) Tiden i sekunder mellem hver måling 0,0001–0,005 Afrundet til 0,005. 1500<x<16000 Afrundet til 1500.

sample#

L1 Vælger dataindsamlingstilstand

REALTIME=NO

1–512 (

trigger

0 Begynder målingerne uden trigger. 1 (standard) Begynder målingerne, når der trykkes på ¤. 7 Venter 10 sekunder og begynder derefter målingerne.

record_tid

0 (standard) Intet

REALTIME=NO

filter

(se kommando 1, operation)

0 (standard) Ingen filtrering

REALTIME=NO

1 (

REALTIME=NO

2 (

REALTIME=NO

3 (

REALTIME=NO

4 (

REALTIME=NO

5 (

REALTIME=NO

6 (

REALTIME=YES

7 (

REALTIME=YES

8 (

REALTIME=YES

9 (

) Tager fra 1 til 512 målinger.

) Absolut tid (starter til tiden 0 og justerer derefter måletiden) ) Relativ tid (starter til tiden 0 og justerer derefter måletiden)

) 5-punkts Savitzsky-Golay-udglatning ) 9-punkts Savitzsky-Golay-udglatning ) 17-punkts Savitzsky-Golay-udglatning ) 29-punkts Savitzsky-Golay-udglatning ) 3-punkts medianudjævningsfilter ) 5-punkts medianudjævningsfilter

) Svagt sporingsfilter ) Middel sporingsfilter ) Kraftigt sporingsfilter

Resultater

data_type

Resultater

sample_tid,sample#,trigger

Resultater

operation,efter_behandling

CBR

returnerer {

CBR

returnerer {

CBR

returnerer {

CBR

returnerer {

CBR

returnerer {

CBR

returnerer {

CBR

returnerer {

àdt2 (anden afledede)

afstand,@tid afstand,@tid afstand,@tid afstand,hastighed,@tid afstand,hastighed,@tid afstand,hastighed,acceleration,@tid afstand,hastighed,acceleration,@tid

,0,0,0,0,0,0,0}

(REALTIME=YES)

temperatur_konvertering

,0,

} } }

} }

,0,0,0,0,

REALTIME=YES

record_tid,filter

}

} }

}

OM GODT I GANG MED

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

Programmeringskommandoer

(forts.)

Kommando 4 Temperaturkompensation {4,

ligning#

lignings_type

temperatur

enheder

Kommando 5 (

første_kanal

data_valg

data_start

data_slut

0 (standard) Nulstiller alle ligninger. 4 Vælger ligning 4.

0 (standard) Nulstiller ligningen. 13 Vælger temperaturkompensation.

flydende decimaltal Sætter den aktuelle temperatur.

0 (standard) Intet (ignoreres af 1 Sætter enheden for temperatur til Fahrenheit. 2 Sætter enheden for temperatur til Celsius. 3 Sætter enheden for temperatur til Kelvin. 4 Sætter enheden for temperatur til Rankin (R = F + 459.7).

REALTIME=NO

0 (standard) Vælger den laveste aktive kanal. 1, 2, 3, 11, 21 Angiver lydkanal. M1 Registrerer tidsliste.

0 Filter data {afstand} 1 Filter data dàdt {hastighed} 2 Filter data d 3 Grunddata {afstand} 4 Grunddata dàdt {hastighed} 5 Grunddata d

1–512 Første dataelement for GET

0–512 Sidste dataelement for GET (0 = sidste måling)

) Dataområde {5,

Resultater

Kommando 6 Systems options {6,

system_kommando

0 Stopper målingerne (af hensyn til kompatibilitet med CBL). 2 (standard) Stopper målingerne. 3 Slår lyden fra (lyden er slået til ved start). 4 Slår lyden til (lyden er slået til ved start). 5 Sætter ID ( 6 Anvender et nyt filter på eksisterende data (

operation

flydende decimaltal ID på formen 0–6 Nyt filter til eksisterende data (

Resultater

Kommando 7 Status {7}

Returnerer en liste, der indeholder:

10.rrrr DeviceCode.RomVersion 0–99 Sidste fejlkode (0 = ingen fejl) 0–2 Batteriets tilstand (0 = OK; 1 = lav under måling; 2 = altid lav) 11 Lydkanal-ID sample_tid Aktuelt måleinterval i sekunder trigger_condition Aktuel trigger-indstilling funktion Aktuel kanalfunktion (1–9) post_processing Aktuel efterbehandlingsindstilling (0–2) filter Aktuelt filtreringsniveau (0–9) samples Antal målinger til rådighed; 0–512 (

recorded_tid Indstilling for registreret tid (0–2) temperature Aktuel temperatur (¡C) piezo_flag 0 = lyd slået fra; 1 = lyd slået til system_state 1 = ingen opsætning; 2 = klar til måling; 3 = der er trykket på

window_start 0 = ingen kommando 5 endnu; 1–512 window_end 0 = brug antal elementer; 1–512 id_number ID (6 cifre) (standard 0.00000) indstillet med kommando 6

ligning#,lignings_type,temperatur,enheder

CBR

). Sætter måleenheden for T til grader Celsius.

første_kanal,data_valg,data_start,data_slut

àdt2 {acceleration}

system_kommando[,operation]

operation

n.nnnnn

kræves).

system_kommando

(

}

operation

= 5)

system_kommando

REALTIME=NO)

REALTIME=YES)

(

trigger/måling i gang; 4 = færdig

system_kommando

(

= 5)

}

kræves).

= 6)

; M1

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

Batterier

Batteritype

-enheden bruger 4 AA-batterier.

CBR

er tilsluttet til et

Isætning af batterier

Når du holder

-system.

CBL

-enheden med oversiden nedad, kan du skubbe batteridækslet mod

CBR

-enheden kan kun køre uden batterier, hvis den

CBR

bagsiden med tommelfingeren. Anbring batterierne som vist på diagrammet på indersiden af rummet til batterierne. De to batterier skal have den positive ende i den

De to andre batterier skal have den negative ende i den side,

side, der er mærket med +. der er mærket med -.

Skyd dækslet på plads igen.

er nu klar til at begynde

CBR

målingerne.

Advarsel om, at batterierne er ved at være flade

har to mekanismer til at advare om, at batterierne er ved at være flade:

CBR

RANGER

-programmet viser en advarsel på skærmen på regneren, mens den prøver at

indsamle data.

Den røde lampe blinker, mens

Oplysninger om batteristatus

Du kan kontrollere batterierne, før du starter målingerne. Vælg

, og vælg

Sikkerhedsforanstaltninger i forbindelse med batterierne

CBR STATUS

. Batteristatus vises (OK eller

indsamler data.

CBR

REPLACE)

TOOLS

i menuen

MAIN

Udskift alle fire batterier samtidigt. Bland ikke batterier af forskellige fabrikater eller typer sammen.

Installer batterierne som vist på diagrammet på indersiden af rummet til batterierne.

Bortskaf straks brugte batterier korrekt i henhold til gældende forskrifter. Sørg for, at børn ikke kan komme til dem.

Undgå at opvarme, brænde eller stikke hul på batterierne. Batterier indeholder farlige kemikalier, som kan eksplodere eller lække.

Bland ikke genopladelige batterier og almindelige batterier.

Forsøg ikke at genoplade almindelige batterier.

OM GODT I GANG MED

CBR

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

Hvis der opstår problemer

Hvis du har dette problem: Så prøv følgende:

Problem med at overføre

RANGER

-programmet eller med at

indsamle data

CBR

begynder automatisk at

indsamle data af sig selv

Fejlmeddelelsen

LINK ERROR

Kontroller, om der er en løs forbindelse mellem re Skub altid begge ender af kablet helt ind i stikkene.

Kontroller, om batterierne er ved at være flade (se side 42). Hvis du lægger CBR-enheden fra dig med

denne knap blive tr Tryk på

Afslut

RANGER

programmer, før du lægger

CBR

Tilslut

-enheden til regneren med kablet til at forbinde en regner og CBR-

kket ind og målingerne blive aktiveret ved en fejltagelse.

igen for at stoppe målingerne.

-programmet (med

QUIT)

CBR

-enheden bort.

og eventuelle andre

enheden. Kontroller, om der er en løs forbindelse mellem re

Skub altid begge ender af kablet helt ind i stikkene. Hvis du ikke vil (eller kan) tilslutte

for at bryde ud af programmet og vælge

på

CBR

-enheden til regneren, kan du trykke

Ikke nok hukommelse Der skal være tilstrækkelig meget hukommelse til

datalisterne. Programmerne og listerne kræver typisk ca. 17.500 byte. Slet nogle programmer og/eller data.

Regneren reagerer ikke som beskrevet i opgaverne

Data ser forkerte ud:

punkterne ligger ikke på kurven

takkede grafer

flade grafer

afbrudte grafer

Denne vejledning gælder for alle de TI-regnere, der kan bruges sammen med

CBR

, så det kan forekomme, at nogle af navnene på menuer, skærmbilleder

eller taster i denne ve

ner. Vælg det, der ligger nærmest. Hvis vejledningen f.eks. siger “Væl

DISTANCE MATCH

Genta

målingen, og sørg for, at CBR-enheden er rettet direkte mod

ledning ikke svarer nøjagtigt til dem på den aktuelle

”, skal du vælge

DIST MATCH

på TI-83.

objektet. Læs på side 6–12, hvordan du opnår gode data fra målingerne. Kontroller, at der ikke er elever, borde eller andre objekter i det frie område. Når du bru

er to

CBR

-enheder samtidigt i det samme lokale, skal den ene

gruppe elever gøre deres målinger færdig, før de andre begynder deres. Kontroller, om der er en løs forbindelse mellem re

Skub altid begge ender af kablet helt ind i stikkene. Kontroller, om batterierne er ved at være flade (se side 42). Sørg for, at graden af udglatning hverken er for stor eller for lille.

CBR

fungerer ikke sammen med

en bestemt TI

Kablet til at forbinde regner o CBR-enheden er blevet væk

Kontroller, at der står “ som tegn på kompatibilitet med

85 kan ikke lave statistiske grafer, så nogle undersøgelser (f.eks.

anvendelse af



Du kan i stedet bru med hinanden, som ful med hinanden er me

CBL

” i slutningen af serienummeret bag på regneren

CBL

CBR

på de afbildede data) kan ikke foretages på TI-85.

e det kabel, der er beregnet på at forbinde to regnere

te med regneren (kablet til at forbinde to regnere

et kortere end det, der er beregnet på at forbinde

regneren med CBR, så det er nok en god idé at bestille et nyt kabel).

Batterierne bliver hele tiden flade Afslut

pro regneren, før du lægger

Der sker ingenting, når du prøver at køre

RANGER

-programmet

Hvis du har redi minutter for re

RANGER

-programmet (med

rammer, og fjern derefter forbindelsen mellem

CBR

eret eller vist

neren at gøre programmet klar til at køre næste gang. Det er

QUIT)

og eventuelle andre

-enheden bort.

RANGER

-programmet, kan det tage op til to

helt normal.

Fejlmeddelelse om, at variablen er låst eller besk

92)

ttet (kun på

Lås op for variablene L1, L2, L3, L4 og L5. Se håndbogen til regneren.

neren og

CBR

-enheden.

-knappen nedad, kan

CBR-

eller

neren og

QUIT

RANGER

neren og

CBR

-enheden.

-programmet o

CBR

-enheden.

CBR-

eller

-enheden o

CBL

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

Oplysninger om TI-produktservice og garanti

Produkt- og serviceoplysninger

Kontakt TI via e-post, eller se TI’s hjemmeside på Internettet: E-postadresse:ti-cares@ti.com Internetadresse:http://www.ti.com/calc

Service og garantioplysninger

Se garantierklæringen, som fulgte med dette produkt, eller kontakt den lokale Texas Instruments forhandler/distributør for at få oplysninger om garantibetingelser, garantiens varighed eller om produktservice.

OM GODT I GANG MED

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

CBR

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

EXAS INSTRUMENTS INCORPORATED

RANGE

MAIN MENU

SETUP / SAMPLE

SET DEFAULTS

NO YES

1-99 (REALTIME=NO)

DISTANCE VELOCITY ACCELERATION

[ENTER] [TRIGGER] DELAY

NONE LIGHT MEDIUM HEAVY

METERS FEET

APPLICATIONS

REALTIME=NO

PLOT MENU

REALTIME=YES

TOOLS

QUIT

APPLICATIONS

UNITS METERS FEET

DISTANCE-TIME VELOCITY-TIME ACCELERATION-TIME PLOT TOOLS REPEAT SAMPLE MAIN MENU QUIT

SHOW PLOT SELECT DOMAIN REPEAT SAMPLE MAIN MENU QUIT

TOOLS GET CBR DATA GET CALC DATA CBR STATUS STOP/CLEAR CBR MAIN MENU

DISTANCE MATCH VELOCITY MATCH BALL BOUNCE MAIN MENU

PLOT TOOLS SELECT DOMAIN SMOOTH DATA PLOT MENU

DATA SMOOTHING LIGHT MEDIUM HEAVY NONE

OPTIONS SAME MATCH NEW MATCH APPLICATIONS MAIN MENU QUIT

ENNE SIDE MÅ KOPIERES, FORUDSAT AT

EXAS INSTRUMENTS INCORPORATED

S MEDDELELSE OM COPYRIGHT MEDTAGES

TI'

OM GODT I GANG MED

CBR

Texas instruments CBR User Manual [da]

Specifications and Main Features

Frequently Asked Questions

User Manual