Texas instruments CBR User Manual [pt]

Download

85-86

TRIGGER

CBR

)

Calculator-Based Ranger (CBR

™

)

™

NTRODUÇÃO AO

CBR™

INCLUINDO

ATIVIDADES PARA ALUNOS

CBR

)

TRIGGER

85-86

CBR

)

TRIGGER

85-86

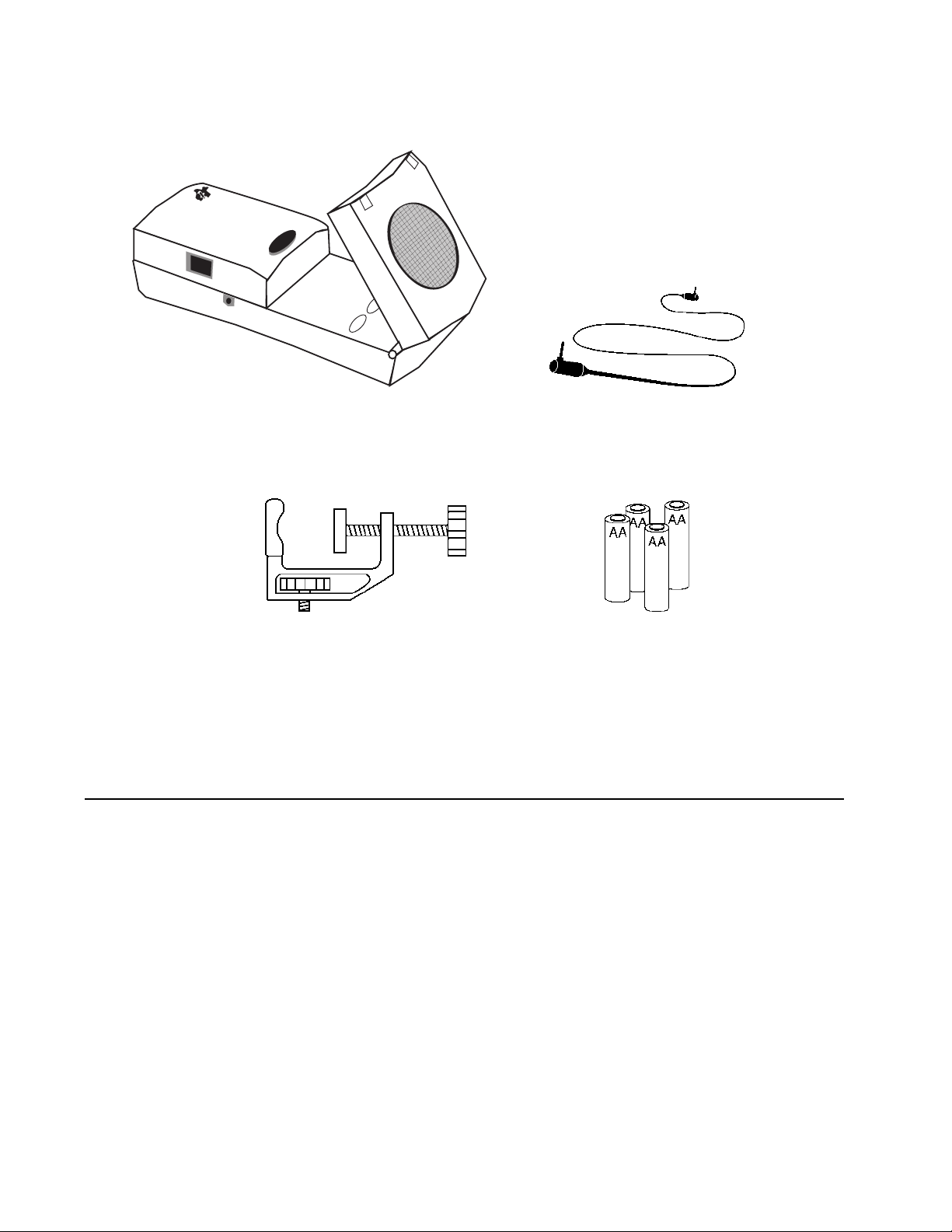
Calculator-Based Rangeré (CBRé) Cabo de calculadora-para-CBR

grampo 4 baterias AA

Observação importante referente aos materiais do manual

A Texas Instruments não fornece garantia, seja expressa ou implícita, incluindo, mas não limitando as garantias implícitas de mercado e adequação a um determinado objetivo, referentes aos programas ou materiais do manual e torna esses materiais disponíveis apenas na base “como está”. Em nenhum caso, a Texas Instruments será responsável por danos específicos, indiretos, acidentais ou subseqüentes juntamente com ou resultantes da aquisição desses materiais e, a responsabilidade única e exclusiva da Texas Instruments, independentemente da forma de ação, não excederá o valor de aquisição desse manual. Além disso, a Texas Instruments não será responsável por nenhum tipo de reivindicação, qualquer que seja, contra o uso desses materiais por parte de terceiros.



1997 Texas Instruments Incorporated.

A permissão, por meio desta, é concedida a professores para imprimirem novamente ou fotocopiarem em salas de aula, workshops ou seminários o número de páginas ou folhas nesse trabalho que contenham observação de copyright da Texas Instruments. Essas páginas destinam-se à reprodução por parte de professores para o uso em salas de aula, workshops ou seminários, contanto que cada cópia feita contenha a observação de copyright. Tais cópias não poderão ser vendidas e outro tipo de distribuição é expressamente proibido. Exceto conforme autorizado acima, deve ser obtida uma permissão prévia por escrito da Texas Instruments Incorporated para a reprodução ou divulgação desse trabalho ou partes dele, de qualquer outra forma ou por outros meios, eletrônicos ou mecânicos, incluindo sistemas de armazenamento ou recuperação de informações, a menos que seja expressamente permitido pela lei federal de copyright. Envie comentários à Texas Instruments Incorporated, PO Box 149149, Austin, TX, 78714

9149, M/S 2151, Attention: Contracts Manager.

Índice

CBR

)

Introdução

O que é CBR? 2 Introdução ao CBR — É tão fácil como 1, 2, 3 4 Dicas para uma coleta de dados eficaz 6

Atividades com notas para professores e folhas de atividades dos alunos

TRIGGER

85-86

Atividade 1 — Correspondência de gráficos linear 13

Atividade 2 — Carrinho de brinquedo linear 17

Atividade 3 — Pêndulo senoidal 21

Atividade 4 — Bola que salta parabólica 25

Atividade 5 — Rolagem da bola parabólica 29

Informações para os professores 33

Informações técnicas

Os dados do CBR são armazenados em listas 37 Definições do RANGER 38 Uso do CBR com o CBL ou com programas de CBL 39 Comandos de programação40

Informações sobre assistência técnica

Baterias 42 Em caso de dificuldade 43 Informações sobre Garantia e Serviços aos Produtos TI 44

Mapa do menu do RANGER

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

na contracapa

NTRODUÇÃO AO

CBR

O que é CBR?

proporciona coleta de dados do mundo real e análise na sala de aula

o RANGER, programa versátil, é tão simples como apertar um botão

os programas MATCH e BOUNCING BALL estão incluídos no RANGER

O que o CBR faz?

Com o de movimentos, sem que sejam necessárias medidas maçantes e “plotagem” manual.

O CBR

velocidade, aceleração e tempo, usando os dados coletados de atividades desempenhadas por eles. Os alunos podem explorar conceitos matemáticos e científicos, tais como:

CBRé (Calculator-Based Rangeré

)

detector sônico de movimentos

CBL

usar com TI-82, TI-83, TI-85/

, TI-86 e TI-92

fácil de utilizar, independente

não é necessária nenhuma programação

Inclui o programa RANGER

os parâmetros principais de amostragem são fáceis de definir

e uma calculadora gráfica, os alunos podem coletar, visualizar e analisar dados

CBR

permite que os alunos explorem as relações matemáticas e científicas entre distância,

movimento:

gráfico: eixos de

funções:

cálculo:

análise estatística e de dados:

distância, velocidade, aceleração

linear, quadrática, exponencial, senoidal

derivadas, integrais

O que este manual contém?

Introdução ao CBR

experiência com calculadoras ou com programação. Ele inclui iniciação rápida para o uso do

, dicas para uma coleta de dados eficaz e cinco atividades de sala de aula para a

CBR

exploração de funções básicas e propriedades de movimento. As atividades (consulte as páginas 13–32) incluem:

notas para professores para cada atividade e informações gerais para professores

instruções passo a passo

uma atividade básica de coleta de dados apropriada para todos os níveis

explorações que examinam os dados mais detalhadamente, incluindo situações

hipotéticas sugestões para tópicos avançados, apropriadas para alunos de pré-cálculo e cálculo

uma folha de atividades do aluno, reproduzível, com perguntas abertas, apropriada para

uma ampla faixa de níveis escolares

coordenadas, inclinações, intercepções

métodos de coleta de dados, análise estatística

foi designado para orientar professores que não possuem uma ampla

NTRODUÇÃO AO

CBR

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

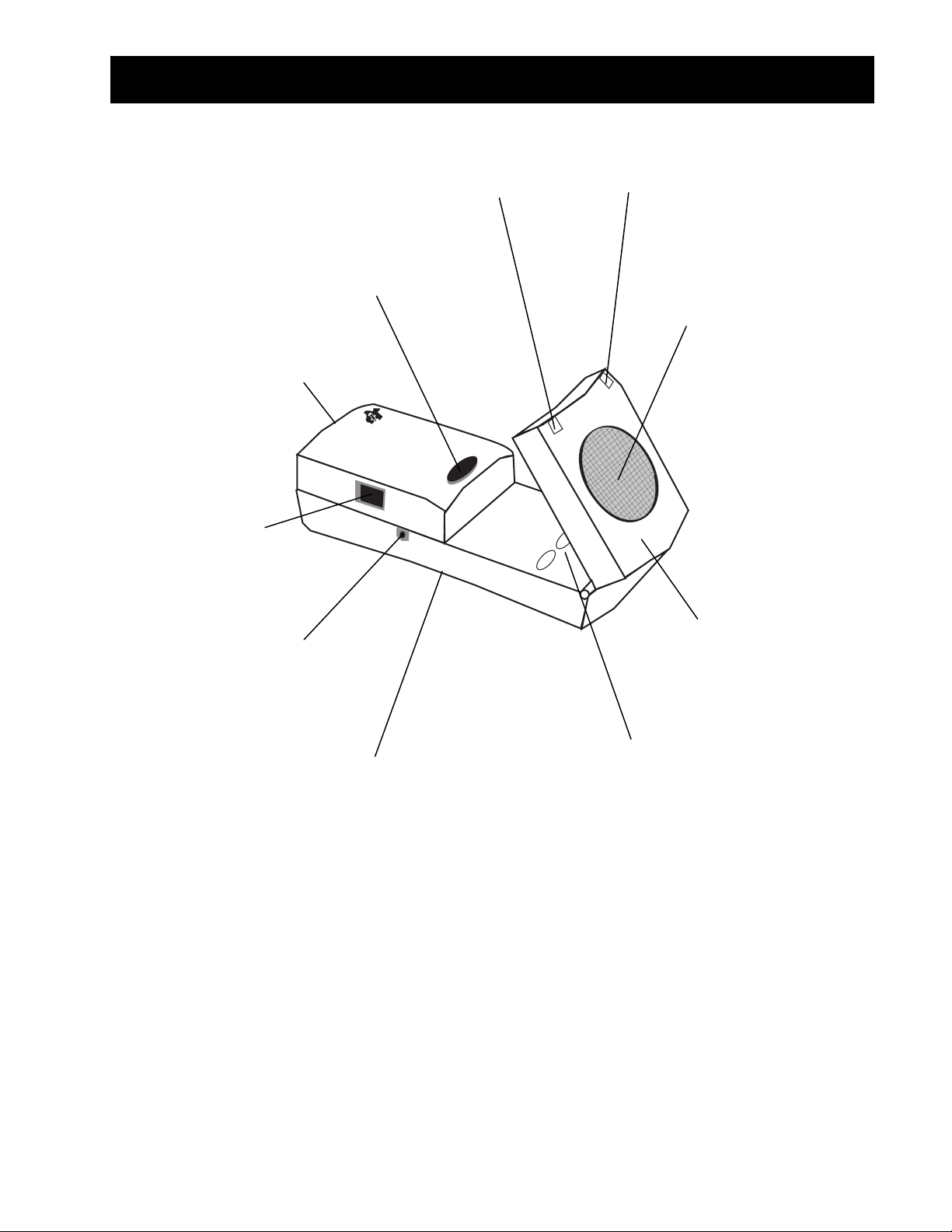
O que é CBR?

s s

(7,

(cont.)

luz verde para indicar quando a coleta de dados está ocorrendo (som também disponível)

botão

para iniciar amostragem

porta da bateria (parte de baixo)

porta para conexão ao CBL (se desejado)

porta para conexão às calculadoras gráficas da TI usando o cabo de 2,25-metros

5-pés) fornecido

luz vermelha para indicar condições especiais

ensor sônico para gravar até 200 amostras por segundo numa distância entre 0,5 metro e 6 metros (1,5 pés e 18 pés)

CBR

)

TRIGGER

85-86

cabeça de articulação para posicionar o sensor adequadamente

oquete padrão rosqueado para conectar um tripé ou o grampo de montagem

botões para transferir o programa RANGER para calculadoras

fornecido (atrás)

contém tudo o que você precisa para começar as atividades em sala de aula de forma fácil e

O CBR

rápida — basta conectá-lo a calculadoras gráficas TI (e acessórios facilmente disponíveis para algumas atividades).

detector sônico de movimentos 0cabo de calculadora-para-

programa RANGER no

CBR

4 baterias AA

CBR

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

grampo de montagem

5 atividades para sala de aula

NTRODUÇÃO AO

CBR

Introdução ao CBR—É tão fácil como 1, 2, 3

Com o

, você está apenas a três passos da primeira amostra de dados!

CBR

Conexão

Conecte o gráfica TI usando o cabo de calculadora-para-

Pressione extremidades para fazer a conexão.

O cabo curto de calculadora-

Nota:

para-calculadora que vem com a mesma calculadora também serve.

a uma calculadora

CBR

firmemente

nas duas

Transferência

RANGER

no calculadora.

Primeiro, prepare a calculadora para receber o programa (consulte as seqüências de teclas abaixo).

, um programa personalizado para cada calculadora, está incluído

. É fácil transferir o programa apropriado do

CBR

para uma

CBR

TI-82 ou TI-83 TI-85/CBL ou TI-86 TI-92

LINK

[

Em seguida, abra a cabeça de articulação no apropriado de transferência de programa no

Durante a transferência, a calculadora exibe a mensagem

›

]

[

LINK

]

CBR CBR

Vá para a tela Inicial.

e pressione o botão .

RECEIVING

(Recebendo) (exceto a TI-92). Quando a transferência é concluída, a luz verde do exibe a mensagem no

pisca uma vez, o

CBR

DONE

pisca duas vezes e o

CBR

Após transferir o programa

emite um sinal sonoro e a tela da calculadora

CBR

(Pronto). Se houver algum problema, a luz vermelha

emite dois sinais sonoros.

CBR

RANGER

para uma calculadora, não será

CBR

necessário transferi-lo novamente para essa calculadora, a menos que você o elimine da memória.

O programa e os dados requerem aproximadamente 17.500 bytes de

Nota:

memória. Poderá ser necessário eliminar programas e dados da calculadora. É possível salvar os programas e os dados primeiro, transferindo-os para um

computador, utilizando TI-Graph Linké ou para outra calculadora, utilizando um cabo de calculadora-para-calculadora ou o cabo de calculadora-para-

CBR

(consulte o manual da calculadora).

NTRODUÇÃO AO

CBR

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

Introdução ao CBR—É tão fácil como 1, 2, 3

Execução

(cont.)

Para resultados rápidos, tente uma das atividades para sala de aula deste guia!

Execute o programa

TI-82 ou TI-83 TI-85/CBL ou TI-86 TI-92

Pressione Selecione Pressione

RANGER

›

RANGER

(consulte as seqüências de teclas abaixo).

Pressione Selecione Pressione

^ A

RANGER

›

É exibida a tela de abertura. Pressione

MAIN MENU

SETUPàSAMPLE SET DEFAULTS APPLICATIONS PLOT MENU TOOLS QUIT

MAIN MENU,

›. É exibido o

& & & & &

selecione

MAIN MENU

visualizar/alterar definições antes da amostragem alterar as definições para definições padrão

DISTANCE MATCH, VELOCITY MATCH, BALL BOUNCE

opções de “plotagem”

GET CBR DATA, GET CALC DATA, STATUS, STOPàCLEAR

SET DEFAULTS

(Menu Principal).

(Definir Padrões). É exibida a tela (Configuração). Pressione › para selecionar Configure a atividade e, em seguida, pressione de dados. É fácil!

Informações importantes

Pressione L [ Selecione Pressione ¨

START NOW

› para começar a coleta

VAR-LINK

RANGER

›

(Iniciar Agora).

SETUP

Este manual aplica-se a todas as calculadoras gráficas TI que podem ser utilizadas com o

, por isso, você descobrirá que alguns dos nomes de

CBR

menus não correspondem exatamente aos de sua calculadora.

Ao configurar as atividades, certifique-se de que o

esteja seguramente

CBR

apoiado e que o fio não possa estar enroscado.

Sempre saia do programa

RANGER

Isto garante que o

executa uma saída adequada do

será inicializado corretamente na próxima vez em

CBR

RANGER

usando a opção

quando você seleciona

CBR

. O programa

QUIT

que for utilizado.

Desconecte sempre o

da calculadora antes de guardá-lo.

CBR

QUIT

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

NTRODUÇÃO AO

CBR

Dicas para uma coleta de dados eficaz

Obtenção de melhores amostras

Como funciona o CBR?

Entender como funciona um detector sônico de movimentos pode ajudá-lo a obter melhores “plotagens” de dados. O detector de movimentos envia um pulso ultra-sônico e, em

seguida, calcula o tempo gasto para o retorno desse pulso depois de bater no objeto mais próximo.

, como qualquer outro detector sônico de movimentos, calcula o intervalo de tempo

O CBR

entre a transmissão do pulso ultra-sônico e o primeiro eco retornado, mas o microprocessador interno que faz muito mais. Quando os dados são coletados, o a distância do objeto ao calcula a primeira e a segunda derivadas dos dados da distância referentes ao tempo para obtenção dos dados da velocidade e da aceleração. Ele armazena esses resultados nas listas

L1, L2, L3 e L4.

usando um cálculo de velocidade do som. Em seguida, ele

CBR

possui um

CBR

calcula

Efetuar os mesmos cálculos que o

Colete uma amostra de dados no modo

➊

programa Use os tempos da amostra em

➋

RANGER

efetua é uma atividade interessante em sala de aula.

CBR

REALTIME=NO

juntamente com os dados da distância em L2 para

(Tempo Real=Não). Saia do

calcular a velocidade do objeto em cada instante da amostra. Em seguida, compare os

)à2

n-1

diminui as chances de uma leitura

CBR

resultados com os dados da velocidade em

(

Use os dados da velocidade em L3 (ou os valores calculados pelo aluno) juntamente com

➌

n+1

os tempos de amostra em

)à2 N (

n+1

para calcular a aceleração do objeto em cada instante da

amostra. Em seguida, compare os resultados com os dados da aceleração em

Tamanho do objeto

Usar um objeto pequeno a uma longa distância do exata. Por exemplo, a 5 metros, há uma probabilidade maior de detectar uma bola de futebol do que uma bola de pingue-pongue.

Distância mínima

Quando o

envia um pulso, ele bate no objeto, retorna e é recebido pelo

CBR

CBR.

Se um objeto estiver a menos de 0,5 metro (1,5 pés), os pulsos consecutivos poderão se sobrepor e serem mal identificados pelo

. A “plotagem” seria imprecisa, por isso, posicione o

CBR

pelo menos a 0,5 metro do objeto.

NTRODUÇÃO AO

Distância máxima

Conforme o pulso se desloca pelo ar, ele perde sua força. Depois de aproximadamente 12 metros (6 metros no percurso até o objeto e 6 metros no percurso de volta ao retorno poderá ser muito fraco para ser detectado de forma segura pelo distância confiável do

CBR

ao objeto a menos de 6 metros (19 pés).

CBR

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

CBR

EXAS INSTRUMENTS INCORPORATED

), o eco de

CBR

. Isso limita a

SEJA INCLUÍDA

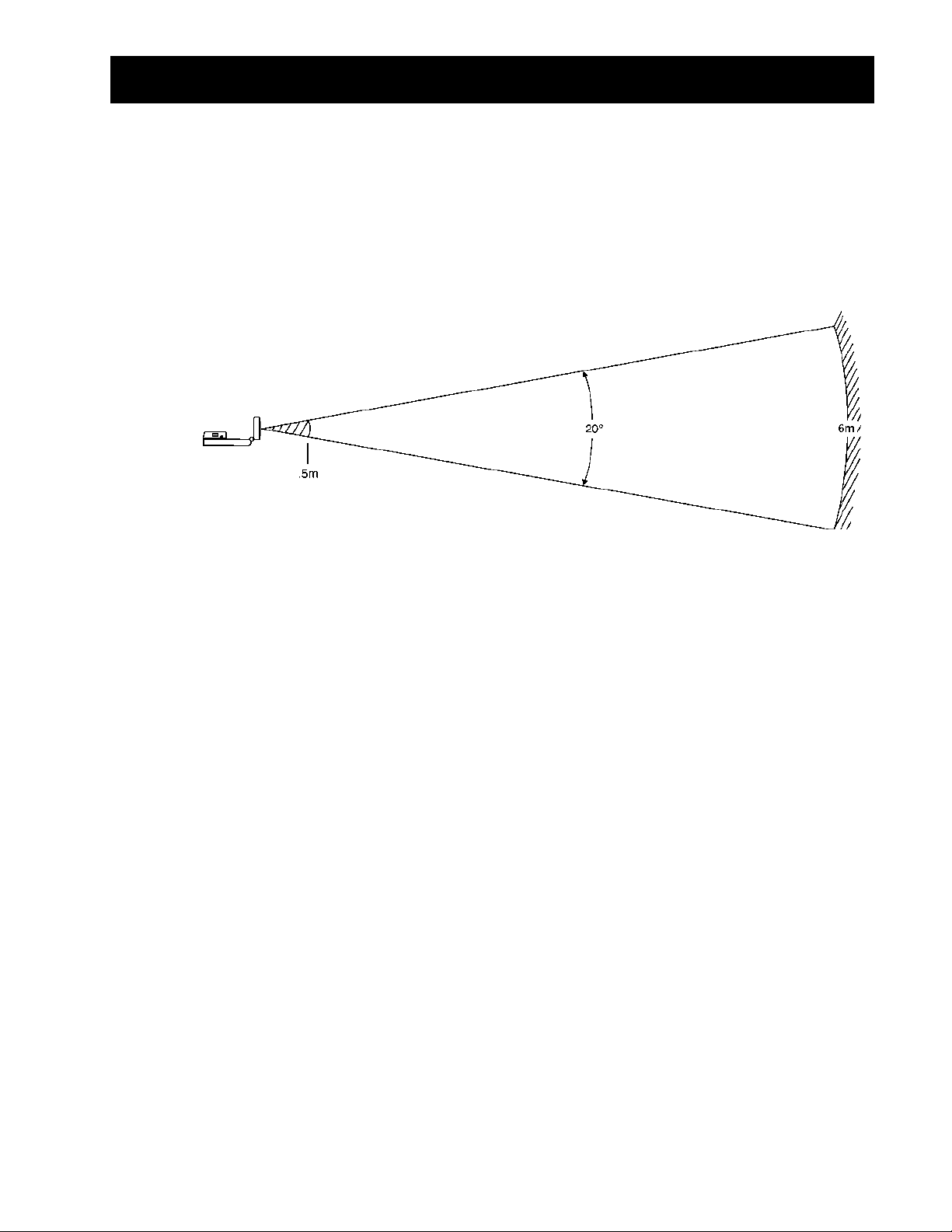
Dicas para uma coleta de dados eficaz

A área livre

(cont.)

O caminho do fluxo de ondas do

não é um fluxo de ondas estreito, em forma de feixe

CBR

luminoso, mas espalha-se em todas as direções até 10°, como um fluxo de ondas em forma de cone.

Para evitar interferência de outros objetos ao redor, tente estabelecer uma caminho do fluxo de ondas do não sejam registrados pelo

Superfícies refletivas

CBR

. Isto ajuda a garantir que objetos que não sejam o alvo

CBR

. O

registra o objeto mais próximo na área livre.

CBR

área livre

Algumas superfícies refletem os pulsos de maneira melhor que outras. Por exemplo, você poderá ver resultados melhores com uma bola de superfície relativamente dura e lisa do que com uma bola de tênis. De forma contrária, as amostras tiradas em um espaço cheio de superfícies duras e refletivas têm maior probabilidade de mostrar pontos de dados dispersos. As medidas de superfícies irregulares (como um carro de brinquedo ou um aluno segurando uma calculadora enquanto caminha) podem parecer desiguais.

Uma “plotagem” de Distância-Tempo de um objeto imóvel poderá ter pequenas diferenças nos valores de distância calculados. Se algum desses valores for mapeado para um pixel diferente, a linha reta esperada poderá apresentar marcas ocasionais. A “plotagem” de Velocidade-Tempo poderá parecer muito mais irregular, porque a alteração na distância entre dois pontos no decorrer do tempo é, por definição, a velocidade. Você poderá aplicar um grau apropriado de aplainamento dos dados.

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

NTRODUÇÃO AO

CBR

Dicas para uma coleta de dados eficaz

Definições do RANGER

Tempos da amostra

representa o tempo total, em segundos, para completar toda a amostragem. Digite um

TIME

número inteiro entre 1 segundo (para objetos com movimento mais rápido) e 99 segundos (para objetos com movimento mais lento). Para sempre de 15 segundos.

REALTIME=YES

(cont.)

(Tempo Real=Sim),

TIME

será

Quando exemplo, quando

for um número inferior, o objeto deverá estar mais próximo ao

TIME

TIME=1 SECOND

1,75 metros (5,5 pés) do

Início e fim

A tela

(Configuração) no programa

SETUP

CBR

(Tempo=1 Segundo), o objeto não poderá estar a mais de

RANGER

fornece várias opções para iniciar e

CBR

. Por

finalizar a amostragem.

BEGIN ON

(Começar em)

: [ENTER]

. Inicia a amostragem com a tecla

da calculadora

›

quando a pessoa que está iniciando a amostragem estiver mais próxima da calculadora.

BEGIN ON: [TRIGGER]

. Inicia e finaliza a amostragem com o botão

pessoa que está começando a amostragem estiver mais próxima do Nesta opção, você também pode optar por desconectar o

configure a amostra, desconecte o cabo do

Use

, obtenha a amostra, reconecte o

BEGIN ON: [TRIGGER]

quando o fio não for longo o suficiente ou quando puder

CBR

, leve o

CBR

e pressione

CBR

onde está a ação, pressione

CBR

›

interferir na coleta de dados. Ele não está disponível no modo aplicação

BEGIN ON: DELAY

MATCH

segundos a partir do momento em que for pressionado

(Correspondência)).

(Retardamento). Inicia a amostragem após um retardamento de 10

›

. Isso permite que você

para transferir os dados.

REALTIME=YES

. É muito útil quando apenas

CBR

quando a

CBR

(como a

uma pessoa está realizando uma atividade.

Botão Trigger

NTRODUÇÃO AO

O efeito de

inicia a amostragem, mesmo que

varia dependendo das definições.

BEGIN ON: [ENTER]

BEGIN ON: DELAY

esteja selecionado. Ele também finaliza a amostragem mas, normalmente, você irá querer uma amostra completa.

REALTIME=NO

(Tempo Real=Não), após o término da amostragem,

repete automaticamente a amostra mais recente, mas não transfere os dados para a calculadora. Para transferir esses dados, no e, em seguida, selecione uma amostra selecionando “Plotagem”) ou

START NOW

GET CBR DATA

REPEAT SAMPLE

(Iniciar Agora) na tela

CBR

MAIN MENU

(Obter Dados do

(Menu Principal), selecione

(Você também pode repetir

CBR).

(Repetir Amostra) no

SETUP

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

PLOT MENU

(Ferramentas)

TOOLS

(Menu

SEJA INCLUÍDA

EXAS INSTRUMENTS INCORPORATED

Dicas para uma coleta de dados eficaz

Aplainamento

(cont.)

Os recursos de aplainamento criados no programa

RANGER

podem reduzir o efeito de sinais dispersos ou variações nas medidas de distância. Evite aplainamento excessivo. Comece sem aplainamentos ou com aplainamento

(Suave). Aumente o aplainamento até obter

LIGHT

resultados satisfatórios.

Para uma atividade com uma probabilidade acima da média de sinais dispersos, você

poderá aumentar o aplainamento na tela

(Configuração) antes da amostragem

SETUP

(consulte a página 38). Para dados em

REALTIME=NO

aplainamento aos dados. A calculadora deve ser conectada ao (Ferramentas de “Plotagem”) no

(Tempo Real=Não) já coletados, você poderá aplicar

. Selecione

PLOT MENU

CBR

(Menu “Plotagem”), selecione

PLOT TOOLS

SMOOTH DATA

(Aplainar Dados) e, em seguida, selecione o grau de aplainamento.

Ruído—o que é e como livrar-se dele?

Quando o

recebe sinais refletidos de objetos que não sejam o alvo principal, a

CBR

“plotagem” mostra pontos de dados incorretos (picos de ruídos) que não estão de acordo com o padrão geral da “plotagem”. Para minimizar o ruído:

Certifique-se de que o

cabeça do sensor enquanto visualiza uma amostra em até obter bons resultados antes de coletar uma amostra em

Tente obter uma amostra em um espaço sem interferências (consulte a

esteja apontado diretamente para o alvo. Tente ajustar a

CBR

REALTIME=YES

REALTIME=NO

(Tempo Real=Sim)

área livre

descrita

a página 7). Escolha um objeto maior, mais refletivo ou mova o objeto para mais perto do

CBR

(mas

deixe-o a mais de 0,5 metro). Quando usar mais de um

em uma sala, um grupo deve concluir uma amostra antes

CBR

que o próximo grupo comece a coletar sua amostra. Para uma amostra em

REALTIME=YES

com ruídos, repita utilizando um grau maior de aplainamento até obter resultados satisfatórios. (Você não pode alterar o aplainamento nas aplicações

DISTANCE MATCH

(Correspondência de Velocidade) ou Para uma amostra em

REALTIME=NO

(Correspondência de Distância),

BALL BOUNCE

(Bola que Salta)).

VELOCITY MATCH

com ruídos, você poderá aplicar um grau maior de

aplainamento aos dados originais.

Velocidade do som

A distância aproximada até o objeto é calculada assumindo-se uma velocidade nominal do som. Entretanto, a velocidade real do som varia por vários fatores, mais notavelmente a temperatura do ar. Para atividades de movimentos relativos, este fator não é importante. Para atividades que exigem medidas altamente precisas, pode ser usado um comando de programação para especificar a temperatura do ambiente (consulte as páginas 40–41).

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

NTRODUÇÃO AO

CBR

Dicas para uma coleta de dados eficaz

REALTIME=YES (Tempo Real=Sim)

(cont.)

Use o modo

para objetos mais lentos

para ver os resultados à medida que eles vão sendo coletados

quando precisar coletar ou plotar apenas um tipo de dados (distância, velocidade ou

REALTIME=YES

aceleração) para uma amostra

No modo

REALTIME=YES, o CBR

processa os dados de “plotagem” solicitados (distância, velocidade ou aceleração), que são transferidos para a calculadora, seguindo cada medida de distância individual. Em seguida, o

RANGER

faz a “plotagem” de um único pixel para esse

pulso. Como todas essas operações devem ser concluídas antes que a próxima amostra possa ser

solicitada, a taxa máxima em que os dados podem ser amostrados no modo

REALTIME=YES

limitada. São gastos aproximadamente 0,080 segundos apenas para fazer a amostragem, processar e

transferir os dados para um único ponto de dados. É necessário um tempo adicional para operações como “plotagem” do ponto, que diminui a taxa de amostragem eficaz para aproximadamente 0,125 segundos no

REALTIME=NO (Tempo Real=Não)

Use o modo

para objetos mais rápidos

quando for necessário o aplainamento (consulte a página 9)

para operar o

quando precisar coletar ou plotar todos os tipos de dados (distância, velocidade e

REALTIME=NO

CBR

no modo desconectado (consulte a página 11)

RANGER

aceleração) para uma amostra

NTRODUÇÃO AO

No modo

REALTIME=NO

, os dados são armazenados no

e não são transferidos para a

CBR

calculadora até que toda a amostragem seja concluída. A taxa de amostra pode ser tão rápida quanto uma vez a cada 0,005 segundos para objetos próximos. Os dados de tempo, distância, velocidade e aceleração são transferidos para a calculadora.

Como os dados são armazenados no

, você pode transferi-los do

CBR

para uma

CBR

calculadora várias vezes.

Toda vez que o aplainamento é alterado, o

aplica o novo fator de aplainamento,

CBR

transfere os dados ajustados para a calculadora e armazena os valores aplainados nas listas.

A seleção de um domínio altera as listas armazenadas na calculadora. Se precisar, você

poderá recuperar os dados originais no

RANGER

Dados do Você também pode compartilhar os mesmos dados com vários alunos, mesmo que eles

, selecione

CBR

TOOLS

(Ferramentas). No menu

CBR

. No

MAIN MENU

TOOLS

(Menu Principal) no programa

, selecione

GET CBR DATA

(Obter

estejam usando tipos diferentes de calculadoras gráficas TI. Isso permite que todos os alunos participem das atividades de análise de dados usando os mesmos dados (consulte a página 11).

CBR

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

Dicas para uma coleta de dados eficaz

O uso do CBR no modo desconectado

(cont.)

Como o

não pode enviar imediatamente dados para a calculadora no modo

CBR

desconectado, são necessárias algumas definições. Na tela

Defina

O programa

REALTIME=NO BEGIN ON

RANGER

reconectado. Não são necessários procedimentos especiais.

Compartilhamento de dados

E se você desejar que a classe inteira analise os mesmos dados ao mesmo tempo? Com o

você pode propagar os dados em

CBR,

Transfira o programa

➊

dados. Colete os dados com o

➋

Peça ao(à) primeiro(a) aluno(a) para conectar sua calculadora ao

➌

calculadora-paraNo

➍

➎

MAIN MENU

TRANSFERRING...

TOOLS

, selecione

Pressione › para retornar ao selecione

QUIT

(Tempo Real=Não).

(Começar em)

=[TRIGGER]

informa quando o

RANGER

ou o cabo de calculadora-para-calculadora.

CBR

para as calculadoras de todos os alunos antes da coleta de

no modo

CBR

(Menu Principal) no programa

GET CBR DATA

. deve ser desconectado e quando deve ser

CBR

REALTIME=NO

rapidamente em uma sala de aula.

RANGER,

(Obter Dados do

(Transferindo) e aparece a “plotagem”.

PLOT MENU

(Menu “Plotagem”) e, em seguida,

(Sair). Desconecte o cabo.

(Configuração):

SETUP

usando o cabo de

CBR

selecione

). É exibida a mensagem

CBR

(Ferramentas). No

TOOLS

Conecte outra calculadora (do mesmo tipo) à calculadora que contém os dados. Na

➏

segunda calculadora, no

, selecione

TOOLS

GET CALC DATA

MAIN MENU

(Obter Dados de Cálculo). As listas L1, L2, L3,

no programa

RANGER

, selecione

TOOLS

. No menu

L4 e L5

transferidas automaticamente para a segunda calculadora. Transfira os dados para a calculadora de outro aluno no

➐

enquanto outros alunos

CBR

continuam as transferências de calculadora-para-calculadora.

Assim que todos os alunos tiverem os mesmos dados, eles podem analisar esses dados no

RANGER

usando

PLOT MENU

ou fora do

RANGER

usando a lista e os recursos gráficos da

calculadora. Para compartilhar dados na TI-85, use o recurso

LINK

fora do

RANGER

para transferir as listas.

são

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

NTRODUÇÃO AO

CBR

Dicas para uma coleta de dados eficaz

Além da simples coleta de dados

(cont.)

Após ter coletado e plotado os dados no

RANGER

, você poderá explorá-los em relação a uma função. Como os dados são coletados em forma de listas e exibidos como uma “plotagem” estatística, você pode usar

No RANGER

Explore as “plotagens” usando

, 

TRACE

œ para explorar essa relação.

, que é acionado automaticamente. (Na TI-85, use o

cursor com movimentos livres.) Manipule o conjunto de dados, incluindo o aplainamento desses dados ou selecionando o

domínio de interesse.

Fora do RANGER

Explore os dados usando o editor de listas da calculadora.

Monte manualmente uma função para os dados usando o editor Y= da calculadora.

Determine automaticamente a equação que melhor se adaptar aos dados usando os

recursos de regressão da calculadora.

Outras relações podem ser exploradas além das representadas pelas opções de “plotagem” no

RANGER

podem ser visualizadas como “plotagens” estatísticas. No programa

. Por exemplo, “plotagens” simultâneas de Distância-Tempo e Velocidade-Tempo

(Menu Principal) no

como L1 versus L2 e

Plot2

RANGER

, selecione

(Sair) e, em seguida, defina

QUIT

MAIN MENU

Plot1

como L1 versus L3. (Pode ser necessário que você ajuste a Janela.) Os dados e as “plotagens” podem ser enviados a um computador usando o TI-Graph Link.

Isso é muito útil quando os alunos criam relatórios mais relacionados às descobertas de suas atividades.

O uso do CBR sem o programa RANGER

Você pode usar o programas diferentes do

Para obter informações sobre o uso do

Para obter informações sobre a obtenção de programas e atividades, consulte a página

como um detector sônico de movimentos com o

CBR

RANGER

36. Para obter informações sobre os comandos de programação para escrever seus próprios

programas, consulte as páginas 40–41.

ou com

CBL

CBR

com o

, consulte a página 39.

CBL

NTRODUÇÃO AO

CBR

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

Atividade 1—Correspondência de gráficos

notas p/ professores

Conceitos

Função explorada: linear.

MATCH

(Correspondência) introduz conceitos de tempo e distância do mundo real—ou mais precisamente, o conceito de distância

versus

tempo. À medida que os alunos tentam construir gráficos correspondentes ao caminhar enquanto vêem seu movimento plotado, o conceito de posição pode ser explorado.

Nas explorações, é solicitado que os alunos convertam a taxa de caminhada de metros por segundo para quilômetros por hora.

Após os alunos terem aprendido a fazer a correspondência Distância-Tempo, desafie-os para uma correspondência Velocidade-Tempo.

Materiais

calculadora

CBR

Ÿ Ÿ

cabo de calculadora-para-calculadora

Um TI ViewScreené permite que outros alunos observem—e proporciona a maior parte da diversão dessa atividade.

Dicas

Os alunos realmente gostam dessa atividade. Planeje o tempo adequado, pois todos vão querer tentar!

Essa atividade funciona melhor quando o aluno que está caminhando (e a classe inteira) podem ver seus movimentos projetados em uma parede ou na tela usando o TI ViewScreen.

Oriente os alunos para caminharem alinhados com o CBR; às vezes, eles tentam caminhar de um lado (perpendicular à linha do CBR) ou até mesmo pular!

As instruções sugerem que a atividade seja feita em metros, para corresponder às perguntas na folha de atividades dos alunos.

Consulte as páginas 6–12 para obter dicas para uma coleta de dados eficaz.

“Plotagens” comuns

Respostas comuns

1. tempo (do início da amostra); segundos; 1 segundo; distância (do CBR ao objeto); metros; 1 metro

2. a intercepção em y representa a distância inicial

3. varia dependendo do aluno

4. para trás (aumentar a distância entre o CBR e o objeto)

5. para frente (diminuir a distância entre o CBR e o objeto)

6. ficar parado; a inclinação zero não requer alterações em y (distância)

7. varia dependendo do gráfico; @yà3,3

8. varia dependendo do gráfico; @yà1

9. o segmento com a maior inclinação (positiva ou negativa)

10.essa é uma pergunta intrigante—o segmento plano, porque você não se move!

11.velocidade da caminhada; quando mudar a direção e/ou velocidade

12.velocidade escalar (ou vetorial)

13.varia dependendo do gráfico (exemplo: 1,5 metros em 3 segundos)

14.varia dependendo do gráfico; exemplo: 0,5 metrosà1 segundo

exemplo: (0,5 metros à 1 segundo) Q (60 segundos

1 minuto) = 30 metros à minuto

exemplo: (30 metros à 1 minuto) Q (60 minutos 1 hora) = 1800 metros à hora

exemplo: (1800 metros à 1 hora) Q (1 quilômetro 1000 metros) = 1,8 quilômetros à hora.

Peça aos alunos para compararem os últimos números com a velocidade de um veículo, digamos 96 quilômetros à hora (60 milhas por hora).

15.varia dependendo do gráfico; a soma de @y para cada segmento de reta.

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

NTRODUÇÃO AO

CBR

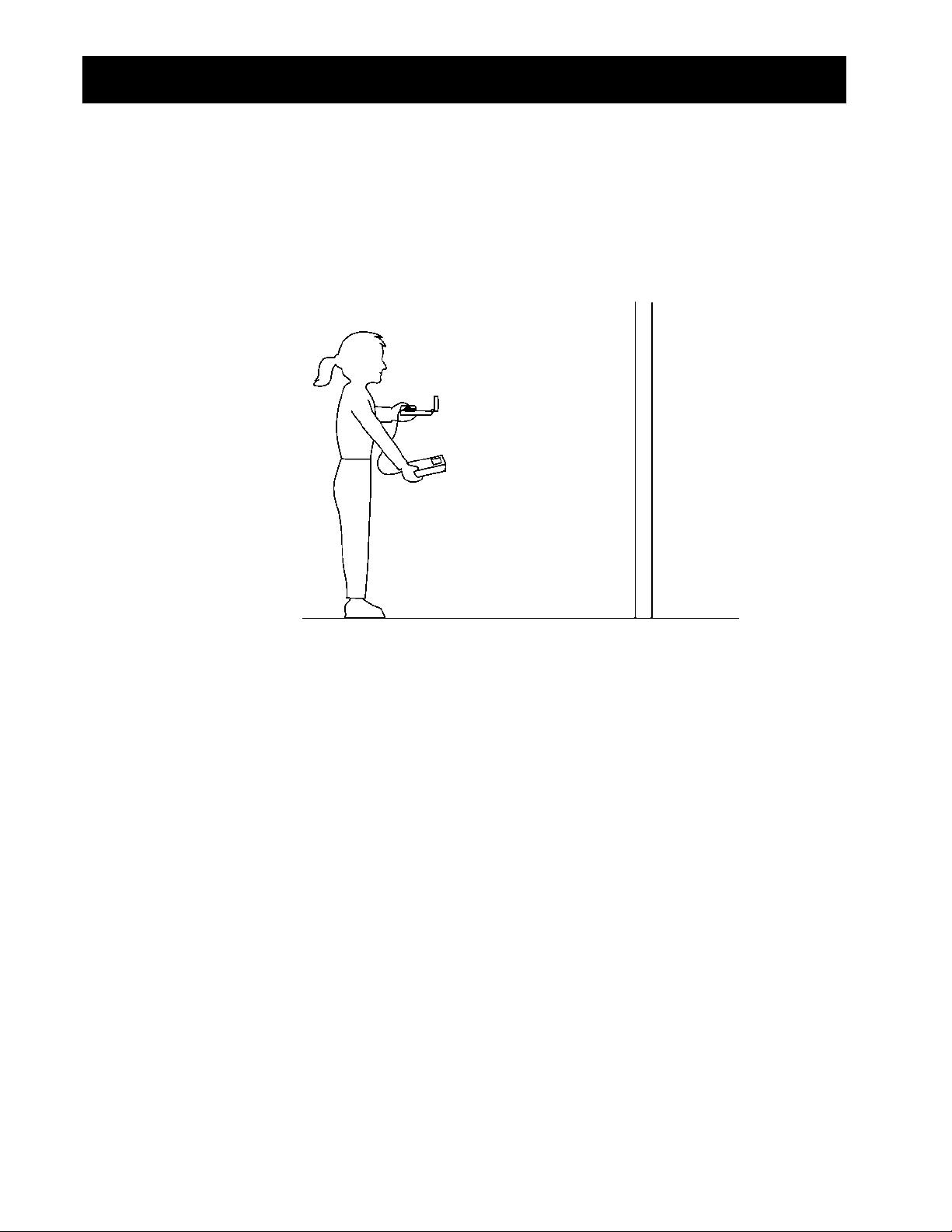
Atividade 1—Correspondência de gráficos linear

Coleta de dados

Mantenha o

➊

em uma mão e a calculadora na outra. Aponte o sensor diretamente

CBR

para uma parede.

A distância máxima de qualquer gráfico é de 4 metros (12 pés) do

Dicas:

distância mínima é de 0,5 metro (1,5 pés). Certifique-se de que não haja nada na

(consulte a página 7).

livre

CBR

. A

área

Execute o programa

➋

RANGER

(consulte a página 5 para obter as seqüências de teclas

para cada calculadora).

➌

MAIN MENU

(Menu Principal), selecione

APPLICATIONS

(Aplicações). Selecione

(Metros). No menu

➍

APPLICATIONS,

exibidas as instruções gerais. Pressione › para exibir o gráfico correspondente. Estude o gráfico por um

➎

momento. Posicione-se onde você achar que o gráfico começa. Pressione › para começar a

➏

Responda as perguntas 1 e 2 na folha de atividades.

selecione

DISTANCE MATCH

faz as definições automaticamente.

(Correspondência de Distância). São

coleta de dados. Você pode ouvir o som de um clique e ver a luz verde à medida que os dados são coletados.

Caminhe para trás e para a frente e tente construir o gráfico correspondente. Sua

➐

posição é “plotada” na tela. Quando terminar a amostra, examine como foi a correspondência entre sua

➑

“caminhada” e o gráfico e, em seguida, Pressione › para exibir o menu

➒

responda a pergunta 3

OPTIONS

(Opções) e selecione

Correspondência). Tente melhorar sua técnica de caminhada e, em seguida,

SAME MATCH

responda

as perguntas 4, 5 e 6.

METERS

(Mesma

NTRODUÇÃO AO

CBR

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

Atividade 1—Correspondência de gráficos

Explorações

(cont.)

linear

DISTANCE MATCH

três segmentos de reta.

Pressione › para exibir o menu

➊

Correspondência). Estude o primeiro segmento e Estude o gráfico inteiro e

➋

Posicione-se onde você achar que o gráfico começa, pressione › para começar a

➌

coleta de dados e tente construir o gráfico correspondente. Quando terminar a amostragem,

➍

Pressione › para exibir o menu

➎

Estude o gráfico e

➏

Pressione › para exibir o menu

➐

MAIN MENU RANGER

Explorações avançadas

Os gráficos gerados por (Correspondência de Velocidade), em que você deve corresponder uma “plotagem” de Velocidade-Tempo. Essa é difícil!

(Correspondência de Distância), todos os gráficos são constituídos de

OPTIONS

(Opções) e selecione

responda as perguntas 9 e 10

responda as perguntas 11 e 12

OPTIONS

e selecione

responda as perguntas 13, 14 e 15

OPTIONS

. Se desejar, repita a atividade ou retorne ao

(Menu Principal) e, em seguida, selecione

DISTANCE MATCH

eram todos retas. Agora, tente a

NEW MATCH (

Nova

responda as perguntas 7 e 8

NEW MATCH

para sair do programa

QUIT

VELOCITY MATCH

MATCH

é um programa muito popular. Podem estar disponíveis versões adicionais que

explorem gráficos mais complicados (consulte a página 36).

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

NTRODUÇÃO AO

CBR

Atividade 1—Correspondência de gráficos

Nome __________________

Coleta de dados

Qual a propriedade física representada no eixo x? _____________________________________________

Quais são as unidades? A que distância estão as unidades de graduação? __________ Qual a propriedade física representada no eixo y? _____________________________________________ Quais são as unidades? A que distância estão as unidades de graduação? __________ A que distância do

Você começou muito perto, muito longe ou na distância correta? ________________________________

Você deve caminhar para a frente ou para trás para um segmento que é “inclinado para cima”?

você deve ficar para começar? _________________________________________

CBR

Por quê? ___________________________________________ Você deve caminhar para a frente ou para trás para um segmento que é “inclinado para baixo”?

Por quê? ___________________________________________ O que você deve fazer para obter um segmento não “inclinado”? ________________________________

Por quê? ________________________________________________________________________________

Explorações

Se você der um passo a cada segundo, qual deve ser o tamanho desse passo? _____________________

Se, em vez disso, você der passos de 1 metro (ou 1 pé), quantos passos você deve dar? ______________

Para qual segmento você terá que se mover mais rapidamente? _________________________________

Por quê? ________________________________________________________________________________ Para qual segmento você terá que se mover mais lentamente? ___________________________________

10.

Por quê? ________________________________________________________________________________ Além de escolher se o movimento será para a frente ou para trás, que outros fatores estão incluídos

11.

para atingir uma correspondência exata entre os gráficos? ______________________________________

________________________________________________________________________________________

Qual a propriedade física que a inclinação ou o grau de inclinação do segmento de reta representa? ___

12.

________________________________________________________________________________________

Para o primeiro segmento de reta, quantos metros você deve caminhar em quantos segundos? _______

13.

Converta o valor na pergunta 13 (a velocidade) para metrosà1 segundo: __________________________

14.

Converta para metrosàminuto: _____________________________________________________________ Converta para metrosàhora:________________________________________________________________ Converta para quilômetrosàhora: ___________________________________________________________ Qual a distância que você realmente caminhou? _______________________________________________

15.

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

NTRODUÇÃO AO

CBR

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

Atividade 2—Carrinho de brinquedo notas p/ professores

Conceitos

Função explorada: linear. O movimento de um carrinho de brinquedo

motorizado é usado para ilustrar o conceito de velocidade constante do mundo real.

Materiais

calculadora

CBR

Ÿ Ÿ

cabo de calculadora-para-

carrinho de brinquedo movido a bateria

TI ViewScreen (opcional)

CBR

Dicas

Os carrinhos de brinquedo variam muito em tamanho, forma e ângulo de reflexão do som ultra-sônico incidente. Portanto, as “plotagens” resultantes podem variar em qualidade. Alguns veículos podem exigir uma superfície refletiva adicional para a obtenção de boas “plotagens”. Tente fixar um cartão retangular no veículo a fim de garantir um bom alvo para o sensor.

Você poderá experimentar uma variedade de veículos para que os alunos possam explorar esses efeitos.

Os carrinhos de brinquedo mais lentos (como os fabricados para crianças menores) são melhores para essa atividade. Procure um carro que pareça manter uma velocidade constante.

Consulte as páginas 6–12 para obter dicas para uma coleta de dados eficaz.

Explorações

A inclinação da “plotagem” de Distância-Tempo de um objeto a qualquer momento determina a velocidade do objeto nesse momento. Assim, para um objeto que está se movimentando a uma velocidade constante, a inclinação da “plotagem” de Distância- Tempo será constante. Isso ocorre porque a “plotagem” de Distância-Tempo exibe uma relação linear.

Se começar a coleta de dados antes que o carrinho comece a se movimentar, você perceberá que a “plotagem” de Distância-Tempo não é linear no início da “plotagem”. Por quê? O carrinho inicialmente se encontra em repouso (v = 0). Ele não consegue alcançar sua velocidade constante instantaneamente. A aceleração é determinada por:

∆

Para que o objeto vá instantaneamente do estado de repouso para sua velocidade constante, isso implica aceleração infinita, o que não é fisicamente possível. (De fato, pela Segunda Lei de Newton, F = ma, uma aceleração infinita só poderia

∆

= 0. Mas,

ser resultante de uma força infinita, o que é igualmente impossível.) Por isso, devemos observar o objeto em aceleração (aumentando sua velocidade) até que sua velocidade se torne constante durante um período de tempo limitado.

“Plotagens” comuns

Respostas das perguntas

1. a primeira ou a última “plotagem”; a distância aumenta a uma taxa constante

2. os alunos completam com os valores obtidos com

TRACE

3. os valores de distância aumentam de forma constante

4. velocidade é a taxa de variação da distância em função do tempo; os valores são os mesmos para um mesmo incremento de tempo.

5. o aluno obtém um valor semelhante aos valores calculados para m

semelhante a m m representa a velocidade do carrinho

6. b é a intercepção de y; exemplo: y = 2x + 0

7. varia; por exemplo, se m = 2, distância (y) = 20 metros após 10 segundos (y = 2 Q 10 + 0); para 1 minuto, y = 120 metros

Explorações Avançadas

A inclinação de uma “plotagem” de VelocidadeTempo para a velocidade constante é zero. Portanto, a “plotagem” de Aceleração-Tempo indica que a = 0 (no caso ideal) durante o período de tempo onde a velocidade é constante.

A área resultante indica o deslocamento do objeto (a distância real de deslocamento) durante o intervalo de tempo entre t

Para estudantes de cálculo, o deslocamento pode ser obtido de:

onde s indica o deslocamento do objeto no intervalo entre t

e t2.

svdt

∫

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

NTRODUÇÃO AO

CBR

Atividade 2—Carrinho de brinquedo linear

Coleta de dados

Posicione o carrinho a pelo menos 0,5 metro (1,5 pés) do

➊

em uma linha reta.

CBR

Aponte o sensor diretamente para o carro e certifique-se de que não haja nada

Dicas:

área livre

Antes de iniciar a coleta de dados,

➋

Execute o programa

➌

(consulte a página 7).

RANGER

(consulte a página 5 para obter as seqüências de teclas

responda a pergunta 1 na folha de atividades.

para cada calculadora).

➍

MAIN MENU

(Menu Principal), selecione

SETUPàSAMPLE

essa atividade, as definições devem ser:

, em direção contrária ao

CBR

(Configuração/Amostra). Para

REALTIME: NO

TIME (S): 5 SECONDS

DISPLAY: DISTANCE

BEGIN ON: [ENTER]

SMOOTHING: LIGHT

UNITS: METERS

As instruções para alterar uma definição estão na página 38. Selecione

➎

Pressione › quando estiver pronto para começar. Ligue o carrinho e saia

➏

START NOW

rapidamente da sendo coletados e a mensagem

Quando a coleta de dados estiver concluída, a calculadora exibirá automaticamente

➐

(Iniciar Agora).

área livre

. Você pode ouvir o som de um clique conforme os dados vão

TRANSFERRING...

(Transferindo) é exibida na calculadora.

uma “plotagem” de Distância-Tempo dos pontos de dados coletados. Compare os resultados da “plotagem” de dados com sua previsão na

➑

resposta 1

semelhanças e diferenças.

para

NTRODUÇÃO AO

CBR

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

Atividade 2—Carrinho de brinquedo

Explorações

Os valores para x (tempo) em intervalos de meio segundo estão na primeira coluna da

➊

pergunta 2.

(distância) na segunda coluna.

“plotagem”. Pode ser necessário que você desconsidere dados inconsistentes do início da coleta de dados. Além disso, pode ser necessário que você aproxime a distância (a calculadora poderá fornecer a distância de 0,957 e 1,01 segundos em vez de exatamente 1 segundo). Escolha o mais próximo ou dê seu melhor chute.

Trace a “plotagem” e coloque os valores de y correspondentes

Inclua resultados apenas da parte linear da

Nota:

(cont.) linear

➋

Responda as perguntas 3 e 4

Calcule as variações na distância e no tempo entre cada ponto para preencher a terceira

➌

e a quarta colunas. Por exemplo, para calcular @Distância (metros) para 1,5 segundos, subtraia a Distância em 1 segundo da Distância em 1,5 segundos.

A função ilustrada por essa atividade é y = mx + b. m indica a inclinação de uma reta. É

➍

calculada por:

A intercepção de y representa b. Calcule m para cada ponto.

➎

Responda as perguntas 5, 6 e 7

Explorações Avançadas

O cálculo da inclinação de uma “plotagem” de Distância-Tempo em qualquer instante determina a velocidade aproximada do objeto nesse instante. O cálculo da inclinação de uma “plotagem” de Velocidade-Tempo determina a aceleração aproximada do objeto nesse instante. Se a velocidade for constante, qual é o valor da aceleração?

Faça uma previsão do aspecto da “plotagem” de Aceleração-Tempo para essa “plotagem” de Distância-Tempo.

distância

tempo

distância

tempo

distância

tempo

Complete a tabela da pergunta 2.

Encontre a área entre a “plotagem” de Velocidade-Tempo e o eixo x entre dois tempos convenientes quaisquer, retângulos, cada um com uma área determinada por:

Qual a importância física da área resultante?

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

. Isso pode ser feito somando-se as áreas de um ou mais

)

NTRODUÇÃO AO

SEJA INCLUÍDA

área

v∆t

= v(

CBR

Atividade 2—Carrinho de brinquedo

Nome ____________________________

Coleta de dados

Qual desses gráficos você acha que corresponderá à “plotagem” de Distância-Tempo do carrinho de

brinquedo?

Por quê? ________________________________________________________________________________

Tempo Distância

1 xxx xxx xxx

1.5 2

2.5 3

3.5 4

4.5 5

O que você observa nos valores de Distância? _________________________________________________ Como esses resultados indicam que o carrinho de brinquedo tinha uma velocidade constante?

Distância

Tempo

________________________________________________________________________________________

Calcule

distânciaà@tempo

entre Tempo = 2 e Tempo = 4. ____________________________________

O que você observou nesse resultado? _______________________________________________________ O que você acha que m representa? _________________________________________________________ Para a equação linear y = mx + b, o que é o valor b? ___________________________________________

Escreva a equação da reta na forma y = mx + b , usando valores para m e b._______________________ Qual a distância percorrida pelo carrinho em 10 segundos? _____________________________________

Em 1 minuto? ___________________________________________________________________________

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

NTRODUÇÃO AO

CBR

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

Atividade 3—Pêndulo notas p/ professores

Conceitos

Função explorada: senoidal. Explore o movimento harmônico simples observando

um pêndulo que balança livremente.

Materiais

calculadora

CBR

Ÿ Ÿ

cabo de calculadora-para-

grampo de montagem

cronômetro

pêndulo

trena

TI ViewScreen (opcional)

CBR

Sugestões para pêndulos:

bolas com tamanhos diferentes (≥ 2" diâmetro)

latas de refrigerante (vazias e cheias)

sacos de feijão

Dicas

Consulte as páginas 6–12 para obter dicas para uma coleta de dados eficaz.

Conexões físicas

Um objeto que executa um movimento periódico resultante de uma força de restauração proporcional ao seu deslocamento de sua posição de equilíbrio (repouso) é dito que exibe um movimento harmônico simples (MHS). O MHS pode ser descrito por duas quantidades.

O período T indica o tempo para um ciclo completo.

A amplitude A indica o deslocamento máximo do objeto de sua

posição de equilíbrio

(a posição do

pêndulo quando está em repouso).

Para um único pêndulo, o período de T é determinado por:

= 2p

onde L indica o comprimento da corda e g indica a aceleração da gravidade. T não depende da massa do objeto ou da amplitude de seu movimento.

A freqüência f (número de ciclos completos por segundo) pode ser encontrada a partir de:

f =

, onde f está em hertz (Hz) quando T está em

segundos. As derivadas de uma “plotagem” senoidal também

são senoidais. Observe especialmente a relação da fase entre a posição e a velocidade do pêndulo.

“Plotagens” comuns

Respostas comuns

1. varia (em metros)

2. varia (em metros)

3. varia (em segundos); T (um período) = tempo total de 10 períodosà10; calcular uma média sobre uma amostra maior tende a minimizar os erros inerentes de medidas

4. o comprimento total da curva, que deve ser aproximadamente 4 vezes a resposta da pergunta 2; porque uma curva é maior que uma reta

5. senoidal, repetitivo, periódico; distância do eixo x à posição de equilíbrio

6. cada ciclo é propagado horizontalmente; uma “plotagem” medida em 10 segundos deve conter mais ciclos na mesma quantidade de espaço da tela, portanto os ciclos parecerão estar mais próximos uns dos outros

7. (nº total de ciclos)à(5 segundos) = ciclosàsegundo; mais fácil visualizar ciclos completos e erros de medidas menores

8. f = 1

T, onde T indica o tempo para 1 período

9. diminui o período, aumenta o período (O comprimento do pêndulo é diretamente

proporcional ao tempo do período; quanto maior a corda, maior o período. Os alunos podem explorar essa relação usando o editor de listas da calculadora, onde eles podem calcular o período para diversos valores de L.)

10.A (amplitude) = ¼ da distância total percorrida pelo pêndulo em 1 período

11.ambas senoidais; as diferenças estão na amplitude e na fase

12.posição de equilíbrio

13.quando posição = valor máximo ou mínimo (quando o pêndulo está na maior distância possível do equilíbrio).

14.Não afeta. T depende apenas de L e g, não da massa.

Explorações avançadas

Coleta de dados: a “plotagem” de L2 versus L3 forma uma elipse.

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

NTRODUÇÃO AO

CBR

Atividade 3—Pêndulo senoidal

Coleta de dados

Monte o pêndulo. Alinhe o pêndulo para que ele balance em linha reta com o

➊

Posicione o

Dicas:

pêndulo. Certifique-se de que não haja nada na

Usando uma trena, meça a distância do

➋

a pelo menos 0,5 metro (1,5 pés) da posição mais próxima do

CBR

área livre

amplitude

posição equilíbrio

à posição de equilíbrio.

CBR

(consulte a página 7).

Responda a

pergunta 1 na folha de atividades.

Meça a distância entre a posição de abandono do pêndulo e a posição de equilíbrio.

Responda a pergunta 2.

CBR

Um ciclo de um pêndulo (um período) consiste em um movimento completo de ida e

➌

volta. Usando um cronômetro, marque dez períodos completos.

perguntas 3 e 4

Execute o programa

➍

RANGER

(consulte a página 5 para obter as seqüências de teclas

Responda as

para cada calculadora). Um método eficiente é uma pessoa balançar o pêndulo enquanto a outra opera a calculadora e o selecione

Pressione › para exibir as definições. Para essa atividade, elas devem ser:

➎

REALTIME: NO

BEGIN ON: [ENTER]

SMOOTHING: LIGHT

As instruções para alterar uma definição estão na página 38. Quando elas estiverem

➏

SETUPàSAMPLE

TIME (S): 10 SECONDS

DISPLAY: DISTANCE

UNITS: METERS

corretas, selecione Pressione › quando estiver pronto para começar. Você pode ouvir o som de um

➐

(Configuração/Amostra).

START NOW

(Iniciar Agora).

CBR

. No

MAIN MENU

clique à medida que os dados vão sendo coletados e a mensagem

(Menu Principal),

TRANSFERRING...

(Transferindo) é exibida na calculadora. Quando a coleta de dados estiver concluída, a calculadora exibirá automaticamente a

➑

“plotagem” de Distância-Tempo dos pontos de dados coletados.

Responda a

pergunta 5.

NTRODUÇÃO AO

CBR

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

Atividade 3—Pêndulo

Explorações

Coleta de dados 2

(cont.)

senoidal

MAIN MENU

, altere o tempo de 10 para 5 segundos. Repita a coleta de dados. Observe a

SETUP

“plotagem”. A quantidade determinada (ciclos por segundo) é chamada

calculado a freqüência na pergunta 7 usando a “plotagem”, você poderá encontrá-la matematicamente a partir de:

onde T indica o período em segundos e f indica a freqüência em hertz (Hz).

f =

Responda a pergunta 8.

Coleta de dados 3 e 4

Repita a coleta de dados de 5 segundos mais duas vezes. Primeiro, reduza a corda. Depois, aumente-a. Após observar essas “plotagens”,

Outra importante medida de distância que afeta o movimento do pêndulo é a A resposta da pergunta 2 era a amplitude do movimento do pêndulo.

pergunta 10.

Explorações avançadas

Coleta de dados 5

PLOT MENU

as perguntas 11, 12 e 13.

(Menu Principal), selecione

SETUPàSAMPLE

Responda as perguntas 6 e 7.

(Menu “Plotagem”), selecione

(Configuração/Amostra). Na tela

freqüência

responda a pergunta 9

VELOCITY-TIME

(Velocidade-Tempo).

. Embora tenha

amplitude

Responda a

Responda

Coleta de dados 6

Repita a coleta de dados com um pêndulo significantemente mais leve ou mais pesado e, em seguida,

responda a pergunta 14.

Modele o comportamento distância-tempo do pêndulo usando a fórmula de uma função senoidal, indica a freqüência,

S = A sin (wt +

indica o ângulo da fase e t indica o tempo. A freqüência, w, está

relacionada ao período, T, por

, onde S indica a posição instantânea, A indica a amplitude,

)

pà

w = 2

Digite essa equação no editor Y= usando os valores calculados de A e w. Simultaneamente, trace o gráfico da curva dessa função e a “plotagem” estatística de

(tempo) versus

(distância). Ajuste os valores de A, w e d até que seja obtido um bom ajuste. Na TI-83 ou TI-86, use a regressão do seno para determinar os valores.

Explore a relação entre a posição e a velocidade, plotando

(distância) versus

(velocidade). Como você prevê o aspecto da “plotagem” resultante? Compare o resultado real com sua previsão.

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

NTRODUÇÃO AO

CBR

Atividade 3—Pêndulo

Coleta de dados

Nome _______________________________________

Qual é a distância do

A que distância você afastará o pêndulo da posição de equilíbrio? ________________________________

Qual foi o tempo para dez períodos? ________________________________________________________

à posição de equilíbrio? _____________________________________________

CBR

Calcule o tempo gasto (em segundos) para completar um período. _______________________________ Qual a vantagem de se calcular dez períodos completos em vez de apenas um? ____________________ Use a resposta da pergunta 2 e dê a distância total aproximada percorrida em um ciclo. _____________

Por que esse valor é menor que a distância real percorrida em um ciclo? __________________________ O que você observou na forma da “plotagem”? _______________________________________________

Como é o valor da pergunta 1 representado na “plotagem”? ___________________________________

Explorações

Como é alterado o aspecto da “plotagem”? Por quê? __________________________________________

________________________________________________________________________________________

Usando dados coletados de sua “plotagem”, calcule o número de ciclos completos por segundo.

________________________________________________________________________________________

Por que é mais fácil determiná-lo usando a segunda “plotagem” (ao final de 5 segundos) em vez da primeira (ao final de 10 segundos)?__________________________________________________________

Calcule a freqüência para um período usando a equação. _______________________________________

Como a redução do comprimento da corda afeta o período do pêndulo? __________________________

Como o aumento da corda afeta o período do pêndulo?

. Qual a relação entre a amplitude do movimento do pêndulo e a distância total que o pêndulo percorre

________________________________________

em um período? _________________________________________________________________________

________________________________________________________________________________________

Explorações avançadas

Compare a “plotagem” de Distância-Tempo com a “plotagem” de Velocidade-Tempo. Relacione as

11.

semelhanças e diferenças.__________________________________________________________________

________________________________________________________________________________________

Em qual posição está a velocidade máxima do pêndulo? ________________________________________

12.

Em que posição está a velocidade mínima do pêndulo? _________________________________________

13.

Como a alteração do peso afeta a “plotagem”? Por quê? _______________________________________

14.

________________________________________________________________________________________

NTRODUÇÃO AO

CBR

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

Atividade 4—Bola que salta notas p/ professores

Conceitos

Função explorada: função do 2º grau. Os conceitos do mundo real como, objetos em queda

livre e que saltam, gravidade e aceleração constante são exemplos de funções do 2º grau. Essa atividade possibilita a investigação dos valores de altura, tempo e o coeficiente A na equação quadrática, Y=A(X–H)

+K,

que descreve o comportamento de uma bola que pula.

Materiais

calculadora

CBR

Ÿ Ÿ

cabo de calculadora-para-

bola grande de borracha (22 cm)

TI ViewScreen (opcional)

CBR

Dicas

Essa atividade é melhor desempenhada com dois alunos, um para segurar a bola e o outro para pressionar

Consulte as páginas 6–12 para obter dicas para uma coleta de dados eficaz.

A “plotagem” deve ter o aspecto de uma bola que salta. Se não tiver, repita a amostra, certificando-se de

CBR

que o

esteja posicionado diretamente para a bola.

Recomenda-se uma bola grande.

“Plotagens” comuns

de distância para que a “plotagem” corresponda da melhor forma às percepções dos alunos sobre o comportamento da bola. y = 0 na “plotagem” é realmente o ponto em que a bola está mais

CBR

distante do

, quando a bola bate no chão.

4. Os alunos devem entender que o eixo x representa o tempo, não a distância horizontal.

7. O gráfico para A = 1 é invertido e maior que a “plotagem”.

8. A < -1

9. concavidade da parábola para cima; concavidade para baixo; linear

12.é o mesmo; matematicamente, o coeficiente A representa a extensão da curvatura da parábola; fisicamente, A depende da aceleração da gravidade, que permanece constante em todos os saltos.

Explorações avançadas

A altura de um determinado salto da bola (altura máxima para determinado salto) é aproximada por:

, onde

y indica a altura de um determinado salto

h indica a altura de onde a bola é solta

p indica uma constante que depende das características físicas da bola e superfície do chão

x indica o número do salto

Explorações

Depois que um objeto é solto, ele age somente pela gravidade (desconsiderando a resistência do ar). Por isso, A depende da aceleração da gravidade, -9,8

metrosàsegundo

(-32 pésàsegundo2). O sinal negativo

indica que a aceleração está sendo para baixo. O valor para A é de aproximadamente a metade da

aceleração da gravidade ou -4,9 metrosàsegundo

pésàsegundo

(-16

Respostas comuns

1. tempo (do início da amostra); segundos; altura distância da bola do chão; metros ou pés

2. altura inicial da bola do chão (os picos representam a altura máxima de cada salto); o chão é representado por y = 0.

3. A “plotagem” de Distância-Tempo para essa atividade não representa a distância do

BALL BOUNCE

bola.

(Bola que Salta) move os dados

CBR

até a

Para uma determinada bola e uma altura inicial, a altura de um determinado salto diminui exponencialmente em cada salto sucessivo. Quando x = 0, y = h e assim a intercepção de y representa a altura inicial de abandono da bola.

Os alunos audaciosos podem encontrar os coeficientes nessa equação usando os dados coletados. Repita a atividade para alturas iniciais diferentes ou com uma bola ou superfície diferente.

Depois de ajustar manualmente a curva, os alunos podem usar a análise de regressão para encontrar a função que melhor representa os dados. Selecione um

único salto usando “Plotagem”),

seguida,

QUIT

PLOT TOOLS

SELECT DOMAIN

(Saia) do

MAIN MENU

(Ferramentas de

(Selecionar Domínio). Em

(Menu Principal). Siga

os procedimentos de operação da calculadora para

efetuar uma regressão quadrática nas listas

e L2.

Extensões

Complete a “plotagem” de Velocidade-Tempo, fornecendo o deslocamento (distância real percorrida) para qualquer intervalo de tempo selecionado. Lembrese de que o deslocamento é zero para qualquer salto completo (a bola começa e termina no chão).

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

NTRODUÇÃO AO

CBR

Atividade 4—Bola que salta parabólica

Coleta de dados

Comece com um salto de teste. Solte a bola (não jogue-a).

➊

Dicas:

Posicione o

a pelo menos 0,5 metro (1,5 pés) acima da altura do salto mais

CBR

alto. Mantenha o sensor diretamente sobre a bola e certifique-se de que não haja nada na

área livre

Execute o programa

➋

(consulte a página 7).

RANGER

(consulte a página 5 para obter as seqüências de teclas

para cada calculadora). No

➌

(Metros) ou

MAIN MENU

(Menu Principal), selecione

(Pés).

FEET

APPLICATIONS

(Aplicações). Selecione

METERS

No menu

➍

APPLICATIONS,

instruções gerais. Segure a bola com os braços estendidos. Pressione ›. Agora, o programa

➎

está no modo Trigger. Nesse momento, você poderá desconectar o Pressione ¤. Quando a luz verde começar a piscar, solte a bola e, em seguida, dê

➏

um passo para trás. (Se a bola saltar para o lado, mova-se para manter o diretamente sobre a bola mas, tenha cuidado para

selecione

BALL BOUNCE

(Bola que Salta). São exibidas as

estabelece as definições automaticamente.

da calculadora.

CBR

mudar a altura do

não

CBR

Você pode ouvir o som de um clique à medida que os dados vão sendo coletados. Os dados são coletados para o tempo e a distância e calculados para a velocidade e a aceleração. Se você tiver desconectado o

, reconecte-o quando a coleta de dados

CBR

estiver concluída. Pressione ›. (Se a “plotagem” não parecer boa, repita a amostra.) Estude a

➐

“plotagem”. Observe que o

➑

as perguntas 3 e 4

Responda as perguntas 1 e 2 na folha de atividades.

BALL BOUNCE

moveu automaticamente os dados de distância.

RANGER

Responda

NTRODUÇÃO AO

CBR

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

Atividade 4—Bola que salta

Explorações

A “plotagem” da Distância-Tempo do salto forma uma parábola.

(cont.)

parabólica

Pressione ›. Em

➊

PLOT MENU

de “Plotagem”) e, em seguida,

(Menu “Plotagem”), selecione

SELECT DOMAIN

(Selecionar Domínio). Desejamos

PLOT TOOLS

(Ferramentas

selecionar o primeiro salto completo. Mova o cursor para a base do início do salto e pressione

›. A “plotagem” é traçada novamente, focalizando um único salto.

A “plotagem” está no modo

➋

pergunta 5

Pressione › para retornar ao

➌

Selecione A

➍

fórmula do vértice

análise. Pressione Digite a fórmula do vértice da equação quadrática:

Na tela Inicial, armazene o valor registrado na pergunta 5 para a altura na variável K;

➎

›. Mova o cursor para a base do final desse salto e, em seguida, pressione

. Determine o vértice do salto.

TRACE

Responda a

na folha de atividades.

QUIT

(Sair).

da equação quadrática

œ. No editor

PLOT MENU

, desative todas as funções que estão selecionadas.

. Selecione

Y = A(X – H)

Yn=A

MAIN MENU

+ K

(X–H)^2+K

…

(Menu Principal).

, é apropriada para essa

armazene o tempo correspondente na variável H; armazene 1 na variável A. Pressione  para exibir o gráfico.

➏

Tente A = 2, 0, –1.

➐

responda a pergunta 9

Escolha você mesmo valores para A até conseguir uma boa correspondência para a

➑

“plotagem”.

Complete a primeira parte do quadro na pergunta 8 e

Registre suas opções para A no quadro da pergunta 8.

Responda as perguntas 6 e 7.

Repita a atividade mas, desta vez, selecione o último salto completo da bola (o que está

➒

mais à direita).

Explorações avançadas

Repita a coleta de dados, mas não selecione uma única parábola.

➊

Registre o tempo e a altura para cada salto sucessivo.

➋

Determine a relação entre as alturas para cada salto sucessivo.

➌

Explique o significado, se houver algum, dessa relação.

➍

Responda as perguntas 10, 11 e 12

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

NTRODUÇÃO AO

CBR

Atividade 4—Bola que salta

Nome _______________________________________

Coleta de dados

Qual propriedade física está representada no eixo x? ___________________________________________

Quais são as unidades? ____________________________________________________________________ Qual propriedade física está representada no eixo y? ___________________________________________ Quais são as unidades? ____________________________________________________________________ O que representa o ponto mais alto na “plotagem”? ___________________________________________

E o ponto mais baixo? ____________________________________________________________________ Por que o programa

Por que a “plotagem” tem o mesmo aspecto da bola que saltou no chão? ________________________

BALL BOUNCE

move a “plotagem”? ________________________________________

Explorações

Registre a altura máxima e o tempo correspondente para o primeiro salto completo. ________________

O gráfico para A = 1 correspondeu à sua “plotagem”? _________________________________________

Por que sim ou por que não? _______________________________________________________________

Complete o quadro abaixo.

A Compare a “plotagem” de dados e o gráfico de Yn

1 2 0

O que implica um valor positivo para A? _____________________________________________________

O que implica um valor negativo para A? _____________________________________________________ O que implica um valor zero para A? ________________________________________________________ Registre a altura máxima e o tempo correspondente para o último salto completo. __________________

10.

Você acha que A será maior ou menor para o último salto? _____________________________________

11.

Compare A. _____________________________________________________________________________

12.

O que você acha que A pode representar? ___________________________________________________

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

NTRODUÇÃO AO

CBR

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

Atividade 5—Rolagem da bola notas p/ professores

Conceitos

Função explorada: função do 2º grau. Fazer a “plotagem” de uma bola que está rolando

sobre uma rampa com inclinações variadas cria um conjunto de curvas, que pode ser modelado por uma série de equações quadráticas. Essa atividade possibilita a investigação dos valores dos coeficientes na equação quadrática, y = ax

+ bx + c.

Materiais

calculadora

CBR

Ÿ Ÿ

cabo de calculadora-para-

grampo de montagem

bola grande de plástico (22 cm)

rampa longa (pelo menos 2 metros ou 6 pés—

CBR

uma tábua leve funciona bem)

transferidor para medir os ângulos

livros para apoiarem a rampa

TI ViewScreen (opcional)

Dicas

Discuta como medir o ângulo da rampa. Deixe que os alunos sejam criativos aqui. Eles poderão usar um cálculo trigonométrico, uma folha dobrada ou um transferidor.

Consulte as páginas 6–12 para obter dicas para uma coleta de dados eficaz.

“Plotagens” comuns

3. varia (deve ser a metade de uma parábola, concavidade para cima)

4. uma parábola (quadrática)

5. varia

6. varia (deve ser parabólica com curvatura aumentada)

7. 0¡ é plano (a bola não pode rolar); 90¡ é o mesmo que uma bola em queda livre (caindo)

Explorações

O movimento de um corpo que se desloca apenas pela gravidade é um assunto comum em um estudo de física. Geralmente, esse movimento é expresso por uma fórmula particular da equação quadrática,

t + s

s = ½at

0 0 0 0

+ v

s indica a posição de um objeto no tempo t a indica sua aceleração

indica sua velocidade inicial

indica sua posição inicial

Na equação quadrática y = ax y representa a distância do

onde

+ bx + c,

CBR

até a bola no tempo x se a posição inicial da bola for c, a velocidade inicial b e a aceleração 2a.

Explorações avançadas:

Desde que a bola esteja em repouso quando for solta, b deve aproximar-se de zero para cada tentativa. c deve aproximar-se da distância inicial, 0,5 metro (1,5 pés). a aumenta conforme o ângulo de inclinação aumenta.

Respostas comuns

1. a terceira “plotagem”

2. tempo; segundos; distância do objeto ao CBR; pés ou metros

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

Se os alunos “montarem” a equação

y = ax

+ bx + c manualmente, poderá ser necessário dar dicas para os valores b e c. Também será possível orientá-los a efetuarem uma regressão

L1, L2

quadrática nas listas

usando suas calculadoras. A aceleração da bola é devida à gravidade da terra. Por isso, quanto mais inclinada a rampa (maior o ângulo de inclinação), maior o valor de a. O valor a máximo ocorre para q = 90¡, mínimo para q = 0¡. De fato, a é proporcional ao seno de q.

NTRODUÇÃO AO

CBR

Atividade 5—Rolagem da bola parabólica

Coleta de dados

➊

Responda a pergunta 1 na folha de atividades

15°. Conecte o grampo à borda superior da rampa. Conecte o

. Ajuste a rampa a uma inclinação de

ao grampo. Abra a

CBR

cabeça do sensor e posicione-o perpendicularmente à rampa. Conecte a calculadora ao

CBR

Coloque uma marca na rampa a 0,5 metro (1,5 pés) do

. Peça a um aluno para

CBR

segurar a bola nessa marca enquanto outro segura a calculadora.

Aponte o sensor diretamente para a bola e certifique-se de que não haja nada

Dicas:

área livre

Execute o programa

➋

para cada calculadora). No

(consulte a página 7).

RANGER

(consulte a página 5 para obter as seqüências de teclas

MAIN MENU

(Menu Principal), selecione

SETUPàSAMPLE

(Configuração/Amostra). Pressione › para exibir as definições. Para essa atividade, elas devem ser:

➌

REALTIME: NO

TIME (S): 3 SECONDS

DISPLAY: DISTANCE

BEGIN ON: [ENTER]

SMOOTHING: LIGHT

UNITS: METERS

As instruções para alterar uma definição estão na página 38. Quando as definições estiverem corretas, selecione

➍

› para começar a amostragem.

Ao ouvir um clique, solte a bola imediatamente (não empurre) e dê um passo para trás.

➎

Quando a amostra estiver concluída, a “plotagem” de Distância-Tempo será exibida

➏

automaticamente. Pressione › para exibir o

➐

(Ferramentas de “Plotagem”) e, em seguida,

Responda as perguntas 2 e 3.

PLOT MENU

(Menu “Plotagem”). Selecione

START NOW

SELECT DOMAIN

o cursor para onde a bola foi solta e, em seguida, pressione onde a bola atingiu o fim da rampa e, em seguida, pressione

(Iniciar Agora). Pressione

PLOT TOOLS

(Selecionar Domínio). Mova

›. Mova o cursor para

›. A “plotagem” é

traçada novamente, focalizando a parte da amostra correspondente à rolagem da bola na rampa.

Responda as perguntas 4 e 5.

NTRODUÇÃO AO

CBR

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

Atividade 5—Rolagem da bola

Explorações

Observe o que acontece com inclinações diferentes.

Faça uma previsão sobre o que acontecerá se a inclinação aumentar.

➊

pergunta 6.

Ajuste a inclinação para 30¡. Repita as etapas de 2 a 6.

➋

quadro da pergunta 6, nomeado

Repita as etapas de 2 a 6 para inclinações de 45¡ e 60¡ e inclua no gráfico.

➌ ➍

Responda a pergunta 7.

Explorações avançadas

Ajuste os valores de tempo de modo que x = 0 para a altura inicial (o tempo em que a bola foi solta). Você pode fazer isso manualmente, subtraindo o valor de x para o primeiro ponto em todos os pontos de sua “plotagem” ou pode digitar

(cont.)

parabólica

Responda a

Inclua essa “plotagem” no

L1(1)"A:L1NA"L1

Calcule os valores para a, b e c para a família de curvas de fórmula

➊

y = ax

0¡, 15¡, 30¡, 45¡, 60¡, 90¡. Quais são os valores mínimo e máximo para a? Por quê?

➋

Escreva uma expressão descrevendo a relação matemática entre a e o ângulo de

➌

inclinação.

+ bx + c

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

NTRODUÇÃO AO

CBR

Atividade 5—Rolagem da bola

Coleta de dados

Nome _____________________________________

Qual dessas “plotagens” você acha que melhor corresponde à “plotagem” de

Distância-Tempo

bola rolando em uma rampa?

Qual propriedade física está representada no eixo x? ___________________________________________

Quais são as unidades? ____________________________________________________________________ Qual propriedade física está representada no eixo y? ___________________________________________ Quais são as unidades? ____________________________________________________________________ Esboce o aspecto real da “plotagem”. Nomeie o eixo. Nomeie a plotagem nos pontos em que a bola foi

solta e quando atingiu o final da rampa.

de uma

Qual o tipo de função representada por essa “plotagem”? ______________________________________

Discuta a mudança na sua compreensão entre o gráfico selecionado na pergunta 1 e a curva esboçada

na pergunta 3. ___________________________________________________________________________

________________________________________________________________________________________

Explorações

Esboce o aspecto que você imagina que a “plotagem” com uma inclinação maior terá. (Nomeie-o como

previsão

Esboce e nomeie as “plotagens” para 0¡ e 90¡:

NTRODUÇÃO AO

CBR

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

Informações para os professores

Como suas aulas podem mudar com o CBR?

é um sistema de fácil utilização, com recursos que ajudam a integrá-lo em seus

O CBR

planejamentos de aulas de forma rápida e fácil.

oferece melhoras significativas sobre outros métodos de coleta de dados que você

O CBR

pode ter usado anteriormente. Sucessivamente, isso poderá conduzir a uma reestruturação de como você usa o tempo em classe, à medida que os alunos ficam mais entusiasmados em usar dados do mundo real.

Você descobrirá que seus alunos sentirão um maior senso de propriedade dos dados

porque eles realmente participam no processo da coleta de dados, em vez de usarem dados de livros-texto, periódicos ou resumos estatísticos. Isso afeta-os porque os conceitos explorados em classe são ligados ao mundo real e não são apenas idéias abstratas. Mas isso também significa que cada aluno(a) desejará ser um(a) participante na coleta de dados.

A coleta de dados com o

é, de forma considerável, mais eficaz do que a criação de

CBR

cenários e a obtenção manual de medidas com uma régua e um cronômetro. Visto que mais pontos de amostragem proporcionam uma resolução maior e um detector sônico de movimentos é altamente preciso, a forma das curvas ficará com uma aparência melhor. Você precisará de menos tempo para a coleta de dados e terá mais tempo para análise e exploração.

Com o

os alunos podem explorar a possibilidade de repetição das observações e

CBR,

variações em cenários hipotéticos. Perguntas como “A parábola será a mesma se soltarmos a bola de uma altura maior?” e “A parábola será a mesma tanto para o primeiro como para o último salto?” serão naturais e com extensões valiosas.

A capacidade de visualização permite que os alunos associem rapidamente os dados

plotados da lista às propriedades físicas e funções matemáticas descritas pelos dados.

Ocorrerão outras mudanças quando forem coletados dados de eventos do mundo real. O

permite que os alunos explorem relações destes eventos tanto numérica quanto

CBR

graficamente.

Exploração de dados de forma gráfica

Use “plotagens” de distância, velocidade e aceleração geradas automaticamente, relacionadas ao tempo para explorações, como por exemplo:

Qual a importância física da intercepção em y? da intercepção em x? da inclinação? do

máximo? do mínimo? das derivadas? das integrais? Como reconhecemos a função (linear, do 2º grau, etc.) representada pela “plotagem”?

Como devemos montar os dados com uma função representativa? Qual a importância

dos diversos coeficientes na função (p.e. AX

Exploração de dados de forma numérica

Os alunos podem empregar métodos estatísticos (média, mediana, moda, desvio padrão, etc.) apropriados a seus níveis para explorarem os dados numéricos. Quando você sai do programa

REALTIME=NO

RANGER,

aparece um prompt para lembrá-lo das listas onde os dados em

(Tempo Real=Não) para tempo, distância, velocidade e aceleração estão

armazenados.

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

+ BX + C)?

NTRODUÇÃO AO

CBR

Informações para os professores

(cont.)

“Plotagens” do CBR—conexão do mundo físico com a matemática

As “plotagens” criadas a partir dos dados coletados pelo

RANGER

são uma representação visual das relações entre as descrições físicas e matemáticas de movimento. Os alunos devem ser encorajados ao reconhecimento, análise e discussão da forma de “plotagem” em termos de física e matemática. Diálogos e descobertas adicionais são possíveis quando as funções são digitadas no editor Y= e exibidas com as “plotagens” dos dados.

Uma “

(distância do

plotagem” de Distância-Tempo

) a cada instante no tempo quando uma amostra é coletada. As

CBR

representa a posição aproximada de um objeto

unidades do eixo y indicam metros ou pés; as unidades do eixo x indicam segundos. Uma “

plotagem” de Velocidade-Tempo

objeto (relativa a e na direção do

representa a velocidade aproximada de um

) a cada instante da amostragem. As unidades do

CBR

eixo y indicam metrosàsegundo ou pésàsegundos; as unidades do eixo x indicam segundos.

Uma “

plotagem” de Aceleração-Tempo

velocidade de um objeto (relativa a e na direção do As unidades do eixo y indicam metrosàsegundo

representa a taxa de variação aproximada na

) a cada instante da amostragem.

CBR

ou pésàsegundo2; As unidades do eixo x

indicam segundos. A

primeira derivada

(taxa instantânea) de qualquer ponto na “plotagem” Distância-

Tempo indica a velocidade nesse instante. A

primeira derivada

(taxa instantânea) de qualquer ponto na “plotagem” VelocidadeTempo indica a aceleração nesse instante. Essa é também a segunda derivada de qualquer ponto na “plotagem” Distância-Tempo.

Uma

integral definida

(área entre a “plotagem” e o eixo x entre dois pontos quaisquer) na

“plotagem” Velocidade-Tempo é igual ao deslocamento (distância real percorrida) pelo

objeto durante esse intervalo de tempo. Geralmente,

velocidade escalar e velocidade vetorial

são usadas sem distinção. Elas são grandezas diferentes, embora estejam relacionadas. Velocidade escalar representa uma grandeza

escalar

por segundo.” Velocidade vetorial representa uma grandeza

; possui um valor, mas nenhuma direção especificada, como em “6 pés

vetorial

; possui uma direção

especificada bem como um valor, como em “6 pés por segundo ao Norte.” Uma “plotagem” comum Velocidade-Tempo do

representa de fato a velocidade

CBR

escalar, não a vetorial. Apenas o valor (que pode ser positivo, negativo ou zero) é fornecido. A direção está apenas incluída. Um valor positivo de velocidade vetorial indica movimento para longe do

calcula a distância apenas em uma linha reta a partir do detector. Dessa forma, se

CBR

; um valor negativo indica movimento para perto do

CBR

um objeto estiver se movendo em um ângulo com a reta, ele calculará somente o componente de velocidade vetorial paralela a essa reta. Por exemplo, um objeto movendo-se perpendicularmente à reta do

mostra velocidade vetorial zero.

CBR

NTRODUÇÃO AO

CBR

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

Informações para os professores

A matemática de distância, velocidade e aceleração

média

instantânea

lim

@t"

= inclinação da “plotagem” de Distância-Tempo

(

d(s)

)

onde s = distância

”plotagem” de Distância-Tempo

(cont.)

plotagem” de Velocidade-Tempo

média

instantânea

lim

@t"

= inclinação da “plotagem” de Velocidade-Tempo

(

)

A área na “plotagem” de Velocidade-Tempo de

entre

Então,

(distância real percorrida).

t=2

v(@t)

(

∑

t=1

)

t=2

⌠

⌡

t=1

v(dt)

para

= (

) = deslocamento

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

”plotagem” de Aceleração-Tempo

NTRODUÇÃO AO

CBR

Informações para os professores

Recursos do site na Web

(cont.)

Em nosso site na web,

uma listagem de materiais complementares para serem usados com o

calculadoras gráficas TI uma biblioteca de programas para serem usados com o

uma página de atividades com aplicações desenvolvidas e compartilhadas por professores

como você programas do

informações mais detalhadas sobre as definições e comandos de programação do

Recursos adicionais

Os livros da série relacionado às calculadoras gráficas TI, incluindo livros com atividades em sala de aula para o

apropriadas para aulas de matemática e ciências no ginásio e segundo grau.

CBR,

http:ààwww.ti.comàcalc

que acessam recursos adicionais do

CBR

Explorations

da Texas Instruments fornecem material complementar

, você encontrará:

CBR, CBL

CBR

CBR, CBL

e calculadoras gráficas TI

CBR

NTRODUÇÃO AO

CBR

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

Os dados do CBR são armazenados em listas

Os dados coletados são armazenados nas listas L1, L2, L3 e L4

Quando o

coleta os dados, ele transfere-os automaticamente para a calculadora e

CBR

armazena-os em listas. Toda vez que sair do programa os dados estão armazenados.

contém dados de tempo.

contém dados de distância.

contém dados de velocidade.

contém dados de aceleração.

Por exemplo, o 5º elemento na lista L1 representa o tempo em que o 5º ponto dos dados foi coletado, e o 5º elemento na lista

REALTIME=YES

(Tempo Real=Sim), apenas os dados da “plotagem” solicitada (distância, velocidade ou aceleração) são calculados e transferidos. Em todos os dados são calculados e transferidos.

As definições são armazenadas na lista L5

A tela

RANGER SETUP

mais usados do Quando o programa

(Configuração do Ranger) facilita a alteração da maioria dos parâmetros

(consulte a página 38).

CBR

RANGER

é transferido do

uma nova lista contendo os padrões. Consulte as páginas 40–41 para obter informações sobre os comandos de programação que

alteram outras definições.

RANGER,

representa a distância do 5º ponto dos dados.

, a L5 é automaticamente substituída por

CBR

você será lembrado de onde

REALTIME=NO

(Tempo Real=Não),

Uso das listas de dados

As listas não são apagadas quando você sai do programa disponíveis para explorações e análises gráficas, estatísticas e numéricas adicionais.

Você pode plotar as listas umas com as outras, exibi-las no editor de listas, usar a análise da regressão e executar outras atividades analíticas. Por exemplo, você pode coletar os dados do movimento do pêndulo usando o Velocidade-Aceleração para explorar funções elípticas. (Também poderá ser necessário ajustar a Janela.)

RANGER

, sair do

RANGER

. Assim, elas ficam

e, em seguida, plotar a

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

NTRODUÇÃO AO

CBR

Definições do RANGER

Alteração das definições do RANGER

O RANGER

➊

exibe as definições mais usadas antes do início da coleta de dados.

MAIN MENU

(Menu Principal) do programa

RANGER,

selecione

SETUPàSAMPLE

(Configuração/Amostra). São exibidas as definições atuais. 4 indica a localização do cursor.

UNITS:

›

START NOW

YES

TOTAL TIME

DISTANCE, VELOCITY

[ENTER], [TRIGGER],

NONE, LIGHT, MEDIUM

METERS

= 1–99

FEET

SECONDS

ACCELERATION

10-SECOND DELAY

HEAVY

(apenas quando

para percorrer as opções disponíveis. Quando a opção estiver correta,

(Tempo), digite 1 ou 2

TIME

MAIN MENU

REALTIME:

TIME (S):

DISPLAY:

BEGIN ON:

SMOOTHING:

Pressione c ou b para ir para a definição que deseja alterar.

➋

Pressione

➌

pressione c para ir para a próxima opção. Para alterar dígitos e, em seguida, pressione c ou b.

Quando todas as definições estiverem corretas, pressione c ou b até que o cursor

➍

esteja sobre

Para continuar, pressione

Para retornar ao

START NOW

(Iniciar Agora).

›

MAIN MENU

, pressione e e, em seguida, pressione

›

REALTIME=NO

)

As novas definições permanecerão, a menos que você selecione Padrões), execute uma aplicação ou outro programa que altere as definições. Se você alterar

fora do programa

próxima vez em que o

RANGER

ou apagá-la, as definições padrão poderão ser restauradas na

for executado.

Restauração das definições padrão do RANGER

As definições padrão são apropriadas para uma ampla variedade de situações de amostragem. Se não tiver certeza sobre as melhores definições, comece com as definições padrão e, em seguida faça o ajuste.

➊

MAIN MENU

do programa

RANGER,

As definições são alteradas para os padrões e a tela Se desejar alterar uma definição do padrão, siga as etapas acima.

➋

Para continuar, pressione

➌

quando o cursor estiver sobre

›

Outras definições do RANGER

O programa

RANGER

acessa as definições mais comumente alteradas. O definições adicionais. Consulte as páginas 40–41 para obter informações sobre os comandos de programação que alteram essas definições.

selecione

SET DEFAULTS

(Configuração) é exibida.

SETUP

SET DEFAULTS

START NOW

possui

CBR

(Definir

NTRODUÇÃO AO

CBR

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

Uso do CBR com o CBL ou com programas de CBL

Uso do CBR como um detector convencional de movimentos com o CBL

pode ser usado como um detector convencional de movimentos com o sistema

CBR

(Calculator-Based Laboratoryé) da Texas Instruments.

CBL

Não conecte o deve ser conectada ao

CBR

quando o

CBL

CBR

Poderá ser necessário alterar o programa

RANGER

não funciona com o

CBL

Uso do CBR com programas escritos para o CBL

Você pode usar o

com a maioria dos programas

CBR

de movimentos sem alterações ou fazendo apenas pequenas alterações no programa.

Para finalizar a amostragem:

REALTIME=YES

(Tempo Real=Sim), o

Com alguns programas

CBR

encerrar a coleta de dados no final do tempo da amostra, você pode proceder de uma das seguintes formas:

Cabo de

CBR

-para-

CBL:

estiver conectado a uma calculadora. A calculadora

conforme mencionado abaixo. O programa

CBL

escritos para apenas um detector

CBL

usando a coleta de dados em

CBL

continua a amostragem indefinidamente. Para

Pressionar ¤ no

Incluir instruções no programa instrução deve estar após a transferência e a exibição dos dados. Por exemplo:

{6,0}"L6:SEND L6

Para desativar ou ativar o som:

existente para enviar o comando {6,3} ao coleta de dados. Por exemplo:

{6,3}"L6:SEND L6

Para ativar o som, simplesmente execute o programa

Em caso de dificuldade:

está respondendo ou está travado, execute o programa web (consulte a página 36), que poderá ter uma versão atualizada do programa

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

CBR

existente para enviar o comando {6,0} ao

CBL

Para desativar o som, inclua instruções no programa

. A instrução deve estar antes do início da

CBR

RANGER.

Se você executar um programa

SEJA INCLUÍDA

e se parecer que o

CBL

RANGER

. Verifique o site da TI na

CBR

CBL.

NTRODUÇÃO AO

. A

CBL

não

CBR

Comandos de programação

Comando 0 Limpa e redefine o sistema {0}

0 Limpa tudo. Redefine padrões de ativação. Seleciona automaticamente o canal 11.

Comando 1 Limpa canal {1,0}

Limpa canal.

Comando 1 Canal {1,11,

operação

REALTIME=NO

operação

REALTIME=YES

pós_processamento

0 (padrão) Nenhum 1( 2(

conversão_da_temperatura

0 (padrão) Desativa o equilíbrio da temperatura. 1 Ativa o equilíbrio da temperatura.

REALTIME=NO REALTIME=NO

) Limpa tudo. Redefine padrões ativação. ) Metros ) Metros )Pés

) Limpa tudo. Redefine padrões ativação. ) Metros, ) Metros, )Pés, ) Metros, )Pés, ) Metros, )Pés,

)dàdt (derivada de 1ª ordem) )d

Comando 2 Configuração de dados {2,

tipo_de_dados

1 (padrão) Lista

Comando 3 Amostra/Trigger {

tempo_de_amostra

0,005–1500 (0.1) Tempo em segundos entre cada amostra 0,0001–0,005 Arredonda para 0,005. 1500<x<16000 Arredonda para 1500.

nº amostra

L1 Seleciona o modo de coleta de dados

REALTIME=NO

1–512 (

trigger

0 Inicia a amostragem sem trigger. 1 (padrão) Inicia a amostragem em 7 Atrasa 10 segundos e, em seguida, inicia a amostragem.

tempo_de_registro

0 (padrão) Nenhum

REALTIME=NO

filtro

(consulte o comando 1, campo operação)

0 (padrão) Sem filtragem

REALTIME=NO

1 (

REALTIME=NO

2 (

REALTIME=NO

3 (

REALTIME=NO

4 (

REALTIME=NO

5 (

REALTIME=NO

6 (

REALTIME=YES

7 (

REALTIME=YES

8 (

REALTIME=YES

9 (

) Obtém de 1 a 512 amostras.

) Tempo absoluto (inicia no tempo 0 e ajusta o tempo de amostra) ) Tempo relativo (inicia no tempo 0 e ajusta o tempo de amostra)

) Aplainamento Savitzsky-Golay de 5 pontos ) Aplainamento Savitzsky-Golay de 9 pontos ) Aplainamento Savitzsky-Golay de 17 pontos ) Aplainamento Savitzsky-Golay de 29 pontos ) Filtro de supressão mediano de 3 pontos ) Filtro de supressão mediano de 5 pontos

) Filtro de rastreamento suave de ) Filtro de rastreamento médio de ) Filtro de rastreamento intenso de

Resultados

tipo_de_dados

Resultados

tempo_de_amostra,nº amostra,trigger

Resultados

operação,pós_processamento

CBR

retorna {

CBR

retorna {

CBR

retorna {

CBR

retorna {

CBR

retorna {

CBR

retorna {

CBR

retorna {

(derivada de 2ª ordem)

àdt

distância,@tempo distância,@tempo

distância,@tempo

distância,velocidade,@tempo

distância,velocidade,aceleração,@tempo

,0,0,0,0,0,0,0}

REALTIME=YES

conversão_da_temperatura

,0,

} }

}

tempo_de_registro,filtro

,0,0,0,0,

REALTIME=YES

}

NTRODUÇÃO AO

CBR

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

Comandos de programação

(cont.)

Comando 4 Equilíbrio da temperatura {4,

nº equação

tipo_de_equação

temperatura

unidades

Comando 5 (

primeiro_canal

seleção_de_dados

dados_iniciais

dados_finais

0 (padrão) Limpa todas as equações. 4 Designa a equação 4.

0 (padrão) Limpa a equação. 13 Designa o equilíbrio da temperatura.

número de ponto flutuante Define a temperatura atual.

0 (padrão) Nenhum (ignorado pelo 1 Define graus = Fahrenheit. 2 Define graus = Celsius. 3 Define graus = Kelvin. 4 Define graus = Rankin onde R = F + 459,7.

REALTIME=NO

0 (padrão) Seleciona o canal ativo mais inferior. 1, 2, 3, 11, 21 Especifica o canal sônico. M1 Registra a lista de tempos.

0 Dados filtro {distância} 1 Dados filtro dàdt {velocidade} 2 Dados filtro d 3 Dados brutos {distância} 4 Dados brutos dàdt {velocidade} 5 Dados brutos d

1–512 Primeiro elemento de dados para GET

0–512 Último elemento de dados para GET (0 = última amostra)

) Config. faixa dados {5,

Resultados

Comando 6 Opções do sistema {6,

comando_do_sistema

0 Interrompe a amostragem (para compatibilidade do CBL). 2 (padrão) Encerra a amostragem. 3 Desativa o som (o som é ativado no “power on”). 4 Ativa o som (o som é ativado no “power on”). 5 Define o Número de Identificação ( 6 Aplica novo filtro aos dados anteriores (

operação

número de ponto flutuante Número_de_Identificação na forma 0–6 Novo filtro para dados coletados anteriormente (

Resultados

Comando 7 Status de pedido {7}

Retorna uma lista contendo:

10.rrrr Código_Dispositivo.Versão_Rom 0–99 Último código de erro (0 = nenhum erro) 0–2 Condição da bateria (0 = OK; 1= baixa durante amostras; 2= sempre baixa) 11 Identificador sônico de canais tempo_de_amostra Intervalo atual de amostras em segundos condição_de_trigger Opção de ativação atual em uso função Função atual do canal (1–9) pós_processamento Opção atual pós-processamento (0–2) filtro Nível de filtragem atual (0–9) amostras Nº de amostras disponíveis; 0–512 tempo_registrado Opção de tempo registrado (0–2) temperatura Temperatura em uso (¡C) sinalizador_piezo 0 = som desativado; 1 = som ativado estado_do_sistema 1 = não-conf.; 2 = preparado; 3 = ativado/amostragem; 4 = pronto início_da_janela 0 = ainda sem o comando 5; 1–512 final_da_janela 0 = uso de nº de elementos; 1–512 número_de_identificaçãoNº Ident. 6 díg. (padrão 0.00000) def.p/comando 6 (

nº equação,tipo_de_equação,temperatura,unidades

CBR

). Define a T para graus Celsius.

}

primeiro_canal,seleção_de_dados,dados_iniciais,dados_finais

{aceleração}

àdt

{aceleração}

àdt

comando_do_sistema

operação

[

]

}

operação

n.nnnnn

obrigatória).

comando_do_sistema

(

REALTIME=NO

obrigatória).

comando_do_sistema

REALTIME=YES

; M1

comando_sistema

= 5)

= 6)

= 5)

}

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

NTRODUÇÃO AO

CBR

Baterias

Tipo das baterias

foi designado para operar com 4 baterias alcalinas AA. O

O CBR

baterias, apenas se estiver conectado a um

Instalação das baterias

Mantendo o

de cabeça para baixo, use seu polegar para deslizar a tampa do

CBR

compartimento de baterias próximo à parte posterior do

CBL

. Posicione as baterias de

CBR

acordo com o diagrama no interior do compartimento de baterias do encaixam com o pólo positivo para cima na lateral marcada com +. encaixam com o pólo negativo para cima na lateral marcada com -. tampa. O

Avisos sobre baterias fracas no CBR

possui dois mecanismos para informá-lo de que as baterias estão fracas:

O CBR

O programa

está pronto para começar a amostragem.

CBR

RANGER

exibe uma mensagem de aviso na tela da calculadora durante a

pode ser executado sem

CBR

. Duas baterias

CBR

Duas baterias se

Deslize novamente a

tentativa de coletar dados.

A luz vermelha pisca de forma intermitente enquanto o

está coletando dados da

CBR

amostra.

Status de carga das baterias do CBR

Você pode verificar a carga da bateria antes de começar a amostragem. No (Menu Principal), selecione do

). É exibido o status da bateria, OK ou

CBR

(Ferramentas) e, em seguida, selecione

TOOLS

REPLACE

(Substituir).

CBR STATUS

MAIN MENU,

(Status

Cuidados com as baterias

Substitua as quatro baterias ao mesmo tempo. Não misture marcas de baterias. Não misture tipos de uma marca de baterias.

Instale as baterias de acordo com os diagramas no interior do compartimento de baterias.

Elimine imediatamente e de forma adequada as baterias usadas. Não deixe-as ao alcance de crianças.

Não aqueça, queime ou perfure as baterias. Elas contêm produtos químicos perigosos e podem explodir ou vazar.

Não misture baterias recarregáveis ou não-recarregáveis.

Não coloque baterias não-recarregáveis em um recarregador de baterias.

NTRODUÇÃO AO

CBR

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

Em caso de dificuldade

Se tiver esse problema: Tente:

Dificuldade em transferir o programa

RANGER

ou coletar

dados O próprio

CBR

começa a coletar

dados

Verifique se a conexão da calculadora-ao-

firmemente

as duas extremidades do cabo. Verifique se as baterias estão fracas (consulte a página 42). Se você definir o CBR com o botão

ficar pressionado e ativar a amostragem. Pressione

CBR

está incorreta. Pressione sempre

empurrado, o botão

encerrar a amostragem.

CBR,

saia adequadamente do programa

CBR

CBL

à calculadora com o cabo da calculadora-para-

CBR

está incorreta. Pressione sempre

as duas extremidades do cabo.

CBR

à calculadora, pressione

QUIT

ensagem

LINK ERROR

Antes de guardar o

QUIT)

ou de qualquer outro programa

Conecte o

CBR

Verifique se a conexão da calculadora-ao-

firmemente

Se não desejar (ou não puder) conectar o

sair do programa e, em seguida, selecione

Memória insuficiente Você deve ter memória suficiente para o programa

Os programas e listas requerem aproximadamente 17.500 bytes. Elimine os programas e/ou dados.

A calculadora não corresponde as instruções das atividades

Este manual aplica-se a todas as calculadoras TI que podem ser usadas com o

CBR

, por isso, você perceberá que alguns dos nomes de menus, telas ou teclas nesse manual não correspondem exatamente ao de sua calculadora. Selecione a correspondência mais próxima. Por exemplo, se as instruções indicarem

DISTANCE MATCH

DIST MATCH

(Correspondência de Distância),” na TI-83 você

CBR

ao mesmo tempo na mesma sala, um grupo

as duas extremidades do cabo.

CBR

está incorreta. Pressione sempre

Os dados parecem incorretos:

os pontos não estão na curva

“plotagens” irregulares

“plotagens” planas

“plotagem” interrompida

“Selecionar

selecionará Repita a amostra, certificando-se de que o CBR esteja posicionado diretamente

para o objeto. Leia as páginas 6–12 para obter boas amostras de dados. Verifique se a área livre não contém alunos, mesas ou outros objetos. Ao usar duas unidades do

deverá concluir uma amostra antes que o próximo grupo comece a sua. Verifique se a conexão da calculadora-ao-

firmemente

Verifique se as baterias estão fracas (consulte a página 42). Verifique se o grau de aplainamento não está muito elevado ou muito baixo.

O CBR

não funciona com uma

TI-85

Verifique se aparece “ calculadora para indicar a compatibilidade com

CBL

” no final do número de série na parte de trás da

A TI-85 não possui recursos de “plotagens” estatísticas, por isso, algumas



em dados plotados) não são possíveis na TI-85.

O cabo da calculadora-parafoi perdido

CBR

explorações (como o uso de Você pode usar o cabo da calculadora-para-calculadora, fornecido com a

calculadora. (O cabo da calculadora-para-calculadora é muito mais curto, por isso, você poderá solicitar um cabo para substituição.)

Baterias freqüentemente fracas Antes de guardar o

QUIT)

ou de qualquer outro programa

CBR,

saia adequadamente do programa

CBR

CBL

calculadora.

Quando você tenta executar o programa

RANGER,

não acontece

nada Mensagem de erro: Variable is

locked or protected (A variável

Se você editar ou visualizar o programa lo, poderá demorar até dois minutos para a calculadora preparar o programa para execução. Isso é normal.

Você deve desbloquear as variáveis L1, L2, L3, L4 e L5. Consulte o manual da calculadora.

RANGER

, na próxima vez em que executá-

está bloqueada ou protegida) (apenas na TI-92)

novamente para

RANGER

CBL

RANGER

e as listas de dados.

CBR

RANGER

e desconecte o

CBR

(usando

CBR

poderá

para

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

NTRODUÇÃO AO

CBR

Informações sobre Garantia e Serviços aos Produtos TI

Informações sobre os produtos e serviços da TI

Para mais informações sobre os produtos e serviços da TI, contate a TI através de correio eletrônico ou visite a home page das calculadoras TI na World Wide Web.

ti-cares@ti.com http://www.ti.com/calc

Informações sobre a assistência e garantia

Para obter informações sobre a duração e termos da garantia ou sobre a assistência a produtos, consulte a declaração de garantia incluída neste produto ou contate o revendedor/distribuidor Texas Instruments mais próximo.

NTRODUÇÃO AO

CBR

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

SMOO

STOP/CLEAR C

[

ACC

ATC

ACC

1-99 (REA

RANGE

SHO

AT SA

MAIN MENU

SETUP / SAMPLE

SET DEFAULTS

NO YE

LTIME=N

DISTANCE VELOCITY

ELERATION

ENTER] TRIGGER]

DEL

NONE LIGHT MEDIUM

METERS FEET

APPLICATIONS

REALTIME=N

PLOT MENU

REALTIME=YE

TOOLS

QUIT

UNITS METERS FEET

DISTANCE-TIME

ITY-TIME

VEL

ELERATION-TIME T TOOLS

PL REPEAT SAMPLE

IN MENU

UIT

W PLOT

ELECT DOMAIN REPE MAIN MENU

UIT

TOOLS

ET CBR DATA

ET CALC DATA

BR STATUS

IN MENU

MPLE

PPLICATIONS DISTANCE MATCH VELOCITY MATCH

LL BOUNCE

IN MENU

PLOT TOOLS

ELECT DOMAIN

TH DATA

T MENU

DATA SMOOTHING LIGHT MEDIUM

PTIONS

ME MATCH

NEW M

MAIN MENU

PPLICATIONS

UIT

ÓPIA PERMITIDA, CONTANTO QUE A NOTA DE COPYRIGHT DA

EXAS INSTRUMENTS INCORPORATED

SEJA INCLUÍDA

NTRODUÇÃO AO

CBR

Texas instruments CBR User Manual [pt]

Specifications and Main Features

Frequently Asked Questions

User Manual