Texas instruments CBR User Manual [de]

Download

85-86

TRIGGER

CBR

)

Calculator-Based Ranger

™

(CBR

™

)

INFÜHRUNG IN DIEINFÜHRUNG IN DIE

ERWENDUNG DES ERWENDUNG DES

MITMIT

CBR™CBR™

5 S5 S

CHÜLEREXPERIMENTENCHÜLEREXPERIMENTEN

CBR

)

TRIGGER

85-86

CBR

)

TRIGGER

85-86

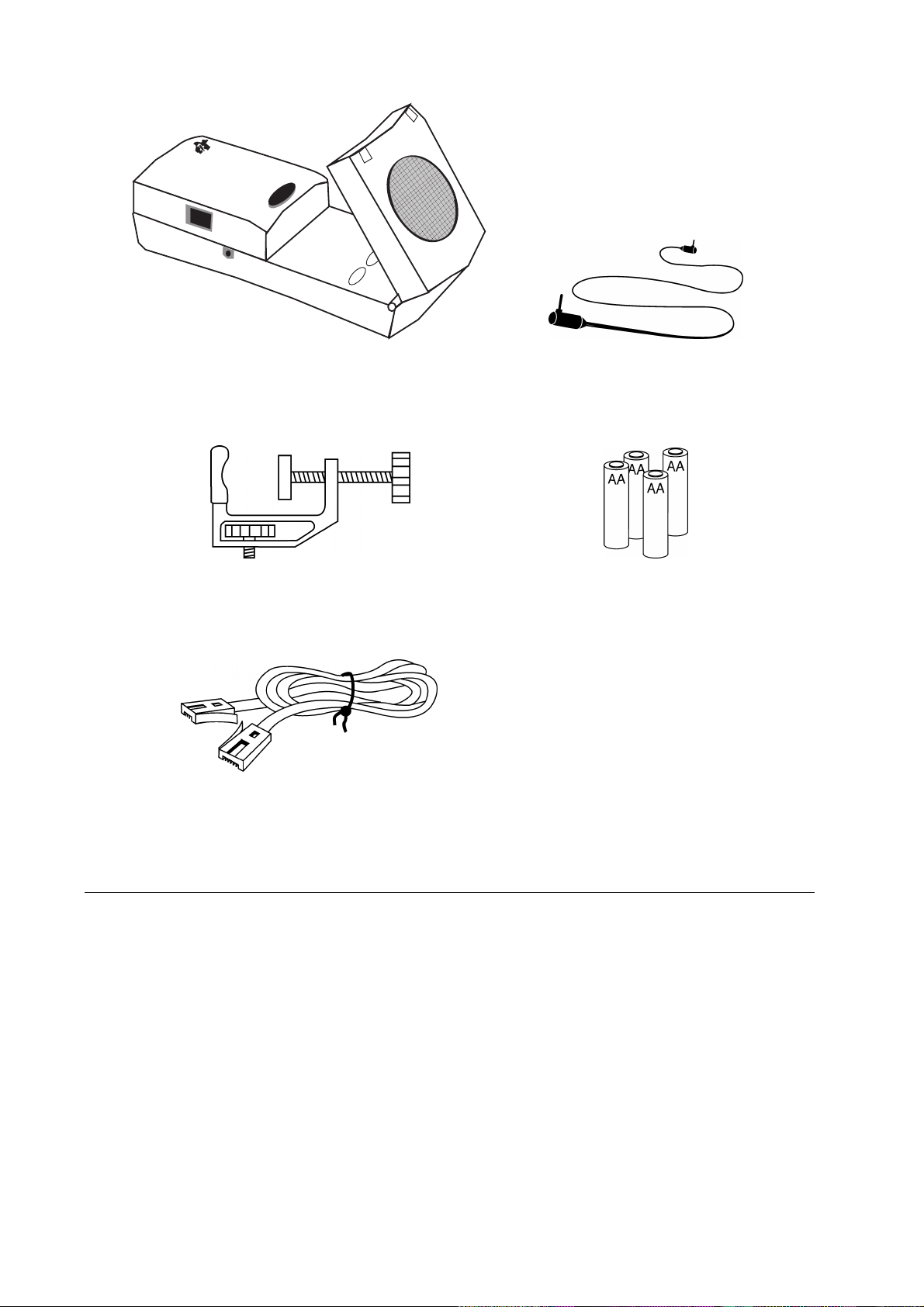
Calculator-Based Rangeré (CBRé) Verbindungskabel CBR-Taschenrechner

(Taschenrechnerbasierter Abstandsmesser)

Schelle 4 AA-Batterien

CBL-CBR-Verbindungskabel

Wichtig

Texas Instruments übernimmt keine Gewährleistung, weder ausdrücklich noch stillschweigend, einschließlich, aber nicht beschränkt auf implizierte Gewährleistungen bezüglich der handelsüblichen Brauchbarkeit und Geeignetheit für einen speziellen Zweck, was sich auch auf die Programme und Handbücher bezieht, die ohne eine weitere Form der Gewährleistung zur Verfügung gestellt werden.

In keinem Fall haftet Texas Instruments für spezielle begleitende oder zufällige Beschädigungen in Verbindung mit dem Kauf oder der Verwendung dieser Materialien. Die einzige und exklusive Haftung von Texas Instruments übersteigt unabhängig von deren Art nicht den Kaufpreis des Geräts. Darüber hinaus übernimmt Texas Instruments keine Haftung gegenüber Ansprüchen Dritter.



1997 Texas Instruments Incorporated.

Texas Instruments gestattet Lehrern hiermit, die in diesem Werk enthaltenen Seiten mit einem Copyright-Vermerk von Texas Instruments in für den Unterricht benötigten Mengen zu kopieren oder zu reproduzieren. Diese Seiten sind für die Reproduktion und Verwendung im Unterricht gedacht, solange jede Kopie den Copyright-Vermerk trägt. Diese Kopien dürfen nicht verkauft werden, und jede Weiterverbreitung ist ausdrücklich untersagt. Sofern nicht wie oben oder gesetzlich ausdrücklich erlaubt bedarf die Reproduktion dieses Werks oder Teilen dieses Werks oder die Überführung in eine andere Form, sei es auf elektronischem oder mechanischem Weg, einschließlich der Einspeisung in Informationssysteme, der vorherigen schriftlichen Genehmigung von Texas Instruments. Richten Sie diesbezügliche Anfragen an Texas Instruments Incorporated, PO Box 149149, Austin, TX, 78714-9149, M/S 2151, z.H. Contracts Manager.

Inhalt

CBR

)

Einleitung

Was ist der CBR? 2

Einführung in die Verwendung des CBR - ganz einfach 4

Tips für effektive Messungen 6

Experimente mit didaktischen Hinweisen und Schüler-Arbeitsblättern

TRIGGER

85-86

Experiment 1 - Graph treffen linear 13

Experiment 2 - Spielzeugauto linear 17

Experiment 3 - Pendel sinusförmig 21

Experiment 4 - Springender Ball parabolisch 25

Experiment 5 - Rollender Ball parabolisch 29

Informationen für den Lehrer 33

Technische Informationen

CBR-Daten werden in Listen gespeichert 37

RANGER-Einstellungen 38 CBR-Einsatz mit dem CBL oder mit CBL-Programmen 39 Programmierbefehle 40

Service-Informationen

Batterien 42

Problembehebung 43

TI-Service und Garantie 44

RANGER Menü-Übersicht Hintere innere Umschlagseite

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Was ist der CBR?

Bringt reale Messungen und Analysen ins Klassenzimmer

Das vielseitige Programm RANGER steht auf Knopfdruck bereit

RANGER beinhaltet bereits die Programme MATCH und BOUNCING BALL

Grundlegende Meßparameter sind einfach einzustellen

Wozu dient der CBR?

Mit Hilfe des aufwendige Messungen und manuelles Auftragen Bewegungsdaten sammeln, sinusförmig und analysieren.

Der

ermöglicht den Schülern anhand selbstgesammelter Daten das Erforschen der

CBR

Zusammenhänge zwischen Weg, Geschwindigkeit, Beschleunigung und Zeit. Die Schüler können so die folgenden mathematischen und physikalischen Konzepte erforschen:

CBRCBRé (Calculator-Based RangerCalculator-Based Rangeré

Schall-Bewegungsdetektor

CBL

Einsetzbar mit TI-82, TI-83, TI-85/

, TI-86 und TI-92

Leicht verwendbares, abgeschlossenes System

Keine Programmierung notwendig

Beinhaltet das Programm RANGERBeinhaltet das Programm RANGER

und eines graphischen TI-Taschenrechners können Schüler ohne

CBR

)

Bewegung: Weg (Abstand), Geschwindigkeit, Beschleunigung

Graphische Darstellung: Koordinatenachsen, Steigung, Schnittpunkte

Funktionen: linear, quadratisch, exponentiell, sinusförmig

Analysis: Ableitungen, Integrale

Statistik und Datenanalyse: Meßmethoden, statistische Analysen

Was enthält diese Einführung?

Einführung in die Verwendung des CBR

Erfahrung im Umgang mit Taschenrechnern und in der Programmierung entworfen. Er enthält Kurzanweisungen für die Verwendung des sowie fünf Experimente zur Erforschung der Grundfunktionen und der Eigenschaften von Bewegung. Die Experimente auf den Seiten 13–32 umfassen:

Didaktische Hinweise zu jedem einzelnen Experiment sowie allgemeine didaktische

Informationen für Lehrer. Schrittweise Anleitungen.

Für alle Jahrgangsstufen geeignete grundlegende Datenerhebungen.

Detailliertere Untersuchungen der erhobenen Daten einschließlich Was-wäre-wenn-

Szenarios. Anregungen für fortgeschrittenere Experimente für die Oberstufe.

Zur Vervielfältigung gedachte Arbeitsblätter mit offenen Fragestellungen für einen

weiten Jahrgangsstufenbereich.

wurde als Leitfaden für Lehrer mit geringer

, Tips für effektive Messungen

CBR

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

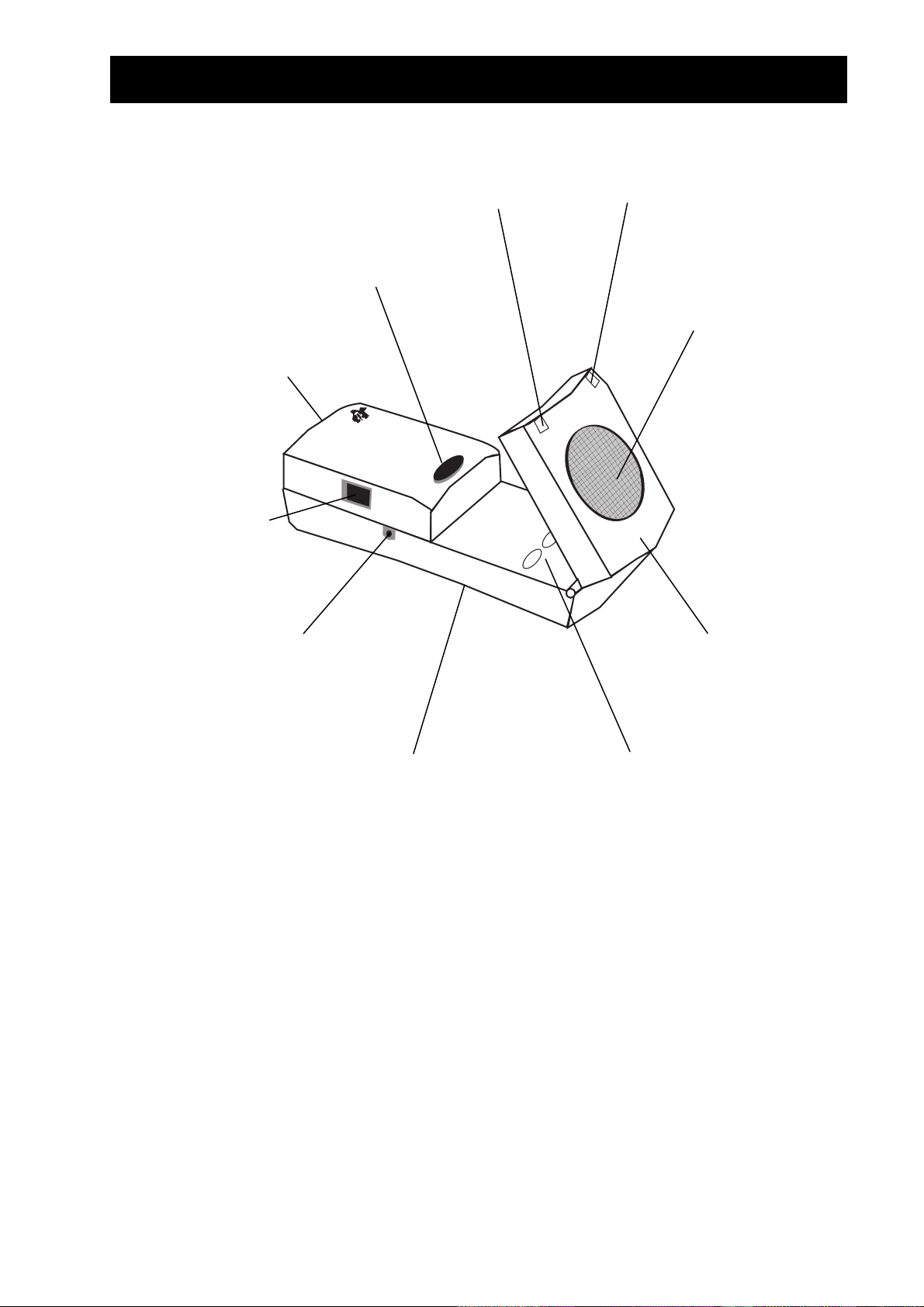
Was ist der CBR?

(Forts.)

Start der Messung

Batteriefachdeckel (unten)

CBL-Anschluß

nschluß zur Verbindung mit einem graphischen TITaschenrechner mit Hilfe des mitgelieferten Kabels (2,25m)

Das grüne Licht gibt an, daß eine Datenerfassung läuft (ein akustisches Signal ist ebenfalls verfügbar)

-Taste zum

CBR

)

Das rote Licht weist auf

pezielle

Betriebsbedingungen hin

Der Ultraschallsensor nimmt bis zu 200 Messungen je Sekunde vor (Meßbereich 0,5m bis 6m)

TRIGGER

85-86

Schwenkkopf, um mit dem Sensor akkurat

u zielen

Standardgewinde für ein Stativ oder die mitgelieferte Befestigungsschelle

Tasten zur Übertragung des Programms RANGER

u einem

Taschenrechner

Der

enthält bereits alles, um schnell und einfach im Klassenraum mit Experimenten beginnen zu

CBR

können - Sie benötigen nur noch einen graphischen TI-Taschenrechner (sowie für einige Experimente einige leicht zu besorgende Gegenstände):

Schall-Bewegungsdetektor

Befestigungsschelle

4 AA-Batterien

Verbindungskabel Taschenrechner-CBR

RANGER

5 vergnügliche Klassenraumexperimente

-Programm im

CBR

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

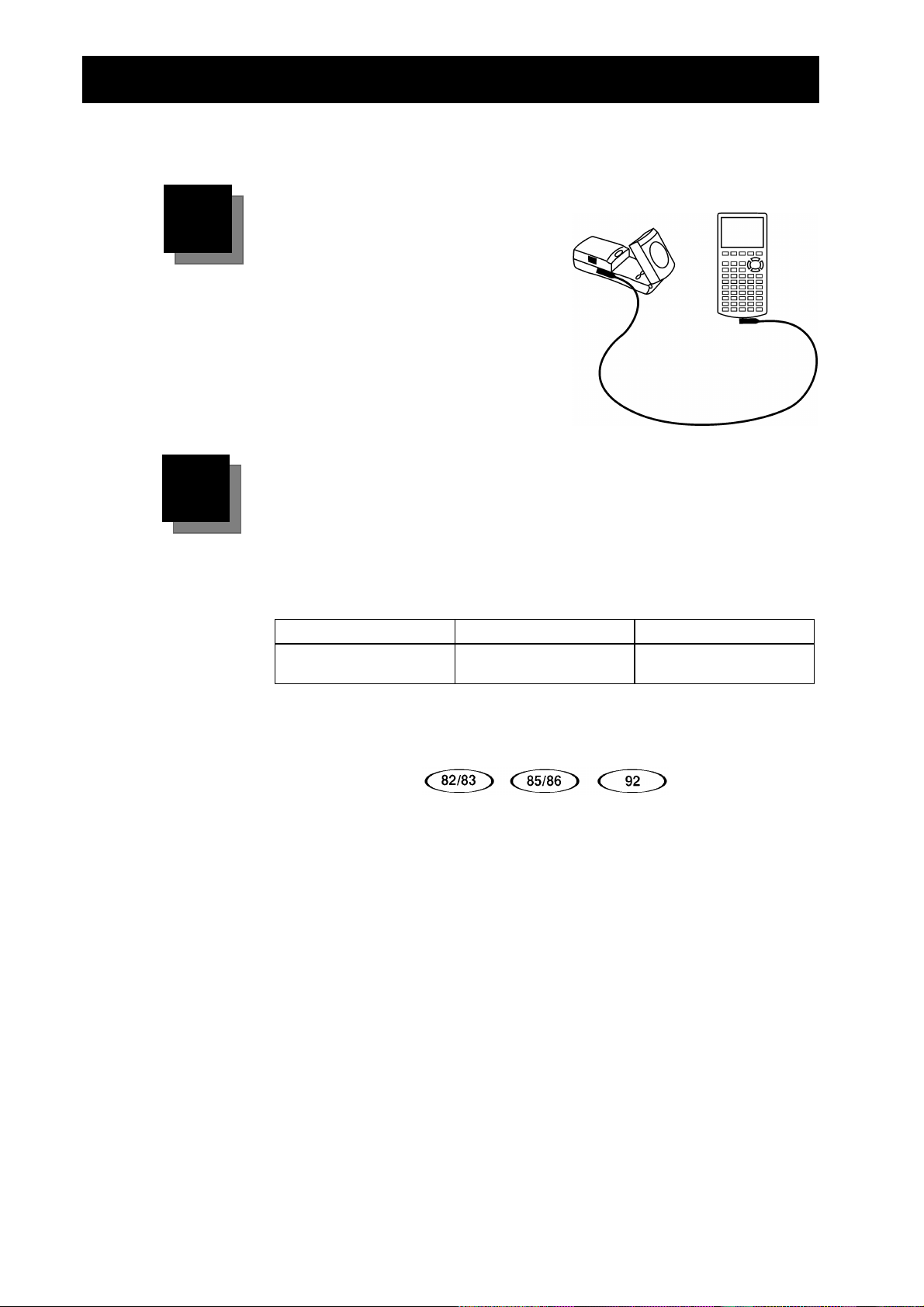
Einführung in die Verwendung des CBR - ganz einfach

Es sind nur drei Schritte zur ersten Messung mit dem

Verbinden

Verbinden Sie den mitgelieferten Verbindungskabels mit einem graphischen TITaschenrechner.

Drücken Sie die Stecker an beiden Anschlüssen fest in die Buchsen.

Sie können auch das

Anmerkun

kurze Verbindungkabel verwenden, das Ihrem Taschenrechner beilag.

mit Hilfe des

CBR

Übertragen

Im CBR ist das für die einzelnen Taschenrechner angepaßte Programm

RANGER

Taschenrechner übertragen.

Bereiten Sie zunächst den Taschenrechner auf den Empfang des Programms vor (siehe die folgenden Tasteneingaben).

enthalten. Sie können dieses leicht vom

CBR

in den

CBR

TI-82 oder TI-83 TI-85/CBL oder TI-86 TI-92

LINK

[

Öffnen Sie nun den Schwenkkopf des sprechende Programmübertragungstaste des

Während der Übertragung zeigt der Taschenrechner (außer TI-92)

RECEIVING

einmal auf, und der

CBR

an. Sollten Probleme auftreten, so blinkt das rote Licht des

DONE

zweimal auf, und der

Sie müssen das Taschenrechner übertragen, wenn Sie es aus dem Speicher des Taschenrechners löschen sollten.

Anmerkung:

Möglicherweise müssen Sie zuvor Programme und/oder Daten aus dem Speicher des Taschenrechners löschen. Sie können Programme und Daten zuvor speichern, indem Sie diese mittels TI-Graph Linké auf einen Computer oder mit Hilfe des Verbindungskabels des Taschenrechners oder des das Handbuch des Taschenrechners).

CBR

›

]

an. Ist die Übertragung beendet, so blinkt das grüne Licht des

piepst einmal; der Taschenrechner zeigt

CBR

piepst zweimal.

CBR

RANGER

Programm und Daten benötigen ca. 17.500 Byte Speicher.

auf einen anderen Taschenrechner übertragen (siehe dazu

-Programm nur dann erneut vom

[

LINK

]

und drücken Sie die ent-

CBR,

CBR

Gehen Sie zum

Hauptbildschirm

CBR

in den

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

Einführung in die Verwendung des CBR - ganz einfach

Starten

(Forts.)

Starten Sie das

TI-82 oder TI-83 TI-85/CBL oder TI-86 TI-92

Drücken Sie Wählen Sie Drücken Sie

RANGER

›

-Programm (siehe die folgenden Tasteneingaben).

Drücken Sie Wählen Sie Drücken Sie

RANGER

›

Drücken Sie L [

LINK

]. Wählen Sie Drücken Sie ¨

Der Anfangsbildschirm wird angezeigt.

Drücken Sie nun

MAIN MENU

SETUPàSAMPLE SET DEFAULTS APPLICATIONS PLOT MENU TOOLS QUIT

Wählen Sie im Menü

wird angezeigt. Drücken Sie ›, und wählen Sie so

SETUP

›. Das Menü

Einsehen/Ändern der Einstellungen vor der Messung

Wiederherstellen der Standardeinstellungen

DISTANCE MATCH, VELOCITY MATCH, BALL BOUNCE

Diagrammoptionen

GET CBR DATA, GET CALC DATA, STATUS, STOPàCLEAR

MAIN MENU

den Eintrag

wird angezeigt.

SET DEFAULTS

Richten Sie das Experiment ein, und drücken Sie dann Messung zu starten. Mehr ist nicht notwendig!

VAR-

RANGER

›

. Der Bildschirm

START NOW

›, um die

Mit den Experimenten dieser Anleitung kommen Sie schnell zu Ergebnissen!

Wichtige Informationen

Dieses Handbuch ist für alle mit dem

verwendbaren graphischen

CBR

Taschenrechner konzipiert; möglicherweise stimmen daher die angegebenen Menünamen nicht exakt mit denen Ihres Taschenrechners überein.

Achten Sie beim Vorbereiten eines Experiments darauf, daß der sicher befestigt ist und daß niemand über das Verbindungskabel stolpern kann.

Verlassen Sie das

RANGER-

Programm nimmt bei Wahl der Option

RANGER

gemäßen Abschluß des

bei der nächsten Verwendung ordnungsgemäß initialisiert ist.

CBR

Lösen Sie die Verbindung zwischen dem

-Programm immer mit der Option einen ordnungs-

QUIT

vor; dadurch wird sichergestellt, daß der

CBR

und dem Taschenrechner,

CBR

QUIT

bevor Sie die Geräte verstauen.

CBR

. Das

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Tips für effektive Messungen

So erhalten Sie bessere Messungen

Wie funktioniert der CBR?

Das Verständnis der Funktionsweise eines Schall-Bewegungsdetektors kann Ihnen helfen, bessere Messungen zu erhalten. Der Bewegungsdetektor sendet einen Ultraschallimpuls aus und mißt die Zeit, bis der Impuls nach Reflexion am nächstgelegenen Objekt wieder zurückkehrt.

Wie jeder andere Schall-Bewegungsdetektor mißt auch der dem Absenden des Ultraschallimpulses und der Ankunft des ersten Echos; der

den Zeitraum zwischen

CBR

hat jedoch einen eingebauten Mikroprozessor, der noch viel mehr macht. Beim Sammeln der Daten berechnet der vom

. Anschließend berechnet er die erste und zweite Ableitung der Entfernungs-

CBR

anhand der Schallgeschwindigkeit die Entfernung des Objekts

CBR

daten nach der Zeit und erhält so Geschwindigkeits- und Beschleunigungsinformationen. Diese Meßwerte speichert er in den Listen

L1, L2, L3

Es ist eine interessante Übung, die Berechnungen des

Sammeln Sie Beispieldaten im Modus

➊

REALTIME=NO

und L4.

selbst nachzuvollziehen.

CBR

. Verlassen Sie das

RANGER-

Programm.

Berechnen Sie anhand der erfaßten Zeiten in

➋

Entfernungsdaten in

die Geschwindigkeit des Objekts zu jedem Meßzeitpunkt.

Vergleichen Sie dann Ihre Ergebnisse mit den Geschwindigkeitsdaten in

(

Berechnen Sie anhand der Geschwindigkeitsdaten in L3 (oder der von Ihnen

➌

n+1

)à2 N (

n+1

berechneten Werten) und der zugehörigen Zeiten in

und der zugehörigen

)à2

n-1

die Beschleunigung des

Objekts zu jedem Meßzeitpunkt. Vergleichen Sie dann Ihre Ergebnisse mit den Beschleunigungsdaten in

Größe des Objekts

Die Verwendung eines kleinen Objekts in großer Entfernung vom

reduziert die

CBR

Wahrscheinlichkeit einer exakten Messung. Auch Sie können aus fünf Metern Entfernung eher einen Fußball als einen Golfball entdecken.

Minimalabstand

Wenn der wieder vom können aufeinanderfolgende Impulse sich überlagern und vom

einen Impuls aussendet, so trifft dieser auf ein Objekt, wird reflektiert und

CBR

empfangen. Ist das Objekt weniger als einen halben Meter entfernt, so

CBR

falsch identifiziert

CBR

werden. Da die Messung in diesem Fall falsch wäre, sollten Sie einen Mindestabstand von einem halben Meter zwischen dem

Maximalabstand

und dem Objekt einhalten.

CBR

Beim Fortpflanzen durch die Luft verliert der Impuls an Energie. Nach etwa zwölf Metern (sechs Meter vom Echo möglicherweise zu schwach, um vom beschränkt die typische zuverlässige Reichweite des

bis zum Objekt und sechs Meter Rückweg) ist das zurückkehrende

CBR

zuverlässig entdeckt zu werden. Dies

CBR

auf maximal sechs Meter.

CBR

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

Tips für effektive Messungen

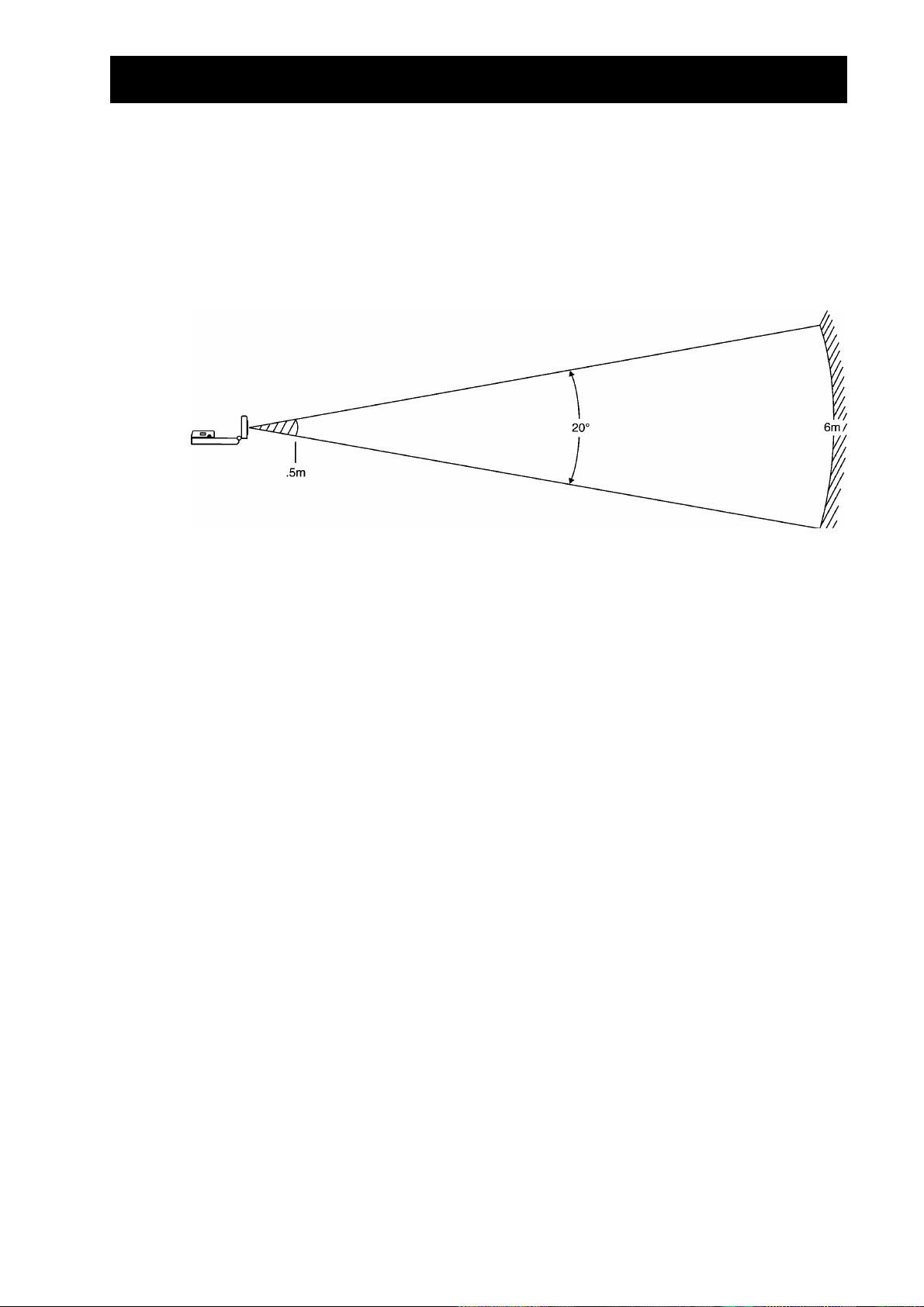
Der freie Bereich

(Forts.)

Der Impuls des

breitet sich nicht strahlförmig nur in eine Richtung aus, sondern

CBR

bildet einen Kegel mit einem Öffnungswinkel von 20°.

Um Interferenzen mit anderen Objekten in der Nähe zu vermeiden, sollte dieser Kegel möglichst ein freier Bereich ohne weitere Objekte sein. Dadurch wird gewährleistet, daß nur die Bewegungen des Zielobjekts vom

aufgezeichnet werden. Der

CBR

zeichnet

CBR

die Daten des nächstgelegenen Objekts im freien Bereich auf.

Reflektierende Oberflächen

Manche Oberflächen reflektieren Ultraschallimpulse besser als andere. Beispielsweise werden Sie mit einem vergleichsweise harten, glatten Ball bessere Ergebnisse erhalten als mit einem Tennisball. Im Gegenzug erhalten Sie bei Messungen in Räumen mit harten, gut reflektierenden Oberflächen wesentlich eher Ausreißer aufgrund von Streumessungen. Messungen an unregelmäßigen Oberflächen (z.B. Spielzeugautos oder umhergehende Personen) erscheinen möglicherweise unregelmäßig.

Wenn Sie den Abstand eines unbeweglichen Objekts über die Zeit auftragen, ergeben sich möglicherweise leichte Schwankungen in den berechneten Abstandswerten. Entspricht einer dieser Werte einem anderen Pixel als die anderen Werte, so zeigt die erwartete gerade Linie möglicherweise Ausreißer. Die Darstellung der Geschwindigkeit über die Zeit sieht dann vermutlich noch wesentlich unruhiger aus, da die Änderung des Abstands zwischen zwei Meßpunkten definitionsgemäß eine Geschwindigkeit impliziert. Sie sollten in diesem Fall eine gewisse Glättung der Meßwerte vornehmen.

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Tips für effektive Messungen

RANGER-Einstellungen

Meßzeiten

legt die gesamte Meßzeit in Sekunden fest. Geben Sie einen ganzzahligen Wert

TIME

zwischen 1 (für sich schnell bewegende Objekte) und 99 (für sich langsam bewegende Objekte) ein. Bei

REALTIME=YES

ist

TIME

(Forts.)

stets 15 Sekunden.

Bei kleinen Werten für

SECOND

Starten und Stoppen

Der

darf das Objekt maximal 1,75 Meter vom

-Bildschirm des

SETUP

muß sich das Objekt näher am

TIME

RANGER-

Programms bietet verschiedene Optionen für Start und

entfernt sein.

CBR

befinden. Für

CBR

Stop von Messungen.

BEGIN ON: [ENTER]

. Die Messung beginnt mit Drücken der Taste

des Taschen-

›

rechners. Diese Option ist geeignet, wenn die die Messung durchführende Person dem Taschenrechner näher als dem

BEGIN ON: [TRIGGER]

des

CBR

. Diese Option ist geeignet, wenn die die Messung durchführende Person dem

CBR

näher ist als dem Taschenrechner.

. Die Messung beginnt und endet mit Drücken der Taste

Bei dieser Option können Sie wahlweise auch die Verbindung zum können so die Messung einrichten, das Kabel vom mitnehmen und dort mittels wieder anschließen und mittels

BEGIN ON: [TRIGGER]

, wenn das Kabel nicht lang genug ist oder bei der Messung stören

›

würde. Diese Option ist im Modus

ist.

CBR

lösen. Sie

CBR

lösen, den

CBR

zur Meßstelle

CBR

die Messung starten, anschließend den

die Daten übertragen. Verwenden Sie daher

REALTIME=YES

(z.B. in der Anwendung

MATCH

verfügbar.

BEGIN ON: DELAY

. Startet die Messung 10 Sekunden nach dem Drücken von Diese Option ist besonders dann hilfreich, wenn die Messung von einer einzelnen Person durchgeführt wird.

TIME=1

CBR

›

) nicht

Trigger-Taste

Der Effekt der

DELAY

beginnt die Messung, auch wenn die Option

ausgewählt wurde. Sie können mit dieser Taste die Messung auch beenden,

-Taste hängt von den Einstellungen ab.

BEGIN ON: [ENTER]

oder

BEGIN ON:

aber normalerweise sollten Sie eine Messung bis zum Ende laufen lassen. Nach Beendung der Messung wiederholt

im Modus

REALTIME=NO

automatisch die letzte Messung, überträgt die Daten aber nicht zum Taschenrechner. Zum Übertragen der Daten wählen Sie im Menü

CBR DATA MENU

. (Sie können eine Messung auch wiederholen, indem Sie im Menü

den Eintrag

REPEAT SAMPLE

oder im

MAIN MENU

-Bildschirm den Befehl

SETUP

den Eintrag

TOOLS

und dann

PLOT

START NOW

wählen.)

GET

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

Tips für effektive Messungen

Glätten

(Forts.)

Die in das

RANGER-

Programm eingebauten Glättungsmöglichkeiten können die Auswirkungen von Streusignalen oder Variationen in Abstandsmessungen reduzieren. Vermeiden Sie jedoch exzessives Glätten. Beginnen Sie ohne oder mit nur leichter ( Glättung, und erhöhen Sie den Glättungsgrad, bis Sie zufriedenstellende Ergebnisse erhalten.

Bei einer Messung mit erhöhter Wahrscheinlichkeit von Streusignalen sollten Sie vor

Beginn der Messung den Glättungsgrad im Sie können auf bereits im Modus

REALTIME=NO

anwenden. Dazu muß der Taschenrechner mit dem im Menü

PLOT MENU

den Eintrag

PLOT TOOLS

-Bildschirm erhöhen (siehe Seite 38).

SETUP

erhobene Daten eine Glättung

verbunden sein. Wählen Sie

CBR

und dann

SMOOTH DATA,

und wählen Sie

den gewünschten Glättungsgrad.

Rauschen - Was ist das, und wie kann es vermieden werden?

Wenn der

Signale empfängt, die von einem anderen Objekt als dem Zielobjekt

CBR

reflektiert wurden, so zeigt die graphische Darstellung falsche Datenpunkte (Rauschspitzen), die nicht dem allgemeinen Muster des Diagramms entsprechen. Beachten Sie die folgenden Punkte, um das Rauschen zu minimieren:

Stellen Sie sicher, daß der

Messung im Modus

REALTIME=YES

erhalten, bevor Sie eine Messung im Modus Versuchen Sie nach Möglichkeit, die Messung in einem möglichst freien Umfeld

direkt auf das Ziel weist. Versuchen Sie, während einer

CBR

den Kopf so zu kippen, daß Sie gute Ergebnisse

REALTIME=NO

starten.

vorzunehmen (siehe die Skizze des freien Bereichs auf Seite 7). Wählen Sie ein größeres, stärker reflektierendes Objekt, oder bewegen Sie das Objekt

näher zum Werden in einem Raum mehrere

(aber keinesfalls näher als einen halben Meter).

CBR

verwendet, so sollte eine Gruppe ihre Messung

CBR

beenden, bevor die nächste Gruppe mit ihrer Messung beginnt. Wiederholen Sie verrauschte Messungen im Modus

REALTIME=YES

solange mit immer höheren Glättungsgraden, bis Sie befriedigende Ergebnisse erhalten. (In den Anwendungen

DISTANCE MATCH, VELOCITY MATCH

und

BALL BOUNCE

können Sie die

Glättung nicht ändern.) Bei verrauschten Messungen im Modus

REALTIME=NO

können Sie auf die Originaldaten

einen höheren Glättungsgrad anwenden.

LIGHT)

Schallgeschwindigkeit

Der Abstand zum Objekt wird anhand einer nominalen Schallgeschwindigkeit berechnet. Die tatsächliche Schallgeschwindigkeit hängt jedoch von verschiedenen Faktoren, insbesondere der Lufttemperatur ab. Für Messungen relativer Bewegung ist dieser Faktor nicht von Bedeutung. Sind jedoch hochgenaue Messungen vonnöten, so kann mit Hilfe eines Programmierbefehls die aktuelle Umgebungstemperatur spezifiziert werden (siehe Seite 40–41).

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Tips für effektive Messungen

REALTIME=YES

(Forts.)

Verwenden Sie den Modus

für langsamere Objekte

um die Ergebnisse bereits bei der Erfassung zu sehen

wenn Sie bei einer Messung nur einen Datentyp (Abstand, Geschwindigkeit oder

REALTIME=YES

Beschleunigung) erheben oder graphisch darstellen möchten.

Im Modus

REALTIME=YES

verarbeitet der

die gewünschten Daten für das Diagramm

CBR

(Abstand, Geschwindigkeit oder Beschleunigung) und überträgt diese nach jeder einzelnen Abstandsmessung an den Taschenrechner.

RANGER

zeichnet dann für diesen

Impuls ein einzelnes Pixel.

Die maximale Meßrate im Modus

REALTIME=YES

ist beschränkt, da alle diese Operationen

vor der nächsten Einzelmessung abgeschlossen sein müssen.

Das Messen, Verarbeiten und Übertragen dauert für einen Datenpunkt ca. 0,08 Sekunden. Für Operationen wie das Zeichnen des Punktes wird zusätzliche Zeit benötigt, wodurch die effektive Meßrate im

RANGER

auf eine Messung in ca. 0,125 Sekunden

sinkt.

REALTIME=NO

Verwenden Sie den Modus

für schnellere Objekte

wenn Glättung benötigt wird (siehe Seite 9)

um den

wenn Sie alle Datentypen (Abstand, Geschwindigkeit und Beschleunigung) eines

im nicht angeschlossenen Modus zu betreiben (siehe Seite 11)

CBR

REALTIME=NO

Vorgangs erfassen oder graphisch darstellen möchten.

Im Modus

REALTIME=NO

werden die Daten im

gespeichert und erst nach vollendeter

CBR

Messung an den Taschenrechner übertragen. Die Meßrate kann für nahe Objekte bis auf eine Messung in 0,005 Sekunden ansteigen. Anschließend werden die Daten für die Zeit, den Abstand (Weg), die Geschwindigkeit und die Beschleunigung an den Taschenrechner übertragen.

Da die Daten im

gespeichert sind, können Sie diese immer wieder an den Taschen-

CBR

rechner übertragen.

Bei jeder Änderung der Glättung wendet der

den neuen Glättungfaktor an, über-

CBR

trägt die geglätteten Werte an den Taschenrechner und speichert die geglätteten Werte in den Listen.

Wenn Sie einen Bereich auswählen, werden die im Taschenrechner gespeicherten

Listen verändert. Bei Bedarf können Sie die Originaldaten vom Wählen Sie dazu im Menü dann

GET CBR DATA

Sie können Daten auch mit anderen gemeinsam nutzen, selbst wenn Sie verschiedene

MAIN MENU

des

RANGER-

Programms den Befehl

wiederherstellen.

CBR

TOOLS

und

graphische TI-Taschenrechner verwenden. Dadurch können alle Schüler mit den gleichen Daten an der Datenanalyse teilnehmen (siehe Seite 11).

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

Tips für effektive Messungen

(Forts.)

Verwendung des CBR im nicht angeschlossenen Modus

Da der

im nicht angeschlossenen Modus die Daten nicht direkt an den Taschen-

CBR

rechner übertragen kann, sind gewisse Einstellungen notwendig. Nehmen Sie diese im

-Bildschirm vor:

SETUP

Setzen Sie

Das

RANGER-

REALTIME=NO BEGIN ON=[TRIGGER]

Programm informiert Sie, wann Sie die Verbindung mit dem wann Sie diese wiederherstellen sollen. Dazu sind keine weiteren speziellen Vorgehensweisen vonnöten.

Gemeinsame Nutzung von Daten

Wie gehen Sie vor, wenn die ganze Klasse zur gleichen Zeit die gleichen Daten auswerten soll? Mit dem

CBR

in der Klasse zu verteilen.

Übertragen Sie vor der Datenerfassung das

➊

Taschenrechner der Schüler.

Erheben Sie die Daten im Modus

➋

Lassen Sie den ersten Schüler seinen Taschenrechner mit Hilfe des

➌

Verbindungskabels für den anschließen.

ist es möglich, im Modus

RANGER-

REALTIME=NO

oder einen anderen Taschenrechner an den

CBR

REALTIME=NO

Programm auf alle

lösen und

CBR

erhobene Daten schnell

CBR

Wählen Sie im Menü

➍

Sie im Menü

TOOLS

MAIN MENU

den Eintrag

des

RANGER-

GET CBR DATA

Programms den Befehl

. Es wird nun

TRANSFERRING...

TOOLS

. Wählen

angezeigt

und die graphische Darstellung aufgebaut.

Drücken Sie ›, um zum Menü

➎

. Lösen Sie das Kabel.

QUIT

Verbinden Sie einen anderen Taschenrechner (des gleichen Typs) mit dem Taschen-

➏

PLOT MENU

zurückzukehren, und wählen Sie dann

rechner, der die Daten bereits erhalten hat. Wählen Sie auf dem zweiten Taschenrechner im Menü

GET CALC DATA

. Die Listen L1, L2, L3, L4 und L5 werden nun automatisch auf den

MAIN MENU

des

RANGER-

Programms den Befehl

TOOLS

und dann

zweiten Taschenrechner übertragen.

Übertragen Sie die Daten vom

➐

auf den Taschenrechner eines anderen Schülers,

CBR

während die Schüler die Übertragungen zwischen den Taschenrechnern vornehmen.

Haben alle Schüler die gleichen Daten erhalten, können sie diese im mittels

PLOT MENU

oder außerhalb des

RANGER-

Programms mit Hilfe der Graphik- und

RANGER-

Programm

Listenfunktionen des Taschenrechners analysieren.

Zur gemeinsamen Nutzung von Daten auf dem TI-85 verwenden Sie außerhalb des

RANGER-

Programms das Feature

zum Übertragen der Listen.

LINK

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Tips für effektive Messungen

Weitergehende Möglichkeiten

(Forts.)

Nachdem Sie die Daten erhoben und mittels

RANGER

graphisch dargestellt haben, können Sie deren Beziehung zu einer Funktion untersuchen. Da die Daten in Listen gespeichert und als statistische Diagramme dargestellt werden, können Sie diese Beziehung mittels

Innerhalb des RANGER-Programms

Untersuchen der Diagramme im automatisch gesetzten

,  und œ erforschen.

TRACE-

Modus (beim TI-85

verwenden Sie den frei positionierbaren Cursor). Manipulieren des Datensatzes durch Glätten oder Auswahl eines interessierenden

Bereichs.

Außerhalb des RANGER-Programms

Untersuchen der Daten mit Hilfe des Listeneditors des Taschenrechners.

Manuelles Anpassen einer Funktion an die Daten mit Hilfe des Y=-Editors des

Taschenrechners. Automatische Bestimmung der den Daten am ehesten entsprechenden Gleichung mit

Hilfe der Regressionsfunktionen des Taschenrechners.

Weiterhin können mit Hilfe der Zeichenoptionen des Programms

RANGER

weitergehende Beziehungen erforscht werden. So können Sie beispielsweise simultan ein Weg/ZeitDiagramm und ein Geschwindigkeit/Zeit-Diagramm als statistische Diagramme darstellen. Wählen Sie dazu im Menü Sie dann

als L1 gegen L2 und

Plot1

MAIN MENU

Plot2

des Programms

RANGER

als L1 gegen L3. (Möglicherweise müssen Sie die

den Befehl

QUIT

; setzen

Fenstereinstellungen anpassen.)

Mit Hilfe von TI-Graph Link können Daten und Diagramme an einen Computer übertragen werden. Diese Möglichkeit ist besonders dann von Nutzen, wenn anhand der erhobenen Daten ausführlichere Berichte erstellt werden sollen.

Verwendung des CBR ohne das RANGER-Programm

Sie können den Programmen als

Informationen über die Verwendung des

Informationen zu Bezugsquellen für andere Programme finden Sie auf Seite 36.

Informationen zu den Programmierbefehlen zum Erstellen eigener Programme finden

als Ultraschall-Bewegungsdetektor mit dem

CBR

RANGER

verwenden.

Sie auf den Seiten 40–41.

mit dem

CBR

oder mit anderen

CBL

finden Sie auf Seite 39.

CBL

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

Experiment 1 - Graph treffen Didaktische Hinweise

Konzepte

Untersuchte Funktion: linear.

MATCH

führt in die Konzepte von Weg und Zeit -

oder genauer in das Konzept von Weg gegen Zeit ein. Das Konzept der Position wird untersucht, wenn die Schüler versuchen, beim Umhergehen und Auftragen ihrer Bewegung Übereinstimmung mit einem Graphen herzustellen.

Bei den Untersuchungen sollen die Schüler ihre Gehgeschwindigkeit von Meter pro Sekunde in Kilometer pro Stunde umrechnen.

Nachdem die Schüler die Abstand/Zeit-Aufgabe bewältigt haben, können Sie Ihnen die Geschwindigkeit/Zeit-Aufgabe stellen.

Materialien

 Taschenrechner

CBR

  Verbindungskabel

Mit Hilfe eines TI ViewScreené können die anderen Schüler zuschauen - und das Experiment wird sehr viel amüsanter.

Tips

Schüler lieben dieses Experiment. Planen Sie ausreichend Zeit ein, denn jeder wird es durchführen wollen!

Das Experiment funktioniert am besten, wenn der es durchführende Schüler (und die gesamte Klasse) die mit Hilfe des TI ViewScreen an die Wand projizierte Bewegung des Schülers verfolgen kann.

Weisen Sie die Schüler darauf hin, sich auf einer Linie mit dem CBR zu bewegen. Manchmal neigen Schüler dazu, sich seitwärts zu bewegen oder sogar hochzuspringen!

Auf den Seiten 6–12 finden Sie Tips für effektive Messungen.

Typische Diagramme

Typische Antworten

1. Zeit (vom Beginn der Meßsequenz); Sekunden; 1 Sekunde; Abstand (vom CBR zum Objekt); Meter; 1 Meter

2. Der Anfangsabstand wird durch den YAchsenabschnitt definiert

3. Variiert je nach Schüler

4. Zurück (vergrößert den Abstand zwischen dem CBR und dem Objekt)

5. Vorwärts (vermindert den Abstand zwischen dem CBR und dem Objekt)

6. Stehenbleiben. Eine Steigung von 0 bedarf keiner Änderung des y-Wertes (Abstand)

7. Variiert je nach Graph; @yà3,3

8. Variiert je nach Graph; @yà1

9. Beim Segment mit der größten Steigung (positiv oder negativ)

10. Das ist eine Fangfrage - beim konstanten Segment, da hier überhaupt keine Bewegung stattfindet!

11. Gehgeschwindigkeit; Zeitpunkt des Richtungsund Geschwindigkeitswechsels

12. Geschwindigkeit

13. Variiert je nach Graph (Beispiel: 1,5 Meter in 3 Sekunden)

14. Variiert je nach Graph (Beispiel: 0,5 Meter je Sekunde)

Beispiel: (0,5 Meterà1 Sekunde) Q (60 Sekundenà1 Minute) = 30 MeteràMinute

Beispiel: (30 Meterà1 Minute) Q (60 Minutenà1 Stunde) = 1800 MeteràStunde

Beispiel: (1800 Meterà1 Stunde) Q (1 Kilometerà 1000 Meter) = 1,8 KilometeràStunde.

Lassen Sie die Schüler die letzte Zahl mit der Geschwindigkeit eines Autos (z.B. 100 Kilometer/Stunde) vergleichen.

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

15. Variiert je nach Graph; Summe der @y der einzelnen Liniensegmente.

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Experiment 1 - Graph treffen linear

Datenerfassung

Halten Sie den

➊

in einer Hand und den Taschenrechner in der anderen. Richten

CBR

Sie den Sensor direkt gegen eine Wand.

vier Meter, der

Für jeden Graphen beträgt der maximale Abstand vom

Tips:

CBR

minimale Abstand einen halben Meter. Achten Sie darauf, daß sich im freien Bereich (siehe Seite 7) keine Objekte befinden.

Starten Sie das

➋

RANGER-

Programm (auf Seite 5 finden Sie die Tasteneingaben für die

verschiedenen Taschenrechner).

Wählen Sie aus dem Menü

➌

Wählen Sie aus dem Menü

➍

allgemeine Anweisungen angezeigt.

MAIN MENU

APPLICATIONS

den Eintrag

APPLICATIONS

den Eintrag

DISTANCE MATCH

und dann

DISTANCE MATCH

. Nun werden

kümmert sich automatisch um

die Einstellungen.

Drücken Sie ›, um den zur Übereinstimmung zu bringenden Graphen

➎

anzuzeigen. Nehmen Sie sich einen Moment Zeit, den Graphen zu studieren.

Beantworten Sie die Fragen 1 und 2 des Arbeitsblattes.

Stellen Sie sich an die Stelle, von der Sie annehmen, daß der Graph dort beginnt.

➏

Drücken Sie

›, um mit der Meßsequenz zu beginnen.Während der Meßsequenz

hören Sie ein klickendes Geräusch und sehen das grüne Licht leuchten.

Gehen Sie vor und zurück, und versuchen Sie, den Graphen zur Übereinstimmung

➐

zu bringen. Ihre Position wird auf dem Bildschirm aufgezeichnet.

Untersuchen Sie nach Ende der Meßsequenz, wie gut Sie den Graphen getroffen

➑

haben, und beantworten Sie dann Frage 3.

Drücken Sie ›, um das Menü

➒

SAME MATCH

. Versuchen Sie, Ihre Gehtechnik zu verbessern, und beantworten Sie

OPTIONS

aufzurufen, und wählen Sie den Eintrag

dann die Fragen 4, 5 und 6.

METERS

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

Experiment 1 - Graph treffen

Untersuchungen

(Forts.)

linear

Im Programm

Drücken Sie ›, um das Menü

➊

NEW MATCH

DISTANCE MATCH

. Untersuchen Sie das erste Segment, und beantworten Sie die Fragen

7 und 8.

Untersuchen Sie den gesamten Graphen, und beantworten Sie die Fragen 9

➋

und 10.

Stellen Sie sich an die Stelle, von der sie annehmen, daß der Graph dort beginnt.

➌

Drücken Sie

›, um die Meßsequenz zu starten, und versuchen Sie, den Graphen

zur Übereinstimmung zu bringen.

Nach dem Ende der Meßsequenz beantworten Sie die Fragen 11 und 12.

➍

Drücken Sie ›, um das Menü

➎

NEW MATCH

Untersuchen Sie den Graphen, und beantworten Sie die Fragen 13, 14 und 15.

➏

Drücken Sie ›, um das Menü

➐

Wunsch das Experiment, oder kehren Sie zum Menü Sie dort

zum Verlassen des

QUIT

Weitergehende Untersuchungen

Die von Sie nun

DISTANCE MATCH

VELOCITY MATCH

keit/Zeit-Diagramm herstellen, was wesentlich schwieriger ist.

bestehen alle Graphen aus drei geradlinigen Segmenten.

OPTIONS

RANGER-

aufzurufen, und wählen Sie den Eintrag

aufzurufen. Wiederholen Sie je nach

MAIN MENU

zurück, und wählen

Programms.

erzeugten Graphen bestanden aus geraden Linien. Versuchen

. Hier müssen Sie Übereinstimmung mit einem Geschwindig-

MATCH

ist ein sehr populäres Programm. Möglicherweise sind bereits zusätzliche Versionen verfügbar, mit denen kompliziertere Graphen untersucht werden (siehe Seite 36).

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Experiment 1 - Graph treffen

Name ____________________________________

Datenerhebung

1. Welche physikalische Größe wird auf der X-Achse aufgetragen? ______________________________

Welche Einheit wird verwendet? Wie ist der Abstand der Skalenmarkierungen? ____

Welche physikalische Größe wird auf der Y-Achse aufgetragen? ______________________________

Welche Einheit wird verwendet? Wie ist der Abstand der Skalenmarkierungen? ____

2. Wie weit entfernt vom

sollten Sie Ihrer Meinung nach zu Beginn stehen? ___________________

CBR

3. Standen Sie zu Beginn zu nah, zu weit oder genau richtig? ___________________________________

4. Sollten Sie bei einem steigenden Segment vor oder zurück gehen? ____________________________

Warum? _____________________________________________________________________________

5. Sollten Sie bei einem fallenden Segment vor oder zurück gehen? ______________________________

Warum? _____________________________________________________________________________

6. Wie sollten Sie sich bei einem konstanten Segment verhalten? ________________________________

Warum? _____________________________________________________________________________

Untersuchungen

7. Wie lang sollte ein Schritt sein, wenn Sie jede Sekunde einen Schritt machen? ___________________

8. Wieviele Schritte müssen Sie machen, wenn Sie stattdessen Schritte von

einem Meter (oder 25 cm) machen? ______________________________________________________

9. Bei welchem Segment müssen Sie sich am schnellsten bewegen? _____________________________

Warum? _____________________________________________________________________________

10. Bei welchem Segment müssen Sie sich am langsamsten bewegen?_____________________________

Warum? _____________________________________________________________________________

11. Welche weiteren Faktoren (neben der Entscheidung für eine Bewegung vorwärts oder rückwärts) fließen bei einer exakten Übereinstimmung mit dem Graphen ein? ____________________________

_____________________________________________________________________________________

12. Welche physikalische Größe repräsentiert die Steigung (bzw. der Abfall) eines Liniensegments?

_____________________________________________________________________________________

13. Wieviele Meter müssen Sie in wievielen Sekunden für das erste Liniensegment gehen? ___________

14. Wandeln Sie den Wert aus Frage 13 (die Geschwindigkeit) in Meter

Wandeln Sie den Wert in Meter

Wandeln Sie den Wert in Kilometer

àMinute um: ______________________________________________

Stunde um: ______________________________________________

Stunde um: ___________________________________________

àSekunde um: _______________

15. Welchen Weg haben Sie tatsächlich zurückgelegt? _________________________________________

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

Experiment 2 - Spielzeugauto Didaktische Hinweise

Konzepte

Untersuchte Funktion: linear. Das Konzept der konstanten Geschwindigkeit wird

anhand der Bewegung eines motorisierten Spielzeugautos illustriert.

Materialien

 Taschenrechner

CBR

  Verbindungskabel  Batteriebetriebenes Spielzeugauto  TI ViewScreen (optional)

Hinweise

Spielzeugautos unterscheiden sich in Größe, Form und Reflexionswinkel des auftreffenden Ultraschalls. Die sich ergebenden Diagramme können daher in ihrer Qualität variieren. Für manche Autos ist möglicherweise eine zusätzliche reflektierende Fläche anzubringen, um gute Ergebnisse zu erhalten. Versuchen Sie, eine Karteikarte an dem Auto zu befestigen, um ein gutes Ziel für den Sensor zu garantieren.

Sie sollten mehrere dieser Spielzeugautos ausprobieren, damit die Schüler diese Effekte untersuchen können.

Langsamere Spielzeugautos (für jüngere Kinder) sind für dieses Experiment besser geeignet. Suchen Sie nach einem Auto mit annähernd konstanter Geschwindigkeit.

Auf den Seiten 6–12 finden Sie Tips für effektive Messungen.

Untersuchungen

Die Steigung im Weg/Zeit-Diagramm eines beliebigen Objekts gibt dessen Geschwindigkeit zum jeweiligen Zeitpunkt an. Für ein sich mit konstanter Geschwindigkeit bewegendes Objekt ist daher die Steigung des Weg/Zeit-Diagramms konstant. Das Weg/Zeit-Diagramm zeigt damit eine lineare Beziehung.

Wenn Sie vor Beginn der Bewegung des Autos mit der Meßsequenz beginnen, werden Sie festellen, daß das Weg/Zeit-Diagramm zu Beginn nicht linear ist. Warum? Die Bewegung des Autos beginnt aus dem Stillstand (v = 0), und es kann nicht sofort seine konstante Geschwindigkeit erreichen. Die Beschleunigung ergibt sich zu:

∆

unendliche Beschleunigung nur aus einer unendlichen, physikalisch ebenfalls unmöglichen Kraft resultieren.) Daher stellen wir in einem bestimmten Zeitraum eine Beschleunigung des Objekts auf seine konstante Geschwindigkeit fest.

Typische Diagramme

Antworten auf die Fragen

1. Das erste oder das letzte Diagramm; der Weg steigt mit einer konstanten Rate an.

TRACE

2. Die Schüler sollen die mittels

ermittelten

Werte eintragen.

3. Die Weg-Werte werden um einen konstanten Betrag größer.

4. Geschwindigkeit ist die Änderungsrate des Wegs über die Zeit; die Werte sind für jedes gleiche Zeitintervall die gleichen.

5. Die Schüler sollten einen Wert ähnlich dem für m berechneten Wert erhalten.

Ähnlich zu m. m steht für die Geschwindigkeit des Autos.

6. b ist der Y-Achsenabschnitt; Beispiel: y = 2x + 0

7. Variiert; ist m beispielsweise = 2, so gilt Weg (y) = 20 Meter nach 10 Sekunden (y = 2 × 10 + 0); für eine Minute gilt y = 120 Meter.

Weitergehende Untersuchungen

Die Steigung des Geschwindigkeit/Zeit-Diagramms ist bei konstanter Geschwindigkeit gleich Null. Das Beschleunigung/Zeit-Diagramm sollte daher (im Idealfall) während der konstanten Geschwindigkeit a = 0 zeigen.

Die Fläche entspricht der Verschiebung des Objekts (tatsächlich zurückgelegte Entfernung) im Zeitintervall von t

Sofern den Schülern die Integralrechnung bereits bekannt ist, kann diese Verschiebung folgendermaßen berechnet werden:

bis t2.

svdt

∫

Damit das Objekt unmittelbar aus dem Stand seine konstante Geschwindigkeit erreicht, müßte ∆t = 0 gelten. Dies jedoch bedingt eine unendliche, physikalisch unmögliche Beschleunigung. (Nach dem zweiten Newtonschen Gesetz (F = ma) könnte eine

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

wobei s die Verschiebung des Objekts im Zeitintervall von t

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

bis t2 ist.

CBR

Experiment 2 - Spielzeugauto linear

Datenerfassung

Positionieren Sie das Auto mindestens einen halben Meter so vom

➊

es vom

Tips:

in einer geraden Linie wegweist.

CBR

Zielen Sie mit dem Sensor direkt auf das Auto, und stellen Sie sicher, daß sich

keine Objekte im freien Bereich (siehe Seite 7) befinden.

Bevor Sie mit der Messung beginnen, beantworten Sie die Frage 1 des

➋

Arbeitsblatts.

Starten Sie das

➌

RANGER-

Programm (auf Seite 5 finden Sie die Tasteneingaben für die

verschiedenen Taschenrechner).

Wählen Sie aus dem Menü

➍

MAIN MENU

den Eintrag

SETUPàSAMPLE

Experiment gelten folgende Einstellungen:

entfernt, daß

CBR

. Für dieses

REALTIME: NO

TIME (S): 5 SECONDS

DISPLAY: DISTANCE

BEGIN ON: [ENTER]

SMOOTHING: LIGHT

UNITS: METRES

Anweisungen zum Ändern der Einstellungen finden Sie auf Seite 38.

Wählen Sie

➎

Wenn Sie soweit sind, drücken Sie ›. Starten Sie das Auto, und entfernen Sie

➏

START NOW

sich aus dem freien Bereich. Während der Datenerfassung hören Sie ein klickendes Geräusch; auf dem Taschenrechner wird

Nach Ende der Meßsequenz zeigt der Taschenrechner automatisch ein Weg/Zeit-

➐

TRANSFERRING...

angezeigt.

Diagramm der gesammelten Datenpunkte an.

Vergleichen Sie das Diagramm mit Ihrer Vorhersage aus Frage 1, und bestimmen

➑

Sie Ähnlichkeiten und Unterschiede.

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

Experiment 2 - Spielzeugauto

Untersuchungen

In der Tabelle zu Frage 2 stehen in der ersten Spalte die Werte für x (Zeit) in

➊

Halbsekundenintervallen. Verfolgen Sie das Diagramm, und geben Sie in die zweite Spalte die entsprechenden y-Werte (Abstand, Weg) ein.

Anmerkung:

Möglicherweise müssen Sie inkonsistente Daten vom Beginn der Messung ignorieren. Außerdem müssen Sie den Abstand möglicherweise annähern (der Taschenrechner gibt Ihnen möglicherweise keinen Wert für exakt die erste Sekunde, sondern einen für 0,957 und einen für 1,01 Sekunden). Nehmen Sie den nächstgelegenen Wert oder eine gute Mittelung.

➋

Beantworten Sie die Fragen 3 und 4.

Berechnen Sie die Änderungen im Weg und in der Zeit zwischen den einzelnen

➌

Datenpunkten, um die dritte und die vierte Spalte auszufüllen. Um beispielsweise @Weg (Meter) für 1,5 Sekunden zu berechnen, subtrahieren Sie den Weg für 1 Sekunde von dem Wert für 1,5 Sekunden.

Die in diesem Experiment illustrierte Funktion lautet y = mx + b. m ist die Steigung

➍

einer Gerade und wird folgendermaßen berechnet:

Geben Sie nur die Werte aus dem linearen Teil des Diagramms ein.

(Forts.) linear

Der Y-Achsenabschnitt repräsentiert b.

Berechnen Sie m für jeden Punkt. Geben Sie die Werte in die Tabelle zu Frage 2

ein.

➎

Beantworten Sie die Fragen 5, 6 und 7.

Weitergehende Untersuchungen

Die Berechnung der Steigung in einem Entfernung/Zeit-Diagramm zu einem beliebigen Zeitpunkt ergibt die ungefähre Geschwindigkeit des Objekts zu diesem Zeitpunkt. Die Berechnung der Steigung eines Geschwindigkeit/Zeit-Diagramms ergibt die ungefähre Beschleunigung des Objekts zu diesem Zeitpunkt. Welche Beschleunigung ergibt sich bei konstanter Geschwindigkeit?

Welches Beschleunigung/Zeit-Diagramm erwarten Sie für dieses Entfernung/ZeitDiagramm?

Bestimmen Sie für zwei sinnvolle Zeitpunkte t Geschwindigkeit/Zeit-Diagramm und der X-Achse. Diese ergibt sich beispielsweise als Summe der Flächen eines oder mehrerer Rechtecke, deren Fläche sich folgendermaßen berechnet:

@Weg @Zeit

oder

Weg Zeit

N Weg

N Zeit

oder

und t2 die Fläche zwischen dem

N y

x2 N x

Fläche= v∆t = v(t

Welche physikalische Größe repräsentiert die sich ergebende Fläche?

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

)

2Nt1

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Experiment 2 - Spielzeugauto

Name _________________________________

Datenerfassung

1. Welches der folgenden Diagramme erwarten Sie als Entfernung/Zeit-Diagramm des Spielzeugautos?

Warum?______________________________________________________________________________

Zeit Weg

1 xxx xxx xxx

1.5 2

2.5 3

3.5 4

4.5 5

Weg

Zeit

3. Was fällt Ihnen bei den Weg-Werten auf? _________________________________________________

4. Wie erkennt man aus diesen Ergebnissen, daß sich das Spielzeugauto mit konstanter

Geschwindigkeit bewegte?______________________________________________________________

5. Berechnen Sie

= @

zwischen Zeit = 2 und Zeit = 4. ______________________________

Wegà@Zeit

Was fällt Ihnen bei diesem Ergebnis auf? __________________________________________________

Wofür steht Ihrer Meinung nach

6. Welchen Wert hat

in der linearen Gleichung y = mx + b? __________________________________

? ______________________________________________________

Notieren Sie die Gleichung für die Gerade in der Form

= mx + b mit Werten für m und b.________

7. Wie weit wird sich das Spielzeugauto in 10 Sekunden bewegen? _____________________________

In einer Minute? ______________________________________________________________________

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

Experiment 3 - Pendel Didaktische Hinweise

Konzepte

Untersuchte Funktion: sinusförmig. Untersuchung einer einfachen harmonischen

Bewegung durch Beobachtung eines frei schwingenden Pendels.

Materialien

 Taschenrechner

CBR

  Verbindungskabel  Befestigungsschelle  Stoppuhr  Pendel  Metermaß  TI ViewScreen (optional)

Vorschläge für Gewichte:

Bälle verschiedener Größe (Durchmesser ≥ 5 cm).

Getränkedosen (leere und volle).

Sandsäckchen

Hinweise

Auf den Seiten 6–12 finden Sie Tips für effektive Messungen.

Physikalische Zusammenhänge

Die periodische Bewegung eines der Auslenkung von der Ruheposition proportionale Rückstellkraft erfahrenden Objekts wird als einfache harmonische Schwingung bezeichnet. Sie kann durch zwei Größen beschrieben werden:

Die Periode T ist die Dauer eines vollständigen

Zyklus. Die Amplitude A ist die maximale Auslenkung des

Objekts aus seiner Ruheposition.

Bei einem einfachen Pendel ergibt sich die Periode T wie folgt:

T = 2p

wobei L die Länge des Fadens und g die Erdbeschleunigung (die durch die Erdanziehung hervorgerufene Beschleunigung) ist. T hängt weder von der Masse des Objekts noch von der Amplitude seiner Bewegung ab.

Die Frequenz f (Anzahl vollständiger Zyklen je Sekunde) ergibt sich wie folgt:

f =

, (f in Hertz (Hz), T in Sekunden)

Die Ableitungen sinusförmiger Funktionen sind wiederum sinusförmig. Beachten Sie insbesondere die Phasenbeziehung zwischen Position und Geschwindigkeit des Gewichts.

Typische Diagramme

Typische Antworten

1. variiert (in Meter)

2. variiert (in Meter)

3. variiert (in Sekunden); T (eine Periode) = Gesamtdauer von 10 Zyklenà10; die Mittelwertbildung über einen längeren Zeitraum reduziert Meßfehler.

4. Die Gesamtlänge des Kreisbogens, welche etwa das Vierfache der Antwort zu Frage 2 ist; weil ein Kreisbogen länger ist als eine gerade Linie.

5. sinusförmig, wiederholend, periodisch; Abstand von der X-Achse zur Ruheposition

6. Jeder Zyklus wird horizontal gedehnt; ein über 10 Sekunden gehendes Diagramm muß im gleichen Bildschirmplatz mehr Zyklen darstellen, daher erscheinen die Zyklen näher beieinander.

7. (Gesamtzahl der Zyklen)à(5 Sekunden) = ZyklenàSekunde; es ist leichter, ganze Zyklen zu erkennen, und es gibt weniger Meßfehler

8. f = 1àT, wobei T die Zeit für einen Zyklus ist.

9. verkürzte Periode, verlängerte Periode (Die Periodendauer hängt unmittelbar mit der

Länge des Pendels zusammen: je länger das Pendel, desto länger die Periode. Die Schüler können diesen Zusammenhang mit Hilfe des Listeneditors des Taschenrechners ermitteln, wo sie die Periode für verschiedene Werte von L berechnen können)

10. A (Amplitude) = ¼ des vom Pendel in einem Zyklus zurückgelegten Wegs.

11. Beide sind sinusförmig; Unterschiede bestehen in Amplitude und Phase.

12. In der Ruheposition

13. Wenn die Position den größten oder kleinsten Wert hat (wenn das Gewicht seine größte Entfernung von der Ruheposition hat).

14. Keine Auswirkungen. T hängt nur von L und g ab, nicht jedoch von der Masse.

Weitergehende Untersuchungen

Datenerfassung: Das Diagramm von L2 gegen L3 bildet eine Ellipse.

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Experiment 3 - Pendel sinusförmig

Datenerfassung

Bauen Sie das Pendel auf. Richten Sie das Pendel so aus, daß es in einer direkten

➊

Linie mit dem

schwingt.

CBR

Hinweise:

Positionieren Sie den

mindestens einen halben Meter von der

CBR

nächstliegenden Position des Gewichts entfernt. Achten Sie darauf, daß sich keine Objekte im freien Bereich (siehe Seite 7) befinden.

Amplitude

Ruheposition

Bestimmen Sie mit Hilfe eines Metermaßes die Entfernung zwischen dem

➋

der Ruheposition. Beantworten Sie die Frage 1 des Arbeitsblatts. Messen Sie, wie weit Sie das Gewicht aus der Ruheposition auslenken werden.

Beantworten Sie die Frage 2.

CBR

und

Ein Pendelzyklus besteht aus einem vollständigen Hin- und Zurückschwingen.

➌

Bestimmen Sie mit Hilfe einer Stoppuhr die Dauer von zehn vollständigen Zyklen. Beantworten Sie die Fragen 3 und 4.

Starten Sie das

➍

RANGER-

Programm (auf Seite 5 finden Sie die Tasteneingaben für die verschiedenen Taschenrechner). Am effizientesten ist es, wenn einer das Pendel startet, während ein anderer den Taschenrechner und den im Menü

Drücken Sie ›, um die Einstellungen anzuzeigen. Für dieses Experiment gelten

➎

MAIN MENU

den Eintrag

SETUPàSAMPLE

bedient. Wählen Sie

CBR

folgende Einstellungen:

REALTIME: NO

TIME (S): 10 SECONDS

DISPLAY: DISTANCE

BEGIN ON: [ENTER]

SMOOTHING: LIGHT

UNITS: METRES

Anweisungen zum Ändern der Einstellungen finden Sie auf Seite 38. Stimmen die

➏

Einstellungen, so wählen Sie Wenn Sie bereit sind, drücken Sie ›. Während der Datenerfassung hören Sie ein

➐

START NOW

klickendes Geräusch; auf dem Taschenrechner wird Nach Ende der Meßsequenz zeigt der Taschenrechner automatisch ein

➑

TRANSFERRING...

angezeigt.

Entfernung/Zeit-Diagramm der gesammelten Daten an. Beantworten Sie die

Frage 5.

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

Experiment 3 - Pendel

Untersuchungen

Meßsequenz 2

(Forts.)

sinusförmig

Wählen Sie im Menü Bildschirm die Zeit von 10 auf 5 Sekunden. Wiederholen Sie die Meßsequenz. Untersuchen Sie das Diagramm. Beantworten Sie die Fragen 6 und 7.

Der von Ihnen bestimmte Meßwert (Zyklen je Sekunde) wird als Frequenz bezeichnet. Während Sie die Frequenz in Frage 7 mit Hilfe des Diagramms ermittelt haben, können Sie diese auch folgendermaßen mathematisch bestimmen:

wobei T die Periode in Sekunden und f die Frequenz in Hertz (Hz) ist.

f =

Beantworten Sie die Frage 8.

Meßsequenzen 3 und 4

Wiederholen Sie die 5-Sekunden-Meßsequenz zwei weitere Male. Kürzen Sie zunächst den Faden, und verlängern Sie ihn dann. Beantworten Sie nach Untersuchung der

Diagramme die Frage 9.

Eine weitere wichtige die Bewegung des Pendels beschreibende Meßgröße ist die Amplitude. Die Antwort zu Frage 2 war die Amplitude dieses Pendelschwungs.

Beantworten Sie die Frage 10.

Weitergehende Untersuchungen

Meßsequenz 5

MAIN MENU

den Eintrag

SETUPàSAMPLE

. Ändern Sie im

SETUP

Wählen Sie im Menü

PLOT MENU

den Eintrag

VELOCITY-TIME

. Beantworten Sie die

Fragen 11, 12 und 13.

Meßsequenz 6

Wiederholen Sie die Meßsequenz mit einem deutlich schwereren oder leichteren Gewicht, und beantworten Sie dann die Frage 14.

Modellieren Sie das Abstand/Zeit-Verhalten des Pendels mit Hilfe der Formel für eine sinusförmige Funktion: S = A sin (

die Kreisfrequenz, d den Phasenwinkel und t die Zeit bezeichnet. Die

Amplitude, Kreisfrequenz

ergibt sich folgendermaßen aus der Periode T:

t + d), wobei S die aktuelle Position, A die

= 2 pàT.

Geben Sie diese Gleichung mit den berechneten Werten für A und w in den Y= Editor ein. Stellen Sie diese Funktion und das statistische Diagramm von

(Zeit) gegen

(Abstand) simultan dar. Ändern Sie die Werte für A, w und d, bis Sie eine gute Übereinstimmung erhalten. Verwenden Sie auf dem TI-83 oder TI-86 zur Bestimmung dieser Werte eine sinusartige Regression.

Untersuchen Sie das Verhältnis zwischen Position und Geschwindigkeit, indem Sie

(Abstand) gegen L3 (Geschwindigkeit) graphisch darstellen. Welches Aussehen erwarten Sie von dem sich ergebenden Diagramm? Vergleichen Sie das tatsächliche Ergebnis mit Ihren Erwartungen.

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Experiment 3 - Pendel

Datenerfassung

Name ____________________________________

1. Wie groß ist der Abstand vom

zur Ruheposition? _______________________________________

CBR

2. Wie weit werden Sie das Pendel aus der Ruheposition entfernen? _____________________________

3. Wie lange dauerten zehn Zyklen? ________________________________________________________

Bestimmen Sie die Dauer eines vollständigen Zyklus (in Sekunden)._____________________________

Welchen Vorteil bringt es, zehn Zyklen statt nur einen zu stoppen? ____________________________

4. Schätzen Sie unter Verwendung der Antwort zu Frage 2 den in einem Zyklus zurückgelegten Gesamtweg. __________________________________________________________________________

Warum ist dieser Wert geringer als der tatsächlich in einem Zyklus zurückgelegte Weg? __________

5. Was fällt Ihnen an der Form des Diagramms auf? ___________________________________________

Wie wird der Wert aus Frage 1 im Diagramm repräsentiert? __________________________________

Untersuchungen

6. Wie ändert sich das Aussehen des Diagramms? Warum? ____________________________________

_____________________________________________________________________________________

7. Bestimmen Sie anhand der Datenpunkte in Ihrem Diagramm die Anzahl vollständiger Zyklen je Sekunde. ____________________________________________________________________________

_____________________________________________________________________________________

Warum ist diese anhand des zweiten Diagramms (mit einer Zeitspanne von 5 Sekunden) leichter zu ermitteln als anhand des ersten Diagramms (mit einer Zeitspanne von 10 Sekunden)?_____________

8. Berechnen Sie unter Verwendung der Gleichung die Frequenz. ________________________________

9. Welchen Einfluß hat die Verkürzung des Fadens auf die Periode des Pendels?____________________

Welchen Einfluß hat die Verlängerung des Fadens auf die Periode des Pendels? __________________

10. Welche Beziehung besteht zwischen der Amplitude des Pendelschwungs und dem Gesamtweg des

Pendels in einer Periode? _______________________________________________________________

_____________________________________________________________________________________

Weitergehende Untersuchungen

11. Vergleichen Sie das Entfernung/Zeit-Diagramm mit dem Geschwindigkeit/Zeit-Diagramm. Führen Sie Ähnlichkeiten und Unterschiede auf. ______________________________________________________

_____________________________________________________________________________________

12. In welcher Position hat das Gewicht die größte Geschwindigkeit?______________________________

13. In welcher Position hat das Gewicht die geringste Geschwindigkeit? ___________________________

14. Wie beeinflußt eine Änderung des Gewichts das Diagramm? Warum? _________________________

_____________________________________________________________________________________

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

EXAS INSTRUMENTS INCORPORATED

TI-

Experiment 4 - Springender Ball Didaktische Hinweise

Konzepte

Untersuchte Funktion: parabolisch. Konzepte wie frei fallende und springende Objekte,

die Gravitation sowie konstante Beschleunigung sind Beispiele für parabolische Funktionen. In diesem Experiment werden die Werte für Höhe, Zeit und der Koeffizient A der quadratischen Gleichung

Y = A(X  H)

+ K untersucht, die das Verhalten

eines springenden Balls beschreibt.

Materialien

 Taschenrechner

CBR

  Verbindungskabel  Großer Ball (25 cm)  TI ViewScreen (optional)

Tips

Dieses Experiment wird am besten von zwei Schülern durchgeführt: Einer hält den Ball und der andere drückt ¤.

Auf den Seiten 6–12 finden Sie Tips für effektive Messungen.

Das Diagramm sollte wie ein springender Ball aussehen. Ist dies nicht der Fall, so wiederholen Sie die Messung und achten darauf, daß der

CBR

unmittelbar senkrecht auf den Ball weist. Es wird empfohlen, einen großen Ball zu verwenden.

Typische Diagramme

Untersuchungen

Wird ein Objekt fallengelassen, so wirkt (unter Vernachlässigung des Luftwiderstands) nur noch die Schwerkraft auf dieses ein. A hängt also von der Erdbeschleunigung N9,8 MeteràSekunde

ab. Das negative Vorzeichen gibt an, daß diese Beschleunigung nach unten gerichtet ist.

Der Wert für A ist etwa die halbe Erdbeschleunigung, also N4,9 MeteràSekunde

Typische Antworten

1. Zeit (seit Beginn der Messung); Sekunden;

HöheàAbstand des Balls vom Boden; Meter

2. Anfangshöhe des Balls (die Spitzen

repräsentieren die Maximalhöhe der einzelnen Sprünge); der Boden wird durch y = 0 repräsentiert.

3. In diesem Experiment repräsentiert das

Entfernung/Zeit-Diagramm nicht den Abstand zwischen dem

CBR

und dem Ball. invertiert die Abstandsdaten, so daß das Diagramm eher den Wahrnehmungen der Schüler

BALL BOUNCE

entspricht. Im Diagramm ist y = 0 (Bodenberührung des Balls) in Wirklichkeit der Punkt des größten Abstands zwischen Ball und

CBR

4. Die Schüler sollten sich darüber im klaren sein, daß die X-Achse keinen horizontalen Weg, sondern die Zeit repräsentiert.

7. Der Graph für A = 1 ist im Verhältnis zum Diagramm invertiert und breiter.

8. A < L1

9. Parabolisch konkav aufwärts; konkav abwärts; linear

12. Identisch; mathematisch gesehen repräsentiert der Koeffizient A den Krümmungsgrad der Parabel; physikalisch gesehen hängt A von der durch die Gravitation verursachten Beschleunigung ab, die während des gesamten Experiments konstant bleibt.

Weitergehende Untersuchungen

Die Sprunghöhe des Balls (maximale Höhe für einen Sprung) ergibt sich näherungsweise zu:

; dabei gilt:

y ist die Sprunghöhe.

h ist die Höhe, aus der der Ball fallen gelassen

wurde. p ist eine von den physikalischen Eigenschaften

des Balls und des Untergrunds abhängige Konstante. x ist die Nummer des Sprungs.

Bei gegebenem Ball und Anfangshöhe nimmt die Sprunghöhe mit jedem Sprung exponentiell ab. Für x = 0 ist y = h; der Y-Achsenabschnitt repräsentiert somit die Höhe, aus der der Ball fallengelassen wurde.

Interessierte Schüler können aus den erhobenen Daten die Koeffizienten dieser Gleichung bestimmen. Wiederholen Sie das Experiment mit verschiedenen Anfangshöhen, anderen Bällen und/oder anderem Untergrund.

Nach der manuellen Angleichung der Kurve können die Schüler mit Hilfe einer Regressionsanalyse die Funktion ermitteln, die die Daten am besten modelliert. Wählen Sie dazu mittels

SELECT DOMAIN

einen einzelnen Sprung aus.

Verlassen Sie dann das Menü

QUIT

. Befolgen Sie die Betriebsanweisungen des

PLOT TOOLS

MAIN MENU

mittels

Taschenrechners zur Durchführung einer quadratischen Regression auf den Listen

und L2.

Ergänzungen

Durch Integration des Geschwindigkeit/ZeitDiagramms erhalten Sie den zurückgelegten Weg für ein beliebiges Zeitintervall. Wie Sie feststellen können, ist dieser Weg für einen vollständigen Sprung (vom Boden bis zurück zum Boden) gleich Null.

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Experiment 4 - Springender Ball parabolisch

Datenerfassung

Beginnen Sie mit einem Test. Lassen Sie den Ball fallen (werfen Sie ihn nicht).

➊

mindestens einen halben Meter über der Höhe des

Positionieren Sie den

Tips:

höchsten Sprungs. Halten Sie den Sensor direkt über den Ball und achten Sie darauf, daß sich keine Objekte im freien Bereich (siehe Seite 7) befinden.

CBR

Starten Sie das

➋

RANGER-

Programm (auf Seite 5 finden Sie die Tasteneingaben für die

verschiedenen Taschenrechner).

Wählen Sie aus dem Menü

➌

Wählen Sie aus dem Menü

➍

allgemeine Anweisungen angezeigt.

MAIN MENU

APPLICATIONS

den Eintrag

BALL BOUNCE

APPLICATIONS

BALL BOUNCE

. Wählen Sie

. Nun werden

setzt automatisch die richtigen

Einstellungen.

Halten Sie den Ball an ausgestreckten Armen. Drücken Sie ›. Das

➎

RANGER-

Programm ist nun im Trigger-Modus. Sie können die Verbindung zwischen Taschenrechner nun lösen.

Drücken Sie ¤. Wenn das grüne Licht anfängt zu blinken, lassen Sie den Ball

➏

los und gehen Sie zurück. (Wenn der Ball zur Seite springt, gehen Sie so mit, daß der Höhe des

weiterhin unmittelbar über dem Ball ist, aber achten Sie dabei darauf, die

CBR

nicht zu ändern.)

CBR

Während der Erfassung der Daten hören Sie ein klickendes Geräusch. Die Daten für Abstand und Zeit werden erfaßt, die Daten für Geschwindigkeit und Beschleunigung werden berechnet. Sofern Sie die Verbindung zum

CBR

haben, stellen Sie diese nach beendeter Datenerfassung wieder her.

Drücken Sie ›. (Wiederholen Sie die Messung, wenn das Diagramm nicht

➐

sonderlich gut aussieht.) Untersuchen Sie das Diagramm. Beantworten Sie die Fragen 1 und 2 des Arbeitsblatts.

CBR

gelöst

METER.

und

Beachten Sie, daß

➑

Beantworten Sie die Fragen 3 und 4.

INFÜHRUNG IN DIE VERWENDUNG DES

BALL BOUNCE

CBR

die Abstandsdaten automatisch invertiert hat.

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

Experiment 4 - Springender Ball

Untersuchungen

Das Entfernung/Zeit-Diagramm eines Sprungs bildet eine Parabel.

(Forts.)

parabolisch

Drücken Sie ›. Wählen Sie im Menü

➊

dann

SELECT DOMAIN

. Wir wollen den ersten vollständigen Sprung auswählen.

PLOT MENU

den Eintrag

PLOT TOOLS

Verschieben Sie den Cursor an den Anfang des Sprungs, und drücken Sie Verschieben Sie nun den Cursor auf der Nullinie an das Ende dieses Sprungs, und drücken Sie wiederum

›. Das Diagramm wird nun neu gezeichnet und ist auf

einen einzelnen Sprung fokussiert.

Das Diagramm befindet sich nun im

➋

-Modus. Bestimmen Sie den Scheitel des

TRACE

Sprungs. Beantworten Sie die Frage 5 des Arbeitsblatts.

Drücken Sie ›, um zum Menü

➌

und dann

Die Scheitelform der quadratischen Gleichung Y = A(X  H)

➍

Analyse angemessen. Drücken Sie

QUIT

PLOT MENU

œ. Deaktivieren Sie im

zurückzukehren. Wählen Sie

+ K ist für diese

Editor alle eventuell

angewählten Funktionen. Geben Sie die Scheitelform der quadratischen Gleichung ein: Yn=A(XH)^2+K.

Speichern Sie im Hauptbildschirm den in Frage 5 für die Höhe festgehaltenen Wert

➎

in der Variablen K und den zugehörigen Zeitwert in der Variablen H; speichern Sie in der Variablen A den Wert 1.

Drücken Sie , um den Graphen anzuzeigen. Beantworten Sie die Fragen 6

➏

und 7.

Versuchen Sie die Werte A = 2, 0, –1. Vervollständigen Sie den ersten Teil der

➐

Tabelle zu Frage 8 und beantworten Sie die Frage 9.

und

›.

MAIN

Wählen Sie selbst Werte für A, bis Sie eine gute Übereinstimmung mit dem

➑

Diagramm finden. Halten Sie die von Ihnen gewählten Werte für A in der Tabelle zu Frage 8 fest.

Wiederholen Sie das Experiment, aber wählen Sie diesmal den letzten vollständigen

➒

Sprung (rechts außen) aus. Beantworten Sie die Fragen 10, 11 und 12.

Weitergehende Untersuchungen

Wiederholen Sie die Meßsequenz, wählen Sie aber diesmal nicht nur eine Parabel

➊

aus.

Bestimmen Sie den Zeitpunkt und die Sprunghöhe der aufeinanderfolgenden

➋

Sprünge.

Bestimmen Sie das Verhältnis zwischen den aufeinanderfolgenden Sprunghöhen.

➌

Erläutern Sie die Bedeutung dieses Verhältnisses, sofern es eine hat.

➍

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Experiment 4 - Springender Ball

Name ________________________________

Datenerfassung

1. Welche physikalische Größe wird auf der X-Achse aufgetragen?_______________________________

Welche Einheit wird verwendet? _________________________________________________________

Welche physikalische Größe wird auf der Y-Achse aufgetragen? ______________________________

Welche Einheit wird verwendet? _________________________________________________________

2. Wofür steht der höchste Punkt im Diagramm? _____________________________________________

Der tiefste Punkt? _____________________________________________________________________

3. Warum hat das Programm

BALL BOUNCE

das Diagramm invertiert? ____________________________

4. Warum sieht das Diagramm aus wie ein Ball, der über den Boden springt? ______________________

Untersuchungen

5. Ermitteln Sie die maximale Höhe und die zugehörige Zeit für den ersten vollständigen Sprung. _____

6. Entspricht der Graph für

= 1 Ihrem Diagramm? ___________________________________________

7. Warum oder warum nicht? _____________________________________________________________

8. Vervollständigen Sie die folgende Tabelle.

A Wie verhalten sich das Datendiagramm und der Yn-Graph zueinander?

1 2 0

9. Was besagt ein positiver Wert für

Was besagt ein negativer Wert für

Was besagt der Wert 0 für

? ___________________________________________________________

? _____________________________________________________

? ____________________________________________________

10. Ermitteln Sie die maximale Höhe und die entsprechende Zeit für den letzten vollständigen Sprung. _

11. Glauben Sie, daß

12. Wie verhält sich

Welche Bedeutung hat

INFÜHRUNG IN DIE VERWENDUNG DES

für den letzten Sprung größer oder kleiner sein wird? ______________________

? ____________________________________________________________________

Ihrer Meinung nach? _____________________________________________

CBR

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

Experiment 5 - Rollender Ball Didaktische Hinweise

Konzepte

Untersuchte Funktion: parabolisch. Die graphische Darstellung eines Balls, der

Rampen mit verschiedenen Steigungen herabrollt, ergibt eine Familie von Kurven, die durch eine Folge von quadratischen Gleichungen modelliert werden können. In diesem Experiment werden die Werte der Koeffizienten der quadratischen Gleichung y = ax

+ bx + c erforscht.

Materialien

 Taschenrechner

CBR

  Verbindungskabel  Befestigungsschelle  großer (25 cm) Ball  Lange Rampe (mindestens 2 Meter; eine

leichte Tafel eignet sich hierfür gut)

 Winkelmesser  Bücher zum Aufbocken der Rampe  TI ViewScreen (optional)

Tips

Diskutieren Sie, wie der Winkel der Rampe gemessen werden kann. Lassen Sie die Schüler hier kreativ sein. Möglichkeiten zur Bestimmung des Winkels sind trigonometrische Berechnungen, gefaltetes Papier oder die Verwendung eines Winkelmessers.

Auf den Seiten 6–12 finden Sie Tips für effektive Messungen.

Typische Diagramme

Typische Antworten

1. Das dritte Diagramm

2. Zeit; Sekunden; Abstand des Objekts vom CBR; Meter

3. variiert (sollte eine aufwärts gerichtete parabolische Kurve sein)

4. Eine Parabel (quadratisch)

5. variiert

6. variiert (sollte eine Parabel mit zunehmender Krümmung sein)

7. 0¡ ist flach (der Ball kann nicht rollen); 90¡ entspricht dem freien Fall eines Balls

Untersuchungen

In der Physik ist die Bewegung eines nur der Erdanziehungskraft ausgesetzten Körpers ein populäres Thema. Derartige Bewegungen werden typischerweise durch eine bestimmte Form der quadratischen Gleichung s = ½at

+ v

t + s

ausgedrückt, wobei folgendes gilt:

s ist die Position eines Objekts zum Zeitpunkt t

a ist seine Beschleunigung

ist seine Anfangsgeschwindigkeit

ist seine Anfangsposition

In der quadratischen Gleichung y = ax repräsentiert y den Abstand zwischen

+ bx + c

CBR

und dem Ball zum Zeitpunkt x, sofern die Anfangsposition des Balls c, seine Anfangsgeschwindigkeit b und die Beschleunigung 2a ist.

Weitergehende Untersuchungen:

Da sich der Ball beim Loslassen in Ruhe befindet, sollte b bei jedem Versuch nahezu 0 sein. c sollte etwa der Anfangsabstand (0,5 Meter) sein. a steigt mit dem Winkel der Rampe.

Wenn die Schüler die Gleichung y = ax manuell modellieren, müssen Sie möglicherweise Hinweise auf die Werte von b und c geben. Möglicherweise müssen Sie sie auch anleiten, mit ihren Taschenrechnern eine quadratische Regression der Listen

und L2 durchzuführen. Die Beschleunigung des Balls wird durch die Erdanziehungskraft bewirkt. Je stärker demnach die Rampe nach unten weist (je größer der Neigungswinkel der Rampe), desto größer wird der Wert für a. Der maximale Wert für a tritt bei einem Winkel von q = 90¡ auf, der kleinste Wert bei q = 0¡. Tatsächlich ist a proportional zu sin q.

+ bx + c

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Experiment 5 - Rollender Ball parabolisch

Datenerfassung

➊

Beantworten Sie die Frage 1 des Arbeitsblatts. Stellen Sie die Rampe auf einen Winkel von 15° ein. Montieren Sie die Schelle am oberen Ende der Rampe, und befestigen Sie den positionieren Sie diesen parallel zu Rampe. Verbinden Sie den Taschenrechner mit

CBR

dem

an der Klemme. Öffnen Sie den Sensorkopf, und

CBR

Markieren Sie in einer Entfernung von einem halben Meter vom

einen Punkt auf

CBR

der Rampe. Lassen Sie einen Schüler den Ball an dieser Marke festhalten, während ein zweiter Schüler den Taschenrechner hält.

Zielen Sie mit dem Sensor direkt auf den Ball, und achten Sie darauf, daß sich

Tip:

keine Objekte im freien Bereich (siehe Seite 7) befinden.

Starten Sie das

➋

RANGER-

verschiedenen Taschenrechner). Wählen Sie aus dem Menü

SETUPàSAMPLE

Drücken Sie ›, um die Einstellungen anzuzeigen. Für dieses Experiment gelten

➌

Programm (auf Seite 5 finden Sie die Tasteneingaben für die

MAIN MENU

den Eintrag

folgende Einstellungen:

REALTIME: NO

TIME (S): 3 SECONDS

DISPLAY: DISTANCE

BEGIN ON: [ENTER]

SMOOTHING: LIGHT

UNITS: METRES

Anweisungen zum Ändern der Einstellungen finden Sie auf Seite 38.

Wenn die Einstellungen stimmen, so wählen Sie

➍

START NOW

. Drücken Sie ›, um

mit der Meßsequenz zu beginnen.

Wenn das klickende Geräusch beginnt, lassen Sie den Ball sofort los (ohne diesem

➎

einen Impuls zu geben) und treten zurück.

Nach Vollendung der Meßsequenz wird automatisch das Entfernung/Zeit-Diagramm

➏

angezeigt. Beantworten Sie die Fragen 2 und 3.

Drücken Sie ›, um das Menü

➐

dann

SELECT DOMAIN

. Verschieben Sie den Cursor zu dem Punkt, an dem der Ball los-

gelassen wurde, und drücken Sie dann

PLOT MENU

anzuzeigen. Wählen Sie

›. Verschieben Sie den Cursor nun zu

PLOT TOOLS

dem Punkt, an dem der Ball das Ende der Rampe erreichte, und drücken Sie erneut

›. Das Diagramm wird neu gezeichnet und zeigt nun den zu der Bewegung des

Balls auf der Rampe gehörenden Teil der Messung. Beantworten Sie die Fragen 4 und 5.

und

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

Experiment 5 - Rollender Ball

Untersuchungen

Untersuchen Sie, was bei unterschiedlichen Winkeln geschieht.

Machen Sie eine Vorhersage, was bei steigendem Winkel passiert. Beantworten Sie

➊

die Frage 6.

Ändern Sie den Winkel der Rampe auf 30¡, und wiederholen Sie die Schritte 2 bis 6.

➋

Übertragen Sie das Diagramm in Ihre Skizze zu Frage 6, und beschriften Sie es mit 30¡.

Wiederholen Sie die Schritte 2 bis 6 für die Winkel 45¡ und 60¡, und übertragen Sie

➌

die Diagramme in die Skizze.

➍

Beantworten Sie die Frage 7.

Weitergehende Untersuchungen

Passen Sie die Zeitwerte so an, daß bei der Anfangshöhe (als der Ball losgelassen wurde) x = 0 gilt. Sie können dazu beispielsweise den x-Wert für den ersten Punkt von Hand von allen anderen Punkten Ihres Diagramms abziehen oder die Anweisung eingeben.

Berechnen Sie die Werte von a, b und c für die Kurvenfamilie der Form

➊

y = ax

+ bx + c bei den Winkeln 0¡, 15¡, 30¡, 45¡, 60¡, 90¡.

(Forts.)

parabolisch

L1(1)"A:L1NA"L1

Welcher ist der kleinste und welcher der größte Wert für a? Warum?

➋

Suchen Sie einen Ausdruck, der den mathematischen Zusammenhang zwischen a

➌

und dem Neigungswinkel ausdrückt.

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Experiment 5 - Rollender Ball

Name ____________________________________

Datenerfassung

1. Von welchem dieser Diagramme nehmen Sie an, daß es am besten mit dem Entfernung/Zeit- Diagramm eines eine Rampe herabrollenden Balls übereinstimmt?

2. Welche physikalische Größe wird auf der X-Achse aufgetragen?_______________________________

Welche Einheit wird verwendet? _________________________________________________________

Welche physikalische Größe wird auf der Y-Achse aufgetragen? ______________________________

Welche Einheit wird verwendet? _________________________________________________________

3. Skizzieren Sie, wie das Diagramm wirklich aussieht. Beschriften Sie die Achsen. Markieren Sie im Diagramm den Punkt, an dem der Ball losgelassen wurde und an dem er das Ende der Rampe erreichte.

4. Welche Art von Funktion wird durch dieses Diagramm dargestellt? ____________________________

5. Diskutieren Sie, warum sich das von Ihnen in Frage 1 ausgewählte Diagramm von dem in Frage 3

skizzierten unterscheidet. _______________________________________________________________

_____________________________________________________________________________________

Untersuchungen

6. Skizzieren Sie, wie das Diagramm Ihrer Meinung nach bei einem größeren Neigungswinkel aussieht (beschriften Sie es mit Vorhersage).

7. Skizzieren und beschriften Sie die Diagramme für 0

¡ und 90¡:

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

Informationen für den Lehrer

Wie ändert sich Ihr Unterricht mit dem CBR?

Der

ist ein leichtverwendbares System mit Funktionen, die Sie dabei unterstützen, es

CBR

schnell und einfach in Ihren Unterrichtsplan zu integrieren.

Der

bietet gegenüber den in der Vergangenheit verwendeten Datenerfassungs-

CBR

methoden signifikante Verbesserungen. Diese können zu einer Änderung der Unterrichtseinteilung führen, da die Schüler großes Interesse an der Verwendung realer Daten zeigen.

Sie werden feststellen, daß Ihre Schüler eine stärkere Beziehung zu den Daten ent-

wickeln werden, da sie diese nicht dem Lehrbuch oder ähnlichen Quellen entnehmen müssen, sondern an der Datenerhebung beteiligt sind. Dies führt dazu, daß Sie die von Ihnen untersuchten Konzepte als real und nicht nur als abstrakte Ideen begreifen. Allerdings führt es auch dazu, daß alle Schüler an der Erhebung der Daten beteiligt sein möchten.

Die Datenerfassung mit dem

ist wesentlich effektiver als Messungen mit

CBR

Metermaß und Stoppuhr. Aufgrund der durch die höhere Anzahl von Meßwerten bedingten höheren Auflösung und der hohen Genauigkeit eines Ultraschallsensors ergibt sich die Form der Kurven wesentlich eher. So werden Sie weniger Zeit für die Datenerfassung benötigen und haben somit mehr Zeit für die Analyse und Untersuchung.

Mit dem

können die Schüler die Wiederholbarkeit von Beobachtungen sowie

CBR

Variationen in Was-wäre-wenn-Szenarios untersuchen. Fragen wie „Ergibt sich die gleiche Parabel, wenn wir den Ball aus einer größeren Höhe fallen lassen?“ und „Ist die Parabel des ersten Sprungs identisch mit der des letzten Sprungs?“ ergeben sich als wertvolle Ergänzung ganz von selbst.

Die Macht der Visualisierung bewirkt, daß die Schüler die graphisch dargestellten

Listendaten schnell mit den durch sie beschriebenen physikalischen Größen und mathematischen Funktionen assoziieren.

Weitere Änderungen ergeben sich, sobald Daten aus realen Ereignissen erfaßt werden. Der

ermöglicht es Ihren Schülern, die zugrundeliegenden Beziehungen numerisch

CBR

und graphisch zu erforschen.

Graphische Erforschung von Daten

Die automatisch erstellten Diagramme von Abstand (Weg), Geschwindigkeit und Beschleunigung gegen die Zeit können Sie für Fragestellungen wie die folgenden verwenden:

Welche physikalische Bedeutung hat der Y-Achsenabschnitt? Welche der

X-Achsenabschnitt? Welche die Steigung, das Maximum, das Minimum? Welche die Ableitungen, die Integrale?

Welcher Funktionstyp (linear, parabolisch usw.) wird durch das Diagramm dargestellt?

Wie könnten wir die Daten mit einer repräsentativen Funktion modellieren? Welche

Bedeutung haben die verschiedenen Koeffizienten der Funktion (z.B. AX

Numerische Erforschung von Daten

+ BX + C)?

Ihre Schüler können zur Erforschung der numerischen Daten ihrem Wissensstand entsprechende statistische Methoden (Mittelwert, Median, Standardabweichung usw.) einsetzen. Wenn Sie das

RANGER

Listen, in denen im Modus

-Programm verlassen, erinnert Sie eine Meldung an die

REALTIME=NO

die Daten für Zeit, Weg, Geschwindigkeit und

Beschleunigung gespeichert sind.

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Informationen für den Lehrer

(Forts.)

CBR-Diagramme verbinden die reale Welt mit der Mathematik

Die aus den mittels

RANGER

erhobenen Daten erstellten Diagramme bilden eine visuelle Repräsentation der Beziehungen zwischen der physikalischen und der mathematischen Beschreibung von Bewegung. Die Schüler sollten ermuntert werden, die Form des Diagramms zu erkennen, zu analysieren und in physikalischen und mathematischen Begriffen zu diskutieren. Zusätzliche Möglichkeiten zu Entdeckungen ergeben sich, wenn im Y= Editor Funktionen eingegeben und gemeinsam mit den Datendiagrammen dargestellt werden.

Entfernung/Zeit-Diagramme stellen die ungefähre Position eines Objekts (Abstand zum

) zu jedem Zeitpunkt während der Datenerhebung dar. Die Einheit der Y-Achse ist

CBR

dabei Meter, die der X-Achse Sekunde.

Geschwindigkeit/Zeit-Diagramme stellen die ungefähre Geschwindigkeit eines Objekts (relativ und in Richtung zum

) zu jedem Zeitpunkt während der Datenerhebung

CBR

dar. Die Einheit der Y-Achse ist dabei Meter/Sekunde, die der X-Achse Sekunde.

Beschleunigung/Zeit-Diagramme stellen die ungefähre Beschleunigung (Änderungsrate der Geschwindigkeit) eines Objekts (relativ und in Richtung zum

) zu jedem

CBR

Zeitpunkt während der Datenerhebung dar. Die Einheit der Y-Achse ist dabei

Meter/Sekunde

Die erste Ableitung (aktuelle Steigung) in jedem Punkt eines Entfernung/Zeit-

, die der X-Achse Sekunde.

Diagramms ist die Geschwindigkeit zu diesem Zeitpunkt.

Die erste Ableitung (aktuelle Steigung) in jedem Punkt eines Geschwindigkeit/Zeit-

Diagramms ist die Beschleunigung zu diesem Zeitpunkt. Sie ist gleich der zweiten Ableitung im entsprechenden Punkt des Entfernung/Zeit-Diagramms.

Das bestimmte Integral (Fläche zwischen dem Diagramm und der X-Achse zwischen

zwei beliebigen Punkten) eines Geschwindigkeit/Zeit-Diagramms entspricht der Verschiebung (zurückgelegte Wegstrecke) des Objekts in diesem Zeitintervall.

Beachten Sie, daß es verschiedene Bedeutungen von Geschwindigkeit gibt. Im

täglichen Sprachgebrauch wird Geschwindigkeit als skalare Größe verwendet, beispielsweise „20 Meter/Sekunde“; physikalisch gesehen ist Geschwindigkeit jedoch ein Vektor, sie hat also eine Richtung: „20 Meter/Sekunde Richtung Norden“.

Ein typisches

-Geschwindigkeit/Zeit-Diagramm enthält jedoch nur skalare Größen.

CBR

Es wird nur der Betrag der Geschwindigkeit (der positiv, negativ oder Null sein kann) dargestellt. Die Richtung ergibt sich implizit. Eine positive Geschwindigkeit steht für eine Bewegung vom

mißt den Abstand nur in direkter Linie zum Detektor. Bewegt sich ein Objekt also

CBR

weg, eine negative für eine Bewegung auf den

CBR

zu.

in einem Winkel, so wird nur die zu der direkten Linie parallele Komponente der Bewegung erfaßt. Beispielsweise zeigt ein sich quer zur direkten Linie zum

CBR

bewegendes Objekt keine Geschwindigkeit.

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

Informationen für den Lehrer

(Forts.)

Die Mathematik von Weg (Abstand), Geschwindigkeit und Beschleunigung

Mittel

N d

= Steigung im Entfernung/Zeit-Diagramm

N t

Entfernung/Zeit-Diagramm

aktuell

lim

(

@t"

d(s)

)

wobei s der Abstand ist

Geschwindigkeit/Zeit-Diagramm

N v

Mittel

aktuell

lim

@t"

= Steigung im Geschwindigkeit/Zeit-Diagramm

N t

(

)

Die Fläche unter dem Geschwindigkeit/Zeit-Diagramm zwischen den Zeitpunkten t1 und

ergibt sich zu @d = (d

und t2.

Es gilt daher @d =

t=2

(

t=1

) als die Verschiebung (zurückgelegte Wegstrecke) zwischen

2Nd1

t=2

v(@t)

∑

oder @d =

)

⌠

⌡

t=1

v(dt)

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

Beschleunigung/Zeit-Diagramm

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Informationen für den Lehrer

Internet und Word Wide Web (WWW)

(Forts.)

Auf unserer Web-Site

Eine Liste zusätzlicher Materialien zur Verwendung mit dem

graphischen TI-Taschenrechnern. Eine Bibliothek von Programmen zur Verwendung mit dem

graphischen TI-Taschenrechnern. Eine Aktivitäten-Seite mit Anwendungen, die von Lehrern wie Ihnen entwickelt und

freigegeben wurden.

-Programme, die zusätzliche Funktionen des

CBR

Detailliertere Informationen über die Einstellungen und Programmierbefehle des

Zusätzliche Quellen

Die Übungsbücher von Texas Instruments enthalten zusätzliche Materialien zu den graphischen TI-Taschenrechnern. Dazu gehören auch Bücher mit cbr-Experimenten für Mathematik- und Physikkurse der Mittel- und Oberstufe.

http:ààwww.ti.comàcalc

finden Sie unter anderem:

, dem

CBR

nutzen.

CBR

, dem

CBL

und

CBR

INFÜHRUNG IN DIE VERWENDUNG DES

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

CBR

EXAS INSTRUMENTS INCORPORATED

TI-

CBR-Daten werden in Listen gespeichert

Die erhobenen Daten werden in den Listen L1, L2, L3 und L4 gespeichert

Bei der Erfassung von Daten überträgt der wo sie in Listen gespeichert werden. Jedesmal, wenn Sie das verlassen, werden Sie daran erinnert, wo die Daten gespeichert sind.

enthält Zeitdaten

enthält Entfernungsdaten

enthält Geschwindigkeitsdaten

enthält Beschleunigungsdaten

So repräsentiert beispielsweise das fünfte Element der Liste L1 den Zeitpunkt, zu dem der fünfte Meßwert erfaßt wurde, und das fünfte Element der Liste Entfernung des Objekts zu diesem Zeitpunkt.

Im Modus

REALTIME=YES

werden nur die Daten für das angeforderte Diagramm (Weg,

Geschwindigkeit oder Beschleunigung) berechnet und übertragen. Im Modus

REALTIME=NO

werden alle Daten berechnet und übertragen.

Einstellungen werden in der Liste L5 gespeichert

Der Bildschirm

-Parameter (siehe Seite 38).

CBR

Wenn Sie das

RANGER SETUP

RANGER

-Programm vom

gestattet die einfache Änderung der meistgebrauchten

CBR

neue Liste mit den Standardwerten ersetzt.

diese automatisch zum Taschenrechner,

CBR

RANGER

-Programm

repräsentiert die

übertragen, wird L5 automatisch durch eine

Auf den Seiten 40–41 finden Sie Informationen über Programmierbefehle zur Änderung der anderen Einstellungen.

Verwendung der Datenlisten

Die Listen werden beim Verlassen des somit für zusätzliche graphische, statistische und numerische Untersuchungen und Analysen zur Verfügung.

Sie können die Listen graphisch gegeneinander auftragen, sie im Listeneditor betrachten und Regressionsanalysen und andere analytische Verfahren durchführen. So könnten Sie beispielsweise mittels verlassen und dann zur Untersuchung elliptischer Funktionen die Geschwindigkeit gegen die Beschleunigung auftragen. (In diesem Fall müssen Sie möglicherweise das Fenster anpassen.)

RANGER

-Programms nicht gelöscht. Sie stehen

die Daten einer Pendelbewegung erfassen,

RANGER

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

RANGER-Einstellungen

Ändern der RANGER-Einstellungen

RANGER

➊

zeigt vor Beginn der Datenerfassung die gebräuchlichsten Einstellungen an.

Wählen Sie im Menü

MAIN MENU

des

RANGER

-Programms den Eintrag

SETUPàSAMPLE

Nun werden die aktuellen Einstellungen angezeigt. 4 bezeichnet die Position des Cursors.

UNITS:

START NOW

oder

= 1–99

FEET

SEKUNDEN

ACCELERATION

oder

10-SECOND DELAY

oder

(

nur bei

HEAVY

REALTIME=NO

)

YES

TOTAL TIME

DISTANCE, VELOCITY

[ENTER], [TRIGGER],

NONE, LIGHT, MEDIUM

METRES

, um durch die verfügbaren Optionen zu blättern. Drücken Sie bei

›

MAIN MENU

REALTIME:

TIME (S):

DISPLAY:

BEGIN ON:

SMOOTHING:

Drücken Sie c oder b, um zu der zu ändernden Einstellung zu gelangen.

➋

Drücken Sie

➌

der richtigen Einstellung c, um zur nächsten Option zu gelangen. Zum Ändern der Zeit geben Sie eine oder zwei Ziffern ein und drücken c oder b.

Wenn alle Einstellungen stimmen, drücken Sie c oder b, bis der Cursor auf

➍

START NOW

Um fortzufahren, drücken Sie

Um zum Menü

steht.

MAIN MENU

›

zurückzukehren, drücken Sie e und dann

›

Die neuen Einstellungen bleiben erhalten, bis Sie aufrufen oder ein anderes Programm starten, das die Einstellungen ändert. Wenn Sie außerhalb des Aufruf des

RANGER-

RANGER

-Programms L5 ändern oder löschen, können beim nächsten

Programms die Standardeinstellungen wiederhergestellt werden.

Wiederherstellen der Standardeinstellungen des RANGER

Die Standardeinstellungen eignen sich für eine Vielzahl von Meßsituationen. Wenn Sie sich über die besten Einstellungen nicht klar sein sollten, so beginnen Sie mit den Standardeinstellungen, und ändern Sie diese schrittweise.

Wählen Sie im Menü

➊

MAIN MENU

des

RANGER

Die Einstellungen werden auf die Standardwerte gesetzt, und der wird angezeigt.

Zum Ändern von Einstellungen folgen Sie den obigen Anweisungen.

➋

Um fortzufahren, positionieren Sie den Cursor auf

➌

Andere RANGER-Einstellungen

Zwar hat das verfügt der

CBR

RANGER

-Programm Zugriff auf die gebräuchlichsten Einstellungen, doch

über weitere Einstellungen. Auf den Seiten 40–41 finden Sie

Informationen über Programmierbefehle zur Änderung der anderen Einstellungen.

SET DEFAULTS

oder eine Anwendung

-Programms den Eintrag

SETUP

START NOW

und drücken

SET DEFAULTS

-Bildschirm

›

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

CBR-Einsatz mit dem CBL oder mit CBL-Programmen

Verwendung des CBR als konventioneller Bewegungsdetektor mit dem CBL

Der

kann im Zusammenhang mit dem Texas Instruments

CBR

based laboratory, taschenrechnerbasiertes Labor) als konventioneller Bewegungsdetektor eingesetzt werden.

Das zur Verbindung des dem wird mitgeliefert.

Verbinden Sie den

nicht mit dem

CBR

, wenn der

CBL

mit einem Taschenrechner

CBR

verbunden ist. In dieser Konfiguration muß der Taschenrechner mit dem werden

Möglicherweise müssen Sie das

RANGER

-Programm wie im folgenden erläutert ändern. Das

CBL

-Programm funktioniert mit dem

CBL

nicht.

Verwendung des CBR mit für das CBL geschriebenen Programmen

Sie können ohne oder mit nur geringen Programmänderungen den für nur einen Bewegungsdetektor geschriebenen

-Programmen verwenden.

CBL

é-System (calculator

CBL

benötigte Spezialkabel

CBL

mit den meisten

CBR

mit

CBR

verbunden

Stoppen der Messung: Bei einigen

REALTIME=YES

betreiben, hört der

CBR

-Programmen, die Datenerfassung im Modus

CBL

nicht mehr mit der Messung auf. Sie haben die

beiden folgenden Möglichkeiten, die Meßsequenz am Ende der Meßzeit zu stoppen:

Drücken Sie ¤ auf dem

Fügen Sie dem vorhandenen

an den

CBR zu

senden. Diese Anweisungen müssen ausgeführt werden, nachdem die

CBR

-Programm Anweisungen hinzu, um den Befehl {6,0}

CBL

Daten übertragen und angezeigt wurden. Ein Beispiel:

{6,0}"L6:SEND L6

Ein- und Ausschalten des akustischen Signals: Zum Ausschalten des akustischen Signals können Sie dem vorhandenen Befehl {6,3} an den

CBR zu

senden. Diese Anweisungen müssen vor Beginn der Daten-

-Programm Anweisungen hinzufügen, um den

CBL

erfassung ausgeführt werden. Ein Beispiel:

{6,3}"L6:SEND L6

Zum Einschalten des akustischen Signals starten Sie einfach das

Bei Schwierigkeiten: Wenn Sie ein

-Programm laufen lassen, und der

CBL

RANGER

nicht zu reagieren oder scheint sich aufgehängt zu haben, so starten Sie das

-Programm.

scheint

CBR

RANGER

Programm. Auf der TI Web-Site (siehe Seite 36) finden Sie möglicherweise eine aktualisierte Version des

-Programms.

CBL

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Programmierbefehle

Befehl 0 System löschen und rücksetzen {0}

Löscht alles und stellt die Standardeinschaltwerte wieder her. Kanal 11 wird automatisch ausgewählt.

Befehl 1 Kanal löschen {1,0}

Löscht kanal.

Befehl 1 Kanal {1,11,

Operation

REALTIME=NO

Operation

REALTIME=YES

Nachverarbeitung

0 (Standard) Keine

REALTIME=NO

Temperaturkompensation

0 (Standard) Deaktiviert die Temperaturkompensation 1 Aktiviert die Temperaturkompensation

) Löscht alles und stellt die Einschalt-Standardwerte wieder her. ) Meter ) Meter ) Fuß

) Löscht alles und stellt die Einschalt-Standardwerte wieder her. ) Meter, ) Meter, ) Fuß, ) Meter, ) Fuß, ) Meter, ) Fuß,

)dàdt (Erste Ableitung) )d

Befehl 2 Einrichten der Daten {2,

Datentyp

1 (Standard) Liste

Befehl 3 Messung/Trigger {3,

Meßzeit

0.005–1500 (0.1) Zeit in Sekunden zwischen den Einzelmessungen

0.0001–0.005 Wird auf 0.005 gerundet 1500<x<16000 Wird auf 1500 gerundet

Messungen

L1 Wählt den Datenerfassungsmodus

REALTIME=NO

1–512 (

Trigger

0 Beginnt die Messungen ohne Trigger 1 (Standard) Beginnt bei Druck auf ¤ mit den Messungen 7 Wartet 10 Sekunden und beginnt dann mit den Messungen

Zeitaufzeichnung

0 (Standard) Keine

REALTIME=NO

Filter

(siehe auch Befehl 1, Feld 0 (Standard) Keine Filterung

REALTIME=NO

1 (

REALTIME=NO

2 (

REALTIME=NO

3 (

REALTIME=NO

4 (

REALTIME=NO

5 (

REALTIME=NO

6 (

REALTIME=YES

7 (

REALTIME=YES

8 (

REALTIME=YES

9 (

) 1 bis 512 Messungen

) Absolute Zeit (startet beim Zeitpunkt 0 und paßt dann die Meßzeit an) ) Relative Zeit (startet beim Zeitpunkt 0 und paßt dann die Meßzeit an)

Operation

) 5-Punkt-Glättung nach Savitzsky-Golay ) 9-Punkt-Glättung nach Savitzsky-Golay ) 17-Punkt-Glättung nach Savitzsky-Golay ) 29-Punkt-Glättung nach Savitzsky-Golay ) 3-Punkt-Median-Schneidefilter ) 5-Punkt-Median-Schneidefilter

) Schwacher ) Mittlerer ) Starker

)

Auswirkungen

Datentyp

Auswirkungen

Meßzeit,Messungen,Trigger

Auswirkungen

Operation,Nachverarbeitung

CBR CBR

CBR

àdt2 (Zweite Ableitung)

Abstand,@Zeit

gibt {

Abstand,@Zeit

gibt {

Abstand,@Zeit

gibt {

Abstand,Geschwindigkeit,@Zeit

gibt {

Abstand,Geschwindigkeit,@Zeit

gibt {

Abstand,Geschwindigkeit,Beschleunigung,@Zeit

gibt {

Abstand,Geschwindigkeit,Beschleunigung,@Zeit

gibt {

} zurück } zurück

} zurück

,0,0,0,0,0,0,0}

REALTIME=YES

Tracking-Filter

Temperaturkompensation

,0,

} zurück

,0,0,0,0,

Zeitaufzeichnung,Filter

REALTIME=YES

aus

}

} zurück

}

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

Programmierbefehle

(Forts.)

Befehl 4 Temperaturkompensation {4,

Befehl 5

GleichungsNr

0 (Standard) Löscht alle Gleichungen 4 Wählt Gleichung 4 aus

Gleichungstyp

0 (Standard) Löscht die Gleichung 13 Wählt die Temperaturkompensation aus

Temperatur

Gleitkommazahl Setzt die aktuelle Temperatur

Einheiten

0 (Standard) Keine (wird vom 1 Setzt die Temperatureinheit auf Fahrenheit 2 Setzt die Temperatureinheit auf Celsius 3 Setzt die Temperatureinheit auf Kelvin 4 Setzt die Temperatureinheit auf Rankin (R = F + 459,7)

REALTIME=NO

(

ErsterKanal

Datenauswahl

Datenanfang

Datenende

)

Einrichten des Datenbereichs {5,

0 (Standard) Wählt den untersten aktiven Kanal aus 1, 2, 3, 11, 21 Legt den Ultraschallkanal fest M1 Hält die Zeitliste fest

0 Filterdaten {Abstand} 1 Filter dàdt-Daten {Geschwindigkeit} 2 Filter d 3 Rohdaten {Abstand} 4 Rohdaten dàdt {Geschwindigkeit} 5 Rohdaten d

1–512 Erstes Datenelement für GET

0–512 Letztes Datenelement für GET (0 = letzte Messung)

Auswirkungen

Befehl 6 Systemoptionen {6,

Systembefehl

0 Stoppt die Messung (zwecks Kompatibilität mit dem CBL) 2 (Standard) Stoppt die Messung 3 Deaktiviert das beim Einschalten aktivierte akustische Signal 4 Aktiviert das beim Einschalten aktivierte akustische Signal 5 Setzt die ID-Nummer ( 6 Wendet auf die vorherigen Daten einen neuen Filter an (

Operation

Gleitkommazahl ID-Nummer der Form 0–6 Neuer Filter für die zuvor erhobenen Daten (

Auswirkungen

Befehl 7 Statusabfrage {7}

Ergibt eine Liste mit dem folgenden Inhalt:

10.rrrr Gerätecode.Romversion 0–99 Letzter Fehlercode (0 = kein Fehler) 0–2 Batteriezustand (0 = OK; 1 = schwach während der Messung; 2 = immer

11 Bezeichner des Ultraschallkanals Meßzeit Aktuelle Meßzeit in Sekunden Triggerzustand Aktuell verwendete Triggeroption Funktion Aktuelle Kanalfunktion (1–9) Nachverarbeitung Aktuelle Nachverarbeitungsoption (0–2) Filter Aktuelle Filterebene (0–9) Messungen Anzahl verfügbarer Messungen; 0–512 bei

Zeitaufzeichnungsoption Zeitaufzeichnungsoption(0–2) Temperatur verwendete Temperatur (¡C) Signal 0 = akustisches Signal deaktiviert; 1 = akustisches Signal aktiviert Systemzustand 1 = nicht eingerichtet; 2 = eingerichtet; 3 = messend; 4 = fertig Fensteranfang 0 = bisher noch kein Befehl 5 ausgeführt; 1–512 Fensterende 0 = Anzahl der Elemente verwenden; 1–512 ID-Nummer sechsstellige ID-Nummer (Standard = 0.00000), die durch Befehl 6

GleichungsNr,Gleichungstyp,Temperatur,Einheiten

CBR

ignoriert). Setzt die Temperatureinheit auf Celsius

ErsterKanal,Datenauswahl,Datenanfang,Datenende

àdt2-Daten {Beschleunigung}

àdt2 {Beschleunigung}

Systembefehl[,Operation]

notwendig)

schwach)

REALTIME=YES

Systembefehl

(

= 5) gesetzt wurde

Operation

n.nnnnn

}

notwendig)

Systembefehl

(

= 5)

Systembefehl

REALTIME=NO

Operation

= 6)

; M1 bei

}

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Batterien

Batterietyp

Der mit einem

Einsetzen der Batterien

Halten Sie den deckel mit dem Daumen zur Rückseite des

wurde für den Betrieb mit vier AA-Alkaline-Batterien entworfen. Wenn der

CBR

verbunden ist, funktioniert er auch ohne Batterien.

CBL

mit der Oberseite nach unten und schieben Sie den Batteriefach-

CBR

. Legen Sie die Batterien entsprechend der

CBR

Skizze im Batteriefach ein. Zwei Batterien müssen mit dem Pluspol nach oben in die mit + bezeichneten Positionen eingelegt werden, zwei Batterien mit dem Minuspol nach oben in die mit - markierten Positionen. Schieben Sie den Batteriefachdeckel wieder zu. Der

Warnungen bei schwachen Batterien

Der

ist nun für Messungen bereit.

CBR

warnt auf zweierlei Weise bei schwachen Batterien:

CBR

Das

RANGER

-Programm zeigt beim Versuch einer Messung auf dem Bildschirm des

Taschenrechners eine Warnung an.

Das rote Licht blitzt regelmäßig auf, während der

Überprüfung des Batteriezustands

Meßdaten sammelt.

CBR

Vor dem Beginn einer Messung können Sie den Zustand der Batterien überprüfen. Wählen Sie dazu im Menü der Batteriestatus

Vorsichtsmaßnahmen beim Umgang mit Batterien

oder

MAIN MENU

REPLACE

den Eintrag

(Austauschen) angezeigt.

TOOLS

und dann

CBR STATUS

. Es wird

Tauschen Sie immer alle vier Batterien auf einmal aus. Mischen Sie keine verschiedenen Batteriemarken oder Batterietypen einer Marke.

Legen Sie die Batterien entsprechend den Skizzen im Batteriefach ein.

Sorgen Sie für eine ordnungsgemäße Entsorgung verbrauchter Batterien. Halten Sie diese von Kindern fern.

Sie dürfen Batterien nicht erhitzen, verbrennen oder öffnen. Batterien enthalten gefährliche Chemikalien und können explodieren oder auslaufen.

Mischen Sie keine wiederaufladbaren und nicht wiederaufladbaren Batterien.

Versuchen Sie nicht, nicht wiederaufladbare Batterien wieder aufzuladen.

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

Problembehebung

gsg

Problem: Mögliche Abhilfe:

Probleme beim Übertragen des

RANGER

-Programms oder bei der

Datenerfassung

CBR

beginnt von selbst mit der

Erfassung von Daten

Meldung

LINK ERROR

Überprüfen Sie die Verbindun Sie immer beide Enden des Kabels fest ein.

Überprüfen Sie den Batteriezustand (siehe Seite 42). Wenn Sie den CBR mit der

-Taste gedrückt werden und die Messung auslösen. Zum Stoppen der

Messung drücken Sie erneut auf Verlassen Sie vor dem Verstauen des

Programm (mittels

QUIT)

Verbinden Sie mit Hilfe des Verbindungkabels den

zwischen Taschenrechner und

-Taste nach unten ablegen, kann die

CBR

ordnungsgemäß das

bzw. jedes andere

Taschenrechner. Überprüfen Sie die Verbindun

zwischen Taschenrechner und

Sie immer beide Enden des Kabels fest ein.

QUIT

CBR

nicht mit dem Taschenrechner verbinden möchten (oder

zum Abbruch

Wenn Sie den nicht können), so drücken Sie Sie dann

Ungenügender Speicher Sie benötigen ausreichend Speicher für das

Datenlisten. Pro

ramm und Listen benötigen etwa 17.500 Bytes. Löschen Sie

ggf. andere Programme und/oder Daten.

Taschenrechner entspricht nicht den Anweisun

en in den

Experimenten

Dieses Handbuch werden können. Es kann daher vorkommen, daß manche der in diesem Handbuch erwähnten Menünamen, Bildschirme oder Tastenbezeichnun

ilt für alle TI-Taschenrechner, die mit dem

nicht exakt mit denen Ihres Taschenrechners übereinstimmen. Nehmen Sie in

ende Auswahl. Wenn es in der Anweisung beispiels-

DISTANCE MATCH

CBR

-Geräte gleichzeitig verwendet, so sollte

beenden, bevor die zweite Gruppe mit ihrer

Daten sehen falsch aus:

Punkte sind nicht auf der Kurve

zerklüftete Diagramme

flache Diagramme

unterbrochene Diagramme

diesem Fall die nächstlie weise heißt: „Wählen Sie den Eintrag

DIST MATCH

Wiederholen Sie die Meßsequenz und stellen Sie sicher, daß der CBR direkt auf das Objekt zielt.

Beachten Sie die Seiten 6–12 zur effektiven Messung. Überprüfen Sie, daß sich im freien Bereich keine Schüler, Tische oder

sonstigen Objekte befinden. Werden im

leichen Raum zwei die erste Gruppe ihre Messun Messung beginnt.

Überprüfen Sie die Verbindun

zwischen Taschenrechner und

Sie immer beide Enden des Kabels fest ein. Überprüfen Sie den Batteriezustand (siehe Seite 42). Überprüfen Sie, ob der Glättungsgrad nicht zu hoch oder niedrig gesetzt ist.

CBR

Der einem TI

Das Taschenrechner-

funktioniert nicht mit

CBR

Verbindungskabel ging verloren

Überprüfen Sie, ob die Seriennummer auf der Rückseite des Taschenrechners

CBL“

mit „ Der TI

manche Untersuchun dargestellten Daten) mit dem TI

endet. Dies kennzeichnet die Kompatibilität mit

85 verfügt über keine statistischen Diagrammfunktionen; daher sind

en (wie die Verwendung von

85 nicht möglich.

Sie können das mit Ihrem Taschenrechner gelieferte Kabel zur Verbindun von Taschenrechnern untereinander verwenden. (Dieses Verbindungskabel ist jedoch wesentlich kürzer, daher sollten Sie ein Ersatzkabel bestellen.)

Häufig leere Batterien Vor dem Verstauen des

ordnun Pro

emäß (mittels

ramme) und die Verbindung zwischen dem

CBR

sollten Sie das

QUIT)

beenden (ebenso alle anderen

lösen.

Beim Aufruf des

RANGER

Programms geschieht nichts

Wenn Sie das Taschenrechner beim nächsten Aufruf bis zu zwei Minuten zur Vorbereitun

RANGER

-Programm bearbeiten oder betrachten, benötigt der

des Programms. Dies ist völlig normal.

Fehlermeldung: Variable is locked

or protected (nur TI

92)

Sie müssen die Variablen L1, L2, L3, L4 und L5 entsperren. Beachten Sie dazu das Handbuch zum Taschenrechner.

CBR

. Stecken

CBR

- oder

CBR

CBL

-Programm.

mit dem

RANGER

CBR

. Stecken

des Programms, und wählen

RANGER

-Programm und die

CBR

verwendet

“, so wählen Sie auf dem TI-83

CBR

. Stecken

RANGER

CBR

CBL



auf graphisch

-Programm

und dem Taschenrechner

und

CBR

- oder

CBL

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Hinweise zu TI Produktservice und Garantieleistungen

Informationen über Produkte und Dienstleistungen von TI

Wenn Sie mehr über das Produkt- und Serviceangebot von TI wissen möchten, senden Sie uns eine E-Mail oder besuchen Sie uns im World Wide Web.

E-Mail-Adresse:ti-cares@ti.com Internet-Adresse:http://www.ti.com/calc

Service- und Garantiehinweise

Informationen über die Garantiebedingungen oder über unseren Produktservice finden Sie in der Garantieerklärung, die dem Produkt beiliegt. Sie können diese Unterlagen auch bei Ihrem Texas Instruments Händler oder Distributor anfordern.

INFÜHRUNG IN DIE VERWENDUNG DES

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

CBR

EXAS INSTRUMENTS INCORPORATED

TI-

RANGE

MAIN MENU

SETUP / SAMPLE

SET DEFAULTS

NO YES

1-99 (REALTIME=NO)

DISTANCE VELOCITY ACCELERATION

[ENTER] [TRIGGER] DELAY

NONE LIGHT MEDIUM HEAVY

METERS FEET

APPLICATIONS

REALTIME=NO

PLOT MENU

REALTIME=YES

TOOLS

QUIT

APPLICATIONS

UNITS METERS FEET

DISTANCE-TIME VELOCITY-TIME ACCELERATION-TIME PLOT TOOLS REPEAT SAMPLE MAIN MENU QUIT

SHOW PLOT SELECT DOMAIN REPEAT SAMPLE MAIN MENU QUIT

TOOLS GET CBR DATA GET CALC DATA CBR STATUS STOP/CLEAR CBR MAIN MENU

DISTANCE MATCH VELOCITY MATCH BALL BOUNCE MAIN MENU

PLOT TOOLS SELECT DOMAIN SMOOTH DATA PLOT MENU

DATA SMOOTHING LIGHT MEDIUM HEAVY NONE

OPTIONS SAME MATCH NEW MATCH APPLICATIONS MAIN MENU QUIT

IESE SEITE DARF KOPIERT WERDEN, VORAUSGESETZT SIE ENTHALT DEN VERMERK

EXAS INSTRUMENTS INCORPORATED

TI-

INFÜHRUNG IN DIE VERWENDUNG DES

CBR

Texas instruments CBR User Manual [de]

Specifications and Main Features

Frequently Asked Questions

User Manual