Texas instruments CBR User Manual [es]

Download

85-86

TRIGGER

CBR

)

Calculator-Based Ranger

™

(CBR

™

)

CONCEPTOS BÁSICOS DEL CONCEPTOS BÁSICOS DEL

INCLUYEINCLUYE

ACTIVIDADES PARAACTIVIDADES PARA

5 5

ESTUDIANTESESTUDIANTES

CBR™CBR™

CBR

)

TRIGGER

85-86

CBR

)

TRIGGER

85-86

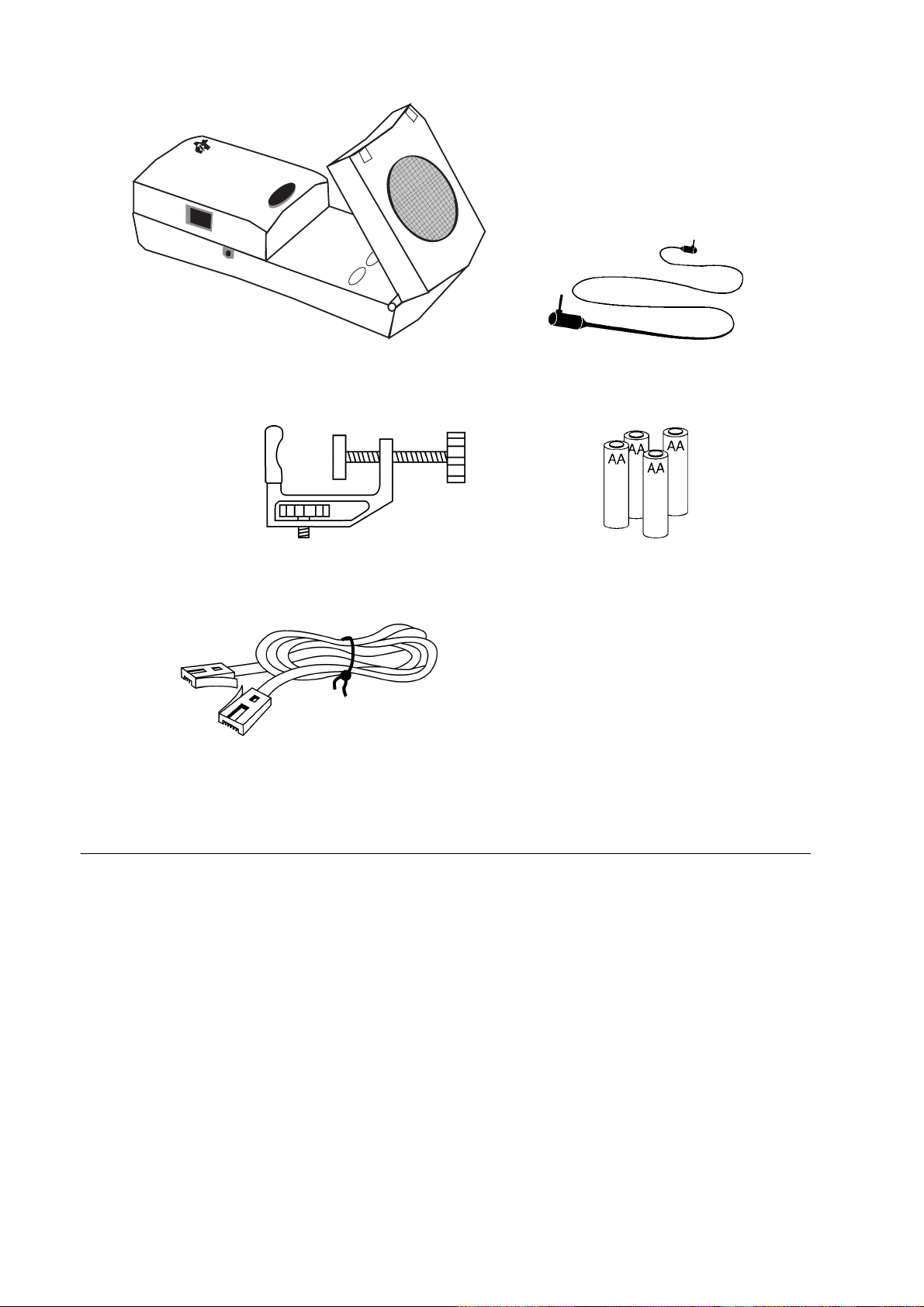
Calculator-Based Rangeré (CBRé) cable de calculadora a CBR

abrazadera 4 pilas AA

Cable CBL a CBR

Importante

Texas Instruments no ofrece garantía alguna, ya sea explícita o implícita, incluidas, sin limitarse a ellas, garantías implícitas de comerciabilidad o idoneidad para un uso concreto, en lo que respecta a los programas o manuales y ofrece dichos materiales únicamente “tal y como son”. En ningún caso Texas Instruments puede hacerse responsable ante cualquier persona por daños especiales, colaterales, accidentales o consecuentes relacionados o causados por la adquisición o el uso de los materiales mencionados, y la responsabilidad única y exclusiva de Texas Instruments, independientemente de la forma de acción, no sobrepasará el precio de compra de este equipo. Asimismo, Texas Instruments no puede hacerse responsable de las reclamaciones de cualquier clase contra el uso de dichos materiales por cualquier otra parte.



1997 de Texas Instruments Incorporated.

Por la presente, se concede permiso a los profesores para reimprimir o fotocopiar en clases, talleres o seminarios las páginas u hojas de esta publicación que contengan el aviso de derechos de copyright de Texas Instruments. Estas páginas están diseñadas para que los profesores puedan reproducirlas y utilizarlas en sus clases, talleres o seminarios, siempre que cada copia que se haga contenga el aviso de copyright. Tales copias no pueden venderse y su distribución está expresamente prohibida. Con excepción de lo autorizado anteriormente, será necesario obtener un permiso previo por escrito de Texas Instruments para reproducir o transmitir esta publicación o partes de la misma por cualquier otro medio electrónico o mecánico, incluyendo cualquier sistema de almacenamiento o recuperación de información, a menos que esté expresamente permitido por las leyes federales de copyright. Dirija sus preguntas y solicitudes a Texas Instruments Incorporated, PO Box 149149, Austin, TX, 78714-9149, M/S 2151, Attention: Contracts Manager.

Índice de materias

CBR

)

Introducción

¿Qué es el CBR? 2 Conceptos básicos del CBR — Es tan sencillo como 1, 2, 3 4 Sugerencias para una captura efectiva de datos 6

Actividades con notas del profesor y hojas de actividades del estudiante

TRIGGER

85-86

Actividad 1. Aproximación a la gráfica lineal 13

Actividad 2. Coche de juguete lineal 17

Actividad 3. Péndulo sinusoidal 21

Actividad 4. Pelota botando parabólico 25

Actividad 5. Pelota rodante parabólico 29

Información para el profesor 33

Información técnica

Los datos del CBR se almacenan en listas 37 Ajustes del RANGER 38 Utilización del CBR con CBL o con programas de CBL 39 Órdenes de programación 40

Información de asistencia

Pilas 42 En caso de dificultad 43 Asistencia y garantía de TI 44

Mapa de menús del RANGER dentro de la contraportada

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

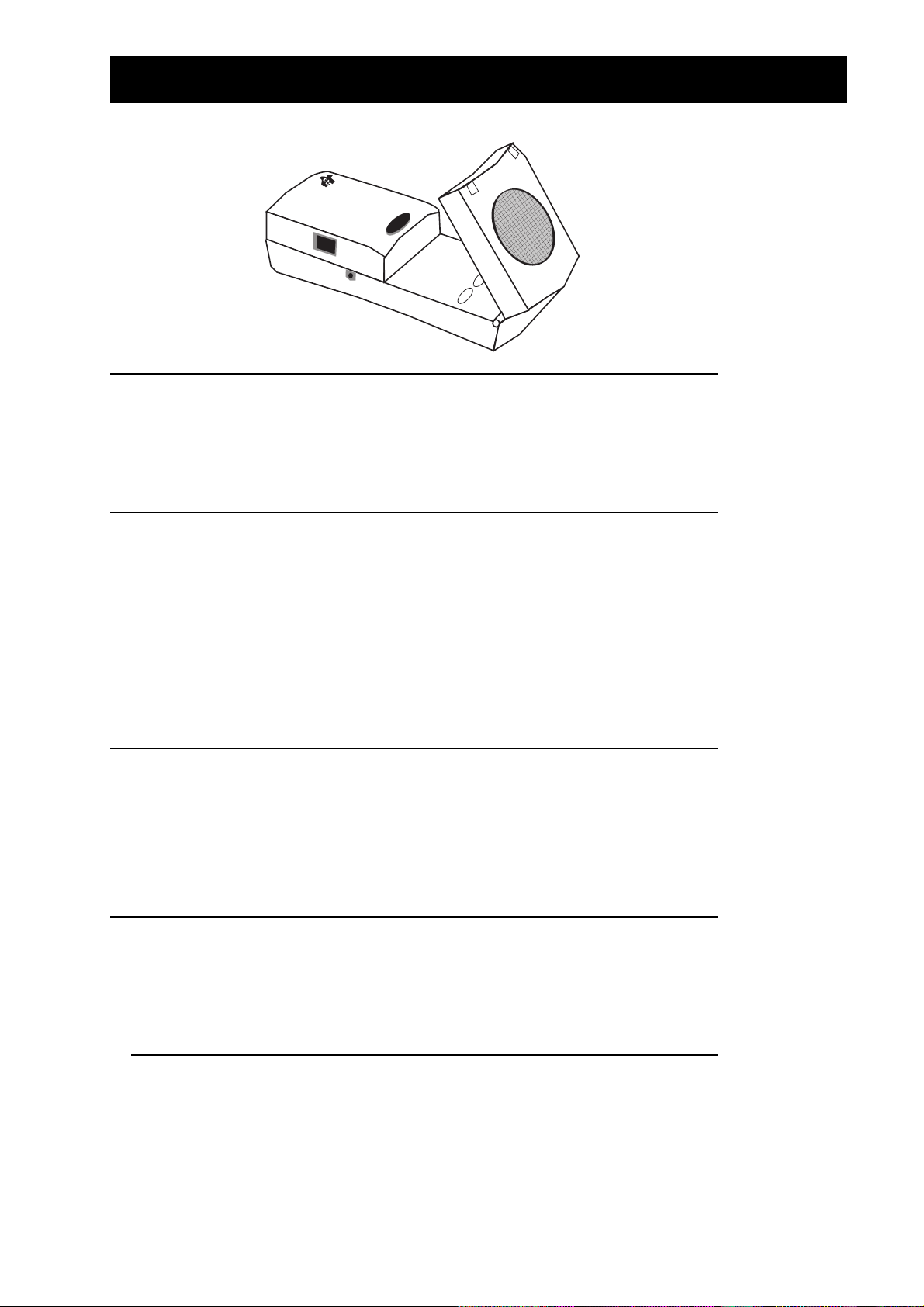
¿Qué es el CBR?

aporta al aula la posibilidad de capturar y analizar datos reales

el versátil programa RANGER está a su alcance con solo apretar un botón

los programas MATCH y BOUNCING BALL vienen incorporados en RANGER

los parámetros primarios de toma de datos son fáciles de ajustar

¿Qué hace el CBR?

Con

CBR

datos de movimiento sin tomar medidas ni hacer dibujos a mano que pueden resultar tediosos.

permite a los estudiantes explorar las relaciones matemáticas y científicas existentes

CBR

entre distancia, velocidad, aceleración y tiempo utilizando los datos de las actividades llevadas a cabo. Los estudiantes pueden explorar conceptos matemáticos y científicos tales como:

CBRCBRé (Calculator-Based RangerCalculator-Based Rangeré

)

detector sónico de movimiento

CBL

para su utilización con TI-82, TI-83, TI-85/

, TI-86 y TI-92

fácil de usar, autoexplicativo

no requiere programación

Incluye el programa RANGERIncluye el programa RANGER

y una calculadora gráfica TI, los estudiantes pueden capturar, ver y analizar

movimiento: distancia, velocidad, aceleración

representación gráfica: ejes de coordenadas, pendiente, cortes con los ejes

funciones: lineal, cuadrática, exponencial, sinusoidal

análisis matemático: derivadas, integrales

análisis estadísticos y de datos: métodos de captura de datos, análisis estadístico

Contenido de esta guía

Conceptos básicos de CBR

mucha experiencia con calculadoras o con programación. Incluye instrucciones para aprender a utilizar rápidamente el cinco actividades de aula para explorar las funciones y propiedades básicas del movimiento. Las actividades incluyen (consulte las páginas 13-22):

notas para el profesor sobre cada actividad, más información general para el profesor

instrucciones paso a paso

una actividad básica de captura de datos, adecuada para todos los niveles

exploraciones que examinan los datos en profundidad, permitiendo realizar hipótesis

sugerencias para temas avanzados, adecuadas para estudiantes de cálculo (o que se

están preparando para esa asignatura) una hoja de actividades de estudiantes reproducible con cuestiones abiertas y con una

amplia gama de niveles de dificultad

está pensada como una guía para profesores que no tienen

, sugerencias para la captura efectiva de datos y

CBR

ONCEPTOS BÁSICOS DEL

CBR

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

EXAS INSTRUMENTS INCORPORATED

TI.

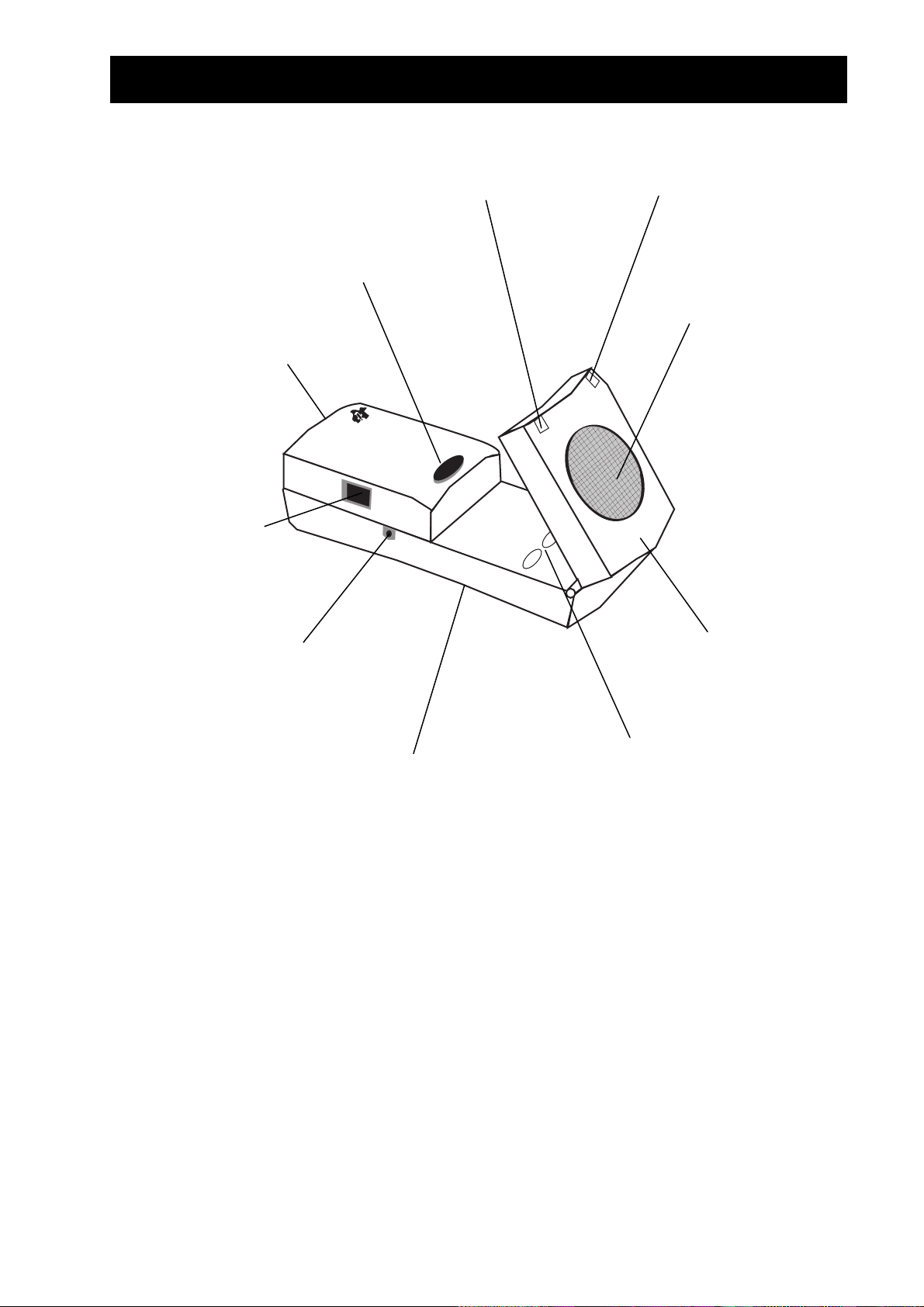
¿Qué es el CBR?

z s

(cont.)

para iniciar la toma de datos

puerta de la pila (en parte inferior)

puerto para conectar al CBL (si se necesita)

puerto para conectar a calculadoras gráficas TI con el cable de 2,2 m que se incluye

luz verde para indicar cuándo

e produce la captura de datos

(también dispone de sonido)

botón

CBR

)

luz roja para indicar condiciones especiales

ensor sónico para registrar hasta 200 datos por segundo con un rango de 0,5 m a 6 m

TRIGGER

85-86

cabezal pivotante para orientar el sensor con precisión

ócalo roscado estándar para montarlo en un trípode o en la abrazadera que se incluye (en

botones para transferir el programa RANGER a las calculadoras

la parte posterior)

incluye todo lo que necesita para iniciar las actividades en el aula sencilla y rápidamente. No

CBR

tiene más que añadir una calculadora gráfica TI (y accesorios fácilmente disponibles para algunas actividades).

detector sónico de movimiento

programa

RANGER

en el

CBR

cable de calculadora a

4 pilas AA

CBR

abrazadera de montaje

5 divertidas actividades

de clase

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

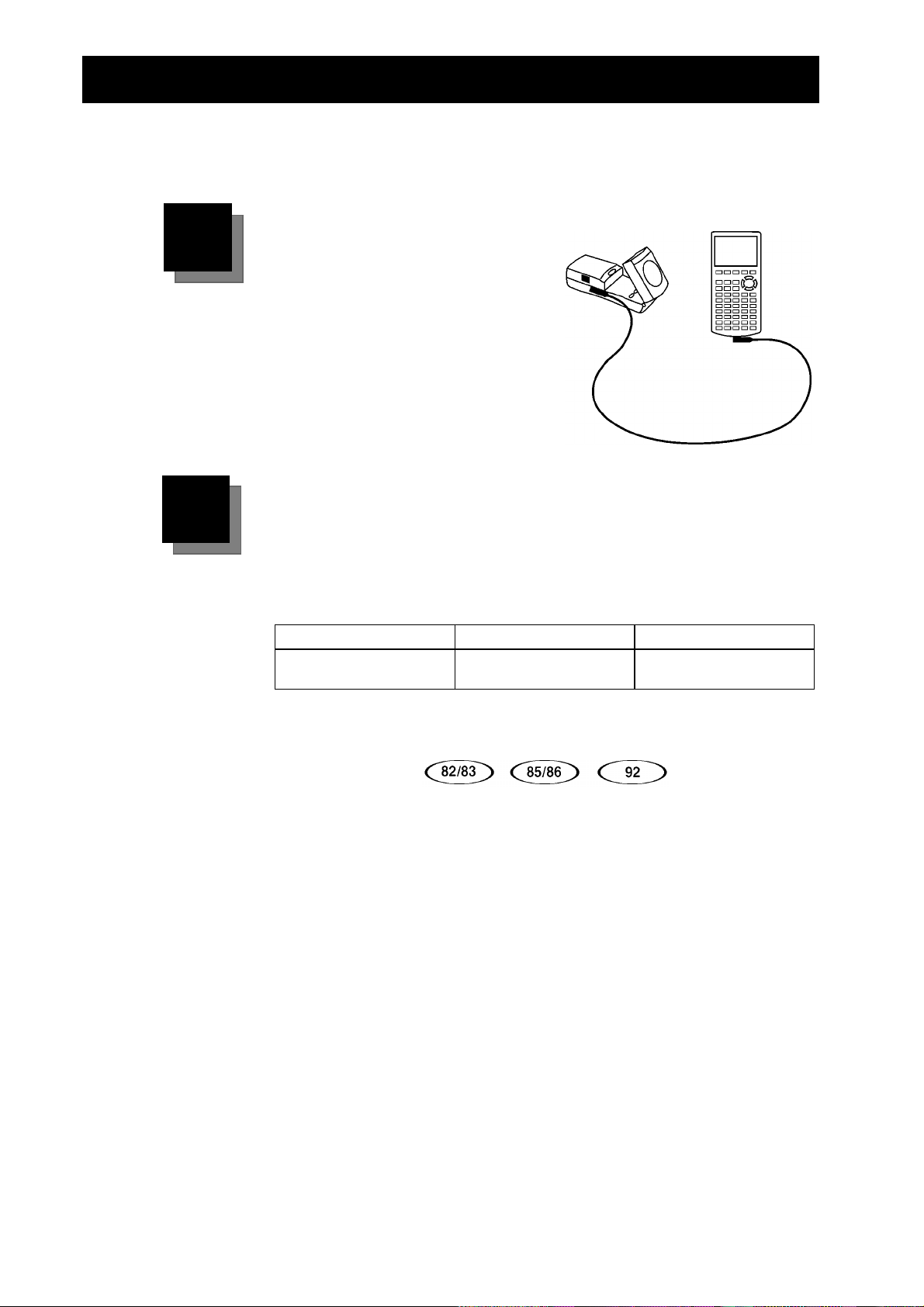
Conceptos básicos del CBR—Es tan sencillo como 1, 2, 3

Con

CBR

de datos!

, ¡sólo tiene que seguir tres sencillos pasos para comenzar con la primera toma

Conexión

Conecte el gráfica TI utilizando el cable correspondiente.

Apriete para asegurar la conexión.

Nota:

calculadora que acompaña a la calculadora también sirve.

firmemente

El cable corto calculadora-

a una calculadora

CBR

ambos extremos

Transferencia

RANGER

Es fácil transferir el programa adecuado desde el En primer lugar, prepare la calculadora para recibir el programa (consulte

las combinaciones de teclas que aparecen a continuación).

, un programa personalizado para cada calculadora, está en el

a una calculadora.

CBR

TI-82 o TI-83 TI-85/CBL o TI-86 TI-92

LINK

[

Seguidamente, abra el cabezal pivotante del botón adecuado de transferencia de programas en el

Durante la transferencia, la calculadora muestra en pantalla la palabra

RECEIVING

la luz verde del de la calculadora muestra el mensaje roja del

Una vez que ha transferido el programa calculadora, no tendrá que volver a transferirlo a la misma a menos que lo borre de su memoria.

Nota:

de memoria. Quizá tenga que borrar programas y datos de la calculadora. Puede guardar los programas y datos transfiriéndolos a un ordenador por medio de Graph Linké de TI o a otra calculadora usando un cable calculadora-calculadora o el cable calculadora a CBR (consulte el manual de la calculadora).

CBR

El programa y los datos necesitan aproximadamente 17.500 bytes

›

]

(excepto la TI-92). Cuando finaliza el proceso de transferencia,

parpadea una vez,

CBR

parpadea dos veces y el

LINK

[

]

CBR

emite un pitido y la pantalla

CBR

. Si hay un problema, la luz

DONE

emite dos pitidos.

CBR

RANGER

Vaya a la pantalla

principal.

y, después, pulse el

CBR

desde el

CBR

a una

ONCEPTOS BÁSICOS DEL

CBR

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

EXAS INSTRUMENTS INCORPORATED

TI.

Conceptos básicos del CBR—Es tan sencillo como 1, 2, 3

Ejecución

Ejecute el programa

RANGER

aparecen a continuación).

TI-82 o TI-83 TI-85/CBL o TI-86 TI-92

Pulse Seleccione Pulse

›

RANGER

Aparece la pantalla de apertura. Pulse

›. Aparece el menú principal

MAIN MENU

SETUPàSAMPLE SET DEFAULTS APPLICATIONS PLOT MENU TOOLS QUIT

& & & & &

(consulte las combinaciones de teclas que

^ A

Pulse Seleccione

›

Pulse

RANGER

MAIN MENU

Pulse L [

Seleccione Pulse ¨

VAR-LINK RANGER

›

ver/cambiar los ajustes antes de la toma de datos cambiar los ajustes a los valores por defecto

DISTANCE MATCH, VELOCITY MATCH, BALL BOUNCE

opciones de dibujo

GET CBR DATA, GET CALC DATA, STATUS, STOPàCLEAR

(cont.)

Para resultados rápidos, realice una de las actividades para el aula que se incluyen en esta guía

En el menú principal pantalla

. Pulse › para seleccionar

SETUP

actividad y pulse

Información importante

Esta guía sirve para todas las calculadoras gráficas de TI que pueden utilizarse con

MAIN MENU,

› para iniciar la captura de datos. ¡Así de sencillo!

, por lo que puede ocurrir que algunos de los

CBR

seleccione

SET DEFAULTS

START NOW

. Aparece la

. Configure la

nombres de menú no coincidan exactamente con los de su calculadora.

Cuando vaya a comenzar una actividad, asegúrese de que el bien sujeto y que no se puede tropezar con el cable.

Salga siempre del programa programa selecciona del

CBR

Desconecte siempre el

RANGER

QUIT

la próxima vez que lo utilice.

realiza un apagado correcto del

. De esta manera se garantiza la correcta inicialización

RANGER

de la calculadora antes de guardarlo.

CBR

utilizando la opción

cuando

CBR

QUIT

CBR

. El

está

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

Sugerencias para una captura efectiva de datos

Obtención de mejores datos

¿Cómo funciona el CBR?

La comprensión del funcionamiento de un detector sónico de movimiento puede ayudarle a obtener mejores gráficas de datos. El detector de movimiento envía una señal ultrasónica y posteriormente mide el tiempo que tarda dicha señal en volver después de chocar con el objeto más cercano.

, al igual que cualquier otro detector sónico de movimiento, mide el intervalo de

CBR

tiempo entre la transmisión de la señal ultrasónica y el primer eco devuelto, pero dispone de un microprocesador incorporado que hace mucho más. Cuando se capturan los datos, el

calcula la distancia del objeto al

CBR

cuenta la velocidad del sonido. Después calcula la primera y segunda derivada con respecto al tiempo de los datos de la distancia para obtener la velocidad y la aceleración. Almacena estas medidas en las listas

L1, L2, L3

utilizando operaciones que tienen en

CBR

y L4.

Una interesante actividad de aula consiste en realizar los mismos cálculos que hace

Capturar los datos del experimento en modo

➊

RANGER

Utilizar los tiempos tomados en el experimento, que aparecen en

➋

datos de la distancia, en Comparar los resultados con los de la lista

Utilizar los datos de la velocidad, en L3 (o los valores calculados por los estudiantes),

➌

junto con los datos del tiempo, en

para calcular la velocidad del objeto en cada momento.

L2,

(

n+1

)à2 N (

n+1

, para calcular la aceleración del objeto en cada

REALTIME=NO

n-1

. Salir del programa

)à2

junto con los

L1,

momento del experimento. Comparar después los resultados con los de la lista

Tamaño del objeto

Si coloca un objeto pequeño muy lejos del

, la precisión de las lecturas disminuirá. Por

CBR

ejemplo, a 5 metros, es mucho más fácil detectar un balón de fútbol que una pelota de ping-pong.

Intervalo mínimo

Cuando el

Si un objeto está a menos de 0,5 metros, las señales consecutivas pueden solaparse

CBR.

y es posible que el debe colocar el

envía una señal, la misma choca con el objeto, rebota y es recibida por el

CBR

las identifique mal. La gráfica sería incorrecta, de manera que

CBR

a más de 0,5 metros del objeto.

CBR

Intervalo máximo

Al desplazarse la señal por el aire, va perdiendo intensidad. Tras recorrer 12 metros (6 de ida y 6 de vuelta al lo detecte bien. Esto limita la distancia efectiva para obtener resultados fiables a un máximo de 6 metros de distancia al

ONCEPTOS BÁSICOS DEL

CBR

), puede que el eco de vuelta sea demasiado débil para que el

CBR

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

EXAS INSTRUMENTS INCORPORATED

CBR

TI.

Sugerencias para una captura efectiva de datos

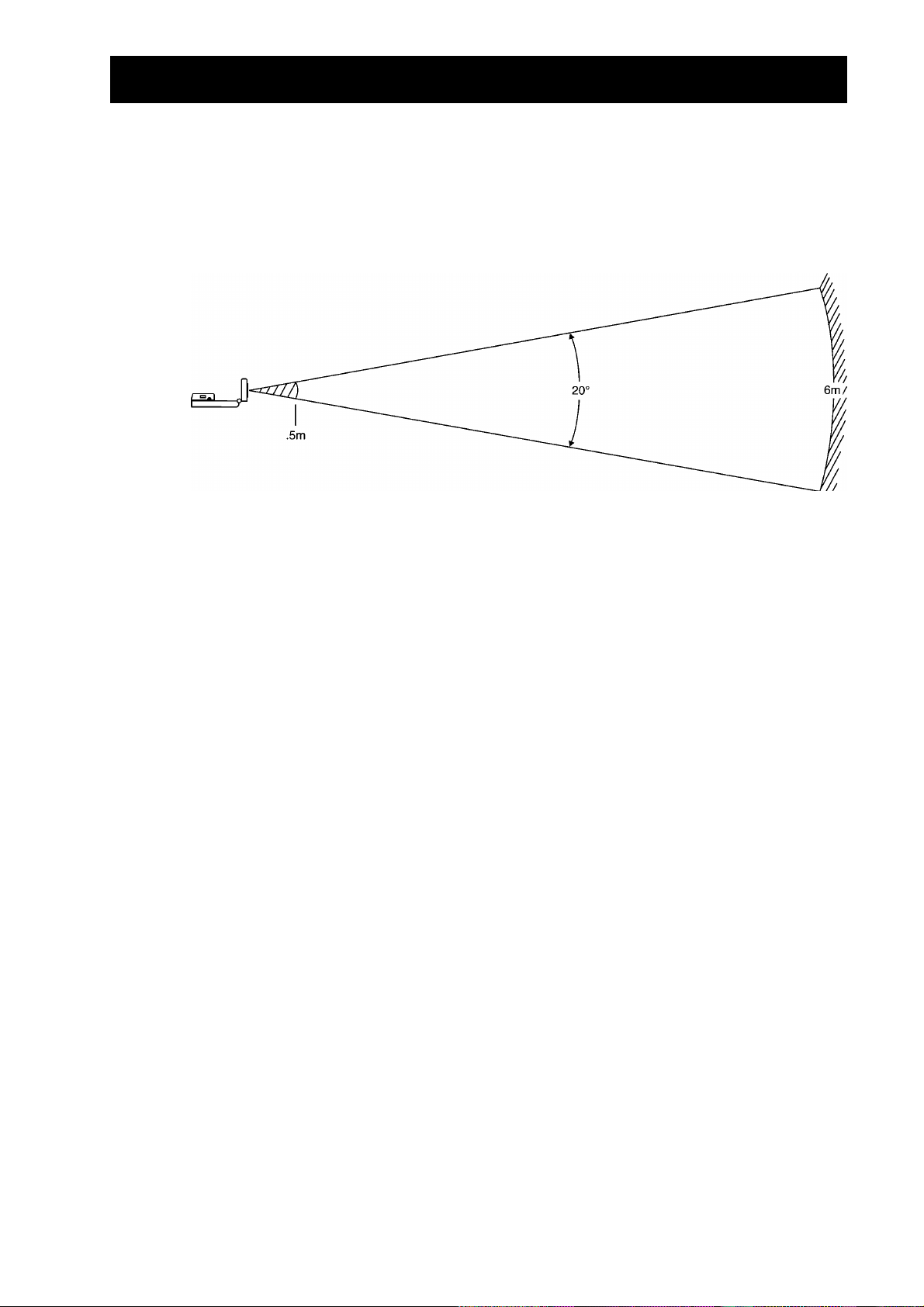
La zona despejada

(cont.)

El haz que emite el

es cónico formando un ángulo de 10°.

CBR

Para evitar interferencias con otros objetos próximos, intente establecer una zona despejada en la trayectoria del haz. Esto ayuda a evitar que el sean el objetivo. El

Superficies reflectantes

registra el objeto más próximo de la zona despejada.

CBR

registre objetos que no

CBR

Algunas superficies reflejan las señales mejor que otras. Por ejemplo, puede que vea mejores resultados con una pelota de superficie relativamente dura y uniforme que con una pelota de tenis. A la inversa, los datos tomados en habitaciones provistas de superficies duras y reflectantes son más proclives a presentar puntos de datos dispersos. Las medidas llevadas a cabo en superficies irregulares (como un coche de juguete o un estudiante sujetando una calculadora mientras va caminando) pueden resultar irregulares.

Una gráfica distancia-tiempo de un objeto inmóvil puede presentar pequeñas diferencias en los valores calculados para la distancia. Si alguno de estos valores se asigna a un píxel diferente, la línea horizontal prevista puede presentar pequeñas irregularidades. La gráfica velocidad-tiempo puede resultar aún más dentada, puesto que el cambio de la distancia entre dos puntos frente al tiempo es, por definición, la velocidad. Puede que desee aplicar cierto grado de suavizado a los datos.

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

Sugerencias para una captura efectiva de datos

Ajustes del RANGER

Tiempos del experimento

es el tiempo total en segundos necesario para completar todo el experimento.

TIME

Introduzca un entero entre 1 segundo (para movimiento rápido) y 99 segundos (para movimiento lento). Cuando

REALTIME=YES, TIME

es siempre 15 segundos.

(cont.)

Cuando ejemplo, cuando

Inicio y detención

La pantalla

es un número más pequeño, el objeto debe estar más cerca del

TIME

TIME=1 SECOND

del programa

SETUP

, el objeto no puede estar a más de 1,75 metros del

RANGER

proporciona varias opciones para iniciar y detener

CBR

. Por

la toma de datos.

BEGIN ON: [ENTER]

. Inicia la toma de datos con la tecla

de la calculadora cuando la

›

persona que inicia la misma está más próxima a la calculadora.

BEGIN ON: [TRIGGER]

. Inicia y detiene la toma de datos con el botón

cuando la persona que inicia la misma está más próxima al En esta opción, también puede seleccionar desconectar el

configurar la toma de datos, desconectar el cable del acción, pulsar

para transferir los datos. Utilice

, realizar la toma de datos, volver a conectar el

BEGIN ON: [TRIGGER]

cuando el cable no sea

, llevar el

CBR

. Esto le permite

CBR

del

CBR

donde esté la

y pulsar

CBR

suficientemente largo o cuando pudiera interferir con la captura de datos. Esta opción no está disponible en modo

BEGIN ON: DELAY

. Inicia la toma de datos tras un intervalo de 10 segundos desde el

momento en que se pulsa

REALTIME=YES

. Es especialmente útil cuando la actividad la realiza

›

(como la aplicación

MATCH

una sola persona.

Botón de activación

El efecto de

varía en función de los ajustes.

CBR

›

ON: DELAY

inicia la toma de datos, incluso si está seleccionado

BEGIN ON: [ENTER]

. También detiene la toma de datos, aunque normalmente se realizará ésta

hasta el final. Si

REALTIME=NO

, una vez detenida la toma de datos,

repite automáticamente la más reciente, pero no transfiere los datos a la calculadora. Para transferirlos, seleccione

TOOLS

en el menú

MAIN MENU

puede repetir una toma de datos seleccionando o

START NOW

en la pantalla

SETUP

, y después seleccione

REPEAT SAMPLE

GET CBR DATA

en el menú

BEGIN

(también

PLOT MENU

ONCEPTOS BÁSICOS DEL

CBR

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

EXAS INSTRUMENTS INCORPORATED

TI.

Sugerencias para una captura efectiva de datos

Suavizado

(cont.)

Las posibilidades de suavizado incorporadas en el programa

RANGER

pueden reducir el efecto de las señales dispersas o de las variaciones en las medidas de distancia. Evite un suavizado excesivo. Comience sin suavizado o con un suavizado

Aumente el grado

LIGHT.

de suavizado hasta que obtenga resultados satisfactorios.

Para una actividad con una alta probabilidad de señales dispersas (inservibles), puede

que desee aumentar el suavizado en la pantalla

antes de realizar la toma de

SETUP

datos (consulte la página 38). Para datos ya capturados con

REALTIME=NO

La calculadora debe estar conectada al

, elija

Ruido. ¿Qué es y cómo eliminarlo?

Cuando el

SMOOTH DATA

recibe señales reflejadas de objetos que no sean el objetivo principal, la

CBR

y, seguidamente, seleccione el grado de suavizado.

, puede aplicar el suavizado a los mismos. . Seleccione

CBR

PLOT TOOLS

en el menú

PLOT

gráfica muestra puntos de datos erráticos (picos de ruido) que no se ajustan al patrón general del dibujo. Para minimizar el ruido:

Compruebe que el

sensor mientras ve un dato en modo resultados antes de capturar un dato en modo

Intente realizar una toma de datos en un espacio libre de obstáculos (consulte el

apunta directamente al objetivo. Intente ajustar el cabezal del

CBR

REALTIME=YES

hasta que obtenga buenos

REALTIME=NO

dibujo de la zona despejada que aparece en la página 7). Seleccione un objeto mayor y más reflectante o acerque el objeto al

(pero no a

CBR

menos de 0,5 metros). Cuando utilice más de un

en una habitación, un grupo debe completar la toma de

CBR

datos antes de que el siguiente grupo comience con la suya. Para una toma de datos con ruido en modo

REALTIME=YES

, repita la misma utilizando un grado de suavizado más alto hasta que obtenga resultados satisfactorios (no puede cambiar el suavizado en las aplicaciones

BOUNCE

Para una toma de datos con ruido en modo

DISTANCE MATCH, VELOCITY MATCH

REALTIME=NO

, puede aplicar un grado

BALL

mayor de suavizado a los datos originales (consulte la página 9).

Velocidad del sonido

La distancia aproximada al objeto se calcula asumiendo la velocidad teórica del sonido. Sin embargo, la velocidad real del sonido depende de varios factores, principalmente de la temperatura del aire. Para actividades de movimiento relativo, este factor no es importante. Para actividades en que las medidas han de ser muy precisas, puede utilizarse una orden de programación para especificar la temperatura ambiente (consulte las páginas 40–41).

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

Sugerencias para una captura efectiva de datos

REALTIME=YES

(cont.)

Utilice el modo

para objetos lentos

para ver los resultados según se van capturando

cuando tiene que capturar o representar un solo tipo de datos (distancia, velocidad o

REALTIME=YES

aceleración) para un experimento

En modo

REALTIME=YES

, el

procesa los datos de la gráfica que se desea (distancia,

CBR

velocidad o aceleración) que se transfieren a la calculadora a medida que se van midiendo los datos individuales de la distancia. Después,

RANGER

dibuja un píxel

individual para esa señal. Puesto que todas estas operaciones deben completarse antes de realizar la toma

siguiente, hay un límite de velocidad de toma de datos en modo

REALTIME=YES

Para un único dato, se emplean aproximadamente 0,080 segundos en capturarlo, procesarlo y transferirlo. Se necesita un tiempo adicional para operaciones como dibujar el punto, lo cual hace disminuir la velocidad efectiva de la toma de datos con el

RANGER

aproximadamente 0,125 segundos.

REALTIME=NO

Utilice el modo

para objetos rápidos

cuando es necesario el suavizado (consulte la página 9)

para trabajar con el

cuando necesita capturar o representar todos los tipos de datos (distancia, velocidad y

REALTIME=NO

en modo desconectado (consulte la página 11)

CBR

aceleración) para un experimento

En modo

REALTIME=NO

, los datos se almacenan en el

y no se transfieren a la

CBR

calculadora hasta que se completa el experimento. La velocidad de la toma de datos puede ser de hasta una cada 0,005 segundos para objetos cercanos. Los datos del tiempo, distancia, velocidad y aceleración se transfieren a la calculadora.

Puesto que los datos se almacenan en el

, puede transferirlos desde él a una

CBR

calculadora tantas veces como quiera.

Cada vez que cambia el suavizado, el

aplica el nuevo factor de suavizado,

CBR

transfiere los datos ajustados a la calculadora y almacena los valores suavizados en las listas.

Al seleccionar un dominio cambian las listas almacenadas en la calculadora. Si es

necesario, puede recuperar los datos originales del programa

También puede compartir los mismos datos con muchos estudiantes, incluso aunque

RANGER

, seleccione

TOOLS

. En el menú

. Desde el menú

CBR

, seleccione

TOOLS

MAIN MENU

GET CBR DATA

estén utilizando diferentes tipos de calculadoras gráficas de TI. Esto permite a los estudiantes participar en actividades de análisis de datos utilizando los mismos datos (consulte la página 11).

del

ONCEPTOS BÁSICOS DEL

CBR

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

EXAS INSTRUMENTS INCORPORATED

TI.

Sugerencias para una captura efectiva de datos

Utilización del CBR en modo desconectado

(cont.)

Puesto que el

CBR

desconectado, son necesarios ciertos ajustes. En la pantalla

Ajuste

El programa

REALTIME=NO BEGIN ON=[TRIGGER]

RANGER

No es necesario ningún procedimiento especial.

Uso compartido de datos

¿Qué hacer si desea que toda la clase analice los mismos datos al mismo tiempo? Con el

puede distribuir los datos de

CBR

Transfiera el programa

➊

capturar los datos. Capture los datos con el

➋

Conecte la calculadora del primer estudiante al

➌

o calculadora-calculadora.

CBR

En el menú

➍

seleccione Pulse › para volver al menú

➎

no puede enviar datos a la calculadora inmediatamente en modo

SETUP

le indica cuándo desconectar el

REALTIME=NO

RANGER

MAIN MENU

GET CBR DATA. TRANSFERRING...

del programa

a las calculadoras de todos los estudiantes antes de

en modo

CBR

RANGER

PLOT MENU

rápidamente en una clase.

REALTIME=NO

, seleccione

se muestra en pantalla y aparece la gráfica.

y seleccione

y cuándo volver a conectarlo.

CBR

por medio del cable calculadora

CBR

. En el menú

TOOLS

. Desconecte el cable.

QUIT

TOOLS

Conecte otra calculadora (del mismo tipo) a la calculadora que tiene los datos. En la

➏

segunda calculadora, en el menú

TOOLS

. En el menú

TOOLS

, seleccione

MAIN MENU

GET CALC DATA

del programa

. Las listas L1, L2, L3, L4 y L5 se

RANGER

, seleccione

transfieren automáticamente a la segunda calculadora. Transfiera los datos desde el

➐

a la calculadora de otro estudiante mientras otros

CBR

estudiantes continúan transfiriendo los datos entre calculadoras.

Cuando todos los estudiantes tengan los mismos datos, podrán analizar los datos de

RANGER

por medio de

PLOT MENU

o fuera de

RANGER

por medio de las funciones de listas

y gráficas de la calculadora. Para compartir datos de la TI-85, utilice la función

LINK

fuera de

RANGER

para transferir

las listas.

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

Sugerencias para una captura efectiva de datos

Más allá de la simple captura de datos

(cont.)

Una vez que ha capturado y representado datos en el

RANGER

, puede comprobar si se distribuyen según algún tipo de función. Puesto que los datos se capturan como listas y se muestran en gráficas estadísticas, puede utilizar

,  y œ para encontrar esa

posible relación.

Dentro de RANGER

Explore las gráficas utilizando

, que está ajustado automáticamente (en la TI-85,

TRACE

utilice el cursor de libre desplazamiento.) Manipule el conjunto de datos, incluyendo el suavizado de datos, o la selección del

dominio de los mismos.

Fuera de RANGER

Explore los datos por medio del editor de listas de la calculadora.

Ajuste manualmente una función a los datos por medio del editor Y= de la

calculadora. Determine automáticamente la función que mejor se ajusta a los datos utilizando las

posibilidades que en cuanto a regresión posee la calculadora.

Pueden explorarse otras relaciones aparte de las representadas por las opciones gráficas de

RANGER

Velocidad-Tiempo como gráficas estadísticas. En el menú

RANGER

. Por ejemplo, pueden verse gráficas simultáneas del tipo Distancia-Tiempo y

del programa

como

Plot2

, seleccione

y después establezca

QUIT

MAIN MENU

como L1 frente a L2 y

Plot1

frente a L3 (puede que también necesite ajustar la ventana). Los datos y gráficas pueden enviarse a un ordenador por medio de Graph Link de TI. Esto

es especialmente útil cuando los estudiantes generan informes más detallados de los resultados obtenidos.

Utilización de CBR sin el programa RANGER

Puede utilizar diferentes de

Para obtener información sobre la utilización de

Para obtener información sobre la obtención de programas y actividades, consulte la

como un detector sónico de movimiento con

CBR

RANGER

página 36. Para obtener información sobre órdenes de programación para escribir sus propios

programas, consulte las páginas 40–41.

CBR

con

o con programas

CBL

, consulte la página 39.

CBL

ONCEPTOS BÁSICOS DEL

CBR

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

EXAS INSTRUMENTS INCORPORATED

TI.

Actividad 1. Aproximación a la gráfica notas para el pr ofesor

Conceptos

Función explorada: lineal.

MATCH

introduce los conceptos de distancia y

tiempo; o, para ser más precisos, el concepto de distancia frente al tiempo. A medida que los estudiantes intentan reproducir gráficas caminando mientras ven representado su movimiento, puede explorarse el concepto de posición.

En las exploraciones, se pide a los estudiantes que conviertan la velocidad de sus pasos de metros por segundo a kilómetros por hora.

Una vez que hayan entendido la relación DistanciaTiempo, pase a la relación Velocidad-Tiempo.

Materiales

 calculadora

CBR



 cable calculadora-calculadora

Un ViewScreené de TI permite a los otros estudiantes observar la actividad, haciéndola muy divertida.

Ideas

Los estudiantes realmente disfrutan con esta actividad. ¡Todos querrán participar!

Como mejor funciona esta actividad es utilizando ViewScreen de TI para que el estudiante que está caminando (y el resto de la clase) pueda ver su movimiento reflejado en una pared o pantalla.

Indique a los estudiantes que caminen en línea recta, alejándose o acercándose al CBR, pues a veces intentan caminar de lado (perpendicularmente) o dando saltos.

Las instrucciones recomiendan que la actividad se realice en metros, para que concuerde con la preguntas de las hojas de actividades del estudiante.

Consulte las páginas 6–12 para obtener sugerencias sobre la captura efectiva de datos.

Gráficas normales

Respuestas habituales

1. tiempo (desde el comienzo de la toma de datos); segundos; 1 segundo; distancia (desde el CBR al objeto); metros; 1 metro

2. la ordenada en el origen representa la distancia inicial

3. varía con el estudiante

4. hacia atrás (aumentar la distancia entre el CBR y el objeto)

5. hacia delante (disminuir la distancia entre el CBR y el objeto)

6. inmóvil; pendiente cero significa que no hay cambio en y (distancia)

7. varía con la gráfica; @yà3.3

8. varía con la gráfica; @yà1

9. el segmento de mayor pendiente (positiva o negativa)

10.ésta es una pregunta con truco; el segmento es horizontal, puesto que no hay movimiento

11.velocidad al caminar; al cambiar de dirección y/o la velocidad

12.velocidad

13.varía con la gráfica (ejemplo: 1,5 metros en 3 segundos)

14.varía con la gráfica; ejemplo: 0,5 metros à 1 segundo

ejemplo: (0,5 metros à 1 segundo) Q (60 segundos à 1 minuto) = 30 metros à minuto

ejemplo: (30 metros à 1 minuto) Q (60 minutos à 1 hora) = 1800 metros à hora

ejemplo: (1800 metros à 1 hora) Q (1 kilómetro à 1000 metros) = .18 kilómetros à hora.

Haga que los estudiantes comparen este último número con la velocidad de un vehículo, por ejemplo 96 kilómetros à hora.

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

15.varía con la gráfica; suma de los @y para cada segmento.

TI.

ONCEPTOS BÁSICOS DEL

CBR

Actividad 1. Aproximación a la gráfica lineal

Captura de datos

➊

Sujete el

en una mano y la calculadora en la otra. Apunte el sensor

CBR

directamente hacia una pared.

Ayuda:

La distancia máxima para cualquier gráfica es de 4 metros desde el distancia mínima es de 0,5 metros. Compruebe que no hay nada en la zona despejada (consulte la página 7).

CBR

. La

Ejecute el programa

➋

RANGER

(consulte la página 5 para obtener las combinaciones

de tecla para cada calculadora). En el menú

➌

En el menú

➍

generales. Pulse › para mostrar la gráfica que va a reproducir. Dedique un momento a

➎

MAIN MENU APPLICATIONS,

DISTANCE MATCH

seleccione

APPLICATIONS

DISTANCE MATCH

. Seleccione

. Aparecen instrucciones

se ocupa automáticamente de los ajustes.

METERS

estudiar la gráfica. Responda a las preguntas 1 y 2 de la hoja de actividades. Colóquese donde piensa que comienza la gráfica. Pulse › para comenzar la

➏

captura de datos. Escuchará un clic y verá la luz verde a medida que se capturan los datos.

Camine hacia atrás y hacia adelante, e intente aproximarse a la gráfica. Su posición

➐

aparece representada en la pantalla. Una vez terminado el experimento, examine lo bien que su “paseo” se ha ajustado a

➑

la gráfica y, después, conteste la pregunta 3. Pulse › para mostrar en pantalla el menú

➒

OPTIONS

y seleccione

SAME MATCH

Intente mejorar su técnica al caminar y, después, conteste las preguntas 4, 5 y 6.

ONCEPTOS BÁSICOS DEL

CBR

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

EXAS INSTRUMENTS INCORPORATED

TI.

Actividad 1. Aproximación a la gráfica

Exploraciones

(cont.)

lineal

DISTANCE MATCH

Pulse › para mostrar el menú

➊

segmento y conteste las preguntas 7 y 8. Estudie toda la gráfica y conteste las preguntas 9 y 10.

➋

Colóquese donde piensa que comienza la gráfica, pulse › para comenzar la

➌

captura de datos, e intente reproducir la gráfica. Cuando finalice el experimento, conteste las preguntas 11 y 12.

➍

Pulse › para mostrar el menú

➎

Estudie la gráfica y conteste las preguntas 13, 14 y 15.

➏

Pulse › para mostrar el menú

➐

menú

MAIN MENU

Exploraciones avanzadas

Las gráficas generadas por en el que debe reproducir una gráfica Velocidad-Tiempo. ¡Esto es más difícil!

MATCH

es un programa muy conocido. Puede disponer de versiones adicionales que

exploran gráficas más complicadas (consulte la página 36).

, todas las gráficas están formadas por tres segmentos.

OPTIONS

y seleccione después

DISTANCE MATCH

y seleccione

NEW MATCH

. Repita la actividad si lo desea, o vuelva al

para salir del programa

QUIT

eran rectas. Ahora pruebe

. Estudie el primer

RANGER

VELOCITY MATCH

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

Actividad 1. Aproximación a la gráfica

Nombre ___________________

Captura de datos

1. ¿Qué propiedad física se representa en el eje X? ____________________________________________ ¿En qué unidades? ¿Cuál es la distancia entre las marcas? ___________ ¿Qué propiedad física se representa en el eje Y? ____________________________________________ ¿En qué unidades? ¿Cuál es la distancia entre las marcas? ___________

2. ¿A qué distancia del

piensa que debería empezar? ______________________________________

CBR

3. ¿Comenzó demasiado cerca, demasiado lejos o a la distancia adecuada? _______________________

4. ¿Debería caminar hacia adelante o hacia atrás para un segmento de pendiente positiva? __________

¿Por qué? ____________________________________________________________________________

5. ¿Debería caminar hacia adelante o hacia atrás para un segmento de pendiente negativa? _________ ¿Por qué? ____________________________________________________________________________

6. ¿Qué debe hacer para un segmento de pendiente nula? _____________________________________ ¿Por qué? ____________________________________________________________________________

Exploraciones

7. Si da un paso cada segundo, ¿qué longitud deberían tener los pasos? _________________________

8. Si, en vez de ello, da pasos de 1 metro de longitud, ¿cuántos pasos debe dar? __________________

9. ¿Para qué segmento deberá moverse más rápidamente? _____________________________________

¿Por qué? ____________________________________________________________________________

10. ¿Para qué segmento deberá moverse más lentamente? ______________________________________ ¿Por qué? ____________________________________________________________________________

11. Además de elegir si tiene que moverse hacia adelante o hacia atrás, ¿qué otros factores hay que considerar para reproducir exactamente la gráfica? _________________________________________

_____________________________________________________________________________________

12. ¿Qué propiedad física representan las pendientes de los segmentos? __________________________

13. Para el primer segmento, ¿cuántos metros debe caminar y en cuántos segundos? _______________

segundo: ________________________

14. Convierta el valor de la pregunta 13 (la velocidad) en metros

Conviértalo en metros/minuto: __________________________________________________________ Conviértalo en metros/hora: _____________________________________________________________ Conviértalo en kilómetros/hora: __________________________________________________________

15. ¿Qué distancia recorrió realmente? _______________________________________________________

ONCEPTOS BÁSICOS DEL

CBR

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

EXAS INSTRUMENTS INCORPORATED

TI.

Actividad 2. Coche de juguete notas para el profesor

Conceptos

Función explorada: lineal. Se utiliza el movimiento de un coche de juguete

motorizado para ilustrar el concepto de velocidad constante.

Materiales

 calculadora

CBR



 cable calculadora a

CBR

 coche de juguete con funcionamiento a pilas  ViewScreen de TI (opcional)

Sugerencias

Los coches de juguete varían mucho en cuanto a tamaño, forma y ángulo de reflexión del sonido ultrasónico incidente. Por tanto, los resultados varían en calidad. Algunos vehículos pueden necesitar una superficie reflectante adicional para obtener buenos resultados. Intente montar una ficha en el vehículo para asegurar un buen blanco (objetivo) para el sensor.

Puede que desee probar varios vehículos para que los estudiantes exploren estos efectos.

Los coches de juguete más lentos (como los diseñados para niños pequeños) son mejores para esta actividad. Busque un coche que parezca mantener una velocidad constante.

Consulte las páginas 6–12 para obtener sugerencias sobre la captura efectiva de datos.

Exploraciones

La pendiente de la gráfica Distancia-Tiempo de un objeto en un momento dado da como resultado la velocidad del objeto en ese momento. Por tanto, para un objeto que se desplaza a velocidad constante, la pendiente de su gráfica DistanciaTiempo es constante. Esta es la razón por la que la gráfica representa una relación lineal.

Si comienza a capturar datos antes de que el coche comience a moverse, observará que la gráfica Distancia-Tiempo no es lineal al principio. ¿Por qué? El coche está parado al principio (v = 0). No puede adquirir instantáneamente su velocidad constante. La aceleración viene dada por:

∆

Para que el objeto adquiriera instantáneamente su velocidad constante partiendo de un estado de inmovilidad debería ser, ∆t = 0. Pero esto implica una aceleración infinita, lo cual no es físicamente posible (de hecho, según la Segunda Ley de Newton, F = ma, una aceleración infinita sólo puede

proceder de una fuerza infinita, lo cual es igualmente imposible). Por tanto, observaremos una aceleración del objeto (aumento de velocidad), hasta que alcance su velocidad constante en un tiempo finito.

Gráficas normales

Respuestas a las preguntas

1. la primera o la última gráfica; la distancia aumenta de manera constante

2. los estudiantes introducen valores desde

TRACE

3. los valores de la distancia aumentan en una cantidad constante

4. la velocidad es la variación de la distancia con respecto al tiempo; los valores son los mismos para cada incremento igual de tiempo

5. el estudiante debe obtener un valor similar a los valores calculados para m

similar a m m representa la velocidad del coche

6. b es la ordenada en el origen; ejemplo: y = 2x + 0

7. varía; por ejemplo, si m = 2, distancia (y) = 20 metros después de 10 segundos (y = 2 Q 10 + 0); para 1 minuto, y = 120 metros

Exploraciones avanzadas

La pendiente de una gráfica Velocidad-Tiempo con velocidad constante es cero. Por tanto, la gráfica Aceleración-Tiempo muestra a = 0 (en el caso ideal) para el periodo de tiempo en que la velocidad es constante.

El área resultante es el camino recorrido por el objeto (distancia neta) durante el intervalo de tiempo que va de t

Para estudiantes de cálculo, el recorrido puede calcularse a partir de:

donde s es el recorrido del objeto en el intervalo que va de t

a t2.

svdt

∫

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

Actividad 2. Coche de juguete lineal

Captura de datos

Coloque el coche a más de 0,5 metros del

➊

CBR

Sugerencias:

Apunte el sensor directamente hacia el coche y asegúrese de que no

, en línea recta en dirección contraria

CBR

hay nada en la zona despejada (consulte la página 7).

Antes de empezar a capturar datos, conteste la pregunta 1 de la hoja de

➋

actividades. Ejecute el programa

➌

RANGER

(consulte la página 5 para obtener las combinaciones

de teclas para cada calculadora). En el menú

➍

MAIN MENU

seleccione

SETUPàSAMPLE

. Para esta actividad, los ajustes

deben ser:

REALTIME: NO

TIME (S): 5 SECONDS

DISPLAY: DISTANCE

BEGIN ON: [ENTER]

SMOOTHING: LIGHT

UNITS: METERS

En la página 38 dispone de instrucciones para los cambios de ajustes. Seleccione

➎

Pulse › cuando esté preparado para comenzar. Arranque el coche y salga

➏

START NOW

rápidamente de la zona despejada. Oirá un clic según se van capturando los datos y el mensaje

Una vez finalizada la captura de datos, la calculadora muestra automáticamente una

➐

TRANSFERRING...

aparecerá en la calculadora.

gráfica Distancia-Tiempo de puntos de los datos capturados. Compare la gráfica resultante de los datos extraídos con su hipótesis realizada en la

➑

pregunta 1 para ver las similitudes y las diferencias.

ONCEPTOS BÁSICOS DEL

CBR

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

EXAS INSTRUMENTS INCORPORATED

TI.

Actividad 2. Coche de juguete

Exploraciones

Los valores para x (tiempo) en intervalos de medio segundo aparecen en la primera

➊

columna de la pregunta 2. Represente la gráfica e introduzca los correspondientes valores y (distancia) en la segunda columna.

sólo los resultados de la parte lineal de la gráfica. Puede que necesite eliminar datos inconsistentes al comienzo de la captura de datos. Asimismo, puede que sea necesario aproximar la distancia (puede que la calculadora le dé la distancia para 0,957 y para 1,01 segundos, pero no para 1 segundo). Tome el valor más cercano o su mejor estimación.

➋

Conteste las preguntas 3 y 4. Calcule los cambios en la distancia y el tiempo entre cada punto de datos para

➌

completar las columnas tercera y cuarta. Por ejemplo, para calcular @Distancia (metros) para 1,5 segundos, reste Distancia en 1 segundo a Distancia en 1,5 segundos.

La función representada en esta actividad es y = mx + b. m es la pendiente de una

➍

recta. Se calcula por medio de:

(cont.) lineal

Incluya

Nota:

po b es la ordenada en el origen. Calcule m para todos los puntos. Introduzca los valores en la tabla de la

pregunta 2.

➎

Responda a las preguntas 5, 6 y 7.

Exploraciones avanzadas

El cálculo de la pendiente de una gráfica Distancia-Tiempo en cualquier momento proporciona la velocidad aproximada del objeto en ese momento. El cálculo de la pendiente de una gráfica Velocidad-Tiempo da como resultado la aceleración aproximada del objeto en ese momento. Si la velocidad es constante, ¿cuál es la aceleración?

Haga una hipótesis sobre el aspecto de la gráfica Aceleración-Tiempo correspondiente a esta gráfica Distancia-Tiempo.

Busque el área incluida en la gráfica Velocidad-Tiempo y el eje X entre dos tiempos dados, t

y t2. Esto puede hacerse sumando las áreas de uno o más rectángulos, cada uno

de ellos con un área dada por:

@distancia

@tiempo

distancia

tiempo

área = v∆t = v(t

N distancia

N tiempo

)

2Nt1

N y

x2 N x

¿Cuál es el significado físico del área resultante?

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

Actividad 2. Coche de juguete

Nombre _______________________________

Captura de datos

1. De las siguientes gráficas, ¿cuál representa la gráfica Distancia-Tiempo del coche de juguete?

¿Por qué? ____________________________________________________________________________

Tiempo Distancia

1 xxx xxx xxx

1,5

2,5

3,5

4,5

Distancia

Tiempo

3. ¿Qué ha observado en los valores de la Distancia?___________________________________________

4. ¿Cómo muestran estos resultados que el coche tenía velocidad constante? ______________________

5. Calcule

distanciaà@tiempo

entre Tiempo = 2 y Tiempo = 4. ________________________________ ¿Qué ha observado en este resultado? ____________________________________________________ ¿Qué representa

6. Para la función lineal

? ___________________________________________________________________

= mx + b, ¿cuál es el valor de b? _____________________________________

Escriba la función de la recta en la forma

= mx + b, utilizando valores para m y para b.__________

7. ¿Qué distancia alcanzaría el coche en 10 segundos? ________________________________________ ¿Y en 1 minuto? ______________________________________________________________________

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

ONCEPTOS BÁSICOS DEL

CBR

EXAS INSTRUMENTS INCORPORATED

TI.

Actividad 3. Péndulo notas para el profesor

Conceptos

Función explorada: sinusoidal. Exploración del movimiento armónico simple

mediante la observación de un péndulo libre.

Materiales

 calculadora

CBR



 cable calculadora a

CBR

 abrazadera de montaje  cronómetro  péndulo  cinta métrica  ViewScreen de TI (opcional)

Como pesos puede utilizar:

bolas de diferentes tamaños (≥ 2" diámetro)

latas de bebidas (vacías y llenas)

latas de conservas

Sugerencias

Consulte las páginas 6–12 para obtener sugerencias sobre la captura efectiva de datos.

Fundamentos de física

Un objeto sujeto al movimiento periódico resultante de una fuerza proporcional al desplazamiento desde su posición de equilibrio (reposo) se dice que presenta un movimiento armónico simple (MAS). Dicho movimiento puede describirse con dos magnitudes.

El periodo T es el tiempo empleado en completar

un ciclo. La amplitud A es el desplazamiento máximo del

objeto desde su posición de equilibrio (la posición del peso cuando está en reposo).

Para un péndulo simple, el periodo T viene dado por:

T = 2p

donde L es la longitud del péndulo y g es la aceleración de la gravedad. T no depende de la masa del objeto ni de la amplitud de su movimiento.

La frecuencia f (número de ciclos por segundo) puede hallarse a partir de:

, donde f viene en hertzios (Hz) y T en

f =

segundos.

Las derivadas de una gráfica sinusoidal son también sinusoidales. Observe en particular la relación de fase entre la posición del peso y la velocidad.

L g

Gráficas normales

Respuestas habituales

1. varía (en metros)

2. varía (en metros)

3. varía (en segundos); T (un periodo) = tiempo total de 10 periodosà10; al promediar sobre una muestra mayor se tiende a minimizar los errores de medición inherentes

4. la longitud total del arco, que debe ser aproximadamente 4 veces la respuesta a la pregunta 2, ya que un arco mide más que una recta

5. sinusoidal, repetitiva, periódica; distancia del eje x a la posición de equilibrio

6. cada ciclo aparece desplegado horizontalmente; una gráfica que incluya 10 segundos debe contener más ciclos en la misma pantalla, por lo que los ciclos aparecen más próximos

7. (núm. total de ciclos)à(5 segundos) = ciclosàsegundo; es más fácil ver ciclos completos, y menos errores de medición

8. f = 1àT, donde T es el tiempo para 1 periodo

9. periodo disminuido; periodo aumentado (la longitud del péndulo está directamente

relacionada con el tiempo del periodo; cuanto más largo sea el péndulo, mayor será el periodo. Los estudiantes pueden explorar esta relación utilizando el editor de listas de la calculadora, con el que pueden calcular el periodo para diferentes valores de L)

10.A (amplitud) = ¼ distancia total que recorre el péndulo en 1 periodo

11.ambos sinusoidales; las diferencias están en la amplitud y en la fase

12.posición de equilibrio

13.cuando posición = valor máximo o mínimo (cuando el peso está a la distancia máxima del equilibrio).

14.No. T sólo depende de L y de g, no de la masa.

Exploraciones avanzadas

Captura de datos: la gráfica de L2 frente a L3 forma una elipse.

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

Actividad 3. Péndulo sinusoidal

Captura de datos

Prepare el péndulo. Alinéelo de manera que se balancee en línea con el

➊

Sugerencias:

Coloque el

a una distancia tal que en el punto de acercamiento

CBR

máximo el peso no quede a menos de 0,5 metros. Compruebe que no hay nada en la zona despejada (consulte la página 7).

amplitud

posición de equilibrio

Utilice una cinta métrica para medir la distancia del

➋

a la posición de equilibrio.

CBR

Conteste la pregunta 1 de la hoja de actividades.

Mida la distancia máxima a la que va a llegar el peso desde la posición de equilibrio.

Conteste la pregunta 2.

Un ciclo de péndulo (un periodo) consiste en una oscilación completa (hacia

➌

adelante y hacia atrás). Con un cronómetro, mida el tiempo empleado en completar diez periodos. Conteste las preguntas 3 y 4.

Ejecute el programa

➍

RANGER

(consulte la página 5 para obtener combinaciones de teclas para cada calculadora). Un método eficaz consiste en que una persona haga oscilar el péndulo mientras otra hace funcionar la calculadora y el

MAIN MENU,

Pulse › para mostrar los ajustes. Para esta actividad, deben ser los siguientes:

➎

REALTIME: NO

TIME (S): 10 SECONDS

DISPLAY: DISTANCE

BEGIN ON: [ENTER]

SMOOTHING: LIGHT

En la página 38 dispone de instrucciones para cambiar un ajuste. Cuando sean

➏

correctos, seleccione Pulse › cuando esté preparado para comenzar. Podrá oír un clic a medida que se

➐

seleccione

UNITS: METERS

SETUPàSAMPLE

START NOW

capturan los datos y el mensaje

TRANSFERRING...

aparecerá en la calculadora.

. En el menú

CBR

➑

ONCEPTOS BÁSICOS DEL

Una vez finalizada la captura de datos, la calculadora muestra automáticamente la gráfica Distancia-Tiempo de los puntos de datos capturados. Conteste la

pregunta 5.

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

CBR

EXAS INSTRUMENTS INCORPORATED

TI.

Actividad 3. Péndulo

Exploraciones

Segunda captura de datos

(cont.)

sinusoidal

En el menú

MAIN MENU

de 10 a 5 segundos. Repita la captura de datos. Estudie la gráfica. Conteste las

preguntas 6 y 7.

La cantidad que ha determinado (ciclos por segundo) se denomina frecuencia. Aunque ha calculado la frecuencia en la pregunta 7 utilizando la gráfica, puede calcularla matemáticamente a partir de:

donde T es el periodo en segundos y f la frecuencia en hertzios (Hz).

f =

Conteste la pregunta 8.

Tercera y cuarta capturas de datos

Repita la captura de datos de 5 segundos dos veces más. Primero, acorte el péndulo. Después, alárguelo. Observe las gráficas correspondientes y conteste la pregunta 9.

Otra medida importante de distancia que afecta al movimiento del péndulo es la amplitud. La respuesta a la pregunta 2 era la amplitud de esa oscilación del péndulo.

Conteste la pregunta 10.

Exploraciones avanzadas

Quinta captura de datos

En el menú

PLOT MENU,

seleccione

SETUPàSAMPLE

VELOCITY-TIME

. En la pantalla

, cambie el tiempo

SETUP

. Conteste las preguntas 11, 12 y 13.

Sexta captura de datos

Repita la captura de datos con un peso bastante más ligero o más pesado y después

conteste la pregunta 14.

Haga un modelo de la relación distancia-tiempo del péndulo utilizando la función sinusoidal S = A sin (wt + d), donde S es la posición instantánea, A es la amplitud, w es la frecuencia, d es el ángulo de fase y t es el tiempo. La frecuencia, w, está relacionada con el periodo, T, mediante la relación w = 2 pàT.

Introduzca esta función en el editor Y= utilizando los valores calculados de A y w. Simultáneamente, represente gráficamente esta función y la gráfica estadística de

(tiempo) frente a L2 (distancia). Ajuste los valores de A, w y d hasta obtener un buen ajuste. En la TI-83 o TI-86, utilice la regresión del seno para determinar los valores.

Explore la relación entre posición y velocidad representando

(distancia) frente a

(velocidad). ¿Cuáles son sus hipótesis respecto al aspecto de la gráfica resultante? Compare el resultado real con sus hipótesis.

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

Actividad 3. Péndulo

Captura de datos

Nombre ____________________________________

1. ¿Cuál es la distancia del

a la posición de equilibrio? _____________________________________

CBR

2. ¿A qué distancia va a separar el péndulo de la posición de equilibrio? __________________________

3. ¿Cuál ha sido el tiempo para diez periodos? _______________________________________________

Calcule el tiempo (en segundos) empleado en completar un periodo. __________________________ ¿Qué ventajas tiene calcular el tiempo de diez periodos completos en vez del de uno solo? ________

4. Utilizando la respuesta a la pregunta 2, calcule aproximadamente la distancia total recorrida en un ciclo. ________________________________________________________________________________

¿Por qué es más pequeño este valor que la distancia real recorrida en un ciclo? __________________

5. ¿Qué ha observado respecto a la forma de la gráfica? _______________________________________ ¿Cómo está representado en la gráfica el valor de la pregunta 1? _____________________________

Exploraciones

6. ¿Cómo cambia el aspecto de la gráfica? ¿Por qué? _________________________________________

_____________________________________________________________________________________

7. Utilizando los datos capturados de la gráfica, calcule el número de ciclos completos por segundo.

_____________________________________________________________________________________

¿Porqué resulta más fácil determinar esto utilizando la segunda gráfica (correspondiente a 5 segundos) en vez de la primera (correspondiente a 10 segundos)? _____________________________

8. Calcule la frecuencia para un periodo utilizando la función.___________________________________

9. ¿En qué manera afecta al periodo del péndulo el acortamiento de la longitud del mismo? _________ ¿En qué manera afecta al periodo del péndulo el alargamiento de la longitud del mismo? _________

10. ¿Cuál es la relación entre la amplitud de la oscilación del péndulo y la distancia total que recorre el

péndulo en un periodo? ________________________________________________________________

_____________________________________________________________________________________

Exploraciones avanzadas

11. Compare la gráfica Distancia-Tiempo con la gráfica Velocidad-Tiempo. Enumere las similitudes y las diferencias. ___________________________________________________________________________

_____________________________________________________________________________________

12. ¿En qué posición es máxima la velocidad del peso?__________________________________________

13. ¿En qué posición es mínima la velocidad del peso? __________________________________________

14. ¿En qué manera afecta el cambio de peso a la gráfica? ¿Por qué? _____________________________

_____________________________________________________________________________________

ONCEPTOS BÁSICOS DEL

CBR

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

EXAS INSTRUMENTS INCORPORATED

TI.

Actividad 4. Pelota botando notas para el profesor

Conceptos

Función explorada: parabólica. Conceptos reales como caída libre, objetos que

rebotan, gravedad y aceleración constante son ejemplos de funciones parabólicas. En esta actividad se investigan los valores de altura, de tiempo y del coeficiente A en la función cuadrática,

Y = A(X  H)

+ K, que describe el comportamiento

de una pelota al botar.

Materiales

 calculadora

CBR



 cable calculadora a

CBR

 pelota grande de jugar (9 pulgadas)  ViewScreen de TI (opcional)

Sugerencias

Esta actividad se realiza mejor con dos estudiantes, uno para sujetar la pelota y el otro para pulsar ¤.

Consulte las páginas 6–12, donde encontrará sugerencias para una captura efectiva de los datos.

La gráfica debe parecerse a una pelota botando. Si no es así, repita la toma de datos, asegurándose que

CBR

apunta a la pelota. Se aconseja utilizar una

pelota grande.

Gráficas normales

BALL BOUNCE

invierte los datos de distancia para que la gráfica se ajuste mejor al movimiento de la pelota que perciben los estudiantes. y = 0 en la gráfica es realmente el punto en que la pelota está a máxima distancia del

CBR

, cuando golpea

el suelo.

4. Los estudiantes deben observar que el eje X representa el tiempo, no la distancia horizontal.

7. La gráfica para A = 1 está invertida y es más ancho que la gráfica.

8. A < L1

9. parábola cóncava hacia arriba; cóncava hacia abajo; lineal

12.igual; matemáticamente, el coeficiente A representa el grado de curvatura de la parábola; físicamente, A depende de la aceleración de la gravedad, que es la misma para todos los botes.

Exploraciones avanzadas

La altura de rebote de la pelota (altura máxima para un bote dado) es aproximadamente:

, donde

y es la altura de rebote

h es la altura desde la que se suelta la pelota

p es una constante que depende de las

características físicas de la pelota y de la superficie del suelo x es el número de bote

Exploraciones

Una vez que se suelta un objeto, sobre él actúa únicamente la aceleración de la gravedad (se desprecia la resistencia del aire). Por tanto, A depende de la aceleración debida a la gravedad, N9,8 metrosàsegundo

. El signo negativo indica que

la aceleración es hacia abajo. El valor de A es aproximadamente la mitad de la

aceleración debida a la gravedad, o N4,9 metrosàsegundo

Respuestas habituales

1. tiempo (desde el principio del experimento); segundos; altura à distancia de la pelota al suelo; metros

2. altura inicial de la pelota sobre el suelo (los picos representan la altura máxima de cada bote); el suelo está representado por y = 0.

3. La gráfica Distancia-Tiempo para esta actividad no representa la distancia del

CBR

a la pelota.

Para una pelota y una altura inicial dadas, la altura de rebote disminuye exponencialmente para cada bote sucesivo. Cuando x = 0 es, y = h, de manera que la ordenada en el origen representa la altura inicial.

Los estudiantes que estén muy interesados pueden encontrar los coeficientes de la función utilizando los datos capturados. Repita la actividad para diferentes alturas iniciales o con una pelota o superficie de suelo diferente.

Después de ajustar manualmente la curva, los estudiantes pueden utilizar un análisis de regresión para encontrar la función que mejor reproduce los datos. Seleccione un único bote utilizando

TOOLS

menú

SELECT DOMAIN

MAIN MENU

. Después seleccione

. Siga los procedimientos de

PLOT

QUIT

en el

funcionamiento de la calculadora para realizar una regresión cuadrática en las listas

y L2.

Extensiones

Integre la gráfica Velocidad-Tiempo, obteniendo el desplazamiento (distancia neta recorrida) para cualquier intervalo de tiempo. Observe que el desplazamiento es cero para un bote completo (la pelota empieza y acaba en el suelo).

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

Actividad 4. Pelota botando parabólico

Captura de datos

Comience con un bote de prueba. Suelte la pelota (no la lance al suelo).

➊

a más de 0,5 metros por encima de la altura del bote

Sugerencias:

Coloque el más alto. Sujete el sensor directamente sobre la pelota y compruebe que no hay nada en la zona despejada (consulte la página 7).

CBR

Ejecute el programa

➋

RANGER

(consulte la página 5 para obtener combinaciones de

teclas para cada calculadora). En el menú

➌

En el menú

➍

BALL BOUNCE

Sujete la pelota con los brazos extendidos. Pulse ›. El programa

➎

MAIN MENU APPLICATIONS

se ocupa automáticamente de los ajustes.

seleccione

APPLICATIONS

BALL BOUNCE

. Seleccione

METERS

FEET

. Aparecen instrucciones generales.

RANGER

ahora en modo de activador (Trigger). En este momento, puede desconectar el de la calculadora.

Pulse ¤. Cuando la luz verde comienza a parpadear, suelte la pelota y

➏

retroceda (si la pelota bota hacia un lado, mueva el

para mantenerlo

CBR

directamente por encima de la pelota, pero tenga cuidado de no cambiar su altura). Podrá escuchar un clic a medida que se capturan los datos. Se capturan datos de

tiempo y distancia, y se calculan para la velocidad y la aceleración. Si ha desconectado el

Pulse › (si la gráfica no tiene el aspecto deseado, repita el experimento). Estudie

➐

, vuelva a conectarlo cuando termine de capturar los datos.

CBR

la gráfica. Conteste las preguntas 1 y 2 de la hoja de actividades. Observe que

➑

BALL BOUNCE

invierte automáticamente los datos de distancia.

Conteste las preguntas 3 y 4.

está

CBR

ONCEPTOS BÁSICOS DEL

CBR

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

EXAS INSTRUMENTS INCORPORATED

TI.

Actividad 4. Pelota botando

Exploraciones

La gráfica Distancia-Tiempo del bote forma una parábola.

(cont.)

parabólico

Pulse ›. En el menú

➊

PLOT MENU

, seleccione

PLOT TOOLS

y después

SELECT DOMAIN

Queremos seleccionar el primer bote completo. Mueva el cursor hasta la base del comienzo del bote y pulse y pulse

La gráfica está en modo

➋

›. Se vuelve a dibujar la gráfica, enfocando un sólo bote.

›. Mueva el cursor hasta la base del final de ese bote

. Determine el vértice del bote. Conteste la

TRACE

pregunta 5 de la hoja de actividades. Pulse › para volver al menú

➌

La forma en función del vértice de la función cuadrática, Y = A(X  H)

➍

adecuada para este análisis. Pulse

PLOT MENU

œ. En el editor

. Seleccione

, desactive cualquier función

MAIN MENU

. Seleccione

+ K, resulta

que esté seleccionada. Introduzca la forma en función del vértice de la función cuadrática: Yn=A(XH)^2+K.

En la pantalla principal, almacene en la variable K el valor que ha registrado en la

➎

pregunta 5 para la altura; almacene el tiempo correspondiente en la variable H; almacene 1 en la variable A.

Pulse  para mostrar la gráfica. Conteste las preguntas 6 y 7.

➏

Pruebe A = 2, 0, –1. Complete la primera parte de la tabla en la pregunta 8 y

➐

conteste la pregunta 9. Escoja sus propios valores para A hasta conseguir una buena concordancia para la

➑

gráfica. Registre las opciones para A en la tabla de la pregunta 8.

QUIT

Repita la actividad, pero en esta ocasión elija el último (más a la derecha) bote

➒

completo. Conteste las preguntas 10, 11 y 12.

Exploraciones avanzadas

Repita la captura de datos, pero no seleccione una sola parábola.

➊

Registre el tiempo y la altura de botes sucesivos.

➋

Determine la relación entre las alturas de botes sucesivos.

➌

Explique el significado, si lo hay, de esta relación.

➍

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

Actividad 4. Pelota botando

Nombre ____________________________________

Captura de datos

1. ¿Qué propiedad física se representa en el eje X? ____________________________________________ ¿En qué unidades? ____________________________________________________________________ ¿Qué propiedad física se representa en el eje Y? ____________________________________________ ¿En qué unidades? ____________________________________________________________________

2. ¿Qué representa el punto más alto de la gráfica? ___________________________________________ ¿Y el punto más bajo? _________________________________________________________________

3. ¿Por qué dio la vuelta a la gráfica el programa

BALL BOUNCE

? _________________________________

4. ¿Por qué parece representar la gráfica el movimiento de botes de la pelota por el suelo? __________

Exploraciones

5. Registre la altura máxima y el tiempo correspondiente al primer bote completo. _________________

6. ¿Coincide la gráfica para

= 1 con su gráfica? _____________________________________________

7. ¿Por qué o por qué no? ________________________________________________________________

8. Complete la tabla que aparece a continuación.

A ¿Cómo se comparan la gráfica de datos y la gráfica Yn?

1 2 0

9. ¿Qué implica un valor positivo de ¿Qué implica un valor negativo de ¿Qué implica un valor cero de

? _____________________________________________________

? ____________________________________________________

? ________________________________________________________

10. Registre la altura máxima y el tiempo correspondiente para el último bote completo. _____________

11. ¿Piensa que

12. ¿Cómo se compara

¿Qué piensa que puede representar

ONCEPTOS BÁSICOS DEL

será mayor o menor para el último bote? _____________________________________

? _________________________________________________________________

? ___________________________________________________

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

CBR

EXAS INSTRUMENTS INCORPORATED

TI.

Actividad 5. Pelota rodante notas para el profesor

Conceptos

Función explorada: parabólica. La representación del movimiento de bajada de

una pelota por una rampa con diferentes inclinaciones crea una familia de curvas, que pueden aproximarse por una sucesión de funciones cuadráticas. En esta actividad se investigan los valores de los coeficientes de las funciones cuadráticas, y = ax

+ bx + c.

Materiales

 calculadora

CBR



 cable calculadora a

CBR

 abrazadera de montaje  pelota grande de jugar (20-25 cm)  rampa larga (de al menos 2 metros, por

ejemplo un tablero ligero)

 transportador para medir ángulos  libros para crear la pendiente  ViewScreen de TI (opcional)

Sugerencias

Discutan la manera de medir el ángulo de la rampa. Deje que los estudiantes muestren su creatividad. Pueden utilizar la trigonometría o un transportador.

Consulte las páginas 6–12 para obtener sugerencias para una captura efectiva de los datos.

Gráficas normales

3. varía (debería ser la mitad de una parábola, cóncava hacia arriba)

4. una parábola (cuadrática)

5. varía

6. varía (debería ser parabólico con curvatura creciente)

7. 0¡ es horizontal (la pelota no rueda); 90¡ es igual a la caída libre de la pelota

Exploraciones

El movimiento de un cuerpo sujeto únicamente a la fuerza de la gravedad es un tema muy estudiado en física. Este tipo de movimiento se expresa normalmente mediante una forma particular de la función cuadrática,

s = ½at

0 0 0 0

En la función cuadrática y = ax y representa la distancia del

+ v

t + s

donde

s es la posición de un objeto en el tiempo t a es su aceleración

es su velocidad inicial

es su posición inicial

+ bx + c,

CBR

a la pelota en el tiempo x si la posición inicial de la pelota era c, la velocidad inicial era b y la aceleración es 2a.

Exploraciones avanzadas:

Puesto que la pelota está en reposo cuando se suelta, b debe aproximarse a cero en cada prueba. c debe aproximarse a la distancia inicial, 0,5 metros. a aumenta con el ángulo de inclinación.

Respuestas habituales

1. la tercera gráfica

2. tiempo; segundos; distancia del objeto al CBR; metros

Si los estudiantes aproximan la función

y = ax

+ bx + c manualmente, puede que deba proporcionarles sugerencias para los valores de b y c. También puede indicarles que realicen una regresión cuadrática en las listas

L1, L2

utilizando sus calculadoras. La aceleración de la pelota se debe a la gravedad. Por ello cuanto más inclinada esté la rampa (mayor sea el ángulo de inclinación), mayor será el valor de a. El máximo de a se da para q = 90¡, el mínimo para q = 0¡. De hecho, a es proporcional al seno de q.

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

Actividad 5. Pelota rodante parabólico

Captura de datos

➊

Conteste la pregunta 1 de la hoja de actividades. Incline la rampa 15°. Ponga la abrazadera en el borde superior de la rampa. Enganche el el sensor y colóquelo perpendicularmente a la rampa. Conecte la calculadora al

a la abrazadera. Abra

CBR

Marque un punto en la rampa a 0,5 metros del

. Elija a un estudiante para que

CBR

sujete la pelota en esta marca mientras otro sujeta la calculadora.

Sugerencias:

Apunte el sensor directamente hacia la pelota y compruebe que no

hay nada en la zona despejada (consulte la página 7).

Ejecute el programa

➋

RANGER

teclas para cada calculadora). En el menú Pulse › para mostrar los ajustes. Para esta actividad, deberían ser:

➌

REALTIME: NO

TIME (S): 3 SECONDS

DISPLAY: DISTANCE

BEGIN ON: [ENTER]

SMOOTHING: LIGHT

UNITS: METERS

(consulte la página 5 para obtener combinaciones de

MAIN MENU

seleccione

SETUPàSAMPLE

En la página 38 dispone de instrucciones para cambiar los ajustes. Cuando los ajustes sean correctos, seleccione

➍

START NOW

. Pulse › para comenzar

la toma de datos. Cuando empiece a oírse el sonido clic, suelte la pelota inmediatamente (sin

➎

empujarla) y retroceda. Una vez finalizada la toma de datos, aparecerá automáticamente la gráfica

➏

Distancia-Tiempo. Conteste las preguntas 2 y 3. Pulse › para mostrar el menú

➐

seleccione

›. Mueva el cursor al punto en que la pelota alcanzó el final de la rampa y pulse ›. Se vuelve a dibujar la gráfica, enfocada ahora en la parte que corresponde a

SELECT DOMAIN

. Mueva el cursor al punto en que se soltó la pelota y pulse

PLOT MENU

. Seleccione

PLOT TOOLS

y, después,

la caída de la pelota por la rampa. Conteste las preguntas 4 y 5.

ONCEPTOS BÁSICOS DEL

CBR

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

EXAS INSTRUMENTS INCORPORATED

TI.

Actividad 5. Pelota rodante

Exploraciones

Examine lo que ocurre para diferentes inclinaciones.

Realice una hipótesis de lo que ocurrirá si aumenta la inclinación. Conteste la

➊

pregunta 6. Ajuste la inclinación en 30¡. Repita los pasos 2 a 6. Añada esta gráfica al dibujo

➋

de la pregunta 6, denominándolo 30¡. Repita los pasos 2 a 6 para inclinaciones de 45¡ y 60¡ y añádalos al dibujo.

➌ ➍

Conteste la pregunta 7.

Exploraciones avanzadas

Ajuste los valores de tiempo de manera que x = 0 para la altura inicial (el tiempo en que se suelta la pelota). Puede hacerlo manualmente restando el valor de x para el primer punto a todos los puntos de la gráfica, o puede introducir

(cont.)

parabólico

L1(1)"A:L1NA"L1

Calcule los valores de a, b y c para la familia de curvas de la forma y = ax

➊

en 0¡, 15¡, 30¡, 45¡, 60¡, 90¡. ¿Cuáles son los valores mínimos y máximos para a? ¿Por qué?

➋

Escriba una expresión que describa la relación matemática entre a y el ángulo de

➌

inclinación.

+ bx + c

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

Actividad 5. Pelota rodante

Nombre ____________________________________

Captura de datos

1. ¿Cuál de estas gráficas se ajusta mejor a la gráfica Distancia-Tiempo de una pelota rodando por una rampa?

2. ¿Qué propiedad física se representa en el eje X? ____________________________________________ ¿En qué unidades? ____________________________________________________________________ ¿Qué propiedad física se representa en el eje Y? ____________________________________________ ¿En qué unidades? ____________________________________________________________________

3. Haga un bosquejo de la gráfica real. Etiquete el eje. Etiquete la gráfica en los puntos en que se suelta la pelota y en que alcanza el final de la rampa.

4. ¿Qué tipo de función representa esta gráfica? _____________________________________________

5. Discuta las diferencias de concepto que hay entre la gráfica seleccionada en la pregunta 1 y la curva

dibujada en la pregunta 3. ______________________________________________________________

_____________________________________________________________________________________

Exploraciones

6. Dibuje la gráfica que corresponde a una mayor inclinación (llámela predicción.)

7. Dibuje y etiquete las gráficas para 0

¡ y 90¡:

ONCEPTOS BÁSICOS DEL

CBR

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

EXAS INSTRUMENTS INCORPORATED

TI.

Información para el profesor

¿Cómo pueden cambiar sus clases con el CBR?

es un sistema fácil de utilizar con funciones que le ayudan a integrarlo en sus planes

CBR

de estudio de manera rápida y sencilla.

ofrece mejoras significativas sobre otros métodos de captura de datos que pueda

CBR

haber utilizado en el pasado. Esto, por su parte, puede llevar a una reestructuración de la utilización del tiempo en clase, a medida que los estudiantes vayan adquiriendo más interés en la utilización de datos reales.

Descubrirá que los estudiantes adquieren el sentido de trabajar con sus propios datos

puesto que participan realmente en su captura en vez de utilizar datos de libros de texto, resúmenes estadísticos u otras publicaciones. Esto les convence de que los conceptos tratados en clase están conectados con el mundo real y no son ideas abstractas. Pero también significa que cada estudiante deseará participar en la captura de datos.

La captura de datos con

es bastante más efectiva que la creación de casos

CBR

particulares y la toma manual de medidas con una regla y un cronómetro. Puesto que la resolución mejora cuanto mayor es la toma de datos y dado que el detector sónico de movimiento es muy preciso, la forma de las curvas se manifiesta de manera sencilla. Necesitará menos tiempo para la captura de datos y dispondrá de más tiempo para el análisis y la exploración.

Con el

los estudiantes pueden explorar la repetitividad de las observaciones y

CBR

variaciones en diversas situaciones. Preguntas tales como “¿Será la misma parábola si tiro la pelota desde mayor altura?” y “¿Se trata de la misma parábola para el primer y para el último bote?” se convierten en ampliaciones naturales y de gran valor.

La posibilidad de visualización permite a los estudiantes asociar rápidamente los datos

de lista representados con las propiedades físicas y las funciones matemáticas que describen los datos.

También tienen lugar otros cambios una vez se capturan datos de sucesos reales.

CBR

permite a los estudiantes explorar las relaciones subyacentes tanto numérica como gráficamente.

Exploración gráfica de datos

Utilice las gráficas de distancia, velocidad y aceleración con respecto al tiempo generadas automáticamente para exploraciones del tipo:

¿Cuál es el significado físico de la ordenada en el origen? ¿y el del corte con el eje X?

¿y el de la pendiente? ¿y el del máximo? ¿y el del mínimo? ¿y el de las derivadas? ¿y el de las integrales?

¿Cómo se reconoce la función (lineal, parabólica, etc.) representada por la gráfica?

¿Cómo podemos ajustar los datos a una función representativa? ¿Cuál es el

significado de los coeficientes de la función (p.ej., AX

Exploración numérica de datos

Los estudiantes pueden emplear los métodos estadísticos (media, mediana, moda, desviación típica, etc.) que conozcan para explorar los datos numéricos. Cuando sale del programa

REALTIME=NO

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

RANGER

NCORPORATED C

+ BX + C)?

, un indicador le recuerda las listas en que se almacenan los datos de

para tiempo, distancia, velocidad y aceleración.

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

Información para el profesor

(cont.)

Gráficas de CBR: conexión entre el mundo físico y las matemáticas

Las gráficas creadas a partir de los datos capturados por

RANGER

son una representación visual de las relaciones entre las descripciones físicas y matemáticas del movimiento. Se debe animar a los estudiantes para que reconozcan, analicen y discutan la forma de la gráfica tanto en términos físicos como matemáticos. Para proseguir la discusión y descubrir más cosas, introduzca las funciones en el editor Y= y muéstrelas con las gráficas de datos.

Una gráfica Distancia-Tiempo representa la posición aproximada de un objeto

(distancia al

) en cada instante de tiempo cuando se realiza un experimento. Las

CBR

unidades del eje Y son metros; las unidades del eje X son segundos. Una gráfica Velocidad-Tiempo representa la velocidad aproximada de un objeto

(relativa al

y en su dirección) durante el tiempo de realización de un experimento.

CBR

Las unidades del eje Y son metros/segundo; las unidades del eje X son segundos. Una gráfica Aceleración-Tiempo representa el índice de cambio aproximado de la

velocidad de un objeto (relativa al realización de un experimento. Las unidades del eje Y son metros/segundo

y en su dirección) durante el tiempo de

CBR

; las

unidades del eje X son segundos. La primera derivada (pendiente instantánea) en cualquier punto de la gráfica

Distancia-Tiempo es la velocidad en ese instante. La primera derivada (pendiente instantánea) en cualquier punto de la gráfica

Velocidad-Tiempo es la aceleración en ese instante. La aceleración también es la segunda derivada en cualquier punto de la gráfica Distancia-Tiempo.

Una integral definida (área encerrada por la gráfica y el eje X entre dos puntos

cualesquiera) en la gráfica Velocidad-Tiempo equivale al recorrido (distancia neta recorrida) del objeto en ese intervalo de tiempo.

Una gráfica normal Velocidad-Tiempo de

representa únicamente la magnitud de

CBR

la velocidad (que puede ser positiva, negativa o cero). La dirección viene implícita. Un valor positivo de la velocidad indica movimiento de alejamiento del negativo indica movimiento de acercamiento al

mide la distancia sólo a lo largo de una línea que sale del detector. Por tanto, si un

CBR

; un valor

CBR

objeto se mueve con un ángulo respecto a dicha línea, sólo calculará el componente de la velocidad paralelo a la misma. Por ejemplo, un objeto que se mueve perpendicularmente a esa línea muestra velocidad cero.

ONCEPTOS BÁSICOS DEL

CBR

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

EXAS INSTRUMENTS INCORPORATED

TI.

Información para el profesor

(cont.)

Las matemáticas de distancia, velocidad y aceleración

media

N d

= pendiente de la gráfica Distancia-Tiempo

N t

Gráfica Distancia-Tiempo

instantánea

lim

@t"

(

d(s)

)

donde s = distancia

Gráfica Velocidad-Tiempo

N v

media

instantánea

lim

@t"

= pendiente de la gráfica Velocidad-Tiempo

N t

(

)

El área que queda bajo la gráfica Velocidad-Tiempo entre t1 y t2 = @d = (d recorrido desde t

Por tanto, @d =

a t2 (distancia neta recorrida).

t=2

⌠

⌡

t=1

v(dt)

(

t=2

∑

t=1

v(@t)

o @d =

)

2Nd1

) =

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

Gráfica Aceleración-Tiempo

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

Información para el profesor

Recursos en la Web

(cont.)

En nuestro espacio en la web,

una lista de material complementario para su utilización con

gráficas de TI una biblioteca de programas para su utilización con

de TI una página de actividades con aplicaciones desarrolladas por profesores como usted

programas de

información más detallada sobre ajustes de

Recursos adicionales

Los libros Explorations de Texas Instruments proporcionan material suplementario relacionado con las calculadoras gráficas de TI, incluyendo libros con actividades de clase con el

CBR

http:ààwww.ti.comàcalc

que dan acceso a funciones adicionales de

CBR

y órdenes de programación

CBR

, podrá encontrar:

CBR, CBL

y calculadoras gráficas

CBR

y calculadoras

pensados para clases de matemáticas y física en colegios e institutos.

ONCEPTOS BÁSICOS DEL

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

CBR

EXAS INSTRUMENTS INCORPORATED

TI.

Los datos del CBR se almacenan en listas

Los datos capturados se almacenan en las listas L1, L2, L3 y L4

Cuando el

captura datos, los transfiere automáticamente a la calculadora y los

CBR

almacena en listas. Cada vez que sale del programa almacenados los datos.

contiene los datos de tiempo.

contiene los datos de distancia.

contiene los datos de velocidad.

contiene los datos de aceleración.

Por ejemplo, el 5º elemento de la lista L1 representa el tiempo en que fue tomado el 5º dato, y el 5º elemento de la lista correspondiente al 5º dato.

En modo

REALTIME=YES

, sólo se calculan y transfieren los datos para la gráfica solicitada (distancia, velocidad o aceleración). En modo todos los datos.

Los ajustes se almacenan en la lista L5

La pantalla de

utilizados más a menudo (consulte la página 38).

CBR

RANGER SETUP

permite realizar fácilmente la modificación de los parámetros

Cuando transfiere el programa por una nueva lista que contiene los valores por defecto.

RANGER

representa la distancia a que está el punto

REALTIME=NO

RANGER

desde el

, se sustituye automáticamente

CBR

, se le recuerda dónde están

, se calculan y transfieren

Consulte las páginas 40–41 para obtener información sobre las órdenes de programación que cambian otros ajustes.

Utilización de las listas de datos

Las listas no se eliminan al salir del programa hacer otras exploraciones y análisis gráficos, estadísticos y numéricos.

Puede representar unas listas frente a otras, mostrarlas en el editor de listas, utilizar análisis de regresión y realizar otras actividades analíticas. Por ejemplo, puede capturar los datos del movimiento del péndulo utilizando representar la gráfica Velocidad-Aceleración para explorar funciones elípticas (es posible que también tenga que ajustar la ventana).

RANGER

. Por tanto, están disponibles para

, salir del programa y, después,

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

Ajustes del RANGER

Cambio de los ajustes del RANGER

RANGER

➊

muestra los ajustes más utilizados antes de comenzar la captura de datos.

En el menú

MAIN MENU

del programa

RANGER

, seleccione

SETUPàSAMPLE

los ajustes actuales. 4 indica la posición del cursor.

MAIN MENU

REALTIME:

TIME (S):

DISPLAY:

BEGIN ON:

SMOOTHING:

Pulse c o b para desplazarse hasta el ajuste que desea cambiar.

➋

Pulse

➌

›

START NOW

YES

= 1–99

FEET

SECONDS

, o

TOTAL TIME DISTANCE, VELOCITY [ENTER], [TRIGGER], NONE, LIGHT, MEDIUM METERS

ACCELERATION

10-SECOND DELAY

, o

HEAVY

(

REALTIME=NO

UNITS:

& & & & & &

para alternar entre las opciones disponibles. Cuando esté situado en la opción correcta, pulse c para pasar a la siguiente opción. Para cambiar 1 o 2 dígitos y pulse c o b.

Cuando todos los ajustes sean correctos, pulse c o b hasta que el cursor esté en

➍

START NOW

Para continuar, pulse

Para volver al menú

Los nuevos ajustes permanecen, salvo que seleccione aplicación o ejecute otro programa que los cambie. Si manipula

RANGER

o elimina L5, es posible que se recuperen los ajustes por defecto la primera vez

que vuelva a ejecutar

›

MAIN MENU

RANGER

, pulse e y, después, pulse

SET DEFAULTS

›

, ejecute una fuera del programa

. Aparecen

solamente

, escriba

TIME

)

Recuperación de los valores por defecto de los ajustes de RANGER

Los ajustes por defecto son apropiados para una gran variedad de situaciones de toma de datos. Si no está seguro de cuáles son los mejores ajustes, comience con los ajustes por defecto y después modifíquelos.

En el menú

➊

MAIN MENU

del programa

RANGER

, seleccione Los ajustes cambian a sus valores por defecto y aparece la pantalla Si desea cambiar un ajuste por defecto, siga los pasos descritos arriba.

➋

Para continuar, pulse

➌

cuando el cursor esté en

›

START NOW

Otros ajustes del RANGER

El programa

RANGER

accede a los ajustes que se modifican con más frecuencia. otros ajustes. Consulte las páginas 40–41 para obtener información sobre las órdenes de programación que cambian estos ajustes.

SET DEFAULTS

SETUP

tiene

CBR

ONCEPTOS BÁSICOS DEL

CBR

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

EXAS INSTRUMENTS INCORPORATED

TI.

Utilización del CBR con CBL o con programas de CBL

Utilización de CBR como un detector de movimiento convencional con CBL

puede utilizarse como un detector de movimiento convencional con el sistema

CBR

é (Calculator-Based Laboratoryé)de Texas Instruments.

CBL

Se incluye el cable especial necesario para conectar el

CBL

CBR

No conecte el calculadora debe estar conectada al

Puede que necesite cambiar el programa

RANGER

no funciona con

CBR

al mismo tiempo que el

CBL

Utilización de CBR con programas escritos para CBL

Puede utilizar el

con la mayoría de los programas de

CBR

detector de movimiento sin hacer ningún cambio o, en todo caso, con pequeños cambios en el programa.

Para interrumpir la toma de datos: Con algunos programas de modo de captura de datos

REALTIME=YES, CBR

Para detener la captura de datos cuando finalice el experimento, puede hacer lo siguiente:

Pulse ¤ en el

Añada instrucciones en el programa de

orden {6,0} al

CBR

. La instrucción debe estar después de que los datos se hayan

transferido y hayan aparecido en pantalla. Por ejemplo:

{6,0}"L6:SEND L6

Para activar o desactivar el sonido: Para desactivar el sonido, añada instrucciones al programa de

con el que esté trabajando para enviar la orden {6,3} al

CBL

instrucción debe estar antes de comenzar la captura de datos. Por ejemplo:

se conecta a la calculadora. La

CBR

según se detalla más adelante. El programa

escritos sólo para un

CBL

que utilizan el

CBL

continúa el experimento indefinidamente.

con el que esté trabajando para enviar la

CBL

. La

CBR

{6,3}"L6:SEND L6

Para activar el sonido, basta con ejecutar el programa En caso de dificultad: Si ejecuta un programa de

bloqueado, ejecute el programa la página 36) hay una versión actualizada del programa de

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

RANGER

OPYRIGHT DE

parece no responder o estar

CBR

CBL

RANGER

. Compruebe si en el espacio web de TI (consulte

CBL

TI.

ONCEPTOS BÁSICOS DEL

CBR

Órdenes de programación

Orden 0 Borra y reinicia el sistema {0}

Borra todo. Restablece los valores por defecto en el encendido. Canal 11 seleccionado automáticamente.

Orden 1 Borra canal {1,0}

Borra canal.

Orden 1 Canal {1,11,

operación

REALTIME=NO

operación

REALTIME=YES

post_proceso

conversión_temperatura

0 (por defecto) Ninguno

REALTIME=NO

0 (por defecto) Desactiva la compensación de temperatura. 1 Activa la compensación de temperatura.

) Borra todo. Restablece valores por defecto en el encendidos. ) Metros ) Metros ) Pies

) Borra todo. Restablece valores por defecto en el encendidos. ) Metros, ) Metros, ) Pies, ) Metros, ) Pies, ) Metros, ) Pies,

)dàdt (derivada de primer orden) )d

Orden 2 Configuración de datos {2,

tipo_dato

1 (por defecto) Lista

Orden 3 Toma de datos/Activador {3,

tiempo_toma datos

0.005–1500 (0.1) Tiempo en segundos entre cada toma de datos

0.0001–0.005 Redondea a 0,005. 1500<x<16000 Redondea a 1500.

núm.datos

L1 Selecciona el modo de captura de datos

REALTIME=NO

1–512 (

activador

0 Comienza la toma de datos sin activador. 1 (por defecto) Comienza la toma de datos con ¤. 7 Tras 10 segundos, comienza la toma de datos.

tiempo_registro

0 (por defecto) Ninguno

REALTIME=NO

filtro

(consulte Orden 1, campo operación)

0 (por defecto) Sin filtro

REALTIME=NO

1 (

REALTIME=NO

2 (

REALTIME=NO

3 (

REALTIME=NO

4 (

REALTIME=NO

5 (

REALTIME=NO

6 (

REALTIME=YES

7 (

REALTIME=YES

8 (

REALTIME=YES

9 (

) Toma de 1 a 512 datos.

) Tiempo absoluto (comienza en tiempo 0, después ajusta el tiempo del ) Tiempo relativo (comienza en tiempo 0, después ajusta el tiempo del

) Suavizado Savitzsky-Golay de 5 puntos ) Suavizado Savitzsky-Golay de 9 puntos ) Suavizado Savitzsky-Golay de 17 puntos ) Suavizado Savitzsky-Golay de 29 puntos ) Filtro de poda mediana de 3 puntos ) Filtro de poda mediana de 5 puntos

) Filtro de seguimiento ligero ) Filtro de seguimiento medio ) Filtro de seguimiento fuerte

Resultados

tipo_dato

Resultados

tiempo_tomadatos,núm.datos,activador

tiempo_registro,filtro

Resultados

experimento) experimento)

Resultados

operación,post_proceso

CBR

devuelve {

CBR

devuelve {

CBR

devuelve {

CBR

devuelve {

CBR

devuelve {

àdt2 (derivada de segundo orden)

distancia,@tiempo

devuelve {

distancia,velocidad,@tiempo

devuelve {

distancia,velocidad,aceleración,@tiempo

,0,

distancia,@tiempo distancia

distancia,velocidad,@tiempo

distancia,velocidad,aceleración,@tiempo

,,@

,0,0,0,0,0,0,0}

}

REALTIME=YES

conversión_temperatura

}

tiempo

}

,0,0,0,0,

REALTIME=YES

}

ONCEPTOS BÁSICOS DEL

CBR

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

EXAS INSTRUMENTS INCORPORATED

TI.

Órdenes de programación

(cont.)

Orden 4 Compensación de temperatura {4,

núm.función

0 (por defecto) Borra todas las funciones. 4 Designa la función 4.

tipo_función

0 (por defecto) Borra la función. 13 Designa la compensación de temperatura.

temperatura

número con coma flotante Ajusta la temperatura actual.

unidades

0 (por defecto) Ninguno (ignorado por 1 Pasa los grados a = Fahrenheit. 2 Pasa los grados a = Celsius. 3 Pasa los grados a = Kelvin. 4 Pasa los grados a = Rankin, donde R = F + 459,7.

Resultados

Orden 5 Configuración del rango de datos {5,

REALTIME=NO

(

)

primer_canal

0 (por defecto) Selecciona el canal activo más bajo. 1, 2, 3, 11, 21 Especifica el canal de sonido. M1 Registra la lista de tiempos.

selección_datos

0 Datos sin filtro {distancia} 1 Datos sin filtro dàdt {velocidad} 2 Datos sin filtro d 3 Datos sin procesar {distancia} 4 Datos sin procesar dàdt {velocidad} 5 Datos sin procesar d

dato_inicial

1–512 Primer elemento de datos para GET

dato_final

0–512 Último elemento de datos para GET (0 = último experimento)

Resultados

Orden 6 Opciones del sistema {6,

orden_sistema

0 Detiene el experimento (para compatibilidad con CBL). 2 (por defecto) Detiene el experimento. 3 Desactiva el sonido (el sonido se activa en el encendido). 4 Activa el sonido (el sonido se activa en el encendido). 5 Define el número de ID ( 6 Aplica un nuevo filtro a datos anteriores (

operación

número con coma flotante Número_ID del tipo 0–6 Nuevo filtro para datos capturados anteriormente (

Resultados

Orden 7 Estado de petición {7}

Devuelve una lista que contiene:

10.rrrr CódigoDispositivo.VersiónRom 0–99 Último código de error (0 = sin error) 0–2 Estado de pilas (0 = Bien;1 = bajas durante la toma de datos;2 = siempre

11 Identificador de canal de sonido tiempo_experimento Intervalo del experimento actual en segundos condición_activador Opción de activación actual en uso función Función de canal actual (1–9) post_proceso Opción de post-proceso actual (0–2) filtro Nivel de filtro actual (0–9) datos núm. de datos disponibles; 0–512 tiempo_registrado Opción de tiempo registrado (0–2) temperatura Temperatura en uso (¡C) indicador_piezo 0 = sonido desactivado; 1 = sonido activado estado_sistema 1 = no configurado; 2 = armado; 3 = activado/toma de datos; 4 = hecho ventana_inicio 0 = sin orden 5 aún; 1–512 ventana_final 0 = utilizar núm. de elementos; 1–512 número_id núm. de ID de 6 dígitos (por defecto 0.00000) definido por la orden

núm.función,tipo_función,temperatura,unidades

CBR

). Ajusta los grados T a Celsius.

}

primer_canal,selección_datos,dato_inicial,dato_final

àdt2 {aceleración}

orden_sistema[,operación]

n.nnnnn

bajas)

}

operación

(

es necesaria).

operación

orden_sistema

REALTIME=NO

necesaria).

= 5)

orden_sistema

REALTIME=YES

;M1

}

=6)

6 (

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

Pilas

Tipo de pila

está diseñado para funcionar con 4 pilas AA alcalinas. El

CBR

sin pilas si está conectado a un

Instalación de las pilas

Sujete el parte posterior del

boca abajo y deslice la cubierta del compartimiento de las pilas hacia la

CBR

. Coloque las pilas tal como se muestra en el diagrama que hay

CBR

CBL

sólo puede funcionar

CBR

dentro del compartimiento de las pilas. Dos pilas con el polo + hacia arriba y las otras dos con el polo - hacia arriba. Vuelva a colocar la cubierta. El

está listo para comenzar la

CBR

toma de datos.

Advertencias de CBR de pilas gastadas

tiene dos mecanismos para indicarle que las pilas tienen poca carga:

CBR

El programa

RANGER

muestra un mensaje de advertencia en la pantalla de la

calculadora mientras intenta capturar los datos.

La luz roja se enciende intermitentemente mientras el

recoge datos del

CBR

experimento.

Estado de carga de las pilas del CBR

Puede comprobar el estado de las pilas antes de empezar el experimento. En el menú

MAIN MENU

seleccione

las pilas, que puede ser

Precauciones con las pilas

y, después, seleccione

TOOLS

(bien) o

REPLACE

CBR STATUS

(sustituir).

. Se muestra el estado de

Sustituya las cuatro pilas al mismo tiempo. No mezcle marcas diferentes de pilas. No mezcle tipos diferentes de la misma marca.

Instale las pilas de acuerdo con el diagrama situado dentro del compartimiento de las mismas.

Deshágase adecuada e inmediatamente de las pilas usadas. No las deje al alcance de los niños.

No caliente, queme ni perfore las pilas, pues contienen productos químicos peligrosos y pueden explotar o derramarse.

No mezcle pilas recargables y no recargables.

No coloque pilas no recargables en un cargador de pilas.

ONCEPTOS BÁSICOS DEL

CBR

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

EXAS INSTRUMENTS INCORPORATED

TI.

En caso de dificultad

Si tiene este problema: Haga esto:

Dificultad transfiriendo el pro

rama

o capturando

RANGER

datos

CBR

comienza a capturar datos

por sí solo

Compruebe la conexión calculadora a extremos del cable.

Compruebe el estado de las pilas (consulte la página 42). Si ha dejado el CBR con el botón

haber presionado

activar la toma de datos. Pulse

CBR

. Apriete

hacia abajo, el botón se puede

detener la toma de datos.

CBR,

salga adecuadamente del programa

o de cualquier otro programa

CBR

a la calculadora con el cable calculadora a

CBR

. Apriete

Mensaje

LINK ERROR

Antes de medio de

Conecte el

uardar el

QUIT)

CBR

Compruebe la conexión calculadora a extremos del cable.

Si no desea (o no puede) conectar el

CBR

a la calculadora, pulse

interrumpir el programa y, después, seleccione

Memoria insuficiente Debe tener memoria suficiente para el programa

datos. El pro

rama y las listas necesitan aproximadamente 17.500 bytes.

Borre programas y/o datos.

Las opciones que aparecen en las instrucciones de actividades no coinciden con las opciones de la calculadora

Los datos no tienen buen aspecto:

puntos fuera de la curva

gráficas dentadas

gráficas planas

gráficas discontinuas

uía se aplica a todas las calculadoras TI que puedan utilizarse con

Esta por lo que puede que conten

a algunos nombres de menú, pantallas o teclas que no coincidan exactamente con los de su calculadora. Seleccione la opción que más se aproxime. Por e “Seleccione

Repita el experimento, ase

DISTANCE MATCH

urándose de que el CBR apunta directamente al

emplo, si las instrucciones dicen

,” en la TI-83 deberá seleccionar

objeto. Lea las páginas 6–12 para la obtención de buenas muestras de datos. Compruebe que en la zona despe

ada no haya estudiantes, mesas u otros

objetos. Cuando utilice dos unidades

CBR

a la vez en la misma habitación, un grupo deberá completar su experimento antes de que el con el suyo.

Compruebe la conexión calculadora a

CBR

. Apriete

extremos del cable. Compruebe el estado de las pilas (consulte la página 42). Compruebe que el

rado de suavizado no es demasiado intenso ni

demasiado ligero.

CBR

no funciona con una TI-85 Compruebe que aparece “

CBL

” al final del número de serie en la parte

posterior de la calculadora, lo cual indica la compatibilidad con La TI

85 no tiene capacidad para realizar gráficas estadísticas, por lo que

unas exploraciones (como la utilización de



pueden realizarse en ella.

Se ha perdido el cable calculadora a

CBR

Puede utilizar el cable calculadora-calculadora que viene incluido con la calculadora (el cable calculadora-calculadora es mucho más corto, por lo que puede ser conveniente pedir el cable que se ha perdido).

Las pilas están bajas con frecuencia

Antes de guardar el (utilizando

QUIT)

CBR,

salga adecuadamente del programa

o de cualquier otro programa

CBR

de la calculadora.

Cuando intenta ejecutar el pro

rama

, no ocurre

RANGER

nada Mensaje de error: La variable está

bloqueada o prote

92)

ida (sólo

Si edita o ve el pro minutos la próxima vez que lo e su ejecución. Esto es normal.

Debe desbloquear las variables L1, L2, L3, L4 calculadora.

rama

RANGER

, la calculadora puede tardar hasta dos

ecute, pues debe preparar el programa para

L5. Consulte el manual de la

firmemente

CBL

firmemente

QUIT

RANGER

y las listas de

ambos

de nuevo para

RANGER

CBR

(por

ambos

para

DIST MATCH

rupo siguiente comience

firmemente

ambos

CBL

CBR

en datos trazados) no

RANGER

CBL

y desconecte el

CBR

STA PÁGINA PUEDE COPIARSE A CONDICIÓN D

EXAS INSTRUMENTS

NCORPORATED C

E QUE SE INCLUYA EL AVISO DE

OPYRIGHT DE

TI.

ONCEPTOS BÁSICOS DEL

CBR

Información sobre productos, servicios y garantías de TI

Información sobre productos y servicios de TI

Para obtener más detalles acerca de los productos y servicios de TI, póngase en contacto mediante correo electrónico o acceda a la página inicial de calculadoras en la world wide web.

dirección de correo electrónico: ti-cares@ti.com dirección de internet:http://www.ti.com/calc

Información sobre servicios y garantías

Para obtener más detalles acerca de la duración y las condiciones de la garantía o sobre el servicio de asistencia a productos, consulte la declaración de garantía que se adjunta a este producto o póngase en contacto con su distribuidor o minorista de Texas Instruments.

ONCEPTOS BÁSICOS DEL

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

CBR

EXAS INSTRUMENTS INCORPORATED

TI.

RANGE

MAIN MENU

SETUP / SAMPLE

SET DEFAULTS

NO YES

1-99 (REALTIME=NO)

DISTANCE VELOCITY ACCELERATION

[ENTER] [TRIGGER] DELAY

NONE LIGHT MEDIUM HEAVY

METERS FEET

APPLICATIONS

REALTIME=NO

PLOT MENU

REALTIME=YES

TOOLS

QUIT

APPLICATIONS

UNITS METERS FEET

DISTANCE-TIME VELOCITY-TIME ACCELERATION-TIME PLOT TOOLS REPEAT SAMPLE MAIN MENU QUIT

SHOW PLOT SELECT DOMAIN REPEAT SAMPLE MAIN MENU QUIT

TOOLS GET CBR DATA GET CALC DATA CBR STATUS STOP/CLEAR CBR MAIN MENU

DISTANCE MATCH VELOCITY MATCH BALL BOUNCE MAIN MENU

PLOT TOOLS SELECT DOMAIN SMOOTH DATA PLOT MENU

DATA SMOOTHING LIGHT MEDIUM HEAVY NONE

OPTIONS SAME MATCH NEW MATCH APPLICATIONS MAIN MENU QUIT

STA PÁGINA PUEDE COPIARSE A CONDICIÓN DE QUE SE INCLUYA EL AVISO DE COPYRIGHT DE

EXAS INSTRUMENTS INCORPORATED

TI.

ONCEPTOS BÁSICOS DEL

CBR

Texas instruments CBR User Manual [es]

Specifications and Main Features

Frequently Asked Questions

User Manual