Texas instruments CBR User Manual [nl]

Download

85-86

TRIGGER

CBR

)

Calculator-Based Ranger

™

(CBR

™

)

AN DE SLAG MET AN DE SLAG MET

INCLUSIEFINCLUSIEF

ACTIVITEITEN VOORACTIVITEITEN VOOR

5 5

STUDENTENSTUDENTEN

CBR™CBR™

CBR

)

TRIGGER

85-86

CBR

)

TRIGGER

85-86

Calculator-Based Rangeré (CBRé) calculator-CBR-kabel

montageklem 4 AA-batterijen

CBL-CBR-kabel

Belangrijk

Texas Instruments biedt geen enkele garantie, hetzij impliciet hetzij uitdrukkelijk, met inbegrip van en niet uitsluitend beperkt tot welke impliciete garanties dan ook wat betreft de geschiktheid voor verkoop en een specifiek gebruik, voor de programma’s of documentatie en stelt deze documentatie slechts ter beschikking “as-is”.

Texas Instruments kan in geen geval aansprakelijk worden gesteld voor speciale, indirecte, toevallige of resulterende schade die in verband zou staan met of het gevolg is van de aankoop of het gebruik van deze produkten; de enige en uitsluitende aansprakelijkheid, ongeacht de wijze van de juridische procedure, die door Texas Instruments wordt gedragen, zal beperkt blijven tot het bedrag van de aankoopprijs van deze apparatuur. Bovendien kan Texas Instruments niet aansprakelijk worden gesteld indien een eis tot schadevergoeding wordt ingediend, ongeacht de aard ervan, tegen het gebruik van deze produkten door een andere persoon.



1997 Texas Instruments Incorporated.

Leraars krijgen hierbij de toestemming om in klaslokalen, workshops of tijdens seminaries de pagina's of bladen in dit werk te herdrukken of te kopiëren waarop het Texas Instrument copyright is vermeld. Die pagina's mogen door leraars worden gereproduceerd voor gebruik in het klaslokaal, in workshops en tijdens seminaries, op voorwaarde dat het copyright op elk exemplaar is vermeld. De kopieën mogen niet worden verkocht en verdere verspreiding is uitdrukkelijk verboden. Behalve in de gevallen hierboven vermeld, is een voorafgaande schriftelijke toestemming van Texas Instruments vereist om dit werk of gedeelten ervan te reproduceren of te verzenden in gelijk welke andere vorm of op gelijk welke elektronische of mechanische manier, inclusief systemen voor het opslaan en opvragen van informatie, behalve als dit uitdrukkelijk toegestaan is door de desbetreffende wetgeving. Meer informatie kunt u krijgen bij Texas Instruments Incorporated, PO Box 149149, Austin, TX, 787149149, M/S 2151, ter attentie van: Contracts Manager.

Inhoudsopgave

CBR

)

Inleiding

Wat is de CBR? 2 Aan de slag met CBR — Eenvoudiger kan het niet 4 Tips voor een goede meting 6

Activiteiten met aantekeningen voor docenten en leerling-werkbladen

TRIGGER

85-86

Activiteit 1 — De grafiek nadoen lineaire functie 13

Activiteit 2 — Speelgoedauto lineaire functie 17

Activiteit 3 — Slinger sinusfunctie 21

Activiteit 4 — Stuiterende bal parabolische functie 25

Activiteit 5 — Rollende bal parabolische functie 29

Informatie voor de docent 33

Technische informatie

CBR-gegevens worden opgeslagen in lijsten 37 RANGER instellingen 38 Het gebruik van CBR met CBL of met CBL programma’s 39 Programmeercommando’s 40

Onderhoudsinformatie

Batterijen 42 Bij moeilijkheden 43 TI service en garantie 44

Overzicht RANGER menu’s binnenzijde achterblad

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

Wat is de CBR?

om de metingen en -analyse uit de werkelijkheid in de klas te brengen

het veelzijdige RANGER programma is een druk op de knop verwijderd

MATCH en BOUNCING BALL programma’s ingebouwd in de RANGER

de voornaamste parameters voor de metingen zijn gemakkelijk in te stellen

Wat doet de CBR?

Met de verzamelen, bekijken en analyseren zonder lastige metingen en handmatig maken van grafieken.

Met

CBR

snelheid, versnelling en tijd verkennen met gegevens die verzameld zijn tijdens activiteiten die zij zelf hebben uitgevoerd. Hierdoor kunnen leerlingen van wiskundige en natuurwetenschappelijk concepten onderzoeken zoals:

CBRCBRé (Calculator-Based RangerCalculator-Based Rangeré

)

ultrasone afstandssensor

CBL

voor gebruik met TI-82, TI-83, TI-85/

, TI-86 en TI-92

gemakkelijk te bedienen, op zichzelf staand

geen programmeerwerk vereist

Inclusief het RANGER programmaInclusief het RANGER programma

en een TI grafische calculator kunnen leerlingen gegevens over bewegingen

CBR

kunnen leerlingen de wiskundige en wetenschappelijke relaties tussen afstand,

beweging: afstand, snelheid, versnelling

grafieken: coördinaatassen, hellingshoek, bijbehorende x- of y-waarde

functies: lineair, kwadratisch, exponentieel, sinusfunctie

differentiaal- en integraalrekening: afgeleiden, integralen

statistiek en analyse van gegevens: methodes voor data acquisitie, statistische analyse

Wat staat in deze handleiding?

Aan de slag met CBR

met calculators of met programmeren. Hierin vindt u instructies om snel aan de slag te gaan met de

, aanwijzingen over effectieve data acquisitie en vijf activiteiten voor in

CBR

de klas, waarbij de basisfuncties en -eigenschappen van bewegingen kunnen worden onderzocht. Deze activiteiten (zie pagina 13–32) bevatten o.a.:

aantekeningen voor docenten voor elke activiteit, plus algemene informatie voor de

docent instructies om stap voor stap te werk te gaan

een basismeting die geschikt is voor alle niveau’s

verkenningen om de gegevens nader te bestuderen, waaronder “wat-als” scenario’s

suggesties voor onderwerpen voor gevorderden, geschikt voor leerlingen die

integraalrekening al dan niet beheersen reproduceerbare leerling-werkblad met open vragen die passen bij een breed

spectrum van onderwijsniveau’s

is bedoeld als handleiding voor docenten zonder veel ervaring

AN DE SLAG MET

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

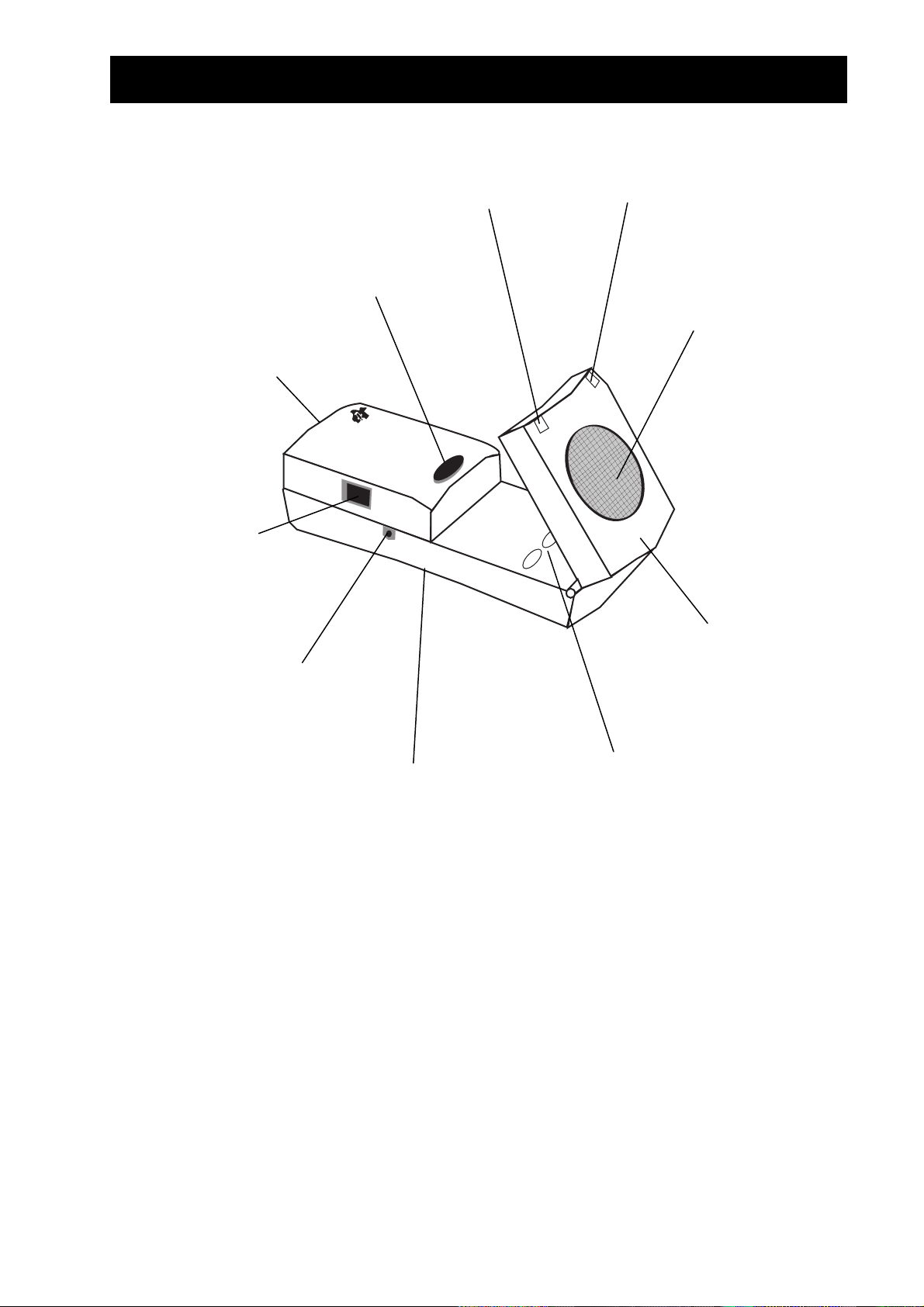
Wat is de CBR?

Z s

s g

g s

g g

(verv.)

de meting te

tarten

batterijklepje (onder)

poort voor aansluiting op CBL (indien

ewenst)

poort voor aansluiting van TI

rafische calculators met de

bijgeleverde kabel van 2,25 m

roen lampje om aan te even wanneer de meting

bezig is (ook met

eluidssignaal mogelijk

knop om

CBR

)

rood lampje om een

peciale toestand

aan te duiden

onic sensor voor max. 200 metingen per s met een bereik tussen 0,5 m en 6 m

TRIGGER

85-86

wenkkop om sensor

nauwkeurig te richten

knoppen voor overdracht van RANGER programma naar calculators

voet met standaard schroefdraad voor bevestiging aan

tatief of aan de meegeleverde

montageklem (achterkant)

bevat alles wat u nodig hebt om gemakkelijk en snel van start te gaan met activiteiten in de

CBR

klas— er is alleen nog een TI grafische calculator bij nodig (en verkrijgbare attributen voor sommige activiteiten).

ultrasone afstandssensor

RANGER

programma in de

CBR

kabel tussen calculator en

4 AA batterijen

CBR

montageklem

5 leuke activiteiten

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

Aan de slag met CBR—Eenvoudiger kan het niet

Met

maakt u in drie stappen uw eerste meting!

CBR

Aansluiten

Met de calculator-CBR-kabel sluit u de calculator.

Druk de kabel aan weerszijden vast.

Opmerkin

calculator-kabel die bij de calculator geleverd wordt is ook bruikbaar.

aan op een grafische TI-

CBR

De korte calculator-

Zenden van programma

In de CBR bevindt zich RANGER, een programma dat voor iedere calculator anders is. Dit programma kan eenvoudig van de CBR naar de calculator worden overgebracht

Zorg er eerst voor dat de calculator klaar is om het programma te ontvangen. Dat gaat met de onderstaande opdrachten.

stevi

TI-82 of TI-83 TI-85/CBL of TI-86 TI-92

LINK

[

Open vervolgens de scharnierende kop van de CBR en druk op de juiste knop om het programma over te sturen.

Tijdens de overdracht toont de calculator overdracht voltooid is, dan knippert het groene lampje op de keer, de Is er een probleem, dan knippert het rode lampje op de CBR twee keer en piept de

Nadat u het overgestuurd, hoeft u het niet opnieuw naar die calculator te sturen zolang u het niet uit het geheugen van de calculator verwijdert.

Opmerking:

bytes geheugen nodig. Het kan nodig zijn programma’s en gegevens uit het geheugen van de calculator te verwijderen. U kan de programma’s en gegevens eerst bewaren door ze met TI-Graph Linké naar een computer te sturen of met een calculator-calculator-kabel naar een andere calculator te sturen (zie de handleiding van de calculator).

CBR

›

]

piept één keer, en het scherm van de calculator toont twee keer.

RANGER-

Voor het programma en de gegevens zijn ongeveer 15500

programma van de

[

LINK

]

RECEIVING

naar een calculator heeft

CBR

Ga naar het Home-

scherm.

(behalve TI-92). Als de

CBR

één

DONE

AN DE SLAG MET

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

Aan de slag met CBR—Eenvoudiger kan het niet

(verv.)

Starten

Probeer voor een snel resultaat eens een van de kant-en-klare activiteiten in deze handleiding

Start het

Druk op Kies Druk op

RANGER-

TI-82 of TI-83 TI-85/CBL of TI-86 TI-92

RANGER

›

programma met de opdrachten hieronder

Druk op Kies Druk op

^ A

RANGER

›

Druk op L [

RANGER

Kies Druk op ¨

›

VAR-LINK

Het openingsscherm wordt getoond. Druk op

MAIN MENU

SETUPàSAMPLE SET DEFAULTS APPLICATIONS PLOT MENU TOOLS QUIT

Op het getoond. Druk op druk op

›. U ziet het

& & & & &

MAIN MENU

› om met het verzamelen van de gegevens te beginnen. Zo

kiest u

› om

MAIN MENU

bekijk en verander de instellingen voor het meten verander de instellingen in de standaardinstellingen

DISTANCE MATCH, VELOCITY MATCH, BALL BOUNCE

grafiek opties

GET CBR DATA, GET CALC DATA, STATUS, STOPàCLEAR

SET DEFAULTS

START NOW

. Het

scherm wordt

SETUP

te kiezen. Stel de activiteit in en

eenvoudig is dat!

Belangrijke informatie

Deze handleiding is van toepassing op alle grafische TI-calculators die met

gebruikt kunnen worden. Het kan dus gebeuren dat sommige

CBR

menu’s op uw calculator een andere naam hebben.

Beëindig het

RANGER

kiest dan zorgt het afgesloten. Hierdoor is verzekerd dat

programma altijd met de

RANGER-

programma ervoor dat

goed geïnitialiseerd wordt als

CBR

optie. Als u QUIT

QUIT

correct wordt

CBR

u hem de volgende keer gebruikt.

Maak de verbinding tussen

en calculator altijd los voordat u de

CBR

opbergt.

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

Tips voor een goede meting

Betere metingen verrichten

Hoe werkt de CBR?

De CBR zendt een ultrasone puls uit en meet hoe lang het duurt voor er een echo terugkomt van het dichtstbijzijnde voorwerp.

meet, zoals iedere detector die gebruik maakt van geluidsgolven, de tijd die

CBR

verloopt tussen het uitzenden van de ultrasone puls en de eerste echo die terugkomt, maar de gegevens verzameld worden, berekent de

heeft een ingebouwde microprocessor die veel meer doet. Terwijl de

CBR

de afstand naar het voorwerp met behulp

CBR

van de bekende geluidssnelheid. Daarna differentieert hij de afstand één en twee keer naar de tijd om de snelheid en de versnelling te bepalen. Deze gegevens worden opgeslagen in de lijsten

L1, L2, L3

Het is interessant om de leerlingen dezelfde berekeningen als de

Verricht metingen in de mode

➊

Gebruik de tijden in

➋

, en L4.

te laten uitvoeren.

CBR

REALTIME=NO

. Verlaat het

RANGER-

programma.

in combinatie met de afstand in L2 om de snelheid van het

object bij iedere meting te bepalen. Vergelijk de resultaten met de

(

n+1

)à2 N (

n+1

om de versnelling van het object bij iedere meting te

n-1

)à2

snelheidsgegevens in

Gebruik de snelheidsgegevens in L3 (of de door de leerling berekende waarden) in

➌

combinatie met de tijden in bepalen. Vergelijk de resultaten met de versnellingsgegevens in

Grootte van het object

Werkt u met een klein object op een grote afstand, dan zijn de kansen op een nauwkeurig resultaat geringer. Bijvoorbeeld, op een afstand van 5 meter detecteert u een voetbal heel wat makkelijker dan een pingpongbal.

Minimumbereik

zendt een puls uit, de puls bereikt het object, kaatst terug en wordt door de

CBR

ontvangen. Als het object dichterbij is dan een halve meter, dan kunnen de opeenvolgende pulsen elkaar overlappen, waardoor ze door geïnterpreteerd worden. De grafiek wordt dan onnauwkeurig. Zet

CBR

verkeerd

dus op een

CBR

afstand van minstens een halve meter van het object.

Maximumbereik

Naarmate de puls verder moet reizen, verliest hij zijn kracht. Na ongeveer 12 meter (6 meter heen naar het object en 6 meter terug naar de betrouwbaar gedetecteerd te kunnen worden. Dit beperkt de afstand waarop de

), wordt de echo te zwak om

CBR

betrouwbaar werkt tot 6 meter.

CBR

AN DE SLAG MET

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

Tips voor een goede meting

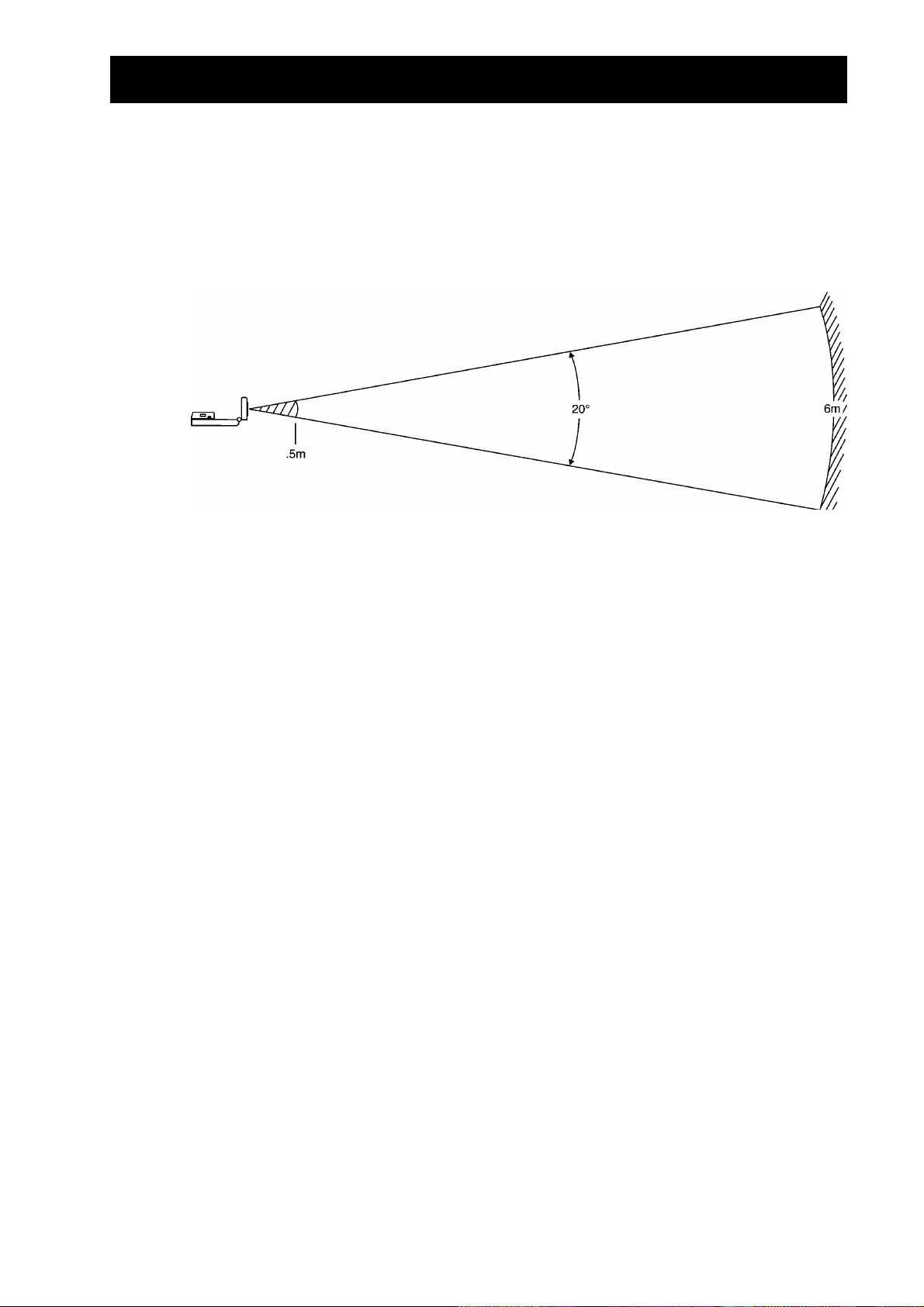
De vorm van de bundel

(verv.)

De bundel van de

heeft de vorm van een kegel met een hoek van 10°.

CBR

Om te vermijden dat andere objecten in de omgeving de uitlezing verstoren, is het gewenst dat er geen andere objecten zijn in het pad van de ervoor dat andere objecten niet door

worden opgemerkt.

CBR

bundel. Hiermee zorgt u

CBR-

ziet alleen het

CBR

dichtstbijzijnde object binnen het gebied van de bundel.

Reflecterende oppervlakken

Sommige oppervlakken reflecteren de pulsen beter dan andere. Bijvoorbeeld: met een harde gladde bal krijgt u betere resultaten dan met een tennisbal. En als u werkt in een ruimte waarin zich veel harde reflecterende voorwerpen bevinden, dan zult u veel onbedoelde metingen zien. Metingen van onregelmatige oppervlakken (zoals een speelgoedauto of een leerling die loopt met een calculator in zijn hand) zullen onduidelijk zijn.

Een afstand-tijd grafiek van een stilstaand object kan kleine verschillen vertonen in de berekende afstanden. Als deze waarden resulteren in een ander pixel, dan zal de verwachte horizontale lijn kleine onregelmatigheden vertonen. Een afstand-tijd grafiek zal nog onregelmatiger worden, want de verandering in afstand tussen twee punten is, per definitie, de snelheid. Het kan dus nodig zijn dat u de gegevens enigszins “gladstrijkt”.

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

Tips voor een goede meting

Instellingen van RANGER

Frequentie van de meting

is de totale tijd in seconden waarin de meting wordt gedaan. Geef hier een geheel

TIME

getal op tussen 1 seconde (voor snel bewegende objecten) en 99 seconden (voor langzaam bewegende objecten). Bij

(verv.)

REALTIME=YES

, is

altijd 15 seconden.

TIME

Naarmate Bijvoorbeeld, als

zijn.

CBR

Starten en stoppen

Het

SETUP-

een lager getal is, moet het object zich dichter bij de

TIME

TIME=1 SECOND

scherm in het

RANGER

, dan kan het object niet verder dan 1,75 meter van de

-programma heeft diverse mogelijkheden om het meten

CBR

te starten en te stoppen.

BEGIN ON: [ENTER]

. Start de meting met de

-toets van de calculator als de

›

opstelling bediend wordt door iemand die in de buurt van de calculator zit.

BEGIN ON: [TRIGGER]

. Start en stopt de meting met de

opstelling bediend wordt door iemand die in de buurt van de Met deze optie kunt u de

verbindingskabel los, neem de op

›

, verricht de meting, verbind de

om de gegevens over te sturen. Gebruik

loskoppelen. Verzorg eerst de instellingen, maak de

CBR

naar de plaats waar gemeten moet worden, druk

CBR

weer met de calculator en druk op

CBR

BEGIN ON: [TRIGGER]

knop van de

zit.

CBR

als de kabel te kort is of de meting zou kunnen verstoren. Dit is niet mogelijk in de mode (zoals de

BEGIN ON: DELAY

MATCH-

toepassing).

. Start de meting tien seconden nadat u op

drukt. Dit is handig

›

als één persoon alle handelingen moet verrichten.

Start-knop

Het effect van

hangt af van de instellingen.

bevinden.

als de

CBR

REALTIME=YES

start de meting, zelfs als

BEGIN ON: [ENTER]

BEGIN ON: DELAY

geselecteerd is. Deze knop stopt de meting ook, maar meestal zult u willen wachten tot de meting voltooid is.

REALTIME=NO

kunt u, nadat de meting voltooid is,

gebruiken om de laatste meting automatisch te herhalen, zonder de gegevens naar de calculator te sturen. Om de gegevens over te sturen opent u het

GET CBR DATA PLOT MENU

. (U kunt een meting ook herhalen door

START NOW

op het

SETUP

scherm)

MAIN MENU

en kiest u

REPEAT SAMPLE

, en vervolgens

TOOLS

te kiezen op het

AN DE SLAG MET

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

Tips voor een goede meting

Filteren

(verv.)

Het

RANGER

-programma kan de gegevens filteren, waardoor het effect van storende signalen en variaties in de metingen verminderd wordt. Overdrijf het filteren niet. Begin zonder filtering of met

filtering. Verhoog het filteren tot het resultaat bevredigend

LIGHT

Is het zeer waarschijnlijk dat er storende signalen optreden, verhoog dan de filtering

op het Heeft u al gegevens met

toepassen. Daarvoor moet de calculator met de op het

Ruis—wat is het en hoe kom je ervan af?

Als de

CBR

scherm voordat u met de meting begint (zie pagina 38).

SETUP

verzameld, dan kunt u naderhand filtering

verbonden zijn. Kies

CBR

PLOT TOOLS

, en kies de graad van filtering.

PLOT MENU

, kies

SMOOTH DATA

REALTIME=NO

signalen ontvangt van andere objecten dan het object dat u bedoeld had, dan toont de grafiek onjuiste punten (ruis) die niet overeenkomen met het algemene patroon van de grafiek. Om ruis te verminderen:

Let erop dat de

naar een een

Probeer te meten in een ruimte met weinig vreemde voorwerpen (zie de tekening van

REALTIME=YES-

REALTIME=NO-

direct op het doel wordt gericht. Stel de sensorkop in terwijl u

CBR

meting kijkt totdat u goede resultaten krijgt. Daarna kunt u

meting verrichten.

de vorm van de bundel op pagina 7). Kies een groter object dat beter reflecteert, of zet het object dichter bij de

CBR

(maar

niet dichter dan een halve meter). Gebruikt u meer dan één

in een ruimte, dan moet de ene groep klaar zijn met de

CBR

meting voordat de andere groep begint. Is er veel ruis bij een

REALTIME=YES

-meting, herhaal de meting dan met een hogere filteringsgraad tot de resultaten bevredigend zijn. (U kunt de filtering niet veranderen in de toepassingen

Is er veel ruis bij een

DISTANCE MATCH, VELOCITY MATCH

REALTIME=NO

-meting, gebruik dan een hogere filteringsgraad met

, en

BALL BOUNCE

de oorspronkelijke gegevens.

Geluidssnelheid

De afstand naar het object wordt bij benadering gevonden met behulp van de standaard ingestelde geluidssnelheid. Evenwel, de geluidssnelheid is van diverse factoren afhankelijk, vooral van de luchttemperatuur. Voor metingen waarbij alleen de relatieve bewegingen van belang zijn, is deze factor niet van belang. Zijn nauwkeurige resultaten vereist, dan kan een programmeercommando worden gebruikt om de omgevingstemperatuur in te stellen. (zie pagina 40–41).

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

Tips voor een goede meting

REALTIME=YES

(verv.)

Gebruik de

voor langzame objecten

om de resultaten te zien terwijl ze gemeten worden

als u slechts één soort gegevens (afstand, snelheid of versnelling) wilt zien

REALTIME=YES-

mode berekent de

mode:

de gevraagde plotgegevens (afstand, snelheid of

CBR

versnelling) direct van elk afzonderlijk meetpunt en verstuurt deze naar de calculator.

RANGER

tekent dan voor dat meetpunt een enkel pixel in de grafiek.

Omdat al deze bewerkingen voltooid moeten zijn voordat het volgende meting kan worden gedaan, is de meetfrequentie in de

REALTIME=YES-

mode beperkt.

Er zijn ongeveer 0,080 seconden nodig voor een enkel meetpunt samen met de verwerking en de overdracht van de gegevens. Er is extra tijd nodig voor het tekenen van de grafiek, waardoor de benodigde tijd in

REALTIME=NO

Gebruik de

voor snellere objecten

als filtering nodig is (zie pagina 9)

als de

als u alle gegevenssoorten (afstand, snelheid en versnelling) van de meting wil weten.

REALTIME=NO-

niet permanent met de calculator verbonden is (zie pagina 11)

CBR

mode:

RANGER

stijgt tot ongeveer 0,125 seconden.

REALTIME=NO

-mode, worden de gegevens in de

opgeslagen en pas naar de

CBR

calculator gezonden als de hele meting voltooid is. De meetfrequentie kan voor dichtbijzijnde objecten 200 metingen per seconde zijn. De gegevens van tijd, snelheid en versnelling worden naar de calculator gestuurd.

Omdat de gegevens in de

worden opgeslagen, kunt u ze steeds weer naar de

CBR

calculator overzenden.

Elke keer als u de filtering verandert, past de

de nieuwe filteringsfactor toe, stuurt

CBR

de gewijzigde gegevens naar de calculator, en slaat de nieuwe waarden op in de lijsten.

Kiest u een domein dan verandert dat de lijsten die in de calculator opgeslagen zijn.

Desgewenst kunt u de oorspronkelijke gegevens terughalen. Open het het

RANGER

U kunt ook dezelfde gegevens met meerdere leerlingen gebruiken, zelfs als ze

-programma, kies

TOOLS

. Kies in het

TOOLS

GET CBR DATA

MAIN MENU

verschillende grafische TI-calculatoren gebruiken. Hierdoor kunnen alle leerlingen met dezelfde gegevens verwerkingsopdrachten uitvoeren. (zie pagina 11).

AN DE SLAG MET

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

Tips voor een goede meting

Gebruik van CBR zonder calculator

(verv.)

Omdat de

niet direct gegevens naar de calculator kan sturen als hij niet met de

CBR

calculator verbonden is, zijn bepaalde instellingen vereist. Maak op het volgende instellingen:

REALTIME=NO

BEGIN ON=[TRIGGER]

Het

RANGER-

programma zegt u wanneer u de

moet worden aangesloten. Er is geen speciale procedure nodig.

Gemeenschappelijk gebruik van gegevens

Wilt u dat de hele klas dezelfde gegevens op hetzelfde moment analyseert? Met kunt u de

Stuur het

➊

REALTIME=NO

RANGER-

-gegevens snel over de leerlingen verdelen.

programma naar de calculator van iedere leerling voordat u begint

met de meting. Meet de gegevens met de

➋

Sluit de calculator van de eerste leerling aan op de

➌

CBR

of de calculator-calculator-kabel.

➍

Open het menu

GET CBR DATA

MAIN MENU

in het

. Er staat nu

verschijnt

REALTIME=NO-

RANGER

-programma en kies

TRANSFERRING...

scherm de

SETUP

mag loskoppelen en wanneer hij weer

CBR

mode.

met de calculator-

CBR

TOOLS

. Kies in het

CBR-

TOOLS

op het scherm en de grafiek

CBR

kabel

Druk op › om terug te gaan naar het

➎

PLOT MENU

, en kies

. Maak de kabel

QUIT

los. Sluit een andere calculator (van het zelfde type) aan op de calculator waarin de

➏

gegevens zich bevinden. Open op de tweede calculator het

RANGER L1, L2, L3, L4

Stuur de gegevens van de

➐

-programma en kies , en L5 worden automatisch naar de tweede calculator overgestuurd.

CBR

. Kies in het

TOOLS

naar de calculator van een andere leerling terwijl de

-menu

MAIN MENU

GET CALC DATA

in het

andere leerlingen de gegevens van calculator naar calculator aan elkaar doorgeven.

Als alle leerlingen dezelfde gegevens hebben, dan kunnen ze de gegevens in

PLOT MENU

analyseren, en zonder

RANGER

met de mogelijkheden van de calculator om

lijsten en grafieken te maken. Om gegevens op de TI-85 gezamenlijk te gebruiken, gebruikt u de

niet

RANGER)

om de lijsten over te sturen.

-faciliteit, (dus

LINK

. Lijsten

RANGER

met

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

Tips voor een goede meting

Niet alleen gewoon gegevens verzamelen

(verv.)

Nadat u met

RANGER

grafieken gemaakt heeft, kunt u de gegevens met een functie

verder verwerken. Omdat de gegevens als lijsten worden verzameld en als een statistische grafiek worden getoond, kunt u

, , en œ gebruiken om de relatie

tussen de gegevens te onderzoeken.

Binnen RANGER

Onderzoek grafieken met

, wat automatisch wordt ingesteld. (Op de TI-85

TRACE

gebruikt u de vrijbewegende cursor.) Bewerk de gegevens, bijvoorbeeld door filtering of door een deel te selecteren.

Buiten RANGER

Onderzoek de gegevens met de list-editor van de calculator.

Maak handmatig een functie-fit met de Y= editor van de calculator.

Fit automatisch de functie die het best met de gegevens overeenstemt door gebruik te

maken van de regressiemogelijkheden van de calculator.

Er kunnen nog veel meer verbanden onderzocht worden dan er worden geboden door de plotopties in

RANGER

tegelijk worden getoond. In het daarna geeft u op:

. Bijvoorbeeld kunnen de afstand-tijd en snelheid-tijd grafieken als L1 versus L2 en

Plot1

MAIN MENU

van het

Plot2

RANGER

als L1 versus L3. (Het kan ook nodig zijn

-programma kiest u

QUIT

, en

om het venster bij te stellen) Gegevens en grafieken kunnen met behulp van een TI-Graph Link naar een computer

worden gestuurd. Dat is vooral handig als de leerlingen uitgebreide verslagen produceren van hun bevindingen.

Gebruik van CBR zonder het RANGER-programma

U kunt

RANGER

Voor informatie over het gebruik van

Voor informatie over het verkrijgen van programma’s en activiteiten, zie pagina 36.

Voor informatie over de programmeercommando’s waarmee u uw eigen

ook als afstandssensor gebruiken met

CBR

programma’s kunt schrijven, zie pagina’s 40–41.

met

of met andere programma’s dan

CBL

, zie pagina 39.

CBL

AN DE SLAG MET

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

Activiteit 1—De grafiek nadoen aantekeningen voor docenten

Concepten

Te verkennen functie: lineaire functie.

MATCH

introduceert de concepten afstand en tijd— of, nauwkeuriger: het concept van afstand versus tijd uit de werkelijkheid. Terwijl leerlingen proberen om grafieken te reproduceren door te lopen, terwijl zij hun eigen beweging in een grafiek zien, kan het concept positie worden verkend.

In “Verkenning” wordt aan leerlingen gevraagd om de loopsnelheid om te zetten van m/s in km/uur.

Als de leerlingen het nadoen van Afstand-tijdgrafieken onder de knie hebben, kunt u een nieuwe uitdaging voor hen vinden in het nadoen van Snelheid-tijd-grafieken.

Materiaal

 calculator

CBR



 calculator-to-calculator cable

Met een TI ViewScreené kunnen andere leerlingen meekijken—waardoor deze activiteit nog leuker wordt.

Aanwijzingen

Leerlingen vinden deze activiteit echt boeiend. Neem genoeg tijd want iedereen wil aan de beurt komen!

Deze activiteit werkt het beste als de leerling die loopt (evenals de hele klas) ziet hoe zijn/haar beweging op een muur of scherm wordt geprojecteerd.

Laat de leerlingen in één lijn met de CBR lopen, want soms lopen zij zijwaarts (loodrecht op de lijn naar de CBR) of springen omhoog!

De instructies stellen voor om de activiteit te laten meten in meters, omdat dat overeenkomt met de vraag op het leerling-werkblad.

Zie pagina 6–12 voor aanwijzingen over goede metingen.

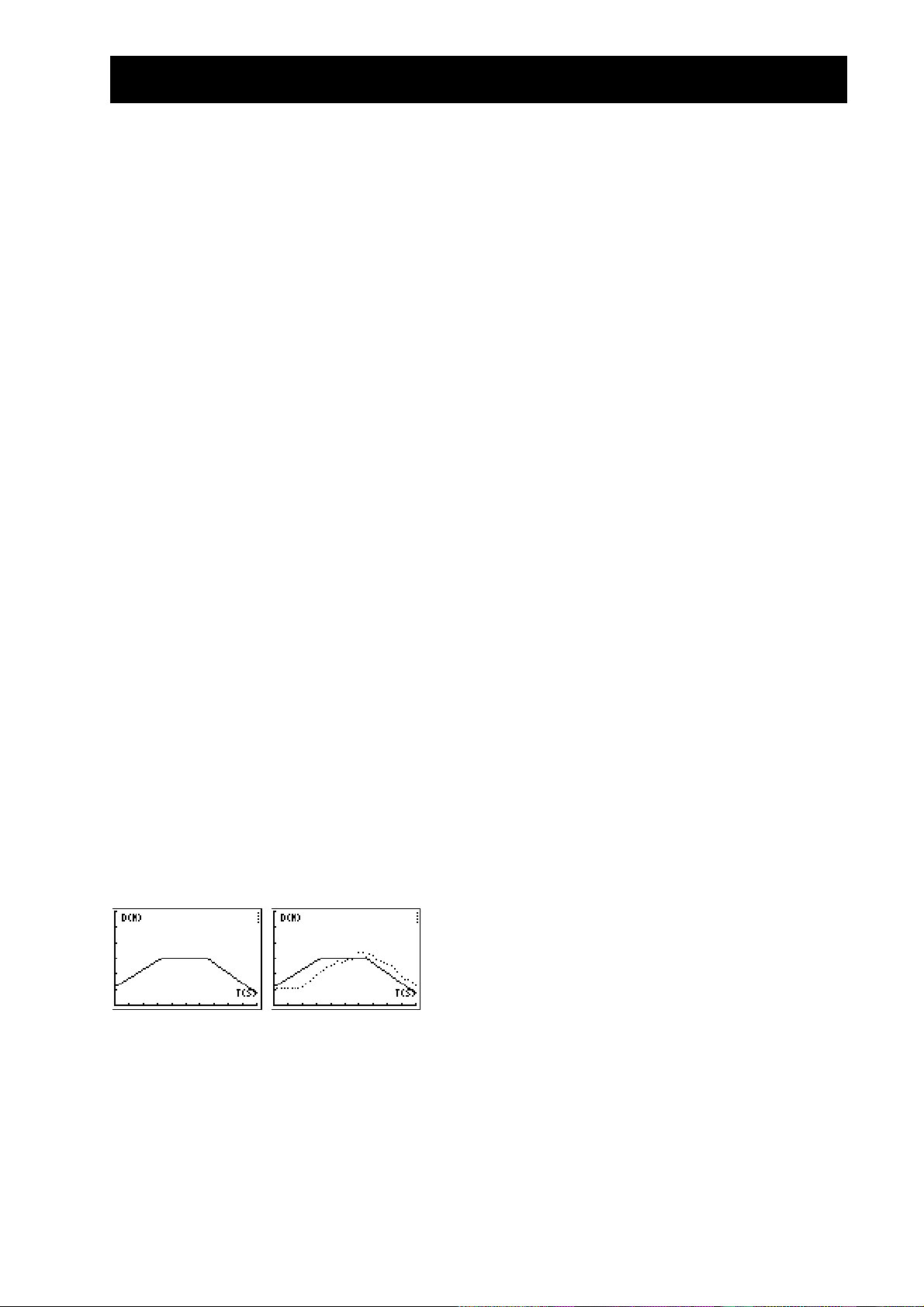
Te verwachten grafieken

Te verwachten antwoorden

1. tijd (vanaf begin meting); seconden; 1 seconde; afstand (vanaf de CBR tot het voorwerp); meter; 1 meter

2. de overeenkomende waarde van y is de waarde van de beginafstand

3. verschillend per leerling

4. achteruit (vergroot de afstand tussen de CBR en het voorwerp)

5. vooruit (verklein de afstand tussen de CBR en het voorwerp)

6. blijf stilstaan; hellingshoek nul houdt in: geen wijziging van y (afstand)

7. verschillend per diagram; @yà3,3

8. verschillend per diagram; @yà1

9. het gedeelte met de grootste hellingshoek (positief of negatief)

10.dit is een strikvraag—het vlakke gedeelte, want je beweegt helemaal niet!

11.loopsnelheid; wanneer je van richting en/of van snelheid verandert

12.snelheid (of snelheidsvector)

13.verschillend per diagram (voorbeeld: 1,5 meter in 3 seconden)

14.verschillend per diagram; voorbeeld: 0,5 meterà1 seconde

voorbeeld: (0,5 meter à 1 seconde) Q (60 seconden à 1 minuut) = 30 meter à minuut

voorbeeld: (30 meter à 1 minuut) Q (60 minuten à 1 uur) = 1800 meter à uur

voorbeeld: (1800 meter à 1 uur) Q (1 kilometer à 1000 meter) = 1,8 kilometer à uur.

Laat leerlingen dit laatste getal vergelijken met de snelheid van een auto. bijv. 96 kilometer à uur.

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

15.verschillend per diagram; som van de @y voor elk lijnsegment.

AN DE SLAG MET

CBR

Activiteit 1—De grafiek nadoen lineaire functie

Metingen

Houd de

➊

CBR

op een muur.

Hints:

De maximale afstand van elk diagram is 4 meter vanaf de

afstand is 0,5 meter.

in één hand en de calculator in de andere. Richt de sensor rechtstreeks

. De minimale

CBR

➋

Start het

RANGER

programma (zie pagina 5 voor de toetsaanslagen voor elke

calculator). Kies uit het

➌

Kies uit het

➍

instructies. Druk op › om het na te doen diagram weer te geven. Neem even de tijd om het

➎

MAIN MENU: APPLICATIONS APPLICATIONS

DISTANCE MATCH

menu:

zorgt automatisch voor de instellingen.

. Kies dan

DISTANCE MATCH

METERS

. Er verschijnen algemene

diagram te bestuderen. Beantwoord vraag 1 en 2 op het werkblad. Ga naar de plaats waar je denkt dat het diagram begint. Druk op › om te

➏

beginnen met metingen. Je hoort een klikkend geluid en je ziet het groene lampje terwijl er gegevens worden verzameld.

Loop achteruit en vooruit en probeer de grafiek na te doen. Je positie wordt op het

➐

scherm geplot. Bestudeer, als de meting afgelopen is, hoe goed jouw “loopje” overeenkomt het

➑

diagram en beantwoord dan vraag 3. Druk op › om het

➒

OPTIONS

menu weer te geven en kies

SAME MATCH

. Probeer

jouw looptechniek te verbeteren en beantwoord dan vraag 4, 5 en 6.

AN DE SLAG MET

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

Activiteit 1—De grafiek nadoen

Verkenning

(verv.)

lineaire functie

DISTANCE MATCH

Druk op › om het

➊

het eerste gedeelte en beantwoord vraag 7 en 8. Bestudeer het hele diagram en beantwoord vraag 9 en 10.

➋

Ga naar de plaats waar je denkt dat het diagram begint, druk op › om te

➌

beginnen met metingen en probeer de grafiek na te doen. Als de meting afgelopen is beantwoordt u vraag 11 en 12.

➍

Druk op › to display the

➎

Bestudeer de grafiek en beantwoord vraag 13, 14 en 15.

➏

Druk op › om het

➐

gewenst, of ga terug naar het programma te verlaten.

Vervolgverkenning

De grafieken die door Probeer nu is pas moeilijk!

MATCH

is een erg gewild programma. Er kunnen extra versies die ingewikkelder

grafieken verkennen, beschikbaar komen. (zie pagina 36).

, bestaan alle grafieken uit 3 del en met rechte lijnen.

DISTANCE MATCH

VELOCITY MATCH

OPTIONS

menu weer te geven en kies

menu en kies

NEW MATCH

menu weer te geven. Herhaal de activiteit indien

MAIN MENU

en kies dan

QUIT

om het

. Bestudeer

RANGER

zijn gegenereerd, bestaan alle uit rechte lijnen

, waarbij je probeert een Snelheid-Tijd grafiek na te doen. Dit

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

Activiteit 1—De grafiek nadoen

Naam _____________________________

Metingen

1. Welke natuurkundige grootheid staat langs de x-as? ________________________________________ Wat is de eenheid? Hoe ver staan de streepjes uit elkaar? ____________ Welke natuurkundige grootheid staat langs de y-as? ________________________________________ Wat is de eenheid? Hoe ver staan de streepjes uit elkaar? ____________

2. Hoe ver van de

moet je volgens jou beginnen? _________________________________________

CBR

3. Ben je te dichtbij, te ver of op de juiste plaats begonnen? ____________________________________

4. Moet je vooruit of achteruit lopen voor een gedeelte met een hellingshoek omhoog? ____________

Waarom? ____________________________________________________________________________

5. Moet je vooruit of achteruit lopen voor een gedeelte met een hellingshoek omlaag? _____________ Waarom? ____________________________________________________________________________

6. Wat moet je doen om een vlak gedeelte te krijgen? _________________________________________ Waarom? ____________________________________________________________________________

Verkenning

7. Als je één stap per seconde zet, hoe groot moet die stap dan zijn? ____________________________

8. Als je in plaats daarvan stappen van 1 meter neemt, hoeveel stappen moet u dan doen? __________

9. Bij welk gedeelte moet je het snelst lopen? ________________________________________________

Waarom? ____________________________________________________________________________

10. Bij welk gedeelte moet je het langzaamst lopen? ___________________________________________ Waarom? ____________________________________________________________________________

11. Welke andere factoren komen erbij kijken om precies de grafiek na te doen naast de beslissing om vooruit of achteruit te lopen? ___________________________________________________________

_____________________________________________________________________________________

12. Voor welke natuurkundige grootheid staat de hellingshoek van het lijngedeelte? ________________

13. Hoeveel meter moet je lopen, in hoeveel seconden, voor het eerste lijngedeelte? ________________

1 seconde: _____________________________

14. Zet de waarde in vraag 13 (de snelheid) om in meter Converteer naar meter Converteer naar meter Converteer naar kilometer

minuut: _________________________________________________________

àuur: _____________________________________________________________

àuur: _________________________________________________________

15. Hoe ver heb je feitelijk gelopen? _________________________________________________________

AN DE SLAG MET

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

Activiteit 2—Speelgoedauto aantekeningen voor docenten

Concepten

Te verkennen functie: lineaire functie. Aan de hand van de beweging van een

gemotoriseerde speelgoedauto wordt geïllustreerd wat het concept van een constante snelheid is.

Materiaal

 calculator

CBR



CBR

 calculator-

snoertje

 speelgoedauto die op batterijen werkt  TI ViewScreen (optioneel)

Aanwijzingen

Speelgoedauto’s verschillen aanzienlijk is grootte, vorm en weerkaatsingshoek van het invallende ultrasone geluid. Daarom kunnen de grafieken die het resultaat zijn, verschillen in kwaliteit. Sommige auto’s hebben misschien een extra weerkaatsingsoppervlak nodig om een goede grafiek te krijgen. Probeer eens een stuk karton aan de auto te bevestigen om een goed doelwit voor de sensor te krijgen.

Misschien wilt u een aantal auto’s uitproberen om de leerlingen een kans te geven deze effecten te verkennen.

Langzamer speelgoedauto’s (bijv. voor jonge kinderen) zijn beter geschikt voor deze activiteit. Zoek een auto uit met een constante snelheid.

Zie pagina 6–12 voor hints over goede metingen.

Verkenning

De hellingshoek van de Afstand-tijd grafiek van een voorwerp op een gegeven moment geeft de snelheid van het voorwerp weer op dat moment. Daarom is bij een voorwerp dat zich met een constante snelheid beweegt, de hellingshoek in de bijbehorende Afstand-tijd grafiek constant. Dit is de reden waarom de Afstand-tijd grafiek lineair is.

Als u begint met gegevens te verzamelen voordat de auto begint te rijden, merkt u dat de Afstand-tijd grafiek niet lineair is aan het begin van de grafiek. Waarom? De auto begint bij rust (v = 0). De constante snelheid kan niet ineens worden bereikt. Versnelling wordt weergegeven door:

Te verwachten grafieken

Antwoorden op vragen

1. de eerste of de laatste grafiek; de afstand neemt constant toe

2. de leerlingen voeren waarden in vanuit

TRACE

3. de waarde van de afstand neemt met een constant getal toe

4. snelheid is de mate van verandering van afstand, gemeten gedurende een gegeven tijd; de waarden zijn gelijk voor elke gelijke toename van de tijd

5. de leerling zou een waarde moeten vinden die lijkt op de waarden, berekend voor m

lijkt op m m staat voor de snelheid van de auto

6. b is de gevonden waarde van y; bijv,: y = 2x + 0

7. varieert; bijvoorbeeld, als m = 2, is afstand (y) = 20 meter na 10 seconden (y = 2 Q 10 + 0); bij 1 minuut is y = 120 meter

Vervolgverkenning

De hellingshoek van een Snelheid-Tijd grafiek bij constante snelheid is nul. Daarom geeft de Versnelling-Tijd grafiek een a = 0 (in het ideale geval) gedurende de tijd dat de snelheid constant is.

De oppervlakte die het resultaat vormt, is de verplaatsing van het voorwerp (netto afgelegde afstand) gedurende tijdinterval t

Voor leerlingen die integraalrekening beheersen, kan verplaatsing worden gevonden uit:

svdt

∫

tot t2.

∆

Als het voorwerp ineens vanuit rust naar een constante snelheid zou gaan, zou ∆t = 0 zijn. Maar dit impliceert oneindige versnelling, hetgeen in de praktijk niet mogelijk is. (In feite zou op grond van de tweede Wet van Newton, F = ma, een oneindige versnelling slechts kunnen resulteren uit een oneindige kracht, die eveneens onmogelijk is.) Daarom moeten wij het voorwerp observeren, terwijl het versnelt (de snelheid verhoogt) tot de constante snelheid gedurende een eindige tijd.

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

waarbij s de verplaatsing van het voorwerp is gedurende tijdinterval t

tot t2.

AN DE SLAG MET

CBR

Activiteit 2—Speelgoedauto lineaire functie

Metingen

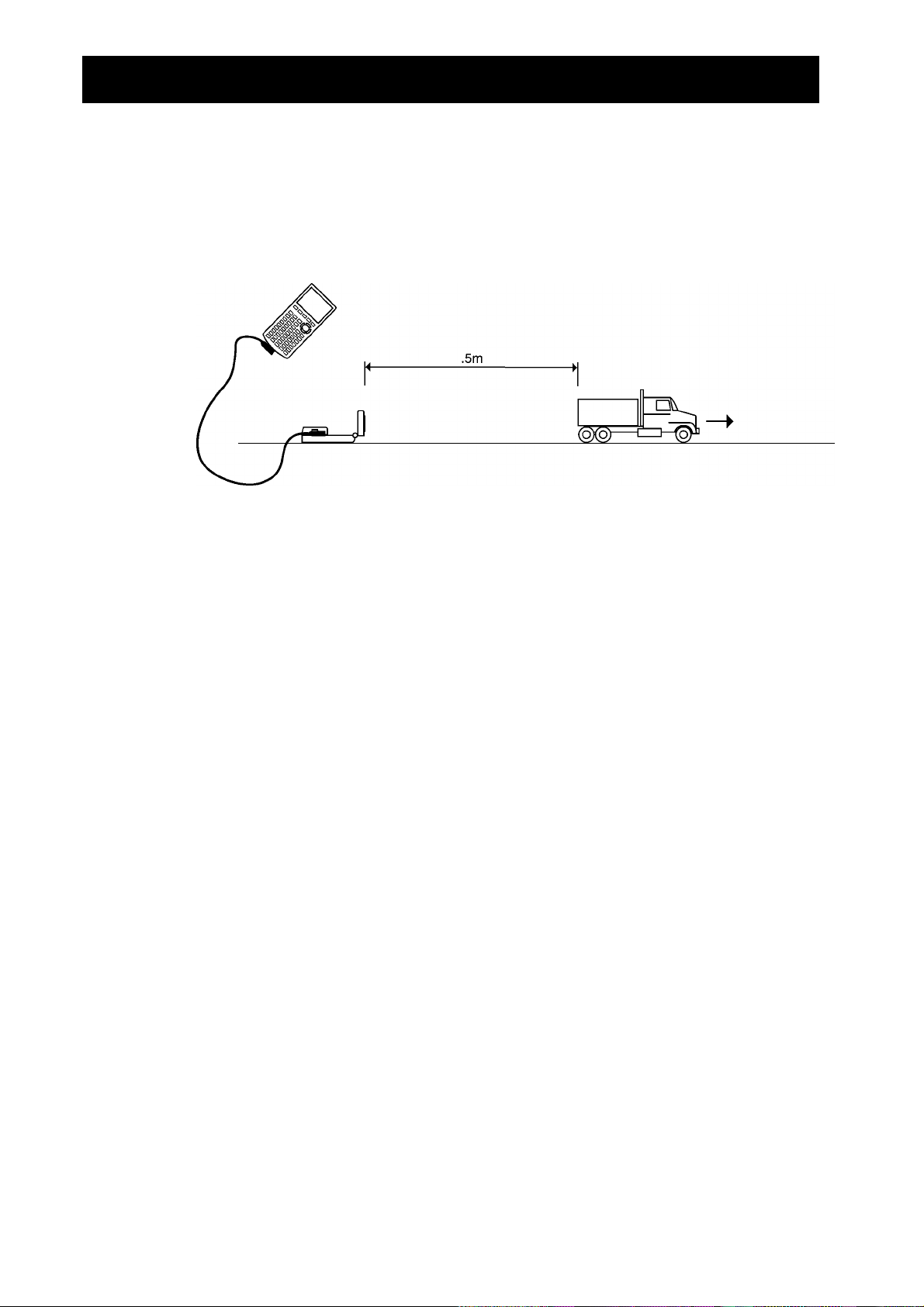
Plaats de auto tenminste 0,5 meter van de

➊

, met de voorkant van de

CBR

een rechte lijn.

Richt de sensor rechtstreeks op de auto en zorg ervoor dat er niets tussen de

Hints:

sensor en de auto staat (zie pagina 7).

Voordat u begint met metingen, beantwoord je eerst vraag 1 op het werkblad.

➋ ➌

Start het

RANGER

programma (zie pagina 5 voor de toetsaanslagen voor elke

calculator). Kies vanuit het

➍

MAIN MENU: SETUPàSAMPLE

. Bij deze activiteit hebt u de volgende

instellingen nodig:

CBR

af in

REALTIME: NO

TIME (S): 5 SECONDEN

DISPLAY: DISTANCE

BEGIN ON: [ENTER]

SMOOTHING: LIGHT

UNITS: METERS

De instructies voor het wijzigen van een instelling vindt u op pagina 38. Kies

➎ ➏

START NOW

Druk op › als je wilt beginnen. Start de auto en laat deze snel uit de clear zone

rijden. Je hoort een klikkend geluid tijdens het verzamelen van gegevens en je ziet de melding

Nadat de gegevens verzameld zijn, geeft de calculator automatisch een Afstand-tijd

➐

TRANSFERRING...

op de calculator.

grafiek van de verzamelde meetpunten weer. Vergelijk de grafiek van de meetresultaten met je prognose in antwoord 1 wat

➑

betreft overeenkomsten en verschillen.

AN DE SLAG MET

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

Activiteit 2—Speelgoedauto

Verkenning

De waarden van x (tijd) met tussenpozen van een halve seconde staan in de eerste

➊

kolom in vraag 2. Loop de grafiek na en vul de overeenkomende waarden van y (afstand) in de tweede kolom. gedeelte van de grafiek. Het is mogelijk dat je gegevens die niet kloppen met de rest, aan het begin van de meting, buiten beschouwing moet laten. Het is ook mogelijk dat je de afstand moet afronden (als de calculator de waarde van de afstand na 0,957 of 1,01 seconde geeft in plaats van na exact 1 seconde). Kies het dichtstbijzijnde getal of het meest voor de hand liggende getal.

➋

Beantwoord vraag 3 en 4. Bereken de veranderingen in afstand en tijd tussen elk van de punten en vul zo de

➌

derde en vierde kolom in. Om bijvoorbeeld de @Afstand (in meter) te berekenen na 1,5 seconde, trek je de afstand na 1 seconde af van de afstand na 1,5 seconde.

De functie die door deze activiteit wordt geïllustreerd is y = mx + b. m is de

➍

hellingshoek van een lijn. Deze wordt als volgt berekend:

(verv.)

Vul alleen resultaten in uit het lineaire

N.B.:

lineaire functie

De overeenkomende waarde van y is de waarde van b. Bereken m voor elk punt. Vul de waarden in de tabel bij vraag 2.

➎

Beantwoord vraag 5, 6 en 7.

Vervolgverkenning

Door de hellingshoek van een Afstand-tijd grafiek op een gegeven moment te berekenen, verkrijg je de snelheid (bij benadering) van het voorwerp op dat moment. Door de hellingshoek van een Snelheid-Tijd grafiek te berekenen, verkrijg je de versnelling (bij benadering) van het voorwerp op dat moment. Als de snelheid constant is, wat is dan de waarde van de versnelling?

Maak een prognose van de vorm van de Versnelling-Tijd grafiek bij deze Afstand-tijd grafiek.

Bereken de oppervlakte tussen de Snelheid-Tijd grafiek en de x-as, tussen twee gemakkelijke tijdstippen t rechthoeken bij elkaar op te tellen, waarvan elk de volgende oppervlakte heeft:

@afstand

@tijd

en t2. Dit is mogelijk door de oppervlakten van een of meer

afstand

oppervlakte = v∆t = v(t

tijd

N afstand

N tijd

2Nt1

)

N y

x2 N x

Wat is de natuurkundige betekenis van de berekende oppervlakte?

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

Activiteit 2—Speelgoedauto

Naam ____________________________

Metingen

1. Welk van de onderstaande illustraties komt volgens u overeen met de Afstand-tijd grafiek van de speelgoedauto?

Waarom?_____________________________________________________________________________

Tijd Afstand

1 xxx xxx xxx

1,5

2.5 3

3.5 4

4.5 5

Afstand

Tijd

3. Wat valt je op aan de waarden voor de afstand?____________________________________________

4. Hoe blijkt uit deze resultaten dat de speelgoedauto een constante snelheid had?_________________

5. Bereken

tussen Tijd = 2 en Tijd = 4. ________________________________________

afstandà@tijd

Wat valt je op aan dit resultaat? _________________________________________________________ Waar staat

6. Wat is in de lineaire vergelijking

volgens jou voor? _________________________________________________________

= mx + b, de waarde van b? _______________________________

Noteer de vergelijking voor de lijn in de vorm

= mx + b en gebruik de waarden van m en b.______

7. Welke afstand zou de speelgoedauto in 10 seconden afleggen? ______________________________ In 1 minuut? _________________________________________________________________________

AN DE SLAG MET

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

Activiteit 3—Slinger aantekeningen voor docenten

Concepten

Te verkennen functie: sinusfunctie. Verkenning van een enkelvoudige harmonische

beweging door waarneming van een vrij bewegende slinger.

Materiaal

 calculator

CBR



CBR

 calculator-

snoertje

 montageklem  stopwatch  slinger  lineaal  TI ViewScreen (optioneel)

Suggesties voor gewichten:

ballen van verschillende afmetingen (≥ 5 cm

diameter) frisdrankblikjes (leeg en vol)

zakken met bonen

Aanwijzingen

Zie pagina 6–12 voor hints over goede metingen.

Natuurkundige verbanden

Een voorwerp voert een harmonische beweging periodiek uit als gevolg van een terugwerkende kracht die evenredig is met de verplaatsing van het voorwerp uit de evenwichts- (rust)positie. Deze beweging kan door twee grootheden worden beschreven.

De tijdsduur T is de tijd benodigd voor een

volledige periode. De amplitude A is de maximale verplaatsing van

het voorwerp uit de evenwichtspositie (de plaats waar het gewicht zich in rust bevindt).

Voor een enkelvoudige slinger is de tijdsduur T:

T = 2p

waarbij L de lengte van het koord is en g de grootte van de versnelling door de zwaartekracht. T hangt niet af van de massa van het voorwerp of van de amplitude van de beweging die het voorwerp uitvoert.

De frequentie f (het aantal volledige periode per seconde) wordt gevonden door:

f =

, waarbij f in hertz (Hz) wordt uitgedrukt als

T in seconden wordt uitgedrukt.

Een afgeleide van een sinusoïde grafiek is ook een sinusoïde. Let met name op de relatie tussen de fasen van de plaats van het gewicht en de snelheid ervan.

L g

Te verwachten grafieken

Te verwachten antwoorden

1. verschillend (in meter)

2. verschillend (in meter)

3. verschillend (in seconden); T (een periode) = totale tijd: 10 periodenà10; het nemen van een gemiddelde van meer metingen geeft een vermindering van de meetfouten

4. de totale booglengte, die ca. 4x het antwoord op vraag 2 moet zijn; omdat een boog langer is dan een rechte lijn

5. sinusoïde, herhalend, periodiek; afstand van de x-as tot de evenwichtspositie

6. elke periode wordt horizontaal “uitgesmeerd”; een grafiek over 10 seconden moet meer perioden in dezelfde grootte van het scherm weergeven, daarom komen deze dichter bij elkaar

7. (totaal aantal perioden)à(5 seconden) = periodenàseconde; het is gemakkelijker om volledige perioden te bekijken; minder meetfouten

8. f = 1àT, waarbij T is de tijd gedurende 1 periode

9. verkleinde periode; vergrote periode (De slingerlengte is rechtstreeks gerelateerd aan

de periode; hoe langer het koord, des te langer de periode. Leerlingen kunnen deze relatie verkennen door middel van de list editor van de calculator, waarbij zij de tijdsduur voor verschillende waarden van L kunnen berekenen.)

10.A (amplitude) = ¼ van de totale afstand die de slinger aflegt in 1 periode

11.beide sinusoïden; verschillen in amplitude en fase

12.evenwichtspositie

13.als positie = maximum- of minimumwaarde (wanneer het gewicht zich op de grootste afstand van het evenwichtspunt bevindt).

14.Niet. T hangt alleen van L en g af, niet van de massa.

Vervolgverkenning

Meting: de grafiek van L2 versus L3 vormt een ellips.

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

Activiteit 3—Slinger sinusfunctie

Metingen

Plaats de slinger. Richt de slinger zó, dat deze in een rechte lijn met de

➊

tenminste 0,5 meter van het dichtstbijzijnde punt van het

Hints:

Plaats the

CBR

gewicht. Zorg ervoor dat er niets in de clear zone staat (zie pagina 7).

amplitude

evenwichtspositie

Meet met een lineaal de afstand vanaf de

➋

tot de evenwichtspositie.

CBR

Beantwoord vraag 1 op het werkblad.

CBR

beweegt.

Meet vanaf hoever je het gewicht van de evenwichtspositie af laat bewegen.

Beantwoord vraag 2.

Een periode is de tijd die de slinger nodig heeft voor een volledige beweging naar

➌

voor en naar achter. Meet met een stopwatch de tijdsduur, nodig voor tien volledige periodes. Beantwoord vraag 3 en 4.

➍

Start het

RANGER

programma (zie pagina 5 voor de toetsaanslagen voor elke calculator). Een efficiënte methode is dat één persoon de slinger start terwijl iemand anders de calculator en

Druk op › om de instellingen weer te geven. Bij deze activiteit moeten deze als

➎

bedient. Kies vanuit het

CBR

MAIN MENU: SETUPàSAMPLE

volgt zijn:

REALTIME: NO

TIME (S): 10 SECONDEN

DISPLAY: DISTANCE

BEGIN ON: [ENTER]

SMOOTHING: LIGHT

UNITS: METERS

De instructies voor het wijzigen van een instelling vind je op pagina 38. Kies,

➏

wanneer deze juist zijn, Druk op › als je wilt beginnen. Je hoort een klikkend geluid tijdens het

➐

START NOW

verzamelen van gegevens en u ziet de melding

TRANSFERRING...

op de calculator.

AN DE SLAG MET

Nadat de gegevens verzameld zijn, geeft de calculator automatisch een Afstand-tijd

➑

grafiek van de verzamelde meetpunten weer. Beantwoord vraag 5.

OPIËREN TOEGESTAAN MITS VERMELDING VAN

CBR

EXAS INSTRUMENTS INCORPORATED

Activiteit 3—Slinger

Verkenning

Meting 2

(verv.)

sinusfunctie

Kies vanuit het seconden. Herhaal de meting. Kijk naar de grafiek. Beantwoord vraag 6 en 7.

De hoeveelheid die je hebt vastgesteld (perioden per seconde) heet de frequentie. Hoewel je de frequentie in vraag 7 hebt berekend met behulp van de grafiek, kun je deze wiskundig berekenen uit:

f =

Beantwoord vraag 8.

Metingen 3 en 4

Herhaal de meting gedurende 5 seconden nog twee maal. Maak bij de eerste meting het koord korter. Maak bij de tweede meting het koord langer. Beantwoord vraag 9 nadat je deze grafieken hebt bestudeerd.

Een andere belangrijke afstands die invloed heeft op de beweging van de slinger is de amplitude. Het antwoord op vraag 2 was de amplitude van die slingeruitlslag.

Beantwoord vraag 10.

Vervolgverkenning

Meting 5

Kies vanuit het

MAIN MENU: SETUPàSAMPLE

waarbij T de tijdsduur in seconden is en f de frequentie is in hertz (Hz).

PLOT MENU: VELOCITY-TIME

. Wijzig in het

. Beantwoord vraag 11, 12 en 13.

scherm de tijd van 10 in 5

SETUP

Meting 6

Herhaal de meting met een aanzienlijk lichter of zwaarder gewicht en beantwoord daarna vraag 14.

Fit de afstand-tijd grafiek van de slinger met behulp van de formule voor een sinusfunctie, S = A sin (wt + d), waarbij S de positie van het moment is, A de amplitude is, w de frequentie is, d de fasehoek is en t de tijd is. De frequentie, w, is gerelateerd aan de periode, T, door w = 2 pàT.

Voer deze vergelijking in in de Y= editor met de berekende waarden van A en w. Maak gelijktijdig een diagram van deze functie en de statistische grafiek van

(tijd) versus

(afstand). Pas de waarden van A, w en d aan totdat er een goede “fit” ontstaat. Op de TI-83 of TI-86 kunt u de sinusregressie gebruiken om de waarden vast te stellen.

Verken de relatie tussen positie en snelheid door een grafiek te maken van versus

(snelheid). Hier zal de resulterende grafiek er naar je mening uit zien? Vergelijk

(afstand)

het uiteindelijke resultaat met jouw voorspelling.

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

Activiteit 3—Slinger

Meting

Naam ____________________________________

1. Wat is de afstand vanaf de

tot de evenwichtspositie? ____________________________________

CBR

2. Hoe ver ga je de slinger vanuit de evenwichtspositie brengen? ________________________________

3. Wat was de tijd voor tien periodes? ______________________________________________________

Bereken hoe lang (in seconden) het duurt om een periode te voltooien. ________________________ Wat is het voordeel van het meten van tien volledige perioden i.p.v. slechts één? ________________

4. Schat de totale afstand die in één periode wordt afgelegd met behulp van het antwoord op vraag 2. _____________________________________________________________________________________

Waarom is deze waarde lager dan de werkelijke afstand die in één periode wordt afgelegd? ______

5. Wat valt je op aan de vorm van de grafiek? ________________________________________________

Hoe wordt de waarde uit vraag 1 weergegeven in de grafiek? ________________________________

Verkenning

6. Hoe verandert de vorm van de grafiek? Waarom ? __________________________________________ _____________________________________________________________________________________

7. Bereken met behulp van d gegevens uit de grafiek, het aantal volledige perioden per seconde. ____

Waarom is het gemakkelijker om dit vast te stellen met de tweede grafiek (over 5 seconden) dan met de eerste (over 10 seconden)?________________________________________________________

8. Bereken de frequentie voor een periode met de vergelijking.__________________________________

9. Welke invloed heeft het verkorten van de lengte van het koord op de tijdsduur van de slinger?_____

Welke invloed heeft het verlengen van het koord op de periode van de slinger?__________________

10. Wat is de relatie tussen de amplitude van de slingeruitslag en de totale afstand die de slinger aflegt

in een periode? _______________________________________________________________________

_____________________________________________________________________________________

Vervolgverkenning

11. Vergelijk de Afstand-tijd grafiek met de Snelheid-Tijd grafiek. Som de overeenkomsten en

verschillen.____________________________________________________________________________

_____________________________________________________________________________________

12. In welke positie is de snelheid van het gewicht maximaal? ____________________________________

13. In welke positie is de snelheid minimaal? __________________________________________________

14. Welke invloed heeft het veranderen van het gewicht op de grafiek? Waarom? __________________

_____________________________________________________________________________________

AN DE SLAG MET

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

Activiteit 4—Stuiterende bal aantekeningen voor docenten

Concepten

Te verkennen functie: parabolische functie. Concepten uit de werkelijkheid zoals vrij vallende en

stuiterende voorwerpen, zwaartekracht en eenparige versnelling zijn voorbeelden van parabolische functies. Deze activiteit onderzoekt de waarden van hoogte, tijd en de coëfficiënt A in de kwadratische vergelijking, Y = A(X  H)

+ K, de

het gedrag van een stuiterende bal beschrijft.

Materiaal

 calculator

CBR



CBR

 calculator-

snoertje

 grote speelbal (20 cm)  TI ViewScreen (optioneel)

Aanwijzingen

Deze activiteit kan het beste door twee leerlingen worden uitgevoerd, waarbij de een de bal vasthoudt en de ander op ¤ drukt.

Zie pagina 6–12 voor hints over goede metingen. De grafiek moet eruit zien als een stuiterende bal. Zo

niet, moet de meting worden herhaald, waarbij je controleert of de

CBR

loodrecht op de bal is gericht.

Een grote bal is aan te bevelen.

Te verwachten grafieken

de bal. y = 0 is in de grafiek in feite het punt waar de bal zich het verst van de

CBR

bevindt,

wanneer de bal de grond raakt.

4. Leerlingen dienen zich ervan bewust te zijn dat de x-as de tijd voorstelt en niet de horizontale afstand.

7. Het diagram voor A = 1 is zowel geïnverteerd als breder dan de grafiek.

8. A < L1

9. parabool holle kant omhoog; holle kant omlaag; lineair

12.hetzelfde; wiskundig staat coëfficiënt A voor de mate van kromming van de parabool; natuurkundig hangt A af van de versnelling door de zwaartekracht, die tijdens de hele proef constant blijft.

Vervolgverkenning

De stuiterhoogte van de bal (maximale hoogte voor een gegeven stuitering) is bij benadering:

, waarbij

y de stuiterhoogte is

h de hoogte is waarvan de bal wordt losgelaten

p een constante is die afhangt van de fysieke

kenmerken van de bal en de oppervlakte van de grond x is het volgnummer van de stuitering

Verkenning

Nadat een voorwerp is losgelaten, werkt de zwaartekracht erop (waarbij de luchtweerstand wordt verwaarloosd). Dus hangt A af van de versnelling door de zwaartekracht, N9,8 meteràseconde

. Het minteken geeft aan dat de

versnelling omlaag gericht is. De waarde van A is ca. de helft van de versnelling

door de zwaartekracht, of N4.9 meteràseconde

Te verwachten antwoorden

1. tijd (vanaf het begin van de meting); seconden; hoogte à afstand van de bal boven de grond; meter

2. starthoogte van de bal boven de grond (de pieken staan voor de maximale hoogte van elke stuitering); de grond staat voor y = 0.

3. De Afstand-tijd grafiek bij deze activiteit geeft niet de afstand vanaf de

BALL BOUNCE

draait de afstandsgegevens om zodat de grafiek beter overeenkomt met de waarneming van leerlingen van het gedrag van

CBR

tot de bal weer.

Bij een gegeven bal en beginhoogte neemt de stuiterhoogte exponentieel af bij elke opeenvolgende stuitering. Wanneer x = 0, is y = h, dus staat de overeenkomende waarde van y voor de beginhoogte.

Ambitieuze leerlingen kunnen de coëfficiënten in deze vergelijking uitzoeken op grond van de verzamelde gegevens. Herhaal de activiteit voor verschillende beginhoogten of met een andere bal of op een andere oppervlakte.

Nadat er handmatig een “fit” van de kromme is uitgevoerd, kunnen leerlingen de regressie- analyse gebruiken om de functie te zoeken die het beste model van de gegevens oplevert. Kies één enkele stuitering met Vervolgens

PLOT TOOLS, SELECT DOMAIN

QUIT

uit het

MAIN MENU

. Ga te werk volgens de bedieningsinstructies van de calculator voor het uitvoeren van een kwadratische regressie

op list

en L2.

Uitbreidingen

Integreer onder de Snelheid-Tijd grafiek; dit geeft de verplaatsing (netto afgelegde afstand)o voor een willekeurig gekozen tijdsinterval. N.B.: de verplaatsing is nul voor elke volledig uitgevoerde stuitering (de bal begint en eindigt op de grond).

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

Activiteit 4—Stuiterende bal parabolische functie

Meting

Begin met stuiteren bij wijze van test. Laat de bal vallen (niet gooien).

➊

tenminste 0,5 meter boven de hoogte van de hoogste

Hints:

Plaats de stuitering. Houd de sensor rechtstreeks boven de bal en zorg ervoor dat zich niets in de clear zone bevindt (zie pagina 7).

CBR

➋

Start het

RANGER

programma (zie pagina 5 voor de toetsaanslagen voor elke

calculator). Kies vanuit het

➌

Kies vanuit het

➍

BALL BOUNCE

Houd de bal vast met gestrekte armen. Druk op ›. Het

➎

MAIN MENU: APPLICATIONS APPLICATIONS

zorgt automatisch voor de instellingen.

nu in Trigger mode. Op dit moment, kun je de Druk op ¤. Als het groene lampje begint te knipperen, laat u de bal los en

➏

doet u een stap achteruit. (Ga, als de bal opzij stuitert, mee zodat de boven de bal blijft, maar zorg ervoor dat de hoogte van de

. Kies

BALL BOUNCE

METERS

. Er volgen algemene instructies.

RANGER

van de calculator loskoppelen.

CBR

programma staat

CBR

niet verandert.)

Je hoort een klikkend geluid tijdens het verzamelen van gegevens. Er worden gegevens verzameld over de tijd en afstand en er worden gegevens berekend over snelheid en versnelling. Als je de

hebt losgekoppeld, sluit je deze nu weer aan

CBR

nadat de metingen klaar zijn. Druk op ›. (Als de grafiek er niet goed uitziet, herhaal je de meting.) Bestudeer

➐

de grafiek. Beantwoord vraag 1 en 2 op het werkblad.

❽

Let op:

BALL BOUNCE

heeft automatisch de afstandsgegevens omgedraaid.

Beantwoord vraag 3 en 4.

recht

AN DE SLAG MET

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

Activiteit 4—Stuiterende bal

Verkenning

De Afstand-tijd grafiek van de stuitering heeft de vorm van een parabool.

(verv.)

parabolische functie

Druk op ›. Kies vanuit het

➊

PLOT MENU: PLOT TOOLS

en dan

SELECT DOMAIN

willen de eerste volledige stuitering selecteren. Breng de cursor naar de basis van het begin van de stuitering en druk op einde van die stuitering en druk op

›. Breng de cursor naar de basis aan het

›. De grafiek wordt opnieuw getekend,

waarbij slechts één stuitering in aanmerking wordt genomen. De grafiek staat in

➋

mode. Bepaal de top van de stuitering. Beantwoord

TRACE

vraag 5 op het werkblad. Druk op › om terug te gaan naar het

➌

De formule voor de top van de kwadratische vergelijking, Y = A(X  H)

➍

bij deze analyse. Druk op

œ. Schakel in de

PLOT MENU

editor, eventueel geselecteerde

. Kies

MAIN MENU

. Kies

+ K, past

functies uit. Vul de formule voor de top van de kwadratische vergelijking: Yn=A(XH)^2+K.

Sla in het Home scherm de waarde op die je in vraag 5 voor de hoogte hebt

➎

vastgesteld, in variabele K; sla de tijd die ermee overeenkomt op in variabele H; sla 1 op in variabele A.

Druk op  om het diagram weer te geven. Beantwoord vraag 6 en 7.

➏

Probeer A = 2, 0, –1. Vul het eerste deel van de tabel in vraag 8 in en

➐

beantwoord vraag 9. Kies eigen waarden voor A totdat er een goede match ontstaat voor de grafiek. Leg

➑

uw keuzes voor A vast in de tabel in vraag 8.

. Wij

QUIT

Herhaal de activiteit, maar kies nu de laatste (rechter) volledige stuitering.

➒

Beantwoord vraag 10, 11 en 12.

Vervolgverkenning

Herhaal de meting, maar kies niet één enkele parabool.

➊

Leg de tijd en hoogte van elke opeenvolgende stuitering vast.

➋

Bepaal de verhouding tussen de hoogten van elke opeenvolgende stuitering.

➌

Leg de betekenis (voorzover aanwezig) van deze verhouding uit.

➍

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

Activiteit 4—Stuiterende bal

Naam ______________________________

Meting

1. Voor welke natuurkundige grootheid staat de x-as? _________________________________________ Wat zijn de eenheden? _________________________________________________________________ Voor welke natuurkundige grootheid staat de y-as? _________________________________________ Wat zijn de eenheden? _________________________________________________________________

2. Waarvoor staat het hoogste punt van de grafiek? __________________________________________ En het laagste punt? ___________________________________________________________________

3. Waarom heeft het

BALL BOUNCE

programma de grafiek omgedraaid? __________________________

4. Waarom lijkt het op de grafiek alsof de bal over de grond is gestuiterd? ________________________

Verkenning

5. Leg de maximale hoogte en overeenkomstige tijd vast voor de eerste volledige stuitering. _________

6. Komt het diagram voor

= 1 overeen met uw grafiek? _____________________________________

7. Waarom of waarom niet? ______________________________________________________________

8. Vul onderstaande tabel in.

A Wat levert een vergelijking van de data plot en het Yn diagram op?

1 2 0

9. Waarop duidt een positieve waarde voor Waarop duidt een negatieve waarde voor Waarop duidt een waarde nul voor

? _______________________________________________

? ______________________________________________

? ____________________________________________________

10. Leg de maximale hoogte en overeenkomstige tijd voor de laatste volledige stuitering vast. ________

11. Denk je dat

12. Wat levert de vergelijking van waarden van

Waarvoor denk je dat

AN DE SLAG MET

groter of kleiner is bij de laatste stuitering? ____________________________________

op? __________________________________________

zou kunnen staan? _______________________________________________

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

Activiteit 5—Rollende bal aantekeningen voor docenten

Concepten

Te verkennen functie: parabolische functie. Het plotten van een bal die van een helling, met

diverse hellingshoeken, afrolt, levert een reeks krommen op, die kunnen worden weergegeven door een reeks kwadratische vergelijkingen. Deze activiteit onderzoekt de waarden van de coëfficiënten in de kwadratische vergelijking,

y = ax

+ bx + c.

Materiaal

 calculator

CBR



CBR

 calculator-

snoertje

 montageklem  grote speelbal (20 cm)  lange helling (tenminste 2 meter—een

lichtgewicht plaat voldoet goed)

 gradenboog om de hoek te meten  boeken als ondersteuning voor de helling  TI ViewScreen (optioneel)

Aanwijzingen

Bespreek hoe de hellingshoek wordt gemeten. Laat leerlingen hun eigen creativiteit hierin ontwikkelen. Het is mogelijk om een trigonometrische berekening, gevouwen papier of een gradenboog te gebruiken.

Zie pagina 6–12 voor hints over goede metingen.

Te verwachten grafieken

4. een parabool (kwadratisch)

5. verschillend

6. verschillend (moet zijn parabool met toenemende kromming)

7. 0¡ is vlak (de bal kan niet rollen); 90¡ is gelijk aan een bal in vrije val

Verkenning

De beweging van een lichaam waarop alleen de zwaartekracht werkt, is een populair onderwerp bij een natuurwetenschappelijke studie. Zo’n beweging wordt meestal uitgedrukt door een specifieke vorm van de kwadratische vergelijking

s = ½at

0 0 0 0

In de kwadratische vergelijking y = ax

+ v

t + s

waarbij

s de positie is van een voorwerp op tijd t a de versnelling ervan is

de beginsnelheid ervan is

de beginpositie ervan is

+ bx + c,

staat y voor de waarde van de afstand vanaf de

CBR

tot de bal op tijd x als de beginpositite van de bal c was, de beginsnelheid b was en versnelling 2a is.

Vervolgverkenning:

Aangezien de bal in rust is bij het loslaten, zou b dicht bij nul moeten liggen bij elke poging. c zou de beginafstand moeten benaderen, nl. 0,5 meter. a neemt toe naarmate de hellingshoek toeneemt.

Te verwachten antwoorden

1. de derde grafiek

2. tijd; seconden; afstand van het voorwerp vanaf CBR; meter

3. verschillend (moet zijn de helft van een parabool, holle kant omhoog)

Als leerlingen handmatig een fit voor de vergelijking y = ax

+ bx + c zoeken, moet u misschien aanwijzingen geven voor de waarden van b en c. U kunt hen ook opdragen een kwadratische regressie op lijst

L1, L2

te maken met behulp van hun calculators. De versnelling van de bal is te danken aan de zwaartekracht. Dus, hoe steiler de helling (d.w.z. hoe groter de hellingshoek), des te groter wordt de waarde van

a. a is maximaal als q = 90¡, en minimum bij q = 0¡. In wezen is a evenredig met de sinus van q.

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

Activiteit 5—Rollende bal parabolische functie

Meting

➊

Beantwoord vraag 1 op het werkblad. Stel de helling in op een hoek van 15°. Bevestig de klem aan de bovenkant van de helling. Bevestig de Open de kop van de sensor en plaats deze loodrecht op de helling. Bevestig de calculator aan de

CBR

aan de klem.

CBR

Maak een merkteken op de helling, op 0,5 meter van de

. Laat één leerling de

CBR

bal op dit punt vasthouden, terwijl een tweede leerling de calculator vasthoudt.

Richt de sensor rechtstreeks op de bal en zorg ervoor dat zich niets in de

Hints:

clear zone bevindt (zie pagina 7).

Start het

➋

RANGER

calculator). Kies uit het Druk op › om de instellingen weer te geven. Voor deze activiteit moeten deze

➌

programma (zie pagina 5 voor de toetsaanslagen voor elke

MAIN MENU: SETUPàSAMPLE

als volgt zijn:

REALTIME: NO

TIME (S): 3 SECONDEN

DISPLAY: DISTANCE

BEGIN ON: [ENTER]

SMOOTHING: LIGHT

UNITS: METERS

AN DE SLAG MET

De instructies voor het wijzigen van een instelling vind je op pagina 38. Kies, als de instellingen juist zijn,

➍

START NOW

. Druk op › om te beginnen met de

metingen. Laat, wanneer je een klikgeluid hoort, de bal onmiddellijk los (zonder duwen) en

➎

doe een stap achteruit. Nadat de meting voltooid is, wordt de Afstand-tijd grafiek automatisch

➏

weergegeven. Beantwoord vraag 2 en 3. Druk op › om het

➐

SELECT DOMAIN

›. Breng de cursor naar de plaats waar de bal het einde van de helling

op bereikte en druk op

PLOT MENU

. Breng de cursor naar de plaats waar de bal werd losgelaten en druk

›. De grafiek wordt opnieuw getekend, waarbij alleen dat

weer te geven. Kies

PLOT TOOLS

en kies daarna

gedeelte van de meting wordt weergegeven dat overeenkomt het afrollen van de helling. Beantwoord vraag 4 en 5.

OPIËREN TOEGESTAAN MITS VERMELDING VAN

CBR

EXAS INSTRUMENTS INCORPORATED

Activiteit 5—Rollende bal

Verkenning

Onderzoek wat er gebeurt bij verschillende hellingshoeken.

Voorspel wat er gebeurt als de hellingshoek toeneemt. Beantwoord vraag 6.

➊

Stel de hellingshoek in op 30¡. Herhaal stap 2 t/m 6. Voeg deze grafiek toe aan

➋

de tekening bij vraag 6, met het label 30¡. Herhaal stap 2 t/m 6 voor hellingshoeken van 45¡ en 60¡ en voeg deze toe aan de

➌

tekening.

➍

Beantwoord vraag 7.

Vervolgverkenning

Stel de tijdwaarden zó in dat x = 0 voor de beginhoogte (de tijd waarop de bal werd losgelaten). Je kunt dit handmatig doen door de x-waarde van het eerste punt van alle punten op de grafiek af te trekken, of je kunt invoeren

Bereken de waarden van a, b en c voor de familie van krommen in de formule

➊

y = ax

Wat zijn de minimale en maximale waarden van a? Waarom?

➋

+ bx + c bij 0¡, 15¡, 30¡, 45¡, 60¡, 90¡.

(verv.)

parabolische functie

L1(1)"A:L1NA"L1

Geef de wiskundige relatie tussen a en de hellingshoek.

➌

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

Activiteit 5—Rollende bal

Naam __________________________________

Meting

1. Welk van de onderstaande illustraties geeft volgens jou het beste de Afstand-tijd grafiek van een bal weer die van een helling afrolt?

2. Welke natuurkundige geeft de x-as weer? _________________________________________________ Wat zijn de eenheden? _________________________________________________________________ Welke natuurkundige grootheid geeft de y-as weer? ________________________________________ Wat zijn de eenheden? _________________________________________________________________

3. Maak een schets van de grafiek zoals die er echt uitziet. Maak een schaalindeling langs de assen. Markeer de punten waarop de bal losgelaten werd en waar deze het einde van de helling bereikte.

4. Welk type functie geeft deze grafiek weer? ________________________________________________

5. Bespreek hoe je begrip is veranderd tussen het diagram gekozen bij vraag 1 en de kromme die je bij

in vraag 3 hebt geschetst. ______________________________________________________________

_____________________________________________________________________________________

Verkenning

6. Maak een schets van hoe de grafiek er volgens jou uitziet bij een grotere hellingshoek. (Vermeld hierbij prognose.)

7. Maak een schets van de bij 0

¡ en 90¡ en vermeld deze hellingshoeken erbij:

AN DE SLAG MET

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

Informatie voor de docent

Hoe zou uw les kunnen veranderen door CBR?

is een gemakkelijk te gebruiken systeem met functies die u helpen om de

CBR

snel

en gemakkelijk te integreren in uw lesplan.

biedt aanzienlijke verbeteringen ten opzichte van andere methodes voor het

CBR

verzamelen van gegevens, die u misschien in het verleden hebt gebruikt. Dit kan op zijn beurt leiden tot een herstructurering van het gebruik van de lestijd, omdat uw leerlingen enthousiaster worden voor het gebruik van gegevens uit reële situaties.

U zult constateren dat uw leerlingen zich meer betrokken gaan voelen tot de

gegevens omdat zij werkelijk deelnemen aan het verzamelen ervan in plaats van gegevens uit boeken, tijdschriften of statische overzichten te halen. Dit maakt ze duidelijk dat de concepten die u tijdens de les onderzoekt, te maken hebben met de werkelijkheid en niet slechts abstracte ideeën zijn. Maar dit houdt ook in dat elke leerling aan de beurt wil komen bij het verzamelen van de gegevens.

Het verzamelen van gegevens met de

is aanzienlijk effectiever dan het maken van

CBR

scenario’s en handmatig meten met een meetlat en een stopwatch. Aangezien meer metingen een grotere resolutie opleveren en aangezien een ultrasone afstandssensor zeer nauwkeurig is, is de vorm van de krommen sneller duidelijk. U hebt minder tijd nodig voor het verzamelen van gegevens en hebt meer tijd voor analyse en verkenning.

Met

kunnen leerlingen de herhaalbaaarheid van waarnemingen en variaties bij

CBR

“wat-als” scenario’s verkennen. Vragen zoals “Is het dezelfde parabool als we de bal van een grotere hoogte laten vallen?” en “Is de parabool dezelfde bij de eerste keer dat de bal stuitert en bij de laatste keer?” worden natuurlijke en waardevolle uitbreidingen.

De kracht van visuele afbeeldingen stelt leerlingen in staat, snel de geplotte gegevens

te associëren met de natuurkundige eigenschappen en wiskundige functies die de gegevens beschrijven.

Andere veranderingen treden op nadat de gegevens uit de werkelijkheid zijn verzameld. Met

kunnen uw leerlingen onderliggende relaties zowel numeriek als grafisch

CBR

verkennen.

Gegevens grafisch verkennen

Het gebruik van automatisch gegenereerde grafieken met afstand, snelheid en versnelling in relatie tot tijd voor verkenningen zoals:

Wat is de natuurkundige betekenis van de bijbehorende y-waarde? de bijbehorende x-

waarde? de hellingshoek? het maximum? het minimum? de afgeleiden? de integralen?

Hoe herkennen we de functie (lineair, parabolisch, etc.) die de grafiek voorstelt?

Hoe zouden we een model van de gegevens maken met een representatieve functie?

Wat is de betekenis van de afzonderlijke coëfficiënten in de functie (bijv. AX

+ BX

+ C)?

Gegevens numeriek verkennen

Uw leerlingen kunnen gebruik maken van statistische methodes (gemiddelde, mediaan, standaarddeviatie, enz.) die past bij hun niveau, om de numerieke gegevens te verkennen. Als u het waarin

REALTIME=NO

RANGER

gegevens voor tijd, afstand, snelheid en versnelling zijn opgeslagen.

programma verlaat, herinnert een prompt u aan de lijsten

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

Informatie voor de docent

(verv.)

CBR grafieken—het verband tussen de fysieke wereld en wiskunde

De grafieken die op basis van de verzamelde gegevens door

RANGER

zijn gemaakt, zijn een visuele weergave van de relaties tussen de natuurkundige en wiskundige omschrijvingen van beweging. Leerlingen hebben aanmoediging nodig om de vorm van de grafiek te herkennen, analyseren en bespreken in termen van zowel natuurkunde als die van wiskunde. Extra dialoog en ontdekkingen zijn mogelijk als er functies worden ingevoerd in de Y= editor en weergegeven met de grafieken.

Een Afstand-tijd grafiek stelt de positie (bij benadering) van een voorwerp voor

(afstand vanaf de

) op elk moment wanneer een meting wordt genomen. de y-as

CBR

wordt in meters uitgedrukt; de x-as wordt in seconden uitgedrukt. Een Snelheid-tijd grafiek geeft de snelheid (bij benadering) van een voorwerp weer

(ten opzichte van en in de richting van de

) op elk moment wanneer een meting

CBR

wordt verricht. De y-as wordt in meteràseconde uitgedrukt; de x-as wordt in seconden uitgedrukt.

Een Versnelling-tijd grafiek geeft de mate van verandering van snelheid van een

voorwerp (ten opzichte van en in de richting van de meting wordt verricht. De y-as wordt in meteràseconde

) op elk moment wanneer een

CBR

uitgedrukt; de x-as wordt in

seconden uitgedrukt. De eerste afgeleide (helling van het moment) is op elk punt van de Afstand-tijd grafiek

de snelheid op dat moment. De eerste afgeleide (helling van het moment) is op elk punt van de Snelheid-tijd

grafiek de versnelling op dat moment. Dit is ook de tweede afgeleide op elk punt van de Afstand-tijd grafiek.

Een bepaalde integraal (oppervlakte onder de grafiek tussen twee gegeven punten) op

de Snelheid-tijd grafiek is gelijk aan de verplaatsing (netto afgelegde afstand) door het voorwerp gedurende dat tijdsinterval.

Snelheid en snelheidsvector kunnen gemakkelijk met elkaar worden verward. Dit zijn afzonderlijke, maar met elkaar verband houdende, grootheden. Snelheid kan op een schaal worden uitgedrukt; er is een grootte maar geen specifieke richting aan verbonden, bijv. “6 meter per seconde.” Snelheidsvector is een vector; deze heeft een specifieke richting en een grootte, bijv. “6 meter per seconde richting Noord.”

Snelheid-tijd grafiek geeft in feite de snelheid weer, niet de

Een gemiddelde

CBR

snelheidsvector. Alleen de grootheid (die positief, negatief of nul kan zijn) wordt gegeven. Richting wordt slechts geïmpliceerd. Een positieve waarde voor de snelheid geeft aan dat de beweging van de de beweging naar de

meet afstand slechts langs een lijn vanaf de detector. Daardoor wordt, als een

CBR

toe gaat.

CBR

af gaat; een negatieve waarde geeft aan dat

CBR

voorwerp zich met een hoek op deze lijn beweegt, slechts de component van de snelheid parallel aan deze lijn berekend. Een voorwerp dat zich bijvoorbeeld loodrecht op de lijn vanaf de

beweegt, zal met snelheid 0 worden waargenomen.

CBR

AN DE SLAG MET

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

Informatie voor de docent

(verv.)

De wiskunde van afstand, snelheid en versnelling

gemiddeld

N d

= hellingshoek van Afstand-tijd grafiek

N t

Afstand-tijd grafiek

momentaan

lim

@t"

(

d(s)

)

waarbij s = afstand

Snelheid-Tijd grafiek

N v

gemiddeld

momentaan

lim

@t"

(

= hellingshoek van Snelheid-tijd grafiek

N t

)

De oppervlakte onder de Snelheid-tijd grafiek van t1 tot t2 = @d = (d van t

tot t2 (netto afgelegde afstand).

t=2

⌠

⌡

t=1

v(dt)

Daarom is @d =

(

t=2

∑

t=1

v(@t)

of @d =

)

) = verplaatsing

2Nd1

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

Versnelling-Tijd grafiek

AN DE SLAG MET

CBR

Informatie voor de docent

Web-site informatiebronnen

(verv.)

Op onze web site,

een opsomming van aanvullend materiaal voor gebruik met

calculators een bibliotheek met programma’s voor gebruik bij

een activiteitenpagina met toepassingen, ontwikkeld voor en door docenten zoals u

programma’s die toegang bieden tot extra

CBR

meer gedetailleerde informatie over

Extra informatiebronnen

De Explorations boeken van Texas Instruments bevatten extra materiaal dat verband houdt met TI grafische calculators, waaronder boeken met activiteiten in de klas voor

geschikt voor middelbare school, HBO- en universitair onderwijs.

CBR,

http:ààwww.ti.comàcalc

instellingen en programmeercommando’s

CBR-

, vindt u:

CBR

CBR, CBL

functies

CBR, CBL

en TI grafische

en TI grafische calculators

AN DE SLAG MET

OPIËREN TOEGESTAAN MITS VERMELDING VAN

CBR

EXAS INSTRUMENTS INCORPORATED

CBR-gegevens worden opgeslagen in lijsten

Verzamelde gegevens worden opgeslagen in de lijsten L1, L2, L3 en L4

Tijdens het verzamelen van gegevens zendt de waar deze in lijsten worden opgeslagen. Telkens wanneer u het verlaat, wordt u eraan herinnerd waar de gegevens zijn opgeslagen.

bevat gegevens over tijd.

bevat gegevens over afstand.

bevat gegevens over snelheid.

bevat gegevens over versnelling.

Het vijfde element in lijst L1 is bijvoorbeeld de waarde van de tijd toen het 5de meetpunt werd verzameld en het vijfde element in lijst vijfde meetpunt.

Bij

REALTIME=YES

worden slechts de gegevens voor de geselcteerde grafiek (afstand, snelheid of versnelling) berekend en verzonden. Bij berekend en overgedragen.

Instellingen worden opgeslagen in lijst L5

Met het

RANGER SETUP

scherm is het gemakkelijk om de meest gebruikte

te wijzigen (zie pagina 38). Als u het

RANGER

programma vanaf de

door een nieuwe lijst met de standaardwaarden.

deze automatisch naar de calculator,

CBR

RANGER

is de waarde van de afstand van het

REALTIME=NO

verzendt, wordt L5 automatisch vervangen

CBR

worden alle gegevens

programma

parameters

CBR

Zie pagina 40–41 voor informatie over programmeercommando’s die de overige instellingen wijzigen.

De lijsten met gegevens gebruiken

De lijsten worden niet verwijderd wanneer u het blijven deze beschikbaar voor extra grafische, statistische en numerieke verkenning en analyses.

U kunt de lijsten tegen elkaar afzetten en plotten, deze in de list editor weergeven, regressie-analyse toepassen evenals andere analytische activiteiten uitvoeren. U kunt bijvoorbeeld de gegevens van de slingerbeweging verzamelen met behulp van dan

RANGER

verlaten en tenslotte een grafiek van de Snelheid-versnelling maken om

elliptische functies te verkennen. (Het is mogelijk dat u het venster moet aanpassen)

RANGER

programma verlaat. Daardoor

RANGER

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

RANGER instellingen

RANGER instellingen wijzigen

RANGER

➊

geeft de meest gebruikte instellingen weer voordat de meting begint.

Kies uit het

MAIN MENU

in het

RANGER

programma:

SETUPàSAMPLE

. De huidige

instellingen worden weergegeven. 4 geeft de plaats van de cursor aan.

UNITS:

›

START NOW

YES

TOTAL TIME

DISTANCE, VELOCITY

[ENTER], [TRIGGER],

NONE, LIGHT, MEDIUM

METER

= 1–99

SECONDEN

, or

ACCELERATION

10-SECOND DELAY

, of

HEAVY

(

slechts bij

REALTIME=NO

om de beschikbare opties te doorlopen. Druk op c om naar de

MAIN MENU

REALTIME:

TIME (S):

DISPLAY:

BEGIN ON:

SMOOTHING:

Druk op c of b om naar de gewenste instelling te gaan.

➋

Druk op

➌

volgende optie door te gaan als de waarde van de optie juist is. Om de waarde van

te wijzigen, voert u 1 of 2 getallen in en drukt u op c of b.

TIME

Wanneer alle instellingen juist zijn, drukt u op c of b totdat de cursor op

➍

staat.

NOW

Druk op

Druk op e om terug te gaan naar het

De nieuwe instellingen blijven van kracht tenzij u

om door te gaan.

›

MAIN MENU

en druk dan op

SET DEFAULTS

kiest, een applicatie

›

START

uitvoert, of een ander programma uitvoert waardoor de instellingen worden gewijzigd. Als u met

werkt buiten het

RANGER

standaard instellingen worden hersteld als u

programma of als u L5 verwijdert, kunnen de

RANGER

de volgende keer uitvoert.

)

De RANGER instellingen terugzetten op de standaardwaarden

De standaardinstellingen zijn geschikt voor een groot aantal meetsituaties. Als u niet zeker weet wat de beste instellingen zijn, kunt u beginnen met de standaardinstellingen en deze vervolgens aanpassen.

Kies uit het

➊

MAIN MENU

in het

RANGER

programma:

De instellingen worden veranderd in de standaardwaarden en het wordt weergegeven.

Als u een standaardinstelling een andere waarde dan de standaardwaarde wilt

➋

geven, gaat u te werk zoals hierboven aangegeven.

➌

Druk op

als de cursor op

›

START NOW

staat, om door te gaan.

Andere RANGER instellingen

Het

RANGER

programma biedt toegang tot de meest gewijzigde instellingen. nog andere instellingen. Zie pagina 40–41 voor informatie over programmeercommando’s waardoor deze instellingen worden gewijzigd.

SET DEFAULTS

SETUP

scherm

heeft

CBR

AN DE SLAG MET

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

Het gebruik van CBR met CBL of met CBL programma’s

Het gebruik van CBR als conventionele afstandssensor met CBL

De Instruments

is geschikt voor gebruik als conventionele afstandssensor met het Texas

CBR

é (Calculator-Based Laboratoryé) systeem.

CBL

De speciale kabel die vereist is voor aansluiting van de wordt meegeleverd.

Sluit de calculator moet zijn aangesloten op de

Het is mogelijk dat u het

RANGER

niet op de

CBR

aan als de

CBL

programma moet wijzigen (zie instructies hieronder). Het

CBL

programma werkt niet met de

al op een calculator is aangesloten. De

CBR

CBL

Het gebruik van CBR met programma’s die zijn geschreven voor CBL

U kunt de

gebruiken met de meeste

CBR

programma’s die uitsluitend zijn geschreven

CBL

voor een afstandssensor zonder wijzigingen of slechts minimale wijzigingen aan het programma.

op de CBL

CBR

De meting stoppen: Bij sommige

REALTIME=YES

gegevensverzameling gaat de

programma’s die gebruik maken van de

CBL

door met meetpunten. Ga op een van

CBR

de hierna beschreven manieren te werk om het verzamelen van gegevens aan het eind van de meettijd te stoppen:

Druk op ¤ op de

Voeg “statements” toe aan het bestaande

naar de

te zenden. Dit statement moet staan na het moment waarop de gegevens

CBR

programma om het commando {6,0}

CBL

zijn verzonden en weergegeven. Bijvoorbeeld:

{6,0}"L6:SEND L6

Geluid aan of uitzetten: Om het geluid uit te zetten, voegt u statements toe aan het bestaande

programma om het commando’ {6,3} naar de

CBL

te zenden. Het

CBR

statement moet staan voordat het verzamelen van gegevens begint. Bijvoorbeeld:

{6,3}"L6:SEND L6

Om het geluid aan te zetten. hoeft u het Bij problemen: Als u een

programma uitvoert en het erop lijkt dat de

CBL

reageert of geblokkeerd is, start u het

RANGER

pagina 36), waar mogelijk een bijgewerkte versie van het

programma alleen te starten.

niet

CBR

programma. Bezoek de TI web site (zie

programma staat.

CBL

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

Programmeercommando’s

Command 0 Wist het system en voert een reset uit {0}

Wist alles. Stelt de standaardwaarden bij aanzetten in. Kanaal 11 wordt automatisch geselecteerd.

Command 1 Wist Kanaal {1,0}

Wist kanaal.

Command 1 Kanaal {1,11,

bewerking

REALTIME=NO

bewerking

REALTIME=YES

post_processing

0 (standaard) Geen 1( 2(

temperatuurconversie

0 (standaard) Schakelt temperatuurcompensatie uit. 1 Schakelt temperatuurcompensatie in.

REALTIME=NO REALTIME=NO

) Wist alles. Stelt de standaardwaarden bij aanzetten in. ) Meter, de ) Meter, de ) Voet, de

) Wist alles. Stelt de standaardwaarden bij aanzetten in. ) Meter, de ) Meter, de ) Voet, de ) Meter, de CBR geeft { ) Voet, de ) Meter, de ) Voet, de

)dàdt (1e afgeleide) )d

Command 2 Data setup {2,

data_type

1 (standaard) Lijst

Command 3 Meting/Trigger {3,

meting_tijd

0.005–1500 (0.1) Tijd in seconden tussen elke meting

0.0001–0.005 Rondt af naar 0,005. 1500<x<16000 Rondt af naar 1500.

sample#

L1 Selecteert

REALTIME=NO

1–512 (

trigger

0 Begint met meten zonder trigger. 1 (standaard) Begint met meten bij ¤. 7 Wacht 10 seconden en begint met meten.

record_time

0 (standaard) Geen

REALTIME=NO

filter

(zie command 1, bewerkingsveld)

0 (standaard) Geen filtering

REALTIME=NO

1 (

REALTIME=NO

2 (

REALTIME=NO

3 (

REALTIME=NO

4 (

REALTIME=NO

5 (

REALTIME=NO

6 (

REALTIME=YES

7 (

REALTIME=YES

8 (

REALTIME=YES

9 (

) Neemt van 1 tot 12 steekproeven.

) Absolute tijd (start bij tijd 0 en past de meettijd aan) ) Relatieve tijd (start bij tijd 0 en past de meettijd aan)

) 5-punts Savitzsky-Golay effening ) 9-punts Savitzsky-Golay effening ) 17-punts Savitzsky-Golay effening ) 29-punts Savitzsky-Golay effening ) 3- punts filter voor vaststellen van mediaan ) 5- punts filter voor vaststellen van mediaan

) Light ) Medium ) Heavy

bewerking,post processing

Resultaten

CBR

Resultaten

CBR

CBR CBR

CBR

Resultaten

àdt2 (2e afgeleide)

Resultaten

data_type

Resultaten

meting_tijd, metingnr.,trigger

Resultaten

REALTIME=YES

Resultaten

REALTIME=YES

,0,

afstand,@tijd

geeft {

afstand,@tijd

geeft {

afstand,@tijd

geeft {

afstand,@tijd

geeft {

afstand,@tijd

geeft {

afstand,@tijd

geeft {

afstand,snelheid,@tijd

geeft {

afstand,snelheid,versnelling,@tijd

geeft {

afstand,snelheid,versnelling,@tijd

geeft {

} }

}

} }

}

,0,0,0,0,0,0,0}

meetmode.

tracking filter

temperatuurconversie

}

,0,0,0,0,

record_tijd,filter

}

AN DE SLAG MET

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

Programmeercommando’s

(verv.)

Command 4 Temperatuurcompensatie {4,

equation#

equation_type

temperatuur

units

Command 5 (

first_channel

data_select

data_begin

data_end

0 (standaard) Wist alle vergelijkingen. 4 Wijst vergelijking 4 toe.

0 (standaard) Wist de vergelijking. 13 Wijst temperatuurcompensatie toe.

floating-point number Stelt de huidige temperatuur in.

0 (standaard) Geen (genegeerd door 1 Stelt graden = Fahrenheit. 2 Stelt graden = Celsius. 3 Stelt graden = Kelvin. 4 Stelt graden = Rankin where R = F + 459.7.

REALTIME=NO

0 (standaard) Selecteert het laagste actieve kanaal. 1, 2, 3, 11, 21 Specificeert ultrasoon kanaal. M1 Registreert tijdlijst.

0 Filter gegevens {afstand} 1 Filter dàdt gegevens {snelheid} 2 Filter d 3 Ruwe gegevens {afstand} 4 Ruwe dàdt gegevens {snelheid} 5 Ruwe d

1–512 Eerste gegevenselement van GET

0–512 Laatste gegevenselement van GET (0 = laatste meting)

) Data range setup {5,

Resultaten

Command 6 Systems options {6,

system_command

0 Stopt met meten (voor compatibiliteit met CBL). 2 (standaard) Stopt met meten. 3 Schakelt geluid uit (geluid staat aan bij aanzetten). 4 Schakelt geluid in (geluid staat aan bij aanzetten). 5 Stelt ID-nummer in ( 6 Stelt nieuw filter in op eerdere gegevens (

bewerking

floating-point number ID_Nummer van form 0–6 Nieuw filter voor eerder verzamelde gegevens (

Resultaten

Command 7 Request status {7}

Geeft een lijst met:

10.rrrr DeviceCode.RomVersie 0–99 Laatste foutcode (0 = geem fout) 0–2 Batterijstatus (0 = OK; 1 = laag tijdens meting; 2 = altijd laag) 11 Identificatie ultrasoon kanaal sample_time Huidig meetinterval in seconden trigger_condition Huidige trigger-optie function Huidige kanaalfunctie (1–9) post_processing Huidige post-processing optie (0–2) filter Huidige filteringniveau (0–9) samples Aantal bescjhikbare metinge; 0–512 recorded_time Geregistreerde tijdoptie (0–2) temperature Temperatuur (¡C) piezo_flag 0 = geluid uit; 1 = geluid aan system_state 1 = geen setup; 2 = klaar om te starten; 3 = triggered/meten; 4 = klaar window_start 0 = nog geen command 5; 1–512 window_end 0 = gebruik xx elementen; 1–512 id_number 6-cijferig ID-nr (standaard 0.00000) ingesteld door commando 6

vergelijking#,vergelijking_type,temperatuur,units

CBR

). Stelt T graden in op Celsius.

first_channel,data_select,data_begin,data_end

àdt2 gegevens {versnelling}

system_command[,bewerking]

bewerking

n.nnnnn

}

vereist).

bewerking

system_command

(

REALTIME=NO

system_command

(

= 5)

}

vereist).

= 5)

system_command

REALTIME=YES

; M1

}

= 6)

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

Batterijen

Batterij type

De batterijen werken als deze op een

Batterijen plaatsen

Terwijl u de achterkant van de het met de aanduiding +. met de aanduiding -.

is ontworpen voor gebruik met 4 AA alkali-batterijen. De

CBR

is aangesloten.

CBL

ondersteboven houdt, duwt u het kapje van de batterijhouder naar de

CBR

. Plaats de batterijen volgens de tekening aan de binnenkant van

CBR

batterijhouder. Er passen twee batterijen in met de +-kant omhoog, aan de kant

CBR

Er passen twee batterijen in met de - -kant omhoog aan de kant

Schuif het kapje weer op de plaats. De

CBR

kan alléén zonder

CBR

is klaar om te beginnen

met meten,

Waarschuwing dat de batterijen van de CBR (bijna) leeg zijn

beschikt over twee waarschuwingsmechanismen voor het geval dat de batterijen

CBR

(bijna) leeg zijn:

Het

RANGER

programma geeft een waarschuwingsmelding op de display van de

calculator weer tijdens het verzamelen van gegevens.

Het rode lampje knippert met tussenpozen tijdens het verzamelen van gegevens.

Status van de CBR batterijen

U kunt de status van de batterijen controleren voordat u begint met meten. Kies uit het

MAIN MENU: TOOLS

en kies dan

CBR STATUS

. De batterijstatus, OK of

REPLACE

, wordt dan

weergegeven.

Voorzorgsmaatregelen bij batterijen

Vervang alle 4 batterijen tegelijk. Gebruik geen verschillende merken batterijen door elkaar. Gebruik geen verschillende batterijtypes van hetzelfde merk.

Plaats de batterijen volgens de aanduidingen in de batterijhouder.

Breng gebruikte batterijen onmiddellijk naar het daarvoor bestemde verzamelpunt. Laat batterijen niet liggen binnen het bereik van kinderen.

Batterijen mogen niet worden verwarmd, verbrand of lekgeprikt. Batterijen bevatten gevaarlijke chemische stoffen die kunnen leiden tot een explosie of lekkage van deze stoffen.

Gebruik geen oplaadbare en niet-oplaadbare batterijen door elkaar.

Plaats batterijen die niet oplaadbaar zijn, NIET in een batterijlader.

AN DE SLAG MET

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

Bij moeilijkheden

Als dit probleem zich

Probeert u dit:

voordoet:

Problemen bij het overdragen van het of bi

RANGER

het verzamelen van

programma

gegevens

CBR

begint vanzelf met het

verzamelen van gegevens

Controleer of de verbindin aangesloten. Duw beide uiteinden van de kabel altijd stevig aan.

Controleer of de batterijen (bijna) leeg zijn (zie pagina 42). Als u de CBR neerzet met de

worden in

edrukt, waardoor de meting begint. Druk nog eens op

van de calculator met de

knop omlaag, kan de

om te stoppen met de meting.

RANGER

van de calculator met de

LINK ERROR

Verlaat op de

CBR

opbergt, verlaat op de juiste manier het

melding Koppel de

Controleer of de verbindin

uiste manier het

CBR

aan de calculator met de kabel van de calculator naar de

aangesloten. Duw beide uiteinden van de kabel altijd stevig aan. Als u de

om het

CBR

niet wilt (of kunt) aansluiten op de calculator, drukt u op

programma te verlaten en kiest u daarna

Onvoldoende geheugen Er moet voldoende geheugen voor het

lists aanwezi

zijn. De programma’s en lijsten hebben ca. 17.500 bytes

nodig. Verwijder (zo nodig) programma’s en/of gegevens.

Meldingen op de calculator komen niet overeen met de instructies bij de activiteit

Deze handleidin kunnen worden gebruikt; daarom kan het zijn dat sommige menunamen, schermen of toetsen in deze handleidin

is van toepassing voor alle TI calculators die met de

die van uw calculator. Kies de menunaam, het scherm of de toets die het meest in de buurt komt. Als de instructies bi

Gegevens zien er niet goed uit:

punten staan niet op de kromme

gerafelde grafieken

vlakke grafieken

gebroken grafiek

MATCH

,” zou u op de TI-83:

Herhaal de metin

, waarbij u controleert dat de CBR rechtstreeks op het

voorwerp gericht is. Lees pagina 6–12 over het krijgen van goede gegevensmetingen. Controleer of er geen leerlingen, tafels of iets anders in de clear zone staat. Wanneer twee

roep de meting afronden voordat de volgende groep begint met de

één

CBR

units tegelijkertijd worden gebruikt in een vertrek, moet

meting. Controleer of de verbindin

DIST MATCH

van de calculator met de

aangesloten. Duw beide uiteinden van de kabel altijd stevig aan. Controleer of de batterijen (bijna) leeg zijn (zie pagina 42). Controleer of de mate van smoothing niet te groot of te klein is.

CBR

werkt niet met een TI-85 Controleer of er “

CBL

” staat aan het einde van het serienummer op de

achterkant van de calculator; dit staat voor compatibiliteit met De TI

85 heeft geen mogelijkheden tot het maken van statistische grafieken

en daarom zi

n sommige verkenningen (zoals het gebruik van

geplotte gegevens) niet mogelijk op de TI-85.

Kabel van de calculator naar de

CBR

is zoek

U kunt de kabel van de calculator naar een andere calculator die bi calculator is

eleverd, gebruiken. (Deze kabel is veel korter, dus het kan

raadzaam zijn om een nieuwe kabel te bestellen.)

Batterijen zijn vaak (bijna) leeg Voordat u de

QUIT)

of enig ander

CBR

opbergt, dient u het

CBR

CBL

programma te verlaten en de

calculator los te koppelen.

Bij het starten van het

RANGER

programma gebeurt er niets

Nadat u het

ende keer wanneer u dit programma start, maximaal twee minuten

vol duren voordat de calculator het pro

RANGER

programma hebt bewerkt of bekeken, kan het bij de

ramma klaar heeft om te starten. Dit is

niets bijzonders.

Foutmelding: Variabele is

eblokkeerd of beschermd

(uitsluitend bij TI

92)

Deblokkeer de variabelen L1, L2, L3, L4 en L5. Zie de handleidin calculator.

CBR

goed is

knop

voordat u de

CBR

programma (met

CBR

CBL

CBR

QUIT

RANGER

programma en voor de data

QUIT)

programma.

goed is

niet (helemaal) overeenkomen met

voorbeeld luiden “Kies

DISTANCE

kiezen.

CBR

goed is

CBL



CBR

RANGER

programma (met behulp van

CBR

van de

bij de

CBR

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

Productinformatie, service en garantie TI

Product en serviceinformatie TI

Voor meer informatie over producten van en service door TI, kan per E-mail contact worden opgenomen met TI. Ook is informatie te vinden op de TI-pagina op het World Wide Web.

E-mailadres:ti-cares@ti.com Internetadres:http://www.ti.com/calc

Informatie service over garantie

Raadpleeg voor informatie over de garantievoorwaarden en -periode of over service, de garantiebepalingen die bij dit product worden geleverd of neem contact op met het verkooppunt waar u dit TI-product heeft gekocht.

AN DE SLAG MET

OPIËREN TOEGESTAAN MITS VERMELDING VAN

CBR

EXAS INSTRUMENTS INCORPORATED

RANGE

MAIN MENU

SETUP / SAMPLE

SET DEFAULTS

NO YES

1-99 (REALTIME=NO)

DISTANCE VELOCITY ACCELERATION

[ENTER] [TRIGGER] DELAY

NONE LIGHT MEDIUM HEAVY

METERS FEET

APPLICATIONS

REALTIME=NO

PLOT MENU

REALTIME=YES

TOOLS

QUIT

APPLICATIONS

UNITS METERS FEET

DISTANCE-TIME VELOCITY-TIME ACCELERATION-TIME PLOT TOOLS REPEAT SAMPLE MAIN MENU QUIT

SHOW PLOT SELECT DOMAIN REPEAT SAMPLE MAIN MENU QUIT

TOOLS GET CBR DATA GET CALC DATA CBR STATUS STOP/CLEAR CBR MAIN MENU

DISTANCE MATCH VELOCITY MATCH BALL BOUNCE MAIN MENU

PLOT TOOLS SELECT DOMAIN SMOOTH DATA PLOT MENU

DATA SMOOTHING LIGHT MEDIUM HEAVY NONE

OPTIONS SAME MATCH NEW MATCH APPLICATIONS MAIN MENU QUIT

OPIËREN TOEGESTAAN MITS VERMELDING VAN

EXAS INSTRUMENTS INCORPORATED

AN DE SLAG MET

CBR

Texas instruments CBR User Manual [nl]

Specifications and Main Features

Frequently Asked Questions

User Manual