Texas instruments CBR User Manual [no]

Download

85-86

TRIGGER

CBR

)

Calculator-Based Ranger

™

(CBR

™

)

OMME I GANG MED OMME I GANG MED

MEDMED

ELEVØVELSERELEVØVELSER

5 5

CBR™CBR™

CBR

)

TRIGGER

85-86

CBR

)

TRIGGER

85-86

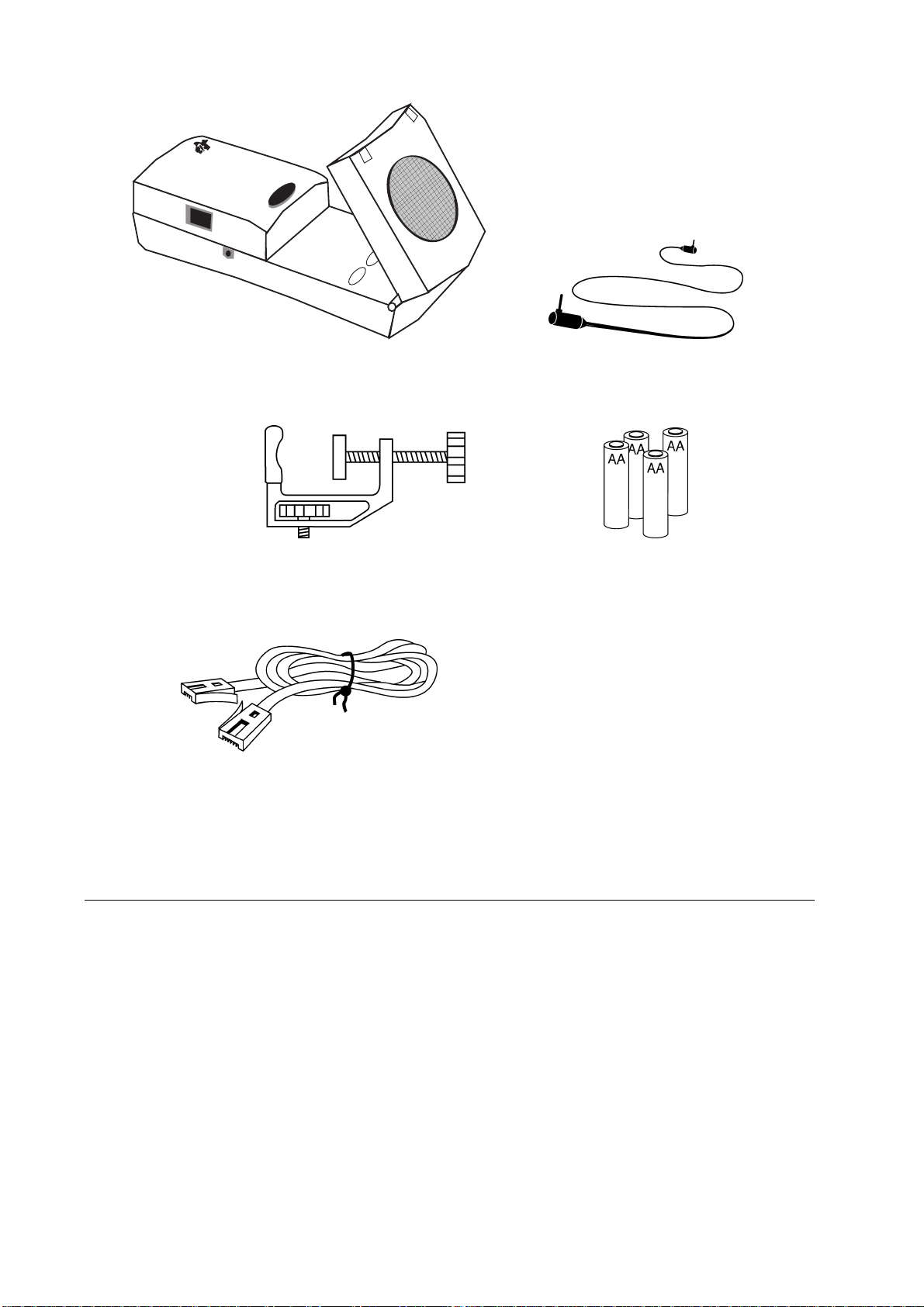
Kalkulatorbasert Rangeré (CBRé) kalkulator-til-CBR-kabel

festeklemme 4 AA batterier

CBL-til-CBR-kabel

Viktig

Texas Instruments gir ingen garantier, verken eksplisitt eller implisitt, heller ikke implisitte garantier for salgbarhet eller egnethet for et bestemt formål, for programmer eller dokumentasjon, og gjør dette materialet tilgjengelig bare i den tilstand det foreligger.

Texas Instruments påtar seg ikke under noen omstendigheter erstatningsansvar for direkte eller indirekte tap som måtte oppstå i forbindelse med eller som følge av kjøp eller bruk av dette materialet. Texas Instruments er heller ikke ansvarlig for krav som fremsettes av en annen part, om begrensning av bruksretten til disse materialene.



1997 Texas Instruments Incorporated.

Med enerett.

Lærere gis hermed tillatelse til å trykke opp eller kopiere de sider eller ark i dette verket som inneholder en melding om opphavsrett for Texas Instruments, i et egnet antall for bruk i klasserom, verksted eller seminarer. Disse sidene er beregnet på reproduksjon av lærere for bruk i klasser, kurs eller seminarer, men bare om hver side inneholder melding om opphavsrett. Slike kopier kan ikke selges, og videre distribusjon er eksplisitt forbudt. Med unntak av den bruk som angitt ovenfor, må det innhentes skriftlig tillatelse fra Texas Instruments Incorporated for reproduksjon eller overføring av dette materialet eller deler av det i noen annen form eller på noen annen elektronisk eller mekanisk måte, inkludert lagrings- eller gjenfinningssystemer, med mindre dette er eksplisitt tillatt i henhold til nasjonal opphavsrettslov. Henvendelser sendes til Texas Instruments Incorporated, PO Box 149149, Austin, TX, 78714

9149, M/S 2151, Attention: Contracts Manager.

Innholdsfortegnelse

CBR

NS T R

)

Innledning

Hva er CBR? 2

Komme i gang med CBR – på 1, 2, 3 4

Hint for effektiv datainnsamling 6

Øvelser med merknader til læreren og oppgaveark for elevene

TRIGGER

85-86

Øvelse 1 — Kopier grafen lineær 13

Øvelse 2 — Lekebil lineær 17

Øvelse 3 — Pendel sinuskurve 21

Øvelse 4 — Sprettende ball parabel 25

Øvelse 5 — Rullende ball parabel 29

Lærerveiledning 33

Teknisk informasjon

CBR-data lagres i lister 37

RANGER-innstillinger 38 Bruke CBR med CBL eller CBL-programmer 39 Programmeringskommandoer 40

Vedlikeholdsinformasjon

Batterier 42

Hvis det oppstår problemer 43

TI service og garanti 44

Menykart for RANGER på innsiden av bakre omslag

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

Hva er CBR?

Hva gjør CBR?

Med uten tidkrevende måling og manuell plotting.

Med CBR

avstand, fart, akselerasjon og tid ved hjelp av data som er samlet inn på grunnlag av aktiviteter de utfører. Elevene kan undersøke matematiske og vitenskapelige begreper som:

CBRCBRé (Calculator-Based RangerCalculator-Based Rangeré

)

ultralyd bevegelsessensor

CBL

brukes med TI-82, TI-83, TI-85/

, TI-86 og TI-92

ta virkelig datainnsamling og dataanalyse med inn i klasserommet

lett å bruke, selvstendig enhet

krever ingen programmering

Inneholder programmet RANGERInneholder programmet RANGER

det allsidige programmet RANGER er bare et tastetrykk unna

programmene MATCH og BOUNCING BALL er bygd inn i RANGER

primærparametere for datainnsamling er enkle å stille inn

og en TI grafkalkulator kan elever samle inn, vise og analysere bevegelsesdata

CBR

kan elevene utforske de matematiske og vitenskapelige forholdene mellom

bevegelse: avstand, fart, akselerasjon

grafer: koordinatakser, helling, skjæringspunkter

funksjoner: lineær, kvadratisk, eksponentiell, sinuskurve

matematisk analyse: differensialkvotienter, integraler

statistikk og dataanalyse: datainnsamlingsmetoder, statistisk analyse

Hva finner jeg i denne boken?

Komme i gang med CBR

erfaring med bruk av kalkulatorer eller programmering. Den inneholder instruksjoner som får deg raskt i gang, hint om effektiv innsamling av data og fem elevøvelser som viser de grunnleggende funksjonene og egenskapene for bevegelse. Øvelsene (se side 13–32) inneholder:

merknader til læreren for hver øvelse, pluss en generell lærerveiledning

trinnvise instruksjoner

grunnleggende aktiviteter for datainnsamling på alle nivåer

undersøkelser som utforsker dataene nærmere, inkludert hva-hvis-scenarier

forslag til avanserte emner egnet for elever innen matematisk analyse

et oppgaveark som kan kopieres til elevene, med åpne spørsmål som passer for de

fleste klassetrinn

er utformet som en veiledning til lærere som ikke har særlig

OMME I GANG MED

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

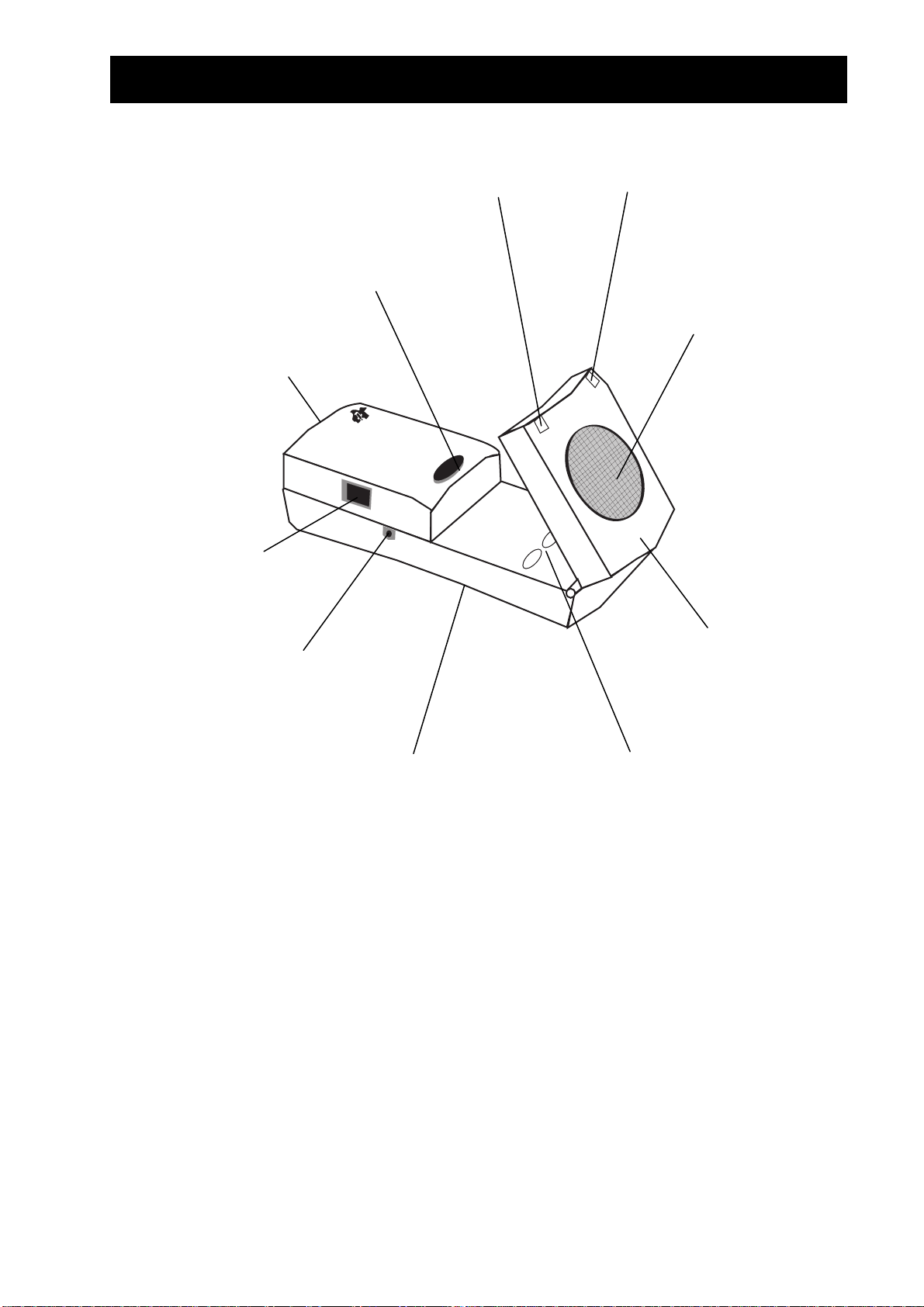
Hva er CBR?

(forts.)

tarter innsamling

batterilokk (under)

Utgang for kobling til CBL (hvis ønskelig)

Utgang for kobling til TI

rafkalkulatorer med den vedlagte 2,25-meters kabelen (7,5-fot)

Grønt lys viser når datainnsamling pågår (lyd er også tilgjengelig)

knapp som

CBR

)

Rødt lys viser

pesielle forhold

Lydsensor som registrerer opptil 200 lydprøver per

ekund med en avstand på mellom 0,5 og 6 meter (1,5 til 18 fot)

TRIGGER

85-86

Bevegelig hode for nøyaktig sensorretning

Standardfeste for trefotsstativ eller den vedlagte festeklemmen (på baksiden)

inneholder alt du trenger for å begynne elevøvelser enkelt og raskt – bare legg til

CBR

Knapper for overføring av RANGERprogrammet til kalkulatorer

TI grafkalkulatorer (og lett tilgjengelig tilbehør for enkelte øvelser).

ultralyd bevegelsessensor

RANGER

-program i

CBR

kalkulator-til-

4 AA-batterier

CBR

-kabel

festeklemme

5 morsomme elevøvelser

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

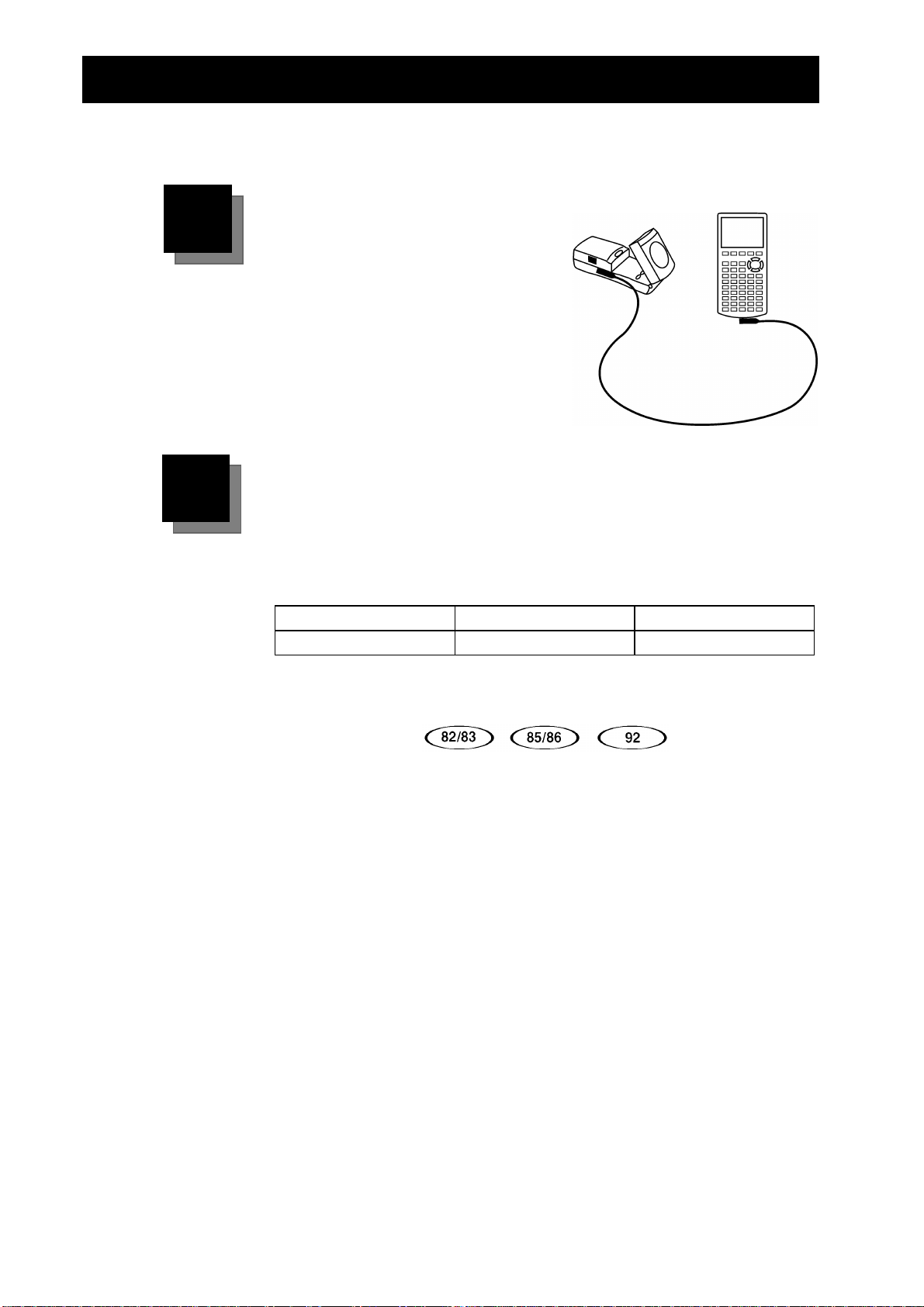
Komme i gang med CBR – på 1, 2, 3

Med

er du bare tre enkle trinn unna den første datainnsamlingen!

CBR

Koble

Koble med kalkulator-til-

Trykk den at kontakten sitter.

Merk:

kalkulator-kabelen som følger med kalkulatoren, kan også brukes.

til en TI grafkalkulator

CBR

abelen.

CBR-k

inn i begge ender slik

odt

Den korte kalkulator-til-

Overfør

RANGER

overføre det riktige programmet fra

Først gjør du klar kalkulatoren til å motta programmet (se tastekombinasjonene nedenfor).

, et eget program for hver kalkulator, ligger inne i

til en kalkulator.

CBR

. Det er lett å

CBR

TI-82 eller TI-83 TI-85/CBL eller TI-86 TI-92

[

LINK

›

]

Så åpner du det bevegelige hodet på overføringstasten på

CBR

Under overføringen viser kalkulatoren overføringen er fullført, blinker det grønne lyset på piper en gang, og kalkulatorskjermen viser problemer, blinker det røde lyset på

LINK

[

]

og trykker på den riktige

CBR

RECEIVING

to ganger og

CBR

Gå til Home-skjermbildet.

(unntatt TI-92). Når

én gang,

CBR

. Hvis det oppstår

DONE

CBR

piper to

ganger.

Når du har overført

RANGER

-programmet fra

til en kalkulator, trenger

CBR

du ikke å overføre det på nytt med mindre du sletter det fra minnet i kalkulatoren.

Merk:

Programmet og dataene krever omtrent 17 500 byte minne. Du kan bli nødt til å slette andre programmer og data fra kalkulatoren. Du kan lagre programmer og data først ved å overføre dem til en datamaskin ved hjelp av TI-Graph Linké, eller til en annen kalkulator ved hjelp av en

-kabelen (se

kalkulator-til-kalkulator-kabel eller kalkulator-til-

CBR

håndboken for kalkulatoren).

OMME I GANG MED

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

Komme i gang med CBR – på 1, 2, 3

Kjør

RANGER

Trykk på Vel Trykk på

Vises åpningsskjermen.

-programmet (se tastekombinasjonene nedenfor).

TI-82 or TI-83 TI-85/CBL or TI-86 TI-92

RANGER

›

kk på

RANGER

Vel Trykk på

(forts.)

^ A

›

kk på L [

RANGER

Vel Trykk på ¨

VAR-LINK

›

Vis resultater raskt med én av elevøvelsene i denne boken!

Trykk på

MAIN MENU

SETUP / SAMPLE SET DEFAULTS APPLICATIONS PLOT MENU TOOLS QUIT

Velg å velge

›.

SET DEFAULTS

START NOW

MAIN MENU

(hovedmenyen) vises.

vis/endre innstillinger før innsamling

endre innstillinger tilbake til standard

DISTANCE MATCH, VELOCITY MATCH, BALL BOUNCE

plottevalg

GET CBR DATA, GET CALC DATA, STATUS, STOPàCLEAR

på

MAIN MENU

. Skjermen

vises. Trykk på › for

SETUP

. Gjør klart alt du trenger til øvelsen, og trykk på ›

for å begynne å samle inn data. Så enkelt er det!

Viktig informasjon

Denne veiledningen gjelder alle grafkalkulatorer fra TI som kan brukes

med

, så det kan hende at noen av menynavnene ikke stemmer

CBR

helt overens med navnene på din kalkulator.

Mens du gjør klart til øvelsene må du passe på at

er forsvarlig

CBR

festet og at ingen kan snuble i ledningen.

Gå alltid ut av

RANGER-

programmet stenger av

Dette sikrer at

Koble alltid kalkulatoren fra

CBR

programmet ved hjelp av valget

riktig og forsvarlig når du velger

CBR

QUIT. RANGER

QUIT

blir riktig initialisert neste gang du skal bruke den.

før du legger den til side.

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

Hint for effektiv datainnsamling

Få bedre data

Hvordan fungerer CBR?

Når du forstår hvordan en ultralyd bevegelsessensor fungerer, blir det enklere å få gode grafer av data. Bevegelsessensoren sender ut ultralydsignaler og måler hvor lang tid det tar før signalet reflekteres tilbake fra nærmeste objekt.

måler, som alle andre ultralyde bevegelsessensorer, tidsintervallet fra utsending av

CBR

ultralydsignalet til første ekko kommer tilbake, men mikroprosessor som gjør mye mer. Når dataene samles inn, beregner objektet til andre derivat av avstandsdataene for å finne farts- og akselerasjonsdata. Disse målingene lagres i listene

Det kan være en interessant elevøvelse å prøve å utføre de samme beregningene som

utfører.

CBR

ved hjelp av lydhastighetsberegninger. Deretter beregner den første og

CBR

L1, L2, L3

og L4.

har også en innebygd

CBR

avstanden fra

CBR

Samle inn eksempeldata i

➊

Bruk eksempeltidene i

➋

REALTIME=NO

sammen med avstandsdataene i L2 til å beregne farten på

-modus. Gå ut av

RANGER-

programmet.

objektet ved hvert prøvetidspunkt. Sammenlign deretter resultatene med fartsdataene i

Bruk fartsdataene i L3 (eller verdiene elevene har kommet fram til) sammen med

➌

eksempeltidene i prøvetidspunkt. Sammenlign deretter resultatene med akselerasjonsdataene i

Objektstørrelse

Hvis du bruker et lite objekt langt fra

(

n+1

til å beregne akselerasjonen for objektet på hvert

)à2 N (

CBR,

n+1

reduseres muligheten for nøyaktige målinger.

n-1

)à2

Ved 5 meter vil det for eksempel være langt mer sannsynlig at du kan peile inn en fotball enn en bordtennisball.

Minimumsavstand

Når Hvis objektet er mindre enn 0,5 meter fra hverandre og feiltolkes av

sender ut et signal, treffer signalet objektet, returneres og blir mottatt av

CBR

, vil etterfølgende signaler kunne overlappe

CBR

. Grafen vil bli unøyaktig. Plasser derfor

CBR

CBR.

minst

0,5 meter fra objektet.

OMME I GANG MED

Maksimumsavstand

Når signalet går gjennom luften, reduseres styrken i det. Etter omtrent 12 meter (6 meter til objektet og 6 meter tilbake til

) vil ekkoet være for svakt til at

CBR

opp. Dette begrenser den pålitelige og effektive avstanden mellom

kan fange det

CBR

og objektet til

CBR

mindre enn 6 meter.

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

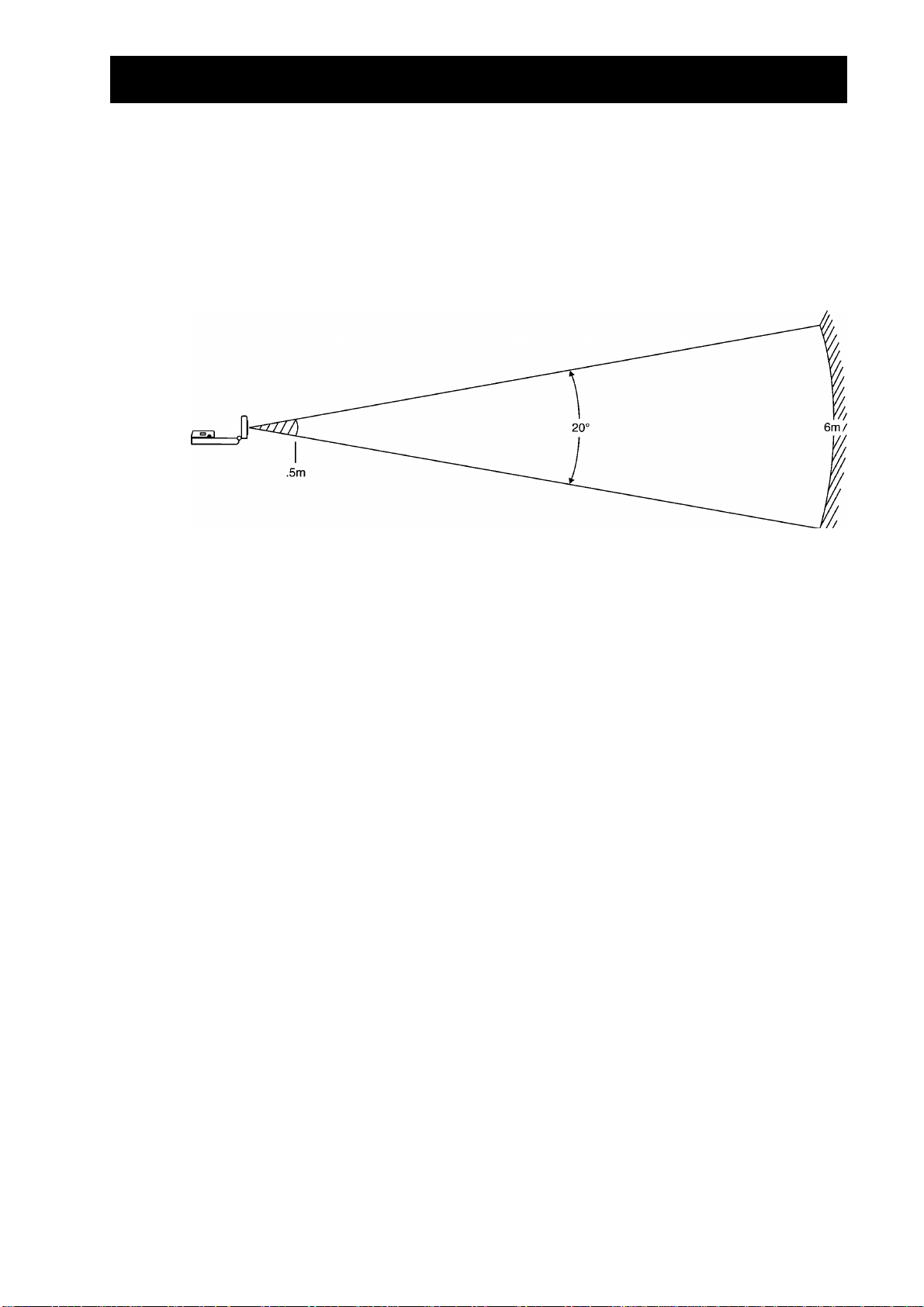
Hint for effektiv datainnsamling

Klar sone

(forts.)

Banen for

-signalet er ikke en smal, enkel stråle, men sendes ut i alle retninger

CBR

innenfor en kjegleformet stråle på opptil 10°.

For å unngå forstyrrelser fra andre objekter i nærheten, bør du prøve å opprette en klar sone for banen til målobjektet blir registrert av

-signalet. Slik hjelper du til å sikre at ikke andre objekter enn

CBR

CBR. CBR

registrerer det nærmeste objektet i den klare

sonen.

Reflekterende overflater

Enkelte overflater reflekterer signalene bedre enn andre. Du kan for eksempel vente bedre resultater med en relativt hard og glatt ball enn med en tennisball. Av samme årsak vil innsamlinger gjort i et rom fylt med harde, reflekterende flater oftere inneholde ugyldige datapunkter. Målinger av uregelmessige overflater (for eksempel en lekebil eller en elev som holder en kalkulator og går over gulvet) kan bli ujevne.

En avtand-tid-graf av et ikke-bevegelig objekt kan inneholde små forskjeller i de beregnede avstandsverdiene. Hvis noen av disse verdiene plottes på en annen piksel, kan den ventede, rette linjen vise små ujevnheter. Fart-tid-grafen kan virke enda mer ujevn fordi endringer i avstand mellom to gitte punkter over tid per definisjon er fart. Det kan hende at du bør bruke en passende grad av glatting på dataene.

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

Hint for effektiv datainnsamling

RANGER-innstillinger

Innsamlingstid

er den samlede tiden det tar å samle inn alle data, målt i sekunder. Skriv inn et

TIME

heltall mellom 1 sekund (for objekter i rask bevegelse) og 99 sekunder (for objekter i sakte bevegelse). For

REALTIME=YES

TIME

(forts.)

alltid 15 sekunder.

Når

TIME=1 SEKUND

Starte og stoppe

SETUP-

er et lavere tall, må objektet være nærmere

TIME

, må objektet ikke være mer enn 1,75 meter fra

skjermen i

RANGER

-programmet inneholder flere valg for hvordan du kan starte og

. For eksempel hvis

CBR

stoppe datainnsamlingen.

BEGIN ON: [ENTER]

. Starter innsamlingen ved trykk på

-tasten på kalkulatoren hvis

›

personen som setter i gang insamlingen, er nærmest kalkulatoren.

BEGIN ON: [TRIGGER]

hvis personen som setter i gang prøven, er nærmest

CBR

Med dette valget kan du også velge å koble fra trekke ut kabelen fra inn dataene, koble til

ON: [TRIGGER]

Dette er ikke tilgjengelig i

. Starter og stopper innsamlingen ved trykk på

CBR

. Slik kan du sette opp prøven,

CBR

, ta med

CBR

igjen og trykke på

CBR

til der tingene skjer, trykke på

CBR

for å overføre dataene. Bruk

›

når kabelen ikke er lang nok eller vil være i veien ved innsamling av data.

REALTIME=YES

-modus (som for eksempel ved bruk av

programmet).

BEGIN ON: DELAY

på

Trigger-tasten

. Dette er spesielt nyttig hvis du arbeider alene.

›

Virkningen av

. Starter innsamlingen etter 10 sekunder fra tidspunktet når du trykker

varierer avhengig av innstillingene.

CBR

-tasten på

, samle

BEGIN

MATCH

Trykk på

starter datainnsamling, selv om

BEGIN ON: [ENTER]

eller

BEGIN ON: DELAY

er valgt. Den kan også brukes til å stoppe innsamlingen, men vanligvis vil du ønske å la den fortsette til den er ferdig.

REALTIME=NO

, etter at innsamlingen er ferdig, vil trykk på

automatisk gjenta den siste innsamlingen, men dataene overføres ikke til kalkulatoren. Hvis du vil overføre disse dataene, velger du

TOOLS

fra

MAIN MENU

kan også gjenta en datainnsamling ved å velge

START NOW

på

SETUP

-skjermen.)

REPEAT SAMPLE

og deretter

fra

GET CBR DATA

PLOT MENU

eller

. (Du

OMME I GANG MED

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

Hint for effektiv datainnsamling

Glatting

(forts.)

Glattingsmulighetene som er innebygd i

RANGER

-programmet kan redusere effekten av ugyldige signaler eller variasjoner i avstandsmålinger. Unngå stor grad av glatting før du har lært å få gode resultater uten.

For en aktivitet med større enn gjennomsnittlig sjanse for ugyldige signaler, vil du

kanskje øke glattingsverdien på På

REALTIME=NO

-data som allerede er samlet inn, kan du også bruke glatting.

Kalkulatoren må da være koblet til

SMOOTH DATA

Støy – hva er det og hvordan bli kvitt det?

Når

mottar signaler som er reflektert fra andre objekter enn hovedmålet, viser grafen

CBR

, og velg deretter et glattingsnivå.

-skjermen før datainnsamlingen (se side 38).

SETUP

CBR

. Velg

PLOT TOOLS

fra

PLOT MENU

, velg

avvikende datapunkter (støypunkter) som ikke passer inn i det generelle mønsteret i grafen. Slik minimeres støyen:

Pass på at

på en

REALTIME=YES

peker rett mot målet. Prøv å justere sensorhodet mens du følger med

CBR

-prøve til du får gode resultater, før du samler inn

REALTIME=NO

data. Prøv å samle inn data i et tomt rom (se illustrasjonen klar sone på side 7).

Velg et større, mer reflekterende objekt eller flytt objektet nærmere

(men ikke

CBR

nærmere enn 0,5 meter). Ved bruk av flere

i et rom bør én gruppe gjøre seg ferdig med sin datainnsamling

CBR

før den neste gruppen begynner. Hvis en

REALTIME=YES

-prøve blir full av støy, kan du gjenta med høyere grad av glatting

til du får tilfredsstillende resultater. (Du kan ikke endre glattingen i programmene

DISTANCE MATCH, VELOCITY MATCH

Hvis en

REALTIME=NO

-prøve blir full av støy, kan du bruke en høyere grad av glatting

BALL BOUNCE

på de opprinnelige dataene.

Lydens hastighet

Den antatte avstanden til objektet beregnes ut fra antagelsen om en nominell lydhastighet. Lydens faktiske hastighet varierer imidlertid med flere faktorer, hvorav lufttemperaturen er den mest merkbare. For aktiviteter med relative bevegelser er denne faktoren ikke så viktig. For aktiviteter som krever særlig nøyaktige målinger, kan en programmeringskommando brukes til å angi miljøtemperaturen (se side 40-41).

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

Hint for effektiv datainnsamling

REALTIME=YES

(forts.)

Bruk

REALTIME=YES

med objekter i langsom bevegelse

når du vil se resultatene etter hvert som dataene samles inn

når du bare trenger å samle inn eller plotte én type data (avstand, fart eller

-modus:

akselerasjon) for en prøvetaking

REALTIME=YES

-modus behandler

akselerasjon), og overfører dem til kalkulatoren etter hver enkelt avstandsmåling.

dataene som skal plottes (avstand, fart eller

CBR

RANGER

tegner deretter inn én enkelt piksel for det overførte signalet.

Fordi alle disse operasjonene må fullføres før neste prøve kan tas, er maksimumsfarten for datainnsamling i

REALTIME=YES

-modus begrenset.

Det tar tilnærmet lik 0,080 sekunder bare å sende og motta et signal, behandle resultatet og overføre dataene for ett enkelt datapunkt. I tillegg kreves det tid til for eksempel å plotte punktet, noe som reduserer farten til tilnærmet lik 0,125 sekunder i

RANGER

REALTIME=NO

Bruk

REALTIME=NO

-modus:

med objekter i rask bevegelse når glatting er nødvendig (se side 9) når du bruker

i frakoblet modus (se side 11)

CBR

når du trenger å samle eller plotte alle typer data (avstand, fart og akselerasjon) for en prøvetaking

REALTIME=NO

-modus blir dataene lagret i

og ikke overført til kalkulatoren før etter

CBR

at datainnsamlingen er fullført. Farten på innsamlingen kan være så rask som hvert 0,005 sekund for objekter nær

. Data for tid, avstand, fart og akselerasjon overføres

CBR

til kalkulatoren.

Fordi dataene lagres i

Hver gang du endrer glattingen, bruker

, kan du overføre dem fra

CBR

til en kalkulator flere ganger.

CBR

den nye glattingsfaktoren, overfører de

justerte dataene til kalkulatoren og lagrer de glattede verdiene i listene. Når du velger et område, endres listene som er lagret i kalkulatoren. Hvis det er

nødvendig, kan du gjenopprette de opprinnelige dataene fra

MAIN MENU

Flere elever kan også dele de samme dataene, selv om de bruker forskjellige typer

RANGER

-programmet. Velg deretter

GET CBR DATA

CBR

fra

. Velg

TOOLS

fra

TOOLS

-menyen

grafkalkulatorer fra TI. På denne måten kan alle elevene delta i analyseoppgaver med de samme dataene (se side 11).

OMME I GANG MED

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

Hint for effektiv datainnsamling

Bruke CBR i frakoblet modus

(forts.)

Dele data

Fordi enkelte innstillinger endres. Velg følgende på

REALTIME=NO

BEGIN ON=[TRIGGER]

RANGER

ikke kan sende data til kalkulatoren med en gang når den er frakoblet, må

CBR

-skjermen:

SETUP

-programmet sier fra når du kan koble fra

og når du kan koble den til igjen.

CBR

Det kreves ingen spesialprosedyrer for dette.

Hvordan skal du kunne gjennomføre en øvelse der hele klassen skal analysere de samme dataene samtidig? Med

Overfør

➊

Samle inn dataene med

➋

Koble kalkulatoren til den første eleven til

➌

RANGER

-programmet til alle elevenes kalkulatorer før datainnsamlingen.

kan du raskt distribuere

CBR

REALTIME=NO

-modus.

med enten kalkulator-til-

CBR

-data i klassen.

CBR

-kabelen

eller kalkulator-til-kalkulator-kabelen.

Velg

➍

➎

TOOLS

Trykk på › for å gå tilbake til

fra

MAIN MENU

-menyen. Ordet

RANGER

TRANSFERRING...

-programmet. Velg deretter

PLOT MENU

vises, og grafen plottes.

, og velg deretter

GET CBR DATA

. Koble fra

QUIT

fra

kabelen.

Koble til en annen kalkulator (av samme type) til kalkulatoren med dataene. Velg

➏

fra

TOOLS

deretter

MAIN MENU

GET CALC DATA

RANGER

fra

-programmet på den andre kalkulatoren. Velg

-menyen. Listene L1, L2, L3, L4 og L5 overføres

TOOLS

automatisk til den andre kalkulatoren.

Overfør data fra

➐

til en annen elevkalkulator mens andre elever fortsetter

CBR

overføringen fra kalkulator til kalkulator.

Når alle elevene har de samme dataene, kan de analysere dem i

MENU,

eller utenfor

RANGER

Hvis du skal dele data på TI-85, bruker du

ved hjelp av liste- og graffunksjonene i kalkulatoren.

-funksjonen utenfor

LINK

RANGER

ved hjelp av

RANGER

listene.

PLOT

til å overføre

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

Hint for effektiv datainnsamling

Utover enkel datainnsamling

(forts.)

Når du har samlet inn og tegnet inn dataene i

RANGER

, kan du undersøke dataene i forhold til en funksjon. Fordi dataene er samlet i lister og vist som en statistisk graf, kan du bruke

Inne i RANGER

Undersøk grafer ved hjelp av

,  og œ til å undersøke dette forholdet.

, som blir stilt inn automatisk. (På TI-85 bruker du

TRACE

den frie markøren.) Manipuler datasettet, også ved å glatte ut dataene eller velge ut det mest interessante

området.

Utenfor RANGER

Undersøk dataene ved hjelp av kalkulatorens listeredigeringsfunksjon.

Lag din egen funksjon manuelt ved hjelp av kalkulatorens Y=-editor.

Finn automatisk fram til ligningen som passer best til dataene ved hjelp av

kalkulatorens regresjonsmuligheter.

Andre forhold kan undersøkes, også de som ikke plottes med grafvalgene i

RANGER

. For eksempel kan samtidige inntegninger av avstand-tid og fart-tid vises som statistiske grafer. Velg

som L1 mot L3. (Det kan hende at du må justere vinduet.)

Plot2

QUIT

fra

MAIN MENU

RANGER

-programmet, og angi deretter

som L1 mot

Plot1

Data og grafer kan overføres til en datamaskin ved hjelp av TI-Graph Link. Dette er særlig nyttig når elevene skal skrive større rapporter om det de har funnet ut.

Bruke CBR uten RANGER-programmet

Du kan bruke programmer enn

Du finner mer informasjon om å bruke

Du finner mer informasjon om hvordan du får tak i programmer og øvelser på side 36.

Du finner mer informasjon om programmeringskommandoer og hvordan du lager

som en ultralyd bevegelsessensor med

CBR

RANGER

egne programmer på side 40–41.

CBR

med

CBL

på side 39.

CBL

eller med andre

OMME I GANG MED

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

Øvelse 1 – Kopier grafen merknader til læreren

Begreper

Funksjon som undersøkes: lineær.

MATCH

presenterer de virkelige begrepene avstand

og tid – eller mer nøyaktig, begrepet avstand i forhold til tid. Når elevene prøver å kopiere en graf ved å gå mens de ser sin egen bevegelse plottes, kan begrepet posisjon undersøkes.

I Undersøkelser blir elevene bedt om å konvertere gangfarten i meter per sekund til kilometer per time.

Når de har fått taket på avstand-tid-forholdet, kan du utfordre elevene med forholdet fart-tid.

Materialer

 kalkulator

CBR

  kalkulator-til-kalkulator-kabel

Med en TI ViewScreené kan de andre elevene følge med på og oppleve det som er morsomst med denne øvelsen.

Hint

Elevene liker vanligvis denne øvelsen godt. Sett av rikelig med tid, slik at alle som vil, får prøve seg!

Denne øvelsen fungerer best når eleven som går (og hele klassen) kan se bevegelsen inntegnet på en vegg eller storskjerm ved hjelp av TI ViewScreen.

Fortell elevene at de må gå på rett linje med CBR. De prøver av og til å gå til siden (vinkelrett på linjen fra CBR) eller til og med hoppe opp og ned!

Instruksjonene anbefaler at øvelsen gjøres i meter (ikke fot), som samsvarer med spørsmålene på elevenes oppgaveark.

Se side 6–12 for flere hint om effektiv datainnsamling.

Vanlige grafer

Mulige svar

1. tid (fra starten av datainnsamlingen); sekunder; 1 sekund; avstand (fra CBR til objektet); meter; 1 meter

2. skjæringspunktet for y representerer startavstanden

3. varierer fra elev til elev

4. bakover (øk avstanden mellom CBR og objekt)

5. framover (reduser avstanden mellom CBR og objekt)

6. stå stille; nullkurve krever ingen endringer i y (avstand)

7. varierer fra graf til graf; @yà3.3

8. varierer fra graf til graf; @yà1

9. segmentet med størst helling (positiv eller negativ)

10. dette spørsmålet er en felle – det flate segmentet, fordi du ikke beveger deg i det hele tatt!

11. gangfart; når eleven skal endre retning og/eller fart

12. fart

13. varierer fra graf til graf (eksempel: 1,5 meter på 3 sekunder)

14. varierer fra graf til graf; eksempel: 0,5 meterà1 sekund

eksempel: (0,5 meter à 1 sekund) Q (60 sekunder à 1 minutt) = 30 meter à minutt

eksempel: (30 meter à 1 minutt) Q (60 minutter à 1 time) = 1800 meter à time

eksempel: (1800 meter à 1 time) Q (1 kilometer à 1000 meter) = 18 kilometer à time.

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

Få elevene til å sammenligne dette siste tallet med farten for et kjøretøy, for eksempel 96 kilometer à time.

15. varierer fra graf til graf; summen av @y for hvert linjesegment.

INKLUDERES

OMME I GANG MED

CBR

Øvelse 1 – Kopier grafen lineær

Datainnsamling

➊

Hold

i en hånd og kalkulatoren i den andre. Pek rett mot veggen med

CBR

sensorhodet.

. Minimumsavstander

Maksimumsavstanden for alle grafene er 4 meter fra

Hint:

CBR

er 0,5 meter. Pass på at det ikke finnes noe annet i den klare sonen (se side 7).

Kjør

➋ ➌ ➍

RANGER

Velg

APPLICATIONS

Velg

DISTANCE MATCH

instruksjoner. Med

Trykk på › for å vise grafen for dataene. Bruk et øyeblikk på å se på grafen.

➎

-programmet (se side 5 for tastekombinasjoner for hver kalkulator).

fra

MAIN MENU

fra

APPLICATIONS

DISTANCE MATCH

. Velg

METERS

-menyen. Skjermen viser generelle

angis innstillinger automatisk.

Svar på spørsmål 1 og 2 på oppgavearket.

Still deg der du tror grafen begynner. Trykk på › for å starte datainnsamlingen.

➏

Du hører et klikk og ser et grønt lys mens dataene samles inn.

Gå fram og tilbake og prøv å lage en kopi av grafen. Posisjonen din plottes på

➐

skjermen.

Når datainnsamlingen er ferdig, undersøker du hvor godt "spaserturen" din

➑

stemmer overens med grafen. Svar på spørsmål 3.

Trykk på › for å vise

➒

OPTIONS

-menyen, og velg

SAME MATCH

. Prøv å forbedre

bevegelsene dine, og svar deretter på spørsmål 4, 5 og 6.

OMME I GANG MED

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

Øvelse 1 – Kopier grafen

Undersøkelser

(forts.)

lineær

DISTANCE MATCH

Trykk på › for å vise

➊

segmentet, og svar på spørsmål 7 og 8.

Se på hele grafen, og svar på spørsmål 9 og 10.

➋

Still deg der du tror grafen begynner, trykk på › for å begynne

➌

datainnsamlingen, og prøv å lage en tilsvarende graf.

Når du er ferdig med datainnsamlingen, svarer du på spørsmål 11 og 12.

➍

Trykk på › for å vise

➎

Se på grafen, og svar på spørsmål 13, 14 og 15.

➏

Trykk på › for å vise

➐

til

MAIN MENU

Avanserte undersøkelser

Grafene som ble generert med

VELOCITY MATCH

MATCH

er et veldig populært program. Andre versjoner som undersøker mer avanserte

grafer kan være tilgjengelig (se side 36).

består alle grafer av tre rette linjesegmenter.

og velg

OPTIONS

for å gå ut av

QUIT

DISTANCE MATCH,

-menyen, og velg

NEW MATCH

-menyen. Gjenta øvelsen hvis du vil, eller gå tilbake

RANGER

-programmet.

bestod av bare rette linjer. Prøv med

. Se på det første

, hvor du skal kopiere en fart-tid-graf. Det er vanskelig!

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

Øvelse 1 – Kopier grafen

Navn ____________________________________

Datainnsamling

1. Hvilken fysisk enhet representeres langs x-aksen? ___________________________________________

Hva er målenheten? Hvor langt fra hverandre er avmerkingene ? ______

Hvilken fysisk størrelse representeres langs y-aksen? ________________________________________

Hva er målenheten? Hvor langt fra hverandre er avmerkingene ? ______

2. Hvor langt fra

tror du du bør stå på begynnelsen? ______________________________________

CBR

3. Begynte du for langt fra, for nær eller akkurat passe? _______________________________________

4. Skal du gå framover eller bakover for et segment som heller oppover ? ________________________

Hvorfor? _____________________________________________________________________________

5. Skal du gå framover eller bakover for et segment som heller nedover? _________________________

Hvorfor? _____________________________________________________________________________

6. Hva skal du gjøre for et segment som er flatt? _____________________________________________

Hvorfor? _____________________________________________________________________________

Undersøkelser

7. Hvis du tar ett skritt hvert sekund, hvor langt må det skrittet være ? ___________________________

8. Hvis du i stedet tar skritt på 1 meter, hvor mange må du ta? _________________________________

9. For hvilket segment må du bevege deg raskest? ____________________________________________

Hvorfor? _____________________________________________________________________________

10. For hvilket segment må du bevege deg saktest? ____________________________________________

Hvorfor? _____________________________________________________________________________

11. I tillegg til å velge om du vil bevege deg framover eller bakover, hvilke andre faktorer må du ta hensyn til for å lage en nøyaktig samsvarende graf? _________________________________________

_____________________________________________________________________________________

12. Hvilken fysisk størrelse representerer hellingen (hvor bratt linjen er)? ___________________________

13. Hvor mange meter må du gå på hvor mange sekunder for det første linjesegmentet? ____________

sekund: ___________________________________

14. Konverter verdien i spørsmål 13 (farten) til meter

Konverter til meter

Konverter til kilometer

minutt: _____________________________________________________________

àtime: _______________________________________________________________

àtime: ____________________________________________________________

15. Hvor langt gikk du faktisk? _____________________________________________________________

OMME I GANG MED

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

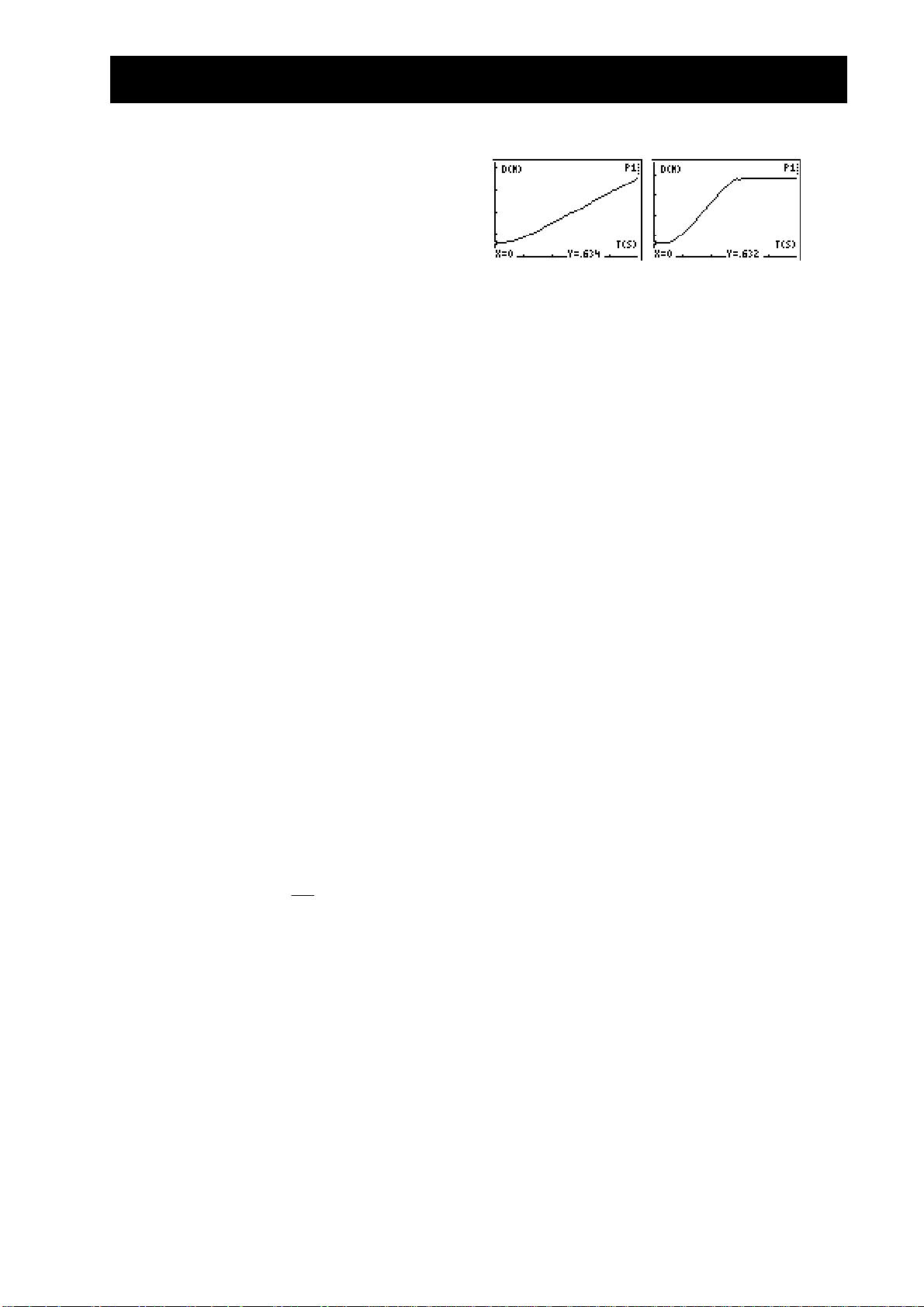
Øvelse 2 – Lekebil merknader til læreren

Begreper

Funksjon som undersøkes: lineær. Bevegelsen på en motorisert lekebil brukes til å

illustrere det fysiske begrepet konstant fart.

Materialer

 kalkulator

CBR



CBR

 kalkulator-til-

-kabel

 batteridrevet lekebil  TI ViewScreen (valgfritt)

Hint

Lekebiler varierer sterkt i størrelse, form og refleksjonsvinkel for ultralydsignalene. De ferdige grafene vil derfor variere i kvalitet. Enkelte biler kan kreve en ekstra reflekterende overflate for å få gode inntegninger. Prøv å lime et kartotekkort e.l. på bilen slik at den fungerer bedre som mål for sensoren.

Du kan også prøve flere typer biler slik at elevene kan undersøke disse virkningene.

Lekebiler som beveger seg sakte (for eksempel biler laget for små barn) passer best til denne øvelsen. Se etter en bil som ser ut til å ha konstant fart.

Se side 6–12 for flere hint om effektiv datainnsamling.

Undersøkelser

Hellingen på en avstand-tid-graf på et gitt tidspunkt angir objektets fart ved dette tidspunktet. For et objekt som beveger seg med konstant fart skal hellingen på avstand-tid-grafen altså være konstant. Derfor viser avstand-tid-grafen et lineært forhold.

Hvis du begynner å samle inn data før bilen begynner å bevege seg, vil du legge merke til at avstand-tid-grafen ikke er lineær på begynnelsen. Hvorfor? Bilen begynner på nullfart (v = 0). Den kan ikke øyeblikkelig oppnå sin vanlige, konstante fart. Akselerasjon beregnes slik:

∆

Vanlige grafer

Svar på spørsmålene

1. første eller siste plotting, avstanden øker konstant

2. elevene skriver inn verdier fra

TRACE

3. avstandsverdiene øker med en konstant mengde

4. fart er mengde avstandsendring over tid, verdiene er de samme for hvert like tidsintervall

5. eleven bør få en verdi i nærheten av den som er beregnet for m

i nærheten av m m representerer farten på bilen

6. b er skjæringspunktet for y; eksempel: y = 2x + 0

7. varierer; for eksempel: hvis m = 2, avstand (y) = 20 meter etter 10 sekunder (y = 2 Q 10 + 0); vil y = 120 meter for 1 minutt

Avanserte undersøkelser

Hellingen for en fart-tid-graf for konstant fart er null. Derfor vil akselerasjon-tid-grafen vise a = 0 (i ideelle tilfeller) for tidsrommet når farten er konstant.

Resultatområdet er objektets forflytning (nettoavstand fra start- til sluttposisjon) i løpet av tidsrommet t

For avanserte matematikkelever: Forflytningen kan finnes med ligningen:

til t2.

svdt

∫

For at bilen skal kunne gå øyeblikkelig fra nullfart til sin konstante fart, må ∆t = 0. Men dette angir en uendelig akselerasjon, som ikke er fysisk mulig. (Etter Newtons andre lov, F = ma, kan en uendelig akselerasjon bare være resultat av en uendelig kraft, som er akkurat like umulig.) Derfor må vi se at objektet akselererer (øker farten) til sin konstante fart over et avgrenset tidsrom.

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

hvor s er objektets forflytning i tidsrommet t1 til t2.

INKLUDERES

OMME I GANG MED

CBR

Øvelse 2 – Lekebil lineær

Datainnsamling

Plasser bilen minst 0,5 meter fra

➊

med fronten bort fra

CBR

slik at den vil kjøre i

CBR,

en rett linje bort fra den.

Still sensorhodet rett mot bilen og pass på at det ikke finnes noe annet i den

Hint:

klare sonen (se side 7).

Før du begynner datainnsamlingen, svarer du på spørsmål 1 på oppgavearket.

➋

Kjør

➌ ➍

RANGER

Velg

SETUPàSAMPLE

REALTIME: NO

TIME (S): 5 SECONDS

DISPLAY: DISTANCE

BEGIN ON: [ENTER]

SMOOTHING: LIGHT

-programmet (se side 5 for tastekombinasjoner for hver kalkulator).

fra

UNITS: METERS

MAIN MENU

. For denne øvelsen skal innstillingene være:

Du finner instruksjoner for endring av innstillinger på side 38.

Velg

➎ ➏

START NOW

Trykk på › når du er klar til å begynne. Start bilen og skynd deg ut av den klare

sonen. Du hører en klikkelyd mens dataene samles inn, og meldingen

TRANSFERRING...

Når datainnsamlingen er ferdig, viser kalkulatoren automatisk en avstand-tid-graf av

➐

vises på kalkulatoren.

de innsamlede datapunktene.

Sammenlign grafen av dataresultatene med din egen forutsigelse i svar 1, og se

➑

etter likheter og forskjeller.

OMME I GANG MED

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

Øvelse 2 – Lekebil (forts.) lineær

Undersøkelser

Verdiene for x (tid) i halvsekundsintervaller vises i den første kolonnen i spørsmål 2.

➊

Følg grafen og skriv inn de tilsvarende y-verdiene (avstand) i den andre kolonnen.

antakelig overse springende data på begynnelsen av datainnsamlingen. Det kan også hende at du må angi tilnærmede avstandstall (kalkulatoren kan gi deg en avstand ved 0,957 eller 1,01 sekunder i stedet for nøyaktig 1 sekund). Ta nærmeste heltall eller gjett deg fram.

➋

Sva på spørsmål 3 og 4.

Beregn endringene i avstand og tid mellom hvert datapunkt for å fylle ut kolonne

➌

tre og fire. Du beregner for eksempel @Avstand (meter) for 1,5 sekunder ved å trekke fra Avstand ved 1 sekund fra Avstand ved 1.5 sekunder.

Funksjonen som illustreres med denne øvelsen, er y = mx + b. m er hellingen på en

➍

linje. Den beregnes slik:

Ta bare med resultater fra den lineære delen av grafen. Du må

Merk:

Skjæringspunktet for y representerer b.

Beregn m for hvert punkt. Skriv inn verdiene i tabellen i spørsmål 2.

➎

Svar på spørsmål 5, 6 og 7.

Avanserte undersøkelser

Beregning av hellingen på avstand-tid-grafen på et hvilket som helst tidspunkt viser objektets fart på dette tidspunktet. Beregning av hellingen på fart-tid-grafen viser objektets tilnærmede akselerasjon på dette tidspunktet. Hvis farten er konstant, hva blir da akselerasjonen?

Forutsi akselerasjon-tid-grafen for denne avstand-tid-grafen.

Finn området mellom Fart-tid-grafen og x-aksen mellom to passende tidspunkter, t

. Dette kan gjøres ved å summere områdene i ett eller flere rektangler som hver har et

areal på:

Hva er den fysiske betydningen av resultatområdet?

@avstand

@tid

eller

avstand

tid

areal = v∆t = v(t

N avstand N tid

)

2Nt1

eller

N y

x2 N x

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

Øvelse 2 – Lekebil

Navn ____________________________________

Datainnsamling

1. Hvilken av disse tror du er mest lik avstand-tid-grafen for lekebilen ?

Hvorfor? _____________________________________________________________________________

Tid Avstand

Avstand

Tid

1 xxx xxx xxx

1,5

2,5

3,5

4,5

3. Hva legger du merke til med Avstand-verdiene? ____________________________________________

4. Hvordan viser disse resultatene at lekebilen hadde konstant fart? ______________________________

5. Beregn

avstandà@tid

mellom Tid = 2 og Tid = 4. _________________________________________

Hva legger du merke til med dette resultatet ? _____________________________________________

Hva tror du

6. For den lineære ligningen

står for? _________________________________________________________________

= mx + b, hva er verdien for b? __________________________________

Skriv ligningen for linjen på formen

= mx + b med verdier for m og b. ________________________

7. Hvor langt ville lekebilen gått på 10 sekunder? _____________________________________________

Og på 1 minutt? ______________________________________________________________________

OMME I GANG MED

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

Øvelse 3 – Pendel merknader til læreren

Begreper

Funksjon som undersøkes: sinuskurve. Undersøke enkel harmonisk bevegelse ved å

observere en fritt svingende pendel.

Materialer

 kalkulator

CBR



CBR

 kalkulator-til-

-kabel

 festeklemme  stoppeklokke  pendel  metermål  TI ViewScreen (valgfritt)

Ideer til lodd:

baller i forskjellige størrelser (≥ 5 cm diameter)

brusbokser (tomme og fylte)

erteposer

Hint

Se side 6–12 for flere hint om effektiv datainnsamling.

Fysiske sammenhenger

Et objekt som utsettes for periodisk bevegelse som resultat av en gjenskapende kraft som er proporsjonal med objektets forlytning fra likevektposisjon (hvileposisjon), sies å utvise enkel harmonisk bevegelse (SHM). SHM kan beskrives ved to enheter.

Perioden T er tiden for én fullstendig svingning.

Svingningsutslaget (amplityden) A er den største

forflytningen av objektet fra likevektposisjon (posisjonen av loddet i hvilestilling).

For en enkel pendel gis perioden T ved:

T = 2p

hvor L er lengden på loddsnoren og g er størrelsen på akselerasjonen på grunnlag av tyngdekraften. T avhenger ikke av objektets masse eller størrelsen på bevegelsen.

Frekvensen f (antall fullstendige svingninger per sekund) kan beregnes ved:

f =

, hvor f er i hertz (Hz) når T er i sekunder.

Differensialkvotienten av en sinuskurvegraf er også en sinuskurve. Legg spesielt merke til faseforholdet mellom loddets plassering og fart.

Vanlige grafer

Mulige svar

1. varierer (i meter)

2. varierer (i meter)

3. varierer (i sekunder); T (én periode) = samlet tid for 10 perioder/10; med gjennomsnitt over flere perioder er sjansen mindre for målingsfeil

4. samlet buelengde, som skal være tilnærmet lik 4 ganger svaret på spørsmål 2, fordi en bue er lengre enn en rett linje

5. sinuskurve, repetitiv, periodisk, avstand fra x-aksen til likevektposisjon

6. hver svingning spres ut vannrett, en graf som går over 10 sekunder må passe inn flere svingninger på samme mengde skjermplass, og svingningene vil derfor se ut til å ligge nærmere sammen

7. (samlet antall svingninger)à(5 sekunder) = svingningeràsekund; lettere å vise fullstendige svingninger og færre målingsfeil

8. f = 1àT, hvor T er tiden for 1 periode

9. redusert periode; økt periode (Pendellengden står i direkte forhold til

periodetiden; jo lengre loddsnor, jo lengre periode. Elevene kan undersøke denne sammenhengen ved hjelp av listeredigeringsfunksjonen i kalkulatoren, hvor de kan beregne perioden for forskjellige verdier for L.)

10. A (svingningsavstand) = ¼ samlet avstand som pendelen beveger seg på 1 periode

11. begge er sinuskurver; forskjellene ligger i svingningsavstand og fase

12. likevektposisjon

13. når posisjon = maksimums- eller minimumsverdi (når loddet er lengst mulig vekk fra likevektposisjon).

14. ikke i det hele tatt. T avhenger bare av L og g, ikke av masse.

Avanserte undersøkelser

Datainnsamling: grafen av L2 mot L3 former en ellipse.

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

Øvelse 3 – Pendel sinuskurve

Datainnsamling

Sett opp pendelen. Plasser den slik at den svinger i rett linje med

➊

minst 0,5 meter fra punktet hvor loddet er nærmest. Pass på at det

Hint:

Plasser

CBR

ikke finnes noe annet i den klare sonen (se side 7).

amplityden

likevektposisjonen

Bruk et metermål til å måle avstanden fra

➋

til likevektposisjonen. Svar på

CBR

spørsmål 1 på oppgavearket.

CBR

Mål hvor langt du vil dra loddet bort fra likevektposisjon. Svar på spørsmål 2.

En pendelsvingning (en periode) består av en fullstendig svingning fram og tilbake.

➌

Bruk en stoppeklokke til å ta tiden på ti fullstendige perioder. Svar på spørsmål 3 og 4.

➍

Kjør

RANGER

-programmet (se side 5 for tastekombinasjoner for hver kalkulator). Det er mest effektivt hvis én person starter pendelen mens en annen opererer kalkulatoren og

Trykk på › for å vise innstillingene. For denne øvelsen skal de være slik:

➎

REALTIME: NO

TIME (S): 10 SECONDS

DISPLAY: DISTANCE

BEGIN ON: [ENTER]

SMOOTHING: LIGHT

UNITS: METERS

Du finner instruksjoner for endring av innstillinger på side 38. Når de er riktige,

➏

velger du

Trykk på › når du er klar til å begynne. Du hører en klikkelyd mens dataene

➐

START NOW

samles inn, og meldingen

Når datainnsamlingen er ferdig, viser kalkulatoren automatisk en avstand-tid-graf av

➑

CBR

. Velg

SETUP/SAMPLE

TRANSFERRING...

fra

MAIN MENU

vises på kalkulatoren.

de innsamlede datapunktene. Svar på spørsmål 5.

OMME I GANG MED

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

Øvelse 3 – Pendel

Undersøkelser

Datainnsamling 2

(forts.)

sinuskurve

Velg

SETUPàSAMPLE

Gjenta datainnsamlingen. Se på grafen. Svar på spørsmål 6 og 7.

Mengden du anga (svingninger per sekund) kalles frekvens. Du beregnet frekvensen i spørsmål 7 ved hjelp av grafen. Nå kan du også beregne den matematisk med ligningen:

f =

Svar på spørsmål 8.

Datainnsamling 3 og 4

Gjenta 5-sekunders-datainnsamlingen to ganger til. Første gang forkorter du loddsnoren, deretter forlenger du den. Etter å ha sett på disse grafene, svarer du på spørsmål 9.

Et annet viktig avstandsmål som påvirker pendelen, er svingningsutslaget (amplityden). Svaret på spørsmål 2 var svingningsutslaget (amplityden) for den pendelsvingningen.

Svar på spørsmål 10.

Avanserte undersøkelser

Datainnsamling 5

Velg

VELOCITY-TIME

Datainnsamling 6

fra

MAIN MENU

. Endre tiden fra 10 til 5 sekunder på

SETUP

-skjermen.

hvor T er perioden i sekunder, og f er frekvensen i hertz (Hz).

fra

PLOT MENU

. Svar på spørsmål 11, 12 og 13.

Gjenta datainnsamlingen med et betydelig lettere eller tyngre lodd, og svar på

spørsmål 14.

Beregn avstand-tid-adferden for pendelen ved hjelp av ligningen for en sinus-funksjon, S = A sin (wt + d), hvor S er øyeblikksposisjonen, A er svingningsutslaget, w er frekvensen, d er fasevinkelen, og t er tiden. Frekvensen, w, er relatert til perioden, T, med w = 2 pàT.

Skriv inn denne ligningen i Y=-editoren med de beregnede verdiene for A og w. Tegn inn en graf for denne funksjonen sammen med en statistisk graf for

(tid) mot L2 (avstand).

Juster verdiene for A, w og d til alt stemmer. På TI-83 eller TI-86 bruker du sinusregresjon til å bestemme verdiene.

Undersøk forholdet mellom posisjon og fart ved å plotte

(avstand) mot L3 (fart).

Hvordan tror du den ferdige grafen vi se ut? Sammenlign det faktiske resultatet med din egen forutsigelse.

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

Øvelse 3 – Pendel

Datainnsamling

Navn ____________________________________

1. Hva er avstanden mellom

og likevektposisjon? _________________________________________

CBR

2. Hvor langt fra likevektposisjon skal du dra pendelen? _______________________________________

3. Hvor lang tid tok ti perioder? ____________________________________________________________

Beregn hvor lang tid (i sekunder) det tok å fullføre én periode. ________________________________

Hva er fordelen med å ta tiden på ti perioder i stedet for bare én? _____________________________

4. Bruk svaret på spørsmål 2 til å beregne en tilnærmet avstand som tilbakelegges i en hel svingning.

_____________________________________________________________________________________

Hvorfor er dette talle mindre enn den faktiske avstanden som tilbakelegges i en svingning? _______

5. Hva legger du merke til med formen på grafen? ____________________________________________

Hvordan vises verdien fra spørsmål 1 i grafen? _____________________________________________

Undersøkelser

6. Hvordan endres utseendet på grafen? Hvorfor ? ____________________________________________

_____________________________________________________________________________________

7. Bruk data fra grafen til å beregne antall fullstendige svingninger per sekund. ____________________

Hvorfor er det enklere å avgjøre dette med den andre grafen (over 5 sekunder) enn med den første (over 10 sekunder)? ____________________________________________________________________

8. Beregn frekvensen for én periode ved hjelp av ligningen. _____________________________________

9. Hvordan påvirkes pendelen når loddsnoren blir kortere?______________________________________

Hvordan påvirkes pendelen når loddsnoren blir lengre? ______________________________________

10. Hva er forholdet mellom svingningsutslaget (amplityden) og den samlede avstanden som pendelen

tilbakelegger i en periode? ______________________________________________________________

_____________________________________________________________________________________

Avanserte undersøkelser

11. Sammenlign avstand-tid-grafen med fart-tid-grafen. Angi likheter og forskjeller. _________________

_____________________________________________________________________________________

12. På hvilket punkt er loddets fart størst? ____________________________________________________

13. På hvilket punkt er loddets fart minst?_____________________________________________________

14. Hvordan påvirkes grafen når loddet endres? Hvorfor? _______________________________________

_____________________________________________________________________________________

OMME I GANG MED

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

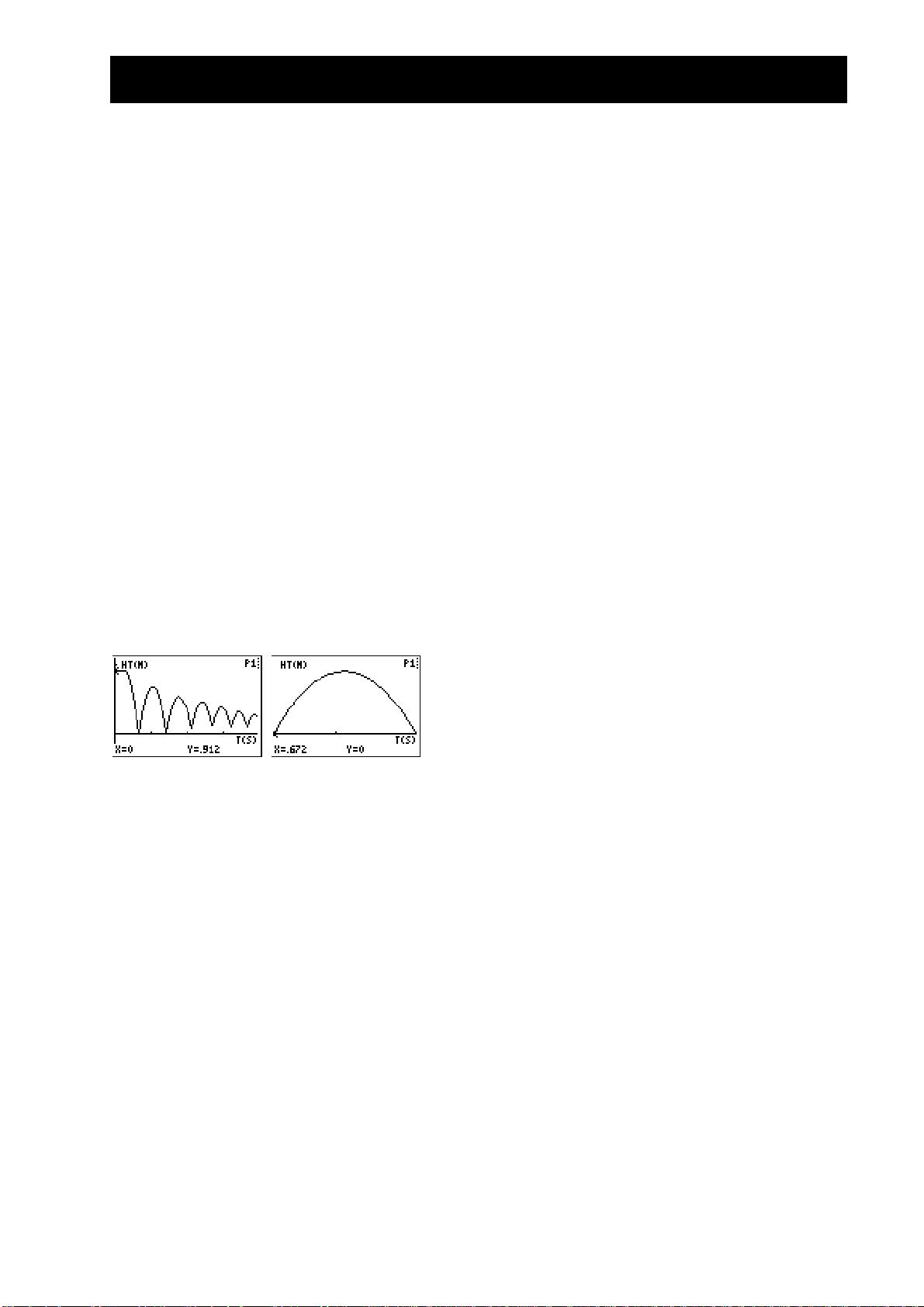
Øvelse 4 – Sprettende ball merknader til læreren

Begreper

Funksjon som undersøkes: parabel. Virkelige begreper som frittfallende objekter som

spretter, tyngdekraft og konstant akselerasjon er eksempler på parabelfunksjoner. I denne øvelsen undersøkes verdiene for høyde, tid og koeffisienten

A i annengradsligningen Y = A(X  H)

+ K, som

beskriver adferden for en sprettende ball.

Materialer

 kalkulator

CBR



CBR

 kalkulator-til-

-kabel

 stor ball (ca 20 cm diameter)  TI ViewScreen (valgfritt)

Hint

Denne øvelsen utføres best i grupper på to elever, en som holder ballen mens den andre trykker på ¤.

Se side 6–12 for flere hint om effektiv datainnsamling.

Grafen skal se ut som en sprettende ball. Hvis den ikke gjør det, må innsamlingen gjentas. Pass på at

CBR

er rettet rett mot ballen. Vi anbefaler å bruke en

forholdsvis stor ball.

Vanlige grafer

3. Avstand-tid-grafen for denne øvelsen representerer ikke avstanden fra

BALL BOUNCE

snur avstandsdataene slik at grafen

CBR

til ballen.

passer bedre til elevenes forventninger om ballens adferd. y = 0 på grafen er faktisk det punktet det ballen er lengst fra

CBR

, nå den

treffer gulvet.

4. Elevene bør innse at x-aksen representerer tid, ikke vannrett avstand.

7. Grafen for A = 1 er både omvendt og bredere enn inntegningen.

8. A < L1

9. parabel konkav opp; konkav ned; lineær

12. samme; matematisk representerer koeffisienten A utstrekningen av krumningen av parabelen; fysisk avhenger A av tyngdekraftens akselerasjon, som forblir konstant i alle sprettene.

Avanserte undersøkelser

Spretthøyden for ballen (maksimumshøyden for et bestemt sprett) kan beregnes slik:

, hvor

y er spretthøyden

h er høyden ballen ble sluppet fra

p er en konstant som avhenger av de fysiske

egenskapene til ballen og gulvets overflate x er sprettens nummer i rekken

Undersøkelser

Etter at et objekt blir sluppet, virker tyngdekraften på det (vi ser bort fra luftmotstanden). Så A avhenger av tyngdens akselerasjon, L9.8 meter/sekund

. Det negative fortegnet indikerer at

akselerasjonen er rettet nedover. Verdien for A er tilnærmet lik halvparten av

tyngdens akselerasjon, eller L4.9 meter/sekund

Mulige svar

1. tid (fra starten av datainnsamlingen); sekunder; høyde/avstand mellom ballen og gulvet; meter

2. utgangshøyden for ballen fra gulvet (toppunktene representerer øverste punkt i hver sprett); gulvet representeres av y = 0.

For en gitt ball og starthøyde vil spretthøyden minske eksponentielt for hver påfølgende sprett. Når x = 0, y = h, vil skjæringspunktet for y representere utgangshøyden.

Ivrige elever kan finne koeffisientene i denne ligningen ved hjelp av de innsamlede dataene. Gjenta øvelsen med forskjellige utgangshøyder eller med annen ball eller gulvoverflate.

Etter å ha tilpasset kurven manuelt, kan elevene bruke regresjonsanalyse til å finne funksjonen som best gjengir dataene. Velg ut én enkelt sprett ved hjelp av

QUIT

PLOT TOOLS, SELECT DOMAIN MAIN MENU

fra

. Følg prosedyrene for

. Velg deretter

kalkulatoren for å utføre en kvadratisk regresjonsanalyse på listene

og L2.

Tillegg

Integrer fart-tid-grafen, for forflytningen (samlet tilbakelagt avstand) for et fritt valgt tidsintervall. Legg merke til at forflytningen er null for et helt sprett (ballen begynner og slutter på gulvet).

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

Øvelse 4 – Sprettende ball parabel

Datainnsamling

Begynn med en testsprett. Slipp ballen (ikke kast den!).

➊

minst 0,5 meter over høyden for den høyeste spretten. Hold

Plasser

Hint:

sensoren rett over ballen og pass på at det ikke finnes noe annet i den klare sonen (se side 7).

CBR

Kjør

➋ ➌ ➍

➎

RANGER

Velg

APPLICATIONS

Velg

BALL BOUNCE

Hold ballen med utstrakte armer. Trykk på ›. Trigger-modus. Nå kan du koble

Trykk på ¤. Når det grønne lyset begynner å blinke, slipper du ballen og tar et

➏

skritt tilbake. (Hvis ballen spretter til siden, må du flytte deg slik at rett over den, men pass på at du ikke endrer høyden på

-programmet (se side 5 for tastekombinasjoner for hver kalkulator).

fra

MAIN MENU

fra

APPLICATIONS

. Velg

METERS

eller

FEET

-menyen. Det vises generelle instruksjoner.

angir innstillinger automatisk.

RANGER

fra kalkulatoren hvis du vil.

CBR

-programmet er nå i

hele tiden er

CBR

Du hører en klikkelyd mens dataene samles inn. Data for tid og avstand samles inn og fart og akselerasjon blir deretter beregnet. Hvis du har koblet

CBR

fra

kalkulatoren, må du koble dem sammen igjen når datainnsamlingen er fullført.

Trykk på ›. (Hvis grafen ikke ser bra ut, gjentar du fosøket.) Se på grafen. Svar

➐

på spørsmål 1 og 2 på oppgavearket.

Legg merke til at

➑

BALL BOUNCE

automatisk snudde avstandsdataene. Svar på

spørsmål 3 og 4.

OMME I GANG MED

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

Øvelse 4 – Sprettende ball

Undersøkelser

Avstand-tid-grafen for en sprett utgjør en parabel.

(forts.)

parabel

Trykk på ›. Velg

➊

PLOT TOOLS

fra

PLOT MENU

, og deretter

SELECT DOMAIN

velge ut den første fullstendige spretten. Flytt markøren til grunnlinjen for begynnelsen av spretten, og trykk på sprett, og trykk på

Grafen er i

➋

TRACE

›. Grafen tegnes på nytt med fokus på én enkelt sprett.

-modus. Bestem toppunktet for spretten. Svar på spørsmål 5 på

›. Flytt markøren til slutten på samme

oppgavearket.

Trykk på › for å gå tilbake til

➌ ➍

Toppunktet beregnes med annengradsligningen Y = A(X  H)2 + K som er egnet for denne analysen. Trykk på

PLOT MENU

œ. Slå av alle valgte funksjoner i

. Velg

MAIN MENU

. Velg

-editoren. Beregn

QUIT

toppunktet med annengradsligningen Yn=A(XH)^2+K.

Lagre verdien du registrerte i spørsmål 5 for høyden i variabelen K på Home-

➎

skjermbildet, lagre den tilsvarende tiden i variabel H, og lagre 1 i variabel A.

Trykk på  for å vise grafen. Svar på spørsmål 6 og 7.

➏

Prøv A = 2; 0; –1. Fullfør første del av tabellen i spørsmål 8, og svar på

➐

spørsmål 9.

Velg dine egne verdier for A til du har tall som stemmer overens med grafen.

➑

Registrer valgene dine for A i tabellen i spørsmål 8.

Gjenta øvelsen, men velg denne gangen ut den siste fullstendige spretten (lengst til

➒

høyre). Svar på spørsmålene 10, 11 og 12.

. Vi vil

Avanserte undersøkelser

Gjenta datainnsamlingen, men ikke velg ut én enkelt parabel.

➊

Registrer tid og høyde for hver påfølgende sprett.

➋

Bestem forholdet mellom høydene for de påfølgende sprettene.

➌

Forklar betydningen, hvis noen, av dette forholdet.

➍

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

Øvelse 4 – Sprettende ball

Navn ____________________________________

Datainnsamling

1. Hvilken fysisk størrelse representeres langs x-aksen? ________________________________________

Hva er målenheten? ___________________________________________________________________

Hvilken fysisk størrelse representeres langs y-aksen? ________________________________________

Hva er målenheten? ___________________________________________________________________

2. Hva representerer grafens høyeste punkt? _________________________________________________

Og det laveste? _______________________________________________________________________

3. Hvorfor ble grafen snudd av programmet

BALL BOUNCE

? _____________________________________

4. Hvorfor ser grafen ut som om ballen spratt bortover gulvet ? _________________________________

Undersøkelser

5. Registrer maksimumshøyden og den tilsvarende tiden for den første fullstendige spretten. ________

6. Stemte grafen for

= 1 med din graf? ___________________________________________________

7. Hvorfor eller hvorfor ikke? ______________________________________________________________

8. Fyll ut diagrammet nedenfor.

A Hvordan blir samsvaret mellom datagrafen og Yn-grafen?

9. Hva tyder en positiv verdi for

Hva tyder en negativ verdi for

Hva tyder en nullverdi for

på? ______________________________________________________

på? _________________________________________________________

10. Registrer maksimumshøyden og den tilsvarende tiden for den siste fullstendige spretten. _________

11. Tror du

12. Hvordan ble

Hva tror du

OMME I GANG MED

blir større eller mindre for den siste spretten? _____________________________________

egentlig? ________________________________________________________________

kan representere? _________________________________________________________

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

Øvelse 5 – Rullende ball merknader til læreren

Begreper

Funksjon som undersøkes: parabel. Å tegne en graf for en ball som ruller nedover et

skråplan med varierende helling gir en gruppe kurver som kan beregnes med en serie annengradsligninger. I denne øvelsen undersøkes verdiene av koeffisientene i annengradsligningen

y = ax

+ bx + c.

Materialer

 kalkulator

CBR



CBR

 kalkulator-til-

-kabel

 festeklemme  stor ball (ca. 20 cm. diameter)  langt skråplan (minst 2 meter – en

kryssfinerplate fungerer bra)

 transportør  bøker til å byge op skråplanet med  TI ViewScreen (valgfritt)

Hint

Diskuter hvordan dere skal måle vinkelen på skråplanet. La elevene bruke fantasien her. De kan bruke trigonometrisk beregning, brettet papir eller en transportør.

Se side 6–12 for flere hint om effektiv datainnsamling.

Vanlige grafer

Mulige svar

1. den tredje grafen

2. tid; sekunder; avstanden mellom objektet og CBR; meter

3. varierer (skal være en halv parabel, konkav opp)

4. en parabel (kvadratisk)

5. varierer

6. varierer (skal være en parabel med økende krumning)

7. 0¡ er flat (ballen kan ikke rulle); 90¡ er det samme som fritt fall (fallende ball)

Undersøkelser

Et legemes bevegelse bare påvirket av tyngdekraften er et populært emne i fysikken. Slik bevegelse uttrykkes vanligvis med en bestemt form av annengradsligningen

s = ½at

0 0 0 0

I annengradsligningen y = ax representerer y avstanden mellom

+ v

t + s

hvor

s er et objekts posisjon ved tidspunktet t a er akselerasjonen

er utgangsfarten

er utgangsposisjonen

+ bx + c,

CBR

og ballen ved tidspunktet x hvis ballens utgangsposisjon var c, utgangsfart var b og akselerasjonen er 2a.

Avanserte undersøkelser:

Siden ballen er i ro når den slippes, skal b være tilnærmet lik null ved hvert forsøk. c skal være tilnærmet lik utgangsavstanden, 0,5 meter. a øker med hellingsvinkelen.

Hvis elevene bruker ligningen y = ax manuelt, bør du kanskje gi dem hint om mulige verdier for b og c. Du kan også lede dem til å utføre en kvadratisk regresjon på listene med kalkulatorene. Ballens akselerasjon er forårsaket av jordens tyngdekraft, så jo mer skråplanet peker nedover (jo større hellingsvinkel), jo større verdi for a. Maksimum a oppstår for q = 90¡, minimum for q = 0¡. a er faktisk proporsjonal med sinus av q.

+ bx + c

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

Øvelse 5 – Rullende ball parabel

Datainnsamling

➊

Svar på spørsmål 1 på oppgavearket. Sett opp skråplanet med 15° helling. Fest klemmen til øverste kant av skråplanet. Fest plasser det vinkelrett i forhold til skråplanet. Koble kalkulatoren til

til klemmen. Åpne sensorhodet og

CBR

Merk et punkt på skråplanet 0,5 meter fra

. Få én elev til å holde ballen på dette

CBR

merket, mens en annen holder kalkulatoren.

Still sensoren inn rett mot ballen og pass på at det ikke finnes noe annet i den

Hint:

klare sonen (se side 7).

Kjør

➋

➌

RANGER

SETUP/SAMPLE

Trykk på › for å vise innstillingene. For denne øvelsen skal de være slik:

REALTIME: NO

TIME (S): 3 SECONDS

DISPLAY: DISTANCE

BEGIN ON: [ENTER]

SMOOTHING: LIGHT

-programmet (se side 5 for tastekombinasjoner for hver kalkulator). Velg fra

MAIN MENU

UNITS: METERS

Du finner instruksjoner for endring av innstillinger på side 38.

Når innstillingene er riktige, velger du

➍

START NOW

. Trykk på › for å begynne

datainnsamlingen.

Når klikkelyden begynner, slippes ballen øyeblikkelig (ikke dytt den), og eleven tar et

➎

skritt tilbake.

Når innsamlingen er ferdig, vises avstand-tid-grafen automatisk. Svar på spørsmål 2

➏

og 3.

Trykk på › for å vise

➐

PLOT MENU

Flytt markøren til der ballen ble sluppet, og trykk på ballen nådde bunnen av skråplanet, og trykk på

. Velg

PLOT TOOLS

›. Grafen plottes på nytt med

og deretter

›. Flytt markøren til der

SELECT DOMAIN

fokus på den delen av forsøket som tilsvarer ballens vei nedover skråplanet. Svar på

spørsmål 4 og 5.

OMME I GANG MED

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

Øvelse 5 – Rullende ball

Undersøkelser

Undersøk hva som skjer ved endring av hellingsvinkel.

Forutsi hva som vil skje hvis hellingen økes. Svar på spørsmål 6.

➊

Juster hellingen til 30¡. Gjenta trinn 2 til og med 6. Legg inn denne grafen på

➋

tegningen i spørsmål 6 med navnet 30¡.

Gjenta trinn 2 til og med 6 for hellinger på 45¡ og 60¡ og legg dem inn i tegningen.

➌ ➍

Svar på spørsmål 7.

Avanserte undersøkelser

Juster tidsverdiene slik at x = 0 for utgangshøyden (tidspunktet da ballen ble sluppet). Du kan gjøre dette manuelt ved å trekke x-verdien for det første punktet fra alle punktene i grafen, eller du kan skrive inn

Beregn verdiene for a, b og c for gruppen med kurver etter ligningen

➊

y = ax

Hva er største og minste mulige verdi for a? Hvorfor?

➋

+ bx + c ved 0¡, 15¡, 30¡, 45¡, 60¡, 90¡.

(forts.)

L1(1)"A:L1NA"L1

parabel

Skriv et uttrykk som beskriver det matematiske forholdet mellom a og

➌

hellingsvinkelen.

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

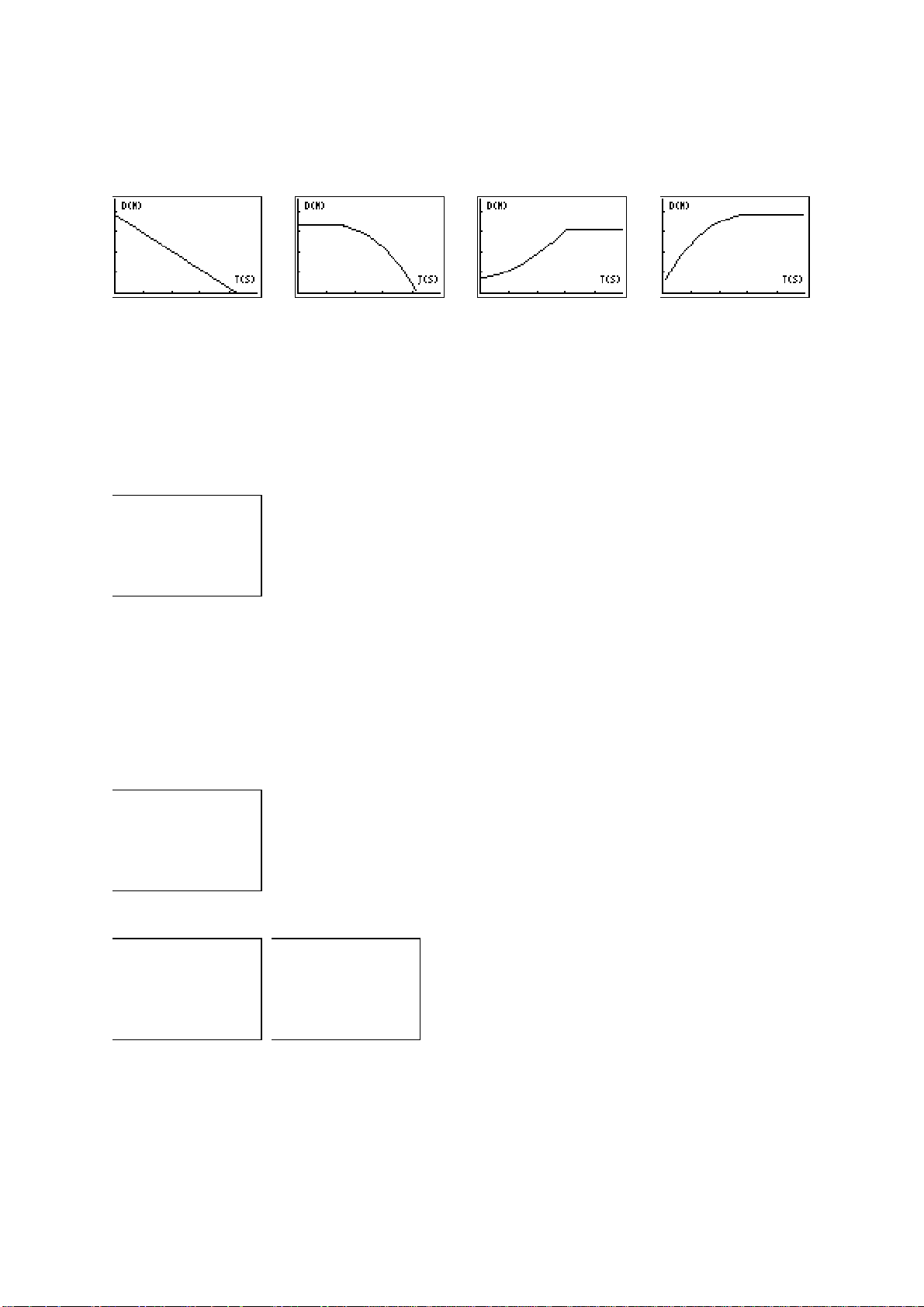
Øvelse 5 – Rullende ball

Navn ____________________________________

Datainnsamling

1. Hvilken av disse grafene tror du best tilsvarer avstand-tid-grafen for en ball som ruller nedover et skråplan?

2. Hvilken fysiske egenskap representeres langs x-aksen? ______________________________________

Hva er målenheten? ___________________________________________________________________

Hvilken fysiske egenskap representeres langs y-aksen? ______________________________________

Hva er målenheten? ___________________________________________________________________

3. Tegn inn hvordan grafen faktisk ser ut. Sett navn på aksene. Merk grafen der ballen ble sluppet og der den kom til bunnen av skråplanet.

4. Hvilke funksjonstype representerer denne grafen? __________________________________________

5. Diskuter hvordan du har endret din forståelse fra grafen du valgte i spørsmål 1 til kurven du tegnet

inn i spørsmål 3. ______________________________________________________________________

_____________________________________________________________________________________

Undersøkelser

6. Tegn inn kurven slik du tror den vil se ut med større helling. (Gi den navnet forutsagt.)

7. Tegn inn og sett navn på grafene for 0

¡ og 90¡:

OMME I GANG MED

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

Lærerveiledning

Hvordan kan undervisningen forandres med CBR?

er et lettbrukt system med funksjoner som gjør at det går enkelt og raskt å

CBR

innarbeide den i undervisningen.

Med

får du betydelige forbedringer i forhold til andre datainnsamlingsmetoder du

CBR

kanskje har brukt tidligere. Dette kan i sin tur lede til en omstrukturering av tidsbruken i klasserommet, etter hvert som elevene blir ivrigere til å ville bruke virkelige data.

Du vil raskt se at elevene føler sterkere tilhørighet til dataene fordi de faktisk deltar i

innsamlingsprosessen i stedet for å bruke data fra lærebøker, tidsskrifter eller statistiske tabeller. Dette gir dem en sterkere opplevelse av at de begrepene de undersøker i klasserommet, er en del av den virkelige verden og ikke bare abstrakte ideer. Men det betyr også at hver elev vil ønske å delta praktisk i innsamlingen av data.

Datainnsamling med

er betydelig mer effektivt enn å sette opp forsøk og måle

CBR

manuelt med linjal og stoppeklokke. Siden flere datapunkter gir bedre oppløsning, og siden en ultralyd bevegelsessensor er svært nøyaktig, blir formen på kurvene tydeligere. Du trenger mindre tid til datainnsamling, og får dermed mer tid til analyse og undersøkelser.

Med

kan elevene gjøre gjentatte observasjoner og undersøke variasjoner i hva-

CBR

hvis-scenarier. Spørsmål som “Er parabelen den samme for første og siste sprett?” blir naturlige og verdifulle tillegg.

Med den styrken som ligger i visualiseringen, kan elevene raskt assosiere de

inntegnede listedataene med de fysiske størrelsene og de matematiske funksjonene som dataene beskriver.

Andre endringer oppstår når data fra virkelige hendelser samles inn.

lar elevene

CBR

undersøke de underliggende forholdene både numerisk og grafisk.

Undersøke data grafisk

Bruk automatisk genererte grafer for avstand, fart og akselerasjon i forhold til tid for undersøkelser som:

Hva er den fysiske betydningen av skjæringspunktet for y? og for x? hellingen?

maksimum? minimum? den deriverte? integralene?

Hvordan gjenkjenner vi hvilken funksjonstype (lineær, parabel osv.) grafen

representerer?

Hvordan ville vi beregne dataene med en representativ funksjon? Hva er betydningen

av de forskjellige koeffisientene i funksjonen (f.eks. AX

Undersøke data numerisk

+ BX + C)?

Elevene kan bruke statistiske metoder (middeltall, medianer, modalverdi, standardavvik osv.) som tilsvarer deres kunnskapsnivå, til å undersøke de numeriske dataene. Når du går ut av

RANGER

-programmet, får du en påminnelse om listene hvor

REALTIME=NO

dataene for tid, avstand, fart og akselerasjon er lagret.

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

Lærerveiledning

(forts.)

CBR-grafer – binder den fysiske verden og matematikken sammen

Grafene som blir tegnet på grunnlag av dataene som blir samlet inn med

RANGER,

er en visuell framstilling av forholdene mellom den fysiske og den matematiske beskrivelsen av bevegelse. Elevene bør oppmuntres til å gjenkjenne, analysere og diskutere formen på en graf både med fysiske og matematiske begreper. Mer samtale og flere oppdagelser er mulig når funksjonene legges inn i Y=-editoren og vises sammen med grafene.

En avstand-tid-graf representerer tilnærmet posisjon for et objekt (avstand fra

CBR

) ved hvert øyeblikk i tid mens en måling gjøres. Y-aksens målenhet er meter, x-aksens målenhet er sekunder.

En fart-tid-graf representerer den tilnærmede farten på objektet (i forhold til og i

retning av

) på hvert prøvetidspunkt. Y-aksens målenhet er meteràsekund,

CBR

x-aksens målenhet er sekunder.

En akselerasjon-tid-graf representerer tilnærmet mål på endring i fart for et objekt

(i forhold til og i retning av

meter/sekund

Den første deriverte av et hvilket som helst punkt på avstand-tid-grafen er farten i det

, x-aksens målenhet er sekunder.

) på hvert prøvetidspunkt. Y-aksens målenhet er

CBR

angitte øyeblikket.

Den andre deriverte av et hvilket som helst punkt på fart-tid-grafen er akselerasjonen i det angitte øyeblikket. Dette finnes også med den andre deriverte i et hvilket som helst punkt på avstand-tid-grafen.

En bestemt integral (området mellom grafen og x-aksen mellom to fritt valgte

punkter) på fart-tid-grafen tilsvarer forflytningen (netto avstand tilbakelagt) i det angitte tidsrommet.

En vanlig fart-tid-graf med

representerer fart uten retning. Bare størrelsen (som

CBR

kan være positiv, negativ eller null) blir gitt. Retningen angis bare implisitt. En positiv fartsverdi angir bevegelse bort fra

måler avstand bare langs en rett linje fra sensoren. Hvis et objekt beveger seg i en

CBR

vinkel i forhold til denne linjen, vil

og en negativ verdi angir bevegelse mot

CBR,

derfor bare beregne den komponenten av

CBR

farten som er parallell med denne linjen. Et objekt som beveger seg vinkelrett på denne linjen, vil for eksempel vise en fart lik null.

CBR

OMME I GANG MED

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

Lærerveiledning

(forts.)

Avstand, fart og akselerasjon i matematikken

gjennomsnitt

N d

= helling på avstand-tid-graf

N t

Avstand-tid-graf

punkt

lim

@t"

(

d(s)

)

hvor s = avstand

Fart-tid-graf

N v

gjennomsnitt

punkt

lim

@t"

(

)

= helling på fart-tid-graf

N t

Arealte under fart-tid-grafen fra t1 til t2 = @d = (d avstand tilbakelagt).

t=2

⌠

⌡

t=1

v(dt)

Så, @d =

(

t=2

∑

t=1

v(@t)

or @d =

)

) = forflytning fra t1 til t2 (netto

2Nd1

Akselerasjon-tid-graf

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

Lærerveiledning

Web-ressurser

(forts.)

På vår web-adresse,

en liste over tilleggsmateriale for bruk med

et bibliotek med programmer for bruk med

en side med øvelser og programmer utviklet og lagt inn av lærere som deg selv

CBR

nærmere informasjon om innstillinger og programmeringskommandoer for

Andre ressurser

Texas Instruments’ Explorations-bøker inneholder tilleggsmateriale for TI grafkalkulatorer, inkludert bøker med elevøvelser for naturfagundervisning i de øvre klassene på ungdomsskolen og videregående skole.

http:ààwww.ti.comàcalc

, finner du:

CBR, CBL

og TI grafkalkulatorer

-programmer som gir tilgang til tilleggsfunksjoner i

som passer for matematikk- og

CBR

OMME I GANG MED

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

CBR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

CBR-data lagres i lister

Innsamlede data lagres i listene L1, L2, L3 og L4

Når

samler inn data, overføres dataene automatisk til kalkulatoren og lagres i lister.

CBR

Hver gang du går ut av lagret.

inneholder tidsdata.

inneholder avstandsdata.

inneholder fartsdata.

inneholder akselerasjonsdata.

Som eksempel representerer det femte elementet i listen L1 tidspunktet da det femte datapunktet ble samlet inn, og det femte elementet i listen for det femte datapunktet.

REALTIME=YES-

modus blir bare dataene for den ønskede grafen (avstand, fart eller akselerasjon) beregnet og overført. I overført.

Innstillinger lagres i listen L5

Med

RANGER SETUP

(se side 38).

Når du overfører

RANGER

med standardinnstillinger.

RANGER

-programmet, får du en påminnelse om hvor dataene er

representerer avstanden

REALTIME=NO-

modus blir alle dataene beregnet og

-skjermen er det enkelt å endre de vanligste parameterne på

-programmet fra

, blir L5 automatisk erstattet av en ny liste

CBR

Se side 40–41 hvis du vil ha informasjon om programmeringskommandoer som endrer andre innstillinger.

Bruke datalistene

Listene slettes ikke når du går ut av annen grafisk, statistisk og numerisk undersøkelse og analyse.

Du kan plotte listene mot hverandre, vise dem i listeredigering, bruke regresjonsanalyse og utføre andre analyser. Du kan for eksempel samle dataene fra pendelbevegelsen ved hjelp av undersøke elliptiske funksjoner. (Det kan hende at du også må justere vinduet.)

RANGER

, gå ut av

RANGER

-programmet. De er derfor tilgjengelige for

og deretter plotte fart-akselerasjon-grafen for å

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

RANGER-innstillinger

Endre innstillinger for RANGER

RANGER

➊

viser de vanligste innstillingene før datainnsamlingen begynner.

Velg

SETUPàSAMPLE

fra

MAIN MENU

RANGER

-programmet. Gjeldende innstillinger

vises. 4 angir plasseringen av markøren.

UNITS:

›

START NOW

eller

= 1–99

FEET

SECONDS

ACCELERATION

eller

10-SECOND DELAY

eller

HEAVY

eller

(

bare ved

REALTIME=NO

YES

TOTAL TIME

DISTANCE, VELOCITY

[ENTER], [TRIGGER]

NONE, LIGHT, MEDIUM

METERS

for å gå gjennom alle tilgjengelige valg. Når riktig alternativ vises,

MAIN MENU

REALTIME:

TIME (S):

DISPLAY:

BEGIN ON:

SMOOTHING:

Trykk på c eller b for å gå til den innstillingen du vil endre.

➋

Trykk på

➌

trykker du på c for å gå til neste innstilling. Hvis du vil endre innstilling for skriver du inn ett eller to sifre og trykker på c eller b.

Når alle innstillingene er riktige, trykker du på c eller b til markøren er på

➍

START NOW

Hvis du vil fortsette, trykker du på

Hvis du vil gå tilbake til

De nye innstillingene blir stående med mindre du velger

›

MAIN MENU

, trykker du på e og deretter på

SET DEFAULTS

›

eller kjører en

applikasjon eller et program som endrer innstillingene. Hvis du gjør endringer i

RANGER

gang du kjører

-programmet eller sletter L5, kan standardinnstillingene bli gjenopprettet neste

RANGER

TIME

utenfor

)

Gjenopprette standardinnstillinger for RANGER

Standardinnstillingene passer til de fleste prøvesituasjoner. Hvis du er usikker på hvilke innstillinger du skal bruke, bør du begynne med standardinnstillingene og justere derfra.

➊

Velg

SET DEFAULTS

fra

MAIN MENU

Innstillingene endres til standard, og

Hvis du vil endre en innstilling fra standarden, følger du instruksjonene ovenfor.

➋

Hvis du vil fortsette, trykker du på

➌

Andre RANGER-innstillinger

Med

RANGER

-programmet har du tilgang til de innstillingene det er vanligst å endre. har også andre innstillinger. På side 40–41 finner du nærmere informasjon om programmeringskommandoer som endrer disse innstillingene.

RANGER

›

programmet.

-skjermen vises.

SETUP

når markøren er på

START NOW

CBR

OMME I GANG MED

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

Bruke CBR med CBL eller med CBL-programmer

Bruke CBR som en vanlig bevegelsessensor med CBL

kan brukes som en vanlig bevegelsessensor med Texas Instruments

CBR

(Kalkulatorbasert laboratoriumé).

Du må ikke koble sammen Kalkulatoren må være koblet til

Du må kanskje endre fungerer ikke med

CBL

CBR

CBL

-programmet som angitt nedenfor.

Bruke CBR med programmer skrevet for CBL

Du kan bruke

med de fleste

CBR

CBL

bevegelsessensor, uten endringer eller med bare minimale endringer i programmet.

Stopp datainnsamlingen: Med enkelte datainnsamling fortsetter

å samle inn data til du stanser den på en av følgende

CBR

måter:

\\Den spesielle kabelen som kreves for å koble sammen følger med.

samtidig som

CBL

er koblet til en kalkulator.

CBR

RANGER

-programmer som er skrevet for en

-programmer med

CBL

REALTIME=YES-

system

CBL

CBR

-programmet

CBL,

Trykk på ¤ på

Legg inn utsagn i det eksisterende

. Utsagnet må være på et punkt etter at dataene er overført og vist. For eksempel:

CBR {6,0}"L6:SEND L6

CBR

-programmet til å sende kommandoen {6,0} til

CBL

Slå lyden av og på: Hvis du vil slå av lyden, legger du inn utsagn i det eksisterende programmet som sender kommandoen {6,3} til

. Utsagnet må være på et punkt før

CBR

datainnsamlingen begynner. For eksempel:

{6,3}"L6:SEND L6

Hvis du vil slå på lyden, kjører du bare

RANGER

Hvis det oppstår problemer: Hvis du kjører et reagere eller har låst seg, kjører du

RANGER

(se side 36) om du kan finne en oppdatert versjon av

-programmet.

-program og

CBL

ikke ser ut til å

CBR

-programmet. Se etter på TIs web-side

-programmet.

CBL

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

Programmeringskommandoer

Kommando 0 Gjenoppretter og tilbakestiller {0}

Fjerner alt. Tilbakestiller standarder. Kanal 11 velges automatisk.

Kommando 1 Fjerner kanal {1,0}

Fjerner kanal.

Kommando 1 Kanal {1,11,

operasjon

REALTIME=NO

operasjon

REALTIME=YES

etterbehandling

0 (standard) Ingen 1( 2(

temperaturkonvertering

0 (standard) Deaktiverer temperaturkompensasjon 1 Aktiverer temperaturkompensasjon.

REALTIME=NO REALTIME=NO

) Fjerner alt. Tilbakestiller standarder. ) Meter ) Meter ) Fot

) Fjerner alt. Tilbakestiller standarder. ) Meter, ) Meter, ) Fot, ) Meter, ) Fot, ) Meter, ) Fot,

)dàdt (første deriverte) )d

Kommando 2 Dataoppsett {2,

datatype

1 (standard) Liste

Kommando 3 Prøve/Trigger {3,

prøvetid

0,005–1500 (0.1) Tid i sekunder mellom hver prøve 0,0001–0.005 Avrunder til 0,005 1500<x<16000 Avrunder til 1500

prøve#

L1 Velger

REALTIME=NO

1–512 (

trigger

0 Begynner innsamling uten Trigger-tasten 1 (standard) Begynner innsamling ved trykk på ¤. 7 Venter 10 sekunder før innsamlingen begynner

registreringstid

0 (standard) Ingen

REALTIME=NO

filter

(se kommando 1,

0 (standard) Ingen filtrering

REALTIME=NO

1 (

REALTIME=NO

2 (

REALTIME=NO

3 (

REALTIME=NO

4 (

REALTIME=NO

5 (

REALTIME=NO

6 (

REALTIME=YES

7 (

REALTIME=YES

8 (

REALTIME=YES

9 (

) Tar fra 1 til 512 prøver.

) Absolutt tid (starter ved tid 0 og justerer deretter prøvetiden ) ) Relativ tid (starter ved tid 0 og justerer deretter prøvetiden )

operasjon

-feltet)

) 5-punkts Savitzsky-Golay-glatting ) 9-punkts Savitzsky-Golay-glatting ) 17-punkts Savitzsky-Golay-glatting ) 29-punkts Savitzsky-Golay-glatting ) 3-punkts medianbeskjæringsfilter ) 5-punkts medianbeskjæringsfilter

) Lett ) Middels ) Tungt

Resultater

datatype

Resultater

prøvetid,prøve#,trigger

Resultater

operasjon,etterbehandling

CBR

returnerer {

CBR

returnerer {

CBR

returnerer {

CBR

returnerer {

CBR

returnerer {

CBR

returnerer {

CBR

returnerer {

àdt2 (andre deriverte)

avstand,@tid avstand,@tid

avstand,@tid

avstand,fart,@tid

avstand,fart,akselerasjon,@tid

,0,0,0,0,0,0,0}

,0,0,0,0,

REALTIME=YES

-modus for datainnsamling

sporingsfilter

temperaturkonvertering

,0,

} }

}

registreringstid,filter

}

OMME I GANG MED

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

Programmeringskommandoer

(forts.)

Kommando 4 Temperaturkompensasjon {4,

ligning_nummer

ligningstype

temperatur

enheter

Kommando 5 (

første_kanal

datautvalg

data_begynn

data_slutt

0 (standard) Gjenoppretter alle formler 4 Tilordner ligning 4.

0 (standard) Fjerner ligning 13 Tilordner temperaturkompensasjon.

flytende punkttall Angir gjeldende temperatur.

0 (standard) Ingen (ignoreres av 1 Angir grader = Fahrenheit. 2 Angir grader = Celsius. 3 Angir grader = Kelvin. 4 Angir grader = Rankin hvor R = F + 459,7.

REALTIME=NO

0 (standard) Velger laveste aktive kanal 1, 2, 3, 11, 21 Angir lydkanal M1 Registrerer tidsliste

0 Filterdata {avstand} 1 Filterdata dàdt {fart} 2 Filterdata d 3 Rådata {avstand} 4 Rådata dàdt- {fart} 5 Rådata d

1–512 Første dataelement for GET

0–512 Siste dataelement for GET (0 = siste prøve)

) Dataområdeoppsett {5,

Resultater

Kommando 6 Systemvalg {6,

systemkommando

0 Stopper datainnsamling (for CBL-kompatibilitet). 2 (standard) Stopper datainnsamling 3 Slår av lyd (lyd av ved strømtilkobling). 4 Slår på lyd (lyd på ved strømtilkobling). 5 Angir ID-nummer ( 6 Bruker nytt filter på tidligere data (

operasjon

Flytende punkttall ID-nummer på formen 0–6 Nytt filter på tidligere innsamlede data (

Resultater

Kommando 7 Ønsket status {7}

Returnerer en liste som inneholder:

10.rrrr Enhetskode.Rom-Versjon 0–99 Siste feilkode (0 = ingen feil) 0–2 Batteritilstand (0 = OK; 1 = lav under datainnsamling; 2 = lav hele tiden) 11 identifikator for lydkanal prøvetid Gjeldende prøveintervall i sekunder triggervilkår Gjeldende triggervalg i bruk funksjon Gjeldende kanalfunksjon (1–9) etterbehandling Gjeldende valg for etterbehandling (0–2) filter Gjeldende filtreringsnivå (0–9) prøver # av tilgjengelige prøver; 0–512 registreringstid Registrert tidsvalg (0–2) temperatur Temperatur i bruk (¡C) piezo_flagg 0 = lyd av; 1 = lyd på systemtilstand 1 = ikke oppsett; 2 = aktivert; 3 = trigger/innsamling; 4 = ferdig vindu_start 0 = ingen kommando 5 ennå; 1–512 vindu_slutt 0 = bruk # av elementer; 1–512 id_nummer 6-sifret ID # (standard 0,00000) fra kommando 6

ligningnummer,ligningtype,temperatur,enheter

CBR

). Konverterer T-grader til Celsius.

første_kanal,datautvalg,data_begynn,data_slutt

àdt2 {akselerasjon}

systemkommando[,operasjon]

operasjon

n.nnnnn

systemkommando

(

= 5)

}

kreves).

operasjon

systemkommando

(

REALTIME=NO

kreves).

systemkommando

REALTIME=YES

; M1

}

= 5)

= 6)

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

Batterier

Batteritype

er beregnet for bruk med 4 AA alkaliske batterier.

CBR

bare hvis den er koblet til en

Installere batterier

Hold

opp-ned, og bruk tommelen til å skyve batteridekselet mot bakre ende av

CBR

CBL

kan brukes uten batterier

CBR

Plasser batteriene i henhold til illustrasjonen inne i batterirommet. To batterier skal ha positiv side opp på siden merket +.

Skyv på plass dekselet.

CBR-advarsler ved lite strøm

har to mekanismer for å varsle deg om at batteriene har lite strøm:

CBR

RANGER

-programmet viser en advarsel på kalkulatorskjermen under forsøk på å samle

er klar til å begynne datainnsamlingen.

CBR

To batterier skal ha negativ side opp på siden merket

inn data.

Den røde lampen blinker under innsamling av data.

CBR-batteristatus

Du kan kontrollere batterienes tilstand før du begynner å samle inn data. Velg

MAIN MENU,

Forsiktighetsregler for batterier

Bytt alltid alle fire batterier samtidig. Ikke bland batterimerker. Ikke bland batterityper

og velg deretter

CBR STATUS

. Battery status OK eller

REPLACE

vises.

TOOLS

av samme merke.

Installer batteriene etter illustrasjonene inne i batterirommet.

Lever inn brukte batterier til mottak for farlig avfall med én gang. Oppbevar dem utilgjengelig for barn.

Ikke varm opp, brenn eller stikk hull på batterier. Batterier inneholder farlige kjemikalier og kan eksplodere eller lekke.

Ikke bland batterier som kan lades med batterier som ikke kan lades.

Ikke plasser batterier som ikke kan lades, i en batterilader.

CBR

fra

OMME I GANG MED

CBR

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

Hvis det oppstår problemer

Hvis du har dette problemet: Prøver du dette:

Problemer med å overføre

RANGER-

programmet eller samle inn data

Se etter at kalkulatoren o kontaktene godt inn på begge ender av kabelen.

Sjekk strømmen i batteriene (se side 42).

CBR

begynner å samle inn data på

egen hånd

Hvis du plasserer CBR med

dermed aktivere datainnsamling. Trykk på

inn o stanse datainnsamlingen.

CBR,

LINK ERROR

Før du le

QUIT)

-melding Koble

er fra deg

og eventuelle andre

CBR

til kalkulatoren med kalkulator-til-

Se etter at kalkulatoren o kontaktene godt inn på begge ender av kabelen.

Hvis du ikke vil (eller kan) koble

gå ut av programmet

, og deretter velger du

Ikke nok minne Du må ha nok minne til

rammene og listene krever omtrent 17 500 byte. Slett programmer

Pro og/eller data.

Kalkulatoren har ikke samme kommandoer som i beskrivelsene av øvelsene

Dataen ser feil ut:

Punktene ligger ikke på kurven

ujevne grafer

flate grafer

brutte grafer

Denne veilednin

CBR

, så det kan hende at noen av menynavnene, skjermene eller tastene

her ikke stemmer nø

er nærmest. Hvis det for eksempel står i instruksjonen “Velg

MATCH

”, må du på TI-83 velge Gjenta prøven, og pass på at CBR er rettet rett mot objektet. Les side 6–12 om hvordan du samler inn gode dataprøver. Kontroller at den klare sonen ikke inneholder elever, bord eller andre

objekter. Når du bruker to

seg ferdig med datainnsamlingen før den neste begynner.

en gjelder alle de TI-kalkulatorene som kan brukes med

aktig med det du ser på din kalkulator. Velg det som

CBR

-enheter samtidig i samme rom, bør én gruppe gjøre

Se etter at kalkulatoren o kontaktene godt inn på begge ender av kabelen.

Sjekk strømmen i batteriene (se side 42). Se etter om graden av glatting er for høy eller lav.

CBR

fungerer ikke med TI-85 Se etter om bokstavene “

kalkulatoren for å angi kompatibilitet med TI

85 inneholder ikke muligheter for tegning av statistiske grafer, så

enkelte undersøkelser (som bruk av

85.

Mistet kalkulator-til-

utføres med TI

CBR

-kabel Du kan bruke kalkulator-til-kalkulator-kabelen som fulgte med kalkulatoren. (Kalkulator-til-kalkulator-kabelen er m kanskje bestille en ny kabel.)

Ofte lite strøm i batteriene Før du legger bort

QUIT)

og eventuelle andre

CBR,

kalkulatoren.

Når du prøver å kjøre programmet, skjer ingenting

RANGER

Hvis du redigerer eller viser minutter for kalkulatoren å klar du vil bruke det. Dette er normalt.

Feilmelding: Variable is locked or

protected (gjelder bareTI

92)

Du må låse opp variablene L1, L2, L3, L4 o kalkulatoren.

CBR

er skikkelig koblet sammen. Trykk alltid

-tasten ned, kan

må du gå riktig ut av

CBR-

CBR

RANGER

CBR

CBL

eller

-programmer.

er skikkelig koblet sammen. Trykk alltid

CBR

til kalkulatoren, trykker du på

-programmet og datalistene.

DIST MATCH

er skikkelig koblet sammen. Trykk alltid

” vises på slutten av serienummeret bak på

CBL



på inntegnede data) kan ikke

CBR

QUIT

RANGER

-kabelen.

CBR

-tasten bli trykt

på nytt for å

-programmet (med

e kortere, så du vil

må du gå riktig ut av

CBR-

RANGER

CBL

eller

-programmet, kan det ta opptil to

RANGER

-programmet (med

-programmer og koble

øre programmet for kjøring neste gan

L5. Se håndboken for

DISTANCE

CBR

fra

for å

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

Informasjon om service og garanti på TI-produkter

Informasjon om service for TI-produkter

Nærmere informasjon om service for TI-produkter fås ved henvendelse til TI via elektronisk post eller ved å slå opp på hjemmeside for TI-kalkulatorer på Internett.

Elektronisk post:ti-cares@ti.com Internettadresse:http://www.ti.com/calc

Informasjon om service og garantibetingelser

Du kan lese mer om garantibetingelser, garantitid samt om produktservice på garantierklæringen som medfølger dette produkt. Du kan også henvende deg til din lokale forhandler/distributør for Texas Instruments.

OMME I GANG MED

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

CBR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

RANGE

MAIN MENU

SETUP / SAMPLE

SET DEFAULTS

NO YES

1-99 (REALTIME=NO)

DISTANCE VELOCITY ACCELERATION

[ENTER] [TRIGGER] DELAY

NONE LIGHT MEDIUM HEAVY

METERS FEET

APPLICATIONS

REALTIME=NO

PLOT MENU

REALTIME=YES

TOOLS

QUIT

APPLICATIONS

UNITS METERS FEET

DISTANCE-TIME VELOCITY-TIME ACCELERATION-TIME PLOT TOOLS REPEAT SAMPLE MAIN MENU QUIT

SHOW PLOT SELECT DOMAIN REPEAT SAMPLE MAIN MENU QUIT

TOOLS GET CBR DATA GET CALC DATA CBR STATUS STOP/CLEAR CBR MAIN MENU

DISTANCE MATCH VELOCITY MATCH BALL BOUNCE MAIN MENU

PLOT TOOLS SELECT DOMAIN SMOOTH DATA PLOT MENU

DATA SMOOTHING LIGHT MEDIUM HEAVY NONE

OPTIONS SAME MATCH NEW MATCH APPLICATIONS MAIN MENU QUIT

ENNE SIDEN KAN KOPIERES UNDER FORUTSETNING AV AT MERKNAD OM COPYRIGHT FOR

EXAS INSTRUMENTS INCORPORATED

INKLUDERES

OMME I GANG MED

CBR

Texas instruments CBR User Manual [no]

Specifications and Main Features

Frequently Asked Questions

User Manual