Texas instruments CBL 2 GETTING STARTED

Download

RINCIPES D

RINCIPES DRINCIPES D

DUDU

5 5

CBR

CBR 2™

CBRCBR

OUVEMENT À

OUVEMENT À OUVEMENT À

EXERCICES POUR LES E

EXERCICES POUR LES ELEVES

EXERCICES POUR LES EEXERCICES POUR LES E

’’’’

UTILISATION

UTILISATION UTILISATION

2™ D

2™ 2™

AVEC

AVECAVEC

ÉTECTEUR DE

ÉTECTEUR DE ÉTECTEUR DE

LTRASONS

LTRASONSLTRASONS

LEVES

LEVESLEVES

Important

Texas Instruments ou tout autre fournisseur tiers n’offre aucune garantie, expresse ou tacite, concernant notamment, mais pas exclusivement, la qualité de ses produits ou leur capacité à remplir quelque application que ce soit, qu’il s’agisse de programmes ou de documentation imprimée. Ces produits sont en conséquence vendus “tels quels”.

En aucun cas Texas Instruments Instruments ou tout autre fournisseur tiers ne pourra être tenu pour responsable des préjudices directs ou indirects, de quelque nature que ce soit, qui pourraient être liés ou dûs à l’achat ou à l’utilisation de ces produits. La responsabilité unique et exclusive de Texas Instruments, quelle que soit la nature de l’action, ne devra pas excéder le prix d’achat du présent équipement. En outre, Texas Instruments décline toute responsabilité en ce qui concerne les plaintes d’utilisateurs tiers.

Les professeurs sont expressément autorisés à reproduire ou à photocopier, en quantités limitées aux besoins de leurs cours, ateliers ou séminaires, les pages de cet ouvrage portant la mention de copyright Texas Instruments. Ces pages sont destinées à être reproduites par les professeurs pour l'usage exclusif de leurs cours, ateliers ou séminaires, à la seule condition que la mention de copyright figure sur chaque page. Les copies réalisées ne peuvent être ni vendues ni distribuées en dehors du contexte auquel elles sont destinées. En dehors des cas précités, une autorisation écrite préalable doit être obtenue de Texas Instruments Incorporated pour toute reproduction ou transmission, partielle ou totale, de cet ouvrage, par quelque moyen que ce soit, électronique ou mécanique, y compris tout système de stockage ou de récupération de données, sauf autorisation expresse stipulée par les lois fédérales sur le copyright. Veuillez envoyer vos demandes à Texas Instruments Incorporated, 7800 Banner Drive, M/S 3918; Dallas, TX 75251; Attention: Manager, Business Services

L’exercice 1 (Représenter graphiquement votre déplacement) et l’exercice 3 (Descente rapide en toboggan) sont utilisés avec l’autorisation de Vernier Software and Technology. Ces exercices ont été adaptés de l’ouvrage Middle School Science with Calculators écrit par Don Volz et Sandy Sapatka.

Table des matières

Introduction

En quoi consiste le CBR 2™ ? 2

Principes d’utilisation du compter jusqu’à 3 4

Conseils pour collecter efficacement des données 6

Exercices : notes pédagogiques et feuilles d’exercice pour les élèves

CBR 2™ : C’est aussi simple que de

³ Exercice 1 — Représenter graphiquement votre déplacement

linéaire 10

³ Exercice 2 — Suivre le graphique linéaire 14 ³ Exercice 3 — Descente rapide en toboggan parabolique 18 ³ Exercice 4 — Balle qui rebondit parabolique 24 ³ Exercice 5 — Balle qui roule parabolique 28

Informations pour le professeur 32

Informations techniques

Les données du CBR 2™ sont enregistrées dans des listes 36

Paramètres de l’application EasyData 37

Utilisation du programmes

CBR 2™ avec le CBL 2™ ou avec des

CBL 2™ 38

Informations de maintenance

Piles 40

En cas de problème 41

Organigramme des menus de l’application EasyData 42

Assistance et garantie de TI 43

En quoi consiste le CBR 2™ ?

CBR

CBR 2™ (Calculator

CBRCBR

TI-83 Plus Silver Edition, TI-84 Plus, et TI-84 Plus Silver Edition

- apprend aux élèves à collecter et à analyser des données réelles

Que fait le CBR 2™ ?

En connectant le CBR 2™ à une calculette graphique TI, les élèves peuvent collecter, visualiser et analyser des données de mouvement sans avoir à effectuer des mesures fastidieuses et à tracer manuellement des graphiques.

CBR 2™ permet d’explorer les relations physiques et mathématiques existant entre

distance, vitesse, accélération et temps. Pour cela, on utilise les données collectées pour résoudre les exercices proposés. Les élèves peuvent ainsi étudier les concepts mathématiques et physiques suivants :

2™ (Calculator----Based Ranger™)

2™ (Calculator2™ (Calculator

détecteur de mouvement à ultrasons

- utilisable avec les calculettes TI-83 Plus,

simple d’emploi

Based Ranger™)

Based Ranger™)Based Ranger™)

0 mouvement : distance, vitesse, accélération 0 représentation graphique : coordonnées, pente, intersections 0 fonctions : linéaires, quadratiques, exponentielles, sinusoïdales 0 calculs : dérivées, intégrales 0 analyse statistique des données : méthodes de collecte de données, analyse statistique 0 physique : déplacement, mouvement guidé, analyse du mouvement

d’oscillateurs mécaniques, position, vitesse, accélération

0 expérimentation : études de mouvements

Quel est l’objectif de ce manuel

Ce manuel intitulé Principes d’utilisation du CBR 2™ est conçu pour les professeurs qui n’ont pas d’expérience approfondie ou de l’utilisation d’une calculette. Il propose des instructions d’exploitation rapide du cinq exercices permettant d’étudier les fonctions et les propriétés de base du mouvement. En complément des exercices (voir pages 10 à 31), vous trouverez les informations suivantes :

0 des notes pédagogiques spécifiques à chaque exercice, plus des informations générales

pour le professeur

0 des instructions pas à pas 0 un exercice élémentaire adapté à tout niveau pour apprendre à collecter des données 0 des indications pour analyser les données, y compris des scénarios du type “Que se passe-

t-il si

?”

0 des pistes pour des études plus approfondies 0 une feuille d’exercice photocopiable avec des questions ouvertes adaptées à plusieurs

niveaux

CBR 2™, des conseils pour collecter efficacement des données et

pour

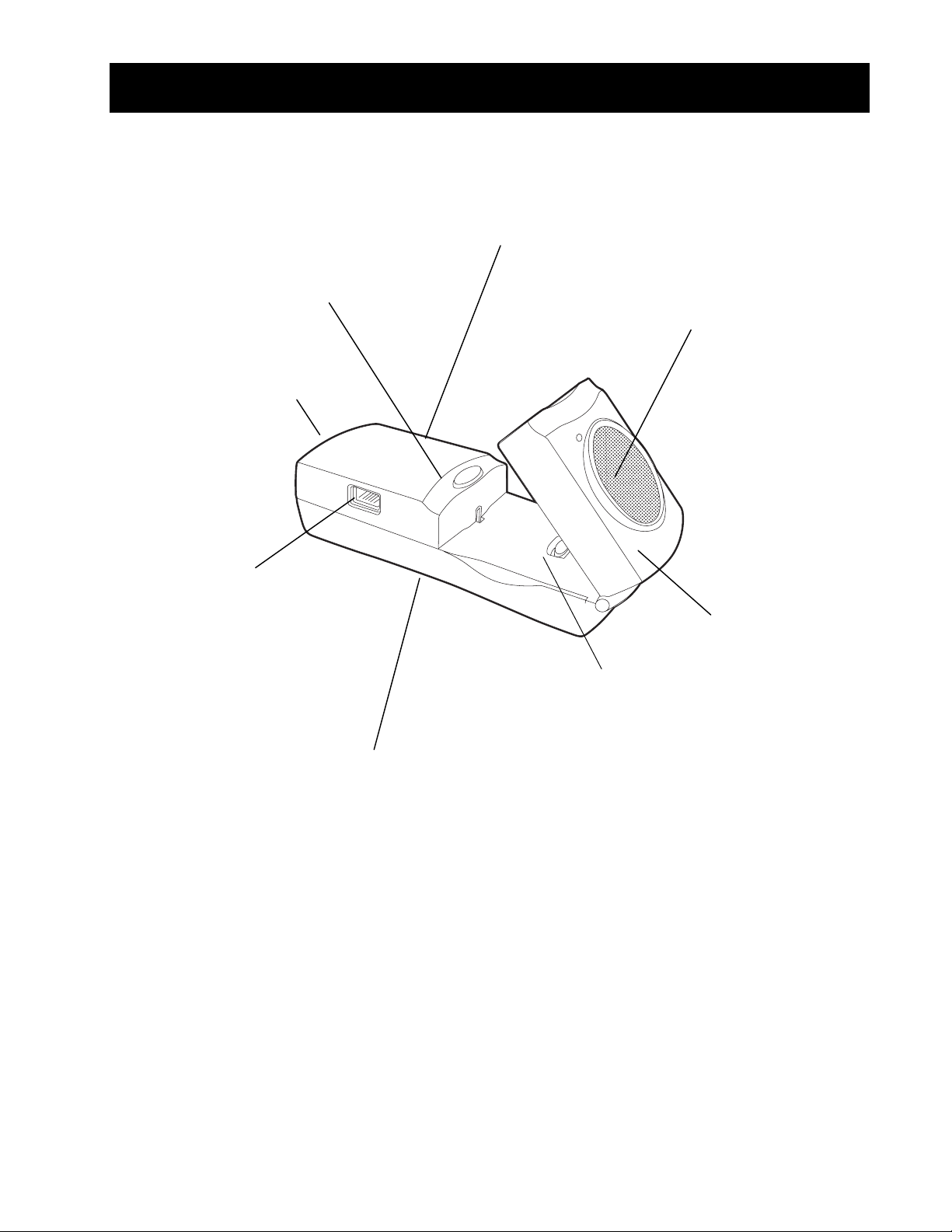
En quoi consiste le CBR 2™ ?

bouton

initialiser

l’échantillonnage

(suite)

accès piles (en bas)

ort pour connecter une calculette graphique TI à l’aide d’un câble de 2,25 m (fourni)

détecteur à ultra-sons : 200 mesures par

econdes entre

15 centimètres et 6 m

ort BT (British Telecom)

our connecter le CBR 2™ à un CBL™, CBL 2™ ou LabPro®

électeur de sensibilité réglable

en mode Normal ou Track (voir

age 7)

oint de fixation normalisé

our installer un trépied ou le serre-joint de montage inclu

CBR 2™ fournit tout ce dont vous avez besoin pour commencer rapidement et facilement vos cours

tête pivotante pour ajuster précisément la

osition du détecteur

et vos exercices. Il vous suffit de le connecter à une calculette graphique TI (vous pouvez également vous procurer aisément les accessoires indispensables à la réalisation de certains exercices).

0 détecteur de mouvement à

ultrasons

0 5 exercices d’application

amusants

0 4 piles AA 0 câble d’E/S de calculette à

calculette

0 câble USB standard B/Mini-A

(calculette/

CBR 2™)

Utilisation du CBR 2™ : aussi simple que de compter jusqu’à 3

Avec le CBR 2™, vous collectez votre premier échantillon de données en 2 ou 3 étapes !

Téléchargement

Votre calculette graphique peut être livrée avec un certain nombre d’applications pré-installées, y compris l’application EasyData. Appuyez sur Œ pour afficher le nom des applications installées sur votre calculette. Si l’application EasyData n’est pas installée, vous pouvez télécharger la dernière version de cette application à partir du site education.ti.com. Si nécessaire, téléchargez EasyData dès à présent.

Connexion

Connectez le CBR 2™ à votre calculette graphique TI au moyen du câble USB standard B/Mini-A (calculette/ calculette en veillant à bien enfoncer chaque extrémité dans les appareils pour établir la connexion.

Réglez le sélecteur de sensibilité sur le mode marche, de jet de balle, de mouvement de pendule, etc. ou sur le mode pour les exercices de mouvements guidés et de déplacements de chariots.

Le câble calculette/

0 doit exclusivement être utilisé avec l’application EasyData. 0 permet de lancer automatiquement l’application EasyData lorsqu’il est

utilisé pour connecter un

0 offre une meilleure connexion physique et une plus grande fiabilité que le

câble d’E/S de calculette à calculette.

0 ne doit pas être utilisé avec RANGER, DataMate ni d’autres applications

similaires.

CBR 2™ :

CBR 2™) ou du câble d’E/S de calculette à

Normal pour les exercices de

Track

CBR 2™ à une TI-84 Plus.

1111 3

Exécution

Exécutez l’application EasyData sur la calculette graphique connectée au

CBR 2™.

Passez à l’étape 1 si vous utilisez une calculette TI-83 Plus. Si vous connectez une TI-84 Plus au moyen d’un câble calculette/

1. Allumez la calculette et affichez l’écran d’accueil.

2. Appuyez sur Œ pour afficher la liste des applications installées sur

votre calculette graphique.

3. Choisissez EasyData et appuyez sur Í. L’écran d’ouverture s’affiche pendant 2 à 3 secondes, puis l’écran

principal apparaît.

4. Sélectionnez Start (appuyez sur q) à partir de l’écran principal pour

commencer la collecte de données.

CBR 2™, effectuez les étapes 1 et 4.

Utilisation du CBR 2™ : aussi simple que de compter jusqu’à 3

Pour obtenir des résultats rapidement, essayez un des ateliers proposés dans ce manuel !

Informations importantes

0 Ce manuel est valable pour toutes les calculettes graphiques TI qui

peuvent être raccordées à un que certains libellés de menu ne correspondent pas exactement à ceux qui apparaissent sur l’écran de votre calculette.

0 Lorsque vous configurez les exercices, veillez à ce que le CBR 2™ soit

bien stable et que personne ne risque de trébucher sur le cordon.

0 Sortez toujours de l’application EasyData en activant l’option Quit. qui

permet à EasyData de lancer une procédure d’arrêt correct du Ceci garantit au

CBR 2™ une initialisation adéquate pour la prochaine

utilisation.

0 Déconnectez toujours le CBR 2™ de la calculette avant de le ranger. 0 L’application EasyData se lance automatiquement lorsque le câble

calculette/ un

CBR 2™.

CBR 2™ relie une TI-84 Plus ou une TI-84 Plus Silver Edition à

CBR 2™ (voir page 2). Il se peut cependant

CBR 2™.

Conseils pour collecter efficacement des données

Comment obtenir de meilleurs échantillons ?

Description du fonctionnement du CBR 2™

Si vous comprenez le fonctionnement d’un détecteur de mouvement à ultrasons, il vous sera plus facile d’obtenir de meilleures mesures pour tracer de meilleures courbes. Le détecteur de mouvement envoie une impulsion ultrasonique, puis mesure le temps que met cette impulsion à revenir après réflexion sur l’objet le plus proche.

CBR 2™, comme tout détecteur de mouvement à ultrasons, mesure la durée écoulée

entre l’instant où l’impulsion ultrasonique a été transmise et l’instant où le premier écho a été renvoyé. Mais le microprocesseur intégré. Lorsque les mesures sont collectées, le laquelle se trouve l’objet à l’aide d’un programme utilisant la vitesse du son. Puis il calcule la dérivée première et seconde des distances par rapport au temps pour obtenir les vitesses et les accélérations. Il enregistre ces mesures dans les listes.

Taille de l’objet

CBR 2™ dispose de bien d’autres fonctionnalités gérées par son

CBR 2™ calcule la distance à

Plus l’objet est petit et loin du CBR 2™, moins la lecture est précise. Par exemple, à une distance de 5 mètres il vous est plus facile de détecter un ballon de football plutôt qu’une balle de ping-pong.

Distance minimale

Lorsque le CBR 2™ envoie une impulsion, celle-ci arrive sur l’objet, est réfléchie vers le CBR 2™ qui la reçoit. Si l’objet est situé à moins de 15 centimètres, des impulsions successives peuvent se chevaucher et être mal identifiées par le donc préférable de placer le

Distance maximale

CBR 2™ à 15 centimètres minimum de l’objet visé

CBR 2™ et la courbe sera inexacte. Il est

Au fur et à mesure que l’impulsion progresse dans l’air, elle perd de sa force (elle s’amortit). Après avoir parcouru environ 12 mètres (6 mètres pour aller vers l’objet et 6 mètres pour revenir jusqu’au détecté par le

CBR 2™), l’écho renvoyé peut être trop faible pour être correctement

CBR 2™. Ceci limite la distance de détection fiable entre l’objet et le CBR 2™ à

moins de 6 mètres.

Sélecteur de sensibilité

Le sélecteur de sensibilité permet d’activer deux modes d’utilisation : Track et Normal. Le mode Track s’utilise dans le cadre d’exercices de mouvements guidés et de

Track Normal

% &

déplacements de chariots, tandis que le mode Normal convient à tous les autres types d’exercices (marche, jet ou rebond de balle, mouvement de pendule, etc.).

Si le niveau de bruit collecté avec vos données est élevé, il est probable que le sélecteur de sensibilité est réglé sur le mode Normal. L’activation du mode Track réduit la sensibilité du détecteur et peut fournir de meilleurs résultats.

Conseils pour collecter efficacement des données

La zone libre

(suite)

Le faisceau du CBR 2™ n’est pas un faisceau rectiligne cylindrique. Au contraire, il forme un faisceau conique d’angle 30°.

Pour éviter toute interférence avec des objets situés aux alentours, essayez de maintenir une zone libre sur le trajet du faisceau du autres que l’objet ciblé ne seront pas détectés par le

CBR 2™. Ceci vous permet d’être sûr que les objets

CBR 2™. Le CBR 2™ détecte l’objet le

plus proche dans la zone libre.

30°

15 centimètre

Surfaces réfléchissantes

Certaines surfaces réfléchissent les impulsions mieux que d’autres. Vous obtenez par exemple de meilleurs résultats avec une balle dont la surface est relativement dure ou lisse qu’avec une balle de tennis. En revanche, des échantillons prélevés dans une pièce remplie de surfaces réfléchissantes dures ont plus de chances de présenter des points de données parasites. Des mesures de surfaces irrégulières (telles qu’une voiture miniature ou un élève se déplaçant en tenant une calculette) peuvent apparaître irrégulières.

La courbe Distance-Temps d’un objet immobile peut présenter quelques petites différences au niveau des valeurs de distance calculées. Si chacune de ces valeurs correspond à un pixel différent, la courbe plate attendue peut présenter quelques accidents. Quant à la courbe Vitesse-Temps, elle peut paraître encore plus accidentée car la différence de la distance entre deux points quelconques dans le temps correspond, par définition, à la vitesse et de plus la vitesse s’obtient par un calcul numérique avec les imprécisions d’un tel calcul.

Conseils pour collecter efficacement des données

(suite)

Paramètres de l’application EasyData

Configuration de la collecte de données pour l’option Time Graph

La durée de l’expérience correspond à la durée totale, exprimé en secondes, requise pour la réalisation complète de l’échantillonnage. Elle est calculée en multipliant le nombre d’échantillons par la durée d’échantillonnage.

Entrez un nombre compris entre 0,05 (pour les objets se déplaçant rapidement) et 0,5 secondes (pour les objets se déplaçant lentement).

Remarque : Reportez-vous à la section “Pour configurer la calculette pour la collecte de données”, page 12, pour des informations détaillées concernant la modification des paramètres.

Menu Description Paramètre par défaut

Sample Interval Mesure le temps en secondes écoulé entre les

échantillons.

Number of Samples Nombre total d’échantillons à collecter. 100

Experiment Length Durée de l’expérience exprimée en secondes. 5

Démarrage et arrêt

0,05

Pour commencer l’échantillonnage, sélectionnez Start (appuyez sur q). L’échantillonnage s’arrête automatiquement lorsque le nombre d’échantillons défini dans le menu Time Graph Settings est atteint. Le

CBR 2™ affiche ensuite un graphique représentant

les données collectées.

Pour interrompre l’échantillonnage avant son arrêt automatique, sélectionnez Stop (appuyez sur q et maintenir la touche enfoncée) à tout moment pendant le processus d’échantillonnage. Une fois ce dernier arrêté, un graphique représentant les données collectées s’affiche.

Bruit : De quoi s’agit-il et comment l’éliminer ?

Lorsque le CBR 2™ reçoit des signaux réfléchis par des objets autres que la cible principale, la courbe présente des points de données erratiques (points aberrants) qui ne sont pas conformes à l’allure générale de la courbe. Pour minimiser le bruit, vous devez :

0 Veillez à ce que le CBR 2™ soit directement pointé sur la cible. Essayez de régler la tête du

détecteur tout en visualisant les données collectées en temps réel sur l’écran d’accueil de mesure. Assurez-vous d’obtenir des résultats satisfaisants avant de commencer un exercice ou une expérience.

0 Essayez d’échantillonner dans un espace sans signaux parasites (voir le schéma de la zone

libre à page 7).

0 Choisissez un objet plus grand et donc susceptible de mieux réfléchir les impulsions, ou

déplacez l’objet plus près du

0 Lorsque plusieurs CBR 2™ sont utilisés dans la même pièce, chaque groupe doit avoir

CBR 2™ (mais à une distance supérieure à 15 centimètres).

terminé son échantillonnage avant que le suivant ne commence le sien.

0 Essayez de régler le sélecteur de sensibilité sur le mode Track pour réduire la sensibilité du

détecteur.

Conseils pour collecter efficacement des données

Vitesse du son

(suite)

La distance approximative de l’objet est calculée en supposant une vitesse nominale du son. Cependant, la vitesse réelle du son varie en fonction de plusieurs facteurs et plus particulièrement en fonction de la température ambiante. Pour des exercices impliquant un certain mouvement, ce facteur n’est pas important.

CBR 2™ est équipé d’un capteur de température intégré qui lui permet de compenser

automatiquement les variations de vitesse du son dues à la température ambiante. La conversion de température de 0 à 40° Celsius, pour une pression standard, est pratiquement linéaire à environ +0,6 mètres/seconde par degré Celsius. La vitesse du son augmente d’environ de 331 mètres/seconde à 0° Celsius à 355 mètres/seconde à 40° Celsius. Ces vitesses tiennent compte d’une humidité relative de 35 % (air sec).

Lorsque l’application EasyData est utilisée avec le

CBR 2™, cette compensation de

température survient lors de la collecte des données de mouvement. Le capteur se trouve sous les orifices situés à l’arrière du

CBR 2™. C’est pourquoi, lors de la collecte de données, il

convient de ne pas recouvrir ces orifices d’un quelconque objet de température différente de la température ambiante.

Utilisation du CBR 2™ sans l’application EasyData

Vous pouvez utiliser le CBR 2™ comme détecteur de mouvement à ultrasons avec le CBL 2™ ou des programmes autres que EasyData.

Le câble d’E/S de calculette à calculette permet d’utiliser le

CBR 2™ avec des calculettes

graphiques sur lesquelles l’application EasyData n’est pas installée, mais qui disposent de l’application fonctionnalités qu’un et/ou le programme

L’application

CBL/CBR et/ou du programme RANGER. Le CBR 2™ offre les mêmes

CBR™ lorsque les données sont collectées via l’application CBL/CBR

RANGER.

CBL/CBR peut être utilisée sur la plupart des anciens modèles de calculette TI-83

Plus. Elle peut être téléchargée à partir du site education.ti.com pour assurer la collecte des données de mouvement sur le

Le programme

RANGER, qui fait partie de l’application CBL/CBR et qui est disponible pour

CBR 2™ au moyen du câble d’E/S de calculette à calculette.

d’autres calculettes, permet de collecter des données de mouvement via le câble d’E/S de calculette à calculette. De nombreux manuels TI consacrés aux Explorations utilisent le programme

Vous pouvez également utiliser le de collecte de données faire fonctionner le

RANGER.

CBR 2™ comme détecteur de mouvement avec votre unité

CBL 2™. Utilisez l’application DataMate fournie avec le CBL 2™ pour

CBR 2™ avec votre CBL 2™. Un câble spécial CBL/CBR est nécessaire pour

pouvoir utiliser ce système. Pour plus d’informations sur ce câble, visitez la boutique TI sur education.ti.com.

Exercice 1 : Représenter graphiquement votre

déplacement notes pédagogiques

Concepts

Fonction étudiée : linéaire

Cet exercice requiert l’utilisation de l’application EasyData.

Matériel nécessaire

Ÿ calculette (voir page 2 la liste des modèles

disponibles)

Ÿ CBR 2™ Ÿ câble calculette/CBR 2™ ou câble d’E/S de

calculette à calculette

Ÿ application EasyData Ÿ ruban adhésif Ÿ mètre

Conseils

Cet exercice peut être la première occasion pour vos élèves d’utiliser le détecteur de mouvement CBR 2™. Prendre le temps de les initier maintenant à son fonctionnement leur sera très utile dans la mesure où ils auront à utiliser le CBR 2™ à plusieurs reprises au cours de l’année. Les conseils suivants sont destinés à favoriser une utilisation efficace du CBR 2™:

0 Avec le CBR 2™, il est important de comprendre

que l’impulsion ultrasonique est émise dans un cône d’environ 30° de large. Tout objet situé à l’intérieur de ce cône peut occasionner une réflexion et, par conséquent, une mesure accidentelle. L’un des problèmes courants liés à l’utilisation d’un détecteur de mouvement réside dans la génération de réflexions indésirables occasionnées par la présence d’un bureau ou d’une chaise dans la pièce.

0 Ces réflexions indésirables peuvent être réduites la

plupart du temps en inclinant légèrement le CBR 2™.

0 Si vous commencez par représenter une courbe de

vitesse ou d’accélération et que l’affichage obtenu est confus, tentez d’afficher une courbe de distance et observez sa pertinence. Si celle-ci n’est pas satisfaisante, il est possible que le CBR 2™ ne pointe pas correctement sur la cible.

0 Le CBR 2™ ne détecte pas correctement les objets

situés à moins de 15 cm. La plage maximum est d’environ 6 m, mais la détection d’objets isolés dans la partie large du cône de détection peut être difficile à cette distance.

0 Il peut arriver qu’une cible n’offre pas une réflexion

suffisante de l’impulsion ultrasonique. Par exemple, si la cible est une personne vêtue d’un pull-over épais, la courbe obtenue peut paraître irrégulière.

0 Si les courbes de vitesse et d’accélération

présentent un niveau de bruit élevé, tentez d’augmenter l’intensité de la réflexion ultrasonique à partir de la cible en augmentant la zone de celleci.

Vous pouvez demander aux élèves de tenir un livre devant eux tout en marchant face au CBR 2™. Vous obtiendrez ainsi de meilleures courbes car le déplacement sera plus régulier.

Courbes typiques

Courbe Distance-Temps

Courbe de correspondance Distance-Temps

Réponses aux questions

9. La pente de la portion de la courbe correspondant au déplacement est plus importante pour l’essai réalisé à plus vive allure.

Les résultats obtenus peuvent varier d’un groupe à

l’autre car leur vitesse de déplacement peut varier.

Tout déplacement en direction du détecteur de

mouvement produira une pente négative, alors que tout déplacement s’éloignant du détecteur génèrera une pente positive.

12. Notez que la pente est presque nulle (voire nulle) si la cible reste immobile. La pente obtenue doit être nulle, mais de légères variations sont possibles en fonction des données collectées.

Exercice 1 : Représenter graphiquement votre

déplacement linéaire

Les graphiques réalisés à l’aide d’un CBR 2™ peuvent être utilisés pour étudier les mouvements. Au cours de cet exercice, vous allez apprendre à utiliser votre représentant votre propre déplacement.

Objectifs

Dans le cadre de cet exercice, vous devrez :

0 utiliser un détecteur de mouvement pour mesurer une distance et une vitesse ; 0 générer des graphiques représentant votre déplacement ; 0 analyser les graphiques générés.

Collecte de données : courbes Distance-Temps

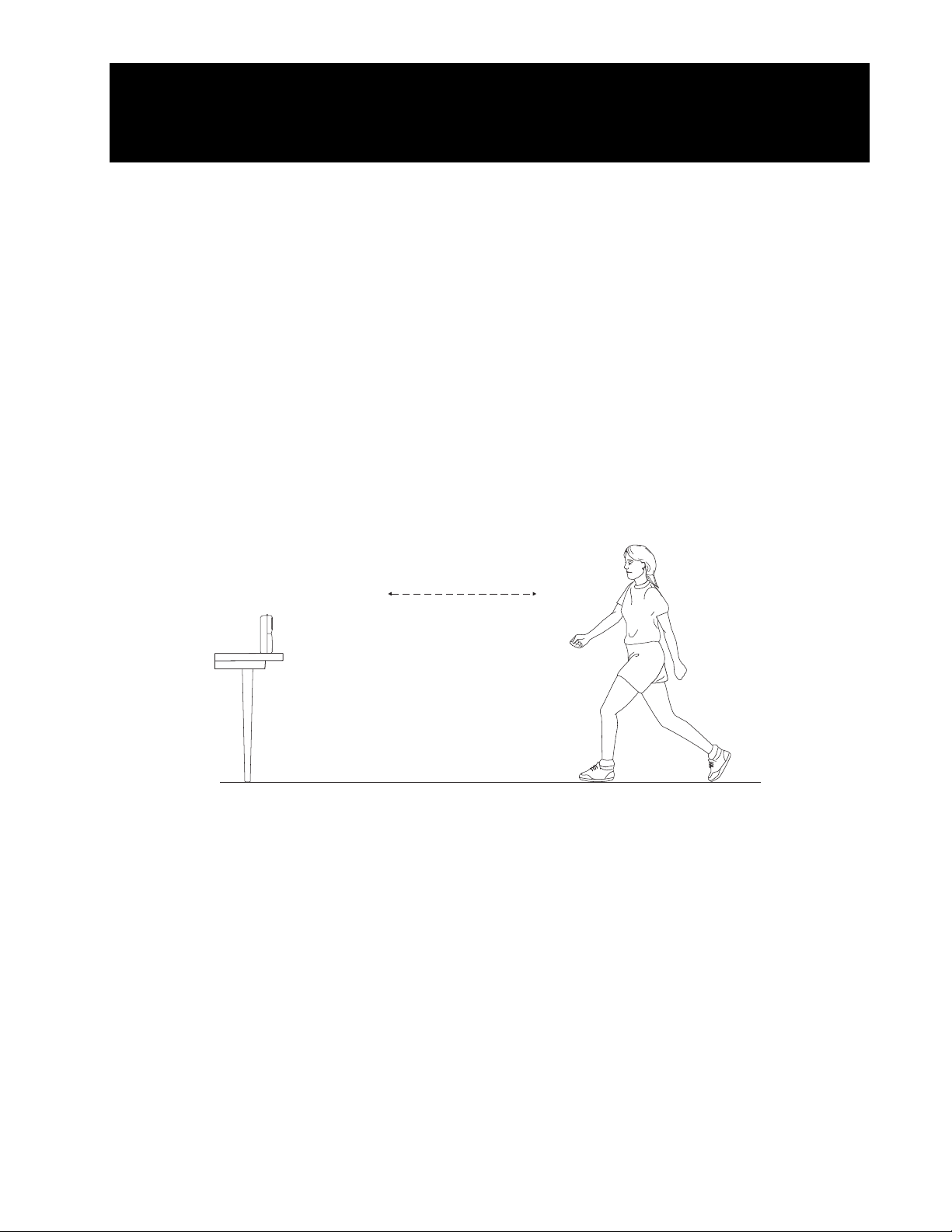
Ê Posez le CBR 2™ sur une table, en l’orientant vers une zone libre, entièrement dégagée

de tout meuble ou autre objet. Le d’environ 15 centimètres au niveau de votre poitrine.

CBR 2™ doit se trouver à une hauteur supérieure

CBR 2™ pour créer des graphiques

Avancez et reculez face

au CBR 2™

Ë Utilisez le ruban adhésif pour effectuer le marquage au sol des distances correspondant

à 1 m, 2 m, 3 m et 4 m du

CBR 2™.

Ì Connectez le CBR 2™ à votre calculette en utilisant le câble approprié (voir ci-dessous)

en veillant à bien enfoncer chacune des extrémités du câble dans les appareils.

0 Avec une TI-83 Plus, utilisez le câble d’E/S de calculette à calculette.

0 Avec une TI-84 Plus, utilisez un câble USB standard B/Mini-A (calculette/CBR 2™).

Í Sur la calculette, appuyez sur Œ et sélectionnez EasyData pour lancer l’application

EasyData.

Remarque : L’application EasyData démarre automatiquement lorsque le

connecté à une TI-84 Plus au moyen d’un câble calculette/

CBR 2™.

CBR 2™ est

Exercice 1 : Représenter graphiquement votre

déplacement

(suite)

Î Pour configurer la calculette pour la collecte de données :

a. Sélectionnez Setup (appuyez sur p) pour ouvrir le

menu Setup.

b. Appuyez sur 2 pour sélectionner 2: Time Graph et afficher

l’écran Time Graph Settings.

c. Sélectionnez Edit (appuyez sur q) pour ouvrir la boîte de

dialogue Sample Interval.

d. Entrez 0,1 pour régler le temps qui doit s’écouler entre les

échantillons sur 1/10 de seconde.

e. Sélectionnez Next (appuyez sur q) pour afficher la boîte

de dialogue Number of Samples.

f. Entrez 50 pour définir le nombre d’échantillons à collecter.

La durée de l’expérience sera de 5 secondes (nombre

d’échantillons multiplié par le nombre d’échantillons par seconde).

linéaire

g. Sélectionnez Next (appuyez sur q) pour afficher le

récapitulatif des nouveaux paramètres.

h. Sélectionnez OK (appuyez sur s) pour revenir à l’écran

principal.

Ï Explorez la fonction de génération de courbes de distance en

fonction du temps.

a. Placez-vous sur la marque au sol correspondant à la distance

de 1 m, face au

b. Demandez à un élève de sélectionner Start (appuyer sur

p).

c. Déplacez-vous lentement en direction de la marque des 2,5

m et arrêtez-vous.

d. Une fois les données collectées, une courbe s’affiche.

CBR 2™.

Exercice 1 : Représenter graphiquement votre

déplacement

e. Réalisez une représentation fidèle de la courbe affichée dans

f. Sélectionnez deux points sur cette courbe et déterminez la

Point 1 :________ Point 2 : ________ Pente :___________

g. Sélectionnez Main (appuyez sur r) pour revenir à

(suite)

la zone prévue à cet effet.

pente à partir de l’axe des x et des y.

l’écran principal.

Ð Répétez l’étape 6, en partant cette fois de la marque des 2,5 m

et en vous déplaçant vers la marque de 1 m. Procédez en deux temps : une première fois en vous déplaçant lentement, puis une deuxième fois en vous déplaçant plus rapidement.

Point 1 :________ Point 2 : ________ Pente :___________

Ñ Réalisez une reproduction fidèle des nouvelles courbes dans la

zone prévue à cet effet.

Ò Décrivez les différences observées entre les courbes générées (à l’étape 6e et 8) :

linéaire

___________________________________________________________________________

Ó Répétez l’étape 6, en vous plaçant sur la marque des 2,5 m, sans

bouger.

Ô Réalisez une reproduction fidèle de la nouvelle courbe dans la

zone prévue à cet effet.

Õ Calculez une pente approximative pour toutes les courbes

générées.

Exercice 2 : Suivre le graphique notes pédagogiques

Concepts

Fonction étudiée : linéaire.

Match présente des concepts réels de distance et de

temps, ou plus précisément le concept de distance par rapport au temps.

Au cours de ces explorations, les élèves doivent convertir leur vitesse de déplacement de mètre(s)/seconde en kilomètre(s)/heure.

Une fois qu’ils maîtrisent bien la correspondance Distance-Temps, demandez-leur d’étudier la relation Vitesse-Temps.

Matériel nécessaire

Ÿ calculette (voir page 2 la liste des modèles

disponibles)

Ÿ CBR 2™ Ÿ câble calculette/CBR 2™ ou câble d’E/S de

calculette à calculette

Ÿ application EasyData

TI ViewScreené permet aux autres élèves de suivre l’exercice sur un écran de visualisation, et par conséquent de le rendre plus vivant.

Conseils

En général, cet exercice plaît beaucoup aux élèves. Prévoyez une durée adéquate car tout le monde voudra essayer.

Cet exercice est mieux réussi lorsque l’élève qui se déplace (et l’ensemble de la classe) peut suivre ses déplacements projetés sur un écran mural ou de visualisation à l’aide de TI ViewScreené.

Conseillez aux élèves de se déplacer en ligne droite avec le CBR 2™ ; ils essaient quelquefois de marcher sur le côté (perpendiculairement au faisceau du CBR 2™) ou même de sauter.

Les consignes de déroulement de l’exercice prévoient que les mesures soient effectuées en mètres, pour assurer la cohérence avec les questions posées aux élèves sur les feuilles d’exercice.

Pour quelques conseils sur la façon de collecter efficacement des données, voir pages 6 à 9.

Courbes typiques

Réponses typiques

1. temps (depuis le début de l’échantillon) ; secondes ; 1 seconde ; distance (du CBR 2™ à l’objet) ; mètres ; 1 mètre

2. l’intersection avec l’axe y représente la distance de départ

3. varie en fonction de l’élève

4. en arrière (augmenter la distance entre le CBR 2™ et l’objet)

5. en avant (diminuer la distance entre le CBR 2™ et l’objet)

6. ne pas bouger ; une pente nulle n’exige aucune modification de y (distance)

7. varie selon le graphique ; @yà3,3

8. varie selon le graphique ; @yà1

9. le segment avec la pente la plus grande (positive ou négative)

10. question piège : le segment plat car vous ne bougez pas du tout

11. vitesse de déplacement ; quand changer de direction et/ou de vitesse

12. vitesse

13. varie selon le graphique (exemple : 1,5 mètre en 3 secondes)

14. varie selon le graphique ; exemple : 0,5 mètre à 1 seconde

exemple : (0,5 mètre à 1 seconde) Q (60 secondes

à 1 minute) = 30 mètres à minute

exemple : (30 mètres à 1 minute) Q (60 minutes à

1 heure) = 1800 mètres à heure

exemple : (1800 mètres à 1 heure) Q (1 kilomètre

à 1000 mètres) = 1,18 kilomètre à heure.

Demandez aux élèves de comparer ce dernier

chiffre à la vitesse d’un véhicule, qui se déplacerait par exemple à la vitesse de 96 kilomètres à heure.

15. varie selon le graphique ; somme de @y pour chaque segment de ligne.

Courbe Distance-Temps Courbe de correspondance

Distance-Temps

Exercice 2 : Suivre le graphique linéaire

Collecte de données

Ê Tenez le CBR 2™ dans une main et la calculette dans l’autre. Pointez le détecteur droit

sur un mur.

Conseils : La distance maximum pour n’importe quel graphique est 6 mètres du

CBR 2™. La portée minimum du CBR 2™ est de 15 centimètres. Veillez à ce que la zone

libre soit entièrement dégagée (voir page 7).

Ë Démarrez l’application EasyData.

Ì Dans le menu Setup, sélectionnez 3:Distance Match.

L’option Distance Match gère automatiquement les paramètres.

Í Sélectionnez Start (appuyez sur q) et suivez les instructions

affichées à l’écran.

Tentez de suivre le graphique affiché sur l’écran suivant.

Î Sélectionnez Next (appuyez sur q) pour afficher le graphique

à suivre. Prenez le temps d’examiner ce graphique. Répondez aux questions 1 et 2 de la feuille d’exercice.

Remarque : Le graphique à suivre sera différent chaque fois que

les étapes 4 et 5 seront effectuées.

Exercice 2 : Suivre le graphique

Ï Positionnez-vous à l’endroit où vous pensez que le graphique débute. Sélectionnez Start

(appuyez sur p) pour commencer la collecte des données. Quand celle-ci est en cours, un cliquetis se fait entendre et le voyant vert s’allume.

Ð Avancez et reculez ; essayez de suivre le graphique. Votre position est reproduite sur

l’écran.

Ñ Lorsque l’échantillon est terminé, examinez la façon dont vous avez suivi le graphique

en marchant et répondez à la question 3.

Ò Sélectionnez Retry (appuyez sur q) pour afficher à nouveau le même graphique à

suivre. Essayez d’améliorer votre technique de déplacement, puis répondez aux questions 4, 5 et 6.

Explorations

Dans Distance Match, chaque graphique comportent trois segments de droite au maximum.

Ê Sélectionnez New (appuyez sur p) pour afficher un autre graphique à suivre.

Etudiez le premier segment et répondez aux questions 7 et 8.

Ë Etudiez l’ensemble du graphique et répondez aux questions 9 et 10.

(suite)

linéaire

Ì Positionnez-vous à l’endroit où vous pensez que le graphique commence, appuyez sur

Start pour commencer la collecte des données, et essayez de suivre le graphique.

Í Lorsque l’échantillonnage s’arrête, répondez aux questions 11 et 12.

Î Sélectionnez New (appuyez sur p) pour afficher un autre graphique à suivre.

Ï Etudiez le graphique et répondez aux questions 13, 14 et 15.

Ð Sélectionnez New (appuyez sur p) et recommencez l’exercice, le cas échéant, ou

sélectionnez Main (appuyez sur r) pour revenir à l’écran principal.

Ñ Sélectionnez Quit (appuyez sur s), puis OK (appuyez sur s) pour fermer

l’application EasyData.

Exercice 2 : Suivre le graphique

Nom __________________________________

Collecte de données

1. Quelle grandeur physique est représentée le long de l’axe des x ? ____________________________

Quelles sont les unités ? _______________________________________________________________

A quelle distance se trouvent les marques les unes des autres ? ______________________________

Quelle grandeur physique est représentée le long de l’axe des y ? ____________________________

Quelles sont les unités ? _______________________________________________________________

A quelle distance se trouvent les marques les unes des autres ? ______________________________

2. A quelle distance du

3. Avez-vous commencé trop près, trop loin ou étiez-vous bien placé ? __________________________

4. Pour un segment qui monte, devez-vous avancer ou reculer ? ________________________________

Pourquoi ? __________________________________________________________________________

5. Pour un segment qui descend, devez-vous avancer ou reculer ? ______________________________

Pourquoi ? __________________________________________________________________________

6. Que devez-vous faire si le segment est horizontal ? _________________________________________

CBR 2™ pensez-vous devoir vous tenir pour commencer ? _________________

Pourquoi ? __________________________________________________________________________

Explorations

7. Si vous faites un pas toutes les secondes, quelle doit être la longueur de ce pas ? _______________

8. Si, à l’inverse, vous faites des pas de 1 mètre de long, combien de pas devez-vous faire en tout ?

____________________________________________________________________________________

9. Quel est le segment où vous devez vous déplacer le plus vite ? _______________________________

Pourquoi ? __________________________________________________________________________

10. Quel est le segment où vous devez vous déplacer le plus lentement ? _________________________

Pourquoi ? __________________________________________________________________________

11. Outre votre choix entre avancer ou reculer, quels autres facteurs ont eu une influence pour vous permettre de suivre exactement le graphique ? ____________________________________________

____________________________________________________________________________________

12. Quelle grandeur physique représente la pente du segment ? _________________________________

13. En ce qui concerne le premier segment de ligne, de combien de mètres devez-vous avancer et en

combien de secondes ? ________________________________________________________________

14. Convertissez la valeur obtenue à la question 13 (vitesse) en mètres par seconde : _______________

Convertissez en mètres àminute : _______________________________________________________

Convertissez en mètres àheure : ________________________________________________________

Convertissez en kilomètres à heure : _____________________________________________________

15. Quelle distance avez-vous réellement parcouru ? ___________________________________________

Exercice 3 : Descente rapide en toboggan notes pédagogiques

Concepts

Fonction étudiée : quadratique

Le mouvement de descente sur un toggoban est utilisé pour illustrer le concept réel de variation de vitesse due au champ de la pesanteur et aux forces de frottement.

Matériel nécessaire

Ÿ calculette (voir page 2 la liste des modèles

disponibles)

Ÿ CBR 2™ Ÿ câble calculette/CBR 2™ ou câble d’E/S de

calculette à calculette

Ÿ application EasyData Ÿ toboggan

Conseils

Le choix d’une aire de jeux avec plusieurs toboggans est préférable pour cet exercice. Les toboggans doivent être droits, même si des toboggans d’autres formes peuvent être utilisés dans le cadre d’une extension. Pour des raisons de sécurité, demandez à vos élèves de ne pas se doubler en montant à l’échelle d’accès au toboggan.

Vous pouvez transporter les calculettes et les détecteurs de mouvement dans une malette ou des boîtiers jusqu’à l’aire de jeux, puis les distribuer aux élèves une fois sur place. Rappelez-leur que le détecteur de mouvement ne détecte pas correctement les objets situés à moins de 15 cm.

Suivant le type de toboggans utilisés, vous pouvez demander aux élèves de se positionner différemment pour la collecte des données. Certaines installations sont équipées de larges plates-formes sur lesquelles l’élève tenant le détecteur de mouvement et celui en charge de la calculette peuvent se placer.

Dans le cadre de cet exercice, les élèves peuvent utiliser du papier ciré, des tissus glissants, du sable et d’autres matériaux afin d’accroître leur vitesse. Pour une meilleure préparation, informez-les à l’avance du déroulement en deux parties de l’exercice et des objectifs correspondants.

Courbes typiques

Descente rapide en toboggan

Réponses typiques

1. Consultez les résultats de l’échantillonnage.

2. Suivant les résultats de l’échantillonnage, la vitesse observée pour la Partie 2 est supérieure de 0,90 m/s à celle enregistrée pour la Partie 1. Du papier ciré a été utilisé pour réduire les frottements et accroître la vitesse.

3. Les réponses varient car les vitesses diffèrent en fonction de facteurs tels que la surface de contact, le poids, le lissage et l’utilisation de matériaux réducteurs de frottements.

4. Les réponses varient.

5. L’augmentation de la hauteur de glisse accroît la vitesse de descente.

6. La pierre lancée du haut du toboggan doit toucher le sol en premier car les frottements et l’inclinaison du toboggan ralentissent davantage la descente de la pierre qui roule.

7. La partie inférieure à l’horizontale des toboggans ralentit les descentes afin de prévenir toute blessure.

Extensions

Elaborez un autre exercice visant à mesurer la vitesse sur une autre installation d’aire de jeux.

Organisez un concours pour déterminer quel élève de la classe ou du groupe réalise le meilleur temps de descente.

Résultats de l’échantillonnage

Vitesse (m/s)

Essai 1 Essai 2 Essai 3 Moyenne

Partie 1

Partie 2

1,97 2,02 2,00 2,00

2,80 3,07 2,82 2,90

Exercice 3 : Descente rapide en toboggan parabolique

Les aires de jeux et les toboggans vous sont familiers depuis votre enfance. Sous l’action de la gravité, votre corps glisse sur un toboggan, tandis que les frottements ralentissent votre descente. Dans la première partie de cet exercice, vous devrez utiliser le descente sur un toboggan. Dans la seconde partie, vous découvrirez différentes façons d’accroître votre vitesse de descente.

Objectifs

Dans le cadre de cet exercice, vous devrez :

0 utiliser le CBR 2™ pour déterminer votre vitesse de descente sur un toboggan ; 0 explorer différentes façons permettant d’accroître votre vitesse de descente ; 0 expliquer vos résultats.

Collecte de données, Partie 1, Vitesse de descente

Ê Connectez le CBR 2™ à votre calculette en utilisant le câble approprié (voir ci-dessous)

en veillant à bien enfoncer chacune des extrémités du câble dans les appareils.

CBR 2™ pour déterminer votre vitesse de

0 Avec une TI-83 Plus, utilisez le câble d’E/S de calculette à calculette.

0 Avec une TI-84 Plus, utilisez un câble USB standard B/Mini-A (calculette/CBR 2™).

Ë Sur la calculette, appuyez sur Œ t et sélectionnez EasyData pour lancer l’application

EasyData.

Remarque : L’application EasyData démarre automatiquement lorsque le

connecté à une TI-84 Plus au moyen d’un câble calculette/

CBR 2™.

Î Pour configurer la calculette pour la collecte de données :

CBR 2™ est

a. Sélectionnez Setup (appuyez sur p) pour ouvrir le

menu Setup.

b. Appuyez sur 2 pour sélectionner 2: Time Graph et afficher

l’écran Time Graph Settings.

Exercice 3 : Descente rapide en toboggan

c. Sélectionnez Edit (appuyez sur q) pour ouvrir la boîte de

dialogue Sample Interval.

d. Entrez 0,2 pour définir l’intervalle de temps exprimé en

secondes entre les échantillons.

e. Sélectionnez Next (appuyez sur q) pour afficher la boîte

de dialogue Number of Samples.

f. Entrez 25 comme nombre d’échantillons. La durée de la

collecte des données sera de 5 secondes.

g. Sélectionnez Next (appuyez sur q) pour afficher le

récapitulatif des nouveaux paramètres.

h. Sélectionnez OK (appuyez sur s) pour revenir à l’écran

principal.

Í Placez-vous aux positions de départ pour la collecte de données.

parabolique

a. Un élève doit se placer en haut du toboggan. b. Un deuxième élève, tenant le

du toboggan de façon à pouvoir pointer le choisi pour la descente.

c. Un troisième élève doit se positionner au bas du toboggan, avec la calculette et

l’interface.

CBR 2™, doit monter suffisamment haut sur l’échelle

CBR 2™ en direction du dos de l’élève

Î Placez-vous aux positions finales pour la collecte de données.

a. L’élève désigné pour la descente doit s’avancer suffisamment, sans entamer sa

glissade, de façon à ce que le

b. L’élève tenant le

choisi pour la descente.

c. L’élève chargé de tenir la calculette et l’interface doit se positionner de façon à ne

pas exercer de traction sur le câble du

CBR 2™ doit pointer celui-ci directement sur le dos de l’élève

CBR 2™ se trouve à 15 cm de son dos.

CBR 2™.

Ï Collectez les données.

a. Sélectionnez Start (appuyez sur q) pour commencer la collecte des données. b. L’élève choisi pour la descente peut entamer sa descente dès qu’un cliquetis se fait

entendre.

c. Une fois la collecte des données terminée pour cet essai, l’élève tenant le

peut descendre de l’échelle du toboggan.

CBR 2™

Attention : Les élèves ne doivent pas se doubler lorsque l’un d’entre eux se trouve sur l’échelle d’accès au toboggan.

Exercice 3 : Descente rapide en toboggan

Ð Déterminez la vitesse de l’élève effectuant la descente.

a. Une fois le processus de collecte des données arrêté et le

graphique de distance en fonction du temps affiché, sélectionnez Plots (appuyez sur p).

b. Appuyez sur 2 pour sélectionner 2: Vel vs Time et afficher la

courbe de vitesse en fonction du temps.

c. Utilisez la touche ~ pour afficher les points de données sur la courbe. A mesure

que vous déplacez le curseur vers la droite et la gauche, les valeurs de temps (x) et de vitesse (y) associées à chaque point de données s’affichent au-dessus de la courbe. Le point le plus haut sur la courbe correspond à la vitesse la plus élevée atteinte au cours de la descente. Notez cette valeur dans le tableau de données. Arrondissez-la au 0,01 m/s le plus proche. (Dans l’exemple ci-contre, la vitesse la plus élevée est 2 m/s.)

d. Sélectionnez Main (appuyez sur r) pour revenir à l’écran principal.

Répétez les étapes 4 à 7 deux fois ou plus.

(suite)

parabolique

Exercice 3 : Descente rapide en toboggan

Nom ________________________

Collecte de données, Partie 2, Descente rapide en toboggan

1. Définissez une stratégie pour augmenter la vitesse de descente.

a. Testez les différentes suggestions visant à accroître la vitesse de descente. Vous ne

pouvez pas recouvrir le toboggan d’une quelconque substance nécessitant un nettoyage ultérieur.

b. Décidez de la meilleure stratégie à adopter pour augmenter la vitesse de descente.

c. Décrivez votre stratégie dans la section Stratégie d’augmentation de la vitesse de

descente ci-dessous.

2. Testez votre stratégie en effectuant les étapes 4 à 8 de la Partie 1 de cet exercice.

Stratégie d’augmentation de la vitesse de descente

Données

Vitesse (m/s)

Essai 1 Essai 2 Essai 3 Moyenne

Partie 1

Partie 2

Traitement des données

1. Calculez la vitesse moyenne pour les trois essais effectués dans le cadre de la Partie 1 de l’exercice. Notez la valeur moyenne calculée dans la colonne du tableau de données prévue à cet effet. Calculez et reportez la vitesse moyenne atteinte lors des essais de la Partie 2.

2. Soustrayez la vitesse moyenne de la Partie 1 de la vitesse moyenne de la Partie 2 pour calculer l’augmentation de vitesse réalisée par votre groupe.

3. Quelles méthodes les autres groupes ont-ils utilisées pour accroître leur vitesse ?

Exercice 3 : Descente rapide en toboggan

4. Quelle méthode a fourni les meilleurs résultats ? Pourquoi ?

5. S’il était possible d’augmenter la hauteur de descente, de quelle façon cela affecterait-il

la vitesse de descente ?

6. Si une pierre est lancée du haut du toboggan alors qu’on fait rouler simultanément une autre pierre semblable du haut du toboggan, laquelle des deux pierres atteindra le sol la première ? Pourquoi ?

7. A quoi sert la portion inférieure à l’horizontale de nombreux toboggans ?

(suite)

Exercice 4 : Balle qui rebondit notes pédagogiques

Concepts

Fonction étudiée : quadratique.

Des expériences réelles tels que les objets qui tombent en chute libre et qui rebondissent sont des exemples de fonctions quadratiques. Cet exercice permet d’analyser les valeurs de hauteur, de temps et le coefficient A de l’équation quadratique,

Y = A(X – H)

+ K, qui décrit le comportement d’une

balle qui rebondit.

Matériel nécessaire

Ÿ calculette (voir page 2 la liste des modèles

disponibles)

Ÿ CBR 2™ Ÿ câble calculette/CBR 2™ ou câble d’E/S de

calculette à calculette

Ÿ application EasyData Ÿ balle de jeu (23 cm) Ÿ TI ViewScreené (facultatif)

Conseils

Cet exercice est plus facile à réaliser avec deux élèves. Un des élèves tient la balle et l’autre sélectionne Start sur la calculette.

Pour quelques conseils sur la façon de collecter efficacement des données, voir pages 6 à 9.

La courbe doit avoir l’aspect d’une balle qui rebondit. Si ce n’est pas le cas, répétez l’échantillon en veillant à ce que le

CBR 2™ soit placé bien en face de la balle.

Nous vous recommandons d’utiliser une grande balle.

Courbes typiques

Explorations

Lorsqu’un objet est lâché, seule la gravité a un effet sur lui (résistance de l’air négligeable). En conséquence, A dépend de l’accélération due à la gravité, N9.8 m/s

. Le signe négatif indique que

l’accélération est dirigée vers le bas. La valeur de A est égale à environ la moitié de

l’accélération due à la gravité, soit N4,9 m/s

Réponses typiques

1. temps (depuis le début de l’échantillon) ; secondes ;

hauteur à distance de la balle au sol ; mètres

2. hauteur initiale de la balle au sol (les pointes représentent la hauteur maximum de chaque rebond) ; le sol est représenté par y = 0.

3. La courbe Distance-Temps de cet exercice ne représente pas la distance du

CBR 2™ à la balle.

L’option Ball Bounce (rebond de la balle) inverse les données de distance de façon à ce que la courbe corresponde mieux à la perception qu’ont les élèves du comportement de la balle. Sur la courbe, y = 0 est en fait le point où la balle est la plus éloignée du

CBR 2™ lorsque celle-ci touche le sol.

4. Les élèves doivent bien réaliser que l’axe des x représente le temps et non une distance horizontale.

7. Le graphique de A = 1 est à la fois inversé et plus large que la courbe.

8. A < L1

9. parabole concave tournée vers le haut ; concave tournée vers le bas ; linéaire

12. semblable ; mathématiquement, le coefficient A représente l’extension de courbure de la parabole ; physiquement, A dépend de l’accélération due à la gravité, qui reste constante durant tous les rebonds.

Explorations évoluées

La hauteur de rebond de la balle (hauteur maximum d’un rebond donné) est approchée par la formule :

y = hp

0 y est la hauteur de rebond 0 h est la hauteur de laquelle la balle est lâchée 0 p est une constante qui dépend des caractéristiques

, où

physiques de la balle et de la surface du sol.

0 x est le nombre de rebonds

Pour une balle et une hauteur initiale données, la hauteur de rebond décroît de façon exponentielle pour chaque rebond successif. Si x = 0, y = h, alors l’intersection avec y représente la hauteur initiale de lâchage.

Les élèves ambitieux peuvent trouver les coefficients de cette équation à l’aide des données collectées. Répétez l’exercice pour des hauteurs initiales variables ou en utilisant des balles ou des surfaces de sol différentes.

Après avoir ajusté manuellement la courbe, les élèves peuvent utiliser l’analyse de régression pour trouver la fonction qui modélise le mieux les données. Choisissez ensuite Quit dans le menu principal Main. Suivez les procédures d’exploitation de la calculette pour effectuer une régression quadratique sur les listes

L1 et L2.

Extensions

Intégrez sous la courbe Vitesse-Temps, suivant le déplacement (distance nette parcourue) pour chaque intervalle de temps choisi. Notez que le déplacement est nul pour tout rebond complet (la balle part du sol et finit sur le sol).

Exercice 4 : Balle qui rebondit parabolique

Collecte de données

Ê Commencez par un rebond d’essai. Lâchez la balle (ne la jetez pas).

Conseils : Positionnez le

supérieure à la hauteur du rebond le plus haut. Pointez le détecteur droit sur la balle et veillez à ce que la zone libre soit entièrement dégagée (voir page 7).

CBR 2™ à une distance de 0,5 mètre et à une hauteur

Ë Exécutez l’application EasyData.

Ì Dans le menu Setup, sélectionnez 4:Ball Bounce, puis Start (appuyez sur q).

Des instructions générales s’affichent. L’option Ball Bounce gère automatiquement les

paramètres.

Í Demandez à un élève de tenir la calculette et le CBR 2™, alors qu’un autre élève place la

balle sous le détecteur.

Î Sélectionnez Start (appuyez sur q). Lorsque le CBR 2™ émet un cliquetis, lâchez la

balle, puis reculez. (Si la balle rebondit sur le côté, bougez pour garder le directement pointé au-dessus de la balle, mais faites attention à ne pas modifier sa hauteur).

CBR 2™

Ï Lorsque le cliquetis s’arrête, les données collectées sont transférées sur la calculette et

une courbe Distance-Temps s’affiche.

Ð Si la courbe ne paraît pas correcte, sélectionnez Main, Start, Start pour répéter

l’échantillonnage. Etudiez la courbe. Répondez aux questions 1 et 2 sur la feuille d’exercice.

Ñ Observez que Ball Bounce a inversé automatiquement les données de distance.

Répondez aux questions 3 et 4.

Exercice 4 : Balle qui rebondit

Explorations

La courbe Distance-Temps du rebond forme une parabole.

Ê La courbe est en mode TRACE. Appuyez sur ~ pour déterminer le sommet du premier

rebond satisfaisant (de forme correcte, avec un niveau de bruit réduit). Répondez à la question 5 sur la feuille d’exercice.

Ë Sélectionnez Main pour revenir à l’écran principal. Choisissez Quit, puis sélectionnez OK

pour fermer l’application EasyData.

Ì La “formule du sommet” de l’équation quadratique, Y = A(X –

Remarque : Si l’application Transformation Graphing est

+ K, est appropriée pour cette analyse. Appuyez sur œ.

Dans l’éditeur Entrez la formule du sommet de l’équation quadratique : Yn=A…(X–H)^2+K.

installée sur votre calculette, cette manipulation s’effectue plus simplement en modifiant la valeur des coefficients sur l’écran graphique.

Y=, désactivez toutes les fonctions sélectionnées.

(suite)

parabolique

Í Dans l’écran initial, enregistrez la valeur obtenue à la question 5 pour la hauteur dans la

variable K ; enregistrez le temps correspondant dans la variable H ; enregistrez 1 dans la variable A.

Par exemple : Appuyez sur 4 v t K Í, 2.5 v t H Í, 1 v

t A Í pour définir la valeur des variables comme suit : K=4, H=2,5 et A=1.

Î Appuyez sur  pour afficher le graphique. Répondez aux questions 6 et 7.

Ï Essayez A = 2, 0, –1. Complétez la première partie du tableau de la question 8 et

répondez à la question 9.

Ð Choisissez vos propres valeurs pour A jusqu’à ce que vous obteniez une courbe

satisfaisante. Enregistrez vos choix pour A dans le tableau de la question 8.

Ñ Répétez l’exercice, mais choisissez cette fois le dernier rebond complet (le plus à droite).

Répondez aux questions 10, 11 et 12.

Explorations évoluées

Ê Répétez la collecte des données, mais ne choisissez pas une seule parabole.

Ë Enregistrez le temps et la hauteur de chaque rebond successif.

Ì Déterminez le ratio entre les hauteurs de chaque rebond successif.

Í Expliquez, le cas échéant, la signification de ce ratio.

Exercice 4 : Balle qui rebondit

Nom __________________________________

Collecte de données

1. Quelle grandeur physique est représentée le long de l’axe des x ? ____________________________

Quelles sont les unités ? _______________________________________________________________

Quelle grandeur physique est représentée le long de l’axe des y ? ____________________________

Quelles sont les unités ? _______________________________________________________________

2. Que représente le point le plus haut de la courbe ? _________________________________________

Le point le plus bas ? __________________________________________________________________

3. Pourquoi l’application Ball Bounce a-t-elle inversé la courbe ? ________________________________

4. Pourquoi la courbe a-t-elle l’apparence d’une balle qui rebondit sur le sol ? ____________________

Explorations

5. Enregistrez la hauteur maximum et le temps correspondant pour le premier rebond complet ? ____

6. Est-ce que le graphique obtenu pour A = 1 correspond à la courbe de données du premier rebond

complet ? ____________________________________________________________________________

7. Si oui, pourquoi ? Si non, pourquoi ? ____________________________________________________

8. Complétez le tableau ci-dessous.

A Quelle comparaison peut-on faire entre la courbe de données et le

graphique Yn ?

-1

9. Qu’implique une valeur positive pour A ? _________________________________________________

Qu’implique une valeur négative pour A ? ________________________________________________

Qu’implique une valeur nulle pour A ? ___________________________________________________

10. Enregistrez la hauteur maximum et le temps correspondant pour le dernier rebond complet. ______

11. Pensez-vous que la valeur de A sera supérieure ou inférieure pour le dernier rebond ? ___________

12. A quoi peut-on comparer A ? ___________________________________________________________

Que représente, selon vous, A ? _________________________________________________________

Exercice 5 : Balle qui roule notes pédagogiques

Concepts

Fonction étudiée : quadratique.

Si vous étudiez le mouvement d’une balle roulant sur divers plan inclinés, vous obtenez toute une famille de courbes qui peuvent être modélisées par une série d’équations quadratiques. Cet exercice analyse les valeurs des coefficients de l’équation quadratique y = ax

+ bx + c.

Matériel nécessaire

Ÿ calculette (voir page 2 pour la liste des modèles

disponibles)

Ÿ CBR 2™ Ÿ câble calculette/CBR 2™ ou câble d’E/S de

calculette à calculette

Ÿ application EasyData Ÿ grande balle de jeu (23 cm) Ÿ rampe longue (une planche légère d’au moins 2

mètres)

Ÿ rapporteur pour mesurer les angles Ÿ livres pour soutenir la rampe Ÿ TI ViewScreené (facultatif)

Conseils

Discutez avec vos élèves de la méthode à utiliser pour mesurer l’angle de la rampe. Laissez-les faire preuve de créativité. Ils peuvent, par exemple, utiliser un calcul trigonométrique ou un papier plié.

Pour les angles à forte pente (supérieurs à 60º), il est possible d’utiliser le dispositif de fixation pour CBR 2™ (vendu séparément).

Pour quelques conseils sur la façon de collecter efficacement des données, voir pages 6 à 9.

Courbes typiques

15¡ 30¡

Réponses typiques

1. la troisième courbe

2. temps ; secondes; distance entre l’objet et le CBR 2™ ; mètres

3. varie (doit correspondre à la moitié d’une parabole, concavité tournée vers le haut)

4. une parabole (quadratique)

5. varie

6. varie (doit être parabolique avec une courbure croissante)

7. 0¡ est plat (la balle ne peut rouler) ; 90¡ est identique à une balle (qui tombe) en chute libre

Explorations

Le mouvement d’un corps sur lequel ne s’exerce que la force de gravité est un problème bien connu dans l’étude des sciences physiques. Un tel mouvement est typiquement exprimé par une forme particulière de l’équation quadratique,

s = ½at

0 s est la position d’un objet au temps t 0 a est son accélération 0 v 0 s

Dans l’équation quadratique y = ax y représente la distance du

+ vit + si où

est sa vitesse initiale

est sa position initiale

+ bx + c,

CBR 2™ à la balle au

temps x si la position initiale de la balle était c, si la vitesse initiale était b, et si l’accélération est égale à 2a.

Explorations évoluées :

Comme la balle est au repos lorsqu’elle est lâchée, b doit tendre vers zéro à chaque essai. c doit tendre vers la distance initiale de 0,5 mètre. a augmente au fur et à mesure que l’angle d’inclinaison croît.

Si les élèves modélisent manuellement l’équation

y = ax des conseils pour les valeurs de b et c. Vous pouvez également leur demander d’effectuer une régression quadratique sur les listes moyen de leur calculette. L’accélération de la balle est due à la force de gravité terrestre. Donc, plus la rampe est inclinée (plus l’angle d’inclinaison est grand), plus la valeur de a est grande. La valeur maximum de a est atteinte lorsque q = 90¡, et son minimum lorsque q = 0¡. En fait, a est proportionnelle au sinus de q.

+ bx + c, vous pouvez être amené à donner

L1 et L2 au

Exercice 5 : Balle qui roule parabolique

Collecte de données

Ê Répondez à la question 1 sur la feuille d’exercice. Utilisez le rapporteur pour

incliner la rampe à 15°. Fixez le perpendiculairement à la rampe.

CBR 2™ à la rampe et positionnez la tête du détecteur

Faites une marque sur la rampe à 15 centimètres du

maintenir la balle sur cette marque tandis qu’un autre élève tient la calculette et

CBR 2™.

Conseils : Pointez le détecteur droit sur la balle et veillez à ce que la zone libre soit

entièrement dégagée (voir page 7).

CBR 2™. Demandez à un élève de

Ë Exécutez l’application EasyData.

Ì Pour configurer la calculette pour la collecte de données :

a. Sélectionnez Setup (appuyez sur p) pour afficher le

menu Setup.

b. Appuyez sur

l’écran Time Graph Settings.

c. Sélectionnez Edit (appuyez sur q) pour ouvrir la boîte de

dialogue Sample Interval.

d. Entrez 0,1 pour définir l’intervalle en secondes entre les

échantillons.

e. Sélectionnez Next (appuyez sur q) pour ouvrir la boîte

de dialogue Number of Samples.

f. Entrez 30 comme nombre d’échantillons. La durée de la

collecte de données sera de 3 secondes.

2 pour sélectionner 2: Time Graph et afficher

Exercice 5 : Balle qui roule

g. Sélectionnez Next (appuyez sur q) pour afficher le

récapitulatif des nouveaux paramètres.

h. Sélectionnez OK (appuyez sur s) pour revenir à l’écran

principal.

Í Lorsque les paramètres définis sont satisfaisants, sélectionnez Start (appuyez sur q)

pour commencer l’échantillonnage.

Î Dès que vous entendez le cliquetis, lâchez immédiatement la balle (ne lui donnez pas

d’élan) et reculez.

Ï Quand l’échantillonnage est terminé, la courbe Distance-Temps s’affiche

automatiquement. Répondez aux questions 2, 3, 4 et 5.

Explorations

Observez ce qui se passe pour des plans inclinés de façons différentes.

Ê Effectuez une prédiction du résultat d’une augmentation d’inclinaison. Répondez à la

question 6.

(suite)

parabolique

Ë Réglez l’inclinaison à 30¡. Répétez la procédure, de l’étape 2 à l’étape 6. Ajoutez cette

courbe au schéma de la question 6, en l’identifiant par 30¡.

Ì Répétez la procédure, de l’étape 2 à l’étape 6, pour des plans inclinés à 45¡ et 60¡.

Ajoutez les courbes obtenues au schéma.

Í Répondez à la question 7.

Explorations évoluées

Ajustez les valeurs de temps telles que x = 0 pour la hauteur initiale (le temps où la balle a été lâchée). Vous pouvez effectuer ceci manuellement en soustrayant la valeur x du premier point de tous les points de votre courbe, ou vous pouvez entrer

Ê Calculez les valeurs de a, b et c pour la famille de courbes de la formule

y = ax

+ bx + c à 0¡, 15¡, 30¡, 45¡, 60¡, 90¡.

Ë Quelles sont les valeurs minimum et maximum de a ? Pourquoi ?

Ì Ecrivez une expression décrivant la relation mathématique entre a et l’angle

d’inclinaison.

L1(1)"A:L1NA"L1.

Exercice 5 : Balle qui roule

Nom ___________________________________

Collecte de données

1. Laquelle de ces courbes correspond selon vous le mieux à la courbe Distance-Temps d’une balle roulant le long d’une rampe ?

2. Quelle grandeur physique est représentée le long de l’axe des x ? ____________________________

Quelles sont les unités ? _______________________________________________________________

Quelle grandeur physique est représentée le long de l’axe des y ? ____________________________

Quelles sont les unités ? _______________________________________________________________

3. Réalisez une reproduction fidèle de la courbe. Identifiez les axes. Identifiez les points de la courbe où la balle a été lâchée et où cette balle a atteint l’extrémité de la rampe.

4. Quel type de fonction représente cette courbe, entre les deux points que vous avez identifiés ? ____

5. Dites pourquoi vous avez changé d’avis entre le graphique que vous avez choisi à la question 1 et la

courbe que vous avez esquissée à la question 3. ___________________________________________

____________________________________________________________________________________

Explorations

6. Faites une reproduction de la courbe telle que vous l’imaginez avec une inclinaison plus importante de la rampe. (Intitulez-la prédiction).

7. Reproduisez et identifiez des courbes pour 0¡ et 90¡ :

Informations pour le professeur

Comment un CBR 2™ peut-il changer la physionomie de vos cours ?

Le CBR 2™ est un système simple d’emploi comportant des fonctions qui vous permettent de l’intégrer facilement et rapidement dans vos cours.

CBR 2™ offre des perfectionnements importants par rapport aux autres méthodes de

Le collecte de données que vous pouvez avoir été amené à utiliser par le passé. Ce système peut vous conduire à restructurer vos cours (réorganisation du temps) car les élèves sont en général plus enthousiastes à manipuler des données réelles.

0 Vous vous rendrez compte que vos élèves s’approprient véritablement les données qu’ils

ont eux-mêmes collectées et qu’ils les préfèrent à celles extraites de manuels, journaux périodiques ou articles de statistiques. Le fait que vous exploriez en cours des concepts directement reliés au monde réel a sur eux plus d’impact que des idées abstraites. Mais ceci suppose bien entendu que chaque élève puisse effectuer lui-même sa collecte de données.

0 Il est considérablement plus efficace d’employer un CBR 2™ pour réaliser une collecte de

données que de créer des scénarios et relever manuellement des mesures à l’aide d’une règle et d’un chronomètre. Comme une quantité supérieure de points d’échantillonnage offre une plus grande résolution et comme un détecteur de mouvement à ultrasons est hautement précis, la forme des courbes est tout de suite plus évidente. Le temps gagné au niveau de la collecte de données peut être utilisé en analyse, en exploration et en modélisation.

0 Avec le CBR 2™, les élèves peuvent étudier la répétabilité des observations ainsi que les

variations introduites dans divers scénarios. Des questions telles que “Obtenons-nous la même parabole si nous lâchons la balle d’une hauteur supérieure ?” et “La parabole du premier rebond est-elle identique à celle du dernier rebond ?” s’imposent naturellement et sont les prolongements naturels et précieux de l’expérience.

0 La possibilité de visualiser immédiatement permet aux élèves d’associer rapidement les

données de liste représentées par des courbes aux propriétés physiques et aux fonctions mathématiques décrites par les données.

D’autres changements se produisent une fois que des données réelles sont collectées. Le

CBR 2™ permet à vos élèves d’étudier de façon numérique et graphique des relations sous-

jacentes.

Exploration graphique de données

Utilisez des courbes de distance, de vitesse et d’accélération en fonction du temps, automatiquement générées, pour les explorations du type suivant :

0 Quelle est la signification physique de l’intersection de l’axe y ? de l’axe x ? de la pente ?

du maximum ? du minimum ? des dérivées ? des intégrales ?

0 Comment reconnaissons-nous la fonction (linéaire, quadratique, etc.) représentée par la

courbe ?

0 Comment pourrions-nous modéliser les données avec une fonction représentative ?

Quelle est la signification des divers coefficients de la fonction (ex., AX

+ BX + C) ?

Informations pour le professeur

Exploration numérique de données

(suite)

Vos élèves peuvent employer des méthodes statistiques (moyenne, médiane, écart type etc.) appropriées à leur niveau pour étudier les données numériques. Lorsque vous quittez l’application EasyData, un message vous rappelle les listes dans lesquelles les données de temps (L1), distance (L2), vitesse (L3) et accélération (L4) ont été enregistrées.

Courbes du CBR 2™ : Elles relient le monde physique aux mathématiques

Les courbes créées à partir des données collectées par l’application EasyData sont une représentation visuelle des relations entre la description physique et mathématique d’un mouvement. Vous devez encourager les élèves à reconnaître, analyser et commenter la forme d’une courbe à la fois en termes de physique et de mathématiques. Un dialogue et des découvertes supplémentaires sont possibles quand les fonctions sont entrées dans l’éditeur Y= et affichées avec les courbes de données.

A titre d’exercice d’application en classe, il est intéressant d’effectuer les mêmes calculs que le CBR 2™.

1. Collectez un échantillon. Quittez l’application EasyData.

2. Utilisez les temps d’échantillonnage de de

L2 pour calculer la vitesse de l’objet pour chaque temps d’échantillonnage.

Comparez ensuite les résultats aux données de vitesse de

L1 conjointement avec les données de distance

L3.

(L2

3. Utilisez les données de vitesse de conjointement avec les temps d’échantillonnage de

+ L2n)à2 N (L2n + L2

n+1

N L1n

n+1

L3 (ou les valeurs calculées par les élèves)

)à2

n-1

L1 pour calculer l’accélération de

l’objet pour chaque temps d’échantillonnage. Comparez ensuite les résultats aux données d’accélération de

0 Une courbe Distance-Temps représente la position approximative d’un objet (distance

CBR 2™) à chaque instant du temps où un échantillon est collecté. Les unités de l’axe

L4.

des y sont des mètres ; celles de l’axe de x sont des secondes.

0 Une courbe Vitesse-Temps représente la vitesse approximative d’un objet (par rapport

CBR 2™ et en direction de celui-ci) à chaque temps d’échantillonnage. Les unités de

l’axe des y sont des mètresàseconde ; celles de l’axe des x sont des secondes.

0 Une courbe Accélération-Temps représente le taux approximatif de changement de

vitesse d’un objet (par rapport au

CBR 2™ et en direction de celui-ci) à chaque temps

d’échantillonnage. Les unités de l’axe des y sont des mètresàseconde² ; celles de l’axe des x sont des secondes.

0 La dérivée première (pente instantanée) de tout point sur la courbe Distance-Temps est

la vitesse à cet instant précis.

0 La dérivée première (pente instantanée) de tout point sur la courbe Vitesse-Temps est

l’accélération à cet instant précis. C’est également la dérivée seconde de tout point sur la courbe Distance-Temps.

0 Une intégrale définie (zone comprise entre la courbe et l’axe des x entre deux points

quelconques) sur la courbe Vitesse-Temps est égale au déplacement (distance nette parcourue) de l’objet durant cet intervalle de temps.

Informations pour le professeur

0 Les données acquises avec CBR 2™ permettent uniquement d’étudier les vitesses des

(suite)

mobiles en mouvement. Ces vitesses sont des grandeurs scalaires. La direction du mouvement est la droite qui joint CBR 2™ et le mobile. Le sens se traduira sur les courbes de variation de la distance en fonction du temps par une pente positive (le mobile s’éloigne du capteur) ou une pente négative (le mobile se rapproche du capteur).

Une courbe typique Vitesse-Temps du

CBR 2™ représente uniquement les variations de la

vitesse. Le sens du mouvement est donné par la courbe de variation de la distance en fonction du temps. Une valeur de vitesse positive indique un accroissement de la vitesse, une valeur de vitesse négative indique un diminution de la vitesse et une valeur constante traduit une vitesse uniforme.

CBR 2™ ne mesure la distance que le long d’une droite qui part du détecteur. Ainsi,

lorsqu’un objet se déplace en faisant un angle avec cette droite, le CBR 2™ ne calcule que la coordonnée de la vitesse parallèle à cette droite. Par exemple, un objet qui se déplace perpendiculairement à la droite du CBR 2™ semble avoir une vitesse nulle.

Les concepts mathématiques de distance, vitesse et accélération

Courbe Distance-Temps

moyenne

instantanée

1 t2

lim

@t"

(

N d

t2 N t

) =

= pente de la courbe Distance-Temps

d(s)

où s = distance

Courbe Vitesse-Temps

1 t2

moyenne

instantanée

lim

@t"

t2 N t

(

N v

= pente de la courbe Vitesse-Temps

) =

Informations pour le professeur

La zone sous la courbe Vitesse-Temps de t1 à t2 = @d = (d2Nd1) = déplacement de t1 à t2 (distance nette parcourue).

t=2

Donc,

d = (

1 t2

∑

t=1

Ressources disponibles sur notre site Web

Visitez notre site Web, education.ti.com, pour trouver :

0 une liste du matériel complémentaire à utiliser avec le CBR 2™, le CBL et les calculettes

graphiques

0 une page d’exercices avec des applications développées et partagées par des professeurs

comme vous

0 des programmes CBR 2™ permettant d’accéder à d’autres fonctions du CBR 2™ 0 des informations plus détaillées à propos des paramètres du CBR 2™ et des commandes

de programmation.

t)) ou

t=2

d =

v(dt)

⌠

⌡

t=1

Courbe Accélération-Temps

(suite)

Autres ressources

Les manuels de Texas Instruments consacrés aux Explorations fournissent des éléments supplémentaires sur les calculettes graphiques TI, y compris des cahiers proposant des exercices classes de collèges et de lycées.

CBR 2™ à faire en cours de mathématiques et de sciences avec des élèves des

Les données du CBR 2™ sont enregistrées dans des listes

Les données collectées sont enregistrées dans les listes L1, L2, L3 et L4

Lorsque le CBR 2™ collecte des données, il les transfère automatiquement sur la calculette et les enregistre dans des listes. Chaque fois que vous quittez l’application EasyData, un message vous spécifie la liste où sont enregistrées les données.

0 L1 contient les données de temps. 0 L2 contient les données de distance. 0 L3 contient les données de vitesse. 0 L4 contient les données d’accélération.

Par exemple, le 5ème élément de la liste données a été collecté, et le 5ème élément de la liste 5ème point de données.

Utilisation des listes de données

Lorsque vous quittez l’application EasyData, les listes ne s’effacent pas. Ainsi, elles sont disponibles pour d’autres explorations graphiques, statistiques et numériques, et pour des analyses.

Vous pouvez reproduire les listes l’une après l’autre, les afficher dans l’éditeur de liste, utiliser l’analyse de régression et effectuer d’autres exercices analytiques. Par exemple, vous pouvez collecter les données de déplacement d’un élève s’éloignant du demander aux élèves de trouver une droite de régression en utilisant la fonction d’ajustement linéaire manuel de la TI-84 Plus.

L1 représente le temps au moment où le point de

L2 représente la distance du

CBR 2™, puis

Paramètres de l’application EasyData

Modification des paramètres de l’application EasyData

L’application EasyData affiche les paramètres les plus fréquemment utilisés avant le début de la collecte des données.

Ê A partir de l’écran principal de l’application EasyData, choisissez Setup > 1: Dist ou 2:

Time Graph. Les paramètres courants s’affichent sur la calculette.

Remarque : Les paramètres utilisés pour les options Distance Match et Ball Bounce du

menu Setup sont prédéfinis et ne peuvent pas être modifiés.

Ë Sélectionnez Next (appuyez sur q) pour afficher le paramètre à modifier.

Ì Répétez cette opération pour chacune des options disponibles. Lorsque le paramétrage

de l’option vous convient, sélectionnez

Í Pour changer la valeur d’un paramètre, entrez 1 ou 2 chiffres, puis sélectionnez Next.

Î Lorsque tous les paramètres sont correctement définis, sélectionnez OK (appuyez sur

s) pour revenir à l’écran principal.

Next pour passer à l’option suivante.

Les nouveaux paramètres restent actifs jusqu’à ce que vous rétablissiez les paramètres par défaut de l’application EasyData, jusqu’à ce que vous exécutiez une application ou une autre activité qui modifie le paramétrage. Si vous manipulez L5 en dehors de l’application EasyData ou si vous effacez L5, les paramètres par défaut peuvent être restaurés la fois suivante où vous exécuterez EasyData.

Restauration des paramètres EasyData à leurs valeurs par défaut

Le paramétrage par défaut est approprié à une grande variété de situations d’échantillonnage. Si vous hésitez sur le paramétrage le plus adéquat, commencez avec les valeurs par défaut, puis ajustez les paramètres en fonction des besoins spécifiques de votre activité.

0 Pour restaurer les paramètres par défaut de l’application EasyData lorsque le CBR 2™ est

connecté à la calculette, choisissez File > 1:New.

0 Pour modifier les paramètres de l’application, suivez la procédure décrite ci-dessus.

0 Sélectionnez Start (appuyez sur q) pour commencer la collecte des données.

Utilisation du CBR 2™ avec le CBL 2™ ou avec des

programmes CBL 2™

Utilisation du CBR 2™ comme un détecteur traditionnel de mouvement avec le CBL 2™

Le CBR 2™ peut être utilisé comme un détecteur traditionnel de mouvement avec le système

CBL 2™

(Calculator-Based Laboratoryé) de Texas Instruments.

Un câble spécial pour connecter le

CBR 2™ au CBL 2™ est inclus.

Ne connectez pas le calculette doit être connectée au

Vous pouvez être amené à modifier le programme du programme

RANGER ne fonctionne pas avec le CBL 2™.

CBR 2™ au CBL 2™ si le CBR 2™ est déjà connecté à une calculette. La

CBL 2™.

CBL 2™ tel qu’indiqué ci-dessous. Le

Collecte de données de mouvement avec le CBR 2™ et le système CBL 2™

Ê Insérez les piles dans le CBL 2™.

Ë Connectez le CBL 2™ à une calculette graphique TI au moyen du câble d’E/S de

calculette à calculette.

Ì Connectez le détecteur CBR 2™ au port DIG/SONIC du CBL 2™ en

utilisant un câble CBL/CBR (vendu séparément).

Í Exécutez l’application DataMate à partir du menu Apps de la

calculette TI-83 Plus ou TI-84 Plus.

Î L’application DataMate identifie automatiquement les capteurs du CBL 2™, charge les

facteurs de calibrage appropriés et affiche le nom du capteur (“Motion”, dans ce cas), ainsi que la distance courante exprimée en mètres. Elle charge également un processus d’échantillonnage de mouvement par défaut de 5 secondes.

Utilisation du CBR 2™ avec le CBL 2™ ou avec des

programmes CBL 2™

Ï Commencez la collecte de données avec le processus

d’échantillonnage par défaut.

Tenez le détecteur de mouvement dans votre main et

sélectionnez 2: START pour commencer la collecte de données.

Ð Marchez en direction d’un mur tout en pointant le CBR 2™ sur

celui-ci.

Une fois la manipulation terminée, le graphique obtenu doit être

semblable à celui reproduit ci-contre.

Piles

Type de piles

Le CBR 2™ est conçu pour fonctionner avec des piles alcalines 4 AA. S’il est connecté à un

CBL, le CBR 2™ peut marcher sans piles.

Mise en place des piles

Quittez l’application EasyData avant de procéder au remplacement des piles.

1. Retournez le

CBR 2™ et, en appuyant à l’aide de

votre pouce sur le couvercle du compartiment à piles, faites-le coulisser vers l’arrière du

CBR 2™.

2. Positionnez les piles en respectant le schéma dessiné à l’intérieur du compartiment à piles du

CBR 2™.

3. Deux piles doivent être installées, pôles positifs vers le haut, du côté marqué + ; et deux piles, pôles négatifs vers le haut, du côté marqué -.

4. Remettez en place le couvercle du compartiment à piles du l’échantillonnage.

CBR 2™. Le CBR 2™ est prêt à commencer

Les piles du CBR 2™ sont déchargées : deux types d’avertissement

Le CBR 2™ dispose de deux mécanismes pour vous prévenir que les piles sont déchargées :

0 L’application EasyData affiche un message d’avertissement sur l’écran de la calculette tout

en essayant de collecter des données.

0 Le voyant lumineux rouge clignote de façon intermittente tandis que le CBR 2™ tente de

collecter des données.

Précautions à prendre pour les piles

0 N’utilisez pas de piles rechargeables. 0 Remplacez les quatre piles en même temps. Ne mélanger pas plusieurs marques de piles.

N’utilisez pas différents types de piles de la même marque.

0 Installez les piles en respectant les schémas dessinés à l’intérieur du compartiment à piles. 0 Débarrassez-vous immédiatement des piles usagées. Ne les laissez pas à la portée des

enfants.

0 Les piles ne doivent être ni chauffées, ni brûlées, ni percées. Elles contiennent des produits

chimiques nocifs qui peuvent fuir ou exploser.

0 Ne mélangez pas piles jetables et piles rechargeables. 0 N’essayez pas de recharger des piles jetables dans un chargeur de piles.

En cas de problème

Si vous avez ce problème : Essayez ceci :

Difficulté pour collecter des données

Vérifiez la connexion de la calculette au CBR 2™. Enfoncez toujours fermement les extrémités du câble dans les appareils.

Vérifiez le niveau des piles (voir page 40).

Le CBR 2™ commence à collecter lui-même des données

Si vous avez mal enfoncé le bouton ¤ du CBR 2™ pour le désactiver, il se peut que le bouton se soit relâché et qu’il ait donc déclenché l’échantillonnage. Appuyez à nouveau sur le bouton

¤ pour arrêter

l’échantillonnage.

CBR 2™, quittez correctement l’application EasyData (à

CBR 2™ ou CBL actif.

CBR 2™ sont perdues.

Le CBR 2™ n’arrête pas la collecte

des données

Avant de ranger le l’aide de Quit) ou tout autre programme

Appuyez sur ¤ pour arrêter l’échantillonnage. Répétez la manipulation. Si le problème persiste, retirez l’une des piles, puis remettez-la en place. Remarque : Toutes les données stockées sur le

Erreur de communication Connectez le CBR 2™ à la calculette au moyen du câble USB standard B/Mini-

A (calculette/ Vérifiez la connexion de la calculette au

CBR 2™).

CBR 2™. Enfoncez toujours

fermement les extrémités du câble dans les appareils. Si vous ne voulez pas (ou ne pouvez pas) connecter le

CBR 2™ à la calculette,

quittez l’application EasyData.

Mémoire insuffisante Vous devez disposer d’un espace suffisant de mémoire pour l’application

EasyData et les listes de données. EasyData requiert 5 000 octets pour fonctionner efficacement. Si nécessaire, effacez des éléments de la mémoire de la calculette.

Sur la calculette TI, appuyez sur y L 2:Mem Mgmt./Del. Choisissez les éléments à effacer et appuyez sur la touche DEL pour supprimer les éléments sélectionnés.

La calculette ne correspond pas aux instructions de l’exercice

Ce manuel s’applique à toutes les calculettes TI pouvant exécuter l’application EasyData. Il est donc possible que certains libellés de menu, certains écrans ou touches mentionnés dans ce guide ne correspondent pas exactement à ceux affichés sur votre calculette. Si vous utilisez Ranger ou d’autres programmes, choisissez la correspondance la plus proche. Par exemple, si les instructions disent “Choisissez DIstance match”, sur la calculette TI-83, vous devez sélectionner DIst match.

Les données n’ont pas l’air correct :

0 les points ne sont pas sur la

courbe

0 les courbes sont en dents de

scie

0 les courbes sont plates 0 la courbe est interrompue

Répétez l’échantillon, en veillant à ce que le sur l’objet.

Lire les pages 6 à 9 pour obtenir plus d’informations sur la manière de bien collecter les échantillons de données.

Vérifiez qu’il n’y ait ni élèves, ni tables, ni autres objets dans la zone libre. Lorsque deux

CBR 2™ sont utilisés en même temps dans la même pièce, il faut

attendre qu’un groupe ait fini de manipuler, avant qu’un autre groupe ne commence à échantillonner.

Vérifiez la connexion de la calculette au

CBR 2™ soit directement pointé

CBR 2™. Enfoncez toujours

fermement les extrémités du câble dans les appareils. Vérifiez le niveau des piles (voir page 40)..

Câble calculette/CBR 2™ égaré Vous pouvez utiliser le câble d’E/S de calculette à calculette fourni avec la

calculette. (Le câble calculette/

CBR 2™ permet d’exécuter automatiquement

l’application EasyData et offre une connexion plus fiable ; vous pouvez, si vous le désirez, commander un câble de remplacement.)

Batteries souvent déchargées Avant de ranger le CBR 2™, sortez correctement de l’application EasyData (à

l’aide de l’option Quit) ou de tout autre programme déconnectez le

CBR 2™ de la calculette.

CBR 2™ ou CBL, et

Organigramme des menus de l'application EasyData

Au bas de chaque écran de l'application s'affiche une ou plusieurs options. Pour sélectionner une option, appuyez sur la touche graphique indiquée directement sous l'option.

Pour afficher les menus dans l'ordre suivant, sélectionnez les options indiquées par la marque .

o p q r s

Par exemple, appuyez sur s pour sélectionner l'option Quit.

indique que la collecte des données est en cours.

Main Menu File Menu Setup Menu Quit Menu

1: Dist Unité

2: Time Graph Déf. int. échant. Déf. nbre échant. Mode Time Graph Courbe échant.

3: Distance Match Instructions Graphique à suivre Corresp. échant

4 :Ball Bounce Instructions Courbe échant

Informations sur les services et la garantie TI

Informations sur les produits et les services TI

Pour plus d’informations sur les produits et les services TI, contactez TI par e-mail ou consultez la page principale des calculatrices TI sur le world-wide web.

adresse e-mail : ti-cares@ti.com

adresse internet : education.ti.com

Informations sur les services et le contrat de garantie

Pour plus d’informations sur la durée et les termes du contrat de garantie ou sur les services liés aux produits TI, consultez la garantie fournie avec ce produit ou contactez votre revendeur Texas Instruments habituel.

Texas instruments CBL 2 GETTING STARTED

Specifications and Main Features

Frequently Asked Questions

User Manual

Important

Table des matières

En quoi consiste le CBR 2™ ?

Que fait le CBR 2™ ?

Quel est l’objectif de ce manuel

Utilisation du CBR 2™ : aussi simple que de compter jusqu’à 3

Téléchargement

Connexion

Exécution

Informations importantes

Conseils pour collecter efficacement des données

Comment obtenir de meilleurs échantillons ?

Description du fonctionnement du CBR 2™

Taille de l’objet

Distance minimale

Distance maximale

Sélecteur de sensibilité

La zone libre

Surfaces réfléchissantes

Paramètres de l’application EasyData

Configuration de la collecte de données pour l’option Time Graph

Démarrage et arrêt

Bruit : De quoi s’agit-il et comment l’éliminer ?

Vitesse du son

Utilisation du CBR 2™ sans l’application EasyData

Objectifs

Collecte de données : courbes Distance-Temps

Collecte de données

Explorations

Collecte de données

Explorations

Résultats de l’échantillonnage

Objectifs

Collecte de données, Partie 1, Vitesse de descente

Collecte de données, Partie 2, Descente rapide en toboggan

Stratégie d’augmentation de la vitesse de descente

Données

Traitement des données

Collecte de données

Explorations

Explorations évoluées

Collecte de données

Explorations

Collecte de données

Explorations

Explorations évoluées

Collecte de données

Explorations

Informations pour le professeur

Comment un CBR 2™ peut-il changer la physionomie de vos cours ?

Exploration graphique de données

Exploration numérique de données

Courbes du CBR 2™ : Elles relient le monde physique aux mathématiques

Les concepts mathématiques de distance, vitesse et accélération

Ressources disponibles sur notre site Web

Autres ressources

Les données du CBR 2™ sont enregistrées dans des listes

Les données collectées sont enregistrées dans les listes L1, L2, L3 et L4

Utilisation des listes de données

Paramètres de l’application EasyData

Modification des paramètres de l’application EasyData

Restauration des paramètres EasyData à leurs valeurs par défaut

Utilisation du CBR 2™ comme un détecteur traditionnel de mouvement avec le CBL 2™

Collecte de données de mouvement avec le CBR 2™ et le système CBL 2™

Piles

Type de piles

Mise en place des piles

Les piles du CBR 2™ sont déchargées : deux types d’avertissement

Précautions à prendre pour les piles

En cas de problème

Organigramme des menus de l'application EasyData

Informations sur les services et la garantie TI

Informations sur les produits et les services TI

Informations sur les services et le contrat de garantie