Teledyne DFP2 User Manual

Digital Filter Package 2
(DFP2)

Software

Instruction Manual

Digital Filter Package 2 Software Instruction Manual

© 2013 Teledyne LeCroy, Inc. All rights reserved.

Unauthorized duplication of Teledyne LeCroy documentation materials other than for internal sales and distribution pur­poses is strictly prohibited. However, clients are encouraged to distribute and duplicate Teledyne LeCroy documentation
for their own internal educational purposes.

Digital Filter Package 2 and Teledyne LeCroy are registered trademarks of Teledyne LeCroy, Inc. Windows is a registered
trademark of Microsoft Corporation. Other product or brand names are trademarks or requested trademarks of their
respective holders. Information in this publication supersedes all earlier versions. Specifications are subject to change
without notice.

923134 Rev A
June 2013

DFP2 Option

INTRODUCTION...................................................................................................3

The Need..........................................................................................................................................3

The Solution.....................................................................................................................................3

Enhanced Solutions.........................................................................................................................4

Kinds of Filters .................................................................................................................................5

Communications Channel Filters.....................................................................................................7

IIR Filters..........................................................................................................................................9

FILTER SETUP ...................................................................................................10

To Set Up a DFP Filter...................................................................................................................10

MULTIRATE FILTERS........................................................................................11

Description ..................................................................................................................................... 11

Example..................................................................................................................................11

CUSTOM FILTERS.............................................................................................13

Custom Filter Setup .......................................................................................................................13

Example 1: Creating an FIR Filter Coefficient File Using Mathcad........................................13

Writing Data to a Data File......................................................................................................15

Example 2: Creating an IIR Filter Coefficient File Using Mathcad .........................................17

Writing Data to a Data File......................................................................................................19

SPECIFICATIONS..............................................................................................19

923134 Rev A ISSUED: June 2013 1

BLANK PAGE

2 ISSUED: June 2013 923134 Rev A

DFP2 Option

INTRODUCTION

The Need

In today's complex environment, data is frequently composed of a mixture of analog and digital
components spread over a broad range of frequencies. In many applications, the relevant data is
encoded or obscured. Capturing the right signals becomes a challenge. Engineers find it
increasingly difficulty to examine only those parts of the data they are interested in. Tradition al (or
even smart) oscilloscope triggering cannot always provide a satisfactory answer.

For example, servo motors from disk drives add a low frequency component to the high
frequency data output. It is hard to achieve an accurate analysis of data unless the low
component is removed.

Another common example is switched power supply units, which inject the switching frequency
component into many system parts. Viewing digital signals mixed with this switching frequency
component could be very difficult. Filtering is definitely required.

Yet another example is in ADSL residential connectivity, where data is transmitted over 256
narrow bands. Each band is only 4.7 kHz wide, and the gap between two adjacent bands is also

4.7 kHz. Examining such complex waveforms with regular DSOs is almost impossible; filtering out
unwanted frequency components is necessary.

The Solution

At present, these needs are addressed in two ways. One way is building analog filters and
placing them in front of the oscilloscope, providing an already filtered signal to the DSO. The
disadvantages of this approach are many. Analog filters depend heavily on the accuracy and
stability of analog components. Although in some cases analog filters are easily implemented,
they are quite impractical for low (< 100 Hz) or high (> 100 MHz) frequency ranges. In
comparison, digital filters can provide the desired results in those cases.

The second approach, practiced by many engineers, is using the DSO as a digitize r. The digitized
data output is then transferred to a PC for processing. This solution freque ntly provides the
required results, but it might be too slow or too limited in flexibility for some applications.

With Digital Filter Package 2 (DFP2), Teledyne LeCroy provides a solution that combines the
best of both worlds. This package includes seven of the most useful finite impulse response
filters (FIR), in addition
(IIR) filter types (Butterworth, Chebyshev, Inverse Chebyshev, Bessel). You can easily set the
Cutoff Frequency in addition to the Stop Band Attenuation and Pass Band Ripple for each filter.

It is even possible to use single filters or multiple filters cascaded for even more complex filtering.
Once filtered, waveforms include mostly relevant frequency components, undesired parts being
greatly attenuated.

If you want filters with special characteristics, the custom design feature allows you to design
unique filters tailored to your specific needs. The required filter can be designed with a digital filter

923134 Rev A ISSUED: June 2013 3

to a custom design feature. It also includes four infinite impulse response

gn or with a math package such as MATLAB or Mathcad. Filter coefficients can be directly

desi
downloaded from the program into the scope, using the DSOFilter utility. It is also possible to
specify the filter coefficients on an Excel spreadsheet and to use DSOFilter to download them
from the spreadsheet to the scope.

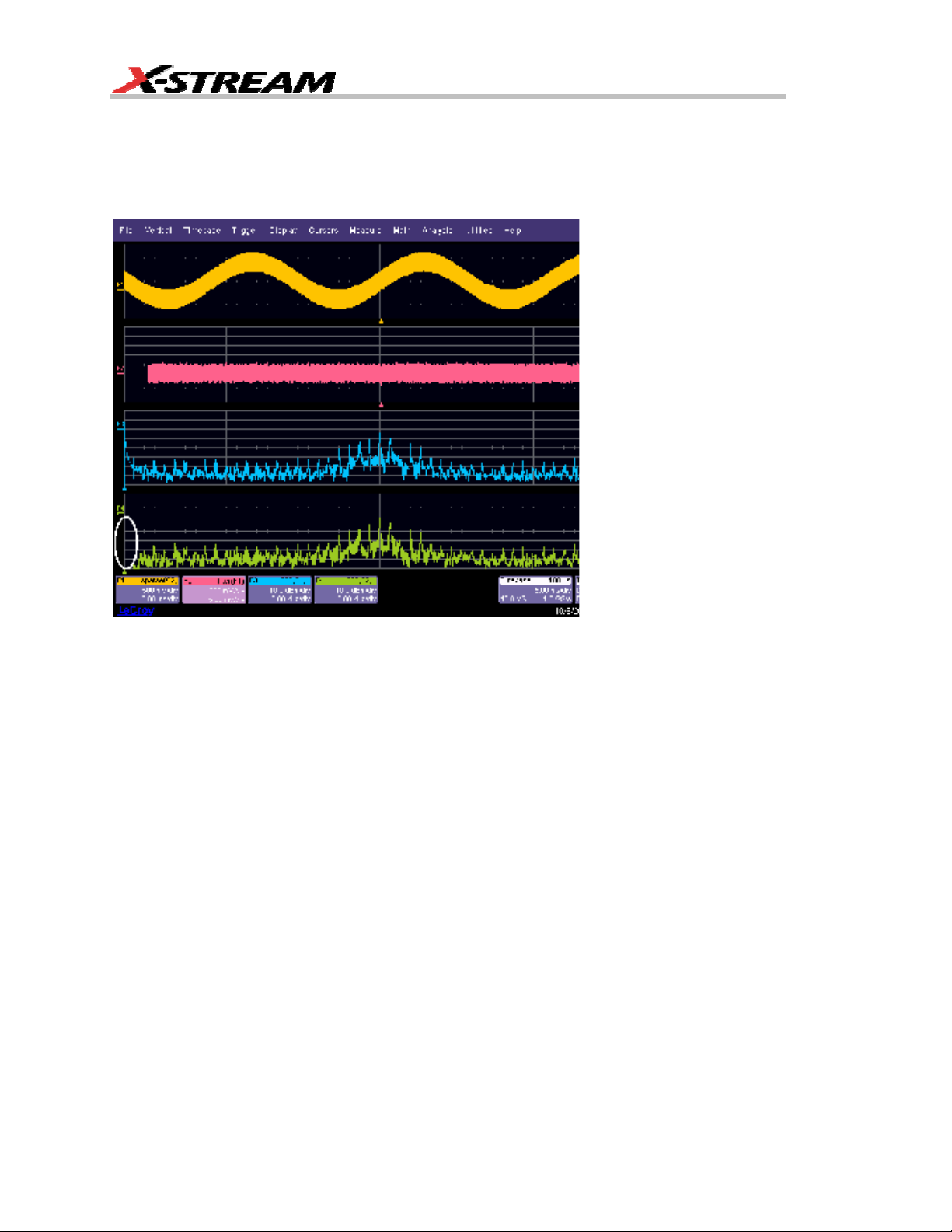
DFP2's flexibility is shown by the following example:

1. A 25 kHz square
with an unwanted 60 Hz sinusoidal
component.

2. A high-pass filter set to attenuate
signals lower than 1 kHz is applied
to remove the unwanted 60 Hz
component.

3. FFT of the unfiltered trace.

4. FFT of the filtered trace. Note the
absence of the 60 Hz component.

wave combined

Enhanced Solutions

DFP2 can be coupled with other Teledyne LeCroy software products such as JTA2 or DDM2 to
enhance the capabilities of these products and to provide improved solutions. For Jitter
Measurement, for example, the DFP2 Band-pass Filter can be coupled with the JTA2 package to
measure jitter over a narrow frequency range.

4 ISSUED: June 2013 923134 Rev A

DFP2 Option

Kinds of Filters

Low-pass Filter

High-pass Filter

1

Low-p

ass filters are useful for eliminating accumulated
high-frequency noise and interference, and for
canceling high-frequency background noise.

Sample applications are in datacom,
telecommunications, and disk drive and optical
recording analysis for accurate RF signal detection.

Band 1: Pass Band — DC to top of the transition
region; signal passes unattenuated.

Band 2: Transition Region — edge frequency to edge
frequency plus width; increasing attenuation.

Band 3: Stop Band — above end of transition region;
signal is highly attenuated.

-pass filters are useful for eliminating DC and low-

High
frequency components. Sample applications include
Disk Drive and Optical Recording analysis (emulation
of the SLICING function).

Band 1: Stop Band — DC to bottom of the transition
region; highly attenuated.

Band 2: Transition Region — edge frequency minus
width to edge frequency; decreasing attenuation.

Band 3: Pass Band — above edge frequency; signal
passes unattenuated.

1

1. Filters are optimal FIR filters of less than 2001 taps, according to the Parks-MacLellan algorithm described in Digital
Filter Design and Implementation by Parks and Burrus, John Wiley & Sons, Inc., 1987, and then adjusted by windowing
the start and end 20% with a raised cosine for improved time domain characteristics and better ultimate rejection in the
frequency domain, slightly increasing 1

923134 Rev A ISSUED: June 2013 5

st

stop-band ripple height.

Band-pass Filter

Band-p

ass filters are useful for emphasizing a selected
frequency band. Sample applications include radio
channel identification, broadband transmission, ADSL,
clock generators (i.e., eliminating the central frequency
and displaying harmonics only), and
telecommunications (Jitter measurement over a
selected frequency range).

Band 1: First Stop Band — DC to bottom of first
transition region; highly attenuated.

Band 2: First Transition Region — lower corner minus
width to lower corner; decreasing attenuation.

Band 3: Pass Band — signal passes unattenuated.
Band 4: Second Transition Region — upper corner to

upper corner plus width; increasing attenuation.
Band 5: Second Stop Band — signal highly attenuated.

Band-stop Filter

Band-stop filters a

re useful for eliminating a narrow
band of frequencies. Sample applications include
medical equipment, such as ECG monitors where the
dominant ripple at 50/60 Hz is rejected, leaving the low
energy biological signals intact. Digital troubleshooting:
the inherent frequency of the switched power supply is
blocked, revealing power line voltage drops and
glitches caused by the system clock generator.

Band 1: First Pass Band — DC to bottom of first
transition region; signal passes unattenuated.

Band 2: First Transition Region — lower corner minus
width to lower corner; increasing attenuation.

Band 3: Stop Band — signal is highly attenuated.
Band 4: Second Transition Region — upper corner to

upper corner plus width; decreasing attenuation.
Band 5: Second Pass Band — signal passes

unattenuated.

6 ISSUED: June 2013 923134 Rev A

Communications Channel Filters

DFP2 Option

Raised Cosine (a low-pass filter)

These filters
a variety of shapes). Raised cosine is one of a class of
filters used to minimize intersymbol interference: the
time domain impulse response crosses zero at all bit
time intervals except the one with the impulse.

Applying raised root cosine twice (or at the sending
and receiving end of a signal, for example) results in a
raised cosine filter effect. Sample applications include
wireless cellular communications such as WCDMA,
datacom, telecommunications, disk drive and optical
drive analysis.

Band 1: Pass Band — DC to corner frequency minus
half width; signal passes unattenuated.

Band 2: Transition Region —corner minus half width to
corner plus half width; attenuation increases with
frequency with a rolloff shape of 0.5cos(a) + 0.5, where
a ranges from 0 to p over the transition region. This
region is determined by b, which is specified as a
percentage of the corner frequency.

Band 3: Stop Band — above corner frequency plus half
width; highly attenuated.

The impulse function for the raised cosine filter is:

belong to the low-pass filter category (with

923134 Rev A ISSUED: June 2013 7

Raised Root Cosine (a low-pass filter)

Band 1: Pass Band — DC

to corner frequency minus

half width; signal passes unattenuated.
Band 2: Transition Region —corner minus half width to

corner plus half width; attenuation increases with
frequency with a rolloff shape of 0.5[cos(a) + 0.5]½,
where a ranges from 0 to p over the transition region.
This region is determined by b, which is specified as a
percentage of the corner frequency.

Band 3: Stop Band: — above corner fre quency plus
half width; signal is highly attenuated.

The impulse function for the square-root raised cosine
filter is:

Gaussian

Band 1: Pass Band — DC

to half power bandwidth%
times modulation frequency, pass; 3 dB down at half
power bandwidth.

The shape of a Gaussian filter’s frequency response is
a Gaussian distribution centered at DC. The signal
becomes more attenuated with increasing frequency. It
is not possible to specify a transition region or a stop
band for Gaussian filters. However, the BT value, a
fraction of the symbol frequency, determines the filter’s
width, where:

B = half power bandwidth
T = bit (or modulation period)

8 ISSUED: June 2013 923134 Rev A

DFP2 Option

IIR Filters

Infinite Impulse Response (IIR) filters are digital filters that emulate analog filters. The four types
offered by the DFP2 option are as follows:

• Butterworth

• Chebyshev

• Inverse Chebyshev

• Bessel

The Butterworth or "maximally flat" filter has the flattest amplitude response of all the available
filters. The Bessel filter is noted for its uniform phase response as a function of frequency. The
following figure shows a comparison between Butterworth and Bessel filters. Note that the Bessel
filter has a wider transition bandwidth, but linear phase within the pass ban d.

If you need the fastest rollo
given number of stages. However, the Chebyshev filter has ripple in the pass band, while the
Inverse Chebyshev filter exhibits a flat pass band response, but has ripple in the stop band.

923134 Rev A ISSUED: June 2013 9

ff, the Chebyshev filters have the narrowest transition region for a

In the setup of these filters, you have control of cutoff frequencies, transition region width, and
stop band attenuation.

FILTER SETUP

To Set Up a DFP Filter

1. Touch Math in the menu bar then Math Setup... in the drop-down menu.

2. Touch the Fx tab (F1
your filtered

ouch the Single function

3. T

waveform.

button

the trace, or touch the Dual function button

for example) for the math trace you want to display

if you want to perform just one filtering function on

to perform math on, or apply another

filter to, the filter output.

4.

Touch inside the Source1 field and select a source waveform from the pop-up m

5.

Touch inside the Operaor1 field and select

Filter

from the pop-up menu. A mini-dialog

enu.

to set up the filter will open at right.

Note: Other math choices in the Operator1 menu include Boxcar, ERES, and interpolation. The boxcar "filter" is a simple
average taken over a user-specified number of points (the "length").

6. Touch inside the FIR/IIR field and select finite or infinite response filter FIR (n on-recursive)
filters require a limited number of multiplications, additions, and memory location
other ha
theory require an infinite number

Whether you selected FIR or IIR, touch inside the Filter Kind field and sele

7.
operation. So

If you selected FIR, touch inside the Type field and choose an FIR filter type.

8.
insid
Alternatively
scope

Ty

enter a value,
Length ch
numbe

nd, IIR (recursive) filters, which are dependent on previous input or output values, in

of each..

e the Taps

me choices are not availabl

2

data entry field and enter a value, using the pop-up numeric keypad.

e for IIR.

, you can touch the Auto Length checkbox; the Taps field is grayed

calculates the optimum number of coefficients. If you selected IIR, touch inside

pe field and choose an IIR filter type. Then touch inside the Stages data en

using the pop-up numeric keypad. Alternatively, you can touch the

eckbox; the Stages field is grayed out and the scope calculates the op

r of sta

ges.

s. On the

ct a filtering

Then touch

out and the

the

try field and

Auto

timum

2

The number of coefficients. The number of coefficients. The suggested number of taps is a minimal suggestion: using
even more taps can give a more desirable response. Using less than the suggested number of taps will not meet the
requested specifications.

10 ISSUED: June 2013 923134 Rev A

DFP2 Option

9. Touch the Frequencies tab.

10. Depending on the class (FIR/IIR) and kind of filter you selected, and whether or not Auto
Length is enabled, you can change the cutoff frequencies, transition width (edge width), stop
band attenuation, and pass band ripple.

MULTIRATE FILTERS

Description

In many of today's development environments, digital filter design has become most

hallenging. Specifications typically require higher order filters, implying increased storage

c
capacity for filter
difficult, if not impossible, to design. In applications such as 3G wireless systems, for example,
at the receiver end data must be filtered very tightly in order to be processed.

Although the Teledyne LeCroy DFP option provides many filter types, the correlation between
edge

frequencies and sample rate may be a limiting factor: edge frequencies are limited from
1% to 49.5% of the sample rate, while the minimum transition width region is 1% of the sample
rate.

Multirate, multistage filters are a practical solution for the design and implementation of FIR
filters with narrow spectral constraints. Multirate filters change the input data rate at one or more
intermediate
input rate. This approach provides a solution with greatly reduced filter lengths, as compared to
standard single-rate filters.

coefficients and higher processing power. Moreover, high-order filters can be

points within the filter itself, while maintaining an output rate that is identical to the

This can be achieved in two or more simple steps. First, a filter (with a relatively limited edge
frequency)
decimated waveform, substantially reducing the lower edge frequency limit.

Example

A sine wave with a frequency of 3 MHz has a higher frequency noise component. A low-pass
filter is required to remove the noise component. The sample rate of the scope is 2 GS/s. The
minimum edge frequency of the low-pass filter for this sample rate is 20 MHz. While this filter is
sufficient for removing part of the noise, it cannot remove the high frequency component
c

ompletely. In such a case, the problem can be solved in two stages.

923134 Rev A ISSUED: June 2013 11

is applied and the results are decimated. Then, a second filter is applied to the

1. A noisy sine wave with a frequency of 3 MHz.

2. The first low-pass filter with 20 MHz edge frequency
and 30 MHz transition region is applied.

3. A sparsed version of trace A.

4. A second low­MHz and a transi
the sparsed trace in 3.

pass filter with an edge frequenc

tion region width of 6 MHz is applied to

The last trace shows the zoomed signal, which was filtered by a multistage filtering method.
Notice that all high frequency noise components were removed.

y of 5

12 ISSUED: June 2013 923134 Rev A

DFP2 Option

CUSTOM FILTERS

Custom Filter Setup

If the standard filters provided with DFP2 are not sufficient for you r needs, you can create filters
with virtually any characteristic, up to 2000 taps.

The required custom filter can be designed with a digital filter design or math package such as
MATLAB or Mathcad. The filter coefficients can then be loaded into the scope from an ASCII file.
The file consists of numbers separated by spaces, tabs, or carriage returns.

Note: Do not use commas as separators.

For a custom IIR filter there needs to be a multiple of 6. Each stage consists of 3 numbers for the
numerator polynomial followed by 3 numbers for the denominator polynomial. They are in the
order a b c where the polynomial is of the form: a + b * z

Example 1: Creating an FIR Filter Coefficient File Using Mathcad

N := 200 i := 0..N
sinx(x) := sin(x)/x

-1

+ c * z-2.

200 poi

nt sin(x)/x, a low-pass filter .

Note: Real world filters would either be windowed or made by the Remez exchange algorithm.
The point of this example is to show how to transfer a filter to the scope.

che

ck = 0.987 This is the DC gain of the filter

923134 Rev A ISSUED: June 2013 13

No

w create an ASCII file containing the coefficients: FirFilter.txt

14 ISSUED: November 2003 DFP2-OM-E Rev A

DFP2 Option

Writing Data to a Data File

To write values from Mathcad version 11 to a data file, you can use the File Read/Write
component, as follows:

Click in the blank spot in your workshee

1.

t.

2. Cho

ose Insert, Data, File Output from t

he menu.

DFP2-OM-E Rev A ISSUED: November 2003 15

3. This opens the File Options wizard:

4. From

5. Press

the File Format drop-down list choose "Tab Deli

Finish.
to the data file unde
Mathcad vari

The File Output component icon will ap

r it. Underneath that, the cursor is on a placeholder for the

able containing the data to be written to the data file. Enter the na

mited Text".

pear in your spreadsheet, with the path

name of the

me of the

variable.

When you cli

ck outside the component, the values in the Mathcad variable will be written to the

filename you specified. Each time you calculate the worksheet, the data file is rewritten.
On the instrument, when the Custom filter kind is selected, a file selection box will appear. Select

the file saved from Mathcad; the coefficients will be used in the filter.

16 ISSUED: June 2013 923134 Rev A

Example 2: Creating an IIR Filter Coefficient File Using Mathcad

⎛

⎜

⎜

⎝⎞⎠

Note: This example uses the Mathcad Signal Processing Extension Pack.

order6:=

fcutoff .1:=
A iirlow butter order( ) fcutoff,():=

DFP2 Option

0.083

A

0.166

=

0.083

x 0 .001, .5..:=

gain A x,()

1

1.404−

0.736

0.067

0.135

0.067

1

1.143−

0.413

0.061

0.122

0.061

1

1.032−

0.276

1

1

0.5

0

0

0 0.1 0.2 0.3 0.4 0.5

Now create an ASCII file containing the coefficients: IirFilter.txt

0.50 x

Note: The diskette icon, the file name, and the "A" below it are the representation of a Mathcad "File Output" component.
It is inserted by selecting Insert, Data, File Output. You must specify the file name ("IirFilter.txt" in the example) and fill in
the variable name that is the source of the data ("A" in the example). Be sure to specify a complete path for the file.

DFP2-OM-E Rev A ISSUED: November 2003 17

Note: In the example above, because “A” has a predefined meaning (as a unit) in Mathcad 11, it appears with a green
underline. However, earlier versions of Mathcad give no warning about using "A" as a variable name, and it may still be
used for this purpose.

What gets written to lirfilter.txt is as follows:

0.0828825751812225 1 0.0674552738890719 1 0.0609096342883086 1

0.165765150362445 -1.40438489047158 0.134910547778144 -1.1429805025399 0.121819268576617 -1.03206940531971

0.0828825751812225 0.735915191196472 0.0674552738890719 0.412801598096189 0.0609096342883086 0.275707942472944

18 ISSUED: June 2013 923134 Rev A

DFP2 Option

Writing Data to a Data File

To write values from Mathcad to a data file, you can use the File Read/Write component, as
follows:

1. Click in the blank spot in your worksheet.

2. Choose Component from the Insert menu.

3. Select File Read or Write from the list and click Next. This launches the first part of the File
Read or Write Setup Wizard.

4. Choose Write to a data source and press Next to go to the second page of the Wizard:
From the File Format drop-down list in this Wizard, choose Tab Delimited Text.

5. Type the p ath to the data file you want to write, or click the Browse button to locate it.

6. Press Finish. You'll see the File Read or Write component icon and the path to the data file.
In the place holder that appears at the bottom of the component, enter the transposed name
of the Mathcad variable containing the data that will be written to the data file. It is important
to transpose the variable (Ctl + 1) so that the variables appear in the correct order.

When you click outside the component, the values in the Mathcad variable will be written to the
filename you specified. Each time you calculate the worksheet, the data file is rewritten.

On the instrument, when the Custom filter kind is selected, a file selection box will appear. Select
the file saved from Mathcad; the coefficients will be used in the filter.

SPECIFICATIONS

• The pass-band gain of all filters (except custom) is normalized to 1.

• FIR Coefficients: 2001 max.

• IIR Stages: 2 9 max.

• Filter Kinds: high pass, low pass, band pass, band stop, raised cosine, raised-root cosine,

Gaussian, custom

• IIR Filter Types: Butterworth, Chebyshev, Inverse Chebyshev, Bessel

§ § §

923134 Rev A ISSUED: June 2013 19