Page 1

Signals and Measurements for
Wireless Communications Testing
Page 2

2
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1
Analog Carriers and Modulation
1 Basic Sine Wave Amplitude Modulation (AM) . . . . . . . . . . . . . . .3
2 AM with Adjacent Carriers . . . . . . . . . . . . . . . . . . . . . . . . . .5
3 Multi-Tone Testing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7
4 Frequency Modulation . . . . . . . . . . . . . . . . . . . . . . . . . . . .9
5 FM with Dual-Tone Modulation . . . . . . . . . . . . . . . . . . . . . . . .10
6 FM Stereo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .12
7 Adding Noise to a Carrier Signal — AWG Noise Characteristics . . . . . . . . . . .14
Digital Modulation
8 Digital Phase Modulation — PSK . . . . . . . . . . . . . . . . . . . . . . .17
9 Baseband Digital Patterns . . . . . . . . . . . . . . . . . . . . . . . . . .19
10 Digital AM — OOK and BPSK . . . . . . . . . . . . . . . . . . . . . . . . .20
11 Digital FM — FSK . . . . . . . . . . . . . . . . . . . . . . . . . . . . .21
12 Quadrature Modulation . . . . . . . . . . . . . . . . . . . . . . . . . . .23
13 Filtering Out Unwanted Sidebands . . . . . . . . . . . . . . . . . . . . . . .25
14 Direct Sequence Spread Spectrum . . . . . . . . . . . . . . . . . . . . . .28
For More Information on Tektronix Instrumentation . . . . . . . . . . . . . . . . . .29
AWG 2000 Series Arbitrary Waveform Generators . . . . . . . . . . . . . . . .30
TDS 744A Digitizing Oscilloscope . . . . . . . . . . . . . . . . . . . . . . .31
Table of Contents
Note: Each signal and waveform screen in this application note originates from one of three types of instruments: an
arbitrary waveform generator, a digital storage oscilloscope, or a spectrum analyzer. Each illustration is annotated
with a symbol indicating its origin:
AWG
Oscilloscope (DSO)
Spectrum Analyzer
Page 3

3
One of the most challenging tasks in designing
wireless communications products is the development of a rational approach to characterizing and
testing components, assemblies, and sub-systems.
Baseband modulation and RF signal characteristics
are becoming increasingly complex as standards
and common sense force more efficient use of the
finite electromagnetic spectrum. In addition,
manufacturers must often make equipment that is
capable of switching between different modes with
differing signal characteristics. As before, realistic
test signals are needed to simulate nominal and
worst case conditions. Yet traditional signal generators with limited modulation capabilities are
inadequate and it is not always feasible to have a
test department develop customized systems.
Test equipment has historically allowed two
approaches. If a standard has reached a threshold
of maturity, then you could obtain a
generator/analyzer that addresses that standard—
from a traditional FM broadcast to a digital PCS
system. Or you could concoct a combination of
signal, RF, and pattern generators to simulate the
desired test signal. The former approach is excellent for production and field service applications
but lacks flexibility for development applications.
The latter approach often turns into an expensive
kluge providing both inconsistent performance and
limited flexibility.
More recently, test equipment manufacturers have
filled the gap between the two approaches with the
arbitrary waveform generator (AWG). The AWG is
the signal generator equivalent to the computer
spreadsheet; you can create limitless “what-if”
waveforms to more thoroughly evaluate or test new
concepts, prototype circuits, or production subassemblies. Like a spreadsheet, the power of the
AWG comes from the ability to define and redefine a signal’s value as a function of time. But a
blank spreadsheet is of little use—how do you get
the first waveform to appear at the BNC connector?
The most straightforward method is the recordplayback technique. A live signal is recorded into
the memory of a digital oscilloscope, and the
record is transferred to the AWG for playback. This
method is expedient but has limited flexibility.
Creating and editing a customized signal is a more
powerful technique and is the focus of this note:
once created, re-creating a complex signal at a later
date is as simple as retrieving it from memory—
rather than re-cabling and re-configuring an assortment of interconnected generators.
Ironically, the flexibility of an AWG can make it
difficult to select a model that fits a given application. For example, you will not find a specification
that explicitly defines an AWG’s ability to generate
a particular modulation type. In general, an AWG’s
ability to generate a specific signal must be demonstrated by example.
In this paper, we begin with examples of basic
AM-FM analog signals and introduce variations
such as multiple carriers and multiple modulation
signals (e.g., FM stereo). Then we demonstrate that
digital modulation generation is a straightforward
extension of basic analog modulation.
Throughout this application tutorial, we have used
the Tektronix AWG 2021 Arbitrary Waveform
Generator as the signal source, and the Tektronix
TDS 744A oscilloscope to capture and analyze
signals. The AWG 2021 provides the signal capabilities, modulation features, and bandwidth
essential to effective wireless communications
testing. The TDS 744A is an ideal complement to
the AWG 2021 and is unique in its ability to
capture signal minutiae.
Certain test setups described in this book may
require external RF generators to provide carrier
signals, which are then modulated by the baseband
signal from the AWG 2021. There are many appropriate RF signal sources available today, including
products from Tektronix, Rohde & Schwarz, and
others. For more information about RF sources,
contact your local Tektronix representative.
Introduction
Signals and Measurements for
Wireless Communications Testing
Page 4

4
Page 5

5
The best introduction to the
AWG is to parallel the procedure
of generating a carrier with a
conventional signal generator.
With a signal generator, one
simply enters the carrier
frequency and the output amplitude, such as 1000 kHz at
0 dBm. With an AWG, one
creates a sequence of points to
represent the waveform:
A sin
ωct
where A is the peak amplitude
and ωcis the frequency. Since a
0 dBm sinusoid has a peak
amplitude of 0.316 V
(0.224 Vrms), the carrier is:
0.316 sin (2π 1000e3 t) Volts.
For a continuous sinusoid this
equation applies for all time, but
the signal can also be defined as
a single cycle sinusoid with a
period of 1 µs that repeats every
1 µs. The unique or arbitrary
part of the signal is a 1 µs series
of points defined by the above
equation. If amplitude modulation is enabled on a signal
generator, one enters the tone
modulation frequency and
depth, such as 1000 Hz at 50%.
Similarly, with an AWG, one
adds the modulation to the waveform description:
(1+ k sin(ωmt)) A sin ωct ,
where k is the modulation depth
between 0 and 1, and ωmis the
sinusoidal modulation frequency.
Thus, our example waveform
becomes:
(1+ 0.5 sin(2π 1000 t) )
x 0.316 sin (2π 1000e3 t) Volts.
This waveform description can
be entered in the AWG’s equation editor to describe our
modulated carrier (Figure 1).
The unique or arbitrary part of
the continuous waveform is now
1 ms, so one defines a time range
of 0 to 1 ms. For convenience,
define several constants, k0, k1,
and k2, so that the modulation
parameters are easily altered.
Finally, a record length of
20,000 points is selected,
keeping in mind the basic AWG
relationship:
Record length (points)
= Waveform period (seconds)
x Sample rate (points/sec).
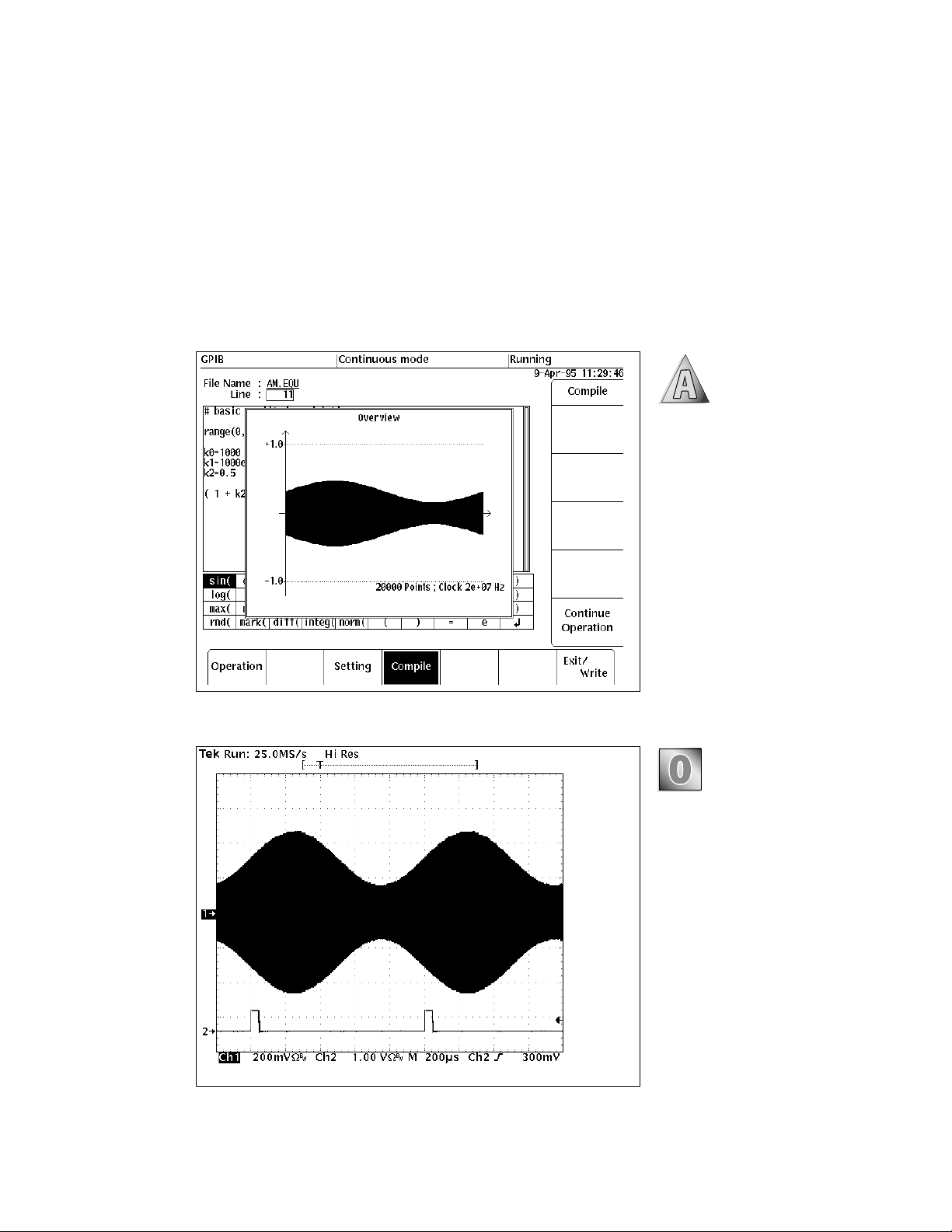
Basic Sine Wave Amplitude Modulation (AM)
1
Figure 1. The AWG’s equation editor permits
direct entry of the mathematical representation of
the modulated carrier. Constants k0, k1, and k2
are used to simplify alterations to modulation
parameters. The user can directly specify the
record length — 20,000 points in this case.
Analog Carriers and Modulation
Page 6
6
A record length must be selected
that has an adequate number of
points to reconstruct the desired
waveform. The waveform period
is 1 ms and there are 1000
carrier cycles in this period. A
record length of 20,000 points
would allocate 20 points per
cycle, which adequately oversamples the ideal waveform.
Any sampling system must
sample at least twice as fast as
the analog bandwidth of the
underlying signal (i.e.,
1000 kHz). A sample rate of
20 MHz meets this criterion and
would require a record length of
20,000 points. In general, to
obtain reasonable results the
sample rate should be at least 3
times the analog bandwidth of
the underlying signal.
The AWG equation compiler
converts the waveform definition to a 1 ms series of 20,000
points (Figure 2). The AWG can
repetitively generate this series
to create the AM carrier in
Figure 3. The TDS 744A scope
captures the resulting waveform.
To aid in scope triggering, the
AWG was programmed to generate a marker signal once per
period on a separate output.
Figure 2. The AWG’s compiler converts the modulation equation into a series of points that will
become the output record. The graphical display
provides an oscilloscope-like overview of the
record.
Figure 3. This is a TDS 744A oscilloscope display
of the modulated waveform; two complete AWG
records are shown in this two millisecond display.
The scope is triggered on one of the two marker
outputs from the AWG. The marker output was
programmed to generate a pulse once per record.
Page 7

7
A simple addition to the AM
signal demonstrates the flexibility
of equation-based waveform
descriptions. A common task in
evaluating receiver performance
is to evaluate the effect of adjacent carriers. For the basic AM
signal, one can easily add modulated carriers 10 kHz above and
below the original signal
(Figure 4). One simply adds two
copies of the basic AM equation
to the original equation. The
modulation frequency of the
adjacent carriers was changed to
3 kHz for later identification,
and the carrier frequencies were
altered accordingly. In this case,
the amplitudes are not explicitly
selected, and the AWG’s
normalization function (last
line) is used to automatically
scale the peak values encountered in the equation to ensure
that there is no clipping within
the AWG when the signals are
added together. The output level
can be set as needed using the
AWG’s setup menu (Figure 5). In
this case the signal amplitude is
set to 1 V peak-to-peak. The
setup menu summarizes key
waveform parameters such as
the 20 MHz sampling rate and
20,000 point record length. The
resulting spectrum of the three
modulated carriers is shown in
Figure 6 (on the following page).
Figure 5. The AWG’s setup menu allows direct
entry of the peak-to-peak waveform amplitude.
The record of the 3-carrier signal is graphically
displayed.
AM with Adjacent Carriers
2
Figure 4. Two additional carriers are added
10 kHz above and below the original carrier. The
“v” term in the equation is a place holder with the
current value of the equation. This allows adding
additional terms on separate lines in the equation
editor. The cosine operator was used in this
example. We can still use the 1 millisecond period
since exactly 3 periods of the 3 kHz adjacent
channel modulation tones occur in 1 millisecond.
Page 8
8
Frequency (kHz
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
980 985 990 995 1000 1005 1010 1015 1020
Figure 6. Spectrum analyzer plot of the 3 carriers.
There are 3 kHz AM on the adjacent carriers and
1 kHz AM on the original carrier. Note the low
level of close-in spurious components.
Magnitude (dBm)
Page 9
9
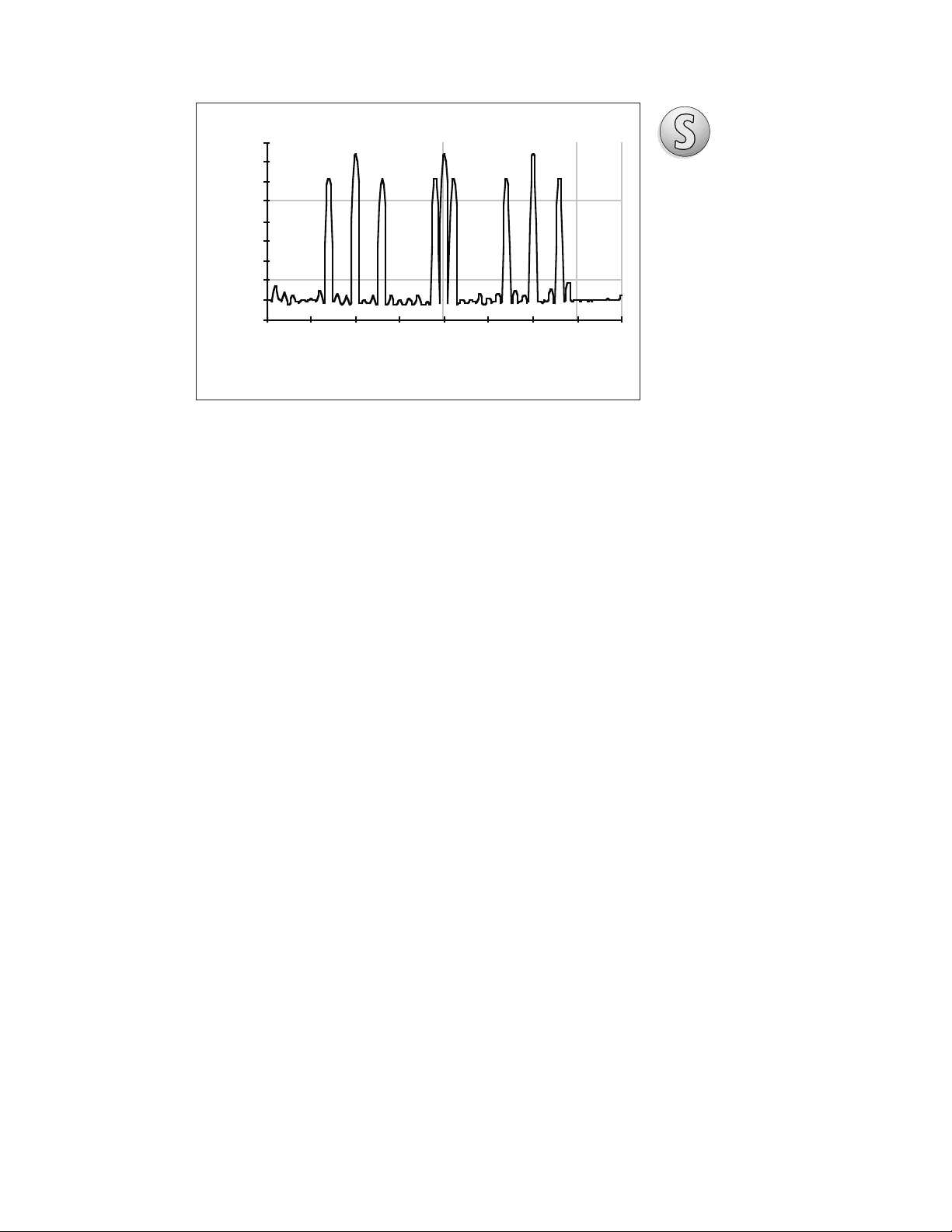
Multi-Tone Testing
3
The logical extension of adjacent
carrier testing is multi-tone testing. In addition to simulating
multiple carriers in a multichannel system, multi-tones can
quickly test filter response when
a scalar or network analyzer is
not available, or they can identify intermodulation products
resulting from saturation or nonlinearities in supposedly linear
component stages. Traditionally,
multi-tone testing requires
assembling as many signal
generators as desired tones. And
while the generators can be
phase-locked to a common
reference, the phase relationship
between the independent signals
is not absolute.
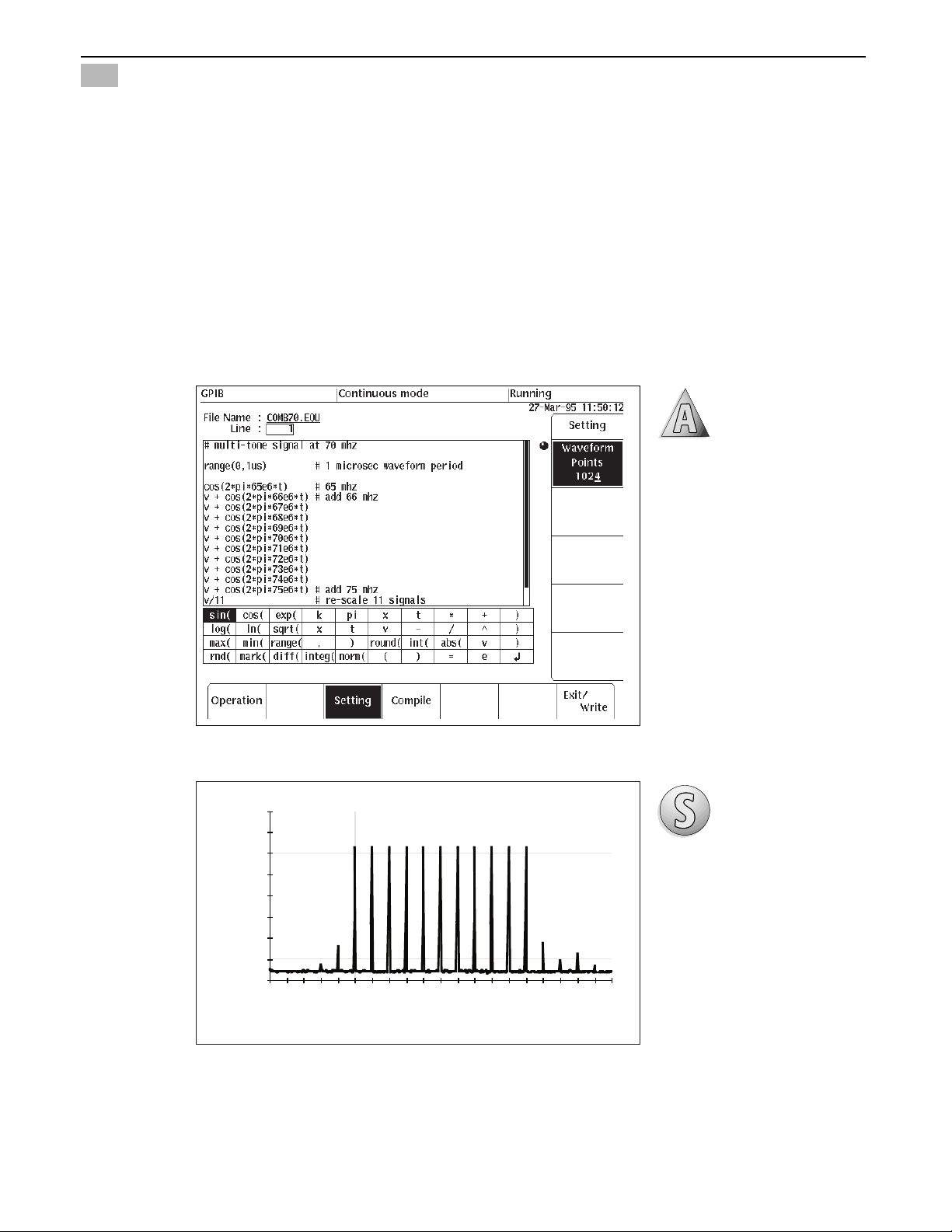
When creating a multi-tone
using an AWG, the relationship
between carrier phase is implicit
in the multi-tone equation.
Figure 7 shows the AWG equation editor specifying 11 tones
centered at 70 MHz in 1 MHz
steps (from 65 MHz through
75 MHz). In this case, the 1 MHz
steps suggest a waveform period
of 1 µs such that the record
repeats at a 1 MHz rate. Thus,
the 65 MHz tone is generated by
65 complete cycles in the 1 µs
record. The 66 MHz tone is
generated by 66 complete cycles
in the record and so on. Thus,
when the record repeats,
all the
tones are continuous in phase. A
spectrum analyzer plot of the
multi-tone signal is shown in
Figure 8.
Figure 7. Eleven tones are added together. The
record length of 1024 points and a waveform
period of 1 µs requires a sample rate of
1.024 GHz. All the tones are in-phase such that
the maximum value of the multi-tone occurs at
t=0 (the beginning of the record) when all the
cosine terms have a value of 1.
Frequency (MHz
-80
-70
-60
-50
-40
-30
-20
-10
0
60 65 70 75 80
Figure 8. Spectrum analyzer plot of the 11
carriers. The tone levels were flat to better
than 0.25 dB.
Magnitude (dBm)
Page 10
10
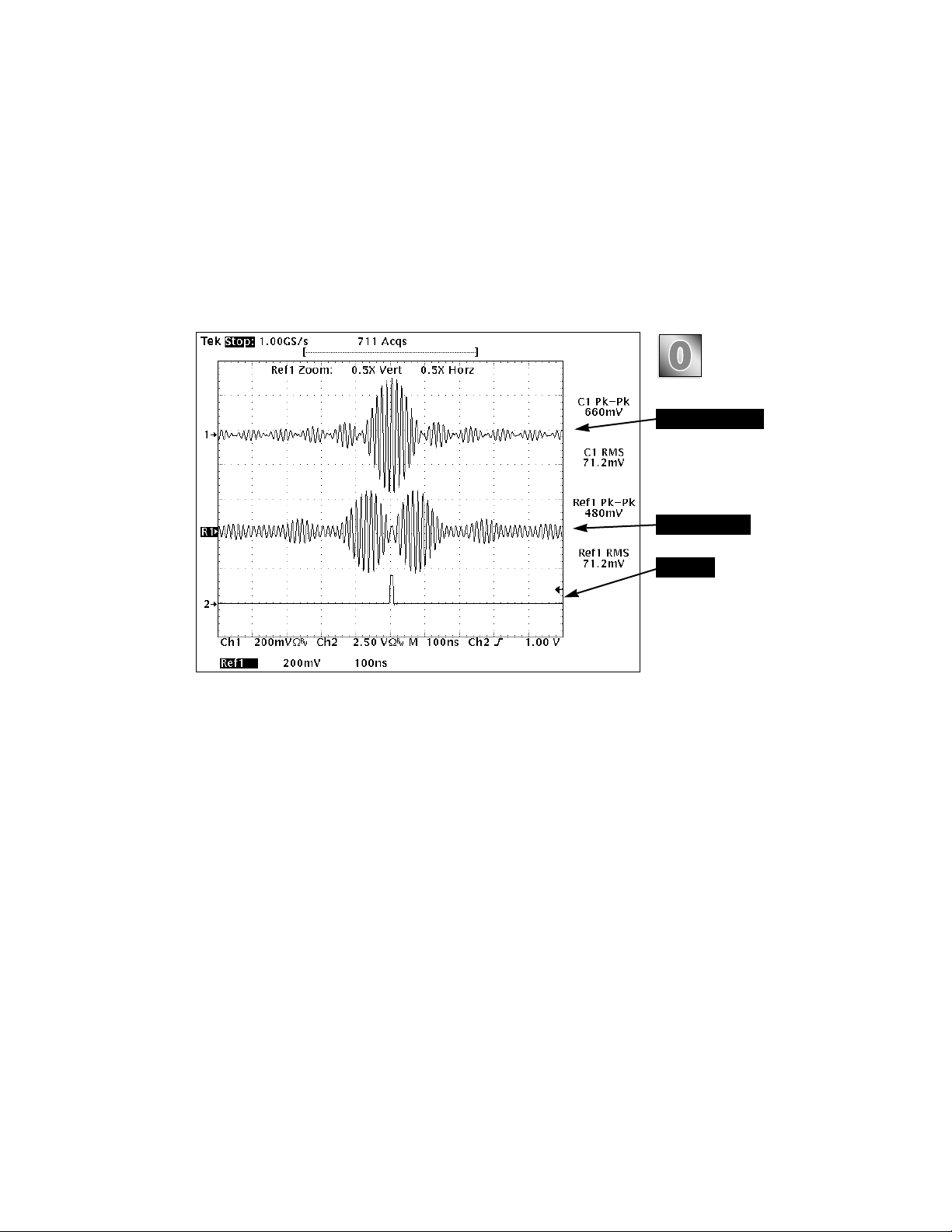
The 11 tone equation was then
modified so that the last 5 tones
(71 through 75 MHz) are
inverted. The two different
multi-tone results are shown in
Figure 9. The scope shows that
the rms levels of the two signals
are identical, but the peak-topeak values are different. All
eleven tones in the original
signal added in-phase at t=0.
This was not the case with the
second signal where 5 of the
carriers were inverted at t=0.
Thus, the crest factor (peak-torms ratio) of the two signals
changed from 4.6 (original) to
3.4 (modified). This difference
can have dramatic results when
using multi-tones to test for saturation in transmitter or receiver
stages. While both signals have
the same power level, the peak
levels are quite different.
Absolute control of phase relationships means that the AWG
can ensure repeatable worst case
testing, which is not possible
with a non-coherent collection
of signal generators. The AWG’s
marker output can simplify incircuit performance characterization since a scope can be
triggered at the exact instant of
the test signal’s peak value.
Figure 9. Scope plot of the original multi-tone
(top trace) and multi-tone signal with five tones
inverted (center trace). The rms levels are the
same, but the peak-to-peak amplitudes differ.
The bottom trace is the AWG marker output
identifying the beginning of the record.
Multi-tone signal
Inverted tones
Marker
Page 11
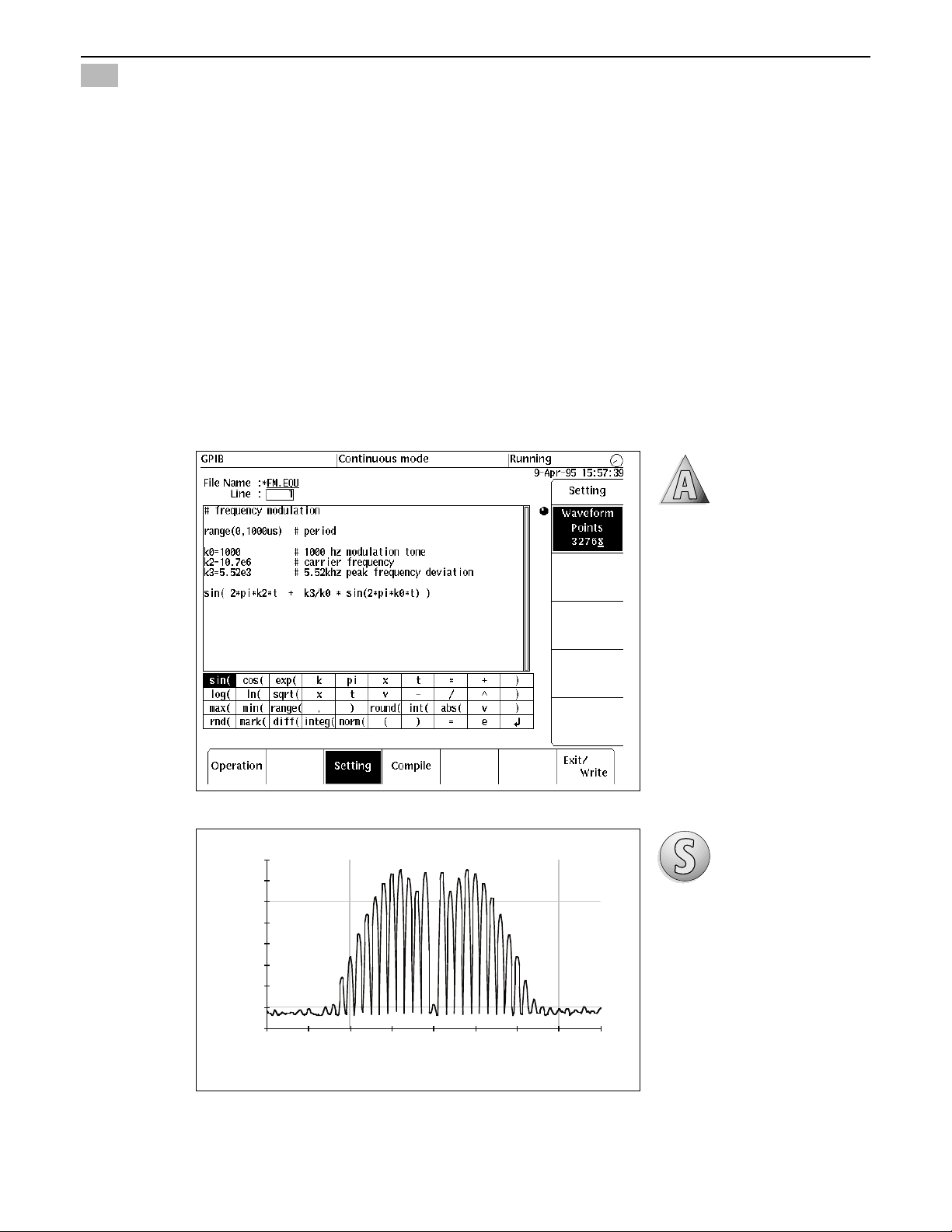
11
Frequency modulation introduces
control of the phase argument,
Φ, in the basic carrier equation:
A sin (ωct + Φ ).
FM is implemented by varying
Φ in direct proportion to the
integral of the modulating
signal. Thus, for a modulating
signal m(t), the FM signal can be
written:
A sin (ωct + k ∫ m(x) dx )
where k sets the peak frequency
deviation. For the special case of
a modulating tone cos (ωmt), the
phase argument becomes:
k/ωmsin (ωmt ),
where k is the peak frequency
deviation and k/ωmis the FM
modulation index.
The FM equation is entered
directly into the AWG’s equation
editor (Figure 10). The modulation tone is 1000 Hz, so the
unique or arbitrary portion of
the signal repeats every 1 ms.
Choosing a common FM IF
carrier frequency of 10.7 MHz,
note that the carrier frequency is
a multiple of the modulating
frequency. This means that the
carrier signal will be phase
continuous when the 1 ms
record repeats.
Figure 11 shows a spectrum
analyzer plot of the modulated
signal. The peak deviation of
5.52 kHz was selected because a
modulation index of 5.52 causes
the carrier component in the
modulated signal to vanish. This
is confirmed by noting that the
0th order Bessel function for a
modulation index of 5.52,
J
0
(5.52), is zero.
Frequency Modulation
4
Frequency (kHz
-80
-70
-60
-50
-40
-30
-20
-10
0
10680 10685 10690 10695 10700 10705 10710 10715 10720
Figure 11. Spectrum analyzer plot of the FM
signal. The carrier component vanishes for a
modulation index of 5.52. The carrier would also
vanish for indices of 2.40, 8.65, and 11.79. This
is a simple way to verify that the peak deviation of
an FM signal has been set properly.
Figure 10. AWG equation for FM single-tone
modulation. The peak deviation is 5.52 kHz with a
modulating tone of 1000 Hz. The carrier
frequency is 10.7 MHz. A 1 ms period is used
with a 32,768 point record length; this sets the
AWG sampling rate to 32.768 MHz.
Magnitude (dBm)
Page 12

12
While basic single-tone FM is a
built-in function of virtually all
conventional signal generators,
dual-tone FM modulation clearly
contrasts the flexibility of the
AWG approach. Dual-tone
modulation tests can be used to
measure intermodulation products in a noise reduction
compandor (compressorexpander) in FM receivers such
as cordless phones. Standard
dual-tone compandor test
frequencies are 900 Hz and
1020 Hz and a typical minimum
requirement is that intermodulation products should be 26 dB
below the per tone levels. This
test used to be performed at
audio frequencies since compandors work in the audio band. But
highly integrated receivers may
not offer direct access to the
compandor circuit, so the dualtone signal must be injected as a
modulated IF signal.
The apparently odd combination
of tone frequencies means that
the AWG waveform parameters
must be carefully selected. The
first step is to recognize that
900 Hz and 1020 Hz are both
integer multiples of 60 Hz. Thus
a waveform period of 16.666 ms
will exactly fit an integer
number of cycles for each tone
(15 and 17 respectively). The
next step is to ensure that the
carrier frequency itself is phase
continuous in a 16.666 ms
record. If one wants to inject at
an IF frequency of 455 kHz, one
must consider that 455 kHz is
not an integer multiple of 60 Hz.
However, with a carrier of
454.98 kHz, exactly 7583 cycles
of the carrier frequency fit in the
16.666 ms period. The 20 Hz
error, less than 50 ppm, is irrelevant for all practical purposes.
Figure 12 shows the waveform
definition in the AWG’s equation
editor. We take advantage of an
equation compiler function
which allows the parameter “x”
to represent a dummy variable
that takes on values between 0
and 1 in direct proportion to the
location within the 16.666 ms
record. For example, the 17
cycles of the 1020 Hz tone can be
expressed as sin(2π 17 x). This
takes the time variable “t” out of
the equation and is particularly
useful for fitting exact numbers
of cycles within an AWG record.
First, the two tones are added to
make the modulating signal.
Next the modulating signal is
integrated using the AWG’s integration function. The integrated
signal must be scaled by the time
between each point since the
integrator integrates point-topoint without regard to sample
rate (which can be changed).
With a record length of 32768
points, the 16.666 ms period
leads to a sample rate of
1.966 MHz. Finally, the integrated
modulating signal is inserted
into the phase argument of the
basic carrier equation with a
peak deviation of 3 kHz per tone.
FM with Dual-Tone Modulation
5
Figure 12. Description of a dual-tone FM signal.
The modulating tones are 900 Hz and 1020 Hz
on a 455 kHz carrier. The record length is
32,768 points, the waveform period is 16.666 ms,
and the sample rate is 1.966 MHz. This FM signal
is used to test the intermodulation distortion
performance of a syllabic expander in an FM
receiver.
Page 13

13
Figure 13. The TDS 744A shows the intermodulation performance with expanders disabled and
enabled. There is no distortion with the expander
disabled. The first order intermodulation products
are about 35 dB below the fundamental tones
with expanders enabled.
Figure 13 shows the demodulated output from an FM
receiver with the expander
disabled and enabled. The top
two traces show the unexpanded
two-tone signal and its spectrum
as calculated by the TDS 744A
FFT function. The lower two
traces show the same signals
with the expander enabled. The
intermodulation products are
now significant, with the first
order products about 35 dB
below the fundamental tones.
Demodulated output, unexpanded
Demodulated output, expanded
Unexpanded spectrum
Expanded spectrum
Page 14

14
A final example of conventional
analog modulation combines
most of the above techniques to
simulate the stereo modulation
used in broadcast FM. The
modulating signal consists of
three components, 1) the
composite audio which is the
sum of the left and right (L+R)
channels, 2) the stereo pilot
signal which is a 19 kHz tone,
and 3) the difference (L-R) signal
which amplitude modulates a
38 kHz carrier. These three
components are summed
together and modulate the
carrier using conventional FM.
Figure 14 shows the waveform
definition in the AWG’s equation editor. This example uses a
5 ms waveform period, a 32768
point record, and a sampling
rate of 6.5536 MHz. The carrier
will be 455 kHz, which can be
mixed externally to an appropriate IF frequency.
The left channel signal is an
800 Hz tone and the right channel signal is a 1000 Hz tone. The
composite audio signal (L+R) is
made by summing the two tones.
The 19 kHz pilot tone is then
summed at half the amplitude of
the audio tones. The (L-R) signal
amplitude modulates a 38 kHz
carrier which is phase-locked
(implicit in the equation definition) to the 19 kHz pilot. Unlike
the previous AM example,
suppressed carrier modulation is
used, where the carrier is
suppressed if there is no modulating signal (the “1” term is
absent from the modulation
product term). The three terms
are integrated to implement FM
modulation; the integration
output is scaled by the sampling
rate as described earlier. Finally,
the integrator output is inserted
into the phase term of the sinusoidal carrier with a peak deviation of 10 kHz per audio tone.
FM Stereo
6
Figure 14. Definition of the stereo FM signal. The
waveform period was 5 ms. All the modulating
components have an integer number of cycles
within the record (i.e., they are multiples of
200 Hz) so the signal is phase continuous.
Page 15

15
The resulting 455 kHz signal is
mixed up to the broadcast band
and inserted into a stereo
receiver. The stereo indicator is
turned on, and the resulting left
and right output signals are
captured on the TDS 744A scope
(Figure 15). The upper two
traces are the right channel
(1000 Hz) signal and spectrum.
The lower two traces are from
the left channel (800 Hz). The
stereo encoding was successful
with the receiver separating the
two tones by over 35 dB. The
38 kHz sub-carrier in FM broad-
cast is not unique. Higher subcarriers are commonly used to
encode specialized audio
channels or pager data to take
advantage of the coverage of
commercial FM transmitters.
Figure 15. After demodulation by an FM receiver,
the TDS 744A displays the left and right channels
and their spectra. The receiver separated the
800 Hz and 1000 Hz tones by over 35 dB
(spectrum scales are 250 Hz/div horizontal and
20 dB/div vertical).
Right channel and spectrum
Left channel and spectrum
Page 16

16
Although the removal of noise is
a common design goal, a noise
source can be an extremely
useful test stimulus or signal
impairment. The AWG 2041
provides a built-in noise function, but its characteristics are
quite different than traditional
sources such as noise diodes. An
AWG
1
noise waveform is actually a calculated series of
pseudo-random numbers. There
are two key properties of the
AWG noise function. First, the
AWG noise signal is actually a
series of voltages that changes
once per clock period. This has
definite implications for the
spectral characteristics of the
signal. The second property
arises because an AWG noise
waveform is simply another precalculated record that must
eventually repeat to obtain a
continuous signal.
Calculating Noise
The AWG provides a built-in
function to calculate the noise
waveform of a specified record
length. In Figure 16, the AWG
creates a 32768 point noise
waveform. Digital random
number generators typically
produce uniformly distributed
values, but circuit noise is better
modeled with a Gaussian distribution. In practice, the AWG
actually calculates a noise value
by averaging 12 consecutive
random numbers. Thus, by the
central-limit theorem, the noise
values will more closely approximate a Gaussian distribution
than the underlying uniform
distribution.
The top trace in Figure 17 shows
the resulting noise output. The
key feature relating to the clock
is that the waveform appears to
be a staircase function. The
sharp edges can be removed by
Adding Noise to a Carrier Signal — AWG Noise Characteristics
7
Figure 17. Upper waveform is a pseudo-random
sequence with a 32.768 MHz clock. The second
waveform is the same signal filtered by the
AWG’s 10 MHz Bessel low-pass filter. The lower
two traces are the calculated FFT spectra. The
horizontal scale of the spectra is 10 MHz per
division.
Figure 16. The noise waveform is a built-in function in the AWG. In this case, the 32768 point
record length specifies a pseudo-random series
of values. The values are approximately Gaussian
in distribution with a crest factor of about 3 to 1.
1
AWG refers to Arbitrary Waveform Generator as opposed to Additive White Gaussian, an unfortunate coincidence in this context.
Pseudo-random noise sequence
Filtered and unfiltered spectra
Filtered sequence
Page 17

17
the AWG’s 10 MHz low-pass
filter (middle trace). The
TDS 744A FFT spectra for the
two signals are overlaid below
the time domain waveforms. The
salient characteristic of the
unfiltered noise spectrum is that
it rolls off with a (sin x)/x function with the first null at the
32.768 MHz clock frequency and
subsequent nulls at multiples of
the clock rate. If the goal is to
add this noise waveform to the
10.7 MHz FM carrier, then noise
density is required only in the
vicinity of 10.7 MHz. The
filtered noise signal is a suitable
bandwidth-limited source. Thus,
when using the AWG noise
function, one consideration is to
account for the clock rate dependent roll-off.
Maximizing “Randomness”
The second property to consider
when using the AWG noise
waveform is to observe that the
noise waveform itself is a precalculated series of points that
will repeat at each period of the
record length. The period of the
32K point noise waveform at a
32.768 MHz sample rate is 1 ms
and the exact noise waveform
repeats at a rate of 1 kHz. This
periodicity translates into the
resulting noise spectrum. The
ideal noise waveform would
exhibit no periodicity (i.e., no
repetition). While this is not an
option with pre-calculated AWG
waveforms, the effect of the periodicity can be reduced by
increasing the period of the
noise waveform relative to the
corresponding signal waveform.
Figure 18 shows how the AWG’s
sequence editor converts the
32K point FM waveform into a
256K point waveform which is
simply 8 concatenated copies of
the same waveform. Thus, if the
same clock waveform of
32.768 MHz is used, the resulting
signal waveform is identical.
However, if a 256K noise waveform is generated, then the
period of the noise waveform is
increased by a factor of 8.
Figure 18. The 32K point FM waveform can be
converted to a 256K point waveform by simply
sequencing or concatenating 8 copies of the
original 32K waveform. This expansion means
that a 256K noise waveform can be added to the
FM waveform instead of a 32K noise waveform.
Page 18

18
The AWG’s graphical waveform
editor provides a variety of
mathematical operators for existing waveforms. Waveforms can
be combined with other
waveforms, or a waveform can
be squared, scaled, differentiated, integrated, etc.
Combining the Noise
with the Carrier
The signal and noise waveforms
are summed using the AWG’s
waveform editor (Figure 19).
The spectra of the 32K point
waveform and the 256K point
waveform are overlaid in
Figure 20. Recall that the period
of the 32K point waveform is
1 ms. You can see that the noise
“floor” of the spectrum of the
32K point waveform is a series
of discrete components spaced
1 kHz apart. Thus, even though
the objective is to define signal
waveforms with the minimum
number of record points, noise
waveforms should be created
with the maximum number of
record points! The two objectives are resolved by creating a
longer version (to match the
noise record length) of the signal
waveform by sequencing multiple
copies of itself.
Frequency (kHz
-90
-80
-70
-60
-50
-40
-30
-20
10670 10680 10690 10700 10710 10720 10730
Figure 20. Spectrum analyzer plots of the
32K point FM carrier plus noise (lighter) and the
256K point FM carrier plus noise. Longer noise
waveforms repeat less often so the noise density
characteristics will be flatter.
Figure 19. The 32K point FM waveform is added
to the 32K point noise waveform.
Magnitude (dBm)
Page 19

19
Digital Phase Modulation — PSK
8
The modulating signals in the
foregoing examples have been
sinusoidal or continuous waveforms. A simple step to digital
modulation is made with a slight
variation to sinusoidal modulation. Figure 21 shows one cycle
of a sinewave that has been
quantized into steps between
–0.5 and +0.5. The equation
defining these steps is shown in
Figure 22. The second line
simply quantizes a cosine wave
by rounding and scaling the
continuous waveform to the
nearest eighth. This quantized
modulating pattern is then
directly inserted in the phase
argument of a cosine carrier.
Thus, the phase argument takes
on values between –π to +π in
π/4 steps. If the polar graphical
representation of the signal is
used, a family of eight points of
equal magnitude is defined,
spaced around the circle in π/4
or 45° phase increments.
Figure 21. The sinusoidal modulating pattern is
quantized into discrete steps. The steps are
equally spaced in amplitude and will shift the
phase of the carrier in π/4 or 45° increments.
Digital Modulation
Page 20

20
The record length of 1024 points
and a waveform period of 1 µs
requires a sampling rate of
1.024 GHz. The resulting carrier
frequency is 50 MHz. Since each
level represents one of eight
states or symbols, 3-bits of data
can be transmitted per symbol.
Of course, no data per se is
associated with this particular
modulating pattern since a
sinusoid was quantized without
regard to the symbol or baud rate.
Figure 23 shows the resulting
AWG output. The top trace is
the marker output generating a
scope trigger pulse once per
record. The second trace is the
phase modulated waveform. The
third trace is the carrier waveform without the phase modulation. That is, the phase argument
was removed from the final
equation line on the AWG in
Figure 22, leaving just the
expression cos (2*pi*50*x). This
waveform was captured separately by the TDS 744A but is
synchronized to the same trigger
Figure 23. Scope plot of the marker output (top
trace) and the phase modulated 50 MHz carrier
(2nd trace). The 3rd trace is the carrier without
the modulation. The bottom trace is the product
of the unmodulated carrier (constant Φ=0) and
the modulated carrier.
Marker (trigger)
Carrier waveform
Product
Phase modulated waveform
Figure 22. The equation defining the quantized
1 MHz modulating pattern and its subsequent
insertion into the phase argument of the 50 MHz
carrier. The modulating pattern shown in Figure
21 is the result of the rounding definition.
Page 21

21
Baseband Digital Patterns
9
Before continuing with examples of digital modulation, it is
important to establish a method
of creating arbitrary test data
patterns. Figure 24 shows direct
entry of a 28-bit binary pattern.
In this case, the 0 or 1 value of
each data bit is repeated for 1000
points in the record, which
requires a record length of
28,000 points. A binary data
pattern requires only one bit of
the AWG’s dynamic range.
Multi-level digital encoding can
be used by altering more than
one bit at each record point. In
addition to direct data entry, the
AWG can automatically generate
pseudo-random data streams.
Figure 25 shows the setup for a
length = 9 linear feedback shift
register that repeats only after
511 data bits. As with direct
entry, the number of record
points per data bit can be specified. In this case, each bit
repeats for 32 data points,
requiring a record length of
16,352 points.
In some applications, the data
pattern itself is the desired
output signal for the AWG. For
example, the data pattern can be
the baseband modulation signal
to an external RF generator or
modulator. However, the
following examples use the
simple 28-bit, 28,000 point
record as the baseband signal in
demonstrating several digital
modulation techniques.
Figure 24. A binary or hex (4-bit) data pattern
can be directly entered from the keypad. The
AWG directly translates a variety of encoding
formats such as NRZ, RZ, and NRZI. The number
of record points that each bit interval occupies
can be specified.
Figure 25. The pseudo-random generator
supports register lengths from 2 to 32 bits. The
binary output stream from the generator can be
assigned to a specific bit in the output range or to
one of the marker bits.
Page 22

22
The simplest example of digital
modulation is to turn the carrier
on or off, depending on the state
of the modulation data. On-off
keying (OOK) can be directly
implemented by multiplying a
carrier by the 1 or 0 value of the
data pattern. This example uses a
10.7 MHz carrier created in a
28,000 point record to match the
record length of the data pattern.
The AWG sampling rate is
40 MHz so the record period is
700 µs. Since each of the 28 data
values occupies 1000 record
points, the data rate is 40 kbaud.
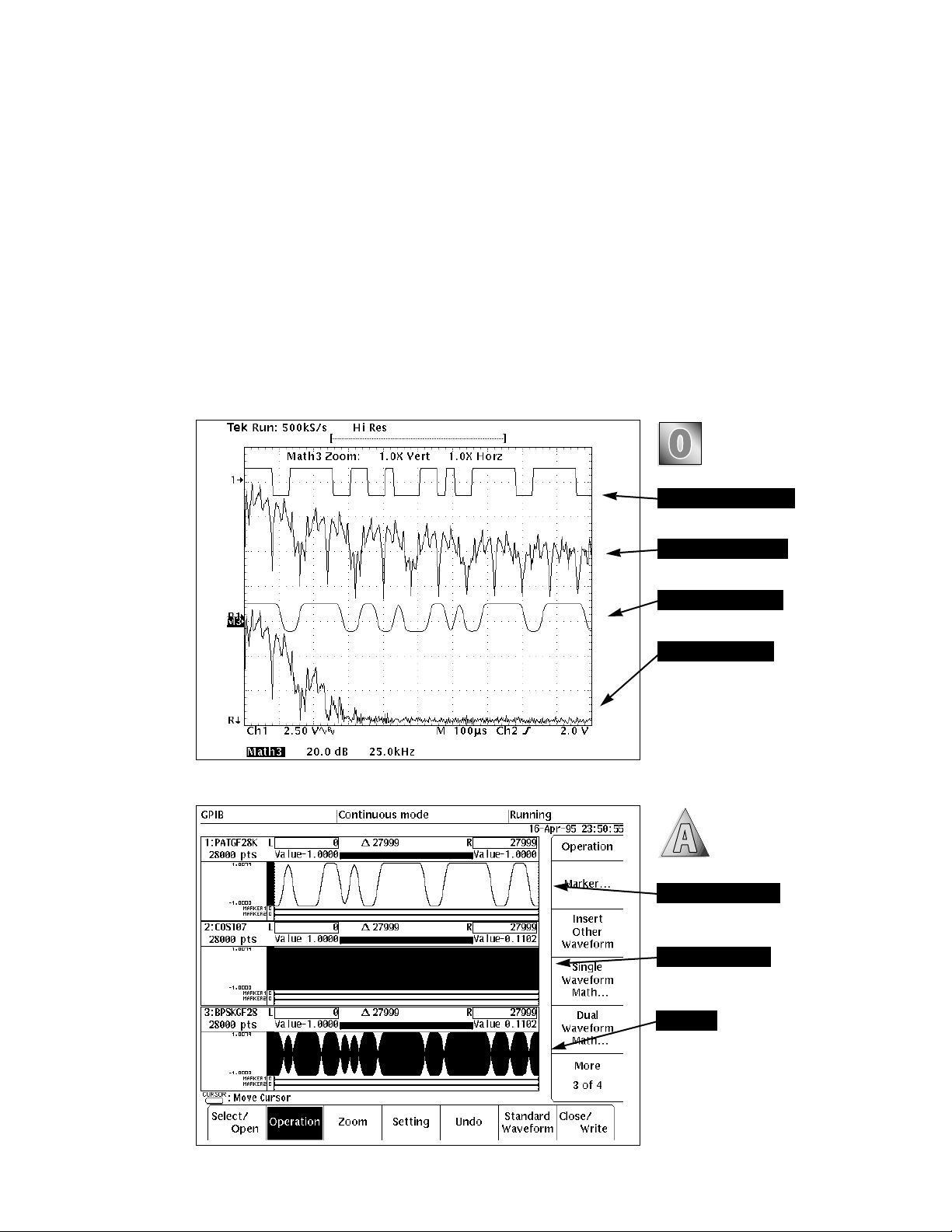
Figure 26 shows how the AWG’s
dual waveform math capability
multiplies the data pattern (top
display) and the 10.7 MHz carrier
(middle) to produce the modulated carrier (bottom). Since
10.7 MHz is a popular receiver IF
frequency, these signals can be
directly injected at the appropriate receiver point to characterize
demodulator performance. The
AWG’s sequencing and triggering
capabilities are particularly
useful in OOK remote-control
device simulations. The AWG
can generate single or occasional
bursts with varying parameters
such as carrier frequency offset or
data rate. The burst itself can be
amplitude modulated with
another waveform to simulate the
power ramping found in many
battery-powered transmitters.
If the data pattern is simply
shifted vertically so that it takes
on bipolar values of –1 and +1,
instead of 0 and 1, then the
modulation inverts the sign of
the carrier. Since inverting the
sign is equivalent to shifting the
phase argument of the carrier by
π, this implements two-state or
binary phase-shift keying
(BPSK). Figure 27 illustrates the
same AWG setup except that the
modulating pattern is offset
using the shift and scale functions. The resulting BPSK has a
constant envelope since the
magnitude of the multiplier is
always 1.
Figure 26. OOK: The “1” and “0” values of the
data pattern turn the carrier on and off. The
carrier frequency is 10.7 MHz. The data rate is
40 kbaud.
Figure 27. BPSK: The 28-bit data pattern is
shifted and scaled to generate a bipolar pattern.
This implements BPSK modulation when multiplied by the carrier. The BPSK waveform has a
constant envelope.
Digital AM — OOK and BPSK
10
Data pattern
Carrier
Modulated carrier (output signal)
Data pattern
Carrier
Modulated carrier (output signal)
Page 23

23
The modulating data alters the
carrier frequency in
frequency-shift keying (FSK). A
digital modulation index of 0.5
is used in this example; that is,
the frequency shift will be
1
⁄2 the
40 kbaud data rate or 20 kHz. If
the carrier remains centered at
10.7 MHz, this results in the two
data frequencies of 10.710 MHz
and 10.690 MHz. Figure 28
shows one way to implement
binary FSK to take advantage of
the AWG’s mathematical precision. First, a second 28-bit data
pattern is generated which is the
1’s complement of the original
pattern. Then two 28,000 point
carriers are generated at
10.690 MHz and 10.710 MHz.
Note that the carriers are phase
continuous since exactly 7483
and 7497 cycles, respectively, of
the carriers fit in the 700 µs
record. The upper waveform is
the 10.690 MHz carrier
multiplied by the original data
pattern, and the middle waveform is the 10.710 MHz carrier
multiplied by the complemented
pattern. If the two waveforms are
added (bottom trace), then the
carrier shifts between the two
frequencies exactly at the data
transitions. The spectra of the
two unmodulated carriers and
the modulated FSK signal are
shown in Figure 29.
Figure 28. FSK: Upper waveform is the
10.690 MHz carrier amplitude modulated by the
data pattern. Middle waveform is the 10.710 MHz
carrier modulated by the complemented pattern.
The sum of the two waveforms shifts between the
two frequencies at data transitions.
Frequency (kHz
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10650 10670 10690 10710 10730 10750
Figure 29. Spectrum analyzer plots of the two
unmodulated carriers, at 10.690 MHz and
10.710 MHz, and an overlay of the FSK signal
with the 28-bit modulation.
Digital FM — FSK
11
Sum
Carrier x data pattern
Carrier x data complement
Page 24

24
As previously mentioned, the
AWG’s two binary marker
output signals can be modulated
with a data pattern. Figure 30
shows how this can be used as a
tool for testing or troubleshooting
digital receivers. One marker
output is programmed to
generate a trigger pulse at the
beginning of each 700 µs record
(top trace). The second marker is
programmed with the 28-bit data
pattern (second trace). The two
marker signals are generated in
real time with the AWG’s main
signal output. The third trace is
the FSK modulated signal with
no indication of modulation
since it is a constant envelope
waveform. However, a coherent
copy (using a marker pulse at
the same record point) of the
10.710 MHz unmodulated
carrier is captured and saved in
the TDS 744A reference
memory. The lower trace is the
real-time product of the FSK
signal and the coherent reference
carrier. When the data is 0, the
FSK signal is at 10.710 MHz and
the coherent demodulation
yields a positive-only component. When the data is 1 (e.g,
between the cursors), the
frequencies are not equal and a
constant frequency difference
during the interval generates a
beat component at 20 kHz. Note
that the time between peaks, or
the period of the beat product, is
50 µs or 20 kHz.
Figure 30. The TDS 744A triggers on AWG’s once
per record marker output (top trace). The TDS
744A multiplies the FSK signal by one of the
reference frequencies (lower trace). The data
pattern can be demodulated by inspection and
verified by the actual data pattern generated by
the AWG’s second marker output (second trace).
Trigger pulse
28-bit data pattern
FSK modulated signal
Reference copy of unmodulated carrier
FSK signal x carrier
Page 25

25
Multi-level data modulation
splits the amplitude, frequency,
or phase of the carrier into more
than two discrete states. 8-PSK
previously demonstrated direct
control of the phase Φ in the
equation A cos(ωct + Φ); A was
constant. The eight symbols
were equally spaced points
around the polar axes.
Alternatively, the I-Q mapping
can be used by noting the
relationship:
A cos(ωct + Φ)
= A cos Φ cos(ωct) – A sin Φ sin(ωct)
That is, any symbol location can
be expressed as a vector sum of
an in-phase (I) component and
an orthogonal quadrature
component (Q). Thus, if we
select 16 equally spaced points
to send 4 bits of information per
symbol, then we can easily
transmit the symbols by amplitude modulation of two carriers.
For example, the I component
could be –
3
⁄4, –1⁄4, 1⁄4, or 3⁄4 times
cos(ωct). The Q component
would be one of the same
multipliers applied to sin(ωct).
Figure 31 illustrates a 28-symbol
pattern, each with one of these
four multipliers. Each quadrature component carries 2 bits of
information. Figure 32, on the
following page, illustrates the
creation of the quadrature amplitude modulated carrier using the
AWG’s waveform editor. The top
waveform is the I pattern modulating the 10.7 MHz cosine
carrier. A separate 28-symbol
Q pattern was created and
modulates the 10.7 MHz sine
carrier in the middle waveform.
The two waveforms are
combined in the third pattern.
Signal impairments are easily
generated with this approach.
The cosine or sine carrier (before
modulation) can be altered
relative to each other in phase or
amplitude to simulate errors in
the modulated signal. For example, the cosine carrier could be
altered from cos(ωct) to
cos(ωct+δ) where δ is a small
offset to move the two carriers
out of quadrature. Or the levels
of the baseband data pattern can
be altered in the waveform
editor to corrupt the uniform
spacing of the 16 symbols. To
accomplish quadrature modulation at appropriate frequencies,
it may be necessary to couple
the AWG with a specialized
dual-input RF signal generator
designed to handle I and Q
information. Figure 33 depicts
the interconnection of the two
instruments, as well as the other
elements of the test setup.
Figure 31. The AWG’s waveform editor was used
to generate this 28-symbol data pattern which
has four potential uniformly spaced levels per
symbol.
Quadrature Modulation
12
Page 26

26
Figure 32. Quadrature amplitude modulated
(QAM) signal generated by combining an
amplitude modulated cosine carrier (upper) and
an amplitude modulated sine carrier. There are
16 symbols, so this is 16-QAM.
I In
I/Q Modulated RF Out
Discrete Q Signal
Discrete I Signal
Ch. 2 Out
Ch. 1 Out
AWG
RF Generator
Controller (PC)
Oscilloscope (DSO)
Q In
DUT
Figure 33. This block
diagram shows the
setup for quadrature
modulation. For more
information about
suitable RF sources,
contact your local
Tektronix
representative.
I pattern x carrier
Q pattern x carrier
Sum
Page 27

27
One effect of the edge transitions
in digital modulation patterns is
a wider than desired occupied
spectrum of the transmitted
signal. The solution is to filter
the baseband digital signal
before it modulates the carrier.
The two most common filter
types for this application are
Gaussian and Nyquist filters.
Application of the Gaussian
filter is illustrated here, though
the process for applying any
filter type is the same. The baseband modulating pattern is
filtered by convolving it with the
impulse response of the desired
filter in the time-domain. The
AWG directly performs the
convolution function. Figure 34
shows the convolution setup.
The upper left waveform is the
28,000 point data pattern, while
the lower left waveform is the
2000 point Gaussian impulse
response. The result of the
convolution process is shown at
the right.
The impulse response of the
Gaussian filter is defined by:
h(t) = exp {–t
2
/2s2},
where s = PW50/(2 √(2 ln(2)).
PW50is the half-width for the
pulse and is approximately
equal to 0.31/B, where B is the
filter bandwidth in Hz. Figure 35
shows the implementation in the
AWG’s equation editor. The key
parameter to select is the halfwidth. This example uses a BT
parameter of 0.5, where B is the
filter bandwidth and T is the
data period (25 µs). This means
the bandwidth must be 20 kHz
and the PW50= 15.5 µs. By trial
and error it is determined that a
50 µs total pulse interval defines
the total response so that both
tails drop to zero within the
interval. For the sample rate of
40 MHz, this requires a record
length of 2000 points.
Figure 34. The data pattern (upper left) is
convolved with the Gaussian impulse response
(lower left). The result is the filtered data pattern.
The convolution of the two waveforms produces a
new waveform that is 30,000 points long. This is
the sum of the two individual waveform lengths
and is a by-product of the convolution process.
Figure 35. The Gaussian impulse response is
defined by the pulse half-width, which is approximately equal to 0.31/B, where B is the –3 dB filter
bandwidth. The constant k1 offsets the peak of
the impulse response to the center of the record.
Filtering Out Unwanted Sidebands
13
Data pattern
Gaussian impulse response
Resulting convolved signal
Page 28
28
The convolution result is 30,000
points long. Note that the
impulse response is 2000 points
long, which is longer than the
1000 points per data bit. This
means that each data bit affects
more than the 1000 points that it
immediately occupies. Hence, a
possible anomaly must be
accounted for in the convolution
process. The AWG assumes that
the data before and after the data
pattern is 0. It does not “know”
that the data pattern is to repeat
over and over. However, a
continuous signal is being
created by adjoining copies of
the same waveform record. What
is to be done with the extra 2000
points? In the example, a data
pattern was selected in which
the last two bits are 00. This
means that the last two bits
(2000 points) do not contribute
to the convolved response, and
it matches the convolution
assumption that the data before
the first bit in the pattern is 0.
Thus, the 2000 points can be
simply removed from the 30,000
point record, and the 28,000
point record will not have any
discontinuities when concatenated.
Of course this was a selected
example. The general solution to
insuring that a convolved
pattern can be concatenated is to
add extra bits to the ends of the
pattern before convolution. The
extra bits simply duplicate the
bits that would be there for a
repeating pattern. In other
words, add the first few bits of
the data pattern to the end of the
pattern. The number of bits to
add depends on the length of the
impulse response.
Figure 36. The TDS 744A captures the filtered and
unfiltered data patterns and calculates their FFT
spectra. The data rate is 40 kbaud, and the
Gaussian filter has a 20 kHz bandwidth. The horizontal scale on the spectra is 25 kHz per division.
Figure 37. BPSK with filtered data: The AWG
waveform editor performs the BPSK modulation
of the 10.7 MHz carrier with the Gaussian filtered
28-bit data pattern. Compare to Figure 27 where
the data was unfiltered: the transition time
between the two complementary phases has been
dramatically increased.
Unfiltered data pattern
FFT of unfiltered data
Filtered data pattern
Filtered data pattern
Carrier (10.7 MHz)
Product
FFT of filtered data
Page 29

29
Figure 36 compares the original
and filtered data patterns. The
upper two traces are the unfiltered data pattern and its spectrum. The lower two traces are
the filtered data pattern and its
spectrum. Note how the spectrum of the filtered version rolls
off more quickly. The spectrum
of a modulated carrier shows the
same results. Figure 37 shows
the filtered baseband pattern
modulating (BPSK) the
10.7 MHz carrier, as in Figure 27.
Figure 38 shows the difference
in their spectra.
The convolution operator can be
applied to multi-level patterns.
Figure 39 shows Gaussian
filtered I and Q baseband
patterns for the 16-QAM signal
in Figure 32. (The unfiltered I
pattern is shown in Figure 31.)
The falling edge of the data
clock output defines the center
of the symbol period. Using the
marker output as a data clock
provides a convenient reference
when characterizing the performance of symbol timing recovery circuits. Careful attention
was given to wrapping data at
the ends of the data patterns so
that the convolution result
would be continuous across the
seams.
Frequency (kHz
-80
-70
-60
-50
-40
-30
-20
-10
0
10500 10550 10600 10650 10700 10750 10800 10850 10900
Figure 38. Spectrum analyzer plots of unfiltered
(upper) and BT=0.5 Gaussian filtered (lower)
BPSK carriers at 10.7 MHz. The data rate is
40 kbaud. Compare the roll-off to the baseband
roll-off in Figure 35.
Figure 39. Gaussian filtered multi-level baseband
modulation is shown. The AWG generated a data
clock output on one of its marker outputs. The
bottom trace is the other AWG marker output
generating a once per pattern pulse for scope
triggering.
AWG data clock output
I baseband pattern
Q baseband pattern
Magnitude (dBm)
Page 30

30
The final example of digital
modulation spreads the energy
in a BPSK signal by amplitude
modulating the carrier with a
spreading pattern. In the same
way that the baseband data
pattern spreads the energy of an
unmodulated carrier, a spreading pattern further spreads the
energy of a modulated carrier.
Pseudo-random sequences are
generally used as the spreading
pattern, with a bit rate or chipping rate that is much higher
than the data bit rate. The
511-bit pseudo-random
sequence generated in Figure 25
is used as the spreading
sequence—the assumption being
that a receiver would use the
same sequence to de-spread the
signal. Since the data pattern is
28 bits, one can directly implement a chipping rate to data rate
ratio of 18.25 or (power reduction of 12.6 dB) by simply
mapping the 511-bit sequence
into 28,000 AWG record points.
Figure 40 shows how the AWG’s
waveform editor can horizontally
interpolate a waveform into
another record size. The spreading is implemented by using the
AWG waveform editor to multiply the spreading sequence and
the modulated BPSK carrier
from Figure 37. The spectra of
the original and spread signals
are shown in Figure 41. The first
null in the spread signal occurs
at the chipping rate of 730 kHz,
which is 18.25 times the 40 kHz
data rate.
Figure 40. The AWG waveform editor performs
horizontal scaling of the 511-bit spreading
sequence. The original record length was
16,352 points. A “new” size of 28,000 points is
entered, and the AWG expands and interpolates
the waveform by a factor of 1.71.
Frequency (kHz
-80
-70
-60
-50
-40
-30
-20
-10
0
9700 10200 10700 11200 11700
Figure 41. Spectrum analyzer plots of the BPSK
carrier at 10.7 MHz before and after a 511-bit
pseudo-random spreading sequence. The data
rate is 40 kbaud and the chipping rate is 730 kHz.
The original spectrum is the same as the filtered
spectrum in Figure 38, but it is displayed here at
a wider span.
Direct Sequence Spread Spectrum
14
Magnitude (dBm)
Page 31

31
For More Information on Tektronix Instrumentation
Tektronix offers a broad line of signal sources and electronic measurement products for engineering,
service, and evaluation requirements in virtually every industry.
For detailed information about the Tektronix tools used in developing this booklet, consult the
appropriate brochures and data sheets for the respective products:
Signal Sources brochure . . . . . . . . . . . . . . . . . . . . . . . . . . .11252
AWG 2005 data sheet . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11372
AWG 2021 data sheet . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11561
AWG 2041 data sheet . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11371
AFG 2020 data sheet . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11297
Signals and Measurements for Disk Drive Design . . . . . . .11478
TDS 700A family brochure . . . . . . . . . . . . . . . . . . . . . . . . .11483
TDS 700A family data sheet . . . . . . . . . . . . . . . . . . . . . . . .11031
To order any of these documents:
From within the U.S.A., call 1-800-426-2200; when prompted press “3” and ask for Code 454.
Outside of the U.S.A., call the nearest Tektronix sales office.
Page 32

32
Tektronix AWG Arbitrary
Waveform Generators give the
most extensive capabilities for
editing waveforms, with 8 or 12
bits of vertical resolution and
waveform frequencies to
500 MHz. AWGs contain a high
speed, high resolution digital to
analog convertor with sophisticated triggering and mode
settings, plus up to 4 megabytes
of internal memory in which to
create and edit waveforms.
You can import a waveform
from a scope or disk, select one
of the AWG’s standard waveforms, or define your own from
scratch. Using their powerful
editing tools, you can edit the
waveform right on the screen,
then clock it out at rates up to
1 GS/s.
For computer-controlled production test applications demanding
high throughput, the AWG 2021
is available in VXI format as the
VX4792. This uncompromised
signal source delivers the same
bandwidth and accuracy as the
AWG 2021, and its waveform
record formats are identical to
those of the benchtop unit. As
such, the VX4792 allows easy
movement of waveforms and
instructions from the design lab
to the production line.
Where the utmost signal purity
is required, the AFG 2020
Arbitrary Function Generator
offers direct digital synthesized
waveforms with exceptionally
low distortion and high
frequency agility.
AWG 2000 Series Arbitrary Waveform Generators
AWG 2041 AWG 2021 AWG 2005
Clock Rate 1 GS/s 250 MS/s 20 MS/s
Max Output Waveform Frequency 500 MHz 125 MHz 10 MHz
Region Shift Yes Yes Yes
Direct Waveform Transfer TDS, 2000 Series, 11000 Series, Same as AWG 2041 Same as AWG 2041
from DSOs DSA, RTD 700 Series, and others
External Clock Clock In & Out Same as AWG 2041 Same as AWG 2041
Graphical Waveform Editing Draws, Timing Table, Equation; Same as AWG 2041; Same as AWG 2041;
FFT (Opt. 09), Digital Word/Pattern TTL Digital Word Generator Digital Word/Pattern Generator option
Generator (Opt. 03) (Opt. 03) not available
Max P–P Amplitude into 50 Ω 2 V 5 V 10 V
Memory: Execution per Channel 1 MB; expandable to 4 MB (Opt. 01) 256 kB per channel 64 kB per channel
Memory: Non-Volatile 512 kB 512 kB 512 kB
External Modulation AM AM AM
Output Channels 1 Analog & Complement; 1 Analog; 2 Analog;
8 ECL Digital (Opt. 03) 2 Analog (Opt. 02); 4 Analog (Opt. 02);
12 ECL Digital (Opt. 03); 24 TTL Digital (Opt. 04);
24 TTL Digital (both Opt. 02 and 04)
Predefined Waveforms Synthesized, 10 MHz Synthesized, 2.5 MHz Synthesized, 2.5 MHz
Sweep Sequencer and Equation Editor Same as AWG 2041 Linear; Log; User-defined (Opt. 05)
used to create sweep
Time Base Accuracy 1 ppm 50 ppm 5 ppm
Vertical Resolution 8 bits 12 bits 12 bits
Built-In Floppy Drive Yes Yes Yes
Page 33

33
The TDS 744A represents the
next generation of digitizing
scope performance. This versatile general-purpose instrument
introduces Tek’s new InstaVu
™
acquisition feature and sets a
benchmark in waveform capture
rate for DSOs. The TDS 744A
can display more than 400,000
acquisitions per second—a rate
2,500 times faster than the most
advanced DSOs available.
Other TDS 744A features
include advanced triggering,
graphical user interface,
high-speed signal processing,
complementary probing, and
sophisticated documentation
capability.
With its long record length and
high bandwidth, the TDS 744A
is an ideal complement to the
2000 Series AWGs for wireless
communications testing.
TDS 744A Digitizing Oscilloscope
TDS 744A
Bandwidth 500 MHz
Input Channels 4
Sample Rate per Channel
1 channel 2 GS/s
2 channels 1 GS/s
3 or 4 channels 500 MS/s
Vertical Resolution 8 bits;
> 12 bits with Hi-Res;
11 bits with Averaging
Record Length 500 to 50,000 points per channel
Max. 500,000 points (optional)
DC Gain Sensitivity ± 1.0%
Vertical Sensitivity 1 mV to 10 V/div;
50 Ω: 1 mV to 1 V/div
Automatic Measurements 25
Triggering System Edge, Pulse (Width, 1 ns Glitch, Runt, and Slew Rate),
Logic (Pattern, State, and Setup and Hold Time
Violation), HDTV Video (optional)
Special Features InstaVu, Dual Window Zoom, FFT, Differentiation,
Integration, Color Monitor, 31⁄2" Floppy Drive
Page 34

343536
Page 35

Page 36

4/97 WCI 76W–10555–1
Copyright © 1997, Tektronix, Inc. All rights reserved. Tektronix products are covered by U.S. and foreign patents, issued and pending. Information in this
publication supersedes that in all previously published material. Specification and price change privileges reserved. TEKTRONIX and TEK are registered
trademarks of Tektronix, Inc. All other tradenames referenced are the service marks, trademarks or registered trademarks of their respective companies.
For further information, contact Tektronix:
World Wide Web:
http://www.tek.com;
ASEAN Countries
(65) 356-3900;
Australia & New Zealand
61 (2) 888-7066;
Austria, Eastern Europe, & Middle East
43 (1) 7 0177-261;
Belgium
32 (2) 725-96-10;
Brazil and South America
55 (11) 3741 8360;
Canada
1 (800) 661-5625;
Denmark
45 (44) 850700;
Finland
358 (9) 4783 400;
France & North Africa
33 (1) 69 86 81 08;
Germany
49 (221) 94 77-400;
Hong Kong (
852) 2585-6688;
India
91 (80) 2275577;
Italy
39 (2) 250861;
Japan
(Sony/Tektronix Corporation) 81 (3) 3448-4611;
Mexico, Central America, & Caribbean
52 (5) 666-6333;
The Netherlands
31 23 56 95555;
Norway
47 (22) 070700;
People’s Republic of China (
86) 10-62351230;
Republic of Korea
82 (2) 528-5299;
Spain & Portugal
34 (1) 372 6000;
Sweden
46 (8) 629 6500;
Switzerland
41 (41) 7119192;
Taiwan
886 (2) 765-6362;
United Kingdom & Eire
44 (1628) 403300;
USA
1 (800) 426-2200
From other areas, contact: Tektronix, Inc. Export Sales, P.O. Box 500, M/S 50-255, Beaverton, Oregon 97077-0001, USA (503) 627-1916
 Loading...
Loading...