ST LS404 User Manual

LS404

HIGH PERFORMANCE

QUAD OPERATIONAL AMPLIFIER

■ SINGLE OR SPLIT SUPPLY OPERATION

■ LOW POWER CONSUMPTION

■ SHORT CIRCUIT PROTECTION

■ LOW DISTORTION, LOW NOISE

■ HIGH GAIN-BANDWIDTH PRODUCT

■ HIGH CHANNEL SEPARATION

DESCRIPTION

The LS404 is a high performance quad operation­al amplifier with frequenc y and phas e compe nsa­tion built into the chip. The internal phase compen­sation allows stable operation as voltage follower
in spite of its high Gain-Bandwidth Product.

The circuit presents very stable electrical charac­teristics over the entire supply voltage range, and
is particularly intended for professional and tele­com applications (active filter, etc).

The patented input stage circuit allows small input
signal swings below the negative supply voltage
and prevents phase inversion when the inputs are
over drivers.

N

DIP14

(Plastic Package)

D

SO14

(Plastic Micropacka ge)

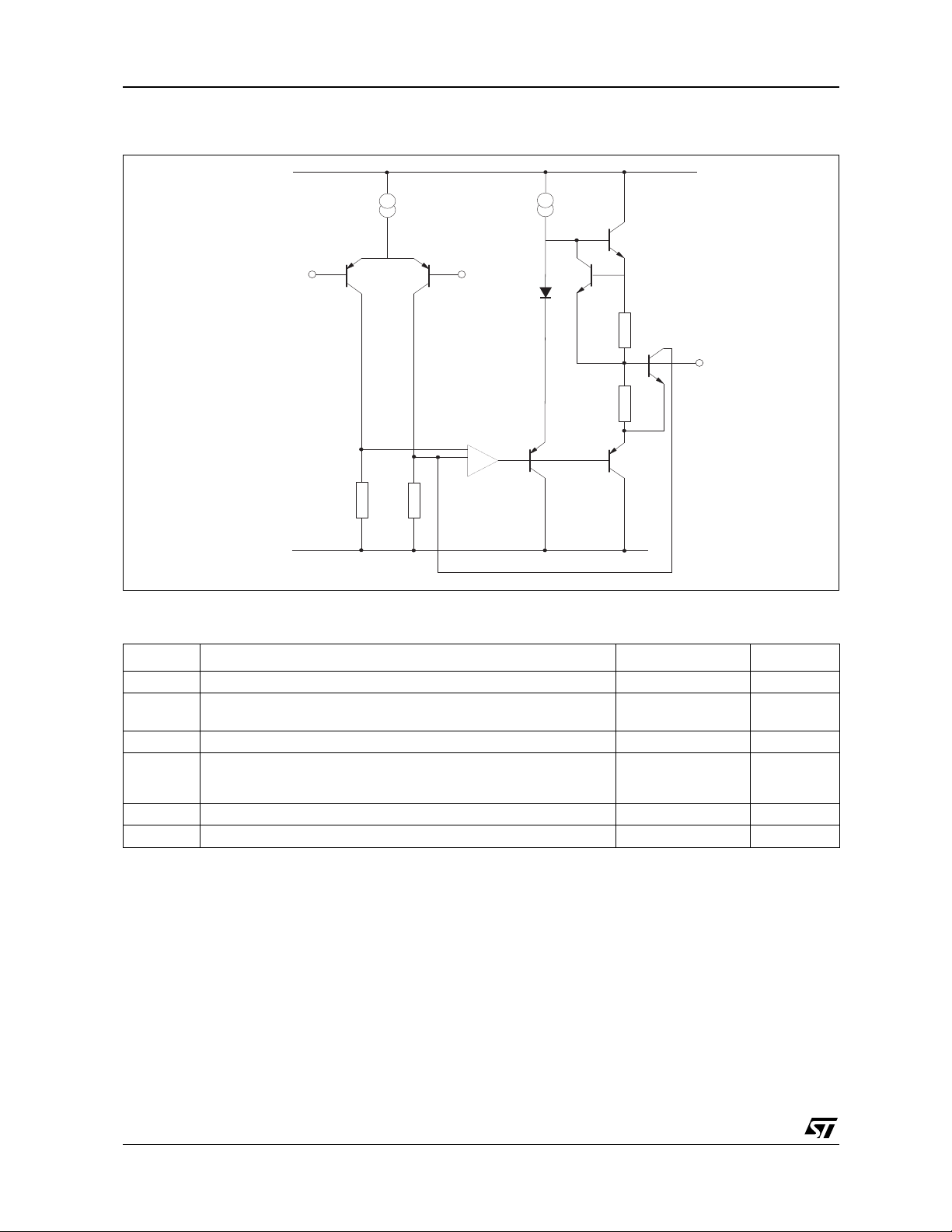
PIN CONNECTIONS (top view)

ORDER CODE

Part Number Temperature Range

LS404C 0°C, +70°C
LS404I -40°C, +105°C
LS404M -55°C, +125°C

Example : LS204CN

N = Dual in Line Package (D IP)
D = Small Outline Package (SO) - also available in Tape & Reel (DT)

November 2001

Package

ND

••

••

••

Output 1

Inverting Input 1

Non-inverting Input 1

V

CC

Non-inverting Input 2

Inverting Input 2

Output 2

1

2

-

+

3

+

4

5

+

-

6

7

14

13

-

+

12

11

10

+

­9

8

Output 4

Inverting Input 4

Non-inverting Input 4

-

V

CC

Non-inverting Input 3

Inverting Input 3

Output 3

1/11

LS404

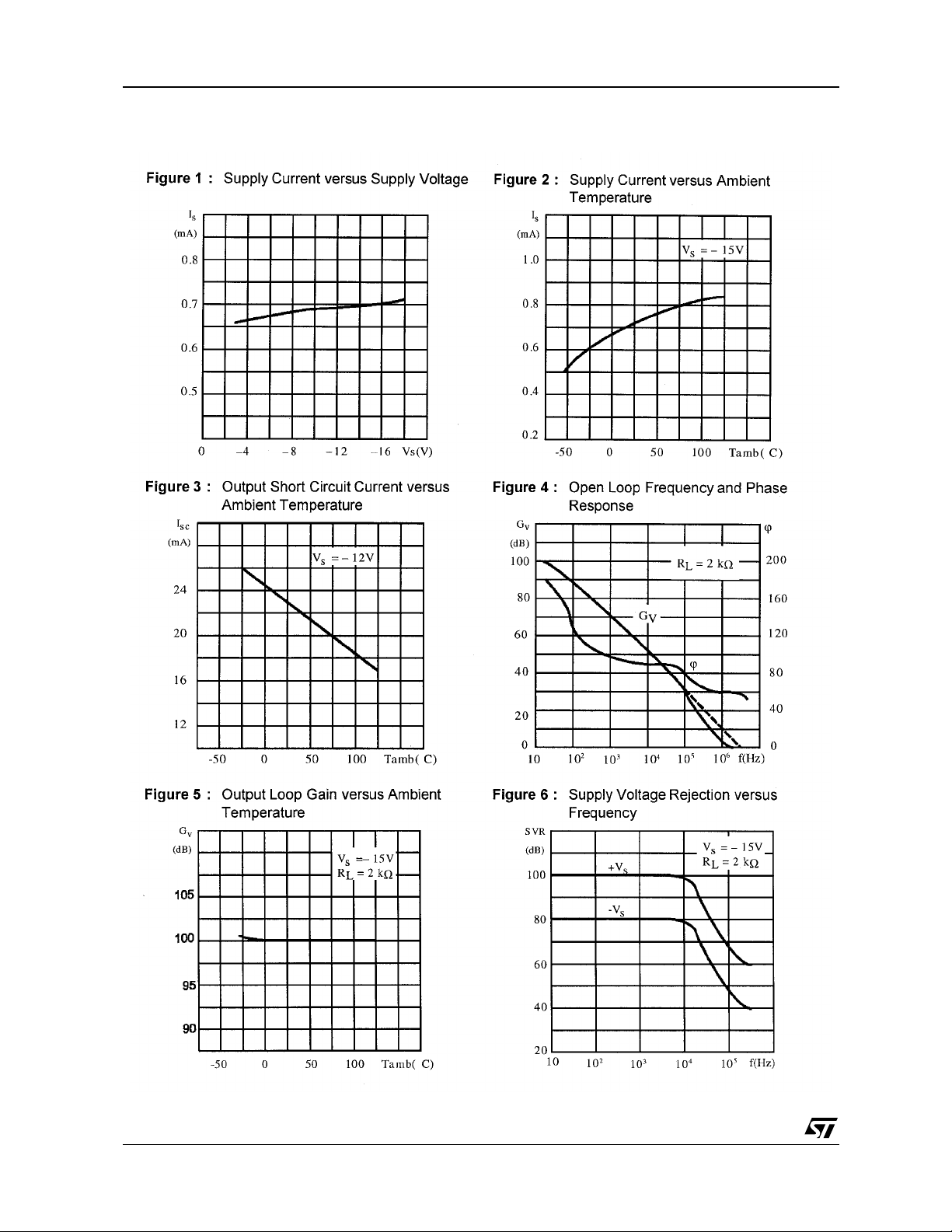
SCHEMATIC DIAGRAM (1/4 LS404)

Inverting input

Non-inverting

input

Output

ABSOLUTE MAXIMUM RATINGS

Symbol Parameter Value Unit

V

T

V

V

oper

P
T

Supply voltage ±18 V

CC

Input Voltage Positive

i

Differential Input Voltage

id

Negative

Operating Temperature Range LS204C

LS204I
LS204I

Power Dissipation at T

tot

Storage Temperature Range -65 to +150 °C

stg

amb

= 70°C

+V

CC

-VCC - 0.5
±(V

-1)

CC

0 to +70

-40 to +105

-55 to +125
400 mW

V
V

°C

2/11

ELECTRICAL CHARACTERISTICS

V

= ±15V, T

CC

Symbol Parameter

I

Supply Current 1.3 2 1.5 3 mA

cc

Input Bias Current

I

ib

R

Input Resistance (f = 1kHz) 1 1 M

i

Input Offset Voltage (Rs ≤ 10kΩ)

V

io

DV

Input Offset Voltage Drift (Rs ≤ 10kΩ)

io

Input Offset Current

I

io

Input Offset Current Drift

DI

io

I

Output Short-circuit Current 23 23 mA

os

Large Signal Voltage Gain

A

vd

GBP

Gain Bandwith Product

Equivalent Input Noise Voltage

e

n

Total Harmonic Distortion

THD

Output Voltage Swing

±V

opp

Large Signal Voltage Swing

V

opp

Slew Rate (R

SR

SVR

CMR

V

o1/Vo2

Supply Voltage Rejection Ratio

Common Mode Rejection Ratio

Channel Separation (f= 1kHz) 100 120 120 dB

= 25°C (unless otherwise specified)

amb

T

< Top < T

min

< Top < T

T

min

R

= 2kΩ, VCC = ±15V

L

V

= ±4V

CC

f =100kHz, R

max

max

= 2k, CL = 100pF

L

f = 1kHz,

= 50

R

Ω

s

R

= 1k

Ω

s

= 10k

R

Ω

s

Unity Gain

= 2k

Ω,

Vo = 2V

pp

R

L

f = 1kHz
f = 20kHz

= 2kΩ, VCC = ±15V

R

L

V

= ±4V

CC

f = 10kHz, R

= 1k

R

L

V

= 1V, f = 100Hz

ic

V

= 10V

ic

= 10k

Ω

L

Ω

= 2kΩ, unity gain)

L

LS404

LS404I - LS404M LS404C

Min. Typ. Max. Min. Typ. Max.

50 200 100 300 nA

0.7 2.5 0.5 5 mV

55

10 40 20 80 nA

0.08 0.1 nA/°C

90

100

95

86 100

95

1.8 3 1.5 2.5 MHz

8
10
18

0.01

0.03

±13

±3

22
20

15 10

12
20

0.4 0.01

0.03

±13

±3

22
20

0.8 1.5 1 V/µs

90 94 86 90

90 94 86 90

Unit

µV/°C

dB

nV

----------- -

Vpp

dB

dB

Ω

Hz

%

V

3/11

LS404

4/11

LS404

5/11

LS404

APPLICATION INFORMATION: Active low-pass filter
BUTTERWORTH

The Butterworth is a "maximally flat" amplitude re­sponse filter (figure 10) Butterworth filters are
used for filtering signals in data acquisition sys­tems to prevent aliasing errors in samples-data
applications and for ge neral purpose l ow-pass fil­tering.

The cut-off frequency Fc, is the frequency at which
the amplitude response is down 3d B. The attenu­ation rate beyond the cutoff frequency is n6 dB per
octave of frequency where n is t he orde r (num ber
of poles) of the filter.

Other characteristics :

❑ Flattest possible amplitude response
❑ Excellent gain accuracy at low frequency

end of passband

BESSEL

The Bessel is a type of “linear ph ase” filter. Be­cause of their linear phase characteristics, these
filters approximate a constant time delay over a
limited frequency range. Be ssel filters pass tran­sient waveforms with a minimum of distortion.
They are also used to provide time delays for low
pass filtering of modulated waveforms and as a
“running average” type filter.

The maximum phase shift is radians where

n is the order (number of poles) of the filter. The
cut-off frequency fc, is defined as the frequency at
which the phase shift is one half of this value.

The table below shows the typical overshoot and setting time response of the low pass filters to a step
input.

Butterworth

Bessel

Chebyschev (ripple ±0.25dB)

Chebyschev (ripple ±1dB)

n

π–

---------- ­2

Number of Poles

2
4
6
8

2
4
6
8

2
4
6
8

2
4
6
8

For accurate delay, the cut-off frequency should
be twice the maximum signal frequency.

The following table can be used to obtain the -3dB
frequency of the filter.

2 Pole 4 Pole 6 Pole 8 Pole

-3dB Frequency 0.77fc 0.67fc 0.57fc 0.50fc

Other characteristics :

❑ Selectivity not as great as Chebyschev or

Butterworth

❑ V ery little overshoot response to step inputs
❑ Fast rise time

CHEBYSCHEV

Chebyschev filters have greater selectivity than ei­ther Bessel ro Butterworth at the expense of ripple
in the passband (figure 11).

Chebyschev filters are normally designed with
peak-to-peak ripple values from 0.2dB to 2dB.

Increased ripple in the passband allows increased
attenuation above the cut-off frequency.

The cut-off frequ ency is defin ed as the frequency
at which the amplitude res ponse passes through
the specificed maximum ripple band and enters
the stop band.

Other characteristics :

❑ Greater selectivity
❑ Very non-linear phase response
❑ High overshoot response to step inputs

Peak

Overshoot

% Overshoot ±1% ±0.1% ±0.01%

4
11
14
14

0.4

0.8

0.6

0.1

11
18
21
23

21
28
32
34

Settling Time (% of final value)

1.1Fc sec.

1.7/fc

2.4/fc

3.1/fc

0.8/fc

1.0/fc

1.3/fc

1.6/fc

1.1/fc

3.0/fc

5.9/fc

8.4/fc

1.6/fc

4.8/fc

8.2/fc

11.6/fc

1.7Fc sec.

2.8/fc

3.9S/fc

5.1/fc

1.4/fc

1.8/fc

2.1/fc

2.3/fc

1.6/fc

5.4/fc

10.4/fc

16.4/fc

2.7/fc

8.4/fc

16.3/fc

24.8/fc

1.9Fc sec.

3.8/fc

5.0S/fc

7.1/fc

1.7/fc

2.4/fc

2.7/fc

3.2/fc

-

-

-

-

-

-

-

Design of 2nd order acti ve low pass f ilt er (Sallen a nd Key configuration uni ty gain op-am p)

6/11

Fixed R = R1 = R2, we have (see figure 13)

1

----

R

-------

ω

ζ

c

C

1 =

Figure 13 : Filter Configuration

C

2 =

C2

1

----

R

1

-----------

ξω

LS404

c

Vin

Three parameters are needed to characterize the
frequency and phase respons e o f a 2n d order ac­tive filter: the gain (Gv), the da mping factio (ξ) or
the Q factor (Q = 2 ξ)

1

), and the cuttoff f requency

(fc).

R2R1

C1

Vout

The higher order response are obtained with a se­ries of 2nd order sections. A simple RC section is
introduced when an odd filter is required.

The choice of ’ξ' (or Q factor) determines the filter
response (see table 1).

Table 1

Filter Response

Bessel

Butterworth Frequency at which Gv = -3dB

Chebyschev

------ -

------ -

------ -

ξ

3

2

2

2

2

2

Q Cuttoff Frequency fc

Frequency at which Phase Shift is -90°C

1

------ ­3

1

------ ­2

Frequency at which the amplitude response
passes through specified max. ripple band and

1

------ ­2

enters the stop bank.

EXAMPLE

Figure 14 : 5th Order Low-pass Filter (Butterworth) with Unity Gain configuration

C2

Ri

Ci

R2R1

C1

R4R3

C3

C4

7/11

LS404

In the circuit of figure 14, for fc = 3.4kHz and Ri =
R1 = R2 = R3 = 10kΩ, we obtain:

1

Ci = 1.354

C1 = 0.421

C2 = 1.753

C3 = 0.309

C4 = 3.325

1

--- -

------------ = 6 .33n F

R

fc

2 π

1

1

--- -

------------ = 1 . 9 7nF

R

fc

2 π

1

1

--- -

------------ = 8 . 2 0nF

R

fc

2 π

1

1

--- -

------------ = 1 . 4 5nF

R

fc

2 π

1

1

--- -

------------ = 1 5 .14nF

R

fc

2 π

The attenuation of the filter is 30dB at 6.8kHz and
better than 60dB at 15kHz.

The same method , referring to table 2 and figure
15 is used to design high-pass filter. In this case
the damping facto r is found by taking the recipro­cal of the numbers in table 2. For fc = 5kHz and Ci
= C1 = C2 = C3 = 1nF we obtain:

1

1

Ri =

R1 =

R2 =

R3 =

R4 =

-------------- -

0.354
1

-------------- -

0.421
1

-------------- -

1.753

1

-------------- -

0.309
1

-------------- -

3.325

1

--- -

----------- - = 25. 5k Ω

C

fc

2π

1

1

--- -

------------ = 75. 6k Ω
2π

C

fc

1

1

--- -

------------ = 18. 2k Ω

C

fc

2π

1

1

----

------------ = 103k Ω

C

fc

2π

1

1

--- -

------------ = 9 . 6 k Ω

C

fc

2π

Table 2 : Damping Factor for Low-pass Butterworth Filters

Order Ci C1 C2 C3 C4 C5 C6 C7 C8

2 0.707 1.41
3 1.392 0.202 3.54
4 0.92 1.08 0.38 2.61
5 1.354 0.421 1.75 0.309 3.235
6 0.966 1.035 0.707 1.414 0.259 3.86
7 1.336 0.488 1.53 0.623 1.604 0.222 4.49
8 0.98 1.02 0.83 1.20 0.556 1.80 0.195 5.125

Figure 15 : 5th Order High-pass Filter (Butterworth) with Unity Gain configuration

R2

8/11

Ci

Ri

C1

C2

R1

C3

C4

R3

R4

Figure 16 : Multiple Feedback 8-pole Bandpass Filter

LS404

C3

C1

R1

IN

0.1 Fm

Vcc

R2

22kW

22kW

R3

R5

C2

2

R4

3

LS404

R6

¼

1

4

C4

0.1 Fm

C6

R8

C5

6

R7

5

C7

220 Fm

LS404

R9

¼

7

11

C13

0.22 Fm

C9

R11

C8

9

LS404

R10

10

R12

8

¼

C11

R14

C10

R13

C12

13

0.1 Fm

14

¼

LS404

12

Out

Figure 17 : Six pole 355Hz Low-pass Filter (chebychev type)

10kΩ

10kΩ

3.54nF

60nF

220nF

0.47 Fµ

56kΩ

10kΩ

10kΩ

86.1nF

161nF

10kΩ

10kΩ

16.3nF

This is a - pole Chebychev type with ±0.25dB ripple in the passband. A decoupling stage is used to avoid
the influence of the input impedance on the filter’s characteristics. The attenuation is about 55dB at 710Hz
and reaches 80dB at 1065Hz. the in band attenuation is limited in practise to the ±0.25dB ripple and does
not exceed 0.5dB at 0.9fc.

Figure 18 : Subsonic Filter (Gv = 0dB)

10kΩ

C

C

22kΩ

Figure 19 : High Cut filter (Gv = 0dB)

C2

10kΩ

Vin

10kΩ

C1

Fc (Hz)

15

Vout

22
30
55

100

Fc (Hz)

3

1

Vout

2

3

5
10
15

C ( F)

µ

0.68

0.47

0.33

0.22

0.10

C1 (nF)

3.9

2.2

1.2

0.68

C2 (nF)

6.8

4.7

2.2

1.5

9/11

LS404

PACKAGE MECHANICAL DATA
14 PINS - PLASTIC PACKAGE

Dimensions

Min. Typ. Max. Min. Typ. Max.

a1 0.51 0.020

B 1.39 1.65 0.055 0.065
b 0.5 0.020

b1 0.25 0.010

D 20 0.787
E 8.5 0.335
e 2.54 0.100

e3 15.24 0.600

F 7.1 0.280

i 5.1 0.201
L 3.3 0.130
Z 1.27 2.54 0.050 0.100

Millimeters Inches

10/11

PACKAGE MECHANICAL DATA
14 PINS - PLASTIC MICROPACKAGE (SO)

a2

LG

A

C

LS404

c1

b

e3

D

14

e

s

a1

b1

E

M

8

F

1

Millimeters Inches

Dimensions

Min. Typ. Max. Min. Typ. Max.

A 1.75 0.069

a1 0.1 0.2 0.004 0.008
a2 1.6 0.063

b 0.35 0.46 0.014 0.018

b1 0.19 0.25 0.007 0.010

C 0.5 0.020

c1 45° (typ.)

D (1) 8.55 8.75 0.336 0.344

E 5.8 6.2 0.228 0.244
e 1.27 0.050

e3 7.62 0.300

F (1) 3.8 4.0 0.150 0.157

G 4.6 5.3 0.181 0.208
L 0.5 1.27 0.020 0.050

M 0.68 0.027

S 8° (max.)

Note : (1) D and F do not include mold flash or protrusions - Mold flash or pr otrusions shall not exceed 0.15mm (.066 inc) ONLY FOR DATA BOOK.

Information furnished is bel ieved to be accurate and reliable. However, STMicroe lectronics assumes no responsibility for the
consequences of use of such information nor for any infringement of patents or other rights of third parties which may result from
its use. No li cense is granted by i mp lication or otherwise under any patent or patent rights of STMicroelectronics. Specifications
mentioned in this publication ar e subject to change without notice. This publication supersedes and replaces all information
previously supplied. S TMicroelectronics products are not authorized for use as critica l components in life suppo rt devices or
systems without express written approval of STMicroelectronics.

© The ST logo is a registered trademark of STMicroelectronics

7

© 2001 STM icroelectronics - P rinted in Italy - All Righ ts Reserv ed

STMicr o el ectronics GROUP OF COMPA NI E S

Australi a - Brazil - Canada - China - Finland - France - Germ any - Hong Kong - India - Is rael - Italy - Japan - Malay sia

Malta - Mor occo - Singapore - Spain - Sweden - Swi tzerland - United Kingdom - United States

© http://www.st.com

11/11