ST AN533 Application note

AN533

Application note

SCRs, TRIACs, and AC switches,

thermal management precautions for handling and mounting

Introduction

The behavior of a semiconductor device depends on the temperature of its silicon chip. This
is why electrical parameters are given at a specified temperature.

To sustain the performance of a component and to avoid failure, the temperature has to be
limited by managing the heat transfer between the chip and the ambient atmosphere. The
aim of this note is to show how to calculate a suitable heatsink for a semiconductor device
and the precautions needed for handling, mounting and soldering techniques.

March 2008 Rev 3 1/22

www.st.com

Contents AN533

Contents

1 Through-hole packages . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

1.1 Thermal resistance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

1.2 Thermal impedance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

1.3 Insulating materials . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

1.4 Insulated components . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

1.5 Handling and mounting techniques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

1.6 Through-hole package wave soldering . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

2 Surface mount packages . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

2.1 Thermal resistance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

2.2 Thermal impedance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

2.3 Mounting techniques and R

2.4 Reflow soldering information . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17

th(j-a)

3 Revision history . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

2/22

AN533 Through-hole packages

1 Through-hole packages

1.1 Thermal resistance

1.1.1 Review

The thermal resistance of semiconductor assembly is the parameter which characterizes its
resistance to the heatflow generated by the junction during operation. A temperature
exceeding the maximum junction temperature curtails the electrical performance and may
damage the device.

The maximum dissipated power capability is:

T

P

max

Where:

● T

max

j

● T

● R

The R

is the ambient air temperature in degrees ( °C)

a

(j-a)

th

th(j-a)

An analogy between Ohm’s law and the thermal equivalent circuit can be made:

● Electrical resistance corresponds to thermal resistance

● Current corresponds to dissipated power

● Voltage corresponds to temperature

jmax-Ta

=

R

th(j-a)

is the maximum junction temperature of the semiconductor in degrees ( °C)

is the thermal resistance between junction and ambient air in °C/W

takes into account all materials between the junction and ambient air.

Thus: V = R . I corresponds to ΔT = R

th

. P

1.1.2 Dissipated power for a thyristor or a TRIAC

The maximum power dissipation versus average on-state current (for SCRs) or RMS on­state current (for TRIACs) is given in the datasheet for each product.

However, a more accurate result is obtained by using the V
following calculation:

P = V

. I

to

T(AV)

+ Rd . I

Where:

● V

● R

● I

● I

is the threshold voltage specified in the datasheet

to

is the dynamic on-state resistance specified as Rd in the datasheet

d

is the average on-state current

T(AV)

is the RMS on-state current

T(RMS)

Figure 1 shows the RMS

2

T(RMS)

and average values for different waveforms of current.

and Rd values with the

to

3/22

Through-hole packages AN533

Figure 1. RMS and average currents

T

I

T(AV)

A

I

p

t

0

B

I

p

T/2

C

I

p

t

0

T/2

1

= i(t)dt

∫

T

0

T

T

T

t

t

t

²

I

I

T(AV)

I

T(AV)

²

I

T(RMS)

I

T(AV)

T(RMS)

2 . Ip.t

=

2 . I

=

=

2 . I

=

π

T

1

i²(t)dt

=

∫

T

0

0

²

I

.Tπ

p

²

I

p

(

2

cos t0.

p .

T(RMS)

²

I

T(RMS)

2 . t

1 - + . sin

²

(

=

0

T

2 . π

π

T

π

(

²

I

.t

p

0

=

2 . T

²

I

p

2

1

4 . . t

(

π

0

((

T

1.1.3 Dissipated power in a TRIAC

A TRIAC is made up of two thyristors connected back to back. This means we consider the
sum of the dissipated power of both thyristors.

The following formula gives the total dissipated power versus I
TRIAC (see Figure 1 C with t

2 . 2√

P =

π

.I

T(RMS).Vt0

For a phase angle conduction the RMS

= 0):

0

+ Rd.I

current is given in Figure 1 C.

1.1.4 TRIAC without external heatsink

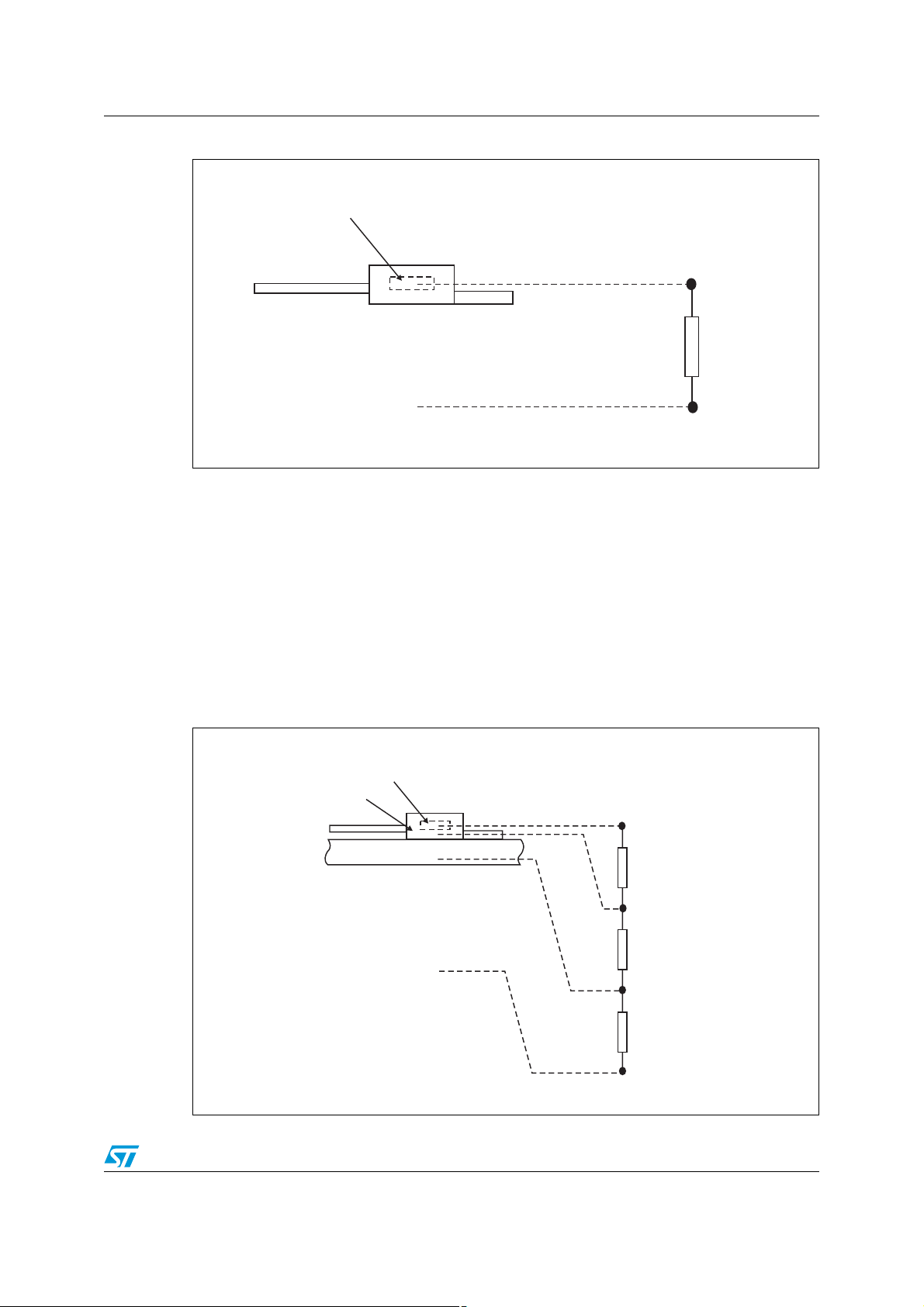
Figure 2 shows the thermal equivalent diagram for a TRIAC without external heatsink.

In practice the imposed parameters are:

● T

● R

● P: dissipated power in the TRIAC depending on the used TRIAC and on the load

The following equation defines the junction temperature depending on these parameters:

: ambient air temperature where the TRIAC is located

a

: thermal resistance between junction and ambient air given in the datasheet

th(j-a)

current

T

= P . R

j

th(j-a)

+ T

a

2

T(RMS)

current through the

T(RMS)

4/22

AN533 Through-hole packages

Figure 2. Thermal equivalent diagram

Junction

T

j

R

th(j-a)

Ambient air

1.1.5 TRIAC with external heatsink

If the estimated junction temperature is higher than the maximum junction temperature
specified in the datasheet, a heatsink has to be used.

Recommendation: this calculation has to be made in the worst case scenario i.e with the
maximum dissipated power, load and line voltage dispersions. We have to consider the
maximum ambient temperature around the component i.e. inside the box where the TRIAC
is located.

The same approach as presented in the previous section allows a suitable heatsink to be
defined. Figure 3 shows the thermal equivalent diagram.

Figure 3. Thermal equivalent diagram with external heatsink

Junction

Case

Heatsink

T

j

R

th(j-c)

T

a

Ambient air

T

c

Rth(c-h)

Th

Rth(h-a)

T

a

5/22

Through-hole packages AN533

The formula to calculate the thermal resistance between heatsink and ambient air is the
following:

Tj-Ta

R

th(h-a)

=

- R

P

th(j-c)

- R

th(c-h)

Where:

● T

● P is the maximum dissipated power in W

● R

R

is the junction temperature in °C

j

is the thermal resistance between junction and case in °C/W

th(j-c)

) is the thermal resistance between case and heatsink in °C/W, depending on the

th(c-h

contact case/heatsink.

Since the current alternates in a TRIAC, we have to consider the R
current which is different to the R

This difference is due to the die of the TRIAC. The first half of the silicon die works when the
current is positive, the second when the current is negative. Because of the thermal coupling
between these two parts, this gives the following equation.

R

th(j-c)AC

= 0.75 . R

1.1.6 Choice of heatsink

Choosing a heatsink depends on several parameters; the thermal characteristic, the shape
and the cost.

However, in some applications a flat heatsink can be sufficient. Figure 4 shows the curve
Rth(h-a) versus the length of a flat square heatsink for different materials and thickness.

Some applications need heatsinks with an optimized shape where the thermal resistances
are not known.

For this, the best solution involves measuring the case temperature of the component in the
worst case scenario and keeping to the following formula:

T

< T

c

Where:

● T

● T

● P is the dissipated power in the component

● R

is the case temperature

c

jmax

th(j-c)

- P . R

jmax

th(j-c)

is the maximum junction temperature

is the thermal resistance between junction and case.

th(j-c)DC

in direct current.

th(j-c)

in alternating

th(j-c)

6/22

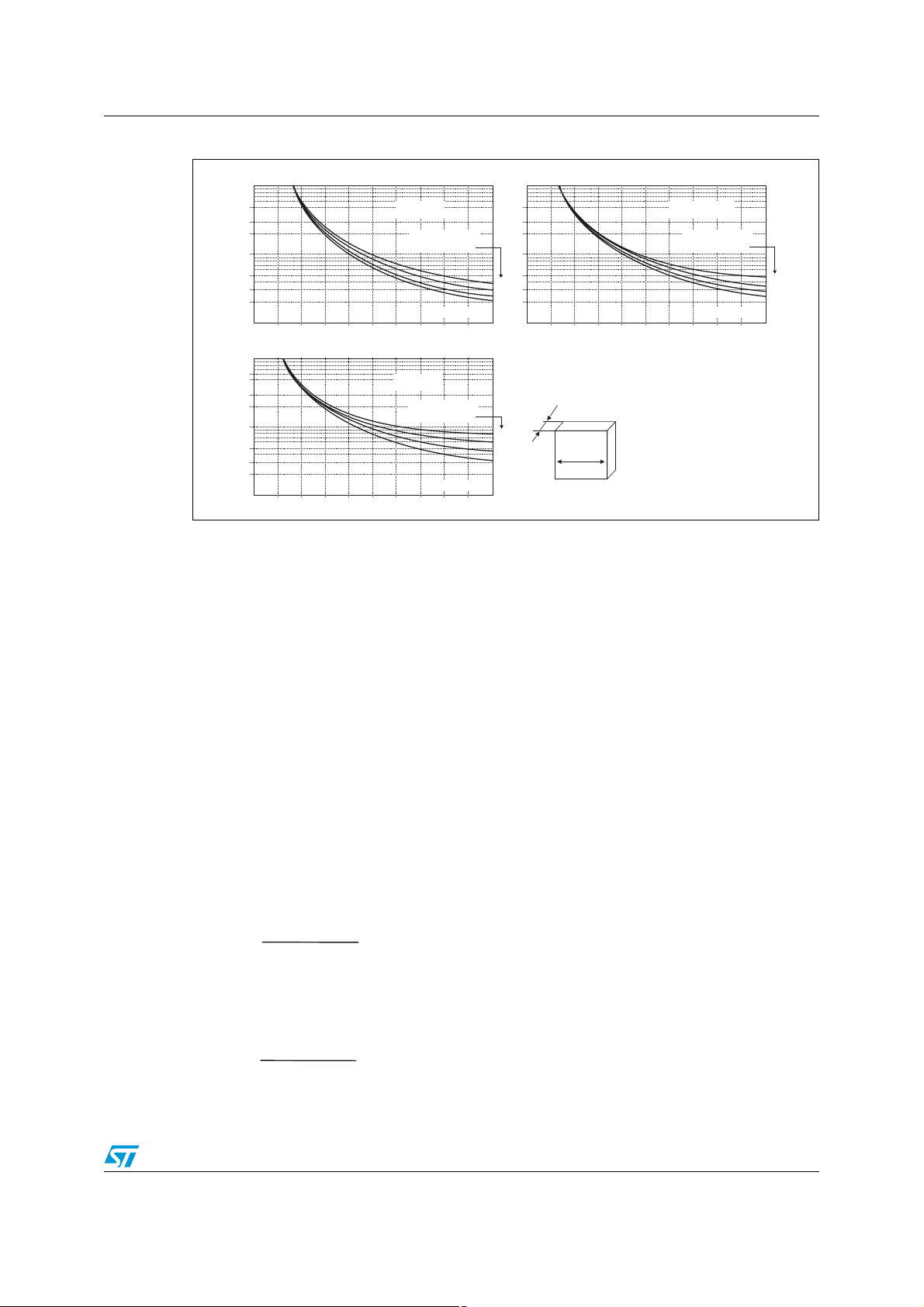
AN533 Through-hole packages

Figure 4. R

100

50
30
20

10

5

3
2

1

100

50
30
20

10

5

3
2

1

R

0

R

0

th(h-a)

2

th(h-a)

2

th(h-a)

(°C/W)

(°C/W)

1.1.7 Forced cooling

For high power or very high power applications, a forced-air or liquid cooling heatsink may
be required. Heatsink manufacturers give a coefficient depending on the air or liquid flow.

versus the length of a flat square heatsink

(°C/W)

R

th(h-a)

100

(cm)

(cm)

50
30
20

10

5

0.5
1

3

2
5

2

1

0

2

Thermal model for calculation

e

0.5
1
2
5

8

based on square heatsink

- Semiconductor device
in the center

L

- Bare convector (no ventilation)

- Vertical position

COPPER

Thickness of
the plate in mm

Length

8

10 166

8

10 166

144

12

STEEL

Thickness of
the plate in mm

144

12

18 20

Length

18 20

10 166

ALUMINIUM

Thickness of
the plate in mm

144

12

Length

(cm)

18 20

0.5
1
2

5

However, in some applications like vacuum cleaners, dissipated power is only a few watts
and air flow cooling is available. This allows a very small heatsink to be used, very often a
flat aluminium heatsink. In this case it is necessary to measure the case temperature in the
worst case scenario and to check the following formula:

T

< T

c

jmax

- P . R

th(j-c)

1.2 Thermal impedance

In steady state, a thermal equivalent circuit can be made only with thermal resistances.
However, for pulse operation it can be useful to consider the thermal impedance, especially
when the component is on during a time lower than the time to reach the thermal resistance.
The thermal impedance value versus pulse duration is given in the datasheets (see an
example in Figure 5), in the form of the relationship Z

For example, BTA08-600SW is able to dissipate

T

jmax-Tamax

P =

Z

th(j-a) (1 s)

can be obtained from the datasheet by reading the value of the ratio Zth/Rth from the

Z

th(j-a)

curve (in the case of this product the ratio is 0.06 as seen in Figure 5) and multiplying the
ratio by the value of R

P =

125 - 25

60 x 0.06

from the datasheet. For this example R

th(j-a)

= 27.5 W

plotted against pulse duration.

th/Rth

≈ 27 W without heatsink during 1 s:

is 60 °C/W

th(j-a)

7/22

Through-hole packages AN533

In steady state, with the same ambient temperature, the same TRIAC is able to dissipate:

P =

125 - 25

60

= 1.7 W

Figure 5. Thermal transient impedance of a BTA08-600SW.

K=[Zth/Rth]

1E+0

Z

th(j-c)

1E-1

0.06

1E-2

TO-220AB

Z

th(j-a)

1E-3

1E-3 1E-2 1E-1

1.3 Insulating materials

We can classify them in 3 types as following:

Mica insulators

This has been the most commonly used insulator for many years. Its insulating quality is
good, but due to its rigidity the thermal interface is not very good, and needs contact grease
on both sides. Because of its rigidity it can be easily broken.

Ceramic insulators

More expensive than mica, their thermal resistances are lower. Due to their rigidity, they also
need contact grease. However, they can be easily broken, as they are less fragile than mica.

Silicone insulators

These materials are not rigid and therefore do not need contact grease. They assume the
shape of the component and of the heatsink if sufficient pressure is applied. The problems
previously explained disappear. According to manufacturers, the stability in time is much
better than with contact grease. However the thermal resistance is higher than the
combination of the mica + grease.

1 s

tp(s)

1E+1 1E+2 5E+2

8/22

AN533 Through-hole packages

Table 1 . R

°C 0.5 1.7 4 2.6

R

th(c-h)

for different materials for TO-220AB package

th(c-h)

Contact grease

Mica + grease

thickness = 80 µm

thickness = 80 µm

Mica dry

Silicone insulator

Ta bl e 1 shows the thermal resistance for different TO-220AB insulators and for a given

pressure (F = 30 N).

1.4 Insulated components

Most of the thyristors and TRIACs manufactured by STMicroelectronics are available in
insulated and non-insulated packages. For insulated packages, insulation can be achieved
in two different ways:

● ceramic between the die pad and the heatsink of the component (TO-220AB / TOP3 /

RD91 packages)

● resin used for encapsulation (ISOWATT220AB / TO-220FPAB packages)

All insulated packages delivered by STMicroelectronics are in accordance with UL1557
recognition applicable for "electrically isolated semiconductors". The added material
increases the thermal resistance between the junction and the case, but the total thermal
resistance (R
external insulating material. In addition, it simplifies assembly and reduces the cost.

) is lower than the one when using a non insulated component with an

th(j-a)

For two 16 A TRIACs in TO-220AB package, R

Table 2. Comparison of R

BTA16-600C

(insulated version)

2.1 device 1.2 device

+ 0.5 grease + 1.7 mica + grease

= 2.6 total = 2.9 total

for sample insulated and non-insulated products

th(j-c)

th(j-c)AC

1.5 Handling and mounting techniques

The use of inappropriate techniques or unsuitable tools during handling and mounting can
affect the long term reliability of the device, or even damage it.

1.5.1 Bending and cutting leads

Lead bending must be done carefully. The lead must be firmly held between the plastic
package and the bending point during lead operation. If the package / lead interface is
strained, the resistance to humidity is impaired and in addition mechanical stress is inflicted
on the die. This damage can affect the long term reliability of the devices.

values ( °C/W) are shown in Ta b le 2 :

BTB16-600C

(non-insulated version)

9/22

Through-hole packages AN533

✓

✓

There are six basic rules to bear in mind:

1. Never clamp the plastic package (Figure 6).

Figure 6. Clamping the lead not the package

✘

Lead forming or

Clamp mechanism

Plastic package

cutting mechanism

Clamp mechanism

✘

2. Clamp the leads firmly between the plastic package and the bend / cut point (Figure 7).

Figure 7. Clamping the lead between the package and the bend / cut point

Correct

3. Bend the leads at least 3 mm from the plastic package (Figure 8).

Figure 8. Bending the lead at least 3 mm from the plastic package

3 mm

Spaced

Incorrect

Correct

10/22

Incorrect

AN533 Through-hole packages

4. Never bend the leads laterally (Figure 9).

Figure 9. Bending the leads laterally (not allowed)

Incorrect

5. Never bend the leads more than 90° and never bend more than once.

6. Make sure that the bending / cutting tool does not damage the leads.

1.5.2 Using a heatsink

Mounting surface preparation

● The mounting surface should be flat, clean and free of burrs and scratches.

● The use of a thin layer of thermal silicone grease ensures a very low contact thermal

resistance between the component and the heatsink. An excessively thick layer or a
excessively viscous silicone grease may have the opposite effect and cause the
deformation of the tab.

● The planarity of the contact surface between device and heatsink must be very low

(less than 50 µm for TO-220AB).

Insertion

If the heatsink is mounted on the PC board, it should be attached to the component before
the soldering process of the leads.

Mounting techniques

Mounting must be done carefully. Excessive stress may induce distortion of the tab and as a
consequence mechanical damage on the die.

Soldering: It is not recommended for through-hole packages.

11/22

Through-hole packages AN533

With rivets: Pop rivets should never be used for the following reasons:

● A too rigorous expansion of the metal can lead to a distortion of the heatsink hole and

induce mechanical stresses on the die.

● High crimping shock can damage the die.

Press rivets can be used with caution provided they are of a soft metal like aluminium. The
crimping force must be applied slowly and carefully in order to avoid shock and deformation
of the heatsink.

Figure 10. Assembly with rivet

Rivet

Component

Heatsink

Contact
grease

With clips: Care should be taken with the contact area between the plastic case and the

clip: the maximum pressure allowed on plastic is 150 N/mm2. Over this value, cracks may
be induced in the package. Therefore, the clips have to be round or smooth in the contact
area to avoid concentrated loads on the plastic body. The force applied on the component
depends on the heatsink and the component thickness, so they must be specially designed
to take this value into account. Screw assembly is preferred to clip assembly for insulated
packages.

Figure 11. Clip assembly

Clip

d

Component

Contact grease

12/22

Heatsink

AN533 Through-hole packages

With screws: The following precautionary measures should be taken:

● To avoid tab distortion, a rectangular washer must be put between the screw head and

the tab, and a compression washer must be put between the tab and the nut.

Figure 12. Correct assembly

M3 screw

Washer

Component

Heatsink

Washer
Lock washer

Nut

● Take care to avoid mechanical shock during screwing.

● Keep the screw straight.

● Appropriate screwing torque should be used, excessive screwing torque may cause the

Contact
grease

distortion of the tab and induce bad thermal contact. In addition it can generate cracks
in the die.

Figure 13. Incorrect assembly

M3 screw

Washer

Component

Bad thermal
contact

Heatsink

Washer
Lock washer
Nut

The thermal contact resistance depends on the force generated by the applied torque on the
screw:

2 . T . π

F =

P + r . D . π

Where:

● T is applied torque on the screw in N.m

● P is pitch in m

● D is screw diameter in m

● r is rubbing factor: # 0.12 for steel-steel with grease and # 0.2 for steel-aluminium

The relative variation of the R

, compared with the value of R

th(c-h)

at 0.6 Nm versus the

th(c-h)

torque for an M3 screw used for the TO220AB is given in Figure 14.

13/22

Through-hole packages AN533

Figure 14. Relative variation of R

compared with R

th(c-h)

at 0.6 Nm versus

th(c-h)

torque for TO-220AB

R

th(c-h)/Rth(c-h)

2.00

1.75

1.50

1.25

1.00

0.75

0.50

0.1

Table 3. Recommended torque and thermal contact resistance

Package Torque (Nm)

TO-220AB / PENTAWATT 0.4 to 0.6

at 0.6 Nm

0.2

Torque (Nm)

0.4

Thermal contact resistance

(1)

0.6

(°C/W)

0.5

ISOWATT220 / TO-220FPAB 0.4 to 0.6 0.5

TOP3 / TOP3I 0.9 to 1.2 0.1

RD91 0.9 to 1.2 0.1

1. For BTB20-xxx, BTB24-xxx and TYNxx40, the maximum torque is 0.5 Nm.

14/22

AN533 Through-hole packages

1.6 Through-hole package wave soldering

The lead-free through-hole devices may be soldered with lead-free solder pastes or alloys
(Sn-Ag-Cu based alloys). The typical soldering temperature is 260 °C.

Alternatively these devices may be soldered with SnPb based solder pastes. The soldering
temperature is then typically around 220 °C.

Interface adherences on through-hole package structures are qualified to sustain only 3
consecutive dips of their connections in a solder pot at 260 °C (-0 °C / +5 °C) .

● immersion duration: 10 seconds each

● delay between 2 dippings: 5 minutes

● minimum distance solder to package plastic body: according to packages, by default

1mm

Lead-free devices are described in an internal specification defining:

● their characteristics: lead-free connection coating, solderability and identification

features

● their reliability such as soldering resistance, reliability performances, whiskers risk

prevention.

This specification is available for ST customers upon request (Title: ECOPACK
Components Definition & Characteristics). Please consult that document for further
information.

®

ECOPACK is a registered trademark of STMicroelectronics

15/22

Surface mount packages AN533

2 Surface mount packages

2.1 Thermal resistance

The thermal resistance of a semiconductor device characterizes the device’s capability to
dissipate the heat generated by the chip during operation. This parameter allows us to
calculate the junction temperature, taking into account the device environment (load current,
ambient temperature, mounting conditions etc...).

For surface mounted devices (SMDs), the thermal resistance between junction and ambient,
called R
giving the relation between R

- 35 µm copper thickness.

Figure 15. Rth(j-a) versus copper surface under tabs (FR4 board -

SOT-223 DPAK

Rth(j-a) (°C/W)

130
120
110
100

90
80
70
60
50
40
30
20
10

0

012345

, depends on the copper surface used under the tab. Figure 15 shows curves

th(j-a)

and the copper surface under the tab for an FR4 board

th(j-a)

copper thickness = 35 µm) for several typical packages

Rth(j-a) (°C/W)

100

80

60

40

20

S(Cu) (cm²)

0

02468101214161820

D2PA K

Rth(j-a) (°C/W)

80

70

60

50

40

30

20

10

0

0 4 8 1216202428323640

S(Cu) (cm²)

S(Cu) (cm²)

2.2 Thermal impedance

When dealing with short duration pulses, the thermal impedance must be considered to
calculate the junction temperature. Depending on the time scale, the following elements are
thermally prevalent:

● t

< 10 ms: die influence

p

● t

< 0.1 s: package influence

p

● t

< 10 s: PCB influence

p

● above 10 s: thermal exchange board-air (example: with / without forced cooling)

Figure 16 shows the Z

2

and D

16/22

PA K .

/ Rth ratio for SMD packages and Figure 17 shows Z

th

th(j-a)

for DPAK

AN533 Surface mount packages

Figure 16. Relative variation of thermal impedance junction to ambient versus pulse

duration

Zth(j-a)/ Rth(j-a)

1.00

0.10

0.01
1E-3 1E-2 1E-1 1E+0 1E+1 1E+2

Figure 17. Typical Z

Z

th(j-a)

50

20
10

5

2
1

0.5

0.2

0.1

0.001 0.01 0.1 1 10 100 1,000

Zth(j-a) / Rth(j-a)

1.00

0.10

tp(s)

0.01
1E-3 1E-2 1E-1 1E+0 1E+1 1E+2 5E+2

tp(s)

SOT-23 SOT-223

for DPAK and D2PAK

th(j-a)

INFINITE HEATSINK IMS FLOATING IN AIR FR4

die

package board board/air

influence of the various mounting elements

2.3 Mounting techniques and R

R

varies with the printed circuit board technology. Different technologies can be used

th(j-a)

depending on the performance required in the design. Four techniques are commonly used:

● FR4 - Copper

● IMS (Insulated Metal Substrate)

● FR4 board with copper filled through holes + HEATSINK

● IMS + HEATSINK.

17/22

th(j-a)

Surface mount packages AN533

Figure 18. Mounting techniques for power SMDs

Footprints

Copper
foil

FR4 board

1

Copper-filled

through-holes

FR4 board

Heatsink

3

Insulation

Copper
foil

Copper
foil

Aluminium / copper

2

Insulation

Copper
foil

Aluminium / copper

Heatsink

4

As the FR4 board is commonly used in surface mounting techniques, there are several ways
of overcoming its low thermal performance:

● use of large heat spreader areas (heat sink) at the copper layer of the PCB

● use of copper-filled through holes in addition to an external heatsink for an even better

thermal management

However, due to its power dissipation limitation, using the FR4 board with these techniques
is advisable only for currents up to 8 A max.

A technology available today is Insulated Metallic Substrate (IMS). This offers greatly
enhanced thermal characteristics for surface mount components. IMS is a substrate
consisting of three different layers:

● base material which is available as an aluminum or a copper plate

● thermal conductive dielectric layer

● copper foil, which can be etched as a circuit layer.

Even if a higher power is to be dissipated, an external heatsink can be applied leading to an
R

of 4.5 °C/W (see Ta b le 4 ). This is commonly applied in practice, leading to

th(j-a)

reasonable heatsink dimensions. Often, power devices are defined by considering the
maximum junction temperature of the device. In practice, however, this is far from being fully
exploited.

The designer should carefully consider which is appropriate mounting method (see Ta bl e 4 )
to be used according to the dissipated power. The type of board will influence the thermal
performance of the system. Ta bl e 4 shows the R
techniques for DPAK and D²PAK.

18/22

depending on the mounting

th(j-a)

AN533 Surface mount packages

Table 4 . R

FR4 70 °C/W 50 °C/W

FR4 with 10 cm² heatsink on board 40 °C/W 35 °C/W

FR4 with copper filled holes and external heatsink 13 °C/W 12 °C/W

IMS (40 cm²) in free air 9 °C/W 8 °C/W

IMS with external heatsink 4.5 °C/W 3.5 °C/W

for DPAK and D2PAK according to mounting method

th(j-a)

Mounting method

DPAK D

Rth (j-a)

2

PAK

2.4 Reflow soldering information

The surface mount assembly is a 4-step process.

1. solder paste printing

2. component placement on the board

3. reflow soldering

4. cleaning (optional)

The soldering process causes considerable thermal stress to a semiconductor component.
This has to be minimized to assure a reliable and extended lifetime of the device. SOT-23,
SOT-223, SO-8 and DPAK packages can be exposed to a maximum temperature of 260 °C
for 10 to 30 seconds. For the D

2

PAK package the maximum temperature is 245 °C.
Overheating during the reflow soldering process may damage the device, therefore any
solder temperature profile should be within these limits. Reflow techniques are most
common in surface mounting. Typical heating profiles for leadfree solder (ST ECOPACK) are
given in Figure 19 for small packages (SOT-23, SOT-223, DPAK), either for mounting on a
FR4 or on metal-backed boards (IMS). Please refer to the IPC/JEDEC J-STD-020C
standard for further information about “small” and “large” component definitions.

Note: Soldering profile defined in IPC/JEDEC J-STD-020C standard is used for reliability

assessment and typically describes warmest profiles used for component mounting, not the
necessary temperatures to achieve good soldering.

Wave soldering is not advisable for DPAK and D²PAK because it is almost impossible to
contact the whole package slug during the process.

19/22

Surface mount packages AN533

Figure 19. ST ECOPACK recommended soldering reflow profile for small packages

Temperature (°C)

Temperature (°C)

260°C max

260°C max

255°C

255°C

220°C

220°C

180°C

180°C

125 °C

125 °C

3°C/s max

3°C/s max

0

0

012345 67

012345 67

10-30 sec

10-30 sec

90 to 150 sec

90 to 150 sec

90 sec max

90 sec max

2°C/s recommended

2°C/s recommended

6°C/s max

6°C/s max

Time (min)

Time (min)

For each individual board, the appropriate heat profile has to be adjusted experimentally.
The current proposal is just a starting point. In every case, the following precautions have to
be considered:

● Always preheat the device. The purpose of this step is to minimize the rate of

temperature rise to less than 3 °C per second (recommended 2 °C/s) to minimize the
thermal shock on the component.

● Dryout section, after preheating, ensures that the solder paste is fully dried before

starting reflow step. Also, this step allows the temperature gradient on the board to be
evened out.

● Peak temperature should be at least 30 °C higher than the melting point of the solder

alloy chosen to ensure the reflow quality. In any case the peak temperature should not
exceed 260 °C.

Lead-free devices are described in an internal specification defining:

● their characteristics: lead-free connection coating, solderability and identification

features

● their reliability such as soldering resistance, reliability performances, whiskers risk

prevention.

This specification is available for ST customers upon request (Title: ECOPACK Components
Definition & Characteristics). Please consult that document for further information about
reflow and wave soldering.

Voids pose a difficult reliability problem for large surface mount devices. Such voids under
the package result in poor thermal contact and the high thermal resistance leads to
component failures.

Coplanarity between the substrate and the package can be easily verified. The quality of the
solder joints is very important for two reasons:

● Poor quality solder joints directly result in poor reliability.

● Solder thickness affects the thermal resistance significantly. Thus, tight control of this

parameter results in thermally efficient and reliable solder joints.

20/22

AN533 Revision history

3 Revision history

Table 5. Revision history

Date Revision Changes

Nov-1997 1 Initial release.

Oct-2000 2 Latest update

10-Mar-2008 3

Reformatted to current standards. General update of all equations,
and graphics.

21/22

AN533

Please Read Carefully:

Information in this document is provided solely in connection with ST products. STMicroelectronics NV and its subsidiaries (“ST”) reserve the
right to make changes, corrections, modifications or improvements, to this document, and the products and services described herein at any
time, without notice.

All ST products are sold pursuant to ST’s terms and conditions of sale.

Purchasers are solely responsible for the choice, selection and use of the ST products and services described herein, and ST assumes no
liability whatsoever relating to the choice, selection or use of the ST products and services described herein.

No license, express or implied, by estoppel or otherwise, to any intellectual property rights is granted under this document. If any part of this
document refers to any third party products or services it shall not be deemed a license grant by ST for the use of such third party products
or services, or any intellectual property contained therein or considered as a warranty covering the use in any manner whatsoever of such
third party products or services or any intellectual property contained therein.

UNLESS OTHERWISE SET FORTH IN ST’S TERMS AND CONDITIONS OF SALE ST DISCLAIMS ANY EXPRESS OR IMPLIED
WARRANTY WITH RESPECT TO THE USE AND/OR SALE OF ST PRODUCTS INCLUDING WITHOUT LIMITATION IMPLIED
WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE (AND THEIR EQUIVALENTS UNDER THE LAWS
OF ANY JURISDICTION), OR INFRINGEMENT OF ANY PATENT, COPYRIGHT OR OTHER INTELLECTUAL PROPERTY RIGHT.

UNLESS EXPRESSLY APPROVED IN WRITING BY AN AUTHORIZED ST REPRESENTATIVE, ST PRODUCTS ARE NOT
RECOMMENDED, AUTHORIZED OR WARRANTED FOR USE IN MILITARY, AIR CRAFT, SPACE, LIFE SAVING, OR LIFE SUSTAINING
APPLICATIONS, NOR IN PRODUCTS OR SYSTEMS WHERE FAILURE OR MALFUNCTION MAY RESULT IN PERSONAL INJURY,
DEATH, OR SEVERE PROPERTY OR ENVIRONMENTAL DAMAGE. ST PRODUCTS WHICH ARE NOT SPECIFIED AS "AUTOMOTIVE
GRADE" MAY ONLY BE USED IN AUTOMOTIVE APPLICATIONS AT USER’S OWN RISK.

Resale of ST products with provisions different from the statements and/or technical features set forth in this document shall immediately void
any warranty granted by ST for the ST product or service described herein and shall not create or extend in any manner whatsoever, any
liability of ST.

ST and the ST logo are trademarks or registered trademarks of ST in various countries.

Information in this document supersedes and replaces all information previously supplied.

The ST logo is a registered trademark of STMicroelectronics. All other names are the property of their respective owners.

© 2008 STMicroelectronics - All rights reserved

STMicroelectronics group of companies

Australia - Belgium - Brazil - Canada - China - Czech Republic - Finland - France - Germany - Hong Kong - India - Israel - Italy - Japan -

Malaysia - Malta - Morocco - Singapore - Spain - Sweden - Switzerland - United Kingdom - United States of America

www.st.com

22/22