ST AN2657 Application note

AN2657

Application note

An innovative verilog model for predicting

LDMOS DC, small and large signal behavior

Introduction

To reduce the design cycle time and cost for wireless applications it is useful to ha v e models that can help RF Engineers predict and simulate the behavior of RF power transistors. Recently, STMicroelectronics has been strongly focused on developing new models for RF LDMOS power transistors.

The model introduced here is simple in concept, and describes with good approximation DC, small signal S-parameter and large signal behavior, and could be a starting point for designers in dev eloping their ne w applications . This model has been implemen ted in Agilent Advanced Design System, in verilog Language, and includes the parasitic elements of the package, as well as a thermal node which takes self heating effects into account.

In this applicatio note we will briefly describe how to extract the model parameters for the PD54003L-E device, which is a 3 W - 7.2 V - 500 MHz LDMOS housed in a PowerFLAT plastic package (5 x 5 mm). As an internally unmatched device, the PD54003L-E can be used in various portable applications ov er HF, VHF and UHF frequency bands. At the end of this note we will validate this ne w model using ST's DB-54003L-175 demoboard, especially designed for 2-way portable radio applications using PD54003L- E over the 135-175 MHz frequency band.

Thanks to their cost effectiveness and high performance, LDMOS devices are widely used in radio frequency applications, ranging from digital communication infrastructures (cellular base stations) to low cost portable radios (private mobile radios) commonly known as walkie-talkies.

November 2007 Rev 1 1/18

www.st.com

Contents AN2657

Contents

1 Model description and parameter extraction . . . . . . . . . . . . . . . . . . . . . 4

2 Conclusions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

3 References . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

4 Revision history . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17

2/18

AN2657 List of figures

List of figures

Figure 1. Model schematic. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

Figure 2. R

Figure 3. Gate-drain charge variation vs. Vds . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10

Figure 4. Generic internal RF package structure . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11

Figure 5. PowerFLAT cross-section. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11

Figure 6. Simulated version of the PowerFLAT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

Figure 7. S-parameters of the simulated package. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

Figure 8. Overall model schematic . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

Figure 9. Measured C

Figure 10. Measured S-parameters vs. simulated parameters (Vds= 7.2 V; Idq= 100 mA) . . . . . . . . 14

Figure 11. Measured input and output DC curves vs. simulated curves . . . . . . . . . . . . . . . . . . . . . . . 14

Figure 12. DB-54003L-175 demoboard . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

Figure 13. Measured RF demonstration board performance vs simulated performance. . . . . . . . . . . 15

vs. Vds. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

jfet

, C

iss

oss

vs. simulated parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

rss

3/18

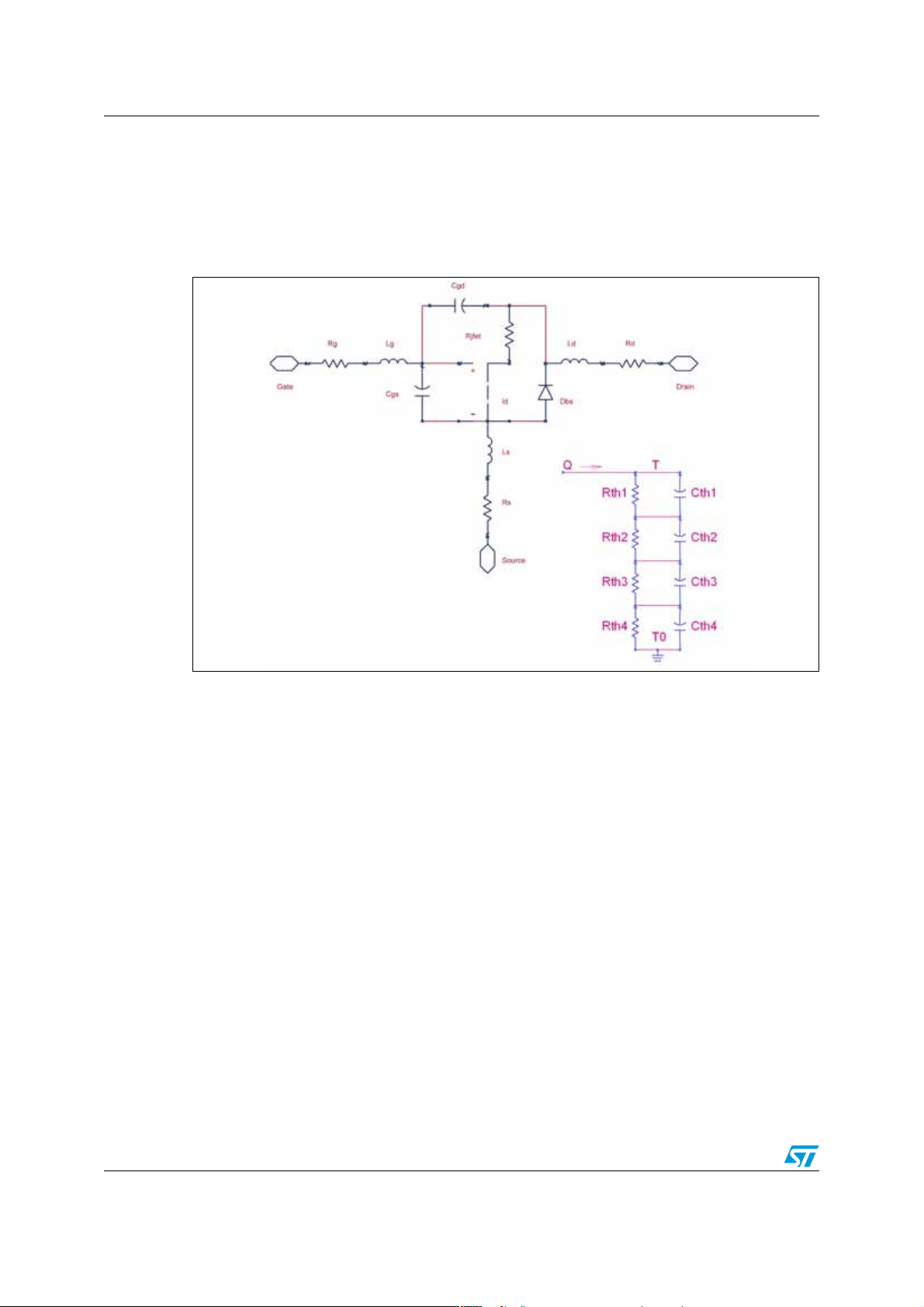
Model description and parameter extraction AN2657

1 Model description and parameter extraction

The model introduced in this application note is a behavioral model with the equations written in verilog language [1] [2].

Figure 1. Model schematic

By observing the equivalent model schematic of Figure 1, the following elements can be noted:

● Parasitic elements associated with the device

● Nonlinear current generator

● JFET resistance

● Substrate-body diode

Parasitic elements

To model the parasitic elements of the device, a resistor and an inductor are place d in series at each terminal. The model can change the resistance and inductance v alu es accord ing to the simulation temperature.

Parameter P in Equation 1 is the temperature dependence, where T coefficient, T is the temperature used in the simu lation and Tnom is the temper ature used to measure the parameter value.

Equation 1

PT() PT

()1TCTT

NOM

–()⋅+()⋅=

NOM

is its temperature

4/18

AN2657 Model description and parameter extraction

Nonlinear current generator

The nonlinear current generat or controlled by Vgs and Vds is the most important factor used to calculate the static and dynamic current of the device. Moreover, the static current is required to define the working region of the MOS.

Table 1. Parameters required for the extraction of the current generator equations

Name Description

VT0 Threshold voltage [V] ETA Drain induce barrier lowering (DIBL) [V-1]

-2

KP0 Transconduttance [A*V

THETA Mobility degradation [V

VGTHETA Mobility degradation exponent [-]

THETA2..9 From 2nd to 9th degradation polynomial factor [V

XN Slope subthreshold current [V

DEL Body effect linearization coefficient [-]

DELVG Body effect linearization coefficient independent of Vgs [V-1]

L0 Critical length [m]

L Channel length [m]

]

-VGTHETA

]

-2

]

-1

]

EPS Output conductance factor if L0>L [m]

KE Output conductance factor if L0<L [Vm]

DT_KP Mobility thermal coefficient [-]

-1

DT_VT Thermal coefficient of threshold voltage [°C

]

Table 1 reports all the parameters required to extract the equat ions of th e current ge nerat or.

To get the generator current equation, a set of equations must be defined. An important parameter to consider is the threshold voltage of the device shown in Equation 2.

Equation 2

THVT0

η VDSDVVT T T

–()⋅+⋅–=

NOM

Moreover, a new threshold voltage formula is necessary to describe the weak and strong inversion region in a single equation (Equation 3).

Equation 3

VR V

2XNU

⋅⋅–=

KT⋅

--------------=

To describe both reg io ns, a new gate voltage can be defined as in Equation 4.

Equation 4

⎧ ⎪

VTH2XNUTHe

⎨

⎪ ⎩

⋅⋅⋅+

VgsVR–

------------------------------------ -

2XNU

⋅⋅

5/18

Model description and parameter extraction AN2657

Equation 5

KP KP0

T ° K()

⎛⎞

--------------------------- -

⋅=

⎝⎠

NOM

DTKP

° K()

Another important parameter to define is the gain factor with zero bias . Referring to

Equation 5, 6 and 7, the gain factor degrades according to the V

voltage (mobility

degradation). Equation 8 and 9, which define the drain satu ration voltage, complete the set of equations needed to define the generator current (Equation 10 and 11).

Equation 6

()

gst

⎧ ⎪ ⎪

⎨

1TV

⎪ ⎪ ⎩

vgT

gst

+⋅+

∑

I2=

TIV

⋅

gst

0≤

gst

Equation 7

EFF

------------------- -=

()

gst

Equation 8

Equation 9

Equation 10

Equation 11

AL0

CKEL

δ∆∆VG Vgg⋅+= D

⎧

EFF

⎪

⎨ ⎪ ⎩

IDSS KP

2L2

–=

-- -

L02⋅=

⋅=

BA–()Vgg VTH–()C1δ–()⋅–⋅=

4C VggV

VDSAT

Vds V( gg VTH– 0.05 Vds 1 ∆+())⋅⋅–⋅⋅

IDSS 1 A

⎛⎞

⋅

⎝⎠

VDSAT Vgg VTH– 0.5 VDSAT 1 ∆+()⋅⋅–()⋅⋅=

EFF

δ∆∆VG Vgg⋅+=

–()1 δ+()0.5 A B–⋅()⋅⋅ ⋅ ⋅–=

----------------------------------------------------- -=

1 δ+()2BA–⋅()⋅

Vds VDSAT–

------------------------------------------ -

⋅+

BVDSATC+⋅

2D1

VDSAT<

VDSAT≥

The automatic ADS optimizer was used to extract the parameters for the current gener ator. The threshold voltage and the gain f a ctor ha v e been e xt racted from th e input char acteristics with Vds at a low voltage level. Concerning mobility degradation, the transconductance parameter was used varying Vds and with Vgs at a high voltage level. The sub-threshold voltage was extracted from the input characteristics with a gate voltage lev el below the threshold voltage level.

6/18

AN2657 Model description and parameter extraction

L is the physical channel length of the MOS, while L0 influences the output conductance which depends on KE and EPS. DEL and DELVG affect the VDSAT and are extracted from the output characteristics in the satura tion region. As mentioned pre viously, all the equations have been implemented in verilog language.

JFET resistance

The quasi-saturation region is modeled by a nonlinear JFET resistor. The mathematical empirical equation is defined in Equation 12, where pres depends on t he current and on the drop voltage across R

Equation 12

RjfVds Vgs,()gpres()hT()⋅⋅=

Figure 2. R

vs. Vds

jfet

Useful to delete any convergence problem, Figure 2 shows the resistor law for the variation of Vds (using the right hand function approach) (Equation 13). A similar graph and function can be obtained by v arying Vgs [3].

Equation 13

Vds VDI–

----------------------------

RjVds()RI0 SR FSI Log10110

⎛⎞

⎜⎟ ⎝⎠

FSI

FSF Log

⋅–⋅⋅+=

Vds VDF–

------------------------------

⎛⎞

110

⎜⎟ ⎝⎠

FSF

The function g(pres) was created to bind the Rj to the current Id. This is accomplished by introducing a new parameter link ed to the dissipated po we r on R

(Equation 14), where pres

is linked to the dissipated power on Rj through RPWR.

Equation 14

gpres()1 PCR1 PCR2 pres⋅+()pres⋅+=

h(T) (Equation 15), introduces the temperature dependence of R

, where TCR1 and TCR2

are temperature coefficients in the linear region. R

is extracted from the DC output characteristics in the linear region with high bias current.

7/18

Model description and parameter extraction AN2657

Equation 15

hT() 1TT

–()TCR1 T T

NOM

–()TCR2⋅+()⋅+=

NOM

Substrate-body diode

The body-substrate diode is emplo yed to describe the breakdo wn, the drain current leakage and the capacitance between the dr ain and source.

The thermal variations are shown by Equation 16.

Equation 16

CjT CJ 1 T+ CCJ T T VjT VJ 1 T+ CVJ T T

CjkparT CJPAR 1 T+ CCJPAT T T

BVT BV 1 TCBV T T

BVVGT BVVG 1 TCBVVG T T R

LEAKT

LEAK

1( TCR

To include the temperature in the saturation current refer to Equation 17.

Equation 17

XTI

---------------

NOM

----------

exp⋅⋅

dIs

⎛⎞

--------

⎝⎠

T200

qEG⋅

⎛⎞

-------------------

⎝⎠

T ° K()T200–()⋅+

IsT

⎧

⎛⎞

⎪

⎝⎠

⎪

⎨ ⎪ ⎪

Is200

⎩

–()⋅()⋅=

NOM

–()⋅()⋅=

NOM

–()⋅()⋅=

–()⋅+()⋅=

NOM

–()⋅+()⋅=

LEAK

⋅

–())⋅+⋅=

NOM

⎛⎞

---------------

⎝⎠

NOM

---–

NOM

T 200≤

T 200>

°C

The diode current is implemented in Equation 18, 19, 20, 21 and 22. The cha rge equation is given by Equation 23.

Equation 18

⎧

⎛⎞

IsT

⋅

⎪

⎝⎠

⎨ ⎪

Ir1 Ir2 Ir3++

⎩

⎛⎞

-----------------

⎝⎠

NVt⋅

1–exp

Equation 19

⎛⎞

Ir1 IsT

-----------------

⎝⎠

NVt⋅

1–exp⋅=

Equation 20

Ir2

--------------------=

LEAKT

Equation 21

Vd BVT BVVGT Vgs⋅++

Ir3 Vd()Ibv

⎛⎞

exp⋅⋅sgn=

------------------------------------------------------------------------–

⎝⎠

NBV Vt⋅

8/18

AN2657 Model description and parameter extraction

Equation 22

Ibv

⎧

⎪

⎨

------- -

⋅

⎪

⎩

0A>

0A≤

Equation 23

⎧⎫ ⎪⎪ ⎪⎪ ⎪⎪

Qd TT Id f1 1

⎪⎪ ⎪⎪ ⎪⎪ ⎨⎬ ⎪⎪ ⎪⎪ ⎪⎪ ⎪⎪ ⎪⎪ ⎪⎪

Qd TT Id f1 f2 Vd 0.5

⎩⎭

f2 1 FCP 1 MJ+()⋅–=

⎛⎞ ⎝⎠

CjT VjT⋅

-------------------------- -=

1MJ–

VjT

CjT

1MJ–()

⋅

MJ Vd

------------------------- -

⋅+⋅

VjT

CjlparT Vd⋅+⋅+⋅=

1Vd–

⎛⎞

---------------- -

⎝⎠

--------------------------------------------=

1FCP–()

VDFCP≤

FCP>

The remaining model parameters are the capacita n ces Cgs an d Cg d of th e MO SF ET. The gate-source capacitance is modeled with a constant capacitance, because it is related to a highly doped MOSFET (Equation 24).

Equation 24

Qgs CgsT Vgs⋅=

Moreover, the gate-drain capacitance can be considered as a classic MOSFET model capacitance, where the equation s of th e charged capacit ance (Eq uation 25 , 26, 27, 28) can be divided into four r egions (Figure 3). Even in this case, capacitance variation depe nds on temperature (Equation 29).

Equation 25

Cgx0

---------------------------------------------------- CgdovlT+= Vgx VFB–

⎛⎞

---------------------------- -–

⎝⎠

Vjx

⎛⎞

–

⎝⎠

VFB Vgx–

---------------------------- -+

Vjx

Mjx

1Mjx–

CgdovlT Vgd⋅+⋅=

Qgd

Cgx0 Vjx⋅

------------------------------ -

1Mjx–

Cgd

1Mjx–

VFB

⎛⎞

----------- -+

⎝⎠

Vjx

Equation 26

Cgx0 Vjx⋅

Qgd Cgx0 Vgd VFB–()

------------------------------ -

1Mjx–

⎛⎞

⎝⎠

VFB

----------- -+

Vjx

1Mjx–

1–

CgdovlT Vgd⋅+⋅+⋅=

Equation 27

Cgx0

---------------------------------------------------- CgdovlT+= Vgx VFB–

⎛⎞

---------------------------- -–

⎝⎠

Vjx

VFB Vgx–

⎛⎞

---------------------------- -+

⎝⎠

Vjx

Mjx

1Mjx–

1–

CgdovlT Vgd⋅+⋅+⋅=

Qgd Cgx0 VFB

Cgd

Cgx0 Vjx⋅

------------------------------ -

1Mjx–

Equation 28

Cgd Cgx0 CgdovlT+=

Qgd Cgx0 CgdovlT+()Vgd⋅=

9/18

Model description and parameter extraction AN2657

Equation 29

GgxT CGX0 1 CGXTC1 T T

VfbT VFB 1 VFBTC1X T T

CgdovlT CGDOVL 1 CGDOVLTC T T

–()CGXTC2 T T

NOM

–()⋅+()⋅=

NOM

–()⋅+()⋅=

–()

⋅+⋅+()⋅=

NOM

Figure 3. Gate-drain charge variation vs. Vds

To extract the capacitance variables, a classic configuration has been used to measure the C

, C

iss

oss

and C

rss

Thermal node

A "thermal node" has been introduced to consider the self-heating effect (Figure 1). The voltage between the external thermal circuit port and the source node is related to the

junction temperature rise. The current source of the circuit is equal to the dissipated power [4] [5]. In this first model implementation we have not considered the temperature dependent variables.

Package simulation

To include all the parasitic elements of the package in the model, several electromagnetic simulations were performed [6].

10/18

AN2657 Model description and parameter extraction

Figure 4. Generic internal RF package structure

Figure 5. PowerFLAT cross-section

The molding resin has a dielectric constant equal to 4 a nd a dielect ric loss tangent of 0.005. The leads of the package are made of copper, while the bonding wires are made of gold.

During the simulation, the device contact pads and the paddle are considered as a PEC (perfect electric conductive surface lossless). Instead, along the external sides of the air bo x containing the package, an electric and magnetic field total wave absorption condition was set to consider the radiation losses (Equation 30).

Equation 30

∇ E×()

tan

-----

∇

tan

∇

tan

×()×

tan

-----

∇

tan

∇

tan

⋅()×⋅+⋅–⋅=

tan

During the simulation lumped ports were used to excite the fields (Figure 6) [7]. The package simulation performed was in the frequency range from 1 MHz to 50 GHz.

11/18

Model description and parameter extraction AN2657

eq, G

Figure 6. Simulated version of the PowerFLAT

To minimize the simulation time and increase accur acy, the structure was split into two parts (drain and gate). In this way, the reciprocal coupling between the input and output parts are not considered. To take into account such effect, an extra capacitor (Cgd-package) has been used. To complete the package model an extra inductor (Lvia) associated with the source has been added. This inductor represents the effect created by the "via holes"[8] [9]. The S-parameters concerning the electromagnetic simulation of the gate section of the package are shown in Figure 7.

Figure 7. S-parameters of the simulated package

Input Ref lection Coeffic ient

S(1,1)

S(2,2)

freq (1.000MHz to 50.00GHz)

2 0

-2

-4

-6

-8

dB(S(2,1))

-10

-12

-14

-16

Forward T ransmission, dB

5 1015202530354045050

freq, GHz

200 150 100

-50

phase(S(2,1))

-100

-150

-200

Forward T ransmission, phase

5 1015202530354045050

Moreover, using the measured S-parameters of the packaged device, it was possible to extract the Cgd-package and the Lvia. Observing Figure 8, it is possible to see the circuit representing the union between the package model and the device model.

12/18

AN2657 Model description and parameter extraction

Figure 8. Overall model schematic

DC and RF small signal validation

Figure 9, 10, and 11 compare the measured DC and RF small signal parameters with the

simulated parameters (C curves). The simulations predict with good app ro ximat ion the abo v e mentioned p ara meters , including S21 and S22 which are the most difficult to predict.

iss

, C

oss

, C

, low signal S-parameters, and input and output DC

rss

Figure 9. Measured C

iss

, C

oss

, C

vs. simulated parameters

rss

13/18

Model description and parameter extraction AN2657

fficient

Figure 10. Measured S-parameters vs. simulated parameters (Vds= 7.2 V;

Idq= 100 mA)

S(1,1)

nput Reflection Coe

S(1,2)

S(3,4)

-0.04

-0.03

-0.05

Rev er se Tr ansmission

-0.02

-0.01

0.00

0.01

0.02

0.03

0.04

0.05

freq (1.000MHz t o 3.000GHz)

Forwar d Transmission

-60 -40 -20 0 20 40 60-80 80

S(2,1)

S(4,3)

freq ( 1. 0 00MHz t o 3.000GHz)

freq (1.000MHz to 3.00 0GHz)

utput ReflectionCoe

S(2,2)

freq (1.000MHz to 3.00 0GHz)

Figure 11. Measured input and output DC curves vs. simulated curves

14/18

AN2657 Model description and parameter extraction

Large signal validation

Using the ADS with harmonic balance engine simulator [10], the model has been simulated in conjunction with the DC network and the input and output matching network of ST's demonstration board DB-54003L-175 (Figure 12).

The DB-54003L-175 demonstration board was developed to demonstrate the best broadband performance of PD54003L-E.

Figure 12. DB-54003L-175 demoboard

In the harmonic balance simulations we used all the information relative to the board and the S-parameters of the lumped capacitors and inductors. Figure 13 compares the simulations and measurements of the demonstration boar d at 155 MHz, varying the power delive re d by the generator at the input port.

is the power available from the generator, Nd is the drain efficiency, IRL (input return

loss) is the ratio between the power reflected from the device and the power available from the generator , and G ain is the ratio be tween the p ower dissipated on the load an d the pow er available from the generator.

Figure 13. Measured RF demonstration board performance vs simulated

performance

15/18

Conclusions AN2657

2 Conclusions

Thanks to this new verilog model, customers will now be able to predict and simulate the behavior of STMicroelectronics' RF DMOS and LDMOS products, reducing design cycle time and time-to-market.

3 References

1. "Beha vioral Modeling with the verilog-a Language," Springer, Oct. 1997.

2. "Behavioral Modeling of Nonlinear RF and Microwave Devices," Artech House Publishers, Nov. 1999.

3. "Lumped Element Behavioural High Voltage MOS Model," Mixed Design of Integrated Circuits and System, 2006. MIXDES 2006. Proceedings of the International Conference, June 2006.

4. "Analysis and Simulation of Self-Heating Effects on RF L DMOS Devices ," Simulation of Semiconductor Processes and Devices , 2005. SISPAD 2005. International Conference on, Sept. 2005.

5. "New LDMOS Model Delivers Powerful Transistor Library - The CMC Model," www. highfrequencyelectronics.com, Oct. 2004.

6. "User's guide - high frequency structure simulator," Ansoft.

7. "Port tutorial series - high frequency structure simulator," Ansoft.

8. "RF package characterization and modeling," University/ Government/Industry Microelectronics Symposium, 1999. Proceedings of the Thi rteenth Biennial, June 1999.

9. "Electrical modeling of rfic packages up to 12 ghz," Electronic Components and Technology Conference, June 1999.

10. "Guide to Harmonic Balance Simulation in ADS," Agilent.

16/18

AN2657 Revision history

4 Revision history

Table 2. Document revision history

Date Revision Changes

27-Nov-2007 1 Initial release

17/18

AN2657

Please Read Carefully:

Information in this document is provided solely in connection with ST products. STMicroelectronics NV and its subsidiaries (“ST”) reserve the right to make changes, corrections, modifications or improvements, to this document, and the products and services described herein at any time, without notice.

All ST products are sold pursuant to ST’s terms and conditions of sale. Purchasers are solely res ponsibl e fo r the c hoic e, se lecti on an d use o f the S T prod ucts and s ervi ces d escr ibed he rein , and ST as sumes no

liability whatsoever relati ng to the choice, selection or use of the S T products and services described herein. No license, express or implied, by estoppel or otherwise, to any intellectual property rights is granted under this document. If any part of this

document refers to any third pa rty p ro duc ts or se rv ices it sh all n ot be deem ed a lice ns e gr ant by ST fo r t he use of su ch thi r d party products or services, or any intellectua l property c ontained the rein or consi dered as a warr anty coverin g the use in any manner whats oever of suc h third party products or servi ces or any intellectual property contained therein.

UNLESS OTHERWISE SET FORTH IN ST’S TERMS AND CONDITIONS OF SALE ST DISCLAIMS ANY EXPRESS OR IMPLIED WARRANTY WITH RESPECT TO THE USE AND/OR SALE OF ST PRODUCTS INCLUDING WITHOUT LIMITATION IMPLIED WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICUL AR PURPOS E (AND THEIR EQUIVALE NTS UNDER THE LAWS OF ANY JURISDICTION), OR INFRINGEMENT OF ANY PATENT, COPYRIGHT OR OTHER INTELLECTUAL PROPERTY RIGHT.

UNLESS EXPRESSLY APPROVED IN WRITING BY AN AUTHORIZED ST REPRESENTATIVE, ST PRODUCTS ARE NOT RECOMMENDED, AUTHORIZED OR WARRANTED FOR USE IN MILITARY, AIR CRAFT, SPACE, LIFE SAVING, OR LIFE SUSTAINING APPLICATIONS, NOR IN PRODUCTS OR SYSTEMS WHERE FAILURE OR MALFUNCTION MAY RESULT IN PERSONAL INJ URY, DEATH, OR SEVERE PROPERTY OR ENVIRONMENTAL DAMAGE. ST PRODUCTS WHICH ARE NOT SPECIFIED AS "AUTOMOTIVE GRADE" MAY ONLY BE USED IN AUTOMOTIVE APPLICATIONS AT USER’S OWN RISK.

Resale of ST products with provisions different from the statements and/or technical features set forth in this document shall immediately void any warranty granted by ST fo r the ST pro duct or serv ice describe d herein and shall not cr eate or exten d in any manne r whatsoever , any liability of ST.

ST and the ST logo are trademarks or registered trademarks of ST in various countries.

Information in this document su persedes and replaces all informatio n previously supplied.

The ST logo is a registered trademark of STMicroelectronics. All other names are the property of their respective owners.

STMicroelectronics group of compan ie s

Australia - Belgium - Brazil - Canada - China - Czech Republic - Finland - France - Germ any - Hong Kong - India - Israel - Italy - Japan -

Malaysia - Malta - Morocco - Singapore - Spain - Sweden - Switzerland - United Kingdom - United States of America

www.st.com

18/18

ST AN2657 Application note

Specifications and Main Features

Frequently Asked Questions

User Manual

1 Model description and parameter extraction

Figure 1. Model schematic

Table 1. Parameters required for the extraction of the current generator equations

Figure 3. Gate-drain charge variation vs. Vds

Figure 4. Generic internal RF package structure

Figure 5. PowerFLAT cross-section

Figure 6. Simulated version of the PowerFLAT

Figure 7. S-parameters of the simulated package

Figure 8. Overall model schematic

Figure 11. Measured input and output DC curves vs. simulated curves

Figure 12. DB-54003L-175 demoboard

2 Conclusions

3 References

4 Revision history

Table 2. Document revision history