ST AN2653 APPLICATION NOTE

AN2653

Application note

Operational amplifier stability compensation methods

for capacitive loading applied to TS507

Introduction

Who has never experienced oscillations issues when using an operational amplifier? Op­amps are often used in a simple voltage follow e r co nf igu r at ion . Howev er, this is not the b est
configuration in terms of capacitive loading and potential risk of oscillations.

Capacitive loads have a big impact on the stability of operational amplifier-based
applications. Several compensation methods exist to stabilize a standard op-amp. This
application note describes the most common ones, which can be used in most cases.

The general theory of each comp en sa tio n me th od is explained, and based on this, specific
data is provided fo r the TS507. The TS507 is a high precision rail-to-rail amplifier, with very
low input offset volta ge, and a 1.9 MHz gain bandwidth product, which is available in
SOT23-5 and SO-8 packages.

This document simplifies the task of designing an application that includes the TS507. It
spares you the time-consuming effort of trying numerous combinations on bench, and it is
also much more accurate than using Spice models which are not designed to study system
stability, even though they can give a general trend.

November 2007 Rev 1 1/22

www.st.com

Contents AN2653

Contents

1 Stability basics . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

1.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

1.2 Operational amplifier modeling for stability study . . . . . . . . . . . . . . . . . . . . 4

2 Stability in voltage follower configuration . . . . . . . . . . . . . . . . . . . . . . . 6

3 Out-of-the-loop compensation method . . . . . . . . . . . . . . . . . . . . . . . . . . 8

3.1 Theoretical overview . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

3.2 Application on the TS507 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

4 In-the-loop compensation method . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

4.1 Theoretical overview . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

4.2 Application on the TS507 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

5 Snubber network compensation method . . . . . . . . . . . . . . . . . . . . . . . 16

5.1 Theoretical overview . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

5.2 Application on the TS507 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17

6 Conclusion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20

7 Revision history . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

2/22

AN2653 Stability basics

1 Stability basics

1.1 Introduction

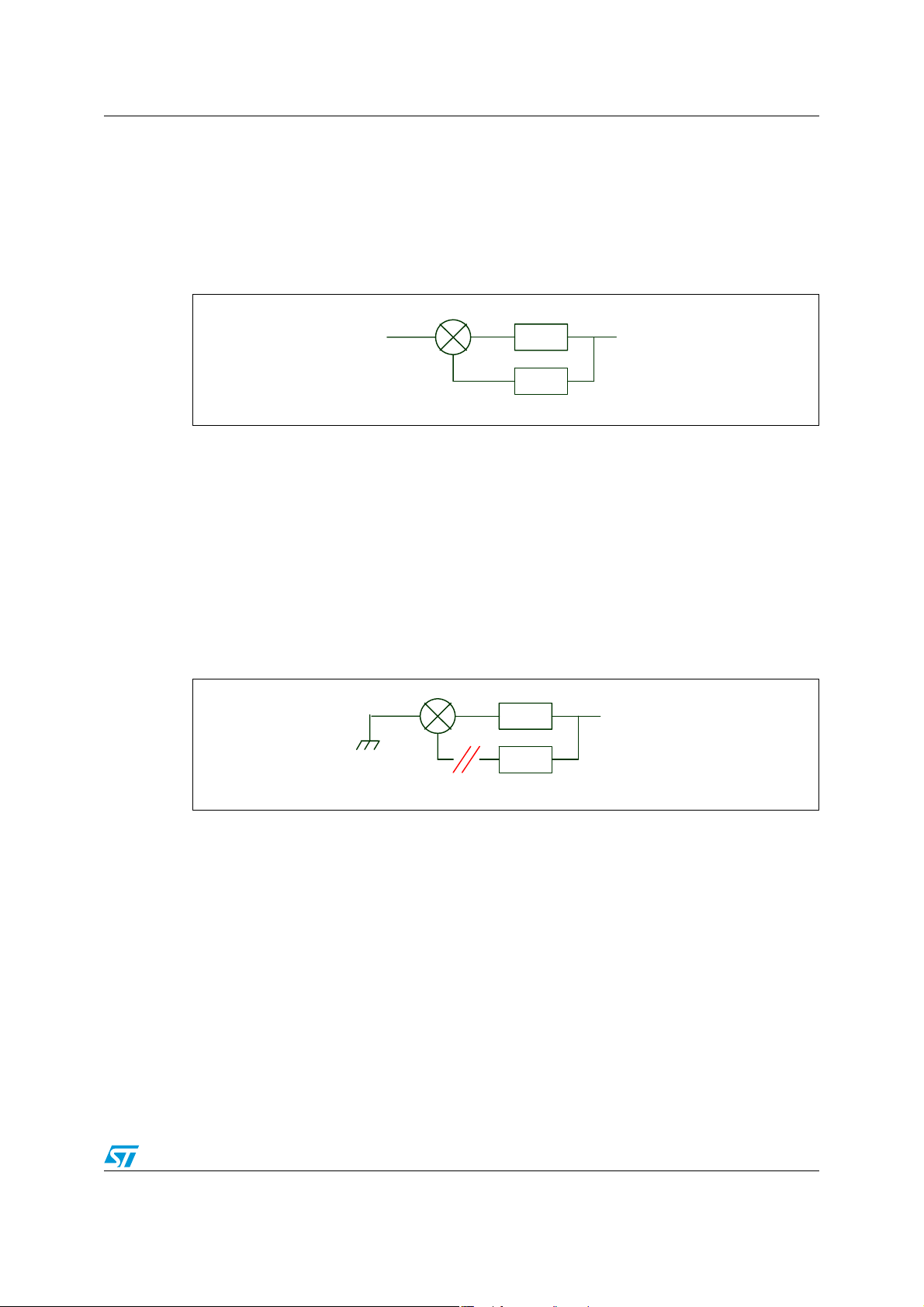
Consider a linear system modeled as shown in Figure 1.

Figure 1. Linear system with feedback model

Vin Vout

-

The model in Figure 1 gives the following equation:

out

---------------- -

1Aβ+

V

A

---------------- -

1Aβ+

is named closed loop gain.

From this equation, it is e vident that f or Aβ = -1, the circuit is unstable (V
V

).

in

Aβ is the loop gain.

A

ß

A

⋅=

V

in

is independent of

out

To evaluate it, the loop is opened and -V

is calculated as shown in Figure 2.

r/Vs

Figure 2. Loop gain calculation

A

Vout

-

Vs

Opening the loop leads to the following equation:

If a small signal V
amplitude above t hat of V
then the system oscillates and is unstable.

This leads to the definition of the gain mar gin, which is the opposite of the loop gain (in dB)
at the frequency for which its phase equals -180°. The bigger the gain margin, the more
stable the system. In addition, the phase margin is defined as the phase of the loop gain
plus 180° at the frequency for which its gain equals 0 dB. Therefore, from the value of Aβ it
is possible to determine the stability of the system.

is sourced into the system, and if Vr comes back in phase with it with an

s

(which means that Aβ is a real number g reater than or e qual to 1)

s

Vr

V

------– Aβ=
V

s

ß

r

3/22

Stability basics AN2653

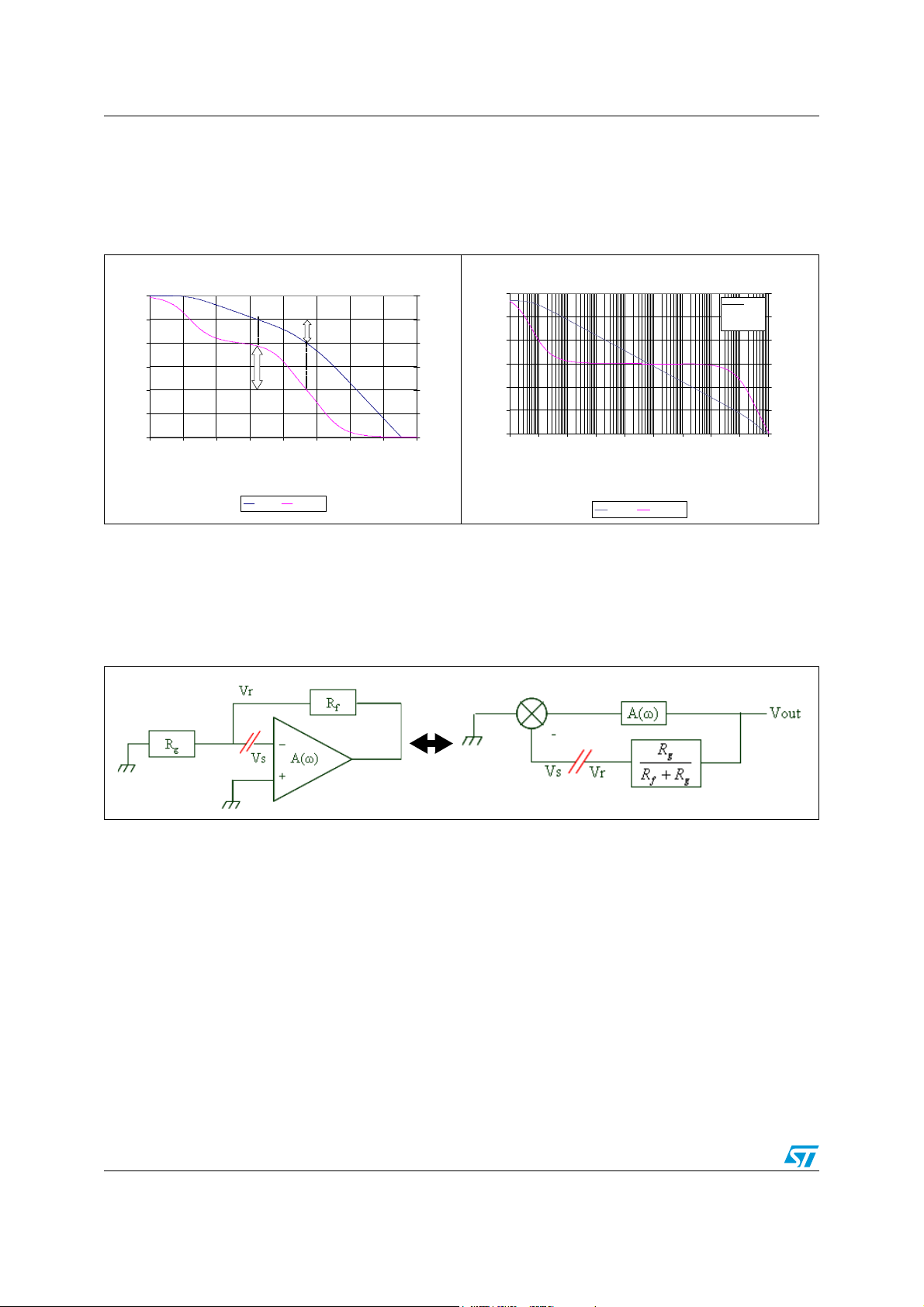
1.2 Operational amplifier modeling for stability study

Figure 3 illustrates the definition of phase and gain margins in a gain configuration.

Figure 3. Illustration of phase and gain

Figure 4. TS507 open loop gain

margins

Gain (dB)

-40

-80

-120

-160

-200

Loop Gain

40

0

Phase Margin

1.E+00

1.E+01

1.E+02

1.E+03

Frequency (Hz )

Gain Phase

1.E+04

Gain Marg in

1.E+05

1.E+06

0

-45

-90

-135

-180

-225

-270

1.E+07

1.E+08

160

130

100

70

Phase (°)

Gain (dB)

40

10

-20

1.E-02

1.E-01

To apply this stability approach to operational amplifier based applications, it is necessary to
know the gain of the operation al amplifier when no f e edbac k and n o loads are used. I t is the
open loop gain (A(ω)) of the amplifier (shown in Figure 4 for the TS507). From this
parameter, it is possible to model the amplifier and to study the stability of any gain
configuration.

Figure 5. Equivalence between schematics and b lock diagram

TS507 Open Loop Gain

1.E+00

1.E+01

1.E+02

Frequency (Hz )

Gain Phase

TS507 :
Vcc = 5 V
Vicm = 2.5 V
T = 25 °C

1.E+03

1.E+04

1.E+05

0

-30

-60

-90

Phase (°)

-120

-150

-180

1.E+06

1.E+07

The loop gain is:

V

r

------– A ω()
V

s

This equation shows the impact of the gain on the stability: if R
loop gain of the system increases and the loop gain decrease s. Because the phase remains
the same, the gain margin increases and stability is improved.

In addition, if you consider the case of a second order system such as the one shown in

Figure 6, a decrease of the loop gain allows to pass the 0 dB axis before the second pole

occurs. It minimize s the ef fect of the phase drop due to t his po le, and as a result, the phase
margin is higher. Therefore, a voltage follower configuration is the worst case for stability.

4/22

------------------ -

⋅=

RfRg+

R

g

increases, the closed

f/Rg

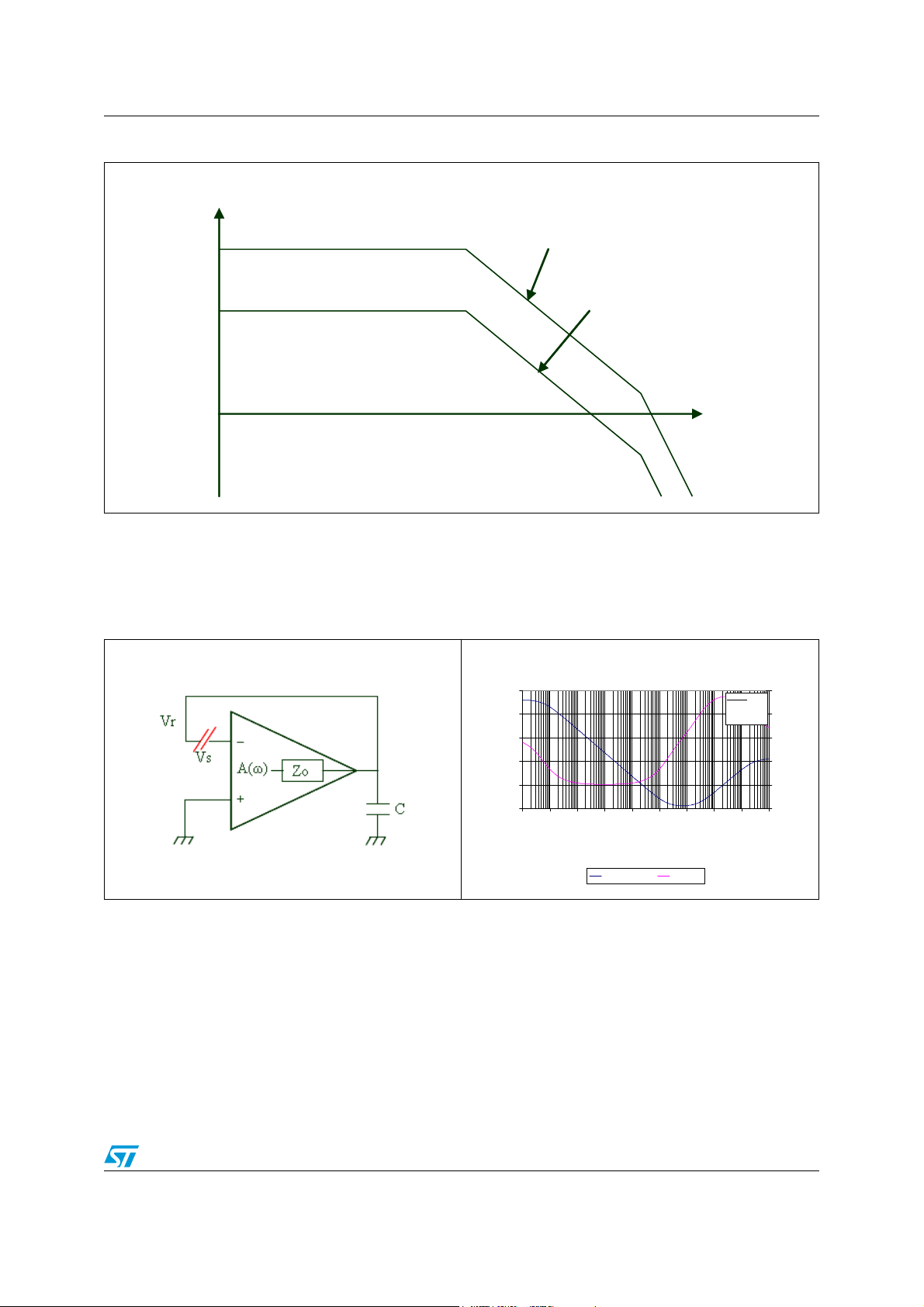
AN2653 Stability basics

Figure 6. Impact of closed loop gain on stability

G

loop gain

(dB)

0

Closed Loop Gain (Case1) < Closed Loop Gain (Case 2)

Another parameter that impacts stability is the amplifier output impedance Z
this parameter in the model of the amplifier leads to t he model shown in Figure 7.

Figure 7. Follower configuration model with

capacitive load for loop gain
calculation

Case 1

Case 2

f

. Including

o

Figure 8. TS507 output impedance Zo

TS507 Output Impedance (Zo)

1.E+05

1.E+04

1.E+03

1.E+02

Impedance ( Ohm)

1.E+01

1.E+00

TS507 :
Vcc = 5 V
Vicm = 2,5 V
T = 25 °C

1.E-02

1.E-01

1.E+00

1.E+01

1.E+02

1.E+03

1.E+04

Frequency (Hz )

Impedanc e Phase

1.E+05

90

45

0

-45

-90

-135

1.E+06

1.E+07

Zo is neither constant over frequency nor purely resistive. Figure 8 shows how the output
impedance varies with the frequ ency in t he case o f the TS507 . Thes e variations complicate
the stability study.

Finally, to study the stability of an op-amp based system, two parameters need to be taken
into account in order to better fit reality: th e amplifier open-loop g ain and the amplifier ou tput
impedance. Then, a calculation of the loop gain indicates how stable the system is.

Phase (°)

5/22

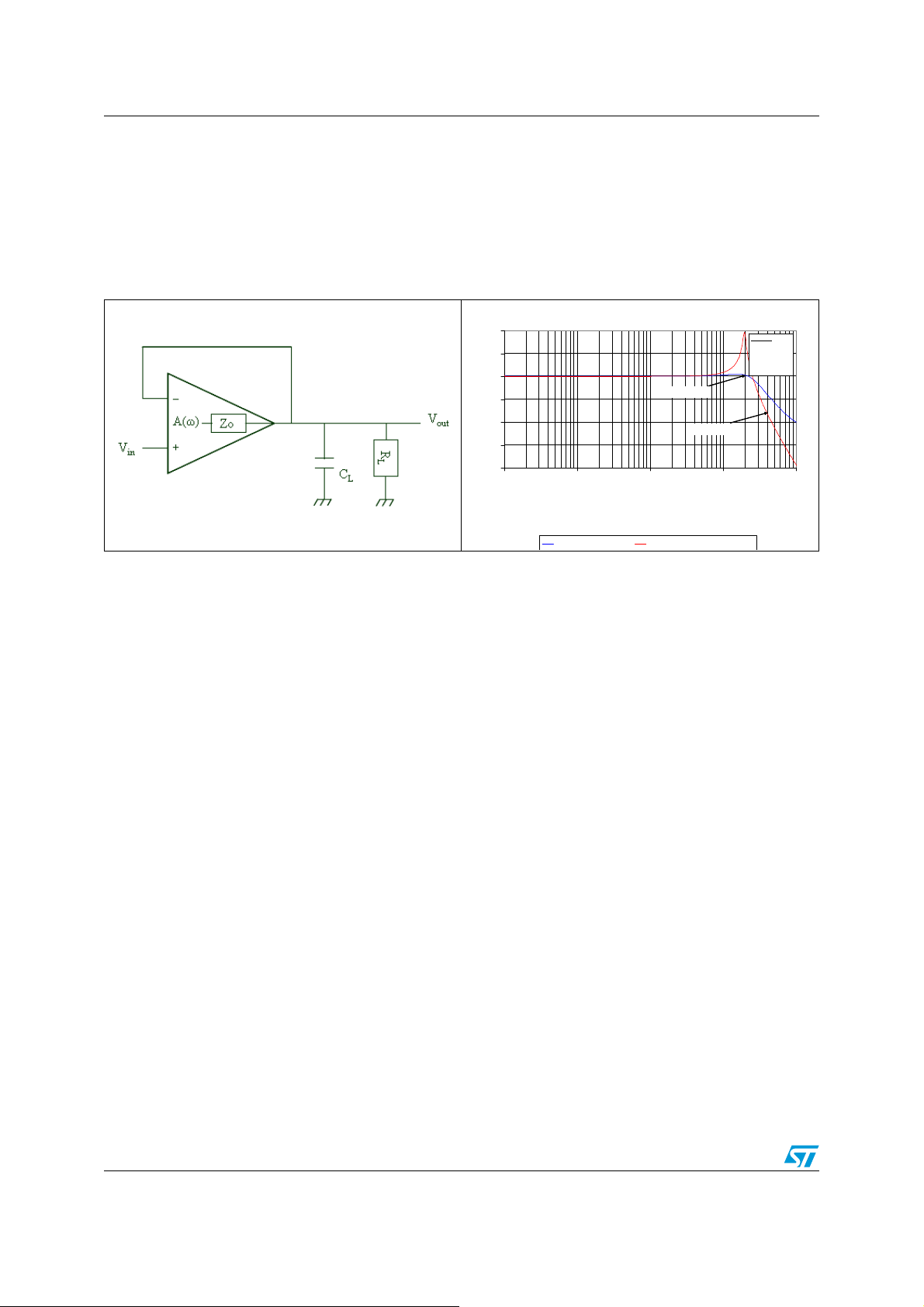
Stability in voltage follower configuration AN2653

2 Stability in voltage follower configuration

This section examines a v o ltage follower configuration because it is the worst case scenario
for stability (compared with a gain configuration).

Figure 9. Voltage follower configuration Figure 10. Closed loop gain measured for a

voltage follower configuration

Voltage Follower Configuration - Closed Loop Gain

20

10

0

-10

Gain (dB)

-20

-30

-40

Without CL

CL=550 pF

TS507 :
Vcc = 5 V
Vicm = 2,5 V
T = 25 °C
RL = 10 kΩ

1.E+03

1.E+04

Gain without CL Gain with CL = 550 pF

1.E+05

Frequency (Hz )

1.E+06

1.E+07

In voltage follower configuration, the loop gain is:

V

r

------–

V

s

----------------------------------------- -=

1

A ω()

Z

o

------ - jZoCLω++
R

L

The capacitive load adds a pole to the loop gain that impacts the stability of the system. The
higher the frequency of this pole, the greater the stability. In fact, if the pole frequency is
lower than or close to the unity gain freq uency, the pole can have a significant negative
impact on phase and gain margins. It means that the stability decreases when the
capacitive load increases.

Without C

, the system is stable. Howe ver, Figure 11 and Figure 12 show , f or the TS507, t he

L

oscillations due to instability with and without an AC input signal for a capacitive load of
550 pF. The oscillation frequency is in line with the peaking frequency observed in a closed
loop gain configuration (approximately 1.9 MHz according to Figure 10).

6/22

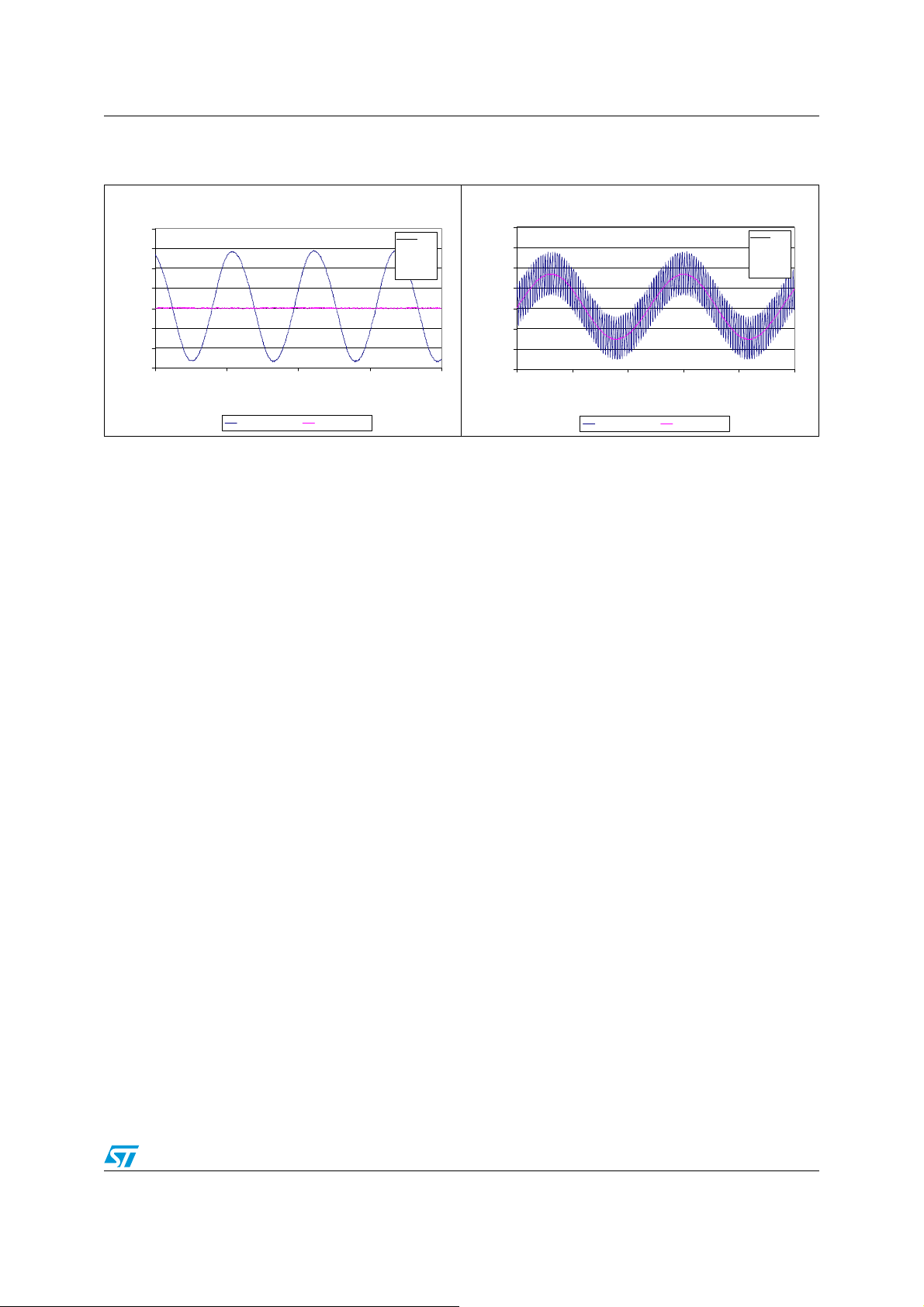
AN2653 Stability in voltage follower configuration

Figure 11. Input and output signals measured

with grounded input

Voltage Follower Configuration -

0.08

0.06

0.04

Output Signal with Input Grounded

TS507 :
Vcc = 5 V
Vicm = 2,5 V
T = 25 °C
RL = 10 kΩ
CL = 550pF

0.02

0

Amplitude (V)

-0.02

-0.04

-0.06

0.00 0.50 1.00 1.50 2.00

Time (μs)

Output Si gnal Input Signa l

To remove this instability and work with higher capacitive loads, many compensation
methods exist, and this applicatio n note examines some of them. By adding zeroes and
poles to the loop gain, stability can be improved.

However, compensation components have to be chos en carefully. A compensation scheme
can indeed improve stability, but can also lead the system to instability, depending on the
choice of component values . Similarly, a compensation configuration can work f or a specific
load, but modifying this load can affect stability.

Figure 12. Input and output signals measured

for an AC input signal

Voltage Follower -

0.2

0.15

0.1

0.05

0

Amplitude (V)

-0.05

-0.1

-0.15
0 100 200 300 400 500

Input and Output Signals

Time (μs)

Output Si gnal Input Signal

TS507 :
Vcc = 5 V
Vicm = 2,5 V
T = 25 °C
RL = 10 kΩ
CL = 550 pF

7/22

Out-of-the-loop compensation method AN2653

3 Out-of-the-loop compensation method

3.1 Theoretical overview

A simple compensation method, using only one extra component, consists in adding a
resistor in series between the output of the amplifier and its load (see Figure 13). It is often
referred to as the out-of-the-loop compensation method because the additional component
(R

) is added outside of the feedback loop. The resistor isolates the op-amp feedback

OL

network from the capacitive load.

Figure 13. Out-of-the-loop compensation

schematics

Figure 14. Out-of-the-loop equivalent

schematics for loop gain
calculation

From Figure 14, the loop gain with this compensation method is:

R

OL

⎛⎞

V

------–

V

r

s

A ω() 1

---------------------------------------------------------------------------------=

R

OLZo

1

----------------------- - jZoROL+()CLω++

---------- - jROLCLω++

⋅

⎝⎠

R

L

+

R

L

This compensation introduces a zero in the loop gain, just after the pole caused by the
capacitive load, at:

------------------------------------------------

2π R

1

||

⋅ RLC

OL

L

This pole is also unfortunately shifted to lower frequencies at:

----------------------------------------------------------------- -

2π Z

1

||

+()⋅ RLC

oROL

L

Howev er, due to the zero , the eff ect of the pole is minimiz ed and the stability is improv ed. To
obtain a good level of stability, R

must be chosen such that the frequency of the zero

OL

occurs at least one decade before unity-gain frequency. It then allows a significant shift of
the phase and therefore increase phase and gain margins.

The previous equation sh ows that if R
In that case, pole and zero occur at the same frequency. Howev er , the v alue of R
by the load impedance, R

and RL acting as a a divider bridge from the operational

OL

amplifier output. Therefore, in order to minimize the er ror on V
compared to R

(for example, a maximum of 1%, but this criterion depends on the required

L

>> Zo, then -Vr/Vs= A(ω), and the circuit is stable.

OL

, ROL must be very small

out

is limited

OL

accuracy).
Finally, this compensation method is effective, but the drawback is a limitation on the

accuracy of V

8/22

depending on the resistive load value.

out

AN2653 Out-of-the-loop compensation method

3.2 Application on the TS507

This compensation method brings very good results in terms of stability, improving strongly
the phase and gain margins. Table 1 and Table 2 show t he results obtained for differen t load
conditions, in the case of v oltage f ollo wer and gain configur ations . Note tha t R
1% of R

Table 1. Results of out-of-the-loop compensation f or diff er ent lo ad condi tions in the cas e of a

even though better results can be obtained with higher values of ROL.

L

voltage follower configuration for TS507

RL=1kΩ RL=10kΩ RL=100kΩ

C

L

R

(Ω)

OL

f

u/fz

(1)

Mg

(dB)

(2)

(2)

Mϕ

(degree)

ROL

(Ω)

f

u/fz

(1)

Mg

(dB)

(2)

(2)

Mϕ

(degree)

ROL
(kΩ)

f

u/fz

is limited to

OL

(2)

Mg

(dB)

(degree)

Mϕ

(2)

1nF

-4.1 -28.5 -5 -34.1 -5.1 -34.4

10 0.11 -2.5 -16.8 100 1.13 16 26.9 1 11.3 22.4 52.1

-22.2 -78.4 -22.9 -79.5 -23 -79.6

10 nF

10 1.13 -14 -32.4 100 11.3 23 37 1 112.3 22.6 52.3

-34.1 -84.4 -34.4 -84.6 -34.5 -84.6

100 nF

10 11.3 17.1 6.8 100 113.3 23.4 39.4 1 1126 22.6 52.3

1. fu/fz cells are shaded when the value is lower than 10, which is not the best case due to ROL limitation.

2. Negative values indicate instability.

Table 2. Results of out-of-the-loop compensation f or diff er ent lo ad condi tions in the cas e of a

gain configuration of either -10 or +11 (R

= 100 Ω and Rf = 1 kΩ) for TS507

g

RL=1kΩ RL=10kΩ RL=100kΩ

C

L

R

(Ω)

OL

f

u/fz

(1)

Mg

(dB)

(2)

(2)

Mϕ

(degree)

ROL

(Ω)

f

u/fz

(1)

Mg

(dB)

(2)

(2)

Mϕ

(degree)

ROL
(kΩ)

f

u/fz

Mg

(dB)

(2)

(2)

Mϕ

(degree)

17.6 84.7 16.8 85.1 16.7 85.2

1nF

10

0.11 19 84.7 100 1.13 36.9 85.1 1 11.3 43.4 85

-0.6 -16.1 -1.3 -25.7 -1.4 -25.9

10 nF

10

1.13 7.2 81.2 100 11.3 43.9 81.4 1 112.6 43.4 84.8

-13 -69.2 -13.3 -69.8 -13.3 -69.9

100 nF

10 11.3 38 41 100 113.3 44.3 80.6 1 1126 43.4 84.8

1. fu/fz cells are shaded when the value is lower than 10, which is not the best case due to ROL limitation.

2. Negative values indicate instability.

As expected, Table 1 and Table 2 show that the higher the value of ROL, the better the
compensation (because the best R

is always its maximum value RL/100).

OL

These results also show that, f or a v oltage f ollo wer configur ation, this compen sation method
does not work with low R

(and low CL), because the zero frequency cannot b e one decade

L

before the unity-gain fr equency of the o pen loop gain. I n the case of the TS507, it works well
only if the R

product is above 10-6.

OL.CL

9/22

Out-of-the-loop compensation method AN2653

Figure 15 and Figure 16 show the loop gain and closed loop gain respectively. These curves

are plotted for R

=10kΩ and CL =1nF.

L

Figure 15. Loop gain Figure 16. Measured closed loop gain

Voltage Follower Configuration - Loop Gain

Compensation with the Out-of-the-Loop Technique

150
130
110

90
70
50

Gain (dB)

30

10

-10

-30

1.E-02

1.E-01

1.E+00

1.E+01

1.E+02

1.E+03

Frequency (Hz)

Gain without Compensation Gain with ROL = 100 Ω
Phase without Compensation Phase with ROL = 100 Ω

1.E+04

Both figures further demonstrates the stability improvement.
Note that the fact that Z

presence of peaking in the loop gain curve, depending on the load capacitor. This is
because the denominator is equal to

with Z

= jL(ω)ω.

o

It leads to a resonance frequency of approximately

Voltage Follower Configuration - Closed Loop Gain
Compensation with the Out-of-the-Loop Technique

20

10

0

With Out-of-the-Loop Compensation Technique

-10

-20

-30

-40

1.E+03

Gain without Compensation Gain with ROL = 100 Ω

L ω()CLω

–++

1.E+04

Without Compensation

1.E+05

Frequency (Hz )

2

1

L

1.E+06

TS507 :
Vcc = 5 V
Vicm = 2,5 V
T = 25 °C
RL = 10 k Ω
CL = 1 n F

1.E+06

1

0

-30

-60

-90

-120

-150

Phase (°)

-180

-210

-240

-270

1.E+07

R

OL

---------- - j
R

L

Gain (dB)

L ω()

⎛⎞

----------- ROLCLω+

⎝⎠

R

L

TS507 :
Vcc = 5 V
Vicm = 2,5 V
T = 25 °C
RL = 10 k Ω
CL = 1 n F

1.E+05

is almost a self at high frequencies (for the TS507) explains the

o

------------------------------------ -

2π L ω()C

⋅

1.E+07

For the peaking frequency

f

the damping is given by the term:

When there is no compensation, it is only:

With the compensation, at the resonance frequency,

therefore the peaking is attenuated.
To help implement the compensation, the abacus given in Figure 17 to Figure 20 provide t he

value to choose fo r a given CL and phase/gain margins. These abacus are plotted in

R

OL

the case of a voltage follower configuration and a gain configuration of -10 or +11, with a
load resistor of 10 kΩ..

10/22

------------------------------------ -=

⋅

2π L ω()C

L ω()

----------- ROLCLω+
R

L

L ω()

-----------

R

L

L ω()

----------- ROLCLω«

R

L

1

L

AN2653 Out-of-the-loop compensation method

V

Figure 17. Gain margin abacus in the case of a

voltage follower configuration

Volta ge F ollo wer Co nfig ura tio n - Ga in Ma rgin Ab acu s

Applied for Out-of-the-Loop Compensation Method

100

STABLE

10

1

ROL (Ω)

1.E-09

UNSTABLE

1.E-08

CL (F)

1.E-07

0.01

0.1

1.E-11

1.E-10

TS507 :
Vcc = 5 V
Vicm = 2,5 V
T = 25 °C
RL = 10 kΩ

1.E-06

1.E-05

R1 (0 dB) R1 (4 dB) R1 (8 dB) R1 (12 dB) R1 (16 dB)

Figure 19. Gain margin abacus in the case of a

gain configuration of -10 or +11

Gain Configuration of either -10 or +11 - Gain Margin Abacus

Applied for Out-of-the-Loop Compensation Method

100

10

1

ROL (Ω)

0.1

STABLE

UNSTABLE

TS507 :
Vcc = 5 V
Vicm = 2,5 V
T = 25 °C
RL = 10 kΩ

Figure 18. Phase margin abacus in the case of

a voltage follower configuration

oltage Follower Configuration - Phase Margin Abacus

Applied for Out-of-the-Loop Compensation Method

100

10

1

ROL (Ω)

0.1

0.01

1.E-04

1.E-10

1.E-09

UNSTABLE

1.E-08

CL (F)

1.E-07

STABLE

1.E-06

TS507 :
Vcc = 5 V
Vicm = 2,5 V
T = 25 °C
RL = 10 k Ω

1.E-05

R1 (0 °) R1 (10 °) R1 (20 °) R1 (30 °) R1 (40 °)

Figure 20. Phase margin abacus in the case of

a gain configuration of -10 or +11

Gain Configuration of either -10 or +11 - Phase Margin Abacus

Applied for Out-of-the-Loop Compensation Method

100

10

ROL (Ω)

0.1

STABLE

1

UNSTABLE

TS507 :
Vcc = 5 V
Vicm = 2,5 V
T = 25 °C
RL = 10 k Ω

1.E-04

0.01

1.E-11

1.E-10

1.E-09

1.E-08

1.E-07

CL (F)

R1 (0 dB) R1 (10 dB) R1 (20 dB) R1 (30 dB)

0.01

1.E-06

1.E-05

1.E-04

1.E-10

1.E-09

1.E-08

CL (F)

1.E-07

1.E-06

1.E-05

1.E-04

R1 (0 °) R1 (20 °) R1 (40 °) R1 (60 °)

11/22

In-the-loop compensation method AN2653

4 In-the-loop compensation method

4.1 Theoretical overview

Figure 21 shows a commonly used compensation method, often called in-the-loop, because

the additional components (a resistor and a capacitor) used to improve the stability are
inserted in the feedback loop.

Figure 21. In-the-loop compensation

schematics

Figure 22. In-the-loop equivalent schematics

for loop gain calculation

The loop gain in this configuration, corresponding to Figure 22, is the following:

V

r

------–

----------------------------------------------------------------------------------------------------------------------------------------------------------------------------- -=

V

s

Z

+

oRIL

1

--------------------- jZoRIL+()CLω jRIL1
R

L

It adds a zero and splits the pole caused by the capacitive load into two poles in the loop
gain. This compensation method allows, by a good choice of compensation compo nents, to
compensate the original pole (caused by the capacitive load), and then to improve stability.

The main drawback of this circuit is the reduction of the output swing, because the isolation
resistor is in the signal path.

Note that, for the following cases, R

IL

configuration) even if better results can be obtained with higher R
But because the feedback loop is taken directly on V

create inaccuracy on V

as it does with the out-of-the-loop method.

out

4.2 Application on the TS507

In the case of the TS507, the first pole of the loop gain caused by the feedback occurs
around:

+

Z

oRIL

---------------------+

1

R

----------------------------------------------------------------------------------------------------

2π ZoRIL+()CLRIL1

L

+⋅

A ω() 1jR

ω+[]⋅

ILCIL

Z

o

⎛⎞

------ -+

⎝⎠

CILω ZoRILCILCLω

R

L

–++ +

2

is limited to 10% of RL (or Rf // RL in the case of a gain

values.

IL

Z

o

⎛⎞

------ -+

C

⎝⎠

IL

R

L

, the R

out

---------------------------------------------------------------------- -

≈

2π R

/ RL divider bridge does not

IL

1

||

()CILCL+()⋅

ILRL

12/22

AN2653 In-the-loop compensation method

The second one occurs at higher frequencies where its impact on stability is limited. The
goal of the first pole is to decrease the loop gain to get closer to 0 dB, just before the zero,
occurring at

1

------------------------------- -

2π RILC

⋅

IL

whose goal is to minimize the phase shift caused by the pole. The stability is increased as
the loop gain crosses the 0 dB axis with a limited phase shift. It minimizes the effect of the
second pole caused by the feedback, which is also pushed toward higher fr equencies.

Although this compensation method ma y se em diffic ult to se t up, it brings very good results,
as shown in Table 3 and Table 4, for the TS507 operational amplifier.

Table 3. Results of in-the-loop compensation for different load conditions in the case of a

voltage follower configuration for TS507

RL=1kΩ RL=10kΩ RL=100kΩ

C

L

(1)

R

IL

(Ω)

C

IL

(nF)

Mg

(dB)

(2)

(2)

Mϕ

(degree)

R

(kΩ)

(1)

IL

C

IL

(nF)

Mg

(dB)

(2)

(2)

Mϕ

(degree)

(1)

R

IL

(kΩ)

C

IL

(nF)

Mg

(dB)

(2)

(2)

Mϕ

(degree)

1nF

-4.1 -28.5 ° -5 -34.1 ° -5.1 -34.4 °

100 1 4.7 24.5 ° 1 0.4 15.2 53.9 ° 10 0.2 24.3 71.9 °

-22.2 -78.4 ° -22.9 -79.5 ° -23 -79.6 °

10 nF

100 2 6 21.9 ° 1 1.26 13.6 61.2 ° 5 1.26 13.3 79.2 °

-34.1 -84.4 ° -34.4 -84.6 ° -34.5 -84.6 °

100 nF

79.4 7.9 6.5 34.3 ° 0.5 6.3 6.5 66.9 ° 0.63 6.3 6.2 70.6 °

1. RIL cells are shaded when its value is clamped to RL/10.

2. Negative values indicate instability.

Table 4. Results of in-of-the-loop compensation for different load conditions in the case of a

gain configuration of either -10 or +11 (R

= 100 Ω and Rf = 1 kΩ) for TS507

g

RL=1kΩ RL=10kΩ RL=100kΩ

C

L

(1)

R

IL

(Ω)

C

IL

(pF)

Mg

(dB)

(2)

(2)

Mϕ

(degree)

(1)

R

IL

(Ω)

C

IL

(pF)

Mg

(dB)

(2)

(2)

Mϕ

(degree)

(1)

R

IL

(Ω)

C

IL

(pF)

Mg

(dB)

(2)

(2)

Mϕ

(degree)

17.6 84.7 ° 16.8 85.1 ° 16.7 85.2 °

1nF

100 126 39 89 ° 100 126 39 88.1 ° 100 126 39 88 °

-0.6 -16.1 ° -1.3 -25.7 ° -1.4 -25.9 °

10 nF

39.8 251 40.2 78.6 ° 31.6 316 40.3 84.9 ° 31.6 316 40.3 84.8 °

-13 -69.2 ° -13.3 -69.8 ° -13.3 -69.9 °

100 nF

10 631 44.5 66.2 ° 10 631 44.5 65.6 ° 10 631 44.5 65.6 °

1. RIL cells are shaded when its value is clamped to (RL// Rf)/10.

2. Negative values indicate instability.

In a gain configuration, when considering the loop gain, the output is loa ded by a resistive
load of R

// (Rf + Rg), where Rf and Rg are the resistors used for the gain. If Rf + Rg << RL,

L

the loop gain and therefore the stability parameters are the same whatever the value of R
This is visible in Table 4 where R

+ Rg = 1.1 kΩ with RL = 10 kΩ and RL = 100 kΩ..

f

13/22

.

L

In-the-loop compensation method AN2653

Table 5 and Table 6 help you to choose the best compensation components for different

ranges of load capacitors (and with R

= 10 kΩ) in voltage follower configuration and in a

L

gain configuration of either -10 or +11.
However, each case of load can be improve d by choosing specific components (seeTable 3

and Table 4).

Table 5. Best compensation components for different load capacitor ranges in voltage

Load capacitor range RIL (kΩ)C

10 pF to 100 pF 1 251 16.8 54.9 °

100 pF to 1 nF 1 251 15.8 42.1 °

1 nF to 10 nF 1 631 10.9 27 °

10 nF to 100 nF 1 2500 3.8 18.4 °

follower configuration for TS507 (with R

(pF)

IL

= 10 kΩ)

L

Minimum gain

margin (dB)

Minimum phase
margin (degree)

Table 6. Best compensation components for different load capacitor ranges in a gain

Load capacitor range RIL (Ω)C

configuration of either -10 or +11 (R

= 100 Ω and Rf = 1 kΩ) for TS507 (with RL = 10 kΩ)

g

IL

(pF)

Minimum gain

margin (dB)

Minimum phase
margin (degree)

10 pF to 100 pF 1000 40 39.2 88.8 °

100 pF to 1 nF 39.8 63 37.2 86.8 °

1 nF to 10 nF 63 251 36.5 70.7 °

10 nF to 100 nF 15.8 631 39.1 63.1 °

These tables are very valuable because almost all the follower and gain configuration
applications requiring compen sa tio n have capacitive loads in the range of 100 pF to 1 nF.
Thus, a simple combination of (R

, CIL), depending on RL can cover all these cases with a

IL

very good stability.
The loop gain shown in Figure 23, plotted for a voltage follower configur at ion with C

and R

= 10 kΩ, shows the instability without compensation. This can also be observed in

L

Figure 24 with the peaking present on closed loop. Both figures show the benefits of

compensation.

Figure 23. Loop gain Figure 24. Measured closed loop gain

Voltage Follower Configuration - Loop Gain

150
130
110

Gain (dB)

-10

-30

Gain without Compensation Gain with RIL = 1 kΩ and CIL = 470 pF
Phase without Compensation Phase with RIL = 1 kΩ and CIL = 470 pF

Compensation with the In-the-Loop Technique

90
70
50
30
10

1.E-02

1.E-01

1.E+00

1.E+01

1.E+02

Frequency (Hz )

TS507 :
Vcc = 5 V
Vicm = 2,5 V
T = 25 °C
RL = 10 kΩ
CL = 1 nF

1.E+03

1.E+04

1.E+05

0

-30

-60

-90

-120

-150

-180

-210

-240

-270

1.E+06

1.E+07

Phase (°)

Gain (dB)

Voltage Follower Configuration - Closed Loop Gain

20

10

-10

-20

-30

-40

Compensation with the In-the-Loop Technique

0

With In-the-Loop Compensation Technique

Without Co mpensation

1.E+03

Gain without CL Gain with RIL = 1 kΩ and CIL = 470 pF

1.E+04

1.E+05

Frequency (Hz )

1.E+06

TS507 :
Vcc = 5 V
Vicm = 2,5 V
T = 25 °C
RL = 10 kΩ
CL = 1 nF

= 1 nF

L

1.E+07

14/22

AN2653 In-the-loop compensation method

The zero and the pole introduced by the compensation are visible on the loop gain.
Introducing first the pole at

()CILCL+()⋅

1

||

ILRL

---------------------------------------------------------------------- - 125kHz=
2π R

leads to a gain fal l (with a slope of - 40 dB/de cade with com pensa tion) which allo ws t o come
closer to unity gain. The zero, occurring at

1

------------------------------- - 400kHz=
2π R

⋅

ILCIL

leads to an upturn of the phase so that when unity gain is reached, the effect of the first
poles are limited in terms of phase shifting. Thus, the circuit is stable with a good phase
margin. Furthermore, it leads to an excellent gain margin, because t he gain keeps falling
whereas the phase increases due to the zero, before finally decreasing to reach the -180°
point.

15/22

Snubber network compensation method AN2653

5 Snubber network compensation method

5.1 Theoretical overview

Figure 25 shows another way to stabilize an operational amplifier driving a capacitive load.

The snubber network compensation method consists in adding an RC series circuit
connected between the output and the ground. It is particularly recommended for lower
voltage applications, where the full output swing is needed.

Figure 25. Snubber network schematics Figure 26. Snubber network equivalent

schematics for loop gain
calculation

Introducing a second load resistor RSN in the circuit decreases the resistive load, and as a
result, pushes the pole caused by the capacitive load to higher frequencies, from

------------------------------------------------

2π Z

1

||

()C

⋅

o

R

L

L

to

-------------------------------------------------------------------- -

⋅

2π Z

1

|| ||

()C

oRL

R

SN

L

Therefore, stability is increased.
Furthermore, adding a serial capacitor C
On one hand, C

R

at the frequencies where RSN plays its role of stabilizer.

SN

On the other hand, R

must be big enough to consider that its impedance is small compared to

SN

being very small, CSN must be small enough because when the

SN

frequency increases, the system becomes limited by the current flowing through R
C

(depending on the output voltage swing).

SN

Therefore, in the following examples, C

with RSN removes the impact of R

SN

I

SN

V

------------------------------- -=

R

SN

j

--------------–

ω

C

SN

is limited to 100 nF in order to not limit the

SN

in DC.

and

SN

frequency range.

16/22

AN2653 Snubber network compensation method

In fact, this compensation introdu ces a zero and an additional pole into the loop gain:

V

r

------–

--------------------------------------------------------------------------------------------------------------------------------------------------------------------------- -=

Z

o

1

------ - jZoCLCSN+()ωj1
R

L

Because Z

V

s

is not a pure resistance over frequency, choosing the minimum RSN is not

o

always the best case.

5.2 Application on the TS507

For the TS507, according to the abacus in Figure 27 and Figure 28, this compensation
method in the case of a voltage follower configuration, works only if the capacitive load is
less than 1 nF, in order to obtain (at least) a phase margin of 20°.

Figure 27. Gain margin abacus in a voltage

1.E-06

1.E-07

1.E-08

1.E-09

CL (F)

1.E-10

1.E-11

1.E-12

1.E+00 1.E+01 1.E+02 1.E+03 1.E+04 1.E+05 1.E+06 1.E+07

follower configuration

Voltage Follower Configuration - Load Abacus

Gain Margin

UNSTABLE

STABLE

RL (Ω)

0 dB 10 dB 20 dB 30 dB

TS507 :
Vcc = 5 V
Vicm = 2,5 V
T = 25 °C

A ω() 1jR

Z

o

⎛⎞

------ -+

⎝⎠

R

L

ω+()⋅

SNCSN

RSNCSNω ZoRSNCLCSNω

–++ +

2

Figure 28. Phase margin abacus in a voltage

follower configuration

Voltage Follower Configuration - Load Abacus

1.E-06

1.E-07

1.E-08

1.E-09

CL (F)

1.E-10

1.E-11

1.E-12

1.E+00 1.E+01 1.E+02 1.E+03 1.E+04 1.E+05 1.E+06 1.E+07

0 ° C1 (10 °) 20 ° C1 (30 °) 40 °

Phase Margin

UNSTABLE

RL (Ω)

STABLE

TS507 :
Vcc = 5 V
Vicm = 2,5 V
T = 25 °C

Figure 29 and Figure 30 are the same abacus in case of a gain of either -10 or +11.

Figure 29. Gain margin abacus in a ga in

configuration of either -10 or +11

Gain Configuration of either -10 or +11 - Load Abacus

1.E-06

1.E-07

1.E-08

1.E-09

CL (F)

1.E-10

1.E-11

1.E-12

1.E+00 1.E+01 1.E+02 1.E+03 1.E+04 1.E+05 1.E+06 1.E+07

0 dB 10 dB 20 dB 30 dB 40 dB 50 dB

Gain Marg in

UNSTABLE

STABLE

RL (Ω)

TS507 :
Vcc = 5 V
Vicm = 2,5 V
T = 25 °C

You can use the abacus in Figure 27 to Figure 30 to determine the best RSN value.

Figure 30. Phase margin abacus in a gain

configuration of either -10 or +11

Gain Configuration of either -10 or +11 - Load Abacus

1.E-06

1.E-07

1.E-08

1.E-09

CL (F)

1.E-10

1.E-11

1.E-12

1.E+00 1.E+01 1.E+02 1.E+03 1.E+04 1.E+05 1.E+06 1.E+07

17/22

Phase Margin

UNSTABLE

STABLE

RL (Ω)

0 ° 20 ° 40 ° 60 ° 80 °

TS507 :
Vcc = 5 V
Vicm = 2,5 V
T = 25 °C

Snubber network compensation method AN2653

Table 7 to Table 10 give the results of compensation in a follower configuration and several

gain configurations for different load conditions.

T ab le 7. Results of snubber network compensation fo r diff erent loa d conditions in the cas e of

a voltage follower configuration for TS507

RL=1kΩ RL=10kΩ RL=100kΩ

C

L

R

(Ω)

SN

C

SN

(nF)

Mg

(dB)

(1)

(1)

Mϕ

(degree)

RSN

(Ω)

C

SN

(nF)

Mg

(dB)

(1)

(1)

Mϕ

(degree)

RSN

(Ω)

C

SN

(nF)

Mg

(dB)

(1)

(1)

Mϕ

(degree)

1nF

-4.1 -28.5 ° -5 -34.1 ° -5.1 -34.4 °

34.4 100 7.3 16.9 ° 31.6 100 7.7 16.7 ° 31.6 100 7.7 16.8 °

-22.2 -78.4 ° -22.9 -79.5 ° -23 -79.6 °

10 nF

13.5 100 -7.5 -18.3 ° 13.5 100 -7.6 -18.5 ° 13.5 100 -7.7 -18.5 °

1. Negative values indicate instability.

T ab le 8. Results of snubber network compensation fo r diff erent loa d conditions in the cas e of

a gain configuration of either -1 or +2 (R

= Rg = 1 kΩ) for TS507

f

RL=1kΩ RL=10kΩ RL=100kΩ

C

L

R

(Ω)

SN

C

SN

(nF)

Mg

(dB)

(1)

(1)

Mϕ

(degree)

RSN

(Ω)

C

SN

(nF)

Mg

(dB)

(1)

(1)

Mϕ

(degree)

RSN

(Ω)

C

SN

(nF)

Mg

(dB)

(1)

(1)

Mϕ

(degree)

2.4 28.7 ° 1.5 19.4 ° 1.4 19.6 °

1nF

58.9 100 11 37.6 ° 56.2 100 10.9 37.6 ° 58.9 100 10.6 37.6 °

-15.7 -70.9 ° -16.5 -72.4 ° -16.6 -72.6 °

10 nF

13.5 100 -1.5 -4 ° 13.5 100 -1.6 -4.1 ° 13.5 100 -1.6 -4.1 °

1. Negative values indicate instability.

T ab le 9. Results of snubber network compensation fo r diff erent loa d conditions in the cas e of

a gain configuration of either -10 or +11 (R

= 100 Ω and Rf = 1 kΩ) for TS507

g

RL=1kΩ RL=10kΩ RL=100kΩ

C

L

R

(Ω)

SN

C

SN

(nF)

Mg

(dB)

(1)

(1)

Mϕ

(degree)

RSN

(Ω)

C

SN

(nF)

Mg

(dB)

(1)

(1)

Mϕ

(degree)

RSN

(Ω)

C

SN

(nF)

Mg

(dB)

(1)

(1)

Mϕ

(degree)

1nF

17.6 84.7 ° 16.8 85.1 ° 16.7 85.2 °

171.1 100 21.6 81.8 ° 149.1 100 21.6 81.8 ° 146.8 100 21.6 81.8 °

-0.6 -16.1 ° -1.3 -25.7 ° -1.4 -25.9 °

10 nF

26.1 100 11.3 60.6 ° 25.7 100 11.3 60.7 ° 25.5 100 11.3 60.6 °

-13 -69.2 ° -13.3 -69.8 ° -13.3 -69.9 °

100 nF

17.1 100 -5.2 -33.3 ° 15.3 100 -5.4 -31.7 ° 15.3 100 -5.4 -31.7 °

1. Negative values indicate instability.

18/22

AN2653 Snubber network compensation method

T ab le 10. Results of snubber network compensation f or diff erent loa d conditions in the cas e of

a gain configuration of either -30 or +31 (R

= 100 Ω and Rf = 3 kΩ) for TS507

g

RL=1kΩ RL=10kΩ RL=100kΩ

C

L

R

(Ω)

SN

C

SN

(nF)

Mg

(dB)

(1)

(1)

Mϕ

(degree)

RSN

(Ω)

C

SN

(nF)

Mg

(dB)

(1)

(1)

Mϕ

(degree)

RSN

(Ω)

C

SN

(nF)

Mg

(dB)

(1)

(1)

Mϕ

(degree)

26 88.2 ° 25.2 88.4 ° 25.1 88.4 °

1nF

198 100 29.8 87.3 ° 168.5 100 29.8 87.3 ° 166 100 29.8 87.3 °

7.9 87.9 ° 7.2 88 ° 7.1 88.1 °

10 nF

30.7 100 19.6 82.7 ° 30 100 19.2 82.7 ° 30 100 19.1 82.8 °

-4.2 -44.7 ° -4.5 -45.8 ° -4.5 -45.9 °

100 nF

16.6 100 3.4 63.8 ° 16.5 100 3.3 64 ° 16.5 100 3.3 64.1 °

1. Negative values indicate instability.

The results are almost the same whether RL = 1 kΩ, 10 kΩ or 100 kΩ because in all cases, at
the frequency range that has a significant impact on stability, the resistive load on the
amplifier is R

// RL ≅ RSN.

SN

From Table 7, you can see that, in the case of a voltage follower configuration, this
compensation method doesn’t work for capacitive loads higher than 1 nF because C
limited to 100 nF. Figure 27 and Figure 28 show that lower R
results. Howe v er , in this case , these abacus are not v alid because the C
negligible compared with R

For R

= 10 kΩ and CL = 1 nF, the snubber network compensation method gives the loop

L

at the frequency range where RSN plays its role of stabilizer.

SN

values would give better

SN

impedance is not

SN

SN

is

gain and closed loop gain shown in Figure 31 and Figure 32 respectively.

Figure 31. Loop gain Figure 32. Measured closed loop gain

Voltage Follower Configuration - Loop Gain

Compensation with the Snubber Network Technique

150
130
110

90
70
50

Gain (dB )

30
10

-10

-30

1.E-02

1.E-01

1.E+00

1.E+01

1.E+02

1.E+03

Frequency (Hz)

Gain without Compensation Gain with RSN = 30 Ω and CSN = 100 nF
Phase without Compensation Phase with RSN = 30 Ω and CSN = 100 nF

TS507 :
Vcc = 5 V
Vicm = 2,5 V
T = 25 °C
RL = 10 kΩ
CL = 1 nF

1.E+04

1.E+05

0

-30

-60

-90

-120

-150

-180

-210

-240

-270

1.E+06

1.E+07

This compensation has the main advantage of neither reducing the output swing nor the
gain accuracy, unlike the two other compensation methods. Nevertheless, for the TS507,
this method is limited to capacitive loads lower than 1 nF in a voltage follow er config uration,
and the stability improvement provided by the compensation is not as good as with the two
other methods.

Voltage Follower Configuration - Closed Loop Gain

Compensation with the Snubber Network Technique

20

10

0

With Snubber Network Compensation Technique

-10

Phase (°)

Gain (dB)

-20

-30

-40

1.E+03

Gain without Compensation Gain with RSN = 30 Ω and CSN = 1 00 nF

1.E+04

Without Compensation

1.E+05

Frequency (Hz )

1.E+06

TS507 :
Vcc = 5 V
Vicm = 2,5 V
T = 25 °C
RL = 10 k Ω
CL = 1 n F

19/22

1.E+07

Conclusion AN2653

6 Conclusion

Based on the results of the three compensation methods described in this application note,
it can be stated that the best compensation solu tion f or the TS507 is th e in-the-loop met hod.
This is the most complex solution to understand, but a pick-up table is provided in order to
choose the most appropriate components for your application. The main drawback of this
compensation method is a limited output swing.

The out-of-the-loop compensation method is easy to implement because it requires only
one extra component . The way it works is also easy to understand. However, its main
limitation is an inaccuracy on the output volt age because the load is pa rt of a divider bridge.
An abacus is provided to choose the component you need for your application.

Finally, the snubber method is easy to understand and use. It does not have the drawbacks
of the first two solutions. But because the loop gain cannot be considered as a pure third­order system (because of the ope n loop gain of the amplifier and the variations of the output
impedance which is not purely resistive and constant over frequency), it does not lead to
great improvements, and it is limited to load capacitors lower than 1 nF in the case of the
TS507. An abacus is also provided for this compensation method. Another dr a wba c k of t his
solution is that it potentially limits the frequency range of the application for large output
signals due to a strong current flowing through the compensation elements. This
compensation method is not really useful for the TS507.

In conclusion, for the TS507, whenever possible, we recommend to use the in-the -loop
compensation method.

Note, that this document provides typical values for the TS507 at ambient temperature.
Therefore, your chosen solution must in any case be checked on bench.

20/22

AN2653 Revision history

7 Revision history

Table 11. Document revision history

Date Revision Changes

7-Nov-2007 1 Initial release.

21/22

AN2653

Please Read Carefully:

Information in this document is provided solely in connection with ST products. STMicroelectronics NV and its subsidiaries (“ST”) reserve the
right to make changes, corrections, modifications or improvements, to this document, and the products and services described herein at any
time, without notice.

All ST products are sold pursuant to ST’s terms and conditions of sale.
Purchasers are solely res ponsibl e fo r the c hoic e, se lecti on an d use o f the S T prod ucts and s ervi ces d escr ibed he rein , and ST as sumes no

liability whatsoever relati ng to the choice, selection or use of the ST products and services described herein.
No license, express or implied, by estoppel or otherwise, to any intellectual property rights is granted under this document. If any part of this

document refers to any third pa rty p ro duc ts or se rv ices it sh all n ot be deem ed a lice ns e gr ant by ST fo r t he use of su ch thi r d party products
or services, or any intellectua l property c ontained the rein or consi dered as a warr anty coverin g the use in any manner whats oever of suc h
third party products or servi ces or any intellectual propert y contained therein.

UNLESS OTHERWISE SET FORTH IN ST’S TERMS AND CONDITIONS OF SALE ST DISCLAIMS ANY EXPRESS OR IMPLIED
WARRANTY WITH RESPECT TO THE USE AND/OR SALE OF ST PRODUCTS INCLUDING WITHOUT LIMITATION IMPLIED
WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICUL AR PURPOS E (AND THEIR EQUIVALE NTS UNDER THE LAWS
OF ANY JURISDICTION), OR INFRINGEMENT OF ANY PATENT, COPYRIGHT OR OTHER INTELLECTUAL PROPERTY RIGHT.

UNLESS EXPRESSLY APPROVED IN WRITING BY AN AUTHORIZED ST REPRESENTATIVE, ST PRODUCTS ARE NOT
RECOMMENDED, AUTHORIZED OR WARRANTED FOR USE IN MILITARY, AIR CRAFT, SPACE, LIFE SAVING, OR LIFE SUSTAINING
APPLICATIONS, NOR IN PRODUCTS OR SYSTEMS WHERE FAILURE OR MALFUNCTION MAY RESULT IN PERSONAL INJ URY,
DEATH, OR SEVERE PROPERTY OR ENVIRONMENTAL DAMAGE. ST PRODUCTS WHICH ARE NOT SPECIFIED AS "AUTOMOTIVE
GRADE" MAY ONLY BE USED IN AUTOMOTIVE APPLICATIONS AT USER’S OWN RISK.

Resale of ST products with provisions different from the statements and/or technical features set forth in this document shall immediately void
any warranty granted by ST fo r the ST pro duct or serv ice describe d herein and shall not cr eate or exten d in any manne r whatsoever , any
liability of ST.

ST and the ST logo are trademarks or registered trademarks of ST in various countries.

Information in this document su persedes and replaces all information previously supplied.

The ST logo is a registered trademark of STMicroelectronics. All other names are the property of their respective owners.

© 2007 STMicroelectronics - All rights reserved

STMicroelectronics group of compan ie s

Australia - Belgium - Brazil - Canada - China - Czech Republic - Finland - France - Germany - Hong Kong - India - Israel - Italy - Japan -

Malaysia - Malta - Morocco - Singapore - Spain - Sweden - Switzerland - United Kingdom - United States of America

www.st.com

22/22