ST AN2644 Application note

AN2644

Application note

An introduction to LLC resonant

half-bridge converter

Introduction

Although in existence for many years, only recently has the LLC resonant converter, in particular in its half-bridge implementation, gained in the popularity it certainly deserves. In many applications, such as flat panel TVs, 85+ ATX PCs or small form factor PCs, where the requirements on efficiency and power density of their SMPS are getting tougher and tougher, the LLC resonant half-bridge with its many benefits and very few drawbacks is an excellent solution. One of the major difficulties that engineers are facing with this topology is the lack of information concerning the way it operates. The purpose of this application note is to provide insight into the topology and help familiarize the reader with it, therefore, the approach is essentially descriptive.

Figure 1. LLC resonant topology schematics and waveforms

September 2008 Rev 2 1/64

www.st.com

Contents AN2644

Contents

1 Classification of resonant converters . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

2 The LLC resonant half-bridge converter . . . . . . . . . . . . . . . . . . . . . . . . . 7

2.1 General overview . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

2.2 The switching mechanism . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

2.3 Fundamental operating modes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20

2.3.1 Operation at resonance (f = fR1) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

Remarks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .23

2.3.2 Operation above resonance (f > fR1) . . . . . . . . . . . . . . . . . . . . . . . . . . . 24

CCMA operation at heavy load. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .25

Remarks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .26

DCMA at medium load . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .28

Remarks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .28

DCMAB at light load . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .29

Remarks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .29

2.3.3 Operation below resonance (fR2 < f < fR1, R>R

DCMAB at medium-light load . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .30

DCMB at heavy load. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .30

Remarks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .33

2.3.4 Capacitive-mode operation below resonance (fR2 < f < fR1, R<R

Remarks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .36

) . . . . . . . . . . . . . . . . 30

crit

) . . . 34

crit

2.4 No-load operation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37

2.5 Overload and short circuit operation . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37

2.6 Converter's startup . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39

2.7 Analysis of power losses . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41

2.8 Small-signal behavior . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42

2.8.1 Operation above resonance (f > fR1) . . . . . . . . . . . . . . . . . . . . . . . . . . . 43

2.8.2 Operation below resonance (f

2.8.3 Operation at resonance (f = f

< f < fR1, R>R

R2

) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44

R1

) . . . . . . . . . . . . . . . . 44

crit

3 Conclusion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46

4 References . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47

Appendix A Power MOSFET driving energy in ZVS operation . . . . . . . . . . . . . . 48

2/64

AN2644 Contents

Appendix B Resonant transitions of half-bridge midpoint . . . . . . . . . . . . . . . . . 50

Appendix C Power MOSFET effective C

and half-bridge midpoint's transition

oss

times . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54

Appendix D Power MOSFETs switching losses at turn-off. . . . . . . . . . . . . . . . . 59

Appendix E Input current in LLC resonant half-bridge with split resonant

capacitors . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61

Revision history . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63

3/64

List of figures AN2644

List of figures

Figure 1. LLC resonant topology schematics and waveforms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1

Figure 2. General block diagram of a resonant inverter, the core of resonant converters. . . . . . . . . . 5

Figure 3. LLC resonant half-bridge schematic . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

Figure 4. LLC resonant half-bridge with split resonant capacitor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

Figure 5. Equivalent schematic of a real transformer (left, tapped secondary; right, single

secondary) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

Figure 6. Example of high-leakage magnetic structures (cross-section) . . . . . . . . . . . . . . . . . . . . . . . 9

Figure 7. Equivalent schematic of a transformer including parasitic capacitance . . . . . . . . . . . . . . . 12

Figure 8. Power MOSFET totem-pole network driving a resonant tank circuit in a half-bridge

converter . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

Figure 9. Detail of Q1 ON-OFF and Q2 OFF-ON transitions with soft-switching for Q2 . . . . . . . . . . 14

Figure 10. Q2 gate voltage at turn-on: with soft-switching . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14

Figure 11. Q2 gate voltage at turn-on: with hard-switching (no ZVS) . . . . . . . . . . . . . . . . . . . . . . . . . 14

Figure 12. Q1 ON-OFF and Q2 OFF-ON transitions with hard switching for Q2 and recovery for

DQ1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

Figure 13. Bridge leg transitions in the neighborhood of inductive-capacitive regions boundary . . . . 17

Figure 14. Bridge leg transitions under no-load conditions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

Figure 15. Reference LLC converter for the analysis of the fundamental operating modes . . . . . . . . 21

Figure 16. Operation at resonance (f = f Figure 17. Operation above resonance (f > f Figure 18. Operation above resonance (f > f

load . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27

Figure 19. Operation above resonance (f > f

load . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30

Figure 20. Operation below resonance (f

operation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31

Figure 21. Operation below resonance (f Figure 22. Capacitive mode operation below resonance (f

Figure 23. No-load operation (cutoff): main waveforms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36

Figure 24. Circuit's equivalent schematic under: no-load conditions . . . . . . . . . . . . . . . . . . . . . . . . . . 38

Figure 25. Circuit's equivalent schematic under: short-circuit conditions. . . . . . . . . . . . . . . . . . . . . . . 38

Figure 26. Converter's startup: main waveforms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40

Figure 27. High-side driving with bootstrap approach and bootstrap capacitor charge path. . . . . . . . 41

Figure 28. Frequency compensation with an isolated type 3 amplifier (3 poles + 2 zeros) . . . . . . . . 45

Figure 29. Comparison of gate-charge characteristics with and without ZVS . . . . . . . . . . . . . . . . . . . 48

Figure 30. Equivalent circuit to analyze the transitions of the half-bridge midpoint node when Q2

turns off . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50

Figure 31. Voltage of HB node vs time (see Equation 32). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53

Figure 32. Resonant current vs time (see Equation 34) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53

Figure 33. Capacitance associated to the half-bridge midpoint node . . . . . . . . . . . . . . . . . . . . . . . . . 54

Figure 34. C

capacitances vs. half-bridge midpoint's voltage . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55

oss

Figure 35. Simplified schematic to analyze transition times of the node HB when Q2 turns off . . . . . 56

Figure 36. Schematization of Q2 turn-off transient . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57

Figure 37. Input current components in a split-capacitor LLC resonant half-bridge. . . . . . . . . . . . . . . 61

Figure 38. Timing diagram showing currents flow in the converter of Figure 37 . . . . . . . . . . . . . . . . . 61

): main waveforms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

R1

): main waveforms in CCMA operation at heavy load 25

R1

): main waveforms in DCMA operation at medium

R1

): main waveforms in DCMAB operation at light

R1

< f < fR1 , R>R

R2

< f < fR1, R>R

R2

): main waveforms in DCMAB

crit

): main waveforms in DCMB2 operation 32

crit

< f < fR1, R<R

R2

): main waveforms . . . 35

crit

4/64

AN2644 Classification of resonant converters

1 Classification of resonant converters

Resonant conversion is a topic that is at least thirty years old and where much effort has

been spent in research in universities and industry because of its attractive features: smooth

waveforms, high efficiency and high power density. Yet the use of this technique in off-line

powered equipment has been confined for a long time to niche applications: high-voltage

power supplies or audio systems, to name a few. Quite recently, emerging applications such

as flat panel TVs on one hand, and the introduction of new regulations, both voluntary and

mandatory, concerning an efficient use of energy on the other hand, are pushing power

designers to find more and more efficient AC-DC conversion systems. This has revamped

and broadened the interest in resonant conversion. Generally speaking, resonant

converters are switching converters that include a tank circuit actively participating in

determining input-to-output power flow. The family of resonant converters is extremely vast

and it is not an easy task to provide a comprehensive picture. To help find one's way, it is

possible to refer to a property shared by most, if not all, of the members of the family. They

are based on a "resonant inverter", i.e. a system that converts a DC voltage into a sinusoidal

voltage (more generally, into a low harmonic content ac voltage), and provides ac power to a

load. To do so, a switch network typically produces a square-wave voltage that is applied to

a resonant tank tuned to the fundamental component of the square wave. In this way, the

tank will respond primarily to this component and negligibly to the higher order harmonics,

so that its voltage and/or current, as well as those of the load, will be essentially sinusoidal

or piecewise sinusoidal. As shown in Figure 2, a resonant DC-DC converter able to provide

DC power to a load can be obtained by rectifying and filtering the ac output of a resonant

inverter.

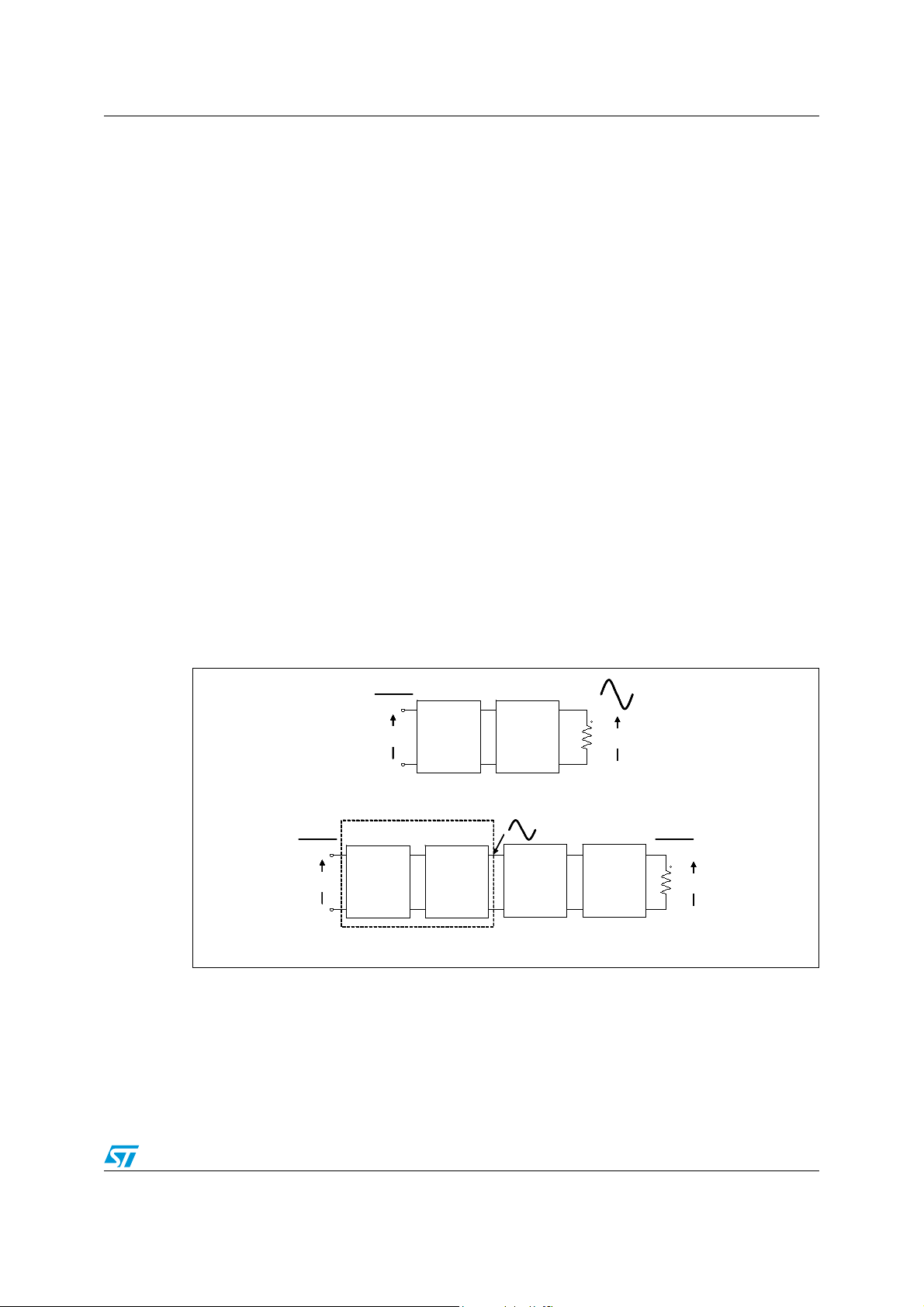
Figure 2. General block diagram of a resonant inverter, the core of resonant

converters

Resonant

tank circuit

Rectifier

Vout

ac

Low-pass

filter

Vout

dc

Vin

dc

Vin

dc

Resonant Inverter

Switch

network

Switch

network

Resonant Inverter

Resonant

tank circuit

Resonant Converter

Different types of DC-AC inverters can be built, depending on the type of switch network and

on the characteristics of the resonant tank, i.e. the number of its reactive elements and their

configuration [1].

As to switch networks, we will limit our attention to those that drive the resonant tank

symmetrically in both voltage and time, and act as a voltage source, namely the half-bridge

and the full-bridge switch networks. Borrowing the terminology from power amplifiers,

5/64

Classification of resonant converters AN2644

switching inverters driven by this kind of switch network are considered part of the group

called "class D resonant inverters".

As to resonant tanks, with two reactive elements (one L and one C) there are a total of eight

different possible configurations, but only four of them are practically usable with a voltage

source input. Two of them generate the well-known series resonant converter and parallel

resonant converter considered in [2] and thoroughly treated in literature.

With three reactive elements the number of different tank circuit configurations is thirty-six,

but only fifteen can be used in practice with a voltage source input. One of these, commonly

called LCC because it uses one inductor and two capacitors, with the load connected in

parallel to one C, generates the LCC resonant inverter commonly used in electronic lamp

ballast for gas-discharge lamps. Its dual configuration, using two inductors and one

capacitor, with the load connected in parallel to one L, generates the LLC inverter.

As previously stated, for any resonant inverter there is one associated DC-DC resonant

converter, obtained by rectification and filtering of the inverter output. Predictably, the above-

mentioned class of inverters will originate the "class D resonant converters". Considering

off-line applications, in most cases the rectifier block will be coupled to the resonant inverter

through a transformer to guarantee the isolation required by safety regulations. To maximize

the usage of the energy handled by the inverter, the rectifier block can be configured as

either a full-wave rectifier, which needs a center tap arrangement of transformer's secondary

winding, or a bridge rectifier, in which case tapping is not needed. The first option is

preferable with a low voltage / high current output; the second option with a high voltage /

low current output. As to the low-pass filter, depending on the configuration of the tank

circuit, it will be made by capacitors only or by an L-C type smoothing filter. The so-called

"series-parallel" converter described in [2], typically used in high-voltage power supply, is

derived from the previously mentioned LCC resonant inverter. Its dual configuration, the LLC

inverter, generates the homonymous converter, addressed in [3], [4] and [5], that will be the

subject of the following discussion. In particular we will consider the half-bridge

implementation, illustrated in Figure 3, but the extension to the full-bridge version is quite

straightforward.

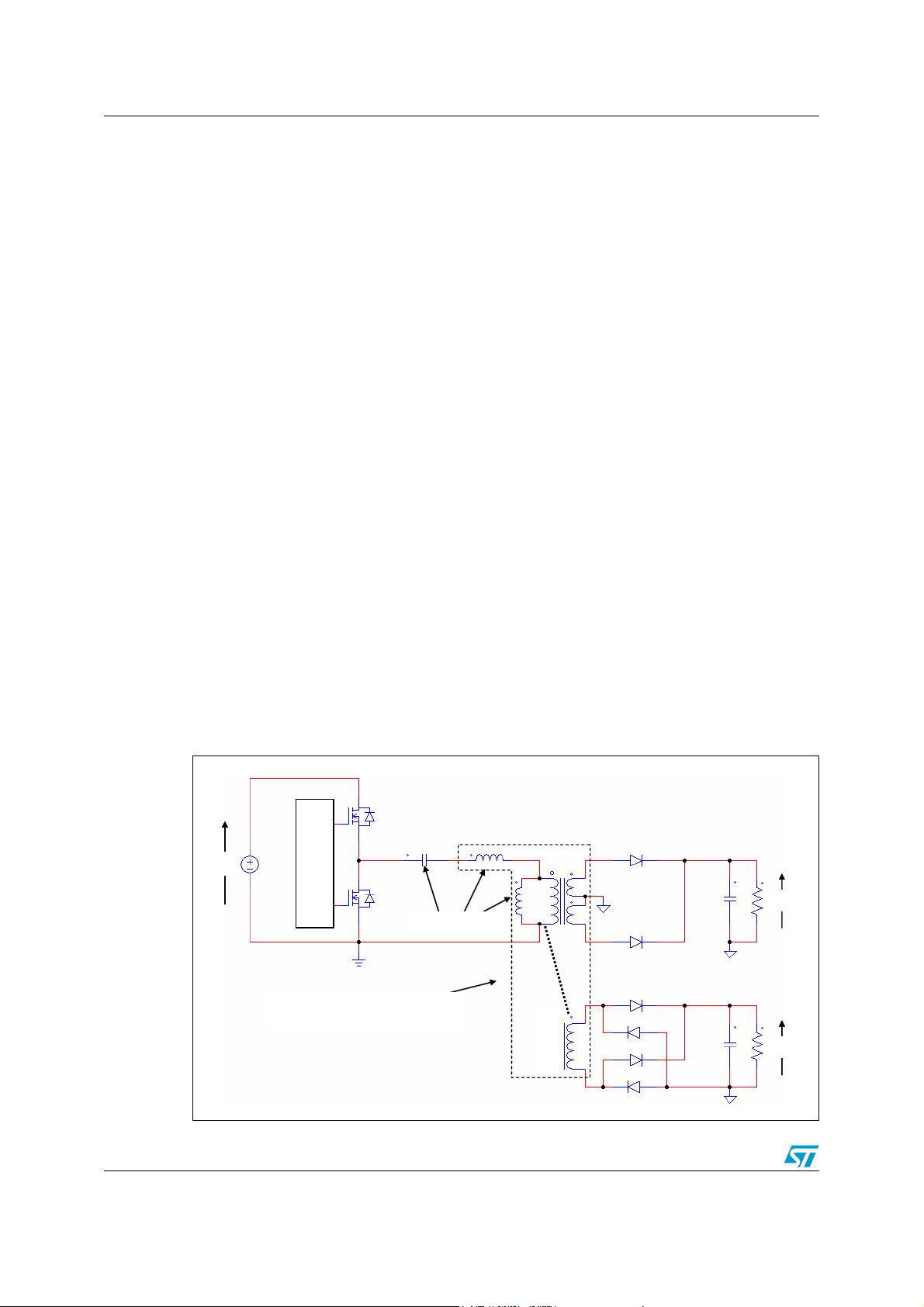
Figure 3. LLC resonant half-bridge schematic

Q1

Cr

VinVin

Preferably integrated into a single

Driver

Half-bridge

magnetic structure

Q2

LLC tank circuit

6/64

Ls

Lp

a:1

Center-tapped output with full-wave

(low voltage and high current)

a:1:1

D4

D2

rectification

D1

D2

Single-ended output with bridge

rectification

(high voltage and low current)

D1

D3

R

Vout

R

VoutVout

AN2644 The LLC resonant half-bridge converter

In resonant inverters (and converters too) power flow can be controlled by the switch

network either by changing the frequency of the square wave voltage, or its duty cycle, or

both, or by special control schemes such as phase-shift control. In this context we will focus

on power flow control by frequency modulation, that is, by changing the frequency of the

square wave closer to or further from the tank circuit's resonant frequency while keeping its

duty cycle fixed.

2 The LLC resonant half-bridge converter

2.1 General overview

According to another way of designating resonant converters, the LLC resonant half-bridge

belongs to the family of multiresonant converters. Actually, since the resonant tank includes

three reactive elements (Cr, Ls and Lp, shown in Figure 3), there are two resonant

frequencies associated to this circuit. One is related to the condition of the secondary

winding(s) conducting, where the inductance Lp disappears because dynamically shorted

out by the low-pass filter and the load (there is a constant voltage a V

Equation 1

f

R1

1

---------------------------- -=

2π Ls Cr⋅

across it):

out

the other resonant frequency is relevant to the condition of the secondary winding(s) open,

where the tank circuit turns from LLC to LC because Ls and Lp can be unified in a single

inductor:

Equation 2

1

It will be of course f

LLC resonant tank, while f

> fR2. Normally, fR1 is referred to as the resonance frequency of the

R1

is sometimes called the second (or lower) resonance

R2

frequency. The separation between f

f

-------------------------------------------=

R2

2π Ls Lp+()Cr

and fR2 depends on the ratio of Lp to Ls. The larger

R1

this ratio is, the further the two frequencies will be and vice versa. The value of Lp/Ls

(typically > 1) is an important design parameter.

It is possible to show that for frequencies f > f

tank is inductive and that for frequencies f < f

frequency region f

< f < fR1 the impedance can be either inductive or capacitive depending

R2

on the load resistance R. A critical value R

impedance will be capacitive, inductive for R> R

the input impedance of the loaded resonant

R1

the input impedance is capacitive. In the

R2

exists such that if R < R

crit

. For a given tank circuit the value of R

crit

then the

crit

depends on f. More precisely, in [6] it is shown that for any tank circuit configuration (then for

the LLC in particular):

Equation 3

where Zo

R

crit

and Zo∞ are the resonant tank output impedances with the source input short-

0

Zo0Zo∞⋅=

circuited and open-circuited, respectively.

7/64

The LLC resonant half-bridge converter AN2644

For certain reasons that will be clarified in the following sections, the LLC resonant

converter is normally operated in the region where the input impedance of the resonant tank

has inductive nature, i.e. it increases with frequency. This implies that power flow can be

controlled by changing the operating frequency of the converter in such a way that a

reduced power demand from the load produces a frequency rise, while an increased power

demand causes a frequency reduction.

The Half-bridge Driver switches the two power MOSFETs Q1 and Q2 on and off in phase

opposition symmetrically, that is, for exactly the same time. This is commonly referred to as

"50% duty cycle" operation even if the conduction time of either power MOSFET is slightly

shorter than 50% of the switching period. In fact, a small deadtime is inserted between the

turn-off of either switch and the turn-on of the complementary one. The role of this deadtime

is essential for the operation of the converter. It goes beyond ensuring that Q1 and Q2 will

never cross-conduct and will be clarified in the next sections as well. For the moment it will

be neglected, and the voltage applied to the resonant tank will be a square-wave with 50%

duty cycle that swings all the way from 0 to V

. Before going any further, however, it is

in

important to make one concept clear.

Figure 4. LLC resonant half-bridge with split resonant capacitor

Q1

Cr / 2

Ls

a:1:1

Vin

Half-bridge

Driver

Q2

a:1:1

Lp

Cr / 2

A few paragraphs above, the impedance of the tank circuit was mentioned. Impedance is a

concept related to linear circuits under sinusoidal excitation, whereas in this case the

excitation voltage is a square wave.

However, as a consequence of the selective nature of resonant tanks, most power

processing properties of resonant converters are associated with the fundamental

component of the Fourier expansion of voltages and currents in the circuit. This applies in

particular to the input square wave and is the foundation of the First Harmonic

Approximation (FHA) modeling methodology presented in [2] as a general approach and

used in [4] and [5] for the LLC resonant converter specifically. This approach justifies the

usage of the concept of impedance as well as those coming from complex ac circuit

analysis.

Coming back to the input square wave excitation, it has a DC component equal to V

/2. In

in

the LLC resonant tank the resonant capacitor Cr is in series to the voltage source and under

steady state conditions the average voltage across inductors must be zero. As a result, the

DC component V

/2 of the input voltage must be found across Cr which consequently plays

in

the double role of resonant capacitor and DC blocking capacitor.

It is possible to see, especially at higher power levels, a slightly modified version of the LLC

resonant half-bridge converter, where the resonant capacitor is split as illustrated in

Figure 4. This configuration can be useful to reduce the current stress in each capacitor

8/64

AN2644 The LLC resonant half-bridge converter

and, in certain conditions, the initial imbalance of the V·s applied to the transformer at start

up (see "Converter's start-up" section). Additionally, it makes the input current to the

converter look like that of a full-bridge converter, as shown in Appendix E, with a resulting

reduction in both the input differential mode noise and the stress of the input capacitor.

Obviously, the currents through Q1 and Q2 will be unchanged. It is easy to recognize that

the two Cr/2 capacitors are dynamically in parallel, so that the total resonant tank's

capacitance is again Cr.

The system appears quite bulky, with its three magnetic components. However, the LLC

resonant topology lends itself well to magnetic integration. With this technique inductors and

transformers are combined into a single physical device to reduce component count, usually

with little or no penalty to the converter's characteristics, sometimes even enhancing its

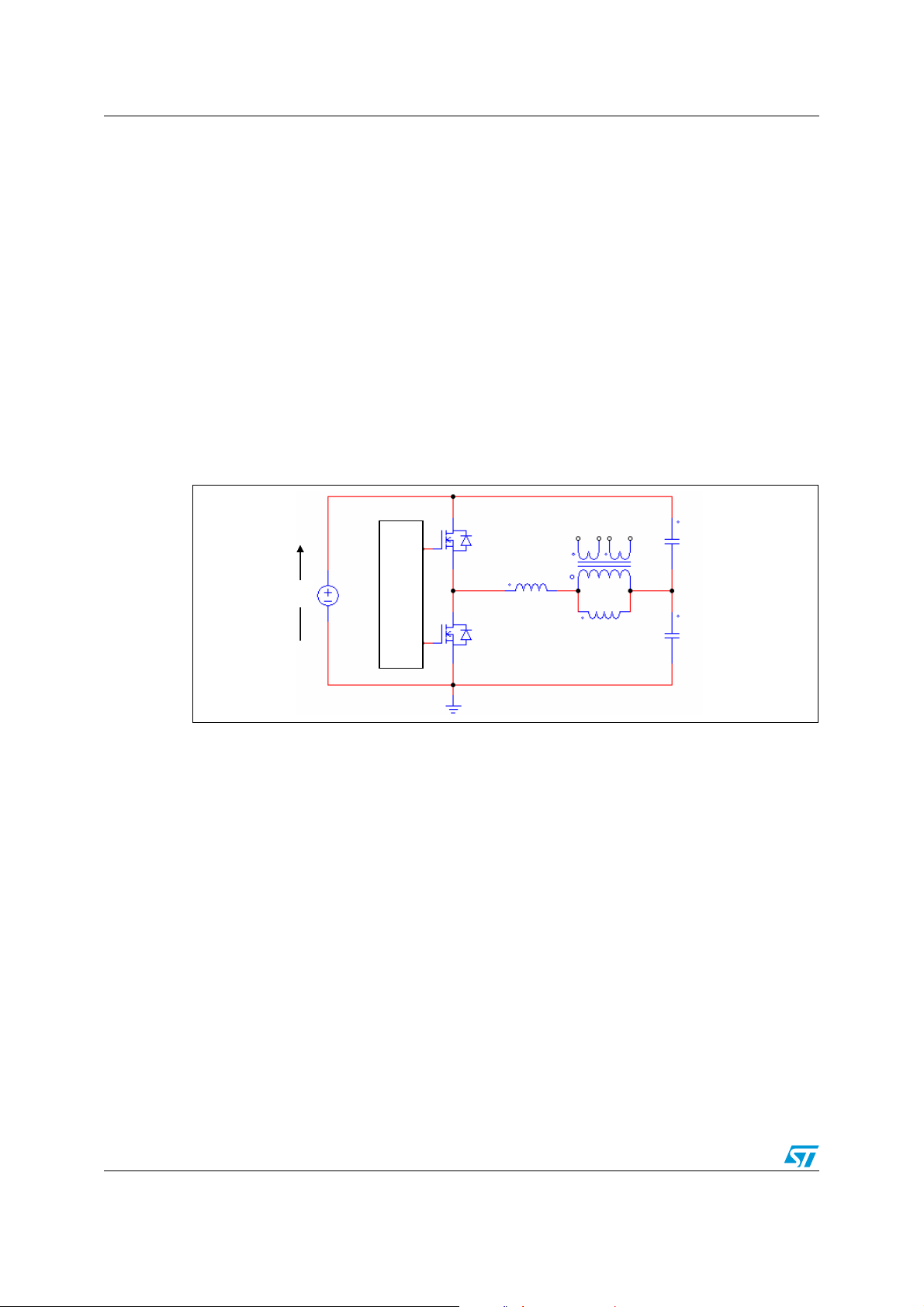
operation. To understand how magnetic integration can be done, it is worth looking at the

well-known equivalent schematics of a real transformer in Figure 5 and comparing them to

the inductive component set of Figure 3.

Lp occupies the same place as the magnetizing inductance L

primary leakage inductance L

. Then, assuming that we are going to use a ferrite core plus

L1

, Ls the same place as the

M

bobbin assembly, Lp can be used as the magnetizing inductance of the transformer with the

addition of an air gap into the magnetic circuit and leakage inductance can be used to make

Ls.

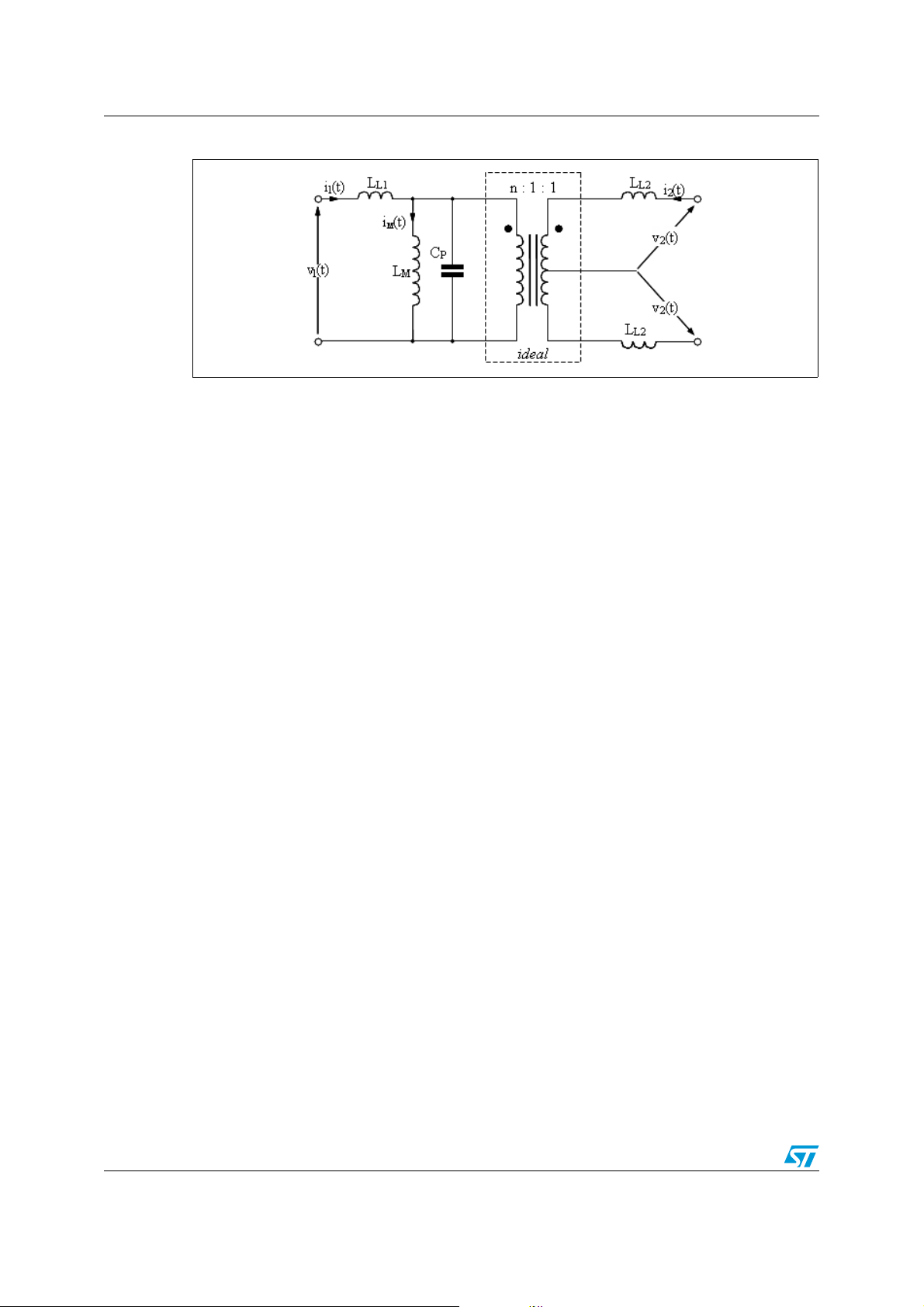
Figure 5. Equivalent schematic of a real transformer (left, tapped secondary; right,

single secondary)

L

i1(t)

L

L1

iM(t)

L

M

n : 1

ideal

L

L2

i2(t)

v2(t)

v2(t)v2(t)

v1(t)

v1(t)v1(t)

i1(t)

L

L1

iM(t)

L

M

n : 1 : 1

ideal

L

L2

i2(t)

v2(t)

v2(t)v2(t)

v1(t)

v1(t)v1(t)

v2(t)

v2(t)v2(t)

L

L2

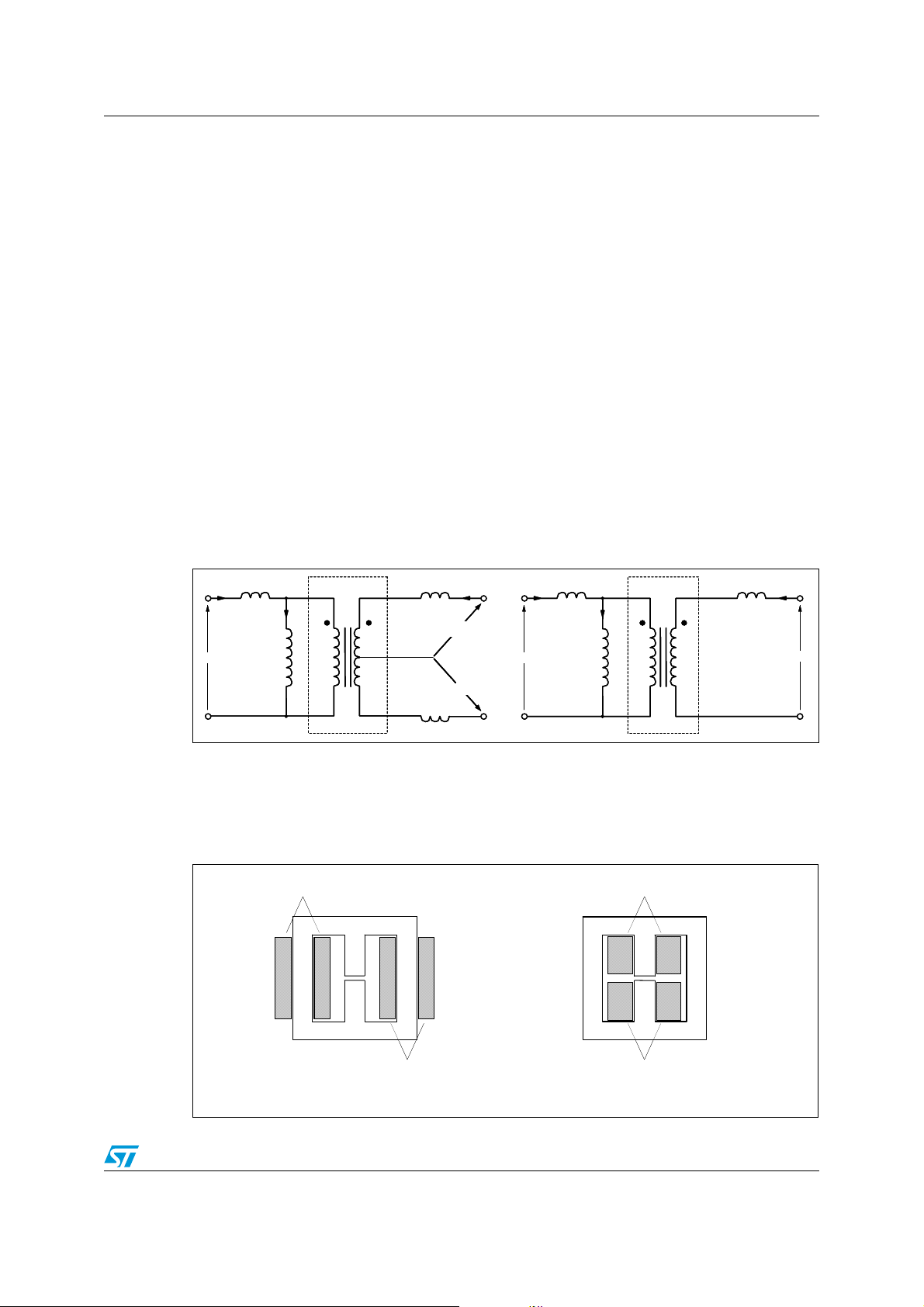
To do so, however, a leaky magnetic structure is needed, which is contrary to the traditional

transformer design practice that aims at minimizing leakage inductance. The usual

concentric winding arrangement is not recommended here, although higher leakage

inductance values can be achieved by increasing the space between the windings.

Figure 6. Example of high-leakage magnetic structures (cross-section)

Primary

Primary winding

winding

Primary

Primary winding

winding

Secondary

winding

Windings on separate legs of an EE core

Secondary

winding

Side-by-side windings (EE or pot core)Windings on separate legs of an EE core

Side-by-side windings (EE or pot core)

9/64

The LLC resonant half-bridge converter AN2644

It is difficult, however to obtain reproducible values, because they depend on parameters

(such as winding surface irregularities or spacer thickness) difficult to control. Other fashions

are recommended, such as placing the windings on separate core legs (using E or U cores)

or side by side on the same leg which is possible with both E and pot cores and shown in

Figure 6. They permit reproducible leakage inductance values, because related to the

geometry and the mechanical tolerances of the bobbin, which are quite well controlled. In

addition, these structures possess geometric symmetry, so they lead to magnetic devices

with an excellent magnetic symmetry.

However, in the real transformer model of Figure 5 there is the secondary leakage

inductance L

that is not considered in the model of Figure 3. The presence of LL2 is not a

L2

problem from the modeling point of view because the transformer's equivalent schematic

can be manipulated so that L

incorporated in L

). This is exactly what has been done in the transformer model shown in

L1

disappears (it is transferred to the primary side and

L2

Figure 3. Then, it is important to underline that Ls and Lp are not real physical inductances

(L

, LM and LL2 are), their numerical values are different (Ls ≠ LL1, Lp ≠ LM), and, finally, the

L1

turn ratio a is not the physical turn ratio n=N

interpretation. L

is the inductance of the primary winding measured with the secondary

s

. Ls and Lp can be given a physical

1/N2

winding(s) shorted, while Lp is the difference between the inductance of the primary winding

measured with the secondary windings open and L

However, L

is not free from side effects. For a given impressed voltage, LL2 decreases the

L2

voltage available on the secondary winding, which carries a current i

.

s

, by the drop LL2·di2/dt.

2

This is an effect that is taken into account by the above mentioned manipulation of the

transformer model. In addition, in multioutput converters, where there is leakage inductance

associated to each output winding, cross-regulation between the various outputs will be

adversely affected because of their decoupling effect.

Finally, there is one more adverse effect to consider in the center-tapped output

configuration. With reference to Figure 3 and 5, when one half-winding is conducting, the

voltage v

(t) externally applied to that half-winding is V

2

(VF is the rectifier forward drop

out+VF

of the conducting diode). With no secondary leakage inductance, this voltage will be found

across the secondary winding of the ideal transformer and then coupled one-to-one to the

nonconducting half-winding. Consequently, the reverse voltage applied to the reverse-

biased rectifier will be 2·V

L

·di2/dt adds up to V

L2

out+VF

the reverse voltage applied to the nonconducting rectifier will be increased by L

. If now we introduce the leakage inductance LL2, the drop

out+VF

. and is reflected to the other half-winding as well. As a result,

·di2/dt.

L2

Note that in case of single-winding secondary with bridge rectification, the voltage applied to

reverse-biased diodes of the bridge is only V

that the negative voltage of the secondary winding is fixed at -V

and is not affected by LL2. The reason is

out+VF

externally and is not

F

determined by internal coupling like in the case of tapped secondary.

It is worth pointing out that the 50% duty cycle operation of the LLC half-bridge equalizes

the stress of secondary rectifiers both in terms of reverse voltage - as just seen - and

forward conduction current. In fact, each rectifier carries half the total output current under

all operating conditions. Then, if compared to similar PWM converters (such as the ZVS

Asymmetrical Half-bridge, or the Forward converter), in the center-tapped output

configuration the equal reverse voltage typically allows the use of lower blocking voltage

rating diodes. This is especially true when using common cathode diodes housed in a single

package. A lower blocking voltage means also a lower forward drop for the same current

rating, and then lower losses.

It must be said, however, that in the LLC resonant converter the output current form factor is

worse, so the output capacitor bank is stressed more. Although the stress level is

10/64

AN2644 The LLC resonant half-bridge converter

considerably lower than that in a flyback converter, as shown in Ta bl e 1 , this is one of the

few real drawbacks of the topology.

Table 1. Output stress for LLC resonant half-bridge vs. PWM topologies @ 50% duty cycle

Output current form factors Forward - ZVS AHB LLC resonant HB Flyback (CCM-DCM boundary)

Peak-to-DC ratio ≈1.05÷1.15

Rms-to-DC ratio ≈1

AC-to-DC ratio ≈0.03÷0.09

π

-- -

≈ 1.57=

2

π

---------- -

≈ 1.11=

22

2

π

----- - 1–≈ 0.48= 8

8

-- - 1.63≈ 3

8

-- - 1– 1.29≈ 3

4

Additional details concerning power losses will be discussed in Analysis of power losses on

page 41.

To complete the general picture on the LLC resonant converter, there is another aspect that needs to be addressed concerning parasitic components which affect the behavior of the circuit.

The first parasitic element to consider is the capacitance of the midpoint of the half-bridge structure, the node common to the source of the high-side power MOSFET and to the drain of the low-side power MOSFET. Its effect is that the transitions of the half-bridge midpoint will require some energy and take a finite time to complete. This is linked to the previously mentioned deadtime inserted between the turn-off of either switch and the turn-on of the complementary one, and will be discussed in more detail in Section 2.2.

The second parasitic element to consider is the distributed capacitance of transformer's windings. This capacitance, which exists for both the primary and the secondary windings, in combination with windings' inductance, originates what is commonly designated as the transformer "self-resonance". In addition to this capacitance one needs to consider also the junction capacitance of the secondary rectifiers, which adds up to that of the secondary windings and lowers the resulting self-resonance frequency (loaded self-resonance).

The effect of all this parasitic capacitance can be modeled with a single capacitor C connected in parallel to L turns from LLC to LLCC. This 4 the transformer's loaded self-resonance (f considerably lower than f than f

and if the load impedance is high enough, its effect starts making itself felt,

R1

as illustrated in Figure 7. The resonant tank, as a consequence,

M

th

- order tank circuit features a third resonance frequency at > fR1). When the operating frequency is

the effect of CP is negligible. However, at frequencies greater

LSR

P

eventually resulting in reversing the transferable power vs. frequency relationship as frequency approaches f

. Power now increases with the switching frequency, feedback

LSR

becomes positive and the converter loses control of the output voltage. The onset of this "feedback reversal" in closed-loop operation is revealed by a sudden frequency jump to its maximum value as the load falls below a critical value (i.e. the frequency exceeds a critical value) and a simultaneous output voltage rise.

In some way, either appropriately choosing the operating frequency range (<< f increasing f

, the converter must work away from feedback reversal. This usually sets the

LSR

) or

practical upper limit to a converter's operating frequency range.

11/64

The LLC resonant half-bridge converter AN2644

Figure 7. Equivalent schematic of a transformer including parasitic capacitance

2.2 The switching mechanism

Still another way of classifying resonant converters would include the LLC resonant halfbridge in the family of "resonant-transition" converters. This nomenclature refers to the fact that in this class of converters power switches are driven in such a way that a resonant tank circuit is stimulated to create a zero-voltage condition for them to turn-on.

To understand how this can be achieved in the LLC half-bridge, it is instructive to consider the circuits illustrated in Figure 8 where the switches Q1 and Q2 that generate the square wave input voltage to the resonant tank are power MOSFETs. Their body diodes DQ1, DQ2 are pointed out because they play an important role. In circuit a), the drain-to-source parasitic capacitances C changes of the node HB are concerned, the parasitic capacitances Cgd and Cds are effectively in parallel, then Cgd+Cds=C

Additionally, other contributors to the parasitic capacitance of the node HB (e.g. that formed between the case of the power MOSFETs and the heat sink, the intrawinding capacitance of the resonant inductor, etc.) are lumped together in the capacitor C C

, is connected between the node HB and a node having a fixed voltage (Vin for C

oss2

ground for C

). Then, as far as voltage changes of the node HB are concerned, C

oss2

effectively connected in parallel to C together in a single capacitor C

oss1

, C

are pointed out as well. In fact, as far as voltage

oss2

has to be considered.

oss

. Note that C

Stray

and C

oss2

from the node HB to ground, as shown in the circuit b):

HB

. It is convenient to lump all of them

Stray

oss1

, like

oss1

is

,

Equation 4

C

HB

C

which we will refer to in the following discussion. Note also that C linear capacitors, i.e. their value is a function of the drain-to-source voltage. It is intended that their time-related equivalent value will be considered (see Appendix A).

12/64

++=

OSS1COSS2CStray

oss1

and C

oss2

are non-

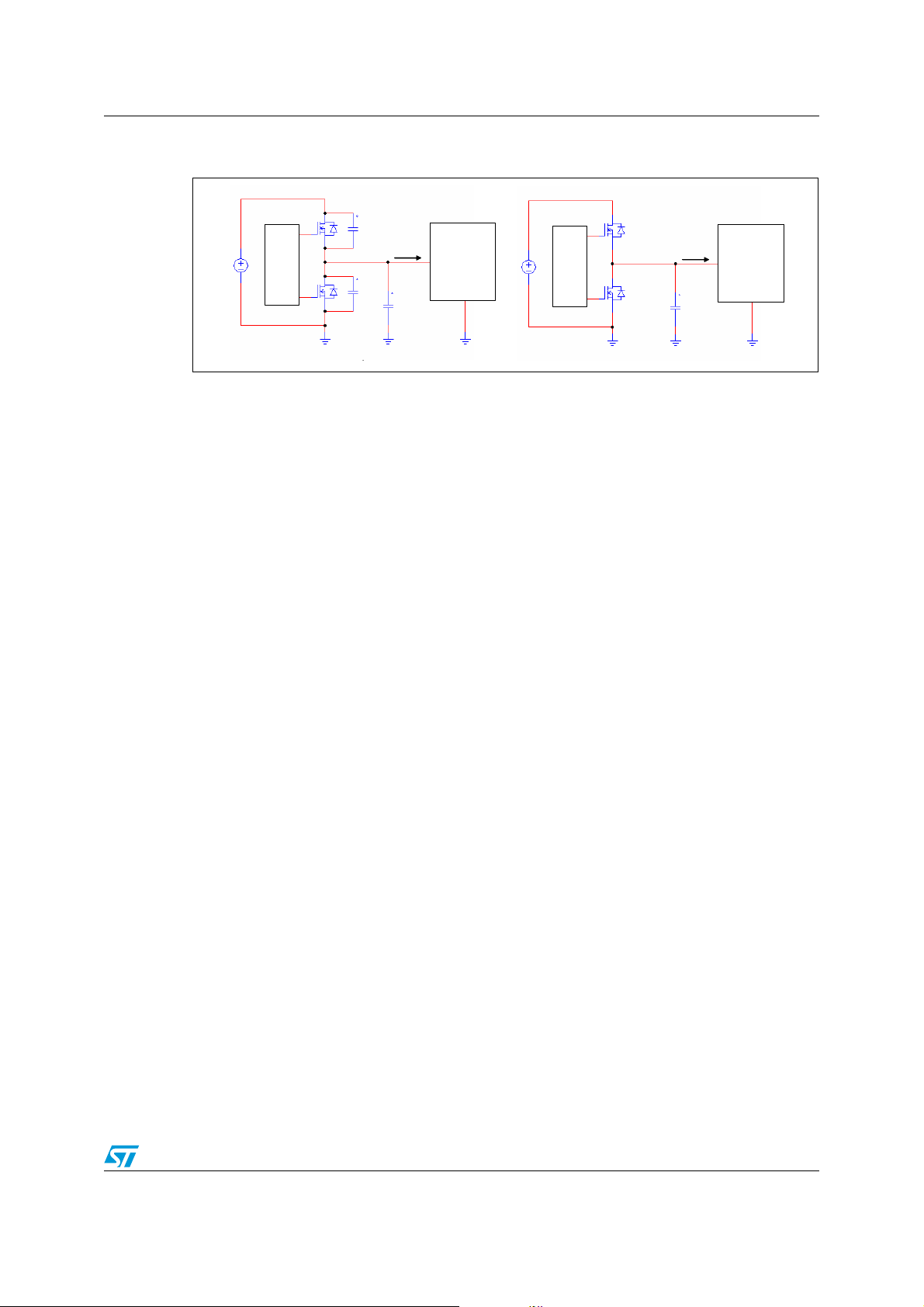
AN2644 The LLC resonant half-bridge converter

Figure 8. Power MOSFET totem-pole network driving a resonant tank circuit in a

half-bridge converter

Q1

Coss

1

DQ1

Vin

Node

HB

Q2

HB Driver

DQ1

DQ2

Coss

2

C

Stray

I

IRI

R

Resonant

Tank &

Load

Vin

Q1

DQ1

Node

HB

Q2

HB Driver

DQ2

C

HB

I

IRI

R

Resonant

Tank &

Load

a)

b)

As previously stated, there is no overlap between the conduction of Q1 and Q2. Additionally, a deadtime T

between the transitions from one state to the other of either

D

switch, where they both are open, is intentionally inserted. It is intended that when Q1 is closed and Q2 is open, the voltage applied to the resonant tank circuit is positive. Similarly we will define as negative the voltage applied to the resonant tank circuit when Q1 is open and Q2 is closed. Consistently with two-port circuits sign convention, the input current to the resonant tank, I

Let us assume Q1 closed and Q2 open. It is then I to the circuit is positive (V reactive elements. Let us suppose that I instant t

when Q1 opens, and refer to the timing diagram of Figure 9.

0

The current through Q1 falls quickly and becomes zero at t = t

, will be positive if entering the circuit, negative otherwise.

R

= I(Q1). Despite that the voltage applied

= Vin), IR can flow in either direction since we are in presence of

HB

is entering the tank circuit (positive current) in the

R

. Q2 is still open and IR must

1

keep on flowing almost unchanged because of the inductance of the resonant tank that acts as a current flywheel. The electrical charge necessary to sustain I C

, initially charged at Vin, which will be now discharged. Provided IR(t1) is large enough,

HB

the voltage of the node HB will then fall at a certain rate until t = t

will come initially from

R

, when its voltage

2

becomes negative and the body diode of Q2, DQ2, becomes forward biased, thus clamping the voltage at a diode forward drop V the remaining part of the deadtime T DQ2. When this occurs, the voltage across Q2 is -V input voltage V

. In the end, this is what is called zero-voltage switching (ZVS): the turn-on

in

below ground. IR will go on flowing through DQ2 for

F

until t = t3, when Q2 turns on and its R

D

, a value negligible as compared to the

F

DS(on)

shunts

transition of Q2 is done with negligible dissipation due to voltage-current overlap and with C

already discharged, there will be no significant capacitive loss either. Note, however,

HB

that there will be nonnegligible power dissipation associated to Q1's turn-off because there will be some voltage-current overlap during the time interval t

- t1.

0

13/64

The LLC resonant half-bridge converter AN2644

Figure 9. Detail of Q1 ON-OFF and Q2 OFF-ON transitions with soft-switching for

Q2

Dead-time

Dead-timeDead-time

t0–t1Q1 current fall time;

voltage-current overlap for Q1

Node HB transition time

t

0–t2

t

Q2’ body diode conduction time

2–t3

Vc = Resonant capacitor voltage

VHB= Node HB voltage

IR= Tank circuit’s current

I(Lp) = Lp (magnetizing) current

I(Q1) = MOSFET Q1 current

I(CHB) = CHBcurrent

V

HB

I

R

Q2 OFF

Q1’s current

falls to zero

Q1 ON

Low turn-off losses

I(Q1)

I(CHB)

I(Q1)

I(CHB)

Q1 OFF

Q2 OFF

Tank circuit’s current

is positive

t

0 t1t2 t3

Q1 OFF

Q2 ON

Q2 is switched on with essentially

zero drain-to-source volt age: ZVS!

Magnetizing current equals

tank circuit’s current

HB node’s parasitic capa-

HB node’s parasitic capacitance discharge current

citance discharge current

There is an additional positive side effect in turning on Q2 with zero drain-to-source voltage. It is the absence of the Miller effect, normally present in power MOSFETs at turn-on when hard-switched. In fact, as the drain-to-source voltage is already zero when the gate is supplied, the drain-to-gate capacitance Cgd cannot "steal" the charge provided to the gate. The so-called "Miller plateau", the flat portion in the gate voltage waveform, as well as the associated gate charge, is missing here and less driving energy is therefore required. Note that this property provides a method to check if the converter is running with soft-switching or not by looking at the gate waveform of Q2 (which is more convenient because it is sourcegrounded), as shown in Figure 10 and 11.

Figure 10. Q2 gate voltage at turn-on: with

soft-switching

HB node is falling down

here; current due to Cgd

With similar reasoning it is possible to understand that the same ZVS mechanism occurs to Q1 when it turns on if I

is flowing out of the resonant tank circuit (negative current).

R

In the end we can conclude that, if the tank current at the instant of half-bridge transitions has the same sign as the impressed voltage, both switches will be "soft-switched" at turn-on, i.e. turned on with zero voltage across them (ZVS). It is intuitive that this sign coincidence

Figure 11. Q2 gate voltage at turn-on: with

hard-switching (no ZVS)

Current injection through

Cgd due to hard-switching

Miller effect

14/64

AN2644 The LLC resonant half-bridge converter

occurs if the tank current lags the impressed voltage (e.g. it is still positive while voltage has already gone to zero), which is a condition typical of inductors. In other words, ZVS occurs if the resonant tank input impedance is inductive. The frequency range where tank current lags the impressed voltage is therefore called the "inductive region".

It is worth emphasizing the essential role of DQ1 and DQ2 in ensuring continuity to current flow and clamping the voltage swing of the node HB at V

and -VF respectively (the LLC

in+VF

resonant half-bridge belongs to the family of ZVS clamped-voltage topologies). Power MOSFETs, with their inherent body diodes are therefore the best suited power switches to be used in this converter topology. Other types of switches, such as BJT or IGBT, would need the addition of external diodes.

Going back to the state when Q1 is closed and Q2 open, let us now assume that at the instant t

when Q1 opens, current is flowing out of the resonant tank towards the input

0

source, i.e. it is negative. This operation is shown in the timing diagrams of Figure 12.

With Q1 now open the current will go on flowing through DQ1 throughout the deadtime, and will eventually be diverted through Q2 only when Q2 closes at t = t

, the end of the

1

deadtime. As far as Q1 is concerned, then, there will be no loss associated to turn-off because the voltage across it does not change significantly (it is essentially the same situation seen at turn-on when the converter works in the inductive region).

Q2, instead, will experience now a totally different situation. As DQ1 is conducting during the deadtime, the voltage across Q2 at t = t considerable voltage-current overlap but the energy of C R happens in PWM-controlled converters at turn-on. The associated power dissipation ½C

as well. In this respect, it is a "hard-switching" condition identical to what normally

DS(on)

2

f may be considerably higher than that normally dissipated under "soft-switching"

HBVin

equals Vin+VF so that there will be not only a

1

will be dissipated inside its

HB

conditions and this may easily lead to Q1 overheating, since heat sinking is not usually sized to handle this abnormal condition.

In addition to that, at t = t

the body diode of Q1, DQ1, is conducting current and its voltage

1

is abruptly reversed by the node HB being forced to ground by Q2. Hence, DQ1 will keep its low impedance and there will be a condition equivalent to a shoot-through between Q1 and Q2 until it recovers (at t = t

).

2

It is well-known the power MOSFET's body diodes do not have brilliant reverse recovery characteristics. Hence DQ1 will undergo a reverse current spike large in amplitude (it can be much larger than the forward current it was carrying at t=t

) and relatively long in duration

1

(in the hundred ns) that will go through Q2 as well. This spike, in fact, cannot flow through the resonant tank because Ls does not allow for abrupt current changes.

This is a potentially destructive condition not only because of the associated power dissipation that adds up to the others previously considered, but also due to the current and voltage of DQ1 which are simultaneously high during part of its recovery. In fact, there will be an extremely high dv/dt (many tens of V/ns!) experienced by Q1 as DQ1 recovers and the voltage of the node HB goes to zero. This dv/dt may exceed Q1 rating and lead to an immediate failure because of the second breakdown of the parasitic bipolar transistor intrinsic in power MOSFET structure. Finally, it is also possible that Q1 is parasitically turned on if the current injected through its Cgd and flowing through the gate driver's pull down, which is holding the gate of Q1 low, is large enough to raise the gate voltage close to the turn-on threshold (see the spike after turn-off in the graph of Figure 11). This would cause a lethal shoot-through condition for the half-bridge leg.

An additional drawback of this operation is the large and energetic negative voltage spikes induced by the recovery of DQ1 because of the unavoidable parasitic inductance of the PCB

15/64

The LLC resonant half-bridge converter AN2644

subject to its di/dt, which may damage any control IC coupled to the half-bridge leg, not to mention the big EMI generation.

Similarly, it is possible to show that the same series of adverse events will happen to Q1 and Q2, with exchanged roles, when Q2 is turned off if I

is flowing into the resonant tank circuit

R

(positive current).

The obvious conclusion is that, if the tank current and the impressed voltage at the instant of half-bridge transitions have opposite signs, both switches will be hard-switched and the reverse recovery of their body diodes will be invoked, with all the resulting negative effects. It is intuitive that this sign opposition occurs if the tank current leads the impressed voltage, which is typical of capacitors and then occurs if the resonant tank input impedance is capacitive. This kind of operation is often termed "capacitive mode" and the frequency range where tank current leads the impressed voltage is called the "capacitive region".

Figure 12. Q1 ON-OFF and Q2 OFF-ON transitions with hard switching for Q2 and

recovery for DQ1

Dead-time

t0–t1Q2’ body diode conduction time;

coinciding with dead-time

Q1’s body diode recovery time

t

1–t2

Vc = Resonant capacitor voltag e

VHB= Node HB voltage

IR= Tank circuit’s current

I(Lp) = Lp (magnetizing) c urrent

I(Q1) = MOSFET Q1 current

V

HB

Node HB voltage

I

R

Q1 ON

Q2 OFF

I(Q1)

I(Q2)

I(Q1)

I(Q2)

Tank circuit’s current

is negative

Q1 OFF

Q2 OFF

t

0 t1t2

Q1 OFF

Q2 ON

Q2 is hard-switchedQ1 has soft turn-off

Resonant capacitor voltage

High dv/dt

Q1’s body diode

is recovered

Current is circulating

through Q1’s body diode

Then, the converter must be operated in the region where the input impedance is inductive (the inductive region), that is, for frequencies f > f load resistance R is such that R> R

. This is a necessary condition in order for Q1 and Q2

crit

to achieve ZVS, which is evidently a crucial point for the good operation of the LLC resonant half-bridge.

To summarize, ZVS brings the following benefits:

1. low switching losses: either high efficiency can be achieved if the half-bridge is operated at a not too high switching frequency (for example < 100 kHz) or high switching frequency operation is possible with a still acceptably high efficiency (definitely out of reach with a hard-switched converter);

2. reduction of the energy needed to drive Q1 and Q2, thanks to the absence of Miller effect at turn-on. Not only is turn-on speed unimportant because there is no voltagecurrent overlap but also gate charge is reduced, then a small source capability is required from the gate drivers.

3. low noise and EMI generation, which minimizes filtering requirements and makes this converter extremely attractive in noise-sensitive applications.

4. all of the above-mentioned adverse effects of capacitive mode, which not only impair efficiency but also jeopardize the converter, are prevented.

16/64

or in the range fR2 < f < fR1 provided the

R1

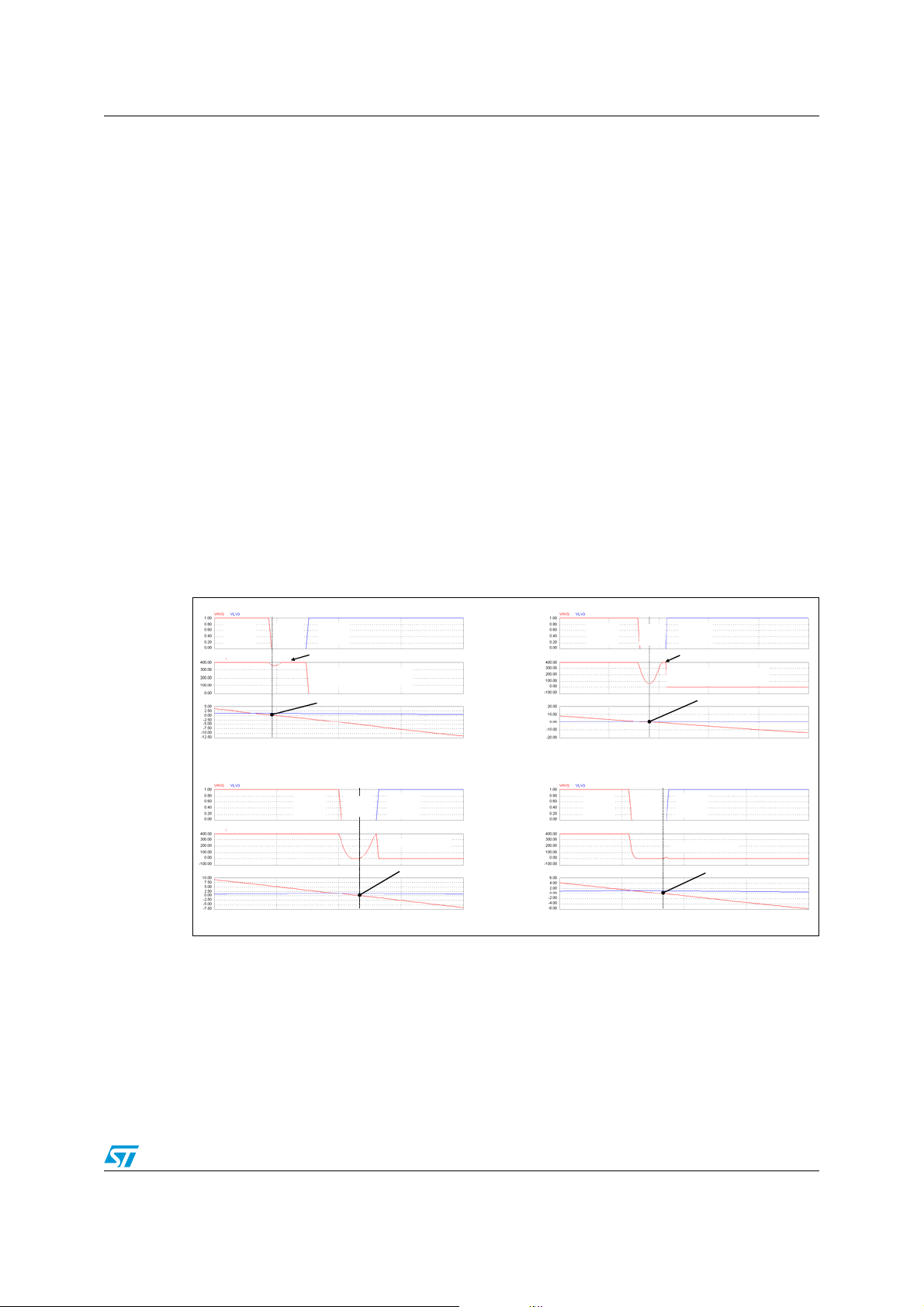
AN2644 The LLC resonant half-bridge converter

Note, however, that working in the inductive region is not a sufficient condition in order for ZVS to occur.

In the above discussion, it has been said that the voltage of the node HB could swing from V

to zero "provided IR is large enough". Of course the same holds if we consider node HB's

in

swing from zero up to V is that the associated inductive energy level of the resonant tank circuit is maintained at the expense of the energy contained in the capacitance C greater than that owned by C the node HB will be able to reach -V

. What actually happens when Q1 turns off with positive IR current

in

2

) is

R

HB

. If the inductive energy (∝ I

(∝ V

2

) CHB will be completely depleted and the voltage of

in

, injecting DQ2 and allowing Q2 to turn-on with

F

HB

essentially zero drain-to-source voltage. Similarly, when Q2 turns off with negative current, part or all of the associated inductive energy will be transferred to C inductive energy is greater than that needed to charge C

up to Vin+VF, the node HB will be

HB

. If the available

HB

allowed to swing all the way up until DQ1 is injected, thus clamping the voltage, and Q1 will be able to turn-on with essentially zero drain-to-source voltage.

Seen from a different perspective, the inductive part of the tank circuit resonates with C and this is the origin of the term "resonant transition" used for designating resonant converters having this property. This "parasitic" tank circuit active during transitions is formed by C

with the series inductance Ls if during the half-bridge transition there is

HB

current circulating on the secondary side (so that Lp is shorted out) or with the total inductance Ls + Lp if there is no current conduction on the secondary side.

Figure 13. Bridge leg transitions in the neighborhood of inductive-capacitive

Q1 ON

Q2 OFF

V

HB

IRI(Lp)

V

HB

IRI(Lp)

regions boundary

Q1 OFF

Q2 OFF

Q2 ON

Q1’s body diode conduction

Q2 is hard switched

Q2 is hard switched Q1’s body diode is recovered

Q1’s body diode is recovered

IR = 0

a)

Q1 ON

Q1 OFF

Q2 OFF

Q1 OFF

Q2 OFF

Q2 is hard switched

c)

Q1 OFF

Q2 ON

IR = 0

VHB= Node HB

voltage

IR= Tank circuit’s

current

I(Lp) = Lp (magnetizing)

current

VHB= Node HB

voltage

IR= Tank circuit’s

current

I(Lp) = Lp (magnetizing)

current

V

HB

IRI(Lp)

V

HB

IRI(Lp)

Q1 ON

Q2 OFF

Q1 ON

Q2 OFF

Q1 OFF

Q2 ON

Q2 OFF

Q1’s body diode conduction

Q2 is hard switched

Q2 is hard switched Q1’s body diode is recovered

Q1’s body diode is recovered

b)

Q1 OFF

Q2 ON

Q2 OFF

Q2 is soft switched

d)

IR = 0

HB

,

The above mentioned energy balance considerations, however, are not still sufficient to guarantee ZVS under all operating conditions. There is an additional element that needs to be considered, the duration of the deadtime T

.

D

The first obvious consideration is that the duration of the deadtime represents an upper limit to the time the node HB takes to swing from one rail to the other: in order for the mosfet that is about to turn on to achieve ZVS (i.e. to be turned on with zero drain-to-source voltage), the transition has to be completed within T

as depicted in Figure 9. However, the way the

D

17/64

The LLC resonant half-bridge converter AN2644

deadtime and ZVS are related is actually more complex and depends on converter's operating conditions.

It is instructive to see this in Figure 13, which shows typical node HB waveforms occurring when working in the inductive region but too close to the capacitive region, so that ZVS is not achieved. They refer to the Q1 →OFF, Q2 → ON transition; those related to the opposite transition are obviously turned upside down.

● Case a) is very close to the boundary between inductive and capacitive regions. Tank

current reverses just after Q1 is switched off, a portion of node HB ringing appears as a small "dip", then the tank current becomes negative enough to let the body diode of Q1 start conducting. When Q2 turns on there are capacitive losses and the recovery of the Q1's body diode with all the related issues.

● Case b) is slightly more in the inductive region but still I

crosses zero within the

R

deadtime. The node HB ringing becomes larger and the body diode of Q1 still conducts for a short time and its recovery is invoked as Q2 turns on.

● Case c) Is even more in the inductive region but still not sufficiently away from the

capacitive-inductive boundary. The ringing of the node HB is large enough to reach zero but I

reverses within the deadtime and the voltage goes up again. At the end of

R

the deadtime the voltage does not reach Vin, hence the body diode of Q1 does not conduct and Q2, when turned on, will experience only capacitive losses.

● Case d) Is further in the inductive region and I

crosses zero nearly at the end of the

R

deadtime. Q2 is now almost soft-switched with no losses. This can be considered as the boundary of the operating region where ZVS can be achieved with the given duration of T

.

D

Note that the resonant tank's current during node HB ringing is lower than the one flowing through Lp. This means that their difference is flowing into the transformer and, consequently, that one of the secondary half-windings is conducting. Therefore, C

HB

is

resonating with Ls only.

This analysis shows that there is a "border belt" in the inductive region, close to the boundary with the capacitive region (f

< f < fR1, R = R

R2

) and that as converter's operation

crit

is moved away from the capacitive-inductive boundary and pushed more deeply in the inductive region there is a progressive behavior change from hard-switching to softswitching. In the cases a and b the inductive energy in the resonant tank is too small to let the node HB even swing "rail-to-rail"; moving away from the boundary, as shown in case c, the energy is higher and allows a rail-to-rail swing, but it is not large enough to keep the node HB "hooked" to the rail throughout the deadtime T

. If the converter is operated in this

D

border belt, Q1 and Q2 will be hard-switched at turn-on and, in cases such as case a and case b, the body diode of the just turned off power MOSFET is injected and then recovered as the other power MOSFET turns on.

Case b and, especially, case c highlight that it is possible to look at the deadtime T from another standpoint: looking at those waveforms, one might conclude that the current I

also

D

R

at the beginning of the deadtime is too low or, conversely, that the deadtime is too long. In case c, for example, if the dead-time had been approximately half the value actually shown, Q2 would have been soft-switched at turn-on. Of course, the more appropriate interpretation depends on whether T

is fixed or not.

D

These cases are related to heavy load conditions.

Figure 14 shows a case typical of no-load conditions, where ZVS is not achieved because of

a too slow transition of the node HB so that it does not swing completely within the deadtime T

. In this case the situation seems less stressful than operating in the capacitive region.

D

18/64

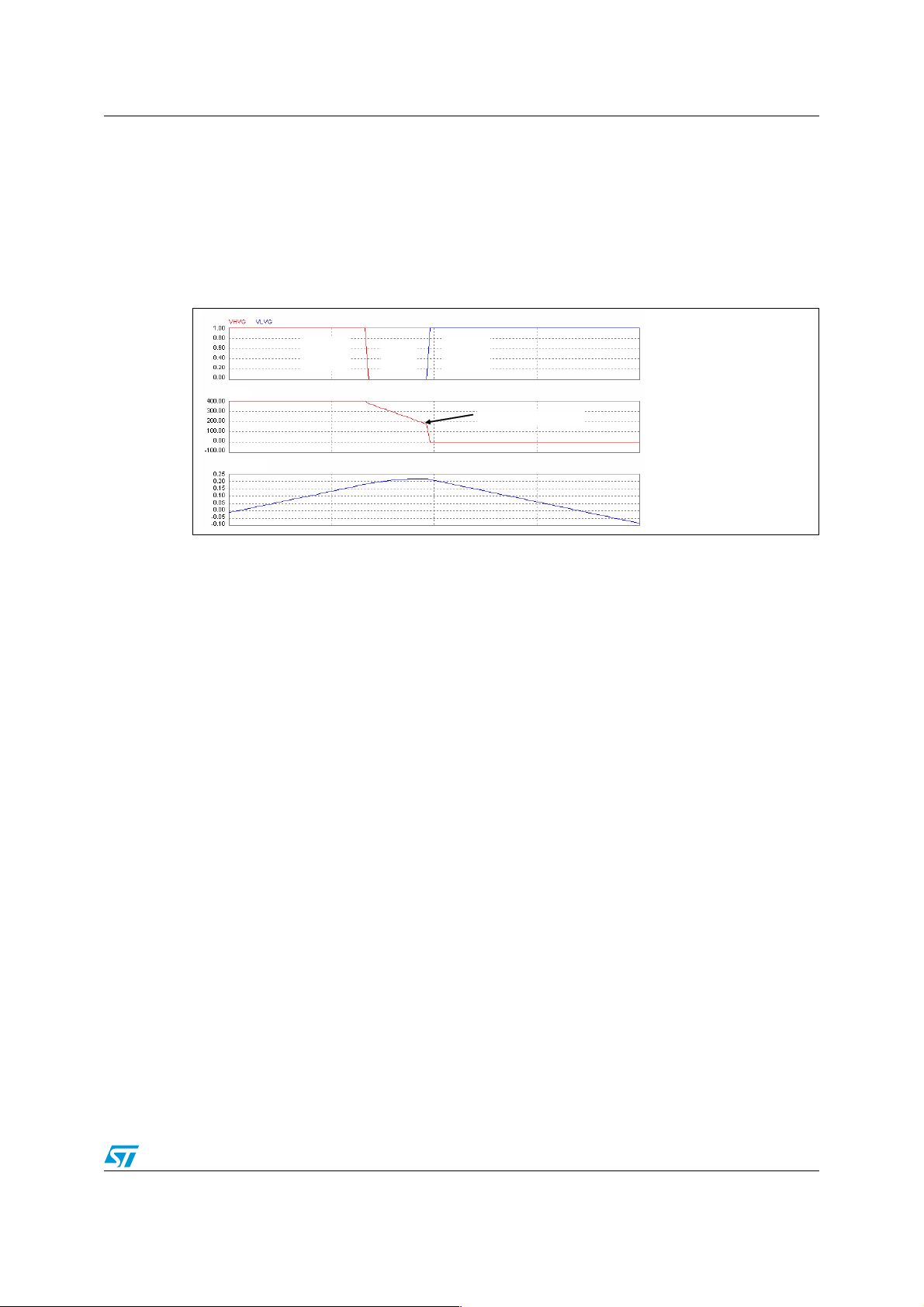
AN2644 The LLC resonant half-bridge converter

There is no body diode conduction and, consequently, no recovery. Q1 will be almost softswitched at turn-off, while Q2 will have capacitive losses at turn-on. It is true that the turn-on voltage is lower than V

, thus the associated energy of CHB is lower, but at no-load the

in

operating frequency is usually considerably higher than in the capacitive region, then these power losses may easily overheat Q1 and Q2. Finally, note in Figure 14 that I(Lp) is exactly superimposed on I

, then the secondary side of the transformer is open and CHB is

R

resonating with the total inductance Ls+Lp.

Figure 14. Bridge leg transitions under no-load conditions

V

HB

IRI(Lp)

Q1 ON

Q2 OFF

Q1 OFF

Q2 OFF

Q1 OFF

Q2 ON

Q2 is hard switched

VHB= Node HB voltage

IR= Tank circuit’s current

I(Lp) = Lp (magnetizing) current

From what we have seen we can conclude that the conditions in order for the half-bridge switches to achieve ZVS are:

1. Under heavy load conditions, as one switch turns off, the tank current must have the same sign as the impressed voltage and be large enough so that both the rail-to-rail transition of the node HB is completed and the current itself does not reverse before the end of the deadtime, when the other switch turns on.

2. With no-load, the tank current at the moment one switch turns off (which has definitely the same sign as the impressed voltage) must be large enough to complete the node HB transition within the deadtime, before the other switch turns on.

Both conditions can be translated into specifying a minimum current value I to be switched when either power MOSFET turns off. In general, different I

that needs

Rmin

values are

Rmin

needed to ensure ZVS at heavy load and at no-load. One can simply pick the greater one to ensure ZVS under any operating condition by design. On the other hand, this minimum required amount of current is to the detriment of efficiency.

At light or no-load a significant current must be kept circulating in the tank circuit, just to maintain ZVS, in spite of the current delivered to the load that is close to zero or zero. Using ac-analysis terminology, a certain amount of reactive energy is required even with no active energy.

Finally, also at heavy load the value of I

to be specified is the result of a trade-off. In fact,

Rmin

its value is directly related to the turn-off losses of both Q1 and Q2. The higher the switched current is, the larger the switching loss due to voltage-current overlap will be.

The discussion on the switching mechanism has been focused on the primary-side switches, and the conditions in order for them to achieve soft-switching (ZVS at turn-on, precisely) have been found. One important merit of the LLC resonant converter is that also the rectifiers on the secondary side are soft-switched. They feature zero-current switching (ZCS) at both turn-on and turn-off. In fact, at turn-on the initial current is always zero and ramps up with a relatively low di/dt, so that forward recovery does not come into play. At turn-off they become reverse biased when their forward current is already zero, so that their

19/64

The LLC resonant half-bridge converter AN2644

reverse recovery is not invoked. This topic will be addressed in Section 2.3, where it will be shown that this property is inherent in the topology, hence it occurs regardless of converter's design or operating conditions.

2.3 Fundamental operating modes

The LLC resonant half-bridge converter features a considerable number of different operating modes, which stem from its multiresonant nature. Essentially, the term "multiresonant" means that the configuration of the resonant tank may change within a single switching cycle. We have seen that there are two resonant frequencies, one (the higher) associated to either of the secondary rectifiers conducting, the lower one associated to both rectifiers non-conducting. Then, depending on the input-to-output voltage ratio, the output load and the characteristics of the resonant tank circuit, the secondary rectifiers can be always conducting (with the exception of a single point in time), which is referred to as CCM (Continuous Conduction Mode) like in PWM converters, or there can be finite time intervals during which neither of the secondary rectifiers is conducting. This will obviously be called a DCM (Discontinuous Conduction Mode) operating mode.

Different kinds of CCM and DCM operating modes exist, although not all of them can be seen in a given converter, some are not even recommended, like those associated with capacitive mode operation. However, in all CCM modes the parallel inductance Lp is always shunted by the load resistance reflected back to the primary side, so that it never participates in resonance, rather it acts as an additional load to the remaining LC resonant circuit. Similarly, in all DCM modes, there will be some finite time intervals where Lp, being no longer shunted from the secondary side, becomes part of resonance.

In the following we will consider four fundamental operating modes and use the nomenclature defined in [3]:

1. Operation at resonance, when the converter works exactly at f = f

2. Above-resonance operation, when the converter works at a frequency f > f

R1

;

. Moving

R1

away from resonance, we will consider three sub-modes:

a) CCMA operation at heavy load;

b) DCMA operation at medium load;

c) DCMAB operation at light load;

3. Below-resonance operation, when the converter works at a frequency f a load resistor R > R

. Moving away from resonance, we will consider two sub-modes:

crit

< f < fR1 with

R2

a) DCMAB operation at medium-light load;

b) DCMB operation at heavy load;

4. Below-resonance operation, when the converter works at a frequency f a load resistor R < R

(capacitive mode), corresponding to the CCMB operating mode

crit

< f < fR1 with

R2

defined in [3];

In addition, two extreme operating conditions will be considered:

1. No-load operation (cutoff)

2. Output short-circuit operation

It is interesting to point out that, unlike PWM converters where DCM operation is invariably associated to light load operation and CCM to heavy load operation, in the LLC resonant converter this combination does not hold.

20/64

AN2644 The LLC resonant half-bridge converter

To illustrate the above-mentioned operating modes we will refer to the reference converter shown in Figure 15. The discussion will start from the inspection of the main waveforms in a switching cycle, highlighting each subinterval where the circuit assumes a topological state and deducing the properties of the converter when operated in that mode from those waveforms. Half-bridge leg transitions are considered instantaneous. Their features have been already discussed.

Figure 15. Reference LLC converter for the analysis of the fundamental operating

modes

Q1

Driver

+

CTRL

I(Q1)I(Q1)

I(Q2)

Coss1

100 pF

IRI

Q2

R

Coss2

100 pF

22 nF

HB

Ls

200 uH

VcVc

Cr

I(Lp)

Lp

500 uH

8.33:1:1

D1

I(D1)

I(D2)

D2

Cout

24 Vdc

300W

VoutVout

Isolated

feedback

360 to 420

Vdc

VinVin

2.3.1 Operation at resonance (f = fR1)

In this operating mode it is possible to distinguish six fundamental time subintervals within a switching cycle, which are illustrated in Figure 16.

The first subinterval and, then, the instant t instant when, with Q1 conducting and Q2 open, the tank current I zero-crossing.

a) t

→ t1. Q1 is ON and Q2 is OFF. This is the "energy taking" phase, when current

0

flows from the input source to the tank circuit, so that energy is positive and both refills the resonant tank and supplies the load. The operating point of Q1 is in the first quadrant (current is flowing from drain to source). D2 is reverse-biased with a voltage -2·V leakage inductance L reflected back to the primary side and the voltage across it is fixed at a·V then, is not participating in resonance and Cr is resonating with Ls only. I portion of a sinusoid having a frequency f = f when Q1 is switched off at t=t decaying. Note that at t=t

b) t

→ t2. This is the deadtime during which both Q1 and Q2 are OFF. At t=t1

1

I(Q1)=I(Lp)=I swing from V to flow. The voltage across Lp reverses to -a·V changes sign. D2 starts conducting while D1 is reverse biased with a negative voltage approximately equal to 2·V shown). This phase ends when Q2 is switched on at t=t

c) t

→ t3. Q1 is OFF and Q2 is ON. At t=t2 IR is diverted from DQ2 to the R

2

Q2, so that no significant energy is lost during the turn-on transient. Note that now

(it is actually larger because of the contribution from the secondary

out

is greater than zero and provides the energy to let the node HB

R

to 0, so that the body diode of Q2, DQ2, is injected. This allows IR

in

). D1 is conducting, so Lp is shorted by the output load

L2

1

=I(Lp) and then I(D1)=0.

1 IR

can be chosen quite arbitrarily. We fix t0 as the

0

. During this phase, which ends

R1

has a positive-going

R

out

. Lp,

is a

R

, IR reaches its maximum value, after that it starts

and the slope of its current

out

(plus the contribution from LL2, here not

out

.

2

DS(on)

of

21/64

The LLC resonant half-bridge converter AN2644

the operating point of Q2 is in the third quadrant, current is flowing from the source to drain. D2 keeps on conducting and the voltage across Lp is -a·V is not participating in resonance and Cr is resonating with Ls only. I of a sinusoid having a frequency f = f

d) t

→ t4. Q1 is OFF and Q2 is ON. Tank circuit current, which is zero at t=t3

3

. This phase ends when IR=0 at t=t3.

R1

, so that Lp

out

is a portion

R

becomes negative. D1 is non-conducting and its reverse voltage is approximately 2·V

(plus the contribution from LL2, here not shown). Lp's current has a

out

negative slope, so the voltage across Lp must be negative. Since the diode D2 is conducting, this voltage will be equal to -a·V resonance, Cr is resonating with Ls only and I frequency f = f I

reaches its minimum value, after that it starts increasing. Note that at t=t4

R

I

=I(Lp) and then I(D2)=0.

R

e) t

→ t5. This is the deadtime during which both Q1 and Q2 are OFF. At t=t4

4

I(Q2)=-I(Lp)=-I swing from 0 to V

. During this phase, which ends when Q2 is switched off at t=t4,

R1

is greater than zero and provides the energy to let the node HB

R

, so that the body diode of Q1, DQ1, is injected. This allows IR

in

to flow back to the input source. The voltage across Lp reverses to a V

. Lp, then, is not participating in

out

is a portion of a sinusoid having a

R

and its

out

current slope changes sign. D1 starts conducting while D2 is reverse biased with a negative voltage approximately equal to 2·V here not shown). This phase ends when Q1 is switched on at t=t

(plus the contribution from LL2,

out

.

5

Figure 16. Operation at resonance (f = f

t0t

0

Q1 ON

Q2 OFF

): main waveforms

R1

t1t1t2t

t3t

2

3

Q1 OFF

Q2 ON

t5t

t6t

t4t

5

6

4

Q1 ON

Q2 OFF

I(D1) = D1 currentV(D1) = D1 anode voltageI(Q1) = Q1 currentIR = Tank circuit’s currentVHB = Node HB voltageHVG= Q1 gate

I(D2) = D2 currentV(D2) = D2 anode voltageI(Q2) = Q2 currentI(Lp) = Lp (magnetizing) currentVc = Resonant capacitor voltageLVG = Q2 gate

→ t6. Q1 is ON and Q2 is OFF. At t=t5 IR is diverted from DQ1 to the R

f) t

5

Q1, so that no significant energy is lost during the turn-on transient. Note that now the operating point of Q1 is in the third quadrant, current is flowing from the source to drain. This phase, along with the preceding one can be referred to as the "external energy recirculation phase": current is negative (coming out of the input terminal) despite that the impressed voltage is positive so that the input energy is

22/64

DS(on)

of

AN2644 The LLC resonant half-bridge converter

negative, i.e. it is returned to the input source. D1 keeps on conducting and the voltage across Lp is a·V resonating with Ls only. I This phase ends when I

, so that Lp is not participating in resonance and Cr is

out

is a portion of a sinusoid having a frequency f = fR1.

R

=0 at t=t6 and another switching cycle starts.

R

Remarks

1. Parallel inductor Lp never resonates and its current is essentially triangular (note: the real magnetizing current is sinusoidal and cannot be seen on the oscilloscope). The LLC converter, then, can be regarded as a series LC resonant half-bridge (composed by Ls and Cr) that supplies a reactive RL load (composed by Lp and R ac resistor loading the converter, as defined in [2] and reflected back to the primary side). This standpoint provides considerable insight into the operation of the converter, as shown in some of the following remarks.

2. In a resistively loaded series LC tank operating at resonance, the impressed voltage and the tank current are exactly in-phase, hence the switched current is zero and, thereby, ZVS cannot be achieved. The effect of adding an inductor (Lp) in parallel to the resistive load is to provide tank current with the phase shift (lagging) necessary to switch a current greater than zero, so that ZVS becomes now possible at resonance. As shown in the diagrams of Figure 16, the tank circuit current lags the impressed voltage by an angle ϕ equal to:

, the equivalent

ac

Equation 5

–

t

6t4

--------------

ϕ 2π

=

t

–

6t0

so that they have the same sign at half-bridge leg transitions. Furthermore, the switched currents I within the deadtimes (t

) and IR(t4) are large enough to complete the HB node swing well

R(t1

, t2) and (t4, t5) respectively. It is not difficult to recognize that

1

the angle ϕ is the phase of the input impedance of the loaded resonant tank evaluated at f=f

. Additionally, since the impedance of a series LC tank operating at resonance

R1

is zero, it is possible to state that the input impedance of the LLC resonant tank at resonance equals the impedance of the RL load.

3. Generally speaking, in a series LC tank operating at resonance, the voltage drop across L is equal in module and opposite in sign to the drop across C at all times (this is why its impedance is zero). In our specific case the drop across the series Cr-Ls will be zero, so that it is possible to write the following voltage balance equations:

Equation 6

V

in

------- -

V

=–

in

2

V

in

------- -– aV⋅

–=

2

aV⋅

out

Q1 ON, Q2 OFF

Q1 OFF, Q2 ON

both of them resulting in the following relationship:

Equation 7

V

in

------- - aV 2

This is a fundamental property of the LLC resonant half-bridge: operating at f=f

⋅=

out

R1

implies that input and output voltages fulfill (1) and, vice versa, if input and output voltages meet Equation 7 the converter is operating at f=f converter operates at resonance or not, for a given output voltage V

. Then, the fact that the

R1

and a given turn

out

23/64

The LLC resonant half-bridge converter AN2644

ratio a (n), depends only on the input voltage, not on the load and on the parameters of the resonant tank. From the design point of view, since V

and V

in

are specified, one

out

can decide the input voltage where to operate at resonance by choosing the turns ratio a. V

/2=a·V

in

considered as the 1:1 conversion ratio for the LLC resonant half-bridge.

out

4. The logical consequence of LLC converter's ability to operate at resonance independently of the output load is that the LLC resonant half-bridge can deliver any power if operated at resonance. This can be seen also in another way. As the impedance of the series Cr-Ls is zero, the RL load R

//Lp "sees" the impressed

ac

voltage directly or, in other words, it is supplied by an ideal voltage source. This is a "singularity" in LLC converter's operation, sometimes referred to as the "loadindependent" point, where the usual energy vs. frequency relationship does not hold. Actually, the inevitable voltage drops across the resistive elements of the real-world circuit (such as power MOSFETs' R

, winding resistance, secondary rectifier's

DS(on)

drop, etc.) cause a slight dependence of the frequency on the load. Note that this is a situation analog to that of CCM-operated PWM converters, where duty cycle is ideally independent of the load, in reality slightly dependent because of losses.

5. Energy is taken from the input source only from t for less than half the switching period, while from t

to t1, the "energy taking" phase, then

0

to t4 energy recirculates internally

1

to allow energy flow to the load while Q1 is not conducting. This low "duty cycle" of the input current can be a limiting factor in terms of power handling capability, especially if the input voltage is low. This consideration suggests the use of the half-bridge topology in high input voltage applications (e.g. with a PFC front-end, which provides a 400 V input rail). The natural improvement to this limitation is the full-bridge topology, where phase d) becomes active as well.

6. Tank circuit current lag ϕ originates the external energy recirculation phase from t

to t6

4

during which energy flow is negative (impressed voltage and input current have opposite signs). This energy subtracts to that drawn from the input during the energy taking phase a), hence reducing the net energy flow from the input source to the load each cycle. This energy can be regarded as reactive energy and cos ϕ as the input power factor. Making ϕ as small as possible (i.e. increasing Lp) would shorten the duration of the external energy recirculation phase and reduce the amount of reactive energy, thus improving the energy transfer process. This, however, would also reduce I

) and IR(t4), hence ϕ can be reduced as long as ZVS is maintained.

R(t1

7. Recalling that the current switched at turn-off by Q1, I

) and by Q2, IR(t4) determine

R(t1

their switching losses, it is straightforward that keeping ϕ to the minimum value that ensures ZVS of Q1 and Q2 provides an optimum design. Of course, component tolerance must be adequately accounted for, thus ϕ must be larger than the minimum required and the typical operation will be suboptimal.

8. The secondary rectifiers D1 and D2 start conducting as Q2 and Q1 turn-off respectively. The initial current is zero and also its di/dt is low, thus they have a soft turn-on. D1 and D2 cease to conduct exactly when Q1 and Q2 turn-off, respectively. These are also the moments when the voltages across D1 and D2 reverse. As a result, neither D1 nor D2 experience a voltage reversal while conducting a forward current. Reverse recovery, with all its adverse effects, does not occur. Note that, in this respect, this is a situation identical to that of a PWM converter operating on the boundary between CCM and DCM.

2.3.2 Operation above resonance (f > fR1)

In this operating mode the converter exhibits its usual frequency vs. load characteristic. We will consider three submodes where, in a closed-loop regulated system, CCM operation

24/64

AN2644 The LLC resonant half-bridge converter

progressively turns into DCM operation as the output load is reduced and frequency is moved away from resonance.

CCMA operation at heavy load

Also in this case it is possible to identify six fundamentals subintervals. The relevant waveforms are illustrated in the timing diagram of Figure 17. Again, t with Q1 conducting and Q2 open, the tank current I

a) t

→ t1. Q1 is ON and Q2 is OFF. This is the "energy taking" phase. It is identical

0

has a positive-going zero-crossing.

R

to the corresponding phase seen in the operation at resonance with the only difference that at the end of this phase, at t=t

b) t

→ t2. This is the deadtime during which both Q1 and Q2 are OFF. At t=t1 IR is

1

, it is still IR > I(Lp) and then I(D1)>0.

1

greater than zero and provides the energy to let the node HB swing from V so that the body diode of Q2, DQ2, is injected. This allows I changes to a higher negative value, so that it quickly approaches I(Lp), which is still increasing with the same slope. D1 conducts until I becomes reverse biased, with a negative voltage equal to 2·V contribution from L

, here not shown), I(Lp) slope changes sign and D2 starts

L2

conducting. This phase ends when Q2 is switched on at t=t Tz needed for I t=t

and not to the duration of the deadtime TD. Here it is Tz = TD just by chance.

1

to hit I(Lp) is related to their values at t=t1 and their slopes after

R

is the instant when,

0

to flow; IR slope

R

equals I(Lp), and then

R

(plus the

out

. Note that the time

2

in

to 0,

Figure 17. Operation above resonance (f > f

at heavy load

t0t

0

Q1 ON

Q2 OFF

): main waveforms in CCMA operation

R1

t1t1t2t

t3t

2

3

Q1 OFF

Q2 ON

t5t

t4t

t6t

5

6

4

Q1 ON

Q2 OFF

I(D1) = D1 currentV(D1) = D1 anode voltageI(Q1) = Q1 currentIR = Tank circuit’s currentVHB = Node HB voltageHVG= Q1 gate

I(D2) = D2 currentV(D2) = D2 anode voltageI(Q2) = Q2 currentI(Lp) = Lp (magnetizing) currentVc = Resonant capacitor voltageLVG = Q2 gate

c) t

→ t3. Q1 is OFF and Q2 is ON. At t=t2 IR is diverted from DQ2 to the R

2

Q2, so that no significant energy is lost during the turn-on transient. This phase, which ends when I

=0 at t=t3, is identical to the (t2, t3) phase of the operation at

R

resonance.

DS(on)

25/64

of

The LLC resonant half-bridge converter AN2644

d) t3 → t4. Q1 is OFF and Q2 is ON. It is identical to the phase (t3, t4) seen in the

operation at resonance with the only difference that at the end of this phase, at t=t

, it is still IR < I(Lp) and then I(D2)>0.

4

e) t

→ t5. This is the deadtime during which both Q1 and Q2 are OFF. At t=t4 IR is

4

(in absolute value) greater than zero and provides the energy to let the node HB swing from 0 to V to flow back to the input source. I

, so that the body diode of Q1, DQ1, is injected. This allows IR

in

changes to a higher slope, so that it quickly

R

approaches I(Lp), which is still decreasing with the same slope. D2 conducts until I

equals I(Lp), after that it becomes reverse biased, with a negative voltage

R

approximately equal to 2·V

(plus the contribution from LL2, here not shown),

out

I(Lp) slope changes sign and D1 starts conducting. This phase ends when Q1 is switched on at t=t equal to T

f) t

→ t6. Q1 is ON and Q2 is OFF. At t=t5 IR is diverted from DQ1 to the R

5

as shown.

D

. Again, the time Tz needed for IR to hit I(Lp) is only by chance

5

DS(on)

of Q1, so that no significant energy is lost during the turn-on transient. This phase, which ends when I

=0 at t=t6, is identical to the (t5, t6) phase of the operation at

R

resonance.

Remarks

1. In this "above-resonance" CCM submode the parallel inductor Lp never resonates and the LLC converter can be regarded as a series LC resonant half-bridge supplying a reactive RL load.

2. As shown in the diagrams of Figure 17, the tank circuit current lags the impressed voltage by an angle ϕ equal to:

Equation 8

t6t4–

--------------

=

ϕ 2π

t

–

6t0

so that they have the same sign at half-bridge leg transitions. Furthermore, the switched currents I within the deadtimes (t impedance of the loaded resonant tank evaluated at f=f

) and IR(t4) are large enough to complete the HB node swing well

R(t1

, t2) and (t4, t5) respectively. Still ϕ is the phase of the input

1

, but now since the

R1

impedance of the series LC tank is no longer zero, it is different from the impedance of the RL load.

3. In the series Cr-Ls tank circuit operating above resonance the voltage drop across it is positive (the inductive reactance is larger in module than the capacitive reactance), i.e. the plus sign is located on the side of the node HB. The obvious conclusion is that:

Equation 9

V

in

out

------- -

<⋅

2

aV

Then, when operating above resonance, for a given input voltage the LLC resonant half-bridge will provide an output voltage lower than that available at resonance and vice versa, with a given output voltage the LLC resonant half-bridge will operate above resonance with an input voltage greater than 2·n·V

. In this case the conversion ratio,

out

intended as previously mentioned is < 1, then the LLC is said to have a "step-down" or "buck" characteristic when operating above resonance.

4. When operating above resonance, the Thevenin-equivalent schematic of the LLC resonant tank as seen by the load has finite impedance (no more zero as when operating at resonance). When the load current increases, for a given frequency (open-

26/64

AN2644 The LLC resonant half-bridge converter

loop operation) the voltage conversion ratio diminishes. For a given V

(closed-loop

out

operation) operating frequency needs to get back closer to resonance.

5. The secondary rectifiers D1 and D2 start conducting as Q1 and Q2 turn-on respectively. The initial current is zero and also its di/dt is low, thus they have a soft turn-on. D1 and D2 cease to conduct when tank circuit's current I I(Lp). The transformer's secondary current is a·[I

-I(Lp)], then the equality IR = I(Lp)

R

equals Lp's current

R

means that the secondary rectifiers current is zero as well. Unlike when operating at resonance, this does not happen synchronously with the half-bridge leg transitions (I

< I(Lp) at t=t1 and IR > I(Lp) at t=t4). However as the leg transition occurs IR and

R

I(Lp) are "forced" to become equal, then the current of the conducting diode goes to zero. The physical reason for that is the presence of Ls. When there is a transition of the half-bridge leg the resulting voltage change is not immediately directly impressed on the transformer (C can be considered as a short circuit during transitions, i.e. the voltage across it can be considered constant) but falls across Ls that acts as a "shock absorber". This leaves I(Lp) unchanged but pushes I

towards I(Lp), forcing a rate of

R

change that is approximately:

Equation 10

⎧⎫

Vc a V

⋅+

Only when I

Ls

out

⋅+

out

⎪⎪

dI

R

--------

dt

equals I(Lp) and no current is flowing through the secondary rectifier

R

-------------------------------- -–

⎪⎪

≈

⎨⎬

Vc– aV

V

⎪⎪

in

---------------------------------------------- -

⎪⎪ ⎩⎭

t ∈

t ∈(t

(t1, t2)

, t5)

4

previously conducting can the voltage across the primary winding of the transformer reverse and hence also the voltage across the secondary rectifiers. In the end, also in this case they are reverse-biased only when their current has gone to zero, thus ensuring ZCS.

Figure 18. Operation above resonance (f > f

at medium load

t

t0t

0

Q1 ON

Q2 OFF

t1t

t1t1t2t

t

t4t

t

t3t

4

2

3

2

3

Q1 OFF

Q2 ON

): main waveforms in DCMA operation

R1

t

t6t

t

t5t

6

5

t

t7t

t8t

7

8

7

8

Q1 ON

Q2 OFF

I(D1) = D1 currentV(D1) = D1 anode voltageI(Q1) = Q1 currentIR = Tank circuit’s currentVHB = Node HB voltageHVG= Q1 gate

I(D2) = D2 currentV(D2) = D2 anode voltageI(Q2) = Q2 currentI(Lp) = Lp (magnetizing) currentVc = Resonant capacitor voltageLVG = Q2 gate

27/64

The LLC resonant half-bridge converter AN2644

DCMA at medium load

In this "above-resonance" DCM submode it is possible to identify eight fundamentals subintervals. The relevant waveforms are illustrated in the timing diagram of Figure 18.

Two new subintervals, namely (t bridge leg transitions (t

, t2), (t5, t6), respectively. The other six phases are exactly identical

1

, t3) and (t6, t7), appear just after the deadtimes of the half-

2

to those of the CCM above-resonance mode.

a) t

→ t3. Q1 is OFF and Q2 is ON. At t=t2 IR is diverted from DQ2 to the R

2

DS(on)

Q2, so that no significant energy is lost during the turn-on transient. Note that the operating point of Q2 is in the third quadrant, current is flowing from the source to drain. D1 is nonconducting but the voltage across the secondary windings is still too low to let D2 conduct, then still I frequency f = f

b) t

→ t7. Q1 is ON and Q2 is OFF. At t=t6 IR is diverted from DQ1 to the R

6

. This phase ends when D2 starts conducting at t=t3.

R2

= I(Lp) is a portion of a sinusoid having a

R

DS(on)

Q1, so that no significant energy is lost during the turn-on transient. Note that the operating point of Q1 is in the third quadrant, current is flowing from the source to drain. D2 is nonconducting but the voltage across the secondary windings is still too low to let D1 conduct, then still I frequency f = f

. This phase ends when D1 starts conducting at t=t7.

R2

= I(Lp) is a portion of a sinusoid having a

R

Remarks

1. In this "above-resonance" DCM submode the multiresonant nature of the LLC converter shows up. In a switching cycle there are two time intervals just after bridgeleg transitions during which no current is flowing on the secondary side (hence this is DCM operation), then the entire transformer's primary inductance Ls+Lp resonates and the second resonance frequency f the resonant current I

is still slightly greater than I(Lp) in absolute value, so it takes a

R

very small portion of the deadtimes for the two currents to equal each other. Then, the first one starts as I starts slightly after t

equals I(Lp) slightly after t1 and ends at t= t3. The second one

R

and ends at t= t7.

5

2. As shown in the diagrams of Figure 18, the tank circuit current is still lagging the impressed voltage, so that they have the same sign at half-bridge leg transitions. Furthermore, the switched currents I HB node swing well within the deadtimes (t compared to CCM mode, the duration of the energy taking phase (t external recirculation phase is longer and the displacement angle ϕ:

appears. At the transitions of the half-bridge leg

R2

) and IR(t5) are large enough to complete the

R(t1

, t2) and (t5, t6) respectively. However, as

1

, t1) is shorter, the

0

of

Equation 11

gets close to π/2. Using ac terminology, the active energy is lower and the reactive energy is higher.

3. The secondary rectifiers D1 and D2 start conducting during the conduction period of Q1 and Q2, respectively. Both the initial current and also its di/dt are zero, thus they have a soft turn-on. D1 and D2 cease to conduct when tank circuit's current I Lp's current I(Lp). In this case this is almost synchronous with either switch turn-off. Again, only when I

equals I(Lp) and no current is flowing through the secondary

R

rectifier previously conducting can the voltage across the primary winding of the transformer reverse and hence also the voltage across the secondary rectifiers. In the

28/64

=

ϕ 2π

t8t6–

--------------

t

–

8t0

equals

R

AN2644 The LLC resonant half-bridge converter

end, also in this case they are reverse-biased only when their current has gone to zero, thus ensuring ZCS.

4. Essentially, the reason why D2 does not conduct during (t (t

, t7) is that the voltage across the transformer (given by Vin - Vc) is not large enough

6

, t3) and D1 does not during

2

so that the voltage developed across Lp (given by the inductive divider ratio Lp/(Ls+Lp)) and reflected to the secondary side can forward-bias D2 or D1. In formulae, this is expressed as:

Equation 12

Lp

Vint() Vc t()–()

------------------- -

Ls Lp+

aV

⋅≤

out

DCMAB at light load

In this "above-resonance" DCM sub-mode it is possible to identify ten fundamental subintervals. The relevant waveforms are illustrated in the timing diagram of Figure 19.

Two more new subintervals, namely (t half-bridge leg transitions (t

, t3), (t7, t8), respectively. The remaining eight phases are

2

, t2), (t6, t7) appear just before the deadtimes of the

1

exactly identical to those of the DCMA above-resonance mode.

a) t

→ t2. Q1 is ON and Q2 is OFF. At t=t1 IR equals I(Lp) and then I(D1) becomes

1

zero before Q1 turns off at t=t During this interval the Equation 12 is met and the current I a sinusoid having a frequency f = f

b) t

→ t7. Q1 is OFF and Q2 is ON. At t=t6 IR equals I(Lp) and then I(D2) becomes

6

zero before Q2 turns off at t=t During this interval the Equation 12 is met and the current I a sinusoid having a frequency f = f

, when this phase ends, and remains zero until t=t2.

2

.

R2

, when this phase ends, and remains zero until t=t7.

7

.

R2

= I(Lp) is a portion of

R

= I(Lp) is a portion of

R

Remarks

1. The transition between this DCMAB mode and the previous DCMA is marked by the I

= I(Lp) condition occurring exactly at t = t1 of Figure 18.

R

2. In this "above-resonance" DCM submode, in a switching cycle there are two time intervals (t is DCM operation) and then the entire transformer's primary inductance Ls+Lp resonates and f appear at the beginning and the end.

3. As shown in the diagrams of Figure 19, the tank circuit current is still lagging the impressed voltage, so that they have the same sign at half-bridge leg transitions. Furthermore, the switched currents I HB node swing well within the deadtimes (t to DCMA mode, the duration of the energy taking phase (t external recirculation phase is longer and the displacement angle ϕ:

, t4), (t6, t9) during which no current flows on the secondary side (hence this

1

appears. Considering each half-cycle, nonconductive intervals

R2

) and IR(t6) are large enough to complete the

R(t2

, t3) and (t7, t8) respectively. As compared

2

, t1) is even shorter, the

0

Equation 13

t10t8–

-----------------

ϕ 2π

=

t

10t0

–

is even closer to π/2. Most of the energy in the tank circuit is reactive.

4. As to the secondary rectifiers, they start conducting during the conduction period of Q1 and Q2, respectively. Both the initial current and also its di/dt are zero, thus they have a

29/64

The LLC resonant half-bridge converter AN2644

soft turn-on. They cease to conduct before the transitions of the half-bridge. The operation is DCM, then ZCS occurs by definition.

Figure 19. Operation above resonance (f > f

operation at light load

t0t

0

Q1 ON

Q2 OFF

t1t1t3t

t4t

t2t

4

2

3

Q1 OFF

Q2 ON

): main waveforms in DCMAB

R1

t5t

5

t6t6t8t8t9t

t7t

7

t10t

9

10

Q1 ON

Q2 OFF

I(D1) = D1 currentV(D1) = D1 anode voltageI(Q1) = Q1 currentIR = Tank circuit’s currentVHB = Node HB voltageHVG= Q1 gate

I(D2) = D2 currentV(D2) = D2 anode voltageI(Q2) = Q2 currentI(Lp) = Lp (magnetizing) currentVc = Resonant capacitor voltageLVG = Q2 gate

2.3.3 Operation below resonance (fR2 < f < fR1, R>R

In this operating mode the converter still exhibits its usual frequency vs. load characteristic. We will consider two submodes where, in a closed-loop regulated system, DCM operation gets deeper and deeper as the output load is increased and frequency is moved away from resonance.

DCMAB at medium-light load

This "below-resonance" DCM submode is exactly equal to the above-resonance DCMAB submode previously considered. The waveforms are shown in Figure 20 and it is possible to see that they match those shown in Figure 19.

Note only that in this case the condition I power level than in the case of the above-resonance DCMAB submode (2:1 in the example shown).

DCMB at heavy load

This "below-resonance" DCM submode, which is unique to below resonance operation, actually comprises two submodes (DCMB2 & DCMB1) as frequency goes away from resonance. Their waveforms do not differ much, only those of DCMB2 will be shown. It is possible to identify eight fundamentals

= I(Lp) at t=t1 occurs at a considerably higher

R

subintervals and the relevant waveforms are

crit

)

30/64

AN2644 The LLC resonant half-bridge converter

illustrated in the timing diagram of Figure 21. Again, t0 is the instant when, with Q1 conducting and Q2 open, the tank current I

has a positive-going zero-crossing.

R

Figure 20. Operation below resonance (f

DCMAB operation

t

t0t

0

Q2 OFF

Q1 ON

t

t2t

t

t1t

2

1

< f < fR1 , R>R

R2

t

t4t

t

t3t

3

t

t5t

4

5

Q1 OFF

Q2 ON

): main waveforms in

crit

t

t8t

t

t6t

t8t8t9t

t7t

6

7

6

7

9

Q1 ON

Q2 OFF

I(D1) = D1 currentV(D1) = D1 anode voltageI(Q1) = Q1 currentIR = Tank circuit’s currentVHB = Node HB voltageHVG= Q1 gate

I(D2) = D2 currentV(D2) = D2 anode voltageI(Q2) = Q2 currentI(Lp) = Lp (magnetizing) currentVc = Resonant capacitor voltageLVG = Q2 gate

t

t10t

10

→ t1. Q1 is ON and Q2 is OFF. This is the "energy taking" phase, when current

a) t

0

flows from the input source to the tank circuit, so that energy is positive. The operating point of Q1 is in the first quadrant (current is flowing from drain to source). D2 is nonconducting and its reverse voltage is approximately 2·V the contribution from L voltage across Lp is a V resonating with Ls only. I During this phase, which ends when I

, here not shown). D1 is conducting as well, so the

L2

. Lp, then, is not participating in resonance and Cr is

out

is a portion of a sinusoid having a frequency f = fR1.

R

equals I(Lp) and, then, I(D1)=0 at t=t1, IR

R

reaches its maximum value, after that it starts decaying.

b) t

→ t2. Q1 is ON and Q2 is OFF. At t=t1 I(D1) becomes zero and IR equals I(Lp),

1

that is before the conduction time of Q2 ends. Both D1 and D2 are nonconducting and Lp, no longer shunted by the load reflected to the primary side, goes effectively in series to Ls and participates to resonance. I sinusoid having a frequency f = f

. Depending on the tank circuit's parameters

R2

is a portion of a

R

and on the operating conditions, this portion can be similar to a straight line, as shown in the diagrams of Figure 21. This phase ends when Q1 is switched off at t=t

.

2

c) t

→ t3. This is the deadtime during which both Q1 and Q2 are OFF. At t=t2

2

I(Q1)=I(Lp)=I swing from V allows I

is greater than zero and provides the energy to let the node HB

R

to ground, so that the body diode of Q2, DQ2, is injected. This

in

to flow. The voltage across Lp reverses to -a·V

R

. D2 starts conducting

out

while D1 is reverse biased with a negative voltage approximately equal to 2·V

out

(plus

out

31/64

The LLC resonant half-bridge converter AN2644

(plus the contribution from LL2, not shown here). This phase ends when Q2 is switched on at t=t

d) t

→ t4. Q1 is OFF and Q2 is ON. At t=t3 IR is diverted from DQ2 to the R

3

.

3

of

DS(on)

Q2, so that no significant energy is lost during the turn-on transient. Note that now the operating point of Q2 is in the third quadrant, current is flowing from the source to drain. D2 keeps on conducting and the voltage across Lp is -a·V is not participating in resonance and Cr is resonating with Ls only. I a sinusoid having a frequency f = f

. This phase ends when IR=0 at t=t4.

R1

, so that Lp

out

is a portion of

R

Figure 21. Operation below resonance (f

DCMB2 operation

t

t0t

0

Q1 ON

Q2 OFF

t

t2t

t

t3t

t

t3t

t1t

t3t3t4t

2

1

< f < fR1, R>R

R2

4

Q1 OFF

Q2 ON

): main waveforms in

crit

t

t7t

t

t5t

5

t

t7t

t

t7t7t6t

t8t

6

8

6

8

6

8

Q1 ON

Q2 OFF

I(D1) = D1 currentV(D1) = D1 anode voltageI(Q1) = Q1 currentIR = Tank circuit’s currentVHB = Node HB voltageHVG= Q1 gate

I(D2) = D2 currentV(D2) = D2 anode voltageI(Q2) = Q2 currentI(Lp) = Lp (magnetizing) currentVc = Resonant capacitor voltageLVG = Q2 gate

→ t5. Q1 is OFF and Q2 is ON. The tank circuit current, which is zero at t=t4

e) t

4

becomes negative. D1 is nonconducting and its reverse voltage is approximately 2·V

(plus the contribution from LL2, here not shown). Lp's current has a

out

negative slope, so the voltage across Lp must be negative. Since the diode D2 is conducting this voltage will be equal to -a·V resonance, Cr is resonating with Ls only and I frequency f = f thereby, I(D2) is zero at t=t

. During this phase, which ends when IR equals I(Lp) and,

R1

15. IR

increasing.

f) t

→ t6. This phase mirrors (t1, t2). At t=t5 I(D2) becomes zero and IR equals I(Lp),

5

that is before the conduction time of Q1 ends. Both D1 and D2 are nonconducting and Lp, no longer shunted by the load reflected to the primary side, goes effectively in series to Ls and participates to resonance. I sinusoid having a frequency f = f t=t

.

6

32/64

. Lp, then, is not participating in

out

is a portion of a sinusoid having a

R

reaches its minimum value, after that it starts

is now a portion of a

. This phase ends when Q2 is switched off at

R2

R

AN2644 The LLC resonant half-bridge converter

g) t6 → t7. This is the deadtime during which both Q1 and Q2 are OFF. At t=t6

I

= I(Lp) is (in absolute value) greater than zero and provides the energy to let the

R

node HB swing from 0 to V allows I V

out

to flow back to the input source. The voltage across Lp reverses to a

R

, D1 starts conducting while D2 is reverse biased with a negative voltage approximately equal to 2·V This phase ends when Q1 is switched on at t=t

h) t

→ t8. Q1 is ON and Q2 is OFF. At t=t7 IR is diverted from DQ1 to the R

7

, so that the body diode of Q1, DQ1, is injected. This

in

(plus the contribution from LL2, here not shown).

out

.

7

DS(on)

of Q1, so that no significant energy is lost during the turn-on transient. Note that now the operating point of Q1 is in the third quadrant, current is flowing from the source to drain. This phase, along with the preceding one is the "external energy recirculation phase": current is negative (coming out of the input terminal) despite that the impressed voltage is positive so that the input energy is negative, i.e. it is returned to the input source. D1 is still conducting and the voltage across Lp is a V

, so that Lp is not participating in resonance anymore and Cr is resonating with

out

Ls only. I ends when I

is again a portion of a sinusoid having a frequency f = fR1. This phase

R

=0 at t=t8 and another switching cycle begins.

R

Remarks

1. Also in this "below-resonance" DCM submode the multiresonant nature of the LLC converter shows up. From t open and the second resonance frequency f advantages of the LLC resonant converter over the traditional LC series-resonant converter. In fact it helps keep operation away from capacitive mode. Although the tank circuit current I

lags the impressed voltage (being R>R

R

have the same sign at half-bridge leg transitions, the switching period is longer than the resonant period,1/f

. Then IR, which is decaying (in absolute value), might come close

R1

to zero or even reverse if it still evolved according to the same sinusoid at frequency f=f

(see the extrapolated black lines drawn in (t1, t2) and (t5, t6)). This lower frequency

R1

sinusoid "holds up" the tank current, hence ensuring that the switched currents I and I

) do not change sign and have amplitude large enough to complete the HB

R(t6

node swing well within the deadtimes (t

2. In the series LC tank Ls-Cr operating below resonance with R>R across the L-C series is negative (the capacitive reactance is larger in module than the inductive reactance), i.e. a minus sign is located at the node HB. As a result:

to t2 and from t5 to t6 the secondary rectifiers are both

1

2

appears. This is one of the fundamental

R2

by assumption) so that they

crit

, t3) and (t6, t7) respectively, i.e. ZVS.

the voltage drop

crit

R(t2

)

Equation 14

V

in

------- -

out

>⋅

2

aV

Then, when operating below resonance, for a given input voltage, the LLC resonant half-bridge will provide an output voltage higher than that available at resonance, and vice versa, with a given output voltage the LLC resonant half-bridge will operate below a resonance if the input voltage is lower than 2·V

. In other words, the conversion

out

ratio, intended as previously mentioned, is > 1, then the LLC is said to have a "step-up" characteristic when operating below resonance.

3. The secondary rectifiers D1 and D2 start conducting when Q2 and Q1 are switched off, respectively. The initial current is zero and its di/dt is low, thus they have a soft turn-on.

33/64

The LLC resonant half-bridge converter AN2644

They cease to conduct before the transitions of the half-bridge. The operation is DCM, then ZCS occurs by definition.

4. Essentially, the reason why D2 does not conduct during (t (t

, t6) is that during these subintervals the condition expressed by Equation 12 is met.

5

5. The waveforms in DCMB1 are very similar, only the portion of sinusoid at f = f to zero more quickly. While DCMB2 is characterized by the duration of the intervals (t t

) and (t5, t6) that gets longer as frequency is reduced, in DCMB1 the duration of these

2

, t2) and D1 does not during

1

decays

R2

1

intervals starts decreasing quite rapidly to reach zero at the boundary with capacitive mode operation. The "border belt" adjacent to the capacitive region is included in the region where DCMB1 occurs, thus it can be a good design practice to limit the operation of the converter to the DCMB1-DCMB2 boundary.

,

2.3.4 Capacitive-mode operation below resonance (fR2 < f < fR1, R<R

In this operating mode, unique to below-resonance operation and corresponding to the CCMB operating mode defined in [3], it is possible to distinguish six fundamental time subintervals within a switching cycle, as illustrated in the timing diagrams of Figure 22.

In this case it is convenient to define t

a) t

→ t1. The tank current IR(t0) as Q1 is switched on is already positive: this

0

means that in the just finished deadtime it was flowing through the body diode of Q2, DQ2. Actually, this is confirmed by the voltage V which was previously zero and is abruptly pulled up to V large dv/dt. The body diode DQ2 is then reverse-recovered and a large current spike flows through Q1 and DQ2 until the latter recovers completely. Functionally this is similar to a cross-conduction of the half-bridge leg. Very high di/dt may occur and, as a result, large voltage spikes are generated across the parasitic inductances experiencing this large di/dt. The voltage V positive overshoots. During this phase when energy is taken from the input source, the tank current reaches its maximum value and then decays. The phase ends

b) t

when I

1

=I(Lp) and, then, I(D1)=0 at t=t1.

R

→ t2. Unlike what happens in the below-resonance DCMB2 submode, where there was insufficient voltage across the resonant capacitor to forward-bias D2, here Vc is much larger and D2 starts conducting immediately at t=t decreasing, becoming lower than I(Lp) and eventually crosses zero before Q1 turns off, which marks the end of the this phase at t=t

c) t

→ t3. This is the deadtime during which both Q1 and Q2 are OFF. During this

2

phase I

is already negative and further decreasing. Since Q1 is off, it is flowing

R

through DQ1. Note that the voltage of the half-bridge midpoint V change. This phase ends when Q2 turns on at t=t

as the instant when Q1 is switched on.

0

of the half-bridge midpoint

HB

exactly at t=t0 with a

in

may have large

HB

.

2

.

3

HB

. IR starts

1

does not

crit

)

34/64

AN2644 The LLC resonant half-bridge converter

Figure 22. Capacitive mode operation below resonance (fR2 < f < fR1, R<R

waveforms

t0t

0

Q1 ON

Q2 OFF

t1t

1

t2t

t3t

2

3

Q1 OFF

Q2 ON

t4t

t5t5t

4

I(D1) = D1 currentV(D1) = D1 anode voltageI(Q1) = Q1 currentIR = Tank circuit’s currentVHB = Node HB voltageHVG= Q1 gate

I(D2) = D2 currentV(D2) = D2 anode voltageI(Q2) = Q2 currentI(Lp) = Lp (magnetizing) currentVc = Resonant capacitor voltageLVG = Q2 gate

crit

6

): main

d) t

→ t4. The tank current IR(t3) as Q2 is switched on is already negative and

3

flowing through the body diode of Q1, DQ1. The voltage of the half-bridge midpoint, V

, is abruptly pulled down to ground at t=t3 with a large dv/dt. The

HB

body diode DQ1 is then reverse-recovered and a large current spike flows through Q2 and DQ1 until the latter recovers completely. Again there is a condition functionally equivalent to a cross-conduction of the half-bridge leg. Very high di/dt may occur and, as a result, large voltage spikes are generated across the parasitic inductances experiencing this large di/dt. The voltage V

may have large

HB

negative undershoots. During this phase energy is internally recirculated, the tank current reaches its minimum value and then increases. The phase ends when I

=I(Lp) and, then, I(D2)=0 at t=t4.

R

e) t

→ t5. This phase mirrors exactly (t1, t2). The voltage across the resonant

4

capacitor is so large that D1 is forward-biased and, thereby, starts conducting immediately at t=t

. IR starts increasing, becoming higher than I(Lp) and

4

eventually crosses zero before Q2 turns off, which marks the end of this phase at t=t

.

5

f) t

→ t6. This is the deadtime during which both Q1 and Q2 are OFF. During this

5

phase I DQ2. Note again that the voltage of the half-bridge midpoint V change. This phase ends when Q2 turns on at t=t

is already positive and increasing. Since Q2 is off, it is flowing through

R

and another switching cycle

3

does not

HB

begins.

35/64

The LLC resonant half-bridge converter AN2644

Remarks

1. In the below-resonance capacitive mode operation, since current is continuously flowing on the secondary side, this is a CCM mode (as already stated, it corresponds to the CCMB mode defined in [3].

2. The physical reason of this CCMB operation is, as previously pointed out, the large voltage developed across the resonant capacitor. A large energy level must be circulating in the tank circuit and this is consistent with R<R capacitive mode to take place. Capacitive operating mode is then likely to occur under heavy load, overload or short circuit conditions and appropriate countermeasures must be taken to handle this.

3. Note that in all the inductive modes the absolute value of the switched currents (i.e. the current I

when either power MOSFET is switched off) is always greater than (in CCM

R

mode above resonance) or equal to (in all DCM modes) the current I(Lp). In the capacitive mode, instead, the absolute value of the switched currents is lower than that in Lp. This consideration is useful when analyzing the transitions of the node HB.

4. Unlike the other modes, in capacitive mode the secondary rectifiers D1 and D2 start conducting during the conduction period of Q2 and Q1, respectively. The initial current is zero and its di/dt is low, thus they have a soft turn-on. Also in this case the voltage across the secondary rectifiers reverses as a result of their currents going to zero. Then, ZCS is maintained even under these conditions and it is possible to conclude that the secondary rectifiers are soft-switched at both turn-on and turn-off under all operating conditions and that this property is inherent in the topology. In fact no assumption has been made about the tank circuit's parameters.

condition in order for the

crit

Figure 23. No-load operation (cutoff): main waveforms

t

t0t

0

Q1 ON

Q2 OFF

t1t

t1t1t2t

t

Q1 OFF

Q2 ON

t3t

3

2

t

t4t

4

t

t5t

5

Q1 ON

Q2 OFF

t

t6t

6

I(D1) = D1 currentV(D1) = D1 anode voltageI(Q1) = Q1 currentIR = Tank circuit’s currentVHB = Node HB voltageHVG= Q1 gate

I(D2) = D2 currentV(D2) = D2 anode voltageI(Q2) = Q2 currentI(Lp) = Lp (magnetizing) currentVc = Resonant capacitor voltageLVG = Q2 gate

36/64

AN2644 The LLC resonant half-bridge converter

2.4 No-load operation

The ability to operate under no-load conditions is another peculiar characteristic of the LLC resonant half-bridge converter. The typical waveforms in this operating mode, called also "cutoff" mode, which can occur at frequencies both above, below and at the resonant frequency f

Note that it is I by portions of sinusoid at f=f this operation to occur, the voltage developed across Lp and reflected to the secondary side has to be lower than the output voltage throughout the entire switching cycle, so that either secondary rectifier cannot be forward-biased. In other words, Equation 12 has to be met for t ∈(t

, t6). The ability of the converter to operate with no-load can be easily deducted by

0

Equation 12 itself. However big the peak value of V

zero, it is possible to find a value of Lp that meets condition (α). In the end, no-load operation is not an intrinsic property of the LLC resonant converter (like ZCS for the secondary rectifiers) but it can be achieved with an appropriate design of the tank circuit.

, as demonstrated in [3], are illustrated in the timing diagrams of Figure 23.

R1

=I(Lp), then I(D1)=I(D2)=0, throughout the entire switching cycle. IR is made

R

, but looks very much like a triangular waveform. In order for

R2

(t)-Vc(t) is and provided a·V

in

out

is not

The difference with respect to the LC series resonant converter is apparent. If Lp →

∞ the

LLC converter turns into the LC one but Vc → 0 because there is no current through the resonant tank and the only possible equilibrium condition is V

= a·V

in

. If the input and

out

output voltage have a different ratio, output voltage regulation will be impossible.

Seen from a different standpoint, under no load conditions and at a frequency considerably higher than f

, the resonant capacitor Cr "disappears" (Vc(t) ≈ Vin/2) and the output voltage

R1

is given by the inductive divider made up by Ls and Lp as shown by the equivalent circuit of

Figure 24. Then, if the voltage conversion ratio is greater than the inductive divider ratio,

regulation will be possible at some finite frequency, otherwise it will not be. From Equation

12, substituting V

= Vin and, then, Vc(t) = Vin/2, it is possible to find a necessary condition

in(t)

in order for the converter to be able to regulate at zero load:

Equation 15

aV

≤

⋅

------------------ -

2

V

out

in

Lp

------------------- -

Ls Lp+

Lp, then, plays a key role. It not only makes zero load operation possible but allows softswitching under these conditions too, as already discussed. The price to pay for that is the considerable tank current I

=I(Lp) circulating in the circuit and illustrated in Figure 23. This

R

circulation is not lossless. Power is dissipated in power MOSFET, the resonant capacitor and the transformer.

This prevents the LLC resonant converter from achieving extremely low input power levels at no load, unless appropriate countermeasures are taken. The most effective way to reduce no-load consumption to a very low level is to let the converter operate intermittently ("burstmode" or "pulse-skipping" operation). In this way, the average value of the tank current can be reduced at an almost negligible value. Furthermore, the average switching frequency will be considerably lowered thus minimizing the residual turn-off switching losses.

2.5 Overload and short circuit operation

The equivalent schematic of the converter under short circuit conditions is illustrated in

Figure 25. The inductance Lp is actually shunted by an extremely low impedance, so that

the LLC circuit reduces to a series LC circuit. The transformer will work as a "current transformer", so that the output current will be a times the primary (input) current Iin. It is

37/64

The LLC resonant half-bridge converter AN2644

intuitive that the impedance of the Ls-Cr resonant tank plays a key role. Note that this impedance becomes zero at f = f

. Two cases will be considered:

R1

1. The converter always works above resonance (some means is provided to bottom-limit the operating frequency at a value f output voltage regulated, will reduce the switching frequency to the minimum value f

> fR1). The control loop, in the attempt to keep the

m

In this case the converter still operates in the inductive region (CCM submode) and ZVS is ensured. However, the impedance of the Ls-Cr tank circuit can be very low and then the current Iin can reach very high values, the closer the minimum frequency to f

is, the lower the impedance and the higher the current will be.

R1

2. The converter can operate below resonance (some means is provided to bottom-limit the operating frequency at a value f

such that fR2 < fm < fR1). Again, the control loop,

m

in the attempt to keep the output voltage regulated, will reduce the switching frequency to the minimum value f of the Ls-Cr tank circuit at a value that is as lower as f

. In this case, the input current will be limited by the impedance

m

is lower. However the capacitive

m

region is entered and ZVS is lost, with all the consequent troubles previously mentioned. The waveforms will be similar to those in Figure 22.

.

Figure 24. Circuit's equivalent schematic

under: no-load conditions

Ls

Lp

Vin

VinVin

a·Vout

a·Vouta·Vout

Lp

a:1

Vout

VoutVout

It is interesting to see what happens under short circuit if the converter is operating at resonance (f = f

). Tank circuit's impedance is zero, then the short circuit is directly

R1

connected across the input source and the current Iin is theoretically unlimited. Theoretically, switching frequency should not change (the system is working in the loadindependent point). In real-world operation, Iin, though reaching very high values, will be limited by the parasitic resistance of the short-circuit mesh, the ESR of Cr and by transformer's nonidealities. Additionally, the drop across the secondary rectifiers does not reflect a true short circuit on the primary side. Because of the parasitic resistances, the output voltage will drop and the control loop will react pushing the operating frequency to the minimum f

, which, realistically, must be lower than fR1 if operation at resonance is allowed.

m

In the end this will fall into case 2.

Figure 25. Circuit's equivalent schematic

under: short-circuit conditions

Iin

Cr Ls

Vin

Still with reference to case 2, it is worth remembering that the capacitive region is entered and ZVS for MOSFETs is lost as , well before short circuit.

R

crit

From the above analysis it is possible to draw the following conclusions:

1. Two major issues arise under overload or short circuit conditions: very high current levels, and capacitive mode operation (with loss of ZVS, etc.). This makes the operation of the LLC resonant converter under overload or short circuit inherently unsafe if no overcurrent protection (OCP) is used, just like in conventional PWM-controlled converters. OCP will have to prevent not only the tank current from exceeding unsafe

38/64

Zo0Zo∞⋅=

AN2644 The LLC resonant half-bridge converter

values but also ZVS from being lost. In principle, its setpoint must be such that the condition R>R

is always fulfilled.

crit

2. Limiting the minimum operating frequency of the converter is not always effective. It prevents losing ZVS under overload or short circuit only if this minimum value is above the resonant frequency f

. Thereby, relying on just limiting the minimum operating

R1

frequency would force giving up the below-resonance operating region and its interesting properties, severely limiting the usability range of the converter. Furthermore, the problem of having too high circulating current would be still unsolved.

3. Converters are often specified to have peak load demands that are considerably higher than the maximum continuous power, and whose duration is such that it cannot be averaged by the output capacitor bank. While these peak loads may be thermally irrelevant, from the electrical standpoint they must be considered as steady-state. OCP circuits must not be triggered and the converter must be designed so that the condition R>R

is not violated under these transient conditions as well.

crit

The inspection of the waveforms under heavy load conditions shows that, unlike PWMcontrolled converters, the peak current in a switching cycle is not reached at the end of the conduction time of either MOSFET. This suggests that the usual cycle-by-cycle current limitation so widely used in PWM-controlled converters is not applicable to LLC resonant converters.

The simplest and also most immediate action to take in response to the detection of an overload or short circuit condition is to increase the operating frequency. It is advantageous to push the frequency well above the resonance frequency f

, so that the converter

R1

definitely operates in the inductive region, and ZVS is maintained, with the input current kept under control by the inductive reactance of the tank circuit.

However, this frequency rise is not typically sufficient to effectively limit the short-circuit output current at safe values. In fact, on one hand, the input impedance of the tank circuit in the inductive region is essentially proportional to frequency. Since there are practical limits on the maximum operating frequency (it rarely exceeds 3-4 times f current can still be considerably large. On the other hand, as the output voltage drops because of the action of the OCP circuits, the voltage reflected across Lp becomes smaller and smaller. Then, less and less current flows through Lp and the transformer tends to transfer all the primary current to the output.

As a consequence, the short circuit output current can be still much higher than the nominal full-load current and the resulting stress, especially for the secondary rectifiers, might be unacceptable. In addition to current limiting it is therefore advisable to provide some timed shutdown protection that either forces an intermittent operation of the converter to drastically reduce the average value of the output current or latches it off if the OCP circuits are active for more than some time.

2.6 Converter's startup

Like in PWM-controlled converters, startup is quite a critical moment that needs to be properly handled in LLC resonant converter as well. When the converter is first switched on (or also while it is recovering after a protection shutdown) the energy flow should be progressively increased to allow a slow buildup in output current and voltage. This is commonly known as "soft-start". Doing otherwise, high and potentially destructive currents might be drawn from the input source and through the power devices in an attempt to charge the output capacitors and bring the output voltage to the regulated value.

), the short circuit tank

R1

39/64

The LLC resonant half-bridge converter AN2644

Since at startup the output capacitors are discharged, the startup phase can be regarded as a "temporary short circuit" (where, however, the output voltage is allowed to increase) and actually it has to be handled like a short circuit as mentioned in the previous section. To minimize energy flow, the initial switching frequency will have to be much higher than the resonance frequency f

, so that the converter operates in the inductive region, ZVS is

R1

maintained and the input current is kept under control by the inductive reactance of the tank circuit. The frequency will be allowed to progressively decay until the output voltage comes close to the regulated value and the control loop closes and takes over.

Some typical waveforms at startup for the converter of Figure 15 are shown in Figure 26, where the initial frequency is set at 300 kHz (against f

≈ 76 kHz).

R1

In the LLC resonant converter there is an additional phenomenon that shows up just at the very beginning and causes higher resonant tank current to flow and ZVS loss.

As mentioned in the Section 2, the resonant capacitor Cr plays the double role of resonant capacitor and DC blocking capacitor. This essentially means that the resonant voltage on Cr is superimposed on a DC value that equals V duty cycle. As a result, the primary of the transformer is symmetrically driven by a ±V

/2 because the half-bridge is driven with 50%

in

/2

in

square wave. This is true when steady-state operation has been reached.

At startup the initial voltage across Cr is zero and for the first few cycles the voltage seen by the transformer when the high-side power MOSFET Q1 is on is considerably different from the voltage seen when Q2 is on. The transformer driving voltage will tend to become symmetrical as switching cycles follow one another and Cr is charged at the steady state DC level. During the Cr charge transient the v·s unbalance can be quite high and this makes the tank current irregular in the first few cycles, with peak values that can be considerably higher than the steady-state peak-to-peak current expected at the starting frequency. Additionally, the fundamental ZVS conditions ("when one switch turns off, the tank current must have the same sign as the impressed voltage") may be violated so that even capacitive mode operation can be observed.

Figure 26. Converter's startup: main waveforms

I(D1) = D1 currentV(D1) = D1 anode voltageI(Q1) = Q1 currentIR = Tank circuit’s currentVHB = Node HB voltageHVG= Q1 gate

I(D2) = D2 currentV(D2) = D2 anode voltageI(Q2) = Q2 currentI(Lp) = Lp (magnetizing) currentVc = Resonant capacitor voltageLVG = Q2 gate

40/64

AN2644 The LLC resonant half-bridge converter

This phenomenon is well-known in push-pull and half-bridge topologies and is sometimes referred to as "flux doubling" because the transformer's magnetic flux excursion, which normally swings by 2B goes from 0 to 2B

from -Bpk to +Bpk under steady state operation, in the first cycle

pk

. Fortunately, if the integrated magnetics approach is used, there will be

pk

no risk of saturation. Flux doubling will concern only the resonant inductor Ls, which is mostly associated to the transformer's leakage inductance that, by definition, cannot saturate because the relevant flux is developed in air.

Although not inherently hazardous, (capacitive mode and ZVS loss will typically occur in the first two-three cycles, then the associated stress level is practically negligible) this phenomenon is not nice to see. To eliminate or, at least, minimize it, the split capacitor configuration of Figure 4 can be used in some cases. In fact, the initial voltage across each capacitor will be close to V

/2 (equal to Vin/2 if the two capacitors had exactly the same

in

value), then there will be only a minimum transient.

However, this is ineffective with many control ICs with high-side MOSFET driving capability using capacitive bootstrap. To guarantee an adequate precharge of the bootstrap capacitor to correctly drive the high-side MOSFET Q1 since the first cycle, the low-side MOSFET Q2 is turned on for some time before starting to operate (as shown in Figure 26), which discharges completely the lower Cr/2 capacitor. This bootstrap precharge mechanism, shown in Figure 27, makes ineffective also any pull-up that could precharge Cr.

In this case the initial current peak cannot be completely eliminated, just reduced by either using a higher starting frequency or by forcing the duty cycle to start from a value considerably smaller than 50% and letting it widen progressively.

Figure 27. High-side driving with bootstrap approach and bootstrap capacitor

charge path

Vin

D

BOOT

BOOTDBOOT

I

BOOTCHARGE

Vcc

Level

Shifter

Vcc

Control

Logic

2.7 Analysis of power losses

Conduction power losses on the primary side are located in the power MOSFETs, in the resonant capacitor Cr and the transformer (for convenience the secondary winding losses can be incorporated). On the secondary side, losses will be essentially located in the secondary rectifiers, although those in the output capacitors cannot be neglected, at least as far as capacitor selection is concerned.

C

BOOT

BOOTCBOOT

Q1

Q2

Ls

a:1:1

Lp

Cr / 2

41/64

The LLC resonant half-bridge converter AN2644

⎧⎫

Unless the converter is running at very high frequency, which would make turn-off losses dominant, R

is usually the major source of power loss in power MOSFET. In the total

DS(on)

loss budget, however, the power wasted in power MOSFETs is usually a minor contributor, especially when the converter is powered from the output of a PFC preregulator (400 V typ.). It is not uncommon to see power MOSFETs running cool with minimum heat sinking.

The resonant capacitor Cr dissipates because of its own ESR. For this reason, especially when very high efficiency is required, Cr should be a low-loss one, suited for AC/pulse applications. Polypropylene film capacitors are the preferred choice.

Concerning the transformer, high frequency copper losses need to be particularly addressed. In fact, eddy currents and proximity losses are considerable, especially in the side-by-side winding arrangement because of the high transverse flux. Litz-type or multistrand wire is a must for both primary and secondary windings.

Switching losses are essentially located in the power MOSFET Q1 and Q2. As previously stated, the value of the switched current at heavy load (I

) is a trade-off between the

Rmin

need for ensuring ZVS for both Q1 and Q2 and their turn-off losses. The higher the switched current is, the higher the margin for ZVS will be, but at the expense of larger switching loss due to voltage-current overlap. It is intuitive that the optimum design, in terms of total dynamic losses minimization, is the one that uses for I

the minimum value

Rmin

necessary to achieve ZVS. It still provides zero capacitive turn-on losses with minimum switching losses at turnoff. Since component tolerance must be accounted for, and losing ZVS must be avoided not only for efficiency reasons but also to prevent troubles, adequate margin needs to be considered and the typical operation will be suboptimal.

Secondary rectifiers are usually the components where the majority of power losses occur. Assuming the rectifiers are identical, their cumulative conduction losses are given by:

Equation 16

V

⎪⎪

thIout dc–

=

⎨⎬ ⎪⎪

2V

⎩⎭

where V

Pd

is the rectifier's threshold voltage and Rd its dynamic resistance. With bridge

th

rectification, losses are almost double because there are always two diodes in the conduction path (we say "almost" because of the lower blocking voltage rating, so that V and R

are expected to be slightly lower for the same current rating). Hence this

d

arrangement is preferred when the output voltage is high. Firstly, the efficiency loss due to the rectifiers (which is ∝ 2 V

F/Vout

output voltage is, the more a lower blocking voltage requirement becomes beneficial.

As compared to the ZVS Asymmetrical Half-bridge and the Forward converter, conduction losses (for the same technology and blocking voltage) would be slightly greater because of the worse current form factor that would increase the term, but this is compensated by the absence of recovery and its associated losses. In the end, considering also that in the LLC resonant half-bridge there is no secondary choke with its associated losses, it is expected that the total secondary losses will be lower.

2.8 Small-signal behavior

thIout dc–

2

RdI

+

out rms–

2

RdI

+()

out rms–

full - wave rectification

bridge rectification

) becomes less significant. Secondly, the higher the

th

It is essential to know the small-signal behavior of the LLC resonant converter to be able to design the feedback loop. In line with the approach followed to describe its steady-state

42/64

AN2644 The LLC resonant half-bridge converter

operation, here only a qualitative description will be given, which is the result of a characterization by simulation [7] (refer to Section 4).

As stated many times, the operating frequency is the parameter that allows regulation of the input-to-output energy flow. The control-to-output transfer function G(j

ω) that characterizes

the small-signal behavior of the LLC resonant converter will then be defined as:

Equation 17

^

V

o

------ Gjω()=

^

f

In the overall converter's dynamics it is convenient to separate the contribution of the "inverter" part and that of the rectifying and filtering block that transforms the inverter in a converter. This is quite a useful concept of superposition because it gives considerable physical insight. Regardless of the operating mode of the inverter and, then, of its contribution to converter's dynamics, the rectifying and filtering block always introduces a low frequency pole associated to the output capacitor, the load resistance and the openloop output impedance Zo

of the resonant tank, plus a zero due to the output capacitor and

0

its ESR (equivalent series resistor). This pole moves with the load (frequency is higher at heavy load, lower at light load) because of the changes in Zo essentially fixed frequency, exactly like in PWM converters.

Different types of dynamic behavior, corresponding to different pole distributions of G(j can be observed depending on the operating mode. Again we will consider operation at, above and below resonance.

2.8.1 Operation above resonance (f > fR1)

In this operating mode the converter features a special characteristic typical of resonant converters, the so-called "beat frequency double pole", i.e. two complex and conjugate poles having their imaginary part at the difference between the switching frequency f and the resonant frequency f there is the pole-zero pair associated to the output filter. If f is significantly higher than f the system can be regarded as a single-pole system.

. In addition to this double pole, contributed by the inverter part,

R1

, while the zero is at an

0

ω),

R1

,

As switching frequency moves close to resonant frequency, the beat frequency double pole will move to lower frequency. When the switching frequency is very close to resonant frequency, the beat frequency double pole will eventually split and become two real poles. One moves to higher frequencies and the other moves to lower frequencies as switching frequency gets closer and closer to resonant frequency. Finally, the split pole moving to low frequency will merge with the low frequency pole caused by the output filter and form a double pole. This type of characteristic is very similar to that of the conventional series LC converter.

Provided the converter is not operating too close to resonance, as long as it runs in CCM, the pole distribution tends not to change significantly. In DCM operation, instead, the beat frequency double pole will more pronouncedly move to higher frequencies and the low frequency pole to lower frequencies. At light load, the converter can then be regarded as a single-pole system.

Concerning how the resonant tank characteristics affect the small-signal behavior, the parallel inductor Lp has no practical effect. Conversely, increasing the impedance of the resonant tank (i.e. increasing Ls and reducing Cr while keeping the same f

), the DC gain

R1

will increase. Also the low frequency pole changes with the resonant tank impedance (it

43/64

The LLC resonant half-bridge converter AN2644

gets higher at low impedance). In fact, the low frequency pole is not determined by the load resistor alone but by the output impedance of the tank circuit as well.

2.8.2 Operation below resonance (fR2 < f < fR1, R>R

In this operating mode the converter's dynamics changes considerably. In the left half-plane, there are three poles and one zero but no beat frequency double pole. The pole distribution is quite insensitive to switching frequency as compared to that in the above resonance operation. The pole that in the above resonance operation was moving to higher frequency when switching frequency was approaching resonance here moves back to lower frequencies as switching frequency is further reduced going away from resonance. Its position, however does not change much. The low-frequency double pole is minimally affected too.

A Right Half Plane Zero (RHPZ) can be observed that moves with switching frequency but, fortunately, it stays typically away from the low frequency region of interest in the design of the feedback loop.

Approaching capacitive region, beat frequency dynamics tends to appear again. The phase has an abrupt 180º shift just beyond the capacitive region threshold (feedback from negative turns into positive).

Starting from heavy load conditions, at first the Q associated to the low frequency double pole decreases. The RHPZ shifts to higher frequencies and leaves the stage. Further reducing the load, the Q of the low frequency double pole increases. At very light load the low frequency double pole splits, one moves to higher frequencies and the other to lower frequencies. Again, at very light load the converter can be regarded as a single-pole system.

Unlike in the above resonance operation, in this case the parallel inductor Lp has a considerable impact on the DC gain of the converter. Additionally, it affects the RHPZ as well. Larger values for Lp tends to shift it to lower frequencies. As far as the impedance of the resonant tank is concerned, the effect is the same as in the above resonance operation.

crit

)

2.8.3 Operation at resonance (f = fR1)

Operation at resonance can be regarded as the borderline between the two previously considered operating modes. The behavior will not be different from that seen just above (and just below) resonance: two low-frequency poles, one high-frequency pole and the ESR zero. The same behavior can be seen as far as load dependence is concerned.

The compensation of the error amplifier must consider the different types of small-signal behavior that the converter can exhibit, especially if it is designed to operate both above and below resonance. The challenge comes essentially from its second-order behavior exhibited in its operation close to resonance frequency due to the low frequency double pole. To properly compensate that, the best option is a type 3 amplifier, i.e. a compensator with one pole at the origin plus two poles and two zeros at finite frequencies. The pole at the origin gives excellent load and line regulation characteristics. The two zeros are placed at low frequency to compensate the double pole of the control-to-output transfer function, by counteracting their phase lag. The poles are placed to compensate the ESR zero and provide more attenuation at switching frequency. A practical implementation of this compensator is shown in Figure 28 along with the relationship between the component values and its transfer function.

44/64

AN2644 The LLC resonant half-bridge converter

Figure 28. Frequency compensation with an isolated type 3 amplifier (3 poles + 2

zeros)

Vo

RF2

RB1

Ic

CF3

RF3

RB1

CTR

TL431

CF2

RB2

CF1

RF1

R1

R2

Equation 18

^

I

C

------

^

V

o

CTR

-------------------------------------------------

sR1 RB1 CF1⋅⋅()

1sRB1RF2+()CF2+

------------------------------------------------------------ -

⋅⋅=

1sRF2CF2⋅+

1 s R1 RF1+()CF1+

--------------------------------------------------------

1sRF3CF3⋅+

45/64

Conclusion AN2644

3 Conclusion

The operation of the LLC resonant converter has been examined in detail and its most important properties have been deduced by inspection of its salient waveforms under different operating conditions. To summarize, the most significant merits of this topology are:

● Soft-switching of all semiconductor devices: ZVS (zero-voltage switching) at turn-on for

the MOSFETs and ZCS (zero-current switching) at both turn-on and turn-off for the secondary rectifiers. The first property results from a correct design of the resonant tank. The second one is a natural feature of the topology.

● Ability to accommodate an extremely broad load range, including zero load, with an

acceptable frequency variation. Also this property results from a correct design of the resonant tank.

● Magnetic integration, which allows the combination of different magnetic devices into a

single physical device.

● Smooth waveforms: the current is piecewise sinusoidal with no steep edges. The

voltage, although a square wave, does not have very high dv/dt edges. EMI emissions are considerably low and filtering requirements are relatively loose.

● As a result of all the above merits, high-efficiency, high switching frequency capability,

high power density are typical characteristics of the converters based on this topology.

The most significant facts concerning the design of an LLC resonant converter are:

● The quantities that determine whether the converter operates at resonance, above

resonance or below resonance are essentially the input and the output voltages and the transformer's turn ratio. There is just a second-order dependence on the load current due to the variation of the voltage drop across parasitic elements such as winding resistance, rectifier drop, etc.

● Operation at resonance looks like the preferred operating point, where load regulation

is ideally zero, where tank current is maximally sinusoidal and where CCM operation minimizes peak tank current for a given power throughput. Whenever possible (e.g. when the LLC converter is powered by a PFC preregulator) it seems a good design strategy to design the converter to work at resonance under nominal conditions, and use below resonance operation to handle mains voltage dips and above resonance operation to handle light load or transient overshoots of the input voltage.

● The ability to operate under no-load conditions and to ensure ZVS operation depend

essentially on the transformer's magnetizing inductance. Its value has to be traded off against the switching losses at full load operation and the input consumption at no-load.

● Avoiding capacitive mode operation is a must. It is a too risky operating mode and any

design procedure should not leave this fundamental aspect out of consideration.

● Overcurrent and short circuit protection must be provided. They will not only have to

prevent excessive currents from flowing in both the resonant tank, the transformer and the output rectifiers but also avoid entering capacitive mode operation.

● Soft-start is highly recommended. At startup there is a situation very similar to a short

circuit and, if not properly controlled, potentially destructive currents might flow in the half-bridge leg and the resonant tank.

46/64

AN2644 References

4 References

1. "Resonant Converter Topologies with Three and Four Energy Storage Elements", IEEE Trans. on Power Electronics, Vol. 9, No. 1, 1994, Pages 64 - 73

2. "A Comparison of Half Bridge Resonant Converter Topologies", IEEE Trans. on Power Electronics, 1988. Pages: 174 - 182.

3. "Steady-state Analysis of the LLC Resonant Converter", Applied Power Electronics Conference and Exposition, 2001. APEC 2001. Pages: 728 - 735

4. "First harmonic approximation including design constraints", Telecommunications Energy Conference, 1998. INTELEC. Pages: 321 - 328

5. "Design Optimization for an LCL-Type Series Resonant Converter", http://www.powerpulse.net/features/techpaper.php?paperID=76

6. "Fundamentals of Power Electronics", 2

7. "Topology Investigation for Front End DC/DC Power Conversion for Distributed Power System", PhD dissertation, Virginia Polytechnic Institute and State University, 2003.

nd

edition, Kluwer, 2001

47/64

Power MOSFET driving energy in ZVS operation AN2644

Appendix A Power MOSFET driving energy in ZVS

operation

When power MOSFETs are switched on under ZVS conditions, i.e. when their drain-tosource is already zero, Miller effect due to drain-to-source voltage modulation is absent. This reduces the gate charge required to turn the power MOSFET fully on, the turn-on energy, as well as the total driving energy. This can be conveniently examined on the gatecharge characteristic of the device (see Figure 29).

Figure 29. Comparison of gate-charge characteristics with and without ZVS

The black curve is the normal piecewise-linear gate-charge curve. The first portion is that related to the charge of the input capacitance C bring the gate voltage up to the plateau value V specified current. The flat portion is the so-called "Miller plateau", where the gate voltage does not increase because the drain-to-source voltage is falling and C charge supplied to the gate until the charge Qgd has been supplied. The third rising portion is related to the overcharge of C

GS+CGD

this line is lower than that of the first portion. This is due to the modulation of C now considerably larger (C

is essentially constant). The total gate charge supplied to the

GS

gate to bring its voltage up to the final value V specified on the datasheet for given V

GS

The grey-hatched area included between the gate-charge curve and the V is the energy lost in the gate driver to charge the gate up to the final value V power MOSFET fully on. Its value can be found with simple geometric considerations:

Equation 19

1

-- -

E

ONHS

-

48/64

2

QgsV

GS+CGD

that lets the power MOSFET carry the

M

, and Qgs is the charge needed to

needed to minimize R

is Qg. The values of Qgs, Qgd, Qg are

GS

, VDS, ID.

Qg Qgs Qgd++()VGSVM–()+[]=

M

is wiping out the

GD

. Note that the slope of

DS(on)

horizontal line

GS

and turn the

GS

, which is

GD

AN2644 Power MOSFET driving energy in ZVS operation

The grey-shaded area below the gate charge curve represents the energy lost in the gate driver to discharge the gate from V

to zero. Its value can be simply found from the

GS

difference of the total driving energy, represented by the rectangle enclosed by the Q-V axes and the Qg and V

GS

lines:

Equation 20

E

HS

Qg VGS⋅=

and E

ON_HS

:

Equation 21

E

OFFHS

-

Qg VGSE

–⋅=

ONHS

-

In case of ZVS, instead, the associated gate-charge curve is the red line. Its slope is equal to that of the third portion of the normal gate-charge characteristic, because C final value since the beginning. By geometrical considerations, the total gate charge Qg

has the

GD

Z

to

provide in this case will be:

Equation 22

V

GS

Z

------------------------ -

V

–

GSVM

Qg Qgs Qgd+()–[]=

and turn

GS

Qg

while the energy lost in the gate driver to charge the gate up to the final value V the power MOSFET fully on and represented by the red-shaded area will be:

Equation 23

2

E

ONZVS

1

-- -

Qg

-

ZVGS

2

1

-- -

------------------------ -

2

V

GSVM

V

GS

Qg Qgs Qgd+()–[]⋅==

–

At turn-off, the Miller effect will be present but to a lower degree. In fact, the operating point will initially move along the red line until the gate voltage reaches the Miller plateau V

(that

M

associated to the switched current at turn-off). From that point on, it will move along the black curve. The energy associated to turn-off will be:

Equation 24

E

OFFZVS

-

1

--------------------------------- -

–()

2V

GSVM

2

V

GS

2

V

+()Qg Qgd–()VGSVGSVM+()Qgs–[]=

M

and the total driving energy:

Equation 25

E

1

--------------------------------- -

ZVS

2VGSVM–()

2V

2

V

+()Qg Qgd–()VGS2V

GS

M

+()Qgs–[]=

GSVM

For the power MOSFET used in the example of Figure 29 (STP14NK60Z), the datasheet specifies: Qgs = 13.2 nC, Qgd = 38.6 nC, Qg = 75 nC @ V values and V nJ, E

OFF_HS

= 5.8 Vin (Equation 19) to (Equation 25) we find: E

M

= 445 nJ, QgZ = 55 nC, E

ON_ZVS

= 276 nJ, E

= 10 V. Substituting these

GS

ON_HS

OFF_ZVS

= 305 nJ, EHS = 750

= 331 nJ and E

ZVS

= 607 nJ. Then, the total gate charge is decreased by 20 nC (-27%) and the total gate driving energy by 143 nJ (-19%).

49/64

Resonant transitions of half-bridge midpoint AN2644

Appendix B Resonant transitions of half-bridge midpoint

To analyze the transitions of the half-bridge midpoint node HB when either Q1 or Q2 is turned off, it is necessary to schematize the equivalent circuit during the transient. For simplicity only the turn-off of Q2 will be considered, being obvious that the turn-off of Q1 will be exactly mirror-symmetrical. Different circuits need to be considered, depending on whether the converter is operated in a DCM mode or a CCM mode. These equivalent circuits are shown in Figure 30.

Figure 30. Equivalent circuit to analyze the transitions of the half-bridge midpoint

node when Q2 turns off

V

Ls

a·(Vout+VF)

ON

t = 0

OFF

V

VCV

C

I

IRI

R

Cr CrLs Ls

LpC

V

VHBV

HB

DCM operation CCM operation

VLV

LpC

L

ON

t = 0

OFF

I

IRI

R

C

V

VHBV

HB

V

VCV

C

In fact, in the case of DCM operation, since the secondary windings are open, Lp is part of the circuit and is effectively in series to Ls to form a single inductor Ls+Lp. In CCM operation, instead, since the secondary windings are conducting there is a constant voltage equal to ±a·(V

) across Lp and then this can be replaced by a voltage generator

out+VF

(placed as shown in Figure 30 in the case under consideration). In either circuit, Q2 is replaced by an ideal switch that opens at t=0.

Resonant tanks are again involved during the transitions, hence the denomination "resonant transitions" given to the swings of the node HB. Considering the operation of the LLC resonant converter in its entirety, then, there are four associated resonant frequencies.

C

is the total parasitic capacitance of the node HB already discussed in Section 2.2: The

HB

switching mechanism and illustrated in Figure 8 and that will be the topic of the next section.

Note that during the transient Cr and C Cr>>C the changes of the V assume V V

C

The value of V

(typically, two orders of magnitude), the combined capacitance will be ≈CHB and

HB

= VC(0) during the transient and replace Cr with a constant voltage generator

C

voltage during the transient can be neglected, so that it is possible to

C

(0).

(0) can be determined on the basis of the following considerations. The

C

value of at the end of the conduction cycle of Q1, V

are effectively in series. However, since normally

HB

(Ts/2), is given by:

C

Equation 26

Ts

⎛⎞

------ -

V

C

⎝⎠

2

50/64

Ts

------ -

1

2

V

------

0()

+=

C

Cr

∫

IRt() td

0

AN2644 Resonant transitions of half-bridge midpoint

Note that the integral in Equation 26 is the total charge provided to Cr during the conduction time of Q1, when the converter draws current from the input source. This charge can be expressed also as the product of the DC input current Iin times the switching period, then:

Equation 27

V

C

Ts

⎛⎞

------ -

⎝⎠

2

V

Iin

------ -

0()

Cr

Ts+=

C

On the other hand, remembering that V

has a DC value equal to Vin/2, for symmetry the

C

following identity holds true:

Equation 28

V

C

Ts

⎛⎞

------ -

⎝⎠

2

------- -

2

in

V

in

------- - V 2

0()–=–

C

By combination of (Equation 39) and (28) we find:

Equation 29

VC0()

Ts

⎛⎞

------ -

V

C

⎝⎠

2

1

-- -

=

2

=

Iin

⎛⎞

------ -

V

⎝⎠

1

⎛⎞

-- -

⎝⎠

2

Ts–

in

Cr

Iin

------ -

V

Ts+

in

Cr

After some algebraic manipulations, it is possible to find that the equations governing the operation of the circuits in Figure 30 are:

Equation 30

d2V

⎧

-----------------

⎪ ⎪ ⎨

2

⎪

d

⎪

-----------------

⎩

V

dt

HB

dt

HB

1

------------------------------------

Ls Lp+()

C

HB

1

----------------- -

V

HB

Ls

HB

C

V

HB

VC0() aV

-----------------------------------------------------------=+

VC0()

------------------------------------=+

C

Ls Lp+()

HB

outVF

C

Ls

HB

DCM

+()⋅–

CCM

with the following initial conditions:

Equation 31

VHB0() 0

The solutions of these equations are:

Equation 32

VHBt()

⎧

=

⎨

V

⎩

CC

with

Equation 33

1

ω

DD

ϕ

CC

----------------------------------------

Ls Lp+()C

HB

VC0() aV

⎛⎞

1–

-----------------------------------------------------------

⎜⎟ ⎝⎠

tan

ϕ

DD

+()⋅–

outVF

0()

I

R

dV

HB

--------------

dt

DD

ωDDt ϕDD–()VC0()+sin

V

ωCCt ϕCC–()VC0() aV

VC0()

⎛⎞

1–

--------------- -

⎜⎟ ⎝⎠

I

R

0()

C

HB

---------- -

Ls

------------------- -

Ls Lp+

V

IR0()

-------------=,=

C

t0=

C

HB

VC0() aV

-----------------------------------------------------------=,tan=

CC

HB

outVF

VC0()

-------------------

V

DD

sin

ϕ

sin

+()⋅–+sin

ϕ

DD

outVF

CC

DCM

CCM

ω

CC

LsC

,=,=,=,=

HB

1

----------------------

+()⋅–

51/64

Resonant transitions of half-bridge midpoint AN2644

The expression of the tank current will be:

Equation 34

0()

I

R

---------------------

ω

cos

DD

0()

I

R

---------------------

cos

ω

CC

ωDDt ϕDD–()cos=cos⋅⋅⋅

t ϕCC–()cos=cos⋅⋅⋅

ω

CC

DCM

CCM

IRt() C

dVHBt()

---------------------

HB

dt

⎧

C

⎪

HBVDDωDD

⎪

==

⎨ ⎪

CHBVCCω

⎪ ⎩

CC

ωDDt ωDD–()

ωCCt ωCC–()

Equations (Equation 30) to (34) apply in the time interval (0, T needed for the voltage V

to reach Vin. TT can be calculated from (Equation 32) taking (33)

HB

), where TT is the time

T

into account; the result is:

Equation 35

⎧ ⎪ ⎪

T

=

⎨

T

⎪

1

---------- -

⎪

ω

CC

⎩

To achieve ZVS, the value of T

1

---------- -

ϕ

DD

ω

DD

VinVC0()– aV

1–

⎛⎞

ϕ

CC

given by (Equation 35) must not exceed the deadtime TD to

T

------------------------------------------------------------------------- -

sin+

⎝⎠

VinVC0()–

1–

⎛⎞

----------------------------- -

sin+

⎝⎠

V

DD

V

CC

+()⋅+

outVF

DCM

CCM

make sure that Q1 is turned on with zero drain-to-source voltage.

Note that in CCM operation there may be an additional constraint on the time interval where equations (Equation 30) to (34) are applicable. The current I

Equation 34 either until T

whichever condition occurs first. We will assume that I

or until it equals the current flowing through Lp (see Figure 9),

T

R

With the usual values of all the involved quantities, the phase angles ϕ considerably less than unity, then it is possible to use the approximation ϕ

(t) will be described by

R

(t)=I(Lp) occurs after TT.

and ϕDD are both

CC

≈ sin ϕ ≈ tan ϕ

for both of them. With this simplification (Equation 35) can be expressed as:

Equation 36

V

in

-------------

IR0()

C

HB

T

=

T

for both CCM and DCM modes, which is equivalent to considering C constant current I

R

(0).

Considering that in CCM operation above resonance it is V that V and decays in (0, T V

(0) ≤ Vin/2, ϕCC is always negative. As a result, IR(t) has its peak for negative t values

C

(0) > 0 and, then, ϕDD positive. Thereby, IR(t) has its peak for positive t values, thus it

C

). In DCM operation, if the input current is lower than a critical value, it is

T

initially increases and then decays in (0,T with no load, the approximation I

(t) = IR(0) is excellent. Still in DCM operation, but with an

R

input current exceeding that critical value, it is V happens below resonance at heavy load. However, as compared to what happens in CCM operation, the associated resonance period is longer, thus the change in I the approximation I

52/64

(t) = IR(0) is still good. This is illustrated in Figure 31 and 32.

R

charged by a

HB

> 2·a·(V

in

). In this case, which happens at light load and

T

(0) < 0 and, then, ϕDD negative, which

C

+ VF) and, again,

out

(t) is lower and

R

AN2644 Resonant transitions of half-bridge midpoint

Figure 31. Voltage of HB node vs time (see

Equation 32)

In the end, the approximation (Equation 36) provides a relationship that is sufficiently accurate for design purposes under all operating conditions. Fortunately the conditions where accuracy is worst (CCM) are not critical as far as ZVS is concerned because the switched current I

(0) is greater than it is under all other conditions.

R

To achieve ZVS for both switches, a necessary condition is that T constraint comes from the condition that the tank current I during the time interval (0, T

). Should the current become zero in that interval, the body

D

diode of Q1 would not be forward biased any more and the voltage V constrained to Vin, would experience oscillations at an angular frequency equal to either

ω

or ωCC. Q1 would then be turned on with a drain-to-source voltage in general greater

DD

then zero.

Figure 32. Resonant current vs time (see

Equation 34)

. An additional

T≤TD

has to keep its sign unchanged

R

, no longer

HB

In practical cases, when the converter is operated at or above resonance the tank current crosses zero with a considerable delay after the end of the deadtime, especially in DCM modes, where the phase lag ϕ described by Equation 5 or 8 or 11 or 13 tends to π /2; hence, this constraint can be disregarded. It becomes significant when working below resonance and close to the boundary between the capacitive and the inductive mode (CCMB mode).

Under the assumption T I

is again a portion of sinusoid having frequency fR1, which can be described by an

R

< TD, in the time interval (TT, TD) Equation 34 no longer apply and

T

equation of the type:

Equation 37

IRt() I

Rpk

-

sin 2π fR1t ϕ–()=

In order for the tank current to keep the same sign during the remainder of the deadtime, the following condition must be fulfilled:

Equation 38

2π fR1TDϕ 0>–

53/64

Power MOSFET effective C

and half-bridge midpoint's transition times AN2644

oss

Appendix C Power MOSFET effective C

midpoint's transition times

Unlike linear capacitors, which have a capacitance value independent of the applied voltage, power MOSFET C source voltage V approximation the C

Equation 39

Power MOSFETs manufacturers usually specify the value of C at 1 MHZ), From (Equation 39) the C

Equation 40

Generally speaking, C MOSFET:

1. at turn-on C MOSFET's R significant in the LLC resonant converter because power MOSFETs are operated in ZVS and capacitive losses are zero, and then it will not be considered.

2. at turn-off the rate of rise of its voltage determines the voltage-current overlap that originates switching losses. This is significant in the LLC resonant converter.

is a nonlinear capacitance, i.e. its value is a function of the drain-to-

oss

. Assuming a p-n step junction for the body-drain diode, with good

DS

vs. VDS relationship can be expressed as:

oss

C

()

ossVDS1

-------------------------------

C

()

ossVDS2

at a given voltage VDS will be:

oss

C

()C

ossVDS

has a twofold role in switching losses mechanism in power

oss

is discharged and the energy stored in it is dissipated inside the

oss

, thus giving origin to the so-called "capacitive losses". This is not

DS(on)

oss25

25

---------- -

V

DS

V

------------- -≈

V

==

DS2

DS1

-------------- -

5

V

DS

and half-bridge

oss

at VDS = 25 V (with VGS=0

oss

C

oss25

Figure 33. Capacitance associated to the half-bridge midpoint node

Q1

Coss

1

V

DS1

Resonant

I

C

IRI

R

Stray

Vin

Node

HB

Q2

HB Driver

It is worth noticing that, although the C

Coss

2

V

DS2

of the two power MOSFETs in the half-bridge are

oss

effectively connected in parallel, however they experience different V If V

is the DC input voltage, and with reference to the circuit shown in Figure 33, the

in

Resonant

Tank &

Load

voltages at any time.

DS

following relationship holds true:

Equation 41

V

DS1

V–

DS2

Vin=

54/64

AN2644 Power MOSFET effective C

and half-bridge midpoint's transition times

oss

Then, assuming that the two MOSFETs are identical to one another (so that C C individual C

oss25-2

= C

), and referring to the voltage of the half-bridge midpoint VHB (= V

oss25

will be:

oss

oss25-1

DS2

= ), their

Equation 42

C

oss1

5

----------------- -

V

DS1

C

oss25

---------------------------- -

==

V

inVHB

5

C

–

oss25

Equation 43

C

oss2

5

----------------- -

V

DS2

C

oss25

==

5

-------------- -

V

HB

C

oss25

and their instantaneous cumulative value will be:

Equation 44

Coss VHB()C

oss1Coss2

1

5

-------------- -

=+=

⎜⎟ ⎝⎠

V

HB

-----------------------------+

V

1

–

inVHB

C

oss25

⎛⎞

The diagram of equations (Equation 43) and (Equation 44) are shown in Figure 34. The branch-constitutive equation of the capacitor C

oss

:

Equation 45

dV

HB

I

t() C

C

oss

ossVHB

--------------

()

dt

I

C

oss

t()dt C

=⇒=

()dV

ossVHB

HB

can be integrated by variable separation.

Figure 34. C

capacitances vs. half-bridge midpoint's voltage

oss

F

3.10

2.25.10

1.5.10

7.5.10

10

11

0

0 100 200 300 400

Coss

V

HB

2

Coss

(= V

Coss

DS2

1

C

stray

)

V

55/64

Power MOSFET effective C

Figure 35. Simplified schematic to analyze transition times of the node HB when Q2

turns off

Vin

and half-bridge midpoint's transition times AN2644

oss

I

C

HB (VHB

I

R0

)

Coss

1

Coss

1

I

R0

=

2

C

Stray

=

⎞

⎛

⎞

⎛

⎞

⎛

t

⎟

⎜

⎟

⎜

⎟

⎜

1II

−=

0R2Q

⎟

⎜

⎟

⎜

⎟

⎜

T

f

⎠

⎝

⎠

⎝

⎠

⎝

IR0–I

Q2

DQ

1

⎞

⎛

⎞

⎛

⎞

⎛

t

⎟

⎜

⎟

⎜

⎟

⎜

−=

1II

0R2Q

⎟

⎜

⎟

⎜

⎟

⎜

T

f

⎠

⎝

⎠

⎝

⎠

⎝

Assuming that V

it is possible to write:

HB|t=0

Equation 46

tf

I

C

∫

oss

0

Note that the left-hand side is the total charge Q voltage up to the level V

. Substituting (Equation 44) in (Equation 46) and developing, it is

HB

V

τ()τ C

HB

=d

∫

0

V()Vd

oss

oss(VHB

) supplied to C

oss(VHB

) to raise its

possible to find:

Equation 47

Qoss VHB()10 V

=

HB

V

in

VinVHB––+()C

oss25

Considering again the turn-off of Q2, as a consequence of the discussion of the previous section, the equivalent schematic of the circuit during the turn-off of Q2 is illustrated in

Figure 35, where the tank circuit is then replaced by a constant current source equal to the

switched current I

. Additionally, the turn-off of Q2 is assumed to be linear in time:

R0

Equation 48

where T

⎧

IR01

⎪

I

=

⎨

Q2

⎪ ⎩

is the time the current IQ2 takes to become zero. The total capacitance of the node

f

t

⎛⎞

---- -–

⎝⎠

T

f

0

0tT

≤≤

f

tT

>

f

HB will be:

Equation 49

()C

C

HBVHB

C

will be charged by the current I

HB

DQ1 turns on, thus clamping V voltage of the node HB to reach V

CHB

at Vin. Let us assume that the time TT needed for the

HB

is greater than Tf. The main quantities during the

in

transient are illustrated in Figure 36. The total charge Q (0, T

) will be:

T

Equation 50

1

-- -

Q

56/64

I

T

R0TfIR0TTTf

2

StrayCossVHB

()+=

= IR0 - IQ2 until VHB equals the input voltage Vin and

delivered to CHB in the interval

T

f

⎛⎞

=+=

–()IR0T

---- -–

T

⎝⎠

2

AN2644 Power MOSFET effective C

Figure 36. Schematization of Q2 turn-off transient

I

HB

C

I

R0

I

Q2

I

R0

V

HB

Vin

Approx.

Actual

and half-bridge midpoint's transition times

oss

Q

T

t

T

f

This charge will be partly stored in C obviously be C substituting V

Stray·Vin

in VHB:

in

, then the one stored in C

T

and partly in C

Stray

t

. The charge in C

oss

will be given by (Equation 47)

oss

Stray

will

Equation 51

A linear capacitance C

equivalent to CHB(Vin) will have the same total charge QT stored in

HB

it when its voltage equals V

Qoss Vin()20 VinC

. Then it is possible to write:

in

=

oss25

Equation 52

QTC

StrayVin

20 VinC

=+=

oss25CHBVin

which yields:

Equation 53

C

HB

C

Stray

+=

----------- -

V

C

oss25

in

20

The capacitance value defined by (Equation 53) has to be used in calculations related to transition time of the node HB, as far as ZVS is concerned.

As previously stated, to achieve ZVS the transition of the node HB must be completed within the deadtime T switch, that is, T

inserted between the transitions from one state to the other of either

D

≤ TD. Combining (Equation 46) and (Equation 48) and solving for TT:

T

Equation 54

C

T

StrayVin

f

---------------------------------------------------------------------

---- -

T

2

20 VinC

+

I

R0

oss25

T

---- -

2

f

CHBV

-------------------

I

R0

in

≤+=+=

T

D

Depending on the data available, (Equation 54) can be used for finding either the minimum value of I T

.

D

(called I

R0

in the text) or the maximum value of CHB or the minimum value of

Rmin

57/64

Power MOSFET effective C

In datasheets of many power MOSFET manufacturers, it is customary to find an "equivalent output capacitance" denoted with C giving the same charging time as C 0 to 80% of the rated voltage V

From the above discussion it is easy to recognize that the linear capacitance equivalent to the C

of a single MOSFET charged at a voltage VDS is:

oss

Equation 55

then, as per the above definition:

Equation 56

The actual value provided in the datasheet can be different from the theoretical value given by (Equation 56), depending on the silicon cell design and density of the particular power MOSFET. For an assigned power MOSFET, whose C (Equation 55), equation (Equation 53) can be re-written as:

and half-bridge midpoint's transition times AN2644

oss

and defined as a constant equivalent capacitance

osseq

when the drain-to-source voltage VDS increases from

oss

.

DSS

10

DSS

=

C

-------------- -

V

oss25

DS

C

oss25

11.2

------------------

≈⋅=

osseq

C

oss25

V

DSS

is specified, by combining with

C

osseq

C

()

osseqVDS

10

-------------------------------

0.8 V

⋅

Equation 57

C

HBCStray

+=

2

V

DSS

-------------- C V

in

osseq

58/64

AN2644 Power MOSFETs switching losses at turn-off

Appendix D Power MOSFETs switching losses at turn-off

The nonlinearity of C

(refer to Figure 34) makes the voltage of the node HB increase

oss

slowly at its low values and its high values, and much faster when it is half way in its swing (see the solid V

waveform labeled "Actual" in Figure 36). Typically, the current through

HB

either Q1 or Q2 during their respective turn-off transients flows during the initial part of the transition of the node HB, i.e. when its value is changing more slowly. This reduces the voltage-current overlap and, consequently, the associated power loss with respect to a linear capacitor. However, the mathematical expression of the loss is extremely complex, therefore it is more useful to provide a conservative estimate using the equivalent linear capacitance C labeled "Approx." in Figure 36 (under the assumption T

defined by (Equation 53). The associated VHB curve is the dotted one

HB

< TT).

f

Again with reference to the turn-off of Q2, the voltage on the node HB can be found by integration of the branch-constitutive equation of C

HB

:

Equation 58

dV

HB

I

t() C

C

HB

--------------

dt

t()

=⇒=

V

HB

1

---------- -

C

HB

t

t() t

I

C

∫

0

=d

HB

1

---------- -

C

HB

t

∫

0

I

R0IQ2

t()–[]td

Power loss due to voltage-current overlap (switching loss) will occur only during the time interval (0, T

) where IQ2 is non-zero, then (Equation 54) will be considered in this interval

f

only; substituting (Equation 48) in (Equation 58) we find:

Equation 59

t

I

1

R0

---------- -

V

t()

=

HB

------- -

tt

∫

C

T

0

HB

f

----------------------------

=d

2CHBT

⋅⋅

I

R0

2

t

f

t∈ (0,T

)

f

Note that in the remainder interval (T because charged by the constant current I

, TT) the voltage VHB will change linearly with time

f

. The energy lost because of voltage-current

R0

overlap will be calculated by integration of the product of (Equation 59) times (Equation 48):

Equation 60

2

T

Q2() IQ2t() VHBt()⋅ t

E

off

f

=

∫

0

------------------------

=d

2CHBTf⋅

I

R0

T

f

2

⎛⎞

1

t

∫

⎝⎠

0

⋅()

R0Tf

HB

2

t

---- -–

T

I

t

----------------------

=d

24C

f

Power loss will be obtained multiplying the energy loss given by (Equation 60) by the operating frequency f

sw

:

Equation 61

P

off

Q2()E

off

Q2()f

IR0Tf⋅()

-------------------------==

sw

24C

2

HB

The same loss occurs to the high-side power MOSFET Q1 as well, thereby, the total switching loss will be:

Equation 62

12C

HB

2

⋅=

f

sw

IR0Tf⋅()

TOT

-------------------------

P

off

59/64

Power MOSFETs switching losses at turn-off AN2644

A more accurate analysis could be done observing in Figure 34 that C

oss1

(C

in case we

oss2

consider Q1's turn-off) changes little during the first portion of the transient, so that it might be considered constant. With this approach, from (Equation 44) it is possible to assume:

Equation 63

C

()5

ossVHB

1

-------------- -

≈

⎜⎟ ⎝⎠

V

HB

1

----------- -+

C

oss25

V

in

⎛⎞

and, from (Equation 49), taking (Equation 63) into account:

Equation 64

CHBVHB()C

Stray

⎛⎞

1

5

-------------- -

⎜⎟ ⎝⎠

V

HB

1

----------- -+

C

oss25

V

in

⎛⎞

C

Stray

⎝⎠

+

5

----------- -

V

Coss

in

5

-------------- -

+=+≈

25

C

oss25

V

HB

Designating:

Equation 65

C

HBF

C

-

substituting (Equation 64) in (Equation 46), integrating both sides and solving for V

Stray

+=

----------- -

V

C

oss25

in

it is

HB

5

possible to find:

Equation 66

VHBt()

1

--------------

C

HBF

I

R0

--------------

2TF⋅

t210

–=

C

⎛⎞

oss25

----------------- -

C

HBF

--

⋅ 5C

25 C

⎜⎟ ⎝⎠

2

oss25

C

HBFIR0

-

---------------------- -

2TF⋅

2

t

–

oss25

Inserting this result in (Equation 60) and integrating would yield the turn-off energy, however the result is complex and of little practical use, hence it will not be provided.

60/64

AN2644 Input current in LLC resonant half-bridge with split resonant capacitors

Appendix E Input current in LLC resonant half-bridge with

split resonant capacitors

An interesting property of the LLC resonant half-bridge with split resonant capacitors is the shape of the input current. Unlike the single capacitor version, where the input current Iin equals the current through the high-side switch Q1, I(Q1), in this case Iin is given by the superposition of I(Q1) and the current through the high-side resonant capacitor I(Cr), as shown in Figure 37.

Figure 37. Input current components in a split-capacitor LLC resonant half-bridge

AM01349v1

The current I(Cr) with the direction defined in Figure 37 is in phase opposition to I(Q1) and to the current through the series resonant inductor I(Ls); also, its instantaneous amplitude is half that of I(Ls) since it is equally split between the two resonant capacitors. As a result, when Q1 is ON, I(Cr) is negative and Iin equals I(Q1) diminished by I(Cr); when Q1 is OFF and I(Q1)=0, Iin = I(Cr) is positive and provides a continuous input current flow. This is shown in the timing diagrams of Figure 38.

Figure 38. Timing diagram showing currents flow in the converter of Figure 37

AM01350v1

61/64

Input current in LLC resonant half-bridge with split resonant capacitors AN2644

Note that the input current is the same as in a full-bridge converter, where during each half switching period there is a conducting path drawing current from the input source.

With the same DC value of Iin, then, the split capacitor configuration makes its peak and squared rms values are cut in half. Unlike bridge converters, however, the currents I(Q1) and I(Q2) keep the same value as in the single capacitor half-bridge version.

It is then advantageous to use the split capacitor configuration to reduce not only the ac current requirements on the resonant capacitors but also the ac current in the input capacitor and the differential-mode conducted noise. It is then easy to find this solution at higher power levels but it is advisable to use it also when there is no front-end PFC preregulator. In this case, in fact, the differential-mode noise that the input EMI filter is required to mitigate is that generated by the resonant half-bridge converter (whereas, with a PFC front-end the noise generated by this stage would be largely dominant), thus it is possible to maximally benefit from the reduction of its differential-mode component.

62/64

AN2644 Revision history

Revision history

Table 2. Document revision history

Date Revision Changes

06-May-2008 1 Initial release

15-Sep-2008 2

Modified: Section 2.1, 2.2, Appendix B Added: Appendix E

63/64

AN2644

Please Read Carefully:

Information in this document is provided solely in connection with ST products. STMicroelectronics NV and its subsidiaries (“ST”) reserve the right to make changes, corrections, modifications or improvements, to this document, and the products and services described herein at any time, without notice.

All ST products are sold pursuant to ST’s terms and conditions of sale.

Purchasers are solely responsible for the choice, selection and use of the ST products and services described herein, and ST assumes no liability whatsoever relating to the choice, selection or use of the ST products and services described herein.

No license, express or implied, by estoppel or otherwise, to any intellectual property rights is granted under this document. If any part of this document refers to any third party products or services it shall not be deemed a license grant by ST for the use of such third party products or services, or any intellectual property contained therein or considered as a warranty covering the use in any manner whatsoever of such third party products or services or any intellectual property contained therein.

UNLESS OTHERWISE SET FORTH IN ST’S TERMS AND CONDITIONS OF SALE ST DISCLAIMS ANY EXPRESS OR IMPLIED WARRANTY WITH RESPECT TO THE USE AND/OR SALE OF ST PRODUCTS INCLUDING WITHOUT LIMITATION IMPLIED WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE (AND THEIR EQUIVALENTS UNDER THE LAWS OF ANY JURISDICTION), OR INFRINGEMENT OF ANY PATENT, COPYRIGHT OR OTHER INTELLECTUAL PROPERTY RIGHT.

UNLESS EXPRESSLY APPROVED IN WRITING BY AN AUTHORIZED ST REPRESENTATIVE, ST PRODUCTS ARE NOT RECOMMENDED, AUTHORIZED OR WARRANTED FOR USE IN MILITARY, AIR CRAFT, SPACE, LIFE SAVING, OR LIFE SUSTAINING APPLICATIONS, NOR IN PRODUCTS OR SYSTEMS WHERE FAILURE OR MALFUNCTION MAY RESULT IN PERSONAL INJURY, DEATH, OR SEVERE PROPERTY OR ENVIRONMENTAL DAMAGE. ST PRODUCTS WHICH ARE NOT SPECIFIED AS "AUTOMOTIVE GRADE" MAY ONLY BE USED IN AUTOMOTIVE APPLICATIONS AT USER’S OWN RISK.

Resale of ST products with provisions different from the statements and/or technical features set forth in this document shall immediately void any warranty granted by ST for the ST product or service described herein and shall not create or extend in any manner whatsoever, any liability of ST.

ST and the ST logo are trademarks or registered trademarks of ST in various countries.

Information in this document supersedes and replaces all information previously supplied.

The ST logo is a registered trademark of STMicroelectronics. All other names are the property of their respective owners.

STMicroelectronics group of companies

Australia - Belgium - Brazil - Canada - China - Czech Republic - Finland - France - Germany - Hong Kong - India - Israel - Italy - Japan -

Malaysia - Malta - Morocco - Singapore - Spain - Sweden - Switzerland - United Kingdom - United States of America

www.st.com

64/64

ST AN2644 Application note

Specifications and Main Features

Frequently Asked Questions

User Manual

Figure 1. LLC resonant topology schematics and waveforms

1 Classification of resonant converters

Figure 3. LLC resonant half-bridge schematic

2 The LLC resonant half-bridge converter

2.1 General overview

Figure 4. LLC resonant half-bridge with split resonant capacitor

Figure 6. Example of high-leakage magnetic structures (cross-section)

Table 1. Output stress for LLC resonant half-bridge vs. PWM topologies @ 50% duty cycle

Figure 7. Equivalent schematic of a transformer including parasitic capacitance

2.2 The switching mechanism

Figure 14. Bridge leg transitions under no-load conditions

2.3 Fundamental operating modes

2.3.1 Operation at resonance (f = fR1)

2.3.2 Operation above resonance (f > fR1)

Figure 23. No-load operation (cutoff): main waveforms

2.4 No-load operation

2.5 Overload and short circuit operation

2.6 Converter's startup

Figure 26. Converter's startup: main waveforms

2.7 Analysis of power losses

2.8 Small-signal behavior

2.8.1 Operation above resonance (f > fR1)

2.8.3 Operation at resonance (f = fR1)

3 Conclusion

4 References

Figure 29. Comparison of gate-charge characteristics with and without ZVS

Appendix B Resonant transitions of half-bridge midpoint

Figure 33. Capacitance associated to the half-bridge midpoint node

Figure 36. Schematization of Q2 turn-off transient

Appendix D Power MOSFETs switching losses at turn-off

Figure 37. Input current components in a split-capacitor LLC resonant half-bridge

Figure 38. Timing diagram showing currents flow in the converter of Figure 37

Revision history

Table 2. Document revision history