ST AN2388 Application note

AN2388

Application note

Sensor field oriented control (IFOC)

of three-phase AC induction motors using ST10F276

Introduction

AC Induction motors are the most widely used motors in industrial motion control systems,
as well as in home appliances thanks to their reliability, robustness and simplicity of control.

Until a few years ago the AC motor could either be plugged directly into the mains supply or
controlled by means of the well-known scalar V/f method. When power is supplied to an
induction motor at the recommended specifications, it runs at its rated speed. With this
method, even simple speed variation is impossible and its system integration is highly
dependent on the motor design (starting torque vs maximum torque, torque vs inertia,
number of pole pairs). However many applications need variable speed operation. The
scalar V/f method is able to provide speed variation but does not handle transient condition
control and is valid only during a steady state. This method is most suitable for applications
without position control requirements or the need for high accuracy of speed control and
leads to over-currents and over-heating, which necessitate a drive which is then oversized
and no longer cost effective. Examples of these applications include heating, air
conditioning, fans and blowers.

During the last few years the field of electrical drives has increased rapidly due mainly to the
advantages of semiconductors in both power and signal electronics and culminating in
powerful microcontrollers and DSPs. These technological improvements have allowed the
development of very effective AC drive control with lower power dissipation hardware and
increasingly accurate control structures. The electrical drive controls become more accurate
with the use of three-phase currents and voltage sensing.

This application note describes the most efficient scheme of vector control: the Indirect Field
Oriented Control (IFOC). Thanks to this control structure, the AC machine, with a
speed/position sensor coupled to the shaft, acquires every advantage of a DC machine
control structure, by achieving a very accurate steady state and transient control, but with
higher dynamic performance.

In this document we will look at the complete software integration and also the theoretical
and practical aspects of the application.

October 2006 Rev 1 1/54

www.st.com

Contents AN2388

Contents

1 Background . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

1.1 AC induction motor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

1.1.1 Stator . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

1.1.2 Rotor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

1.2 Three-phase induction motor and classical AC drives . . . . . . . . . . . . . . . . 6

2 Vector control of AC induction machines . . . . . . . . . . . . . . . . . . . . . . . . 9

2.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

2.2 Theory on vector control . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

2.2.1 Space vector definition and projection . . . . . . . . . . . . . . . . . . . . . . . . . . 10

2.2.2 The (a,b,c)(α,β) projection (Clark transformation) . . . . . . . . . . . . . . . . . 11

2.2.3 The (α,β)(d,q) projection (Park transformation) . . . . . . . . . . . . . . . . . . . 12

2.2.4 The (d,q)(α,β) projection (inverse Park transformation) . . . . . . . . . . . . . 13

2.3 Block diagram of the vector control . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14

2.4 The current model (rotor flux estimator) . . . . . . . . . . . . . . . . . . . . . . . . . . 14

2.5 Space vector modulation (SVPWM) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

3 Hardware design . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

3.1 System configuration . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

3.2 MDK-ST10 control board . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

3.3 Three-phase high voltage power stage (powerBD-1000) . . . . . . . . . . . . . 23

3.3.1 Power stage . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24

3.3.2 Auxiliary supply . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25

3.4 Gate driver board . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

3.5 Current sensing board . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

3.6 The 3-phase AC induction motor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30

4 Software design . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32

4.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32

4.2 Software organization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32

4.3 Software variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35

4.4 Base values and PU model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36

4.4.1 Magnetizing current . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36

2/54

AN2388 Contents

4.4.2 Numerical considerations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37

4.4.3 ST10-DSP features . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37

4.5 Analog value scaling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39

4.5.1 Current sensing and scaling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39

4.5.2 Rotor mechanical position sensing . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40

4.5.3 The PI regulator . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43

4.6 Clark and Park transformation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44

4.6.1 (a,b)->(α,β) projection (Clark transformation) . . . . . . . . . . . . . . . . . . . . 44

4.6.2 The (α,β)-> (d,q) projection (Park transformation) . . . . . . . . . . . . . . . . . 45

4.6.3 The Current model implementation (rotor flux estimator) . . . . . . . . . . . 45

4.6.4 Generation of sine and cosine values . . . . . . . . . . . . . . . . . . . . . . . . . . 46

4.6.5 The space vector modulation module . . . . . . . . . . . . . . . . . . . . . . . . . . 47

5 References . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52

6 Revision history . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53

3/54

Background AN2388

1 Background

1.1 AC induction motor

The AC induction motor is a rotating electric machine designed to operate from a 3-phase
source of alternating voltage. Asynchronous motors are based on induction. The cheapest
and most widely used is the squirrel cage motor in which aluminum conductors or bars are
cast into slots in the outer periphery of the rotor. These conductors or bars are shorted
together at both ends of the rotor by cast aluminum end rings. For variable speed drives, the
source is normally an inverter that uses power switches to produce approximately sinusoidal
voltages and currents controllable in terms of frequency and magnitude.

Like most motors, an AC induction motor has a fixed outer portion, called the stator and a
rotor that spins inside with a well-optimized air gap between the two.

Virtually all electrical motors use magnetic field rotation to spin their rotors. A three-phase
AC induction motor is the only type where the rotating magnetic field is generated naturally
in the stator because of the nature of the supply.

In an AC induction motor, one set of electromagnets is formed in the stator because the AC
supply is connected to the stator windings. The alternating nature of the supply voltage
induces an Electromagnetic Force (EMF) in the rotor (just like the voltage is induced in the
secondary transformer) as per Lenz’s law, thus generating another set of electromagnets;
hence the name “induction motors”.

Interaction between the magnetic field of these electromagnets generates a revolving force,
or torque. As a result, the motor rotates in the direction of the resultant torque.

1.1.1 Stator

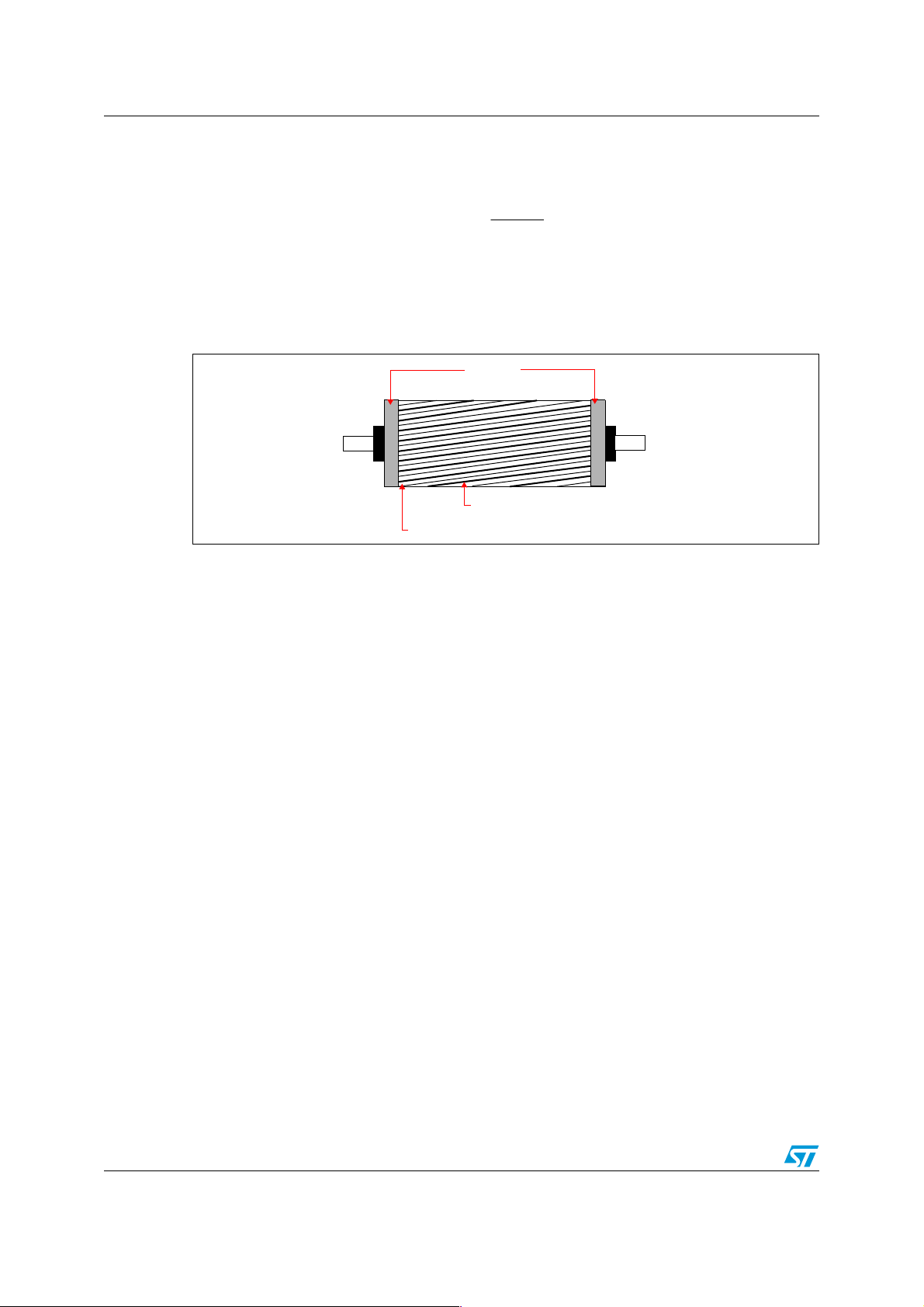
The stator is made up of several thin laminations of aluminum or cast iron. They are
punched and clamped together to form a hollow cylinder (stator core) with slots as shown in

Figure 1. Coils of insulated wires are inserted into these slots. Each grouping of coils,

together with the core it surrounds, forms an electromagnet (a polar pair) on the application
of AC supply.

The number of poles of an AC induction motor depends on the internal connection of the
stator windings. Internally they are connected in such a way, that when an AC supply is
applied, a rotating magnetic field is created.

4/54

AN2388 Background

Figure 1. Stator core and windings

1.1.2 Rotor

The rotor is made up of several thin steel laminations with spaced bars, which are made up
of aluminum or copper, along the periphery. In the most popular type of rotor (squirrel cage
rotor), these bars are connected mechanically at the ends and electrically by the use of
rings. The rotor consists of a cylindrical laminated core with an axially placed parallel slot for
carrying the conductors. Each slot carries a copper, aluminum or alloy bar. These rotor bars
are permanently short-circuited at both ends by means of the end rings. The rotor slots are
not exactly parallel to the shaft in order to decrease magnetic hum and slot harmonics.
Moreover this reduces the locking tendency of the rotor. In fact, the rotor teeth tend to
remain locked under the stator teeth due to direct magnetic attraction between the two. This
happens when the number of stator teeth are equal to the number of rotor teeth.

The rotor is mounted on the shaft using bearings on each end. One end of the shaft is
usually kept longer than the other for driving the load. Some motors may have
position/speed sensing devices. Between the stator and the rotor exists an air-gap, through
which, due to induction, the energy is transferred from the stator to the rotor like a
transformer. The generated torque forces the rotor and then the load to rotate.

The magnetic field created in the stator rotates at a synchronous speed (N

N ×= 60

s

where:

N

= synchronous speed in RPM

s

= the number of pole pairs

p

p

f = the supply frequency in Hertz

f

p

p

).

s

The magnetic field produced in the rotor is alternating in nature because of the induced
voltage. The frequency of the induced EMF is the same as the supply frequency. Its
magnitude is proportional to the relative velocity between synchronous speed (stator
frequency) and rotor speed. Since the rotor bars are shorted at the ends, the EMF induced
produces a current in the rotor conductors.

When the magnetic field is generated the rotor starts to run in the same direction trying to
reach the same speed. The rotor revolves slower than the speed of the stator field. This
difference is called slip (s). The slip varies with the load so that an increasing of the load

5/54

Background AN2388

causes the rotor to slow down (or slip increasing). On the contrary, a decreasing of the load
causes the rotor to speed up (or slip decreasing). The slip is expressed as a percentage and
can be determined with the following formula:

−

NN

rs

=

Slip

where;

N

= synchronous speed in RPM

s

N

= rotor speed in RPM

r

100% ×

N

s

Figure 2. Rotor structure

Rings

Shaft

Conductors

Skewed slots

Slots in the inner periphery of the stator accommodate 3-phase winding a, b, c. The turns in
each winding produces an approximately sinusoidally-distributed flux density around the
periphery of the air gap. When three currents that are sinusoidally varying in time, but
displaced in phase by 120° from each other, flow through the three symmetrically placed
windings, a radially directed air gap flux density is produced that is also sinusoidally

distributed around the gap and rotates at an angular velocity equal to the angular frequency

ω

of the stator currents.

s

The flux produced by the stator current is a sinusoidally-distributed wave. This flux revolves
and collides with the rotor bars, generating rotor current in the short-circuited rotor bars.
Because of the low resistance of these shorted bars, only a small relative angular velocity ω
between the angular velocity ω

of the flux wave and the mechanical angular velocity ω of

s

the two pole rotor is required to produce the necessary rotor current.

The relative angular velocity ω

is called the slip velocity. The interaction of the sinusoidally

r

distributed air gap flux density and induced rotor currents produces a torque on the rotor.

1.2 Three-phase induction motor and classical AC drives

Three-phase AC induction motor are widely used in many fields. They are classified in two
categories:

● Squirrel cage motor

● Wound-rotor motor

90% of the three-phase AC Induction motors are squirrel cage motors because of their lower
cost and the possibility of starting heavier loads with respect to wound-rotor motors. The
range of power ratings goes from one-third to hundred horsepower.

r

The wound-rotor motor is a variation of the squirrel cage induction motor. While the stator is
the same as that the squirrel cage, it has a set of windings on the rotor which are not short-

6/54

AN2388 Background

circuited, but are terminated to a set of slip rings. These are helpful in adding external
resistors and contactors.

In fact, it is possible to demonstrate that the slip frequency producing the maximum torque
(pull-out torque) is directly proportional to the rotor resistance. In wound-rotor motors, the
real rotor resistance can be increased by connecting external resistors through the slip
rings. This possibility allows for higher slip and hence, the pull-out torque at lower speed. A
particularly high resistance can deliver a high pull-out torque starting from zero speed. As
the motor accelerates, the value of the resistance can be reduced so that the motor
characteristic can follow the load requirement at different speeds. Once the motor reaches
the nominal speed, external resistors are removed from the motor coming back to work as
the standard induction motor.

This motor type (when external resistors are connected with the rotor) is ideal for very high
inertia loads, where it is necessary to generate the pull-out torque at almost zero speed and
accelerate to full speed in the minimum time with minimum current consumption.

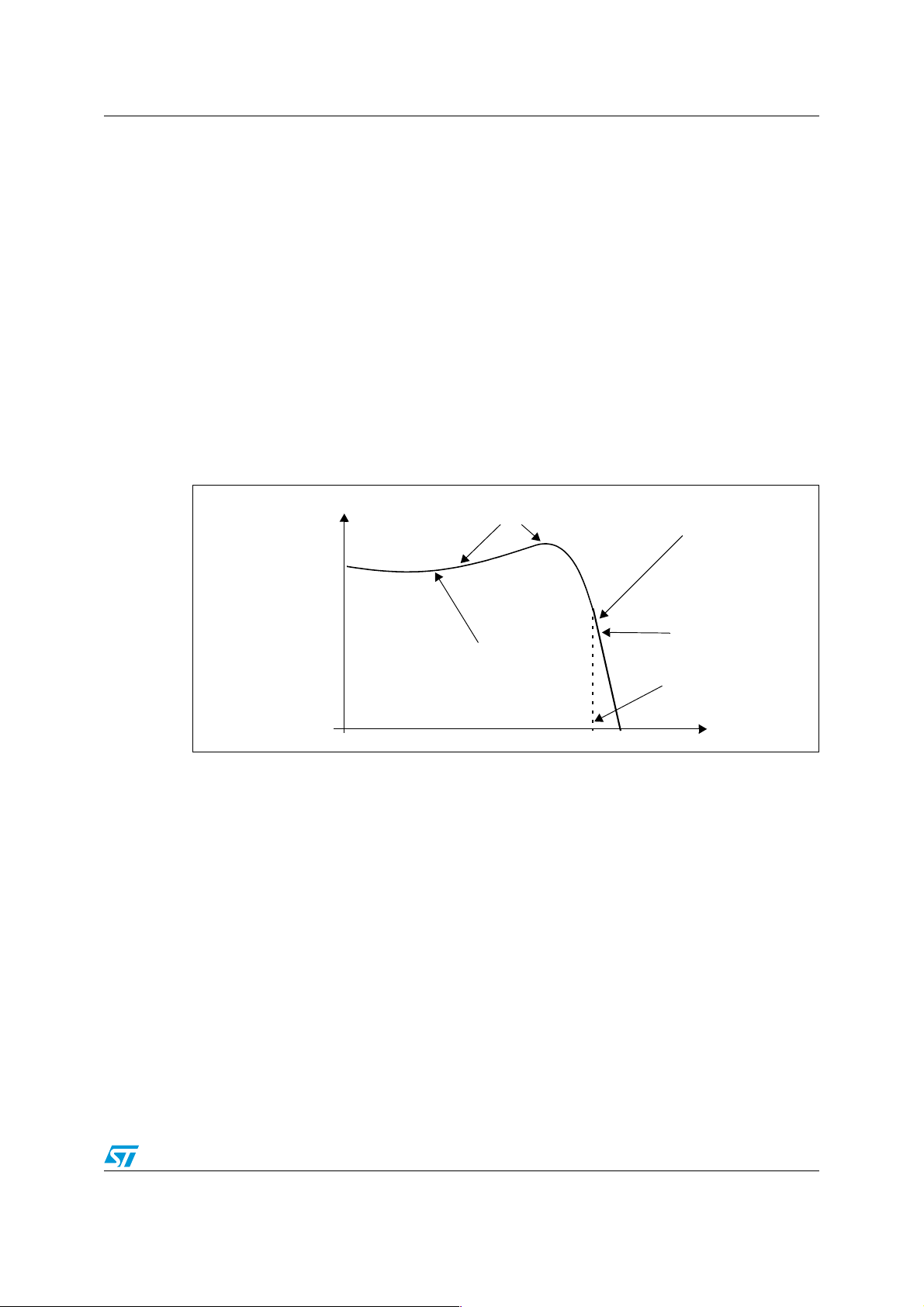
The typical speed-torque characteristic of an induction motor is shown in Figure 3

Figure 3. Speed-torque characteristic

Pull-out Torque

Locked Rotor Torque (LRT)

1.5

Flux decreases

Stable zone

T, r a t e d

1.0

Unstable points

Slip Speed

Flux = rated

Rotor speed

Nb Ns

The X axis shows speed and slip. The Y axis shows the torque. During start-up the motor
needs seven times the rated current and this depends on the interaction between stator and
rotor flux, the losses in the stator and rotor windings and losses in the bearing due to friction.
This over-current produces the torque necessary to spin the motor from zero speed.

During start-up, the motor is able to delivers 1.5 times the rated torque. This torque is called
locked rotor torque (LRT). Once the speed increases, the current that flows in the motor
reduces slightly. When the motor runs at approximately 80% of the synchronous speed, the
load can increase up to 2.5 times the rated torque. Any further growth in term of load could
take the motor to a stall condition.

As seen in the speed-torque characteristics, torque is highly nonlinear as the speed varies.
In all applications where it is necessary to regulate the speed a control strategy must be
used which is able to vary the frequency. One of the best known strategies is the simple
open loop method called Variable Voltage Variable Frequency or simply V/f method. This
method doesn’t allow management of the quantities in terms of phase but modifies only the
magnitude of the stator flux.

7/54

Background AN2388

φ

The torque delivered by the motor is directly proportional to the magnetic field produced by
the stator. The flux produced by the stator is proportional to the ratio of applied voltage and
frequency of the supply. By varying the frequency it is possible to control the speed motor.

If the ratio of voltage to frequency is kept constant, the torque delivered by the motor
remains constant under the condition of no torque load variation.

[][ ]

=∝

e

fVelocityAngularStatorFluxVVoltageStator

πφωφ

2*)(*)()(

or

V

=

f

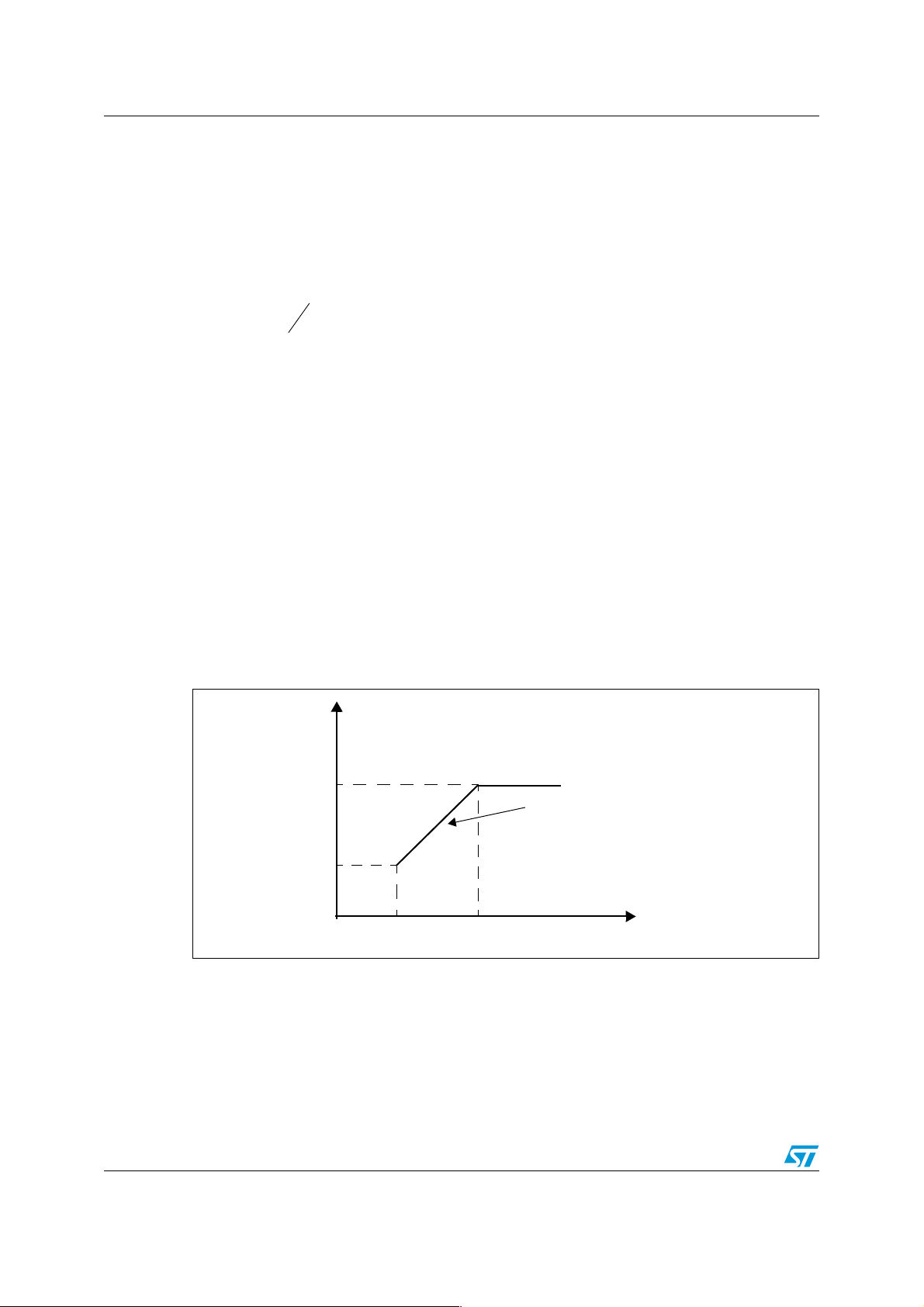
Figure 4 shows the relation between the voltage and torque versus frequency. At base

speed, the voltage and frequency reach their nominal values. The motor can be driven
beyond base speed by increasing the frequency. The applied voltage cannot be increased
beyond the V

voltage. Only the frequency can be increased. Above base speed losses,

max

mechanical friction and other complex factors increase significantly. The torque curve
becomes nonlinear respect to speed or frequency.

The Voltage on frequency is based on steady-state characteristics of the motor and the
assumption that the stator voltages and currents are sinusoidal. Its field of application is the
majority of existing variable-speed AC drives by means of an open-loop constant V/f voltage
source converter. No inner current controllers are required. The advantages of this control
technique is its simplicity, it is quick and easy to program and doesn’t require any highly
complex calculations.

The major drawback is the high reaction time for load variations and the efficiency during
these operation points. This is the reason why it is often used in fans and pumps where the
torque load is approximately constant.

Figure 4. Voltage frequency characteristic

Vs

Vmax

φ = constant

Vmin

f

minimum frequency rated frequency (stator frequency)

8/54

AN2388 Vector control of AC induction machines

2 Vector control of AC induction machines

2.1 Introduction

The performance of an AC induction motor is strongly dependant on its control. The recent
advances of powerful microcontrollers with DSP functions has enhanced complex and real­time algorithms. In particular, the use of a powerful microcontroller brings the following:

● system cost reduction by an efficient control and right dimensioning power devices as

well

● the removal of speed or position sensors by the implementation of sensorless

algorithms that need higher complexity calculations

● a reduction of current harmonics using enhanced algorithms

● a reduction in the number of look-up tables which reduces the amount of memory

required

● real-time generation of torque and flux profiles and move trajectories, resulting in

better-performance

Thanks to the capability of such modern microcontrollers it is possible to implement
sophisticated controls like Vector Control.

Vector control refers not only to the magnitude but also to the phase of variables. Matrix and
vectors are used to represent the control quantities. This method takes into account not only
successive steady-states but real mathematical equations that describe the motor itself, so
that the obtained results have a better dynamic for torque variations in a wider speed range.

The Field Oriented Control (FOC) offers a solution to circumvent the need to solve high
order equations with a large number of variables and nonlinearities and achieve an efficient
control with high dynamic.

This approach needs more calculations than other standard control schemes and has the
following advantages:

● full motor torque capability at low speed

● better dynamic behavior

● higher efficiency for each operation point in a wide speed range

● decoupled control of torque and flux

● short term overload capability

● four quadrant operation

2.2 Theory on vector control

FOC involves controlling the components of the motor stator currents, represented by a
vector, in a rotating reference frame (with a d-q coordinate system). In a special reference
frame, the expression for the electromagnetic torque of the smooth-air-gap machine is
similar to the expression for the torque of the separately excited DC machine. In the case of
induction machines, the control is normally performed in a reference frame aligned to the
rotor flux space vector. To perform the alignment on a reference frame revolving with the
rotor flux requires information on the modulus and the space angle (position) of the rotor flux

9/54

Vector control of AC induction machines AN2388

space vector. In order to estimate the rotor flux vector is possible to use two different
strategies:

● DFOC (Direct Field Oriented Control): rotor flux vector is either measured by means of

a flux sensor mounted in the air-gap or measured using the voltage equations starting
from the electrical machine parameters.

● IFOC (Indirect Field Oriented Control): rotor flux vector is estimated using the field

oriented control equations (current model) requiring a rotor speed measurement.

The usual terminology “Sensorless” specifies that no position/speed feedback devices are
used.

With these algorithms, the stator currents of the induction machine are separated into flux
and torque producing components by utilizing transformation to the d-q coordinate system.
On this reference frame the torque component is on the q axis and the flux component is on
the d axis. The vector control system requires the dynamic model equations of the induction
motor and returns to the instantaneous currents and voltages in order to calculate and
control the variables.

The technique described in this application note is IFOC. Indirect vector control of the rotor
currents can be implemented using the following data:

● Instantaneous stator phase currents, i

●

Rotor mechanical position

● Rotor electrical time constant

, ib, and i

a

c

The motor must be equipped with sensors to monitor the three-phase stator currents and a
rotor position feedback device. An encoder is normally mounted on the shaft rotor for this
purpose but in order to have a cheaper solution is possible to use a speed feedback device
such as a tachometer.

The key for understanding how vector control works is to explain the coordinate reference
transformation process. From the perspective of the stator, a sinusoidal input current is
forced to the stator. This time variant signal causes the generation of a rotating magnetic
flux. The speed of the rotor is a function of the rotating flux vector. From a stationary
perspective, the stator currents and motor and the rotating flux vector look like AC
quantities.

Keep in mind that the rotor flux speed is not equal to the revolving magnetic field, produced
by the stator phase windings, during the transient conditions. Looking at the motor from this
perspective during steady state conditions, the stator currents become constant.

2.2.1 Space vector definition and projection

The three-phase voltages, currents and fluxes of AC-motors can be deeply studied in terms
of complex space vectors. Assuming that i
phases we can define the stator current vector i

2

π

j

where and represent the spatial operators.

α

3

e=

α

4

π

j

2

3

e=

, ib, ic are the instantaneous currents in the stator

a

by:

s

2

iiii

αα

++=

cbas

This current space vector describes the three phase sinusoidal system.

10/54

AN2388 Vector control of AC induction machines

As discussed above, this three phase system can be transformed into a two time invariant
co-ordinate system. This transformation can be split in two steps:

● (a,b,c) -> (α,β) (the Clark transformation) which outputs a two co-ordinate time variant

system

● (α,β) -> (d,q) (the Park transformation) which outputs a two co-ordinate time invariant

system

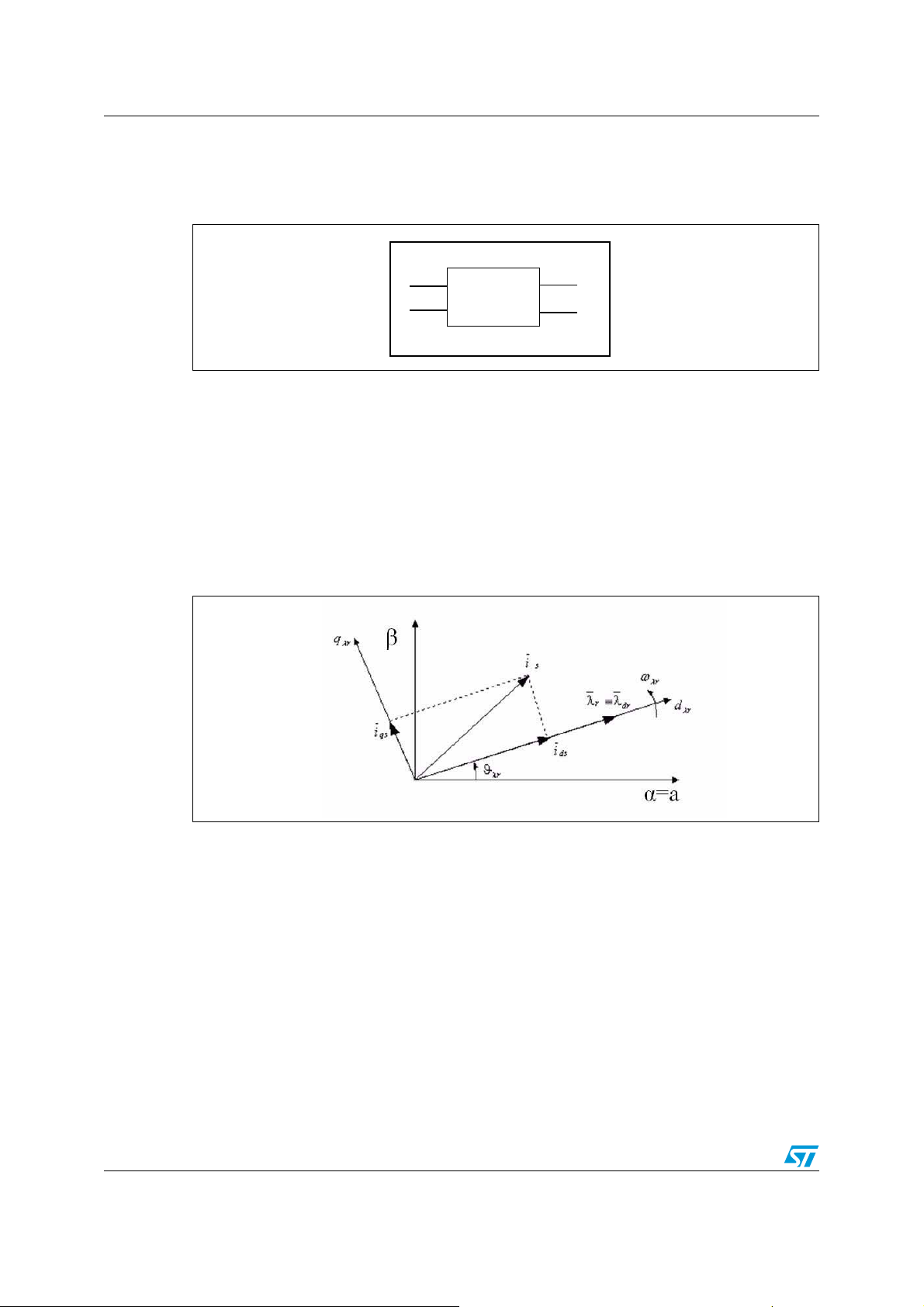
2.2.2 The (a,b,c)(α,β) projection (Clark transformation)

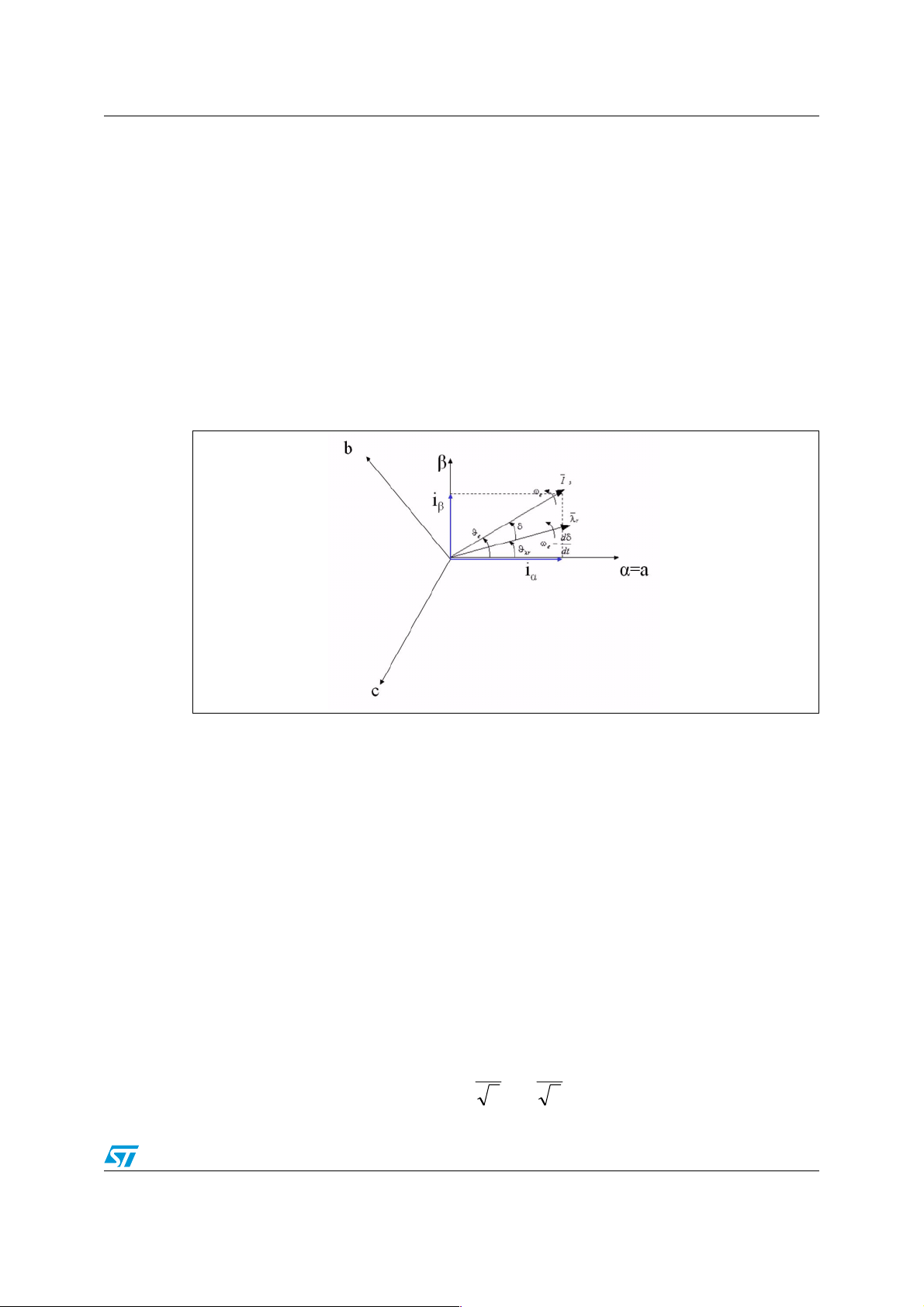
The space vector can be reported in another reference frame with only two orthogonal axis
called (α, β). Assuming that the axis a and the axis α are in the same direction we have the
following vector diagram:

Figure 5. Stator space vector in 2-orthogonal axis (Clark components) in a

reference frame aligned with the stator

where:

θ

is the rotor flux position

λr

θ

is the revolving magnetic field position

e

ω

is the revolving magnetic field angular speed

e

δ is an angle that depends on torque load transitions

Take into consideration that δ doesn’t change in steady state so the rotor flux speed revolves
with the same speed of revolving magnetic field.

Basically the transformation moves from a 3-axis, 2-dimensional coordinate system
referenced to the stator of the motor to a 2-axis system also referenced to the stator.

The projection that modifies the three phase system into the (α,β) two-dimensional
orthogonal system is presented below.

ii

=

⎧

as

α

⎪
⎨

⎪
⎩

1

β

3

11/54

2

iii

+=

bas

3

Vector control of AC induction machines AN2388

We obtain a two co-ordinate system that still depends on time and speed.

Figure 6. Clark transformation module

i

⎛

⎞

s

⎜

⎟

⎜

⎟

i

βαs

⎝

⎠

ia

ib

Clarke

ic=-ia-ib

ialfa

ibeta

2.2.3 The (α,β)(d,q) projection (Park transformation)

This is the most important transformation in the FOC. In fact this projection modifies

a two phase orthogonal system (α,β) in the d, q rotating reference frame. Thanks to this
information it is possible to fix a component of the stato current on a d-axis responsible of
flux. If we consider the d-axis aligned with the rotor flux, the next diagram (Figure 7) shows,
for the current vector, the relationship from the two reference frames:

Figure 7. Stator Space vector in a reference frame revolving with the rotor flux

vector λ

r

where θλr is the rotor flux position. The flux and torque components of the current vector are
determined by the following equations:

⎧

⎪
⎨
⎪

⎩

These components depend on the current vector (α,β) components and on the rotor flux
position ; knowing the right rotor flux position, then make constant the d,q
component.

The two co-ordinate system obtained using a Park transformation has the advantages
of being time invariant and has separate torque and flux components for stator currents.

12/54

()

θ

r

λ

i

⎞

⎛

ds

⎟

⎜

⎟

⎜

i

qs

⎠

⎝

() ()

+=

iii

() ()

+−=

θθ

sincos

rsrsds

λβλα

iii

θθ

cossin

rsrsqs

λβλα

AN2388 Vector control of AC induction machines

Figure 8. Park transformation module

i

α

i

β

Rotor Flux Position

Park

θ

l

q

l

d

λ

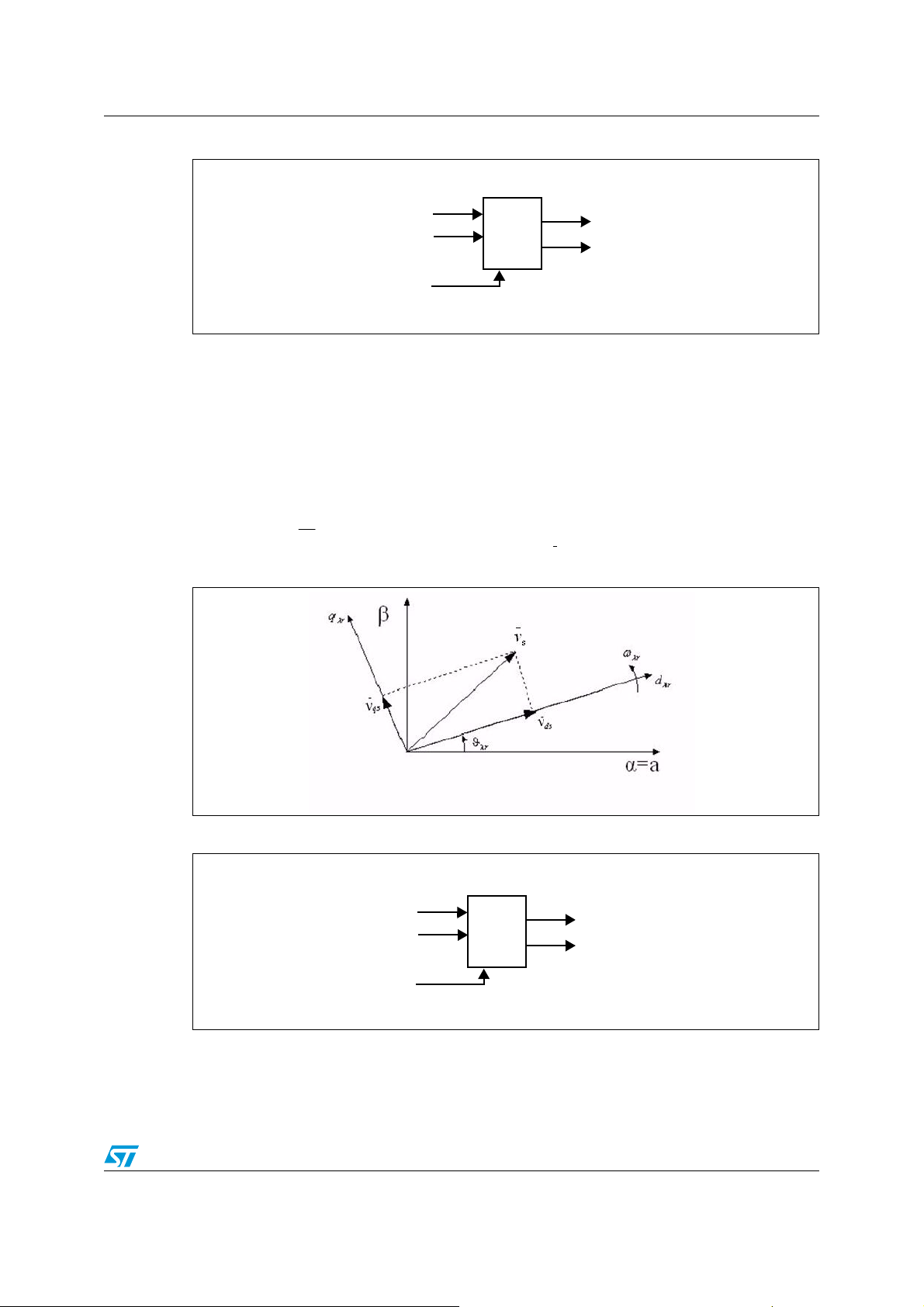
2.2.4 The (d,q)(α,β) projection (inverse Park transformation)

The equations presented here transform the stator voltage expressed in a d,q rotating
reference frame into a

The outputs of this block are the components of the reference vector to be applied to the
motor phases ( ) through space vector modulation.

V

(α,β) orthogonal system:

⎧

⎪
⎨
⎪

⎩

r

() ()

−=

VVV

() ()

−=

VVV

θθ

sincos

rqrefrdrefref

λλα

θθ

sinsin

rqrefrdrefref

λλβ

Figure 9. Voltage components in inverse Park transformation

Figure 10. Inverse Park transformation module

V

d

V

Inverse

q

Park

θ

r

λ

Rotor Flux Position

v

α

v

β

13/54

Vector control of AC induction machines AN2388

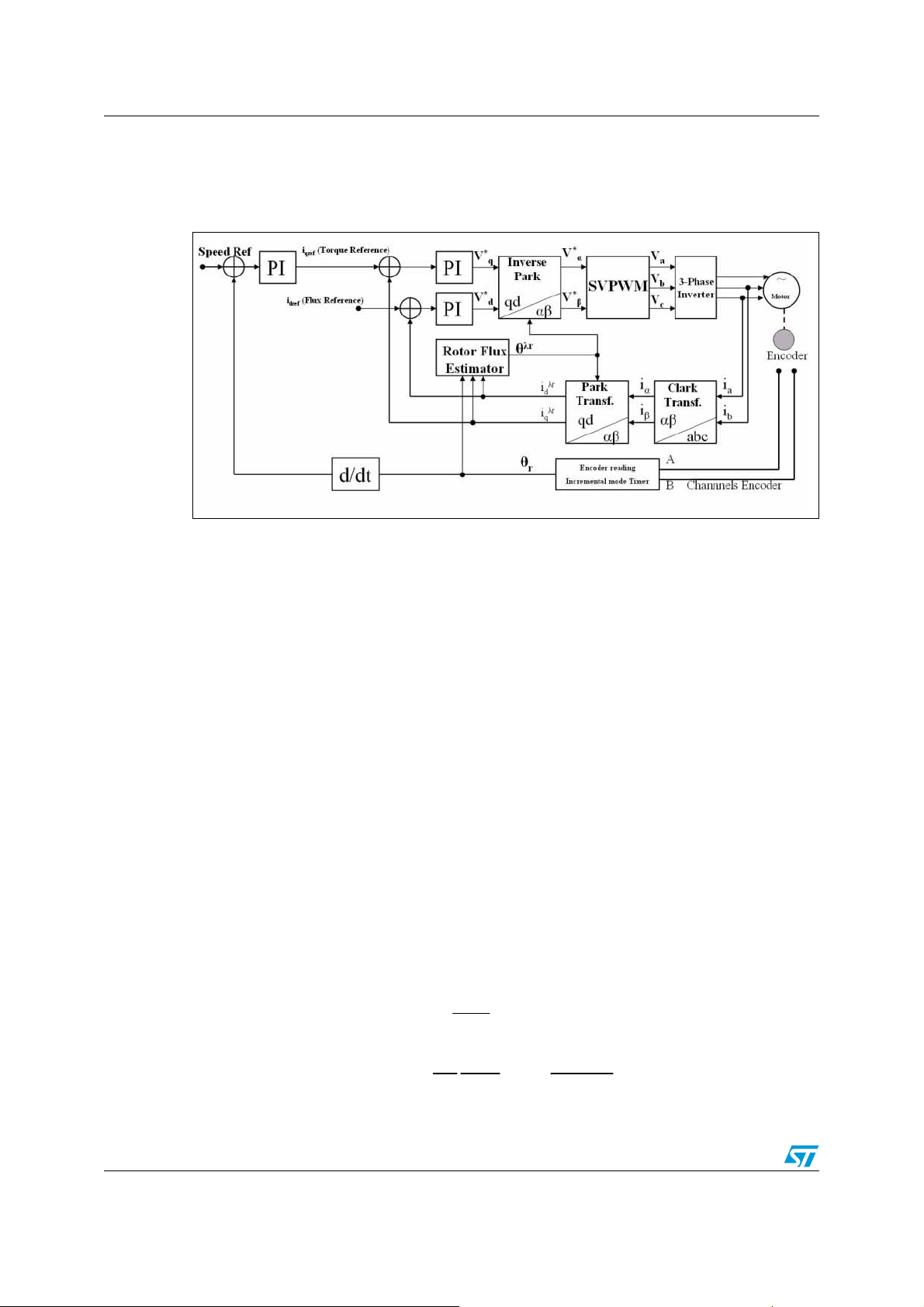
2.3 Block diagram of the vector control

The basic scheme of torque control with IFOC is shown below:

Figure 11. Block diagram of I.F.O.C.

Two phase currents go into some transformation module (Clarke and Park). The projection
outputs of the Clark block are indicated with i
current provide the input of the Park transformation that gives the current in the
reference frame aligned with the rotor flux vector. The exact rotor flux angular position (θ
is necessary to calculate the two components i
compared to the references i
torque command i
the right rotor flux command for every speed reference within the nominal value. The current
regulator outputs are V
transformation. The outputs of this are V
stator vector voltage in the α,β orthogonal reference frame. These are the inputs of the
Space Vector PWM. The outputs of this block are the gate signals that drive the inverter.
The main block of the vector control is the
resistance and rotor inductance as parameters and knowledge of these, with the highest
accuracy, greatly affects the performance of the control.

is the output of the speed regulator. The flux command i

qref

dref

(the flux reference) and i

dref

and V

. They are processed into the inverse Park

qref

αref

and isβ. These two components of the

sα

and i

ds

and V

Current Model block. This block needs the rotor

The ids and iqs components are

qs.

(the torque reference). The

qref

, which are the components of the

βref

d,q rotating

indicates

dref

λr

)

2.4 The current model (rotor flux estimator)

Knowledge of the rotor flux space vector magnitude and position are key for the AC
induction motor vector control. Knowing the rotor magnetic angular position allows to
establish, in fact, the rotational co-ordinate system (d, q). .

The current model consists of implementing the following two equations of the motor in the
d-q reference frame:

di

mR

+=

dt

d

θ

dt

i

mR

i

λ

r

n

qs

+==

iT

Ti

rds

1

f

s

ω

b

14/54

ω

bmRr

AN2388 Vector control of AC induction machines

L

where θλr is the rotor flux position, imR the magnetizing current and the rotor time

T =

constant.

r

r

R

r

The knowledge of this constant is critical for the proper functioning of the overall FOC since
it is strictly tied to the rotor flux speed that is integrated to get the rotor flux position.

Assuming the previous equation can be discretized as follows:

ii ≈

qSqS

+1

kK

mR

mR

+

T

k

T

r

1

+=

1

T

ω

ωθθ

r

λλ

k

−+=

mRds

KK

i

qs

K

i

mR

br

1

k

+

⋅⋅+=

sb

1

k

+

ii

k

1

+

nf

ks

k

1

+

r

k

1

+

eqii

eq

eqTf

1.)(

2.

3.

where:

i

= magnetizing current

mR

f

=rotor flux speed

s

T = sampling time

n = rotor mechanical speed

T

= Lr / Rr (Rotor time constant)

r

θλr = rotor flux position

ω

= electrical nominal flux speed

b

During the steady state condition, the Id current component is responsible for generating the
rotor flux. For transient changes, there is a low-pass filtered relationship between the
measured I
component of I

Under steady-state conditions, I

current component and the rotor flux. The magnetizing current, ImR, is the

d

that is responsible for producing the rotor flux.

d

is equal to ImR. This equation is dependent upon accurate

d

knowledge of the rotor electrical time constant.

Essentially, the equation of the magnetizing current corrects the flux producing component
of I

during transient changes.

d

The computed I
frequency is a function of the rotor electrical time constant, I

value is then used to compute the slip frequency (eq.2) The slip

mR

, ImR and the current rotor

q

velocity.

Equation 3 is the final flux estimator equation. It expresses the new flux angle based on the
slip frequency calculated in Equation 2 and the previously calculated flux angle.

If the slip frequency and stator currents have been related by Equation1 and Equation 2,
then motor flux and torque have been specified. Furthermore, these two equations ensure
that the stator currents are properly oriented to the rotor flux. If proper orientation of the
stator currents and rotor flux is maintained, then flux and torque can be controlled
independently. The I

current component controls motor torque. Already explained is the

d

principle of the indirect vector control.

15/54

Vector control of AC induction machines AN2388

2.5 Space vector modulation (SVPWM)

Space vector modulation is a sophisticated PWM method that provides advantages to the
application when compared to classical sinusoidal weighted modulation PWM:

● Higher bus voltage utilization (86%)

● Lower THD%

One common way to represent the phase voltages A, B, C is the space vector model. The
three legs of the three phase inverter can connect the phases of the motor to positive or
negative terminal of DC bus voltage. Considering that one and only one switch per leg must
be closed, 8 different states are possible. It is possible to associate a reference vector to
each of the 8 states. In order to generate a rotating field, the inverter has to be switched in
six of the eight states. This mode of operation is called six-step mode. The remaining two
states are called zero vectors because in these states the voltage applied in the motor
windings is null due to the middle point of each leg is connected to GND or to the DC bus
voltage. The zero vectors, located in the middle of the hexagon, see Figure 17, can be used
to regulate the amplitude of the space vector. The angle between any two vectors is 60°.

Note that whenever transistor T1 is on, transistor T2 is off, and vice versa. This makes it
easy to adopt a simple notation to describe the state of the inverter. For example, the state
when transistors T1, T4 and T6 are “on” (and of course T2, T3, and T5 are “off”) can be
represented with the notation (+,-,-). The state where transistors T2, T3, T6 are on is
denoted by (-, +, -).

Thanks to this notation is possible to determine the following states related to the power
switches of the inverter.

(+, -, -), (+, +, -), (-, +, -), (-, +, +), (-, -, +), (+, -, +),

Running the inverter through this switching sequence will produce the line-to-neutral
voltages shown in Figure 12.

16/54

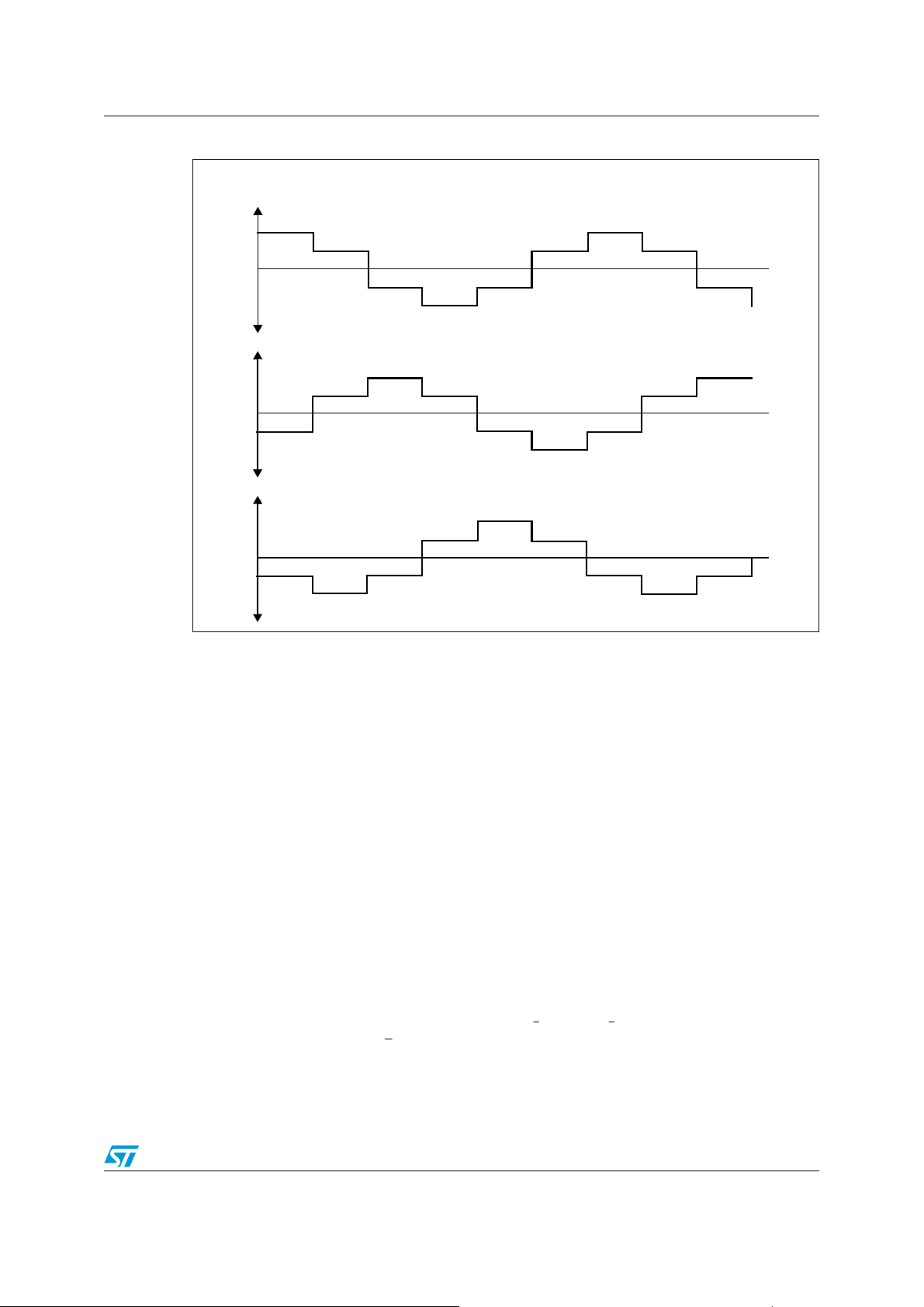
AN2388 Vector control of AC induction machines

Figure 12. Line to neutral voltage in “six-step mode”

Van

(+,-,-) (+,+,-) (-,+,-) (-,+,+) (-,-,+) (+,-,+)

Vbn

(+,-,-) (+,+,-) (-,+,-) (-,+,+) (-,-,+) (+,-,+)

Vcn

(+,-,-) (+,+,-) (-,+,-) (-,+,+) (-,-,+) (+,-,+)

This strategy of operation is called “six-step mode”. Operating in this mode allows you to use
the full capabilities of the inverter. The amplitude of the fundamental frequency in six-step
mode is actually greater than the inverter rail voltage.

Space vector modulation uses six-step mode, but smoothes out the steps through some
sophisticated averaging techniques. For example, if a voltage is required between two step
voltages, the corresponding inverter states can be activated in such a way that the average
of the step voltages produces the desired output. To develop the equations needed to
generate this averaging effect, the problem is transformed into an equivalent geometrical
problem. The first step in this re-definition is to transform the inverter voltages of six-step
mode into a space vector.

Space vectors are similar to phasors and they are denoted by a magnitude and an angle. It’s
important to note that space vectors are not phasors. Phasors are used to represent a
single time varying sinusoid. Space vectors are used to represent three spatially separated
time variant quantities. If there are three time varying quantities, which sum to zero and are
spatially separated by 120°, then these quantities can be expressed as a single space
vector.

Since the three line-to-neutral voltages sum to zero, they can easily be converted into a
space vector (u

) using the following transformation:

s

⎛
⎜
⎜
⎝

0

j

an

bn

2

j

3

++=

2

−

j

⎞

3

⎟

)()()(

etVetVetVu

cn

⎟
⎠

Since the components of space vectors are projected along constant angles (0,-2π/3, and
2π/3), it is easy to graphically represent a space vector as shown in

Figure 14.

17/54

Vector control of AC induction machines AN2388

Figure 13. Three-phase inverter

T1

T3

T5

A

+

Vdc

_

T2

T4

B

T6

Table 1.

State C On Devices Van Vbn Vcn

0 T2, T4,T6 0 0 0 0

1 T1,T4, T6 2Vdc/3 -Vdc/3 -Vdc/3 U

2 T1,T3, T6 Vdc/3 Vdc/3 -2Vdc/3 U

3 T3,T2, T6 -Vdc/3 2Vdc/3 -Vdc/3 U

4 T2,T3, T5 -2Vdc/3 Vdc/3 Vdc/3 U

5 T2,T4, T6 -Vdc/3 -Vdc/3 2Vdc/3 U

6 T1,T4, T5 Vdc/3 -2Vdc/3 Vdc/3 U

7T1,T3, T50000

U

N

V

C

W

Space Voltage

Vector

(-,-,-)

000

(+,-,-)

0

(+,+,-)

60

(-,+,-)

120

(-,+,+)

180

(-,-,+)

240

(+,-,+)

300

(+,+,+)

111

Figure 14. Transforming 3 quantities into a single space vector

Usually, when creating space vectors, the three time-varying quantities are sinusoids of the
same amplitude and frequency that have 120° phase shifts. When this is the case, the
space vector at any given time maintains its magnitude. As time increases, the angle of the

18/54

AN2388 Vector control of AC induction machines

space vector increases, causing the vector to rotate with a frequency equal to the frequency
of the sinusoid.

Figure 15 shows the values that the space vector obtains as time increases.

The purpose of space vector modulation is to generate the appropriate PWM signals so that
any vector (u
defined by u
and u

for a percentage of time (t2) such that:

2

) can be produced. Consider a space vector voltage u

s

and u2. We can approximate us by applying u1 for a percentage of time (t1)

1

**

0

1

2

uutut =+

60

s

located in the sector

out

This leads to the following formulas for t

2

1

where (Modulation index)

α

uU =

out

u∠=

s

and t2:

1

⎛

⎞

1

⎜

=

2

Ut

⎜

3

⎝

⎡

Ut

⎢
⎣

)sin(

α

⎟

⎟
⎠

)cos(

⎟

⎜

−=

⎟

⎜

3

⎠

⎝

⎞

⎛

1

⎤

)sin(

αα

⎥
⎦

So, given a space vector of angle α, bounded by u0, u60 and modulation index U, the
approximation can be constructed by applying vectors u
and t

respectively. If the vector is in another sector it can be rotated by a multiple of π/3

2

and u60 for percentage of times t1

0

radians until it is inside the first sector. No over-modulation condition has been implemented
in this application note.

Figure 15. Approximation of Us

Figure 15 shows how any vector in the sector bounded by u

To approximate u
seconds, and the inverter state that corresponds to u

the inverter state that corresponds to u0 should be active for t1*T0

s

60

When the modulation index is sufficiently small (less than 0.866), the sum of t
less than one. This means that t
the PWM frequency. That’s why T

1*T0+t2*T0

will be indicated as T

0

is less than T0. T0 is the sampling time, typically

voltage should be applied to the motor. The remaining time will be referred to as t

and u60 can be approximated.

0

should be active for t2*T0 seconds.

and t2 will be

1

. So for the left over time no

pwm

.

0

To be more formal:

)1(

ttTt

−−=

pwm

210

There are two ways to apply no voltage to the motor. The first way is to simply connect all
three phases to the negative rail of the inverter. This will be called inverter state 0 and the

19/54

Vector control of AC induction machines AN2388

corresponding switching pattern is (-, -, -). The second way to apply no voltage to the motor
is to connect all three phases to the positive rail of the inverter. This will be called inverter
state 7 and the corresponding switching pattern is (+, +, +).

To approximate the voltage u

during the PWM carrier period, the pulses and timing shown

s

in Figure 16 should be used.

This uses a symmetric or center-aligned space vector modulation in order to reduce the
THD%

Figure 16.

1

When the modulation index exceeds (0.866), the value of t
(depending on the angle). As it is not possible to apply one of the zero vectors for negative

3

2

can become negative

0

time, the maximum modulation index for space vector modulation is approximately 0.866.
unless an over-modulation additional block is implemented in the SVPWM routine. However
such a block is not implemented in this application note.

Graphically, this means that for space vector modulation to work properly, the magnitude of
the reference space vector, u

, must be totally contained inside the hexagon shown in

s

Figure 17.

20/54

AN2388 Vector control of AC induction machines

Figure 17.

Each of the vectors U
by the inverter where the zero voltages 0

, U60, etc., in the diagram represent the six voltage steps developed

0

000

and 0

are located at the origin. At each of

111

these states the inverter transistors are in steady state. In order to develop a sine wave at
the motor then we must devise a switching pattern that produces a voltage at not only the six
vectors states but also one which transitions in between these states. This effectively means
producing a continuously rotating vector Uout that transition smoothly from state to state.

SVPWM seeks to average out the adjacent vectors for each sector. Using the appropriate
PWM signals a vector is produced that transitions smoothly between sectors and thus
provide sinusoidal line to line voltages to the motor.

21/54

Hardware design AN2388

3 Hardware design

3.1 System configuration

The application is designed to drive the 3-phase AC motor. It consists of:

● MDK-ST10 Control Board

● 3-phase AC/BLDC High Voltage Power Stage

● Gate driver Stage

● Current Sensing Board

● 3-phase AC Induction motor

3.2 MDK-ST10 control board

The MDK-ST10 control board is used to demonstrate the capabilities of the ST10F276
microcontroller and to provide a hardware tool allowing applications development.
ST10F276 is a 16-bit MCU with MAC unit (DSP features), 832 Kbytes of flash memory and
68 Kbytes of RAM. Its main characteristics are: 64MHz CPU, 31.25ns instruction cycle,
multiply/accumulate unit (MAC) with 40-bit accumulator 8 PWM channels, 24 A/D converter
channels (10-bit 3µsec of conversion time), CAP/COM peripherals with 16-bit timer
(100nsec of maximum resolution, 111 GPI/O, I
of the micro is shown in Figure 18. Please refer to ST10F276 datasheet or user manual for
more details.

2

C, SCI, 2 CAN peripherals. The architecture

The MDK-ST10 is an evaluation module board that includes a ST10F276 part, peripheral
expansion connectors (3 general purpose motor connectors + 1 standard MC connector
vector control-based) and CAN interface. The expansion connectors have been placed for
signal monitoring and user feature expandability.

Figure 18. ST10F276 block diagram

16

16

IRAM

2K

Watchdog

Oscillator

32kHz

Oscillator

PLL

5V-1.8V
Voltage

Regulator

PWM

CAPCOM2

CAPCOM1

16

Por t 2

16

16

8

XFLASH

320K

XRAM

48K

XRAM

16K

(STBY)

XRAM

2K

(PEC)

XI2C

XCAN1

Por t 0Po rt 1Por t 4

16

16

16

16 16

16 16

16 16

16

16

IFLASH

XPWM

XCAN2

External Bus

512K

XRTC

XASC

XSSC

Controller

32

CPU-Core and MAC Unit

16

16

Interrupt Controller

10-bit ADC

GPT1 / GPT2

BRG BRG

PEC

ASC0

SSC0

Por t 6

81615 8 8

Por t 5

22/54

Port 3 Port 7 Por t 8

AN2388 Hardware design

Figure 19.

MC Connector

3 G/P

Motor

Connectors

CAN 2.0

RS 232

DIP Configuration
Switches

The general purpose motor connectors are here below shown:

Figure 20. General purpose motor connectors (DC and BLDC motors)

Clock Configuration

3.3 Three-phase high voltage power stage (powerBD-1000)

For this purpose, the power stage has been chosen able to manage power requirements up
to 1000 watt. For other power ratings, it is possible to use PowerBD-300 (300 watt) or
PowerBD-3000. The power boards can work directly from AC or DC power supply (only DC
for the PowerBD-3000). The auxiliary supplies are located on the Power boards and are
usable with applications above 24V
Design Kit (UM0122, available from the ST website, http://www.st.com/mcu).

. For more details see the Motor Drive Reference

DC

Original partitioning between the Power board and Gate Driver Board contributes to system
noise immunity.

23/54

Hardware design AN2388

3.3.1 Power stage

The board is designed to fit TO220 packages. For the right part numbers see the details in
the following table:

Table 2.

PowerBD-300 PowerBD-1000 PowerBD-3000

Power board parameters

min max min max min max

AC input voltage range with on
board auxiliary supply & double
rectification

AC input voltage range with on
board auxiliary supply & voltage
doubler

DC input voltage range with on
board auxiliary supply

External auxiliary supply source 13V 18V 13V 18V 13V 18V

50V 260V 50V 260V 50V 260V

250V 135V 25V 135V 25V 135V

70V 370V 70V 370V 70V 370V

Recommended Power switches
at 12V

input voltage

DC

Recommended Power switches
at 24V

input voltage

DC

Recommended Power switches
at 42V

input voltage

DC

Recommended Power switches
at 120V

input voltage (with

AC

voltage doubler) or 230VAC
input voltage

STD35NF06
STB80NF55-08

STD25NF06
STB80NFFF-08

STD25NF10
STB75NF75

STGB3NB60HD
STGB3NB60KD
STGB7NB60HD
STGB7NB60KD
STGB7NC60HD
STGB7NC60KD

Not relevant Not relevant

Not relevant Not relevant

Not relevant Not relevant

STGP3NB60HDFP
STGP7NB60HDFP
STGP3NB60KDFP
STGP7NB60KDFP

1

STGP7NC60HDFP

1

STGP7NC60KDFP
STGP12NB60HD
STGP12NB60KD

Note: 1 New devices not included in the kit, available on request

2 New devices available ‘on request’, soon also in this package

The figure below shows the board:

1

STGW20NB60HD
STGW20NB60KD

1

STGW20NC60VD
STGW30NB60HD

2

STGY40NC60VD

2

STGY50NB60HD

1

1

24/54

AN2388 Hardware design

Figure 21. Components placement

Motor output

Tacho inputs

_

+

V

DC

15V supply BEMF & Hall sensor

AC inputs

3.3.2 Auxiliary supply

This Buck converter uses a VIPer12A providing start-up capability, integrated PWM
controller as well as thermal and over-current protection. This PWM controller is very simple
and does not require any external feedback compensation networking. The regulation circuit
is decoupled from the supply circuit, using a separate diode D2 and capacitor C2 to supply
the zener diode D3 on the FB pin. The diode D2 is a low voltage diode (1N4148) and allows
the voltage on Vdd to reach the start-up value. D2 and C2 together form a peak detector for
the output voltage.

To prevent disturbance resulting in possible output over-voltage or incorrect start-up, a zener
D6 is connected across the output. For further details please refer to the application notes
AN1317 and AN1357

An axial insulated inductor can be used. An inductor of this type meets low cost
considerations but features a high series resistance that affects the efficiency of the
converter. The current capability of this kind of inductor is determined, for a given package,
by its series resistance. For example, a 1.5mH inductor has a current capability of about
100mA since its series resistance is about 30R. The 5V is supplied from the 15V using a
L78L05 three-terminal positive regulator. It provides internal current limiting and thermal
shutdown. The 5V Zener diode D5 decreases the voltage regulator temperature in lifetime
sensitive applications.

Note: When the line voltage is lower than 44V, an external 15V auxiliary supply is mandatory. It

must be plugged to CON2 while removing J14 & J8

25/54

Hardware design AN2388

Figure 22. PowerBD-1000 schematic

00

ve
Rre

113

t
e
eh

S

tiK ecn

00
2

00

,

DC

92

0

e

b

re

1

M

ts

-

mu

f

D

ugu

e

N
tnemuco

Br
R
ngiseD

A

e

,

woP

y
adirF

D

:e

:e

l

ez

tiT

taD fo

i
S

D

1

E

2R ,02R

LLAT

S
NI T

,

K

12R

91R

7
.4

O
N

K

02R

7

V5+

.4

K7.4

91R

V

Fn001

5
+

V05

9
C

V51

+

5

1

2

123

4

1NOC

2NOC

TXE

-

CDV5

1

1
2
3
4
5
6
7
8
9

10
11
12
13

'F
B

1
2

'
EB

1
2
3
4

'DB

s

1

sent

2

'CB

su
bor lacinahcem

1
2
3

'
B
B

1
2

'
A
B

rof

CDV+

3
2R

100K-1/2W

100K-1/2W

1
R

1
C

1
T
S
F

4PT

7R

213

31J

21J

esneS tnerruC-sH

V5+

3

4

2-A516HFS

42

3

1U

1

1

2

8R

K2.2

740.0

W5.2

V004 Fn22

11C

213

2Q

1Q

esne

S
tnerruC-sH

1

2

AB

1

1

4y
a

l
e
R

4

123

BB

2X-V572 Fu22.0

01C

1F

5P

A 8

T

6PT

K0142R

A esahP

4TSF

8C

213

3Q

CB

3TSF

ESAHP

7PT

F
n
001

2

C
A
V

­03

2
/
0
2
1

6TSF

V004

1

LARTUE

N

B esahP

7TSF

8P
T

213

4Q

4

DB

9R

V51+

5TSF

C esahP

740.0

W5.2

01R

5
2R

123

001

2
U

9PT

moC

V004 F

n

2

22

1
C

213

213

5Q

K
0
1

1

2

E

FB

B

CONTROL BOARD

8414

8D

N1

7
Q

1 2

1

2

DELLA

A21Y

T
SN

AL

I
TON

E
R

5

3

4

3yale

4yaleR

R

3

4

W2/1-K021

W2/1-K02161R

W2

601HTTS11D

601HTTS

/
1-

K

2

60

021
1
HTTS

9

3

D

1R

1 2

K1

W2

/1

-K
7
2R

6
521R

6Q

V51+

gnir

6

V5+

2

R

o
tinoM V

H

41R

123

45678

9

011121

31

11

K
0
1

R

52-733CB

81R

01
D

1

1 2

W2/1-K6571R

K1

W2/1-

K192R

82

K
6551R

R

K0
1

K33

8TSF

9
T

1

2

3

SF

3NO

C

ROSNE

S
ERU

d
e
su ton fi p

T
AREPM

a
rtS

E
T

%

1< EB T
SR
O

T
S
I

S
SE

UM
R

E

YC
H

A
T

RUCCA
L

L
A

FFO

/
N
O

2
1

R
EP

4

I

1

V

J

12

841

4
N1

1D

1 2

60
1

H
T
T
S

2

J

1
J

C
D
V

­2
4/

4
2
/
2
1

V51

+

5
6
7
8

4

3C

2
C

2
D

3
J

1

1

1

4
D

1

2TSF

K
0

2R

8
6

2PT

1
P
T

PIDA

2
1R

E

1

PI

CI

V

NIAR

TES

S

D

ER

+

-

V3

D

2

D

.0

V

Fu

3

V5

0

3

1

51C48

3D

X
Z
B

1 2

F
u

V

2
.

5

2

2

1 2

lisnar

1R

t

T

6
J

1

1

5
J

1

4
J

2

3

CDV

-

gnirotinoM VH

3PT

K033

3R

4R

6C

V
5+

3

tuoV

ZCA50L87L

DNG

2CI

niV

1

1V5C58XZB

12

5D

5C

21

8J

99400 OKOT

Hm1

1L

2
1

ECRUOS

BF

Fn22

V05

4C

launam ees

11J

7J

1

1

1

01J

5R

1

22R

9J

4

-+

3yaleR

3

K21

Fu1

2

61C

5
8XZB

6D

Fu001

V52

7D

7C

100K-1/2W

100K-1/2W

V61

1 2

601HTTS

6R

3.4 Gate driver board

Each half bridge is driven by a high voltage integrated circuit L6386. It is able to operate at
voltage up to 600V. The logic inputs are CMOS logic compatible and the driving stages can
source up to 400mA and sink 600mA. It integrates one upper and one lower side channel
with two under-voltage lockout circuits and a comparator referred to 0.5V.

26/54

AN2388 Hardware design

The bootstrap auxiliary supply is integrated inside the IC helping to reduce the number of
PCB parts and to increase the layout flexibility. This function is normally accomplished by a
high voltage fast recovery diode. In the L6386 a patented integrated structure replaces the
external diode. It is realized by a high voltage DMOS, driven synchronously with the low side
driver (LVG) (refer to AN1299 for further information). An internal charge pump provides the
DMOS driving voltage. The diode connected in series to the DMOS has been added to
avoid unwanted switching on. An external fast recovery diode normally used for this purpose
can be avoided (this diode usually exhibits great leakage current). The gate drive resistors
R2, R6, R13 R18 R27 and R32 have been set at 100 Ohms. This value must be adapted
according to power device characteristics.

Figure 23. Gate driver board schematic

D

r
e

BA1

BA2

BB3

BB1

BB2
th
o

1
B

1

123

2

ch

rs in

BA1

B

a

o

e
n

nnect

GQ1

Q1

co
6

line

5
2

07-

itch betwee
p

C8
B

R4

.08 mm
5

1

0R
0
1

R2

.M)
(N

uF

V

2

16

C4

2.

uF

V
6

.2

1

2

C3

14

M
N.

2

D
6

BOOT

8

V

08A

63

1

L

D2

N

I

1

L

C1

STTH

I

12345

2

4

F

3

0n

C5

0
1

4
1

8
0

A

C
H

U2

+5Vdc

74

1

2

16V
F
n

C2

1

0W

3

7

13

S
A

K

B

3

.
3

1

0W

R

1

AS7

D1

B

3

D3

1A
U

100nF
8
C4

7

8
c
Vd
+5

0
30

2

4

L

1

P
O
S

HC

I

2

1

F
p
0
0
1

C1

R3

r
o
t

ec
n
n
o

rc
o

ot

Rm
O
T
C
E
V

5

L

L

L

1

2

3
_

M_

M

PW

PWM_

PW

0R
2
2

1 2

C5

3
1

HVGOUT

SDHINVCC

15Vcc
+

6

U2B

4

R5

6

3

K
3

3.

l
o
r
t

con

n

te

w
do

_

AND-ga

shut
t_

aul

f

1GQ2
EQ

100pF

12

5

C6

K
.3
3

4HC04
7

e
s
n
e
S
t
n

rre

-Cu
Hs

V
6
1
F

1n

5

4

7-25
0

BC8

e
s

HSCS

n
e
S
t
n

rre
Cu

Hs-

11109

CNC
N

HC08
4
7

D4

2
O
IS

F

100p

C7

2
EQ

GQ3

Q2

5
2

07­C8

B

11

R8

220R

0pF

C

10

R
0

0R
0

R131

R6 10

.M)
(N

uF

4

2

C1

16V

2.
F

u

3

6V

.2

C1

2

1

8

N.M

VG

A

L

GND

8
0
1

TTH

N

S

1 2

GND

DIAGCI

D6

6

7

4.7k

R10

0

F
n
1

C1

F
n

V

9

0

C

25

47

F

C8

1n

G
A
DI

CS
HS

11

8

HC08
4
7

D

C

U2

U2

0

9

12

1

V

nF 16

C121

1

AS70W
B

K
3

3.

W
70

3

9
R

13

AS
B

D5

4

B

HC04
4
7

U1

F

3

00n
1

C49

5

678

00
3

L2
P
C
H

4

2

3

1

3K

.

73
R

tage

l

_vo
s
u
B

4

6

2

8

21416
1

10

315

3

5

J1

1

7911

1

sense_phaseA
_

t_sense_phaseB
n

Curre

Current

c
Vc

5
+

D

BC1

D
6

38
6

C2 L

I

1820222

17

R14

3
1

ISO3

C
e

has
p

sense_
_
nt

rre
Cu

BC2

2

4
1

VBOOT

LINSD

123

5
1
C

3K

.
3
2

R1

PL2300
C
H

1921

BD1

BC1

1

3
Q

0R
22

13

HVG

R15

c
d
V

+5

7

8
C0
4H

7

6V
1

1nF

C501

1

F
0p

0
1

6
C1

current_sense
_

ow_side

l

6

4

2

325
2

+5Vcc

BD4

BD2

BD3

BD1

1

234

EQ3

GQ4

4
Q

5
2

EQ4

07­C8

B

pF

0R

R19

22

C21

C17

100

00pF
1

0R
10

R18

e­ns

Rse

0
1

9

8

12

11

C

3

NC

N

LVG

OUT

GND

R2

D
N

I

IN

VCC

DIAG

C

H

GN

456

7

nF
7

C20

4.

41nF
C2

c

1K

Vc

3
2

+15

C

K
0
1

R11

3

6

8
C0

U5A

4H
7

4

1

2

F16V
n
1

C19

W
70

13

S

K

BA

3

.

3
7
1

0W

R

7

13

7

S

D

A
B

R22

D8

0nF

U1C

0

5 6

678

5

8

00
3
2

PL
HC

SO4

I

2

3

4

1

F
0p

0

1
K
3

3.

C22
6
R1

ex
d
n

i
r_
de

c

o
c

Vc
5
+

En

4

2830323

A
4

9

3

27

31

3

CON3

2

er_A

der_B

d

o
c

En

Enco

F
1u

.

C18

0

BE2

BE1

E1

1

2

B

GQ5

EQ5

Q5

25

-

BC807

R29

220R

C30

LSCS

K
1

0

R21

12

0nF
7

25V

4

U5B

5

16V

5

F
2
C

1n

K
.3
3

74HC04

c
d

+5V

2

4

R2

nrush_protection

I

Rigenerative_brake_control

100pF

27

G

100R

S

R

R32

16V

C29

2.2uF(N.M)

V

.2uF

16

C28

2

3

12

14

1

11

N.M

T

2

6D

NC

O

38

OUT

HVG

O

6
L

VB

08A
1

D9

N

I

IC3

1

LINSDH

VCC

STTH

123

456

D
S

74HC08

SD

R30

1K

IP

uF
1

C26

0.

BD
T

R31

2

3

1

567

5
O
IS

8

3

4

0
0
1

00nF

R28 100

C51

1

c

+5Vc

ndex

i

B
r_

er_

e

d

cod
n

Encoder_A

Enco

E

K

0

1

R2

R25

1K

x

R261K

Teudx

Index

Tin

Vcc
5
+

2CON

7

J

345

C2

0.1uF

C C

R

100

10

NC

DIAGCINGND

15Vcc
+

1

2

+5Vdc

14

6
5
C

c
Vd

5
+

1

F

1

n

100

5D
U

12

100nF

53

U4

R60

cc
V

+5

A

v

vCode>
e

P

PN

C46CA

)
l
o

0"

contr

.1.

d

R

riente
o

E
V

field
t

tle

i
T

.C.

C. (indirec

O

O.
F.

.
I

"I.F.

or
it

mon

ED

down

D11

L

ut­sh

R62

1K

8

D
1

74HC04

U

9

LS

R56

68K

6
0

39
N

Q14

2

2

8

4

0

5

1

R

2N390

1

0
_
1

/
0

PD1PD2

20

NR­HC

5 4367

6
90

3
N
2

Q13

321

613
1

10K

R57

2N

F
u
1

.

C45

0

<R

f
o

11Fri

1

5
0

,20
7
0
r

rRe

obe

mbe

ct

u
tN

n

ay,O
d

>

cume
o

<Doc

<Title>

ize D
S

Date: Sheet

2

3

4

5

D
N
G

7

CC
V

74HC08

3
1

5Vdc
+

D
S

4

74V1G03

1

2

D

TBD

C57

TB

10R

R61

S1

Reset PUSH-BUTTON

.1uF

C44

0

10K

R55

+5Vdc

Q12

3

2

1

8

C
N

NC

SO

I

8

K
8

K

R54

6

10

R53

70
4

R52

Q11

321

A

0

2

4

F1

F7

F3

B

BF12

BF1

BF

BF13

BF11

BF9

BF

B

BF5

BF6

B

BF8

1
F
B

GQ6

Q6
5
2
7-

C80
B

3

R

R3

220

9

8

G
V
L

GND

7

7
C3

1nF
6
C3

nF

C35

0
47

+5Vdc

R34

+5Vdc

4

8

0
0

CPL23
H

ISO6

567

1

F

4

100p

C3

C33T

2
C3

C31

5

2

9

111

1

6

10

13

2

345

8

7

EQ6

c

7

d

R4

5V
+

C38

100pF

TS

%
1

R37

1%

R

nF

0

1

82

6
R3

V
25

D10

LED

2.2K

2

5
R3

BD

D
TB

D
B
T

+15Vcc

K

4.7

90R

R38

3

C390.1uF

3

100

K
0
1

IP

LS

0
C4

%
1

+5Vdc

K

6.8
9
R3

CS
S
L

C
RB

0
4

K
1

R

F
n

100

C53

8

567

HCPL2 300

9
O
S

I

4

2

1

F
0p

C52

10

R59100

cc
V

+5

R
O
T
C
E

NN
O

RC
E
D
O
C
N
E

C
RB

F
n
0
0
1

84

1%
K

R44

10

e
l
b
a

dis
e/

enabl
e

D-gat
AN

C47

2

0

1

1

4
0
C
H

1E

4
7

U1F74

U

3

11

1

1

IC4A

TS272N

%

+

-

K1
0

3

2

10

R50

R46

10K 1%

nse­e
s
R

nnections
o

short

c

+5Vdc

567

HCPL2 300

K
0
1

R42

3

4

470

R41

B

A

eC

e

s

se

a
ha
p

e_ph

s
ense_

sen
_s

t_
nt

en

r

re

uF

r
u

Current_sense_phas

C

Cur

0.1

3
J

B B

LSCS

c
d

5V
+

C04
H

C55

7

ISO

12345678910

C43

53

C41

K
0
1

R45

1

NC

3
R4

7
Q

3

CON10

U5C

22pF

100nF

3
U

uF
.1
0

2

NC

68K

2

9

1

G
A
DI

Q82

3

PD1PD

2

1

8

10

2N
7

B

S2

4

T

C

I

84

4

2

R48

Q102

2

1

5 43678

Q9

2N1613

C42

8
C5

+5Vdc

C08
H
4
7

5

6

+

-

7

G03
1

74V

LSCS

68K

N3906

51

10

R

N3904

0

0/1_
0
2

-

HCNR

N3906
2

321

10K

R49

0.1uF

27/54

Hardware design AN2388

The comparator integrated in the L6386 is used to provide an over-current protection. The
board includes also an opto-isolation stage for separating the high voltage of the power
stage from the low voltage of the control board. Moreover, electrical insulation is also useful
to eliminate ground loop currents and for producing a noise-robust system architecture. Two
different kinds of opto-isolators have been used. Linear opto (HCNR-200) for the A/D
converter signal and switch (HCPL-2300) for the control.

Control signals come from the MDK-ST10 thanks to a 34 pin connector (standard MC
connector). This is an ST standard for all applications in motor control and has pin-out
shown in Figure 25.

The encoder signals, channels A, B, and Z (Pulse per Revolution) are filtered here with a
simple RC network. The best-fit value to set the right cut-off frequency of the low-pass filter
has to be fixed in relation with the feedback device signals. The encoder channels are
passed to the dedicated peripheral for encoder reading.

Figure 24. Evaluation of the incremental encoder signals

A

A

B

B

ENCODER

T0

T0

Signal Conditioning

Figure 25. MC (motor control) standard connector

A

B

T0

T3input

ST10F276

T3input

Interrupt

In order to obtain the highest noise immunity, most of the control and sensing signals are
referred to their own GND voltage. To further increase the noise immunity, it is also
suggested to use a shielded flat cable with the shield connected to the control section GND.
The delay times are neglected (<300ns)

28/54

AN2388 Hardware design

A

The cell made of Q1-C5-R4 is used to separate the issues of cancelling of the switching
cross-conduction and control of the winding dV/dt regardless of the operating conditions and
IGBT junction temperature. In particular, the cell provides a low impedance path to the Miller
current when the adjacent power switch turns on, canceling any cross-conduction current.
So the half-bridge turn-on switching dV/dt is only defined by the gate drive resistor value
(R2, R6, R13, R18, R27 & R32). The comparator integrated in the L6386 (IC2) is used to
provide an over-current protection. If the voltage applied on pin 6 reaches 0.5V typical, the
Diag output (pin 5) is pulled down as well as the shut-down input (pin 2). Then the three half­bridges are shut-down. In regulator operation this protection never triggers as the micro­controller limits the motor current to the pre-set values.

The same circuit has also been implemented to provide over-temperature protection. This is
done via the IC3 comparator input. An OR function is made paralleling the diagnostic output
of IC2 and IC3. A third protection can be implemented using the IC1 input comparator, for
example a high side over-current protection with the PowerBD-1000 or the PowerBD-3000.

3.5 Current sensing board

The current sensing board has been designed to sense the line currents. Only two phase
current in this application are detected. The full schematic is shown in Figure 26.

Figure 26. Current sensing board schematic

C

1TBD

R1

K

100

nt_

seA

sense_pha

+5_V

+5_

V

Curre

+5_V

C4

0nF

10

Current_sense_phaseB

+5_V

Current_sense_phase

r

C

rent_sense_phase

u

+5_V

B

-

2

1

+

3

8 4

TS272

U1A

C

5

D

TB

R4 100K

-

6

7

+

5

f

8 4

T

272

S

U1B

J

1

9

10

7

8

5

6

3

V_ref

4

2

CON5A

J4

2
1

CON

1

2

J

CON2

J5

CON2

2

2
1

2
1

+5_V

C

S1

LEM LTSR6-NP/LT S6-NP

654

Ref

out
out

0

0
+5V
+5V

123

100

2

CS

LEM LTSR6-NP/LT S6-NP

654

Ref

out
ou

t
0
0

+5V
+5V

123

100n

0

R1

1

5K

C12
100nF

2 1

T

/TL431

TS824AI

-

L

2.1

R

V_re

3

1

2

1
9

1

1
7

0

1
8

C3

nF

13
12
9
11
7
10
8

2

C7

F

R1
NM

3

-

2

f

10K

C2

3.3uF

12

J3

+5_V

R5

V_ref

10K

C6

3

F

.3

u

1

J6

+5_V

R1

10

R

2

C14
1

13

NM

0

0nF

C13
330uF

R3

K

10

V_ref

R6

K

10

V_re

2

1

J

9

The working principle of the above circuitry is very simple: two Hall effect (LTSR 6NP)
current sensors measure the phase currents i
to the related current. This voltage is then

, ib producing an output voltage proportional

a

amplified (see Figure 27) in order to obtain a rail
to rail voltage in steady state condition. An external voltage reference has been used. This is
necessary to force into the current sensor the same offset value. Although the sensor has
got an embedded voltage reference, this is not as stable as the external one. The voltage
signals proportional to the three-phase current are then passed to the Gate Driver Board
through a shielded flat cable.

29/54

Hardware design AN2388

Figure 27. Voltage characteristic

V

[V]

OUT

5

4.5

3.125

-I

PMAX

2.5

-I

PN

1.875

0.5

I

[At]

0

PMAX

PN

I

I

P

3.6 The 3-phase AC induction motor

The AC induction machine used in this platform is a single cage three phase Y connected
motor. The rated value and the parameters of this motor are as follows:

Rated Power P

Rated Voltage V

Rated Current I

Rated Speed n

= 410W

n

= 400V

n

=1A

n

=3000 rpm

n

Pole Pairs 2

Slip 205

Rated Torque

M

nom

rpm

ω

P

nom

nom

3.1==

Nm

The electric motor equivalent circuit (IEEE) is here shown with the electric machine
parameters estimated by standard tests (No Load and locked Rotor test).

30/54

AN2388 Hardware design

Figure 28. Electric motor equivalent circuit (IEEE)

No Load Test

Frequency 50.00 Hz

Voltage 399.90 V

Average current 0.53 A

Input power 0.08 kW

Short Circuit Test (Locked Rotor)

Frequency 50.00 Hz

Voltage 87.30 V

Average current 0.92 A

Input power 0.11 kW
Average resistance of a phase 21.85 Ω

No Load Test

Phase voltage 230.882 V
No load impedance 435.627 Ω
No load resistance 71.200 Ω
No load reactance 429.769 Ω

Tes t

Calculations

Short Circuit Test (Locked Rotor)

Locked rotor resistance 43.321 Ω
Rotor resistance related to the stator 21.671 Ω

Phase voltage 50.40 V
Locked rotor impedance 54.786 Ω
Locked rotor reactance 33.538 Ω
Rotor reactance related to the stator 33.538 Ω
Stator reactance 16.769 Ω
Magnetizing reactance 413.000 Ω

Report

I’

2

I

1

V

1

R

1

X

I

1

Φ

E

1

X’

2

X

m

R

21.6500 Ω

1

16.7688 Ω

X

1

R’

2

s

X

m

X’

2

R’

2

413.0004 Ω

16.7688 Ω

21.6767 Ω

An embedded incremental encoder is also provided with this motor. This is capable of 1000
pulses per revolution and is used in this application to obtain the rotor mechanical position
feedback.

31/54

Software design AN2388

4 Software design

4.1 Introduction

This section describes the software design of the AC induction vector control drive
application. In particular, the software organization is outlined as well as the utilization of
different variables and the handling of the DSP-based micro functions used in this
application in order to speed-up the execution time. A short explanation on numerical
considerations is also provided inherent within fixed-point calculation.

4.2 Software organization

The software is organized in two different modules: the initialization module and the run
module. The first is performed only once at the beginning. The second module consists of a
“Waiting Loop” of Interrupt event. The interrupt (PWM ISR) is served every PWM Timer
underflow. The complete FOC algorithm is computed within the PWM ISR and thus runs at
the same frequency as the chopping frequency chosen to drive the power devices.

An overview of the software is given in the flow chart below:

Figure 29. Main organization flow chart

Start

µC Initialization

(Peripherals)

Software

Initialization

Waiting

Loop

Loop

PWM ISR

The micro peripheral PWM Unit is used to generate the necessary pulsed signal to the
power electronics board. It is programmed to generate symmetrical PWM signals at a
frequency of 16kHz (@64MHz, 15.6ns of resolution).

The following figure illustrates the time diagram for the initialization and the operating.

32/54

AN2388 Software design

Figure 30. Time diagram

Initialization routine

************************************************************************************
**************************INIT ROUTINE*
************************************************************************************
*************************
void Configure_PWM(void)// PWM module configuration
{
Set Direction Port PWM CHANNEL 1,2,3 : Outputs
Set PWM MODE : CENTER ALIGNED MODE
Set PWM FREQUENCY ;//16 kHz @ 64MHz

Enable PWM INTERRUPT
Enable Channels;
}

void Configure_ADC(void)// Configure AD module
{
Set AD Conversion Mode: Single Conversion;
Set Channel : channel1, channel2 ;
}

void Configure_Encoder(void)
{
Configure Timer T3: Timer for encoder reading sets for any transition counting

Enable Timer;
}
void Configure_TIMERS(void)
{
T01CON = 0x0206 ; // Timer 1 enabled, T1M=0(Timer Mode) T1I=011 --//>prescaler=32
,Tres=0.5uS with 64MHz

Tres=16uS with 64MHz

T1IC=0x0007 // T1 interrupt priority levelxxx , group level x
T1IE = 1 // Enable interrupts
T1 = 0 ; // T1 starts from 0
T1R = 1; //Timer 1 for speed sensing
T0IC=0x0009 // T1 interrupt priority levelxxx , group level x
T0IE = 1 // Enable interrupts
T0 = 0 // T1 starts from 0
T0R = 1; //Timer 1 for speed sensing
}

// Timer 0 enabled, T1M=0(Timer Mode) T1I=111 -->prescaler=1024 //

33/54

Software design AN2388

************************************************************************************
**************************END INIT ROUTINE*
************************************************************************************
*************************

IFOC control loop (PWM ISR)

The entire control loop is executed inside the PWM ISR. The loop is performed in about
40µs and it is executed approximately every 62 µs. This is the reason why there is a “Wait
State” before updating the new value with the next control loop.

The basic steps, required for the indirect vector control, are summarized as follows:

1. 2 out of the 3-phase stator currents are measured by means of the two Hall effect

current sensors. These measurements provide i

.

iii −−=

bac

2.

The 3-phase currents are converted into a 2-axis time variant system. This conversion
provides the variables i

and iβ starting from ia, ib and ic (Clark Transformation). This

α

transformation allows the number of variables to be reduced in the voltage equations of
the electrical machinery. In particular all mutual-inductances in the stator windings are
neglected

3. The 2-axis time variant coordinate system (i

frame aligned with the rotor flux. The knowledge of the rotor flux angle is necessary to
execute this transformation that provides the I
conditions, I

and Iq will be constant.

d

4. Error signals are computed starting from the reconstructed value of I

reference values. The I

reference controls rotor flux while the Iq reference controls the

d

torque output of the motor. The error signals constitute the input of the PI controllers
which provide as output V

and Vq, that are voltage vector to be applied to the motor.

d

5. The rotor mechanical position, rotor electrical time constant, I

the current model block that estimates the new rotor flux position.

6.

Vd and Vq values are rotated back to the stator reference frame using the rotor flux
position only just calculated. This calculation provides quadrature voltage values V
and V

7. The V

.

β

and Vβ values are transformed back to 3-phase values V

α

constituting the voltage reference for the SVPWM block which will take care of
calculating and applying the new PWM duty cycle values to be applied to the motor.

, ib while ic is computed as

a

, iβ) is projected in a time invariant rotating

α

and Iq components. For steady state

d

and from their

d, Iq

and Iq are the inputs for

d

α

, V

ref2

, V

ref3

ref1

34/54

AN2388 Software design

Figure 31. PWM interrupt service routine (IFOC control loop)

PWM ISR

Currents Sensing

Clark Transf.

Position/Speed Sensing

Update Flux Angle

Park Transf.

FOC Equations

(Flux Estimator)

Flux & Torque Regulator

Reverse Park Transf.

Main Program

4.3 Software variables

The following lines show the different variables used in this control software and in the
equations and schemes presented here.

i

, ib, ic phase currents

a

i

, i

alfa

iq, id stator current flux and torque component

Flux_ref, Torque_ref flux and torque command

Teta_cm rotor flux position

f

s

i

mR

v

d

v

alfa

stator current (α,β) components

beta

, v

q

, v

beta

Wait State in

Sine Generating with

SVPWM Technique

rotor flux speed

magnetizing current

(d, q) components of the stator voltage

(α, β) components of the stator voltage (input of the
SVPWM)

Vn_V

V

n_Vdc

V

ref1

dc

_inverse Constant using in the SVPWM

, V

, V

ref2

ref3

Vn/DC bus voltage

Voltage reference used for SV sector determination

Sector sector variable used in SVPWM

t

, t

1

2

time vector application in SVPWM

Time_A, Time_B, Time_C PWM commutation instant

35/54

Software design AN2388

ϕ

X, Y, Z SVPWM variables

Low_Limit_Flux, Up_Limit_Flux Flux range in PI regulator

Low_Limit_Torque, Up_Limit_TorqueTorque range in PI regulator

4.4 Base values and PU model

Since the ST10F276 is a fixed point microcontroller with DSP features, a Per Unit (PU)
model of the motor has been used. In this model all quantities are referred to base values.
The base values are determined from the nominal values by using the following equations,
where I
voltage and the nominal frequency in a star-connected induction motor:

and where Ib, Vb are the nominal values of the phase nominal current and voltage; ωb is the
electrical nominal rotor flux speed; φ

The base values of the motor used in this asynchronous drive are stated below:

, Vn, fn are respectively the phase nominal current, the phase to neutral nominal

n

II

=

2

nb

VV

=

2

nb

πω

f

=

2

nb

V

b

=

b

ω

b

is the base flux.

b

AII

41.11*22

nb

nb

πω

f

==

nb

V

b

ϕ

==

b

ω

b

===

VVV

310220*22

===

rad

15.3142
sec

Wb

98.0

4.4.1 Magnetizing current

In the normal speed range (where speed is lower or equal to the nominal speed) the IFOC
structure requires the magnetizing current as input to estimate the rotor flux component.
Thanks to the following motor equivalent circuit, valid only in stationary steady state, the
magnetizing current may be first estimated.

Figure 32. Equivalent electrical circuit

36/54

AN2388 Software design

4.4.2 Numerical considerations

The PU model has been developed in order to represent some quantities that reach nominal
value in certain condition. Take into consideration that during the transient the current might
reach higher values than the nominal current (I

The numeric format consideration

Integer data is inherently represented as a signed two’s complement value, where the most
significant bit is defined as a sign bit. Generally, the range of an N-bit two’s complement
integer is -2
(0x7FFF), including 0. Fractional data is represented as a two’s complement number where
the most significant bit is defined as a sign bit, and the radix point is implied to lie just after
the sign bit. This format is commonly referred to as 1.15 (or Q15) format, where 1 is the
number of bits used to represent the integer portion. The range of an N-bit two’s
complement fraction with this implied radix point is -1.0 to (1-2

1.15 data range is -1.0 (0x8000) to 0.999969482 (0x7FFF), including 0.0 .

The resolution in this format is:

N-1

N-1

to 2

-1. For a 16-bit integer, the data range is -32768 (0x8000) to 32767

1

=

15

2

).

b

1-N

). For a 16-bit fraction, the

5

−

10*01518.3

In normal saturation mode, the 32-bit accumulators use a 1.31 format, which enhances the
precision to 4.6566*10

-10

.

An example of different representations (positive and negative numbers) are shown below:

1.15 Fractional Format

0 00000000000011

-1

-202

.

Implied radix point

0x4001 = 2-1 + 2

1.15 Fractional Format (negative number)

1 00000000000101

-1

-202

.

Implied radix point

0xC002 = -2

-15

= 0.000301518 = 0.500301518

0

+ 2-1 + 2

-14

= -1.0 + 0.5 + 0.000061035 = -0.499938965

-15

2

-15

-14

2

2

4.4.3 ST10-DSP features

ST10 is a combined CPU and DSP.

As a CPU, it is a powerful real time oriented 16-bit CPU.

As a DSP, it is a single MAC 16 by 16-bit multiplier with a 40-bit accumulator

37/54

Software design AN2388

Harvard architecture

ST10-DSP has an Harvard architecture to allow on every instruction cycle:

● 1 opcode fetch

● 2 operand reads

● 1 optional operand write

Real time aspects

The ST10-DSP is both a real time CPU and a DSP. Code developed for ST10-DSP can be
interrupted at any time (including during repeat sequences) and execution resumed after the
interrupt routine. During the interrupt, bit MR remains set to indicate that a repeated
instruction has been interrupted.

Latency: there is no added latency on interrupts when DSP functions are used.

Interrupt Routine Requirements: the only requirement for interrupt routines that are using
DSP and that are interrupting a DSP function is to save and restore the MAC registers at the
entry point and exit point of the routine. This control can be automatically done by TASKING
(ST10 C Compiler) tool chain by using “#PRAGMA savemac” on each task using DSP
functions (for details, refer to Tasking user’s manual).

DSP library

In order to have all the benefit of this powerful micro, the MAC unit has been used to perform
the arithmetical equations. Take into consideration that the DSP library uses the fractional
format q1.15 (further information can be found in the DSP Library Technical Note)

See below in detail the DSP functions used:

Multiplication

The multiplication of two real 16-bit fractional operands is calculated by (LeftOp*RightOp =
Output):

mul_q15_q15_q31(short LeftOp, short RightOp, long *Output)

where:

LeftOp Left operand

RightOp Right operand

Output Output pointer

Assembly source code:

mul_q15_q15_q31.asm

Code size and cycles:

Size: 22 bytes, Instruction cycles: 10

Note: Keep into consideration that the Output format is in q1.31 format. A 16-right shift must be

executed if you want the result in the same format.

Division

The division of two real fractional inputs is calculated by

38/54

AN2388 Software design

div_q31_q15_q15( short LeftOpMsb, short LeftOpLsb, short RightOp, short *Output)

where:

LeftOpMsb Left operand most significant bits

LeftOpLsb Left operand least significant bits

RightOp Right operand

Output Output pointer

Assembly source code:

div_q31_q15_q15.asm

Code size and cycles:

Size: 98 bytes

Instruction cycles: 216

Note: The dividend must be smaller than the divisor for a valid result.

Divisions on limits (for example, division of 1 by 1 or of -1 by -1) are not computed by this
routine.

The algorithm implemented does not allow integer division. For dividing two integers
(dividend in 32.0 format and divisor in 16.0), shift the dividend one bit to the left (into 31.1
format) before dividing.

4.5 Analog value scaling

The AC induction motor vector control application uses a fractional representation for all real
quantities, except time. The following equation shows the relationship between a real and a
fractional representation:

ValueFractional =

4.5.1 Current sensing and scaling

The FOC algorithm requires two phase currents as input. In this application a current
voltage transducer Hall effect based (LEM type) sense these two current. The current
sensor output therefore needs to be rearranged and scaled so that it can be used by the
control software as q1.15 format values

Figure 33. Current sensing block diagram

Scaling

Factor (q1.15)

i

fractional value

Note that the real quantity range used in the fractional value represents the maximum
measurable current, which is not necessarily equal to the maximum phase current. This is

Range

adjustment

ST10F2756

A/D

ValuealRe

Conditioning

circuitry

RangeQuantityalRe

i

phase

Current Sensor

39/54

Software design AN2388

the reason why the current gain has been set to have the maximum wide range voltage
during the transient stage, avoiding any saturation.

The two phase currents are sampled through the microcontroller and converted using the
ADC module. The channels of the A/D peripheral are multiplexed and the time of conversion
is 3µs per channel. A complete conversion (two phase currents) needs 6µs.

In this application, channel 0 (port 5.0) and channel 1 (port 5.1) have been configured as
inputs for A/D conversion.

Figure 34. Phase current detection

As can be seen in the Figure 34 a slight offset appears on the two phase currents acquired
by Hall effect sensors. Many reasons could explain it (offset voltage on the op-amp and
conditioning circuitry) and in order to compensate for it there are some offset values
introduced in the current sensing routine. The offset value fixes the output voltage, coming
out from the current sensor, in order to have a 2.5V mean value.

4.5.2 Rotor mechanical position sensing

In this AC induction drive a 1024 pulse incremental encoder produces the rotor position.

The two sensor output channels (A and B) are wired directly to the incremental interface
mode for the core timer T3 selected by setting bit-field T3M in register T3CON to ‘110’. In
incremental interface mode the two inputs associated with timer T3 (T3IN, T3EUD) are used
to interface to an incremental encoder. T3 is clocked by each transition on one or both of the
external input pins which gives 2-fold or 4-fold resolution to the encoder input

40/54

AN2388 Software design

Figure 35. Core timer T3 in incremental interface mode

T3R

T3IN
P3.6

Edge detect

T3

T3IR

Up/Down

T3EUD
P3.4

Figure 36. T3CON register configuration for incremental encoder reading

Phase detect

T3UD

XOR

MUX

T3OTL

T3OE

T3OUT
P3.3

T3CON (FF42h/A1h) SFR Reset Value: 0000h

151413121110 9 8 7 6 543210

- - - - - T3OTL T3OE T3UDE T3UD T3R T3M T3I

RW RW RW RW RW RW RW RW RW RW RW

Bit Function

T3I Timer 3 Input Selection Depends on the operating mode, see respective sections.

Timer 3 Mode Control (Basic Operating Mode)

0 0 0 : Timer Mode
0 0 1 : Counter Mode

T3M

0 1 0 : Gated Timer with Gate active low
0 1 1 : Gated Timer with Gate active high
1 0 X : Reserved. Do not use this combination
1 1 0 : Incremental Interface mode
1 1 1 : Reserved. Do not use this combination

Timer 3 Run Bit

T3R

T3R = ‘0’: Timer / Counter 3 stops
T3R = ‘1’: Timer / Counter 3 runs

T3UD Timer 3 Up / Down Control *

T3UDE Timer 3 External Up/Down Enable *

Alternate Output Function Enable

T3OE

T3OE = ‘0’: Alternate Output Function Disabled
T3OE = ‘1’: Alternate Output Function Enabled

T3OTL

Timer 3 Output Toggle Latch

Toggles on each overflow / underflow of T3. Can be set or reset by software.

41/54

Software design AN2388

Figure 37. GPT1 core timer T3 (incremental interface mode) input edge selection

T3I Triggering Edge for Counter Increment/Decrement

000 None. Counter stops.

001 Any transition (rising or falling edge) on T3IN

010 Any transition (rising or falling edge) on T3EUD

011 Any transition (rising or falling edge) on T3 input (T3IN or T3EUD)

1XX Reserved. Do not use this combination

Figure 38. Timer 3 operating in incremental interface mode automatically provides

information on the sensor’s current position. Dynamic information
(speed, acceleration, deceleration) may be obtained.

forward jitter backward jitter forward

T3IN

T3EUD

Contents
of T3

up down up

Note: This example shows the timer behavior assuming that T3 counts upon any transition on any

input, T3I=’011b’

The typical waveforms of the Incremental encoder are shown below in Figure 39.

Figure 39. Encoder channels

Ch.A (T3IN)

Ch.B (T3EUD)

11024

Position counter values

one revolution

1024 1

In this application, the maximum count per transition has been set in order to have the
maximum resolution (T3I=”011”)

In a single mechanical revolution there are 4096 pulses

2

π

4096

==

3−

pulseradstepmechanical /10*53.1

The flow of the rotor mechanical sensing routine is shown below.

The value of the incremental timer for the encoder reading (T3) is assigned to a variable in
every sample time

42/54

AN2388 Software design

Figure 40. Mechanical rotor angle estimation block diagram

T3IN

Mechanical_Rotor_Angle Pulses Encoder

Scaling factor

Incremental

Timer

ST10F276

Channel A

T3EUD

Channel B

4.5.3 The PI regulator

Introduction

PID has a fundamental importance in the industrial controller field due to the simplicity of
approach, the robustness of control and the immediacy of calibration.

In this regulator, the variable “error”, the derivative and the integral errors are performed to
calculate the output variable that has the following representation:

A complete discussion of Proportional Integral Derivative (PID) controllers is beyond the
scope of this application, but this section will provide the basics of PID operation.

A digital PID controller is executed at a periodic sampling interval. It is assumed that the
controller is executed frequently enough so that the system can be properly controlled. The
error signal is formed by subtracting the desired setting of the parameter. The sign of the
error indicates the direction of change required by the control input.

The Proportional term (P) of the controller is formed by multiplying the error signal by a P
gain, causing the PID controller to produce a control response that is a function of the error
magnitude. As the error signal becomes larger, the P term of the controller follows and
grows to provide more correction. The effect of the P term tends to reduce the overall error
as time elapses. In most systems, the error of the controlled parameter gets very close but
does not converge so it remains a small steady state error.

The Integral (I) term of the controller is used to eliminate small steady state errors. The I
term calculates a continuous running total of the error signal. Therefore a small steady state
error accumulates into a large error value over time. This accumulated error signal is
multiplied by an I gain factor and becomes the I output term of the PID controller.

The Differential (D) term of the PID controller is used to enhance the speed of the controller
and responds to the rate of change of the error signal. The D term input is calculated by
subtracting the present error value from a prior value. This delta error value is multiplied by a
D gain factor that becomes the D term of the controller. The D term of the controller
produces more control output the faster when the system error is changing.

This application doesn’t use the D terms due to the relatively slow response time of motor
speed changes. In this case, the D term could cause excessive changes in PWM duty cycle
that could affect the operation of the algorithm and produce over current trips.

The PI (Proportional-Integral) regulators are implemented with output saturation. Keep in
mind that all the variables are in 1.15 format.

43/54

Software design AN2388

Adjusting the PI gain

The gains of the controller set the overall system response. At the beginning when the P
gain is set, the I term should be set to zero . The P gain can then be increased until the
system responds well to set-point changes without excessive overshoot or oscillations. After
a reasonable P gain is selected, the I term gain can be slowly increased to force the system
error to zero. Only a small amount of I gain is required in most systems. This application
includes a term to limit integral wind-up which will occur if the integrated error saturates the
output parameter. Any further increase in the integrated error won’t effect the output.

Take into consideration that the PI regulator for the Flux components is essentially the same
as that for the torque.

4.6 Clark and Park transformation

In the next two paragraphs, the ST10F276 code for Clark and Park transformation is
presented. The corresponding theoretical background explanations have already been
handled.

4.6.1 (a,b)->(α,β) projection (Clark transformation)

In the following code the considered constant and variables are implemented in 1.15 format.

************************************************************************************
*************************
* Clark Transformation *
* (a, b) ->(alfa, beta) *

* iSalfa = ia .....*

* iSbeta = (2*ib+ia)/sqrt(3) *
void Clark (void)
{

qIalfa=qIa; //qIalfa component in Q1.15 format

mul_q15_q15_q31 (qSqrt3, qIa, &qIa_Sqrt3_tmp);

mul_q15_q15_q31 (qSqrt3, qIb, &qIb_Sqrt3_tmp);

qI_tmp_a = (short) (qIa_Sqrt3_tmp>>16);

qI_tmp_b = (short) (qIb_Sqrt3_tmp>>16);

I_beta_tmp = (qI_tmp_a+qI_tmp_b+qI_tmp_b);

qIbeta = I_beta_tmp;// qIbeta component in Q1.15 Format

}
************************************************************************************
*************************
* END Routine *
************************************************************************************
************************

where qSqrt3 is the following constant:

1

3

44/54

⇔==

finExqSqrt 15.16490577.0

AN2388 Software design

4.6.2 The (α,β)-> (d,q) projection (Park transformation)

In the following code the constant and variables under consideration are implemented in

1.15 format. The quantity Teta_cm represents the rotor flux position calculated by the
current model.

************************************************************************************
**************************Park Transformation *
* (alfa, beta) ->(d,q) *

* iSd = iSalfa*Cos_Teta_cm+iSbeta*Sin_Teta_cm.....*

* iSq = -iSalfa*Sin_Teta_cm+iSbeta*Cos_Teta_cm *

void Park(void)
{

mul_q15_q15_q31(qIalfa,Cos_Teta_cm,&qId_tmp_1);
mul_q15_q15_q31(qIbeta,Sin_Teta_cm,&qId_tmp_2);
qId_1 = (short)(qId_tmp_1>>16);// Q1.31 ->Q1.15 conversion

qId_2 = (short)(qId_tmp_2>>16);// Q1.31 ->Q1.15 conversion

qId = (qId_1+qId_2);//Id component in Q1.15 format

mul_q15_q15_q31(qIalfa,Sin_Teta_cm,&qIq_tmp_1); //Sin_Teta_cm is the tabled

value Sin_Cos_Table[Sin_Index]

mul_q15_q15_q31(qIbeta,Cos_Teta_cm,&qIq_tmp_2);//Cos_Teta_cm is the

tabled value Sin_Cos_Table[Sin_Index+64]

qIq_1 = (short) (qIq_tmp_1>>16);// Q1.31 ->Q1.15 conversion

qIq_2 = (short) (qIq_tmp_2>>16);// Q1.31 ->Q1.15 conversion

qIq = (-qIq_1)+(qIq_2);//Iq component in Q1.15 Format

}

SinTeta_cm and cosTeta_cm indicate respectively the Teta_cm sine and cosine values.

The modalities required to determine these values are explained later in this document.

4.6.3 The Current model implementation (rotor flux estimator)

This chapter represents the core module of the Field Oriented Control (FOC).

This module takes as input i
equations, the numerical considerations, code is also be shown.

, iq plus the rotor electrical speed. In addition to the essential

d

45/54

Software design AN2388

The theoretical background explanations have already been handled and assuming that

the current model equations can be discretized as follows:

ii ≈

qSqS

+1

KK

mR

ii

k

1

+

nf

ks

1

k

+

mR

+

λλ

T

k

T

r

1

+=

1

T

ω

ωθθ

−+=

mRds

KK

i

qs

K

i

mR

br

1

k

+

⋅⋅+=

sbrr

11

kkK

++

eq

1.)(

eqii

2.

3.

eqTf

Take into consideration that all variables are in q1.15 format.

In the above equations, appear two constants:

where = sampling time=PWM period

T

L

r

T

==

r

R

r

TT,

r

176.106

mH

671.21

=

Ω

3

−

10*89.4

In the following code the constants are converted in the new numerical form:

⎛

T

⎜

qK

qK

void Calc_theta(void)
{
mul_q15_q15_q31(K_incr, q_Flux_Speed,&Theta_cm_tmp);
Teta_cm_new = (short)(Teta_cm_tmp>>16);

Theta_cm = Theta_cm+Theta_cm_new;
Theta_cm=Theta_cm+q_Mechanical_Rotor_Angle; //Rotor Flux Angle
Theta_cm=Theta_cm+q_Mechanical_Rotor_Position
}

************************************************************************************
**************************End Calc Teta calculation*
************************************************************************************
************************

==

r

⎜

T

r

⎝

⎛
⎜

t

==

⎜

ω

T

br

⎝

⎞

µ

S

4.62

89.4

mS

PU

⎟

⎯→⎯

⎟
⎠

11

3

−

⋅

⎞

PU

⎟

⎯→⎯

⎟

5.314*1089.4

⎠

fFx

15.10190

fex

15.15290

4.6.4 Generation of sine and cosine values

In order to generate sine and cosine values, a sine table and indirect addressing mode have
been implemented. In order to have the best performance in term of position accuracy and
the used memory minimization, this table contains 2
range. The above computed position (16-bit integer value) therefore needs to be shifted 8
positions to the right. This new position (8-bit integer value) is used as a pointer (Index_Sin
or Index_Cos) to access this table. The outputs of the table are the Sin_Teta_cm and
Cos_Teta_cm value represented in Q1.15 format.

The following figure below shows how the sine value calculation is handled:

46/54

8

=256 values to represent the [0;2π]

AN2388 Software design

Figure 41. Generation of Sin and Cos values

Sin_Cos_Table [Index_Sin]

0x0000

0x0001

Rotor Flux
Position (θ

λΓ

)

8-bit Shift

Index_Sin

............

............

0xFFFF

0

π

π/2

3π/2

2π

Keep in mind that to have the cosine value 256/4=64 (OFFSET variable) must be added to
the Index_Sin.

The C code is shown below:

************************************************************************************
**************************Calc_Sin_Cos_Routine*
************************************************************************************
************************
void Calc_Cos_Sin(void)
{
Index_Sin = (((Theta_cm+32768))>>8);

Index_Cos = (((Theta_cm+32768)>>8)+OFFSET);

if (Index_Cos > 255)
{
Index_Cos = (Index_Cos-255);
}
Sin_Theta_cm = Sin_Cos_Table[Index_Sin];

Cos_Theta_cm = Sin_Cos_Table[Index_Cos];
}

4.6.5 The space vector modulation module

The Space Vector modulation is a highly efficient way to generate the six pulsed signals
necessary at the power stage.

Before estimating and calculating the best value of PWM duty cycle to be provided to the
power stage it is necessary to go through complementary inverse transformations to get
back to the 3-phase motor voltage. First it must be transformed from the 2-axis rotating d-q
reference frame to the 2-axis stationary frame α-β. This transformation uses the Inverse
Park Transformation and uses the output of the PI regulator V
implemented in this block are:

Valfa = Vd*Cos_Theta_cm-Vq*Sin_Theta_cm

Vbeta = Vd*Sin_Theta_cm+Vq*Cos_Theta_cm

. The relations

d Vq

The inputs for the space vector modulation module are the reference voltages ,
the DC bus voltages, and gives the three PWM patterns as output. These values are once

VV ,

betaalfa

47/54

Software design AN2388

again expressed in PU quantities, so they may be implemented in 1.15 format by the DSP
software library provided with the entire code.

Inside the SVPWM module it is necessary to estimate the 3 reference voltages to
discriminate the right place (Sector) where to place the proper space vector.

This is done using the Calc_Ref routine,:

************************************************************************************
**************************Reference Voltages calculation*
* Vref1 = Vbeta *
* Vref2 = (Vbeta+Sqrt(3)*Valfa)/2*
* Vref3 = (-Vbeta-Sqrt(3)*Valfa)/2*
************************************************************************************
***********************

void Calc_Ref(void)
{
qVref1 = qVbeta;

mul_q15_q15_q31(qSqrtd2,qValfa,&qVref2_tmp1);

mul_q15_q15_q31(q0dot5,qVbeta,&qVref2_tmp2);

qVref2_1=(short)(qVref2_tmp1>>16);

qVref2_2=(short)(qVref2_tmp2>>16);

qVref2=(qVref2_1-qVref2_2);

mul_q15_q15_q31(qSqrtd2,qValfa,&qVref3_tmp1);

mul_q15_q15_q31(q0dot5,qVbeta,&qVref3_tmp2);

qVref3_1=(short)(qVref3_tmp1>>16);

qVref3_2=(short)(qVref3_tmp2>>16);

qVref3 = (-qVref3_1-qVref3_2);
************************************************************************************
**************************End Routine *
************************************************************************************
*************************

The conversions of the inputs necessary for the SVPWM module, to the required numerical
format:

V

400

VdcV

_

n

n

n

V

DCbus

inverseVdcV

__

325

23.1

===

1

VdcV

_*2

n

⎯→⎯==

fx

15.134080

48/54

AN2388 Software design

_

inverseqSqrt

_2

inverseqSqrt

_23

inversedq

************************************************************************************
**************************SVPWM Calculation Block Diagram*
************************************************************************************
************************

3

__

n

inverseVdcV

3

__*2

n

inverseVdcV

3

inverseVdcV

__*2

n

15.11150

⎯→⎯==

fAx

15.1020

⎯→⎯==

⎯→⎯==

fFDx

fCEx

15.1040

Calculate voltage reference

Evaluate sector and duration of two

boundary vectors

Compute the 3 necessary duty

cycles assigning to the right

motor phase according to the sector

The right sector can be found it by means this simple rule.

Sector determination:

if V

>0 THEN A_Sector=1, ELSE A_Sector=0;

ref1

if V

>0 THEN B_Sector=1, ELSE B_Sector=0;

ref2

if V

>0 THEN C_Sector=1, ELSE C_Sector=0;

ref3

Sector= A_Sector+2* B_Sector+4*C_Sector

Inside the proper sector, it must be calculated the duration of the two sector boundary
vectors application as shown below:

Timing calculation

The final step is to compute the three necessary duty cycle to provide to power devices
depending on which sector the voltage vector defined by .

VV ,

βα

49/54

Software design AN2388

TimeTimeperiodpwm

⎧

t

=

a

⎪
⎪

⎪
⎨

⎪
⎪

⎪

⎩

Timett

+=

ab

Timett

+=

bc

2

1_

2_

−−

2_1__

The following table shows how to proceed to assign the right duty cycle to the right motor
phase.

Table 3. PWM value per each sector

Sector

Phase

123456

PWM0 Time B Time A Time A Time C Time C Time B

PWM1 Time A Time C Time B Time B Time A Time C

PWM2 Time C Time B Time C Time A Time B Time A

Figure 42. Typical waveforms of the SVPWM modulation

50/54

AN2388 Software design

Figure 43. Typical waveforms of the SVPWM modulation

51/54

References AN2388

5 References

[1] – D. W Novotny and T.A. Lipo “Vector Control and Dynamics of AC Drives, Oxford
Science Publications, ISBN 0-19-856439-2

[2] –Werner Leonard, “Control of Electrical Drives”, 2
Edition, Springer, ISBN 3-540-59380-2

nd

Completely Revised and Enlarged

52/54

AN2388 Revision history

6 Revision history

Table 4. Document revision history

Date Revision Changes

03-Oct-2006 1 Initial release.

53/54

AN2388

Please Read Carefully:

Information in this document is provided solely in connection with ST products. STMicroelectronics NV and its subsidiaries (“ST”) reserve the
right to make changes, corrections, modifications or improvements, to this document, and the products and services described herein at any
time, without notice.

All ST products are sold pursuant to ST’s terms and conditions of sale.

Purchasers are solely responsible for the choice, selection and use of the ST products and services described herein, and ST assumes no
liability whatsoever relating to the choice, selection or use of the ST products and services described herein.

No license, express or implied, by estoppel or otherwise, to any intellectual property rights is granted under this document. If any part of this
document refers to any third party products or services it shall not be deemed a license grant by ST for the use of such third party products
or services, or any intellectual property contained therein or considered as a warranty covering the use in any manner whatsoever of such
third party products or services or any intellectual property contained therein.

UNLESS OTHERWISE SET FORTH IN ST’S TERMS AND CONDITIONS OF SALE ST DISCLAIMS ANY EXPRESS OR IMPLIED
WARRANTY WITH RESPECT TO THE USE AND/OR SALE OF ST PRODUCTS INCLUDING WITHOUT LIMITATION IMPLIED
WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE (AND THEIR EQUIVALENTS UNDER THE LAWS
OF ANY JURISDICTION), OR INFRINGEMENT OF ANY PATENT, COPYRIGHT OR OTHER INTELLECTUAL PROPERTY RIGHT.

UNLESS EXPRESSLY APPROVED IN WRITING BY AN AUTHORIZED ST REPRESENTATIVE, ST PRODUCTS ARE NOT
RECOMMENDED, AUTHORIZED OR WARRANTED FOR USE IN MILITARY, AIR CRAFT, SPACE, LIFE SAVING, OR LIFE SUSTAINING
APPLICATIONS, NOR IN PRODUCTS OR SYSTEMS WHERE FAILURE OR MALFUNCTION MAY RESULT IN PERSONAL INJURY,
DEATH, OR SEVERE PROPERTY OR ENVIRONMENTAL DAMAGE. ST PRODUCTS WHICH ARE NOT SPECIFIED AS "AUTOMOTIVE
GRADE" MAY ONLY BE USED IN AUTOMOTIVE APPLICATIONS AT USER’S OWN RISK.

Resale of ST products with provisions different from the statements and/or technical features set forth in this document shall immediately void
any warranty granted by ST for the ST product or service described herein and shall not create or extend in any manner whatsoever, any
liability of ST.

ST and the ST logo are trademarks or registered trademarks of ST in various countries.

Information in this document supersedes and replaces all information previously supplied.

The ST logo is a registered trademark of STMicroelectronics. All other names are the property of their respective owners.

© 2006 STMicroelectronics - All rights reserved

STMicroelectronics group of companies

Australia - Belgium - Brazil - Canada - China - Czech Republic - Finland - France - Germany - Hong Kong - India - Israel - Italy - Japan -

Malaysia - Malta - Morocco - Singapore - Spain - Sweden - Switzerland - United Kingdom - United States of America

www.st.com

54/54