ST AN1126 Application note

AN1126

V

®

APPLICATION NOTE

CURRENT SHARING OF THE L4973

IN A MULTIPHASE APPLICATION

by Domenico Arrigo & Giuseppe Gattavari

INTRODUCTION

The L4973 family is a 3.5A monolithic s tep-down dc-dc converter, available in POWERDIP18( 12+3+3)
and SO20L (12+4+4) plastic packages. The operating input supply voltage range is f rom 8V to 55V, and
the output ranges from 3.3V (L4973D3.3) and 5.1V(L4973D5.1) to 40V. Other regulated outputs below

3.3V are also possible (See Application Note AN938).
Using two L4973D is possible to deliver up to 7A with a good sharing between the two sections or a re-

dundant 3.5A. The two devices work at a switching frequency of 200kHz. At Vcc = 24V, V o = 5.1V at 7A
the efficiency is 87%. At 3.5A output, the efficiency is 90%.

Electrical Specifications

Input Voltage range 8V-30V
Output Voltage 5.1V ±3% (Line, Load and Temperature)
Output Voltage Ripple 47mV (0.92%/Vo)
Output Current range 0 to 7A
Max Output Ripple current 15%
Min Iomax Current limit 8A
Switching frequency 200kHz

Current Sharing Operating Principle

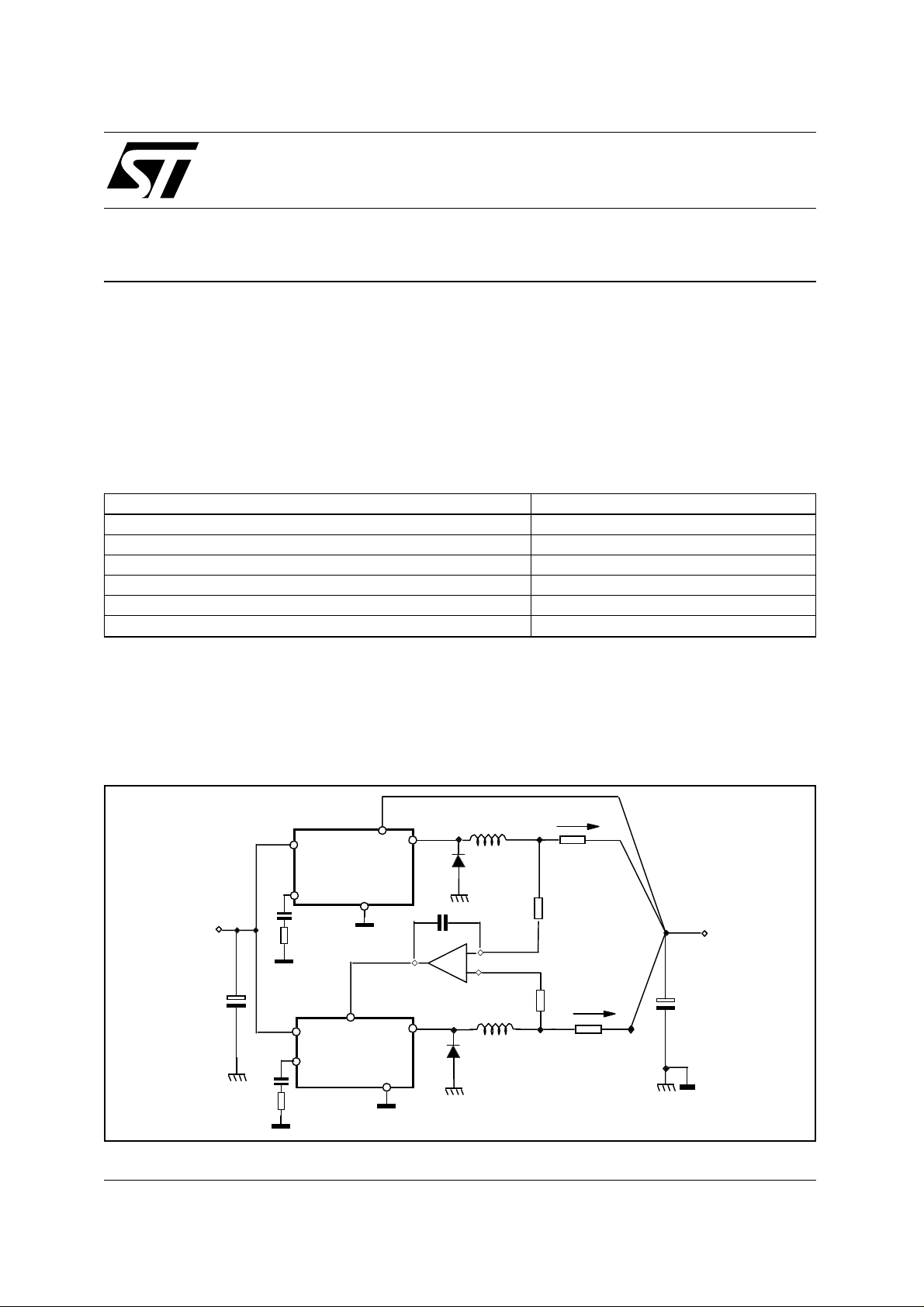
The current sharing configuration, shown in fig. 1, is based upon two L497x devices U1 and U2. Any de­vice in the L497x family can be used for this purpose.
The U1 regulator acts as a master which regulates the output voltage.
The second section U2 works as a current follower. Its task is to deliver an output current equal to the

Figure 1. Current Sharing Operating Princi ple

Rint

I -FB

Rs

Vout

I +

Rs

Cout

Vcc

U1

COMP

cc

Vcc

COMP

L497x

FB

U2
L497x

GND

OUT

Cint

OP-AMP

OUT

GND

L

­+

L

May 1999

1/16

AN1126 APPLICATION NOTE

current delivered from the first section. An op-amp compares the voltage drop through Rs which is pro­portional to the cur rent deliv er ed from the U2 section with the voltage drop across Rs proportional to the
current delivered from the U1 section. T he Cin and Rin components introduce a pole and a zero in the
current loop which allows integration of the error signal. The current loop regulates I
result the output current delivered to the load is Iout = 2I- = 2I+ for every load condition.

Current Sharing Accuracy

The accuracy of the current sharing between the two sections depends on the op-amp offset voltage,
Voff, and the value of Rs and its ac curacy . The of fset voltage introduce an error in the sensing voltage ,
Vs=Rs Iout/2 . The relative percentage current error due to the offset is given by :

e%= (∆ I/I) ⋅ 100 = (Voffset ⋅ 100) / (Rs ⋅ Iout)

This error is minimum at maximum load. The larger the value of Rs, the smaller the error. Rs must be
chosen as a compromise between error minimization and system efficiency.

For example with Iout = 7A choosing Rs = 25mΩ ,considering a maximum offset voltage of 3mV
(LM358A), the maximum relative percentage error is 1.7% (120mA @ Iout = 7A).

The total error is given by the sum of this error plus the error due to the sensing resistor ( which corre­sponds to its accuracy of 1% ). So the maximum error is 2.7% (190mA @Iout = 7A)

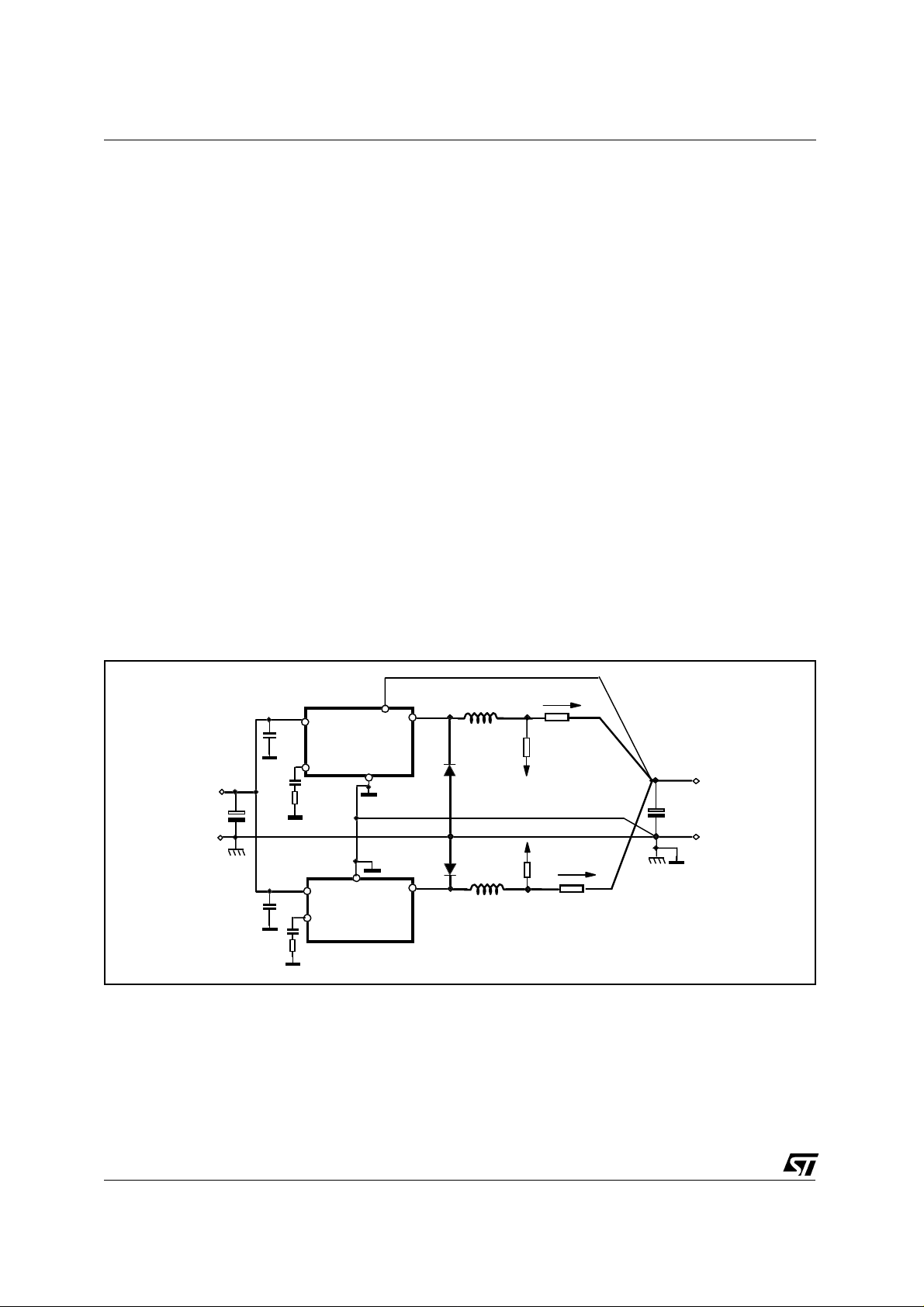
Layout Hints

The PCB layout requires some care. The power paths of the two sections must be as short and sym­metrical as possible. The current sensing wires must be parallel and s hort to avoid induced noises. The
sensing resistor must be non induct ive. The ground pins of the two devices must be at the same voltage
and connected to the output ground point.

Figure 2. Layout hints.

+

equal to I- . As a

to the
current
FB

I -FB

Rs

to the
current
FB

Vout

Cout

GND

I +

Rs

Vcc

GND

COMP

Vcc

Vcc

COMP

U1
L497x

U2
L497x

L

OUT

GND

GND

L

OUT

Syncronization or Multiphase

In a current sharing application the two sections c an be synchronized. This permits a reduction of noise
induced from one section to another. In this case a single RC network can be used for both the oscilla­tors and the two SYNC pins are connected.

In many application, instead of synchronizing the two oscillator, it is useful to introduce a delay between
the two PWM signals in order to achieve a multiphase application. The phase shift between the two
PWM signals can be easily achieved by two methods :

2/16

AN1126 APPLICATION NOTE

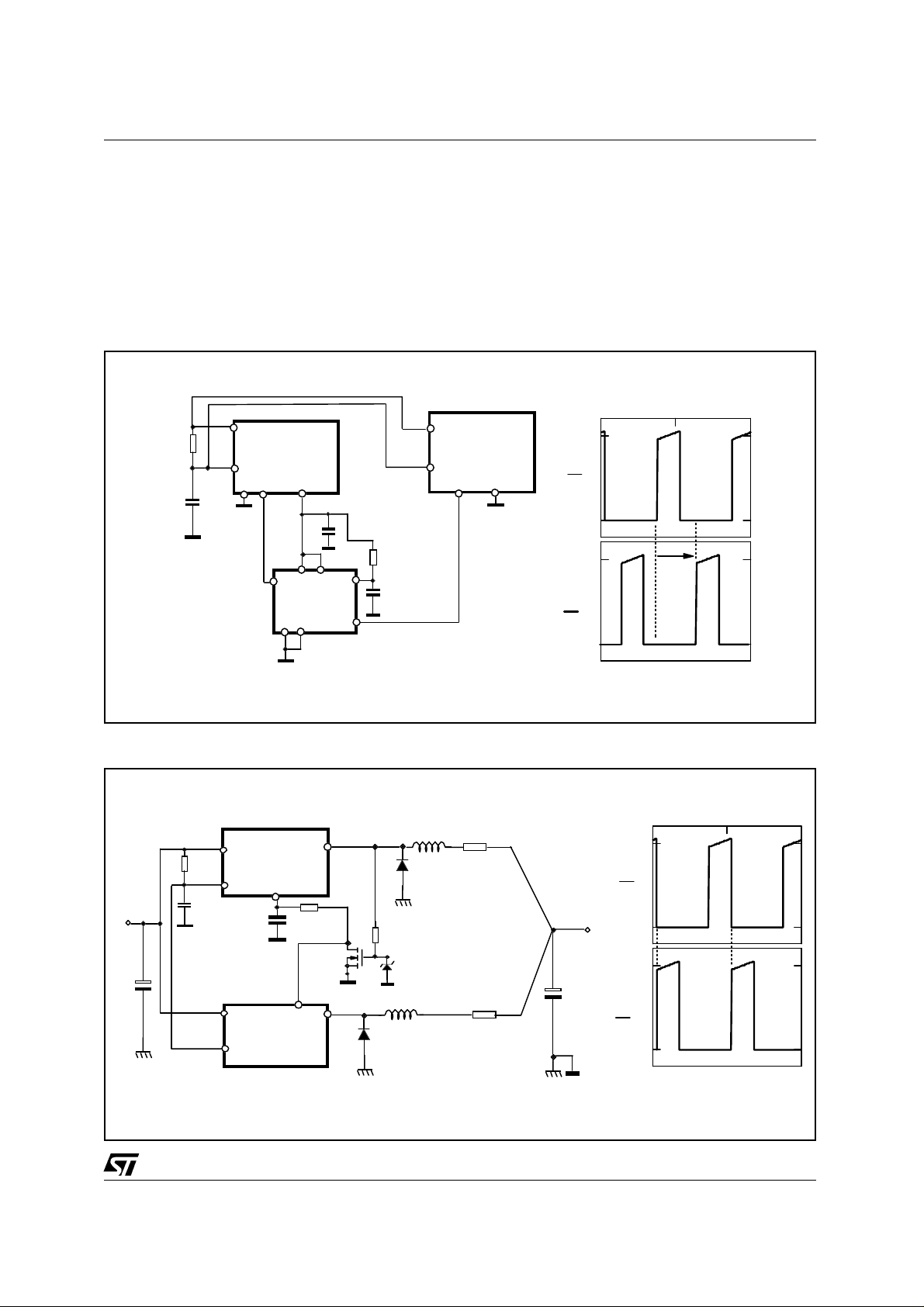
Case 1)

Programmable Phase Delay.

Fig. 3 shows how to program a phase delay with a monostable multivibrator whos e on time is equal to
the desired phase delay.

Case 2)

Fixed Phase Delay.

Figure 3 shows a method of setting a delay time for the 2nd PWM section to be slightly larger than the
ON-time of the 1st PWM section.

Figure 3. Case 1) Programmable Phase Delay.

Vcc

R1

OSC

GND

U1
L4973D3.3

SYNC

Vcc

1B

M74HC123

1A

GND

Vref=5.1C2

CLR

_
1Q

Vcc

OSC

U2
L4973D3.3

SYNC

U1

GND

U2

PWM OUTPUTS

0

α

0

Figure 4. Case 2) Programmable Phase Delay.

L

18V

*

L

Vcc

necessary if Vcc>18V

*

OUT1

OUT2

Vcc

R1

OSC

C2

Vcc

OSC

U1
L4973D3.3

Vref=5.1

SYNC

U2
L4973D3.3

t

PWM OUTPUTS

Rs

Vout

Cout

Rs

U1

0

U2

0

t

3/16

AN1126 APPLICATION NOTE

Multiphase Benefits

The main benefits are :

Minimization of the RMS current through the input capacitor therefore increasing of the efficiency and
reducing of the capacitor cost and size.

Minimization of ripple current through the output capacitor and ground path.
Fast load transient response.
Improved reliability /MTBF.

RMS current through the input capacitor are equivalent in Case 1) and Case 2). Even though the cir­cuitry of Case 2) is simplifier than Case 1), Case 1) provides the opportunity to optimize this ripple cur­rent.

Minimization of the RMS Current Through the Input Capacitor.

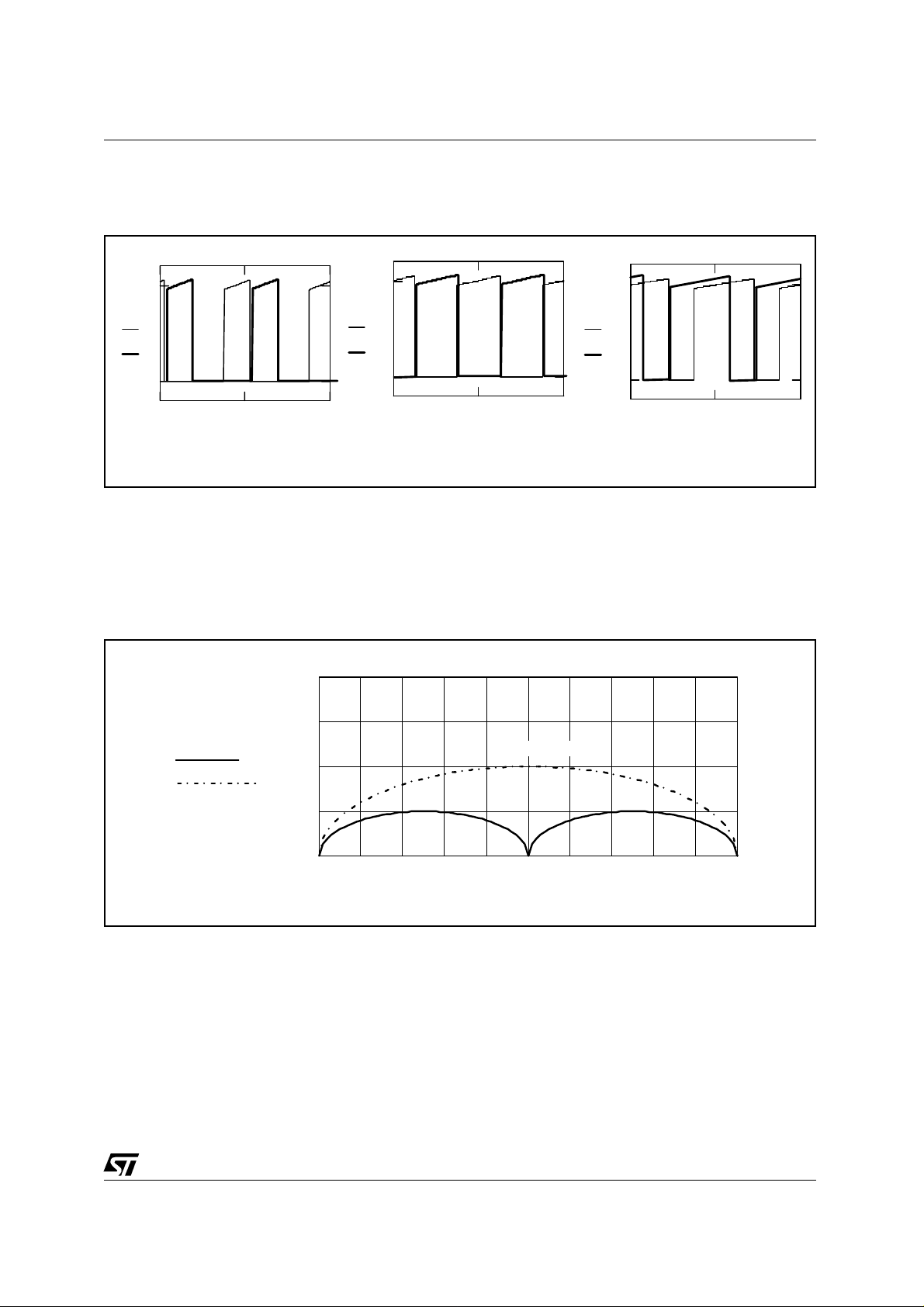
In Case 1) , Figure 3 shows the RMS current through the input capacitor, referred to the output current
(Iout), for various phase delays, α , of the two PWM sections. This assumes a duty cycle of 0.5 and a
ripple current through the coil of 0.1⋅ Iout.

For α equal to a half period (180 degrees of phase delay) the RMS current is approximately zero. If the
two PWM signals are synchronized the RMS value is Irms = Iout/2. For example if Vout = 5V and
Iout = 7A the Output Power is 35W. If the Input capacitor has an ESR of 100mOhm the phase delay
allows a savings of 1.23W which corresponds to the 3.5% of the power delivered to the load.

Figure 5. RMS current through the input capacitor for a different phase delay, α , with a duty

cycle of 0.5.

[ A ]

α=120

°

Iout/2

0

- Iout/2

α=40

0

Assuming the same duty cycle for the two sections, the RMS Current through the input filter for different
duty cycle, considering a phase delay of the second PWM signal equal to the Ton of the first section (
Case 2) ), is given approximately (the output c urrent ripple can be negleted for this calculation) by the
following formula:

2





− (Iout ⋅

I

RMS

(α)



Iout



√ 




=



⋅

√2 ⋅ δ



2






Iout



√



where δ = duty cycle



2



(3

⋅

2

⋅ δ −1)

√

⋅

α=180

°

δ

2



− (iout ⋅




2

)

°

if

δ)

α=90

°

α=0

time

0.5

δ ≤

2

if δ > 0.5

°

Multiphase (1)

4/16

AN1126 APPLICATION NOTE

Iout is the total output current equal to the sum of the individual output currents delivered from the two
sections.

Figure 6. Input current of the two sections for different dut y cycle.

PWM1

PWM2

PWM1

PWM2

1

0

0

t

δ=0.5

1

0

0

t

δ<0.5

1

PWM1

PWM2

0

0

t

δ>0.5

If the PWM signals are synchronized without any delay, the RMS current through the input filter as a
function of duty cycle is :

Irmssync



(Iout

(δ) =

√

⋅ √δ )

2

− (Iout ⋅

2

synchronized (2)

δ)

Figure 7. RMS current through the input capacitor with synchronizat ion and with multiphase.

Iout

[ A ]

3Iout/4

δ

Irms ( )

Irmssync ( )

δ

Iout/2

Irms

Iout/4

Irmssync

0

0 0.1 0.2 0.3 0 .4 0.5 0.6 0.7 0.8 0.9 1

δ

Figure 7 shows Equations (1) and (2) versus the duty cycle.
The maximum RMS current with synchronized PWMs is 1/2 of the total output current and it is obtained

for δ = 0.5.
In contrast, considering the multiphase PWM,

RMS value is 1/4 of the total output current.

the RMS value is 0 with δ = 0.5

So the maximum RMS current with multiphased PWMs

and the max value of the

is a half of that syncronized PWMs.

For every duty cycle condition the RMS current with multiphase application is lower than the case with
synchronized PWMs and it is quite regular for different duty cycles.

It allows to optimize the input capacitor for the real working condition. In the synchronized case the input
capacitor has to be dimensioned f or the worst case of δ = 0.5 that can be far from the real working con­ditions.

5/16

AN1126 APPLICATION NOTE

If Psync is the wasted power on the input capacitor with synchronized PWMs, given by :

Psync = ESR ⋅ Irmssync

2

and Pmulti is the wasted power with multiphased PWMs, given by :

Pmulti = ESR ⋅ Irms

2

the power saved using the multiphase instead of the synchronized method for various duty cycle is :

Psaved (δ) = ESR ⋅ (Irmssyn c

ESR

Psaved

(δ) =







ESR

I

⋅

out

2

⋅ I

out

2

2

2 ⋅

⋅

2

(δ) - Irms2 (δ))

δ if

1

if δ >

δ)

(

−

δ

≤

0.5

0.5

For example considering an input capacitor ESR of 0.1 Ohm and an output current of 7A the power
saved using the multiphase instead of the synchronized method for different duty cycle is shown in fig.8.

Figure 8. Power saved using the multiphase instead of the synchronized method for various

duty cycle.

2

[W]

1.5

1

Psaved (δ)
Psync

Pmulti

(δ)

(δ)

Psync

0.5

0

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Figure 9. Power saved vs. Vout

[W]

2

Vin=12V

Ω

Iout=10A

Iout=7A

Vout [ V ]

6/16

Psaved

ESR=60m

1.5

1

0.5

0

3 3.5 4 4.5 5 5.5 6 6.5 7 7.5 8

Iout=5A

Psaved

Pmulti

δ

[W]

Psaved

2

Vin=12V

Iout=7A

1.5

1

0.5

0

33.544.555.566.577.58

ESR=100m

Vo u t [ V ]

Ω

ESR=75m

ESR=50m

Ω

Ω

Figure 10. Power saved vs. Iout.

AN1126 APPLICATION NOTE

Psaved
[ W ]

Psave( ),,,Iout 5.1 12 0.05

Psave( ),,,Iout 5.1 12 0.085

Psave( ),,,Iout 5.1 12 0.1

2

Vcc=12V
Vo=5.1V

1.5

fsw=200kHz

1

0.5

0

0 1 2 3 4 5 6 7 8 9 10

ESR=100m

Iout

[ A ]

Ω

85m

50m

Ω

Ω

The gained power as a percentage of the output power using the multiphase PWMs instead of synchro­nized PWMs is :

∆P%(δ) =

∆P%(δ) =

Psaved

ESR

(δ)

⋅ 100

Po

Iout

⋅ 100

⋅

2

Vcc

So the percentage gained power, ∆P%, for a fixed Iout, Vcc and ESR does not change with the output
voltage.

For example if the input capacitor has an ESR of 100mOhm for a 12V/3.3V or 12V/5V power conversion,
with Iout = 7A, there is in both cases a ∆P% gain of 3% .

Table1 shows in details the major tips for different output voltages.

Table 1. Vcc = 12V , Iout = 7A, ESR=100mΩ.

Vo
(V)

3.3 3.13 1.74 1.39 0.98 0.3 0.68 3%

5.1 3.46 1.25 2.21 1.2 0.16 1.04 3%
6 3.5 0 3.5 1.23 0 1.23 3%

Irmssync

(A)

Irmsmulti

(A)

Irms

∆

(A)

Psync

(W)

Pmulti

(W)

Psaved

(W)

P%

∆

Gained

The gained power ∆P% versus duty cycle is shown in figure 10.

7/16

]

AN1126 APPLICATION NOTE

Figure 11. ∆P% vs. duty cycle.

6
5
4

∆

P%(δ)

3
2
1

0

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Figure 12. ∆P%

∆

P%=(Psaved/Po) · 100

∆

P%

6

ESR=60m

5

4

3

2

1

Ω

Vcc=8V

δ

Vcc=12V

Vcc=24V

∆

P%

10

8

6

4

2

The gained power ∆P% as a function
of input voltage, output voltage, output
current and input capacitor ESR is
shown in figure 12.

Figure 12 shows the measured effi­ciency with the L4973D board , with
Vin = 12V, Vout = 5.1V, fsw = 200kHz,
using a input capacitor 470µF/50V
ROE with an ESR = 85mΩ. Using the
multiphase application with a phase
delay, α, equal to half period, case1) ,
there is a gained efficiency of 2%
compared to the synchronous applica­tion. So it is possible to maintain high
efficiency values using low cost and
size capacitor.

∆

P%=(Psaved/Po) · 100

Vcc=12V

ESR=100m

Ω

50m

75m

Ω

Ω

0

02468101214161820

Iout [ A ]

Figure 13. Efficiency vs. Output Current.

V

⋅ I

O

VIN ⋅ I

O

⋅ 100

IN

η

=

[%]

95

Cin = 470µF/50V ROE EKE
ESR = 85 m Ohm

Multiphase

α=180

90

synchronous

85

Vcc = 12V
Vo = 5.1V

fsw = 200kHz

80

012345678

Io [A

02 4 6 8 101214161820

Iout [ A ]

Conclusions

To sum up in application in which the duty
cycle is between 0.2 and 0.8 t here is a big
advantage using the multiphase PWMs, in
terms of dissipated power on the input ca­pacitor compared with the added circuitry to
achieve it. The more the output current is
the more this advantage increases.

Applications with δ = 0.5, using a half period
of multiphase phase delay, gives the best
benefit because the RMS current through
the input capacitor is approximately zero.

Minimization of the Ripple Current
Through the Output Capac itor.

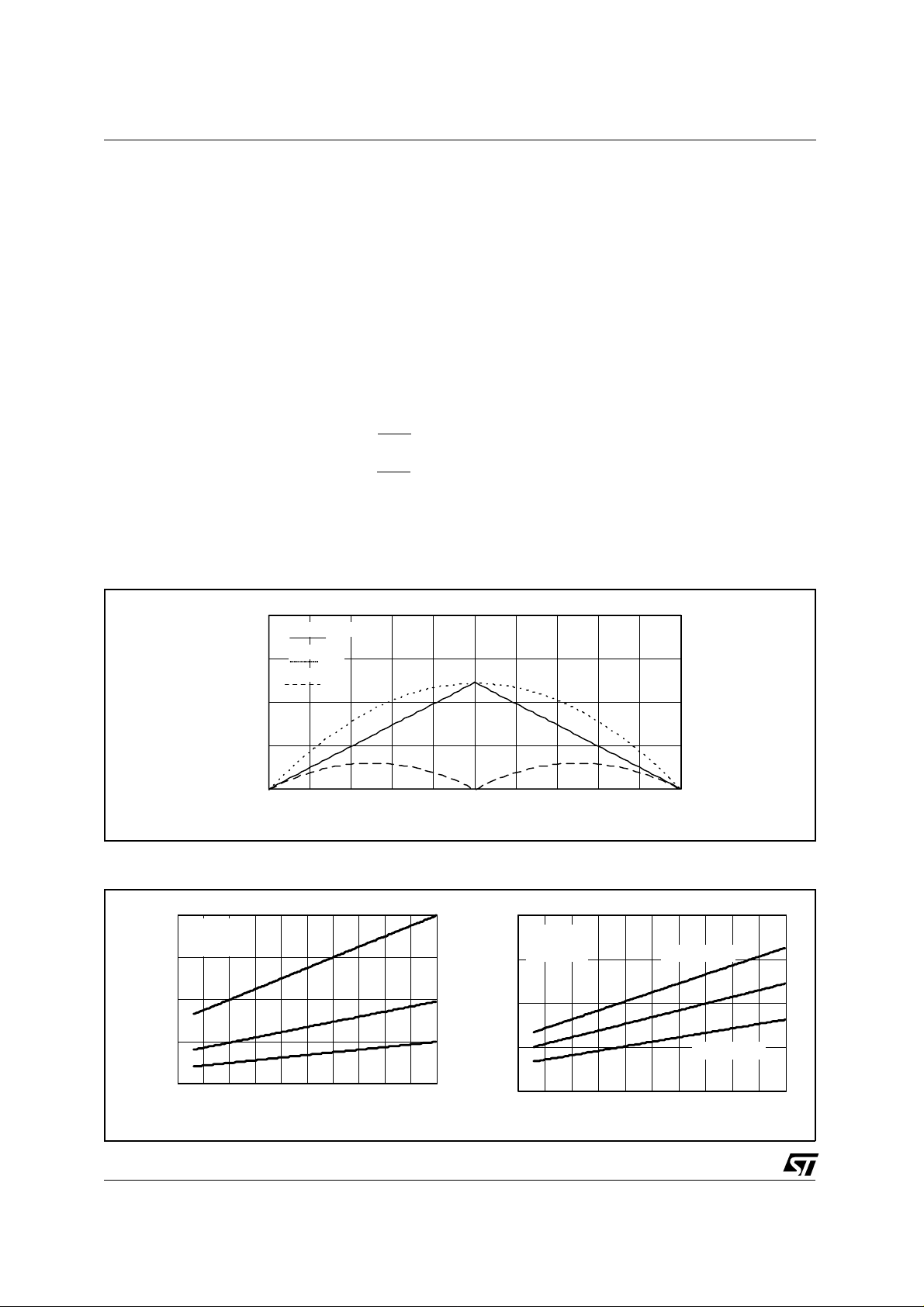
Figure 13 shows the current ripple through
the output filter for different phase delay, α,
of the two PWMs considering a duty cycle of

0.5.

8/16

AN1126 APPLICATION NOTE

For α equal to half period (180 degrees

Figure 14. Ripple current through the output

of phase delay) the ripple current is ap­proximately zero.

This allows to chose low cost output filtering
capacitor. Or, with the same ESR, to re­duce drastically the output voltage ripple.

The phase shift between the two PWM sig­nals can be easily achieved in two way.

If the duty cycle is far from 0.5, the ripple
current through the output capacitor is
higher in Case 2 than in Case 1 in which
the delay time can be programmed.

−∆Ιο/2

Current Sharing Evaluation Board for L4973D
Figure 15. Current sharing schematic diagram.

+∆Ιο/2

capacitor for different phase delay, α.

α=40

α=0

α=90

°

°

α=180

0

α=120

°

0

°

°

t

α=240

°

Vcc (8V to 30V)

C1

680uF
35V

C3
680uF

35V

C7
220nF

220nF

C17

C2

1.2nF

J2

INH1

Vcc

22k

R1

OSC

OSC

Vcc

INH2

J3

1uF

C20

INH

V5.1

8,9

1111
19

SS

15nF

SYNC

1
8,9
11

18

FB

INH

11

U1
L4973D

20

SYNC

C5

20

U2
L4973D

19

SS

13

V5.1

C10
1uF

1/2
LM358
SO8

FB

13

4,..,7
14,..,17

C15

15nF

BOOT

18

Vcc

4,..,7
14,..,17

7

R7*

BOOT

COMPGND
C16

4.7nF
R8

10K

GND

Z1*

220nF

C6

10

OUT

2,3

12

COMP

C4

22nF

R2

10K

C14

Cin=10nF

4

­+

8

C13

100nF

220nF

C18

10

2,3

OUT

D2
STPS
640CB

12

C19
220pF

D1
STPS
640CB

6

5

C9
220pF

R11

Rin=10K

10K

L1 43uH
(77120) N=34

R5

L2 43uH
(77120) N=34

25m

R6

25m

C12
220nF

Iout=7A

Ω

R3

C8
220uF

R4

Ω

R9

C21

220uF

C23

220nF

* Z1 and R1 are necessary only if Vcc>25V

9/16

AN1126 APPLICATION NOTE

Electrical Specifications and Performance:

Input Voltage range 8V-30V
Output Voltage 5.1V ±3% (Line, Load and Temperature)
Output Voltage Ripple 47mV (0.92%/Vo)
Output Current range 0 to 7A
Max Output Ripple current 15%
Min Iomax Current limit 8A
Switching frequency 200kHz
Efficiency 87% @ 7A Vin = 24V

Figure 16. Board efficiency vs. output current.

η

[%]

95

Vcc=8V

10V
12V

90

15V

20V

85

24V

Table 2. Output voltage selection

L4973D3.3

Vo (V) R3 (KΩ)R4 (K

3.3 0 4.7

5.1 2.7 4.7

L4973D5.1

5.1 0 4.7

)

Ω

80

Main Components Description.

Vo=5.1V

75

fsw=200kHz

It follows a description of the chosen out­put and input capacitor and of the i nduc­tor for each of the two sections.

70

012345678

Io [A ]

Input Capacitors

The input capacitors have t o be able to support the maximum input operating voltage of the device and
the maximum RMS input current.

At full load, Io = 7A and duty cycle of 50% the RMS current flowing through the input capacitors is
maximum and is given by Io/2 . So the RMS current to be sustained is 3.5A.

The two selected capacitor, FA 680µF/50V Panasonic, are able to support this current.

Inductor Selection

The minimum duty cycle is:

Dmin = (Vo + Vf )/(Vin max + Vf )= 0.184

where Vf is the freewheeling diode forward voltage.
The inductor ripple current is fixed at 15% of Iomax and it is 0.525A.
The inductor needed for each of the two sections is:

The L ⋅ Io

Vo

(

L =

2

is 0.533 and the size cor e chose is 77120 (125µ) Magnetics KoolMµ material. In order t o

+ Vf

1 – D

⋅ (

)

f

I

⋅

∆

o

sw

min

)

= 43µH

compensate a 40% reduction of in ductance at full load due to t he DC current level, it is necessary to
wire 34 turns, which correspond to 84µH of inductance at light load.

10/16

AN1126 APPLICATION NOTE

With this choice the core losses are approximately 280mW. The temperature increasing of the core is
12°C approximately.

Output Capacitor

The selection of Cout is driven by the output ripple voltage required, 1% of Vo. This is defined by the
ESR of the output capacitance and by the maximum ripple current (0.525A).

The maximum ESR is:

ESR = ∆Vo/∆Io = 0.051/0.525 = 97m

Ω

The selected capacitance is 220µF/35V FA Panasonic with ESR = 90mW and the ripple voltage is

0.92% of Vo (47mV).

Bill of Material

C1, C3 680µF / 35V FA PANASONIC 16x15 Irms=1690mA
C2 1.2nF/35V SMD 1206
C4 22nF SMD 1206
C16 4.7nF SMD 1206
C13 100nF/35V SMD 1206
C5,C15 15nF/35V SMD 1206
C6,C7,C12,C17,C18,C23 220nF/50V SMD 10% Kemet 1206 X7R
C8,C21 220µF/35V FA PANASONIC 8x15
C10,C20 1µF/10V electrolitic (not SMD)
C11,C22 not used
C14 10nF/35V SMD 1206
C9,C19 220pF SMD 1206
U1,U2 L4973D3.3
R1 22k SMD 1% 1206, 0.25W
R2 9.1k SMD 1% 1206, 0.25W
R3,R10 2.7k SMD 1% 1206, 0.25W
R4,R12 4.7k SMD 1% 1206, 0.25W
R6,R9 0.025 Ohm 1W 1% DALE WSL-2512
R7 0 SMD 1206
R11,R5,R8 10K SMD 1% 1206, 0.25W
D1 STPS640CB (DPAK)
D2 STPS640CB (DPAK)
U3 LM358 SO8 ST
Z1 Diodo Zener 25V SOT23
L1,L2 43µH KoolMu Magnetics core 77120 34 Turns d(mm)=0.91 AWG19

Stability Analysis of the Current Loop.

In the current sharing configuration the U1 regulator acts as a master in order to regulate the output
voltage. The second section U2 works as current follower. Its task is to deliver an output current equal to
the current delivered from the first section. For the analysis of the stability, see Fig. 21, the current loop
of the U2 section can be considered as a separated loop from the voltage loop of the U1 section, consid­ering that the current loop is quite faster than the voltage one.

11/16

AN1126 APPLICATION NOTE

For the stability of the voltage loop see the AN938.

The open loop transfer functions is composed of the following blocks :

- Error amplifier and compensation block :

R

⋅ C

)

c

c

1

)

+

c

A

=

(s)

2

s

⋅ Ro ⋅ C

o

R

⋅

c

Avo ⋅ (1 + s ⋅

C

+ s ⋅ (Ro ⋅ Cc + Ro ⋅ Co + Rc ⋅ C

⋅

c

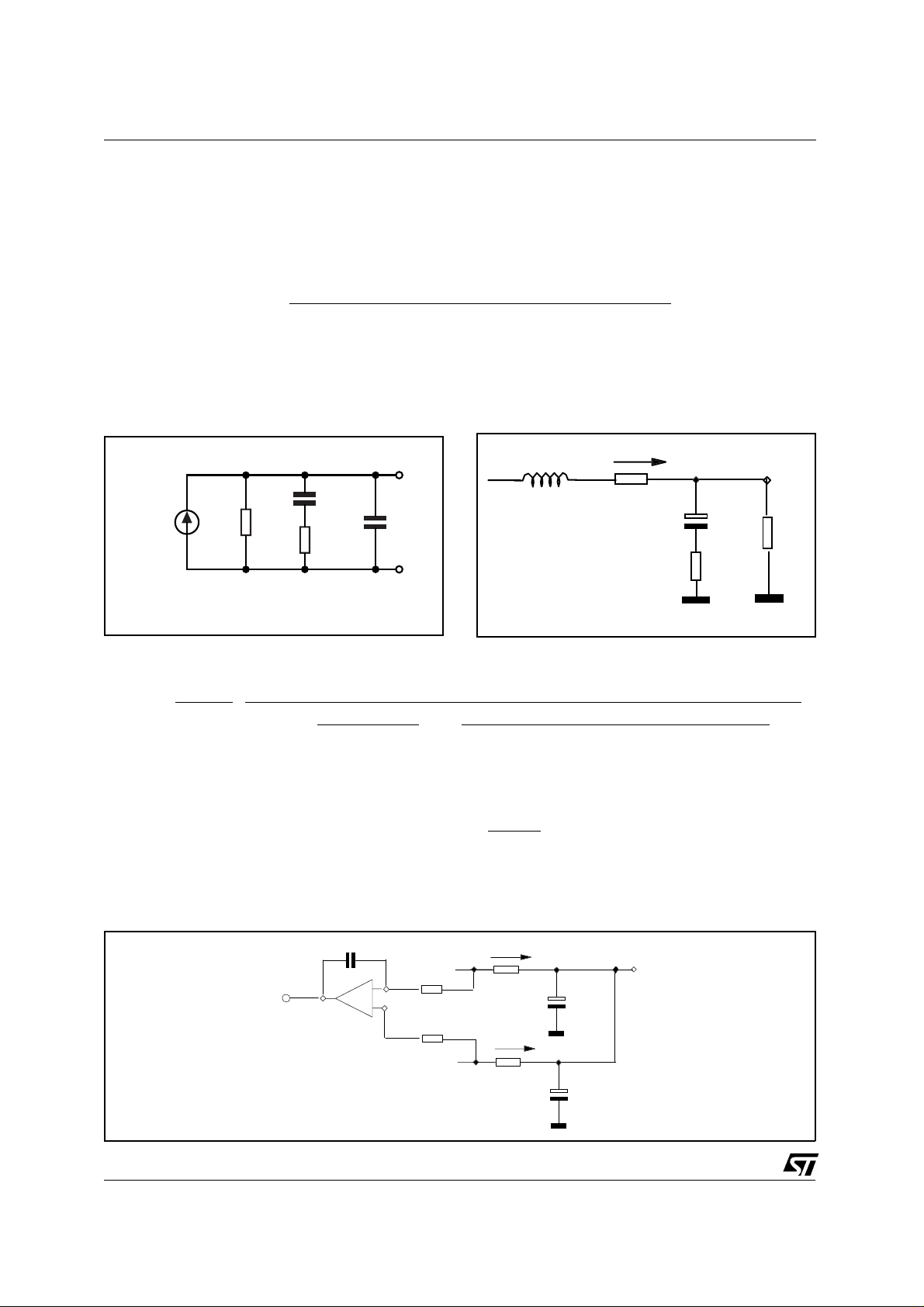
in which Ro = 1.2MΩ and Co = 220pF are internal capacitance and resistance of the Error Amplifier
while R

Figure 17. Error Amplifier Compensation Cir-

and Cc are the compensation values.

c

Figure 18. Output filter

cuit

L

Cc

Rogm

Rc

Co

D99IN1022

I +

Vout

Rs

Cout

ESR

RL

- Output LC filter:

Gfil

(s)

=

RL

1

+

Rs

Cout ⋅

+ s ⋅

⋅

Cout





⋅

2

Cout

s

⋅

ESR + RL) ⋅ L

(

⋅

RL + Rs

⋅

ESR

RL

(

+

Rs

RL + ESR) + L + RL ⋅ ESR ⋅ Cout

⋅ (

) +

1

RL + Rs



1

+




s

Rs is the sensing resistor, RL is the load resistance.

PWM gain:

=

Gpwm

Vcc

where Vct is the peak to peak saw tooth oscillator.

Figure 19. Current feedback.

Cint

6

­+

Rint

5

R

12/16

FB

7

LM358

Vct =

⁄

Vcc

Vcc

I -

Rs

I +

⋅ 6

6

≈

1

−

Vout

Cout

Rs

Cout

AN1126 APPLICATION NOTE

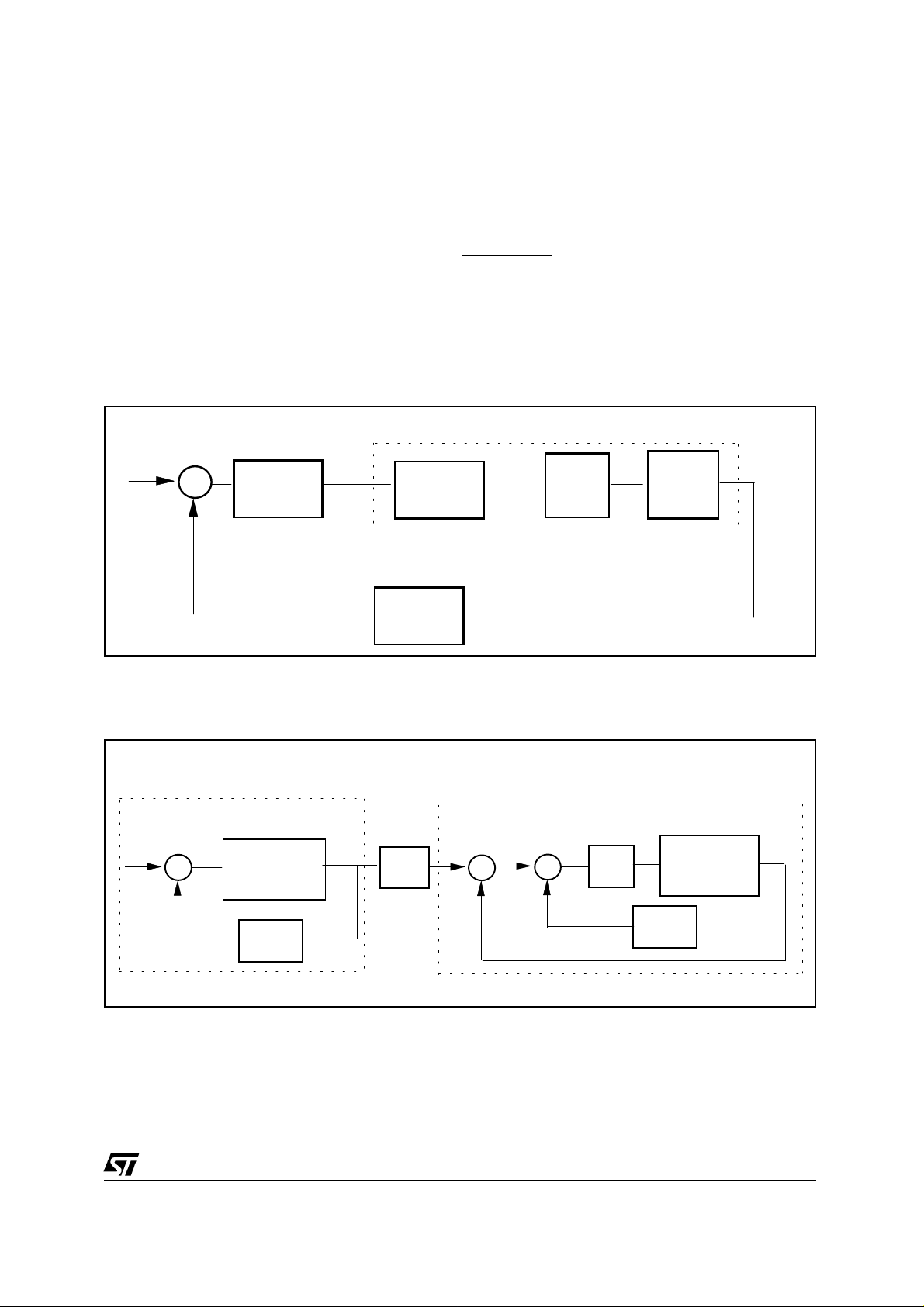
The LM358 configured as an integrator introduces a gain given by Rs , a pole in Gint(s) and a zero in
Z(s) :

Vfb= ( Rs / s ⋅ Cint ⋅ Rint )[ (I

Assuming :

Gint

(s) =

and :

H(s) = (1 + s ⋅ Rint ⋅ Cint)

the current control loop block diagram can be considered as shown in Figure 20.

Figure 20. Block diagram of the current loop

+

) ⋅ (1 + s ⋅ Cint ⋅ Rint) - (I-) ]

s

Rint

⋅

1

Cint

⋅

Rs ⋅

G(s) ( Compensated E/A, PWMGain, Output Filter )

I-

Gint(s)

Current

integrator

Current
Feedback

Vfb

A(s)

Compensated

E/A

H(s)

PWM
Gain

The complete block diagram of the current sharing loop is shown is figure 21.

Figure 21. Complete block diagram of the current sharing loop

U1 section (Volt age Loop )

Vref

∆ V

Vfb

G(s)

( Compensated E/A,

PWMGain,

Output Filter )

Av

Vout

1/Rload

Iout

I-

-

I+

∆ I

Gint(s)

-

Gfilt(s)
Output
Filter

U2 section ( Current Loop )

G(s)

( Compensated E/A,

PWMGain,

Output Filter )

H(s)

I+

I+

The open loop function of the current loop is given by :

F(s) := GpwmZint(s) ⋅ Gfil(s) ⋅ A(s)

In figures 22 and 23 are shown t he open loop Gain and Phase Bode plot . The capacitor C5 does not
influence the system stability but is useful only to reduce the noise. The cut off f requency and a phase
margin are: Fc = 8KHz; Angle = 40°

13/16

AN1126 APPLICATION NOTE

Figure 22. Gain Bode open loop plot.

120

[ dB ]

100

80
60
40
20

0

-20
110100110

Figure 23. Phase Bode open loop plot.

0

[ ° ]

-20

-40

-60

-80

-100

-120

-140

-160

-180
1 10 100 1 10

| F |

f [ Hz ]

φ

F

f [ Hz ]

3

3

110

110

4

4

110

110

5

5

Figure 24. Load transient response.

14/16

Load Transient Response

Figure 24 shows the load transient be­havior of the schematic circuit of Fig­ure 15.

In Figure 24 are shown the current de­liveder from the two sections, the load
current and the drop voltage on the
output . After 20µs the total current de­livered from the two section is equal to
the current required from the load. So
the response time of the application is
20µs approximately for a load transient
from 1A to 6A.

TEST CONDITIONS (fig 24):
Vin = 5V, Vout = 3.3V, Load transient

form 1A to 6A, dIout/dt = 20A/µs.

AN1126 APPLICATION NOTE

Figure 25. PCB Layout top view: Silk, component side and bottom layer (1:1.25 scale).

15/16

AN1126 APPLICATION NOTE

Information furnished is bel i eved to be accurat e and reliable. However, STMicroelec tronics assumes no responsibility for the consequences
of use of such inform ation nor for any infringement of patents or other rights of third parties which may result from its use. No license is
granted by implication or otherw ise under any patent or patent rights of STMic roelectronics . Specification mentioned in this publi cation are
subject to c hange without notice. Thi s publication supersedes and replac es all information previously su ppl ie d. S TMicroelectroni cs products
are not authorized for use as critical components in life support devices or systems without express written approval of STMicroelectronics.

The ST logo is a registered trademark of STMicroelectronics

© 1999 STMicroelectronics – Printed in Italy – All Rights Reserved

STMicroel ec tr on i c s GRO U P OF COMPANIES

Australia - Brazil - Canada - China - France - Germany - Italy - Japan - Korea - Malaysia - Malta - Mexico - Morocco - The Netherlands -

Singapore - Spain - Sweden - Switzerland - Taiwan - Thailand - United Kingdom - U.S.A.

http://www.st.com

16/16